(完整版)分式混合运算练习题(中考题汇编).docx
分式的混合运算练习题

分式的混合运算练习题分式是数学中的一种常见表示形式,它由分子和分母构成,表示了两个数之间的比例关系。
混合运算则是指同时进行多种运算,如加减乘除等。
本文将提供一些分式的混合运算练习题,以帮助读者巩固和练习相关的数学知识。
1. 请计算以下分式的值:(a) $\frac{3}{4} + \frac{1}{2}$(b) $\frac{5}{6} - \frac{1}{3}$(c) $\frac{2}{3} \times \frac{4}{5}$(d) $\frac{2}{5} \div \frac{1}{4}$解答:(a) $\frac{3}{4} + \frac{1}{2} = \frac{3 \times 2 + 4 \times 1}{4 \times 2} = \frac{6+4}{8} = \frac{10}{8} = \frac{5}{4}$(b) $\frac{5}{6} - \frac{1}{3} = \frac{5 \times 3 - 6 \times 1}{6 \times 3} = \frac{15-6}{18} = \frac{9}{18} = \frac{1}{2}$(c) $\frac{2}{3} \times \frac{4}{5} = \frac{2 \times 4}{3 \times 5} =\frac{8}{15}$(d) $\frac{2}{5} \div \frac{1}{4} = \frac{2}{5} \times \frac{4}{1} =\frac{2 \times 4}{5 \times 1} = \frac{8}{5}$2. 请化简以下分式:(a) $\frac{9}{12}$(b) $\frac{15}{20}$(c) $\frac{24}{36}$(d) $\frac{16}{24}$解答:(a) $\frac{9}{12} = \frac{3 \times 3}{4 \times 3} = \frac{3}{4}$(b) $\frac{15}{20} = \frac{5 \times 3}{4 \times 5} = \frac{3}{4}$(c) $\frac{24}{36} = \frac{6 \times 4}{6 \times 6} = \frac{4}{6} = \frac{2}{3}$(d) $\frac{16}{24} = \frac{8 \times 2}{8 \times 3} = \frac{2}{3}$3. 请计算以下分式的和及差:(a) $\frac{1}{2} + \frac{3}{4} - \frac{1}{8}$(b) $\frac{3}{5} - \frac{3}{10} + \frac{1}{2}$(c) $\frac{5}{6} + \frac{2}{3} - \frac{1}{4}$(d) $\frac{7}{8} - \frac{1}{2} + \frac{3}{16}$解答:(a) $\frac{1}{2} + \frac{3}{4} - \frac{1}{8} = \frac{4 \times 4 + 3 \times 2 - 1}{8} = \frac{16+6-1}{8} = \frac{21}{8}$(b) $\frac{3}{5} - \frac{3}{10} + \frac{1}{2} = \frac{6 \times 2 - 3 \times 1 + 5}{10} = \frac{12-3+5}{10} = \frac{14}{10} = \frac{7}{5}$(c) $\frac{5}{6} + \frac{2}{3} - \frac{1}{4} = \frac{5 \times 2 + 2\times 4 - 3}{6 \times 4} = \frac{10+8-3}{24} = \frac{15}{24} =\frac{5}{8}$(d) $\frac{7}{8} - \frac{1}{2} + \frac{3}{16} = \frac{14 \times 2 - 8\times 1 + 3}{16} = \frac{28-8+3}{16} = \frac{23}{16}$4. 请计算以下分式的乘积及商:(a) $\frac{2}{3} \times \frac{3}{4} \times \frac{4}{5}$(b) $\frac{5}{6} \div \frac{1}{2} \div \frac{2}{3}$(c) $\frac{3}{4} \times \frac{1}{2} \div \frac{2}{5}$(d) $\frac{4}{3} \div \frac{3}{2} \times \frac{2}{5}$解答:(a) $\frac{2}{3} \times \frac{3}{4} \times \frac{4}{5} = \frac{2 \times 3 \times 4}{3 \times 4 \times 5} = \frac{24}{60} = \frac{2}{5}$(b) $\frac{5}{6} \div \frac{1}{2} \div \frac{2}{3} = \frac{5}{6} \times \frac{2}{1} \times \frac{3}{2} = \frac{5 \times 2 \times 3}{6 \times 1 \times 2} = \frac{30}{12} = \frac{5}{2}$(c) $\frac{3}{4} \times \frac{1}{2} \div \frac{2}{5} = \frac{3 \times 1 \times 5}{4 \times 2 \times 2} = \frac{15}{16}$(d) $\frac{4}{3} \div \frac{3}{2} \times \frac{2}{5} = \frac{4}{3}\times \frac{2}{3} \times \frac{2}{5} = \frac{4 \times 2 \times 2}{3 \times 3 \times 5} = \frac{16}{45}$通过以上练习题,我们可以巩固和练习分式的混合运算。
中考数学专项练习分式的混合运算(含解析)

中考数学专项练习分式的混合运算(含解析)【一】单项选择题1.计算的结果是〔〕A.B.C.x2+1D.x2﹣12.化简分式〔x-y+〕〔x+y-〕的结果为〔〕A.y2-x2B.x2-y2C.x2-4y2D.4x2-y23.x﹣=﹣y,且x+y≠0,那么xy的值为〔〕A.-1B.0C.1D.24.化简÷〔1+ 〕的结果是〔〕A.B.C.D.5.化简:〔1+ 〕÷结果为〔〕A.4xB.3xC.2xD.x6.化简〔1﹣〕÷的结果是〔〕A.〔x+1〕2B.〔x﹣1〕2C.D.7.以下运算结果为x﹣1的是〔〕A.1﹣B.•C.÷D.8.化简的结果是〔〕A.B.C.x+1D.x﹣19.假设分式□运算结果为x,那么在〝□〞中添加的运算符号为〔〕A.+B.﹣C.+或×D.﹣或÷10.化简的结果是()A.1B.C.D.-111.计算〔﹣〕÷的结果为〔〕A.B.C.D.12.以下等式成立的是〔〕A.+ =B.=C.=D.=﹣【二】填空题13.化简:〔1+ 〕÷的结果为________.14.÷·=________÷·________.15.化简:=________.16.有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:那么第n次运算的结果yn=________〔用含字母x和n的代数式表示〕.17.计算:=________.【三】计算题18.计算:〔1〕;〔2〕.19.计算:〔1〕〔2〕.20.计算:①;②﹣a﹣1;③.21.计算:.22.计算或化简:①计算〔﹣〕÷.②a≠0,且满足a2﹣3a+1=0,求a2+ 的值.23.计算或化简:〔1〕.〔2〕.24.计算:.25.计算:〔1〕÷;〔2〕〔1+ 〕÷.【四】解答题26.:y= ,试说明不论x为任何有意义的值,y值均不变.27.化简:÷.【一】单项选择题1.计算的结果是〔〕A.B.C.x2+1D.x2﹣1【考点】分式的混合运算【解析】【解答】解:原式=[+ ]•〔x+1〕〔x﹣1〕=2x+〔x﹣1〕2=x2+1,应选C【分析】原式括号中两项通分并利用同分母分式的加法法那么计算,同时利用除法法那么变形,约分即可得到最简结果.2.化简分式〔x-y+〕〔x+y-〕的结果为〔〕A.y2-x2B.x2-y2C.x2-4yD.4x2-y2【考点】分式的混合运算【解析】【分析】先算小括号里的,再算乘法,把分子因式分解,化简即可.【解答】〔x-y+)〔x+y-)===x2-y2 .应选B、【点评】当整式与分式相加减时,一般可以把整式看作分母为1的分式,与其它分式进行通分运算.需注意:〔x+y)2-4xy=〔x-y)2 ,〔x-y)2+4xy =〔x+y)2的应用.3.x﹣=﹣y,且x+y≠0,那么xy的值为〔〕A.-1B.0C.1D.2【考点】分式的混合运算【解析】【解答】解:∵x﹣=﹣y,∴x+y=+= ,∵x+y≠0,∴xy=1,应选C【分析】等式移项变形,整理后根据x+y不为0求出xy的值即可.4.化简÷〔1+ 〕的结果是〔〕A.B.D.【考点】分式的混合运算【解析】【解答】解:原式=÷= •=,应选C【分析】原式括号中两项通分并利用同分母分式的加法法那么计算,同时利用除法法那么变形,约分即可得到结果.5.化简:〔1+ 〕÷结果为〔〕A.4xB.3xC.2xD.x【考点】分式的混合运算6.化简〔1﹣〕÷的结果是〔〕A.〔x+1〕2B.〔x﹣1〕2C.D.【考点】分式的混合运算【解析】【解答】解:〔1﹣〕÷===〔x﹣1〕2 ,应选B、【分析】先对括号内的式子通分,然后再将除法转化为乘法即可解答此题.7.以下运算结果为x﹣1的是〔〕A.1﹣B.•C.÷D.【考点】分式的混合运算【解析】【解答】解:A、1﹣= ,故此选项错误;B、原式= •=x﹣1,故此选项正确;C、原式= •〔x﹣1〕= ,故此选项错误;D、原式= =x+1,故此选项错误;应选:B、【分析】根据分式的基本性质和运算法那么分别计算即可判断.8.化简的结果是〔〕A.B.C.x+1D.x﹣1【考点】分式的混合运算9.假设分式□运算结果为x,那么在〝□〞中添加的运算符号为〔〕A.+B.﹣C.+或×D.﹣或÷【考点】分式的混合运算【解析】【解答】解:A、根据题意得:+ = ,不符合题意;B、根据题意得:﹣= =x,不符合题意;C、根据题意得:×= ,不符合题意;D、根据题意得:﹣= =x;÷= •=x,符合题意;应选D【分析】将运算符号放入原式,计算即可得到结果.10.化简的结果是()A.1B.C.D.-1【考点】分式的混合运算11.计算〔﹣〕÷的结果为〔〕A.B.C.D.【考点】分式的混合运算【解析】【解答】解:原式=÷= •=.应选A、【分析】首先把括号内的式子通分、相减,然后把除法转化为乘法,进行通分即可.12.以下等式成立的是〔〕A.+ =B.=C.=D.=﹣【考点】分式的混合运算【解析】【解答】解:A、原式= ,错误;B、原式不能约分,错误;C、原式= = ,正确;D、原式= =﹣,错误,应选C【分析】原式各项计算得到结果,即可做出判断.【二】填空题13.化简:〔1+ 〕÷的结果为________.【考点】分式的混合运算14.÷·=________÷·________.【考点】分式的混合运算15.化简:=________.【考点】分式的混合运算【解析】【解答】解:=1﹣=1﹣= = .【分析】把第二个分式的分子分母先因式分解,再把除法统一成乘法化简,最后算减法.16.有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:那么第n次运算的结果yn=________〔用含字母x和n的代数式表示〕.【考点】分式的混合运算17.计算:=________.【考点】分式的混合运算【三】计算题18.计算:〔1〕;〔2〕.【考点】分式的混合运算【解析】【分析】〔1〕原式利用除法法那么变形,约分即可得到结果;〔2〕原式先计算乘方运算,再计算除法运算,最后算加减运算即可得到结果.19.计算:〔1〕〔2〕.【考点】分式的混合运算【解析】【分析】〔1〕原式通分并利用同分母分式的加法法那么计算,即可得到结果;〔2〕原式括号中通分并利用同分母分式的减法法那么计算,同时利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果.20.计算:①;②﹣a﹣1;③.【考点】分式的混合运算【解析】【分析】①原式利用除法法那么变形,约分即可得到结果;②原式两项通分并利用同分母分式的减法法那么计算即可得到结果;③原式括号中两项通分并利用同分母分式的加减法那么计算,约分即可得到结果.21.计算:.【考点】分式的混合运算【解析】【分析】原式括号中三项通分并利用同分母分式的减法法那么计算,约分即可得到结果.22.计算或化简:①计算〔﹣〕÷.②a≠0,且满足a2﹣3a+1=0,求a2+ 的值.【考点】分式的混合运算【解析】【分析】①原式括号中两项通分并利用同分母分式的减法法那么计算,同时利用除法法那么变形,约分即可得到结果;②等式整理求出a + 的值,再利用完全平方公式即可求出所求式子的值.23.计算或化简:〔1〕.〔2〕.【考点】分式的混合运算【解析】【分析】〔1〕、〔2〕根据分式混合运算的法那么进行计算即可.24.计算:.【考点】分式的混合运算【解析】【分析】先把括号内通分,再把分子分母因式分解和除法运算化为乘法运算,然后约分即可.25.计算:〔1〕÷;〔2〕〔1+ 〕÷.【考点】分式的混合运算【解析】【分析】〔1〕原式利用除法法那么变形,约分即可得到结果;〔2〕原式括号中两项通分并利用同分母分式的加法法那么计算,同时利用除法法那么变形,约分即可得到结果.【四】解答题26.:y= ,试说明不论x为任何有意义的值,y值均不变.【考点】分式的混合运算【解析】【分析】先算乘除,约分化为最简分式,后算加减,得到不论x为任何有意义的值,y值均不变.27.化简:÷.【考点】分式的混合运算【解析】【分析】利用分式的混合运算顺序求解即可.。
分式混合运算(习题及答案)

分式混合运算(习题及答案)混合运算(题)例1:混合运算:解:原式可以化简为:frac{4-x}{x-2} \div \frac{12}{x+2-x^2}$$frac{4-x}{x-2} \times \frac{x+2-x^2}{12}$$frac{-(x-4)}{(x-2)(x+4)}$$例2:先化简,然后在$-2\leq x\leq 2$的范围内选取一个合适的整数$x$代入求值.解:先化简原式:frac{x(x+1)}{(x-1)(1-x)} \div \frac{2x}{x+1}$$frac{x(x+1)}{(x-1)(x-1)} \times \frac{x+1}{2x}$$frac{1}{2}$$由于$-2\leq x\leq 2$,且$x$为整数,因此使原式有意义的$x$的值为$-2$,$-1$或$2$。
代入计算可得:当$x=2$时,原式为$-2$。
巩固练1.计算:1)$$\frac{x-y}{x+2y} \div \frac{1}{2x+4y}$$化简原式:frac{x-y}{x+2y} \times \frac{2x+4y}{1}$$frac{2(x-y)}{x+2y}$$2)$$\frac{\frac{a}{a-1}-1}{a^2-2a+1} \div \frac{1}{a+1}$$ 化简原式:frac{\frac{a}{a-1}-1}{(a-1)^2} \times (a+1)$$frac{a-2}{(a-1)^2}$$3)$$\frac{2a-2ab}{a^2-b^2} \div \frac{a+b}{a+b}$$化简原式:frac{2a-2ab}{a^2-b^2} \times \frac{a+b}{a+b}$$frac{2a-2ab}{(a-b)(a+b)} \times \frac{a+b}{1}$$frac{2(1-b)}{a-b}$$4)$$\frac{y-1-\frac{8}{y-1}}{y^2+y} \div\frac{1}{y(y+1)}$$化简原式:frac{y-1-\frac{8}{y-1}}{y(y+1)} \times \frac{y(y+1)}{1}$$ frac{(y-1)^2-8}{y(y+1)^2}$$5)$$\frac{a^2-2ab+b^2}{b}\div \frac{1}{a-b}-1$$化简原式:frac{(a-b)^2}{b} \times \frac{a-b}{1}-1$$frac{(a-b)^3}{b}-1$$6)$$\frac{x^2-4x+4}{x(x-1)} \div \frac{x+2}{x-1}$$化简原式:frac{(x-2)^2}{x(x-1)} \times \frac{x-1}{x+2}$$frac{(x-2)^2}{x(x+2)}$$7)$$\frac{2}{(x-1)^2} - \frac{1}{(x-1)^2(x+1)}$$化简原式:frac{2(x+1)-1}{(x-1)^2(x+1)}$$frac{2x+1}{(x-1)^2(x+1)}$$8)$$\frac{3-x}{2(x-2)} \div \frac{5}{x-2}-\frac{5}{x-3}$$ 化简原式:frac{3-x}{2(x-2)} \times \frac{x-2}{5} - \frac{5}{x-3}$$ frac{(x-3)(x-1)}{2(x-2)5} - \frac{5}{x-3}$$frac{x^2-4x+7}{10(x-2)(x-3)}$$9)$$\frac{x-1}{x+1} \div \frac{x-3}{x-2} - \frac{5}{x^2-3x}$$化简原式:frac{(x-1)(x-2)}{(x+1)(x-3)} - \frac{5}{x(x-3)}$$frac{x^2-3x-2}{x(x-3)(x+1)(x-3)} - \frac{5(x+1)}{x(x-3)(x+1)(x-3)}$$frac{x^2-3x-2-5x-5}{x(x-3)(x+1)(x-3)}$$frac{x^2-8x-7}{x(x-3)(x+1)^2}$$10)$$\frac{1}{(x-1)(x+1)}-\frac{1}{x(x-1)}$$化简原式:frac{x-(x-1)}{x(x-1)(x+1)}$$frac{1}{x(x+1)}$$11)$$\frac{2}{x+y} - \frac{1}{y-x} \times \frac{y^2-x^2}{11}$$化简原式:frac{2(y-x)}{(y-x)(x+y)} - \frac{y+x}{11(x+y)}$$frac{y-x-2}{11(x+y)}$$2.化简求值:1)先化简,再求值:$\frac{x^2+2x+1}{x+2x+2} \div \frac{1}{x+2}$,其中$x=3-1$。
分式混合运算练习题

分式混合运算练习题分式混合运算练习题在数学学习中,分式混合运算是其中一个重要的知识点。
它不仅在数学领域中有着广泛的应用,还在科学、工程和经济学等领域中发挥着重要作用。
为了帮助学生更好地掌握分式混合运算的技巧,本文将提供一些练习题并提供详细的解答过程。
首先,我们来看一下分式混合运算的基本规则。
当进行分式运算时,我们需要遵循以下规则:1、分式乘法:分式与分式相乘时,把分子相乘,分母相乘,作为新的分母。
2、分式除法:分式除以一个分式时,分母与分母相乘,分子与分子相除,作为新的分子。
3、分式乘方:分式的乘方等于分式的分子和分母分别乘方。
现在让我们来看一些练习题:例1:计算 $\frac{x}{y} \div \frac{y}{x}$解: $\frac{x}{y} \div \frac{y}{x} = \frac{x}{y} \times\frac{x}{y} = \frac{x^{2}}{y^{2}}$例2:计算 $\frac{a}{b} \times \frac{c}{d}$解: $\frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd}$例3:计算 $\frac{a}{b} \div \frac{c}{d}$解: $\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times\frac{d}{c} = \frac{ad}{bc}$以上是分式混合运算的基本规则和练习题。
通过不断地练习,学生可以逐步掌握分式混合运算的技巧,提高解题能力。
学生还可以通过参考答案来检查自己的解题过程和结果,进一步加深对分式混合运算的理解。
分数混合运算应用题练习题一分数混合运算应用题练习题一分数混合运算是一种常见的数学问题,它涉及到分数的加减乘除以及各种应用场景。
下面我们通过一道例题来讲解分数混合运算的解题方法和技巧。
例题:某班共有40名学生,其中男生占1/2,女生占1/2。
分式混合运算(习题及答案)

分式混合运算(习题)例题示范例1:混合运算:. 412222x x x x -⎛⎫÷+- ⎪--⎝⎭【过程书写】 2244122241622422(4)(4)14x x x x x x x x x x x x x x ---=-÷----=-÷----=-⋅-+-=-+解:原式例2:先化简,然后在的范围内选取一个你认为(1)211x x x x x x+⎡⎤+÷⎢⎥--⎣⎦22x -≤≤合适的整数x 代入求值. 【过程书写】 2221122112x x x x x x xx x x x x++--=⋅--=⋅-=-解:原式∵,且x 为整数22x -≤≤∴使原式有意义的x 的值为-2,-1或2当x =2时,原式=-2巩固练习1. 计算:(1); 22221244x y x y x y x xy y---÷+++(2);211121a a a a ⎛⎫-÷ ⎪--+⎝⎭(3);22221aa b a ab a b ⎛⎫-÷ ⎪--+⎝⎭(4);2286911y y y y y y ⎛⎫-+--÷ ⎪-+⎝⎭(5); (6);2221122a ab b a b b a -+⎛⎫÷- ⎪-⎝⎭24421x x x x -+⎛⎫÷- ⎪⎝⎭(7); 2234221121x x x x x x ++⎛⎫-÷ ⎪---+⎝⎭(8); (9); 352242x x x x -⎛⎫÷+- ⎪--⎝⎭253263x x x x --⎛⎫÷-- ⎪--⎝⎭(10); 211(1)111x x x ⎛⎫--- ⎪-+⎝⎭(11). 22221113x y x y x y x xy x y ⎛⎫⎛⎫--⋅÷-- ⎪ ⎪+--⎝⎭⎝⎭2. 化简求值:(1)先化简,再求值:,其中. 2121122x x x x ++⎛⎫-÷ ⎪++⎝⎭1x =(2)先化简,再求值:,其中 2222225321x y x x y y x x y xy ⎛⎫++÷ ⎪---⎝⎭,.x =+y =(3)先化简,然后在 22212211211x x x x x x x x ++-⎛⎫+÷+ ⎪--+-⎝⎭22x -≤≤的范围内选取一个合适的整数x 代入求值.(4)已知.222111x x xA x x ++=---①化简A ;②当x 满足不等式组,且x 为整数时,求A 的值.1030x x -⎧⎨-<⎩≥3. 不改变分式的值,把分子、分母中各项系数化为整数,结果是2132113x yx -+( )A .B .263x yx -+218326x yx -+C .D . 2331x y x -+218323x y x -+4. 把分式中的分子、分母的值同时扩大为原来的2倍,则分式的值32a b ab-( )A .不变B .扩大为原来的2倍C .扩大为原来的4倍D .缩小为原来的125. 把分式中a ,b 的值都扩大为原来的2倍,则分式的值() 34a bab -A .不变 B .扩大为原来的2倍C .扩大为原来的4倍D .缩小为原来的126. 把分式中x ,y 的值都扩大为原来的2倍,则分式的值()222xyx y +A .不变 B .扩大为原来的2倍C .扩大为原来的4倍D .缩小为原来的12 7. 已知,则A =_______,B =_______.47(2)(3)23x ABx x x x +=+-+-+【参考答案】巩固练习1. (1)yx y -+(2)1a -(3)21a (4)22(1)(27)(1)(3)y y y y y y +----(5)2ab (6)2x -+(7)11x x -+ (8)126x -+ (9)124x -+ (10)23x -+(11)y x y-+2. (1)原式,当时,原式11x =+1x =-=(2)原式=3xy ,当,时,原式=3 x =+y =(3)原式,当x =2时,原式=0 241x x -=+(4)①;②1 11x -3.B 4.A 5.D 6.A 7. 3,1。
分式混合运算专题目练习(经典集合)

合用标准文案分式的乘除乘方运算一、基础知识点:1.约分把一个分式的分子与分母的公因式约去,叫做约分.约分的依照是分式的根本性质 .假设分式的分子、分母是多项式,必定先把分子、分母分解因式,尔后才能约去公因式.分子与分母没有公因式的分式,叫做最简分式,又叫做既约分式.分式的运算结果必然要化为最简分式.2.分式的乘法乘法法测:a·c=ac.b d bd3.分式的除法除法法那么:a÷c=a · d = adb d bc bc4.分式的乘方求 n 个相同分式的积的运算就是分式的乘方,用式子表示就是a n () . b分式的乘方,是把分子、分母各自乘方.用式子表示为:(a n a n) =n (n 为正整数 ) b b二、典型例题例 1、以下分式15bc,3( a b) 2 a 2 b 2a2b2). 12a b,2(a,a中最简分式的个数是 (a b)b例 2. 计算:(1)4xy(2)a212a(3)3xy 26y2 3y 2x3 a 2a2x(4)a 2a 1 a 21例3、假设x y zxy yz zx的值 . 4a 4 a24 2 34,求x 2y 2z2例 4、计算〔 1〕〔2a2b 3x2)2(y23(y4 c3〕〔2〕())y x x〔 3〕( 2a2bc)3(3a3b2x 2y 2)2( x2xy)3(xy2 )〔4〕()例5计算:11248x 1 x 1 x2 1 x4 1 x81112x 4 x38x7练习: 1.计算:2x 2 a 4x 4a8x8a x a x a例 6.计算:11111324351719182011111练习 1、x 2 x 3x 3 x 4x 100 x 101 x 1 x 2例 7、2x 1A B( x 1)( x 2)x 1x 2,求 A. B 的值。
针对性练习: 1. 计算以下各题 :〔 1〕x 3yx 2 y 2x 3 y〔2〕 a23a11. x2y 2x 2y2y 2x2 a 2 1a1(3)16(4)x2- x- 1(5)a-a6+3 ,a 3 9 a2x 1 a 3 a23a a(6)2xy x y2b2⑻313 2⑺ a b211x 2 y 2 ⑽x 2x 1〕 ( a aa 24⑼xy2-2 〔 11).x y x yx 2x x 4 x 4a 2 a 2a2. x 为整数,且2 22 x 18为整数,求所有的吻合条件的 x 的值的和.x 3 3 x x 293、混杂运算:⑴ (2x 3 x 293x x 2x a 1a11)⑵x 2 x 2x 24⑶a 2 2a 1axxa 1⑷ ( a 25a 2 1)a 24 ⑸x 2 2x 1(1 x 3)a 2a 24a 4x 2 1x 1⑹x3 (x 2 5 ) ⑺1 1 x 1x 2x 2x 1 x 2 1 x 2 2x 1x 2 4x 4 x 22x 11⑼xy 1 1⑻24x 2x 2 y 2x y x yxx⑽ (a 2b 2a 2b 2x x 3 x 2 2x 1+2) ÷⑾x 21x 3ab a bx 1⑿ ( x2 x 1 ) x 2 16(13)、 (x 2)2 ( y 2 )3 ( y ) 4 x 22x x 2 4x 4 x 24xy x x〔 14 〕、3 m(m 25 ) 〔 15〕、2x 6 ( x 3)x 2x 6 2m 4m 24 4x x 23 x1 a 1b 2213b 2 c〔 16〕、22b 3〔 17〕、2x 2 18 3 x2a4 4xx22 x4. 算:( x 2x 1)4 x,并求当 x3 原式的 .x 2 2x x 2 4x 4 x5、先化 ,3xxx 21再取一个你喜 的数代入求 :x 1 x 1 xx 22x 1÷x 1 6、有 一道 : “ 算21x 2 x x-x 的 ,其中 x=2 004 〞甲同学把“ x=2 004 〞 抄成“ x=2 040 〞,但他的 算 果也正确,你 是怎么回事?11+117、 算、++⋯+。
分式混合运算专题练习(经典集合)
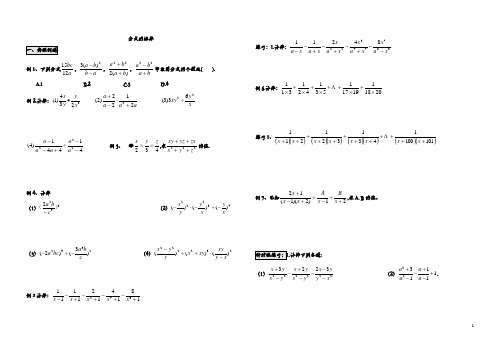
分式的运算一、典型例题例1、下列分式a bc 1215,a b b a --2)(3,)(222b a b a ++,b a b a +-22中最简分式的个数是( ).A.1B.2C.3D.4例2.计算:3234)1(x y y x ∙ a a a a 2122)2(2+⋅-+ x y xy 2263)3(÷41441)4(222--÷+--a a a a a 例3、 若432z y x ==,求222zy x zxyz xy ++++的值.例4、计算(1)3322)(c b a - (2)43222)()()(xy x y y x -÷-⋅-(3)2332)3()2(c b a bc a -÷- (4)232222)()()(xy xy xy x y y x -⋅+÷-例5计算:1814121111842+-+-+-+--x x x x x练习:1.计算:8874432284211x a x x a x x a x x a x a --+-+-+--例6.计算:2018119171531421311⨯+⨯++⨯+⨯+⨯练习1、()()()()()()()()1011001431321211++++++++++++x x x x x x x x例7、已知21)2)(1(12++-=+-+x Bx A x x x ,求A. B 的值。
针对性练习:1.计算下列各题:(1)2222223223xy yx y x y x y x y x ----+--+ (2)1111322+-+--+a a a a .(3)29631a a --+ (4) 21x x --x -1 (5)3a a --263a a a +-+3a ,(6)xy yy x x y x xy --++-222 ⑺b a b b a ++-22 ⑻293261623x x x -+--+⑼xy y x y x y x 2211-⋅⎪⎪⎭⎫ ⎝⎛+-- ⑽ 222x x x +--2144x x x --+(11)a a a a a a 4)22(2-⋅+--.2.已知x 为整数,且918232322-++-++x x x x 为整数,求所有的符合条件的x 的值的和.3、混合运算:⑴2239(1)x x x x ---÷ ⑵232224xx x x x x ⎛⎫-÷ ⎪+--⎝⎭⑶ a a a a a a 112112÷+---+⑷ 444)1225(222++-÷+++-a a a a a a ⑸ )1x 3x 1(1x 1x 2x 22+-+÷-+-⑹ )252(23--+÷--x x x x ⑺ 221111121x x x x x +-÷+--+⑻2224421142x x x x x x x -+-÷-+-+ ⑼2211xy x y x y x y ⎛⎫÷- ⎪--+⎝⎭⑽ (ab b a 22++2)÷ba b a --22 ⑾22321113x x x x x x x +++-⨯--+⑿ x x x x x x x x x 416)44122(2222+-÷+----+ (13)、22234()()()x y y y x x-⋅-÷-(14)、)252(423--+÷--m m m m (15)、x x x x xx x --+⋅+÷+--36)3(446222(16)、 ()3212221221------⎪⎭⎫ ⎝⎛ba cb b a (17)、⎪⎭⎫ ⎝⎛---÷⎪⎪⎭⎫ ⎝⎛+--x x x x x 23441823224.计算:x xx x x x x x -÷+----+4)44122(22,并求当3-=x 时原式的值.5、先化简,x x x x x x11132-⋅⎪⎭⎫ ⎝⎛+--再取一个你喜欢的数代入求值:6、有这样一道题:“计算22211x x x -+-÷21x x x -+-x 的值,其中x=2 004”甲同学把“x=2 004”错抄成“x=2 040”,但他的计算结果也正确,你说这是怎么回事?7、计算、)1(1+a a +)2)(1(1++a a +)3)(2(1++a a +…+)2006)(2005(1++a a 。
分式的混合运算练习题及答案

分式的混合运算练习题及答案分式的混合运算练习题及答案分式是数学中常见的一种数形式,它由分子和分母组成,分子表示被分割的部分,分母表示总共的部分。
在实际生活中,我们经常会遇到需要进行分式的混合运算的情况,比如在购物时计算折扣、在烹饪中调整食材的比例等等。
下面我将给大家提供一些分式的混合运算练习题及答案,希望对大家的数学学习有所帮助。
1. 小明有1/4千克的苹果,他打算分给5个朋友,每人分多少千克?解答:将1/4千克除以5,即1/4 ÷ 5 = 1/4 × 1/5 = 1/20千克。
所以每人分到的苹果重量为1/20千克。
2. 一桶果汁有3/5升,小红喝了1/4升后,还剩下多少升?解答:将3/5升减去1/4升,即3/5 - 1/4 = 12/20 - 5/20 = 7/20升。
所以还剩下7/20升果汁。
3. 小明用1/2小时走完了全程,他一共用了多少分钟?解答:将1/2小时转换成分钟,即1/2 × 60 = 30分钟。
所以小明一共用了30分钟。
4. 一辆汽车以每小时80公里的速度行驶,行驶了1/4小时后停下来休息,此时汽车行驶了多少公里?解答:将每小时80公里的速度乘以1/4小时,即80 × 1/4 = 20公里。
所以汽车行驶了20公里。
5. 一张长方形的纸片的长是2/3米,宽是1/4米,求纸片的面积。
解答:将长和宽相乘,即2/3 × 1/4 = 2/12 = 1/6平方米。
所以纸片的面积为1/6平方米。
通过以上的练习题,我们可以看到分式的混合运算并不复杂,只需要将题目中的分式进行相应的运算即可得到答案。
在进行分式的混合运算时,我们需要注意分式的基本运算规则,比如分数的加减乘除运算规则,以及分数的化简等等。
熟练掌握这些规则,我们就能够轻松地解决分式的混合运算问题。
当然,在实际生活中,我们还会遇到更加复杂的分式混合运算问题,比如多个分式的加减乘除运算,或者分式与整数的混合运算等等。
分式混合运算专项练习158题(有答案)26页

分式混合运算专项练习158题(有答案)(1)(2)+﹣(3)(4)(5)(﹣)•÷(+)(6).(7)(8)(9)(10).(11)(12).(13)•÷(14)(﹣)÷.(15)(16)(17)(1+)÷(18)(19)(20)()2•+÷(21)(22)(23)(24)(25)(26)(27)(28).(29)(30).(31)(32)÷•.(33)()÷.(34)(35)(36)(37)(38)(39)(40).(41)(42)(43)(44)(﹣)÷(45)(46)(47)+(48)(49)(50).(51)(52).(53)(54).(55)÷•(56)1﹣÷.(57)(58)(59)÷(60)(61).(62)(63).(64)(+1)÷(1﹣)(65)(66)•﹣÷(67)(68).(69)(70)[﹣(﹣x﹣y)]÷(71)﹣÷x.(72)(73)(74)÷(x+3)•(75)(a ﹣)÷•(76)()÷•(2﹣x)2(77)•(﹣)2(78)(79)(80)(81)(82)(83)(84)(85)(86)(87)(88).(89)(90).(91)(92).(93)[+÷(+)2]•(94)(95)(96)(97)(98)(99)x﹣(100)(101)(102).(103).(104)(105).(106)(x2﹣y2)•÷(107)+﹣(108).(109)÷﹣.(110)(111).(112).(113)(114).(115).(116)(117)(118)(119)(120)(x2y﹣1)﹣3•(﹣x﹣2)﹣3÷(xy)﹣1.(121)(122)(﹣)•.(123)(124).(125).(126).(127).(128).(129)﹣(130)(131)1﹣÷.(132)(﹣)3÷•(﹣)2(133).(134)(135).(136).(137)(138).(139)(140).(141).(142)(143).(144).(145).(146).(147)(148)(149).(150)(151)(152)(153).(154)(155)(156).(157)(158).分式混合运算158题参考答案:(1)=﹣=(2)+﹣=++==(3)=﹣=2x+6﹣x+3=x+9 (4)=÷(﹣)=•(﹣)=﹣.(5)原式===.(6)原式===(7)原式==x+y(8)原式==a﹣1(9)原式==y﹣3(10)==3(x+2)﹣(x﹣2)=3x+6﹣x+2=2x+8.(11)原式==(12)原式==(﹣1)==(13)解:原式==(14)解:原式==(15)原式=÷•=••=.(16)原式=•=﹣=﹣=.(17)原式===.(18)===﹣y.(19)原式==1﹣==(20)原式===.(21)原式=××=.(22)原式==(23)原式==﹣1(24)原式===(25)=+﹣=,===(26)=﹣••=﹣(27)=﹣•,=﹣==﹣(28),=(﹣)•,=﹣,=,=,=﹣.(29)原式==(a+1)﹣(a﹣1)=2(30)原式=(31)原式==(32)原式==.(33)()÷=•=(34)原式===.(35)原式=•(a﹣1)2=a﹣1.(36)原式=×=(37)原式=×=(38)原式=×==(39)原式==a4b(40)原式==(41)=×=2(m﹣3)﹣(m+3)=m﹣9.(42)原式==﹣.(43)原式=﹣+=1﹣x+x2=x2﹣x+1.(44)原式=(﹣)×=×=.(45)原式===3(1+x)(46)原式==.(47)原式=×+=+=.(48)原式=﹣==(49)原式=••=.(50)原式=====.(51)原式=====(52)原式===.(53)原式==(54)原式=×=(55)原式=•=(56)原式=1﹣=1﹣==.(57)原式=﹣÷(58)原式=×=.(59)原式=÷(﹣)=÷=×=.(60)原式=﹣===﹣(61)原式=﹣•=﹣==.(62)原式=(63)原式=××(m+n)(m﹣n)=(m+n)2.(64)原式=÷=×=.(65)原式=﹣×=﹣=.(66)原式=×﹣×=﹣==.(67)原式==0(68)原式=+=(69)原式=(×=.(70)=.(71)===.(72)原式===(73)原式=﹣+====(74)原式=××=(75)原式=××=(76)原式=[﹣]ו(2﹣x)2=ו(2﹣x)2=(77)原式=××=(78)原式===.(79)=﹣+,==(80),=÷=•=﹣(81)原式==(82)原式==(83)原式=×= (84)原式=+﹣==. (85)原式=(x+1)(x ﹣1)(﹣﹣), =x+1﹣x+1﹣(x+1)(x ﹣1)=﹣x 2+3.(86)原式=﹣×=﹣=0.(87)原式=÷(﹣)=.(88)原式=(﹣)÷=×=.(89)原式=﹣×(m ﹣1)=﹣=﹣2m . (90)===(91)原式= (92)原式=.(93)原式=[+×]×=[+]×=(94) 原式==.(95)原式=(x+y )•﹣==x+y(96)原式==(97)原式=••=(98)原式=•+•=+==(99)原式==(100)原式===.(101)原式=﹣===(102)原式=•=•=.(103)原式=1﹣×=1﹣=﹣.(104)=×=(105)=××=x.(106)原式=(x+y)(x﹣y)××=y(107)原式=﹣﹣=﹣﹣==(108)=••==.(109)原式=•﹣=﹣==(110)=+=+﹣==(111)=﹣+=﹣+1=1.(112)原式=+•=+==1.(113)原式=﹣==(114)原式=•=•=•=y+9 (115)原式=1﹣•=1﹣===﹣(116)原式==x﹣y.(117)原式==(118)原式===(119)原式====﹣(120)原式=x﹣6y3•(﹣x6)÷x﹣1y﹣1=﹣y3÷x﹣1y﹣1=﹣xy4(121)原式=++==﹣(122)原式=(﹣)•=3(x+2)﹣(x﹣2)=3x+6﹣x+2=2x+8(123)原式=•=•=x﹣2(124)原式=1﹣÷[﹣]=1﹣÷=1﹣•=1﹣==﹣.(125)原式=﹣×=﹣==.(126)原式=[﹣]÷=[﹣]×x=×x=﹣.(127)原式=[]÷=[﹣]÷=×=(128)原式=[]•=•=y+9.(129)原式==(130)原式==0(131)原式=1﹣=.(132)原式=﹣••=﹣(133)原式=•﹣=﹣=原式=••=(134)(135)原式=[﹣]•=[﹣]•=•=(136)原式==﹣=(137)=(138)=,==.(139)=•=(x+y)(x﹣y)=x2﹣y2(140)=++===(141)原式=====(142)原式====2(143)原式=÷=•=.(144)原式=÷=•=.(145)原式=4a﹣1﹣+=﹣==(146)原式=×+=+==1.(147)==﹣(148)原式=+•=+=﹣=﹣(149)原式===0(150)原式=•=(151)原式=•=(152)原式=﹣===﹣(153)原式=[﹣]•=•=•=(154)原式===(155)原式=•=(156)原式=﹣a2b6••=﹣b5(157)原式===﹣(x+y)=﹣x﹣y(158)原式=÷=•=。
分式混合运算专项理解练习158题(有答案解析)

.
(127)
.
(123) (124) (125)
(128)
.
.
(129)
﹣
.
(130)
分式混合运算---- 13
(131)1﹣
÷
.
(136)
.
(132)(﹣ )3÷ •(﹣ )2;
(137)
(133)
.
(138)
.
(134) (135)
(139)
.
(140)
.
分式混合运算---- 14
(141)
•
﹣
=
﹣
=
(134)原式= •
•=
(135)原式=[
﹣
=
•
=
]•
=[
﹣
]•
(136) 原式=
(137)
=
=
﹣
=
;
(138)
=
,
分式混合运算---- 26
= (139) (140) = (141)原式=
= (142)原式=
=
.
=
•
=(x+y)(x﹣y)=x2﹣y2;
= =
+
+
=
=
=
=
= =
=2;
(143)原式=
.
(104)
;
(109)
÷﹣
.
(105)
.
(110)
分式混合运算---- 11
(111)
.
(116)
(112)
.
(117)
(113)
(118)
(114)
.
(119)
(115)
(word完整版)八年级下册分式混合运算练习题

9-(宀盹)4(乙」乙血-)(乙).i -工~T~:直44 (車菲乙00乙)L(6 -(Mx^soos)乙q B+q 町+j £” qg 产[外-泸'q 「Q:直44 (別邈900乙) :凰肘(音日*施注00乙)中字己(悬)手己(占)•g:直44 26+口9+泸.£+呂r +乔10. (2001?常州)”1+—a+l& ( 2005?宜 昌)计算:9. (2001?吉林)计算: (1)12.计算:一一-a - 1.13.计算: (1)(2)12 2m 2 - 9 3_m14.计算:a - 2+ °15.计算: 3 _ 6_ 时 5% I Tx 2 Xa+2(2)xy2 2x y17.已知ab=1,试求分式:丄+■上7的值.a+1 b+119. (2010?新疆)计算: (子一^20.I _ 11 _ K X _ 1.6(3) x 的取值范围.21 ]a 2-la- 116.化简:18计算:23. (2009?江苏)计算:(1)卜2卜(1+念)°+石;(2009?太原)化简:21. (2009?上海)计算: 22. (2009?眉山)化简:.a 2 - 2a+laa(2)24. (2009?东营)化简:18. 先化简代数式 门 U 门,然后选取一个使你喜欢的X 的值代入求值.25. (2008?白银)化简:26. (2007?南昌)化简:27. (2007?巴中)计算:(1+f T/ -甌+128. (2006?宜昌)计算:29. (2006?十堰)化简:〔;% - _ 、aH-2 a-230.(2006?南充)计算:x - 2)、填空、选择题:x 21•以下是方程xn 匚I 去分母的结果'其中正确的是 —A. x2X 1)1 B . i 2x2 1 C .空 2<2fx D . >< 2x 2 X x2 •在下列方程中,关于x 的分式方程的个数有.IA 、1B 、土 1C 、1D 、-1分式方程练习题①】x 2 2x 4 0234;④.-9 1;⑤6;x 3x 22.A.2 个B.3 个C.4 个D.53.分式一J 的值为1时,m 的值是. m 5A . 2B . - 2C . - 3D . 34 .不解下列方程,判断下列哪个数是方程7.赵强同学借了一本书,共280页,要在两周借期内读完,当他读了一半时, 发现平时每天要多读21页才能在借期内读完.他读了前一半时,平均每天读多少 页?如果设读前一半时,平均每天读x 页,则下列方程中,正确的是.A 、140 140 14B 、 280 280LJ >A AC 、10 10 1D 、140140141414xx 21 x x 21x x 21x x 212ax 3 8.关于x 的方程a x 5 4的根为x=2,则a 应取值A.1B.3C. -2D.-3A . x=1B . x=-1 .x=3 D . x=-3若分式 x 2-12(x+1) 的值等于8. ____________________________________________ 关于x 的方程2ax 3 5的根为x=2,则a 应取值 ___________________________________ .a x 410. “五一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面 包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,设参加游览的同学共 x 人,则所列方程为一、填空题:13. 若分式 也 的值为0,则x 的值等于x 1------------------14. 若分式方程 竺 5— 无解,那么m 的值应为x 22 x16.阅读材料:方程丄1二 1的解为x 1,x 1 x x 2 x 3方程1 丄」 匚的解为x=2,x x 1 x 3 x 4方程—1 1—的解为x 3,x 1 x 2 x 4 x 5请写出能反映上述方程一般规律的方程,并直 接写出这个方程的解 是 _____________二、解答题:x17.解方程3 x 1(x 1)(x 2)19.若方程 空 a 1的解是正数,求a 的取值范围x 2A.1B.3C. —2D. —3A180竺 3x x 2B . 180 180 3 CF"2 V180 180 3x x 2180 180 x 2 xmx20. 若解关于x的分式方程x 27—4 x 2会产生增根,求m的值21. A、B两地的距离是80公里,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,结果小汽车比公共汽车迟20分钟到达B地,求两车的速度.22. 华联商厦进货员在苏州发现一种应季衬衫,预料能畅销市场,就用80000元购进所有衬衫,还急需2倍这种衬衫,经人介绍又在上海用了176000元购进所需衬衫,只是单价比苏州贵4元,商厦按每件58元销售,销路很好,最后剩下的150件按八折销售,很快销售完,问商厦这笔生意赢利多少元?23. 现有一项工程由甲乙两个工程队来做,若甲队先做10天,余下的由乙队单独完成还需30天;若甲队先做9天后,因故抽走甲队一半去做其它工作,剩下任务由乙队和甲队剩余人员合做18天完成。
