高考预测模拟试题以及答案理汇总

合集下载

模拟高考各科试题及答案

模拟高考各科试题及答案一、语文试题及答案1. 阅读下面一段文言文，完成（1）-（3）题。

（1）下列词语解释不正确的一项是：A. 觥筹交错（酒杯和酒筹相互错杂）B. 箪食瓢饮（用瓢盛水喝）C. 夙兴夜寐（早起晚睡）D. 箪食壶浆（用壶盛酒）答案：D（2）下列句子中，加点词的意义和用法相同的一项是：A. 吾谁与归B. 吾从子游C. 吾与点也D. 吾谁欺答案：A（3）翻译文中划线的句子。

句子：不以物喜，不以己悲。

翻译：不因为物质的得失而感到高兴或悲伤。

2. 现代文阅读，回答问题。

（1）文章中“他”为什么坚持要回家？答案：因为他思念家乡和亲人。

（2）文章中“她”对“他”的态度是怎样的？答案：她对“他”既关心又有些无奈。

（3）文章的主题是什么？答案：文章的主题是思乡之情。

二、数学试题及答案1. 已知函数f(x)=2x^2-3x+1，求f(2)的值。

答案：f(2)=2*(2^2)-3*2+1=52. 解方程：x^2-5x+6=0。

答案：x=2或x=33. 计算定积分：∫(0到1) (2x+3)dx。

答案：(2/2)x^2+3x | 0到1 = 2+3-0 = 5三、英语试题及答案1. 根据句意，选择填空。

I don't think it is necessary to ________ the matter.A. look intoB. look upC. look outD. look over答案：A2. 翻译句子。

句子：他决定去旅行，放松一下。

翻译：He decided to go on a trip to relax.3. 阅读理解，回答问题。

（1）文章中提到了哪些旅游目的地？答案：文章提到了巴黎、伦敦和纽约。

（2）作者对旅游的态度是什么？答案：作者认为旅游是一种放松和学习的方式。

四、物理试题及答案1. 已知一个物体的质量为2kg，受到的重力为19.6N，求物体的加速度。

答案：a=F/m=19.6N/2kg=9.8m/s^22. 一个电容器的电容为4μF，通过它的电流为2A，求电容器的电压。

天津市2024届高考模拟预测物理高频考点试题(三)(强化版)

天津市2024届高考模拟预测物理高频考点试题（三）（强化版）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题电导率是电阻率ρ的倒数，即。

用国际单位制中基本单位表示正确的是（）A．B．C．D．第(2)题如图所示，理想变压器原、副线圈的匝数比，原线圈通过理想交流电流表接入正弦式交变电流，副线圈两端接两个阻值均为的电阻和，已知电流表的示数为0.1A，下列说法正确的是（）A．电阻中的电流的最大值为2AB．原线圈接入的正弦式交变电流的电压的有效值为200VC．电阻消耗的电功率为40WD．当电源的输入功率增大使通过电流表的电流增大时，通过电阻的电流减小第(3)题下列关于原子物理相关知识说法正确的是（）A．粒子散射实验现象能够作为“原子核可再分”的依据B．在裂变反应中，钡核的平均结合能比铀核的平均结合能大C．β衰变中产生的β射线是原子核外电子挣脱原子核束缚后形成的D．核反应属于α衰变第(4)题如图所示为研究高压带电体周围绝缘试验的电场分布图，由于试验线路比较短，在大的空间尺度下高压带电体A可以等效为点电荷，B、C、D是其周围的三个金属导体，均已处于静电平衡状态，P、S是导体C上的两点，M、N是A附近的两点，下列说法正确的是（）A．电场强度B．电场强度C．正电荷在点的电势能大于其在S点的电势能D．负电荷在点的电势能大于其在点的电势能第(5)题2022年9月2日，印度科钦造船厂建造的首艘航母“维克兰特”号正式服役。

“滑跃式”起飞甲板比“电磁弹射式”起飞甲板建造技术更为简单，印度该艘航母选择装配“滑跃式”起飞甲板。

如图所示，舰载飞机起飞时，先在水平甲板上加速后冲上圆弧形的甲板，运动过程中受到垂直于运动方向的升力，升力的大小与速度成正比，在离开圆弧甲板时，舰载飞机与甲板之间没有相互作用力则可以正常起飞，此时舰载飞机的动能为E0，已知圆弧轨道的水平长度为L，圆弧半径为R，舰载飞机的重力为G，舰载飞机可视为质点，则下列说法正确的是（）A．舰载飞机在圆弧形甲板上运动时处于失重状态B．舰载飞机在圆弧轨道的底端对甲板的压力一定大于舰载飞机的重力C．起飞时，舰载飞机受到的升力为D．若舰载飞机在离开甲板时的动能E<E0，则仍然可以正常起飞第(6)题义乌某中学学生用图甲装置进行趣味实验，其原理如图乙所示，在一块平板玻璃上放置一平薄凸透镜，在两者之间形成厚度不均匀的空气膜，让一束单一波长的光垂直入射到该装置上，结果在上方观察到如图丙所示的同心、内疏外密的圆环状干涉条纹，称为牛顿环，现将a、b两束单色光分别进行实验，结果发现同等条件下a光的圆环状干涉条纹平均间距大于b光的间距。

2024届江苏省泰州中学高三模拟预测地理试题含答案

江苏省泰州中学2023-2024学年高三年级高考模拟测试地理试卷（满分100分，考试时间75分钟）命题人：高三地理备课组2024.5.25一、单项选择题：共23题，每题2分，共46分。

每题只有一个选项最符合题意。

太阳辐射照度，是指到达某表面的单位面积单位时间内的太阳辐射能量。

图1为某地日光温室示意图，图2为该地夏至日测量的室内墙体和室内地面太阳辐射照度数据。

完成下面小题。

1．该地最可能位于（）A．黑龙江B．贵州C．新疆D．宁夏2．该日室内墙体和地面有太阳辐射照度的时长比昼长短，其影响因素是（）①太阳方位②地势高低③温室朝向④天气状况A．①③B．①④C．②③D．③④天山石林属典型的砾岩地貌，位于天山山脉西段。

石林周围冰川雪峰遍布，云雾变幻，巨岩耸立，似塔如堡。

下图为天山石林地理位置及天山石林景观图。

据此完成下面小题。

3．天山石林形成的主要地质作用是（）A．化学风化、风力侵蚀、流水溶蚀B．物理风化、风力侵蚀、流水侵蚀C．物理风化、冰川侵蚀、流水溶蚀D．化学风化、冰川侵蚀、流水侵蚀4．推测图中甲河径流量日变化最大的季节是（）由于湖陆热力差异，鄱阳湖周边形成明显的湖陆风环流。

湖陆风起止时刻具有季节变化。

下图是鄱阳湖甲监测站2010-2015年湖陆风起止时刻及其频次统计图，四条曲线表示湖风开始、湖风停止、陆风开始、陆风停止时刻。

据此完成下面小题。

5．四条曲线中，表示陆风停止时刻的是（）A．①B．②C．③D．④6．与夏季相比，鄱阳湖冬季湖风起止时刻（）A．开始晚，结束晚B．开始晚，结束早C．开始早，结束晚D．开始早，结束早7．鄱阳湖附近城市推进绿色生态发展，对湖陆风强度的影响的是（）A．湖风减弱，陆风增强B．湖风陆风均减弱C．湖风增强，陆风减弱D．湖风陆风均增强盐水楔是指在河流入海口处，密度大的海水沿河床底部侵入河口形成的界面清晰、形态稳定的楔形水体。

下图示意河口盐水楔，据此完成下面小题。

8．推测下列河流入海口处盐水楔不明显的是（）A．尼罗河B．密西西比河C．湄公河D．亚马孙河9．盐水楔的变化特点是（）A．河口越宽，盐水层越厚B．越深入河口，盐水层越厚C．盐淡水密度差大，入侵距离远D．水下地形坡度大，入侵距离远索诺拉沙漠位于美国和墨西哥交界处，冬夏两季降水，年降水量超过300m，高于北部的莫哈维沙漠。

高考数学模拟试题含答案详解

高考数学模拟试题含答案详解一、选择题1. 已知函数 $ f(x) = x^2 4x + 3 $，求 $ f(2) $ 的值。

答案：将 $ x = 2 $ 代入函数 $ f(x) $，得 $ f(2) = 2^2 4\times 2 + 3 = 1 $。

2. 已知等差数列 $\{a_n\}$ 的首项为 $a_1 = 3$，公差为 $d = 2$，求第 $n$ 项 $a_n$ 的表达式。

答案：等差数列的通项公式为 $a_n = a_1 + (n 1)d$，代入$a_1 = 3$ 和 $d = 2$，得 $a_n = 3 + (n 1) \times 2 = 2n + 1$。

3. 已知等比数列 $\{b_n\}$ 的首项为 $b_1 = 2$，公比为 $q = 3$，求第 $n$ 项 $b_n$ 的表达式。

答案：等比数列的通项公式为 $b_n = b_1 \times q^{n1}$，代入 $b_1 = 2$ 和 $q = 3$，得 $b_n = 2 \times 3^{n1}$。

4. 已知三角形的两边长分别为 $a = 5$ 和 $b = 8$，夹角为$60^\circ$，求第三边长 $c$。

答案：利用余弦定理 $c^2 = a^2 + b^2 2ab \cos C$，代入 $a = 5$，$b = 8$，$C = 60^\circ$，得 $c^2 = 5^2 + 8^2 2 \times5 \times 8 \times \cos 60^\circ = 49$，所以 $c = 7$。

5. 已知函数 $ g(x) = \frac{1}{x} $，求 $ g(x) $ 的定义域。

答案：由于 $x$ 不能为 $0$，所以 $g(x)$ 的定义域为 $x \neq 0$。

二、填空题1. 已知函数 $ h(x) = \sqrt{4 x^2} $，求 $ h(x) $ 的定义域。

答案：由于根号内的值不能为负，所以 $4 x^2 \geq 0$，解得$2 \leq x \leq 2$。

2024年浙江省山东省高考模拟题汇编+答案解析

2024新高考模拟试卷综合一一．选择题（共23小题）1．十二生肖是中国特有的文化符号，有着丰富的内涵，它们是成对出现的，分别为鼠和牛、虎和免、龙和蛇、马和羊、猴和鸡、狗和猪六对．每对生肖相辅相成，构成一种完美人格．现有十二生肖的吉祥物各一个，按照上面的配对分成六份．甲、乙、丙三位同学依次选一份作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学所有的吉祥物都喜欢，如果甲、乙、丙三位同学选取的礼物中均包含自己喜欢的生肖，则不同的选法种数共有（）A．12种B．16种C．20种D．24种2．把物体放在空气中冷却，如果物体原来的温度是θ1℃，空气的温度是θ0℃，那么tmin后物体的温度θ（单位：℃）满足公式（其中k为常数）．现有52℃的物体放在12℃的空气中冷却，2min后物体的温度是32℃．则再经过4min该物体的温度可冷却到（）A．12℃B．14.5℃C．17℃D．22℃3．已知双曲线的左、右顶点分别为A，B，其中一条渐近线与以线段AB为直径的圆在第一象限内的交点为P，另一条渐近线与直线PA垂直，则C 的离心率为（）A．3B．2C．D．4．关于函数f（x）＝sin|x|+|sin x|有下述四个结论：①f（x）是偶函数②f（x）在区间（，π）单调递增③f（x）在[﹣π，π]有4个零点④f（x）的最大值为2其中所有正确结论的编号是（）A．①②④B．②④C．①④D．①③5．已知三棱锥P﹣ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，则球O的体积为（）A．8πB．4πC．2πD．π6．2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式，孪生素数猜想是希尔伯特在1900年提出的23个问题之一，可以这样描述：存在无穷多个素数p使得p+2是素数，素数对（p，p+2）称为孪生素数．从10以内的素数中任取两个，其中能构成孪生素数的概率为（）A．B．C．D．7．著名数学家华罗庚先生被誉为“中国现代数学之父”，他倡导的“0.618优选法“在生产和科研实践中得到了非常广泛的应用，黄金分割比t＝≈0.618还可以表示成2sin18°，则＝（）A．4B．﹣1C．2D．8．在等腰梯形ABCD中，AB∥CD，且AB＝2AD，AB＞CD，若双曲线E以A，B为焦点，且过C，D两点，则双曲线E的离心率的取值范围为（）A．B．C．D．9．在正三棱台ABC﹣A1B1C1中，AB＝3AA1＝A1B1＝6，D是BC的中点，设A1D与BC、BB1、BA所成角分别为α，β，γ，则（）A．α＜γ＜βB．a＜β＜γC．β＜γ＜αD．γ＜β＜α10．已知实数x，y满足x2+y2＝1，0＜x＜1，0＜y＜1，当取最小值时，的值为（）A．B．C．D．111．十三世纪意大利数学家列昂那多•斐波那契从兔子繁殖中发现了“斐波那契数列”，斐波那契数列{a n}满足以下关系：a1＝1，a2＝1，a n＝a n﹣1+a n﹣2（n≥3，n∈N*），记其前n项和为S n，若a2020＝m（m为常数），则S2018的值为（）A．m﹣2B．m﹣1C．m D．m+112．三棱锥P﹣ABC的顶点都在球O的球面上，AC⊥BC，AC＝2，BC＝4．若三棱锥P﹣ABC的体积的最大值为，则球O的体积为（）A．B．33πC．D．36π13．设函数f a（x）＝sin a x+cos a x，a∈N*，记f a（x）的最小正周期为T a，则（）A．T3＝πB．T6＝πC．D．14．已知平面向量，，满足||＝2|﹣|＝2|﹣|＝2||＝2，则•的取值范围是（）A．[1，2]B．C．D．15．如图所示，等边三角形ABC的边长为2，D，E分别是AC，AB上的点，满足DE∥BC，将△ADE沿直线DE折到△FDE，则在翻折过程中，下列说法正确的个数是（）①；②∃G∈FE，使得BG∥平面FCD；③若存在平面FBC⊥平面FDE，则AD＜DC．A．0B．1C．2D．316．两位教师和两位学生排成一排拍合照，记ξ为两位学生中间的教师人数，则E（ξ）＝（）A．B．C．D．17．在棱长为1的正方体ABCD﹣A1B1C1D1中，E为线段B1C的中点，F是棱C1D1上的动点，若点P为线段BD1上的动点，则PE+PF的最小值为（）A．B．C．D．18．已知等差数列{a n}的前n项和为S n，满足sin（a4﹣1）+2a4﹣5＝0，sin（a8﹣1）+2a8+1＝0，则下列结论正确的是（）A．S11＝11，a4＜a8B．S11＝11，a4＞a8C．S11＝22，a4＜a8D．S11＝22，a4＞a819．函数y＝sin x+e x ln|x|的图象可能是（）A．B．C．D．20．一只小虫从数轴上的原点出发爬行，若一次爬行过程中，小虫等概率地向前或向后爬行1个单位，设爬行n次后小虫所在位置对应的数为随机变量ξn，则下列说法错误的是（）A．E（ξn）＝0B．D（ξn）＝nC．P（ξ2020＝0）＜P（ξ2020＝2）D．P（ξ2020＝0）＜P（ξ2018＝0）21．对于任意集合A，设f A（x）＝，已知集合S，T⊆X，则对任意的x∈X，下列说法错误的是（）A．S⊆T⇔f S（x）≤f T（x）B．f（x）＝1﹣f S（x）C．f S∩T（x）＝f S（x）•f T（x）D．f S∪T（x）＝f S（x）+f T（x）22．如图所示，平面α∩平面β＝l，二面角α﹣l﹣β∈[，]，已知A∈α，B∈β，直线AB 与平面α，平面β所成角均为θ，与l所成角为γ，若sin（γ+θ）＝1，则sin（γ﹣θ）的最大值是（）A．B．C．D．23．设等差数列{a n}的前n项和为S n，若S6＜S7＜S5，则满足S n＞0时正整数n的最小值为（）A．11B．12C．13D．14二．多选题（共2小题）24．如图，在正四棱柱ABCD﹣A1B1C1D1中，AA1＝2AB＝2，点P为线段AD1上一动点，则下列说法正确的是（）A．直线PB1∥平面BC1DB．三棱锥P﹣BC1D的体积为C．三棱锥D1﹣BC1D外接球的表面积为D．直线PB1与平面BCC1B1所成角的正弦值的最大值为25．声音是由物体振动产生的声波，其中包含着正弦函数．纯音的数学模型是函数y＝A sinωt，我们听到的声音是由纯音合成的，称之为复合音．若一个复合音的数学模型是函数，则下列结论正确的是（）A．2π是f（x）的一个周期B．f（x）在[0，2π]上有3个零点C．f（x）的最大值为D．f（x）在上是增函数三．填空题（共11小题）26．已知直线l与抛物线C：y2＝8x相切于点P，且与C的准线相交于点T，F为C的焦点，连接PF交C于另一点Q，则△PTQ面积的最小值为；若|TF|＝5，则|PQ|的值为．27．已知{|a n|}是首项和公差均为1的等差数列，S n为数列{a n}的前n项和，记m n为|S n|的所有可能取值中的最小值，则m1+m2+…+m2020＝．28．已知P为椭圆上的一点，过P作直线l交圆x2+y2＝4于A，B两点，则|PA|•|PB|的最大值是．29．已知平面向量，是不共线的单位向量，记，的夹角为θ，若平面向量满足||＝，且对于任意的正实数k，|﹣+k|≥恒成立，则cosθ的最大值为．30．甲、乙、丙、丁和戊5名学生进行劳动技术竞赛并决出1至5名，赛后甲、乙去询问成绩，老师对甲说：“很遗憾，你和乙都没有得到冠军．”；对乙说：“你当然不是最差的．”则5人的名次排列可能有种．31．已知直线l与双曲线Γ的两条渐近线交于与A，B两点，与x轴交于点C，若O是坐标原点，OA＝OC，BC＝2AB，则Γ的离心率是．32．设数列a1，a2，a3，a4满足前三项成等比数列且和为m，后三项成公差不为0的等差数列且和为12，若满足条件的数列个数大于1，则m的取值范围是．33．已知实数a，b满足对任意的实数x，不等式（|x|﹣a）（|x|﹣b）（|x|﹣2a2﹣1）≥0恒成立，则|x﹣a|+|x﹣b|的最小值是．34．已知函数f（x）＝sin2x+|sin x﹣a|+（a，b∈R），若对于任意x∈R，均有|f（x）|≤1，则a+b的最大值是．35．在一个不透明的摸奖箱中有五个分别标有1，2，3，4，5号码的大小相同的小球，现甲、乙、丙三个人依次参加摸奖活动，规定：每个人连续有放回地摸三次，若得到的三个球编号之和恰为4的倍数，则算作获奖．记获奖的人数为X，则X的数学期望为．36．已知||＝||＝1，若存在m，n∈R，使得m+与n+夹角为60°，且|（m+）﹣（n+）|＝，则||的最小值为．四．解答题（共4小题）37．已知函数f（x）＝e ax﹣1•cos x（a＞0），其中e＝2.71828……为自然对数的底数．（Ⅰ）若a＝，求f（x）在（0，）上的极值点；（Ⅱ）（ⅰ）证明：f（x）在（0，）上单调递增；（ⅱ）讨论函数g（x）＝f（x）﹣e在[0，]上的零点个数．38．已知抛物线C：y2＝2px的焦点为F（1，0），斜率为k的直线l1过点P（0，m）（m＞0），直线l1与抛物线C相交于A，B两点．（1）求抛物线C的方程；（2）直线l2过点P（0，m）（m＞0），且倾斜角与l1互补，直线l2与抛物线C交于M，N两点，且△FAB与△FMN的面积相等，求实数m的取值范围．39．已知椭圆C1：＝1，拋物线C2：y2＝2px（p＞0），点A（﹣1，0），斜率为k的直线l1交拋物线于B、C两点，且＝，经过点C的斜率为﹣k的直线l2与椭圆相交于P、Q两点．（1）若拋物线的准线经过点A，求拋物线的标准方程和焦点坐标：（2）是否存在p，使得四边形APBQ的面积取得最大值？若存在，请求出这个最大值及p的值；若不存在，请说明理由．40．已知函数f（x）＝e x﹣ax﹣1（1）讨论函数g（x）＝在其定义域内的单调性；（2）若f（x）≥0对任意的x∈R恒成立，设h（x）＝e x f（x），证明：h（x）在R上存在唯一的极大值点t，且h（t）＜．2024新高考模拟试卷高考综合二一．选择题（共23小题）1．十二生肖是中国特有的文化符号，有着丰富的内涵，它们是成对出现的，分别为鼠和牛、虎和免、龙和蛇、马和羊、猴和鸡、狗和猪六对．每对生肖相辅相成，构成一种完美人格．现有十二生肖的吉祥物各一个，按照上面的配对分成六份．甲、乙、丙三位同学依次选一份作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学所有的吉祥物都喜欢，如果甲、乙、丙三位同学选取的礼物中均包含自己喜欢的生肖，则不同的选法种数共有（）A．12种B．16种C．20种D．24种【解答】解：由题意可得：①甲选鼠和牛，乙同学有2中选法，丙同学有4种选法，共有2×4＝8，②甲选马和羊，乙同学有2中选法，丙同学有4种选法，共有2×4＝8，综上共有8+8＝16种，故选：B．2．把物体放在空气中冷却，如果物体原来的温度是θ1℃，空气的温度是θ0℃，那么tmin后物体的温度θ（单位：℃）满足公式（其中k为常数）．现有52℃的物体放在12℃的空气中冷却，2min后物体的温度是32℃．则再经过4min该物体的温度可冷却到（）A．12℃B．14.5℃C．17℃D．22℃【解答】解：由题意知，32＝12+（52﹣12）e﹣2k，∴e﹣2k＝，再经过4min该物体的温度可冷却到θ＝12+（32﹣12）e﹣4k＝12+20•（e﹣2k）2＝12+20×＝17℃，故选：C．3．已知双曲线的左、右顶点分别为A，B，其中一条渐近线与以线段AB为直径的圆在第一象限内的交点为P，另一条渐近线与直线PA垂直，则C的离心率为（）A．3B．2C．D．【解答】解：双曲线的渐近线方程为y＝±x，由可得P（，），则﹣•＝﹣1，化为b2＝ac+a2，即为c2﹣a2＝ac+a2，即（c﹣a）（c+a）＝a（a+c），可得c﹣a＝a，即c＝2a，所以e＝＝2，故选：B．4．关于函数f（x）＝sin|x|+|sin x|有下述四个结论：①f（x）是偶函数②f（x）在区间（，π）单调递增③f（x）在[﹣π，π]有4个零点④f（x）的最大值为2其中所有正确结论的编号是（）A．①②④B．②④C．①④D．①③【解答】解：f（﹣x）＝sin|﹣x|+|sin（﹣x）|＝sin|x|+|sin x|＝f（x）则函数f（x）是偶函数，故①正确，当x∈（，π）时，sin|x|＝sin x，|sin x|＝sin x，则f（x）＝sin x+sin x＝2sin x为减函数，故②错误，当0≤x≤π时，f（x）＝sin|x|+|sin x|＝sin x+sin x＝2sin x，由f（x）＝0得2sin x＝0得x＝0或x＝π，由f（x）是偶函数，得在[﹣π，0）上还有一个零点x＝﹣π，即函数f（x）在[﹣π，π]有3个零点，故③错误，当sin|x|＝1，|sin x|＝1时，f（x）取得最大值2，故④正确，故正确是①④，故选：C．5．已知三棱锥P﹣ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，则球O的体积为（）A．8πB．4πC．2πD．π【解答】解：如图，由PA＝PB＝PC，△ABC是边长为2的正三角形，可知三棱锥P﹣ABC为正三棱锥，则顶点P在底面的射影O1为底面三角形的中心，连接BO1并延长，交AC于G，则AC⊥BG，又PO1⊥AC，PO1∩BG＝O1，可得AC⊥平面PBG，则PB⊥AC，∵E，F分别是PA，AB的中点，∴EF∥PB，又∠CEF＝90°，即EF⊥CE，∴PB⊥CE，得PB⊥平面PAC，∴正三棱锥P﹣ABC的三条侧棱两两互相垂直，把三棱锥补形为正方体，则正方体外接球即为三棱锥的外接球，其直径为D＝＝＝＝．半径为，则球O的体积为．故选：D．6．2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式，孪生素数猜想是希尔伯特在1900年提出的23个问题之一，可以这样描述：存在无穷多个素数p使得p+2是素数，素数对（p，p+2）称为孪生素数．从10以内的素数中任取两个，其中能构成孪生素数的概率为（）A．B．C．D．【解答】解：依题意，10以内的素数共有4个，从中选两个共包含＝6个基本事件，而10以内的孪生素数有（3，5），（5，7）两对，包含2个基本事件，所以从10以内的素数中任取两个，其中能构成孪生素数的概率P＝＝＝．故选：A．7．著名数学家华罗庚先生被誉为“中国现代数学之父”，他倡导的“0.618优选法“在生产和科研实践中得到了非常广泛的应用，黄金分割比t＝≈0.618还可以表示成2sin18°，则＝（）A．4B．﹣1C．2D．【解答】解：∵由题意可得：t＝2sin18°，∴．故选：D．8．在等腰梯形ABCD中，AB∥CD，且AB＝2AD，AB＞CD，若双曲线E以A，B为焦点，且过C，D两点，则双曲线E的离心率的取值范围为（）A．B．C．D．【解答】解：设|AB|＝2m（m＞0），∠BAD＝θ，，则|AD|＝m，在△ABD中，由余弦定理知，|BD|2＝|AB|2+|AD|2﹣2|AB|•|AD|cos∠BAD＝4m2+m2﹣2•2m•m•cosθ＝5m2﹣4m2•cosθ，∴|BD|＝，由双曲线的定义知，|BD|﹣|AD|＝2a，∴2a＝﹣m，∴离心率＝＝，又，∴cosθ∈（0，1），∴﹣1∈（0，﹣1），∴．故选：B．9．在正三棱台ABC﹣A1B1C1中，AB＝3AA1＝A1B1＝6，D是BC的中点，设A1D与BC、BB1、BA所成角分别为α，β，γ，则（）A．α＜γ＜βB．a＜β＜γC．β＜γ＜αD．γ＜β＜α【解答】解：如图1，令B1C1的中点为D1，连接A1D1，DD1，在平面ADD1A1中，过A1作DD1的平行线A1E得图2，在平面BCC1B1中，连接B1D得图3，过B1作B1F⊥BC，由题意可得BF＝1，BB 1＝2，所以DD，∠B＝60°，又因为DF＝2，所以B，在△BCB 1中，B，则在图2中，AD＝3，DE＝2，所以AE＝，又因为AA 1＝2，A，所以在三角形AA1E中由余弦定理可得：cos，在三角形AA 1D中由余弦定理可得：cos∠A1AD＝，解得A，①连接A 1C，则在三角形A1DC中，A，DC＝3，A，所以cos，所以∠A1DC＝90°，即α＝90°；②过A1作A1M∥BB1，则AM＝2，在三角形AMD中，∠MAD＝30°，AD＝3，则由余弦定理可得MD＝，在三角形A 1MD中，A1M＝2，MD＝，所以cos，所以cos，③在三角形A 1B1D中，A，所以cos，即cos，因为y＝cos x在（0，]单调递减，且cosγ＞cosβ＞cosα，所以α＞β＞γ，故选：D．10．已知实数x，y满足x2+y2＝1，0＜x＜1，0＜y＜1，当取最小值时，的值为（）A．B．C．D．1【解答】解：令z＝，由x2+y2＝1，所以＝＝，令，则，所以，通过题中选项给出的数据，可得当t＝时，f'(t)＝0，故当t＝时，f(t)取得最小值，即当的值为时，取最小值．故选：A．11．十三世纪意大利数学家列昂那多•斐波那契从兔子繁殖中发现了“斐波那契数列”，斐波那契数列{a n}满足以下关系：a1＝1，a2＝1，a n＝a n﹣1+a n﹣2（n≥3，n∈N*），记其前n项和为S n，若a2020＝m（m为常数），则S2018的值为（）A．m﹣2B．m﹣1C．m D．m+1【解答】解：因为a1＝1，a2＝1，a n＝a n﹣1+a n﹣2（n≥3，n∈N*)，所以数列{a n}的前2018项和为a1+a2+a3+a4+…+a2018＝a2+a1+a2+a3+a4+…+a2018﹣1＝a3+a2+a3+a4+…+a2018＝a4+a3+a4+…+a2018﹣1＝a5+a4+a5+…+a2018﹣1＝a6+a5+a6+…+a2018﹣1＝a2020﹣1＝m﹣1．故选：B．12．三棱锥P﹣ABC的顶点都在球O的球面上，AC⊥BC，AC＝2，BC＝4．若三棱锥P﹣ABC的体积的最大值为，则球O的体积为（）A．B．33πC．D．36π【解答】解：因为AC⊥BC，且AC＝2，BC＝4，所以，过AB的中点M作平面ABC的垂线MN，则球心O在直线MN上，设OM＝h，球O的半径为r，则棱锥的高的最大值为r+h，所以，解得r+h＝5①，在Rt△OAM中，OA2＝OM2+AM2，则②，由①②解得r＝3，h＝2，所以球O的体积为．故选：D．13．设函数f a（x）＝sin a x+cos a x，a∈N*，记f a（x）的最小正周期为T a，则（）A．T3＝πB．T6＝πC．D．【解答】解：选项A：因为f3（x+π）＝sin3（π+x）+cos3（π+x）＝﹣sin3x﹣cos3x≠f3（x），所以A错误；选项B：因为f6（+x）＝sin6（+x）+cos6（+x）＝sin6x+cos6x＝f（x），所以T6≠π，B错误；选项C：f4（x）＝sin4x+cos4x＝（sin2x+cos2x）2﹣2sin2x cos2x＝1﹣2（sin2x）2＝1﹣sin22x，因为sin22x∈[0，1]，则1﹣，即f4（x），C错误；选项D：f8（x）＝sin8x+cos8x＝（sin2x）4+（cos2x）4＝（sin4x+cos4x）2﹣2sin4x cos4x＝[（sin2x+cos2x）2﹣2sin2x cos2x]2﹣2sin4x cos4x＝（1﹣2sin2x cos2x）2﹣2sin4x cos4x＝2sin4x cos4x﹣4sin2x cos2x+1，令t＝sin2x cos2x＝（sin2x）2＝sin22x，则f8（x）＝g（t）＝2t2﹣4t+1在t上单调递减，所以g（t）max＝g（0）＝1，g（t）min＝g（）＝，所以f8（x）∈[，1]，D正确，故选：D．14．已知平面向量，，满足||＝2|﹣|＝2|﹣|＝2||＝2，则•的取值范围是（）A．[1，2]B．C．D．【解答】解：设＝，＝，＝，则由题意可知PA＝2，AB＝1，PC＝1，BC ＝1，以PA为x轴，以PA的中垂线为y轴建立平面直角坐标系O﹣xy，则B点在圆A：（x﹣1）2+y2＝1上，C点在圆P：（x+1）2+y2＝1上，设B（1+cosα，sinα），C（﹣1+cosβ，sinβ），则＝＝（2+cosα，sinα），＝＝（cosβ，sinβ），∴＝2cosβ+cosαcosβ+sinαsinβ，∵BC＝1，∴||＝1，∴+﹣2＝1，即（1+cosα）2+sin2α+（﹣1+cosβ）2+sin2β﹣2（1+cosα）（﹣1+cosβ）﹣2sinαsinβ＝1，整理可得：cosαcosβ+sinαsinβ＝+2cosα﹣2cosβ，∴＝+2cosα，∵|BC|＝1，∴以B为圆心，以1为半径的圆B与圆P有公共点，故1≤|PB|≤2，即1≤（2+cosα）2+sin2α≤4，∴﹣2≤2cosα≤﹣，∴≤≤2．故选：C．15．如图所示，等边三角形ABC的边长为2，D，E分别是AC，AB上的点，满足DE∥BC，将△ADE沿直线DE折到△FDE，则在翻折过程中，下列说法正确的个数是（）①；②∃G∈FE，使得BG∥平面FCD；③若存在平面FBC⊥平面FDE，则AD＜DC．A．0B．1C．2D．3【解答】解：①可知当平面FDE⊥平面BCDE时，四棱锥F﹣BCDE的体积最大，设DE＝x（0＜x＜2），则DC＝2﹣x，则等腰梯形BCDE的高为＝﹣x，＝（x+2）（﹣x）＝﹣x2，故梯形BCDE的面积为S梯形BCDE点F到平面BCDE的距离即点F到DE的距离为x，所以四棱锥F﹣BCDE的体积V＝×（﹣x2）×x＝﹣x3+x，0＜x＜2，则V′＝﹣x2+＝﹣（x+）（x﹣），当x∈（0，）时，V′＞0，当x∈（，2）时，V′＜0，所以当x＝时，V取得最大值为，≤，故①正确，故V F﹣BCDE②如图，在EF上任取一点G，过点G作GH∥ED，交FD于H，连接BG，CH，因为DE∥BC，且DE＜BC，又GH∥DE，且GH＜DE，所以GH∥BC，且GH≠BC，故四边形BCHG为梯形，所以BG与CH相交，因为CH⊂平面FCD，故BG与平面FCD相交，故②错误，③如图，取BC中点M，DE中点N，连接FM，FN，连接MN并延长至A，设平面FBC∩平面FDE＝l，则由DE∥BC，可得DE∥平面FBC，则DE∥l，即GE∥BC∥l，因为FD＝FE，所以FN⊥DE，FN⊥l，因为FC＝FB，所以FM⊥BC，FM⊥l，则∠MFN即为平面FBC与平面FDE所成角，因为平面FBC⊥平面FDE，所以∠MFN＝90°，所以FN＜MN，因为AN＝FN，所以AN＜MN，因为＝，所以AD＜DC，故③正确．故选：C．16．两位教师和两位学生排成一排拍合照，记ξ为两位学生中间的教师人数，则E（ξ）＝（）A．B．C．D．【解答】解：随机变量ξ的可能取值为0，1，2，P（ξ＝0）＝＝，P（ξ＝1）＝＝，P（ξ＝2）＝＝，∴E（ξ）＝0×+1×+2×＝，故选：C．17．在棱长为1的正方体ABCD﹣A1B1C1D1中，E为线段B1C的中点，F是棱C1D1上的动点，若点P为线段BD1上的动点，则PE+PF的最小值为（）A．B．C．D．【解答】解：连接BC1，则BC1∩B1C＝E，点P、E、F在平面BC1D1中，且BC1⊥C1D1，C1D1＝1，BC1＝，如图1所示；在Rt△BC1D1中，以C1D1为x轴，C1B为y轴，建立平面直角坐标系，如图2所示；则D1（1，0），B（0，），E（0，）；设点E关于直线BD1的对称点为E′，∵BD1的方程为x+＝1①，＝﹣＝，∴k EE′∴直线EE′的方程为y＝x+②，由①②组成方程组，解得，直线EE′与BD1的交点M（，）；所以对称点E′（，），∴PE+PF＝PE′+PF≥E′F＝．故选：D．18．已知等差数列{a n}的前n项和为S n，满足sin（a4﹣1）+2a4﹣5＝0，sin（a8﹣1）+2a8+1＝0，则下列结论正确的是（）A．S11＝11，a4＜a8B．S11＝11，a4＞a8C．S11＝22，a4＜a8D．S11＝22，a4＞a8【解答】解：sin（a4﹣1）+2a4﹣5＝0，sin（a8﹣1）+2a8+1＝0，∴sin（a4﹣1）+2（a4﹣1）﹣3＝0，sin（1﹣a8）+2（1﹣a8）﹣3＝0，令f（x）＝sin x+2x﹣3，可得f′（x）＝cos x+2＞0，因此函数f（x）在R上单调递增．又f（1）＝sin1﹣1＜0，f（2）＝sin2+1＞0，因此函数f（x）在（1，2）内存在唯一零点．∴a4﹣1＝1﹣a8，1＜a4﹣1＜2，1＜1﹣a8＜2，∴a4+a8＝2，2＜a4＜3，﹣1＜a8＜0，∴S11＝＝＝11，a4＞a8，故选：B．19．函数y＝sin x+e x ln|x|的图象可能是（）A．B．C．D．【解答】解：当x＜0时，e x＜1，ln|x|∈（﹣∞，+∞），﹣1≤sin x≤1∴sin x+e x ln|x|＝0，有很多解，故排除AC，当x→+∞时，e x→+∞，ln|x|→+∞，﹣1≤sin x≤1，则y→+∞，故排除D；故选：B．20．一只小虫从数轴上的原点出发爬行，若一次爬行过程中，小虫等概率地向前或向后爬行1个单位，设爬行n次后小虫所在位置对应的数为随机变量ξn，则下列说法错误的是（）A．E（ξn）＝0B．D（ξn）＝nC．P（ξ2020＝0）＜P（ξ2020＝2）D．P（ξ2020＝0）＜P（ξ2018＝0）【解答】解：由题意知：设爬行n次后小虫所在位置对应的数为随机变量ξn∈[﹣n，n]，且小虫向前或向后爬行1个单位的概率均为，∴爬行n次后小虫一共向前爬行r次，则向后爬行n﹣r次，有ξn＝r﹣[﹣（n﹣r）]＝2r ﹣n；故P（ξn＝2r﹣n）＝∁n r（）n，则：1、E（ξn）＝＝0，D（ξn）＝E（ξn2）﹣E（ξn）2＝E（ξn2）﹣＝n，故A、B正确，2、P（ξ2020＝0）＝（）2020，P（ξ2020＝2）＝（）2020，即＝＞1，P（ξ2020＝0）＞P（ξ2020＝2），故C错误，3、P（ξ2018＝0）＝（）2018，即＝＜1，故P（ξ2020＝0）＜P（ξ2018＝0），故D正确，故选：C．21．对于任意集合A，设f A（x）＝，已知集合S，T⊆X，则对任意的x∈X，下列说法错误的是（）A．S⊆T⇔f S（x）≤f T（x）B．f（x）＝1﹣f S（x）C．f S∩T（x）＝f S（x）•f T（x）D．f S∪T（x）＝f S（x）+f T（x）【解答】解：对于A，因为S⊆T，可得x∈S则x∈T，∵f A（x）＝，所以f S（x）＝＝，f T（x）＝，而∁X S中可能有T的元素，但∁X T中不可能有S的元素∴f S（x）≤f T（x），即对于任意x∈X，都有f S（x）≤f T（x）故A正确；∵f（x）＝，结合f S（x）的表达式，可得f T（x）＝1﹣f S（x），即f S（x）+f T（x）＝1，故B正确；（x）＝＝＝对于C，f S∩T•＝f S（x）•f T（x），故C正确；（x）＝，∵f S∪T（x）＝1，当某个元素x在S中但不在T中，由于它在S∪T中，故f S∪T而f S（x）＝1且f T（x）＝0，可得f S∪T（x）≠f S（x）•f T（x），由此可得D不正确．故错误的是D．故选：D．22．如图所示，平面α∩平面β＝l，二面角α﹣l﹣β∈[，]，已知A∈α，B∈β，直线AB 与平面α，平面β所成角均为θ，与l所成角为γ，若sin（γ+θ）＝1，则sin（γ﹣θ）的最大值是（）A．B．C．D．【解答】解：∵θ∈[0，]，γ∈[0，]，sin（γ+θ）＝1，∴γ+θ＝，过A作AC⊥l，过B作BD⊥l，垂足分别为C，D，过A作AE∥l，过B作BF∥l，设AA1⊥β，BB1⊥α，延长CA1交BF于F，延长DB1交AE于E，则∠ACF和∠BDE为二面角α﹣l﹣β的平面角，∠ABA1为AB与平面β所成角，∠BAB1为AB与平面α所成角，∠ABF和∠EAB为AB与l所成角，∴sinθ＝＝，cosγ＝＝，∴AA1＝BB1＝BF＝AE，∴△AA1C≌△BB1D，∴AC＝BD＝CF，即△ACF是等腰三角形，设∠ACF＝α，则α∈[，]，∴sin（γ﹣θ）＝sin[γ﹣（﹣γ）]＝﹣cos2γ＝sin2γ﹣cos2γ＝＝1﹣，显然当tanγ取得最大值时，sin（γ﹣θ）取得最大值，而tanγ＝＝，故当∠AFA1取得最小值时，tanγ取得最大值，又△ACF是等腰三角形，故∠AFA1＝，∴当α＝时，∠AFA1取得最小值，∴tanγ的最大值为，∴sin（γ﹣θ）的最大值为1﹣＝，故选：B．23．设等差数列{a n}的前n项和为S n，若S6＜S7＜S5，则满足S n＞0时正整数n的最小值为（）A．11B．12C．13D．14【解答】解：∵等差数列{a n}的前n项和为S n，S6＜S7＜S5，∴＜7＜，∴a6＜0，a7＞0，a6+a7＜0，∴S13＝＝13a7＞0，＝6（a6+a7）＜0．∴满足S n＞0的正整数n的最小值为13．故选：C．二．多选题（共2小题）24．如图，在正四棱柱ABCD﹣A1B1C1D1中，AA1＝2AB＝2，点P为线段AD1上一动点，则下列说法正确的是（）A．直线PB1∥平面BC1DB．三棱锥P﹣BC1D的体积为C．三棱锥D1﹣BC1D外接球的表面积为D．直线PB1与平面BCC1B1所成角的正弦值的最大值为【解答】解：作辅助线如图．对于A，因为AD1∥BC1，∥AB1∥DC1∥，所以平面AB1D1∥平面BC1D，PB1⊂平面AC1D1从而直线PB1∥平面BC1D，则A对；对于B，由A知，平面AB1D1∥平面BC1D，P点在平面AC1D1，所以＝；则B对；对于C，三棱锥D1﹣BC1D外接球的半径R＝，所以三棱锥D1﹣BC1D外接球的表面积为S＝，则C错；对于D，因为当B1P⊥AD1时，B1P最短，此时直线PB1与平面BCC1B1所成角的正弦值的最大，先用等面积法求B1P，⇒B1P＝⇒直线PB1与平面BCC1B1所成角的正弦的最大值为，则D对；故选：ABD．25．声音是由物体振动产生的声波，其中包含着正弦函数．纯音的数学模型是函数y＝A sinωt，我们听到的声音是由纯音合成的，称之为复合音．若一个复合音的数学模型是函数，则下列结论正确的是（）A．2π是f（x）的一个周期B．f（x）在[0，2π]上有3个零点C．f（x）的最大值为D．f（x）在上是增函数【解答】解：∵y＝sin x的周期为2π，y＝的周期为π，∴的周期为2π，故A正确；由＝0，得sin x+sin x cos x＝0，得sin x＝0或cos x＝﹣1，∵x∈[0，2π]，∴x＝0，x＝π，x＝2π，则f（x）在[0，2π]上有3个零点，故B正确；函数的最大值在[0，]上取得，由f′（x）＝cos x+cos2x＝2cos2x+cos x﹣1＝0，可得cos x＝，当x∈（0，）时，cos x 单调递减，原函数单调递增，当x∈（，）时，cos x单调递减，原函数单调递减，则当x＝时，原函数求得最大值为sin+＝，故C正确；∵f（）＝sin+＝＞1，f（）＝sin＝1，∴f（x）在上不是增函数，故D错误．故选：ABC．三．填空题（共11小题）26．已知直线l与抛物线C：y2＝8x相切于点P，且与C的准线相交于点T，F为C的焦点，连接PF交C于另一点Q，则△PTQ面积的最小值为16；若|TF|＝5，则|PQ|的值为．【解答】解：设直线PQ的方程为x＝ny+2（恒过定点F（2，0））与抛物线联立，可得y2﹣8ny﹣16＝0，所以△＝64n2+64＞0恒成立，设P（x1，y1），Q（x2，y2），则有y1+y2＝8n，y1y2＝﹣16，设抛物线在点P处的切线为x＝my+t，与抛物线方程联立，可得y2﹣8my﹣8t＝0，切线与抛物线只有一个公共点，所以△＝64m2+32t＝0，解得t＝﹣2m2，方程可变为y2﹣8my+16m2＝0，故y＝4m，所以，抛物线在点P处的切线为，因为点T在抛物线的准线上，则有，，所以点T的坐标为（﹣2，4n），设点T到直线PQ的距离为d，将直线PQ写成一般式即x﹣ny﹣2＝0，故，所以，有最小值16，所以当n＝0时，S△TPQ点T的坐标为（﹣2，4n），F（2，0），所以，所以16n2+16＝25，即，故PQ＝PF+QF＝（x1+2）+（x2+2）＝（ny1+4）+（ny2+4）＝，所以．故答案为：16；．27．已知{|a n|}是首项和公差均为1的等差数列，S n为数列{a n}的前n项和，记m n为|S n|的所有可能取值中的最小值，则m1+m2+…+m2020＝1010．【解答】解：{|a n|}是首项和公差均为1的等差数列，∴|a n|＝1+n﹣1＝n．∴a n＝±n．S n为数列{a n}的前n项和，则S n的取值可能为，﹣1，……，1﹣，﹣．|S n|的取值可能为：，﹣1，……．记m n为|S n|的所有可能取值中的最小值，则m1＝1，m2＝1，m3＝0，m4＝0，m5＝1，m6＝1，m7＝0，m8＝0，……．∴m1+m2+…+m2020＝505×（1+1+0+0）＝1010．故答案为：1010．28．已知P为椭圆上的一点，过P作直线l交圆x2+y2＝4于A，B两点，则|PA|•|PB|的最大值是3．【解答】解：由P为椭圆上的一点，可设P（2cosα，sinα）（0≤α＜2π），设直线AB的参数方程为（t为参数，θ为倾斜角），代入圆圆x2+y2＝4，可得4cos2α+t2cos2θ+4t cosαcosθ+sin2α+t2sin2θ+2t sinαsinθ＝4，化为t2+2t（2cosαcosθ+sinαsinθ）+4cos2α+sin2α﹣4＝0，可得t1t2＝4cos2α+sin2α﹣4＝﹣3sin2α，所以|PA|•|PB|＝3sin2α≤3，当α＝时，上式取得等号．即|PA|•|PB|的最大值是3，故答案为：3．29．已知平面向量，是不共线的单位向量，记，的夹角为θ，若平面向量满足||＝，且对于任意的正实数k，|﹣+k|≥恒成立，则cosθ的最大值为．【解答】解：因为（k﹣）2＝k22﹣2k•+2＝k2+1﹣2k cosθ，由|﹣+k|≥，得2+2•（k﹣）+（k﹣）2＝+|k﹣|cos＜，k﹣＞+|k﹣|2≥，所以|k﹣|≥﹣cos＜，k﹣＞，由题意可得|k﹣|≥，所以k2+1﹣2k cosθ≥，即k2﹣2k cosθ+≥0对于任意的正实数k恒成立，所以cosθ≤0或，解得cosθ≤，故cosθ的最大值为．故答案为：．30．甲、乙、丙、丁和戊5名学生进行劳动技术竞赛并决出1至5名，赛后甲、乙去询问成绩，老师对甲说：“很遗憾，你和乙都没有得到冠军．”；对乙说：“你当然不是最差的．”则5人的名次排列可能有54种．【解答】解：根据题意，甲、乙都不是第一名且乙不是最后一名，则乙的可以为第二、三、四名，有3种情况；再排甲，不能为第一名，也有3种情况；余下3人有A33种排法．故共有3•3•A33＝54种不同的情况，故答案为：5431．已知直线l与双曲线Γ的两条渐近线交于与A，B两点，与x轴交于点C，若O是坐标原点，OA＝OC，BC＝2AB，则Γ的离心率是4或．【解答】解：如图所示，分别过点B、A，作BD⊥x轴，作AE⊥x轴，垂足D、E，则BD∥AE，∴＝，由渐近线性质可知∠BOD＝∠AOE，故△BOD∽△AOE，∴＝，设OD＝2m，则OE＝3m，CD＝10m，若双曲线焦点在x轴上，则直线OA的方程为y＝，∴AE＝，∴OA＝，∵OC＝OA，∴12m＝，化简可得：＝15，∴双曲线的离心率e＝＝4，若若双曲线焦点在y轴上，则直线OA的方程为y＝x，∴AE＝，∴OA＝，∵OC＝OA，∴12m＝，化简可得：＝15，∴双曲线的离心率e＝＝＝，故答案为：4或．32．设数列a1，a2，a3，a4满足前三项成等比数列且和为m，后三项成公差不为0的等差数列且和为12，若满足条件的数列个数大于1，则m的取值范围是m＞3且m≠4，m≠12．【解答】解：设后三项成公差d不为0的等差数列且和为12，设a3＝x，可得a2＝x﹣d，a4＝x+d且x﹣d+x+x+d＝12，解得x＝4，由前三项成等比数列，可得a1a3＝a22，则a1＝＝，且m＝+4﹣d+4＝d2﹣3d+12＝（d﹣6）2+3，当d＝6时，m取得最小值3，由于d≠0，且满足条件的数列个数大于1，可得m＞3且m≠4，m≠12．故答案为：m＞3且m≠4，m≠12．33．已知实数a，b满足对任意的实数x，不等式（|x|﹣a）（|x|﹣b）（|x|﹣2a2﹣1）≥0恒成立，则|x﹣a|+|x﹣b|的最小值是1．【解答】解：设|x|＝t≥0，则（t﹣a）（t﹣b）（t﹣2a2﹣1）≥0对t∈[0，+∞）恒成立，令（t﹣a）（t﹣b）（t﹣2a2﹣1）＝0，解得t1＝a，t2＝b，，∵恒成立，∴t3＞t1，令t＝0，（﹣a）（﹣b）（﹣2a2﹣1）＝﹣ab（2a2+1）≥0，∴ab≤0；①当a＝0时，则2a2+1＝1，若b≤0，则当t∈（0，1）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；若0＜b＜1，则当t∈（b，1）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；若b＝1＝2a2+1，（t﹣a）（t﹣b）（t﹣2a2﹣1）≥0恒成立，符合题意；若b＞1，则当t∈（1，b）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；②当b＝0时，若a≤0，则当t∈（0，2a2+1）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；若0＜a＜2a2+1，则当t∈（a，2a2+1）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；③当b＜0＜a时，则当t∈（a，2a2+1）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；④当a＜0＜b时，若0＜b＜2a2+1，则当t∈（b，2a2+1）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；若b＝2a2+1，（t﹣a）（t﹣b）（t﹣2a2﹣1）≥0恒成立，符合题意；若b＞2a2+1，则当t∈（2a2+1，b）时，（t﹣a）（t﹣b）（t﹣2a2﹣1）＜0，不合题意；综上，若不等式恒成立，则需满足a≤0且b＝2a2+1，∴|x﹣a|+|x﹣b|≥|（x﹣a）﹣（x﹣b）|＝|b﹣a|＝|2a2﹣a+1|（当且仅当a＜x＜b时），∵a≤0，∴当a＝0时，|2a2﹣a+1|min＝1，故答案为：1．34．已知函数f（x）＝sin2x+|sin x﹣a|+（a，b∈R），若对于任意x∈R，均有|f（x）|≤1，则a+b的最大值是﹣1．【解答】解：令t＝sin x∈[﹣1，1]，函数f（x）可化为g（t）＝，①a≥1时，g（t）＝＝，故时，，t＝﹣1时，．因为|g（t）|≤1，所以，解得．②a≤﹣1时，g（t）＝＝，故时，；t＝1时，．所以，解得，又a≤﹣1，所以a+b≤﹣3．③﹣1＜a＜1时，，当时，g（t）在[﹣1，a）上单调递减，在上单调递减，在[]上单调递增；当时，g（t）在[﹣1，a）单调递减，在[a，1]上单调递增；当时，g（t）在单调递减，在上单调递增，在（a，1]上单调递增．所以g（t）在[﹣1，1]上先减后增，故g（t）的最大值为g（﹣1）或g（1）．所以⇒，所以a+b≤﹣1．综上可知，a+b≤﹣1恒成立，即a+b的最大值为﹣1．故答案为：﹣1．35．在一个不透明的摸奖箱中有五个分别标有1，2，3，4，5号码的大小相同的小球，现甲、乙、丙三个人依次参加摸奖活动，规定：每个人连续有放回地摸三次，若得到的三个球编号之和恰为4的倍数，则算作获奖．记获奖的人数为X，则X的数学期望为．【解答】解：三个球号码和的取值范围是3~15中的整数，其中4的倍数可能为4，8，12，则三个球编号之和恰为4的倍数的基本事件：（112）有3种，（125）有6种，（134）有6种，（224）有3种、（332）有3种，（345）有6种、（552）有3种、（444）有1种，共有31种，所有基本事件有5×5×5＝125种，所以每个人获得纪念品的概率为，又X~B（3，），所以EX＝3×＝．故答案为：．36．已知||＝||＝1，若存在m，n∈R，使得m+与n+夹角为60°，且|（m+）﹣（n+）|＝，则||的最小值为．【解答】解：由题意，，令，，故有A，A′，B，B′共线，∵为定值，在△A′OB′中，由余弦定理可得，＝，当且仅当时，取最大值，此时△A′OB′面积最大，则O到AB距离最远，即当且仅当A′、B′关于y轴对称时，最小，此时O到AB的距离为，∴，即．故答案为：．四．解答题（共4小题）37．已知函数f（x）＝e ax﹣1•cos x（a＞0），其中e＝2.71828……为自然对数的底数．（Ⅰ）若a＝，求f（x）在（0，）上的极值点；（Ⅱ）（ⅰ）证明：f（x）在（0，）上单调递增；（ⅱ）讨论函数g（x）＝f（x）﹣e在[0，]上的零点个数．【解答】解：（Ⅰ）易知f′（x）＝（a cos x﹣sin x）e ax﹣1＝（a﹣tan x）cos x•e ax﹣1，若a＝，则f′（x）＝（﹣tan x）cos x•e ax﹣1，x，f′（x），f（x）的变化如下：x（0，）（，）f′（x）+0﹣f（x）递增极大值递减∴函数f（x）在（0，）递增，在（，）递减，∴函数f（x）的极大值点是，无极小值点；（Ⅱ）（i）证明：∵a＞0，∴在（0，）上必存在唯一实数x0，使得tan x0＝a，∴函数f（x）在（0，x0）递增，在（x0，）递减，欲证明f（x）在（0，）递增，只需证明≤x0，∵tan x0＝a，∴＝sin x0，故只需证明sin x0≤x0，令g（x）＝sin x﹣x，x∈[0，），则g′（x）＝cos x﹣1≤0，∴函数g（x）在[0，）递减，∴当x0∈（0，）时，g（x0）＜g（0）＝0，∴sin x0﹣x0＜0，即sin x0＜x0，亦即＜x0，∴函数f（x）在（0，）递增；（ii）先证明当x≥0时，有e x≥1+x，令h（x）＝e x﹣x﹣1，（x≥0），则h′（x）＝e x﹣1≥0，（x≥0），∴函数h（x）在[0，+∞）递增，∴当x≥0时，h（x）≥0，即e x≥1+x，再证明函数f（x）的最大值f（x0）＞，显然tan x0＝a，∴cos x0＝，sin x0＝，∵≥ax0＞a sin x0，∴f（x0）＝cos x0＞a sin x0cos x0＝，下面证明＞，令t＝﹣，则t＜0，即证明＞e t（t＜0），即证明（1+t2）e t﹣1＜0（t＜0），令F（t）＝（1+t2）e t﹣1，则F′（t）＝（1+t）2e t≥0，∴函数F（t）是单调递增函数∴当t＜0时，F（t）＜F（0）＝0，∴（1+t2）e t﹣1＜0（t＜0），∴f（x0）＞，令函数G（x）＝cos xe ax﹣1﹣，x∈[0，]，（ii）先求函数G（x）在（x0，]上的零点个数，∵G（）＝﹣＜0，G（x0）＞0，且函数G（x）在（x0，]上单调递减，∴G（x）在（x0，]上有唯一零点，即函数G（x）在（x0，]上的零点个数是1个，再求函数G（x）在[0，x0]上的零点的个数，∵G（0）＝﹣，G（x0）＞0，且G（x）在[0，x0]递增，∴①当0＜a＜1时，＞，即G（0）＞0，故函数G（x）在[0，x0]上没有零点，即函数G（x）在[0，x0]上的零点个数是0个，②a≥1时，≤，即G（0）≤0，故函数G（x）在[0，x0]上有唯一零点，即函数G（x）在[0，x0]上的零点个数是1个，综上，当0＜a＜1时，函数G（x）1个零点，a≥1时，函数G（x）2个零点，∴0＜a＜1时，关于x的方程f（x）＝在[0，]上的实数解的个数是1个，a≥1时，关于x的方程f（x）＝在[0，]上的实数解的个数是2个．38．已知抛物线C：y2＝2px的焦点为F（1，0），斜率为k的直线l1过点P（0，m）（m＞0），直线l1与抛物线C相交于A，B两点．（1）求抛物线C的方程；（2）直线l2过点P（0，m）（m＞0），且倾斜角与l1互补，直线l2与抛物线C交于M，N两点，且△FAB与△FMN的面积相等，求实数m的取值范围．【解答】解：（1）抛物线C：y2＝2px的焦点为F（1，0），即＝1，解得p＝2，则抛物线C的方程为y2＝4x；（2）设直线l1的方程为y＝kx+m（m＞0），代入y2＝4x，得k2x2+（2km﹣4）x+m2＝0，△＝（2km﹣4）2﹣4k2m2＞0，得1﹣km＞0，由题意得，直线l2的方程为y＝﹣kx+m，同理可得1+km＞0，即有﹣1＜km＜1，设A（x1，y1），B（x2，y2），则x2+x2＝，x2x2＝，∴|AB|＝•＝•＝•，点F到AB的距离为d＝，则△FAB的面积为d•|AB|＝，同理△FMN的面积为，由已知得＝，化简得k2+m2＝2，则m2＜2，即0＜m＜，又k2m2＜1，即有（2﹣m2）m2＜1，又直线AB不过F（1，0），即k+m≠0，即m≠1，解得0＜m＜1或1＜m＜，综上，m的取值范围为（0，1）∪（1，）．39．已知椭圆C1：＝1，拋物线C2：y2＝2px（p＞0），点A（﹣1，0），斜率为k的直线l1交拋物线于B、C两点，且＝，经过点C的斜率为﹣k的直线l2与椭圆相交于P、Q两点．（1）若拋物线的准线经过点A，求拋物线的标准方程和焦点坐标：（2）是否存在p，使得四边形APBQ的面积取得最大值？若存在，请求出这个最大值及p的值；若不存在，请说明理由．。

湖南省2024-2025学年高三高考模拟试题含解析

湖南省2024-2025学年高三高考模拟试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、单项选择题：本题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、一质点做速度逐渐增大的匀加速直线运动，在时间间隔t 内位移为s ，速度变为原来的2倍，该质点的加速度为（）A ．2s tB ．22s tC ．223s tD ．232s t 2、如图，两束单色光A 、B 分别沿半径方向由空气射入半圆形玻璃砖，出射时合成一束复色光P ，下列说法正确的是A ．A 光的频率小于B 光的频率B ．在玻璃砖中A 光的传播速度小于B 光的传播速度C ．玻璃砖对A 光的折射率大于对B 光的折射率D ．两种单色光由玻璃射向空气时，A 光的临界角较小3、在一大雾天，一辆小汽车以30m/s 的速度行驶在高速公路上，突然发现正前方30m 处有一辆大卡车以10m/s 的速度同方向匀速行驶，小汽车紧急刹车，刹车过程中刹车失灵。

如图所示a 、b 分别为小汽车和大卡车的v －t 图像，以下说法正确的是（）A ．因刹车失灵前小汽车已减速，不会追尾B ．在t ＝5s 时追尾C ．在t ＝2s 时追尾D．若刹车不失灵不会追尾4、如图所示，薄纸带放在光滑水平桌面上，滑块放在薄纸带上，用水平恒外力拉动纸带，滑块落在地面上A点；将滑块和纸带都放回原位置，再用大小不同的水平恒外力拉动纸带，滑块落在地面上B点。

2023-2024学年四川省成都市高三高考冲刺卷(一)数学(理)模拟试题(含解析)

2023-2024学年四川省成都市高三高考冲刺卷（一）数学（理）模拟试题一、单选题1．已知集合2{|60},{|4}A x x x B y y x =+-≥=≤≤，则集合()A B =R ð（）A ．(,0)[2,)-∞⋃+∞B ．(,0)(2,)-∞+∞C ．(,3][2,)-∞-+∞UD ．(,3](2,)-∞-+∞ 【正确答案】A【分析】根据题意，将集合,A B 分别化简，然后结合集合的运算，即可得到结果.【详解】因为{2{|60}2A x x x x x =+-≥=≥或}3x ≤-，且{}{|4}02B y y x y x ==≤≤=≤≤，则()(),02,B =-∞+∞R ð，所以(,0)[2(),)A B -∞⋃+=∞R ð.故选：A2．走路是最简单优良的锻炼方式，它可以增强心肺功能，血管弹性，肌肉力量等，甲、乙两人利用手机记录了去年下半年每个月的走路里程（单位：公里），现将两人的数据绘制成如图所示的折线图，则下列结论中正确的是（）A ．甲走路里程的极差等于10B ．乙走路里程的中位数是26C ．甲下半年每月走路里程的平均数小于乙下半年每月走路里程的平均数D ．甲下半年每月走路里程的标准差小于乙下半年每月走路里程的标准差【正确答案】C【分析】根据折线图，得到甲、乙下半年的走路历程数据，根据极差、中位数、平均数以及标准差与数据稳定性之间的关系求解.【详解】对于A 选项，712-月甲走路的里程为：31、25、21、24、20、30，甲走路里程的极差为312011-=公里，A 错；对于B 选项，712-月乙走路的里程为：29、28、26、28、25、26，由小到大排列分别为：25、26、26、28、28、29，所以，乙走路里程的中位数是2628272+=，B 对；对于C 选项，甲下半年每月走路里程的平均数31252124203015166+++++=，乙下半年每月走路里程的平均数为2928262825261622766+++++==，所以，甲下半年每月走路里程的平均数小于乙下半年每月走路里程的平均数，C 对；对于D 选项，由图可知，甲下半年走路里程数据波动性大于乙下半年走路里程数据，所以甲下半年每月走路里程的标准差大于乙下半年每月走路里程的标准差，D 错.故选：C.3．已知平面向量||2a = ，||1b = ，,a b 的夹角为60 ，)a tb t +=∈R ，则实数t （）A ．1-B ．1C ．12D ．1±【正确答案】A【分析】对a tb +=两边平方，再由数量积公式计算可得答案.【详解】因为a tb += ，所以22223a a b t t b +⋅⋅+= ，即2422cos603t t +⨯⨯+= ，解得1t =-.故选：A.4．若直线y ax =是曲线2ln 1y x =+的一条切线，则实数=a A ．12e -B ．122e -C ．12e D ．122e 【正确答案】B【分析】设出切点坐标，求出函数的导数，利用导数的几何意义求出切线方程，进行比较建立方程关系进行求解即可．【详解】数的定义域为（0，+∞），设切点为（m ，2lnm+1），则函数的导数2f x x'=（），则切线斜率2k m =，则对应的切线方程为22122y lnm x m x m m-+=-=-（）（），即221y x lnm m=+-，2y ax a m=∴= ，且210lnm -=，即12lnm =，则12m e =，则121222a ee-=，故选B ．本题主要考查函数的导数的几何意义的应用，求函数的导数，建立方程关系是解决本题的关键．5．函数1e ()sin 1e xxf x x -=⋅+的部分图象大致形状是（）A ．B ．C．D．【正确答案】C【分析】先判断函数的奇偶性，结合对称性以01x <<时的函数值的正负判断可得答案.【详解】由1e ()sin 1e xxf x x -=⋅+，x ∈R ，定义域关于原点对称，得()()()()1e e 11e sin sin sin 1e e 11ex x xx x x f x x x x f x ------=⋅-=⋅-=⋅=+++，则函数()f x 是偶函数，图象关于y 轴对称，排除BD ；当01x <<时，1e 0x-<，1e 0x+>，sin 0x >，所以()1e sin 01e xxf x x -=⋅<+，排除A.故选：C.6．已知正方体1111ABCD A B C D -(如图1)，点P 在棱1DD 上(包括端点).则三棱锥1B ABP -的侧视图不可能．．．是（）A ．B ．C ．D ．【正确答案】D【分析】根据题意结合三视图逐项分析判断.【详解】对于选项A ：当点P 于点D 重合，则1B ABP -的侧视图如选项A 所示，故A 正确；对于选项B ：当点P 于点1D 重合，则1B ABP -的侧视图如选项B 所示，故B 正确；对于选项C ：当点P 为线段1DD 的中点，则1B ABP -的侧视图如选项C 所示，故C 正确；对于选项D ：因为点P 在棱1DD 上运动，则侧视图中右边的一条边与底边垂直，且右边的一条边的边长与正方体的棱长相等，所以1B ABP -的侧视图如不可能如选项D 所示，故D 错误；故选：D.7．已知抛物线24y x =的焦点和椭圆的一个焦点重合，且抛物线的准线截椭圆的弦长为3，则椭圆的标准方程为（）A ．22132x y +=B ．22143x y +=C ．22154x y +=D ．22165x y +=【正确答案】B【分析】根据椭圆的焦点以及31,2⎛⎫-± ⎪⎝⎭在椭圆上，即可求解,,a b c 的值.【详解】抛物线24y x =的焦点为()1,0，准线为=1x -，设椭圆的方程为()222210x y a b a b +=>>，椭圆中，1c =，当=1x -时，32y =，故229141,a b+=又222a b c =+，所以2,a b ==，故椭圆方程为22143x y +=，故选：B8．已知()()sin f x x ωϕ=+（0,ωϕ>为常数），若()f x 在ππ,62⎛⎫⎪⎝⎭上单调，且π5ππ263f f f ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则ϕ的值可以是（）A ．5π6-B ．π6-C ．π3D ．2π3【正确答案】A【分析】根据()f x 在ππ,62⎛⎫⎪⎝⎭上单调，可得03ω<≤，再由π5ππ263f f f ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭求得()f x 的一条对称轴和一个对称中心，进而求得2ω=，再求ϕ的值.【详解】对于函数()()sin f x x ωϕ=+，0ω>，因为()f x 在ππ,62⎛⎫⎪⎝⎭上单调，所以πππ262T ω-≤=，即03ω<≤.又π5ππ263f f f ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以π5π2π2623x +==为()f x 的一条对称轴，且ππ23,02⎛⎫+ ⎪ ⎪ ⎪⎝⎭即5π,012⎛⎫⎪⎝⎭为()f x 的一个对称中心，因为2π5πππ312432T-=<≤，所以2π3x =和5π,012⎛⎫⎪⎝⎭是()f x 同一周期内相邻的对称轴和对称中心，则2π5π4312T =-，即πT =，所以(]2π20,3Tω==∈，所以()()sin 2f x x ϕ=+，又5π,012⎛⎫⎪⎝⎭为()f x 的一个对称中心，则5π2π12k ϕ⨯+=，Z k ∈，则5ππ6k ϕ=-+，Z k ∈，当0k =时，5π6ϕ=-.故选：A.9．如图，在矩形ABCD 中，E F 、分别为边AD BC 、上的点，且3AD AE =，3BC BF =，设P Q 、分别为线段AF CE 、的中点，将四边形ABFE 沿着直线EF 进行翻折，使得点A 不在平面CDEF 上，在这一过程中，下列关系不能．．成立的是（）A ．直线//AB 直线CD B ．直线AB ⊥直线PQC ．直线//PQ 直线ED D ．直线//PQ 平面ADE【正确答案】C【分析】画出翻折之后的立体图形，根据点线面之间的位置关系以及平行与垂直的相关定理，可以证明或证伪相关命题.【详解】翻折之后如图所示：①因为3AD AE =，3BC BF =，所以//AB EF 且//EF CD ，因此//AB CD ，故选项A 成立；②连接FD ，因为P Q 、分别为FA FD 、的中点，所以//PQ AD ，又因为AB AD ⊥，所以AB PQ ⊥，故选项B 成立；③因为//PQ AD ，⋂=ED AD D ，所以PQ 与ED 不平行，故选项C 不成立；④因为//PQ AD ，且PQ ⊄平面ADE ，AD ⊂平面ADE ，所以//PQ 平面ADE ，故选项D 成立.故选：C10．筒车是我国古代发明的一种水利灌溉工具，因其经济又环保，至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（图1所示）.假定在水流量稳定的情况下，筒车上的每一个盛水筒都做逆时针匀速圆周运动，筒车转轮的中心O 到水面的距离h 为1.5m ，筒车的半径r 为2.5m ，筒车每秒转动rad 12π，如图2所示，盛水桶M 在0P 处距水面的距离为3m ，则2s 后盛水桶M 到水面的距离近似为（）A ．3.2mB ．3.4mC ．3.6mD ．3.8m【正确答案】D设ts 后盛水桶M 到水面的距离h 关于t 的函数解析式为()()()sin 0,0h t A t b A ωϕω=++>>，根据题中信息求出函数()h t 的解析式，再令2t =即可得解.【详解】设ts 后盛水桶M 到水面的距离h 关于t 的函数解析式为()()()sin 0,0h t A t b A ωϕω=++>>，由题意可得()()max min 41.52.51h t A b h t A b ⎧=+=⎪⎨=-=-=-⎪⎩，解得 2.51.5A b =⎧⎨=⎩，由于筒车每秒转动rad 12π，所以，函数()h t 的最小正周期为()22412T s ππ==，所以，212T ππω==，则() 2.5sin 1.512t h t πϕ⎛⎫=++ ⎪⎝⎭，由于盛水桶M 在0P 处距水面的距离为3m ，则()0 2.5sin 1.53h ϕ=+=，可得3sin 5ϕ=，由于函数()h t 在0=t 附近单调递增，则ϕ为第一象限角，所以，4cos 5ϕ=，所以，()12 2.5sin 1.5 2.5cos 1.5622h πϕϕϕ⎛⎫⎛⎫=++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭()2.5 1.5 3.8m =≈.故选：D.思路点睛：建立三角函数模型解决实际问题的一般步骤：（1）审题：审清题目条件、要求、理解数学关系；（2）建模：分析题目变化趋势，选择合适的三角函数模型；（3）求解：对所建立的数学模型进行分析研究，从而得出结论.11．已知双曲线C 的方程为22221(0,0)x y a b a b -=>>l 与圆2220(0)x y mx m +-=>相切于M ，与双曲线C 的两条渐近线分别相交于A ，B ，且M 为AB中点，则双曲线C 的离心率为（）A ．2BCD【正确答案】B 【分析】.设出直线l 的方程，求出A ，B 的坐标，从而可得点M 的坐标，代入圆方程中即可求离心率【详解】依题意，设直线l的方程为(0)y n n =+>，圆2220(0)x y mx m +-=>的方程可化为222()x m y m -+=，即圆心坐标为(,0)m ，半径为m ，因为直线l 与圆相切于Mm =，由0n >可化简得m =，则直线l的方程为()3y x m =+，双曲线C 的两条渐近线分别为b y x a =，b y x a =-，由)y x m b y xa ⎧=+⎪⎪⎨⎪=⎪⎩得A，同理可得B ，因为M 为AB中点，由中点坐标公式可得222(3ma M b a -，M 在圆上，将M 的坐标代入圆方程可得222222())3ma m m b a -+=-，化简整理得222()0a b -=，从而可得a b =，则双曲线C 的离心率ce a==故选：B12．已知函数(),()f x g x 的定义域均为R ，且满足(1)(3)4,(1)(3)6---=++-=f x g x g x f x ，(2)g x +为奇函数，则1071()n f n ==∑（）A ．5350-B ．5250-C ．5150-D ．5050-【正确答案】A【分析】由条件通过赋值，结合周期函数的定义证明()()h x f x x =+为周期为2的周期函数，再求()()0,1h h ，结合周期函数性质求1071()n h n =∑，由此可得结论.【详解】因为函数(2)g x +为奇函数，所以()()220g x g x ++-+=，在(1)(3)4f x g x ---=中将x 代换为1x +可得()(2)4f x g x --=①，在(1)(3)6g x f x ++-=中将x 代换为1x +可得(2)(2)6g x f x ++-=②，①②两式相减可得()()(2)(2)22g x f x f x g x ++--+-+=，所以()(2)2f x f x --=，即()(2)2f x x f x x -+-=+，设()()h x f x x =+，则()()2h x h x +=，所以函数()()h x f x x =+为周期为2的周期函数，由()()220g x g x ++-+=取0x =可得()20g =，由()(2)4f x g x --=取0x =可得(0)(2)4f g -=，所以(0)4f =，在()(2)2f x f x --=中取1x =可得()(1)12f f --=，在()(2)4f x g x --=中取1x =可得(1)(1)4f g -=④，在()(2)4f x g x --=中取=1x -可得(1)(3)4f g --=⑤，在()()220g x g x ++-+=中取1x =可得()()310g g +=⑥，将④⑤⑥相加可得()(1)18f f -+=，又()(1)12f f --=，所以()13f =，又(0)4f =，()()h x f x x =+，所以()()0004h f =+=，()()1114h f =+=，又函数()()h x f x x =+为周期为2的周期函数，所以()()()()1071()1231074107428n h n h h h h ==+++⋅⋅⋅+=⨯=∑，所以()()()()()1071()112210710742812107n h n n h h h =-=-+-+⋅⋅⋅+-=-++⋅⋅⋅+∑，所以()()()10711107107428428577853502n h n n =+⨯-=-=-=-∑，所以1071()5350n f n ==-∑.故选：A.知识点点睛：本题考查奇函数的性质，周期函数的定义，周期函数的性质，组合求和法，等差数列求和，考查赋值法，属于综合题，考查学生的逻辑推理能力和运算求解能力.二、填空题13．若复数z 满足(2i)12i z +=-，则z 的共轭复数z 的虚部为________.【正确答案】1【分析】根据复数的除法运算化简复数，即可由共轭复数的概念以及虚部概念求解.【详解】由(2i)12i z +=-得()()()()12i 2i 12i 2i 4i 2i 2i 2i 2i 5z ------====-++-，故i z =，且虚部为1，故114．在[]4,4-之间任取一个实数m ，使得直线0x y m ++=与圆222x y +=有公共点的概率为________.【正确答案】12/0.5【分析】利用直线与圆的位置关系求出m 的取值范围，再利用几何概型的概率公式可求得所求事件的概率.【详解】圆222x y +=因为直线0x y m ++=与圆222x y +=≤，解得22m -≤≤，因此，所求事件的概率为()()221442P --==--.故答案为.1215．已知正三棱柱111ABC A B C -所有顶点都在球O 上，若球O 的体积为32π3，则该正三棱柱体积的最大值为________.【正确答案】8【分析】由条件结合球的体积公式求球的半径，设正三棱柱的底面边长为x ，求出三棱柱的高，结合棱柱的体积求三棱柱的体积，再利用导数求其最大值.【详解】设正三棱柱111ABC A B C -的上，下底面的中心分别为12,O O ，连接12O O ，根据对称性可得，线段12O O 的中点O 即为正三棱柱111ABC A B C -的外接球的球心，线段OA 为该外接球的半径，设OA R =，由已知3432ππ33R =，所以2R =，即2OA =，设正三棱柱111ABC A B C -的底面边长为x ，设线段BC 的中点为D ，则2AD x =，1223323AO AD ==⨯=，在1Rt AO O △中，1OO ==所以12O O =，0x <<，又ABC 的面积1122S BC AD x =⋅=⨯=所以正三棱柱111ABC A B C -的体积242x V x =⨯设t ，则22123x t =-，02t <<，所以)2123V t t =-，02t <<，所以)2129V t '=-，令0V '=，可得3t =或3t =-，舍去，所以当0t <<0V '>，函数)2123V t t =-在0,3⎛⎫ ⎪ ⎪⎝⎭上单调递增，当2323t <<时，0V '<，函数()231232V t t =-在23,23⎛⎫ ⎪ ⎪⎝⎭上单调递减，所以当233t =时，()231232V t t =-取最大值，最大值为8，所以当22x =时，三棱柱111ABC A B C -的体积最大，最大体积为8.故答案为.816．在ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若cos cos a C c A b c -=-，且1a c +=，则当边c 取得最大值时，ABC 的周长为________.【正确答案】33/33【分析】由正弦定理结合两角和的正弦公式可求得cos A 的值，结合角A 的取值范围可得出角A 的值，利用正弦定理可求得c 的最大值及其对应的C 的值，进而可求得b 的值，由此可得出ABC 的周长.【详解】因为cos cos a C c A b c -=-，由正弦定理可得sin cos cos sin sin sin A C A C B C -=-，即()sin cos cos sin sin sin sin cos cos sin sin A C A C A C C A C A C C -=+-=+-，整理可得2cos sin sin A C C =，因为A 、()0,πC ∈，所以，sin 0C >，则1cos 2A =，故π3A =，由正弦定理可得)231sin sin 332c a c c C A =-，整理可得2332332sin 31sin 23sin Cc C C C=+++因为2π03C <<，当π2C =时，c 取最大值，且c 4323=-+，此时，(1143a c =-=--=，π6B =，所以，22c b ==因此，当边c 取得最大值时，ABC的周长为()((32423a b c ++=+-+-=-.故答案为.3三、解答题17．设等比数列{}n a 的前n 项和为n S ，且()*231n n S a n N =-∈．()1求{}n a 的通项公式；()2若()()1311nn n n b a a +=++，求{}n b 的前n 项和n T ．【正确答案】(1)13n n a -=．(2)311 2231n n T ⎛⎫=- +⎝⎭．【分析】()1利用数列的递推关系式的应用求出数列的通项公式．()2利用()1的结论，进一步利用裂项相消法求出数列的和．【详解】() 1等比数列{}n a 的前n 项和为n S ，且()*231.n n S a n N =-∈①当1n =时，解得11a =．当2n ≥时11231n n S a --=-②-①②得1323n n n a a a --=，所以13(nn a a -=常数)，故11133n n n a --=⋅=．()2由于13n n a -=，所以()()1133111123131n n n n n n b a a -+⎛⎫==- ⎪++++⎝⎭，所以011311113112313131312231n n n n T -⎛⎫⎛⎫=-+⋯+-=- ⎪ ⎪+-+++⎝⎭⎝⎭．本题考查的知识要点：数列的通项公式的求法及应用，裂项相消法在数列求和中的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题型．18．“五一黄金周”期间，某商场为吸引顾客，增加顾客流量，推出购物促销优惠活动，具体优惠方案有两种：方案一：消费金额不满300元，不予优惠；消费金额满300元减60元；方案二：消费金额满300元，可参加一次抽奖活动，活动规则为：从装有3个红球和3个白球共6个球的盒子中任取3个球（这些小球除颜色不同其余均相同），抽奖者根据抽到的红球个数不同将享受不同的优惠折扣，具体优惠如下：抽到的红球个数0123优惠折扣无折扣九折八折七折(1)现有甲乙两位顾客各获得一次抽奖活动，求这两位顾客恰好有一人获得八折优惠折扣的概率；(2)若李女士在该商场消费金额为x 元（300x >），请以李女士实付金额的期望为决策依据，对李女士选择何种优惠方案提出建议.【正确答案】(1)99200(2)答案见解析【分析】（1）先求事件抽奖的顾客获得八折优惠的概率，再根据独立重复试验的概率公式求两位顾客恰好有一人获得八折优惠折扣的概率；（2）在300x >条件下，分别求两种方案下李女士实付金额的期望，由此提出建议.【详解】（1）设事件A ：抽奖的顾客获得八折优惠，则213336C C 9()C 20P A ⋅==；由于甲乙两位顾客获得八折优惠的概率均为920，设甲乙两位顾客恰好一人获得八折优惠的概率P ，则129999C (12020200P =⨯-=；所以甲乙两位顾客恰好一人获得八折优惠的概率为99200.（2）方案一：设实付金额1ξ，则160x ξ=-,（300x >）.方案二：设实付金额2ξ，则2ξ的可能取值有：x ，0.9x ，0.8x ，0.7x ；（300x >）.03236C 1()C 20P x ξ===；1233236C C 9(0.9)C 20P x ξ===；29(0.8)20P x ξ==；33236C 1(0.7)C 20P x ξ===；所以()219998178520201020102010100E x x x x x ξ=+⨯+⨯+⨯=.①若8560100x x -<，解得300400x <<，选择方案一；②若8560100x x -=，解得400x =，选择方案一或方案二均可；③若8560100x x ->，解得400x >，选择方案二.，所以当消费金额大于300且小于400时，选择方案一；当消费金额等于400时，选择方案一或方案二均可；当消费金额大于400时，选择方案二.19．如图，在直三棱柱111ABC A B C -中，点E ，F 分别是BC ，11AC 中点，平面11ABB A 平面AEF l =．(1)证明：l EF ∥；(2)若AB AC ==，平面11ACC A ⊥平面11ABB A ，且1AB EF ⊥，求直线l 与平面11A B E 所成角的余弦值．【正确答案】(1)证明过程见详解【分析】（1）取AB 中点G ，连接EG ，1A G ，先证明四边形1EGA F 为平行四边形，再证明EF ∥平面11ABB A ，再根据直线与平面平行的性质即可证明l EF ∥；（2）根据题意先证明11AC ，11A B ，1AA 两两垂直，从而建立空间直角坐标系，再根据1AB EF ⊥求得1AA 的值，再利用线面角的向量求法即可求解．【详解】（1）取AB 中点G ，连接EG ，1A G ，∵E ，G 分别是BC ，AB 中点，∴EG AC ∥且12EG AC =，又∵1A F AC ∥且112A F AC =，∴1A F EG ∥且1=A F EG ，∴四边形1EGA F 为平行四边形，∴1EF A G ∥，又EF ⊄平面11ABB A ，1AG ⊂平面11ABB A ，∴EF ∥平面11ABB A ，∵EF ⊂平面AEF ，平面AEF ⋂平面11ABB A l =，∴EF l ∥．（2）由三棱柱为直棱柱，∴1AA ⊥平面111A B C ，∴111AA AC ⊥，111AA A B ⊥，∵平面11ACC A ⊥平面11ABB A ，平面11ACC A 平面111ABB A AA =，11AC ⊂平面11ACC A ，∴11A C ⊥平面11ABB A ，∴1111A C A B ⊥，故以1A 为坐标原点，以11A C ，11A B ，1AA 分别为x ，y ，z 轴建立空间直角坐标系，设1AA a =，则1B ，F ，)E a ，(0,0,)A a ，所以1)AB a =- ，(0,)EF a =-，又1AB EF ⊥，则10AB EF ⋅=，解得2a =，所以2)E ，(0,0,2)A，则11A B =，12)A E =，设平面11A B E 法向量为(,,)n x y z =，所以11100n A B n A F ⎧⋅=⎪⎨⋅=⎪⎩，即020z ⎧=⎪+=，取x =，得1)n =- ，由（1）知直线EF l ∥，则l方向向量为(0,2)EF =-，设直线l 与平面11BCC B 所成角为α，则sin cos ,3n EF n EF n EF α⋅===⋅，则cos α=所以直线l 与平面11BCC B所成角的余弦值为3．20．已知抛物线C ：22y x =，过(1,0)P 的直线与C 相交于A ，B 两点，其中O 为坐标原点.(1)证明：直线OA ，OB 的斜率之积为定值；(2)若线段AB 的垂直平分线交y 轴于M ，且12tan 5AMB ∠=，求直线AB 的方程.【正确答案】(1)证明见解析(2)10x -=或10x -=【分析】（1）直线与抛物线方程联立，利用韦达定理表示斜率乘积；（2）结合二倍角公式，求||4||3AB MN =，以及弦长公式求AB ，并利用韦达定理表示MN ，利用比值，即可求直线方程.【详解】（1）设1222(,),(,)A x y B x y ，设直线AB ：x =my +1.联立221y x x my ⎧=⎨=+⎩化简可得：2220.y my --=由韦达定理可得：12122,2y y m y y +==-；所以1212221212124222OA OB y y y y k k y y x x y y ⋅====-⋅，所以直线OA ，OB 的斜率之积为定值2-.（2）设线段AB 的中点N ，设AMN θ∠=.则22tan 12tan tan 21tan 5AMB θθθ∠===-，解得2tan 3θ=，所以||2||3AN MN =，即||4||3AB MN =；所以12|||AB y y =-=又线段AB 的中点N ，可得122N y y y m +==，所以211N N x my m =+=+.因为MN AB ⊥，所以MN k m =-，所以2|||1)N M MN x x m =-=+.所以||4||3AB MN =，解得m =所以直线AB 的方程为：10x -=或10x +-=.21．已知()ln 1(R)f x x kx k =-+∈，()(e 2)x g x x =-.(1)求()f x 的极值；(2)若()()g x f x ≥，求实数k 的取值范围.【正确答案】(1)答案见解析(2)1k ≥【分析】（1）根据题意，求导得()f x '，然后分0k ≤与0k >讨论，即可得到结果.（2）根据题意，将问题转化为1n 2e l xx k x+≥-+在0x >恒成立，然后构造函数1ln ()e 2xx h x x+=-+，求得其最大值，即可得到结果.【详解】（1）已知1()ln 1,(),0f x x kx f x k x x'=-+=->（），当0k ≤时，()0f x '≥恒成立，()f x 无极值，当0k >时，1()kx f x x -'=，()f x 在10k ⎛⎫⎪⎝⎭，上单调递增，在1,k ⎛+∞⎫ ⎪⎝⎭单调递减，当1x k =时，()f x 有极大值，1(ln f k k=-，无极小值，综上：当0k ≤时，()f x 无极值；当0k >时，极大值为1()ln f k k=-，无极小值；（2）若()()g x f x ≥，则(e 2)ln 10x x x kx --+-≥在0x >时恒成立，l 2e 1n x x k x +∴≥-+恒成立，令()()221ln ln e e 2,xx x x x h x h x x x '+--=-+=，令2ln e x x x x φ=--（），则21(2)e 0(0)x x x x x xφ'=--+<>（），()x φ在()0+∞，单调递减，又12e 11e 0,(1)e 0e φφ-⎛⎫=->=-< ⎪⎝⎭，由零点存在定理知，存在唯一零点01,1e x ⎛⎫∈ ⎪⎝⎭，使得()00x φ=，即0001ln 20000000111ln e lne ,ln e e x x x x x x x x x x x -===，，令e (0),()(1)e 0,()x x x x x x x x ωωω'=>=+>（）在()0+∞，上单调递增，000011ln(),ln x x x x ωω⎛⎫=∴= ⎪⎝⎭，即00ln x x -=∴当0(0,)x x ∈时，()h x 单调递增，0(,)x x ∈+∞单调递减，()()0000max 0001ln 11e 221x x x h x h x x x x +-==+=-+=，0()1k h x ∴≥=，即k 的取值范围为1k ≥.关键点睛：本题主要考查了用导数研究函数极值问题，难度较难，解答本题的关键在于分离参数，然后构造函数，将问题转化为最值问题.22．在直角坐标系xOy 中，已知曲线1C的参数方程为：1cos x y φφ⎧=⎪⎨⎪=⎩（φ为参数），曲线2C 的参数方程为：sin 2sin cos x ty t t =⎧⎨=+⎩（t 为参数）.(1)将曲线12,C C 化为普通方程；(2)若曲线2C 与y 轴相交于,A B ，与x 轴相交于C ，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，射线π:(0)6l θρ=≥与曲线2C 相交于P ，求四边形ACBP 的面积.【正确答案】(1)2212y x -=；21y x =+，[1,1]x ∈-(2)1【分析】（1）根据关系2221sin 1cos cos φφφ-=消去曲线1C 的参数可得其普通方程，根据平方关系消去参数t 可得曲线2C 的普通方程，（2）先求点,,,A B C P 的坐标，再求四边形ACBP 面积即可.【详解】（1）曲线1C的参数方程为：1cos x y φφ⎧=⎪⎨⎪=⎩（φ为参数）可得222221cos sin 2cos x y φφφ⎧=⎪⎪⎨⎪=⎪⎩（φ为参数）消去参数φ可得：2212y x -=，所以曲线1C 的普通方程为.2212y x -=曲线2C 的参数方程为sin 2sin cos x t y t t =⎧⎨=+⎩（t 为参数）可得22sin cos 12sin cos x t ty t t=⎧⎨=+⎩（t 为参数）消去参数t 可得21y x -=，又因为sin 2[1,1]t ∈-，所以[1,1]x ∈-.所以曲线2C 的普通方程为：21y x =+，[1,1]x ∈-.（2）易得曲线2C 与y 轴交于(0,1)±，与x 轴交于(1,0)-.将射线π:(0)6l θρ=≥化为直角坐标方程.(0)3y x =≥联立()22012y x y x ⎧=≥⎪⎪⎨⎪-=⎪⎩解得x y ⎧=⎪⎪⎨⎪=⎪⎩，所以四边形ACBP 的面积()112ACB ACPC P S S SAB x x =+=+=+所以四边形ACBP的面积为123．设,,x y z 均为正数，且1x y z ++=，证明：（Ⅰ）13xy yz zx ++≤（Ⅱ）22212x y z y z x z x y ++≥+++【正确答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析．【分析】（1）先由基本不等式可得222x y z xy yz xz ++≥++，再结合()2x y z ++的展开式即可证明原式成立；（2）利用柯西不等式[]2222()()()()1x y z x y y z x z x y z y z x z x y ⎛⎫+++++++≥++= ⎪+++⎝⎭证明.【详解】证明：（Ⅰ）：因为()()()2222222222xy y z x z x y z xy yz xz+++++++=≥++所以22221()2223()x y z x y z xy yz xz xy yz zx =++=+++++≥++故13xy yz zx ++≤，当且仅当x y z ==时“=”成立.（Ⅱ）,,x y z 均为正数，由柯西不等式得：2222[()()()]()1x y z x y y z x z x y z y z x z x y ⎛⎫+++++++≥++= ⎪+++⎝⎭即22221x y z y z x z x y ⎛⎫++≥ ⎪+++⎝⎭，故22212x y z y z x z x y ++≥+++，当且仅当x y z ==时“=”成立.本题考查利用基本不等式、柯西不等式等证明不等式，难度一般.证明时，利用整体思想，注意“1”的巧妙代换.。

高考模拟卷(二)备战2024年高考地理阶段性模拟仿真冲刺卷(山东专用)试题含答案解析

备战2024年高考地理阶段性模拟仿真冲刺卷（山东专用）高考模拟卷（二）（本卷共19小题，满分100分，考试用时90分钟）第I卷（选择题）一、单项选择题:本题共15小题,每小题3分,共45分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

近年来屋顶光伏发电发展迅速，但在具体安装中，工程要考虑屋顶坡度、前后排光伏板的距离、建筑物遮挡及自然地理环境等多个影响因素。

下图示意辽宁省西部某处厂房房屋的屋顶光伏板安装结构，完成下面小题。

1．该地光伏板的最低点距离屋面的高度（H）不宜过高或过低，主要考虑的自然因素是（）A．最大降水量B．最大积雪深度C．最大太阳高度角D．最大风速2．为保证最佳发电效果，若图示屋面倾角α变小，则安装倾角θ和光伏板间的距离L应（）A．θ不变，L变大B．θ变小，L变大C．θ不变，L变小D．θ变小，L变小在空气中水汽含量不变，保持气压一定的情况下，空气因冷却而达到饱和时的温度，称为露点温度。

其数值越大，反映空气中水汽含量越大。

一般情况下，温度相同时湿空气要比干空气密度小。

两个温度相近的干、湿气团相遇所形成的锋，称为干线。

下图为我国河套平原及其附近地区6月某日14时主要气象要素分布形势示意图。

完成下面小题。

3．与乙、丙气团相比，甲气团的物理性质是（）A．暖湿B．冷湿C．暖干D．冷干4．最易出现扬沙天气的地点是（）A．甲B．乙C．丙D．丁疏勒河从祁连山流出，形成昌马洪积-冲积扇，河流则潜行至冲积扇边缘出露（古称冥水），之后西行。

党河则是疏勒河的最大支流。

月牙泉原为党河的一部分，是河流改道后留下的一部分河湾。

月牙泉水深仅五米，是一处天然淡水湖泊。

读图，完成下面小题5．冥水（）A．在土层薄的冲积扇边缘流出成河B．落差大，河流的汇水速度快C．夏季蒸发旺盛，形成季节性断流D．是地下溶洞中流动的地下水6．党河（）A．春季流量最大，冬季流量最小B．流量季节变化小，泥沙多C．为内流河，主要是冰雪融水补给D．干流基本为西北流向东南7．月牙泉是淡水湖的主要原因是其（）A．周边沙土中的含盐率很低B．有地下径流进出，可平衡盐分C．没有径流注入和带入盐分D．常受党河洪水侵袭，带走盐分冬克玛底河是长江上游通天河的二级支流，流域内的河谷为平坦开阔的稀疏草地，地表植被矮，多在5～10cm，根系深度主要集中于0～40cm。

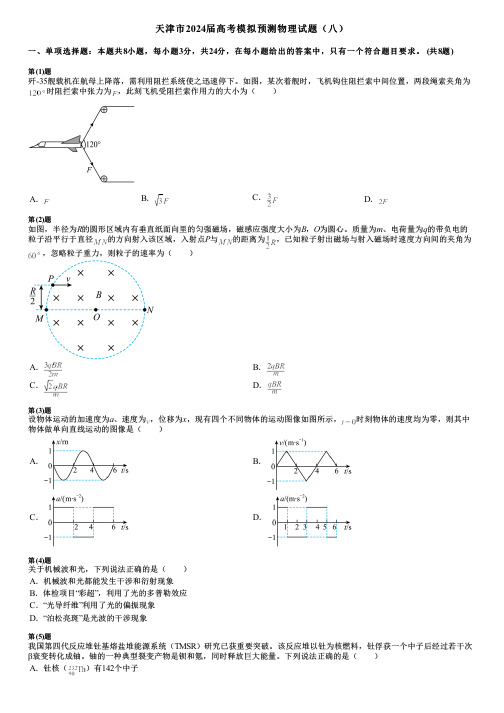
天津市2024届高考模拟预测物理试题(八)

天津市2024届高考模拟预测物理试题（八）一、单项选择题：本题共8小题，每小题3分，共24分，在每小题给出的答案中，只有一个符合题目要求。

(共8题)第(1)题歼-35舰载机在航母上降落，需利用阻拦系统使之迅速停下。

如图，某次着舰时，飞机钩住阻拦索中间位置，两段绳索夹角为时阻拦索中张力为，此刻飞机受阻拦索作用力的大小为（）A．B．C．D．第(2)题如图，半径为R的圆形区域内有垂直纸面向里的匀强磁场，磁感应强度大小为B，O为圆心。

质量为m、电荷量为q的带负电的粒子沿平行于直径的方向射入该区域，入射点P与的距离为，已知粒子射出磁场与射入磁场时速度方向间的夹角为，忽略粒子重力，则粒子的速率为（）A．B．C．D．第(3)题设物体运动的加速度为a、速度为，位移为x，现有四个不同物体的运动图像如图所示，时刻物体的速度均为零，则其中物体做单向直线运动的图像是（）A．B．C．D．第(4)题关于机械波和光，下列说法正确的是（）A．机械波和光都能发生干涉和衍射现象B．体检项目“彩超”，利用了光的多普勒效应C．“光导纤维”利用了光的偏振现象D．“泊松亮斑”是光波的干涉现象第(5)题我国第四代反应堆钍基熔盐堆能源系统（TMSR）研究已获重要突破。

该反应堆以钍为核燃料，钍俘获一个中子后经过若干次β衰变转化成铀。

铀的一种典型裂变产物是钡和氪，同时释放巨大能量。

下列说法正确的是（）A．钍核（）有142个中子B．针核（）经过4次衰变后转化成铀（）C．钍核（）衰变后核子的比结合能减小D．钍核（）的半衰期与钍核的数量有关第(6)题如图甲所示是一种门后挂钩，相邻挂钩间的距离相等，均为。

图乙所示的单肩包底边长度，包和包内物品的总质量，柔软肩带长100，肩带与挂钩间的摩擦可忽略不计。

现要挂包时两边肩带受到的拉力最小（带的两端与包的接点间的距离始终保持与底边的长度相等），需将挂包肩带跨挂在（）A．2个挂钩上B．3个挂钩上C．4个挂钩上D．5个挂钩上第(7)题我国计划在2030年前实现载人登月，开展科学探索。

2024年浙江省新高考普通高校招生考试9月预测模拟卷物理试题(基础必刷)

2024年浙江省新高考普通高校招生考试9月预测模拟卷物理试题（基础必刷）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题在如图所示的空间直角坐标系中，一不计重力且带正电的粒子从坐标为处以某一初速度平行y轴正方向射出，经时间t，粒子前进的距离为L，在该空间加上匀强电场，粒子仍从同一位置以相同的速度射出，经相同时间t后恰好运动到坐标原点O，已知粒子的比荷为k，则该匀强电场的场强大小为（）A．B．C．D．第(2)题正电子发射型计算机断层显像（PET）的基本原理：将放射性同位素注入人体，在人体内衰变放出的正电子与人体内的负电子相遇而湮灭转化为一对光子，光子被探测器探测后经计算机处理产生清晰图像，下列说法正确的是（）A．在人体内衰变的方程是B．正负电子湮灭的方程式是C．正负电子相遇而湮灭违背了能量守恒定律D．在PET中，的主要用途是参与人体的代谢过程第(3)题平时我们所处的地球表面，实际上存在场强大小为100 V/m的电场，可将其视为匀强电场，在地面立一金属杆后空间中的等势面如图所示。

空间中存在a、b、c三点，其中a点是电势为300V等势面的最高点，b、c等高。

则下列说法正确的是（）A．b、c两点的电势差B．a点场强大小等于100V/mC．a点场强方向沿竖直方向D．a点的电势低于c点第(4)题如图所示，为远距离输电的示意图，发电机组发出的电首先经过升压变压器（T1）升压后再向远距离输电，到达用电区后，首先在一次高压变电站（T2）降压，在更接近用户地点再由二次变电站（T3）降压后，一部分电能送到大量用电的工业用户（工厂），另一部分经过低压变电站（T4）降到220V/380V，送给其他用户。

假设变压器都是理想变压器，只考虑远距离输电线电阻，其他电阻不计，则下列说法正确的是（）A．T1的输出电压和T2的输入电压相等B．增加其他用户负载，T2的输出电压减小C．增加其他用户负载，T3的输出电压不变D．增加工业用户负载，T4的输出电压不变第(5)题伽利略通过斜面理想实验得出了（）A．力是维持物体运动的原因B．物体的加速度与外力成正比C．物体运动不需要力来维持D．力是克服物体惯性的原因第(6)题如图所示，两等量异种点电荷固定在、两点，以、连线的中点为原点，沿、连线的中垂线建立轴。

湖南省衡阳市第八中学2024届高三下学期高考模拟预测化学试题(含答案与解析)_5509

湖南省衡阳市第八中学2024届高三下学期高考模拟预测卷化学试题时量75分钟满分：100分注意事项：1．答卷前，考生务必将自己的姓名､准考证号填写在答题卡上．2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上，写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．相对原子质量：H1 C12 O16 N14 S32一、单选题：本题包括14小题，每小题3分，共42分，在每小题给出的四个选项种，只有一项是符合题目要求的。

1. 2023年10月26日11时14分，神舟十七号载人飞船点火升空成功发射，我国航天航空事业再次迎来飞速发展。

下列有关说法错误的是A. 神舟十七号宇宙飞船返回舱所用高温结构陶瓷属于新型无机非金属材料B. 返回舱降落回收过程中使用了芳纶制作的降落伞，芳纶是有机高分子材料C. 神舟十七号载人飞船所用燃料偏二甲肼[(CH3)2N-NH2]，属于烃的衍生物D. 神舟十七号使用砷化镓(GaAs)太阳能电池，供电时的能量转化形式为化学能转化为电能2. 下列关于HCHO及构成微粒的化学用语或图示表达错误的是A. HCHO的分子结构模型：B. H原子电子的电子云轮廓图：C. C原子杂化轨道示意图：D. 基态氧原子的轨道表示式为：3. 已知反应：3323232CH COOH CH CH OH CH COOCH CH H O ++△浓硫酸，设A N 为阿伏加德罗常数的值，下列有关说法正确的是A. 标准状况下，2.24L 乙酸含有的σ键数目为A 0.8NB. 向足量乙醇中加入2.3g 金属钠，转移电子数为A 0.1NC. 1mol 乙醇与等量乙酸充分发生上述反应，生成乙酸乙酯分子的数目为A ND. 0.1mol 醋酸钠溶于稀醋酸中使溶液呈中性，混合溶液中3CH COO -数目小于A 0.1N 4. 下列实验能达到实验目的是(图中部分夹持装置略)实验实验目的A ．证明1-溴丁烷发生消去反应生成丁烯B ．证明苯环使羟基活化实验实验目的 C ．实验室制备并收集乙酸乙酯D ．证明乙炔可使溴的四氯化碳溶液褪色A. AB. BC. CD. D5. 下列对物质性质解释合理的是的选项性质解释A 热稳定性：22H O(g)H S(g)> 2H O 中存在氢键B 熔点：晶体硅<碳化硅碳化硅中分子间作用力较大C酸性：22F CH COOH Cl CH COOH -->-- 电负性：F Cl > D 熔点：22Br I <Br Br -键较强A. AB. BC. CD. D6. “律动世界”国际化学元素周期表主题年活动报告中，提到了一种具有净水作用的物质，它由Q 、W 、X 、Y 、Z 五种原子序数依次增大的元素组成。

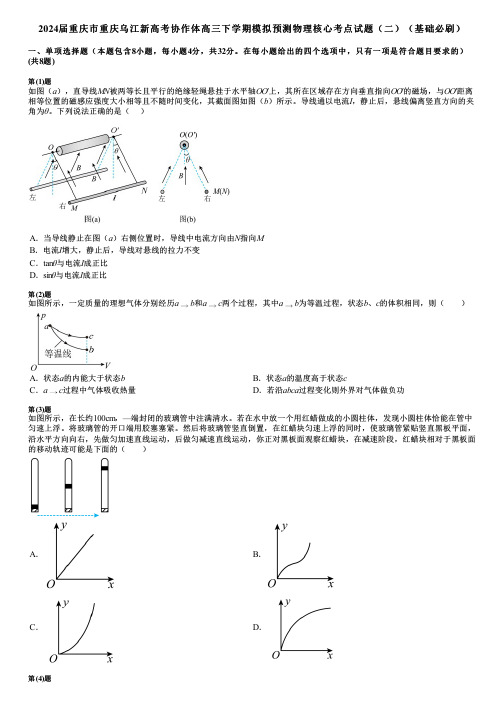
2024届重庆市重庆乌江新高考协作体高三下学期模拟预测物理核心考点试题(二)(基础必刷)

2024届重庆市重庆乌江新高考协作体高三下学期模拟预测物理核心考点试题（二）（基础必刷）一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图（a），直导线MN被两等长且平行的绝缘轻绳悬挂于水平轴OO′上，其所在区域存在方向垂直指向OO′的磁场，与OO′距离相等位置的磁感应强度大小相等且不随时间变化，其截面图如图（b）所示。

导线通以电流I，静止后，悬线偏离竖直方向的夹角为θ。

下列说法正确的是（）A．当导线静止在图（a）右侧位置时，导线中电流方向由N指向MB．电流I增大，静止后，导线对悬线的拉力不变C．tanθ与电流I成正比D．sinθ与电流I成正比第(2)题如图所示，一定质量的理想气体分别经历a b和a c两个过程，其中a b为等温过程，状态b、c的体积相同，则（）A．状态a的内能大于状态b B．状态a的温度高于状态cC．a c过程中气体吸收热量D．若沿abca过程变化则外界对气体做负功第(3)题如图所示，在长约100cm，—端封闭的玻璃管中注满清水。

若在水中放一个用红蜡做成的小圆柱体，发现小圆柱体恰能在管中匀速上浮。

将玻璃管的开口端用胶塞塞紧。

然后将玻璃管竖直倒置，在红蜡块匀速上浮的同时，使玻璃管紧贴竖直黑板平面，沿水平方向向右，先做匀加速直线运动，后做匀减速直线运动，你正对黑板面观察红蜡块，在减速阶段，红蜡块相对于黑板面的移动轨迹可能是下面的（）A．B．C．D．第(4)题如图所示，A、B、C、D、E、F、G、H是正方体的八个顶点。

则下列说法错误的是（）A．只在F、D两点放置等量异种点电荷，则A、G两点电势相等B．只在B、D两点放置等量异种点电荷，则E、C两点电势相等C．只在A、B两点放置等量异种点电荷，则H、G两点电场强度大小相等D．在八个顶点均放置电荷量为+q的点电荷，则立方体每个面中心的电场强度大小相等第(5)题一根柔软轻绳水平静止，A、B、C、D、E为绳上标记的5个点，彼此间隔1米排成一条直线，如图甲所示。

2024-2025学年浙江省高考模拟卷及参考答案

2024-2025学年浙江省高考模拟卷及参考答案一、现代文阅读(35分) 2024.11(一) 现代文阅读Ⅰ (本题共5小题，19分)阅读下面的文字，完成1~5题。

材料一：“科技向善”一词最早由影响力投资者保罗·米勒于2013年正式提出，并很快得到了科技企业的广泛认同和响应。

所谓科技向善，就是企业在追求科技创新的同时，主动且负责任地利用科技创新解决社会问题，如生态环境、公共健康、教育、就业、医疗、安全等方面的社会需求和薄弱环节。

近年来，政府、社会和企业界对科技向善的关注度逐渐提高，这一方面是源于对科技伦理认识的深化。

当前，新一轮科技革命和产业变革突飞猛进，新技术、新业态、新模式不断涌现，给经济社会发展带来了深远的影响，科技创新从未像今天这样深刻影响着国家实力和人民福祉。

但如何才能确保科技为人服务、造福人民? 面对这个问题，党的十八大以来，中国逐步明确了科技造福人民的价值取向，以及科技发展为了人民、依靠人民，科技成果由人民共享的科技伦理观。

2024年4月，三大交易所正式发布《上市公司可持续发展报告指引(试行)》，《指引》强调了科技创新的作用，并明确提出“鼓励披露主体积极践行创新驱动发展战略，持续提升创新能力和竞争力，在创新决策和实践中遵守科学伦理规范，尊重科学精神，发挥科学技术的正面效应”。

方向已经明确，共识业已建立。

但企业在践行科技向善的过程中依然面临着很多矛盾。

首先，需要平衡国家发展战略需要与企业资源有限的矛盾。

在当前推动中国式现代化的进程中，科技创新将发挥更大的作用。

然而；在某一特定时间、空间，企业的资源是有限的，这就需要企业从战略角度思考如何在保障企业生存成长的前提下，坚持长期主义，加大科技创新投入。

其次，作为行业龙头企业成关键企业，需要平衡产业可持续发展和自身可持续发展的关系，通过带动产业链上下游企业高质量发展，提升企业自身的可持续竞争力。

第三，需要平衡追求利润最大化与承担社会责任的关系，在企业发展的同时积极回报社会，增进社会民生福祉。

高考各科模拟试题及答案

高考各科模拟试题及答案一、语文（一）现代文阅读1. 下列句子中，没有语病的一项是：A. 经过认真研究，我们决定采纳他的建议。

B. 他不仅学习好，而且品德高尚。

C. 这个问题，我们还需要进一步探讨。

D. 他的到来，给我们的团队带来了活力。

答案：D（二）古诗文鉴赏2. 下面这首诗的作者是谁？春眠不觉晓，处处闻啼鸟。

夜来风雨声，花落知多少。

答案：孟浩然二、数学（一）选择题1. 下列哪个选项是不等式x^2 - 4x + 4 ≤ 0的解？A. x > 4B. x < 2C. x ∈ [-2, 2]D. x ≥ 2答案：C（二）填空题2. 若f(x) = x^2 - 6x + 5，求f(3)的值。

答案：-4三、英语（一）阅读理解1. 根据文章内容，下列哪项陈述是正确的？A. The author is a teacher.B. The author enjoys traveling.C. The author dislikes reading.D. The author is a student.答案：B（二）完形填空2. In the passage, the word "inspire" is closest in meaning to:A. EncourageB. AnnoyC. DisappointD. Surprise答案：A四、物理（一）选择题1. 根据牛顿第二定律，下列哪个公式是正确的？A. F = maB. F = mvC. F = m/aD. F = a/m答案：A（二）计算题2. 一个物体的质量为2kg，受到的力为10N，求物体的加速度。

答案：5 m/s²五、化学（一）选择题1. 下列哪个元素属于碱金属？A. NaB. ClC. OD. He答案：A（二）实验题2. 在实验室中，如何正确地使用滴定管？答案：使用滴定管时，应确保滴定管清洁，避免污染。

高考模拟演练考试题及答案

高考模拟演练考试题及答案一、语文题阅读理解(一)“我们与大自然的关系何尝不是一种恩赐？大自然会赋予我们生命和物质，我们也应该尊重和保护它。

”这是一位环保志愿者在接受采访时的回答。

她坚信人与自然的关系是平等和互惠的。

1. 此文段主要表达了什么观点？2. 你对于人与自然的关系有什么看法？请结合自身经验或观察进行论述。

答案：1. 此文段主要表达了人与自然关系是平等和互惠的观点。

2. (回答因个人观点和经验而异)(二)鲁迅先生曾说过：“只有痛定思痛，才能自救。

”意思是在痛苦中醒悟并反思，人才能够自救。

他认为痛苦可以激发人们的反抗精神和改造自我的欲望。

1. 请阐述你对这句话的理解。

2. 你在生活中是否有过痛定思痛的经历？如果有，请具体描述。

答案：1. 我理解这句话是指只有当人们在痛苦中意识到问题并进行深刻的思考时，才能够从中找到解决问题的方法，实现自救。

2. (回答因个人经历而异)作文题请根据以下提示，写一篇不少于800字的文章。

题目：追寻梦想的力量提示：1. 梦想是人们前进的动力，它可以激励我们勇敢面对困难和挑战；2. 通过追寻梦想，我们可以发现自己的潜力，并将其变成现实；3. 追寻梦想的过程可能会遇到阻碍和挫折，但正是这些困难使我们变得更加坚强和自信；4. 在追寻梦想的过程中，我们需要付出努力和奋斗，同时也需要坚持和耐心；5. 最重要的是，追寻梦想能够让我们过上更加有意义和充实的生活。

参考答案：追寻梦想的力量梦想，是一种无形的力量，它存在于每个人的内心深处，可以激励人们不断前进，勇敢面对困难和挑战。

正是这股力量，让我们在追寻梦想的道路上不断奋发努力，不断超越自我。

通过追寻梦想，我们可以发现自己的潜力，并将其变成现实。

追寻梦想不仅是个人的奋斗，更是对自己的信心和勇气的肯定。

每个人都有自己独特的梦想，只有通过努力和坚持，我们才能够将梦想变成现实，开创属于自己的一片天地。

追寻梦想的过程可能会遇到阻碍和挫折，但正是这些困难使我们变得更加坚强和自信。

2023年新高考仿真模拟预测卷语文试题及参考答案

2023年新高考仿真模拟预测卷语文试题及参考答案一、现代文阅读（35分）（一）现代文阅读（本题共5小题，17分）阅读下面的文字，完成1至5题。

材料一：中国人的最高信仰，乃是天、地、人三者之合一。

借用耶教术语来说，便是天、地、人之“三位一体”。

在中国，天地可合称为天，人与天地合一，便是所谓“天人合一”。

中国的社会风俗里面也有“三位一体”的信仰之存在。

如言时令，有二十四个节气，但同时有人造的节日。

中国人把此二项混合看待，不加区别，如清明、冬至是自然节，端午、中秋、重阳是人造节。

中国人在节日中，又多增添一些神话故事，使得人文自然益加亲密配合，社会礼俗随着天时节气而多彩多姿。

这亦是一种天人相应，把我们的日常生活推衍到大自然变化中而与之呼应。

这就是那人文参加进自然里面而演化成为一体了。

此中有信仰、有希望、有娱乐，极富礼乐意义，极富艺术性，亦极富传统性，极富有关于民族文化信仰之启示性与教育性。

但到最近，大家对自己文化无了解、无信心，因此对此种节日亦觉无趣味、无意义。

中国社会上之新年节日不废而渐废，耶诞节日代之而兴。

中国社会并非一耶教社会，中国文化亦非一耶教文化，而中国人则追步西方，来过耶诞节日。

这里面自不免夹杂着许多无情无理之盲目效颦。

再讲中国的艺术，一幅山水画，就是天、地、人三位一体的一种结构。

一幅画上定有空白，有春、夏、秋、冬四季分别，那都是天。

一座山、一溪水、一栋房子、一座亭榭，那都是地。

中间画着一渔翁，或是赶着骡子做生意的，或是读书弹琴的，或是倚着一杖在那里看天看地的，这都是人。

这是画中之主。

天有气象，地有境界，人有风格。

在此气象境界之中有此风格，配合起来，这是一个艺术的世界。

中国画便要此“气象”“境界”与“风格”之三者合一。

.中国画也不愿酷肖自然，而要把人文意境融入，另成一天地。

如画梅、兰、竹、菊，只是自然，但有生命，而且有人文理想作衬托，故称“四君子”。

天地大自然，一切是景，里面有了主人，有了生意，便有了“情”。

高考预测模拟试题以及答案(理)汇总

一. 选择题：1. 复数i+12的共轭复数是（） A. i +1 B. i -1 C. i 22+ D. i 22-2. 已知AB 是圆2522=+y x 的弦，AB 的中点是（1，2），则直线AB 的方程是（） A. 02=-y x B. 042=-+y x C. 022=+-y xD. 052=-+y x3. 命题P ：“012,≤+∈∃x R x ”，则命题P 的否定是（） A. 012,>+∈∃x R x B. 012,>+∈∀x R x C. 012,≥+∈∃x R xD. 012,≥+∈∀x R x4. 已知函数()x f 是奇函数，当0>x 时，()x x f x2log 2+=，则()2-f 的值为（） A. 5 B. 43-C. －5D. 无意义 5. 在△ABC 中，角A 、B 、C 所对的边为c b a ,,，若角CAb aC 2sin sin ,3=>π，则关于△ABC 的两个判断“① 一定锐角三角形 ② 一定是等腰三角形”中（）A. ①②都正确B. ①正确②错误C. ①错误②正确D. ①、②都错误6. 已知y x ,是正数，且⎩⎨⎧≤+≥+24362054y x y x ，则y x 93+的取值范围是（）A. ]22,15(B. )36,22[C. )72,22[D. ()72,36 7. 如果执行下图的程序框图，那么输出的S=（） A. 6 B. 15 C.61 D. 1518. 已知平面向量,,-=+===221b ++的最大值是（） A. 5 B. 25- C. 25+ D. 33+9. 如图，正方体1111D C B A ABCD -的棱长是2，E 为BC 的中点，G 为B 1C 1中点，F 为正方形A 1B 1C 1D 1内（包括边界）的点，则使EF=6，GF ⊥AC 的点F 有（）A. 0个B. 1个C. 2个D. 无数个10. 已知函数()()012>+-=a x ax x f ，对函数()x f 作变换()t g x =，得到函数()()[]t g f t F =。

2024年高考押题预测模拟测试卷01(新题型地区专用)(解析版)

2024年高考押题预测模拟测试卷01（新题型地区专用）（满分150分，考试用时120分钟）一、选择题1．若复数()5i 1i z =+，则复数 z 在复平面上对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C 【分析】由复数的乘法运算化简复数，再由共轭复数的定义和复数的几何意义即可得出答案.【解析】因为()()523i =i i =1i i ⋅-⋅-=，()()52i 1i =i 1i i i i 1z =++=+=-，所以i 1z =--，所以复数z 在复平面上对应的点为()1,1--，位于第三象限.故选：C.2．已知集合(){}lg 3A x y x ==-，{B y y ==，则A B = （）A ．(,3]-∞B ．(3),-∞C ．[0,3]D ．[0,3)3．已知α，β是两个不同的平面，m ，n 是两条不同的直线，则下列说法正确的是（）A ．若m n ⊥，m α⊥，n β⊥，则αβ⊥B ．若//m n ，//m α，//n β，则//αβC ．若m n ⊥，//m α，αβ⊥，则n β⊥D ．若//m n ，m α⊥，αβ⊥，则//n β【答案】A【分析】由空间中线线、线面、面面之间的位置关系逐一判定各选项即可.【解析】若m α⊥，n β⊥，设,αβ对应法向量分别为,m n ，也是m ,n 的方向向量，由m n ⊥，即m n ⊥，则αβ⊥，故A 正确；若//m n ，//m α，//n β，则α与β可能平行或相交，故B 错误；若m n ⊥，//m α，αβ⊥，则n β⊂，或//n β，或n 与β相交，故C 错误；若//m n ，m α⊥，则n α⊥，又αβ⊥，则//n β或n β⊂，D 错误.故选：A4．某市高三年级男生的身高X (单位：cm)近似服从正态分布()2175,5N .现随机选择一名本市高三年级男生，则该男生身高不高于170cm 的概率是（）参考数据：()0.6827P x μσμσ-≤≤+≈A ．0.6827B ．0.34135C ．0.3173D ．0.158655．已知正项等比数列{}n a 中，23a =，427a =，设2n S 为该数列的前2n 项和，n T 为数列{}1n n a a +的前n 项和，若2n n S kT =，则实数k 的值为（）．A ．13B C ．23D ．436．已知()()()()()()451121101211111222x x x a a x a x a x ++++++=+++++++ ，则02410a a a a ++++ 的值是（）A ．680B ．680-C ．1360D ．1360-7．已知()22cos cos ,sin 124αβαβ-=--=，则()cos 22αβ+=（）A ．79-B ．79C ．29-D ．298．已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ，过点F 且斜率为()0k k ≠的直线l 交双曲线于A 、B 两点，线段AB 的中垂线交x 轴于点D .若AB ≥，则双曲线的离心率取值范围是（）A．⎛ ⎝⎦B．(C．)+∞D．⎫+∞⎪⎪⎣⎭【解析】设双曲线的右焦点为()()()1122,0,,,,F c A x y B x y ，则直线():l y k x c =-，故选：A.【点睛】方法定睛：双曲线离心率(离心率范围)的求法求双曲线的离心率或离心率的范围，关键是根据已知条件确定a ，b ，c 的等量关系或不等关系，然后把b 用a ，c 代换，求e 的值（或范围）．二、多选题9．某服装公司对1-5月份的服装销量进行了统计，结果如下：月份编号x 12345销量y （万件）5096142185227若y 与x 线性相关，其线性回归方程为 7.1y bx=+ ，则下列说法正确的是（）A ．线性回归方程必过()3,140B ．44.3b= C ．相关系数0r <D ．6月份的服装销量一定为272.9万件10．已知函数()2sin 2sin 20)33f x x x x ωωωω⎛⎫⎛⎫=++-+> ⎪ ⎪⎝⎭⎝⎭，则下列结论正确的是（）A ．若()f x 相邻两条对称轴的距离为π2，则2ω=B ．当1ω=，π0,2⎡⎤∈⎢⎥⎣⎦x 时，()f x 的值域为⎡⎤⎣⎦C ．当1ω=时，()f x 的图象向左平移π6个单位长度得到函数解析式为π2cos 26y x ⎛⎫=+ ⎪⎝⎭D ．若()f x 在区间π0,6⎡⎤⎢⎥上有且仅有两个零点，则58ω≤<11．已知函数()f x 和其导函数()g x 的定义域都是R ，若()f x x -与(21)g x +均为偶函数，则（）A ．(0)0f =B ．()f x x关于点(0,1)对称C ．(2023)1g =D ．((1)1)((2)1)((2)1)((3)1)((2023)1)((2024)1)0g g g g g g -⨯++-⨯+++-⨯+= 【答案】BD若(2)()2f a x f x b -+=，则()f x 关于点(),a b 中心对称；周期性结论：若()()f x T f x +=，则函数()f x 的周期为T .三、填空题12．已知向量(1,3)a =- ，(,1)b m =r ，若()a b b -⊥，则正数m 的值为.【答案】1【分析】根据向量垂直的坐标形式可得m 的方程，故可得正数m 的值.【解析】由题意得，(1,2)a b m -=--，()a b b -⊥ ，(1)20m m ∴--+=，解得2m =-（舍去）或1m =.故答案为：1.13．在三棱锥-P ABC 中，底面ABC 为等腰三角形，120ABC ∠=︒，且AC PA =，平面PAC ⊥平面,ABC PA BC ⊥，点Q为三棱锥-P ABC 外接球O 上一动点，且点Q 到平面PAC 的距离的最大值为1则球O 的表面积为．【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径；③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可；14．在锐角ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，S 为ABC 的面积，且()222S a b c =--，则22b c bc+的取值范围为.四、解答题15．已知函数()2e xx xf x +=．(1)求函数()f x 的极值点；(2)记曲线():C y f x =在0x =处的切线为l ，求证，l 与C 有唯一公共点．-中，四边形ABCD是菱形，平面ABCD⊥平面PAD，点M在DP上，且16．如图，在四棱锥P ABCD==∠=︒．2,,120DM MP AD AP PAD(1)求证：BD ⊥平面ACM ；(2)若60ADC ∠=︒，求平面ACM 与平面ABP 夹角的余弦值．【答案】(1)证明见解析(2)55【分析】（1）由余弦定理结合勾股定理逆定理可得MA AD ⊥，后结合平面ABCD ⊥平面PAD ，可得MA BD ^，后结合AC BD ⊥可得结论；（2）由（1）结合题意建立如图所示的空间直角坐标系，分别求出平面ACM 与平面ABP 的法向量，即可得答案.【解析】（1）不妨设3,120,2AD AP PAD DM MP ==∠=︒= ，33,23,3DP DM PM ∴===，由余弦定理得222cos303AM AP MP AP MP =+-⋅︒=，在ADM △中，222,AD AM DM MA AD +=∴⊥，平面ABCD ⊥平面PAD ，平面ABCD ⋂平面,PAD AD MA =⊂平面PAD ，MA ∴⊥平面ABCD ．BD ⊂Q 平面,ABCD MA BD ∴⊥，四边形ABCD 是菱形，AC BD ∴⊥，又AC MA A = ，且AC ⊂平面,ACM MA ⊂平面,ACM BD ∴⊥平面ACM ．（2）在平面ABCD 内，过点B 作AD 的垂线，垂足为N ，平面ABCD ⊥平面PAD ，平面ABCD ⋂平面PAD AD =，BN ∴⊥平面ADP ，又四边形ABCD 是菱形，60,30ADC BDA ∠=︒∴∠=︒，,ACD ABC ∴△△均为等边三角形，以点A 为坐标原点，,AD AM 及过点A 平行于NB 的直线分别为,,x y z 轴，17．在某数字通信中，信号的传输包含发送与接收两个环节．每次信号只发送0和1中的某个数字，由于随机因素干扰，接收到的信号数字有可能出现错误，已知发送信号0时，接收为0和1的概率分别为()01αα<<，1α-；发送信号1时，接收为1和0的概率分别为(01),1βββ<<-．假设每次信号的传输相互独立．(1)当连续三次发送信号均为0时，设其相应三次接收到的信号数字均相同的概率为()f α，求()f α的最小值；(2)当连续四次发送信号均为1时，设其相应四次接收到的信号数字依次为1234,,,x x x x ，记其中连续出现相同数字的次数的最大值为随机变量X （1234,,,x x x x 中任意相邻的数字均不相同时，令1X =），若23β=，求X 的分布列和数学期望．18．已知椭圆方程E ：22143x y +=的左焦点为F ，直线y kx =（0k >）与椭圆E 相交于A ，B ，点A 在第一象限，直线BF 与椭圆E 的另一点交点为C ，且点C 关于原点O 的对称点为D ．(1)设直线BC ，AC 的斜率分别为1k ，2k ，证明：12k k ⋅为常数；(2)求BCD △面积的最大值．所以三角形OBC 的面积为S 222163623434m m m ⎛⎫=+= ⎪++⎝⎭令21t m =+，1t ≥，19．在数列{}n a 中，若存在常数t ，使得()*1123n n a a a a a t n +=+∈N 恒成立，则称数列{}n a 为“()H t 数列”．(1)若11n c n=+，试判断数列{}n c 是否为“()H t 数列”，请说明理由；(2)若数列{}n a 为“()H t 数列”，且12a =，数列{}n b 为等比数列，且2121log ni n n i aa b t +==+-∑，求数列{}n b 的通项公式；(3)若正项数列{}n a 为“()H t 数列”，且11a >，0t >，证明：ln 1n n a a <-．【答案】(1)数列{}n c 不是“()H t 数列”。

语文高考模拟试题及答案

语文高考模拟试题及答案一、阅读理解（共30分）阅读下面的文章，完成1-5题。

在古代，人们对于时间的概念与今天大相径庭。

他们没有现代的钟表来精确计量时间，而是通过观察自然现象来感知时间的流逝。

例如，日出日落、月圆月缺、季节更替等自然现象，都是古人用来划分时间的重要依据。

这种对时间的感知方式，不仅影响了他们的生活方式，也深刻地影响了他们的文化和哲学思想。

1. 文中提到的古人感知时间的方式是什么？（6分）答：古人通过观察自然现象来感知时间的流逝，如日出日落、月圆月缺、季节更替等。

2. 古人对时间的感知方式对他们产生了哪些影响？（6分）答：古人对时间的感知方式影响了他们的生活方式，并深刻地影响了他们的文化和哲学思想。

3. 根据文章内容，以下哪项不是古人感知时间的方式？（6分）A. 观察日出日落B. 使用钟表计量时间C. 观察月圆月缺D. 观察季节更替答：B4. 文章中提到的“自然现象”包括哪些？（6分）答：自然现象包括日出日落、月圆月缺、季节更替。

5. 古人对时间的感知方式与今天人们的方式有何不同？（6分）答：古人没有现代的钟表来精确计量时间，而是通过观察自然现象来感知时间的流逝，而现代人则依赖于钟表等精确的时间计量工具。

二、古诗文鉴赏（共20分）阅读下面的古诗，完成6-8题。

春夜喜雨杜甫好雨知时节，当春乃发生。

随风潜入夜，润物细无声。

野径云俱黑，江船火独明。

晓看红湿处，花重锦官城。

6. 这首诗的作者是谁？（5分）答：杜甫7. 诗中描述的是哪一个季节的景象？（5分）答：春季8. 诗人是如何描绘雨的？（10分）答：诗人通过“好雨知时节，当春乃发生”来描绘雨的及时，通过“随风潜入夜，润物细无声”来描绘雨的细腻和无声，通过“野径云俱黑，江船火独明”来描绘雨夜的宁静和江船的明亮，最后通过“晓看红湿处，花重锦官城”来描绘雨后花朵的鲜艳和城市的繁荣。

三、作文（共50分）请以“时间的价值”为题，写一篇不少于800字的文章。