[八个有趣模型]搞定空间几何体的外接球与内切球
八个有趣模型——搞定空间几何体的外接球与内切球(教师版)复习过程

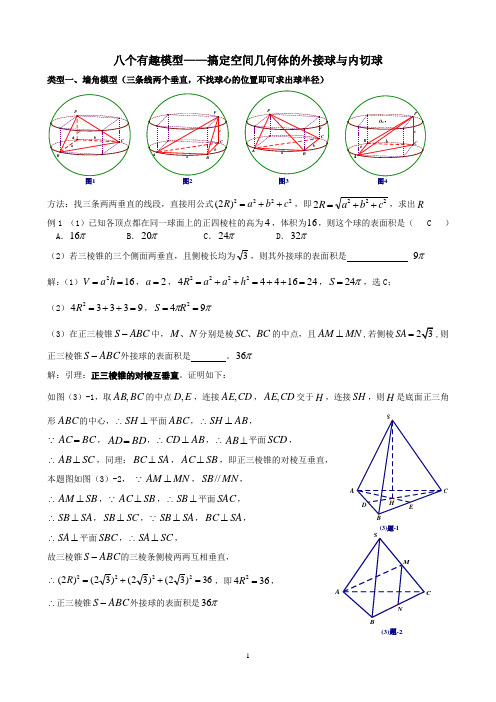
八个有趣模型——搞定空间几何体的外接球与内切球(教师版)复习过程八个有趣模型——搞定空间几何体的外接球与内切球一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).初图1初图22.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法).四、与台体相关的,此略.五、八大模型第一讲柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)图1-1图1-2图1-3图1-4方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32 解: 162==h a V ,2=a ,24164442222=++=++=h a a R ,π24=S ,选C ;(2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是π9 解:933342=++=R ,ππ942==R S ;(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是.π36 解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1,取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,ΘBC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD ,∴S C AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2,ΘMN AM ⊥,MN SB //,∴SB AM ⊥,ΘSB AC ⊥,∴⊥SB 平面SAC ,∴SA SB ⊥,SC SB ⊥,ΘSA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理)AC(3)题-2(解答图)AC(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠?AB AC SA BAC 则该四面体的外接球的表面积为( D )π11.A π7.B π310.C π340.D 解:在ABC ?中,7120cos 2222=??-+=οBC AB AB AC BC ,7=BC ,ABC ?的外接球直径为372237sin 2==∠=BAC BC r ,∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是解:由已知得三条侧棱两两垂直,设三条侧棱长分别为c b a ,,(+ ∈R c b a ,,),则===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S ,(6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为解:3)2(2222=++=c b a R ,432=R ,23=Rπππ2383334343=?==R V 球,类型二、对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =)第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,=+=+=+222222222z a c y c b x b a ?2)2(2222222z y x c b a R ++=++=,补充:图2-1中,abc abc abc V BCD A 31461=?-=-. (6)题图(6)题直观图P图2-1第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .思考:如何求棱长为a 的正四面体体积,如何求其外接球体积?例2(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解:对棱相等,补形为长方体,如图2-1,设长宽高分别为c b a ,,,110493625)(2222=++=++c b a ,55222=++c b a ,5542=R ,π55=S(1)题图B(2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为 .π229 解:如图2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S (3)正四面体的各条棱长都为2,则该正面体外接球的体积为(3)解答题解:正四面体对棱相等的模式,放入正方体中,32=R ,23=R ,ππ2383334=?=V (4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解:如解答图,将正四面体放入正方体中,截面为1PCO ?,面积是2.类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1图3-2 图3-3题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ?的外心,则⊥1OO 平面ABC ;第二步:算出小圆1O 的半径r AO =1,h AA OO 2 12111==(h AA =1也是圆柱的高);第三步:勾股定理:21212O O A O OA +=?222)2(r hR +=?22)2(hr R +=,解出R例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为解:设正六边形边长为a ,正六棱柱的高为h ,底面外接圆的半径为r ,则21=a ,正六棱柱的底面积为833)21(4362=??=S ,89833===h Sh V 柱,∴3=h ,4)3(14222=+=R 也可1)21()23( 222=+=R ),1=R ,球的体积为34π=球V ;(2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=?,则此球的表面积等于 .解:32=BC ,4120sin 322==οr ,2=r ,5=R ,π20=S ;(3)已知EAB ?所在的平面与矩形ABCD 所在的平面互相垂直,=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为.π16 解:折叠型,法一:EAB ?的外接圆半径为31=r ,11=OO ,231=+=R ;法二:231=M O ,21322==D O r ,4413432=+=R ,2=R ,π16=表S ;法三:补形为直三棱柱,可改变直三棱柱的放置方式为立式,算法可同上,略.换一种方式,通过算圆柱的轴截面的对角线长来求球的直径:162)32()2(222=+=R ,π16=表S ;(4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为 .π3160解:法一:282164236162=?-+=BC ,72=BC ,37423722==r ,372=r , 3404328)2(2122=+=+=AA r R ,π3160=表S ;法二:求圆柱的轴截面的对角线长得球直径,此略.第二讲锥体背景的模型类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)图4-1图4-2图4-3图4-41.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ?的外心?三棱锥ABC P -的三条侧棱相等?三棱ABC P -的底面ABC ?在圆锥的底上,顶点P 点也是圆锥的顶点. 解题步骤:第一步:确定球心O 的位置,取ABC ?的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);(3)题第三步:勾股定理:21212O O A O OA +=?222)(r R h R +-=,解出R ;事实上,ACP ?的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=?22)2(2r PA R +=;②2122OO r R +=?212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径) 21212O O C O OC +=?2122O O r R +=?2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ?的外心,即PAC ?的外接圆是大圆,先求出小圆的直径r AC 2=;第二步:在PAC ?中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R . 例4 (1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为 . 解:法一:由正弦定理(用大圆求外接球直径);法二:找球心联合勾股定理,72=R ,ππ4942==R S ;(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为解:方法一:找球心的位置,易知1=r ,1=h ,r h =,故球心在正方形的中心ABCD 处,1=R ,3 4π=V 方法二:大圆是轴截面所的外接圆,即大圆是SAC ?的外接圆,此处特殊,SAC Rt ?的斜边是球半径,22=R ,1=R ,34π=V . (3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是() A .433 B .33 C .43 D .123解:高1==R h ,底面外接圆的半径为1=R ,直径为22=R ,设底面边长为a ,则260sin 2==οaR ,3=a ,433432==a S ,三棱锥的体积为4331==Sh V ;(4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为ο60,则该三棱锥外接球的体积为() A .π B.3π C. 4π D.43π 解:选D ,由线面角的知识,得ABC ?的顶点C B A ,,在以23=r 为半径的圆上,在圆锥中求解,1=R ;(5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ?是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为()AA.6 BC.3 D.2解:36)33(12221=-=-=r R OO ,362=h ,62362433131=??==Sh V 球类型五、垂面模型(一条直线垂直于一个平面)1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ?画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ?的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=;第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=?22)2(2r PA R +=;②2122OO r R +=?212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ?的外心?三棱锥ABC P -的三条侧棱相等?三棱锥ABC P -的底面ABC ?在圆锥的底上,顶点P 点也是圆锥的顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤:第一步:确定球心O 的位置,取ABC ?的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);第三步:勾股定理:21212O O A O OA +=?222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示,则该几何体外接球的表面积为( )C A .π3 B .π2 C .316πD .以上都不对解:选C ,法一:(勾股定理)利用球心的位置求球半径,球心在圆锥的高线上,221)3(R R =+-,32=R ,ππ31642==R S ;法二:(大圆法求外接球直径)如图,球心在圆锥的高线上,故圆锥的轴截面三角形PMN 的外接圆是大圆,于是3460sin 22==οR ,下略;第三讲二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)俯视图侧视图正视图解答图图6第一步:先画出如图6所示的图形,将BCD ?画在小圆上,找出BCD ?和BD A '?的外心1H 和2H ;第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,;第三步:解1OEH ?,算出1OH ,在1OCH Rt ?中,勾股定理:22121OC CH OH =+ 注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 .解:如图,3460sin 22221===οr r ,3221==r r ,312=H O , 35343121222=+=+=r H O R ,315=R ;法二:312=H O ,311=H O ,1=AH , 352121222=++==O O H O AH AO R ,315=R ;(2)在直角梯形ABCD 中,CD AB //,ο90=∠A ,ο45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为π4(2)题-2(2)题-1→A(3)题解:如图,易知球心在BC的中点处,π4=表S ;(1)题(3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为π6 解:如图,法一:33)2cos(cos 211-=+∠=∠πO OO B SO , 33sin 21=∠O OO ,36cos 21=∠O OO , 22cos 21211=∠=O OO O O OO ,232112=+=R ,ππ642==R S ;法二:延长1BO 到D 使111r BO DO ==,由余弦定理得6=SB ,2=SD ,大圆直径为62==SB R ;(4)在边长为32的菱形ABCD 中,ο60=∠BAD ,沿对角线BD 折成二面角C BD A --为ο120的四面体ABCD ,则此四面体的外接球表面积为π28解:如图,取BD 的中点M ,ABD ?和CBD ?的外接圆半径为221==r r ,ABD ?和CBD ?的外心21,O O 到弦BD 的距离(弦心距)为121==d d ,法一:四边形21MO OO 的外接圆直径2=OM ,7=R ,π28=S ;法二:31=OO ,7=R ;法三:作出CBD ?的外接圆直径CE ,则3==CM AM , 4=CE ,1=ME ,7=AE ,33=AC ,72147227167cos -=??-+=∠AEC ,7233sin =∠AEC ,72723333sin 2==∠=AEC AC R ,7=R ;(4)题图(5)在四棱锥ABCD 中,ο120=∠BDA ,ο150=∠BDC ,2==BD AD ,3=CD ,二面角CBD A --的平面角的大小为ο120,则此四面体的外接球的体积为解:如图,过两小圆圆心作相应小圆所在平面的垂线确定球心,→抽象化(5)题解答图-2(5)题解答图-11B32=AB ,22=r ,弦心距32=M O ,13=BC ,131=r ,弦心距321=M O ,∴2121=O O ,72120sin 21==οO O OM ,法一:∴292222=+==OM MD OD R ,29=R ,∴329116π=球V ;法二:2522222=-=M O OM OO ,∴29222222=+==OO r OD R ,29=R ,∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设:如图7,ο90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 2 1====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为()A .π12125B .π9125C .π6125D .π3125解:(1)52==AC R ,25=R ,6125812534343πππ=?==R V ,选C(2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCDA -的外接球的表面积为.解:BD 的中点是球心O ,132==BD R ,ππ1342==R S .第四讲多面体的内切球问题模型类型八、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径. 第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ?的高;第三步:由POE ?相似于PDH ?,建立等式:PDPODH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ?的高;第三步:由POG ?相似于PFH ?,建立等式:PFPOHF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=?r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ?+++=?+?+?+?=-)(3131313131第三步:解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 (1)棱长为a 的正四面体的内切球表面积是 62a π,解:设正四面体内切球的半径为r ,将正四面体放入棱长为2a的正方体中(即补形为正方体),如图,则2622313133a a V V ABCP =?==-正方体,又Θr a r a Sr V ABC P 223343314314==?=-,D图8-1A图8-2∴263332a r a =,62a r =,∴内切球的表面积为6422a r S ππ==表(注:还有别的方法,此略)(2)正四棱锥ABCD S -的底面边长为2,侧棱长为37解:如图,正四棱锥ABCD S -的高7=h ,正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ,正四棱锥ABCD S -的表面积为284+=表S ,正四棱锥ABCD S -的体积为r r S V ABCDS ?+==-328431表,∴3743284=?+r , 771427)122(7221728474-=-=+=+=r (3)三棱锥ABC P -中,底面ABC ?是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则32解:如图,3=?ABC S ,2==??ACP ABP S S ,7=?BCP S ,743++=表S ,三棱锥ABC P -的体积为332=-ABC P V ,另一表达体积的方式是r r S V ABC P ?++==-347331表,∴3323473=?++r ,∴47332++=r习题:1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为() A.3 B.6 C.36 D.9 解:【A 】616164)2(2=++=R ,3=R【三棱锥有一侧棱垂直于底面,且底面是直角三角形】【共两种】2.三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于 . 332π(2)题(3)题B解:260sin 32==οr ,16124)2(2=+=R ,42=R ,2=R ,外接球体积332834ππ=? 【外心法(加中垂线)找球心;正弦定理求球小圆半径】3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 .解:ABC ?外接圆的半径为,三棱锥ABC S -的直径为3460sin 22==οR ,外接球半径32=R ,或1)3(22+-=R R ,32=R ,外接球体积2733233834343πππ===R V , 4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:PAC ?的外接圆是大圆,3460sin 22==οR ,32=R , 5.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:973324992cos 222=??-+=?-+=∠PC PA AC PC PA P ,81 216)97(1sin 22?=-=∠P ,924sin =∠P ,42922992422===R ,829=R 6.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABCP -外接球的半径为 .解:AC 是公共的斜边,AC 的中点是球心O ,球半径为1=R。
八个无敌模型——全搞定空间几何的外接球和内切球问题

八个有趣模型——搞定空间几何体的外接球与内切球文:付雨楼、段永建今天给大家带来8个求解立体几何内切球与外接球半径的模型,本文最开始源自付雨楼老师分享的模型,教研QQ 群(群号:9)成员段永建老师进一步作图编辑优化分享。
类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径)图2图3方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32 {(2)若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是 π9解:(1)162==h a V ,2=a ,24164442222=++=++=h a a R ,π24=S ,选C ; (2)933342=++=R ,ππ942==R S(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =则正三棱锥ABC S -外接球的表面积是 。
π36 解:引理:正三棱锥的对棱互垂直。
证明如下:如图(3)-1,取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD ,∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC ,-∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,(3)题-1A∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( D )π11.A π7.Bπ310.C π340.D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是(6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为 》解析:(4)在ABC ∆中,7120cos 2222=⋅⋅-+=BC AB AB AC BC ,7=BC ,ABC ∆的外接球直径为372237sin 2==∠=BAC BC r , ∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)三条侧棱两两生直,设三条侧棱长分别为c b a ,,(+∈R c b a ,,),则⎪⎩⎪⎨⎧===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S , (6)3)2(2222=++=c b a R ,432=R ,23=Rπππ2383334343=⋅==R V ,·类型二、垂面模型(一条直线垂直于一个平面) 1.题设:如图5,⊥PA 平面ABC 解题步骤:图5ADPO 1OCB(3)题-2MNASAP第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ; 第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=^2.题设:如图6,7,8,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点图6PADO 1OCB图7-1PAO 1O CB图7-2PAO 1O CB图8PAO 1OCB图8-1DPOO 2ABC图8-2POO 2ABC图8-3DPOO 2AB解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆。
八个有趣模型——搞定空间几何体的外接球与内切球(教师版)

八个有趣模型——搞定空间几何体的外接球与内切球(教师版)相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法).四、与台体相关的,此略.五、八大模型第一讲柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)c ab图1-1CP A Babc 图1-2P CBAabc 图1-3CBPAa bcPCB A方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R例 1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32 解: 162==h a V ,2=a ,24164442222=++=++=h a a R,π24=S ,选C ;(2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 π9 解:933342=++=R,ππ942==RS ;(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱23SA =,则正三棱锥ABCS -外接球的表面积是 .π36解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1,(3)题-1(引理)HEDBACS取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH , 则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD , ∴SCAB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R,∴正三棱锥ABC S -外接球的表面积是π36.(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( D )π11.A π7.B π310.C π340.D 解:在ABC ∆中,7120cos 2222=⋅⋅-+= BC AB AB AC BC ,7=BC ,ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ,∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是(3)题-2(解答图)MNABCS解:由已知得三条侧棱两两垂直,设三条侧棱长分别为cb a ,,(+∈R c b a ,,),则⎪⎩⎪⎨⎧===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S ,(6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为 解:3)2(2222=++=c b a R ,432=R,23=Rπππ2383334343=⋅==R V 球,类型二、对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =) 第一步:画出一个长方体,标出三组互为异面直线的对棱;(6)题图(6)题直观图APyc z zyxDCA第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,yCD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=,补充:图2-1中,abcabc abc VBCDA 31461=⨯-=-.第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .思考:如何求棱长为a 的正四面体体积,如何求其外接球体积?例2(1)如下图所示三棱锥A BCD-,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解:对棱相等,补形为长方体,如图2-1,设长宽高分别为c b a ,,,110493625)(2222=++=++c b a ,55222=++c b a ,5542=R ,π55=S(1)题图BDA(2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为 .π229解:如图2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a,422=+c b ,1622=+a c∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a,229222=++c b a ,22942=R,π229=S (3)正四面体的各条棱长都为2,则该正面体外接球的体积为(3)解答题CP解:正四面体对棱相等的模式,放入正方体中,32=R ,23=R ,ππ2383334=⋅=V(4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三 角形(正四面体的截面)的面积是 .(4)题解答图(4)题CPBO 1OO 2A解:如解答图,将正四面体放入正方体中,截面为1PCO ∆,面积是2.类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1C 1B 1AEFA 1O 1OO 2BC图3-2C 1B 1AA 1O 1OO 2BC图3-3C 1B 1AEFA 1O 1O O 2BC题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ;第二步:算出小圆1O 的半径rAO=1,h AA OO212111==(h AA =1也是圆柱的高);第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(h r R +=,解出R例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为解:设正六边形边长为a ,正六棱柱的高为h ,底面外接圆的半径为r ,则21=a , 正六棱柱的底面积为833)21(4362=⋅⋅=S ,89833===h Sh V 柱,∴3=h ,4)3(14222=+=R也可1)21()23(222=+=R),1=R ,球的体积为34π=球V;(2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 .解:32=BC ,4120sin322==r ,2=r ,5=R ,π20=S ;(3)已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为 .π16 解:折叠型,法一:EAB ∆的外接圆半径为31=r ,11=OO,231=+=R ; 法二:231=M O ,21322==D O r,4413432=+=R,2=R ,π16=表S;r 1R r 2r 1R (3)题O O 2MAO 1法三:补形为直三棱柱,可改变直三棱柱的放置方式为立式,算法可同上,略.换一种方式,通过算圆柱的轴截面的对角线长来求球的直径:162)32()2(222=+=R ,π16=表S;(4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为 .π3160 解:法一:282164236162=⋅⋅⋅-+=BC,72=BC ,37423722==r ,372=r ,3404328)2(2122=+=+=AA r R ,π3160=表S; 法二:求圆柱的轴截面的对角线长得球直径,此略.第二讲 锥体背景的模型类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)图4-1PAO 1OCB图4-2AO 1OCBP图4-3O O 1A CBP图4-4ACBP1.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点. 解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径rAO=1,再算出棱锥的高hPO=1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ;事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R+=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径) 21212OO C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=;第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin===,求出R .例 4 (1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为 . 解:法一:由正弦定理(用大圆求外接球直径);法二:找球心联合勾股定理,72=R ,ππ4942==RS ;(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为 解:方法一:找球心的位置,易知1=r ,1=h ,r h =,故球心在正方形的中心ABCD 处,1=R ,34π=V方法二:大圆是轴截面所的外接圆,即大圆是SAC ∆的外接圆,此处特殊,SAC Rt ∆的斜边是球半径,22=R ,1=R ,34π=V . (3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( )A .433B .33C .43D .123解:高1==R h ,底面外接圆的半径为1=R ,直径为22=R , 设底面边长为a ,则260sin 2==a R ,3=a ,433432==a S ,三棱锥的体积为4331==Sh V ;(4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60,则该三棱锥外接球的体积为( )A .π B.3π C. 4πD.43π解:选D ,由线面角的知识,得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上,在圆锥中求解,1=R ;(5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )AA .26B 3C .23D .22解:36)33(12221=-=-=r R OO ,362=h ,62362433131=⋅⋅==Sh V球类型五、垂面模型(一条直线垂直于一个平面) 1.题设:如图5,⊥PA 平面ABC ,求外接球半径.ADPO 1OCB解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=;第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R+=⇔212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.图5-1PAO 1O CB图5-2PAO 1O CB图5-3PAO 1O CB图5-4PADO 1OCB图5-6DPOO 2ABC图5-7POO 2ABC图5-8DPOO 2AB解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径rAO=1,再算出棱锥的高hPO=1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径.例 5 一个几何体的三视图如图所示,则该几何体外接球的表面积为( )CA .π3B .π2C .316π D .以上都不对解:选C ,2222俯视图侧视图正视图22RR 11解答图PMNO 1O法一:(勾股定理)利用球心的位置求球半径,球心在圆锥的高线上,221)3(R R =+-,32=R ,ππ31642==RS ;法二:(大圆法求外接球直径)如图,球心在圆锥的高线上,故圆锥的轴截面三角形PMN 的外接圆是大圆,于是3460sin 22==R ,下略;第三讲 二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)图6H 1EACOB D A'H 2第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ;第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,;第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 . 解:如图,3460sin 22221=== rr ,3221==rr ,312=H O ,35343121222=+=+=r H O R ,315=R ;法二:312=H O ,311=H O ,1=AH ,352121222=++==O O H O AH AO R ,315=R ;(2)在直角梯形ABCD 中,CD AB //,90=∠A ,45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为 π4(2)题-2(2)题-1→MADA'22r 111R r 2(3)题22DO 1SBO 2O解:如图,易知球心在BC 的中点处,π4=表S ;(3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角BAC S --的余弦值为33-,则四面体ABC S -的外接球表面积为π6(1)题O H A O 2O 1解:如图,法一:33)2cos(cos 211-=+∠=∠πOOO B SO ,33sin 21=∠O OO ,36cos 21=∠OOO , 22cos 21211=∠=O OO O O OO ,232112=+=R,ππ642==RS ;法二:延长1BO 到D 使111r BO DO==,由余弦定理得6=SB ,2=SD ,大圆直径为62==SB R ;(4)在边长为32的菱形ABCD 中,60=∠BAD ,沿对角线BD 折成二面角C BD A --为120的四面体ABCD ,则此四面体的外接球表面积为 π28解:如图,取BD 的中点M ,ABD ∆和CBD ∆的外接圆半径为221==r r ,ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离(弦心距)为121==d d ,R r 2d 2d 1r 1R(4)题图M BDAO 2O 1O法一:四边形21MO OO 的外接圆直径2=OM ,7=R ,π28=S ;法二:31=OO,7=R ;法三:作出CBD ∆的外接圆直径CE ,则3==CM AM , 4=CE ,1=ME ,7=AE ,33=AC ,72147227167cos -=⋅⋅-+=∠AEC ,7233sin =∠AEC ,72723333sin 2==∠=AECAC R ,7=R ;(5)在四棱锥ABCD 中,120=∠BDA ,150=∠BDC ,2==BD AD ,3=CD ,二面角C BD A --的平面角的大小为120,则此四面体的外接球的体积为解:如图,过两小圆圆心作相应小圆所在平面的垂线确定球心,→抽象化(5)题解答图-2(5)题解答图-1MMDAO 2O 11O 2BDO32=AB ,22=r ,弦心距32=M O ,13=BC ,131=r ,弦心距321=M O ,∴2121=O O ,72120sin21==OO OM , 法一:∴292222=+==OM MD OD R ,29=R ,∴329116π=球V;法二:2522222=-=M O OM OO ,∴29222222=+==OO r OD R ,29=R ,∴329116π=球V .类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7OBP题设:如图7,90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为( )A .π12125B .π9125C .π6125D .π3125解:(1)52==AC R ,25=R ,6125812534343πππ=⋅==R V ,选C(2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为 .解:BD 的中点是球心O ,132==BD R ,ππ1342==R S .第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径.第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高; 第三步:由POE ∆相似于PDH ∆,建立等式:PDPODH OE =,解出r2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高; 第三步:由POG ∆相似于PFH ∆,建立等式:PFPO HF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半图8-1HDAPOE图8-2FE H A POG径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步:先画出四个表面的面积和整个锥体体积; 第二步:设内切球的半径为r,建立等式:PBCO PACO PABO ABCO ABCP V V V V V -----+++=⇒rS S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABC O ABCP S S S SV r -----+++=3例8 (1)棱长为a 的正四面体的内切球表面积是 62a π,解:设正四面体内切球的半径为r ,将正四面体放入棱长为2a的正方体中(即补形为正方体),如图,则2622313133a a V V ABCP =⋅==-正方体,又 ra r a Sr VABCP 223343314314=⋅⋅⋅=⋅=-,∴263332a r a =,62a r =,∴内切球的表面积为6422a r Sππ==表(注:还有别的方法,此略)(2)正四棱锥ABCD S -的底面边长为2,侧棱长为3,则其内切球的半径为2217+(1)题CBD解:如图,正四棱锥ABCD S -的高7=h ,正四棱锥ABCD S -的体积为374=-ABCDS V侧面斜高221=h ,正四棱锥ABCD S -的表面积为284+=表S,正四棱锥ABCD S -的体积为rr S V ABCD S ⋅+==-328431表,∴3743284=⋅+r ,771427)122(7221728474-=-=+=+=r (3)三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则该三棱锥的内切球半径为47332++解:如图,3=∆ABCS,2==∆∆ACP ABPS S ,7=∆BCPS,743++=表S ,三棱锥ABC P -的体积为332=-ABC P V , 另一表达体积的方式是r r S V ABC P ⋅++==-347331表,∴3323473=⋅++r ,∴47332++=r习题: 1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ) A.3 B.6 C.36 D .9 解:【A 】616164)2(2=++=R ,3=Rhh 1(2)题MHAS(3)题BA【三棱锥有一侧棱垂直于底面,且底面是直角三角形】【共两种】2. 三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于 . 332π解:260sin 32==r ,16124)2(2=+=R ,42=R,2=R ,外接球体积332834ππ=⋅ 【外心法(加中垂线)找球心;正弦定理求球小圆半径】3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 . 解:ABC ∆外接圆的半径为 ,三棱锥ABC S -的直径为3460sin 22==R ,外接球半径32=R , 或1)3(22+-=R R,32=R ,外接球体积2733233834343πππ=⋅==RV ,4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:PAC ∆的外接圆是大圆,3460sin 22==R ,32=R ,5. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ,81216)97(1sin 22⋅=-=∠P ,924sin =∠P , 42922992422===R ,829=R6. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:AC 是公共的斜边,AC 的中点是球心O ,球半径为1=R。
八个有趣模型——搞定空间几何体的外接球与内切球

八个有趣模型一一搞定空间几何体的外接球与内切球当讲到付雨楼老师于2018年1月14日总第539期微文章,我如获至宝.为有了教学的实施,我以付老师的文章主基石、框架,增加了我个人的理解及例题,形成此文,仍用文原名,与各位同行分享•不当之处,敬请大家批评指正•—、有关定义1•球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球2•外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球•3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球•二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2 :经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5 :在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心)2.结论:结论1 :长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2 :若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论&圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直•(与直线切圆的结论有一致性)2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等•(类比:与多边形的内切圆)•3.正多面体的内切球和外接球的球心重合4.正棱锥的内切球和外接球球心都在高线上,但不一定重合5.基本方法:(3)在正三棱锥 S ABC 中,M 、N 分别是棱SC 、BC 的中点,且 AMMN ,若侧棱SA 2・3则正三棱锥S ABC 外接球的表面积是解:引理:正三棱锥的对棱互相垂直 .证明如下:如图(3) -1 , 取AB,BC 的中点D,E ,连接AE,CD , AE,CD 交于H ,连接SH , 则H 是底面正三角形ABC 的中心,SH 平面ABC : ,SH AB ,AC BC , ADBD , CD AB ,AB 平面SCD ,AB SC ,同理: BC SA , ACSB , 即正三棱锥的对棱互垂直, 本题图如图(3) -2 ,AM MN ,SB//MN , AM SB , AC SB , SB平面SAC ,SB SA , SB SC , SB SA ,BC SA ,SA 平面SBC , SA SC ,故三棱锥 S ABC 的三棱条侧棱两两互相垂直,(2R )2 !(2、3)2r — r~(2、、3)2(2、、36 2即4R 2 36 ,正三棱锥S ABC 外接球的表面积是36(4)在四面体S ABC 中,SA 平面ABC , BAC 120 ,SA AC 2, AB 1,则该四面体的外接(1) 构造三角形利用相似比和勾股定理;(2) 体积分割是求内切球半径的通用做法( 等体积法) 四、 与台体相关的,此略• 五、 八大模型第一讲柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)方法:找三条两两垂直的线段,直接用公式 2(2R)..a 2 b 2 c 2,求出 R例1 ( 1)已知各顶点都在同一球面上的正四棱柱的高为 4,体积为16,则这个球的表面积是( A. 16 B . 20C . 24D . 32(2)若三棱锥的三个侧面两两垂直,且侧棱长均为,3,则其外接球的表面积是 _________________PbCB图1-1图1-2图1-3 图1-4C(3)题-1(引理)球的表面积为(求出R .球的表面积为 _________________ ,球的表面积为 ____________ . __________A11 B.7C.- 3(5) 如果三棱锥的三个侧面两两垂直,它们的面积分别为 (6) 已知某几何体的三视图如图所示,三视图是腰长为何体外接球的体积为 ________________D.40 6、4、3,那么它的外接球的表面积是1的等腰直角三角形和边长为 1的正方形,则该几类型二、对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等, 第一步:画出一个长方体,标出三组互为异面直线的对棱; 求外接球半径(AB第二步:设出长方体的长宽高分别为a,b,c , AD BC x ,AB CD AC BD z ,列方程组,2a b 2 2cb 22 c2a2 x2 y 2z2(2R) 2 . 2 2abcx 2补充: 2-1 中, V A BCDabc - abc6 -abc . 3第三步:根据墙角模型,2Ra 2b 2c 2R 2CD ,AD BC ,AC BD )2 2y __ j R 8 ,R2 2 2x y z { 8 ,例2( 1)如下图所示三棱锥A BCD ,其中 AB CD 5,ACBD 6, AD BC 7,则该三棱锥外接(2)在三棱锥A BCD 中,AB CD 2,AD BC 3,AC BD 4,则三棱锥A BCD 外接A(1)题图(3)正四面体的各条棱长都为 ______________________________ 2,则该正面体外接球的体积为(4) 棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三 角形(正四面体的截面)的面积是类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1 图3-2 图3-3题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是 任意三角形) 第一步:确定球心 0的位置,01是 ABC 的外心,则001 平面ABC ; 11第二步:算出小圆 0<!的半径A01r ,001 AA 1h ( AA , h 也是圆柱的高);2 2 第三步:勾股定理: OA 2 01A 20102R 2(-)2 r 2 Rv r2(-)2,解出 R . 2V 2例3( 1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,9且该六棱柱的体积为 -,底面周长为3,则这个球的体积为 __________________________8(2)直三棱柱 ABC A 1B 1C 1的各顶点都在同一球面上,若ABAC AA 2, BAC120,则此球的表面积等于(3)已知 EAB 所在的平面与矩形 ABCD 所在的平面互相垂直,EA EB 3, AD 2,AEB 60,则多面体E ABCD 的外接球的表面积为.(4)在直三棱柱 ABC A 1B 1C 1 中,AB 4, AC 6, A孑AA 14, 则直三棱柱ABC A 1B 1C 1的外接球的表面积为r!,BccooAA2o第二讲锥体背景的模型1.如图4-1,平面PAC 心 三棱锥P ABC 的三条侧棱相等 锥的顶点.解题步骤:BC (即AC 为小圆的直径),且P 的射影是P ABC 的底面 ABC 在圆锥的底上,顶点确定球心 O 的位置,取 ABC 的外心01,则三点共线;图4-4图4-1图4-2 图4-3类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径一一正弦定理求大圆直径是通法) 平面ABC ,且AB三棱 ABC 的外 P 点也是圆第一步: 第二步: 先算出小圆 O i 的半径AO ir ,再算出棱锥的高 PO 1 h (也是圆锥的高);第三步: 勾股定理:OA 2 O 1A 2 O 1O 2R 2 (h R)2 r 2,解出 R ;事实上,2.如图 ACP 的外接圆就是大圆,直接用 正弦定理也可求解出R .4-2,平面PAC 平面ABC , 且AB BC (即AC 为小圆的直径),且PAAC ,则利用勾股定理求三棱锥的外接球半径:① (2R)2PA 2 (2r)2 2R PA 2 (2r)2② R 2 r 2 OO 12 OO 123.如图4-3,平面PAC平面 ABC , 且ABBC (即AC 为小圆的直径) OC 2 O 1C 2 O 1O 2R 2 r 2 O 1O 2AC 2 R 2 O 1O 2平面ABC ,且AB BC (即AC 为小圆的直径) PAC 的外接圆是大圆,先求出小圆的直径第二步:在 PAC中,可根据正弦定理 — b— 2R ,求出R . sin A sin B sin C 4.题设:如图 4-4,平面 第一步:易知球心 O 必是PAC PAC 的外心,即 aAC 2r ;例4 (1)正四棱锥的顶点都在同一球面上, 若该棱锥的高为1,底面边长为2 3 ,则该球的表面积为 (2)正四棱锥S ABCD 的底面边长和各侧棱长都为 2,各顶点都在同一球面上,则此球体积为(3) —个正三棱锥的四个顶点都在半径为三棱锥的体积是( )A .沁B .旦1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正^3 12(4)在三棱锥P ABC 中,PA PB PC . 3 ,侧棱PA 与底面ABC 所成的角为60 ,则该三棱锥外接球的体积为(类型五、垂面模型(一条直线垂直于一个平面) 1. 题设:如图5, PA 平面ABC ,求外接球半径解题步骤:第一步:将 ABC 画在小圆面上, A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心0 ;第二步:01为 ABC 的外心,所以 00^! 平面ABC ,算出小圆01的半径01D r (三角形的外接圆直 径算法:利用正弦定理,得 -^―-^―2r ),0011PA ;sin A sin B sinC2第三步:利用勾股定理求三棱锥的外接球半径:①(2R )2 PA 2 (2r )22R . PA 2 (2r )2 ;② R 2 r 2 0012R ... r 2 00:.2•题设:如图5-1至5-8这七个图形,P 的射影是 ABC 的外心 三棱锥P ABC 的 三条侧棱相等 三棱锥P ABC 的底面 ABC 在圆锥的底上,顶点 P 点也是圆锥的 顶点•33(5)已知三棱锥 S ABC 的所有顶点都在球 0的求面上,ABC 是边长为1的正三角形,SC 为球0的直径,且SC 2,则此棱锥的体积为( )A •二B .C.1!D.迈6 6 3 2A . B.C. 4D.P图5-1OCA Oi BPP图5-4OCA DBO i P图5-6图5-7图5-8解题步骤:第一步:确定球心0的位置,取ABC的外心O i,则P,O,O i三点共线;第二步:先算出小圆O i的半径AO i r,再算出棱锥的高PO i h (也是圆锥的高)第三步:勾股定理:OA2 O i A2 O i O2R2(h R)2 r2,解出R方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径.例5 一个几何体的三视图如图所示,则该几何体外接球的表面积为A. 3B. 2C.i63D.以上都不对第三讲二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)图6第一步:先画出如图6所示的图形,将BCD画在小圆上,找出BCD和ABD的外心H1和H2;第二步:过H i和H2分别作平面BCD和平面ABD的垂线,两垂线的交点即为球心0,连接OE,OC ;第三步:解OEH i,算出OH i,在Rt OCH i中,勾股定理:OH; CH; 0C2注:易知O,H i,E,H2四点共面且四点共圆,证略•例6( 1)三棱锥P ABC中,平面PAC 平面ABC,△ PAC和厶ABC均为边长为2的正三角形,贝U 三棱锥P ABC外接球的半径为____________________________ .(2)在直角梯形ABCD中,AB//CD , A 90 , C 45 , AB AD 1,沿对角线BD折成四面体A BCD,使平面ABD 平面BCD,若四面体A BCD的顶点在同一个球面上,则该项球的表面积为(3)在四面体S ABC中,AB BC , AB BC 匹,二面角S AC B的余弦值为—贝y四3 面体S ABC的外接球表面积为____________________(4)在边长为2..3的菱形ABCD中,BAD 60,沿对角线BD折成二面角A BD C为120的四面体ABCD,则此四面体的外接球表面积为 ____________________(5)在四棱锥ABCD 中,BDA 120 , BDC 150 , AD BD 2, CD . 3,二面角A BD C的平面角的大小为120,则此四面体的外接球的体积为 ________________类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型题设:如图7, APB ACB 90,求三棱锥P ABC 外接球半径(分析:取公共的斜边的中点O ,1连接OP,OC ,则OA OB OC OP -AB , O 为三棱锥P ABC 外接球球心,然后在 OCP 中 2求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都 为定值•例7 (1)在矩形ABCD 中,AB 4, BC则四面体ABCD 的外接球的体积为(3,沿AC 将矩形ABCD 折成一个直二面角 BAC D ,).125D6125 3A125DA . B.121259C(2)在矩形ABCD 中,AB 2, BC 3, 沿BD 将矩形ABCD 折叠,连接AC , 所得三棱锥A BCD的外接球的表面积为 ___________________第四讲多面体的内切球问题模型类型八、锥体的内切球问题第一步:先现出内切球的截面图,E,H 分别是两个三角形的外心;1第二步:求DH -BD , PO PH r , PD 是侧面 ABP 的高;3第三步:由 POE 相似于 PDH ,建立等式: 坐 竺,解出rDH PD2. 题设:如图8-2,四棱锥P ABC 是正四棱锥,求其内切球的半径3. 题设:三棱锥 P ABC 是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等1.题设:如图8-1,三棱锥P ABC 上正三棱锥,求其内切球的半径第一步: 先现出内切球的截面图,P,O, H 三点共线;第二步: 求 1FH 丄 BC2 ,PO PH r , PF 是侧面PCD 的高;第三步:由POG 相似于 PFH OG ,建立等式:HF PO ,解出PFPCACB图8-1PGOHFC图8-2D第一步:先画出四个表面的面积和整个锥体体积;3V P ABCS O ABC S O PAB S O PACS O PBC 例8 ( 1)棱长为a 的正四面体的内切球表面积是 ________________________(2)正四棱锥S ABCD 的底面边长为2,侧棱长为3,则其内切球的半径为 _________________(3)三棱锥P ABC 中,底面 ABC 是边长为2的正三角形,PA 底面ABC ,PA 2, 则该三棱锥的内切球半径为 ___________________习题:1 •若三棱锥S ABC 的三条侧棱两两垂直,且SA 2,SB SC 4,则该三棱锥的外接球半径为 ()A. 3B. 6C. 36D. 9 2.三棱锥S ABC 中,侧棱SA 平面ABC ,底面ABC 是边长为..3的正三角形,SA 2 3,则该三 棱锥的外接球体积等于 . 3•正三棱锥S ABC 中,底面ABC 是边长为 3的正三角形,侧棱长为 2,则该三棱锥的外接球体积等 于4 •三棱锥P ABC 中,平面PAC 平面ABC ,△ PAC 边长为2的正三角形, AB BC ,则三棱锥 P ABC 外接球的半径为5. 三棱锥 P ABC 中,平面 PAC 平面ABC ,AC 2,PA PC 3,AB BC ,则三棱锥P ABC 外接球的半径为6. 三棱锥P ABC 中,平面PAC 平面ABC ,AC 2,PA PC ,AB BC ,则三棱锥P ABC第二步:设内切球的半径为 建立等式:V p ABC ABC V O PAB VO PAC V O PBC 1 V P ABC S ABC 3 11 PAB r S pAC 33 1 PBC 3 1 (S ABC S PAB S PAC S PBC ) r 3 第三步:解出r外接球的半径为_______ .。
八个有趣模型——搞定空间几何体的外接球与内切球(学生版)

八个有趣模型——搞定空间几何体的外接球与内切球当讲到付雨楼老师于2018年1月14日总第539期微文章,我如获至宝.为有了教学的实施,我以付老师的文章主基石、框架,增加了我个人的理解及例题,形成此文,仍用文原名,与各位同行分享.不当之处,敬请大家批评指正.一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).初图1初图22.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法). 四、与台体相关的,此略. 五、八大模型第一讲 柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)图1-1图1-2图1-3图1-4方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( ) A .π16 B .π20C .π24D .π32 (2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 (3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1, 取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH , 则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD ,∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直, 本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC , ∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥, ∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理)AC(3)题-2(解答图)AC(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( )π11.A π7.B π310.C π340.D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是 (6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为类型二、对棱相等模型(补形为长方体) 题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =) 第一步:画出一个长方体,标出三组互为异面直线的对棱; 第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=, 补充:图2-1中,abc abc abc V BCD A 31461=⨯-=-. 第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .例2(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .(1)题图B(6)题图图2-1(2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为 . (3)正四面体的各条棱长都为2,则该正面体外接球的体积为(4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是 .(4)题类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1图3-2 图3-3题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ; 第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高); 第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=,解出R .例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为 (2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 .(3)已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为 .(4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为 .第二讲 锥体背景的模型类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)图4-1图4-2图4-3图4-41.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点. 解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ;事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则 利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=; 第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R . 例4 (1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为 .(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为 (3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( )A .433 B .33 C .43 D .123(4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60,则该三棱锥外接球的体积为( ) A .π B.3π C. 4π D.43π (5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )ABD类型五、垂面模型(一条直线垂直于一个平面)1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.图52.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的 三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的 顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示,则该几何体外接球的表面积为( ) A .π3 B .π2 C .316πD .以上都不对俯视图侧视图正视图第三讲 二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)图6第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ; 第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,; 第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+ 注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 .(2)在直角梯形ABCD 中,CD AB //, 90=∠A ,45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为(3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为(4)在边长为32的菱形ABCD 中,60=∠BAD ,沿对角线BD 折成二面角C BD A --为120的四面体ABCD ,则此四面体的外接球表面积为(5)在四棱锥ABCD 中, 120=∠BDA , 150=∠BDC ,2==BD AD ,3=CD ,二面角C BD A -- 的平面角的大小为120,则此四面体的外接球的体积为类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设:如图7,90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为( )A .π12125 B .π9125 C .π6125 D .π3125(2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为 .第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径. 第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高;第三步:由POE ∆相似于PDH ∆,建立等式:PDPODH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高; 第三步:由POG ∆相似于PFH ∆,建立等式:PFPOHF OG =,解出图8-1A图8-23.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 (1)棱长为a 的正四面体的内切球表面积是(2)正四棱锥ABCD S -的底面边长为2,侧棱长为3,则其内切球的半径为(3)三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则该三棱锥的内切球半径为习题: 1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ) A.3 B.6 C.36 D.9 2. 三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于 . 3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 .4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .5. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 . 6. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABCP -外接球的半径为 .。
八个有趣模型搞定空间几何体的外接球与内切球(教师版)

八个有趣模型——搞定空间几何体的外接球与内切球一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).初图1初图22.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法).四、与台体相关的,此略.五、八大模型第一讲柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)图1-1图1-2图1-3方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32解: 162==h a V ,2=a ,24164442222=++=++=h a a R ,π24=S ,选C ;(2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 π9 解:933342=++=R ,ππ942==R S ;(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .π36 解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1, 取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD , ∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,(3)题-1(引理)AC(3)题-2(解答图)AC∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36. (4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( D )π11.A π7.B π310.C π340.D 解:在ABC ∆中,7120cos 2222=⋅⋅-+=BC AB AB AC BC ,7=BC ,ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ,∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是 解:由已知得三条侧棱两两垂直,设三条侧棱长分别为c b a ,,(+∈R c b a ,,),则⎪⎩⎪⎨⎧===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S , (6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为解:3)2(2222=++=c b a R ,432=R ,23=Rπππ2383334343=⋅==R V 球,类型二、对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =)(6)题图(6)题直观图P第一步:画出一个长方体,标出三组互为异面直线的对棱; 第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=, 补充:图2-1中,abc abc abc V BCD A 31461=⨯-=-.第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .思考:如何求棱长为a 的正四面体体积,如何求其外接球体积?例2(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解:对棱相等,补形为长方体,如图2-1,设长宽高分别为c b a ,,,110493625)(2222=++=++c b a ,55222=++c b a ,5542=R ,π55=S(1)题图B(2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为 .π229 解:如图2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S (3)正四面体的各条棱长都为2,则该正面体外接球的体积为图2-1(3)解答题解:正四面体对棱相等的模式,放入正方体中,32=R ,23=R ,ππ2383334=⋅=V (4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解:如解答图,将正四面体放入正方体中,截面为1PCO ∆,面积是2.类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)图3-1图3-2图3-3题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ; 第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高); 第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=,解出R例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为 解:设正六边形边长为a ,正六棱柱的高为h ,底面外接圆的半径为r ,则21=a ,正六棱柱的底面积为833)21(4362=⋅⋅=S ,89833===h Sh V 柱,∴3=h ,4)3(14222=+=R 也可1)21()23(222=+=R ),1=R ,球的体积为34π=球V ; (2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 . 解:32=BC ,4120sin 322==r ,2=r ,5=R ,π20=S ;(3)已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为 .π16 解:折叠型,法一:EAB ∆的外接圆半径为31=r ,11=OO ,231=+=R ;法二:231=M O ,21322==D O r ,4413432=+=R ,2=R ,π16=表S ; 法三:补形为直三棱柱,可改变直三棱柱的放置方式为立式,算法可同上,略.换一种方式,通过算圆柱的轴截面的对角线长来求球的直径:162)32()2(222=+=R ,π16=表S ;(4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接(3)题球的表面积为 .π3160解:法一:282164236162=⋅⋅⋅-+=BC ,72=BC ,37423722==r ,372=r , 3404328)2(2122=+=+=AA r R ,π3160=表S ;法二:求圆柱的轴截面的对角线长得球直径,此略.第二讲 锥体背景的模型类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)图4-1图4-2图4-3图4-41.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点. 解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ; 事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则 利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=; 第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R . 例4 (1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为 . 解:法一:由正弦定理(用大圆求外接球直径);法二:找球心联合勾股定理,72=R ,ππ4942==R S ;(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为 解:方法一:找球心的位置,易知1=r ,1=h ,r h =,故球心在正方形的中心ABCD 处,1=R ,34π=V 方法二:大圆是轴截面所的外接圆,即大圆是SAC ∆的外接圆,此处特殊,SAC Rt ∆的斜边是球半径,22=R ,1=R ,34π=V . (3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( ) A .433 B .33 C .43 D .123解:高1==R h ,底面外接圆的半径为1=R ,直径为22=R , 设底面边长为a ,则260sin 2==aR ,3=a ,433432==a S ,三棱锥的体积为4331==Sh V ; (4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60,则该三棱锥外接球的体积为( ) A .π B.3π C. 4π D.43π 解:选D ,由线面角的知识,得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上,在圆锥中求解,1=R ; (5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )AA.6 BC.3 D.2解:36)33(12221=-=-=r R OO ,362=h ,62362433131=⋅⋅==Sh V 球 类型五、垂面模型(一条直线垂直于一个平面) 1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的 三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的 顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示,则该几何体外接球的表面积为( )C A .π3 B .π2 C .316πD .以上都不对俯视图侧视图正视图解答图解:选C ,法一:(勾股定理)利用球心的位置求球半径,球心在圆锥的高线上,221)3(R R =+-,32=R ,ππ31642==R S ;法二:(大圆法求外接球直径)如图,球心在圆锥的高线上,故圆锥的轴截面三角形PMN 的外接圆是大圆,于是3460sin 22==R ,下略;第三讲 二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)图6第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ; 第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,; 第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+ 注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为.(1)题解:如图,3460sin 22221===r r ,3221==r r ,312=H O , 35343121222=+=+=r H O R ,315=R ; 法二:312=H O ,311=H O ,1=AH , 352121222=++==O O H O AH AO R ,315=R ; (2)在直角梯形ABCD 中,CD AB //,90=∠A ,45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为 π4(2)题-2(2)题-1→A(3)题解:如图,易知球心在BC 的中点处,π4=表S ; (3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为 π6 解:如图,法一:33)2cos(cos 211-=+∠=∠πO OO B SO , 33sin 21=∠O OO ,36cos 21=∠O OO , 22cos 21211=∠=O OO O O OO ,232112=+=R ,ππ642==R S ; 法二:延长1BO 到D 使111r BO DO ==,由余弦定理得6=SB ,2=SD ,大圆直径为62==SB R ;(4)在边长为32的菱形ABCD 中, 60=∠BAD ,沿对角线BD 折成二面角C BD A --为120的四面体ABCD ,则此四面体的外接球表面积为 π28解:如图,取BD 的中点M ,ABD ∆和CBD ∆的外接圆半径为221==r r ,ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离(弦心距)为121==d d , 法一:四边形21MO OO 的外接圆直径2=OM ,7=R ,π28=S ;法二:31=OO ,7=R ;法三:作出CBD ∆的外接圆直径CE ,则3==CM AM , 4=CE ,1=ME ,7=AE ,33=AC ,72147227167cos -=⋅⋅-+=∠AEC ,7233sin =∠AEC ,72723333sin 2==∠=AEC AC R ,7=R ;(5)在四棱锥ABCD 中, 120=∠BDA ,150=∠BDC ,2==BD AD ,3=CD ,二面角CBD A --的平面角的大小为120,则此四面体的外接球的体积为(4)题图解:如图,过两小圆圆心作相应小圆所在平面的垂线确定球心,→抽象化(5)题解答图-2(5)题解答图-11B32=AB ,22=r ,弦心距32=M O ,13=BC ,131=r ,弦心距321=M O , ∴2121=O O ,72120sin 21==O O OM , 法一:∴292222=+==OM MD OD R ,29=R ,∴329116π=球V ; 法二:2522222=-=M O OM OO ,∴29222222=+==OO r OD R ,29=R ,∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设:如图7,90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为( ) A .π12125 B .π9125 C .π6125 D .π3125解:(1)52==AC R ,25=R ,6125812534343πππ=⋅==R V ,选C (2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCDA -的外接球的表面积为 .解:BD 的中点是球心O ,132==BD R ,ππ1342==R S .第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径. 第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高;第三步:由POE ∆相似于PDH ∆,建立等式:PDPODH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高;第三步:由POG ∆相似于PFH ∆,建立等式:PFPOHF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3图8-1A图8-2例8 (1)棱长为a 的正四面体的内切球表面积是 62a π,解:设正四面体内切球的半径为r ,将正四面体放入棱长为2a的正方体中(即补形为正方体),如图,则 2622313133aa V V ABC P =⋅==-正方体,又 r a r a Sr V ABC P 223343314314=⋅⋅⋅=⋅=-, ∴263332a r a =,62a r =,∴内切球的表面积为6422a r S ππ==表(注:还有别的方法,此略)(2)正四棱锥ABCD S -的底面边长为2,侧棱长为37解:如图,正四棱锥ABCD S -的高7=h ,正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ,正四棱锥ABCD S -的表面积为284+=表S ,正四棱锥ABCD S -的体积为r r S V ABCDS ⋅+==-328431表, ∴3743284=⋅+r , 771427)122(7221728474-=-=+=+=r (3)三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则32解:如图,3=∆ABC S ,2==∆∆ACP ABP S S ,7=∆BCP S ,743++=表S ,(2)题(1)题D(3)题B三棱锥ABC P -的体积为332=-ABC P V , 另一表达体积的方式是r r S V ABC P ⋅++==-347331表, ∴3323473=⋅++r ,∴47332++=r习题:1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ) A.3B.6C.36D.9解:【A 】616164)2(2=++=R ,3=R【三棱锥有一侧棱垂直于底面,且底面是直角三角形】【共两种】2. 三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于 . 332π解:260sin 32==r ,16124)2(2=+=R ,42=R ,2=R ,外接球体积332834ππ=⋅ 【外心法(加中垂线)找球心;正弦定理求球小圆半径】3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 .解:ABC ∆外接圆的半径为 ,三棱锥ABC S -的直径为3460sin 22==R ,外接球半径32=R ,或1)3(22+-=R R ,32=R ,外接球体积2733233834343πππ=⋅==R V , 4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:PAC ∆的外接圆是大圆,3460sin 22==R ,32=R , 5. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .解:973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ,81216)97(1sin 22⋅=-=∠P ,924sin =∠P ,42922992422===R ,829=R 6. 三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABCP -外接球的半径为 .R 解:AC是公共的斜边,AC的中点是球心O,球半径为1。
八个有趣模型搞定外接球内切球问题学生版本.doc

实用标准八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径)PPPPO 2ccccA CbC baCbBCabABAaBaBA图1 图 2 图 3 图4方法:找三条两两垂直的线段,直接用公式(2R)2a 2b 2c 2 ,即 2Ra 2b 2c 2 ,求出 R例 1 ( 1)已知各顶点都在同一球面上的正四棱柱的高为4 ,体积为 16 ,则这个球的表面积是()A . 16B . 20C. 24D. 32( 2)若三棱锥的三个侧面两垂直,且侧棱长均为3 ,则其外接球的表面积是( 3)在正三棱锥 S ABC 中, M 、 N 分别是棱 SC 、 BC 的中点,且 AM MN , 若侧棱 SA 2 3 , 则正三棱锥 SABC 外接球的表面积是( 4)在四面体 S ABC 中, SA平面 ABC , BAC 120 , SA AC 2, AB 1, 则该四面体的外接球的表面积为()10 40 A.11B.7C.D.33( 5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6 、 4 、 3,那么它的外接球的表面积是( 6)已知某几何体的三视图如图所示, 三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为类型二、垂面模型(一条直线垂直于一个平面) 1.题设:如图 5, PA 平面 ABC解题步骤:第一步:将 ABC 画在小圆面上, A 为小圆直径的一个端点,作小圆的直径AD ,连接 PD ,则 PD 必过球心 O ;PO第二步: O 1 为 ABC 的外心,所以 OO 1 平面 ABC ,算出小圆 O 1 的半CAO 1 D径 O 1D r (三角形的外接圆直径算法:利用正弦定理,得Ba b c1图 52r ), OO 1sin A sin B sin C PA ;2第三步:利用勾股定理求三棱锥的外接球半径:① (2R)2 PA 2(2r )22RPA 2(2r )2 ;② R 2r 2 OO 12 Rr 2 OO 1 22.题设: 如图 6,7,8, P 的射影是 ABC 的外心 三棱锥 P ABC 的三条侧棱相等三棱锥 PABC 的底面 ABC 在圆锥的底上,顶点 P 点也是圆锥的顶点PPPPOOOOCCCCA1DAO 1BAO 1O 1OBABB图 6图 7-1 图 7-2图 8PPPAAABCO 2O 2O 2DBCDBOOO图 8-1 图8-2图 8-3解题步骤:第一步:确定球心O 的位置,取ABC 的外心 O1,则 P,O, O1三点共线;第二步:先算出小圆O1的半径 AO1r ,再算出棱锥的高PO1h (也是圆锥的高);第三步:勾股定理:OA2O1 A2O1O 2R2(h R) 2r 2,解出R方法二:小圆直径参与构造大圆。
高中数学的八个有趣模型——搞定空间几何体的外接球与内切球
八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径)图2图3图4方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32 (2)若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是 π9 解:(1)162==h a V ,2=a ,24164442222=++=++=h a a R ,π24=S ,选C ; (2)933342=++=R ,ππ942==R S(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 。
π36 解:引理:正三棱锥的对棱互垂直。
证明如下:如图(3)-1,取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD ,∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC , ∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥, ∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36(3)题-1A(3)题-2A(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( D )π11.A π7.B π310.C π340.D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是(6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为 解析:(4)在ABC ∆中,7120cos 2222=⋅⋅-+=BC AB AB AC BC ,7=BC ,ABC ∆的外接球直径为372237sin 2==∠=BAC BC r , ∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)三条侧棱两两生直,设三条侧棱长分别为c b a ,,(+∈R c b a ,,),则⎪⎩⎪⎨⎧===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S , (6)3)2(2222=++=c b a R ,432=R ,23=Rπππ2383334343=⋅==R V ,类型二、垂面模型(一条直线垂直于一个平面) 1.题设:如图5,⊥PA 平面ABC 解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直 径AD ,连接PD ,则PD 必过球心O ; 第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=图5ADPO 1OCBAP2.题设:如图6,7,8,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点图6PADO 1OCB图7-1PAO 1O CB图7-2PAO 1O CB图8PAO 1OCB图8-1DPOO 2ABC图8-2POO 2ABC图8-3DPOO 2AB解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆。
八个有趣模型——搞定空间几何体的外接球与内切球(学生版)

八个有趣模型——搞定空间几何体的外接球与内切球文:付雨楼段永建一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:外接球球心到多面体各顶点的距离均相等,均为球的半径;性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(结论类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).2.结论:结论1:长方体的外接球的球心在长方体的体对角线的交点处,即长方体的体对角线中点是外接球的球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆直径,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的上下两底面圆的圆心连线段的中点是的外接球球心;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面(等腰三角形)的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.多面体的内切球球心到多面体各面的距离均相等,(类比:多边形的内切圆);多面体的外接球球心到多面体各顶点的距离均相等(类比:多边形的外接圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法).四、与台体相关的,此略.五、八大模型(共四讲):第一讲柱体背景的模型类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R【例1】在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是.π36解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1,取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD ,∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.【变式1】已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是()A .π16B .π20C .π24D .π32【变式2】若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是【变式3】在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为()π11.A π7.B π310.C π340.D 【变式4】如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是【变式5】已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为类型二、对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =)第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=,补充:图2-1中,abc abc abc V BCD A 31461=⨯-=-.第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .思考:如何求棱长为a 的正四面体体积,如何求其外接球体积?【例2】(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为.(2)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是.【变式1】BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为.【变式2】正四面体的各条棱长都为2,则该正面体外接球的体积为类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ;第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高);第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(h r R +=,解出R .【例3】一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为【变式1】直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于.【变式2】在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为.【变式3】已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,3==EB EA ,2=AD ,︒=∠60AEB ,则多面体ABCD E -的外接球的表面积为.第二讲锥体背景的模型类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)1.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ;事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=;第二步:在PAC ∆中,可根据正弦定理R Cc B b A a 2sin sin sin ===,求出R .【例4】正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为.【变式1】已知正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为【变式2】一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是()A .433B .33C .43D .123【变式3】在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为 60,则该三棱锥外接球的体积为()A .π B.3πC.4πD.43π【变式4】已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为()A .6B .6C .3D .2类型五、垂面模型(一条直线垂直于一个平面)1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=;第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径.【例5】一个几何体的三视图如图所示,则该几何体外接球的表面积为()A .π3B .π2C .316πD .以上都不对【变式1】(2018全国卷III 第10题)设D C B A ,,,是一个半径为4的球面上的四点,ABC ∆为等边三角形且其面积为39,则三棱锥ABC D -体积的最大值为()A .312B .318C .324D .354第三讲二面角背景的模型类型六、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1O 和2O ;第二步:过1O 和2O 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,;第三步:解1OEO ∆,算出1OO ,在1OCO Rt ∆中,勾股定理:22121OC CO OO =+.注:易知21,,,O E O O 四点共面且四点共圆,证略.【例6】三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为.【变式1】在直角梯形ABCD 中,CD AB //, 90=∠A ,45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该球的表面积为【变式2】在四面体ABC S -中,BC AB ⊥,2==BC AB ,2==SC SA ,且二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为【变式3】在边长为32的菱形ABCD 中, 60=∠BAD ,沿对角线BD 折成二面角C BD A --为 120的四面体ABCD ,则此四面体的外接球表面积为【变式4】(自编题)在四面体ABCD 中, 120=∠BDA , 150=∠BDC ,2==BD AD ,3=CD ,二面角C BD A --的平面角的大小为120,则四面体ABCD 的外接球的体积为【变式5】如图,在ABC ∆中,6==BC AB , 90=∠ABC ,点D 为AC 的中点,将ABD ∆沿BD 折起,使PD PC =,连接PC ,得到三棱锥BCD P -,若该三棱锥的所有点都在同一个球面上,则该的表面积是()A .πB .π3C .π5D .π7【变式6】某棱锥的三视图如图所示,则该项棱锥的外接球的表面积为【变式7】已知菱形ABCD 的边长为6,60=∠A ,沿对角线BD 将该菱形折成锐二面角C BD A --,连接AC .若三棱锥BCD A -的体积为3227,则三棱锥的外接球的表面积为【变式8】在平面四边形ABCD 中,AD AB ⊥,CD BD ⊥,BCD ∆的面积为3,将其沿对角线BD折成四面体ABCD ,满足C BD A --为60.若四面体ABCD 的顶点在同一个球面上,则该球的表面积的最小值是()A .π4B .π34C .π8D .π38类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型题设:如图7,90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.【例7】在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为()A.π12125B.π9125C.π6125D.π3125【变式1】在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为.【变式2】已知球的直径为6=SC ,A 、B 是球面上的两点,且3===SB SA AB ,则三棱锥ABC S -的体积为第四讲多面体的内切球问题模型类型八、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径.第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高;第三步:由POE ∆相似于PDH ∆,建立等式:PDPO DH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高;第三步:由POG ∆相似于PFH ∆,建立等式:PF PO HF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABC O ABC P S S S S V r -----+++=3【例8】棱长为a 的正四面体的内切球表面积是【变式1】正四棱锥ABCD S -的底面边长为2,侧棱长为3,则其内切球的半径为【变式2】三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则该三棱锥的内切球半径为【变式3】如图,已知正方形ABCD 的边长为22,将ABC ∆沿对角线AC 折起,使平面⊥ABC 平面ACD ,得到如图所示的三棱锥ACD B -.若O 为AC 的中点,N M ,分别是线段BO DC ,上的动点(不包括端点),且CM BN =.当三棱锥AMC N -的体积最大时,三棱锥ADC N -的内切球的半径为习题:1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为()A.3B.6C.36D.92.三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于.3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于.4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为.5.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为.6.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABCP -外接球的半径为.7.中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑.如图为一个阳马与一个鳖臑的组合体,已知三棱锥ADE P -为鳖臑,且⊥PA 平面ABCD ,2=AB ,2=AD ,3=EC ,该鳖臑的外接球的表面积为π9,则阳马的外接球的体积为A .23πB .33πC .42πD .43π8.鲁班锁是中国传统的智力玩具,起源一中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱分成三组,经90榫卯起来.若正棱柱的高为5,底面正方形边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为(容器壁的厚度忽略不计,结果保留π)9.若在三棱锥ABC P -中,1==AC AB ,AC AB ⊥,⊥PA 平面ABC ,且直线PA 与平面PBC 所成角的正切值为21,则三棱锥ABC P -的外接球的表面积为()A .π4B .π8C .π16D .π3210.四棱锥ABCD P -的底面ABCD 是边长为6的正方形,且PD PC PB PA ===,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是()A .6B .5 C.29 D.4911.(2017·全国I )已知三棱锥ABC S -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面⊥SCA 平面SCB ,AC SA =,BC SB =,三棱锥ABC S -的体积为9,则球O 的表面积为.12.(2017·江苏)如图,在圆柱21O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱21O O 的体积为1V ,球O 的体积为2V ,则21V V 的值是.13.在正三棱锥ABC S -中,点M 是SC 的中点,且SB AM ⊥,底面边长22=AB ,则正三棱锥ABCS -的外接球的表面积为()A .π6B .12C .32D .3614.已知半径为1的球O 中内接一个圆柱,当圆柱的侧面积最大时,球的体积与圆柱的体积的比值为.。
(完整)八个有趣模型搞定外接球内切球问题(学生版))

八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径)图2图3方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( ) A .π16 B .π20 C .π24D .π32(2)若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( )π11.A π7.B π310.C π340.D(5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是(6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为类型二、垂面模型(一条直线垂直于一个平面) 1.题设:如图5,⊥PA 平面ABC 解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=; ②2122OO r R +=⇔212OO r R +=2.题设:如图6,7,8,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点图6PADO 1OCB图7-1PAO 1O CB图7-2PAO 1O CB图8PAO 1OCB图5ADP O 1OCB图8-1DPOO 2ABC图8-2POO 2ABC图8-3DPOO 2AB解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高); 第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆。
高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型墙角模型是指三条线段两两垂直的几何体,通过公式(2R) = a + b + c,即2R = a^2 + b^2 + c^2,可以求出其外接球半径R。
例1:1)已知顶点都在同一球面上的正四棱柱的高为4,体积为16,求该球的表面积。
解:由V = ah = 16,得a = 2,4R = a + a + h = 4 + 4 + 16 = 24,S = 24π,答案为C。
2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,求其外接球的表面积。
解:由2R = a + b + c = 3 + 3 + 3 = 9,得R = 9/4,S =4πR^2 = 9π。
3)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA = 23,求正三棱锥S-ABC外接球的表面积。
解:由墙角模型的特点可知,正三棱锥的对棱互垂直。
连接AB、BC的中点D、E,连接AE、CD,交于H,则H是底面正三角形ABC的中心。
由AM⊥MN,SB//MN,可得AM⊥SB,AC⊥SB,故SB⊥平面SAC,SB⊥SA,SB⊥SC,即SB⊥SA,BC⊥SA,故SA⊥平面SBC,SA⊥SC。
因此,三棱锥S-ABC的三棱条侧棱两两互相垂直,由2R^2 = 23^2 + 23^2 + 23^2 = 36,得R^2 = 9,S = 36π。
类型二、棱台模型棱台模型是指上底面和下底面都是正多边形,且两底面中心连线与侧棱垂直的几何体。
通过勾股定理和相似三角形,可以求出其外接球半径R和内切球半径r。
例2:1)已知棱台的上底面和下底面都是正三角形,上底边长为3,下底边长为6,侧棱长为5,求其外接球半径R和内切球半径r。
解:由勾股定理可得棱台的高为4√3.设外接球半径为R,内切球半径为r,则有R/r = (a + b + c)/(a + b - c) = (3 + 6 +5)/(3 + 6 - 5) = 7,解得R = 7r。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
, r2
O2 D
13 2
,
R2
3 4
13 4
4
,
R
2
, S表
16
.
法三:补形为直三棱柱,可改变直三棱柱的放置方式为立式,算法可同上,略.
法三:补形为直三棱柱,通过算圆柱的轴截面的对角线长来求球的直径: (2R)2 (2 3)2 22 16 ,
S表 16 .
6
第二讲 锥体背景的模型
类型四、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)
体,这个球是这个多面体的外接球. 3.内切球的定义:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,
这个球是这个多面体的内切球. 二、外接球的有关知识与方法 1.性质:
性质 1:外接球球心到多面体各顶点的距离均相等,均为球的半径; 性质 1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等; 性质 2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆; 性质 3:过球心与小圆圆心的直线垂直于小圆所在的平面(结论类比:圆的垂径定理); 性质 4:球心在大圆面和小圆面上的射影是相应圆的圆心; 性质 5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,
则正三棱锥 S ABC 外接球的表面积是
. 36
解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1,
取 AB, BC 的中点 D, E ,连接 AE, CD , AE, CD 交于 H ,连接 SH ,
则 H 是底面正三角形 ABC 的中心, SH 平面 ABC , SH AB , AC BC , AD BD , CD AB , AB 平面 SCD , AB SC ,同理: BC SA , AC SB ,即正三棱锥的对棱互垂直, 本题图如图(3)-2, AM MN , SB // MN , AM SB , AC SB , SB 平面 SAC , SB SA , SB SC , SB SA , BC SA , SA 平面 SBC , SA SC , 故三棱锥 S ABC 的三棱条侧棱两两互相垂直,
第一讲 柱体背景的模型
类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)
方法:找三条两两垂直的线段,直接用公式 (2R)2 a2 b2 c2 ,即 2R a2 b2 c2 ,求出 R
【例 1】在正三棱锥 S ABC 中, M、N 分别是棱 SC、BC 的中点,且 AM MN ,若侧棱 SA 2 3 ,
b2 c2 4 , c2 a2 16 2(a2 b2 c2 ) 9 4 16 29 , 2(a2 b2 c2 ) 9 4 16 29 ,
a2 b2 c2 29 , 4R2 29 , S 29 .
2
2
2
【变式 2】正四面体的各条棱长都为 2 ,则该正面体外接球的体积为
A.11
B.7
C.10 3
D. 40 3
解:可补形为三棱柱,进一步可补形为圆柱体,在 ABC 中,BC 2 AC 2 AB2 2 AB BC cos120 7 ,
BC
7
, ABC
的外接球直径为 2r
BC sin BAC
7
2
7
,
33
2
(2R)2 (2r)2 SA2 ( 2 7 )2 4 40 , S 40 ,选 D。
就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆; 结论 4:圆柱体的上下两底面圆的圆心连线段的中点是的外接球球心; 结论 5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径; 结论 6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球; 结论 7:圆锥体的外接球球心在圆锥的高所在的直线上; 结论 8:圆锥体轴截面(等腰三角形)的外接圆是大圆,该三角形的外接圆直径是球的直径; 结论 9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球. 3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度); 三、内切球的有关知识与方法 1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性). 2.多面体的内切球球心到多面体各面的距离均相等,(类比:多边形的内切圆);多面体的外接球球心到
abc
1 6
abc 4
1 3
abc
.
第三步:根据墙角模型,2R
a2 b2 c2
x2 y 2 z 2 ,R2 x2 y 2 z 2 ,R
x2 y2 z2
,
2
8
8
求出 R . 思考:如何求棱长为 a 的正四面体体积,如何求其外接球体积?
【例 2】(1)如下图所示三棱锥 A BCD ,其中 AB CD 5, AC BD 6, AD BC 7, 则该三棱锥
1.如图 4-1,平面 PAC 平面 ABC ,且 AB BC (即 AC 为小圆的直径),且 P 的射影是 ABC 的外 心 三棱锥 P ABC 的三条侧棱相等 三棱 P ABC 的底面 ABC 在圆锥的底上,顶点 P 点也是圆
锥的顶点. 解题步骤:
第一步:确定球心 O 的位置,取 ABC 的外心 O1 ,则 P, O, O1 三点共线;
【变式 3】已知 EAB 所在的平面与矩形 ABCD 所在的平面互相垂直, EA EB 3 , AD 2 ,
AEB 60 ,则多面体 E ABCD 的外接球的表面积为
.16
解:折叠型,
法一: EAB 的外接圆半径为 r1 3 , OO1 1, R 1 3 2 ;
法二: O1M
3 2
两相交弦的中垂线交点是圆心).
2.结论: 结论 1:长方体的外接球的球心在长方体的体对角线的交点处,即长方体的体对角线中点是外接球的球心; 结论 2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同; 结论 3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆直径,换言之,
解:正四面体对棱相等的模式,放入正方体中, 2R 3 , R 3 ,V 4 3 3 3 .
2
38 2
类型三、汉堡模型(直棱柱的外接球、圆柱的外接球)
题设:如图 3-1,图 3-2,图 3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任 意三角形)
第一步:确定球心 O 的位置, O1 是 ABC 的外心,则 OO1 平面 ABC ;
3
3
3
【变式 4】如果三棱锥的三个侧面两两垂直,它们的面积分别为 6 、 4 、 3 ,那么它的外接球的表面积是
解:由已知得三条侧棱两两垂直,设三条侧棱长分别为 a, b, c ( a, b, c R ),则
ab 12 bc 8 , abc 24 , a 3 , b 4 , c 2 , (2R)2 a2 b2 c2 29 , S 4R2 29 。 ac 6
第二步:算出小圆
O1 的半径
AO1
r
, OO1
1 2
AA1
1 2
h
(
AA1
h
也是圆柱的高);
第三步:勾股定理: OA2
O1 A2
O1O 2
R2
(h)2 2
r2
R
r 2 ( h )2 ,解出 R 。 2
【例 3】一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,
且该六棱柱的体积为 9 ,底面周长为 3 ,则这个球的体积为 8
外接球的表面积为
.
解:对棱相等,补形为长方体,如图 2-1,设长宽高分别为 a, b, c , 2(a2 b2 c2 ) 25 36 49 110 ,
a2 b2 c2 55 , 4R2 55 , S 55 。
(2)棱长为 2 的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三
角形(正四面体的截面)的面积是
.
解:如解答图,将正四面体放入正方体中,截面为 PCO1 ,面积是 2 .
4
【变式 1】 A BCD 中, AB CD 2 , AD BC 3 , AC BD 4 ,则三棱锥 A BCD 外接球的
表面积为
. 29 2
解:如图 2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为 a, b, c ,则 a2 b2 9 ,
1
多面体各顶点的距离均相等(类比:多边形的外接圆). 3.正多面体的内切球和外接球的球心重合. 4.正棱锥的内切球和外接球球心都在高线上,但不一定重合. 5.基本方法: (1)构造三角形利用相似比和勾股定理; (2)体积分割是求内切球半径的通用做法(等体积法). 四、与台体相关的,此略. 五、八大模型(共四讲):
第一步:画出一个长方体,标出三组互为异面直线的对棱;
第二步:设出长方体的长宽高分别为 a, b, c , AD BC x ,
AB CD y , AC BD z ,列方程组,
a2 b2 x2
b
2
c2
y2
(2R)2
a2
b2
c2
x2
y2
z2
,
c2 a2 z 2
2
补充:图
2-1
中, V A BCD
解:设正六边形边长为 a ,正六棱柱的高为 h ,底面外接圆的半径为 r ,则 a 1 , 2
5
正六棱柱的底面积为 S 6
3 4
( 1 )2 2
33 8
,V柱
Sh
33 8
hLeabharlann 9 8,h
3 ,4R2 12 ( 3)2 4
也可 R2
(
3 )2 (1)2
2
2
1 ), R 1,球的体积为V球
,
AA1
4 ,则直三棱柱
