高中数学空间几何体的内切球与外接球问题
立体几何中球的内切和外接问题(完美版)
则这个球的表面积是( )
A.16π
B.20π
C.24π
D.32π
4
举一反三-突破提升
2.正六棱柱的底面边长为 4,高为 6,则它的外接球的表面积为
A. 20 B. 25 C. 100 D. 200
4
举一反三-突破提升
已知正三棱锥 P-ABC 的主视图和俯视图如图所 示,
则此三棱锥的外接球的表面积为 ( )
ห้องสมุดไป่ตู้
切(如图).求:
(1)这个正三棱锥的表面积; (2)这个正三棱锥内切球的表面积与体积.
考点一 考点二 考点三
4
举一反三-突破提升
-30-
解:(1)底面正三角形中心到一边的距离为1 × 3×2 6 = 2,则正棱锥
32
侧面的斜高为 12 + ( 2)2 = 3.
∴S 侧=3×12×2 6 × 3=9 2.
,五个顶点都在同一个球面上,
P
设外接球半径为 R,在△OO1A 中有
D
解得 . ∴ .
O1
O C
A B
6
测棱相等的锥体顶点的投影在底面外接圆心
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形,AB=2,
SA=SB=SC=2,则该三棱锥的外接球的球心到平面 ABC 的距离为( )
B、体积为 3
D、外接球的表面积为 16
3
1正视图
1
3 1 侧视图
俯视图
点 A、B、C、D 均在同一球面上,其中
是正三角形,
AD 平面 ABC,AD=2AB=6,则该球的体积为 ( )
(A)
(B)
(C)
(D)
平面四边形 ABCD中, AB AD CD1, BD 2, BD CD ,
高考数学空间几何体的外接球与内切球常见题型

高考数学空间几何体的外接球与内切球常见题型本文介绍了空间几何体的外接球与内切球的经典类型,其中第一种类型为墙角模型,即三条棱两两垂直,不需要找球心的位置即可求出球半径。
具体方法是找到三条两两垂直的线段,然后使用公式2R=a+b+c或2R=a^2+b^2+c^2来求出R。
例如,在已知各顶点都在同一球面上的正四棱柱的高为4,体积为16的情况下,可以求出该球的表面积为32π。
第二种类型为对棱相等模型,补形为长方体。
在这种情况下,需要找到对棱相等的空间几何体,并补成长方体。
例如,如果三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积为36π。
除此之外,文章还给出了一些具体的例子,如正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA=23,则正三棱锥S-ABC外接球的表面积为36π。
同时,文章还提到了一些需要注意的引理,如正三棱锥的对棱互相垂直等。
需要注意的是,文章中存在一些格式错误和明显有问题的段落,需要进行删除或修改。
题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD,AD=BC,AC=BD)首先,我们可以画出一个长方体,标出三组互为异面直线的对棱,如图2-1所示。
设出长方体的长宽高分别为a,b,c,AD=BC=x,AB=CD=y,AC=BD=z,列方程组:a^2+b^2=x^2b+c=yc^2+a^2=z^2根据墙角模型,我们可以得到2R=a+b+c=2(x^2+y^2+z^2)/(x^2+y^2+z^2),化简得到R=sqrt(2)/2*(x^2+y^2+z^2)/(x^2+y^2+z^2),求出R即可。
例2(1)如下图所示三棱锥A-BCD,其中AB=CD=5,AC=BD=6,AD=BC=7,则该三棱锥外接球的表面积为。
2)在三棱锥A-BCD中,AB=CD=2,AD=BC=3,AC=BD=4,则三棱锥A-BCD外接球的表面积为。
3)正四面体的各条棱长都为2,则该正面体外接球的体积为。
专题——几何体的外接球和内切球问题

B.112π
C.1 000π 9
D.5 000 10π 81
※内切球问题 1.正棱锥的内切球.
第一步:先现出内切球的截面图, E, H 分别是两个三角形的外心; 第二步:由 POE 相似于 PDH ,建立等式: OE PO ,解出 r
DH PD
2.任意多面体的内切球:等体积法,
例 3 非直二面角类型
(1)内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
专题——几何体的外接球和内切球问题
※基础知识:
1.常见平面图形:正方形,长方形,正三角形的外接圆和内切圆
长方形(正方形)的外接圆半径为对角线长的一半,正方形的内切圆半径为边长的一半;
正三角形的内切圆半径: 3 a 6
外接圆半径: 3 a 3
面体的外接球的球心。 由定义,给出以下简单多面体外接球的球心的结论。
结论 1:正方体或长方体的外接球的球心就是其体对角线的中点,即其外接球的半径 R 满足:
2R2 a2 b2 c2 ,即 R a2 b2 c2
2 结论 2:正棱柱的外接球的球心是上下底面中心的连线的中点,即正棱柱的外接球的半径 R 为: R h 2 r 2 (其中 h 为正棱柱的侧棱长, r 是底面多边形的外接圆的半径)
(1)已知边长为 2 3 的菱形 ABCD 中,BAD 60 ,沿对角线 BD 折成二面角 A BD C 的大
小为120 的四面体,则该四面体的外接球的表面积为
。
第一步:先求出多面体的表面积和体积; 第二步:解出 r 3V S表
例 1、正方体的内切球与其外接球的体积之比为( )
球。
3.球的截面:
用一平面 去截一个球 O ,设 OO 是平面 的垂线段,O 为垂 足,且 OO d ,所得的截面是以球心在截面内的射影为圆心,以
立体几何中球的内切和外接问题完美版

性质
内切球的球心位于旋转体 的轴线上,且球的半径等 于旋转体半径。
应用
在几何和工程领域中,内 切球常用于研究旋转体的 体积和表面积。
旋转体的外接球
定义
旋转体的外接球是指与旋 转体外侧相切的球。
性质
外接球的球心位于旋转体 外侧,且球的半径等于旋 转体轴线到旋转体外侧的 垂直距离。
应用
在几何ቤተ መጻሕፍቲ ባይዱ工程领域中,外 接球常用于研究旋转体的 空间位置和关系。
立体几何中球的内 切和外接问题完美 版
目 录
• 球与多面体的内切和外接问题 • 球与旋转体的内切和外接问题 • 球与几何体的内切和外接问题实例 • 总结与展望
01
CATALOGUE
球与多面体的内切和外接问题
多面体的内切球
01
02
03
04
多面体的内切球是指与多面 体的所有顶点和面都相切的
球。
内切球半径的求法:设多面体的 每个面为$S_i$,内切球的半径
03
CATALOGUE
球与几何体的内切和外接问题实例
多面体内切球实例
总结词
多面体内切球是指一个球完全内切于一个多面体,且与多面体的每个面都相切 。
详细描述
多面体内切球的问题可以通过几何定理和公式来解决,例如欧拉公式和球内切 定理。例如,一个正方体的内切球就是其中心,半径等于正方体边长的一半。
旋转体外接球实例
外接球的性质:外接球与 多面体的每个顶点都相切 ,且外接球的直径等于多 面体的对角线长度。
外接球的应用:在几何、 物理和工程领域中,外接 球的概念被广泛应用于研 究多面体的性质和计算。
02
CATALOGUE
球与旋转体的内切和外接问题
第08讲 拓展一:空间几何体内接球与外接球问题 (讲)(含答案解析)

第08讲拓展一:空间几何体内接球与外接球问题(讲)第08讲拓展一:空间几何体内接球与外接球问题(精讲)高频考点一:空间几何体的内切球问题建立模型球的内切问题(等体积法)例如:在四棱锥P ABCD -中,内切球为球O ,求球半径r .方法如下:P ABCD O ABCD O PBC O PCD O PAD O PABV V V V V V ------=++++即:1111133333P ABCD ABCD PBC PCD PAD PAB V S r S r S r S r S r -=⋅+⋅+⋅+⋅+⋅,可求出r .典型例题例题(2022·江苏·苏州外国语学校高一期末)1.在三棱锥S ABC -中,SA ⊥平面,90ABC ABC ∠= ,且3,4,5SA AB AC ===,若球O 在三棱锥S ABC -的内部且与四个面都相切(称球O 为三棱锥S ABC -的内切球),则球O 的表面积为()A .169πB .49πC .3227πD .1681π【答案】A解:因为SA ⊥平面,90ABC ABC ∠= ,AB ⊂平面ABC ,AC ⊂平面ABC ,BC ⊂平面ABC ,所以SA AB ⊥,SA AC ⊥,SA BC ⊥,又,BC AB SA AB A ⊥= ,所以BC ⊥平面SAB ,所以BC SB ⊥,所以,,SAB ABC SAC SBC ,均为直角三角形,设球O 的半径为r ,则()1+++3S ABC SAB CAB SAC SBC V S S S S r -=⋅ ,而11334632S ABC V -=⨯⨯⨯⨯=,11156,35222SAB CAB SAC SBC S S SA AB S S ==⋅===⨯⨯= ,所以115156+6++6322r ⎛⎫⋅= ⎪⎝⎭,解得23r =,所以球O 的表面积为221644239r S πππ⎛==⨯=⎫ ⎪⎝⎭,故选:A .例题(2022·全国·高一)2.某学校开展手工艺品展示活动,小明同学用塑料制作了如图所示的手工艺品,其外部为一个底面边长为6的正三棱柱,内部为一个球,球的表面与三棱柱的各面均相切,则该内切球的表面积为___________,三棱柱的顶点到球的表面的最短距离为___________.【答案】12π解:依题意如图过侧棱的中点作正三棱柱的截面,则球心为MNG 的中心,因为6MN =,所以MNG 内切圆的半径13r OH MH ====即内切球的半径R 2412S R ππ==,又正三棱柱的高12AA R ==所以23OM OH ==AO =所以A 到球面上的点的距离最小值为AO R -故答案为:12π例题(2022·全国·高一专题练习)3.如图,直三棱柱111ABC A B C -有外接圆柱1OO ,点O ,1O 分别在棱AB 和11A B 上,4AB =.(1)若AC BC =,且三棱柱111ABC A B C -有一个内切球,求三棱柱111ABC A B C -的体积;【答案】(1))161-(1)O ,1O 是圆柱的上下底面圆心,而且点O ,1O 分别在棱AB 和11A B 上,由此可知ABC 是AB 为斜边的直角三角形.4,AB AC BC =∴==11422ABC S AC BC =⋅=⨯= 设ABC 的内切圆的半径为r ,则由等面积法,可知:()1122AB BC AC r AC BC ++⋅=⋅,)21r ∴=,故三棱柱111ABC A B C -的内切球的半径也是)21,故三棱柱的高)241h r ==,进而三棱柱111ABC A B C -的体积))441161ABC V S h =⋅=⨯-=- .题型归类练(2022·全国·高一)1.已知点O 到直三棱柱111ABC A B C -各面的距离都相等,球O 是直三棱柱111ABC A B C -的内切球,若球O 的表面积为16π,ABC 的周长为4,则三棱锥1A ABC -的体积为()A .43B .163C .3D .3(2022·湖南·高一期末)2锥的底面和侧面均相切)的表面积为______.(2022·全国·高三专题练习(文))3.若正四棱锥P ABCD -内接于球O ,且底面ABCD 过球心O ,则球O 的半径与正四棱锥P ABCD -内切球的半径之比为__________.(2022·广西玉林·模拟预测(理))4.若正四棱锥P ABCD -内接于球O ,且底面ABCD 过球心O ,球的半径为4,则该四棱锥内切球的体积为_________.高频考点二:空间几何体的外接球问题模型1:长(正)方体模型——公式法建立模型正方体或长方体的外接球的球心为其体对角线的中点(1)设长方体一个顶点出发的三条边长分别为a ,b ,c ,则外接球半径2r =;(2)设正方体边长为a ,则外接球半径2r a =;典型例题例题(2022·贵州黔西·高二期末(理))1.若一个长方体的长、宽,高分别为4,2,3,则这个长方体外接球的表面积为______________.【答案】29π由题知,长方体的体对角线即为外接球的直径,所以2222(2)42329R =++=,所以2294R =所以外接球的表面积2429S R ππ==.故答案为:29π例题(2022·新疆·乌苏市第一中学高一期中)2.正方体1111ABCD A B C D -的棱长为2,则此正方体外接球的表面积是______.【答案】12π因为正方体的体对角线长度等于长方体外接球的直径,又正方体1111ABCD A B C D -的棱长为2,所以正方体外接球的直径为则该正方体外接球的表面积是2412ππ==S r .故答案为:12π.题型归类练(2022·全国·高一期末)5.正方体的外接球与内切球的表面积之比是()A .13B .3C .D (2021·河北·深州长江中学高三期中)6.已知某正方体外接球的表面积为3π,则该正方体的棱长为______.(2021·福建·莆田锦江中学高一期中)7.已知正方体的棱长为2,则其外接球的表面积为______.模型2:墙角型,对棱相等型——补形法(补长方体或正方体)建立模型①墙角模型(三条线两个垂直)题设:三条棱两两垂直(重点考察三视图)②对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB CD =,AD BC =,AC BD =)典型例题例题(2022·全国·高一)1.若三棱锥-P ABC 的三条侧棱PA ,PB ,PC 两两互相垂直,且PA PB PC ===则其外接球的表面积为()()A .6πB .12πC .18πD .24π【答案】A侧棱PA ,PB ,PC 两两互相垂直,且PA PB PC ===PA ,PB ,PC 作为正方体的棱长,如图:设外接球的半径为R ,则正方体的对角线的长2R =所以R =,所以外接球的表面积为246S R ππ==.故选:A例题(2022·江苏·南京师大附中高一期末)2.在三棱锥-P ABC 中,5PA BC ==,PB AC ==PC AB ==锥外接球的表面积为_________;外接球体积为_________.【答案】26π由题意,该三棱锥的对棱相等,可知该三棱锥可置于一个长方体中,如图所示:记该长方体的棱长为,,a b c ,则222222101725a b a c b c ⎧+=⎪+=⎨⎪+=⎩,即22226a b c ++=,所以r =,23442633S r V r πππ====,.故答案为:26π题型归类练(2022·辽宁·本溪高中高一阶段练习)8.已知正三棱锥S ABC -,则此三棱锥的外接球的表面积为()A .πB .3πC .6πD .9π(2022·安徽·高一阶段练习)9.鳖臑是我国古代对四个面均为直角三角形的三棱锥的称呼.如图,三棱锥A BCD -是一鳖臑,其中AB BC ⊥,AB BD ⊥,BC CD ⊥,AC CD ⊥,且3BC DC ==,4AB =.则三棱锥A BCD -外接球的表面积是()A.25πB .34πC .100πD .3(2022·河北·沧县中学高一期中)10.三棱锥-P ABC 中,已知,,PA PB PC 两两垂直,且1,2PA PB PC ===,则三棱锥-PABC 的外接球的表面积为___________.(2022·贵州·清华中学高三阶段练习(理))11.四棱锥ABCD 中,2,======AB CD AD BC AC BD A ,B ,C ,D 的外接球的表面积是__________.模型3:单面定球心法(定+算)建立模型单面定球心法(定+算)步骤:①定一个面外接圆圆心:选中一个面如图:在三棱锥-P ABC 中,选中底面ABC ∆,确定其外接圆圆心1O (正三角形外心就是中心,直角三角形外心在斜边中点上,普通三角形用正弦定理定外心2sin ar A=);②过外心1O 做(找)底面ABC ∆的垂线,如图中1PO ⊥面ABC ,则球心一定在直线(注意不一定在线段1PO 上)1PO 上;③计算求半径R :在直线1PO 上任取一点O 如图:则OP OA R ==,利用公式22211OA O A OO =+可计算出球半径R .典型例题例题(2022·山西省长治市第二中学校高一期末)1.在四面体ABCD 中,,ABD BCD 都是边长为2的等边三角形,且平面ABD ⊥平面BCD ,则该四面体外接球的表面积为_________.【答案】203π依题意作图,取BD 的中点P ,连接AP ,CP ,取ABD △的中心E ,BCD △的中心G ,分别作平面ABD 和平面BCD 的垂线,得交点H ,则H 点就是四面体ABCD 外接球的球心,CH 就是球的半径r ,AP CP HG PE CG =====,222253r CH CG GH ==+=,外接球的面积为22043S r ππ==;故答案为:203π.例题(2023·山西大同·高三阶段练习)2.球内接直三棱柱1111,1,120,2ABC A B C AB AC BAC AA -===︒∠=,则球表面积为___________.【答案】8π设三角形ABC 和三角形111A B C 的外心分别为D ,E .可知其外接球的球心O 是线段DE 的中点,连结OC ,CD ,设外接球的半径为R ,三角形ABC 的外接圆的半径r ,1,120,AB AC BAC =∠=︒=可得BC =,由正弦定理得,21sin120r r ︒=∴=,而在三角形OCD 中,可知222||||||CO OD CD =+,即2212R r =+=,因此三棱柱外接球的表面积为248S R ππ==.故答案为:8π例题(2022·广西贺州·高一期末)3.已知ABC ∆的三个顶点都在球O 上,AC BC ⊥,2AC BC ==,且三棱锥3O ABC V -=,则球O 的体积为()A .π3B .32π3C .π3D .36π【答案】D△ABC 中,AC BC ⊥,2AC BC ==,则AB =取AB 中点H ,连接OH ,则点H 为△ABC 所在小圆圆心,OH ⊥平面ABC则112232O ABC V OH -=⨯⨯⨯⋅,解之得OH则球O 的半径3OA 则球O 的体积为34π3=36π3⋅故选:D例题(2022·河南开封·高二期末(理))4.已知球O 为三棱锥D ABC -的外接球,球O 的体积为256π3,正三角形ABC 的外接圆半径为D ABC -的体积的最大值为______.【答案】设ABC 外接圆的圆心为1O ,因为正三角形ABC 的外接圆半径为23,即123O B =,由正弦定理243sin 60ACR ==︒,得6AC =,所以166sin 60932ABC S =⨯⨯⨯︒= ,要使三棱锥D ABC -的体积最大,则1O D ⊥平面ABC ,且球心O 在线段1O D 上,因为球O 的体积为34π256π33R =,所以球O 的半径为4R =.在1Rt OO B 中,由勾股定理得221116122OO R O B =-=-=,所以三棱锥D ABC -体积的最大值()()111932418333ABC V S OO R =⋅+=⨯⨯+=△.故答案为:183题型归类练(2022·河北·衡水市第十三中学高一阶段练习)12.在正四棱锥P ABCD -中,4AB =,6PA =,则平面PAB 截四棱锥P ABCD -外接球的截面面积是()A .655πB .365πC .12πD .36π(2022·安徽·巢湖市第一中学模拟预测(文))13.已知三棱锥S ABC -中,平面SAC ⊥平面ABC ,且AB AC ⊥,30SCA ∠=︒,若4AB SA ==,则三棱锥S ABC -外接球的表面积为()A .64πB .128πC .40πD .80π(2022·重庆市万州第二高级中学高一期中)14.在ABC 中,角A ,B ,C 所对的边为a ,b ,c ,且3a =,π3A =.又点A ,B ,C 都在球O 的球面上,且点O 到平面ABC 5O 的体积为()A .642π3B 635π3C .643π3D 636π3(2022·河南·汝州市第一高级中学模拟预测(文))15.已知点,,,A B C D在同一个球的球面上,1AB =,BC =,2AC =,若四面体ABCD)A .14425πB .24825πC .57625πD .67625π(2022·全国·高三专题练习)16.已知球O 是正三棱锥A BCD -的外接球,3BC =,AB =E 在线段BD 上,且6BD BE =,过点E 作球O 的截面,则所得截面圆面积的取值范围是___________.模型4:双面定球心法(两次单面定球心)建立模型如图:在三棱锥-P ABC 中:①选定底面ABC ∆,定ABC ∆外接圆圆心1O ②选定面PAB ∆,定PAB ∆外接圆圆心2O ③分别过1O 做面ABC 的垂线,和2O 做面PAB 的垂线,两垂线交点即为外接球球心O .典型例题例题(2022·全国·高三专题练习)1.已知点A 、B 、C 、D 都在球O 的球面上,AB AC =,BCD ∆是边长为1的等边三角形,AD 与平面BCD 所成角的正弦值为3,若2AD =,且点D 在平面BCD 上的投影与D 在BC 异侧,则球O 的表面积为()A .πB .4πC .8πD .16π【答案】B由题设,若E 是BC 的中点,则O '是△BCD 的中心,连接DE ,如图示:由题设知:DE BC ⊥,AE BC ⊥,又AE DE E = ,则BC ⊥面AED ,而BC ⊂面BCD ,即面BCD ⊥面AED ,过A 作AF ⊥面BCD ,则F 必在直线DE 上,易知:ADF ∠为AD 与平面BCD 所成角的平面角,又AD 与平面BCD ,2AD =,可得DF =.过O '作OO DE '⊥交AD 于O ,易知:OD OB OC ==,而O D '=12O D DF '=,又//AF OO ',故O 为AD 的中点,OD OA =,∴OD OB OC OA ===,即O 是球心,故球O 的半径为1,∴球O 的表面积为4π.故选:B例题(2022·全国·高三专题练习(理))2.已知平面四边形ABCD 中,4AB AD BD =====,现沿BD 进行翻折,使得A 到达A '的位置,连接A C ',此时二面角A BD C '--为150°,则四面体A BCD '外接球的半径为()A .3B .3C D .3【答案】C解:取BD 的中点E ,连接A E ',CE ,因为4AB AD BD =====即BC CD ==所以CE BD ⊥,A E BD '⊥,A EC '∠即为二面角A BD C '--的平面角,且90BCD ∠=︒,所以BCD △外接圆的圆心为E ,设A BD ' 外接圆的圆心为1O ,则1O E =过点1O ,E 分别作平面A BD ',平面BDC 的垂线,交于点O ,则O 即为四面体A BCD '外接球的球心.因为二面角A BD C '--的平面角为150︒,即150A EC '∠=︒,则160∠=︒OEO .在1Rt OO E △中,3cos603OE ==︒,连接OB ,则OB 即为外接球的半径R ,则2222283R OB OE BE ==+=,即3R =,故选:C .题型归类练(2022·湖南·邵阳市第二中学高一期末)17.一边长为4的正方形ABCD ,M 为AB 的中点,将AMD ,BMC △分别沿MD ,MC 折起,使MA ,MB 重合,得到一个四面体,则该四面体外接球的表面积为().A .763πB .48πC .81πD .9(2022·广东梅州·高一阶段练习)18.如图,在三棱锥-P ABC ,PAC △是以AC 为斜边的等腰直角三角形,且CB =AB AC ==,二面角P AC B --的大小为120︒,则三棱锥-P ABC 的外接球表面积为()AB .10πC .9πD .(4π+参考答案:1.B【分析】设三棱柱111ABC A B C -的高为h ,内切球O 的半径为r ,通过内切球的半径可求出h ,再求得ABC S ,由体积公式即可求解三棱锥1A ABC -的体积.【详解】解:设直三棱柱111ABC A B C -的高为h ,AB =c ,BC =a ,AC =b ,内切球O 的半径为r ,则h =2r ,由题意可知球O 的表面积为2164r ππ=,解得r =2,∴h =4,又△ABC 的周长为4,即a +b +c =4,∴连接OA ,OB ,OC ,111,,OA OB OC 可将直三棱柱111ABC A B C -分成5个棱锥,即三个以原来三棱柱侧面为底面,内切球球心为顶点的四棱锥,两个以原来三棱柱底面为底面,内切球球心为顶点的的三棱锥,∴由体积相等可得直三棱柱111ABC A B C -的体积为ABC S h =13ahr +13bhr +13chr +2×13ABC S r ,即4ABC S =13(a +b +c )hr +43ABC S ,∴ABC S =4,∴三棱锥1A ABC -的体积为13ABC S h =13×4×4=163.故选:B .2.4π【分析】根据已知先求母线长,再结合轴截面可得半径,然后可得.【详解】有题意可知,PA π⋅=,所以PA =所以,圆锥的轴截面是边长为23的正三角形,圆锥的内切球的半径等于该正三角形的内切圆的半径,所以tan 3tan 301R OD AD OAD ==⋅∠=⨯︒=,所以该圆锥的内切球的表面积为4π.故答案为:4π331+##13+【分析】根据外接球的性质,结合正四棱锥的性质、内切球的性质进行求解即可.【详解】设外接球半径为R ,由题意可知,OA =OB =OC =OD =OP =R ,设四棱锥P -ABCD 的内切球半径为r ,设正方形ABCD 的边长为a ,因为底面ABCD 过球心O 2222a a R a R +=⇒=,2222116()2242R a R R R +=+⋅=,设该正四棱锥的表面积为S ,由等体积法可知:2211161(224)(2),(31)33223V Sr R R r R R R r ==+⋅⨯==+,314.6435)3π【分析】利用等体积法可求出四棱锥内切球的半径,从而可求出其体积【详解】因为正四棱锥P ABCD -内接于球O ,且底面ABCD 过球心O ,球的半径为4,所以4OA OB OC OD OP =====,所以42AB BC CD DA PA PB PC PD ========,所以正四棱锥P ABCD -的表面积为((22432S =+=,正四棱锥P ABCD -的体积为(21128433V =⨯⨯=设正四棱锥P ABCD -内切球的半径为r,则1112832)333V Sr r ==+=,解得1)r =,所以该四棱锥内切球的体积为334464(35)1)333r ππ⎡⎤=⨯=⎣⎦,故答案为:645)3π5.B【分析】设正方体的棱长为a ,求出其外接球的半径和内切球的半径,再根据表面积公式可得结果.【详解】设正方体的棱长为a,则其外接球的半径为2a ,内切球的半径为12a ,所以正方体的外接球与内切球的表面积之比是224142a ππ⎫⋅⎪⎝⎭⎛⎫⋅ ⎪⎝⎭3=.故选:B 6.1【分析】根据球的表面积公式,求得球的半径,结合正方体的对角线长等于外接球的直径,列出方程,即可求解.【详解】设正方体的棱长为a ,外接球的半径为R ,2R =,由243R ππ=,可得R22=⨯,解得1a =.故答案为:1.7.12π【分析】由于正方体的外接球直径等于正方体的体对角线,所以求出正方体的体对角线的长,可求出球的半径,从而可求出外接球的表面积【详解】解:设正方体外接球的半径为R ,则由题意可得()2222222212R =++=,即2412R =,所以外接球的表面积为2412R ππ=,故答案为:12π8.C【分析】根据题意,把三棱锥S ABC -外接球的半径,进而求得外接球的表面积,即可求解.【详解】由题意,正三棱锥S ABC -此三棱锥S ABC -的正方体,三棱锥S ABC -设正方体的外接球的半径为R ,可得2R =,即R =,所以此三棱锥的外接球的表面积为224π4π6πS R ==⨯=⎝⎭.故选:C.9.B【分析】结合长方体外接球的性质可知三棱锥A BCD -外接球的直径为AD ,进而可得结果.【详解】易得三棱锥A BCD -外接球的直径为AD ,则AD ,故三棱锥A BCD -外接球的半径R =所以24342S ππ⎛⎫=⨯= ⎪⎪ ⎭⎝,故选:B.10.9π【分析】将三棱锥-P ABC 放在长方体中,则长方体的外接球与三棱锥的外接球相同,即可求解.【详解】以线段,,PA PB PC 为相邻的三条棱为长方体,连接AB ,BC ,AC ,即为三棱锥-P ABC ,∵如图所示,长方体的外接球与三棱锥的外接球相同,∴则其外接球直径为长方体对角线的长,设外接球的半径为R ,则2222222(2)1229R PA PB PC =++=++=,解得32R =,则294π4π9π4S R ==⨯=.故答案为:9π.11.13π【分析】由题意将此四棱锥补成一个长方体,则经过A ,B ,C ,D 的外接球即为长方体的外接球,然后求出长方体的对角线的长即可得外接球的直径,从而可求出其表面积【详解】解:因为四棱锥ABCD 的对棱相等,所以将四棱锥ABCD 补成如图所示的长方体,则经过A ,B ,C ,D 的外接球即为长方体的外接球,所以球的直径为长方体的对角线的长,设长方体的长、宽、高分别为,,a b c ,因为2,======AB CD AD BC AC BD ,所以22222241012a b a c b c ⎧+=⎪+=⎨⎪+=⎩,解得13a b c =⎧⎪=⎨⎪=⎩所以球的半径r =所以球的表面积为2244132r πππ=⨯=⎝⎭,故答案为:13π12.B【分析】先作出辅助线,求出外接球半径,求出球心到截面的距离,从而得到截面圆的半径,求出截面的面积.【详解】如图,作PO '⊥平面ABCD ,垂足为O ',则O '是正方形ABCD 外接圆的圆心,从而正四棱锥P ABCD -外接球的球心O 在PO '上,取棱AB 的中点E ,连接,,,O D O E OD PE '',作OH PE ⊥,垂足为H .由题中数据可得2,4O D O E PE O P '''====,设四棱锥P ABCD -外接球的半径为R ,则()22222R O D O O OP O P O O =+='-'='',即()22284R O O O O =+='-',解得3R =.由题意易证OPH EPO ' ∽,则PH OPO P PE=',故PH =故所求截面圆的面积是236ππ5PH ⋅=.故选:B 13.D【分析】三棱锥补成三棱柱,问题转化为三棱柱的外接圆,利用球心到底面圆的距离为12AB ,截面圆的半径为12sin 30SA ⋅︒,由222R d r =+求球半径即可.【详解】由题意得,BA ⊥平面SAC ,将三棱锥补成三棱柱11SAC S BC -,如图,则三棱柱11SAC S BC -的外接球即为所求.设外接球的球心为O ,则SAC 的外心为1O ,则1122OO AB ==,又1142sin SAO A SCA=⨯=∠,则外接球的半径R =表面积2480S R ππ==,故选:D 14.A【分析】依据截面圆半径和球心距即可求得球半径,进而求得球O 的体积.【详解】ABC的外接圆半径2sin 2ar A===则球O 的半径2R=则球O 的体积为(3344πR π33V ===3故选:A 15.D【分析】由已知得到ABC 为直角三角形,得到ABC 所以直角ABC 所在截面小圆的半径1r =,设点D 到平面ABC 的距离为h ,结合题意求得5h =,设四面体ABCD 的外接球半径为R ,球心O 到截面的距离为d ,当D 到底面ABC 距离最远时,即h R d =+时,求得135R =,进而求得球的表面积.【详解】由1,2AB BC AC ===,可得222AB BC AC +=,所以ABC 为直角三角形,其面积为112S ==,所以直角ABC 所在截面小圆的半径112r AC ==,设点D 到平面ABC 的距离为h ,因为四面体ABCD 体积取得最大值为6,所以113263D ABC ABC S h h V -=⨯==⨯ ,解得5h =,设四面体ABCD 的外接球半径为R ,球心O 到截面的距离为d ,当D 到底面ABC 距离最远时,即h R d =+时,四面体ABCD 的体积取得最大值,因为d ==5R +=,解得135R =,所以球的表面积为2136764525S ππ⎛⎫== ⎪⎝⎭.故选:D.16.5,44ππ⎡⎤⎢⎥⎣⎦【分析】设BDC 的中心为1O ,球O 的半径为R ,连接1O D ,OD ,1O E ,OE ,可得223(3)R R =+-,解得2R =,过点E 作圆O 的截面,当截面与OE 垂直时,截面的面积最小,当截面过球心时,截面面积最大,即可求解.【详解】解:如图,设BDC 的中心为1O ,球O 的半径为R ,连接1O D ,OD ,1O E ,OE ,则123sin 603O D =︒⨯=13AO =,在Rt 1OO D 中,223(3)R R =+-,解得2R =,6BD BE = , 2.5DE ∴=,在1DEO 中,12O E ==,OE ∴===过点E 作圆O 的截面,当截面与OE 垂直时,截面的面积最小,,最小面积为54π,当截面过球心时,截面面积最大,最大面积为4π.∴所得截面圆面积的取值范围是5,44ππ⎡⎤⎢⎥⎣⎦,故答案为:5,44ππ⎡⎤⎢⎥⎣⎦.17.A【分析】先判断出MA ⊥平面ACD ,△ACD 为等边三角形.利用球内截面的性质,过△ACD 的中心O1作平面ACD 的垂线l1,过线段MC 的中点O2作平面MAC 的垂线l2,记12l l O =∩,则O 即为三棱锥M 一ACD 外接球的球心.利用勾股定理求出半径R ,即可求出外接球的表面积.【详解】如图所示,由图可知在四面体A -CDM 中,由正方形,ABCD M 为AB 的中点,可得MA ⊥AD ,MA ⊥AC ,AC ∩AD =A ,故MA ⊥平面ACD .将图形旋转得到如图所示的三棱锥M -ACD ,其中△ACD 为等边三角形,过△ACD 的中心O1作平面ACD 的垂线l1,过线段MC 的中点O2作平面MAC 的垂线l2,由球内截面的性质可得直线l1与l2相交,记12l l O =∩,则O 即为三棱锥M 一ACD 外接球的球心.设外接球的半径为R ,连接OC ,O1C ,可得111O C ==.在Rt △OO1C 中,222211193OC OO O C R =+==,故该外接球的表面积219764433S R πππ==⨯=.故选:A.18.B【分析】由题作出图形,易得PAC △外接圆圆心在AC 中点,结合正弦定理可求ABC 外接圆半径,结合图形知,()()222222R AO AO OO ==+,再结合二面角大小求出2OO ,进而得解.【详解】根据题意,作出图形,如图所示,因为PAC △是以AC 为斜边的等腰直角三角形,所以PAC △的外心在AC 中点,设为2O ,设ABC 的外心为1O ,BC 中点为E ,11AO r =,因为AB AC ==,所以1O 必在AE 连线上,则123sin AB ABr AEC AC===,即132r =,因为两平面交线为AC ,1O 为平面ABC 所在圆面中心,所以12O O AC ⊥,()221212O O r AO =-又因为二面角P AC B --的大小为120︒,2PO AC ⊥,所以2121120,30PO O OO O ∠=︒∠=︒,所以2121OO O O =⨯,锥体-P ABC 外接球半径()()2222222512R AO AO OO ==+=+=⎝⎭,则三棱锥-P ABC 的外接球表面积为2410S R ππ==,故选:B。
高中数学几何体的外接球与内切球的6个题型!-掌门1对1

高中数学几何体的外接球与内切球的6个题型!-掌门1对1 今天掌门1对1在线一对一小编老师给大家总结了一些常见的外接球与内切球的问题,请同学们好好研究一下,难度不大,有一些规律要注意!另外,小编老师答应用嘟嘟星xi 给的题目做例题的,但是小编老师用几何画板的能力还需要加强,所以,时间有限,没有整理出来!等节后,小编老师一定再分析一下那几道例题!一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点,此类问题实质是解决球的半径尺或确定球心0的位置问题,其中球心的确定是关键.(一)由球的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.结论4:正棱锥的外接球的球心在其高上,具体位置可通过计算找到.结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.(二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.以下是常见的、基本的几何体补成正方体或长方体的途径与方法.途径1:正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体.途径2:同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体.途径3:若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.途径4:若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.(三) 由性质确定球心利用球心O与截面圆圆心O1的连线垂直于截面圆及球心O与弦中点的连线垂直于弦的性质,确定球心.二、内切球问题若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
八个模型全搞定空间几何的外接球和内切球问题(学生版)

1八个模型搞定空间几何体的外接球与内切球一、直棱柱模型1.已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是。
2.一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为。
3.直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于。
4.在直三棱柱ABC A B C 111中,AB 4,AC 6,,A 3AA 14则直三棱柱ABC A B C 111的外接球的表面积为。
5.若三棱锥S ABC 的三条侧棱两两垂直,且SA 2,SB SC 4,则该三棱锥的外接球半径为。
6.三棱锥S ABC 中,侧棱SA 平面ABC ,底面ABC的正三角形,SA ,则该三棱锥的外接球体积等于。
,则其外接球的表面积是。
8.在四面体S ABC -中,SA ABC 平面,,,,BAC SA AC AB 12021则该四面体的外接球的表面积为。
二、棱锥所有侧棱相等模型1、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是。
2.正三棱锥S ABC 中,底面ABC侧棱长为2,则该三棱锥的外接球体积等于。
3、在三棱锥P ABC中,PA PB PC ,侧棱PA 与底面ABC 所成的角为60 ,2则该三棱锥外接球的体积为。
三、侧面与底面垂直模型1.三棱锥P ABC 中,平面PAC 平面ABC ,AC 2,PA PC 3,AB BC ,则三棱锥P ABC 外接球的半径为。
2.三棱锥P ABC 中,平面PAC 平面ABC ,△PAC 边长为2的正三角形,AB BC ,则三棱锥P ABC 外接球的半径为。
3.已知EAB 所在的平面与矩形ABCD 所在的平面互相垂直,,EA EB AD AEB 3260,则多面体E ABCD 的外接球的表面积为。
高考数学立体几何体的外接球与内切球常见题型

高考数学立体几何体的外接球与内切球常见题型介绍在高考数学中,立体几何是一个重要的考点。
其中,经常涉及到求解立体几何体的外接球和内切球的问题。
本文将介绍几种常见的题型以及解题方法,帮助考生更好地理解和应对这类题目。
以下是具体内容。
外接球的题型题型1:求立体几何体的外接球的半径或直径这类题型要求求解一个给定立体几何体的外接球的半径或直径。
解题的关键是找到立体几何体的特性和几何关系。
解题步骤:1. 确定给定立体几何体的特性,如边长、角度等。
2. 根据立体几何体的几何关系,得出外接球与立体几何体的关系。
3. 利用几何关系,建立方程。
4. 求解方程,得到外接球的半径或直径。
题型2:求多个立体几何体的共同外接球的半径或直径这类题型要求求解多个给定立体几何体的共同外接球的半径或直径。
解题的关键是找到多个立体几何体之间的共同特性和几何关系。
解题步骤:1. 确定给定立体几何体的特性,如边长、角度等。
2. 找到多个立体几何体之间的共同特性和几何关系。
3. 根据几何关系,建立方程。
4. 求解方程,得到共同外接球的半径或直径。
内切球的题型题型1:求立体几何体的内切球的半径或直径这类题型要求求解一个给定立体几何体的内切球的半径或直径。
解题的关键是找到立体几何体的特性和几何关系。
解题步骤:1. 确定给定立体几何体的特性,如边长、角度等。
2. 根据立体几何体的几何关系,得出内切球与立体几何体的关系。
3. 利用几何关系,建立方程。
4. 求解方程,得到内切球的半径或直径。
题型2:求多个立体几何体的共同内切球的半径或直径这类题型要求求解多个给定立体几何体的共同内切球的半径或直径。
解题的关键是找到多个立体几何体之间的共同特性和几何关系。
解题步骤:1. 确定给定立体几何体的特性,如边长、角度等。
2. 找到多个立体几何体之间的共同特性和几何关系。
3. 根据几何关系,建立方程。
4. 求解方程,得到共同内切球的半径或直径。
总结本文介绍了高考数学立体几何体的外接球和内切球常见题型,并给出了解题的步骤和方法。
立体几何中球内切和外接问题(完美版)

则这个球的表面积是( )
A.16π
B.20π
C.24π
D.32π
4
举一反三-突破提升
2.正六棱柱的底面边长为 4,高为 6,则它的外接球的表面积为
A. 20 B. 25 C. 100 D. 200
4
举一反三-突破提升
已知正三棱锥 P-ABC 的主视图和俯视图如图所 示,
则此三棱锥的外接球的表面积为 ( )
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形,AB=2,
SA=SB=SC=2,则该三棱锥的外接球的球心到平面 ABC 的距离为( )
S
A.
B.
C.1
D.
答案:D.
O
,即
.
C
A
M
B
7
若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
例 9、已知三棱锥的四个顶点都在球 的球面上,
4
内切球半径:r 6 a
12
结论:正四面体与球的接切问题,可通过线面关系证出,内切球 和外接球的两个球心是重合的,为正四面体高的四等分点,即定 有内切球的半径 r 1(为h 正四面体的高),且外接球的半径 .R 3r
4
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不 重合。
C 求正多面体外接球的半径
A B
O D
C
求正方体外接球的半径
4
直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
例 4、(2014)已知三棱柱 若该棱柱的体积为
的侧棱垂直于底面,各顶点都在同一球面上,
.
ቤተ መጻሕፍቲ ባይዱ
球的内切、外接问题

P
球的表面积.
解1:作出截面图如图示. 由图可知,
3
AD
a,
2
2
3
AO AD
a.
3
3
a
6
2
2
∴PO PA AO
a.
3
6
∴OO PO PO
a R.
3
P
a
R
R
A
A
R O•
O•
•
O′
解得R
时,球内切于圆锥,如图所示,
O为球心,M为球O与母线PB的切点,E为底面圆心,
设球O的半径为R,底面圆E的半径为r,
因为圆锥侧面积为2π,
LOGO
(4)正棱锥、圆锥 ②外接球
例8 正四棱锥的五个顶点在同一个球面上,若该正
四棱锥的底面边长为4,侧棱长为2 6,求这个球
P
的表面积. 36π
PO′= 4,OO′=4-R,AO=R
2 6
AO2 = OO′ 2 + AO′ 2,
R=3
•
O′
R
R
A
O
O•
•
O′
O′
•
O
LOGO
(4)正棱锥、圆锥 ②外接球
正棱锥外接球半径求法——轴截面法
1.球心在棱锥的高所在的直线上
2.球心到底面外接圆圆心的距离d等于锥体的高h 减去球半径R的绝对值
d= |h -R |
P
3. R 2 r 2 (h R ) 2
4
9
O
1
, 解得r= 3
轴截面法
2023届高三数学一轮复习专题 空间几何体的外接球与内切球问题 讲义 (解析版)

空间几何体的外接球与内切球问题高考分析: 球与几何体的切接问题是近几年高考的高频考点,常以选择题和填空题的形式出现,以中档题和偏难题为主. 一、几种常见几何体的外接与内切球 1.长方体的外接球 (1)球心:体对角线的交点;(2)半径:R =a 2+b 2+c 22(a ,b ,c 为长方体的长、宽、高).2.正方体的外接球、内切球及与各条棱相切的球 (1)外接球:球心是正方体的中心;半径R =32a(a 为正方体的棱长); (2)内切球:球心是正方体的中心;半径r =2a(a 为正方体的棱长);(3)与各条棱都相切的球:球心是正方体的中心;半径=2r a (a 为正方体的棱长). 3.正四面体的外接球与内切球(1)外接球:球心是正四面体的中心;半径R (a 为正四面体的棱长);(2)内切球:球心是正四面体的中心;半径r (a 为正四面体的棱长).求外接球问题常用方法:1.补体法。
将几何体补形成长方体正方体等常见模型去求解2.外接球的球心都在过底面外接圆圆心的垂线上(注意球体可以滚动所以可以选择较为方便计算的那一面作为底面)3.利用外接球球心到几何体各顶点距离都等于半径4.球心与截面圆圆心的连线垂直于截面圆求外接球的关键是确定球心位置,进而计算出外接球半径。
题型一:柱体的外接球1.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为_________.2.已知三棱柱111ABC A B C -的底面是边长为6的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12 ,则该三棱柱的体积为_________.3.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )A .16πB .20πC .24πD .32π4.已知圆柱的底面半径为12,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4 C.π2 D.π4题型二:锥体的外接球5.求棱长为1的正四面体外接球的体积为_________.6.已知正四棱锥P -ABCD 内接于一个半径为R 的球,则正四棱锥P -ABCD 体积的最大值是( )A.16R 381B.32R 381C.64R 381 D .R 3 7.如图,在四棱锥P -ABCD 中,底面ABCD 为菱形,PB ⊥底面ABCD ,O 为对角线AC 与BD 的交点,若PB =1,∠APB =∠BAD =π3,则三棱锥P -AOB 的外接球的体积是_________.8.已知△ABC 是面积为的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( ) A.B.C. 1D.9.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A. 64πB. 48πC. 36πD. 32π10.《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵.将一堑堵沿其一顶点与相对的棱切开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均是直角三角形的四面体).在如图所示的堑堵ABC -A 1B 1C 1中,AA 1=AC =5,AB =3,BC =4,则阳马C 1-ABB 1A 1的外接球的表面积是( )A .25πB .50πC .100πD .200π11.已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为 A .68πB .64πC .62πD .6π12.已知正三棱锥的所有顶点都在球O 的球面上,其底面边长为3,E,F ,G 分别为为侧棱AB,AC,AD 的中点.若O 在三棱锥A -BCD 内,且三棱锥A -BCD 的体积是三棱锥O -BCD 体积的3倍,则平面EFG 截球O 所得截面的面积为微专题 球与几何体的切接问题——内切球1.半径为R 的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为_________,体积为_________.2.若正四面体的棱长为a ,则其内切球的半径为_________.3.已知正三棱锥的高为6,内切球(与四个面都相切)的表面积为16π,则其底面边长为( ) A .18 B .12 C .6 3 D .434.将半径为3,圆心角为2π3的扇形围成一个圆锥(接缝处忽略不计),则该圆锥的内切球的体积为( )A.2π3 B.3π3 C.4π3D .2π 5.如图,已知球O 是棱长为1的正方体ABCD -A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为( )A.66π B.π3 C.π6 D.33π题型三 最值问题6.已知底面是正六边形的六棱锥P -ABCDEF 的七个顶点均在球O 的表面上,底面正六边形的边长为1,若该六棱锥体积的最大值为3,则球O 的表面积为_________.7.四棱锥S -ABCD 的所有顶点都在同一球面上,底面ABCD 是正方形且和球心O 在同一平面内,当此四棱锥的体积取得最大值时,其表面积等于8+83,则球O 的体积等于( )A.32π3B.322π3 C .16π D.162π38.已知SAB 是边上为2的等边三角形,045ACB ∠=,则三棱锥体积最大时,CA = ;其外接球的表面积为。
(word完整版)高考数学中的内切球和外接球问题

高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.考查学生的空间想象能力以及化归能力.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法(公式法)1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为.例2一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24 ,则该球的体积为.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为.例4已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为().A. 16B. 20C. 24D. 323.求多面体的外接球的有关问题例5一个六棱柱的底面是正六边形, 其侧棱垂直于底面,已知该 六棱柱的顶点都在同一个球面上,且该六棱柱的体积为9,底面周长 为3,则这个球的体积为.解设正六棱柱的底面边长为x ,高为h ,则有 6x 3 9 会 3 2.6 — x h 8 4的半径的常用公式二、构造法(补形法)1、构造正方体例5若三棱锥的三条侧棱两两垂直,且侧棱长均为 V 3 ,则其外 接球的表面积是.例3若三棱锥的三个侧面两两垂直,且侧棱长均为V 3 ,则其外 接球的表面积是.故其外接球的表面积S 4 r 2 9 .小结:一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分 别为a,b,c ,则就可以将这个三棱锥补成一个长方体, 于是长方体的体 对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则 有2R va 2 b 2 c 2.出现“墙角”结构利用补形知识,联系长方体。
高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型墙角模型是指三条线段两两垂直的几何体,通过公式(2R) = a + b + c,即2R = a^2 + b^2 + c^2,可以求出其外接球半径R。
例1:1)已知顶点都在同一球面上的正四棱柱的高为4,体积为16,求该球的表面积。
解:由V = ah = 16,得a = 2,4R = a + a + h = 4 + 4 + 16 = 24,S = 24π,答案为C。
2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,求其外接球的表面积。
解:由2R = a + b + c = 3 + 3 + 3 = 9,得R = 9/4,S =4πR^2 = 9π。
3)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA = 23,求正三棱锥S-ABC外接球的表面积。
解:由墙角模型的特点可知,正三棱锥的对棱互垂直。
连接AB、BC的中点D、E,连接AE、CD,交于H,则H是底面正三角形ABC的中心。
由AM⊥MN,SB//MN,可得AM⊥SB,AC⊥SB,故SB⊥平面SAC,SB⊥SA,SB⊥SC,即SB⊥SA,BC⊥SA,故SA⊥平面SBC,SA⊥SC。
因此,三棱锥S-ABC的三棱条侧棱两两互相垂直,由2R^2 = 23^2 + 23^2 + 23^2 = 36,得R^2 = 9,S = 36π。
类型二、棱台模型棱台模型是指上底面和下底面都是正多边形,且两底面中心连线与侧棱垂直的几何体。
通过勾股定理和相似三角形,可以求出其外接球半径R和内切球半径r。
例2:1)已知棱台的上底面和下底面都是正三角形,上底边长为3,下底边长为6,侧棱长为5,求其外接球半径R和内切球半径r。
解:由勾股定理可得棱台的高为4√3.设外接球半径为R,内切球半径为r,则有R/r = (a + b + c)/(a + b - c) = (3 + 6 +5)/(3 + 6 - 5) = 7,解得R = 7r。
空间几何体的外接球与内切球问题(学生版)

空间几何体的外接球与内切球问题目录一、必备秘籍二、典型题型题型一:内切球等体积法题型二:内切球独立截面法题型三:外接球公式法题型四:外接球补型法题型五:外接球单面定球心法题型六:外接球双面定球心法三、专项训练一、必备秘籍1.球与多面体的接、切定义1;若一个多面体的各顶点都在一个球面上,则称这个多面体是这个球的内接多面体,这个球是多面体的外接球。
定义2;若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是多面体的内切球。
类型一球的内切问题(等体积法)例如:在四棱锥P-ABCD中,内切球为球O,求球半径r.方法如下:V P-ABCD=V O-ABCD+V O-PBC+V O-PCD+V O-PAD+V O-PAB即:V P-ABCD=13S ABCD⋅r+13S PBC⋅r+13S PCD⋅r+13S PAD⋅r+13S PAB⋅r,可求出r.类型二球的外接问题1、公式法正方体或长方体的外接球的球心为其体对角线的中点2、补形法(补长方体或正方体)①墙角模型(三条线两个垂直)题设:三条棱两两垂直(重点考察三视图)②对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD,AD=BC,AC=BD) 3、单面定球心法(定+算)步骤:①定一个面外接圆圆心:选中一个面如图:在三棱锥P-ABC中,选中底面ΔABC,确定其外接圆圆心O1(正三角形外心就是中心,直角三角形外心在斜边中点上,普通三角形用正弦定理定外心2r=asin A);②过外心O1做(找)底面ΔABC的垂线,如图中PO1⊥面ABC,则球心一定在直线(注意不一定在线段PO1上)PO1上;③计算求半径R:在直线PO1上任取一点O如图:则OP=OA=R,利用公式OA2=O1A2+OO12可计算出球半径R.4、双面定球心法(两次单面定球心)如图:在三棱锥P-ABC中:①选定底面ΔABC,定ΔABC外接圆圆心O1②选定面ΔPAB,定ΔPAB外接圆圆心O2③分别过O1做面ABC的垂线,和O2做面PAB的垂线,两垂线交点即为外接球球心O.二、典型题型题型一:内切球等体积法1(22·23·全国·专题练习)正三棱锥P-ABC的三条棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为()A.1:3B.1:3+3C.3+1 :3D.3-1 :32(22·23下·朔州·阶段练习)正四面体的内切球、棱切球(与各条棱均相切的球)及外接球的半径之比为.3(23·24上·萍乡·期末)已知球O 是棱长为1的正四面体的内切球,AB 为球O 的一条直径,点P 为正四面体表面上的一个动点,则PA ⋅PB的取值范围为.4(22·23上·张家口·期中)球O 为正四面体ABCD 的内切球,AB =4,PQ 是球O 的直径,点M 在正四面体ABCD 的表面运动,则MP ⋅MQ的最大值为.5(22·23上·河南·阶段练习)已知正四面体ABCD 的棱长为12,球O 内切于正四面体ABCD ,E ,F 是球O 上关于球心O 对称的两个点,则AE ⋅BF的最大值为.6(22·23上·扬州·期中)中国古代数学名著《九章算术》中将底面为矩形且有一条侧棱垂直于底面的四棱锥称为“阳马”.现有一“阳马”的底面是边长为3的正方形,垂直于底面的侧棱长为4,则该“阳马”的内切球表面积为,内切球的球心和外接球的球心之间的距离为.题型二:内切球独立截面法1(23·24上·淮安·开学考试)球M 是圆锥SO 的内切球,若球M 的半径为1,则圆锥SO 体积的最小值为()A.43π B.423π C.83π D.4π2(22·23下·咸宁·期末)已知球O 内切于圆台(即球与该圆台的上、下底面以及侧面均相切),且圆台的上、下底面半径r 1:r 2=2:3,则圆台的体积与球的体积之比为()A.32B.1912C.2D.1963(22·23·全国·专题练习)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为.4(23·24上·佛山·开学考试)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的体积为4π3,当该圆锥体积取最小值时,该圆锥的表面积为.5(22·23下·成都·阶段练习)已知圆锥的底面半径为2,高为42,则该圆锥的内切球表面积为.题型三:外接球公式法1(16·17·全国·单元测试)若长方体从一个顶点出发的三条棱长分别为3,4,5,则该长方体的外接球表面积为 ()A.50πB.100πC.150πD.200π2(22·23·全国·专题练习)设球O 是棱长为4的正方体的外接球,过该正方体的棱的中点作球O 的截面,则最小截面的面积为()A.3πB.4πC.5πD.6π3(14·15上·佛山·阶段练习)正方体的外接球(正方体的八个顶点都在球面上)与其内切球(正方体的六个面都与球相切)的体积之比是.题型四:外接球补型法1(23·24上·成都·开学考试)在三棱锥P -ABC 中,PA =PB =PC =2,PA ⊥PB ,PA ⊥PC ,PB ⊥PC ,则该三棱锥的外接球的表面积为()A.43πB.12πC.48πD.323π2(22·23下·揭阳·期中)在三棱锥S -ABC 中,SA =BC =5,SB =AC =41,SC =AB =34,则该三棱锥的外接球表面积是()A.50πB.100πC.150πD.200π3(23·24上·成都·开学考试)已知四面体ABCD 满足AB =CD =3,AD =BC =5,AC =BD =2,且该四面体ABCD 的外接球的表面积是()A.2πB.6πC.6π11D.4π4(22·23下·黔西·阶段练习)正三棱锥P -ABC 的三条棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为.5(22·23下·黔西·期中)如图,已知在三棱锥P -ABC 中,PA ⊥PB ,PB ⊥PC ,PC ⊥PA ,且PA =2PB =2PC =2,求该三棱锥外接球的表面积是.题型五:外接球单面定球心法1(23·24上·汉中·模拟预测)如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,PA =6,BC =3,∠CAB =π6,O为△ABC 外接圆的圆心,O 为三棱锥P -ABC 外接球的球心,OQ ⊥PA ,则三棱锥P -ABC 的外接球O 的表面积为.2(23·24上·秦皇岛·开学考试)三棱锥P-ABC中,AB⊥BC,P在底面的射影O为△ABC的内心,若AB=4,BC=3,PO=5,则四面体PABC的外接球表面积为.3(22·23下·石家庄·阶段练习)已知球O是正四面体P-ABC的外接球,E为棱PA的中点,F是棱PB上的一点,且FC=2EF,则球O与四面体P-EFC的体积比为.4(22·23下·淄博·期末)已知四棱锥P-ABCD的底面ABCD是矩形,侧面PAD为等边三角形,平面PAD⊥平面ABCD,其中AD=2,AB=3,则四棱锥P-ABCD的外接球表面积为.题型六:外接球双面定球心法1(22·23上·抚州·期中)已知菱形ABCD的各边长为2,∠D=60°.如图所示,将△ACD沿AC折起,使得点D到达点S的位置,连接SB,得到三棱锥S-ABC,此时SB=3.若E是线段SA的中点,点F在三棱锥S-ABC的外接球上运动,且始终保持EF⊥AC则点F的轨迹的面积为.2(22·23·赣州·模拟预测)如图,正三角形ABC中,D,E分别为边AB,AC的中点,其中AB=4,把△ADE沿着DE翻折至△A DE的位置,得到四棱锥A -BCED,则当四棱锥A -BCED的体积最大时,四棱锥A -BCED外接球的球心到平面A BC的距离为.3(22·23下·湖南·期末)为加强学生对平面图形翻折到空间图形的认识,某数学老师充分利用习题素材开展活动,现有一个求外接球表面积的问题,活动分为三个步骤,第一步认识平面图形:如图(一)所示的四边形PABC中,AB=BC=2,PA=PC,∠ABC=60°,PA⊥PC.第二步:以AC为折痕将△PAC折起,得到三棱锥P-ABC,如图(二).第三步:折成的二面角P-AC-B的大小为120°,则活动结束后计算得到三棱锥P-ABC外接球的表面积为.三、专项训练一、单选题1(22·23下·河南·模拟预测)已知直六棱柱的所有棱长均为2,且其各顶点都在同一球面上,则该球的表面积为( ).A.16πB.20πC.24πD.25π2(22·23下·宁德·期中)正四面体ABCD的外接球的半径为2,过棱AB作该球的截面,则截面面积的最小值为()A.2π3B.4π3C.8π3D.3π3(23·24上·河北·开学考试)长方体的一个顶点上三条棱长是3,4,5,且它的八个顶点都在同一球面上,这个球的体积是()A.12523π B.1252π C.50π D.125π4(22·23下·临夏·期末)已知四棱锥P-ABCD的体积为83,侧棱PA⊥底面ABCD,且四边形ABCD是边长为2的正方形,则该四棱锥的外接球的表面积为()A.12πB.8πC.4πD.2π5(23·24上·广东·阶段练习)如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△DCF分别沿DE,EF,DF折起,使得A,B,C三点重合于点A ,若三棱锥A -EFD的所有顶点均在球O的球面上,则球O的表面积为()A.2πB.3πC.6πD.8π6(23·24上·安徽·开学考试)在封闭的等边圆锥(轴截面为等边三角形)内放入一个球,若球的最大半径为1,则该圆锥的体积为()A.3πB.6πC.9πD.12π7(23·24上·莆田·阶段练习)三棱锥P-ABC中,△ABC是边长为23的正三角形,PA=4,PA⊥AB,D为BC中点且PD=5,则该三棱锥外接球的表面积为()A.16πB.32πC.48πD.64π8(22·23·九江·一模)三棱锥A-BCD中,△ABD与△BCD均为边长为2的等边三角形,若平面ABD ⊥平面BCD,则该三棱锥外接球的表面积为()A.8π3B.20π3C.8πD.20π二、填空题9(23·24·柳州·模拟预测)已知圆锥的底面直径为23,轴截面为正三角形,则该圆锥内半径最大的球的体积为.10(22·23·唐山·二模)已知某圆台的上、下底面的圆周在同一球的球面上,且圆台上底面半径为1,下底面半径为2,轴截面的面积为3,则该圆台的外接球的体积为.11(22·23·大同·模拟预测)四个面都为直角三角形的四面体称之为鳌臑.在鳌臑P-ABC中,PA⊥平面ABC,PA=4,AB=BC=2,鳌臑P-ABC的四个顶点都在同一个球面上,则该球的表面积是.12(23·24上·辽宁·阶段练习)已知圆锥的底面半径为2,侧面展开图的面积为8π,则该圆锥的内切球的体积为.13(23·24上·成都·阶段练习)已知三棱锥S-ABC底面ABC是边长为2的等边三角形,平面SAB⊥底面ABC,SA=SB=2,则三棱锥S-ABC的外接球的表面积为.14(23·24上·遂宁·阶段练习)已知正三棱柱ABC-A1B1C1的六个顶点在球O1上,又球O2与此三棱柱的5个面都相切,则球O1与球O2的表面积之比为.15(22·23下·赣州·阶段练习)已知圆锥的内切球半径为1,若圆锥的侧面展开图恰好为一个半圆,则该圆锥的体积为.。
高中数学立体几何中的外接球与内切球问题

高中数学立体几何中的外接球与内切球问题
在高中数学的立体几何中,外接球与内切球问题是一个重要的探讨点。
这个问
题涉及到如何在一个给定的立体图形中,找到一个外切于该图形的球和一个内切于该图形的球。
首先,让我们来看外接球问题。
在立体几何中,给定一个多面体,如正方体或
正四面体,我们想找到一个球,使得该球恰好外接于该多面体的每一个面上。
所谓外接,即球与每一个面都有且只有一个公共点,这个点是每个面的外接圆心。
以正方体为例,我们可以观察到正方体的每一个面都是正方形,而正方形的外
接圆心恰好位于该正方形的中心点。
因此,我们可以得出结论:正方体的外接球的圆心与该正方体的每个面的外接圆心重合。
接下来,让我们来看内切球问题。
在立体几何中,给定一个多面体,如正方体
或正四面体,我们想找到一个球,使得该球恰好内切于该多面体的每一个面上。
所谓内切,即球与每一个面都有且只有一个公共点,这个点是每个面的内切圆心。
以正方体为例,我们可以观察到正方体的每一个面都是正方形,而正方形的内
切圆心恰好位于该正方形的中心点。
因此,我们可以得出结论:正方体的内切球的圆心与该正方体的每个面的内切圆心重合。
总结起来,对于任何一个给定的多面体,我们可以找到一个外接球和一个内切球。
外接球的圆心与每个面的外接圆心重合,而内切球的圆心与每个面的内切圆心重合。
这个问题在高中数学的立体几何中十分重要,理解了外接球和内切球的性质,可以帮助我们更好地理解和解决相关的几何问题。
空间几何体的外接球内切球问题

P DS CAO空间几何体的外接球、内切球问题外接球问题一.棱锥的外接球三棱锥都有外接球;底面有外接圆的任意棱锥都有外接球。
1.确定棱锥外接球球心的通法先找到棱锥底面的外接圆的圆心D ,过D 作底面的垂线DP交一侧棱的中垂面于O ,点O 即为外接球的球心。
练习:1.三棱锥S-ABC 的各顶点都在同一球面上,若SB ⊥平面ABC ,SB=6,AB=AC=2120BAC ∠=︒,则此球的表面积等于 。
2. 点A 、B 、C 、D 均在同一球面上,其中△ ABC 是正三角形,AD ⊥平面ABC ,AD=2AB=6则该球的体积为 。
3.四面体ABCD 的四个顶点在同一球面上,AB=BC=CD=DA=3,32=AC ,6=BD ,则该球的表面积为 ( )A . π14 B.π15 C.π16 D.π182.补成长方体或正方体,再利用体对角线是外接球直径这一结论求解。
练习:1.三棱锥O ABC -中,,,OA OB OC 两两垂直,且22OA OB OC a ===,则三棱锥O ABC -外接球的表面积为( )A .26a πB .29a πC .212a πD .224a π2.已知,,,S A B C 是球O 表面上的点,SA ABC ⊥平面,AB BC ⊥,1SA AB ==,BC =O 表面积等于(A )4π (B )3π (C )2π (D )π3.,四个顶点在同一个球面上,则此球的表面积为( )A.3πB.4πD.6π4.3.公共边所对的两个角为直角确定球心法 练习1.在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积为 A.12512π B.1259π C.1256π D.1253π2.空间四边形ABCD中,1,AB BC AD DC ====ABCD 的外接球的表面积为4.利用轴截面截球为大圆确定球半径正四、六、八棱锥的外接球的一个轴截面为大圆,该圆的半径等于外接球的半径. 练习:1.正四棱锥S ABCD -S A B C D 、、、、都在同一球面上,则此球的体积为 .2.正六棱锥EF S ABCD -的底面边长为1S A B C D 、、、、、E 、F 都在同一球面上,则此球的表面积为 .3.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为_ C_ A_ O_ D _ BA.3B.13π C.23π D.3二.棱柱的外接球底面有外接圆的直棱柱才有外接球。
立体几何中球的内切和外接问题(完美版)
C 1
注意:①割补法,② V多面体 3 S全 r内切球
变式训练:一个正方体内接于一个球,过球心作一截面,如 图所示,则截面的可能图形是( )
①
②
③
④
• A .①② B.②④ C.①②③ D.②③④
D A
D1 A1
C
B O
C1 B1
球的内接正方体的对角线等于球直径。
变式训练:已知正四面体内接于一个球,某人画出四 个过球心的平面截球与正四面体所得的图形如下,
的动点,当弦 MN 的长度最大时, PM • PN 的取值范围是
.
感谢阅读
• 感谢阅读
• 感谢阅读
• 感谢阅读
• 感谢阅读
2023最新整理收集 do something
球与多面体的内切、外接
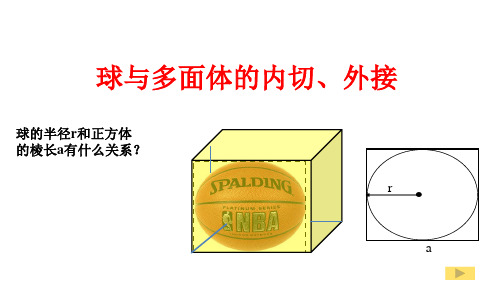
球的半径r和正方体 的棱长a有什么关系?
.r
a
一、 球体的体积与表面积
①
②
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上,
则称这个多面体是这个球的内接多面体,
这个球多是面这体个的外接球
。
定义2:若一个多面体的各面都与一个球的球面相切,
,即 为该四面体的外接球的球心
A
O
C
所以该外接球的体积为
03
破译规律-特别提
醒
2 例题剖析-针对讲 解
04
举一反三-突破提
升
4 举一反三-突破提 升 1、(2015 海淀二模)已知斜三棱柱的三 视图如图所示,该斜三棱柱的体积为 ______.
4 举一反三-突破提 升
2、(2015 郑州三模) 正三角形ABC的2 边3 长
5 正棱锥的外接球的球心是在其 高上
高中数学立体几何之外接球与内切球问题常见模型归纳(完整版)
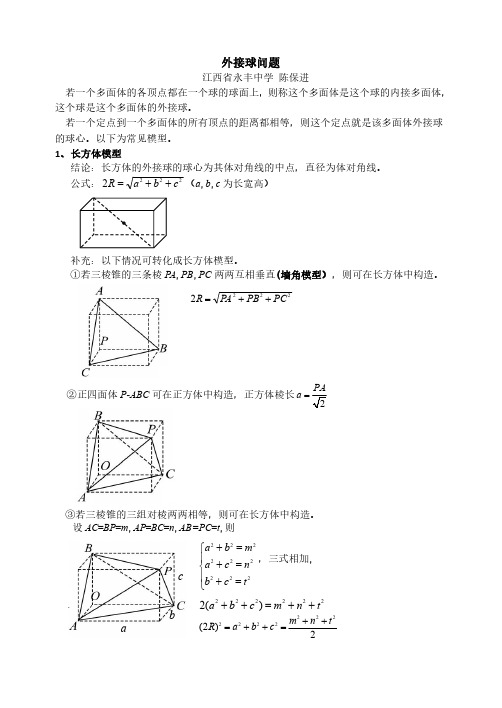
外接球问题江西省永丰中学陈保进若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
若一个定点到一个多面体的所有顶点的距离都相等,则这个定点就是该多面体外接球的球心。
以下为常见模型。
1、长方体模型结论:长方体的外接球的球心为其体对角线的中点,直径为体对角线。
公式:2222c b a R ++=(a ,b ,c 为长宽高)补充:以下情况可转化成长方体模型。
①若三棱锥的三条棱PA ,PB ,PC 两两互相垂直(墙角模型),则可在长方体中构造。
2222PC PB P A R ++=②正四面体P -ABC 可在正方体中构造,正方体棱长2=PA a ③若三棱锥的三组对棱两两相等,则可在长方体中构造。
设AC =BP =m ,AP =BC =n ,AB=PC =t ,则⎪⎩⎪⎨⎧=+=+=+222222222t c b n c a m b a ,三式相加,222222)(2t n m c b a ++=++2)2(2222222t n m c b a R ++=++=abc2、直三棱柱模型结论:直三棱柱外接球的球心是上、下底面外心连线的中点,222()2hR r =+r 为底面三角形外接圆的半径,可用正弦定理求,h 为直三棱柱的高。
补充:有一条侧棱垂直底面的三棱锥可补成直三棱柱,如图P -ABC 中,PA ⊥平面ABC ,则可补成直三棱柱PB 1C 1-ABC ,外接球半径公式同上。
提醒:底面具有外接圆的直棱柱才有外接球,比如正棱柱,且球心在上、下底面外心连线的中点,底面无外接圆的直棱柱,以及所有斜棱柱均无外接球。
3、共斜边模型四面体D-ABC 中,DC AD ⊥,BC AB ⊥,AC 为公共的斜边,O 为AC 的中点,则O 为四面体D-ABC 外接球的球心。
4、正棱锥模型外接球的球心在正棱锥的高所在直线上,如图正三棱锥A-BCD 中,作AO 1⊥平面BCD ,则易得BO 1=CO 1=DO 1,所以O 1为△BCD 的外心,设O 为其外接球球心,半径为R ,则BO =AO =R ,设AO 1=h ,BO 1=r ,则由BO 2=BO 12+OO 12,得R 2=r 2+(h-R )2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体的内切球与外接球问题1.[2016·全国卷Ⅱ] 体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )A .12π B.323π C .8π D .4π[解析]A 因为正方体的体积为8,所以正方体的体对角线长为23,所以正方体的外接球的半径为3,所以球的表面积为4π·(3)2=12π. 2.[2016·全国卷Ⅲ] 在封闭的直三棱柱ABC - A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4π B.9π2 C .6π D.32π3[解析]B 当球与三侧面相切时,设球的半径为r 1,∵AB ⊥BC ,AB =6,BC =8,∴8-r 1+6-r 1=10,解得r 1=2,不合题意;当球与直三棱柱的上、下底面相切时,设球的半径为r 2,则2r 2=3,即r 2=32.∴球的最大半径为32,故V 的最大值为43π×⎝⎛⎭⎫323=92π.3.[2016·郑州模拟] 在平行四边形ABCD 中,∠CBA =120°,AD =4,对角线BD =23,将其沿对角线BD 折起,使平面ABD ⊥平面BCD ,若四面体ABCD 的顶点在同一球面上,则该球的体积为________.答案:2053π;解析:因为∠CBA =120°,所以∠DAB =60°,在三角形ABD 中,由余弦定理得(23)2=42+AB 2-2×4·AB ·cos 60°,解得AB =2,所以AB ⊥BD .折起后平面ABD ⊥平面BCD ,即有AB ⊥平面BCD ,如图所示,可知A ,B ,C ,D 可看作一个长方体中的四个顶点,长方体的体对角线AC 就是四面体ABCD 外接球的直径,易知AC =22+42=25,所以球的体积为2053π.4.[2016·山西右玉一中模拟] 球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大值为( )A .33B . 3C .2 3D .4 选A ;[解析] (1)由于平面SAB ⊥平面ABC ,所以点S 在平面ABC 上的射影H 落在AB 上,根据球的对称性可知,当S 在“最高点”,即H 为AB 的中点时,SH 最大,此时棱锥S -ABC 的体积最大.因为△ABC 是边长为2的正三角形,所以球的半径r =OC =23CH =23×32×2=233.在Rt △SHO 中,OH =12OC =33,所以SH =⎝⎛⎭⎫2332-⎝⎛⎭⎫332=1, 故所求体积的最大值为13×34×22×1=33.5.[2016·赣州模拟] 如图7-38-19所示,设A ,B ,C ,D 为球O 上四点,AB ,AC ,AD 两两垂直,且AB =AC =3,若AD =R(R 为球O 的半径),则球O 的表面积为( )图7-38-19A .πB .2πC .4πD .8π选D ;解析:因为AB ,AC ,AD 两两垂直,所以以AB ,AC ,AD 为棱构建一个长方体,如图所示,则长方体的各顶点均在球面上,AB =AC =3,所以AE =6,AD =R ,DE =2R ,则有R 2+6=(2R )2,解得R =2,所以球的表面积S =4πR 2=8π.6.[2016·安徽皖南八校三联] 如图所示,已知三棱锥A -BCD 的四个顶点A ,B ,C ,D 都在球O 的表面上,AC ⊥平面BCD ,BC ⊥CD ,且AC =3,BC =2,CD =5,则球O 的表面积为( )A .12πB .7πC .9πD .8π[解析]A 由AC ⊥平面BCD ,BC ⊥CD 知三棱锥A -BCD 可以补成以AC ,BC ,CD 为三条棱的长方体,设球O 的半径为R ,则有(2R )2=AC 2+BC 2+CD 2=3+4+5=12,所以S 球=4πR 2=12π.7.[2016·福建泉州质检] 已知A ,B ,C 在球O 的球面上,AB =1,BC =2,∠ABC =60°,且点O 到平面ABC 的距离为2,则球O 的表面积为________.答案:20π [解析] 在△ABC 中用余弦定理求得AC =3,据勾股定理得∠BAC 为直角,故BC 的中点O 1即为△ABC 所在小圆的圆心,则OO 1⊥平面ABC ,在直角三角形OO 1B 中可求得球的半径r =5,则球O 的表面积S =4πr 2=20π.8. [2016·河南中原名校一联] 如图K3816所示,ABCD -A 1B 1C 1D 1是边长为1的正方体,S -ABCD 是高为1的正四棱锥,若点S ,A 1,B 1,C 1,D 1在同一个球面上,则该球的表面积为( )图K3816A.916πB.2516πC.4916πD.8116π选D ;[解析] 如图所示作辅助线,易知球心O 在SG 1上,设OG 1=x ,则OB 1=SO =2-x ,同时由正方体的性质知B 1G 1=22,则在Rt △OB 1G 1中,由勾股定理得OB 21=G 1B 21+OG 21,即(2-x)2=x 2+⎝⎛⎭⎫222,解得x =78,所以球的半径R =2-78=98,所以球的表面积S =4πR 2=8116π.9.[2013·课标全国Ⅰ]如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,如果不计容器的厚度,则球的体积为( )A.500π3 cm 3B.866π3 cm 3C.1 372π3cm 3D.2 048π3cm 3解析:设球半径为R ,由题可知R ,R -2,正方体棱长一半可构成直角三角形,即△OBA 为直角三角形,如图.BC =2,BA =4,OB =R -2,OA =R , 由R 2=(R -2)2+42,得R =5,所以球的体积为43π×53=5003π(cm 3),故选A 项.答案:A10.已知正四棱锥的侧棱与底面的边长都为32,则这个四棱锥的外接球的表面积为( )A .12πB .36πC .72πD .108π选B ;解析:依题意得,该正四棱锥的底面对角线长为32×2=6,高为 (32)2-⎝⎛⎭⎫12×62=3,因此底面中心到各顶点的距离均等于3,所以该四棱锥的外接球的球心为底面正方形的中心,其外接球的半径为3,所以其外接球的表面积等于4π×32=36π. 11.[2014·石家庄质检一]已知球O ,过其球面上A 、B 、C 三点作截面,若O 点到该截面的距离是球半径的一半,且AB =BC =2,∠B =120°,则球O 的表面积为( )A.64π3B.8π3 C .4π D.16π9解析:如图,球心O 在截面ABC 的射影为△ABC 的外接圆的圆心O ′.由题意知OO 1=R2,OA =R ,其中R 为球O 的半径.在△ABC 中, AC =AB 2+BC 2-2AB ·BC ·cos120° =22+22-2×2×2×⎝⎛⎭⎫-12=2 3. 设△ABC 的外接圆半径为r ,则2r =AC sin120°=2332=4,得r =2,即O ′A =2.在Rt △OO 1A中,OO 21+O 1A 2=OA 2,即R 24+4=R 2,解得R 2=163,故球O 的表面积S =4πR 2=64π3,故选A.答案:A12.[2014·郑州模拟]在三棱锥A -BCD 中,AB =CD =6,AC =BD =AD =BC =5,则该三棱锥的外接球的表面积为__________.解析:依题意得,该三棱锥的三组对棱分别相等,因此可将该三棱锥补形成一个长方体,设该长方体的长、宽、高分别为a 、b 、c ,且其外接球的半径为R ,则⎩⎪⎨⎪⎧a 2+b 2=62,b 2+c 2=52,c 2+a 2=52,得a 2+b 2+c 2=43,即(2R )2=a 2+b 2+c 2=43,易知R 即为该三棱锥的外接球的半径,所以该三棱锥的外接球的表面积为4πR 2=43π.答案:43π13.[2014·全国卷] 正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π4答案:A ; [解析] 如图所示,E 为AC 与BD 的交点.因为正四棱锥的底面边长为2,所以AE =12AC = 2.设球心为O ,球的半径为R ,则OE =4-R ,OA =R .又因为△AOE 为直角三角形,所以OA 2=OE 2+AE 2,即R 2=(4-R )2+2,解得R =94,所以该球的表面积S =4πR 2=4π⎝⎛⎭⎫942=81π4.14.[2016·湖南八校联考] 如图是一个几何体的三视图, 则这个几何体外接球的表面积为( )A .8πB .16πC .32πD .64π答案:C ; [解析] 该几何体为一个四棱锥,其外接球的球心为底面正方形的中心,所以半径为22,表面积为4π×(22)2=32π.15.已知四棱锥S -ABCD 的所有顶点在同一球面上,底面ABCD 是正方形且球心O 在此平面内,当四棱锥的体积取得最大值时,其表面积等于16+163,则球O 的体积等于( )A.42π3B.162π3C.322π3D.642π3答案:D ; [解析] 由题意,当此四棱锥的体积取得最大值时,四棱锥为正四棱锥.设球O 的半径为R ,则AC =2R ,SO =R ,∴AB =2R ,则有(2R )2+4×12×2R ·⎝⎛⎭⎫22R 2+R 2=16+163,解得R =22,∴球O 的体积是43πR 3=6423π.16.[2016·武汉调研] 已知直三棱柱ABC -A 1B 1C 1的各顶点都在同一球面上,若AB =AC =AA 1=2,∠BAC =90°,则该球的体积等于________.答案:43π; [解析] 设该球的球心为O ,△ABC 所在圆面的圆心为O 1,则OO 1⊥平面ABC 且OO 1=1.在△ABC 中,因为AB =AC =2,∠BAC =90°,所以△ABC 外接圆的半径r =12BC =12AB 2+AC 2=2,所以该球的半径R =r 2+O 1O 2=(2)2+12=3,所以该球的体积V =43πR 3=43π.。
