应力强度因子
应力强度因子的计算

2b
2b
ZII ( )
sin ( a)
2b
[sin ( a)]2 (sin a )2
2b
2b
10
KⅡ
lim
0
2 ZII ( )
a
2b tan a a 2b
3.Ⅲ型裂纹应力强度因子的普遍表达形式(无限大板):
KⅢ
lim
0
[( a)2 b2 ] ( 2a)
KⅠ
lim
0
2 Z ( )
2P a
(a2 b2)
4
2.在无限大平板中,具有长度为 2a 的穿透板厚的裂纹表 面上,在距离 x a1 的范围内受均布载荷q作用
利用叠加原理
集中力 qdx dKⅠ
2q a dx
K lim 2 2 x(Z ) 0
26
若采用
Z a K 2 2 lim z ax(z) za
选择 x(z) 满足具体问题的应力边界条件
f F1(Z ) F1(Z ) ZF4 (Z ) ZF4 (Z )
---复变解析函数表达的双调和函数的普遍形式 或复变应力函数为普遍形式
)
1 4
在椭圆的短轴方向上,即 ,有
2
KI KImax
--椭圆片状深埋裂纹的应力强度因子
当a
c
时,
2
KI
2
a
--圆片状深埋裂纹应力强度因子
18
§2-3 半椭圆表面裂纹的应力强度因子计算
一、表面浅裂纹的应力强度因子
裂纹 应力强度因子

裂纹应力强度因子裂纹是各种材料中的一种常见缺陷,对材料的机械性能以及使用寿命都会产生一定的影响。
因此,如何准确地评估裂纹的危害程度及其生长速率,成为了材料科学研究中的一个重要问题。
在研究裂纹时,应力强度因子是一个重要的概念。
1. 什么是裂纹?裂纹是材料中的一种线状缺陷,它是由于材料内部缺陷的存在而引起的,主要表现为材料表面出现的一条或多条细长的开裂。
2. 什么是应力强度因子?应力强度因子是一种描述裂纹尖端应力场变化的物理量。
简单来说,它是应力和裂纹尖端处的几何因素的函数。
根据裂纹尖端处的应力分布,应力强度因子可分为模式I、模式II和模式III三种。
3. 应力强度因子的意义是什么?应力强度因子是评估裂纹的危害程度以及预测裂纹扩展速率的重要参数。
根据弹性力学理论,当一个裂纹存在时,裂纹尖端处的应力场会出现奇异性,这就需要用应力强度因子来描述裂纹尖端的应力分布,并据此评估裂纹的危害程度。
4. 应力强度因子和材料力学性质的关系应力强度因子和材料力学性质是密切相关的。
在理论研究中,人们通常用应力强度因子来表示材料的断裂韧性。
而在实际应用中,通常使用裂纹扩展速率与应力强度因子的关系来描述材料的裂纹生长行为,从而评估其在不同应力条件下的使用寿命。
5. 应力强度因子的计算方法计算应力强度因子需要使用复杂的数学方法,如奇异积分等。
对于实际问题,通常使用有限元分析等计算方法来模拟裂纹的扩展过程,从而得到相应的应力强度因子。
此外,还可以通过实验的方式来测定裂纹的扩展速率,并结合应力强度因子的计算结果来预测材料的寿命。
综上所述,应力强度因子在材料科学和工程中具有重要的作用。
在今后的研究中,人们将继续深入探究应力强度因子的理论基础,开发更加精确和高效的计算方法,以更好地为材料设计和工程应用服务。
应力场强度因子

应力场强度因子
应力场强度因子是研究材料断裂行为的重要参数之一。
它是描述材料在受到外力作用下,裂纹尖端应力场的强度和分布情况的物理量。
应力场强度因子的大小和方向对材料的断裂行为有着重要的影响。
应力场强度因子的计算方法有多种,其中最常用的是Williams和Landel的方法。
该方法基于线弹性力学理论,通过对裂纹尖端应力场的分析,得出了应力场强度因子的计算公式。
该公式中包含了裂纹尖端应力场的强度和分布情况,因此可以用来预测材料的断裂行为。
应力场强度因子的大小和方向对材料的断裂行为有着重要的影响。
当应力场强度因子达到一定的临界值时,裂纹尖端的应力场会达到材料的断裂强度,从而导致材料的断裂。
因此,应力场强度因子可以用来预测材料的断裂强度和断裂模式。
除了预测材料的断裂行为外,应力场强度因子还可以用来优化材料的设计和制备。
通过对应力场强度因子的分析,可以确定材料的最大承载能力和断裂模式,从而优化材料的设计和制备过程。
应力场强度因子是研究材料断裂行为的重要参数之一。
它可以用来预测材料的断裂行为、优化材料的设计和制备过程,对于提高材料的性能和可靠性具有重要的意义。
应力强度因子的计算
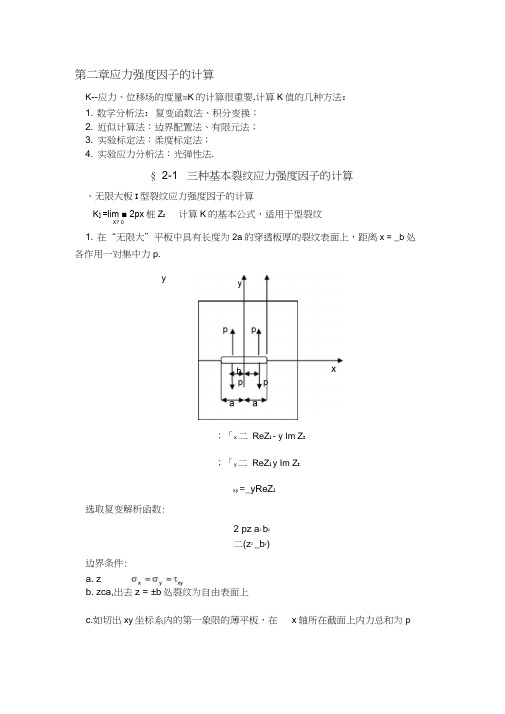
第二章应力强度因子的计算K--应力、位移场的度量=K的计算很重要,计算K值的几种方法:1. 数学分析法:复变函数法、积分变换;2. 近似计算法:边界配置法、有限元法;3. 实验标定法:柔度标定法;4. 实验应力分析法:光弹性法.§ 2-1 三种基本裂纹应力强度因子的计算、无限大板I型裂纹应力强度因子的计算K] =lim ■ 2px桩Z I计算K的基本公式,适用于型裂纹X? 01. 在“无限大”平板中具有长度为2a的穿透板厚的裂纹表面上,距离x = _b处各作用一对集中力p.y;「x 二ReZ i - y Im Z I;「y 二ReZ i y Im Z Ixy =_yReZ l选取复变解析函数:2 pz a2b2二(z2_b2)边界条件:a. zb. zca,出去z = ±b处裂纹为自由表面上c.如切出xy坐标系内的第一象限的薄平板,在x轴所在截面上内力总和为p2 p (匕 +a) Ja 2+孑二[(a)2-b 2] ; (2a)2p 、、 a二(a 2-b 2)2. 在无限大平板中,具有长度为2a 的穿透板厚的裂纹表面上,在距离x= _印的 范围内受均布载荷q 作用.yb.11yqn____ r~Kq 1旺x------ ►J 2 a利用叠加原理:a2q\a i . ---------------- dxo _ / 2 2、二(a -x )令x=acos : a 2-x 2= acosv , dx = acos 二当整个表面受均布载荷时,c -• a. =K i = 2^-s in3. 受二向均布拉力作用的无限大平板,在x 轴上有一系列长度为2a ,间距为2b的裂纹.以新坐标表示:K i微段 > 集中力qdx > dK i2q烏 dx 护(a 2_x 2)-K isin 4(J)广;)竺吗=a cos^二0, -a ::: x ::: a, -a 二2b ::: x ::: a 二2b 在区间内;-y =°,,xy =c.所有裂纹前端;匚y.匚单个裂纹时又Z应为2b的周期函数采用新坐标:=z-an ..-sin ( a) 2b当© t 0时,sin 二© =厶Jcos 厶© =12b 2b 2b迟JL乜JL JL乜= sin——( a) =sin—— cos一a cos一sin — a 2b2b 2b 2b 2b边界条件是周期的:a. z —二二xb.在所有裂纹内部应力为零.y~2 2z - a-sin2b二a、2(Sin" %2b 仙2b)JI u 31ji.二 a 二 sin - 2b 1 -a . -a ——cos ——sin — 2b 2b 2b =;「2b tan a \ 2b—a, 2b tan :aYn a2b2a 1若裂纹间距离比裂纹本身尺寸大很多(兰乞丄)可不考虑相互作用,按单个裂纹2b 5计算•二、无限大平板n>m 型裂纹问题应力强度因子的计算1. u 型裂纹应力强度因子的普遍表达形式(无限大板):心计吋(人尹2. 无限大平板中的周期性的裂纹,且在无限远的边界上处于平板面内的纯剪切 力作用.JT JT cos a sin a 2b 2b2bfTTfTTfTTfTTHTfTTfTT.. 2 ■22 2[sin (a)] = ( ) cos a 2 cos a sin a (sin a) 2b2b 2b 2b 2b 2b2b•2::.2[%(a)] -(sin2b a)JI=2 -2bn Jicos asin a2b 2b:二 sin2b—2/ ?.a .二 acos ——sin2b 2b2b 修正系数,大于1,表示其他裂纹存在对K ]的影响.二a 2 药)心=帆 J 2 兀©Z (©) = i V^a J^tan 舒3.川型裂纹应力强度因子的普遍表达形式(无限大板):4.周期性裂纹:sin二z 2b n : …sin ( a) 2bZ()二訓n 2?+a)]2-伽訝H Z 2伽亦)一伽§ 2-2 深埋裂纹的应力强度因子的计算1950年,格林和斯内登分析了弹性物体的深埋的椭圆形裂纹邻域内的应力 和应变,得到椭圆表面上任意点,沿y 方向的张开位移为:2 2 1x z . 2 y =y 0(1 2 2)a c2(1 -」2);「a 其中:yo =(丘丿.-为第二类椭圆积分•有Ji | 2 2=o 2、1-c;asin 2d 「(于仁东书丿匹 a^2 二 2[sin 2「(-)2cos 2] d (王铎书丿 0c1962年,lrwin 利用上述结果计算在这种情况下的应力强度因子xz2 2 2 2 2N 二 Qcos : ,x ,-『sin :2 2 X i 乙-2~~2acacc 2sin 2「a 2cos 2假设:椭圆形裂纹扩展时,其失径「的增值r 与「成正比.边缘上任一点p (x ,z ),有:x j (「r)sin 炉=(1 f^?sin 》=(1 f)x iz = r)cos 即=(1 f )z 1=■ p (x ;z), p (M,Z i )均在 y=0 的平面内.— ,:2 ・2-2 24 2 2・2 ・2=c x a z (i f)ac a c=新的裂纹面仍为椭圆•长轴c =(i • f)c ,短轴a '=(i • f)a .=y 向位移2 2原有裂纹面:二 二,上)2=ia c y o2 2扩展后裂纹面:笃•务•(工)2=i a c y o以x'x i , z'z,代入=原有裂纹面的边缘y 向位移y ,有原裂纹面y o2(i 」2)二 a2(i-」2)ri f)aE=(i f)y oc 2片2a 2zj 二 a 2c 2sin 2「亠 a 2cos2 :2 2 2 2 2 2「-(1-2门笃一(1一2门刍=1一笃一乌2f (笃吕)ac a ca c=2f二 y 2=2fy °2=2f (1 f )2y o 2L 2fy 。
应力强度因子的数值计算方法

应力强度因子的数值计算方法一、引言数值计算方法通过将裂纹尖端的应力场分布模拟为一个虚拟的数学模型,利用计算机进行数值求解来得到应力强度因子的数值。
数值计算方法通常分为两种类型:直接方法和间接方法。
1.直接方法直接方法是指直接通过有限元分析软件求解裂纹尖端的应力场分布,并通过一些后处理技术来计算应力强度因子。
其中最常用的方法是J积分法和节点法。
(1)J积分法:J积分法是一种常用的裂纹应力强度因子计算方法,它通过在裂纹尖端附近引入一个虚拟断裂面,将裂纹尖端附近的应力场分布(由有限元分析得到)转化为裂纹尖端处的应力强度因子。
具体计算方法较为复杂,一般需要通过数值积分的方法求解。
(2)节点法:节点法是一种基于有限元网格节点的方法,其基本思想是通过增加节点对裂纹尖端附近的应力场进行离散,利用节点处的应力场计算应力强度因子。
节点法相对于J积分法计算简单,但适用条件较为有限。
2.间接方法间接方法是指通过已知应力场的变化率来计算应力强度因子的方法。
常用的间接方法有格里菲斯准则法、欠奇性法和EOS法。
(1)格里菲斯准则法:格里菲斯准则法是最早提出的计算裂纹扩展的方法之一,基于弹性力学理论和线弹性断裂力学基本假设,通过对裂纹尖端周围应力场的分析,得到应力强度因子与裂纹尖端形状和尺寸以及应力场的关系。
(2)欠奇性法:欠奇性法是一种基于能量原理的裂纹尖端应力强度因子计算方法,通过构造合适的应变能表达式和裂纹尖端应力强度因子的定义,利用应变能的分式展开求解裂纹尖端处的应力强度因子。
(3)EOS法:EOS法是一种在裂纹尖端周围选取合适的控制体,通过求解控制体内外表面的应力分布,建立应力强度因子与表面应力之间的关系,从而计算裂纹尖端处的应力强度因子。
三、应用场景1.断裂力学:数值计算方法可以用于预测和分析裂纹扩展行为,在断裂力学领域中有着重要的应用。
通过计算裂纹尖端的应力强度因子,可以评估材料的断裂韧性和脆性。
2.疲劳分析:3.材料破坏:数值计算方法可以用于分析材料的破坏机理和破坏行为。
dyna 应力强度因子

dyna 应力强度因子Dyna 应力强度因子引言:在材料力学中,应力强度因子是衡量裂纹尖端应力场的一种参数,可用于预测裂纹扩展的可能性和速率。
Dyna 应力强度因子是一种动态应力强度因子,考虑了载荷速率对裂纹尖端应力场的影响。
在工程实践中,准确地确定动态应力强度因子对于评估材料的断裂行为和结构的寿命至关重要。
1. 动态载荷对应力强度因子的影响动态载荷是指载荷在时间上的变化,对于裂纹尖端应力场的影响是不可忽视的。
在动态载荷下,裂纹尖端附近的应力场会发生明显的变化,从而导致动态应力强度因子的变化。
当载荷速率增加时,动态应力强度因子会增大,这意味着裂纹的扩展速率也会增加。
因此,准确地计算和评估动态应力强度因子对于预测材料的疲劳寿命至关重要。
2. 动态应力强度因子的计算方法计算动态应力强度因子需要考虑载荷的变化率和载荷的频率。
常用的计算方法包括线性弹性法、弹塑性法和有限元法。
线性弹性法适用于裂纹尖端附近应力场近似为线性弹性的情况,可以通过解析方法或数值方法进行计算。
弹塑性法考虑了材料的非线性行为,适用于裂纹尖端附近应力场存在明显的塑性区域的情况。
有限元法是一种广泛应用的数值方法,可以对复杂的裂纹形状和载荷条件进行计算。
通过这些方法可以得到动态应力强度因子的近似解,为评估材料的断裂行为提供了重要的参考。
3. 动态应力强度因子的工程应用动态应力强度因子在工程实践中具有重要的应用价值。
首先,准确地计算动态应力强度因子可以预测材料的疲劳寿命,帮助工程师优化设计和维护策略。
其次,动态应力强度因子对于评估材料的断裂韧性和抗裂纹扩展能力也是至关重要的。
通过实验和数值模拟,可以获得不同材料在不同载荷下的动态应力强度因子,从而为工程实践提供可靠的数据支持。
4. 动态应力强度因子的研究进展随着材料科学和工程技术的发展,对动态应力强度因子的研究也得到了广泛关注。
研究者们通过实验和数值模拟,探索了不同载荷速率、不同载荷类型和不同材料性质对动态应力强度因子的影响。
应力强度因子的计算.

以1x x '=, 1z z '=,代入⇒原有裂纹面的边缘y向位移y ',有
22222
11112222222
011(1 (1 x z x z y y a c f a f c
'=-+=--'''++
222222
1111112222221(12 (12 12( x z x z x z f f f a c a c a c
r f ρ= (f远小于
1
r
f ρ
⇒=
=
边缘上任一点(, p x z ''',有:
1(sin (1 sin (1 x r f f x ρϕρϕ'=+=+=+
1(cos (1 z r f z ρϕ'=+=+
11(, , (, p x z p x z '''⇒均在0y =的平面内. 222242222(1 c x a z f a c a c ''''''⇒+=+=
a. , 0x y xy z σστ→∞===.
b. , z a <出去z b =±处裂纹为自由表面上0, 0y xy στ==。
c.如切出xy坐标系内的第一象限的薄平板,在x轴所在截面上内力总和为p。
y '
以新坐标表示:
Z =
⇒( K Z ξ→==
Ⅰ
2.在无限大平板中,具有长度为2a的穿透板厚的裂纹表面上,在距离1x a =±的范围内受均布载荷q作用.
⇒新的裂纹面仍为椭圆.长轴(1 c f c '=+,短轴(1 a f a '=+. ⇒y向位移
应力强度因子

应力强度因子应力强度因子是力学领域中一个重要的概念,用来描述材料在裂纹尖端的应力集中情况。
在材料工程和断裂力学中,应力强度因子的概念被广泛应用。
应力强度因子的理论基础是线弹性断裂力学,该理论描述了材料在发生破裂时的应力和位移场。
应力强度因子的定义在裂纹尖端处的应力场通常是复杂的,而应力强度因子是一种在裂纹尖端的应力场附近对应力的特定描述。
它通常用符号K表示,可根据裂纹尖端的应力场表达式得出。
应力强度因子是衡量材料裂纹尖端应力集中程度的物理量。
应力强度因子的计算计算应力强度因子的方法主要有解析解法、半解析解法和数值解法。
解析解法适用于简单几何形状和边界条件的情况,可以通过应力场的解析解来计算应力强度因子。
半解析解法则是在解析解法的基础上引入数值计算方法解决更为复杂的情况。
数值解法则通过数值模拟来近似计算裂纹尖端的应力场和应力强度因子。
应力强度因子的应用应力强度因子的应用可以帮助工程师和科学家更好地理解材料的断裂行为。
通过计算裂纹尖端的应力强度因子,可以预测材料的疲劳寿命、裂纹扩展速率等参数,进而指导材料设计和使用。
此外,在材料选用、损伤评估、结构安全性评估等方面,应力强度因子也扮演着重要的角色。
结论应力强度因子作为描述裂纹尖端应力集中的重要参数,在材料断裂力学和工程实践中发挥着至关重要的作用。
深入理解和准确计算应力强度因子,对于改善材料性能、提高结构安全性具有重要意义。
在未来的研究和工程实践中,应该进一步探讨应力强度因子的计算方法和应用,为材料工程领域的发展做出新的贡献。
以上是对应力强度因子的简要介绍,希望对读者有所帮助。
应力场强度因子

应力场强度因子
应力场强度因子是一种用于描述裂纹尖端应力场的物理量。
它通常用K表示,也称为裂纹尖端强度因子。
在材料科学领域中,应力场强度因子被广泛应用于研究材料的断裂行为和疲劳寿命。
在理解应力场强度因子之前,需要先了解什么是裂纹。
裂纹是指材料中的一条细小的缝隙或裂缝,它可以是由于外部载荷、化学腐蚀或热应力等原因造成的。
当外部载荷作用于材料时,这些裂纹会扩展并最终导致材料的断裂。
应力场强度因子是描述这种断裂行为的关键参数之一。
它表示在单元长度上施加一个单位载荷所产生的最大应力值。
具体来说,如果一个材料中存在一个长度为a的直线裂纹,则其尖端处的应力场可以由下式计算得出:
σ = K√(πa)
其中,σ表示尖端处的应力值,K表示应力场强度因子。
应力场强度因子K是一个与材料性质、载荷类型和几何形状等因素相关的物理量。
它通常使用有限元分析等数值方法来计算。
在实验中,
可以通过测量裂纹尖端的应力场分布来确定应力场强度因子。
应力场强度因子在材料科学中具有广泛的应用。
例如,在疲劳寿命研究中,可以使用应力场强度因子来预测材料在不同载荷下的寿命。
此外,它还可以用于评估材料缺陷的大小和形状,以及设计结构件的安全性。
总之,应力场强度因子是描述裂纹尖端应力场的重要物理量。
它对于理解材料断裂行为和设计结构件具有重要意义,并且在实际工程中得到了广泛应用。
应力强度因子与应力的关系

应力强度因子与应力的关系大家好,今天咱们聊聊一个听起来有点高深的东西——应力强度因子和应力的关系。
你可能会想,这是什么鬼?别着急,咱们一步步来,轻松点,别让这些专业名词吓到你,搞得像在看科幻电影一样。
这个话题跟咱们的日常生活其实是有点关系的,搞懂了它,你以后遇到一些小问题也能大大提高你解决问题的效率。
咱得搞清楚什么是“应力”。
大家都知道,咱们在生活中很多时候都会遇到“压力”,有的是来自工作上的,有的是来自家庭的,还有的来自你喜欢的那个女孩儿——压力山大啊!不过,“应力”这个词在物理学里面就有点不一样了,它是用来表示物体内部承受外力作用时产生的内力。
举个例子,当你按住一个软球时,球的表面就会受到你手指的挤压,这个挤压就叫应力。
你想想看,咱们生活中是不是常常面临着各种“应力”?只不过生活中的压力看不见摸不着,而这应力,像是潜藏在物体里面的一种能量,压得它喘不过气来,随时准备爆发。
再说到应力强度因子,这就有点儿学术味了。
它用来表示裂纹尖端的应力集中程度。
简单点讲,就是在物体裂开的一瞬间,裂纹尖端那地方的应力有多大。
想象一下,当你把一根竹签折断时,竹签的中心断裂处就是应力最集中的地方。
这个地方就像是物体受力的“最弱点”,有点像咱们人的心理,压力过大,一不小心就崩溃了。
物体也是,受力不均匀的时候,某些地方的应力会像开玩笑一样集中过来,一点小小的裂缝都能让它崩溃。
你想,物体上出现裂纹,哪怕是个小裂缝,可能就能导致整个结构的垮塌,这就是为什么应力强度因子这么重要的原因。
好啦,我们说到这里,可能你有点儿晕头转向,别急,咱继续往下看。
应力强度因子和应力之间的关系,实际上就是两者是息息相关的。
就拿咱们自己来说,生活中我们每个人都面临着不同程度的“压力”,有时候工作压力大,身体上就开始感觉到不适,像肩膀酸痛,头疼脑热。
对物体来说也是一样的,当外部应力加大时,物体内部的应力强度因子就会随之增大,尤其是裂缝所在的地方,那里几乎是“压力”的源头。
材料裂尖的应力强度因子

材料裂尖的应力强度因子材料裂尖的应力强度因子是用于描述材料断裂过程中裂纹尖端处应力状态的一个重要参数。
裂纹是材料中常见的缺陷,在应力作用下裂纹可能引发材料的断裂事故。
因此,研究裂尖应力强度因子可以指导我们在工程中预测和控制裂纹的扩展,从而提高材料的可靠性和安全性。
应力强度因子是由Ernst G. Williams在20世纪50年代提出的,用来描述环境下裂纹尖端处应力的分布情况,即裂纹尖端处的应力强度。
它通过定义一些适当的应力分量,将裂纹尖端处的应力分为两个部分,一部分是正应力,另一部分是剪应力。
这两部分应力分别对应于裂尖处的拉伸和剪切应力。
应力强度因子K的大小表示其所代表的应力强度,它是由以下公式计算得出:K=σ√πa (1)其中,σ是裂纹尖端处的应力场强度,a是裂纹的长度。
这个公式说明了裂纹尖端处的应力强度与裂纹长度和应力场强度有关。
应力强度因子K的计算可通过解析或数值方法得出。
对于平面应力情况下的裂纹,通常使用Williams解析方法或Newman-Raju数值方法进行计算。
而对于三维应力情况下的裂纹,则需要使用更为精细的数值方法进行计算。
应力强度因子K描述了裂纹尖端处的应力状态,它对材料的裂纹扩展过程起着重要的作用。
根据线弹性断裂力学理论和现代断裂力学理论,当K达到一定的数值时材料就会发生裂纹扩展的过程。
这一临界值Kc,也被称作材料的断裂韧性,它是描述材料抗裂纹扩展的能力的参数。
理论上,当裂纹尖端处的应力强度因子K小于断裂韧性Kc时,裂纹就会停止扩展。
而当应力强度因子K达到或超过Kc时,裂纹就会以较快的速度扩展,导致材料的破坏。
在实际工程中,我们常常需要确定裂纹扩展的问题。
对于这个问题,可以使用K-Δa曲线来预测裂纹扩展的过程。
K-Δa曲线表示应力强度因子K和裂口扩展量Δa之间的关系,它是测试材料断裂过程中的重要参数。
通过K-Δa曲线,我们可以确定裂纹扩展的临界值Kc和裂口扩展速率da/dN,这对于材料裂纹扩展过程的控制非常重要。
应力强度因子的意义

应力强度因子的意义1. 你知道吗,应力强度因子的意义重大着呢!就好比一座大桥,它的坚固程度靠什么来保证?不就是各种结构因素嘛,应力强度因子就像是其中关键的一环。
比如,当车辆在桥上行驶时,它能决定桥是否能承受住压力而不出现问题呀!2. 嘿,想想看,应力强度因子的意义多重要啊!就像一个团队中的核心人物,能起到关键的作用。
比如说制造一架飞机,要是不考虑应力强度因子,那飞机还能安全飞行吗?这可太让人担心了!3. 哇塞,应力强度因子的意义简直超乎想象!好比是人体的骨骼强度,要是出了问题那可不得了。
就像运动员进行高强度训练,如果不关注这个,受伤的风险不就大大增加了嘛!4. 哎呀呀,应力强度因子的意义可不能小瞧啊!它就像汽车的发动机性能一样,直接影响整体表现。
比如在恶劣路况下行驶,没有合适的应力强度因子保障,那得多危险呀!5. 嘿哟,应力强度因子的意义真的好关键呀!可以类比为电脑的核心处理器,决定了整体的运行能力。
像在一些高精密仪器中,它的作用可太明显了,不然怎么能保证精确运行呢?6. 哇哦,应力强度因子的意义那是相当重要啊!如同建筑的根基,要是不牢固可不行。
就像盖高楼的时候,不重视它,这楼能盖得稳吗?7. 哎呀,应力强度因子的意义太突出啦!就像是船在大海中航行的稳定性因素,不可或缺呀!比如遇到大风大浪,没有良好的应力强度因子支持,那不就危险啦?8. 嘿呀,应力强度因子的意义真的太特别啦!可以想象成是电路中的保险丝,关键时刻起大作用。
像一些复杂的机械系统中,要是没有它,那不是随时可能出问题嘛!9. 哇,应力强度因子的意义真的很惊人啊!好比是运动员的体能储备,至关重要。
例如在一场激烈的比赛中,没有足够的应力强度因子来支撑,怎么能取得好成绩呢?10. 哟呵,应力强度因子的意义绝对不容小觑啊!它就像是心脏对于人体的重要性一样。
比如在一些高负荷的工程中,不重视它的话,后果简直不敢想象呀!我觉得应力强度因子真的是在很多领域都有着极其关键的作用,我们必须要高度重视它呀!。
dyna 应力强度因子

dyna 应力强度因子Dyna 应力强度因子应力强度因子是研究材料断裂行为和疲劳寿命的重要参数之一。
在动态加载下,应力强度因子的计算对于分析材料的疲劳寿命和断裂行为具有重要意义。
本文将重点介绍Dyna 应力强度因子的概念、计算方法以及其在工程实践中的应用。
一、概念Dyna 应力强度因子是指在动态加载条件下,应力场中应力的局部最大值与裂纹尖端处的应力强度之比。
它是描述材料断裂行为的重要参数,可以用于预测材料的断裂韧性和疲劳寿命。
二、计算方法计算Dyna 应力强度因子的方法有多种,常用的方法包括应力分析法、能量法和位移法等。
其中,应力分析法是最常用的计算方法之一。
该方法基于弹性理论,通过对裂纹周围应力场的分析,计算得到裂纹尖端处的应力强度因子。
三、应用Dyna 应力强度因子在工程实践中有着广泛的应用。
首先,它可以用于评估材料的断裂韧性。
通过计算Dyna 应力强度因子,可以得到材料在不同加载条件下的断裂韧性参数,进而评估材料的断裂性能。
其次,Dyna 应力强度因子还可以用于预测材料的疲劳寿命。
根据Dyna 应力强度因子和材料的疲劳裂纹扩展速率,可以预测材料在不同加载条件下的疲劳寿命。
此外,Dyna 应力强度因子还可以用于优化工程设计。
通过对Dyna 应力强度因子的计算和分析,可以得到不同结构参数对应的应力分布情况,从而优化工程设计,提高结构的安全性和可靠性。
总结:Dyna 应力强度因子是研究材料断裂行为和疲劳寿命的重要参数,它可以用于评估材料的断裂韧性、预测材料的疲劳寿命以及优化工程设计。
在工程实践中,通过计算和分析Dyna 应力强度因子,可以得到材料在不同加载条件下的断裂性能和疲劳寿命,为工程设计提供科学依据。
因此,研究Dyna 应力强度因子的计算方法和应用具有重要意义。
低周疲劳应力强度因子

低周疲劳应力强度因子低周疲劳应力强度因子是指在低周疲劳试验中,对材料进行加载时,引起疲劳破裂的应力强度。
它是研究材料疲劳性能的重要参数,对于工程结构的设计和寿命评估具有重要意义。
低周疲劳是指在应力幅值较大、循环次数较少的情况下,材料发生疲劳破裂的现象。
相比高周疲劳,低周疲劳的循环次数较少,但应力幅值较大,因此对材料的疲劳性能要求更高。
在低周疲劳试验中,我们通常会对材料施加不同的应力幅值,然后观察材料的疲劳寿命。
疲劳寿命是指在特定的应力幅值下,材料能够承受的循环次数。
通过对不同应力幅值下的疲劳寿命进行统计分析,可以获得材料的低周疲劳性能曲线。
低周疲劳应力强度因子是评估材料低周疲劳性能的重要指标之一。
它是指在低周疲劳试验中,引起疲劳破裂的应力强度。
在试验中,我们可以通过测量应力幅值和材料疲劳寿命,计算出低周疲劳应力强度因子的数值。
低周疲劳应力强度因子的计算方法有多种,常见的有应力幅值法、应力比法和应力强度因子法等。
这些方法根据试验条件和材料特性的不同,选择不同的计算方式。
在实际工程中,我们可以根据具体情况选择合适的方法进行计算。
低周疲劳应力强度因子的数值是评估材料低周疲劳性能的重要依据。
一般来说,低周疲劳应力强度因子越大,材料的低周疲劳性能越好。
因此,在工程实践中,我们通常会选择低周疲劳应力强度因子较大的材料,以保证结构的安全和可靠。
除了低周疲劳应力强度因子,还有其他一些参数也可以用来评估材料的低周疲劳性能,如低周疲劳极限、低周疲劳裂纹扩展速率等。
这些参数可以提供更全面的疲劳性能评估,帮助工程师选择合适的材料和设计更安全可靠的工程结构。
低周疲劳应力强度因子是评估材料低周疲劳性能的重要指标之一。
它可以通过对材料的低周疲劳试验进行测量和计算得到。
在工程实践中,我们可以根据低周疲劳应力强度因子的数值来选择合适的材料和设计更安全可靠的工程结构。
同时,还可以结合其他参数来进行全面的疲劳性能评估,以确保工程结构的安全和可靠性。
应力强度因子变程

应力强度因子变程,即应力强度因子的变程范围,指的是在疲劳裂纹扩展过程中,裂纹尖端应力强度因子的变化范围。
裂纹尖端的应力强度因子变程包括最小值(Kmin)和最大值(Kmax),两者之差即为应力强度因子变程的差值(△K)。
应力强度因子变程是描述裂纹扩展行为的重要参数,其大小直接影响到裂纹的扩展速率和材料的疲劳寿命。
在裂纹扩展过程中,应力强度因子变程的差值越大,裂纹扩展速率越快,材料的疲劳寿命越短。
因此,通过控制应力强度因子变程的差值,可以有效地控制裂纹扩展行为,提高材料的疲劳寿命。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
断裂与损伤力学应力强度因子数值计算方法综述2013年6月第一章应力强度因子求解方法概述含有裂纹的工程结构的断裂力学分析一直是一个重要问题,在断裂力学理论中应力强度因子是线弹性断裂力学中最重要的参量。
它是由构件的尺寸、形状和所受的载荷形式而确定。
由于裂尖应力场强度取决于应力强度因子,因此在计算各种构件或试件的应力强度因子是线弹性断裂力学的一项重要任务。
由于应力强度因子在裂纹体分析中的中心地位,它的求解自断裂力学问世以来就受到了高度的重视。
迄今为止,已经产生了众多的理论和致值解法。
70年代中期以前的有关工作在文献中已有相当全面的总结,近20年来,求解的方法又得刭了明显的发展与完善。
下文将穿透裂纹问题(二维)与部分穿透裂纹问题(三维)分开讨论。
第二章 二维裂纹问题2.1 复变函数法由Muskhelishvili 的复变函数法,应力函数为:_])()()([2/1)]()(Re[z z z z z z z z χψψχψ++=+=Φ平面应变情况下的应力与位移为: )]('Re[42222z yx y x ϕφφσσ=∂∂+∂∂=+ )]('')(''[22z z z i xy y x χϕτσσ+=+-)](')('[21)(243x z z z iv u χϕμϕμμ+--=+ 可以证明,在裂纹尖端区域:)]('lim[220z z z iK K K I ϕπ-=-=∏由上式可见。
由于k 仅与)(z φ有关,因此只需确定一个解析函数)(z φ,就能求得k I ,这一方法一般只能用来解无限体裂纹问题。
对于含孔边裂纹的无限大板,通常可利用复变函数的保角映射原理来简化解题过程。
如采用复变(解析)变分方法,则可求解具有复杂几何形状的含裂纹有限大板的应力强度因子。
2.2 积分方程法弹性边值问题可以变为求解下列形式的积分方程:)())(()().,(r f dt t b a t t P t r M -=--⎰ 由积分方程解出沿裂纹的坐标的函数,便能直接求出应力强度因子k 。
这个积分方程在有些特殊情况下可用普通的Gauss-Chebyshellr 积分或它的修正形式来求解。
2.3边界配置法边界配置法是求解各类边值问题的一种半解析半数值方法。
用应力函数法求解二维裂纹问题,关键是选择合适的满足全部边界条件的双调和应力函数,而对有限体或裂纹分布较复杂的情况,封闭形式的应力函数是很难选取的。
边界配置法克服了这一困难,它的基本思路是选择以级数展开形式的函数作为满足双调和方程和裂纹面边界条件的应力函数,通过边界条件来确定含有限项的级数中的待定系数。
这些待定系数可以通过求解满足边界上的应力,载葡或位移的一组线性代数方程而确定。
求解中可以在指定点上精确地满足,也可以在最小均方差的意义上满足边界条件。
这样得到的级致解一般能精确满足域内的给定条件,并且近似地满足其余边界上的条件。
在裂纹问题的边界配置法中有两种基本的应力函数可供选择,即Williams 的应力函数和Muskhelishyili的复变应力函数,从发展过程看,前者一般用在边缘裂纹问题中,后者可用于内埋裂纹与边缘裂纹的情况。
边界配置法的求解精度较高。
它的不足之处是:对于不同类型的裂纹问题,应力函数必须改变。
而建立这些新的应力函数的工作量将是很大的,对于较复杂的几何与载荷情况,应力函数所应满足的边界条件很难确定,另外,解的收敛性还没有得到严格的证明。
2.4边界力法边界力法通过利用无限体中有限数量的集中力和集中力矩的叠加来求解边值问题。
这种解法以无限体中集中力和集中力矩的弹性解为基本解,对于不含裂纹的板,基本解取Muskhelishyili的解,对于含裂纹的板,则取Erdogan的解作为基本解。
由于Erdogan的解精确地满足了裂纹面应力为零的条件,所以裂纹面就不再需要作为边界的一一部分加以考虑。
因为基本解满足了物体内部的所有弹性力学方程,余下所需满足的条件只是边界条件。
这些边界条件则是通过在相应于真实裂纹体的假想边界上施加一系列的集中力和集中力矩来满足的,先把假想的边界离散化为一组线段,在每一段的中心,在离开假想边界处加上一对集中力和力矩,这些力和力矩的值可通过近似地满足边界条件得以确定。
与其他数值方法相比,边界力法有其明显的优点。
由于这一方法已精确地满足了裂纹面上的边界条件,所以它不需要像边界元法那样把裂纹面视为边界的一部分。
另外,它也克服了边界配位法中所需要的对每一类裂纹问题都要建立新的应力函数的缺点。
这种解法只要较小的自由度就能达到相当高的精度。
因此它在求解几何形体复杂的裂纹向题中有着明显的优点,但在处理复杂载荷的能力方面,则远非如权函数法那样灵活。
2.5权函数法权函数法是一种求解在任意受载条件下裂纹应力强度因子的高效方法。
这种解法的高效性在于它把影响应力强度因子的两个因素,即载荷与几何,作了变量分离。
权函数仅反映了裂纹体的几何特性,它可以根据一种受载情况下的已知解确定。
一经导出,它就能被用来不受限制地求解任意加载条件下的k 值,求解中只需作一个积分运算:dx x x a m K a )().,(0σ⎰= 式中m(a,x)为权函数,)(x σ为无裂纹体中假想裂纹处的应力分布。
除了灵活通用,简单经济等特点外,这一方法所得的结果有高的可靠性。
2.6 有限元法有限元法在断裂力学中有着非常广泛的应用,它不受解析方法常遇到的因裂纹体几何或载荷的复杂性的限制。
这种方法的基本思路是用一系列离散化的,区段连续的场变量来对任何连续的场交量作逼近。
这些区段称为单元,单元间由结点互相连结。
因为单元内的场变量的变化规律是未知的,所以要用某些近似函数来描述它们在单元内的行为。
这些近似函数称为插值函数。
求解以有限矩阵形式出现的场的方程,便能得到整个系统的单元结点的场变量值,进而确定单元内的变量值,关于这一方法本身的理论可另见有关专著,这里只对利用有限元法求解裂纹体应力强度因子作一简单介绍。
除了极少数特殊设计的专用程序能在有限元输出结果中直接给出应力强度因子k 以外,一般的有限元计算结果都需要再通过一定的中间运算才能最终确定k 值,目前在文献中用有限元法求解应力强度因子大致可以分成直接法和间接法两种,直接法是指由有限元计算输出的应力或位移求k 值。
间接法则是通过有限元求出某些中间量,进而导出k 值。
2.6.1 直接法常用的直接法一般有以下三种:(l)采用非奇异元的位移法有限元计算所得的结点位移,通过近裂纹尖端区位移与应力强度因子之间的关系,求得一组应力强度因子值。
一般建议用由裂尖起始的,沿θ为常数(通常取θ=180)的射线上的结点位移。
在裂纹面上取若干结点的位移,作出k-r/a 的关系图。
在r/a=0的小区域内,由于采用常规单元体体现不了裂纹尖端的奇异性,可能会出现k 的异常变化,为了提高求解精度,可将k-r/a 的直线段外延到与纵轴k 的交点,交点的值即为所求的k 。
(2)采用非奇异元的应力法与位移法类似,可利用裂尖区应力场与应力强度因子的关系求k 值。
)(2θπσij ij f r K = 以有限元结点或高斯点的应力值代入上式。
并采用与位移法类似的由k-r/a 直线段外推到,r/a=0,便能确定应力强度因子值。
对于基于位移假设的有限元解法,由干位移的计算精度比应力的精度高,而且裂尖区应力的奇异性在常规元中又不能体现,所以通常都是由位移解来导出应力强度因子值。
(3)裂尖奇异元用常规的非奇异元来求解裂纹问题的一大困难是需要用很细的网格,即大量的自由度,才能使应力强度因子解达到一定的精度水平,为了压缩计算工作量,发展了各类具有r /1奇异性的裂尖奇异元,这些奇异元自身所具有的应力与应变r /1奇异性使得用较小的自由度便能达刭一定的求解精度,然而这些奇异元在某些方面也有着不足之处,如:缺乏刚性位移,与常规元不易协调,在通用的结构分析有限元程序中并不具备,因此应用起来较麻烦等等。
后来出现的一种新的奇异元则克服了以上的不足,这种新的奇异元就是由广为使用的二次等参元退化而成的四分之一结点奇异元。
四分之一结点的四边形单元的这种奇异性只在单元的两个侧边上才存在。
而在单元内部,任一条自裂尖起始的射线上奇异性并不存在。
然而,如果把四边形的一条边压缩成位于裂尖的一个点,并把两侧边的中结点向裂尖移到四分之一边长的位置,则沿自裂尖出发的任一条射线,这种经畸变后的裂失单元通常称为畸变的(或退化的)四分之一结点奇异元。
由于一般的有限元程序中都含有8结点二次等参元(三维则为20结点六面体等参元),所以采用这种四分之一结点奇异元能够在一般的有限元程序中实现,且不需对程序作任何修改。
所需要做的只是在输入文件中写进畸变后单元的结点坐标(而其他类型的裂尖奇异元法则需要有限元程序本身就具有这些裂尖奇异元,这就大大地限制了它们的使用范围)。
另外,这种四分之一结点奇异元不存在与周围的非奇异元不相容的问蹲。
由于这些明显的优点,这种裂尖元得到了非常广泛的应用。
2.6.2 间接法应用直接法遇到的一个主要问题是:由于裂纹尖端的奇异性,应力在r=0时以r/1。
方式趋于无穷。
为了保证解的精度,在用常规非奇异元时需要把网格划得很细,从而导致自由度和计算量的增加,解决这一问题除了上面已讨论的奇异元外,还可以采用各种间接法,如能量释放率,J积分,刚度导数等方法间接地导出应力强度因子。
(1)能量释放率法线弹性断裂力学的理论已证明,应力强度因子k与裂纹体能量释放率G之间有如下关系。
K'=EG'2ν-E=E)1/(计算G的一个简单方法是进行两次有限元计算,在一个计算中取裂纹长度为a,在另一个计算中释放紧靠裂纹尖端的一个结点,用公式计算应变能。
取两个计算之差值,可得能量释放率,由此便能得到k值。
这种方法的优点是对网格细化的程度要求较低。
(2)J 积分法J 积分为应力强度因子的求解提供了另一种数值方法,积分是沿着包围裂纹尖端的某路径的一个线积分,其定义是⎰∂∂-=).(ds xu T wdy J 式中w 为应变能密度,T 为积分路径的外法线方向的面力矢量,U 为位移矢量,ds 是沿积分路径的弧长。
Rice 已经证明了J 积分的路径无关性。
这一特性为J 积分的计算带来很大方便。
由于积分路径可选在近裂尖区以外,因而就降低了对裂尖区单元及其密度的要求。
在线弹性条件下,J 积分与应变能释放率G 是等同的,因此由J 积分可得应力强度因子k 。
为了计算J 积分,必须有一个根据其定义式建立的一个专用的计算机后处理程序,并要有一个描述数值积分路径的子程序。
如果在计算机中采用的是二次等参元,则最好选择通过单元Gauss 点(而不是结点)的路径。
在大多数情况下,用2x2的积分比用高阶积分所得的结果会更好些。
