方腔顶盖驱动流动
4.2 顶盖驱动流(8)

4.2顶盖驱动流4.2.1物理模型在一个正方形的二维空腔中充满等密度的空气,方腔每边长为0.1m,其顶板以0.1m/s 的速度向右移动,同时带动方腔内流体的流动,流场内的流体为层流。
计算区域示意图如图4-2-1所示。
图4-2-1 计算区域示意图4.2.2在Gambit中建立模型Step1:启动Gambit并选择求解器为Fluent5/6。
Step2:创建面操作:→→打开对话框如图4-2-2所示。
输入长度和宽度10,在Direction中选择XY Centered。
图4-2-2 创建面设置对话框Step3:划分面网格操作:→→打开对话框如图4-2-3所示,Shift+鼠标左键选择正方形面,Internal size=0.5,其它保留默认,点击Apply确认。
划分后的网格如图4-2-4所示。
图4-2-3 网格划分设置对话框图4-2-4 计算区域网格图Step4:设置边界类型操作:→●在Name栏输入边界名称wall-1,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔顶部边线。
●在Name栏输入边界名称wall-2,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔其它三条边线。
Step5:输出网格文件操作:Fil m→export→mesh打开对话框如图4-2-5所示,选中Export 2-D mesh 前面的复选框,输出网格文件。
图4-2-5 网格文件输出对话框4.2.3求解计算Step1:启动Fluent选择2d单精度求解器,点击Run,如图4-2-6所示。
图4-2-6 启动求解器图4-2-7 网格尺寸设置对话框Step2:导入并检查网格1.读入网格文件操作:Fil e→Read→Case...找到文件后,单击OK按键确认。
2.检查网格操作:Grid→Check网格读入后,一定要进行网格检查,注意最小体积不能为负值。
3.网格比例设置操作:Grid→Scale...在Gambit中,生成网格使用的单位是cm,在Grid Was Created In下拉菜单中,选取cm,如图4-2-7所示,然后单击Scale,关闭对话框。
方腔流动
边界条件
流函数边界条件:根据已知条件,在四个壁上流函数均为 0,上边界平板速度 1,根据不可 滑移条件确定流函数偏导数条件。
涡量边界条件,采用(1):
(1)可以用 Taylor 展开建立一般形式的 Thom 公式。假设某壁面切向速度 v ,沿其内法
向 n 有一节点,距离壁面距离为 h, 此点上的流函数为1 ,如果壁面上的流函数值为 0 ,那么
0
(1
0 2h2
v h)
时间导数采用向前 Euler 法,空间导数项可以用中心差分格式离散
计算步骤 1、计算 n + 1 时刻内点的涡量,需要考虑时间步长和空间步长和粘性项的关系。
2、计算 n + 1 时刻的流函数 n1 ,超松弛迭代法,松弛因子为-1.8。
3、计算 n + 1 时刻边界上的涡量
计算流体力学作业
题目
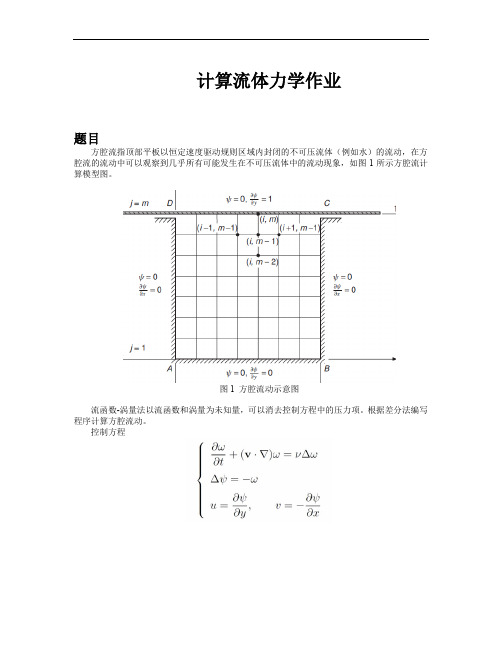
方腔流指顶部平板以恒定速度驱动规则区域内封闭的不可压流体(例如水)的流动,在方 腔流的流动中可以观察到几乎所有可能发生在不可压流体中的流动现象,如图 1 所示方腔流计 算模型图。
图 1 方腔流动示意图 流函数-涡量法以流函数和涡量为未知量,可以消去控制方程中的压力项。根据差分法编写 程序计算方腔流动。 控制方程
-0.5
0
0.5
1
1.5
3.995s 方腔速度矢量图
0
0.5
1
x0=0; x1=1; dx=(x1-x0)/(N-1); %空间步长 y0=0; y1=1; dy=(y1-y0)/(M-1); %空间步长
Thom 公式
1
0.8
0.6
0.4
0.2
0
-0.2
0
0.2
0.4
顶盖驱动方舱流的动力学模态分解

航空航天科学技术科技创新导报 Science and Technology Innovation Herald1二维顶盖驱动方舱流动,可以用于简化由某一壁面引起的空腔内部环流[1]。
从热力学角度分析,是典型的功热转化过程。
该文选用二维顶盖驱动方舱流动模型作为D N S 方法研究的载体。
N a v i e r -S t o k e s 方程具有抛物型和椭圆型两个特性,尽管控制方程具有混合特性,但采用M a c C o r m a c k 格式进行时间推进求解是适定的。
M acCor m ack格式是L a x-We nd rof f格式的一个变种,在时间和空间上都具有二阶精度的显式有限差分格式[2]。
由于M acC or m ack 格式是最容易理解和实现的格式,同时得到的结果在很多实际应用中都有令人满意的结果,所以该文选用M acCor m ack格式直接求解Nav ier-S toke s方程。
当雷诺数为6 000~8 000时,流动为转捩状态;当雷诺数达到10 000时,流动为局部湍流[3]。
为了分析流场振荡产生的原因,该文应用动力学模态分解(D M D)技术对原流场进行处理[4-7]。
1 数值模拟该文考虑二维剪切力驱动方舱流动,方舱为长宽均为=1 m m 的正方形区域,雷诺数(=ρV L /μ=9 000),壁面为无滑移恒定壁温边界条件,理想气体初始压力为101 k Pa。
顶盖运动方向与右侧壁面交接处被称为DUE,右侧壁面与下壁面的夹角处被称为DSE,左侧壁面与下壁面的夹角处被称为USE,顶盖运动反方向与左侧壁面交接处被称为UUE,4个区域如图1所示。
求解忽略体积力和体积热的二维守恒形式N a v i e r -S t o k e s 方程:定义为单位体积动能和内能的和,正应力与剪切应力为、、、,由Fou r ie r 定律得到热交换率。
采用M acC or m ac k显示时间推进求解离控制方程,并运用预测校正两步法保证在时间和空间上都具有两阶精度。
方腔驱动流源代码(SIMPLE算法)

p
pi, j
x 0
编号为(i,j)的速度修正量 u , v 不仅与压力修正量
p 有关,还与邻近点的速度修正
量有关。SIMPLE 算法的重要假定:速度的改变只与压力的改变有关,忽略邻近点对速度修 正的影响。因而得到如下速度修正量
u i, j vi, j
本算例采用求解不可压缩流动的经典算法, 即 SIMPLE 算法, 求解方腔内粘性不可压缩 流体运动的定常解。 SIMPLE 算法的全称为 Semi-Implicit Method for Pressure-Linked Equations, 即求解压力关联方程的半隐式算法。 采用 SIMPLE 算法时, 为了避免中心差分格式将 “棋盘” 型参量分布误认为是均匀分布, 需要用交错网格对计算域进行离散。
xy M 1 M 1 1 1 M 1 M 1 ui , j ui , j Fi ,1j Fi y 0 1, j y Gi , j Gi , j 1 x pi 1, j pi , j t
Y 方向动量方程在速度 v 控制体上离散,时间采用前差
1 2 2 xy 1 M M M M aiu, j y uiM x viM 1, j u i 1, j , j vi 1, j vi , j 1 vi 1, j 1 Re x Re y t 4 4
以上是 SIMPLE 算法中离散化的动量方程
三、SIMPLE 算法基本思想
SIMPLE 算法是一种解决压力-速度耦合问题的“半隐式”算法。首先给定 M 时刻猜测 的速度场 u 估计值 值u
方腔顶盖驱动流动
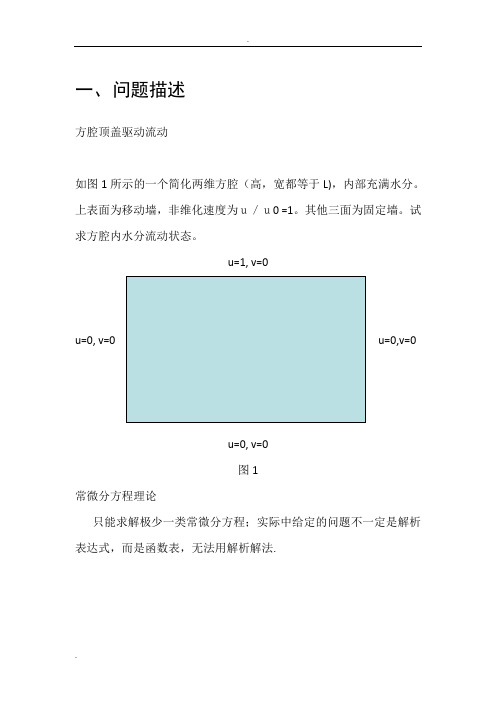
一、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0 u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1) y n +1 , 称为局部截断误差.截断误差: 实际上,y (x n ) ? y n , y n 也有误差,它对y n +1的误差也有影响,见下图。
但这里不考虑此误差的影响,仅考虑方法或公式本身带来的误差,因此称为方法误差或截断误差。
局部截断误差的分析:由于假设y n = y (x n ) ,即y n 准确,因此分析局部截断误差时将y (x n +1) 和 y n +1都用点x n 上的信息来表示,工具:Taylor 展开。
显式欧拉公式一阶向前差商近似一阶导数推导如下:223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+隐式欧拉公式xn +1点向后差商近似导数 推导如下:几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
方腔顶盖驱动流动

一、二、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1)y n +1 , 称为局部截断误差.显式欧拉公式一阶向前差商近似一阶导数223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+推导如下:隐式欧拉公式x n +1点向后差商近似导数 推导如下:1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+11()()()n n n y x y x y x h++-'≈11()()()()n n n n ny x y x hy x y x y ++'≈+↑≈几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
OpenFOAM顶盖驱动流详解!使用手册

OpenFOAM顶盖驱动流详解!使用手册引言这是开源场运算和操作c++库类(openfoam)的使用指南。
他详细描述了OpenFOAM的基本操作。
首先通过第二章一系列教程练习。
然后通过对更多的独立组件的更详细的描述学习openfoam。
Of 首先主要是一个c++库类,主要用于创建可执行文件,比如应用程(application)。
应用程序分成两类:求解器,都是为了解决特定的连续介质力学问题而设计的;公用工程,这些是为了执行包括数据操作等任务而设计的。
Of 包括了数量众多的solver和utilities,牵涉的问题也比较广泛。
将在第三章进行详尽的描述。
Of 的一个强项是用户可以通过必要的预备知识(包括数学,物理和编程技术)创建新的solvers 和utilities。
Of 需要前处理和后处理环境。
前处理、后处理接口就是of本身的实用程序(utilities),以此确保协调的数据传输环境。
图是of总体的结构。
第4章和第五章描述了前处理和运行of 的案例。
既包括用of提供的mesh generator划分网格也包括第三方软件生成的网格数据转换。
第六章介绍后处理。
Chapter 2指导手册在这一章中我们详细描述了安装过程,模拟和后进程处理一些OpenFOAM测试案例,以引导用户运行OpenFOAM的基本程序。
$FOAM_TUTORIALS 目录包含许多案件演示of提供的所有求解器以及许多共用程序的使用,在试图运行教程之前,用户必须首先确保他们已经正确地安装了OpenFOAM。
该教程案件描述 blockMesh预处理工具的使用,paraFoam案例设置和运行OpenFOAM求解器及使用paraFoam进行后处理。
使用OpenFOAM支持的第三方后处理软件的用户可以选择:他们要么可以按照教程使用paraFoam,或当需要后处理时参阅第六章的第三方软件使用说明。
OpenFOAM安装目录下的tutorials目录中所有的指导手册都是可复制的。
顶驱结构和原理

顶驱构造及原理
顶驱构造 顶驱旳构成: 1、综合游 车
VACRO 综合游动滑车组提供六个额定载荷为500T, 外径为50 in旳滑轮。整个游车高 。
2、钻井装置总成
• 钻井电动机是一种1000hp旳分流电动机。电动机是 由电枢空心轴和垂直止推轴承构成。
• 单速行星变速器 IDS 单速行星变速器由下列主要原件构成: 内齿合齿轮和齿轮箱 电机小齿轮
顶驱构造及原理
顶驱构造
6、有延伸入口旳现场谷风机冷却系统。
该系统向钻井电动机提供现场冷却空气。该系统由带有导管旳原则型局部 鼓风机和一根向马达方向旳延伸旳软管构成,鼓风机上旳导管能将进口安 装在大钩和游动滑车上。 C.PH-60型管子处理装置 管子处理装置涉及 1、整体吊卡 2、安全阀(IBOPS)
❖ 每3个月对顶驱齿轮箱旳润滑油进行更换,油品标号为 MOBIL626。油量为12加仑。
❖ 每3个月对机械手泵站旳液压油进行更换,油品为N32抗磨 液压油,油量32加仑。
❖ 每日对顶驱旳各个连接螺栓及开口销进行检验,对发觉旳问 题及时处理。
顶驱构造及原理
顶驱构造及原理
顶驱构造及原理
顶驱简介
据悉,目前我国赴国外工作旳钻井队,如钻机未安装顶部驱动 钻井装置者,投标竞争中不允许中标,可见顶部驱动钻井装置 已到了非用 不可旳地步。图片
❖目前,石油钻井中使用旳顶驱有两大类:电动顶驱和液动顶 驱。其中电动顶驱又按照电机分为直流电动顶驱和液动变频顶 驱,我们平台现用旳是直流电动顶驱。 ❖a.顶驱钻井系统特点 ❖ 能够节省钻井时间20%-50 %,能够大大降低卡钻事故能够 控制井涌防止井喷,用于深井超深井、斜井以及高难度旳定向 钻井,其综合效益尤为明显。
顶驱构造及原理
高雷诺数三维顶盖驱动方腔流实验研究

高雷诺数三维顶盖驱动方腔流实验研究在流体动力学中,顶盖驱动方腔流是重要的研究方向之一,可获取流动特性及流场模型,为汽车、航空、船舶等结构设计提供指导。
然而,传统的顶盖方腔主要分析了低雷诺数的平面流动,无法模拟三维流动过程。
为此,开展高雷诺数三维顶盖驱动方腔流的实验研究具有重要意义。
一、介绍(1)定义高雷诺数三维顶盖驱动方腔流,是指采用高雷诺数的环境,以三维顶盖的形式对方腔内的流体进行驱动,观察流体在方腔内运动轨迹,以研究三维顶盖方腔流动特性及流场模型。
(2)研究内容高雷诺数三维顶盖驱动方腔流的实验研究,主要涉及到两个方面:第一,研究调节顶盖尺寸和高度、边界条件及内外温度差等参数,探讨流动特性及流场模型。
第二,研究流体运动轨迹,以研究运动情况,揭示顶盖驱动方腔流动的实际机理,以优化设计及实现流体动力学性能。
二、实验条件(1)实验装置实验装置主要包括高雷诺数气体序列量程器、定压泵、三维顶盖驱动方腔、蒸汽源、温度计、密度计、压力计等。
(2)实验参数实验参数主要包括顶盖尺寸及高度、边界条件、内外温度差等参数。
三、实验和结果研究高雷诺数三维顶盖驱动方腔流的实验,主要运用基本物理测量方法,确定实验参数,调节顶盖尺寸和高度,监测内外温度差、流速等参数,对方腔内部流动进行观测,收集流场实验数据,以便研究顶盖驱动方腔流动特性及流场模型。
实验结果表明,在各种不同参数设定下,测量到的方腔内部流场均能受到高雷诺数三维顶盖的影响,流经方腔内流动具有不同的轨迹。
运用流体动力学理论,根据实验数据,建立顶盖驱动方腔流动的数学模型,以实现对方腔内流场形态的解析和分析。
四、结论本次实验通过高雷诺数三维顶盖驱动方腔流的实验研究,发现了方腔内流动特性与顶盖参数设定的关系,揭示了顶盖驱动方腔流动的实际机理,并建立了顶盖驱动方腔流动的数学模型,为汽车、航空、船舶等结构设计提供指导,有助于更好地了解流体动力学。
格子玻尔兹曼方法顶盖驱动流

格子玻尔兹曼方法顶盖驱动流格子玻尔兹曼方法(LBM)是一种近年来在流体力学模拟中被广泛应用的数值模拟方法。
该方法可以在复杂的几何和边界条件上精确地模拟各种流体现象。
其中的顶盖驱动流模拟,是一种受到广泛关注的研究领域。
1.什么是顶盖驱动流?顶盖驱动流是指由上端盖板施加外力所形成的流场,它是在一个密闭的正方形边界中进行模拟。
流场通常是由重力和顶部盖板的驱动力组成的。
对于使用LBM计算的顶盖驱动流,由于模型简单,计算效率高,因此已取得了广泛的应用。
2.LBM是如何模拟顶盖驱动流的?LBM的基本原理是通过在大量的离散速度上进行策略性模拟,以模拟物质运动。
与传统的流体动力学方法不同,LBM使用离散的速度和密度来描述流体的运动,因此它可以非常方便的用于复杂的几何和边界条件下的流体模拟。
在顶盖驱动流模拟中,LBM将二维正方形边界分为许多离散化的小单元格,并在每个单元格上施加离散速度和压力值来模拟流体行为。
3.顶盖驱动流模拟的应用领域是什么?顶盖驱动流模拟在许多领域具有广泛的应用,包括地质、生物学、工程学和环境科学等领域。
在地质学中,它被用于模拟岩石的岩石圈运动并对流体流动的地质效应进行分析。
在工程学中,它被用于模拟汽车空气动力学和水力学作用以及结构物的振动和熱传导等现象。
4.顶盖驱动流模拟存在的挑战是什么?尽管顶盖驱动流模拟为模拟流体行为提供了强有力的工具,但仍然存在一些挑战。
例如,该方法需要高度离散化的速度空间和网格结构,这可能会导致计算效率低下和计算成本高昂。
此外,顶盖驱动流模拟还需要对物理设置和计算参数进行大量的调整和测试,才能使模拟结果更加准确和可靠。
总之,格子玻尔兹曼方法顶盖驱动流是一种新兴的数值模拟方法,在流体力学和其他领域的应用越来越广泛。
将来,随着计算机硬件和软件的不断发展,顶盖驱动流模拟将进一步提高计算精度和计算效率,为工程学、生物学和环境科学等领域能提供更准确的解决方案。
格子Boltzmann方法三种边界格式的对比分析

格子Boltzmann方法三种边界格式的对比分析刘连国;杨帆;王宏光【摘要】采用格子Boltzmann方法(Lattice Boltzmann Method- LBM)对二维顶盖驱动方腔流动进行数值模拟.在计算中分别使用半步长反弹、非平衡反弹、以及非平衡外推三种边界处理格式,并得到了不同格式对应的流线分布,流函数最小值、涡心坐标、几何中心线速度分布等.通过将所得结果与基准解进行比较,就三种边界格式的计算效率,计算精度、以及计算稳定性等方面进行了讨论和分析,为LBM计算中边界格式的选择提供了有益的参考.【期刊名称】《机械研究与应用》【年(卷),期】2012(000)001【总页数】5页(P18-22)【关键词】格子Boltzmann方法;边界处理格式;半步长反弹格式;非平衡反弹格式;非平衡外推格式【作者】刘连国;杨帆;王宏光【作者单位】上海理工大学能源与动力工程学院,上海200093;上海理工大学能源与动力工程学院,上海200093;上海理工大学能源与动力工程学院,上海200093【正文语种】中文【中图分类】O357.11 引言格子Boltzmann方法(LBM)是近年来迅速发展的一种新型数值计算方法。
边界条件的处理是LBM实施中一项非常关键的内容。
实际计算表明:选取不同的边界条件会对数值计算的精度、稳定性以及效率产生很大影响。
作为LBM的一个基本问题,边界条件的处理一直是流体力学一个重要的研究方面。
根据边界条件的类型,可将之分为两类:压力边界和速度边界[1],其中的速度边界又可细分为:平直边界和曲面边界。
笔者从经典的流体力学问题二维顶盖方腔流模拟入手,对三种平直边界格式进行对比和分析,为LBM计算中边界格式的选择提供了有益的参考。
2 二维九点格子Boltzmann模型目前最常用的格子Boltzmann模型为LBGK模型,通过引入“单一弛豫时间”来简化Boltzmann方程中碰撞项的计算[2]。
九点格子LBGK模型的演化方程为:式中:(x,t)是在t时刻、x处的平衡态分布函数;τ为单一弛豫时间因子;eα为网格点各方向上的粒子速度。
顶部驱动钻井系统课件

9、便于维修。钻井马达清晰可见。熟练的现场人员约12小时就能 将其组装和拆卸。
10、使用常规的水龙头部件。顶部驱动装置可使用650吨常规水龙 头的一些部件,特殊设计后维修难度没有增加。
11、下套管。顶部驱动钻井装置的提升能力很大(650吨),在套 管和主轴之间加一个转换头(大小头)就可以在套管中进行压力循 环。套管可以旋转和循环入井,从而减少缩径井段的摩阻力。
但在延续百多年的转盘钻井方式中,有两个突出的矛盾未能得 到有效的解决:其一、起下钻时不能及时实现循环旋转的功能,遇 上复杂地层或是岩屑沉淀,往往造成卡钻。其二、方钻杆的长度限 制了钻进的深度(每次只能接单根),降低了效率,增加了劳动的 强度,降低了安全系数。
二十世纪七十年代,出现了动力水龙头,改革了驱动的方式,在 相当的程度上改善了工人的操作条件,加快了钻井的速度以及同期 出现的“铁钻工”装置、液气大钳等等,局部解决了钻杆位移、连 接等问题,但远没有达到石油工人盼望的理想程度。
该系统是当前钻井设 备自动化发展更新的突 出阶段成果之一。经实 践证明:这种系统可节 省钻井时间20%到30%, 并可预防卡钻事故,用 于钻高难度的定向井时 经济效果尤为显著。
顶部驱动钻井系统
二、顶部驱动系统的研制过程:
1、钻井自动化进程推动了顶部驱动钻井法的诞生。
二十世纪初期,美国首先使用旋转钻井法获得成功,此种方 法较顿钻方法是一种历史性的飞跃,据统计,美国有63%的石油 井是用旋转法钻井打成的。
顶部驱动钻井系统
20世纪80年代,美国首先研 制了顶部驱动钻井系统TDS-3S 投入石油钻井的生产。80年代 末期新式高扭矩马达的出现为 顶驱注入了新的血液和活力。 TDS—3H、TDS—4应运而生, 直至后来的TDS-3SB、TDS4SB、TDS-6SB。
方腔顶盖驱动流数值模拟

方腔顶盖驱动流数值模拟张鑫(浙江理工大学 动力工程 2013G0502003)摘 要:在计算流体力学的研究中,通常要计算方腔驱动流问题来检验各种N-S 数值方法的有效性。
本文利用Fluent 软件对标准计算流体力学测试算例——方腔驱动流问题进行了模拟分析,其计算结果与文献中的标准解符合的比较好。
关键字:N-S 方程 方腔驱动流 Fluent 数值求解0引言流体流动的数值模拟广泛应用于气象、航天、机械、采矿等自然研究和工程计算的各个领域。
近年来,随着高性能计算与通信的迅速发展,针对流体流动的数值模拟以及求解相应Navier -Stokes 方程(简称N-S 方程)的高级算法研究现已成为目前国内外备受关注的热点和前沿课题。
Fluent 软件是用于模拟具有复杂外形的流体流动以及热传导的计算机程序,可以有效地模拟方腔驱动流问题,为计算流体力学的算法理论研究提供仿真参考。
高殿荣等学者采用液压冲击进行了分析;韩善玲等分析流体在空腔内的运动规律和物理机制,指出微小的凹凸是引起噪声的原因之一。
杨晶用Fluent 软件对方腔驱动流动进行了模拟分析,研究了不同雷诺数对计算结果的影响。
1模型介绍下图描述了本文所研究的物理模型,模型为边长等于0.1m 的正方形,上壁面为有一定速度的水,两侧壁面及地面均固定。
流体材料为水,密度为998.2kg/m3,黏度310005.1-⨯=u 。
2数值计算2.1、N-S 方程本文控制方程采用纳维司托克斯方程,纳维司托克斯方程是描述粘性不可压缩流体动量守恒的运动方程。
简称N-S 方程。
在直角坐标系中,可表达为如下所示: 连续方程:0=∂∂+∂∂yv x u 动量方程:)(yu x u x p y u v x u u 22221∂∂+∂∂+∂∂-=∂∂+∂∂υρ )(yv x v x p y v v x v u 22221∂∂+∂∂+∂∂-=∂∂+∂∂υρ 2.2、网格划分及边界条件设置在gambit 软件中建立模型划分网络,由于模型几何形状比较规则,故全部采用四边形的的结构化网格,如下图所示。
4.2 顶盖驱动流(8)

4.2顶盖驱动流4.2.1物理模型在一个正方形的二维空腔中充满等密度的空气,方腔每边长为0.1m,其顶板以0.1m/s 的速度向右移动,同时带动方腔内流体的流动,流场内的流体为层流。
计算区域示意图如图4-2-1所示。
图4-2-1 计算区域示意图4.2.2在Gambit中建立模型Step1:启动Gambit并选择求解器为Fluent5/6。
Step2:创建面操作:→→打开对话框如图4-2-2所示。
输入长度和宽度10,在Direction中选择XY Centered。
图4-2-2 创建面设置对话框Step3:划分面网格操作:→→打开对话框如图4-2-3所示,Shift+鼠标左键选择正方形面,Internal size=0.5,其它保留默认,点击Apply确认。
划分后的网格如图4-2-4所示。
图4-2-3 网格划分设置对话框图4-2-4 计算区域网格图Step4:设置边界类型操作:→●在Name栏输入边界名称wall-1,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔顶部边线。
●在Name栏输入边界名称wall-2,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔其它三条边线。
Step5:输出网格文件操作:Fil m→export→mesh打开对话框如图4-2-5所示,选中Export 2-D mesh 前面的复选框,输出网格文件。
图4-2-5 网格文件输出对话框4.2.3求解计算Step1:启动Fluent选择2d单精度求解器,点击Run,如图4-2-6所示。
图4-2-6 启动求解器图4-2-7 网格尺寸设置对话框Step2:导入并检查网格1.读入网格文件操作:Fil e→Read→Case...找到文件后,单击OK按键确认。
2.检查网格操作:Grid→Check网格读入后,一定要进行网格检查,注意最小体积不能为负值。
3.网格比例设置操作:Grid→Scale...在Gambit中,生成网格使用的单位是cm,在Grid Was Created In下拉菜单中,选取cm,如图4-2-7所示,然后单击Scale,关闭对话框。
格子玻尔兹曼方法顶盖驱动流

格子玻尔兹曼方法顶盖驱动流
格子玻尔兹曼方法是一种用于数值模拟流体动力学的方法,适用于微观尺度上的非平衡流体系统。
其中一个经典的案例是顶盖驱动流。
顶盖驱动流是一种实验室中常见的流体力学现象,其涉及到一个长方形的容器,其中底部被加热,顶部被保持在常温下。
流体在容器内自然对流,并产生了一个横向的流动。
这种流动很适合用格子玻尔兹曼方法来模拟。
在模拟过程中,首先需要将流体分割成小的区域,然后在每个区域中计算流体的速度、密度和分布函数。
通过这些值的计算和更新,可以模拟出流体的运动和演化过程。
针对顶盖驱动流,需要在容器的顶部施加一个固定的速度场,以模拟顶部的运动。
通过格子玻尔兹曼方法的模拟,可以得出流体的速度场、温度场和压力场等信息,从而更好地理解和预测顶盖驱动流的行为。
这对于流体力学的研究和应用都具有重要意义。
- 1 -。
顶盖驱动流 谱方法

顶盖驱动流谱方法
顶盖驱动流谱方法(Top Hat driven flow spectroscopy method)是一种常用于表征复杂流体动力学行为的流体力学方法。
顶盖驱动流谱方法通过在流体上方施加一个顶盖运动,并通过监测流体中的扩散和剪切变形来评估流体的流动性质。
顶盖驱动流谱方法的基本原理是利用顶盖的运动来引起流体的流动。
通过在流体上方施加一个顶盖的运动,可以在流体中引入额外的扩散和剪切变形。
顶盖的运动可以通过不同的方式实现,如旋转、振荡或往复移动。
同时,在顶盖运动的影响下,流体中的粒子或标记物会发生位移和旋转,这些运动可以通过光学、电学或其他检测方法进行监测和分析。
顶盖驱动流谱方法可以用于研究不同流体性质的变化,如黏度、流变特性和颗粒浓度等。
通过测量扩散和剪切变形的程度,可以得到关于流体动力学行为的定量信息。
这种方法在生命科学领域的应用也很广泛,可以用于研究细胞运动、颗粒流和微流体中的流动等。
与传统的流体力学方法相比,顶盖驱动流谱方法具有一些优势。
首先,它可以对复杂、非牛顿流体的性质进行研究,而传统方法往往只适用于牛顿流体。
其次,顶盖驱动流谱方法可以用于研究微观尺度下的流体行为,可以探索纳米和微米尺度上的流动现象。
此外,这种方法还可以与其他技术相结合,如荧光标记、微流控等,进一步拓展其应用范围。
总之,顶盖驱动流谱方法是一种有效的流体力学方法,可以用
于研究复杂流体的动力学行为。
其原理简单,应用范围广泛,有望在生物医学和纳米技术等领域发挥重要作用。
数值传热学-CMAC算法-答辩PPT

aW 0
b Ui, j Ui1, j Vi, j1 Vi, j1
2X
2Y
(4)i=M-1&j=2时
aE 0 aS 0
b Ui1, j Ui, j Vi, j Vi, j1
2X
2Y
方程离散
(5)i=M-1&j=N-1时:
aW 0 aN 0
b Ui1, j Ui, j Vi, j1 Vi, j
对U的控制方程进行离散:
U
U n1 i, j
U
n i,
j
U
U X
Un i, j
U U n i1, j
n i1, j
2X
V
U Y
Vn i, j
U U n i, j 1
n i, j 1
2Y
P
P n 1 i1, j
Pn1 i-1, j
X
2X
2U Y 2
U
n i,
j
1
2U
n i,
j
Y 2
U
n i,
j
1
n1 i, j
X
(4)
V n1 i, j1 2
Vi, j
n
+ Vi, j1 2
n
P P n1 i, j
n1 i, j1
Y
(5)
V n1 i, j1 2
Vi, j1
n + Vi, j 2
n
P P n1 i, j1
n1 i, j
Y
(6)
方程离散
将(3)、(4)、(5)、(6)带入连续性方程可得:
方程离散
上述压力泊松方程对内点成立,对边界邻点需要进行特殊 处理,将边界邻点划分为8区域,分别进行讨论,如图所示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、问题描述
方腔顶盖驱动流动
如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0
u=0, v=0
u=0,v=0
u=0, v=0
图1
常微分方程理论
只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.
二、离散格式
数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点
a = x 0< x 1<…<
x n = b 处的近似值
)
,...,1()
(n i x y y i i =≈
节点间距
为步长,通常采
用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法
1(,) 0,1,...
n n n n y y h f x y n +=+=
几何意义
在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1)
y n +1 , 称为局部截
截断误差: 实际上,y (x n )
y n , y n 也有误差,它对y n +1的误差也有影响,见下
图。
但这里不考虑此误差的影响,仅考虑方法或公式本身带来的误差,因此称为
断误差.
显式欧拉公式
一阶向前差商近似一阶导数
22
3
1112
3
2
()[()()()()]
[ (,)] ()()
h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=
+
推导如下:
隐式欧拉公式
x n +1点向后差商近似导数 推导如下:
1()()
()n n n y x y x y x h
+-'≈
111()()() ()()(,)
n n n n n
n n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+11()()
()n n n y x y x y x h
++-'≈
111111()()()
()()(,)
n n n n n
n n n n n y x y x hy x y x y y x y y h f x y ++++++'≈+↑≈≈=+
几何意义
设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
比较 显式公式和隐式公式及其局部截断误差
显式公式
1(,) 0,1,...
n n n n y y h f x y n +=+=23
1112
()()()
h n n n n R y x y y x O h +++''=-=
+
隐式公式
中点欧拉公式
中心差商近似导数
h x y x y x y 2)
()()(021-≈
'
1
,...,1),(211-=+=-+n i y x f h y y i i i i
111(,)
n n n n y y h f x y +++=+2
3
1112
()()()
h n n n n R y x y y x O h +++''=-=-+))
(,(2)()(1102x y x f h x y x y +≈P n+1
x y
y(
控制方程
交错网格
因为方腔顶盖驱动流动的流动不均与性,u、v及压力p的变化存在交错的现象。
P 点位置
u 点位置
v 点位置
P 点控制微元体u点控制微元体v点控制微元体
守恒形式N-S方程
动量方程离散(x-方向)
方程(1)
推导过程:
⎪⎪
⎭
⎫
⎝
⎛
+
=
+
-j
i
j
i
j
i
u
u
u
,
2
1
,
2
1
,2
1
综上有:
动量方程离散(y-方向)
方程(2)
三、压力修正的基本思想
压力修正方程推导
方程(1)
欧拉显式
方程(3)
方程(2)欧拉显式
方程(4)
压力修正方程
U*,V*,P* 中间值
方程(5)U’,V’,P’修正值(N+1时间步)U N+1,V N+1,P N+1,满足连续方程的值
方程(6)
方程(7)
方程(8)
综合方程3,5,6,可得
方程(9)
综合方程4,5,7,可得
方程(10)将方程9,10,5 代入方程8,可得
方程(11)
四、SIMPLE算法流程图
M程序语言:
已知条件
L=H; 方腔的宽,高
u=1, v=0;方腔上表面的速度
u=0, v=0;方腔左表面的速度
u=0, v=0;方腔右表面的速度
u=0, v=0;方腔下表面的速度
网格划分
Y方向网格数为:M。
节点在Y方向序号变量为i。
1< =i<= M
X方向网格数为:N。
节点在X方向序号变量为j。
1<= j<= N
节点矩阵:
OT=zeros(M,N); OT 旧值某个节点OT(i, j)
NT=zeros(M,N); NT 新值间距
dx=L/(N-1); X方向间距dy=H/(M-1); Y方向间距控制方程离散
方程(11)。
