三角形手拉手模型-专题讲义(无答案)
人教版八年级数学 全等三角形之手拉手模型和半角模型 专题讲义

八年级数学全等三角形之手拉手模型和半角模型专题讲义
一、什么叫半角模型
定义:我们习惯把过等腰三角形顶角的顶点引两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
常见的图形为正方形,正三角形,等腰直角三角形等,解题思路一般是将半角两边的三角形通过旋转到一边合并形成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得出线段之间的数量关系,从而解决问题。
二、基本模型(1)——正方形内含半角
如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF。
三、基本模型(2)——等边三角形内含半角
四、基本模型(3)——等腰直角三角形内含半角
手拉手模型。
人教版数学八年级上册 综合专题2—全等三角形手拉手模型

长线交 CE 于 F 点.
证明重要结论:
C
① △ABD≌△ACE;
FD
② BD = CE;
③ BD 的延长线 BF⊥CE;
EA
B
解:∵△ABC、△ADE 都是等腰直角三角形, ∴ AB = AC,AD = AE. 在△ABD 和△ACE 中,
∴ △ABD≌△ACE(SAS). ∴ BD = CE. ∴ ∠ABD = ∠ACE. ∵ ∠BDC = ∠ABD + ∠BAC
E
① △ABD≌△ACE
② BD = CE
③ ∠BFC = ∠BAC = ∠DAE B
F D G
C
解:∵△ABC、△ADE 都是等腰三角形,
∴ AB = AC,AD = AE.
又∵∠BAC = ∠DAE,
A
∴∠BAC + ∠CAD =∠DAE +∠CAD,
即∠BAD = ∠CAE.
在△ABD 和△ACE 中
BE 交于点 O,AD 与 BC 交于点 P,BE 与 CD 交于点
Q,连接 PQ,则有以下五个结论: B ① AD = BE; ② PQ∥AE;
③ AP = BQ; ④ DE = DP;
⑤∠AOB = 60°.
P
OD Q
其中正确的结论有__①__②__③__⑤___.
A
C
E
=∠ACE + ∠BFC, ∴ ∠BFC = ∠BAC = 90°. ∴ BF⊥CE.
C FD
EA
B
练一练
2. 如图,△ABC、△ADE 都是等腰直角三角形,
∠BAC = ∠DAE = 90°,连接 BD、CE 交于点 F.
(1) 求证:BD = CE; (2) 求证:BD⊥CE. C
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)
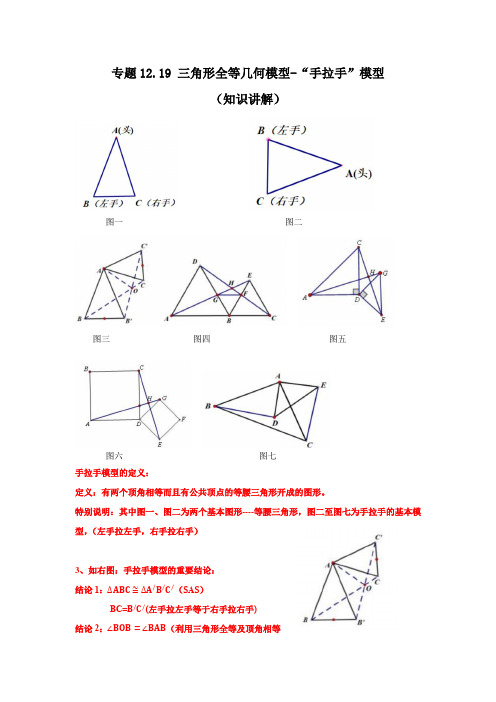
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)图一图二图三图四图五图六图七手拉手模型的定义:定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)3、如右图:手拉手模型的重要结论:结论1:∆ABC≅∆A/B/C/(SAS)BC=B/C/(左手拉左手等于右手拉右手)结论2:∠BOB=∠BAB(利用三角形全等及顶角相等的等腰三角形底角相等)结论3:AO平分∠B O C/(利用三角形全等面积相等,再利用角平分线性质定理证明)典型例题讲练:在学习全等三角形知识时、教学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究:(1)如图1、两个等腰三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE,连接BD、CE、如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和△ADB 全等的三角形是,此线BD和CE的数量关系是(2)如图2、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和CE的数量关系和位置关系,并说明理由:(3)如图3,已知△ABC、请完成作图:以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等,三个角都等于60°),连接BE,CD,两线交于点P,并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】(1)△AEC,BD=CE;(2)BD=CE且BD△CE,理由见解析;(3)作图见解析,BE=CD,△PBC+△PCB=60°.【分析】(1)根据SAS证明两个三角形全等即可证明;(2)通过条件证明△DAB△△EAC(SAS),得到△DBC+△ECB=90°,即可证明BD△CE,从而得到结果;≅即可得到证明;(3)根据已知条件证明DAC BAE解:(1)△AB=AC,AE=AD,△BAC=△DAE,∠+∠=∠+∠,△DAE EAB BAC EAB即DAB EAC ∠=∠,△()△△ADB AEC SAS ≅,△BD=CE ;(2)BD=CE 且BD△CE ;理由如下:因为△DAE=△BAC=90°,如图2.所以△DAE+△BAE=△BAC+△BAE .所以△DAB=△EAC .在△DAB 和△EAC 中,,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC (SAS ).所以BD=CE ,△DBA=△ECA .因为△ECA+△ECB+△ABC=90°,所以△DBA+△ECB+△ABC=90°.即△DBC+△ECB=90°.所以△BPC=180°-(△DBC+△ECB )=90°.所以BD△CE .综上所述:BD=CE 且BD△CE .(3)如图3所示,BE=CD ,△PBC+△PCB=60°.由图可知60DAB EAC ∠=∠=︒,AD=AB ,AE=AC ,△+DAB BAC EAC BAC ∠∠=∠+∠,即DAC BAE ∠=∠,△()△DAE △BAE SAS ≅,△BE=CD ,ABE ADC ∠=∠,又△60BDA ∠=︒,△60ADC BDC ABE BDC ∠+∠=∠+∠=︒,△120BPC ABP BDC BDA ∠=∠+∠+∠=︒,△△PBC+△PCB=60°.【点拨】本题主要考查了全等三角形的知识点应用,准确分析图形是解题的关键. 举一反三变式1:如图,AC △BC ,DC △EC ,AC =BC ,DC =EC ,AE 与BD 交于点F .(1)求证:AE =BD ;(2)求△AFD 的度数.【答案】(1)详情见解析;(2)90AFD ∠=︒【分析】(1)利用角的等量代换求出ACE BCD ∠=∠,再判断ACE ≌BCD △即可求解; (2)利用全等三角形的性质得到E D ∠=∠,再通过角的等量代换求解即可.解:(1)△AC BC ⊥,DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =(2)设BD 与CE 的交点为G ,如图所示:△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠,180GCD CGD D ++=︒∠∠∠,且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定,灵活运用角的等量代换是解题的关键.例题2.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;△AD =BE △△EFD =60° △MC =NC △△AMB =△END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示. △问:(1)中的正确结论哪些还成立?若成立,请说明理由;△连接FC ,如图3所示,求证:FC 平分△BFD【答案】(1)△△△;(2)△ △△;△见解析.【分析】(1)△根据等边三角形的性质得CA =CB ,CD =CE ,△ACB =60°,△DCE =60°,则△ACE =60°,利用“SAS ”可判断△ACD △△BCE ,则AD =BE ;△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论; △连接MN ,证明△MCN 是等边三角形即可得出结论;△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠,而AC ≠CD 得CAD CDA ∠≠∠,从而可得出结论;(2)△方法同(1),逐个结论进行证明即可;△作,CG BE CH AD ⊥⊥于点G ,H ,证明△BGC △△AHC ,△CGF △△CHF 可得△CFG CFH =∠,从而可得结论.解:(1)△△ABC ,△ECD 是等边三角形,△AC=BC ,CE=CD ,△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ,故△正确;△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°,故△正确;又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ,故△正确;又△△AMB=△ACB+△ECB=60°+△ECB ,△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠,故△错误;故答案为:△△△;(2)△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ,CE=CD△△ACD△△BCE△AD=BE,故△正确;△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°,故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ,△MC≠NC ,故△错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)△知,△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ,△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.举一反三变式:如图,在ABC∆中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则AOB∠的度数为()A.100︒B.120︒C.130︒D.150︒【答案】B【分析】先证明△DCB△△ACE,求出△CAE=△CDB,再利用“8字型”证明△AOH=△DCH =60°即可解决问题.解:如图:AC与BD交于点H,△△ACD,△BCE都是等边三角形,△CD=CA,CB=CE,△ACD=△BCE=60°,△△DCB=△ACE,在△DCB和△ACE中,CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩===,△△DCB△△ACE,△△CAE=△CDB,△△DCH+△CHD+△BDC=180°,△AOH+△AHO+△CAE=180°,△DHC=△OHA,△△AOH=△DCH=60°,△△AOB=180°−△AOH=120°.故选:B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.例题3.(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若△BAC=△DAE,AB=AC,AD=AE,则△ABD△△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:△BD=EC;△△BOC=60°;△△AOE=60°;△EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,△ABC=△BDC=60°,试探究△A与△C的数量关系.【答案】(1)证明见解析;(2)△△△;(3)△A+△C=180°.【分析】(1)利用等式的性质得出△BAD=△CAE,即可得出结论;(2)同(1)的方法判断出△ABD△△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出△BOC=60°,再判断出△BCF△△ACO,得出△AOC=120°,进而得出△AOE=60°,再判断出BF<CF,进而判断出△OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,△DBP=60°,进而判断出△ABD△△CBP(SAS ),即可得出结论.(1)证明:△△BAC=△DAE ,△△BAC+△CAD=△DAE+△CAD , △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ;(2)如图2,△△ABC 和△ADE 是等边三角形, △AB=AC ,AD=AE ,△BAC=△DAE=60°, △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ,△BD=CE ,△正确,△ADB=△AEC , 记AD 与CE 的交点为G ,△△AGE=△DGO ,△180°-△ADB -△DGO=180°-△AEC -△AGE , △△DOE=△DAE=60°,△△BOC=60°,△正确,在OB上取一点F,使OF=OC,△△OCF是等边三角形,△CF=OC,△OFC=△OCF=60°=△ACB,△△BCF=△ACO,△AB=AC,△△BCF△△ACO(SAS),△△AOC=△BFC=180°-△OFC=120°,△△AOE=180°-△AOC=60°,△正确,连接AF,要使OC=OE,则有OC=12 CE,△BD=CE,△CF=OF=12 BD,△OF=BF+OD,△BF<CF,△△OBC>△BCF,△△OBC+△BCF=△OFC=60°,△△OBC>30°,而没办法判断△OBC大于30度,所以,△不一定正确,即:正确的有△△△,故答案为△△△;(3)如图3,延长DC至P,使DP=DB,△△BDC=60°,△△BDP 是等边三角形,△BD=BP ,△DBP=60°,△△BAC=60°=△DBP ,△△ABD=△CBP ,△AB=CB ,△△ABD△△CBP (SAS ),△△BCP=△A ,△△BCD+△BCP=180°,△△A+△BCD=180°.【点拨】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.举一反三变式:如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;①//PQ AE ;①60AOB ∠=︒;①CPQ 是等边三角形,恒成立的是______.【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形,可知AC=BC ,CD=CE ,△ACB=△DCE=60°,所以△ACD=△BCE=120°,所以△ACD△△BCE (SAS ),从而AD=BE ,故△正确;△△由△ACD△△BCE 得△CBE=△DAC ,加之AC=BC ,易得△ACB=△BCQ=60°,可证△CQB△△CPA (ASA ),从而CP=CQ ,再加之△PCQ=60°,可推出△PCQ 为等边三角形,易得△PQC=60°=△DCE ,根据内错角相等,两直线平行,可知△△正确;△结合△ACD△△BCE 和三角形的外角的性质,可得△AOB=60°,故△正确.解:△△等边△ABC 和等边△CDE ,△AC=BC ,CD=CE ,△ACB=△DCE=60°,△△ACB+△BCD=△DCE+△BCD ,即△ACD=△BCE ,△在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===△△ACD△△BCE (SAS ),△AD=BE ,故△正确;△△△△ACD△△BCE ,△△CBE=△DAC ,△由△ACB=△DCE=60°得△BCD=60°,△△ACP=△BCQ ,又△AC=BC ,△△CQB△△CPA (ASA ),△CP=CQ ,又△△PCQ=60°△△PCQ 为等边三角形,△△PQC=60°,△△PQC=60°=△DCE△PQ△AE故△△正确;△△△ACD△△BCE (SAS ),△△CAD=△CBE ,△△AOB=△CAD+△CEB=△CBE+△CEB ,又△△ACB=△CBE+△CEB=60°,△△AOB=△ACB=60°,故△正确.故答案为:△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质,熟练应用三角形全等的判定是解题的关键.。
2020年中考备考专题复习讲义------手拉手模型(PDF版无答案)

手拉手模型类型一、旋转型全等1.等边三角形条件:如图1,△OAB ,△OCD 均为等边三角形.结论:①△OAC ≌△OBD ;②∠AEB =60°;③EO 平分∠AED .④O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:如图2,∵△OAB ,△OCD 均为正△∴OA=OB ,OC =OD ,∠AOB =∠COD =60°∴∠AOB+∠BOC =∠COD+∠BOC ∴∠AOC=∠BOD ∴△OAC ≌△OBD∴∠OAC=∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO=120°∴∠AEB =60°作OM 、ON 分别⊥AC 、BD 于点M 、N∵S △OAC =S △OBD ,AC =BD∴OM =ON∴EO 平分∠AED ∴∠OEA =∠OED =∠OBA =∠OCD =60°∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆;点E 为△OBC 的费马点(仅图2)2.等腰直角三角形条件:如图3,△OAB ,△OCD 均为等腰直角三角形.结论:①△OAC ≌△OBD ;②∠AEB =90°;③EO 平分∠AED.④O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:如图4,∵△OAB ,△OCD 均为等腰Rt △∴OA=OB ,OC =OD ,∠AOB =∠COD =90°∴∠AOB+∠BOC =∠COD+∠BOC ∴∠AOC=∠BOD ∴△OAC ≌△OBD ∴∠OAC=∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO=90°∴∠AEB =90°作OM 、ON 分别⊥AC 、BD 于点M 、N∵S △OAC =S △OBD ,AC =BD ∴OM =ON ∴EO 平分∠AED∴∠OEA =∠OED =∠OBA =∠OCD =45°∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆(四边形OMEN 是正方形)OB DAC EO BD A C E图1OB DACE OBD ACE图3O B DA CE N M 图2OBD A CEN M 图43.任意等腰三角形条件:如图5,△OAB ,△OCD 均为等腰三角形,OA=OB ,OC=OD ,∠AOB=∠COD.结论:①△OAC ≌△OBD ;②∠AEB=∠AOB ;③EO 平分∠AED.④O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:证明:如图6,∵OA=OB ,OC=OD ,∠AOB=∠COD∴∠AOB+∠BOC =∠COD+∠BOC∴∠AOC=∠BOD ∴△OAC ≌△OBD∴∠OAC=∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO∴∠AEB =∠AOB作OM 、ON 分别⊥AC 、BD 于点M 、N∵S △OAC =S △OBD ,AC =BD ∴OM =ON∴EO 平分∠AED∴∠OEA =∠OED =∠OBA =∠OCD∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆模型二、旋转型相似1.一般情况条件:如图7,CD //AB ,将△OCD 旋转至右图位置.结论:①△OCD ∽△OAB ,△OAC ∽△OBD ;②延长AC 交BD 于点E ,则∠BEC=∠BOA.③O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:∵CD //AB ,旋转∴△OCD ∽△OAB ,∠COD =∠AOB∴∠COD -∠COB =∠AOB -∠COB ,OC :OA =OD :OB ∴∠AOC =∠BOD ∴△OAC ∽△OBD∴∠OAC =∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO ∴∠BEC=∠BOA=∠DOC ∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆2.特殊情况条件:如图9,CD //AB ,∠AOB=90°,将△OCD 旋转至右图位置.结论:右图中①△OCD ∽△OAB ,△OAC ∽△OBD ;②连接AC ,BD 交于点E ,则∠BEC =∠BOA ;③BD AC =OD OC =OBOA =tan ∠OCD ;④BD ⊥AC ;⑤连接AD ,BC ,则AD 2+BC 2=AB 2+CD 2;⑥S 四边形ABCD =12AC ·BD (对角线互相垂直的四边形).⑦O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆(证明可参考以上方法)O BDA CE OBD A CE图5OB D ACOB D ACE 图9OB D AC OBD AC图7E O B DACENM 图6OBD AC图8E中考真题1.[2019·滨州]如图,在△OAB 和△OCD 中,OA =OB ,OC =OD ,OA >OC ,∠AOB =∠COD =40°,连接AC ,BD 交于点M ,连接OM .下列结论:①AC =BD ;②∠AMB =40°;③OM 平分∠BOC ;④MO 平分∠BMC .其中正确的个数为()DBCAMOA .4B .3C .2D .12.[2018·东营]如图,点E 在△DBC 的边DB 上,点A 在△DBC 内部,∠DAE =∠BAC =90°,AD =AE ,AB =AC .给出下列结论:①BD =CE ;②∠ABD +∠ECB =45°;③BD ⊥CE ;④BE 2=2(AD 2+AB 2)﹣CD 2.其中正确的是()DBCAEA .①②③④B .②④C .①②③D .①③④3.[荆门]如图,点A ,B ,C 在一条直线上,△ABD ,△BCE 均为等边三角形,连接AE 和CD ,AE 分别交CD ,BD 于点M ,P ,CD 交BE 于点Q ,连接PQ ,BM ,下面结论:①△ABE ≌△DBC ;②∠DMA =60°;③△BPQ 为等边三角形;④MB 平分∠AMC ,其中结论正确的有()CDB MAEQPA .1个B .2个C .3个D .4个4.[2016·贺州]如图,在△ABC 中,分别以AC 、BC 为边作等边三角形ACD 和等边三角形BCE ,连接AE 、BD 交于点O ,则∠AOB 的度数为.DC AEBO5.[2018·包头]如图,在Rt △ACB 中,∠ACB =90°,AC =BC ,D 是AB 上的一个动点(不与点A ,B 重合),连接CD ,将CD 绕点C 顺时针旋转90°得到CE ,连接DE ,DE 与AC 相交于点F ,连接AE .下列结论:①△ACE ≌△BCD ;②若∠BCD =25°,则∠AED =65°;③DE 2=2CF ·CA ;④若AB =32,AD =2BD ,则AF =53.其中正确的结论是.(填写所有正确结论的序号)D CA EBF6.[柳州]如图,在△ABC 中,分别以AC ,BC 为边作等边△ACD 和等边△BCE .设△ACD 、△BCE 、△ABC 的面积分别是S 1、S 2、S 3,现有如下结论:①S 1:S 2=AC 2:BC 2;②连接AE ,BD ,则△BCD ≌△ECA ;③若AC ⊥BC ,则S 1·S 2=34S 32.其中结论正确的序号是.DCA EB7.[2019·宜宾]如图,△ABC 和△CDE 都是等边三角形,且点A 、C 、E 在同一直线上,AD 与BE 、BC 分别交于点F 、M ,BE 与CD 交于点N .下列结论正确的是(写出所有正确结论的序号).①AM =BN ;②△ABF ≌△DNF ;③∠FMC +∠FNC =180°;④1MN =1AC +1CEA DCF EBMN8.[2019·襄阳]如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点C ,点D 在AB 上,∠BAC =∠DEC =30°,AC 与DE 交于点F ,连接AE ,若BD =1,AD =5,则CF EF=.D CAEBF9.[2017·包头]如图,在△ABC 与△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,且点D 在AB 上,点E 与点C 在AB 的两侧,连接BE ,CD ,点M 、N 分别是BE 、CD 的中点,连接MN ,AM ,AN .下列结论:①△ACD ≌△ABE ;②△ABC ∽△AMN ;③△AMN 是等边三角形;④若点D 是AB 的中点,则S △ABC =2S △ABE .其中正确的结论是.(填写所有正确结论的序号)DC AE BMN10.[烟台]如图,△ABC 与△AEF 中,AB =AE ,BC =EF ,∠B =∠E ,AB 交EF 于D .给出下列结论:①∠AFC =∠C ;②DE =CF ;③△ADE ∽△FDB ;④∠BFD =∠CAF 其中正确的结论是.D CABFE11.[鄂州]在平面内正方形ABCD 与正方形CEFH 如图放置,连DE ,BH ,两线交于M .求证:(1)BH =DE .(2)BH ⊥DE .M DHFECBA12.[莱芜]如图,△ABC 是等腰直角三角形,∠ACB =90°,分别以AB ,AC 为直角边向外作等腰直角△ABD 和等腰直角△ACE ,G 为BD 的中点,连接CG ,BE ,CD ,BE 与CD 交于点F .(1)判断四边形ACGD 的形状,并说明理由.(2)求证:BE =CD ,BE ⊥CD .DCHEBFGA13.[2019·无锡]如图,在Rt △ABC 中,AC =BC =4,∠ACB =90°,正方形BDEF 的边长为2,将正方形BDEF 绕点B 旋转一周,连接AE 、BE 、CD .(1)请找出图中与△ABE 相似的三角形,并说明理由;(2)求当A 、E 、F 三点在一直线上时CD 的长;(3)设AE 的中点为M ,连接FM ,试求FM 长的取值范围.DCAEBFBA备用题C。
专题05 手拉手模型构造全等三角形(学生版)
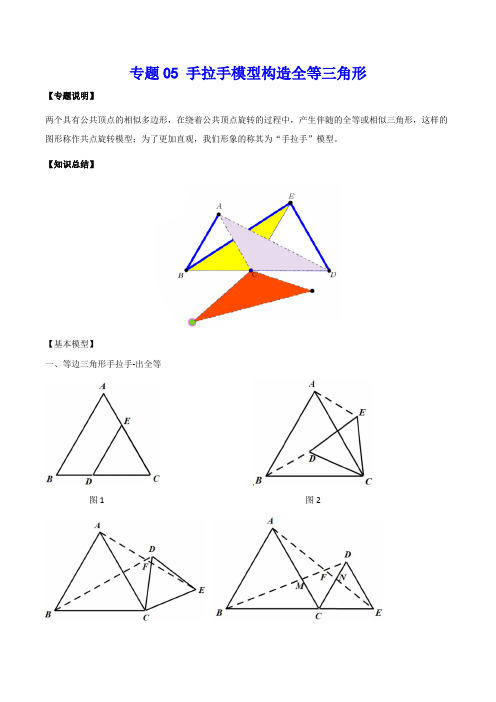
专题05 手拉手模型构造全等三角形【专题说明】两个具有公共顶点的相似多边形,在绕着公共顶点旋转的过程中,产生伴随的全等或相似三角形,这样的图形称作共点旋转模型;为了更加直观,我们形象的称其为“手拉手”模型。
【知识总结】【基本模型】一、等边三角形手拉手-出全等图1 图2图3 图4二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形,绕点C旋转过程中(B、C、D不共线)始终有①△BCD≌△ACE;②BD⊥AE(位置关系)且BD=AE(数量关系);③FC平分∠BFE;图1图2图3图41、如图,点C在线段AB上,△DAC和△DBE都是等边三角形,求证:△DAB≌△DCE;DA∥EC.2、已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连结AE,BD交于点O,AE与DC交于点0,AE与DC交于点M,BD与AC交于点N.3、已知,在△ABC中,AB=AC,点P平面内一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP,⑴若点P在△ABC内部,求证BQ=CP;⑵若点P在△ABC外部,以上结论还成立吗?4、如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=√2,AG=1,则EB=________________.5、已知正方形ABCD和正方形AEFG有一个公共点,点G、E分别在线段AD、AB上,若将正方形AEFG 绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长度始终相等?并说明理由。
6、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠BDC=45°;④BE2=2(AD2+AB2)其中结论正确的个数是_______【基础训练】1、已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.如图1,当点D在边BC上时,求证:△ABD≌△ACE;直接判断结论BC=DC+CE是否成立(不需要证明);如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC、DC、CE之间存在的数量关系,并写出证明过程.2、如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.若DE=13,BD=12,求线段AB的长.3、如图,点A、B、C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM.下面结论:△ABE≌△DBC;∠DMA=60°;△BPQ为等边三角形;MB平分∠AMC.其中正确的有____________4、如图1,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.求证:BE=AD;用含α的式子表示∠AMB的度数;当α=90°时,取AD、BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.【巩固提升】1、已知△ABC和△BDE都是等腰直角三角形,∠ACB=∠BED=90°,AB=2BD,连接CE.(1)如图1,若点D在AB边上,点F是CE的中点,连接BF.当AC=4时,求BF的长;(2)如图2,将图1中的△BDE绕点B按顺时针方向旋转,使点D在△ABC的内部,连接AD,取AD 的中点M,连接EM并延长至点N,使MN=EM,连接CN.求证:CN⊥CE.2、如图,△ABC中AB=AC=5,tan∠ACB=,点D为边BC上的一动点(不与点B、C重合),将线段AD绕点A顺时针旋转得AE,使∠DAE=∠BAC,DE与AB交于点F,连接BE.(1)求BC的长;(2)求证∠ABE=∠ABC;(3)当FB=FE时,求CD的长.3、如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.(1)求证:△BCD≌△ACE;(2)如图2,连接ED,若CD=2,AE=1,求AB的长;(3)如图3,若点F为AD的中点,分别连接EB和CF,求证:CF⊥EB.4、如图,△ABC和△EDC都是等腰直角三角形,C为它们的公共直角顶点,连接AD、BE,点F为线段AD的中点,连接CF.(1)如图1,当D点在BC上时,试判断线段BE、CF的关系,并证明你的结论;(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变时,请探究BE、CF的关系并直接写出结论.5、如图1,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转a角(0°<a<180°),得到△AB′C′(如图2),连接DB',EC'.(1)探究DB'与EC'的数量关系,并结合图2给予证明;(2)填空:①当旋转角α的度数为时,则DB'∥AE;②在旋转过程中,当点B',D,E在一条直线上,且AD=时,此时EC′的长为.6、如图,∠AOB=120°,OC平分∠AOB,∠MCN=60°,CM与射线OA相交于M点,CN与直线BO相交于N点.把∠MCN绕着点C旋转.(1)如图1,当点N在射线OB上时,求证:OC=OM+ON;(2)如图2,当点N在射线OB的反向延长线上时,OC与OM,ON之间的数量关系是(直接写出结论,不必证明)。
全等三角形之手拉手模型

全等三角形之手拉手模型5一、知识点睛 1、全等型手拉手模型两等边三角形或等腰直角三角形或两正方形共端点(两个相同图形,有公共顶点且它两邻边相等),图示如下2、全等型手拉手模型的常见结论结论1:△ABC ≌△AB 'C ' BC=B 'C '(左手拉左手等于右手拉右手) 结论2:AO 平分∠BOC' 二、典型例题1.(1)熟悉模型:如图(1),已知△ABC 与△ADE 都是等腰三角形,AB =AC ,AD =AE ,且∠BAC =∠DAE ,求证:BD =CE ;(2)运用模型:如图(2),P 为等边△ABC 内一点,且P A :PB :PC =3:4:5,求∠APB 的度数.A D BCE(1)BP (2)(3)深化模型:如图(3),在四边形ABCD 中,AD =4,CD =3,∠ABC =∠ACB =∠ADC =45°,求BD 的长.2. 已知在△ABC 中,AB =AC ,D 是BC 上一点,连接AD ,在直线AD 的右侧作等腰△ADE , AD=AE.(1) 如图1,∠BAC =∠DAE =90°,连接CE ,求证:BD=CE 。
(2) 如图2,∠BAC =∠DAE =120°,AB =AC=2,取AC 边的中点F ,连接EF . 当D 点从B 点运动到C 点过程中,求线段EF 长度的最小值,并直接写出它的最大值。
(3) 如图3,四边形ABCD 中,∠BAD =∠BC D =90°,AB=AD ,DC=1,连接AC ,已知2230+=AC ,求AB 的长。
(3)图2FACDE图1图3ABCD3.如图,在△ABC中,∠BAC=90°,点D、E分别在AB、AC上,且AD=AE.连接BE、CD,点M是BE的中点,连接AM.(1)观察猜想:如图①,若AB=AC,线段AM与CD的数量关系是,位置关系是.(2)类比探究:在(1)的条件下,将△ADE绕点A逆时针旋转α(0°<α<360°)至图②的位置,试判断线段AM和CD的数量关系和位置关系,并给出证明;4.(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A位于_______________时,线段AC的长取得最大值,且最大值为_________ (用含a,b的式子表示)(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②写出线段BE长的最大值.(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0)点P为线段AB外一动点,且P A=2,PM=PB,∠BPM=90°,请写出线段AM长的最大值及此时点P的坐标.。
人教版八年级上册第十二章全等三角形专题手拉手模型讲义(无答案)
全等三角形专题------手拉手模型不积跬步,无以至千里;不积小流,无以成江海。
荀子——《劝学》学习目标:1、认识并学会识别手拉手模型2、掌握手拉手模型的证明3、学会运用手拉手模型解题手拉手:Ⅰ顶角相等的两个等腰三角形Ⅱ顶点相同手拉手模型:1、识别:顶角相等的等腰三角形,顶点相同常见图形【例1】如图在直线ABC的同一侧作两个等边三角形ABD∆,连结AE与CD,∆与BCE证明以下常用结论:1、DBC∆ABE∆≅2、DCAE=3、AE与DC之间的夹角为︒60(底边夹角等于顶角)4、DFB∆AGB∆≅5、CFB≅∆EGB∆6、连接GF,则B GF∆为等边三角形7、BH平分AHC∠8、ACGF//9、AH=DH+BH,CH=EH+BH(截长补短法)【变式精练1】如图两个等边三角形ABD∆,连结AE与CD,∆与BCE证明(1)DBC∆ABE∆≅(2)DCAE=60(3)AE与DC之间的夹角为︒(4)AE与DC的交点设为H,BH平分AHC∠【变式精练2】如图两个等边三角形ABD∆,连结AE与CD,∆与BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠【例2】如图,两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H 问:(1)CDE∆是否成立?≅ADG∆(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分AHE∠?【例3】如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?【例4】两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,问:(1)DBC ABE ∆≅∆是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?(4)HB 是否平分AHC ∠?综合练习1、如图,C 为线段AE 上一动点(不与点A 、E 重合),在AE 同侧分别作正∆ABC 和正∆CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ ,以下五个结论: ①AD=BE ②PQ∥AE ③AP=BQ④DE=DP ⑤∠AOB=60°恒成立的结论有 __________________ (填序号)分别是线段 BE 和AD 的中点,则△CPM 是()A.钝角三角形B.直角三角形C.等边三角形D.非等腰三角形3、如图,△DAC 和△EBC 均是等边三角形,AE、BD 分别与CD、CE 交于点 M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是()A.3 个B.2 个C.1 个D.0 个4、如图,四边形ABCD、BEFG 均为正方形,连接AG、CE.(1)求证:AG=CE;(2)求证:AG⊥CE.5、、(1)问题发现如图 1,△ACB 和△DCE 均为等边三角形,点A,D,E 在同一直线上,连接BE.填空:①∠AEB 的度数为___________;②线段 AD,BE 之间的数量关系为_________ (2)拓展探究如图 2,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点 A,D,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接 BE,请判断∠AEB 的度数及线段CM, AE,BE 之间的数量关系,并说明理由.。
初中数学模型【讲义】全等“手拉手”模型(上)

全等“手拉手”模型一、模型背景全等“手拉手”模型:两个顶角相等的等腰三角形,若顶点重合,则构成全等“手拉手”模型,其中连接左、右对应的底角顶点所得线段,称为“拉手线”(如图中BE和CF)全等“手拉手”模型,主要是利用全等三角形的知识,判断拉手线之间的数量关系和位置关系(夹角度数)二、模型内容(一)等边三角形的“手拉手”模型1. 共线型(特例)如图,已知等边三角形ABC与等边三角形ADE,其中C、A、D三点共线,连接BD、CE交于点H.问题1. 判断BD与CE的数量关系;问题2. 求∠BHC的度数(BD与CE的夹角)【证明】2. 不共线型(一般情况)如图,已知等边三角形ABC与等边三角形ADE,连接BD、CE交于点H.问题1. 判断BD与CE的数量关系;问题2. 求∠BHC的度数(BD与CE的夹角)【证明】引申:(判断以下结论哪些依然满足,哪些不满足,无需证明)(1)全等关系:△ABD≌△ACE;△ACM≌△ABN;△AEM≌△ADN(2)线段相等:BD=CE;BN=CM;EM=DN(3)角度:∠BHC=60°;∠DHE=60°;∠MHN=120°(4)角平分线:AH平分∠CHD(5)等边三角形:△AMN是等边三角形(6)平行:MN∥CD(7)截长补短线段相等:CH=BH+AH;DH=EH+AH;MH+NH=AH(8)四点共圆:A、M、H、N四点共圆;A、C、B、H四点共圆;A、D、E、H四点共圆(二)等腰直角三角形的“手拉手”模型如图,已知等腰直角三角形ABC与等腰直角三角形ADE,连接BD、CE交于点H.问题1. 判断BD与CE的数量关系;问题2. 求∠BHC的度数(BD与CE的夹角)(三)正方形的“手拉手”模型如图,已知正方形ABCD与正方形AEFG,连接BE、DG交于点H,连接AH.(四)等腰三角形的“手拉手”模型(类型一、二、三的一般情况)如图,已知等腰三角形ABC与等腰三角形ADE,AB=AC,AD=AE,∠BAC=∠DAE=α,连接BD、CE.问题1. 判断BD与CE的数量关系;问题2. 延长BD和CE相交于点H,求∠BHC的度数(BD与CE的夹角)。
专题03 手拉手模型(从全等到相似)(解析版)

专题03 手拉手模型(从全等到相似)全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就手拉手模型进行梳理及对应试题分析,方便掌握。
模型1.手拉手模型(全等模型)【模型解读】将两个三角形绕着公共顶点(即头)旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等,常用“边角边”判定定理证明全等。
【常见模型及证法】(等腰)(等边)(等腰直角)公共顶点A 记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
对应操作:左手拉左手(即连结BD ),右手拉右手(即连结CE ),得ABD ACE ≅。
1.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形. (1)问题发现:如图1,若ABC 和ADE 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =; (2)解决问题:如图2,若ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,点A ,D ,E 在同一条直线上,CM 为DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE ∠=︒;2AE AD DE BE CM =+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ∠∠CAE ,即可得出结论;(2)同(1)的方法判断出△BAD ∠∠CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论. 【解析】(1)证明:∠ABC 和ADE 是顶角相等的等腰三角形,∠AB AC =,AD AE =,BAC DAE ∠=∠,∠BAC CAD DAE CAD ∠-∠=∠-∠,∠BAD CAE ∠=∠.在BAD 和CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∠()BAD CAE SAS ≌△△,∠BD CE =.(2)解:90AEB =︒∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE ,∠AD BE =,ADC BEC ∠∠=,∠CDE △是等腰直角三角形,∠45CDE CED ∠=∠=︒,∠180135ADC CDE ∠=︒-∠=︒,∠135BEC ADC ∠=∠=︒,∠1354590AEB BEC CED ∠=∠-∠=︒-︒=︒.∠CD CE =,CM DE ⊥,∠DM ME =.∠90DCE ∠=︒,∠DM ME CM ==,∠2DE CM =.∠2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ∠∠BCE 是解本题的关键. 2.(2022·黑龙江·中考真题)ABC 和ADE 都是等边三角形.(1)将ADE 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接P A ,猜想线段P A 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接P A ,猜想线段P A 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC +=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,P A =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE ≌(SAS ),得ABD ACE ∠=∠,再证明CAP BAF ≌△△(SAS ),得CAP BAF ∠=∠,AF AP =,然后证明AFP 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE ≌(SAS ),得ABD ACE ∠=∠,再证明BAP CAF ≌△△(SAS ),得出CAF BAP ∠=∠,AP AF =,然后证明AFP 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∠∠ABC 是等边三角形,∠AB =AC ,∠点P 与点A 重合,∠PB =AB ,PC =AC ,P A =0,∠PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC =+证明:在BP 上截取BF CP =,连接AF ,∠ABC 和ADE 都是等边三角形,∠AB AC =,AD AE =,60BAC DAE ∠=∠=︒∠BAC CAD DAE CAD ∠+∠=∠+∠,∠BAD CAE ∠=∠,∠BAD CAE ≌(SAS ),∠ABD ACE ∠=∠,∠AC =AB ,CP =BF , ∠CAP BAF ≌△△(SAS ),∠CAP BAF ∠=∠,AF AP =,∠CAP CAF BAF CAF ∠+∠=∠+∠,∠60FAP BAC ∠=∠=︒,∠AFP 是等边三角形,∠PF AP =,∠PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∠ABC 和ADE 都是等边三角形,∠AB AC =,AD AE =,60BAC DAE ∠=∠=︒∠BAC BAE DAE BAE ∠+∠=∠+∠,∠BAD CAE ∠=∠,∠BAD CAE ≌(SAS ),∠ABD ACE ∠=∠,∠AB =AC ,BP =CF ,∠BAP CAF ≌△△(SAS ),∠CAF BAP ∠=∠,AP AF =,∠BAF BAP BAF CAF ∠+∠=∠+∠,∠60FAP BAC ∠=∠=︒,∠AFP 是等边三角形,∠PF AP =,∠PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.3.(2022·吉林·九年级期末)如图①,在ABC 中,90C ∠=︒,6AC BC ==D ,E 分别在边AC ,BC 上,且2CD CE =AD BE =,AD BE ⊥成立.(1)将CDE △绕点C 逆时针旋转90︒时,在图②中补充图形,并直接写出BE 的长度;(2)当CDE △绕点C 逆时针旋转一周的过程中,AD 与BE 的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)将CDE △绕点C 逆时针旋转一周的过程中,当A ,D ,E 三点在同一条直线上时,请直接写出AD 的长度. 【答案】(1)补充图形见解析;22BE =;(2)AD BE =,AD BE ⊥仍然成立,证明见解析;(3)51AD =-或51=+AD .【分析】(1)根据旋转作图的方法作图,再根据勾股定理求出BE 的长即可;(2)根据SAS 证明E ACD BC ≅∆∆得AD =BE ,∠1=∠2,再根据∠1+∠3+∠4=90°得∠2∠3+∠4=90°,从而可得出结论;(3)分两种情况,运用勾股定理求解即可.【详解】解:(1)如图所示,根据题意得,点D 在BC 上,∠BCE ∆是直角三角形,且BC =6,CE =2由勾股定理得,2222(2)(6)22BE CE BC =+=+=;(2)AD BE =,AD BE ⊥仍然成立. 证明:延长AD 交BE 于点H ,∠90ACB DCE ∠=∠=︒,ACD ACB BCD ∠=∠-∠,BCE DCE BCD ∠=∠-∠,∠ACD BCE ∠=∠,又∠CD CE =,AC BC =,∠ACD BCE ≅△△,∠AD BE =,12∠=∠,在Rt ABC 中,13490∠+∠+∠=︒,∠23490∠+∠+∠=︒,∠90AHB ∠=︒,∠AD BE ⊥.(3)①当点D 在AC 上方时,如图1所示,同(2)可得ACD BCE ≅△△∠AD =BE同理可证BE AE ⊥在Rt △CDE 中,2CD CE ==∠DE=222+=CD CE在Rt△ACB中,6==AC BC∠2223=+=AB AC BC设AD=BE=x,在Rt△ABE中,222+=BE AE AB∠222++=(2)(23)x x解得,51x=-∠ 51AD=-②当点D在AC下方时,如图2所示,同(2)可得ACD BCE△△≅∠AD=BE同理可证BE AE⊥在Rt△CDE中,2==CD CE∠DE=222+=CD CE在Rt△ACB中,6==AC BC∠2223=+=AB AC BC设AD =BE =x ,在Rt △ABE 中,222BE AE AB +=∠222(2)(23)x x +-=解得,5+1x =∠ 51=+AD .所以,AD 的值为51-或5+1【点睛】本题考查了旋转的性质,全等三角形的判定与性质,勾股定理等知识,熟练解答本题的关键.模型2.手拉手模型(旋转相似模型)【模型解读与图示】旋转放缩变换,图中必有两对相似三角形.1.(2022·四川达州·中考真题)某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形ABC 和等腰直角三角形CDE ,按如图1的方式摆放,90ACB ECD ∠=∠=︒,随后保持ABC 不动,将CDE △绕点C 按逆时针方向旋转α(090α︒<<︒),连接AE ,BD ,延长BD 交AE 于点F ,连接CF .该数学兴趣小组进行如下探究,请你帮忙解答:(1)【初步探究】如图2,当ED BC ∥时,则α=_____;(2)【初步探究】如图3,当点E ,F 重合时,请直接写出AF ,BF ,CF 之间的数量关系:_________;(3)【深入探究】如图4,当点E ,F 不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.(4)【拓展延伸】如图5,在ABC 与CDE △中,90ACB DCE ∠=∠=︒,若BC mAC =,CD mCE =(m 为常数).保持ABC 不动,将CDE △绕点C 按逆时针方向旋转α(090α︒<<︒),连接AE ,BD ,延长BD 交AE 于点F ,连接CF ,如图6.试探究AF ,BF ,CF 之间的数量关系,并说明理由.【答案】(1)45︒(2)2BF AF CF =(3)2BF AF CF =仍然成立,理由见解析(4)21BF m FC mAF =++【分析】(1)根据等腰直角三角形的性质,可得AC BC ⊥,根据题意可得AC ED ⊥,根据等原三角形的性质可得AC 平分ECD ∠,即可得45ACE ∠=︒,根据旋转的性质可知ECA α∠=;(2)证明ACE ≌BCD △,可得AE DB =,根据等腰直角三角形可得2ED CE =,由BE BD ED =+,即可即可得出2BF AF CF =;(3)同(2)可得ACE ≌BCD △,过点C ,作CH FC ⊥,交BF 于点H ,证明FEC HDC ≌,AFC △≌BHC △,可得BH AF =,即可得出2BF AF CF =+;(4)过点C 作CG CF ⊥,交BF 于点G ,证明ACE BCD △∽△,可得BG mAF =,GC mFC =,在Rt FCG 中,勾股定理可得21FG m FC +,即可得出21BF m FC mAF ++.(1)等腰直角三角形ABC 和等腰直角三角形CDE ,90ECD ∴∠=︒,AC BC ⊥ED BC ∥ED AC ∴⊥45ACE α∴∠==︒故答案为:45︒(2)90∠=∠=︒ACB ECD ACE ACD ACD BCD ∴∠+∠=∠+∠ACE BCD ∴∠=∠在ACE 与BCD △中,AC BC ACE BCD EC DC =⎧⎪∠=∠⎨⎪=⎩ACE ≌BCD △∴AE DB =BE BD ED ∴=+ 又2ED CE =2BE AE CE ∴= ,E F 重合,2BF AF CF ∴=故答案为:2BF AF CF =(3)同(2)可得ACE ≌BCD △AE DB ∴=,EAC DBC ∠=∠过点C ,作CH FC ⊥,交BF 于点H ,则90ECF FCD FCD DCH ∠+∠=∠+∠=︒,∴ECF DCH ∠=∠,在FEC 与HDC △中,FEC HDC EC CD ECF DCH ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴FEC HDC ≌, FC CH ∴=,CFH ∴是等腰直角三角形,2FH FC ∴=,CH FC =,90,90FCH ACF ACH ACB BCH ACH ∴∠=∠+∠=︒∠=∠+∠=︒,ACF BCH ∴∠=∠,在AFC △与BHC △中,FC HC ACF BCH AC BC =⎧⎪∠=∠⎨⎪=⎩,∴AFC △≌BHC △, BH AF ∴=,2BF FH BH CF AF ∴=+=+,即2BF AF CF =+,(4)过点C 作CGCF ⊥,交BF 于点G ,BC mAC =,CD mCE =,BC CD AC CE ∴=,AC BC EC DC∴=, ACE BCD α∠=∠=,ACE BCD ∴△△∽,CBG CAF ∴∠=∠,FCA ACG GCB ACG ∠+∠=∠+∠,∴FCA GCB ∠=∠,AFC BGC ∴∽,BG GC BC AF FC AC∴==m =, BG mAF ∴=,GC mFC =, Rt FCG 中,2221FG FC CG m FC =++,∴21BF FG GB m FC mAF =+=++,即21BF mFC mAF ++.【点睛】本题考查了等腰直角三角形的性质,旋转的性质,全等三角形的性质与判定,相似三角形的性质与判定,掌握全等三角形的性质与判定,相似三角形的性质与判定是解题的关键.2.(2022·山东烟台·中考真题)(1)【问题呈现】如图1,∠ABC 和∠ADE 都是等边三角形,连接BD ,CE .求证:BD =CE .(2)【类比探究】如图2,∠ABC 和∠ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .请直接写出BD CE 的值.(3)【拓展提升】如图3,∠ABC 和∠ADE 都是直角三角形,∠ABC =∠ADE =90°,且AB BC=AD DE =34.连接BD ,CE .①求BD CE 的值;②延长CE 交BD 于点F ,交AB 于点G .求sin∠BFC 的值. 【答案】(1)见解析235;②45 【分析】(1)证明△BAD ∠∠CAE ,从而得出结论;(2)证明△BAD ∠∠CAE ,进而得出结果;(3)①先证明△ABC ∠∠ADE ,再证得△CAE ∠∠BAD ,进而得出结果;②在①的基础上得出∠ACE =∠ABD ,进而∠BFC =∠BAC ,进一步得出结果.(1)证明:∠∠ABC 和△ADE 都是等边三角形,∠AD =AE ,AB =AC ,∠DAE =∠BAC =60°,∠∠DAE ﹣∠BAE =∠BAC ﹣∠BAE ,∠∠BAD =∠CAE ,∠∠BAD ∠∠CAE (S A S ),∠BD =CE ;(2)解:∠∠ABC 和∠ADE 都是等腰直角三角形,2AB AB AE AC ∴==∠DAE =∠BAC =45°,∠∠DAE ﹣∠BAE =∠BAC ﹣∠BAE ,∠∠BAD=∠CAE,∠∠BAD∠∠CAE,22BD ABCE AC∴==(3)解:①34AB ADAC DE==,∠ABC=∠ADE=90°,∠∠ABC∠∠ADE,∠∠BAC=∠DAE,35 AB ADAC AE==,∠∠CAE=∠BAD,∠∠CAE∠∠BAD,35 BD AD CE AE∴==;②由①得:∠CAE∠∠BAD,∠∠ACE=∠ABD,∠∠AGC=∠BGF,∠∠BFC=∠BAC,∠sin∠BFC45 BCAC==.【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是熟练掌握“手拉手”模型及其变形.3.(2022·山东·东营市一模)【提出问题】(1)如图1,在等边∠ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边∠AMN,连结CN.求证:∠ABC=∠ACN.【类比探究】(2)如图2,在等边∠ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰∠ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰∠AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.【答案】(1)证明见解析;(2)成立,理由见解析;(3)∠ABC=∠CAN,理由见解析.【分析】(1)利用SAS可证明∠BAM∠∠CAN,继而得出结论.(2)也可以通过证明∠BAM∠∠CAN,得出结论,和(1)的思路完全一样.(3)首先得出∠BAC=∠MAN,从而判定∠ABC∠∠AMN,得到AB ACAM AN=,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定∠BAM∠∠CAN,得出结论.【详解】解:(1)证明:∠∠ABC、∠AMN是等边三角形,∠AB=AC,AM=AN,∠BAC=∠MAN=60°.∠∠BAM=∠CAN.∠在∠BAM和∠CAN中,AB ACBAM CANAM AN=⎧⎪∠=∠⎨⎪=⎩,∠∠BAM∠∠CAN(SAS).∠∠ABC=∠ACN.(2)结论∠ABC=∠ACN仍成立.理由如下:∠∠ABC、∠AMN是等边三角形,∠AB=AC,AM=AN,∠BAC=∠MAN=60°.∠∠BAM=∠CAN.∠在∠BAM和∠CAN中,AB ACBAM CANAM AN=⎧⎪∠=∠⎨⎪=⎩,∠∠BAM∠∠CAN(SAS),∠∠ABC=∠ACN.(3)∠ABC=∠ACN.理由如下:∠BA=BC,MA=MN,顶角∠ABC=∠AMN,∠底角∠BAC=∠MAN,∠∠ABC∠∠AMN,∠AB ACAM AN=,又∠∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∠∠BAM=∠CAN,∠∠BAM∠∠CAN,∠∠ABC=∠ACN.4.(2022·山西长治·九年级期末)问题情境:如图1,在∠ABC中,AB=6,AC=5,点D,E分别在边AB,AC上,且∥DE BC.数学思考:(1)在图1中,BD CE的值为 ;(2)图1中∠ABC 保持不动,将∠ADE 绕点A 按逆时针方向旋转到图2的位置,其它条件不变,连接BD ,CE ,则(1)中的结论是否仍然成立?并说明理由;(3)拓展探究:在图2中,延长BD ,分别交AC ,CE 于点F ,P ,连接AP ,得到图3,探究∠APE 与∠ABC 之间有何数量关系,并说明理由;(4)若将∠ADE 绕点A 按逆时针方向旋转到图4的位置,连接BD ,CE ,延长BD 交CE 的延长线于点P ,BP 交AC 于点F ,则(3)中的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠APE 与∠ABC 之间的数量关系. 【答案】(1)65(2)(1)中结论仍然成立,理由见解析(3)∠APE =∠ABC ,理由见解析 (4)结论不成立,∠APE +∠ABC =180°,理由见解析【分析】(1)根据平行线分线段成比例定理求解即可;(2)根据旋转的性质得到∠BAD =∠CAE ,由(1)可证明∠BAD ∠∠CAE ,从而可证∠APE +∠ABC 得到65BD AB CE AC ==;(3)由(2)可证∠ABD =∠ACE ,证明∠AFB ∠∠PFC 和∠AFP ∠∠BFC 即可得到结论; (4)证明∠ABD =∠ACE ,推出A 、B 、C 、P 四点共圆即可得到结论;(1)解:∠∥DE BC ,∠BD CE AB AC=,∠65BD AB CE AC ==; (2)解:中结论仍然成立,理由如下:∠旋转的性质,∠∠ADE =∠ABC ,∠AED =∠ACB ,∠∠ADE ∠∠ABC ,∠AD AE AB AC=, 在图2中,由旋转的性质可知,∠BAC =∠DAE ,∠∠BAD=∠CAE,∠∠BAD∠∠CAE,∠65 BD ABCE AC==;(3)解:∠APE=∠ABC,理由如下:由(2)得∠BAD∠∠CAE,∠∠ABD=∠ACE,又∠∠AFB=∠PFC,∠∠AFB∠∠PFC,∠AF BFBAC BPCPF CF==,∠∠,∠AF PFBF CF=,又∠∠AFP=∠BFC,∠∠AFP∠∠BFC,∠∠CBF=∠P AF,∠∠APE=∠ACE+∠P AF,∠ABC=∠ABF+∠CBF,∠∠APE=∠ABC;(4)解:(3)结论不成立,∠APE+∠ABC=180°,理由如下:由(2)知,∠BAD∠∠CAE,∠∠ABD=∠ACE,∠A、B、C、P四点共圆,∠∠APE+∠ABC=180°.【点睛】本题主要考查了平行线分线段成比例,旋转的性质,相似三角形的性质与判定,圆内接四边形的性质等等,熟练掌握相关三角形的性质与判定是解题的关键.课后专项训练:1.(2022·湖南·中考真题)如图,点O 是等边三角形ABC 内一点,2OA =,1OB =,3OC =AOB ∆与BOC ∆的面积之和为( )A 3B 3C 33D 3【答案】C【分析】将AOB ∆绕点B 顺时针旋转60︒得BCD ∆,连接OD ,得到BOD 是等边三角形,再利用勾股定理的逆定理可得90COD ∠=︒,从而求解.【详解】解:将AOB ∆绕点B 顺时针旋转60︒得BCD ∆,连接OD ,OB OD ∴=,60BOD ∠=︒,2CD OA ==,BOD ∴∆是等边三角形, 1OD OB ∴==,∵2222134OD OC +=+=,2224CD ==,222OD OC CD ∴+=,90DOC ∴∠=︒,AOB ∴∆与BOC ∆的面积之和为2313311342BOC BCD BOD COD S S S S +=+=+⨯=C . 【点睛】本题主要考查了等边三角形的判定与性质,勾股定理的逆定理,旋转的性质等知识,利用旋转将AOB ∆与BOC ∆的面积之和转化为BOC BCD S S +,是解题的关键.2.(2022·四川宜宾·中考真题)如图,ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,点D 是BC 边上的动点(不与点B 、C 重合),DE 与AC 交于点F ,连结CE .下列结论:①BD CE =;②DAC CED ∠=∠;③若2BD CD =,则45CF AF =;④在ABC 内存在唯一一点P ,使得PA PB PC ++的值最小,若点D 在AP 的延长线上,且AP 的长为2,则23CE =( )A .①②④B .①②③C .①③④D .①②③④ 【答案】B【分析】证明BAD CAE ≌,即可判断①,根据①可得ADB AEC ∠=∠,由180ADC AEC ∠+∠=︒可得,,,A D C E 四点共圆,进而可得DAC DEC ∠=∠,即可判断②,过点A 作AG BC ⊥于G ,交ED 的延长线于点H ,证明FAH FCE ∽,根据相似三角形的性质可得45CF AF =,即可判断③,将APC △绕A 点逆时针旋转60度,得到AB P ''△,则APP '是等边三角形,根据当,,,B P P C ''共线时,PA PB PC ++取得最小值,可得四边形ADCE 是正方形,勾股定理求得DP , 根据CE AD AP PD ==+即可判断④.【详解】解:ABC 和ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒, ,,AB AC AD AE BAD CAE ∴==∠=∠BAD CAE ∴△≌△BD CE ∴=故①正确;BAD CAE ≌ADB AEC ∴∠=∠180ADC AEC ∴∠+∠=︒,,,A D C E ∴四点共圆,CD CD =DAC DEC ∴∠=∠故②正确;如图,过点A 作AG BC ⊥于G ,交ED 的延长线于点H ,BAD CAE ≌,45,45ACE ABD ACB ∴∠=∠=︒∠=︒90DCE ∴∠=︒FC AH ∴∥ 2BD CD =,BD CE =1tan2DC DEC CE ∴∠==,13CD BC = 设6BC a =,则2DC a =,132AG BC a ==,24EC DC a == 则32GD GC DC a a a =-=-=FC AH ∥1tan 2GD H GH ∴==22GH GD a ∴==325AH AG GH a a a ∴=+=+= AH ∠CE ,FAH FCE ∴∽ CF CE AF AH ∴=4455CF a AF a ∴==则45CF AF =;故③正确 如图,将ABP 绕A 点逆时针旋转60度,得到AB P ''△,则APP '是等边三角形,PA PB PC PP P B PC B C '''+++∴'+=≥,当,,,B P P C ''共线时,PA PB PC ++取得最小值,此时180********CPA APP '∠=-∠=︒-=︒︒︒,180********APB AP B AP P ∠=∠=︒-∠=︒-︒='''︒,360360*********BPC BPA APC ∠=︒-∠-∠=︒-︒-︒=︒,此时120APB BPC APC ∠=∠=∠=︒,AC AB AB '==,AP AP '=,APC AP B ''∠=∠,AP B APC ''∴≌,PC P B PB ''∴==,60APP DPC '∠=∠=︒,DP ∴平分BPC ∠,PD BC ∴⊥,,,,A D C E 四点共圆,90AEC ADC ∴∠=∠=︒,又AD DC BD ==,BAD CAE ≌,AE EC AD DC ∴===,则四边形ADCE 是菱形,又90ADC ∠=︒,∴四边形ADCE 是正方形,9060150B AC B AP PAC P AP ''''∠=∠+∠+∠=︒+︒=︒,则'B A BA AC ==,()1180152B ACB B AC '''∠=∠=︒-∠=︒, 30PCD ∠=︒,3DC PD ∴=,DC AD =,2AP =,则()312AP AD DP DP =-==,3131DP ∴==-, 2AP =,33CE AD AP PD ∴==+=,故④不正确,故选B .【点睛】本题考查了旋转的性质,费马点,圆内接四边形的性质,相似三角形的性质与判定,全等三角形的性质与判定,勾股定理,解直角三角形,正方形的性质与判定,掌握以上知识是解题的关键.3.(2022·湖北·襄阳市樊城区青泥湾中学九年级阶段练习)如图,已知AOB 和MON 都是等腰直角三角形(22OA <OM =ON ),∠AOB =∠MON =90°.(1)如图①,连接AM ,BN ,求证:AOM ∠BON ;(2)若将MON 绕点O 顺时针旋转,①如图②,当点N 恰好在AB 边上时,求证:22220BN AN N +=;②当点A ,M ,N 在同一条直线上时,若OB =4,ON =3,请直接写出线段BN 的长. 【答案】(1)见解析;(2)①见解析;②46322+或46322-.【分析】(1)利用SAS 定理证明AOM BON ≌即可;(2)①连接AM ,证明AOM BON ≌,即可证2222BN AN ON =+;②当点N 在线段AM 上时,连接BN ,在Rt ANB 中构造勾股定理的等量关系;当点M 在线段AN 上时,同理即可求得.(1)证明:90AOB MON ︒∠=∠=,MON AON AOB AON ∴∠+∠=∠+∠,即AOM BON ∠=∠.MON 和AOB 是等腰直角三角形,,OM ON OA OB ∴==,AOM BON ∴≌(SAS) .(2)解:①证明:如图,连接AM .90AOB MON ︒∠=∠=,MON AON AOB AON ∴∠-∠=∠-∠,即AOM BON ∠=∠.MON 和AOB 是等腰直角三角形,,,45OM ON OA OB OAB OBA ︒∴==∠=∠=,.()AOM BON SAS ∴≌45,MAO OBA AM BN ︒∴∠=∠==,90MAN ︒∴∠=,222AM AN MN ∴+=.MON 是等腰直角三角形,222MN ON ∴=,2222BN AN ON =∴+.②46322+或46322-.∠△AOB 和△MON 都是等腰直角三角形,OB =4,ON =3,∠42,32AB MN ==.当点N 在线段AM 上时,如图,连接BN ,设BN x =,由(1)可知AOM BON ≌.∠OAM OBN ∠=∠,AM BN x ==.∠NAB ABN OAM OAB ABN OBN ABN OAB∠+∠=∠+∠+∠=∠+∠+∠18090OBA OAB AOB =∠+∠=︒-∠=︒,∠()18090ANB NAB ABN ∠=︒-∠+∠=︒,∠ANB 是直角三角形,222+=AN BN AB .又∠32AN AM MN BN MN x =-=-=-,∠222(32)(42)x x -+=,解得:1246324632,22x x +-+==(舍去)∠46322BN +=;当点M 在线段AN 上时,如图,连接BN ,设BN x =,由(2)①可知AOM BON ≌.∠OAM OBN ∠=∠,AM BN x ==.∠NAB ABN OAM OAB ABN OBN ABN OAB∠+∠=∠+∠+∠=∠+∠+∠18090OBA OAB AOB =∠+∠=︒-∠=︒,∠()18090ANB NAB ABN ∠=︒-∠+∠=︒,∠ANB 是直角三角形,222+=AN BN AB .又∠32AN AM MN BN MN x =+=+=+,∠222(32)(42)x x ++=,解得: 1246324632,22x x ---==(舍去)∠46322BN -=综上所述:BN 的长为46322+或46322-. 【点睛】本题主要考查全等三角形的判定与性质、等腰直角三角形的性质,三点共线分类讨论,对几何题目的综合把握是解题关键.4.(2022·山西朔州·九年级期末)综合与实践问题情境:在数学课上老师出了这样一道题:如图1,在ABC 中6AB AC ==,30BAC ∠=︒,求BC 的长.(1)探究发现:如图2,勤奋小组经过思考后,发现:把ABC 绕点A 顺时针旋转90︒得到ADE ,连接BD ,BE ,利用直角三角形的性质即可求解,请你根据勤奋小组的思路,求BC 的长;(2)探究拓展:如图3,缜密小组的同学在勤奋小组的启发下,把ABC 绕点A 顺时针旋转120︒后得到ADE ,连接BD ,CE 交于点F ,交AB 于点G ,请你判断四边形ADFC 的形状并证明;(3)奇异小组的同学把图3中的BGF 绕点B 顺时针旋转,在旋转过程中,连接AF ,发现AF 的长度在不断变化,直接写出AF 的最大值和最小值.【答案】(1)BC 的长是3632-,见解析;(2)四边形ADFC 是菱形,见解析;(3)AF 的最大值是63,AF 的最小值是1263-,见解析.【分析】(1)过点B 作BH DE ⊥交DE 的延长线于点H .由旋转性质进一步得AEB △是等边三角形, EBH △是等腰直角三角形,ABD △是等腰直角三角形,45BDA ∠=︒,在Rt EBH △中由勾股定理,1832HE HB ===,在Rt BDH 中,62BD =.在Rt BDH 中,求得36=DH ,进而得解; (2)利用旋转的性质得到相关结论,进一步证明四边形ADFC 是平行四边形.又有AD AC =,得证四边形ADFC 是菱形;(3)作AH ∠BD 于点H ,则90AHB ∠=︒,利用解直角三角形求得BF 的长,分两种情况进行分析,即可得解.(1)解:如图4,延长CB 、DE 交于点H .∠ABC 绕点A 顺时针旋转90︒得到ADE ∠ABC ADE △≌△,90CAE BAD ∠=∠=︒,∠H =90°, ∠AB AD ==6,AC AE ==6,DAE BAC ∠=∠,DE BC =∠6AB AC ==,30BAC ∠=︒∠∠ABC 是等腰三角形,60∠=∠-∠=︒BAE CAE BAC ∠180752-=︒∠∠=︒BAC ABC , ∠=6AE AB = ∠AEB △是等边三角形∠6BE AB ==,60ABE ∠=︒∠18045∠=︒-∠-∠=︒EBH ABE ABC ∠EBH △是等腰直角三角形∠HE HB =.∠AD AB =,90DAB ∠=︒.∠ABD △是等腰直角三角形,45BDA ∠=︒.在Rt EBH △中,由勾股定理,得222+=HE HB BE .∠2226+=HE HB =36.∠HE 2=HB 2=18∠1832HE HB ===.在BDH 中,90H ∠=︒,30∠=∠-∠=∠=︒-∠BDH EDA BDA ABC BDA .在Rt BDH 中,1322==BH BD .∠62BD =. 在Rt BDH 中,tan ∠=BH BDH DH ,∠3233=DH , ∠36=DH .∠3632=-=-DE DH EH .∠DE BC =,∠BC 的长是3632-.(2)解:四边形ADFC 是菱形.理由如下:∠ABC 绕点A 顺时针旋转120︒得到ADE ,AB AC =,30BAC ∠=︒,∠ABC ADE △≌△,120∠=∠=︒BAD CAE .∠AC AE =,AB AD =,30BAC DAE ∠=∠=︒.∠AC AE AB AD ===.∠∠ACE 是等腰三角形∠180302︒-∠=︒∠=∠=CAE ACE AEC .同理可得:30ABD ADB ∠=∠=︒.∠180752-=︒∠∠=︒BAC ACB . ∠45∠=∠-∠=︒BCG ACB ACE ,105∠=∠+∠=︒FBC ABC ABF .∠在BFC △中,18030∠=︒-∠-∠=︒BFG FBC BCG .∠∠=∠BFG ACF ,∠=∠BFG ADB .∠∥DB AC ,∥FC AD .∠四边形ADFC 是平行四边形.∠AD AC =,∠四边形ADFC 是菱形.(3)如图5,作AH ∠BD 于点H ,则90AHB ∠=︒∠ABC 绕点A 顺时针旋转120︒得到ADE , ∠ABC ADE △≌△,120BAD ∠=︒∠AB AD ==6∠∠ABD 是等腰三角形∠BH =DH =12BD∠180302BAD ABD ADB ︒-∠∠=∠==︒ .在Rt △ABH 中,∠AHB =90°,∠ABH =30°, AB =6∠cos cos30BH ABH AB ==︒∠∠BH =33∠BD =2 BH =63 由(2)知四边形ADFC 是菱形∠DF =AD =6 ∠BF =BD -DF =63-6当BGF 绕点B 顺时针旋转,在旋转过程中,当旋转到A 、B 、F 第一次三点共线时,如图6, ∠=BF ''BF 此时AF 有最小值,此时AF =AF ''=AB -BF ''=AB -BF =6-(63-6)=12-63当旋转到A 、B 、F 第二次三点共线时,如图7,BGF ''△≌△BG F ,∠=BF 'BF此时AF 有最大值,此时AF =AB +BF '=AB +BF =6+63-6=63故AF 的最大值是63,AF 的最小值是1263-【点睛】本题以图形的变换——旋转为载体考查了全等三角形的性质和判定,菱形的判定,线段长度的最值问题等知识点,综合性较强,准确作出辅助线是解题的关键.5.(2022·湖北武汉·八年级期末)已知ABC 中,∠BAC =60°,以AB 和BC 为边向外作等边ABD 和等边BCE .(1)连接AE、CD,如图1,求证:AE=CD;(2)若N为CD中点,连接AN,如图2,求证:CE=2AN(3)若AB∠BC,延长AB交DE于M,DB23,则BM=_______(直接写出结果)【答案】(1)见解析(2)见解析(3)2 2【分析】(1)先判断出∠DBC=∠ABE,进而判断出∠DBC∠∠ABE,即可得出结论;(2)先判断出∠ADN∠∠FCN,得出CF=AD,∠NCF=∠AND,进而判断出∠BAC=∠ACF,即可判断出∠ABC∠∠CF A,即可得出结论;(3)先判断出∠ABC∠∠HEB(ASA),得出22BH AC==,AB EH=,再判断出∠ADM∠∠HEM (AAS),得出AM=HM,即可得出结论.(1)解:∠∠ABD和∠BCE是等边三角形,∠BD=AB,BC=BE,∠ABD=∠CBE=60°,∠∠ABD+∠ABC=∠CBE+∠ABC,∠∠DBC=∠ABE,∠∠ABE∠∠DBC(SAS),∠AE=CD;(2)解:如图,延长AN使NF=AN,连接FC,∠N 为CD 中点,∠DN =CN ,∠∠AND =∠FNC ,∠∠ADN ∠∠FCN (SAS ),∠CF =AD ,∠NCF =∠AND ,∠∠DAB =∠BAC =60°∠∠ACD +∠ADN =60°∠∠ACF =∠ACD +∠NCF =60°,∠∠BAC =∠ACF ,∠∠ABD 是等边三角形,∠AB =AD ,∠AB =CF ,∠AC =CA ,∠∠ABC ∠∠CF A (SAS ),∠BC =AF ,∠∠BCE 是等边三角形,∠CE =BC =AF =2AN ;(3)解: ∠∠ABD 是等边三角形,∠2AB AD DB ===,∠BAD =60°,在Rt ∠ABC 中,∠ACB =90°-∠BAC =30°,∠222AC AB ==, 如图,过点E 作EH // AD 交AM 的延长线于H ,∠∠H =∠BAD =60°,∠∠BCE 是等边三角形,∠BC =BE ,∠CBE =60°,∠∠ABC =90°,∠∠EBH =90°-∠CBE =30°=∠ACB ,∠∠BEH =180°-∠EBH -∠H =90°=∠ABC ,∠∠ABC ∠∠HEB (ASA ),∠22BH AC ==,AB EH =,∠AD =EH ,∠∠AMD =∠HME ,∠∠ADM ∠∠HEM (AAS ),∠AM =HM ,∠()()1111122222BM AM AB AH AB AB BH AB BH AB BH AB =-=-=+-=-=- ∠22BH =,2AB =,∠22BM =.故答案为:22. 【点睛】此题是三角形综合题,主要考查了等边三角形的性质,含30°角的直角三角形的性质,全等三角形的判定和性质,构造出全等三角形是解本题的关键.6.(2022·湖南·长沙市湘郡培粹实验中学八年级阶段练习)如图1,在Rt ∠ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE 2.(1)如图2,将∠BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是 ;(2)如图3,DE ∠BC ,连接AE ,判断∠EAC 的形状,并求出EC 的长;(3)继续旋转∠BDE ,当∠AEC =90°时,请直接写出EC 的长.【答案】(1)EC =AD ,EC ∠AD (2)等腰三角形,10(3)151±【分析】(1)延长CE 交AD 于F ,交AB 于O ,证明∠ABD ∠∠CBE (SAS ),得∠BCE =∠BAD ,CE =AD ,再由∠AOF =∠BOC ,可得∠AFC =∠ABC =90°,即可得到结论;(2)设DE 与AB 的交点为H ,可得AB 是DE 的垂直平分线,利用勾股定理可求出AE 的长,由(1)知CE =AD ,从而得出答案;(3)分当点E 在BC 上方时和当点E 在BC 下方时,分别画图,利用勾股定理计算即可.(1)EC与AD垂直且相等,理由如下:延长CE交AD于F,交AB于O,∠∠BDE和△ABC都是等腰直角三角形,∠BD=BE,AB=BC,∠DBE=∠ABC=90°,∠∠ABD=∠CBE,∠∠ABD∠∠CBE(SAS),∠∠BCE=∠BAD,CE=AD,∠∠AOF=∠BOC,∠∠AFE=∠ABC=90°,∠AD∠CE,∠故答案为:EC=AD,EC∠AD;(2)设DE与AB的交点为H,∠DE∠BC,∠∠AHE=∠ABC=90°,∠BD=BE,∠AB是DE的垂直平分线,∠AD =AE ,由(1)知AD =CE ,∠AE =CE ,∠∠ACE 是等腰三角形,∠BE =2,∠BH =HE =1,∠AH =AB ﹣BH =4﹣1=3,在Rt △AHE 中,由勾股定理得:AE =2210AH HE +=,∠CE =AE =10;(3)如图4,当点E 在BC 上方时,过点B 作BG ∠DE 于G ,∠∠AEC =90°,CE ∠AD ,∠A 、E 、D 三点共线,∠AG =2215AB BG -=,∠AD =AG +DG =151+,∠CE =AD =15+1;如图,当点E 在BC 下方时,同理可得CE =CG ﹣GE =15﹣1.综上:CE =15+1或15﹣1.【点睛】本题主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,旋转的性质,勾股定 理等知识,根据前面探索的结论解决新的问题是解题的关键.7.(2022·广东·惠州一中八年级期中)ABC 为等边三角形,4AB =,AD BC ⊥于点D .E 为线段AD 上一点,3AE =AE 为边在直线AD 右侧构造等边AEF .连结CE ,N 为CE 的中点.(1)如图1,EF 与AC 交于点G ,①连结NG ,求线段NG 的长;②连结ND ,求DNG ∠的大小. (2)如图2,将AEF 绕点A 逆时针旋转,旋转角为α.M 为线段EF 的中点.连结DN 、MN .当30120α︒<<︒时,猜想DNM ∠的大小是否为定值,并证明你的结论.【答案】(1)①72;②120︒;(2)120DNM ∠=︒,证明见解析 【分析】(1)①根据等边三角形的性质,AD BC ⊥,可得60,30AEF EAG ∠=︒∠=︒,NG 是Rt EGC △斜边EC 上的中线,勾股定理在Rt EDC 中可求得EC 的长,进而求得NG 的长;②根据①的结论可得NG NC ND ==,根据120NGC NCG NCD NDC ∠+∠+∠+∠=︒=GND ∠,即可求得GND ∠的度数; (2)连接,BE FC ,证明BAE CAF ≌,进而可得ABE ACF ∠=∠,则120EBC BCF ABC ABE ACB ACF ABC ACB ∠+∠=∠-∠+∠+∠=∠+∠=︒,进而根据D 为BC 的中点,N 为EC 的中点,M 为EF 的中点,根据三角形中位线定理可得,DN BE MN CF ∥∥,进而可得MNE DNE ∠+∠=FCE DCE ∠+∠120=︒【详解】(1)①ABC 是等边三角形,4,AB AD BC =⊥222,23DB DC AD AC DC ∴===-=,60BAC ∠=︒3AE =3ED AD AE ∴=-=AEF 是等边三角形,60AEG ∴∠=︒1302DAG DAB CAB ∠=∠=∠=︒90EGC ∴∠=︒ N 为CE 的中点()22221117322222NG EC DE DC ∴==+=+= ②如图,连接DN ,11,22NG EC NC DN EC ===NG NC ND ∴== ==NGC NCG NCD NDC ∴∠∠∠∠,()2=2120NGC NCG NCD NDC NCD NCG BCA ∴∠+∠+∠+∠=∠+∠=︒NGC NCG NCD NDC GNE DNE GND ∠+∠+∠+∠=∠+∠=∠120GND ∴∠=︒;(2)120DNM ∠=︒,理由如下,如图,连接,BE FC ABC ,AEF 为等边三角形,,AB AC AE AF ∴==,60BAE BAC CAE CAE ∠=∠+∠=︒+∠60CAF CAE EAF CAE ∠=∠+∠=︒+∠BAE CAF ∴∠=∠BAE CAF ∴△≌△∴ABE ACF ∠=∠则120EBC BCF ABC ABE ACB ACF ABC ACB ∠+∠=∠-∠+∠+∠=∠+∠=︒D 为BC 的中点,N 为EC 的中点,M 为EF 的中点,DN BE MN CF ∴∥∥,MNE FCE EBC NDC ∴∠=∠∠=∠END NDC NCD ∠=∠+∠∴DNM DNE MNE NDC ACB ACN ECF∠=∠+∠=∠+∠+∠+∠120EBC ACB ACF EBC BCF =∠+∠+∠=∠+∠=︒120DNM ∴∠=︒【点睛】本题考查了等边三角形的性质,勾股定理,三线合一,直角三角形斜边上的中线等于斜边的,勾股定理,中位线定理,三角形全等的性质与判定,旋转的性质,综合运用以上知识是解题的关键.8.(2022•新乡中考模拟)在△ABC中,CA=CB=m,在△AED中,DA=DE=m,请探索解答下列问题.【问题发现】(1)如图1,若∠ACB=∠ADE=90°,点D,E分别在CA,AB上,则CD与BE的数量关系是,直线CD与BE的夹角为;【类比探究】(2)如图2,若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图2所示的位置,则CD 与BE之间是否满足(1)中的数量关系?说明理由.【拓展延伸】(3)在(1)的条件下,若m=2,将△AED绕点A旋转过程中,当B,E,D三点共线.请直接写出CD的长.【分析】(1)根据等腰直角三角形的性质得到AB=AC=m,AE=AD=m,计算即可;(2)过点C作CH⊥AB于H,延长CD、BE交于点F,根据直角三角形的性质得到AB=AC,AE=AD,证明△CAD∽△BAE,根据相似三角形的性质解答即可;(3)分点E在线段BD上、点D在线段BE上两种情况,根据相似三角形的性质计算即可.【解答】解:(1)∵∠ACB=∠ADE=90°,CA=CB,DA=DE,∴∠A=∠B=∠DEA=45°,∴AB=AC=m,AE=AD=m,∴CD=AC﹣AD=m,BE=AB﹣AE=m,∴BE=CD,∵∠A=45°,∴直线CD与BE的夹角为45°,故答案为:BE=CD,45°;(2)不满足,BE=CD,直线CD与BE的夹角为30°,理由如下:如图2,过点C作CH⊥AB于H,延长CD、BE交于点F,∵CA=CB,∴AH=HB,∵∠ACB=∠ADE=120°,CA=CB,DA=DE,∴∠CAB=∠CBA=30°,∠DAE=∠DEA=30°,∴AC=2CH,∠CAD=∠BAE,由勾股定理得:AH=AC,∴AB=AC,同理可得:AE=AD,∴=,∵∠CAD=∠BAE,∴△CAD∽△BAE,∴==,∠ACD=ABE,∴BE=CD,∠F=∠CAB=30°,∴BE=CD,直线CD与BE的夹角为30°;(3)如图3,点E在线段BD上,∵m=2,∴AD=DE=1,AB=2,由勾股定理得:BD==,∴BE=BD﹣DE=﹣1,∴CD=BE=,如图4,点D在线段BE上,BE=BD+DE=+1,∴CD=BE=,综上所述:当B,E,D三点共线.CD的长为或.【点评】本题考查的是相似三角形的判定和性质、直角三角形的性质、等腰三角形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.9.(2022•虹口区期中)如图,在△ABC和△ADE中,△BAD=△CAE,△ABC=△ADE.(1)求证:△ABC△△ADE;(2)判断△ABD与△ACE是否相似?并证明.。
相似三角形重要模型-手拉手模型(解析版)-初中数学

相似三角形重要模型-手拉手模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型,在实际的应用和解题当中出现时,对于同学们来说,都比较困难。
而深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。
手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义:如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。
1)手拉手相似模型(任意三角形)条件:如图,∠BAC =∠DAE =α,AD AB =AE AC=k ;结论:△ADE ∽△ABC ,△ABD ∽△ACE ;EC BD =k .2)手拉手相似模型(直角三角形)条件:如图,∠AOB =∠COD =90°,OC OA =OD OB =k (即△COD ∽△AOB );结论:△AOC ∽△BOD ;BD AC =k ,AC ⊥BD ,S ABCD =12AB ×CD .3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点;结论:△BME ∽△CMF ;BE CF =3.条件:△ABC 和ADE 是等腰直角三角形;结论:△ABD ∽△ACE .1(2023秋·福建泉州·九年级校考期末)问题背景:(1)如图①,已知△ABC ∽△ADE ,求证:△ABD ∽△ACE ;尝试应用:(2)如图②,在△ABC 和△ADE 中,∠BAC =∠DAE =90°,∠ABC =∠ADE =60°,AC 与DE相交于点F ,点D 在BC 边上,DF CF=233,求AD BD 的值;拓展创新:(3)如图③,D 是△ABC 内一点,∠BAD =∠CBD =30°,∠BDC =90°,AB =4,AC =23,求AD 的长.【答案】(1)见解析;(2)AD BD =2;(3)AD =5【分析】问题背景(1)由题意得出AB AD =AC AE ,∠BAC =∠DAE ,则∠BAD =∠CAE ,可证得结论;尝试应用(2)连接EC ,证明△ABC ∽△ADE ,由(1)知△ABD ∽△ACE ,由相似三角形的性质得出AE AD =EC BD =3,∠ACE =∠ABD =∠ADE ,可证明△ADF ∽△ECF ,得出DF CF =AD CE=233,则可求出答案.拓展创新(3)过点A 作AB 的垂线,过点D 作AD 的垂线,两垂线交于点M ,连接BM ,证明△BDC ∽△MDA ,由相似三角形的性质得出BD MD =DC DA ,证明△BDM ∽△CDA ,得出BM CA =DM AD=3,求出BM =6,由勾股定理求出AM ,最后由直角三角形的性质可求出AD 的长.【详解】问题背景(1)证明:∵△ABC ∽△ADE ,∴AB AD =AC AE ,∠BAC =∠DAE ,∴∠BAD =∠CAE ,AB AC =AD AE,∴△ABD ∽△ACE ;尝试应用(2)解:如图,连接EC ,∵∠BAC=∠DAE=90°,∠ABC=∠ADE=60°,∴△ABC∽△ADE,AE=3AD由(1)知△ABD∽△ACE,∴AEAD=ECBD=3,∠ACE=∠ABD=∠ADE=60°,∴AEEC=ADBD,∵∠AFD=∠AEFC∴△ADF∽△ECF∴DFCF =ADCE∵DF CF =233∴DFCF=ADCE=233∴AD=233CE∴AE=3AD=2CE∴ADBD=AEEC=2,拓展创新(3)解:如图2,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,∵∠BAD=30°,∴∠DAM=60°,∴∠AMD=30°,∴∠AMD=∠DBC,又∵∠ADM=∠BDC=90°,∴△BDC∽△MDA,∴BDMD=DCDA,又∠BDC=∠ADM,∴∠BDC+∠CDM=∠ADM+∠CDM,即∠BDM=∠CDA,∴△BDM∽△CDA,∴BMCA=DMAD=3,∵AC=23,∴BM=23×3=6,∴AM=BM2-AB2=62-42=25,∴AD=12AM=5.【点睛】此题是相似形综合题,考查了直角三角形的性质,勾股定理,相似三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质是解题的关键.2(2023秋·江苏无锡·九年级校考阶段练习)【模型呈现:材料阅读】如图,点B,C,E在同一直线上,点A,D在直线CE的同侧,△ABC和△CDE均为等边三角形,AE,BD 交于点F,对于上述问题,存在结论(不用证明):(1)△BCD≌△ACE(2)△ACE可以看作是由△BCD绕点C旋转而成;⋯【模型改编:问题解决】点A ,D 在直线CE 的同侧,AB =AC ,ED =EC ,∠BAC =∠DEC =50°,直线AE ,BD 交于F ,如图1:点B 在直线CE 上,①求证:△BCD ∽△ACE ; ②求∠AFB 的度数. 如图2:将△ABC 绕点C 顺时针旋转一定角度.③补全图形,则∠AFB 的度数为;④若将“∠BAC =∠DEC =50°”改为“∠BAC =∠DEC =m °”,则∠AFB 的度数为.(直接写结论)【模型拓广:问题延伸】如图3:在矩形ABCD 和矩形DEFG 中,AB =2,AD =ED =23,DG =6,连接AG ,BF ,求BF AG 的值.图1 图2 图3【答案】【模型改编:问题解决】①见解析;②65°;③图见解析,115°;④90°+m °2【模型拓广:问题延伸】233【分析】【模型改编:问题解决】①先证明△ABC ∽△EDC ,可得AC EC =BC DC,再证明∠ACE =∠BCD ,可得△BCD ∽△ACE ;②由△BCD ∽△ACE ,可得∠DBC =∠EAC ,再结合三角形的外角可得答案;③连接EA 并延长交BD 于F ,同理可得:△BCD ∽△ACE ,∠CEF =∠BDC ,再结合三角形的外角可得答案;④先求解∠CDE =∠DCE =12180°-m ° =90°-12m °,结合③的思路可得答案;【模型拓广:问题延伸】连接BD 、DF ,先证明△ADB ∽△GDF ,可得∠ADB =∠GDF ,AD DG =BD DF ,证明∠ADG =∠BDF ,可得△BDF ∽△ADG ,可得BF AG =BD AD,从而可得答案.【详解】【模型改编:问题解决】①∵AB =AC ,ED =EC ,∠BAC =∠DEC =50°,∴∠ABC =∠ACB =180°-50° ÷2=65°,∠EDC =∠ECD =180°-50° ÷2=65°,∴△ABC ∽△EDC ,∴AC EC =BC DC,∵∠ACE =180°-∠ACB =115°,∠BCD =180°-∠DCE =115°,∴∠ACE =∠BCD ,∴△BCD ∽△ACE ;②由①知,△BCD ∽△ACE ,∴∠DBC =∠EAC ,∴∠AFB =∠DBC +∠CEA =∠EAC +∠CEA =∠ACB =65°③补图如下:连接EA 并延长交BD 于F ,图2同理可得:△BCD ∽△ACE ∴∠CEF =∠BDC ,∴∠AFB =∠BDC +∠CDE +∠DEF =∠CEF +∠CDE +∠DEF =∠CED +∠CDE =50°+65°=115°,④∵∠BAC =∠DEC =m °,CE =DE ,∴∠CDE =∠DCE =12180°-m ° =90°-12m °,同理③可得∠AFB =∠CED +∠CDE =m °+90°-12m °=90°+m °2,故答案为:90°+m °2;【模型拓广:问题延伸】连接BD 、DF ,图3∵在矩形ABCD 和矩形DEFG 中,AB =2,AD =ED =FG =23,DG =6,∴AB AD =GF DG =33,又∵∠BAD =∠DGF =90°,∴△ADB ∽△GDF ,∴∠ADB =∠GDF ,AD DG=BD DF ,∵∠ADG =∠GDF +∠ADF ,∠BDF =∠ADB +∠ADF ,∴∠ADG =∠BDF ,∴△BDF ∽△ADG ,∴BF AG =BD AD,∵AD =23,AB =2,∴BD =AB 2+AD 2=4,∴BF AG =BD AD =423=233.【点睛】本题考查的是等腰三角形的性质,矩形的性质,勾股定理的应用,相似三角形的判定与性质,熟练的证明三角形相似是解本题的关键.3(2023春·湖北黄冈·九年级专题练习)【问题呈现】△CAB 和△CDE 都是直角三角形,∠ACB =∠DCE =90°,CB =mCA ,CE =mCD ,连接AD ,BE ,探究AD ,BE 的位置关系.(1)如图1,当m =1时,直接写出AD ,BE 的位置关系:;(2)如图2,当m ≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.【拓展应用】(3)当m =3,AB =47,DE =4时,将△CDE 绕点C 旋转,使A ,D ,E 三点恰好在同一直线上,求BE 的长.【答案】(1)BE ⊥AD (2)成立;理由见解析(3)BE =63或43【分析】(1)根据m =1,得出AC =BC ,DC =EC ,证明△DCA ≌△ECB ,得出∠DAC =∠CBE ,根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ,求出∠GAB +∠ABG =90°,即可证明结论;(2)证明△DCA ∽△ECB ,得出∠DAC =∠CBE ,根据∠GAB +∠ABG =∠DAC +∠CAB +∠ABG ,求出∠GAB +∠ABG =90°,即可证明结论;(3)分两种情况,当点E 在线段AD 上时,当点D 在线段AE 上时,分别画出图形,根据勾股定理求出结果即可.【详解】(1)解:∵m =1,∴AC =BC ,DC =EC ,∵∠DCE =∠ACB =90°,∴∠DCA +∠ACE =∠ACE +∠ECB =90°,∴∠DCA =∠ECB ,∴△DCA ≌△ECB ,∴∠DAC =∠CBE ,∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG,=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°-∠ACB=90°,∴∠AGB=180°-90°=90°,∴BE⊥AD;故答案为:BE⊥AD.(2)解:成立;理由如下:∵∠DCE=∠ACB=90°,∴∠DCA+∠ACE=∠ACE+∠ECB=90°,∴∠DCA=∠ECB,∵DC CE =ACBC=1m,∴△DCA∽△ECB,∴∠DAC=∠CBE,∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG,=∠CBE+∠CAB+∠ABG =∠CAB+∠CBA=180°-∠ACB=90°,∴∠AGB=180°-90°=90°,∴BE⊥AD;(3)解:当点E在线段AD上时,连接BE,如图所示:设AE=x,则AD=AE+DE=x+4,根据解析(2)可知,△DCA∽△ECB,∴BE AD =BCAC=m=3,∴BE=3AD=3x+4=3x+43,根据解析(2)可知,BE⊥AD,∴∠AEB=90°,根据勾股定理得:AE2+BE2=AB2,即x2+3x+432=472,解得:x=2或x=-8(舍去),∴此时BE=3x+43=63;当点D在线段AE上时,连接BE,如图所示:设AD=y,则AE=AD+DE=y+4,根据解析(2)可知,△DCA∽△ECB,∴BE AD =BCAC=m=3,∴BE=3AD=3y,根据解析(2)可知,BE⊥AD,∴∠AEB=90°,根据勾股定理得:AE 2+BE 2=AB 2,即y +4 2+3y 2=47 2,解得:y =4或y =-6(舍去),∴此时BE =3y =43;综上分析可知,BE =63或43.【点睛】本题主要考查了全等三角形的判定和性质,相似三角形的判定和性质,三角形内角和定理的应用,勾股定理,解题的关键是熟练掌握三角形相似的判定方法,画出相应的图形,注意分类讨论.4(2023秋·福建泉州·九年级校考阶段练习)如图,已知△ABC 中,AB =AC ,∠BAC =α.点D 是△ABC 所在平面内不与点A 、C 重合的任意一点,连接CD ,将线段CD 绕点D 顺时针旋转α得到线段DE ,连接AD 、BE .(1)如图1,当α=60°时,求证:BE =AD .(2)当α=120°时,请判断线段BE 与AD 之间的数量关系是,并仅就图2的情形说明理由.(3)当α=90°时,且BE ⊥AB 时,若AB =8,BE =2,点E 在BC 上方,求CD 的长.【答案】(1)见解析,(2)BE =3AD ,理由见解析(3)82【分析】(1)先证明△ABC 和△DCE 是等边三角形,再证明△ADC ≌△BEC ,可推出BE =AD ;(2)过A 作AH ⊥BC 与H ,先根据含30°的直角三角形的性质,等腰三角形的性质以及勾股定理可求出BC =3AC ,同理求出CE =3CD ,可得出BC EC =3AC 3DC=AC DC ,证明∠DCA =∠BCE ,然后证明△EBC ∽△DAC 即可求解;(3)过E 作EF ⊥BC 于F ,可判断△BEF 是等腰直角三角形,然后可求出EF ,BF ,CF 的长度,由(2)同理可证出△EBC ∽△DAC ,最后根据相似三角形的性质即可求解.【详解】(1)解:∵旋转,∴CD =ED ,当α=60°时,又AB =AC ,∴△ABC 和△DCE 是等边三角形,∴AC =BC ,DC =EC ,∠DCE =∠ACB =60°,∴∠ACD =∠BCE ,∴△ADC ≌△BEC ,∴AD =BE ;(2)解:BE =3AD 过A 作AH ⊥BC 与H ,∵AB =AC ,∠BAC =α=120°,∴∠ACB =30°,CH =12BC ,∴AC =2AH ,又由勾股定理得AH 2+CH 2=AC 2,∴CH =32AC ,∴BC =3AC ,同理CE =3CD ,∵DC =EC ,∠CDE =α=120°,∴∠DCE =30°=∠ACB ,∴∠DCA =∠BCE ,∵BC =3AC ,CE =3CD ,∴BC EC =3AC 3DC =AC DC ,∴△EBC ∽△DAC ,∴BE AD =BC AC =3,即BE =3AD (3)解:如图,过E 作EF ⊥BC 于F ,当α=90°时,∵AC =AB =8,∴∠ACB =45°,BC =AB 2+AC 2=2AC =82,∵BE ⊥AB ,∴∠EBF =45°=∠BEF ,∴BF =EF ,∵BE =EF 2+BF 2=2EF =2,∴EF =BF =2,∴CF =BF +BC =92,∴CE =EF 2+CF 2=241,由(2)同理可证△EBC ∽△DAC ,∴EC DC =BC AC=2,即241DC =2,∴DC =82.【点睛】本题属于三角形综合题,考查了等边三角形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键在于正确寻找全等三角形或相似三角形.5(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.(1)发现问题:如图1,在△ABC 和△AEF 中,AB =AC ,AE =AF ,∠BAC =∠EAF =30°,连接BE ,CF,延长BE交CF于点D.则BE与CF的数量关系:,∠BDC=°;(2)类比探究:如图2,在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点D.请猜想BE与CF的数量关系及∠BDC的度数,并说明理由;(3)拓展延伸:如图3,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线上,过点A作AM⊥BF,垂足为点M.则BF,CF,AM之间的数量关系:;(4)实践应用:正方形ABCD中,AB=2,若平面内存在点P满足∠BPD=90°,PD=1,则S△ABP=.【答案】(1)BE=CF,30(2)BE=CF,∠BDC=60°,证明见解析(3)BF=CF+2AM(4)7+74或7-74【分析】(1)根据已知得出∠BAE=∠CAF,即可证明△BAE≌△CAF,得出BE=CF,∠ABE=∠ACF,进而根据三角形的外角的性质即可求解;(2)同(1)的方法即可得证;(3)同(1)的方法证明△BAE≌△CAF SAS,根据等腰直角三角形的性质得出AM=12EF=EM=MF,即可得出结论;(4)根据题意画出图形,连接BD,以BD为直径,BD的中点为圆心作圆,以D点为圆心,1为半径作圆,两圆交于点P,P1,延长BP至M,使得PM=DP=1,证明△ADP∽△BDM,得出PA=22BM,勾股定理求得PB,进而求得BM,根据相似三角形的性质即可得出PA=221+7=2+142,勾股定理求得BQ,PQ,进而根据三角形的面积公式即可求解.【详解】(1)解:∵∠BAC=∠EAF=30°,∴∠BAE=∠CAF,又∵AB=AC,AE=AF,∴△BAE≌△CAF,∴BE=CF,∠ABE=∠ACF设AC,BD交于点O,∵∠AOD=∠ACF+∠BDC=∠ABE+∠BAO∴∠BDC=∠BAO=∠BAC=30°,故答案为:BE= CF,30.(2)结论:BE=CF,∠BDC=60°;证明:∵∠BAC=∠EAF=120°,∴∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF,又∵AB=AC,AE=AF,∴△BAE≌△CAF∴BE=CF,∠AEB=∠AFC∵∠EAF=120°,AE=AF,∴∠AEF=∠AFE=30°,∴∠BDC=∠BEF-∠EFD=∠AEB+30°-∠AFC-30°=60°,(3)BF=CF+2AM,理由如下,∵∠BAC=∠EAF=90°,∴∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF,又∵△ABC和△AEF均为等腰直角三角形∴AB=AC,AE=AF,∴△BAE≌△CAF SAS,∴BE= CF,在Rt △AEF 中,AM ⊥BF ,∴AM =12EF =EM =MF ,∴BF =BE +EF =CF +2AM ;(4)解:如图所示,连接BD ,以BD 为直径,BD 的中点为圆心作圆,以D 点为圆心,1为半径作圆,两圆交于点P ,P 1,延长BP 至M ,使得PM =DP =1,则△MDP 是等腰直角三角形,∠MDP =45°∵∠CDB =45°,∴∠MDB =∠MDP +∠PDC +∠CDB =90°+∠PDC =∠ADP ,∵AD DB =12,DP DM =12,∴△ADP ∽△BDM ∴PA BM =12=22,∴PA =22BM ,∵AB =2,在Rt △DPB 中,PB =DB 2-DP 2=22 2-12=7,∴BM =BP +PM =7+1∴PA =221+7 =2+142过点P 作PQ ⊥AB 于点Q ,设QB =x ,则AQ =2-x ,在Rt △APQ 中,PQ 2=AP 2-AQ 2,在Rt △PBQ 中,PQ 2=PB 2-BQ 2∴AP 2-AQ 2=PB 2-BQ 2∴2+142 2-2-x 2=7 2-x 2解得:x =7-74,则BQ =7-74,设PQ ,BD 交于点G ,则△BQG 是等腰直角三角形,∴QG =QB =7-74在Rt △DPB ,Rt △DP 1B 中,DP =DP 1DB =DB ∴Rt △DPB ≌Rt △DP 1B ∴∠PDB =∠P 1DB又PD =P 1D =1,DG =DG ∴△PGD ≌△P 1DG ∴∠PGD =∠P 1GD =45°∴∠PGP 1=90°,∴P 1G ∥AB ∴S △ABP 1=12AB ×QG =12×2×7-74=7-74,在Rt △PQB 中,PQ =PB 2-BQ 2=7 2-7-74 2=7+74∴S△ABP =12AB ×PQ =12×2×7+74=7+74,综上所述,S△ABP=7+74或7-74故答案为:7+74或7-74.【点睛】本题考查了全等三角形的性质与判定,相似三角形的性质与判定,正方形的性质,勾股定理,直径所对的圆周角是直角,熟练运用已知模型是解题的关键.6(2023·山东济南·九年级统考期中)问题背景:一次小组合作探究课上,小明将一个正方形ABCD和等腰Rt△CEF按如图1所示的位置摆放(点B、C、E在同一条直线上),其中∠ECF=90°.小组同学进行了如下探究,请你帮助解答:初步探究(1)如图2,将等腰Rt△CEF绕点C按顺时针方向旋转,连接BF,DE.请直接写出BF与DE的关系;(2)如图3,将(1)中的正方形ABCD和等腰Rt△CEF分别改成菱形ABCD和等腰△CEF,其中CE=CF,∠BCD=∠FCE,其他条件不变,求证:BF=DE;深入探究:(3)如图4,将(1)中的正方形ABCD和等腰Rt△CEF分别改成矩形ABCD和Rt△CEF,其中∠ECF=90°且CECF =CDBC=34,其它条件不变.①探索线段BF与DE的关系,说明理由;②连接DF,BE若CE=6,AB=12,直接写出DF2+BE2=.【答案】(1)BF=DE,BF⊥DE;(2)见解析;(3)①DEBF=34,DE⊥BF,见解析;②500【分析】(1)由正方形的性质,等腰直角三角形的性质,得到BC=CD,CE=CF,证明△BCF≌DCE,得到BF=DE,∠CBF=∠CDE,结合对顶角相等,即可得到BF⊥DE;(2)由菱形的性质,旋转的性质,先证明ΔBCF≌ΔDCE,即可得到结论成立;(3)①由矩形的性质,直角三角形的性质,先证明ΔBCF∽ΔDCE,得到BF与DE的数量关系,再由余角的性质证明位置关系即可;②连接BD,先求出矩形的边长,直角三角形的边长,与(1)同理先证明BF⊥DE,然后利用勾股定理,等量代换,即可得到DF2+BE2=500.【详解】解:(1)如图:∵正方形ABCD和等腰Rt△CEF中,∴BC=CD,CE=CF,∠BCD=∠ECF=90°,∴∠BCD+∠DCF=∠ECF+∠DCF,即∠BCF=∠DCE,∴△BCF≌DCE,∴BF=DE,∠CBF=∠CDE,∵∠BGC=∠DGF,∴∠BCG=∠DFG=90°∴BF⊥DE.(2)证明:如图:∵∠BCD=∠FCE,∴∠BCF=∠DCE,∵四边形ABCD为菱形∴BC=CD,又∵CE=CF∴△BCF≌△DCE(SAS),∴BF=DE;(3)①∵在矩形ABCD中,∠BCD=90°,∴∠BCD=∠FCE∴∠BCF=∠DCE,又∵CECF=CDBC=34∴△BCF∽△DCE,∴DEBF=CECF=34;∴∠CBF=∠CDE,设CD与BF交于点G∵∠BGC=∠DGF∴180°-∠CBF-∠BGC=180°-∠CDE-∠DGF,∴∠DQB=∠BCD=90°∴DE⊥BF.②如图:连接BD在矩形ABCD中,CD=AB=12,∵CE=6,6CF =12BC=34,∴CF=8,BC=16,∵△BCF∽△DCE,∴∠CBF=∠CDE,∵∠BGC=∠DGF,∴∠BCG=∠DQG=90°,∴BF⊥DE;在直角△BCD中,有BD2=BC2+CD2=162+122=400,在直角△BDQ中,BD2=BQ2+DQ2=400;在直角△CEF中,EF2=CE2+CF2=62+82=100,在直角△EFQ中,EF2=EQ2+FQ2=100;∴BQ2+DQ2+EQ2+FQ2=400+100=500;在直角△BEQ和直角△DFQ中,由勾股定理,则∵BQ2+EQ2=BE2,DQ2+FQ2=DF2,∴DF2+BE2=BQ2+DQ2+EQ2+FQ2=500;故答案为:500.【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,旋转的性质,勾股定理,以及等腰直角三角形的性质等知识,解题的关键是熟练掌握所学的知识,正确的作出辅助线,找到证明三角形相似和三角形全等的条件进行解题.7(2023春·广东·九年级专题练习)已知在△ABC中,O为BC边的中点,连接AO,将△AOC绕点O顺时针方向旋转(旋转角为钝角),得到△EOF,连接AE,CF.(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)如图2,当∠BAC =90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.【答案】(1)AE=CF;(2)成立,证明见解析;(3)511 3【分析】(1)结论AE=CF.证明ΔAOE≅ΔCOF(SAS),可得结论.(2)结论成立.证明方法类似(1).(3)首先证明∠AED=90°,再利用相似三角形的性质求出AE,利用勾股定理求出DE即可.【详解】解:(1)结论:AE=CF.理由:如图1中,∵AB=AC,∠BAC=90°,OC=OB,∴OA=OC=OB,AO⊥BC,∵∠AOC=∠EOF=90°,∴∠AOE=∠COF,∵OA=OC,OE=OF,∴ΔAOE≅ΔCOF(SAS),∴AE=CF.(2)结论成立.理由:如图2中,∵∠BAC=90°,OC=OB,∴OA=OC=OB,∵∠AOC=∠EOF,∴∠AOE=∠COF,∵OA=OC,OE=OF,∴ΔAOE≅ΔCOF(SAS),∴AE=CF.(3)如图3中,由旋转的性质可知OE =OA ,∵OA =OD ,∴OE =OA =OD =5,∴∠AED =90°,∵OA =OE ,OC =OF ,∠AOE =∠COF ,∴OA OC =OE OF ,∴ΔAOE ∽ΔCOF ,∴AE CF =OA OC,∵CF =OA =5,∴AE 5=53,∴AE =253,∴DE =AD 2-AE 2=102-253 2=5113.【点睛】本题属于几何变换综合题,考查了旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考压轴题.课后专项训练1(2023秋·北京顺义·九年级校考期中)如图,△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .则BD CE的值为()A.12B.22C.2D.2【答案】B 【分析】由等腰直角三角形的性质可推出∠DAE =∠BAC =45°,AE =2AD ,AC =2AB ,从而可得出∠EAC =∠DAB ,AE AD =AC AB=2,证明△DAB ∽△EAC 即可得出结论.【详解】解:∵△ABC 和△ADE 都是等腰直角三角形,∴∠DAE =∠BAC =45°,AE =2AD ,AC =2AB ,∴∠EAC =∠DAB ,AE AD =AC AB =2,∴△DAB ∽△EAC ,∴BD CE =AD AE=22.故选B .【点睛】本题考查等腰直角三角形的性质,勾股定理,相似三角形的判定和性质.掌握三角形相似的判定条件是解题关键.2(2023春·浙江金华·九年级校考期中)如图,在Rt △ABC 中,∠ABC =90°,以AB ,AC 为边分别向外作正方形ABFG 和正方形ACDE ,CG 交AB 于点M ,BD 交AC 于点N .若GM CM =12,则CG BD=() A.12 B.34 C.255 D.13013【答案】D【分析】设AG =a =AB ,BC =2a ,由“AAS ”可证△ABC ≌△CHD ,可得AB =CH =a ,DH =BC =2a ,利用勾股定理分别求出CG ,BD 的长,即可求解.【详解】解:如图,过点D 作DP ⊥BC ,交AC 的延长线于点P,交BC 的延长线于点H ,∵AG ∥BF ,∴△AGM ∽△BCM ,∴AG BC =GM CM=12,∴设AG =a =AB ,BC =2a ,∴CG =GF 2+FC 2=a 2+(3a )2=10a ,∵DH ⊥BC ,AB ⊥BC ,∴∠DHC =∠ABC =∠ACD =90°,AB ∥DH ,∴∠DCH +∠ACB =90°=∠ACB +∠BAC ,∴∠DCH =∠BAC ,在△ABC 和△CHD 中,∠ABC =∠DHC ∠BAC =∠DCH AC =CD,∴△ABC ≌△CHD (AAS ),∴AB =CH =a ,DH =BC =2a ,∴BD =BH 2+DH 2=(3a )2+(2a )2=13a ,∴CG BD =10a 13a =13013.故选:D .【点睛】本题考查了相似三角形的判定和性质,正方形的性质,全等三角形的判定和性质,添加恰当辅助线构造相似三角形是解题的关键.3(2023春·浙江丽水·九年级专题练习)如图,在△ABC 中,过点C 作CD ⊥AB ,垂足为点D ,过点D 分别作DE ⊥AC ,DF ⊥BC ,垂足分别为E ,F .连接EF 交线段CD 于点O ,若CO =22,CD =32,则EO ⋅FO 的值为( ).A.63B.4C.56D.6【答案】B【分析】由题意易得出∠DEC=∠DFC=90°,即说明点C,E,D,F四点共圆,得出∠DEO=∠FCO,从而易证△DOE∽△FOC,得出EOCO=DOFO.由题意可求出DO=CD-CO=2,即可求出EO⋅FO=CO⋅DO=4.【详解】解:∵DE⊥AC,DF⊥BC,∴∠DEC=∠DFC=90°,∴点C,E,D,F四点共圆,∴∠DEF=∠FCD,即∠DEO=∠FCO.又∵∠DOE=∠FOC,∴△DOE∽△FOC,∴EOCO=DOFO,∴EO⋅FO=CO⋅DO.∵CO=22,CD=32,∴DO=CD-CO=2,∴EO⋅FO=CO⋅DO=22×2=4.故选B.【点睛】本题考查相似三角形的判定和性质,四点共圆的知识,圆周角定理.确定点C,E,D,F四点共圆,从而可得出证明△DOE∽△FOC的条件是解题关键.4(2022·广西梧州·统考一模)如图,在△ABC中,∠C=45°,将△ABC绕着点B逆时针方向旋转,使点C的对应点C′落在CA的延长线上,得到△A′BC′,连接AA′,交BC′于点O.下列结论:①∠AC′A′= 90°;②AA′=BC′;③∠A′BC′=∠A′AC′;④△A′OC′∽△BOA.其中正确结论的个数是()A.1B.2C.3D.4【答案】C【分析】利用旋转的性质和等腰三角形的性质推出∠AC A =90°,即可判断①的正确性;通过点A 、B、A、C 四点共圆可以判断出②③④的正确性.【详解】解:由题意可得:BC=BC ,∠C=∠A C B∵∠C=45°∴∠BC A=45°∵∠AC A =∠A C B+∠BC A∴∠AC A =90°,故①正确;∵∠BC A=∠C=45°∴∠C BC=90°∵∠ABC=∠A BC ∴∠A BA=90°∴∠A BA+∠AC A =180°,∠C AB+∠C A B=180°∴点A 、B、A、C 四点共圆∵∠AC A =90°,∠BAC ≠90°∴A A是直径,BC 不是直径∴A A≠BC ,故②错误;∵点A 、B、A、C 四点共圆∴∠A BC =∠A AC ,故③正确;∵点A 、B、A、C 四点共圆∴∠AA C =∠ABC ,∠A C B=∠A AB∴△A OC ∽△BOA,故④正确;∴正确结论的个数是3个故选C.【点睛】本题考查了图形的旋转、等腰三角形的性质、四点共圆、圆周角定理的推论以及相似的判定等知识点,灵活运用这些知识点是解题的关键.5(2023·广东深圳·校联考模拟预测)如图,已知▱ABCD ,AB =3,AD =8,将▱ABCD 绕点A 顺时针旋转得到▱AEFG ,且点G 落在对角线AC 上,延长AB 交EF 于点H ,则FH 的长为.【答案】558【分析】先利用平行四边形的性质得到CD =AB =3,BC =AD =8,∠D =∠ABC ,再根据旋转的性质得到∠DAG =∠BAE ,AE =AB =3,EF =BC =8,∠E =∠ABC ,接着证明△ADC ∽△AEH ,然后利用相似比求出EH ,从而得到FH 的长.【详解】解:∵四边形ABCD 为平行四边形,∴CD =AB =3,BC =AD =8,∠D =∠ABC ,∵将▱ABCD 绕点A 顺时针旋转得到▱AEFG ,且点G 落在对角线AC 上,∴∠DAG =∠BAE ,AE =AB =3,EF =BC =8,∠E =∠ABC ,∴∠E =∠D ,∵∠DAC =∠HAE ,∴△ADC ∽△AEH ,∴AD AE =DC EH ,∴83=3EH ,∴EH =98,∴FH =EF -EH =8-98=558,故答案为:558.【点睛】本题考查了平行四边形的性质,旋转、三角形相似的判定利用三角形相似比求线段的长,根据旋转的性质得到∠DAG =∠BAE ,然后根据两组对应角分别相等的两三角形相似得出AD AE=DC EH 是本题的关键.6(2022·安徽·模拟预测)如图,将边长为3的菱形ABCD 绕点A 逆时针旋转到菱形AB C D 的位置,使点B 落在BC 上,B C 与CD 交于点E .若BB =1,则CE 的长为.【答案】34/0.75【分析】延长D D 交BC 的延长线于点M ,过点C 作CN ∥DM 交B C 于点N ,根据菱形的性质和旋转的性质证明△ABB ≌△ADD ≌△DCM ≌B C M ,求得C D =B C =2,CM =C M =1,再根据CN ∥DM ,得CN MC =B C B M ,CN DC=CE DE ,代入即可求解.【详解】解:如图,延长D D 交BC 的延长线于点M ,过点C 作CN ∥DN 交B C 于点N ,∵四边形ABCD是菱形∴AB=BC=CD=AD=3,∠B=∠ADC=∠D ,AB∥CD∴∠DCM=∠B由旋转的性质得:AB =AB=3,AD =AD=3,∠BAB =∠DAD =∠MB C ,B C =D C =3,∠ADC=∠D ,∴△ABB ≌△ADD ∴DD =BB =1∴DC =D C -DD =2∵∠CDM+∠ADC=∠DAD +∠D ∴∠BAB =∠DAD =∠CDM∴△ABB ≌△DCM≌B C M,∴DM=AB =3,∠M=∠AB B∴C M=CM=3-2=1∵CN∥DM∴△B CN∽△B MC ∴CNMC =B CB M∵B C=BC-BB =2∴CN1=23∴CN=23∵CN∥DM∴△CNE∽△DC E∴CNDC =CEDE∴232=CE3-CE∴CE=34故答案为:34【点睛】本题考查菱形的性质,旋转的性质,全等三角形的判定与性质,相似三角形的判定与性质,综合性较强,作辅助线构造全等三角形和相似三角形是解题的关键.7(2021·湖南益阳·统考中考真题)如图,Rt△ABC中,∠BAC=90°,tan∠ABC=32,将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB C ,连接BB ,CC ,则△CAC 与△BAB 的面积之比等于.【答案】9:4【分析】先根据正切三角函数的定义可得ACAB=32,再根据旋转的性质可得AB=AB,AC=AC ,∠BAB=∠CAC =α,从而可得ACAC =ABAB=1,然后根据相似三角形的判定可得△CAC ∼△BAB ,最后根据相似三角形的性质即可得.【详解】解:∵在Rt△ABC中,∠BAC=90°,tan∠ABC=32,∴ACAB=32,由旋转的性质得:AB=AB ,AC=AC ,∠BAB =∠CAC =α,∴ACAC=ABAB=1,在△CAC 和△BAB 中,ACAC=ABAB∠CAC =∠BAB,∴△CAC ∼△BAB ,∴S△CACS△BAB=ACAB2=94,即△CAC 与△BAB 的面积之比等于9:4,故答案为:9:4.【点睛】本题考查了正切三角函数、旋转的性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.8(2023秋·山东济南·九年级校考阶段练习)如图,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°.(1)求证:△ACD∽△BCE;(2)若AC=3,AE=8,求AD.【答案】(1)见详解(2)AD=103 3【分析】(1)根据30°的正切值得ACBC=DCEC,即可证明相似.(2)先证明∠BAE=90°,进而求出BE=10,再根据△ACD∽△BCE得出ADBE=ACBC=DCEC=33,即可求出AD=33BE=1033.【详解】(1)∵∠ACB=∠DCE=90°∴∠ACD=∠BCE∵∠ABC=∠CED=∠CAE=30°∴tan∠ABC=ACBC =33,tan∠CED=DCEC=33∴AC BC =DCEC∴△ACD∽△BCE(2)∵由(1),△ACD∽△BCE∴ADBE =ACBC=DCEC=33∵∠ABC=∠CED=∠CAE=30°∴∠BAC=60°∴∠BAE=90°∵AC=3,∠ABC=30°∴AB=2AC=6∵AE=8∴BE=10∴AD=33BE=1033【点睛】本题考查相似三角形的判定、特殊角三角函数值及勾股定理,根据特殊角得出对应线段成比例是解题关键.9(2023·安徽滁州·九年级校考阶段练习)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P、M.求证:(1)△BAE∽△CAD;(2)MP⋅MD=MA⋅ME.【答案】(1)证明见解析(2)证明见解析【分析】(1)由题意可得AC=2AB,AD=2AE,∠BAE=∠CAD=135°,即可证△BAE∽△CAD;(2)由△BAE∽△CAD可得∠BEA=∠CDA,即可证△PME∽△AMD,可得MP⋅MD=MA⋅ME.【详解】(1)证明:∵等腰Rt △ABC 和等腰Rt △ADE ,∴AB =BC ,AE =DE ,∠BAC =∠DAE =45°,∴AC =2AB ,AD =2AE ,∠BAE =∠CAD =135°,∴AC AB =AD AE=2,∴△BAE ∽△CAD ,(2)∵△BAE ∽△CAD ,∴∠BEA =∠CDA ,且∠PME =∠AMD ,∴△PME ∽△AMD ,∴ME MD =MP AM,∴MP ⋅MD =MA ⋅ME .【点睛】本题考查了相似三角形的判定和性质,等腰直角三角形性质,勾股定理的应用,熟练运用相似三角形的判定是本题的关键.10(2023秋·湖北孝感·九年级校联考阶段练习)问题背景:如图1,在△ABC 中,∠ACB =90°,AC =BC ,AD 是BC 边上的中线,E 是AD 上一点,将△CAE 绕点C 逆时针旋转90°得到△CBF ,AD 的延长线交BF 于点P .问题探究:(1)当点P 在线段BF 上时,证明EP +FP =2BP .①先将问题特殊化,如图2,当CE ⊥AD 时,证明:EP +FP =2BP ;②再探究一般情形,如图1,当CE 不垂直AD 时,证明:EP +FP =2BP ;拓展探究:(2)如图3,若AD 的延长线交BF 的延长线于点P 时,直接写出一个等式,表示EP ,FP ,BP 之间的数量关系.【答案】(1)①见解析,②见解析(2)EP -FP =2PB【分析】①结论:PE +PF =2PB .根据旋转的性质△ACE ≌△BCF ,再证明四边形CEPF 是正方形,可得结论.②结论不变,如图2中,过点C 作CG ⊥AD 于点G ,过点C 作CH ⊥BF 交BF 的延长线于点H .证明△CHF ≌△CGE ,可以推出FH =EG ,再利用正方形的性质解决问题即可.(2)结论:EP -FP =2PB ,证明方法类似②.【详解】(1)①证明:∵CE ⊥AD ,∴∠AEC =∠PEC =90°,在△ABC 中,∠ACB =90°,AC =AB ,∵将△CAE 绕点C 逆时针旋转90°得到△CBF ,∴△ACE ≌△BCF ,CF =CE ,∠ECF =90°,∠BFC =∠AEC =90°,∴∠BFC =∠ECF =∠PEC =90°,∴四边形CEPF 是矩形,∵CE =CF ,∴四边形CEPF 是正方形,∴CE =EP =FP =CF ,∠EPF =90°,∴∠BPD =90°=∠CED ,∵AD 是△ABC 中BC 边上的中线,∴BD =CD =12BC ,在△CED 和△BPD 中,∴∠CED =∠BPD∠CDE =∠BDP CD =BD,∴△CED ≌△BPD (AAS ),∴CE =BP ,∴BP =EP =CE =FP ,∴EP +FP =2BP②结论成立,证明:过点C 作CG ⊥AD 于点G ,过点C 作CH ⊥BF 交BF 的延长线于点H .则∠CGE =∠CGD =∠CHF =90°.由旋转性质可知,△CBF≌△CAE,∴CF=CE,∠CFB=∠CEA,∠ACE=∠BCF,∵∠CFH=180°-∠CFB,∠CEG=180°-∠CEA,∴∠CFH=∠CEG,∴△CHF≌△CGE,∴∠FCH=∠ECG,CH=CG,FH=EG.∴∠FCH+∠BCF+∠DCG=∠ECG+∠ACF+∠DCG=90°.∴∠HCG=90°.∴四边形CGPH是正方形.∴CG=GP=PH,∴EP+FP=GP+PH=2CG.∵CD=BD,∠CGD=∠BPD=90°,∠CDG=∠BDP,∴△CDG≌△BDP.∴CG=BP.∴EP+FP=2PB.(2)解:EP-FP=2PB.理由:如下图所示,过C作CN∥BP交AP于点N,CM∥DP交BP的延长线于点M,则四边形CNPM是平行四边形,△BPD∽△BMC,∴CN=PM,CM=PN,BPBM =BDBC=12,∴BM=2BP,∴PM=BP,∵∠APB=90°,∴∠NPM=90°,∴四边形CNPM是矩形,∴∠M=∠CNE=∠CNP=90°,在△CFM和△CEN中,∠H=∠CNE=90°∠CFH=∠CEN CF=CE,∴△CFM≌△CEN(AAS),∴CM=CN,FM=EN,∴四边形CNPM是正方形,∴PM=CN=PN,∴EP-FP=PN+EN-FP=PN+FM-FP=PN +PM=2PM,∴EP-FP=2BP.【点睛】本题属于几何变换综合题,考查相似三角形的判定和性质,等腰直角三角形的性质,全等三角形的判定和性质,正方形的判定和性质等知识,解题关键是正确寻找全等三角形解决问题,属于中考压轴题.11(2022·河南·九年级专题练习)规定:有一角重合,且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”,如图,四边形ABCD和AMPN就是嵌套四边形.(1)问题联想:如图①,嵌套四边形ABCD,AMPN都是正方形,现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',连接BM',DN'交于点O,则BM'与DN'的数量关系为,位置关系为;(2)类比探究:如图②,将(1)中的正方形换成菱形,∠BAD=∠MAN=60,其他条件不变,则(1)中的结论还成立吗?若成立,请说明理由;若不成立,请给出正确的结论,并说明理由;(3)拓展延伸:如图3,将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形,旋转角换成α(90°<α<180°),其他条件不变,请直接写出BM'与DN'的数量关系和位置关系.【答案】(1)BM =DN ,BM ⊥DN ;(2)BM =DN 成立,BM ⊥DN 不成立,BM 与DN 相交,且夹角为60°.理由见解析;(3)BM =2DN ,BM ⊥DN .【分析】(1)根据SAS证明△ABM'≌△AND',进而得到BM =DN ,∠ABM'=∠ADN',再利用三角形内角和可推出∠BOD=90°,即BM ⊥DN ;(2)根据旋转和菱形的性质证明ΔABM ≌ΔADN ,再推出∠BOD=∠BAD=60°,故可求解;(3)根据旋转和矩形的性质证明ΔABM ∼ΔADN ,得到BM =2DN ,再推出∠BOD=∠BAD=90°即可求解.【详解】(1)如图设AB,DN 交于点H,,∵四边形ABCD,AMPN都是正方形,把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',∴AB=AD,AM'=AD', ∠BAM =∠DAN =150°∴△ABM'≌△AND',∴BM =DN ,∠ABM'=∠ADN',∵∠ADN'+∠DHA+∠DAH=180°,∠ABM'+∠BHO+∠BOD=180°,又∠DHA=∠BHO∴∠BOD=∠BAD=90°,即BM ⊥DN 故答案为:BM =DN ,BM ⊥DN ;(2)BM =DN 成立,BM ⊥DN 不成立,BM 与DN 相交,且夹角为60°.理由:设AB,DN 交于点E,由旋转的性质可得∠BAM =∠DAN =150°.∵四边形ABCD,AM P N 都是菱形,∴AB=AD,AM =AN ,∴ΔABM ≌ΔADN ,∴BM =DN ,∠ABM =∠ADN .。
第四章三角形专题二全等三角形-考点1“手拉手”模型(教案)

(五)总结回顾(用时5分钟)
今天的学习,我们了解了“手拉手”模型的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对“手拉手”模型的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解“手拉手”模型的基本概念。“手拉手”模型是指在全等三角形中,通过对应边和对应角的相互关系来判定两个三角形是否全等。它是几何学中非常重要的一个部分,广泛应用于实际问题中。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了如何运用“手拉手”模型解决实际问题,以及它如何帮助我们解决问题。
- “手拉手”模型的定义及特点;
- “手拉手”模型在全等三角形中的应用;
-通过实际案例分析,掌握“手拉手”模型的应用方法;
-练习相关的习题,巩固所学知识。
二、核心素养目标
本节课的核心素养目标主要包括以下方面:
1.培养学生的几何直观与空间想象能力,通过“手拉手”模型的探究,使学生能够直观感知全等三角形之间的关系,提高空间思维能力。
第四章三角形专题二全等三角形-考点1 “手拉手”模型(教案)
一、教学内容
本节课选自教材第四章“三角形”中的专题二“全等三角形-考点1‘手拉手’模型”。教学内容主要包括以下部分:
1.掌握“手拉手”模型的基本概念及性质。
2.理解全等三角形中对应边、对应角的关系。
3.学会运用“手拉手”模型解决实际问题。
具体内容包括:
五、教学反思
在今天的教学中,我发现学生们对“手拉手”模型的概念和应用表现出很大的兴趣。通过引入日常生活中的实例,他们能够更直观地理解全等三角形的相关知识。在理论讲授环节,我注意到有些学生对对应边、对应角的判定方法掌握得还不够扎实,这是需要我在今后的教学中进一步强调和巩固的地方。
专题12 全等三角形中的手拉手模型(解析版)

专题12全等三角形中的手拉手模型【模型1】等腰三角形中的手拉手全等模型如图,△ABC 与△ADE 均为等腰三角形,且∠BAC =∠DAE ,连接BD 、CE ,则△ABD ≌△ACE。
【证明】∠BAC =∠DAECAEBAD ∠=∠∴又△ABC 与△ADE 均为等腰三角形∴在ABD ∆和ACE ∆中⎪⎩⎪⎨⎧=∠=∠=AE AD CAE BAD AC AB ∴△ABD ≌△ACE【模型2】等边三角形中的手拉手全等模型如图,△ABC 与△CDE 均为等边三角形,点B 、C 、E 三点共线,连接AE 、BD ,则△BCD≌△ACE。
【模型3】一般三角形中的手拉手全等模型如图,在任意△ABC 中,以AB 为边作等边△ADB ,以AC 为边作等边△ACE ,连接DC 、BE ,则△ADC ≌△ACE .【模型4】正方形中的手拉手全等模型如图,在任意△ABC中,以AB为边作正方形ABDE,以AC为边作正方形ACFG,连接EC、BG,则△AEC≌△ABG.【例1】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下结论错误的是()A.∠AOB=60°B.AP=BQC.PQ∥AE D.DE=DP【答案】D【分析】利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,得出A正确;根据△CQB≌△CPA (ASA),得出B正确;由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,得出C正确;根据∠CDE=60°,∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,可知∠DQE ≠∠CDE ,得出D 错误.【解析】解:∵等边△ABC 和等边△CDE ,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠BCD =∠DCE +∠BCD ,即∠ACD =∠BCE ,在△ACD 与△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠DAC ,又∵∠ACB =∠DCE =60°,∴∠BCD =60°,即∠ACP =∠BCQ ,又∵AC =BC ,在△CQB 与△CPA 中,ACP BCQ AC BC PAC CBQ ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△CQB ≌△CPA (ASA ),∴CP =CQ ,又∵∠PCQ =60°可知△PCQ 为等边三角形,∴∠PQC =∠DCE =60°,∴PQ ∥AE ,故C 正确,∵△CQB ≌△CPA ,∴AP =BQ ,故B 正确,∵AD =BE ,AP =BQ ,∴AD -AP =BE -BQ ,即DP =QE ,∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,∠CDE =60°,∴∠DQE ≠∠CDE ,故D 错误;∵∠ACB =∠DCE =60°,∴∠BCD =60°,∵等边△DCE ,∠EDC =60°=∠BCD ,∴BC ∥DE ,∴∠CBE =∠DEO ,∴∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°,故A 正确.故选:D .【例2】如图,ABC 是边长为5的等边三角形,BD CD =,120BDC ∠=︒.E 、F 分别在AB 、AC 上,且60EDF ∠=︒,则三角形AEF 的周长为______.【答案】10【分析】延长AB 到N ,使BN =CF ,连接DN ,求出∠FCD =∠EBD =∠NBD =90°,根据SAS 证△NBD ≌△FCD ,推出DN =DF ,∠NDB =∠FDC ,求出∠EDF =∠EDN ,根据SAS 证△EDF ≌△EDN ,推出EF =EN ,易得△AEF 的周长等于AB +AC .【解析】解:延长AB 到N ,使BN =CF ,连接DN,∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,∵BD =CD ,∠BDC =120°,∴∠DBC =∠DCB =30°,∴∠ACD =∠ABD =30°+60°=90°=∠NBD ,∵在△NBD 和△FCD 中,BD DC NBD FCD BN CF =⎧⎪∠=∠⎨⎪=⎩,∴△NBD ≌△FCD (SAS ),∴DN =DF ,∠NDB =∠FDC ,∵∠BDC =120°,∠EDF =60°,∴∠EDB +∠FDC =60°,∴∠EDB +∠BDN =60°,即∠EDF =∠EDN ,在△EDN 和△EDF 中,DE DE EDF EDN DN DF =⎧⎪∠=∠⎨⎪=⎩,∴△EDN ≌△EDF (SAS ),∴EF =EN =BE +BN =BE +CF ,即BE +CF =EF .∵△ABC 是边长为5的等边三角形,∴AB =AC =5,∵BE +CF =EF ,∴△AEF 的周长为:AE +EF +AF =AE +EB +FC +AF =AB +AC =10,故答案为:10.【例3】如图1,B 、C 、D 三点在一条直线上,AD 与BE 交于点O ,△ABC 和△ECD 是等边三角形.(1)求证:△ACD ≌△BCE ;(2)求∠BOD 的度数;(3)如图2,若B 、C 、D 三点不在一条直线上,∠BOD 的度数是否发生改变?(填“改变”或“不改变”)【答案】(1)证明见解析(2)∠BOD =120°(3)不改变,理由见解析【分析】(1)根据“SAS ”证明△ACD ≌△BCE 即可;(2)由全等三角形的性质得∠ADC =∠BEC ,再由三角形的外角性质得∠AOB =60°,即可求解;(3)同(1)得:△ACD ≌△BCE ,得出∠DAC =∠EBC ,根据三角形外角求出∠AOE =120°,即可得出答案.【解析】(1)证明:∵△ABC 和△ECD 是等边三角形,∴∠ACB =∠ECD =60°,BC =AC ,EC =CD ,∴∠ACB +∠ACE =∠ECD +∠ACE ,∴∠BCE =∠ACD ,在△BCE 和△ACD 中∵BC AC BCE ACD CE CD =⎧⎪∠=∠⎨⎪=⎩,∴△BCE ≌△ACD (SAS ).(2)解:∵△BCE ≌△ACD ,∴∠ADC =∠BEC ,∵∠AOB =∠EBC +∠ADC ,∴∠AOB =∠EBC +∠BEC =∠DCE =60°,∵∠AOB +∠BOD =180°,∴∠BOD =120°.(3)解:不改变,理由如下:同(1)得:△ACD ≌△BCE (SAS ),∴∠DAC =∠EBC ,∵∠AOE =∠ABO +∠OAB=∠ABO +∠DAC +∠BAC=∠ABO +∠EBC +∠BAC=∠ABC +∠BAC=120°∴∠BOD =∠AOE =120°,即∠BOD 的度数不改变.故答案为:不改变.一、单选题1.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中,正确的结论有()①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S四边形BCDE =12BD•CE;⑤BC2+DE2=BE2+CD2.A.1个B.2个C.3个D.4个【答案】C【分析】根据等腰直角三角形的性质可得AB=AC,AD=AE,然后求出∠BAD=∠CAE,再利用“边角边”证明△ABD和△ACE全等,根据全等三角形对应边相等可得CE=BD,判断①正确;根据全等三角形对应角相等可得∠ABD=∠ACE,从而求出∠BCG+∠CBG=∠ACB+∠ABC=90°,再求出∠BGC=90°,从而得到BD⊥CE,根据四边形的面积等于两个三角形的面积之和可判断出④正确;根据勾股定理表示出BC2+DE2,BE2+CD2,得到⑤正确;再求出AE CD∥时,∠ADC=90°,判断出②错误;∠AEC与∠BAE 不一定相等判断出③错误.【解析】解:∵,△ABC和△ADE都是等腰直角三角形,∴AB=AC,AD=AE,∵∠BAD=∠BAC+∠CAD=90°+∠CAD,∠CAE=∠DAE+∠CAD=90°+∠CAD,∴∠BAD=∠CAE,∴△ABD≌△ACE(SAS),∴CE=BD,∠ABD=∠ACE,故①正确;∴∠BCG+∠CBG=∠ACB+∠ABC=90°,在△BCG中,∠BGC=180°-(∠BCG+∠CBG)=180°-90°=90°,∴BD⊥CE,∴S四边形BCDE =11··22BCE DCES S CE BG CE DG+=+=12BD•CE,故④正确;由勾股定理,在Rt△BCG中,BC2=BG2+CG2,在Rt△DEG中,DE2=DG2+EG2,∴BC2+DE2=BG2+CG2+DG2+EG2,在Rt△BGE中,BE2=BG2+EG2,在Rt△CDG中,CD2=CG2+DG2,∴BE 2+CD 2=BG 2+CG 2+DG 2+EG 2,∴BC 2+DE 2=BE 2+CD 2,故⑤正确;从题干信息没有给出,AC AD =所以只有AE CD ∥时,DAE ADC ∠=∠=90°,无法说明AE CD ∥,更不能说明,CD AD =故②错误;∵△ABD ≌△ACE ,∴∠ADB =∠AEC ,条件不足以证明,CAE BAE ≌∴∠AEC 与∠AEB 相等无法证明,∴∠ADB =∠AEB 不一定成立,故③错误;综上所述,正确的结论有①④⑤共3个.故选:C .2.如图,正ABC 和正CDE △中,B 、C 、D 共线,且3BC CD =,连接AD 和BE 相交于点F ,以下结论中正确的有()个①60AFB ∠=︒②连接FC ,则CF 平分BFD ∠③3BF DF =④BF AF FC=+A .4B .3C .2D .1【答案】A【分析】根据“手拉手”模型证明BCE ACD ≌,从而得到CBE CAD ∠=∠,再结合三角形的外角性质即可求解60AFB ACB ∠=∠=︒,即可证明①;作CM BE ⊥于M 点,CN AD ⊥于N 点,证明CEM CDN ≌,结合角平分线的判定定理即可证明②;利用面积法表示BCF △和DCF 的面积,然后利用比值即可证明③;利用“截长补短”的思想,在AD 上取点Q ,使得FC FQ =,首先判断出FCQ 为等边三角形,再结合“手拉手”模型推出BCF ACQ ≌即可证明④.【解析】解:①∵ABC 和CDE △均为等边三角形,∴60ACB ECD ∠=∠=︒,AC BC =,EC DC =,∴ACB ACE ECD ACE ∠+∠=∠+∠,∴BCE ACD ∠=∠,在BCE 和ACD △中,BC AC BCE ACD EC DC =⎧⎪∠=∠⎨⎪=⎩∴()BCE ACD SAS ≌,∴CBE CAD ∠=∠,∵AFB CBE CDA ∠=∠+∠,ACB CDA CAD ∠=∠+∠,∴60AFB ACB ∠=∠=︒,故①正确;②如图所示,作CM BE ⊥于M 点,CN AD ⊥于N 点,则90CME CND ∠=∠=︒,∵BCE ACD ≌,∴CEM CDN ∠=∠,在CEM 和CDN △中,CME CND CEM CDN CE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CEM CDN AAS ≌,∴CM CN =,∴CF 平分BFD ∠,故②正确;③如图所示,作FP BD ⊥于P 点,∵1122BCF SBF CM BC FP ==,1122DCF S DF CN CD FP ==,∴11221122BCFDCF BF CM BC FP SS DF CN CD FP ==,∵CM CN =,∴整理得:BF BC DF CD =,∵3BC CD =,∴33BF CD DF CD==,∴3BF DF =,故③正确;④如图所示,在AD 上取点Q ,使得FC FQ =,∵60AFB ACB ∠=∠=︒,CF 平分BFD ∠,∴120BFD ∠=︒,1602CFD BFD ∠=∠=︒,∴FCQ 为等边三角形,∴60FCQ ∠=︒,CF CQ =,∵60ACB ∠=︒,∴ACB ACF FCQ ACF ∠+∠=∠+∠,∴BCF ACQ ∠=∠,在BCF △和ACQ 中,BC AC BCF ACQ CF CQ =⎧⎪∠=∠⎨⎪=⎩∴()BCF ACQ SAS ≌,∴BF AQ =,∵AQ AF FQ =+,FQ FC =,∴BF AF FC =+,故④正确;综上,①②③④均正确;故选:A.3.如图,在直线AC 的同一侧作两个等边三角形△ABD 和△BCE ,连接AE 与CD 交于点H ,AE 与DB 交于点G ,BE 与CD 交于点F ,下列结论:①AE =CD ;②∠AHD =60°;③△AGB ≌△DFB ;④BH 平分∠GBF ;⑤GF ∥AC ;⑥点H 是线段DC 的中点.正确的有()A .6个B .5个C .4个D .3个【答案】C 【分析】连接GF ,过点B 作BM ⊥AE 于M ,BN ⊥CD 于N ;结合题意,利用等边三角形、全等三角形的性质,推导得AE =CD ,∠AHD =∠ABG =60°;再根据等边三角形、角平分线的性质分析,即可得到答案.【解析】连接GF ,过点B 作BM ⊥AE 于M ,BN ⊥CD 于N∵△ABD ,△BCE 都是等边三角形,∴∠ABD =∠EBC =60°,BA =BE ,BE =BC ,∴∠ABE =∠DBC ,在△ABE 和△DBC 中,BA BD ABE DBC BE BC =⎧⎪∠∠⎨⎪=⎩=∴△ABE ≌△DBC (SAS ),∴AE =CD ,故①正确;∵△ABE ≌△DBC ,∴∠BAE =∠BDC ,∵∠AGB =∠DGH ,∴∠AHD =∠ABG =60°,故②正确;在△AGB 和△DFB 中,60BAG BDF AB DB ABG DBF ∠=∠⎧⎪=⎨⎪∠∠︒⎩==∴△AGB ≌△DFB (ASA ),故③正确;∵△AGB ≌△DFB ,∴BG =BF ,∵∠GBF =60°,∴△BGF 是等边三角形,∴∠FGB =∠ABD =60°,∴FG ∥AC ,故⑤正确;∵△ABE ≌△DBC ,BM ⊥AE ,BN ⊥CD ,∴BM=BN,∴BH平分∠AHC,但不一定平分∠GBF,故④错误;根据题意,无法判断DH=CH,故⑥错误.故选:C.4.如图,点C是线段AE上一动点(不与A,E重合),在AE同侧分别作等边三角形ABC 和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,有以下5个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中一定成立的结论有()个A.1B.2C.3D.4【答案】D【分析】①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;③由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ(ASA),所以AP=BQ;故③正确;②根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.【解析】①∵等边△ABC和等边△DCE,∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60∘,∴∠ACD=∠BCE,在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,DC=CE,∴△ACD≌△BCE(SAS),∴AD=BE;故①正确;③∵△ACD≌△BCE(已证),∴∠CAD=∠CBE,∵∠ACB=∠ECD=60°(已证),∴∠BCQ=180°-60°×2=60°,∴∠ACB=∠BCQ=60°,在△ACP与△BCQ中,∠CAD=∠CBE,AC=BC,∠ACB=∠BCQ=60°,∴△ACP≌△BCQ(ASA),∴AP=BQ;故③正确;②∵△ACP≌△BCQ,∴PC=QC,∴△PCQ是等边三角形,∴∠CPQ=60∘,∴∠ACB=∠CPQ,∴PQ∥AE;故②正确;④∵AD=BE,AP=BQ,∴AD−AP=BE−BQ,即DP=QE,∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,∴∠DQE≠∠CDE,∴DE≠QE,则DP≠DE,故④错误;⑤∵∠ACB=∠DCE=60°,∴∠BCD=60°,∵等边△DCE,∠EDC=60°=∠BCD,∴BC∥DE,∴∠CBE=∠DEO,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.故⑤正确;综上所述,正确的结论有:①②③⑤,错误的结论只有④,故选D.5.如图,在ABC 中,AB AC =,点D 、F 是射线BC 上两点,且AD AF ⊥,若AE AD =,15BAD CAF ∠=∠=︒;则下列结论中正确的有()①CE BF ⊥;②ABD ACE △≌△;③ABC ADCE S S =四边形△;④122BC EF AD CF -=-A .1个B .2个C .3个D .4个【答案】D 【分析】由AD ⊥AF ,∠BAD=∠CAF ,得出∠BAC=90°,由等腰直角三角形的性质得出∠B=∠ACB=45°,由SAS 证得△ABD ≌△ACE (SAS ),得出BD=CE ,∠B=∠ACE=45°,S △ABC =S 四边形ADCE ,则∠ECB=90°,即EC ⊥BF ,易证∠ADF=60°,∠F=30°,由含30°直角三角形的性质得出EF=2CE=2BD ,DF=2AD ,则BD=12EF ,由BC-BD=DF-CF ,得出BC-12EF=2AD-CF ,即可得出结果.【解析】∵AD ⊥AF ,∠BAD=∠CAF ,∴∠BAC=90°,∵AB=AC ,∴∠B=∠ACB=45°,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩,∴△ABD ≌△ACE (SAS ),∴BD=CE ,∠B=∠ACE=45°,S △ABC =S 四边形ADCE ,∴∠ECB=90°,∴EC ⊥BF ,∵∠B=45°,∠BAD=15°,∴∠ADF=60°,∴∠F=30°,∴EF=2CE=2BD ,DF=2AD ,∴BD=12EF ,∵BC-BD=DF-CF ,∴BC-12EF=2AD-CF,∴①、②、③、④正确.故选:D.6.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM,下列结论:①△AOC≌△BOD;②AC=BD;③∠AMB=40°;④MO平分∠BMC.其中正确的个数为()A.4B.3C.2D.1【答案】A【分析】由题意易得∠AOC=∠BOD,然后根据三角形全等的性质及角平分线的判定定理可进行求解.【解析】解:∵∠AOB=∠COD=40°,∠AOD是公共角,∴∠COD+∠AOD=∠BOA+∠AOD,即∠AOC=∠BOD,∵OA=OB,OC=OD,∴△AOC≌△BOD(SAS),∴AC=BD,∠OAC=∠OBD,∠ODB=∠OCA,故①②正确;过点O作OE⊥AC于点E,OF⊥BD于点F,BD与OA相交于点H,如图所示:∵∠AHM=∠OHB,∠AMB=180°-∠AHM-∠OAC,∠BOA=180°-∠OHB-∠OBD,∴∠AMB=∠BOA=40°,∴∠OEC=∠OFD=90°,∵OC=OD,∠OCA=∠ODB,∴△OEC≌△OFD(AAS),∴OE=OF,∴OM平分∠BMC,故③④正确;所以正确的个数有4个;故选A .二、填空题7.如图,在正方形ABCD 中,E 是对角线BD 上一点()BE DE <,将线段CE 绕点C 按顺时针方向旋转90︒得到线段CE ',连接AE ,DE ',EE '.下列结论:①若20BAE ∠=︒,则70DE E ∠='︒;②2222BE DE AE +=;③若30BAE ∠=︒,则DE;④若BC =,10EC =,则9sin 10DEC ∠=.其中正确的结论有___________(填正确的序号)【答案】①②④【分析】证明△BCE ≌△E CD ',可得AE CE =,BE DE '=,==45CDE EBC '∠∠,根据三角形内角和定理可判断①正确;在Rt △E CE '中,2222=2E E CE CE CE ''+=,即2222BE DE AE +=,从而判断②正确;③证明DE ',故可判断③错误;连接AC 与BD 交于点O ,计算可得CO =9,根据正弦定理可判断④正确.【解析】解:∵四边形ABCD 是正方形,∴BC =CD ,∠BCD =90°,∵线段CE 绕点C 按顺时针方向旋转90︒得到线段CE ',∴CE CE '=,=90ECE '∠,∴△ECE '是等腰直角三角形,∴==45EE C E EC ''∠∠,∴=BCD ECD ECE ECD '--∠∠∠∠,即=BCE E CD '∠∠,在△BCE 和△E CD '中,=BC CD BCE E CD CE CE =⎧'∠'⎪∠⎨⎪=⎩∴△BCE ≌△DCE '(SAS ),∴==45CDE EBC '∠∠,=BE E D ',∴=454590EDE '+=∠,即△EDE '是直角三角形,∵四边形ABCD 是正方形,E 在对角线BD 上,∴=BCE BAE ∠∠,∴=DEC DEE E EC EBC BCE ''+=+∠∠∠∠∠,==45E EC EBC '∠∠,∴DEE BCE BAE '==∠∠∠,∵=20BAE ∠,∴9070DE E DEE ''==∠-∠,故①正确;在Rt △E CE '中,2222=2E E CE CE CE ''+=,在Rt △E DE '中,22222=E E DE DE BE DE ''+=+,∴2222BE DE AE +=,故②正确;若=30BAE ∠,则=30DEE BCE BAE '==∠∠∠,在在Rt △E DE '中,DE ',∵BE DE '=,DE ,故③错误;连接AC 与BD 交于点O ,如图,∵四边形ABCD 是正方形,∴∠EOC =90°,且BOC 是等腰直角三角形,∵BC =∴CO =22922BC ⨯==,∵10EC =,∴sin ∠DEC =9=10CO BC ,故④正确.故答案为:①②④.8.如图,O 是正ABC 内一点,3,4,5OA OB OC ===,将线段BO 以点B 为旋转中心逆时针旋转60︒得到线段BO ',下列结论:①点O 与O '的距离为4;②150AOB ∠=︒;③6ABC AOC S S -=;④64AOC AOB S S +=+△△其中正确的结论是____________.(只填序号)【答案】①②④【分析】由题意可得△BOC ≌△BAO ',△BOO '是等边三角形,可得AO '=CO =5,OO '=4,可判断△AOO '是直角三角形.可判断①②③,由S 四边形AOBO ′=S △AOO '+S △OO 'B =S △BOC +S △AOC ,可判定③④.【解析】解;连接OO ',如图1,BO BO '=,60OBO '∠=︒,BOO '∴∆是等边三角形,4OO BO '∴==,故①正确;60OBO ABC '∠=∠=︒,ABO ABC '∴∠=∠且OB OB '=,AB AC =,()ABO BOC SAS '∴∆≅∆,5AO CO '∴==,225O A '=,2225AO O O '+=,222O A AO O O ''∴=+,90AOO '∴∠=︒,150AOB ∴∠=︒,故②正确;△OO B '是等边三角形,3AO =,4OO '=,3BOO S '∆∴=,6AOO S '∆=,=+=643ABC AOC ABC ABO AOBO S S S S S '∴-=+四边形如图2,AOC ∆绕A 点顺时针旋转60︒到ABO '∆位置,同理可得9364AOC AOB S S ∆∆+=+,故④正确;故答案为:①②④.9.在ABC 中,90ACB ∠=︒,60B ∠=︒,4AB =,点D 是直线BC 上一动点,连接AD ,在直线AD 的右恻作等边ADE ,连接CE ,当线段CE 的长度最小时,则线段CD 的长度为__________.【答案】3【分析】以AC 为边向左作等边三角形ACF ,连接DF ,先根据直角三角形中30°所对的直角边是斜边的一半求出BC 的长,再由勾股定理求出AC 的长,根据作的辅助线证明()ACE AFD SAS ≅,则CE DF =,当DF BC ⊥时,DF 的长是最小的,即CE 的长最小,求出此时CD '的长即可.【解析】解:如图,以AC 为边向左作等边三角形ACF ,连接DF ,∵90ACB ∠=︒,60B ∠=︒,∴30BAC ∠=︒,∵4AB =,∴122BC AB ==,∴2223AC AB BC =-=∵ACF 是等边三角形,∴CF AC AF ===60FAC ∠=︒,∵ADE 是等边三角形,∴AD AE =,60DAE ∠=︒,∵FAC DAC DAE DAC ∠-∠=∠-∠,∴CAE FAD ∠=∠,在ACE 和AFD V 中,AC AF CAE FAD AE AD =⎧⎪∠=∠⎨⎪=⎩,∴()ACE AFD SAS ≅,∴CE DF =,当DF BC ⊥时,DF 的长是最小的,即CE 的长最小,∵906030FCD '∠=︒-︒=︒,Rt CFD ',∴12D F CF '==3CD '==,∴当线段CE 的长度最小时,则线段CD 的长度为3.故答案是:3.10.如图,在ABC 中,45ABC ︒∠=,3AB =,AD BC ⊥于点D ,BE AC ⊥于点F .1AE =,连接DE ,将AED 沿直线AE 翻折至ABC 所在的平面,得AEF ,连接DF .过点D 作DG DE ⊥交BE 于点G ,则四边形DFEG 的周长为________.【答案】2+【分析】先证BDG DE ∆≅∆,得出1AE BG ==,再证DGE ∆与EDF ∆是等腰直角三角形,在直角AEB ∆中利用勾股定理求出BE 的长,进一步求出GE 的长,可通过解直角三角形分别求出GD ,DE ,EF ,DF 的长,即可求出四边形DFEG 的周长.【解析】∵45ABC ︒∠=,AD BC ⊥于点D ,∴9045BAD ABC ︒︒∠=-∠=,∴ABD ∆是等腰直角三角形,∴AD BD =,∵BE AC ⊥,∴90GBD C ︒∠+∠=,∵90EAD C ︒∠+∠=,∴GBD EAD ∠=∠,∵90ADB EDG ︒∠=∠=,∴ADB ADG EDG ADG ∠-∠=∠-∠,即BDG ADE ∠=∠,∴()BDG ADE ASA ∆≅∆,∴1BG AE ==,DG DE =,∵90EDG ︒∠=,∴EDG ∆为等腰直角三角形,∴9045135AED AEB DEG ︒︒︒∠=∠+∠=+=,∵AED ∆沿直线AE 翻折得AEF ∆,∴AED AEF ∆≅∆,∴135AED AEF ︒∠=∠=,ED EF =,∴36090DEF AED AEF ︒︒∠=-∠-∠=,∴DEF ∆为等腰直角三角形,∴EF DE DG ==,在Rt AEB ∆中,BE ===∴1GE BE BG =-=,在Rt DGE ∆中,22222DG GE ==,∴222EF DE ==-,在Rt DEF ∆中,1DF ==-,∴四边形DFEG 的周长为:GD EF GE DF+++221)2⎛=-+ ⎝⎭2=+,故答案为:2+.11.如图ABD △和ACE 是ABC 外两个等腰直角三角形,90BAD CAE ∠∠==,下列说法正确的是:________.①CD BE =,且DC BE ⊥;②22222DE BC BD EC +=+;③FA 平分DFE ∠;④取BC 的中点M ,连MA ,则MA DE ⊥.【答案】①③④【分析】①由ABD △与ACE 是等腰直角三角形,AD AB =,AC AE =,DAB EAC ∠=∠可证(SAS)ADC ABE △≌△,CD BE =,AEB ACD ∠=∠且ARE FRC ∠∠=,90EAR ∠=︒AER ARE FCR FRC ∠∠∠∠+=+,即可退出;②由DC BE ⊥,由勾股定理222DF EF DE +=,222+=BF CF BC ,()()22222222=DE BC DF BF CF EF BD EC ++++=+,即可;③过点A 作AS DC ⊥,AG BE ⊥,可证(AAS)ADS ABG ≌,由性质得AS AG =,结合AS DC ⊥,AG BE ⊥,即可;④取BC 中点M ,使得AM MN =,易证(SAS)BMN CMA ≌,推出BN AC =,再证(SAS)DAE ABN ≌,推出BAN ADH ∠∠=,由90DAH BAN ∠∠+=︒,推出90DAH ADH ∠+∠=︒即可.【解析】ABD 与ACE 是等腰直角三角形,AD AB ∴=,AC AE =,DAB EAC ∠=∠,DAC EAB ∴∠=∠,∴在ADC 与ABE △中,AD AB DAC EAB AC AE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADC ABE ∴≌,CD BE ∴=,设BE 交AC 于点R ,由①可知AEB ACD ∠=∠且ARE FRC ∠∠=,AER ARE FCR FRC ∠∠∠∠∴+=+,90EFC EAR ∠∠∴==︒,即DC BE ⊥,故①符合题意.②DC BE ⊥,222DF EF DE ∴+=,222+=BF CF BC ,222222DF EF BF CF DE BC ∴+++=+,且222DF BF BD +=,222CF EF CE +=,2222DE BC BD CE ∴+=+.故②不符合题意.③证明,过点A 作AS DC ⊥,AG BE ⊥,由①可知ADS ABG ∠∠=,且AD AB =,ASD AGB ∠∠=,∴在ADS △与ABG 中,ADS ABG ASD AGB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)ADS ABG ∴≌,AS AG ∴=,且AS DC ⊥,AG BE ⊥,FA ∴平分DFE ∠,故③符合题意.④作BC 中点M ,倍长AM ,使得AM MN =,∴在BMN △与CMA 中,BM MC BMN CMA MN AM =⎧⎪∠=∠⎨⎪=⎩,(SAS)BMN CMA ∴≌,则BN AC =,AC AE =,BN AE ∴=,180BAC DAE ∠∠︒+=,180BAC ABN ∠∠+=︒,DAE ABN ∠∠∴=,∴在DAE △与ABN 中,AD AB DAE ABN AE BN =⎧⎪∠=∠⎨⎪=⎩,(SAS)DAE ABN ∴≌,BAN ADH ∠∠∴=,90DAH BAN ∠∠︒+=,90DAH ADH ∠∠∴+=︒,∠90AHD ∴=︒,即AM DE ⊥,故④符合题意.故答案为:①③④.12.(1)如图(1),在四边形ABCD 中,AB AD =,180B D ︒∠+∠=,E ,F 分别是,BC CD 上的动点,且12EAF BAD ∠=∠,求证:EF BE DF =+.(2)如图(2),在(1)的条件下,当点E ,F 分别运动到,BC CD 的延长线上时,,,EF BE DF 之间的数量关系是______.【答案】(1)详见解析;(2)EF BE DF=-【分析】(1)延长FD 到点G ,使DG BE =,连接AG ,先证明()ABE ADG SAS ∆∆≌,得到AE AG BAE DAG =∠=∠,,然后证明AEF AGF ∆∆≌,得到EF FG =,根据FG DG DF BE DF =+=+,可得EF BE DF =+;(2)在BC 上截取BG DF =,连接AG ,先证明△ABG ≌△ADF (SAS ),得到AG=AF ,∠BAG=∠DAF ,再证明△EAG ≌△EAF (SAS ),得到EG=EF ,根据BG=DF ,即可得EF=BE-BG=BE-DF .【解析】(1)如图,延长FD 到点G ,使DG BE =,连接AG.180B ADF ADG ADF ︒∠+∠=∠+∠=,B ADG ∴∠=∠,又AB AD =,BE DG =,∴()ABE ADG SAS ∆∆≌,,AE AG BAE DAG ∴=∠=∠,12EAF BAD ∠=∠,GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠.,,AE AG EAF GAF AF AF =∠=∠=,∴AEF AGF ∆∆≌,EF FG ∴=.FG DG DF BE DF =+=+,EF BE DF ∴=+;(2)EF BE DF =-.如图,在BC 上截取BG DF =,连接AG,180B ADC ADC ADF ︒∠+∠=∠+∠=,B ADF ∴∠=∠,在△ABG 和△ADF 中AB AD B ADF BG DF ⎧⎩=⎪==⎪⎨∠∠,∴△ABG ≌△ADF (SAS ),∴AG=AF ,∠BAG=∠DAF ,∠BAD=2∠EAF ,∴∠BAG+∠GAE+∠EAD=∠EAD+∠DAF+∠EAD+∠DAF ,∴∠GAE=∠EAF ,在△EAG 和△EAF 中AG AF EAG EAF AE AE ===⎧⎪⎨⎪⎩∠∠,∴△EAG ≌△EAF (SAS ),∴EG=EF ,∵BG=DF ,∴EF=BE-BG=BE-DF .三、解答题13.如图,若ABD △和ACE 都是等边三角形,求BOC ∠的度数.【答案】120°.【分析】利用等边三角形的性质可得AD =AB ,AC =AE ,∠DAB =∠CAE =60°,利用SAS 即可证明△DAC ≌△BAE ,从而得出∠ABE =∠ADC ,设AB 与CD 交于点F ,根据三角形内角和定理和等量代换即可求出∠BOF ,利用平角的定义即可求出结论.【解析】证明:∵△ABD 、△AEC 都是等边三角形,∴AD =AB ,AC =AE ,∠DAB =∠CAE =60°,∵∠DAC =∠BAC +60°,∠BAE =∠BAC +60°,∴∠DAC =∠BAE ,在△DAC 和△BAE 中,AD AB DAC BAE AC AE ⎧⎪∠∠⎨⎪⎩===,∴△DAC ≌△BAE (SAS ),∴∠ABE =∠ADC设AB 与CD 交于点F ,∵∠BFO=∠DFA∴∠BOF=180°-∠ABE -∠BFO=180°-∠ADC -∠DFA=∠DAB=60°∴∠BOC=180°-∠BOF=120°.14.如图,ACB △和ECD 都是等腰直角三角形,,,CA CB CD CE ACB ==△的顶点A 在ECD 的斜边DE 上,连接BD.(1)求证:BD AE =.(2)若3cm,6cm AE AD ==,求AC 的长.【答案】(1)证明见解析;(2)310cm 2AC =.【分析】(1)根据同角的余角相等得出∠BCD=∠ACE ,然后根据SAS 定理证明△BCD ≌△ACE ,从而得出结论;(2)根据全等三角形的性质得出∠BDC=∠AEC ,然后结合等腰直角三角形的性质求得∠BDA 是直角三角形,从而利用勾股定理求解.【解析】(1)∵ACB △和ECD 都是等腰直角三角形,∴90ACB ECD ∠=∠=︒,∴90,90ACD BCD ACD ACE ∠+∠=︒∠+∠=︒,∴BCD ACE ∠=∠,在BCD △和ACB △中,CB CA BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩∴()BCD ACE SAS V V ≌,∴BD AE =.(2)∵BCD ACE ≌,∴BDC AEC ∠=∠,又∵ECD 是等腰直角三角形,∴45CDE CED ∠=∠=︒,∴45BDC ∠=︒,∴90BDC CDE ∠+∠=︒,∴BDA ∠是直角三角形,∴22222223645AB BD AD AE AD =+=+=+=,在等腰直角三角形ACB 中,22222AB AC BC AC =+=,∴2AC =.15.如图,△ACB 和△DCE 均为等腰三角形,∠ACB=∠DCE=90°,点A ,D ,E 在同一条直线上,连接BE .(1)求证:AD=BE ;(2)若∠CAE=15°,AD=4,求AB的长.【答案】(1)见解析;(2)8【分析】(1)直接证明≌ACD BCE V V ,即可得出结论;(2)由(1)可进一步推出AEB △为直角三角形,且30EAB ∠=︒,从而由2AB BE =求解即可.【解析】(1)△ACB 和△DCE 均为等腰三角形,∠ACB=∠DCE=90°,ADC BCE ∴∠=∠,在ACD △与BCE 中,AC BC ACD BCE DC EC =⎧⎪∠=∠⎨⎪=⎩()ACD BCE SAS ∴≌,AD BE ∴=;(2)ABC 是等腰直角三角形,45ABC ∴∠=︒,由(1)可知,15CAE CBE ∠=∠=︒,4BE AD ==,451560ABE ABC CBE ∴∠=∠+∠=︒+︒=︒,90ABE ACB ∴∠=∠=︒,则在Rt AEB 中,30EAB ∠=︒,28AB BE ∴==.16.如图,在△ABC 中,AB =BC ,∠ABC =120°,点D 在边AC 上,且线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,点F 是ED 与AB 的交点.(1)求证:AE =CD ;(2)若∠DBC =45°,求∠BFE 的度数.【答案】(1)证明见解析;(2)∠BFE =105°.【分析】(1)根据旋转的性质证明△ABE ≌△CBD (SAS ),进而得证;(2)由(1)得出∠DBC=∠ABE=45°,BD=BE ,∠EBD=120°,最后根据三角形内角和定理进行求解即可.【解析】(1)证明:∵线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,∴BD =BE ,∠EBD =120°,∵AB =BC ,∠ABC =120°,∴∠ABD+∠DBC =∠ABD+∠ABE =120°,∴∠DBC =∠ABE ,∴△ABE ≌△CBD (SAS ),∴AE =CD ;(2)解:由(1)知∠DBC =∠ABE =45°,BD =BE ,∠EBD =120°,∴∠BED =∠BDE =12(180°﹣120°)=30°,∴∠BFE =180°﹣∠BED ﹣∠ABE=180°﹣30°﹣45°=105°.17.ABC 和ADE 如图所示,其中,,ABC ACB ADE AED BAC DAE ∠=∠∠=∠∠=∠.(1)如图①,连接BE CD 、,求证:BE CD =;(2)如图②,连接BE CD BD 、、,若60BAC DAE ∠=∠=︒,CD AE ⊥,3AD =,5CD =,求BD 的长.【答案】(1)见解析;34【分析】(1)只需证ABE ACD ∆∆≌,即可得到结论;(2)先证明BED ∆是直角三角形,再用勾股定理求BD .【解析】(1)证明:ABC ACB ∠=∠,ADE AED ∠=∠,AB AC ∴=,AE AD =,,BAC DAE ∠=∠,BAE CAD ∴∠=∠,()ABE ACD SAS ∴∆∆≌,BE CD ∴=.(2)解:ADE AED ∠=∠,AE AD ∴=,60DAE ∠=︒,DAE ∴∆是等边三角形,3AD ED ∴==,60AED ADE ∠=∠=︒,CD AE ⊥,160302ADC ∴∠=⨯︒=︒,由(1)知:ABE ACD ∆∆≌,5BE CD ∴==,30AEB ADC ∠=∠=︒,90BED ∴∠=︒,2234BD BE ED ∴+18.问题:如图1,在等边三角形ABC 内,点P 到顶点A 、B 、C 的距离分别是3,4,5,求∠APB 的度数?探究:由于PA 、PB 、PC 不在同一个三角形中,为了解决本题,我们可以将△ABP 绕点A 逆时针旋转60°到△ACP ′处,连结P P ′,这样就将三条线段转化到一个三角形中,从而利用全等的知识,求出∠APB 的度数.请你写出解答过程:应用:请你利用上面的方法解答:如图2,△ABC 中,∠CAB =90°,AB =AC ,E 、F 为BC 上的点,且∠EAF =45°,求证:222BE FC EF +=【答案】探究:∠APB =150°,应用:见解析【分析】探究:运用旋转的性质,以及全等三角形的性质得对应角相等,对应边相等,得出∠PAP ′=60°,再利用等边三角形的判定得出△APP ′为等边三角形,即可得出∠APP ′的度数,即可得出答案;应用:利用已知首先得出△AEG ≌△AFE ,即可把EF ,BE ,FC 放到一个直角三角形中,从而根据勾股定理即可证明.【解析】探究:解:将△ABP 绕顶点A 旋转到△ACP ′处,∴△BAP ≌△CAP ′,∴AB =AC ,AP =AP ′,∠BAP =∠CAP ′,∴∠BAC =∠PAP ′=60°,∴△APP ′是等边三角形,∴∠APP ′=60°,因为BPP ′不一定在一条直线上,∴P ′C =PB =4,PP ′=PA =3,P ′C =PC =5,∴∠PP ′C =90°,∴△PP ′C 是直角三角形,∴∠APB =∠AP ′C =∠APP ′+∠P ′PC =60°+90°=150°,∴∠BPA =150°;应用:证明:把△ACF 绕点A 顺时针旋转90°,得到△ABG .连接EG .则△ACF ≌△ABG .∴AG =AF ,BG =CF ,∠ABG =∠ACF =45°.∵∠BAC =90°,∠GAF =90°.∴∠GAE =∠EAF =45°,在△AEG 和△AFE 中,AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△AEG ≌△AFE (SAS ).∴EF =EG ,又∵∠GBE =90°,∴BE 2+BG 2=EG 2,即BE 2+CF 2=EF 2.19.【探究发现】(1)如图1,在四边形ABCD 中,对角线AC BD ⊥,垂足是O ,求证:2222AB CD AD BC +=+.【拓展迁移】(2)如图2.以三角形ABC 的边AB 、AC 为边向外作正方形ABDE 和正方形ACFG ,求证:CE BG ⊥.(3)如图3,在(2)小题条件不变的情况下,连接GE ,若90EGA ∠=︒,6GE =,8AG =,则BC 的长_____________.(直接填写答案)【答案】(1)见解析;(2)见解析;(3)【分析】(1)根据AC BD ⊥,利用勾股定理分别求出22AB CD +和22AD BC +即可证明结论;(2)利用正方形的性质证明△CAE ≌△GAB (SAS ),可得∠CEA =∠GBA ,根据∠GBA +∠ANB =90°等量代换求出∠EMN =90°即可;(3)利用勾股定理分别求出AE 、CG 和BE ,然后利用(1)中结论求出BC 即可.【解析】解:(1)∵AC BD ⊥,∴∠AOD =∠AOB =∠COD =∠BOC =90°,由勾股定理得:222222AB CD OA OB OD OC +=+++,222222AD BC OA OD OB OC +=+++,∴2222AB CD AD BC +=+;(2)∵在正方形ABDE 和正方形ACFG 中,AC =AG ,AE =AB ,∠CAG =∠EAB =90°,∴∠CAG +∠GAE =∠EAB +∠GAE ,即∠CAE =∠GAB ,∴△CAE ≌△GAB (SAS ),∴∠CEA =∠GBA ,∵∠GBA +∠ANB =90°,∠ANB =∠MNE ,∴∠CEA +∠MNE =90°,∴∠EMN =90°,∴CE BG ⊥;(3)如图3,连接CG ,BE ,∵90EGA ∠=︒,6GE =,8AG =,∴AC =8,AE 10=,∴AB =10,∴CG =BE =,∵CE BG ⊥,∴由(1)可知:2222GE BC CG BE +=+,即236128200BC +=+,∵BC >0,∴BC =故答案为:20.△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形.(1)问题发现:如图1,若点A,D,E在同一直线上,连接AE,BE.①求证:△ACD≌△BCE;②求∠AEB的度数.(2)类比探究:如图2,点B、D、E在同一直线上,连接AE,AD,BE,CM为△DCE中DE 边上的高,请求∠ADB的度数及线段DB,AD,DM之间的数量关系,并说明理由.(3)拓展延伸:如图3,若设AD(或其延长线)与BE的所夹锐角为α,则你认为α为多少度,并证明.【答案】(1)①见解析;②∠AEB=60°;(2)∠ADB=60°,2DM+BD=AD,理由见解析;(3)α=60°,证明见解析【分析】(1)①由△ACB和△DCE是等边三角形知AC=BC,CD=CE,∠ACD=60°-∠DCB=∠BCE,据此即可得证;②由△ACD≌△BCE知∠ADC=∠BEC=120°,结合∠CED=60°可得∠AEB=60°;(2)证△ACD≌△BCE得∠CDA=∠CED=60°,由∠ADB+∠CDA=∠DCE+∠CED知∠ADB=60°,根据CM⊥BE,且△CDE为等边三角形可得DE=2DM,DE+BD=BE=AD;(3)同理知△ACD≌△BCE,据此得∠BEC=∠ADC,继而知∠CDF+∠CEF=180°,即∠ECD+∠DFE=180°,从而得出答案.【解析】(1)①证明:∵△ACB和△DCE是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=60°-∠DCB=∠BCE,∴△ACD≌△BCE(SAS);②∵△ACD≌△BCE,∴∠ADC=∠BEC=180°-∠CDE=120°,又∵∠CED=60°,∴∠AEB=60°;(2)解:∠ADB=60°,2DM+BD=AD,理由如下;∵AC =BC ,CD =CE ,∠ACD =60°+∠DCB =∠BCE ,∴△ACD ≌△BCE (SAS ),∴∠CDA =∠CED =60°;∵∠ADB +∠CDA =∠DCE +∠CED ,∴∠ADB =60°;又∵CM ⊥BE ,且△CDE 为等边三角形,∴DE =2DM ,∴2DM +BD =BE =AD ;(3)解:α=60°,理由如下:同理可证△ACD ≌△BCE ,∴∠BEC =∠ADC ,∴∠CDF +∠CEF =180°,∴∠ECD +∠DFE =180°,而α+∠DFE =180°,∴α=∠ECD =60°.21.定义:我们把两条对角线互相垂直的四边形称为“垂美四边形”.(1)特例感知:如图1,四边形ABCD 是“垂美四边形”,如果13OA OD OB ==,2OB =,60OBC ∠=︒,则22AD BC +=______,22AB CD +=______.(2)猜想论证:如图1,如果四边形ABCD 是“垂美四边形”,猜想它的两组对边AB ,CD 与BC ,AD 之间的数量关系并给予证明.(3)拓展应用:如图2,分别以Rt ACB △的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连接CE ,BG ,GE ,已知4AC =,60BAC ∠=︒,求GE 长.【答案】(1)1529,1529(2)2222AB CD AD BC +=+,证明见解析(3)EG =【分析】(1)利用含30°角的直角三角形的性质得4BC =,OC =可得出答案;(2)由“垂美四边形”得90AOD BOC ∠=∠=︒,再根据勾股定理得22222222AB CD OA OB OD OC AD BC +=+++=+;(3)连接CG ,BE ,首先利用SAS 证明GAB CAE ∆≅∆,得GAB ACE ∠=∠,说明BG CE ⊥,从而得出2222BC GE CG BE +=+,进而解决问题.【解析】(1)解:13OA OD OB ==,2OB =,23OA OD ∴==,四边形ABCD 是“垂美四边形”,90AOD BOC ∴∠=∠=︒,60OBC ∠=︒,30BCO ∴∠=︒,4BC ∴=,OC =22222222152(2439AD BC OA OD BC ∴+=++=⨯+=,222222221529AB CD OA OB OD OC AD BC +=+++=+=,故答案为:1529,1529;(2)结论:2222AB CD AD BC +=+,证明:∵AC BD ⊥于点O ,∴90AOD ∠=︒,∴222AD OA OD =+.同理可得222AB OA OB =+,222BC OB OC =+,222CD OC OD =+∴2222AB CD AD BC +=+(3)解:如图:连接CG 、BE ,∵90GAC BAE ∠=∠=°,∴GAC CAB BAE CAB ∠+∠=∠+∠,∴GAB CAE ∠=∠,在GAB △和CAE V 中,AG AC GAB CAE AB AE =⎧⎪∠=∠⎨⎪=⎩,∴GAB CAE V V ≌,∴AGB ACE ∠=∠,∵90AGB AMG ∠+∠=°,AMG BMC ∠=∠,∴90ACE CMB ∠+∠=°,∴BG CE ⊥,∴四边形GCBE 为垂美四边形,由(2)中结论可知2222EG BC CG BE +=+,∵4AC =,60BAC ∠=︒,∴30ABC ∠=︒,∴8AB =,B C =,∴22232CG AC ==,222128BE AB ==,∴24832128EG +=+,∴2112EG =,根据线段为正数可知EG =22.在ABC 中,90BAC ∠=︒,AB AC =,点D 是射线CB 上的动点(点D 不与点B 、C 重合),连接AD ,AE AD ⊥,且AE AD =,连接DE ,过点D 作DF BC ⊥,且DF BD =,连接CF.(1)如图1,当点D 是BC 中点时,DE 与CF 的数量关系是,位置关系是;(2)如图2,当点D 是线段BC 上任意一点时,(1)中的两个结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;(3)若722AB =,3BD =时,请直接写出线段DE 的长.【答案】(1)DE CF =;DE CF∥(2)成立,证明见解析(3)5【分析】(1)由等腰直角三角形的性质得出AD =BD =CD ,证出CF ,DE ,∠ADE =45°,则可得出结论;(2)证明△ABD ≌△ACE (SAS ),由全等三角形的性质得出BD =CE ,∠ABD =∠ACE ,由直角三角形的性质及平行线的判定可证出结论;(3)分类讨论,当D 在线段BC 上时,当D 在CB 的延长线上时,由勾股定理可求出答案.【解析】(1)解:数量关系:DE CF =;位置关系:DE CF ∥;∵∠BAC =90°,AB =AC ,D 为BC 的中点,∴AD =BD =CD ,∵DF ⊥BD ,DF =BD ,∴∠FDC =90°,DF =CD ,∴CF CD ,∵EA ⊥AD ,AE =AD ,∴DE AD ,∠ADE =45°,∴CF =DE ,∵CD =DF ,∠CDF =90°,∴∠F =45°,∴∠ADE =∠F ,∴DE ∥CF .故答案为:DE =CF ,DE ∥CF ;(2)成立证明:如图2,连接CE .∵90BAC ∠=︒,AE AD ⊥,∴90BAD DAC CAE DAC ∠+∠=∠+∠=︒,∴BAD CAE ∠=∠,又∵AB AC =,AE AD =,∴()SAS ABD ACE △≌△,∴BD CE =,ABD ACE ∠=∠,∵90BAC ∠=︒,AB AC =,∴45ABC ACB ∠=∠=︒,∴45ACE ∠=︒,∴454590BCE ACB ACE ∠=∠+∠=︒+︒=︒,∴BC CE ⊥,∵DF BC ⊥,DF BD =,∴DF CE =,DE CF ∥,∴四边形DECF 是平行四边形,∴DE CF =,DE CF ∥;(3)∵AB =AC =22,∠BAC =90°,∴BC 27222=7,如图2,当D 在线段BC 上时,∵BD =DF =3,DF ⊥BC ,∴DC =BC ﹣BD =7﹣3=4,∴CF 5,由(2)可知,DE =CF =5.如图3,当D 在CB 的延长线上时,同理BC =7,DB =DF =3,∴DC =BC +DB =10,∴CF 连接CE ,同理可证四边形DCEF 为平行四边形,∵∠FDC =90°,∴四边形DCEF 为矩形,∴DE =CF综上所述,DE 5.23.如图1,90ACD ∠=︒,AC DC =,MN 是过点A 的直线,过点D 作DB MN ⊥于点B ,连接CB ;过点C 作CE CB ⊥,与MN 交于点E .(1)连接AD ,AD 是AC 的______倍;(2)直线MN 在图1所示位置时,可以得到线段BD 和AE 的数量关系是______,BD BA -与BC 之间的数量关系是______,请证明你的结论;(3)直线MN 绕点A 旋转到图2的位置,若2BD =,BCAB 的长为______(直接写结果);(4)直线MN 绕点A 旋转到图3的位置时,直接写出线段BA ,BC ,BD 之间的数量关系______.【答案】(2)AE =BD ,BD ﹣ABBC ;(3)4;(4)BA +BD BC【分析】(1)由90ACD ∠=︒,AC DC =,根据勾股定理可直接得出答案;(2)先证明△ACE ≌△DCB ,确定△ECB 为等腰直角三角形,即可得出答案;(3)先证明△ACE ≌△DCB ,CE =BC ,得到△BCE 为等腰直角三角形,得到AB =BD ,即可得出答案;(4)先证明△ACE ≌△DCB ,确定△ECB 为等腰直角三角形即可得出答案.【解析】(1)解:连接AD ,设AC =a ,则DC =a ,∴AD ===,即AD 是AC .(2)如图1,设AC 与BD 交于O ,由题可知,∠BCE =90°=∠ACD ,∴∠ACE =∠BCD ,∵BD ⊥MN ,∴∠ABD =90°=∠ACD ,∵∠AOB =∠DOC ,∴∠BAC =∠CDB ,∵AC =DC ,∴△ACE ≌△DCB (ASA ),∴CE =BC ,AE =BD ,∵∠BCE =90°,∴△ECB 为等腰直角三角形,∴BE BC ,∵BE =AE ﹣AB =BD ﹣AB ,∴BD ﹣AB BC ;故答案为:AE =BD ;BD ﹣AB ;(3)解:如图2,设CD 与MN 交于O ,由题可知,∠BCE =90°=∠ACD ,∴∠ACE =∠BCD ,∵BD ⊥MN ,∴∠ABD =90°=∠ACD ,∵∠AOC =∠DOB ,∴∠BAC =∠CDB ,∵AC =DC ,∴△ACE ≌△DCB (ASA ),∴CE =BC ,AE =BD ,∵∠BCE=90°,∴BE BC ,∵BE =AB ﹣AE =AB ﹣BD ,∴AB =BD ,∵BD =2,BC ,∴AB =BD=4,故答案为:4.(4)∴∠BCE =90°=∠ACD ,∴∠ACE =∠DCB ,∠CEB +∠CBE =90°,∵BD ⊥MN ,∴∠ABD =90°,∴∠CBE +∠CBD =90°,∴∠CEB =∠CBD ,∵AC =DC ,∴△ACE ≌△DCB (AAS ),∴CE =BC ,AE =BD ,∵∠BCE =90°,∴BEBC ,∵BE =AE +BA =BD +BA ,∴BA +BD,故答案为:BA +BDBC .24.两个顶角相等的等腰三角形,如果具有公共的顶角顶点,并将它们的底角顶点分别对应连接起来得到两个全等三角形,我们把这样的图形称为“手拉手”图形.如图1,在“手拉手”图形中,AB =AC ,AD =AE ,∠BAC =∠DAE ,连接BD ,CE ,则△ABD ≌△ACE.(1)请证明图1的结论成立;(2)如图2,△ABC 和△AED 是等边三角形,连接BD ,EC 交于点O ,求∠BOC 的度数;(3)如图3,AB =BC ,∠ABC =∠BDC =60°,试探究∠A 与∠C 的数量关系.【答案】(1)见解析(2)60°(3)∠A +∠BCD =180°,理由见解析【分析】(1)利用等式的性质得出∠BAD =∠CAE ,即可得出结论;(2)同(1)的方法判断出△ABD ≌△ACE ,得出∠ADB =∠AEC ,再利用对顶角和三角形的内角和定理判断出∠BOC =60°,即可得出答案;(3)先判断出△BDP 是等边三角形,得出BD =BP ,∠DBP =60°,进而判断出△ABD ≌△CBP (SAS ),即可得出结论.【解析】(1)解:证明:∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS );。
全等三角形之手拉手模型讲义

全等三角形-----------手拉手模型一、手拉手模型基本含义定义:所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
二、基本图形:△ABC和△ADE均是等腰三角形,其中AC=AB,AD=AE,且∠BAC=∠DAE手拉手左手拉左手、右手拉右手基本特征:① ;② ;③ ;基本三、典例精析:➢类型一:共顶点的等边三角形中手拉手例1:在直线ABC的同一侧作两个等边三角形△ABD和△BCE,连接AE与CD,(1)证明:△ABE≌△DBC;(2)证明:AE=DC;(3)求线段AE和线段DC所夹∠AFD的度数.变式练习1:在例1的基础上,将△BEC绕点B逆时针旋转一定角度,连接AE,CD,如图.(1)证明:AE=DC;(2)求线段AE所在直线和线段DC所在直线之间的夹角.➢共顶点的等腰直角三角形的手拉手例2:如图,ACB∆均为等腰直角三角形,且90∆和DCEACB DCE∠=∠=︒,连接AD,BE.判断线段AD与线段BE之间的关系,请说明理由变式练习2:如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE、GC.(1)试猜想AE与GC有怎样的数量位置关系,并证明你的结论;(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC. 你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.总结归纳:如下图△ABC和△ADE均是等腰三角形,其中AC=AB,AD=AE,且∠BAC=∠DAE=α,则∠BEC 的大小是多少?GEFDABCOE DA BCA B CD E 321AB DE全等三角形-----------手拉手模型课后练习1.如图,AB=AC ,AD=AE ,∠BAC=∠DAE ,∠1=25°,∠2=30°,则∠3=__________.2.如图,△ABD ,△AEC 都是等边三角形,BE 交CD 于点O ,求△DOE 的度数.3.如图,四边形ABCD ,BEFG 均为正方形,连接AG ,CE.(1)求证:AG=CE ;(2)求证:AG△CE.4.如图,AC=BC ,DC=EC ,∠ACB=∠ECD=90°,且∠EBD=42°,求∠AEB 的度数.。
正三角形中的手拉手模型

正三角形中的手拉手模型我们常常会遇到这样的问题:问题的背景是正三角形,然后又会出现一个正三角形绕着原正三角旋转,这时往往会出现全等三角形,从而出现等角或等线段。
我们形象地将这两个等边三角形称为“手拉手三角形”。
如上图所示,手拉手三角形不仅仅存在与共顶点等边三角形中,只要两个图形(正三角形、正方形、等腰直角三角形、等腰三角形)是“相似”的,即对应边成比例,对应角相等,那么联结对应顶点,就会出现全等三角形。
解法分析:本题中的▲ABC和▲COD是共顶点的相似的“手拉手”等边三角形,由此产生了一组全等三角形,即▲BOC≌▲ADC,由此可以用含α的代数式表示出∠OAD、∠ADO的度数,继而达到①判定▲AOD的形状;②判定▲AOD是等腰三角形(从角出发分类讨论:∠OAD=∠AOD,∠OAD=∠ADO,∠AOD=∠ADO)。
链接:等腰三角形的存在性问题讨论(根据已知条件,确定到底是从角出发分类讨论还是从边出发分类讨论)解法分析:本题中的▲OAB和▲CBD是共顶点的相似的“手拉手”等边三角形,由此产生了一组全等三角形,即▲BOC≌▲ABD,由这组全等三角形,得到∠BAD=∠AOB,可以得到∠CAD的度数。
由于OC>1,则▲EAC为钝角三角形,若▲EAC为等腰三角形,有且仅有EA=AC的情况,而∠EAO=60°,因此得到EA=2。
解法分析:本题中的▲ABC和▲MDN虽然不是共顶点的等边三角形,但是联结DE、DF、EF后,即可将▲ABC分割成4个全等的等边三角形,由此可以得到一组全等三角形,即:▲DNE≌▲DMF,利用全等三角形对应角相等,得到∠DEC=∠DFN=60°,从而说明点F在线段EN上。
第2、第3问中,虽然点M在线段BC或线段BC延长线上,但是仍旧有▲DNE≌▲DMF,线段间的等量关系依旧存在。
再次说明了不论点在线段或其延长线上,辅助线的添加方法或解法思路是完全一致的。
学习单:正三角形中的手拉手模型。
全等三角形之手拉手模型

全等三角形之手拉手模型专题手拉手模型:定义:所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
基本模型:例题:已知,△ABB和厶ACC都是等腰三角形,AB二AB;AC二AC;且/ BAB'二/CAC。
三个结论结论1: △ABC^A ABC(SAS)BC=B'C'结论2:Z BOB'二/ BAB'结论3: AO平分/ BOC'共顶点的等腰直角三角形中的手拉手变式精练1、下图,△ABC ffiA ADE是等腰直角三角形,/ BAC K DAE=90 ,求证:⑴BD=CE ⑵BD丄CEE共顶点的等边三角形中的手拉手变式精练2:如图,点A为线段BD上一点,△ABC ffiA ADE匀是等边三角形,求: (1) CD二BE (2) / DAE^Z模型应用1:如图,分别以厶ABC的边AB AC同时向外作等腰直角三角形,其中AB =AE , AC =AD Z BAE =Z CAD=90,点G为BC中点,点F 为BE 中点,点H为CD中点。
探索GF与GH的位置及数量关系并说明理由。
(选讲)模型应用2:如图,在五边形ABCDE K/ ABC二/ AED =90,/ BAC二/EAD a, F为CD的中点。
求证:(1)BF=EFB E课堂小测:练习1:如图,两个正方形ABCD与DEFG连结CE AG,二者相交于点H。
求:(1)AG=CE (2)AG与CE之间的夹角为多少度?(3)HD平分/ AHE欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
专题 相似三角形手拉手模型(老师版)

专题03相似三角形中的重要模型-手拉手模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型,在实际的应用和解题当中出现时,对于同学们来说,都比较困难。
而深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。
手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义:如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。
1)手拉手相似模型(任意三角形)条件:如图,∠BAC=∠DAE=α,AD AE k AB AC ==;结论:△ADE ∽△ABC ,△ABD ∽△ACE ;EC k BD=.2)手拉手相似模型(直角三角形)条件:如图,90AOB COD ∠=∠=︒,OC OD k OA OB==(即△COD ∽△AOB );结论:△AOC ∽△BOD ;BD k AC =,AC ⊥BD ,12ABCD S AB CD =⨯.3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点;结论:△BME ∽△CMF ;BE CF =条件:△ABC 和ADE 是等腰直角三角形;结论:△ABD ∽△ACE.例1.(2022·山西长治·九年级期末)问题情境:如图1,在△ABC 中,AB =6,AC =5,点D ,E 分别在边AB ,AC 上,且∥DE BC .数学思考:(1)在图1中,BD CE 的值为;(2)图1中△ABC 保持不动,将△ADE 绕点A 按逆时针方向旋转到图2的位置,其它条件不变,连接BD ,CE ,则(1)中的结论是否仍然成立?并说明理由;(3)拓展探究:在图2中,延长BD ,分别交AC ,CE 于点F ,P ,连接AP ,得到图3,探究∠APE 与∠ABC 之间有何数量关系,并说明理由;(4)若将△ADE 绕点A 按逆时针方向旋转到图4的位置,连接BD ,CE ,延长BD 交CE 的延长线于点P ,BP 交AC 于点F ,则(3)中的结论是否仍然成立,若成立,请说明理由;若不成立,请直接写出∠APE 与∠ABC 之间的数量关系.例2.(2022·山东济南·八年级期末)某校数学活动小组探究了如下数学问题:(1)问题发现:如图1,ABC 中,90BAC ∠=︒,AB AC =.点P 是底边BC 上一点,连接AP ,以AP 为腰作等腰Rt APQ △,且90PAQ ∠=︒,连接CQ 、则BP 和CQ 的数量关系是______;(2)变式探究:如图2,ABC 中,90BAC ∠=︒,AB AC =.点P 是腰AB 上一点,连接CP ,以CP 为底边作等腰Rt CPQ △,连接AQ ,判断BP 和AQ 的数量关系,并说明理由;(3)问题解决:如图3,在正方形ABCD 中,点P 是边BC 上一点,以DP 为边作正方形DPEF ,点Q 是正方形DPEF两条对角线的交点,连接CQ .若正方形DPEF ,CQ =ABCD 的边长.∵四边形ABCD 与四边形DPEF ∴22QD CD PD BD ==,BDC ∠=∠∴BDP CDQ △∽△,∴QD CD PD BD =设CD x =,则2CP x =-,又∵正方形例3.(2022·河南信阳·九年级期末)如图1,在Rt △ABC 中,∠C =90°,∠A =30°,BC =1,点D ,E 分别为AC ,BC 的中点.△CDE 绕点C 顺时针旋转,设旋转角为α(0°≤α≤360°),记直线AD 与直线BE 的交点为点P .(1)如图1,当α=0°时,AD 与BE 的数量关系为______,AD 与BE 的位置关系为______;(2)当0°<α≤360°时,上述结论是否成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)△CDE 绕点C 顺时针旋转一周,请直接写出运动过程中P 点运动轨迹的长度和P 点到直线BC 距离的最大值.【答案】(1)AD=3BE,AD⊥BE(2)结论仍然成立,证明见解析(3)P点运动轨迹的长度是43π;P点到直线BC距离的最大值是32【分析】(1)分别求出AD、BE的长即可解答;(2)先证明△BCE∽△ACD,可得AD ACBE BC==3,∠CBO=∠CAD即可解答;(3)利用锐角三角函数可求∠EBC=30°,由弧长公式可求P点运动轨迹的长度,由直角三角形的性质可求P点到直线BC距离的最大值即可.(1)解:在Rt△ABC中,∠C=90°,∠A=30°,BC=1∴AC=3BC=3,AB=2BC=2,AD⊥BE∵点D,E分别为AC,BC的中点∴AD=CD=12AC=32,BE=EC=12BC=12∴AD=3BE.故答案为:AD=3BE,AD⊥BE.(2)解:结论仍然成立,理由如下:∵AC=3,BC=1,CD=32,EC=12,∴33BCAC=,ECCD=33,∴BC ECAC DC=,∵△CDE绕点C顺时针旋转,∴∠BCE=∠ACD,∴△BCE∽△ACD,∴AD ACBE BC==3,∠CBO=∠CAD,∴AD=3BE,∵∠CBO+∠BOC=90°,∴∠CAD+∠AOP=90°,∴∠APO=90°,∴BE⊥AD.(3)解:∵∠APB=90°,∴点P在以AB为直径的圆上,如图3,取AB的中点G,作⊙G,以点C为圆心,CE为半径作⊙C,当BE是⊙C切线时,点P到BC的距离最大,过点P作PH⊥BC,交BC的延长线于H,连接GP,60∠=︒,2DAEAD=.将ADE绕点A按顺时针方向旋转一周.(1)当AD、AE分别在AC、AB边上,连结OD、OE,求ODE的面积;(2)设DE所在直线与ABC的边AB或AC交于点F,当O、D、E三点在一条直线上,求AF的长;(3)连结CE,取CE中点M,连结DM,DM的取值范围为_________.∵O是等边△ABC的中心∴∠OBM=30°,BM=MC,AM⊥BC∴OM=11=22OB OA=3∴==2AEBE∴EO∥BM延长EO交AC于N,则△AEN为等边三角形∵EO∥BM∴4==2 AE ANBE NC∴ON=OE,CN=DN=AD=2∴OD EN=2∴11=S==222ODE ODN DENS S∆∆∆⨯⨯是等边△ABC的中心∴∠OBA=30°,OA(3)取AE的中点N,连接MN,DN,∵D,N在⊙A的圆上∴当D、即MN-DN≤DM≤DN+MN,∴MN-2≤DM≤MN+2当D、M、N三点共线如图1时,△AND为等边三角形,∴∠NDA=∵M,N为中点∴MN=1=32AC∴DM≥1当D、M、N三点共线如图2时,△AND为等边三角形,∴∠NDA=例5.(2022·山东烟台·中考真题)(1)【问题呈现】如图1,△ABC 和△ADE 都是等边三角形,连接BD ,CE .求证:BD =CE .(2)【类比探究】如图2,△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°.连接BD ,CE .请直接写出BD CE 的值.(3)【拓展提升】如图3,△ABC 和△ADE 都是直角三角形,∠ABC =∠ADE =90°,且AB BC=AD DE =34.连接BD ,CE .①求BD CE的值;②延长CE 交BD 于点F ,交AB 于点G .求sin ∠BFC 的值.【答案】(1)见解析(2)2(3)①35;②45【分析】(1)证明△BAD ≌△CAE ,从而得出结论;(2)证明△BAD ∽△CAE ,进而得出结果;(3)①先证明△ABC ∽△ADE ,再证得△CAE ∽△BAD ,进而得出结果;②在①的基础上得出∠ACE =∠ABD ,进而∠BFC =∠BAC ,进一步得出结果.(1)证明:∵△ABC 和△ADE 都是等边三角形,∴AD =AE ,AB =AC ,∠DAE =∠BAC =60°,∴∠DAE ﹣∠BAE =∠BAC ﹣∠BAE ,∴∠BAD =∠CAE ,∴△BAD ≌△CAE (S A S ),∴BD =CE ;(2)解:∵△ABC 和△ADE 都是等腰直角三角形,AB AB AE AC ∴==DAE =∠BAC =45°,∴∠DAE ﹣∠BAE =∠BAC ﹣∠BAE ,∴∠BAD =∠CAE ,∴△BAD ∽△CAE ,22BD AB CE AC ∴==;(3)解:①34AB AD AC DE ==,∠ABC =∠ADE =90°,∴△ABC ∽△ADE ,∴∠BAC =∠DAE ,35AB AD AC AE ==,∴∠CAE =∠BAD ,∴△CAE ∽△BAD ,35BD AD CE AE ∴==;②由①得:△CAE ∽△BAD ,∴∠ACE =∠ABD ,∵∠AGC =∠BGF ,∴∠BFC =∠BAC ,∴sin ∠BFC 45BC AC ==.【点睛】本题考查了等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是熟练掌握“手拉手”模型及其变形.例6.(2023·四川·成都九年级期中)如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明:四边形CEGF是正方形;(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=9,GH=,求BC的长.=课后专项训练1、如图,AB =3,AC =2,BC =4,AE =3,AD =4.5,DE =6,∠BAD =20°,则∠CAE 的度数为()A .10°B .20°C .40°D .无法确定【答案】B【解答】AC AE =23,AB AD =34.5=23,BC DE =46=23,∴AC AE =AB AD =BC DE ,∴△ABC ∽△ADE ,∴∠BAC =∠DAE ,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC ,∴∠CAE =∠BAD =20°,故选:B .2、如图,△ABC ∽△ADE ,∠BAC =∠DAE =90°,AB 与DE 交于点O ,AB =4,AC =3,F 是DE 的中点,连接BD ,BF ,若点E 是射线CB 上的动点,下列结论:①△AOD ∽△FOB ,②△BOD ∽△EOA ,③∠FDB+∠FBE =90°,④BF =56AE ,其中正确的是()A .①②B .③④C .②③D .②③④【解答】∵△ABC ∽△ADE ,∴∠ADO =∠OBE ,∵∠AOD =∠BOE ,∴△AOD ∽△EOB ,∴OD OB =OA OE ,∴OD OA =OB OE ,∵∠BOD =∠AOE ,∴△BOD ∽△EOA ,故②正确,∵△AOD ∽△EOB ,△BOD ∽△EOA ,∴∠ADO =∠EBO ,∠AEO =∠DBO ,∵∠ADO+∠AEO=90°,∴∠DBE=∠DBO+∠EBO=90°,∵DF=EF,∴FD=FB=FE,∴∠FDB=∠FBD,∴∠FDB+∠FBE=∠FBD+∠FBE=90°,故③正确,在Rt△ABC中,∵AB=4,AC=3,∴BC=32+42=5,∵△ABC∽△ADE,∴DE AE=BC AC=53,∵BF=12DE,∴2BF AE=53,∴BF=56AE,故④正确,∵∠ADO=∠OBE,∴∠ADO≠∠OBF,∴无法判断△AOD∽△FOB,故①错误.故选:D.3、如图,△ABC中,∠C=90°,∠B=30°,AC=7,D、E分别在边AC、BC上,CD=1,DE∥AB,将△CDE 绕点C旋转,旋转后点D、E对应的点分别为D′、E′,当点E′落在线段AD′上时,连接BE′,此时BE′的长为()A.23B.33C.27D.37【分析】如图,作CH⊥BE′于H,设AC交BE′于O.首先证明∠CE′B=∠D′=60°,解直角三角形求出HE′,BH 即可解决问题.【详解】解:如图,作CH⊥BE′于H,设AC交BE′于O.∵∠ACB=90°,∠ABC=30°,∴∠CAB=60°,∵DE∥AB,∴CDCA=CECB,∠CDE=∠CAB=∠D′=60°∴'CDCA='CECB,∵∠ACB=∠D′CE′,∴∠ACD′=∠BCE′,∴△ACD′∽△BCE′,∴∠D′=∠CE′B=∠CAB,在Rt△ACB中,∵∠ACB=90°,AC=7,∠ABC=30°,∴AB=2AC=27,BC=3AC=21,∵DE∥AB,∴CDCA=CECB,∴17=21CE,∴CE=3,∵∠CHE′=90°,∠CE′H=∠CAB=60°,CE′=CE=3∴E′H=12CE′=32,CH=3HE′=32,∴BH=22BC CH-=9214-532∴BE′=HE′+BH=3B.【点拨】本题考查了相似三角形的综合应用题,涉及了旋转的性质、平行线分线段成比例、相似三角形的性质与判定等知识点,解题的关键是灵活运用上述知识点进行推理求导.4、已知正方形DEFG 的顶点F 在正方形ABCD 的一边AD 的延长线上,连结AG ,CE 交于点H ,若3AB =,2DE =,则CH 的长为________.【分析】连接EG ,与DF 交于N ,设CD 和AH 交于M ,证明△ANG ∽ADM ,得到DM AD NG AN=,从而求出DM 的长,再通过勾股定理算出AM 的长,通过证明△ADG ≌△CDE 得到∠DAG=∠DCE ,从而说明△ADM ∽△CHM ,得到AD AM CH CM=,最后算出CH 的长.【详解】解:连接EG ,与DF 交于N ,设CD 和AH 交于M ,∴∠GNA=90°,DN=FN=EN=GN ,∵∠MAD=∠GAN ,∠MDA=∠GNA=90°,∴△ANG ∽ADM ,∴DM AD NG AN=,∵2DE =,∴DF=EG=2,∴DN=NG=1,∵AD=AB=3,∴3131DM =+,解得:DM=34,∴MC=94,22317AD DM +,∵∠ADM+∠MDG=∠EDG+∠CDG ,∴∠ADG=∠EDC ,在△ADG 和△CDE 中,AD CD ADG CDE DG DE =⎧⎪∠=∠⎨⎪=⎩,∴△ADG ≌△CDE (SAS ),∴∠DAG=∠DCE ,∵∠AMD=∠CMH ,∴∠ADM=∠CHM=90°,∴△ADM ∽△CHM ,∴AD AM CH CM =,即3494CH =,解得:.【点拨】本题考查了全等三角形的判定和性质,相似三角形的判定和性质,正方形的性质,勾股定理,综合性较强,解题的关键是找到合适的全等三角形和相似三角形,通过其性质计算出CH 的长.5.(2022·浙江国·九年级课时练习)观察猜想(1)如图1,在等边ABC 中,点M 是边BC 上任意一点(不含端点B 、C ),连接AM ,以AM 为边作等边AMN ,连接CN ,则ABC ∠与ACN ∠的数量关系是______.(2)类比探究:如图2,在等边ABC 中,点M 是BC 延长线上任意一点(不含端点C ),(1)中其它条件不变,(1)中结论还成立吗?请说明理由.(3)拓展延伸:如图3,在等腰ABC 中,BA BC =,点M 是边BC 上任意一点(不含端点B 、C ),连接AM ,以AM 为边作等腰AMN ,使顶角AMN ABC ∠=∠.连按CN .试探究ABC ∠与ACN ∠的数量关系,并说明理由.6.(2022湖北·九年级专题练习)如图,ABC 为等边三角形,D 为AC 边上一点,连接BD ,M 为BD 的中点,连接AM .(1)如图1,若AB =,∠ABD =45°,求AMD 的面积;(2)如图2,过点M 作MN AM ⊥与AC 交于点E ,与BC 的延长线交于点N ,求证:AD =CN ;(3)如图3,在(2)的条件下,将ABM 沿AM 翻折得'AB M ,连接B'N ,当B'N 取得最小值时,直接写出BN DE MN-的值.(2)如解图2,过点A 作AG ∵△ABC 为等边三角形,∴∵BM =DM ,∴//MG AC ,∴∴AGM AGB BGM ∠=∠-∠又∵AM MN ⊥,AG BC ⊥(3)取AC 的中点Q ,连接BQ ,取∵将△ABM 沿AM 翻折得△AB 'M ∴BAM MAB '∠=∠,AB AB AC '==又∵BAM CAN =∠∠,∴MAB '∠∴MAN CAN MAN MAB ∠-∠=∠-∠又∵30ANM ∠=︒,1122AQ AC ==【点睛】本题主要考查了三角形综合,涉及了等边三角形、全等三角形、相似三角形的性质和判定以及解三角形等知识点,难度大,综合性强,需要平时积累和训练.解题关键是根据题目的已知条件添加辅助线构造适当的三角形转化线段和角的关系.7.(2023·广西·九年级课时练习)某校数学活动小组在一次活动中,对一个数学问题作如下探究:(1)问题发现:如图1,在等边ABC 中,点P 是边BC 上任意一点,连接AP ,以AP 为边作等边APQ ,连接CQ ,BP 与CQ 的数量关系是________;(2)变式探究:如图2,在等腰ABC 中,AB BC =,点P 是边BC 上任意一点,以AP 为腰作等腰APQ ,使AP PQ =,APQ ABC ∠=∠,连接CQ ,判断ABC ∠和ACQ ∠的数量关系,并说明理由;(3)解决问题:如图3,在正方形ADBC 中,点P 是边BC 上一点,以AP 为边作正方形APEF ,Q 是正方形APEF 的中心,连接CQ .若正方形APEF 的边长为5,22CQ =,求正方形ADBC 的边长.【答案】(1)BP CQ =;(2)ABC ACQ ∠=∠;理由见解析;(3)4.,根据全等三角形的性质解答;∵四边形ADBC 是正方形,∴2AB AC=,∠解得,14x =-(舍去),23x =,∴正方形ADBC 的边长为:314+=.【点睛】本题考查的是正方形的性质、三角形全等的判定和性质、三角形相似的判定和性质、勾股定理的应用,掌握相似三角形的判定定理和性质定理、正方形的性质是解题的关键.8.(2022·河南开封·九年级期末)某数学兴趣小组在学习了尺规作图、等腰三角形和相似三角形的有关知识后,在等腰△ABC 中,其中AB AC =,如图1,进行了如下操作:第一步,以点A 为圆心,任意长为半径画弧,分别交BA 的延长线和AC 于点E ,F ,如图2;第二步,分别以点E ,F 为圆心,大于12EF 的长为半径画弧,两弧相交于点D ,作射线AD ;第三步,以D 为圆心,DA AE 于点G ;(1)填空;写出∠CAD 与∠GAD 的大小关系为___;(2)①请判断AD 与BC 的位置关系,并说明理由.②当6,2AB AC BC ===时,连接DG ,请直接写出AD AG =___;(3)如图3,根据以上条件,点P 为AB 的中点,点M 为射线AD 上的一个动点,连接PM ,PC ,当CPM B ∠=∠时,求AM 的长.由(1)(2)可得NAM CAM B ∠=∠=∠设AN x =则3AM MN x ==∵点P 为AB ∵CPM B ∠=∠∴CPM B N∠=∠=∠∴BCP MPN NPC B ∠=∠=∠-∠∴BPC∴P P MN B BC N =∴3233x x =+,解得3x =∴【点睛】本题考查尺规作图中的作角平分线以及相似三角形的判定与性质,解题的关键是能根据尺规作图的步骤判断是作角平分线.9.(2022·山东济南·一模)在Rt ABC 中与Rt DCE 中,90,30ACB DCE BAC DEC ∠=∠=︒∠∠=∠=︒,AC DC =Rt DCE 绕点C 顺时针旋转,连接,BD AE,点,F G 分别是,BD AE 的中点,连接,CF CG .(1)观察猜想:如图1,当点D与点A重合时,CF与CG的数量关系是__________,位置关系是__________;(2)类比探究:当点D与点A不重合时,(1)中的结论是否成立?如果成立,请仅就图2的情形给出证明;如果不△的面积的最大值与最小值.成立,请说明理由.(3)问题解决在Rt DCE旋转过程中,请直接写出CFG的面积10.(2022•莱芜区一模)在△ACB中,∠ACB=120°,AC=BC,点P在AB边上,AP=AB,将线段AP绕点P顺时针旋转至PD,记旋转角为a,连接BD,以BD为底边,在线段BD的上方找一点E,使∠BED=120°,ED =EB,连接AD、CE.(1)如图1,当旋转角a=180°时,请直接写出线段CE与线段AD的数量关系;(2)当0<a<180°时,①如图2,(1)中线段CE与线段AD的数量关系是否还成立?并说明理由.②如图3,当点A、D、E三点共线时,连接CD,判断四边形CDBE的形状,并说明理由.【分析】(1)作EH⊥AB于H,利用含30°角的直角三角形的性质得BD=BE,再利用平行线分线段成比例定理可得答案;(2)利用△ABD∽△CBE,可得;(3)设AE与BC交于F,作PQ⊥AD于Q,BH⊥AD,交AD的延长线于H,与(2)知,△ABD∽△CBE,得∠BAD=∠BCE,可证明CE∥BD,设EH=x,则BE=2x,BH=x,DE=BE=2x,BD=2x,再利用平行线分线段成比例可得AD=6x,从而证明CE=BD,进而解决问题.【解答】解:(1)AD=CE,理由如下:∵∠BED=∠ACB=120°,∴DE∥AC,∴,∴,作EH⊥AB于H,∵BE=DE,∠BED=120°,∴∠B=30°,BD=2BH,∴,∴BD=BE,∴,∴AD=CE;(2)仍然成立,∵∠ABC=∠DBE=30°,∴∠ABD=∠CBE,由(1)知,,∴△ABD∽△CBE,∴,∴AD=CE;(3)四边形CDBE是平行四边形,理由如下:设AE与BC交于F,作PQ⊥AD于Q,BH⊥AD,交AD的延长线于H,与(2)知,△ABD∽△CBE,∴∠BAD=∠BCE,∴∠CEF=∠ABC=30°,∵∠BDE=30°,∴∠BDE=∠,∴CE∥BD,∵∠BED=120°,∴∠BEH=60°,设EH=x,则BE=2x,BH=x,∴DE=BE=2x,BD=2x,∵AP=PD,PQ⊥AD,∴AQ=DQ,∵AP=AB,PQ∥BH,∴AQ=QH,∴AQ=DQ=DH=3x,∴AD=6x,由(2)知,AD=CE,∴CE=2x,∴CE=BD,∴四边形CDBE是平行四边形.【点评】本题是四边形综合题,主要考查了等腰三角形的性质,平行线分线段成比例定理,相似三角形的判定与性质,平行四边形的判定等知识,证明CE=BD是解决问题(3)的关键.11.(2022·江苏·九年级课时练习)观察猜想(1)如图1,在等边ABC中,点M是边BC上任意一点(不含端点B、C),连接AM,以AM为边作等边AMN,连接CN ,则ABC ∠与ACN ∠的数量关系是______.(2)类比探究:如图2,在等边ABC 中,点M 是BC 延长线上任意一点(不含端点C ),(1)中其它条件不变,(1)中结论还成立吗?请说明理由.(3)拓展延伸:如图3,在等腰ABC 中,BA BC =,点M 是边BC 上任意一点(不含端点B 、C ),连接AM ,以AM 为边作等腰AMN ,使顶角AMN ABC ∠=∠.连按CN .试探究ABC ∠与ACN ∠的数量关系,并说明理由.12、如图1,在Rt ABC 中,90C ∠=︒,30A ∠=︒,1BC =,点D ,E 分别为AC ,BC 的中点.CDE △绕点C 顺时针旋转,设旋转角为α(0360α︒≤≤︒,记直线AD 与直线BE 的交点为点P .(1)如图1,当0α=︒时,AD 与BE 的数量关系为_________,AD 与BE 的位置关系为_______;(2)当0360α<≤︒︒时,上述结论是否成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)CDE △绕点C 顺时针旋转一周,请直接写出运动过程中P 点运动轨迹的长度和P 点到直线BC 距离的最大值.【分析】(1)分别求出AD ,BE 的长,即可求解;(2)通过证明△BCE ∽△ACD ,可得AD ACBE BC==,∠CBO=∠CAD ,可得结论;(3)利用锐角三角函数可求∠EBC=30°,由弧长公式可求P 点运动轨迹的长度,由直角三角形的性质可求P 点到直线BC 距离的最大值.【详解】解:(1)∵在Rt △ABC 中,∠C=90°,∠A=30°,BC=1,∴AB=2BC=2,AD ⊥BE ,∵点D ,E 分别为AC ,BC 的中点,∴AD=CD=12AC=32,BE=EC=12BC=12,∴BE ,故答案为:BE ,AD ⊥BE ;(2)结论仍然成立,理由如下:∵BC=1,EC=12,∴3BC AC =,3EC CD =,∴BC EC AC DC =,∵△CDE 绕点C 顺时针旋转,∴∠BCE=∠ACD ,∴△BCE ∽△ACD ,∴AD ACBE BC==,∠CBO=∠CAD ,∴BE ,∵∠CBO+∠BOC=90°,∴∠CAD+∠AOP=90°,∴∠APO=90°,∴BE ⊥AD ;(3)∵∠APB=90°,∴点P 在以AB 为直径的圆上,如图3,取AB 的中点G ,作⊙G ,以点C 为圆心,CE 为半径作⊙C ,当BE 是⊙C 切线时,点P 到BC 的距离最大,过点P 作PH ⊥BC ,交BC 的延长线于H ,连接GP ,∵BE 是⊙C 切线,∴CE ⊥BE ,∵sin ∠EBC=12EC BC =,∴∠EBC=30°,∴∠GBP=30°,∵GB=GP ,∴∠GBP=∠GPB=30°,∴∠BGP=120°,∵点P 的运动轨迹为点C→点P→点C→点B→点C ,∴P 点运动轨迹的长度=120121803ππ︒⨯⨯=︒,∵∠ABP=30°,BP ⊥AP ,∴AP=12AB=1,33∵∠CBP=30°,PH ⊥BH ,∴PH=12BP=32.∴P 点到直线BC 距离的最大值32.【点拨】本题考查了直角三角形的性质,相似三角形的判定和性质,旋转的性质,锐角三角函数等知识,确定点P 的运动轨迹是本题的关键.13、尝试:如图①,ABC 中,将ABC 绕点A 按逆时针方向旋转一定角度得到AB C '',点B 、C 的对应点分别为B ′、C ',连接BB '、CC ',直接写出图中的一对相似三角形_______;拓展:如图②,在ABC 中,90C ∠=︒,AC BC =,将ABC 绕点A 按逆时针方向旋转一定角度得到AB C '',点B 、C 的对应点分别为B ′、C ',连接BB '、CC ',若8BB '=,求CC '的长;应用:如图③,在Rt ABC △中,90ACB ∠=︒,2AB =,30ABC ∠=︒,将ABC 绕点A 按逆时针方向旋转一周,在旋转过程中,当点B 的对应点B ′恰好落在Rt ABC △的边所在的直线上时,直接写出此时点C 的运动路径长.【详解】尝试:''ABB ACC △△;【解法提示】∵''ABC AB C ≅△△,∴'AB AB =,'AC AC =,''BAC B AC ∠=∠,∴''BAB CAC ∠=∠,''AB AB AC AC =,∴''ABB ACC △△.拓展:∵在ABC 中,90C ∠=︒,AC BC =,∴45ABC ∠=︒,∴2sin 452AC AB ︒==,易得''ABB ACC △△,∴22CC'AC BB'AB ==.又∵'8BB =,∴'42CC =.应用:3π或43π或23π或π或2π.【解法提示】在Rt ABC 中,2AB =,30ABC ∠=︒,∴1AC =,60BAC ∠=︒,当点'B 落在AC 所在直线上时,有两种情况:①若点'B 在AC 延长线上时,如解图①,'60CAC BAC ∠=∠=︒,∴弧60'11803CC ππ⨯==;②若点'B 在CA 的延长线上时,如解图②,此时点B ,'C ,'B 三点共线,∴旋转角360260240=︒-⨯=︒,∴弧240141803'CC ππ⨯==;当点'B 落在边BC 所在直线上时,如解图③,'260120CAC ∠=⨯︒=︒,∴弧120121803CC'ππ⨯==;当点'B 落在边AB 所在直线上时,如解图④,此时点C ,A ,'C 三点共线,旋转角为180︒,∴弧1801180CC'ππ⨯==.当点'B 与点B 重合时,点C 旋转一周,∴弧'22CC AC ππ=⨯=.∴当点B 的对应点'B 恰好落在Rt ABC 的边所在直线上时,点C 的运动路径长为3π或43π或23π或π或2π.图①图②图③图④14、问题背景:如图(1),已知A ABC DE ∽△△,求证:ABD ACE ∽;尝试应用:如图(2),在ABC 和ADE 中,90BAC DAE ︒∠=∠=,30ABC ADE ︒∠=∠=,AC 与DE 相交于点F .点D 在BC 边上,3AD BD=,求DFCF 的值;拓展创新:如图(3),D 是ABC 内一点,30BAD CBD ︒∠=∠=,90BDC ︒∠=,4AB =,23AC =,直接写出AD 的长.【分析】问题背景:通过A ABC DE ∽△△得到AB AC AD AE =,AB ACAD AE=,再找到相等的角,从而可证ABD ACE ∽;尝试应用:连接CE ,通过BAC DAE ∽可以证得ABD ACE ∽,得到BD ADCE AE=,然后去证AFE DFC ∽△△,ADF ECF ∽△△,通过对应边成比例即可得到答案;拓展创新:在AD 的右侧作∠DAE=∠BAC ,AE 交BD 延长线于E ,连接CE ,通过BAC DAE ∽,BAD CAE ∽,然后利用对应边成比例即可得到答案.【详解】问题背景:∵A ABC DE ∽△△,∴∠BAC=∠DAE ,AB ACAD AE=,∴∠BAD+∠DAC=CAE+∠DAC ,∴∠BAD=∠CAE ,∴ABD ACE ∽;尝试应用:连接CE ,∵90BAC DAE ︒∠=∠=,30ABC ADE ︒∠=∠=,∴BAC DAE ∽,∴AB ADAC AE=,∵∠BAD+∠DAC=CAE+∠DAC ,∴∠BAD=∠CAE ,∴ABD ACE ∽,∴BD ADCE AE=,由于30ADE ︒∠=,90DAE ︒∠=,∴3303AE tan AD ︒==,即3BD AD CE AE =,∵3AD BD=3ADCE =,∵90BAC DAE ︒∠=∠=,30ABC ADE ︒∠=∠=,∴60C E ︒∠=∠=,又∵AFE DFC ∠=∠,∴AFE DFC ∽△△,∴AF EFDF CF =,即AF DF EF CF=,又∵AFD EFC ∠=∠∴ADF ECF ∽△△,∴3DF AD CF CE==;拓展创新:5AD =如图,在AD 的右侧作∠DAE=∠BAC ,AE 交BD 延长线于E ,连接CE ,∵∠ADE=∠BAD+∠ABD ,∠ABC=∠ABD+∠CBD ,30BAD CBD ︒∠=∠=,∴∠ADE=∠ABC ,又∵∠DAE=∠BAC ,∴BAC DAE ∽,∴AB AC BCAD AE DE==,又∵∠DAE=∠BAC ,∴∠BAD=∠CAE ,∴BAD CAE ∽,∴=BD AB AD CE AC AE ==设CD=x ,在直角三角形BCD 中,由于∠CBD=30°,∴BD =,2BC x =,∴32CE x =,∴2DE x =,∵AB BCAD DE =,∴452AD =,∴AD =【点拨】本题考查了相似三角形的综合问题,熟练掌握相似三角形的判定和性质是解题的关键15、如图,四边形ABCD 和四边形AEFG 都是正方形,C ,F ,G 三点在一直线上,连接AF 并延长交边CD 于点M .(1)求证:△MFC ∽△MCA ;(2)求证△ACF ∽△ABE ;(3)若DM=1,CM=2,求正方形AEFG的边长.【分析】(1)由正方形的性质得45ACD AFG ∠=∠=︒,进而根据对顶角的性质得CFM ACM ∠=∠,再结合公共角,根据相似三角形的判定得结论;(2)根据正方形的性质得AF ACAE AB=,再证明其夹角相等,便可证明ACF ABE ∽△△;(3)由已知条件求得正方形ABCD 的边长,进而由勾股定理求得AM 的长度,再由MFC MCA △∽△,求得FM ,进而求得正方形AEFG 的对角线长,便可求得其边长.【详解】解:(1)四边形ABCD 是正方形,四边形AEFG 是正方形,45ACD AFG ∴∠=∠=︒,CFM AFG ∠=∠,CFM ACM ∴∠=∠,CMF AMC ∠=∠,MFC MCA ∴△∽△;(2)四边形ABCD 是正方形,90ABC ∴∠=︒,45BAC ∠=︒,AC ∴=,同理可得AF =,∴AFACAE AB=45EAF BAC ∠=∠=︒,CAF BAE ∴∠=∠,ACF ABE ∴△∽△;(3)1DM =,2CM =,123AD CD ∴==+=,AM ∴=MFC MCA △∽△,∴CM FMAM CM =2FM =,5FM ∴=,5AF AM FM ∴=-=,∴AG ==AEFG .【点拨】本题主要考查了正方形的性质,相似三角形的性质与判定,勾股定理,关键是掌握相似模型及证明方法和正方形性质.16.(2022•南山区校级一模)(1)【问题发现】如图①,正方形AEFG 的两边分别在正方形ABCD 的边AB 和AD 上,连接CF .填空:①线段CF 与DG 的数量关系为;②直线CF 与DG 所夹锐角的度数为.(2)【拓展探究】如图②,将正方形AEFG 绕点A 逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.(3)【解决问题】如图③,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,AB =AC =10,O 为AC 的中点.若点D 在直线BC 上运动,连接OE ,则在点D 的运动过程中,线段OE 长的最小值为(直接写出结果).【分析】(1)连接AF ,由正方形的性质可得点A 、F 、C 三点共线,AC =,AF =AG ,从而得出答案;(2)连接AF ,AC ,利用△CAF ∽△DAG ,得CF =DG ,∠ACF =∠ADG ,从而解决问题;(3)连接CE ,利用SAS 证明△BAD ≌△CAE ,得∠ABD =∠ACE =45°,则∠DCE =90°,可知当OE ⊥CE 时,OE 最小,再利用等腰直角三角形的性质求出答案.【解答】解:(1)连接AF ,∵四边形AEFG 、ABCD 是正方形,∴∠GAF =45°,∴点A 、F 、C 三点共线,∴AC =,AF =AG ,∴CF =GD ,故答案为:CF =GD ,45°;(2)仍然成立,连接AF ,AC ,∵∠CAD =∠FAG =45°,∴∠CAF =∠DAC ,,∴△CAF ∽△DAG ,∴CF =DG ,∠ACF =∠ADG ,∴∠COD =∠CAD =45°,∴(1)中的结论仍然成立;(3)连接CE ,∵∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,∵AB =AC ,AD =AE ,∴△BAD ≌△CAE (SAS ),∴∠ABD =∠ACE =45°,∴∠DCE =90°,∴当OE ⊥CE 时,OE 最小,∵AC =10,O 为AC 的中点.∴OC =5,∵∠OCE =45°,∴OE =OC=,故答案为:.【点评】本题是四边形综合题,主要考查了正方形的性质,等腰直角三角形的性质,相似三角形的判定与性质,全等三角形的判定与性质等知识,熟练掌握旋转型相似是解题的关键.17、某校数学活动小组在一次活动中,对一个数学问题作如下探究:(1)问题发现:如图1,在等边ABC 中,点P 是边BC 上任意一点,连接AP ,以AP 为边作等边APQ ,连接CQ ,BP 与CQ 的数量关系是________;(2)变式探究:如图2,在等腰ABC 中,AB BC =,点P 是边BC 上任意一点,以AP 为腰作等腰APQ ,使AP PQ =,APQ ABC ∠=∠,连接CQ ,判断ABC ∠和ACQ ∠的数量关系,并说明理由;(3)解决问题:如图3,在正方形ADBC 中,点P 是边BC 上一点,以AP 为边作正方形APEF ,Q 是正方形APEF 的中心,连接CQ .若正方形APEF 的边长为5,CQ =ADBC 的边长.【分析】(1)利用SAS 定理证明BAP CAQ △≌△,根据全等三角形的性质解答;(2)先证明BAC PAQ △∽△,得到AB AP AC AQ=,再证明BAP CAQ △≌△,根据相似三角形的性质解答即可;(3)连接AB 、AQ ,根据相似三角形的性质求出BP ,根据勾股定理列出方程,解方程得到答案.【详解】解:(1)问题发现:∵ABC ∆和APQ ∆都是等边三角形,∴A B AC =,AP AQ =,60BAC PAQ ∠=∠=︒,∴BAP CAQ ∠=∠,在BAP △和CAQ ∆中,AB AC BAP CAQ AP AQ =⎧⎪∠=∠⎨⎪=⎩,∴()BAP CAQ SAS ≌△△,∴BP CQ =,故答案为:BP CQ =;(2)变式探究:ABC ACQ ∠=∠,理由如下:∵AB BC =,∴1802ABC BAC -∠︒∠=,∵AP PQ =,∴1802APQ PAQ ︒-∠∠=,∵APQ ABC ∠=∠,∴BAC PAQ ∠=∠,∴BAC PAQ △∽△,∴AB AP AC AQ=,∵BAP PAC PAC CAQ ∠+∠=∠+∠,∴BAP CAQ ∠=∠,∴BAP CAQ ∽△△,∴ABC ACQ ∠=∠;(3)解决问题:连接AB 、AQ ,如图所示:∵四边形ADBC 是正方形,∴AB AC=,45BAC ∠=︒,∵Q 是正方形APEF 的中心,∴AP AQ =,45PAQ ∠=︒,∴BAP PAC PAC CAQ ∠+∠=∠+∠,即BAP CAQ ∠=∠,∵AB APAC AQ =,∴ABP ACQ △∽△,∴CQ AC BP AB ==∵2CQ =,∴1BP =,设PC x =,则1BC AC x ==+,在Rt APC △中,222AP AC PC =+,即()22251x x =++,解得,14x =-(舍去),23x =,∴正方形ADBC 的边长为:314+=.【点拨】本题考查的是正方形的性质、三角形全等的判定和性质、三角形相似的判定和性质、勾股定理的应用,掌握相似三角形的判定定理和性质定理、正方形的性质是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
手拉手模型1、等边三角形条件:△OAB,△OCD均为等边三角形结论:;;导角核心:八字导角2、等腰直角三角形条件:△OAB,△OCD均为等腰直角三角形结论:;;导角核心:3、任意等腰三角形条件:△OAB,△OCD均为等腰三角形,且∠AOB = ∠COD结论:;;核心图形:核心条件:;;例题讲解:A类1:在直线ABC的同一侧作两个等边三角形△ABD和△BCE,连接AE与CD, 等边三角形要得到哪些结论?要联想到什么模型?证明:(1)△ABE≌△DBC;(2)AE=DC;(3)AE与DC的夹角为60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB;(6)BH平分∠AHC;解题思路:1:出现共顶点的等边三角形,联想手拉手模型2:利用边角边证明全等;3:八字导角得角相等;2:如图两个等腰直角三角形ADC与EDG,连接AG,CE,二者相交于H. 等腰直角三角形要得到哪些结论?要联想到什么模型?问 (1)△ADG≌△CDE是否成立?(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分∠AHE?解题思路:1:出现共顶点的等腰直角三角形,联想手拉手模型2:利用边角边证明全等;3:八字导角得角相等;3:如图,分别以△ABC 的边AB、AC同时向外作等腰直角三角形,其中AB =AE,AC =AD,等腰直角三角形要得到哪些结论?要联想到什么模型?∠BAE=∠CAD=90°,点G为BC中点,点F为BE 中点,点H 为CD中点。
探索GF与多个中点,一般考虑什么?GH 的位置及数量关系并说明理由。
解题思路:1:有两个共顶点的等腰直角三角形,联想手拉手全等,连接BD,CE,△BAD≌△EAC2:多个中点,联想中位线,得线段关系B类1:如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD任意一点(P与A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E. (1)如图1,猜想∠QEP=_______°;旋转60°,要做什么?出现等边三角形,要想到哪些?(2)如图2,3,若当∠DA C是锐角或钝角时,其它条件不变,猜想∠QEP 的度数,选取一种情况加以证明;(3)如图3,若∠DA C=135°,∠A CP=15°,且AC=4,求BQ 的长.解题思路:1:旋转60°,出现等边三角形2:两个共顶点的三角形,联想手拉手全等 3:求线段长度,利用勾股定理2:在ABC ∆中,2AB BC ==,90ABC ∠=︒,BD 为斜边A C上的中线,将ABD ∆绕点D顺时针旋转α(0180α︒<<︒)得到EFD ∆,其中点A 的对应点为点E ,点B 的对应点为点F,等腰直角三角形斜边的中线可以得到什么?求线段长有哪些方法? 有特殊的钝角,需要做什么?BE与FC相交于点H.(1)如图1,直接写出BE与FC的数量关系:____________;(2)如图2,M、N分别为EF、BC的中点.求证:MN CF22;(3)连接BF,CE,如图3,直接写出在此旋转过程中,线段BF、CE与AC之间的数量关系:.解题思路:1:等腰直角三角形斜边的中线把三角形分成两个相同的等腰直角三角形2:等腰直角三角形绕顶点旋转,联想手拉手模型3:等腰直角三角形中出现中点,联想斜边中点线段的关系都有哪些?出现中点要想到什么?等腰直角三角形绕顶点旋转,是什么模型?4:利用勾股定理得线段关系3:在Rt △ABC 中,90ACB ∠=︒,D 是AB 的中点,DE ⊥BC于E,连接CD .(1)如图1,如果30A ∠=︒,那么DE 与C E之间的数量关系是___________.(2)如图2,在(1)的条件下,P是线段CB 上一点,连接DP ,将线段D P绕点D 逆时针旋转60°,得到线段DF,连接BF ,请猜想DE 、BF 、BP 三者之间的数量关系,并证明你的结论.(3)如图3,如果A α∠=(090α︒<<︒),P 是射线CB 上一动点(不与B 、C 重合),连接DP ,将线段DP 绕点D逆时针旋转2α,得到线段DF ,连接BF,请直接写出D E、BF 、BP 三者之间的数量关系(不需证明).解题思路:线段关系,一般有哪些?旋转60°,要做什么,还要联想什么?直角+中点,联想什么?1:直角三角形斜边的中线是斜边的一半2:30°的直角三角形,得到等边三角形3:线段关系一般有和差倍,勾股定理4:等腰三角形共顶点旋转,联想手拉手模型C类1:已知:在△ABC中,∠BAC=60°.(1)如图1,若AB=AC,点P在△ABC内,且∠APC=150°,PA=3,PC=4,把△APC绕着点A顺时针旋转,使点C旋转到点B处,得到△ADB,连接DP旋转60°,要做什么,还要联想什么?①依题意补全图1;②直接写出PB的长;(2)如图2,若AB=AC,点P在△ABC外,且PA=3,PB=5,PC=4,求∠APC的度数;给出共顶点的三条线段,要做什么?当看到3,4,5,要来你想什么?(3)如图3,若AB=2AC,点P在△ABC内,且PA=3,PB=5,∠APC=120°,请直接写出PC的长.图1 图2图3解题思路:1:共点的三条线段,利用旋转,构造手拉手模型,使之放在同一三角形中2:勾股定理,勾股数3:沿用前两问思路,构造手拉手相似2:在□ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG =AG+BG;(2)如图2,当EF与AB相交时,若∠EAB= α(0º﹤α﹤90º),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.解题思路:1:有60°角,联想等边三角形,联想手拉手2:线段和差,联想截长补短3:等腰三角形,构造手拉手模型4:三条线段的关系:和差倍、勾股定理课堂练习A类1:如图,已知ABC∆都是等边三角形,B、C、D在一条直线上,试说明CE与∆和ADE+相等的理由.AC CD2:如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.(1)求证:AE=BD;(2)求证:MN∥AB.3:已知:如图,△ABC 、△CD E都是等边三角形,AD 、BE 相交于点O,点M 、N 分别是线段AD 、BE的中点.(1)求证:AD=BE;(2)求∠D OE 的度数;(3)求证:△MN C是等边三角形.B 类1:在ABC △中,AB AC =,BAC ∠=α()060︒<α<︒,将线段BC 绕点B 逆时针旋转60︒得到线段B D.(1)如图1,直接写出ABD ∠的大小(用含α的式子表示);(2)如图2,150BCE ∠=︒,60ABE ∠=︒,判断ABE △的形状并加以证明;(3)在(2)的条件下,连结DE ,若45DEC ∠=︒,求α的值2.如图1,在四边形ABCD中,BA=BC,∠ABC=60°,∠ADC=30°,连接对角线BD. (1)将线段CD绕点C顺时针旋转60°得到线段CE,连接AE.①依题意补全图1;②试判断AE与BD的数量关系,并证明你的结论;(2)在(1)的条件下,直接写出线段DA、DB和DC之间的数量关系;(3)如图2,F是对角线BD上一点,且满足∠AFC=150°,连接FA和FC,探究线段FA、FB和FC之间的数量关系,并证明.(图1) (图2)3.如图,在△ABC中,∠ACB=90°,AC=BC=CD,∠ACD=α,将线段CD绕点C顺时针旋转90°得到线段CE,连接DE,AE,BD.(1)依题意补全图1;(2)判断AE与BD的数量关系与位置关系并加以证明;(3)若0°<α≤64°,AB=4,AE与BD相交于点G,求点G到直线AB的距离的最大值.请写出求解的思路(可以不写出计算结果)..........C类1:已知:2,4PA PB ==,以AB 为一边做正方形ABCD ,使P 、D 两点落在直线AB 的两侧。
(1)如图,当45APB ∠=时,求AB 及PD 的长(2)当APB ∠变化, 且其它条件不变时,求PD 的最大值,及相应的APB ∠的大小方法总结:手拉手辅助线构造方法:_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________。
