水的动力粘滞系数η、粘滞系数比η_rη_20
20度水的粘滞系数

20度水的粘滞系数
摘要:
1.水的粘滞系数定义
2.20 度水的粘滞系数实验结果
3.影响粘滞系数的因素
4.20 度水粘滞系数在实际应用中的意义
正文:
水的粘滞系数是一个描述液体内部阻力大小的物理量。
在20 度(即摄氏20 度)时,水的粘滞系数约为0.0009 Pa·s。
这一数值是通过实验测量得到的,实验过程中,将水置于一个恒定的温度环境,并通过特定的仪器测量水的粘滞系数。
在实验中,科学家们发现,水的粘滞系数受多种因素影响,包括温度、压力、剪切速率等。
在温度一定的情况下,压力的增大和剪切速率的增加都会导致粘滞系数的减小。
反之,压力的降低和剪切速率的减小则会使粘滞系数增大。
在实际应用中,20 度水的粘滞系数对于许多工程领域具有重要意义。
例如,在水利工程中,了解水的粘滞系数可以帮助工程师们更好地设计水电站、水渠等设施,以确保水流畅通、减小阻力。
此外,在化工、生物医学等领域,对粘滞系数的了解也有助于优化生产过程和实验条件。
总之,20 度水的粘滞系数是一个与温度、压力、剪切速率等因素密切相关的物理量,它在实际应用中具有重要意义。
粘滞系数 -回复

粘滞系数 -回复粘滞系数是指在液体流动时,单位时间内液体内部分子间相互粘滞力的大小。
在科学研究和工业生产中,粘滞系数是液体物理性质的重要参数之一,尤其是在流体力学、化学工程、生物科学等领域中有着广泛的应用。
由于液体分子内部相互作用力的不同,不同液体的粘滞系数范围有所差异。
水的粘滞系数约为0.001 Pa•s,而甘油的粘滞系数则约为1.5 Pa•s。
在工业生产中,合理地选择液体的粘滞系数可以提高生产效率和质量,避免因粘度过高或过低而导致的工艺问题。
液体的粘滞系数通常通过沿不同方向施加切应力来测量。
当我们在液体中施加一个平行于液体平面的切应力时,液体分子会发生形变,形成横向位移。
粘滞系数即为单位宽度上的剪应力与剪变速率之比。
表达式为:η=τ/(du/dy)η为粘滞系数,τ为剪应力,du/dy为剪变速率。
在这个表达式中,剪应力与剪变速率成正比,即剪应力越大,粘滞系数越大。
剪变速率是液体形变速度的一个衡量,剪变速率越大,粘滞系数越小。
粘滞系数是一个和温度、压力、液体性质等因素有关的物理量。
粘滞系数的测量可以采用多种方法,常见的有旋转圆盘法、旋转圆缸法、悬线法、带负载弹性板法等。
旋转圆盘法和旋转圆缸法是测量粘度最常用的方法之一。
这两种方法都是通过液体与旋转盘或旋转圆柱的摩擦力来测量液体的粘滞系数,但两种方法的测量原理不同,适用于不同的液体类型。
在实际应用中,液体的粘滞系数对于流动稳定性、摩擦等现象有着重要的影响。
在工业生产中,当液体的粘滞系数增大时,液体的摩擦力也随之增大,这可能导致一些不稳定的现象发生,如流量减小、流速降低、甚至出现管道堵塞等。
了解液体粘滞系数的变化规律,具有十分重要的实际意义。
液体的粘滞系数不仅与液体的性质有关,还受到温度、压力等外部因素的影响。
对于大多数液体而言,随着温度升高,粘滞系数会降低。
这是因为在高温下,液体分子间距离增大,分子的运动变得更加自由,因此液体的流动性能会提高。
同样地,在高温下粘滞系数降低,液体在流动时热量的带走也增多,这会对液体产生一定的冷却作用,从而降低了液体的温度。
液体粘滞系数的测定

液体粘滞系数的测定在稳定流动的液体中,由于各层液体的流速不同,在相邻两层流体之间存在相对运动而产生切向力,流速快的一层给流速慢的一层以拉力,流速慢的一层给流速快的层以阻力,液层间的这一作用称为内摩擦力或粘滞力,流体这一性质称为粘滞性。
液体的粘滞性在液体(例如石油)管道输送以及医药等方面都有重要的应用。
现代医学发现,许多心脑血管疾病与血液粘度有关,血液粘滞会使流人人体器官和组织的血流量减少、血流流速减缓,使人体处于供血和供氧不足的状态中,可能引发多种心脑血管疾病,所以,血粘度大小成了人体血液健康的重要标志之一。
实验证明,粘滞力f 的大小与两液层间的接触而积△s 和该处的速度空间变化率dyd υ(常称为速度的梯度)的乘积成正比,即 s dyd f ∆=υη (5—1) 式(5-1)就是决定流体内摩擦力大小的粘滞定律,式中的比例系数η称为液体的内摩擦系数或粘滞系数。
它决定于液体的性质和温度,在润滑油选择、液压传动以及液体质研究等很多方面是一项主要技术指标,其国际制单位是:“帕斯卡·秒”(Pa·s )。
[实验目的](1)用落针法测定液体的粘度。
(2)熟悉各仪器的使用方法。
[实验仪器]本仪器采用落针法测量液体粘度(粘滞系数),既适于牛顿液体,又适于非牛顿液体,还可测量液体的密度。
实验中使中空细长圆柱体(针)在待测液体中垂直下落,通过测量针的收尾速度,确定粘度。
本仪器采用霍尔传感器和多功能毫秒计(单片机计时器)测量落针的速度,并可自动计算后将粘度显示出来。
巧妙的取针装置和投针装置,使测量过程极为简便。
仪器由本体、落针、霍尔传感器、单片机计时器和恒温控制等部分组成。
见下图: 如图5-1,待测液体(例如蓖麻油)装在被玻璃恒温水套包围的玻璃圆筒容器中,圆筒竖直固定在机座上,机座底部有调水平的螺丝,机座上竖立一个铝合金支架。
其上装有霍尔传感器、提针装置(未画出)。
装在液体容器顶部的盖子上有投针装置发射器,它包括喇叭形的导杯和带永久磁钢的拉杆。
运动粘滞系数和运动粘度的关系

运动粘滞系数和运动粘度的关系运动粘滞系数和运动粘度是流体力学中常用的两个概念,用于描述流体的流动性质和阻力大小。
运动粘滞系数是指流体内部分子之间相互作用的强度,而运动粘度则是流体流动时所表现出的阻力大小。
本文将从理论和实验两个方面探讨运动粘滞系数和运动粘度的关系。
我们来了解一下运动粘滞系数的概念。
运动粘滞系数,也称为动力粘滞系数,是指单位面积上单位时间内单位切应力的变化率。
它是描述流体内部摩擦阻力大小的物理量,通常用希腊字母μ表示。
运动粘滞系数越大,表示流体的内部分子之间相互作用越强,流体的黏稠度也就越高。
而运动粘度,则是指单位面积上单位速度梯度的变化率。
它是描述流体流动性质的物理量,通常用希腊字母η表示。
运动粘度越大,表示流体流动时所表现出的阻力越大,流体的黏稠度也就越高。
根据流体力学理论,运动粘滞系数和运动粘度之间存在着一定的关系。
根据牛顿运动定律和流体的层流流动假设,可以推导出运动粘滞系数与运动粘度之间的关系式:运动粘滞系数等于运动粘度乘以密度。
在实验中,我们可以通过一些方法来测量流体的运动粘滞系数和运动粘度。
常用的方法有:旋转圆柱法、平板法、毛细管法等。
这些方法都是通过测量流体在不同条件下的流动情况,利用流体动力学的原理来计算运动粘滞系数和运动粘度。
实验结果表明,运动粘滞系数和运动粘度之间存在着一定的线性关系。
当流体的密度不变时,运动粘滞系数与运动粘度成正比。
也就是说,当运动粘度增加时,运动粘滞系数也会相应增加。
这说明了运动粘度对运动粘滞系数的影响是显著的。
运动粘滞系数和运动粘度的大小还与流体本身的性质有关。
不同的流体具有不同的运动粘滞系数和运动粘度。
例如,水的运动粘滞系数和运动粘度较小,而某些高黏度液体如糖浆、胶体等的运动粘滞系数和运动粘度较大。
运动粘滞系数和运动粘度在工程实践中具有重要的应用价值。
在流体力学、化学工程、地质勘探等领域,我们常常需要对流体的流动性质和阻力进行研究和计算。
土力学试验指导书

土力学试验指导书-CAL-FENGHAI.-(YICAI)-Company One11一、 含水量试验(一)试验仪器设备1. 烘箱:能控制温度为105~110℃。
2. 天平:精度为0.01g 。
3. 称量合(铝土合):合盖和合体有相同的编号。
(二)试验步骤1.取有代表性试样,粘性土为15~20g ,砂性土、有机质土为50g ,放入称量合内,盖上合盖,称湿土+称量合质量(m 0);2.打开合盖,将合置于烘箱内,在105~110℃的恒温下烘干。
烘干时间对粘性土不得少于8h ,对砂性土不得少于6h 。
对含有机质超过5%的土,应将温度控制在65~70℃的恒温下烘干;3.将称量合从烘箱中取出,盖上合盖,放入干燥容器内冷却至室温,称干土+称量合质量(m d )。
(三)含水量计算试样的含水量计算,按下式计算,精确至%,mm m m d d--=00ω (1—1)式中,m —称量合的质量。
含水量试验应进行两次平行测定,两次测定的差值,当含水量小于40%时不得大于1%;当含水量等于、大于40%时不得大于2%。
取两次测值的平均值。
2二、 密度试验测定土的密度方法有环刀法、蜡封法、灌水法和灌砂法,环刀法适用于粘土,蜡封法适用于和形状不规则的坚硬土,灌水法和灌砂法适用于现场测定原状砂和砾质土的密度。
这里只介绍环刀法。
(一)试验仪器设备1.环刀:内径为±0.15mm 和±0.15mm ,高度为20±0.016mm 。
2.天平:称量500g ,感量0.1g ;称量200g ,感量0.01g 。
(二)试验步骤1.试样切取。
根据试验要求用环刀切取试样时,应在环刀内壁涂一薄层凡士林,刃口向下放在土样上,将环刀垂直下压,并用切土刀沿环刀外侧切削土样,边压边削至土样高出环刀,用钢丝锯整平环刀两端土样,擦净环刀外壁。
2.称环刀和土的总质量,并取余土测定含水量。
(三) 密度计算试样的密度按下式计算:Vm00=ρ (2—1)试样的干密度按下式计算:11ωρρ+=d (2—2) 式(1)、(2)中,m 0 — 湿土的质量(g ); V — 土的体积(cm 3);ρ0 — 土的湿密度(g/cm 3);ρd — 土的干密度(g/cm 3) ω1 — 土的含水量。
《工程地质与土力学》第七章:土的渗透性

第七章 土的渗透性
图1 坝、闸渗透示意图 (a)土坝渗透: (b)闸基渗透
第七章 土的渗透性 二、达西定律
1856年,法国科学家达西对不同粒径砂土作试验时,发现水流在层 流状态时,水的渗透速度与水力坡度成正比。其表达式为:
Q k i A
v k h k i L
式中:
次;
v
i
h ——水力坡降,是水头差h与渗透路径L之比,即 ,无因 L
20
式中
kT k 20
——ToC和20oC时土的渗透系数;
η T 、η 20——ToC和20oC时水的动力粘滞系数,见《土工 试验方法标准》(SL237-1999)。
第七章 土的渗透性 ⑷封闭气体含量
土中封闭气体含量愈多,会使土的渗透通路愈小,渗透系数减小。故试 验时应充分饱和土样降低土中封闭气体的影响。
第 2节
• • • •
渗透力和渗透变形
教学目的与要求: 掌握渗透力、 临界水力坡度的计算方法、 理解渗透变形的主要形式、 了解防止渗透变形的主要措施
第七章 土的渗透性 一、渗透力
水流在渗透过程中会遇到土颗粒的阻力作用。
根据牛顿第三定律,水对土颗粒必将产生一个相等的反作用力。 我们将渗流作用在单位土体上的力称为单位渗透力,简称渗透力,以j 表示。见图7 则 式中: j= w
n——孔隙率;
k
通常要求
——渗透系数,cm/s。
i
≤
[
i ],方法同流土。
第七章 土的渗透性
四、 防止渗透变形的措施
根据渗透变形的机理可知,土体发生渗透破坏的原因有两个方面一
是渗流特征,即上下游水位差形成的水力坡降,二是土的类别及组成特
性。即土的性质及颗粒级配。 故防止渗透变形的工程措施基本归结为: 1) 延长渗径,减小下游出逸口水力坡降,降低渗透力; 2) 增强渗流出逸处土体抗渗能力。 具体措施如下: • 1、上游设置垂直和水平防渗体,以延长渗径,减小水力坡降
土工合成材料测试规程

1 总则1.0.1为推动土工合成材料在工程建设中的应用,统一材料测试的技术要求,特制定本规程。
1.0.2本规程适用于水利、铁路、公路、水运、建筑、环境等工程中所用的土工合成材料的测试。
1.0.3土工合成材料性状受试验方法、荷载性质、试样尺寸、加荷速率、试验温度等因素的影响,测试时应按本规程有关规定进行。
1.0.4土工合成材料的测试除应遵守本规程的规定外,尚应符合国家现行有关标准、规范的规定。
2 术语和符号2.1 术语2.1.1 等效孔径(或称表观孔径)以土工织物为筛布对颗粒料进行筛析,当一种颗粒料的过筛率(通过织物的颗粒料重量与颗粒料总重量之比)为5%时,则该颗粒粒径尺寸定为土工织物的等效孔径。
2.1.2 垂直渗透系数水流垂直于土工织物平面水力梯度等于1时的渗透流速。
2.1.3透水率水流垂直于土工织物平面水位差等于1时的渗透流速。
2.1.4水平渗透系数水流沿土工织物平面水力梯度等于l时的渗透流速。
2.1.5导水率水力梯度等于1时水流沿土工织物平面单位宽度内输导的水量。
2.1.6抗拉强度试样拉伸时能承受的最大拉力,发生在断裂时或断裂前。
2.1.7延伸率试样拉伸时对应最大拉力时的应变。
2.1.8 握持强度在试样宽度范围内试样在局部被夹持的条件下进行拉伸的过程中出现的最大拉力。
2.1.9撕裂强度试样沿规定的切缝逐渐扩展裂口至整个试样的过程中出现的最大撕裂力。
2.1.10胀破强度在试样的垂直方向上施加液压,使试样扩张直至破坏,破坏时的液压称为胀破强度。
2.1.11 CBR顶破强度一直径50mm的圆柱顶杆垂直顶人试样过程中的最大顶压力。
2.1.12刺破强度一直径8mm的刚性顶杆垂直刺人试样过程中最大刺破力。
2.1.13压屈强度塑料排水带的芯带在外力作用下抵抗压裂、倾倒破坏的能力。
2.1.14 排水带通水量排水带的芯带与滤膜复合体在侧压力作用下沿排水带截面的纵向通水能力。
2.1.15 扁平率软式透水管在上复压力作用下透水管的径向变形量与管径之比。
液体粘滞系数实验原理 -回复

液体粘滞系数实验原理 -回复液体粘滞系数是衡量流体黏性的指标。
当液体通过管道或通道时,粘滞力会对流体产生阻力。
粘滞系数越大,阻力越大,液体运动越缓慢。
粘滞系数是设计和优化流体力学系统的重要参数。
本文将介绍液体粘滞系数实验的原理和常用测量方法。
一、实验原理液体粘滞系数实验的原理基于史托克斯定律。
根据史托克斯定律,在液体中移动的小球所受到的粘滞力与小球速度成正比,且与小球大小和液体粘度成正比。
可以用下列公式表示:F = 6πrvF是粘滞力,r是小球半径,v是小球速度。
过程中,对于流过管道的流体,粘滞力可以描述为:F = ηA(dv/dx)F是管道内两平面之间粘滞力对流体运动的阻力,η是液体粘滞系数,A是管道横截面积,dv/dx是速度梯度,单位为m/s/m。
通过测量流体从细管中流出的速度并与细管直径和运动距离相关联的数据,可以计算出液体粘滞系数。
二、实验设备和仪器1. 细管或毛细管细管或毛细管通常是通过其内部流体的速度和通过管道的液体流量测量液体粘滞系数的主要工具。
2. 数字计时器数字计时器可以准确地测量流体通过细管或毛细管的运动时间,帮助我们计算液体的平均速度。
3. 数字天平数字天平用于测量细管或毛细管的质量,以及在实验中使用的液体的质量。
4. 液体容器用于装载实验需要的液体。
通常用玻璃瓶或塑料瓶来存储液体。
5. 温度计温度计用于测量液体的温度。
因为液体的粘度随温度而变化,所以必须在一定的温度区间内进行实验,并将数据进行校正。
三、实验步骤1. 准备实验设备和仪器,并确保它们已经校准。
2. 准备实验室环境,确保无风和震动的影响。
3. Weigh the liquid to be tested, and record its mass.4. Set up the glass tube or capillary pipette in the experimental setup, and take a measurement of the capillary diameter.5. 将液体轻轻地注入细管或毛细管,注入液体时要小心,确保不会引入气泡。
水文地质学基础实验指导书
实验二 渗透试验一般规定1. 常水头渗透试验适用于粗粒土,变水头渗透试验适用于细粒土。
2. 本试验采用的纯水,应在试验前用抽气法或煮沸法脱气。
试验时的水温宜高于试验室温度3~4℃。
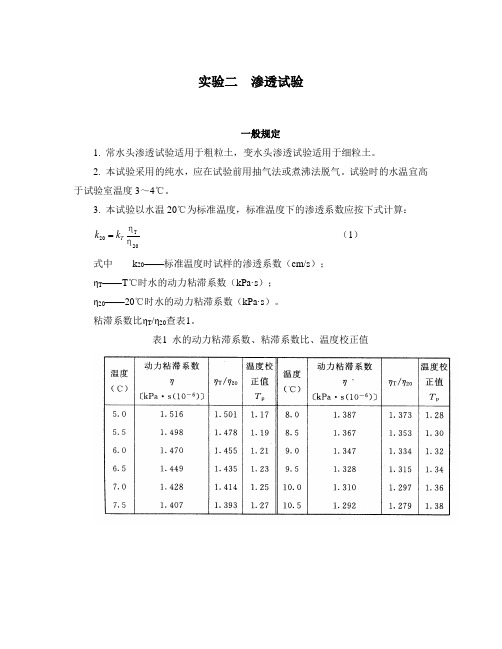
3. 本试验以水温20℃为标准温度,标准温度下的渗透系数应按下式计算: 20T k k T 20ηη (1) 式中 k 20——标准温度时试样的渗透系数(cm/s );ηT ——T ℃时水的动力粘滞系数(kPa·s );η20——20℃时水的动力粘滞系数(kPa·s )。
粘滞系数比ηT /η20查表1。
表1 水的动力粘滞系数、粘滞系数比、温度校正值续表 14. 根据计算的渗透系数,应取3~4个在允许差值范围内的数据的平均值,作为试样在该孔隙比下的渗透系数(允许差值不大于2×10-n)。
5. 当进行不同孔隙比下的渗透试验时,应以孔隙比为纵坐标,渗透系数的对数为横坐标,绘制关系曲线。
常水头渗透试验一、实验目的和意义(1)通过稳定流条件下的渗流实验,掌握均匀砂渗透系数的测定方法。
进一步理解渗流基本定律——达西定律,加深对岩石渗透系数的认识。
(2)了解达西实验装置,加深理解渗流速度、水力梯度、渗透系数之间的关系,并熟悉实验室测定渗透系数的方法,从而提高对直线渗透定律的理解。
(3)渗透系数是进行井孔、矿坑涌水量及水库,渠道渗流量计算时不可缺少的重要水文地质参数。
二、实验方法确定渗透系数的方法很多,在室内常用达西仪,戚姆仪及渗压仪等方法测定。
在野外常用井孔抽水,注水及试坑渗水、压水试验等方法,所得资料可靠精度高,但效率低,成本高。
本次实验采用达西仪测定岩石的渗透系数。
三、实验原理岩石渗透系数是定量描述岩石透水性能的物理指标,岩石空隙越大、连通性越好,则渗透系数越大,单位时间内通过过水断面的水量越多。
其物理含义是当水力坡度等于1时,渗透系数就等于渗透速度。
常水头渗透系数应按下式计算:T QLkAHt(2)式中k T——水温为T℃时试样的渗透系数(cm/s);Q——时间t秒内的渗出水量(cm3);L——两测压管中心间的距离(cm);A——试样的断面积(cm2);H——平均水位差(cm);t——时间(s)。
水的运动粘滞系数随温度变化的经验公式

水的运动粘滞系数随温度变化的经验公式全文共四篇示例,供读者参考第一篇示例:水的运动粘滞系数是描述水在运动过程中阻力大小的物理量,而这一属性会随着水的温度变化而有所不同。
在日常生活中,我们经常可以观察到水的不同温度会导致其具有不同的流动性质,这是由于水的分子在不同温度下运动方式的变化所致。
研究水的运动粘滞系数随温度变化的规律具有一定的重要性。
我们需要了解一下水的运动粘滞系数的定义。
运动粘滞系数是衡量一种流体在单位时间内通过单位横截面积在单位长度上的流动速度梯度产生的剪切应力的大小的物理量。
对于水而言,其运动粘滞系数是一个重要的物理指标,它不仅在实际生产中有重要应用,同时也对科学研究有一定的指导意义。
在讨论水的运动粘滞系数随温度变化的规律时,我们首先需要了解水的性质随温度的变化规律。
一般来说,随着温度的升高,水的分子将会具有更大的平均动能,运动速度将增加,分子之间的作用力也会减弱,这导致了水的黏度随温度升高而减小。
这是由于在较高温度下,水分子之间的相互作用力受到热运动的影响而减弱,分子之间的距离增大,导致流体的内部摩擦减小,流动性增加。
在实验数据的基础上,我们可以尝试拟合出水的运动粘滞系数与温度的关系的经验公式。
一般而言,水的运动粘滞系数与温度之间可以用指数函数的形式来进行拟合。
根据已有的研究数据,可以得到如下经验公式:μ = A*exp(B/T)μ代表水的运动粘滞系数,A和B为待定系数,T代表水的温度。
这一经验公式可以较好地描述水的运动粘滞系数随温度变化的规律,为后续研究提供了重要的参考依据。
水的运动粘滞系数随温度变化的规律是一个重要的研究课题。
通过实验数据和经验公式的拟合,我们可以更好地理解水的运动特性,并为工程应用提供相关的参考依据。
对于水的运动粘滞系数的研究也有助于科学家们更加深入地理解流体力学的基本规律,推动相关领域的研究不断取得新的突破和进展。
希望本文能够为读者对水的运动粘滞系数随温度变化这一问题有更深入的了解和认识。
粘度知识以及粘度单位换算

粘度知识以及粘度单位换算发布日期:[2011-1-21] 共阅[2905]次粘度知识以及粘度单位换算表概述液体在流动时,在其分子间产生内摩擦的性质,称为液体的黏性,粘性的大小用黏度表示,粘度又分为动力黏度与运动黏度度。
粘度基础知识:粘度分为动力粘度,运动粘度和条件粘度。
黏度简介将流动着的液体看作许多相互平行移动的液层, 各层速度不同,形成速度梯度(dv/dx),这是流动的基本特征.(见图)由于速度梯度的存在,流动较慢的液层阻滞较快液层的流动,因此.液体产生运动阻力.为使液层维持一定的速度梯度运动,必须对液层施加一个与阻力相反的反向力.在单位液层面积上施加的这种力,称为切应力τ(N/m2).切变速率(D)D=d v /d x (S-1)切应力与切变速率是表征体系流变性质的两个基本参数牛顿以图4-1的模式来定义流体的粘度。
两不同平面但平行的流体,拥有相同的面积”A”,相隔距离”dx”,且以不同流速”V1”和”V2”往相同方向流动,牛顿假设保持此不同流速的力量正比于流体的相对速度或速度梯度,即:τ= ηdv/dx =ηD(牛顿公式)其中η与材料性质有关,我们称为“粘度”。
黏度定义将两块面积为1m2的板浸于液体中,两板距离为1米,若加1N的切应力,使两板之间的相对速率为1m/s,则此液体的粘度为1Pa.s。
牛顿流体:符合牛顿公式的流体。
粘度只与温度有关,与切变速率无关,τ与D为正比关系。
非牛顿流体:不符合牛顿公式τ/D=f(D),以ηa表示一定(τ/D)下的粘度,称表观粘度。
又称黏性系数、剪切粘度或动力粘度。
流体的一种物理属性,用以衡量流体的粘性,对于牛顿流体,可用牛顿粘性定律定义之:式中μ为流体的黏度;τyx为剪切应力;ux为速度分量;x、y为坐标轴;d ux/d y为剪切应变率。
流体的粘度μ与其密度ρ的比值称为运动粘度,以v表示。
粘度随温度的不同而有显著变化,但通常随压力的不同发生的变化较小。
液体粘度随着温度升高而减小,气体粘度则随温度升高而增大。
动力粘滞系数与运动粘滞系数的关系

动力粘滞系数与运动粘滞系数的关系1.引言1.1 概述动力粘滞系数和运动粘滞系数是物理学中重要的概念,它们可以描述物质在运动中受到的粘滞作用。
粘滞力常常在流体力学、固体力学以及相关工程领域中起着重要的作用。
动力粘滞系数是指在物质受到外力作用下,流动速度发生变化时所表现出的阻力大小。
它可以通过测量物质在外力作用下的变形速率与应力大小的关系来求得。
动力粘滞系数的数值越大,表示物质的流动阻力越大,即粘滞效应越明显。
运动粘滞系数是指物质在恒定外力作用下,持续运动时所表现出的阻力大小。
它可以通过测量物质受到的静态应力与运动速度的关系来求得。
运动粘滞系数与动力粘滞系数有着相似的物理意义,但是它们所描述的运动状态不同。
本文将探讨动力粘滞系数与运动粘滞系数之间的关系。
我们将详细介绍动力粘滞系数和运动粘滞系数的定义和特点,并分析它们之间的联系和区别。
同时,我们将探讨影响动力粘滞系数和运动粘滞系数的因素,以便更好地理解它们的物理本质和应用范围。
通过深入研究动力粘滞系数和运动粘滞系数的关系,我们可以更好地理解物质在运动中所受到的粘滞效应。
这对于工程领域的流体力学问题、材料疲劳分析以及自然界中的地质现象等都具有重要的意义。
因此,通过本文的研究,我们将有助于推动相关领域的发展,并为解决相关问题提供参考和指导。
1.2 文章结构【文章结构】本文将从概述、动力粘滞系数的定义和特点、运动粘滞系数的定义和特点、动力粘滞系数与运动粘滞系数的关系以及影响动力粘滞系数和运动粘滞系数的因素等几个方面进行叙述和分析。
在引言部分,我们将对本文的研究内容进行概述,介绍研究的目的以及文章的结构。
在正文部分的第一节,将详细介绍动力粘滞系数的定义和特点。
首先,我们将给出动力粘滞系数的定义,并解释其物理意义。
其次,我们将讨论动力粘滞系数的特点,包括其计算方法、影响因素以及在实际运用中的应用。
在正文部分的第二节,将详细介绍运动粘滞系数的定义和特点。
我们将首先给出运动粘滞系数的定义,并解释其物理意义。
210990393_探究水在0~10℃粘滞系数的变化规律

科学研究创探究水在0~10℃粘滞系数的变化规律兰国栋卢佳枫王晓悦张婷媛谢超然冯志芳∗(北京化工大学数理学院北京100029)摘 要:粘滞系数是描述液体内摩擦力性质的一个重要物理量,笔者利用毛细管法和虹吸原理制成一套测量水粘滞系数的实验装置,这套装置利用半导体制冷机与温控器取代恒温箱,实现温度的精准控制。
笔者用该装置测量水在0~10℃的粘滞系数,重点探究了4℃附近粘滞系数的变化特点,观察发现,水的粘滞系数在0~ 10℃范围随温度的升高而逐渐降低,且在4℃左右不存在反常变化。
关键词:粘滞系数泊肃叶公式半导体制冷机虹吸原理中图分类号:T Q645.1文献标识码:A文章编号:1674-098X(2022)07(c)-0027-04 Study on the Variation Law of Viscosity Coefficient of Waterat 0-10℃LAN Guodong LU Jiafeng WANG Xiaoyue ZHANG Tingyuan XIE Chaoran FENG Zhifang∗(College of Mathematics and Physics, Beijing University of Chemical Technology, Beijing, 100029 China) Abstract: The viscosity coefficient is an important physical quantity to describe the nature of friction force in liq-uid. The author has made a set of experimental device to measure the viscosity coefficient of water using capillary method and siphon principle. The device uses semiconductor refrigerator and temperature controller to replace the constant temperature box to realize accurate temperature control. The viscosity coefficient of water at 0-10°C was measured by this device, and the variation characteristics of viscosity coefficient near 4°C were mainly explored. It was observed that the viscosity coefficient of water decreased gradually with the increase of temperature in the range of 0-10°C, and there was no abnormal change at about 4°C.Key Words: Viscosity coefficient; Poiseuille formula; Semiconductor refrigerator; Siphon principle液体的粘性力主要是由分子间吸引力造成的,当温度升高时,分子距离加大,引力减小,使粘性力减弱,粘度降低,导致液体的粘滞系数随温度的升高而降低。
液体粘滞阻力公式

液体粘滞阻力公式咱们先来说说液体粘滞阻力这回事儿。
在我们的日常生活中,其实到处都能见到和液体粘滞阻力相关的现象。
就比如,你倒蜂蜜的时候,那缓慢流淌的样子,跟倒水可完全不一样,这就是因为蜂蜜的粘滞阻力大。
咱们要深入了解液体粘滞阻力,那就得先搞清楚这个公式。
液体粘滞阻力公式是:F = 6πηrv 。
这里面的 F 代表粘滞阻力,η是液体的粘滞系数,r 是物体在液体中的半径,v 是物体在液体中的运动速度。
那这个公式到底咋用呢?咱们来举个例子。
假设在一个装满了油的大桶里,有一个小球在匀速下落。
油的粘滞系数咱们假设是 0.5 Pa·s,小球的半径是 2 厘米,下落速度是 0.1 米每秒。
那根据公式,粘滞阻力F 就等于 6×3.14×0.5×0.02×0.1,算出来大概是 0.01884 牛。
在科学实验里,液体粘滞阻力的研究也特别重要。
我记得有一次在实验室里,我们做一个关于不同液体粘滞阻力的对比实验。
准备了水、食用油还有蜂蜜,让同样大小的小球在这几种液体里下落。
那场面可热闹了,水里面的小球“唰”地一下就下去了,食用油里的小球慢了一些,而蜂蜜里的小球,简直就是在“艰难前行”。
再来说说这个公式在实际生活中的应用。
比如汽车的发动机里,机油的选择就和粘滞阻力有关。
粘滞系数太大的机油,会让发动机运转起来更费劲,增加能耗;粘滞系数太小呢,又可能起不到良好的润滑作用。
所以,工程师们就得根据发动机的特点,选好合适粘滞系数的机油,这里面可都是学问呐!还有在医学领域,血液在血管里的流动也会受到粘滞阻力的影响。
要是血液变得黏稠,粘滞阻力增大,那心血管系统的负担就加重了,可能就会引发各种疾病。
咱们学习液体粘滞阻力公式,可不是为了光背个公式应付考试。
而是要真正理解它背后的原理,能把它用到生活里,解决实际问题。
就像我前面说的那些例子,从实验室的小实验,到汽车发动机,再到我们身体里的血液循环,液体粘滞阻力都在悄悄地发挥着作用。
