三角恒等变换专题复习带答案

合集下载

专题12 简单的三角恒等变换（解析版）

于是 b + c = 2R (sinB + sinC )
=
43 3
sinB
+
sin
2 3
−
B
=
43 3
3 sinB + 2
3 2
cosB
=
4sin
B
+
6
.
因为 ABC 是锐角三角形且 A = ， 3
所以由 C
2
，得
2 3
−
B
2
，因此
B
的取值范围是
6
,
2
.
6/7
( 而由
；（2）
−
2 2
,1
.
【解析】（1）由正弦定理得： sinA = sinBcosC + sinCsinB
因为： sinA = sin ( B + C ) = sinBcosC + cosBsinC
故 cosBsinC = sinCsinB 因为 sinC 0 ，所以 cosB = sinB 因为 0 B ，所以 B =
2
2
∴ A .
6
4
) ∵
a
=
2
，∴
a sinA
2
2,4
.又 b + c = a ， sinB + sinC sinA
3/7
( ) ∴ b + c 2 2, 4 . sinB + sinC
( ) 故答案为 2 2, 4
7．（三角恒等变换在实际中的运用）如图，有一壁画，最高点 A 处离地面 6m，最低点 B 处离地面 3.5m.若从离地高 2m 的 C 处观赏它，则离墙______m 时，视角最大.

新高考一轮复习特训三角恒等变换 (含答案)高中数学高考专区一轮复习

2025届新高考一轮复习特训三角恒等变换一、选择题1．在ABC △中，D 为边BC 上一点，DAC ∠=4AD =，2AB BD =，且ADC △的面积为ABD ∠=( )2．sin20cos40cos20cos50+︒︒︒︒的值是( )C.3．若π0,2α⎛⎫∈ ⎪⎝⎭=α=( )4．已知25cos 2cos αα+=,()cos 2αβ+=π0,2⎛⎫∈ ⎪⎝⎭,ππ3,22β⎛⎫∈ ⎪⎝⎭,则cos β的值为( )A.cos 0θθ-=,则tan 2θ=( )A.-6．已知α为锐角，cos α=2α=( )7．已知()sin αβ-=3tan αβ=,则()sin αβ+=( )8．已知πcos6α⎛⎫-=⎪⎝⎭π26α⎛⎫+=⎪⎝⎭( )A.C.二、多项选择题9．在ABC△中，内角A，B，C所对的边分别为a，b，c，已知sin()sin()3sin2BA B A A-++=，且c==A.22cos15︒ B.sin27cos3cos27sin3︒︒+︒︒C.2sin15sin75︒11．下列化简正确是( )A.sin45cos451︒︒=B.22ππcos sin1212-=4040sin80︒+︒=三、填空题12．已知tanα，tanβ是方程2330x x--=的两个实数根，()tan22αβ+=________. 13．(1tan13)(1tan32)+︒+︒=________.14．已知()()4tan114tan17A B+-=,则()tan A B-=________.四、解答题15．已知sinα=π0,2⎛⎫∈ ⎪⎝⎭（1）求πsin4α⎛⎫+⎪⎝⎭的值；（2）若tanβ=tan2()αβ-的值.16．在ABC△=的12=（1）求C ;（2）若32a b c +=且,求的外接圆半径.17．记ABC △1sin A =+.(1)若A B =,求C ；18．在ABC △中，内角A ，B ，C 的对边分别为a ，b ，c ，且a =5=，cos A =（1）求B ；（2）设D 是AB 边上点，且3AB AD =，求证：CD AB ⊥.19．在ABC △中,角A ,B,C 的对边分别为a ,b ,c ,且cos b A c+=（1）求B 的大小;（2）若c =2b +=,求ABC △的面积.（3）已知πsin 3α⎛⎫+= ⎪⎝⎭π6α⎛⎫- ⎪⎝⎭的值.3a =ABC △参考答案1．答案：A解析：因为11sin 422ADC S AD AC DAC AC =⋅∠=⨯⨯=△4AC =，所以ADC △为等腰三角形，则ADC ∠=在△=sin DBBAD =∠，解得sin BAD ∠=因为ADB ∠=BAD为锐角，所以cos BAD ∠==所以()πsin sin sin 6ABD ADC BAD BAD ⎛⎫∠=∠-∠=-∠ ⎪⎝⎭ππsin cos cos sin 66BAD BAD -∠==∠故选：A 2．答案：A解析：原式sin20cos40cos20sin 40sin 60=︒︒︒︒=︒=+故选：A.3．答案：B解析：因为tan2α==π0,2⎛⎫∈ ⎪⎝⎭，所以sin02α≠，所以22cos 2cos α-=cos 1cos αα-=+，所以cos α=π0,2α⎛⎫∈ ⎪⎝⎭，所以α=α=解析：25cos 2cos αα+= ,210cos cos 30αα∴--=,cos α∴=因为π0,2α⎛⎫∈ ⎪⎝⎭,所以3cos 5α=432255α=⨯⨯=ππ,42α⎛⎫∴∈ ⎪⎝⎭(2π,3π)αβ+∈,coscos(22)cos(2)cos 2sin(2)sin 2βαβααβααβα∴=+-=+++故选：B.5．答案：Bcos 0θθ-=,得tan θ=则22tan tan 21tan θθθ===-故选:B.6．答案：D解析：法一：由题意，，又为锐角，所以，所以法二：由题意，2cos 12sin α==-22α=，将选项逐个代入验证可知D 选项满足，故选D.sin α∴=222cos sin ααα=-=()cos 2αβ+=()3sin 25αβ∴+=47324525525=-⨯+⨯=2cos 12sin α==-22sin 2α===αsin 02α>sin2α=解析：由tan 3tan αβ==cos 3cos sin αβαβ=,又()sin sin cos cos sin αβαβαβ-=-=sin αβ=cos αβ=所以()sin sin cos cos sin αβαβαβ+=+=8．答案：A解析：ππππsin 2cos 2cos 2cos26336αααα⎛⎫⎛⎫⎛⎫⎛⎫+=-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22ππ1cos22cos 121663αα⎛⎫⎛⎫⎛⎫=-=--=⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭9．答案：AD解析：因为sin()sin()3sin 2B A B A A -++=，所以sin cos cos sin sin cos cos sin 32sin cos B A B A B A B A A A -++=⨯，即sin cos 3sin cos B A A A =.当cos 0A =，即A ===sin c C ==当cos 0A ≠时，sin 3sin B A =，由正弦定理可得3b a =，由余弦定理可得22222(3)7cos 223a b c a a C ab a a +-+-===⋅1=（负值舍去）.综上，1a =或a =10．答案：BCD解析：选项A ：22cos 151cos301︒=+︒=选项B ：sin 27cos3cos 27sin 3sin 30︒︒+︒︒=︒=选项C ：2sin15sin 752sin15cos15sin 30︒=︒︒=︒=212tan 22.51tan 4521tan 22.52︒=⋅=⋅︒=-︒故选：BCD.11．答案：BCD解析：A:因为()11sin 45cos 45sin 245sin 9022︒︒=⨯︒=︒=所以本选项不正确;B:因22ππππcos sin cos 2cos 1212126⎛⎫-=⨯== ⎪⎝⎭所以本选项正确;()4040cos 60sin 40sin 60cos 40sin 6040︒︒=︒︒+︒︒=︒+︒()sin 18080sin 80=︒-︒=︒,所以本选项正确;()11tan 222.5tan 4522=⨯︒=︒=所以本选项正确,故选:BCD 解析：tan ,tan αβ是方程2330x x --=的两个实数根，则有tan tan 3αβ+=，tan tan 3αβ=-，因此()tan tan tan 1tan tan αβαβαβ++==-()()()232tan22291tan 116αβαβαβ++===-+-.13．答案：2解析：因为()tan13tan 32tan 45tan 133211tan13tan 32︒+︒︒=︒+︒==-︒︒,整理得tan13tan 32tan13tan 321︒+︒+︒︒=,所以(1tan13)(1tan 32)1tan 32tan13tan 32tan13112+︒+︒=+︒+︒+︒︒=+=.故答案为:214．答案：4为解析：因为()()4tan 114tan 17A B +-=,所以()tan tan 41tan tan A B A B -=+⋅,所以()tan tan tan 41tan tan A BA B A B--==+⋅,故答案为:4（2）13tan(2)9αβ-=解析：（1）因为sin α=π0,2⎛⎫∈ ⎪⎝⎭，所以cos α==所以ππsin sin cos cos 44ααα⎛⎫+=+ ⎪⎝⎭3455==（2）由（1）tan α=232tan 291tan 116ααα===--所以()241tan2tan73tan 22411tan2tan 173αβαβαβ---===++⨯16．答案：（1）2π3C ==sin 2sin cos A B C B +=,且()sin sin sin cos cos sin A B C B C B C =+=+,即2sin cos 2cos sin sin 2sin cos B C B C B C B ++=,则2sin cos sin 0B C B +=,且()0,πB ∈,则sin 0B ≠,可得cos C =且()0,πC ∈,所以C =（2）因为32a b c +=且3a =,则290b c =->,可得c >由余弦定理可得2222cos c a b ab C =+-,即()()22192923292c c c ⎛⎫=+--⨯-⨯- ⎪⎝⎭,整理可得210210c c -+=,解得7c =或3c =（舍去）,所以ABC△的外接圆半径2sin cR C===17．答案：（1）答案见解析（2）()0,1解析：（1）由A B=1sin A =+1sin A =+,则()2cos 1sin sin A A A =+整理得22sin sin 10AA +-=,解之得sin A =1A =-又0A <<A =B =2π3=（2）A ,B 为ABC△的内角,则1sin 0A +>1sin =+0>,则A 、B 均为锐角222cos sin 1tancos π222tan tan 1sin 42(sin cos )1tan222A A AA AB A A A A --⎛⎫====- ⎪+⎝⎭++又0B <<π42A <-<π4B =π4B <<则π22A B =-,则πsin sin 2cos 22A B B ⎛⎫=-= ⎪⎝⎭22sin 2cos 22cos 112cos 2cos 2cos cos cos b A b B B B b B b B B B-====-令cos t B =π04B ⎛<< ⎝1t <<又()2f t t =⎫⎪⎪⎭单调递增,0f =,(1)1f =可得1021t t <-<,则2cos B -)0,1,)0,1（2）详见解析解析：（1）在ABC △中，内角A，B ，C 的对边分别为a ，b ，c ，cos 0A=>，∴sin A ==5=，∴sin sinb A B a ===又5ba =>=，A B >，∴B=（2） ()sin sin C A B =+=+=∴sin sin a Cc A===∵23CD BD BC BA BC =-=-∴(222220333CD BA BA BC BA BA BC BA ⎛⎫⋅=-⋅=-⋅=⨯-= ⎪⎝⎭，∴CD BA ⊥ ，∴CD AB ⊥.19．答案：（1）π6B =解析：（1）cos b A c = ,∴由正弦定理可得sin cos sin B A A C +=,又()sin sin sin cos cos sin ,C A B A B A B =+=+sin cos A A B =sin 0A ≠,cos B ∴=()0,πB ∈ ,π6B ∴=;（2）π6B = ,c =∴由余弦定理可得cosB ==2233b a -+=,又2a b +=,解得1a b ==,111cos 1222ABC S a B ∴==⨯=△;（3）因为απ5π36α<+<又因为π4πsin sin 353α⎛⎫+=<= ⎪⎝⎭，所以α则π3cos ,35α⎛⎫+==- ⎪⎝⎭ππππ3sin sin cos 63235ααα⎛⎫⎛⎫⎛⎫-=+-=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.。

三角恒等变换专题复习带答案

三角恒等变换专题复习教学目标：1、能利用单位圆中的三角函数线推导出 απαπ±±,2的正弦、余弦、正切的诱导公式；2、理解同角三角函数的基本关系式：；3、可熟练运用三角函数见的基本关系式解决各种问题; 教学重难点：可熟练运用三角函数见的基本关系式解决各种问题基础知识一、同角的三大关系：① 倒数关系 tan α•cot α=1 ② 商数关系 sin cos αα= tan α ； cos sin αα= cot α ③ 平方关系 22sin cos 1αα+=温馨提示：1求同角三角函数有知一求三规律,可以利用公式求解,最好的方法是利用画直角三角形速解;来源:学+科+网2利用上述公式求三角函数值时,注意开方时要结合角的范围正确取舍“±”号;二、诱导公式口诀：奇变偶不变,符号看象限用诱导公式化简,一般先把角化成,2k z α+∈的形式,然后利用诱导公式的口诀化简如果前面的角是90度的奇数倍,就是 “奇”,是90度的偶数倍,就是“偶”；符号看象限是,把α看作是锐角,判断角2k πα+在第几象限,在这个象限的前面三角函数的符号是 “+”还是“--”,就加在前面;用诱导公式计算时,一般是先将负角变成正角,再将正角变成区间0(0,360)的角,再变到区间00(0,180)的角,再变到区间00(0,90)的角计算;三、和角与差角公式：sin()sin cos cos sin αβαβαβ±=±; cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=变用 tan α±tan β=tan α±β1 tan αtan β四、二倍角公式：sin 2α= 2sin cos αα.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-五、注意这些公式的来弄去脉这些公式都可以由公式cos()cos cos sin sin αβαβαβ±=推导出来;六、注意公式的顺用、逆用、变用;如：逆用sin cos cos sin sin()αβαβαβ±=± 1sin cos sin 22ααα=变用22cos 1cos 2αα+=22cos 1sin 2αα-= 21cos 4cos 22αα+= 七、合一变形辅助角公式把两个三角函数的和或差化为“一个三角函数,一个角,一次方”的 B x A y ++=)sin(ϕϖ形式;()22sin cos αααϕA +B =A +B +,其中tan ϕB=A．八、万能公式ααα2tan 1tan 22sin += ααα22tan 1tan 12cos +-= ααα2tan 1tan 22tan -=九、用αsin ,αcos 表示2tanααααααsin cos 1cos 1sin 2tan-=+=十、积化和差与和差化积积化和差 )]sin()[sin(cos sin βαβαβα-++=； )]sin()[sin(sin cos βαβαβα--+=；)]cos()[cos(cos cos βαβαβα-++=； )]cos()[cos(sin sin βαβαβα--+=.和差化积 2cos2sin2sin sin ϕθϕθϕθ-+=+2sin 2cos 2sin sin ϕθϕθϕθ-+=- 2cos 2cos 2cos cos ϕθϕθϕθ-+=+ 2sin 2sin 2cos cos ϕθϕθϕθ-+=-十一、方法总结1、三角恒等变换方法观察角、名、式→三变变角、变名、变式1 “变角”主要指把未知的角向已知的角转化,是变换的主线,如α=α+β－β=α－β+β, 2α=α+β+ α－β, 2α=β+α－β－α,α+β=2·错误! , 错误! = α－错误!－错误!－β等.2“变名”指的是切化弦正切余切化成正弦余弦sin cos tan ,cot cos sin αααααα==, 3“变式’指的是利用升幂公式和降幂公式升幂降幂,利用和角和差角公式、合一变形公式展开和合并等; 2、恒等式的证明方法灵活多样①从一边开始直接推证,得到另一边,一般地,如果所证等式一边比较繁而另一边比较简时多采用此法,即由繁到简.②左右归一法,即将所证恒等式左、右两边同时推导变形,直接推得左右两边都等于同一个式子. ③比较法, 即设法证明: "左边－右边=0" 或" 错误! =1";④分析法,从被证的等式出发,逐步探求使等式成立的充分条件,一直推到已知条件或显然成立的结论成立为止,则可以判断原等式成立.例题精讲例1 已知α为第四象限角,化简：ααααααcos 1cos 1sin sin 1sin 1cos +-++-解：1因为α为第四象限角所以原式=αααααα2222cos 1)cos 1(sin sin 1)sin 1(cos --+-- ()ααααααααααsin cos cos 1sin 1sin cos 1sin cos sin 1cos -=---=--+-=例2 已知360270<<α,化简α2cos 21212121++ 解：360270<<α,02cos,0cos <>∴αα所以原式2111cos211cos 22222αα++=+21cos cos cos 222ααα+===- 例3 tan20°+4sin20°解：tan20°+4sin20°=0020cos 40sin 220sin +=0sin(6040)2sin 40cos 20-+00003340sin 403cos 20223cos 20+=== 例4 05天津已知727sin()2425παα-==,求sin α及tan()3πα+．解：解法一：由题设条件,应用两角差的正弦公式得)cos (sin 22)4sin(1027ααπα-=-=,即57cos sin =-αα ①由题设条件,应用二倍角余弦公式得)sin (cos 57)sin )(cos sin (cos sin cos 2cos 25722ααααααααα+-=+-=-== 故51sin cos -=+αα ② 由①和②式得53sin =α,54cos -=α因此,43tan -=α,由两角和的正切公式11325483343344331433tan 313tan )3tan(-=+-=+-=-+=+ααπα 解法二：由题设条件,应用二倍角余弦公式得αα2sin 212cos 257-==, 解得 259sin 2=α,即53sin ±=α 由1027)4sin(=-πα可得57cos sin =-αα由于0cos 57sin >+=αα,且057sin cos <-=αα,故α在第二象限于是53sin =α,从而5457sin cos -=-=αα 以下同解法一小结：1、本题以三角函数的求值问题考查三角变换能力和运算能力,可从已知角和所求角的内在联系均含α进行转换得到．2、在求三角函数值时,必须灵活应用公式,注意隐含条件的使用,以防出现多解或漏解的情形．例 5 已知,,A B C 为锐角ABC ∆的三个内角,两向量(22sin ,cos sin )p A A A =-+,(sin cos ,q A A =-1sin )A +,若p 与q 是共线向量.1求A 的大小；2求函数232sin cos()2C By B -=+取最大值时,B 的大小. 解：122// 2(1)(1+)- p q sinA sinA sin A cos A ∴-=22220 120cos A cos A cos A ∴+=∴+= 1cos 2A 2∴=-0<2A<π,002A 120 A=60∴=∴200A=60 B+C=120∴ 2013y=2sin B+cos(602B)1cos 2B+cos 2B sin 2B 22-=-+31 =sin 2B cos 2B+1=sin(2B )1226π--+ , 2B B 623πππ-=当时，即=．小结：三角函数与向量之间的联系很紧密,解题时要时刻注意例6 设关于x 的方程sinx ＋3cosx ＋a ＝0在0, 2π内有相异二解α、β.1求α的取值范围; 2求tan α＋β的值. 解: 1∵sinx ＋3cosx ＝221sinx ＋23cosx ＝2 sinx ＋3π, ∴方程化为sinx ＋3π＝－2a.∵方程sinx ＋3cosx ＋a ＝0在0, 2π内有相异二解, ∴sinx ＋3π≠sin 3π＝23 .又sinx ＋3π≠±1 ∵当等于23和±1时仅有一解, ∴|－2a |<1 . 且－2a≠23. 即|a |<2且a ≠－3.∴ a 的取值范围是－2, －3∪－3, 2.2 ∵α、 β是方程的相异解, ∴sin α＋3cos α＋a ＝0 ①. sin β＋3cos β＋a ＝0 ②. ①－②得sin α－ sin β＋3 cos α－ cos β＝0. ∴ 2sin2βα-cos2βα+－23sin2βα+sin2βα-＝0, 又sin2βα+≠0, ∴tan2βα+＝33.∴tan α＋β＝2tan22tan22βαβα+-+＝3.小结：要注意三角函数实根个数与普通方程的区别,这里不能忘记0, 2π这一条件. 例7 已知函数()x x m x f cos sin 2-=在区间⎪⎭⎫⎝⎛2,0π上单调递减,试求实数m 的取值范围．解：已知条件实际上给出了一个在区间⎪⎭⎫⎝⎛2,0π上恒成立的不等式．任取∈21,x x ⎪⎭⎫⎝⎛2,0π,且21x x <,则不等式()()21x f x f >恒成立,即>-11cos sin 2x x m 22cos sin 2x x m -恒成立．化简得()()2112sin 2cos cos x x x x m ->- 由2021π<<<x x 可知：0cos cos 12<-x x ,所以()1221cos cos sin 2x x x x m --<上式恒成立的条件为：()上的最小值，在区间⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛--<20cos cos sin 21221πx x x x m . 由于()2sin 2cos 22sin 2sin 22cos 2sin4cos cos sin 22121212121211221x x x x x x x x x x x x x x x x +-=-+--=-- 2sin2cos 2cos 2sin 2sin 2sin 2cos 2cos 221212121x x x x x x x x +⎪⎭⎫ ⎝⎛+=2tan2tan 2tan 2tan 122121x x x x +⎪⎭⎫ ⎝⎛+=且当2021π<<<x x 时,42,2021π<<x x ,所以 12tan ,2tan 021<<x x , 从而 02tan 12tan 12tan 2tan 2tan 2tan1212121>⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+x x x x x x , 有 22tan2tan 2tan 2tan 122121>+⎪⎭⎫ ⎝⎛+x x x x , 故 m 的取值范围为]2,(-∞.基础精练1．已知α是锐角,且sin 错误!＝错误!,则sin 错误!的值等于A.错误! B ．－错误! C.错误! D ．－错误!2．若－2π＜α＜－错误!,则错误!的值是A ．sin 错误!B ．cos 错误!C ．－sin 错误!D ．－cos 错误!3.错误!·错误!等于A.－sinαB.－cosαC.sinαD.cosα4.已知角α在第一象限且cosα＝错误!,则错误!等于A.错误!B.错误!C.错误!D.－错误!5.定义运算错误!＝ad －bc.若cosα＝错误!,错误!＝错误!,0<β<α<错误!,则β等于A.错误!B.错误!C.错误!D.错误!6.已知tanα和tan 错误!－α是方程ax 2＋bx ＋c ＝0的两个根,则a 、b 、c 的关系是A.b ＝a ＋cB.2b ＝a ＋cC.c ＝b ＋aD.c ＝ab7.设a ＝错误!sin56°－cos56°,b ＝cos50°cos128°＋cos40°cos38°,c ＝错误!,d ＝错误!cos80°－2cos 250°＋1,则a,b,c,d 的大小关系为A.a ＞b ＞d ＞cB.b ＞a ＞d ＞cC.d ＞a ＞b ＞cD.c ＞a ＞d ＞b8．函数y ＝错误!sin2x ＋sin 2x,x ∈R 的值域是A.错误!B.错误!C.错误!D.错误!9.若锐角α、β满足1＋错误!tanα1＋错误!tanβ＝4,则α＋β＝ .10.设α是第二象限的角,tanα＝－错误!,且sin 错误!<cos 错误!,则cos 错误!＝ .11.已知sin-4πx=135,0<x<4π,求)4cos(2cos x x +π的值;12.若),0(,πβα∈,31tan ,507cos -=-=βα,求α+2β;拓展提高1、设函数fx ＝sin 错误!－错误!－2cos 2错误!＋11求fx 的最小正周期.2若函数y ＝gx 与y ＝fx 的图像关于直线x ＝1对称,求当x ∈0,错误!时y ＝gx 的最大值2.已知向量a ＝cosα,sinα,b ＝cosβ,sinβ,|a －b|＝错误!1求cosα－β的值；2若0<α<错误!,－错误!<β<0,且sinβ＝－错误!,求sinα.3、求证：αβαsin 2sin ）（+－2cos α+β=αβsin sin .基础精练参考答案4．C 解析原式＝错误!＝错误!＝错误!＝2×cosα＋sinα＝2×错误!＋错误!＝错误!. 5.D 解析依题设得：sinα·cosβ－cosα·sinβ＝sin α－β＝错误!.∵0<β<α<错误!,∴cosα－β＝错误!. 又∵cosα＝错误!,∴sinα＝错误!.sinβ＝sinα－α－β＝sinα·cosα－β－cosα·sinα－β ＝错误!×错误!－错误!×错误!＝错误!,∴β＝错误!.6.C 解析tan tan()4,tan tan(),4b a c a πααπαα⎧+-=-⎪⎪⎨⎪-=⎪⎩∴tan 错误!＝tan 错误!－α＋α＝错误!＝1,∴－错误!＝1－错误!,∴－b ＝a －c,∴c ＝a ＋b.7.B 解析a ＝sin56°－45°＝sin11°,b ＝－sin40°cos52°＋cos40°sin52°＝sin52°－40°＝sin12°,c ＝错误!＝cos81°＝sin9°,d ＝错误!2cos 240°－2sin 240°＝cos80°＝sin10°∴b ＞a ＞d ＞c.8.C 解析y ＝错误!sin2x ＋sin 2x ＝错误!sin2x －错误!cos2x ＋错误!＝错误!sin 错误!＋错误!,故选择C. 9. 错误!解析由1＋错误!tanα1＋错误!tanβ＝4,可得错误!＝错误!,即tanα＋β＝错误!. 又α＋β∈0,π,∴α＋β＝错误!.10. －错误!解析：∵α是第二象限的角,∴错误!可能在第一或第三象限,又sin 错误!<cos 错误!,∴错误!为第三象限的角, ∴cos 错误!<0.∵tanα＝－错误!,∴cosα＝－错误!,∴cos 错误!＝－错误!＝－错误!.12.解析∵),0(,πβα∈,507cos -=α∴),0,33(71tan -∈-=α),0,33(31tan -∈-=β∴),65(,ππβα∈,α+2β)3,25(ππ∈,又tan2β=43tan 1tan 22-=-ββ,12tan tan 12tan tan )2tan(-=-+=+βαβαβα,来源:Zxxk ∴α+2β=411π拓展提高参考答案1、解析 1fx ＝sin 错误!cos 错误!－cos 错误!sin 错误!－cos 错误!x ＝错误!sin 错误!x －错误!cos 错误!x＝错误!sin 错误!x －错误!,故fx 的最小正周期为T ＝错误!＝82法一：在y ＝g x 的图象上任取一点 x,gx,它关于x ＝1的对称点2－x,gx.由题设条件,点2－x ,gx 在y ＝fx 的图象上,从而gx ＝f2－x ＝错误!sin 错误!2－x －错误! ＝错误!sin 错误!－错误!x －错误!＝错误!cos 错误!x ＋错误!,当0≤x≤错误!时, 错误!≤错误!x ＋错误!≤错误!,因此y ＝gx 在区间0,错误!上的最大值为gx max ＝错误!cos 错误!＝错误!.法二：因区间0,错误!关于x ＝1的对称区间为错误!,2,且y ＝gx 与y ＝fx 的图象关于x ＝1对称,故y ＝gx 在0,错误!上的最大值为y ＝fx 在错误!,2上的最大值,由1知fx ＝错误!sin 错误!x －错误!, 当错误!≤x ≤2时,－错误!≤错误!x －错误!≤错误!,因此y ＝gx 在0,错误!上的最大值为gx max ＝错误!sin 错误!＝错误!.2、解析1∵a ＝cos α,sinα,b ＝cosβ,sinβ, ∴a －b ＝cosα－cosβ,sinα－sinβ. ∵|a －b|＝错误!,∴错误!＝错误!, 即2－2cosα－β＝错误!,∴cosα－β＝错误!.2∵0<α<错误!,－错误!<β<0,∴0<α－β<π,∵cosα－β＝错误!,∴sinα－β＝错误! ∵sin β＝－错误!,∴cosβ＝错误!,∴sinα＝sinα－β＋β＝sinα－βcosβ＋cosα－βsinβ＝错误!·错误!＋错误!·－错误!＝错误!。

三角恒等变换含答案

三角恒等变换一、单选题1．已知α是第二象限角，tan()74πα-=-，则sin()3πα+=（）A B C D 2．已知锐角θ满足2sin 263θπ⎛⎫+= ⎪⎝⎭，则5cos 6πθ⎛⎫+⎪⎝⎭的值为（）A ．19-B C ．19D ． 3．2002年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形。

如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么cos2θ的值等于（）A ．45B ．725C ．725-D ．354．已知锐角α满足3cos()65πα+=，则sin(2)3πα+=（） A ．1225B ．1225±C ．2425D ．2425±5．sin 3πα⎛⎫-= ⎪⎝⎭，0,2πα⎛⎫∈ ⎪⎝⎭，则cos α=（）A B C D6．已知22ππαβ--＜＜，sin 2cos 1αβ-=，2cos sin αβ+=则3s i n πβ⎛⎫-= ⎪⎝⎭ （）A ．3B ．3C ．3±D ．3±7．若,αβ都是锐角，且cos 5α=，3sin()5αβ+=，则cos β= （）A B C D 8．已知方程x 2+3ax +3a +1=0（a ＞1）的两根分别为tanα，tanβ，且22ππαβ⎛⎫∈- ⎪⎝⎭，，，则α+β=（）. A ．34π或34π-B ．4π-或4πC ．4π D ．34π-9．已知角,αβ均为锐角，且cos αβ==αβ-的值为（） A ．3πB ．4π C ．4π-D ．4π或4π-10．已知 πsin()4α+=，则 3πsin()4α-的值为 ( )．A ．B ．2C ．－12D ．1211．已知函数()212cos 2f x x x =+-，若其图象是由sin 2y x =图象向左平移ϕ（0ϕ>）个单位得到，则ϕ的最小值为（） A ．6πB ．56π C ．12πD ．512π 12．已知函数()sin sin 3f x x x =-，[0,2]x πÎ，则()f x 的所有零点之和等于（） A ．5πB ．6πC ．7πD ．8π13．若函数()sin cos f x a x b x =+在3x π=处取得最大值4，则ab=（）A ．1B C ．2D ．314．已知函数()sin f x a x x =-图象的一条对称轴为6x π=-，若()()124f x f x ⋅=-，则12x x +的最小值为（）A ．3π B ．πC ．23π D ．43π二、填空题15．计算：tan 20tan 40tan120tan 20tan 40++=_______________.16．cos102cos20cos10-⋅=____________． 17．已知()2sin 3αβ+=，()2sin 5αβ-=，则tan tan αβ的值为__________；18．已知αβ，均为锐角，1sin())663ππαβ-=+=，cos()αβ+=________. 19．函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为_________. 20．若奇函数()f x 在其定义域R 上是单调减函数，且对任意的R x ∈，不等式()()cos2sin sin 0f x x f x a ++-≤恒成立，则a 的最大值是_____．21．已知等腰三角形顶角的余弦值为725-，则这个三角形底角的正切值．．．为______ 22．o o oosin58+cos60sin2cos2=____________.23．已知π1sin cos 63αα⎛⎫--=⎪⎝⎭，则πcos 23α⎛⎫+= ⎪⎝⎭__________．24．设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则sin 2θ=______．25．若函数2()4sin sin cos 2(0)42x f x x x πωωωω⎛⎫=⋅++>⎪⎝⎭在2,23ππ⎡⎤-⎢⎥⎣⎦上是增函数，则ω的取值范围是____________.26．如图，某园林单位准备绿化一块直径为BC 的半圆形空地，ABC ∆外的地方种草，ABC ∆的内接正方形PQRS 为一水池，其余的地方种花，若BC a =，ABC θ∠=，设ABC ∆的面积为1S ，正方形PQRS 的面积为2S ，当a 固定，θ变化时，则12S S 的最小值是__________．27．已知函数()()()cos sin sin cos f x a x b x =-没有零点，则22a b +的取值范围是_______三、解答题 28．（1cos103sin10-；（2）求值tan 70tan 503tan 70tan 50+-= 29．已知()222x x x f x sincos sin a ⎛⎫=⋅++ ⎪⎝⎭ （1）求实数a 的值；（2）若443f f ππαα⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭，求2141tan παα⎛⎫-+ ⎪⎝⎭+的值． 30．（1）已知51sin π123α⎛⎫+=⎪⎝⎭，求πsin 12α⎛⎫- ⎪⎝⎭的值．（2）已知角α的终边过点()43P ,-，β为第三象限角，且4tan 3β=，求()c o s αβ-的值.31．（1）求值: sin 7cos15sin8cos7sin15sin8︒+︒︒︒-︒︒；（2）已知10sin cos ,25x x x π-<<+=，，求sin cos x x -的值. 32．已知1tan()2αβ-=，1tan 7β=-，且,(0,)αβπ∈，求2αβ-的值 33．已知32ππα<<，32ππβ<<，sin α=，cos β=αβ-的值. 34．已知α，β为锐角，且17cos α=，()1114cos αβ+=-．求sinβ的值． 35．计算（1）已知2sin cos 0αα-=，求sin cos sin cos sin cos sin cos αααααααα-+++-的值；（2）求()214cos 102sin10︒+︒-︒的值. 36．已知2sin cos 3αα+=，且2παπ<<，求下列各式的值（1）sin cos αα-（2）cos()24sin()4πααπα+++37．已知sin(2)7αβ-=11cos(2)14αβ-=-， 042ππβα<<<<，(1)求tan(2)αβ-的值； (2)求cos()αβ+以及αβ+的值38．计算（1）23sin12(4cos 122)--；（240sin 50(13tan10).701cos 40+++39．已知函数2()2cos cos cos .22x xf x x x =+ (1)求函数f (x )的最小正周期； (2)求函数f (x )在区间,64ππ⎡⎤-⎢⎥⎣⎦上的值域.40．已知函数2()sinsin 1(02f x x x x πωωωω⎫⎛⎫=+⋅+-> ⎪⎪⎝⎭⎭的相邻两条对称轴之间的距离为2π．（1）求ω的值；（2）当,122x ππ⎡⎤∈-⎢⎥⎣⎦时，求函数()f x 的值域. 41．如图，OPQ 是半径为2，圆心角为3π的扇形，C 是扇形弧上的一动点，记COP θ∠=，四边形OPCQ 的面积为S ．（1）找出S 与θ的函数关系；（2）试探求当θ取何值时，S 最大，并求出这个最大值．42．已知函数2()sin cos (0)f x x x x =>ωωωω的最小正周期为2π，（1）求函数()f x 的单调递减区间；（2）若函数()()g x =f x +m 在区间0,4⎡⎤⎢⎥⎣⎦π上有两个零点，求实数m 的取值范围. 43．为迎接2020年奥运会，某商家计划设计一圆形图标，内部有一“杠铃形图案”（如图阴影部分），圆的半径为1米，AC ，BD 是圆的直径，E ，F 在弦AB 上，H ，G 在弦CD 上，圆心O 是矩形EFGH 的中心，若23EF =米，2AOB θ∠=，5412ππθ≤≤.（1）当3πθ=时，求“杠铃形图案”的面积；（2）求“杠铃形图案”的面积的最小值.参考答案1．C 【解析】由tan 74πα⎛⎫-=- ⎪⎝⎭，得171tan tan αα-=-+，解得34tan α=-. 又α是第二象限角，可得34sin ,cos 55αα==-.则314sin 333525sin cos cos sin πππααα⎛⎫+=+=⨯-= ⎪⎝⎭. 故选C. 2．D 【解析】分析：由二倍角公式得cos 3πθ⎛⎫+⎪⎝⎭，再由5cos ?cos sin 6323ππππθθθ⎛⎫⎛⎫⎛⎫+=++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，结合同角三角函数关系可得解.详解：由2sin 263θπ⎛⎫+=⎪⎝⎭，得28112sin 12699θπ⎛⎫-+=-= ⎪⎝⎭，即1cos 39πθ⎛⎫+= ⎪⎝⎭，由θ为锐角，且1cos 039πθ⎛⎫+=> ⎪⎝⎭，所以3πθ+因为锐角，所以sin 03πθ⎛⎫+> ⎪⎝⎭.5cos cos sin 6323ππππθθθ⎛⎫⎛⎫⎛⎫+=++=-+== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故选D.点睛：解决三角变换中的给值求值问题时，一定要注意先化简再求值，同时要注意所给条件在解题中的整体作用． 3．B 【解析】【分析】根据两个正方形的面积求出两个正方形的边长,进而用三角函数表示边长求出三角函数值,再利用二倍角公式求解即可. 【详解】由大正方形面积为25,小正方形面积为1.易得大正方形边长为5,小正方形边长为1.由图有15cos 5sin 1cos sin 5θθθθ-=⇒-=,故221cos sin 5cos sin 1θθθθ⎧-=⎪⎨⎪+=⎩ ,因为较小的锐角为θ,故4cos 53sin 5θθ⎧=⎪⎪⎨⎪=⎪⎩.故2247cos 22cos 121525θθ⎛⎫=-=⨯-= ⎪⎝⎭ 故选：B 【点睛】本题主要考查了由图像求解三角函数值的问题,需要根据图像到三角函数的关系式再求解,属于中等题型. 4．C 【解析】【分析】利用诱导公式，求得sin()6πα+的值，再利用倍角公式，即可求解.【详解】因为锐角α满足3cos()65πα+=，所以6πα+也是锐角，由三角函数的基本关系式可得4sin()65πα+==，则24sin(2)2sin()cos()36625πππααα+=++=，故选C. 【点睛】本题主要考查了三角函数的化简求值问题，其中解答中熟记三角函数的诱导公式和三角函数的倍角公式，准确运算是解答的关键，着重考查了推理与运算能力，属于基础题. 5．B 【解析】【分析】根据sin 3πα⎛⎫-= ⎪⎝⎭和0,2πα⎛⎫∈ ⎪⎝⎭，得到sin 3πα⎛⎫- ⎪⎝⎭和cos 3πα⎛⎫- ⎪⎝⎭的值，将所求的cos α转化为cos 33ππα⎡⎤⎛⎫-+ ⎪⎢⎥⎝⎭⎣⎦，利用两角和的余弦公式，得到答案.【详解】因为sin 33πα⎛⎫-=⎪⎝⎭，所以sin 33πα⎛⎫-=- ⎪⎝⎭，因为0,2πα⎛⎫∈ ⎪⎝⎭，所以cos 33πα⎛⎫-==⎪⎝⎭，所以cos cos 33ππαα⎡⎤⎛⎫=-+⎪⎢⎥⎝⎭⎣⎦cos cos sin sin 3333ππππαα⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭12⎛=- ⎝⎭36+=. 故选：B. 【点睛】本题考查同角三角函数关系，两角和的余弦公式，属于简单题. 6．B 【解析】【分析】两式平方相加利用两角和与差的公式可化为()54sin 3αβ--=，再根据22ππαβ-<-<得出6παβ=+，代入2cos sin αβ+=.【详解】将两个等式两边平方可得2222sin 4sin cos 4cos 1cos 4cos sin 4sin 2ααββααββ⎧-⋅+=⎨+⋅+=⎩，两式相加可得()54sin 3αβ--=，所以()1sin 2αβ-=， 22ππαβ-<-<，6παβ∴-=，即6παβ=+，代入2cos sin αβ+=3sin 2ββ+=，所以sin 63πβ⎛⎫+= ⎪⎝⎭，故选：B 【点睛】本题主要考查三角函数的化简求值，需熟记两角和与差的公式以及常见的三角函数值，属于中档题. 7．A 【解析】【分析】先计算出()cos αβ+，再利用余弦的和与差公式，即可. 【详解】因为,αβ都是锐角，且1cos 2α=<，所以,32ππα<<又()31sin 52αβ+=>，所以2παβπ<+<，所以()4cos 5αβ+==-sin α==，cos β=()()()cos cos cos sin sin αβααβααβα+-=+++ 25=，故选A.【点睛】本道题考查了同名三角函数关系和余弦的和与差公式，难度较大。

三角恒等变换(含答案)

2
4
4
4
从而 sin
−
4
=
−
4 5
，因此
tan
−
4
=
−
4 3
．故填
−
4 3
．
评注：此处的角还可由 cos
−
4
=
3 5
缩小至 2k +
2
−
4
2k
+
7 4
(k
Z)
，但没必要．
另外，还可利用
tan
−
π 4
tan
+
π 4
=
−1 来进行处理，或者直接进行推演，即由题意
cos
+
4
4
5
（A） 7 25
（B） 1 5
（C） − 1 5
（D） − 7 25
【解析】因为
cos
π 4
−
=
3 5
，
2 (cos + sin ) = 3，所以 cos + sin = 3
2
5
5
2 ，两边平方得，
1+sin 2 = 18 sin 2 = 7 ．故选 D．
25
25
2
解法二：
cos 2
4
= − 1 ．选 A 2
2
1+
cos
2
22
2
2
2
4．【2010 新课标文 10】若 sin = − 4 ，是第三象限的角，则 sin( + ) = （）
5
4
（A） − 7 2 10
（B） 7 2 10
（C） − 2 10

三角恒等变换综合 (详细答案)

题一函数f (x )=sin x (cos x －sin x )的最小正周期是( ) A.π4 B. π2C. πD. 2π 答案：注意公式选用同类题一题面：函数y ＝2cos x (sin x ＋cos x )的最大值和最小正周期分别是( ) A ．2，π B.2＋1，π C ．2,2πD.2＋1,2π答案：B. 详解：y ＝2cos x sin x ＋2cos 2x ＝sin 2x ＋cos 2x ＋1＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4＋1，所以当2x ＋π4＝2k π＋π2(k ∈Z )，即x ＝k π＋π8(k ∈Z )时取得最大值2＋1，最小正周期T ＝2π2＝π.同类题二题面：函数f (x )＝cos ⎝ ⎛⎭⎪⎫－x 2＋sin ⎝ ⎛⎭⎪⎫π－x 2，x ∈R . 求f (x )的最小正周期；答案：4π.详解：f (x )＝cos ⎝⎛⎭⎪⎫－x 2＋sin ⎝⎛⎭⎪⎫π－x 2＝sin x 2＋cos x 2＝2sin ⎝ ⎛⎭⎪⎫x 2＋π4.∴f (x )的最小正周期T ＝2π12＝4π.题二题面：设θ为第二象限角，若π1tan()42θ+=，则sin cos θθ+=______．答案：同类题一题面：若tan θ＋1tan θ＝4，则sin 2θ＝()A.15 B.14 C.13 D.12答案：D. 详解：∵tan θ＋1tan θ＝4，∴sin θcos θ＋cos θsin θ＝4，∴sin2θ＋cos2θcos θsin θ＝4，即2sin 2θ＝4，∴sin 2θ＝1 2.同类题二题面：已知tan θ＝2，则sin⎝⎛⎭⎪⎫π2＋θ－cos π－θsin⎝⎛⎭⎪⎫π2－θ－sin π－θ＝()A．2 B．－2C．0 D.2 3答案：B. 详解：原式＝cos θ＋cos θcos θ－sin θ＝21－tan θ＝21－2＝－2.题一题面：在△ABC中，若2cos B sin A=sin C，则△ABC的形状一定是( )A. 等腰直角三角形B. 直角三角形C. 等腰三角形D.等边三角形答案：C同类题一题面：已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，a ＝80，b ＝100，A ＝30°，则此三角形( )A ．一定是锐角三角形B ．一定是直角三角形C ．一定是钝角三角形D ．可能是直角三角形，也可能是锐角三角形答案：C. 详解：依题意得a sin A ＝b sin B ，sin B ＝b sin A a ＝100sin 30°80＝58，12<58<32，因此30°<B <60°，或120°<B <150°.若30°<B <60°，则C ＝180°－(B ＋30°)>90°，此时△ABC 是钝角三角形；若120°<B <150°，此时△ABC 仍是钝角三角形．因此，此三角形一定是钝角三角形，选C.同类题二题面：在三角形ABC 中，若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫32π＋B tan (C －π)<0，求证：三角形ABC 为钝角三角形．答案：见详解.详解：若cos ⎝ ⎛⎭⎪⎫π2＋A sin ⎝ ⎛⎭⎪⎫32π＋B tan (C －π)<0，则(－sin A )(－cos B )tan C <0，即sin A cos B tan C <0，∵在△ABC 中，0<A <π，0<B <π，0<C <π， ∴sin A >0，⎩⎨⎧ cos B <0，tan C >0或⎩⎨⎧tan C <0，cos B >0，∴B 为钝角或C 为钝角，故△ABC 为钝角三角形．题二题面：设π,2Zkkα≠∈，sin tancos cotTαααα+=+，则( )A. T < 0B. T ≤ 0C. T > 0D. T的值可正可负答案：同类题一题面：三角形ABC是锐角三角形，若角θ终边上一点P的坐标为(sin A－cos B，cosA－sin C)，则sin θ|sin θ|＋cos θ|cos θ|＋tan θ|tan θ|的值是()A．1 B．－1C．3 D．4答案：B.详解：因为三角形ABC是锐角三角形，所以A＋B>90°，即A>90°－B，则sin A>sin(90°－B)＝cos B，sin A－cos B>0，同理cos A－sin C<0，所以点P在第四象限，sin θ|sin θ|＋cos θ|cos θ|＋tan θ|tan θ|＝－1＋1－1＝－1，故选B.同类题二题面：已知α为第二象限角，则cos α1＋tan2α＋sin α1＋1tan2α＝________.答案：0. 详解：原式＝cos α1＋sin2αcos2α＋sin α1＋cos2αsin2α＝cos α1cos2α＋sin α1sin2α＝cos α1－cos α＋sin α1sin α＝0.题三题面：求值：oo o o tan 20tan 4020tan 40++.答案： 3同类题一题面：若α＋β＝3π4，则(1－tan α)(1－tan β)的值是________．答案：2. 详解：－1＝tan 3π4＝tan(α＋β)＝tan α＋tan β1－tan αtan β，∴tan αtan β－1＝tan α＋tan β. ∴1－tan α－tan β＋tan αtan β＝2，即(1－tan α)(1－tan β)＝2.同类题二题面：若tan α＝lg(10a )，tan β＝lg ⎝ ⎛⎭⎪⎫1a ，且α＋β＝π4，则实数a 的值为( )A ．1B.110 C ．1或110D ．1或10答案：C. 详解：tan(α＋β)＝1⇒tan α＋tan β1－tan αtan β＝lg 10a ＋lg ⎝ ⎛⎭⎪⎫1a 1－lg 10a ·lg ⎝ ⎛⎭⎪⎫1a ＝1⇒lg 2a ＋lg a ＝0，所以lg a ＝0或lg a ＝－1，即a ＝1或110.题四题面：设当x θ=时，函数f (x )=sin x －2cos x 取得最大值，则cos θ=______答案：5-同类题一题面：当函数y ＝sin x －3cos x (0≤x <2π)取得最大值时，x ＝________. 答案：56π. 详解：利用正弦函数的性质求解． ∵y ＝sin x －3cos x (0≤x <2π)， ∴y ＝2sin ⎝ ⎛⎭⎪⎫x －π3(0≤x <2π)．由0≤x <2π知，－π3≤x －π3<5π3，∴当y 取得最大值时，x －π3＝π2，即x ＝56π.同类题二题面：函数f (x )＝sin x －cos ⎝ ⎛⎭⎪⎫x ＋π6的值域为( )A ．[－2,2]B ．[－3，3]C ．[－1,1] D.⎣⎢⎡⎦⎥⎤－32，32答案：[－3，3]．详解：将函数化为y ＝A sin(ωx ＋φ)的形式后求解．∵f (x )＝sin x －cos ⎝ ⎛⎭⎪⎫x ＋π6＝sin x －cos x cos π6＋sin x sin π6＝sin x －32cos x ＋12sin x ＝3⎝ ⎛⎭⎪⎫32sin x －12cos x＝3sin ⎝ ⎛⎭⎪⎫x －π6(x ∈R )，∴f (x )的值域为[－3，3]．题五题面：已知1sin cos ()1sin cos x xf x x x+-=++，(1)计算f (x )+ f (－x )的值； (2)判断函数f (x )的奇偶性.答案：同类题一题面：已知sin(2α＋β)＝3sin β，设tan α＝x ，tan β＝y ，记y ＝f (x )． (1)求证：tan(α＋β)＝2tan α； (2)求f (x )的解析式．答案： (1)略. (2) f (x )＝x1＋2x 2详解：(1)证明：由sin(2α＋β)＝3sin β，得sin [(α＋β)＋α]＝3sin [(α＋β)－α]，即sin(α＋β)cos α＋cos(α＋β)sin α＝3sin(α＋β)cos α－3cos(α＋β)sin α， ∴sin(α＋β)cos α＝2cos(α＋β)sin α. ∴tan(α＋β)＝2tan α.(2)由(1)得tan α＋tan β1－tan αtan β＝2tan α，即x ＋y1－xy＝2x ，∴y ＝x 1＋2x 2，即f (x )＝x1＋2x 2.同类题二题面：已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫x ＋7π4＋cos ⎝ ⎛⎭⎪⎫x －3π4，x ∈R .(1)求f (x )的最小正周期和最小值；(2)已知cos(β－α)＝45，cos(β＋α)＝－45，0＜α＜β≤π2，求证：[f (β)]2－2＝0. 答案：(1)－2.(2)略. 详解：(1)∵f (x )＝sin ⎝ ⎛⎭⎪⎫x ＋7π4－2π＋cos ⎝ ⎛⎭⎪⎫x －π4－π2＝sin ⎝ ⎛⎭⎪⎫x －π4＋sin ⎝ ⎛⎭⎪⎫x －π4＝2sin ⎝ ⎛⎭⎪⎫x －π4，∴T ＝2π，f (x )的最小值为－2.(2)证明：由已知得cos βcos α＋sin βsin α＝45， cos βcos α－sin βsin α＝－45. 两式相加得2cos βcos α＝0.∵0＜α＜β≤π2，∴β＝π2.∴[f (β)]2－2＝4sin 2π4－2＝0.题一题面：在△ABC 中，若tan A +tan B +tan C >0，则△ABC 是( )A ．直角三角形B ．钝角三角形C ．锐角三角形D ．形状不确定答案：C同类题一题面：在△ABC 中a ，b ，c 分别为内角A ，B ，C 的对边，且2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C .(1)求A 的大小；(2)若sin B ＋sin C ＝1，试判断△ABC 的形状．答案：(1) A ＝120°.(2)等腰的钝角三角形．详解：(1)由已知，根据正弦定理得2a 2＝(2b ＋c )·b ＋(2c ＋b )c ，即a 2＝b 2＋c 2＋bc . 由余弦定理得a 2＝b 2＋c 2－2bc cos A ，故cos A ＝－12，∵0<A <180°，∴A ＝120°. (2)由(1)得sin 2A ＝sin 2B ＋sin 2C ＋sin B sin C ＝34. 又sin B ＋sin C ＝1，解得sin B ＝sin C ＝12.∵0°<B <60°，0°<C <60°，故B ＝C ， ∴△ABC 是等腰的钝角三角形．同类题二题面：已知△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，向量m ＝(4，－1)，n ＝⎝ ⎛⎭⎪⎫cos 2A 2，cos 2A ，且m ·n ＝72.(1)求角A 的大小；(2)若b ＋c ＝2a ＝23，试判断△ABC 的形状．答案：(1)A ＝π3.(2)△ABC 为等边三角形．详解：(1)∵m ＝(4，－1)，n ＝⎝ ⎛⎭⎪⎫cos 2A 2，cos 2A ，∴m ·n ＝4cos 2A2－cos 2A ＝4·1＋cos A 2－(2cos 2A －1)＝－2cos 2A ＋2cos A ＋3. 又∵m ·n ＝72，∴－2cos 2A ＋2cos A ＋3＝72，解得cos A ＝12. ∵0<A <π，∴A ＝π3.(2)在△ABC 中，a 2＝b 2＋c 2－2bc cos A ，且a ＝3， ∴(3)2＝b 2＋c 2－2bc ·12＝b 2＋c 2－bc .①又∵b ＋c ＝23，∴b ＝23－c ，代入①式整理得c 2－23c ＋3＝0，解得c ＝3，∴b ＝ 3，于是a ＝b ＝c ＝ 3，即△ABC 为等边三角形．题二题面：oo 4cos50tan 40- = ( )A B ．2+ C D ．1-答案：C同类题一题面：sin 47°－sin 17°cos 30°cos 17°＝( )A ．－32 B ．－12 C.12 D.32.答案：C.详解：原式＝sin 30°＋17° －sin17°cos 30°cos 17°＝sin 30°cos 17°＋cos 30°sin 17°－sin 17°cos 30°cos 17°＝sin 30°cos 17°cos 17°＝sin 30°＝12.同类题二题面：计算：cos 10°＋3sin 10°1－cos 80°＝________.答案： 2.详解：cos 10°＋3sin 10°1－cos 80° ＝2 s in 30°cos 10°＋cos 30°sin 10° 2sin 240°＝2sin 40°2sin 40°＝ 2.题一题面：方程x 2－2a sin(cos x )+a 2=0仅有一个解，求a 的值.答案：0或2sin1同类题一题面：若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两根，则m 的值为()A ．1＋ 5B ．1－ 5C ．1±5D ．－1－ 5答案：B.详解：由题意知：sin θ＋cos θ＝－m 2，sin θcos θ＝m 4，又(sin θ＋cos θ)2＝1＋2sin θcos θ，∴m 24＝1＋m 2，解得：m ＝1±5，又Δ＝4m 2－16m ≥0，∴m ≤0或m ≥4，∴m ＝1－ 5.同类题二题面：已知sin θ、cos θ是关于x 的方程x 2－ax ＋a ＝0的两根，则a ＝________. 答案：1－ 2详解：由题意知，原方程判别式Δ≥0，即(－a )2－4a ≥0，∴a ≥4或a ≤0.∵⎩⎨⎧sin θ＋cos θ＝a ，sin θcos θ＝a ，又(sin θ＋cos θ)2＝1＋2sin θcos θ，∴a 2－2a －1＝0，∴a ＝1－2或a ＝1＋2(舍去)．。

专题12 三角恒等变换(纯答案)

专题12三角恒等变换答案例1、【答案】A【解析】3cos28cos 5αα-=，得26cos 8cos 80αα--=，即23cos 4cos 40αα--=，解得2cos 3α=-或cos 2α=（舍去），又(0,),sin 3αα∈π∴==. 故选：A ．变式1、【答案】35；13 【解析】2222222222cos sin 1tan 123cos 2cos sin cos sin 1tan 125θθθθθθθθθ---=-====-+++， tan 1211tan()41tan 123πθθθ---===++，故答案为：31,53- 变式2、【解析】由()tan 1tan tan tan 2tan 1πtan 13tan 1tan 4αααααααα-===-++⎛⎫+ ⎪-⎝⎭，得23tan 5tan 20αα--=，解得tan 2α=，或1tan 3α=-. πππsin 2sin 2cos cos 2sin 444ααα⎛⎫+=+ ⎪⎝⎭()22222sin cos cos sin sin 2cos 2=22sin cos αααααααα⎫+-=+⎪+⎝⎭222tan 1tan =2tan 1ααα⎛⎫+- ⎪+⎝⎭，当tan 2α=时，上式222212==22110⎛⎫⨯+- ⎪+⎝⎭ 当1tan 3α=-时，上式=22112()1()33[]=1210()13⨯-+---+综上，πsin 2410α⎛⎫+= ⎪⎝⎭ 变式3、【解析】 (1)因为cos 2β＝－35，cos 2β＝2cos 2β－1，所以 2cos 2β－1＝－35，解得cos 2β＝15.(2分) 因为β为钝角，所以cos β＝－55. 从而sin β＝1－cos 2β＝1－15＝255.(5分) 所以tan β＝sin βcos β＝255－55＝－2.(7分) (2)因为α为钝角，sin α＝35，所以cos α＝－1－sin 2α＝－2531⎪⎭⎫ ⎝⎛-＝－45. (9分) 所以 sin 2α＝2sin αcos α＝2×35×⎪⎭⎫ ⎝⎛-54＝－2425，cos 2α＝1－2sin 2α＝1－2×⎪⎭⎫ ⎝⎛532＝725. (11分) 从而cos (2α＋β)＝cos 2αcos β－sin 2αsin β＝725×⎪⎪⎭⎫ ⎝⎛-55－⎪⎭⎫ ⎝⎛-2524×255 ＝415125.(14分)题型二、变角问题例2、【答案】17【解析】因为sin cos 11cos 2ααα=-，所以2sin cos 2sin ααα=且cos 0α≠，所以1tan 2α=；又1tan()3αβ-=，所以()()()11tan tan 123tan tan 11tan tan 716ααββααβααβ---=--===⎡⎤⎣⎦+-+. 故答案为：17. 变式1、【解析】（1）因为4tan 3=α，sin tan cos =ααα，所以4sin cos 3=αα．因为22sin cos 1+=αα，所以29cos 25=α，因此，27cos 22cos 125=-=-αα．（2）因为,αβ为锐角，所以(0,)+∈παβ．又因为cos()+=αβ，所以sin()+==αβ，因此tan()2+=-αβ．因为4tan 3=α，所以22tan 24tan 21tan 7==--ααα，因此，tan 2tan()2tan()tan[2()]1tan 2tan()11-+-=-+==-++ααβαβααβααβ．变式2、【答案】A【解析】0,2πα⎛⎫∈ ⎪⎝⎭，,444πππα⎛⎫-∈- ⎪⎝⎭4cos 45πα⎛⎫-== ⎪⎝⎭， cos cos cos cos sin sin 444444ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫=-+=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦43525210=⨯-⨯=. 故选：A题型三、求角问题例3、【解析】 (1) 由cos α＝437，α∈⎪⎭⎫ ⎝⎛2,0π，得sin α＝1－cos 2α＝27341⎪⎪⎭⎫ ⎝⎛-＝17.(2分) 所以sin ⎪⎭⎫ ⎝⎛+απ4＝sin π4cos α＋cos π4sin α(4分) ＝22×437＋22×17＝46＋214.(6分) (2) 因为α，β∈⎪⎭⎫ ⎝⎛2,0π，所以α＋β∈(0，π)．又cos (α＋β)＝1114，则sin (α＋β)＝1－cos 2（α＋β）＝214111⎪⎭⎫ ⎝⎛-＝5314.(8分) 所以sin β＝sin (α＋β－α)＝sin (α＋β)cos α－cos (α＋β)sin α(10分)＝5314×437－1114×17＝12.(12分) 因为β∈⎪⎭⎫ ⎝⎛2,0π，所以β＝π6.(14分) 变式【解析】因为锐角α的终边与单位圆交于点A ，且点A 的横坐标是31010，所以由任意角的三角函数的定义可知cos α＝31010，从而sin α＝1－cos 2α＝1010.(2分) 因为钝角β的终边与单位圆交于点B ，且点B 的纵坐标是255，所以sin β＝255，从而cos β＝－1－sin 2β＝－55.(4分) (1) cos(α－β)＝cos αcos β＋sin αsin β＝31010×⎪⎪⎭⎫ ⎝⎛-55＋1010×255＝－210.(8分) (2) sin(α＋β)＝sin αcos β＋cos αsin β＝1010×⎪⎪⎭⎫ ⎝⎛-55＋31010×255＝22.(11分)因为α为锐角，β为钝角，所以α＋β∈⎪⎭⎫⎝⎛232ππ，，所以α＋β＝3π4.(14分) 易错警示求角的大小，经常会因为忽略角的取值范围而导致增解．另外，在求角的大小时，一般地，应首先确定所求角的范围，然后根据角的范围来确定求角的哪个三角函数，通常所选择的那个三角函数应该在范围内是单调的．1、【答案】B 【解析】2217cos 212sin 12()39αα=-=-⨯=. 故选B.2、【答案】D【解析】方法一：由α为第四象限角，可得3222,2k k k απ+π<<π+π∈Z ，所以34244,k k k απ+π<<π+π∈Z此时2α的终边落在第三、四象限及y 轴的非正半轴上，所以sin 20α<，故选：D ．方法二：当6απ=-时，cos 2cos 03απ⎛⎫=-> ⎪⎝⎭，选项B 错误；当3απ=-时，2cos 2cos 03απ⎛⎫=-< ⎪⎝⎭，选项A 错误；由α在第四象限可得：sin 0,cos 0αα<>，则sin 22sin cos 0ααα=<，选项C 错误，选项D 正确；故选：D ．3、【答案】D 【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭，tan 12tan 71tan θθθ+∴-=-，令tan ,1t t θ=≠，则1271t t t+-=-，整理得2440t t -+=，解得2t =，即tan 2θ=. 故选：D ．4、【答案】B【解析】2sin 2cos21αα=+，24sin cos 2cos .0,,cos 02αααααπ⎛⎫∴⋅=∈∴> ⎪⎝⎭，sin 0,α>2sin cos αα∴=，又22sin cos 1αα+=，2215sin 1,sin 5αα∴==，又sin 0α>，sin 5α∴=，故选B ． 5、【答案】13【解析】221sin ())(1sin 2)42παααα+=+=+ 121(1sin 2)sin 2233αα∴+=∴= 故答案为：136、【答案】12- 【解析】因为sin cos 1+=αβ，cos sin 0+=αβ，所以()()221sin cos 1,-+-=αα所以11sin ,cos 22==αβ， ()22111111sin sin cos cos sin cos 1sin 1.224442+=+=⨯-=-+=-+=-αβαβαβαα7、【答案】【解析】由于1sin 4x =，x 为第二象限角，所以cos x ==所以1sin 22sin cos 2448x x x ⎛==⨯⨯-=- ⎝⎭.故答案为：8、【答案】A【解析】2π2π2πππcos 2cos π2cos 2cos 22sin 133333ααααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=--=--=--=-- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 1721168=⨯-=-．故选A ．。

三角恒等变换专题练习(含答案)

三角恒等变换2020.21．若α为第四象限角，则可以化简为（）A．B．C．D．﹣2tanα【解答】解：∵α为第四象限角，∴＝﹣＝﹣＝＝﹣2tanα．故选：D．2．已知cos（13°+α）＝﹣，则sin（﹣64°+2α）的值为（）A．B．C．D．【解答】解：∵cos（13°+α）＝﹣，则sin（﹣64°+2α）＝﹣cos[90°+（﹣64°+2α）]＝﹣cos（26°+2α）＝﹣2cos2（13°+α）+1＝﹣，故选：A．3．已知α，β为锐角，且cosα＝，cosβ＝，则α+β的值是（）A．B．C．或D．或【解答】解：α，β为锐角，且cosα＝，cosβ＝，∴sinα＝，sinβ＝，且α+β∈（0，π），则cos（α+β）＝cosαcosβ﹣sinαsinβ＝，＝，则α+β＝，故选：B．4．已知cos（﹣+α）＝﹣，则cos（﹣α）＝（）A．B．C．D．【解答】解：由于cos（﹣+α）＝﹣，所以cos（﹣α）＝﹣cos（﹣+α）＝，故选：B．5．已知tan（π+α）＝2，则＝（）A．B．C．D．【解答】解：∵tan（π+α）＝2，∴tanα＝2，∴＝．故选：D．6．下列四个等式：①tan25°+tan35°+；②＝1；③cos2；④＝4，其中正确的是（）A．①④B．①②C．②③D．③④【解答】解：对①：，故tan25°+tan35°+，故正确；对②：，故，故错误；对③：，故错误；对④：＝，故正确．故选：A．7．已知，则sin2α＝（）A．B．C．D．【解答】解：，故：，解得tanα＝2．所以＝＝．故选：D．8．已知，则2sin2α﹣sinαcosα＝（）A．B．C．D．2【解答】解：∵，∴﹣cosα﹣2cosα＝sinα，可得sinα＝﹣3cosα，∴sin2α+cos2α＝9cos2α+cos2α＝10cos2α＝1，可得cos2α＝，∴2sin2α﹣sinαcosα＝18cos2α﹣（﹣3cosα）cosα＝21cos2α＝．故选：A．9．若cos（α﹣β）＝，且α，β均为锐角，α＜β，则α+β＝（）A．B．C．D．【解答】解：∵α+β＝2α﹣（α﹣β）∴cos（α+β）＝cos[2α﹣（α﹣β）]＝cos2αcos（α﹣β）+sin2αsin （α﹣β），∵α，β均为锐角，α＜β，∴0＜2α＜π，﹣＜α﹣β＜0，则sin2α＝＝＝，sin（α﹣β）＝﹣，则cos（α+β）＝×﹣×＝﹣＝，则α+β＝，故选：C．10．已知函数f（x）＝sin（x+）sin x﹣（π+x）+，当0＜α＜时，f（α）＝，则cos2α＝（）A．B．C．D．【解答】解：由题可知＝＝＝，则．因为，所以，，所以由可知，则＝，则＝＝＝，故选：C．11．若sin（﹣α）＝，则sin（2α﹣）＝（）A．B．﹣C．D．﹣【解答】解：因为sin（﹣α）＝，所以，所以sin（2α﹣）＝＝．故选：A．12．已知角α，β∈（0，π），tan（α+β）＝，cosβ＝，则角2α+β＝（）A．B．C．D．【解答】解：∵cosβ＝，∴sinβ＝＝，则tanβ＝，则tanα＝tan（α+β﹣β）＝＝＝，tan（2α+β）＝tan（α+β+α）＝＝＝1，∵0＜tan（α+β）＜1，0＜tanα＜1，∴0＜α+β＜，0＜α＜，则0＜2α+β＜，则2α+β＝，故选：D．13．若cosθ﹣2sinθ＝1，则tanθ＝（）A．B．C．0或D．0或【解答】解：∵cosθ﹣2sinθ＝1，且sin2θ+cos2θ＝1，∴5sin2θ+4sinθ＝0，∴，∴，则tanθ＝0或，故选：C．14．已知锐角α满足3cos2α＝1+sin2α，则cosα＝（）A．B．C．D．【解答】∵3cos2α＝1+sin2α，∴3（cos2α﹣sin2α＝（cosα+sinα）2，∴3（cosα﹣sinα）（cosα+sinα）＝（cosα+sinα）2，∵α为锐角，可得cosα+sinα＞0，∴3（cosα﹣sinα）＝cosα+sinα，可得cosα＝2sinα，即tanα＝，∴cosα＝＝＝．故选：A．15．若，则＝（）A．1B．C．D．﹣3【解答】解：∵，∴tanαtan＝2，则＝＝﹣＝﹣＝﹣＝﹣＝，故选：C．16、，则的值为（）A．﹣4B．﹣2 C．2 D．4【解答】解：已知，所以＝，令g（x）＝故g（x）＝﹣g（x），所以函数g（x）为奇函数．则═﹣1﹣1＝﹣2故选：A．17．若θ∈（0，π），且2cosθ+sinθ＝2，则tan＝（）A．﹣B．C．D．【解答】解：∵θ∈（0，π），∴∈（0，），由2cosθ+sinθ＝2，得，即，整理得，∴tan＝0（舍）或tan．故选：C．18．若sin78°＝m，则sin6°＝（）A．B．C．D．【解答】解：∵sin78°＝m，∴cos12°＝m，即1﹣2sin26°＝m得2sin26°＝1﹣m，sin26°＝，则sin6°＝，故选：B．19．＝（）A．8B．﹣8C．D．【解答】解：原式＝﹣＝﹣＝＝＝＝＝＝﹣8，故选：C．20．化简的结果是（）A．sin 2B．﹣cos 2C．﹣cos 2D．sin 2【解答】解：＝＝．故选：D．21．已知当x＝θ时函数f（x）＝sin x﹣2cos x取得最小值，则＝（）A．﹣5B．5C．D．【解答】解：函数f（x）＝sin x﹣2cos x＝（sin x﹣cos x）＝sin（x﹣α），其中，cosα＝，sinα＝，故当x＝2kπ+α﹣，k∈z时，函数取得最小值为﹣，此时x＝θ＝2kπ+α﹣，k∈z，∴sinθ＝﹣cosα＝，cosθ＝sinα＝，则tanθ＝，tan2θ＝．则＝．故选：D．22．＝（）A．B．1C．D．2【解答】解：＝＝＝．故选：C．23．化简＝（）A．cos4B．sin4C．sin4+cos4D．﹣sin4﹣cos4【解答】解：∵sin4＜0，cos4＜0，∴＝＝＝﹣sin4﹣cos4．故选：D．。

三角恒等变换(含答案)

三角恒等变换
一、单选题(共10道，每道10分)
1.的值为( )
A. B.1
C.-1
D.
答案：B
解题思路：
试题难度：三颗星知识点：两角和与差的正切公式
2.的值为( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：二倍角的余弦
3.已知，是第三象限角，则的值是( )
A. B.
C. D.
答案：B
解题思路：
试题难度：三颗星知识点：两角和与差的余弦公式
4.已知，，则的值是( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：两角和与差的正弦公式
5.已知，则的值为( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：两角和与差的正切公式
6.已知，，则的值为( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：二倍角的正弦
7.已知，，则的值为( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：二倍角的正切
8.若，则=( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：二倍角的余弦
9.已知，则的值域是( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：二倍角的正弦
10.设，则函数的最值是( )
A. B.
C. D.
答案：B
解题思路：
试题难度：三颗星知识点：形如asinx+bcosx的化简。

2025新高考数学计算题型精练专题09 三角恒等变换(解析版)

2025新高考数学计算题型精练三角恒等变换1．cos70cos20sin70sin160︒︒-︒︒=（）A．0B．12C D．1【答案】A【详解】cos20cos70sin160sin70︒︒-︒︒()cos20cos70sin18020sin70=︒︒-︒-︒︒cos20cos70sin20sin70=︒︒-︒︒()cos2070cos900=︒+︒=︒=．故选：A．2．sin40°cos10°+cos140°sin10°＝（）A B C．﹣12D．12【答案】D【详解】sin40°cos10°+cos140°sin10°，=sin40°cos10°-cos40°sin10°，=sin（40°-10°），=sin30°＝12.故选：D3．sin20cos40cos20sin140︒︒︒︒+=A．B．2C．12-D．12【答案】B【详解】sin20cos40cos20sin140sin20cos40cos20sin40sin(2040)sin60︒︒+︒︒=︒︒+︒︒=︒+︒=︒故选B4．已知π1cos63α⎛⎫-=⎪⎝⎭，则πsin26α⎛⎫+=⎪⎝⎭（）A．79-B．79C．3-D．3【答案】A【详解】因为π1 cos63α⎛⎫-=⎪⎝⎭，故2πππππ27sin 2sin 2()cos 2()2cos ()116626699αααα⎛⎫⎡⎤+=-+=-=--=-=- ⎪⎢⎥⎝⎭⎣⎦，故选：A 5．若cos tan 3sin ααα=-，则sin 22πα⎛⎫+= ⎪⎝⎭（）A ．23B ．13C ．89D ．79【答案】D【详解】因为cos tan 3sin ααα=-，所以sin cos cos 3sin αααα=-，即223sin sin cos ααα-=，所以223sin sin cos 1ααα=+=，即1sin 3α=，所以27sin 2cos212sin 2π9ααα⎛⎫+==-= ⎪⎝⎭，故选：D ．6．sin 20cos 40sin 70sin 40︒︒+︒︒=（）AB ．12C．2D ．1【答案】A【详解】已知可化为：()sin 20cos 40cos 20sin 40sin 20402︒︒︒+︒=︒+︒=.故选：A7．若πtan 28α⎛⎫-= ⎪⎝⎭，则πtan 24α⎛⎫-= ⎪⎝⎭（）A ．34B ．34-C ．43D ．43-【答案】D【详解】由2π2tan()π448tan 2π41431tan ()8ααα-⎛⎫-===- ⎪-⎝⎭--.故选：D8．已知π0,2α⎛⎫∈ ⎪⎝⎭π2sin 4αα⎛⎫=+ ⎪⎝⎭，则sin 2α=（）A ．34-B ．34C ．1-D ．1【答案】B【详解】π2sin(4αα=+Q，)22(sin cos )2cos sin αααα=+-Q,1(cos sin )(cos sin )02αααα∴+--=，又π0,2α⎛⎫∈ ⎪⎝⎭，则sin 0,cos 0αα>>，即cos sin 0αα+>所以1cos sin 2αα-=，因为π0,2α⎛⎫∈ ⎪⎝⎭，所以2(0,π)α∈，sin 20α>.由1cos sin 2αα-=平方可得11sin 24α-=，即3sin 24α=，符合题意.综上，3sin 24α=.故选：B.9．已知5π4sin 125θ⎛⎫+= ⎪⎝⎭，则πsin 23θ⎛⎫+= ⎪⎝⎭（）A ．2425-B ．725-C ．725D ．2425【答案】C【详解】5ππππ4sin sin cos 12212125θθθ⎡⎤⎛⎫⎛⎫⎛⎫+=--=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，所以22πππ47cos 2cos 22cos 1216612525θθθ⎛⎫⎛⎫⎛⎫⎛⎫-=-=--=⨯-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，得ππππ7sin 2sin 2cos 2326625θθθ⎡⎤⎛⎫⎛⎫⎛⎫+=+-=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故选：C.10．已知tan 2α=，则213cos sin2αα-=（）A ．12B ．14C ．2D ．4【答案】A【详解】因为tan 2α=，所以222213cos sin 2cos tan 221sin22sin cos 2tan 42αααααααα---====，故选：A.11．化简：()22sin πsin 22cos 2ααα-+=（）A ．sin αB ．sin 2αC ．2sin αD ．sin2α【答案】C【详解】根据题意可知，利用诱导公式可得()222sin πsin 22sin sin 22cos 2cos 22αααααα-++=再由二倍角的正弦和余弦公式可得()()222sin 1cos 2sin 1cos 2sin sin 22sin 1cos 2cos2cos22αααααααααα+++===+，即()22sin πsin 22sin 2cos2αααα-+=.故选：C12．cos78cos18sin 78sin18︒︒+︒︒的值为（）A ．12B ．13CD【答案】A【详解】依题意由两角差的余弦公式可知，()1cos78cos18sin 78sin18cos 7818cos602︒︒+︒︒=︒-︒==.故选：A13．若tan 2θ=-，则()()()πsin 1sin22sin πcos πθθθθ⎛⎫+- ⎪⎝⎭=-++____________【答案】35-/-0.6【详解】()()()()22πsin 1sin2cos sin cos 2cos sin cos sin πcos πsin cos θθθθθθθθθθθθ⎛⎫+- ⎪-⎝⎭==--++-22222tan 1213cos sin 1tan 1(2)5cossin cos θθθθθθ-=---===-+++-，故答案为：35-14．已知ππ2θ<<，且4cos 5θ=-，则tan 2θ=______．【答案】247-【详解】4cos 5θ=-，3sin 5θ==±，ππ2θ<< ，3sin 5θ∴=.sin 3tan cos 4θθθ∴==-,232tan 242tan 291tan 7116θθθ-===---.故答案为：247-.15．已知cos 24π7sin 4αα=⎛⎫+ ⎪⎝⎭，则sin 2α的值是______．【答案】4149【详解】22cos 2442cos sin π777sin 422αααα=⇒⇒-=⎛⎫+ ⎪⎝⎭228841cos 2sin cos sin 1sin 2sin 2494949αααααα⇒-+=⇒-=⇒=，故答案为：414916．已知()0,απ∈，若sin 6πα⎛⎫-= ⎪⎝⎭cos 26πα⎛⎫+= ⎪⎝⎭_________.【答案】3±【详解】因为sin 63πα⎛⎫-= ⎪⎝⎭，()0,απ∈，所以cos 6πα⎛⎫-== ⎪⎝⎭所以sin 2=2sin cos =6663πππααα⎛⎫⎛⎫⎛⎫---±⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以cos 2cos 2cos 2sin 2=6326263ππππππαααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=-+=--± ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故答案为：17．若3,0,sin 25⎛⎫∈-=- ⎪⎝⎭x x π，则tan 2x =________.【答案】247-【详解】343,0,sin cos ,tan 2554x x x x π⎛⎫∈-=-∴==-⎪⎝⎭Q 232tan 242tan 291tan 7116x x x -∴===---故答案为：247-18．已知(),2αππ∈，cos 3sin 1αα-=，则cos 2α=_______________________．【答案】【详解】因为(),2αππ∈，所以,22αππ⎛⎫∈ ⎪⎝⎭，由cos 3sin 1αα-=可得212sin 6sin cos 1222ααα--=，整理可得sin 3cos 22αα=-，22sin 3cos 22sin cos 12222ααααπαπ⎧=-⎪⎪⎪+=⇒⎨⎪⎪<<⎪⎩cos 2α=故答案为：19．若πcos 0,,tan 22sin αααα⎛⎫∈= ⎪⎝⎭，则α=__________.【答案】6π/16π【详解】依题意，πcos 0,,tan 22sin αααα⎛⎫∈= ⎪⎝⎭，所以2222tan 1,2tan 1tan 1tan tan ααααα==--，21tan 3α=，而α为锐角，所以πtan 6αα=.故答案为：π620．已知tan 3α=，则sin 2α=______．【答案】35【详解】22222sin cos 2tan 233sin 2sin cos tan 1315ααααααα⨯====+++.故答案为：3521．已知α是第二象限的角，1cos24α=，则tan α=________．【答案】5/【详解】因为21cos 212sin 4αα=-=，又α是第二象限的角，所以6sin 4α=，cos 4α=，所以5tan α=-.故答案为：5-22．已知22cos 5sin 10αα-+=，则cos 2=α______．【答案】12/0.5【详解】解：已知()2222cos 5sin 121sin 5sin 12sin 5sin 30αααααα-+=--+=--+=，即()()22sin 5sin 32sin 1sin 30αααα+-=-+=，解得1sin 2α=或sin 3α=-（舍），211cos 212sin 1242αα∴=-=-⨯=，故答案为：12.23．若tan 2θ=，则sin cos 2cos sin θθθθ=-_________.【答案】65/1.2/115【详解】()()22sin cos sin sin cos 2sin cos sin cos sin cos sin θθθθθθθθθθθθ-==+--222222sin cos sin tan tan 246sin cos sin sin cos tan 155θθθθθθθθθθθ+++=+====++.故答案为：65.24．函数()sin 2sin 1cos x xf x x=+的值域__________．【答案】14,2⎛⎤- ⎥⎝⎦【详解】因为()()222221cos cos sin 2sin 2sin cos 11=2cos 2cos 2cos 1cos 1cos 1cos 22x x x x x x f x x x x x x x -⎛⎫===-+=--+ ⎪+++⎝⎭，因为1cos 1x -≤≤，当1cos 2x =时，()f x 取得最大值12，当cos 1x =-时，()f x 取得最小值4-，又因为1cos 0x +≠，所以()f x 的值域为14,2⎛⎤- ⎝⎦．故答案为：14,2⎛⎤- ⎥⎝⎦.25．已知sin 2cos αα=，π0,2α⎛⎫∈ ⎪⎝⎭，tan α=________．【详解】sin 2cos 2sin cos αααα==，π0,2α⎛⎫∈ ⎪⎝⎭，则cos 0α≠，1sin 2α=，π6α=，故tan α=26．（1）计算：cos157sin 97sin 60cos 97︒+︒︒︒；（2）已知tan 1α=-，求2cos 2sin cos 1ααα--的值．【答案】（1）12；（2）12【详解】（1）cos157sin 97sin 60cos97︒+︒︒︒()cos 9760sin 97sin 60cos 97︒+︒+︒︒=︒cos 97cos 60sin 97sin 60sin 97sin 60cos 97︒︒-︒︒+︒︒=︒cos 60=︒12=．（2）2cos 2sin cos 1ααα--222cos 2sin cos 1cos sin ααααα-=-+212tan 11tan αα-=-+()()2121111-⨯-=-+-12=．。

专题5.5 三角恒等变换(解析版)

专题5.5三角恒等变换（一）两角和与差的正弦、余弦、正切公式1．C (α－β)：cos(α－β)＝cos αcos β＋sin αsin β；C (α＋β)：cos(α＋β)＝cos αcos_β－sin_αsin β；S (α＋β)：sin(α＋β)＝sin αcos β＋cos αsin β；S (α－β)：sin(α－β)＝sin_αcos_β－cos αsin β；T (α＋β)：tan(α＋β)＝tan α＋tan β1－tan αtan β；T (α－β)：tan(α－β)＝tan α－tan β1＋tan αtan β.2．变形公式：tan α±tan β＝tan(α±β)(1∓tan αtan β)；4sin(2cos sin πααα±=±.sin αsin β＋cos(α＋β)＝cos αcos β，cos αsin β＋sin(α－β)＝sin αcos β，3．辅助角公式：函数f(α)＝acos α＋bsin α(a ，b 为常数)，可以化为f(α)＝a 2＋b 2sin(α＋φ)或f(α)＝a 2＋b 2cos(α－φ)，其中φ可由a ，b 的值唯一确定．（二）二倍角的正弦、余弦、正切公式1.S 2α：sin 2α＝2sin αcos α；C 2α：cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α；T 2α：tan 2α＝2tan α1－tan 2α2.变形公式：（1）降幂公式：cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2，sin αcos α＝12sin 2α.（2）升幂公式1＋cos α＝2cos 2α2；1－cos α＝2sin 2α2；1＋sin αα2＋cos ；1－sin αα2－cos .（3）配方变形：1＋sin 2α＝(sin α＋cos α)2,1－sin 2α＝(sin α－cos α)21±sin αsin α2±cos 1＋cos α＝2cos 2α2，1－cos α＝2sin 2α2（4）sin 2α＝2sin αcos αsin 2α＋cos 2α＝2tan α1＋tan 2α；cos 2α＝cos 2α－sin 2αcos 2α＋sin 2α＝1－tan 2α1＋tan 2α.tanα2＝sin α1＋cos α＝1－cos αsin α.（三）常见变换规律(1)角的变换：明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角)，熟悉角的变换技巧，及半角与倍角的相互转化，如：2α＝(α＋β)＋(α－β)，α＝(α＋β)－β＝(α－β)＋β，40°＝60°－20°＝π2，α2＝2×α4等．(2)名的变换：明确各个三角函数名称之间的联系，常常用到同角关系、诱导公式，把正弦、余弦化为正切，或者把正切化为正弦、余弦．一、单选题1．sin 40sin 50cos 40cos50︒︒-︒︒等于（）A ．1-B ．1C ．0D ．cos10-︒【答案】C【解析】由两角和的余弦公式得：()()sin 40sin 50cos 40cos50cos 40cos50sin 40sin 50cos 4050cos900︒︒-︒︒=-︒︒-︒︒=-+=-=故选：C2．已知()5cos 2cos 22παπα⎛⎫-=+ ⎪⎝⎭，且()1tan 3αβ+=，则tan β的值为（）A ．7-B ．7C ．1D ．1-【答案】D【解析】：因为()5cos 2cos 22παπα⎛⎫-=+ ⎪⎝⎭，所以sin 2cos αα=，所以sin tan 2cos ααα==，又()1tan 3αβ+=，所以()()()12tan tan 3tan tan 111tan tan 123αβαβαβααβα-+-=+-===-⎡⎤⎣⎦+++⨯.故选：D3．已知,αβ均为锐角，且1sin 2sin ,cos cos 2αβαβ==，则()sin αβ-=（）A ．35B ．45C．3D ．23【答案】A【解析】：因为1sin 2sin ,cos cos 2αβαβ==，所有22221sin cos 4sin cos 14ααββ+=+=，则2153sin 44β=，又,αβ均为锐角，所以sin β=cos β=所以sin αα==所以()3sin sin cos cos sin 5αβαβαβ-=-=.故选：A.4．已知()1sin 5αβ+=，()3sin 5αβ-=，则tan tan αβ的值为（）A ．2B ．2-C ．12D ．12-【答案】B【解析】()()1sin sin cos cos sin 53sin sin cos cos sin 5αβαβαβαβαβαβ⎧+=+=⎪⎪⎨⎪-=-=⎪⎩，解得2sin cos 51cos sin 5αβαβ⎧=⎪⎪⎨⎪=-⎪⎩，所以tan sin cos 2tan cos sin ααββαβ==-.故选：B5．已知sin sin 13πθθ⎛⎫++= ⎪⎝⎭，则tan 6πθ⎛⎫+= ⎪⎝⎭（）ABC ．D ．±22【答案】D【解析】sin sin()13πθθ++=，则1sin sin cos 122θθθ++=，即3sin 122θθ+=，故1sin cos 223θθ+=，所以sin 6πθ⎛⎫+= ⎪⎝⎭cos 63πθ⎛⎫+=± ⎪⎝⎭，所以tan 62πθ⎛⎫+=± ⎪⎝⎭故选：D6．下面公式正确的是（）A ．3sin cos 2πθθ⎛⎫+= ⎪⎝⎭B ．2cos212cos θθ=-C ．3cos sin 2πθθ⎛⎫+=- ⎪⎝⎭D ．cos()sin 2πθθ-=【答案】D 【解析】对A ，3sin cos 2πθθ⎛⎫+=- ⎪⎝⎭，故A 错误；对B ，2cos 22cos 1θθ=-，故B 错误；对C ，3cos sin 2πθθ⎛⎫+= ⎪⎝⎭，故C 错误；对D ，cos()sin 2πθθ-=，故D 正确；故选：D7．已知2tan()5αβ+=，1tan()44πβ-=，则tan()4πα+的值为（）A ．16B ．322C ．2213D ．1318【答案】B【解析】：因为2tan()5αβ+=，1tan()44πβ-=，所以()tan()tan 44ππααββ⎡⎤⎛⎫+=+-- ⎪⎢⎥⎝⎭⎣⎦()()tan tan 41tan tan 4παββπαββ⎛⎫+-- ⎪⎝⎭=⎛⎫++- ⎪⎝⎭213542122154-==+⨯.故选：B 8．设1cos1022a =-，22tan131tan 13b =+，c =，则a ，b ，c 大小关系正确的是（）A ．a b c <<B ．c b a <<C ．a c b <<D ．b c a<<【答案】C【解析】()1cos10cos 6010cos 70sin 202a =︒=︒+︒=︒=︒，2222sin132tan13cos132sin13cos13sin 26sin 131tan 131cos 13b ︒︒︒===︒︒=︒︒+︒+︒，sin 25c =，因为函数sin y x =在0,2π⎛⎫⎪⎝⎭上是增函数，故sin 20sin 25sin 26<<，即a c b <<.故选：C.9．已知sin()63πα+=-，则2cos(2)3πα-=（）A ．23-B ．13-C ．23D ．13【答案】B 【解析】：因为sin()6πα+=2cos 2cos 263παππα⎡⎤⎛⎫⎛⎫-=-⎪ ⎪⎢⎥⎝⎭⎣+⎭⎝⎦6cos 2πα⎪+⎛⎫=- ⎝⎭212n 6si πα⎡⎤⎛⎫=-- ⎪⎢⎥⎭⎣+⎝⎦21123⎡⎤⎛⎢⎥=--=- ⎢⎥⎝⎭⎣⎦故选：B 10．若11tan ,tan()72βαβ=+=，则tan =α（）A ．115B ．112C ．16D ．13【答案】D【解析】：因为11tan ,tan()72βαβ=+=，所以()()()11tan tan 127tan =tan 111tan tan 3127αββααββαββ-+-+-===⎡⎤⎣⎦+++⨯.故选：D.11．已知3cos 16παα⎛⎫--= ⎪⎝⎭，则sin 26πα⎛⎫+= ⎪⎝⎭（）A ．13-B ．13C．3-D．3【答案】B【解析】：因为3cos 16παα⎛⎫--= ⎪⎝⎭，即3cos cos sin sin 166ππααα⎛⎫-+= ⎪⎝⎭，即13cos sin 122ααα⎫-+=⎪⎪⎝⎭3sin 12αα-=1cos 123πααα⎫⎛⎫=+=⎪ ⎪⎪⎝⎭⎭，所以cos 3πα⎛⎫+= ⎪⎝⎭所以sin 2cos 2662πππαα⎛⎫⎛⎫+=-++ ⎪ ⎪⎝⎭⎝⎭2cos 22cos 133ππαα⎡⎤⎛⎫⎛⎫=-+=-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦21213⎡⎤⎢⎥=--=⎢⎥⎝⎭⎣⎦.故选：B 12．已知4sin 5α=，π5,π,cos ,213αββ⎛⎫∈=- ⎪⎝⎭是第三象限角，则()cos αβ-=（）A ．3365-B ．3365C ．6365D ．6365-【答案】A【解析】由4sin 5α=，π,π2α⎛⎫∈ ⎪⎝⎭，可得3cos 5α=-由5cos ,13ββ=-是第三象限角，可得12sin 13β=-则()3541233cos cos cos sin sin 51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故选：A13．若sin 25α=，()sin 10βα-=，且,4απ⎡⎤∈π⎢⎥⎣⎦，3,2βππ⎡⎤∈⎢⎥⎣⎦，则αβ+的值是（）A ．54πB ．74πC ．54π或74πD ．54π或94π【答案】B【解析】,,2,242ππαπαπ⎡⎤⎡⎤∈∴∈⎢⎥⎢⎥⎣⎦⎣⎦，又∵sin 2,2,,,242πππααπα⎡⎤⎡⎤=∴∈∈⎢⎥⎢⎥⎣⎦⎣⎦，∴cos 25α==-.又∵35,,,224πππβπβα⎡⎤⎡⎤∈∴-∈⎢⎥⎢⎥⎣⎦⎣⎦，∴()cos βα-==，于是()()()()cos cos 2cos 2cos sin 2sin αβαβααβααβα+=+-=---⎡⎤⎣⎦5105102⎛⎛⎫=---= ⎪ ⎪⎝⎭⎝⎭，易得5,24αβπ⎡⎤+∈π⎢⎥⎣⎦，则74αβπ+=.故选：B.14．)sin20tan50=（）A ．12B ．2C D ．1【答案】D【解析】原式()()()()sin20sin 50cos502sin 20sin 50602sin 20sin 9020cos50cos50cos 9050++===-2sin 20cos 20sin 401sin 40sin 40===.故选：D.15．若1cos ,sin(),0722ππααβαβ=+=<<<<，则角β的值为（）A ．3πB ．512πC ．6πD ．4π【答案】A 【解析】∵0,022ππαβ<<<<，0αβπ∴<+<，由1cos 7α=，()sin αβ+=，得sin α=11cos()14αβ+=±，若11cos()14αβ+=，则sin sin[()]βαβα=+-sin()cos cos()sin αβααβα=+-+1110714=-<，与sin 0β>矛盾，故舍去，若11cos()14αβ+=-，则cos cos[()]βαβα=+-cos()cos sin()sin αβααβα=+++111147147=-⨯+⨯12=，又(0,)2πβ∈，3πβ∴=.故选：A.16．若7171212ππα<<，且7cos 268πα⎛⎫+=- ⎪⎝⎭，则5cos 12πα⎛⎫-=⎪⎝⎭（）A ．B ．CD ．14-【答案】A【解析】由27cos 212sin 6128ππαα⎛⎫⎛⎫+=-+=- ⎪ ⎪⎝⎭⎝⎭，得215sin 1216πα⎛⎫+= ⎪⎝⎭．因为7171212ππα<<，所以233122πππα<+<，所以sin 122πα⎛⎫⎛⎫+∈- ⎪ ⎪ ⎪⎝⎭⎝⎭，所以15sin 124πα⎛⎫+= ⎪⎝⎭所以5cos cos sin 1221212ππππααα⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭故选：A17．已知sin cos αα-=0απ≤≤，则sin 23πα⎛⎫-= ⎪⎝⎭（）A B ．34410-C ．D 【答案】D【解析】：因为sin cos αα-=()22sin cos αα-=⎝⎭，即222sin 2sin cos cos 5αααα-+=，即21sin 25α-=，所以3sin 25α=，又sin cos 45πααα⎛⎫-=-=⎪⎝⎭，即2sin 42πα⎛⎫-= ⎪⎝⎭，因为0απ≤≤，所以3444πππα-≤-≤，所以044ππα<-≤，即42ππα<≤，所以22παπ<≤，所以4cos 25α==-，所以sin 2sin 2cos cos 2sin333πππααα⎛⎫-= ⎪⎝⎭23145252⎛⎫=⨯--⨯ ⎪⎝⎭故选：D18．若10,0,cos ,cos 2243423ππππβαβα⎛⎫⎛⎫<<-<<+=-= ⎪ ⎪⎝⎭⎝⎭，则cos 2βα⎛⎫+= ⎪⎝⎭（）A B ．C D ．【答案】C 【解析】cos cos cos cos sin sin 2442442442βππβππβππβαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+--=+-++- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，因为0,022ππαβ<<-<<所以3,444πππα⎛⎫+∈ ⎪⎝⎭，,4242πβππ⎛⎫-∈ ⎪⎝⎭，因为1cos 43πα⎛⎫+= ⎪⎝⎭，cos 423πβ⎛⎫-= ⎪⎝⎭所以sin 4πα⎛⎫+ ⎪⎝⎭sin 42πβ⎛⎫-= ⎪⎝⎭则122cos 233βα⎛⎫+=+ ⎪⎝⎭C 19．已知π43cos sin 65αα⎛⎫-+= ⎪⎝⎭，则2πcos 3α⎛⎫+ ⎪⎝⎭的值是（）A ．45-B ．45C ．5-D ．5【答案】A【解析】由πcos sin 6αα⎛⎫-+= ⎪⎝⎭ππ3πcos cossin sin sin sin 6623αααααα⎛⎫++=+=-=⎪⎝⎭，所以，π4cos 35α⎛⎫-= ⎪⎝⎭，所以，2πππ4cos cos πcos 3335ααα⎛⎫⎛⎫⎛⎫⎛⎫+=--=--=-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选：A.20．已知,2παπ⎛⎫∈ ⎪⎝⎭，且2sin 45πα⎛⎫+= ⎪⎝⎭，则cos()α-=（）A ．10B ．10C ．10-D ．222110【答案】C【解析】因为,2παπ⎛⎫∈ ⎪⎝⎭，所以35,444πππα⎛⎫+∈ ⎪⎝⎭．又2sin 45πα⎛⎫+= ⎪⎝⎭，所以cos 45πα⎛⎫+==- ⎪⎝⎭，cos()cos cos cos cos sin sin 44444410ππππππααααα⎡⎤⎛⎫⎛⎫⎛⎫-==+-=+++=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦故选：C.二、多选题21．对于函数()sin 22f x x x =，下列结论正确的是（）A ．()f x 的最小正周期为πB ．()f x 的最小值为2-C ．()f x 的图象关于直线6x π=-对称D ．()f x 在区间,26ππ⎛⎫-- ⎪⎝⎭上单调递增【答案】AB【解析】()1sin 222(sin 2cos 2)2sin(2)223f x x x x x x π=+=+=+，22T ππ==，A 正确；最小值是2-，B 正确；(2sin()0633f πππ-=-+=，C 错误；(,26x ππ∈--时，22(,0)33x ππ+∈-，232x ππ+=-时，()f x 得最小值2-，因此函数不单调，D 错误，故选：AB ．22）A ．222cos2sin 1212ππ-B ．1tan151tan15+︒-︒C ．cos 75︒︒D ．cos15︒︒【答案】ABC【解析】A ：222cos 2sin 2cos 12126πππ-==B ：1tan15tan 45tan15tan 601tan151tan 45tan15+︒︒+︒==︒=-︒-︒︒C ：cos 754sin15230︒︒=︒︒=︒=D ：cos152sin(3015)2sin15︒︒=︒-︒=︒.故选：ABC23．已知函数2()sin 222x x xf x =-，则下列结论正确的有（）A ．()f x 的最小正周期为4πB ．直线23x π=-是()f x 图象的一条对称轴C ．()f x 在0,2π⎛⎫⎪⎝⎭上单调递增D ．若()f x 在区间,2m π⎡⎤-⎢⎥⎣⎦上的最大值为12，则3m π≥【答案】BD【解析】：()21cos 1cos sin sin 222262x x x xf x x x π-⎛⎫=-=-=+- ⎪⎝⎭，所以()f x 的最小正周期为2,π故A 不正确；因为2362πππ-+=-，所以直线23x π=-是()f x 图象的一条对称轴，故B 正确；当02x π<<时，2+663x πππ<<，而函数sin y x =在2,63ππ⎛⎫⎪⎝⎭上不单调，故C 不正确；当2x m π-≤≤时，++366x m πππ-≤≤，因为()f x 在区间,2m π⎡⎤-⎢⎥⎣⎦上的最大值为12，即11sin 622x π⎛⎫+-≤ ⎪⎝⎭，所以sin 16x π⎛⎫+≤ ⎪⎝⎭，所以+62m ππ≥，解得3m π≥，故D 正确.故选：BD.24．已知函数22()cos cos sin (0)f x x x x x ωωωωω=+->的周期为π，当π[0]2x ∈，时，()f x 的（）A ．最小值为2-B ．最大值为2C ．零点为5π12D ．增区间为π06⎡⎤⎢⎥⎣⎦，【答案】BCD【解析】22()cos cos sin (0)f x x x x x ωωωωω=+->2cos 2x xωω=+2sin 26x πω⎛⎫=+ ⎪⎝⎭，因为()f x 的周期为π，所以22ππω=，得1ω=，所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭，当π[0]2x ∈，时，72,666x πππ⎡⎤+∈⎢⎥⎣⎦，所以1sin 2126x π⎛⎫-≤+≤ ⎪⎝⎭，所以12sin 226x π⎛⎫-≤+≤ ⎪⎝⎭，所以()f x 的最小值为1-，最大值为2，所以A 错误，B 正确，由()2sin 206f x x π⎛⎫=+= ⎪⎝⎭，72,666x πππ⎡⎤+∈⎢⎥⎣⎦，得26x ππ+=，解得512x π=，所以()f x 的零点为5π12，所以C 正确，由2662x πππ≤+≤，得06x π≤≤，所以()f x 的增区间为π06⎡⎤⎢⎣⎦，，所以D 正确，故选：BCD25．关于函数()cos 2cos f x x x x =-，下列命题正确的是（）A ．若1x ，2x 满足12πx x -=，则()()12f x f x =成立；B ．()f x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增；C ．函数()f x 的图象关于点π,012⎛⎫⎪⎝⎭成中心对称；D ．将函数()f x 的图象向左平移7π12个单位后将与2sin 2y x =的图象重合．【答案】ACD 【解析】()1cos 2cos cos 222cos 222f x x x x x x x x ⎛⎫=-== ⎪ ⎪⎝⎭π2cos 23x ⎛⎫=+ ⎪⎝⎭，对于A ，若1x ，2x 满足12πx x -=，则()()()1222ππ2cos 2π2cos 233f x x x f x ⎡⎤⎛⎫=++=+= ⎪⎢⎥⎣⎦⎝⎭成立，故A 正确；对于B ，由ππ2π22π2π,3k x k k Z +≤+≤+∈，得：π5πππ,36k x k k +≤≤+∈Z ，即()f x 在区间π5π,36⎡⎤⎢⎣⎦上单调递增，故B 错误；对于C ，因为πππ2cos 2012123f ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭，所以函数()f x 的图象关于点π,012⎛⎫⎪⎝⎭成中心对称，故C 正确；对于D ，将函数()f x 的图象向左平移7π12个单位后得到7π7ππ3π2cos 22cos 22sin 2121232y f x x x x ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，其图象与2sin 2y x =的图象重合，故D 正确．故选：ACD 三、解答题26．求下列各式的值(1)cos54cos36sin54sin36⋅-⋅(2)sin7cos37cos(7)sin(37)⋅+-⋅-(3)ππcos sin 1212⋅(4)22ππsincos 88-【答案】(1)0；(2)12-；(3)14；(4)2-.【解析】(1)cos54cos36sin54sin36cos(5436)cos900⋅-⋅=+==.(2)sin7cos37cos(7)sin(37)sin7cos37cos7sin37⋅+-⋅-=⋅-⋅1sin(737)sin(30)2=-=-=-.(3)ππ1π1cossin 1212264⋅==.(4)22πππsin cos cos 8842-=-=-.27．已知3sin 5α=，其中2απ<<π.(1)求tan α；(2)若0,cos 2πββ<<=()sin αβ+的值.【答案】(1)34-(2)5-【解析】(1)由3sin 5α=可得4cos 5α=±，因为2απ<<π，故4cos 5α=-，进而sin 3tan cos 4ααα==-(2)π0,cos 2ββ<<=，故sin β==；()34sin =sin cos cos sin 55αβαβαβ++==28．已知角α为锐角，2πβαπ<-<，且满足1tan23=α，()sin 10βα-=(1)证明：04πα<<；(2)求β.【答案】(1)证明见解析(2)3.4πβ=【解析】(1)证明：因为1tan23α=，所以2122tan332tan 1tan 1441tan 129απαα⨯===<=--，因为α为锐角且函数tan y x =在0,2π⎛⎫⎪⎝⎭上单调递增，所以04πα<<(2)由22sin 3tan cos 4sin cos 1ααααα⎧==⎪⎨⎪+=⎩，结合角α为锐角，解得3sin 5α=，4cos 5α=，因为2πβαπ<-<，且()sin 10βα-=所以()cos βα-==()()()sin sin sin cos cos sin βαβααβααβα⎡⎤=+-=-+-⎣⎦3247225105102⎛=⨯-+⨯ ⎝⎭又5224πππαβπα<+<<+<，所以3.4πβ=29．已知α，β为锐角，π33sin 314α⎛⎫-=⎪⎝⎭，()11cos 14αβ+=-．(1)求cos α的值；(2)求角β．【答案】(1)17(2)π3【解析】(1)因为π0,2α⎛⎫∈ ⎪⎝⎭，所以ππ336πα⎛⎫-∈ ⎪⎝⎭-，，又π33sin 314α⎛⎫-=⎪⎝⎭所以π13cos 314α⎛⎫-== ⎪⎝⎭所以ππcos =cos +33αα⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦ππππ1cos cos sin sin =33337αα⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭(2)因为α，β为锐角，所以0αβ<+<π，则()sin 0αβ+>，因为()11cos 14αβ+=-，所以()sin 14αβ+==．又α为锐角，1cos 7α=，所以sin α==，故()()()sin sin sin cos cos sin βαβααβααβα=+-=+-+⎡⎤⎣⎦111714=+=因为β为锐角，所以π3β=．30．已知sincos22αα-=(1)求sin α的值；(2)若αβ，都是锐角，()3cos 5αβ+=，求sin β的值.【答案】(1)12【解析】(1)解：2221sin cos sin 2sin cos cos 1sin 2222222a αααααα⎛⎫-=-+=-= ⎪⎝⎭，1sin 2a =.(2)因为αβ，都是锐角,所以0αβ<+<π，()4sin 5αβ+==，13sin cos 22a a =⇒=，()()()43sin cos c 0s 13si o 55n sin sin 221αβααβααββα-=-+=+-=+-=⨯⨯⎡⎤⎣⎦31．已知tan ,tan αβ是方程23570x x +-=的两根，求下列各式的值：(1)()tan αβ+(2)()()sin cos αβαβ+-；(3)()cos 22αβ+.【答案】(1)12-(2)54(3)35【解析】（1）由题意可知：57tan tan ,tan tan 33αβαβ+=-=-()5tan tan 13tan 71tan tan 213αβαβαβ-++===--+（2）()()5sin sin cos cos sin tan tan 537cos cos cos sin sin 1tan tan 413αβαβαβαβαβαβαβαβ-+++====-++-（3）()22222211cos ()sin ()1tan ()34cos 221cos ()sin ()1tan ()514αβαβαβαβαβαβαβ-+-+-++====++++++。

三角恒等变换复习题答案

（1）求（2）求
值．
的值；
【分析】（1）由已知利用诱导公式可求cosα+sinα＝﹣ ，两边平方可得2cosαsinα＝ ﹣ ，进而利用同角三角函数基本关系式化简所求即可得解．（2）由（1）可得cosα+sinα＝﹣ ，结合角的范围利用同角三角函数基本关系式可
求cosα，sinα的值，即可计算得解．
第10页（共14页）
求得0＜ω≤ ，或 ≤ω≤ ，
故选：D．
【点评】本题主要考查两角和差的三角公式，函数y＝Asin（ωx+φ）的变换规律，属于中档题．二．填空题（共4小题）
13．已知tanα＝2，则
＝ ﹣ ．
【分析】由已知利用诱导公式，二倍角的正弦函数公式，同角三角函数基本关系式化简所求即可计算得解．
【解答】解：（1）∵α∈（0，π），且
，
第14页（共14页）
∴可得：﹣cosα﹣sinα＝，即cosα+sinα＝﹣ ，两边平方可得：1+2cosαsinα＝
，可得2cosαsinα＝﹣ ，
∴α为钝角，cosα＜0， ∴
＝cosα
+sinα
＝
﹣（1+sinα）+1+cosα＝cosα﹣sinα＝﹣
16．不等式sin2x﹣cos2x≥0的解集为 [kπ+ ，kπ+ ]，k∈Z ．
【分析】利用二倍角的余弦函数公式化简可得cos2x≤0，进而根据余弦函数的图象和性质即可求解．【解答】解：∵sin2x﹣cos2x＝﹣cos2x≥0，
∴cos2x≤0，可得2kπ+ ≤2x≤2kπ+ ，k∈Z，解得kπ+ ≤x≤kπ+ ，k∈Z，

方法技巧专题19 三角恒等变换(解析版)

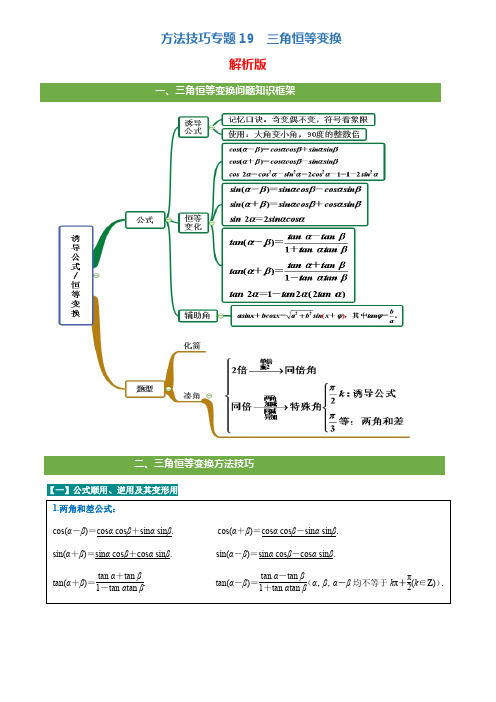
方法技巧专题19 三角恒等变换解析版一、三角恒等变换问题知识框架【一】公式顺用、逆用及其变形用1.例题【例1】计算：(1)cos(－15°)； (2)cos 15°cos 105°＋sin 15°sin 105°. 【解析】(1)方法一原式＝cos(30°－45°)＝cos 30°cos 45°＋sin 30°sin 45°＝32×22＋12×22＝6＋24. 方法二原式＝cos 15°＝cos(45°－30°)＝cos 45°cos 30°＋sin 45°sin 30°＝22×32＋22×12＝6＋24. (2)原式＝cos(15°－105°)＝cos(－90°)＝cos 90°＝0. 【例2】(1)计算：cos 2π12－sin 2π12；【解析】原式＝cos π6＝32.(2)计算：1－tan 275°tan 75°；【解析】 1－tan 275°tan 75°＝2·1－tan 275°2tan 75°＝2·1tan 150°＝－2 3.(3)计算：cos 20°cos 40°cos 80°.【解析】原式＝12sin 20°·2sin 20°cos 20°cos 40°cos 80°＝12sin 20°·sin 40°·cos 40°cos 80°＝122sin 20°sin 80°cos 80°＝123sin 20°·sin 160°＝sin 20°23sin 20°＝18.【例3】(1)1＋tan 15°1－tan 15°＝________.【解析】3 原式＝tan 45°＋tan 15°1－tan 45°tan 15°＝tan(45°＋15°)＝tan 60°＝ 3.(2)化简：tan 23°＋tan 37°＋3tan 23°tan 37°. 【解析】方法一 tan 23°＋tan 37°＋3tan 23°tan 37° ＝tan(23°＋37°)(1－tan 23°tan 37°)＋3tan 23°tan 37° ＝tan 60°(1－tan 23°tan 37°)＋3tan 23°tan 37°＝ 3. 方法二 ∵tan(23°＋37°)＝tan 23°＋tan 37°1－tan 23°tan 37°，∴3＝tan 23°＋tan 37°1－tan 23°tan 37°，∴3－3tan 23°tan 37°＝tan 23°＋tan 37°， ∴tan 23°＋tan 37°＋3tan 23°tan 37°＝ 3. （3）已知sin θ＝45，5π2＜θ＜3π，求cos θ2和tan θ2.【解析】 ∵sin θ＝45，且5π2＜θ＜3π，∴cos θ＝－1－sin 2θ＝－35.由cos θ＝2cos 2θ2－1，得cos 2θ2＝1＋cos θ2＝15.∵5π4＜θ2＜3π2，∴cos θ2＝－ 1＋cos θ2＝－55. tan θ2＝sin θ1＋cos θ＝2.2.巩固提升综合练习【练习1】化简cos 15°cos 45°＋cos 75°sin 45°的值为( )A.12B.32 C ．－12 D ．－32【解析】Bcos 15°cos 45°＋cos 75°sin 45°＝cos 15°cos 45°＋sin 15°sin 45°＝cos(15°－45°)＝cos(－30°)＝32.【练习2】1－3tan 75°3＋tan 75°＝________.【解析】－1原式＝33－tan 75°1＋33tan 75°＝tan 30°－tan 75°1＋tan 30°tan 75°＝tan(30°－75°)＝－tan 45°＝－1.【练习3】在△ABC 中，A ＋B ≠π2，且tan A ＋tan B ＋3＝3tan A tan B ，则角C 的值为( )A.π3B.2π3C.π6D.π4 【解析】A∵tan A ＋tan B ＋3＝3tan A tan B ⇔tan(A ＋B )·(1－tan A tan B )＝3(tan A tan B －1)．(*) 若1－tan A tan B ＝0，则cos A cos B －s in A sin B ＝0，即cos(A ＋B )＝0. ∵0<A ＋B <π，∴A ＋B ＝π2与题设矛盾．∴由(*)得tan(A ＋B )＝－3，即tan C ＝ 3.又∵0<C <π，∴C ＝π3.【练习4】若sin α＋cos α＝13，则sin 2α= .【解析】由题意，得(sin α＋cos α)2＝19，∴1＋2sin αcos α＝19，即1＋sin 2α＝19，∴sin 2α＝－89.1.例题【例1】已知31)3sin(=-πα，则)6cos(πα+ 的值为( ) A ．－13 B.13 C.223 D ．－223【答案】A 【解析】∵sin )3(πα-＝13，∴cos )6(πα+＝cos )]3(2[παπ-+＝－sin )3(πα-＝－13.【例2】已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点⎪⎭⎫⎝⎛--54,53P . 若角β满足sin(α＋β)＝513，则cos β的值为________．【答案】－5665或1665【解析】由角α的终边过点⎪⎭⎫⎝⎛--54,53P ，得sin α＝－45，cos α＝－35. 由sin(α＋β)＝513，得cos(α＋β)＝±1213.由β＝(α＋β)－α，得cos β＝cos(α＋β)cos α＋sin(α＋β)sin α，所以cos β＝－5665或cos β＝1665.【例3】若1sin 63πα⎛⎫-= ⎪⎝⎭，则2cos 23πα⎛⎫+= ⎪⎝⎭（） A ．13 B ．13-C ．79D ．79-【答案】D 【解析】222πππcos 22cos 12cos 13326πααα⎡⎤⎛⎫⎛⎫⎛⎫+=+-=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦2π272sin 11699α⎛⎫=--=-=- ⎪⎝⎭2.巩固提升综合练习【练习1】已知33)6tan(=-απ，则=+)65tan(απ________. 【答案】－33【解析】tan )65(απ+＝tan )6(αππ+-＝tan )]6([αππ--＝－tan )6(απ-＝－33. 【练习2】若1027)4sin(=+πA ，A ∈),4(ππ，则sin A 的值为( ) A.35 B.45C.35或45D.34【答案】B 【解析】∵A ∈),4(ππ，∴A ＋π4∈)45,2(ππ， ∴cos （A ＋π4）＝－1－sin 2⎝⎛⎭⎫A ＋π4＝－210， ∴sin A ＝sin[（A ＋π4）- π4]＝sin （A ＋π4）cos π4－cos （A ＋π4）sin π4＝45.【练习3】已知sin(α−3π10)=35，则cos(α+π5)=（） A.−45 B.45C.−35D.35【答案】C【解析】因为sin(α−3π10)=35，则cos(α+π5)=cos[π2+(α−3π10)]=−sin(α−3π10)=−35．故应选C ．【练习4】若sin （3x π-）=23，则cos （23x π+）=（）A ．79B ．19C ．19-D ．79-【答案】C 【解析】令3x πθ=-，则223x ππθ+=-，所以()21cos 2cos 2cos 22sin 139x ππθθθ⎛⎫+=-=-=-=- ⎪⎝⎭，故选C ．【练习5】已知3sin 245x π⎛⎫-= ⎪⎝⎭，则sin 4x 的值为（） A ．1825B ．1825±C ．725D ．725±【答案】C【解析】由题意得：297cos 412sin 212242525x x ππ⎛⎫⎛⎫-=--=-⨯=⎪ ⎪⎝⎭⎝⎭7sin 4cos 4225x x π⎛⎫∴=-= ⎪⎝⎭本题正确选项：C1.例题【例1】已知02απ<<，cos()4απ+= （1）求tan()4απ+的值；（2）求sin(2)3απ+的值．【解析】（1）∵02απ<<，cos()4απ+= ∴sin()4απ+==， ∴sin()4tan()24cos()4αααπ+π+==π+．（2）∵tan 1tan()241tan αααπ++==-，∴1tan 3α=， ∴2222sin cos 2tan 3sin 2sin cos tan 15ααααααα===++，2222cos sin cos 2sin cos ααααα-=+221tan 4tan 15αα-==+，3sin(2)sin 2cos cos 2sin 33310αααπππ++=+=．【例2】已知△ABC 中,137cos sin -=+A A ,则tanA= . 【解析】解法一：列出方程组⎪⎩⎪⎨⎧=+-=+1cos sin 137cos sin 22A A A A由第一个方程得,A A sin 137cos --=,代入第二个方程得1)sin 137(sin 22=--+A A ，即016960sin 137sin 2=-+A A ，解得135sin =A 或1312sin -=A ，因为△ABC 中0<A<π, 所以sinA>0,135sin =A ，1312cos -=A ，所以125tan -=A . 答案:125-. 解法二：由已知得sinA>0, cosA<0, |sin A|<|cos A|, tanA>-1, 由137cos sin -=+A A 两边平方,整理得16960cos sin -=⋅A A ，即16960cos sin cos sin 22-=+⋅A A A A ，分子分母同除以A 2cos 得169601tan tan 2-=+A A ，解得125tan -=A .2.巩固提升综合练习【练习1】已知a ∈R ，sina +2cosa =√102，则tan2a =（）A ．−34或−35 B ．−34C ．34D ．−35【答案】B 【解析】因为sina +2cosa =√102，所以(sina +2cosa )2=52，所以sin 2a +4cos 2a +4sinacosa =52，所以sin 2a+4cos 2a+4sin acosasin 2a+cos 2a=52，即tan 2a+4+4tanatan 2a+1=52，解得tana =3或者tana =−13，当tana =3时，tan2a =2tana1−tan 2a =−34，当tana =−13时，tan2a =2tana 1−tan 2a =−34，综上所述，tan2a =−34，故选B 。

高三复习数学32_三角恒等变换(有答案)

3.2 三角恒等变换一、解答题。

1. 和、差角公式：sin(α±β)=________；cos(α±β)=________；tan(α±β)=________．2. 二倍角公式：sin2α=________；cos2α=________=________=________；tan2α=________．当tanα、tanβ或tan(α±β)的值不存在时，不能使用公式Tα±β处理有关问题，应改用诱导公式或其它方法来解．3. 如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为√210,2√5 5．求tan(α+β)的值；求α+2β的值．4. 已知sin(α−π4)=√55,α∈(π2,5π4)，则sinα=（）A.3√1010B.−√1010C.±√1010D.−√1010或3√10105. 已知α∈(0,π2)，2sin2α=cos2α+1，则sinα=（）A.1 5B.√55C.√33D.2√556. 设α∈(0,π2)，β∈(0,π4)，且tanα=1+sin2βcos2β，则下列结论中正确的是（）A.α−β=π4B.α+β=π4C.2α−β=π4D.2α+β=π47. sin40∘(tan10∘−√3)=________．8. 在锐角△ABC中，若sin A=2sin B sin C，则tan A tan B tan C的最小值是________.9. 已知函数f(x)=2cos2x−sin2x+2，则（）A.f(x)的最小正周期为π，最大值为3B.f(x)的最小正周期为π，最大值为4C.f(x)的最小正周期为2π，最大值为3D.f(x)的最小正周期为2π，最大值为410. 若cos(π4−α)=35，则sin2α=（）A.7 25B.15C.−15D.−72511. 若tanα=34，则cos2α+2sin2α=（）A.64 25B.4825C.1D.162512. 设函数f(x)=sin2x+b sin x+c，则f(x)的最小正周期（）A.与b有关，且与c有关B.与b有关，但与c无关C.与b无关，且与c无关D.与b无关，但与c有关13. 已知α为第二象限角，sinα+cosα=√33，则cos2α=（）A.−√53B.−√59C.√59D.√5314. 2cos10∘−sin20∘sin70∘的值是( )A.1 2B.√32C.√2D.√315. 函数f(x)=4cos x sin(x+π6)−1在区间[−π6,π4]上值域为________．16. 已知α,β∈(3π4,π)，sin(α+β)=−35，sin(β−π4)=1213，则cos(α+π4)=________．17. 已知sin(π6−α)=√23，那么cos2α+√3sin2α=________．18. 在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2A−B2cos B−sin(A−B)sin B+cos(A+C)=−35．求cos A的值．19. 求函数y=7−4sin x cos x+4cos2x−4cos4x的最大值与最小值．20. 在△ABC中，内角A，B，C所对的边分别为a，b，c．已知b+c=2a cos B．证明：A=2B；若△ABC的面积S=a 24，求角A的大小．参考答案与试题解析3.2 三角恒等变换一、解答题。

三角恒等变换复习答案

三角恒等变换复习答案1解析由tan θ＋1tan θ＝sin θcos θ＋cos θsin θ＝1sin θcos θ＝4，得sin θcos θ＝14，则sin 2θ＝2sin θcos θ＝2×14＝12.2答案 A 解析方法一 ∵sin α＋cos α＝33，∴(sin α＋cosα)2＝13，∴2sin αcos α＝－23，即sin 2α＝－23.又∵α为第二象限角且sin α＋cos α＝33>0，∴2k π＋π2<α<2k π＋34π(k ∈Z)，∴4k π＋π<2α<4k π＋32π(k ∈Z)，∴2α为第三象限角，∴cos 2α＝－1－sin 22α＝－53.方法二由sin α＋cos α＝33，两边平方得1＋2sin αcos α＝13，∴2sin αcos α＝－23.∵α为第二象限角，∴sin α>0，cos α<0，∴sin α－cos α＝sin α－cos α2＝1－2sin αcos α＝153.由⎩⎪⎨⎪⎧sin α＋cos α＝33，sin α－cos α＝153，得⎩⎪⎨⎪⎧sin α＝3＋156，cos α＝3－156.∴cos 2α＝2cos 2α－1＝－53.3答案 A 解析由于α，β都为锐角，所以cos α＝1－sin 2α＝255，cos β＝1－sin 2β＝31010.所以cos(α＋β)＝cos α·cos β－sin α·sin β＝22，所以α＋β＝π4.4答案 D 解析 ∵α∈⎝ ⎛⎭⎪⎪⎫0，π2，且sin 2α＋cos 2α＝14，∴sin 2α＋cos 2α－sin 2α＝14，∴cos 2α＝14，∴cos α＝12或－12(舍去)，∴α＝π3，∴tan α＝3.5答案 B 解析由sin α＋cos αsin α－cos α＝12，等式左边分子、分母同除cos α得，tan α＋1tan α－1＝12，解得tan α＝－3，则tan 2α＝2tan α1－tan 2α＝34. 6答案 A 解析 sin(π4＋θ)＝22(sin θ＋cos θ)＝13，将上式两边平方，得12(1＋sin 2θ)＝19，∴sin 2θ＝－79. 7答案 D 解析 ∵θ∈⎣⎢⎢⎡⎦⎥⎥⎤π4，π2，∴2θ∈⎣⎢⎢⎡⎦⎥⎥⎤π2，π.∴cos 2θ＝－1－sin 22θ＝－18，∴sin θ＝1－cos 2θ2＝34. 8答案 C 解析因为α＋π4＋β－π4＝α＋β，所以α＋π4＝(α＋β)－⎝⎛⎭⎪⎪⎫β－π4，所以tan ⎝ ⎛⎭⎪⎪⎫α＋π4＝tan ⎣⎢⎢⎡⎦⎥⎥⎤α＋β－⎝ ⎛⎭⎪⎪⎫β－π4＝tan α＋β－tan ⎝ ⎛⎭⎪⎪⎫β－π41＋tan α＋βtan ⎝⎛⎭⎪⎪⎫β－π4＝322.9答案 D 解析f (x )＝sin x ＋3cos x ＝2⎝ ⎛⎭⎪⎪⎫12sin x ＋32cos x ＝2sin ⎝ ⎛⎭⎪⎪⎫x ＋π3，由－π2≤x ≤π2，得－π6≤x ＋π3≤5π6.所以当x ＋π3＝π2时，f (x )有最大值2，当x ＋π3＝－π6时，f (x )有最小值－1.10 空11答案54解析由诱导公式及倍角公式，得cos 275°＋cos 215°＋cos 75°cos 15°＝sin 215°＋cos 215°＋sin 15°cos 15°＝1＋12sin 30°＝54. 12答案－43解析原式＝3sin 12°cos 12°－322cos 212°－1sin 12°＝23⎝ ⎛⎭⎪⎪⎫12sin 12°－32cos 12°cos 12°2cos 24°sin 12°＝23sin－48°2cos 24°sin 12°cos 12°＝－23sin 48°sin 24°cos 24°＝－23sin 48°12sin 48°＝－4 3.13答案 π2解析 ∵α、β∈⎝⎛⎭⎪⎪⎫0，π2，∴α＋β∈(0，π)，∴cos α＝45，sin β＝45，∴cos(α＋β)＝45×35－35×45＝0，∴α＋β＝π2.14答案713解析由sin(α＋β)＝sin αcos β＋cos αsin β＝23， sin(α－β)＝sin αcos β－cos αsin β＝－15，得sin αcos β＝730，cos αsin β＝1330，所以sin αcos βcos αsin β＝tan αtan β＝713.15答案 17250解析 ∵α为锐角且cos ⎝ ⎛⎭⎪⎪⎫α＋π6＝45，∴sin ⎝⎛⎭⎪⎪⎫α＋π6＝35.∴sin ⎝ ⎛⎭⎪⎪⎫2α＋π12＝sin ⎣⎢⎢⎡⎦⎥⎥⎤2⎝⎛⎭⎪⎪⎫α＋π6－π4＝sin 2⎝ ⎛⎭⎪⎪⎫α＋π6cos π4－cos 2⎝ ⎛⎭⎪⎪⎫α＋π6sin π4＝2sin ⎝ ⎛⎭⎪⎪⎫α＋π6cos ⎝ ⎛⎭⎪⎪⎫α＋π6－22⎣⎢⎢⎡⎦⎥⎥⎤2cos 2⎝ ⎛⎭⎪⎪⎫α＋π6－1＝2×35×45－22⎣⎢⎢⎡⎦⎥⎥⎤2×⎝ ⎛⎭⎪⎪⎫452－1 ＝12225－7250＝17250.16解因为1＋sin α1－sin α－1－sin α1＋sin α＝1＋sin α2cos 2α－1－sin α2cos 2α＝|1＋sin α||cos α|－|1－sin α||cos α|＝1＋sin α－1＋sin α|cos α|＝2sin α|cos α|，所以2sin α|cos α|＝－2tan α＝－2sin αcos α.所以sin α＝0或|cos α|＝－cos α>0.故α的取值集合为{α|α＝k π或2k π＋π2<α<2k π＋π或2k π＋π<α<2k π＋3π2，k ∈Z}．17解 (1)因为sin α2＋cos α2＝62，两边同时平方，得sin α＝12.又π2<α<π，所以cos α＝－32.(2)因为π2<α<π，π2<β<π，所以－π<－β<－π2，故－π2<α－β<π2.又sin(α－β)＝－35，得cos(α－β)＝45.cos β＝cos[α－(α－β)]＝cos αcos(α－β)＋sin αsin(α－β) ＝－32×45＋12×⎝ ⎛⎭⎪⎪⎫－35＝－43＋310.18思维启迪：(1)拆分角：α＋β2＝⎝⎛⎭⎪⎪⎫α－β2－⎝ ⎛⎭⎪⎪⎫α2－β，利用平方关系分别求各角的正弦、余弦．(2)2α－β＝α＋(α－β)；α＝(α－β)＋β.解 (1)∵0<β<π2<α<π，∴－π4<α2－β<π2，π4<α－β2<π，∴cos ⎝ ⎛⎭⎪⎪⎫α2－β＝1－sin 2⎝ ⎛⎭⎪⎪⎫α2－β＝53，sin ⎝ ⎛⎭⎪⎪⎫α－β2＝1－cos 2⎝ ⎛⎭⎪⎪⎫α－β2＝459，∴cos α＋β2＝cos ⎣⎢⎢⎡⎦⎥⎥⎤⎝ ⎛⎭⎪⎪⎫α－β2－⎝ ⎛⎭⎪⎪⎫α2－β＝cos ⎝ ⎛⎭⎪⎪⎫α－β2cos ⎝ ⎛⎭⎪⎪⎫α2－β＋sin ⎝ ⎛⎭⎪⎪⎫α－β2sin ⎝ ⎛⎭⎪⎪⎫α2－β＝⎝ ⎛⎭⎪⎪⎫－19×53＋459×23＝7527，∴cos(α＋β)＝2cos 2α＋β2－1＝2×49×5729－1＝－239729. (2)∵tan α＝tan[(α－β)＋β]＝tan α－β＋tan β1－tanα－βtan β＝12－171＋12×17＝13>0，∴0<α<π2，又∵tan 2α＝2tan α1－tan 2α＝2×131－⎝ ⎛⎭⎪⎪⎫132＝34>0，∴0<2α<π2，∴tan(2α－β)＝tan 2α－tan β1＋tan 2αtan β＝34＋171－34×17＝1.∵tan β＝－17<0，∴π2<β<π，－π<2α－β<0，∴2α－β＝－3π4.19答案 ⎣⎢⎢⎡⎦⎥⎥⎤－π8＋k π，3π8＋k π (k ∈Z)解析 f (x )＝2sin 2x ＋2sin x cos x ＝2×1－cos 2x2＋sin 2x ＝sin 2x －cos 2x ＋1＝2sin ⎝⎛⎭⎪⎪⎫2x －π4＋1，由－π2＋2k π≤2x －π4≤π2＋2k π，k ∈Z ，得－π8＋k π≤x ≤3π8＋k π，k ∈Z.所以所求区间为⎣⎢⎢⎡⎦⎥⎥⎤－π8＋k π，3π8＋k π (k ∈Z)．审题视角 (1)问首先化为形如y ＝A sin(ωx ＋φ)的形式，由T ＝2πω求得；(2)问由x ∈⎣⎢⎢⎡⎦⎥⎥⎤－π6，π4求得ωx ＋φ的范围，从而求得最值．20解 (1)因为f (x )＝4cos x sin ⎝ ⎛⎭⎪⎪⎫x ＋π6－1＝4cos x ⎝ ⎛⎭⎪⎪⎫32sin x ＋12cos x －1＝3sin 2x ＋2cos 2x －1＝3sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎪⎪⎫2x ＋π6，[4分]所以f (x )的最小正周期为π.[6分](2)因为－π6≤x ≤π4，所以－π6≤2x ＋π6≤2π3.[8分]于是，当2x ＋π6＝π2，即x ＝π6时，f (x )取得最大值2；[10分]当2x ＋π6＝－π6，即x ＝－π6时，f (x )取得最小值－1.[12分]21解 (1)因为f (x )＝3sin ⎝ ⎛⎭⎪⎪⎫2x －π6＋1－cos 2⎝ ⎛⎭⎪⎪⎫x －π12＝2[32sin ⎝ ⎛⎭⎪⎪⎫2x －π6－12cos ⎝⎛⎭⎪⎪⎫2x －π6]＋1＝2sin ⎣⎢⎢⎡⎦⎥⎥⎤⎝⎛⎭⎪⎪⎫2x －π6－π6＋1＝2sin ⎝ ⎛⎭⎪⎪⎫2x －π3＋1，所以f (x )的最小正周期T ＝2π2＝π.(2)当f (x )取得最大值时，sin ⎝⎛⎭⎪⎪⎫2x －π3＝1，此时2x －π3＝2k π＋π2(k ∈Z)，即x ＝k π＋5π12 (k ∈Z)，所以所求x 的集合为{x |x ＝k π＋5π12，k ∈Z}．补偿训练1、若2π-≤x ≤2π，则()3sin cos f x x x =+的取值范围是（）Ａ．[2,2]- Ｂ．[2,3]- Ｃ．[3,2]- Ｄ．[3,3]-3、ω为正实数，函数1()sincos222xxf x ωω=在[,]34ππ-上为增函数，则( )Ａ．0ω<≤32 Ｂ．0ω<≤2 Ｃ．0ω<≤247Ｄ．ω≥2 4、函数sin()cos 6y x x π=-的最小值________。

简单的三角恒等变换专题及答案

简单的三角恒等变换专题及答案简单的三角恒等变换专题一、选择题1.已知sinα＝5115，则cos(π－2α)＝()。

答案：B。

通过sinα和cos(π－2α)的关系，可以得到cos(π－2α)＝－sinα＝－(1/5115)。

2.sin70°/(2cos10°－sin20°)的值是()。

答案：C。

通过三角函数的恒等变换，可以将sin70°/(2cos10°－sin20°)化简为sin70°/cos80°，再使用tan的定义式，得到tan70°=sin70°/cos70°=sin70°/sin10°cos80°=sin70°/sin10°sin10°=1/sin10°=3.3.若sin76°＝m，用含m的式子表示cos7°为()。

答案：B。

通过三角函数的恒等变换，可以得到cos(π/2－76°)＝sin76°＝m，即cos14°＝m，再通过三角函数的恒等变换，可以得到cos7°＝2cos2(7°)－1＝2cos2(14°)cos(π/2－14°)－1＝2(1－sin2(14°))－1＝1－2sin2(14°)＝1－2(cos14°)2＝1－2m2.4.若cos2α＝－2，则sinα＋cosα的值为sin(7π/4)()。

答案：B。

通过cos2α的值可以得到sin2α＝1－cos2α＝3，再通过三角函数的恒等变换，可以得到sinα＋cosα＝√2sin(π/4＋α)＝√2sin(π/4＋α－2π)＝√2sin(7π/4－α)。

5.已知f(x)＝2tanx－2/(x＋π/12)，则f(π/6)的值为()。

答案：D。

三角恒等变换-复习-答案

必修四第三章三角恒等变形单元测试(时间：120分钟，满分：150分)一、选择题(本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．)1．sin105°cos105°的值为( ) A.14 B ．－14C.34D ．－34 解析：原式＝12sin210°＝－12sin30°＝－14.答案：B2．若sin2α＝14，π4<α<π2，则cos α－sin α的值是( )A.32B ．－32C.34 D ．－34解析：(cos α－sin α)2＝1－sin2α＝1－14＝34.又π4<α<π2， ∴cos α<sin α，cos α－sin α＝－34＝－32. 答案：B3．sin15°sin30°sin75°的值等于( ) A.14 B.34 C.18D.38解析：sin15°sin30°sin75° ＝sin15°cos15°sin30° ＝12sin30°sin30°＝12×12×12＝18. 答案：C4．在△ABC 中，A ＝15°，则3sin A －cos(B ＋C )的值为( )A. 2B.22C.32D ．2解析：在△ABC 中，A ＋B ＋C ＝π， 3sin A －cos(B ＋C ) ＝3sin A ＋cos A ＝2(32sin A ＋12cos A ) ＝2cos(60°－A )＝2cos45°＝ 2. 答案：A5．已知tan θ＝13，则cos 2θ＋12sin2θ等于( )A ．－65B ．－45C.45D.65解析：原式＝cos 2θ＋sin θcos θcos 2θ＋sin 2θ＝1＋tan θ1＋tan 2θ＝65.答案：D6．在△ABC 中，已知sin A cos A ＝sin B cos B ，则△ABC 是( ) A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等腰三角形或直角三角形解析：∵sin2A ＝sin2B ，∴A ＝B 或A ＋B ＝π2.答案：D 7．设a ＝22(sin17°＋cos17°)，b ＝2cos 213°－1，c ＝32，则( ) A ．c <a <b B ．b <c <a C ．a <b <c D ．b <a <c解析：a ＝22sin17°＋22cos17°＝cos(45°－17°)＝cos28°， b ＝2cos 213°－1＝cos26°， c ＝32＝cos30°， ∵y ＝cos x 在(0,90°)内是减函数，∴cos26°>cos28°>cos30°，即b >a >c .答案：A8．三角形ABC 中，若C >90°，则tan A ·tan B 与1的大小关系为( ) A ．tan A ·tan B >1 B ．tan A ·tan B <1 C ．tan A ·tan B ＝1D ．不能确定解析：在三角形ABC 中，∵C >90°，∴A 、B 分别都为锐角．则有tan A >0，tan B >0，tan C <0. 又∵C ＝π－(A ＋B )，∴tan C ＝－tan(A ＋B )＝－tan A ＋tan B 1－tan A ·tan B <0，易知1－tan A ·tan B >0 即tan A ·tan B <1. 答案：B9．函数f (x )＝sin 2⎝⎛⎭⎫x ＋π4－sin 2⎝⎛⎭⎫x －π4是( ) A ．周期为π的奇函数 B ．周期为π的偶函数 C ．周期为2π的奇函数 D ．周期为2π的偶函数解析：f (x )＝sin 2⎝⎛⎭⎫x ＋π4－sin 2⎝⎛⎭⎫x －π4 ＝cos 2⎝⎛⎭⎫π4－x －sin 2⎝⎛⎭⎫x －π4 ＝cos 2⎝⎛⎭⎫x －π4－sin 2⎝⎛⎭⎫x －π4 ＝cos ⎝⎛⎭⎫2x －π2 ＝sin2x . 答案：A10．y ＝cos x (cos x ＋sin x )的值域是( ) A ．[－2,2] B.⎣⎢⎡⎦⎥⎤1＋22，2C.⎣⎢⎡⎦⎥⎤1－22，1＋22D.⎣⎡⎦⎤－12，32 解析：y ＝cos 2x ＋cos x sin x ＝1＋cos2x 2＋12sin2x ＝12＋22⎝⎛⎭⎫22sin2x ＋22cos2x＝12＋22sin(2x ＋π4)．∵x ∈R ， ∴当sin ⎝⎛⎭⎫2x ＋π4＝1时，y 有最大值1＋22；当sin ⎝⎛⎭⎫2x ＋π4＝－1时，y 有最小值1－22. ∴值域为⎣⎢⎡⎦⎥⎤1－22，1＋22.答案：C11．已知θ为第二象限角，sin(π－θ)＝2425，则cos θ2的值为( )A.335 B.45 C ．±35D ．±45解析：由sin(π－θ)＝2425，得sin θ＝2425.∵θ为第二象限的角，∴cos θ＝－725.∴cos θ2＝±1＋cos θ2＝± 1－7252＝±35. 答案：C12．若α、β为锐角，cos(α＋β)＝1213，cos(2α＋β)＝35，则cos α的值为( )A.5665 B.1665C.5665或1665D ．以上都不对解析：∵0<α＋β<π，cos(α＋β)＝1213>0，∴0<α＋β<π2，sin(α＋β)＝513.∵0<2α＋β<π，cos(2α＋β)＝35>0，∴0<2α＋β<π2，sin(2α＋β)＝45.∴cos α＝cos[(2α＋β)－(α＋β)]＝cos(2α＋β)cos(α＋β)＋sin(2α＋β)sin(α＋β) ＝35×1213＋45×513＝5665. 答案：A13．计算2sin 14°·cos 31°＋sin 17°等于( )．A.22 B ．－22 C.32 D ．－32 解析原式＝2sin 14°cos 31°＋sin(31°－14°) ＝sin 31°cos 14°＋cos 31°sin 14°＝sin 45°＝22. 答案 A14．设向量a ＝(cos 25°，sin 25°)，b ＝(sin 20°，cos 20°)，若t 是实数，且c ＝a ＋t b ，则|c |的最小值为( )．A. 2 B ．1 C.22 D.12 解析 c ＝a ＋t b ＝(cos 25°，sin 25°)＋(t sin 20°，t cos 20°) ＝(cos 25°＋t sin 20°，sin 25°＋t cos 20°)， ∴|c |＝(cos 25°＋t sin 20°)2＋(sin 25°＋t cos 20°)2 ＝1＋t 2＋2t sin 45°＝t 2＋2t ＋1 ＝⎝⎛⎭⎪⎫t ＋222＋12，∴当t ＝－22时，|c |最小，最小值为22. 答案 C15．设△ABC 的三个内角为A ，B ，C ，向量m ＝(3sin A ，sin B )，n ＝(cos B ，3cos A )，若m ·n ＝1＋cos(A ＋B )，则C 的值为( )． A.π6 B.π3 C.2π3 D.5π6解析 ∵m ·n ＝3sin A cos B ＋3cos A sin B ＝3sin(A ＋B )＝1＋cos(A ＋B )，∴3sin(A ＋B )－cos(A ＋B )＝3sin C ＋cos C ＝2sin ⎝ ⎛⎭⎪⎫π6＋C ＝1.∴sin ⎝ ⎛⎭⎪⎫π6＋C ＝12，∴π6＋C ＝56π或π6＋C ＝π6(舍去)，∴C ＝23π. 答案 C二、填空题(本大题共4小题，每题5分，共20分．将答案填在题中横线上．) 13．若1＋tan α1－tan α＝2010，则1cos2α＋tan2α＝______.解析：1cos2α＋tan2α＝1＋sin2αcos2α＝sin 2α＋cos 2α＋2sin αcos αcos 2α－sin 2α＝tan 2α＋1＋2tan α1－tan 2α＝(tan α＋1)21－tan 2α＝1＋tan α1－tan α＝2010.答案：201014．已知cos2α＝13，则sin 4α＋cos 4α＝________.解：∵cos2α＝13，∴sin 22α＝89.∴sin 4α＋cos 4α＝(sin 2α＋cos 2α)2－2sin 2αcos 2α ＝1－12sin 22α＝1－12×89＝59.答案：5915.sin (α＋30°)＋cos (α＋60°)2cos α＝________.解析：∵sin(α＋30°)＋cos(α＋60°)＝sin αcos30°＋cos αsin30°＋cos αcos60°－sin αsin60°＝cos α.∴原式＝cos α2cos α＝12.答案：1216．关于函数f (x )＝cos(2x －π3)＋cos(2x ＋π6)，则下列命题：①y ＝f (x )的最大值为2； ②y ＝f (x )最小正周期是π；③y ＝f (x )在区间⎣⎡⎦⎤π24，13π24上是减函数；④将函数y ＝3cos2x 的图象向右平移π24个单位后，将与已知函数的图象重合．其中正确命题的序号是________．解析：f (x )＝cos ⎝⎛⎭⎫2x －π3＋cos ⎝⎛⎭⎫2x ＋π6 ＝cos ⎝⎛⎭⎫2x －π3＋sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫2x ＋π6 ＝cos ⎝⎛⎭⎫2x －π3－sin ⎝⎛⎭⎫2x －π3 ＝2⎣⎡⎦⎤22cos ⎝⎛⎭⎫2x －π3－22sin ⎝⎛⎭⎫2x －π3 ＝2cos ⎝⎛⎭⎫2x －π3＋π4 ＝2cos ⎝⎛⎭⎫2x －π12， ∴y ＝f (x )的最大值为2，最小正周期为π，故①、②正确．又当x ∈⎣⎡⎦⎤π24，13π24时，2x －π12∈[0，π]，∴y ＝f (x )在⎣⎡⎦⎤π24，13π24上是减函数，故③正确．由④得y ＝2cos2⎝⎛⎭⎫x －π24＝2cos ⎝⎛⎭⎫2x －π12，故④正确．答案：①②③④11．若cos 2αsin ⎝ ⎛⎭⎪⎫α－π4＝－22，则sin α＋cos α＝________. 解析原式可化为cos 2α－sin 2α22(sin α－cos α)＝(cos α＋sin α)(cos α－sin α)22(sin α－cos α)＝－22，∴sin α＋cos α＝12. 答案 1212．已知向量m ＝(3sin x ，cos x )，p ＝(23，1)．若m ∥p ，则sin x ·cos x ＝________. 解析 ∵m ∥p ，∴3sin x ＝23cos x ，tan x ＝2， ∴sin x ·cos x ＝sin x ·cos x sin 2x ＋cos 2x ＝tan x 1＋tan 2x ＝25.答案 2514．已知tan(α＋β)＝35，tan ⎝ ⎛⎭⎪⎫β－π4＝14，那么tan(α＋π4)的值为________．解析 tan(α＋π4)＝tan ⎣⎢⎡⎦⎥⎤(α＋β)－⎝ ⎛⎭⎪⎫β－π4＝tan (α＋β)－tan ⎝ ⎛⎭⎪⎫β－π41＋tan (α＋β)tan ⎝ ⎛⎭⎪⎫β－π4＝35－141＋35×14＝723. 答案 723三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．) 17．(10分)已知tan α＝2，tan β＝－13，其中0<α<π2，π2<β<π.(1)求tan(α－β)的值； (2)求α＋β的值．解：(1)∵tan α＝2，tan β＝－13，∴tan(α－β)＝tan α－tan β1＋tan αtan β＝2＋131－23＝7.(2)∵tan(α＋β)＝tan α＋tan β1－tan αtan β＝2－131＋23＝1，且0<α<π2，π2<β<π，∴π2<α＋β<3π2， ∴α＋β＝5π4.15．(10分)对任意实数x 和整数n ，已知f (sin x )＝sin[(4n ＋1)x ]，求f (cos x )．解 f (cos x )＝f ⎣⎢⎡⎦⎥⎤sin ⎝ ⎛⎭⎪⎫π2－x ＝sin ⎣⎢⎡⎦⎥⎤(4n ＋1)·⎝ ⎛⎭⎪⎫π2－x ＝sin ⎣⎢⎡⎦⎥⎤2n π＋π2－(4n ＋1)x ＝sin ⎣⎢⎡⎦⎥⎤π2－(4n ＋1)x ＝cos[(4n ＋1)x ]．18．(12分)已知向量m ＝⎝⎛⎭⎫cos α－23，－1，n ＝(sin α，1)，m ，n 为共线向量，且α∈⎝⎛⎭⎫－π2，0. 求sin α－cos α的值．解：由m ，n 共线可得：⎝⎛⎭⎫cos α－23×1－(－1)sin α＝0，∴cos α＋sin α＝23. 平方得：2sin αcos α＝－79.∴(sin α－cos α)2＝1－2sin αcos α＝1＋79＝169，∵α∈⎝⎛⎭⎫－π2，0，∴sin α<0，cos α>0， ∴sin α－cos α<0， ∴sin α－cos α＝－43.19．(12分)(2010·北京高考)已知函数f (x )＝2cos2x ＋sin 2x －4cos x . (1)求f ⎝⎛⎭⎫π3的值；(2)求f (x )的最大值和最小值．解：(1)f ⎝⎛⎭⎫π3＝2cos 2π3＋sin 2π3－4cos π3 ＝2×⎝⎛⎭⎫－12＋⎝⎛⎭⎫322－4×12 ＝－1＋34－2＝－94.(2)f (x )＝2(2cos 2x －1)＋(1－cos 2x )－4cos x ＝3cos 2x －4cos x －1＝3⎝⎛⎭⎫cos x －232－73， ∵x ∈R ，cos x ∈[－1,1]，∴当cos x ＝－1时，f (x )有最大值6；当cos x ＝23时，f (x )有最小值－73.20．(12分)(2009·湖北高考)已知向量a ＝(cos α，sin α)，b ＝(cos β，sin β)，c ＝(－1,0)． (1)求向量b ＋c 的长度的最大值； (2)设α＝π4，且a ⊥(b ＋c )，求cos β的值．解：(1)解法1：b ＋c ＝(cos β－1，sin β)，则 |b ＋c |2＝(cos β－1)2＋sin 2β＝2(1－cos β)． ∵－1≤cos β≤1，∴0≤|b ＋c |2≤4，即0≤|b ＋c |≤2，当cos β＝－1时，|b ＋c |＝2， ∴向量b ＋c 的长度的最大值为2.解法2：∵|b |＝1，|c |＝1，|b ＋c |≤|b |＋|c |＝2. 当cos β＝－1时，有b ＋c ＝(－2,0)，即|b ＋c |＝2. ∴向量b ＋c 的长度的最大值为2.(2)解法1：由已知可得b ＋c ＝(cos β－1，sin β)， a ·(b ＋c )＝cos α(cos β－1)＋sin αsin β ＝cos(α－β)－cos α.∵a ⊥(b ＋c )，∴a ·(b ＋c )＝0，即cos(α－β)＝cos α.当α＝π4时，得cos ⎝⎛⎭⎫π4－β＝cos π4，∴β－π4＝2k π±π4(k ∈Z )，∴β＝2k π＋π2或β＝2k π(k ∈Z )，于是cos β＝0或cos β＝1.解法2：若α＝π4，则a ＝⎝⎛⎭⎫22，22，又由b ＝(cos β，sin β)，c ＝(－1,0)得 a ·(b ＋c )＝⎝⎛⎭⎫22，22·(cos β－1，sin β) ＝22cos β＋22sin β－22. ∵a ⊥(b ＋c )，∴a ·(b ＋c )＝0，∴cos β＋sin β＝1.又cos 2β＋sin 2β＝1，解得cos β＝0或cos β＝1.经检验知，cos β＝0或cos β＝1即为所求．21．(12分)已知cos ⎝⎛⎭⎫x －π4＝210，x ∈⎝⎛⎭⎫π2，3π4. (1)求sin x 的值； (2)求sin ⎝⎛⎭⎫2x ＋π3的值．解：(1)解法1：∵x ∈⎝⎛⎫π2，3π4，∴x －π4∈⎝⎛⎭⎫π4，π2，于是sin ⎝⎛⎭⎫x －π4＝1－cos 2⎝⎛⎭⎫x －π4＝7210.sin x ＝sin ⎣⎡⎦⎤⎝⎛⎫x －π4＋π4 ＝sin ⎝⎛⎭⎫x －π4cos π4＋cos ⎝⎛⎭⎫x －π4sin π4＝7210×22＋210×22＝45. 解法2：由题设得22cos x ＋22sin x ＝210，即cos x ＋sin x ＝15. 又sin 2x ＋cos 2x ＝1，从而25sin 2x －5sin x －12＝0，解得：sin x ＝45或sin x ＝－35，因为x ∈⎝⎛⎭⎫π2，3π4，所以sin x ＝45.(2)∵x ∈⎝⎛⎭⎫π2，3π4，故cos x ＝－1－sin 2x ＝－1－⎝⎛⎭⎫452＝－35. sin2x ＝2sin x cos x ＝－2425. cos2x ＝2cos 2x －1＝－725. ∴sin ⎝⎛⎭⎫2x ＋π3 ＝sin2x cos π3＋cos2x sin π3 ＝－24＋7350. 22．(12分)(2009·重庆高考)设函数f (x )＝(sin ωx ＋cos ωx )2＋2cos 2ωx (ω>0)的最小正周期为2π3. (1)求ω的值；(2)若函数y ＝g (x )的图象是由y ＝f (x )的图象向右平移π2个单位长度得到的．求y ＝g (x )的单调增区间．解：(1)f (x )＝sin 2ωx ＋cos 2ωx ＋2sin ωx cos ωx ＋1＋cos2ωx＝sin2ωx ＋cos2ωx ＋2＝2sin ⎝⎛⎭⎫2ωx ＋π4＋2. 依题意得T ＝2π2ω＝2π3，∴ω＝32. (2)依题意得g (x )＝2sin ⎣⎡⎦⎤3⎝⎛⎭⎫x －π2＋π4＋2 ＝2sin ⎝⎛⎭⎫3x －5π4＋2 由2k π－π2≤3x －5π4≤2k π＋π2(k ∈Z )，解得23k π＋π4≤x ≤23k π＋7π12(k ∈Z )．故g (x )的单调增区间为⎣⎡⎦⎤23k π＋π4，23k π＋7π12(k ∈Z )．。

三角恒等变换专题复习带答案

专题12 简单的三角恒等变换（解析版）

新高考一轮复习特训 三角恒等变换 (含答案)高中数学 高考专区 一轮复习

三角恒等变换专题复习带答案

三角恒等变换含答案

三角恒等变换(含答案)

三角恒等变换综合 (详细答案)

专题12 三角恒等变换(纯答案)

三角恒等变换专题练习(含答案)

三角恒等变换(含答案)

2025新高考数学计算题型精练专题09 三角恒等变换(解析版)

专题5.5 三角恒等变换(解析版)

三角恒等变换复习题答案

方法技巧专题19 三角恒等变换(解析版)

高三复习数学32_三角恒等变换(有答案)

三角恒等变换复习答案

简单的三角恒等变换专题及答案

三角恒等变换-复习-答案

新高考一轮复习特训三角恒等变换 (含答案)高中数学高考专区一轮复习