高中数学《二面角的平面角及求法》练习
高考数学试卷二面角

一、选择题1. 下列关于二面角的叙述中,正确的是()A. 二面角是由两个平面相交形成的角B. 二面角是由两个平面相交形成的两条线段所夹的角C. 二面角是由两个平面相交形成的两条射线所夹的角D. 二面角是由两个平面相交形成的两条直线所夹的角答案:C2. 在二面角中,一个平面内两条相交直线与另一个平面所成的角分别为α和β,则二面角的度数是()A. α + βB. α - βC. |α - β|D. 90°答案:C3. 若二面角的平面角为θ,那么这个二面角的度数范围是()A. 0° < θ < 90°B. 0° ≤ θ ≤ 180°C. 0° < θ ≤ 180°D. 90° < θ ≤ 180°答案:C4. 下列图形中,能表示二面角的是()A. 一个等腰三角形B. 一个等边三角形C. 一个矩形D. 一个正方形答案:C5. 若二面角的平面角为60°,则其补角的度数是()A. 60°B. 120°C. 180°D. 240°答案:B二、填空题6. 在二面角中,若一个平面内两条相交直线与另一个平面所成的角分别为α和β,则二面角的平面角为______。
答案:|α - β|7. 若二面角的平面角为θ,那么这个二面角的度数范围是______。
答案:0° < θ ≤ 180°8. 若一个二面角的平面角为45°,则其补角的度数是______。
答案:135°三、解答题9. 已知二面角的平面角为60°,求这个二面角的补角的度数。
解答过程:根据题意,设二面角的平面角为θ,则有:θ = 60°由补角的定义可知,二面角的补角为180° - θ,因此:补角= 180° - 60° = 120°所以,这个二面角的补角的度数是120°。
五种方法法求二面角及限时练习

从而可得本解法。(答案:二面角 P BD A 的大小为 arctan
三.补棱法
本法是针对在解构成二面角的两个半平面没有明确交线
的求二面角题目时,要将两平面的图形补充完整,使之有明
确的交线(称为补棱),然后借助前述的定义法与三垂线法解
题。即当二平面没有明确的交线时,一般用补棱法解决
例 3(2008 湖南)如图所示,四棱锥 P-ABCD 的底面 ABCD
面角解之。(Ⅰ)证略
解: (Ⅱ)延长 AD、BE 相交于点 F,连结 PF.
过点 A 作 AH⊥PB 于 H,由(Ⅰ)知
平面 PBE⊥平面 PAB,所以 AH⊥平面 PBE.
在 Rt△ABF 中,因为∠BAF=60°,
所以,AF=2AB=2=AP.
在等腰 Rt△PAF 中,取 PF 的中点 G,连接 AG.
解(II):利用二面角的定义。在等边三角形 ABM 中过点 B 作 BF AM 交 AM 于
点 F ,则点 F 为 AM 的中点,过 F 点在平面 ASM 内作 GF AM ,GF 交 AS 于 G,
连结 AC,∵△ADC≌△ADS,∴AS-AC,且 M 是 SC 的中点,
∴AM⊥SC, GF⊥AM,∴GF∥AS,又∵ F 为 AM 的中点,
五种方法求二面角及练习题
一、 定义法: 从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这
两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂 线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。如例 1 中从二面角 S—AM—B 中半平面 ABM 上的一已知点(B)向棱 AM 作垂线,得垂足(F);在另一半平面 ASM 内过该垂足 (F)作棱 AM 的垂线(如 GF),这两条垂线(BF、GF)便形成该二面角的一个平面角, 再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。
第8章立体几何专题8 二面角的求解-人教A版(2019)高中数学必修(第二册)常考题型专题练习

二面角的求解【方法总结】二面角A-BC-D 的求法:1、先确定两个平面,面ABC 及面BCD 和其两面的交线BC ,根据题意过点A 或点D 作交O 线BC 的垂线(一般情况选择在等腰三角形中作垂线AB=AC 时,或者在直角三角形中作垂线∠BAC=900时,应该过点A 作BC 垂线);2、1)反连OD ,证明OD ⊥BC ;2)若OD 不垂直于BC ,看面BCD 内是否有与交线BC 垂直的直线,若有直线l ⊥BC ,则直接过点O 作l 的平行线;3、若两个平面上没有对应的等腰三角形则看两平面是否有垂直于交线BC 的直线若有可将两垂线平移至相交直线,求其夹角。
【巩固练习】1、在长方体''''ABCD A B C D -中,若AB AD =='CC =,则二面角'C BD C --的大小为( )A .30B .45C .60D .90【答案】A【解析】如图所示,AB AD =∵BCD ∆, 'BC D ∆为等腰三角形,∴OC BD ⊥, 'OC BD ⊥,则'C OC ∠是二面角'C BD C --的平面角,30,故选2.已知矩形ABCD 的两边3AB =,4=AD ,PA ⊥平面ABCD ,且45PA =,则二面角A BD P --的正切值为( )A .12B .13C .12-D .13- 【答案】B【解析】如图所示,在平面PBD 内,过P 作BD 的垂线,垂足为E ,连接AE , 因为PA ⊥平面ABCD ,BD ⊂ 平面ABCD ,所以PA BD ⊥,因为PE BD ⊥,PA PE P = ,故BD ⊥平面PAE ,因为AE ⊂平面PAE ,故AE BD ⊥,所以PEA ∠为A BD P --的平面角,3.如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆翻折成A CD '∆,所成二面角A CD B '--的平面角为α,则A.A DB α'∠≤B.A DB α'∠≥C.A CB α'∠≤D.A CB α'∠≥ B 【解析】解法一 设ADC θ∠=,2AB =,则由题意知1AD BD A D '===. 在空间图形中,连结A B ',设A B '=t .过A '作A N DC '⊥,过B 作BM DC ⊥,垂足分别为N M 、.连结,A P BP ',则A NP '∠就是二面角A CD B '--的平面角,所以A NP α'∠=. 在ΔRt A ND '中,cos cos DN A D A DC θ''=∠=,sin sin A N A D A DC θ'''=∠=. 同理,sin BM PN θ==,cos DM θ=,故2cos BP MN θ==.显然BP ⊥平面A NP ',故BP A P '⊥.在ΔRt A BP '中,222222(2cos )4cos A P A B BP t t θθ''=-=-=-.2π时取等号)因为α,[0,]A DB π'∠∈,而cos y x =在[0,]π上为递减函数,所以A DB α'∠≤,故选B .解法二 若CA CB ≠,则当απ=时,A CB π'∠<,排除D ;当0α=时,0A CB '∠>,0A DB '∠>,排除A 、C ,故选B .4、如图,在直棱柱111ABC A B C -中,AB AC ⊥,12AB AC AA ===,则二面角11A BC C --的平面角的正弦值为____.【解析】过1A 作111A D B C ⊥交11B C 于D ,过D 作1DE BC ⊥,交1BC 于E ,连接1A E .由于三棱柱为直三棱柱,故11CC A D ⊥,所以1A D ⊥平面11BCC B ,所以111,A D BC A D DE ⊥⊥,因此1BC ⊥平面1A DE ,所以11BC A E ⊥.故1DEA ∠是二面角11A BC C --的平面角的补角,由于AB AC ⊥,12AB AC AA ===,故5.如图所示,在四棱锥P ABCD -中,底面是边长为a 的正方形,侧棱PD a PA PC ===,,则二面角P BC D --的大小为___________.【答案】45.【解析】由题意,四棱锥P ABCD -中,底面是边长为a 的正方形,PDa , PD DC , 同理PD DA ⊥,因为DA DC D =,所以PD ⊥平面ABCD ,则PD BC ⊥,又BC DC ⊥,且PD DC D =,所以BC ⊥平面PDC ,则BC PC ⊥,所以PCD ∠为二面角P BC D --的平面角,在Rt PDC △中,PD DC a ==,所以45PCD ∠=,所以二面角P BC D --的大小为45.6、如图,已知在直四棱柱1111ABCD A B C D -中,AD DC ⊥,//AB DC ,122DC DD AD AB ===.(1)求证:DB ⊥平面11B BCC ;(2)求二面角11A BD C --的正弦值.【解析】(1)设E 是DC 的中点,连结BE ,则四边形DABE 为正方形, 90,即BD 又1BD BB ⊥,1.B B BC B ⋂=BD ∴⊥平面11BCC B ,(2)由(I )知DB ⊥平面11BCC B ,又1BC ⊂平面11BCC B ,1BD BC ∴⊥,取DB 的中点F , 连结1A F ,又11A D A B =,则1A F BD ⊥.取1DC 的中点M ,连结FM ,则1FMBC ,FM BD ∴⊥.∴BD ⊥平面1A FM 1A FM ∴∠为二面角11A BD C --的平面角. ,在1A FM 中,212BC =+取11D C 的中点H ,连结1A H ,HM , 1Rt A HM 中,1A H =7、已知四棱柱1111ABCD A B C D -的底面为菱形,12AB AA ==,3BAD π∠=,AC BD O =,AO ⊥平面1A BD ,11A BA D =.(1)证明:1//B C 平面1A BD ;(2)求钝二面角1B AA D --的余弦值.【解析】 (1)证明:连接1AB 交1A B 于点Q ,易知Q 为1AB 中点,∵OQ ⊂平面1A BD ,1B C ⊄平面1A BD , ∴1//B C 平面1A BD .(2)∵AO ⊥平面1A BD ,∴1AO A O ⊥,∵11A B A D =且O 为BD 的中点,∴1AO BD ⊥, ∵AO BD ⊂、平面ABCD 且AO BD O =,∴1A O ⊥平面ABCD ,如图,建立空间直角坐标系O xyz -.∴(1AA =-,(AB =-设平面1A AB 的一个法向量为(),,n x y z =, 1n AA n AB ⎧⊥⎨⊥⎩,∴⎧-⎪⎨⎪⎩1=,得y z =∴(1,3,n =的一个法向量为(1,m =-1,7m nm n m n ⋅<>==,8、如图,在椎体P-ABCD 中,ABCD 是边长为1的棱形,且∠DAB =60,PB =2,E ,F 分别是BC ,PC 的中点. (Ⅰ)证明:AD 平面DEF;(Ⅱ)求二面角P -AD -B 的余弦值. 【解析】法一:(Ⅰ)证明:取AD 中点G ,连接PG ,BG ,BD .因P A =PD ,有PG AD ⊥,在ABD ∆中,1,60AB AD DAB ==∠=︒,有ABD ∆为等边三角形,因此,BG AD BG PG G ⊥⋂=,所以AD ⊥平面PBG ,.AD PB AD GB ⇒⊥⊥又PB //EF ,得AD EF ⊥,而DE //GB 得AD ⊥DE ,又FE DE E ⋂=,所以AD ⊥平面DEF 。
高二数学二面角专项练习题及参考答案(精品)

高二数学二面角专项练习题及参考答案班级_____________姓名_____________一、定义法:直接在二面角的棱上取一点,分别在两个半平面内作棱的垂线,得出平面角. 例1 在四棱锥P-ABCD 中,ABCD 是正方形,PA ⊥平面ABCD ,PA=AB=a ,求二面角B-PC-D 的大小。
二、垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;例2 在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面ABCD ,PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的正切。
三、垂面法:作棱的垂直平面,则这个垂面与二面角两个面的交线所夹的角就是二面角的平面角 例3 在四棱锥P-ABCD 中,ABCD 是正方形,PA ⊥平面ABCD ,求B-PC-D 的大小。
四、投影面积法:一个平面α上的图形面积为S ,它在另一个平面β上的投影面积为S',这两个平面的夹角为θ,则S'=Scos θ或cos θ=/SS .例4 在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
五、补形法:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。
例5、在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
方法归纳:二面角的类型和求法可用框图展现如下: [基础练习]1. 二面角是指 ( ) A 两个平面相交所组成的图形B 一个平面绕这个平面内一条直线旋转所组成的图形C 从一个平面内的一条直线出发的一个半平面与这个平面所组成的图形D 从一条直线出发的两个半平面所组成的图形2.平面α与平面β、γ都相交,则这三个平面可能有 ( ) A 1条或2条交线 B 2条或3条交线C 仅2条交线D 1条或2条或3条交线3.在300的二面角的一个面内有一个点,若它到另一个面的距离是10,则它到棱的距离是( )A 5B 20C 210 D225 4.在直二面角α-l-β中,RtΔABC 在平面α内,斜边BC 在棱l 上,若AB 与面β所成的角为600,则AC 与平面β所成的角为 ( ) A 300 B 450 C 600 D 1200 5.如图,射线BD 、BA 、BC 两两互相垂直,AB=BC=1,BD=26, 则弧度数为3的二面角是( ) A D-AC-B B A-CD-BC A-BC-D D A-BD-C6.△ABC 在平面α的射影是△A 1B 1C 1,如果△ABC 所在平面和平面α成θ,则有( ) A S △A1B1C1=S △ABC ·sinθ B S △A1B1C1= S △ABC ·cosθC S △ABC =S △A1B1C1·sinθD S △ABC =S △A1B1C1·cosθ7.如图,若P 为二面角M-l-N 的面N 内一点,PB ⊥l ,B 为垂足,A 为l 上一点,且∠PAB=α,PA 与平面M 所成角为β,二面角M-l-N 的 大小为γ,则有 ( )A.sinα=sinβsinγB.sinβ=sinαsinγC.sinγ=sinαsinβ D 以上都不对AB C DAB M NP l C1A1B1D8.在600的二面角的棱上有两点A 、B ,AC 、BD 分别是在这个二面角的两个面内垂直于AB 的线段,已知:AB=6,AC=3,BD=4,则CD= 。
解二面角问题三种方法(习题及答案)

C A B DA A 1B DC C 1 B 1 解二面角问题(一)寻找有棱二面角的平面角的方法和求解。
(1)定义法:利用二面角的平面角的定义,在二面角的棱上取一点,过该点在两个半平面内作垂直于棱的射线,两射线所成的角就是二面角的平面角,这是一种最基本的方法。
要注意用二面角的平面角定义的三个“主要特征”来找出平面角,当然这种找出的角要有利于解决问题。
下面举几个例子来说明。
例1:如图,立体图形V -ABC 的四个面是全等的正三角形,画出二面角V -AB -C 的平面角并求出它的度数。
例2:在三棱锥P-ABC 中,∠APB=∠BPC=∠CPA=600,求二面角A-PB-C 的余弦值。
这样的类型是不少的,如下列几道就是利用定义法找出来的:1、在正方体ABCD -A 1B 1C 1D 1中,找出二面角B -AC -B 1的平面角并求出它的度数。
2、.边长为a 的菱形ABCD ,∠ACB=600,现沿对角线BD 将其折成才600的二面角,则A 、C 之间的距离为 。
(菱形两条对角线互相垂直,对折后的一条对角线成两条线段仍都垂直于另一条对角线,则所成的角是二面角的平面角)3、正三棱柱ABC —A 1B 1C 1的底面边长是4,过BC 的一个平面与AA 1交于D ,若AD =3,求二面角D ―BC ―A 的正切值。
总之,能用定义法来找二面角的平面角的,一般是图形的性质较好,能够较快地找到满足二面角的平面角的三个主要特征。
并且能够很快地利用图形的一些条件来求出所要求的。
在常见的几何体有正四面体,正三棱柱,正方体,以及一些平面图形,正三角形,等腰三角形,正方形,菱形等等,这些有较好的一些性质,可以通过它们的性质来找到二面角的平面角。
至于求角,通常是把这角放在一个三角形中去求解。
由图形及题目的已知条件来求这个三角形的边长或者角,再用解三角形的知识去求解。
(2)三垂线法:是利用三垂线的定理及其逆定理来证明线线垂直,来找到二面角的平面角的方法。
五种方法法求二面角及限时练习

五种方法求二面角及练习题之杨若古兰创作一、定义法:从一条直线出发的两个半平面所构成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角.本定义为解题提供了添辅助线的一种规律.如例1中从二面角S—AM—B中半平面ABM上的一已知点(B)向棱AM作垂线,得垂足(F);在另一半平面ASM内过该垂足(F)作棱AM的垂线(如GF),这两条垂线(BF、GF)便构成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题.例1(2009全国卷Ⅰ理)如图,四棱锥S ABCD-中,底面ABCD为矩形,SD⊥底面ABCD,2AD===,点M在侧棱SC上,ABMDC SD2∠=60°(I)证实:M在侧棱SC的中点(II)求二面角S AM B--的大小.证(I)略解(II):利用二面角的定义.在等边三角形ABM中过点B 作BF AM⊥交AM于点F,则点F为AMGF面ASM 内作GF AM ⊥,GF 交AS 于G ,连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点,∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点,∴GF 是△AMS 的中位线,点G 是AS 的中点.则GFB ∠即为所求二面角. ∵2=SM ,则22=GF ,又∵6==AC SA ,∴2=AM∵2==AB AM,060=∠ABM ∴△ABM 是等边三角形,∴3=BF在△GAB 中,26=AG ,2=AB ,090=∠GAB ,∴211423=+=BG366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG∴二面角S AM B --的大小为)36arccos(-练习1(2008山东)如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC , PC 的中点. (Ⅰ)证实:AE ⊥PD ;(Ⅱ)若H 为PD 上的动点,EH 与平面PAD 所成最大角FGE —AF —C 的余弦值.分析:第1题容易发现,可通过证AE ⊥AD 后推出AE ⊥平面APD ,使命题获证,而第2题,则首先必须在找到最大角正切值有关的线段计算出各线段的长度以后,考虑到应用在二面角的棱AF 上找到可计算二面角的平面角的顶点S ,和两边SE 与SC ,进而计算二面角的余弦值.(答案:二二、三垂线法三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上则通经常使用三垂线定理法求二面角的大小.本定理亦提供了另一种添辅助线的普通规律.如(例2)过二面角中半平面BFC 上的一已知点B 作另一半平面FC 1C 的垂线,得垂足O ;再过该垂足O 作棱FC 1的垂线,得垂足P ,连结起点与起点得斜线段PB ,便构成了三垂线定理的基本构图(斜线PB 、垂线BO 、射影OP ).再解直角三角形求二面角的度数.例2.(2009山东卷理)如图,在直四棱柱EABCFE 1 A 1B 1C 1D 1D中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2, AA 1=2, E 、E 1、F 分别是棱AD 、AA 1、AB 的中点.(1) 证实:直线EE 1//平面FCC 1; (2)求二面角B-FC 1-C 的余弦值.证(1)略解(2)由于AB=4, BC=CD=2, 、F 是棱AB 的中点,所以BF=BC=CF,△BCF 为正三角形,取CF 的中点O,则OB ⊥CF,又由于直四棱柱ABCD-A 1B 1C 1D 1中,CC 1⊥平面ABCD,所以CC 1⊥BO,所以OB ⊥平面CC 1F,过O 在平面CC 1F 内作OP ⊥C 1F,垂足为P,连接BP,则∠OPB 为二面角B-FC 1-C 的一个平面角, 在△BCF 为正三角形中,3OB =,在Rt △CC 1F 中, △OPF ∽△CC 1F,∵11OP OF CC C F=∴22122222OP =⨯=+, 在Rt △OPF 中22114322BP OP OB =+=+=,272cos 7142OP OPB BP ∠===,所以二面角B-FC 1-C 的余弦值为77. 练习2(2008天津)如图,在四棱锥ABCD P -中,底面ABCD 是矩形.EAB CFE 1A 1B 1C 1D 1DF 1O P已知60,22,2,2,3=∠====PAB PD PA AD AB .(Ⅰ)证实⊥AD 平面PAB ;(Ⅱ)求异面直线PC 与AD 所成的角的大小;(Ⅲ)求二面角A BD P --的大小.分析:本题是一道典型的利用三垂线定理求二面角成绩,在证实AD ⊥平面PAB 后,容易发现平面PAB ⊥平面ABCD ,点P 就是二面角P-BD-A 的半平面上的一个点,因而可过点P 作棱BD 的垂线,再作平面ABCD 的垂线,因而可构成三垂线定理中的斜线与射影内容,从而可得本解法.(答案:二面角A BD P --的大小为439arctan)三.补棱法本法是针对在解构成二面角的两个半平面没有明确交线的求二面角题目时,要将两平面的图形弥补完好,使之有明确的交线(称为补棱),然后借助前述的定义法与三垂线法解题.即当二平面没有明确的交线时,普通用补棱法解决例3(2008湖南)如图所示,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的AB CEDP中点,PA⊥底面ABCD,PA=2.(Ⅰ)证实:平面PBE⊥平面PAB;(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的大小.分析:本题的平面PAD和平面PBE没有明确的交线,依本法明显要弥补完好(耽误AD、BE订交于点F,连结PF.)再在完好图形中的PF.上找一个适合的点构成二面角的平面角解之.(Ⅰ)证略解: (Ⅱ)耽误AD、BE订交于点F,连结PF.过点A作AH⊥PB于H,由(Ⅰ)知平面PBE⊥平面PAB,所以AH⊥平面PBE.在Rt△ABF中,由于∠BAF=60°,所以,AF=2AB=2=AP.在等腰Rt△PAF中,取PF的中点G,连接AG.则AG⊥PF.连结HG,由三垂线定理的逆定理得,PF⊥HG.所以∠AGH是平面PAD和平面PBE所成二面角的平面角(锐角).在等腰Rt△PAFABCEDPFGH在Rt △PAB 中,所以,在Rt △AHG故平面PAD 和平面PBE 所成二面角(锐角)的大小是练习3已知斜三棱柱ABC —A 1B 1C 1的棱长都是a ,侧棱与底面成600的角,正面BCC 1B 1⊥底面ABC.(1)求证:AC 1⊥BC ;(2)求平面AB 1C 1与平面 ABC 所成的二面角(锐角)的大小.提示:本题须要补棱,可过A 点作CB 的平行线L (答案:所成的二面角为45O )四、S射影凡二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的都可利用射影面积公式(.例4.(2008北京理)如图,在三棱锥ACBPACBB 1C 1A 1L分析:本题请求二面角B —AP —C 的大小,如果利用射影面积法解题,不难想到在平面ABP 与平面ACP 中建立一对原图形与射影图形并分别求出S 原与S 射 因而得到上面解法.解:(Ⅰ)证略∴△ACE 是△ABE 在平面ACP 内的射影,因而可求得:,,则设二面角的大小为,则A CBEPA 1D 1 B 1C 1EDBC A图5∴二面角B AP C --的大小为33arccos=ϑ练习4:如图5,E 为正方体ABCD -A 1B 1C 1D 1的棱CC 1的中点,求平面AB 1E 和底面A 1B 1C 1D 1所成锐角的余弦值.分析 平面AB 1E 与底面A 1B 1C 1D 1交线即二面角的棱没有给出,要找到二面角的平面角,则必须先作两个平面的交线,这给解题带来必定的难度.考虑到三角形AB 1E 在平面A 1B 1C 1D 1上的射影是三角形A 1B 1C 1,从而求得两个三角形的面积即可求得二面角的大小.(答案:所求二面角的余弦值为cos θ=32).五、向量法向量法解立体几何中是一种十分简捷的也是非常传统的解法,可以说所有的立体几何题都可以用向量法求解,用向量法解立体几何题时,通常要建立空间直角坐标系,写出各点的坐标,然后将几何图中的线段写成用坐标法暗示的向量,进行向量计算解题.例4:(2009天津卷理)如图,在五面体ABCDEF 中,FA⊥平面ABCD, AD//BC//FE ,AB ⊥AD ,M 为EC 的中点,AF=AB=BC=FE=12AD(I) 求异面直线BF 与DE 所成的角的大小;(II) 证实平面AMD ⊥平面CDE ; 求二面角A-CD-E 的余弦值.此刻我们用向量法解答:如图所示,建立空间直角坐标系,以点A为坐标原点.设,1=AB 依题意得(),,,001B (),,,011C (),,,020D (),,,110E (),,,100F(I )(),,,解:101BF -=(),,,110DE -= 所以异面直线BF 与DE 所成的角的大小为060. (II)证实:,,,由⎪⎭⎫ ⎝⎛=21121AM (),,,101CE -=()0AM CE 020AD =•=,可得,,,(III )⎪⎩⎪⎨⎧=•=•=.0D 0)(CDE E u CE u z y x u ,,则,,的法向量为解:设平面 又由题设,平面ACD 的一个法向量为).100(,,=v 练习5、(2008湖北)如图,在直三棱柱111ABC A B C -中,平面ABC ⊥正面11A ABB . (Ⅰ)求证:AB BC ⊥;(Ⅱ)若直线AC 与平面1A BC 所成的角为θ,二面角1A BC A --的大小为ϕ,试判断θ与ϕ的大小关系,并予以证实.分析:由已知条件可知:平面ABB 1A 1⊥平面BCC 1B 1⊥平面ABC 因而很容易想到以B 点为空间坐标原点建立坐标系,并将相干线段写成用坐标暗示的向量,先求出二面角的两个半平面的法向量,再利用两向量夹角公式求解.总之,上述五种二面角求法中,前三种方法可以说是三种增加辅助线的普通规律,后两种是两种分歧的解题技巧,考生可选择使用.1. 如图,的中点,(Ⅰ)(Ⅱ)(Ⅲ) 所成角的余弦值2.如图,已知正方形ABCD 和正方形ABEF 所在平面成600的二面角,求直线BD 与平面ABEF 所成角的正弦值.3.如图,在棱长为a 的正方体ABCD —(1)面A 1ABB 1与面ABCD (2)二面角C 1—BD —C 的正切值 (31A A设PA=AB=a ,(1)求二面角B PCD 的大小;(2)求二面角C-PD-A5. 如图所示,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的中点,PA ⊥底面ABCD ,PA =3.(1) 证实: BE ⊥平面PAB ; (2) 求二面角A -BE -P 的大小 (3)PB 与面PAC 的角6如图,在底面为直角梯形的四棱锥,//,BC AD ABCD P 中-,90︒=∠ABCABCD PA 平面⊥,32,2,3===AB AD PA ,BC=6(1) 求证:;PAC BD 平面⊥(2) 求二面角A BD P --的大小. (3)求二面角B-PC-A 的大小7.如图,直二面角D —AB —E 中,四边形ABCD 是边长为2的正方形,AE=EB ,F 为CE 上的点,且BF ⊥平面ACE. (Ⅰ)求证AE ⊥平面BCE ;(Ⅱ)求二面角B —AC —E 的大小; (Ⅲ)求点D 到平面ACE 的距离.8.如图,在四棱锥P ABCD -中,底面ABCD 是矩形.已知3AB =,2AD =,2PA =,ADPEPABcDFED BA。
二面角习题及标准答案

二面角习题及答案————————————————————————————————作者:————————————————————————————————日期:二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
解:DPC A BE DB ASCS R NMO B DPA CB A EC5.已知正方体 AC',M 、N 分别是BB',DD'的中点,求截面 AMC'N 与面ABCD ,CC'D'D 所成的角。
解:6.如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:7. 三棱锥 A-BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9. 如图所示,四棱锥P —ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD.(2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小. 解析:D BD ACBAC M N B F E ACDDOA BC10. 如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC 上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.11. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a. (1)求证:AF ⊥A1C(2)求二面角C —AF —B 的大小12.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A 所成二面角的大小.13. 在正方体1111D C B A ABCD -中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM 与ABCD 所成角的大小.14. 如图,将边长为a 的正三角形ABC 按它的高AD 为折痕折成一个二面角C AD C --'. (1)若二面角C AD C --'是直二面角,求C C '的长; (2)求C A '与平面CD C '所成的角;(3)若二面角C AD C --'的平面角为120°,求二面角D C C A -'-的平面角的正切值.参考答案解:由已知条件,D 是BC 的中点∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC ∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2、解:∵ BS =BC ,又DE 垂直平分SC ∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60° 3、解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2, 过 N 作 NR ⊥BD 于 R ,连MR , 则 ∠MRN 即为二面角 M-BD-C 的平面角 过 C 作 CE ⊥BD 于S则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴ 58BD BC CD CE =⋅=DPCA BE DBASCS R N MO B DPA C∴ 54RN =25RN MN MRN tan ==∠ ∴ 25arctanMRN =∠ 4. 解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴ △EBD 为△ABD 在面BCD 内的射影设 AB =a 则AE =DE =ABsin60°=a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴ 22ABD a 815415a 21S =⨯=∆ 又 a 21BE = ∴ 2BDE a 83a 21a 2321S =⋅⋅=∆ ∴ 55S S cos ABD BDE ==θ∆∆ 5. 解:设边长为a ,易证 ANC'N 是菱形 且MN =a 2,A'C =a 3 ∴S□AMC'N = 2a 26'AC 21MN =⋅由于AMC'N 在面ABCD 上的射影即 为正方形ABCD ∴ S□ABCD =2aD B D AC BAC MN∴ 36a 26a cos 221==θ ∴ 36arccos1=θ 取CC'的中点M',连结DM'则平行四边形DM'C'N 是四边形AMC'N 在CC'D'D 上的射影,S□DM'C'M =2a 21 ∴ 66a 26a21cos 222==θ ∴66arccos2=θ 6. 解:作DF ⊥AB 于F ,CE ⊥AB 于E , ∵ AC =CD =1 ∠ABC =30° ∴ AD =2,BC =3 , AB =2, BD =2 在Rt △ABC 中, 23231AB BC AC CE =⨯=⋅=,同理 1222ABBDAD DF =⨯=⋅= ∴ 1DF BD BF 22=-=21CE AC AE 22=-= ∴ 212112EF =--= ∴ θ⋅-++=cos DF EF 2EF DF CE CD 2222∴ 33cos =θ BF E ACD即所求角的大小为33arccos。
空间二面角的求法

立体几何二面角求法练习题1、正方形ABCD-A 1B 1C 1D 1中,二面角B-A 1C-A 的大小为___ _;2、将∠A 为60°的棱形ABCD 沿对角线BD 折叠,使A 、C 的距离等于BD ,则二面角A-BD-C 的余弦值是 __;3、正四棱柱ABCD —A 1B 1C 1D 1中对角线BD 1=8,BD 1与侧面B 1BCC 所成的为30°,则二面角C 1—BD 1—B 1的大小为____ __;4、从点P 出发引三条射线PA 、PB 、PC ,每两条的夹角都是60°,则二面角B-PA-C 的余弦值是___ ___;5、二面角α-l -β的平面角为120°,A 、B ∈l ,AC ⊂α,BD ⊂β,AC ⊥l ,BD ⊥l ,若AB=AC=BD=1,则CD 的长___ ___;6、ABCD 为菱形,∠DAB =60°,PD ⊥面ABCD ,且PD =AD ,则面PAB 与面PCD 所成的锐二面角的大小为___ ___。
7、空间三条射线CA 、CP 、CB ,∠PCA=∠PCB=600,∠ACB=900,求二面角B-PC-A 的大小。
8、如图:Rt ∠ABC 中,斜边AB 在平面α内,C ∉α,AC 、BC 与α所成角分别为450和300,求平面ABC 与α所成角。
P BαCAE FDDαC BAH1、P 是二面角βα--AB 的棱AB 上一点,分别在βα,上引射线PM 、PN ,若o45=∠=∠BPN BPM ,o 60=∠MPN ,则二面角βα--AB 的大小为( )A. o30 B. o45 C. o60 D. o902、正方体1111D C B A ABCD -中二面角111A D C A --的大小为 。
3、在一个o45的二面角的一个面内有一条直线与二面角的棱成o45,则此直线与二面角的另一个面所成的角为 。
4、如图,立体图形V-ABC 的四个侧面是全等的正三角形,则二面角V-AB-C 的度数为( )A. 31arccosB. 32arccosC. 33arccosD.61arccos5、如图,若P 为二面角M-l-N 的面N 内一点,PB ⊥l ,B 为垂足,A 为l 上一点,且∠P AB=α,PA 与平面M 所成角为β,二面角M-l-N 的大小为γ,则有 ( )A sinα=sinβsinγB sinβ=sinαsinγC sinγ=sinαsinβD 以上都不对 6、在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面ABCD ,PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的大小。
34 高中数学立体几何(解答题)二面角计算专题训练

专题3高中数学立体几何(解答题)二面角计算专题训练【方法总结】 1.二面角(1)如图①,AB ,CD 是二面角α-l -β的两个面内与棱l 垂直的直线,则二面角的大小θ=<AB →,CD →>.(2)如图②③,n 1,n 2分别是二面角α-l -β的两个半平面α,β的法向量,则二面角的大小θ满足|cos θ|=|cos <n 1,n 2>|,二面角的平面角大小是向量n 1与n 2的夹角(或其补角).2.平面与平面的夹角如图,平面α与平面β相交,形成四个二面角,我们把四个二面角中不大于90°的二面角称为平面α与平面β的夹角.若平面α,β的法向量分别是n 1和n 2,则平面α与平面β的夹角即为向量n 1和n 2的夹角或其补角.设平面α与平面β的夹角为θ,则cos θ=|cos <n 1,n 2>|=|n 1·n 2||n 1||n 2|. 3.利用空间向量计算二面角大小的常用方法(1)找法向量:分别求出二面角的两个半平面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角的大小;(2)找与棱垂直的方向向量:分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小就是二面角的大小.【高考真题】1.(2022新高考Ⅰ卷)如图,直三棱柱111ABC A B C 的体积为4,1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1A C 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C --的正弦值.2.(2022新高考Ⅱ卷)如图,PO 是三棱锥P ABC -的高,PA PB =,AB AC ⊥,E 是PB 的中点.(1)证明://OE 平面PAC ;(2)若30ABO CBO ︒∠=∠=,3PO =,5PA =,求二面角C AE B --的正弦值. 【题型突破】1.(2020·全国Ⅲ改编)如图,在长方体ABCD -A 1B 1C 1D 1中,点E ,F 分别在棱DD 1,BB 1上,且2DE =ED 1,BF =2FB 1.(1)证明:点C 1在平面AEF 内;(2)若AB =2,AD =1,AA 1=3,求平面AEF 与平面EF A 1夹角的正弦值.2.(2019·全国Ⅲ)图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE = BF =2,∠FBC =60°.将其沿AB ,BC 折起使得BE 与BF 重合,连接DG ,如图2. (1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的二面角B -CG -A 的大小.3.(2019·全国Ⅱ)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B-EC-C1的正弦值.4.(2019·全国Ⅰ改编)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求平面AMA1与平面MA1N夹角的正弦值.5.(2020·全国Ⅰ)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD.△ABC是底面的内接正三角形,P为DO上一点,PO=66DO.(1)证明:P A⊥平面PBC;(2)求二面角B-PC-E的余弦值.6.(2021·全国新Ⅱ)在四棱锥Q-ABCD中,底面ABCD是正方形,若AD=2,QD=QA=5,QC=3.(1)证明:平面QAD ⊥平面ABCD ; (2)求二面角B -QD -A 的平面角的余弦值.7.(2021·全国乙)如图,四棱锥P —ABCD 的底面是矩形,PD ⊥底面ABCD ,PD =DC =1,M 为BC 的 中点,且PB ⊥AM . (1)求BC ;(2)求二面角A -PM -B 的正弦值.8.(2018·全国Ⅲ)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD ︵ 所在平面垂直,M 是CD ︵上异 于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M -ABC 体积最大时,求面MAB 与面MCD 所成二面角的正弦值.9.(2021·全国新Ⅰ)如图,在三棱锥A -BCD 中,平面ABD ⊥平面BCD ,AB =AD ,O 为BD 的中点. (1)证明:OA ⊥CD ;(2)若△OCD 是边长为1的等边三角形,点E 在棱AD 上,DE =2EA ,且二面角E -BC -D 的大小为45°,求三棱锥A -BCD 的体积.DABCQDABCPM10.(2021·全国甲)已知直三棱柱ABC -A 1B 1C 1中,侧面AA 1B 1B 为正方形,AB =BC =2,E ,F 分别为AC和CC 1的中点,D 为棱A 1B 1上的点,BF ⊥A 1B 1. (1)证明:BF ⊥DE ;(2)当B 1D 为何值时,面BB 1C 1C 与面DFE 所成的二面角的正弦值最小?11.(2021·北京)已知正方体ABCD -A 1B 1C 1D 1,点E 为A 1D 1中点,直线B 1C 1交平面CDE 于点F .(1)证明:点F 为B 1C 1的中点;(2)若点M 为棱A 1B 1上一点,且二面角M -CF -E 的余弦值为53,求A 1M A 1B 1的值.12.如图所示的几何体由平面PECF 截棱长为2的正方体得到,其中P ,C 为原正方体的顶点,E ,F 为原 正方体侧棱长的中点,正方形ABCD 为原正方体的底面,G 为棱BC 上的动点. (1)求证:平面APC ⊥平面PECF ;(2)设BG →=λBC →(0≤λ≤1),当λ为何值时,平面EFG 与平面ABCD 所成的角为π3?ABCDOEBACA 1B 1C 1D FEBAD CA 1B 1C 1D 1E FM13.如图,已知直三棱柱ABC -A 1B 1C 1中,AA 1=AB =AC =1,AB ⊥AC ,M ,N ,Q 分别是CC 1,BC ,AC的中点,点P 在直线A 1B 1上运动,且A 1P →=λA 1B 1→(λ∈[0,1]). (1)证明:无论λ取何值,总有AM ⊥平面PNQ ;(2)是否存在点P ,使得平面PMN 与平面ABC 的夹角为60°?若存在,试确定点P 的位置,若不存在,请说明理由.14.已知在四棱锥P -ABCD 中,平面PDC ⊥平面ABCD ,AD ⊥DC ,AB ∥CD ,AB =2,DC =4,E 为PC的中点,PD =PC ,BC =22. (1)求证:BE ∥平面P AD ;(2)若PB 与平面ABCD 所成角为45°,点P 在平面ABCD 上的射影为O ,问:BC 上是否存在一点F ,使平面POF 与平面P AB 所成的角为60°?若存在,试求点F 的位置;若不存在,请说明理由.15.如图所示,在梯形ABCD 中,AB ∥CD ,∠BCD =120°,四边形ACFE 为矩形,且CF ⊥平面ABCD ,AD =CD =BC =CF . (1)求证:EF ⊥平面BCF ;(2)点M 在线段EF 上运动,当点M 在什么位置时,平面MAB 与平面FCB 所成的锐二面角最大,并求此时二面角的余弦值.16.如图所示,正方形AA 1D 1D 与矩形ABCD 所在平面互相垂直,AB =2AD =2,点E 为AB 的中点.(1)求证:BD 1∥平面A 1DE ;(2)设在线段AB 上存在点M ,使二面角D 1-MC -D 的大小为π6,求此时AM 的长及点E 到平面D 1MC的距离.17.(2017·全国Ⅱ)如图,四棱锥P -ABCD 中,侧面P AD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD ,∠BAD =∠ABC =90°,E 是PD 的中点. (1)证明:直线CE ∥平面P AB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为45°,求二面角M -AB -D 的余弦值.18.如图所示的几何体中,四边形ABCD 是等腰梯形,AB ∥CD ,∠ABC =60°,AB =2BC =2CD ,四边形DCEF 是正方形,N ,G 分别是线段AB ,CE 的中点. (1)求证:NG ∥平面ADF ;(2)设二面角A -CD -F 的大小为θ⎝⎛⎭⎫π2<θ<π,当θ为何值时,二面角A -BC -E 的余弦值为1313?19.已知三棱锥P -ABC (如图1)的平面展开图(如图2)中,四边形ABCD 为边长等于2的正方形,△ABE和△BCF 均为正三角形.在三棱锥P -ABC 中: (1)证明:平面P AC ⊥平面ABC ;(2)若点M 在棱P A 上运动,当直线BM 与平面P AC 所成的角最大时,求二面角P -BC -M 的余弦值.20.如图所示,在四棱锥P-ABCD中,侧面P AD⊥底面ABCD,侧棱P A=PD=2,P A⊥PD,底面ABCD 为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD的中点.(1)求直线PB与平面POC所成角的余弦值;(2)求B点到平面PCD的距离;(3)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为63若存在,求出PQQD的值;若不存在,请说明理由.。
高中数学例题:二面角

高中数学例题:二面角例6.已知Rt△ABC,斜边BCα⊂,点Aα∉,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,求二面角A-BC-O的大小。
【答案】60°【解析】如图所示,在平面α内,过O作OD⊥BC,垂足为D,连接AD。
设OC=a,∵AO⊥α,BC⊂α,∴AO⊥BC。
又∵AO∩OD=O,∴BC⊥平面AOD。
而AD⊂平面AOD,∴AD⊥BC,∴∠ADO是二面角A-BC-O的平面角。
由AO⊥α,OB⊂α,OC⊂α知AO⊥OB,AO⊥OC。
又∠ABO=30°,∠ACO=45°,∴AO=a,AC=,AB=2a。
在Rt△ABC中,∠BAC=90°,∴BC==,∴3AB ACADBC⋅===。
在Rt△AOD中,sin AOADOAD∠===。
∴∠ADO=60°,即二面角A-BC-O的大小是60°。
【总结升华】本题是用垂线法作二面角的平面角,求二面角的平面角关键是找出(或作出)平面角,再把平面角放到三角形中求解。
举一反三:【变式1】如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD ∠BAD=∠CDA=45°。
(1)求异面直线CE与AF所成角的余弦值;(2)证明:CD⊥平面ABF;(3)求二面角B—EF—A的正切值。
【答案】(1)3(2)略(3)14【解析】(1)因为//FA DE,所以CE与DE所成的角就是异面直线CE与AF所成角,余弦值为3。
(2)如右图,过点B作BG∥CD,交AD于点G,则∠BGA=∠CDA=45°。
由∠BAD=45°,可得BG⊥AB。
从而CD⊥AB。
又CD⊥FA,FA∩AB=A,所以CD⊥平面ABF。
(3)如图,MN与NG所成的角即为二面角B—EF—A的平面角,所以二面角B—EF—A的正切值为14。
高中数学二面角的平面角及求法精选题

二面角的平面角及求法一.选择题(共14小题)1.已知四棱锥S﹣ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S﹣AB﹣C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ12.如图长方体中,AB=AD=2,CC1=,则二面角C1﹣BD﹣C的大小为()A.30°B.45°C.60°D.90°3.将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个结论:①AC⊥BD;②△ACD是等边三角形;③AB与平面BCD所成的角为60°;④AB与CD所成的角为60°.其中错误的结论是()A.①B.②C.③D.④4.已知菱形ABCD的边长为2,∠BAD=60°,沿对角线BD将菱形ABCD折起,使得二面角A﹣BD﹣C的余弦值为,则该四面体ABCD外接球的体积为()A.B.8πC.D.36π5.如图,在四棱锥P﹣ABCD中,P A⊥底面ABCD,底面ABCD是边长为1的正方形,P A=1,则侧面PCD与底面ABCD所成的二面角的大小是()6.如图,三棱锥V﹣ABC的侧棱长都相等,底面ABC与侧面VAC都是以AC为斜边的等腰直角三角形,E为线段AC的中点,F为直线AB上的动点,若平面VEF与平面VBC所成锐二面角的平面角为θ,则cosθ的最大值是()A.B.C.D.7.已知矩形ABCD,AD=AB,沿直线BD将△ABD折成△A′BD,使点A′在平面BCD上的射影在△BCD内(不含边界).设二面角A′﹣BD﹣C的大小为θ,直线A′D,A′C与平面BCD所成的角分别为α,β,则()A.α<θ<βB.β<θ<αC.β<α<θD.α<β<θ8.如图,在三棱柱ABC﹣A1B1C1中,AB,AC,AA1两两互相垂直,AB=AC=AA1,M,N是线段BB1,CC1上的点,平面AMN与平面ABC所成(锐)二面角为,当|B1M|最小时,∠AMB=()A.B.C.D.9.如图,在大小为45°的二面角A﹣EF﹣D中,四边形ABFE与CDEF都是边长为1的正方形,则B与D两点间的距离是()A.B.C.1D.10.直角△ABC中,AB=AC=,D为BC边上一点,沿AD将△ACD折起,使点C在平面ABD内的正投影H 恰好在AB上,若AH=1,则二面角C﹣AD﹣B的余弦值是()A.B.C.D.11.已知点E是正方形ABCD的边AD上一动点(端点除外),现将△ABE沿BE所在直线翻折成△A′BE,并连结A′C,A′D.记二面角A′﹣BE﹣C的大小为α(0<α<π).则()A.存在α,使得BA′⊥面A′DE B.存在α,使得BA′⊥面A′CDC.存在α,使得EA′⊥面A′CD D.存在α,使得EA′⊥面A′BC12.如图,在直三棱柱ABC﹣A 1B1C1中,AB=AC=1,,点E,O分别是线段C1C,BC的中点,,分别记二面角F﹣OB1﹣E,F﹣OE﹣B1,F﹣EB1﹣O的平面角为α,β,γ,则下列结论正确的是()A.γ>β>αB.α>β>γC.α>γ>βD.γ>α>β13.如图,在单位正方体ABCD﹣A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:①异面直线A1P与BC1间的距离为定值;②三棱锥D﹣BPC1的体积为定值;③异面直线C1P与直线CB1所成的角为定值;④二面角P﹣BC1﹣D的大小为定值.其中真命题有()A.1个B.2个C.3个D.4个14.如图,已知BD是圆O的直径,A,C在圆上且分别在BD的两侧,其中BD=2,AB=CD.现将其沿BD折起使得二面角A﹣BD﹣C为直二面角,则下列说法不正确的是()A.A,B,C,D在同一个球面上B.当AC⊥BD时,三棱锥A﹣BCD的体积为C.AB与CD是异面直线且不垂直D.存在一个位置,使得平面ACD⊥平面ABC二.填空题(共17小题)15.在四面体ABCD中,AB=AD=2,∠BAD=60°,∠BCD=90°,二面角A﹣BD﹣C的大小为150°,则四面体ABCD外接球的半径为.16.已知正方体ABCD﹣A1B1C1D1中,E为BC的中点,在平面A1B1C1D1内,直线l∥B1D1,设二面角A﹣l﹣E的平面角为θ,当θ取最大值时,cosθ=.17.已知矩形ABCD,AB=20,BC=15,沿对角线AC将△ABC折起,使得BD=,则二面角B﹣AC﹣D的大小是.18.如图,在正四棱锥P﹣ABCD中,∠APC=60°,则二面角A﹣PB﹣C的平面角的余弦值为.19.如图,在四面体A﹣BCD中,已知棱AC的长为,其余各棱长都为1,则二面角A﹣CD﹣B的平面角的余弦值为.20.已知直二面角α﹣l﹣β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足.若AB=2,AC=BD=1,则D21.矩形ABCD中,AB=,BC=1,现将△ACD沿对角线AC向上翻折,得到四面体D﹣ABC,则该四面体外接球的体积为;设二面角D﹣AC﹣B的平面角为θ,当θ在[,]内变化时,|BD|的范围为.22.在边长为2的菱形ABCD中,A=60°,沿对角线BD折起,使二面角A﹣BD﹣C的大小为120°,这时点A,B,C,D在同一个球面上,则该球的表面积为・23.正三棱锥P﹣ABC高为2,侧棱与底面所成角为45°,则二面角P﹣AB﹣C的正切值是,点A到侧面PBC的距离是.24.在三棱锥P﹣ABC中,P A⊥AB,P A=4,AB=3,二面角P﹣AB﹣C的大小为30°,在侧面△P AB内(含边界)有一动点M,满足M到P A的距离与M到平面ABC的距离相等,则M的轨迹的长度为.25.如图,在三棱柱ABC﹣A1B1C1中,AC⊥CC1,AC⊥BC,AC=BC=2,∠C1CB=60°,CC1=3,点D,E分别在棱AA1和棱CC1上,且AD=1,CE=2,则二面角B﹣B1E﹣D的正切值.26.若四棱锥P﹣ABCD的侧面P AB内有一动点Q,已知Q到底面ABCD的距离与Q到点P的距离之比为正常数k,且动点Q的轨迹是抛物线,则当二面角P﹣AB﹣C平面角的大小为30°时,k的值为.27.四棱锥V﹣ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为的等腰三角形,则二面角V﹣AB﹣C的平面角为.28.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A﹣BCD,则在三棱锥A﹣BCD中,下列判断正确的是.(写出所有正确的序号)①平面ABD⊥平面ABC②直线BC与平面ABD所成角是45°③平面ACD⊥平面ABC29.小明在研究三棱锥的时候,发现下面一个真命题,在三棱锥A﹣BCD中,已知∠BAC=α,∠CAD=β,∠DAB =γ(如图),设二面角B﹣AC﹣D的大小为θ,则cosθ=,其中f(γ)是一个与γ有关的代数式,请写出符合条件的f(γ)=.30.将边长为1的正方形ABCD沿对角线AC折叠,使得点B和D的距离为1,则二面角B﹣AC﹣D的大小为.31.如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是.三.解答题(共5小题)32.如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面P AB⊥平面P AD;(2)若P A=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.33.如图,四棱锥P﹣ABCD中,侧面P AD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC =90°,E是PD的中点.(1)证明:直线CE∥平面P AB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.34.如图,在三棱锥P﹣ABC中,AB=BC=2,P A=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M﹣P A﹣C为30°,求PC与平面P AM所成角的正弦值.35.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.36.如图,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A﹣MA1﹣N的正弦值.二面角的平面角及求法精选题36道参考答案与试题解析一.选择题(共14小题)1.已知四棱锥S﹣ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S﹣AB﹣C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1【分析】作出三个角,表示出三个角的正弦或正切值,根据三角函数的单调性即可得出三个角的大小.【解答】解:∵由题意可知S在底面ABCD的射影为正方形ABCD的中心.过E作EF∥BC,交CD于F,过底面ABCD的中心O作ON⊥EF交EF于N,连接SN,取AB中点M,连接SM,OM,OE,则EN=OM,则θ1=∠SEN,θ2=∠SEO,θ3=∠SMO.显然,θ1,θ2,θ3均为锐角.∵tanθ1==,tanθ3=,SN≥SO,∴θ1≥θ3,又sinθ3=,sinθ2=,SE≥SM,∴θ3≥θ2.故选:D.【点评】本题考查了空间角的计算,三角函数的应用,属于中档题.2.如图长方体中,AB=AD=2,CC1=,则二面角C1﹣BD﹣C的大小为()A.30°B.45°C.60°D.90°【分析】取BD的中点E,连接C1E,CE,根据已知中AB=AD=2,CC1=,我们易得△C1BD及△CBD 均为等腰三角形,进而得到C1E⊥BD,CE⊥BD,则∠C1EC即为二面角C1﹣BD﹣C的平面角,解△C1EC即可求也二面角C1﹣BD﹣C的大小.【解答】解:取BD的中点E,连接C1E,CE由已知中AB=AD=2,CC1=,易得CB=CD=2,C1B=C1D=根据等腰三角形三线合一的性质,我们易得C1E⊥BD,CE⊥BD则∠C1EC即为二面角C1﹣BD﹣C的平面角在△C1EC中,C1E=2,CC1=,CE=故∠C1EC=30°故二面角C1﹣BD﹣C的大小为30°故选:A.【点评】本题考查的知识点是二面角平面角及求法,其中根据三垂线定理找出二面角的平面角是解答本题的关键.3.将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,有如下四个结论:①AC⊥BD;②△ACD是等边三角形;③AB与平面BCD所成的角为60°;④AB与CD所成的角为60°.其中错误的结论是()【分析】取BD的中点E,则AE⊥BD,CE⊥BD.根据线面垂直的判定及性质可判断①的真假;求出AC长后,可以判断②的真假;求出AB与平面BCD所成的角可判断③的真假;建立空间坐标系,利用向量法,求出AB与CD所成的角,可以判断④的真假;进而得到答案.【解答】解:取BD的中点E,则AE⊥BD,CE⊥BD.∴BD⊥面AEC.∴BD⊥AC,故①正确.设正方形边长为a,则AD=DC=a,AE=a=EC.∴AC=a.∴△ACD为等边三角形,故②正确.∠ABD为AB与面BCD所成的角为45°,故③不正确.以E为坐标原点,EC、ED、EA分别为x,y,z轴建立直角坐标系,则A(0,0,a),B(0,﹣a,0),D(0,a,0),C(a,0,0).=(0,﹣a,﹣a),=(a,﹣a,0).cos<,>==∴<,>=60°,故④正确.故选:C.【点评】本题考查的知识点是线面垂直的判定与性质,空间两点距离,线面夹角,异面直线的夹角,其中根据已知条件将正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,结合立体几何求出相关直线与直线、直线与平面的夹角,及线段的长是关键.4.已知菱形ABCD的边长为2,∠BAD=60°,沿对角线BD将菱形ABCD折起,使得二面角A﹣BD﹣C的余弦值为,则该四面体ABCD外接球的体积为()A.B.8πC.D.36π【分析】正确作出图形,利用勾股定理建立方程,求出四面体的外接球的半径,即可求出四面体的外接球的体积.【解答】解:如图所示,取BD中点F,连结AF、CF,则AF⊥BD,CF⊥BD,∴∠AFC是二面角A﹣BD﹣C的平面角,过A作AE⊥平面BCD,交CF延长线于E,∴cos∠AFC=﹣,cos,AF=CF==3,∴AE=2,EF=1,设O为球,过O作OO′⊥CF,交F于O′,作OG⊥AE,交AE于G,设OO′=x,∵O′B=CF=2,O′F==1,∴由勾股定理得R2=O′B2+OO'2=4+x2=OG2+AG2=(1+1)2+(2﹣x)2,解得x=,∴R2=6,即R=,∴四面体的外接球的体积为V=πR3==8π.故选:B.【点评】本题考查四面体的外接球的体积的求法,考查四面体、球等基础知识,考查运用求解能力、空间想象能力、探索能力、转化与化归思想、函数与方程思想,是中档题.5.如图,在四棱锥P﹣ABCD中,P A⊥底面ABCD,底面ABCD是边长为1的正方形,P A=1,则侧面PCD与底面ABCD所成的二面角的大小是()A.30°B.45°C.60°D.90°【分析】由已知利用直线与平面垂直的判定证明CD⊥平面P AD,可知∠PDA为侧面PCD与底面ABCD所成的二面角的平面角,再由已知结合直角三角形得答案.【解答】解:∵P A⊥底面ABCD,CD⊂平面ABCD,∴CD⊥P A,又底面ABCD是正方形,∴CD⊥AD,而P A∩AD=A,∴CD⊥平面P AD,得CD⊥PD,可知∠PDA为侧面PCD与底面ABCD所成的二面角的平面角.在Rt△P AD中,由P A=AD=1,可得∠PDA=45°.即侧面PCD与底面ABCD所成的二面角的大小是45°.故选:B.【点评】本题考查二面角的平面角的求法,考查空间想象能力与思维能力,是中档题.6.如图,三棱锥V﹣ABC的侧棱长都相等,底面ABC与侧面VAC都是以AC为斜边的等腰直角三角形,E为线段AC的中点,F为直线AB上的动点,若平面VEF与平面VBC所成锐二面角的平面角为θ,则cosθ的最大值是()A.B.C.D.【分析】连接BE,以E为坐标原点,分别以EB,EC,EV所在直线为x,y,z轴建立空间直角坐标系.求出平面VBC与平面VEF的一个法向量,由两法向量所成角的余弦值求解.【解答】解:由底面ABC与侧面VAC都是以AC为斜边的等腰直角三角形,得Rt△ABC≌Rt△AVC,∴VA=VC=BA=BC.设VA=VC=BA=BC=2,由E为线段AC的中点,可得VE=EB=.由VE2+BE2=VB2,可得VE⊥EB.以E为坐标原点,分别以EB,EC,EV所在直线为x,y,z轴建立空间直角坐标系.则C(0,,0),B(,0,0),V(0,0,),设F(x,x﹣,0),,,,.设平面VBC的一个法向量为,由,取x=1,得;设平面VEF的一个法向量为,由,取y1=1,得.平面VEF与平面VBC所成锐二面角的平面角为θ,则cosθ==.令f(x)=.当x=时,f(x)min=3.∴cosθ的最大值为.故选:D.【点评】本题考查利用空间向量法求二面角,考查空间想象能力与运算求解能力,关键是建立恰当的空间直角坐标系,是中档题.7.已知矩形ABCD,AD=AB,沿直线BD将△ABD折成△A′BD,使点A′在平面BCD上的射影在△BCD内(不含边界).设二面角A′﹣BD﹣C的大小为θ,直线A′D,A′C与平面BCD所成的角分别为α,β,则()A.α<θ<βB.β<θ<αC.β<α<θD.α<β<θ【分析】由题意画出图形,由两种特殊位置得到点A′在平面BCD上的射影的情况,由线段的长度关系可得三个角的正弦的大小,则答案可求.【解答】解:如图,∵四边形ABCD为矩形,∴BA′⊥A′D,当A′点在底面上的射影O落在BC上时,有平面A′BC⊥底面BCD,又DC⊥BC,可得DC⊥平面A′BC,则DC⊥BA′,∴BA′⊥平面A′DC,在Rt△BA′C中,设BA′=1,则BC=,∴A′C=1,说明O为BC的中点;当A′点在底面上的射影E落在BD上时,可知A′E⊥BD,设BA′=1,则,∴A′E=,BE=.要使点A′在平面BCD上的射影F在△BCD内(不含边界),则点A′的射影F落在线段OE上(不含端点).可知∠A′EF为二面角A′﹣BD﹣C的平面角θ,直线A′D与平面BCD所成的角为∠A′DF=α,直线A′C与平面BCD所成的角为∠A′CF=β,可求得DF>CF,∴A′C<A′D,且,而A′C的最小值为1,∴sin∠A′DF<sin∠A′CF<sin∠A′EO,则α<β<θ.故选:D.【点评】本题考查二面角的平面角,考查空间想象能力和思维能力,训练了正弦函数单调性的应用,是中档题.8.如图,在三棱柱ABC﹣A1B1C1中,AB,AC,AA1两两互相垂直,AB=AC=AA1,M,N是线段BB1,CC1上的点,平面AMN与平面ABC所成(锐)二面角为,当|B1M|最小时,∠AMB=()A.B.C.D.【分析】以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出∠AMB 的大小.【解答】解:以A为原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,设CN=b,BM=a,则N(0,1,b),M(1,0,a),A(0,0,0),B(1,0,0),=(1,0,a),=(0,1,b),设平面AMN的法向量=(x,y,z),,取z=1,得=(﹣a,﹣b,1),平面ABC的法向量=(0,0,1),∵平面AMN与平面ABC所成(锐)二面角为,∴cos==,解得3a2+3b2=1,∴当B1M|最小时,b=0,BM=a=,∴tan∠AMB===,∴∠AMB=.故选:B.【点评】本题考查角的大小的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.9.如图,在大小为45°的二面角A﹣EF﹣D中,四边形ABFE与CDEF都是边长为1的正方形,则B与D两点间的距离是()A.B.C.1D.【分析】由=,利用数量积运算性质展开即可得出.【解答】解:∵四边形ABFE与CDEF都是边长为1的正方形,∴==0,又大小为45°的二面角A﹣EF﹣D中,∴•=1×1×cos(180°﹣45°)=﹣.∵=,∴=+++=3﹣,∴=.故选:D.【点评】本题考查了数量积运算性质、向量的多边形法则、空间角,考查了推理能力与计算能力,属于中档题.1的正方形,则B与C两点间的距离是()改为则B与D两点间的距离是(?10.直角△ABC中,AB=AC=,D为BC边上一点,沿AD将△ACD折起,使点C在平面ABD内的正投影H 恰好在AB上,若AH=1,则二面角C﹣AD﹣B的余弦值是()A.B.C.D.【分析】由题意画出图形,求解三角形求出BD的长度,进一步求得三角形ACD与三角形AHD的面积,再由三角形AHD是三角形ACD在平面ABC上的射影,利用面积比值求解.【解答】解:如图,在直角△ABC中,由AB=AC=,得BC=.设BD=x,则CD=,由CH⊥AB,AC=,AH=1,可得CH=.在△BDH中,由BH=,BD=x,∠DBH=45°,得=.在Rt△CHD中,有DH2+CH2=CD2,即,解得x=.即DB=,CD=.则=.=.设二面角C﹣AD﹣B的平面角为θ,则cosθ=.故选:A.【点评】本题考查二面角的平面角及其求法,考查空间想象能力与思维能力,考查运算求解能力,是中档题.11.已知点E是正方形ABCD的边AD上一动点(端点除外),现将△ABE沿BE所在直线翻折成△A′BE,并连结A′C,A′D.记二面角A′﹣BE﹣C的大小为α(0<α<π).则()A.存在α,使得BA′⊥面A′DE B.存在α,使得BA′⊥面A′CDC.存在α,使得EA′⊥面A′CD D.存在α,使得EA′⊥面A′BC【分析】Rt△ABE绕BE旋转的几何体是两个圆锥的组合体,能推导出某个位置存在母线A′E⊥AE,即A′E ⊥BC,从而得到存在α,使得EA′⊥面A′BC.【解答】解:作AF⊥BE于F,交DC于G,则当折叠时,A′的投影在FG上设正方形的边长为1,则A′B=1,BD=,∵A′E+ED=1>A′D,∴∠BA′D≠90°,故A和B错误;∵如果EA’⊥平面A’CD,则EA’⊥A’C,EA’⊥A’D,而EA’⊥A’B,但A’B,A’C,A’D不共面,∴不可能存在α,使得EA′⊥面A′CD,故C错误;Rt△ABE绕BE旋转的几何体是两个圆锥的组合体,∵∠A′BE<45°,45°<∠A′EB<90°,∴某个位置存在母线A′E⊥AE,即A′E⊥BC,∵二面角A′﹣BE﹣C的大小为α(0<α<π),∴存在α,使得EA′⊥面A′BC,故D正确.故选:D.【点评】本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.12.如图,在直三棱柱ABC﹣A1B1C1中,AB=AC=1,,点E,O分别是线段C1C,BC的中点,,分别记二面角F﹣OB1﹣E,F﹣OE﹣B1,F﹣EB1﹣O的平面角为α,β,γ,则下列结论正确的是()A.γ>β>αB.α>β>γC.α>γ>βD.γ>α>β【分析】以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法求解二面角的余弦值得答案.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,则F(1,0,),O(,,0),E(0,0,),B1(1,1,),,,,,,设平面OB1E的法向量=(x,y,z),则,取x=1,得=(1,﹣1,0),同理可求平面OB1F的法向量,平面OEF的法向量,平面EFB1的法向量.∴,,.∴γ>α>β.故选:D.【点评】本题考查二面角的大小的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.13.如图,在单位正方体ABCD﹣A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:①异面直线A1P与BC1间的距离为定值;②三棱锥D﹣BPC1的体积为定值;③异面直线C1P与直线CB1所成的角为定值;④二面角P﹣BC1﹣D的大小为定值.其中真命题有()A.1个B.2个C.3个D.4个【分析】对于①由题意及三棱锥的体积的算法中可以进行顶点可以轮换性求解体积,和点P的位置及直线AD1与平面BDC1的位置即可判断正误;对于②三棱锥的底面DBC1为定值,判断P到平面DBC1的距离是否是定值,即可判断正误;对于③由题意及图形利用异面直线所成角的概念及求异面直线间的方法及可求解;对于④由题意及平面具有延展性可知实质为平面ABC1D1与平面BDC1所成的二面角;【解答】解:对于①三棱锥D﹣BPC1的体积还等于三棱锥的体积P﹣DBC1的体积,而平面DBC1为固定平面且大小一定,又因为P∈AD1,而AD1∥平面BDC1,所以点A到平面DBC1的距离即为点P到该平面的距离,所以三棱锥的体积为定值,所以①正确;对于②三棱锥的底面DBC1为定值,因为AD1∥BC1,所以AD1∥平面DBC1,P⊂AD1,所以P到平面DBC1的距离是定值,所以三棱锥D﹣BPC1的体积为定值;故②正确;对于③因为在棱长为1的正方体ABCD﹣A1B1C1D1中,点P在线段AD1上运动,有正方体及题意易有B1C⊥平面ABC1D1,而C1P⊂平面ABC1D1,所以B1C⊥C1P,故这两个异面直线所成的角为定值90°,故③正确;对于④因为二面角P﹣BC1﹣D的大小,实质为平面ABC1D1与平面BDC1所成的二面角,而这两个平面为固定的不变的平面所以夹角也为定值,故④正确;故选:D.【点评】本题重点考查了异面直线所成角的概念及求异面直线间的方法;平面具有延展性及二面角的求法及其定义;三棱锥的体积的体积计算可以进行顶点轮换及线面平行时,直线上任意一点到平面的距离都行等这一结论;考查计算能力,空间想象能力.14.如图,已知BD是圆O的直径,A,C在圆上且分别在BD的两侧,其中BD=2,AB=CD.现将其沿BD折起使得二面角A﹣BD﹣C为直二面角,则下列说法不正确的是()A.A,B,C,D在同一个球面上B.当AC⊥BD时,三棱锥A﹣BCD的体积为C.AB与CD是异面直线且不垂直D.存在一个位置,使得平面ACD⊥平面ABC【分析】选项A,易知∠BAD=∠BCD=90°,而O为BD的中点,故OA=OB=OC=OD,从而判断选项A;选项B,当AC⊥BD时,由三垂线定理的逆定理可知,AC在面BCD内的投影m垂直于BD,从而推出AO⊥平面BCD,点A为弧BD的中点,再由三棱锥A﹣BCD的体积V=AO•S△BCD可判断选项B;选项C,易知AB与CD是异面直线;但当AC⊥CD时,由线面垂直的判定定理可证得CD⊥平面ABC,此时有CD⊥AB,可判断选项C;选项D,由选项C可知,当AC⊥CD时,CD⊥平面ABC,再由面面垂直的判定定理可判断选项D.【解答】解:选项A,由题可知,∠BAD=∠BCD=90°,∵O为BD的中点,∴OA=BD=OC,即OA=OB=OC=OD,∴A,B,C,D都在以O为球心的球面上,即选项A正确;选项B,∵二面角A﹣BD﹣C为直二面角,∴平面ABD⊥平面BCD,当AC⊥BD时,由三垂线定理的逆定理可知,AC在面BCD内的投影m垂直于BD,∵OC⊥BD,∴m与OC重合,∴AO⊥平面BCD,即点A为弧BD的中点,∵AB=CD,∴△ABD和△BCD均为等腰直角三角形.三棱锥A﹣BCD的体积V=AO•S△BCD=×1××1×2=,即选项B正确;选项C,∵AB⊂平面ABD,CD∩平面ABD=D,∴AB与CD是异面直线.∵∠BCD=90°,即BC⊥CD,∴若AC⊥CD,由于AC∩BC=C,AC、BC⊂平面ABC,则CD⊥平面ABC,∴CD⊥AB,即选项C错误;选项D,由选项C可知,当AC⊥CD时,CD⊥平面ABC,∵CD⊂平面ACD,∴平面ACD⊥平面ABC,即选项D正确.故选:C.【点评】本题主要考查空间中线与面的垂直关系,熟练掌握空间中线面、面面垂直的判定定理与性质定理是解题的关键,考查学生的空间立体感和逻辑推理能力,属于中档题.二.填空题(共17小题)15.在四面体ABCD中,AB=AD=2,∠BAD=60°,∠BCD=90°,二面角A﹣BD﹣C的大小为150°,则四面体ABCD外接球的半径为.【分析】利用已知条件画出图形,判断球心的位置,转化求解球的半径即可.【解答】解:在四面体ABCD中,AB=AD=2,∠BAD=60°,∠BCD=90°,二面角A﹣BD﹣C的大小为150°,四面体ABCD外接球,如图:则△BCD在求出一个小圆上,BD的中点为圆心N,△ABD是正三角形,也在球的一个小圆上,圆心为M,作OM⊥平面ABD,ON⊥平面BCD,O为球心,二面角A﹣BD﹣C的大小为150°,作NP⊥BD,则∠ANP=150°,可得∠ONM=60°,MN=,则ON=,BN=1,外接球的半径为:=.故答案为:.【点评】本题考查球的内接体,二面角的平面角的应用,球与平面相交的性质的应用,考查空间想象能力以及计算能力.16.已知正方体ABCD﹣A1B1C1D1中,E为BC的中点,在平面A1B1C1D1内,直线l∥B1D1,设二面角A﹣l﹣E的平面角为θ,当θ取最大值时,cosθ=.【分析】找到二面角的平面角,转化成平面图形后建立坐标系借助直线斜率的知识处理.【解答】解:如图,设正方体的棱长为1,l与A1B1,A1D1分别交于I,H两点,取CD的中点F,连接EF,则EF∥BD,又因为BD∥B1D1,∴EF∥B1D1,又因为直线l∥B1D1,∴直线l∥EF,即EFHI在同一平面内,设平面EFHI与AC交于G,在正方形A1B1C1D1中,B1D1⊥A1C1,又知道AA1⊥B1D1,AA1∩A1C1.所以B1D1⊥平面AA1C1C,又因为HI∥B1D1,所以HI⊥平面AA1C1C,设HI∩A1C1=O,连接OA,OG,则∠AOG即为二面角A﹣l﹣E的平面角θ,且θ为锐角.因为EF为三角形BCD的中位线,故G是AC的四等分点,即AG=,取出截面AA1C1C如图,以A为坐标原点,AC为x轴,建立如图坐标系,设O点坐标为(x,1),x∈(0,).直线OA的斜率为k OA=,直线OG的斜率k OG=,∴tanθ====,当θ取得最大值时,tanθ取得最大值,故当x=时,tanθ最大,即O点坐标为(,1),∴OA=OG==,所以由余弦定理cosθ====.故填:.【点评】本题考查了二面角的求法,且为二面角余弦值的最值的求法,将二面角的平面角转化的平面内建系后用到角公式处理是比较简单的方法,本题属于难题.17.已知矩形ABCD,AB=20,BC=15,沿对角线AC将△ABC折起,使得BD=,则二面角B﹣AC﹣D的大小是.【分析】作出二面角的平面角,建立空间坐标系,设二面角为α,表示出B,D两点坐标,根据距离公式列方程解出α.【解答】解:在矩形ABCD中,作DE⊥AC于点O,交AB于点E,作BF⊥AC于点F,∵AB=20,BC=15,∴AC==25,∴DO=BF==12,AO=CF==9,∴OF=25﹣9×2=7,在翻折后,以O为原点,以OE,OC所在直线为x轴,y轴建立空间直角坐标系O﹣xyz,则∠DOE为二面角B﹣AC﹣D的平面角,设∠DOE=α(0<α<π),则D(12cosα,0,12sinα),B(12,7,0),∴|BD|===,∴cosα=﹣,∴α=,故答案为:.【点评】本题考查了二面角计算,作出二面角的平面角是关键,建系代入坐标运算可使计算简便,属于中档题.18.如图,在正四棱锥P﹣ABCD中,∠APC=60°,则二面角A﹣PB﹣C的平面角的余弦值为.【分析】过点A作AE⊥PB于点E,连接CE、AC,易知∠AEC即为所求.设底面ABCD的边长为a,则AC==P A=PC=PB,在△P AB中,由可求得△P AB的面积,再由等面积法求出AE的值,最后在△ACE中,由余弦定理知,cos∠AEC=,代入数据即可得解.【解答】解:过点A作AE⊥PB于点E,连接CE、AC,由题可知,△P AB≌△PCB,∴CE⊥PB,∴∠AEC即为二面角A﹣PB﹣C的平面角.设底面ABCD的边长为a,则AC=,∵P A=PC,∠APC=60°,∴△P AC为等边三角形,P A=PC==PB,在△P AB中,=,由等面积法可知,,∴AE==CE,在△ACE中,由余弦定理知,cos∠AEC==.由题可知,二面角A﹣PB﹣C为钝二面角,∴二面角A﹣PB﹣C的平面角的余弦值为.故答案为:.【点评】本题考查二面角的求法,理解二面角的定义是解题的基础,考查学生的空间立体感和运算能力,属于基础题.19.如图,在四面体A﹣BCD中,已知棱AC的长为,其余各棱长都为1,则二面角A﹣CD﹣B的平面角的余弦值为.【分析】过A作AO⊥平面BCD,垂足为O,连结OD,推导出AD⊥CD,OD⊥CD,OB⊥BC,从而∠ADO是二面角A﹣CD﹣B的平面角,由△BCD是等边三角形,得∠BOD=120°,由余弦定理得求出BD=,由此能求出二面角A﹣CD﹣B的平面角的余弦值.【解答】解:过A作AO⊥平面BCD,垂足为O,连结OD,∵在四面体A﹣BCD中,棱AC的长为,其余各棱长都为1,∴AD⊥CD,∴OD⊥CD,∴OB⊥BC,∴∠ADO是二面角A﹣CD﹣B的平面角,∴△BCD是等边三角形,∴∠BOD=120°,设PO=x,OB=OD=y,由余弦定理得:BD2=OB2+OD2﹣2OB•OD•cos120°,即1=y2+y2﹣2y2cos120°,解得y=,x==,∴cos∠ADO==.∴二面角A﹣CD﹣B的平面角的余弦值为.故答案为:.【点评】本题考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想,是中档题.20.已知直二面角α﹣l﹣β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足.若AB=2,AC=BD=1,则D到平面ABC的距离等于.【分析】由题意通过等体积法,求出三棱锥的体积,然后求出D到平面ABC的距离.【解答】解:由题意画出图形如图:直二面角α﹣l﹣β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,则D到平面ABC的距离转化为三棱锥D﹣ABC的高为h,所以AD=,CD=,BC=由V B﹣ACD=V D﹣ABC可知×AC•CD•BD=×AC•BC•h所以,h=故答案为:【点评】本题考查点到平面的距离,考查转化思想的应用,考查计算能力,等体积法是求解点到平面距离的基本方法之一.21.矩形ABCD中,AB=,BC=1,现将△ACD沿对角线AC向上翻折,得到四面体D﹣ABC,则该四面体外接球的体积为;设二面角D﹣AC﹣B的平面角为θ,当θ在[,]内变化时,|BD|的范围为[,].【分析】设AC中点为O,则O为四面体外接球球心,求出OA=1,即可求解V球;取CO中点E,取CD三等分点F,且F靠近点C,连BE、EF、BF,通过求解三角形转化求解BD的范围即可.【解答】解:设AC中点为O,则O为四面体外接球球心,半径OA=1,故V球=;取CO中点E,取CD三等分点F,且F靠近点C,连BE、EF、BF,此时∠BEF=θ,余弦定理求得BF2=EF2+BE2﹣2EF•BE•cosθ=,△CBF中,用余弦定理求得cos∠BCF==,△BCD中,余弦定理求得BD2=CD2+BC2﹣2BC•CD cos∠BCF=4﹣,根据θ∈[,],即可确定≤BD≤.故答案为:,[,].【点评】本题考查空间点线面距离的求法,几何体的外接球的体积的求法,考查空间想象能力,转化思想以及计算能力.22.在边长为2的菱形ABCD中,A=60°,沿对角线BD折起,使二面角A﹣BD﹣C的大小为120°,这时点A,B,C,D在同一个球面上,则该球的表面积为28π・【分析】正确作出图形,利用勾股定理建立方程,求出四面体的外接球的半径,即可求出四面体的外接球的表面积.【解答】解:如图所示,∠AFC=120°,∠AFE=60°,AF==3∴AE=,EF=,设OO′=x,则∵O′B=2,O′F=1,∴由勾股定理可得R2=x2+4=(+1)2+(﹣x)2,∴R2=7,∴四面体的外接球的表面积为4πR2=28π,故答案为:28π.【点评】本题考查四面体的外接球的表面积,考查学生的计算能力,正确求出四面体的外接球的半径是关键,考。
(完整)二面角习题及答案
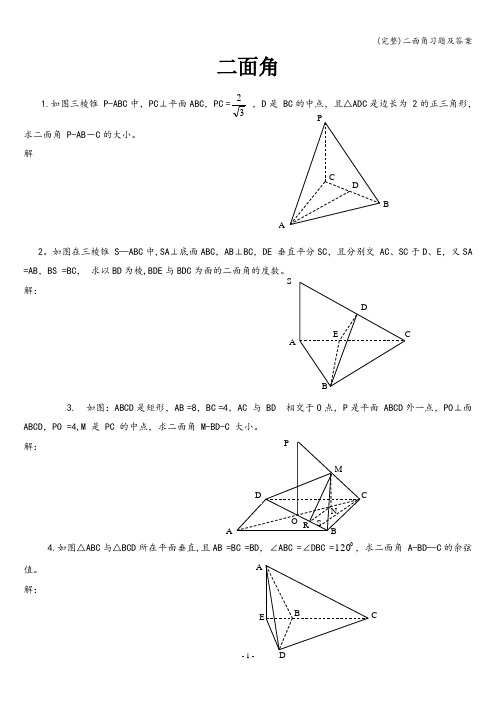
二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2。
如图在三棱锥 S —ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =,求二面角 A-BD —C 的余弦值。
解:ABAC5.已知正方体 AC ’,M 、N 分别是BB ’,DD'的中点,求截面 AMC'N 与面ABCD ,CC'D ’D 所成的角. 解:6。
如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:7。
三棱锥 A —BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9。
如图所示,四棱锥P-ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD,PC =a ,E 是PA 的中点。
(1)求证平面BDE ⊥平面ABCD 。
(2)求点E 到平面PBC 的距离。
(3)求二面角A —EB —D 的平面角大小. 解析:10。
如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.D ’B ’DAC ’BA ’CMNBF EACDDOABC11。
【最新精选】二面角的基本求法例题及练习
C1C1一、平面与平面的垂直关系1.判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
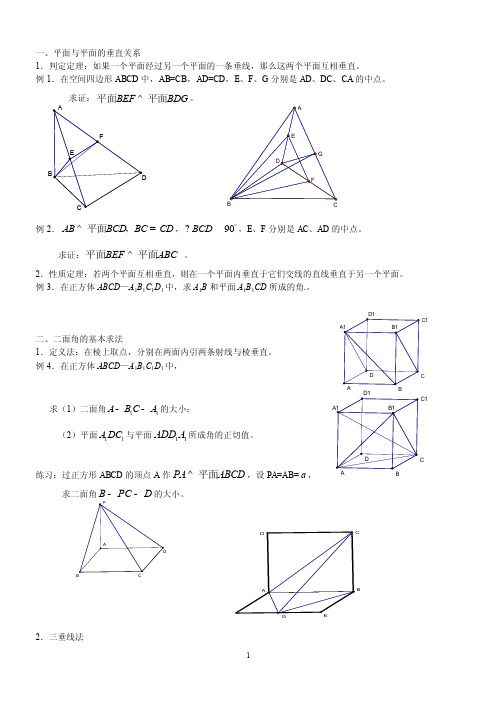
例1.在空间四边形ABCD 中,AB=CB ,AD=CD ,E 、F 、G 分别是AD 、DC 、CA 的中点。
求证:BEF BDG ^平面平面。
例2.AB BCD BC CD ^=平面,,90BCD °,E 、F 分别是AC 、AD 的中点。
求证:BEF ABC ^平面平面 。
2.性质定理:若两个平面互相垂直,则在一个平面内垂直于它们交线的直线垂直于另一个平面。
例3.在正方体ABCD —A 1B 1C 1D 1中,求A 1B 和平面A 1B 1CD 所成的角.。
二、二面角的基本求法1.定义法:在棱上取点,分别在两面内引两条射线与棱垂直。
例4.在正方体ABCD —A 1B 1C 1D 1中,求(1)二面角11A B C A --的大小;(2)平面11A DC 与平面11ADD A 所成角的正切值。
练习:过正方形ABCD 的顶点A 作PA ABCD ^平面,设PA=AB=a ,求二面角B PC D --的大小。
2.三垂线法C例5.ABCD ABEF ABCD ^平面平面,是正方形,ABEF 是矩形且AF=12AD=a ,G 是EF 的中点,(1)求证:AGC BGC ^平面平面; (2)求GB 与平面AGC 所成角的正弦值; (3)求二面角B AC G --的大小。
例6.点P 在平面ABC 外,ABC 是等腰直角三角形,90ABC°,PAB 是正三角形,PA BC ^。
(1)求证:^平面PA B 平面A BC ; (2)求二面角P AC B --的大小。
练习:正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是AD 的中点,求二面角1A BD P --的大小。
B13.垂面法例7.SA ABC AB BC SA AB BC ^^==平面,,, (1)求证:SB BC ^;(2)求二面角C SA B --的大小;(3)求异面直线SC 与AB 所成角的余弦值。
高考数学二面角专题训练

高考数学二面角专题训练1.(06某某卷)如图,P 是边长为1的正六边形ABCDEF 所在平面外一点,1PA =,P 在平面ABC 内的射影为BF 的中点O 。
(Ⅰ)证明PA ⊥BF ;(Ⅱ)求面APB 与面DPB 所成二面角的大小。
解:(Ⅰ)在正六边形ABCDEF 中,ABF 为等腰三角形,∵P 在平面ABC 内的射影为O ,∴PO ⊥平面ABF ,∴AO 为PA 在平面ABF 内的射影;∵O 为BF 中点,∴AO ⊥BF ,∴PA ⊥BF 。
(Ⅱ)∵PO ⊥平面ABF ,∴平面PBF ⊥平面ABC ;而O 为BF 中点,ABCDEF 是正六边形 ,∴A 、O 、D 共线,且直线AD ⊥BF ,则AD ⊥平面PBF ;又∵正六边形ABCDEF 的边长为1,∴12AO =,32DO =,BO =。
过O 在平面POB 内作OH ⊥PB 于H ,连AH 、DH ,则AH ⊥PB ,DH ⊥PB ,所以AHD ∠为所求二面角平面角。
在AHO 中,,1tan AO AHO OH ∠==。
在DHO中,3tan 27DO DHO OH ∠===;而tan tan()AHD AHO DHO ∠=∠+∠== (Ⅱ)以O 为坐标原点,建立空间直角坐标系,P(0,0,1),A(0,12-,0),B(2,0,0),D(0,2,0),∴1(0,,1)2PA =--,3(1)2PB =-,(0,2,1)PD =-设平面PAB 的法向量为111(,,1)n x y =,则1n PA ⊥,1n PB⊥,得111102102y x ⎧--=⎪⎪-=⎪⎩,123(2,1)3n =-;设平面PDB 的法向量为222(,,1)n x y =,则2n PD ⊥,2n PB ⊥,得22210102y x -=⎧-=⎩,2231(,1)32n =;121212cos ,||||n n n n n n ⋅<>==⋅2. (06卷)如图,在底面为平行四边表的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点.(Ⅰ)求证:AC PB ⊥;(Ⅱ)求证://PB 平面AEC ; (Ⅲ)求二面角E AC B --的大小.解法一:(Ⅰ)PA ⊥平面ABCD ,∴AB 是PB 在平面ABCD 上得射影, 又AB ⊥AC ,AC ⊂平面ABCD , ∴AC ⊥PB.(Ⅱ)连接BD ,与AC 相交与O ,连接EO , ABCD 是平行四边形 ∴O 是BD 的中点 又E 是PD 的中点, ∴EO PB.又PB ⊄平面AEC ,EO ⊂平面AEC , ∴PB 平面AEC ,(Ⅲ)取BC 中点G ,连接OG ,则点G 的坐标为,,022a b ⎛⎫ ⎪⎝⎭,0,,02b OC ⎛⎫= ⎪⎝⎭又(,0,0),OE AC a =b b=(0,-,),220,0,OE AC OG AC ∴==,,OE AC OG AC ∴⊥⊥EOG ∴∠是二面角E AC B -=的平面角。
新教材高中数学第1章二面角学案含解析新人教B版选择性必修第一册

新教材高中数学:1.2.4 二面角学习目标核心素养1.掌握二面角的概念,二面角的平面角的定义,会找一些简单图形中的二面角的平面角.(重点)2.掌握求二面角的方法、步骤.(重点、难点) 1.通过学习二面角的概念及二面角的平面角,培养数学抽象素养.2.借助求二面角的方法和步骤的学习,提升逻辑推理、数学运算素养.同学们可能经常谈论某某同学是白羊座的,某某同学是双子座的,可是你知道十二星座的由来吗?我们知道,地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面交角(二面角的平面角)约为23°26′,它与天球相交的大圆为“黄道”,黄道及其附近的南北宽8°以内的区域为黄道带,黄道带内有十二个星座,称为“黄道十二宫”,从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、金牛座、双子座等等,这便是星座的由来,今天我们研究的问题便是二面角的平面角问题.1.二面角的概念(1)半平面:平面内的一条直线把平面分为两部分,其中的每一部分都叫做半平面.(2)二面角:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面.棱为l,两个面分别为α,β的二面角的面,记作αlβ,若A∈α,B∈β,则二面角也可以记作AlB,二面角的范围为[0,π].(3)二面角的平面角:在二面角αlβ的棱上任取一点O,以O为垂足,分别在两半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角αlβ的平面角.提醒:二面角的大小等于它的平面角大小,平面角是直角的二面角称为直二面角.思考:如何找二面角的平面角?[提示](1)定义法由二面角的平面角的定义可知平面角的顶点可根据具体题目选择棱上一个特殊点,求解用到的是解三角形的有关知识.(2)垂面法作(找)一个与棱垂直的平面,与两面的交线就构成了平面角.(3)三垂线定理(或逆定理)作平面角,这种方法最为重要,其作法与三垂线定理(或逆定理)的应用步骤一致.2.用空间向量求二面角的大小如果n 1,n 2分别是平面α1,α2的一个法向量,设α1与α2所成角的大小为θ.则θ=〈n 1,n 2〉或θ=π-〈n 1,n 2〉,sin θ=sin 〈n 1,n 2〉.1.思考辨析(正确的打“√”,错误的打“×”) (1)二面角的范围是⎣⎢⎡⎦⎥⎤0,π2.( )(2)若二面角αl β的两个半平面的法向量分别为n 1,n 2,则二面角的平面角与两法向量夹角〈n 1,n 2〉一定相等.( ) (3)二面角的大小通过平面角的大小来度量. ( )[答案] (1)× (2)× (3)√ [提示] (1)× 不是.是[0,π]. (2)× 不一定.可能相等,也可能互补. (3)√2.(教材P 52练习B②改编)在正方体ABCD A 1B 1C 1D 1中,二面角A 1BC A 的余弦值为( ) A .12 B .23 C .22 D .33 C [易知∠A 1BA 为二面角A 1 BC A 的平面角, cos∠A 1BA =AB A 1B =22.] 3.已知二面角αl β,其中平面α的一个法向量m =(1,0,-1),平面β的一个法向量n =(0,-1,1),则二面角αl β的大小可能为________.60°或120° [cos 〈m ,n 〉=m ·n |m |·|n |=-12·2=-12,∴〈m ,n 〉=120°,∴二面角αl β的大小为60°或120°.]4.在正方体ABCD A 1B 1C 1D 1中,二面角A 1BD C 1的余弦值是________. 13[如图,建立空间直角坐标系,设正方体的棱长为1,则D (0,0,0),B (1,1,0),A 1(1,0,1),DA 1→=(1,0,1),DB →=(1,1,0). 设n =(x ,y ,z )是平面A 1BD 的一个法向量, 则⎩⎪⎨⎪⎧n ·DA 1→=0,n ·DB →=0,即⎩⎪⎨⎪⎧x +z =0,x +y =0,令x =1,则y =-1,z =-1,∴n =(1,-1,-1). 同理,求得平面BC 1D 的一个法向量m =(1,-1,1), 则cos 〈m ,n 〉=m·n |m||n|=13,所以二面角A 1BD C 1的余弦值为13.]用定义法求二面角【例1】 如图,设AB 为圆锥PO 的底面直径,PA 为母线,点C 在底面圆周上,若△PAB 是边长为2的正三角形,且CO ⊥AB ,求二面角P AC B 的正弦值.[解] 如图,取AC 的中点D ,连接OD ,PD ,∵PO ⊥底面,∴PO ⊥AC , ∵OA =OC ,D 为AC 的中点, ∴OD ⊥AC , 又PO ∩OD =O ,∴AC ⊥平面POD ,则AC ⊥PD , ∴∠PDO 为二面角P AC B 的平面角. ∵△PAB 是边长为2的正三角形,CO ⊥AB , ∴PO =3,OA =OC =1,OD =22, 则PD =32+⎝ ⎛⎭⎪⎫222=142. ∴sin∠PDO =PO PD=3142=427, ∴二面角P AC B 的正弦值为427.用定义求二面角的步骤(1)作(找)出二面角的平面角(作二面角时多用三垂线定理). (2)证明所作平面角即为所求二面角的平面角. (3)解三角形求角.[跟进训练]1.已知矩形ABCD 的两边AB =3,AD =4,PA ⊥平面ABCD ,且PA =45,则二面角A BD P的正切值为________.13[过A 作AO ⊥BD ,交BD 于O ,连接PO ,∵矩形ABCD 的两边AB =3,AD =4,PA ⊥平面ABCD ,且PA =45,∴BD =32+42=5,PO ⊥BD , ∴∠POA 是二面角A BD P 的平面角, ∵12×BD ×AO =12×AB ×AD , ∴AO =AB ×AD BD =125, ∴tan∠POA =PA AO =45125=13.∴二面角A BD P 的正切值为13.]用向量法求二面角[探究问题1.构成二面角的平面角有几个要素?[提示] (1)角的顶点在二面角的棱上;(2)角的两边分别在表示二面角的两个半平面内;(3)角的两边分别和二面角的棱垂直.2.二面角的大小与其两个半平面的法向量的夹角有何关系? [提示] 条件平面α,β的法向量分别为u ,v ,α,β所构成的二面角的大小为θ,〈u ,v 〉=φ图形关系 θ=φθ=π-φ计算cos θ=cos φcos θ=-cos φ【例2】 如图所示,四棱柱ABCD A 1B 1C 1D 1的所有棱长都相等,AC ∩BD =O ,A 1C 1∩B 1D 1=O 1,四边形ACC 1A 1和四边形BDD 1B 1均为矩形.(1)证明:O 1O ⊥底面ABCD ;(2)若∠CBA =60°,求二面角C 1OB 1D 的余弦值.[思路探究] (1)充分利用图形中的垂直关系,用传统的方法(综合法)可证. (2)利用垂直关系建立空间直角坐标系,用法向量求二面角的余弦值.[解] (1)证明:因为四边形ACC 1A 1和四边形BDD 1B 1均为矩形,所以CC 1⊥AC ,DD 1⊥BD , 又CC 1∥DD 1∥OO 1,所以OO 1⊥AC ,OO 1⊥BD ,因为AC ∩BD =O ,所以O 1O ⊥底面ABCD . (2)因为四棱柱的所有棱长都相等,所以四边形ABCD 为菱形,AC ⊥BD ,又O 1O ⊥底面ABCD ,所以OB ,OC ,OO 1两两垂直.如图,以O 为原点,OB ,OC ,OO 1所在直线分别为x ,y ,z 轴,建立空间直角坐标系.设棱长为2,因为∠CBA =60°,所以OB =3,OC =1, 所以O (0,0,0),B 1(3,0,2),C 1(0,1,2), 平面BDD 1B 1的一个法向量为n =(0,1,0), 设平面OC 1B 1的法向量为m =(x ,y ,z ),则由m ⊥OB 1→,m ⊥OC 1→,所以3x +2z =0,y +2z =0, 取z =-3,则x =2,y =23,所以m =(2,23,-3), 所以cos 〈m ,n 〉=m·n |m||n|=2319=25719.由图形可知二面角C 1OB 1D 的大小为锐角, 所以二面角C 1OB 1D 的余弦值为25719.1.(变问法)本例(2)条件不变,求二面角B A 1C D 的余弦值. [解] 如图建立空间直角坐标系.设棱长为2,则A 1(0,-1,2),B (3,0,0),C (0,1,0),D (-3,0,0). 所以BC →=(-3,1,0),A 1C →=(0,2,-2),CD →=(-3,-1,0). 设平面A 1BC 的法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧ n 1·A 1C →=0,n 1·BC →=0,即⎩⎨⎧2y 1-2z 1=0,-3x 1+y 1=0,取x 1=3,则y 1=z 1=3,故n 1=(3,3,3).设平面A 1CD 的法向量为n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧n 2·A 1C →=0,n 2·CD →=0,即⎩⎨⎧2y 2-2z 2=0,-3x 2-y 2=0,取x 2=3,则y 2=z 2=-3,故n 2=(3,-3,-3).所以cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=-1521=-57.由图形可知二面角B A 1C D 的大小为钝角,所以二面角B A 1C D 的余弦值为-57.2.(变条件、变问法)本例四棱柱中,∠CBA =60°改为∠CBA =90°,设E ,F 分别是棱BC ,CD 的中点,求平面AB 1E 与平面AD 1F 所成锐二面角的余弦值.[解] 以A 为坐标原点建立空间直角坐标系,如图所示,设此棱柱的棱长为1,则A (0,0,0),B 1(1,0,1),E ⎝ ⎛⎭⎪⎫1,12,0,D 1(0,1,1),F ⎝ ⎛⎭⎪⎫12,1,0,AE →=⎝⎛⎭⎪⎫1,12,0,AB 1→=(1,0,1),AF →=⎝ ⎛⎭⎪⎫12,1,0,AD 1→=(0,1,1).设平面AB 1E 的法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧ n 1·AB 1→=0,n 1·AE →=0,即⎩⎪⎨⎪⎧x 1+z 1=0,x 1+12y 1=0,令y 1=2,则x 1=-1,z 1=1, 所以n 1=(-1,2,1).设平面AD 1F 的法向量为n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧n 2·AD 1→=0,n 2·AF →=0,即⎩⎪⎨⎪⎧y 2+z 2=0,12x 2+y 2=0.令x 2=2,则y 2=-1,z 2=1.所以n 2=(2,-1,1). 所以平面AB 1E 与平面AD 1F 所成锐二面角的余弦值为|n 1·n 2||n 1||n 2|=|-1,2,1·2,-1,1|-12+22+12·22+-12+12=|-1×2+2×-1+1×1|6×6=12.利用坐标法求二面角的步骤设n 1,n 2分别是平面α,β的法向量,则向量n 1与n 2的夹角(或其补角)就是两个平面夹角的大小,如图.用坐标法的解题步骤如下:(1)建系:依据几何条件建立适当的空间直角坐标系. (2)求法向量:在建立的坐标系下求两个面的法向量n 1,n 2.(3)计算:求n1与n2所成锐角θ,cos θ=|n1·n2||n1|·|n2|.(4)定值:若二面角为锐角,则为θ;若二面角为钝角,则为π-θ.提醒:确定平面的法向量是关键.空间中的翻折与探索性问题【例3】如图甲,在直角梯形ABCD中,AB∥CD,AB⊥BC,CD=2AB=2BC=4,过A点作AE⊥CD,垂足为E,现将△ADE沿AE折叠,使得DE⊥EC.取AD的中点F,连接BF,CF,EF,如图乙.甲乙(1)求证:BC⊥平面DEC;(2)求二面角CBFE的余弦值.[思路探究](1)根据线面垂直的判定定理即可证明BC⊥平面DEC;(2)建立空间坐标系,利用向量法即可求二面角CBFE的余弦值.[解](1)证明:如图,∵DE⊥EC,DE⊥AE,AE∩EC=E,∴DE⊥平面ABCE,又∵BC⊂平面ABCE,∴DE⊥BC,又∵BC⊥EC,DE∩EC=E,∴BC⊥平面DEC.(2)如图,以点E为坐标原点,分别以EA,EC,ED为x,y,z轴建立空间坐标系Exyz,∴E(0,0,0),C(0,2,0),B(2,2,0),D(0,0,2),A(2,0,0),F(1,0,1),设平面EFB的法向量n1=(x1,y1,z1),由EF →=(1,0,1),EB →=(2,2,0),所以⎩⎪⎨⎪⎧x 1+z 1=0,2x 1+2y 1=0,∴取x 1=1,得平面EFB 的一个法向量n 1=(1,-1,-1), 设平面BCF 的一个法向量为n 2=(x 2,y 2,z 2), 由CF →=(1,-2,1),CB →=(2,0,0),所以⎩⎪⎨⎪⎧x 2=0,x 2-2y 2+z 2=0,∴取y 2=1,得平面BCF 的一个法向量n 2=(0,1,2), 设二面角C BF E 的大小为α,则cos α=|n 1·n 2||n 1|·|n 2|=|-1-2|5·3=155.1.与空间角有关的翻折问题的解法要找准翻折前后的图形中的不变量及变化的量,再结合向量知识求解相关问题. 2.关于空间角的探索问题的处理思路利用空间向量解决空间角中的探索问题,通常不需要复杂的几何作图、论证、推理,只需先假设结论成立,设出空间的坐标,通过向量的坐标运算进行推断,把是否存在问题转化为点的坐标是否有解的问题来处理.[跟进训练]2.如图1,在等腰梯形ABCD 中,AD ∥CB ,AD =2CB =4,∠ABC =120°,E 为AD 的中点,现分别沿BE ,EC 将△ABE 和△ECD 折起,使得平面ABE ⊥平面BCE ,平面ECD ⊥平面BCE ,连接AD ,如图2.(1)若在平面BCE 内存在点G ,使得GD ∥平面ABE ,请问点G 的轨迹是什么图形?并说明理由.(2)求平面AED 与平面BCE 所成锐二面角的余弦值.图1 图2[解] (1)点G 的轨迹是直线MN . 理由如下:如图,分别取BC 和CE 的中点N 和M ,连接DM ,MN ,ND ,则MN ∥BE ,又MN ⊄平面BEA ,BE ⊂平面BEA , ∴MN ∥平面BEA ,依题意有△ABE ,△BCE ,△ECD 均为边长为2的正三角形, ∴MD ⊥CE ,又平面ECD ⊥平面BCE ,则MD ∥平面BEA , ∴平面NMD ∥平面BEA ,∴点G 的轨迹是直线MN .(2)如图,以点M 为坐标原点,MB 为x 轴,MC 为y 轴,MD 为z 轴,建立空间直角坐标系,则E (0,-1,0),D (0,0,3),A ⎝⎛⎭⎪⎫32,-12,3,∴EA →=⎝ ⎛⎭⎪⎫32,12,3,ED →=(0,1,3),设平面AED 的法向量n =(x ,y ,z ),则⎩⎨⎧n ·ED →=y +3z =0,n ·EA →=32x +12y +3z =0,取x =3,得n =(3,3,-3), 取平面BCE 的一个法向量m =(0,0,1), 则cos 〈n ,m 〉=n ·m |n |·|m |=-55,∴平面AED 与平面BCE 所成锐二面角的余弦值为55.1.学会利用空间向量求二面角与定义法求二面角的方法.2.利用向量法求二面角的基本思想是把空间角转化为求两个向量之间的关系.首先要找出并利用空间直角坐标系或基向量(有明显的线面垂直关系时尽量建系)表示出向量,然后运用向量的运算即可,其次要理清要求角与两个向量夹角之间的关系.1.三棱锥A BCD 中,平面ABD 与平面BCD 的法向量分别为n 1·n 2,若〈n 1,n 2〉=π3,则二面角A BD C 的大小为( )A .π3B .2π3C .π3或2π3D .π6或π3C [当二面角A BD C 为锐角时,它等于〈n 1,n 2〉=π3.当二面角A BD C 为钝角时,它应对等于π-〈n 1,n 2〉=π-π3=2π3.]2.已知△ABC 和△BCD 均为边长为a 的等边三角形,且AD =32a ,则二面角A BC D 的大小为( )A .30°B .45°C .60°D .90° C [如图取BC 的中点为E ,连接AE ,DE ,由题意得AE ⊥BC ,DE ⊥BC , 且AE =DE =32a ,又AD =32a , ∴∠AED =60°,即二面角A BC D 的大小为60°.]3.如图所示,在正四棱锥P ABCD 中,若△PAC 的面积与正四棱锥的侧面面积之和的比为6∶8,则侧面与底面所成的二面角为( )A .π12B .π4C .π6D .π3D [设正四棱锥的底面边长为a ,侧面与底面所成的二面角为θ,高为h ,斜高为h ′,则12×2ah 4×12ah ′=68,∴h h ′=32,∴sin θ=32,即θ=π3.]4.在正方体ABCD A 1B 1C 1D 1中,E 为BB 1的中点,则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为________.23 [建系如图,设正方体的棱长为1,则D (0,0,0),A 1(1,0,1),E ⎝ ⎛⎭⎪⎫1,1,12,∴DA 1→=(1,0,1),DE →=⎝⎛⎭⎪⎫1,1,12.设平面A 1ED 的一个法向量为n =(x ,y ,z ),则n ·DA 1→=0,且n ·DE →=0.即⎩⎪⎨⎪⎧x +z =0,x +y +12z =0,令x =1,得y =-12,z =-1.∴n =⎝ ⎛⎭⎪⎫1,-12,-1,又平面ABCD 的一个法向量为DD 1→=(0,0,1).则cos 〈n ,DD 1→〉=|n ·DD 1→||n ||DD 1→|=23.] 5.三棱锥P ABC ,PA =PB =PC =73,AB =10,BC =8,CA =6,求二面角P AC B 的大小. [解] 如图在三棱锥P ABC 中,PA =PB =PC =73,AB =10,BC =8,CA =6,∴AC 2+BC 2=AB 2,∴△ABC 是以AB 为斜边的直角三角形,∴P 在底△ABC 的射影D 是△ABC 的外心, 即斜边AB 的中点D 是P 在底△ABC 的射影, 作DE ⊥AC ,交AC 于点E ,连接PE , 则∠PED 是所求的二面角的平面角,由题意得DE =4,PE =8,cos∠PED =DE PE =12,∴∠PED =60°,∴二面角P AC B 的大小为60°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学《二面角的平面角及求法》练习1. 如图,直三棱柱中,=,=,,分别为、的中点.(1)证明:平面;(2)已知与平面所成的角为,求二面角的余弦值.2. 已知三棱锥的展开图如图二,其中四边形为边长等于的正方形,和均为正三角形,在三棱锥中.证明:平面平面;若是的中点,求二面角的余弦值.3. 如图,正方形所在平面与四边形所在平面互相垂直,是等腰直角三角形,=,=,=.(1)求证:平面;(2)设线段、的中点分别为、,求与所成角的正弦值;(3)求二面角的平面角的正切值.4. 如图所示,正四棱锥中,为底面正方形的中心,侧棱与底面所成的角的正切值为.(1)求侧面与底面所成的二面角的大小;(2)若是的中点,求异面直线与所成角的正切值;(3)问在棱上是否存在一点,使侧面,若存在,试确定点的位置;若不存在,说明理由.5. 如图,在平行四边形中,=,=,=,平面平面,且=,=.(1)在线段上是否存在一点,使平面,证明你的结论;(2)求二面角的余弦值.6. 如图,在边长为的正方形中,点,分别是,的中点,点在上,且.将,分别沿,折叠使,点重合于点,如图所示.(1)试判断与平面的位置关系,并给出证明;(2)求二面角的余弦值.7. 如图,四棱锥中,平面,底面是边长为的正方形,=,为中点.(1)求证:;(2)求二面角的正弦值.8. 已知四棱柱中,底面为菱形,=,=,=,为中点,在平面上的投影为直线与的交点.(1)求证:;(2)求二面角的正弦值.9. ((1)如图,已知四棱锥的底面是边长为的正方形,,分别是棱、的中点,=,,直线与平面所成的角的正弦值为.证明:平面;(2)求二面角的余弦值.10. 如图,在四面体中,,分别是线段,的中点,==,,==Ⅰ,直线与平面所成的角等于.Ⅱ证明:平面平面;求二面角的余弦值.11. 如图,在正方形中,,分别是,的中点,将正方形沿着线段折起,使得=,设为的中点.(1)求证:平面;(2)求二面角的余弦值.12. 已知三棱柱中,==,侧面底面,是的中点,=,.Ⅰ求证:为直角三角形;Ⅱ求二面角的余弦值.13. 如图,在三棱柱中,侧面是菱形,=,是棱的中点,=,在线段上,且=.(1)证明:面;(2)若,面面,求二面角的余弦值.14. 如图,在四棱锥中,平面底面,其中底面为等腰梯形,,===,,=,为的中点.(1)证明:平面;(2)求二面角的余弦值.参考答案一、解答题1.证明:以为坐标原点,射线为轴的正半轴,建立如图所示的直角坐标系.设=,=,则,,,,,,,,.∵,,∴,,又=,∴平面;设平面的法向量,则,又,故,取=,得.∵与平面所成的角为,,∴,解得,∴.由(1)知平面的法向量,∴.∴二面角的余弦值为.2.证明:设的中点为,连结,,如图:由题意得,,,∵在中,,为的中点,∴,∵在中,,,,∴,∴.∵,,平面,∴平面.,∵平面,∴平面平面.解:由知平面,∴,,,以为原点,,,所在直线分别为,,轴,建立空间直角坐标系,如图:则,,,,,,,,,设平面的法向量,则取,得.设平面的法向量,则取,得.设二面角的平面角为,则.∴二面角的余弦值为.3.因为平面平面,平面,,平面平面=,所以平面.所以.因为为等腰直角三角形,=,所以=又因为=,所以==,即.因为平面,平面,=,所以平面.取的中点,连结,,则,所以为平行四边形,所以.所以与所成角即为所求,正方形所在平面与四边形所在平面互相垂直,是等腰直角三角形,=,设=,.=,,在直角三角形中,.由,平面平面,易知,平面.作,交的延长线于,则.从而,平面.作于,连结,则由三垂线定理知,.因此,为二面角的平面角.因为=,=,所以=,=.设=,则=,..在中,=,,.在中,.故二面角的平面角的正切值为.4.取中点,连接,,依条件可知,,则为所求二面角的平面角.∵面,∴为侧棱与底面所成的角.∴,设=,,∴=,.∴=.连接,,∵,∴为异面直线与所成的角.∵,,∴平面.又平面,∴.∵,∴;延长交于,取中点,连,,.∵,,∴平面∴平面平面.又=,=,∴为正三角形.∴.又平面平面=,∴平面.∴是的等分点,靠近点的位置.5.存在点,点为的中点,证明:当点为的中点时,连结交于,∵平行四边形,∴为的中点,连结,则,∵在平面,不在平面,∴平面;∵===,===,=,∴,∴,∴=,∴,又∵平面平面,∴平面,平面,∴过点作,垂足为,连结,∴平面,∴,则为二面角的平面角,在中,,∴,∴二面角的余弦值为.6.平面.证明如下:在图中,连接,交于,交于,则,在图中,连接交于,连接,在中,有,,∴.∵平面,平面,故平面;图中的三角形与三角形分别是图中的与,∴,,又=,∴平面,则,又,∴平面,则为二面角的平面角.可知,则在中,=,,则.在中,=,,由余弦定理,得.∴二面角的余弦值为.7.证明:∵底面是边长为的正方形,=,为中点,∴,.∵平面,平面,∴.∵=,∴平面,∵平面,∴,∵=,∴平面,∵平面,∴;以为原点,为轴,为轴,为轴建立如图空间直角坐标系.则,,,,,,,设平面的一个法向量,则,取=,得;设平面的一个法向量为,则,取=,得,∴,∴二面角的正弦值为.8.证明:四棱柱中,底面为菱形,连结、,则,,∵在平面上的投影为直线与的交点,∴平面,∵平面平面,∴平面,∵平面,∴,∵=,∴平面,∴平面,∵平面,∴.连结,则四边形是平行四边形,∴平面,以为原点,在平面中过作的垂线为轴,为轴,为轴,建立空间直角坐标系,则,,,,,,,设平面的法向量,则,取,得,设平面的法向量,则,取=,得,设二面角的平面角为,则.∴二面角的正弦值.9.证明:取中点,连接,,在中,,分别为,的中点,则,且,又底面为正方形,为的中点,则,且,∴,∴四边形为平行四边形,∴,又不在平面内,在平面内,∴平面;∵,,且=,都在平面内,∴平面,取中点,则,∴平面,∴为直线与平面所成的角,∴,∵、、分别为、、的中点,底面边长为,=,∴,且,∵平面,在平面内,∴平面平面,且交线为,又,且在平面内,∴平面,在平面内作于点,则,又∵=,,在平面内,∴平面,再作于点,如图,则为所求二面角的平面角,在正方形中可求得,∴二面角的余弦值为.10.证明:Ⅰ在中,是斜边的中点,所以.因为,是,的中点,所以,且,所以=,,又因为,,所以,且=,故平面因为平面,所以平面平面.(2)方法一:取中点,则因为,所以.又因为,所以平面,故平面因此是直线与平面所成的角,,所以,过点作于,则平面,,过点作于,连接,则为二面角的平面角,因为,所以因此二面角的余弦值为.方法二:如图所示,在平面中,作轴,以为坐标原点,,为,轴建立空间直角坐标系.因为(同方法一,过程略)则,,,所以,,设平面的法向量则即取=,得,设平面的法向量则即取=,得所以,因此二面角的余弦值为.11.证明:∵,分别为正方形的边,的中点,∴,,又平面,平面,=,∴平面,∵平面,∴,∵=,=,∴是等边三角形,∵为的中点,∴,又,面,面,=,∴平面.设中点为,连结,则,,两两垂直,不妨设=.以为原点,以,,为坐标轴建立空间直角坐标系如图:则,,,,∴,,设平面的法向量为,则,令=,得,而为平面的一个法向量,∴,故二面角的余弦值为.12.(1)取的中点,连接,,在中,=,=,故是等边三角形,∴,又,而与相交于,∴平面,故,又,∴,∴为;(2)以为坐标原点,分别以,,为,,轴建立空间直角坐标系,可令===,则,,,,,∴,,,,设平面的法向量为,由题意有,令=,则=,,∴,又侧面底面,可得平面,可得平面的法向量为,,,二面角的平面角为钝角,可得二面角的余弦值为.13.连接交于点,连接.………因为,所以,又因为,所以,所以,……又面,面,所以面………过作于,因为=,所以是线段的中点.因为面面,面面=,所以面.连接,因为是等边三角形,是线段的中点,所以.如图以为原点,分别为轴,轴,轴的正方向建立空间直角坐标………分不妨设=,则,,,,,由,得,的中点,,设面的一个法向量为,则,即,得方程的一组解为,即面的一个法向量为,则所以二面角的余弦值为.………14.证明:取中点,连结,,∵,是,的中点,∴,且,∵,=,∴,∴,∴=,又,∴,∴为平行四边形,∴,又平面,且平面,∴平面.取中点,连结,取的中点,连结,,设=,由(1)得===,∴为等边三角形,∴,同理,,∵平面平面,平面平面=,平面,∴平面,以为坐标原点,分别以,,所在直线为轴,轴,轴,建立空间直角坐标系,则,,,,,,设平面的法向量,则,取,得,平面的法向量,∴,由图得二面角的平面角为钝角,∴二面角的余弦值为.第21页共22页◎第22页共22页。
