单一参数的交流电路.共31页文档
合集下载
单一参数交流电路
i
90° ）
u
i
I
90
t
U
u 2U sin t
i 2U C sin(t 90 )
I
1 I 3. 有效值 I U C 或 U C
定义：
1 XC C
容抗（Ω ）
则：
U I XC
4. 相量关系
u 2U sin t
i 2U C sin(t 90 ) U0 设： U I I90 U C90
1 （X C ） 容抗 是频率的函数， 表示电容 C
波有效。
1 Xc C
E
•
+
-e
ω＝0 时
ω
+ E -E
Xc
直流
电容电路中的功率
1. 瞬时功率 p
i
u
i 2 I sin t u 2U sin(t 90 )
p i u U I sin2t
p i u U I sin2t
是一个运算工具。
U
L C
U L
U C
I Z U
在正弦交流电路中，只要物理量用相量
表示, 元件参数用复数阻抗表示，则电路
方程式的形式与直流电路相似。
（二）
关于复数阻抗 Z 的讨论
由复数形式的欧姆定律
（１）Z和总电流、总电压的关系
I Z U
I
U 1 则： 90 C I
U
1 X U I 90 jI C C
电容电路中复数形式的 欧姆定律
U I j X C
I
其中含有幅度和相位信息
第3章 交流回路 (交流电路)
（初相位）
i
位相 初期位相
u
ψu =－60
°
O
30°
ωt
60°
位相差:同じ周波数の二つの正弦波交流の位相角の差。
（同频率的正弦电量的初相位之差）
大連理工大学電気工程学院
目録
3.1 正弦波交流の基本概念
位相差（相位差） =ψu－ψi =－60 °－30°=－90°
電気回路
基準量（参考量）：初期位相が0となる正弦波交流物理量。
(直交形式)
(三角形式) (指数形式) (極形式)
目録
（仮にa, b>0）
大連理工大学電気工程学院
3.2 正弦波交流のフェーザ表示法
電気回路
二、正弦波交流のフェーザ表示
+j
ω
ψ O
p Um +1 O ψ
u=Um sin (ωt +ψ)
ωt
ベクトルは角速度ωで反時計方向に回転し、 c sin（ωt＋ψ）は Op の虚軸への射影である。 [ Op 在虚轴上的投影为 c sin （ωt＋ψ)] 回転ベクトルは正弦波形で表されるし、逆に 正弦波形は回転ベクトルで表されるといえる。
U m 2U
大連理工大学電気工程学院
目録
3.2 正弦波交流のフェーザ表示法
電気回路
二、正弦波交流のフェーザ表示
jI +j
I
i=Imsin(ωt +ψ)
ψ O -jI +1
e j90°= cos 90°+ j sin 90°= j e -j90° cos 90°- j sin 90°= -j = j I と I の関係は？
目録
（仮にa, b>0）
i
位相 初期位相
u
ψu =－60
°
O
30°
ωt
60°
位相差:同じ周波数の二つの正弦波交流の位相角の差。
（同频率的正弦电量的初相位之差）
大連理工大学電気工程学院
目録
3.1 正弦波交流の基本概念
位相差（相位差） =ψu－ψi =－60 °－30°=－90°
電気回路
基準量（参考量）：初期位相が0となる正弦波交流物理量。
(直交形式)
(三角形式) (指数形式) (極形式)
目録
（仮にa, b>0）
大連理工大学電気工程学院
3.2 正弦波交流のフェーザ表示法
電気回路
二、正弦波交流のフェーザ表示
+j
ω
ψ O
p Um +1 O ψ
u=Um sin (ωt +ψ)
ωt
ベクトルは角速度ωで反時計方向に回転し、 c sin（ωt＋ψ）は Op の虚軸への射影である。 [ Op 在虚轴上的投影为 c sin （ωt＋ψ)] 回転ベクトルは正弦波形で表されるし、逆に 正弦波形は回転ベクトルで表されるといえる。
U m 2U
大連理工大学電気工程学院
目録
3.2 正弦波交流のフェーザ表示法
電気回路
二、正弦波交流のフェーザ表示
jI +j
I
i=Imsin(ωt +ψ)
ψ O -jI +1
e j90°= cos 90°+ j sin 90°= j e -j90° cos 90°- j sin 90°= -j = j I と I の関係は？
目録
（仮にa, b>0）
单一参数正弦交流电路分析
ui u
i
0
i +u-
t
I
相量图
U
T
T
2
2
电阻元件的关联参考方向、波形图和相量图
(2) 纯电阻电路的功率 p u, i
p
▪ 瞬时功率
p ui
P
I 2 sin tU 2 sin t
Pm=UmIm u
P=UI
2UI sin 2t
0
i
t
UI UI cos 2t
T
▪ 平均功率
【讨论】 指出下列各式中哪些是对的，哪些是错的？
在电阻电路中： 在电感电路中：
在电容电路中：
IU R
i U R
i u R
I U R
i u XL
U jωL I
I U ωL
U I
jX L
U I
X
L
u
L
di dt
i u ωL
UIωC
ui XC
IUjωC
1
C
1
2fC
容抗XL的单位为欧姆（Ω）。XC与ω成反比，频率愈 高，XC愈小，在一定电压下，I愈大。
在直流情况下，ω＝0，XC=∞ ，电容相当于开路； 在交流电路中电容元件具有隔直通交和通高频阻低频
的特性。
电容电压的相量表达式 U jXCI
(2) 纯电容电路的功率
▪ 瞬时功率
设 i 0
u L di dt
电感两端的电压与通过该电 感中电流的变化率成正比。
uN +
i
ψL=N
L
2.正弦交流电路中的电感元件
i
（1）电压、电流关系
正弦交流电路的分析—单一元件电路分析
I U
u、 i 同相 U IR
UI
0
纯电阻交流电路
✓ 思考
在电阻R=100Ω的电路中，加上 u=311sin(314t+300)V的电压，求 该电路中电流值及电流的解析式，并 画出电压和电流的相量图。
01
正弦交流电的三要素
02
正弦交流电的表示
03 单一参数正弦交流电路的分析
04
简单正弦交流电路的分析
3
解： 电流i(瞬时值)：
i 10 2 sin (200t+ 2 ) A
3
功率：P=UI=11010=1100W
纯电阻交流电路
✓ 小结
电路图 基本 (正方向) 关系
复数 阻抗
电压、电流关系
功率
瞬时值 有效值 相量图 相量式 有功功率 无功功率
R
i u
u iR
R
u 2U sint
U IR
i 2I sin t
01
正弦交流电的三要素
02
正弦交流电的表示
03 单一参数正弦交流电路的分析
04
简单正弦交流电路的分析
01
纯电阻交流电路
✓ 电压与电流关系
✓ 电阻元件的功率
纯电阻交流电路
✓ 电压与电流关系
交流电路中如果只有线性电阻，这种电路叫做纯电阻电路。
根据 欧姆定律：u=iR
i
设 u 2 U sin t
i
设
U
L
u
u L di jX L i 2I sint U IX L
dt jL u
X L L
I U IjX L
0
2IL sin(t 90)
u领先 i 90°
单相正弦交流电路—单一参数元件的电路
幅角:
i 90o
二、 C元件电路的功率
1. 瞬时功率 p
i
u
i
u
C
2 I sin t
2U sin( t 90 )
p i u U I sin 2 t
在关联参考方向下，功率有时大于零，有时小于零，电容元件在电路中的作
用是怎样的呢？
p i u iU I sin2ut
o
U I R
三、 R元件电路的功率
1. 瞬时功率 p：瞬时电压与瞬时电流的乘积
i
u
i I m sin ( t )
u U m sin ( t )
R
U m Im
p u i U m I m sin t
(1 cos 2t )
2
UI (1 cos 2t ) UI UI sin(2t 900 )
U IL
3. 有效值
电压、电流波
形图
u
i
90
定义：
t
X L L 2 fL
则：
U I XL
感抗（Ω）
关于感抗的讨论
感抗（ XL ωL 2πfL）是频率的函数，频率越高,感抗越大,频率越低,感抗越
小。电感有通低频，阻高频的特性。
UL I X L
R
+
_
f=0时
e
L
0.45 / 60o ( A)
R
484
i 0.45 2 sin(314t 60o )( A)
P UI 220 0.45 100(W )
在关联参考方向下，功率有时大于零，有时小于零，电感元件在电路中的作
用是怎样的呢？
单一参数的交流电路
R
•
I
波
Im
向 量 图
0
I• U•
Re
形 图
0
t
i
i
i = Imsin t +
u = Umsin t u
R
–
i、u、p
瞬时功率：电路在某一瞬间吸收 或放出的功率
u
p = u i =UI(1– cos2 t )
i
平均功率：瞬时功率在一周内的平均值 0
P = I U = I2 R
转换成的热能 W= P t
平均功率 P =0
i
无功功率 Q =UI=XC I2 =
U2 XC
波形图
u
电容与电源之间能量交换的规模
0
t
称为无功功率。其值为瞬时功
率的最大值，单位为(Var) 乏。
p
+
+
电容不消耗功率，它是储能元件。 0
–
– t
解：由线圈两端电压的解析式 u 100 2 sin 314tV可以得到
U=100V， 314rad / s, 0,
•
U 1000V
线圈的感抗为
X L L 314 0.01 3.14
•
•
I
U
100 0
31.85(90) A
jX L 190 3.14
因此通过线圈的电流瞬时值表达式为
i 31.85 2 sin(314t 90) A
i = Imsin( t + 90)
i u
波 形 图0
Im
• I
• U
t 0
Re
相量图
电流超前电压 90
电压与电流大小关系 U = I XC
单一参数的交流电路
U jX LI
C
jXC
j
1 ωC
i C du dt
U jXC I
相量图
I U
U
I I
U
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 (参考方向) 关系
阻抗
电压、电流关系
功率
瞬时值
有效值 相量图 相量式 有功功率 无功功率
i
+
Ru
u iR R
设
i 2Isinωt
则
U IR
I
设：u 2 U sin ω t dt
i
+
u
C
_
则：i C du 2 UC ω cos ω t 电流与电压
dt
的变化率成
2 U ωC sin(ω t 90) 正比。
ui
ui
① 频率相同
② I =UC
ωt ③电流超前电压90
90
相位差 ψu ψi 90
u 2Usinω t i 2Uω C sin( ω t 90)
有效值 I U ωC 或 U 1 I
定义：
XC
1 ωC
1 2π fC
ωC
容抗（Ω）
则: U I XC
XC
1 2π f
C
直流：XC ，电容C视为开路
交流：f
XC
所以电容C具有隔直通交的作用
XC
1 2π fC
容抗XC是频率的函数
由：u 2Usinω t
I , XC
XC
1 ωC
I U (2 π f C)
电阻的标称值 = 标称值10n
电阻器的色环表示法
四环
五环
倍 有效 率
第8次课 单一参数交流电路教案
［例 3］ 把一个 0.1 H 的电感接到 10 V、50 HZ 的工频交流电源上，电流 是多少？若接到 10 V、5 000 HZ 的交流电源上，电流是多少？
解：（1）接到 10 V、50 HZ 的工频交流电源上
X L = 2π fL = 2π × 50 × 0.1 Ω = 31.4 Ω
课次 8
共7页
3．电压、电流有效值之间的关系：U = RI
4．电压、电流相量之间的关系
I& = I ∠0o
U& = U ∠0o
U& I&
=
U ∠0o I ∠0o
=U I
∠0o
= R∠0o
=
R
U& = RI&
U& 和 I& 的相位相同，如图 3.3.1（b）所示。
5．瞬时功率 p
p
=
ui
=
UmIm
sin 2
ωt
=
UmIm 2
课次 8
共7页
第4页
解：（1）接到 10 V、50 HZ 的工频交流电源上
XC
=1 2π fC来自=1 2π ×50 × 25×10−6
Ω = 127.4 Ω
I = U = 10 A = 0.078 A XC 127.4
Q = UI = 10× 0.078 var = 0.78 var
(2)接到 10 V、5 000 HZ 的交流电源上
=
UmIm
sin
ωt
cos ωt
=
Um Im 2
sin
2ωt
=
UI
sin
2ωt
7．平均功率 P
∫ ∫ P = 1
T pdt = 1
解：（1）接到 10 V、50 HZ 的工频交流电源上
X L = 2π fL = 2π × 50 × 0.1 Ω = 31.4 Ω
课次 8
共7页
3．电压、电流有效值之间的关系：U = RI
4．电压、电流相量之间的关系
I& = I ∠0o
U& = U ∠0o
U& I&
=
U ∠0o I ∠0o
=U I
∠0o
= R∠0o
=
R
U& = RI&
U& 和 I& 的相位相同，如图 3.3.1（b）所示。
5．瞬时功率 p
p
=
ui
=
UmIm
sin 2
ωt
=
UmIm 2
课次 8
共7页
第4页
解：（1）接到 10 V、50 HZ 的工频交流电源上
XC
=1 2π fC来自=1 2π ×50 × 25×10−6
Ω = 127.4 Ω
I = U = 10 A = 0.078 A XC 127.4
Q = UI = 10× 0.078 var = 0.78 var
(2)接到 10 V、5 000 HZ 的交流电源上
=
UmIm
sin
ωt
cos ωt
=
Um Im 2
sin
2ωt
=
UI
sin
2ωt
7．平均功率 P
∫ ∫ P = 1
T pdt = 1
单一元件交流电路资料
QL
UI
I2XL
UL2 XL
为和有功功率相区别，无功功率的单位定义为 乏尔[Var]。
【例】在电压为220V、工频50Hz的电力网内，接 入电感L=0.127H、而电阻可忽略不计的电感线圈。 试求电感线圈的感抗、电感线圈中电流的有效值及 无功功率。
解： X L 2 fL 23.14500.127 40()
p
i
p ui
ωt
u
说明：（1） p>0，电感线圈吸取电能，并以磁能的方式 储存起来 （2） p<0，电感线圈把储存的磁能转换为电能， 还给电路
2）平均功率 P
P 0 电感元件不耗能！
3）无功功率 Q
电感元件虽然不耗能，但它与电源之间的能量交
换始终在进行，这种电能和磁场能之间交换的规模 可用无功功率来衡量。即：
b 串联电容的总电容的倒数等于各个电容
的倒数之和。
即： 1 1 1 1
C C1 C2
Cn
3)电容器的容抗 电容器的导电原理
+q E -q
+
US
－
正弦交流电的电压和电流的大小、方向是变化的，
使得电容器极板上的电荷也随之变化，电荷的变化
形成了电流。
即： i q C u t t
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
相量关系式
I
U
U0
U
0
I0
RRR
相量图
U I
（2）电阻元件上的功率关系
单一参数的正弦交流电路 教案11
T0
T0
R
可见，平均功率的计算公式与直流电路功率计
算公式相同，只不过交流电路计算式中的U和I是
指电压、电流的有效值而已。在一些交流用电设
备的铭牌上以瓦或千瓦标注的功率都是指设备的
额定有功功率。
正弦交流电路
二、电感交流电路：
1、电压、电流关系： 若在理想电感中流过电流i=Imsinωt，在u、i
的假定正方向一致的情况下（如图所示），由式 可知：
为欧姆。感抗是反映电感对电流流动阻碍能力大 小的物理量。它跟电感L、电流频率f的大小成正比。 同样一个电感L，处在不同频率的交流电路中所呈 现出的感抗是不同的。对于直流电流，由于f=0， 故XL=0，即电感对直流电流没有阻碍作用。频率 愈高则感抗愈大，即电感阻碍电流的作用愈大。
这是电感的重要性质之一。感抗的频率特性如图 所示。
p=ui=Um Imsin2ωt=2UIsin2ωt=UI（1cos2ωt）=UI-UI cos2ωt。
正弦交流电路
可见，电阻元件的瞬时功率由两部分组成：第 一部分是电压，电流有效值的乘积，它是一个常 数；第二部分是一个幅值为UI、频率为2ω的余弦 函数。瞬时功率p的波形如图所示。因为ui同相， 即同时为正或同时为负，所以瞬时功率总是正值。 由此可见，电阻元件总是从电路吸取电能，然后 又把电能转化热能，而且这种转化过程是不可逆 的。
③、正负瞬时功率幅值相等，正负半周曲线所 包围的面积相等。
（2）、平均功率P：
瞬时功率在一个周期中的平均值称为平均功率 或有功功率。在纯电感电路中其值为：
正弦交流电路
P
1 T
T
0
pdt
1 T
T
0
UI
单一参数的交流电路
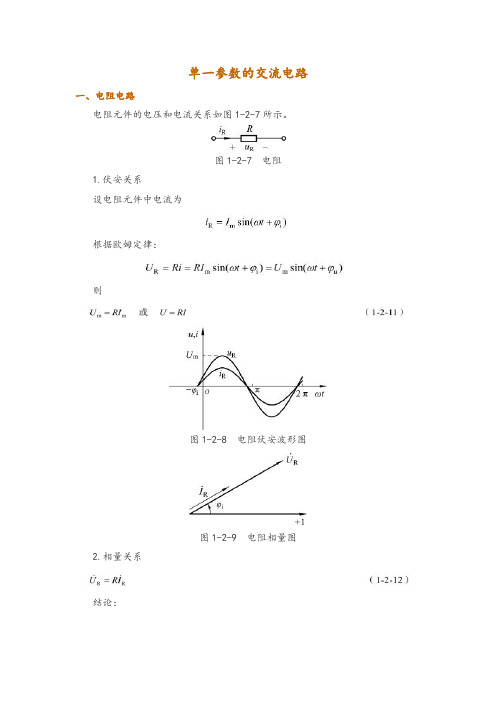
单一参数的交流电路一、电阻电路电阻元件的电压和电流关系如图1-2-7所示。
图1-2-7 电阻1.伏安关系设电阻元件中电流为根据欧姆定律：则图1-2-8 电阻伏安波形图图1-2-9 电阻相量图2.相量关系结论：（1）电阻元件两端的电压和电流的相量值、瞬时值、最大值、有效值均服从欧姆定律。
（2）电阻两端的电压与电流同相（电压电流的复数比值为一实数）。
二、电阻元件的功率1.瞬时功率（instantaneous power）该电阻元件的电流：设则：其波形如图1-2-10所示。
由图1-2-10可见，电阻元件的瞬时功率大于（等于）零。
图1-2-10 电阻瞬时功率波形图2.平均功率（有功功率）瞬时功率在一个周期内的平均值（见图1-2-11）：图1-2-11 电阻平均功率波形图注意：通常铭牌数据或测量的功率均指有功功率。
【例2.9】电阻元件电压、电流的参考方向关联。
＝1.414sin（ωt＋30）A 已知：电阻R＝100 Ω，通过电阻的电流iR求：（1）电阻元件的电压和u ；RP ；（2）电阻消耗的功率R（3）画相量图。
解：（1）（2）（3）相量图如图1-2-12所示。
三电感电路（一）电磁感应定律1831 年，法拉第从一系列实验中总结出：当穿过某一导电回路所围面积的磁通发生变化时，回路中即产生感应电动势及感应电流，感应电动势的大小与磁通对时间的变化率成正比。
这一结论称为法拉第定律。
这种由于磁通的变化而产生感应电动势的现象称为电磁感应现象。
1834 年，楞次进一步发现：闭合导体回路中的感应电流，其流向总是企图使感应电流自己激发的穿过回路面积的磁通量能够抵消或补偿引起感应电流的磁通量的增加或减少。
这一结论即是楞次定律。
法拉第定律经楞次补充后，完整地反映了电磁感应的规律。
电磁感应定律指出：如果选择磁通Φ的参考方向与感应电动势e 的参考方向符合右手螺旋关系，如右图所示。
对一匝线圈来说，其感应电动势可以描述为式中，磁通的单位为韦伯（Wb），时间的单位为秒（s），电动势的单位为伏特（V）。
单一参数的交流电路.PPT文档共33页
1
0
、
倚
南
窗
以
寄
傲
，
审
容
膝
之
易
安
。
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
文 家 。汉 族 ，东 晋 浔阳 柴桑 人 （今 江西 九江 ） 。曾 做过 几 年小 官， 后辞 官 回家 ，从 此 隐居 ，田 园生 活 是陶 渊明 诗 的主 要题 材， 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
单一参数的交流电路.
6
、
露
凝
无
游
氛
，
天
高
风
景
澈
。
7、翩翩新 来燕，双双入我庐 ，先巢故尚在，相 将还旧居。
8
、
吁
嗟
身
后
名
，
于
我
若
浮
烟
。
9、 陶渊 明（ 约 365年 —427年 ），字 元亮， （又 一说名 潜，字 渊明 ）号五 柳先生 ，私 谥“靖 节”， 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
单一参数交流电路的分析计算PPT课件
L C2
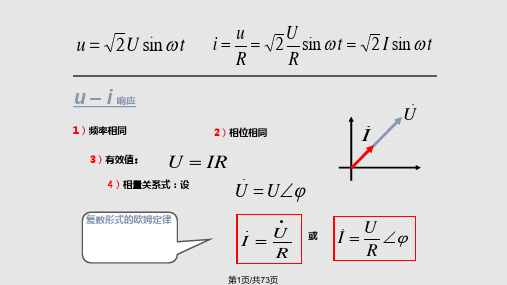
B 求：i = ？ u
=？
U = +UAB= UC+1
1V00
00
100 -900
第15页/共73页
1. 相量方程式
U U R U L UC
设：i 2 Isin t
或 I I0
i
R uR u L uL
C uC
则： U R IR , U L I jX L , UC I jX C
U IR I jX L I jXC
IR jX L XC
第16页/共73页
总电压与总电流的关系 式
jX C
U C
U I(R jX L jX C )
------ 相量形式的欧姆定律
第29页/共73页
二. 复杂交流电路的计算方法
1、保持电路结构不变，将电路中的正弦量用相 量表示，电路参数用复数阻抗表示。
R
R
L
jXL
C
-jXC
u
U
i
I
即：将正弦交流电路转换成相应的相量模型图。
2、用电路的基本定律（基氏定律）、定理（迭加 定理、电源等效定理、戴维南定理）、和分析 方法（支路电流）对交流电路的相量模型，列 相量方程式分析计算。
i
dt
复阻抗 j jX
C c
功率 有功功率: 0
无功功率: UI I2XC
瞬时值
电压、电流关系
有效值
相量图
相量式
设 u 2U sint
则i 2 U 1
C
U IX C
XC
1
C
I U
U
I jXC
u落后i90°
sin(t 90)
第14页/共73页
单一参数正弦交流电路的分析计算
S U
Q
I
R U R
L U L
C
U C
P
（二）一般正弦交流电路的解题步骤
1、据原电路图画出相量模型图（电路结构不变）
RR、LjXL、CjXC uU、iI、 eE
2、根据相量模型列出相量方程式或画相量图 3、用复数符号法或相量图求解 4、将结果变换成要求的形式
正弦交流电路的功率问题
RL
1 4
0.25S
t≥0 R C 0 .0S 3 R L 0 .2S 5
零输入响应
2 1 K
2
u 0
t
uC uC(0)e RC
4A
t
u
2
t>0
uC 0.01F 2
iL
1H
iL iL(0)e RL
零状态响应
完全响应
t≥0 R C 0 .0S 3 R L 0 .2S 5
R'C
5. t<0时电路处于稳态，t=0时开关Ｋ打开，试求 t≥0
时的uC 、iL、u的零输入响应、零状态响应和完全响
应。
2 1 K
2
t=0
4A u
iL
2 uC 0.01F 2
1H
初始状态值 t≥0
iL (0)iL (0)1 A uC(0+)=uC(0-) =2V
RC
三相交流电路的小结（1）--三相电源
e 三相四线制 A
e （Y形联接） C
A
三相电源
N 一般都是
eB
对称的，
B C
称三相对 称电源
三相三线制（Y形联接）
eA
A
eC
eB
B
C
第5讲单一参数的交流电路、简单交流电路的分析
例：把一个25μ F的电容元件接到频率为50Hz，电压 有效值为10V的正弦电源上，问电流是多少？如保持 电压值不变，而电源频率改为5000Hz，这时电流将 为多少？
解：当f = 50Hz时
XC 1 2πfC
当f = 5000Hz时
XC
1
1 2fC
1 2 3.14 5000 25 10
S UI
S P Q
2 2
S
P S cos Q S sin
Q
P
arctan
Q P
功率三角形
S
Z R (X L XC )
2 2
U
Z
U L UC
R Z cos
X Z sin
U U R (U L U C )
2 2
Q
I
C
I jC
I
⑸相量图
U
⒉ 功率关系
⑴ 瞬时功率
p ui U m I m sin ω t sin ( ω t 90)
U m I m sin ω t cos ω t UmIm 2 sin 2 ω t
UI sin 2ωt
交变量
⑵ 平均功率
P
T
1
T
p dt
6
2 3. 50 25 10 14
6
127.4Ω
I U XC 10 127.4 78mA
I
1.274
U XC 10 1.274 7.8A
2.4 简单交流电路的分析
U 0
①直流电路中基尔霍夫定律的形式 ②交流电路中基尔霍夫定律的形式
单一参数的正弦交流电路 教案12
正弦交流电路
p=ui= Um Imsinωt sin（ωt+900） （ =UmImsinωtcosωt =UmImsin2ωt/2=UI sin2ωt 瞬时功率的波形图如图所示。 瞬时功率的波形图如图所示。与电感电路瞬 时功率相似，它有如下特点： 时功率相似，它有如下特点：
正弦交流电路
①、瞬时功率的幅值为UI，频率为 ； 瞬时功率的幅值为 ，频率为2ω； 当电压、电流同符号， ②、当电压、电流同符号，如图中第一个和第 三个T/4时段 为正，说明这段时间内， 时段p为正 三个 时段 为正，说明这段时间内，电源把电 荷送入电容器中，电容被充电， 荷送入电容器中，电容被充电，电容吸取电能并 把电能转换成电场能储存在电场中。 把电能转换成电场能储存在电场中。当u，i符号相 ， 符号相 反时，如图中第二、四个T/4周期 周期， 为负值 为负值， 反时，如图中第二、四个 周期，p为负值，这 段时间内电容把电场能释放出来转换成电能， 段时间内电容把电场能释放出来转换成电能，此 时电容放电并向电路提供能量。 时电容放电并向电路提供能量。 ③、正负瞬时功率的幅值相等，波形图中正负 正负瞬时功率的幅值相等， 半周的面积相等。 半周的面积相等。 ）、平均功率 （2）、平均功率 ： ）、平均功率P：
d (U m sin ωt ) du i=c =c = ωcU m cos ωt = I m sin ωt + 90 0 dt dt
正弦交流电路
(
)
电压电流的波形图如图所示。由此可知， 电压电流的波形图如图所示。由此可知，电容 两端的电压和电流之间的关系是： 两端的电压和电流之间的关系是：
）、电流与电压为同频率的正弦量 （1）、电流与电压为同频率的正弦量； ）、电流与电压为同频率的正弦量； ）、在相位上电流超前于电压 （2）、在相位上电流超前于电压 0； ）、在相位上电流超前于电压90
相关主题