材料力学求形心位置例题
材料力学 中国建筑工业出版社 第五章 截面的几何性质 习题解答

5-1 试用积分法确定图示平面图形的形心位置。
解:(1)建立极坐标极坐标(α,ρ),取微面积dA d d ραρ=⋅。
则cos y ρα=, (2)求形心位置222322cos ()cos 43434rrACd d d d ydA r r r y AArππραρραρρααπππ⋅⋅⋅⋅=====⎰⎰⎰⎰⎰由对称性可知:43C rz π=。
图形形心为(43r π,43r π)。
700图题5-1b 图题5-2b5-2 确定图示平面图形力的形心位置。
解:(1)选取通过矩形I 的形心C 1,矩形II 形心C 2,矩形III 形心C 3 (2)求形心位置 由于截面左右对称,故:400mm Cz =。
3131150400150150800200400150500150700222mm=305mm 150800200400500150i Cii C ii A yy A==⎛⎫⎛⎫⨯⨯+⨯⨯++⨯⨯- ⎪ ⎪⎝⎭⎝⎭==⨯+⨯++⨯∑∑图形形心为(305,400)。
5-4(a)题5-4图解:(1)矩形341212z bh a I ==(2)箱形箱形与方形面积,即:22226 5.4 5.4a a bt at t ==→=333322224(0.9)(1.8)(0.9)(1.8)()(2)()(2)5.4 5.4 5.4 5.4121212120.4567z a a a a a a a a b t b t b t b t I a ++--++--=-=-= (3)工字形截,即:面23332 1.62 5.2a a at at t =⨯+→= 工字形截面方形面积33333341.6(22)(1.6)81.6(22)(1.6)8 5.2 5.2121212120.8695z a a a a a a a a t a t aI a +⨯-+-=-=-=10.45670.869515.4810.4312z z z I I I ==工方箱::::::5-8图示矩形h=2b=200mm ,(1)试求矩形通过坐标原点O 1的主惯性轴的位置及主惯性矩。
求图示平面图形的形心位置及形心主惯性矩
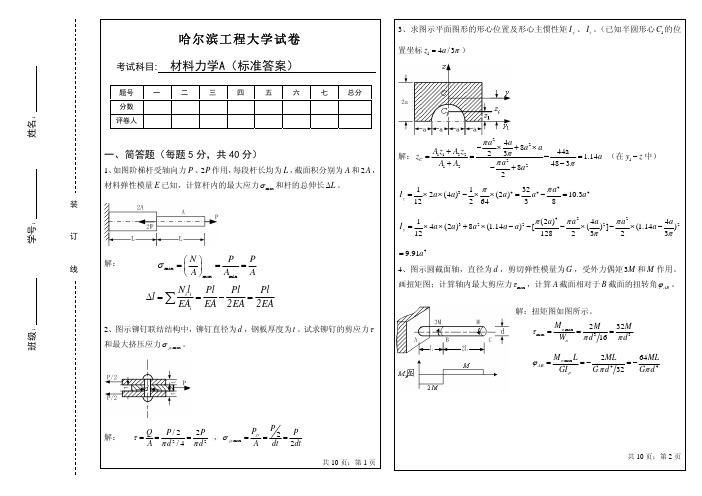
σ x +σ y
2
± (
σ x −σ y
2
) 2 + τ xy 2
j
= 2v A , kd = 1 + 1 +
2H
j
= 1+ 1+
H vA
σ max = ⎨
min
⎧130MPa ⎩30MPa
σ d max = kd i2σ B max
vd = kd
⎛ H⎞ = 2 ⎜1 + 1 + ⎟ σ B max ⎜ vA ⎟ ⎝ ⎠
(δ B )水平
M ∂M 1 = [∫ ds ]Pf =0 = s EI ∂P EI f
∫
π
2 0
PR 3 PR cos ϕ i R(1 − sin ϕ )i Rdϕ = 2 EI
共 10 页;第 8 页
共 10 页;第 7 页
六、图示传动轴。直径为 d,轮 C、轮 E 直径均为 D。轮 C 受铅垂力 P。轮 E 受水平力 P。试求:⑴作轴的扭矩图,弯矩图。⑵指出危险截面的位置。⑶ 用第三强度理论写出校核该轴强度的相当应力表达式。 10 分) (
δ 22 =
1 ⎛l ⎞ 3l ⎜ × 1 + l × 1⎟ = EI ⎝ 2 ⎠ 2 EI
应用卡氏定理
将以上系数代入式(1) ,经简化可得
l Pl 1 ⎫ X1 − X 2 + = 0⎪ ⎪ 3 2 8 ⎬ 5Pl lX 1 − 3 X 2 + =0⎪ ⎪ 8 ⎭ X1 = − P 8 X2 = P Pl H A = HB = 6 8 RA = RB = P 2 MA = MB = Pl 24
2 3 2 2 2
∂M = R cos ϕ ∂P (δ B )竖直 M ∂M 1 =∫ ds = s EI ∂P EI
材料力学学生习题解答
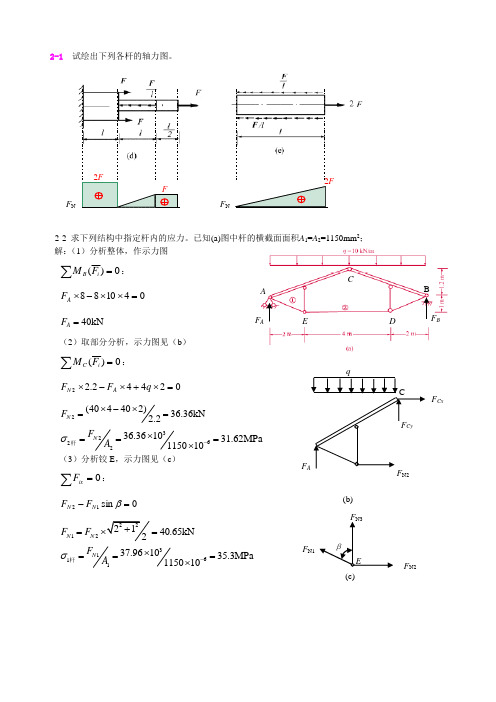
E F N1F N3F N2β(c)2-1 试绘出下列各杆的轴力图。
2-2 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:041088=⨯⨯-⨯A F 40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=⨯+⨯-⨯q F F A N2(404402)36.36kN 2.2N F ⨯-⨯==3262236.361031.62MPa 115010N F A σ-⨯===⨯杆(3)分析铰E ,示力图见(c )∑=0ixF:0sin 12=-βN N F F22122140.65kN 2N N F F +=⨯= 3161137.961035.3MPa 115010N F A σ-⨯===⨯杆F 2F F N 2F F N A ECDB F AF BCF A F CyF CxN2(b)2-3 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F -=+⨯⨯⨯=AB 段最大轴力在A 处6N 1212(0.5300.540)107812.0kN A F -=++⨯+⨯⨯⨯=3N 2612.010400MPa 30mm 3010B B F σ--⨯===⨯ 3N 2612.010300MPa 40mm4010AA F σ--⨯===⨯杆件最大正应力为400MPa ,发生在B 截面。
2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比ν。
材料力学___形心位置确定

46.7mm
20
2
y
100
I I
1 yC
1 12 1
20 1403 20 140 (80 46.7 )
3
2
2 yC
12
100 20 100 20 ( 4 4 1 2 I yC I yC I yC 12.12 10 m
πd
4
x
所以
Ix Iy
64
§ І -3 惯性矩和惯性积的平行移轴公式
组合截面的惯性矩和惯性积
一、 平行移轴公式
x , y ——任意一对坐标轴 C —— 截面形心 a (b , a ) _____ 形心 c 在 xoy 坐标系下的 坐标。 xc , yc ——过截面的形心 c 且与 x , y 轴平 行的坐 标轴(形心轴)
I x Iy
2α 0 在第三象限
2α 0 227.60
0
0
113.8
形心主惯性轴 x0 , y0 分别由 x 轴和 y 轴绕 C点
逆时针转 113.80 得出。
形心主惯形矩为
I x0 I y0 Ix Iy 2 1 2
I
x
Iy
2
4 I xy
2
321 10
4 4
57.4 10
mm
4
Ix Iy 2
1 2
I x
Iy
2
4I
2
xy
过截面上的任一点可以作无数对坐标轴,其中必有 一对是主惯性轴。截面的主惯性矩是所有惯性矩中
的极值。即:Imax = Ix0 ,
Imin = Iy0
求图示平面图形的形心位置及形心主惯性矩
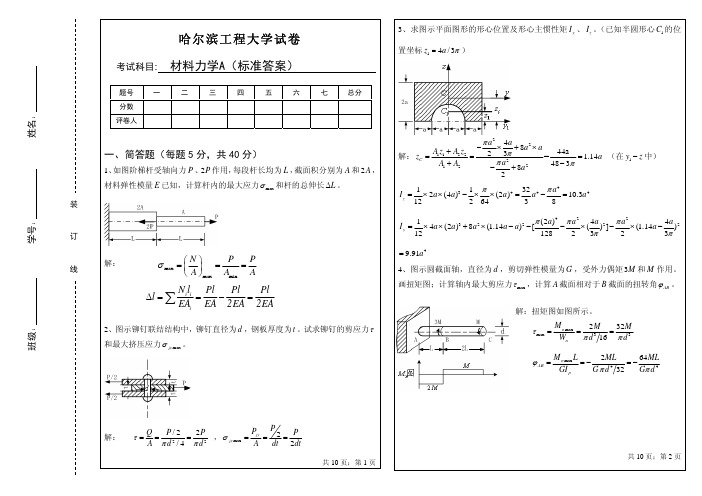
=
−
l2 2EI
δ 22
=
1 EI
⎛ ⎜⎝
l 2
×1+ l ×1⎞⎟⎠
=
3l 2EI
将以上系数代入式(1),经简化可得
l 3
X1
−
1 2
lX1 − 3X
X2 2+
+
0
⎪ ⎪⎭
X1
=
−
P 8
X2
=
Pl 6
HA
= HB
=
P 8
RA
=
RB
=
P 2
MA
=
MB
=
Pl 24
六、图示传动轴。直径为 d,轮 C、轮 E 直径均为 D。轮 C 受铅垂力 P。轮 E 受水平力 P。试求:⑴作轴的扭矩图,弯矩图。⑵指出危险截面的位置。⑶ 用第三强度理论写出校核该轴强度的相当应力表达式。(10 分)
七、图示细长压杆,两端球形铰支,材料弹性模量 E ,试对下面两种情况计 算其临界压力 Plj 。①圆截面,直径 d ,杆长 l 。②矩形截面, h = 2b ,长 l 。 (10 分)
班级:
解:
τ = Q = P / 2 = 2P A πd2 /4 πd2
, σ jy max
=
Pjy A
=
P 2
dt
=
P 2dt
共 10 页;第 1 页
共 10 页;第 2 页
5、图示悬臂梁 AB 。已知当自由端受静载 P 时,自由端的挠度为 vA ,固定端 的最大正应力为σ Bmax 。现有重为 2P 的物体自 H 高度自由落体冲击于自由端, 求此时 A 端的挠度 vd 和梁内最大正应力σ d max 。
材料力学附录I 平面图形的几何性质2形心主轴和形心主惯性矩

i1
i1
i1
材料力学 附录I 平面图形的几何性质
例I-4-1:已知三角形对底边(x1轴)的惯性矩为bh3/12,
求其对过顶点的与底边平行的x2轴的所以不
x2
能直接使用平行移轴公式,需先求出 三角形对形心轴xC的惯性矩,再求对
h xC
h/3
x1
x2轴的惯性矩,即进行两次平行移轴
I
A2 zc
60 1003
12
50 44.72
60 100
404 64
50 44.7
202
202
4.24106 mm4
材料力学 附录I 平面图形的几何性质
§I-5 转轴公式 主惯性轴*
一、 惯性矩和惯性积的转轴定理
y
x1 y1
x cos y sin x sin y cos
材料力学 附录I 平面图形的几何性质
y
1.先求截面的 形心轴
A2
取参考坐标系如图,则:
A1
zc
yc
60100 50 60 100
202 202
70
44.7mm
yc z 2.求截面对形心轴的惯性矩:
I yc
Iy
100 603 12
404 64
1.67 106 mm4
I zc
I A1 zc
12
64 4
d
y
yC
x1
I
yC
I
矩xC
I圆xC
(1.5d )32d 12
d 4
64
0.513
d
4
I xCyC0
2d
O
xC yC轴便是形心主轴
x xC
I xC、I yC便是形心主惯性矩
材料力学作业

三、桥式起重机大梁上的小车的每个轮子对大梁的压力均为 ,试问小车在什么位置时梁内的弯矩为最大?其最大弯矩等于多少?最大弯矩的作用截面在何处?设小车的轮距为 ,大梁的跨度为 。
四、试利用微分关系作出图示各杆的剪力图和弯矩图。
五、已知简支梁的弯矩图如图所示,试作该梁的剪力图和载荷图。
材料力学作业
———————————————————————————————— 作者:
———————————————————————————————— 日期:
ﻩ
一、试作出图示各杆的轴力图。
二、图示结构中,1、2两杆的横截面直径分别为 和 ,试求两杆的应力。设两根横梁皆为刚体。
三、桁架的尺寸及受力如图所示,若 , 杆的横截面面积 ,试求 杆的应力。
四、在图示简易吊车中, 为钢杆, 为木杆。木杆 的横截面面积 ,许用应力 ;钢杆 的横截面面积 ,许用应力 。试求许可吊重 。
五、在低碳钢拉伸实验用的力与变形曲线及应力应变曲线中分别标出 、 、 和 、 、 ,并回答在 曲线中的 、 、 是否是构件中的真实应力,如果不是请另绘出强化阶段与颈缩阶段真实应力曲线的大致形状。
八、重量为 的直梁放置在水平刚性平面上,若受力后未提起的部分保持与平面密合,试求提起部分的长度。
一、在图示应力状态中,试用解析法和图解法求出指定截面上的应力及其主应力并画主单元体(应力单位为 )。
二、受力某点两平面上的应力如图示,求其主应力。应力单位为 。
六、简支梁的剪力图如图所示,已知梁上没有集中力偶作用,试作该梁的弯矩图和载荷图。
七、试作出图示平面刚架的内力图( 、 、 )。
一、把直径 的钢丝绕在直径 的轮缘上,已知材料的弹性模量 ,试求钢丝内的最大弯曲正应力。
材料力学的静矩和形心计算

-
谢谢观看
XXXXX
XXXXX
材料力学的静矩和形心计算
-
第一部分 第二部分 第三部分 第四部分 第五部分
静矩的定义 形心的计算 静矩和形心的关系 静矩和形心在工程中的应用 材料力学中的静矩和形心计算
1
静矩的定义
静矩的定义
这个概念主要在分析物体的稳 定性和强度时使用
在材料力学中,静矩是指一个 物体在受到外力作用时,所产 生的力矩与其对应的位移之商 静矩的计算公式为:S=∫(r × F) dV,其中S为静矩,r为物体 上任意点的位置向量,F为作用 在该点的外力,dV为微小体积
2
形心的计算
形心是物体形受到 的合力为零,那么这个物体 就是处于静力平衡状态。这 时,物体的重心位置就是其 形心。形心的计算方法有多 种,其中一种是利用物体的 质量分布和形状来确定。如 果一个物体具有均匀的密度 分布,那么其形心就是其质
量分布的几何中心
形心的计算
在计算形心时,通常需要将 物体分割成若干个小的体积 元素,并计算每个元素的质 心位置。然后将所有元素的 质心位置进行平均,得到整 个物体的形心位置。如果物 体具有旋转对称性,那么其 形心就是其旋转轴的交点
3
静矩和形心的关系
静矩和形心的关系
1 静矩和形心之间存在一定的关系。对于一个 物体,如果其受到的合力为零,那么其静矩 也为零。这是因为静矩是外力与位移的商, 而当物体处于静力平衡状态时,其位移为零。 因此,静矩也为零
此外,在建筑设计中,也需要计算建筑结构的静矩和形心位置,以确 保建筑结构的强度和稳定性。在机械设计中,需要计算零件的静矩和 形心位置,以确保零件的强度和稳定性
材料力学形心位置确定课件

其中,(x1, y1), (x2, y2), ..., (xn, yn) 是图 形各点的坐标,n 是 图形的顶点数。
图表:通过在坐标系 中绘制图形,可以直 观地显示形心的位置 。例如,对于矩形、 三角形等简单图形, 可以通过作图软件计 算并绘制出其形心的 位置。
立体图形形心位置的相关公式与图表
• 公式:对于三维图形,形心位置的坐标可以通过对图形各点坐标的加权平均来计算。假设三维空间中有一个点集 {P1(x1, y1, z1), P2(x2, y2, z2), ..., Pn(xn, yn, zn)},那么形心坐标 (xc, yc, zc) 可以通过以下公式计算
THANKS
感谢观看
VS
组合截面对形心的位置可以通过将各部分 形心位置加总得到。如果各部分形心位置 不在同一直线上,则需要通过坐标系转换 和线性代数的方法进行计算。
思考题及答案解析
问题5
举例说明形心在材料力学中的应用。
• 答案
形心在材料力学中有着广泛的应用,如组合 截面对形心的计算、截面应力的计算等。例 如,在组合截面对形心的计算中,可以通过 对各部分形心位置的计算,得到组合截面对 形心的位置,从而得到截面的内力和应力。
06
复习与思考题
本章重点回顾
理解截面内力和截 面应力的概念和计 算方法
掌握组合截面对形 心的计算方法
掌握形心的定义和 计算方法
熟悉静矩、惯性矩 、极惯性矩、惯性 积的计算和意义
理解形心在材料力 学中的重要性及应 用
思考题及答案解析
问题1
什么是形心?其重要性是什么?
• 答案
形心是指截面的几何中心,即截面上各点到截面几何中心点 的距离相等。形心在材料力学中有着重要的应用,如组合截 面对形心的计算、截面应力的计算等。
材料力学附录I 平面图形的几何性质2形心主轴和形心主惯性矩

10 150yC x1
x
由于对称知: xC=0
材料力学 附录I 平面图形的几何性质
§I-2 惯性矩和惯性半径
一、惯性矩
Iz
y 2 d A,
A
Iy
z2dA
A
工程中常把惯性矩表示为平面图 形的面积与某一长度平方的乘积, 即
Iy A iy2
或
iy
Iy A
Iz A iz2
或
iz
Iz A
4
③ 建立形心坐标系;求:IyC , IxC , I xCy
材料力学 附录I 平面图形的几何性质
I xC I矩xC I圆xC I矩x A矩 y 2[I圆x1A圆 (0.5dy)2 ]
1.5d
(2d )3
3d 2 (0.177 d )2
d 4
[
d 2
(0.5d
0.177 d )2 ]
0.685 d 4
A
dA
zdy
h1
y2 b2
dy
dz
z
yC C y
O b
A
y
dA
A
b 0
h1
y2 b2
dy
2bh 3
材料力学 附录I 平面图形的几何性质
z
h yC C z O y dy
b
Sz
y
ydA
A
b 0
yh1
y2 b2
dy
b2h 4
yC
Sz A
3b 8
z
dz
z
yC C y
y
O b
Sy
4bh2 15
材料力学 附录I 平面图形的几何性质
§I-1 静矩和形心 §I-2 惯性矩和惯性半径 §I-3 惯性积 §I-4 平行移轴公式 §I-5 转轴公式 主惯性轴
【材料力学】第五章 截面的几何性质习题答案

5-1 试用积分法确定图示平面图形的形心位置。
解:(1)建立极坐标极坐标(α,ρ),取微面积dA d d ραρ=⋅。
则cos yρα=,(2)求形心位置222322cos ()cos 43434r r AC d d d d ydA rrr y AA rππραρραρρααπππ⋅⋅⋅⋅=====⎰⎰⎰⎰⎰由对称性可知:43Cr z π=。
图形形心为(43r π,43r π)。
y700图题5-1b 图题5-2b5-2 确定图示平面图形力的形心位置。
解:(1)选取通过矩形I 的形心C 1,矩形II 形心C 2,矩形III 形心C 3 (2)求形心位置 由于截面左右对称,故:400m mCz=。
3131150400150150800200400150500150700222m m =305m m150800200400500150i C ii C ii A y y A ==⎛⎫⎛⎫⨯⨯+⨯⨯++⨯⨯- ⎪ ⎪⎝⎭⎝⎭==⨯+⨯++⨯∑∑图形形心为(305,400)。
5-4(a)题5-4图解:(1)矩形341212z bhaI ==(2)箱形箱形与方形面积,即:22226 5.4 5.4a a bt at t ==→=333322224(0.9)(1.8)(0.9)(1.8)()(2)()(2)5.45.45.45.4121212120.4567z a a a a a a a a b t b t b t b t I a++--++--=-=-=(3)工字形截,即:面23332 1.62 5.2a a at at t =⨯+→=工字形截面方形面积33333341.6(22)(1.6)81.6(22)(1.6)8 5.25.2121212120.8695z a aa a a aa a t a t aI a+⨯-+-=-=-=10.45670.869515.4810.4312z z z I I I ==工方箱::::::5-8图示矩形h=2b=200mm ,(1)试求矩形通过坐标原点O 1的主惯性轴的位置及主惯性矩。
材料力学作业参考解答

2-3答:以B点为研究对象,由平面汇交力系的平衡条件
2-2求下列结构中指定杆内的应力。已知(a)图中杆的横截面面积A1=A2=1150mm2;
解:(1)分析整体,作示力图
:
(2)取部分分析,示力图见(b)
:
(3)分析铰E,示力图见(c)
:
2-3求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB的横截面积为40mm2,下段BC的横截面积为30mm2,杆材料的ρg=78kN/m3。
解:(1)求①、②杆轴力
由平衡方程可以求出:
(2)求杆的变形
(压缩)
(拉伸)
(压缩)
(3)由几何关系: (下降)
2-9答:任一截面上轴力为F,由
得面积为
伸长量为
2-11图示一挡水墙示意图,其中AB杆支承着挡水墙,各部分尺寸均已示于图中。若AB杆为圆截面,材料为松木,其容许应力[σ]=11MPa,试求AB杆所需的直径。
:
(2)由强度条件求
2-14图示AB为刚性杆,长为3a。A端铰接于墙壁上,在C、B两处分别用同材料、同面积的①、②两杆拉住,使AB杆保持水平。在D点作用荷载F后,求两杆内产生的应力。设弹性模量为E,横截面面积为A。
解:
1.本题为超静定问题,
见图(a),设AB杆产生角位移 ,则
,
2.由Hooke定律:
由平衡条件可知:
所以B,C截面相对位移为
3-1试作下列各杆的扭矩图。
3-2一直径d=60mm的圆杆,其两端受外力偶矩T=2kN·m的作用而发生扭转。试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。(G=80GPa)。
解:横截面上切应力大小沿半径线性分布,方向垂直半径
1材料力学习题解答(平面图形几何性质).docx
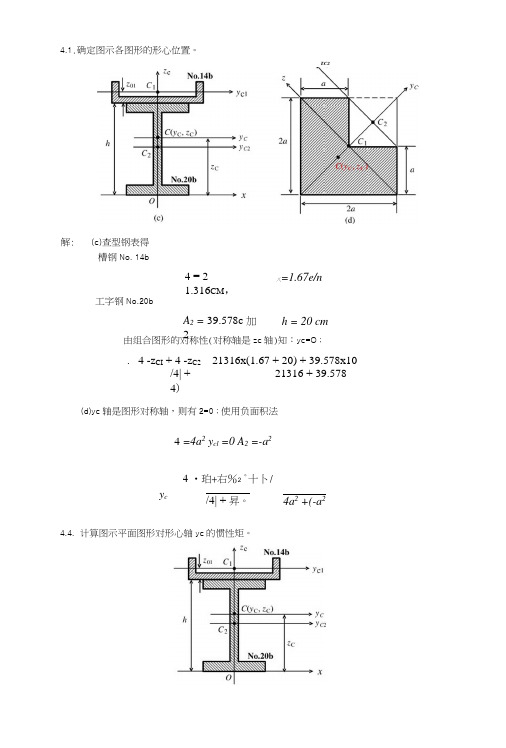
由组合图形的对称性(对称轴是zc轴)知:yc=O;._ 4 -z CI + 4 -z C2 _ 21316x(1.67 + 20) + 39.578x10(d)yc轴是图形对称轴,则有2=0;使用负面积法4 =4a2 y cl =0 A2 =-a24.4.计算图示平面图形对形心轴yc的惯性矩。
ZC24.1.确定图示各图形的形心位置。
(c)查型钢表得槽钢No. 14b解:4 = 21.316CM,八=1.67e/n 工字钢No.20bA2 = 39.578c 加2h = 20 cm/4| +4)=14.09c 加21316 + 39.578y c4 •珀+右%2 °十卜//4| + 昇。
4a2 +(-a2解:(c)(1)查型钢表得槽钢No 14bA x = 21.316C/H2I y =61.1c/n4z(ll = 1.61cm 工字钢No20b4 =39.578c 亦I v=2500C7H4方=20c 加2>C2(2)形心位置(由题4.1知)y c =0 z c = 14.09c 加(3)用平行移轴公式计算图形1、2对比轴的惯性矩-------- 20r]}Vc = I Vc, +CC, 4 =61.1+(1.67 + 20-14.09)2x21.316 =1285.8 cw4I2)Vc =I Vc^ +CO A2 = 2500 + (14.09- 10)2 x39.578= 3162.1 cm4⑷ 求纽•合图形对)z轴的惯性矩4.5.计算半圆形对形心轴兀的惯性矩。
(1)求图形旳彫八人I人坛. •如饰lH7hJ . “s y _ 2/Z3 _ 4rA岔2/2 3龙⑵求图形对);轴惯性矩£ z dA = £(psin&) [pdOdp]=[p'dp f sin2OdO =—⑶应用平行移轴定理¥ 一(謝穴/ 2)£一斜宀0」098宀0.00686十4.6.计算图示图形对y、z轴的惯性积。
《材料力学》附录I 截面的几何性质 习题解
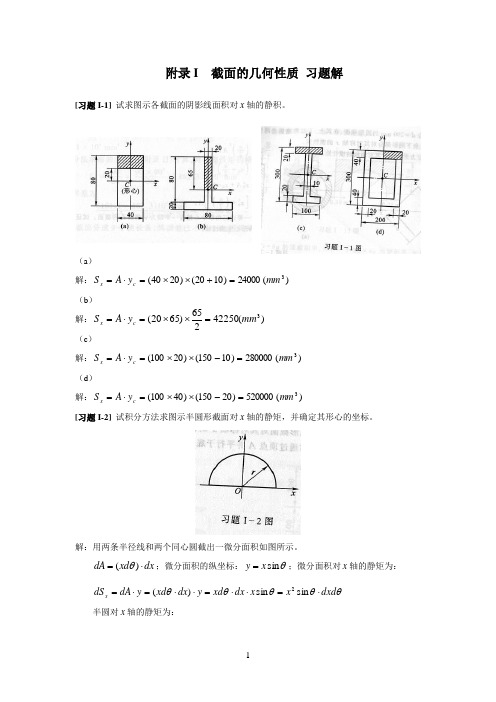
附录I 截面的几何性质 习题解[习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。
(a )解:)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅=(b )解:)(42250265)6520(3mm y A S c x =⨯⨯=⋅= (c )解:)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅=(d )解:)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅=[习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩,并确定其形心的坐标。
解:用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的静矩为: θθθθθdxd x x dx xd y dx xd y dA dS x ⋅=⋅⋅=⋅⋅=⋅=sin sin )(2半圆对x 轴的静矩为:32)]0cos (cos [3]cos []3[sin 33003002r r x d dx x S r rx =--⋅=-⋅=⋅=⎰⎰πθθθππ因为c x y A S ⋅=,所以c y r r ⋅⋅=232132π π34ry c = [习题I-3] 试确定图示各图形的形心位置。
(a ) 解:解:[习题I-4] 试求图示四分之一圆形截面对于x 轴和y 轴的惯性矩x I 、y I 和惯性积xy I 。
解:用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ;微分面积的纵坐标:θsin x y =;微分面积对x 轴的惯性矩为: θθθθθdxd x dx xd x dx xd y dA y dI x ⋅=⋅⋅=⋅==232222sin sin )(四分之一圆对x 轴的惯性矩为: ⎰⎰⎰-⋅==2/0042/02322c o s 1]4[s i n ππθθθθd x d dx x I r rx)]2(2cos 21[2142/02/04θθθππd d r ⎰⎰-⋅= }]2[sin 212{82/04πθπ-=r 164r ⋅=π由圆的对称性可知,四分之一圆对y 轴的惯性矩为:164r I I x y ⋅==π微分面积对x 轴、y 轴的惯性积为:xydA dI xy =8)42(21]42[21)(21444042222022r r r x x r dx x r x ydx xdx I r rx r rxy =-=-=-==⎰⎰⎰- [习题I-5] 图示直径为mm d 200=的圆形截面,在其上、下对称地切去两个高为mm 20=δ的弓形,试用积分法求余下阴影部分对其对称轴x 的惯性矩。
材料力学附录A-例题4

II 100
y AI yI AII yII 140 20 (70 10) 100 20 0 46.7mm
AI AII
140 20 100 20
(2) 截面对其形心轴的惯性矩:
因为 y 轴过两个矩形的形心,截面对 y 轴的惯性矩就等于
两个矩形对其形心轴惯性矩之和。
1
Iy
I yI
I yII
140 203 12
20 1003 12
1.76106 mm 4
利用平行移轴公式可得到截面对 zC 轴的惯性矩
I zC
II zC
I
II zC
(I zCI
aI2 AI ) (I zCII
aI2I AII )
201403
12
(80
46.7)2
20140
100 203
12
46.72
100 20
例题
与教材 P411 例 II.6 相似
T 形截面如图所示。试确定其形心 C 的位置,并计算图形对其形心轴 的惯性矩。
解
(1) 形心 C 的位置:
把截面看成 I、II 两个矩形的组成, 建立如图所示坐标系。
截面形心必在对称轴 y 上,只需确 定形心在 y 轴上的位置。
20
140
y
I 20
C zC y
12.12106 mm 4
小结:
通常把组合图形分解为几个矩形或圆形,利用这些基本图
形的形心位置及对其形心轴的惯性矩,并利用平行移轴公式,
即可求组合图形的形心位置及惯性矩。本题仍可用“负面积
法”,可以试做一下。
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学求形心位置例题
对于一个物体,定位其形心位置是物体力学中的基本问题之一。
形心位置是一个物体整体
平衡的位置,也可以被认为是物体质量的重心。
通过求解形心位置,可以帮助我们更好地理解
物体的平衡状态和运动性质。
下面我们来看一个求解形心位置的例题。
例题:一个均匀的长方形板有边长为a和b,其质量密度为ρ。
求解板的形心位置。
解答:为了求解板的形心位置,我们需要用到物体的质量和质量元的概念。
质量(m)可以通过
物体的质量密度(ρ)和物体体积(V)相乘得到,即m = ρV。
对于一个均匀的长方形板,可以将其
看作无数个宽度微小但高度为b的质量元叠加而成。
首先,我们将长方形板沿着宽度(b)方向进行切割,得到宽度为Δx的无数个矩形质量元。
然后,对于每个质量元,我们需要确定其质量(dm)和距离形心位置的距离(x)。
由于板的质量密度为ρ,那么每个矩形质量元的质量(dm)可以表示为dm = ρΔx。
而每个质量元
距离形心位置的距离(x)可以表示为x = Δx/2。
然后,我们可以将质量元质量(dm)和距离形心位置的距离(x)相乘,然后将所有的质量元的乘积累加起来得到形心位置的坐标。
形心位置的x坐标可以表示为x_cm = Σ(dm*x) / Σ(dm)。
而形心位置的y坐标则与矩形板的宽
度(b)无关,即y_cm = 0。
接下来,我们将上面的表达式代入求解。
解得,形心位置的x坐标为x_cm = (b/2) * (a/3) = ab/6。
因此,长方形板的形心位置为(ab/6, 0)。
通过求解形心位置,我们可以得到长方形板的形心位置坐标。
这个结果说明,在一个均匀的长
方形板上,形心位置位于长方形的重心位置,且形心位置的x坐标与长方形的长和宽有关,y
坐标为0。
在实际问题中,求解形心位置对于分析物体的平衡和运动至关重要。
对于复杂的物体形状,求
解形心位置可能需要更加复杂的数学方法,但其基本原理是相同的。
形心位置的求解是物体力
学中的一个基础知识点,对于学习物理学的人来说具有重要意义。
