材料力学精选题1
材料力学 考试题集 含答案

材料力学考试题集含答案《材料力学》考试题集一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关 (B)只与构件的形状尺寸有关(C)与二者都有关 (D)与二者都无关2.向来拉杆如图所示,在P力作用下。
(A) 横截面a 上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上,各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中,图所示杆是轴向拉伸杆。
(A)P(C) (D)5.图示拉杆承受轴向拉力P的作用,歪截面m-m的面积为A,则σ=P/A为。
(A)横截面上的正应力(B)歪截面上的剪应力(C)歪截面上的正应力(D)歪截面上的应力6.解除外力后,消逝的变形和遗留的变形。
(A)分不称为弹性变形、塑性变形(B)通称为塑性变形(C)分不称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍,则抗拉。
(A)强度和刚度分不是原来的2倍、4倍(B)强度和刚度分不是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示,已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面,则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等,正负号相同(B)绝对值相等,正负号别同(C)绝对值别等,正负号相同(D)绝对值别等,正负号别同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内;(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上,各个截面上的。
(A)剪力相同,弯矩别同(B)剪力别同,弯矩相同(C)剪力和弯矩均相同(D)剪力和弯矩均别同13.当横向力作用于杆件的纵向对称面内时,对于杆件横截面上的内力与应力有以下四个结论。
材料力学习题及答案
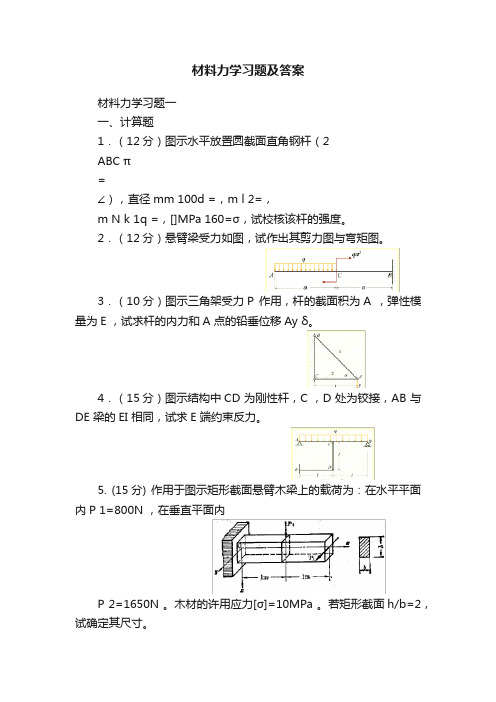
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 导电性答案:D2. 根据胡克定律,当材料受到正应力时,其应变与应力成正比,比例系数称为:A. 杨氏模量B. 剪切模量C. 泊松比D. 屈服强度答案:A3. 在材料力学中,材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料发生弹性变形的应力D. 材料发生脆性断裂的应力答案:A4. 材料的疲劳寿命与下列哪一项无关?A. 材料的疲劳极限B. 应力循环次数C. 材料的弹性模量D. 应力循环的幅度答案:C5. 在材料力学中,下列哪一项不是材料的力学性能指标?A. 硬度B. 韧性C. 密度D. 冲击韧性答案:C二、简答题(每题5分,共10分)6. 简述材料力学中弹性模量和剪切模量的区别。
答:弹性模量,也称为杨氏模量,是描述材料在受到正应力作用时,材料的纵向应变与应力成正比的比例系数。
剪切模量,也称为刚度模量,是描述材料在受到剪切应力作用时,材料的剪切应变与剪切应力成正比的比例系数。
7. 什么是材料的疲劳寿命,它与哪些因素有关?答:材料的疲劳寿命是指材料在反复加载和卸载过程中,从开始加载到发生疲劳断裂所需的循环次数。
它与材料的疲劳极限、应力循环的幅度、材料的微观结构和环境因素等有关。
三、计算题(每题15分,共30分)8. 一根直径为20mm的圆杆,材料的杨氏模量为200GPa,当受到100N的拉力时,求圆杆的伸长量。
答:首先计算圆杆的截面积A = π * (d/2)^2 = π * (0.02/2)^2m^2 = 3.14 * 0.01 m^2。
然后根据胡克定律ΔL = F * L / (A * E),其中 L 为杆长,假设 L = 1m,代入数值得ΔL = 100 * 1 / (3.14* 0.01 * 200 * 10^9) m = 7.96 * 10^-6 m。
材料力学试题(附完整答案)

大 连 理 工 大 学课 程 名 称:材料力学 试 卷: A一.选择题:(每小题3分,共15分) 1. 图示简支梁挠曲线大致形状为 A 。
2. 某梁横截面形状有四种,如图所示。
若外力作用线与图中虚线重合,则发生斜弯曲变形的梁为 D 。
3. 下列说法正确的是 C 。
A. 拉压杆内不存在切应力。
B. 拉压杆内各点的应力应变关系满足胡克定律。
姓名: 学号: 院系: 级 班题一、1图(B)(C)(A)(D)C. 杆件受压后体积会变小。
D. 滑移线是由切应力造成的。
4. 混凝土立柱所受压力的作用线与轴线平行但不重合,若力的作用点在截面核心区域内,则横截面上 B 。
A. 只存在拉应力。
B. 只存在压应力。
C. 既存在拉应力,又存在压应力。
D. 既存在正应力,又存在切应力。
5. 图示平面刚架分别受到集中力(图a )和集中力偶(图b )的作用,若F 与e M 数值上相等,则 D 。
A. b a B C θθ=b a B C w w =b a B C w 和θ数值相等 D. b a B C w θ和数值相等二、(15分)图示结构中杆AB 、CD 材料相同,横截面也相同,均为矩形截面,截面的高08=h mm ,宽03=b mm 。
材料的100P =λ,600=λ,206=E GPa ,304=a MPa ,12.1=b MPa ,若规定稳定安全因数3=w n ,试根据稳定条件求结构的许可荷载[q ]。
CD 杆为压杆 8.8003.0289.017.0=⨯⨯==ilμλ题一、5图F(a)(b)p 0λλλ<<为中长杆kN 7.51303.008.010)8.8012.1304()(6cr =⨯⨯⨯⨯-=-=A b a F λ171.2kN 37.513][cr cr ===w n F F取AB 杆为对象,列平衡方程∑=0A M ,075.0][5.11][cr =⨯-⨯q F ,kN/m 152][=q三、(15分)作图示外伸梁的剪力图和弯矩图,方法不限。
材料力学精选练习题

材料力学精选练习题1.梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
42.铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心。
已知Iz=60125000mm,yC=157.5mm,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa。
试求:①画梁的剪力图、弯矩图。
②按正应力强度条件校核梁的强度。
3.传动轴如图所示。
已知Fr=2KN,Ft=5KN,M=1KN·m,l=600mm,齿轮直径D=400mm,轴的[σ]=100MPa。
试求:①力偶M的大小;②作AB轴各基本变形的内力图。
③用第三强度理论设计轴AB的直径d。
4.图示外伸梁由铸铁制成,截面形状如图示。
已知Iz=4500cm,y1=7.14cm,y2=12.86cm,材料许用压应力[σc]=120MPa,4许用拉应力[σt]=35MPa,a=1m。
试求:①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
5.如图6所示,钢制直角拐轴,已知铅垂力F1,水平力F2,实心轴AB的直径d,长度l,拐臂的长度a。
试求:①作AB轴各基本变形的内力图。
②计算AB轴危险点的第三强度理论相当应力。
6.图所示结构,载荷P=50KkN,AB?a href=“http:///fanwen/shuoshuodaquan/”target=“_blank” class=“keylink”>说闹本禿=40mm,长度l=1000mm,两端铰支。
已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=1.12MPa,稳定安全系数nst=2.0,[σ]=140MPa。
试校核AB杆是否安全。
7.铸铁梁如图5,单位为mm,已知Iz=10180cm4,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa,试求:①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 硬度D. 韧性2. 材料在拉伸过程中,当应力达到屈服点后,材料将:A. 断裂B. 产生永久变形C. 恢复原状D. 保持不变3. 材料的弹性模量是指:A. 材料的密度B. 材料的硬度C. 材料的抗拉强度D. 材料在弹性范围内应力与应变的比值4. 根据材料力学的胡克定律,下列说法正确的是:A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成线性关系5. 材料的疲劳寿命是指:A. 材料的总寿命B. 材料在循环加载下达到破坏的周期数C. 材料的断裂寿命D. 材料的磨损寿命6. 材料的屈服强度是指:A. 材料在弹性范围内的最大应力B. 材料在塑性变形开始时的应力C. 材料的抗拉强度D. 材料的极限强度7. 材料的断裂韧性是指:A. 材料的硬度B. 材料的抗拉强度C. 材料抵抗裂纹扩展的能力D. 材料的屈服强度8. 材料力学中的泊松比是指:A. 材料的弹性模量B. 材料的屈服强度C. 材料在拉伸时横向应变与纵向应变的比值D. 材料的断裂韧性9. 在材料力学中,下列哪一项是衡量材料脆性程度的指标?A. 弹性模量B. 屈服强度C. 断裂韧性D. 泊松比10. 材料在受力过程中,当应力超过其极限强度时,将:A. 发生弹性变形B. 发生塑性变形C. 发生断裂D. 恢复原状答案1. C2. B3. D4. A5. B6. B7. C8. C9. C10. C试题二、简答题(每题10分,共30分)1. 简述材料力学中材料的三种基本力学性质。
2. 解释什么是材料的疲劳现象,并简述其对工程结构的影响。
3. 描述材料在拉伸过程中的四个主要阶段。
答案1. 材料的三种基本力学性质包括弹性、塑性和韧性。
弹性指的是材料在受到外力作用时发生变形,当外力移除后能够恢复原状的性质。
塑性是指材料在达到一定应力水平后,即使外力移除也无法完全恢复原状的性质。
材料力学复习题1
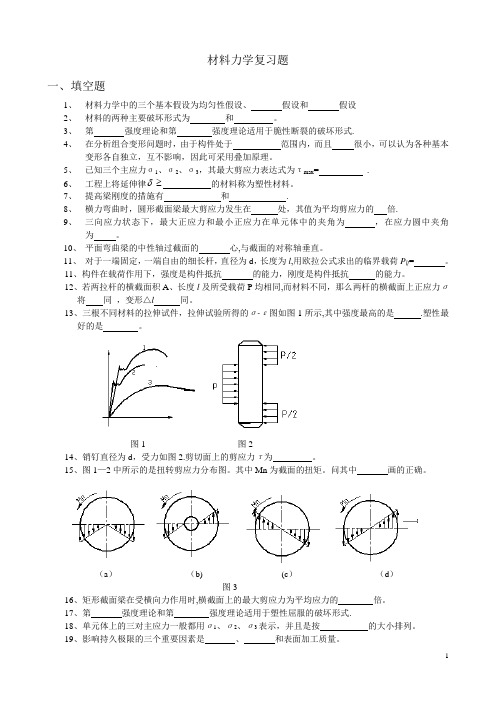
材料力学复习题一、填空题1、材料力学中的三个基本假设为均匀性假设、假设和假设2、材料的两种主要破坏形式为和。
3、第强度理论和第强度理论适用于脆性断裂的破坏形式.4、在分析组合变形问题时,由于构件处于范围内,而且很小,可以认为各种基本变形各自独立,互不影响,因此可采用叠加原理。
5、已知三个主应力σ1、σ2、σ3,其最大剪应力表达式为τmax= .δ的材料称为塑性材料。
6、工程上将延伸律≥7、提高梁刚度的措施有和.8、横力弯曲时,圆形截面梁最大剪应力发生在处,其值为平均剪应力的倍.9、三向应力状态下,最大正应力和最小正应力在单元体中的夹角为,在应力圆中夹角为。
10、平面弯曲梁的中性轴过截面的心,与截面的对称轴垂直。
11、对于一端固定,一端自由的细长杆,直径为d,长度为l,用欧拉公式求出的临界载荷P lj= 。
11、构件在载荷作用下,强度是构件抵抗的能力,刚度是构件抵抗的能力。
12、若两拉杆的横截面积A、长度l及所受载荷P均相同,而材料不同,那么两杆的横截面上正应力σ将同,变形△l同。
13、三根不同材料的拉伸试件,拉伸试验所得的σ-ε图如图1所示,其中强度最高的是.塑性最好的是。
图1 图214、销钉直径为d,受力如图2.剪切面上的剪应力τ为。
15、图1—2中所示的是扭转剪应力分布图。
其中Mn为截面的扭矩。
问其中画的正确。
(a)(b) (c)(d)图316、矩形截面梁在受横向力作用时,横截面上的最大剪应力为平均应力的倍。
17、第强度理论和第强度理论适用于塑性屈服的破坏形式.18、单元体上的三对主应力一般都用σ1、σ2、σ3表示,并且是按的大小排列。
19、影响持久极限的三个重要因素是、和表面加工质量。
20、弹性体的变形能的大小,只取决于载荷的最终值,而与 无关。
21、在强度计算中,低碳钢的破坏应力一般用的是 ,铸铁的破坏应力一般用的是 .22、 柔度λ综合地反映了压杆的 、 以及横截面形状和大小对压杆承载能力的影响。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,弹性模量E的单位是()。
A. N/mB. N·mC. PaD. m/N答案:C2. 材料力学中,材料的屈服强度通常用()表示。
A. σyB. σsC. σbD. E答案:A3. 根据胡克定律,当应力超过材料的弹性极限时,材料将()。
A. 保持弹性B. 发生塑性变形C. 发生断裂D. 无法预测答案:B4. 材料力学中,第一强度理论认为材料破坏的原因是()。
A. 最大正应力B. 最大剪应力C. 最大正应变D. 最大剪应变答案:A5. 下列哪种材料不属于脆性材料()。
A. 玻璃B. 铸铁C. 混凝土D. 铝答案:D6. 材料力学中,梁的弯曲应力公式为()。
A. σ = Mc/IB. σ = Mc/IbC. σ = Mc/ID. σ = Mc/Ib答案:C7. 在材料力学中,梁的剪应力公式为()。
A. τ = VQ/IB. τ = VQ/ItC. τ = VQ/ID. τ = VQ/It答案:B8. 材料力学中,梁的挠度公式为()。
A. δ = (5PL^3)/(384EI)B. δ = (5PL^3)/(384EI)C. δ = (PL^3)/(48EI)D. δ = (PL^3)/(48EI)答案:C9. 材料力学中,影响材料屈服强度的因素不包括()。
A. 材料的微观结构B. 加载速度C. 温度D. 材料的密度答案:D10. 材料力学中,影响材料疲劳强度的因素不包括()。
A. 应力集中B. 表面粗糙度C. 材料的硬度D. 材料的导热性答案:D二、填空题(每题2分,共20分)1. 材料力学中,材料在外力作用下,其形状和尺寸发生的变化称为______。
答案:变形2. 材料力学中,材料在外力作用下,其内部产生的相互作用力称为______。
答案:应力3. 材料力学中,材料在外力作用下,其内部产生的相对位移称为______。
答案:应变4. 材料力学中,材料在外力作用下,其内部产生的单位面积上的力称为______。
材料力学试题及答案

材料力学试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是均匀的D. 材料是线弹性的答案:A2. 在材料力学中,下列哪个公式表示杆件的正应力?A. σ = F/AB. τ = F/AC. σ = F/LD. τ = F/L答案:A3. 当材料受到轴向拉伸时,下列哪个选项是正确的?A. 拉伸变形越大,材料的强度越高B. 拉伸变形越小,材料的强度越高C. 拉伸变形与材料的强度无关D. 拉伸变形与材料的强度成正比答案:B4. 下列哪种材料在拉伸过程中容易发生断裂?A. 钢材B. 铸铁C. 铝合金D. 塑料答案:B5. 下列哪个选项表示材料的泊松比?A. μ = E/GB. μ = G/EC. μ = σ/εD. μ = ε/σ答案:C二、填空题(每题10分,共30分)6. 材料力学研究的是材料在______作用下的力学性能。
答案:外力7. 材料的强度分为______强度和______强度。
答案:屈服强度、断裂强度8. 材料在受到轴向拉伸时,横截面上的正应力公式为______。
答案:σ = F/A三、计算题(每题25分,共50分)9. 一根直径为10mm的圆钢杆,受到轴向拉伸力F=20kN 的作用,求杆件横截面上的正应力。
解:已知:d = 10mm,F = 20kNA = π(d/2)^2 = π(10/2)^2 = 78.5mm^2σ = F/A = 20kN / 78.5mm^2 = 255.8N/mm^2答案:杆件横截面上的正应力为255.8N/mm^2。
10. 一根长度为1m的杆件,受到轴向拉伸力F=10kN的作用,已知材料的弹性模量E=200GPa,泊松比μ=0.3,求杆件的伸长量。
解:已知:L = 1m,F = 10kN,E = 200GPa,μ = 0.3ε = F/(EA) = 10kN / (200GPa × π(10mm)^2) =0.025δ = εL = 0.025 × 1000mm = 25mm答案:杆件的伸长量为25mm。
材料力学试题及答案

材料力学试题及答案一、选择题1. 材料力学中,下列哪个参数是用来描述材料在受力时抵抗变形的能力?A. 弹性模量B. 屈服强度C. 抗拉强度D. 断裂韧性答案:A2. 以下哪种材料在受力后能够完全恢复原状?A. 弹性体B. 塑性体C. 粘弹性体D. 脆性体答案:A3. 应力集中现象主要发生在哪种情况下?A. 材料表面存在缺陷B. 材料内部存在孔洞C. 材料受到均匀分布的载荷D. 材料受到单一集中载荷答案:D4. 根据胡克定律,当应力不超过比例极限时,应力与应变之间的关系是:A. 线性的B. 非线性的C. 指数的D. 对数的答案:A5. 材料的疲劳破坏是指在何种条件下发生的?A. 单次超负荷B. 长期重复载荷C. 瞬间高温D. 腐蚀环境答案:B二、填空题1. 在简单的拉伸和压缩实验中,应力(σ)是力(F)与横截面积(A)的比值,即σ=______。
答案:F/A2. 材料的韧性是指其在断裂前能够吸收的能量,通常通过______试验来测定。
答案:冲击3. 当材料在受力时发生塑性变形,且变形量随时间增加而增加,这种现象称为______。
答案:蠕变4. 剪切应力τ是剪切力(V)与剪切面积(A)的比值,即τ=______。
答案:V/A5. 材料的泊松比是指在单轴拉伸时,横向应变与纵向应变的比值,通常用希腊字母______表示。
答案:ν三、简答题1. 请简述材料弹性模量的定义及其物理意义。
答:弹性模量,又称杨氏模量,是指材料在弹性范围内抵抗形变的能力的量度。
它定义为应力与相应应变的比值。
物理意义上,弹性模量越大,表示材料在受力时越不易发生形变,即材料越硬。
2. 描述材料的屈服现象,并解释屈服强度的重要性。
答:屈服现象是指材料在受到外力作用时,由弹性状态过渡到塑性状态的过程。
在这个过程中,材料首先经历弹性变形,当应力达到某个特定值时,即使应力不再增加,材料也会继续发生显著的塑性变形。
屈服强度是衡量材料开始屈服的应力值,它对于工程设计和材料选择具有重要意义,因为它决定了结构在载荷作用下的安全性和可靠性。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 脆性D. 磁性答案:D2. 根据胡克定律,弹簧的伸长量与所受力的关系是:A. 正比B. 反比C. 无关D. 非线性关系答案:A3. 材料的屈服强度是指:A. 材料开始发生永久变形的应力B. 材料发生断裂的应力C. 材料开始发生弹性变形的应力D. 材料达到最大应力点的应力答案:A4. 材料力学中,应力的定义为:A. 材料单位面积上承受的力B. 材料单位长度上承受的力C. 材料单位体积上承受的力D. 材料单位质量上承受的力答案:A5. 材料的泊松比是描述材料在受力时的:A. 弹性变形能力B. 塑性变形能力C. 横向变形与纵向变形的关系D. 断裂韧性答案:C6. 材料的疲劳寿命与下列哪个因素无关?A. 应力水平B. 材料的疲劳极限C. 温度D. 材料的弹性模量答案:D7. 在材料力学中,剪切应力与正应力的区别在于:A. 作用方向B. 作用面积C. 材料的破坏形式D. 材料的应力-应变曲线答案:A8. 材料的硬度通常通过什么测试来测量?A. 拉伸测试B. 压缩测试C. 冲击测试D. 硬度测试答案:D9. 材料的屈服现象通常发生在:A. 弹性阶段B. 塑性阶段C. 断裂阶段D. 疲劳阶段答案:B10. 材料的疲劳破坏通常发生在:A. 材料表面B. 材料内部C. 材料的接合处D. 材料的任何位置答案:A二、简答题(每题10分,共30分)1. 简述材料力学中材料的弹性模量和剪切模量的区别。
答:弹性模量是描述材料在单轴拉伸或压缩时,应力与应变比值的物理量,反映了材料抵抗变形的能力。
剪切模量则是描述材料在剪切状态下,剪切应力与剪切应变的比值,反映了材料抵抗剪切变形的能力。
2. 解释什么是材料的疲劳破坏,并简述其形成过程。
答:材料的疲劳破坏是指在反复加载和卸载的过程中,即使应力水平低于材料的屈服强度,材料也会逐渐发生损伤并最终导致断裂。
材料力学精选题1

大学材料力学轴向拉压 1. 衡。
设杆CD 截面面积为(A) q gA ρ=(B) (C) (D) 2. (A) …(C) 3. 在A 和B A 和点B (A) 0; (C) 45; 。
4. 可在横梁(刚性杆)为A (A) []2A σ;(C) []A σ;5. 设受力在弹性范围内,问空心圆杆受轴向拉伸时,外径与壁厚的下列四种变形关系中哪一种是正确的(A) 外径和壁厚都增大;(B) 外径和壁厚都减小;-(C) 外径减小,壁厚增大;(D) 外径增大,壁厚减小。
6. 三杆结构如图所示。
今欲使杆3的轴力减小,问应采取以下哪一种措施(A) 加大杆3的横截面面积;(B) 减小杆3的横截面面积;(C) 三杆的横截面面积一起加大;(D) 增大α角。
7. 图示超静定结构中,梁AB示杆1的伸长和杆2的缩短,(A) 12sin 2sin l l αβ∆=∆;(B) 12cos 2cos l l αβ∆=∆;(C) 12sin 2sin l l βα∆=∆;—(D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆1(A) 两杆轴力均减小;(B) 两杆轴力均增大;(C) 杆1轴力减小,杆2轴力增大;(D) 杆1轴力增大,杆2轴力减小。
9. 结构由于温度变化,则:(A) (B) (C) ,(D) 10. 面n-n 上的内力N F 的四种答案中哪一种是正确的(A) pD ;(C) 4pD ; 11. 的铅垂位移12. 截面的形状为13. 一长为l 挂时由自重引起的最大应力14. 图示杆112A A >是N1F F 题1-14答案:— 1. D 2. D 3. C 4. B 5. B 6. B 7. C 8. C 9. B 10. B11. Fl EA ; 12. a b;椭圆形 13. 22gl gl E ρρ, 14. >,= 15. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
材料力学考试试题及答案

材料力学考试试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 硬度2. 材料在拉伸过程中,若应力超过屈服点后继续增加,材料将进入:A. 弹性阶段B. 塑性阶段C. 断裂阶段D. 疲劳阶段3. 材料的弹性模量E表示的是:A. 材料的硬度B. 材料的韧性C. 材料的弹性程度D. 材料的屈服强度4. 根据材料力学理论,下列哪一项不是材料的疲劳破坏特点?A. 疲劳破坏是局部的B. 疲劳破坏是突然的C. 疲劳破坏是可预测的D. 疲劳破坏是累积的5. 在材料力学中,下列哪一项不是材料的失效模式?A. 屈服B. 断裂C. 腐蚀D. 疲劳6. 材料的屈服强度和抗拉强度之间的关系是:A. 屈服强度总是大于抗拉强度B. 屈服强度总是小于抗拉强度C. 屈服强度等于抗拉强度D. 两者之间没有固定关系7. 材料的疲劳寿命与下列哪一项无关?A. 应力水平B. 材料的微观结构C. 环境温度D. 材料的密度8. 材料的冲击韧性通常用下列哪一项来表示?A. 抗拉强度B. 屈服强度C. 硬度D. 冲击吸收能量9. 材料的疲劳寿命与加载频率的关系是:A. 正相关B. 负相关C. 无关D. 先正相关后负相关10. 在材料力学中,下列哪一项不是材料的应力-应变曲线的特点?A. 弹性阶段B. 屈服阶段C. 塑性阶段D. 线性阶段二、简答题(每题10分,共20分)1. 请简述材料的弹性模量和屈服强度的区别和联系。
2. 材料的疲劳破坏与静载下的破坏有何不同?三、计算题(每题15分,共30分)1. 已知一材料的弹性模量E=200 GPa,泊松比ν=0.3。
若材料受到拉伸力F=10 kN,试计算材料的应变ε和应力σ。
2. 某材料的疲劳寿命S-N曲线已知,当应力水平为σ=200 MPa时,疲劳寿命N=1000次。
若应力水平降低到150 MPa,根据Basis Goodman关系,计算新的疲劳寿命。
材料力学试题库试题精选:精选题1

1.衡。
设杆(A) qρ=(B)(C)(D)2.(A)(C)3. 在A和BA和点B(A) 0;(C) 45;。
4. 可在横梁(刚性杆)为A(A) [] 2A σ(C) []Aσ;5.(A)(C)6. 三杆结构如图所示。
今欲使杆3哪一种措施?(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 图示超静定结构中,梁AB 示杆1的伸长和杆2的缩短,(A) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C) 12sin 2sin l l βα∆=∆; (D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆1(A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2轴力增大; (D) 杆1轴力增大,杆2轴力减小。
9. 结构由于温度变化,则:(A) (B) (C) (D) 10. 面n-n 上的内力N F 的四种答案中哪一种是正确的?(A) pD ; (B) 2pD;(C) 4pD ; (D) 8pD 。
1. D2. D3. C4. B5. B6. B7. C8. C9. B 10. B11. Fl EA ;12. ab;椭圆形 13. 22gl gl E ρρ, 14. >,= 15. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()s d πππd d ddddεε+∆-∆=== 证毕。
16. 如图所示,一实心圆杆1在其外表面紧套空心圆管2。
设杆的拉压刚度分别为11E A 和22E A 。
此组合杆承受轴向拉力F ,试求其长度的改变量。
(假设圆杆和圆管之间不发生相对滑动)解: 由平衡条件 N1N2F F F += (1)变形协调条件N1N21122F l F lE A E A = (2) 由(1)、(2)得 N1111122F l F ll E A E A E A ∆==+E,17. 设有一实心钢杆,在其外表面紧套一铜管。
材料力学试卷试题(附参考答案)

材料力学试卷试题(附参考答案)材料力学试卷试题一、选择题(每题共10分,共5题,计50分)1. 下面哪项不属于材料力学的基本假设?A. 弹性材料的应力-应变关系符合胡克定律。
B. 材料的体积不随外力的作用发生改变。
C. 在材料的应力达到极限时将发生塑性变形。
D. 材料在外力作用下会发生应变。
2. 受力体系中,若要使物体保持静止,则下面哪个条件必须满足?A. 所有受力的合力为零。
B. 所有受力的合力的矩为零。
C. 所有受力的合力和合力矩皆为零。
D. 所有受力的大小均为零。
3. 弹簧常数为k,弹簧长度为l,当受到外力F时,弹簧发生形变Δl,弹性势能为U。
则下面哪个公式正确?A. U = F/ΔlB. U = F·ΔlC. U = 1/2k(Δl)^2D. U = k/2Δl4. 一根弹性绳子的上端系在固定点,下端挂着一个质量为m的小球,长度为l。
如果小球偏离平衡位置的距离为x,则绳子受力的大小为多少?A. mgx/lB. mg/lxC. mx/lgD. mg/l5. 压力是物体受到的外力作用面积单位所计算出的量。
压力的计算公式为?A. P = F/AB. P = F×AC. P = F-AD. P = A/F二、简答题(共10分,计20分)1. 什么是材料力学的研究对象?并介绍材料力学的主要内容。
(要求回答清晰明了,条理清晰)2. 说明静力平衡的条件,并举例说明其应用。
(要求回答准确,能说明条件的必要性,并给出具体应用例子)三、计算题(共15分,计30分)1. 一个质量为2kg的物体受到两个力的作用,分别为10N和20N。
这两个力的夹角为60°,求物体所受合力的大小和方向。
(要求列出计算步骤,有清晰的计算过程和结果)2. 一个弹簧的斜率为k,长度为l,质量为m的物体悬挂在该弹簧下方,当物体达到平衡时,弹簧的形变为Δl。
求物体所受重力的大小。
(要求列出计算步骤,有清晰的计算过程和结果)3. 一个桥梁的两个支座分别承受20kN和30kN的垂直压力,支座之间的距离为4m。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学主要研究的是材料在外力作用下的______。
A. 化学变化B. 物理变化C. 力学性质D. 热学性质2. 材料力学中,应力的定义是单位面积上的______。
A. 力B. 位移C. 速度D. 加速度3. 弹性模量是描述材料______的物理量。
A. 弹性B. 塑性C. 韧性D. 硬度4. 材料力学中,材料的屈服强度是指材料在______条件下的应力。
A. 弹性变形B. 永久变形C. 断裂D. 疲劳5. 材料力学中,拉压杆件的承载能力主要取决于其______。
A. 长度B. 直径C. 材料种类D. 表面处理6. 材料力学中,剪切应力的计算公式是______。
A. τ = F/AB. τ = F/LC. τ = Fb/AD. τ = Fb/L7. 材料力学中,梁的弯曲问题主要考虑的是______。
A. 材料的弹性模量B. 梁的截面形状C. 梁的长度D. 梁的重量8. 材料力学中,疲劳破坏是指材料在______作用下发生的破坏。
A. 静载荷B. 动载荷C. 冲击载荷D. 温度变化9. 材料力学中,材料的断裂韧性是指材料在______条件下的抗断裂能力。
A. 静载荷B. 动载荷C. 冲击载荷D. 疲劳10. 材料力学中,安全系数是指实际承载能力与______的比值。
A. 设计载荷B. 最大载荷C. 极限载荷D. 疲劳载荷答案:1-5 C A A B B 6-10 C B B D C二、填空题(每空1分,共10分)1. 材料力学中的______是指材料在受到外力作用时,其形状和尺寸发生改变的能力。
2. 当材料受到的应力超过其______时,材料将发生永久变形。
3. 在材料力学中,______是指材料在受到外力作用时,其内部各点的应力状态。
4. 材料力学中,______是指材料在受到外力作用时,其内部各点的位移状态。
5. 材料力学中,______是指材料在受到外力作用时,其内部各点的应变状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学材料力学1. 衡。
设杆CD 截面面积为(A) q gA ρ=(B) (C) (D)2. (A) (C)3. 在A 和B A 和点B (A) 0; (C) 45; 。
4. 可在横梁(刚性杆)为A (A)[]2A σ;(C) []A σ;5.一种是正确的(A) 外径和壁厚都增大;(B) 外径和壁厚都减小;(C) 外径减小,壁厚增大;(D) 外径增大,壁厚减小。
6. 三杆结构如图所示。
今欲使杆3哪一种措施(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 图示超静定结构中,梁AB 示杆1的伸长和杆2的缩短,(A) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C) 12sin 2sin l l βα∆=∆; (D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆1(A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2轴力增大; (D) 杆1轴力增大,杆2轴力减小。
9. 结构由于温度变化,则:(A) (B) (C) (D) 10. 面n-n 上的内力N F 的四种答案中哪一种是正确的(A) pD ; (B) 2pD;(C) 4pD ; (D) 8pD 。
11.的铅垂位移12. 截面的形状为13. 一长为l 挂时由自重引起的最大应力14. 图示杆112A A >是N1F F 题1-141. D 2. D 3. C 4. B 5. B 6. B 7. C 8. C 9. B 10. B11. Fl EA ;12. ab;椭圆形 13. 22gl gl E ρρ, 14. >,= 15. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()s d πππd d ddddεε+∆-∆=== 证毕。
16. 如图所示,一实心圆杆1在其外表面紧套空心圆管2。
设杆的拉压刚度分别为11E A 和22E A 。
此组合杆承受轴向拉力F ,试求其长度的改变量。
(假设圆杆和圆管之间不发生相对滑动)解: 由平衡条件 N1N2F F F += (1)变形协调条件N1N21122F l F lE A E A = (2) 由(1)、(2)得 N1111122F l F ll E A E A E A ∆==+E,17. 设有一实心钢杆,在其外表面紧套一铜管。
材料的弹性模量和线膨胀系数分别为1E2由18.19.20. 图示为胶合而成的等截面轴向拉杆,杆的强度由胶缝控制,已知胶的许用切应力[]τ为许用正力[]σ的1/2。
问α为何值时,胶缝处的切应力和正应力同时达到各自的许用应力。
解:2cos ασσα=≤[]σsin cos ατσαα=≤[]τ[]1tan []2τασ== 胶缝截面与横截面的夹角 57.26=α21.各杆直径为150 mm d =,许用应力[]σ=门受的水压力与水深成正比,水的质ρ=331.010 kg m ⨯,杆间的最大距离。
(取210 m g =)解:设支杆间的最大距离为x ,闸门底部A 集度为0q 。
闸门AB 的受力如图0A M ∑=,01314cos 2q F α⨯⨯=N F F =≤21[]π4d σ3cos 5α=,0330 kN m q gx x ρ==得:9.42 m x =22. 图示结构中AC 为刚性梁,BD 为斜撑杆,载荷F 可沿梁AC 水平移动。
试问:为使斜杆的重量最小,斜撑杆与梁之间的夹角θ应取何值 解:载荷F 移至C 处时,杆BD 的受力最大,如图。
θcos h FlF BD =A ≥[]cos []BD F Flh σθσ=杆BD 的体积 2sin []sin 2h FlV Aθσθ== 当sin 21θ=时,V 最小即重量最轻,故π454θ==423. 图示结构,BC 为刚性梁,杆1和杆2的横截面面积均为A ,和2[]σ,且12[]2[]σσ=。
载荷F 可沿梁BC (1) 从强度方面考虑,当x 为何值时,许用载荷[]F (2) 该结构的许用载荷[]F 多大 解:(1) 杆BC 受力如图N1F =1[]A σ,N2F =2[]A σmaxN1N22133[][]2F F F A Aσσ=+==3lx =(2) F 在C 处时最不利 N2F F =≤2[]A σ 所以结构的许用载荷 2[][]F A σ=24. 图示结构,杆1和杆模量为E 且[]2[]σσ-+=,载荷F 虑杆的失稳,试求: (1) 结构的许用载荷[]F 。
(2) 当x 为何值时(0x <<解:(1) F 在B N12F F =(压) , N2F F =(拉)结构的许用载荷 [][]F A σ+=(2) F 在CD 正中间时能取得许用载荷最大值,此时N1N22FF F ==(压)-+N2BN2(1)12cot cos sin cos [][]l Fl l F V A A l αααασσ=+=+0d 0d Vααα==,()2200222000sin cos 10sin cos sin ααααα--=, 即22002200sin 2cos 0sin cos αααα-=0tan α=当054.74α=时,V 最小,结构用料最省。
26. 如图所示,外径为D ,壁厚为δ,长为l 的均质圆管,由弹性模量E ,泊松比ν的材料制成。
若在管端的环形横截面上有集度为q 的均布力作用,试求受力前后圆管的长度,厚度和外径的改变量。
解:长度的改变量 l lql l E Eσε∆=== 厚度的改变量 qEδνδεδνεδ'∆==-=-外径的改变量 D qD D D Eνενε'∆==-=-27.正方形截面拉杆,边长为,弹性模量200 GPa E =,泊松比0.3ν=。
当杆受到轴向拉力作用后,横截面对角线缩短了0.012 mm ,试求该杆的轴向拉力F 的大小。
解:对角线上的线应变0.0120.000340ε-'==- 则杆的纵向线应变0.001εεν'=-=杆的拉力160 kN F EA ε==28. 图示圆锥形杆的长度为l ,材料的弹性模量为E ,质量密度为ρ,试求自重引起的杆的伸长量。
解:x 处的轴向内力 ()()()N 13F x gV x g A x x ρρ==⋅杆的伸长量N00()d ()d ()3()l l F x x gA x x l x EA x EA x ρ⋅∆==⎰⎰20d 36l gx x gl E Eρρ==⎰29. 设图示直杆材料为低碳钢,弹性模量200 GPa E =,杆的横截面面积为25 cm A =,杆长 1 m l =,加轴向拉力150 kN F =,测得伸长 4 mm l ∆=。
试求卸载后杆的残余变形。
解:卸载后随之消失的弹性变形e 1.5 mm Fll EA∆== 残余变形为p e 2.5 mm l l l ∆=∆-∆=30. 图示等直杆,已知载荷F ,BC 段长l ,横截面面积A ,弹性模量E ,质量密度ρ,考虑自重影响。
试求截面B 的位移。
解:由整体平衡得43C F gAl ρ=BC 段轴力()N 43F x gA x l ρ⎛⎫=- ⎪⎝⎭截面B 的位移 ()N 020d 453d ()6lB BC l F x xΔl EA gA x l gl x EA Eρρ=∆=⎛⎫- ⎪⎝⎭==-↓⎰⎰ 31. 已知图示结构中三杆的拉压刚度均为EA ,设杆AB 为刚体,载荷F ,杆AB 长l 。
试求点C 的铅垂位移和水平位移。
解:杆AB 受力如图N20F =, N1N32FF F ==132y FlΔl l EA=∆=∆=因为杆AB 作刚性平移,各点位移相同,且N20F =,杆2不变形。
又沿45由A 移至A '。
所以 2x y FlΔΔEA==32. 电子秤的传感器是一个空心圆筒,承受轴向拉伸或压缩。
已知圆筒外径80 mm D =,壁厚9 mm δ=,材料的弹性模量210 GPa E =。
在称某重物时,测得筒壁的轴向应变647610ε-=-⨯,试问该物重多少l=1kNN3'xΔ解:圆筒横截面上的正应力FE Aσε== ()221π4F EA E D d εε==⋅-262 mm d D δ=-= 该物重 200.67 kN F =33. 图示受力结构,AB 为刚性杆,CD 为钢制斜拉杆。
已知杆CD 的横截面面积2100 mm A =,弹性模量200 GPa E =。
载荷1 5 kN F =,210 kN F =,试求: (1) 杆CD 的伸长量l ∆; (2) 点B 的垂直位移B ∆。
解:杆AB 受力如图0A M =∑,N2120F F F --=)N 212F F F =+=N 2 mm F ll EA∆==2 5.66 mm B C ΔΔl ===34. 如图示,直径16 mm d =的钢制圆杆ABB 处铰接。
当D 处受水平力F 0.0009ε=。
已知钢材拉伸时的弹性模量E =(1) 力F 的大小; (2) 点D 的水平位移。
解:折杆BCD 受力如图(1)0C M ∑=,N 1.520F F ⨯-⨯=N1.5 1.528.5kN 22F F E A ε=== (2)0.0018 m 1.8 mm l l ε∆=== 2 1.5Dx Δl∆=2 2.4 mm 1.5Dx Δl ε==11B35. 如图示等直杆AB 在水平面内绕A 端作匀速转动,角速度为ω,设杆件的横截面面积为A ,质量密度为ρ。
则截面C 处的轴力N C F = 。
答:22x A x l ρω⎛⎫- ⎪⎝⎭36. 如图示,两端固定的等直杆AB ,已知沿轴向均匀分布的载荷集度为q ,杆长为l ,拉压刚度为EA ,试证明任意一截面的位移()2x qx l x EA δ-=,最大的位移2max 8ql EA δ=。
证:由平衡条件得0A B F F ql +-=()2 N 0 0d d 2ll AA F qx x F x F l ql l EA EA EA EA-∆===-⎰⎰ 由变形协调条件0l ∆=,得2A qlF =22d 222xA A x F qx F x qx ql x qx x EA EA EA EA EA δ-==-=-=⎰令0x δ'=,20ql qx -= 即当2lx =时,杆的位移最大,2max 2228l l q l qlEA EAδ⎛⎫- ⎪⎝⎭==证毕。
37. 图示刚性梁AB ,在BD 两点用钢丝悬挂,钢丝绕进定滑轮G 、F ,已知钢丝的弹性模量210 GPa E =,横截面面积2100 mm A =,在C处受到载荷20 kN F =的作用,不计钢丝和滑轮的摩擦,求C 点的铅垂位移。
