实验一升余弦滚降系统及眼图
北邮通信原理软件实验报告

通信原理软件实验报告学院:信息与通信工程学院班级:一、通信原理Matlab仿真实验实验八一、实验内容假设基带信号为m(t)=sin(2000*pi*t)+2cos(1000*pi*t),载波频率为20kHz,请仿真出AM、DSB-SC、SSB信号,观察已调信号的波形和频谱。
二、实验原理1、具有离散大载波的双边带幅度调制信号AM该幅度调制是由DSB-SC AM信号加上离散的大载波分量得到,其表达式及时间波形图为:应当注意的是,m(t)的绝对值必须小于等于1,否则会出现下图的过调制:AM信号的频谱特性如下图所示:由图可以发现,AM信号的频谱是双边带抑制载波调幅信号的频谱加上离散的大载波分量。
2、双边带抑制载波调幅(DSB—SC AM)信号的产生双边带抑制载波调幅信号s(t)是利用均值为0的模拟基带信号m(t)和正弦载波c(t)相乘得到,如图所示:m(t)和正弦载波s(t)的信号波形如图所示:若调制信号m(t)是确定的,其相应的傅立叶频谱为M(f),载波信号c(t)的傅立叶频谱是C(f),调制信号s(t)的傅立叶频谱S(f)由M(f)和C(f)相卷积得到,因此经过调制之后,基带信号的频谱被搬移到了载频fc处,若模拟基带信号带宽为W,则调制信号带宽为2W,并且频谱中不含有离散的载频分量,只是由于模拟基带信号的频谱成分中不含离散的直流分量。
3、单边带条幅SSB信号双边带抑制载波调幅信号要求信道带宽B=2W, 其中W是模拟基带信号带宽。
从信息论关点开看,此双边带是有剩余度的,因而只要利用双边带中的任一边带来传输,仍能在接收机解调出原基带信号,这样可减少传送已调信号的信道带宽。
单边带条幅SSB AM信号的其表达式:或其频谱图为:三、仿真设计1、流程图:Array2、实验结果&分析讨论实验仿真结果从上至下依次是AM信号、DSB信号、SSB信号。
从仿真结果看,AM调制信号包络清晰,可利用包络检波恢复原信号,接收设备较为简单。
(完整word版)使用matlab绘制眼图.docx

使用 matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉 MATLAB语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1 所示,要获得良好的基带传输系统,就应该a n t nT s基带传输a n h t nT sn n抽样判决H ( )图 3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为a n t nT s, T s为基带信号的码元周期,则经过n基带传输系统后的输出码元为a n h t nT s。
其中nh(t )1H ()e j t d(3-1 )2理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:,k 0h( kT s)(3-2)0,k为其他整数频域应满足:T s,T s(3-3)H ( )0,其他H ( )T sT sT s图 3-2 理想基带传输特性此时频带利用率为2Baud / Hz , 这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:2 i H2 2 ,(3-4)HH ( ) HT s iT sT sT sT s基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性H ( ) 时是适宜的。
1 sinT s ( ) , (1 ) (1 )2T sT sT sH ( )1, (1 ) 0(3-5)T s0,(1 )T s这里称为滚降系数,1。
所对应的其冲激响应为:sin tcos( t T s )h(t )T s (3-6)t 1 4 2t 2 T s 2T s此时频带利用率降为 2 / (1 ) Baud/ Hz ,这同样是在抽样值无失真条件下,所能达到的最高频率利用率。
通信系统的仿真实验资料
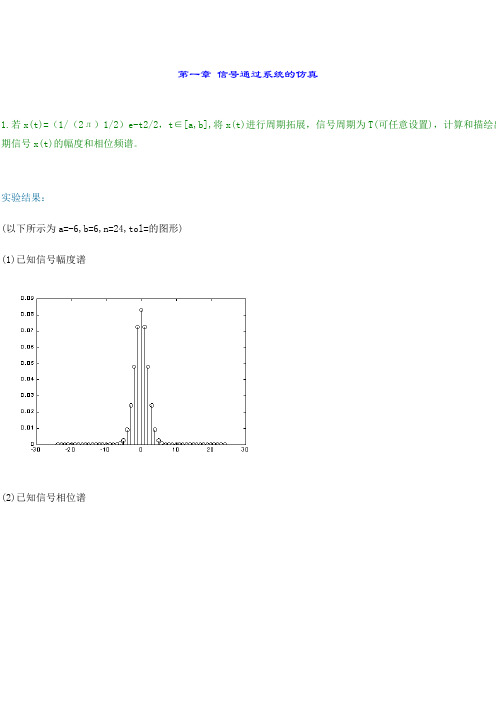
第一章信号通过系统的仿真1.若x(t)=(1/(2л)1/2)e-t2/2,t∈[a,b],将x(t)进行周期拓展,信号周期为T(可任意设置),计算和描绘出期信号x(t)的幅度和相位频谱。
实验结果:(以下所示为a=-6,b=6,n=24,tol=的图形)(1)已知信号幅度谱(2)已知信号相位谱2.信号定义为x(t)= cos(2л*47t)+cos(2л*219t), 0≤t≤100, 其它假设信号以1000抽样/秒进行抽样。
用MATLAB设计一个低通Butterworth滤波器。
确定并绘出输出的功率谱和输入功率谱比较(滤波器的阶数及截频可自行确定)。
实验结果:(以下为阶数=4,截频=100Hz的图形)(1)输入信号功率谱密度(2)输出信号功率谱密度第二章随机过程仿真1.从下式的递归关系中产生一个高斯马尔可夫过程的1000个(等间距)样本的序列Xn=+ωn n=1,2,…1000,式中X0=0,ωn是一个零均值,方差为1,独立的随机变量序列。
绘出序列{ Xn,1≤n≤1000}与时序n的关系及相关函数N-mRx(m)=1/(N-m)ΣXn Xn+m m=0,1,…50 式中N=1000.n-1实验结果:(1)高斯——马尔可夫过程(2)高斯马尔可夫过程的自相关函数2.假设一个具有抽样序列{X(n)}的白噪声过程通过一个脉冲响应如下所示的线性滤波器nh(n)= ,n≥00, n<0求输出过程{Y(n)}的功率谱和自相关函数Ry(τ)。
实验结果:(1)输出的功率谱(2)输出的自相关第三章模拟调制仿真1.用MATLAB软件仿真AM调制。
被调信号为1, (t0/3)>t>0;m(t)=-2, (t0/3)≤t≤(2*t0/3);0, 其它;利用AM 调制方式调制载波。
假设t0=,fc=250hz;调制系数a=。
实验结果:1)调制信号、载波、已调信号的时域波形2)已调信号的频域波形2.被调信号为1, t0/3>t>0;m(t)=-2, t0/3<= t<2*t0/3;0, 其它;采用频率调制方案。
通信原理 (1)

(1 nTs )
P) g1 (t
Pg1(t
nTs nTs
) )
g2 (t nTs ),
(1 P)g2 (t
nTs
以概率P
)
Pg1(t nTs ) g2 (t nTs ),
以概率(1-P)
14
一、数字基带信号的功率谱密度
➢ v(t)的功率谱密度
v(t)
Pg1 t nTs 1 P g2 (t nTs )
Cm 2 ( f mfs )
m
Pv ( f )
fs PG1 mfs 1 PG2 (mfs ) 2 ( f mfs )
m
15
一、数字基带信号的功率谱密度
➢ u(t)的功率谱密度
Pu
(
f
)
lim
N
E
UT
(
(2N
f)2 1)Ts
N
N
uT (t) un (t) an g1(t nTs ) g2 (t nTs )
其中:h(t) 1 H ()e jtd
2
22
二、码间串扰的数学分析
y(t) ak h(t kTs ) nR (t) k
y(t0 jTs ) ak h(t0 jTs kTs ) nR (t0 jTs ) k
ak h ( j k)Ts t0 nR (t0 jTs ) k
G1 (
f
)
Sa (
f)
Ts 2
Sa (
fTs 2
)
当P=0.5时
Ps
(
)
Ts 16
Sa2
(
fTs 2
)
1 16
m
Sa2
(
关于使用matlab绘制眼图

使用matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATLAB 语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该图3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为()nsna t nT δ-∑,sT 为基带信号的码元周期,则经过基带传输系统后的输出码元为()nsna h t nT -∑。
其中1()()2j th t H ed ωωωπ+∞-∞=⎰(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数 (3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 (3-3)图3-2 理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ (3-4)基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性()H ω时是适宜的。
(1)(1)1sin (),2(1)()1,0(1)0,s s s s s s T T T T H T T ππαπαωωαπαωωπαω⎧⎡⎤-+--≤≤⎪⎢⎥⎣⎦⎪⎪-⎪=≤≤⎨⎪⎪+>⎪⎪⎩(3-5)这里α称为滚降系数,01α≤≤。
使用matlab绘制眼图

使用matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATLAB 语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该图3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为()nsna t nT δ-∑,sT 为基带信号的码元周期,则经过基带传输系统后的输出码元为()nsna h t nT -∑。
其中1()()2j th t H ed ωωωπ+∞-∞=⎰(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数 (3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 (3-3)图3-2 理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ (3-4)基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性()H ω时是适宜的。
(1)(1)1sin (),2(1)()1,0(1)0,s s s s s s T T T T H T T ππαπαωωαπαωωπαω⎧⎡⎤-+--≤≤⎪⎢⎥⎣⎦⎪⎪-⎪=≤≤⎨⎪⎪+>⎪⎪⎩(3-5)这里α称为滚降系数,01α≤≤。
实验2 眼图观察测量实验

班级通信1403 学号 201409732 姓名裴振启指导教师邵军花日期实验2 眼图观察测量实验一、实验目的学会观察眼图及其分析方法,调整传输滤波器特性。
二、实验仪器1. 眼图观察电路2.时钟与基带数据发生模块,位号:G3.PSK调制模块,位号A4.噪声模块,位号B5.PSK解调模块,位号C6.复接/解复接、同步技术模块,位号:I7.20M双踪示波器1台三、实验原理在整个通信系统中,通常利用眼图方法估计和改善(通过调整)传输系统性能。
所谓“眼图”,就是由解调后经过接收滤波器输出的基带信号,以码元时钟作为同步信号,基带信号一个或少数码元周期反复扫描在示波器屏幕上显示的波形称为眼图。
干扰和失真所产生的传输畸变,可以在眼图上清楚地显示出来。
因为对于二进制信号波形,它很像人的眼睛故称眼图。
在图2-1中画出两个无噪声的波形和相应的“眼图”,一个无失真,另一个有失真(码间串扰)。
图2-1中可以看出,眼图是由虚线分段的接收码元波形叠加组成的。
眼图中央的垂直线表示取样时刻。
当波形没有失真时,眼图是一只“完全张开”的眼睛。
在取样时刻,所有可能的取样值仅有两个:+1 或-1。
当波形有失真时,“眼睛”部分闭合,取样时刻信号取值就分布在小于+1或大于-1附近。
这样,保证正确判决所容许的噪声电平就减小了。
换言之,在随机噪声的功率给定时,将使误码率增加。
“眼睛”张开的大小就表明失真的严重程度。
眼图图2-1 无失真及有失真时的波形及眼图(a)无码间串扰时波形;无码间串扰眼图(b)有码间串扰时波形;有码间串扰眼图通信工程实验教学中心通信系统原理实验报告在图2-2中给出从示波器上观察到的比较理想状态下的眼图照片。
本实验主要是完成PSK 解调输出基带信号的眼图观测实验。
(a) 二进制系统 (b) 随机数据输入后的二进制系统图2-2实验室理想状态下的眼图四、各测量点和可调元件作用底板右边“眼图观察电路”W06:接收滤波器特性调整电位器。
实验一 升余弦滚降系统及眼图

实验一 升余弦滚降系统及眼图一、实验目的1. 理解无码间串扰系统的原理;2. 理解升余弦滚降系统的工作原理;3.理解眼图的工作原理及实现方法。
二、实验仪器及软件电脑、MATLAB7.0软件三、实验原理 1. 无码间串扰系统若想消除码间串扰,应有()00nsn ka h k n T t ≠-+=⎡⎤⎣⎦∑ (1-1)由于n a 是随机的,要想通过各项相互抵消使码间串扰为0是不行的,这就需要对()h t 的波形提出要求,如果相邻码元的前一个码元的波形到达后一个码元抽样判决时刻时已经衰减到0,如图1-1(a )所示的波形,就能满足要求。
但这样的波形不易实现,因为实际中的()h t 波形有很长的“拖尾”,也正是由于每个码元“拖尾”造成对相邻码元的串扰,但只要让它在0s t T +,02s t T +等后面码元抽样判决时刻上正好为0,就能消除码间串扰,如图1-1(b )所示。
这也是消除码间串扰的基本思想。
著名的奈奎斯特第一准则就给出了无码间串扰时基带传输特性应满足的频率条件:2,s i s s i H T T T ππωω⎛⎫+=≤ ⎪⎝⎭∑ (1-2)图1-1 消除码间串扰显然,满足式(1-2)的系统()H ω并不是唯一的,容易想到的一种就是()H ω为一个理想低通滤波器。
2. 升余弦滚降系统理想低通特性的基带系统具有最大的频带利用率。
但实际上理想低通系统在应用中存在两个问题:一是实现极为困难,二是理想的冲击响应()h t 的“拖尾”很长,衰减很慢,当定时存在偏差时,可能出现严重的码间串扰。
实际使用中常采用升余弦频谱特性的系统,其系统传输特性如下:()1,0111cos ,22210,2sss s s s s s T f T T T H f f T T T f T αππααωαα-⎧≤≤⎪⎪⎪⎡⎤⎛⎫-+⎪=+-<≤⎨⎢⎥ ⎪⎝⎭⎣⎦⎪⎪+⎪>⎪⎩(1-3)其中,α称为滚降系数。
其单位冲激响应为()()()222sin cos 14s s s st T t T h t t T t T παππα=- (1-4) 3.眼图一个实际的基带传输系统尽管经过了十分精心的设计,但要使其传输特性完全符合理想情况是非常困难的,甚至是不可能的。
《现代通信与安全综合实验》实验报告

《现代通信与安全综合实验》---通信基础实验实验一消除码间干扰一、实验目的1.了解码间干扰产生机理;2.加深理解带限通道最佳传输的基本工作原理与升余弦滚降滤波器的使用;3.学会通过调整不同参数观察采样点抑制码间干扰的能力。
二、实验原理升余弦滚降信号用来消除码间干扰,实际实现时采用的方式是由发送端的基带成形滤波器和接收端的匹配滤波器两个环节共同实现。
传输系统的传递函数是二者的乘积,所以每个环节均为平方根升余弦滚降滤波器。
发射端和接收端同时使用根升余弦脉冲成形滤波器可以实现升余弦滤波器的效果,消除码间干扰(ISI),而且是匹配滤波,可以实现最佳接收。
匹配滤波器总的频响为RC谱(无ISI)根升余弦滤波器(RRC)三、实验步骤1.了解ISI用"Vector Source"模块生成了四组序列,每组都是100位0、1组成的序列。
为了方便,四组数据均只包含1比特数据为1,且每组序列中1相互偏移一个位置。
其中,第一组序列内容设置如下通过使用"Interpolation FIR Filter"模块实现sps(sample per second)倍过采样(例如这里sps=4,Interpolation参数为4),并使用了一个均方根升余弦滤波器。
(过采样的数字信号处理起来对低通滤波器的要求相对较低,如果不过采样,滤波的时候滤波器需要很陡峭,指标会很严格。
)Interpolation FIR Filter滤波器参数设置如下:其中eb表示"Excess BW"(带外带宽)因子取值,该参数来调整滤波器的滚降因子系数。
ntaps表示滤波器的抽头数。
其中,QT GUI Time Sink模块的参数设置如下:2. 消除ISI通过使用"Decimating FIR Filter"模块与第一部分的"Interpolation FIR Filter"组合起来形成了一个奈奎斯特升余弦滤波器(匹配滤波器)。
5.5.4 升余弦滚降传输特性[共2页]
![5.5.4 升余弦滚降传输特性[共2页]](https://img.taocdn.com/s3/m/bfde14ddbb68a98271fefaff.png)
通信原理及MATLAB/Simulink 仿真172为s 2π/T 宽度,各段在(s π/T −,s π/T )区间内能叠加成一个矩形频率特性,那么它以s R 速率传输基带信号时,无码间串扰。
如果不考虑系统的频带,从消除码间串扰来看,基带传输特性()H ω的形式并不是唯一的,升余弦滚降传输特性就是使用较多的一类。
5.5.4 升余弦滚降传输特性升余弦滚降传输特性()H ω可表示为12()()()H H H ωωω=+(5.5-16)如图5-14所示。
()H ω就是将1()H ω按2()H ω的滚降特性进行“圆滑”后得到的,这种“圆滑”称之为滚降。
ω(a )(b )(c )11图5-14 升余弦滚降传输特性2()H ω对于1ω具有奇对称的幅度特性,其上、下截止角频率分别为12ωω+、12ωω−。
它的选取可根据需要选择,定义滚降系数为21ωαω=(5.5-17)其中,1ω为无滚降时的截止频率,2ω为滚降部分的截止频率。
不同的α有不同的滚降特性。
图5-15画出了按余弦滚降的3种滚降特性和冲激响应。
具有滚降系数α的余弦滚降特性()H ω为s ss s s s ss(1)ππ(1)π(1)π()1sin ,22(1)π0T T T T H T T T T αωααωωωααω−⎧⎪⎪⎪⎡⎤⎛⎞−+⎪=+−<<⎢⎥⎨⎜⎟⎢⎥⎝⎠⎪⎣⎦⎪+⎪⎪⎩,≤,≥(5.5-18)而相应的()h t 为s s222s s sin π/cos π/()π/14/t T t T h t t T t T αα=−i(5.5-19)实际的()H ω可按不同的α来选取。
由图5-15可以看出:0α=时,就是理想低通特性;1α=时,是实际中常采用的升余弦频谱特性,这时,()H ω可表示为。
通信原理实验报告BPSK传输系统实验

BPSK 传输系统实验一、实验原理(一)基带成型基带传输是频带传输的基础,也是频带传输的等效低通信号表示。
基带传输系统的框图如图1所示。
图1 基带传输系统的框图(二)BPSK 调制解调理论上二进制相移键控(BPSK )可以用幅度恒定,而其载波相位随着输入数据m (1、0码)而改变,通常这两个相位相差180°。
如果每比特能量为E b ,则传输的BPSK 信号为:)2cos(2)(c c bb f T E t S θπ+=其中 ⎩⎨⎧===11800000m m c θ 升余弦滤波器的传递函数为:⎪⎪⎩⎪⎪⎨⎧+>+<<-+-+-≤≤=S S S S S RC T f T f T f T T f f H 2/)1(||02/)1(||2/)1()21|)|2(cos(1[212/)1(||01)(αααααπα其中,α是滚降因子,取值范围为0到1。
一般α=0.25~1时,随着α的增加,相邻符号间隔内的时间旁瓣减小,这意味着增加α可以减小位定时抖动的敏感度,但增加了占用的带宽。
BPSK 的调制工作过程如下:首先输入数据进行Nyquist 滤波,滤波后的结果分别送入I 、Q 两路支路。
因为I 、Q 两路信号一样,本振频率是一样的,相位相差180度, 所以经调制合路之后仍为BPSK方式。
二、实验内容(一)基带成形1.α=0.3升余弦滤波的眼图观察(1)以发送时钟(TPM01)作同步,观测发送信号(TPi03)的波形。
技巧:按下示波器“显示”按钮,将“持续”设置为2秒。
注意不观测眼图时需将示波器“显示”菜单内“持续”设置回关闭。
测量过零率抖动与眼皮厚度(换算成百分数)。
实验现象及分析:上图中CH1黄色波形为TPM01发送时钟,CH2蓝色波形为TPi03眼图。
由图中红框中光标1光标2的时间差可以读出测量值为11.6us。
由上图可以读出T=32us。
理论上发送时钟是32kHz,因而T=1/32kHz=31.25us。
基带信号眼图实验 (2)

实验三 数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATLAB 语言编程。
二、实验预习要求1、复习《数字通信原理》第七章7.1节——奈奎斯特第一准则内容;2、复习《数字通信原理》第七章7.2节——数字基带信号码型内容;3、认真阅读本实验内容,熟悉实验步骤。
三、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该图3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为()nsna t nT δ-∑,sT 为基带信号的码元周期,则经过基带传输系统后的输出码元为()nsna h t nT -∑。
其中1()()2j th t H ed ωωωπ+∞-∞=⎰(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数 (3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 (3-3)图3-2 理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ (3-4)基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性()H ω时是适宜的。
(1)(1)1sin (),2(1)()1,0(1)0,s s s s s s T T T T H T T ππαπαωωαπαωωπαω⎧⎡⎤-+--≤≤⎪⎢⎥⎣⎦⎪⎪-⎪=≤≤⎨⎪⎪+>⎪⎪⎩(3-5)这里α称为滚降系数,01α≤≤。
MATLAB仿真实例(通信原理)

一、实验目的 (1)二、实验题目 (1)三、实验内容 (1)3.1傅里叶变换与傅里叶反变换 (1)3.2题目一:正弦信号波形及频谱 (2)3.2.1仿真原理及思路 (2)3.2.2程序流程图 (3)3.2.3仿真程序及运行结果 (3)3.2.4实验结果分析 (5)3.3题目二:单极性归零(RZ)波形及其功率谱 (5)3.3.1仿真原理及思路 (5)3.3.2程序流程图 (6)3.3.3仿真程序及运行结果 (6)3.3.4实验结果分析 (8)3.4题目三:升余弦滚降波形的眼图及其功率谱 (8)3.4.1仿真原理及思路 (8)3.4.2程序流程图 (8)3.4.3仿真程序及运行结果 (8)3.4.4实验结果分析: (10)3.5题目四:完成PCM编码及解码的仿真 (11)3.5.1仿真原理及思路 (11)3.5.2程序流程图 (12)3.5.3仿真程序及运行结果 (12)3.5.4实验结果分析 (15)3.6附加题一:最佳基带系统的Pe~Eb\No曲线,升余弦滚降系数a=0.5,取样值的偏差是Ts/4 (16)3.6.1仿真原理及思路 (16)3.6.2程序流程图 (16)3.6.3仿真程序及运行结果 (16)3.6.4实验结果分析 (18)3.7附加题二:试作出Pe~Eb/No曲线。
升余弦滚降系数a=0.5,取样时间无偏差,但信道是多径信道,C(f)=|1-0.5-j2 ft|,t=T s/2 (18)3.7.1仿真原理及思路 (18)3.7.2程序流程图 (19)3.7.3仿真程序及运行结果 (19)3.7.4实验结果分析 (21)四、实验心得 (21)一、 实验目的⏹ 学会MATLAB 软件的最基本运用。
MATLAB 是一种很实用的数学软件,它易学易用。
MATLAB 对于许多的通信仿真类问题来说是很合适的。
⏹ 了解计算机仿真的基本原理及方法,知道怎样通过仿真的方法去研究通信问题。
⏹ 加深对通信原理课程有关内容的理解。
通信原理升余弦滚降系统

实验四升余弦滚降系统设计一、代码设计考虑到α的变化,本实验对应产生一个m×N的矩阵保存所有α对应码元信号,同时使用了矩阵参数的fft函数,由于它是按列分别进行变化的,故用列保存对应一个α的码元的。
tic %¿ªÊ¼¼Æʱglobal dt t df Nclose allN=2^15; %²ÉÑùµãÊýL=32; %ÿÂëÔªµÄ²ÉÑùµãÊýM=N/L; %ÂëÔªÊýRb=2; %ÂëËÙÂÊÊÇ2Mb/sW=Rb/2;Ts=1/Rb; %ÂëÔª¼ä¸ôdt=Ts/L; %ʱÓò²ÉÑù¼ä¸ôdf=1/(N*dt); %ƵÓò²ÉÑù¼ä¸ôT=N*dt; %½Ø¶Ìʱ¼äBs=N*df/2; %ϵͳ´ø¿íNa=4; %ʾ²¨Æ÷ɨÃè¿í¶ÈΪ4¸öÂëÔªAgain=10;alpha=[0.05,0.5,1]'; %alpha±ä»¯²ÎÊý£¬¿É·½±ãÐ޸ģº£©Nalpha=length(alpha);t=[-T/2+dt/2:dt:T/2]; %ʱÓòºá×ø±êf=[-Bs+df/2:df:Bs]; %ƵÓòºá×ø±êtempalpha=ones(Nalpha,1); %tempalpha£½[1,1,1]£¬ËùÒÔtempalpha* tΪ3*1ÏòÁ¿Óë1*NÏòÁ¿£½3¡ÁNÏòÁ¿£¬g1=sin(tempalpha*pi*t/Ts)./(tempalpha*pi*t/Ts);%g2=cos(alpha*pi*t/Ts)./(1-(2*alpha*t/Ts).^2);g=g1.*g2; %ÉýÓàÏÒÂö³å²¨ÐÎg=g'; %ÓÃN*3¾ØÕó°´Áб£´æÒ»ÖÖalpha¶ÔÓ¦µÄgG= fft(g); %fft(3*N¾ØÕó)½«°´ÁнøÐÐfft±ä»»G=[G(N/2+1:N,:);G(1:N/2,:)]*dt;SumP=zeros(length(f),Nalpha)+eps;for jj=1:Again%²úÉú³å»÷ÐòÁÐa=sign(randn(M,Nalpha))+1; %Öµ0,2imp=zeros(N,Nalpha); %Éú³å¼¤ÐòÁÐfigure(3)for indexalpha=1:Nalphaimp(L/2:L:N,indexalpha)=a(:,indexalpha)/dt;subplot(Nalpha,1,indexalpha);title(['\alpha=',num2str(alpha(indexalpha)),'ʱµÄÑÛͼ']);hold onend%µÃµ½½ÓÊÕ¶ËÊä³öÐźţ¬Í¬Ê±¹Û²ìÑÛͼ%ÓÉÓÚimpÊÇN*3µÄÊý×飬¹Ê²»ÄÜÖ±½Óµ÷ÓÃt2fH=fft(imp);H=[H(N/2+1:N,:);H(1:N/2,:)]*dt;S= H.*G ; %ÉýÓàÏÒÐźŵĸµÊϱ任SumP=SumP+S.*conj(S)/T;S=[S(N/2+1:N,:);S(1:N/2,:)];s=real(ifft(S)/dt); %µÃµ½½ÓÊÕ¶ËÊä³öÐźÅtt=[0:dt:Na*L*dt];if jj==1 %Ϊ¼Ó¿ìÔËÐÐËٶȣ¬Ö»¹Û²ìÒ»´ÎÑÛͼfigure(3)for jj=1:Na*L:N-Na*Lfor indexalpha=1:Nalphasubplot(Nalpha,1,indexalpha);plot(tt,s(jj:jj+Na*L,indexalpha));hold onendendendendP=SumP/Again;for ii=1:Nalpha%»-²»Í¬alphaʱµÄʱÓòg(t)ÓëƵÓòG(f)figure(1);subplot(3,2,2*ii-1)plot(t/Ts,g(:,ii)); %ÓÃTs¶Ôʱ¼ä¹éÒ»»¯axis([-5,5,-0.5,1.2]); %½ØÈ¡¹éÒ»»¯Ê±¼äÖátitle(['\alpha=',num2str(alpha(ii)), 'ʱµÄg(t)-t/Ts'],'fontsize',15); ylabel('g(t)','fontsize',17)subplot(3,2,2*ii)plot(2*f/Rb,Rb*abs(G(:,ii)));axis([-5,5,-0.5,1.2]);ylabel('G(f)','fontsize',17)title(['\alpha=',num2str(alpha(ii)), 'ʱµÄƵÆÕ'],'fontsize',15);%»-²»Í¬alphaʱµÄ¹¦ÂÊÆÕfigure(2);subplot(3,1,ii)plot(2*f/Rb,30+10*log10(P(:,ii)*2*W));axis([-5,5,-50,100]);ylabel('P(f)','fontsize',17)title(['\alpha=',num2str(alpha(ii)), 'ʱµÄ¹¦ÂÊÆÕ'],'fontsize',15); endusetime= toc二、实验图像 Figure 1:-55-0.500.51α=0.05时的g(t)-t/Tsg (t )-55-0.500.51G (f )α=0.05时的频普-55-0.500.51α=0.5时的g(t)-t/Tsg (t )-55-0.500.51G (f )α=0.5时的频普-55-0.500.51α=1时的g(t)-t/Tsg (t )-55-0.500.51G (f )α=1时的频普-5-4-3-2-112345-50050100P (f )α=0.05时的功率普-5-4-3-2-112345-50050100P (f )α=0.5时的功率普-5-4-3-2-112345-50050100P (f )α=1时的功率普Figure 3 :00.20.40.60.81 1.2 1.4 1.6 1.82-505α=0.05时的眼图00.20.40.60.81 1.2 1.4 1.6 1.82-505α=0.5时的眼图00.20.40.60.81 1.2 1.4 1.6 1.82-505α=1时的眼图三、实验总结:当 α=1时候,眼图睁开最大,峰值失真最小。
升余弦滚降系统可以看成是一个的低通和一个的函数的叠加

将G(f)的带宽范围放宽为[-fs,fs],则G(f) 的选择多样,可以选择出具有平缓特性的 G(f)。
升余弦滚降特性的G(f)就是其中常用的一 类。
升余弦滚降成形
频率特性满足
G(
f
)
T 2
1
cos
n
ak g 0 ak m g mTs
m0
抽样点无失真传输
第kTs时刻的抽样值由两部分组成
akg(0):与kTs发送时刻对应的发送值
码间干扰项: akm g mTs
m0
• 其它时刻码元幅值由于波形的原因对kTs码元抽样 值的影响
抽样点无失真条件
f
e j 2 fnTs df
1
G 2Ts 1
k
2Ts
f k / Ts e df j2 f k /Ts nTs
1
G 2Ts
1 2Ts
k
f k / Ts e j2 fnTs df
抽样点无失真传输-频域观点
令
周期函数的傅氏级 数展开
1.2
1
0.8
0.6
0.4
0.2
0
-0.2
-30
-20
-10
0
10
20
30
升余弦滚降成形
信号频宽 B (1)
频带利用率
2
1 2Ts
1
的几何意义
升余弦滚降系统可以看成是一个 0, w1 的低
通和一个 w1 w2 , w1 w2 的函数的叠加
正弦波的源程序

正弦波的源程序:(一),用到的函数1,f2t 函数function x=f2t(X)global dt df t f T N%x=f2t(X)%x 为时域的取样值矢量%X 为x 的傅氏变换%X 与x 长度相同并为2 的整幂%本函数需要一个全局变量dt(时域取样间隔) X=[X(N/2+1:N),X(1:N/2)];x=ifft(X)/dt;end2,t2f 函数。
function X=t2f(x)global dt df N t f T%X=t2f(x)%x 为时域的取样值矢量%X 为x 的傅氏变换%X 与x 长度相同,并为2 的整幂。
%本函数需要一个全局变量dt(时域取样间隔) H=fft(x);X=[H(N/2+1:N),H(1:N/2)]*dt;end(二),主程序。
1 ,% (1)绘出正弦信号波形及频谱global dt df t f Nclose allk=input('取样点数=2^k, k 取10 摆布');if isempty(k), k=10; endf0=input('f0=取1(kz)摆布');if isempty(f0), f0=1; endN=2^k;dt=0.01; %msdf=1/(N*dt); %KHzT=N*dt; %截短期Bs=N*df/2; %系统带宽f=[-Bs+df/2:df:Bs]; %频域横坐标t=[-T/2+dt/2:dt:T/2]; %时域横坐标s=sin(2*pi*f0*t); %输入的正弦信号S=t2f(s); %S 是s 的傅氏变换a=f2t(S); %a 是S 的傅氏反变换a=real(a);as=abs(S);subplot(2,1,1) %输出的频谱plot(f,as,'b');gridaxis([-2*f0,+2*f0,min(as),max(as)]) xlabel('f (KHz)')ylabel('|S(f)| (V/KHz)') %figure(2) subplot(2,1,2)plot(t,a,'black') %输出信号波形画图gridaxis([-2/f0,+2/f0,-1.5,1.5])xlabel('t(ms)')ylabel('a(t)(V)')gtext('频谱图')升余弦滚降系统的源程序:(一),用到的函数f2t 函数和t2f 函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一升余弦滚降系统及眼图
、实验目的
1. 理解无码间串扰系统的原理;
2. 理解升余弦滚降系统的工作原理;
3. 理解眼图的工作原理及实现方法。
、实验仪器及软件
电脑、MATLAB7.0软件
三、实验原理
1. 无码间串扰系统
若想消除码间串扰,应有
a n h k n T s t00 (1-1)
n k
由于a n是随机的,要想通过各项相互抵消使码间串扰为0是不行的,这就需要对h t的波形提出
要求,如果相邻码元的前一个码元的波形到达后一个码元抽样判决时刻时已经衰减到0,如图1-1(a)所示的波形,就能满足要求。
但这样的波形不易实现,因为实际中的h t波形有很长的“拖尾”,也
正是由于每个码元拖尾"造成对相邻码元的串扰,但只要让它在t0 T s,t0 2T s等后面码元抽样判决
时刻上正好为0,就能消除码间串扰,如图1-1(b)所示。
这也是消除码间串扰的基本思想。
著名的奈
奎斯特第一准则就给出了无码间串扰时基带传输特性应满足的频率条件:
(1-2)
图1-1消除码间串扰
显然,满足式(1-2)的系统H 并不是唯一的,容易想到的一种就是H 为一个理想低通滤
波器。
2. 升余弦滚降系统
理想低通特性的基带系统具有最大的频带利用率。
但实际上理想低通系统在应用中存在两个问题: 是实现极为困难,二是理想的冲击响应
h t 的“拖尾”很长,衰减很慢,当定时存在偏差时,可能
出现严重的码间串扰。
实际使用中常采用升余弦频谱特性的系统,其系统传输特性如下:
T s ,0
其中, 称为滚降系数。
其单位冲激响应为
sin t T s cos g 一
tT s y
l 4
3. 眼图
一个实际的基带传输系统尽管经过了十分精心的设计,但要 使其传输特性完全符合理想情况是非常困难的,甚至是不可能的。
码间干扰问题与发送滤波器特性、信道特性、接收滤波器特性等 因素有关,因而计算由于这些因素所引起的误码率就非常困难, 尤其在信道特性不能完全确知的情况下,甚至得不到一种合适的 定量分析方法。
在码间干扰和噪声同时存在的情况下,很难做到 系统性能的定量分析,就是想得到一个近似的结果都是非常繁杂 的,因此,实际应用中需要用简便的实验手段来评价系统的性能, 比较常用的一种方法就是眼图。
所谓眼图就是指通过用示波器观察接收端得基带信号波形, 从而估计和调整系统性能的一种方法。
因为在传输二进制信号波 形时,示波器显示的图形很像人的眼睛,所以称为“眼图”
四、实验步骤
假设随机二进制序列为“” ,“1 ”码对应的基带波形为升余弦
波形,持续时间为 T s ; “0”码对应的基带波形与“ 1”码相反。
(1)通过MATLAB 画出滚降系数分别为 1和 0.5时基
带信号波形及其眼图;
(2)基带信号中加性高斯白噪声,画出合成信号的波形及其眼图。
利用MATLAB 画出基带信号波形及其眼图的流程图如图
1-2所
cos 」 T
S
1
2T s
1 2T s
(1-3)
0, f
1 2T
(1-4)
图1-2升余弦滚降系统眼图程序流程图
示。
1. 生成双极性数字信号
在双极性不归零码中,脉冲的正、负电平分别对应于二进制代码1、0,由于它是幅度相等极性相
反的双极性波形,故当0、1符号等可能出现时无直流分量。
这样,恢复信号的判决电平为0,因而不受信道特性变化的影响,抗干扰能力也较强,故双极性码较单极性码更有利于在信道中传输。
%产生双极性数孚倍号
d = sign (razidn (1 j a));
dd = sigexp and (dj N);
2. 眼图的函数形式
MATLAB中产生眼图的函数为eyediagram函数。
Eyediagram 函数的完整定义格式为eyediagram ( x,n,period,offset,plotstring),表示创建信号
的x的眼图。
其中:
x——信号;n——每个轨迹包括的采样点数;
period ----- 水平轴的坐标范围是[-period/2,period/2];
offset ------ 偏置因子,信号的第(offset+1)个采样值之后每个n个值为一周期,且该周期为period 的整数倍,offset必须是非负整数,其范围是[0,n-1];
plotstring ――绘制眼图时采用的符号、线形和颜色,其格式可参见plot函数的说明前两个参数为必选参数,后三个为可选参数,如不设置的话,采用系统缺省值,详见MATLAB帮助文件。
3. MATLAB中产生高斯白噪声的两个函数
MATLAB中产生高斯白噪声非常方便,可以直接应用两个函数,一个是WGN,另一个是AWGN。
WGN用于产生高斯白噪声,AWGN则用于在某一信号中加入高斯白噪声。
五、实验报告要求
1. 整理实验程序,并画出相关的曲线和波形图。
2. 分析加入高斯白噪声前后基带信号及其相应眼图的变化。
