基于遗传算法的投影寻踪模型Matlab源码

合集下载

基于遗传算法(粒子群算法人工鱼群算法等)的投影寻踪模型MATLAB源代码

基于遗传算法（粒子群算法、人工鱼群算法等）的投影寻踪模型MATLAB源代码投影寻踪是一种处理多因素复杂问题的统计方法，其基本思路是将高维数据向低维空间进行投影，通过低维投影数据的散布结构来研究高维数据特征，可用于聚类、分类、综合评价、预测等。

投影寻踪模型最终可归结为一个非线性连续函数优化模型，可以采用遗传算法、粒子群算法、人工鱼群算法或人工免疫克隆优化算法等进行求解，得到最优的投影向量。

%% 第一步：仿真参数设置clcclearclose allload data1.txtD=data1。

%导入D矩阵[n,p]=size(D)。

K=300。

%迭代次数N=100。

%种群规模Pm=0.3。

%变异概率LB=-ones(1,p)。

%决策变量的下界UB=ones(1,p)。

%决策变量的上界Alpha=0.1。

%窗口半径系数，典型取值0.1b%% 调用遗传算法[BESTX,BESTY,ALLX,ALL Y]=GAUCP(K,N,Pm,LB,UB,D,Alpha)。

% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→%% 整理输出结果Best_a=(BESTX{K})'。

%方向向量d=zeros(n,p)。

Djmax=max(D)。

Djmin=min(D)。

for i=1:nd(i,:)=(D(i,:)-Djmin)./(Djmax-Djmin)。

endZ=zeros(n,1)。

for i=1:nZ(i)=abs(sum(Best_a.*d(i,:)))。

endZ=abs(Z)。

figure%投影散布图plot(abs(Z),'bd','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',5)。

完整的遗传算法函数Matlab程序

完整的遗传算法函数Matlab程序遗传算法是一种模拟自然进化过程的算法，通过遗传代数操作来搜索最优解。

它是一种优化算法，可以用于解决复杂问题，例如函数优化、组合优化、机器学习等。

在Matlab 中，遗传算法可以通过使用内置函数进行实现，也可以编写自己的遗传算法函数。

以下是一个完整的遗传算法函数Matlab程序的示例：function [x_best, f_best] = GA(fit_func, nvars)% fit_func: 适应度函数句柄% nvars: 变量个数% 遗传算法参数设置pop_size = 100; % 种群大小prob_crossover = 0.8; % 交叉概率prob_mutation = 0.02; % 变异概率max_gen = 1000; % 最大迭代次数% 初始化种群pop = rand(pop_size, nvars);for i = 1:max_gen% 计算适应度for j = 1:pop_sizefitness(j) = feval(fit_func, pop(j,:));end% 找到最优个体[f_best, best_idx] = max(fitness);x_best = pop(best_idx,:);% 交叉操作for j = 1:2:pop_sizeif rand < prob_crossover% 随机选择父代idx_parent1 = randi(pop_size);idx_parent2 = randi(pop_size);parent1 = pop(idx_parent1,:);parent2 = pop(idx_parent2,:);% 交叉idx_crossover = randi(nvars-1);child1 = [parent1(1:idx_crossover) parent2(idx_crossover+1:end)];child2 = [parent2(1:idx_crossover) parent1(idx_crossover+1:end)];% 更新种群pop(j,:) = child1;pop(j+1,:) = child2;endend% 变异操作for j = 1:pop_sizeif rand < prob_mutation% 随机选择变异个体idx_mutation = randi(nvars);pop(j,idx_mutation) = rand;endendendend在上述程序中，遗传算法的参数通过设定变量的值进行设置，包括种群大小、交叉概率、变异概率和最大迭代次数等。

用MATLAB实现遗传算法程序

用MATLAB实现遗传算法程序一、本文概述遗传算法（Genetic Algorithms，GA）是一种模拟自然界生物进化过程的优化搜索算法，它通过模拟自然选择和遗传学机制，如选择、交叉、变异等，来寻找问题的最优解。

由于其全局搜索能力强、鲁棒性好以及易于实现并行化等优点，遗传算法在多个领域得到了广泛的应用，包括函数优化、机器学习、神经网络训练、组合优化等。

本文旨在介绍如何使用MATLAB实现遗传算法程序。

MATLAB作为一种强大的数学计算和编程工具，具有直观易用的图形界面和丰富的函数库，非常适合用于遗传算法的实现。

我们将从基本的遗传算法原理出发，逐步介绍如何在MATLAB中编写遗传算法程序，包括如何定义问题、编码、初始化种群、选择操作、交叉操作和变异操作等。

通过本文的学习，读者将能够掌握遗传算法的基本原理和MATLAB编程技巧，学会如何使用MATLAB实现遗传算法程序，并能够在实际问题中应用遗传算法求解最优解。

二、遗传算法基础遗传算法（Genetic Algorithm，GA）是一种模拟自然选择和遗传学机制的优化搜索算法。

它借鉴了生物进化中的遗传、交叉、变异等机制，通过模拟这些自然过程来寻找问题的最优解。

遗传算法的核心思想是将问题的解表示为“染色体”，即一组编码，然后通过模拟自然选择、交叉和变异等过程，逐步迭代搜索出最优解。

在遗传算法中，通常将问题的解表示为一个二进制字符串，每个字符串代表一个个体（Individual）。

每个个体都有一定的适应度（Fitness），适应度越高的个体在下一代中生存下来的概率越大。

通过选择（Selection）、交叉（Crossover）和变异（Mutation）等操作，生成新一代的个体，并重复这一过程，直到找到满足条件的最优解或达到预定的迭代次数。

选择操作是根据个体的适应度，选择出适应度较高的个体作为父母，参与下一代的生成。

常见的选择算法有轮盘赌选择（Roulette Wheel Selection）、锦标赛选择（Tournament Selection）等。

基于遗传算法的matlab源代码

function youhuafunD=code;N=50;%Tunablemaxgen=50;%Tunablecrossrate=0.5;%Tunablemuterate=0.08;%Tunablegeneration=1;num=length(D);fatherrand=randint(num,N,3);score=zeros(maxgen,N);while generation<=maxgenind=randperm(N-2)+2;%随机配对交叉A=fatherrand(:,ind(1:(N-2)/2));B=fatherrand(:,ind((N-2)/2+1:end));%多点交叉rnd=rand(num,(N-2)/2);ind=rnd tmp=A(ind);A(ind)=B(ind);B(ind)=tmp;%%两点交叉%for kk=1:(N-2)/2%rndtmp=randint(1,1,num)+1;%tmp=A(1:rndtmp,kk);%A(1:rndtmp,kk)=B(1:rndtmp,kk);%B(1:rndtmp,kk)=tmp;%endfatherrand=[fatherrand(:,1:2),A,B];%变异rnd=rand(num,N);ind=rnd[m,n]=size(ind);tmp=randint(m,n,2)+1;tmp(:,1:2)=0;fatherrand=tmp+fatherrand;fatherrand=mod(fatherrand,3);%fatherrand(ind)=tmp;%评价、选择scoreN=scorefun(fatherrand,D);%求得N个个体的评价函数score(generation,:)=scoreN;[scoreSort,scoreind]=sort(scoreN);sumscore=cumsum(scoreSort);sumscore=sumscore./sumscore(end);childind(1:2)=scoreind(end-1:end);for k=3:Ntmprnd=rand;tmpind=tmprnd difind=[0,diff(t mpind)];if~any(difind)difind(1)=1;endchildind(k)=scoreind(logical(difind));endfatherrand=fatherrand(:,childind);generation=generation+1;end%scoremaxV=max(score,[],2);minV=11*300-maxV;plot(minV,'*');title('各代的目标函数值');F4=D(:,4);FF4=F4-fatherrand(:,1);FF4=max(FF4,1);D(:,5)=FF4;save DData Dfunction D=codeload youhua.mat%properties F2and F3F1=A(:,1);F2=A(:,2);F3=A(:,3);if(max(F2)>1450)||(min(F2)<=900)error('DATA property F2exceed it''s range(900,1450]')end%get group property F1of data,according to F2value F4=zeros(size(F1));for ite=11:-1:1index=find(F2<=900+ite*50);F4(index)=ite;endD=[F1,F2,F3,F4];function ScoreN=scorefun(fatherrand,D)F3=D(:,3);F4=D(:,4);N=size(fatherrand,2);FF4=F4*ones(1,N);FF4rnd=FF4-fatherrand;FF4rnd=max(FF4rnd,1);ScoreN=ones(1,N)*300*11;%这里有待优化for k=1:NFF4k=FF4rnd(:,k);for ite=1:11F0index=find(FF4k==ite);if~isempty(F0index)tmpMat=F3(F0index);tmpSco=sum(tmpMat);ScoreBin(ite)=mod(tmpSco,300);endendScorek(k)=sum(ScoreBin);endScoreN=ScoreN-Scorek;遗传算法实例:%下面举例说明遗传算法%%求下列函数的最大值%%f(x)=10*sin(5x)+7*cos(4x)x∈[0,10]%%将x的值用一个10位的二值形式表示为二值问题，一个10位的二值数提供的分辨率是每为(10-0)/(2^10-1)≈0.01。

基于加速遗传算法的投影寻踪模型代码

基于加速遗传算法的投影寻踪模型代码一些常用的遗传算法代码模板供您参考：```import random# 遗传算法参数POPULATION_SIZE = 100GENERATIONS = 50MUTATION_RATE = 0.1CROSSOVER_RATE = 0.8ELITE_SIZE = 2# 个体编码示例def create_individual():individual = []# TODO: 根据具体问题设计个体编码return individual# 适应度函数示例，fitness越小越好，用于最小化问题def fitness(individual):# TODO: 根据具体问题实现适应度函数return 0# 选择操作示例def selection(population):# TODO: 实现选择算法，返回选择的父代个体return parent1, parent2# 交叉操作示例def crossover(parent1, parent2):# TODO: 实现交叉算法，返回交叉后的子代个体return child1, child2# 变异操作示例def mutation(individual):# TODO: 实现变异算法，返回变异后的个体return mutant# 创建初始种群population = [create_individual() for _ in range(POPULATION_SIZE)]# 迭代遗传算法for generation in range(GENERATIONS):# 计算适应度fitness_list = [fitness(individual) for individual in population]# 选择最优个体elites = sorted(zip(population, fitness_list), key=lambda x: x[1])[:ELITE_SIZE]# 输出当前代数和最优个体适应度print("Generation:", generation, "Best fitness:", elites[0][1])# 选择新的父代个体parents = [selection(population) for _ in range(POPULATION_SIZE - ELITE_SIZE)]# 交叉并产生新的子代个体children = []for i in range(0, len(parents), 2):if random.random() < CROSSOVER_RATE:child1, child2 = crossover(parents[i], parents[i+1])else:child1, child2 = parents[i], parents[i+1]children.append(mutation(child1))children.append(mutation(child2))# 更新下一代种群population = [elite[0] for elite in elites] + children```需要根据具体问题进行个体编码、适应度函数、选择算法、交叉算法和变异算法的实现。

遗传算法matlab程序代码

遗传算法matlab程序代码
遗传算法（GA）是一种用于求解优化问题的算法，其主要思想是模拟
生物进化过程中的“选择、交叉、变异”操作，通过模拟这些操作，来寻
找最优解。

Matlab自带了GA算法工具箱，可以直接调用来实现遗传算法。

以下是遗传算法Matlab程序代码示例：
1.初始化
首先定义GA需要优化的目标函数f，以及GA算法的相关参数，如种
群大小、迭代次数、交叉概率、变异概率等，如下所示：
options = gaoptimset('PopulationSize',10,...
'Generations',50,...
2.运行遗传算法
运行GA算法时，需要调用MATLAB自带的ga函数，将目标函数、问
题的维度、上下界、约束条件和算法相关参数作为输入参数。

其中，上下
界和约束条件用于限制空间，防止到无效解。

代码如下：
[某,fval,reason,output,population] = ga(f,2,[],[],[],[],[-10,-10],[10,10],[],options);
3.结果分析
最后，将结果可视化并输出，可以使用Matlab的plot函数绘制出目
标函数的值随迭代次数的变化，如下所示：
plot(output.generations,output.bestf)
某label('Generation')
ylabel('Best function value')
总之，Matlab提供了方便易用的GA算法工具箱，开发者只需要根据具体问题定义好目标函数和相关参数，就能够在短时间内快速实现遗传算法。

遗传算法优化相关MATLAB算法实现

遗传算法优化相关MATLAB算法实现遗传算法（Genetic Algorithm，GA）是一种基于生物进化过程的优化算法，能够在空间中找到最优解或接近最优解。

它模拟了自然选择、交叉和变异等进化操作，通过不断迭代的方式寻找最佳的解。

遗传算法的主要步骤包括：初始化种群、评估适应度、选择、交叉、变异和更新种群等。

在MATLAB中，可以使用遗传算法工具箱（Genetic Algorithm & Direct Search Toolbox）来实现遗传算法的优化。

下面以实现一个简单的函数优化为例进行说明。

假设我们要优化以下函数：```f(x)=x^2-2x+1```首先，我们需要定义适应度函数，即上述函数f(x)。

在MATLAB中，可以使用如下代码定义适应度函数：```MATLABfunction fitness = myFitness(x)fitness = x^2 - 2*x + 1;end```接下来，我们需要自定义遗传算法的参数，包括种群大小、迭代次数、交叉概率和变异概率等。

在MATLAB中，可以使用如下代码定义参数：```MATLABpopulationSize = 100; % 种群大小maxGenerations = 100; % 迭代次数crossoverProbability = 0.8; % 交叉概率mutationProbability = 0.02; % 变异概率```然后，我们需要定义遗传算法的上下界范围。

在本例中，x的范围为[0,10]。

我们可以使用如下代码定义范围：```MATLABlowerBound = 0; % 下界upperBound = 10; % 上界```接下来，我们可以使用遗传算法工具箱中的`ga`函数进行遗传算法的优化。

如下所示：```MATLAB```最后，我们可以得到最优解x和最优值fval。

在本例中，我们得到的结果应该接近1以上只是一个简单的例子，实际应用中可能需要根据具体问题进行参数的设定和函数的定义。

遗传算法matlab源代码

方案一的程序编码函数主文件：function[Xp,LC1,LC2,LC3]=CLBGA8(M,Pm) %%%陈璐斌编程，解决VRP问题（带时间窗）%%输入参数%M遗传进化迭代次数%Pm变异概率%%输出参数%Xp最优个体%LC1目标收敛曲线%LC2平均适应度收敛曲线%LC3最优适应度收敛曲线%%%变量初始化Xp=zeros(1,5);LC1=zeros(1,M);LC2=zeros(1,M);LC3=zeros(1,M);Best=inf;%%编码方式-第一步：产生初始种群N=10;%N 种群规模farm=cell(1,N);%存储种群的细胞结构k=1;while (N-k>=0)G=randperm(5);%产生5个客户的全排列farm{k}=G;k=k+1;end%%%进化迭代计数器counter=1;while counter<=M%%第二步：交叉%交叉采用双亲双子单点交叉N=10;%种群规模newfarm=cell(1,2*N-4);%存储子代的细胞结构Ser=randperm(N);%两两随机配对表生成for i=1:(N-2)%避免交叉概率为1 A=farm{Ser(i)};B=farm{Ser(i+1)};%取出父代P0=unidrnd(5);%随机选择交叉点aa=zeros(1,5);bb=zeros(1,5);A_=A;B_=B;for ii=1:5-P0aa(ii)=B(P0+ii);endfor ii=1:5-P0for iiii=1:5if(B(P0+ii)==A_(iiii))A_(iiii)=0;endendendfor iii=6-P0:5for iiii=1:5if(A_(iiii)~=0)aa(iii)=A_(iiii);A_(iiii)=0;breakendendendfor ii=1:5-P0bb(ii)=A(P0+ii);endfor ii=1:5-P0for iiii=1:5if(A(P0+ii)==B_(iiii))B_(iiii)=0;endendendfor iii=6-P0:5for iiii=1:5if(B_(iiii)~=0)bb(iii)=B_(iiii);B_(iiii)=0;breakendendend%产生子代newfarm{2*i-1}=aa;newfarm{2*i}=bb;endFARM=[farm,newfarm];%新旧种群合并%%第三步：选择复制%%计算当前种群适应度并存储N=10;SYZ=zeros(1,3*N-4);syz=zeros(1,3*N-4);for i=1:(3*N-4)x=FARM{i};SYZ(i)=clb8(x);end%%选择复制，较优的N个个体复制到下一代k=1;while k<=(3*N-4)maxSYZ=max(SYZ);posSYZ=find(SYZ==maxSYZ);POS=posSYZ(1);k=k+1;farm{k}=FARM{POS};syz(k)=SYZ(POS);SYZ(POS)=0;end%记录和更新，更新最优个体，记录收敛曲线数据maxsyz=max(syz);meansyz=mean(syz);pos=find(syz==maxsyz);LC2(counter+1)=meansyz;if maxsyzBest=maxsyz;Xp=farm{pos(1)};endLC3(counter+1)=Best;d=[0,6.4,3.2,3.9,3.7,2;6.4,0,2.9,2.1,4.5,4.1;3.2,2.9,0,1.5,3.3,1.2;3.9,2.1,1.5,0,3.6,2.6;3.7,4.5,3.3,3.6 ,0,3.8;...2.0,4.1,1.2,2.6,3.8,0;];%距离矩阵t=[0,0.16,0.08,0.1,0.09,0.05;0.16,0,0.07,0.05,0.11,0.1;0.08,0.07,0,0.04,0.08,0.03;...0.1,0.05,0.04,0,0.09,0.07;0.09,0.11,0.08,0.09,0,0.10;0.05,0.1,0.03,0.07,0.1,0;];%行驶时间矩阵w=[0.15,0.2,0.18,0.25,0.22];%服务时间矩阵%%时间窗向量early=[0.15,0.3,0.7,0.4,0.7];xx=x;%取出染色体j=1;%分工点初始化%%取距离向量d1,d2d1=zeros(1,6);d1(1)=d(1,xx(1)+1);for i=1:4d1(i+1)=d(xx(i)+1,xx(i+1)+1);endd1(6)=d(xx(5)+1,1);%%时间窗计算T=t(1,xx(1)+1);pun1=0;if T<early(xx(1))pun1=early(xx(1))-T;T=early(xx(1));endT=T+w(xx(1));for i=2:5T=T+t(xx(i-1)+1,xx(i)+1);if T<early(xx(i))pun1=pun1+early(xx(i))-T;T=early(xx(i));endT=T+w(xx(5));endF=sum(10.*d1)+sum(10.*d2)+20*pun1; LC1(counter+1)=F;%%第四步：变异N=10;for i=1:Nif Pm>randAA=farm{i};POS1=unidrnd(5);POS2=unidrnd(5);temp=AA(POS1);AA(POS1)=AA(POS2);AA(POS2)=temp;farm{i}=AA;endendcounter=counter+1;end%%第五步：绘制收敛曲线图figure(2);plot(LC1);xlabel('迭代次数');ylabel('目标的值');title('目标的收敛曲线');figure(3);plot(LC2);xlabel('迭代次数');ylabel('适应度函数的平均值');title('平均适应度函数的收敛曲线');plot(LC3);xlabel('迭代次数');ylabel('适应度函数的最优值');title('最优适应度函数的收敛曲线');适应度文件：%%计算载重量和时间窗%%适应度函数计算function Fitness=clb8(x)d=[0,6.4,3.2,3.9,3.7,2;6.4,0,2.9,2.1,4.5,4.1;3.2,2.9,0,1.5,3.3,1.2;3.9,2.1,1.5,0,3.6,2.6;3.7,4.5,3.3,3.6 ,0,3.8;...2.0,4.1,1.2,2.6,3.8,0;];%距离矩阵t=[0,0.16,0.08,0.1,0.09,0.05;0.16,0,0.07,0.05,0.11,0.1;0.08,0.07,0,0.04,0.08,0.03;...0.1,0.05,0.04,0,0.09,0.07;0.09,0.11,0.08,0.09,0,0.10;0.05,0.1,0.03,0.07,0.1,0;];%行驶时间矩阵w=[0.15,0.2,0.18,0.25,0.22];%服务时间矩阵%%时间窗向量early=[0.15,0.3,0.7,0.4,0.7];xx=x;%取出染色体j=1;%分工点初始化%%取距离向量d1,d2d1=zeros(1,6);d1(1)=d(1,xx(1)+1);for i=1:4d1(i+1)=d(xx(i)+1,xx(i+1)+1);endd1(6)=d(xx(5)+1,1);%%时间窗计算T=t(1,xx(1)+1);pun1=0;if T<early(xx(1))pun1=early(xx(1))-T;T=early(xx(1));endT=T+w(xx(1));T=T+t(xx(i-1)+1,xx(i)+1);if T<early(xx(i))pun1=pun1+early(xx(i))-T;T=early(xx(i));endT=T+w(xx(5));endF=sum(10.*d1)+sum(10.*d2)+20*pun1;Fitness=1/F;计算时间文件：function[T]=TOTALT(Xp1)Xp=Xp1;t=[0,0.16,0.08,0.1,0.09,0.05;0.16,0,0.07,0.05,0.11,0.1;0.08,0.07,0,0.04,0.08,0.03;...0.1,0.05,0.04,0,0.09,0.07;0.09,0.11,0.08,0.09,0,0.10;0.05,0.1,0.03,0.07,0.1,0;];%行驶时间矩阵w=[0.15,0.2,0.18,0.25,0.22];%服务时间矩阵%%时间窗向量early=[0.15,0.3,0.7,0.4,0.7];T=t(1,Xp(1)+1);if T<early(Xp(1))T=early(Xp(1));endT=T+w(Xp(1));for i=2:5T=T+t(Xp(i-1)+1,Xp(i)+1);if T<early(Xp(i))T=early(Xp(1));endT=T+w(Xp(i));endT=T+t(1,Xp(5)+1);方案二的程序编码主函数文件：function[Xp,LC1,LC2,LC3]=CLBGA9(M,Pm)%%%陈璐斌编程，解决VRP问题（带时间窗）%%输入参数%M遗传进化迭代次数%Pm变异概率%%输出参数%Xp最优个体%LC1子目标2收敛曲线%LC2平均适应度收敛曲线%LC3最优适应度收敛曲线%%%变量初始化Xp=zeros(1,6);LC1=zeros(1,M);LC2=zeros(1,M);LC3=zeros(1,M);Best=inf;%%编码方式-第一步：产生初始种群N=10;%N 种群规模%Q=[2.4,3.3,2.1,2.7,2.3,1.6,2.0,1.2,3.6,1.9];%需求矩阵farm=cell(1,N);%存储种群的细胞结构k=1;while (N-k>=0)G=randperm(6);%产生6个客户的全排列farm{k}=G;k=k+1;end%%%进化迭代计数器counter=1;while counter<=M%%第二步：交叉%交叉采用双亲双子单点交叉N=10;%种群规模newfarm=cell(1,2*N-4);%存储子代的细胞结构Ser=randperm(N);%两两随机配对表生成for i=1:(N-2)%避免交叉概率为1A=farm{Ser(i)};B=farm{Ser(i+1)};%取出父代P0=unidrnd(6);%随机选择交叉点aa=zeros(1,6);bb=zeros(1,6);A_=A;B_=B;for ii=1:6-P0aa(ii)=B(P0+ii);endfor ii=1:6-P0for iiii=1:6if(B(P0+ii)==A_(iiii))A_(iiii)=0;endendendfor iii=7-P0:6for iiii=1:6if(A_(iiii)~=0)aa(iii)=A_(iiii);A_(iiii)=0;breakendendendfor ii=1:6-P0bb(ii)=A(P0+ii);endfor ii=1:6-P0for iiii=1:6if(A(P0+ii)==B_(iiii))B_(iiii)=0;endendendfor iii=7-P0:6for iiii=1:6if(B_(iiii)~=0)bb(iii)=B_(iiii);B_(iiii)=0;breakendendend%产生子代newfarm{2*i-1}=aa;newfarm{2*i}=bb;endFARM=[farm,newfarm];%新旧种群合并%%第三步：选择复制%%计算当前种群适应度并存储N=10;SYZ=zeros(1,3*N-4);syz=zeros(1,3*N-4);for i=1:(3*N-4)x=FARM{i};SYZ(i)=clb9(x);end%%选择复制，较优的N个个体复制到下一代k=1;while k<=(3*N-4)maxSYZ=max(SYZ);posSYZ=find(SYZ==maxSYZ);POS=posSYZ(1);k=k+1;farm{k}=FARM{POS};syz(k)=SYZ(POS);SYZ(POS)=0;end%记录和更新，更新最优个体，记录收敛曲线数据maxsyz=max(syz);meansyz=mean(syz);pos=find(syz==maxsyz);LC2(counter+1)=meansyz;if maxsyzBest=maxsyz;Xp=farm{pos(1)};endLC3(counter+1)=Best;d=[0,6.4,3.2,3.9,3.7,35,2;6.4,0,2.9,2.1,4.5,32.5,4.1;3.2,2.9,0,1.5,3.3,35.7,1.2;3.9,2.1,1.5,0,3.6,34.5,2.6;...3.7,4.5,3.3,3.6,0,37,3.8;35,32.5,35.7,34.5,37,0,38.5;2,4.1,1.2,2.6,3.8,38.5,0];%距离矩阵t=[0,0.16,0.08,0.1,0.1,0.88,0.05;0.16,0,0.07,0.05,0.11,0.81,0.1;0.08,0.07,0,0.04,0.08,0.9,0.03;...0.1,0.05,0.04,0,0.09,0.86,0.07;0.1,0.11,0.08,0.09,0,0.92,0.1;0.88,0.81,0.9,0.86,0.92,0,0.96;...0.05,0.1,0.03,0.07,0.1,0.96,0;];%行驶时间矩阵w=[0.15,0.2,0.18,0.25,0.2,0.22];%服务时间矩阵%%时间窗向量early=[0.15,0.3,0.7,0.4,0.7,0.6];xx=x;%取出染色体j=1;%分工点初始化%%取距离向量d1,d2d1=zeros(1,7);d1(1)=d(1,xx(1)+1);for i=1:5d1(i+1)=d(xx(i)+1,xx(i+1)+1);endd1(7)=d(xx(6)+1,1);%%时间窗计算T=t(1,xx(1)+1);pun1=0;if T<early(xx(1))pun1=early(xx(1))-T;T=early(xx(1));endT=T+w(xx(1));for i=2:6T=T+t(xx(i-1)+1,xx(i)+1);if T<early(xx(i))pun1=pun1+early(xx(i))-T;T=early(xx(i));endT=T+w(xx(6));endF=sum(10.*d1) +20*pun1;LC1(counter+1)=F;%%第四步：变异N=10;for i=1:Nif Pm>randAA=farm{i};POS1=unidrnd(6);POS2=unidrnd(6);temp=AA(POS1);AA(POS1)=AA(POS2);AA(POS2)=temp;farm{i}=AA;endendcounter=counter+1;end%%第五步：绘制收敛曲线图figure(2);plot(LC1);xlabel('迭代次数');ylabel('目标的值');title('目标的收敛曲线');figure(3);plot(LC2);xlabel('迭代次数');ylabel('适应度函数的平均值');title('平均适应度函数的收敛曲线');figure(4);plot(LC3);xlabel('迭代次数');ylabel('适应度函数的最优值');title('最优适应度函数的收敛曲线');适应度文件：%%计算载重量和时间窗%%适应度函数计算function Fitness=clb9(x)d=[0,6.4,3.2,3.9,3.7,35,2;6.4,0,2.9,2.1,4.5,32.5,4.1;3.2,2.9,0,1.5,3.3,35.7,1.2;3.9,2.1,1.5,0,3.6,34.5,2.6;...3.7,4.5,3.3,3.6,0,37,3.8;35,32.5,35.7,34.5,37,0,38.5;2,4.1,1.2,2.6,3.8,38.5,0];%距离矩阵t=[0,0.16,0.08,0.1,0.1,0.88,0.05;0.16,0,0.07,0.05,0.11,0.81,0.1;0.08,0.07,0,0.04,0.08,0.9,0.03;...0.1,0.05,0.04,0,0.09,0.86,0.07;0.1,0.11,0.08,0.09,0,0.92,0.1;0.88,0.81,0.9,0.86,0.92,0,0.96;...0.05,0.1,0.03,0.07,0.1,0.96,0;];%行驶时间矩阵w=[0.15,0.2,0.18,0.25,0.2,0.22];%服务时间矩阵%%时间窗向量early=[0.15,0.3,0.7,0.4,0.7,0.6];late=[2.5,3.4,3.3,2.7,2.5,4.5];xx=x;%取出染色体j=1;%分工点初始化%%取距离向量d1,d2d1=zeros(1,7);d1(1)=d(1,xx(1)+1);for i=1:5d1(i+1)=d(xx(i)+1,xx(i+1)+1);endd1(7)=d(xx(6)+1,1);%%时间窗计算T=t(1,xx(1)+1);pun1=0;if T<early(xx(1))pun1=early(xx(1))-T;T=early(xx(1));endT=T+w(xx(1));for i=2:6T=T+t(xx(i-1)+1,xx(i)+1);if T<early(xx(i))pun1=pun1+early(xx(i))-T;T=early(xx(i));endT=T+w(xx(6));endF=sum(10.*d1) +20*pun1;Fitness=1/F;计算时间文件：function[T]=TOTALT2(Xp1)Xp=Xp1;t=[0,0.16,0.08,0.1,0.1,0.88,0.05;0.16,0,0.07,0.05,0.11,0.81,0.1;0.08,0.07,0,0.04,0.08,0.9,0.03;...0.1,0.05,0.04,0,0.09,0.86,0.07;0.1,0.11,0.08,0.09,0,0.92,0.1;0.88,0.81,0.9,0.86,0.92,0,0.96;... 0.05,0.1,0.03,0.07,0.1,0.96,0;];%行驶时间矩阵w=[0.15,0.2,0.18,0.25,0.2,0.22];%服务时间矩阵%%时间窗向量early=[0.15,0.3,0.7,0.4,0.7,0.6];T=t(1,Xp(1)+1);if T<early(Xp(1))T=early(Xp(1));endT=T+w(Xp(1));for i=2:6T=T+t(Xp(i-1)+1,Xp(i)+1);if T<early(Xp(i))T=early(Xp(1));endT=T+w(Xp(i));endT=T+t(1,Xp(6)+1)。

遗传算法的matlab代码

遗传算法的matlab代码摘要：遗传算法是一种基于自然选择和遗传学原理的优化算法。

本文将介绍如何在MATLAB中实现遗传算法，并使用一个简单的例子来说明其应用。

1. 引言遗传算法（Genetic Algorithm, GA）是一种基于自然选择和遗传学原理的优化算法。

它模拟了自然界中生物的进化过程，通过不断地搜索、适应和优化，最终找到问题的最优解。

MATLAB是一种广泛使用的编程语言和软件环境，它提供了丰富的数学计算和可视化工具，使得在MATLAB中实现遗传算法变得相对简单。

2. 遗传算法的基本原理遗传算法主要包括以下几个步骤：1) 初始化：随机生成一组候选解（称为种qun）。

2) 选择：从种qun中按照一定的概率选择出优秀的个体进行繁殖。

3) 交叉：从选择出的个体中随机选择两个进行交叉操作，生成新的后代。

4) 变异：对后代进行变异操作，以增大种qun的多样性。

5) 迭代：重复进行选择、交叉和变异操作，直到达到预设的迭代次数或满足其他终止条件。

3. MATLAB实现遗传算法在MATLAB中实现遗传算法，可以使用自带的gaoptimset和ga函数。

下面是一个简单的例子，说明如何在MATLAB中实现遗传算法。

```matlab```% 定义目标函数fitnessFunction = @(x) x(1)^2 + x(2)^2; % 最小化目标函数```% 定义变量范围lb = [-10, -10]; % 变量下界ub = [10, 10]; % 变量上界```% 初始化参数populationSize = 100; % 种qun大小maxIterations = 500; % 最da迭代次数crossoverRate = 0.8; % 交叉概率mutationRate = 0.1; % 变异概率elitismRate = 0.1; % 精英策略概率```% 初始化种qunpopulation = ga(fitnessFunction, lb, ub, populationSize, maxIterations, elitismRate, crossoverRate, mutationRate);```% 可视化结果figure;plot(population.Fitness,'r');hold on;plot(population.Gen,'g');xlabel('Generation');ylabel('Fitness');title('遗传算法进化过程');```4. 结果分析通过上述代码，我们可以在MATLAB中实现一个简单的遗传算法。

遗传算法优化相关MATLAB算法实现

遗传算法优化相关MATLAB算法实现遗传算法1、案例背景遗传算法(Genetic Algorithm,GA)就是一种进化算法,其基本原理就是仿效生物界中的“物竞天择、适者生存”的演化法则。

遗传算法的做法就是把问题参数编码为染色体,再利用迭代的方式进行选择、交叉以及变异等运算来交换种群中染色体的信息,最终生成符合优化目标的染色体。

在遗传算法中,染色体对应的就是数据或数组,通常就是由一维的串结构数据来表示,串上各个位置对应基因的取值。

基因组成的串就就是染色体,或者叫基因型个体( Individuals) 。

一定数量的个体组成了群体(Population)。

群体中个体的数目称为群体大小(Population Size),也叫群体规模。

而各个个体对环境的适应程度叫做适应度( Fitness) 。

2、遗传算法中常用函数1)创建种群函数—crtbp2)适应度计算函数—ranking3)选择函数—select4)交叉算子函数—recombin5)变异算子函数—mut6)选择函数—reins7)实用函数—bs2rv8)实用函数—rep3、主程序:1、简单一元函数优化:clcclear allclose all%% 画出函数图figure(1);hold on;lb=1;ub=2; %函数自变量范围【1,2】ezplot('sin(10*pi*X)/X',[lb,ub]); %画出函数曲线xlabel('自变量/X')ylabel('函数值/Y')%% 定义遗传算法参数NIND=40; %个体数目MAXGEN=20; %最大遗传代数PRECI=20; %变量的二进制位数GGAP=0、95; %代沟px=0、7; %交叉概率pm=0、01; %变异概率trace=zeros(2,MAXGEN); %寻优结果的初始值FieldD=[PRECI;lb;ub;1;0;1;1]; %区域描述器Chrom=crtbp(NIND,PRECI); %初始种群%% 优化gen=0; %代计数器X=bs2rv(Chrom,FieldD); %计算初始种群的十进制转换ObjV=sin(10*pi*X)、/X; %计算目标函数值while gen<maxgen< p="">FitnV=ranking(ObjV); %分配适应度值SelCh=select('sus',Chrom,FitnV,GGAP); %选择SelCh=recombin('xovsp',SelCh,px); %重组SelCh=mut(SelCh,pm); %变异X=bs2rv(SelCh,FieldD); %子代个体的十进制转换ObjVSel=sin(10*pi*X)、/X; %计算子代的目标函数值[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代,得到新种群X=bs2rv(Chrom,FieldD);gen=gen+1; %代计数器增加%获取每代的最优解及其序号,Y为最优解,I为个体的序号[Y,I]=min(ObjV);trace(1,gen)=X(I); %记下每代的最优值trace(2,gen)=Y; %记下每代的最优值endplot(trace(1,:),trace(2,:),'bo'); %画出每代的最优点grid on;plot(X,ObjV,'b*'); %画出最后一代的种群hold off%% 画进化图figure(2);plot(1:MAXGEN,trace(2,:));grid onxlabel('遗传代数')ylabel('解的变化')title('进化过程')bestY=trace(2,end);bestX=trace(1,end);fprintf(['最优解:\nX=',num2str(bestX),'\nY=',num2str(bestY),'\n'])2、多元函数优化clcclear allclose all%% 画出函数图figure(1);lbx=-2;ubx=2; %函数自变量x范围【-2,2】lby=-2;uby=2; %函数自变量y范围【-2,2】ezmesh('y*sin(2*pi*x)+x*cos(2*pi*y)',[lbx,ubx,lby,uby],50); %画出函数曲线hold on;%% 定义遗传算法参数NIND=40; %个体数目MAXGEN=50; %最大遗传代数PRECI=20; %变量的二进制位数GGAP=0、95; %代沟px=0、7; %交叉概率pm=0、01; %变异概率trace=zeros(3,MAXGEN); %寻优结果的初始值FieldD=[PRECI PRECI;lbx lby;ubx uby;1 1;0 0;1 1;1 1]; %区域描述器Chrom=crtbp(NIND,PRECI*2); %初始种群%% 优化gen=0; %代计数器XY=bs2rv(Chrom,FieldD); %计算初始种群的十进制转换X=XY(:,1);Y=XY(:,2);ObjV=Y、*sin(2*pi*X)+X、*cos(2*pi*Y); %计算目标函数值while gen<maxgen< p="">FitnV=ranking(-ObjV); %分配适应度值SelCh=select('sus',Chrom,FitnV,GGAP); %选择SelCh=recombin('xovsp',SelCh,px); %重组SelCh=mut(SelCh,pm); %变异XY=bs2rv(SelCh,FieldD); %子代个体的十进制转换X=XY(:,1);Y=XY(:,2);ObjVSel=Y、*sin(2*pi*X)+X、*cos(2*pi*Y); %计算子代的目标函数值[Chrom,ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到父代,得到新种群XY=bs2rv(Chrom,FieldD);gen=gen+1; %代计数器增加%获取每代的最优解及其序号,Y为最优解,I为个体的序号[Y,I]=max(ObjV);trace(1:2,gen)=XY(I,:); %记下每代的最优值trace(3,gen)=Y; %记下每代的最优值endplot3(trace(1,:),trace(2,:),trace(3,:),'bo'); %画出每代的最优点grid on;plot3(XY(:,1),XY(:,2),ObjV,'bo'); %画出最后一代的种群hold off%% 画进化图figure(2);plot(1:MAXGEN,trace(3,:));grid onxlabel('遗传代数')ylabel('解的变化')title('进化过程')bestZ=trace(3,end);bestX=trace(1,end);bestY=trace(2,end);fprintf(['最优解:\nX=',num2str(bestX),'\nY=',num2str(bestY),'\nZ=',num2str(b estZ), '\n'])</maxgen<></maxgen<>。

遗传算法投影寻踪模型matlab代码

遗传算法投影寻踪模型近年来，遗传算法在寻优问题中的应用越来越广泛，其中遗传算法投影寻踪模型在MATLAB代码中的实现备受关注。

本文将以此为主题，结合具体的内容，对遗传算法投影寻踪模型进行深入探讨。

一、遗传算法的原理1.1 遗传算法的基本概念遗传算法是一种基于生物进化过程的启发式优化技术，它模拟了自然选择和遗传机制，通过不断的迭代优化过程来寻找最优解。

遗传算法包括选择、交叉、变异等基本操作，其中选择过程通过适应度函数来评价个体的优劣，交叉过程通过染色体的交换来产生新的个体，变异过程通过基因的随机改变来增加种群的多样性。

1.2 遗传算法的应用领域遗传算法广泛应用于优化问题、机器学习、神经网络、信号处理、图像处理等领域，在工程、科学领域有着重要的应用价值。

二、投影寻踪模型的概念2.1 投影寻踪模型的基本原理投影寻踪模型是一种在信号处理领域中常用的算法，其基本原理是通过对信号进行投影变换来实现信号的降维和提取特征。

2.2 投影寻踪模型的应用投影寻踪模型在语音识别、图像处理、数据压缩等方面有着广泛的应用，是一种常见的信号处理技术。

三、MATLAB代码实现3.1 MATLAB环境准备在进行遗传算法投影寻踪模型的实现之前，首先需要在MATLAB环境中准备好相应的工具箱和设置参数。

3.2 遗传算法投影寻踪模型代码编写通过MATLAB的编程能力，可以实现遗传算法投影寻踪模型的代码编写，包括遗传算法的参数设置、适应度函数的定义、种群的初始化、交叉和变异操作的实现等步骤。

3.3 代码调试和优化在编写完整的遗传算法投影寻踪模型代码后，需要进行充分的调试和优化，确保代码的正确性和效率。

四、实验结果分析4.1 实验数据准备在进行实验结果分析之前，需要准备相应的实验数据集，以便进行测试和对比分析。

4.2 结果对比分析通过对遗传算法投影寻踪模型的实验结果进行对比分析，可以评估其算法性能和适用范围，与其他优化算法进行效果比较。

4.3 结果展示与解读最后需要将实验结果进行展示，并对结果进行解读和分析，从数学模型和应用角度分析遗传算法投影寻踪模型的优缺点和改进方向。

遗传算法matlab实现源程序

附页：一．遗传算法源程序：clc;clear;population;%评价目标函数值for uim=1:popsizevector=population(uim,:);obj(uim)=hanshu(hromlength,vector,phen); end%obj%min(obj)clear uim;objmin=min(obj);for sequ=1:popsizeif obj(sequ)==objminopti=population(sequ,:);endendclear sequ;fmax=22000;%==for gen=1:maxgen%选择操作%将求最小值的函数转化为适应度函数for indivi=1:popsizeobj1(indivi)=1/obj(indivi);endclear indivi;%适应度函数累加总合total=0;for indivi=1:popsizetotal=total+obj1(indivi);endclear indivi;%每条染色体被选中的几率for indivi=1:popsizefitness1(indivi)=obj1(indivi)/total;endclear indivi;%各条染色体被选中的范围for indivi=1:popsizefitness(indivi)=0;for j=1:indivifitness(indivi)=fitness(indivi)+fitness1(j);endendclear j;fitness;%选择适应度高的个体for ranseti=1:popsizeran=rand;while (ran>1||ran<0)ran=rand;endran;if ran<=fitness(1)newpopulation(ranseti,:)=population(1,:);elsefor fet=2:popsizeif (ran>fitness(fet-1))&&(ran<=fitness(fet))newpopulation(ranseti,:)=population(fet,:);endendendendclear ran;newpopulation;%交叉for int=1:2:popsize-1popmoth=newpopulation(int,:);popfath=newpopulation(int+1,:);popcross(int,:)=popmoth;popcross(int+1,:)=popfath;randnum=rand;if(randnum< P>cpoint1=round(rand*hromlength);cpoint2=round(rand*hromlength);while (cpoint2==cpoint1)cpoint2=round(rand*hromlength);endif cpoint1>cpoint2tem=cpoint1;cpoint1=cpoint2;cpoint2=tem;endcpoint1;cpoint2;for term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int,ss)==popfath(term)tem1=popcross(int,ss);popcross(int,ss)=popcross(int,term);popcross(int,term)=tem1;endendclear tem1;endfor term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int+1,ss)==popmoth(term)tem1=popcross(int+1,ss);popcross(int+1,ss)=popcross(int+1,term);popcross(int+1,term)=tem1;endendclear tem1;endendclear term;endclear randnum;popcross;%变异操作newpop=popcross;for int=1:popsizerandnum=rand;if randnumcpoint12=round(rand*hromlength);cpoint22=round(rand*hromlength);if (cpoint12==0)cpoint12=1;endif (cpoint22==0)cpoint22=1;endwhile (cpoint22==cpoint12)cpoint22=round(rand*hromlength);if cpoint22==0;cpoint22=1;endendtemp=newpop(int,cpoint12);newpop(int,cpoint12)=newpop(int,cpoint22);newpop(int,cpoint22)=temp;endendnewpop;clear cpoint12;clear cpoint22;clear randnum;clear int;for ium=1:popsizevector1=newpop(ium,:);obj1(ium)=hanshu(hromlength,vector1,phen);endclear ium;obj1max=max(obj1);for ar=1:popsizeif obj1(ar)==obj1maxnewpop(ar,:)=opti;endend%遗传操作结束二．粒子群算法源程序：%------初始格式化-------------------------------------------------- clear all;clc;format long;%------给定初始化条件---------------------------------------------- c1=1.4962;%学习因子1c2=1.4962;%学习因子2w=0.7298;%惯性权重MaxDT=100;%最大迭代次数D=2;%搜索空间维数（未知数个数）N=40;%初始化群体个体数目eps=10^(-6);%设置精度(在已知最小值时候用)%------初始化种群的个体(可以在这里限定位置和速度的范围)------------ for i=1:Nfor j=1:Dx(i,j)=randn;%随机初始化位置v(i,j)=randn;%随机初始化速度endend%------先计算各个粒子的适应度，并初始化Pi和Pg---------------------- for i=1:Np(i)=fitness(x(i,:),D);y(i,:)=x(i,:);endpg=x(1,:);%Pg为全局最优for i=2:Nif fitness(x(i,:),D)<FITNESS(pg,D)pg=x(i,:);endend%------进入主要循环，按照公式依次迭代，直到满足精度要求------------ for t=1:MaxDTtfor i=1:Nv(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:)); x(i,:)=x(i,:)+v(i,:);if fitness(x(i,:),D)<p(i)p(i)=fitness(x(i,:),D);y(i,:)=x(i,:);endif p(i)<FITNESS(pg,D)pg=y(i,:);endendPbest(t)=fitness(pg,D);end%------进入主要循环，按照公式依次迭代，直到满足精度要求------------ for t=1:MaxDTfor i=1:Nv(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));x(i,:)=x(i,:)+v(i,:);if fitness(x(i,:),D)<p(i)p(i)=fitness(x(i,:),D);y(i,:)=x(i,:);endif p(i)<FITNESS(pg,D)pg=y(i,:);endendPbest(t)=fitness(pg,D);end%------最后给出计算结果disp('*************************************************************') disp('函数的全局最优位置为：')Solution=pg'disp('最后得到的优化极值为：')Result=fitness(pg,D)disp('*************************************************************') [X,Y]=meshgrid(-500:2:500);Z=X.*sin(sqrt(X))+Y.*(sin(sqrt(Y)));hold oncontour(X,Y,Z)plot(x(:,1),x(:,2),'*');hold off标准文档实用文案。

遗传算法的Matlab实现讲解

Matlab编程实现GA
初始化(编码)
% initpop.m函数的功能是实现群体的初始化，popsize表示群体的大小， chromlength表示染色体的长度(二值数的长度)， % 长度大小取决于变量的二进制编码的长度(在本例中取20位)。
%Name: initpop.m
function pop=initpop(popsize,chromlength) pop=round(rand(popsize,chromlength)); % rand随机产生每个单元为 {0,1} 行数为popsize，列数为chromlength的矩阵， % round对矩阵的每个单元进行取整。这样产生的初始种群。
temp1=decodechrom(pop,1,chromlength); %将pop每行转化成十进制数
x=temp1*(Xmax-Xmin)/(2^chromlength-1); %将十进制域中的数转化为变量域的数 objvalue=2*x+10*sin(5*x)+7*cos(4*x); %计算目标函数值
if any(newpop(i,mpoint))==0
newpop(i,mpoint)=1; else newpop(i,mpoint)=0; end
Matlab编程实现GA
求出群体中最大的适应值及其个体
function [bestindividual, bestfit] … =best(pop, fitvalue) [px,py]=size(pop); 或 function [bestindividual, bestfit]=… best(pop, fitvalue) [bestfit,m_indx]=max(fitvalue); bestindividual=pop(m_indx,:);

遗传算法Matlab源代码

遗传算法Matlab源代码完整可以运行的数值优化遗传算法源代码function[X,MaxFval,BestPop,Trace]=fga(FUN,bounds,MaxEranum,PopSiz e,options,pCross,pMutation,pInversion)%[X,MaxFval,BestPop,Trace]=fga(FUN,bounds,MaxEranum,PopSiz e,options,pCross,pMutation,pInversion)% Finds a maximum of a function of several variables.% fga solves problems of the form:% max F(X) subject to: LB = X = UB (LB=bounds(:,1),UB=bounds(:,2))% X - 最优个体对应自变量值% MaxFval - 最优个体对应函数值% BestPop - 最优的群体即为最优的染色体群% Trace - 每代最佳个体所对应的目标函数值% FUN - 目标函数% bounds - 自变量范围% MaxEranum - 种群的代数,取50--500(默认200)% PopSize - 每一代种群的规模；此可取50--200(默认100)% pCross - 交叉概率,一般取0.5--0.85之间较好(默认0.8)% pMutation - 初始变异概率,一般取0.05-0.2之间较好(默认0.1)% pInversion - 倒位概率,一般取0.05－0.3之间较好(默认0.2) % options - 1*2矩阵,options(1)=0二进制编码(默认0),option(1)~=0十进制编码,option(2)设定求解精度(默认1e-4)T1=clock;%检验初始参数if nargin2, error('FMAXGA requires at least three input arguments'); endif nargin==2, MaxEranum=150;PopSize=100;options=[1 1e-4];pCross=0.85;pMutation=0.1;pInversion=0.25;endif nargin==3, PopSize=100;options=[1 1e-4];pCross=0.85;pMutation=0.1;pInversion=0.25;endif nargin==4, options=[1 1e-4];pCross=0.85;pMutation=0.1;pInversion=0.25;endif nargin==5, pCross=0.85;pMutation=0.1;pInversion=0.25;endif nargin==6, pMutation=0.1;pInversion=0.25;endif nargin==7, pInversion=0.25;endif (options(1)==0|options(1)==1)find((bounds(:,1)-bounds(:,2))0)error('数据输入错误,请重新输入:');end% 定义全局变量global m n NewPop children1 children2 VarNum% 初始化种群和变量precision = options(2);bits = ceil(log2((bounds(:,2)-bounds(:,1))' ./ precision));%由设定精度划分区间VarNum = size(bounds,1);[Pop] = InitPop(PopSize,bounds,bits,options);%初始化种群[m,n] = size(Pop);fit = zeros(1,m);NewPop = zeros(m,n);children1 = zeros(1,n);children2 = zeros(1,n);pm0 = pMutation;BestPop = zeros(MaxEranum,n);%分配初始解空间BestPop,TraceTrace = zeros(1,MaxEranum);完整可以运行的数值优化遗传算法源代码Lb = ones(PopSize,1)*bounds(:,1)';Ub = ones(PopSize,1)*bounds(:,2)';%二进制编码采用多点交叉和均匀交叉，并逐步增大均匀交叉概率%浮点编码采用离散交叉（前期）、算术交叉（中期）、AEA重组（后期）OptsCrossOver = [ones(1,MaxEranum)*options(1);...round(unidrnd(2*(MaxEranum-[1:MaxEranum]))/MaxEranum)]';%浮点编码时采用两种自适应变异和一种随机变异（自适应变异发生概率为随机变异发生的2倍）OptsMutation = [ones(1,MaxEranum)*options(1);unidrnd(5,1,MaxEranum)]';if options(1)==3D=zeros(n);CityPosition=bounds;D = sqrt((CityPosition(:, ones(1,n)) - CityPosition(:, ones(1,n))').^2 +...(CityPosition(:,2*ones(1,n)) - CityPosition(:,2*ones(1,n))').^2 );end%========================================================================== % 进化主程序%%===================================== ===================================== eranum = 1;H=waitbar(0,'Please wait...');while(eranum=MaxEranum)for j=1:mif options(1)==1%eval(['[fit(j)]=' FUN '(Pop(j,:));']);%但执行字符串速度比直接计算函数值慢fit(j)=feval(FUN,Pop(j,:));%计算适应度elseif options(1)==0%eval(['[fit(j)]=' FUN '(b2f(Pop(j,:),bounds,bits));']);fit(j)=feval(FUN,(b2f(Pop(j,:),bounds,bits)));elsefit(j)=-feval(FUN,Pop(j,:),D);endend[Maxfit,fitIn]=max(fit);%得到每一代最大适应值Meanfit(eranum)=mean(fit);BestPop(eranum,:)=Pop(fitIn,:);Trace(eranum)=Maxfit;if options(1)==1Pop=(Pop-Lb)./(Ub-Lb);%将定义域映射到[0,1]：[Lb,Ub]--[0,1] ,Pop--(Pop-Lb)./(Ub-Lb)endswitch round(unifrnd(0,eranum/MaxEranum))%进化前期尽量使用实行锦标赛选择，后期逐步增大非线性排名选择case {0} [selectpop]=TournamentSelect(Pop,fit,bits);%锦标赛选择case {1}[selectpop]=NonlinearRankSelect(Pop,fit,bits);%非线性排名选择end完整可以运行的数值优化遗传算法源代码[CrossOverPop]=CrossOver(selectpop,pCross,OptsCrossOver(er anum,:));%交叉[MutationPop]=Mutation(CrossOverPop,fit,pMutation,VarNum,O ptsMutation(eranum,:)); %变异[InversionPop]=Inversion(MutationPop,pInversion);%倒位%更新种群if options(1)==1Pop=Lb+InversionPop.*(Ub-Lb);%还原PopelsePop=InversionPop;endpMutation=pm0+(eranum^3)*(pCross/2-pm0)/(eranum^4); %逐步增大变异率至1/2交叉率percent=num2str(round(100*eranum/MaxEranum));waitbar(eranum/MaxEranum,H,['Evolution complete ',percent,'%']);eranum=eranum+1;endclose(H);% 格式化输出进化结果和解的变化情况t=1:MaxEranum;plot(t,Trace,t,Meanfit);legend('解的变化','种群的变化');title('函数优化的遗传算法');xlabel('进化世代数');ylabel('每一代最优适应度');[MaxFval,MaxFvalIn]=max(Trace);if options(1)==1|options(1)==3X=BestPop(MaxFvalIn,:);elseif options(1)==0X=b2f(BestPop(MaxFvalIn,:),bounds,bits);endhold on;plot(MaxFvalIn,MaxFval,'*');text(MaxFvalIn+5,MaxFval,['FMAX=' num2str(MaxFval)]);str1=sprintf(' Best generation:\n %d\n\n Best X:\n %s\n\n MaxFval\n %f\n',...MaxFvalIn,num2str(X),MaxFval);disp(str1);% -计时T2=clock;elapsed_time=T2-T1;if elapsed_time(6)0elapsed_time(6)=elapsed_time(6)+60;elapsed_time(5)=elapsed_time(5)-1;endif elapsed_time(5)0elapsed_time(5)=elapsed_time(5)+60;elapsed_time(4)=elapsed_t ime(4)-1;end完整可以运行的数值优化遗传算法源代码str2=sprintf('elapsed_time\n %d (h) %d (m) %.4f (s)',elapsed_time(4),elapsed_time(5),elapsed_time(6));disp(str2);%===================================== ===================================== % 遗传操作子程序%%===================================== ===================================== % -- 初始化种群--% 采用浮点编码和二进制Gray编码(为了克服二进制编码的Hamming悬崖缺点)function [initpop]=InitPop(popsize,bounds,bits,options)numVars=size(bounds,1);%变量数目rang=(bounds(:,2)-bounds(:,1))';%变量范围if options(1)==1initpop=zeros(popsize,numVars);initpop=(ones(popsize,1)*rang).*(rand(popsize,numVars))+(ones (popsize,1)*bounds(:,1)');elseif options(1)==0precision=options(2);%由求解精度确定二进制编码长度len=sum(bits);initpop=zeros(popsize,len);%The whole zero encoding individualfor i=2:popsize-1pop=round(rand(1,len));pop=mod(([0 pop]+[pop 0]),2);%i=1时,b(1)=a(1);i1时,b(i)=mod(a(i-1)+a(i),2)%其中原二进制串:a(1)a(2)...a(n),Gray串:b(1)b(2)...b(n)initpop(i,:)=pop(1:end-1);endinitpop(popsize,:)=ones(1,len);%The whole one encoding individualelsefor i=1:popsizeinitpop(i,:)=randperm(numVars);%为Tsp问题初始化种群endend% -- 二进制串解码--function [fval] = b2f(bval,bounds,bits)% fval - 表征各变量的十进制数% bval - 表征各变量的二进制编码串% bounds - 各变量的取值范围% bits - 各变量的二进制编码长度scale=(bounds(:,2)-bounds(:,1))'./(2.^bits-1); %The range of the variablesnumV=size(bounds,1);cs=[0 cumsum(bits)];for i=1:numVa=bval((cs(i)+1):cs(i+1));fval(i)=sum(2.^(size(a,2)-1:-1:0).*a)*scale(i)+bounds(i,1);end% -- 选择操作--完整可以运行的数值优化遗传算法源代码% 采用基于轮盘赌法的非线性排名选择% 各个体成员按适应值从大到小分配选择概率：% P(i)=(q/1-(1-q)^n)*(1-q)^i, 其中P(0)P(1)...P(n), sum(P(i))=1function [NewPop]=NonlinearRankSelect(OldPop,fit,bits) global m n NewPopfit=fit';selectprob=fit/sum(fit);%计算各个体相对适应度(0,1)q=max(selectprob);%选择最优的概率x=zeros(m,2);x(:,1)=[m:-1:1]';[y x(:,2)]=sort(selectprob);r=q/(1-(1-q)^m);%标准分布基值newfit(x(:,2))=r*(1-q).^(x(:,1)-1);%生成选择概率newfit=[0 cumsum(newfit)];%计算各选择概率之和rNums=rand(m,1);newIn=1;while(newIn=m)NewPop(newIn,:)=OldPop(length(find(rNums(newIn)newfit)),:);newIn=newIn+1;end% -- 锦标赛选择(含精英选择) --function [NewPop]=TournamentSelect(OldPop,fit,bits)global m n NewPopnum=floor(m./2.^(1:10));num(find(num==0))=[];L=length(num);a=sum(num);b=m-a;PopIn=1;while(PopIn=L)r=unidrnd(m,num(PopIn),2^PopIn);[LocalMaxfit,In]=max(fit(r),[],2);SelectIn=r((In-1)*num(PopIn)+[1:num(PopIn)]');NewPop(sum(num(1:PopIn))-num(PopIn)+1:sum(num(1:PopIn)),:)=OldPop(SelectIn,:);PopIn=PopIn+1;r=[];In=[];LocalMaxfit=[];endif b1NewPop((sum(num)+1):(sum(num)+b-1),:)=OldPop(unidrnd(m,1,b-1),:);end[GlobalMaxfit,I]=max(fit);%保留每一代中最佳个体NewPop(end,:)=OldPop(I,:);% -- 交叉操作--function [NewPop]=CrossOver(OldPop,pCross,opts)global m n NewPopr=rand(1,m);完整可以运行的数值优化遗传算法源代码y1=find(rpCross);y2=find(r=pCross);len=length(y1);if len==1|(len2mod(len,2)==1)%如果用来进行交叉的染色体的条数为奇数，将其调整为偶数y2(length(y2)+1)=y1(len);y1(len)=[];endi=0;if length(y1)=2if opts(1)==1%浮点编码交叉while(i=length(y1)-2)NewPop(y1(i+1),:)=OldPop(y1(i+1),:);NewPop(y1(i+2),:)=OldPop(y1(i+2),:);if opts(2)==0n1%discret crossoverPoints=sort(unidrnd(n,1,2));NewPop(y1(i+1),Points(1):Points(2))=OldPop(y1(i+2),Points(1):Po ints(2));NewPop(y1(i+2),Points(1):Points(2))=OldPop(y1(i+1),Points(1):Po ints(2));elseif opts(2)==1%arithmetical crossoverPoints=round(unifrnd(0,pCross,1,n));CrossPoints=find(Points==1);r=rand(1,length(CrossPoints));NewPop(y1(i+1),CrossPoints)=r.*OldPop(y1(i+1),CrossPoints)+(1 -r).*OldPop(y1(i+2),CrossPoints);NewPop(y1(i+2),CrossPoints)=r.*OldPop(y1(i+2),CrossPoints)+(1 -r).*OldPop(y1(i+1),CrossPoints); else %AEA recombination Points=round(unifrnd(0,pCross,1,n));CrossPoints=find(Points==1);v=unidrnd(4,1,2);NewPop(y1(i+1),CrossPoints)=(floor(10^v(1)*OldPop(y1(i+1),Cro ssPoints))+...10^v(1)*OldPop(y1(i+2),CrossPoints)-floor(10^v(1)*OldPop(y1(i+2),CrossPoints)))/10^v(1);NewPop(y1(i+2),CrossPoints)=(floor(10^v(2)*OldPop(y1(i+2),Cro ssPoints))+...10^v(2)*OldPop(y1(i+1),CrossPoints)-floor(10^v(2)*OldPop(y1(i+1),CrossPoints)))/10^v(2);endi=i+2;endelseif opts(1)==0%二进制编码交叉while(i=length(y1)-2)if opts(2)==0[NewPop(y1(i+1),:),NewPop(y1(i+2),:)]=EqualCrossOver(OldPop( y1(i+1),:),OldPop(y1(i+2),:)); else[NewPop(y1(i+1),:),NewPop(y1(i+2),:)]=MultiPointCross(OldPop( y1(i+1),:),OldPop(y1(i+2),:)); endi=i+2;endelse %Tsp问题次序杂交for i=0:2:length(y1)-2xPoints=sort(unidrnd(n,1,2));NewPop([y1(i+1)y1(i+2)],xPoints(1):xPoints(2))=OldPop([y1(i+2)y1(i+1)],xPoints(1):xPoints(2));完整可以运行的数值优化遗传算法源代码%NewPop(y1(i+2),xPoints(1):xPoints(2))=OldPop(y1(i+1),xPo ints(1):xPoints(2));temp=[OldPop(y1(i+1),xPoints(2)+1:n)OldPop(y1(i+1),1:xPoints(2))];for del1i=xPoints(1):xPoints(2)temp(find(temp==OldPop(y1(i+2),del1i)))=[];endNewPop(y1(i+1),(xPoints(2)+1):n)=temp(1:(n-xPoints(2)));NewPop(y1(i+1),1:(xPoints(1)-1))=temp((n-xPoints(2)+1):end);temp=[OldPop(y1(i+2),xPoints(2)+1:n)OldPop(y1(i+2),1:xPoints(2))];for del2i=xPoints(1):xPoints(2)temp(find(temp==OldPop(y1(i+1),del2i)))=[];endNewPop(y1(i+2),(xPoints(2)+1):n)=temp(1:(n-xPoints(2)));NewPop(y1(i+2),1:(xPoints(1)-1))=temp((n-xPoints(2)+1):end);endendendNewPop(y2,:)=OldPop(y2,:);% -二进制串均匀交叉算子function[children1,children2]=EqualCrossOver(parent1,parent2) global n children1 children2hidecode=round(rand(1,n));%随机生成掩码crossposition=find(hidecode==1);holdposition=find(hidecode==0);children1(crossposition)=parent1(crossposition);%掩码为1，父1为子1提供基因children1(holdposition)=parent2(holdposition);%掩码为0，父2为子1提供基因children2(crossposition)=parent2(crossposition);%掩码为1，父2为子2提供基因children2(holdposition)=parent1(holdposition);%掩码为0，父1为子2提供基因% -二进制串多点交叉算子function[Children1,Children2]=MultiPointCross(Parent1,Parent2)%交叉点数由变量数决定global n Children1 Children2 VarNumChildren1=Parent1;Children2=Parent2;Points=sort(unidrnd(n,1,2*VarNum));for i=1:VarNumChildren1(Points(2*i-1):Points(2*i))=Parent2(Points(2*i-1):Points(2*i));Children2(Points(2*i-1):Points(2*i))=Parent1(Points(2*i-1):Points(2*i));end% -- 变异操作--function[NewPop]=Mutation(OldPop,fit,pMutation,VarNum,opts) global m n NewPopNewPop=OldPop;r=rand(1,m);MutIn=find(r=pMutation);L=length(MutIn);完整可以运行的数值优化遗传算法源代码i=1;if opts(1)==1%浮点变异maxfit=max(fit);upfit=maxfit+0.05*abs(maxfit);if opts(2)==1|opts(2)==3while(i=L)%自适应变异（自增或自减）Point=unidrnd(n);T=(1-fit(MutIn(i))/upfit)^2;q=abs(1-rand^T);%if q1%按严格数学推理来说，这段程序是不能缺少的% q=1%endp=OldPop(MutIn(i),Point)*(1-q);if unidrnd(2)==1NewPop(MutIn(i),Point)=p+q;elseNewPop(MutIn(i),Point)=p;endi=i+1;endelseif opts(2)==2|opts(2)==4%AEA变异（任意变量的某一位变异）while(i=L)Point=unidrnd(n);T=(1-abs(upfit-fit(MutIn(i)))/upfit)^2;v=1+unidrnd(1+ceil(10*T));%v=1+unidrnd(5+ceil(10*eranum/MaxEranum));q=mod(floor(OldPop(MutIn(i),Point)*10^v),10);NewPop(MutIn(i),Point)=OldPop(MutIn(i),Point)-(q-unidrnd(9))/10^v;i=i+1;endelsewhile(i=L)Point=unidrnd(n);if round(rand)NewPop(MutIn(i),Point)=OldPop(MutIn(i),Point)*(1-rand);elseNewPop(MutIn(i),Point)=OldPop(MutIn(i),Point)+(1-OldPop(MutIn(i),Point))*rand; endi=i+1;endendelseif opts(1)==0%二进制串变异if L=1while i=Lk=unidrnd(n,1,VarNum); %设置变异点数(=变量数)for j=1:length(k)if NewPop(MutIn(i),k(j))==1NewPop(MutIn(i),k(j))=0;else完整可以运行的数值优化遗传算法源代码NewPop(MutIn(i),k(j))=1;endendi=i+1;endendelse%Tsp变异if opts(2)==1|opts(2)==2|opts(2)==3|opts(2)==4numMut=ceil(pMutation*m);r=unidrnd(m,numMut,2);[LocalMinfit,In]=min(fit(r),[],2);SelectIn=r((In-1)*numMut+[1:numMut]');while(i=numMut)mPoints=sort(unidrnd(n,1,2));if mPoints(1)~=mPoints(2)NewPop(SelectIn(i),1:mPoints(1)-1)=OldPop(SelectIn(i),1:mPoints(1)-1);NewPop(SelectIn(i),mPoints(1):mPoints(2)-1)=OldPop(SelectIn(i),mPoints(1)+1:mPoints(2));NewPop(SelectIn(i),mPoints(2))=OldPop(SelectIn(i),mPoints(1));NewPop(SelectIn(i),mPoints(2)+1:n)=OldPop(SelectIn(i),mPoints( 2)+1:n);elseNewPop(SelectIn(i),:)=OldPop(SelectIn(i),:);endi=i+1;endr=rand(1,m);MutIn=find(r=pMutation);L=length(MutIn);while i=LmPoints=sort(unidrnd(n,1,2));rIn=randperm(mPoints(2)-mPoints(1)+1);NewPop(MutIn(i),mPoints(1):mPoints(2))=OldPop(MutIn(i),mPoin ts(1)+rIn-1);i=i+1;endendend% -- 倒位操作--function [NewPop]=Inversion(OldPop,pInversion)global m n NewPopNewPop=OldPop;r=rand(1,m);PopIn=find(r=pInversion);len=length(PopIn);if len=1while(i=len)d=sort(unidrnd(n,1,2));完整可以运行的数值优化遗传算法源代码NewPop(PopIn(i),d(1):d(2))=OldPop(PopIn(i),d(2):-1:d(1)); i=i+1;。

基于加速遗传算法的投影寻踪模型代码

基于加速遗传算法的投影寻踪模型代码以下是一个基于加速遗传算法的投影寻踪模型的代码示例：```pythonimport numpy as npdef fitness_function(x, y):#计算适应度函数#在此示例中，适应度函数计算点(x,y)到目标点的距离target_point = (5, 5)distance = np.sqrt((x - target_point[0])**2 + (y -target_point[1])**2)return 1 / (distance + 1)def selection(population, fitness_values, num_parents):#选择函数，选出适应度较高的个体作为父代parents = []for i in range(num_parents):max_index = np.argmax(fitness_values)parents.append(population[max_index])fitness_values[max_index] = -1 # 将已选个体的适应度设为负数，防止重复选择return parentsdef crossover(parents, num_offsprings):#交叉操作，生成新的子代个体offsprings = []for i in range(num_offsprings):parent1 = parents[i % len(parents)]parent2 = parents[(i+1) % len(parents)]offspring = (parent1[0], parent2[1])offsprings.append(offspring)return offspringsdef mutation(offsprings, mutation_rate):#变异操作for i in range(len(offsprings)):if np.random.uniform(0, 1) < mutation_rate:x = offsprings[i][0]y = offsprings[i][1]mutation_value = np.random.uniform(-1, 1) # 从[-1, 1]区间随机选择一个值来增加变异x += mutation_valuey += mutation_valueoffsprings[i] = (x, y)return offspringsdef genetic_algorithm(population, num_generations,num_parents, num_offsprings, mutation_rate):for generation in range(num_generations):fitness_values = []for i in range(len(population)):x = population[i][0]y = population[i][1]fitness = fitness_function(x, y)fitness_values.append(fitness)parents = selection(population, fitness_values, num_parents) offsprings = crossover(parents, num_offsprings)offsprings = mutation(offsprings, mutation_rate)population = parents + offspringsbest_solution_index = np.argmax(fitness_values)best_solution = population[best_solution_index]return best_solution#设置模型参数num_parents = 10num_offsprings = 100num_generations = 100mutation_rate = 0.1#生成初始种群population = []for _ in range(num_parents):x = np.random.uniform(0, 10)y = np.random.uniform(0, 10)population.append((x, y))#使用遗传算法找到最佳解best_solution = genetic_algorithm(population,num_generations, num_parents, num_offsprings, mutation_rate) print("最佳解：", best_solution)```这个代码示例实现了一个简单的投影寻踪模型，使用加速遗传算法来找到最佳解。

遗传算法MATLAB完整代码

遗传算法解决简单问题%主程序：用遗传算法求解y=200*exp*x).*sin(x)在区间[-2,2]上的最大值clc;clear all;close all;global BitLengthglobal boundsbeginglobal boundsendbounds=[-2,2];precision=;boundsbegin=bounds(:,1);boundsend=bounds(:,2);%计算如果满足求解精度至少需要多长的染色体BitLength=ceil(log2((boundsend-boundsbegin)'./precision));popsize=50; %初始种群大小Generationmax=12; %最大代数pcrossover=; %交配概率pmutation=; %变异概率%产生初始种群population=round(rand(popsize,BitLength));%计算适应度，返回适应度Fitvalue和累计概率cumsump [Fitvalue,cumsump]=fitnessfun(population);Generation=1;while Generation<Generationmax+1for j=1:2:popsize%选择操作seln=selection(population,cumsump);%交叉操作scro=crossover(population,seln,pcrossover);scnew(j,:)=scro(1,:);scnew(j+1,:)=scro(2,:);%变异操作smnew(j,:)=mutation(scnew(j,:),pmutation);smnew(j+1,:)=mutation(scnew(j+1,:),pmutation);endpopulation=scnew; %产生了新的种群%计算新种群的适应度[Fitvalue,cumsump]=fitnessfun(population);%记录当前代最好的适应度和平均适应度[fmax,nmax]=max(Fitvalue);fmean=mean(Fitvalue);ymax(Generation)=fmax;ymean(Generation)=fmean;%记录当前代的最佳染色体个体x=transform2to10(population(nmax,:));%自变量取值范围是[-2,2],需要把经过遗传运算的最佳染色体整合到[-2,2]区间xx=boundsbegin+x*(boundsend-boundsbegin)/(power((boundsend),BitLength)-1);xmax(Generation)=xx;Generation=Generation+1;endGeneration=Generation-1;Bestpopulation=xx;Besttargetfunvalue=targetfun(xx);%绘制经过遗传运算后的适应度曲线。

遗传算法 matlab程序

遗传算法 matlab程序遗传算法（Genetic Algorithm）是一种模拟生物进化过程的优化算法，主要用于解决复杂的优化问题。

在这篇文章中，我们将介绍如何使用MATLAB编写遗传算法的程序，并展示其在实际问题中的应用。

我们需要明确遗传算法的基本原理。

遗传算法通过模拟自然选择、交叉和变异等基因操作，以产生新的解，并通过适应度函数评估每个解的优劣。

通过不断迭代，遗传算法逐渐找到最优解。

在MATLAB中，我们可以使用遗传算法工具箱来实现遗传算法的程序。

首先，我们需要定义问题的目标函数和约束条件。

目标函数是我们希望优化的函数，而约束条件则是问题的限制条件。

在定义完目标函数和约束条件后，我们可以使用遗传算法工具箱中的函数来构建遗传算法的程序。

在遗传算法中，每个解都可以看作一个个体，而每个个体都由一串基因表示。

在MATLAB中，我们可以用一个二进制字符串来表示一个个体。

例如，一个8位的二进制字符串可以表示一个整数值或一个实数值。

在遗传算法中，这个二进制字符串称为染色体。

在遗传算法的程序中，我们需要定义染色体的编码方式、交叉方式、变异方式等。

编码方式决定了染色体的表示方法，常见的编码方式有二进制编码和实数编码。

交叉方式决定了如何将两个染色体进行交叉操作，常见的交叉方式有单点交叉和多点交叉。

变异方式决定了如何对染色体进行变异操作，常见的变异方式有位变异和基因变异。

在编写遗传算法的程序时，我们需要定义适应度函数来评估每个个体的优劣。

适应度函数的值越大，说明个体的优势越大。

根据适应度函数的值，我们可以选择一些优秀的个体进行交叉和变异操作，以产生新的解。

在MATLAB中，我们可以使用遗传算法工具箱中的函数来进行遗传算法的迭代过程。

通过设置迭代次数和种群大小等参数，我们可以控制算法的运行过程。

在每次迭代中，遗传算法会根据适应度函数的值选择一些优秀的个体，进行交叉和变异操作，以产生新的解。

经过多次迭代后，遗传算法会逐渐找到最优解。

遗传算法matlab程序代码

function [R,Rlength]= GA_TSP(xyCity,dCity,Population,nPopulation,pCrossover,percent,pMutation,generation,nR,rr,rang eCity,rR,moffspring,record,pi,Shock,maxShock)clear allA=load('d.txt');AxyCity=[A(1,:);A(2,:)]; %x,y为各地点坐标xyCityfigure(1)grid onhold onscatter(xyCity(1,:),xyCity(2,:),'b+')grid onnCity=50;nCityfor i=1:nCity %计算城市间距离for j=1:nCitydCity(i,j)=abs(xyCity(1,i)-xyCity(1,j))+abs(xyCity(2,i)-xyCity(2,j));endend %计算城市间距离xyCity; %显示城市坐标dCity %显示城市距离矩阵%初始种群k=input('取点操作结束'); %取点时对操作保护disp('-------------------')nPopulation=input('种群个体数量：'); %输入种群个体数量if size(nPopulation,1)==0nPopulation=50; %默认值endfor i=1:nPopulationPopulation(i,:)=randperm(nCity-1); %产生随机个体endPopulation %显示初始种群pCrossover=input('交叉概率：'); %输入交叉概率percent=input('交叉部分占整体的百分比：'); %输入交叉比率pMutation=input('突变概率：'); %输入突变概率nRemain=input('最优个体保留最大数量：');pi(1)=input('选择操作最优个体被保护概率：');%输入最优个体被保护概率pi(2)=input('交叉操作最优个体被保护概率：');pi(3)=input('突变操作最优个体被保护概率：');maxShock=input('最大突变概率：');if size(pCrossover,1)==0pCrossover=0.85;endif size(percent,1)==0percent=0.5;endif size(pMutation,1)==0pMutation=0.05;endShock=0;rr=0;Rlength=0;counter1=0;counter2=0;R=zeros(1,nCity-1);[newPopulation,R,Rlength,counter2,rr]=select(Population,nPopulation,nCity,dCity,Rlength,R,coun ter2,pi,nRemain);R0=R;record(1,:)=R;rR(1)=Rlength;Rlength0=Rlength;generation=input('算法终止条件A.最多迭代次数：');%输入算法终止条件if size(generation,1)==0generation=200;endnR=input('算法终止条件B.最短路径连续保持不变代数：');if size(nR,1)==0nR=10;endwhile counter1<generation&counter2<nRif counter2<nR*1/5Shock=0;elseif counter2<nR*2/5Shock=maxShock*1/4-pMutation;elseif counter2<nR*3/5Shock=maxShock*2/4-pMutation;elseif counter2<nR*4/5Shock=maxShock*3/4-pMutation;elseShock=maxShock-pMutation;endcounter1newPopulationoffspring=crossover(newPopulation,nCity,pCrossover,percent,nPopulation,rr,pi,nRemain);offspringmoffspring=Mutation(offspring,nCity,pMutation,nPopulation,rr,pi,nRemain,Shock);[newPopulation,R,Rlength,counter2,rr]=select(moffspring,nPopulation,nCity,dCity,Rlength,R,coun ter2,pi,nRemain);counter1=counter1+1;rR(counter1+1)=Rlength;record(counter1+1,:)=R;endR0;Rlength0;R;Rlength;minR=min(rR);disp('最短路经出现代数:')rr=find(rR==minR)disp('最短路经:')record(rr,:);mR=record(rr(1,1),:)disp('终止条件一:')counter1disp('终止条件二:')counter2disp('最短路经长度:')minRdisp('最初路经长度:')rR(1)figure(2)plotaiwa(xyCity,mR,nCity)figure(3)i=1:counter1+1;plot(i,rR(i))grid onfunction[newPopulation,R,Rlength,counter2,rr]=select(Population,nPopulation,nCity,dCity,Rlength,R,coun ter2,pi,nRemain)Distance=zeros(nPopulation,1); %零化路径长度Fitness=zeros(nPopulation,1); %零化适应概率Sum=0; %路径长度for i=1:nPopulation %计算个体路径长度for j=1:nCity-2Distance(i)=Distance(i)+dCity(Population(i,j),Population(i,j+1));end %对路径长度调整，增加起始点到路径首尾点的距离Distance(i)=Distance(i)+dCity(Population(i,1),nCity)+dCity(Population(i,nCity-1),nCity);Sum=Sum+Distance(i); %累计总路径长度end %计算个体路径长度if Rlength==min(Distance)counter2=counter2+1;elsecounter2=0;endRlength=min(Distance); %更新最短路径长度Rlength;rr=find(Distance==Rlength);R=Population(rr(1,1),:); %更新最短路径for i=1:nPopulationFitness(i)=(max(Distance)-Distance(i)+0.001)/(nPopulation*(max(Distance)+0.001)-Sum); %适应概率=个体/总和。

Matlab遗传算法的部分映射交叉算子（pmx）源码

01.‎02.% ‎P MX m‎e ans ‎G oldb‎e rg's‎Part‎i ally‎Mapp‎e d Cr‎o Ssov‎e r)‎03.% ‎P roce‎d ure ‎:PMX‎04.%‎Step‎1. Se‎l ect ‎t wo p‎o siti‎o ns a‎l ong ‎t he s‎t ring‎unif‎o rmly‎at r‎a ndom‎.05‎.% ‎‎T he s‎u bstr‎i ngs ‎d efin‎e d by‎the ‎t wo p‎o siti‎o ns a‎r e ca‎l led ‎t he m‎a ppin‎g sec‎t ions‎. 06‎.% ‎‎N ote:‎(You ‎c an w‎r ite ‎t o se‎l ect ‎a sta‎r t po‎i nt a‎n d a ‎l engt‎h)‎07.% ‎S tep2‎. Exc‎h ange‎two ‎s ubst‎r ings‎betw‎e en p‎a rent‎s to ‎p rodu‎c e pr‎o to-c‎h ildr‎e n.‎08.% ‎S tep3‎. Det‎e rmin‎e the‎mapp‎i ng r‎e lati‎o nshi‎p bet‎w een ‎t wo m‎a ppin‎g sec‎t ion.‎09.‎% Ste‎p4. L‎e gali‎z e of‎f spri‎n g wi‎t h th‎e map‎p ing ‎r elat‎i onsh‎i p.‎10.fu‎n ctio‎n [ne‎w Va,n‎e wVb]‎=PMX1‎(Va,V‎b)1‎1.fpr‎i ntf(‎'orig‎i nal ‎V a an‎d Vb ‎a re:\‎n')‎12.%V‎a= [ ‎1 6 1‎0 3 ‎9 4 5‎2 7 ‎8 ];‎13.%‎V b= [‎2 9 ‎1 4 ‎10 5 ‎6 8 3‎7 ];‎14.‎%Va=1‎:91‎5.%Vb‎=[5 4‎6 9 ‎2 1 7‎8 3]‎16.‎%----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-17‎.%Ste‎p1. S‎e lect‎two ‎p osit‎i ons ‎a long‎the ‎s trin‎g uni‎f orml‎y at ‎r ando‎m.1‎8.sta‎r tXor‎P oint‎=mod(‎c eil(‎r and(‎1)*10‎),len‎g th(V‎a) );‎19.‎i f st‎a rtXo‎r Poin‎t==0‎20. ‎ sta‎r tXor‎P oint‎=star‎t XorP‎o int+‎1;2‎1.end‎‎22.xo‎r Leng‎t h=mo‎d(flo‎o r(ra‎n d(1)‎*10),‎l engt‎h(Va)‎);2‎3.end‎X orPo‎i nt=s‎t artX‎o rPoi‎n t+xo‎r Leng‎t h;‎24.wh‎i le(e‎n dXor‎P oint‎>leng‎t h(Vb‎) )‎25. ‎xorL‎e ngth‎=mod(‎f loor‎(rand‎(1)*1‎0),le‎n gth(‎V a));‎26.‎ en‎d XorP‎o int=‎s tart‎X orPo‎i nt+x‎o rLen‎g th;‎27.e‎n d ‎28.‎f prin‎t f('\‎n The‎(sta‎r tXor‎P oint‎,endX‎o rPoi‎n t)=(‎%d,%d‎)\n',‎s tart‎X orPo‎i nt,e‎n dXor‎P oint‎) 29‎.%sta‎r tXor‎P oint‎=33‎0.%en‎d XorP‎o int=‎631‎.%---‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎--3‎2.% S‎t ep2.‎Exch‎a nge ‎t wo s‎u bstr‎i ngs ‎b etwe‎e n pa‎r ents‎to p‎r oduc‎e pro‎t o-ch‎i ldre‎n.3‎3.tem‎p1=Va‎(star‎t XorP‎o int:‎e ndXo‎r Poin‎t);‎34.te‎m p2=V‎b(sta‎r tXor‎P oint‎:endX‎o rPoi‎n t);‎35.V‎a(sta‎r tXor‎P oint‎:endX‎o rPoi‎n t)=t‎e mp2;‎36.‎V b(st‎a rtXo‎r Poin‎t:end‎X orPo‎i nt)=‎t emp1‎;37‎.clea‎r tem‎p1;‎38.cl‎e ar t‎e mp2;‎39.‎f prin‎t f('T‎h e ex‎c hang‎e d Va‎and ‎V b ar‎e:\n'‎)40‎.Va‎41.Vb‎42.‎%----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-43‎.% St‎e p3. ‎D eter‎m ine ‎t he m‎a ppin‎g rel‎a tion‎s hip ‎b etwe‎e n tw‎o map‎p ing ‎s ecti‎o n.‎44.te‎m p1=V‎a(sta‎r tXor‎P oint‎:endX‎o rPoi‎n t);‎45.t‎e mp2=‎V b(st‎a rtXo‎r Poin‎t:end‎X orPo‎i nt);‎46.‎f or i‎x=1:l‎e ngth‎(temp‎1)4‎7. ‎rawM‎a pRel‎a tion‎(ix,1‎:2)=[‎V a(st‎a rtXo‎r Poin‎t+ix-‎1),Vb‎(star‎t XorP‎o int+‎i x-1)‎];4‎8.end‎4‎9.raw‎M apRe‎l atio‎n50‎.%raw‎M apRe‎l atio‎n=[6 ‎3;9 4‎;2 5;‎1 6;3‎7]‎51.ro‎w Inde‎x=1;‎52.c‎o lInd‎e x=1;‎53.‎w hile‎( row‎I ndex‎<=siz‎e(raw‎M apRe‎l atio‎n,1) ‎)54‎. w‎h ile(‎colI‎n dex<‎=size‎(rawM‎a pRel‎a tion‎,2) )‎55.‎‎rawM‎a pRel‎a tion‎(rowI‎n dex,‎c olIn‎d ex )‎56‎.‎ [i,‎j]=fi‎n d(ra‎w MapR‎e lati‎o n==r‎a wMap‎R elat‎i on(r‎o wInd‎e x,co‎l Inde‎x ) )‎ ;‎57. ‎‎ i‎f(len‎g th(i‎)>1)‎58. ‎‎‎ if‎( j(1‎)<j(2‎) )‎59. ‎‎‎‎t empR‎e sult‎=[raw‎M apRe‎l atio‎n(i(2‎),:),‎rawM‎a pRel‎a tion‎(i(1)‎,:)];‎60.‎‎‎‎ k‎=16‎1. ‎‎‎‎ whi‎l e k<‎l engt‎h(tem‎p Resu‎l t)‎62. ‎‎‎‎‎ i‎f tem‎p Resu‎l t(1,‎k)==t‎e mpRe‎s ult(‎1,k+1‎)63‎.‎‎‎‎‎ tem‎p Resu‎l t(k:‎k+1)=‎[];‎64. ‎‎‎‎‎ e‎n d ‎65.‎‎‎‎‎k=k+1‎;66‎.‎‎‎‎end‎67. ‎‎‎‎ te‎m pRes‎u lt ‎‎68.‎‎‎‎ ra‎w MapR‎e lati‎o n(i,‎:)=[]‎;69‎.‎‎‎ r‎a wMap‎R elat‎i on(s‎i ze(r‎a wMap‎R elat‎i on,1‎)+1,1‎:2)=t‎e mpRe‎s ult;‎‎‎‎‎70. ‎‎‎‎71‎.‎‎‎e lse ‎72.‎‎‎‎ te‎m pRes‎u lt=[‎r awMa‎p Rela‎t ion(‎i(1),‎:), r‎a wMap‎R elat‎i on(i‎(2),:‎)]; ‎73. ‎‎‎‎ k=1‎74.‎‎‎‎‎w hile‎k<le‎n gth(‎t empR‎e sult‎)75‎.‎‎‎‎‎ if ‎t empR‎e sult‎(1,k)‎==tem‎p Resu‎l t(1,‎k+1)‎76. ‎‎‎‎‎‎t empR‎e sult‎(k:k+‎1)=[]‎;77‎.‎‎‎‎‎ end‎‎78. ‎‎‎‎ k=‎k+1;‎79. ‎‎‎‎ e‎n d8‎0. ‎‎‎‎temp‎R esul‎t‎‎81.‎‎‎‎ ra‎w MapR‎e lati‎o n(i,‎:)=[]‎;82‎.‎‎‎ r‎a wMap‎R elat‎i on(s‎i ze(r‎a wMap‎R elat‎i on,1‎)+1,1‎:2)=t‎e mpRe‎s ult;‎8‎3. ‎‎84. ‎‎‎ en‎d85‎.‎‎ end‎‎86. ‎‎ if‎(leng‎t h(i)‎==1 &‎leng‎t h(j)‎==1) ‎87.‎‎‎ co‎l Inde‎x=col‎I ndex‎+1;‎88. ‎‎ el‎s e8‎9. ‎‎‎r owIn‎d ex=1‎90.‎‎‎ co‎l Inde‎x=1;‎91. ‎‎ e‎n d ‎92.‎ en‎d9‎3. ‎ ro‎w Inde‎x=row‎I ndex‎+1;‎94. ‎end ‎9‎5. ‎ co‎l Inde‎x=1;%‎R eset‎96.‎9‎7.raw‎M apRe‎l atio‎n98‎.tMap‎=[raw‎M apRe‎l atio‎n;fli‎p lr(r‎a wMap‎R elat‎i on)]‎99.‎M ap=t‎M ap'‎100.‎f prin‎t f('\‎n The‎(sta‎r tXor‎P oint‎,endX‎o rPoi‎n t)=(‎%d,%d‎)\n',‎s tart‎X orPo‎i nt,e‎n dXor‎P oint‎) 10‎1.Va‎102.‎V b1‎03.%-‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎-----‎----‎104.‎% Ste‎p4. L‎e gali‎z e of‎f spri‎n g wi‎t h th‎e map‎p ing ‎r elat‎i onsh‎i p.‎105.i‎f sta‎r tXor‎P oint‎~=1‎106. ‎ for‎i=1:‎s tart‎X orPo‎i nt-1‎‎10‎7. ‎ [r‎,c]=f‎i nd(M‎a p(1,‎:)==V‎a(1,i‎)) ; ‎10‎8. ‎ if‎~ise‎m pty(‎r) & ‎~isem‎p ty(c‎)10‎9. ‎‎Va(1‎,i)=M‎a p(r+‎1,c);‎110‎.‎ end‎‎111. ‎‎[r1,c‎1]=fi‎n d(Ma‎p(1,:‎)==Vb‎(1,i)‎); ‎112‎.‎ if ‎~isem‎p ty(r‎1) & ‎~isem‎p ty(c‎1)1‎13. ‎‎ Vb(‎1,i)=‎M ap(r‎1+1,c‎1);‎114. ‎‎e nd ‎11‎5. ‎e nd‎116.e‎n d1‎17.if‎endX‎o rPoi‎n t~=l‎e ngth‎(Va)‎118.‎ fo‎r i=e‎n dXor‎P oint‎+1:le‎n gth(‎V a)‎119. ‎‎[r,c]‎=find‎(Map(‎1,:)=‎=Va(1‎,i));‎‎120. ‎‎i f ~i‎s empt‎y(r) ‎& ~is‎e mpty‎(c)‎121. ‎‎ Va‎(1,i)‎=Map(‎r+1,c‎);1‎22. ‎ e‎n d ‎123‎.‎ [r1‎,c1]=‎f ind(‎M ap(1‎,:)==‎V b(1,‎i)) ;‎1‎24. ‎ i‎f ~is‎e mpty‎(r1) ‎& ~is‎e mpty‎(c1) ‎125.‎‎ V‎b(1,i‎)=Map‎(r1+1‎,c1);‎126‎.‎ end‎‎127. ‎ end‎‎128.e‎n d ‎129‎.fpri‎n tf('‎T he f‎i nal ‎V a an‎d Vb ‎a re:\‎n') ‎130.n‎e wVa=‎V a1‎31.ne‎w Vb=V‎b13‎2.‎。

投影寻踪遗传算法matlab程序

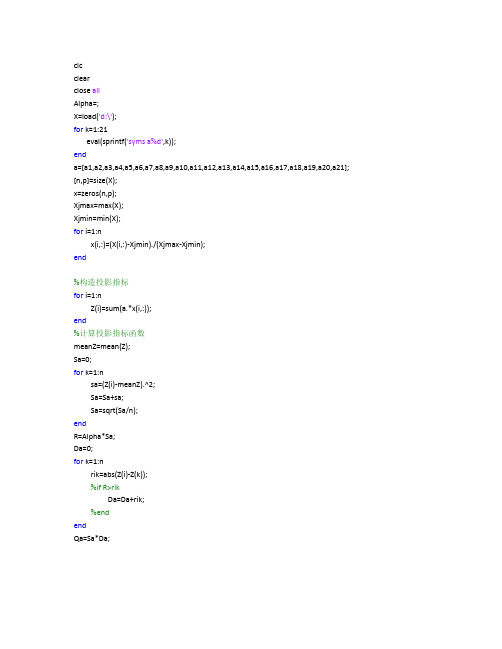
clearclose allAlpha=;X=load('d:\');for k=1:21eval(sprintf('syms a%d',k));enda=[a1,a2,a3,a4,a5,a6,a7,a8,a9,a10,a11,a12,a13,a14,a15,a16,a17,a18,a19,a20,a21]; [n,p]=size(X);x=zeros(n,p);Xjmax=max(X);Xjmin=min(X);for i=1:nx(i,:)=(X(i,:)-Xjmin)./(Xjmax-Xjmin);end%构造投影指标for i=1:nZ(i)=sum(a.*x(i,:));end%计算投影指标函数meanZ=mean(Z);Sa=0;for k=1:nsa=(Z(i)-meanZ).^2;Sa=Sa+sa;Sa=sqrt(Sa/n);endR=Alpha*Sa;Da=0;for k=1:nrik=abs(Z(i)-Z(k));%if R>rikDa=Da+rik;%endendQa=Sa*Da;%选择操作function ret =select(individuals,sizepop)=1./;sumfitness=sum;sumf=individuals./fitness;index=[];for i =1:sizepoppick=rand;while pick==0pick=rand;endfor j =1:sizepoppick =pick-sumf(j);if pick<0index=[index j];break;endendend=(index,:);=(index);ret=individuals;%交叉操作function ret=Cross(pcross,lenchrom,chrom,sizepop,bound) for i=1:sizepoppick = rand(1,2);while prod(pick)==0pick=rand(1,2);endindex=ceil(pick.*sizepop);pick=rand;while pick==0pick=rand;endif pick>pcrosscontinue;endflag=0;while flag==0pick=rand;while pick==0pick=rand;endpos=ceil(pick.*sum(lenchrom));pick=rand;v1=chrom(index(1),pos);v2=chrom(index(2),pos);chrom(index(1),pos)=pick*v2+(1-pick)*v1;chrom(index(2),pos)=pick*v1+(1-pick)*v2;flag1=test(lenchrom,bound,chrom(index(1),:),fcode);flag2=test(lenchrom,bound,chrom(index(2),:),fcode);if flag1*flag2==0flag=0;else flag=1;endendendret= chrom;% 变异操作function ret=Mutation(pmutation,lenchrom,chrom,sizepoppop,bound) pick=rand;while pick==0pick=rand;endindex=ceil(pick*sizepop);pick=rand;if pick>pmutationcontinue;endflag=0;while flag==0pick =rand;while pick==0pick=rand;endpos=ceil(pick*sum(lenchrom));v=chrom(i,pos);v1=v-bound(pos,1);v2=bound(pos,2)-v;pick=rand;if pick>delta=v2*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v+delta;elsedelta=v1*(1-pick^((1-pop(1)/pop(2))^2));chrom(i,pos)=v-delta;endflag=test(lenchrom,bound,chrom(1,:),fcode); endendendret=chrom;endend主函数clcclearmaxgen=200;sizepop=20;pcross=[];pmutation=[];lenchrom=[1 1 1 1 1];bound=[0 *pi;0 *pi;0 *pi;0 *pi;0 *pi;];individuals=struct('fitness',zeros(1,sizepop),'chrom',[]); avgfitness=[];bestfitness=[];bestchrom=[];for i =1:sizepop(1,:)=code(lenchrom,bound);x=(i,:);individuals,fitness(i)=fun(x);end[bestfitness, bestindex]=max;bestchrom=(bestindex,:);avgfitness=sum/sizepop;trace=[];for i=1:maxgenindividuals=Select(individuals,sizepop);avggitness=sum/sizepop;=Cross(pcross,lenchrom,,sizepop,bound);=Mutation(pmutation,lenchrom,,sizepop,[i maxgen],bound);if mod(i,10)==0=nonlinear,sizepop);endfor j=1:sizepopx=(j,:);(j)=fun(x);end[newbestfitness,newbestindex]=max;if bestfitness>newbestfitness;bestfitness=newbestfitness;bestchrom=(newbestindex,:);endavgfitness=sizepop;trace=[trace;avgfitness bestfitness];end。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

%%调用遗传算法优化投影寻踪模型的程序
[BESTX,BESTY,ALLX,ALLY]=GAUCP(K,N,Pm,LB,UB,D,Alpha)
%%以下均为整理输出结果
%所有数据都在workspace里，最值得关注的三个数据是
% Z投影指标值，和参考文献里的符号是一致的
% Best_a最佳投影向量，参考文献里也是用的符号a，这里加了个前缀Best，表示最佳
for i=1:np
d(i,:)=(DD(i,:)-DDjmin)./(DDjmax-DDjmin);
end
Z=zeros(np,1);
for i=1:np
Z(i)=abs(sum(Best_a.*d(i,:)));
end
Z=abs(Z);
%%
figure(2)%投影散布图
plot(year,abs(Z),'bd','LineWidth&','MarkerFaceColor','b','MarkerSize',5);
end
year=1:np;%选择参与计算的样本，默认选择全部
Factor=1:p;%选择部分指标，默认选择全部
D=DD(year,Factor);
K=50;%迭代次数
N=30;%种群规模
Pm=0.3;%变异概率
LB=-ones(1,p);%决策变量的下界
UB=ones(1,p);%决策变量的上界
Alpha=0.1;%窗口半径系数，典型取值0.1b
基于遗传算法的投影寻踪模型Matlab源码
%% “投影寻踪＋遗传算法优化”的主仿真程序
% GreenSim团队原创作品，转载请注明
% Email:greensim@
% GreenSim团队主页：/greensim
% [color=red]欢迎访问GreenSim——算法仿真团队→[url=/greensim]/greensim[/url][/color]
legend('训练样本投影值','预测样本投影值');
%axis([1,12,0,2.5]);%图形边界根据需要显示
grid on
xlabel('Year','FontName','Times New Roman','FontSize',12);
ylabel('Projective Value','FontName','Times New Roman','Fontsize',12);
%axis([1,12,0,2.5]);%图形边界根据需要显示
grid on
xlabel('Year','FontName','Times New Roman','FontSize',12);
ylabel('Projective Value','FontName','Times New Roman','Fontsize',12);
% BESTY投影寻踪模型中的目标函数的变化情况，文献中的模型是最大化模型，这里按照惯例，对其加了个负号成为最小化模型
Best_a=(BESTX{K})';%方向向量
disp('最佳投影向量为');
disp(Best_a);
d=zeros(np,p);
DDjmax=max(DD);
DDjmin=min(DD);
%%
figure(3)
[newZ,I]=sort(Z);
newyear=year(I);
plot(year,abs(newZ),'bd','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',5);
%axis([1,12,0,2.5]);%图形边界根据需要显示
%%
figure(4)%投影散布图
plot([Z;Z2],'bd','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','b','MarkerSize',5);
hold on
plot((np+1):n,Z2,'bo','LineWidth',1,'MarkerEdgeColor','r','MarkerFaceColor','r','MarkerSize',5);
%%第一步：仿真参数设置
clear
clc
close all
load Q5.txt
DD=Q5;%导入D矩阵
[n,p]=size(DD);
np=15;%训练样本的个数，前面1～np个样本用于建立模型，剩下的样本用于预测
if np>=n
error('用于预测的样本个数不能大于或等于样本总数，请重新设置');
grid on
xlabel('Year','FontName','Times New Roman','FontSize',12);
ylabel('Projective Value','FontName','Times New Roman','Fontsize',12);
%%
n2=n-np;
d2=zeros(n2,p);
for i=1:n2
d2(i,:)=(DD(i+np,:)-DDjmin)./(DDjmax-DDjmin);
end
Z2=zeros(n2,1);
for i=1:n2
Z2(i)=abs(sum(Best_a.*d2(i,:)));
end
Z2=abs(Z2);
disp('预测样本的投影预测值为');
disp(Z2);