北师大版九年级上册数学 矩形的判定和性质 同步测试题(含答案)
北师大版九年级数学上册 第1章 1.2 《矩形性质和判定的运用》 同步测试(含答案)

北师版九年级数学上册第一章特殊平行四边形1.2矩形性质和判定的运用同步测试题号 一 二 三 总分 得分第Ⅰ卷(选择题)一、选择题(共10小题,3*10=30)1.点D 是等腰Rt △ABC 斜边BC 上一点,DE ⊥AB 于点E ,DF ⊥AC 于点F ,若BC =2,则四边形AEDF 的周长是( ) A .1 B .2 C .3 D .222.如图,点O 是矩形ABCD 的对角线AC 的中点,OM ∥AB 交AD 于点M ,若OM =3,BC =10,则OB 的长为( )A .5B .4 C.342 D.343.如图,将矩形纸片ABCD 沿直线EF 折叠,使点C 落在AD 边的中点C′处,点B 落在点B′处,其中AB =9,BC =6,则FC′的长为( ) A.103 B .4 C .4.5 D .54.如图,在矩形ABCD 中,AB =2,BC =4,对角线AC 的垂直平分线分别交AD ,AC 于点E ,O ,连接CE ,则CE 的长为()A .3B .3.5C .2.5D .2.85. 如图,在矩形ABCD中,对角线AC,BD相交于点O,且AB=6,BC=8,则△ABO的周长为( ) A.16 B.18 C.20 D.226.如图,在矩形ABCD中,AD=3,M是CD上的一点,将△ADM沿直线AM对折得到△ANM,若AN平分∠MAB,则折痕AM的长为( )A.3 B.2 3C.3 2 D.67.如图,在▱ABCD中,E,F分别是AB,CD的中点,连接AC,AF,CE,当CA=CB时,判断四边形AECF是( )A.平行四边形B.矩形C.菱形D.任意四边形8. 如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=60°,则∠2的度数为( ) A.30°B.45°C.60°D.75°9.如图,四边形ABCD 的对角线AC ,BD 相交于点O ,已知下列6个条件: ①AB ∥CD ;②AB =DC ;③AC =BD ;④∠ABC =90°;⑤OA =OC ; ⑥OB =OD.则不能使四边形ABCD 成为矩形的是( ) A .①②③ B .①②④ C .②⑤⑥ D .④⑤⑥10. 如图,矩形OABC 的顶点O 与原点重合,点A ,C 分别在x 轴、y 轴上,点B 的坐标为(-5,4),点D 为BC 边上一动点,连接OD ,若线段OD 绕点D 顺时针旋转90°后,点O 恰好落在AB 边上的点E 处,则点E 的坐标为( ) A .(-5,3) B .(-5,4) C .(-5,52)D .(-5,2)第Ⅰ卷(非选择题)二.填空题(共8小题,3*8=24)11. 将一个含30°的角的直角三角尺(∠AMF =90°)按如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M 是BC 边的中点,则∠AFE 的度数为____.12. 如图,矩形ABCD 的对角线AC 与BD 相交于点O ,AC =10,P ,Q 分别为AO ,AD 的中点,则PQ 的长度为_______.13.如图,四边形OABC 为矩形,点A ,C 分别在x 轴和y 轴上,连接AC ,点B 的坐标为(4,3),∠CAO 的平分线与y 轴相交于点D ,则点D 的坐标为.14. 如图,矩形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点E,F,已知AD=4 cm,图中阴影部分的面积总和为6 cm2,则对角线AC的长为________cm.15.如图,在矩形ABCD中,BC=20 cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3 cm/s和2 cm/s,则最快____s后,四边形ABPQ成为矩形.16.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B 落在矩形内点F处,连接CF,则CF的长为__________17.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度.18. 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是__________三.解答题(共7小题, 46分)19.(6分) 如图,在四边形ABCD 中,∠A =∠BCD =90°,BC =CD ,CE ⊥AD ,垂足为E.求证:AE =CE.20. (6分) 如图,在菱形ABCD 中,对角线AC 与BD 交于点O.过点C 作BD 的平行线,过点D 作AC 的平行线,两直线相交于点E. (1)求证:四边形OCED 是矩形;(2)若CE =1,DE =2,求菱形ABCD 的面积.21. (6分) 在△ABC 中,D 是BC 边的中点,E ,F 分别在AD 及其延长线上,CE ∥BF ,连接BE ,CF. (1)求证:△BDF ≌△CDE ;(2)若DE =12BC ,试判断四边形BFCE 是怎样的四边形,并证明你的结论.22.(6分) 如图,在▱ABCD中,点P是AB边上一点(不与A,B重合),CP=CD,过点P作PQ⊥CP,交AD边于点Q,连接CQ.(1)若∠BPC=∠AQP,求证:四边形ABCD是矩形;(2)在(1)的条件下,当AP=2,AD=6时,求AQ的长.23.(6分) 如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.24.(8分) 如图,矩形ABCD中,延长AB至点E,延长CD至点F,且BE=DF,连接EF,与BC,AD分别相交于P,Q两点.(1)求证:CP=AQ;(2)若BP=1,PQ=22,∠AEF=45°,求矩形ABCD的面积.25.(8分) 如图,在▱ABCD中,DC>AD,四个角的平分线AE,DE,BF,CF的交点分别是E,F,过点E,F分别作DC与AB间的垂线MM′与NN′,在DC与AB上的垂足分别是M,N与M′,N′,连接EF.(1)求证:四边形EFNM是矩形;(2)已知:AE=4,DE=3,DC=9,求EF的长.参考答案 1-5 BDDCA 6-10 BBCCA 11. 15° 12. 2.5 13. (0,43)14. 5 15. 4 16.18517. 22.5 18. 4.819. 证明:如图,过点B 作BF ⊥CE 于点F.∵CE ⊥AD ,∴∠D +∠DCE =90°. ∵∠BCD =90°, ∴∠BCF +∠DCE =90°, ∴∠BCF =∠D.在△BCF 和△CDE 中,∠BCF =∠D ,∠BFC =∠CED =90°,BC =CD , ∴△BCF ≌△CDE(AAS), ∴BF =CE.∵∠A =90°,CE ⊥AD ,BF ⊥CE , ∴四边形AEFB 是矩形, ∴AE =BF , ∴AE =CE.20. 解:(1)∵四边形ABCD 是菱形, ∴AC ⊥BD , ∴∠COD =90°.∵CE ∥OD ,DE ∥OC , ∴四边形OCED 是平行四边形, 又∠COD =90°, ∴▱OCED 是矩形(2)由(1)知,▱OCED 是矩形, 则CE =OD =1,DE =OC =2. ∵四边形ABCD 是菱形, ∴AC =2OC =4,BD =2OD =2,∴菱形ABCD 的面积为12AC·BD =12×4×2=421. 解:(1)证明:∵CE ∥BF ,∴∠CED =∠BFD. ∵D 是BC 边的中点,∴BD =DC.在△BDF 和△CDE 中,⎩⎪⎨⎪⎧∠BFD =∠CED ,∠BDF =∠CDE ,BD =DC ,∴△BDF ≌△CDE(AAS)(2)四边形BFCE 是矩形.证明:∵△BDF ≌△CDE ,∴DE =DF =12EF.∵BD =DC ,∴四边形BFCE 是平行四边形.∵DE =12BC =12EF ,∴BC =EF ,∴平行四边形BFCE 是矩形22. (1)证明:∵∠BPQ =∠BPC +∠CPQ =∠A +∠AQP , 又∵∠BPC =∠AQP ,∴∠CPQ =∠A.∵PQ ⊥CP , ∴∠CPQ =∠A =90°.又∵四边形ABCD 是平行四边形, ∴四边形ABCD 是矩形(2)∵四边形ABCD 是矩形,∴∠D =∠CPQ =90°.在Rt △CDQ 和Rt △CPQ 中,⎩⎪⎨⎪⎧CQ =CQ ,CD =CP ,∴Rt △CDQ ≌Rt △CPQ(HL).∴DQ =PQ.设AQ =x ,则DQ =PQ =6-x.在Rt △APQ 中,AQ 2+AP 2=PQ 2,∴x 2+22=(6-x)2, 解得x =83.∴AQ 的长是8323. 解:(1)∵四边形ABCD 是矩形, ∴AB ∥CD , ∴∠FAE =∠CDE ,∵E 是AD 的中点, ∴AE =DE ,又∵∠FEA =∠CED , ∴△FAE ≌△CDE , ∴CD =FA , 又∵CD ∥AF ,∴四边形ACDF 是平行四边形 (2)BC =2CD.证明:∵CF 平分∠BCD , ∴∠DCE =45°, ∵∠CDE =90°,∴△CDE 是等腰直角三角形, ∴CD =DE , ∵E 是AD 的中点, ∴AD =2DE =2CD , ∵AD =BC , ∴BC =2CD24. 解:(1)证明:∵四边形ABCD 是矩形, ∴∠A =∠ABC =∠C =∠ADC =90°,AB =CD ,AD =BC ,AB ∥CD ,AD ∥BC ,∴∠E =∠F. ∵BE =DF ,∴AE =CF.在△CFP 和△AEQ 中,⎩⎪⎨⎪⎧∠C =∠A ,CF =AE ,∠F =∠E ,∴△CFP ≌△AEQ(ASA),∴CP =AQ(2)∵AD ∥BC ,∴∠PBE =∠A =90°.∵∠AEF =45°,∴△BEP ,△AEQ 是等腰直角三角形,∴BE =BP =1,AQ =AE ,∴PE =2BP =2,∴EQ =PE +PQ =2+22=32, ∴AQ =AE =3,∴AB =AE -BE =2.∵CP =AQ ,AD =BC ,∴DQ =BP =1,∴AD =AQ +DQ =3+1=4, ∴矩形ABCD 的面积=AB ·AD =2×4=825. 解:(1)过点E ,F 分别作AD ,BC 的垂线,垂足分别是G ,H.∵∠3=∠4,∠1=∠2,EG ⊥AD ,EM ⊥CD ,EM ′⊥AB∴EG =ME ,EG =EM′,∴EG =ME =EM′=12MM′ 同理可证:FH =NF =N′F =12NN′, ∵CD ∥AB ,MM ′⊥CD ,NN ′⊥CD , ∴MM ′=NN′,∴ME =NF =EG =FH ,又∵MM′∥NN′,∴四边形EFNM 为平行四边形, 又∵MM′⊥CD ,∴▱EFNM 是矩形(2)∵DC ∥AB ,∴∠CDA +∠DAB =180°,∵∠3=12∠CDA ,∠2=12∠DAB , ∴∠3+∠2=90°,在Rt △DEA ,∵AE =4,DE =3,∴AD =32+42=5.∵四边形ABCD 是平行四边形,∴∠DAB =∠DCB ,又∵∠2=12∠DAB ,∠5=12∠DCB ,∴∠2=∠5, 由(1)知GE =NF ,在Rt △GEA 和Rt △NFC 中 ⎩⎪⎨⎪⎧∠2=∠5,∠EGA =∠FNC =90°,GE =NF ,∴△GEA ≌△NFC , ∴AG =CN.在Rt △DME 和Rt △DGE 中,∵DE =DE ,ME =GE ,∴△DME ≌△DGE ,∴DG =DM ,∴DM +CN =DG +AG =AD =5,∴MN=CD-DM-CN=9-5=4.∵四边形EFNM是矩形.∴EF=MN=4。
北师大版九年级数学上册--第一章 1.2《矩形的性质和判定》同步练习题(含答案)

1.2《矩形的性质和判定》同步练习1、矩形的对边 ,对角线 且 ,四个角都是 ,即是 图形又是 图形。
2、四边形ABCD 的对角线AC 、BD 互相平分,要使它成为矩形,需要添加的条件是________。
3、已知矩形ABCD 的对角线相交于O ,对角线长8cm ,∠AOD=60°,则AD=________,AB=________。
4、如图,四边形ABCD 是平行四边形,AC 、BD 交于点O ,∠1=∠2,∠BOC=120°,AB=4,则四边形ABCD 的面积=________。
5、矩形的面积是60,一边长为5,则它的一条对角线长等于 。
6、如果矩形的一边长为8,一条对角线长为10,那么这个矩形面积是__________。
7、 矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是___________。
8、已知,如图:在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,点A 、C 的坐标分别为A (10,0)、C (0,4),点D 是OA 的中点,点P 在BC 边上运动,当△ODP 是腰长为5的等腰三角形时,点P 的坐标为 。
题4图 题8图9、若一个直角三角形的两条直角边分别为5和12,则斜边上的中线等于 。
10、平行四边形没有而矩形具有的性质是( )A 、对角线相等B 、对角线互相垂直C 、对角线互相平分D 、对角相等 11、下列叙述错误的是( )A.平行四边形的对角线互相平分B.平行四边形的四个内角相等。
C.矩形的对角线相等。
D.有一个角是90º的平行四边形是矩形12、下列检查一个门框是否为矩形的方法中正确的是( )A .测量两条对角线是否相等B .用曲尺测量对角线是否互相垂直C .用曲尺测量门框的三个角是否都是直角 D.测量两条对角线是否互相平分13、矩形ABCD 的对角线相交于点O ,如果ABC ∆的周长比AOB ∆的周长大10cm ,则AD 的长是( )A 、5cmB 、7.5cmC 、10cmD 、12.5cm14、下列图形中既是轴对称图形,又是中心对称图形的是( )A 、平行四边形B 、等边三角形C 、矩形D 、直角三角形15、如图,四边形的对角线互相平分,要使它成为矩形,需要添加的条件是( )A.B. C. D.题15图 题16图16、如图,在矩形ABCD 中,两条对角线AC 与BD 相交于点O ,AB=6,OA=4,则AD 的长为( )A 、4B 、8C 、33D 、72yxP D CB A O解答题:1、如图,已知矩形ABCD的两条对角线相交于O,︒=∠120AOD,AB=4cm,求此矩形的面积。
2023-2024学年九年级数学上册《第一章 矩形的性质与判定》同步练习题有答案(北师大版)
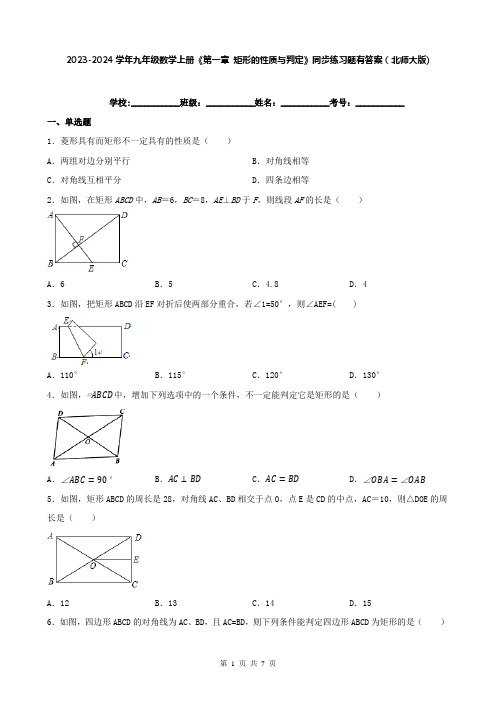
2023-2024学年九年级数学上册《第一章矩形的性质与判定》同步练习题有答案(北师大版)学校:___________班级:___________姓名:___________考号:___________一、单选题1.菱形具有而矩形不一定具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分D.四条边相等2.如图,在矩形ABCD中,AB=6,BC=8,AE⊥BD于F,则线段AF的长是()A.6 B.5 C.4.8 D.43.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=( )A.110°B.115°C.120°D.130°4.如图,▱ABCD中,增加下列选项中的一个条件,不一定能判定它是矩形的是()A.∠ABC=90°B.AC⊥BD C.AC=BD D.∠OBA=∠OAB 5.如图,矩形ABCD的周长是28,对角线AC、BD相交于点O,点E是CD的中点,AC=10,则△DOE的周长是()A.12 B.13 C.14 D.156.如图,四边形ABCD的对角线为AC、BD,且AC=BD,则下列条件能判定四边形ABCD为矩形的是()A.BA=BC B.AC、BD互相平分C.AC⊥BD D.AB∥CD7.如图,在矩形ABCD中,AB=5,BC=8,E是边BC的中点,M是AE的中点,连接CM,则CM的长为()A.6 B.6.5 C.7 D.7.58.如图,在矩形ABCD中,AB=6,BC=8,AC与BD相交于O,E为DC的一点,过点O作OF⊥OE交BC于F.记d=√DE2+BF2,则关于d的正确的结论是()A.d=5 B.d<5 C.d≤5 D.d≥5二、填空题9.如图,矩形ABCD中,∠AOB=60°,BC=3√3,点P是AD边上一动点,则OP的最小值为.10.如图,在菱形ABCD中,AC、BD交于点O,AC=6,BD=8,若DE∥AC,CE∥BD,则OE的长为.11.如图,矩形ABCD沿AF折叠,使点D落在BC边上E处,如果∠BAE=50°,则∠DAF= .12.如图,把矩形ABCD纸片沿着过点A的直线AE折叠,使得点D落在BC边上的点F处,若∠BAF= 40°则∠DAE=°13.如图,矩形ABCD中AB=6,BC=8对角线AC、BD相交于点O,点P是线段AD上任意一点(点Р不与A、D重合),过P作PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于.三、解答题14.如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.求证:四边形ABCD是矩形.15.已知:如图,M为平行四边形ABCD边AD的中点,且MB=MC.求证:四边形ABCD是矩形.16.如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连结AE,交BC于点F,∠AFC=2∠D,连结AC、BE.求证:四边形ABEC是矩形.17.如图,在△ABC中,AB=AC,点D(不与点B重合)在BC上,点E是AB的中点,过点A作AF∥BC交DE延长线于点F,连接AD,BF.(1)求证:△AEF≌△BED.(2)若BD=CD,求证:四边形AFBD是矩形.18.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.参考答案1.D2.C3.B4.B5.A6.B7.B8.D9.3210.511.20°12.2513.24514.解:在□ABCD中,应用平行四边形性质得到AO=CO,BO=DO,又∵∠1=∠2 ,∴BO=CO,∴AO=BO=CO=DO,∴AC=BD,∴□ABCD为矩形.15.证明:∵四边形ABCD是平行四边形∴AB=CD,AB∥CD∴∠A+∠D=180°在△ABM和△DCM中{AM=DM AB=DC BM=CM∴△ABM≌△DCM(SSS)∴∠A=∠D=90°∴平行四边形ABCD是矩形.16.证明:∵四边形ABCD是平行四边形∴AB∥CD,AB=CD∵CE=DC∴AB=EC,AB∥EC∴四边形ABEC是平行四边形∴FA=FE,FB=FC∵四边形ABCD是平行四边形∴∠ABC=∠D又∵∠AFC=2∠D∴∠AFC=2∠ABC∵∠AFC=∠ABC+∠BAF∴∠ABC=∠BAF∴FA=FB∴FA=FE=FB=FC∴AE=BC∴四边形ABEC是矩形.17.证明:(1)∵AF∥BC∴∠AFE=∠EDB∵E为AB的中点∴EA=EB在△AEF和△BED中∴△AEF≌△BED(ASA);(2)∵△AEF≌△BED∴AF=BD∵AF∥BD∴四边形AFBD是平行四边形∵AB=AC,BD=CD∴AD⊥BD∴四边形AFBD是矩形.18.(1)解:BD=CD.理由如下:依题意得AF∥BC ∴∠AFE=∠DCE∵E是AD的中点∴AE=DE在△AEF和△DEC中{∠AFE=∠DCE∠AEF=∠DECAE=DE∴△AEF≌△DEC(AAS)∴AF=CD∵AF=BD∴BD=CD;(2)解:当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD∴四边形AFBD是平行四边形∵AB=AC,BD=CD(三线合一)∴∠ADB=90°∴▱AFBD是矩形。
北师大版九年级数学上册《1.2 矩形的性质与判定》同步练习题-附答案

北师大版九年级数学上册《1.2 矩形的性质与判定》同步练习题-附答案一、选择题1.如图,在矩形ABCD中,两条对角线AC、BD相交于点O,若OB=5.则AC=()A.10 B.8 C.5√3D.52.如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则AB的长度为()A.1 B.√2C.√3D.23.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若∠DAE∶∠BAE=3∶1,则∠EAC 的度数是()A.18°B.36°C.45°D.72°4.如图,在矩形ABCD中E,F分别是AD,CD的中点,连接BE,BF,且G,H分别是BE,BF的中点,已知BD=20,则GH的长为( )A.4B.5C.8D.105.如图∠BAC=90°,AB=6,AC=8,P为边BC上一动点(点P不与点B,C重合),PE⊥AB于点E,PF⊥AC 于点F,则EF的最小值为()A.4 B.4.8C.5.2D.66.如图,在矩形纸片ABCD中AB=10,AD=6点E为AD边上一点,将△ABE沿BE翻折,点A恰好落在CD边上点F处,则AE长为()A.83B.72C.103D.1347.如右图,A,B为5×5的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,则在此图中以A,B为顶点的格点矩形共可以画出()A.1个B.2个C.3个D.4个8.如图,在矩形ABCD中,AB=10,BC=6,点M是AB边的中点,点N是AD边上任意一点,将线段MN绕点M顺时针旋转90°,点N旋转到点N',则△MBN'周长的最小值为()A.15 B.5+5√5C.10+5√2D.18二、填空题9.在矩形ABCD中AB=2,对角线AC与BD相交于点 O,若∠BAO=60°,则边BC的长为.10.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°若AB=3cm,则AC=cm.11.如图所示的长方形纸条ABCD,将纸片沿MN折叠,MB与DN交于点K,若∠1=70°,则∠KNC=°12.如图,在矩形ABCD中AB=2AD=6,点P为AB边上一点,且AP≤3,连接DP,将ΔADP沿DP折叠,点A落在点M处,连接CM,BM,当ΔBCM为等腰三角形时,BP的长为.13.如图,在矩形ABCD中AB=8,BC=12,E为BC上一点,CE=4,M为BC的中点.动点P,Q从E出发,分别向点B,C运动,且PE=2QE.若PD和AQ交于点F,连接MF,则MF的最小值为.三、解答题14.如图,折叠长方形纸片ABCD的一边,使点D落在BC边的D′处AB=6cm,BC=10cm求CE的长.15.如图,在矩形ABCD中,点E在BC边上,点F在CD边上,且AB=4,BE=3,EF=6,AF=√61求三角形AEF的面积.16.如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且AE=CG,BF=DH,连接EG、FH.(1)求证:△AEH≌△CGF;(2)若EG=FH,∠AHE=35°,求∠DHG的度数.17.如图,四边形ABCD中∠DAB=45°,AB=8,AD=3√2,E为AB中点,且CD⊥DE,连接CE.(1)求DE的长度;(2)若∠BEC=∠ADE,求BC的长度.18.已知:如图,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点。
北师大版数学九年级上册:1.2.1 矩形的定义及性质 同步练习(含答案)

1.2.1 矩形的定义及性质一、选择题1.矩形具有而菱形不一定具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分D.两组对角分别相等2.如图K-4-1,在矩形ABCD中,对角线AC,BD相交于点O.已知∠AOB=60°,AC=16,则图中长度为8的线段的条数为()图K-4-1A.4B.6C.8D.103.如图K-4-2,在△ABC中,∠A+∠B=90°,D为AB上一点,AD=DB,CD=3,则AB的长度为()图K-4-2A.3B.4C.5D.64.如图K-4-3,O是矩形ABCD的对角线AC的中点,M是CD边的中点.若AB=12,OM=92,则线段OB的长为()图K-4-3A.7B.8C.152D.1725.如图K-4-4,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C'处,点B落在点B'处,其中AB=9,BC=6,则FC'的长为()图K-4-4A.10B.4C.4.5D.53二、填空题6.如图K-4-5,在Rt△ABC中,∠ABC=90°,D为AC的中点,若∠C=55°,则∠ABD=°.图K-4-57.如图K-4-6,矩形ABCD中,对角线AC,BD交于点O,过点O的直线与AD,BC分别交于点E,F,已知AD=4 cm,图中阴影部分的面积为6 cm2,则对角线AC的长为cm.图K-4-68.如图K-4-7,在矩形ABCD中,对角线AC,BD交于点O,E是直线BC上一点,且BE=OB,连接AE,若∠BAC=60°,则∠CAE的度数是.图K-4-79.如图K-4-8,∠MON=90°,矩形ABCD的顶点A,B分别在边OM,ON上,当点B在边ON上运动时,点A也随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2,运动过程中点D到点O的最大距离是.图K-4-8三、解答题10.如图K-4-9,在矩形ABCD中,E是AB的中点,连接DE,CE.(1)求证:△ADE≌△BCE;(2)若AB=6,AD=4,求△CDE的周长.图K-4-911.如图K-4-10,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,且BE=DF.(1)求证:AE=CF;(2)若AB=6,∠COD=60°,求矩形ABCD的面积.图K-4-1012.如图K-4-11,在四边形ABCD中,AB∥CD,∠ACB=90°,且E是AB的中点,CE∥AD.(1)求证:四边形AECD是菱形;(2)若AC=6,CE=5,求四边形ABCD的面积.图K-4-1113.如图K-4-12,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.(1)求证:BD=BE;(2)若∠DBC=30°,BO=4,求四边形ABED的面积.图K-4-1214.数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图K-4-13①所示,两阴影部分面积相等)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》) 请根据图①完成这个推论的证明过程.证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(+),易证S△ADC=S△ABC,=,=,可得S矩形NFGD=S矩形EBMF.图K-4-13[变式]如图②,P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8,则图中阴影部分的面积为.参考答案1.B2.B [解析] 根据题意可知,△AOB 和△COD 都是边长为8的等边三角形,所以长度为8的线段有6条.3.D [解析] ∵在△ABC 中,∠A+∠B=90°,∴∠ACB=90°. ∵AD=DB ,∴CD 是Rt △ABC 斜边AB 上的中线, ∴AB=2CD=6.故选D .4.C [解析] ∵O 是矩形ABCD 的对角线AC 的中点,M 是CD 边的中点, ∴OM 是△ADC 的中位线,∴AD=2OM=9.∵四边形ABCD 是矩形,AB=12,∴∠D=∠ABC=90°,CD=AB=12, ∴AC=2+CD 215,∴OB=12AC=152.故选C .5.D [解析] 设FC'=x ,则FC=x ,FD=9-x.∵BC=6,四边形ABCD 为矩形,C'为AD 的中点,∴AD=BC=6,C'D=3,∠D=90°.在Rt △FC'D 中,∠D=90°,FC'=x ,FD=9-x ,C'D=3,∴FC'2=FD 2+C'D 2,即x 2=(9-x )2+32,解得x=5.故选D . 6.357.5 [解析] ∵图中阴影部分的面积为6 cm 2,AD=4 cm,则12AD ·CD=12×4×CD=6,∴CD=3(cm).在Rt △ACD 中,AD=4 cm,CD=3 cm,由勾股定理得AC=5 cm,即对角线AC 的长为5 cm . 8.15° [解析] ∵四边形ABCD 是矩形,∴∠ABC=90°,OA=OC ,OB=OD ,AC=BD ,∴OA=OB. 又∵∠BAC=60°,∴△AOB 是等边三角形, ∴AB=OB.又∵BE=OB ,∴AB=BE , ∴△ABE 是等腰直角三角形,∴∠BAE=45°,∴∠CAE=∠BAC-∠BAE=60°-45°=15°.故答案为15°. 9.2+2√210.解:(1)证明:在矩形ABCD 中,AD=BC ,∠A=∠B=90°. ∵E 是AB 的中点,∴AE=BE.在△ADE与△BCE中,∵AD=BC,∠A=∠B,AE=BE,∴△ADE≌△BCE(SAS).(2)由(1),知△ADE≌△BCE,∴DE=CE.AB=3,在Rt△ADE中,AD=4,AE=12由勾股定理,知DE=√AD2+AE2=√42+32=5,∴△CDE的周长=DE+CE+CD=2DE+AB=2×5+6=16.11.解:(1)证明:∵四边形ABCD是矩形,∴OA=OC,OB=OD.又∵BE=DF,∴OE=OF.在△AOE和△COF中,∵OA=OC,∠AOE=∠COF,OE=OF,∴△AOE≌△COF(SAS),∴AE=CF.(2)∵四边形ABCD是矩形,∴OA=OC=OB=OD.又∵∠AOB=∠COD=60°,∴△AOB是等边三角形,∴OA=AB=6,∴AC=2OA=12.在Rt△ABC中,BC=√AC2-AB2=6√3,∴矩形ABCD的面积=AB·BC=6×6√3=36√3.12.解:(1)证明:∵AB∥CD,CE∥AD,∴四边形AECD是平行四边形.∵∠ACB=90°,E是AB的中点,AB,∴四边形AECD是菱形.∴CE=AE=12(2)由(1)知AB=2CE=10.在Rt△ACB中,∠ACB=90°,AC=6,AB=10,∴BC=√AB2-AC2=8,∴S △ABC =12BC ·AC=24.∵E 是AB 的中点,四边形AECD 是菱形, ∴S △AEC =S △EBC =S △ACD =12, ∴S 四边形ABCD =S △ABC +S △ACD =36.13.[解析] (1)根据“矩形的对角线相等”可得AC=BD ,然后证明四边形ABEC 是平行四边形,再根据“平行四边形的对边相等”可得AC=BE ,从而得证;(2)根据矩形的对角线相等且互相平分求出BD 的长度,再根据30°角所对的直角边等于斜边的一半求出CD 的长度,然后利用勾股定理求出BC 的长度,再利用梯形的面积公式列式计算即可得解.解:(1)证明:∵四边形ABCD 是矩形, ∴AC=BD ,AB ∥CD. 又∵BE ∥AC ,∴四边形ABEC 是平行四边形, ∴AC=BE , ∴BD=BE.(2)∵在矩形ABCD 中,BO=4, ∴BD=2BO=2×4=8. ∵∠DBC=30°,∠DCB=90°, ∴CD=12BD=12×8=4, ∴AB=CD=4,∴DE=CD+CE=CD+AB=4+4=8.在Rt △BCD 中,BC=√BD 2-CD 2=√82-42=4√3, ∴AD=BC=4√3,∴四边形ABED 的面积=12×(4+8)×4√3=24√3.14.S △AEF S △FCM S △ANF S △AEF S △FGC S △FCM变式 16。
北师大版数学九年级上册矩形的性质与判定 同步练习题 含答案

第一章特殊平行四边形 1.2 矩形的性质与判定1. 如图,在△ABC中,BD,CE是高,点G,F分别是BC,DE的中点,则下列结论中错误的是( )A.∠DGE=60° B.GF⊥DE C.GF平分∠DGE D.GE=GD2. 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD 的中点,若AB=6 cm,BC=8 cm,则△AEF的周长等于( )A. 7cmB. 8cmC. 9cmD. 10cm3. 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )A. 13B. 14 C, 15 D. 164. 如图,在△ABC中,点D,E,F分别为边BC,AC,AB的中点,AH⊥BC于点H,若FD=8 cm,则HE等于( )A. 11cmB. 10cmC. 9cmD. 8cm5. 矩形具有而一般平行四边形不具有的性质是( )A.对边相等 B.对角线相等 C.对角相等 D.对角线互相平分6. 下列四边形不是矩形的是( )A.有三个角都是直角的四边形B.四个角都相等的四边形C.对角线相等且互相平分的四边形D.一组对边平行,且对角相等的四边形7. 如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )A.AC⊥BD B.AC=BD C.AB∥DC D.AB=DC8. 在数学活动课上, 老师和同学们判断一个四边形门框是否为矩形, 下面是某合作学习小组的4位同学拟订的方案, 其中正确的是( ) A .测量两组对边是否分别相等 B .测量对角线是否相互平分 C .测量其内角是否都为直角 D . 测量对角线是否垂直9. 如图,在矩形ABCD 中(AD >AB),点E 是BC 上一点,且DE =DA ,AF ⊥DE ,垂足为点F ,在下列结论中,不一定正确的是( )A .BE =AD -DFB .AF =12ADC .AB =AFD .△AFD ≌△DCE10. 如图,点P 是矩形ABCD 的边AD 上的一动点,矩形的两条边AB ,BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离之和是( )A .4.8B .5C .6D .7.211. 如图,矩形ABCD 的顶点A ,C 分别在直线a ,b 上,且a∥b,∠1=60°,则∠2=12. 如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,则矩形ABCD的面积=13. 如图,四边形ABCD的对角线AC,BD相交于点O,已知条件:①AB∥CD;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD,则下列条件的组合不能使四边形ABCD成为矩形的选项是 (填序号)14. 在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,2),要使四边形OBCA为矩形,则C点的坐标为________.15. 已知一直角三角形的周长是4+26,斜边的中线长是2,则这个三角形的面积是16. 如图,将△ABC绕AC的中点O顺时针旋转180°得到△CDA,添加一个条件,使四边形ABCD为矩形.17. 如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为18. 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为19. 矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D 是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为20. 如图,在矩形ABCD中,AB=1,点E,F分别为AD,CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD=________.21. 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC 的交点为点O,连接DE.(1)求证:△ADE≌△CED;(2)求证:DE∥AC.22. 如图,在▱ABCD中,E是BC的中点,且EA=ED.(1)求证:四边形ABCD是矩形;(2)若BC=6 cm,AE=5 cm,求S▱ABCD.23. 如图,在矩形ABCD中,点E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.24. 如图,四边形ABCD 的对角线AC ,BD 相交于点O ,已知O 是AC 的中点,AE =CF ,DF∥BE.(1)求证:△BOE≌△DOF;(2)若OD =12AC ,则四边形ABCD 是什么特殊四边形?请证明你的结论.25. 如图,△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=8,CF=6,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.答案:1---10 ACBDB DADBA 11. 60° 12. 4 3 13. ② ⑤ ⑥ 14. (3,2) 15. 5216. ∠B=90°或∠BAC+∠BCA=90° 17. 818. 60°19. (3,43) 20. 221. 解:(1)∵四边形ABCD 是矩形,∴AD =BC ,AB =CD ,由折叠知BC =CE =AD ,AB =AE =CD ,又∵DE =ED ,∴△ADE ≌△CED(SSS ).(2)∵△ADE ≌△CED ,∴∠EDC =∠DEA ,由折叠知∠OAC =∠CAB ,又∵∠OCA =∠CAB ,∴∠OAC =∠OCA ,∵∠EOC =∠EAB ,∴2∠OAC =2∠DEA ,∴∠OAC =∠DEA ,∴DE ∥AC.22. (1)证明:∵四边形ABCD 是平行四边形,∴AB=CD ,又∵EA=ED , BE =EC ,∴△ABE≌△DCE,∴∠B=∠C,∵AB∥CD,∴∠B+∠C=180°,∴∠B=12×180°=90°,∴▱ABCD 是矩形 (2)在Rt△ABE 中,BE =12BC =3(cm), ∴AB=AE 2-BE 2=4(cm),∴S ▱ABCD =AB·BC=4×6=24(cm 2).23. 证明:∵四边形ABCD 是矩形,∴∠B=∠C=∠BAD=90°,AB =CD , ∴∠BEF+∠BFE=90°,∵EF⊥ED,∴∠BEF+∠CED=90°,∴∠BFE=∠CED,同理∠BEF=∠EDC.在△EBF 与△DCE 中,⎩⎪⎨⎪⎧∠BFE=∠CED,EF =ED ,∠BEF=∠EDC,∴△EBF≌△DCE(ASA ).∴BE=CD.∴BE=AB.∴∠BAE=∠BEA=45°.∴∠EAD=45°.∴∠BAE=∠EAD,即AE 平分∠BAD.24. (1)证明:∵DF∥BE,∴∠FDO=∠EBO,∠DFO=∠BEO,∵OA=OC , AE =CF ,∴OE=OF ,∴△BOE≌△DOF(AAS ).(2)若OD =12AC ,则四边形ABCD 是矩形.证明如下:∵△BOE≌△DOF, ∴OB=OD ,又∵OD=12AC ,OA =OC ,∴OA=OB =OC =OD , ∴BD=AC ,∴四边形ABCD 为矩形.25. (1)证明:如图所示,∵MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F ,∴∠2=∠5,∠4=∠6,∵MN ∥BC ,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,∴EO =CO ,FO =CO ,∴OE =OF.(2)∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°,∵CE=8,CF =6,∴EF=82+62=10,∴OC=12EF =5. (3)当点O 在边AC 上运动到AC 中点时,四边形AECF 是矩形.理由如下:当O 为AC 的中点时,AO =CO ,∵EO =FO ,∴四边形AECF 是平行四边形,∵∠ECF =90°,∴平行四边形AECF 是矩形.1、最困难的事就是认识自己。
北师大版九年级数学上册《1.2矩形的性质与判定》同步练习题-附答案

北师大版九年级数学上册《1.2矩形的性质与判定》同步练习题-附答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为()A.60°B.75°C.72° D2.关于矩形的性质、下面说法错误的是()A.矩形的四个角都是直角B.矩形的两组对边分别相等C.矩形的两组对边分别平行D.矩形的对角线互相垂直平分且相等3.在矩形ABCD中,以A为圆心,AD长为半径画弧,交AB于F点,以C为圆心,CD长为半径画弧,交AB于E点,若AD=2,CD=√5则EF=()A.1B.4−√5C.√5−2 D4.顺次连接矩形各边中点得到的四边形是()A.梯形B.矩形C.菱形D.正方形5.如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC边于点E,点F是AE的中点,连接OF,若∠BDC=2∠ADB,AB=1则FO的长度为()A.√32B.12C.√3−1 D6.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=2,则四边形CODE的周长是()A.2.5B.3C.4D.57.如图,已知平行四边形ABCD的对角线AC与BD相交于点O,下列结论中,不正确...的是()A.当AB⊥AD时,四边形ABCD是矩形B.当AC⊥BD时,四边形ABCD是菱形C.当OA=OB时,四边形ABCD是矩形D.当AB=AC时,四边形ABCD是菱形8.依据所标数据,下列四边形不一定为矩形的是()A.B.C.D.二、填空题9.如图,要使平行四边形ABCD是矩形,则应添加的条件是(添加一个条件即可)10.如图,矩形ABCD中,点A坐标是(﹣1,0),点C的坐标是(2,4),则BD的长是;11.如图,在矩形ABCD中,对角线AC与BD相交于点O,CE⊥BD,垂足为点E,CE=5且OE=2DE,则DE的长为.12.矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为cm213.如图,在矩形ABCD中AD=4,AB=6作AE平分∠BAD,若连接BF,则BF的长度为。
北师大版九年级数学上册第一章1.2矩形的性质与判定 同步测试(解析版)

北师大版九年级数学上册第一章1.2矩形的性质与判定同步测试一.选择题1.矩形具有而菱形不一定具有的性质是( )A.对角线互相垂直B.对角线相等C.对角线互相平分D.对角相等【解答】 B ∵矩形和菱形是平行四边形,∴C、D是二者都具有的性质,A是菱形具有的性质,对角线相等是矩形具有而菱形不一定具有的性质.故选B.2.下列说法错误的是( )A.有一个内角是直角的平行四边形是矩形B.矩形的四个角都是直角,并且对角线相等C.对角线相等的平行四边形是矩形D.有两个角是直角的四边形是矩形【解答】 DA.有一个内角是直角的平行四边形是矩形,正确,故本选项不符合题意;B.矩形的四个角都是直角,并且对角线相等,正确,故本选项不符合题意;C.对角线相等的平行四边形是矩形,正确,故本选项不符合题意;D.有两个角是直角的四边形不一定是矩形,可以是直角梯形,故本选项符合题意.故选D.3.(2018•兰州)如图,矩形ABCD中,AB=3,BC=4,EB∥DF且BE与DF之间的距离为3,则AE的长是()A.B.C.D.【解答】解:如图所示:过点D作DG⊥BE,垂足为G,则GD=3.∵∠A=∠G,∠AEB=∠GED,AB=GD=3,∴△AEB≌△GED.∴AE=EG.设AE=EG=x,则ED=4﹣x,在Rt△DEG中,ED2=GE2+GD2,x2+32=(4﹣x)2,解得:x=.故选:C.4.如图,在矩形ABCD中,点O为对角线的交点,E为BC的中点,OE=3,AC=12,则AD=( )A.6√3B.8C.6D.6√2AC=6.【解答】 A ∵四边形ABCD为矩形,∴AD=BC,OB=OC=12∵OB=OC,BE=EC,∴OE⊥BC.∴EC=√OC2-OE2=3√3.∴BC=2EC=6√3.故选A.5.(2019•眉山)如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF ⊥AC交AD于点E,交BC于点F,则DE的长是()A .1B .C .2D .【解答】解:连接CE ,如图所示: ∵四边形ABCD 是矩形,∴∠ADC =90°,CD =AB =6,AD =BC =8,OA =OC , ∵EF ⊥AC , ∴AE =CE ,设DE =x ,则CE =AE =8﹣x ,在Rt △CDE 中,由勾股定理得:x 2+62=(8﹣x )2, 解得:x =, 即DE =; 故选:B .6.如图,矩形ABCD 中,对角线AC,BD 交于点O.若∠AOB=60°,BD=8,则AB 的长为( )A.4B.4√3C.3D.5【解答】 A ∵四边形ABCD 是矩形,∴OA=12AC,OB=12BD=4,AC=BD, ∴OA=OB,∵∠AOB=60°,∴△AOB 是等边三角形,∴AB=OB=4.故选A.7.如图,E,F,G,H 分别是四边形ABCD 四条边的中点,要使四边形EFGH 为矩形,则四边形ABCD 应具备的条件是( )A.一组对边平行而另一组对边不平行B.对角线相等C.对角线互相垂直D.对角线互相平分【解答】 C 要使四边形EFGH 是矩形,则四边形ABCD 应具备的条件是对角线互相垂直.理由:连接AC 、BD,交于点O,由题意可得EF ∥AC,且EF=12AC,GH ∥AC,且GH=12AC, ∴EF ∥GH,且EF=GH,∴四边形EFGH 是平行四边形, ∵E 、H 分别是AB 、AD 的中点,∴EH ∥BD,∵BD ⊥AC,EF ∥AC,∴EH ⊥EF,∴∠HEF=90°,∴平行四边形EFGH 为矩形.故选C. 8. 如图,四边形ABCD 为平行四边形,延长AD 到E ,使DE=AD ,连接EB ,EC ,DB ,添加一个条件,不能使四边形DBCE 成为矩形的是( )A .AB=BEB .DE ⊥DC C .∠ADB=90°D .CE ⊥DE 【答案】B ;【解析】∵四边形ABCD为平行四边形,∴AD∥BC,且AD=BC,又∵AD=DE,∴BE∥BC,且BE=BC,∴四边形BCED为平行四边形,A、∵AB=BE,DE=AD,∴BD⊥AE,∴□DBCE为矩形,故本选项错误;B、∵DE⊥DC,∴∠EDB=90°+∠CDB>90°,∴四边形DBCE不能为矩形,故本选项正确;C、∵∠ADB=90°,∴∠EDB=90°,∴□DBCE为矩形,故本选项错误;D、∵CE⊥DE,∴∠CED=90°,∴□DBCE为矩形,故本选项错误.故选B.9. 矩形一个角的平分线分矩形一边为1cm和3cm两部分,则它的面积为()A.3cm B.4cm C.12cm D.4cm或12cm【答案】D;【解析】矩形的短边可能是1,也可能是3,所以面积为4×1或4×3.10. 如图,矩形ABCG(AB<BC)与矩形CDEF全等,点B、C、D在同一条直线上,∠APE的顶点P在线段BD上移动,使∠APE为直角的点P的个数是( )A.0 B.1 C.2 D.3【答案】C;【解析】当BP=AB或BP=BC时,∠APE是直角.二.填空题11. 如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB 请你添加一个条件,使四边形DBCE是矩形.【答案】EB=DC.【解析】添加EB=DC.理由如下:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴DE∥BC,又∵DE=AD,∴DE=BC,∴四边形DBCE为平行四边形.又∵EB=DC,∴四边形DBCE是矩形.故答案是:EB=DC.12.(2019•徐州)如图,矩形ABCD中,AC、BD交于点O,M、N分别为BC、OC 的中点.若MN=4,则AC的长为16 .【解答】解:∵M、N分别为BC、OC的中点,∴BO=2MN=8.∵四边形ABCD是矩形,∴AC=BD=2BO=16.故答案为16.13.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86厘米,矩形的周长是30厘米,则对角线的长是厘米.【解答】14解析∵四边形ABCD是矩形,∴AB=CD,AD=BC,AC=BD,AO=OC,OD=OB,∴AO=OC=OD=OB,∵矩形ABCD被两条对角线分成的四个小三角形的周长的和是86厘米,∴OA+OD+AD+OD+OC+CD+OC+OB+BC+OA+OB+AB=86厘米,即8OA+2AB+2BC=86厘米,∵矩形ABCD的周长是30厘米,∴2AB+2BC=30厘米,∴8OA=56厘米,∴OA=7厘米,则AC=BD=2OA=14厘米.故答案为14.14. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F 处,折痕为AE,且EF=3,则AB的长为_______.【答案】6;【解析】设AB=AF=,BE=EF=3,EC=5,则CF=4,,解得.15. 如图,矩形ABCD中,AB=3,BC=4,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为_________.【答案】;【解析】BD=5,利用面积法,PE+PF=△AOD中OD边上的高=.16. 矩形ABCD的∠A的平分线AE分BC成两部分的比为1:3,若矩形ABCD的面积为36,则其周长为.【答案】30或10;【解析】∵AE平分∠DAB,∴∠DAE=∠EAB,∵四边形ABCD是矩形,∴AD=BC,DC=AB,AD∥BC,∴∠DEA=∠BEA,∴∠EAB=∠BEA,∴AB=BE,①设BE=x,CE=3x,则AD=4x,AB=x,∵矩形ABCD的面积为36,∴x•4x=36,解得:x=3(负舍),即AD=BC=4x=12,AB=CD=x=3,∴矩形的周长为:AB+BC+CD+AD=2×(3+12)=30;②设BE=3x,CE=x,则AD=4x,AB=3x,∵矩形ABCD的面积为36,∴3x•4x=36,解得:x=(负舍),即AD=BC=4x=4,AB=CD=x=,∴矩形的周长为:AB+BC+CD+AD=2×(4+)=10;故答案为:30或10三.解答题17.如图,已知AB∥DE,AB=DE,AF=CD,∠CEF=90°.求证:(1)△ABF≌△DEC;(2)四边形BCEF是矩形.【解答】证明(1)∵AB∥DE,∴∠A=∠D,在△ABF与△DEC中,{AF=DC,∠A=∠D,AB=DE,∴△ABF≌△DEC(SAS).(2)∵△ABF≌△DEC,∴EC=BF,∠ECD=∠BFA,∴∠ECF=∠BFC,∴EC∥BF,∴四边形BCEF是平行四边形.∵∠CEF=90°,∴四边形BCEF是矩形.18.(2018•沈阳)如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.(1)求证:四边形OCED是矩形;(2)若CE=1,DE=2,ABCD的面积是 4 .【分析】(1)欲证明四边形OCED是矩形,只需推知四边形OCED是平行四边形,且有一内角为90度即可;(2)由菱形的对角线互相垂直平分和菱形的面积公式解答.【解答】(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°.∵CE∥OD,DE∥OC,∴四边形OCED 是平行四边形, 又∠COD=90°,∴平行四边形OCED 是矩形;(2)由(1)知,平行四边形OCED 是矩形,则CE=OD=1,DE=OC=2. ∵四边形ABCD 是菱形, ∴AC=2OC=4,BD=2OD=2,∴菱形ABCD 的面积为: AC •BD=×4×2=4. 故答案是:4.19.如图,矩形ABCD 的对角线AC 、BD 相交于点O.过点A 作AE ∥BD,交CB 的延长线于点E. (1)求证:AC=AE;(2)若∠AOB=120°,AE=8,求BC 的长.【解答】 (1)证明:在矩形ABCD 中,AC=BD,AD ∥BC, 又∵AE ∥BD,∴四边形AEBD 是平行四边形. ∴BD=AE,∴AC=AE.(2)∵∠AOB=120°,∴∠BOC=60°, ∵四边形ABCD 是矩形,∴OB=OC,∴△OBC 是等边三角形,∴BC=OC=12AC=12AE=4.20.(2018•连云港)如图,矩形ABCD 中,E 是AD 的中点,延长CE ,BA 交于点F ,连接AC ,DF .(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.【分析】(1)利用矩形的性质,即可判定△FAE≌△CDE,即可得到CD=FA,再根据CD∥AF,即可得出四边形ACDF是平行四边形;(2)先判定△CDE是等腰直角三角形,可得CD=DE,再根据E是AD的中点,可得AD=2CD,依据AD=BC,即可得到BC=2CD.【解答】解:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠FAE=∠CDE,∵E是AD的中点,∴AE=DE,又∵∠FEA=∠CED,∴△FAE≌△CDE,∴CD=FA,又∵CD∥AF,∴四边形ACDF是平行四边形;(2)BC=2CD.证明:∵CF平分∠BCD,∴∠DCE=45°,∵∠CDE=90°,∴△CDE是等腰直角三角形,∴CD=DE,∵E是AD的中点,∴AD=2CD,∵AD=BC,∴BC=2CD.21.如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.(1)证明:四边形OCED为菱形;(2)若AC=4,求四边形CODE的周长.【解答】(1)证明:∵CE∥BD,DE∥AC,∴四边形CODE为平行四边形,又∵四边形ABCD是矩形,∴OD=OC,∴四边形CODE为菱形.(2)∵四边形ABCD是矩形,∴OC=OD=1AC,2又∵AC=4,∴OC=2,由(1)知,四边形CODE为菱形,∴四边形CODE的周长为4OC=4×2=8.22.(2019•青岛)如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.(1)求证:△ABE≌△CDF;(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF,∵点E,F分别为OB,OD的中点,∴BE=OB,DF=OD,∴BE=DF,在△ABE和△CDF中,,∴△ABE≌△CDF(SAS);(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:∵AC=2OA,AC=2AB,∴AB=OA,∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,同理:CF⊥OD,∴AG∥CF,∴EG∥CF,∵EG=AE,OA=OC,∴OE是△ACG的中位线,∴OE∥CG,∴EF∥CG,∴四边形EGCF是平行四边形,∵∠OEG=90°,∴四边形EGCF是矩形.。
九年级数学上册《第一章 矩形的性质与判定》同步练习题及答案(北师大版)

九年级数学上册《第一章矩形的性质与判定》同步练习题及答案(北师大版)1.如图,点E为矩形ABCD内一点,且EA=EB.求证:∠ECD=∠EDC.2.如图,在矩形ABCD中,点M在CD上,AM=AB,BN⊥AM,垂足为N.(1)求证:△ABN≌△MAD;(2)若AD=3,MN=1,求AB的长.3.如图,在矩形ABCD中,O是对角线AC的中点,过点O作EF⊥AC分别交AD,BC于点E,F.(1)求证:△AOE≌△COF;(2)若AB=8,BC=16,求CF的长.4.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,且FC=AE,连接AF、BF.(1)求证:四边形DEBF是矩形;(2)若AF平分∠DAB,FC=3,DF=5,求BF的长.5.如图,在平行四边形ABCD中,CE⊥AD于点E,延长DA至点F,使得EF=DA,连接BF,CF.(1)求证:四边形BCEF是矩形;(2)若AB=3,CF=4,DF=5,求EF的长.6.如图,在▱ABCD中,点E、F在AD边上,且BF=CE,AE=DF.(1)求证:△ABF≌△DCE;(2)求证:四边形ABCD是矩形.7.已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E,CE=AC.(1)求证:四边形ABCD是矩形;(2)若AB=4,AD=3,求四边形BCED的周长.8.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC 交BC于点E,连接OE.(1)求证:四边形ABCD是矩形;(2)若∠BDE=15°,求∠DOE;(3)在(2)的条件下,若AB=2,求△BOE的面积.9.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.(1)如图1,求证:四边形ABCD为矩形;(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.10.如图,在矩形ABCD中,E为DC边的中点,连接AB,AE的延长线和BC的延长线相交于点F.(1)求证:△ADE≌△FCE;(2)连接AC,与BE相交于点G,若△GEC的面积为2,求矩形ABCD的面积.11.如图,在矩形ABCD中,O为对角线BD的中点,过点O作直线分别与矩形的边AB,CD交于E,F 两点,连接BF,DE.(1)求证:四边形BEDF为平行四边形;(2)若AD=1,AB=3,且EF⊥BD,求AE的长.12.已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.(1)求证:四边形AMCN是平行四边形;(2)当△ABC的边AC、BC满足什么数量关系时,四边形AMCN是矩形,请说明理由.13.如图,过△ABC边AC的中点O,作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD,CE,若CE平分∠ACB,CE⊥BO于点F.(1)求证:OC=BC.(2)四边形ABCD是矩形.14.已知,在四边形ABCD中,AD∥BC,点E为BC的中点,连接AC,DE交于点F,AB=AC,AF=CF.(1)如图1,求证:四边形AECD是矩形;(2)如图2,连接BF,在不添加任何辅助线的情况下,请直接写出图2中与△BEF面积相等的三角形.15.如图,AD是▱ABDE的对角线,∠ADE=90°,延长ED至点C,使DC=ED,连接AC交BD于点O,连接BC.(1)求证:四边形ABCD是矩形;(2)连接OE,若AD=4,AB=2,求OE的长.16.如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1(1)判断△BEC的形状,并说明理由;(2)求证:四边形EFPH是矩形.17.如图△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=4,CF=3,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.18.如图,在平行四边形ABCD中,已知对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向点O运动.(1)当E与F不重合时,四边形DEBF是否是平行四边形?请说明理由;(2)若AC=16cm,BD=12cm,点E,F在运动过程中,四边形DEBF能否为矩形?如能,求出此时的运动时间t的值,如不能,请说明理由.19.如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P 作PQ⊥CP交AD边于点Q,连接CQ.(1)当△CDQ≌△CPQ时,求AQ的长;(2)取CQ的中点M,连接MD,MP,MD⊥MP,求AQ的长.20.如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.(1)求证:△ABE≌△CDF;(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.21.如图,在长方形ABCD中,BC=20cm,P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA 方向在长方形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止,已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当x为何值时,点的运动停止?(2)点P与点N可能相遇吗?点Q与点M呢?请通过计算说明理由.(3)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形?22.如图,AC为矩形ABCD的对角线,BE⊥AC于点E,DF⊥AC于点F.(1)求证:△ABE≌△CDF.(2)求证:四边形BFDE是平行四边形.23.如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线D→C→B→A→D方向以2cm/s 的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.(1)若动点M、N同时出发,经过几秒钟两点相遇?(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?24.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B﹣C﹣D回到点A,设点P运动的时间为t秒.(1)当t=3秒时,求△ABP的面积;(2)当t为何值时,点P与点A的距离为5cm?(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边.参考答案1.证明:∵EA=EB∴∠EAB=∠EBA在矩形ABCD中,∠DAB=∠CBA=90°,AD=BC ∴∠DAB﹣∠EAB=∠CBA﹣∠EBA即∠EAD=∠EBC在△ADE和△BCE中{AD=BC∠DAE=∠CBE EA=EB∴△ADE≌△BCE(SAS).∴ED=EC∴∠ECD=∠EDC.2.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB ∴∠BAN=∠AMD∵BN⊥AM∴∠BNA=90°在△ABN和△MAD中{∠BAN=∠AMD ∠BNA=∠D=90°AB=AM∴△ABN≌△MAD(AAS);(2)解:∵△ABN≌△MAD∴BN=AD=3∵AB2=AN2+BN2∴AB2=(AB﹣1)2+9∴AB=53.(1)证明:∵四边形ABCD是矩形∴AD∥BC∴∠DAC=∠BCA∵点O是AC的中点∴AO=CO在△AEO和△CFO中{∠DAC=∠ACB AO=CO∠AOE=∠COF∴△AEO≌△CFO(ASA);(2)解:如图,连接AF∵AO=CO,EF⊥AC∴AF=FC∵AF2=AB2+BF2∴CF2=(16﹣CF)2+64∴CF=10.4.(1)证明:∵四边形ABCD是平行四边形∴DC∥AB,DC=AB∵FC=AE∴CD﹣FC=AB﹣AE即DF=BE∴四边形DEBF是平行四边形又∵DE⊥AB∴∠DEB=90°∴平行四边形DEBF是矩形;(2)解:∵AF平分∠DAB∴∠DAF=∠BAF∵DC∥AB∴∠DF A=∠BAF∴∠DF A=∠DAF∴AD=DF=5在Rt△AED中,由勾股定理得:DE=√AD2−AE2=√52−32=4由(1)得:四边形DEBF是矩形∴BF=DE=4.5.(1)证明:∵四边形ABCD是平行四边形∴AD∥BC,AD=BC∵EF=DA∴EF=BC,EF∥BC∴四边形BCEF是平行四边形又∵CE⊥AD∴∠CEF=90°∴平行四边形BCEF是矩形;(2)解:∵四边形ABCD是平行四边形∴CD=AB=3∵CF=4,DF=5∴CD2+CF2=DF2∴△CDF是直角三角形,∠DCF=90°∴△CDF的面积=12DF×CE=12CF×CD∴CE=CF×CDDF=4×35=125由(1)得:EF=BC,四边形BCEF是矩形∴∠FBC=90°,BF=CE=12 5∴BC=√CF2−BF2=√42−(125)2=165∴EF=16 5.6.证明:(1)∵四边形ABCD是平行四边形∴AB=CD,AB∥CD∵AE=FD∴AE+EF=FD+EF即AF=DE在△ABF和△DCE中{AB=CD BF=CE AF=DE∴△ABF≌△DCE(SSS);(2)由(1)可知:△ABF≌△DCE∴∠A=∠D∵AB∥CD∴∠A+∠D=180°∴2∠A=180°∴∠A=90°∴▱ABCD为矩形.7.(1)证明:∵四边形ABCD是平行四边形∴AE∥BC∵CE∥BD∴四边形BCED是平行四边形∴CE=BD.∵CE=AC∴AC=BD.∴▱ABCD是矩形;(2)解:∵AB=4,AD=3,∠DAB=90°∴BD=√AB2+AD2=√42+32=5.∵四边形BCED是平行四边形∴四边形BCED的周长为2(BC+BD)=2×(3+5)=16.8.(1)证明:∵AD∥BC∴∠ABC+∠BAD=180°∵∠ABC=90°∴∠BAD=90°∴∠BAD=∠ABC=∠ADC=90°∴四边形ABCD是矩形;(2)解:∵四边形ABCD是矩形,DE平分∠ADC∴∠CDE=∠CED=45°∴EC=DC又∵∠BDE=15°∴∠CDO=60°又∵矩形的对角线互相平分且相等∴OD=OC∴△OCD是等边三角形∴∠DOC=∠OCD=60°∴∠OCB=90°﹣∠DCO=30°∵CO=CE∴∠COE=(180°﹣30°)÷2=75°∴∠DOE=∠DOC+∠COE=60°+75°=135°;(3)解:作OF⊥BC于F.∵四边形ABCD是矩形∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD ∴AO=BO=CO=DO∴BF=FC∴OF=12CD=1∵∠OCB=30°,AB=2∴BC=2√3∵DE平分∠ADC,∠ADC=90°∴∠EDC=45°在Rt△EDC中,EC=CD=2∴△BOE的面积=12•EB•OF=12×(2√3−2)×1=√3−1.9.证明:(1)∵AD∥BC∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°∵∠ABC =∠ADC∴∠BAD =∠BCD∴四边形ABCD 是平行四边形∴OA =OC =12AC ,OB =OD =12BD∵OA =OB∴AC =BD∴四边形ABCD 是矩形;(2)如图,连接OP∵AD =12,AB =5∴BD =√AB 2+AD 2=√144+25=13∴BO =OD =AO =CO =132 ∵S △AOD =14S 矩形ABCD =14×12×5=15∴S △AOP +S △POD =15∴12×132×FP +12×132×EP =15 ∴PE +PF =6013.10.(1)证明:∵四边形ABCD 是矩形∴AD ∥CB ,AD =BC∴∠D =∠FCE ;∵E 为DC 中点∴ED =EC在△ADE 与△FCE 中{∠D =∠FCE DE =CE ∠AED =∠FEC∴△ADE ≌△FCE (ASA );(2)解:∵四边形ABCD 是矩形∴AB ∥CD ,AB =DC∴AB EC =BG EG ,S △ABGS △CEG =(AB EC )2∵DE =CE∴AB =2CE∴BG EG =2,S △ABGS △CEG =(AB EC )2=4∵△GEC 的面积为2∴S △BGC =2S △CEG =4,S △ABG =4S △CEG =8∴S △ABC =S △BGC +S △ABG =4+8=12∴矩形ABCD 的面积=2S △ABC =24.11.(1)证明:∵四边形ABCD 是矩形∴AB ∥CD∴∠OBE =∠ODF∵O 为对角线BD 的中点∴OB =OD在△OBE 和△ODF 中{∠OBE =∠ODF OB =OD ∠BOE =∠DOF∴△OBE ≌△ODF (ASA )∴BE =DF又∵BE ∥DF∴四边形BEDF 为平行四边形;(2)解:∵四边形ABCD 是矩形∴∠A =90°由(1)得:四边形BEDF 为平行四边形∵EF ⊥BD∴平行四边形BEDF 为菱形∴BE =DE设AE =x ,则DE =BE =3﹣x在Rt △ADE 中,由勾股定理得:AD 2+AE 2=DE 2即12+x 2=(3﹣x )2解得:x =43即AE 的长为43. 12.(1)证明∵四边形ABCD 是平行四边形∴AB =CD ,AB ∥CD∵M ,N 分别为AB 和CD 的中点∴AM =12AB ,CN =12CD∴AM =CN∵AB ∥CD∴四边形AMCN 是平行四边形;(2)解:AC =BC 时,四边形AMCN 是矩形证明∵AC =BC ,且M 是BC 的中点∴CM ⊥AB即∠AMC =90°∴四边形AMCN 是矩形.13.证明:(1)∵CE 平分∠ACB∴∠OCE =∠BCE∵BO ⊥CE∴∠CFO =∠CFB =90°在△OCF 与△BCF 中{∠OCE =∠BCE CF =CF ∠CFO =∠CFB△OCF ≌△BCF (ASA )∴OC =BC ;(2)∵点O 是AC 的中点∴OA =OC∵AD ∥BC∴∠DAO =∠BCO ,∠ADO =∠CBO在△OAD 与△OCB 中{∠DAO =∠BCO OA =OC ∠ADO =∠CBO∴△OAD ≌△OCB (ASA )∴AD =BC∵AD ∥BC∴四边形ABCD 是平行四边形∵OE ⊥AC∴∠EOC =90°在△OCE 与△BCE 中{CE =CE ∠OCE =∠BEC OC =BC∴△OCE ≌△BCE (SAS )∴∠EBC =∠EOC =90°∴四边形ABCD 是矩形.14.(1)证明:∵AD ∥BC∴∠F AD =∠FCE ,∠FDA =∠FEC在△ADF 和△CEF 中{∠FAD =∠FCE ∠FDA =∠FEC AF =CF∴△ADF ≌△CEF (AAS )∴AD =CE∵AD ∥CE∴四边形AECD 为平行四边形∵AB =AC ,点E 为BC 的中点∴AE ⊥BC∴∠AEC =90°∴平行四边形AECD 为矩形;(2)解:图2中与△BEF 面积相等的三角形为△AEF ,△ADF ,△CDF ,△CEF .理由如下:∵点E为BC的中点∴S△CEF=S△BEF∵AF=CF∴S△AEF=S△CEF,S△ADF=S△CDF由(1)可知,四边形AECD是矩形∴EF=DF∴S△AEF=S△ADF∴S△CEF=S△BEF=S△AEF=S△ADF=S△CDF即与△BEF面积相等的三角形为△AEF,△ADF,△CDF,△CEF.15.(1)证明:∵四边形ABDE是平行四边形∴AB∥DE,AB=ED∵DC=ED∴DC=AB,DC∥AB∴四边形ABCD是平行四边形∵DE⊥AD∴∠ADC=90°∴四边形ABCD是矩形;(2)解:过O作OF⊥CD于F∵四边形ABCD是矩形,AD=4,AB=2∴DE=CD=AB=2,AD=BC=4,AC=BD,AO=OC,BO=DO ∴OD=OC∵OF⊥CD∴DF=CF=12CD=12×2=1∴OF=12BC=12×4=2,EF=DE+DF=2+1=3∴OE=√EF2+OF2=√32+22=√13.16.解:(1)△BEC是直角三角形:理由是:∵矩形ABCD∴∠ADC=∠ABP=90°,AD=BC=5,AB=CD=2由勾股定理得:CE=√CD2+DE2=√22+12=√5同理BE=2√5∴CE2+BE2=5+20=25∵BC2=52=25∴BE2+CE2=BC2∴∠BEC=90°∴△BEC是直角三角形.(2)∵矩形ABCD∴AD=BC,AD∥BC∵DE=BP∴四边形DEBP是平行四边形∴BE∥DP∵AD=BC,AD∥BC,DE=BP∴AE=CP∴四边形AECP是平行四边形∴AP∥CE∴四边形EFPH是平行四边形∵∠BEC=90°∴平行四边形EFPH是矩形.17.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F ∴∠2=∠5,∠4=∠6∵MN∥BC∴∠1=∠5,∠3=∠6∴∠1=∠2,∠3=∠4∴EO=CO,FO=CO∴OE=OF;(2)解:∵∠2=∠5,∠4=∠6∴∠2+∠4=∠5+∠6=90°∵CE=4,CF=3∴EF=√42+32=5∴OC=12EF=52;(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.证明:当O为AC的中点时,AO=CO∵EO=FO∴四边形AECF是平行四边形∵∠ECF=90°∴平行四边形AECF是矩形.18.解:(1)当E与F不重合时,四边形DEBF是平行四边形.理由:∵四边形ABCD是平行四边形∴OA=OC,OB=OD;∵E、F两动点,分别从A、C两点以相同的速度向点O运动∴AE=CF;∴OE=OF;∴BD、EF互相平分;∴四边形DEBF是平行四边形;(2)四边形DEBF能是矩形.理由:∵四边形DEBF是平行四边形∴当BD=EF时,四边形DEBF是矩形;∵BD=12cm∴EF=12cm;∴OE=OF=6cm;∵AC=16cm;∴OA=OC=8cm;∴AE=2cm由于动点的速度都是1cm/s所以t=2(s)故当运动时间t=2s时,以D、E、B、F为顶点的四边形是矩形.19.解:(1)∵△CDQ≌△CPQ∴DQ=PQ,PC=DC∵AB=DC=5,AD=BC=3∴PC=5在Rt△PBC中,PB=√PC2−BC2=4∴P A=AB﹣PB=5﹣4=1设AQ=x,则DQ=PQ=3﹣x在Rt△P AQ中,(3﹣x)2=x2+12解得x=4 3∴AQ=4 3.(2)方法1,如图2,过M作EF⊥CD于F,则EF⊥AB ∵MD⊥MP∴∠PMD=90°∴∠PME+∠DMF=90°∵∠FDM+∠DMF=90°∴∠MDF=∠PME∵M是QC的中点∴DM=12QC,PM=12QC∴DM=PM在△MDF和△PME中{∠MDF=∠PME ∠DFM=∠MEP DM=PM∴△MDF≌△PME(AAS)∴ME=DF,PE=MF∵EF⊥CD,AD⊥CD∴EF∥AD∵QM=MC∴DF=CF=12DC=52∴ME=5 2∵ME是梯形ABCQ的中位线∴2ME=AQ+BC,即5=AQ+3∴AQ=2.方法2、∵点M是Rt△CDQ的斜边CQ中点∴DM=CM∴∠DMQ=2∠DCQ∵点M是Rt△CPQ的斜边的中点∴MP=CM∴∠PMQ=2∠PCQ∵∠DMP=90°∴2∠DCQ+2∠PCQ=90°∴∠PCD=45°,°∠BCP=90°﹣45°=45°∴∠BPC=45°=∠BCP,∴BP=BC=3∵∠CPQ=90°∴∠APQ=180°﹣90°﹣45°=45°∴∠AQP=90°﹣45°=45°=∠APQ∴AQ=AP=2.20.(1)证明:∵四边形ABCD是平行四边形∴AB=CD,AB∥CD,OB=OD,OA=OC∴∠ABE=∠CDF∵点E,F分别为OB,OD的中点∴BE=12OB,DF=12OD∴BE=DF在△ABE和△CDF中{AB=CD∠ABE=∠CDF BE=DF∴△ABE≌△CDF(SAS);(2)解:当AC=2AB时,四边形EGCF是矩形;理由如下:∵AC=2OA,AC=2AB∴AB=OA∵E是OB的中点∴AG⊥OB∴∠OEG=90°同理:CF⊥OD∴AG∥CF∴EG∥CF由(1)得:△ABE≌△CDF∴AE=CF∵EG=AE∴EG=CF∴四边形EGCF是平行四边形∵∠OEG=90°∴四边形EGCF是矩形.21.解:(1)由题意得x2=20∴x=2√5∴当x为2√5时,点的运动停止;(2)当点P与点N相遇时,2x+x2=20解得x=2√21−1或﹣1﹣2√21(舍去)当点Q与点M相遇时,x+3x=20解得x=5当x=5时,x2=25>20∴点Q与点M不能相遇;(3)∵当点N到达A点时,x2=20∴x=2√5∴BQ=2√5cm,CM=6√5cm∵BQ+CM=8√5<20∴此时M点与Q点还未相遇∴点Q只能在点M的左侧①如图,当点P在点N的左侧时20﹣(x+3x)=20﹣(2x+x2)解得x=0(舍去)或x=2∴当x=2时,以P、Q、M、N为顶点的四边形是平行四边形;②如图,当点P在点N的右侧时20﹣(x+3x)=(2x+x2)﹣20解得x=4或﹣10(舍去)∴当x=4时,以P、Q、M、N为顶点的四边形是平行四边形综上,当x=2或4时,以P、Q、M、N为顶点的四边形是平行四边形.22.证明:(1)∵四边形ABCD是矩形∴AB=CD,AB∥CD∴∠BAE=∠DCF又∵BE⊥AC,DF⊥AC∴∠AEB=∠CFD=90°在△ABE和△CDF中{∠AEB=∠CFD ∠BAE=∠DCF AB=CD∴△ABE≌△CDF(AAS);(2)由(1)得:△ABE≌△CDF∴BE=DF又∵BE⊥AC,DF⊥AC∴BE∥DF∴四边形BFDE是平行四边形.23.解:(1)设t秒时两点相遇根据题意得,t+2t=2(4+8)解得t=8答:经过8秒两点相遇;(2)观察图象可知,点M不可能在AB或DC上.①如图1,点M在E点右侧时,当AN=ME时,四边形AEMN为平行四边形得:8﹣t=9﹣2t解得t=1∵t =1时,点M 还在DC 上∴t =1舍去;②如图2,点M 在E 点左侧时,当AN =ME 时,四边形AEMN 为平行四边形 得:8﹣t =2t ﹣9解得t =173. 所以,经过173秒钟,点A 、E 、M 、N 组成平行四边形.24.解:(1)当t =3时,点P 的路程为2×3=6cm∵AB =4cm ,BC =6cm∴点P 在BC 上∴S △ABP =12AB ⋅BP =4(cm 2).(2)(Ⅰ)若点P 在BC 上∵在Rt △ABP 中,AP =5,AB =4∴BP =2t ﹣4=3∴t =72;(Ⅱ)若点P 在DC 上则在Rt △ADP 中,AP 是斜边∵AD =6∴AP >6∴AP ≠5;(Ⅲ)若点P 在AD 上AP =5则点P 的路程为20﹣5=15∴t=15 2综上,当t=72秒或t=152时,AP=5cm.(3)当2<t<5时,点P在BC边上∵BP=2t﹣4,CP=10﹣2t∴AP2=AB2+BP2=42+(2t﹣4)2由题意,有AD2+CP2=AP2∴62+(10﹣2t)2=42+(2t﹣4)2∴t=133<5即t=13 3.。
北师大版数学九年级上册1.2矩形的性质与判定同步练习有答案

2018-2019学年度北师大版数学九年级上册同步练习1.2 矩形的性质与判定学校:___________姓名:___________班级:___________一.选择题(共15小题)1.已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是()A.24cm2B.32cm2C.48cm2D.128cm22.下面对矩形的定义正确的是()A.矩形的四个角都是直角B.矩形的对角线相等C.矩形是中心对称图形D.有一个角是直角的平行四边形3.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD 于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10 B.12 C.16 D.184.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC,若AC=6cm,则四边形CODE的周长为()A.6 B.8 C.10 D.125.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD,垂足为E,AE=3,ED=3BE,则AB的值为()A.6 B.5 C.2 D.36.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE垂直平分BO,AE=cm,则OD=()A.1cm B.1.5cm C.2cm D.3cm7.下列命题中正确的是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是矩形C.对角线相等的平行四边形是矩形D.对角线互相垂直的平行四边形是矩形8.如图,在平行四边形ABCD中,AC、BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是()A.∠BAC=∠ACB B.∠BAC=∠ACD C.∠BAC=∠DAC D.∠BAC=∠ABD9.如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是()A.AO=OC B.AC=BD C.AC⊥BD D.BD平分∠ABC10.如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是()A.AB=CD,AD=BC,AC=BD B.AC=BD,∠B=∠C=90°C.AB=CD,∠B=∠C=90°D.AB=CD,AC=BD11.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形12.如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F.则线段EF的最小值为()A.B.C.D.13.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是()A.3 B.C. D.414.如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF 是矩形的是()A.∠BAC=90°B.BC=2AE C.DE平分∠AEB D.AE⊥BC15.已知四边形ABCD中,对角线AC与BD相交于点O,AD∥BC,下列判断中错误的是()A.如果AB=CD,AC=BD,那么四边形ABCD是矩形B.如果AB∥CD,AC=BD,那么四边形ABCD是矩形C.如果AD=BC,AC⊥BD,那么四边形ABCD是菱形D.如果OA=OC,AC⊥BD,那么四边形ABCD是菱形二.填空题(共6小题)16.矩形ABCD中,AB=3,BC=4,则AC=,矩形的面积为.17.如图,在▱ABCD中,再添加一个条件(写出一个即可),▱ABCD是矩形(图形中不再添加辅助线)18.如图,设矩形ABCD和矩形AEFC的面积分别为S1、S2,则二者的大小关系是:S1 S2.19.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=5cm,BC=12cm,则EF=cm.20.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加条件,才能保证四边形EFGH是矩形.21.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF ⊥AC于F,M为EF中点,则AM的最小值为.三.解答题(共5小题)22.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,BD=6,求矩形ABCD的面积.23.如图,DB∥AC,且DB=AC,E是AC的中点.(1)求证:BC=DE;(2)连接AD、BE,若∠BAC=∠C,求证:四边形DBEA是矩形.24.已知:如图,菱形ABCD,分别延长AB,CB到点F,E,使得BF=BA,BE=BC,连接AE,EF,FC,CA.(1)求证:四边形AEFC为矩形;(2)连接DE交AB于点O,如果DE⊥AB,AB=4,求DE的长.25.如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD 边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.(1)求证:平行四边形ABCD是矩形;(2)求BF的长;(3)求折痕AF长.26.已知矩形ABCD 和点P ,当点P 在图1中的位置时,则有结论:S △PBC =S △PAC +S △PCD 理由:过点P 作EF 垂直BC ,分别交AD 、BC 于E 、F 两点.∵S △PBC +S △PAD =BC•PF +AD•PE=BC (PF +PE )=BC•EF=S 矩形ABCD .(1)请补全以上证明过程.(2)请你参考上述信息,当点P 分别在图1、图2中的位置时,S △PBC 、S △PAC 、S PCD 又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.参考答案一.选择题(共15小题)1.B.2.D.3.C.4.D.5.C.6.C.7.C.8.D.9.B.10.D.11.D.12.D.13.C.14.D.15.A.二.填空题(共6小题)16.5,12.17.AC=BD18.=.19..20.AC⊥BD.21..三.解答题(共5小题)22.解:∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD,OA=AC,OD=BD,∴OA=OD,∵∠AOD=120°,∴∠ADO=30°∴AB=BD.在直角三角形ABD中,由勾股定理,得AD===3=AB•AD=3×3=9.∴S矩形ABCD23.(1)证明:∵E是AC中点,∴EC=AC.∵DB=AC,∴DB=EC.又∵DB∥EC,∴四边形DBCE是平行四边形.∴BC=DE.(2)证明:∵DB∥AE,DB=AE,∴四边形DBEA是平行四边形.∵∠BAC=∠C,∴BA=BC,∵BC=DE,∴AB=DE.∴▭ADBE是矩形.24.证明:(1)∵BF=BA,BE=BC,∴四边形AEFC为平行四边形,∵四边形ABCD为菱形,∴BA=BC,∴BE=BF,∴BA+BF=BC+BE,即AF=EC,∴四边形AEFC为矩形;(2)连接DB,由(1)可知,AD∥EB,且AD=EB,∴四边形AEBD为平行四边形,∵DE⊥AB,∴四边形AEBD为菱形,∴AE=EB,AB=2AG,ED=2EG,∵矩形ABCD中,EB=AB,AB=4,∴AG=2,AE=4,∴在Rt△AEG中,EG=2,∴ED=4.25.(1)证明:∵把纸片ABCD折叠,使点B恰好落在CD边上,∴AE=AB=10,AE2=102=100,又∵AD2+DE2=82+62=100,∴AD2+DE2=AE2,∴△ADE是直角三角形,且∠D=90°,又∵四边形ABCD为平行四边形,∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);(2)解:设BF=x,则EF=BF=x,EC=CD﹣DE=10﹣6=4cm,FC=BC﹣BF=8﹣x,在Rt△EFC中,EC2+FC2=EF2,即42+(8﹣x)2=x2,解得x=5,故BF=5cm;(3)解:在Rt△ABF中,由勾股定理得,AB2+BF2=AF2,∵AB=10cm,BF=5cm,∴AF==5cm.26.证明:(1)∵S△PAC+S△PCD+S△PAD=S矩形ABCD∴S△PBC +S△PAD=S△PAC+S△PCD+S△PAD,∴S△PBC=S△PAC+S△PCD;(2)猜想结果:图2结论S△PBC=S△PAC+S△PCD;图3结论S△PBC=S△PAC﹣S△PCD.证明:如图,过点P作EF垂直AD,分别交AD、BC于E、F两点.∵S△PBC=BC•PF=BC•PE+BC•EF=AD•PE+BC•EF=S△PAD+S矩形ABCDS△PAC+S△PCD=S△PAD+S△ADC=S△PAD+S矩形ABCD∴S△PBC=S△PAC+S△PCD.。
北师版九上数学1.2矩形的性质与判定 同步练习(含答案)

北师版九上数学1.2矩形的性质与判定同步练习(含答案)一、选择题(共10题;共20分)1.(2分)下列说法正确的是()A.对角线互相垂直的四边形是菱形B.四边相等的四边形是菱形C.一组对边平行的四边形是平行四边形D.矩形的对角线互相垂直2.(2分)如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S△ABC=2S△ABF.其中正确的结论有()A.4个B.3个C.2个D.1个3.(2分)如图,在ABC中,AB=10,AC=8,BC=12,AD⊥BC于D,点E、F分别在AB、AC边上,把ABC沿EF折叠,使点A与点D恰好重合,则DEF的周长是().A.14B.15C.16D.174.(2分)如图,将正方形ABCD的一角折叠,折痕为AE,∠FAD比∠FAE大48°,设∠FAE和∠FAD的度数分别为x°,y°,那么x,y所适合的一个方程组是()A.B.C.D.5.(2分)如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于,则sin∠CAB=()A.B.C.D.6.(2分)如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB 上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°7.(2分)如图,在中,,平分.若则的长为()A.B.C.D.8.(2分)(2011•朝阳)如图,沿Rt△ABC的中位线DE剪切一刀后,用得到的△ADE 和四边形DBCE拼图,下列图形:①平行四边形;②菱形;③矩形;④等腰梯形.一定能拼出的是()A.只有①②B.只有③④C.只有①③④D.①②③④9.(2分)如图,已知⊙O的半径为5,AB⊥CD,垂足为P,且AB=CD=8,则OP的长为()A.3B.4C.3D.410.(2分)如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是﹣1,则对角线AC、BD的交点表示的数是()A. 5.5B.5C.6D. 6.5二、填空题(共5题;共5分)11.(1分)如图,▱ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是________cm.12.(1分)如图,在△ABD中,∠ADB=90°,C是BD上一点,若E、F分别是AC、AB 的中点,△DEF的面积为3.5,则△ABC的面积为________.13.(1分)如图,在四边形ABCD中,,M、N分别是AC、BD的中点,则线段MN的长为________14.(1分)如图,等边三角形AOB的顶点A的坐标为(﹣4,0),顶点B在反比例函数y=(x<0)的图象上,则k=________.15.(1分)如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是________.三、解答题(共5题;共50分)16.(5分)如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.求证:四边形OCED是菱形.17.(20分)如图,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO﹣OC以每秒1个单位长度的速度向终点C运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD 重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).(1)求点N落在BD上时t的值;(2)直接写出点O在正方形PQMN内部时t的取值范围;(3)当点P在折线AD﹣DO上运动时,求S与t之间的函数关系式;(4)直接写出直线DN平分△BCD面积时t的值.18.(10分)猜想与证明:如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM,EM.(1)试猜想写出DM与EM的数量关系,并证明你的结论.拓展与延伸:(2)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则(1)中的结论是否仍然成立?请直接写出你的判断.19.(6分)如图,中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,BF =AC.(1)求证:△BDF≌ADC(2)若∠CAD=20°,则∠ABE=________°.(直接写出结果)20.(9分)一位同学拿了两块45°的三角尺△MNK,△ACB做了一个探究活动:将△MNK 的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为________,周长为________;(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为________,周长为________;(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.参考答案一、选择题(共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题(共5题;共5分)11-1、12-1、13-1、14-1、15-1、三、解答题(共5题;共50分)16-1、17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、20-3、。
2023-2024学年北师大版九年级数学上册《第一章 矩形的性质与判定》同步练习题附答案

2023-2024学年北师大版九年级数学上册《第一章矩形的性质与判定》同步练习题附答案学校:___________班级:___________姓名:___________考号:___________一、选择题(本大题共10小题,共30.0分。
在每小题列出的选项中,选出符合题目的一项)1. 菱形具有而矩形不一定具有的性质是( )A. 对边平行B. 对角线互相平分C. 对角线互相垂直D. 对角互补2. 在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )A. ∠ABC=90∘B. AC=BDC. OA=OBD. OA=AD3. 四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A. AB=CDB. AD=BCC. AB=BCD. AC=BD4. 在Rt△ABC中∠C=90°,斜边AB=8,则斜边上的中线CD=( )A. 2B. 4C. 8D. 165. 如图,在Rt△ABC中∠A=90°,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( )A. 一直增大B. 一直减小C. 先减小后增大D. 先增大后减少6. 如图,用一根绳子检测一个平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量两条对角线就可以判断了.在如下定理中:①两组对边分别相等的四边形是平行四边形②对角线相等的平行四边形是矩形③矩形的四个角都是直角④三个角都是直角的四边形是矩形,这种检测方法用到的数学根据是( )A. ①B. ②C. ③D. ④7. 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AO=2,则AB的长是( )A. 2B. 3C. 4D. 68. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AD的中点,且OE=3,则菱形ABCD的周长为( )A. 9B. 12C. 18D. 249. 如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3则AO 的长为( )A. √ 5B. 32√ 5C. 2√ 5D. 4√ 510. 如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )A. 485B. 325C. 245D. 125二、填空题(本大题共10小题,共30.0分)11. 在Rt△ABC中∠C=90°,D为斜边AB的中点,若CD=2cm,则AB=______cm.12. 在矩形ABCD中,对角线AC,BD交于点O,若∠AOB=100∘,则∠OAB=°.13. 矩形的两条对角线的一个夹角是60°,两条对角线长度的和是8cm,那么矩形的较短边长是______cm.14. 直角三角形中,两直角边长分别为2和4,则斜边上的中线长为______ .15. 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AC=5km,BC=12km,则M、C两点间的距离为km.16. 如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=6则AC的值为________.17. 在四边形ABCD中∠ABC=∠ADC=90°,连接AC,点E为AC的中点,,BC=12则△ABE的周长为______ .连接BE,DE.若DE=13218. 已知矩形纸片ABCD中AB=8cm,AD=16cm将此长方形纸片折叠,使点B与点D重合,折痕为EF,则折痕EF的长为______ cm.19. 如图,矩形ABCD中AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为______.20. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF若MF=AB,则∠DAF=______ 度.三、解答题(本大题共5小题,共40.0分。
2023-2024学年北师大版九年级数学上册《第一章-矩形的性质与判定》同步练习题带答案

2023-2024学年北师大版九年级数学上册《第一章矩形的性质与判定》同步练习题带答案学校:___________班级:___________姓名:___________考号:___________一、选择题(本大题共10小题,共30.0分。
在每小题列出的选项中,选出符合题目的一项)1. 若菱形的周长为48cm,则其边长是( )A. 24cmB. 12cmC. 8cmD. 4cm2. 菱形具有而一般平行四边形不具有的性质是( )A. 两组对边分别相等B. 两条对角线相等C. 四个内角都是直角D. 每一条对角线平分一组对角3. 如图,广场中心菱形花坛ABCD的周长是32米∠A=60°,则A、C两点之间的距离为( )A. 4米B. 4√ 3米C. 8米D. 8√ 3米4. 下列选项中能使▱ABCD成为菱形的是( )A. AB=CDB. AB=BCC. ∠BAD=90°D. AC=BD5. 如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2.则OC的长为( )A. 2B. 3C. 4D. 56. 如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根圆心,大于12据他的作图方法可知四边形ADBC一定是( )A. 矩形B. 菱形C. 正方形D. 等腰梯形7. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )A. 四边形ABCD周长不变B. AD=CDC. 四边形ABCD面积不变D. AD=BC8. 如图,在Rt△ABC中∠C=90°,∠A=30°,AB=2,将△BEF沿EF所在直线翻折得到△DEF,点D为∠ABC的平分线与边AC的交点,则线段EF长度为( )A. 12B. √ 32C. 23√ 3D. 239. 如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )A. 13B. 10C. 12D. 510. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4,OH的长为1.5,则S菱形ABCD=( )A. 24B. 12C. 8D. 6二、填空题(本大题共10小题,共30.0分)11. 菱形的边长为5,则它的周长是.12. 已知菱形的两条对角线长分别是6和8,则这个菱形的面积为.13. 如图,菱形ABCD的对角线AC,BD相交于点O,已知OB=4,菱形ABCD的面积为24,则AC的长为______14. 如图,将菱形纸片ABCD沿过点C的直线折叠,使点D落在射线CA上的点E处,折痕CP交AD于点P.若∠ABC=30°,AP=2则PE的长等于______ .15. 菱形ABCD的边长为2,∠ABC=45°点P、Q分别是BC、BD上的动点,CQ+PQ的最小值为______.16. 如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC若AB=2cm,四边形OACB的面积为5cm2.则OC的长为____cm.17. 已知菱形的一边与两条对角线的夹角之差是18°,则此菱形的各个内角分别是______ .18. 如图,菱形ABCD的边长为10,对角线AC=18,点E、F分别是边CD,BC的中点,连接EF并延长与AB的延长线相交于点G,则EG=______ .19. 如图,在菱形ABCD中∠ABC=60°°,在对角线AC上任取一点P(端点除外),连接PD、PB.在BA的延长线上取一点Q,使PD=PQ.当点P在线段AC上移动时:①∠PDA=PBA②当点P沿CA方向运动时,∠DPQ的度数先变小,后变大③PC=AQ④PB=PD.其中,说法正确的序号是______ .20. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为______.三、解答题(本大题共5小题,共40.0分。
2023-2024学年北师大版九年级数学上册《第一章 矩形的性质与判定》同步练习题附带答案
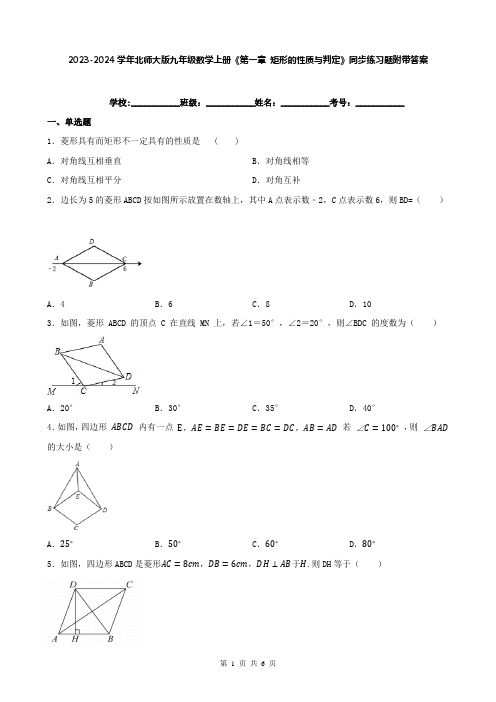
2023-2024学年北师大版九年级数学上册《第一章矩形的性质与判定》同步练习题附带答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.菱形具有而矩形不一定具有的性质是 ( )A.对角线互相垂直B.对角线相等C.对角线互相平分D.对角互补2.边长为5的菱形ABCD按如图所示放置在数轴上,其中A点表示数﹣2,C点表示数6,则BD=()A.4 B.6 C.8 D.103.如图,菱形 ABCD 的顶点 C 在直线 MN 上,若∠1=50°,∠2=20°,则∠BDC 的度数为()A.20°B.30°C.35°D.40°4.如图,四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD若∠C=100∘,则∠BAD 的大小是()A.25∘B.50∘C.60∘D.80∘5.如图,四边形ABCD是菱形AC=8cm,DB=6cm,DH⊥AB于H.则DH等于()A.3.6 B.4.8 C.5 D.10CD长为半径作弧,两弧分别交于点E,6.已知,如图,在菱形ABCD中.(1)分别以C,D为圆心,大于12F;(2)作直线EF,且直线EF恰好经过点A,且与边CD交于点M;(3)连接BM.根据以上作图过程及所作图形,判断下列结论中错误的...是()A.∠ABC=60°B.如果AB=2,那么BM=4C.BC=2CM D.S△ABM=2S△ADM7.如图,将一个长为10cm,宽为8cm的矩形纸片横向对折,再纵向对折后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的图形的面积为()A.10cm2B.20cm2C.40cm2D.80cm28.如图,在平面直角坐标系xOy中,已知点A(2√2,0),B(2,2)若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是()A.向左平移2个单位,再向下平移2个单位B.向左平移(2√2−1)个单位,再向上平移2个单位C.向右平移2个单位,再向上平移2个单位D.向右平移√2个单位,再向上平移2个单位二、填空题9.菱形的两条对角线的长分别是6cm和8cm,则菱形的周长是cm.10.蜜蜂采蜜时,如果蜜源很远它就会跳起“8字舞”,告诉同伴蜜源的方向.如图所示,两个全等菱形的边长为1厘米,一只蜜蜂由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,飞行2020厘米后停下,则这只蜜蜂停在点.11.菱形ABCD的边长为2,∠ABC=60°,E是AD边中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是.12.如图,已知菱形ABCD的顶点A( −√3,0),∠DAB=60°,若动点P从点A出发,沿A→B→C→D→A →B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标为.13.如图,菱形ABCD中,∠DAB=60°,DF⊥AB于点E,且DF=DC,连结PC,则∠DCF的度数为度.三、解答题14.如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,AD=BC,求证:四边形EFGH 是菱形.15.如图,已知菱形ABCD的对角线AC、BD相交于点O,点E是菱形外一点,且DE∥AC,CE∥BD,连接OE.求证:OE=CD.16.如图,点F在平行四边形ABCD的对角线AC上,过点F,B分别作AB,AC的平行线相交于点E、连接BF;若∠ABF=∠FBC+∠DAC.求证:四边形ABEF是菱形.17.□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F,四边形AFCE是否是菱形?为什么?18.求证:对角线互相垂直的平行四边形是菱形.小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.①已知:如图,在▱ABCD中,对角线AC,BD交于点O,.②求证:参考答案1.A2.B3.C4.B5.B6.B7.A8.C9.2010.E11.2√3312.(0,-1)13.4514.证明:∵E ,F 是AB ,BD 的中点 ∴EF =12AD 同理,GH =12AD ,HE =12BC ,FG =12BC ∵AD =BC ∴EF =GH =HE =FG ∴四边形EFGH 是菱形.15.证明:∵DE ∥AC ,CE ∥BD ∴四边形OCED 是平行四边形 ∵四边形ABCD 是菱形 ∴∠COD=90°,AB=BC=CD=AD ∴四边形OCED 是矩形 ∴OE=DC ;16.证明∵EF ∥AB ,BE ∥AF ∴四边形ABEF 是平行四边形 ∵四边形ABCD 是平行四边形 ∴AD ∥BC ∴∠DAC =∠FCB ∵∠ABF =∠FBC +∠DAC ∴∠ABF =∠FBC +∠FCB 又∵∠AFB =∠FBC +∠FCB ∴∠ABF =∠AFB ∴AB =AF ∴▱ABEF 是菱形;即:四边形ABEF 是菱形.17.解:四边形AFCE 是菱形,理由如下:∵四边形ABCD 是平行四边形 ∴AD ∥BC∴∠EAO=∠FCO ,∠AEO=∠CFO ;∵EF 垂直平分AC ∴OA=OC.在△AOE和△COF中∠EAO=∠FCO,∠AEO=∠CFO,OA=OC.∴△AOE≌△COF;∴OE=OF ∴四边形AFCE是平行四边形∵EF⊥AC ∴平行四边形AFCE是菱形.18.解:①AC⊥BD②四边形ABCD是菱形证明:∵四边形ABCD为平行四边形∴BO=DO ∵AC⊥BD ∴AC垂直平分BD ∴AB=AD ∴四边形ABCD为菱形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩形 同步测试题
一.选择题
1.下列关于矩形的说法中正确的是( )
A .对角线相等的四边形是矩形
B .对角线互相平分的四边形是矩形
C .矩形的对角线互相垂直且平分
D .矩形的对角线相等且互相平分
2. 矩形一个角的平分线分矩形一边为1cm 和3cm 两部分,则它的面积为( )
A.32cm
B. 42cm
C. 122cm
D. 42cm 或122
cm 3.已知:如图,四边形ABCD 是平行四边形,延长BA 到点E ,使AE=AB ,联结ED ,EC ,AC ,添加一个条件,能使四边形ACDE 成为矩形的是( )
A .AC=CD
B .AB=AD
C .AD=AE
D .BC=CE
4. 把一张长方形的纸片按如图所示的方式折叠,EM 、FM 为折痕,折叠后的C 点落在B′M 或B′M 的延长线上,那么∠EMF 的度数是( )
A.85°
B.90°
C.95°
D.100°
5.如图,四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°,BE ⊥AD 于点E ,且四边形ABCD 的面积为8,则BE =( )
A.2
B.3
C.22
D.32
6. 矩形的面积为1202cm ,周长为46cm ,则它的对角线长为( )
A.15cm
B.16cm
C.17cm
D.18cm
二.填空题
7.如图,四边形ABCD 是一张矩形纸片,AD =2AB ,若沿过点D 的折痕DE 将A 角翻折,使点A 落在BC 上的A 1处,则∠EA 1B =______°.
8.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连结CE,则CE的长______.
9. 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=4cm,则矩形对角
线AC长为________cm.
10.如图,在矩形ABCD中,点E、F分别在边CD、BC上,DC=3DE=3a,将矩形沿直线EF折
叠,使点C恰好落在AD边上的点P处,则FP=_______.
11.矩形ABCD的∠A的平分线AE分BC成两部分的比为1:3,若矩形ABCD的面积为36,则
其周长为.
12.如图所示,将矩形ABCD沿AE向上折叠,使点B落在DC边上的F处,若△AFD的周长
为9,△ECF的周长为3,则矩形ABCD的周长为___________.
13.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有几个?
14.已知:如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O
既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=1
2
BD,则四边形ABCD是什么特殊四边形?说明理由.
15.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.
求证:AE平分∠BAD.
一.选择题
1.【答案】D ;
2.【答案】D ;
【解析】矩形的短边可能是1,也可能是3,所以面积为4×1或4×3.
3.【答案】D ;
【解析】添加一个条件BC=CE.
理由:∵四边形ABCD 为平行四边形,∴AB ∥CD 且AB=CD ,
∵AE=AB ,∴AE ∥CD 且AE=CD ,∴四边形DEAC 为平行四边形,
∵BC=EC ,AE=AB ,∴∠EAC=90°,∴平行四边形ACDE 是矩形.
4.【答案】B ; 【解析】∠EMF=∠EMB′+∠FMB′=21∠BMC′+21∠CMC′=2
1×180°=90°. 5.【答案】C ;
【解析】过点C 做BE 垂线,垂足为F ,易证△BAE ≌△CBF ,所以BF =AE ,BE =CF ,所以
总面积=AE ×BE +CF ×EF = AE ×BE +BE ×(BE -AE )=28BE =,22BE =.
6.【答案】C ;
【解析】设边长为a b 、,则23,120,a b ab +==解得22
289a b +=,所以对角线为28917=.
二.填空题
7.【答案】60°;
【解析】AD =A 1D =2CD ,所以∠CA 1D =30°,∠EA 1B =60°.
8.【答案】136
; 【解析】设AE =CE =x ,DE =3x -,()22232x x =-+,136
x =. 9.【答案】8;
【解析】由矩形的性质可知△AOB 是等边三角形,∴ AC =2AO =2AB =8cm .
10.【答案】23a ;
【解析】作FM ⊥AD 于M ,如图所示:
则MF=DC=3a ,由题意可得:CE=2a ,
由折叠可得:PE=CE=2a =2DE ,∠EPF=∠C=90°,
∴∠DPE=30°,∴∠MPF=60°,∠MFP=30°,∴FP=2233
a ⨯=. 11.【答案】30或10;
【解析】∵AE 平分∠DAB ,
∴∠DAE=∠EAB ,
∵四边形ABCD 是矩形,
∴AD=BC ,DC=AB ,AD ∥BC ,
∴∠DEA=∠BEA ,
∴∠EAB=∠BEA ,
∴AB=BE ,
①设BE=x ,CE=3x ,则AD=4x ,AB=x ,
∵矩形ABCD 的面积为36,
∴x•4x=36,
解得:x=3(舍负),
即AD=BC=4x=12,AB=CD=x=3,
∴矩形的周长为:AB+BC+CD+AD=2×(3+12)=30;
②设BE=3x ,CE=x ,则AD=4x ,AB=3x , ∵矩形ABCD 的面积为36,
∴3x•4x=36, 解得:x=(舍负), 即AD=BC=4x=4,AB=CD=x=,
∴矩形的周长为:AB+BC+CD+AD=2×(4
+)=10;
故答案为:30或10.
12.【答案】12; 【解析】设BE =EF =x ,CE =b ,CF =a ,DF =y ,则9,3x b y y a x a b ++++=++=,
解得3y =,矩形ABCD 的周长=()()223312y a x b +++=⨯+=.
三.解答题
13.【解析】
解:①正确,连接PC ,可得PC=EF ,PC=PA ,∴AP=EF ;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PD=PF=CE;
⑤正确,PB2+PD2=2PA2.
所以正确的有4个:①②③⑤.
14.【解析】
(1)证明:∵BE⊥AC.DF⊥AC,
∴∠BEO=∠DFO=90°,
∵点O是EF的中点,
∴OE=OF,
又∵∠DOF=∠BOE,
∴△BOE≌△DOF(ASA);
(2)解:四边形ABCD是矩形.理由如下:
∵△BOE≌△DOF,
∴OB=OD,
又∵OA=OC,
∴四边形ABCD是平行四边形,
∵OA=1
2
BD,OA=
1
2
AC,
∴BD=AC,
∴ABCD是矩形.
15.【解析】
证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,AB=CD,
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠BEF+∠CED=90°.
∴∠BFE=∠CED.
又∵EF=ED,
∴△EBF≌△DCE.
∴BE=CD.
∴BE=AB.∴∠BAE=∠BEA=45°.
∴∠EAD=45°.
∴∠BAE=∠EAD.
∴AE平分∠BAD.。
