核数据处理课程设计--能谱谱数据分解方法研究程序
核数据处理课程设计

导数法在γ射线能谱寻峰、边界道的确定、峰面积计算中的应用摘要:本文导数法对平滑后的能谱数据进行寻峰,并比较各阶导数法寻峰、导数法对于能谱数据寻峰、以及比较不同的拟合公式求导后对寻峰以及峰面积结果分析。
关键词:能谱、峰面积、导数法、寻峰、边界道、拟合Abstract:This method of derivative spectroscopy data after smoothing peak search, and compare order derivative France to find the peak derivative method for the spectroscopy data the peak search and compare different fitting formula derivation on the peak search and peak areaanalysis of results.Keywords: spectroscopy, peak area, the derivative method, peak search, boundary Road, fitting.导数是一条光沿曲线上数值的微商或微商函数,在数学上称它为曲线上各点的斜率。
在导数光谱术中导数吸收光谱是指光强度或吸光强度对波长的变化率曲线。
当将原吸收曲线进行一阶、二阶直至四阶求导时,便可得到各阶导数光谱。
导数光谱的基本特征(1)对原曲线的极值求一、二阶导数时通过原点,求二阶导数时为极小值,四阶导数为极大值,并恢复至原位置。
据此特征可以准确的测定最大的吸收峰位。
(2)极值数目随求导阶数的增加而增加。
如当原曲线有一个极大值时 ,求n阶导数就有n+1个极大值和极小值,而原曲线有两个极大值时,则出现n+3个极值。
(3)随求导阶数的增加,谱带变窄和复杂化。
两组分组合的吸收曲线原光小的吸收谱带为大的吸收谱带所掩蔽,经二阶求导之后,原曲线中的小“卫星”峰就变成极小值,四阶导数变为极大值。
核数据处理课程设计报告

核数据处理课程设计报告姓名:学号:班级:2012年月日目录一、设计目的和要求二、设计原理1、探测原理。
2、核数据处理的分析方法:谱光滑、寻峰、求峰面积。
三、任务实现1、计算器2、写数据到文件中3、按钮实现数据的读写4、显示图谱5、寻峰及道址换算6、求峰面积一、设计目的和要求1、掌握核辐射探测的原理及核数据处理的方法;2、了解图形程序的编写技能与技巧;3、掌握文件读写函数的使用;4、理解整个谱数据处理的流程;5、进一步掌握对常用核数据处理的基本方法。
二、设计原理1、探测原理。
什么是核辐射和核辐射探测?所谓核辐射是指在各种核跃迁中,从原子核中释放出来中子、质子、α粒子、β粒子、X射线、γ射线等。
由于它们本身具有波粒二象性,所以也将它们称为粒子或射线。
而核辐射探测主要是用各种类型和规格的核辐射探测器记录粒子数目,测定放射源的活度,确定粒子的质量、电荷、寿命、能量以及动量等。
在核辐射探测原理中,最基本的是利用带电粒子在物质中对物质原子产生的电离和激发效应或快速轻带电粒子穿过物质时的电磁效应。
X射线和γ射线在物质中没有直接电离和激发效应,因此,不能直接被探测到。
只有利用它们在物质中的光电效应、康普顿散射和电子对产生效应等产生的次级电子再引起的电离和激发才能探测到。
射线与物质的相互作用主要有三个过程:光电效应、康普顿效应、电子对效应1.1 光电效应光子通过物质时和物质原子相互作用,光子被原子吸收后发射轨道电子的现象,称为光电效应,也称光电吸收。
光电效应发出来的电子叫做光电子。
光电效应、特征X射线和俄歇电的发射示意图光电子可以从原子的K、L、M等各壳层中发射出来。
在光电效应过程中,因为动量守恒要求,除入射光子和光电外,还必需有第三者参加,即原子核,严格的讲是发射光电子之后余下的整个原子。
所以自由电子不能产生光电效应,而且原子的内层电子由于受到原子核的强束缚更容易满足动量守恒而更容易发射光电子。
一般的说,如果入射光子的能量超过K层电子结合能,那么,大约80%的光电吸收发生在K层电子上。
核磁数据处理方法

核磁数据处理方法核磁共振(NMR)是一种重要的分析技术,广泛应用于化学、生物学和医学等领域。
在进行核磁实验时,我们需要对得到的数据进行处理和分析,以获得实用的信息。
本文将详细介绍核磁数据处理的方法和步骤。
一、数据获取和预处理1. 数据获取:通过核磁共振仪器获取样品的核磁共振谱图。
谱图通常包含两个维度的数据,即横轴表示化学位移,纵轴表示信号强度。
2. 数据预处理:对获得的谱图进行预处理,包括去除噪声、基线校正和相位校正等。
去除噪声可以提高信噪比,基线校正可以消除谱图中的基线漂移,相位校正可以调整信号的相位。
二、数据处理和分析1. 峰识别:通过峰识别算法找出谱图中的峰,并确定其化学位移和峰面积。
常用的峰识别算法包括峰拟合法和峰积分法。
2. 化学位移校正:根据已知的内部标准品或者参考物质的峰位置,对谱图进行化学位移校正,以提高数据的准确性和可比性。
3. 峰归属:通过与数据库或者文献比对,确定峰的归属,即确定峰所代表的化合物或者功能基团。
4. 峰积分和积分校正:对峰进行积分,计算峰的面积。
如果需要,还可以进行积分校正,以消除不同峰的积分因子差异带来的影响。
5. 峰定量:根据峰的面积和浓度关系,进行峰定量分析,计算样品中目标物质的含量。
6. 数据可视化:将处理后的数据进行可视化展示,通常使用谱图或者曲线图来展示数据的特征和变化趋势。
三、常用的数据处理软件和工具1. NMRPipe:是一个常用的核磁数据处理软件,提供了丰富的数据处理和分析功能。
2. MestReNova:是一款功能强大的核磁数据处理软件,可以进行多维数据处理、峰识别和峰归属等操作。
3. TopSpin:是一款广泛应用于核磁实验室的数据处理软件,提供了直观的用户界面和丰富的数据处理功能。
4. MATLAB:是一种常用的科学计算和数据处理工具,可以编写自定义的数据处理算法和脚本。
四、注意事项和常见问题1. 数据质量:核磁数据处理的结果受到数据质量的影响,因此在进行数据处理前,需要确保获得的数据质量良好。
核物理实验数据分析方法

核物理实验数据分析方法在核物理领域,实验数据的分析是理解和揭示原子核内部结构与相互作用的关键环节。
准确、有效的数据分析方法不仅能够从复杂的实验数据中提取有价值的信息,还能为进一步的理论研究和实际应用提供坚实的基础。
核物理实验通常会产生大量的数据,这些数据的来源多种多样,包括粒子探测器、闪烁计数器、能谱仪等等。
数据的类型也丰富多样,可能是能量谱、时间谱、位置信息等等。
面对如此庞大和复杂的数据量,选择合适的分析方法至关重要。
首先,我们来谈谈数据的预处理。
在进行深入分析之前,需要对原始数据进行筛选、清理和校准。
筛选是为了去除明显的错误或无效数据,比如由于仪器故障产生的异常值。
清理则是要消除噪声和干扰,常见的方法有滤波处理。
而校准则是将测量数据与已知的标准进行对比和修正,以确保数据的准确性和可靠性。
接下来是数据的可视化。
将数据以图表的形式呈现出来,能够帮助我们直观地了解数据的分布和特征。
例如,绘制能谱图可以清晰地看到不同能量区间的粒子数量分布;绘制时间谱可以观察到粒子产生或衰变的时间规律。
通过可视化,我们可以快速发现数据中的异常点、趋势和周期性等特征,为后续的分析提供线索。
在数据分析中,常用的方法之一是拟合。
拟合是指通过选择合适的数学函数来描述数据的分布规律。
比如,对于能谱数据,常常使用高斯函数来拟合峰形,从而确定粒子的能量值和能量分辨率。
拟合的过程中,需要根据数据的特点选择合适的函数形式,并通过优化算法来确定函数的参数,使得拟合曲线与实验数据尽可能地吻合。
统计分析也是不可或缺的手段。
通过计算数据的均值、方差、标准差等统计量,可以了解数据的集中趋势和离散程度。
假设检验则可以用来判断实验结果是否具有统计学上的显著性差异。
例如,在比较不同实验条件下的测量结果时,通过假设检验可以确定这些差异是由随机误差引起的还是反映了真实的物理变化。
另外,蒙特卡罗模拟在核物理实验数据分析中也发挥着重要作用。
它通过建立随机模型来模拟实验过程,生成大量的模拟数据。
核磁数据处理方法

核磁数据处理方法
引言概述:
核磁共振(Nuclear Magnetic Resonance,NMR)是一种重要的分析技术,广泛应用于化学、生物、医学等领域。
在核磁实验中,数据处理是不可或缺的一环。
本文将介绍核磁数据处理的方法及其应用。
正文内容:
1. 预处理
1.1 去除噪声
1.2 校正基线
1.3 信号增强
2. 谱图解析
2.1 化学位移测定
2.2 峰归属
2.3 峰面积计算
3. 谱峰拟合
3.1 Lorentz-Gauss线型
3.2 峰形参数拟合
3.3 多峰分析
4. 数据处理
4.1 傅里叶变换
4.2 相位校正
4.3 平滑处理
5. 数据可视化
5.1 谱图绘制
5.2 二维谱图处理
5.3 图像导出
总结:
核磁数据处理方法在核磁共振实验中起着重要的作用。
预处理阶段主要包括去
除噪声、校正基线和信号增强等步骤,以提高数据质量。
谱图解析阶段涉及化学位移测定、峰归属和峰面积计算等内容,对于分析样品结构具有重要意义。
谱峰拟合可以采用Lorentz-Gauss线型进行参数拟合,多峰分析可以帮助识别复杂样品的峰。
数据处理阶段包括傅里叶变换、相位校正和平滑处理等步骤,以进一步优化数据。
最后,数据可视化通过绘制谱图和处理二维谱图等方式,使结果更直观,方便分析和导出。
综上所述,核磁数据处理方法在核磁共振实验中具有重要意义,为研究者提供
了强大的分析工具。
熟练掌握这些方法,能够更准确地解读核磁共振实验结果,进一步推动科学研究的发展。
核数据课程设计

核数据课程设计一、教学目标本课程的教学目标是使学生掌握核数据的基本概念、原理和应用,培养学生对核数据处理和分析的能力。
具体目标如下:1.知识目标:–了解核数据的基本概念和分类。
–掌握核数据的采集、处理和分析方法。
–理解核数据在科学研究和工程应用中的重要性。
2.技能目标:–能够使用核数据处理和分析软件,进行核数据的处理和分析。
–能够根据实际问题,选择合适的核数据处理和分析方法。
–能够对核数据处理和分析结果进行解释和评价。
3.情感态度价值观目标:–培养学生对核数据的科学精神和探究态度。
–培养学生对核数据处理和分析的兴趣和热情。
–培养学生对科学研究和工程应用的责任感和使命感。
二、教学内容本课程的教学内容主要包括核数据的基本概念、原理和应用。
具体内容如下:1.核数据的基本概念:核素的定义、核素的基本性质、核谱等。
2.核数据的采集:核数据采集的方法、设备和技术。
3.核数据的处理:核数据处理的基本方法、核数据处理的软件工具等。
4.核数据的分析:核数据分析的基本方法、核数据分析的软件工具等。
5.核数据的应用:核数据在科学研究和工程应用中的实例和案例。
三、教学方法本课程的教学方法主要包括讲授法、讨论法、案例分析法和实验法。
具体方法如下:1.讲授法:通过教师的讲解,使学生掌握核数据的基本概念和原理。
2.讨论法:通过小组讨论,使学生深入理解核数据的处理和分析方法。
3.案例分析法:通过分析实际案例,使学生了解核数据在科学研究和工程应用中的应用。
4.实验法:通过实验操作,使学生掌握核数据的采集、处理和分析方法。
四、教学资源本课程的教学资源主要包括教材、参考书、多媒体资料和实验设备。
具体资源如下:1.教材:选用权威的核数据教材,为学生提供系统的理论知识。
2.参考书:提供相关的参考书籍,丰富学生的知识体系。
3.多媒体资料:制作多媒体课件,生动形象地展示核数据的基本概念和原理。
4.实验设备:配置核数据采集和分析的实验设备,为学生提供实践操作的机会。
γ能谱的数据处理

2015讲义能谱的数据处理由多道脉冲分析器获取的谱数据需要以一定的数学方法进行处理才能得到实验要求的最终结果。
能谱的数据处理大致可以分为两个步骤。
首先进行峰分析,即由能谱数据中找到全部有意义的峰,并计算出扣除本底之后每个峰的净面积。
第二步是放射性核素的活度或样品中元素浓度的计算,即由峰位所对应的能量识别出被测样品中含有哪些放射性核素或被激发的元素,并且由峰的净面积计算出放射性核素的活度或元素在样品中的浓度。
采用不同的物理实验方法,使用不同的探测器时,能谱的数据处理方法也有所不同。
在本章中首先讨论在各种能谱数据处理中经常用到的峰分析方法,包括谱数据的平滑处理,本底扣除、寻峰、峰净面积计算和函数拟合法解谱。
然后,以γ谱分析为例,讨论基于计算机的多道脉冲分析系统中的谱自动分析软件的工作原理。
第一节 常用的峰分析方法一、谱数据的平滑处理由于射线和探测器中固有的统计涨落、电子学系统的噪声的影响,谱数据有很大的统计涨落。
在每道计数较少时,相对统计涨落更大。
谱数据的涨落将会使谱数据处理产生误差。
其主要表现为在寻峰过程中丢失弱峰或出现假峰、峰净面积计算的误差加大等等。
谱数据的平滑就是以一定的数学方法对谱数据进行处理,减少谱数据中的统计涨落,但平滑之后的谱曲线应尽可能地保留平滑前谱曲线中有意义的特征,峰的形状和峰的净面积不应产生很大的变化。
对谱数据进行平滑处理通常使用数字滤波器。
由信号分析理论的观点出发,我们可以把原始谱数据看成是噪声(即谱数据中的统计涨落)和信号(即峰函数和本底函数)的叠加。
经过数字滤波器的处理可以提高信号噪声比。
如图5-1-1所示,令第x 道的原始谱数据为y (x ),经过数字滤波之后的谱数据为λλ-λ=⎰+∞∞-d x y g x y )()()((5.1.1)其中,)(λg 为数字滤波器的单位冲击响应函数,并有1)(=λλ⎰+∞∞-d g(5.1.2)由于谱数据是离散量,公式(5.1.1)、(5.1.2)的离散量表达形式为∑+-=+=KKj j m j m y g y(5.1.3)2015讲义∑+-==K Kj j g 1(5.1.3)只要选择恰当的数字滤波器响应函数,就能够使平滑后的谱既保留了原始谱中的峰和本底的形状和大小,又得到最佳的信号噪声比。
核数据处理
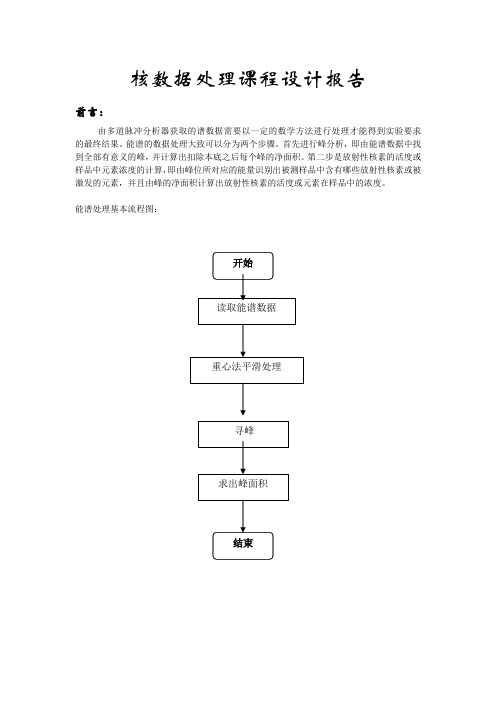
核数据处理课程设计报告前言:由多道脉冲分析器获取的谱数据需要以一定的数学方法进行处理才能得到实验要求的最终结果。
能谱的数据处理大致可以分为两个步骤。
首先进行峰分析,即由能谱数据中找到全部有意义的峰,并计算出扣除本底之后每个峰的净面积。
第二步是放射性核素的活度或样品中元素浓度的计算,即由峰位所对应的能量识别出被测样品中含有哪些放射性核素或被激发的元素,并且由峰的净面积计算出放射性核素的活度或元素在样品中的浓度。
能谱处理基本流程图:一、处理过程原理1、重心法平滑法所谓重心法就是假设光滑后的数据是原来数据的重心。
对某一质点的集合体,由于各质点所受合外力大小方向不同,如果该质点系所受合外力为零,那么该物体重心不变。
对于能谱而言,由于噪声信号的幅度平均值为零。
所以各数据点的重心不变。
选取加权因子和归一化因子,使光滑后的数据成为原来数据的重心。
常见的有5点和7点光滑。
三点重心法:114/12/14/1+-++=i i i y y y i y五点法重心法:)464(16/12112++--++++=i i i i i y y y y y i y2、高斯乘积函数找峰法 描述谱峰形状的函数主要是高斯函数[]2202/)(exp 2)(σσπi i A i G --=则由相邻的数据点定义一个新的函数(第一高斯乘积函数,只与σ2.3556FWHM =有关):2)092.11exp()()2()1()()(2≥=+--+=m Hm m i G i G m i G i G i P m m 是步长(用道表示),是高斯乘积函数的阶数,则Pm(i)称为第m 阶高斯乘积函数。
找峰的灵敏度与m 有关,随m 的增加灵敏度提高。
为避免基线参数的影响,最好扣除本底后,再应用高斯乘积函数找峰。
考虑统计涨落的影响,把判断无峰存在的1变为一个“单位带”。
即峰的判断为:3)/1(/1)(≥⎪⎩⎪⎨⎧+>±≤=k y k y k i P i i m 有峰无峰随着k 的增大,可以减少统计涨落的影响,但k “过大”会漏失真峰。
《核数据处理》1 能谱数据的获取

• γ/X射线 • 中子
本课程在核专业课中的位置
原子核物理
核辐射探测器
核仪器
核电子学
核数据处理
辐射剂量与防护 核环境学 核技术应用
1.1 核辐射探测器
按给出信息分类:
• 粒子进入探测器后,经过一定的处理才给出感官所能接受 的信息;
• 探测器接收到入射粒子后,立即给出/转换成相应的电信号。
按工作原理分类: • 利用射线通过物质产生的荧光现象做成的辐射探测器。
闪烁体闪光越亮越好; 输出信号大,利于后续电路处理
闪烁时间越短越好; 能量线性好。
适于探测强辐射 甄别能量
常见的有:
NaI(Ti) CsI(Ti/Na) BGO LaBr3
ZnS(Ag) 6LiI(Eu) +n/γ
LiI(Eu) 7LiI(Eu) +γ
靶核:中子俘获截面大;
问题: 是否活化完成后立即
生成放射性核素半衰期适中;
测量?
物理、化学性质稳定。
为什么要冷却?冷却 时间如何把握?
1.1 核辐射探测器
按工作原理分类: • 利用射线与物质的相互作用的其它原理制成的辐射探测器 ■ 切伦琴科夫探测器 ■ 热释光探测器
1.2 模拟式能谱仪
谱仪中为什么需要前置放大器:
C
R1
R
VR(t)
R
f
R1
f
R1
R
R1 C
VR
t
RR1 t
V0 e R1
R1
R R1 RC
R R1
VR
t
V0
t
e
1.2 模拟式能谱仪
主放大器:
《核数据处理》4 谱数据的定量分析

iL
(R L 1)
B (dataL dataR )* 2 (410 92)* 23/ 2 5773
A 297005773 23927
峰面积的计算
线性本底法(总峰面积法,TPA法)
面积统计均方差(标准偏差):
A
R iL
datai
R
L 2
1
2
(dataL
dataR
)
R1
datai
实测谱中,各特征峰是叠加在环境本底和康普顿散射 背景之上的。
总面积S:在一个指定的峰区内,各道计数之和 本底面积B:由环境本底和散射造成的计数总和 净峰面积A:由峰的总面积扣除本底面积即可得出净峰面积
即:峰的总面积—本底面积=净峰面积 S - B = A,所以,计算净峰面积,如何确定B最关键!
然后,将此l+1个科沃尔面积 再求和以表示“峰面积”。
…
…
峰面积的计算
Sterlinski(斯托林斯基)峰面 积法——峰面积计算
分别计算n取不同值的Covell峰面 积
i0 k1
1
Ak
datai
ii0 k 1
(k
2)(datai0 k
datai0 k )
i0 k
1
Ak 1
datai
ii0 k
bn1
dataR R
dataL L
(i0
L
n1)
dataL
bn2
dataR R
dataL L
(i0
L
n2 )
dataL
B总 峰(b面n1 积bn的2 ) (计n2 算2n1 1) i0 n2
净峰面积的计算 S datai ii0 n1
核数据——精选推荐

核数据《核数据处理》课程设计报告在本课程设计中,所要做的是对所给的谱数据进⾏⼀系列处理,达到想要的结果。
在对所给的数据进⾏图像成型时,会发现谱线有很多“粗糙”之处,这是由于在实验中得到这些谱数据的时候会有噪声的⼲扰或统计涨落的影响,造成谱数据的不平滑,⽽此就会形成谱线中真峰被湮没。
在此,我们需对谱线进⾏平滑处理和寻峰。
谱数据的平滑就是以⼀定的数学⽅法对谱数据进⾏处理,减少谱数据的统计涨落,但平滑之后的谱曲线应尽可能的保留平滑前谱曲线中有意义的特征,峰的形状、峰的净⾯积和峰的位置不应产⽣很⼤的变化,在进⾏平滑处理时,只要选择合适的滤波⽅法,就能够使平滑后的谱既保留了原始谱中的峰和本底的形状和⼤⼩,⼜得到最佳信噪⽐。
⽽在能谱数据中进⾏寻峰是为了找出各个峰的峰位,再根据各个峰的能量来决定被测样品中是否存在某种核素,其寻峰最关键的⽬的是为了判别是否有峰的存在。
在寻峰之后确定峰的峰位和道址,以及峰位的计数。
寻峰的⽅法有很多种,每种⽅法都有优缺点,但不管哪种⽅法要从谱中正确的找到全部存在的峰是⽐较困难的。
2、实验内容2.1 读取谱数据⽂件,对原始谱数据作图2.2 对所给的谱数据进⾏平滑处理,利⽤各种⽅法处理,再对谱线进⾏平滑前与平滑后的⽐较2.3 在平滑后的谱数据的基础上进⾏寻峰,找出峰位的道址和计数。
3.1 谱平滑处理的⽅法及原理:重⼼法原理:所谓的重⼼法就是假设光滑后的数据是原来数据的重⼼。
对某⼀点的集合体,由于各质点所受到的合外⼒的⼤⼩和⽅向不同,导致各点质向不同⽅向运动不同的距离,如果质点系所受的合外⼒为0,那么该物体的重⼼不变。
对于能谱⽽⾔,由于噪声信号的幅度平均值为0,所以谱线上各数据点的重⼼是不变的。
假设噪声对相邻两道计数的⼲扰相同时,则对于第i 道及第i+1道数据的重⼼应为此两道数据的平均值。
由于能谱中不存在半道,则可以推断重⼼法的3点平滑公式: )2(4121+--++=i i i i y y y y (1)5点平滑公式: )464(1612112++---++++=i i i i i i y y y y y y (2)7点平滑公式: )61520156(641321123+++----++++++=i i i i i i i y y y y y y y y (3)这种平滑⽅式的优点是全因⼦都是正数,平滑之后的谱数据不可能出现负值,从⽽提⾼了光滑之后的谱数据的可靠性。
《核数据处理原理》课件

采用分布式存储架构,将核数据分散存储在多个 节点上,以提高数据可靠性和容错性。
数据备份与恢复
建立完善的数据备份与恢复机制,确保数据安全 可靠。
THANKS
[ 感谢观看 ]
《核数据处理原理》 PPT课件
CONTENTS 目录
• 核数据处理概述 • 核数据采集 • 核数据预处理 • 核数据特征提取 • 核数据分类与回归 • 核数据处理性能优化
CHAPTER 01
核数据处理概述
核数据处理的意义
核数据处理是核科学和技术领域 的重要环节,对于核能、核安全 、核医学、核物理等领域具有重
核医学领域
核数据处理在放射性药物研发、医学影像处理等方面有重要应用。
核物理领域
通过对实验数据的处理和分析,深入了解原子核结构和反应机制等物理现象。
CHAPTER 02
核数据采集
核数据采集的原理
核数据采集是指利用各种探测器、加速器等设备,测量和记录核反应过程中释放的各种信息,如能量 、时间、角度等参数。
基于统计的方法
通过假设检验、相关性分析等方法评估每个 特征的重要性。
交互式特征选择
在特定领域知识的基础上,通过用户与系统 交互来选择特征。
特征提取算法
主成分分析(PCA):通过线 性变换将原始特征转换为新的 特征,新特征按照方差从大到 小排列,保留主要方差成分。
线性判别分析(LDA):寻找 最佳投影方向,使得同类数据 投影后尽可能接近,不同类数
半导体探测法
利用半导体材料中电子和空穴 的运动规律来进行探测。
量子点探测法
利用量子点材料对特定光子的 吸收和荧光现象来进行探测。
核数据采集的设备
闪烁计数器
利用闪烁物质发光的现象进行探测的设备。
核数据处理课程设计报告
核数据处理课程设计报告通过对C语言的复习和深层得掌握其编程。
能够自主地做出以下实验。
(一)计算器制作。
1,先建立一个工程,截图如下2,然后制作计算器的界面3,建立类向导写程序如下。
void CJmxjisuanqiDlg::Onjia(){UpdateData(true);m_Result=m_Firtn+m_Secn; UpdateData(false);}void CJmxjisuanqiDlg::Onjian() {UpdateData(true);m_Result=m_Firtn-m_Secn; UpdateData(false);}void CJmxjisuanqiDlg::Oncheng() {UpdateData(true);m_Result=m_Firtn-m_Secn; UpdateData(false);}void CJmxjisuanqiDlg::Onchu() {UpdateData(true);m_Result=m_Firtn/m_Secn; UpdateData(false);}4,运行得到的的界面和结果(二)按钮实现数据读写。
通过对C语言文件相关函数的掌握并熟悉运用可以写出以下实验。
创立一个工程文件然后对于按钮键编写属性和建立类向导,建立类向导的程序如下。
void CJMXDlg::Onduqushuju(){// TODO: Add your control notification handler code hereFILE *fp;int datanum=0,data[2048];float data_ph[2048];int i;int data1,data2;if((fp=fopen("090623.txt","r"))==NULL){printf("Cannot open the file.\n");exit(0);}while(!feof(fp)){fscanf(fp,"%d %d",&data1,&data2);data[datanum++]=data2;fscanf(fp,"\n");}for(i=0;i<2048;i++){if(i<2||i>2045)data_ph[i]=data[i];elsedata_ph[i]=(data[i-2]+4*data[i-1]+6*data[i]+4*data[i+1]+data[i+2])*1.0/16.0;printf("%f\n",data_ph[i]);}fclose(fp);if((fp=fopen("OUT1.txt","w"))==NULL){printf("file open error.\n");exit(0);}for(i=0;i<2048;i++){fprintf(fp,"%d %f\n",i+1,data_ph[i]);}fclose(fp);}注意:在编程时要把所给的数据文本文件要在所创立的文件下去编写程序。
核数据处理课程设计报告

核数据处理课程设计题目:基于matlab对能谱的处理学生姓名:xx班级:xx学号:xx指导教师:xx核数据处理课程设计报告——基于matlab对能谱的处理摘要:利用matlab对cu05.0au91.7ag3.3能谱数据进行处理,编写程序,对能谱进行平滑,寻峰,峰面积计算和不确定度的计算。
寻峰显示结果为:229.0072,244.0151,282.0407,337.0044,396.9997,716.7143,724.7917。
关键词:能谱平滑寻峰Abstract: the use of MATLAB on the energy spectrum data processing,programming, on the energy spectrum smoothing, peak search, peak areacalculationanduncertaintycalculation.Searchresultsfor:229.0072,244.0151,282.0407,337.0044,396.9997,716.7143,724.7917。
实验目的1、了解能谱各峰的意义2、掌握如何编程对能谱进行平滑,寻峰和计算峰面积3、理解数据处理的基本流程4、进一步掌握对核数据处理的基本方法 编程思想1、获取能谱信息2、对获取的谱进行平滑处理,处理方法原理 重心法:假设光滑后的数据是原来数据的重心。
重心法 假设能谱相邻两道所受统计涨落影响之和为0,根据质心不变,可知)(2/1y y 1i i5.0+++=yi )(2/1y y i1-i 5.0-+=yi由于能谱不存在半道,但 三点重心法)1/2()(2/1y y y 1i i5.00.5-i +++++=yy i i))1/2()(1/2(21/y y y y 1i ii1-i ++++=yy y i ii 11-4/12/141/+++=同理 五点重心法——》2次三点重心法)464(16/1y y y y y 2i 1i i 1-i 2-i ++++++=y i3寻峰协方差法:协方差找峰的基本思想是模拟人们用目测方法找峰的过程,人们通常是用心目中的峰形状对一个能谱数据从始至终进行比较,确定每个区段是否像峰。
有关谱解析的课程设计

有关谱解析的课程设计一、课程目标知识目标:1. 学生能掌握谱解析的基本概念,理解其在化学分析中的应用。
2. 学生能够识别不同类型的谱图,如红外光谱、核磁共振谱等,并描述其特征。
3. 学生能够运用谱解析方法,对简单有机化合物的结构进行推断。
技能目标:1. 学生能够操作谱解析仪器,进行基本的谱图采集。
2. 学生能够运用谱解析软件,对谱图进行处理和分析。
3. 学生能够运用所学的谱解析知识,解决实际问题,提高解决问题的能力。
情感态度价值观目标:1. 学生通过谱解析的学习,培养对化学实验和科研的兴趣,增强探究精神。
2. 学生能够认识到谱解析在科学研究和实际应用中的重要性,增强学习的责任感。
3. 学生在合作学习中,培养团队协作精神,尊重他人意见,学会倾听和表达。
课程性质分析:本课程为化学学科选修课程,旨在帮助学生掌握谱解析的基本知识和技能,提高化学分析能力。
学生特点分析:高二年级学生,具有一定的化学基础知识,思维活跃,对实验和探究感兴趣,但需加强对理论知识的理解和应用。
教学要求:1. 结合课本内容,注重理论与实践相结合,提高学生的实际操作能力。
2. 注重启发式教学,引导学生主动参与,培养学生的思维能力和创新能力。
3. 强化目标导向,关注学生的学习成果,及时进行教学反馈和调整。
二、教学内容本章节教学内容围绕谱解析的基本原理、方法和应用进行组织,具体包括以下部分:1. 谱解析基本原理:- 谱学概述:介绍谱解析的定义、分类及在化学分析中的应用。
- 电磁波与物质相互作用:讲解电磁波与分子之间的相互作用,以及谱图产生的原理。
2. 常见谱图解析方法:- 红外光谱:介绍红外光谱的原理、仪器构造、样品制备和谱图解析方法。
- 核磁共振谱:阐述核磁共振原理、仪器操作、样品制备和谱图分析技巧。
- 紫外-可见光谱:讲述紫外-可见光谱的原理、仪器及谱图解析。
3. 谱解析应用实例:- 有机化合物结构鉴定:通过实际案例,教授如何运用谱解析方法鉴定有机化合物结构。
《核数据处理b》课件
案例分析
核反应堆实例分析
通过实例讲解核反应堆的设计、运行原理以及核数 据在反应堆分析中的应用。
辐射防护实例分析
以具体案例为例,介绍辐射防护设计中所使用的材 料和结构,并分析其效果。
总结
核数据处理在核能源领域扮演着重要的角色,面临着挑战和机遇,科学家们 需要不断创新和发展核数据处理的技术和方法。
MATXS处理与输出
介绍MATXS文件的处理和输出, 它包含了用于核能量谱分析的 重要数据。
核数据应用
1
反应堆物理分析
利用核数据进行反应堆物理参数的计算
辐射防护设计
2
和分析,优化反应堆设计。
基于核数据进行辐射防护材料和结构的
设计,确保工作环境的安全。
3
核能源开发
利用核数据进行核能源的开发和利用, 推动可持续能源的应用。
《核数据处理b》PPT课件
本PPT课件将介绍核数据处理b的主要内容,包括核数据处理的简介、方法、 软件,以及核数据的应用和案例分析。
核数据处理概述
核数据处理是研究和处理核能量谱的方法和技术。它是核能源开发、反应堆物理分析和辐射防护设计的重要工 具。
核数据处理方法
核反应截面测量
通过实验测量核反应截面, 获取核数据的重要信息。
数据评价与推荐
对测量得到的数据进行评价 和推荐,提供高质量的核数 据。
数据组合
将来自不同实验的数据组合 起来,形成更全面、准确的 核数据集。
核数据处理软件ຫໍສະໝຸດ NJOY软件简介介绍NJOY软件,它是一个流行 的核数据处理软件,用于处理 核数据的格式转换和处理。
PENDF处理与输出
详细解释PENDF文件的处理和输 出,它包含了核数据处理的关 键信息。
核数据处理课程设计

核数据处理一、实习目的1、掌握图形程序的编写技能与技巧;2、掌握文件读写函数的使用;3、理解整个谱数据处理的流程;4、进一步掌握对常用核数据处理的基本方法5、掌握软件设计所需的基本动手能力,解决实际问题。
二、实习内容1、读谱数据文件、保存光滑后的谱数据文件,文件名可选2、显示谱数据,各算法要以函数方式实现3、显示分析谱段范围内,寻得的各峰位道址、能量、对应的元素名称4、显示寻峰及峰面积计算结果5、光滑、寻峰宽度2k+1应在5、7之间可选,讨论最佳参数。
三、需求分析1、输入、输出的内容和形式(1)输入:a、打开应用软件,弹出要求输入谱数据文件名对话框。
b、需要刻度谱线时,分别按e键和c键输入元素文件名和能量刻度文件名。
c、人机交互时,采用键盘按键方式将命令传给程序(具体操作:在运行程序后按h键即可弹出操作说明对话框)。
(2)输出:a、屏幕显示谱线;光标位置及光标处的道址、能量和计数;屏幕上方显示“Softwareinstructions please input 'h'”。
b、当谱线被刻度好后,按n键会弹出相应元素对应的能量、面积和净峰面积。
c、按h键弹出应用程序操作说明对话框。
2、预期功能、界面(1)显示输入谱文件名对话框;在文件名输入正确时,能够正确读取文件中的数据。
(2)正确显示谱线以及在刻度后显示道址、能量及计数。
(3)显示相应元素对应的能量、面积和净峰面积对话框。
(4)达到谱数据光滑的效果。
(5)采用键盘输入命令,使屏幕:a、即时显示光标的位置以及对应的道址、能量及计数。
b、即时显示不同幅度放大倍数时的谱线形状。
c、即时显示不同光滑次数处理后的谱线微细结构(只有在幅度放大倍数很大时光滑效果才明显)。
d、即时显示谱线的点和线的切换。
3、测试数据(1)文件读入是否正确。
(2)谱数据段的选择功能是否实现。
(3)move和curse的边界值是否设置妥当。
(5)道址和能量的换算是否正确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%本次课程设计采用的谱数据为iaea-1995文件夹下iaearfnwﻩTSTSPEC%里面的数据。
首先来看看CALIB.ASC。
READ_ME.TXT中说明了这个谱数据包含的部分峰的峰位与对应能量如下:% Channel Energy(keV)%ﻩ301122.06% 1281 511.00%ﻩ1661 661.66% 2097834.84%ﻩ2951 1173.24% 3207 1274.54%ﻩ3353 1332.50%运行程序,其中参数选择为:选择傅里叶变换法平滑输入3,选择高斯滤波器输入2,然后A=1,FWHM=4,对称零面积法的参数是K=2,H=3,b=1寻出来%的峰与READ_ME.TXT中说明的部分峰的峰位与对应能量数据相吻合。
clc;clear;[Filename,Pathname]=uigetfile('*.*','选择谱数据');fid=fopen([Pathname Filename],'r')%fid为文件指针,r表示读操作[array,count]=fscanf(fid,'%d',[1 inf]);%指定格式转换后返回给矩阵array,同时返回成功的读出的数据数量count,1表示读出一个元素到一个列向量,inf表示读到文件结束返回一个与文件数据元素相同的列向量fclose(fid);%%%%下面开始能谱平滑%%%%%%%pinghuaxuanze=input('请选择平滑方法:\n输入1选择重心法平滑\n输入2选择多项式最小二乘移动平滑法\n输入3选择傅里叶变换法\n输入4选择小波变换:\n');%************************重心法平滑****************************if(pinghuaxuanze==1)biaoji=1;for i=1:countarray_z(i)=array(i);endw=input('input the widthof the filter window:'); %w表示w 点平滑公式while mod(w,2)==0 %判断输入的数是否是奇数,不是则重新输入。
w=input('input oddnumber:');endm=floor(w/2);for j=1:mfor i=1:countif(i==1)array_smooth(i)=0.5*(array_z(i)+array_z(i+1)); %能谱左边界做对称镜像处理elseif(i>1&&i<(count-1))array_smooth(i)=0.25*array_z(i-1)+0.5*array_z(i)+0.25*array_z(i+1);elsearray_smooth(i)=0.5*(array_z(count)+array_z(count-1)); %能谱右边界做对称镜像处理endendfori=1:count %将平滑好的数据放回原数组,为下一次做好准备。
array_z(i)=array_smooth(i);endendfor i=1:counta1(i)=array_z(i);end%***********************重心法平滑结束***************************%***********************多项式最小二乘移动平滑法*****************elseif(pinghuaxuanze==2)biaoji=2;w=input('inputthewidth ofthe filter window:');%w为窗口宽度fwk= zeros(w,1); %存储滤波器系数,产生一个1行,w列的零矩阵;当求平滑之后谱的第i点数据时,先在原始数据第i点的左、右各取m个数据点;也就是形成一个共有w=2m+1个数据点的窗口;for i=1:wk=i-ceil(w/2); %调整,计算采用k=- m:m,窗口的中心点为ceil( w/2)点fwk(i)=[1+(15/(w^2-4))*((w^2-1)/12-k^2)]/w;%2次或3次滤波器%fwkz=2.5*(w^2-7)*((w^2-1)/12-k^2)-9*((w^2-1)*(3*w^2-7)/240-k^4); %4次或5次滤波器%fwk(i)=(1+105/(4*(w^2-4)*(w^2-16))*fwkz)/w;%fwk(i)=(1+(15*(3*w^2-7)/((w^2-4)*((w^2-5)^2+4)))*((w^2-1)*(3*w^2-7)/240-k^%4))/w;%箱型滤波器endarray_z = zeros(count+2*floor(w/2),1);%先将数据全部放在array_z数组中,并将边界做镜像处理,即增加2*floor(w/2)个数据for i=1:count+2*floor(w/2)if(i<=floor(w/2))array_z(i)=array(-i+ceil(w/2));elseif(i>count+floor(w/2))array_z(i)=array(-(i-floor(w/2))+2*count+1);elsearray_z(i)=array(i-floor(w/2));endenda1=zeros(1,count);fori=1:count %做矩阵乘法,i=1:count 即完成能谱滤波for j=1:wSMZ(j)=array_z(i+j-1);enda1(i)=SMZ*fwk;end%*************************多项式最小二乘移动平滑结束**************** %*******************************傅里叶变换法开始********************elseif(pinghuaxuanze==3)biaoji=3;y=fft(array,count); %对原始谱进行傅里叶变换lvboqixuanze=input('请选择滤波器:\n输入1选择理想低通滤波器\n输入2选择高斯型滤波器:\n');%*************************理想低通滤波器傅立叶变换程序开始*************************pyy=y.*conj(y);%计算y 的模平方,conj为求复数的共轭ss=0;flag=0; %flag 为噪声幅度最大值ss 的标志for i=floor(count/2*3/4):floor(count/2)if(ss<pyy(i))flag=i;%flag为噪声幅度最大值ss 的标志ss=pyy(i);%找出最大幅度E对应的频率w1endendR=5.0;flag1=0;if(flag1==0)R=R-0.01;tt=R*ss;for i=floor(count/2*3/4)-1:-1:1if(pyy(i)>tt)flag1=i;break;%从最大频率的3/4处向前找出R*w1的点,此点为信号起主要作用的点endendendfor i=flag1:floor(count/2*3/4) %找到信号起主要作用的点,从该点向后找出第一个频率低于w1的点,此点即为切断频率MFCif(pyy(i)<ss)flag=i;break%找到信号的切断频率并放在fl ag 中endendif(lvboqixuanze==1)yli=y;yli(flag+1:count-flag+1)=0;%在截断频率后赋值为0,这里考虑到对称的原因a1=real(ifft(yli,count));%反变换后求实部%***************************理想低通滤波器傅立叶变换程序结束************************%*************************高斯型滤波器开始**************else(lvboqixuanze==2)A=input('请输入A:\n');FWHM=input('请输入半高宽:\n');delta=FWHM/2.355; %delta为高斯宽度for i=1:ceil(count/2)%ceil表示取整if(i>flag)ygao(i)=0;ygao(count-i)=0;elsew=2*pi*i/count;ygao(i)=y(i)*A*exp(-0.5*delta^2*w^2);ygao(count-i+1)=y(count-i+1)*A*exp(-0.5*delta^2*w^2);endendgd=real(ifft(ygao,count));%反变换后求实部for i=1:counta1(i)=gd(i);endend%************************傅立叶变换法结束****************%***********************小波变换开始*******************else(pinghuaxuanze==4)biaoji=4;[c,l]=wavedec(array,3,'sym8');a3=appcoef(c,l,'sym8',3); %提取小波低频系数d3=detcoef(c,l,3);%提取小波高频系数d2=detcoef(c,l,2);d1=detcoef(c,l,1);delta=median(abs(c))/0.6745;THR=delta*sqrt(2*log(count));hardd1=wthresh(d1,'h',THR);%均为硬阈值,大于阈值的加'h',小于阈值的减‘h'hardd2=wthresh(d2,'h',THR);hardd3=wthresh(d3,'h',THR);c2=[a3 hardd3hardd2 hardd1];a1=waverec(c2,l,'sym8');%反变换回来%*************************小波变换结束*****************end%***************平滑结束******************************plot(array,'r-*');xlabel('道址');ylabel('能量');holdon;if biaoji==1plot(a1,'k-');elseifbiaoji==2plot(a1,'k-');elseifbiaoji==3plot(a1,'k-');elseifbiaoji==4plot(a1,'k-');endtitle('平滑前与平滑后的谱');text(4000,8000,'\leftarrow 平滑前后对比','FontSize',20);holdoff;for i=1:count;if a1(i)==0;a1(i)=1;endend%*****************下面开始峰位确定********************* %%%%%%%%%%%%%%%%%%%先采用对称零面积寻峰法(矩形波函数)**** disp('下面开始输入对称零面积法寻峰');disp('下面开始输入对称零面积法的各参数');disp('如果是方波的话有k=1');K=input('请输入参数k=?:\n');H=input('请输入参数半宽度H=?(正奇数):\n');m=((2*K+1)*H-1)/2;w=2*m+1;b=input('请输入参数b=?:\n');a=2*K*b;%K=4;%H=2*K+1;%w=3*H;%b=1;%a=2*K*b;m1=floor(w/2);temporary=zeros((count+2*m1),1); %以下循环为镜像处理数据for i=1:count+2*m1if(i<=m1);temporary(i)=a1(ceil(w/2)-i);elseif(i>(count+m1))temporary(i)=a1(-(i-m1)+2*count+1);elsetemporary(i)=a1(i-m1);endendA=zeros(count,1); %以下循环为对称零面积褶积变换for i=ceil(w/2):count+m1;for j=-(w-1)/2:(w-1)/2;ifabs(j)<=(H-1)/2;T=a;elseT=-b;endA(i-m1,1)=A(i-m1,1)+T*temporary(i+j);endendfori=1:count;%数据转制SSiFENZI(i,1)=A(i,1);endB=zeros(count,1);for i=ceil(w/2):count+m1;forj=-(w-1)/2:(w-1)/2;if abs(j)<=(H-1)/2;T=a^2;elseT=b^2;endB(i-m1,1)=B(i-m1,1)+T*temporary(i+j);endendfori=1:count; %数据转存SSiFENMU(i,1)=B(i,1);endfor i=1:count; %计算SSSS(i,1)=SSiFENZI(i,1)/sqrt(SSiFENMU(i,1));endp=1;q=1;f=30;%灵敏因子或称为找峰阈值for i=1:count; %寻峰if SSiFENZI(i)<0;fpdatablow(p,1)=i;fpdatablow(p,2)=SSiFENZI(i);p=p+1;elseif SS(i)>f;fpdataup(q,1)=i;fpdataup(q,2)=SSiFENZI(i);q=q+1;endendp=1;fori=2:length(fpdataup(:,1))-1;%确定峰位if fpdataup(i,2)>fpdataup(i+1,2)&&fpdataup(i,2)>fpdataup(i-1,2);mpeak(p,1)=fpdataup(i,1);p=p+1;endendfori=1:length(mpeak(:,1)); %确定边界道j=mpeak(i);t=mpeak(i);peak(i)=t+(a1(t+1)-a1(t-1))/(2*a1(t)-a1(t+1)-a1(t-1))/2;%*******************************确定左右边界道******************%*********************************采用0.2倍峰高法确定边界********while a1(j)>0.2*a1(mpeak(i));j=j-1;endpboard(i,1)=j;%左边界道zuobianjie(i)=pboard(i,1);j=mpeak(i);while a1(j)>0.2*a1(mpeak(i));j=j+1;endpboard(i,2)=j; %右边界道youbianjie(i)=pboard(i,2);endfor i=1:length(mpeak)fk(i)=pboard(i,2)-pboard(i,1);enddisp('各峰的道址如下:')sprintf('%d',mpeak)disp('峰所在道址对应的计数:')for i=1:length(mpeak)sprintf('%d ',a1(mpeak(i)))enddisp('各峰的准确道址如下:')sprintf('%d ',peak)disp('各峰的左边界道址如下:')sprintf('%d',zuobianjie)disp('各峰的右边界道址如下:')sprintf('%d',youbianjie)%**********下面开始能量刻度*************disp('如果你是用高斯滤波器A=1,FWHM=4,对称零面积法的参数是K=2,H=3,b=1的话,寻得的峰恰好READ_ME.TXT所示(这里是特殊情况)')biaoji3=input('各参数是否如上所述?是的话请输1,不是的话请输2\n');if biaoji3==1;nengliang=[122.06 511.00 661.66 834.84 1173.24 1274.54 1332.50];p=polyfit(peak,nengliang,1);disp('二次多项式y=kx+b的拟合系数为:这里第一个数据是k,第二个数据是b,x对应道址,y对应能量');sprintf('%f ',p)else daozhi=input('请输入寻得的峰的道址若干:用[]形式输入数据\n');nengliang=input('请输入道址对应的能量:用[]形式输入数据单位kev\n');p=polyfit(daozhi,nengliang,1);disp('二次多项式y=kx+b的拟合系数为:这里第一个数据是k,第二个数据是b,x 对应道址,y对应能量');sprintf('%f ',p)endfor i=1:count;y(i)=p(1)*i+p(2);endfigure;plot(y);xlabel('道址');ylabel('能量kev');title('刻度好的能量刻度方程曲线');%*****************以下是画寻峰之后的得图***************figure;pp=plot(a1);set(pp,'Color','blue','LineWidth',3);xlabel('道址');ylabel('计数');title('寻峰之后的道址与计数的关系图');hold on;hh=axis;for(i=1:length(peak))plot([peak(i),peak(i)],[hh(3),hh(4)],'r');endhold off;%***************************************************biaoji4=input('下面计算峰面积,输入1采用瓦森峰面积法,输入2采用总峰面积法'); ifbiaoji4==1;%******************下面计算峰面积(这里采用瓦森峰面积法)********************disp('计算峰面积:下面采用瓦森峰面积法');n=2;%经调试,取2时deta最小y=zeros(1,10000);s=zeros(1,length(mpeak));fori=1:length(mpeak)B1=zeros(1,length(mpeak));B2=zeros(1,length(mpeak));if(fk(i)/2>n)B1(i)=(a1(youbianjie(i))-a1(zuobianjie(i)))*(mpeak(i)-zuobianjie(i)-n)/fk(i)+a1(zuobianjie(i));B2(i)=(a1(youbianjie(i))-a1(zuobianjie(i)))*(mpeak(i)-zuobianjie(i)+n)/fk(i)+a1(zuobianjie(i));for j=(mpeak(i)-n):(mpeak(i)+n)y(i)=y(i)+a1(j);endelsedisp('您输入的n值不满足fk(i)/2>n的条件');break;ends(i)=y(i)-(2*n+1)*(B1(i)+ B2(i))/2;endelsebiaoji4==2;%******************************************下面用总峰面积法*********************disp('计算峰面积:下面采用总峰面积法');y1=zeros(1,length(mpeak));fori=1:length(mpeak)forj=(zuobianjie(i)+1):(youbianjie(i)-1)y1(i)=y1(i)+a1(j);ends(i)=y1(i)-(youbianjie(i)-zuobianjie(i)-1)*(a1(zuobianjie(i))+a1(youbianjie(i)))/2;endenddisp('各个峰的面积为:');sprintf('%d ',s)。
