自适应PID控制综述(完整版)
自适应PID控制研究概要

概念设计控制器,并能保证在有界噪声和不可量测扰动存在的情况下控制误差是稳定和收敛的。F.Radke和R.Isermann在1984年提出了名为参数逐步优化的自适应PID控制算法,讨论了时域和频域中该种控制器的设计问题。他们提出的算法特点是,能使PID参数在线逐步优化,从而使整个系统的动态性能渐近最优化。A.Holme在1984年从另一角度用二次型性能指标函数方法设计了一种参数自适应PID控制器,这种方法的实时性较强,其不足之处是不能应用于非最小相位的过程控制中。2.2非参数自适应PID控制
1.2/a
2L
L/2
注:a=T k
3.2闭环系统的增益自适应
利用ERCM法确定的PID控制器适合于定常系统,但实际物理系统存在时变性、非线性和不确定性,特别是当用“一阶惯性十纯滞后环节”逼近模型时,理论上己经存在模型误差;另外,将连续系统的研究成果应用于离散系统时,其系统性能会受到采样周期的影响。因此,为了提高PID控制器的自适应能力,有必要在ERCM基础上对其进行探究。
自适应PID控制研究
摘要:PID控制结构简单、可靠性高,在工业控制中得到了广泛的应用。但是实际工业生产过程往往具有大滞后、非线性、时变不确定性,因此常规PID控制经常达不到理想的控制效果。因此,有必要提出一种算法简单且对被控对象数学模型要求不高的自适应PID控制器。本文围绕这一目标,主要作了一些研究工作:首先对扩充响应曲线法进行改进,提出了扩充响应曲线法开环递推求解算法,简化了PID参数的整定过程。研究结果表明这些工作取得了一定的成果。
针对PID离线整定的不足,提出来开环情况下ERCM方法的递推求解方案,无需通过系统响应曲线的面积计算来提取被控对象的特征参数,简化了PID的整定过程;在闭环条件下,对递推算法加以改进,在确保PID控制器零极点不变的条件下,实现了PID增益自适应。
(完整word版)单神经元自适应PID控制算法

单神经元自适应PID 控制算法一、单神经元PID 算法思想神经元网络是智能控制的一个重要分支,神经元网络是以大脑生理研究成果为基础,模拟大脑的某些机理与机制,由人工建立的以有向图为拓扑结构的网络,它通过对连续或断续的输入做状态响应而进行信息处理;神经元网络是本质性的并行结构,并且可以用硬件实现,它在处理对实时性要求很高的自动控制问题显示出很大的优越性;神经元网络是本质性的非线性系统,多层神经元网络具有逼近任意函数的能力,它给非线性系统的描述带来了统一的模型;神经元网络具有很强的信息综合能力,它能同时处理大量不同类型的输入信息,能很好地解决输入信息之间的冗余问题,能恰当地协调互相矛盾的输入信息,可以处理那些难以用模型或规则描述的系统信息。
神经元网络在复杂系统的控制方面具有明显的优势,神经元网络控制和辨识的研究已经成为智能控制研究的主流。
单神经元自适应PID 控制算法在总体上优于传统的PID 控制算法,它有利于控制系统控制品质的提高,受环境的影响较小,具有较强的控制鲁棒性,是一种很有发展前景的控制器。
二、单神经元自适应PID 算法模型单神经元作为构成神经网络的基本单位,具有自学习和自适应能力,且结构简单而易于计算。
传统的PID 则具有结构简单、调整方便和参数整定与工程指标联系紧密等特点。
将二者结合,可以在一定程度上解决传统PID 调节器不易在线实时整定参数,难以对一些复杂过程和参数时变、非线性、强耦合系统进行有效控制的不足。
2.1单神经元模型对人脑神经元进行抽象简化后得到一种称为McCulloch-Pitts 模型的人工神经元,如图2-1所示。
对于第i 个神经元,12N x x x 、、……、是神经元接收到的信息,12i i iN ωωω、、……、为连接强度,称之为权。
利用某种运算把输入信号的作用结合起来,给它们的总效果,称之为“净输入”,用i net 来表示。
根据不同的运算方式,净输入的表达方式有多种类型,其中最简单的一种是线性加权求和,即式 (2-1)。
具有自适应参数的PID控制器设计

具有自适应参数的PID控制器设计PID控制器是现代工业中常用的控制器之一,其具有结构简单、易于调节、可靠性高等特点。
然而,在实际控制过程中,PID控制器的参数常常需要根据被控对象的特性进行调节,以达到较好的控制效果。
因此,在实际工程应用中,具有自适应参数的PID控制器逐渐成为研究热点。
本文将介绍具有自适应参数的PID控制器的设计原理和实现方法。
一、PID控制器的基本原理PID控制器是由比例控制器、积分控制器和微分控制器三个部分组成的。
在控制过程中,比例控制器通过与被控对象的偏差成比例的输出控制信号,积分控制器通过对偏差的时间积分来消除静态误差,微分控制器通过对偏差的变化率进行控制,来减小超调量和提高控制速度。
PID控制器的输出信号可表示为:u(t) = Kp[e(t) + 1/Ti∫e(τ)dτ + Td(de(t)/dt)]其中,e(t)为被控对象的偏差,Kp、Ti、Td为控制器的比例系数、积分时间常数和微分时间常数。
二、PID控制器参数调节问题PID控制器的参数调节对于控制系统稳定性和控制品质的影响非常大。
传统的PID控制器参数调节方法主要有经验调整法、试控法、模型辨识法等。
这些方法都需要对被控对象进行较高的数学建模和系统参数辨识,并且难以处理非线性、时变的被控对象。
因此,针对复杂度高、涉及数学理论较多的问题,基于现代控制理论和人工智能技术的自适应PID控制器应运而生。
三、具有自适应参数的PID控制器原理与设计自适应PID控制器的设计原理是根据被控对象的特性或控制系统的工作状态,通过对PID控制器的参数进行在线自适应调节,以达到控制效果的优化。
具有自适应参数的PID控制器的设计关键是参数选择和规划方法的确定。
常用的自适应PID控制器设计方法主要包括下面几种:1.基于遗传算法的PID控制器设计方法:遗传算法是一种有效的参数优化方法,可根据被控对象的特性和优化目标确定适当的PID控制器参数,以提高控制效果。
PID自适应控制

PID 自适应控制PID Adaptive Control●夏 红 王 慧 李 平Xia Hong Wang Hui Li Ping夏 红,现在浙江大学工业控制研究工作。
地址:杭州市邮政编码:310027收稿日期:1995年9月30日(磁盘来稿)1 引言在PID 控制中,一个关键的问题便是PID 参数整定。
传统的方法是在获取对象数学模型的基础上,根据某一整定原则来确定PID 参数。
然而实际的工业过程往往难以用简单的一阶或二阶系统来描述,且由于噪声、负载扰动等因素的干扰,还可以引起对象模型参数的变化甚至模型结构的改变。
这就要求在PID 控制中,不仅PID 参数的整定不依赖于对象数学模型,而PID 参数能在线调整,以满足实时控制的要求。
本文提出将PID 继电自整定与神经网络相结合,共同完成PID 自适应控制任务。
2 系统构成如图1所示,PID 控制器由一个二层线性网络构造[1,2],网络权的初值由PID 继电自整定法[3]提供。
实施控制时,先将开关T 置于S 处,进行PID 参数整定,将所得的参数做适当的修正后作为网络权的初值,然后将开关T 置于V 处,进入系统自适应控制。
2.1 PID 继电自整定图1PID 自适应控制系统 基于继电反馈的PID 参数自动整定方法用继电特性的非线性环节代替Ziegler ─Nichols 法中的纯比例器,使系统出现极限环,从而获得所需的临界值。
设继电器特性幅值为d ,继电器滞环宽度为h ,且被控过程的广义对象传递函数为G (S ),用N 代表非线性元件的描述函数,则对无滞环的继电器型有 N =(4d/πa )<0(1)对于具有滞环的继电器非线性有 N =2(4d/πa )<-arcsin (h/a )(2)中,a 为继电器型非线性环节输入的一次谐波振幅。
只要满足方程: G (jω)=-(1/N )(3)则系统输出将出现极限环。
得到的临界增益K u 为: Ku =(4d/πa )(4)临界振荡周期tu 通过直接测量相邻两个输出过零的时间值确定。
PID整定综述

PID控制器参数整定综述PID调节器从问世至今已历经了半个多世纪,在这几十年中,人们为它的发展和推广作出了巨大的努力,使之成为工业过程控制中主要的和可靠的技术工具。
即使在微处理技术迅速发展的今天,过程控制中大部分控制规律都未能离开PID,这充分说明PID控制仍具有很强的生命力。
PID控制中一个至关重要的问题,就是控制器三参数(比例系数、积分时间、微分时间)的整定。
整定的好坏不但会影响到控制质量,而且还会影响到控制器的鲁棒性。
此外,现代工业控制系统中存在着名目繁多的不确定性,这些不确定性能造成模型参数变化甚至模型结构突变,使得原参数无法保证系统继续良好的工作,这时就要求整定PID控制器的参数,这是自从使用PID控制以来人们始终关注的重要问题之一。
参数整定的方法很多,下面介绍几种工程上常用的方法。
1、临界比例度法这是目前使用较广的一种方法,它是先通过试验得到临界比例度PB 和临界周期Tk ,然后根据经验公式求出控制器各参数值。
具体做法如下:1)被控系统稳定后,把控制器的积分时间放到最大,微分时间放到零(相当于切除了积分和微分作用,只使用比例作用)。
2)通过外界干扰或使控制器设定值作一阶跃变化,观察由此而引起的测量值振荡。
3)从大到小逐步把控制器的比例度减小,看测量值振荡的变化是发散的还是衰减的,如是衰减的则应把比例度继续减小;如是发散的则应把比例度放大。
4)连续重复2)、3)步骤,直至测量值按恒定幅度和周期发生振荡,即持续4~5 次等幅振荡为止。
此时的比例度示值就是临界比例度PB。
5)从振荡波形图来看,来回振荡1 次的时间就是临界周期Tk,即从振荡波的第一个波的顶点到第二个波的顶点的时间。
如果有条件用记录仪,就比较好观察了,即可看振荡波幅值,还可看测量值输出曲线的峰———峰距离,把该测量值除以记录纸的走纸速度,就可计算出临界周期Tk ;如果是DCS 控制,在趋势记录曲线中可直接得出Tk(如图1)。
得到了临界比例度PB 和临界周期Tk 后,就可根据表1 中的经验公式求出控制器的P、时间Ti、Td 参数值了。
自适应控制中PID控制方法

自适应PID 控制方法1、自适应控制的理论概述设某被控对象可用以下非线性微分方程来描述:'()((),(),,)()((),(),,)x t f x t u t t y t h x t u t t θθ== (1-1)其中x (t),u (t ),y (t )分别为n ,p,m 维列向量。
假设上述方程能线性化、离散化,并可得出在扰动和噪音影响下的方程:(1)(,)()(,)()()()(,)()()X k k X k k U k k Y k H k X k V k θρθωθ+=Φ++=+ (1-2) X(k ),X (k),U(k ),Y(k),V (k)分别为n ,n ,p ,m,m 维列向量;(,)k θΦ、(,)k ρθ、(,)H k θ分别为n ×n 系统矩阵、n ×p 控制矩阵、m ×n 输出矩阵。
那么自适应控制就是研究:在矩阵(,)k θΦ,(,)k ρθ,(,)H k θ中的参数向量,随机{()k ω},{v(k )}的统计特性及随机向量X(0)的统计特性都未知的条件下的控制问题,也就是说自适应控制的问题可归结为在对象及扰动的数学模型不完全确定的条件下,设计控制序列u(0),u(1),…,u (N — 1),使得指定的性能指标尽可能接近最优和保持最优。
自适应控制是现代控制的重要组成部分,它同一般反馈控制相比有如下突出特点:(l)一般反馈控制主要适用于确定性对象或事先确知的对象,而自适应控制主要研究不确定对象或事先难以确知的对象。
(2)一般反馈控制具有抗干扰作用,即它能够消除状态扰动引起的系统误差,而自适应控制因为有辨识对象和在线修改参数的能力,因而不仅能消除状态扰动引起的系统误差,还能消除系统结构扰动引起的系统误差。
(3)自适应控制是更复杂的反馈控制,它在一般反馈控制的基础上增加了自适应控制机构或辨识器,还附加了一个可调系统"1.1模型参考自适应控制系统模型参考自适应控制系统由参考模型、反馈控制器、自适应机构及被控对象组成.此系统的主要特点是具有参考模型,其核心问题可归纳为如何确定自适应调节律及算法。
单神经元自适应PID

单神经元自适应PID一、单神经元神经网络与PID 结合的基础根据前面的推文“神经网络基础”中所介绍的,神经元是多输入单输出的,训练的目的确定权值,从而当给予输入时,能给出理想的输出。
对于PID 控制来讲,以增量式PID 为例,公式如下()()()[]()()()()[]212**1*-+--++--=∆k E k E k E kd k E ki k E k E kp k U输入是()k E 、()1-k E 和()2-k E ,输出是增量()k U ∆,对于PID 来讲,最重要的任务是确定系数。
两者相比较,只要将大量的()k E 、()1-k E 和()2-k E 作为输入,()k U ∆作为输出,确定权值的过程就是确定PID 系数的过程。
二、控制算法单神经元自适应PID 的整体结构如下图以智能车为例,上述参数解释为,()k r 为控制器输入的参考值,K 是神经元比例系数,()k u ∆是增量,()k u 是输出PWM ,()k y 是反馈值,偏差()()()k y k r k e -=。
(1)输入()()()11--=k e k e k x ()()k e k x =2()()()()2123-+--=k e k e k e k x(2)权值根据前面讲的,学习规则有两类有导师学习和无导师学习,其中无导师的Hebb 学习规则,又叫无监督Hebb 学习规则,其公式为()()()()()()k y k y k w k w k w k w i j ij ij ij ij η=∆∆+=+1η是设定的学习速率,()k y j 、()k y i 分别是k 时刻i 神经元与j 神经元的输出。
结合Delta 规则,得到有监督的Hebb 学习规则,其公式为()()()()()()()()[]k y k d k y k y k w k w k w k w j j i j ij ij ij ij -=∆∆+=+η1其中,()k d j 是期望输出,()()k y k d j j -在这里即为()()k e k x =2,。
机器人控制中的自适应PID控制算法研究

机器人控制中的自适应PID控制算法研究随着人工智能和机器人技术的进步,机器人在现代生产、服务和家庭等多个领域中得到了广泛应用。
机器人的运动控制是机器人技术中最核心的部分之一,也是机器人实现各种任务的前提。
PID控制算法作为一种经典的控制方法,一直被广泛使用于机器人控制系统之中。
但是,由于现实环境的复杂性和机器人自身的不确定性,传统的PID控制算法难以满足高精度、高性能的控制需求。
因此,自适应PID 控制算法的发展和应用成为了研究热点之一。
什么是自适应PID控制算法?自适应PID控制就是在PID控制算法的基础上,增加了一些自适应的调节因素,从而能够更好地适应不同的控制环境。
自适应PID控制算法的本质思想就是通过对控制对象的实时观测和自身状态的动态更新,从而实现对控制过程的自适应调节。
自适应PID控制算法的本质特征是在PID算法中增加了自适应项,从而能够使控制系统对输入信号产生更加快速、准确和稳定的响应。
具体而言,自适应PID控制算法会根据控制对象的实际运动状态进行自适应调节,以达到更好的控制效果。
自适应PID控制算法的研究意义自适应PID控制算法是机器人技术发展的必要条件之一。
对于机器人来说,精确合理的运动控制是满足各种实际需求的前提。
传统PID控制算法虽然能够在很大程度上实现基本控制要求,但是在应对复杂环境和不确定性因素时表现不佳。
而自适应PID控制算法能够克服这些问题,使机器人能够更好地适应各种复杂环境。
其次,自适应PID控制算法的研究和应用可以为机器人运动控制领域的发展带来更加深远的影响。
在现实应用中,机器人往往面临着各种各样的运动控制问题,需要不断创新和进步。
自适应PID控制算法的研究和应用,可以为机器人智能化、高效化、精确化发展提供更多的思路和方法。
自适应PID控制算法的实现方法自适应PID控制算法的实现方法主要包括三个方面:自适应增益PID控制算法、自适应模型PID控制算法和自适应混合PID控制算法。
自适应PID

由于PID调节器规律简单、运行可靠、易于实现等特点,PID 控制器仍是目前工业生产过程控制系统中应用最广泛的一类控制器。
然而,随着工业过程对控制性能要求的不断提高,传统的PID 算法已不能完全满足生产实际的要求。
为此不少学者在现代控制理论的基础上建立了一些新的控制算法及PID 参数的自动整定方法,但许多算法在工程应用过程中比较复杂,特别对于多段温度控制系统,在升降温过程中会出现振荡等现象。
为此,将常规PID 控制器与自校正算法相结合并利用人工智能系统使其在系统状态变化的每一时刻自动调节PID 参数,让控制过程时刻处于最优状态是每个编程人员都力争实现的。
为了达到这种目的,笔者利用改进的Z - N 算法与人工智能结合,完成PID 参数的初始值设定,利用测量误差改变调节器步长的方法实现PID 参数的自动整定,在大型加热炉的多段温度曲线控制中取得了非常满意的效果。
1利用Z - N 算法获得PID 参数的初始值Ziegler2Nichols 方法(简称Z - N 算法) 是基于简单的被控过程的Niquist 曲线的临界点计算PID 参数初值的方法。
它采用的整定准则是要求系统的暂态过程衰减率为0.75 ,其最大优点是计算方法简单,使用方便。
但实际过程中,许多工业对象对自动控制系统的要求各不相同,生产过程的暂态衰减率不同于0.75。
因此,本文采用修正的Z - N 整定方法,即利用4∶1 的衰减比性能准则获得PID 参数的初始值。
给系统施加一阶跃输入U (可取U 为40 %功率) ,由于温度控制系统有一S 形响应曲线,可以利用一阶延时系统进行近似:U ( s) / T( s) = Ke - τs/ (1 + Ts)假如温度达到50 %和75 %时所用的时间分别为:t1、t2 ,如图1 —1。
则根据Z - N 调谐器调谐准则:Kp = 1.2U/ ( RL) , Ti = 2L , Td = 0.5L ; (1 —1)按照4∶1 的衰减比,可等到:斜率R = (0.75-0.5)*Tset/ ( t2 - t1) (1 —2)滞后L = t1 - (2 T1 - 4 T0) ( t2 - t1) / Tset (1 —3)利用这种方法可以方便地得到PID 参数中的比例系数Kp、积分时间常数Ti 和微分时间常数Td 的初始值。
自适应PID 经验总结

注:大部分为摘入或加以修改模糊自适应PID 控制器是在常规PID控制器的基础上以偏差E和偏差变化率Ec 作为输入,利用模糊控制规则在线对Kp、Ki、Kd的修改,以满足不同时刻偏差E 和偏差变化率Ec 对PID参数自调整的要求。
模糊控制器是以e 和ec 为输入变量,Kp、Ki、Kd为输出语言变量的双输入三输出的模糊控制器。
在运行中通过不断检测e 和ec,查询模糊控制表得出三个参数Kp、Ki、Kd对P、I、D进行在线修改(得到Kp、Ki、Kd需去模糊化处理,一般采用重心法),以满足不同e 和ec 时对P、I、D的不同要求,从而使被控对象具有良好的动、静态性能。
模糊控制表的规则:(1)当e较大时,为使系统具有较好的跟踪性能,应取较大的Kp与较小的Kd,同时为避免系统响应出现较大的超调,应对积分作用加以限制,通常取Ki=0。
(2)当e处于中等大小时,为使系统响应具有较小的超调,Kp应取得小些。
在这种情况下,Kd的取值对系统响应的影响较大,Ki的取值要适当。
(3)当e较小时,为使系统具有较好的稳定性能,Kp与Ki均应取得大些,同时为避免系统在设定值附近出现振荡,Kd值的选择根据|ec|值较大时,Kd取较小值,通常Kd为中等大小。
具体控制表制作方式:另外主要还得根据系统本身的特性和你自己的经验来整定。
注:E是设定值与实际输入变量的差值,Ec是当前偏差与前一偏差值之差P=KP+KP*(设定的原始值)I=KI+KI*(设定的原始值)D=KD+KD*(设定的原始值)做为PID控制的参数具体做法如下:1,输入输出模糊化及隶属函数的建立偏差e和偏差变化率ec作为模糊运算的输入量,Kp,Ki和Kd模糊运算的输出量。
e 和ec 基本论域均设为(-0.6,0.6),输出量Kp,Ki和Kd的基本论域分别设为(-0.3,0.3), (-0.06,0.06)和(-3,3),都划分为7个等级,即(e,ec,Kp,Ki,Kd)={-3,-2,-1,0,1,2,3},对应其模糊集的语言变量均取7个,{NB,NM,NS,Z,PS,PM,PB},其含义依次为:负大,负中,负小,零,正小,正中,正大。
自适应模糊PID控制

SPLS Templates
SPLS Templates
者的转换由微机程序根据事先给定的偏差范围 自动实现。 这种改进的控制方法的出发点主要是因为 模糊控制器本身消除其稳态误差的能力比较差, 难以达到较高的控制精度。
SPLS Templates
SPLS Templates
SPLS Templates
SPLS Templates
SPLS Templates
完成各部分的参数设置后,点击仿真在示波器 中观看系统的阶跃响应曲线。
SPLS Templates
SPLS Templates
PID子系统
SPLS Templates
SPLS Templates
自适应模糊PID控制阶跃响应
SPLS Templates SPLS Templates
SPLS Templates
SPLS Templates
3.2 模糊控制规则的建立
确定语言控制规则是模糊控制设计的核心 工作,规则的形式很多,象计算机程序设计语 言常用的“If…then…”条件语句。控制规则的 多少可视输入输出物理量数目及所需的控制精 度而定。本文有两个输入量,其中一个输入量 有8种模糊态,另一个是7种模糊态,所以共有 56种模糊控制规则。
SPLS Templates
SPLS Templates
在MATLAB菜单窗口中输入命令fuzzy可进 入FIS编辑器,在FIS编辑器中可以设置输入、 输出变量的模糊隶属度函数和模糊控制规则。 隶属度函数有三角形、梯形、高斯形等不同 种类。如下图所示:
SPS Templates
SPLS Templates
输入及输出的隶属度函数
SPLS Templates
智能控制神经网络的自适应PID控制器综述

HUNAN UNIVERSITY2016 年6 月 25 日课程 智能控制理论题目 基于神经网络的自适应PID控制器的设计学生姓名 学生学号 专业班级 学院名称基于神经网络的自适应PID控制器的设计摘要神经网络由于其固有的自学习、自适应、自组织和大规模并行处理能力,已经在控制及其优化领域取得了广泛的应用。
利用神经网络来可以处理控制系统的非线性、不确定性和逼近系统的辨识函数等问题并取得了大量研究成果。
PID控制是最经典的控制算法,其简单、稳定、高效的性能使其在工业控制领域具有绝对的统治地位。
但是面对现代控制系统规模大,复杂度高的情况,单纯使用传统的PID控制已经无法满足要求。
本文结合神经网络与PID两者的优势,提出了一种基于神经网络的自适应PID控制器的设计的方法。
实验证明该方法具有一定的实际应用价值。
近年来,智能控制在工业领域的应用受到了广泛的关注,硬件性能的不断提高与硬件成本的不断降低起到了至关重要的作用。
目前在工业中单纯使用传统的控制方法具有一定的局限性,在面对复杂系统与大规模控制的情况下不能保证在任何时刻都提供准确无误的控制信号,将传统的PID控制方法结合智能控制中的神经网络控制可以克服信息的不完备性和不确定性,更加准确地控制被控对象,从而做出正确的判断和决策。
1.神经网络控制神经网络用于控制系统设计主要是针对系统的非线性、不确定性和复杂性进行的。
资料显示,国内外将神经网络用于控制系统设计的方式和结构还未有一种统一的分类方法。
目前,对神经网络控制系统比较公认地研究方向可以分为监督控制、神经自适应控制、预测控制和逆控制,这时根据控制系统的结构划分的。
本文利用到的就是神经自适应控制。
本文结合神经网络自适应控制与PID控制,提出了一种有效的控制器设计方法,并在在MA TLAB中进行控制系统仿真。
2.控制器原理根据当前产生误差的输入和输出数据,以及误差的变化趋势作为神经网络的输入条件,神经网络将根据当前PID控制器的误差情况以及过去所有进行的PID控制历史数据,共同作为样本数据,重新进行神经网络的参数的训练,得到神经网络内部传递函数的新的表达式,之后PID参数调整将依据新的神经网络进行自动的控制和调整,从而以实现PID控制器具备自适应调节的能力。
自适应PID控制综述(完整版)

自适应PID控制摘要:自适应PID控制是一门发展得十分活跃控制理论与技术,是自适应控制理论的一个重要组成部分,本文简要回顾PID控制器的发展历程,对自适应PID控制的主要分支进行归类,介绍和评述了一些有代表性的算法。
关键词:PID控制,自适应,模糊控制,遗传算法。
Abstract: The adaptive PID control is a very active developed control theory and technology and is an important part of adaptive control theory.This paper briefly reviews the development process PID controller.For adaptive PID control of the main branches, the paper classifies,introduces and reviews some representative algorithms.Keywords: PID control, adaptive, fuzzy control, genetic algorithm1 引言从问世至今已历经半个世纪的PID控制器广泛地应用于冶金、机械、化工、热工、轻工、电化等工业过程控制之中,PID控制也是迄今为止最通用的控制方法, PID控制是最早发展起来的控制策略之一,因为他所涉及的设计算法和控制结构都很简单,并且十分适用于工程应用背景,所以工业界实际应用中PID控制器是应用最广泛的一种控制策略(至今在全世界过程控制中用的80% 以上仍是纯PID调节器,若改进型包含在内则超过90%)。
由于实际工业生产过程往往具有非线性和时变不确定性,应用常规PID控制器不能达到理想控制效果,长期以来人们一直寻求PID控制器参数的自动整定技术,以适应复杂的工况和高指标的控制要求。
智能PID控制及先进参数自整定综述

课程名称工业自动化专题题目名称智能PID控制综述学生学院自动化学院专业班级10自动化(3)班学号 3110000906学生姓名陈兆国指导教师陈老师智能PID控制及先进参数自整定综述摘要PID控制器因为结构简单、容易实现,并且具有较强的鲁棒性,因而被广泛应用于各种工业过程控制中。
但是传统的PID控制应用于复杂的实际系统时存在一定的局限性,而融合了先进智能控制思想和传统PID构成的智能PID控制器则具有良好的特性。
文中介绍几种常见的智能PID控制器的构成方式和参数整定,包括继电反馈、模糊PID、神经网络PID、参数自整定和专家PID控制及基于遗传算法的PID控制。
关键词:PID控制,智能控制,智能PID, 继电反馈,模糊控制PID,神经网络PID和参数自整定AbstractPID(Proportional, interregnal and differential) controller is used widely in kinds of industry circumstance of its simple structure, easy implementation and strong robustness. However, the conventional PID control is limited when applied to a complex physical system, whereas the intelligent PID control fused by both advanced intelligent control thought and conventional PID control has a favorable characteristic. This paper presents some common kinds of intelligent PID controller including relay Feedback, Fuzzy-PID, Neural-Network PID, Parameters Auto-tuning and PID control based on genetic algorithm, Genetic algorithm PID .Their characteristic are also discussed respectively.Key words: PID controller, intelligent control, intelligent PID,Parameters Auto-tuning, Relay Feedback, Fuzzy-PID, Neural-Network PID, Genetic algorithm PID引言PID控制器是工业过程控制中最常见的一种控制器。
第8章PID自适应控制系统

第8章PID自适应控制系统非线性PID控制安排型自适应PID控制系统滕文春编写1994年1自适应PID控制1.概述1.1.自适应PID控制的提出1.2.自适应PID控制的构成1.3.自适应功能的设计方法概述1.4.自适应PID控制的分类1.4.1.按自适应补偿构成分类1.4.2.按被修正的PID参数分类1.4.3.按适应的变量分类2.自适应功能的设计2.1.过程、远程输入和偏差的自适应功能设计2.2.控制输出自适应功能设计2.3.外部触点输入自适应功能设计2.4.多个变量同时施加自适应功能2.5.自适应响应的限幅(AdaptedResponseLimits)3.过程变量自适应增益(AdaptiveGain)PID控制3.1.一般性过程变量自适应增益PID控制的功能构成3.2.密闭、非线性容器的液位控制3.3.均匀液位控制(AveragingLevelControl)3.4.PH值中和控制4.偏差自适应增益PID控制及其应用4.1.PH值中和控制4.1.1.偏差自乘型自适应控制4.1.2.带低增益区(不灵敏区)的偏差自适应控制4.1.3.偏差自适应增益控制4.2.偏差自适应增益控制应用于非优整定补偿4.3.偏差自适应增益控制应用于降低回路之间的藕合4.4.偏差自适应增益控制用于减小过程噪声4.5.偏差自适应增益控制用于精确设定值控制5.远程输入信号自适应增益控制及其应用5.1.一般性远程输入自适应增益PID控制的功能构成5.2.对热量混合过程的负荷自适应增益控制5.3.物料成份混合过程的负荷自适应增益控制5.4.效率自适应增益控制6.控制输出自适应增益控制(ControlOutputAdaptiveGain) 6.1.一般性控制输出自适应增益PID控制的功能构成6.2.控制输出自适应增益对阀门特性补偿的应用7.触点信号(条件切换)自适应增益控制7.1.触点信号(条件切换)自适应增益控制用于缩短启动时间8.设定值自适应增益控制和多变量的自适应增益控制8.1.设定值自适应增益控制8.2.多变量的自适应增益控制9.自适应积分(AdaptiveReset)的应用9.1.概述9.2.自适应积分功能用于改善批量过程控制的启动特性9.2.1.偏差自适应积分控制9.2.2.触点信号自适应积分控制9.3.自适应积分功能用于连续过程控制10.三个参数全可调整的PID控制非线性PID控制安排型自适应PID控制系统滕文春编写1994年2自适应PID控制1.概述1.1.自适应PID控制的提出就一般在特定操作条件下整定出最佳控制参数的控制器来说,当过程特性变化后,其效能是很低的。
PID自适应控制
G ( ) 一 二
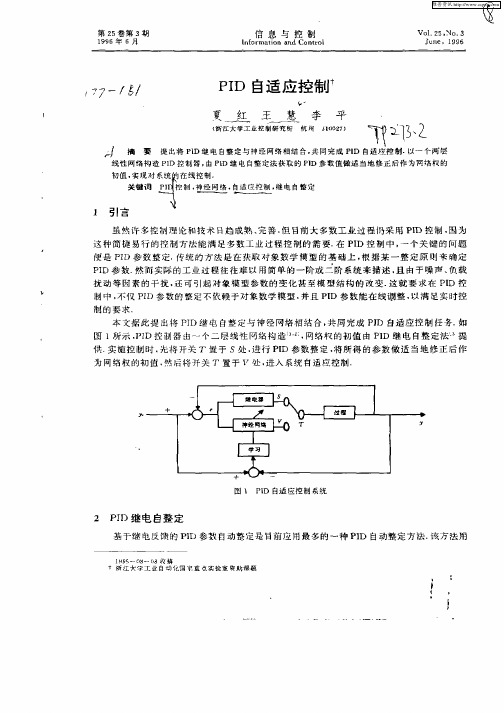
取 k。 一 1, r 一1 , 7 . 一1 .
由图 3可 知 , z N 法的超调量较大 ; 0 — 1法 的 回 复 时 间 较 长 , 并 且 其 负 载 响 应 在 3种 方 法 中 是 最差的 ; P I D 神 经 自适 应 法 用 继 电 自整 定 P I D参 数作 神 经 网络 初 值 , 不 但降低 了超调 量 , 减 弱 了过程响应的振荡程度 , 并使 回 复 时 间 减 短 , 负 载 响 应 质 量 也 有 所 改 善.
Ⅳ ( 0)一 础
Ⅳ2 ( 0)
a k / t .
W ( O )= a k
其中 , 0 < < 1为修 正率 .
4 仿 真 研 究
本 文 选 用 3种 在 实际 工 业 过 程 中较 具代 表 性 的过 程 函 数 , 进行仿真 研究. 并 将 本 文 所 提 出 的P I D 自适 应 控 制 法 , 与应用较 广的 Z i e g l e r — Ni c h o l s法 , 以及 用 ( 0 , 1 ) 之 间 的 随机 值 怍为 神经 网络 P I D控制器初值的控制法 ( 以 下简 0 l法 ) . 进 行 设 定值 改 变 及 负 载 振 动控 制 响 应 的 比较 . 4 . 1 一 阶加 纯滞 后过 程
维普资讯
第2 5卷 第 3期
1 9 9 6年 6月
信 息 与 控 制
I n [ o r ma i f o n a n d Co n t r o |
Vo 1 . 2 5。 No . 3
J u n e,l 9 g 6
, 7 7 -/ /
5 结 论
本 文 提 出 了将 P I D继 电 自整定 与 神 经 网 络 P I D控制器相结合的 P I D 自适 应 控 制 法 . 以 神 经 网络构造 P I D 控制 器 , 解决了 P I D 参 数 在 线调 整 的 问题 , 使P I D控制器适 用范围更广. 以 继 电 自整 定 P I D参 数确定 网络初值 , 使 过 程 响 应 超 调 量 降低 , 回复时 间减短 , 控 制质量 提高 , 仿
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自适应PID控制摘要:自适应PID控制是一门发展得十分活跃控制理论与技术,是自适应控制理论的一个重要组成部分,本文简要回顾PID控制器的发展历程,对自适应PID控制的主要分支进行归类,介绍和评述了一些有代表性的算法。
关键词:PID控制,自适应,模糊控制,遗传算法。
Abstract: The adaptive PID control is a very active developed control theory and technology and is an important part of adaptive control theory.This paper briefly reviews the development process PID controller.For adaptive PID control of the main branches, the paper classifies,introduces and reviews some representative algorithms. Keywords: PID control, adaptive, fuzzy control, genetic algorithm1 引言从问世至今已历经半个世纪的PID控制器广泛地应用于冶金、机械、化工、热工、轻工、电化等工业过程控制之中,PID控制也是迄今为止最通用的控制方法, PID控制是最早发展起来的控制策略之一,因为他所涉及的设计算法和控制结构都很简单,并且十分适用于工程应用背景,所以工业界实际应用中PID 控制器是应用最广泛的一种控制策略(至今在全世界过程控制中用的80% 以上仍是纯PID调节器,若改进型包含在内则超过90%)。
由于实际工业生产过程往往具有非线性和时变不确定性,应用常规PID控制器不能达到理想控制效果,长期以来人们一直寻求PID控制器参数的自动整定技术,以适应复杂的工况和高指标的控制要求。
随着微机处理技术和现代控制理论诸如自适应控制、最优控制、预测控制、鲁棒控制、智能控制等控制策略引入到PID控制中,出现了许多新型PID控制器。
人们把专家系统、模糊控制、神经网络等理论整合到PID控制器中,这样既保持了PID控制器的结构简单、适用性强和整定方便等优点,又通过先进控制技术在线调整PID控制器的参数,以适应被控对象特性的变化。
2 自适应PID控制概念及发展2.1 PID控制器常规PID控制系统原理框图如下图所示,系统由模拟PID控制器和被控对象组成。
PID的标准控制规律:式中:e(t)—控制器偏差输入;u(t)—控制器输出;Kp,Ki,Kd —比例、积分和微分项系数。
2.2 PID控制器的发展1936年,英国诺夫威治市帝国化学有限公司(Imperial Chemical Limited in Northwich, England)的考伦德(Albert Callender)和斯蒂文森(Allan Stevenson)等人给出了一个温度控制系统的PID控制器的方法并于1939年获得美国专利。
从美国专利局的网站上,可以找到当年获得专利的PID计算公式。
这个公式与我们现在使用的PID公式已经没有很大区别。
式中,e代表温度。
只是当时把比例积分微分的增益倍数分开了,可以想象当初这样做的原因:用K1来确定积分的强度(斜率),用K3来确定微分的强度。
面对这个美妙的、简洁的、普适的思想,我们还是多花点时问关注一下她的生日吧。
她的专利的美国存档时问是1936年2月17日。
英国的存档时间:1935年2月13日;1939年10月10日批准美国专利申请。
这说明PID的诞生时问应该在1935年初了,只是出生证明开在1936年。
1940年以后为革新阶段,在革新阶段,PID控制器已经发展成一种鲁棒的、可靠的、易于应用的控制器。
仪表工业的重心是使PID控制技术能跟上工业技术的最新发展。
从气动控制到电气控制到电子控制再到数字控制,PID控制器的体积逐渐缩小,性能不断提高。
一些处于世界领先地位的自动化仪表公司对PID 控制器的早期发展做出重要贡献,甚至可以说PD控制器完全是在实际工业应用中被发明并逐步完善起来的。
PID控制至今仍是应用最广泛的一种实用控制器。
各种现代控制技术的出现并没有削弱PID控制器的应用,相反,新技术的出现对于PID控制技术的发展起了很大的推动作用。
一方面,各种新的控制思想不断被应用于PID控制器的设计之中或者是使用新的控制思想设计出具有PID结构的新控制器,PID控制技术被注入了新的活力。
另一方面,某些新控制技术的发展要求更精确的PID控制,从而刺激了控制器设计与参数整定技术的发展。
2.3 发展中的自适应PID控制PID控制技术经过近几年来的研究和发展,近年来国内外学者越来越多地将智能控制技术引入PID控制器的设计与构成。
下面将介绍这方面的研究、发展和创新。
2.3.1自寻最优PID控制器其控制原理是:系统以积分误差性能指标为准则,当误差性能指标为最小时,即系统为最佳状态,此时PID的各参数为最佳参数。
常用积分误差性能指标有ISE、IAE、ITAE等,可根据不同控制系统选择不同性能指标。
对于随动跟踪控制系统一般可选用ISE积分误差性能指标。
2.3.2模糊PID控制器模糊控制是一类应用模糊集合理论的控制方法。
特别是在一些大滞后、时变、非线性的复杂系统,无法获得系统的精确的数学模型,而模糊控制不需要被控对象的精确数学模型。
这种控制器不但具有PID控制精度高等优点,又兼有模糊控制灵活、适应性强的优点,对复杂控制系统和要求高精度的伺服系统可获得优良的控制效果,是近年来控制领域十分活跃的一支分支。
模糊盒树法自适应PID算法,通过对常规PID控制系统性能品质的分析,提出一种PID控制策略,利用模糊盒树的分枝定界算法,以最少的模糊规则推理实现PID参数的自适应调整。
该方法具有结构简单、鲁棒性强、动态品质优良的特点。
2.3.3神经元自适应PID控制器由Windrow提出的自适应神经元,由于具有自适应学习能力,且结构简单、实时性强、无须对控制对象精确建模等优点。
在神经非模型控制的基础上,结合PID控制的优点,提出了神经非模型自适应PID控制方法,确定了神经元网络的输入信号,设计出自适应系数的在线修正算法,在使控制系统具有良好的动态性能和稳态性能所进行的研究,取得了一定成效。
2.3.4基于遗传算法的PID控制器遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法,其基本思想是将待求解问题转换由个体组成的滨化群体进行操作折一组遗传算子,经历生成一评价一选择一操作的滨化过程,反复进行,自到搜索到最优解。
基于遗传算法的PID参数优化方法,这种方法可简化优化的解析计算过程。
对免疫反馈和遗传机制的免疫遗传算法进行了讨论和研究,基于该研究提出了一种改进的变参数PID控制策略和鲁棒整定的思想,并采用免疫遗传算法进行设计参数的鲁棒优化调整。
2.3.5基于蚁群算法的PID控制器蚁群算法是一种新型模拟进化算法,初步的研究表明该算法具有许多优良的性质。
蚁群算法是受到人们对自然界真实的蚁群集体行为的研究成果的启发而提出的一种基于种群的模拟进化算法,属于随机搜索算法。
由意大利学者M.Dorigo 等人首先提出。
仿生学家经过大量细致的观察研究发现,蚂蚁个体之问是通过一种称之为信息激素的物质进行信息传递。
蚂蚁在运动过程中,在它所经过的路径上留下该种物质,而且蚂蚁在运动过程中能够感知这种物质,并以此指导自己的运动方向。
因此,由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象,某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大,从而增加该路径的信息激素强度,这种选择过程称为蚂蚁的自催化过程,其原理是一种正反馈机制,所以蚂蚁系统也称为增强型学习系统。
2.3.6专家智能自整定PID控制器将专家控制与常规PID控制相结合而具有的自整定、自学习等功能可以用来描述复杂系统的特性,并通过学习和自组织得到相应的控制策略。
一些学者对专家自整定PID控制器设计的方法及应用进行了研究,并针对一般专家自整定PID 控制器的不足之处,加入智能自整定控制,提出采用阶梯信号作为系统输入的思路,这种智能自整定PID控制器由于采用了阶梯信号作为系统输入,避免了系统在参数训练过程中频繁启动的问题,还可以根据实际系统变化的要求,灵活地设定给定信号的阶梯数目,以满足一些特殊场合的控制要求,其具有很强的自整定能力,能允许对象模型的结构和参数在较大范围内变化。
一种改进的单神经元PID控制的方法,采用专家控制调节单神经元PID控制中的比例增益,有效地解决了单神经元PID控制中学习速度较慢,动态响应时问增长等问题。
3 结束语自适应PID控制是随着自适应控制的理论发展和在过程控制上的实践而形成和发展的。
从一开始就带有强烈的应用色彩。
PID控制算法是迄今为止最通用的控制策略,随着计算机技术的迅猛发展,先进控制理论的出现和发展,以及自适应控制技术的引入,使PID控制进入了一个更为深入和广阔的应用大地,自适应PID控制技术将与先进控制理论更为紧密地结合,在先进控制理论推动下,以及微处理器(例如PIC和DSP等)和传感器等硬件的性能的大幅提高,必将是过程控制中极有发展前途的研究和应用方向。
参考文献[1]代军,苏娅芳,张雪.PID算法及其演变[J].辽宁省交通高等专科学校学报2003, (3) :43-45[2]陶水华.新型PID控制及其应用[M].北京:机械上业出版社,2002. 11[3]蒋丽英,李成博,李平.基于最优保留遗传算法的PID参数自寻优[J].仪器仪表学报,2001,22(3):45-46[4]蔡自兴.智能控制一基础与应用[M].国防工业出版社,1998. 10[5]方千山.基于模糊盒树法的自适应PID[J].仪器仪表学报,2002,23(3):378-379[6]腾表芳,秦春林,党建武.神经元自适应PID控制[J].兰州铁道学院学报,2003,22(1):87-89[7]毛敏,于希宁.基于遗传算法的PID参数优化方法[J].中国电力,2002,35(8):48一51[8]詹士昌,吴俊.基于蚁群算法的PID参数优化设计[J].测控技术,2004,23(1):69-72。
