第二章 热力学第一定律分析
热力学第一定律原理分析

热力学第一定律原理分析热力学是研究物质能量转化和守恒的学科,其中最基本的定律被称为热力学第一定律。
热力学第一定律表明能量在物理系统中是守恒的,它是整个热力学理论体系的基础。
本文将对热力学第一定律原理进行分析,探讨其相关概念、表述以及应用。
一、热力学第一定律的基本概念热力学第一定律,也称为能量守恒定律,指的是能量在物理系统中的守恒原理。
按照能量守恒原理,一个系统的内能变化等于从系统中传入的热量减去对外做功的量。
这可用一个简单的数学公式来表示:ΔU = Q - W其中,ΔU表示系统内能的变化,Q表示系统所吸收或放出的热量,W表示系统所做的对外功。
这个公式反映了能量不会自发地消失或产生,只能通过热量传递和对外做功的方式转移。
二、热力学第一定律的表述热力学第一定律可以用不同的形式表述,其中最常见的有以下几种形式:1. 热力学第一定律的简单表述:能量不会自发地产生或消失,只能从一个物体传递到另一个物体或转化为其他形式。
2. 热力学第一定律的数学表述:在一个热力学循环中,系统的内能变化等于循环过程中吸热与放热之间的差值,再减去对外做功的量。
3. 热力学第一定律的微观表述:能量守恒的原理可以通过分子级别的能量转移来解释,即分子间的热运动导致能量传递。
三、热力学第一定律的应用热力学第一定律是研究热力学问题的基础和出发点,它在各个领域都有重要应用,以下是其中的一些常见应用:1. 热力学循环中的工作原理:热力学第一定律揭示了热力学循环中能量的转移与转化,例如内燃机、蒸汽机等均基于这一原理进行工作。
2. 热力学过程中的能量分析:热力学第一定律可以用于分析热传导、热辐射等能量转移过程中的能量转化效率和能源利用率。
3. 热力学平衡条件的确定:热力学第一定律可以用于确定物质在不同温度下的平衡条件,从而对不同系统的热平衡进行分析。
4. 热力学系统的性质研究:热力学第一定律可以帮助研究者了解系统内部的能量分布和转移状况,从而更好地分析系统的性质和行为。
第2章热力学第一定律

技术功:技术上可以利用的功
1 2 wt c gz wi 2
q u w
wt w pv w p2 v2 p1v1
可逆过程
wt pdv p1v1 p2v2 pdv d pv vdp
2 2 2 2 1 1 1 1
第二章 热力学第一定律
本章要求
理解热力学第一定律的实质—能量守恒定律 掌握流动功,轴功及技术功的概念 注意热力学能,焓的引入及定义
掌握热力学第一定律能量方程的基本表达式 及稳定流动能量方程
本章学习流程
热力学第一定律的提出
热力系能量的组成
能量之间的传递和转化 + 焓
闭口系能量方程 + 开口系能量方程 (第一定律数学表达式)
热力学能只取决于热力系内部的状态,且具有 可加性,是一个具有广延性质的状态参数
2
1
du u 2 u1
du 0
2u 2u Tv vT
u u du dT dv T v v T
二.外储存能
工质在参考坐标系中作为一个整体,因有宏观 速度而具有动能,因有高度差而具有位能
热力学能:是指储存于热力系内部的能量. 用U表示,单位是J或 kJ,单位质量工质的热力 学能称为比热力学能,用u表示,单位是J/kg或 kJ/Kg
热力学能是工质的状态参数,完全取决于工 质的初态和终态,与过程的途径无关
热力学能为两个独立状态参数的函数: u=f(T,v)或u=f(T,p)或u=f(p,v)
能量方程式的应用
确定研究对象—选好热力系统
写出所研究热力系对应的能量方程
针对具体问题,分析系统与外界的相互作用, 作出某些假设和简化,使方程简单明了 求解简化后的方程,解出未知量
热工流体第二章 热力学第一定律

第二章 热力学第一定律第一节 第一定律的实质及热力学能和总能能量守恒与转换定律是自然界的基本规律之一,它指出:自然界中的一切物质都具有能量,能量不可能被创造,也不能被消灭;但能量可以从一种形态转变为另一种形态,且在能量的转化过程中能量总量不变。
热力学第一定律是能量守恒与转换定律在热现象中的应用。
它确定了热力过程中热力系统与外界进行能量交换时,各种形态能量数量上的守恒关系。
一、热力学能热力学能是与物质内部粒子的微观运动和粒子的空间位置有关的能量。
它包括分子移动、转动、粒子震动运动的内动能和分子间由于相互作用力的存在而具有的内位能,故又称内能。
内动能取决于分子热运动,是温度的函数,而内位能取决于分子间的距离,是比体积的函数,即u = f ( T, v )二、总能除热力学能外,工质的总能量还包括工质在参考坐标系中作为一个整体,因有宏观运动速度而具有动能、因有不同高度而具有位能。
前一种能量称之为内部储存能,后两种能量则称之为外部储存能。
我们把内部储存能和外部储存能的总和,即热力学能与宏观运动动能和位能的总和,叫做工质的总储存能,简称总能。
即p k E U E E =++ (2-1)E---总能; U---热力学能; E k ---宏观动能; E p ---宏观位能。
第二节 第一定律的基本能量方程及工质的焓一、焓在有关热力计算总时常有U+pV 出现,为了简化公式和计算,把它定义为焓,用符号H 表示,即H=U+pV (2-2)1kg工质的焓值称为比焓,用h表示,即h=u+pv (2-3)焓的单位是J,比焓的单位是J/kg。
焓是一个状态参数,在任一平衡状态下,u、p和v都有一定得值,因而焓h也有一定的值,而与达到这一状态的路径无关。
当1kg工质通过一定的界面流入热力系统时,储存于它内部的热力学能当然随着也进入到系统中,同时还把从外部功源获得的推动功pv带进了系统。
因此系统中因引进1kg工质而获得的总能量是热力学能与推动功之和(u+pv),即比焓。
3第二章热力学第一定律

●闭口热力系统总储存能的变化: △E=△U=U2-U1 闭口热力系统总储存能的变化:
热力学第一定律: 热力学第一定律: Q -W=△E=△U 或 Q =△U+ W
Q
W
一、闭口系统能量方程式
Q = U + W 一 δQ = dU + δW
般 式 q = u + w
Q
W
δq = du + δw δq = du + pdv
2
单位工质
适用条件: ) 适用条件:1)任何工质 2) 任何过程
●过程量
符号w ●符号
轴功
●定义 ●符号 ●实例
系统通过机械轴与外界传递的机械功 ws 规定系统输出轴功为正,输入为负 规定系统输出轴功为正, ws
…………… …………… …………… …………… ……………
ws
闭口系统
开口系统
2-4 焓enthalpy
流动工质传递的总能量 pV + U + 0.5mc2 + mgz h= u + pv 定义焓: 定义焓:H=U+ pV 单位: 单位: J(kJ) kJ) J/kg(kJ/kg) J/kg(kJ/kg) 对理想气体:h=u+pv=u+RT=f( ●H是状态参数 ,对理想气体:h=u+pv=u+RT=f(T) 是 H为广延参数 h为比参数 ● H为广延参数 H=U+pV= m(u+pv)= mh, h为比参数 物理意义: ●物理意义:
(4)热力学第二章1

W Q
循环过程闭口系能量方程式
在一个动力循环中,加入系统的净热量 等于输出的净功量;在一个逆向循环中,系 统放出的净热量等于输入的净功量。 Qnet = Wnet 或 qnet = wnet
特例闭口系能量方程式
Q = dU + W
Q=U+W 绝功系
闭口系统能量方程式
设闭口系统由于温差与 外界交换的热量为Q, 对外作功为W,系统从 状态1变化到状态2
闭口系统与外界无质量交 换;则系统的储存能的增 加为 TH
Q
1
热力系统 W
外界
EC
M1
2
边界 EC
M2
Q W ECM 离开系统的 ECM 2 ECM 1 U E k Ep 进入系统的 系统储存能量 = 能量 能量 的变化
2-2 热力学能和总能
内部储存能
系统储存的能量
外部储存能
内部储存能:只取决于系统本身(内部)的状态
外部储存能:与系统整体运动以及外界重力场有关
内 能
储存于系统内部的能量,称为内能。它与系 统内工质的内部粒子的微观运动和粒子空间位形 有关。 移动 内动能 转动 振动 内位能 内能 化学能 原子能
内能分析
可逆闭口系能量方程
简单可压缩系可逆过程
Q = TdS TdS = dU + pdV
TdS = U + pdV
q = Tds Tds = du + pdv Tds = u + pdv
循环过程闭口系能量方程式
Q = dU + W
p
4 3
1 2 v
∮δQ=∮dU+ ∮δW
第二章 热力学第一定律

(二)热力学第一定律
热力学第一定律实质就是能量守恒和转换 定律在热现象上的应用。 表述1:热可以变为功,功也可以变为热;一 定量的热消灭,必产生一定量的功;消耗一 定量的功时,必出现与之相应数量的热。
表述2:第一类永动机是造不成的
First Law of Thermodynamics
In 1843, at the age of 25, James Prescott Joule did a series of careful experiments to prove the equivalence of heat and work.
A p V
dl
对推进功的说明
1、与宏观流动有关,流动停止,推进功不存在 2、作用过程中,工质仅发生位置变化,无状态变化
3、w推=pv与所处状态有关,是状态量 4、并非工质本身的能量(动能、位能)变化引起, 而由外界(泵与风机)做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之
间所传递的一种机械功,表现为流动工质进 出系统使所携带和所传递的一种能量
4、物理意义:开口系中随工质流动而携带的、取决 于热力状态的能量。
三、稳定流动能量方程
Energy balance for steady-flow systems
稳定流动条件
(P22)
1、
•
•
•
mout min m
2、
•
Q Const
min
uin 1 2
c
2 in
gzin
3、
•
•
Wnet ConstWs
三、总能
热力系统的储存能: 储存于热力系统的能量。 (1)内部储存能———热力学能 (2)外部储存能———宏观动能,宏观位能。
第2 章热力学第一定律

第2章 热力学第一定律一 基本要求:1. 深入理解热力学第一定律的实质,掌握热力学第一定律的表达式——能量方程,并熟练应用热力学第一定律解决工程实际中的有关问题。
2. 掌握储存能、热力学能和焓的概念。
3. 掌握体积变化功、流动功、轴功和技术功的概念,计算他们之间的关系。
二 重点、难点:1. 热力学第一定律的实质。
2. 焓的物理意义。
3. 热力学能及系统总储存能的区分。
4. 开口及闭口系统的能量方程。
5. 技术功、轴功、推动功和膨胀功的联系及区别。
6. 稳定流动能量方程式的应用。
三 典型题精解:例1:气缸内储有完全不可压缩的流体,气缸的一端被封闭,另一端是活塞。
气缸是绝热静止的。
试问:(1) 活塞能否对流体做功? (2) 流体的压力会改变吗?(3) 若使用某种方法把流体从0.2Mpa 提高到4Mpa ,热力学能有无变化?焓有无变化? 解:(1)汽缸活塞系统是闭口系统。
由于流体不可压缩,流体的体积不会变化,因此流体的体积变化功为零,活塞不能对流体做功。
(2)根据牛顿第三定律,流体的压力应与外力时时相等,因而当活塞上的作用力改变时,流体的压力也随之改变。
(3)根据已知条件,汽缸活塞系统与外界无热交换,Q=0,又W=0,由能量方程 Q=∆U+W 知∆U=0,故流体热力学能无变化。
焓H=U+pV ,当U ,V 不变,p 提高时,H 应增大。
讨论:(1) 从本题分析可以看到,闭口系统与外界有无功量交换,不在于压力大小或系统压力有无变化,而在于系统有无体积的变化。
(2) 本题由于系统与外界无热量交换,无功量交换,因而系统的热力学能变化为零,但焓的变化不为零。
应将热力学能和焓的概念加以正确区分。
例2.门窗紧闭的房间内有一台电冰箱正在运行,若敞开冰箱的大门就有一股凉气扑面,感到凉爽。
于是有人就想通过敞开冰箱大门达到降低室内温度的目的,你认为这种想法可行吗? 解:按题意,以门窗禁闭的房间为分析对象,可看成绝热的闭口系统,与外界无热量交换,Q=0,如图2.1(a)所示,当安置在系统内部的电冰箱运转时,将有电功输入系统,根据热力学规定:0<W ,由热力学第一定律W U Q +∆=可知,0>∆U ,即系统的内能增加,也就是房间内空气的内能增加。
02第二章 热力学第一定律 重点和难点

系统内部储能增量: ΔECV
考虑到稳流特征: ΔECV=0 qm1=qm2=qm; 及h=u+pv 有
2 2 cf2 cf1 Q H 2 H1 qm qm g z2 z1 WS 2 2 1 2 q h2 h1 cf2 cf21 g z2 z1 ws 2
3)第一定律第二解析式 把wt的概念代入(B)式,可得第一定律第二解析式
1 2 q h2 h1 cf 2 cf21 g z2 z1 ws 2 ( B)
2
q h wt δq dh δwt
可逆 q h 1 vdp
δq dh vdp
几种功及相互之间的关系
名称 含义 说明
1)当系统可逆时δw=pdv 2)膨胀功是简单可压缩系热变功的源泉 3)膨胀功往往对应闭口系所求的功 1)轴功是开口系所求的功 W 2) 当工质进出口间的动、位能差被忽略时, pdV Wt=Ws此时开口系统所求的功也是技术功
2 1
体积变化 系统体积变化 功W 所完成的功
轴功Ws 流动功 Wf. 系统通过轴与 外界交换的功
开口系付诸于质 量迁移所作的功
流动功是进出口推动功之差, 即Wf=Δ(pV)=p2V2-p1V1
技术功Wt 技术上可资利 用的功
1)Wt与Ws的关系 Wt=m Δ cf2/2+mg Δz+Ws 2) Wt与W,Wf的关系 Wt=W-Wf 3)当过程可逆时, δ W=-Vdp,这也是动、 位能差不计时的最大轴功
2)技术功(technical work)—技术上可资利用的功 wt 1 2 wt ws cf g z 2 由(C)
q u wt p2v2 p1v1 (D)
第二章 热力学第一定律

进入系统的能量-离开系统的能量=系统能量的增加 (2-9) 进入系统的能量-离开系统的能量= - )
1 2 Q = m2 (u2 + cf 2 + gz2 ) + m2 p2 v2 2 1 2 − m1 (u1 + cf 1 + gz1 ) − m1 p1v1 + Wi 2
1 2 wt = (cf 2 − cf21 ) + g ( z 2 − z1 ) + wi 2
比较式(2-10b)和(2-16) 比较式( - 和 - )
(2 − 19)
q = ∆u + w q = ∆h + wt = ∆u + ∆( pv) + wt 1 2 w = ∆( pv) + wt = ∆( pv) + ∆cf + g∆z + wi 2
由于m 由于 1=m2=m, 整理上式得
1 2 Q = m(u2 + p2 v2 + cf 2 + gz2 ) 2 1 2 − m(u1 + p1v1 + cf 1 + gz1 ) + Wi 2 令 H = U + pV 代入上式得
1 Q = ∆H + m∆cf2 + mg∆z + Wi 2 1 2 δQ = dH + mdcf + mgdz + δWi 2
m1 = m2 = m
∆ECV = 0
稳定系统的能量分析: 稳定系统的能量分析: 进入系统的能量: 进入系统的能量:
1 2 Q + E1 + p1V1 = Q + m1 (u1 + cf 1 + gz1 ) + m1 p1v1 2 离开系统的能量: 离开系统的能量: 1 2 E2 + p2V2 + Wi = m2 (u 2 + cf 2 + gz 2 ) + m2 p2 v2 + Wi 2
第二章 热力学第一定律

( )分两次将两堆细砂加上 : b¢
W b¢ = - 2p 0 (1.5V 0 - 3V 0 ) - 3p 0 (V 0 - 1.5V 0 ) = 4.5p 0V 0 = 1.5R T
( c¢)将细砂一粒粒加到活塞上直至加完
2. 可逆体积功的计算
Wr = -
òV
V2
1
V2
1
p dV
(1)理想气体的恒温可逆体积功
W T ,r = -
蝌 V
p dV = -
V2 V1
nR T dV V
V1 = nR T ln V2 p2 = nR T ln p1
例题2-2 不同途径功的计算
§2.5 恒容热、恒压热及焓 1. 恒容热(QV): 热是非状态函数---与途径有关
第二章
热力学第一定律
§2.1
概论
热力学是自然科学中建立最早的学科之一
1. 第一定律:能量守恒,解决过程的能量衡算
问题(功、热、热力学能等) 2. 第二定律:过程进行的方向判据 3. 第三定律:解决物质熵的计算
热力学基本定律是生产经验和科学实验的总结,它们
不能用其它理论方法加以证明,但其正确性毋庸置疑。
(2)状态函数的分类——广度量和强度量
按状态函数的数值是否与物质的数量有关,将其分为广 度量(或称广度性质)和强度量(或称强度性质)。
广度量:具有加和性(如V、m、U) 强度量:没有加和性(如p、T、 ) 注意:由任何两种广度性质之比得出的物理量则为强度 量,如摩尔体积 等
状态函数
(3)平衡态 当系统与环境间的联系被隔绝后,系统的热力学性质 不随时间而变化,就称系统处于热力学平衡态。 热力学研究的对象就是处于平衡态的系统。
第二章热力学第一定律

m out
u pv c / 2 gz min
in
流动时,总一起存在
焓的引入
定义:焓
h = u + pv
Q dEcv / W net u pv c / 2 gz h
2 2 out
m out
u pv c / 2 gz min h
总结: 开口系能量方程一般表达式:
Q =dEcv + ∑(h+ + gz)out mout ∑(h+ c2/2 + gz)in min + Wnet
2/2 c
以流率表示的开口系能量方程:
Q dEcv / W net u pv c / 2 gz h
2 2 out
1 q h c 2 g z ws 2
稳定流动能量方程
1 2 q h c g z ws 2
适用条件:
任何流动工质
任何稳定流动过程
技术功
Wt
1 2 Q mh mc mg z Ws 2 1 2 q h c g z ws 2 动能 位能 轴功 wt 机械能 工程技术上可以直接利用
间所传递的一种机械功,表现为流动工质进 出系统使所携带和所传递的一种能量
开口系能量方程的推导
uin pvin gzin Wnet mout uout pvout 1 2 cout gzout 2 min 1 2 cin 2
Q
Q + min(u + c2/2 + gz)in - mout(u + c2/2 + gz)out - Wnet = dEcv
《工程热力学》第二章 热力学第一定律

6
2-2 热力学能和总能
能量是物质运动的度量,运动有各种不同的 形态,相应的就有各种不同的能量。
系统储存的能量称为储存能,它有内部储存 能与外部储存能之分。系统的内部储存能即为热 力学能
Q U W
Q 0 W ? 0 U 0 即U1 U2
强调:功是通过边界传递的能量。
30
h1 a 2
h1 b 2
2
dh
1
h2 h1
dh 0
21
三、焓的意义:
焓是物质进出开口系统时带入或带出的热力学 能与推动功之和,是随物质一起转移的能量。
焓是一种宏观存在的状态参数,不仅在开口系 统中出现,而且在分析闭口系统时,它同样存 在。
焓是随着质量交换而交换的一种“转移能”, 只有在质量跨越边界的前提下,焓的物理意义 及其能量属性才能体现出来。
第二章 热力学第一定律
1
本章基本要求
深刻理解热能、储存能、功的概念,深刻理解内 能、焓的物理意义;
理解膨胀(压缩)功、轴功、技术功、流动功的 联系与区别;
本章重点
熟练应用热力学第一定律解决具体问题
2
2-1 热力学第一定律的实质
19世纪30-40年代,迈耶,焦耳等发现并确 定了能量转换与守恒定律。恩格斯将这列为19世纪 三大发现之一(细胞学说、达尔文进化论)。
在热能与其它形式能的互相转换过程中,能的 总量始终不变。
不花费能量就可以产生功的第一类永动机是不 可能制造成功的。
4
5
进入系统的能量-离开系统的能量 = 系 统储存能量的变化
在工程热力学的范围内,主要考虑热能与机 械能之间的相互转换与守恒,因此热力学第一定 律可表述为:热可以变为功,功也可以变为热, 在相互转变时能的总量是不变的。
工程热力学与传热学(中文) 第2章 热力学第一定律

∫
2
1
dH = H 2 − H 1
∫ dH
=0
什么条件下,热力学能和焓值可以同时为零”? 什么条件下,热力学能和焓值可以同时为零”
2-4-4 开口系统稳定流动能量方程式
(The first law applied to open system - steady flow) )
dm 2
2. 表示
入口处: δ W f 1 = p1 A1dx1 = p1dV1 = p1v1dm1 入口处: 出口处: 出口处: δ W f 2 = p 2 A2 dx 2 = p 2 dV 2 = p 2 v 2 dm 2 单位质量工质: 单位质量工质: w f 1 =
δW f 1
dm1
= p1v1
例 题
2. 一活塞汽缸中的气体经历了两个过程,从状态 到状态 , 一活塞汽缸中的气体经历了两个过程,从状态1 到状态2, 气体吸热500kJ,活塞对外做功 到状态3 气体吸热 ,活塞对外做功800kJ。从状态 到状态 。从状态2到状态 是一个定压的压缩过程,压力为400kPa,气体向外散热 是一个定压的压缩过程,压力为 , 450kJ。并且已知 1=2000kJ,U3=3500kJ。 。并且已知U , 。 试计算2-3过程中气体体积的变化 过程中气体体积的变化。 试计算 过程中气体体积的变化。
Q
W
a: 一部分用于增加工质的热力学能。 一部分用于增加工质的热力学能。 b: 另一部分以作功的方式传递到外界。 另一部分以作功的方式传递到外界。
∆u
(2)对于1kg工质 :q = w + ∆ u ) (3)适用条件:a: 可逆过程,不可逆过程。 )适用条件: 可逆过程,不可逆过程。
物理化学第二章(第一定律)

热力学
8
系统的性质具有如下特点: 1.系统的性质只决定于它现在所处的状态,而与其过
去的历史无关。 2. 系统的状态发生变化时,它的一系列性质也随之而改
变,改变多少,只决定于系统的开始状态和终了状态, 而与变化的途径无关。
热力学把具有这种特征的系统性质称为状态函数。
或不能使一个自然发生的过程完全复原。
第一类永动机 (能量不守衡)
热源 Q W
第二类永动机
2
根据大量的实验结果和自然现象,得出热力学第一、 二定律。
热力学定律的特点: (1) 大量分子系统
(2)不管物质的微观结构 (3)不管过程的机理
优点:结论绝对可靠, 如从热力学导出纯液体 饱和蒸汽压与温度的关系:
(3) 热分为: 显热(Sensible heat)系统做单纯的pVT变化(没有相 变化),如: 25C水75C水时,系统与环境交换的热量。 潜热(Latent heat)系统发生相变化时,如:
100C水100C水汽时,系统与环境交换的热量。
27
§2-2 热力学第一定律 The First Law of Thermodynamics
活塞
p1 dV
pe
汽缸
如果p1>pe(外压),气体膨胀dV,
则系统对环境做体积功为:dWe= pedV
21
(1) 自由膨胀(Free expansion) 为外压等于零的膨胀,即 pe=0,所以:
We,1 0
(2) 恒外压膨胀pe=const.
We,2
V2
-
pedV
-pe (V2
V1 )
第二章 热力学第一定律及其应用
物理化学第2章热力学第一定律

第二章热力学第一定律2.1 热力学的理论基础与方法1.热力学的理论基础热力学涉及由热所产生的力学作用的领域,是研究热、功及其相互转换关系的一门自然科学。
热力学的根据是三件事实:①不能制成永动机。
②不能使一个自然发生的过程完全复原。
③不能达到绝对零度。
热力学的理论基础是热力学第一、第二、第三定律。
这两个定律是人们生活实践、生产实践和科学实验的经验总结。
它们既不涉及物质的微观结构,也不能用数学加以推导和证明。
但它的正确性已被无数次的实验结果所证实。
而且从热力学严格地导出的结论都是非常精确和可靠的。
不过这都是指的在统计意义上的精确性和可靠性。
热力学第一定律是有关能量守恒的规律,即能量既不能创造,亦不能消灭,仅能由一种形式转化为另一种形式,它是定量研究各种形式能量(热、功—机械功、电功、表面功等)相互转化的理论基础。
热力学第二定律是有关热和功等能量形式相互转化的方向与限度的规律,进而推广到有关物质变化过程的方向与限度的普遍规律。
利用热力学第三定律来确定规定熵的数值,再结合其他热力学数据从而解决有关化学平衡的计算问题。
2.热力学的研究方法热力学方法是:从热力学第一和第二定律出发,通过总结、提高、归纳,引出或定义出热力学能U,焓H,熵S,亥姆霍茨函数A,吉布斯函数G;再加上可由实验直接测定的p,V,T等共八个最基本的热力学函数。
再应用演绎法,经过逻辑推理,导出一系列的热力学公式或结论。
进而用以解决物质的p,V,T变化、相变化和化学变化等过程的能量效应(功与热)及过程的方向与限度,即平衡问题。
这一方法也叫状态函数法。
热力学方法的特点是:(i)只研究物质变化过程中各宏观性质的关系,不考虑物质的微观结构;(ii)只研究物质变化过程的始态和终态,而不追究变化过程中的中间细节,也不研究变化过程的速率和完成过程所需要的时间。
因此,热力学方法属于宏观方法。
2.2 热力学的基本概念1.系统与环境系统:作为某热力学问题研究对象的部分;环境:与系统相关的周围部分;按系统与环境交换内容分为:(1)敞开系统(open system) :体系与环境间既有物质交换又有能量交换的体系。
哈工大工程热力学-(2)热力学第一定律

5、能量方程之间的内在联系、热变功的本质
如果把稳定流动能量方程中流体动能的增量和重力 位能的增量看作是暂存于流体(热力系)本身,并把它 们和轴功合并在一起,合并以后的功也就相当于开 口系能量方程中的技术功 这样,式(2-13)和式(2-11)也就完全一样了,即
如果再把式 (2-14) 中的焓写为热力学能和推 动功之和,把技术功写为进气功、膨胀功及 排气功的代数和,便可以得到式(2-6)
代入式 (2-8) 可得 每千克工质 微分式
适用条件:开口系、任何工质、任何 (无摩擦或摩擦)过程
4、稳定流动的能量方程
稳定流动是指流道中任何位置上流体的流速及 其它状态参数 ( 温度、压力、比体积、比热力 学能等 ) 都不随时间而变化的流动
设有流体流过一复杂通道,虚线(界面)所包围的 开口系研究对象,假定进、出口截面上流体的各个 参数均匀一致,依次为: 进口截面: 出口截面:
归根结底,反映热能和机械能转换的是式 (2-6),将其改写为
在任何情况下,膨胀功都只能从热力系本 身的热力学能储备或从外界供给的热量 转变而来
在闭口系中 - 膨胀功(w)全部向外界输出 在开口系中 - 膨胀功中有一分要用来弥补 排气推动功和进气推动功的差值( p2v2-p1v1 ) 剩下的部分(即为技术功)可供输出
第二章 热力学第一定律
2 - 1 热力学第一定律 的实质及表达式
一、热力学第一定律的实质
实质是能量守恒与转换原理在热力学中 的具体体现
在工程热力学中,热力学第一定律主要 说明热能和机械能在转移和转换时,能 量的总量必定守恒
二、热力学第一定律表达式
1. 一般热力系能量方程
第二章 热力学第一定律

思考
定量气体在等温过程中热力学能不变?
错误。气体的热力学能是温度和比体积的函
数,等温过程中虽然温度不变,但比体积可
能会发生改变,故热力学能也会改变。
思考
理想气体的热力学能只与温度有关。
正确。对于理想气体,因为分子间不存在相
互作用力,因此没有内位能。其热力学能仅 包括分子内动能。因此,理想气体热力学能 只是温度的单值函数。
二、外部储存能
需要用在系统外的参考坐标系测量的
参数来表示的能量,称为外部储存能,
它包括系统的宏观动能和重力位能。
质量为m的物体相对于系统外的参考坐 标以速度c运动时,其具有的宏观动能为:
1 2 Ek mc 2
重力场中质量为m的物体相对于系统外的 参考坐标系的高度为z时,其具有的重力位 能为:
滚球永动机
软臂永动机
19世纪有人设计了一种特殊机 构,它的臂可以弯曲。臂上有 槽,小球沿凹槽滚向伸长的臂 端,使力矩增大。转到另一侧, 软臂开始弯曲,向轴心靠拢。 设计者认为这样可以使机器获 得转矩。然而,他没有想到力 臂虽然缩短了,阻力却增大了, 转轮只能停止在原地。
软臂永动机
阿基米得螺旋永动机
分子热运动形成的内动能。它是温度的函数。
分子间相互作用形成的内位能。它是比体积的函 数。
维持一定分子结构的化学能、原子核内部的原子 能及电磁场作用下的电磁能等。
1、内动能
根据分子运动学说,组成气体的分子是处于不 断运动的状态中,不仅分子本身作直线运动、 旋转运动和相对于其它分子的振动,构成分子 的内部原子也在不断地振动,这些运动着的分 子与原子都具有动能,称为气体的内动能。 气体的内动能与气体的温度有关。气体的温 度越高,内动能越大。
第二章__热力学第一定律

(D) 系统的某一性质改变了,其状态必定发生 改变
11
状态函数特点:
状态改变,状态函数值至少有一个改变 异途同归,值变相等;周而复始,其值不变 系统状态的微小变化引起状态函数 X 的变化用 全微分 dX 表示。
按照热力学系统宏观性质的数值是否与物质的数量有关, 状态函数可分为:
状态函数分类
状态确定
所以,性质是状态的函数
状态函数(state function):鉴于状态与性质 之间的这种对应关系,所以系统处于平衡态
时的热力学性质(如 U、H、p、V、T 等)
称为状态函数。
下面说法错误的是
(
)
(A) 系统的同一状态可具有不同的体积
(B) 系统的不同状态可具有相同的体积
(C) 系统的状态改变了,可能所有的状态函数 都要发生改变
W= -pambV= - pV
δW= -pambdV= - pdV 由热力学第一定律可得:
Qp = U - W = U + pV δQp = dU + d(pV) = d(U + pV) (dp = 0,δW’=0)
3.焓的导出: δQp = d(U + pV)
定义 : H = U + pV 称H为焓,H为状态函数,广度量,单位J 将焓的定义式代入上式有:
35
热力学第一定律的其它表述方法:
要制造一种既产生功又不需消耗能量 的机器(第一类永动机)是不可能的。
隔离系统能量守恒。
3. 焦耳实验 焦耳于1843年进行了低压气体的自由膨胀实验:
温度计
气体
水浴
真空
37
利用热力学第一定律对焦耳实验过程进行分析 理想气体向真空膨胀:W=0;
热力学第一定律与第二定律

热力学第一定律与第二定律热力学是关于能量转化和能量守恒的科学,它研究了物质与能量之间的关系以及能量转化的规律。
在热力学中,有两个基础定律,即热力学第一定律和热力学第二定律。
本文将详细介绍这两个定律的定义、原理和应用。
一、热力学第一定律热力学第一定律又被称为能量守恒定律,它表明能量在系统中的变化量等于系统所做的功加上系统吸收的热量。
简言之,能量是守恒的。
具体来说,热力学第一定律可以用以下方程式表示:ΔU = Q - W其中,ΔU代表系统内能的变化,Q代表系统吸收的热量,W代表系统所做的功。
根据这个定律,我们可以得出以下结论:1. 系统吸收的热量等于系统内能的增加。
热量可以使系统内粒子的动能增加,也可以使分子之间的相互作用增强,从而使内能增加。
2. 系统所做的功等于系统内能的减少。
当一个物体从高温区移动到低温区时,它会做功,从而导致内能减少。
热力学第一定律的应用非常广泛。
例如,在工程领域中,我们可以利用这个定律来计算热机的效率。
在化学反应中,我们可以根据热力学第一定律来判断反应是否放热或吸热,并求出反应的焓变。
总之,热力学第一定律是热力学研究中的基础,对于理解和应用能量转化的过程至关重要。
二、热力学第二定律热力学第二定律是关于物质能量转化方向的定律。
它规定了能量在自然界中传递的方式和限制。
总结起来,热力学第二定律表明热量自发地从高温物体传递到低温物体,而不会自发地从低温物体传递到高温物体。
这个定律可以从以下两个方面解释:1. 热量不会自发地从低温物体传递到高温物体。
这是因为能量在自然界中总是从高能态流向低能态。
如果低温物体能够将热量传递给高温物体,就违背了能量的自发流动方向。
2. 熵增定律。
熵是用来描述系统无序程度的物理量,热力学第二定律指出,一个孤立系统的熵要么保持不变,要么增加。
换句话说,自发过程总是趋于增加系统的熵。
而熵的增加意味着能量的转化趋于不可逆。
根据热力学第二定律的约束,我们可以得出一些重要的结论。
工程热力学(热力学第一定律)
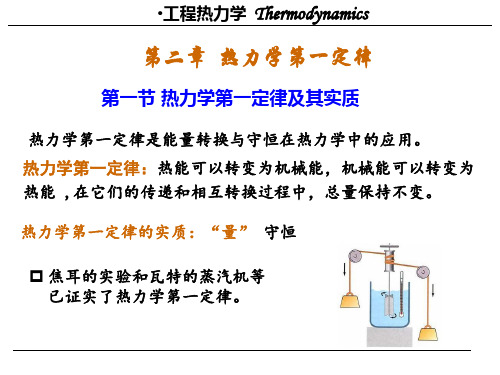
e u 1 c2 gz 2
三、闭口系的能量方程——热力学第一定律基本表达式
Q U W
q u w
可逆: 微元:
2
Q U pdV 1
或
2
q u pdv 1
Q dU W 或 q du w
可逆: Q dU pdV 或 q du pdv
•工程热力学 Thermodynamics
五、 焓
•工程热力学 Thermodynamics
定义式 H U pV
比焓 h H u pv
m
物理意义: 焓是开口系统中流入(或流出)系统工质所携带
的取决于热力学状态的总能量。
•工程热力学 Thermodynamics
第六节 能量方程的应用
一 叶轮式机械 1、动力机(汽轮机,燃气轮机)
气,带动此压气机要用多大功率的电动机?
解(1)系统为闭口系,能量方程为:
q u w
则
w q u 50 150 200 kJ kg
•工程热力学 Thermodynamics
(2)系统 可视为稳定流动系统(如图所示)则能量方程为:
q
h
1 2
c
2
g
z
wsh
由: c2 0, gz 0
得: wsh q h q [u ( pv)] (q u) ( pv)
—热力学第一定律基本表达式
一、能量方程:
Esy U
(e2 m2 e1 m1) 0
Q U W 或
Wtot W
q u w
Q Esy (e2m2 e1m1) Wtot
二、分析 :
Q U W
外热能
内热能
热能
体积变化功
机械能
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热学
19
例题:1mol理想气体,初态的压强、体积和温度 分别为p1、V1和T1。若体系经历一个压强与体积满 足关系p=aV的过程,其中a为常数,试求: (1)用p1、T1和R来表示常数a; (2)若系统经历此过程体积扩大一倍,则系统的 温度T为多少?在此过程中对外所做的功为多少? 解:(1)由理想气体的状态方程,得
热学1ຫໍສະໝຸດ 热学2教学基本要求
一 掌握内能、功和热量等概念 . 理解准静 态过程 .
二 掌握热力学第一定律,能分析、计算理 想气体在等体、等压、等温和绝热过程中的功、 热量和内能的改变量 . 三 理解循环的意义和循环过程中的能量转 换关系,会计算卡诺循环和其他简单循环的效率 .
四 了解可逆过程和不可逆过程,了解热力 学第二定律和熵增加原理 .
11
二、功的表达式(体积功)
1、气体对外界所作的元功为:
所作的总功为:
dA pSdx pdV
A pdV
V1
V2
2、外界对气体所作的功为:
A pdV
V1
热学
V2
12
三、功的图示
注意
当dV>0,即气体体积膨胀时, 则dA>0,作正功,系统对外界作功; 当dV<0,即气体体积压缩时, 则dA<0,作负功,外界对系统作功。
第一章我们从热力学的角度学习了有关 平衡态的一些知识,那么很自然要进一 步讨论系统从一个平衡态变化到另一个 平衡态的过程,在这一过程中状态参量 的变化的规律是什么?从而系统的能量 以及热力学性质会发生什么样的变化? 这种变化在实际中有何意义?这些重要 的问题可以用热力学的方法加以方便地 讨论,从而给出满意的回答。
A
F F
l0
l0+dl
热学
16
2 2、表面张力功
x L A dx F
dA 2ldx dS
σ 是表面张力系数
3、可逆电池所作的功 3
a b
G
dA dq
E
Cu Zn
可 逆 电 池
CuSO4
热学
ZnSO4
17
4、功的一般表达式
dWi Yi dxi
x是 广义坐标,它是广延量,广 延量的特征是:若系统在相同情况下 质量扩大一倍,则广延量也扩大一倍。 如:体积,面积,电极化强度等。 Y是广义力,它是强度量,强度量 的特征是:当系统在相同情况下质量扩 大一倍时,强度量不变。如:压强,表 面张力,电场强度等。
热学
8
显然作为准静态过程中间状 态的平衡态,具有确定的状 态参量值,对于简单系统可 用P—V图上的一点来表示 这个平衡态。系统的准静态 变化过程可用P—V图上的 一条曲线表示,称之为过程 曲线(右图)。 准静态过程是一种理想的极 限,但作为热力学的基础, 我们要首先着重讨论它。
热学
9
外界对系统的作用使系统的状态发生了变化, 这种相互作用的情况用力的情况来反映是不 方便的,有的时候甚至是不可能的,但是作 用的结果是使系统的能量发生了改变,作为 能量变化的量度是功,作为能量变化的主要 形式之一是热量的交换,因此,外界的作用 就是功和热的转移,从而使系统的状态发生 改变,为此,我们以后就以功和热为两条主 要线索来反映系统和外界的相互作用了。
热学
18
七、对功的计算公式,有几点说明:
1、功不但与系统的初、末状态有关,而且与过 程有关,即功是过程量; 2、只适用于无摩擦的准静态过程; 3、用公式来计算功时,必须先找到压强p随体 积V变化的函数关系式p=p(V),然后代入公式, 就可以求出一过程所作的功; 4、我们讨论的都是体积功; 5、功还可以利用p-V图求出作功的大小,在图 中曲线下方所围成的面积就是功的大小,功的 正负由曲线上的箭头来判断。
热学
6
三、准静态过程
如果一个热力学系统过程在始末两平衡态 之间所经历的之中间状态,可以近似当作 平衡态,则此过程为准静态过程。
注意 •准静态过程只有在进行的“无限缓慢” 的条件下才可能实现
•对于实际过程则要求系统状态发生变化的 特征时间远远大于弛豫时间才可近似看作 准静态过程。
热学
7
准静态过程例子 无摩擦准静态过程,其特点是没有摩擦力, 外界在准静态过程中对系统的作用力,可以用 系统本身的状态参量来表示。 [例] 右图活塞与汽缸无摩擦,当气体作准静态 压缩或膨胀时,外界的压强Pe必等于此时气体的 压强P,否则系统在有限压 dx 差作用下,将失去平衡, 称为非静态过程。若有摩 P 擦力存在,虽然也可使过 S Pe 程进行的“无限缓慢”, 但 P e ≠P 。
当热力学系统的状态随时 间变化时,我们就说系统 在经历一个热力学过程, 简称过程。
推进活塞压缩汽缸内的 气体时,气体的体积、 密度、温度或压强都将 变化
热学
5
二、非静态过程
1、弛豫时间:系统由非平衡态到达平衡态所 需要的时间称为弛豫时间。用τ表示 2、弛豫过程:由非平衡态到达平衡态的过程 称为弛豫过程。 3、非静态过程:在热力学过程的发生时,系 统往往由一个平衡状态经过一系列状态变化 后到达另一平衡态。如果中间状态为非平衡 态,则此过程称非静态过程。 作为中间态的非平衡态通常不能用状态参量 来描述。
热学
3
第二章 热力学第一定律
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 热力学系统的过程 功 内能 热量 焦耳热功当量实验 热力学第一定律 理想气体的内能、热容和焓 热力学第一定律对理想气体 几种典型过程的应用 §2.7 循环过程 §2.8 技术上的循环实例
热学
4
§2.1 热力学系统的过程 一、热力学过程
热学
13
四、功是过程量
注意
三种过程的初、末状态相同, 但所作的功不同;说明功不仅 与初、末状态有关,而且与变 化的路径也有关,证明它不是 状态的函数,而是过程量。
热学
14
五、理想气体在几种等值过程中功的计算
等温过程:
等压过程:
等体过程:
热学
15
六、其它形式的功
1、拉伸弹簧棒所作的功
热学
10
§2.2
功
一、功是力学相互作用下的能量转移
力学相互作用:将力学平衡条件被破坏时所产生的对系统 状态的影响。 在力学相互作用过程中系统和外界之间转移的能量就是功。
热力学认为力是一种广义力,所以功也是广义功。
注意:
1)、只有在系统状态变化过程中才有能量转移。
2)、只有在广义力(如压强、电动势等)作用下 产生了广义位移(如体积变化、电量迁移等)后 才作了功。 3)、在非准静态过程中很难计算系统对外作的功。 4)、功有正负之分。 热学
