八年级数学下册错题集
数学八年级下册经典易错题集附答案解析

八年级下易错题集(一)一.选择题(共16小题)1.代数式中,分式的个数是()A.1B.2C.3D.42.已知对任意实数x,式子都有意义,则实数m的取值范围是()A.m>4 B.m<4 C.m≥4 D.m≤4 3.(龙岩模拟)当式子的值为零时,x等于()A.4B.﹣3 C.﹣1或3 D.3或﹣3 4.若分式的值为正,则x的取值范围是()A.x>0 B.x>﹣C.x≠﹣D.x>﹣且x≠05.分式中的x,y同时扩大3倍,则分式的值()A.不变B.是原来的3倍C.是原来的4倍D.是原来的6.下面各分式:,其中最简分式有()个.A.4B.3C.2D.17.(眉山)某种长途电话的收费方式如下:接通电话的第一分钟收费a元,之后的每一分钟收费b元.如果某人打该长途电话被收费8元钱,则此人打长途电话的时间是()A.分钟B.分钟C.分钟D.分钟8.计算的结果为()A.a2B.C.D.9.计算的结果是()A.1B.﹣1 C.D.10.(鸡西)若关于x的分式方程无解,则m的值为()A.﹣1.5 B.1C.﹣1.5或2 D.﹣0.5或﹣1.5 11.(扬州)若方程=1有增根,则它的增根是()A.0B.1C.﹣1 D.1和﹣1 12.如图可作为函数y=f(x)的图象的是()A.B.C.D.13.(金华)小明在一直道上骑自行车,经过起步、加速、匀速、减速之后停车.设小明骑车的时间为t(秒),骑车的路程为s(米),则s关于t的函数图象大致是()A.B.C.D.14.下列函数:①y=﹣8x、②、③y=8、④y=﹣8x2+6、⑤y=﹣0.5x﹣1中,一次函数有()A.1个B.2个C.3个D.4个15.(辽宁)下列图象中,不可能是关于x的一次函数y=mx﹣(m﹣3)的图象的是()A.B.C.D.16.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较二.填空题(共9小题)17.约分:=_________;=_________.18.(清远)计算:(π﹣3)0+2﹣1=_________.19.等腰三角形的周长是16,写出底边长y与一腰长x的函数关系式____,自变量x的取值范围是________.20.(贵州模拟)在函数y=中,自变量的取值范围是_________.21.已知函数y=(k﹣1)x+k2﹣1,当k_________时,它是一次函数,当k=_______时,它是正比例函数.22.(包头)若一次函数y=ax+1﹣a中,y随x的增大而增大,且它的图象与y轴交于正半轴,则|a﹣1|+=_________.23.(襄阳)若一次函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则k的取值范围是_________.24.将直线y=2x沿x轴的正方向平移1个长度单位,得到直线_________.25.直角坐标系中,直线y=2x+3关于原点对称的解析式为_________.三.解答题(共5小题)26.通分:,.27.计算:(1);(2)÷(a2﹣4)•.28.(六合区一模)化简,求值:),其中m=.29.(苏州)解分式方程:+=3.30.(沈阳)甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用的时间与乙加工120个零件所用时间相等,求甲、乙两人每小时各加工多少个机器零件?参考答案与试题解析一.选择题(共16小题)1.代数式中,分式的个数是()A.1B.2C.3D.4考点:分式的定义.分析:找到分母中含有字母的式子的个数即可.解答:解:分式共有2个,故选B.点评:本题主要考查分式的定义,分母中含有字母的式子就是分式,注意π不是字母,是常数.2.已知对任意实数x,式子都有意义,则实数m的取值范围是()A.m>4 B.m<4 C.m≥4 D.m≤4考点:分式有意义的条件.专题:常规题型.分析:先把分母配方,然后根据分母不等于0结合平方数非负数解答即可.解答:解:∵x2﹣4x+m=(x﹣2)2+m﹣4,∵(x﹣2)2≥0,对任意实数式子都有意义,∴m﹣4>0,解得m>4.故选A.点评:本题考查了分式有意义的条件,熟记分式有意义⇔分母不为零,并利用配方法对分母进行整理是解题的关键.3.(龙岩模拟)当式子的值为零时,x等于()A.4B.﹣3 C.﹣1或3 D.3或﹣3考点:分式的值为零的条件.分析:根据分式为零,分子等于0,分母不等于0列式进行计算即可得解.解答:解:根据题意得,|x|﹣3=0,解得x=3或﹣3,又x2﹣2x﹣3≠0,解得x1≠﹣1,x2≠3,所以,x=﹣3.故选B.点评:本题考查了分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.4.若分式的值为正,则x的取值范围是()A.x>0 B.x>﹣C.x≠﹣D.x>﹣且x≠0考点:分式的值.专题:计算题.分析:根据分式的性质列出不等式组解此不等式组即可.解答:解:由分式的性质可得,解得x>﹣且x≠0,故选D.点评:本题考查不等式的解法和分式的取值,注意分式的分母不能为0,比较简单.5.分式中的x,y同时扩大3倍,则分式的值()A.不变B.是原来的3倍C.是原来的4倍D.是原来的考点:分式的基本性质.分析:x,y都扩大3倍就是分别变成原来的3倍,变成3x和3y,用3x和3y代替式子中的x和y,看得到的式子与原来的式子的关系.解答:解:用3x和3y代替式子中的x和y得:,则分式是原来的3倍.故选B.点评:解题的关键是抓住分子、分母变化的倍数.解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.6.下面各分式:,其中最简分式有()个.A.4B.3C.2D.1考点:最简分式.分析:最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.解答:解:;=;;分子分母没有公因式,是最简分式.故选D.点评:判断一个分式是最简分式,主要看分式的分子分母是不是有公因式.7.(眉山)某种长途电话的收费方式如下:接通电话的第一分钟收费a元,之后的每一分钟收费b元.如果某人打该长途电话被收费8元钱,则此人打长途电话的时间是()A.分钟B.分钟C.分钟D.分钟考点:列代数式(分式).专题:应用题.分析:由题意可知收费为=a+(打长途电话的时间﹣1)b.解答:解:设此人打长途电话的时间是x分钟,则有a+b(x﹣1)=8,解得:x=.故选C.点评:注意此题的分类收费方式.找到相应的量的等量关系是解决问题的关键.8.计算的结果为()A.a2B.C.D.考点:分式的乘除法.专题:计算题.分析:先把除法转化成乘法,再根据分式的乘法法则进行计算即可.解答:解:=a2××=.故选B.点评:本题考查了分式的乘除法的应用,主要考查学生的计算能力,题目比较好,但是一道比较容易出错的题目.9.计算的结果是()A.1B.﹣1 C.D.考点:分式的加减法.专题:计算题.分析:几个分式相加减,根据分式加减法则进行运算,如果分式分母互为相反数,则先将其变为同分母分数,然后再直接相加减即可.解答:解:,故选B.点评:在进行分式的加减运算时,应注意分式符号的改变.10.(鸡西)若关于x的分式方程无解,则m的值为()A.﹣1.5 B.1C.﹣1.5或2 D.﹣0.5或﹣1.5考点:分式方程的解.专题:计算题;压轴题.分析:去分母得出方程①(2m+x)x﹣x(x﹣3)=2(x﹣3),分为两种情况:①根据方程无解得出x=0或x=3,分别把x=0或x=3代入方程①,求出m;②求出当2m+1=0时,方程也无解,即可得出答案.解答:解:方程两边都乘以x(x﹣3)得:(2m+x)x﹣x(x﹣3)=2(x﹣3),即(2m+1)x=﹣6,分两种情况考虑:①∵当2m+1=0时,此方程无解,∴此时m=﹣0.5,②∵关于x 的分式方程无解,∴x=0或x﹣3=0,即x=0,x=3,当x=0时,代入①得:(2m+0)×0﹣0×(0﹣3)=2(0﹣3),解得:此方程无解;当x=3时,代入①得:(2m+3)×3﹣3(3﹣3)=2(3﹣3),解得:m=﹣1.5,∴m的值是﹣0.5或﹣1.5,故选D.点评:本题考查了对分式方程的解的理解和运用,关键是求出分式方程无解时的x的值,题目比较好,难度也适中.11.(扬州)若方程=1有增根,则它的增根是()A.0B.1C.﹣1 D.1和﹣1考点:分式方程的增根.专题:压轴题.分析:增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.有增根,那么最简公分母(x+1)(x﹣1)=0,所以增根可能是x=1或﹣1.解答:解:方程两边都乘(x+1)(x﹣1),得6﹣m(x+1)=(x+1)(x﹣1),由最简公分母(x+1)(x﹣1)=0,可知增根可能是x=1或﹣1.当x=1时,m=3,当x=﹣1时,得到6=0,这是不可能的,所以增根只能是x=1.故选B.点评:求增根只需将最简公分母等于0即可,但有两个或两个以上的增根时需进行检验.12.如图可作为函数y=f(x)的图象的是()A.B.C.D.考点:函数的概念.分析:由函数的概念,对每一个x有唯一的y和x对应.反映在图象上,取平行于y轴的直线x=a与图象始终只有一个交点.解答:解:由函数的定义.A、B、C中都存在x有两个y与x对应,不能构成函数.故选D点评:此题主要考查了对函数的概念、函数图象的理解,属基本概念的考查.13.(金华)小明在一直道上骑自行车,经过起步、加速、匀速、减速之后停车.设小明骑车的时间为t(秒),骑车的路程为s(米),则s关于t的函数图象大致是()A.B.C.D.考点:函数的图象.专题:压轴题.分析:随着时间的增大,路程也越来越远.经过起步,加速,匀速以及减速后停车,结合选项可得出答案.解答:解:随着时间的增多,路程越来越远.过程为起步、加速、匀速、减速之后停车.函数图象的形态为:缓,陡,缓,停.故选D.点评:应看清函数图象的横轴和纵轴表示的量,再根据实际情况来判断函数图象.14.下列函数:①y=﹣8x、②、③y=8、④y=﹣8x2+6、⑤y=﹣0.5x﹣1中,一次函数有()A.1个B.2个C.3个D.4个考点:一次函数的定义.分析:根据一次函数的定义进行逐一分析即可.解答:解:①是一次函数;②自变量次数不为1,故不是一次函数;③是常数函数;④自变量次数不为1,故不是一次函数;⑤是一次函数.∴一次函数有2个.故选B.点评:解题关键是掌握一次函数的定义条件:一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.15.(辽宁)下列图象中,不可能是关于x的一次函数y=mx﹣(m﹣3)的图象的是()A.B.C.D.考点:一次函数的图象.专题:压轴题.分析:分别根据四个答案中函数的图象求出m的取值范围即可.解答:解:A 、由函数图象可知,,解得,0<m<3;B 、由函数图象可知,,解得,m=3;C 、由函数图象可知,,解得,m<0,m>3,无解;D、由函数图象可知,解得,m<0.故选C.点评:此题比较复杂,解答此题的关键是根据各选项列出方程组,求出无解的一组.16.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较考点:一次函数图象上点的坐标特征.分析:先根据一次函数的解析式判断出函数的增减性,再根据两点横坐标的大小即可得出结论.解答:解:∵k=﹣<0,∴y随x的增大而减小.∵﹣4<2,∴y1>y2.故选:A.点评:本题考查的是一次函数图象上点的坐标特点,先根据题意判断出一次函数的增减性是解答此题的关键.二.填空题(共9小题)17.约分:=;=.考点:约分.分析:先把分子和分母因式分解,再约去分母与分子的公因式,即可得出答案.解答:解:=;==;故答案为:,.点评:此题考查了约分,用到的知识点是分式的基本性质、平方差公式和完全平方公式,注意把结果化到最简.18.(清远)计算:(π﹣3)0+2﹣1=.考点:负整数指数幂;零指数幂.专题:计算题.分析:本题涉及零指数幂、负整数指数幂两个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:解:原式=(π﹣3)0+2﹣1=1+=.故答案为1.5.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂等考点的运算.19.等腰三角形的周长是16,写出底边长y与一腰长x的函数关系式y=﹣2x+16,自变量x的取值范围是4<x<8.考点:函数关系式.分析:根据等腰三角形的周长、底边和腰长的关系可得函数关系式,根据三角形的两边之和大于第三边,可得自变量x的取值范围.解答:解:由等腰三角形的周长是16,底边长y与一腰长x,可得函数关系式:y=﹣2x+16,∵2x>﹣2x+16,∴自变量x的取值范围是4<x<8,故答案为:y=﹣2x+16,4<x<8.点评:本题考查了函数关系式,三角形的周长减两腰长等于底边长的解析式,三角形两边之和大于第三边得自变量的取值范围.20.(贵州模拟)在函数y=中,自变量的取值范围是x>1.考点:函数自变量的取值范围.分析:根据被开方数大于等于0,分母不等于0列式计算即可得解.解答:解:根据题意得,x﹣1≥0且x2﹣1≠0,解得x≥1且x≠±1,所以x>1.故答案为:x>1.点评:本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.21.已知函数y=(k﹣1)x+k2﹣1,当k≠1时,它是一次函数,当k=﹣1时,它是正比例函数.考点:一次函数的定义;正比例函数的定义.专题:待定系数法.分析:根据正比例函数的定义可得出k的值及取值范围.解答:解:∵函数y=(k﹣1)x+k2﹣1是一次函数,∴k﹣1≠0,即k≠1;函数y=(k﹣1)x+k2﹣1是正比例函数,则k﹣1≠0,k2﹣1=0,∴k=﹣1.点评:本题考查对正比例函数和一次函数的概念理解.形如y=kx,(k≠0)为正比例函数;y=kx+b,(k≠0)为一次函数.22.(包头)若一次函数y=ax+1﹣a中,y随x的增大而增大,且它的图象与y轴交于正半轴,则|a﹣1|+=1.考点:一次函数的性质.专题:计算题.分析:由一次函数y=ax+1﹣a中y随x的增大而增大,可以推出a>0,又由于它的图象与y轴交于正半轴可以得到a<1,最后即可确定a的取值范围,于是可以求出题目代数式的结果.解答:解:∵一次函数y=ax+1﹣a中,y随x的增大而增大,∴a>0,∵它的图象与y轴交于正半轴,∴1﹣a>0,即a<1,故0<a<1;∴原式=1﹣a+a=1.故填空答案:1.点评:一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限,y的值随x的值增大而增大;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限,y的值随x的值增大而增大;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,y的值随x的值增大而减小;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限,y的值随x的值增大而减小.23.(襄阳)若一次函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则k的取值范围是1<k≤2.考点:一次函数图象与系数的关系.专题:计算题.分析:若函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则此函数的x的系数小于0,b≤0.解答:解:∵函数y=2(1﹣k)x+k﹣1的图象不过第一象限,∴2(1﹣k)<0,k﹣1≤0,∴1<k≤2.点评:一次函数的图象经过第几象限,取决于x的系数是大于0或是小于0.24.将直线y=2x沿x轴的正方向平移1个长度单位,得到直线y=2x﹣2.考点:一次函数图象与几何变换.分析:沿x轴正方向平移即是向右平移,根据解析式“左加右减”的平移规律,即可得到平移后的直线解析式.解答:解:将直线y=2x沿x轴的正方向平移1个长度单位,得到直线y=2(x﹣1),即y=2x﹣2.故答案为y=2x﹣2.点评:本题考查一次函数图象与几何变换,掌握解析式的平移规律:左加右减,上加下减是解题的关键.25.直角坐标系中,直线y=2x+3关于原点对称的解析式为y=2x﹣3.考点:中心对称;一次函数图象与几何变换.分析:若两条直线关于原点对称,则这两条直线平行,即k值不变;与y轴的交点关于原点对称,即b值互为相反数.解答:解:直线y=2x+3关于原点对称的解析式为y=2x﹣3.点评:能够数形结合来分析此类型的题,根据图形,发现k和b值之间的关系.三.解答题(共5小题)26.通分:,.考点:通分.专题:计算题.分析:将两分式的分母中的系数取各系数的最小公倍数,相同因式的次数取最高次幂.解答:解:=,=.点评:本题考查了通分.解答此题的关键是熟知找公分母的方法:(1)系数取各系数的最小公倍数;(2)凡出现的因式都要取;(3)相同因式的次数取最高次幂.27.计算:(1);(2)÷(a2﹣4)•.考点:分式的混合运算.专题:计算题.分析:(1)原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果;(2)原式利用除法法则变形,约分即可得到结果.解答:解:(1)原式=1﹣•=1﹣==﹣;(2)原式=••=.点评:此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.28.(六合区一模)化简,求值:),其中m=.考点:分式的化简求值.分析:这道求代数式值的题目,不应考虑把x的值直接代入,通常做法是先把代数式化简,然后再代入求值.分式的四则运算是整式四则运算的进一步发展,是有理式恒等变形的重要内容之一.解答:解:原式======.当m=时,原式==.点评:考查了分式的化简求值,本题的关键是化简,然后把给定的m值代入求值.29.(苏州)解分式方程:+=3.考点:解分式方程.专题:计算题.分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.解答:解:去分母得:x﹣2=3x﹣3,解得:x=,经检验x=是分式方程的解.点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.30.(沈阳)甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用的时间与乙加工120个零件所用时间相等,求甲、乙两人每小时各加工多少个机器零件?考点:分式方程的应用.专题:压轴题.分析:根据“甲加工150个零件所用的时间与乙加工120个零件所用时间相等”可得出相等关系,从而只需表示出他们各自的时间就可以了.解答:解:设乙每小时加工机器零件x个,则甲每小时加工机器零件(x+10)个,根据题意得:=,解得x=40,经检验,x=40是原方程的解,x+10=40+10=50.答:甲每小时加工50个零件,乙每小时加工40个零件.点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.。
八年级下册人教版数学精选大数据易错题集(附解析)

14.
10
15. 已知数 a,b,c 在数轴上的位置如图所示: 化简 a2 a c (c b)2 b 的结果是:______________________.
ca
b
0
【解答】
由图可知,a<0,c<0,b>0, 且|c|<|b|, 所以,a+c<0,c-b<0,
a2 − |a + c| + (c − b)2 − | − b|, =-a+a+c+b-c-b, =0.
3
11. 若 x 的立方根是 4,则 x 的平方根是___________.
的立方根是
的平方根是
故应填:
12. 3 1 x 3 x 1 中的 x 的取值范围是_________, 1 x x 1 中的 x 的取值范围是___________.
13. 27 的立方根与 81 的平方根的和是_____________. ∵ -27 的立方根是-3,√81 的平方根是±3, 所以它们的和为 0 或-6. 故答案:0 或-6.
9. (1)2 的立方根是______________;一个数的立方根是 1 ,则这个数是___________. 10
的立方根是 一个数立方根是 ,则这个数是
故答案为: ;
八下数学 错题本

《分式》单元评价测试题1、填空题:将0.000 000 749保留两个有效字,用科学记数法表示为 。
解答下列问题:2、在和式311⨯+531⨯+751⨯+……中,第六项为 ;第n 项题为 。
3、上述求和的想法是通过逆用 法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以 ,从而达到求和的目的。
第16单元《分式》单元评价测试卷选择题:4、分式a b a 434+,1142--x x ,yx y xy x ++-222,2222b ab ab a -+中,最简分式有( ) A 、1个 B 、2个 C 、3个 D 、4个5、某学校学生进行急行军训练,预计行60千米的路程,下午5时到达目的地,后来由于把速度加快20%,结果于下午4时到达,求原计划行军的速度。
设原计划行军的速度为xkm/h ,则可列方程( )A 、1%206060++=x xB 、1%)201(6060++=x x C 、1%206060-+=x x D 、1%)201(6060-+=x x 6、一个人从甲地去乙地,去时速度为x ,返回时速度则为y ,则这个人往返的平均速度为 ( )。
A 、2y x +B 、y x xy +2C 、y x xy +D 、xyy x )(2+ 做错误的答案: 1、7.49×1016 2、 , )2(1+n n 3、乘法,相减 4、B 5、D 6、A 从分数到分式1、若分式44-+x x 的值为0,则x 的值是( ) A 、-4 B 、4 C 、0 D 、1 2、下列各式中,无论x 取何值,分式都有意义的是( )A 、121-xB 、1222+x x C 、21x x + D 122+x x 3、当x=( )时,xx 12-的值为零。
A 、-1 B 、1 C 、±1 D 、0 4、使分式133+-x 的值为正的条件是( ) A 、x ﹤-31 B 、x 2 -31 C 、x ﹥0 D 、x ﹤0 5、当x 为何值时,分式xx +-11的值为0?6、是否存在x 的值,使分式145.02-+x x 的值为0? 7、a 千克盐水中含盐b 千克,1千克这样的盐水中含盐 千克。
八年级数学下册错题集

易错题考查卷一、选择题1、在下列函数关系中:①y=kx ,②y=错误!未找到引用源。
x ,③y=x 2﹣(x ﹣1)x ,④y=x 2+1,⑤y=22﹣x ,一定是一次函数的个数有( ) A 、3个B 、2个C 、4个D 、5个 2.若=1﹣2x ,则x 的取值范围是( ) A .x ≥B .x ≤C .x >D .x <3、将直线y=2x 向右平移2个单位所得的直线的解析式是( )A 、y=2x+2B 、y=2x ﹣2C 、y=2(x ﹣2)D 、y=2(x+2)4、若函数y=﹣2mx ﹣(m 2﹣4)的图象经过原点,且y 随x 的增大而增大,则( )A 、m=2B 、m=﹣2C 、m=±2D 、以上答案都不对5、已知一组数据-1,x ,0,1,-2的平均数是0,那么这组数据的方差是( ) A.2 B.2 C.4 D.106、如图,在同一坐标系内,直线l 1:y=(k ﹣2)x+k 和l 2:y=kx 的位置可能为( )A 、B 、C 、D 、7、y ﹣2与x 成正比例,且x=1时,y=6,则y 与x 的关系式是( )A 、y=4xB 、y=6xC 、y=4x ﹣2D 、y=4x+28、若顺次连接四边形ABCD 各边中点所得四边形是菱形,则四边形ABCD 一定是( )A 、对角线互相垂直的四边形B 、对角线相等的四边形C 、矩形D 、菱形9、正方形ABCD 在直角坐标系中的位置如下边图表示,将正方形ABCD 绕点C 逆时针方向旋转180°后,B 点的坐标是( ) A .(2,0) B .(3,0) C .(2,-1) D .(-2,-1)10.如图,在菱形ABCD 中,E 是AB 边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF ;②△DEF 是等边三角形;③△BEF 是等腰三角形;④∠ADE=∠BEF ,其中结论正确的个数是( )A .3 B .4 C .1 D .29题 10题 13题 14题 15题二、填空题11 、 已知直角三角形的两边长分别为3、4,求第三边长_______.12、若直线y=3x+b 与两坐标轴所围成的三角形的面积是6,则b 的值是 .13.如图,矩形纸片ABCD 中,AD=1,将纸片折叠,使顶点A 与CD 边上点E 重合,折痕FG 分别与AD 、AB 交于点F 、G ,若DE=33则EF 的长为______. 14、如图,在△ABC 中,AB=6,AC=8,BC=10,P 为边BC 上一动点(且点P 不与点B 、C 重合),PE ⊥AB 于E ,PF ⊥AC 于F .则EF 的最小值为________2选择题答案:1-5:________________:6-10:________________11______ 12_______ 13_______ 14_______15、如图,正方形ABCD 的面积为16,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线BD 上有一点P ,使PC+PE 的和最小,则这个最小值为__________.16、如图,在△A1B1C1中,已知A1B1=6,B1C1=8,A1C1=10,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点,得△A3B3C3,…,则△555C B A 的周长=__________.17、解一元二次方程25x 32=-x18、现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x 千克.(1)请分别写出甲、乙两家快递公司快递该物品的费用y (元)与x (千克)之间的函数关系式;(2)小明选择哪家快递公司更省钱?。
数学八下易错题(含答案)

八年级下册易错题第一章 三角形的证明1.已知等腰三角形的两边长分别为5㎝、2㎝,则该等腰三角形的周长是(D )A .7㎝B .9㎝C .12㎝或者9㎝D .12㎝考查知识点:三角形的基本知识及等腰三角形边的关系:任意两边之和大于第三边,等腰三角形两腰相等,因此只能是:5cm ,5cm,2cm.2.一个等腰三角形的一个角是40°,则它的底角是(D )A .40°B .50°C .60°D .40°或70°考查知识点:三角形的内角和及等腰三角形两底角相等:①当40°是顶角时,底角就是70°;②40°就是一个底角.3.已知△ABC 的三边长分别是6cm 、8cm 、10cm ,则最长边上的高是(D )A.2.4cmB.3cmC.4cmD. 4.8cm提示:设最长边上的高为h,由题意可得△ABC 是直角三角形,利用面积相等求,即h .10.218.6.21 解得h=4.84.等腰三角形一腰上的高与另一腰的夹角为300,腰长为6,则其底边上的高是3或33. 解:①三角形是钝角三角形时,如图1,∵∠ABD=30°∴AD=21AB=21×6=3, ∵AB=AC , ∴∠ABC=∠ACB=21∠BAD=21(90°-30°)=30°, ∴∠ABD=∠ABC ,∴底边上的高AE=AD=3;②三角形是锐角三角形时,如图2,∵∠ABD=30°∴∠A=90°-30°=60°,∴△ABC 是等边三角形,∴底边上的高为23×6=33 综上所述,底边上的高是3或335.到三角形三个顶点的距离相等的点是三角形(B )的交点.A.三个内角平分线B.三边垂直平分线C.三条中线D.三条高考查的知识点:三角形三边垂直平分线的交点到到三角形三个顶点的距离相等【归纳为:点到点距离相等,为垂直平分线上的点】还有一个:三角形三个内角平分线的交点到三角形三边的距离相等【归纳为:点到线的距离相等,为角平分线的交点,此时的距离有“垂直”】 6.如图,在△ABC 中,AB=5,AC=3,BC 的垂直平分线交AB 于D ,交BC 于E ,则△ADC 的周长等于8考查的知识点:垂直平分线上的点到线段两端点的距离相等7. 用反证法证明:一个三角形中至少有一个内角小于或等于60°.答案:已知:△ABC , 求证:△ABC 中至少有一个内角小于或等于60°证明:假设△ABC 中没有一个内角小于或等于60°,即每一内角都大于60°则∠A>60°,∠B>60°,∠C>60°∴∠A+∠B+∠C>60°+60°+60°=180° 即∠A+∠B+∠C>180°,这与三角形的内角和为180度矛盾.假设不成立. ∴△ABC 中至少有一个内角小于或等于60°考查知识:反证法,用反证法进行证明时先写出已知、求证,再假设求证的反面成立,推出与题设、定理等相矛盾的结论,从而肯定原结论成立【注意:反证法一般很少用到,除非是题目要求用反证法证明,否则一般不考虑该方法】8. 如图所示,∠AOB=30°,OC 平分∠AOB,P 为OC 上任意一点,PD∥OA 交OB 于点D ,PE⊥OA 于点E ,若PE=2cm ,则PD=_________cm .解:过点P 作PF ⊥OB 于F ,∵∠AOB=30°,OC 平分∠AOB ,∴∠AOC=∠BOC=15°,∵PD ∥OA ,∴∠DPO=∠AOP=15°,∴∠DPO=∠AOP=15°,∴∠BOC=∠DPO ,∴PD=OD=4cm ,∵∠AOB=30°,PD ∥OA ,∴∠BDP=30°,∴在Rt △PDF 中,PF=21PD=2cm , ∵OC 为角平分线,PE ⊥OA ,PF ⊥OB,∴PE=PF ,∴PE=PF=2cm9.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点E ,过点E 作MN∥BC 交AB 于M ,交AC 于N ,若BM+CN=9,则线段MN 的长为( ) A.6 B.7 C.8 D.9解:∵∠ABC 、∠ACB 的平分线相交于点E ,∴∠MBE=∠EBC ,∠ECN=∠ECB ,∵MN ∥BC ,∴∠EBC=∠EBC ,∠ECN=∠ECB ,∴BM=ME ,EN=CN ,∴MN=BM+CN ,∵BM+CN=9,∴MN=9考查知识点:平行+平分,必有等腰三角形10.如图,AD 是△ABC 的角平分线,DF⊥AB,垂足为F ,DE=DG ,△ADG 和△AED 的面积分别为50和39,则△EDF 的面积为(B ) A.11 B.5.5 C.7 D.3.5解:作DM=DE 交AC 于M ,作DN ⊥AC ,∵在△AED 和△AMD 中∴△AED ≌△AMD∴ADM ADE S S V V∵DE=DG ,DM=DE ,∴DM=DG ,∵AD 是△ABC 的外角平分线,DF ⊥AB ,∴DF=DN ,在Rt △DEF 和Rt △DMN 中,Rt △DEF ≌Rt △DMN (HL ),∵△ADG 和△AED 的面积分别为50和39,∴ADM ADG MDG S S S V V V -==50-39=11MDG DEF DNM S S S V V V 21===21×11=5.5考查知识点:角平分线上的点到角两边的距离相等及三角形的全等11.在Rt△ABC 中,∠C=90°,AC=9,BC=12,则点C 到AB 的距离是(A )A. B. C.D.解:在Rt △ABC 中,AC=9,BC=12,根据勾股定理得:AB=151292222=+=+BC AC过C 作CD ⊥AB ,交AB 于点D ,则由ABC S V =21AC .BC=21AB .CD ,得CD=AB BC AC .=1512x 91=536考查知识:利用面积相等法12.如图,在△ABC 中AD⊥BC,CE⊥AB,垂足分别为D 、E ,AD 、CE 交于点H ,已知EH=EB=3,AE=4,则CH 的长是(A )A.1 B.2 C.3 D.4解:∵AD ⊥BC ,∴∠EAH+∠B=90°,∵CE ⊥AB ,∴∠EAH+∠AHE=90°,∴∠B=∠AHE ,∵EH=EB ,在△AEH 和△CEB 中,∴△AEH ≌△CEB (ASA )∴CE=AE ,∵EH=EB=3,AE=4,∴CH=CE-EH=4-3=1考查知识:利用三角形全等求线段长度.13.如图,在△ABC 中,AD 是中线,AE 是角平分线,CF ⊥AE 于点F ,AB=5,AC=2,则DF 的长为23.解:延长CF 交AB 于点G ,∵AE 平分∠BAC ,∴∠GAF=∠CAF ,∵AF 垂直CG ,∴∠AFG=∠AFC ,在△AFG 和△AFC 中,∴△AFG ≌△AFC (ASA )∴AC=AG ,GF=CF ,又∵点D 是BC 的中点,∴DF 是△CBG 的中位线,∴DF=21BG=21(AB-AG )=21(AB-AC )=23点评:本题考查了三角形的中位线定理,解答本题的关键是作出辅助线,一般出现既是角平分线又是高的情况,我们就需要寻找等腰三角形.14.如图,在△ABC 中,AD 为∠BAC 的平分线,FE 垂直平分AD ,交AD 于E ,交BC 的延长线于F.求证:∠CAF=∠B.解:∠B=∠CAF.∵FE 垂直平分AD ,∴FA=FD ,∴∠FAD=∠ADF ∵AD 为∠BAC 的平分线,∴∠CAD=∠BAD又∵∠CAF=∠FAD=∠CAD ,∠B=∠ADF-∠BAD ,∴∠B=∠CAF点评:此题考查了线段垂直平分线的性质、角平分线的定义及三角形的外角等知识点.15.如图,OA 、OB 表示两条相交的公路,点M 、N 是两个工厂,现在要在∠AOB 内建立一个货物中转站P ,使中转站到公路OA 、OB 的距离相等,并且到工厂M 、N 的距离也相等,用尺规作出货物中转站P 的位置.解:①作∠AOB 的角平分线;②连接MN ,作MN 的垂直平分线,交OM 于一点,交点就是所求货物中转站的位置.16. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.(1)求证:△ACD≌△AED;(2)若∠B=30°,CD=1,求BD的长.(1)证明:∵AD平分∠CAB∴∠CAD=∠EAD∵DE⊥AB,∠C=90°,∴∠ACD=∠AED=90°又∵AD=AD,∴△ACD≌△AED(2)解:∵△ACD≌△AED∴DE=CD=1∵∠B=30°,∠DEB=90°,∴BD=2DE=217.如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:BF=2AE;(2)若CD=,求AD的长.(1)证明:∵AD⊥BC,∠BAD=45°∴∠ABD=∠45°=∠BAD∴AD=BD∵BE⊥AC∴∠CAD+∠AFE=90°∵AD⊥BC∴∠FBD=∠BFD=90°又∠AFE=∠BFD∴∠CAD=∠FBD又∠ADC=∠BDF=90°∴△ADC≌△BDF∴AC=BF∵AB=BC,BE⊥AC∴AC=2AE∴BF=2AE(2)解:设AD=x,则BD=x∴AB=BC=2+x∵△ABD是等腰直角三角形∴AB=2AD∴2+x=2x解得x=2+2即AD=2+218.如图,已知△ABC是等边三角形,D、E分别在BA、BC的延长线上,且AD=BE.求证:DC=DE证明:延长BE至F,使EF=BC∵△ABC是等边三角形∴∠B=60°,AB=BC∴AB=BC=EF∵AD=BE,BD=AB+AD, BF=BE+EF∴BD=BF∴△BDF是等边三角形∴∠F=60°,BD=FD在△BCD和△FED中,BC=EF∠B=∠F=60°BD=FD∴△BCD≌△FED(SAS)∴DC=DE19.如图,在△ABC 中,AC=BC ,∠ACB=90°,D 是AC 上一点,AE ⊥BD 交BD 的延长线于E ,且AE=21BD ,求证:BD 是∠ABC 的角平分线.证明:延长AE 、BC 交于点F∵AE ⊥BE∴∠BEF=90°,又∠ACF=∠ACB=90°∴∠DBC+∠AFC=∠FAC+∠AFC=90°∴∠DBC=∠FAC在△ACF 和△BCD 中∴△ACF ≌△BCD (ASA )∴AF=BD又AE=21BD ∴AE=EF,即点E 是AF 的中点∴AB=BF∴BD 是∠ABC 的角平分线20.如图,在△ABC 中,分别以AC 、AB 为边,向外作正△ACD ,正△ABE ,BD 与AE 相交于F ,连接AF ,求证:AF 平分∠DME证明:过点A 分别作AM ⊥BD,AN ⊥CE,分别交BD ,CE 于M ,N 两点∵△ABE 和△ACD 均为等边三角形,∴∠EAB=∠CAD=60°,AD=AC ,AB=AE∵∠EAC=∠BAD=60°+∠BAC ,∴△EAC ≌△BAD ,∴ AM BD S AN CE S BAD EAC .21.21===V V CE=BD ∴AN=AM∴AF 平分∠DME (在角的内部到角两边距离相等的点在该角的平分线上)21.如图,已知:AB=AC ,∠A=90°,AF=BE,BD=DC.求证:FD ⊥ED.证明:连接AD.∵∠A=90° AB=AC D 是BC 的中点∴AD ⊥BC ∠ADB=90° ∠B=45°=∠CAD AD=BD (直角三角形中,中线等于斜边的一半)且BE=AF∴易证△BED ≌△AFD (SAS )∴∠BDE=∠ADF ∵∠ADE+∠EDB=∠ADB=90°∴∠ADF+∠ADE=90°∴ED ⊥FD如图,在Rt △ABC 中,D ,E 为斜边AB 上的两点,且BD=BC ,AE=AC ,则∠DCE 的大小为_____°.如图,在等腰△ABC 中,AB=AC ,∠BAC=50°,∠BAC 的平分线与AB 的中垂线交于点O ,点C 沿EF 折叠后与点O 重合,则∠OEC 的度数是_____.第二章 不等式(组) 不等式基本性质例:如果x >y ,那么下列各式中正确的是(C )A .x-2<y-2B . 2x <2y C .-2x <-2y D .-x >-y 1.系数含有字母的不等式(组)解题思路:先把字母系数当做已知数,解出未知数的取值范围,再根据题意及不等式的性质或解不等式组的方法进行计算【特别注意:“=”一定要考虑,如果满足题意则要取,不满足题意就不取】【自己做】(1)已知关于x 的方程3k -5x =-9的解是非负数,求k 的取值范围.(2) 已知关于x 的不等式(1-a )x >2的解集为x <a -12 ,则a 的取值范围是a >1. 提示:利用不等式的基本性质三:a-1<0(3)如果不等式组⎩⎨⎧<+>-00b x a x 的解集是3<x <5,那么a=3,b=-5.提示:解得不等式组的解集为:a<x <-b而不等式组的解集为:3<x <5∴a=3,b=-5(4) 如果不等式 ⎩⎨⎧><m x x 8 无解,那么m 的取值范围是 (B ) A .m >8 B.m ≥8 C.m <8 D.m ≤8提示:不等式组无解的条件是:比大的还大,比小的还小;∴m ≥8【“=”一定要考虑,这个题取“=”就满足题意】(5)如果不等式组⎩⎨⎧>-<+m x x x 148的解集是3>x ,则m 的取值范围是(A ).A .m≤3B . m≥3C .m=3D .m <3提示:不等式组解集:同大取大;解不等式组得而该不等式组的解集是3>x ,∴m≤3【“=”一定要考虑,这个题取“=”就满足题意】(6)关于x 的不等式组()⎪⎩⎪⎨⎧->-+--<-325251263x x a x x 有三个整数解,则a 的取值范围是65-<a ≤32-. 解:解该不等式组得∵有三个整数解∴2<x <6a+10∴三个整数解应该是3,4,5∴5<6a+10≤6解得65-<a ≤32- 【自己解答】(7) 若方程组⎩⎨⎧+=++=+3654,2m y x m y x 的解x ,y 均为正数,求m 的取值范围.提示:先将m 当作已知数,将x 、y 用含m 的式子表示出来,然后利用x ,y 均为正数,列出含m 的不等式组,解出m 的取值范围【自己解】2.解不等式(组)【不等式组的结果不能写成大括号的形式】(1)解不等式1213312+-≥+)(x x ,并将解集在数轴上表示出来; (2)解不等式组⎪⎩⎪⎨⎧≤+--+<-1215312)1(315x x x x ,并把它的解集表示在数轴上. 3.一元一次不等式(组)与一次函数利用一次函数解一元一次不等式(组):实质就是比较两个函数y 值得大小,函数值(y )越大,图像越高,函数值(y )越小,图像越高低,这里一般是让求自变量x 的取值范围,找出与x 轴交点的横坐标(指一元一次不等式),看让求图像在x 轴以上的自变量的取值范围(还是图像在x 轴以下的自变量的取值范围);或找出函数交点的横坐标,然后看在该交点以左满足题意还是交点以右满足题意.(1)函数y =kx +b (k 、b 为常数,k ≠0)的图象如图所示,则关于x 的不等式kx+b>0的解集为(C ).A .x>0B .x<0C .x<2D .x>2(2)直线b x k y l +=11:与直线x k y l 22:=在同一平面直角坐标系中的图象如图所示,则关于x 的不等式x k b x k 21>+的解为x<-14.一元一次不等式(组)应用题◆一件商品的进价是500元,标价为600元,打折销售后要保证获利不低于8%,则此商品最多打9折.商品销售中需注意的地方:①“进价”也叫“成本”;“售价”也叫“标价”;②获利是在进价的基础上获利;打折是在售价基础上打折;③打几折就是给售价×10x 解:设可以打x 折.那么(600×10x -500)÷500≥8% 解得x ≥9.故答案为:9.◆某商贩去菜摊买黄瓜,他上午买了30斤,价格为每斤x 元;下午,他又买了20斤.价格为每斤y 元.后来他以每斤2y x +元的价格卖完后,结果发现自己赔了钱,其原因是(B ) <y B .>y C .≤y D .≥y解:根据题意得,他买黄瓜每斤平均价是502030y x + 以每斤2y x +元的价格卖完后,结果发现自己赔了钱,则 502030y x +>2y x + 解得:x >y∴赔钱的原因是x>y(1)某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。
数学八年级下册经典易错题集附答案解析

八年级下易错题集(一)一.选择题(共16小题)1.代数式中,分式的个数是()A.1B.2C.3D.42.已知对任意实数x,式子都有意义,则实数m的取值范围是()A.m>4 B.m<4 C.m≥4 D.m≤4 3.(龙岩模拟)当式子的值为零时,x等于()A.4B.﹣3 C.﹣1或3 D.3或﹣3 4.若分式的值为正,则x的取值范围是()A.x>0 B.x>﹣C.x≠﹣D.x>﹣且x≠05.分式中的x,y同时扩大3倍,则分式的值()A.不变B.是原来的3倍C.是原来的4倍D.是原来的6.下面各分式:,其中最简分式有()个.A.4B.3C.2D.17.(眉山)某种长途电话的收费方式如下:接通电话的第一分钟收费a元,之后的每一分钟收费b元.如果某人打该长途电话被收费8元钱,则此人打长途电话的时间是()A.分钟B.分钟C.分钟D.分钟8.计算的结果为()A.a2B.C.D.9.计算的结果是()A.1B.﹣1 C.D.10.(鸡西)若关于x的分式方程无解,则m的值为()A.﹣1.5 B.1C.﹣1.5或2 D.﹣0.5或﹣1.5 11.(扬州)若方程=1有增根,则它的增根是()A.0B.1C.﹣1 D.1和﹣1 12.如图可作为函数y=f(x)的图象的是()A.B.C.D.13.(金华)小明在一直道上骑自行车,经过起步、加速、匀速、减速之后停车.设小明骑车的时间为t(秒),骑车的路程为s(米),则s关于t的函数图象大致是()A.B.C.D.14.下列函数:①y=﹣8x、②、③y=8、④y=﹣8x2+6、⑤y=﹣0.5x﹣1中,一次函数有()A.1个B.2个C.3个D.4个15.(辽宁)下列图象中,不可能是关于x的一次函数y=mx﹣(m﹣3)的图象的是()A.B.C.D.16.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较二.填空题(共9小题)17.约分:=_________;=_________.18.(清远)计算:(π﹣3)0+2﹣1=_________.19.等腰三角形的周长是16,写出底边长y与一腰长x的函数关系式____,自变量x的取值范围是________.20.(贵州模拟)在函数y=中,自变量的取值范围是_________.21.已知函数y=(k﹣1)x+k2﹣1,当k_________时,它是一次函数,当k=_______时,它是正比例函数.22.(包头)若一次函数y=ax+1﹣a中,y随x的增大而增大,且它的图象与y轴交于正半轴,则|a﹣1|+=_________.23.(襄阳)若一次函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则k的取值范围是_________.24.将直线y=2x沿x轴的正方向平移1个长度单位,得到直线_________.25.直角坐标系中,直线y=2x+3关于原点对称的解析式为_________.三.解答题(共5小题)26.通分:,.27.计算:(1);(2)÷(a2﹣4)•.28.(六合区一模)化简,求值:),其中m=.29.(苏州)解分式方程:+=3.30.(沈阳)甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用的时间与乙加工120个零件所用时间相等,求甲、乙两人每小时各加工多少个机器零件?参考答案与试题解析一.选择题(共16小题)1.代数式中,分式的个数是()A.1B.2C.3D.4考点:分式的定义.分析:找到分母中含有字母的式子的个数即可.解答:解:分式共有2个,故选B.点评:本题主要考查分式的定义,分母中含有字母的式子就是分式,注意π不是字母,是常数.2.已知对任意实数x,式子都有意义,则实数m的取值范围是()A.m>4 B.m<4 C.m≥4 D.m≤4考点:分式有意义的条件.专题:常规题型.分析:先把分母配方,然后根据分母不等于0结合平方数非负数解答即可.解答:解:∵x2﹣4x+m=(x﹣2)2+m﹣4,∵(x﹣2)2≥0,对任意实数式子都有意义,∴m﹣4>0,解得m>4.故选A.点评:本题考查了分式有意义的条件,熟记分式有意义⇔分母不为零,并利用配方法对分母进行整理是解题的关键.3.(龙岩模拟)当式子的值为零时,x等于()A.4B.﹣3 C.﹣1或3 D.3或﹣3考点:分式的值为零的条件.分析:根据分式为零,分子等于0,分母不等于0列式进行计算即可得解.解答:解:根据题意得,|x|﹣3=0,解得x=3或﹣3,又x2﹣2x﹣3≠0,解得x1≠﹣1,x2≠3,所以,x=﹣3.故选B.点评:本题考查了分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.4.若分式的值为正,则x的取值范围是()A.x>0 B.x>﹣C.x≠﹣D.x>﹣且x≠0考点:分式的值.专题:计算题.分析:根据分式的性质列出不等式组解此不等式组即可.解答:解:由分式的性质可得,解得x>﹣且x≠0,故选D.点评:本题考查不等式的解法和分式的取值,注意分式的分母不能为0,比较简单.5.分式中的x,y同时扩大3倍,则分式的值()A.不变B.是原来的3倍C.是原来的4倍D.是原来的考点:分式的基本性质.分析:x,y都扩大3倍就是分别变成原来的3倍,变成3x和3y,用3x和3y代替式子中的x和y,看得到的式子与原来的式子的关系.解答:解:用3x和3y代替式子中的x和y得:,则分式是原来的3倍.故选B.点评:解题的关键是抓住分子、分母变化的倍数.解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.6.下面各分式:,其中最简分式有()个.A.4B.3C.2D.1考点:最简分式.分析:最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.解答:解:;=;;分子分母没有公因式,是最简分式.故选D.点评:判断一个分式是最简分式,主要看分式的分子分母是不是有公因式.7.(眉山)某种长途电话的收费方式如下:接通电话的第一分钟收费a元,之后的每一分钟收费b元.如果某人打该长途电话被收费8元钱,则此人打长途电话的时间是()A.分钟B.分钟C.分钟D.分钟考点:列代数式(分式).专题:应用题.分析:由题意可知收费为=a+(打长途电话的时间﹣1)b.解答:解:设此人打长途电话的时间是x分钟,则有a+b(x﹣1)=8,解得:x=.故选C.点评:注意此题的分类收费方式.找到相应的量的等量关系是解决问题的关键.8.计算的结果为()A.a2B.C.D.考点:分式的乘除法.专题:计算题.分析:先把除法转化成乘法,再根据分式的乘法法则进行计算即可.解答:解:=a2××=.故选B.点评:本题考查了分式的乘除法的应用,主要考查学生的计算能力,题目比较好,但是一道比较容易出错的题目.9.计算的结果是()A.1B.﹣1 C.D.考点:分式的加减法.专题:计算题.分析:几个分式相加减,根据分式加减法则进行运算,如果分式分母互为相反数,则先将其变为同分母分数,然后再直接相加减即可.解答:解:,故选B.点评:在进行分式的加减运算时,应注意分式符号的改变.10.(鸡西)若关于x的分式方程无解,则m的值为()A.﹣1.5 B.1C.﹣1.5或2 D.﹣0.5或﹣1.5考点:分式方程的解.专题:计算题;压轴题.分析:去分母得出方程①(2m+x)x﹣x(x﹣3)=2(x﹣3),分为两种情况:①根据方程无解得出x=0或x=3,分别把x=0或x=3代入方程①,求出m;②求出当2m+1=0时,方程也无解,即可得出答案.解答:解:方程两边都乘以x(x﹣3)得:(2m+x)x﹣x(x﹣3)=2(x﹣3),即(2m+1)x=﹣6,分两种情况考虑:①∵当2m+1=0时,此方程无解,∴此时m=﹣0.5,②∵关于x 的分式方程无解,∴x=0或x﹣3=0,即x=0,x=3,当x=0时,代入①得:(2m+0)×0﹣0×(0﹣3)=2(0﹣3),解得:此方程无解;当x=3时,代入①得:(2m+3)×3﹣3(3﹣3)=2(3﹣3),解得:m=﹣1.5,∴m的值是﹣0.5或﹣1.5,故选D.点评:本题考查了对分式方程的解的理解和运用,关键是求出分式方程无解时的x的值,题目比较好,难度也适中.11.(扬州)若方程=1有增根,则它的增根是()A.0B.1C.﹣1 D.1和﹣1考点:分式方程的增根.专题:压轴题.分析:增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.有增根,那么最简公分母(x+1)(x﹣1)=0,所以增根可能是x=1或﹣1.解答:解:方程两边都乘(x+1)(x﹣1),得6﹣m(x+1)=(x+1)(x﹣1),由最简公分母(x+1)(x﹣1)=0,可知增根可能是x=1或﹣1.当x=1时,m=3,当x=﹣1时,得到6=0,这是不可能的,所以增根只能是x=1.故选B.点评:求增根只需将最简公分母等于0即可,但有两个或两个以上的增根时需进行检验.12.如图可作为函数y=f(x)的图象的是()A.B.C.D.考点:函数的概念.分析:由函数的概念,对每一个x有唯一的y和x对应.反映在图象上,取平行于y轴的直线x=a与图象始终只有一个交点.解答:解:由函数的定义.A、B、C中都存在x有两个y与x对应,不能构成函数.故选D点评:此题主要考查了对函数的概念、函数图象的理解,属基本概念的考查.13.(金华)小明在一直道上骑自行车,经过起步、加速、匀速、减速之后停车.设小明骑车的时间为t(秒),骑车的路程为s(米),则s关于t的函数图象大致是()A.B.C.D.考点:函数的图象.专题:压轴题.分析:随着时间的增大,路程也越来越远.经过起步,加速,匀速以及减速后停车,结合选项可得出答案.解答:解:随着时间的增多,路程越来越远.过程为起步、加速、匀速、减速之后停车.函数图象的形态为:缓,陡,缓,停.故选D.点评:应看清函数图象的横轴和纵轴表示的量,再根据实际情况来判断函数图象.14.下列函数:①y=﹣8x、②、③y=8、④y=﹣8x2+6、⑤y=﹣0.5x﹣1中,一次函数有()A.1个B.2个C.3个D.4个考点:一次函数的定义.分析:根据一次函数的定义进行逐一分析即可.解答:解:①是一次函数;②自变量次数不为1,故不是一次函数;③是常数函数;④自变量次数不为1,故不是一次函数;⑤是一次函数.∴一次函数有2个.故选B.点评:解题关键是掌握一次函数的定义条件:一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.15.(辽宁)下列图象中,不可能是关于x的一次函数y=mx﹣(m﹣3)的图象的是()A.B.C.D.考点:一次函数的图象.专题:压轴题.分析:分别根据四个答案中函数的图象求出m的取值范围即可.解答:解:A 、由函数图象可知,,解得,0<m<3;B 、由函数图象可知,,解得,m=3;C 、由函数图象可知,,解得,m<0,m>3,无解;D、由函数图象可知,解得,m<0.故选C.点评:此题比较复杂,解答此题的关键是根据各选项列出方程组,求出无解的一组.16.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较考点:一次函数图象上点的坐标特征.分析:先根据一次函数的解析式判断出函数的增减性,再根据两点横坐标的大小即可得出结论.解答:解:∵k=﹣<0,∴y随x的增大而减小.∵﹣4<2,∴y1>y2.故选:A.点评:本题考查的是一次函数图象上点的坐标特点,先根据题意判断出一次函数的增减性是解答此题的关键.二.填空题(共9小题)17.约分:=;=.考点:约分.分析:先把分子和分母因式分解,再约去分母与分子的公因式,即可得出答案.解答:解:=;==;故答案为:,.点评:此题考查了约分,用到的知识点是分式的基本性质、平方差公式和完全平方公式,注意把结果化到最简.18.(清远)计算:(π﹣3)0+2﹣1=.考点:负整数指数幂;零指数幂.专题:计算题.分析:本题涉及零指数幂、负整数指数幂两个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.解答:解:原式=(π﹣3)0+2﹣1=1+=.故答案为1.5.点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂等考点的运算.19.等腰三角形的周长是16,写出底边长y与一腰长x的函数关系式y=﹣2x+16,自变量x的取值范围是4<x<8.考点:函数关系式.分析:根据等腰三角形的周长、底边和腰长的关系可得函数关系式,根据三角形的两边之和大于第三边,可得自变量x的取值范围.解答:解:由等腰三角形的周长是16,底边长y与一腰长x,可得函数关系式:y=﹣2x+16,∵2x>﹣2x+16,∴自变量x的取值范围是4<x<8,故答案为:y=﹣2x+16,4<x<8.点评:本题考查了函数关系式,三角形的周长减两腰长等于底边长的解析式,三角形两边之和大于第三边得自变量的取值范围.20.(贵州模拟)在函数y=中,自变量的取值范围是x>1.考点:函数自变量的取值范围.分析:根据被开方数大于等于0,分母不等于0列式计算即可得解.解答:解:根据题意得,x﹣1≥0且x2﹣1≠0,解得x≥1且x≠±1,所以x>1.故答案为:x>1.点评:本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.21.已知函数y=(k﹣1)x+k2﹣1,当k≠1时,它是一次函数,当k=﹣1时,它是正比例函数.考点:一次函数的定义;正比例函数的定义.专题:待定系数法.分析:根据正比例函数的定义可得出k的值及取值范围.解答:解:∵函数y=(k﹣1)x+k2﹣1是一次函数,∴k﹣1≠0,即k≠1;函数y=(k﹣1)x+k2﹣1是正比例函数,则k﹣1≠0,k2﹣1=0,∴k=﹣1.点评:本题考查对正比例函数和一次函数的概念理解.形如y=kx,(k≠0)为正比例函数;y=kx+b,(k≠0)为一次函数.22.(包头)若一次函数y=ax+1﹣a中,y随x的增大而增大,且它的图象与y轴交于正半轴,则|a﹣1|+=1.考点:一次函数的性质.专题:计算题.分析:由一次函数y=ax+1﹣a中y随x的增大而增大,可以推出a>0,又由于它的图象与y轴交于正半轴可以得到a<1,最后即可确定a的取值范围,于是可以求出题目代数式的结果.解答:解:∵一次函数y=ax+1﹣a中,y随x的增大而增大,∴a>0,∵它的图象与y轴交于正半轴,∴1﹣a>0,即a<1,故0<a<1;∴原式=1﹣a+a=1.故填空答案:1.点评:一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限,y的值随x的值增大而增大;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限,y的值随x的值增大而增大;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,y的值随x的值增大而减小;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限,y的值随x的值增大而减小.23.(襄阳)若一次函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则k的取值范围是1<k≤2.考点:一次函数图象与系数的关系.专题:计算题.分析:若函数y=2(1﹣k)x+k﹣1的图象不过第一象限,则此函数的x的系数小于0,b≤0.解答:解:∵函数y=2(1﹣k)x+k﹣1的图象不过第一象限,∴2(1﹣k)<0,k﹣1≤0,∴1<k≤2.点评:一次函数的图象经过第几象限,取决于x的系数是大于0或是小于0.24.将直线y=2x沿x轴的正方向平移1个长度单位,得到直线y=2x﹣2.考点:一次函数图象与几何变换.分析:沿x轴正方向平移即是向右平移,根据解析式“左加右减”的平移规律,即可得到平移后的直线解析式.解答:解:将直线y=2x沿x轴的正方向平移1个长度单位,得到直线y=2(x﹣1),即y=2x﹣2.故答案为y=2x﹣2.点评:本题考查一次函数图象与几何变换,掌握解析式的平移规律:左加右减,上加下减是解题的关键.25.直角坐标系中,直线y=2x+3关于原点对称的解析式为y=2x﹣3.考点:中心对称;一次函数图象与几何变换.分析:若两条直线关于原点对称,则这两条直线平行,即k值不变;与y轴的交点关于原点对称,即b值互为相反数.解答:解:直线y=2x+3关于原点对称的解析式为y=2x﹣3.点评:能够数形结合来分析此类型的题,根据图形,发现k和b值之间的关系.三.解答题(共5小题)26.通分:,.考点:通分.专题:计算题.分析:将两分式的分母中的系数取各系数的最小公倍数,相同因式的次数取最高次幂.解答:解:=,=.点评:本题考查了通分.解答此题的关键是熟知找公分母的方法:(1)系数取各系数的最小公倍数;(2)凡出现的因式都要取;(3)相同因式的次数取最高次幂.27.计算:(1);(2)÷(a2﹣4)•.考点:分式的混合运算.专题:计算题.分析:(1)原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果;(2)原式利用除法法则变形,约分即可得到结果.解答:解:(1)原式=1﹣•=1﹣==﹣;(2)原式=••=.点评:此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.28.(六合区一模)化简,求值:),其中m=.考点:分式的化简求值.分析:这道求代数式值的题目,不应考虑把x的值直接代入,通常做法是先把代数式化简,然后再代入求值.分式的四则运算是整式四则运算的进一步发展,是有理式恒等变形的重要内容之一.解答:解:原式======.当m=时,原式==.点评:考查了分式的化简求值,本题的关键是化简,然后把给定的m值代入求值.29.(苏州)解分式方程:+=3.考点:解分式方程.专题:计算题.分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.解答:解:去分母得:x﹣2=3x﹣3,解得:x=,经检验x=是分式方程的解.点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.30.(沈阳)甲、乙两人加工同一种机器零件,甲比乙每小时多加工10个零件,甲加工150个零件所用的时间与乙加工120个零件所用时间相等,求甲、乙两人每小时各加工多少个机器零件?考点:分式方程的应用.专题:压轴题.分析:根据“甲加工150个零件所用的时间与乙加工120个零件所用时间相等”可得出相等关系,从而只需表示出他们各自的时间就可以了.解答:解:设乙每小时加工机器零件x个,则甲每小时加工机器零件(x+10)个,根据题意得:=,解得x=40,经检验,x=40是原方程的解,x+10=40+10=50.答:甲每小时加工50个零件,乙每小时加工40个零件.点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.。
八年级数学下册错题集

=(anb3﹣an+1b2).故选B.
点评:本题考查的是二次根式的化简.最简二次根式的条件:被开方数中不含开得尽方的因式或因数.点评:解答此题,要弄清二次根式的性质: =|a|,分类讨论的思想.
2.当x<﹣1时,|x﹣ ﹣2|﹣2|x﹣1|的值为()A.2B.4x﹣6C.4﹣4xD.4x+4
解答:解:∵a<﹣4,
∴2a<﹣8,a﹣4<0,
∴2a+3 <﹣8+3 <0原式=|2a+3|+
=|2a+3|+
=﹣2a﹣3 +4﹣a= ﹣3a.
故选 D.
点评:本题考查的是二次根式的化简和绝对值的化简,解此类题目时要充分考虑数的取值范围,再去绝对值,否则 容易计算错误.
4.当x<2y时,化 得() A.x(x﹣2y)B. D.(2y﹣x)
分析:计算时首先要分清运算顺序,先乘方,后加减.二次根式的加减,实质是合并同类二次根式,需要先化简, 再合并.
解答:解: •(﹣ )﹣2﹣(2)0+|﹣|+
= +1+
=2
=7.
点评:计算时注意负指数次幂与 0 次幂的含义,并且理解绝对值起到括号的作用.
十七章《勾股定理》易错题
一、审题不仔细,受定势思维影响
考点:二次根式的性质与化简;点的坐标。 专题:计算题;分类讨论。
分析:先判断出点的横纵坐标的符号,进而判断点所在的象限或坐标轴.解答:解:∵实数a、b满 ,
∴a、b 异号,且 b>0;
故 a<0,或者 a、b 中有一个为 0 或均为 0.
于是点(a,b)在第二象限或坐标轴上.故选 C.
点评:根据二次根式的意义,确定被开方数的取值范围,进而确定 a、b 的取值范围,从而确定点的坐标位置.
八年级下册数学错题集

八年级下册数学错题集一、二次根式部分(5题)1. 化简:√(18)- 错解:√(18)=√(9 + 9)=3 + 3 = 6- 正解:√(18)=√(9×2)=3√(2)。
解析:二次根式化简时,要将被开方数分解成完全平方数与其他数相乘的形式,而不是简单的数字相加分解。
2. 计算:√(8)+√(18)- 错解:√(8)+√(18)=2√(2)+3√(2)=5√(2)√(2)=5×2 = 10- 正解:√(8)+√(18)=2√(2)+3√(2)=5√(2)。
解析:在计算二次根式加法时,最后结果应保留最简二次根式形式,不能再对√(2)进行错误的乘法运算。
3. 若√(x - 1)+√(1 - x)=y + 4,求x,y的值。
- 错解:由√(x - 1)+√(1 - x)=y + 4,得x-1≥0且1 - x≥0,解得x≥1且x≤1,所以x = 1或x = 0,当x = 0时,y=-4;当x = 1时,y=-4。
- 正解:由√(x - 1)+√(1 - x)=y + 4,因为二次根式有意义的条件是被开方数非负,所以x - 1≥0且1 - x≥0,解得x = 1。
把x = 1代入原式得y+4 = 0,解得y=-4。
解析:在确定x的值时,根据二次根式有意义的条件,x只能取1,不能取0。
4. 比较大小:2√(3)和3√(2)- 错解:因为2√(3)=√(12),3√(2)=√(18),所以2√(3)>3√(2)。
- 正解:因为2√(3)=√(12),3√(2)=√(18),所以2√(3)<3√(2)。
解析:比较二次根式大小时,先将它们化为最简二次根式对应的被开方数,再比较被开方数大小。
5. 已知a=√(5)+2,b=√(5)-2,求a^2+b^2的值。
- 错解:- 先求ab=(√(5)+2)(√(5)-2)=5 - 4 = 1。
- 然后a + b=√(5)+2+√(5)-2 = 2√(5)。
八年级数学下错题集1

许竹筠八年级数学下乙本错题集(1—50)1.下列说法正确的是()个。
P1A.8是不等式y-1>6的解。
B.不等式m-1>2的解有无数个。
C.x>4是不等式x+3 >6的解集。
D.不等式x+1<2有两个非负整数解。
2.如果一次函数y=(2-m)x+m的图象经过第一、二、四象限,那么m的取值范围是_______。
P33.某人10点10分离家赶11整的火车,已知他家离车站10公里,他离家后先以3公里/时的速度走了5分钟,然后乘公共汽车去车站,公共汽车每小时至少走__公里才能不误当次火车。
P54.已知机器工作时,每小时耗油9㎏,现油箱中存油多于38㎏但少于45㎏,问这油箱中的油大约可供这台机器工作__小时。
P55.不等式组 x-1≤8-2x的最小正整数解是()。
P72x>-3A.1B.0C.2D.36.若不等式组 x+ a≥0 有解,则a的取值范围是()。
P71-2x>x-2A.a>-1B. a≥-1C. a≤1D. a<17.设一个三角形的三边分别为3、1、-2m 则m 的取值范围是( )。
P7A .0<m <7/2 B.-5<m <-2C.-2<m <5D.-7/2<m <-18.已知关于x 的方程组 3x+2y=p+1 的解满足x >y,求p 的取值范围。
P74x+3y=p-19.一位老师说,他班学生的一半在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足6名学生在操场上踢足球,则这个班的学生共有多少人? P810.一宾馆有二人房、三人房、四人房三种客房供游客租住,某施行团20人准备同时租用这三种客房共7间,如果每个房间都住满,租房方案有( )。
P911.若不等式组 1<x ≤2 有解,则m 的取值范围是___。
P11x >m12.如果不等式x ≤3m 的正整数解是1,2,3,则m 的取值范围是___。
P1113. -1<223x +<2,并把它的解集在数轴是表示出来。
八年级下册人教版数学精选大数据易错题集(附解析)

⼋年级下册⼈教版数学精选⼤数据易错题集(附解析)⼆次根式的定义及性质⼀.选择题1.下列结论正确的是()A.2764的⽴⽅根是34±B.1125-没有⽴⽅根C.有理数⼀定有⽴⽅根D.6(1)-的⽴⽅根是1-2.下列各式计算正确的是()A.30.01250.5±=±B.3273644-=C.3313182=D.3421255-=-【解答】A 、0.53=0.125,故选项错误;BC 、∵112等于3338,∴3338的⽴⽅根等于112,故选项正确;D 、应取正号,故选项错误.故选C3.下列说法中正确的有()个.①负数没有平⽅根,但负数有⽴⽅根②49的平⽅根是23±③827的⽴⽅根是23±④8-的⽴⽅根是2-A .1B .2C .3D .44.下列各数中,⽴⽅根⼀定是负数的是()A .a-B .2a -C .21a --D .21a -+【解答】∵?a 2?1≤-1,∴?a 2?1的⽴⽅根⼀定是负数.故选C .5.下列结论正确的是()A.64的⽴⽅根是4±B.12-是16-的⽴⽅根C.⽴⽅根等于本⾝的数只有0和1D.332727-=-⼆.填空题6.正数的⽴⽅根是__________数;负数的⽴⽅根是________数;0的⽴⽅根是_________.⼀个正数的⽴⽅根是正数,⼀个负数的⽴⽅根是负数,0的⽴⽅根式0.故答案:正,负,0.7.⼀般地,3________a -=.8.64的⽴⽅根是________;364的平⽅根是__________.30.064______=;3216_______=;33(2)_______-=;331(1)______5-=;38_______-=;38_____-=;33()_______a -=.9.2(1)-的⽴⽅根是______________;⼀个数的⽴⽅根是110,则这个数是___________.的⽴⽅根是⼀个数⽴⽅根是,则这个数是故答案为:;10.平⽅根等于本⾝的数是________;⽴⽅根等于本⾝的数是_______.∵平⽅根等于它本⾝的数是0,⽴⽅根都等于它本⾝的数是0,1,-1.故填0;0,±1.11.若x 的⽴⽅根是4,则x 的平⽅根是___________.的⽴⽅根是的平⽅根是故应填:12.3311x x -+-中的x 的取值范围是_________,11x x -+-中的x 的取值范围是___________.13.27-的⽴⽅根与81的平⽅根的和是_____________.∵-27的⽴⽅根是-3,√81的平⽅根是±3,所以它们的和为0或-6.故答案:0或-6.14.若33 0x y +=,则x 与y 的关系是_________.∵3x +3y =0,∴3x =?3y ,∴x=-y ,即x 与y 的关系是互为相反数.故答案为:互为相反数.15.如果344a +=,那么3(67)a -的值是___________.则:答:值为.三.解答题16.出下列各式中的a :(1)若30.343a =,则_______a =;(2)若33213a -=,则_______a =;(3)若31250a +=,则_______a =;(4)若3(1)8a -=,则_______a =.17.已知519x +的⽴⽅根是4,求27x +的平⽅根.∵5x+19的⽴⽅根是4,∴5x+19=64,解得x=9则2x+7=2×9+7=25,∵25的平⽅根是±5故2x+7的平⽅根是±5.18.互为相反数,求ab 的值.【解答】∵32a ?1和31?3b 互为相反数,∴2a-1=-(1-3b),2a=3b ,32a ?1和31?3b 互为相反∴a b =32,故答案为:32.19.已知a 的整数部分,b 是它的⼩数部分,求2a b +的值.因为a 是的整数部分,b 是它的⼩数部分,所以:a=2,a+b=所以:2a+b=。
人教版-八年级数学下册易错题

八年级下册数学易错题一、选择题: 1、如果把分式yx xy +中的x 和y 都扩大2倍,则分式的值( )A 、扩大4倍B 、扩大2倍C 、不变D 、缩小2倍2、下面函数:①y=-3x ;②y=-x8;③y=4x-5;④y=5x -1;⑤xy=81。
其中反比例函数的个数是( ) A 、2 B 、3 C 、4 D 、5 3、下列关系中的两个量成反比例关系的是( )A 、三角形一边的长与这边上的高;B 、三角形的面积与一边上的高;C 、三角形的面积一定时,一边的长与这边上的高;D 、三角形一边的长不变时,它的面积与这边上的高。
4、若反比例函数y=xk的图象经过点(-1,2),则这个函数的图象一定经过点( )A 、(-2,-1)B 、(-21,2)C 、(2,-1)D 、(21,2) 5、当x=-2008时,分式2-11x x +的值为( )A 、2008B 、-2008C 、20081D 、200916、下列各式正确的是( )A 、c b a c b a --=B 、cba c ab ---= C 、c b a c --b a -+=+)( D 、c b a c b a ----= 7、若分式方程3234=++xm mx 的解为x=1,则m 的值为( ) A 、1 B 、2 C 、3 D 、48、若分式11-2+x x 的值为0,则x 的值为( )A 、1B 、-1C 、±1D 、0 9、如果分式)(3)(b a b a a ++的值是零,那么ab 满足的条件是( )A 、a=-bB 、a≠-bC 、a=0D 、a=0且b≠0 10、计算x 2y 3÷(xy)-2的结果为( ) A 、xy B 、x C 、x 4y 5 D 、y11、已知关于x 的函数y=k(x-1)和y=-xk(k≠0),它们在同一坐标系中的图象大致是( )oxyA oxyBoxyC oxyD12、如果把分式224y x xy +中的x 和y 都扩大2倍,则分式的值( )A 、不变B 、扩大2倍C 、扩大4倍D 、缩小2倍13、美是一种感觉,当人体下半身与身高的比值越接近0.618时,越给人一种美感。
八年级数学下册错题集精编版

八年级数学下册错题集集团企业公司编码:(LL3698-KKI1269-TM2483-LUI12689-ITT289-第十六章《二次根式》易错题一、选择题1.当a>0,b>0时,n是正整数,计算的值是()A.(b﹣a)B.(a n b3﹣a n+1b2)C.(b3﹣ab2)D.(a n b3+a n+1b2)错答:D考点:二次根式的性质与化简。
分析:把被开方数分为指数为偶次方的因式的积,再开平方,合并被开方数相同的二次根式.解答:解:原式=﹣=a n b3﹣a n+1b2=(a n b3﹣a n+1b2).故选B.点评:本题考查的是二次根式的化简.最简二次根式的条件:被开方数中不含开得尽方的因式或因数.点评:解答此题,要弄清二次根式的性质:=|a|,分类讨论的思想.2.当x<﹣1时,|x﹣﹣2|﹣2|x﹣1|的值为()A.2 B.4x﹣6 C.4﹣4x D.4x+4错答:C考点:二次根式的性质与化简。
分析:根据x<﹣1,可知2﹣x>0,x﹣1<0,利用开平方和绝对值的性质计算.解答:解:∵x<﹣1∴2﹣x>0,x﹣1<0∴|x﹣﹣2|﹣2|x﹣1|=|x﹣(2﹣x)﹣2|﹣2(1﹣x)=|2(x﹣2)|﹣2(1﹣x)=﹣2(x﹣2)﹣2(1﹣x)=2.故选A.点评:本题主要考查二次根式的化简方法与运用:a>0时,=a;a<0时,=﹣a;a=0时,=0;解决此类题目的关键是熟练掌握二次根式、绝对值等考点的运算.3.化简|2a+3|+(a<﹣4)的结果是()A.﹣3a B.3a﹣C.a+D.﹣3a错答:B考点:二次根式的性质与化简;绝对值。
分析:本题应先讨论绝对值内的数的正负性再去绝对值,而根号内的数可先化简、配方,最后再开根号,将两式相加即可得出结论.解答:解:∵a<﹣4,∴2a<﹣8,a﹣4<0,∴2a+3<﹣8+3<0原式=|2a+3|+=|2a+3|+=﹣2a﹣3+4﹣a=﹣3a.故选D.点评:本题考查的是二次根式的化简和绝对值的化简,解此类题目时要充分考虑数的取值范围,再去绝对值,否则容易计算错误.4.当x<2y时,化简得()A.x(x﹣2y)B. C.(x﹣2y)D.(2y﹣x)错答:C考点:二次根式的性质与化简。
初中数学八年级下册几何易错题集锦(含答案)
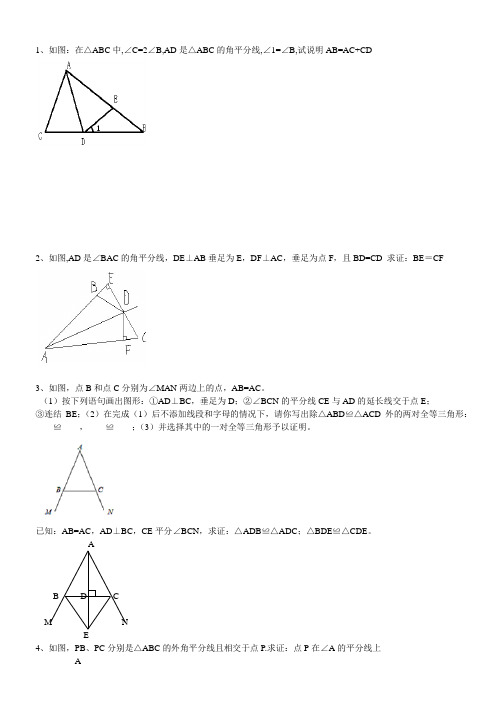
1、如图:在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E,DF⊥AC,垂足为点F,且BD=CD 求证:BE=CF3、如图,点B和点C分别为∠MAN两边上的点,AB=AC。
(1)按下列语句画出图形:①AD⊥BC,垂足为D;②∠BCN的平分线CE与AD的延长线交于点E;③连结BE;(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:____≌____,____≌____;(3)并选择其中的一对全等三角形予以证明。
已知:AB=AC,AD⊥BC,CE平分∠BCN,求证:△ADB≌△ADC;△BDE≌△CDE。
AB D CM NEB CP5、如图,△ABC中,p是角平分线AD,BE的交点. 求证:点p在∠C的平分线上6、下列说法中,错误的是()A.三角形任意两个角的平分线的交点在三角形的内部B.三角形两个角的平分线的交点到三边的距离相等C.三角形两个角的平分线的交点在第三个角的平分线上D.三角形任意两个角的平分线的交点到三个顶点的距离相等7、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC8、如图,AP、CP分别是△ABC外角∠MAC与∠NCA的平分线,它们相交于点P,PD⊥BM于点D,PF⊥BN于点F.求证:BP为∠MBN的平分线。
9、如图,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB 的平分线上.10、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;(2)线段DM与AM有怎样的位置关系?请说明理由.11、八(1)班同学上数学活动课,利用角尺平分一个角(如图所示).设计了如下方案:(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.(Ⅱ)∠AOB是一个任意角,在边OA、OB上分别取OM=ON,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由;PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.ADEBFC12、如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF。
2020-2021学年苏科版八年级数学下册期末复习错题集(1)

2020-2021学年度第二学期初二数学期末复习错题集(1)一.选择题(共13小题)1.如图,正方形纸片ABCD的边长为4cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是()A.2 cm B.4 cm C.cm D.1 cm2.在平面直角坐标系中,点A(1,),B(4,),若点M(a,﹣a),N(a+3,﹣a﹣4),则四边形MNBA的周长的最小值为()A.10+B.5+13C.10+D.5+133.如图,矩形ABCD中,AB=2,对角线AC、BD交于点O,∠AOD=120°,E为BD上任意点,P为AE中点,则PO+PB的最小值为()A.B.1+C.D.34.如图,在菱形ABCD中,∠D=135°,AD=3,CE=2,点P是线段AC上一动点,点F是线段AB上一动点,则PE+PF的最小值()A.2B.3 C.2D.5.如图,在矩形ABCD中,AB=6,AD=3,动点P满足S△P AB=S矩形ABCD,则点P到A、B两点距离之和P A+PB的最小值为()A.2B.2C.3D.6.如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点.且BE=CF,连接BF、DE,则BF+DE的最小值为()A.B.C.D.7.如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE⊥AC于E,PF⊥BC于点F,连接EF,则线段EF的最小值为()A.B.C.D.58.如图,在△ABC中,AC=4,BC=3,AB=5,D为AB上的动点,连接CD以AD、CD 为边作平行四边形ADCE,则DE长的最小值为()A.3 B.4 C.D.9.如图,在▱ABCD中,AB=4,BC=6,∠ABC=60°,点P为▱ABCD内一点,点Q在BC边上,则P A+PD+PQ的最小值为()A.++B.6+2C.5D.1010.如图,在▱ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE 于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是()①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE.A.只有①②B.只有①②③C.只有③④D.①②③④11.在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、F A⊥AE交DP于点F,连接BF,FC.下列结论:①△ABE≌△ADF;②FB=AB;③CF⊥DP;④FC=EF其中正确的是()A.①②④B.①③④C.①②③D.①②③④12.如图,四边形ABCD中,AB与CD不平行,M,N分别是AD,BC的中点,AB=4,DC=2,则MN的长不可能是()A.3 B.2.5 C.2 D.1.513.在平面直角坐标系xOy中,点A(4,3),点B为x轴正半轴上一点,将△AOB绕其一顶点旋转180°,连接其余四个顶点得到一个四边形,若该四边形是一个轴对称图形,则满足条件的点有()A.5个B.4个C.3个D.2个二.填空题(共16小题)14.如图,已知▱ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,则对角线OB长的最小值为.15.如图,在正方形ABCD中,AB=2,E是对角线AC上的动点,以DE为边作正方形DEFG,H是CD的中点,连接GH,则GH的最小值为.16.如图,等腰直角三角形的斜边长AB=8,一直线l绕顶点B任意旋转,过A向l作垂线,垂足为H,则线段CH长的取值范围是.17.如图,▱ABCD中,∠DAB=30°,AB=8,BC=3,P为边CD上的一动点,则PB+PD 的最小值等于.18.如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边上一点,且BD:DC=1:2,以D为一个顶点作正方形DEFG,且DE=BC,连接AE,将正方形DEFG绕点D旋转一周,在整个旋转过程中,当AE取得最大值时AG的长为.19.如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连接CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=4,则BE的最小值为.20.如图,正方形ABCD的边长为4,E为AB上一点,且AE=3,F为BC边上的一个动点,连接EF,以EF为边向左侧作等腰直角三角形FEG,EG=EF,∠GEF=90°,连接AG,则AG的最小值为.21.如图,平面直角坐标系中,点A、B分别是x、y轴上的动点,以AB为边作边长为2的正方形ABCD,则OC的最大值为.22.点C是线段AB上的动点,分别以AC,BC为边向上方作正方形ACDE,正方形CBGF,连接AD,AD,BF的中点M,N,若AB=4,则MN的最小值为.23.如图,在矩形ABCD中,AB=2,BC=,两顶点A、B分别在平面直角坐标系的x 轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则当OC为最大值时,点C的坐标是.24.如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是.(把所有正确结论的序号都填在横线上)①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.25.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为.26.如图,在边长为4的正方形ABCD中,动点E,F分别在CD,BC上移动,CF=DE,AE和DF交于点P,则线段CP的最小值是.27.如图所示,在正方形ABCD中,点E在AB边上,BE=4,M是对角线BD上的一点(∠EMB是锐角),连接EM,EM=5,过点M作MN⊥EM交BC边于点N.过点N作NH⊥BD于H,则△HMN的面积=.28.如图,菱形ABCD的边长为1,∠ABC=60°.E,F分别是BC,BD上的动点,且CE =DF,则AE+AF的最小值为.29.如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是.三.解答题(共8小题)30.已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点(1)写出线段FD与线段FC的关系并证明;(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD 与线段FC的关系是否变化,写出你的结论并证明;(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2,直接写出线段BF的范围.31.如图,在矩形ABCD中,AB=2,AD=m,动点P从点D出发,沿射线DA以每秒1个单位的速度向点A方向运动,连接CP,把△PDC沿PC翻折,得到△PEC.设点P的运动时间为t(s).(1)若m=3,当P,E,B三点在同一直线上时,求t的值;(2)若点E到直线BC的距离等于1,求t的值;(3)若AE的最小值为1,直接写出m值.32.已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P 的运动时间为t秒(1)当t为何值时,四边形PODB是平行四边形?(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.(3)在线段PB上有一点M,且PM=5,当P运动秒时,四边形OAMP的周长最小,并画图标出点M的位置.33.综合与实践:如图1,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想在图1中,线段PM与PN的数量关系是,∠MPN的度数是;(2)探究证明把△ADE绕点A逆时针方向旋转到图2的位置,①判断△PMN的形状,并说明理由;②求∠MPN的度数;(3)拓展延伸若△ABC为直角三角形,∠BAC=90°,AB=AC=10,点DE分别在边AB,AC上,AD =AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图3,请直接写出△PMN面积的最大值.34.我们定义:只有一组对角相等的凸四边形叫做等对角四边形.(1)四边形ABCD是等对角四边形,∠A≠∠C,若∠A=60°,∠B=80°,则∠C =°,∠D=°.(2)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在格点上,按要求以AB、BC为边在图①、图②中各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.(3)如图③,在平行四边形ABCD中,∠A=60°,AB=12,AD=6,点E为AB的中点,过点E作EF⊥DC,交DC于点F.点P是射线FE上一个动点,设FP=x,求以点A、D、E、P为顶点的四边形为等对角四边形时x的值.35.如图(1),抛物线y=ax2+bx+5(a≠0)与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为y=x+5,抛物线的对称轴与x轴交于点E,点D(﹣2,﹣3)在对称轴上.(1)求此抛物线的解析式;(2)如图(1),若点M是线段OE上一点(点M不与点O、E重合),过点M作MN⊥x轴,交抛物线于点N,记点N关于抛物线对称轴的对称点为点F,点P是线段MN上一点,且满足MN=4MP,连接FN、FP,作QP⊥PF交x轴于点Q,且满足PF=PQ,求点Q的坐标;(3)如图(2),过点B作BK⊥x轴交直线AC于点K,连接DK、AD,点H是DK的中点,点G是线段AK上任意一点,将△DGH沿GH边翻折得△D′GH,求当KG为何值时,△D′GH与△KGH重叠部分的面积是△DGK面积的?36.如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.(1)求k,并用t表示h;(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.37.综合与实践:如图1,已知△ABC,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接DC,点P、Q、M分别为DE、BC、DC的中点.(1)观察猜想在图1中,线段PM与QM的数量关系是;(2)探究证明当∠BAC=60°,把△ADE绕点A顺时针方向旋转到图2的位置,判断△PMQ的形状,并说明理由;(3)拓展延伸当∠BAC=90°,AB=AC=5,AD=AE=2,再连接BE,再取BE的中点N,把△ADE 绕点A在平面内自由旋转,如图3,①请你判断四边形PMQN的形状,并说明理由;②请直接写出四边形PMQN面积的最大值.。
八年级下册数学错题摘抄

八年级下册数学错题摘抄一、选择题错题。
题1。
- 题目:下列二次根式中,最简二次根式是()A. √(12)B. √(0.2)C. √(7)D. √(frac{1){3}}- 错选:A。
- 解析:- 对于选项A,√(12)=√(4×3)=2√(3),不是最简二次根式。
- 对于选项B,√(0.2)=√(frac{1){5}}=(√(5))/(5),不是最简二次根式。
- 对于选项C,√(7)不能再化简,是最简二次根式。
- 对于选项D,√(frac{1){3}}=(√(3))/(3),不是最简二次根式。
所以这题正确答案是C。
题2。
- 题目:若在实数范围内有意义,则x的取值范围是()A. x>5B. x≥5C. x≤5D. x≠5- 错选:A。
- 解析:- 要使二次根式√(x - 5)有意义,则被开方数x-5≥0,即x≥5。
所以正确答案是B。
题3。
- 题目:下列计算正确的是()A. √(2)+√(3)=√(5)B. 3√(2)-√(2)=3C. √(6)÷√(3)=√(2)D. √(3)×√(2)=√(5)- 错选:A。
- 解析:- 选项A,√(2)与√(3)不是同类二次根式,不能直接相加,所以A错误。
- 选项B,3√(2)-√(2)=(3 - 1)√(2)=2√(2),所以B错误。
- 选项C,√(6)÷√(3)=√(frac{6){3}}=√(2),C正确。
- 选项D,√(3)×√(2)=√(3×2)=√(6),所以D错误。
正确答案是C。
二、填空题错题。
题4。
- 题目:计算:√(18)-√(8)=___。
- 错误答案:√(10)- 解析:- 先将二次根式化简,√(18)=√(9×2)=3√(2),√(8)=√(4×2)=2√(2)。
- 则√(18)-√(8)=3√(2)-2√(2)=√(2)。
题5。
- 题目:若y=√(x - 3)+√(3 - x)+2,则x^y =___。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档第十六章《二次根式》易错题一、选择题是正整数,计算的值是(n )a>0,b>0时,1.当)+ab(a ﹣b﹣aab)b)D.C.(b(A.b﹣a()B.ab22n+1233nn3n+1D错答:考点:二次根式的性质与化简。
分析:把被开方数分为指数为偶次方的因式的积,再开平方,合并被开方数相同的二次根式.﹣解答:解:原式=a=abb﹣23n+1n)b﹣aa=(b.2nn+13故选B.点评:本题考查的是二次根式的化简.最简二次根式的条件:被开方数中不含开得尽方的因式或因数.点评:解答此题,要弄清二次根式的性质:=|a|,分类讨论的思想.﹣2|﹣2|x﹣|x1|﹣的值为()12.当x<﹣时,C.2A.B.4x﹣64﹣4xD.4x+4C错答:考点:二次根式的性质与化简。
分析:根据x<﹣1,可知2﹣x>0,x﹣1<0,利用开平方和绝对值的性质计算.解答:解:∵x<﹣1∴2﹣x>0,x﹣1<0﹣﹣2|﹣2|x﹣1|∴|x=|x﹣(2﹣x)﹣2|﹣2(1﹣x)=|2(x﹣2)|﹣2(1﹣x)=﹣2(x﹣2)﹣2(1﹣x)精品文档.精品文档=2.故选A.时,=0a=0;时,=﹣a点评:本题主要考查二次根式的化简方法与运用:a>0;时,=a;a<0解决此类题目的关键是熟练掌握二次根式、绝对值等考点的运算.|+(a<﹣4)的结果是(3.化简)|2a+3.﹣.a+D3aAB.﹣3a .3a ﹣C B错答:考点:二次根式的性质与化简;绝对值。
分析:本题应先讨论绝对值内的数的正负性再去绝对值,而根号内的数可先化简、配方,最后再开根号,将两式相加即可得出结论.解答:解:∵a<﹣4,∴2a<﹣8,a﹣4<0,8+3<<﹣0 ∴2a+3|+原式=|2a+3=|2a+3|+a=﹣3a.3+4﹣=﹣2a﹣故选D.点评:本题考查的是二次根式的化简和绝对值的化简,解此类题目时要充分考虑数的取值范围,再去绝对值,否则容易计算错误.时,化简得().当4x<2y)x2y﹣.x﹣2y)D((C 2yxxA .(﹣)B..C错答:考点:二次根式的性质与化简。
分析:本题可先将根号内的分式的分子分解因式,再根据x与y的大小关系去绝对值.精品文档.精品文档2y| =解答:解:原式=|x=﹣∵x<2y).故选D.∴原式=(2y﹣x点评:本题考查的是二次根式的化简,解此类题目时要注意题中所给的范围去绝对值..若=1﹣2x,则x的取值范围是()5<.x>B.xD≤C.xA.x ≥A错答:考点:二次根式的性质与化简。
分析:由于≥0,所以1﹣2x≥0,解不等式即可.=1﹣2x,解答:解:∵≤x.0∴1﹣2x≥,解得故选B.点评:算术平方根是非负数,这是解答此题的关键.,)b)在(、6.如果实数ab,那么点(满足aA.第一象限B.第二象限C.第二象限或坐标轴上D.第四象限或坐标轴上B错答:考点:二次根式的性质与化简;点的坐标。
专题:计算题;分类讨论。
分析:先判断出点的横纵坐标的符号,进而判断点所在的象限或坐标轴.满足、b,解答:解:∵实数a 0;、b异号,且b>a∴或均为0.b0故a<,或者a、中有一个为0 C,b)在第二象限或坐标轴上.故选.a于是点(ba点评:根据二次根式的意义,确定被开方数的取值范围,进而确定、的取值范围,从而确定点的坐标位置.精品文档.精品文档2+ 7..计算:=考点:二次根式的性质与化简;零指数幂;负整数指数幂。
分析:本题涉及零指数幂、负整数指数幂、二次根式化简四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.﹣+2=解答:解:原式+2=2﹣=2+.,次幂都得=1,1点评:本题考查0次幂、负数次幂、二次根式的化简以及合并,任何非零数的0负数次幂可以运用底倒指反技巧,=2=2.1取最大值时,8x= .代数式±2 .考点:二次根式的性质与化简。
专题:计算题。
分析:根据二次根式有意义的条件,求出x的取值即可.解答:解:∵≥0,取得最大值时,取得最小值,∴代数式时原式有最大值,即当=0,得:x=±2=0解答案为±2.点评:本题比较简单,考查了二次根式有意义的条件,即被开方数大于等于0.二、填空题,化简= ﹣a ..若9a<1考点:二次根式的性质与化简。
(1|=|a01aa11|=|a﹣﹣,根据分析:的范围,﹣<,所以﹣﹣a)1﹣,进而得到原式的值.a解答:解:∵1<,精品文档.精品文档,1<0∴a﹣ 1﹣﹣1|=|a∴1 ﹣﹣1)=﹣(a ﹣a.﹣=a+1﹣1=化简,应先将其转化为绝对值形式,再去绝对值符号,即.点评:对于.= <12x ,化简10.若0<x考点:二次根式的性质与化简。
,通过变形化>0,则有﹣x,,又0<x<1分析:由简原式即可得出最终结果.解答:解:原式﹣=.x)=2x=x+﹣(﹣点评:本题考查的是对完全平方公式的灵活使用和对二次根式的化简应用.三、计算题﹣|+)的结果是.﹣(2)+| ﹣11.计算:(?﹣02考点:二次根式的性质与化简;绝对值;零指数幂;负整数指数幂。
分析:计算时首先要分清运算顺序,先乘方,后加减.二次根式的加减,实质是合并同类二次根式,需要先化简,再合并.﹣+|?﹣)解答:解:﹣(2)(02=1+﹣?4+1+﹣|++4=2=7.点评:计算时注意负指数次幂与0次幂的含义,并且理解绝对值起到括号的作用.十七章《勾股定理》易错题精品文档.精品文档一、审题不仔细,受定势思维影响2c?b)?b)(a?(acb,?B,Ca,?A,?)的对边分别为,且1 、在△ABC中,,则(C?B??A)不是直角三角形(D (C)(A)为直角(B)为直角为直角B)选(错解:CC??就一定表示直,因而有同学就习惯性的认为分析:因为常见的直角三角形表示时,一般将直角标注为222222cb?ca?b?a?因根据这该题中的条件应转化为即,,导致错误角,加之对本题所给条件的分析不缜密,..一公式进行判断222222c??b??cbaa.故选(A)正解:,∴2 、已知直角三角形的两边长分别为3、4,求第三边长.22?254?35?.错解:第三边长为分析:因学生习惯了“勾三股四弦五”的说法,即意味着两直角边为3和4时,斜边长为5.但这一理解的前提是3、4为直角边.而本题中并未加以任何说明,因而所求的第三边可能为斜边,但也可能为直角边.正解:(1)当两直角边为3和4时,第三边长为22?25?35?4;(2)当斜边为4,一直角边为3时,第三边长为22?347?.二、概念不明确,混淆勾股定理及其逆定理3 、下列各组数据中的三个数,可作为三边长构成直角三角形的是()222,543,3,4,1,2,35)(3 1(A)、2、B)(C(D)错解:选(B)分析:未能彻底区分勾股定理及其及逆定理,对概念的理解流于表面形式.判断直角三角形时,应将所给数据222cb?a?.进行平方看是否满足的形式??????222321??),故选(正解:因为C60?方向以每小时8B 4 、在港有甲、乙两艘渔船,若甲船沿北偏东海里的速度前进,乙船沿南偏东某个角度以精品文档.精品文档每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?8?2?16(海里)错解:甲船航行的距离为BM=,15?2?30(海里)乙船航行的距离为BP=.22?34?3016(海里)且MP=34(海里)∵?MBP?90?30?方向航行的,∴乙船是沿着南偏东. ∴△MBP为直角三角形,∴分析:虽然最终判断的结果也是对的,但这解题过程中存在问题.勾股定理的使用前提是直角三角形,而本题222c?a?b??C?90错解的原因在于未能,.则.需对三角形做出判断,判断的依据是勾定理的逆定理其形式为“若.充分理解勾股定理及其逆定理的概念,导致错误运用168?2?(海里),正解:甲船航行的距离为BM=30?2?15.(海里)乙船航行的距离为BP=22222211561156,34??30?16MP?BM?BP,,∴∵?MBP?90?30?方向航行的,∴乙船是沿着南偏东为直角三角形,∴∴△MBP.三、混淆勾股定理及其逆定理应用321的周长是△AM=ABC又BC=AD.RT是中线,且°,△5、如图,已知RtABC中,∠BAC=90AD是高,AM323.(6+2)cm.求AD错解∵△ABC是直角三角形,∴AC:AB:BC=3:4:5∴AC∶AB∶BC=3∶4∶5.精品文档.精品文档3?333 AC=(6+2)=∴212326?43 )=AB=(6+2312 3515?53 BC=)=(6+261211AC?ABBC?AD =又∵223236?3??AB?A3∴AD= BC15?536(3?3)?2(3?3) =5(3?3)23=(3+)(cm) 5我们知道,“勾三股四弦五”是直角三角形中三边关系的一种特殊情形,并不能代表一般的直角三角形诊断的三边关系.上述解法犯了以特殊代替一般的错误.23AD正确解法∵AM=32322AD(?3AD)AD∴MD== 33又∵MC=MA,∴CD=MD.∵点C与点M关于AD成轴对称.∴AC=AM,∴∠AMD=60°=∠C.精品文档.精品文档31BC°,AC=BC,AB=∴∠B=30223132.BC+BC=6+BC+∴AC+AB+BC=22∴BC=4.1BC32123(cm)=∵BC=AD, ∴AD=232336、在△ABC中,a∶b∶c=9∶15∶12,试判定△ABC是不是直角三角形.错解依题意,设a=9k,b=15k,c=12k(k>0).∵a+b=(9k)+(15k)=306k,c2=(12k)=144k,2222222∴a+b≠c.∴△ABC不是直角三角形.222诊断我们知道“如果一个三角形最长边的平方等于另外两边的平方和,那么这个三角形是直角三角形”.而上面解答错在没有分辨清楚最长边的情况下,就盲目套用勾股定理的逆定理.正确解法由题意知b是最长边.设a=9k,b=15k,c=12k(k>0).∵a+c=(9k)+(12k)=81k+144k=225k.2222222b2=(15k)=225k,∴a+c=b.22222∴△ABC是直角三角形.7、已知在△ABC中,AB>AC,AD是中线,AE是高.求证:AB-AC=2BC·DE.22精品文档.精品文档如图.错证E,⊥BC于∵AE AE,AB=BE+∴222.=EC+AEAC222 ECAC=BE-∴AB-2222EC) -·(BE=(BE+EC) EC).(BE=BC·-EC.-EC=2DC-∵BD=DC,∴BE=BC .·DE(2DC -EC-EC)=2BC·-∴ABAC=BC22的形状,又没给出图形,因此,这个三角形有可能是锐角三角形,也可能题设中既没明确指出△ABC诊断既可以在形内,也可以与一边重合,还可以在形外,这三种情况都符合题AE是直角三角形或钝角三角形.所以高意.而这里仅只证明了其中的一种情况,这就犯了以偏概全的错误。
