浙教版八年级数学上册错题集及分析
八上数学易错题

八年级上册数学易错题可能涵盖多个知识点,以下是一些典型的易错题及其详细解析,旨在帮助学生更好地理解和避免这些错误。
1 平面直角坐标系
题目:点 A(2,−3) 关于 x 轴对称的点 B 的坐标是 _______。
易错点:混淆关于 x 轴和 y 轴对称的点的坐标变化规则。
解析:点 A(2,−3) 关于 x 轴对称时,横坐标不变,纵坐标取反。
因此,点 B 的坐标为 (2,3)。
2. 一元一次不等式
题目:解不等式 2x−1>3x+2。
易错点:移项时符号处理不当。
解析:首先将不等式两边合并同类项,得−x>3。
然后,两边同时乘以−1,注意不等号方向要反转,得到 x<−3。
3. 函数的图像与性质
题目:函数 y=2x 的图像经过哪几个象限?
易错点:未正确分析函数图像的性质。
解析:函数 y=2x 是一个正比例函数,其图像是一条经过原点的直线。
由于斜率 k=2>0,图像将从第三象限经过原点进入第一象限。
因此,它经过第一、三象限。
4. 数据的集中趋势与离散程度
题目:一组数据 3,5,5,4,2 的众数是 _______。
易错点:混淆众数与中位数、平均数的概念。
解析:众数是一组数据中出现次数最多的数。
在这组数据中,数字 5 出现了两次,而其他数字只出现了一次。
因此,众数是 5。
浙教版八年级数学上册错题集及分析
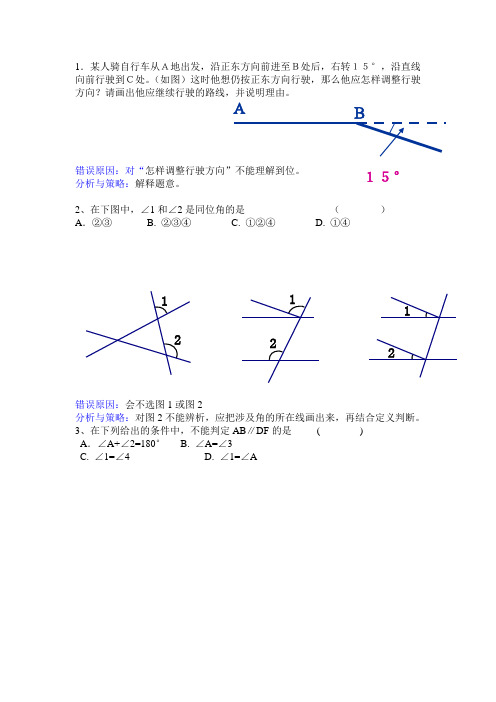
1.某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处。
(如图)这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由。
错误原因:对“怎样调整行驶方向”不能理解到位。
分析与策略:解释题意。
2、在下图中,∠1和∠2是同位角的是 ( ) A .②③ B. ②③④ C. ①②④ D. ①④212121错误原因:会不选图1或图2分析与策略:对图2不能辨析,应把涉及角的所在线画出来,再结合定义判断。
3、在下列给出的条件中,不能判定AB ∥DF 的是 ( ) A .∠A+∠2=180° B. ∠A=∠3 C. ∠1=∠4 D. ∠1=∠A15°A4321F E DCBA错误原因:对所截线不能找到分析与策略:先找AB 和DF ,再找所截线,再利用定义分析4、∠1+∠2+∠3=228°,AB ∥DF ,BC ∥DE ,则∠1的度数是( ) A .48° B.96° C. 84° D. 86°5.已知一等腰三角形三边分别为3x-1、 x+1、5,试求x 的值。
错误原因:一般都是分2种情况讨论对 3x-1= x+1的情况没有考虑 分析与策略:加强分类意识 6.问:如图,下列推理正确吗?错误原因:认为正确,对文字概念转化为图形理解不到位分析与策略:书面语言强化为图形语言 7 1. 已知△ABC 是等边三角形,D,E,F 分别是各边上的一点,且AD=BE=CF.试说明△ DEF 是等边三角形.错误原因:不能正确书写分析与策略:做好板书示范并强调8 .D,E 是△ABC 中BC 上的两点,且BD=DE=EC=AD=AE.求∠ B 与∠ BAC 的度数.ABCD21 ∵∠1=∠2 ∴ BD=DCDC E9. 1 .满足下列条件的ΔABC ,不是直角三角形的是:( ) A. B. ∠C=∠A-∠B C.∠A:∠B:∠C=3:4:5 D.a:b:c=12:9:1510.下列条件中,不能判定两个直角三角形全等的是( ) A.一条直角边和一个角分别相等 B.两条直角边对应相等C.斜边和一条直角边对应相等D.斜边和一个锐角对应相等.10、已知ΔABC 是等腰三角形,BC 边上的高恰好等于 BC 边长的一半,求∠BAC 的度数 错误原因:没有进行分类讨论分析与策略:强化分类意识,教师作好分类引导和板书练习11、根据下列条件,判断下面以a 、b 、 c 为边的三角形是不是直角三角形? (1) a=5,b=7,c=8(3) a=3n ,b=4n ,c=5n (n 是正整数) (4) a: b: c=5:12:13 错误原因:不能正确书写分析与策略:做好板书示范并强调12、如图:在△ABC 中AB=4,BC=2,BD=1,CD= 判断下列结论是否正确,并说明理由 (1) CD ⊥AB;ADE C13、如图,四边形ABCD 中,AB =3,BC=4,CD=12,AD=13, ∠B=90°,求四边形ABCD 的面积.14、1 .满足下列条件的ΔABC ,不是直角三角形的是:( ) A.b 2=a 2-c 2 B. ∠C=∠A-∠BC.∠A:∠B:∠C=3:4:5D.a:b:c=12:9:153. 错误原因:选择C分析与策略:强调3:4:5是边的关系才可以运用逆定理判断15、如图,EA ⊥AB,BC ⊥AB,AB=AE=2BC,D 为AB 中点,有以下判断:(1)DE=AC (2)DE ⊥AC(3) ∠CAB=30° (4) ∠EAF=∠ADE, 其中正确结论的个数是( )DACBDBA CA.1B.2C.3D.416.如果等腰三角形腰上的高线等于腰长的一半,那么这个等腰三角形的顶角度数是( )A.30°B.75°C.150°D.30°或150° 错误原因:没有进行分类讨论分析与策略:强化分类意识,教师作好分类引导和板书练习17、如图,某校A 与公路距离为3000米,又与该公路旁上的某车站D 的距离为5000米,现要在公路边建一个商店C ,使之与该校A 及车站D 的距离相等,则商店与车站的距离约为( ) A.875米 B.3125米 C.3500米 D.3275米 错误原因:计算错误分析与策略:对于复杂计算准确度低,注重技巧和一步步落实到位的解题方法 18、已知:如图,∠C=90°,BC=AC ,D 、E 分别在BC 和AC 上,且BD=CE ,M 是AB 的中点.求证:△MDE 是等腰三角形.FABCDE错误原因:想不到添辅助线分析与策略:强调三线合一这条线的添一等于添三的作用20、已知ΔABC 是等腰三角形,BC 边上的高恰好等于 BC 边长的一半,求∠BAC 的度数。
2022-2023学年浙教版八年级数学上册第2章《特殊三角形》易错题精选(原卷版)

保密★启用前2022-2023学年浙教版八年级数学上册第2章《特殊三角形》易错题精选学校:___________姓名:___________班级:___________考号:___________ 注意事项∶1. 答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2. 所有答案都必须写到答题卷上。
选择题必须使用2B 铅笔填涂;非选择题必须使用黑色字迹的签字笔或钢笔书写,字体要工整,笔迹要清楚。
3.本试卷分试题卷和答题卷两部分,满分100分。
考试时间共90分钟。
一、选择题(本题有10个小题,每小题3分,共30分)1.(本题3分)(2022·浙江衢州·八年级期末)如图图案中,成轴对称图形的是( ) A . B . C . D . 2.(本题3分)(2020·浙江·模拟预测)等腰三角形的两边长为3和8则这个等腰三角形的周长是( )A .14B .19C .14或19D .203.(本题3分)(2021·浙江·八年级期末)如图,在ABC 中,,30AB AC A =∠=︒,直线//,m n 顶点C 在直线n 上,直线m 交AB 于点,D 交AC 于点E ,若1150,∠=︒则2∠的度数是( )A .45B .40C .35D .304.(本题3分)(2020·浙江·绍兴市锡麟中学八年级阶段练习)有下列命题:①对顶角相等;②同位角相等,两直线平行;③若a =b ,则|a|=|b|;④全等三角形的对应角相等.它们的逆命题一定成立的有( )A .①②③④B .①④C .②④D .②5.(本题3分)(2022·浙江杭州·八年级期末)在Rt ABC 中,90ACB ∠=︒,分别以A 点,B 点为圆心以大于12AB 为半径画弧,两弧交于E ,F ,连接EF 交AB 于点D ,连接CD ,以C 为圆心,CD 长为半径作弧,交AC 于G 点,则:CG AB =( )A .B .1:2C .D .6.(本题3分)(2021·浙江杭州·八年级期中)在锐角ABC 中,15AB =,13AC =,高12AD =,则BC 的长度为( )A .16B .15C .14D .137.(本题3分)(2021·浙江湖州·八年级阶段练习)如图,AO ,BO 分别平分CAB ∠,CBA ∠,且点O 到AB 的距离2OD =,ABC 的周长为28,则ABC 的面积为( )A .7B .14C .21D .288.(本题3分)(2022·浙江绍兴·八年级期末)如图,斜靠在墙上的一根竹竿,AB =10m ,BC =6m ,若A 端沿垂直于地面的方向AC 下移2m ,则B 端将沿CB 方向移动的距离是( )米.A .1.6B .1.8C .2D .2.29.(本题3分)(2022·浙江宁波·八年级期末)如图,△ABC 中,90ACB ∠=,以其三边分别向外侧作正方形,然后将整个图形放置于如图所示的长方形中,若要求图中两个阴影部分面积之和,则只需知道( )A .以BC 为边的正方形面积B .以AC 为边的正方形面积 C .以AB 为边的正方形面积D .△ABC 的面积10.(本题3分)(2022·浙江绍兴·八年级期末)在Rt △ABC 中,AC =3,BC =4,∠ACB=90°,点P ,Q 分别是边AB 和BC 上的动点,始终保持AP =BQ ,连接AQ ,CP ,则AQ CP+的最小值为( )A .BC .D .6二、填空题(本题有7个小题,每小题3分,共21分)11.(本题3分)(2021·浙江宁波·八年级期中)等腰三角形的顶角是40°,则底角的度数为________°.12.(本题3分)(2019·浙江杭州·八年级期末)如图,已知O 是等边△ABC 内一点,D 是线段BO 延长线上一点,且 OD OA =,AOB ∠=120°,那么BDC ∠=_____.13.(本题3分)(2022·浙江·台州市书生中学八年级期中)已知直角三角形的两边长分别为3和4,则斜边上的中线长为______.14.(本题3分)(2021·浙江·乐清市英华学校八年级期中)课本第78页阅读材料《从勾股定理到图形面积关系的拓展》中有如下问题:如图①分别以直角三角形的三条边为边,向形外分别作正三角形,则图中的S 1,S 2,S 3满足的数量关系是S 1+S 2=S 3.现将△ABF 向上翻折,如图②,已知S 甲=9,S 乙=8,S 丙=7,则△ABC 的面积是______ .15.(本题3分)(2021·浙江·杭州英特外国语学校八年级期中)如图,在△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB =8cm ,则△BED 的周长是______.16.(本题3分)(2022·浙江·浦江县实验中学八年级期中)图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A 、B 、C 在同一直线上,且∠ACD =90°,图2是小床支撑脚CD 折叠的示意图,在折叠过程中,△ACD 变形为四边形ABC'D',最后折叠形成一条线段BD ''.某家装厂设计的折叠床是AB =4cm ,BC =8cm , (1)此时CD 为_________ cm ;(2)折叠时,当AB ⊥BC′时,四边形ABC′D′的面积为_______cm 2 .17.(本题3分)(2022·浙江宁波·八年级期末)如图,△ABC 中,13AB AC ==,24BC =,点D 在BC 上()BD CD >,△AED 与△ACD 关于直线AD 轴对称,点C 的对称点是点E ,AE 交BC 于点F ,连结BE ,CE . 当DE BC ⊥时,∠ADE 的度数为________,CE 的长为________.三、解答题(请写出必要的解题过程,本题共6个小题,共49分)18.(本题6分)(2019·浙江·八年级期中)如图,在△ABC 中,AB =BC ,∠ABC =90°,点E 在BC 上,点F 在AB 的延长线上,且AE =CF .(1)求证:△ABE ≌△CBF .(2)若∠ACF =70°,求∠EAC 的度数.19.(本题8分)(2022·浙江嘉兴·八年级期末)如图,在7×7的正方形网格中,A ,B 两点都在格点上,连结AB ,请完成下列作图:(1)在图1中找一个格点C,使得△ABC是等腰三角形(作一个即可);(2)在图2中找一个格点D,使得△ABD是以AB为直角边的直角三角形(作一个即可).20.(本题8分)(2022·浙江绍兴·八年级期末)如图,在△ABC中,AB=AC,点D在AC 边上(不与A,C重合),连接BD,BD=AB.(1)设∠C=α,∠ABD=β.①当α=50°时,求β.②直接写出β与α之间的等量关系及α的取值范围.(2)若AB=5,BC=6,求AD的长.21.(本题8分)(2022·浙江宁波·八年级期末)如图,M,N分别为锐角AOB∠边OA,OB上的点,把AOB∠所在平面内的点C处.∠沿MN折叠,点O落在AOB(1)如图1,点C 在AOB ∠的内部,若20CMA ∠=︒,50CNB ∠=︒,求AOB ∠的度数.(2)如图2,若45AOB ∠=︒,ON =折叠后点C 在直线OB 上方,CM 与OB 交于点E ,且MN ME =,求折痕MN 的长.(3)如图3,若折叠后,直线MC OB ⊥,垂足为点E ,且5OM =,3ME =,求此时ON 的长.22.(本题9分)(2022·浙江杭州·八年级期末)如图,C 是线段BD 上的一点,以,BC CD 为斜边在线段BD 同侧作等腰直角三角形ABC 和CDE △,过D 作DF DE ⊥于点D ,且DF AB =,连接AF 交BD 于点G ,连接,AE EF .(1)求证:AGB FGD △≌△;(2)请判断AEF 的形状,并说明理由;(3)请写出CAG ∠与DEF ∠的数量关系,并说明理由.23.(本题10分)(2022·浙江宁波·八年级期末)如果平面内一点到三角形的三个顶点的距离中,最长距离的平方等于另两个距离的平方和,则称这个点为该三角形的勾股点,如图1,平面内有一点P 到△ABC 的三个顶点的距离分别为P A 、PB 、PC ,若,PC PA PC PB >>,且222PC PA PB =+,则点P 就是△ABC 的勾股点.⨯的方格纸中,每个小正方形的边长均为1,△ABC的顶点在格点(小(1)如图2,在32正方形的顶点)上,格点P是△ABC的勾股点吗?请说明理由;(2)如图3,△ABC为等边三角形,过点A作AB的垂线,点E在该垂线上,以CE为边在其右侧作等边△CDE,连结AD.①求证:点A是△CDE的勾股点;②若AC=1AE=,直接写出等边△CDE的边长.。
八年级上册数学错题

八年级上册数学错题八年级上册数学错题集一、三角形错题 1:一个三角形的两边长分别为 3 和 6,第三边长是方程x^2 10x + 21 = 0的根,则三角形的周长为()A. 12B. 16C. 12 或 16D. 不能确定解析:解方程x^2 10x + 21 = 0,即(x 3)(x 7) = 0,解得x = 3或x = 7。
当第三边长为 3 时,因为 3 + 3 = 6,不满足三角形两边之和大于第三边,所以舍去。
当第三边长为 7 时,三角形的周长为 3 + 6 + 7 = 16。
故选 B。
错题 2:在\triangle ABC中,\angle A = 50^{\circ},\angle B = \angle C,则\angle B的度数为()A. 65°B. 50°C. 80°D. 40°解析:因为\angle A + \angle B + \angle C = 180^{\circ},且\angle B = \angle C,所以\angle B = (180^{\circ}50^{\circ})÷ 2 = 65^{\circ}故选 A。
二、全等三角形错题 3:如图,已知AB = AD,那么添加下列一个条件后,仍无法判定\triangle ABC ≌ \triangle ADC的是()A. CB = CDB. ∠BAC = ∠DACC. ∠B = ∠D = 90°D.∠BCA = ∠DCA解析:A 选项,因为AB = AD,CB = CD,AC = AC,根据 SSS 可判定\triangle ABC ≌ \triangle ADC。
B 选项,因为AB = AD,∠BAC = ∠DAC,AC = AC,根据 SAS 可判定\triangle ABC ≌ \triangle ADC。
C 选项,因为AB = AD,∠B = ∠D = 90°,AC = AC,根据 HL 可判定\triangle ABC ≌ \triangle ADC。
完整word版,浙教版八年级上学期数学易错题较难题精华题整理

八年级上册数学易错题较难题整理 一、不等式和不等式组1、以下各式中,是一元一次不等式的是〔〕A.5+4>-≤5.-3x≥02、假设m >5,试用m 表示出不等式(5-m)x >1-m 的解集______.x95x1,3、不等式组m的解集是x >2,那么m 的取值范围是().x1(A)m≤2(B)m≥2(C)m≤1 (D)m≥13x 2y p 1,4、关于x ,y 的方程组3yp 的解满足x >y ,求p 的取值范围.4x 12x y 1 3m, 5、方程组x 2y 1 m① 的解满足 x +y <0,求m 的取值范围.②6、适中选择 a 的取值范围,使 <x <a 的整数解:〔1〕 x 只有一个整数解; 〔2〕x 一个整数解也没有.10k x 的不等式k(x5)7、当2(k3)时,求关于 xk 的解集.348、A =2x 2+3x +2,B =2x 2-4x -5,试比拟 A 与B 的大小.9、a 是自然数,关于3x 4 a, x 的不等式组2 的解集是x >2,求a 的值.xx a 0,5个,求a 的取值范围.10、关于x 的不等式组2x的整数解共有 3 111、假设不等式组有解,那么 a 的取值范围是12、假设不等式组无解,那么 a 的取值范围是13、如果关于x 的不等式组 无解,那么不等式组 的解集是14、不等式组的解集是 3<x <a+2,那么a 的取值范围是15、关于x 的不等式组 的解集是 x >﹣1,那么m=116、如果关于x的不等式〔a﹣1〕x<a+5和2x<4的解集相同,那么a的值为17、如图,如果不等式组的整数解仅为1,2,3,那么适合这个不等式组的整数a,b的有序数对〔a,b〕共有个18、在平面直角坐标系中,点A〔x﹣1,2﹣x〕在第四象限,那么实数x的取值范围是19、假设关于x的不等式(a-1)x-2a+2>0的解集为x<2,那么a的值为20、假设不等式组x a2的解集为1x 1,那么(a b)2006=b2x021、a,b为常数,假设ax+b>0的解集是x 1a0解集是,那么的bx322、韩日“世界杯〞期间,重庆球迷一行56人从旅馆乘出租车到球场为中国队加油,现有A、B两个出租车队,A队比B队少3辆车,假设全部安排乘A队的车,每辆坐5人,车不够,每辆坐6人,有的车未坐满;假设全部安排乘B队的车,每辆车坐4人,车不够,每辆车坐5人,有的车未坐满,那么A队有出租车〔〕辆辆辆辆23、某公司到果品基地购置某种优质水果慰问医务工作者,果品基地对购置量在3000kg以上〔含3000kg〕的顾客采用两种销售方案。
浙教版八年级上数学第二章易错题

浙教版八年级上第二章易错题
1. 等腰三角形的底边长为5cm ,一腰上的中线将其周长分成的两部分的差为3cm ,则腰长为( C )
A .2cm 或8cm B.2cm C.8cm D.5cm
2.下列叙述中,错误的是( C )
A .两个内角是70°和40°的三角形是等腰三角形
B .一个外角的平分线平行于一边的三角形是等腰三角形
C .有两个内角不相等的三角形一定不是等腰三角形
D .不同内角的两个外角相等的三角形是等腰三角形
3.下列条件不能判断△ABC 为直角三角形的有( B )
①∠A -∠B=90°②∠A -∠B=∠C ③∠A=2∠B=3∠C ④∠A :∠B :∠C=2:3:5
A .1个 B.2个 C.3个 D.4个
4.在△ABC 中,不能判定是等腰三角形的是 ( D )
A .∠A:∠B:∠C=1:1:3 B.a:b:c=2:2:3
C. ∠B=500 ,∠C=800
D.2∠A=∠B+∠C
5.若等腰三角形的两边长分别为4和9,则周长为( B )
A .17 B.22 C.13 D.17或22
6.用9根火柴棒首尾顺次想接,能搭成 3 个不同形状的三角形,其中是等腰三角形的有 2 个。
7.已知等腰△ABC 中,AB=AC ,D 是BC 边上一点,连接AD ,若△ACD 与△ABD 都是等腰三角形,则∠C 的度数是 45或36 。
8.在直线l 上依次摆放着七个正方形(如图所示)。
已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4,则S 1+S 2+S 3+S 4等于 4 .
l
321S 4S 3S 2S 1。
初中八年级学生数学错题集

说明:1.题集所收录的是八年级()班学生在日常学习中出现的具有代表性、典型性的题目;2.题集里面的题目无顺序、章节规律;3.对于题集里面出现的题目,拥有人应彻底掌握,再次遇到该题或此类题目不应再犯以前的错误.★1.若aa则,6.122________.错解:1.6 正解:6.1.★2.计算:mm m xx xx223122223.说明:本题并无多大难度,但部分学生在看到题目后会被题目吓倒,不敢下手!出现假不会的现象. 解:原式mm m x x x x 22312222322222222223m m m xxx ★3.若32433212nn ,试求n 的值.说明:本题是资料上所谓的开放探究创新题,说明白些就是资料(ˇ?ˇ)想告诉你本题是具有较大难度的!但真的是这样吗?解:32433212nn 48133322nn(这一步反向利用了同底数幂的乘法公式)4313342n(这一步主要是把公因式n23提出来)2,423343434242nnnn★4.计算3210的结果是【】(A )510(B )610(C )510(D )610说明:有学生选择(C )答案,我想他(她)肯定是将同底数幂的乘法运算和幂的乘方运算弄混淆了,两种运算的公式是不一样的.本题考查的是幂的乘方运算公式.另外,还要用到结论:为奇数)为偶数)n A n A Annn(-(解:63232101010,选择(D ).★5.42m a________.说明:这道题当时居然有人做错,而且不止一人,不过我宽恕了他们!出错的地方是没有利用乘法分配律.解:84424)2(442m m m m aaaa(够详细了).★6.设d c b a dc b a,,,,5,4,3,211223344把按从小到大的顺序排列.说明:本题又是所谓的开放探究创新题,没有一个学生做出来.我们若仔细观察,就会发现d c b a ,,,的指数都是11的倍数,所以我们就往这个方向努力. 解:111141144416222a.516444273331111112112221111311333b ca d d cb 我们在任何时候都不要脱离了课本!★7.201020115775________.分析本题考查公式nm nmaaa 的反向利用,即nmnm a aa.解:2010201157757575175577575577557752010201020102010201012010★8.计算:23104.1.解:原式62321096.1104.1.评注:这道题你们真的没有做错,但你们过程写多了. ★9.若5127,n x xxxnmnm求的值.评注:这道题的正确率并不高,都出现了或多或少的问题.本题只能求出n 的值,m 的值是无法求出的. 解:nmnmxxx x.7127127055n nnm nm x xnm nm (题外话:把本章的公式、结论看看、背背)21第10题DABCE21EDAB C★10.如图所示,点B 、C 、E 在同一条直线上,△ABC 和△DCE 均为等边三角形,连结AE 、BD. (1)求证:AE=BD;(2)若把△DCE 绕点C 顺时针旋转一个角度,(1)中的结论还成立吗?请画出图形进行说明. 解:(1)∵△ABC 和△DCE 都是等边三角形∴∠1=∠2,BC=AC,CD=CE ∴∠1+∠ACD=∠2+∠ACD 即∠BCD=∠ACE 在△BCD 和△ACE 中∵CECDACEBCD ACBC∴△BCD ≌△ACE (SAS )∴BD=AE;(2)如图所示,(1)中的结论还成立. 同理可证:△BCD ≌△ACE (SAS )∴BD=AE.评注:这几个学生的胆子有点小,一看这个题目就不敢做了!如果认真思考、耐心看完题目是完全能够解决这个问题的.★11.已知2322,2y x yx y x 求的值.分析数学这一门学科,公式和定理、公理等都是给定的,我们必须在理解的基础上加以记忆,然后再进行一些适当的练习加以巩固,最终把知识变成我们自己的东西,才能灵活运用.当然,在运用这些定理、公式和公理等解决问题的时候,我们还会得出一些有用的、重要的结论,这些结论的总结其实是我们对知识深刻掌握的产物,是我们学会学习的一种表现.每一个学生都要学会总结结论,虽然每个人总结的结论不尽相同,但对每个人自己确是最适用的.另外,对同一个知识点的考查,有各种各样的题目,这些题目我们是做不完的,我们能做的是进行适当的练习,最终掌握相关的知识点! 解:∵2y x ∴2322yxyx1282444)(2552323yx yxyx y x y x 评注就是这么一个简单的题目,当时却没几个学生能做出来.我想他们还是没有深刻掌握相关的公式和结论等所导致的.他们应该对这个问题引起重视. ★12.已知10210510826的计算结果用科学记数法表示为n a an与求,10的值.分析科学记数法的一般形式为na 10,其中n a ,101为正整数.如8106.3、6108.2等都是合法的表示形式,而71036这样的表示却是不正确的!你们几个犯的就是这样的错误!两个用科学记数法表示的数相乘(除)的方法是:系数与系数相乘(除),同底数幂相乘(除).但要保证结果的系数的绝对值大于或等于1而小于10. 解:10210510826109261081080101010258★13.已知c b a xxx xb c x x a 、、求,34722222的值. 分析这是一个关于多项式相等的问题.我之前给你们总结了一个相关的结论:如果两个多项式相等,则它们对应..的系数相等.如果F Ex DxC Bx Ax22,那么.ECD BC A注意:该结论里面各项之间是相加的.解:34722222xx xx b cx x a 324723472234722347222222222bacb ab a xxbacxb a x b axxb ac x b a x b a x x b bx bx ac ax ax 解之得:115cba.★14.若n mxxxx 284,则n m 、的值分别是【】(A )4 , 32 (B )4 , 32(C )4, 32(D )4,32分析这也是一个考查两个多项式相等的题目,出现的错误比较多!注意结论里面各项之间是相加的.解:nmxxxx 2843243243243243248222222nm n m nmxxx xn mxx x x n mx x x x x 正确答案是【 A 】.★15.若20112,01232xxxx 求的值.分析本题主要考查学生依据题目所给的条件,对要求值的式子进行变形处理的能力. 解:∵012x x ∴12x x ∴2011223x x2012201112011201112011222223x x xx x xxx★16.若n mx xx 21的计算结果中不含2x 项和x 项,则m________,n ________. 分析这是一个关于多项式中不含某项的问题,有这样的结论:若一个多项式中不含某一项,则该项的总系数等于0(总系数是指合并同类项之后的系数). 解:nmx xx 210011223223nmm x x nxn mxmxn mx xnx mx x 项项和其计算结果中不含解之得:11nm .★17.。
浙教版八年级数学上册第一章易错题及解析很好讲解

1.1 同位角、内错角、同旁内角选择题1.(2009•桂林)如图,在所标识的角中,同位角是()2.(2006•梧州)有下列命题:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确命题的个数是()3.(2005•南通)已知:如图,直线AB、CD被直线EF所截,则∠EMB的同位角是()6.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是()8.下列四幅图中,∠1和∠2是同位角的是()9.给出下列说法:(1)两条直线被第三条直线所截,同位角相等;(2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;(3)相等的两个角是对顶角;(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.其中正确的有()10.下列所示的四个图形中,∠1和∠2是同位角的是()12.在图中,∠1与∠2是同位角的有()14.下列说法中正确的有()个①对顶角的角平分线成一条直线;②相邻二角的角平分线互相垂直;③同旁内角的角平分线互相垂直;15.如图,∠1与∠2是()16.如图,与∠B是同旁内角的角有()17.如图,∠ADE和∠CED是()18.下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角.其中正确的有()1.2 平行线的判定选择题2.(2008•十堰)如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是()3.(2007•绍兴)学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有()①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.4.(2006•苏州)如图,给出了过直线外一点画已知直线的平行线的方法,其依据是()5.(2005•潍坊)如图,在△ABC中,D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的()6.(2005•双柏县)如图,∠1=∠2,则下列结论一定成立的是()7.(2004•淄博)如图,下列条件中,不能判断直线l1∥l2的是()9.如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.10.下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;13.如图,不能作为判断AB∥CD的条件是()14.如图,在下列结论给出的条件中,不能判定AB∥DF的是()15.如图所示,下列条件中,能判断直线l1∥l2的是()16.如图,点E在BC的延长线上,由下列条件不能得到AB∥CD的是()17.如图,下列条件中,能判定DE∥AC的是()19.如图,下列说法中,正确的是()20.根据图,下列推理判断错误的是()21.如图,∠1=∠2,∠DAB=∠BCD.给出下列结论(1)AB∥DC,(2)AD∥BC,(3)∠B=∠D,(4)∠D=∠DAC.其中,正确的结论有()个.22.如图,点E在BC的延长线上,下列条件中能判断AB∥CD()23.下面的说法正确的个数为()①若∠α=∠β,则∠α和∠β是一对对顶角;②若∠α与∠β互为补角,则∠α+∠β=180°;③一个角的补角比这个角的余角大90°;④同旁内角相等,两直线平行.24.如图,∠1=∠2,由此可得哪两条直线平行()25.如图,不一定能推出a∥b的条件是()26.如图所示,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2=∠6;④∠4+∠7=180°,其中能说明a∥b的条件有()个.27.已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是()28.如图,E、F在线段BC上,AB=DC,AE=DF,BF=CE.下列问题不一定成立的是()填空题29.如图,BC平分∠DBA,∠1=∠2,填空:因为BC平分∠DBA,所以∠1=∠CBA,所以∠2=∠CBA,所以AB∥CD.30.如图是由五个同样的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有5对平行线.1.3 平行线的性质解答题1.如图,已知:AC∥DE,DC∥EF,CD平分∠BCA.求证:EF平分∠BED.(证明注明理由)2.如图①所示,已知直线m∥n,A,B为直线n上的两点,C,D为直线m上的两点.(1)写出图中面积相等的各对三角形△ABC和△ABD,△AOC和△BOD,△CDA和△CDB;(2)如果A,B,C为三个定点,点D在m上移动,那么无论D点移动到任何位置,总有△ABD与△ABC 的面积相等,理由是平行线间的距离处处相等;解决以下问题:如图②所示,五边形ABCDE是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图③所示的形状,但承包土地与开垦荒地的分界小路(即图中的折线CDE)还保留着.张大爷想过E点修一条直路,使直路左边的土地面积与承包时的一样多,右边的土地面积与开垦荒地面积一样多.请你用相关的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)(3)写出设计方案,并在图③中画出相应的图形;(4)说明方案设计的理由.3.如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.4.如图所示,直线AB∥CD,∠1=75°,求∠2的度数.5.已知:如图,直线AE∥BF,∠EAC=28°,∠FBC=50°,求∠ACB的度数.6.如图,已知∠ABC.请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边与点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.7.如图,按虚线剪去长方形纸片的相邻两个角,并使∠1=120°,AB⊥BC,试求∠2的度数.8.已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论.(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是:∠1=∠2;(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是:∠1+∠2=180°;(3)经过上述证明,我们可以得到一个真命题:如果一个角的两边分别平行与另一个角的两边,那么这两个角相等或互补.9.已知:如图,a∥b,∠1=55°,∠2=40°,求∠3和∠4的度数.10.将一副直角三角尺如图放置,已知AE∥BC,求∠AFD的度数.11.如图,已知AB∥CD,现在要证明∠B+∠C=180°,请你从下列三个条件中选择一个合适的条件来进行证明.你选择①①EC∥FB;②∠AGE=∠B;③∠B+∠EGB=180°(写出证明过程)证明:12.如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F,若BE=3,CF=2,试求EF的值.13.已知:如图,AD∥BE,∠1=∠2,求证:∠A=∠E.14.如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC.理由如下:∵AD⊥BC于D,EG⊥BC于G,(已知)∴∠ADC=∠EGC=90°,(垂直的定义),∴AD∥EG,(同位角相等,两直线平行)∴∠1=∠2,(两直线平行,内错角相等)∠E=∠3,(两直线平行,同位角相等)又∵∠E=∠1(已知),∴∠2=∠3(等量代换)∴AD平分∠BAC(角平分线的定义)15.如图,已知:∠1=∠2,∠D=50°,求∠B的度数.16.如图,∠1+∠2=180°,∠3=108°,求∠4的度数.17.如图所示,∠1=∠2,∠3=118°,求∠4的度数.18.如图,已知直线AB∥CD,求∠A+∠C与∠AEC的大小关系并说明理由.19.已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.问CD与AB有什么关系?20.如图所示,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F的关系,并说明理由.21.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,问直线EF与AB有怎样的位置关系?为什么?22.已知:如图BE∥CF,BE、CF分别平分∠ABC和∠BCD,求证:AB∥CD证明:∵BE、CF分别平分∠ABC和∠BCD(已知)∴∠1=∠ABC∠2=∠BCD(角平分线的定义)∵BE∥CF(已知)∴∠1=∠2(两直线平行,内错角相等)∴∠ABC=∠BCD即∠ABC=∠BCD∴AB∥CD(内错角相等,两直线平行)1=∠∠ABC=∠23.完成下列推理说明:如图,已知AB∥DE,且有∠1=∠2,∠3=∠4,试说明BC∥EF.∵AB∥DE(已知)∴∠1=∠3(两直线平行,同位角相等)∵∠1=∠2,∠3=∠4(已知)∴∠2=∠4(等量代换)∴BC∥EF(同位角相等,两直线平行)24.如图,已知∠A=∠F,∠C=∠D.试问BD是否与CE平行?为什么?25.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.26.如图,已知AB∥CD,AE平分∠BAD,DF平分∠ADC,那么AE与DF有什么位置关系?试说明理由.27.已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.证明:∵DG⊥BC,AC⊥BC(已知)∴∠DGB=∠ACB=90°(垂直定义)∴DG∥AC(同位角相等,两直线平行)∴∠2=∠ACD(两直线平行,内错角相等)∵∠1=∠2(已知)∴∠1=∠ACD(等量代换)∴EF∥CD(同位角相等,两直线平行)∴∠AEF=∠ADC(两直线平行,同位角相等)∵EF⊥AB(已知)∴∠AEF=90°(垂直定义)∴∠ADC=90°(等量代换)∴CD⊥AB(垂直定义)28.如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2.(1)用尺规作图作出光线BC经镜面EF反射后的反射光线CD;(2)试判断AB与CD的位置关系;(3)你是如何思考的.29.如图AB∥DE,∠1=∠2,问AE与DC的位置关系,说明理由.30.已知:如图∠1=∠2,当DE∥FH时,(1)证明:∠EDF=∠HFD;(2)CD与FG有何关系?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处。
(如图)这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由。
错误原因:对“怎样调整行驶方向”不能理解到位。
分析与策略:解释题意。
2、在下图中,∠1和∠2是同位角的是 ( ) A .②③ B. ②③④ C. ①②④ D. ①④
错误原因:会不选图1或图2
分析与策略:对图2不能辨析,应把涉及角的所在线画出来,再结合定义判断。
3、在下列给出的条件中,不能判定AB ∥DF 的是 ( ) A .∠A+∠2=180° B. ∠A=∠3 C. ∠1=∠4 D. ∠1=∠A
2
12
1
2
115°
A
错误原因:对所截线不能找到
分析与策略:先找AB 和DF ,再找所截线,再利用定义分析
4、∠1+∠2+∠3=228°,AB ∥DF ,BC ∥DE ,则∠1的度数是( ) A .48° B.96° C. 84° D. 86°
5.已知一等腰三角形三边分别为3x-1、 x+1、5,试求x 的值。
错误原因:一般都是分2种情况讨论对 3x-1= x+1的情况没有考虑 分析与策略:加强分类意识 6.问:如图,下列推理正确吗?
43
21F E D
C
B
A
错误原因:认为正确,对文字概念转化为图形理解不到位
分析与策略:书面语言强化为图形语言 7 1. 已知△ABC 是等边三角形,D,E,F 分别是各边上的一点,且AD=BE=CF.试说明△ DEF 是等边三角形.
错误原因:不能正确书写
分析与策略:做好板书示范并强调
8 .D,E 是△ABC 中BC 上的两点,且BD=DE=EC=AD=AE.求∠ B 与∠ BAC 的度数.
A
B
C
D
2
1 ∵∠1=∠
2 ∴ BD=DC
D
C E
9. 1 .满足下列条件的ΔABC ,不是直角三角形的是:( ) A. B. ∠C=∠A-∠B C.∠A:∠B:∠C=3:4:5 D.a:b:c=12:9:15
10.下列条件中,不能判定两个直角三角形全等的是( ) A.一条直角边和一个角分别相等 B.两条直角边对应相等
C.斜边和一条直角边对应相等
D.斜边和一个锐角对应相等.
10、已知ΔABC 是等腰三角形,BC 边上的高恰好等于 BC 边长的一半,求∠BAC 的度数 错误原因:没有进行分类讨论
分析与策略:强化分类意识,教师作好分类引导和板书练习
11、根据下列条件,判断下面以a 、b 、 c 为边的三角形是不是直角三角形? (1) a=5,b=7,c=8
(3) a=3n ,b=4n ,c=5n (n 是正整数) (4) a: b: c=5:12:13 错误原因:不能正确书写
分析与策略:做好板书示范并强调
12、如图:在△ABC 中AB=4,BC=2,BD=1,CD= 判断下列结论是否正确,并说明理由 (1) CD ⊥AB;
A
D
E C
13、如图,四边形ABCD 中,AB =3,BC=4,CD=12,AD=13, ∠B=90°,求四边形ABCD 的面积.
14、1 .满足下列条件的ΔABC ,不是直角三角形的是:( ) A.
B. ∠C=∠A-
∠B
C.∠A:∠B:∠C=3:4:5
D.a:b:c=12:9:153. 错误原因:选择C
分析与策略:强调3:4:5是边的关系才可以运用逆定理判断
15、如图,EA ⊥AB,BC ⊥AB,AB=AE=2BC,D 为AB 中点,有以下判断:
(1)DE=AC (2)DE ⊥AC
(3) ∠CAB=30° (4) ∠EAF=∠ADE, 其中正确结论的个数是( )
b 2=a 2-
c 2
D
A
C
B
D
B
A C
A.1
B.2
C.3
D.4
16.如果等腰三角形腰上的高线等于腰长的一半,那么这个等腰三角形的顶角度数是( )
A.30°
B.75°
C.150°
D.30°或150° 错误原因:没有进行分类讨论
分析与策略:强化分类意识,教师作好分类引导和板书练习
17、如图,某校A 与公路距离为3000米,又与该公路旁上的某车站D 的距离为5000米,现要在公路边建一个商店C ,使之与该校A 及车站D 的距离相等,则商店与车站的距离约为( ) A.875米 B.3125米 C.3500米 D.3275米 错误原因:计算错误
分析与策略:对于复杂计算准确度低,注重技巧和一步步落实到位的解题方法 18、已知:如图,∠C=90°,BC=AC ,D 、E 分别在BC 和AC 上,且BD=CE ,M 是AB 的中点.
求证:△MDE 是等腰三角形.
F
A
B
C
D
E
错误原因:想不到添辅助线
分析与策略:强调三线合一这条线的添一等于添三的作用
20、已知ΔABC 是等腰三角形,BC 边上的高恰好等于 BC 边长的一半,求∠BAC 的度数。
错误原因:没有进行分类讨论
分析与策略:强化分类意识,教师作好分类引导和板书练习 21.解不等式:3x-2>5x
错误原因:移项没有变符号 分析与策略:强调、学生间找错 22.解不等式:3x+5>5x-2
A
B
C
D
E
M
23、
错误原因:去分母时常数没有乘分母的最小公倍数,去括号时发生错误
分析与策略:强调、学生间找错
16
1213≥+--x
x 解不等式:。
