贝叶斯分析软件WinBUGS1.3中文使用说明

合集下载

winAMS使用手册(中文版详细版本测试工具)

覆盖大师使用指导一、介绍我们十分感谢你对GAIO单元测试工具CoverageMaster-winAMS的兴趣爱好。

CoverageMaster-winAMS是一种对嵌入式软件进行评估和改善的单元测试工具。

这个试用指导包括为初次使用者制定的练习习题。

跟着指导完成练习，使用者会对CoverageMaster-winAMS的基本使用和特点有一个了解。

覆盖大师概述在开始练习之前，首先会出现一个关于覆盖大师的特点及操作的解释。

1、嵌入式软件单元测试工具CoverageMaster-winAMS是一个嵌入式软件单元测试工具。

它通过使用一个MPU仿真器（系统仿真器）执行软件代码（功能）来执行测试。

MPU仿真器（系统仿真器）通过启动实际交叉编译的MPU代码（对象代码）来操作运行。

由于实际目标代码是在仿真环境中使用，它有可能依据目标微处理器去核实项目行为和检查错误。

2、CoverageMaster-winAMS包含以下组件：SSTManager：管理单元测试操作的基本UI应用。

System-G：MPU仿真器（系统仿真器）包括对多种MPU的支持。

WinAMS：单元测试仿真器。

除了这些项目之外，准备测试源文件需要一个交叉编译或者集成开发环境（IDE）。

二、为测试I/O使用CSV格式的文件为了保证正确率的同时提高单元测试的效率CoverageMaster-winAMS在仿真过程中使用CSV格式文件。

单独单元测试设置，以及变量和根函数的输入输出数据都保存在CSV文件中。

因此，使用CSV文件让目标源代码中不必一定包含专用测试代码或者输入数据。

下面的图片阐明了CoverageMaster-winAMS单元测试的流程。

首先，交叉编译代码被加载到MPU仿真器。

代码必须附上可执行对象代码（被拆开的中间级对象代码不能被使用）下一步，为了测试基础函数（如上文所示）生成一个CSV文件。

文件里有函数信息类似函数名称，输入变量，输出变量，测试条件，以及测试数据（测试容器）。

应用R软件bmeta程序包实现贝叶斯Meta分析与Meta回归

•方法学•应用R软件b m e ta程序包实现贝叶斯M eta分析与M e ta回归石丰豪\孟蕊\芮明军、马爱霞〃1. 中国药科大学国际医药商学院（南京211198)2. 中国药科大学药物经济学评价研究中心（南京211198)【摘要】R软件bm eta程序包是一款通过调用IAGS软件来实现贝叶斯M eta分析和M eta回归的程序包，该程序基于“马尔可夫链-蒙特卡罗”（MCMC)算法来合并不同类型资料（二分类、连续和计数）的各种效应量 (OR、M D和IRR)。

该程序包具有命令函数参数少、提供模型丰富、绘图功能强大、易于理解和掌握等优点。

本文将结合实例介绍展示bmeta程序包实现贝叶斯Meta分析与M eta回归的完整操作流程。

【关键词】R语言；bmeta程序包；贝叶斯Meta分析；M eta回归Perform ing Bayesian m eta-analysis and m eta-regression using bmeta package in R softwareSHIFenghao1，M ENGRui1，RUIMingjun1，M AAixia121. School of I nternational Pharmaceutical Business, China Pharmaceutical University, Nanjing 211198, P.R.China2. Pharmacoeconomic Evaluation Research Center, China Pharmaceutical University, Nanjing211198, P.R.China Correspondingauthor:MAAixia,Email:*****************【Abstract】The R software bmeta package is a package that implements Bayesian meta-analysis and meta-regression by invoking JAGS software. The program is based on the Markov Chain Monte Carlo (MCMC) algorithm to combine various effect quantities (OR, MD and IRR) of different types of data (dichotomies, continuities and counts). The package has the advantages of fewer command function parameters, rich models, powerful drawing function, easy of understanding and mastering. In this paper, an example is presented to demonstrate the complete operation flow of bmeta package to implement bayesian meta-analysis and meta-regression.【Key words 】R language; bmeta package; Bayesian meta-analysis; Meta-regressionM eta分析作为一种整合单个研究效应量进行证据合并的常用统计方法，在循证医学中占有重要地位叭贝叶斯M eta分析是基于贝叶斯统计发展起来的一种的M eta分析方法，主要采用“马尔科夫链一蒙特卡罗 ”（Markov chain Monte C arlo, MCMC)方法，因其在处理复杂随机效应、分层结构或是稀疏数据时比频率学M eta分析方法更有优势，目前越来越受欢迎。

Meta分析系列之五_贝叶斯Meta分析与WinBUGS软件_董圣杰

无法给出恰当的解析解，求解这些积分成为其发展的障碍，因此一直停留在理论阶段。20世纪90年代起MCMC方法为样本 x=(x1,x2,...,xn)的联合条件密度函数，也即似然函数；
广泛应用于贝叶斯统计，成功地解决了限制贝叶斯统计发
展的高维积分运算问题，为贝叶斯统计带来了革命性的突破，进而使其在更多的领域得到应用。在医学领域，贝叶斯方法广泛应用于不同的数据类型统计分析中，如遗传数据、纵向数据、生存数据及缺少数据等；同时也应用于不同的研究方法，如临床试验实施[4]循证医学[5]等。
表1 常用共轭先验分布
总体分布二项分布泊松分布指数分布正态分布（方差已知）正态分布（均数已知）
参数成功概率均值均值的倒数均值方差
共轭先验分布
贝塔分布 beta(α,β) 伽马分布 Ga(α,λ) 伽马分布 Ga(α,λ) 正态分布N(μ,τ2) 倒伽马分布 IGa(α,λ)
③采用Jeffreys原则确定无信息先验分布：Jeffreys对先
中国循证心血管医学杂志2012年10月第4卷第5期 Chin J Evid Based Cardiovasc Med,Oct,2012,Vol.4,No.5
• 397 •
②加载数据（Load data）：将光标移到数据的语句前面的list处，选中list字样，再点击Specification Tool对话框的 load data，若对模型描述的语法正确的话，则窗口底部左下角会提示data loaded（图5）。
验分布的确定做出重大贡献，利用Fisher信息矩阵给出了确
定无信息先验分布的一般方法。Jeffreys原则包括两部分：
一是对先验分布应有一个合理的要求；二是给出一个具体

winbugs操作方法(已翻译)

[例] (引自于W inBUGS软件帮助手册中的Volum I) : George et al (1993) 讨论了分层模型的贝叶斯分析(Bayesian analysis of hierarchical mod2els) 。

其中,第一层采用了共轭先验分布。

该例考虑了相关的10个发电站的水泵,假设发生故障的水泵个数服从Poisson分布,即x i ～Poisson (θi t i ) , i = 1, 2, ⋯10.其中,θi 表示水泵i的发生故障率, t i 表示水泵运行时间的长度(单位:千小时) ,数据见下表:故障率的共轭先验分布假设为θi ～Gamma (α,β) , i = 1, 2, ⋯10.George et al (1993) 对超参数α和β先验假设为α～Exponential (1. 0) β～Gamma (0. 1, 1. 0)他们给出了β的后验分布,但β的标准后验分布无法给出。

因而,他们使用Gibbs samp ler模拟得到α的后验密度。

以上表达式可用贝叶斯图建模方法表示成如下有向关系图(图1) ,在WinBUGS中称作Doodle模型。

(注意:α用alpha表示, x i 用x [ i ]表示,λi用lambda[ i ]表示,其余类似。

启动W inBUGS14,会出现两个窗口,关闭其中一个(L icence Agreement窗口) ,你会看到如下Win2BUGS主窗口(图2) :窗口简单明了,W inBUGS主窗口和W indows常用窗口结构类似,关闭、最小化等基本操作相同。

WinBUGS主窗口最上面一行为标题栏( heading line ) , 下一行是菜单栏(menuheading line ) ———有File, Tools, Edit, Attributes,Info, Model, Inference, Op tions, Doodle, Map,Window, Help———12个菜单,最下面一行是状态栏( status line) 。

WinBUGS在统计分析中的应用

WinBUGS在统计分析中的应用作者：齐韬第一部分开篇词首先非常感谢COS论坛提供了这样一个良好的平台，敝人心存感激之余，也打算把一些学习心得拿出来供大家分享，文中纰漏之处还请各位老师指正。

下面我将以WinBUGS的统计应用为题，分几次来谈一谈WinBUGS这个软件。

其中会涉及到空间数据的分析、GeoBUGS的使用、面向R及SPLUS的接口包R2WinBUGS的使用、GIS与统计分析等等衍生出的话题。

如有问题，请大家留下评论，我会调整内容，择机给予回答。

第一节什么是WinBUGS?WinBUGS对于研究Bayesian统计分析的人来说，应该不会陌生。

至少对于MCMC方法是不陌生的。

WinBUGS (Bayesian inference Using Gibbs Sampling）就是一款通过MCMC方法来分析复杂统计模型的软件。

其基本原理就是通过Gibbs sampling和Metropolis算法，从完全条件概率分布中抽样，从而生成马尔科夫链，通过迭代，最终估计出模型参数。

引入Gibbs抽样与MCMC的好处是不言而喻的，就是想避免计算一个具有高维积分形式的完全联合后验概率公布，而代之以计算每个估计参数的单变量条件概率分布。

具体的算法思想，在讲到具体问题的时候再加以叙述，在此不过多论述。

就不拿公式出来吓人了（毕竟打公式也挺费劲啊）。

第二节为什么要用WinBUGS?第一、因为同类分析软件中它做得最好。

同类的软件：OpenBUGS、JAGS等在成熟度、灵活性以及兼容性方面和它相比还有一定距离。

在处理spatial data的方面，它采用了Gibbs 抽样和MCMC的方法，在模型支持方面又具有极大的灵活性，较之名声大噪的GeoR包，虽然也实现了bayesian的手法，但是灵活性还是不及WinBUGS。

第二、因为它免费。

免费的东西总有吸引人之处。

第三、有各色的R包为WinBUGS实现了针对R的、SPLUS的、Matlab的软件接口。

WinQSB简介及操作说明

WinQSB 简介WinQSB1.0 是在 QSB （ DOS 版）的基础上，升级开发的运行于 WINDOWS 操作系统的管理运筹学应用软件包。

WinQSB1.0 （下简称为 WinQSB1.0 ）的技术成熟，运行稳定，操作方便，对硬件要求较低，非常适合初学者上机使用。

一、系统程序菜单简介在程序安装包里找到 SETUP.EXE 文件双击后开始安装，安装时可选择安装位置，默认安装是在 C 盘的根目录 WinQSB 文件夹里。

安装成功后，系统开始菜单程序栏里会生成 WinQSB 应用程序菜单选项，如图 1 所示。

图 1 WinQSB 系统程序菜单从 WinQSB 系统的菜单选项，可以看出其可用于求解以下管理与决策科学领域的问题：1．Acceptance Sampling Analysis （缩写为 ASA ，接受抽样分析）主要用于各种抽样分析、抽样方案的设计以及假设分析；2．Aggregate Planning （缩写为 AP ，综合计划编制）用于求解具有多时期正常排班、加班、分时段、转包生产量、需求量、储存费用、生产费用等复杂的整体综合生产计划的编制方法，求解思路是将问题归结到求解线性规划模型或运输模型；3．Decision Analysis （缩写为 DA ，决策分析）用于确定型与风险型决策、贝叶斯决策、决策树、二人零和对策、蒙特卡罗模拟等问题的求解；4．Dynamic Programming （缩写为 DP ，动态规划）主要用于最短路问题、背包问题、生产与储存等类问题的求解；5．Facility Location and Layout （缩写为 FLL ，设备场地布局）应用于设备场地设计、功能布局、线路均衡布局等类问题的求解；6．Forecasting and Linear Regression （缩写为 FC ，预测与线性回归）可进行简单平均、移动平均、加权移动平均、线性趋势移动平均、指数平滑、多元线性回归、 Holt-Winters 季节叠加与乘积算法的运算；7．Inventory Theory and System （缩写为 ITS ，存储论与存储系统）用于经济订货批量模型、批量折扣模型、单时期随机模型、多时期动态储存模型、储存控制系统（各种储存策略）等类问题的求解；8．Job Scheduling （缩写为 JOB ，作业调度）用于零件加工排序、流水线车间加工排序等；9．MarKov Process （缩写为 MKP ，马尔科夫过程）用于求解马尔科夫动态过程问题；10．Material Requirements Planning （缩写为 MRP ，物料需求计划）用于求解和分析产品物料的供应链计划，尤其是在自动化生产线中应用广泛；11．Network Modeling （缩写为 NET ，网络模型）用于求解运输、指派、最大流、最短路、最小生成树、货郎担等问题；12．Nonlinear Programming （缩写为 NLP ，非线性规划）用于有（无）条件约束、目标函数或约束条件非线性以及目标函数与约束条件都非线性等类规划的求解与分析；13．PERT-CPM （网络计划）用于路径求解、计划评审技术分析、网络优化、工程完工时间模拟、绘制甘特图与网络图等，有的版本该菜单名为 Project Scheduling ；14．Quality Control Charts （缩写为 QCC ，质量管理控制图）用于分析基于统计数据的产品和服务质量分析与控制；15．Queuing Analysis （缩写为 QA ，排队分析）用于各种排队模型的求解与性能分析、各种分布模型求解、灵敏度分析、服务能力分析、成本分析等；16．Queuing System Simulation （缩写为 QSS ，排队系统模拟）用于进行各种排队系统的仿真模拟与研究分析；17．Linear and Integer Programming （缩写为 LP-ILP ，线性规划与整数线性规划）用于求解线性规划、整数规划、对偶问题等，可进行灵敏度分析、参数分析。

winbugs操作方法(已翻译)

[例] (引自于W inBUGS软件帮助手册中的Volum I) : George et al (1993) 讨论了分层模型的贝叶斯分析(Bayesian analysis of hierarchical mod2els) 。

其中,第一层采用了共轭先验分布。

因而,他们使用Gibbs samp ler模拟得到α的后验密度。

以上表达式可用贝叶斯图建模方法表示成如下有向关系图(图1) ,在WinBUGS中称作Doodle模型。

(注意:α用alpha表示, x i 用x [ i ]表示,λi用lambda[ i ]表示,其余类似。

如何使用贝叶斯网络工具箱

如何使用贝叶斯网络工具箱2004-1-7版翻译：By 斑斑（QQ：23920620）联系方式：banban23920620@安装安装Matlab源码安装C源码有用的Matlab提示创建你的第一个贝叶斯网络手工创建一个模型从一个文件加载一个模型使用GUI创建一个模型推断处理边缘分布处理联合分布虚拟证据最或然率解释条件概率分布列表（多项式）节点Noisy-or节点其它（噪音）确定性节点Softmax（多项式分对数）节点神经网络节点根节点高斯节点广义线性模型节点分类 / 回归树节点其它连续分布CPD类型摘要模型举例高斯混合模型PCA、ICA等专家系统的混合专家系统的分等级混合QMR条件高斯模型其它混合模型参数学习从一个文件里加载数据从完整的数据中进行最大似然参数估计先验参数从完整的数据中（连续）更新贝叶斯参数数据缺失情况下的最大似然参数估计（EM算法）参数类型结构学习穷举搜索K2算法爬山算法MCMC主动学习结构上的EM算法肉眼观察学习好的图形结构基于约束的方法推断函数联合树消元法全局推断方法快速打分置信传播采样（蒙特卡洛法）推断函数摘要影响图 / 制定决策DBNs、HMMs、Kalman滤波器等等安装安装Matlab代码1.下载FullBNT.zip文件。

2.解压文件。

3.编辑"FullBNT/BNT/add_BNT_to_path.m"让它包含正确的工作路径。

4.BNT_HOME = 'FullBNT的工作路径';5.打开Matlab。

6.运行BNT需要Matlab版本在V5.2以上。

7.转到BNT的文件夹例如在windows下，键入8.>> cd C:\kpmurphy\matlab\FullBNT\BNT9.键入"add_BNT_to_path"，执行这个命令。

添加路径。

添加所有的文件夹在Matlab的路径下。

10.键入"test_BNT"，看看运行是否正常，这时可能产生一些数字和一些警告信息。

winQSB教程

即：1Æ4Æ7Æ8，最短路长：8
6.winQSB求解最小部分树问题
[例]求解最小部分树问题：
v2 2
3 2
5
v3 28
v1
3
v4
4 v5
v8
2 4
2 4 v6
23 v7
第 1 步：生成表格选择“程序ÆwinQSBÆNetwork ModelingÆFileÆNew Program”，弹出对话框：
决策变量 x1=6.67,x2=10 目标值：G1=16.67，G2=10，G3=6.67
3.winQSB求解分配问题
[例]求解最小化分配问题：
⎡2 15 13⎤ C = ⎢⎢10 4 14⎥⎥
⎢⎣9 14 16⎥⎦
第 1 步：生成表格选择“程序ÆwinQSBÆNetwork ModelingÆFileÆNew Program”弹出对话框：
第 3 步：求解从系统菜单选择“Solve and AnalyzeÆSolve the Problem”，弹出对话框：
选择左侧“发点”和右侧“收点”，单击“求解（Solve）”生成如下运行结果：
即：
v 2•
13(11) 4(0)
v1•
9(9) •v3
5(5)
•v5
6(4)
5(4)
9(9)
v4 •
问题题头（Problem Title）：没有可不输入；变量数（Number of Variables）：2；约束条件数（Number of Constraints）：3；目标优化条件（Objective Criterion）：最小（Minimization）数据输入格式（Data Entry Format）：矩阵式电子表格式（Spreadsheet Matrix Form）变量类型（Default Variable Type）：非负连续变量选择第 1 个单选按钮（Nonnegative continuous）；非负整型变量选择第 2 个单选按钮（Nonnegative integer）；

WinBUGS软件应用

WinBUGS软件应⽤计算机应⽤?ＷｉｎＢＵＧＳ软件应⽤＊孟海英１刘桂芬２罗天娥２ＷｉｎＢＵＧＳ（ＢａｙｅｓｉａｎＩｎｆｅｒｅｎｃｅＵｓｉｎｇＧｉｂｂｓＳａｍｐｌｉｎｇ）是英国剑桥公共卫⽣研究所的ＭＲＣＢｉｏｓｔａｔｉｓｔｉｃｓＵｎｉｔ推出的⽤马尔可夫链⼀蒙特卡罗（ＭａｒｋｏｖｃｈａｉｎＭｏｎｔｅＣａｒｌｏ，ＭＣＭｃ）⽅法进⾏贝叶斯推断的专⽤软件包。

它可⽅便地对许多常⽤或复杂模型（如分层模型，交叉设计模型、空间和时间作为随机效应的⼀般线性混合模型，潜变量模型，脆弱模型，应变量的测量误差，协变量，截尾数据，限制性估计，缺失值问题）和分布进⾏Ｇｉｂｂｓ抽样，还可⽤简单的有向图模型（ｄｉｒｅｃｔｅｄｇｒａｐｈｉｃａｌｍｏｄｅｌ）进⾏直观的描述，并给出参数的Ｇｉｂｂｓ抽样动态图，⽤Ｓｍｏｏｔｈｉｎｇ⽅法得到后验分布的核密度估计图、抽样值的⾃相关图及均数和置信区间的变化图等，使抽样结果更直观、可靠。

Ｇｉｂｂｓ抽样收敛后，可很⽅便地得到参数后验分布的均数、标准差、９５％置信区间和中位数等信息。

这⾥介绍ＷｉｎＢＵＧＳ软件的基本使⽤⽅法。

⾸先从⽹上下载ＷｉｎＢＵＧＳ软件，安装后即可打开软件主界⾯，点击ｆｉｌｅ—ｎｅｗ，即可根据研究内容创建模型，模型格式如下：ｍｏｄｅｌ｛ｆｏｒ（ｊｉｎ１：Ｔｒｔ）｛ａｌｐｈａ．Ｔｒｔ［ｊ］～ｄｎｏｒｍ（０．０，１．０Ｅ⼀４）｝ｄ?Ｔｒｔ＜⼀ａｌｐｈａ．Ｔｒｔ［１］⼀ａｌｐｈａ．Ｔｒｔ［２］Ｔｒｔ．ｂａｒ＜⼀ｍｅａｎ（Ｔｒｔ［］）｝ｍｏｄｅｌ为模型指⽰语，由｛｝括起来的语句为模型的具体内容，ｆｏｒ语句表⽰循环语句，括号内为循环变量及循环次数。

每个循环语句同样要⽤｛｝括起来才完整。

“～”表⽰随机变量的分布，左边为变量，右边为分布，ｄｎｏ矗表⽰服从正态分布，括号内为该分布的两个参数。

“＜⼀”表⽰变量间的逻辑函数关系，其左右符号含义同“～”。

逻辑关系可⽤逻辑函数如“ｍｅａｎ”，＊：⼭西省⾃然科学基⾦资助（２００５１０９１）１．北京市朝阳区疾病预防控制中⼼２．⼭西医科⼤学卫⽣统计教研室（０３０００１）?３７５?“ｓｕｍ”等或⼀般的运算符号表⽰。

贝叶斯专业软件WinBUGS

alpha beta
Constant node
theta[i] t[i]
Deterministic node Plate
lambda[i]
x[i] for(i IN 1 : N)
Model specification through BUGS language
model { for (i in 1 : N) { theta[i] ~ dgamma(alpha, beta) lambda[i] <- theta[i] * t[i] x[i] ~ dpois(lambda[i]) } alpha ~ dexp(1) beta ~ dgamma(0.1, 1.0) }
– – DoodleBUGS, Direct graphics BUGS language
ቤተ መጻሕፍቲ ባይዱ
• •
Format data and specify initial values Tutorial
The pumps data
PUMP 1 2 3 4 5 6 7 8 9 10
• •
ti 94.5 15.7 62.9 126 5.24 31.4 1.05 1.05 2.1 10.5
How do we use WinBUGS?
Educational Example: Pumps: conjugate Gamma-Poisson hierarchical model • The pumps data • Gamma-Poisson hierarchical model • Model specification in WinBUGS
How do we install WinBUGS?
• Obtaining the key for unrestricted use by registration at

WinQSB软件简介

1 WinQSB软件简介Q S B2.0是Q ua nt i ta ti v e S y st em s fo r Bu s in es s的缩写，早期版本的操作系统在D OS下运行，Wi nQ SB是在W i nd ow s操作系统下运行。

W i nQ SB是一种教学软件，对于非大型的问题一般都能计算，较小的问题还能演示中间的计算过程，特别适合多媒体课堂教学。

该软件可应用于管理科学、决策科学、运筹学及生产运作管理等领域的求解问题，见表1。

表 12 WinQSB操作简介（1）安装与起动安装Wi n QS B软件后，在系统程序中自动生成W i nQ SB应用程序，用户根据不同的问题选择子程序，操作简单方便，与一般W i nd ow s的应用程序操作相同。

进入某个子程序后，第1项工作就是建立新问题或打开已有的数据文件。

每一个子程序系统都提供了典型的例题数据文件，用户可先打开已有数据文件，观察数据输入格式，系统能够解决哪些问题，结果的输出格式等内容。

例如，打开线性规划文件LP.LP P，系统显示图1所示的界面.图一（2）与Of fi ce文档交换数据从电子表(E xc el)或wo rd文档中复制数据到W i nQ SB：电子表中的数据可以复制到W in QS B中，方法是先选中要复制电子表中单元格的数据，点击复制或按“C tr l+C”键，然后在Wi n QS B的电子表格编辑状态下选中要粘贴的单元格，点击粘贴或按“C t rl+V”键完成复制。

注意：粘贴过程与在电子表中粘贴有区别，在W i nQ SB中选中的单元格应与在电子表中选中的单元格（行列数）相同，否则只能复制部分数据。

例如在电子表中复制3行10列，见表2，在W i nQ SB 中选中3行5列粘贴，则只能复制3行5列的数据，见表 3表 2表 3。

MATLAB与WinBUGS在贝叶斯方法测量不确定度评定中的应用

斯测量不确定度评定的关键是复杂计算实现；蒙特卡罗仿真是实现贝叶斯估计的最常用的有
效的方法１。
１ＭＡＢＬＡＢ在贝叶斯方法测量不确定度中的应用
贝叶斯估计的原理是，由先验信息使对未知参数有一定的认识，然后通过试验获取样本，利
分布ｈ（１￣ｌｘ）可以根据先验分布与样本信息确定，
如公式（１）。
不确定度来源繁多、相关性难以确定，复杂的传
递函数与仪器软件不稳定性等口。贝叶斯方法测
（Ｉ）ｏｃ（） × ｌ（ｘ）
式（１）中
ＷｉｎＢＵＧＳｓｏｆｔｗａｒｅ．
Ｋｅｙｗｏｒｄｓ：Ｂａｙｅｓｉａｎａｐｐｒｏａｃｈ；ｕｎｃｅｔａｒｉｎｔｙ；ｍｅｓｕａｒｅｍｅｎｔ
０引言
随着计算机技术运用于测控领域，传统的仪
器正在向计算机化的方向发展。随着基于计算机
用样本对参数的先验分布进行调整，得到后验分
布。设被测量的密度函数为ｆ（ｘ），以被测量的
均值为待估参数，根据贝叶斯理论，的后验
的现代仪器结构１３益复杂，传统的测量不确定度
评定方法面临着巨大的挑战，主要表现在：测量
ＵｎｃｅｒｔａｉｎｔｙＡｓｓｅｓｓｍｅｎｔ
ＹＵＡＮＭｉｎ（１．ＧｕａｎｇｚｈｏｕＣｏｌｌｅｇｅｏｆＳｏｕｔｈＣｈｉｎａＵｎｉｖｅｒｓｉｔｙｏｆＴｅｃｈｎｏｌｏｔｙ，Ｇｕａｎｇｚｈｏｕ５１０８００，Ｃｈｉｎａ）

WINQSB软件介绍

例：
max Z 4.5 x1 3.8 x2 9.5 x3 2 x4 1.5 x5 4x1 6 x2 12 x3 8 x4 x5 20 5 x 4 x 12 x 3x 8 x 15 2 3 4 5 1 x x x 2 1 2 3 x j 0 或 1 ( j 1, 2, ,5)
u12=8
u25=6
u42=2 u45=4
5
u57=9
f
1
u13=7
u23=3
4 3
u65=7
7
u67=8
f
u34=4 u46=3 u36=1
6
2、用WINQSB软件解决网络问题中的最短经问题
1
1
2 10 4 5 2 4
2
5
6 9 5 3 4 8
3
3
7
6
6
7
8
求从1到8的最短路径
§5
用WINQSB软件解决决策分析问题
约束条件：
§1
用WINQSB软件解决线性规划问题—例3
Wyndor Glass 公司生产高质量的玻璃产品，包括窗和玻璃门，拥有3个工厂。铝框架和硬件在工厂1制造，木质框
架在工厂2生产，玻璃生产和产品组装在工厂3完成。现有两
种产品：8英尺玻璃门（产品1），4*6英尺框架（产品2）。产品1需要工厂1和工厂3的生产能力，分别是1小时和3小时，
资源设
产品备
Ⅰ 1 4 0
Ⅱ 2 0 4
拥有量 8台时 16 kg 12 kg
原材料 A 原材料 B
例1的数学模型
目标函数：
max z 2 x1 3 x2 s.t. x1 2 x2 8 4 x1 16 4 x2 12 x1 , x2 0

winqsb使用方法

ProjectScheduling
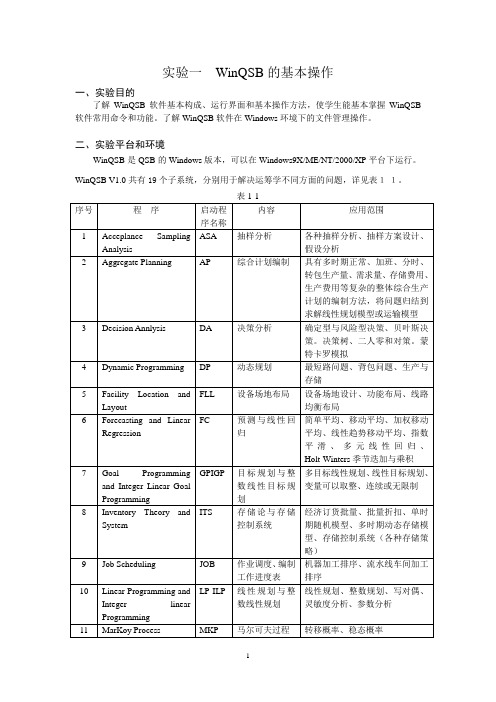
PERT-CPM
网络计划
关键路径法、计划评审技术、网络的优化、工程完工时间模拟、绘制特图与网络图
16
Queqing Programming
QP
二次规划
求解线性约束、目标函数是二次型的一种非线性规划问题，变量可以取整数
17
Queuing Analysis
QA
排队分析
各种排队模型的求解与性能分析、15种分布模型、灵敏度分析、服务能力分析、成本分析
MRP
物料需求计划
物料需求计划的编制、成本核算
13
Network Modeling
Net
图论模型
运输、指派、最大值、最短路、最小支撑树、货郎担等问题
14
Nonlinear Programming
NLP
非线性规划
有（无）条件约束、目标函数或约束条件非线性，目标函数与约束条件都非线性等规划的求解与分析
15
Exit：退出
Edit菜单，如图1-9
图1-9
需要注意的是除了剪切复制等的第一部分和Undo的第二部分外，其它部分的子菜单会由于所选程序的不同而不同。具体见后面实验中各问题的详细解法。
Format菜单，如图1-10
图1-10
Number：选择数字的显示格式。选择此菜单，弹出窗口如图1-11
图1-11
6
Forecasting and Linear Regression
FC
预测与线性回归
简单平均、移动平均、加权移动平均、线性趋势移动平均、指数平滑、多元线性回归、Holt-Winters季节迭加与乘积
7
Goal Programmingand Integer Linear Goal Programming

Winbugs基础操作及使用

Y~ D（μ） μ= α0+ α1*X1+…… αn*Xn αi ~ Di（）

1- 确定模型 2- 输入数据 3- 运行模型 4- 模型初始化 5- generate burn-in values 6- 确定被模拟的参数 7- 运行 8- 检查收敛性及列出结果

The end!
设定DIC之后，再次update模型。单击DIC，则显示此模型的DIC值。DIC主要用来比较模型的优劣，其绝对值没有太大意义。
点击任务栏help，下拉菜单点击examples Vol 1或者 examples Vol 2，则跳出案例菜单，里面包含各种已有的Bayesian模型代码及样本数据。
模型基本结构 (model) 数据 (list) 模型初始化参数 (list)
选中model，然后点击check model，检查模型是否有错。
一，Check model后左下方如果显示 Model is syntactically correct, 则表明模型运行通过，没有语法错误。
二，选中list（即原始data），点击load data，导入数据。左下方显示 data loaded，则数据导入成功。三，点击compile，编译模型
总体信息经典统计样本信息贝叶斯统计
先验信息
联合密度与先验分布，样本分布间的关系
p( , y) p( ) p( y | )
p( , y ) p( ) p( y | ) p( | y) p( y ) p( y )

经典统计模型

Bayesian模型
Y=α0+ α1*X1+…… αn*Xn
李艳丽

R软件R2WinBUGS程序包在网状Meta分析中的应用

R软件R2WinBUGS程序包在网状Meta分析中的应用R软件R2WinBUGS程序包在网状Meta分析中的应用Meta分析是一种系统性综合评价的方法，用于整合多个独立研究的结果，从而获得更准确、稳定的估计结果。

而网状Meta分析则是在传统Meta分析的基础上发展起来的一种方法，能够应对大规模、复杂的研究领域，对于推动科研进展具有重要意义。

在进行网状Meta分析时，统计软件的选择和运用显得尤为关键，而R软件作为一种开源的数据分析工具，以其强大的功能和灵活性在科学研究中广泛应用。

本文将介绍R软件中的R2WinBUGS程序包，并探讨其在网状Meta分析中的应用。

R2WinBUGS是一款在R环境中调用WinBUGS程序的工具包，WinBUGS则是一种基于贝叶斯统计的软件，结合了R和WinBUGS的功能，可以方便地进行网状Meta分析。

首先，我们需要了解一些基础概念。

在Meta分析中，我们通常会使用效应量来衡量研究的结果，常见的效应量包括风险比（Risk Ratio，RR）、比率比（Rate Ratio，RaR）、标准化均值差（Standardized Mean Difference，SMD）等。

而在网状Meta分析中，除了效应量，我们还需要考虑网络图、贝叶斯方法等因素。

R2WinBUGS程序包提供了一系列函数，方便用户进行网状Meta分析的数据准备和分析。

首先，我们可以使用函数“network.data”将研究的原始数据转化为适合进行网状Meta分析的格式。

函数中的参数包括研究的名称、各组别的名称、各组别的样本量、事件数量等，可以方便地生成一个数据框。

接着，我们需要使用函数“network.graph”将数据框转化为网络图，以便更好地展示研究之间的关系。

函数中的参数包括研究名称、颜色、形状等，可以根据需要进行调整。

通过这两个函数，我们可以更好地理解各个研究之间的关系，为后续的分析提供基础。

接下来，我们可以利用贝叶斯方法进行效应量的估计和模型拟合。

winbugs1.3简易使用说明

Step 2
在 update 方塊中鍵入想要 generate posterior samples 的樣本數，如：3000 筆，按下 update 鍵，則 iteration 將由 0 run 至 3000，WinBugs 左下角的狀態列將會顯示 generate posterior samples 所需的時間，如：’ updates took 1 s ’，執行完後關閉 Update Tool 視窗。 refresh=100 表示在 iteration 方塊中，將會以 100 為單位，顯示正在 update
不會有任何作用，亦即更改其中的數值皆不會對 output 有任何影響，在此先省略不談，之後在 simulated value 時將會對這些指令之功用提出簡略的說明。
……
5. Update the Model Step 1 在功能表列中點選：Model → Update，開啟 Update Tool 視窗
例：Seeds: random effects logistic regression (下圖為 WinBugs Examples 中 Seeds 的例子)
Model： ri ~ Binomial(pi, ni) logit(pi) = α0 + α1x1i + α2x2i + α12x1ix2i + bi bi ~ Normal(0, τ)
Step 6 關閉 Specification Tool 視窗
3
4. Monitor 感興趣的參數 Step 1 在功能表列中點選：Inference → Samples，開啟 Sample Monitor Tool 視窗
Step 2
在 node 方塊中輸入想要 monitor 的參數，如：在 Seeds 範例中，欲 generate posterior samples 的參數為：alpha0、alpha1、alpha2、alpha12、tau、sigma，此步驟便是在 node 方塊中輸入這些參數名稱，每輸入一個參數名稱，便按一次 set 鍵，待完全鍵入後，關閉此視窗。 ps:由於此步驟之作用僅在 monitor 參數，視窗中之 beg、end、thin 或 chains 皆