2012-2017年高考文科数学真题汇编:三角函数高考题老师版
2017年全国高考文科数学试题分类汇编之三角函数

2017年全国高考文科数学试题分类汇编之三角函数一、选择题:1.函数f(x)=sin(2x+π/3)的最小正周期为(B)2π2.已知cosx=π/3,则cos2x=(D)-1/23.已知sinα-cosα=4/√2,则sin2α=(C)9/74.函数y=3sin2x+cos2x最小正周期为(B)π5.函数f(x)=5sin(x+π/11)+6的最大值为(A)5/36.设函数f(x)=cos(x+π/3),则下列结论错误的是(D)f(x)的一个零点为x=8π/37.设函数f(x)=2sin(ωx+ϕ),x∈R,其中ω>0,|ϕ|<π,若f(x)的最小正周期大于2π,则(C)ω=2π/3,ϕ=-π/38.函数y=sin2x/(1-cosx)的部分图像大致为(B)V形二、填空题:9.若XXX(α-π/4)=1/6,则tanα=(5/6)10.已知α∈(0,π/2),tanα=2,则cos(α-π/4)=(1/√10)11.函数f(x)=2cosx+sinx的最大值为(2√5)12.在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sinα=1/3,则sinβ=(-1/3)三、解答题:13.已知函数f(x)=3cos(2x-π/4)。
1)f(x)的最小正周期为π/2;2)当x∈[-π/3,π/2]时,f(x)≥-2√2/3.14.已知向量a=(cosx,sinx),b=(3,-3),x∈[0,π]。
1)若a//b,则x=π/4或5π/4;2)记f(x)=a·b,当x=π/4时,f(x)取最大值6√2;当x=5π/4时,f(x)取最小值-6√2.15.已知函数f(x)=sin2x-cos2x-2/3sinxcosx(x∈R)。
1)f(2π)的值为-8/3;2)f(x)的最大值为1,当x=π/4或5π/4时取到;f(x)的最小值为-5/3,当x=3π/4或7π/4时取到.求函数f(x)的最小正周期和单调递增区间。
2012年高考数学 05 三角函数试题解析 教师版 文

2012年高考试题解析数学(文科)分项版之专题05 三角函数--教师版一、选择题:1.(2012年高考某某卷文科5)设命题p :函数sin 2y x =的最小正周期为2π;命题q :函数cos y x =的图象关于直线2x π=对称.则下列判断正确的是(A)p 为真 (B)q ⌝为假 (C)p q ∧为假 (D)p q ∨为真2.(2012年高考某某卷文科8)函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为(A)23- (B)0 (C)-1 (D)13--3.(2012年高考某某卷文科6)已知sin cos 2αα-=α∈(0,π),则sin 2α=(A) -1 (B) 22- (C)22(D) 1 【答案】A 【解析】2sin cos 2,(sin cos )2,sin 21,ααααα-=∴-=∴=-故选A【考点定位】本题主要考查三角函数中的倍角公式以及转化思想和运算求解能力,属于容易题.4. (2012年高考某某卷文科6)在△ABC 中,若∠A =60°,∠B =45°,BC =32AC =A.333325. (2012年高考新课标全国卷文科9)已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ= (A )π4 (B )π3 (C )π2 (D )3π46. (2012年高考某某卷文科6)把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A【解析】由题意,y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即解析式为y=cosx+1,向左平移一个单位为y=cos (x-1)+1,向下平移一个单位为y=cos (x-1),利用特殊点,02π⎛⎫⎪⎝⎭变为1,02π⎛⎫- ⎪⎝⎭,选A. 【考点定位】本题主要考查了三角函数中图像的性质,具体考查了在x 轴上的伸缩变换,在x 轴、y 轴上的平移变化,利用特殊点法判断图像的而变换。
2012年高考数学文科试题分类汇编:三角函数

2012年高考数学文科试题分类汇编:三角函数2012高考文科试题解析分类汇编:三角函数一、选择题 1.【2012高考安徽文7】要得到函数的图象,只要将函数的图象(A)向左平移1个单位(B)向右平移1个单位(C)向左平移个单位(D)向右平移个单位【答案】C 左+1,平移 2.【2012高考新课标文9】已知ω>0,,直线和是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ= (A)π4 (B)π3 (C)π2 (D)3π4 【答案】A 【命题意图】本题主要考查三角函数的图像与性质,是中档题. 【解析】由题设知, = ,∴ =1,∴ = (),∴ = (),∵ ,∴ = ,故选A. 3.【2012高考山东文8】函数的最大值与最小值之和为 (A) (B)0 (C)-1 (D) 【答案】A 考点:三角函数图像与性质解析: ,函数定义域为[0,9],所以,根据三角函数图像最大值为,最小值为,最大值与最小值之和为 4.【2012高考全国文3】若函数是偶函数,则(A)(B)(C)(D)【答案】C 【命题意图】本试题主要考查了偶函数的概念与三角函数图像性质,。
【解析】由为偶函数可知,轴是函数图像的对称轴,而三角函数的对称轴是在该函数取得最值时取得,故,而,故时,,故选答案C。
5.【2012高考全国文4】已知为第二象限角,,则(A)(B)(C)(D)【答案】A 【命题意图】本试题主要考查了同角三角函数关系式的运用以及正弦二倍角公式的运用。
【解析】因为为第二象限角,故,而,故,所以,故选答案A。
6.【2012高考重庆文5】(A)(B)(C)(D)【答案】C 【解析】:【考点定位】本题考查三角恒等变化,其关键是利用7.【2012高考浙江文6】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A 【命题意图】本题主要考查了三角函数中图像的性质,具体考查了在x轴上的伸缩变换,在x轴、y轴上的平移变化,利用特殊点法判断图像的而变换。
2012年高考真题文科数学汇编4:三角函数.pdf

一、主要内容:东胜神州傲来国有一花果山,山顶一石,产下一猴。
石猴求师学艺,得名孙悟空,学会七十二般变化,一个筋斗去可行十万八千里,自称"美猴王"。
他盗得定海神针,化作如意金箍棒,可大可小,重一万三千五百斤。
又去阴曹地府,把猴属名字从生死簿上勾销。
玉帝欲遣兵捉拿,太白金星建议,把孙悟空召入上界,做弼马温。
当猴王得知弼马温只是个管马的小官后,便打出天门,返回花果山,自称"齐天大圣"。
玉帝派天兵天将捉拿孙悟空,美猴王连败巨灵神、哪咤二将。
孙悟空又被请上天管理蟠桃园。
他偷吃了蟠桃,搅闹了王母娘娘的蟠桃宴、盗食了太上老君的金丹,逃离天宫。
玉帝又派天兵捉拿。
孙悟空与二郎神赌法斗战,不分胜负。
太上老君用暗器击中孙悟空,猴王被擒。
经刀砍斧剁,火烧雷击,丹炉锻炼,孙悟空毫发无伤。
玉帝请来佛祖如来,才把孙悟空压在五行山下。
如来派观音菩萨去东土寻一取经人,来西天取经,劝化众生。
观音点化陈玄奘去西天求取真经。
唐太宗认玄奘做御弟,赐号三藏。
唐三藏西行,在五行山,救出孙悟空。
孙悟空被带上观世音的紧箍,唐僧一念紧箍咒,悟空就头疼难忍。
师徒二人西行,在鹰愁涧收伏白龙,白龙化作唐僧的坐骑。
在高老庄,收伏猪悟能八戒,猪八戒做了唐僧的第二个徒弟;在流沙河,又收伏了沙悟净,沙和尚成了唐僧的第三个徒弟。
师徒四人跋山涉水,西去求经。
观音菩萨欲试唐僧师徒道心,和黎山老母、普贤,文殊化成美女,招四人为婿,唐僧等三人不为所动,只有八戒迷恋女色,被菩萨吊在树上。
在万寿山五庄观,孙悟空等偷吃人参果,推倒仙树。
为了赔偿,孙悟空请来观音,用甘露救活了仙树。
白骨精三次变化,欲取唐僧,都被悟空识破。
唐僧不辨真伪,又听信八戒谗言,逐走悟空,自己却被黄袍怪拿住。
八戒、沙僧斗不过黄袍怪,沙僧被擒,唐僧被变成老虎。
八戒在白龙马的苦劝下,到花果山请转孙悟空,降伏妖魔,师徒四人继续西行。
乌鸡国国王被狮精推人井内淹死,狮精变作国王。
2012年高考试题分项解析数学(文科)——专题05三角函数(教师版)

2012年高考试题分项解析数学(文科)专题05 三角函数(教师版)一、选择题:1.(2012年高考山东卷文科5)设命题p :函数sin 2y x =的最小正周期为2π;命题q :函数cos y x =的图象关于直线2x π=对称.则下列判断正确的是 (A)p 为真 (B)q ⌝为假 (C)p q ∧为假 (D)p q ∨为真2.(2012年高考山东卷文科8)函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为(A)2- (B)0 (C)-1 (D)1-3.(2012年高考辽宁卷文科6)已知sin cos αα-=,α∈(0,π),则sin 2α=(A) -1 (B) (C) (D) 1 【答案】A【解析】2sin cos (sin cos )2,sin 21,ααααα-=∴-=∴=-故选A【考点定位】本题主要考查三角函数中的倍角公式以及转化思想和运算求解能力,属于容易题.4. (2012年高考广东卷文科6)在△ABC 中,若∠A =60°,∠B =45°,BC =AC =A. B. C.D.5. (2012年高考新课标全国卷文科9)已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ= (A )π4 (B )π3 (C )π2 (D )3π46. (2012年高考浙江卷文科6)把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A【解析】由题意,y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即解析式为y=cosx+1,向左平移一个单位为y=cos (x-1)+1,向下平移一个单位为y=cos (x-1),利用特殊点,02π⎛⎫⎪⎝⎭变为1,02π⎛⎫- ⎪⎝⎭,选A. 【考点定位】本题主要考查了三角函数中图像的性质,具体考查了在x 轴上的伸缩变换,在x 轴、y 轴上的平移变化,利用特殊点法判断图像的而变换。
2012年高考试题数学文科汇编4三角函数

2012高考试题分类汇编:三角函数一、选择题1.【2012高考安徽文7】要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象 (A ) 向左平移1个单位 (B ) 向右平移1个单位 (C ) 向左平移 12个单位 (D ) 向右平移12个单位 【答案】C2.【2012高考新课标文9】已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=(A )π4 (B )π3 (C )π2 (D )3π4 【答案】A3.【2012高考山东文8】函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为(A)2 (B)0 (C)-1 (D)1--【答案】A4.【2012高考全国文3】若函数()sin ([0,2])3x f x ϕϕπ+=∈是偶函数,则=ϕ (A )2π(B )32π (C )23π (D )35π【答案】C5.【2012高考全国文4】已知α为第二象限角,3sin 5α=,则sin2α= (A )2524- (B )2512- (C )2512 (D )2524【答案】B6.【2012高考重庆文5】sin 47sin17cos30cos17-(A )B )12-(C )12(D 【答案】C7.【2012高考浙江文6】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A8.【2012高考上海文17】在△ABC 中,若222sin sin sin A B C +<,则△ABC 的形状是( ) A 、钝角三角形 B 、直角三角形 C 、锐角三角形 D 、不能确定【答案】A9.【2012高考四川文5】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )(1)10B 、10C 、10D 、15【答案】B10.【2012高考辽宁文6】已知sin cos αα-=α∈(0,π),则sin 2α=(A) -1 (B)- (D) 1 【答案】A【点评】本题主要考查三角函数中的倍角公式以及转化思想和运算求解能力,属于容易题。
20122017年高考文科数学真题汇编基本初等函数老师版

11、(2016年山东)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3-1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f(x +12)=f(x —12).则f(6)=( D ) (A )-2 (B )-1 (C )0 (D )212、(2016年天津)已知)(x f 是定义在R 上的偶函数,且在区间)0,(-∞上单调递增,若实数a 满足)2()2(|1|->-f f a ,则a 的取值范围是( C )(A ))21,(-∞(B )),23()21,(+∞-∞Y (C ))23,21( (D )),23(+∞13、(2016年全国I 卷)若a>b>0,0<c<1,则( B )(A )log a c <log b c (B )log c a <log c b (C )a c <b c (D )c a >c b 14、(2016年全国I 卷高考)函数y =2x 2–e |x |在[–2,2]的图像大致为( D )(A )(B )(C )(D )15、(2016年全国II 卷)下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是( D )(A )y =x (B )y =lg x (C )y =2x (D )1y x=16、(2016年全国III 卷)已知4213332,3,25a b c ===,则( A )(A) b a c << (B)a b c <<(C) b c a << (D) c a b <<17、(2016年江苏)函数y =232x x --的定义域是 []3,1- .18、(2016年江苏)设f (x )是定义在R 上且周期为2的函数,在区间[ −1,1)上,,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R 若59()()22f f -= ,则(5)f a 的值是 25- . 19、(2016年四川高考)若函数f (x )是定义R 上的周期为2的奇函数,当0<x<1时,f (x )=x 4,则f (25-)+f (2)= -2 。
2012-2017年高考文科数学真题汇编:基本初等函数老师版

11、(2016年山东)已知函数f(x )的定义域为R.当x <0时,f(x )=x 3—1;当-1≤x ≤1时,f(-x )= —f(x );当x >12时,f (x +12)=f(x —12)。
则f (6)=( D ) (A )—2 (B )-1 (C)0 (D )212、(2016年天津)已知)(x f 是定义在R 上的偶函数,且在区间)0,(-∞上单调递增,若实数a 满足)2()2(|1|->-f f a ,则a 的取值范围是( C )(A ))21,(-∞(B)),23()21,(+∞-∞(C ))23,21((D )),23(+∞13、(2016年全国I 卷)若a 〉b>0,0〈c<1,则( B )(A )log a c <log b c (B )log c a <log c b (C)a c 〈b c (D )c a >c b 14、(2016年全国I 卷高考)函数y =2x 2–e |x |在[–2,2]的图像大致为( D )(A )(B )(C )(D)15、(2016年全国II 卷)下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是( D )(A )y =x (B )y =lg x (C )y =2x (D )1y x=16、(2016年全国III 卷)已知4213332,3,25a b c ===,则( A )(A) b a c << (B )a b c <<(C) b c a << (D) c a b <<17、(2016年江苏)函数y =232x x --的定义域是 []3,1- 。
18、(2016年江苏)设f (x )是定义在R 上且周期为2的函数,在区间[ −1,1)上,,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R 若59()()22f f -= ,则(5)f a 的值是 25- 。
2012-2017年高考文科数学真题汇编:三角函数高考题老师版

()1求tan4πα⎛⎫+⎪⎝⎭的值;()2求2sin2sin sin cos cos21ααααα+--的值.【答案】(1)3-;(2)1.3、三角函数的图象和性质9、(2016年四川高考)为了得到函数y=sin)3(π+x的图象,只需把函数y=sinx的图象上所有的点( A )(A)向左平行移动3π个单位长度 (B) 向右平行移动3π个单位长度(C) 向上平行移动3π个单位长度 (D) 向下平行移动3π个单位长度10.(2014大纲)设sin33,cos55,tan35,a b c=︒=︒=︒则( C )A.a b c>>B.b c a>>C.c b a>>D.c a b>>11.(2014福建文) 将函数siny x=的图象向左平移2π个单位,得到函数()y f x=的函数图象,则下列说法正确的是( D )()()()()....-022A y f xB y f xC y f x xD y f xπππ==⎛⎫=== ⎪⎝⎭是奇函数的周期为的图象关于直线对称的图象关于点,对称12.(2012山东文)函数2sin(09)63xy xππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为( A )(A)23- (B)0 (C)-1 (D)13--13、(2013山东)将函数y=sin (2x +ϕ)的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为 ( B ) (A )34π (B ) 4π (C )0 (D ) 4π- 14.(2013山东)函数y =x cos x +sin x 的图象大致为( D )15.(2016年全国I 卷)将函数y =2sin (2x +π6)的图像向右平移14个周期后,所得图像对应的函数为( D )(A )y =2sin(2x +π4) (B )y =2sin(2x +π3) (C )y =2sin(2x –π4) (D )y =2sin(2x –π3)16.(2013沪春招)既是偶函数又在区间(0 )π,上单调递减的函数是( B ) (A )sin y x = (B )cos y x = (C )sin 2y x = (D )cos 2y x =【简解】根据偶函数,只能在BD 中选择,(0,π)上单调减,只能选B17.(2013四川)函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是( A )A .2,-π3B .2,-π6C .4,-π6D .4,π318.(2014四川理) 为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点( A )A 、向左平行移动12个单位长度 B 、向右平行移动12个单位长度 C 、向左平行移动1个单位长度 D 、向右平行移动2个单位长度19.(2016年全国II 卷)函数=sin()y A x ωϕ+的部分图像如图所示,则( A )(A )2sin(2)6y x π=- (B )2sin(2)3y x π=-(C )2sin(2+)6y x π= (D )2sin(2+)3y x π=20.(2013天津文) 函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为( B ) A .-1 B .-22 C.22D .0 21.(2014浙江) 为了得到函数x x y 3cos 3sin +=的图象,可以将函数x y 3sin 2=的图象( C )A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 22.(2012大纲)已知α为第二象限角,3sin cos 3αα+=,则cos2α= A .53-B .59- C .59 D .53【简解】原式两边平方可得121sin 2sin 233αα+=⇒=- α是第二象限角,因此sin 0,cos 0αα><,所以2215cos sin (cos sin )133αααα-=--=-+=-225cos 2cos sin (cos sin )(cos sin )3ααααααα∴=-=+-=-23.(2013福建文)将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,若)(),(x g x f 的图象都经过点)23,0(P ,则ϕ的值可以是( ) A .35π B .65π C .2π D .6π[,] 34[,]43[,]34[,]34f(x-1)=f(|x-1|)f(t)≤1/2,得到3/4;代入x天津文) 将函数f(x)=sin xω(其中)的图象向右平移个单位长度,所得图象经过点),则ω的最小值是的最小正值是____38π____. 34.(2012福建文)函数)4sin()(π-=x x f 的图象的一条对称轴是( C )A .4π=x B .2π=x C .4π-=x D .2π-=x35.(2014江苏)函数)42sin(3π+=x y 的最小正周期为 π 。
2012高考文科试题解析分类汇编4(三角函数)

2012高考文科试题解析分类汇编:三角函数一、选择题1.【2012高考安徽文7】要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象 (A ) 向左平移1个单位 (B ) 向右平移1个单位 (C ) 向左平移 12个单位 (D ) 向右平移12个单位【答案】Cc o s 2c o s (2y x y x =→=+左+1,平移122.【2012高考新课标文9】已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=(A )π4 (B )π3 (C )π2 (D )3π4【答案】A【命题意图】本题主要考查三角函数的图像与性质,是中档题.【解析】由题设知,πω=544ππ-,∴ω=1,∴4πϕ+=2k ππ+(k Z ∈), ∴ϕ=4k ππ+(k Z ∈),∵0ϕπ<<,∴ϕ=4π,故选A.3.【2012高考山东文8】函数2sin (09)63x y x ππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为(A)2- (B)0 (C)-1(D)1--【答案】A考点:三角函数图像与性质 解析:1262==ππT ,函数定义域为[0,9],所以,根据三角函数图像最大值为2)5(=f ,最小值为3)0(-=f,最大值与最小值之和为2- 4.【2012高考全国文3】若函数()sin ([0,2])3x f x ϕϕπ+=∈是偶函数,则=ϕ(A )2π(B )32π (C )23π (D )35π【答案】C【命题意图】本试题主要考查了偶函数的概念与三角函数图像性质,。
【解析】由[]()sin(0,2)3x f x ϕϕπ+=∈为偶函数可知,y 轴是函数()f x 图像的对称轴,而三角函数的对称轴是在该函数取得最值时取得,故3(0)sin13()3322f k k k Z ϕϕπππϕπ==±⇒=+⇒=+∈,而[]0,2ϕπ∈,故0k =时,32πϕ=,故选答案C 。
2012年高考文科数学解析分类汇编:三角函数(逐题详解)

2012年高考文科数学解析分类汇编:三角函数一、选择题1 .(2012年高考(重庆文))sin47sin17cos30cos17-()A.2-B.12-C.12D.22 .(2012年高考(浙江文))把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是3 .(2012年高考(天津文))将函数()sin(0)f x xωω=>的图像向右平移4π个单位长度,所得图像经过点3(,0)4π,则ω的最小值是()A.13B.1 C.53D.24 .(2012年高考(四川文))如图,正方形ABCD的边长为1,延长BA至E,使1AE=,连接EC、ED则sin CED∠=()A B C D5 .(2012年高考(上海文))在ABC∆中,若BA222sinsinsin<+()A.钝角三角形. B.直角三角形. C.锐角三角形. D.不能确定.6 .(2012年高考(陕西文))设向量a=(1.cosθ)与b=(-1, 2cosθ)垂直,则cos2θ等于A2B12C.0 D.-17 .(2012年高考(山东文))函数2sin(09)63xy xππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为()A.2B.0 C.-1 D.1--8 .(2012年高考(辽宁文))已知sin cos αα-=,α∈(0,π),则sin 2α= ( )A .-1B .-C D .19 .(2012年高考(课标文))已知ω>0,0ϕπ<<,直线x =4π和x =54π是函数()s i n()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=( )A .π4B .π3C .π2D .3π410.(2012年高考(江西文))若sin cos 1sin cos 2αααα+=-,则tan2α=( )A .-34B .34C .-43D .4311.(2012年高考(湖南文))在△ABC 中,BC=2,B =60°,则BC 边上的高等于( )A B 33C 36+D 12.(2012年高考(湖北文))设ABC ∆的内角,,,A B C 所对的边分别为,,a b c ,若三边的长为连续的三个正整数,且A B C >>,320cos b a A =,则sin :sin :sin A B C 为 ( )A .4∶3∶2B .5∶6∶7C .5∶4∶3D .6∶5∶413.(2012年高考(广东文))(解三角形)在ABC ∆中,若60A ∠=︒,45B ∠=︒,BC =,则AC = ( )A .B .CD 14.(2012年高考(福建文))函数()sin()4f x x π=-的图像的一条对称轴是( )A .4x π=B .2x π=C .4x π=-D .2x π=-15.(2012年高考(大纲文))已知α为第二象限角,3sin 5α=,则sin 2α= ( )A .2425-B .1225-C .1225 D .242516.(2012年高考(大纲文))若函数[]()sin (0,2)3x f x ϕϕπ+=∈是偶函数,则ϕ= ( )A .2π B .23π C .32π D .53π17.(2012年高考(安徽文))要得到函数cos(21)y x =+的图象,只要将函数cos 2y x =的图象( )A .向左平移1个单位B .向右平移1个单位C .向左平移12个单位 D .向右平移12个单位 二、填空题18.(2012年高考(重庆文))设△ABC 的内角A B C 、、 的对边分别为a b c 、、,且1cos 4a b C ==1,=2,,则sin B =____ 19.(2012年高考(陕西文))在三角形ABC 中,角A,B,C 所对应的长分别为a,b,c,若a=2 ,B=6π则b=______ 20.(2012年高考(福建文))在ABC ∆中,已知60,45,BAC ABC BC ∠=︒∠=︒,则AC =_______.21.(2012年高考(大纲文))当函数sin (02)y x x x π=≤<取最大值时,x =____.22.(2012年高考(北京文))在△ABC 中,若3a =,3b =3A π∠=,则C ∠的大小为___________.三、解答题23.(2012年高考(重庆文))(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)设函数()sin()f x A x ωϕ=+(其中0,0,A ωπϕπ>>-<< )在6x π=处取得最大值2,其图象与轴的相邻两个交点的距离为2π(I)求()f x 的解析式; (II)求函数426cos sin 1()()6x x g x f x π--=+的值域.24.(2012年高考(浙江文))在△ABC 中,内角A,B,C 的对边分别为a,b,c,且(1)求角B 的大小;(2)若b=3,sinC=2sinA,求a,c 的值.25.(2012年高考(天津文))在ABC ∆中,内角,,A B C 所对的分别是,,a b c .已知2,,cos 4a c A ==-.(I)求sin C 和b 的值; (II)求cos(2)3A π+的值.26.(2012年高考(四川文))已知函数21()cossin cos 2222x x x f x =--. (Ⅰ)求函数()f x 的最小正周期和值域;(Ⅱ)若()f α=求sin 2α的值.27.(2012年高考(上海文))海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为y 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰在失事船的正南方向12海里A 处,如图. 现假设:①失事船的移动路径可视为抛物线24912x y =;②定位后救援船即刻沿直线匀速前往救援;③救 援船出发t 小时后,失事船所在位置的横坐标为t 7.(1)当5.0=t 时,写出失事船所在位置P 的纵坐标. 若此时 两船恰好会合,求救援船速度的大小和方向;(2)问救援船的时速至少是多少海里才能追上失事船?28.(2012年高考(陕西文))函数()sin()16f x A x πω=-+(0,0A ω>>)的最大值为3, 其图像相邻两条对称轴之间的距离为2π, (1)求函数()f x 的解析式; (2)设(0,)2πα∈,则()22f α=,求α的值.29.(2012年高考(山东文))(本小题满分12分)在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知sin (tan tan )tan tan B A C A C +=. (Ⅰ)求证:,,a b c 成等比数列;(Ⅱ)若1,2a c ==,求△ABC 的面积S .30.(2012年高考(辽宁文))在ABC ∆中,角A 、B 、C 的对边分别为a ,b ,c .角A ,B ,C成等差数列.(Ⅰ)求cos B 的值;(Ⅱ)边a ,b ,c 成等比数列,求sin sin A C 的值.31.(2012年高考(课标文))已知a ,b ,c 分别为ABC ∆三个内角A ,B ,C 的对边,sin sin c C c A -. (Ⅰ)求A ;(Ⅱ)若a =2,ABC ∆求b ,c .32.(2012年高考(江西文))△ABC 中,角A,B,C 的对边分别为a,b,c.已知3cos(B-C)-1=6cosBcosC. (1)求cosA;(2)若a=3,△ABC 的面积为22求b,c.33.(2012年高考(湖南文))已知函数()sin()(,0,02f x A x x R πωϕωω=+∈><<的部分图像如图5所示.(Ⅰ)求函数f(x)的解析式; (Ⅱ)求函数()()()1212g x f x f x ππ=--+的单调递增区间.34.(2012年高考(湖北文))设函数22()sin cos cos ()f x x x x x x R ωωωωλ=+-+∈的图像关于直线x π=对称,其中,ωλ为常数,且1(,1)2ω∈ (1) 求函数()f x 的最小正周期; (2) 若()y f x =的图像经过点(,0)4π,求函数()f x 的值域.35.(2012年高考(广东文))(三角函数)已知函数()cos 46x f x A π⎛⎫=+⎪⎝⎭,x ∈R ,且3f π⎛⎫⎪⎝⎭(Ⅰ)求A 的值;(Ⅱ)设α、0,2πβ⎡⎤∈⎢⎥⎣⎦,4304317f απ⎛⎫+=- ⎪⎝⎭,28435f βπ⎛⎫-= ⎪⎝⎭,求()cos αβ+的值.36.(2012年高考(福建文))某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.(1)2sin 13cos17sin13cos17︒+︒-︒︒ (2)2sin 15cos15sin15cos15︒+︒-︒︒ (3)2sin 18cos12sin18cos12︒+︒-︒︒ (4)2sin (18)cos48sin(18)cos48-︒+︒--︒︒ (5)2sin (25)cos55sin(25)cos55-︒+︒--︒︒ Ⅰ 试从上述五个式子中选择一个,求出这个常数Ⅱ 根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.37.(2012年高考(大纲文))ABC ∆中,内角A.B.C 成等差数列,其对边,,a b c 满足223b ac =,求A .38.(2012年高考(北京文))已知函数(sin cos )sin 2()sin x x xf x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递减区间.39.(2012年高考(安徽文))设ABC ∆的内角,,A B C 所对的边为,,a b c ,且有2s i n c o s s i n c o s c o s sB A AC A C =+ (Ⅰ)求角A 的大小;(II) 若2b =,1c =,D 为BC 的中点,求AD 的长.2012年高考文科数学解析分类汇编:三角函数参考答案一、选择题 1. 【答案】:C【解析】:sin 47sin17cos30sin(3017)sin17cos30cos17cos17-+-=sin 30cos17cos30sin17sin17cos30sin 30cos171sin 30cos17cos172+-====【考点定位】本题考查三角恒等变化,其关键是利用473017=+2. 【答案】A【命题意图】本题主要考查了三角函数中图像的性质,具体考查了在x 轴上的伸缩变换,在x 轴、y 轴上的平移变化,利用特殊点法判断图像的而变换. 【解析】由题意,y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即解析式为y=cosx+1,向左平移一个单位为y=cos(x-1)+1,向下平移一个单位为y=cos(x-1),利用特殊点,02π⎛⎫⎪⎝⎭变为1,02π⎛⎫- ⎪⎝⎭,选A. 3. 【解析】函数向右平移4π得到函数)4sin()4(sin )4()(ωπωπωπ-=-=-=x x x f x g ,因为此时函数过点)0,43(π,所以0)443(sin =-ππω,即,2)443(πωπππωk ==-所以Z k k ∈=,2ω,所以ω的最小值为2,选D.4. [答案]B1010cos 1sin 10103ECED 2CD-EC ED CED cos 1CD 5CB AB EA EC 2AD AE ED 11AE ][22222222=∠-=∠=∙+=∠∴==++==+=∴=CED CED )(,正方形的边长也为解析[点评]注意恒等式sin 2α+cos 2α=1的使用,需要用α的的范围决定其正余弦值的正负情况.5. [解析] 由条件结合正弦定理,得222c b a <+,再由余弦定理,得0cos 2222<=-+abc b a C ,所以C 是钝角,选A.6. 解析:0a b ⋅=,212cos 0θ-+=,2cos 22cos 10θθ=-=,故选C.7. 解析:由90≤≤x 可知67363ππππ≤-≤-x ,可知]1,23[)36sin(-∈-ππx ,则2sin [63x y ππ⎛⎫=-∈ ⎪⎝⎭,则最大值与最小值之和为2答案应选A.8. 【答案】A【解析】2sin cos (sin cos )2,sin 21,ααααα-=∴-=∴=- 故选A 【点评】本题主要考查三角函数中的倍角公式以及转化思想和运算求解能力,属于容易题.9. 【命题意图】本题主要考查三角函数的图像与性质,是中档题.【解析】由题设知,πω=544ππ-,∴ω=1,∴4πϕ+=2k ππ+(k Z ∈), ∴ϕ=4k ππ+(k Z ∈),∵0ϕπ<<,∴ϕ=4π,故选A.10. 【答案】B【解析】主要考查三角函数的运算,分子分母同时除以cos α可得tan 3α=-,带入所求式可得结果. 11. 【答案】B【解析】设AB c =,在△ABC 中,由余弦定理知2222cos AC AB BC AB BC B =+-⋅⋅,即27422cos60c c =+-⨯⨯⨯,2230,(-3)(1)c c c c --=+即=0.又0, 3.c c >∴=设BC 边上的高等于h ,由三角形面积公式11sin 22ABC S AB BC B BC h == ,知1132sin 60222h ⨯⨯⨯=⨯⨯ ,解得2h =. 【点评】本题考查余弦定理、三角形面积公式,考查方程思想、运算能力,是历年常考内容.12. D 【解析】因为,,a b c 为连续的三个正整数,且>>A B C ,可得a b c >>,所以2,1=+=+a c b c ①;又因为已知320cos =b a A ,所以3cos 20bA a=②.由余弦定理可得222cos 2+-=b c a A bc③,则由②③可得2223202b b c aa b c +-=④,联立①④,得2713600--=c c ,解得4=c 或157=-c (舍去),则6=a ,5=b .故由正弦定理可得,sin :sin :sin ::6:5:4==A B C a b c .故应选D.【点评】本题考查正、余弦定理以及三角形中大角对大边的应用.本题最终需求解三个角的正弦的比值,明显是要利用正弦定理转化为边长的比值,因此必须求出三边长.来年需注意正余弦定理与和差角公式的结合应用.13.解析:B.由正弦定理,可得sin 45sin60AC BC=︒︒,所以2AC == 14. 【答案】C【解析】把4x π=-代入后得到()1f x =-,因而对称轴为4x π=-,答案C 正确.【考点定位】此题主要考查三角函数的图像和性质,代值逆推是主要解法. 15.答案A【命题意图】本试题主要考查了同角三角函数关系式的运用以及正弦二倍角公式的运用.【解析】因为α为第二象限角,故cos 0α<,而3sin 5α=,故4cos 5α==-,所以24sin 22sin cos 25ααα==-,故选答案A.16.答案C【命题意图】本试题主要考查了偶函数的概念与三角函数图像性质,. 【解析】由[]()sin(0,2)3x f x ϕϕπ+=∈为偶函数可知,y 轴是函数()f x 图像的对称轴,而三角函数的对称轴是在该函数取得最值时取得,故3(0)sin13()3322f k k k Z ϕϕπππϕπ==±⇒=+⇒=+∈,而[]0,2ϕπ∈,故0k =时,32πϕ=,故选答案C. 17. 【解析】选C cos 2cos(21)y x y x =→=+左+1,平移12二、填空题 18. 【答案】【解析】11,2,cos 4a b C ===,由余弦定理得22212cos 1421244c a b ab C =+-=+-⨯⨯⨯=,则2c =,即B C=,故sin B ==. 【考点定位】利用同角三角函数间的基本关系式求出sin B 的值是本题的突破点,然后利用正弦定理建立已知和未知之间的关系,同时要求学生牢记特殊角的三角函数值.19.解析:由余弦定理得,2222cos 4b a c ac B =+-=,所以2b =. 20.【解析】由正弦定理得sin 45sin 60AC AC =⇒=︒︒【考点定位】本题考查三角形中的三角函数,正弦定理,考醒求解计算能力.21.答案:56π 【命题意图】本试题主要考查了三角函数性质的运用,求解值域的问题.首先化为单一三角函数,然后利用定义域求解角的范围,从而结合三角函数图像得到最值点.【解析】由sin 2sin()3y x x x π==-由502333x x ππππ≤<⇔-≤-<可知22sin()23x π-≤-≤ 当且仅当332x ππ-=即116x π=时取得最小值,32x ππ-=时即56x π=取得最大值.22. 【答案】2π【解析】222cos 232b c a A c bc+-=⇒=而sin sin c a C A =,故sin 12C C π=⇒=. 【考点定位】本小题主要考查的是解三角形,所用方法并不唯一,对于正弦定理和余弦定理此二者会其一都可以得到最后的答案.三、解答题23. 【答案】:(Ⅰ)6πϕ=(Ⅱ)775[1,)(,]4422231cos 1(cos )22x x =+≠因2cos [0,1]x ∈,且21cos 2x ≠故()g x 的值域为775[1,)(,]44224. 【命题意图】本题主要考查了正弦定理、余弦定理、三角形内角和定理,考查考生对基知识、基本技能的掌握情况.【解析】(1) bsinA=acosB,由正弦定理可得sin sin cos B A A B =,即得tan B =3B π∴=.(2)sinC=2sinA,由正弦定理得2c a=,由余弦定理2222cos b a c ac B =+-,229422cos3a a a a π=+-⋅,解得a =2c a ∴==25.解:(1)在ABC ∆中,由cos A =,可得sin A =,又由s i n s i n a c A C =及2a =,c =可得sin 4C =由22222cos 20a b c bc A b b =+-⇒+-=,因为0b >,故解得1b =.所以sin 14C b == (2)由2cos 4A =-,sin 4A =,得23cos 22cos 14A A =-=-,7sin 2sin cos A A A ==所以321cos(2)cos 2cossin 2sin333A A A πππ-++=-=26. [解析](1)由已知,f(x)=212x cos 2x sin 2x cos2-- 21sinx 21cosx 121--+=)( )(4x cos 22π+= 所以f(x)的最小正周期为2π,值域为⎥⎥⎦⎤⎢⎣⎡-22,22, (2)由(1)知,f(α)=,)(10234cos 22=+πα 所以cos(534=+πα). 所以)()(42cos 22cos 2sin πααπα+-=+-=257251814cos 212=-=+-=)(πα, [点评]本小题主要考查三角函数的性质、两角和的正(余)弦公式、二倍角公式等基础知识,考查运算能力,考查化归与转化等数学思想.27. [解](1)5.0=t 时,P 的横坐标x P =77=t,代入抛物线方程24912x y = 中,得P 的纵坐标y P =3 由|AP |=2949,得救援船速度的大小为949海里/时由tan∠OAP =30712327=+,得∠OAP =arctan 307,故救援船速度的方向为北偏东arctan 307弧度(2)设救援船的时速为v 海里,经过t 小时追上失事船,此时位置为)12,7(2t t . 由222)1212()7(++=t t vt ,整理得337)(1442122++=tt v因为2212≥+t t ,当且仅当t =1时等号成立,所以22253372144=+⨯≥v ,即25≥v .因此,救援船的时速至少是25海里才能追上失事船28.29.解:(I)由已知得:sin (sin cos cos sin )sin sin B A C A C A C +=,sin sin()sin sin B A C A C +=,则2sin sin sin B A C =,再由正弦定理可得:2b ac =,所以,,a b c 成等比数列.(II)若1,2a c ==,则22b ac ==,∴2223cos 24a cb B ac +-==,sin C ==,∴△ABC 的面积11sin 1222S ac B ==⨯⨯=. 30. 【答案与解析】(1)由已知12=+,++=,=,cos =32B AC A B C B B ππ∴ (2)解法一:2=b ac ,由正弦定理得23sin sin =sin =4A CB 解法二:2=b ac ,222221+-+-=cos ==222a c b a c acB ac ac,由此得22+-=,a c ac ac 得=a c所以===3A B C π,3sin sin =4A C 【点评】本题主要考查三角形的正弦定理、余弦定理、三角形内角和定理及等差、等比数列的定义,考查转化思想和运算求解能力,属于容易题.第二小题既可以利用正弦定理把边的关系转化为角的关系,也可以利用余弦定理得到边之间的关系,再来求最后的结果.31. 【命题意图】本题主要考查正余弦定理应用,是简单题.【解析】(Ⅰ)由sin sin c C c A =-及正弦定理得sin sin sin sin A C A C C -=由于sin 0C ≠,所以1sin()62A π-=, 又0A π<<,故3A π=.(Ⅱ) ABC ∆的面积S =1sin 2bc A 3故bc =4, 而 2222cos a b c bc A =+- 故22c b +=8,解得b c ==2. 法二:解: 已知:A c C a c cos sin 3⋅-⋅=,由正弦定理得:A C C A C cos sin sin sin 3sin ⋅-⋅=因0sin ≠C ,所以:A A cos sin 31-=,由公式:()⎪⎭⎫ ⎝⎛<=>++=+2,tan ,0sin cos sin 22πϕϕϕa b a x b a x b x a 得:216sin =⎪⎭⎫ ⎝⎛-πA , A 是∆的内角,所以66ππ=-A ,所以:3π=A(2) 1sin 42S bc A bc ==⇔= 2222cos 4a b c bc A b c =+-⇔+=解得:2b c ==32. 【解析】(1)3(cos cos sin sin )16cos cos 3cos cos 3sin sin 13cos()11cos()3B C B C B C B C B C B C A π+-=-=-+=--=-则1cos 3A =. (2) 由(1)得sin 3A =,由面积可得bc=6①,则根据余弦定理 2222291cos 2123b c a b c A bc +-+-===则2213b c +=②,①②两式联立可得32b a =⎧⎪⎨=⎪⎩或32a b =⎧⎪⎨=⎪⎩. 33. 【解析】(Ⅰ)由题设图像知,周期11522(),21212T Tππππω=-=∴==. 因为点5(,0)12π在函数图像上,所以55sin(2)0,sin()0126A ππϕϕ⨯+=+=即. 又55450,,=26636πππππϕϕϕπ<<∴<+<+ 从而,即=6πϕ.又点0,1()在函数图像上,所以s i n 1,26A A π==,故函数f(x)的解析式为()2sin(2).6f x x π=+(Ⅱ)()2sin 22sin 2126126g x x x ππππ⎡⎤⎡⎤⎛⎫⎛⎫=-+-++ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2sin 22sin(2)3x x π=-+12sin 22(sin 22)2x x x =-sin 2x x =2sin(2),3x π=- 由222,232k x k πππππ-≤-≤+得5,.1212k x k k z ππππ-≤≤+∈ ()g x ∴的单调递增区间是5,,.1212k k k z ππππ⎡⎤-+∈⎢⎥⎣⎦【点评】本题主要考查三角函数的图像和性质.第一问结合图形求得周期1152(),1212T πππ=-=从而求得22Tπω==.再利用特殊点在图像上求出,A ϕ,从而求出f(x)的解析式;第二问运用第一问结论和三角恒等变换及sin()y A x ωϕ=+的单调性求得.34. 【解析】(1)因为22()sin cos cos cos 222sin(2)6f x x x x x x x πωωωωλωωλωλ=-++=-++=-+由直线x π=是()y f x =图像的一条对称轴,可得sin(2)16x πω-=±所以2()62x k k Z ππωπ-=+∈,即1()23k k Z ω=+∈又1(,1),2k Z ω∈∈,所以1k =时,56ω=,故()f x 的最小正周期是65π.(2)由()y f x =的图象过点(,0)4π,得()04f π=即52sin()2sin 26264πππλ=-⨯-=-=,即2λ=-故5()2sin()236f x x π=--函数()f x 的值域为[22,2.【点评】本题考查三角函数的最小正周期,三角恒等变形;考查转化与划归,运算求解的能力.二倍角公式,辅助角公式在三角恒等变形中应用广泛,它在三角恒等变形中占有重要的地位,可谓是百考不厌. 求三角函数的最小正周期,一般运用公式2T πω=来求解;求三角函数的值域,一般先根据自变量x 的范围确定函数x ωϕ+的范围.来年需注意三角函数的单调性,图象变换,解三角形等考查.35.解析:(Ⅰ)1cos cos 34364f A A A ππππ⎛⎫⎛⎫=⨯+===⎪ ⎪⎝⎭⎝⎭所以2A =. (Ⅱ)4143042cos 42cos 2sin 3436217f ππαπαπαα⎡⎤⎛⎫⎛⎫⎛⎫+=++=+=-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,所以15sin 17α=.212842cos 42cos 34365f πβπβπβ⎡⎤⎛⎫⎛⎫-=-+== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以4cos 5β=.因为α、0,2πβ⎡⎤∈⎢⎥⎣⎦,所以8c o s n17α=,3sin 5β=,所以()8415313c o s c os c o s s i n s i n 17517585αβαβαβ+=-=⨯-⨯=-. 36. 【考点定位】本题主要考查同角函数关系、两角和与差的三角函数公式、二倍角公式,考查运算能力、特殊与一般思想、化归与转化的思想.解:(1)选择(2)式计算如下213sin 15cos15sin15cos151sin 3024︒+︒-︒︒=-︒= (2)证明:22sin cos (30)sin cos(30)αααα+︒--︒-22sin (cos30cos sin30sin )sin (cos30cos sin30sin )αααααα=+︒+︒-︒+︒2222311sin cos cos sin cos sin 442αααααααα=+++-22333sin cos 444αα=+= 37. 【命题意图】: 本试题主要考查了解三角形的运用.该试题从整体看保持了往年的解题格,依然是通过边角的转换,结合了三角形的内角和定理的知识,以及正弦定理求解三角形中的角的问题.试题整体上比较稳定,思路比较容易想,先利用等差数列得到角B ,然后利用正弦定理与三角求解运算得到答案.【解析】由A.B.C 成等差数列可得2B A C =+,而A B C π++=,故33B B ππ=⇒=且23C A π=- 而由223b ac=与正弦定理可得2222sin 3sin sin 2sin 3sin()sin 33B AC A A ππ=⇒⨯=- 所以可得232223(s 433A A Aππ⨯=-⇒+=⇒1cos 2121sin(2)262A A A π-+=⇒-=,由27023666A A ππππ<<⇒-<-<,故 266A ππ-=或5266A ππ-=,于是可得到6A π=或2A π=.38. 【考点定位】本题考查三角函数,三角函数难度较低,此类型题平时的练习中练习得较多,考生应该觉得非常容易入手.解:(1)由sin 0x ≠得,()x k k Z π≠∈,故()f x 的定义域为{|,}x R x k k Z π∈≠∈. 因为(s()sin x xxf x x-==2cos (sin cos )x x x -=sin 2cos 21x x --=)14x π--,所以()f x 的最小正周期22T ππ==.(2)函数sin y x =的单调递减区间为3[2,2]()22k k k Z ππππ++∈.由3222,()242k x k x k k Z ππππππ+≤-≤+≠∈得37,()88k x k k Z ππππ+≤≤+∈ 所以()f x 的单调递减区间为37[],()88k x k k Z ππππ+≤≤+∈. 39. 【解析】(Ⅰ),,(0,)sin()sin 0A C B A B A C B ππ+=-∈⇒+=>2sin cos sin cos cos sin sin()sin B A A C A C A C B =+=+= 1cos 23A A π⇔=⇔=(II)2222222cos 2a b c bc A a b a c B π=+-⇔==+⇒=在Rt ABD ∆中,AD ===。
2012-2017年高考文科数学真题汇编:坐标系和参数方程老师版

第1页(共 10 页)学科教师辅导教案
学员姓名
年级高三辅导科目数学授课老师
课时数2h 第次课授课日期及时段 2017年月日
:—:1.(2015年广东文)在平面直角坐标系x y 中,以原点为极点,x 轴的正半轴为极轴建立极坐标系.曲
线1C 的极坐标方程为cos
sin 2,曲线2C 的参数方程为222x
t y t (t 为参数),则1C 与2C 交点的直角坐标为2,4.
2.(2015年新课标2文)在直角坐标系xOy 中,曲线1cos ,:sin ,x
t C y t (t 为参数,且0t ),其中0,
在以O 为极点,x 轴正半轴为极轴的极坐标系中
,曲线23:2sin ,:23cos .C C (I )求2C 与3C 交点的直角坐标;(II )若1C 与2C 相交于点A,1C 与3C 相交于点B,求AB 最大值.
试题分析:(I )把2C 与3C 的方程化为直角坐标方程分别为2220x y y ,22230x y x ,联立解
历年高考试题集锦——坐标系和参数方程。
2012年高考真题汇编——文科数学(解析版)4:三角函数

2012高考试题分类汇编:4:三角函数一、选择题1.【2012高考安徽文7】要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象 (A ) 向左平移1个单位 (B ) 向右平移1个单位 (C ) 向左平移 12个单位 (D ) 向右平移12个单位 【答案】C【解析】 cos 2cos(21)y x y x =→=+左+1,平移12。
2.【2012高考新课标文9】已知ω>0,πϕ<<0,直线4π=x 和45π=x 是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=(A )π4 (B )π3 (C )π2 (D )3π4 【答案】A 【解析】因为4π=x 和45π=x 是函数图象中相邻的对称轴,所以2445T=-ππ,即ππ2,2==T T .又πωπ22==T ,所以1=ω,所以)sin()(ϕ+=x x f ,因为4π=x 是函数的对称轴所以ππϕπk +=+24,所以ππϕk +=4,因为πϕ<<0,所以4πϕ=,检验知此时45π=x 也为对称轴,所以选A. 3.【2012高考山东文8】函数2sin (09)63x y x ππ⎛⎫=-≤≤⎪⎝⎭的最大值与最小值之和为(A)2 (B)0 (C)-1 (D)1-【答案】A【解析】因为90≤≤x ,所以6960ππ≤≤x ,369363πππππ-≤-≤-x ,即67363ππππ≤-≤-x ,所以当336πππ-=-x 时,最小值为3)3s i n(2-=-π,当236πππ=-x 时,最大值为22sin2=π,所以最大值与最小值之和为32-,选A.4.【2012高考全国文3】若函数()sin ([0,2])3x f x ϕϕπ+=∈是偶函数,则=ϕ (A )2π (B )32π (C )23π (D )35π【答案】C【解析】函数)33sin(3sin )(ϕϕ+=+=x x x f ,因为函数)33sin()(ϕ+=x x f 为偶函数,所以ππϕk +=23,所以Z k k ∈+=,323ππϕ,又]2,0[πϕ∈,所以当0=k 时,23πϕ=,选C. 5.【2012高考全国文4】已知α为第二象限角,3sin 5α=,则sin 2α=(A )2524- (B )2512- (C )2512 (D )2524【答案】B【解析】因为α为第二象限,所以0cos <α,即54sin 1cos 2-=--=αα,所以25125354cos sin 22sin -=⨯-==ααα,选B.6.【2012高考重庆文5】sin 47sin17cos30cos17-(A )B )12-(C )12 (D【答案】C【解析】sin 47sin17cos30sin(3017)sin17cos30cos17cos17-+-=sin 30cos17cos30sin17sin17cos30sin 30cos171sin 30cos17cos172+-====,选C.7.【2012高考浙江文6】把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是【答案】A【解析】由题意,y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),即解析式为y=cosx+1,向左平移一个单位为y=cos (x-1)+1,向下平移一个单位为y=cos (x-1),利用特殊点,02π⎛⎫⎪⎝⎭变为1,02π⎛⎫- ⎪⎝⎭,选A. 8.【2012高考上海文17】在△ABC 中,若222sin sin sin A B C +<,则△ABC 的形状是( ) A 、钝角三角形 B 、直角三角形 C 、锐角三角形 D 、不能确定【答案】A【解析】根据正弦定理可知由C B A 222sin sin sin <+,可知222c b a <+,在三角形中02cos 222<-+=abc b a C ,所以C 为钝角,三角形为钝角三角形,选A.9.【2012高考四川文5】如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=( )(1)10B 、10C 、10D 、15【答案】B【解析】 2EB EA AB =+=,EC =3424EDC EDA ADC πππ∠=∠+∠=+=,由正弦定理得sin sin 5CED DC EDC CE ∠===∠,所以3sin sin sin 4CED EDC π∠=∠==10.【2012高考辽宁文6】已知sin cos αα-=,α∈(0,π),则sin 2α= (A)-1 (B)(D) 1 【答案】A【解析】2sin cos (sin cos )2,sin 21,ααααα-∴-=∴=-故选A【点评】本题主要考查三角函数中的倍角公式以及转化思想和运算求解能力,属于容易题。
高考全国卷三角函数、解三角形真题汇编(文科)
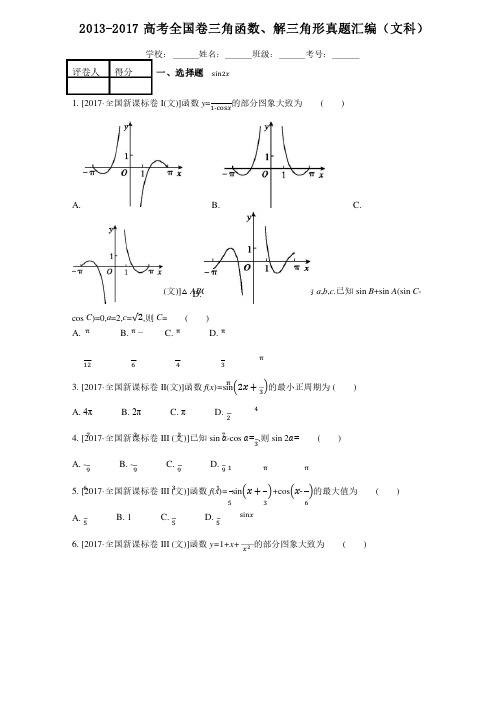
2013-2017 高考全国卷三角函数、解三角形真题汇编(文科)学校: 姓名: 班级: 考号:评卷人评卷人 得分得分一、选择题 1. [2017·全国新课标卷I(文)]函数y =sin2x 1-cosx 的部分图象大致为的部分图象大致为( ) A. B. C.D. 2. [2017·全国新课标卷I(文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知sin B +sin A (sin C -cos C )=0,a =2,c =√2,则C = ( )A. π12B. π6C. π4D. π3 3. [2017·全国新课标卷II(文)]函数f (x )=sin (2x +π3)的最小正周期为 ( ) A. 4π B. 2π C. π D. π24. [2017·全国新课标卷III (文)]已知sin α-cos α=43,则sin 2α= ( )A. -79B. -29C. 29D. 79 5. [2017·全国新课标卷III (文)]函数f (x )=15sin (x +π3)+cos (x (x--π6)的最大值为的最大值为 ( ) A. 65 B. 1 C. 35 D. 15 6. [2017·全国新课标卷III (文)]函数y=1+x+sinx x 2的部分图象大致为的部分图象大致为 ( )A. B.C. D.7. [2016·高考全国新课标卷Ⅰ(文),4]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知a =√5,c =2,cos A =23,则b = ( ) A. √2 B. √3C. 2D. 3 8. [2016·高考全国新课标卷Ⅰ(文),6]将函数y =2sin (2x +π6)的图象向右平移14个周期后,所得图象对应的函数为象对应的函数为 ( ) A. y =2sin (2x +π4) B. y =2sin (2x +π3) C. y =2sin (2x (2x--π4) D. y =2sin (2x (2x--π3) 9. [2016·高考全国新课标卷Ⅰ(文),12]若函数f (x )=x -13sin 2x +a sin x 在(-∞,+∞)单调递增,则a 的取值范围是的取值范围是 ( ) A. [-1,1] B. [-1,13] C. [-13,13] D. [-1,1,--13] 10. [2016·高考全国新课标卷Ⅱ(文),3]函数y =A sin(ωx +φ)的部分图象如图所示,则 ( ) A. y =2sin (2x (2x--π6) B. y =2sin (2x (2x--π3) C. y =2sin (x +π6) D. y =2sin (x +π3)11. [2016·高考全国新课标卷Ⅱ(文),11]函数f (x )=cos2x +6cos (π2-x)的最大值为( ) A. 4 B. 5 C. 6 D. 7 12. [2016·高考全国新课标卷Ⅲ(文),6]若tan θ=-13,则cos 2θ= ( )A. -45B. -15C. 15 D. 45 13. [2016·高考全国新课标卷Ⅲ(文),9]在△ABC 中,B =π4,BC 边上的高等于13BC ,则sin A = ( ) A. 310 B. √1010 C. √55 D. 3√101014. [2015·高考全国新课标卷Ⅰ(文),8]函数f (x )=cos(ωx+φ)的部分图象如图所示,则f (x )的单调递减区间为( )A. (kπ(kπ--14,kπ+34),k ∈Z B. (2kπ(2kπ--14,2kπ+34),k ∈Z C. (k (k--14,k +34),k ∈Z D. (2k (2k--14,2k +34),k ∈Z 15. [2014﹒高考全国新课标卷Ⅰ(文),7]在函数①y =cos|2x |,②y =|cos x |,③y =cos(2x +π6),④y =tan(2x -π4)中,最小正周期为π的所有函数为( )A. ②④B. ①③④C. ①②③D. ①③16. [2013·高考全国新课标卷I(文),9]函数f (x )=(1-cos x )sin x 在[-π,π]的图象大致为( )A. B.C. D. 17. [2013·高考全国新课标卷I(文),10]已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2A+cos2A=0,a=7,c=6,则b=( )A. 10B. 9C. 8D. 518. [2013·高考全国新课标卷II(文),4]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b=2,B=π6,C=π4,则△ABC 的面积为( )A. 2√3+2B. √3+1C. 2√3-2D. √3-1 19. [2013·高考全国新课标卷II(文),6]已知sin2α=23,则cos 2(α+π4)=( ) A. 16 B. 13 C. 12 D. 23 评卷人评卷人 得分得分 二、填空题20. [2017·全国新课标卷I(文)]已知α∈(0,π2),tan α=2,则cos (α(α--π4)= . 21. [2017·全国新课标卷II(文)]函数f (x )=2cos x+sin x 的最大值为 .22. [2017·全国新课标卷II(文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2b cos B=a cos C+c cos A ,则B= .23. [2017·全国新课标卷III (文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知C=60°60°,,b=√6,c=3,则A= .24.[2016·高考全国新课标卷Ⅰ(文),14]已知θ是第四象限角,且sin (θ+π4)=35,则tan (θ(θ--π4)= 25. [2016·高考全国新课标卷Ⅱ(文),15]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A =45,cos C =513,a =1,则b = . 26. [2016·高考全国新课标卷Ⅲ(文),14]函数y =sin x -√3cos x 的图象可由函数y =2sin x 的图象至少向右平移 个单位长度得到.27. [2014﹒高考全国新课标卷Ⅰ(文),16]如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角∠MAN =60°60°,,C 点的仰角∠CAB =45°以及∠MAC =75°;从C 点测得∠MCA =60°60°..已知山高BC =100 m,则山高MN =________m.28. [2014﹒高考全国新课标Ⅱ(文),14]函数f (x )=sin(x +φ)-2sin φcos x 的最大值为________. 29. [2013·高考全国新课标卷I(文),16]设当x=θ时,函数f (x )=sin x-2cos x 取得最大值,则cos θ= .30. [2013·高考全国新课标卷II(文),16]函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移π2个单位后,与函数y=sin(2x+π3)的图象重合,则φ= .。
2012年高考数学真题解答题:三角函数

2012年高考真题解答题:三角函数(文科)1.(2012.x ∈R (1)求A 的值; (2)设,,,求cos (α+β)的值. 2.(2012.天津)在△ABC 中,内角A ,B ,C 所对的分别是a,b ,c 。
已知a=2,(I )求sinC 和b 的值;(II3.(2012.大纲卷)△ABC 中,内角A 、B 、C 成等差数列,其对边a 、b 、c 满足223=b ac ,求A 。
4.(2012.浙江)在△ABC中,内角A,B,C的对边分别为a,b,c,且。
(1)求角B的大小;(2)若b=3,sinC=2sinA,求a,c的值中,角A,B,C的对边分别为a,b,c。
角A,B,C成等差5.(2012.辽宁)在ABC数列。
(Ⅰ)求cos B的值;A C的值。
(Ⅱ)边a,b,c成等比数列,求sin sin6.(2012.福建)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数。
(1)sin213°+cos217°-sin13°cos17°(2)sin215°+cos215°-sin15°cos15°(3)sin218°+cos212°-sin18°cos12°(4)sin2(-18°)+cos248°- sin(-18°)cos48°(5)sin2(-25°)+cos255°- sin(-25°)cos55°Ⅰ试从上述五个式子中选择一个,求出这个常数Ⅱ根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论7.(2012.(Ⅰ)求()f x 的定义域及最小正周期 (Ⅱ)求()f x 的单调递减区间。
8.(2012.山东)在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知s i n (t a n t a n )t a n B A C A C +=. (Ⅰ)求证:,,a b c 成等比数列;(Ⅱ)若1,2a c ==,求△ABC 的面积S.9.(2012. 新课标卷)已知a ,b ,c 分别为ABC ∆三个内角A ,B ,C 的对边,(Ⅰ)求A ;(Ⅱ)若a =2,ABC ∆的面积为,求b ,c .10.(2012.江苏)在ABC ∆中,已知3AB AC BA BC =. (1)求证:tan 3tan B A =;(2A 的值.11.(2012.重庆)设函数()sin()f x A x ωϕ=+(其中0,0,A ωπϕπ>>-<< )在2,I )求()fx 的解析式;(II12.(2012.江西)在△ABC 中,角A B C 、、的对边分别为a b c 、、,已知3cos()16cos cos B C B C --=,(1)求c o s A (2)若3a =,△ABC 的面积为求b c 、13.(2012.四川)(本小题满分12分) (Ⅰ)求函数()f x 的最小正周期和值域;,求sin 2α的值。
2012-2017年高考文科数学真题汇编:坐标系和参数方程老师版

学科教师辅导教案 学员姓名 年 级高三 辅导科目 数 学授课老师课时数2h第 次课授课日期及时段 2017年 月 日 : - :1。
(2015年广东文)在平面直角坐标系x y O 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线1C 的极坐标方程为()cos sin 2ρθθ+=-,曲线2C 的参数方程为222x ty t⎧=⎪⎨=⎪⎩(t 为参数),则1C 与2C 交点的直角坐标为 ()2,4- .2.(2015年新课标2文)在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩(t 为参数,且0t ≠ ),其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ==(I)求2C 与3C 交点的直角坐标; (II )若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.试题分析:(I )把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,22230x y x +-=,联立解历年高考试题集锦——坐标系和参数方程3.(2015年陕西文)在直角坐标版权法xOy 吕,直线l 的参数方程为132(32x t t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数),以原点为极点,x 轴的正半轴为极轴建立极坐标系,C 的极坐标方程为23sin ρθ=.(I)写出C 的直角坐标方程;(II )P 为直线l 上一动点,当P 到圆心C 的距离最小时,求点P 的坐标.试题解析:(I )由23sin ρθ=,得223sin ρρθ=,从而有2223x y y +=所以()2233x y +-=(II)设133,22P t t ⎛⎫+ ⎪⎝⎭,又(0,3)C ,则22213331222PC t t t ⎛⎫⎛⎫=++-=+ ⎪ ⎪⎝⎭⎝⎭,故当0t =时,PC 取得最小值,此时P 点的坐标为(3,0)。
2012-2017年高考文科数学真题汇编:解三角形高考题老师版

14.(2013陕西)设△ABC 的内角A, B, C 所对的边分别为a, b, c, 若cos cos sin b C c B a A +=, 则△ABC 的形状为(A) 锐角三角形(B) 直角三角形(C) 钝角三角形(D) 不确定【简解】sinBcosC+sinCcosB=sinAsinA,sin(B+C)=sin 2A,sinA=1,A=2π.选B 15、(2016年新课标Ⅰ卷文)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a =,2c =,2cos 3A =,则b=(A )2 (B )3 (C )2 (D )3 【答案】D16、(2016年新课标Ⅲ卷文)在ABC △中,π4B,BC 边上的高等于13BC ,则sin A(A )310(B )1010 (C )55 (D )31010试题分析:设BC 边上的高线为AD ,则3,2BC AD DC AD ==,所以225AC AD DC AD =+=.由正弦定理,知sin sin AC BCB A =,即53sin 22AD AD A =,解得310sin 10A =,故选D .17、(2016年高考山东卷文)ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,已知22,2(1sin )b c a b A ,则A =(A )3π4(B )π3(C )π4(D )π6【答案】C考点:余弦定理18、2016年高考北京卷文)在△ABC 中,23A π∠=,a=3c ,则bc =_________.试题分析:由正弦定理知sin 3sin A aC c==,所以2sin13sin 23C π==,则6C π=,所以2366B ππππ=--=,所以b c =,即1bc =.考点:解三角形19、(2016年新课标Ⅱ卷文)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若4cos 5A =,5cos 13C =,a =1,则b =____________. 【解析】因为45cos ,cos 513A C ==,且,A C 为三角形内角,所以312sin ,sin 513A C ==,13sin sin(C)sin cos cos sin 65B A AC A C =+=+=,又因为sin sin a b A B =,所以sin 21sin 13a Bb A ==.20.(2013安徽)设ABC ∆的内角,,A B C 所对边的长分别为,,a b c 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
()1求tan 4πα⎛⎫+⎪⎝⎭的值;()2求2sin 2sin sin cos cos 21ααααα+--的值. 【答案】(1)3-;(2)1.3、三角函数的图象和性质9、(2016年四川高考) 为了得到函数y=sin )3(π+x 的图象,只需把函数y=sinx 的图象上所有的点( A )(A)向左平行移动3π个单位长度 (B) 向右平行移动3π个单位长度 (C) 向上平行移动3π个单位长度 (D) 向下平行移动3π个单位长度10.(2014大纲)设sin33,cos55,tan35,a b c =︒=︒=︒则( C ) A .a b c >> B .b c a >> C .c b a >> D .c a b >> 11.(2014福建文) 将函数sin y x =的图象向左平移2π个单位,得到函数()y f x =的函数图象,则下列说法正确的是 ( D )()()()()....-022A y f x B y f x C y f x x D y f x πππ==⎛⎫=== ⎪⎝⎭是奇函数 的周期为的图象关于直线对称 的图象关于点,对称12.(2012山东文)函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为( A )(A)23- (B)0 (C)-1 (D)13--13、(2013山东)将函数y=sin (2x +ϕ)的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为 ( B ) (A )34π (B ) 4π (C )0 (D ) 4π- 14.(2013山东)函数y =x cos x +sin x 的图象大致为( D )15.(2016年全国I 卷)将函数y =2sin (2x +π6)的图像向右平移14个周期后,所得图像对应的函数为( D )(A )y =2sin(2x +π4) (B )y =2sin(2x +π3) (C )y =2sin(2x –π4) (D )y =2sin(2x –π3)16.(2013沪春招)既是偶函数又在区间(0 )π,上单调递减的函数是( B ) (A )sin y x = (B )cos y x = (C )sin 2y x = (D )cos 2y x =【简解】根据偶函数,只能在BD 中选择,(0,π)上单调减,只能选B17.(2013四川)函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是( A )A .2,-π3B .2,-π6C .4,-π6D .4,π318.(2014四川理) 为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点( A )A 、向左平行移动12个单位长度 B 、向右平行移动12个单位长度 C 、向左平行移动1个单位长度 D 、向右平行移动2个单位长度19.(2016年全国II 卷)函数=sin()y A x ωϕ+的部分图像如图所示,则( A )(A )2sin(2)6y x π=- (B )2sin(2)3y x π=-(C )2sin(2+)6y x π= (D )2sin(2+)3y x π=20.(2013天津文) 函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为( B ) A .-1 B .-22 C.22D .0 21.(2014浙江) 为了得到函数x x y 3cos 3sin +=的图象,可以将函数x y 3sin 2=的图象( C )A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 22.(2012大纲)已知α为第二象限角,3sin cos 3αα+=,则cos2α= A .53-B .59-C .59D .53【简解】原式两边平方可得121sin 2sin 233αα+=⇒=- α是第二象限角,因此sin 0,cos 0αα><,所以2215cos sin (cos sin )133αααα-=--=-+=-225cos 2cos sin (cos sin )(cos sin )3ααααααα∴=-=+-=-23.(2013福建文)将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,若)(),(x g x f 的图象都经过点)23,0(P ,则ϕ的值可以是( ) A .35π B .65π C .2π D .6π 【简解】P 在f(x)上,θ=3π,f(x)=sin(2x+3π);g(x)=sin[2(x-φ)+3π]过点P ,φ=56π满足条件。
选B 24.(2017年新课标Ⅱ文)函数f (x )=sin ⎝⎛⎭⎫2x +π3的最小正周期为( ) A .4πB .2πC .πD .π247 [,] 3412[,]4347[,]3413[,]34f(x-1)=f(|x-1|)f(t)≤1/2,得到3/4;代入x天津文) 将函数f(x)=sin xω(其中)的图象向右平移个单位长度,所得图象经过点),则ω的最小值是35.(2014江苏)函数)42sin(3π+=x y 的最小正周期为 π 。
36.(2014江苏)已知函数cos y x =与sin(2)(0)y x ϕϕ=+<π≤,它们的图象有一个横坐标为3π的交点,则ϕ的值是 6π .37、(2017年新课标Ⅱ文)函数f (x )=2cos x +sin x 的最大值为 . 5 【解析】f (x )=2cos x +sin x ≤22+12=5,∴f (x )的最大值为5. 38、(2017•新课标Ⅰ理)已知曲线C 1:y=cosx ,C 2:y=sin (2x+),则下面结论正确的是( D )A 、把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C 2B 、把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C 2C 、把C 1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C 2D 、把C 1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C 239、( 2017年新课标Ⅱ卷理) 函数()23sin 3cos 4f x x x =+-(0,2x π⎡⎤∈⎢⎥⎣⎦)的最大值是 . 【答案】1【解析】()22311cos 3cos cos 3cos 44f x x x x x =-+-=-++ 23cos 12x ⎛⎫=--+ ⎪ ⎪⎝⎭,0,2x π⎡⎤∈⎢⎥⎣⎦,那么[]cos 0,1x ∈,当3cos 2x =时,函数取得最大值1. 40.(2014大纲)若函数()cos 2sin f x x a x =+在区间(,)62ππ是减函数,则a 的取值范围是 .【简解】()f x '=cosx(a-4sinx)≤0在x ∈(,)62ππ恒成立;a ≤4sinx 。
填(],2-∞. 41.(2013新标2文) 函数y =cos(2x +φ)(-π≤φ≤π)的图象向右平移π2个单位后,与函数y =sin ⎝⎛⎭⎫2x +π3的图象重合,则φ=________.【简解】y =sin ⎝⎛⎭⎫2x +π3向左平移π2个单位,得y =sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎫x +π2+π3=sin ⎝⎛⎭⎫2x +π+π3=-sin ⎝⎛⎭⎫2x +π3=cos ⎝⎛⎭⎫π2+2x +π3=cos ⎝ ⎛⎭⎪⎫2x +5π6,即φ=5π6.64、.(2013浙江文) 函数f (x )=sin x cos x +32cos 2x 的最小正周期和振幅分别是( A ) 65.(2013新标2文) 已知sin 2α=23,则cos 2⎝⎛⎭⎫α+π4=( A ) A.16B.13C.12D.23【简解】cos 2⎝⎛⎭⎫α+π4=1+cos2⎝⎛⎭⎫α+π42=1+cos ⎝⎛⎭⎫2α+π22=1-sin 2α2=16,选A.66.(2014大纲文)函数cos 22sin y x x =+的最大值为32. 67.(2013江西)函数y =sin 2x +23sin 2x 的最小正周期T 为_____π___.68.(2012上海文)若1cos cos sin sin 3x y x y +=,则()cos 22x y -= -7/9 . 69.(2014上海)函数212cos (2)y x =-的最小正周期是 2π .70.(2013四川) 设sin 2α=-sin α,α∈⎝⎛⎭⎫π2,π,则tan 2α的值是________.【简解】∵sin 2α=-sin α,∴sin α(2cos α+1)=0,又α∈⎝⎛⎭⎫π2,π,∴sin α≠0,2cos α+1=0即cos α=-12,sin α=32,tan α=-3,∴tan 2α=2tan α1-tan 2α=-231-(-3)2= 3. 71、已知点P ⎝⎛⎭⎫sin 3π4,cos 3π4落在角θ的终边上,且θ∈[0,2π),则θ的值为 ( ) A.π4B.3π4C.5π4D.7π4解析:tan θ=cos 34πsin 34π=-cosπ4sin π4=-1,又sin 3π4>0,cos 3π4<0,所以θ为第四象限角且θ∈[0,2π),所以θ=7π4.72、已知α∈(-π,0),tan(3π+α)=13,则cos ⎝⎛⎭⎫32π+α的值为( )A.1010B .-1010 C.31010D .-31010答案 B 解析:由tan(3π+α)=13,得tan α=13,cos ⎝⎛⎭⎫32π+α=cos ⎝⎛⎭⎫π2-α=sin α.∵α∈(-π,0),∴sin α=-1010. 73、函数f (x )=sin(ωx +φ)(其中|φ|<π2)的图象如图所示,为了得到g (x )=sin ωx 的图象,则只要将f (x )的图象( )A .向右平移π6个单位B .向右平移π12个单位C .向左平移π6个单位 D .向左平移π12个单位答案 A 解析 由图象可知,T 4=7π12-π3=π4,∴T =π,∴ω=2ππ=2,再由2×π3+φ=π,得φ=π3,所以f (x )=sin ⎝⎛⎭⎫2x +π3.故只需将f (x )=sin 2⎝⎛⎭⎫x +π6向右平移π6个单位,就可得到g (x )=sin 2x . 74.(2013北京文)已知函数21()(2cos 1)sin 2cos 42f x x x x =-+(1)求()f x 的最小正周期及最大值。
