指数函数和对数函数知识点总结
指数函数和对数函数知识点总结

指数函数和对数函数知识点总结适用于高一应届学习及高三一轮复习指数函数和对数函数知识点总结及练习题一.指数函数(一)指数及指数幂的运算a am ar as ar s (ar)s ars (ab)r arbr(二)指数函数及其性质1.指数函数的概念:一般地,形如y a(a 0且a 1)叫做指数函数。
xmn二.对数函数(一)对数1.对数的概念:一般地,如果a N(a 0且a 1),那么x叫做以a为底N的对数,记作x logaN,其中a叫做底数,N叫做真数,logaN叫做对数式。
2.指数式与对数式的互化幂值真数xax log指数对数适用于高一应届学习及高三一轮复习3.两个重要对数(1)常用对数:以10为底的对数lgN(2)自然对数:以无理数e 2.***** 为底的对数lnN(二)对数的运算性质(a 0且a 1,M 0,N 0)①logaM logaN logaMN ②logaM logaN loga③logaM nlogaM ④换底公式:logab 关于换底公式的重要结论:①logamb(三)对数函数1.对数函数的概念:形如y logax(a 0且a 1)叫做对数函数,其中x 是自变量。
M Nnlogcb(c 0且c 1)logcannlogab ②logab logba 1 m适用于高一应届学习及高三一轮复习基本初等函数练习题1.已知集合M { 1,1},N {x|12x 1 4,x Z},则M∩N=()2A.{-1,1}B.{0}C.{-1}D.{-1,0} 2.设11b1a() () 1,则()333abaaabbaabaaA.a a bB.a b aC.a a bD.a b a 3.设y1 40.9,y2 80.48,y3 () 1.5,则()12A.y3 y1 y2B.y2 y1 y3C.y1 y3 y2D.y3 y1 y2 4.若()122a 11()3 2a,则实数a的取值范围是()211A.(1,+∞)B.(,+∞)C.(-∞,1)D.(-∞,)221-5.方程3x1=的解为()9A.x=2B.x=-2C.x=1D.x=-1116.已知实数a,b满足等式(a=()b,则下列五个关系式:①0ba;②ab0;③0ab;23④ba0;⑤a=b。
指数与对数函数知识点小结

指数与对数函数知识点小结1 指数与对数函数是数学中重要的函数类型之一,它们在许多领域都有广泛的应用。
本文将对指数与对数函数的定义、性质、图像以及应用等方面进行详细的介绍和总结。
一、指数函数1. 定义:指数函数是以固定底数为底的幂函数,其中底数为正实数且不等于1,指数为实数。
指数函数的一般形式为f(x) = a^x,其中a为底数,x为指数。
2. 性质:(1) 当底数a大于1时,指数函数是递增函数,即随着指数x的增加,函数值也增加;(2) 当0 < a < 1时,指数函数是递减函数,即随着指数x的增加,函数值减小;(3) 当底数a等于1时,指数函数是常值函数,即函数值始终为1;(4) 当指数x为0时,指数函数的函数值始终为1;(5) 当指数x为正无穷大时,指数函数的函数值趋于正无穷大;(6) 当指数x为负无穷大时,指数函数的函数值趋于0。
3. 图像:指数函数的图像呈现出一种特殊的曲线,当底数a大于1时,曲线从左下方向右上方逼近x轴;当0 < a < 1时,曲线从左上方向右下方逼近x轴;当底数a等于1时,曲线始终与x轴重合。
4. 应用:(1) 经济学中的复利计算就是基于指数函数的原理;(2) 物理学中的指数衰减和指数增长等现象都可以用指数函数来描述;(3) 生物学中的细胞分裂和生物种群增长等现象也可以用指数函数来描述。
二、对数函数1. 定义:对数函数是指数函数的反函数,即对数函数是以固定底数为底的幂函数的反函数。
对数函数的一般形式为f(x) = loga(x),其中a为底数,x为实数。
2. 性质:(1) 对数函数的定义域为正实数集合,值域为实数集合;(2) 当底数a大于1时,对数函数是递增函数,即随着自变量x的增加,函数值也增加;(3) 当0 < a < 1时,对数函数是递减函数,即随着自变量x的增加,函数值减小;(4) 当底数a等于1时,对数函数无定义;(5) 对数函数的反函数是指数函数。
高中数学必修一指数函数对数函数知识点

高中数学必修一指数函数对数函数知识点高中数学必修一中,指数函数和对数函数是重要的知识点。
指数函数是一种以指数为自变量的函数,形式为y = a^x,其中a为底数,x为指数。
而对数函数是指数函数的逆运算,形式为y = loga(x),其中a为底数,x为真数。
以下是关于指数函数和对数函数的具体知识点。
一、指数函数的图像和性质1.指数函数的基本形式:-y=a^x,其中a>0且a≠12.指数函数的基本性质:-当0<a<1时,指数函数呈现递减的图像;-当a>1时,指数函数呈现递增的图像;-当a=1时,指数函数为常数函数y=1二、对数函数的图像和性质1.对数函数的基本形式:- y = loga(x),其中a > 0且a≠12.对数函数的基本性质:- 对数函数与指数函数互为反函数,即loga(a^x) = x,a^loga(x) = x;-对数函数的图像关于直线y=x对称;-对数函数的定义域为正实数集,值域为实数集。
三、指数函数和对数函数的运算性质1.指数函数的运算性质:-a^x*a^y=a^(x+y);- (a^x)^y = a^(xy);- (ab)^x = a^x * b^x;-a^0=1,其中a≠0。
2.对数函数的运算性质:- loga(xy) = loga(x) + loga(y);- loga(x^y) = y * loga(x);- loga(x/y) = loga(x) - loga(y);- loga(1) = 0,其中a≠0。
四、指数函数和对数函数的应用1.指数函数在生活中的应用:-经济增长模型中的应用;-指数衰减与物质的半衰期计算;-大自然中的指数增长现象。
2.对数函数在生活中的应用:-pH值的计算;-放大器的功率增益计算;-数字音乐的音量计算。
综上所述,指数函数和对数函数是高中数学必修一中的重要知识点。
掌握了指数函数和对数函数的基本形式、性质以及运算规律,能够理解其图像特征和在实际问题中的应用。
指数与对数知识点总结

指数与对数知识点总结指数和对数是数学中重要的概念和工具。
它们广泛应用于科学、工程和金融领域,具有重要的理论和实用价值。
本文将对指数和对数的基本概念、性质和应用进行总结。
一、指数的基本概念和性质1.1 指数的定义指数是表示一个数乘积的幂运算。
设 a 是一个非零实数,n 是一个正整数,那么 a 的 n 次幂可以表示为 a^n。
其中,a 称为底数,n 称为指数,a^n 读作“a 的 n 次方”。
1.2 指数的性质(1)指数为正数时,指数运算具有如下性质:a^m * a^n = a^(m + n) (指数相加,底数不变)(a^m)^n = a^(m * n) (指数相乘,底数不变)(ab)^n = a^n * b^n (乘法公式,底数相乘,指数不变)(a/b)^n = a^n / b^n (除法公式,底数相除,指数不变)(2)指数为负数时,指数运算的性质如下:a^(-n) = 1 / a^n (负指数时,求倒数)1.3 底数为 e 的指数函数以自然对数的底数 e 为底的指数函数称为自然指数函数,记为 f(x)= e^x。
1.4 对数的定义和性质对数是指数运算的逆运算。
设 a 是一个正实数,b 是一个正实数且不等于 1,如果 b^x = a,那么称 x 为以 b 为底 a 的对数。
记作 x =log_b(a),读作“以 b 为底 a 的对数”。
(1)对数的基本性质:log_b(1) = 0 (对数的底数为 1 时,值为 0)log_b(b) = 1 (对数的底数为自身时,值为 1)log_b(a * c) = log_b(a) + log_b(c) (对数相乘,变为求和)log_b(a / c) = log_b(a) - log_b(c) (对数相除,变为求差)log_b(a^n) = n * log_b(a) (对数的幂运算,变为乘法)二、指数与对数的应用2.1 指数函数的应用指数函数常用于描述增长或衰减的趋势,如人口增长、金融利率等。
指数函数与对数函数知识点

指数函数与对数函数1、n 次方根与分数指数幂、指数幂运算性质(1)若nx a =,则))n x n =⎪⎩为奇数为偶数;()()a n a n ⎧⎪⎨⎪⎩为奇数为偶数;(3)n a =;(4)*0,,,1)m na a m n N n =>∈>且;(5)*0,,1)mn a a m n N n -=>∈>,且;(6)0的正分数指数幂为0,0的负分数指数幂没有意义.(7)()0,,r s r s a a a a r s R +⋅=>∈;(8)()()0,,r s rs a a a r s R =>∈;(9)()()0,0,,r r r ab a b a b r s R =⋅>>∈.2、对数、对数运算性质(1)()log 0,1x a a N x N a a =⇔=>≠;(2)()log 100,1a a a =>≠;(3)()log 10,1a a a a =>≠;(4);()log0,1a N a N a a =>≠;(5)()log 0,1m a a m a a =>≠;(6)()log ()log log 0,1,0,0a a a MN M N a a =+>≠M >N >; (7)()log log log 0,1,0,0a a a M M N a a N=->≠M >N >; (8)()log log 0,1,0n a a M n M a a =⋅>≠M >; (9)换底公式()log log 0,1,0,0,1log c a c b b a a b c c a =>≠>>≠; (10)()log log 0,1,,*m n a a n b b a a n m N m=>≠∈;(11)()1log log 0,1,0,a a M a a M n R n=>≠>∈; (12)()log log log 10,1,0,1,0,1a b c b c a a a b b c c ⋅⋅=>≠>≠>≠.3、指数函数)1,0(≠>=a a a y x 且及其性质:①定义域为(),-∞+∞; ②值域为()0,+∞;③过定点()0,1;④单调性:当1a >时,函数()f x 在R 上是增函数;当01a <<时,函数()f x 在R 上是减函数; ⑤在y 轴右侧,指数函数的图象“底大图高”.4、对数函数)1,0(log ≠>=a a x y a 且及其性质:①定义域为()0,+∞;②值域为(),-∞+∞;③过定点()1,0;④单调性:当1a >时,函数()f x 在()0,+∞上是增函数;当01a <<时,函数()f x 在()0,+∞上是减函数;⑤在直线1=x 的右侧,对数函数的图象“底大图低”.5指数函数x a y =与对数函数)1,0(log ≠>=a a x y a 且互为反函数,它们的图象关于直线x y =对称.6不同函数增长的差异:线性函数模型)0(>+=k b kx y 的增长特点是直线上升,其增长速度不变;指数函数模型)1(>=a a y x 的增长特点是随着自变量的增大,函数值增大的速度越来越快,呈“指数爆炸”状态;对数函数模型)1(log >=a x y a 的增长特点是随着自变量的增大,函数值增大速度越来越慢,即增长速度平缓;幂函数模型)0(>=n x y n 的增长速度介于指数函数和对数函数之间.7函数的零点:在函数)(x f y =的定义域内,使得0)(=x f 的实数x 叫做函数的零点.8零点存在性定理:如果函数()f x 在区间[],a b 上的图象是连续不断的一条曲线,且有()()0f a f b ⋅<,那么函数()y f x =在区间(),a b 内至少有一个零点,即存在(),c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根.9二分法:对于区间],[b a 上图象连续不断且()()0f a f b ⋅<的函数)(x f y =,通过不断把它的零点所在区间一分为二,使得区间的两个端点逐步逼近零点,进而得到零点近似值的方法.10给定精确度ε,用二分法求函数)(x f y =零点0x 近似值的步骤:⑴确定零点0x 的初始区间[],a b ,验证()()0f a f b ⋅<;⑵求区间[],a b 的中点c ;⑶计算)(c f ,并进一步确定零点所在的区间;①若0)(=c f ,则c 就是函数的零点;②若0)()(<c f a f (此时),(0c a x ∈),则令c b =;③若0)()(<b f c f (此时),(0b c x ∈),则令c a =;⑷判断是否达到精确度ε:若a b ε-<,则得到零点的近似值a (或b );否则重复上面的⑵至⑷.。
指数函数与对数函数例题和知识点总结

指数函数与对数函数例题和知识点总结一、指数函数的定义与性质指数函数的一般形式为$y = a^x$($a > 0$且$a ≠ 1$)。
其中,底数$a$决定了函数的性质。
当$a > 1$时,函数单调递增;当$0 < a < 1$时,函数单调递减。
指数函数的定义域为$R$,值域为$(0, +\infty)$。
例如,函数$y = 2^x$是一个底数为$2$(大于$1$)的指数函数,它在$R$上单调递增。
二、对数函数的定义与性质对数函数是指数函数的反函数,一般形式为$y =\log_a x$($a > 0$且$a ≠ 1$)。
其中,对数的底数$a$同样决定了函数的性质。
当$a > 1$时,函数在$(0, +\infty)$上单调递增;当$0 < a <1$时,函数在$(0, +\infty)$上单调递减。
对数函数的定义域为$(0, +\infty)$,值域为$R$。
例如,函数$y =\log_2 x$是一个底数为$2$(大于$1$)的对数函数,它在$(0, +\infty)$上单调递增。
三、指数函数与对数函数的图象指数函数$y = a^x$($a > 0$且$a ≠ 1$)的图象特点:当$a > 1$时,图象过点$(0, 1)$,从左到右逐渐上升;当$0 < a < 1$时,图象过点$(0, 1)$,从左到右逐渐下降。
对数函数$y =\log_a x$($a > 0$且$a ≠ 1$)的图象特点:当$a > 1$时,图象过点$(1, 0)$,从左到右逐渐上升;当$0 < a < 1$时,图象过点$(1, 0)$,从左到右逐渐下降。
四、指数运算与对数运算的性质指数运算性质:1、$a^m \times a^n = a^{m + n}$2、$\frac{a^m}{a^n} = a^{m n}$3、$(a^m)^n = a^{mn}$4、$a^0 = 1$($a ≠ 0$)对数运算性质:1、$\log_a (MN) =\log_a M +\log_a N$2、$\log_a \frac{M}{N} =\log_a M \log_a N$3、$\log_a M^n = n \log_a M$4、$\log_a a = 1$5、$\log_a 1 = 0$五、例题分析例 1:比较大小比较$2^{03}$和$03^2$的大小。
指数函数与对数函数知识点总结

指数函数与对数函数知识点总结一、指数函数1、指数函数的定义一般地,函数\(y = a^x\)(\(a > 0\)且\(a ≠ 1\))叫做指数函数,其中\(x\)是自变量,函数的定义域是\(R\)。
需要注意的是,底数\(a\)的取值范围,当\(a = 1\)时,函数就变成了\(y = 1^x = 1\),是一个常函数,不符合指数函数的定义;当\(a < 0\)时,对于某些\(x\)的值,\(a^x\)无意义,比如\((-2)^{\frac{1}{2}}\)就没有实数解。
2、指数函数的图象当\(a > 1\)时,指数函数\(y = a^x\)的图象是上升的,经过点\((0, 1)\),在\(R\)上单调递增;当\(0 < a < 1\)时,指数函数\(y = a^x\)的图象是下降的,经过点\((0, 1)\),在\(R\)上单调递减。
我们可以通过几个特殊的点,比如\((0, 1)\)、\((1, a)\)、\((-1, \frac{1}{a})\)等来大致描绘指数函数的图象。
3、指数函数的性质(1)定义域:\(R\)(2)值域:\((0, +∞)\)(3)恒过定点\((0, 1)\)(4)单调性:当\(a > 1\)时,在\(R\)上单调递增;当\(0 <a < 1\)时,在\(R\)上单调递减(5)函数值的变化情况当\(a > 1\)时,若\(x > 0\),则\(a^x > 1\);若\(x = 0\),则\(a^x = 1\);若\(x < 0\),则\(0 < a^x < 1\)。
当\(0 < a < 1\)时,若\(x > 0\),则\(0 < a^x < 1\);若\(x = 0\),则\(a^x = 1\);若\(x < 0\),则\(a^x > 1\)。
4、指数运算的性质(1)\(a^m × a^n = a^{m + n}\)(2)\(\frac{a^m}{a^n} = a^{m n}\)(\(a ≠ 0\))(3)\((a^m)^n = a^{mn}\)(4)\((ab)^n = a^n b^n\)这些运算性质在化简指数表达式和进行指数运算时经常用到。
知识点总结指数函数、对数函数
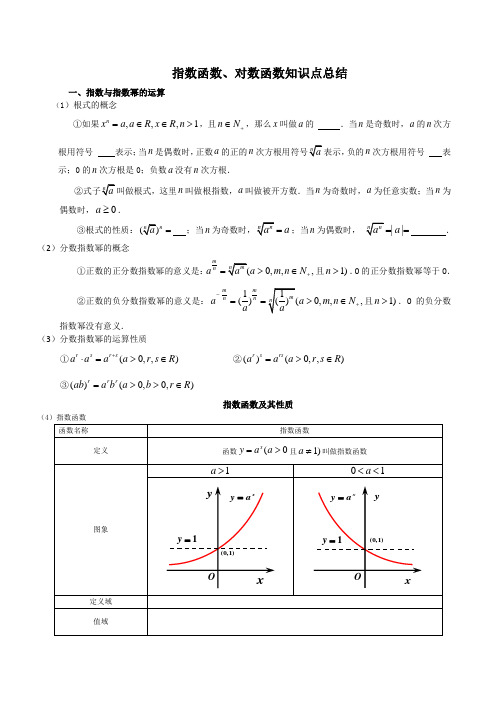
指数函数、对数函数知识点总结一、指数与指数幂的运算 (1)根式的概念①如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的 .当n 是奇数时,a 的n 次方根用符号 表示;当n 是偶数时,正数a 的正的n负的n 次方根用符号 表示;0的n 次方根是0;负数a 没有n 次方根.n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n = ;当na =;当n 为偶数时,||a == .(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是:1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. (3)分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)rr rab a b a b r R =>>∈指数函数及其性质(4)指数函数二、对数函数1,对数与对数运算(1)对数的定义:(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a xN =,其中a 叫做底数,N叫做 .② 数和 没有对数.③对数式与指数式的互化:log (0,1,0)x ax N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式log 1a = ,log a a = ,log b a a = .(3)常用对数与自然对数常用对数: ,即10log N ;自然对数: ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0aa M N >≠>>,那么①加法:log log aa M N += ②减法:log log a a M N -=③数乘:log log ()n aa n M M n R =∈ ④log a N a =2、对数函数及其性质(5)对数函数3、幂函数(1)幂函数的定义一般地,函数 叫做幂函数,其中x 为自变量,α是常数. (2(3①(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点( , ). ③单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.4、二次函数(1)二次函数解析式的三种形式 ①一般式:2()(0)f x ax bx c a =++≠②顶点式:2()()(0)f x a x h k a =-+≠③两根式:12()()()(0)f x a x x x x a =--≠(2)二次函数图象的性质 ①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为 顶点坐标是( , ). ②当0a>时,抛物线开口向上,函数在(,]2b a -∞-上递 ,在[,)2b a -+∞上递 ,当2bx a=-时,2min 4()4ac b f x a-=;当0a<时,抛物线开口向下,函数在 上递增,在 上递减,当2bx a=-时,max ()f x = .。
指数函数和对数函数知识点总结

指数函数和对数函数知识点总结一、指数函数:1.基本概念:指数函数是形如y=a^x(a>0,且a≠1)的函数,其中a称为底数,x 称为指数,a^x称为底数a的x次幂。
2.基本性质:(1)a^0=1,任何数的0次幂等于1;(2)a^x*a^y=a^(x+y),相同底数的指数幂相乘,底数不变,指数相加;(3)a^x÷a^y=a^(x-y),相同底数的指数幂相除,底数不变,指数相减;(4)(a^x)^y=a^(x*y),指数幂的乘积再乘方,指数相乘;(5)a^(-x)=1/(a^x),任何数的负指数满足倒数规律。
3.常见指数函数:(1)指数函数y=2^x:以2为底的指数函数,可以用来描述2的x 次幂关系,是一种常见的指数型增长函数,图像逐渐向上凸起。
二、对数函数:1.基本概念:对数函数是指y=loga(x),其中a>0,且a≠1,a称为底数,x称为真数,y称为以a为底x的对数。
2.基本性质:(1)loga(1)=0,底数为任何正数时,1的对数都是0;(2)loga(a)=1,底数为任何正数时,底数的对数都是1;(3)loga (x*y) = loga(x) + loga(y),对数相乘,真数取乘积,对数相加;(4)loga (x/y) = loga(x) - loga(y),对数相除,真数取商,对数相减;(5)loga(x^k) = k * loga(x),对数乘方,真数取底数的k次方,对数乘以指数。
3.常见对数函数:(1)常用对数函数:y=log10(x),其中底数为10,对数函数可以简写为y=log(x)。
常用对数函数是以10为底的对数函数,输入一个正实数x,输出满足10^y=x的y值。
(2)自然对数函数:y=ln(x),其中底数为e。
自然对数函数是以e 为底的对数函数,输入一个正实数x,输出满足e^y=x的y值。
三、指数函数与对数函数的关系:四、指数函数与对数函数的应用:1.科学中的指数增长:指数函数常常用于描述原子衰变、细胞分裂和放射性物质的衰变等过程。
指数函数与对数函数知识点梳理

指数函数与对数函数知识点梳理一.指数,分数指数幂1. 分数指数幂/负数指数幂/非零实数的零次方2. 奇次偶次根式3. 幂的运算性质4. 平方差,立方差公式,完全平方公式的变形 二.对数及其运算 1.对数的概念2.对数的运算性质及常用结论3.换底公式及相关推论 三.指数函数1.指数函数的概念图像及性质2.指数函数的底与图像的关系3.指数复合函数的定义域,值域,单调性,奇偶性4.指数方程,不等式的解法 四.对数函数1.对数函数的概念性质与图像2.对数函数的底与图像的关系3.指数复合函数的定义域,值域,单调性,奇偶性 4对数不等式,对数方程的解法 5.两边同时取对数 五.常用的解题方法1.把根式转化为分数指数幂进而利用幂的运算性质2.完全平方公式的灵活变化整体求值3.化为同底法4.对数式与指数式之间的互化5.对数运算性质的灵活运用6.对数复合函数奇偶性的判别用定义的变形形式 六.常考题型归纳例1.(1) 化简:;315383327a a a a⋅÷-- (2)322-化为分数指数幂的形式 (3) 化简2115113366221()(3)3a b a b a b ⎛⎫⋅-÷ ⎪⎝⎭变式:1).)4()3(6521332121231----⋅÷-⋅⋅b a b a b a 20,0)a b >>;3)121316324(12427162(8)--+-+-;例2. 已知32121=+-xx ,求32232322-+-+--xx x x 的值变式: 已知42121=--mm ,求下列各式的值:①1-+m m ; ②21212323----mm m m例3.求值: 51log 25() 212log 16() 3lg1000() lg 0.001(4)变式:15log 15(1) 0.4log 1(2) 9log 81(3)2.5log 6.25(4) 7log 343(5) 3log 243(6)例4. 若log 2a m =,log 3a n =,则2m n a +等于变式;例5.求值:(1))39(log 523⨯ (2)51100lg (3)20lg 5lg + (4)4log 36log 33-(5) lg10;-4lg 5.2lg + (6).39log 523)(⨯变式:求值:(1))24(log 572⨯= .(2)5100lg = . (3)25log 20lg 100+= .(4)22log (1log (1++++=____ ____.例6.(1). 求log 84的值; (2)2log (2)log log a a a M N M N -=+,则NM的值为_______ (3).已知23834xy ==,l o g ,则x y +2的值为_______变式:(1).y x yx lg lg 2lg 2+=-,求y x .(2).例7.lg8lg1.2+- (2)0.21log 35-(3)50lg 2lg )5(lg 2⋅+(4)4912log 3log 2log ⋅-变式:(1)lg14-21g 18lg 7lg 37-+ (2)试求2lg 2lg2lg5lg5+⋅+的值(3)11lg 9lg 240212361lg 27lg 35+-+-+; (4)142log 2112log 487log 222--+;例8.(1)若lg 2a =,lg 3b =,用a. b 表示5log 12变式: 45log ,518,8log 3618求==ba (用含a ,b 的式子表示)例9. (1).lg 243lg9= (2)91log 81log 251log 532∙∙= .变式:(1)3109log 28g 的值是 (2) 5361log log 6log 2,______3x x ⋅⋅==若则;例10. (1).设3a =4b =36,求a 2+b1的值 (2). 设a 、b 、c 都是正数,且346a b c==,那么( )A .111c a b =+ B.221c a b=+ C.122c a b=+ D.212c a b=+变式:若R z y x ∈,,,且zyx643==,求代数式xyz y -的值例11. (1)函数f (x )=log 3(2x 2-8x +m )的定义域为R ,则m 的取值范围是________.(2). 若函数的值域为一切实数,求实数的取值范围。
初中数学指数函数与对数函数的性质知识点总结

初中数学指数函数与对数函数的性质知识点总结一、指数函数的性质:1. 定义:指数函数是以指数为自变量,底数固定的函数。
形如f(x) = a^x,其中a是正实数,且a≠1。
2. 指数函数的图像特点:a) 当0<a<1时,函数图像在y轴上方逐渐逼近x轴正半轴;b) 当a>1时,函数图像在y轴下方逐渐逼近x轴正半轴;c) a=1时,指数函数为常数函数,图像为y = 1。
3. 指数函数的性质:a) 当x∈R时,指数函数f(x) > 0,即指数函数的值始终大于0;b) 指数函数的增减性:当x1 < x2时,若a > 1,则a^x1 < a^x2;若0 < a < 1,则a^x1 > a^x2。
4. 指数函数的特殊性质:a) a^0 = 1,任何数的0次方等于1;b) a^m * a^n = a^(m+n),指数的乘法法则;c) (a^m)^n = a^(m*n),幂的乘方法则;d) a^(-n) = 1/(a^n),负指数的倒数性质。
二、对数函数的性质:1. 定义:对数函数是以对数为自变量的函数。
形如f(x) = loga(x),其中a是正实数且不等于1,x为大于0的实数。
2. 对数函数的图像特点:a) 在a>1时,函数的图像在y轴右侧逐渐逼近x轴正半轴;b) 在0<a<1时,函数的图像在y轴左侧逐渐逼近x轴正半轴;c) a=1时,对数函数为常数函数,图像为y = 0。
3. 对数函数的性质:a) 当x∈(0,+∞)时,对数函数f(x) > 0,即对数函数的值始终大于0;b) 对数函数的增减性:当x1 < x2时,若a > 1,则loga(x1) <loga(x2);若0 < a < 1,则loga(x1) > loga(x2)。
4. 对数函数的特殊性质:a) loga(a) = 1,任何数以自身为底的对数等于1;b) loga(1) = 0,任何底数为正数的对数以1为真数的对数等于0;c) loga(M*N) = loga(M) + loga(N),对数的乘法法则;d) loga(M/N) = loga(M) - loga(N),对数的除法法则;e) loga(M^n) = n * loga(M),对数的乘方法则;f) loga(c) = 1/logc(a),对数的换底公式。
(完整版)指数函数与对数函数知识点总结

(一)指数与指数幂的运算
1.根式的概念:一般地,如果 ,那么 叫做 的 次方根,其中 >1,且 ∈ *.
当 是奇数时, ,当 是偶数时,
2.分数指数幂
正数的分数指数幂的意义,规定:
3.实数指数幂的运算性质
(1) · ;
(2) ;
(3) .
(二)指数函数及其性质
1、指数函数的概念:一般地,函数 叫做指数函数,其中x是自变量,函数的定义域为R.
(2) =__________
4、设 ,求 的值__________。
5、若 ,则 等于。
6、已知函数 在 上为增函数,则 的取值范围是。
7、设函数 ,若 ,则
8、函数 且 恒过定点。
9、已知函数 在 上的最大值比最小值多 ,求实数 的值。
幂函数(第15份)
1、下列函数中,是幂函数的是( )
A、 B、 C、 D、
(3) =__________
(4) =__________
(5) =__________
(6) =__________
(7) =__________
(8) =__________
2、已知 ,试用 表示下列各对数。
(1) =__________(2) =__________
3、(1)求 的值__________;
f(1.5625)=0.003
f(1.5562)=-0.029
f(1.5500)=-0.060
据此数据,可得方程 的一个近似解(精确到0.01)为
(1) (2) (3)
5、函数 在区间[ ,2]上的最大值为,最小值为。
函数 在区间[ ,2]上的最大值为,最小值为。
指数对数幂函数知识点汇总

指数函数、对数函数、幂函数知识要点梳理知识点一:指数及指数幂的运算1.根式的概念的次方根的定义:一般地,如果,那么叫做的次方根,其中当为奇数时,正数的次方根为正数,负数的次方根是负数,表示为;当为偶数时,正数的次方根有两个,这两个数互为相反数可以表示为.负数没有偶次方根,0的任何次方根都是0.式子叫做根式,叫做根指数,叫做被开方数.2.n次方根的性质:(1)当为奇数时,;当为偶数时,(2)3.分数指数幂的意义:;注意:0的正分数指数幂等与0,负分数指数幂没有意义.4.有理数指数幂的运算性质:(1) (2) (3)知识点二:指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:且图象过定点,即当.在在变化对图在第一象限内,从逆时针方向看图象,看图象,知识点三:对数与对数运算1.对数的定义(1)若,则叫做以为底的对数,记作,其中叫做底数,叫做真数. (2)负数和零没有对数. (3)对数式与指数式的互化:.2.几个重要的对数恒等式,,.3.常用对数与自然对数常用对数:,即;自然对数:,即(其中…).4.对数的运算性质如果,那么①加法:②减法:③数乘:④⑤⑥换底公式知识点四:对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.且图象过定点,即当时,上是增函数上是减函数变化对图在第一象限内,从顺时针方向看图象,看图象,1.幂函数概念形如的函数,叫做幂函数,其中为常数.2.幂函数的性质(1)图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.(2)过定点:所有的幂函数在都有定义,并且图象都通过点.(3)单调性:如果,则幂函数的图象过原点,并且在上为增函数.如果,则幂函数的图象在上为减函数,在第一象限内,图象无限接近轴与轴.(4)奇偶性:当为奇数时,幂函数为奇函数,当为偶数时,幂函数为偶函数.当(其中互质,和),若为奇数为奇数时,则是奇函数,若为奇数为偶数时,则是偶函数,若为偶数为奇数时,则是非奇非偶函数.(5)图象特征:幂函数,当时,若,其图象在直线下方,若,其图象在直线上方,当时,若,其图象在直线上方,若,其图象在直线下方.。
指数函数与对数函数知识点总结

指数函数与对数函数知识点总结一、指数函数的定义与性质1. 定义指数函数是以底数a(a>0且a≠1)为底的函数,一般表示为y=a^x,其中a是底数,x是指数,y是函数值。
2. 性质⑴当a>1时,指数函数是递增函数,图像上开;当0<a<1时,指数函数是递减函数,图像下降。
⑵当x=0时,a^0=1。
⑶当a>1时,随着x的增大,函数值y=a^x也会增大;当0<a<1时,随着x的增大,函数值y=a^x会减小。
3. 图像当底数a>1时,指数函数的图像是递增的曲线,图像上翘;当0<a<1时,指数函数的图像是递减的曲线,图像下降。
4. 应用指数函数在科学计算、生物增长、财经复利、工程技术等领域都有着重要的应用。
例如在计算机科学中,指数函数常用于指数衰减算法、指数增长算法等;在生物学中,指数函数常用于描述生物的增长规律;在金融领域中,指数函数用以描述利息的复利增长等。
二、对数函数的定义与性质1. 定义对数函数是指数函数的逆运算,一般表示为y=log_a(x),其中a是底数,x是真数,y是对数。
2. 性质⑴对数函数的定义域为x>0,值域为实数集。
⑵对数函数的图像是单调递增的曲线,在0处没有定义。
⑶特殊情况下,当底数a=10时,我们称为常用对数函数,一般表示为y=log(x);当底数a=e时,我们称为自然对数函数,一般表示为y=ln(x)。
3. 图像对数函数的图像是单调递增的曲线,图像在x轴的右侧。
4. 应用对数函数在科学计算、信息论、统计学、工程技术等领域都有着广泛应用。
例如在信息论中,对数函数用于计算信息量、信息熵等;在统计学中,对数函数用于描述正态分布、伯努利分布等;在工程技术中,对数函数用于解决指数增长问题、指数衰减问题等。
三、指数函数与对数函数的关系1. 反函数关系指数函数与对数函数是一对反函数,它们的定义域和值域互为对方的值域和定义域。
具体而言,对数函数y=log_a(x)中,x=a^y。
指数函数和对数函数知识点总结

指数函数和对数函数知识点总结一、指数函数1.定义:指数函数是以正数为底数、自变量为指数的函数。
一般形式为y=a^x,其中a>0且a≠12.特点:(1)当a>1时,指数函数呈递增趋势;(2)当0<a<1时,指数函数呈递减趋势;(3)a>1时,指数函数的图像在x轴的右侧逐渐上升,称为“增长指数函数”;(4)0<a<1时,指数函数的图像在x轴的右侧逐渐下降,称为“衰减指数函数”;(5)当x=0时,指数函数的值恒为1;(6)指数函数与直线y=0平行(若a>1)或经过点(0,1)(若0<a<1)。
3.基本性质:(1)a^m*a^n=a^(m+n);(2) (a^m)^n = a^(mn);(3) (ab)^m = a^m * b^m;(4)(a/b)^m=a^m/b^m。
二、对数函数1. 定义:对数函数是指以正数a(a>0且a≠1)为底数的对数。
一般形式为y=loga(x),其中x>0。
2.特点:(1)对数函数的定义域为正实数集(0,+∞),值域为实数集;(2) 指数函数y=a^x和对数函数y=loga(x)是互逆运算,即y=loga(a^x) = x,x=loga(a^x) = y;(3)当x>1时,对数函数的值大于0;(4)当0<x<1时,对数函数的值小于0;(5)a>1时,对数函数呈递增趋势;(6)0<a<1时,对数函数呈递减趋势;(7)当x=1时,对数函数的值恒为0;(8)对数函数的图像与直线y=x交于点(1,1)。
三、常用公式与性质1.e与自然对数:(1) e的定义:e=lim(1+1/n)^n,其中n为正整数;(2) 自然对数:ln(x)表示以e为底数的对数函数;(3) 自然对数的性质:ln(e^x)=x,e^(lnx)=x;2.指数方程与对数方程:(1)指数方程:a^x=b,其中a>0且a≠1;(2) 对数方程:loga(x)=b,其中a>0且a≠1;(3)指数方程求解的一般步骤:将方程两边取对数,利用对数的性质求解;(4)对数方程求解的一般步骤:将方程两边以a为底取指数,利用指数函数的性质求解。
指数函数和对数函数知识点总结

指数函数和对数函数知识点总结一、指数函数的定义和性质1.定义:指数函数是以一些正数a为底数的函数,形式为f(x)=a^x,其中a>0且a≠1、指数函数的定义域为实数集R,值域为正数集(0,+∞)。
2.指数函数的性质:(1)当a>1时,指数函数是递增函数;当0<a<1时,指数函数是递减函数。
(2)指数函数的图像在直线y=0上方,且与y轴渐近。
(3) 指数函数的反函数是对数函数,即 f(x) = a^x 的反函数是 g(x) = logₐ(x)。
(4)指数函数的图像在(0,+∞)上是光滑的连续曲线。
3.常见的指数函数:(2)以10为底的指数函数:记作f(x)=10^x。
在计算科学领域中经常使用。
(3)以2为底的指数函数:记作f(x)=2^x。
在计算机科学和信息技术领域中广泛应用。
二、对数函数的定义和性质1. 定义:对数函数是指数函数的反函数,形式为 f(x) = logₐ(x),其中 a>0 且a ≠ 1、对数函数的定义域为正数集(0,+∞),值域为实数集 R。
2.对数函数的性质:(1)对数函数的图像与指数函数的图像关于直线y=x对称。
(2)当0<a<1时,对数函数是递增函数;当a>1时,对数函数是递减函数。
(3)对数函数的图像在x轴正半轴上方,且与x轴渐近。
(4) 对数函数的反函数是指数函数,即 f(x) = logₐ(x) 的反函数是g(x) = a^x。
(5) 对数函数的特殊性质:logₐ(1) = 0,logₐ(a) = 1,logₐ(a^x) = x。
3.常见的对数函数:(2) 以 10 为底的对数函数:记作 f(x) = log₁₀(x)。
在计算科学领域中经常使用。
(3) 以 2 为底的对数函数:记作 f(x) = log₂(x)。
在计算机科学和信息技术领域中广泛应用。
三、指数函数和对数函数的应用1.指数函数的应用:(1)复利计算:复利计算公式中的指数函数可以用来计算存款利息、投资收益等。
指数与对数知识点总结

指数与对数知识点总结一、指数(一)指数的定义指数是数学中的一个重要概念,表示一个数自乘若干次的形式。
一般地,对于正整数 n,aⁿ表示 n 个 a 相乘,即aⁿ = a × a ×× a(n 个 a)。
(二)指数的运算性质1、 aᵐ×aⁿ = aᵐ⁺ⁿ(同底数幂相乘,底数不变,指数相加)例如:2³×2²= 2³⁺²= 2⁵= 322、(aᵐ)ⁿ = aᵐⁿ (幂的乘方,底数不变,指数相乘)比如:(2³)²= 2³×²= 2⁶= 643、(ab)ⁿ =aⁿbⁿ (积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘)例如:(2×3)²= 2²×3²= 4×9 = 364、 aᵐ÷aⁿ = aᵐ⁻ⁿ(a ≠ 0,m > n,同底数幂相除,底数不变,指数相减)比如:2⁵÷2³= 2⁵⁻³= 2²= 4(三)指数函数1、定义:一般地,函数 y =aˣ(a > 0 且a ≠ 1)叫做指数函数,其中 x 是自变量,函数的定义域是 R。
2、图像特征:当 a > 1 时,函数图像单调递增,过点(0,1)。
当 0 < a < 1 时,函数图像单调递减,过点(0,1)。
(四)指数方程形如aˣ = b 的方程,其解法通常是将其转化为对数形式求解。
二、对数(一)对数的定义如果aˣ = N(a > 0 且a ≠ 1),那么数 x 叫做以 a 为底 N 的对数,记作 x =logₐN,其中 a 叫做对数的底数,N 叫做真数。
(二)对数的运算性质1、logₐ(MN) =logₐM +logₐN (正数积的对数,等于同一底数的各个因数的对数的和)例如:log₂(4×8) = log₂4 + log₂8 = 2 + 3 = 52、logₐ(M/N) =logₐM logₐN (正数商的对数,等于被除数的对数减去除数的对数)比如:log₃(9/3) = log₃9 log₃3 = 2 1 = 13、logₐMⁿ =nlogₐM (幂的对数等于幂指数乘以底数的对数)例如:log₅2⁵= 5log₅2(三)换底公式logₐb =logₑb /logₑa (其中 e 为自然对数的底数,约等于 2718)(四)常用对数与自然对数1、常用对数:以 10 为底的对数叫做常用对数,简记为 lgN。
指数函数和对数函数复习(有详细知识点和习题详解)

指数函数和对数函数复习(有详细知识点和习题详解)一、指数的性质一)整数指数幂整数指数幂的概念是指:a的n次方等于a乘以a的n-1次方,其中a不等于0,n为正整数。
另外,a的-n次方等于1除以a的n次方,其中a不等于0,n为正整数。
整数指数幂的运算性质包括:(1)a的m次方乘以a的n次方等于a的m+n次方;(2)a的n次方的m次方等于a的mn次方;(3)a乘以b的n次方等于a的n次方乘以b的n次方。
其中,a除以a的n次方等于a的n-1次方,a的m-n次方等于a的m除以a的n次方,an次方根的概念是指,如果一个数的n次方等于a,那么这个数叫做a的n次方根,记作x=√a。
例如,27的3次方根等于3,-27的3次方根等于-3,32的5次方根等于2,-32的5次方根等于-2.a的n次方根的性质包括:如果n是奇数,则a的n次方根等于a;如果n是偶数且a大于等于0,则a的正的n次方根等于a,a的负的n次方根等于负的a;如果n是偶数且a小于0,则a的n次方根没有意义,即负数没有偶次方根。
二)例题分析例1:求下列各式的值:(1)3的-8次方;(2)(-10)的2次方;(3)4的(3-π)次方;(4)(a-b)的2次方,其中a大于b。
例2:已知a小于b且n大于1,n为正整数,化简n[(a-b)/(a+b)]。
例3:计算:7+40+7-40.例4:求值:(59/24)+(59-45)/24 + 25×(5-2)/24.解:略。
二)分数指数幂1.分数指数幂当根式的被开方数能被根指数整除时,根式可以写成分数指数幂的形式,例如:$5\sqrt[10]{a^5}=a^{\frac{1}{2}}$,$3\sqrt[12]{a^3}=a^{\frac{1}{4}}$。
当根式的被开方数不能被根指数整除时,根式也可以写成分数指数幂的形式,例如:$\sqrt[4]{a^5}=a^{\frac{5}{4}}$。
规定:1)正数的正分数指数幂的意义是$a^{\frac{p}{q}}=\sqrt[q]{a^p}$。
指数函数与对数函数知识点总结

指数函数与对数函数知识点总结一、指数与指数幂的运算1.根式的概念注意:负数没有偶次方根;0的任何次方根都是0当n 是奇数时,a a n n =,当n 是偶数时,⎩⎨⎧<≥-==)0()0(||a a a a a a n n 2.分数指数幂正数的分数指数幂的意义,规定:)1,,,0(*>∈>=n N n m a a a n m n m )1,,,0(11*>∈>==-n N n m a a a a n m n mn m0的正分数指数幂等于0,0的负分数指数幂没有意义3.实数指数幂的运算性质.4.达标要求:会进行根式与分数指数幂的相互转化;能够进行指数幂的运算和化简。
5.相关习题:课本54页练习1、2、3;59页2,4 补充:若11225x x -+=,则21x x+的值是 二、指数函数及其性质1、指数函数的概念2、指数函数的图象和性质a 的范围a >1 0<a <1图像定义域 值域单调性奇偶性定点函数值变化情况 当x >0时, 当x <0时, 当x >0时,当x <0时,3、达标要求:理解指数函数的性质(如单调性,定点);能够应用性质进行比较大小,解决与指数函数相关的函数性质问题和图像问题。
4、相关习题:白皮书35页例2,巩固提高1-4;36页例1例2,;37页例4三、对数与对数运算1.对数的概念幂值 真数b a = N ⇔log a N = b底数指数 对数2.对数的运算性质如果0>a ,且1≠a ,0>M ,0>N ,那么:○1 M a (log ·=)N M a log +N a log ; ○2 =NM a log M a log -N a log ; ○3 n a M log n =M a log )(R n ∈. 注意:换底公式ab bc c a log log log = (0>a ,且1≠a ;0>c ,且1≠c ;0>b ). 利用换底公式推导下面的结论 (1)b m n b a n a m log log =;(2)a b b a log 1log =. 3.达标要求:能够进行对数式与指数式的互化,熟练的运用对数法则解决问题。
初中数学指数函数与对数函数的计算知识点总结

初中数学指数函数与对数函数的计算知识点总结指数函数和对数函数是初中数学中重要的概念,学好这两个函数的计算方法对于理解高中数学和实际问题具有重要意义。
本文将对初中数学指数函数与对数函数的计算知识点进行总结。
一、指数函数的计算知识点总结1. 指数幂的定义:对于任意的实数a和正整数n,a^n表示a连乘n 次,其中a称为底数,n称为指数。
2. 同底数幂相乘:当底数相同时,指数幂相乘等于底数不变,指数相加,即a^m * a^n = a^(m+n)。
3. 同底数幂相除:当底数相同时,指数幂相除等于底数不变,指数相减,即a^m / a^n = a^(m-n)。
4. 指数幂的幂:幂的指数就是指数幂的指数,即(a^m)^n = a^(m*n)。
5. 零指数幂:任意非零数的零次方等于1,即a^0 = 1(a ≠ 0)。
6. 负指数幂:任意非零数的负整数次方等于该数的倒数的绝对值的幂,即a^(-n) = 1 / a^n(a ≠ 0)。
二、对数函数的计算知识点总结1. 对数的定义:对于正数a(a ≠ 1),b(b > 0)和正整数n,n称为底数,b称为真数,记作logₐb=n,表示a的n次幂等于b。
2. 换底公式:logₐb = logₐc * log_cb,其中a,b,c为正数,且a,b 不等于1。
3. 常用对数和自然对数:以10为底的对数称为常用对数,记作logb,以自然常数e为底的对数称为自然对数,记作lnb。
三、指数函数与对数函数的性质1. 指数函数与对数函数是互为反函数的关系,即对于a^x = y,有logₐy = x。
2. 指数函数和对数函数的图像是关于直线 y = x 的对称图像。
3. 指数函数的图像随着底数的变化有不同的特征,如当底数大于1时,图像递增;当底数在0和1之间时,图像递减。
4. 对数函数的图像在底数大于1和小于1的情况下有不同的特征,如当底数大于1时,图像递增;当底数在0和1之间时,图像递减。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数函数和对数函数知识点总结及练习题一.指数函数(一)指数及指数幂的运算n m nm a a = s r s r a a a +=⋅ rs s r a a =)( r r r b a ab =)((二)指数函数及其性质1.指数函数的概念:一般地,形如xa y =(0>a 且1≠a )叫做指数函数。
二.对数函数(一)对数1.对数的概念:一般地,如果N a x=(0>a 且1≠a ),那么x 叫做以a 为底N 的对数,记作N x a log =,其中a 叫做底数,N 叫做真数,N a log 叫做对数式。
2.指数式与对数式的互化幂值 真数x N N a a x =⇔=log底数指数 对数3.两个重要对数(1)常用对数:以10为底的对数N lg(2)自然对数:以无理数 71828.2=e 为底的对数N ln(二)对数的运算性质(0>a 且1≠a ,0,0>>N M ) ①MN N M a a a log log log =+ ②NM N M aa a log log log =- ③M n M a na log log = ④换底公式:abb c c a log log log =(0>c 且1≠c ) 关于换底公式的重要结论:①b mnb a na m log log = ②1log log =⋅ab b a(三)对数函数1.对数函数的概念:形如x y a log =(0>a 且1≠a )叫做对数函数,其中x 是自变量。
基本初等函数练习题1.已知集合M }1,1{-=,N },4221|{1Z x x x ∈<<=+,则M ∩N =( ) A.{-1,1} B.{0} C.{-1} D.{-1,0} 2.设1)31()31(31<<<ab ,则( ) A.abab a a << B.baaa b a << C.aabb a a << D.aaba b a << 3.设9.014=y ,48.028=y ,5.13)21(-=y ,则( )A.213y y y >>B.312y y y >>C.231y y y >>D.213y y y >> 4.若a a 2312)21()21(-+<,则实数a 的取值范围是( ) A.(1,+∞) B.(12,+∞) C.(-∞,1) D.(-∞,12)5.方程3x -1=19的解为( )A.x =2B.x =-2C.x =1D.x =-16.已知实数a ,b 满足等式(12)a =(13)b ,则下列五个关系式:①0<b <a ;②a <b <0;③0<a <b ;④b <a <0;⑤a =b 。
其中不.可能成立的有( ) A.1个 B.2个 C.3个 D.4个 7.函数xy -=1)21(的单调增区间为( )A.(-∞,+∞)B.(0,+∞)C.(1,+∞)D.(0,1) 8.函数1-=x a y 的定义域是]0,(-∞,则实数a 的取值范围为( )A.a >0B.a <1C.0<a <1D.a ≠1 9.函数xy π=的值域是( )A.(0,+∞)B.[0,+∞)C.RD.(-∞,0)10.当x >0时,指数函数f (x )=(a -1)x <1恒成立,则实数a 的取值范围是( ) A.a >2 B.1<a <2 C.a >1 D.a ∈R 11.不论a 取何正实数,函数f (x )=a x +1-2恒过点( ) A.(-1,-1) B.(-1,0) C.(0,-1) D.(-1,-3)12.函数y =a x (a >0且a ≠1)在[0,1]上的最大值与最小值的和为3,则a 的值为( )A.12B.2C.4D.1413.方程4x +1-4=0的解是x =________.14.当x ∈[-1,1]时,f (x )=3x -2的值域为________. 15.方程4x +2x -2=0的解是________.16.满足f (x 1)·f (x 2)=f (x 1+x 2)的一个函数f (x )=______ . 17.求适合a 2x +7<a 3x -2(a >0,且a ≠1)的实数x 的取值范围.18.已知2x ≤(14)x -3,求函数y =(12)x 的值域.19.log 63+log 62等于( )A.6B.5C.1D.log 65 20.若102x =25,则x 等于( ) A.51lgB.5lgC.5lg 2D.51lg 2 21.log 22的值为( ) A.2-B. 2C.-12 D.1222.化简12log 612-2log 62的结果为( )A.6 2B.12 2C.log 6 3D.1223.已知lg2=a ,lg3=b ,则log 36=( )A.a +b aB.a +b bC.a a +bD.b a +b24.1log =b a 成立的条件是( )A.a =bB.a =b 且b >0C.a >0且a ≠1D.a >0,a =b ≠1 25.若b N a=log (a >0且a ≠1),则下列等式中正确的是( )A.N =a 2bB.N =2a bC.N =b 2aD.N 2=a b 26.若c b a =7log ,则a 、b 、c 之间满足( )A.b 7=a cB.b =a 7cC.b =7a cD.b =c 7a27.已知2log =x a ,1log =x b ,4log =x c (a ,b ,c ,x >0且≠1),则=)(log abc x ( ) A.47 B.27 C.72 D.7428.如果f (e x )=x ,则f (e)=( )A.1B.ee C.e 2 D.0 29.在b =log (a -2)(5-a )中,实数a 的取值范围是( )A.a >5或a <2B.2<a <3或3<a <5C.2<a <5D.3<a <4 30.若log a 2<log b 2<0,则下列结论正确的是( )A.0<a <b <1B.0<b <a <1C.a >b >1D.b >a >1 31.若log a 2<1,则实数a 的取值范围是( )A.(1,2)B.(0,1)∪(2,+∞)C.(0,1)∪(1,2)D.(0,12)32.下列不等式成立的是( ) A.log 32<log 23<log 25 B.log 32<log 25<log 23 C.log 23<log 32<log 25D.log 23<log 25<log 3233.已知log 12b <log 12a <log 12c ,则( )A.2b >2a >2cB.2a >2b >2cC.2c >2b >2aD.2c >2a >2b 34.在b =log (a -2)3中,实数a 的取值范围是( )A.a <2B.a >2C.2<a <3或a >3D.a >335.有以下四个结论:①lg(lg10)=0;②ln(lne)=0;③若10=x lg ,则x =10;④若x e ln =,则2e x =..其中正确的是( )A.①③B.②④C.①②D.③④ 36.函数x y a log =的图象如图所示,则实数a 的可能取值是( ) A.10 B.e C.12 D.237.函数2log 2-=x y 的定义域是( )A.(3,+∞)B.[3,+∞)C.(4,+∞)D.[4,+∞) 38.函数x x x f -+-=4)1lg()(的定义域为( ) A.(1,4] B.(1,4) C.[1,4] D.[1,4) 39.函数f (x )=log 2(x +x 2+1)(x ∈R )为( )A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数 40.已知2x =5y =10,则1x +1y =________.41.计算:2log 510+log 50.25=________.42.已知log a 2=m ,log a 3=n (a >0且a ≠1),则a 2m +n =________. 43.方程1)12(log 3=-x 的解为x =________.44.已知⎩⎨⎧>≤=0,ln 0,)(x x x e x g x ,则g (g (13))=________.45.函数)1(log 21-=x y 的定义域是________.46.已知集合A }2log |{2≤=x x ,B =(-∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =________.47.函数3)2(log ++=x y a (0>a 且1≠a )的图象过定点________. 48.函数)124(log 231++-=x x y 的值域是________.49.已知集合A ={x |2≤x ≤π},定义在集合A 上的函数x y a log =(0>a 且1≠a )的最大值比最小值大1,求a 的值.。
