全等三角形证明经典试题50道
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
BADBCC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE (AAS )∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=E G ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB 所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC=∠FAC 又因为AC =AC 所以△ADC≌△AFC(SAS ) 所以AD =AF所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF。
所BC DF ADBCBC以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE(AAS)∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BECDB ABA CDF2 1 E证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB 所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF 所以∠B=∠CFE 因为∠B+∠D=180°,∠CFE+∠CFA =180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC=∠FAC 又因为AC =AC 所以△ADC≌△AFC(SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
(完整版)全等三角形证明经典50的题目(含答案详解),推荐文档
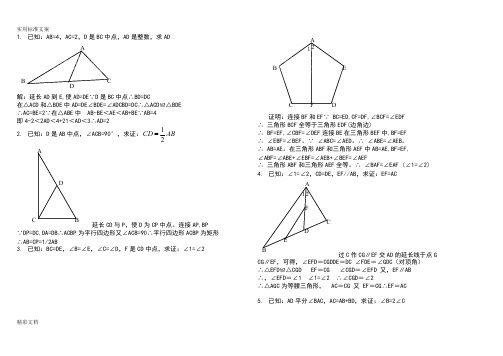
精彩文档1.已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求ADADBC解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE ∴AC=BE=2∵在△ABE 中 AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22.已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BPC ∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3.已知:BC=DE ,∠B=∠E,∠C=∠D,F 是CD 中点,求证:∠1=∠2B证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF。
∵ ∠ABC=∠AED。
∴ ∠ABE=∠AEB。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)4.已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点GBA CDF21ECG∥EF,可得,∠EFD=CGDDE =DC ∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG∴EF=AC 5.已知:AD 平分∠BAC,AC=AB+BD ,求证:∠B=2∠C 建议收藏下载本文,以便随时学习!证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD(SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在ADA精彩文档精彩文档上。
全等三角形经典题型50题带答案

全等三角形证明经典50题(含答案)(一)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB从D 做辅助线3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中, AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
AD B C4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明: 过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2 又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS ) ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明: 在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS ) ∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(有答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E ,使DE=AD ,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB —BE<AE 〈AB+BE 即:10—2〈2AD<10+2 4<AD 〈6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED ,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF ,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF.所以 ∠EBF=∠BEF.又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2).ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS)∴EG=AC ∵EF//AB ∴∠DF E=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案解析)
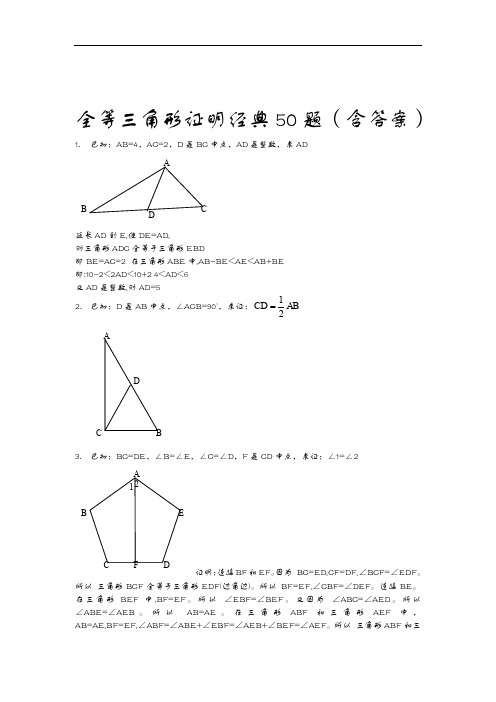
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF和三ADBC角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典50的题目(含答案详解)

1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE ∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=22.已知:D是AB中点,∠ACB=90°,求证:12 CD AB延长CD与P,使D为CP中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB3.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2) 4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC过C作CG∥EF交AD的延长线于点G CG∥EF,可得,∠EFD=CGDDE=DC ∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF=CG ∠CGD=∠EFD 又,EF∥AB∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG 又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CADBCBACDF21E精彩文档证明:延长AB取点E,使AE=AC,连接DE ∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE 证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
全等三角形证明50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=2ADBC2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC∠FDE =∠GDC (对顶角)BA CDF2 1 EEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB∴∠CEB =∠CEF =90° ∵EB =EF ,CE =CE , ∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS ) ∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DEADB C∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=29.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
全等三角形证明经典50题(含答案)

三角形全等经典证明1.已知:AB=4,AC=2,D是BC中点, AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=21. 已知:D是AB中点,∠ACB=90°,求证:延长CD与P,使D为CP中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB2. 已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴ ∠EBF=∠BEF。
∵ ∠ABC=∠AED。
∴ ∠ABE=∠AEB。
∴ AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF和三角形AEF全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
3. 已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC过C作CG∥EF交AD的延长线于点GCG∥EF,可得,∠EFD=CGDDE=DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又 EF=CG∴EF=AC4. 已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE ∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD(SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5. 已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6. 已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=27. 已知:D是AB中点,∠ACB=90°,求证:解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=28. 已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
全等三角形经典题型50题(有答案)
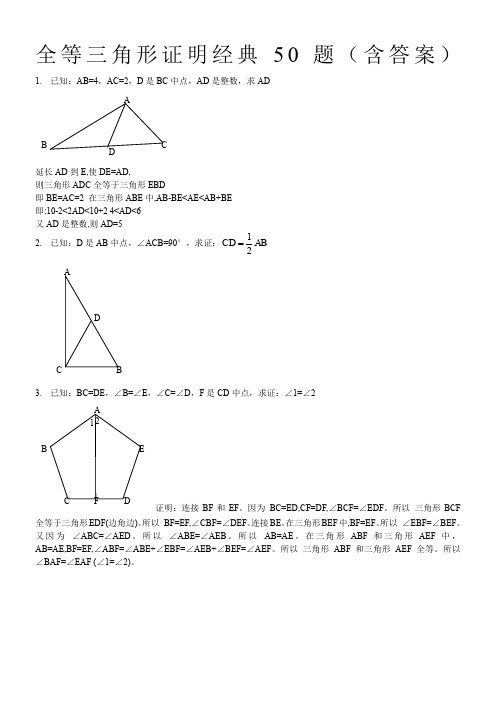
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC 5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C 6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE 12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
(完整版)全等三角形证明经典50题(含答案)
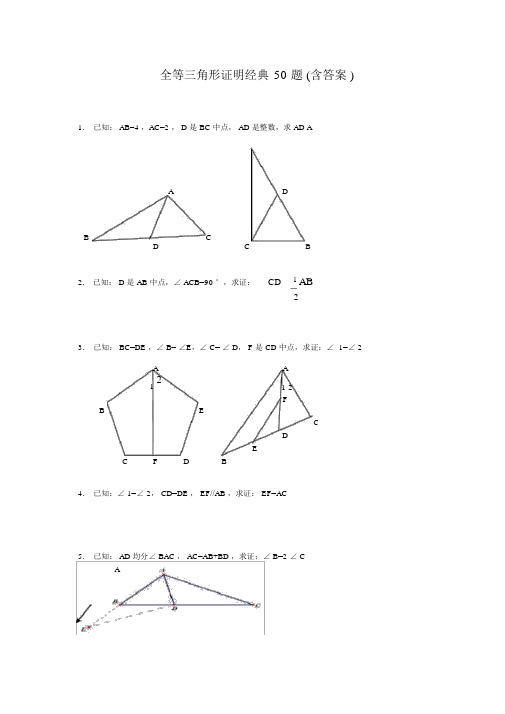
全等三角形证明经典50 题 (含答案 )1.已知: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求 AD AA DB CD C B2. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB23.已知: BC=DE ,∠ B= ∠E,∠ C= ∠ D, F 是 CD 中点,求证:∠ 1=∠ 2A A1 21 2BFECDEC FD B4.已知:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=AC5.已知: AD 均分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CA6.已知: AC 均分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE12.如图,四边形 ABCD 中, AB ∥ DC ,BE、 CE 分别均分∠ ABC 、∠ BCD ,且点 E 在 AD上。
求证: BC=AB+DC 。
E DCFA B13.已知: AB//ED ,∠ EAB= ∠ BDE , AF=CD , EF=BC ,求证:∠ F=∠ C14.P 是∠ BAC 均分线 AD 上一点, AC>AB ,求证: PC-PB<AC-AB CAP DB15. 已知∠ ABC=3 ∠ C,∠ 1=∠2, BE⊥ AE ,求证: AC-AB=2BE16.已知, E 是 AB 中点, AF=BD , BD=5 , AC=7 ,求 DCDF A CE B18.如图,在△ABC 中, BD =DC ,∠ 1=∠ 2,求证: AD⊥BC .19.如图, OM 均分∠ POQ ,MA ⊥ OP,MB⊥ OQ , A、 B 为垂足, AB 交 OM 于点 N.求证:∠ OAB=∠OBA20.( 5 分)如图,已知 AD ∥BC,∠ PAB 的均分线与∠ CBA 的均分线订交于 E, CE 的连线交AP 于 D .求证: AD +BC =AB.PACEDCD BA B21.如图,△ ABC 中, AD 是∠ CAB 的均分线,且AB=AC+CD,求证:∠ C=2∠ B22.( 6 分)如图①, E、F 分别为线段AC 上的两个动点,且DE ⊥AC 于 E, BF⊥AC 于 F ,若 AB=CD , AF=CE, BD 交 AC 于点 M.(1)求证: MB=MD , ME =MF(2)当 E、F 两点挪动到如图②的地点时,其他条件不变,上述结论可否建立?若建立请赐予证明;若不建立请说明原因.23.已知:如图,DC∥ AB,且 DC =AE, E 为 AB 的中点,( 1)求证:△ AED≌△ EBC.( 2)观看图前,在不添协助线的状况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):AE ODB C24.( 7 分)如图,△ ABC 中,∠ BAC=90 线垂直于过 C 点的直线于 E,直线 CE 交求证: BD =2CE.度, AB=AC, BD 是∠ ABC 的均分线, BD 的延伸BA 的延伸线于 F.FAED证明:B C25、如图: DF=CE, AD=BC,∠ D=∠ C。
全等三角形经典题型50题(含答案)
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD/ C= / D, F 是CD 中点,求证:/ 1 = / 2证明:连接BF 和EF。
因为BC=ED,CF=DF, / BCF= / EDF。
所以三角形BCF全等于三角形EDF(边角边)。
所以BF=EF, / CBF= / DEF。
连接BE。
在三角形BEF 中,BF=EF。
所以 / EBF= / BEF。
又因为 / ABC= / AED。
所以 / ABE= / AEB。
所以AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF。
所以三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF (/ 1 = / 2)。
延长AD至U E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知:D是AB中点,/ ACB=90 °,求证:CD1 —AB 2A34. 已知:/ 仁/2, CD=DE , EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于 G 则/ DEG= / DCA , / DGE= / 2 又 •/ CD=DE U ADC 也"GDE ( AAS )••• EG=AC •/ EF//AB /-Z DFE= / 1 v/ 1 = / 2:丄 DFE= / DGE ••• EF=EG •: EF=AC5. 已知:AD 平分Z BAC , AC=AB+BD ,求证:Z B=2 / C证明:在 AC 上截取 AE=AB ,连接 ED •/ AD 平分Z BAC :•/ EAD= Z BAD 又 v AE=AB ,AD=AD :•" AED 6 ABD (SAS )•:Z AED= Z B ,DE=DB v AC=AB+BDAC=AE+CE •: CE=DE :-Z C=Z EDC vZ AED= Z C+ Z EDC=2 Z C -Z B=2 Z C 6. 已知:AC 平分Z BAD , CE 丄 AB , Z B+ Z D=180 °,求证: AE=AD+BE证明:在AE 上取F ,使EF = EB , 连接CF 因为CE 丄AB 所以Z CEB=Z CEF = 90° 因为 EB = EF , CE = CE , 所以△CEBCEF 所以Z B = Z CFE 因为Z B+ Z D = 180°, Z CFE +Z CFA = 180° 所以Z D = Z CFA 因为 AC 平分Z BAD 所以Z DAC=Z FAC 又因为 AC = AC 所以△ ADC AFC (SAS ) 所以 AD = AF 所以 AE = AF + FE=AD + BE12.如图,四边形 ABCD 中,AB // DC , BE 、CE 分别平分Z ABC 、Z BCD ,且点 E 在AD 上。
全等三角形经典题型50题(含答案)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD /即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 ~证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
BADBCC(4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形证明经典试题50道1. (已知:如图,E,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =C F .【答案】∵AD ∥CB∴∠A=∠C又∵AD=CB ,∠D=∠B∴△ADF ≌△CBE∴AF=CE∴AF+EF=CE+EF即AE=CF2. 已知:如图,∠ABC =∠DCB ,BD 、C A 分别是∠ABC 、∠DCB 的平分线.求证:AB =DC 证明:在△ABC 与△DCB 中(ABC DCB ACB DBC BC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩已知)(公共边)(∵AC 平分∠BCD ,BD 平分∠ABC ) ∴△ABC ≌△DCB∴AB =DC3. 如图,点D ,E 分别在AC ,AB 上.(1) 已知,BD =CE ,CD=BE ,求证:AB=AC ;(2) 分别将“BD=CE ”记为①,“CD=BE ” 记为②,“AB=AC ”记为③.添加条件①、③,以②为结论构成命题1,添加条件②、③以①为结论构成命题2.命题1是命题2的 命题,命题2是 命题.(选择“真”或“假”填入空格).【答案】(1) 连结BC,∵BD=CE,CD=BE,BC=CB.∴△DBC≌△ECB (SSS)∴∠DBC =∠ECB∴AB=AC(2) 逆,假;4. 如图,在□ABCD中,分别延长BA,DC到点E,使得AE=AB,CH=CD,连接EH,分别交AD,BC于点F,G。
求证:△AEF≌△CHG.【答案】证明:∵□ABCD∴ AB=CD,∠BAD=∠BCD AB∥CD∴∠EAF=∠HCG ∠E=∠H∵ AE=AB,CH=CD∴ AE=CH∴△AEF≌△CHG.5. 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.【证明】∵AF=DC,∴AC=DF,又∠A=∠D ,AB=DE,∴△ABC≌△DEF,∴∠ACB=∠DFE,∴BC∥EF.6. 两块完全相同的三角形纸板ABC和DEF,按如图所示的方式叠放,阴影部分为重叠部分,点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等?为什么?【答案】解:全等.理由如下:∵两三角形纸板完全相同,∴BC=BF,AB=BD,∠A=∠D,∴AB-BF=BD-BC,即AF=DC.在△AOF和△DOC中,∵AF=DC,∠A=∠D,∠AOF=∠DOC,∴△AOF≌△DOC(AAS).7. 已知:如图,E,F在AC上,AD∥CB且AD=CB,∠D=∠B.求证:AE=CF.【答案】∵AD ∥CB∴∠A=∠C又∵AD=CB ,∠D=∠B∴△ADF ≌△CBE∴AF=CE∴AF+EF=CE+EF即AE=CF8. 在△ABC 中,AB=CB,∠ABC=90º,F 为AB 延长线上一点,点E 在BC 上,且AE=CF.(1)求证:Rt △AB E ≌Rt △CBF;(2)若∠CAE=30º,求∠ACF 度数.【答案】(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.在Rt △ABE 和Rt △CBF 中,∵AE=CF, AB=BC, ∴Rt △ABE ≌Rt △CBF(HL)(2)∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠AC B=45°.∵∠BAE=∠CAB-∠CAE=45°-30°=15°.由(1)知 Rt △ABE ≌Rt △CBF , ∴∠BCF=∠BAE=15°,∴∠ACF=∠BCF+∠ACB=45°+15°=60°.9. 如图6,AB BD ⊥于点B ,ED BD ⊥于点D ,AE 交BD 于点C ,且BC DC =.求证AB ED =. ABC EF 第22题图【答案】(1)证明:∵AB BD ⊥,ED BD ⊥ ∴90ABC D ∠=∠=o在ABC ∆和EDC ∆中ABC D BC DCACB ECD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABC ∆≌EDC ∆∴AB ED =10.如图,在Rt △ABC 中,∠BAC=90°,AC=2AB ,点D 是AC 的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A 、D 重合,连结BE 、EC .试猜想线段BE 和EC 的数量及位置关系,并证明你的猜想.【答案】BE=EC ,BE ⊥EC∵AC=2AB ,点D 是AC 的中点∴AB=AD=CD∵∠EAD=∠EDA=45°∴∠EAB=∠EDC=135°∵EA=ED∴△EAB ≌△EDC∴∠AEB=∠DEC ,EB=EC∴∠BEC=∠AED=90°∴BE=EC ,BE ⊥EC11. 已知:如图,E,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF . A图6 B C DE AB CDE【答案】∵AD∥CB∴∠A=∠C又∵AD=CB,∠D=∠B∴△ADF≌△CBE∴AF=CE∴AF+EF=CE+EF即AE=CF12. 如图,D,E,分别是 AB,AC 上的点,且AB=AC,AD=AE.求证∠B=∠C.【答案】证明:在△ABE和△ACD中,AB=AC∠A=∠A AE=AD∴△ABE≌△ACD∴∠B=∠C13. 如图,在△ABC中,AD是中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.【证明】∵在△ABC中,AD是中线,∴BD=CD,∵CF⊥AD,BE⊥AD,∴∠CFD=∠BED=90°,在△BED与△CFD中,∵∠BED=∠CFD,∠BDE=∠CDF,BD=CD,∴△BED≌△CFD,∴BE=CF.14. 已知:如图,在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=∠B,ED=DC.求证:AB=AC【答案】证明∵AD平分∠EDC,∴∠ADE=∠ADC,又DE=DC,AD=AD,∴△ADE≌△ADC, ∴∠E=∠C,又∠E=∠B,∴∠B =∠C,∴AB=AC.15. 如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F.(1)证明:∠DFA = ∠FAB;(2)证明: △ABE≌△FCE.(第18题图)【答案】证明:(1)∵AB与CD是平行四边形ABC D的对边,∴AB∥CD,(1分)∴∠F=∠FAB.(3分)(2)在△ABE和△FCE中,∠FAB=∠F (4分)∵∠AEB=∠FEC (5分)BE=CE (6分)∴△ABE≌△FCE.(7分)16.如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.(1)求证:△ACD≌△BCE;(2)若∠D=50°,求∠B的度数.【答案】17.如图,已知:点B 、F 、C 、E 在一条直线上,FB =CE ,AC =DF .能否由上面的已知条件证明AB ∥ED ?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适....的条件...,添加到已知条件中,使AB ∥ED 成立,并给出证明. 供选择的三个条件(请从其中选择一个):①AB =ED ;②BC =EF ;③∠ACB =∠DFE .【答案】解:由上面两条件不能证明AB//ED .有两种添加方法.第一种:FB =CE ,AC =DF 添加 ①AB =ED证明:因为FB =CE ,所以BC =EF ,又AC =EF ,AB =ED ,所以V ABC ≅V DEF所以∠ABC =∠DEF 所以AB//ED第二种:FB =CE ,AC =DF 添加 ③∠ACB =∠DFE证明:因为FB =CE ,所以BC =EF ,又∠ACB =∠DFE AC =EF ,所以V ABC ≅V DEF所以∠ABC =∠DEF 所以AB//ED 18.如图,在△ABC 中,D 是BC 边上的点(不与B ,C 重合),F ,E 分别是AD 及其延长线上的点,CF ∥BE . 请你添加一个条件,使△BDE ≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是: ▲ ;(2)证明: AB DEFC(第25题) A CB D F E (第18题图)【答案】 解:(1)DC BD =(或点D 是线段BC 的中点),ED FD =,BE CF =中任选一个即可﹒(2)以DC BD =为例进行证明:∵CF ∥BE ,∴∠FCD ﹦∠EBD .又∵DC BD =,∠FDC ﹦∠EDB ,∴△BDE ≌△CDF .19.如图,分别过点C 、B 作△ABC 的BC 边上的中线AD 及其延长线的垂线,垂足分别为E 、F .求证:BF =CE .【答案】∵CE ⊥AF ,FB ⊥AF ,∴∠DEC =∠DFB =90°又∵AD 为BC 边上的中线,∴BD =CD , 且∠EDC =∠FDB (对顶角相等)∴所以△BFD ≌△CDE (AAS ),∴BF =CE .20.如图,已知AD 是△ABC 的角平分线,在不添加任何辅助线的前提下,要使△AE D ≌△AFD ,需添加一个条件是:_______________,并给予证明.全品中考网【答案】解法一:添加条件:AE =AF ,证明:在△AED 与△AFD 中,∵AE =AF ,∠EAD =∠FAD ,AD =AD ,∴△AED ≌△AFD (SAS ).解法二:添加条件:∠EDA =∠FDA ,证明:在△AED 与△AFD 中, B D CAEF∵∠EAD =∠FAD ,AD =AD ,∠EDA =∠FDA∴△AED ≌△AFD (ASA ).21.已知:如图,点C 是线段AB 的中点,CE=CD ,∠ACD=∠BCE,求证:AE=BD .题20图【答案】证明:∵点C 是线段AB 的中点,∴AC=BC ,∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD, 在△ACE 和△BCD 中,AC BC ACE BCD CE CD ⎧=⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD (SAS ),∴AE=BD.21.已知:如图,点A 、B 、C 、D 在同一条直线上,EA ⊥AD ,FD ⊥AD ,AE =DF ,AB =DC .求证:∠ACE =∠DBF .【答案】证明:∵AB =DC∴AC =DB∵EA ⊥AD ,FD ⊥AD∴∠A =∠D =90°在△EAC 与△FDB 中⎪⎩⎪⎨⎧=∠=∠=DB AC D A FD EA∴△EAC ≌△FDB∴∠ACE =∠DBF .22.如图,点A 、E 、B 、D 在同一条直线上,AE =DB ,AC =DF ,AC ∥DF .请探索BC 与EF 有怎样的位置关系?并说明理由.DO C B A【答案】解:BC ∥EF .理由如下:∵AE =DB ,∴AE +BE =DB +BE ,∴AD =DE .∵AC ∥DF , ∴∠A =∠D ,∵AC =DF , ∴△ACB ≌△DFE ,∴∠FED =∠CBA ,∴BC ∥EF . 23.如图,点B 、D 、C 、F 在一条直线上,且BC = FD ,AB = EF.(1)请你只添加一个条件(不再加辅助线),使△ABC ≌△EFD ,你添加的条件是 ; (2)添加了条件后,证明△ABC ≌△EFD.【答案】(1)∠B = ∠F 或 AB ∥EF 或 AC = ED .(2)证明:当∠B = ∠F 时 在△ABC 和△EFD 中AB EFB F BC FD =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△EFD (SAS) 24.如图,BAC ABD ∠=∠.(1)要使OC OD =,可以添加的条件为: 或 ;(写出2个符合题意的条件即可) (2)请选择(1)中你所添加的一个条件,证明OC OD =. 【答案】解:(1)答案不唯一. 如C D ∠=∠,或ABC BAD ∠=∠,或OAD OBC ∠=∠,或AC BD =. ……4分 说明:2空全填对者,给4分;只填1空且对者,给2分. (2)答案不唯一. 如选AC BD =证明OC=OD. 证明: ∵ BAC ABD ∠=∠,∴ OA=OB. ……………………6分 又 AC BD =,∴ AC-OA=BD-OB ,或AO+OC=BO+OD. ∴ OC OD =. ……………………8分25.八(1)班同学上数学活动课,利用角尺平分一个角(如图).设计了如下方案:FABCDEABCDEFDOCBA B(Ⅰ)∠AOB 是一个任意角,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM=PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线.(Ⅱ)∠AOB 是一个任意角,在边OA 、OB 上分别取OM=ON ,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM=PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线. (1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.(2)在方案(Ⅰ)PM=PN 的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由. 【答案】解:(1)方案(Ⅰ)不可行.缺少证明三角形全等的条件. ……………………………2分(2)方案(Ⅱ)可行. ……………………………3分证明:在△OPM 和△OPN 中⎪⎩⎪⎨⎧===OP OP PN PM OP OM∴△OPM ≌△OPN(SSS)∴∠AOP=∠BOP(全等三角形对应角相等) ……………………………5分 (3)当∠AOB 是直角时,此方案可行. ……………………………6分∵四边形内角和为360°,又若PM ⊥OA,PN ⊥OB, ∠OMP=∠ONP=90°, ∠MPN=90°, ∴∠AOB=90°∵若PM ⊥OA,PN ⊥OB, 且PM=PN∴OP 为∠AOB 的平分线.(到角两边距离相等的点在这个角的角平分线上) 当∠AOB 不为直角时,此方案不可行. …………8分 26.如图,AB 是∠DAC 的平分线,且AD =AC 。
