解一元一次方程同解方程精选试题附答案
解一元一次方程50道练习题(带答案)

解一元一次方程50道练习题(带答案)基础题:1.(1) x = 3.(2) x =2.(3) x = 4.(4) x = 4.(5) x = 1.(6) x = -9.(7) x = 1.(8) 0 = 16 (无解)2.(1) x = -2.5.(2) x = 1.5.(3) x = -2.(4) x = -0.5.(5) x = 0.5.(6) x = -0.5.(7) 0 = 1 (无解)。
(8) x = 13.(1) x = 1.25.(2) x =4.5.(3) x = -9.(4) x = -2.(5) x = 4.(6) x =4.(7) x = -1.(8) x = -8综合题Ⅰ:4.(1) x = 2.(2) 无解。
(3) x = 2.5.(4) x = -1.(5) x = 1.(6) x = -1/2.(7) x = -38.(8) x = 175.(1) x = -2.(2) x = -3.(3) x = -1/3.(4) x = -1/2.(5) 无解。
(6) x = -1/7.(7) x = 94/3.(8) x = 10改写后的文章:这篇文章包含了50个一元一次方程的练题及其答案。
下面按照题目类型分别列出解法。
基础题:1.(1) 解得 x = 3;(2) 解得 x = 2;(3) 解得 x = 4;(4) 解得x = 4;(5) 解得 x = 1;(6) 解得 x = -9;(7) 解得 x = 1;(8) 无解。
2.(1) 解得 x = -2.5;(2) 解得 x = 1.5;(3) 解得 x = -2;(4) 解得 x = -0.5;(5) 解得 x = 0.5;(6) 解得 x = -0.5;(7) 无解;(8) 解得 x = 1.3.(1) 解得 x = 1.25;(2) 解得 x =4.5;(3) 解得 x = -9;(4) 解得 x = -2;(5) 解得 x = 4;(6) 解得 x = 4;(7) 解得 x = -1;(8) 解得 x = -8.综合题Ⅰ:4.(1) 解得 x = 2;(2) 无解;(3) 解得 x = 2.5;(4) 解得 x = -1;(5) 解得 x = 1;(6) 解得 x = -1/2;(7) 解得 x = -38;(8) 解得 x = 17.5.(1) 解得 x = -2;(2) 解得 x = -3;(3) 解得 x = -1/3;(4) 解得 x = -1/2;(5) 无解;(6) 解得 x = -1/7;(7) 解得 x = 94/3;(8) 解得 x = 10.1.答案:(1) x=3.(5) x=7/3;2.答案:(1) x= -5/2.(2) x=2.(6) x=2/3.(2) x=-1;3.答案:(3) x=6/5.(4) x=-3.(5) x=4.(6) x=9;4.答案:(1) x=3.(3) x=64/13.(4) x=29/2;5.答案:(1) x=5.(2) x=13/14.(3) x=-1.(6) x=-3.(7) x=7/8.(8) x=216.注:原文中有很多格式错误和明显的段落问题,已经删除并改写成上述答案)。
解一元一次方程练习题及答案过程

解一元一次方程练习题及答案过程一.解答题 1.解方程:2x+1=.3.解方程:4﹣x=3;解方程:.4.解方程:.5.解方程4﹣3=5;x﹣=2﹣.6.解方程:3=2x+3;解方程:=x﹣.7.﹣=8.解方程:5﹣2=3+x+1;.9.解方程:.110.解方程:4x﹣3=2; =2﹣.11.计算:计算:解方程:12.解方程:13.解方程:14.解方程:5﹣2=+2[3+]=5x﹣115.解方程:5x﹣2=7x+8;解方程:﹣=﹣;解方程:.16.解方程3=9﹣5217.解方程:解方程:4x﹣3=13解方程:x﹣﹣318.计算:﹣42×+|﹣2|3×3计算:﹣12﹣|0.5﹣|÷×[﹣2﹣2]解方程:4x﹣3=2;解方程:.19.计算:×;计算:÷;3解方程:3x+3=2x+7;解方程:.20.解方程﹣0.2=1;.21.解方程:﹣2=9﹣3x. 22.8x﹣3=9+5x.5x+2=9﹣4...23.解下列方程:0.5x﹣0.7=5.2﹣1.3;=﹣2.24.解方程:﹣0.5+3x=10;43x+8=2x+6;2x+3=5﹣4;.25.解方程:.26.解方程:10x﹣12=5x+15;27.解方程:8y﹣3=7.28.当k为什么数时,式子比的值少3.29.解下列方程: 12y﹣2.5y=7.5y+.30.解方程:.5解一元一次方程一、慧眼识金 1.某数的15等于4与这个数的45的差,那么这个数是.4-45-52.若3?2x?11?3x,则x?4的值为.8-8-443.若a?b,则①a?13?b?13;②13a?14b;③?34a??34b;④3a?1?3b?1中,正确的有.1个2个3个4个4.下列方程中,解是x??1的是. ?2?12?2?411x?1?525.下列方程中,变形正确的是.由x?3?4得x?4? 由3=x?2得x?3? 由2-x?5得x?5? 由5?x?2得x?5?26.对于“x?y?a?b”,下列移项正确的是. x?b?y?ax?a?y?ba?x?y?ba?x?b?y .某同学在解关于x 的方程5a?x?13时,误将?x看作?x,得到方程的解为x??2,则原方程的解为. x??3x?0x?2x?18.小丽的年龄乘以3再减去3是18,那么小丽现在的年龄为. 7岁8岁16岁32岁二、画龙点睛1.在x?3,x?5,x?10中,是方程x?x?42?3的解.2.若m是3x?2?2x?1的解,则30m?10的值是.3.当x? 时,代数式12与13的差为10.4.如果5m?14与m?14互为相反数,则m的值为.?6?0是关于x的一元一次方程,则a? .5.已知方程xa?16.如果3x?1?2x?3成立,则x的正数解为.7.已知3x?8?x4?a的解满足x?2?0,则1a? .8.若2x3?2k?2k?4是关于x的一元一次方程,则k?,x?.三、考考你的基本功1.解下列方程?7x?6?22?6x; ?4x?3??5x?2;4x?5?3x;y?7??3y?5.2.x?2是方程ax?4?0的解,检验x?3是不是方程2ax?5?3x?4a的解.3.已知x4.如果?四、同步大闯关方程4x?2m?3x?1和方程3x?2m?4x?1的解相同,求m 的值和方程的解.关于x的方程mx?n?2x?3中,m、n是常数,请你给m、n赋值,并解此时关于x的方程.x3?y4?z6?3,求3x?4y?6z的值.2m?3?6?m是关于x的一元一次方程,试求代数式2008的值.解一元一次方程一、相信你都能选对 1、下列方程中是一元一次方程的是x?12A、x-y=200B、3x-200C、x+x=1D、2x?2=32、下列四组变形中,属于去括号的是1A.5x+3=0,则5x=-B.2x =,则x = 12C.3x-=5,则3x+4x-2=D.5x=1+4,则5x=53、某同学在方程5x-1=□x+3时,把□处的数字看错了,解得x=-4/3,该同学把□看成了A.3B.-C.D. -314、方程x - = +x的解是11A.-2;B.2;C.-2;D.25、下列解方程去分母正确的是x?1?1?x2A.由3,得2x - 1 = -x;x?2B.由2y?1?3x?24y3??1,得2 -x - = -3y?16?yC.由24x??,得3y + =y -y + 1 -y;D.由5?1?y?43,得12x - 1 =y +06、某件商品连续两次9折降价销售,降价后每件商品售价为a元,则该商品每件原价为aaA.0.92aB.1.12aC.1.1D.0.817、一个两位数,个位数字与十位数字的和是9,如果将个位数字与十位数字对调后所得的新数比原数大9,则原来的两位数为 A.5B.2C.7D.458、一个长方形的周长为2cm,这个长方形的长减少1 cm,宽增加cm,就可成为一个正方形,设长方形的长为xcm,可列方程A.x?1?? B.x?1??2C.x?1??2D.x?1??二、相信你填得又快又准、去括号且合并含有相同字母的项:3x+2=8y-6= 10、x =和x = -中,________是方程x - =的解.2?k?111、若代数式3的值是1,则k = _________.3?2x2?x12、当x=________时,式子2与3互为相反数.13、小明买了20本练习本,店主给他八折优惠,结果便宜1.6元,每本练习本的标价是元。
解一元一次方程40题(一)含答案

解一元一次方程40题(一)一.解答题(共40小题)1.已知3x =是方程(1)3[(1)]234x m x -++=的解,求m 的值.2.已知关于x 的方程13(23)322x x +-=和3261x m x +=+的解相同,求:代数式202020193(2)()2m m ---的值.3.解方程(1)2(4)3(1)x x x --=- (2)313142x x-+-=4.某同学在解方程21233x x a-+=-时,方程右边的2-没有乘以3,其它步骤正确,结果方程的解为1x =.求a 的值,并正确地解方程.5.解方程:(1)37322x x +=-; (2)43(20)40x x --+=; (3)352123x x +-=; (4)5415323412y y y +--+=-;6.解方程2191136x x ++-=7.解方程: (1)0.10.2130.020.5x x -+-= (2)312143x x -+-=-8.解方程: (1)132x x --= (2)0.6310.20.4x x--=9.解下列方程:(1)5379x x +=-+ (2)43(20)40x x --+= (3)3157146y y ---= (4)1213323x x x --+=-10.已知12x =是方程21423x m x m ---=的解,求式子211(428)(1)42m m m -+-+-的值.11.(1)计算:225(210)4-⨯--÷ (2)计算:2313()(24)(3)12468-+⨯-+-÷12.解方程:(1)2557x x +=- (2)3(2)25(2)x x -=-+ (3)14223x x +-+= (4)12311463x x x -++-=+13.解下列方程或方程组(1)219x x -=+ (2)52(1)x x +=- (3)43135x x --=- (4)3717245x x -+-=-14.若代数式33x +比344x -的值大4,求x 的值.15.定义:若关于x 的一元一次方程ax b =的解为b a +,则称该方程为“和解方程”,例如:24x =-的解为2x =-,且242-=-+,则该方程24x =-是和解方程. (1)判断934x -=是否是和解方程,说明理由;(2)若关于x 的一元一次方程52x m =-是和解方程,求m 的值.16.解方程(1)412(3)x x +=- (2)3157146y y ---=17.解方程.(1)8(35)20x x -+= (2)1:225%:0.753x = (3)2940%316x ÷=18.解方程 (1)23132x x --+= (2)2321{[1(1)]9}1320.32x xx +----=-19.解方程(1)0.50.7 6.5 1.3x x -=- (2)758143x x -+-=20.解下列方程:(1)3520x x x --=(2)3(56)320x x -=-(3)23[2(1)4]8x x x +--+=(4)2123134x x ---=21.解方程:851217x =22.m 为何值时,0.2m 的值比280.3m -的值大1?23.解方程:(1)34(25)4x x x -+=+; (2)12226x x x -+-=-.24.311(54)1535x -+= 22531277714x +-=25.解方程:(1)2343x x -=- (2)13(1)2x x --=(3)85(1)2x x +-= (4)4320.20.5x x +--=26.解方程:11(26)(8)134x x -=++.27.一元一次方程解答题:已知关于x 的方程23x m mx -=-与12(2)x x l -=-的解互为倒数,求m 的值.28.解方程(1)321x x -=-+ (2)18(1)32(21)x x x -+=-- (3)31571104y y ---=29.解方程:(1)2(100.5)(1.52)x x -=-+; (2)5415523412y y y +--+=-30.(1)将方程123126x x +--=去分母,得到33236x x +--=,错在 A .最简公分母找错 B .去分母时,漏掉乘数项C .去分母时,分子部分没有加括号D .去分母时,各项所乘的数不同(2)解方程:123126x x +--=31.0.1210.30.15x x-=+32.已知方程(21)32a x ax +=-有正整数解,求整数a 的值.33.解方程: (1)2121163x x +--= (2)2(1)35x x -=-34.解方程(1)2(21)(34)2x x +--= (2)1213323x x x --+=-35.先阅读下列解题过程,然后解答后面两个问题. 解方程:|3|2x -=.解:当30x -时,原方程可化为32x -=,解得5x =; 当30x -<时,原方程可化为32x -=-,解得1x =. 所以原方程的解是5x =或1x =. (1)解方程:|32|40x --=. (2)解关于x 的方程:|2|1x b -=+36.(1)684(1)x x -=-+ (2)20.30.410.50.3x x -+-=37.解下列方程:(1)2(2)3(41)9(1)x x x ---=-; (2)2152122362x x x-+--=-38.解方程:(1)432(1)1x x +=-+; (2)23(37)272x x +=-;(3)32[(21)2]223x x ---=; (4)218269x xx --=+.39.解下列方程:(1)369x --= (2)5467x x -=-+ (3)2(1)246x x -+=- (4)223123x x---=.40.小明解方程21152x x a+-+=时,由于粗心大意,在去分母时,方程左边的1没有乘10,求的方程的解为2x =-,试求a 的值.解一元一次方程40题(一)参考答案与试题解析一.解答题(共40小题)1.已知3x =是方程(1)3[(1)]234x m x -++=的解,求m 的值.【分析】把3x =代入方程,即可得出一个关于m 的方程,求出方程的解即可. 【解答】解:3x =是方程(1)3[(1)]234x m x -++=的解,∴代入得:3(31)3[(1)]234m -++=, 解得:83m =-.【点评】本题考查了解一元一次方程和一元一次方程的解,能得出关于m 的一元一次方程是解此题的关键. 2.已知关于x 的方程13(23)322x x +-=和3261x m x +=+的解相同,求:代数式202020193(2)()2m m ---的值.【分析】分别求出两个方程的解,然后根据解相同,列出关于m 的方程,求出m 的值,再将m 的值代入200920103(2)()2m m ---,计算即可求解.【解答】解:解方程13(23)322x x +-=,得:2363x x +-=, 0x ∴=,方程13(23)322x x +-=和3261x m x +=+的解相同,21m ∴=解得:12m =, 所以202020193(2)()2m m ---20202019113(2)()222=-⨯--1(1)=--2=.【点评】本题考查了同解方程的知识,解答本题的关键是能够求解关于x 的方程,要正确理解方程解的含义. 3.解方程(1)2(4)3(1)x x x --=- (2)313142x x-+-=【分析】(1)方程去括号,移项合并,把x 系数化为1,即可求出解; (2)方程去分母,去括号,移项合并,把x 系数化为1,即可求出解. 【解答】解:(1)去括号得:2833x x x -+=-, 移项合并得:25x =-, 解得: 2.5x =-;(2)去分母得:43162x x -+=+, 移项合并得:51x -=, 解得:0.2x =-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键. 4.某同学在解方程21233x x a-+=-时,方程右边的2-没有乘以3,其它步骤正确,结果方程的解为1x =.求a 的值,并正确地解方程.【分析】由题意可知2x =是方程212x x a -=+-的解,然后可求得a 的值,然后将a 的值代入方程求解即可.【解答】解:将1x =代入212x x a -=+-得:112a =+-. 解得:2a =,将2a =代入216x x a -=+-得:2126x x -=+-. 解得:3x =-.【点评】本题主要考查的是一元一次方程的解,明确2x =是方程2(21)3()2x x a -=+-的解是解题的关键. 5.解方程:(1)37322x x +=-; (2)43(20)40x x --+=; (3)352123x x +-=; (4)5415323412y y y +--+=-;【分析】(1)移项,合并同类项,系数化成1即可;(2)去括号,移项,合并同类项,系数化成1即可;(3)去分母,去括号,移项,合并同类项,系数化成1即可;(4)去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)37322x x+=-,32327x x+=-,525x=,5x=;(2)43(20)40x x--+=,460340x x-++=,43604x x+=-,756x=,8x=;(3)去分母得:3(35)2(21)x x+=-,91542x x+=-,94215x x-=--,517x=-,3.4x=-;(4)去分母得:4(54)3(1)24(53)y y y++-=--,2016332453y y y++-=-+,2035243163y y y++=+-+,2814y=,12y=.【点评】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.6.解方程21911 36x x++-=【分析】根据去分母、去括号、移项、合并同类项、系数化为1解答即可.【解答】解:21911 36x x++-=2(21)(91)6x x+-+=42916x x+--=49612x x-=+-55x-=1x=-【点评】此题考查解一元一次方程,关键是根据去分母、去括号、移项、合并同类项、系数化为1解答.7.解方程:(1)0.10.213 0.020.5x x-+-=(2)3121 43x x-+-=-【分析】(1)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)方程整理得:510223x x---=,移项合并得:315x=,解得:5x=;(2)去分母得:934812x x---=-,移项合并得:51x=-,解得:15x=-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.8.解方程:(1)132xx--=(2)0.6310.20.4 x x--=【分析】(1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(2)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去分母得:216x x-+=,解得:5x=;(2)方程整理得:315512xx--=,去分母得:102315x x-=-,移项合并得:255x=,解得:0.2x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.9.解下列方程:(1)5379x x+=-+(2)43(20)40x x--+=(3)3157146 y y---=(4)121 3323x xx--+=-【分析】(1)方程移项合并,把x系数化为1,即可求出解;(2)方程去括号,移项合并,把x系数化为1,即可求出解;(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)移项合并得:126x=,解得:0.5x=;(2)去括号得:460340x x-++=,移项合并得:756x=,解得:8x=;(3)去分母得:93121014y y--=-,移项合并得:1y-=,解得:1y=-;(4)去分母得:18331842x x x+-=-+,移项合并得:2523x=,解得:2325x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.10.已知12x=是方程21423x m x m---=的解,求式子211(428)(1)42m m m-+-+-的值.【分析】把12x =代入方程,求出m 的值,再把代数式进行化简,最后代入求出即可. 【解答】解:把12x =代入方程21423x m x m ---=得:1112423m m ---=, 解得:5m =,211(428)(1)42m m m -+-+- 21112222m m m =-+-+- 2122m =-- 21522=-- 1272=-. 【点评】本题考查了解一元一次方程,一元一次方程的解,整式的混合运算和求值等知识点,能求出m 的值是解此题的关键.11.(1)计算:225(210)4-⨯--÷(2)计算:2313()(24)(3)12468-+⨯-+-÷ 【分析】(1)根据有理数的混合计算解答即可;(2)根据有理数的混合计算解答即可;(3)根据去分母、去括号、移项、合并同类项、系数化为1解答.【解答】解:(1)225(210)4-⨯--÷45(8)4=-⨯--÷202=-+18=-;(2)2313()(24)(3)12468-+⨯-+-÷ 1849912=-+-+÷318494=-+-+ 1224=-; 【点评】此题考查解一元一次方程,关键是根据去分母、去括号、移项、合并同类项、系数化为1解答.12.解方程:(1)2557x x +=-(2)3(2)25(2)x x -=-+(3)14223x x +-+= (4)12311463x x x -++-=+ 【分析】(1)移项,合并同类项,系数化成1即可;(2)去括号,移项,合并同类项,系数化成1即可;(3)去分母,去括号,移项,合并同类项,系数化成1即可;(4)去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)2557x x +=-,2575x x -=--,312x -=-,4x =;(2)3(2)25(2)x x -=-+,362510x x -=--,352106x x +=-+,82x =-,0.25x =-;(3)14223x x +-+=, 3(1)2(4)12x x ++-=,332812x x ++-=,321238x x +=-+,517x =,5.4x =;(4)去分母得:3(1)122(23)4(1)x x x --=+++,33124644x x x --=+++,34464312x x x--=+++,525x-=,5x=-.【点评】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.13.解下列方程或方程组(1)219x x-=+(2)52(1)x x+=-(3)431 35x x--=-(4)3717 245x x-+ -=-【分析】(1)方程移项合并,把x系数化为1,即可求出解;(2)方程去括号,移项合并,把x系数化为1,即可求出解;(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)移项合并得:10x=;(2)去括号得:522x x+=-,移项合并得:7x-=-,解得:7x=;(3)去分母得:2053915x x-=--,移项合并得:844x-=-,解得: 5.5x=;(4)去分母得:401535468x x-+=--,移项合并得:11143x-=-,解得:13x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.14.若代数式33x+比344x-的值大4,求x的值.【分析】根据题意列出方程,求出方程的解即可得到x的值.【解答】解:根据题意得:3344 34x x+--=,去分母得:41291248x x+-+=,移项合并得:524x -=,解得: 4.8x =-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.15.定义:若关于x 的一元一次方程ax b =的解为b a +,则称该方程为“和解方程”,例如:24x =-的解为2x =-,且242-=-+,则该方程24x =-是和解方程.(1)判断934x -=是否是和解方程,说明理由; (2)若关于x 的一元一次方程52x m =-是和解方程,求m 的值.【分析】(1)求出方程的解,再根据和解方程的意义得出即可;(2)根据和解方程得出关于m 的方程,求出方程的解即可.【解答】解:(1)934x -=, 34x ∴=-, 93344-=-, 934x ∴-=是和解方程;(2)关于x 的一元一次方程52x m =-是和解方程,2255m m -∴-+=, 解得:174m =-. 故m 的值为174-. 【点评】本题考查了一元一次方程的解的应用,能理解和解方程的意义是解此题的关键.16.解方程(1)412(3)x x +=-(2)3157146y y ---= 【分析】(1)方程去括号,移项合并,把x 系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把y 系数化为1,即可求出解.【解答】解:(1)去括号得:4162x x +=-,移项合并得:65x =,解得:56x=;(2)去分母得:93121014y y--=-,移项合并得:1y-=,解得:1y=-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.17.解方程.(1)8(35)20x x-+=(2)1:225%:0.75 3x=(3)29 40%316x÷=【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)利用比例的性质化简,计算即可求出x的值;(3)方程整理后,把x系数化为1,即可求出解.【解答】解:(1)去括号得:83520x x--=,移项合并得:525x=,解得:5x=;(2)整理得:1132434x⨯=⨯,整理得:21x=,解得:12x=;(3)方程整理得:9240%163x=⨯,即340%8x=,解得:1516x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.18.解方程(1)231 32x x--+=(2)2321{[1(1)]9}1 320.32x x x+----=-【分析】(1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(2)方程去括号,去分母,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去分母得:42396x x-+-=,移项合并得:11x=;(2)去括号得:2010116132x xx+--+-=-,去分母得:66402063663x x x---+-=-,移项合并得:3162x-=,解得:2x=-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.19.解方程(1)0.50.7 6.5 1.3x x-=-(2)7581 43x x-+-=【分析】(1)方程移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)移项合并得:1.87.2x=,解得:4x=-;(2)去分母得:321203212x x---=,移项合并得:1765x-=,解得:6517x=-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.20.解下列方程:(1)3520x x x--=(2)3(56)320x x-=-(3)23[2(1)4]8x x x+--+=(4)21231 34x x---=【分析】解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1,据此求出每个方程的解即可.【解答】解:(1)3520x x x--=合并同类项,可得:40x-=,系数互为1,可得:0x=;(2)3(56)320x x -=-去括号,可得:1518320x x -=-,移项,可得:1520318x x +=+,合并同类项,可得:3521x =,系数互为1,可得:0.6x =;(3)23[2(1)4]8x x x +--+=,去括号,可得:2366128x x x +-++=移项,可得:2366128x x x +-=--+,合并同类项,可得:10x -=-,系数互为1,可得:10x =;(4)2123134x x ---=, 去分母,可得,4(21)3(23)12x x ---=,去括号,可得:846912x x --+=,移项,可得:864912x x -=-+,合并同类项,可得:27x =,系数互为1,可得:72x =. 【点评】此题主要考查了解一元一次方程的方法,要熟练掌握,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.21.解方程:851217x = 【分析】方程x 系数化为1,即可求出解.【解答】解:方程x 系数化为1得:122178x =⨯, 解得:92x =. 【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.22.m 为何值时,0.2m 的值比280.3m -的值大1? 【分析】根据题意列出方程,求出方程的解即可得到m 的值.【解答】解:根据题意得:281 0.20.3m m--=,整理得:2080513mm--=,去分母得:1520803m m-+=,移项合并得:577m-=-,解得:775m=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.23.解方程:(1)34(25)4x x x-+=+;(2)12226x xx-+-=-.【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去括号得:38204x x x--=+,移项合并得:624x-=,解得:4x=-;(2)去分母得:633122x x x-+=--,移项合并得:47x=,解得:74x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.24.311(54)1 535 x-+=22531277714x+-=【分析】方程移项合并,把x系数化为1,即可求出解;方程去分母,移项合并,把x系数化为1,即可求出解.【解答】解:移项得:3158 515x=,解得:1589x=;去分母得:418383x+-=,移项合并得:423x=,解得:234x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.25.解方程:(1)2343x x-=-(2)1 3(1)2xx--=(3)85(1)2x x+-=(4)432 0.20.5x x+--=【分析】(1)方程移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(3)原式去括号,移项合并,把x系数化为1,即可求出解;(4)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)移项得:2343x x+=+,合并得:57x=,解得:75x=;(2)去分母得:6(1)1x x-=-,去括号得:661x x-=-,移项合并得:55x=,解得:1x=;(3)去括号得:8552x x+-=,移项合并得:33x=-,解得:1x=-;(4)方程整理得:520262x x+-+=,移项合并得:324x=-,解得:8x=-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.26.解方程:11(26)(8)1 34x x-=++.【分析】去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:去分母得:4(26)3(8)12x x-=++,82432412x x -=++,83241224x x -=++,560x =,12x =.【点评】本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.27.一元一次方程解答题:已知关于x 的方程23x m m x -=-与12(2)x x l -=-的解互为倒数,求m 的值.【分析】求出第二个方程的解,确定出第一个方程的解,代入计算即可求出m 的值.【解答】解:方程12(21)x x -=-,去括号得:142x x -=-, 解得:13x =, 将3x =代入方程23x m m x -=-得,3323m m -=-, 去分母得:93182m m -=-,解得:9m =-.【点评】此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.28.解方程(1)321x x -=-+(2)18(1)32(21)x x x -+=--(3)31571104y y ---= 【分析】(1)方程移项合并,把x 系数化为1,即可求出解;(2)方程去括号,移项合并,把x 系数化为1,即可求出解;(3)方程去分母,去括号,移项合并,把y 系数化为1,即可求出解.【解答】解:(1)方程移项合并得:34x =, 解得:43x =; (2)去括号得:1818342x x x -+=-+,移项合并得:2520x =, 解得:45x =;(3)去分母得:62202535y y--=-,移项合并得:1913y-=-,解得:1319y=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.29.解方程:(1)2(100.5)(1.52)x x-=-+;(2)5415523412 y y y+--+=-【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把y系数化为1,即可求出解.【解答】解:(1)去括号得:20 1.52x x-=--,移项合并得:0.522x=-,解得:44x=-;(2)去分母得:2016332455y y y++-=-+,移项合并得:2816y=,解得:47y=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.30.(1)将方程123126x x+--=去分母,得到33236x x+--=,错在CA.最简公分母找错B.去分母时,漏掉乘数项C.去分母时,分子部分没有加括号D.去分母时,各项所乘的数不同(2)解方程:1231 26x x+--=【分析】(1)方程左右两边乘以6得到结果,即可作出判断;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)方程去分母得:3(1)(23)6x x+--=,去括号得:33236x x+-+=,故答案为:C;(2)去分母得:33(23)6x x+--=,去括号得:33236x x+-+=,解得:0x=.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.31.0.1210.30.15x x-=+【分析】方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:方程整理得:12020133x x-=+,去分母得:120320x x-=+,移项合并得:402x=-,解得:120x=-.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.32.已知方程(21)32a x ax+=-有正整数解,求整数a的值.【分析】将原方程整理移项,合并同类项,根据该方程有解,得到关于a得方程的解,结合方程的解为正整数,a为整数,得到两个关于a的一元一次方程,解之即可.【解答】解:(21)32a x ax+=-,移项,合并同类项得:(1)2a x-+=-,因为方程有解,所以(1)0a-+≠,即21xa=-,因为方程有正整数解,且a取整数,所以11a-=或12a-=,解得:2a=或3a=,答:整数a的值为2或3.【点评】本题考查了一元一次方程的解,正确掌握一元一次方程的解法是解题的关键.33.解方程:(1)21211 63x x+--=(2)2(1)35x x-=-【分析】(1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;(2)方程去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去分母得:21426x x+-+=,移项合并得:23x-=,解得:32x =-; (2)去括号得:2235x x -=-,移项合并得:3x =.【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.34.解方程(1)2(21)(34)2x x +--=(2)1213323x x x --+=- 【分析】(1)方程去括号,移项合并,把x 系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x 系数化为1,即可求出解.【解答】解:(1)去括号得:42342x x +-+=,移项合并得:4x =-;(2)去分母得:18331842x x x +-=-+,移项合并得:2523x =, 解得:2325x =. 【点评】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.35.先阅读下列解题过程,然后解答后面两个问题.解方程:|3|2x -=.解:当30x -时,原方程可化为32x -=,解得5x =;当30x -<时,原方程可化为32x -=-,解得1x =.所以原方程的解是5x =或1x =.(1)解方程:|32|40x --=.(2)解关于x 的方程:|2|1x b -=+【分析】(1)首先要认真审题,解此题时要理解绝对值的意义,要会去绝对值,然后化为一元一次方程即可求得.(2)根据绝对值的性质分类讨论进行解答.【解答】解:(1)当320x -时,原方程可化为3240x --=,解得2x =;当320x -<时,原方程可化为(32)40x ---=,解得23x =-. 所以原方程的解是2x =或23x =-.(2)①当10b +<,即1b <-时,原方程无解,②当10b +=,即1b =-时:原方程可化为:20x -=,解得2x =;③当10b +>,即1b >-时:当20x -时,原方程可化为21x b -=+,解得3x b =+;当20x -<时,原方程可化为2(1)x b -=-+,解得1x b =-+.【点评】本题主要考查含绝对值符号的一元一次方程,解题的关键是根据绝对值的性质将绝对值符号去掉,从而化为一般的一元一次方程求解.36.(1)684(1)x x -=-+(2)20.30.410.50.3x x -+-= 【分析】(1)依次去括号,移项,合并同类项,系数化为1,即可得到答案,(2)原方程可整理得:203104153x x -+-=,依次去分母,去括号,移项,合并同类项,系数化为1,即可得到答案.【解答】解:(1)去括号得:6844x x -=--,移项得:4846x x +=-+,合并同类项得:510x =,系数化为1得:2x =,(2)原方程可整理得:203104153x x -+-=, 方程两边同时乘以15得:3(203)5(104)15x x --+=,去括号得:609502015x x ---=,移项得:605015209x x -=++,合并同类项得:1044x =,系数化为1得: 4.4x =.【点评】本题考查了解一元一次方程,正确掌握解一元一次方程的方法是解题的关键.37.解下列方程:(1)2(2)3(41)9(1)x x x ---=-;(2)2152122362x x x -+--=-.【分析】(1)依次去括号,移项,合并同类项,系数化为1,即可得到答案,(2)依次去分母,去括号,移项,合并同类项,系数化为1,即可得到答案.【解答】解:(1)去括号得:2412399x x x--+=-,移项得:2129943x x x-+=+-,合并同类项得:10x-=,系数化为1得:10x=-,(2)去分母得:2(21)(52)3(12)12x x x--+=--,去括号得:42523612x x x---=--,移项得:45631222x x x-+=-++,合并同类项得:55x=-,系数化为1得:1x=-.【点评】本题考查了解一元一次方程,正确掌握解一元一次方程的方法是解题的关键.38.解方程:(1)432(1)1x x+=-+;(2)23 (37)272x x+=-;(3)32[(21)2]2 23x x---=;(4)218269x xx--=+.【分析】(1)先去括号,移项并合并同类项,再把系数化为1即可(2)可以先左右两边乘以14,去分母再去括号,移项并合并同类项,将系数化为1即可(3)先去括号,合并同类项,将系数化为1即可(4)可左右两边同时乘以18,去分母后,移项并合并同类项,将系数化为1即可【解答】解:(1)原式去括号得:4321x x+=-移项并合并同类项得,24x=-系数化为1得,2x=-(2)原式去分母得,4(37)2821x x+=-去括号得,12282821x x+=-移项合并同类项得,330x=系数化为1得,0x=(3)原式去括号得,42x-=移项得,6x=(4)原式去分母得,183(218)236x x x--=+去括号得,18654236x x x-+=+移项合并同类项得,7042x=系数化为1得,35 x=【点评】此题考查的是解一元一次方程,掌握解一元一次方程的步骤是解答此题的关键.解一元一次方程的步骤是:1.去分母:在方程两边都乘以各分母的最小公倍数;2.去括号:先去小括号,再去中括号,最后去大括号;3.移项:把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(注意移项要改变运算的符号);4.合并同类项:把方程化成(0)ax b a=≠的形式;5.系数化成1:在方程两边都除以未知数的系数a,得到方程的解.39.解下列方程:(1)369x--=(2)5467x x-=-+(3)2(1)246x x-+=-(4)2231 23x x---=.【分析】(1)依次移项,合并同类项,系数化为1,即可得到答案,(2)依次移项,合并同类项,系数化为1,即可得到答案,(3)依次去括号,移项,合并同类项,系数化为1,即可得到答案,(4)依次去分母,去括号,移项,合并同类项,系数化为1,即可得到答案.【解答】解:(1)移项得:396x-=+,合并同类项得:315x-=,系数化为1得:5x=-,(2)移项得:4675x x-+=-,合并同类项得:22x=,系数化为1得:1x=,(3)去括号得:22246x x-+=-,移项得:24622x x-=--+,合并同类项得:26x-=-,系数化为1得:3x=,(4)去分母得:3(2)2(23)6x x---=,去括号得:36466x x--+=,移项得:36664x x+=++,合并同类项得:916x=,系数化为1得:169x=.【点评】本题考查了解一元一次方程,正确掌握解一元一次方程的方法是解题的关键.40.小明解方程21152x x a+-+=时,由于粗心大意,在去分母时,方程左边的1没有乘10,求的方程的解为2x=-,试求a的值.【分析】根据一元一次方程的解法即可求出答案.【解答】解:由题意可知:2x=-是方程2110110 52x x a+-⨯+=⨯,(41)215(2)a∴-+⨯+=--,61105a∴-+=--,5105a∴-=--,5105a∴=-+,55a∴=-,1a∴=-;【点评】本题考查一元一次方程的解法,解题的关键是熟练运用一元一次方程的解法,本题属于基础题型.。
解一元一次方程专项练习(含答案)

一、“移项+系数化1”针对练习(1)8x﹣5=3x;(2)6x﹣7=4x﹣5;(3)2x+17=32﹣3x;(4)7x+6=16﹣3x;(5)3x﹣4=2x+5;(6)4x﹣1=2x+5;(7)4﹣3x=6﹣5x;(8).(9)3x+7=32﹣2x;(10)5x+3=﹣2x﹣11;(11)3x﹣8=x+4;(12)5x+2=3x﹣18;(13)2﹣5x=3x+4;(14)5x﹣2x=9;(15)9﹣3y=5y+5.(16)5x﹣8=8x+1;(17)4x﹣1=2x+2.(18)3x+3=8﹣12x;(19)4x﹣2=2x+6;(20)3x﹣2=4x+1;(21)3x﹣6=2x+1;(22)x+4=x﹣2.(23);(24);(25).(26);(27)1.5:6=1:x.(28)6x﹣7=4x﹣5;(29)x+3x=﹣16;(30)9﹣3x=5x+5.(31);(32).(33);(34).(35)6x+6=2x﹣2;(36)3x+9=12;(二)“去括号”针对练习(1)3﹣5(x+1)=2x;(2)3(x﹣3)=x+1;(3)3(1﹣x)=1+2x;(4)8x=﹣2(x+4);(5)7﹣3(x﹣1)=﹣x;(6)2x﹣2(3x+1)=6;(7)5x﹣2(x﹣1)=3;(8)8﹣3(3x+2)=6;(9)x﹣3;(10)7x+2(3x﹣3)=20;(11)4﹣2x=﹣3(2﹣x);(12)4﹣3(2﹣x)=5x;(13)3(x+2)﹣2=x+2;(14)3(x﹣7)+5(x﹣4)=15;(15)x+2(x﹣3)=3(1﹣x);(16)2(3﹣x)=﹣4(x+5);(17)4﹣2(x+4)=2(x﹣1);(18)4(2x﹣1)﹣3(5x+1)=14;(19)3(2x﹣1)=5﹣2(x+2);(20)2((x﹣2)﹣3((4x﹣1)=5((1﹣x).(21)3(20﹣y)=6y﹣4(y﹣11);(22)1﹣3(x+1)=2(1﹣0.5x);(23)3(2x﹣7)=1﹣(x+8);(24);(25)3(x﹣1)+5(x﹣1)=16.(26)7x+2(3x﹣3)=20;(27)3x﹣4(x+1)=6﹣2(2x﹣5);(28)3(x﹣1)﹣2(x+10)=﹣6;(29)3(y﹣7)﹣5(4﹣y)=15;(30)2x﹣3(x﹣1)=5(1﹣x);(31)3x﹣2(x﹣1)=2+3(4﹣x).(32)5(x﹣4)+3(x+6)=14.(33)2(x﹣2)﹣(4x﹣1)=3(1﹣x);(34)2(x+1)=﹣5(x﹣2);(35)x﹣3=2(x﹣3)﹣6(1﹣x);(36)2(x+2)=3(x﹣1);(37)3x﹣2=5(x+2);(38)2(x+4)﹣10=5(x﹣2)+10x;(39)9y﹣2(﹣y+4)=3.(40)2(x﹣3)=1﹣3(x+1);(三)“去分母”针对练习(1);(2).(3).(4).(5)=1.(6);(7).(8).(11).(12).(13).(14).(15).(16).(17).(18).(19).(20).(23).(24).(25);(26).(27)﹣1.(28).(29).(30)5x=2x+5;(31)=.(32).(35).(36).(37)﹣1=.(38)=4.(39).(40).(41).(42)﹣1=.(43)=1.(44).(45)=1﹣.(46).(47).(48).(49).答案与解析(一)“移项+系数化1”针对练习(1)8x﹣5=3x;【解答】解:(1)移项得:8x﹣3x=5,合并同类项得:5x=5,系数化为1得:x=1,∴原方程的解为:x=1;(2)6x﹣7=4x﹣5;【解答】解:(1)移项,可得:6x﹣4x=﹣5+7,合并同类项,可得:2x=2,系数化为1,可得:x=1.(3)2x+17=32﹣3x;【解答】解:(1)2x+3x=32﹣17,5x=15,x=3;(4)7x+6=16﹣3x;【解答】解:(1)7x+6=16﹣3x,移项,得7x+3x=16﹣6,合并同类项,得10x=10,系数化为1,得x=1;(5)3x﹣4=2x+5;【解答】解:(1)3x﹣4=2x+5,移项,得3x﹣2x=5+4,合并同类项,得x=9;(6)4x﹣1=2x+5;【解答】解:(1)4x﹣1=2x+5,移项,得:4x﹣2x=5+1,合并同类项,得:2x=6,系数化为1,得:x=3;(7)4﹣3x=6﹣5x;﹣3x+5x=6﹣4,2x=2,x=1;(8)解方程:.【解答】解:,移项,得,合并同类项,得,系数化为1,得x=.(9)3x+7=32﹣2x;【解答】解:(1)移项合并得:5x=25,解得:x=5;(10)5x+3=﹣2x﹣11;【解答】解:(1)5x+3=﹣2x﹣11,移项,得5x+2x=﹣11﹣3,合并同类项,得7x=﹣14,系数化成1,得x=﹣2;(11)3x﹣8=x+4;【解答】解:(1)3x﹣8=x+4,3x﹣x=4+8,2x=12,x=6;(12)5x+2=3x﹣18;【解答】解:(1)5x+2=3x﹣18,移项,5x﹣3x=﹣18﹣2,合并同类项,2x=﹣20,系数化为1,x=﹣10;(13)2﹣5x=3x+4;移项,得﹣5x﹣3x=4﹣2,合并同类项,得﹣8x=2,系数化为1,得x=;(14)5x﹣2x=9;【解答】解:(1)5x﹣2x=9,合并同类项,得3x=9,系数化为1,得x=3;(15)9﹣3y=5y+5.【解答】(2)9﹣3y=5y+5,移项,得﹣3y﹣5y=5﹣9,合并同类项,得﹣8y=﹣4,系数化为1,得.(16)5x﹣8=8x+1;【解答】解:(1)5x﹣8=8x+1移项得:5x﹣8x=1+8,合并同类项得;﹣3x=9,系数化为1得;x=﹣3;(17)4x﹣1=2x+2.【解答】解:(1)移项,可得:4x﹣2x=2+1,合并同类项,可得:2x=3,系数化为1,可得:x=1.5.(18)3x+3=8﹣12x;【解答】解:(1)3x+3=8﹣12x,移项,得3x+12x=8﹣3,合并同类项,得15x=5,系数化为1,得x=;(19)4x﹣2=2x+6;【解答】解:(1)4x﹣2=2x+6,移项,得4x﹣2x=6+2,合并同类项,得2x=8,系数化为1,得x=4;(20)3x﹣2=4x+1;【解答】解:(1)移项,可得:3x﹣4x=1+2,合并同类项,可得:﹣x=3,系数化为1,可得:x=﹣3.(21)3x﹣6=2x+1;【解答】解:(1)3x﹣6=2x+1,移项,得3x﹣2x=6+1,合并同类项,得x=7;(22)x+4=x﹣2.【解答】(2)x+4=x﹣2,移项,得﹣=﹣2﹣4,合并同类项,得﹣=﹣6,系数化为1,得x=9.(23);【解答】解:(1)移项,可得:x=5%+14,合并同类项,可得:x=14.05,系数化为1,可得:x=.(24);【解答】(2)合并同类项,可得:1.4x=2.1,系数化为1,可得:x=1.5.(25).【解答】(3)∵,∴1.6x=,系数化为1,可得:x=.(26);【解答】解:(1)整理原方程,得:;系数化为1,得:x=;所以原方程的解为:x=;(27)1.5:6=1:x.【解答】(2)整理原方程,得:1.5x=6;系数化为1,得:x=4;所以原方程的解为:x=4.(28)6x﹣7=4x﹣5;【解答】解:(1)6x﹣7=4x﹣5,6x﹣4x=﹣5+7,2x=2,x=1;(29)x+3x=﹣16;【解答】解:(1)4x=﹣16,x=﹣4;(30)9﹣3x=5x+5.【解答】(2)﹣3x﹣5x=5﹣9,﹣8x=﹣4,x=.(31);【解答】解:(1),去分母,得:18x=2,系数化为1,得:x=;(32).【解答】(2).整理方程,得:=12,去分母,得:8x=36,系数化为1,得:x=.(33);【解答】解:(1)x系数化为1得:x=;(34).【解答】(2)方程整理得:x=6×,即x=4,解得:x=8.(35)6x+6=2x﹣2;【解答】解:(1)移项得:6x﹣2x=﹣2﹣6,合并同类项得:4x=﹣8,解得:x=﹣2;(36)3x+9=12;【解答】解:(1)移项得,3x=12﹣9,合并同类项得,3x=3,两边都除以3得,x=1;(二)“去括号”针对练习(1)3﹣5(x+1)=2x;【解答】(1)3﹣5(x+1)=2x,3﹣5x﹣5=2x,﹣5x﹣2x=5﹣3,﹣7x=2,x=﹣;(2)3(x﹣3)=x+1;【解答】解:(2)去括号,得3x﹣9=x+1,移项,得3x﹣x=9+1,合并,得2x=10,系数化为1,得x=5;(3)3(1﹣x)=1+2x;【解答】解:(3)去括号,得3﹣3x=1+2x,移项,得﹣3x﹣2x=1﹣3,合并同类项,得﹣5x=﹣2,解得x=0.4;(4)8x=﹣2(x+4);【解答】(4)去括号,可得:8x=﹣2x﹣8,移项,可得:8x+2x=﹣8,合并同类项,可得:10x=﹣8,系数化为1,可得:x=﹣0.8.(5)7﹣3(x﹣1)=﹣x;【解答】(5)7﹣3(x﹣1)=﹣x,7﹣3x+3=﹣x,﹣3x+x=﹣3﹣7,﹣2x=﹣10,x=5;(6)2x﹣2(3x+1)=6;【解答】解:(6)2x﹣2(3x+1)=6,去括号,得2x﹣6x﹣2=6,移项,得2x﹣6x=6+2,合并同类项,得﹣4x=8,系数化成1,得x=﹣2;(7)5x﹣2(x﹣1)=3;【解答】解:(7)原方程去括号得:5x﹣2x+2=3,移项得:5x﹣2x=3﹣2,合并同类项得:3x=1,系数化为1得:x=;(8)8﹣3(3x+2)=6;【解答】解:(8)去括号得:8﹣9x﹣6=6,移项合并得:﹣9x=4,解得:x=﹣;(9)x﹣3;【解答】(9)x﹣3,5(3x﹣6)=12x﹣90,15x﹣30=12x﹣90,15x﹣12x=﹣90+30,3x=﹣60,x=﹣20;(10)7x+2(3x﹣3)=20;【解答】解:(10)去括号得,7x+6x﹣6=20,移项得,7x+6x=20+6,合并同类项得,13x=26,x的系数化为1得,x=2;(11)4﹣2x=﹣3(2﹣x);【解答】解:(11)4﹣2x=﹣3(2﹣x),去括号得:4﹣2x=﹣6+3x,移项合并得:5x=10,系数化为1得:x=2;(12)4﹣3(2﹣x)=5x;【解答】解:(12)4﹣3(2﹣x)=5x,去括号,得:4﹣6+3x=5x,移项,得:3x﹣5x=﹣4+6,合并同类项,得:﹣2x=2,系数化为1,得:x=﹣1;(13)3(x+2)﹣2=x+2;【解答】解:(13)3(x+2)﹣2=x+2;3x+6﹣2=x+2,3x﹣x=2﹣6+2,2x=﹣2x=﹣1.(14)3(x﹣7)+5(x﹣4)=15;【解答】解:(14)去括号得:3x﹣21+5x﹣20=15,移项、合并同类项得:8x=56,系数化1得:x=7.(15)x+2(x﹣3)=3(1﹣x);【解答】解:(15)x+2(x﹣3)=3(1﹣x),去括号,得:x+2x﹣6=3﹣3x,移项、合并同类项,得:6x=9,系数化为1,得:;(16)2(3﹣x)=﹣4(x+5);【解答】(16)2(3﹣x)=﹣4(x+5),去括号,得6﹣2x=﹣4x﹣20,移项,得4x﹣2x=﹣20﹣6,合并同类项,得2x=﹣26,系数化为1,得x=﹣13;(17)4﹣2(x+4)=2(x﹣1);【解答】解:(17)4﹣2(x+4)=2(x﹣1),去括号得:4﹣2x﹣8=2x﹣2,移项得:2x+2x=4﹣8+2,合并同类项得:4x=﹣2,系数化为1得:;(18)4(2x﹣1)﹣3(5x+1)=14;【解答】解:(18)原方程去括号得:8x﹣4﹣15x﹣3=14,移项得:8x﹣15x=14+4+3,合并同类项得:﹣7x=21,系数化为1得:x=﹣3;(19)3(2x﹣1)=5﹣2(x+2);【解答】解:(19)6x﹣3=5﹣2x﹣4,6x+2x=5﹣4+3,8x=4,x=;(20)2(x﹣2)﹣3(4x﹣1)=5(1﹣x).【解答】(20)2x﹣4﹣12x+3=5﹣5x,2x﹣12x+5x=5+4﹣3,﹣5x=6,x=﹣.(21)3(20﹣y)=6y﹣4(y﹣11);【解答】解:(21)去括号得:60﹣3y=6y﹣4y+44,移项合并得:5y=16,解得:y=3.2;(22)1﹣3(x+1)=2(1﹣0.5x);【解答】(22)1﹣3(x+1)=2(1﹣0.5x),1﹣3x﹣3=2﹣x,﹣3x+x=2+3﹣1,﹣2x=4,x=﹣2;(23)3(2x﹣7)=1﹣(x+8);【解答】解:(23)3(2x﹣7)=1﹣(x+8),6x﹣21=1﹣x﹣86x+x=﹣7+21,7x=14,x=2;(24);【解答】(24),去分母,得2x﹣1+3=18(2x﹣1),去括号,得2x﹣1+3=36x﹣18,移项,得2x﹣36x=﹣18+1﹣3,合并同类项,得﹣34x=﹣20,系数化为1,得x=;(25)3(x﹣1)+5(x﹣1)=16.【解答】解:(25)3(x﹣1)+5(x﹣1)=16,去括号,得3x﹣3+5x﹣5=16,移项,得3x+5x=16+3+5,合并同类项,得8x=24,系数化成1,得x=3;(26)7x+2(3x﹣3)=20;【解答】解:(26)7x+2(3x﹣3)=20,去括号,得7x+6x﹣6=20,移项,得7x+6x=20+6,合并同类项,得13x=26,系数化成1,得x=2;(27)3x﹣4(x+1)=6﹣2(2x﹣5);【解答】解:(27)3x﹣4(x+1)=6﹣2(2x﹣5)去括号得:3x﹣4x﹣4=6﹣4x+10,移项得:3x﹣4x+4x=6+10+4,合并同类项得:3x=20,系数化为1得;;(28)3(x﹣1)﹣2(x+10)=﹣6;【解答】解:(28)去括号得,3x﹣3﹣2x﹣20=﹣6,移项得,3x﹣2x=﹣6+3+20,合并同类项得,x=17;(29)3(y﹣7)﹣5(4﹣y)=15;【解答】解:(29)去括号得,3y﹣21﹣20+5y=15,移项得,3y+5y=15+21+20,合并同类项可得,8y=56系数化为1得,y=7;(30)2x﹣3(x﹣1)=5(1﹣x);【解答】解:(30)2x﹣3(x﹣1)=5(1﹣x),去括号得:2x﹣3x+3=5﹣5x,移项得:2x﹣3x+5x=5﹣3,合并同类项得:4x=2,把系数化为1得:x=.(31)3x﹣2(x﹣1)=2+3(4﹣x).【解答】(31)3x﹣2(x﹣1)=2+3(4﹣x),去括号,得3x﹣2x+2=2+12﹣3x,移项,得3x﹣2x+3x=2+12﹣2,合并同类项,得4x=12,系数化为1,得x=3.(32)5(x﹣4)+3(x+6)=14.【解答】(32)去括号,可得:5x﹣20+3x+18=14,移项,可得:5x+3x=14+20﹣18,合并同类项,可得:8x=16,系数化为1,可得:x=2.(33)2(x﹣2)﹣(4x﹣1)=3(1﹣x);【解答】解:(33)2(x﹣2)﹣(4x﹣1)=3(1﹣x);去括号得:2x﹣4﹣4x+1=3﹣3x移项得:2x﹣4x+3x=3+4﹣1,合并得:x=6;(34)2(x+1)=﹣5(x﹣2);【解答】解:(34)2(x+1)=﹣5(x﹣2),去括号得:2x+2=﹣5x+10,移项得:2x+5x=10﹣2,合并同类项得:7x=8,系数化为1得:;(35)x﹣3=2(x﹣3)﹣6(1﹣x);【解答】解:(35)x﹣3=2(x﹣3)﹣6(1﹣x),去括号,得x﹣3=2x﹣6﹣6+6x,移项,得x﹣2x﹣6x=﹣6﹣6+3,合并同类项,得﹣7x=﹣9,系数化成1,得x=;(36)2(x+2)=3(x﹣1);【解答】(36)去括号得:2x+4=3x﹣3,移项得:2x﹣3x=﹣3﹣4,合并同类项得:﹣x=﹣7,解得:x=7;(37)3x﹣2=5(x+2);【解答】解:(37)去括号得,3x﹣2=5x+10,移项合并得:2x=﹣12,解得:x=﹣6;(38)2(x+4)﹣10=5(x﹣2)+10x;【解答】解:(38)去括号得:2x+8﹣10=5x﹣10+10x,移项得:2x﹣5x﹣10x=﹣10﹣8+10,合并同类项得:﹣13x=﹣8,解得:x=;(39)9y﹣2(﹣y+4)=3.【解答】(39)去括号得:9y+2y﹣8=3,移项得:9y+2y=3+8,合并同类项得:11y=11,解得:y=1.(40)2(x﹣3)=1﹣3(x+1);【解答】解:(40)去括号得:2x﹣6=1﹣3x﹣3,移项得:2x+3x=1﹣3+6,合并同类项得:5x=4,解得:x=0.8;(三)“去分母”针对练习(1);【解答】(1)去分母,可得:3(3y﹣1)﹣12=2(5y﹣7),去括号,可得:9y﹣3﹣12=10y﹣14,移项,可得:9y﹣10y=﹣14+3+12,合并同类项,可得:﹣y=1,系数化为1,可得:y=﹣1.(2).【解答】(2).去分母,可得:4(5y+4)+3(y﹣1)=24﹣(5y﹣5),去括号,可得:20y+16+3y﹣3=24﹣5y+5,移项,可得:20y+3y+5y=24+5﹣16+3,合并同类项,可得:28y=16,系数化为1,可得:y=.(3).【解答】(3)去分母得:4(5y+1)=3(9y+1)﹣8(1﹣y),去括号得:20y+4=27y+3﹣8+8y,移项、合并同类项得:﹣15y=﹣9,系数化1得:.(4).【解答】(4),去分母,得:6﹣2(2x﹣1)=3+x,去括号,得:6﹣4x+2=3+x,移项、合并同类项,得:﹣5x=﹣5,系数化为1,得:x=1.(5)=1.【解答】(5)3(x﹣2)+2(5﹣2x)=6,3x﹣6+10﹣4x=6,3x﹣4x=6+6﹣10,﹣x=2,x=﹣2.(6);【解答】(6),去分母,得2(2x﹣1)=3(3x+5),去括号,得4x﹣2=9x+15,移项,得4x﹣9x=2+15,合并同类项,得﹣5x=17,系数化为1,得x=﹣;(7).【解答】(7),去分母,得2(3x﹣2)﹣(5x+1)=18,去括号,得6x﹣4﹣5x﹣1=18,移项,得6x﹣5x=18+4+1,合并同类项,得x=23.(8).【解答】(8),去分母,得x﹣3﹣2(2x+1)=4,去括号,得x﹣3﹣4x﹣2=4,移项,得x﹣4x=4+3+2,合并同类项,得﹣3x=9,系数化成1,得x=﹣3.(9).【解答】(9)分母化为整数得:,去分母得:3(3x﹣4)+12=2(5x﹣2),去括号得:9x﹣12+12=10x﹣4,即:9x=10x﹣4,移项、合并同类项得:x=4.(10).【解答】(10),去分母,得:2(2x+1)﹣(x﹣1)=6,去括号,得:4x+2﹣x+1=6,移项,合并同类项,得3x=3,系数化为1,得:x=1.(11).【解答】(11)去分母得:2(2x﹣1)﹣(x+2)=12,去括号得:4x﹣2﹣x﹣2=12,移项得:4x﹣x=12+2+2,合并同类项得:3x=16,系数化为1得:,∴原方程的解为:.(12).【解答】(12),3(3x﹣1)=6﹣(x﹣1),9x﹣3=6﹣x+1,9x+x=6+1+3,10x=10,x=1;(13).【解答】(13),4(2x﹣1)﹣12x=3(2x+1)﹣12,8x﹣4﹣12x=6x+3﹣12,8x﹣12x﹣6x=3﹣12+4,﹣10x=﹣5,x=.(14).【解答】(14)原方程去分母得:2(7﹣5x)=4﹣(3x﹣1),去括号得:14﹣10x=4﹣3x+1,移项得:﹣10x+3x=4+1﹣14,合并同类项得:﹣7x=﹣9,系数化为1得:x=.(15).【解答】(15),去分母,得3(x+1)﹣6=2(2﹣3x),去括号,得3x+3﹣6=4﹣6x,移项,得3x+6x=4﹣3+6,合并同类项,得9x=7,系数化成1,得x=.(16).【解答】(16),去分母得,2(2x﹣3)=5(3x﹣1)+10,去括号得,4x﹣6=15x﹣5+10,移项得,4x﹣15x=﹣5+10+6,合并同类项得,﹣11x=11,x的系数化为1得,x=﹣1.(17).【解答】(17)原方程去分母得:3x﹣2=6+2(x﹣1),去括号得:3x﹣2=6+2x﹣2,移项得:3x﹣2x=6﹣2+2,合并同类项得:x=6.(18).【解答】(18)去分母得:3(2x+1)﹣12=12x﹣2(5x﹣3),去括号得:6x+3﹣12=12x﹣10x+6,移项合并得:4x=15,解得:x=.(19).【解答】(19)方程去分母得:18x+3x﹣3=18﹣4x+4,移项合并得:25x=25,解得:x=1.(20).【解答】(20)去分母得:1.2x+9﹣1.2=0.9﹣2x,移项合并得:3.2x=﹣6.9,解得:x=﹣.(21).【解答】(21),去分母,得2x+1=6﹣2(5x﹣2),去括号,得2x+1=6﹣10x+4,移项,得2x+10x=6+4﹣1,合并同类项,得12x=9,系数化成1,得x=.(22).【解答】(22),3(3y﹣1)﹣12=2(5y﹣7),9y﹣3﹣12=10y﹣14,9y﹣10y=﹣14+12+3,﹣y=1,y=﹣1.(23).【解答】(52)去分母得:10y﹣5(y﹣1)=30﹣2(y+2),去括号得:10y﹣5y+5=30﹣2y﹣4,移项得:10y﹣5y+2y=30﹣4﹣5,合并同类项得:7y=21,解得:y=3.(24).【解答】(24),去分母,方程两边同时乘以最小公倍数6,2(2x+1)=3(x﹣1),去括号,4x+2=3x﹣3,移项,合并同类项,4x﹣3x=﹣3﹣2,系数化为1,x=﹣5.(25);【解答】(25),去分母,得3(3y﹣1)﹣2(5y﹣7)=12,去括号,得9y﹣3﹣10y+14=12,移项,得9y﹣10y=12+3﹣14,合并同类项,得﹣y=1,系数化为1,得y=﹣1;(26).【解答】(26),原方程可化为,去分母,得4(x﹣20)+3(30﹣7x)=12,去括号,得4x﹣80+90﹣21x=12,移项,得4x﹣21x=12+80﹣90,合并同类项,得﹣17x=2,系数化为1,得x=﹣.(27)﹣1.【解答】(51)去分母得:4(2y﹣1)=3(y+2)﹣12,去括号得:8y﹣4=3y+6﹣12,移项合并得:5y=﹣2,解得:y=﹣.(28).【解答】(28),去分母,得7(1﹣2x)=3(3x+1)﹣63,去括号,得7﹣14x=9x+3﹣63,移项,得﹣14x﹣9x=3﹣63﹣7,合并同类项,得﹣23x=﹣67,系数化成1,得x=.(29).【解答】(29)去分母得,2(2x﹣1)=3(3x+5)﹣6,去括号得,4x﹣2=9x+15﹣6,移项得,4x﹣9x=15﹣6+2,合并同类项得,﹣5x=11,x的系数化为1得,x=﹣.(30)5x=2x+5;【解答】解:(30)5x=2x+5,5x﹣2x=5﹣,3x=5,x=;(31)=.【解答】(31)=,5x﹣10=2x+2,5x﹣2x=2+10,3x=12,x=4.(32).【解答】(32)整理得:,去分母得:3(3x﹣1)﹣2(2x+9)=﹣48,去括号得:9x﹣3﹣4x﹣18=﹣48,移项得:9x﹣4x=﹣48+18+3,合并同类项得:5x=﹣27,系数化为1得;.(33).【解答】(33)去分母得,4(2x﹣6)﹣3(x+18)=12,去括号得,8x﹣24﹣3x﹣54=12,移项得,8x﹣3x=12+24+54,合并同类项得,5x=90,系数化为1得,x=18.(34).【解答】(34)去分母可得,10(x+2)﹣20(2x﹣1)=﹣2,去括号得,10x+20﹣40x+20=﹣2,移项得,10x﹣40x=﹣2﹣20﹣20,合并同类项得,﹣30x=﹣42,系数化为1得,.(35).【解答】(35),去分母得:3(x+2)﹣2(x﹣1)=12,去括号得:3x+6﹣2x+2=12,移项合并得:x=4.(36).【解答】(36),去分母,得:4x﹣2(2x+3)=24﹣(8﹣x),去括号,得:4x﹣4x﹣6=24﹣8+x,移项,得:4x﹣4x﹣x=24﹣8+6,合并同类项,得:﹣x=22,系数化为1,得:x=﹣22.【解答】(37)﹣1=去分母得:3(x+1)﹣6=2(2﹣3x),去括号得:3x+3﹣6=4﹣6x,移项并合并得:9x=7,系数化为1得:x=.(38)=4.【解答】(38)去分母,可得:3(x﹣3)+2(x﹣1)=24,去括号,可得:3x﹣9+2x﹣2=24,移项,可得:3x+2x=24+9+2,合并同类项,可得:5x=35,系数化为1,可得:x=7.(39).【解答】(39),去分母,得2(2x+1)﹣(5x﹣1)=﹣6,去括号,得4x+2﹣5x+1=﹣6,移项,得4x﹣5x=﹣6﹣1﹣2,合并同类项,得﹣x=﹣9,系数化为1,得x=9.(40).【解答】(40).2(2x+1)﹣(10x+1)=4,4x+2﹣10x﹣1=4,4x﹣10x=4﹣2+1,﹣6x=3.x=﹣0.5.【解答】(41)1﹣=,去分母得:15﹣3(x﹣3)=5(4﹣x),去括号得:15﹣3x+9=20﹣5x,移项得:﹣3x+5x=20﹣15﹣9,合并同类项得:2x=﹣4,把系数化为1得:x=﹣2.(42)﹣1=.【解答】(42)去分母得:3(3y﹣1)﹣12=2(5y﹣7),去括号得:9y﹣3﹣12=10y﹣14,移项得:9y﹣10y=﹣14+3+12,合并得:﹣y=1,解得:y=﹣1.(43)=1.【解答】(43)﹣=1,5(x+2)﹣3(2x﹣3)=15,5x+10﹣6x+9=15,5x﹣6x=15﹣10﹣9,﹣x=﹣4,x=4.(44).【解答】(44),去分母得:3(3x+5)=2×2x,去括号得:9x+15=4x,移项得:9x﹣4x=﹣15,合并同类项得:5x=﹣15,系数化为1得:x=﹣3.(45)=1﹣.【解答】(45)=1﹣,去分母,得2(2x﹣1)=4﹣(3﹣x),去括号,得4x﹣2=4﹣3+x,移项,得4x﹣x=4﹣3+2,合并同类项,3x=3,系数化成1,得x=1.(46).【解答】(46)去分母,得5×3x﹣2(4x﹣2)=﹣10,去括号,得15x﹣8x+4=﹣10,移项,得15x﹣8x=﹣10﹣4,合并同类项,得7x=﹣14,系数化为1,得x=﹣2.(47).【解答】(47)去分母得:2(1+2x)=3(1﹣x),去括号得:2+4x=3﹣3x,移项得:4x+3x=3﹣2,合并同类项得:7x=1,解得:x=.(48)解方程:.【解答】(50)解:,去分母,得2x+3(30﹣x)=30,去括号,得2x+90﹣3x=30,移项,得2x﹣3x=30﹣90,合并同类项,得﹣x=﹣60,系数化为1,得x=60.(49).【解答】(49)去分母,得3(x+2)﹣2(2x﹣3)=24,去括号,得3x+6﹣4x+6=24,移项,得3x﹣4x=24﹣6﹣6,合并,得﹣x=12,系数化为1,得x=﹣12.。
解一元一次方程习题精选含答案解析

一、解方程:(1)=x ﹣.(3).(5).(7)4(x﹣1)﹣3(20﹣x )=5(x﹣2);(9)(11).(13).(2)(x﹣1)=2﹣(x+2).(4)(6)[3(x﹣)+]=5x﹣1 (8)(10)(12)(14)(17)(19)x﹣﹣3(21).(23).20.解方程(1).(2).(I8)12y﹣2.5y=7.5y+5(20).(22).二、计算:(1)(2)÷(4)﹣42×+|﹣2|3×(﹣)3(5)当k为什么数时,式子比的值少3.6.2.4解一元一次方程(三)参考答案与试题解析一.解答题(共30小题)1.(2005•宁德)解方程:2x+1=7考点:解一元一次方程.专题:计算题;压轴题.分析:此题直接通过移项,合并同类项,系数化为1可求解.解答:解:原方程可化为:2x=7﹣1 合并得:2x=6系数化为1得:x=3点评:解一元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.2.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:左右同乘12可得:3[2x﹣(x﹣1)]=8(x﹣1),化简可得:3x+3=8x﹣8,移项可得:5x=11,解可得x=.故原方程的解为x=.点评:若是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.3.(1)解方程:4﹣x=3(2﹣x);(2)解方程:.考点:解一元一次方程.专题:计算题.分析:(1)先去括号,然后再移项、合并同类型,最后化系数为1,得出方程的解;移项得:﹣x+3x=6﹣4,合并得:2x=2,系数化为1得:x=1.(2)去分母得:5(x﹣1)﹣2(x+1)=2,去括号得:5x﹣5﹣2x﹣2=2,移项得:5x﹣2x=2+5+2,合并得:3x=9,系数化1得:x=3.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.4.解方程:.考点:解一元一次方程.专题:计算题.分析:此题两边都含有分数,分母不相同,如果直接通分,有一定的难度,但将方程左右同时乘以公分母6,难度就会降低.解答:解:去分母得:3(2﹣x)﹣18=2x﹣(2x+3),去括号得:6﹣3x﹣18=﹣3,移项合并得:﹣3x=9,∴x=﹣3.点评:本题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.5.解方程(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);(2)x﹣=2﹣.考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项、合并同类项、化系数为1,从而得到方程的解;(2)先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣4﹣60+3x=5x﹣10(2分)移项得:4x+3x﹣5x=4+60﹣10(3分)合并得:2x=54(5分)系数化为1得:x=27;(6分)(2)去分母得:6x﹣3(x﹣1)=12﹣2(x+2)(2分)去括号得:6x﹣3x+3=12﹣2x﹣4(3分)移项得:6x﹣3x+2x=12﹣4﹣3(4分)合并得:5x=5(5分)多项式)作为一个整体加上括号.去括号时要注意符号的变化.6.(1)解方程:3(x﹣1)=2x+3;(2)解方程:=x﹣.考点:解一元一次方程.专题:计算题.分析:(1)是简单的一元一次方程,通过移项,系数化为1即可得到;(2)是较为复杂的去分母,本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)3x﹣3=2x+33x﹣2x=3+3x=6;(2)方程两边都乘以6得:x+3=6x﹣3(x﹣1)x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0.点评:本题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进行,从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.7.﹣(1﹣2x)=(3x+1)考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:﹣7(1﹣2x)=3×2(3x+1)﹣7+14x=18x+6﹣4x=13x=﹣.点评:解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1.此题去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.8.解方程:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+1;(2).点:专题:计算题.分析:(1)可采用去括号,移项,合并同类项,系数化1的方式进行;(2)本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+13x﹣7=4x﹣2∴x=﹣5;(2)原方程可化为:去分母得:40x+60=5(18﹣18x)﹣3(15﹣30x),去括号得:40x+60=90﹣90x﹣45+90x,移项、合并得:40x=﹣15,系数化为1得:x=.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果;(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.9.解方程:.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:,去分母得:2x﹣(3x+1)=6﹣3(x﹣1),去括号得:2x﹣3x﹣1=6﹣3x+3,移项、合并同系数化为1得:x=5.点评:去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.10.解方程:(1)4x﹣3(4﹣x)=2;(2)(x﹣1)=2﹣(x+2).考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,合并同类项,系数化1,即可求出方程的解;(2)先去分母,再去括号,移项,合并同类项,系数化1可求出方程的解.解答:解:(1)4x﹣3(4﹣x)=2去括号,得4x﹣12+3x=2移项,合并同类项7x=14系数化1,得x=2.(2)(x﹣1)=2﹣(x+2)去分母,得5去括号,得5x﹣5=20﹣2x﹣4移项、合并同类项,得7x=21系数化1,得x=3.点评:(1)此题主要是去括号,移项,合并同类项,系数化1.(2)方程两边每一项都要乘各分母的最小公倍数,方程两边每一项都要乘各分母的最小公倍数,切勿漏乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母时,应该将分子用括号括上.11.计算:(1)计算:(2)解方程:考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:(1)根据有理数的混合运算法则计减;(2)两边同时乘以最简公分母4,即可去掉分母.解答:解:(1)原式=,=,=.(2)去分母得:2(x﹣1)﹣(3x﹣1)=﹣4,解得:x=3.点评:解答此题要注意:(1)去分母时最好先去中括号、再去小括号,以减少去括号带来的符号变化次数;(2)去分母就是方程两边同时乘以分母的最简公分母.12.解方程:考点:解一元一次方程.专题:计算题.分析:(1)这是一个带分母的方程,所以要为1,从而得到方程的解.(2)解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.解答:解:(1)去分母得:3(3x﹣1)+18=1﹣5x,去括号得:9x﹣3+18=1﹣5x,移项、合并得:14x=﹣14,系数化为1得:x=﹣1;(2)去括号得:x﹣x+1=x,移项、合并同类项得:x=﹣1,系数化为1得:x=﹣.点评:本题考查解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时“1”也要乘以最小公倍数.13.解方程:(2)考点:解一元一次方程.专题:计算题.分析:(1)去分母、去括号、移项、合并同类项、化系数为1.(2)去分母、去括号、移项、合并同类项、化系数为1.解答:(1)解:去分母得:5(3x+1)﹣2×10=3x﹣2﹣2(2x+3),去括号得:15x+5﹣20=3x﹣2﹣4x﹣6,移项得:15x+x=﹣8+15,合并得:16x=7,解得:;(2)解:,4(x﹣1)﹣18(x+1)=﹣36,4x﹣4﹣18x﹣18=﹣36,﹣14x=﹣14,x=1.点评:本题考查解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时“1”也要乘以最小公倍数.14.解方程:(1)5(2x+1)﹣2(2x﹣3)=6 (2)+2(3)[3(x﹣)+]=5x﹣1考点:解一元一次方程.专题:计算题.分析:(2)通过去括号、移项、合并同类项、系数化为1,解得x的值;(3)乘最小公倍数去分母即可;(4)主要是去括号,也可以把分数转化成整数进行计算.解答:解:(1)去括号得:10x+5﹣4x+6=6移项、合并得:6x=﹣5,方程两边都除以6,得x=﹣;(2)去分母得:3(x﹣2)=2(4﹣3x)+24,去括号得:3x﹣6=8﹣6x+24,移项、合并得:9x=38,方程两边都除以9,得x=;(3)整理得:[3(x﹣)+]=5x﹣1,4x﹣2+1=5x﹣1,移项、合并得:x=0.点评:一元一次方程的解法:一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.解题时,要灵活运用这些步骤.15.(A类)解方程:5x﹣2=7x+8;(B类)解方程:(x﹣1)﹣(x+5)=﹣;(C类)解方程:.考点:解一元一次方程.专题:计算题.分析:通过去分母、去括号、移项、系数化为1等方法,求得各方程的解.解答:解:A类:5x﹣2=7x+8移项:5x﹣7x=8+2化简:﹣2x=10即:x=﹣5;B类:(x﹣1)﹣(x+5)=﹣去括号:x﹣﹣x﹣5=﹣化简:x=5即:x=﹣;C类:﹣=1去分母:3(4﹣x)﹣2(2x+1)=6去括号:12﹣3x﹣4x﹣2=6化简:﹣7x=﹣4即:x=.点评:本题主要考查一元一次方程的解法,比较简单,但要细心运算.16.解方程(1)3(x+6)=9﹣5(1﹣2x)(2)(3)(4)考点:解一元一次方程.专题:计算题.分析:(1)去括号以后,移项,合并同类项,系数化为1即可求解;(2)(3)首先去掉分母,再去括号以后,移项,合并同类项,系数化为1以后即可求解;(4)首先根据分数的基本性质,把第一项分母中的0.3化为整数,再去分母,求解.解答:解:(1)去括号得:3x+18=9﹣5+10x 移项得:3x﹣10x=9﹣5﹣18合并同类项得:﹣7x=﹣14则x=2;(2)去分母得:2x+1=x+3﹣5移项,合并同类项得:x=﹣3;(3)去分母得:10y+2(y+2)=20﹣5(y﹣1)去括号得:10y+2y+4=20﹣5y+5移项,合并同类项得:17y=21系数化为1得:;(4)原方程可以变形为:﹣5x=﹣1去分母得:17+20x﹣15x=﹣3移项,合并同类项得:5x=﹣20系数化为1得:x=﹣4.解方程的过程中要注意每步的依据,这几个题目都是基础的题目,需要熟练掌握.点评:17.解方程:(1)解方程:4x﹣3(5﹣x)=13(2)解方程:x﹣﹣3考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,化系数为1,从而得到方程的解.(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣15+3x=13,移项合并得:7x=28,系数化为1得:得x=4;(2)原式变形为x+3=,去分母得:5(2x﹣5)+3(x﹣2)=15(x+3),去括号得10x﹣25+3x﹣6=15x+45,移项合并得﹣2x=76,系数化为1得:x=﹣38.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.18.(1)计算:﹣42×+|﹣2|3×(﹣)3(2)计算:﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2](3)解方程:4x﹣3(5﹣x)=2;(4)解方程:.考点:解一元一次方程;有理数的混合运算.分析:(1)利用平方和立方的定义进行计算.(2)按四则混合运算的顺序进行计算.(3)主要是去括号,移项合并.乘最小公倍数去分母,再求值.解答:解:(1)﹣42×+|﹣2|3×(﹣)3==﹣1﹣1=﹣2.(2)﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2]====.(3)解方程:4x﹣3(5﹣x)=2去括号,得4x﹣15+3x)=2移项,得4x+3x=2+15合并同类项,得7x=17系数化为1,得.(4)解方程:去分母,得15x﹣3(x﹣﹣3×15去括号,得15x﹣3x+6=10x﹣25﹣45移项,得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项,得2x=﹣76系数化为1,得x=﹣38.点评:前两道题考查了学生有理数的混合运算,后两道考查了学生解一元一次方程的能力.19.(1)计算:(1﹣2﹣4)×;(2)计算:÷;(3)解方程:3x+3=2x+7;(4)解方程:.考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:(1)和(2)要熟练掌握有理数的混合运算;(3)和(4)首先熟悉解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1.解答:解:(1)(1﹣2﹣4)×=﹣=﹣13;(2)原式=﹣1×(﹣4﹣2)×(﹣)=6×(﹣)=﹣9;(3)解方程:3x+3=2x+7移项,得3x﹣2x=7﹣3合并同类项,得x=4;(4)解方程:去分母,得6(x+15)=15﹣10(x﹣7)去括号,得6x+90=15﹣10x+70移项,得6x+10x=15+70﹣90合并同类项,得16x=﹣5系数化为1,得x=.点评:(1)和(2)要注意符号的处理;(4)要特别注意去分母的时候不要发生数字漏乘的现象,熟练掌握去括号法则以及合并同类项法则.20.解方程(1)﹣0.2(x﹣5)=1;(2).考点:解一元一次方程.分析:(1)通过去括号、移项、系数化为1等过程,求得x的值;(2)通过去分母以及去括号、移项、系数化为1等过程,求得x的值.解答:解:(1)﹣0.2(x﹣5)=1;去括号得:﹣0.2x+1=1,∴﹣0.2x=0,∴x=0;(2).去分母得:2(x﹣2)+6x=9(3x+5)﹣(1﹣2x),∴﹣21x=48,∴x=﹣.点评:此题主要考查了一元一次方程解法,解一元一次方程常见的过程有去括号、移项、系数化为1等.21.解方程:(x+3)﹣2(x﹣1)=9﹣3x.考点:解一元一次方程.专题:计算题.分析:先去括号得x+3﹣2x+2=9﹣3x,然后移项、合并同类得到2x=4,然后把x的系数化为1即可.解答:解:去括号得x+3﹣2x+2=9﹣3x,移项得x﹣2x+3x=9﹣3﹣2,合并得2x=4,系数化为1得x=2.点评:本题考查了解一元一次方程:先去分母,再去括号,接着移项,把含未知数的项移到方程左边,不含未知数的项移到方程右边,然后合并同类项,最后把未知数的系数化为1得到原方程的解.22.8x﹣3=9+5x.5x+2(3x﹣7)=9﹣4(2+x)...考点:解一元一次方程.专题:方程思想.分析:本题是解4个不同的一元一次方程,第一个通过移项、合并同类项及系数化1求解.第二个先去括号再通过移项、合并同类项及系数化1求解.第三个先去分母再同第二个.第四个先分子分母乘以10,再同第三个求解.解答:8x﹣3=9+5x,解:8x﹣5x=9+3,3x=12,∴x=4.∴x=4是原方程的解;5x+2(3x﹣7)=9﹣4(2+x),解:5x+6x﹣14=9﹣8﹣4x,5x+6x+4x=9﹣8+14,15x=15,∴x=1.∴x=1是原方程的解..解:3(x﹣1)﹣2(2x+1)=12,3x﹣3﹣4x﹣2=12,3x﹣4x=12+3+2,﹣x=17,∴x=﹣17.∴x=﹣17是原方程的解.,解:,5(10x﹣3)=4(10x+1)+40,50x﹣15=40x+4+40,50x﹣40x=4+40+15,10x=59,∴x=.∴x=是原方程的解.点评:此题考查的知识点是解一元一次方程,关键是注意解方程时的每一步都要认真仔细,如移项时要变符号.23.解下列方程:(1)0.5x﹣0.7=5.2﹣1.3(x﹣1);(2)=﹣2.考点:解一元一次方程.分析:(1)首先去括号,然后移项、合并同类项,系数化成1,即可求解;(2)首先去分母,然后去括号,移项、合并同类项,系数化成1,即可求解解答:解:(1)去括号,得:0.5x﹣0.7=5.2﹣1.3x+1.3移项,得:0.5x+1.3x=5.2+1.3+0.7合并同类项,得:1.8x=7.2,则x=4;(2)去分母得:7(1﹣2x)=3(3x+1)﹣42,去括号,得:7﹣14x=9x+3﹣42,移项,得:﹣14x﹣9x=3﹣42﹣7,合并同类项,得:﹣23x=﹣46,则x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.24.解方程:(1)﹣0.5+3x=10;(2)3x+8=2x+6;(3)2x+3(x+1)=5﹣4(x﹣1);(4).考点:解一元一次方程.分析:(1)移项,合并同类项,然后系数化成1即可求解;(2)移项,合并同类项,然后系数化成1即可求解;(3)去括号、移项,合并同类项,然后系数化成1即可求解;(4)首先去分母,然后去括号、移项,合并同类项,然后系数化成1即可求解.解答:解:(1)3x=10.5,x=3.5;(2)3x﹣2x=6﹣8,x=﹣2;(3)2x+3x+3=5﹣4x+4,2x+3x+4x=5+4﹣3,9x=6,x=;(4)2(x+1)+6=3(3x﹣2),2x+2+6=9x﹣6,2x﹣9x=﹣6﹣2﹣6,﹣7x=﹣14,x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.25.解方程:.考点:解一元一次方程.专题:计算题.分析:方程两边乘以10去分母后,去括号,移项合并,将x系数化为1,即可求出解.解答:解:去分母得:5(3x﹣1)﹣2(5x﹣6)=2,去括号得:15x﹣5﹣10x+12=2,移项合并得:5x=﹣5,解得:x=﹣1.点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.26.解方程:(1)10x﹣12=5x+15;(2)考点:解一元一次方程.专题:计算题.分析:(1)先移项,再合并同类项,最后化系数为1,从而得到方程的解;(2)先去括号,再移项、合并同类项,最后化系数为1,从而得到方程的解.解答:解:(1)移项,得10x﹣5x=12+15,合并同类项,得5x=27,方程的两边同时除以5,得x=;(2)去括号,得=,方程的两边同时乘以6,得x+1=4x﹣2,移项、合并同类项,得3x=3,方程的两边同时除以3,得x=1.点评:本题考查解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.27.解方程:(1)8y﹣3(3y+2)=7(2).考点:解一元一次方程.专题:计算题.分析:(1)根据一元一次方程的解法,去括号,移项,合并同类项,系数化为1即可得解;(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(1)去括号得,8y﹣9y﹣6=7,移项、合并得,﹣y=13,系数化为1得,y=﹣13;(2)去分母得,3(3x﹣1)﹣12=2(5x﹣7),去括号得,9x﹣3﹣12=10x﹣14,移项得,9x﹣10x=﹣14+3+12,合并同类项得,﹣x=1,系数化为1得,x=﹣1.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.28.当k为什么数时,式子比的值少3.考点:解一元一次方程.专题:计算题.分析:先根据题意列出方程,再根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.解答:解:依题意,得=+3,去分母得,5(2k+1)=3(17﹣k)+45,去括号得,10k+5=51﹣3k+45,移项得,10k+3k=51+45﹣5,合并同类项得,13k=91,系数化为1得,k=7,∴当k=7时,式子比的值少3.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.29.解下列方程:(I)12y﹣2.5y=7.5y+5(II).考点:解一元一次方程.专题:计算题.分析:(Ⅰ)根据一元一次方程的解法,移项,合并同类项,系数化为1即可得解;(Ⅱ)是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(Ⅰ)移项得,12y﹣2.5y﹣7.5y=5,合并同类项得,2y=5,系数化为1得,y=2.5;(Ⅱ)去分母得,5(x+1)﹣10=(3x﹣2)﹣2(2x+3),去括号得,5x+5﹣10=3x﹣2﹣4x﹣6,移项得,5x﹣3x+4x=﹣2﹣6﹣5+10,合并同类项得,6x=﹣3,系数化为1得,x=﹣.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.30.解方程:.考点:解一元一次方程.专题:计算题.分析:由于方程的分子、分母均有小数,利用分数的基本性质,分子、分母同时扩大相同的倍数,可将小数化成整数.解答:解:原方程变形为,(3分)去分母,得3×(30x﹣11)﹣4×(40x﹣2)=2×(16﹣70x),(4分)去括号,得90x﹣33﹣160x+8=32﹣140x,(5分)移项,得90x﹣160x+140x=32+33﹣8,(6分)合并同类项,得70x=57,(7分)系数化为1,得.(8分)点评:本题考查一元一次方程的解法.解一元一次方程的一般步骤:去分母,去括号,移项,合并同类项,系数化为1.本题的难点在于方程的分子、分母均有小数,将小数化成整数不同于去分母,不是方程两边同乘一个数,而是将分子、分母同乘一个数.。
专题 一元一次方程的同解、错解、参数等问题(解析版)

七年级上册数学《第三章一元一次方程》专题一元一次方程的同解、错解、参数等问题【例题1】(2022•江阴市模拟)已知x=1是方程x+2a=﹣1的解,那么a的值是()A.﹣1B.0C.1D.2【分析】根据方程解的定义,将方程的解代入方程可得关于字母系数a的一元一次方程,从而可求出a 的值.【解答】解:把x=1代入方程,得:1+2a=﹣1,解得:a=﹣1.故选:A.【点评】已知条件中涉及到方程的解,把方程的解代入原方程,转化为关于字母系数的方程进行求解.可把它叫做“有解就代入”.【变式1-1】(2022秋•秀山县期末)已知x=1是关于x的方程6﹣(m﹣x)=5x的解,则代数式m2﹣6m+2=.【分析】根据一元一次方程的解的定义可知m的值,然后代入求值即可.【解答】解:把x=1代入6﹣(m﹣x)=5x,得6﹣(m﹣1)=5×1.解得m=2.所以m2﹣6m+2=22﹣6×2+2=﹣6.故答案为:﹣6.【点评】本题主要考查了一元一次方程的定义.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.【变式1-2】(2022秋•张家港市期中)已知x=1是关于x的方程3x3﹣2x2+x﹣4+a=0的解,则3a3﹣2a2+a ﹣4的值是()A.1B.﹣1C.16D.14【分析】把x=1代入关于x的方程3x3﹣2x2+x﹣4+a=0可以求得a的值,然后把x=2代入所求的代数式进行求值.【解答】解:∵x=1是关于x的方程3x3﹣2x2+x﹣4+a=0的解,∴3﹣2+1﹣4+a=0,解得,a=2,∴3a3﹣2a2+a﹣4=3×23﹣2×22+2﹣4=14.故选:D.【点评】本题主要考查了方程解的定义,解决本题的关键在于根据方程的解的定义将x=1代入,从而转化为关于a的一元一次方程.【变式1-3】若关于x的方程x+2=2(m﹣x)的解满足方程|x−12|=1,则m的值是()A.14或134B.14C.54D.−12或54【分析】解含绝对值符号的一元一次方程要根据绝对值的性质和绝对值符号内代数式的值分情况讨论,即去掉绝对值符号得到一般形式的一元一次方程,再求解.【解答】解:因为方程|x−12|=1,所以x−12=±1,解得x=32或x=−12,因为关于x的方程x+2=2(m﹣x)的解满足方程|x−12|=1,所以解方程x+2=2(m﹣x)得,m=3r22,当x=32时,m=134,当x=−12时,m=14.所以m的值为:134或14.故选:A.【点评】本题考查了含绝对值符号的一元一次方程,解决本题的关键是解含绝对值符号的一元一次方程要根据绝对值的性质和绝对值符号内代数式的值分情况讨论.【变式1-4】(2022秋•奎屯市校级月考)已知x=4是关于x的一元一次方程﹣3m﹣x=2+3m的解,则m2020+1的值是.【分析】根据一元一元一次方程的解的定义求得m,再解决此题.【解答】解:由题意得,﹣3m﹣4=42+3.∴﹣3m﹣4=2+3m.∴﹣6m=6.∴m=﹣1.∴m2020+1=(﹣1)2020+1=1+1=2.故答案为:2.【点评】本题主要考查一元一次方程的解、有理数的乘方,熟练掌握一元一次方程的解的定义、有理数的乘方是解决本题的关键.【变式1-5】(2022秋•烟台期末)已知x=﹣1是关于x的方程2a+2=﹣1﹣bx的解.求代数式5(2a﹣b)﹣2a+b+2的值.【分析】根据方程解的定义,把x=﹣1代入关于x的方程2a+2=﹣1﹣bx,即可得出代数式5(2a﹣b)﹣2a+b+2的值.【解答】解:当x=﹣1时,2a+2=﹣1+b,即2a﹣b=﹣3,∴5(2a﹣b)﹣2a+b+2=5(2a﹣b)﹣(2a﹣b)+2=﹣15+3+2=﹣10.【点评】本题考查了一元一次方程的解,以及整式的加减,把2a﹣b作为整体,是数学中常用的整体思想.(2023春•长春期中)已知关于x的方程4x+2m=3x+1的解是x=0,试求(−2p2021−(−32)2020【变式1-6】的值.【分析】将x=0代入原方程,可求出m的值,再将m的值代入原式,即可求出结论.【解答】解:将x=0代入原方程得:2m=1,解得:m=12,∴原式=(﹣2×12)2021﹣(12−32)2020,=(﹣1)2021﹣(﹣1)2020=﹣1﹣1=﹣2.【点评】本题考查了一元一次方程的解,牢记“把方程的解代入原方程,等式左右两边相等”是解题的关键.【例题2】(2023秋•东台市期中)如果关于x的方程K43=8−r22的解与方程4x﹣(3a+1)=6x+2a﹣1的解相同,求a的值.【分析】先求出第一个方程的解,然后代入第二个方程得到关于a的一元一次方程,再根据一元一次方程的解法进行求解即可.【解答】解:解方程K43=8−r22得:x=10,由题意:4x﹣(3a+1)=6x+2a﹣1的解为x=10,代入得:4×10﹣(3a+1)=6×10+2a﹣1,解得:a=﹣4.【点评】本题考查了同解方程,同解方程就是解相同的方程,本题先求出第一个方程的解是解题的关键.【变式2-1】(2022秋•长沙期末)若关于x的方程r32−=2的解与方程x+1=m的解相同,求m的值.【分析】先解方程r32−=2可得x=4﹣m,再根据方程同解的含义可得4﹣m+1=m,再解关于m 的方程即可.【解答】解:r32−=2,去分母可得:m+3x﹣2x=4,即x=4﹣m,∵关于x的方程r32−=2的解与方程x+1=m的解相同,∴4﹣m+1=m,解得:=52.【点评】本题考查的是同解方程的含义,选择合适的方程进行变形是解本题的关键.【变式2-2】(2022秋•仙游县校级期末)如果方程2K35=23x﹣2与3a−14=3(x+a)﹣2a的解相同,求(a ﹣3)2的值.【分析】通过解关于x的方程2K35=23x﹣2求得x的值,然后将x的值代入3a−14=3(x+a)﹣2a列出关于a的新方程,通过解该新方程即可求得a的值,再代入计算即可求解.【解答】解:由关于x的方程2K35=23x﹣2,解得x=5.25∵关于x的方程2K35=23x﹣2与3a−14=3(x+a)﹣2a的解相同,∴3a−14=3(5.25+a)﹣2a,解得a=8.∴(a﹣3)2=(8﹣3)2=25.【点评】本题考查了同解方程的定义.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.【变式2-3】(2023春•安岳县校级期中)已知关于x的一元一次方程2r13−5K16=1.(1)求这个方程的解;(2)若这个方程的解与关于x的方程3(x+m)=﹣(x﹣1)的解相同,求m的值.【分析】(1)按照去分母,去括号,移项,合并同类项,系数化为1的步骤解方程即可;(2)根据题意可知x=﹣3是方程3(x+m)=﹣(x﹣1)的解,把x=﹣3代入方程3(x+m)=﹣(x ﹣1)中得到关于m的方程,解方程即可.【解答】解:(1)2r13−5K16=1去分母得:2(2x+1)﹣(5x﹣1)=6,去括号得:4x+2﹣5x+1=6,移项得:4x﹣5x=6﹣1﹣2,合并同类项得:﹣x=3,系数化为1得:x=﹣3;(2)由题意得x=﹣3是方程3(x+m)=﹣(x﹣1)的解,∴3(﹣3+m)=﹣(﹣3﹣1),∴3m﹣9=4,解得=133.【点评】本题主要考查了解一元一次方程,一元一次方程的解,熟知解一元一次方程的步骤是解题的关键.【变式2-4】如果方程K43−8=−r22的解与方程4x﹣(3a+1)=6x+2a﹣1的解相同,求式子a﹣a2的值.【分析】先求得方程方程K43−8=−r22的解,然后将所求的x的值代入方程4x﹣(3a+1)=6x+2a﹣1求得a的值,最后在求代数式的值即可.【解答】解:K43−8=−r22去分母得:2(x﹣4)﹣48=﹣3(x+2)去括号得:2x﹣8﹣48=﹣3x﹣6,移项得:2x+3x=﹣6+8+48,合并同类项得:5x=50,系数化为1得:x=10.将x=10代入方程4x﹣(3a+1)=6x+2a﹣1得:40﹣(3a+1)=60+2a﹣1,去括号得:40﹣3a﹣1=60+2a﹣1,移项得:﹣3a﹣2a=60﹣1﹣40+1,合并同类项得:﹣5a=20,系数化为1得:a=﹣4.a﹣a2=﹣4﹣(﹣4)2=﹣4﹣16=﹣20.【点评】本题主要考查的是同解方程的定义、解一元一次方程、求代数式的值,求得a的值是解题的关键.【变式2-5】(2022秋•巴南区期末)已知方程3K52=5K83的解满足等式10−3(Kp2=3K4−25(3x+m),求m的值.【分析】根据方程的解相同,可得关于m的方程,根据解方程,可得答案.【解答】解:解方程3K52=5K83,3(3x﹣5)=2(5x﹣8),9x﹣15=10x﹣16,9x﹣10x=﹣16+15,x=1,∵方程3K52=5K83的解满足等式10−3(Kp2=3K4−25(3x+m),∴10−3(1−p2=3−4−25×(3+p,2m﹣30(1﹣m)﹣5(3﹣m)﹣8(3+m),2m﹣30+30m=15﹣5m﹣24﹣8m,2m+30m+8m+5m=30+15﹣24,45m=21,解得m=715.【点评】本题考查了同解方程,利用同解方程得出关于m的方程是解题关键.【变式2-6】(2022秋•利州区校级期末)已知方程4x+2m=3x+1和方程3x+2m=6x+1的解相同.(1)求m的值;(2)求代数式(﹣2m)2022−(−32)2021的值.【分析】(1)分别解出两个方程的解,根据解相同列出方程,解方程即可;(2)代入求值即可.【解答】解:(1)由4x+2m=3x+1解得:x=1﹣2m,由3x+2m=6x+1解得:x=2K13,由题知:1﹣2m=2K13,解得:m=12;(2)当m=12时,(﹣2m)2022﹣(m−32)2021=(﹣2×12)2022﹣(12−32)2021=1+1=2.【点评】本题考查了同解方程,解一元一次方程,列出关于m的方程是解题的关键.【例题3】(202秋•沂源县期末)方程2﹣3(x+1)=0的解与关于x的方程r2−3k﹣2=2x的解互为相反数,求k的值【分析】直接解方程得出x=−13,进而得出关于x的方程r2−3k﹣2=2x的解,求出答案即可.【解答】解:∵2﹣3(x+1)=0,∴解得:x=−13,∵方程2﹣3(x+1)=0的解与关于x的方程r2−3k﹣2=2x的解互为相反数,∴关于x的方程r2−3k﹣2=2x的解x=13,∴r132−3k﹣2=23,解得:k=﹣1.【点评】此题主要考查了一元一次方程的解,正确得出x的值是解题关键.【变式3-1】(2022秋•高港区校级月考)已知关于x的方程①:x+1﹣2m=﹣m的解比方程②:32(−p−2=54的解大2.求m的值以及方程②的解.【分析】用含m的式子分别表示出方程①和方程②的解,根据方程①的解比方程②的解大2列出关于m的方程,求解可得m的值,将m的值代入方程②中即可解得x的值.【解答】解:解x+1﹣2m=﹣m得:x=m﹣1,解32(−p−2=54得:=611−811,∵方程①的解比方程②的解大2,∴−1−(611−811)=2,解得:m=5,将m=5代入方程②中得:32(5−p−2=54,解得:x=2.【点评】本题考查了解一元一次方程,熟练掌握解一元一次方程的一般步骤是解题的关键.【变式3-2】(2022秋•石景山区校级期末)已知关于x的方程中,12x﹣a=0的解比a+8x=2+4x的解大1,求a的值.【分析】分别解出关于x的方程12x﹣a=0的解和方程a+8x=2+4x的解,然后根据已知条件“关于x的方程中,12x﹣a=0的解比a+8x=2+4x的解大1”列出关于a的一元一次方程,解方程即可.【解答】解:由方程12x﹣a=0,得x=12,由方程a+8x=2+4x,得x=2−4,又∵关于x的方程中,12x﹣a=0的解比a+8x=2+4x的解大1,∴12−2−4=1,去分母,得a﹣3(2﹣a)=12,去括号,得a﹣6+3a=12,移项,得a+3a=6+12,合并同类项,得4a=18,化系数为1,得a=4.5.【点评】本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.【变式3-3】(2022秋•太仓市期末)已知关于x的一元一次方程2x+10﹣3m=0的解与关于x的一元一次方程r12+2(r1)3=1的解互为相反数,求代数式92m﹣4n﹣1的值.【分析】分别解方程,进而用m,n分别表示出x,再结合相反数的定义得出等式,将原式变形求出答案.【解答】解:2x+10﹣3m=0,则2x=3m﹣10,解得:x=3K102,r12+2(r1)3=1,则3(x+1)+4(n+1)=6,故3x+3+4n+4=6,3x=﹣1﹣4n,解得:x=−1+43,∵关于x的一元一次方程2x+10﹣3m=0的解与关于x的一元一次方程r12+2(r1)3=1的解互为相反数,∴3K102−1+43=0,去分母得:3(3m﹣10)﹣2(1+4n)=0,则9m﹣30﹣2﹣8n=0,故9m﹣8n=32,则92m﹣4n﹣1=12(9m﹣8n)﹣1=12×32﹣1=16﹣1=15.【点评】此题主要考查了一元一次方程的解,正确解方程是解题关键.【变式3-4】(2022秋•亭湖区校级月考)已知关于x的方程3(x﹣2)=x﹣a的解比r2=2K3的解小52,求2a﹣3的值.【分析】先分别求出两个方程的解,根据题意得出关于a的一元一次方程,再求出方程的解,最后求出答案即可.【解答】解:解方程3(x﹣2)=x﹣a得:x=6−2,解方程r2=2K3得:x=5a,∵关于x的方程3(x﹣2)=x﹣a的解比r2=2K3的解小52,∴6−2=5a−52,解得:a=1,∴2a﹣3=2×1﹣3=﹣1.【点评】本题考查了解一元一次方程和一元一次方程的解,能得出关于a的一元一次方程是解此题的关键.【变式3-5】(2022秋•常州期中)已知关于x的方程r12=3x﹣2与K2=x+3的解互为倒数,求m的值.【分析】先求出两方程的解,再由倒数的定义即可得出结论.【解答】解:解方程r12=3x﹣2得,x=1,解方程K2=x+3得,x=−53,∵关于x的方程r12=3x﹣2与K2=x+3的解互为倒数,−53×1=1,解得m=−35.【点评】本题考查的是一元一次方程的解,熟知使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解是解答此题的关键.【变式3-6】(2022秋•武城县期末)已知(|a|﹣1)x2﹣(a+1)x+8=0是关于x的一元一次方程.(1)求a的值,并解出上述一元一次方程;(2)若上述方程的解是方程5x﹣2k=2x解的2倍,求k的值.【分析】(1)根据一元一次方程的定义和解一元一次方程的一般步骤准确计算即可;(2)根据解析(1)得出的方程解,得出方程5x﹣2k=2x解为x=2,然后代入求出k的值即可.【解答】解:(1)由题意得:|a|﹣1=0,﹣(a+1)≠0,∴a=±1且a≠﹣1,∴a=1,将a=1代入方程得:﹣2x+8=0,解得:x=4.答:a的值是1,方程的解是x=4.(2)由题意得:x=4÷2=2,将x=2代入方程得:5×2﹣2k﹣2×2,解得:k=3.答:k的值是3.【点评】本题主要考查了解一元一次方程,方程解的定义,一元一次方程的定义,解题的关键熟练掌握解一元一次方程的方法.【例题4】(2023•平桥区校级开学)王涵同学在解关于x的一元一次方程7a+x=18时,误将+x看作﹣x,得方程的解为x=﹣4,那么原方程的解为()A.x=4B.x=2C.x=0D.x=﹣2【分析】把x=﹣4代入方程7a﹣x=18,得出方程7a+4=18,求出a的值,再代入方程,求出方程的解即可.【解答】解:把x=﹣4代入方程7a﹣x=18得:7a+4=18,解得:a=2,即原方程为14+x=18,解得:x=4.故选:A.【点评】本题考查了解一元一次方程和一元一次方程的解的应用,能得出关于a的一元一次方程是解此题的关键.【变式4-1】(2022秋•椒江区校级期中)小明解方程2K15+1=r2,由于粗心大意,在去分母时,方程左边的1没有乘10,由此求得的解为x=4,试求a的值,并求出方程的正确解.【分析】把x=4代入小明粗心得出的方程,求出a的值,代入方程求出解即可.【解答】解:由题意可知:(在去分母时,方程左边的1没有乘10,由此求得的解为x=4),2(2x﹣1)+1=5(x+a),把x=4代入得:a=﹣1,将a=﹣1代入原方程得:2K15+1=K12,去分母得:4x﹣2+10=5x﹣5,移项合并得:﹣x=﹣13,解得x=13.【点评】此题考查了解一元一次方程,解方程去分母时注意各项都乘以各分母的最小公倍数.【变式4-2】(2022秋•前郭县期末)某同学在解关于y的方程3K4−5K76=1去分母时,忘记将方程右边的1乘以12,从而求得方程的解为y=10.(1)求a的值;(2)求方程正确的解.【分析】(1)根据题意得3(3y﹣a)﹣2(5y﹣7a)=1,将y=10代入方程即可求a的值;(2)当a=1代入原方程再求解即可.【解答】解:(1)该同学去分母时方程右边的1忘记乘12,则原方程变为3(3y﹣a)﹣2(5y﹣7a)=1,∵方程的解为y=10,代入得3(30﹣a)﹣2(50﹣7a)=1.解得a=1.(2)将a=1代入方程3K4−5K76=1,得3K14−5K76=1,解得y=﹣1,即原方程的解为y=﹣1.【点评】本题考查一元一次方程的解,熟练掌握一元一次方程的解与一元一次方程的关系是解题的关键.【变式4-3】(2023•秦皇岛一模)米老鼠在解方程2K13=r2−1的过程中,去分母时方程右边的﹣1忘记乘6,因而求得的解为x=2.(1)请你帮助米老鼠求出a的值;(2)正确地解这个方程.【分析】(1)把x=2代入方程2(2x﹣1)=3(x+a)﹣1得出2×(2×2﹣1)=3(2+a)﹣1,再求出方程的解即可;(2)去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)把x=2代入方程2(2x﹣1)=3(x+a)﹣1得:2×(2×2﹣1)=3(2+a)﹣1,解得:a=13;(2)方程为2K13=r132−1,2(2x﹣1)=3(x+13)﹣6,4x﹣2=3x+1﹣6,4x﹣3x=1﹣6+2,x=﹣3.【点评】本题考查了一元一次方程的解和解一元一次方程,注意:使方程左右两边相等的未知数的值,叫方程的解.【变式4-4】(2022秋•道里区校级月考)小明同学在解方程2K13=r3−2,去分母时,方程右边的﹣2没有乘3,因而求得方程的解为x=3.试求a的值,并正确地解出方程.【分析】先根据题意,得x=3是方程2x﹣1=x+a﹣2的解,然后根据方程解的定义将x=2代入这个方程,从而求出a的值;再把所求得的a的值代入原方程,最后解一元一次方程即可.【解答】解:依题意,x=3是方程2x﹣1=x+a﹣2的解,∴2×3﹣1=3+a﹣2,∴a=4.∴原方程为2K13=r43−2,解方程,得2x﹣1=x+4﹣6,解得x=﹣1.故a=4,原方程的正确的解是x=﹣1.【点评】本题考查了一元一次方程的解和解一元一次方程的知识,解题的关键是掌握相关的定义和解一元一次方程的一般步骤.【变式4-5】小王在解关于x的方程3a﹣2x=15时,误将﹣2x看作2x,得方程的解x=3,(1)求a的值;(2)求此方程正确的解;(3)若当y=a时,代数式my3+ny+1的值为5,求当y=﹣a时,代数式my3+ny+1的值.【分析】(1)把x=3代入方程即可得到关于a的方程,求得a的值;(2)把a的值代入方程,然后解方程求解;(3)把y=a代入my3+ny+1得到m和n的式子,然后把y=﹣a代入my3+ny+1,利用前边的式子即可代入求解.【解答】解:(1)把x=3代入3a+2x=15得3a+6=15,解得:a=3;(2)把a=3代入方程得:9﹣2x=15,解得:x=﹣3;(3)把y=a代入my3+ny+1得27m+3n+1=5,则27m+3n=4,当y=﹣a时,my3+ny+1=﹣27m﹣3n+1=﹣(27m+3n)+1=﹣4+1=﹣3.【点评】本题考查了方程的解的定义,以及代数式的求值,正确理解方程的解的定义,方程的解就是能使方程左右两边相等的未知数的值,是关键.【变式4-6】(2022秋•大余县期末)聪聪在对方程r33−B−16=5−2①去分母时,错误地得到了方程:2(x+3)﹣mx﹣1=3(5﹣x)②,因而求得的解是=52.(1)求m的值;(2)求原方程的解.【分析】(1)将x=52代入方程②,整理即可求出m的值,(2)将m的值代入方程①即可求出正确的解.【解答】(1)把x=52代入2(x+3)﹣mx﹣1=3(5﹣x)中,得:2×(52+3)−52m﹣1=3×(5−52),解得:m=1.(2)当m=1时原方程为r33−K16=5−2,2(x+3)﹣(x﹣1)=3(5﹣x),4x=8,x=2.【点评】此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.【例题5】(2022秋•兴隆县期末)方程mx+2x﹣12=0是关于x的一元一次方程,若此方程的解为正整数,则正整数m的值有几个?()A.2个B.3个C.4个D.5个【分析】根据方程的解是正整数,可得(m+2)是12的约数,根据12的约数,可得关于m的方程,根据解方程,可得答案.【解答】解:由mx+2x﹣12=0,得=12r2,∵方程mx+2x﹣12=0是关于x的一元一次方程,此方程的解为正整数,m是正整数,∴m+2=3或4或6或12,解得m=1或2或4或10,∴正整数m的值有4个.故选:C.【点评】本题考查了一元一次方程的解,正确理解m+2=3或4或6或12是关键.【变式5-1】已知关于x的方程kx=5﹣x,有正整数解,则整数k的值为.【分析】根据方程的解是正整数,可得5的约数.【解答】解:由kx=5﹣x,得x=5r1.由关于x的方程kx=5﹣x,有正整数解,得5是(k+1)的倍数,得k+1=1或k+1=5.解得k=0或k=4,故答案为:0或4.【点评】本题考查了一元一次方程的解,利用方程的解是正整数得出关于k的方程是解题关键.【变式5-2】已知关于x的一元一次方程mx﹣1=2(x+32)的解是正整数,则整数m的值为.【分析】根据方程的解是正整数,可得4的约数,根据4的约数,可得关于m的方程,根据解方程,可得答案.【解答】解:由mx﹣1=2(x+32),得x=4K2,因为关于x的方程mx﹣1=2(x+32)的解是正整数,得m﹣2=1,m﹣2=2,或m﹣2=4.解得m=3,m=4,或m=6.故答案为:3或4或6.【点评】本题考查了一元一次方程的解,利用方程的解是正整数得出关于m的方程是解题关键.【变式5-3】(2022秋•九龙坡区校级期末)若关于x的方程−2−B6=r13的解是整数解,m是整数,则所有m的值加起来为()A.﹣5B.﹣16C.﹣24D.18【分析】根据解一元一次方程的一般步骤表示出x的代数式,分析解答即可.【解答】解:解方程−2−B6=r13,得:=44+,根据题意可知=44+为整数,m是整数,当m的值为0,﹣2,﹣3,﹣5,﹣6,﹣8时,44+为整数,∴0+(﹣2)+(﹣3)+(﹣5)+(﹣6)+(﹣8)=﹣24,故选:C.【点评】本题考查了根据一元一次方程解的情况求参数,熟练掌握解一元一次方程的一半步骤是解本题的关键.【变式5-4】(2022秋•邗江区校级期末)若关于x的方程2ax=(a+1)x+6的解为正整数,求整数a的值.【分析】首先解方程表示出x的值,然后根据解为正整数求解即可.【解答】解:2ax=(a+1)x+6,移项得:2ax﹣(a+1)x=6,合并同类项得:(a﹣1)x=6,系数化为1得:=6K1,∵关于x的方程2ax=(a+1)x+6的解为正整数,∴=6K1为正整数,∴a﹣1=1或a﹣1=2或a﹣1=3或a﹣1=6∴a=2或a=3或a=4或a=7.【点评】本题主要考查方程的解和解一元一次方程,解题的关键是掌握解一元一次方程的基本步骤:去分母、去括号、移项、合并同类项、系数化为1.【变式5-5】设m为整数,且关于x的一元一次方程(m﹣5)x+m﹣3=0.(1)当m=2时,求方程的解;(2)若该方程有整数解,求m的值.【分析】(1)把m=2代入原方程,得到关于x得一元一次方程,解之即可,(2)根据“m≠5,该方程有整数解,且m是整数”,结合一元一次方程的解题步骤,得到关于m的几个一元一次方程,解之即可.【解答】解:(1)当m=2时,原方程为﹣3x﹣1=0,解得,=−13,(2)当m≠5时,方程有解,=3−K5=−1−2K5,∵方程有整数解,且m是整数,∴m﹣5=±1,m﹣5=±2,解得,m=6或m=4或m=7或m=3.【点评】本题考查了一元一次方程的解和一元一次方程的定义,解题的关键:(1)正确掌握一元一次方程的解题步骤,(2)正确掌握一元一次方程的定义和一元一次方程的解题步骤.。
解一元一次方程习题精选附答案

解一元一次方程一.解答题(共30小题)1.解方程:2x+1=72.3.(1)解方程:4﹣x=3(2﹣x);(2)解方程:.4.解方程:.5.解方程(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);(2)x﹣=2﹣.6.(1)解方程:3(x﹣1)=2x+3;(2)解方程:=x﹣.7.﹣(1﹣2x)=(3x+1)8.解方程:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+1;(2).9.解方程:.10.解方程:(1)4x﹣3(4﹣x)=2;(2)(x﹣1)=2﹣(x+2).11.计算:(1)计算:(2)解方程:12.解方程:13.解方程:(1)(2)14.解方程:(1)5(2x+1)﹣2(2x﹣3)=6 (2)+215.(A类)解方程:5x﹣2=7x+8;(B 类)解方程:(x﹣1)﹣(x+5)=﹣;(C 类)解方程:.16.解方程(1)3(x+6)=9﹣5(1﹣2x)(2)(3)(4)17.解方程:(1)解方程:4x﹣3(5﹣x)=13(2)解方程:x ﹣﹣318.(1)计算:﹣42×+|﹣2|3×(﹣)3(2)计算:﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2] (3)解方程:4x﹣3(5﹣x)=2;(4)解方程:.19.(1)计算:(1﹣2﹣4)×;(2)计算:÷;(3)解方程:3x+3=2x+7;(4)解方程:20.解方程(1)﹣0.2(x﹣5)=1;(2).21.解方程:(x+3)﹣2(x﹣1)=9﹣3x.22.8x﹣3=9+5x.5x+2(3x﹣7)=9﹣4(2+x).23.解下列方程:(1)0.5x﹣0.7=5.2﹣1.3(x﹣1);(2)=﹣2.24.解方程:(1)﹣0.5+3x=10;(2)3x+8=2x+6;(3)2x+3(x+1)=5﹣4(x﹣1);(4).25.解方程:.26.解方程:(1)10x﹣12=5x+15;(2)27.解方程:(1)8y﹣3(3y+2)=7(2).28.当k 为什么数时,式子比的值少3.29.解下列方程:(I )12y ﹣2.5y=7.5y+5 (II ).30.解方程:.专题训练(七) 一元一次方程的解法1.解下列方程: (1)3x -5=2x ;(2)56-8x =11+x ;(3)32x =12x +13;(4)0.5y -0.7=6.5-1.3y.2.解下列方程:(1)4x -3(20-2x)=10;(2)2(x -3)+5(2x +1)=11;(3)3(2x +5)=2(4x +3)-3;(4)4y -3(20-y)=6y -7(9-y).3.解下列方程: (1)x -22=4x +15;(2)107x -17-20x 3=1;(3)2x -13-2x -34=1;(4)2(x +3)5=32x -2(x -7)3.4.解下列方程: (1)0.1-2x 0.3=1+x 0.15;(2)2x 0.3-1.6-3x 0.6=31x +83.5.解下列方程: (1)119x +27=29x -57;(2)278(x -3)-463(6-2x)-888(7x -21)=0;(3)32[23(x4-1)-2]-x =2;(4)x -13[x -13(x -9)]=19(x -9).1.解下列方程: ⑴ 8723-=+x x⑵623521-=+x x⑶ x x x 7)25(34=--⑷ 12)1(3=-x⑸ 4)20(34-=--x x⑹ x x 57)53(212-=-- ⑺ )2(512)1(21+-=-x x ⑻352)63(61-=-x x ⑼ 314125=-x x ⑽52221+-=-y y ⑾ 321513223=-⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-x x⑿343883x x =⎪⎭⎫ ⎝⎛+⒀ x x x 432132342=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--⒁165.032.04=--+x x6.2.4解一元一次方程(三)参考答案与试题解析一.解答题(共30小题)1.(2005•宁德)解方程:2x+1=7考点:解一元一次方程.专题:计算题;压轴题.分析:此题直接通过移项,合并同类项,系数化为1可求解.解答:解:原方程可化为:2x=7﹣1 合并得:2x=6系数化为1得:x=3点评:解一元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.2.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:左右同乘12可得:3[2x﹣(x﹣1)]=8(x﹣1),化简可得:3x+3=8x﹣8,移项可得:5x=11,解可得x=.故原方程的解为x=.点评:若是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.3.(1)解方程:4﹣x=3(2﹣x);(2)解方程:.分析:(1)先去括号,然后再移项、合并同类型,最后化系数为1,得出方程的解;(2)题的方程中含有分数系数,应先对各式进行化简、整理,然后再按(1)的步骤求解.解答:解:(1)去括号得:4﹣x=6﹣3x,移项得:﹣x+3x=6﹣4,合并得:2x=2,系数化为1得:x=1.(2)去分母得:5(x﹣1)﹣2(x+1)=2,去括号得:5x﹣5﹣2x﹣2=2,移项得:5x﹣2x=2+5+2,合并得:3x=9,系数化1得:x=3.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.4.解方程:.考点:解一元一次方程.专题:计算题.分析:此题两边都含有分数,分母不相同,如果直接通分,有一定的难度,但将方程左右同时乘以公分母6,难度就会降低.解答:解:去分母得:3(2﹣x)﹣18=2x﹣(2x+3),去括号得:6﹣3x﹣18=﹣3,移项合并得:﹣3x=9,∴x=﹣3.点评:本题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.5.解方程(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);(2)x﹣=2﹣.考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项、合并同类项、化系数为1,从而得到方程的解;(2)先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣4﹣60+3x=5x﹣10(2分)移项得:4x+3x﹣5x=4+60﹣10(3分)合并得:2x=54(5分)系数化为1得:x=27;(6分)(2)去分母得:6x﹣3(x﹣1)=12﹣2(x+2)(2分)合并得:5x=5(5分)系数化为1得:x=1.(6分)点评:去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.去括号时要注意符号的变化.6.(1)解方程:3(x﹣1)=2x+3;(2)解方程:=x﹣.考点:解一元一次方程.专题:计算题.分析:(1)是简单的一元一次方程,通过移项,系数化为1即可得到;(2)是较为复杂的去分母,本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)3x﹣3=2x+33x﹣2x=3+3x=6;(2)方程两边都乘以6得:x+3=6x﹣3(x﹣1)x+3=6x﹣3x+3x﹣6x+3x=3﹣3﹣2x=0∴x=0.点评:本题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进行,从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.7.﹣(1﹣2x)=(3x+1)考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:﹣7(1﹣2x)=3×2(3x+1)﹣7+14x=18x+6﹣4x=13x=﹣.点评:解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1.此题去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.8.解方程:(2).考点:解一元一次方程.专题:计算题.分析:(1)可采用去括号,移项,合并同类项,系数化1的方式进行;(2)本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.解答:解:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+13x﹣7=4x﹣2∴x=﹣5;(2)原方程可化为:去分母得:40x+60=5(18﹣18x)﹣3(15﹣30x),去括号得:40x+60=90﹣90x﹣45+90x,移项、合并得:40x=﹣15,系数化为1得:x=.点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果;(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.9.解方程:.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:,去分母得:2x﹣(3x+1)=6﹣3(x﹣1),3x+3,移项、合并同类项得:2x=10,系数化为1得:x=5.点评:去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.10.解方程:(1)4x﹣3(4﹣x)=2;(2)(x﹣1)=2﹣(x+2).考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,合并同类项,系数化1,即可求出方程的解;(2)先去分母,再去括号,移项,合并同类项,系数化1可求出方程的解.解答:解:(1)4x﹣3(4﹣x)=2去括号,得4x﹣12+3x=2移项,合并同类项7x=14系数化1,得x=2.=2﹣(x+2)去分母,得5(x﹣1)=20﹣2(x+2)去括号,得5x﹣5=20﹣2x﹣4移项、合并同类项,得7x=21系数化1,得x=3.点评:(1)此题主要是去括号,移项,合并同类项,系数化1.(2)方程两边每一项都要乘各分母的最小公倍数,方程两边每一项都要乘各分母的最小公倍数,切勿漏乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母时,应该将分子用括号括上.11.计算:(1)计算:(2)解方程:考点:解一元一次方程;有理数算:先算乘方、后算乘除、再算加减;(2)两边同时乘以最简公分母4,即可去掉分母.解答:解:(1)原式=,=,=.(2)去分母得:2(x﹣1)﹣(3x﹣1)=﹣4,解得:x=3.点评:解答此题要注意:(1)去分母时最好先去中括号、再去小括号,以减少去括号带来的符号变化次数;(2)去分母就是方程两边同时乘以分母的最简公分母.12.解方程:考点:解一元一次先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.(2)解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.解答:解:(1)去分母得:3(3x﹣1)+18=1﹣5x,去括号得:9x﹣3+18=1﹣5x,移项、合并得:14x=﹣14,系数化为1得:x=﹣1;(2)去括号得:x﹣x+1=x,移项、合并同类项得:x=﹣1,系数化为1得:x=﹣.点评:本题考查解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时“1”也13.解方程:(1)(2)考点:解一元一次方程.专题:计算题.分析:(1)去分母、去括号、移项、合并同类项、化系数为1.(2)去分母、去括号、移项、合并同类项、化系数为1.解答:(1)解:去分母得:5(3x+1)﹣2×10=3x﹣2﹣2(2x+3),去括号得:15x+5﹣20=3x﹣2﹣4x﹣6,移项得:15x+x=﹣8+15,合并得:16x=7,解得:;(2)解:,4(x﹣1)﹣18(x+1)=﹣36,4x﹣4﹣18x﹣18=﹣36,﹣14x=﹣14,x=1.程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时“1”也要乘以最小公倍数.14.解方程:(1)5(2x+1)﹣2(2x﹣3)=6 (2)+2(3)[3(x﹣)+]=5x﹣1考点:解一元一次方程.专题:计算题.分析:(2)通过去括号、移项、合并同类项、系数化为1,解得x的值;(3)乘最小公倍数去分母即可;(4)主要是去括号,也可以把分数转化成整数进行计算.解答:解:(1)去括号得:10x+5﹣4x+6=6移项、合并得:6x=﹣5,方程两边都除以6,得x=﹣;(2)去分母得:3(x﹣2)=2(4﹣3x)+24,去括号得:3x﹣6=8﹣6x+24,除以9,得x=;(3)整理得:[3(x﹣)+]=5x﹣1,4x﹣2+1=5x﹣1,移项、合并得:x=0.点评:一元一次方程的解法:一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.解题时,要灵活运用这些步骤.15.(A类)解方程:5x﹣2=7x+8;(B类)解方程:(x﹣1)﹣(x+5)=﹣;(C类)解方程:.考点:解一元一次方程.专题:计算题.分析:通过去分母、去括号、移项、系数化为1等方法,求得各方程的解.解答:解:A类:5x﹣2=7x+8移项:5x﹣7x=8+2B类:(x﹣1)﹣(x+5)=﹣去括号:x﹣﹣x﹣5=﹣化简:x=5即:x=﹣;C类:﹣=1去分母:3(4﹣x)﹣2(2x+1)=6去括号:12﹣3x﹣4x﹣2=6化简:﹣7x=﹣4即:x=.点评:本题主要考查一元一次方程的解法,比较简单,但要细心运算.16.解方程(1)3(x+6)=9﹣5(1﹣2x)(2)(3)(4)考解一元一次方程.点:专计算题.析:(2)(3)首先去掉分母,再去括号以后,移项,合并同类项,系数化为1以后即可求解;(4)首先根据分数的基本性质,把第一项分母中的0.3化为整数,再去分母,求解.解答:解:(1)去括号得:3x+18=9﹣5+10x移项得:3x﹣10x=9﹣5﹣18合并同类项得:﹣7x=﹣14则x=2;(2)去分母得:2x+1=x+3﹣5移项,合并同类项得:x=﹣3;(3)去分母得:10y+2(y+2)=20﹣5(y﹣1)去括号得:10y+2y+4=20﹣5y+5移项,合并同类项得:17y=21系数化为1得:;(4)原方程可以变形为:﹣5x=﹣1去分母得:17+20x﹣15x=﹣3移项,合并同类项得:5x=﹣20系数化为1得:x=﹣4.点评:解方程的过程中要注意每步的依据,这几个题目都是基础的题目,需要熟练掌握.17.解方程:(1)解方程:4x﹣3(5﹣x)=13(2)解方程:x﹣﹣3考点:解一元一次方程.专题:计算题.分析:(1)先去括号,再移项,化系数为1,从而得到方程的解.(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:(1)去括号得:4x﹣15+3x=13,移项合并得:7x=28,系数化为1得:得x=4;形为x+3=,去分母得:5(2x﹣5)+3(x﹣2)=15(x+3),去括号得10x﹣25+3x﹣6=15x+45,移项合并得﹣2x=76,系数化为1得:x=﹣38.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.18.(1)计算:﹣42×+|﹣2|3×(﹣)3(2)计算:﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2] (3)解方程:4x﹣3(5﹣x)=2;(4)解方程:.考点:解一元一次方程;有理数的混合运算.分析:(1)利用平方和立方的定义进行计算.(2)按四则混合运算的顺序进行计算.去括号,移项合并.(4)两边同乘最小公倍数去分母,再求值.解答:解:(1)﹣42×+|﹣2|3×(﹣)3==﹣1﹣1=﹣2.(2)﹣12﹣|0.5﹣|÷×[﹣2﹣(﹣3)2]====.(3)解方程:4x﹣3(5﹣x)=2去括号,得4x﹣15+3x)=2移项,得4x+3x=2+15合并同类项,得7x=17系数化为1,得.(4)解方程:去分母,得15x﹣3(x﹣2)=5(2x﹣5)﹣3×15去括号,得15x﹣3x+6=10x﹣25﹣45移项,得15x﹣3x﹣10x=﹣25﹣45﹣6合并同类项,得2x=﹣76系数化为1,得x=﹣38.点评:前两道题考查了学生有理数的混合运算,后两道考查了学生解一元一次方程的能力.19.(1)计算:(1﹣2﹣4)×;(2)计算:÷;(3)解方程:3x+3=2x+7;(4)解方程:.考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:(1)和(2)要熟练掌握有理数的混合运算;(3)和(4)首先熟悉解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1.解答:解:(1)(1﹣2﹣4)×=﹣=﹣13;(2)原式=﹣1×(﹣4﹣2)×(﹣)=6×(﹣)=﹣9;(3)解方程:3x+3=2x+7移项,得3x﹣2x=7﹣3合并同类项,得x=4;(4)解方程:去分母,得6(x+15)=15﹣10(x﹣7)去括号,得6x+90=15﹣10x+70移项,得6x+10x=15+70﹣90合并同类项,得16x=﹣5系数化为1,得x=.点评:(1)和(2)要注意符号的处理;(4)要特别注意去分母的时候不要发生数字漏乘的现象,熟练掌握去括号法则以及合并同类项法则.20.解方程(1)﹣0.2(x﹣5)=1;(2).考点:解一元一次方程.分析:(1)通过去括号、移项、系数化为1等过程,求得x的值;(2)通过去分母以及去括号、移项、系数化为1等过程,求得x的值.解答:解:(1)﹣0.2(x﹣5)=1;去括号得:﹣0.2x+1=1,∴﹣0.2x=0,∴x=0;(2).去分母得:2(x﹣2)+6x=9(3x+5)﹣(1﹣2x),∴﹣21x=48,∴x=﹣.点评:此题主要考查了一元一次方程解法,解一元一次方程常见的过程有去括号、移项、系数化为1等.21.解方程:(x+3)﹣2(x﹣1)=9﹣3x.考点:解一元一次方程.专题:计算题.分析:先去括号得﹣3x,然后移项、合并同类得到2x=4,然后把x的系数化为1即可.解答:解:去括号得x+3﹣2x+2=9﹣3x,移项得x﹣2x+3x=9﹣3﹣2,合并得2x=4,系数化为1得x=2.点评:本题考查了解一元一次方程:先去分母,再去括号,接着移项,把含未知数的项移到方程左边,不含未知数的项移到方程右边,然后合并同类项,最后把未知数的系数化为1得到原方程的解.22.8x﹣3=9+5x.5x+2(3x﹣7)=9﹣4(2+x)...考点:解一元一次方程.专题:方程思想.分析:本题是解4个不同的一元一次方程,第一个通过移项、合并同类项及系数化1求解.第二个通过移项、合并同类项及系数化1求解.第三个先去分母再同第二个.第四个先分子分母乘以10,再同第三个求解.解答:8x﹣3=9+5x,解:8x﹣5x=9+3,3x=12,∴x=4.∴x=4是原方程的解;5x+2(3x﹣7)=9﹣4(2+x),解:5x+6x﹣14=9﹣8﹣4x,5x+6x+4x=9﹣8+14,15x=15,∴x=1.∴x=1是原方程的解..解:3(x﹣1)﹣2(2x+1)=12,3x﹣3﹣4x﹣2=12,3x﹣4x=12+3+2,﹣x=17,∴x=﹣17.∴x=﹣17是原方程的解.,解:,5(10x﹣3)=4(10x+1)+40,50x﹣15=40x+4+40,50x﹣40x=4+40+15,10x=59,∴x=.∴x=是原方程的解.点评:此题考查的知识点是解一元一次方程,关键是注意解方程时的每一步都要认真仔细,如移项时要变符号.23.解下列方程:(1)0.5x﹣0.7=5.2﹣1.3(x﹣1);(2)=﹣2.考点:解一元一次方程.分析:(1)首先去括号,然后移项、合并同类项,系数化成1,即可求解;(2)首先去分母,然后去括号,移项、合并同类项,系数化成1,即可求解解答:解:(1)去括号,得:0.5x ﹣0.7=5.2﹣1.3x+1.3移项,得:0.5x+1.3x=5.2+1.3+0.7合并同类项,得:1.8x=7.2,则x=4;(2)去分母得:7(1﹣2x)=3(3x+1)﹣42,去括号,得:7﹣14x=9x+3﹣42,移项,得:﹣14x﹣9x=3﹣42﹣7,合并同类项,得:﹣23x=﹣46,则x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.24.解方程:(1)﹣0.5+3x=10;(2)3x+8=2x+6;(3)2x+3(x+1)=5﹣4(x﹣1);(4).考点:解一元一次方程.分析:(1)移项,合并同类项,然后系数化成1即可求解;(2)移项,合并同类项,然后系数化成1即可求解;(3)去括号、移项,合并同类项,然后系数化成1即可求解;(4)首先去分母,然后去括号、移项,合并同类项,然后系数化成1即可求解.解答:解:(1)3x=10.5,x=3.5;(2)3x﹣2x=6﹣8,x=﹣2;(3)2x+3x+3=5﹣4x+4,2x+3x+4x=5+4﹣3,9x=6,x=;(4)2(x+1)+6=3(3x﹣2),2x+2+6=9x﹣6,2x﹣9x=﹣6﹣2﹣6,﹣7x=﹣14,x=2.点评:本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.25.解方程:.考点:解一元一次方程.专题:计算题.分析:方程两边乘以10去分母后,去括号,移项合并,将x系数化为1,即可求出解.解答:解:去分母得:5(3x﹣1)﹣2(5x﹣6)=2,去括号得:15x﹣5﹣10x+12=2,移项合并得:5x=﹣5,解得:x=﹣1.点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.26.解方程:(1)10x﹣12=5x+15;(2)考点:解一元一次方程.专题:计算题.分析:(1)先移项,再合并同类项,最后化系数为1,从而得到方程的解;(2)先去括号,再移项、合并同类项,最后化系数为1,从而得到方程的解.解答:解:(1)移项,得10x﹣5x=12+15,合并同类项,得5x=27,方程的两边同时除以5,得x=;(2)去括号,得=,方程的两边同时乘以6,得x+1=4x﹣2,移项、合并同类项,得3x=3,方程的两边同时除以3,得x=1.点评:本题考查解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.27.解方程:(1)8y﹣3(3y+2)=7(2).考点:解一元一次方程.专题:计算题.分析:(1)根据一元一次方程的解法,去括号,移项,合并同类项,系数化为1即可得解;(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(1)去括号得,8y﹣9y﹣6=7,移项、合并得,﹣y=13,系数化为1得,y=﹣13;(2)去分母得,3(3x﹣1)﹣12=2(5x﹣7),去括号得,9x﹣3﹣12=10x﹣14,移项得,9x﹣10x=﹣14+3+12,合并同类项得,﹣x=1,系数化为1得,x=﹣1.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.28.当k 为什么数时,式子比的值少3.考点:解一元一次方程.专题:计算题.分析:先根据题意列出方程,再根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.解答:解:依题意,得=+3,去分母得,5(2k+1)=3(17﹣k)+45,去括号得,10k+5=51﹣3k+45,移项得,10k+3k=51+45﹣5,合并同类项得,13k=91,系数化为1得,k=7,∴当k=7时,式子比的值少3.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.29.解下列方程:(I)12y﹣2.5y=7.5y+5(II ).考点:解一元一次方程.专题:计算题.分析:(Ⅰ)根据一元一次方程的解法,移项,合并同类项,系数化为1即可得解;(Ⅱ)是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:(Ⅰ)移项得,12y﹣2.5y﹣7.5y=5,合并同类项得,2y=5,系数化为1得,y=2.5;(Ⅱ)去分母得,5(x+1)﹣10=(3x﹣2)﹣2(2x+3),去括号得,5x+5﹣10=3x﹣2﹣4x﹣6,移项得,5x﹣3x+4x=﹣2﹣6﹣5+10,合并同类项得,6x=﹣3,系数化为1得,x=﹣.点评:本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.30.解方程:.考点:解一元一次方程.专题:计算题.分析:由于方程的分子、分母均有小数,利用分数的基本性质,分子、分母同时扩大相同的倍数,可将小数化成整数.解答:解:原方程变形为,(3分)去分母,得3×(30x﹣11)﹣4×(40x﹣2)=2×(16﹣70x),(4分)去括号,得90x﹣33﹣160x+8=32﹣140x,(5分)移项,得90x﹣160x+140x=32+33﹣8,(6分)合并同类项,得70x=57,(7分)系数化为1,得.(8分)点评:本题考查一元一次方程的解法.解一元一次方程的一般步骤:去分母,去括号,移项,合并同类项,系数化为1.本题的难点在于方程的分子、分母均有小数,将小数化成整数不同于去分母,不是方程两边同乘一个数,而是将分子、分母同乘一个数.参考答案1.(1)3x-2x=5,x=5. (2)-8x-x=11-56,-9x =-45,x=5. (3)32x-12x=13,x=13. (4) 0.5y+1.3y =0.7+6.5,1.8y=7.2,y=4.2.(1)4x-60+6x=10,4x+6x=60+10,10x=70,x =7. (2)2x-6+10x+5=11,12x=12,x=1. (3)6x +15=8x+6-3,6x-8x=-15+6-3,-2x=-12,x=6. (4)4y-60+3y=6y-63+7y,3y+4y-6y-7y =60-63,-6y=-3,y=12.3.(1)5(x-2)=2(4x+1),5x-10=8x+2,5x-8x=10+2,-3x=12,x=-4. (2)30x-7(17-20x)=21,30x-119+140x=21,30x+140x=119+21,170x=140,x=1417. (3)4(2x-1)-3(2x-3)=12,8x-4-6x+9=12,8x-6x=4-9+12,2x=7,x=72. (4)12(x +3)=45x-20(x-7),12x+36=45x-20x+140,12x -45x+20x=-36+140,-13x=104,x=-8.4.(1)解法一:原方程整理,得1-20x3=1+100x15.去分母,得5(1-20x)=15+100x.去括号,得5-100x=15+100x.移项,得-100x-100x=15-5.合并同类项,得-200x=10.系数化为1,得x=-0.05.解法二:去分母,得0.15(0.1-2x)=0.045+0.3x.去括号,得0.015-0.3x=0.045+0.3x.移项,得-0.3x-0.3x=0.045-0.015.合并同类项,得-0.6x=0.03.系数化为1,得x=-0.05. (2)20x3-16-30x6=31x+83,40x-(16-30x)=2(31x+8),40x-16+30x=62x+16,40x +30x-62x=16+16,8x=32,x=4.5.(1)119x-29x=-57-27,x=-1. (2)278(x-3)+463×2(x-3)-888×7(x-3)=0,(278+463×2-888×7)(x-3)=0,x=3. (3)x4-1-3-x=2,x=-8. (4)x-13x+19(x-9)=19(x-9),23x=0,x=0.WelcomeTo Download !!!欢迎您的下载,资料仅供参考!。
解一元一次方程专项练习60题+解析答案

解一元一次方程-红老师一.解答题(共60小题)1.解方程:.2.解方程:.3.解方程:.4.解方程:.5.解方程:.6.解方程:(1)2﹣=x﹣;(2).7.解方程:.8.解方程:﹣1=.9.解方程:.10.解方程:.11.解方程:.12.解方程.13.解方程:.14.解方程:.15.解方程:.16.解方程:﹣=1.17.解方程:=1.18.解方程:=1﹣.19.解方程:﹣2=.20.解方程:.21.解方程:.22.解关于x的一元一次方程.23.解方程:.24.解方程:.25.解方程:.26.解方程:y﹣=2﹣27.解方程:.28.解方程:.29.解方程:3x+.30.解方程:.31.解方程:.32.解方程:.33.解方程:.34.解方程:.35.解方程:.36.解方程:.37.解方程:﹣=1.38.解方程:.39.解方程:.40.解方程:.41.解方程:.42.解方程:﹣1=.43.解方程:=1﹣.44.解方程:.45.解方程:.46.解方程.47.解方程:(1)3(5﹣x)=18+2x;(2);(3).48.解方程:(1);(2).49.解方程:(1)2(x﹣4)﹣3(4x﹣1)=5(1﹣x);(2);(3).50.解下列方程(1)(2)51.解方程(1)x=﹣1;(2)﹣=1.52.解方程:(1)3x﹣7(x﹣1)=3﹣2(x+3);(2);(3).53.解方程:(1)3x+=3﹣;(2)+2=.54.解方程(1)4x+3(x﹣20)=8x﹣7(20﹣x)(2)﹣=1.55.解方程:﹣=.56.若3x+1的值比的值少1,求x的值.57.k取何值时,代数式值比的值小1.58.当x为何值时,代数式的值与的值的和等于3?59.已知代数式与代数式.(1)当x为何值时,两个代数式的值相等?(2)当x为何值时,代数式的值比代数式的值大2?60.我们规定一种运算:=ad﹣bc,例如=3×6﹣4×5=﹣2,=4x+6,按照这种运算规定,当x等于多少时,=0.解一元一次方程-红老师参考答案与试题解析一.解答题(共60小题)1.解方程:.【解答】解:去分母得:6﹣2(3﹣5x)=3(3x+1),去括号得:6﹣6+10x=9x+3,移项合并得:x=3.2.解方程:.【解答】解:去分母得:5(3x+1)=2(4x+2),去括号得:15x+5=8x+4,移项得:15x﹣8x=4﹣5,合并同类项得:7x=﹣1,解得:x=﹣.3.解方程:.【解答】解:,去分母,3(2x﹣1)=60﹣5(x﹣5),去括号,6x﹣3=60﹣5x+25,移项,6x+5x=60+3+25,合并同类项,11x=88,化系数为1,x=8.4.解方程:.【解答】解:去分母,得3(x﹣2)=12﹣4x,去括号,得3x﹣6=12﹣4x,移项、合并同类项,得7x=18,系数化为1,得.5.解方程:.【解答】解:去分母得:10x﹣5(x﹣1)=20﹣2(x+18),去括号得:10x﹣5x+5=20﹣2x﹣36,移项合并得:7x=﹣21,解得:x=﹣3.6.解方程:(1)2﹣=x﹣;(2).【解答】解:(1)去分母得:12﹣(x+5)=6x﹣2(x﹣1),去括号得:12﹣x﹣5=6x﹣2x+2,移项得:﹣x﹣6x+2x=2﹣12+5,合并得:﹣5x=﹣5,系数化为1得:x=1;(2)方程整理得:﹣2=,即2x﹣2=5x ﹣2,移项得:2x﹣5x=﹣2+2,合并得:﹣3x=0,系数化为1得:x=0.7.解方程:.【解答】解:去分母,得2(3x﹣2)﹣6=5﹣4x,去括号,得6x﹣4﹣6=5﹣4x,移项,合并同类项,得10x=15,系数化为1,得x=1.5.8.解方程:﹣1=.【解答】解:﹣1=3(x+1)﹣6=2(x﹣2)3x+3﹣6=2x﹣43x﹣2x=﹣1x=﹣1.9.解方程:.【解答】解:去分母得:6x﹣3=12﹣4x﹣8,移项合并得:10x=7,解得:x=0.7.10.解方程:.【解答】解:去分母得:4x﹣10=5﹣2x,移项得:4x+2x=5+10,合并同类项得:6x=15,系数化为1得:x=.11.解方程:.【解答】解:,去分母,得3(x﹣1)+12=4(2x+1),去括号,得3x﹣3+12=8x+4,移项,得3x﹣8x=4+3﹣12,合并同类项,得﹣5x=﹣5,系数化成1,得x=1.12.解方程.【解答】解:去分母得:3(3y﹣1)﹣12=2(5y﹣7),去括号得:9y﹣3﹣12=10y﹣14,移项得:9y﹣10y=﹣14+3+12,合并得:﹣y=1,解得:y=﹣1.13.解方程:.【解答】解:去分母,得3(4x﹣3)﹣15=5(2x﹣2),去括号,得12x﹣9﹣15=10x﹣10,移项,得12x﹣10x=﹣10+9+15,合并同类项,得2x=14,系数化为1,得x=7.14.解方程:.【解答】解:原方程去分母,得:2(3x+2)﹣4=2x ﹣1,去括号,得:6x+4﹣4=2x﹣1,移项,合并同类项,得:4x=﹣1,系数化为1,得:.15.解方程:.【解答】解:4﹣(3x﹣1)=2(3+x),去分母,得4﹣3x+1=6+2x,移项,得﹣3x﹣2x=6﹣4﹣1,合并同类项,得﹣5x=1,系数化1,得x=﹣.16.解方程:﹣=1.【解答】解:方程两边同乘以12得:12×﹣12×=12,则3(x+2)﹣2(2x﹣3)=12,故3x+6﹣4x+6=12,移项合并同类项得:﹣x=0,解得:x=0.17.解方程:=1.【解答】解:,去分母,得4x﹣1=6﹣2(3x﹣1),去括号,得4x﹣1=6﹣6x+2,移项,得4x+6x=6+2+1,合并,得10x=9,系数化为1,得.18.解方程:=1﹣.【解答】解:去分母得:3(x﹣1)=6﹣2(x﹣3),去括号得:3x﹣3=6﹣2x+6,移项得:3x+2x=6+6+3,合并同类项得:5x=15,系数化1得:x=3.19.解方程:﹣2=.【解答】解:去分母:2(x+1)﹣8=x,去括号:2x+2﹣8=x,移项:2x﹣x=8﹣2,合并同类项:x=6.20.解方程:.【解答】解:方程两边同乘以12得:12×﹣12×=12,则3(x+2)﹣2(2x﹣5)=12,故3x+6﹣4x+10=12,移项合并同类项得:﹣x=﹣4,解得:x=4.21.解方程:.【解答】解:,去分母,得2x﹣1﹣6=3(2x+3),去括号,得2x﹣1﹣6=6x+9,移项,得2x﹣6x=9+1+6,合并同类项,得﹣4x=16,系数化为1,得x=﹣4.22.解关于x的一元一次方程.【解答】解:去分母得:3(4x﹣3)﹣15=5(2x﹣2),去括号得:12x﹣9﹣15=10x﹣10,移项得:12x﹣10x=24﹣10,合并同类项得:2x=14,解得:x=7.23.解方程:.【解答】解:,去分母,得2(2x﹣1)+3(x+1)=4,去括号,得4x﹣2+3x+3=4,移项、合并同类项,得7x=3,系数化为1,得.24.解方程:.【解答】解:,去分母得,3(x+2)﹣(4x+3)=6,去括号得,3x+6﹣4x﹣3=6,移项得,3x﹣4x=6﹣6+3,合并同类项得,﹣x=3,系数化为1得,x=﹣3.25.解方程:.【解答】解:去分母得:6x﹣(3x﹣3)=2x+4+6,去括号得:6x﹣3x+3=2x+4+6,移项合并得:x=7.26.解方程:y﹣=2﹣【解答】解:10y﹣5(y﹣1)=20﹣2(y+3),10y﹣5y+5=20﹣2y﹣6,10y﹣5y+2y=20﹣6﹣5,7y=9,y=.27.解方程:.【解答】解:×6﹣×6=2×6,3(x﹣1)﹣2(2﹣x)=12,3x﹣3﹣4+2x=12,5x=19,∴x=.28.解方程:.【解答】解:去分母,得5(1﹣2x)=3(3x+4)﹣15,去括号,得5﹣10x=9x+12﹣15,移项,得﹣10x﹣9x=12﹣15﹣5,合并同类项,得﹣19x=﹣8,系数化为1,得.29.解方程:3x+.【解答】解:去分母得,18x+3(x﹣1)=18﹣2(2x ﹣1),去括号得,18x+3x﹣3=18﹣4x+2,移项得,18x+3x+4x=18+2+3,合并同类项得,25x=23,系数化为1得,x=.30.解方程:.【解答】解:去分母得:3(2x+1)﹣(4x﹣1)=6,去括号得:6x+3﹣4x+1=6,移项得:6x﹣4x=6﹣3﹣1,合并得:2x=2,系数化为1得:x=1.31.解方程:.【解答】解:去分母,可得:3(x﹣3)﹣2(4x+1)=6,去括号,可得:3x﹣9﹣8x﹣2=6,移项,可得:3x﹣8x=6+9+2,合并同类项,可得:﹣5x=17,系数化为1,可得:x=﹣3.4.32.解方程:.【解答】解:去分母,方程两边同时乘以6,得:3(x+2)=12﹣2(x﹣2).去括号,得:3x+6=12﹣2x+4.移项、合并同类项,得:5x=10.未知数的系数化为1,得:x=2.33.解方程:.【解答】解:去分母,可得:3(2x﹣3)﹣12=4(x ﹣4),去括号,可得:6x﹣9﹣12=4x﹣16,移项,可得:6x﹣4x=﹣16+9+12,合并同类项,可得:2x=5,系数化为1,可得:x=2.5.34.解方程:.【解答】解:,去分母,得2(x+1)﹣3(x﹣3)=6,去括号,得2x+2﹣3x+9=6,移项,得2x﹣3x=6﹣9﹣2,合并同类项,得﹣x=﹣5,系数化为1,得x=5.35.解方程:.【解答】解:,去分母,得3(x+1)﹣6=2(3x﹣2),去括号,得3x+3﹣6=6x﹣4,移项,得3x﹣6x=﹣4﹣3+6,合并同类项,﹣3x=﹣1,系数化为1,得.36.解方程:.【解答】解:,3(3y﹣1)﹣12=4(2y+7),9y﹣3﹣12=8y+28,9y﹣8y=28+3+12y=43.37.解方程:﹣=1.【解答】解:2(x﹣3)﹣3(4x+1)=6,2x﹣6﹣12x﹣3=6,2x﹣12x=6+6+3,﹣10x=15,x=﹣.38.解方程:.【解答】解:,去分母,得4(2x+1)﹣(x﹣3)=12,去括号,得8x+4﹣x+3=12,移项,得8x﹣x=12﹣4﹣3,合并同类项,得7x=5,系数化成1,得x=.39.解方程:.【解答】解:去分母得:2x=12+3(2x﹣1),去括号得:2x=12+6x﹣3,移项得:2x﹣6x=12﹣3,合并同类项得:﹣4x=9,系数化为1得:x=﹣.40.解方程:.【解答】解:,去分母,得3(3y+2)﹣12=2(2y﹣1),去括号,得9y+6﹣12=4y﹣2,合并同类项,得9y﹣6=4y﹣2,移项,得9y﹣4y=﹣2+6,合并同类项,得5y=4,系数化为1,得.41.解方程:.【解答】解:去分母得,4(x﹣2)=12﹣3(3x﹣2),去括号得,4x﹣8=12﹣9x+6,移项得,4x+9x=12+6+8,合并同类项得,13x=26,系数化1得,x=2.42.解方程:﹣1=.【解答】解:﹣1=,5x﹣3﹣6=3x,5x﹣3x=3+6,2x=9,x=.43.解方程:=1﹣.【解答】解:方程=1﹣,去分母得:5(2x﹣1)=10﹣2(x﹣3),去括号得:10x﹣5=10﹣2x+6,移项合并得:12x=21,解得:x=.44.解方程:.【解答】解:,两边同时乘以6得:2(2x+1)﹣12=﹣x,整理得:4x﹣10=﹣x,解得x=2,45.解方程:.【解答】解:∵,∴+=3,去分母,可得:2(10x﹣20)+5(10x﹣10)=30,去括号,可得:20x﹣40+50x﹣50=30,移项,可得:20x+50x=30+40+50,合并同类项,可得:70x=120,系数化为1,可得:x=.46.解方程.【解答】解:方程整理得:﹣=1,即﹣2x+1=1,去分母得:2x﹣4﹣6x+3=3,移项得:2x﹣6x=3+4﹣3,合并同类项得:﹣4x=4,解得:x=﹣1.47.解方程:(1)3(5﹣x)=18+2x;(2);(3).【解答】解:(1)去括号得:15﹣3x=18+2x,移项得:﹣3x﹣2x=18﹣15,合并同类项得:﹣5x=3,解得:x=﹣;(2)去括号得:﹣=(x﹣4),去分母得:2﹣(2x﹣5)=x﹣4,去括号得:2﹣2x+5=x﹣4,移项得:﹣2x﹣x=﹣4﹣2﹣5,合并同类项得:﹣3x=﹣11,解得:x=;(3)方程整理得:﹣(2x+4)=1.2,去分母得:10x﹣10﹣3(2x+4)=3.6,去括号得:10x﹣10﹣6x﹣12=3.6,移项得:10x﹣6x=3.6+10+12,合并同类项得:4x=25.6,解得:x=6.4.48.解方程:(1);(2).【解答】解:(1)去分母得:3(3x﹣1)﹣12=2(5x﹣7),去括号得:9x﹣3﹣12=10x﹣14,移项得:9x﹣10x=﹣14+3+12,合并同类项得:﹣x=1,系数化为1得:x=﹣1.(2)化整得:,去分母得:3(3x﹣1)﹣2(2x+9)=﹣36,去括号得:9x﹣3﹣4x﹣18=﹣36,移项得:9x﹣4x=﹣36+3+18,合并同类项得:5x=﹣15,系数化为1得:x=﹣3.49.解方程:(1)2(x﹣4)﹣3(4x﹣1)=5(1﹣x);(2);(3).【解答】解:(1)2(x﹣4)﹣3(4x﹣1)=5(1﹣x),2x﹣8﹣12x+3=5﹣5x,2x﹣12x+5x=5+8﹣3,﹣5x=10,x=﹣2;(2),2(2x+1)﹣6=6x﹣(10x+1),4x+2﹣6=6x﹣10x﹣1,4x﹣6x+10x=﹣1﹣2+6,8x=3,x=;(3),﹣1=,15x﹣6=2(17﹣20x),15x﹣6=34﹣40x,15x+40x=34+6,55x=40,x=.50.解下列方程(1)(2)【解答】解:(1)去分母得:15x﹣10=8x+4﹣10,移项合并得:7x=4,解得:x=;(2)方程整理得:=1+,去分母得:1﹣20x=3+20x,移项合并得:40x=﹣2,解得:x=﹣.51.解方程(1)x=﹣1;(2)﹣=1.【解答】解:(1)去分母,可得:6x+2(1﹣x)=x+2﹣6,去括号,可得:6x+2﹣2x=x+2﹣6,移项,可得:6x﹣2x﹣x=2﹣6﹣2,合并同类项,可得:3x=﹣6,系数化为1,可得:x=﹣2.(2)∵﹣=1,∴﹣=1,去分母,可得:30x﹣7(17﹣20x)=21,去括号,可得:30x﹣119+140x=21,移项,可得:30x+140x=21+119,合并同类项,可得:170x=140,系数化为1,可得:x=.52.解方程:(1)3x﹣7(x﹣1)=3﹣2(x+3);(2);(3).【解答】解:(1)3x﹣7(x﹣1)=3﹣2(x+3),去括号得:3x﹣7x+7=3﹣2x﹣6,移项得:3x﹣7x+2x=3﹣6﹣7,合并同类项得:﹣2x=﹣10,系数化为1得:x=5;(2),去分母得:2(1﹣2x)﹣18x=3(x﹣1)﹣18,去括号得:2﹣4x﹣18x=3x﹣3﹣18,移项得:2+3+18=3x+4x+18x,合并同类项得:25x=23,系数化为1得:x=;(3)﹣=x,分母化为整数得:﹣=x,去分母得:3(3x﹣5)﹣2(12﹣5x)=6x,去括号得:9x﹣15﹣24+10x=6x,移项得:9x+10x﹣6x=15+24,合并同类项得:13x=39,系数化为1得:x=3.53.解方程:(1)3x+=3﹣;(2)+2=.【解答】解:(1)3x+=3﹣,去分母得:18x+3(x﹣1)=18﹣2(2x﹣1),去括号得:18x+3x﹣3=18﹣4x+2,移项得:18x+3x+4x=18+3+2,合并同类项得:25x=23,系数化为1得:x=;(2)+2=化简得,去分母得:3(3x﹣4)+12=2(5x﹣2),去括号得:9x﹣12+12=10x﹣4,移项得:9x﹣10x=﹣4,合并同类项得:﹣x=﹣4,系数化为1得:x=4.54.解方程(1)4x+3(x﹣20)=8x﹣7(20﹣x)(2)﹣=1.【解答】解:(1)去括号得:4x+3x﹣60=8x﹣140+7x,移项合并得:8x=80,解得:x=10;(2)方程整理得:﹣=1,去分母得:30y﹣119+140y=21,解得:y=.55.解方程:﹣=.【解答】解:化简得:﹣=,去分母得:9(30x﹣15)﹣2(20x﹣10)=18(4﹣8x),去括号得:270x﹣135﹣40x+20=72﹣144x,移项合并同类项得:374x=187,系数化为1得:x=0.5.56.若3x+1的值比的值少1,求x的值.【解答】解:由题意,得,去分母,得6x+2=5x+1﹣2,移项合并,得x=﹣3.57.k取何值时,代数式值比的值小1.【解答】解:由题意得:﹣=﹣1,去分母得2(k+1)﹣3(3k+1)=﹣6,去括号得2k+2﹣9k﹣3=﹣6,移项、合并同类项得:﹣7k=﹣5,系数化1得:.58.当x为何值时,代数式的值与的值的和等于3?【解答】解:根据题意得:+=3,去分母得:6﹣3x+2x+2=18,移项合并得:﹣x=10,解得:x=﹣10.59.已知代数式与代数式.(1)当x为何值时,两个代数式的值相等?(2)当x为何值时,代数式的值比代数式的值大2?【解答】解:(1)根据题意列式为:,去分母得:3x=4(2﹣x),去括号得:3x=8﹣4x,移项、合并同类项,得:7x=8,系数化为1得:.(2)根据题意列式为:,去分母得:3x﹣4(2﹣x)=24,去括号得:3x﹣8+4x=24,移项、合并同类项得:7x=32,系数化为1得:.60.我们规定一种运算:=ad﹣bc,例如=3×6﹣4×5=﹣2,=4x+6,按照这种运算规定,当x等于多少时,=0.【解答】解:∵=ad﹣bc,∴(+1)×(﹣1)=(﹣2)x,解得:x=,故当x=时,=0.。
初一七年级一元一次方程30题含答案解析

初一七年级一元一次方程30题〔含答案解析〕一.解答题〔共30小题〕1.〔2005•〕解方程:2*+1=72.3.〔1〕解方程:4﹣*=3〔2﹣*〕;〔2〕解方程:.4.解方程:.5.解方程〔1〕4〔*﹣1〕﹣3〔20﹣*〕=5〔*﹣2〕;〔2〕*﹣=2﹣.6.〔1〕解方程:3〔*﹣1〕=2*+3;〔2〕解方程:=*﹣.7.﹣〔1﹣2*〕=〔3*+1〕8.解方程:〔1〕5〔*﹣1〕﹣2〔*+1〕=3〔*﹣1〕+*+1;〔2〕.9.解方程:.10.解方程:〔1〕4*﹣3〔4﹣*〕=2;〔2〕〔*﹣1〕=2﹣〔*+2〕.11.计算:〔1〕计算:〔2〕解方程:12.解方程:13.解方程:〔1〕〔2〕14.解方程:〔1〕5〔2*+1〕﹣2〔2*﹣3〕=6 〔2〕+2〔3〕[3〔*﹣〕+]=5*﹣115.〔A类〕解方程:5*﹣2=7*+8;〔B 类〕解方程:〔*﹣1〕﹣〔*+5〕=﹣;〔C 类〕解方程:.16.解方程〔1〕3〔*+6〕=9﹣5〔1﹣2*〕〔2〕〔3〕〔4〕17.解方程:〔1〕解方程:4*﹣3〔5﹣*〕=13〔2〕解方程:*﹣﹣318.〔1〕计算:﹣42×+|﹣2|3×〔﹣〕3〔2〕计算:﹣12﹣|0.5﹣|÷×[﹣2﹣〔﹣3〕2] 〔3〕解方程:4*﹣3〔5﹣*〕=2;〔4〕解方程:.19.〔1〕计算:〔1﹣2﹣4〕×;〔2〕计算:÷;〔3〕解方程:3*+3=2*+7;〔4〕解方程:.20.解方程〔1〕﹣0.2〔*﹣5〕=1;〔2〕.21.解方程:〔*+3〕﹣2〔*﹣1〕=9﹣3*.22.8*﹣3=9+5*.5*+2〔3*﹣7〕=9﹣4〔2+*〕...23.解以下方程:〔1〕0.5*﹣0.7=5.2﹣1.3〔*﹣1〕;〔2〕=﹣2.24.解方程:〔1〕﹣0.5+3*=10;〔2〕3*+8=2*+6;〔3〕2*+3〔*+1〕=5﹣4〔*﹣1〕;〔4〕.25.解方程:.26.解方程:〔1〕10*﹣12=5*+15;〔2〕27.解方程:〔1〕8y﹣3〔3y+2〕=7〔2〕.28.当k 为什么数时,式子比的值少3.29.解以下方程:〔I〕12y﹣2.5y=7.5y+5〔II 〕.30.解方程:.6.2.4解一元一次方程〔三〕参考答案与试题解析一.解答题〔共30小题〕1.〔2005•〕解方程:2*+1=7考点:解一元一次方程.专题:计算题;压轴题.分析:此题直接通过移项,合并同类项,系数化为1可求解.解答:解:原方程可化为:2*=7﹣1 合并得:2*=6系数化为1得:*=3点评:解一元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为1等步骤,把一个一元一次方程"转化〞成*=a的形式.2.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:左右同乘12可得:3[2*﹣〔*﹣1〕]=8〔*﹣1〕,化简可得:3*+3=8*﹣8,移项可得:5*=11,解可得*=.故原方程的解为*=.点评:假设是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.3.〔1〕解方程:4﹣*=3〔2﹣*〕;〔2〕解方程:.考点:解一元一次方程.专题:计算题.分析:〔1〕先去括号,然后再移项、合并同类型,最后化系数为1,得出方程的解;〔2〕题的方程中含有分数系数,应先对各式进展化简、整理,然后再按〔1〕的步骤求解.解答:解:〔1〕去括号得:4﹣*=6﹣3*,移项得:﹣*+3*=6﹣4,合并得:2*=2,系数化为1得:*=1.〔2〕去分母得:5〔*﹣1〕﹣2〔*+1〕=2,去括号得:5*﹣5﹣2*﹣2=2,移项得:5*﹣2*=2+5+2,合并得:3*=9,系数化1得:*=3.点评:〔1〕此题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比拟多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进展,从而到达分解难点的效果.〔2〕此题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小假设干倍,值不变.这一性质在今后常会用到.4.解方程:.考点:解一元一次方程.专题:计算题.分析:此题两边都含有分数,分母不一样,如果直接通分,有一定的难度,但将方程左右同时乘以公分母6,难度就会降低.解答:解:去分母得:3〔2﹣*〕﹣18=2*﹣〔2*+3〕,去括号得:6﹣3*﹣18=﹣3,移项合并得:﹣3*=9,∴*=﹣3.点评:此题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进展,从而到达分解难点的效果.5.解方程〔1〕4〔*﹣1〕﹣3〔20﹣*〕=5〔*﹣2〕;〔2〕*﹣=2﹣.考点:解一元一次方程.专题:计算题.分析:〔1〕先去括号,再移项、合并同类项、化系数为1,从而得到方程的解;〔2〕先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:〔1〕去括号得:4*﹣4﹣60+3*=5*﹣10〔2分〕移项得:4*+3*﹣5*=4+60﹣10〔3分〕合并得:2*=54〔5分〕系数化为1得:*=27;〔6分〕〔2〕去分母得:6*﹣3〔*﹣1〕=12﹣2〔*+2〕〔2分〕去括号得:6*﹣3*+3=12﹣2*﹣4〔3分〕移项得:6*﹣3*+2*=12﹣4﹣3〔4分〕合并得:5*=5〔5分〕系数化为1得:*=1.〔6分〕点评:去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子〔如果是一个多项式〕作为一个整体加上括号.去括号时要注意符号的变化.6.〔1〕解方程:3〔*﹣1〕=2*+3;〔2〕解方程:=*﹣.考点:解一元一次方程.专题:计算题.分析:〔1〕是简单的一元一次方程,通过移项,系数化为1即可得到;〔2〕是较为复杂的去分母,此题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进展化简、整理为整数形式,难度就会降低.解答:解:〔1〕3*﹣3=2*+33*﹣2*=3+3*=6;〔2〕方程两边都乘以6得:*+3=6*﹣3〔*﹣1〕*+3=6*﹣3*+3*﹣6*+3*=3﹣3﹣2*=0∴*=0.点评:此题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进展,从而到达分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子〔如果是一个多项式〕作为一个整体加上括号.7.﹣〔1﹣2*〕=〔3*+1〕考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:﹣7〔1﹣2*〕=3×2〔3*+1〕﹣7+14*=18*+6﹣4*=13*=﹣.点评:解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1.此题去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子〔如果是一个多项式〕作为一个整体加上括号.8.解方程:〔1〕5〔*﹣1〕﹣2〔*+1〕=3〔*﹣1〕+*+1;〔2〕.考点:解一元一次方程.专题:计算题.分析:〔1〕可采用去括号,移项,合并同类项,系数化1的方式进展;〔2〕此题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进展化简、整理为整数形式,难度就会降低.解答:解:〔1〕5〔*﹣1〕﹣2〔*+1〕=3〔*﹣1〕+*+13*﹣7=4*﹣2∴*=﹣5;〔2〕原方程可化为:去分母得:40*+60=5〔18﹣18*〕﹣3〔15﹣30*〕,去括号得:40*+60=90﹣90*﹣45+90*,移项、合并得:40*=﹣15,系数化为1得:*=.点评:〔1〕此题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比拟多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进展,从而到达分解难点的效果;〔2〕此题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小假设干倍,值不变.这一性质在今后常会用到.9.解方程:.考点:解一元一次方程.专题:计算题.分析:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:,去分母得:2*﹣〔3*+1〕=6﹣3〔*﹣1〕,去括号得:2*﹣3*﹣1=6﹣3*+3,移项、合并同类项得:2*=10,系数化为1得:*=5.点评:去分母时,方程两端同乘小公倍数时,不要漏乘没有分母的项,同时要把分子〔如果是一个多项式〕作为一个整体加上括号.10.解方程:〔1〕4*﹣3〔4﹣*〕=2;〔2〕〔*﹣1〕=2﹣〔*+2〕.考点:解一元一次方程.专题:计算题.分析:〔1〕先去括号,再移项,合并同类项,系数化1,即可求出方程的解;〔2〕先去分母,再去括号,移项,合并同类项,系数化1可求出方程的解.解答:解:〔1〕4*﹣3〔4﹣*〕=2去括号,得4*﹣12+3*=2移项,合并同类项7*=14系数化1,得*=2.〔2〕〔*﹣1〕=2﹣〔*+2〕去分母,得5〔*﹣1〕=20﹣2〔*+2〕去括号,得5*﹣5=20﹣2*﹣4类项,得7*=21系数化1,得*=3.点评:〔1〕此题主要是去括号,移项,合并同类项,系数化1.〔2〕方程两边每一项都要乘各分母的最小公倍数,方程两边每一项都要乘各分母的最小公倍数,切勿漏乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母时,应该将分子用括号括上.11.计算:〔1〕计算:〔2〕解方程:考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:〔1〕根据有理数的混合运算法则计算:先算乘方、后算乘除、再算加减;〔2〕两边同时乘以最简公分母4,即可去掉分母.解答:解:〔1〕原式=,=,=.〔2〕去分母得:2〔*﹣1〕﹣〔3*﹣1〕=﹣4,解得:*=3.点评:解答此题要注意:〔1〕去分母时最好先去中括号、再去小括号,以减少去括号带来的符号变化次数;〔2〕去分母就是方程两边同时乘以分母的最简公分母.12.解方程:考点:解一元一次方程.专题:计算题.分析:〔1〕这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.〔2〕解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化解答:解:〔1〕去分母得:3〔3*﹣1〕+18=1﹣5*,去括号得:9*﹣3+18=1﹣5*,移项、合并得:14*=﹣14,系数化为1得:*=﹣1;〔2〕去括号得:*﹣*+1=*,移项、合并同类项得:*=﹣1,系数化为1得:*=﹣.点评:此题考察解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时"1〞也要乘以最小公倍数.13.解方程:〔1〕〔2〕考点:解一元一次方程.专题:计算题.分析:〔1〕去分母、去括号、移项、合并同类项、化系数为1.〔2〕去分母、项、合并同类项、化系数为1.解答:〔1〕解:去分母得:5〔3*+1〕﹣2×10=3*﹣2﹣2〔2*+3〕,去括号得:15*+5﹣20=3*﹣2﹣4*﹣6,移项得:15*+*=﹣8+15,合并得:16*=7,解得:;〔2〕解:,4〔*﹣1〕﹣18〔*+1〕=﹣36,4*﹣4﹣18*﹣18=﹣36,﹣14*=﹣14,*=1.点评:此题考察解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时"1〞也要乘以最小公倍数.14.解方程:〔1〕5〔2*+1〕﹣2〔2*﹣3〕=6 〔2〕+2〔3〕[3〔*﹣〕+]=5*﹣1考点:解一元一次方程.专题:计算题.分析:〔2〕通过去括号、移项、合并同类项、系数化为1,解得*的值;〔3〕乘最小公倍数去分母即可;〔4〕主要是去括号,也可以把分数转化成整数进展计算.解答:解:〔1〕去括号得:10*+5﹣4*+6=6移项、合并得:6*=﹣5,方程两边都除以6,得*=﹣;〔2〕去分母得:3〔*﹣2〕=2〔4﹣3*〕+24,去括号得:3*﹣6=8﹣6*+24,移项、合并得:9*=38,方程两边都除以9,得*=;〔3〕整理得:[3〔*﹣〕+]=5*﹣1,4*﹣2+1=5*﹣1,移项、合并得:*=0.点评:一元一次方分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程"转化〞成*=a的形式.解题时,要灵活运用这些步骤.15.〔A类〕解方程:5*﹣2=7*+8;〔B类〕解方程:〔*﹣1〕﹣〔*+5〕=﹣;〔C类〕解方程:.考点:解一元一次方程.专题:计算题.分析:通过去分母、去括号、移项、系数化为1等方法,求得各方程的解.解答:解:A类:5*﹣2=7*+8移项:5*﹣7*=8+2化简:﹣2*=10即:*=﹣5;B类:〔*﹣1〕﹣〔*+5〕=﹣去括号:*﹣﹣*﹣5=﹣化简:*=5即:*=﹣;=1去分母:3〔4﹣*〕﹣2〔2*+1〕=6去括号:12﹣3*﹣4*﹣2=6化简:﹣7*=﹣4即:*=.点评:此题主要考察一元一次方程的解法,比拟简单,但要细心运算.16.解方程〔1〕3〔*+6〕=9﹣5〔1﹣2*〕〔2〕〔3〕〔4〕考点:解一元一次方程.专题:计算题.分析:〔1〕去括号以后,移项,合并同类项,系数化为1即可求解;〔2〕〔3〕首先去掉分母,再去括号以后,移项,合并同类项,系数化为1以后即可求解;〔4〕首先根据分数的根本性质,把第一项分母中的0.3化为整数,再去分母,求解.解答:解:〔1〕去括号得:3*+18=9﹣5+10*移项得:3*﹣10*=9﹣5﹣18合并同类项得:﹣7*=﹣14则*=2;〔2〕去分母得:2*+1=*+3﹣5移项,合并同类项得:*=﹣3;〔3〕去分母得:10y+2〔y+2〕=20﹣5〔y﹣1〕去括号得:10y+2y+4=20﹣5y+5移项,合并同类项得:17y=21系数化为1得:;〔4〕原方程可以变形为:﹣5*=﹣1去分母得:17+20*﹣15*=﹣3移项,合并同类项得:5*=﹣20评:17.解方程:〔1〕解方程:4*﹣3〔5﹣*〕=13 〔2〕解方程:*﹣﹣3 考点:解一元一次方程.专题:计算题.分析:〔1〕先去括号,再移项,化系数为1,从而得到方程的解.〔2〕这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解答:解:〔1〕去括号得:4*﹣15+3*=13,移项合并得:7*=28,系数化为1得:得*=4;〔2〕原式变形为*+3=,去分母得:5〔2*﹣5〕+3〔*﹣2〕=15〔*+3〕,去括号得10*﹣25+3*﹣6=15*+45,移项合并得﹣2*=76,系数化为1得:*=﹣38.点评:此题考察解一元一次方般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.18.〔1〕计算:﹣42×+|﹣2|3×〔﹣〕3〔2〕计算:﹣12﹣|0.5﹣|÷×[﹣2﹣〔﹣3〕2] 〔3〕解方程:4*﹣3〔5﹣*〕=2;〔4〕解方程:.考点:解一元一次方程;有理数的混合运算.分析:〔1〕利用平方和立方的定义进展计算.〔2〕按四则混合运算的顺序进展计算.〔3〕主要是去括号,移项合并.〔4〕两边同乘最小公倍数去分母,再求值.解答:解:〔1〕﹣42×+|﹣2|3×〔﹣〕3==﹣1﹣1〔2〕﹣12﹣|0.5﹣|÷×[﹣2﹣〔﹣3〕2] ====.〔3〕解方程:4*﹣3〔5﹣*〕=2去括号,得4*﹣15+3*〕=2移项,得4*+3*=2+15 合并同类项,得7*=17系数化为1,得.〔4〕解方程:去分母,得15*﹣3〔*﹣2〕=5〔2*﹣5〕﹣3×15去括号,得15*﹣3*+6=10*﹣25﹣45移项,得15*﹣3*﹣10*=﹣25﹣45﹣6合并同类项,得2*=﹣76-点评:前两道题考察了学生有理数的混合运算,后两道考察了学生解一元一次方程的能力.19.〔1〕计算:〔1﹣2﹣4〕×;〔2〕计算:÷;〔3〕解方程:3*+3=2*+7;〔4〕解方程:.考点:解一元一次方程;有理数的混合运算.专题:计算题.分析:〔1〕和〔2〕要熟练掌握有理数的混合运算;〔3〕和〔4〕首先熟悉解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为1.解答:解:〔1〕〔1﹣2﹣4〕×=﹣=﹣13;〔2〕原式=﹣1×〔﹣4﹣2〕×〔﹣〕=6×〔﹣〕=﹣9;〔3〕解方程:3*+3=2*+7合并同类项,得*=4;〔4〕解方程:去分母,得6〔*+15〕=15﹣10〔*﹣7〕去括号,得6*+90=15﹣10*+70移项,得6*+10*=15+70﹣90合并同类项,得16*=﹣5系数化为1,得*=.点评:〔1〕和〔2〕要注意符号的处理;〔4〕要特别注意去分母的时候不要发生数字漏乘的现象,熟练掌握去括号法则以及合并同类项法则.20.解方程〔1〕﹣0.2〔*﹣5〕=1;〔2〕.考点:解一元一次方程.分析:〔1〕通过去括号、移项、系数化为1等过程,求得*的值;〔2〕通过去分母以及去括号、移项、系数化为1等过程,求得*的值.解答:解:〔1〕﹣0.2﹣0.2*+1=1,∴﹣0.2*=0,∴*=0;〔2〕.去分母得:2〔*﹣2〕+6*=9〔3*+5〕﹣〔1﹣2*〕,∴﹣21*=48,∴*=﹣.点评:此题主要考察了一元一次方程解法,解一元一次方程常见的过程有去括号、移项、系数化为1等.21.解方程:〔*+3〕﹣2〔*﹣1〕=9﹣3*.考点:解一元一次方程.专题:计算题.分析:先去括号得*+3﹣2*+2=9﹣3*,然后移项、合并同类得到2*=4,然后把*的系数化为1即可.解答:解:去括号得*+3﹣2*+2=9﹣3*,移项得*﹣2*+3*=9﹣3﹣2,合并得2*=4,点评:此题考察了解一元一次方程:先去分母,再去括号,接着移项,把含未知数的项移到方程左边,不含未知数的项移到方程右边,然后合并同类项,最后把未知数的系数化为1得到原方程的解.22.8*﹣3=9+5*.5*+2〔3*﹣7〕=9﹣4〔2+*〕...考点:解一元一次方程.专题:方程思想.分析:此题是解4个不同的一元一次方程,第一个通过移项、合并同类项及系数化1求解.第二个先去括号再通过移项、合并同类项及系数化1求解.第三个先去分母再同第二个.第四个先分子分母乘以10,再同第三个求解.解答:8*﹣3=9+5*,解:8*﹣5*=9+3,∴*=4是原方程的解;5*+2〔3*﹣7〕=9﹣4〔2+*〕,解:5*+6*﹣14=9﹣8﹣4*,5*+6*+4*=9﹣8+14,15*=15,∴*=1.∴*=1是原方程的解..解:3〔*﹣1〕﹣2〔2*+1〕=12,3*﹣3﹣4*﹣2=12,3*﹣4*=12+3+2,﹣*=17,∴*=﹣17.∴*=﹣17是原方程的解.,解:,5〔10*﹣3〕=4〔10*+1〕+40,50*﹣15=40*+4+ 40,50*﹣40*=4+40+ 15,10*=59,∴*=.∴*=是原方程的解.点评:此题考察的知识点是解一元一次方程,关键是注意解方程时的每一步都要认真仔细,如移项时要变符号.23.解以下方程:〔1〕0.5*﹣0.7=5.2﹣1.3〔*﹣1〕;〔2〕=﹣2.考点:解一元一次方程.分析:〔1〕首先去括号,然后移项、合并同类项,系数化成1,即可求解;〔2〕首先去分母,然后去括号,移项、合并同类项,系数化成1,即可求解解答:解:〔1〕去括号,得:0.5*﹣0.7=5.2﹣1.3*+1.3移项,得:0.5*+1.3*=5.2+1.3+0.7合并同类项,得:1.8*=7.2,则*=4;〔2〕去分母得:7〔1﹣2*〕=3〔3*+1〕﹣42,去括号,得:7﹣14*=9*+3﹣42,移项,得:﹣14*﹣9*=3﹣42﹣7,合并同类项,得:﹣23*=﹣46,则*=2.点评:此题考察解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.24.解方程:〔1〕﹣0.5+3*=10;〔2〕3*+8=2*+6;〔3〕2*+3〔*+1〕=5﹣4〔*﹣1〕;〔4〕.考点:解一元一次方程.分析:〔1〕移项,合并同类项,然后系数化成1即可求解;〔2〕移项,合并同类项,然后系数化成1即可求解;〔3〕去括号、移项,合并同类项,然后系数化成1即可求解;〔4〕首先去分母,然后去括号、移项,合并同类项,然后系数化成1即可求解.解答:解:〔1〕3*=10.5,*=3.5;〔2〕3*﹣2*=6﹣8,*=﹣2;〔3〕2*+3*+3=5﹣4*+4,2*+3*+4*=5+4﹣3,9*=6,*=;〔4〕2〔*+1〕+6=3〔3*﹣2〕,2*+2+6=9*﹣6,2*﹣9*=﹣6﹣2﹣6,﹣7*=﹣14,*=2.点评:此题考察解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.25.解方程:.考点:解一元一次方程.专题:计算题.分析:方程两边乘以10去分母后,去括号,移项合并,将*系数化为1,即可求出解.解答:解:去分母得:5〔3*﹣1〕﹣2〔5*﹣6〕=2,去括号得:15*﹣5﹣10*+12=2,移项合并得:5*=﹣5,解得:*=﹣1.点评:此题考察了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.26.解方程:〔1〕10*﹣12=5*+15;〔2〕考点:解一元一次方程.专题:计算题.分析:〔1〕先移项,再合并同类项,最后化系数为1,从而得到方程的解;〔2〕先去括号,再移项、合并同类项,最后化系数为1,从而得到方程的解.解答:解:〔1〕移项,得10*﹣5*=12+15,合并同类项,得5*=27,方程的两边同时除以5,得*=;〔2〕去括号,得=,方程的两边同时乘以6,得*+1=4*﹣2,移项、合并同类项,得3*=3,方程的两边同时除以3,得*=1.点评:此题考察解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.27.解方程:〔1〕8y﹣3〔3y+2〕=7 〔2〕.考点:解一元一次方程.专题:计算题.分析:〔1〕根据一元一次方程的解法,去括号,移项,合并同类项,系数化为1即可得解;〔2〕这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:〔1〕去括号得,8y﹣9y﹣6=7,移项、合并得,﹣y=13,系数化为1得,y=﹣13;〔2〕去分母得,3〔3*﹣1〕﹣12=2〔5*﹣7〕,去括号得,9*﹣3﹣12=10*﹣14,移项得,9*-﹣10*=﹣14+3+12,合并同类项得,﹣*=1,系数化为1得,*=﹣1.点评:此题主要考察了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子〔如果是一个多项式〕作为一个整体加上括号.28.当k 为什么数时,式子比的值少3.考点:解一元一次方程.专题:计算题.分析:先根据题意列出方程,再根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.解答:解:依题意,得=+3,去分母得,5〔2k+1〕=3〔17﹣k〕+45,去括号得,10k+5=51﹣3k+45,移项得,10k+3k=51+45﹣5,合并同类项得,13k=91,系数化为1得,k=7,∴当k=7时,式子比的值少3.点评:此题主要考察了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子〔如果是一个多项式〕作为一个整体加上括号.29.解以下方程:〔I〕12y﹣2.5y=7.5y+5〔II 〕.考点:解一元一次方程.专题:计算题.分析:〔Ⅰ〕根据一元一次方程的解法,移项,合并同类项,系数化为1即可得解;〔Ⅱ〕是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解答:解:〔Ⅰ〕移项得,12y﹣2.5y﹣7.5y=5,合并同类项得,2y=5,系数化为1得,y=2.5;〔Ⅱ〕去分母得,5〔*+1〕﹣10=〔3*﹣2〕﹣2〔2*+3〕,去括号得,5*+5﹣10=3*﹣2﹣4*﹣6,移项得,5*﹣3*+4*=﹣2﹣6﹣5+10,合并同类项得,6*=﹣3,系数化为1得,*=﹣.点评:此题主要考察了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子〔如果是一个多项式〕作为一个整体加上括号.30.解方程:.考点:解一元一次方程.专题:计算题.分析:由于方程的分子、分母均有小数,利用分数的根本性质,分子、分母同时扩大一样的倍数,可将小数化成整数.解答:解:原方程变形为,〔3分〕去分母,得3×〔30*﹣11〕﹣4×〔40*﹣2〕=2×〔16﹣70*〕,〔4分〕去括号,得90*﹣33﹣160*+8=32﹣140*,〔5分〕移项,得90*﹣160*+140*=32+33﹣8,〔6分〕合并同类项,得70*=57,〔7分〕系数化为1,得.〔8分〕点评:此题考察一元一次方程的解法.解一元一次方程的一般步骤:去分母,去括号,移项,合并同类项,系数化为1.此题的难点在于方程的分子、分母均有小数,将小数化成整数不同于去分母,不是方程两边同乘一个数,而是将分子、分母同乘一个数.。
完整版)解一元一次方程习题精选附答案

完整版)解一元一次方程习题精选附答案6.2.4 解一元一次方程一、解答题(共30小题)1.解方程:2x+1=7.2.删除此题。
3.(1)解方程:4-x=3(2-x);2)解方程:删除此题。
4.解方程:删除此题。
5.解方程:1)4(x-1)-3(20-x)=5(x-2);2)x-1=2(x+1)。
6.(1)解方程:3(x-1)=2x+3;2)解方程:x-1=3(x-2)。
7.-1+2x=3x+1.8.解方程:1)5(x-1)-2(x+1)=3(x-1)+x+1;2)删除此题。
9.解方程:删除此题。
10.解方程:1)4x-3(4-x)=2;2)(x-1)+2=2-(x+2)。
11.(1)计算:删除此题。
2)解方程:删除此题。
12.解方程:删除此题。
13.解方程:1)删除此题。
2)删除此题。
14.解方程:1)5(2x+1)-2(2x-3)=6;2)x+2;3)3(x-1)+2=5x-1.15.(A类)解方程:5x-2=7x+8;B类)解方程:(x-1)-(x+5)=-2;C类)解方程:删除此题。
16.解方程:1)3(x+6)=9-5(1-2x);2)删除此题;3)删除此题;4)删除此题。
17.解方程:1)4x-3(5-x)=13;2)x+3.18.(1)计算:-42x+|-2|3x(-1);2)计算:-12-|0.5-2|÷2×[-2-(-3)2];3)4x-3(5-x)=2;4)(x+1)+2=4(x-1)。
19.(1)计算:-1-2-4×(-2);2)计算:-6÷2;3)3x+3=2x+7;4)2x-3=5x+1.20.解方程:1)-0.2(x-5)=1;2)删除此题。
21.解方程:(x+3)-2(x-1)=9-3x。
22.8x-3=9+5x;5x+2(3x-7)=9-4(2+x)。
23.解下列方程:1)0.5x-0.7=5.2-1.3(x-1);2)x+3=-2.24.解方程:1)-0.5+3x=10;2)x= -1;3)5x+3=1;4)删除此题。
解一元一次方程习题精选附答案

考点:
解一元一次方程.
专题:
计算题.
分析:
这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.
解答:
解:左右同乘12可得:3[2x﹣(x﹣1)]=8(x﹣1),
化简可得:3x+3=8x﹣8,
移项可得:5x=11,
解可得x= .
故原方程的解为x= .
点评:
若是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.
解:(1)5(x﹣1)﹣2(x+1)=3(x﹣1)+x+1
3x﹣7=4x﹣2
∴x=﹣5;
(2)原方程可化为:
去括号得:6﹣3x﹣18=﹣3,
移项合并得:﹣3x=9,
∴x=﹣3.
点评:
本题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.
5.解方程
(1)4(x﹣1)﹣3(20﹣x)=5(x﹣2);
(2)x﹣ =2﹣ .
考点:
解答:
解:(1)3x﹣3=2x+3
3x﹣2x=3+3
x=6;
(2)方程两边都乘以6得:x+3=6x﹣3(x﹣1)
x+3=6x﹣3x+3
x﹣6x+3x=3﹣3
﹣2x=0
∴x=0.
点评:
本题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进行,从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.
解一元一次方程——同解方程精选试题附答案

6.2.6同解方程完成时间:20min一.选择题(共9小题)1.已知关于x的方程7x+3k=12与7x+3=0的解相同,则k的值为()A﹣3 B.3C.﹣5 D.52.关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解,则a、b的关系为()A.a﹣b=3 B.b﹣a=3 C.b+a=3 D.b+a+3=03.已知方程4x=8与x﹣k=1的解相同,则4k2﹣1的值为()A.1B.3C.8D.174.吴云科和孟家福是七年级四班的两名爱好数学的优等生,在学完第三章《一元一次方程》后,吴云科对孟家福说:“方程与方程的解相同,你能求出k的值吗?”孟家福用笔算了一下给出正确答案,聪明的你知道是哪个吗?()A.0B.2C.1D.﹣15.如果方程x=1与2x+a=ax的解相同,则a的值是()A.2B.﹣2 C.3D.﹣36.下列方程中与方程3x=x+1的解相同的是()A.2x=4 B.2x=4x﹣1 C.5x+3=6 D.6x﹣15x=37.如果方程6x+3a=22与方程3x+5=11的解相同,那么a=()A.B.C.﹣D.﹣8.在方程:①3x﹣=1;②;③6x﹣5=2x﹣3;④x+=2x中,与方程2x=1的解相同的方程有()A.1个B.2个C.3个D.4个9.有4个关于x方程:(1)x﹣2=﹣1 (2)(x﹣2)+(x﹣1)=﹣1+(x﹣1)(3)x=0 (4)其中同解的两个方程是()A.(1)与(2)B.(1)与(3)C.(1)与(4)D.(2)与(4)二.填空题(共15小题)10.方程x+2=3的解也是方程ax﹣5=8的解时,则a=_________.11.已知关于x的方程+3=x与方程3﹣2x=1的解相同,则m2=_________.12.若方程2x﹣3=11与关于x的方程4x+5=3k有相同的解,则k的值是_________.13.已知关于x的方程5x+3k=24与5x+3=0的解相同,则k的值为_________.14.已知方程3(x+3)﹣1=2x的解与关于x的方程的解相同,则m2﹣2m+1的值为_________.15.已知关于x的方程=x+与=3x﹣2的解相同,则m=_________.16.如果关于x的方程和方程的解相同,那么k的值_________.17.如果方程与方程3x﹣2a=0的解相同,则a3=_________.18.方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程,则a+b+c=_________;如果关于x的方程2x+1=﹣3和方程=0的解相同,那么k=_________.19.若3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解,则(a﹣b+c)2009=_________.20.若以为未知数的方程3x=5x﹣8和有相同的解,则a=_________.21.已知方程2x﹣3=+x的解满足|x|﹣1=0,则m_________.22.关于x的方程3x=9与x+4=k的解相同,则代数式1﹣2|k|的值为_________.23.关于x的方程3mx+7=0和2 x+3n=0是同解方程,那么(mn)2=_________.24.已知:一元一次方程2x﹣2=3的解是方程的解,则m=_________.三.解答题(共6小题)25.已知:关于x的方程4x﹣k=2与3(2+x)=2k的解相同,求k的值及相同的解.26.已知关于x的方程2x+1=a和2x+2=0的解相同,求的值.27.若关于x的方程2x﹣3=1和=k﹣3x有相同的解,求k的值.28.如果方程的解与方程4y﹣(3m+1)=6y+2m﹣1的解相同,求式子的值.29.方程4+2(x﹣1)=0的解与关于x的方程的解相同,求k的值.30.当k为何值时,方程与方程有相同的解?6.2.6同解方程参考答案与试题解析一.选择题(共9小题)1.已知关于x的方程7x+3k=12与7x+3=0的解相同,则k的值为()A.﹣3 B.3C.﹣5 D.5考点:同解方程.专题:计算题.分析:先解方程7x+3=0,可得x=﹣,根据同解的定义可得x=﹣也是7x+3k=12的解,再把x=﹣代入7x+3k=12中即可求k.解答:解:解方程7x+3=0得,x=﹣,∵7x+3k=12与7x+3=0的解相同,∴x=﹣也是7x+3k=12的解,再把x=﹣代入7x+3k=12中,得7×(﹣)+3k=12,解得k=5.故选D.点评:本题考查了同解方程的定义,解题的关键是先求出x.2.关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解,则a、b的关系为()A.a﹣b=3 B.b﹣a=3 C.b+a=3 D.b+a+3=0考点:同解方程.分析:求出两个方程的解,根据已知得出两个解相等,即可求出答案.解答:解:x+a=2x﹣3,x﹣2x=﹣3﹣a,﹣x=﹣3﹣a,则x=3+a,2x﹣b=x,x=b,∵关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解,∴3+a=b,∴b﹣a=3,故选B.点评:本题考查了对同解方程的理解,关键是求出3+a=b,题目比较好,难度适中.3.已知方程4x=8与x﹣k=1的解相同,则4k2﹣1的值为()A.1B.3C.8D.17考点:同解方程.专题:计算题.分析:先解出方程4x=8的解,然后代入求出k的值,进而可得出答案.解答:解:解方程4x=8,得:x=2,把x=2代入x﹣k=1,得:k=1,∴4k2﹣1=3.故选B.点评:本题考查同解方程的知识,比较简单,解决本题的关键是理解方程解的定义,注意细心运算.4.吴云科和孟家福是七年级四班的两名爱好数学的优等生,在学完第三章《一元一次方程》后,吴云科对孟家福说:“方程与方程的解相同,你能求出k的值吗?”孟家福用笔算了一下给出正确答案,聪明的你知道是哪个吗?()A.0B.2C.1D.﹣1考点:同解方程.专题:方程思想.分析:先解方程,得x=1,因为这个解也是方程的解,根据方程的解的定义,把x代入方程中求出k的值.解答:解:12﹣2(x﹣1)=3(1﹣x)+6(3﹣x)解得:x=1.把x=1代入方程得:4﹣=3k﹣,12﹣k﹣2=9k,解得:k=1.故选C.点评:本题考查了同解方程,解题的关键是正确解一元一次方程.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.5.如果方程x=1与2x+a=ax的解相同,则a的值是()A.2B.﹣2 C.3D.﹣3考点:同解方程.专题:计算题.分析:可以分别解出两方程的解,两解相等,就得到关于a的方程,从而可以求出a的值.解答:解:解第一个方程得:x=3,解第二个方程得:x=∴=3解得:a=3故选C.点评:本题解决的关键是能够求解关于x的方程,要能正确理解方程解的含义.6.下列方程中与方程3x=x+1的解相同的是()A.2x=4 B.2x=4x﹣1 C.5x+3=6 D.6x﹣15x=3考点:同解方程.专题:计算题.分析:求得题目中各个方程的解,即可作出判断.解答:解:方程3x=x+1的解是x=.A、解是x=2,故错误;B、解是x=,故正确;C、解是x=,故错误;D、解是x=﹣,故错误.故选B.点评:本题主要考查了一元一次方程的解法,正确解方程是解题的关键.7.如果方程6x+3a=22与方程3x+5=11的解相同,那么a=()A.B.C.﹣D.﹣考点:同解方程.专题:计算题.分析:先通过方程3x+5=11求得x的值,因为方程6x+3a=22与方程3x+5=11的解相同,把x的值代入方程6x+3a=22,即可求得a的值.解答:解:3x+5=11,移项,得3x=11﹣5,合并同类项,得3x=6,系数化为1,得x=2,把x=2代入6x+3a=22中,得6×2+3a=22,∴a=,故选B.点评:解一元一次方程的一般步骤是去分母,去括号,移项,合并同类项,移项时要变号.因为两方程解相同,把求得x的值代入方程,即可求得常数项的值.8.在方程:①3x﹣=1;②;③6x﹣5=2x﹣3;④x+=2x中,与方程2x=1的解相同的方程有()A.1个B.2个C.3个D.4个考点:同解方程.专题:计算题.分析:求出方程2x=1的解是x=,要判断x=是否是方程的解,就是把它代入方程的左右两边,看是否相等.解答:解:方程2x=1的解是x=A、把x=代入3x﹣=1,左边=﹣=1,左边=右边,因而x=是方程3x﹣=1的解,即与方程2x=1的解相同.B、把x=代入,左边=(+1)=,左边=右边,因而x=是方程的解,即与方程2x=1的解相同.C、把x=代入6x﹣5=2x﹣3,左边=3﹣5=﹣2,右边=1﹣3=﹣2,左边=右边,因而x=是方程6x﹣5=2x﹣3的解,即与方程2x=1的解相同.D、把x=代入x+=2x,左边=+=1,右边=2×=1,因而左边=右边,因而x=是方程6x﹣5=2x﹣3的解,即与方程2x=1的解相同.四个方程都与2x=1的解相同.故选D.点评:本题主要考查判断一个数是否是方程的解的方法.9.有4个关于x方程:(1)x﹣2=﹣1 (2)(x﹣2)+(x﹣1)=﹣1+(x﹣1)(3)x=0 (4)其中同解的两个方程是()A.(1)与(2)B.(1)与(3)C.(1)与(4)D.(2)与(4)考点:同解方程.分析:(1)移项可解出x的值.(2)先去括号在移项合并可得出x的值.(3)直接可得出x的值.(4)直接移项即可,注意分式有意义的条件.解答:解:(1)方程的解为x=1,(2)方程的解为x=1,(3)方程的解为x=0,(4)方程无解.∴只有(1)(2)是同解方程.故选A.点评:本题考查同解方程的知识,关键是正确求出4个方程的解,难度不大,注意要细心运算.二.填空题(共15小题)10.方程x+2=3的解也是方程ax﹣5=8的解时,则a=13.考点:同解方程.专题:计算题.分析:首先解出方程x+2=3的解,代入方程ax﹣5=8中求出a的值即可.解答:解:x+2=3,解得x=1;把x=1代入ax﹣5=8中,得a﹣5=8,解得a=13.点评:本题的关键是正确解一元一次方程.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.11.已知关于x的方程+3=x与方程3﹣2x=1的解相同,则m2=16.考点:同解方程.分析:首先解出方程3﹣2x=1的解,然后把方程的解代入方程+3=x求出m,即可求出m2.解答:解:解方程3﹣2x=1得:x=1,把x=1代入方程+3=x得:+3=1,解得:m=﹣4,则m2=16.故答案为:16.点评:本题考查了同解方程的知识,解答本题的关键是理解方程解得定义.12.若方程2x﹣3=11与关于x的方程4x+5=3k有相同的解,则k的值是11.考点:同解方程;解一元一次方程.专题:计算题.分析:先解方程2x﹣3=11求出x的值,把解得的值代入方程4x+5=3k,就可以得到一个关于k的方程,解方程就可以求出k的值.解答:解:解方程2x﹣3=11得:x=7,把x=7代入4x+5=3k,得:28+5=3k,解得:k=11.故答案为:11.点评:本题考查同解方程的知识,已知条件中涉及到方程的解,把方程的解代入原方程,转化为关于字母系数a 的方程进行求解.13.已知关于x的方程5x+3k=24与5x+3=0的解相同,则k的值为9.考点:同解方程.专题:计算题.分析:首先根据5x+3=0得到5x=﹣3,再把5x=﹣3代入5x+3k=24求出k的值即可.解答:解:∵5x+3=0,∴5x=﹣3,∵方程5x+3k=24与5x+3=0的解相同,∴﹣3+3k=34,解得k=9,故答案为9.点评:本题考查了同解方程.解一元一次方程的一般步骤是去分母,去括号,移项,合并同类项,移项时要变号.因为两方程解相同,把求得x的值代入方程,即可求得常数项的值.14.已知方程3(x+3)﹣1=2x的解与关于x的方程的解相同,则m2﹣2m+1的值为25.考点:同解方程.分析:先求出方程3(x+3)﹣1=2x的解,再根据方程3(x+3)﹣1=2x的解与关于x的方程的解相同,把x的值代入方程中,求出m的值,再把m的值代入要求的式子,即可得出答案.解答:解:3(x+3)﹣1=2x,3x+9﹣1﹣2x=0,x=﹣8,∵方程3(x+3)﹣1=2x的解与关于x的方程的解相同,∴把x=﹣8代入方程得:3×(﹣8)+m=﹣27,解得:m=﹣4,把m=﹣4代入m2﹣2m+1得:(﹣4)2﹣2×(﹣4)+1=16+8+1=25;故答案为:25.点评:此题考查了同解方程,关键是能够求出关于x的方程,根据同解的定义建立方程,求出m的值.15.已知关于x的方程=x+与=3x﹣2的解相同,则m=﹣.考点:同解方程.分析:先求出方程=3x﹣2的解,然后把x的值代入方程=x+求出m的值.解答:解:解方程=3x﹣2,得:x=1,把x=1代入方程=x+得:=1+,解得:m=﹣.故答案为:﹣.点评:本题考查了同解方程,解答本题的关键是能够求解关于x的方程,要正确理解方程解的含义.16.如果关于x的方程和方程的解相同,那么k的值.考点:同解方程.分析:本题可先根据一元一次方程解出x的值,再根据解相同,将x的值代入二元一次方程中,即可解出k的值.解答:解:解方程得:x=﹣,把x=﹣代入方程得:2﹣=0,解得:k=5;故答案为:5.点评:本题考查了二元一次方程与一元一次方程的综合运用.运用代入法,将解出的x的值代入二元一次方程,可解出k的值.17.如果方程与方程3x﹣2a=0的解相同,则a3=.考点:同解方程.分析:根据第一个方程即可求得x=﹣;然后根据同解方程的定义,将其代入第二个方程,列出关于a的方程;最后通过解关于a的方程求得a的值后,把a的值代入所求的代数式并求值.解答:解:∵x+=0,∴x=﹣;根据题意得3×(﹣)﹣2a=0,解得a=﹣,∴a3==.故答案是:.点评:本题考查了同解方程.使方程左右两边相等的未知数的值是该方程的解.因此检验一个数是否为相应的方程的解,就是把这个数代替方程中的未知数,看左右两边的值是否相等,如果左边=右边,那么这个数就是该方程的解;反之,这个数就不是该方程的解.18.方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程,则a+b+c=1;如果关于x的方程2x+1=﹣3和方程=0的解相同,那么k=﹣2.考点:同解方程;一元一次方程的定义.专题:计算题.分析:根据一元一次方程的定义可得出a=0,b=1,c=0,然后计算即可a+b+c;先解出2x+1=3的值,然后代入可得出k.解答:解:∵方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程,∴a=0,2b﹣1=1,c=0,解得:a=0,b=1,c=0,故可得a+b+c=1;方程2x+1=﹣3的解为:x=﹣2,代入可得:=0,解得:k=﹣2.故答案为:1、﹣2.点评:此题考查了同解方程的知识,关键是掌握使方程左右两边相等的未知数的值是该方程的解,难度一般.19.若3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解,则(a﹣b+c)2009=﹣1.考点:同解方程.专题:计算题;整体思想.分析:答题时首先解出一元一次方程的解,把一元一次方程的解代入另一个方程中,求得a﹣b+c的值.解答:解:∵3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解,∴x=1也是ax﹣b+1=﹣c的解,∴a﹣b+c=﹣1,∴(a﹣b+c)2009=﹣1.点评:本题主要考查解一元一次方程,利用整体法求值是解答本题的关键.20.若以为未知数的方程3x=5x﹣8和有相同的解,则a=.考点:同解方程.专题:计算题.分析:解方程3x=5x﹣8就可以求出方程的解,这个解也是方程的解,根据方程的解的定义,把这个解代入就可以求出a的值.解答:解:首先解方程3x=5x﹣8得:x=4;把x=4代入方程,得到2+4a=a﹣5;解得:a=﹣.点评:本题的关键是正确解一元一次方程以及同解方程的意义.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.21.已知方程2x﹣3=+x的解满足|x|﹣1=0,则m﹣6或﹣12.考点:同解方程.分析:通过解绝对值方程可以求得x=±1.然后把x的值分别代入方程2x﹣3=+x来求m的值.解答:解:由|x|﹣1=0,得x=±1..当x=1时,由,得,解得m=﹣6;当x=﹣1时,由,得,解得m=﹣12.综上可知,m=﹣6或﹣12.故答案是:﹣6或﹣12.点评:本题考查了同解方程的定义.如果第一个方程的解都是第二个方程的解,并且第二个方程的解也都是第一个方程的解,那么这两个方程叫做同解方程.22.关于x的方程3x=9与x+4=k的解相同,则代数式1﹣2|k|的值为﹣13.考点:同解方程.专题:计算题.分析:根据3x=9与x+4=k的解相同可得出k的值,代入即可得出答案.解答:解:3x=9,解得:x=3,将x=3代入x+4=k可得:3+4=k,k=7,∴1﹣2|k|=﹣13.故填:﹣13.点评:本题考查同解方程的定义,难度不大,理解同解的概念是关键.23.关于x的方程3mx+7=0和2 x+3n=0是同解方程,那么(mn)2=.考点:同解方程;代数式求值.分析:分别解出两个方程的解,使这两个解相等,即可得出mn的值,从而可得出答案.解答:解:由3mx+7=0与2x+3n=0是关于x的同解方程,可知m≠0,n≠0解得∴,.故填:2.点评:本题考查了同解方程的知识,属于比较简单的题目,注意掌握解答此类题目的方法.24.已知:一元一次方程2x﹣2=3的解是方程的解,则m=.考点:同解方程.分析:先求出方程2x﹣2=3的解,然后把x的值代入方程,求解m的值.解答:解:解方程2x﹣2=3得:x=,把x=,代入方程,得,m+=4,解得:m=.故答案为:.点评:本题考查了同解方程,解决本题的关键是能够求解关于x的方程,要正确理解方程解的含义.三.解答题(共6小题)25.已知:关于x的方程4x﹣k=2与3(2+x)=2k的解相同,求k的值及相同的解.考点:同解方程.专题:计算题.分析:由已知关于x的方程4x﹣k=2与3(2+x)=2k的解相同,所以得关于x、k的方程组,解方程组即可.解答:解:已知:关于x的方程4x﹣k=2与3(2+x)=2k的解相同,∴,解得,,所以k的值为6,相同的解为2.点评:此题考查的知识点是同解方程,本题解决的关键是能够求解关于x的方程,根据同解的定义建立方程组.26.已知关于x的方程2x+1=a和2x+2=0的解相同,求的值.考点:同解方程.专题:计算题.分析:先求出方程2x+2=0的解,代入方程2x+1=a求出a的值,代入代数式即可得出答案.解答:解:2x+2=0,解得:x=﹣1,将x=﹣1代入2x+1=a,得a=﹣1,则=1﹣1=0.点评:本题考查了同解方程的知识,关键是理解方程解得含义,另外在代入计算时要细心,不要出错.27.若关于x的方程2x﹣3=1和=k﹣3x有相同的解,求k的值.考点:同解方程.分析:求出方程2x﹣3=1中x的值,再把k当作已知条件求出方程=k﹣3x中x的值,再根据两方程有相同的解列出关于k的方程,求出k的值即可.解答:解:解方程2x﹣3=1得,x=2,解方程=k﹣3x得,x=k,∵两方成有相同的解,∴k=2,解得k=.点评:本题考查的是同解方程,熟知如果两个方程的解相同,那么这两个方程叫做同解方程是解答此题的关键.28.如果方程的解与方程4y﹣(3m+1)=6y+2m﹣1的解相同,求式子的值.考点:同解方程.分析:求出方程的解y=10,代入第二个方程求出m=﹣4,代入求出即可.解答:解:,2(y﹣4)﹣48=﹣3(y+2),2y﹣8﹣48=﹣3y﹣6,5y=50,y=10,即方程4y﹣(3m+1)=6y+2m﹣1的解也是y=10,代入得:40﹣(3m+1)=60+2m﹣1,m=﹣4,所以=4﹣=.点评:本题考查了一元一次方程的解,解一元一次方程,求出代数式的值的应用,关键是求出y、m的值.29.方程4+2(x﹣1)=0的解与关于x的方程的解相同,求k的值.考点:同解方程.专题:方程思想.分析:先求方程4+2(x﹣1)=0的解,再代入,求得k的值.解答:解:解方程4+2(x﹣1)=0,得x=﹣1,把x=﹣1代入,得﹣3k﹣2=﹣2,解得k=﹣.点评:此题主要考查了一元一次方程解的定义.解答此题的关键是熟知方程组有公共解的含义,考查了学生对题意的理解能力.30.当k为何值时,方程与方程有相同的解?考点:同解方程.分析:先解第二个方程,得x的值,因为这个解也是第一个方程的解,根据方程的解的定义,把x代入第一个方程中求出k的值.解答:解:解方程,得x=1,把x=1代入方程,得4﹣,解得k=﹣13,∴当k=﹣13时,方程与方程有相同的解.点评:此题考查同解方程,关键是正确解方程的解的定义,就是能够使方程左右两边相等的未知数的值.。
解一元一次方程习题精选附答案

解一元一次方程例题精练(爱上学数学)•解答题(共30小题)(2005?宁德)解方程:2X +1=7(2)解方程:普=X-号1 27 .寸1—2x r ( 3x+1)8.解方程:(1) 5 (X — 1)- 2 (X+1) =3 (X — 1) +X+1 ;4.解方程:“5•解方程(1) 4 (X — 1)— 3 (20 — X ) =5 (X — 2); (2) X-=2=2-竺.2 3(2) 0- 02/ - 0・ 1&+0・ 18 _ 1.5- 3號丿 0・ 03 10?12 ~2~9.解方程:3-晋二1-宁.6. (1)解方程:3 (X — 1) =2x+3 ;2. 4 [^4 (mt)]諾(汀1)1. 3. (1)解方程: (2)解方程:4 — X=3 (2 —X );X- 1 _ :t+1 十 ITT10.解方程: (1) 4x - 3 (4 - x ) =2 ;1) =2 -2 (X+2 ).513.解方程:(1) 3x+l _ 2二烫-2 _2^~2' "T"(2) 4 &T)-也二-46 511.计算: (1)计算:(2)解方程: -弓[一 /X (-牛2 — 2]X- 1 3E - 1. --- - ----- =-1 2 414 .解方程:(1) 5 (2X+1)- 2 (2x - 3) =6(2)宀 _4 - 3沉 +24(3) 卫[3 (X -土)+ 上]=5x - 13 2 "⑴耳⑵琨-G-寺]孕12.解方程: 15. (A 类)解方程: (B 类)解方程: (C 类)解方程:5x -2=7x+8 ; (X - 1)-( X+5)=-寺34- X 2x+l T丁■丁=1.16.解方程(1) 3 (X+6) =9 - 5 (1 - 2x )18. (1)计算:2 13 42+1 —2| X(2) 计算: 12—10.5—21』汽—2 —( —3 32]解方程: 4x—3 ( 5 - x)=2;(4) 解方程:(4) 1.了+加0.3 丄二一T0.219. (1)计算: (1- 2-4)“岭);17.解方程:(1)解方程:4x—3 (5—x) =13(2)计算:(-1) (-|) ^-2](2)解方程:X - 2 2it- 5 Cx———5x+2 (3x - 7) =9 - 4 (2+x ).(3) 解方程: 3x+3=2x+7 ;(4) 解方程:23•解下列方程:(1) 0.5x - 0.7=5.2 - 1.3 (x -1);21.解方程:(x+3)- 2 (x - 1) =9 - 3x .20•解方程(1)- 0.2 (x -5)=1;M 3 s+0.1 0・4二0.5也X- 1 2x+l T3 (3計5) 1 - 2s+垃 =—-―^22. 8x - 3=9+5x . 24.解方程:(1)- 0.5+3x=10 ;"“7 咗 g27•解方程:(1) 8y - 3 (3y+2 ) =7(2) 3x+8=2x+6 ;(3) 2x+3 (x+1 ) =5- 4 (x - 1);17一 k 91<+128 •当k 为什么数时,式子 _ 比竺a 的值少3.(4)罰耳29.解下列方程:(I ) 12y -25.解方程:3K - 1 5K -6 —g —0.2.26.解方程: (1) 10x - 12=5x+15 ;30.解方程:智F4x- 0. 2 0.16-0. ?K 0. 06解一元一次方程参考答案与试题解析一.解答题(共30小题)1. (2005?宁德)解方程:2x+1=7考占:V八、、•解一元一次方程. 点评: 计算题;压轴题.此题直接通过移项,合并同类项,系数化为 1可求解.解:原方程可化为:2x=7 - 1 合并得:2x=6 系数化为1得:x=3元一次方程,一般要通过去分母,去括号,移项,合并同类项,未知数的系数化为 元一次方程 转化”成x=a 的形式.解一 1等步骤,把一个2.存込(y-1) ]=-| (/-I)考占:V八、、•解一元一次方程. 计算题.这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为 解:左右同乘 12 可得:3[2x -( X - 1) ]=8 (X - 1), 化简可得:3x+3=8x - 8, 移项可得:5x=11 , 解可得x=31. 51,从而得到方程的解.点评:故原方程的解为x=31.5若是分式方程,先同分母,转化为整式方程后,再移项化简,解方程可得答案.解方程:4 - x=3 (2-x );⑵解方程:启-= 03. (1) 考点:解一元一次方程. 专题:计算题.分析: (1)先去括号,然后再移项、合并同类型,最后化系数为1,得出方程的解;(2)题的方程中含有分数系数,应先对各式进行化简、整理,然后再按(1)的步骤求解.解答: 解: (1)去括号得:4 -x=6 - 3x ,移项得:-x+3x=6 - 4, 合并得:2x=2 ,系数化为1得: (2)去分母得:去括号得:5x - 移项得:5x - 合并得:3x=9 ,x=1. 5 (X - 1)- 2 (X+1 ) =2,5- 2x - 2=2,2x=2+5+2 ,分析:(1)是简单的一元一次方程,通过移项,系数化为1即可得到;系数化1得:x=3 .点评:(1)本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理•因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从 而达到分解难点的效果. (2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在 今后常会用到.4.解方程:号违■罕考点:解一儿 专题:次方程.计算题.分析:此题两边都含有分数,分母不相同,如果直接通分,有一定的难度,但将方程左右同时乘以公分母 会降低. 6,难度就解答:解:去分母得:3 ( 2-x )- 18=2x -( 2x+3 ), 去括号得:6 - 3x - 18=- 3, 移项合并得:-3x=9,■ • x= — 3.点评:本题易在去分母和移项中出现错误,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们 要教会学生分开进行,从而达到分解难点的效果.5.解方程(1) 4 (X — 1)- 3 (20 - x ) =5 (x - 2); (2)x-=2=2-空.23考点:解一元一次方程. 专题:计算题.分析: (1)先去括号,再移项、合并同类项、化系数为* (2)先去分母,再去括号,最后移项,化系数为 解:(1) 移项得: 合并得:系数化为 解答:1,从而得到方程的解; 1,从而得到方程的解. 去括号得:4x - 4 - 60+3x=5x - 10 (2 分)-5x=4+60 - 10 ( 3 分) (5分)x=27; (6 分)6x - 3 (x - 1) =12 - 2 (x+2 ) (2 分) 3x+3=12 - 2x - 4 (3 分)4x+3x 2x=54 1 得: 点评:(2)去分母得: 去括号得:6x -移项得:6x - 3x+2x=12 - 4 - 3 (4 分) 合并得:5x=5 ( 5分) 系数化为1得:x=1 . (6分)去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多 项式)作为一个整体加上括号•去括号时要注意符号的变化.解方程:3 (x - 1) =2x+3 ;Y + gT — 1(2)解方程:^=x -丄J .6 26. (1) 考点:解一元一次方程.专题:计算题.解答:解:(1) 3x - 3=2x+33x - 2x=3+3 x=6 ;(2)方程两边都乘以 6得:x+3=6x - 3 (x - 1)x+3=6x - 3x+3 x - 6x+3x=3 - 3-2x=0•• x=0 .点评:本题易在去分母、去括号和移项中出现错误,还可能会在解题前不知如何寻找公分母,怎样合并同类项,怎样化简,所以要学会分开进行, 从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.7.-£(1 - 2x )現(3x+1)考点:解一元一次方程.专题:计算题.&解方程: (1) 5 (x - 1)- 2 (x+1 ) =3 ( x - 1) +x+1 ;(2)0. Q2x -0・ 18^+0.18 _ 1.5- 3 玄 丿 0・ 03 1 0?l2 ~2~考点:解一元一次方程. 专题:计算题. —分析:(1)可采用去括号,移项,合并同类项,系数化1的方式进行;(2 )本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为 整数形式,难度就会降低.解答:解:(1) 5 (x - 1)- 2 ( x+1) =3 (x - 1) +x+13x - 7=4x - 2 ••• x= - 5;(2)原方程可化为:竿+1竺翼■宅空3 12 20去分母得:40x+60=5 ( 18 - 18x )- 3 (15 - 30x ), 去括号得:40x+60=90 - 90x - 45+90x , 移项、合并得:40x= - 15, 系数化为1得:x=-上.8分析: 解答: 1,从而得到方程的解.点评:这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为 解:-7 (1 - 2x ) =3疋(3x+1)-7+14x=18x+6 -4x=13_ 13 x=-T解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号. 1 .此题去分母时,方程两端(1)此题主要是去括号,移项,合并同类项,系数化 1.(2 )方程两边每一项都要乘各分母的最小公倍数,方程两边每一项都要乘各分母的最小公倍数,切勿漏 乘不含有分母的项,另外分数线有两层意义,一方面它是除号,另一方面它又代表着括号,所以在去分母 时,应该将分子用括号括上.11.计算:点评:(1 )本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理•因为看到小数、分数 比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而 达到分解难点的效果;(2)本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变•这一性质在 今后常会用到.9.解方程:X _ 3H +1二]_ X ~ 13~2~考占: V 八、、• 专题: 分析: 解答: 解一元一次方程. 计算题这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为 ~r ,2x -( 3x+1 ) =6 - 3 (X - 1),2x - 3x - 1=6 - 3x+3,2x=10 ,解: Z-3去分母得:去括号得:点评: 10.解方程: (1) 4x - 3 1,从而得到方程的解.移项、合并同类项得:系数化为1得:x=5 . 去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多 项式)作为一个整体加上括号. (4 - x ) =2 ;⑵-(X - 1)=2 V ( x+2). 考点: 专题:分析: 解一元一次程. 计算题. 解答: (1 )先去括号,再移项,合并同类项,系数化1,即可求出方程的解;(2 )先去分母,再去括号,移项,合并同类项,系数化 1可求出方程的解.解: (1)4x - 3 (4 - X ) =2去括号,得4x - 12+3x=2移项,合并同类项 7x=14 系数化1,得x=2 .(2 )4 (x - 1) =2-4 (x+2 )2 5去分母,得 5 (x - 1) =20 - 2 (x+2 ) 去括号,得 5x - 5=20 - 2x - 4 移项、合并同类项,得 7x=21系数化1,得x=3 .点评:13•解方程:(1) 罗 (2)4(-1)解一元一次方程.(1)计算: (2)解方程: -弓[-沁(普)2-2]X- 1 3K - 1.----- ~ --------- 二 _ I2 4考点: 专题: 分析: 解一元一次方程;有理数的混合运算. ■计算题.(1 )根据有理数的混合运算法则计算:先算乘方、后算乘除、再算加减; (2)两边同时乘以最简公分母 4,即可去掉分母.解答: 点评: 解:(1)原式=—号X (―— 2),=号(-6),4迈.(2)去分母得:2 (x - 1)-( 3x - 1) = - 4,解得:x=3 .解答此题要注意:(1)去分母时最好先去中括号、再去小括号,以减少去括号带来的符号变化次数; 去分母就是方程两边同时乘以分母的最简公分母.12.解方程: 考占: V 八、、• 专题: 分析: 解一元一次方程. 计算题.(1 )这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为 (2 )解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、化系数为 1,从而得到方程的解. 1.解答: 解:(1)去分母得:3 (3x - 1) +18=1 - 5x , 去括号得:9x - 3+18=1 - 5x , 移项、合并得: 系数化为1得:点评: 14x= - 14, x= - 1 ;E 3 卫X ,x+1 = d x ,-34 苍-1,1212 T ______本题考查解一元一次方程^确掌握解一元一次方程的一般步骤,注意移项要变号、去分母时 最小公倍数.(2)去括号得:移项、合并同类项得:系数化为1得:x=1”也要乘以考点:本题考查解一元一次方程,正确掌握解一元一次方程的一般步骤,注意移 项要变号、去分母时 1 ”也要乘以最小公倍数.专题: 分析:计算题.(1) 去分母、去括号、 (2) 去分母、去括号、 移项、合并同类项、化系数为 移项、合并同类项、化系数为1. 1.解答: (1)解:去分母得:去括号得:15X+5 - 20=3x - 2 - 4x - 6,移项得: 合并得: 5 (3x+1 )- 2X10=3x - 2 - 2 (2x+3),15x+x= - 8+15,16x=7 ,7 ;(2)解:° 4-1)_2 (时 1)二_4,解得:94 (x - 1)- 18 (x+1 ) = - 36, 4x - 4 - 18x - 18=- 36,-14x= - 14,14 .解方程:(1) 5 (2x+1 )- 2 (2) ¥¥+2 4 6 (3)星[3 (x -丄)+ 星]=5x - 1 3 2 3 (2x - 3) =6考点: 专题: 分析: 解一元一次方程. 计算题.(2) 通过去括号、移项、合并同类项、系数化为 (3) 乘最小公倍数去分母即可;(4) 主要是去括号,也可以把分数转化成整数进行计算.1,解得x 的值;解答: 解:(1)去括号得:10x+5 - 4x+6=6 移项、合并得: 方程两边都除以 (2)去分母得:去括号得:3x - 6=8 - 6x+24 ,移项、合并得:9x=38 , 方程两边都除以9,得x=』§;96x= - 5, 6,得 x= - 2;63 (x - 2) =2 (4 - 3x ) +24 ,点评:点评:(3)整理得:里[3 ( X-1) +里]=5x - 1 ,3 2 3 X - 2+1=5x - 1, 多项、合并得:x=0 . 一元一次方程的解法:一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为 把一个一元一次方程 转化”成x=a 的形式•解题时,要灵活运用这些步骤.15. (A 类)解方程:5x - 2=7x+8 ; 解方程:—(X - 1)-( X+5)=-丄; 3 3 解方程:匕-空iL.]. 3 (B 类) (C 类) 1等步骤,考占: V 八、、• 专题: 分析: 解答: 解一元一次方程. 计算题.通过去分母、去括号、移项、系数化为 1等方法,求得各方程的解.解:A 类:5x - 2=7x+8 移项:5x - 7x=8+2 化简:-2x=10 即:x= - 5;B 类:-3(X - 1)-( X+5)=--3丄X-1- X - 5=-丄3 33化简:Z x=53即:X=-—;2…4- X 2x+lC 类: --------------- 去括号: =12 3 3 ( 4 -X )- 2 (2x+1) =6 12 - 3x - 4x - 2=67x= - 4点评: 去分母: 去括号: 化简:-即:x=27本题主要考查一元一次方程的解法,比较简单,但要细心运算.16.解方程 (1)3 (X+6) =9 - 5 (1 - 2x )2x+l K +3 _ I (4)5 5 ,y+2—_ y 1 r-文丁0.3 考占: V八、、• 专题: 分析:解一元一次方程. 计算题. (1)去括号以后,移项,合并同类项,系数化为 1即可求解;X -解:(1)去括号得:4x - 15+3x=13 , 移项合并得:7x=28 , 系数化为1得:得x=4 ; (2)原式变形为X +3=^^_A',35去分母得:5 (2x - 5) +3 (x - 2) =15 (x+3), 去括号得 10x - 25+3x - 6=15x+45 ,移项合并得-2x=76 , 系数化为1得:x= - 38.本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数 为1•注意移项要变号.42 +1-2|3X(-+)3(-4)「' (2)解答 (2) (3)首先去掉分母,再去括号以后,移项,合并同类项,系数化为 1以后即可求解;(4)首先根据分数的基本性质,把第一项分母中的 0.3化为整数,再去分母,求解.解: (1) 去括号得:3x+18=9 - 5+10x 移项得:3x - 10x=9 - 5 - 18 合并同类项得:-7x= - 14 则 x=2 ;(2) 去分母得:2x+1=x+3 - 5 移项,合并同类项得:x= - 3;(3) 去分母得:10y+2 ( y+2) =20 - 5 (y - 1) 去括号得:10y+2y+4=20 - 5y+5 移项,合并同类项得:17y=21系数化为1得:尸里; y 17 少绝-5x= - 1 3 去分母得:17+20X - 15x= - 3 移项,合并同类项得:5x= - 20系数化为1得:x= - 4. 占评:解方程的过程中要注意每步的依据,这几个题目都是基础的题目,需要熟练掌握. (4)原方程可以变形为: 17•解方程: (1)解方程: 解方程:4x - 3 (5 - X ) =13 X - 2 2it- 5 _ X ----- = ------ 353考占: V 八、、• 专题: 分析:计算题.(1 )先去括号,再移项,化系数为1,从而得到方程的解.(2 )这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.解一元一次方程.(2)计算: (3)解方程:(4)解方程:9 12-10.5-彳苗汽-2 -( - 3)2]4x - 3 ( 5 - X ) =2 ;X - 2 2z- 5 -12解答: 点评:18. (1) 计算:考占: V八、、• 分析: 解一 (1)(2)(3) (4)儿一次方程;有理数的混合运算.I 利用平方和立方的定义进行计算. I 按四则混合运算的顺序进行计算. I 主要是去括号,移项合并.I 两边同乘最小公倍数去分母,再求值.解答: 解:(1)- 42——i_-+|- 2|3X(-丄)3C-4)2= -rsx^8x(-1=-1 - 1 =-2.(2)- 12-|O.5-2|」X - 2-(- 3)2]3 3=-1-|£-訴余(-2-9)=-l+|x3X ( -11) =_ 11 =1迈13■ —■ =2 .(3 )解方程:4x - 3 (5 -x ) =2 去括号,得4x - 15+3x ) =2 移项,得 4x+3x=2+15 合并同类项,得 系数化为1得(4 )解方程:7x=1717X - 2 2z- 5 -点评: 去分母,得 15x - 3 (x - 2) =5 (2x - 5)- 3X5 去括号,得 15x - 3x+6=10x - 25 - 45 移项,得 15x - 3x - 10x= - 25 - 45 - 6合并同类项,得2x= - 76系数化为1,得x= - 38. _______________________________ 前两道题考查了学生有理数的混合运算,后两道考查了学生解一元一次方程的能力.19. (1) 计算: (2)计算: 2 (-1)如[—3? 乂(-j) -2]- C--| (3)解方程: (4)解方程:3x+3=2x+7 ; g Cx+15)三电Cx-7). 考占: V八、、• 专题: 分析:解一元一次方程;有理数的混合运算. 计算题.(1 )和(2)要熟练掌握有理数的混合运算;(3)和(4)首先熟悉解一元一次方程的步骤:去分母,去括号,移项,合并同类项,系数化为 解:(1) (1 - 2- 4) X (2鱼)5=-哙=-13;⑵原式=-1x (-4-2) x (揺)去括号得: -0.2x+1=1 , ••- 0.2x=0,•• x=0 ;“、x-2 3 (3計5)(2) 丁+垃=去分母得:(X+3)- 2 (X - 1) =9 - 3x .20.解方程(1)-0.2 (X -5) =1 ; X - 23 (3計5) 1 - 2s(2)3 + 垃二 2 6 .考点: 解一元一次方程.分析:(1)通过去括号、移项、系数化为(2 )通过去分母以及去括号、移项、 解答:解: (1)- 0.2 ( X -5) =1 ; 1等过程,求得X 的值;系数化为 1等过程,求得X 的值.点评: 2 (X - 2) +6x=9 •••-21X =48 , ._ _ 16…X= y .此题主要考查了一(3X+5)-( 1 - 2x ),儿一次方程解法,解一元一次方程常见的过程有去括号、移项、系数化为1等.考点:专题:解一元一次方程. 计算题.解答:1.点评:3=6X(-寺=-9;(3 )解方程:3X +3=2X +7 移项,得 3x - 2x=7 - 3合并同类项,得x=4 ;(4)解方程:g &+15) =+ 去分母,得 6 (X+15) =15 - 10 去括号,得 6x+90=15 - 10X+70 移项,得 6x+10x=15+70 - 90 合并同类项,得16x= - 5 系数化为1,得x= -A .16(1 )和(2)要注意符号的处理; 号法则以及合并同类项法则.逍〔…)(X-7)(4)要特别注意去分母的时候不要发生数字漏乘的现象,熟练掌握去括21•解方程:+ 2,分析: 解答: 先去括号得x+3 - 2x+2=9 - 3x ,然后移项、合并同类得到 2x=4,然后把x 的系数化为1即可.点评: 解:去括号得 x+3 - 2x+2=9 - 3x , 移项得 x - 2x+3x=9 - 3 - 2 , 合并得2x=4 , 系数化为1得x=2 . 本题考查了解一元一次方程:先去分母,再去括号,接着移项,把含未知数的项移到方程左边,不含未知 数的项移到方程右边,然后合并同类项,最后把未知数的系数化为 1得到原方程的解. 22. 8x - 3=9+5x . 5x+2 ( 3x - 7) =9 - 4 (2+x ). x- 1 2x+l T s - 0.3 x+0.1 0. 4 考点: 专题: 分析:解一元一次方程. 解答:方程思想. 本题是解4个不同的一元一次方程,第一个通过移项、合并同类项及系数化 1求解.第二个先去括号再通 过移项、合并同类项及系数化 1求解.第三个先去分母再同第二个.第四个先分子分母乘以 10,再同第三 个求解. 8x - 3=9+5x , 解:8x - 5x=9+3 , 3x=12, •• x=4 . • x=4是原方程的解; 5x+2 (3x - 7) =9 - 4 (2+x ),解:5x+6x - 14=9 - 8 - 4x ,5x+6x+4x=9 — 8+14 , 15x=15 , x=1 .••• x=1是原方程的解. x- 1 _ 2x+l TT ~r n .解:3 (x - 1)- 2 (2x+1 ) =12,3x - 3 - 4x - 2=12 ,3x - 4x=12+3+2 ,-x=17 ,••• x= - 17.••• x= - 17是原方程的解.H - 0. 3 计0.10.4 ■ 0.5 解:4 5+2,5 (10x - 3) =4 (1OX+1 ) +40, 50x - 15=40x+4+40 , 50x - 40x=4+40+15 ,10x=59,••• x=-^ 10 点评: ••• x=§?是原方程的解.10比题考查的知识点是解一元一次方程,关键是注意解方程时的每一步都要认真仔细,如移项时要变符号. 23.解下列方程: (1) 0.5x - 0.7=5.2 - 1.3 (x - 1); (2) 1-2 掘=3只+1 — 2 考占: V八、、• 分析: 解答: 解一元一次方程. (1)首先去括号,然后移项、合并同类项,系数化成 1,即可求解;(2)首先去分母,然后去括号,移项、合并同类项,系数化成 1,即可求解解:(1)去括号,得: 0.5x - 0.7=5.2 -1.3X+1.3移项,得:24.解方程:(1)(2)(3)(4)点评: 0.5x+1.3x=5.2+ 1.3+0.7合并同类项, 得:1.8x=7.2 , 则 x=4;(2)去分母得: 7 (1 - 2x ) =3(3x+1 )- 42, 去括号,得:7 -14x=9x+3 -42,移项,得:-14x -9x=3 - 42 -7,合并同类项, 得:-23x=-46, 则 x=2. 本题考查解一 元一次方程,解 一元一次方程 的一般步骤是: 去分母、去括 号、移项、合并 同类项、化系数 为1 .注意移项 要变号.考点: 分析:解答:点评: -0.5+3x=10 ; 3x+8=2x+6 ;2x+3 ( x+1) =5 - 4 (x - 1);i+l ,, 3 K - 2 T 1二 2 . 解一元 (1) (2)(3) (4) 次方程.移项,合并同类项,然后系数化成 1即可 移项,合并同类项,然后系数化成 1即可 去括号、移项,合并同类项,然后系数化首先去分母,然后去括号、移项,合并同 解:(1) 3x=10.5,x=3.5;(2) 3x - 2x=6 - 8, x= - 2;(3) 2x+3x+3=5 - 4x+4 ,2x+3x+4x=5+4 - 3, 9x=6,2 X 込;(4) 2 ( x+1) +6=3 (3x - 2), 2x+2+6=9x - 6, 2x - 9x= - 6 - 2 - 6, -7x= - 14,本题考查解一元一次方程,解 数为1.注意移项要变号.元一 -次方程的一25.解方程:^-^0.2.Z 5考占八、、解一兀一次方程.专题:计算题.分析:方程两边乘以10去分母后,去括号,考点:移项合并,将x系数化为1,即可求出专题:解. 分析:解答:解:去分母得:5 (3x - 1) - 2 (5x - 6)=2,去括号得:15x - 5 - 10x+12=2 ,移项合并得:5x= - 5,解得:x= - 1 . 解答:点评: 26.解方程:考点:专题:分析:解答:点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.(1) 10X- 12=5x+15 ; (2)(,7]誇(込)解一元一次方程.计算题.(1)先移项,再合并同类项,最后化系数为从而得到方程的解;(2 )先去括号,再移项、合并同类项,最后化系数为1,从而得到方程的解.解:(1)移项,得10x - 5x=12+15 , 合并同类项,得5x=27,方程的两边同时除以27X=E ;5,(2)去括号,得a+l_2x - 1 飞~,方程的两边同时乘以x+1=4x - 2,移项、合并同类项,得3x=3 ,方程的两边同时除以6,3,x=1 .本题考查解一元一次方程,一般步骤:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.解一元一次方程的27.解方程:(1) 8y - 3 (3y+2 ) =7解一元一次方程.计算题.(1)根据一元一次方程的解法,去括号,移项,合并同类项,系数化为1即可得解;(2 )这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.解:(1)去括号得,8y- 9y - 6=7 , 移项、合并得,-y=13, 系数化为1得,y= - 13;(2)去分母得,3 ( 3x - 1)- 12=2 (5x - 7),去括号得,9x - 3 - 12=10x - 14, 移项得,9x -10x= - 14+3+12 , 合并同类项得,-x=1 , 系数化为1得,x= - 1 .本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.17 - V28 .当k为什么数时,式子—比宰丄的值少3.5 3点评:考点:专题:分析:解答:点评:29.解下列方程:解一元一次方程.计算题.先根据题意列出方程,再根据一元一次方程的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.解:依题意,得生E ,3 5去分母得,5 (2k+1) =3 ( 17 - k) +45,去括号得,10k+5=51 - 3k+45 ,移项得,10k+3k=51+45 - 5,合并同类项得,13k=91 , 系数化为1得,k=7 ,•••当k=7时,式子土戈比坐2的值5 3少3.本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.(I) 12y -2.5y=7.5y+5考点: 专题: 分析:解答:计算题.(I)根据一元一次方程的解法,移项, 合并同类项,系数化为1即可得解;(n)是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解. 解: (I)移项得,合并同类项得,系数化为1得,12y - 2.5y -7.5y=5 ,2y=5, y=2.5 ;点评: 30.解方程:(n)去分母得,-2)- 2 (2x+3),去括号得,5x+5 - 10=3x - 2 - 4x- 6, 移项得,5x- 3x+4x= - 2 - 6 - 5+10, 合并同类项得,6x= - 3, 系数化为1得,x=-丄2本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.3K - 1.1 _ - 0* 2 0.16 - 0. ¥芷~0.4 ~0.3 -~oToe~.5 (x+1 )- 10= (3x考点:专题: 分析:解答: 解一元一次方程.计算题.由于方程的分子、分母均有小数,利用分数的基本性质,分子、分母同时扩大相同的倍数,可将小数化成整数. 解:原方程变形为30z- 11 40x- 2 16- 70x ’—= -------- 6, (3点评:4分) 去分母,得2) =2 X (16 - 70x) , (4 分)去括号,得90x - 33 - 160x+8=32 -140x, (5 分)移项,得90x - 160x+140x=32+33 - 8,(6分)合并同类项,得70x=57 , ( 7分)57系数化为1,得X喘.(8分)本题考查一元一次方程的解法•解一兀3X(30x - 11)- 4X(40x -一次方程的一般步骤:去分母,去括号,移项,合并同类项,系数化为1•本题的难点在于方程的分子、分母均有小数,将小数化成整数不同于去分母,不是方程两边同乘一个数,而是将分子、分母同乘一个数.。
解一元一次方程50道练习题(带答案)

解一元一次方程50道练习题(带答案)解一元一次方程50道练习题(带答案)
1. 问题:解方程2x + 5 = 9
解答:将已知方程写成标准形式,得到2x = 9 - 5 = 4
将方程两边同时除以2,得到x = 2
答案:x = 2
2. 问题:解方程3(x - 4) = 5
解答:将已知方程通过分配律展开,得到3x - 12 = 5
将方程两边同时加上12,得到3x = 17
将方程两边同时除以3,得到x = 17/3
答案:x = 17/3
3. 问题:解方程4 - 2x = 6x - 8
解答:将已知方程进行整理,得到-2x - 6x = -8 - 4
将方程进行合并,得到-8x = -12
将方程两边同时除以-8,注意要将负号带到分子,得到x = -12/-8
答案:x = 3/2
4. 问题:解方程6(x + 3) = 4(x - 2)
解答:将已知方程展开,得到6x + 18 = 4x - 8
将方程两边同时减去4x,得到2x + 18 = -8
将方程两边同时减去18,得到2x = -8 - 18
将方程两边同时除以2,得到x = -26/2
答案:x = -13
5. 问题:解方程2(x + 1) - 3(x - 2) = 4 - 2x
解答:将已知方程进行整理,得到2x + 2 - 3x + 6 = 4 - 2x 将方程两边同时减去2x,得到-2x + 8 = 4 - 2x
将方程两边同时加上2x,得到8 = 4
答案:此方程无解
......依次类推,解答剩下的题目。
解一元一次方程50道练习题(经典、强化、带答案)
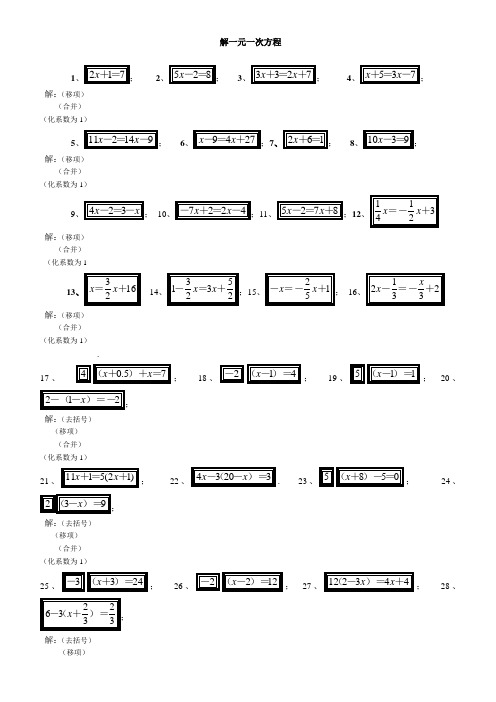
解一元一次方程1234解:(移项)(合并)(化系数为1)5678解:(移项)(合并)(化系数为1)9101112解:(移项)(合并)(化系数为113141516解:(移项)(合并)(化系数为1).17、;18、;19、;20、解:(去括号)(移项)(合并)(化系数为1)21222324、解:(去括号)(移项)(合并)(化系数为1)25;26、;27;28、解:(去括号)(移项)(合并)(化系数为1)293032解:(去分母)(去括号)(移项)(合并)(化系数为1)333435解:(去分母)(去括号)(移项)(合并)(化系数为1363738解:(去分母)(去括号)(移项)(合并)(化系数为139404142解:(去分母)(去括号)(移项)(合并)(化系数为1434445解:(去分母)(去括号)(移项)(合并)(化系数为14647解:(去分母)(去括号)(移项)(合并)(化系数为1484950解:(化整)(去分母)(去括号)(移项)(合并)(化系数为1【参考答案】1、【答案】(1(2(3(4(5(6(7(81.1、【答案】(9(10(11(12(13(14(15(162、【答案】(17(18(19(20(21(22)2.1、【答案】(23(24(25(26(27(28)(29(303、【答案】(31(32(33(34(35(36(37(383.1、【答案】(39(40(41(42(43(44(45(464、【答案】(47(48(49(50。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.2.6同解方程完成时间:20min一.选择题(共9小题)1.已知关于x的方程7x+3k=12与7x+3=0的解相同,则k的值为()A.﹣3 B.3C.﹣5 D.52.关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解,则a、b的关系为()A.a﹣b=3 B.b﹣a=3 C.b+a=3 D.b+a+3=03.已知方程4x=8与x﹣k=1的解相同,则4k2﹣1的值为()A.1B.3C.8D.174.吴云科和孟家福是七年级四班的两名爱好数学的优等生,在学完第三章《一元一次方程》后,吴云科对孟家福说:“方程与方程的解相同,你能求出k的值吗?”孟家福用笔算了一下给出正确答案,聪明的你知道是哪个吗?()A.0B.2C.1D.﹣15.如果方程x=1与2x+a=ax的解相同,则a的值是()A.2B.﹣2 C.3D.﹣36.下列方程中与方程3x=x+1的解相同的是()A.2x=4 B.2x=4x﹣1 C.5x+3=6 D.6x﹣15x=37.如果方程6x+3a=22与方程3x+5=11的解相同,那么a=()A.B.C.﹣D.﹣8.在方程:①3x﹣=1;②;③6x﹣5=2x﹣3;④x+=2x中,与方程2x=1的解相同的方程有()A.1个B.2个C.3个D.4个9.有4个关于x方程:(1)x﹣2=﹣1 (2)(x﹣2)+(x﹣1)=﹣1+(x﹣1)(3)x=0 (4)其中同解的两个方程是()A.(1)与(2)B.(1)与(3)C.(1)与(4)D.(2)与(4)二.填空题(共15小题)10.方程x+2=3的解也是方程ax﹣5=8的解时,则a=_________.11.已知关于x的方程+3=x与方程3﹣2x=1的解相同,则m2=_________.12.若方程2x﹣3=11与关于x的方程4x+5=3k有相同的解,则k的值是_________.13.已知关于x的方程5x+3k=24与5x+3=0的解相同,则k的值为_________.14.已知方程3(x+3)﹣1=2x的解与关于x的方程的解相同,则m2﹣2m+1的值为_________.15.已知关于x的方程=x+与=3x﹣2的解相同,则m=_________.16.如果关于x的方程和方程的解相同,那么k的值_________.17.如果方程与方程3x﹣2a=0的解相同,则a3=_________.18.方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程,则a+b+c=_________;如果关于x的方程2x+1=﹣3和方程=0的解相同,那么k=_________.19.若3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解,则(a﹣b+c)2009=_________.20.若以为未知数的方程3x=5x﹣8和有相同的解,则a=_________.21.已知方程2x﹣3=+x的解满足|x|﹣1=0,则m_________.22.关于x的方程3x=9与x+4=k的解相同,则代数式1﹣2|k|的值为_________.23.关于x的方程3mx+7=0和2 x+3n=0是同解方程,那么(mn)2=_________.24.已知:一元一次方程2x﹣2=3的解是方程的解,则m=_________.三.解答题(共6小题)25.已知:关于x的方程4x﹣k=2与3(2+x)=2k的解相同,求k的值及相同的解.26.已知关于x的方程2x+1=a和2x+2=0的解相同,求的值.27.若关于x的方程2x﹣3=1和=k﹣3x有相同的解,求k的值.28.如果方程的解与方程4y﹣(3m+1)=6y+2m﹣1的解相同,求式子的值.29.方程4+2(x﹣1)=0的解与关于x的方程的解相同,求k的值.30.当k为何值时,方程与方程有相同的解?6.2.6同解方程参考答案与试题解析一.选择题(共9小题)1.已知关于x的方程7x+3k=12与7x+3=0的解相同,则k的值为()A.﹣3 B.3C.﹣5 D.5考点:同解方程.专题:计算题.分析:先解方程7x+3=0,可得x=﹣,根据同解的定义可得x=﹣也是7x+3k=12的解,再把x=﹣代入7x+3k=12中即可求k.解答:解:解方程7x+3=0得,x=﹣,∵7x+3k=12与7x+3=0的解相同,∴x=﹣也是7x+3k=12的解,再把x=﹣代入7x+3k=12中,得7×(﹣)+3k=12,解得k=5.故选D.点评:本题考查了同解方程的定义,解题的关键是先求出x.2.关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解,则a、b的关系为()A.a﹣b=3 B.b﹣a=3 C.b+a=3 D.b+a+3=0考点:同解方程.分析:求出两个方程的解,根据已知得出两个解相等,即可求出答案.解答:解:x+a=2x﹣3,x﹣2x=﹣3﹣a,﹣x=﹣3﹣a,则x=3+a,2x﹣b=x,x=b,∵关于x的方程x+a=2x﹣3与2x﹣b=x有相同的解,∴3+a=b,∴b﹣a=3,故选B.点评:本题考查了对同解方程的理解,关键是求出3+a=b,题目比较好,难度适中.3.已知方程4x=8与x﹣k=1的解相同,则4k2﹣1的值为()A.1B.3C.8D.17考点:同解方程.专题:计算题.分析:先解出方程4x=8的解,然后代入求出k的值,进而可得出答案.解答:解:解方程4x=8,得:x=2,把x=2代入x﹣k=1,得:k=1,∴4k2﹣1=3.故选B.点评:本题考查同解方程的知识,比较简单,解决本题的关键是理解方程解的定义,注意细心运算.4.吴云科和孟家福是七年级四班的两名爱好数学的优等生,在学完第三章《一元一次方程》后,吴云科对孟家福说:“方程与方程的解相同,你能求出k的值吗?”孟家福用笔算了一下给出正确答案,聪明的你知道是哪个吗?()A.0B.2C.1D.﹣1考点:同解方程.专题:方程思想.分析:先解方程,得x=1,因为这个解也是方程的解,根据方程的解的定义,把x代入方程中求出k的值.解答:解:12﹣2(x﹣1)=3(1﹣x)+6(3﹣x)解得:x=1.把x=1代入方程得:4﹣=3k﹣,12﹣k﹣2=9k,解得:k=1.故选C.点评:本题考查了同解方程,解题的关键是正确解一元一次方程.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.5.如果方程x=1与2x+a=ax的解相同,则a的值是()A.2B.﹣2 C.3D.﹣3考点:同解方程.专题:计算题.分析:可以分别解出两方程的解,两解相等,就得到关于a的方程,从而可以求出a的值.解答:解:解第一个方程得:x=3,解第二个方程得:x=∴=3解得:a=3故选C.点评:本题解决的关键是能够求解关于x的方程,要能正确理解方程解的含义.6.下列方程中与方程3x=x+1的解相同的是()A.2x=4 B.2x=4x﹣1 C.5x+3=6 D.6x﹣15x=3考点:同解方程.专题:计算题.分析:求得题目中各个方程的解,即可作出判断.解答:解:方程3x=x+1的解是x=.A、解是x=2,故错误;B、解是x=,故正确;C、解是x=,故错误;D、解是x=﹣,故错误.故选B.点评:本题主要考查了一元一次方程的解法,正确解方程是解题的关键.7.如果方程6x+3a=22与方程3x+5=11的解相同,那么a=()A.B.C.﹣D.﹣考点:同解方程.专题:计算题.分析:先通过方程3x+5=11求得x的值,因为方程6x+3a=22与方程3x+5=11的解相同,把x的值代入方程6x+3a=22,即可求得a的值.解答:解:3x+5=11,移项,得3x=11﹣5,合并同类项,得3x=6,系数化为1,得x=2,把x=2代入6x+3a=22中,得6×2+3a=22,∴a=,故选B.点评:解一元一次方程的一般步骤是去分母,去括号,移项,合并同类项,移项时要变号.因为两方程解相同,把求得x的值代入方程,即可求得常数项的值.8.在方程:①3x﹣=1;②;③6x﹣5=2x﹣3;④x+=2x中,与方程2x=1的解相同的方程有()A.1个B.2个C.3个D.4个考点:同解方程.专题:计算题.分析:求出方程2x=1的解是x=,要判断x=是否是方程的解,就是把它代入方程的左右两边,看是否相等.解答:解:方程2x=1的解是x=A、把x=代入3x﹣=1,左边=﹣=1,左边=右边,因而x=是方程3x﹣=1的解,即与方程2x=1的解相同.B、把x=代入,左边=(+1)=,左边=右边,因而x=是方程的解,即与方程2x=1的解相同.C、把x=代入6x﹣5=2x﹣3,左边=3﹣5=﹣2,右边=1﹣3=﹣2,左边=右边,因而x=是方程6x﹣5=2x﹣3的解,即与方程2x=1的解相同.D、把x=代入x+=2x,左边=+=1,右边=2×=1,因而左边=右边,因而x=是方程6x﹣5=2x﹣3的解,即与方程2x=1的解相同.四个方程都与2x=1的解相同.故选D.点评:本题主要考查判断一个数是否是方程的解的方法.9.有4个关于x方程:(1)x﹣2=﹣1 (2)(x﹣2)+(x﹣1)=﹣1+(x﹣1)(3)x=0 (4)其中同解的两个方程是()A.(1)与(2)B.(1)与(3)C.(1)与(4)D.(2)与(4)考点:同解方程.分析:(1)移项可解出x的值.(2)先去括号在移项合并可得出x的值.(3)直接可得出x的值.(4)直接移项即可,注意分式有意义的条件.解答:解:(1)方程的解为x=1,(2)方程的解为x=1,(3)方程的解为x=0,(4)方程无解.∴只有(1)(2)是同解方程.故选A.点评:本题考查同解方程的知识,关键是正确求出4个方程的解,难度不大,注意要细心运算.二.填空题(共15小题)10.方程x+2=3的解也是方程ax﹣5=8的解时,则a=13.考点:同解方程.专题:计算题.分析:首先解出方程x+2=3的解,代入方程ax﹣5=8中求出a的值即可.解答:解:x+2=3,解得x=1;把x=1代入ax﹣5=8中,得a﹣5=8,解得a=13.点评:本题的关键是正确解一元一次方程.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.11.已知关于x的方程+3=x与方程3﹣2x=1的解相同,则m2=16.考点:同解方程.分析:首先解出方程3﹣2x=1的解,然后把方程的解代入方程+3=x求出m,即可求出m2.解答:解:解方程3﹣2x=1得:x=1,把x=1代入方程+3=x得:+3=1,解得:m=﹣4,则m2=16.故答案为:16.点评:本题考查了同解方程的知识,解答本题的关键是理解方程解得定义.12.若方程2x﹣3=11与关于x的方程4x+5=3k有相同的解,则k的值是11.考点:同解方程;解一元一次方程.专题:计算题.分析:先解方程2x﹣3=11求出x的值,把解得的值代入方程4x+5=3k,就可以得到一个关于k的方程,解方程就可以求出k的值.解答:解:解方程2x﹣3=11得:x=7,把x=7代入4x+5=3k,得:28+5=3k,解得:k=11.故答案为:11.点评:本题考查同解方程的知识,已知条件中涉及到方程的解,把方程的解代入原方程,转化为关于字母系数a 的方程进行求解.13.已知关于x的方程5x+3k=24与5x+3=0的解相同,则k的值为9.考点:同解方程.专题:计算题.分析:首先根据5x+3=0得到5x=﹣3,再把5x=﹣3代入5x+3k=24求出k的值即可.解答:解:∵5x+3=0,∴5x=﹣3,∵方程5x+3k=24与5x+3=0的解相同,∴﹣3+3k=34,解得k=9,故答案为9.点评:本题考查了同解方程.解一元一次方程的一般步骤是去分母,去括号,移项,合并同类项,移项时要变号.因为两方程解相同,把求得x的值代入方程,即可求得常数项的值.14.已知方程3(x+3)﹣1=2x的解与关于x的方程的解相同,则m2﹣2m+1的值为25.考点:同解方程.分析:先求出方程3(x+3)﹣1=2x的解,再根据方程3(x+3)﹣1=2x的解与关于x的方程的解相同,把x的值代入方程中,求出m的值,再把m的值代入要求的式子,即可得出答案.解答:解:3(x+3)﹣1=2x,3x+9﹣1﹣2x=0,x=﹣8,∵方程3(x+3)﹣1=2x的解与关于x的方程的解相同,∴把x=﹣8代入方程得:3×(﹣8)+m=﹣27,解得:m=﹣4,把m=﹣4代入m2﹣2m+1得:(﹣4)2﹣2×(﹣4)+1=16+8+1=25;故答案为:25.点评:此题考查了同解方程,关键是能够求出关于x的方程,根据同解的定义建立方程,求出m的值.15.已知关于x的方程=x+与=3x﹣2的解相同,则m=﹣.考点:同解方程.分析:先求出方程=3x﹣2的解,然后把x的值代入方程=x+求出m的值.解答:解:解方程=3x﹣2,得:x=1,把x=1代入方程=x+得:=1+,解得:m=﹣.故答案为:﹣.点评:本题考查了同解方程,解答本题的关键是能够求解关于x的方程,要正确理解方程解的含义.16.如果关于x的方程和方程的解相同,那么k的值.考点:同解方程.分析:本题可先根据一元一次方程解出x的值,再根据解相同,将x的值代入二元一次方程中,即可解出k的值.解答:解:解方程得:x=﹣,把x=﹣代入方程得:2﹣=0,解得:k=5;故答案为:5.点评:本题考查了二元一次方程与一元一次方程的综合运用.运用代入法,将解出的x的值代入二元一次方程,可解出k的值.17.如果方程与方程3x﹣2a=0的解相同,则a3=.考点:同解方程.分析:根据第一个方程即可求得x=﹣;然后根据同解方程的定义,将其代入第二个方程,列出关于a的方程;最后通过解关于a的方程求得a的值后,把a的值代入所求的代数式并求值.解答:解:∵x+=0,∴x=﹣;根据题意得3×(﹣)﹣2a=0,解得a=﹣,∴a3==.故答案是:.点评:本题考查了同解方程.使方程左右两边相等的未知数的值是该方程的解.因此检验一个数是否为相应的方程的解,就是把这个数代替方程中的未知数,看左右两边的值是否相等,如果左边=右边,那么这个数就是该方程的解;反之,这个数就不是该方程的解.18.方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程,则a+b+c=1;如果关于x的方程2x+1=﹣3和方程=0的解相同,那么k=﹣2.考点:同解方程;一元一次方程的定义.专题:计算题.分析:根据一元一次方程的定义可得出a=0,b=1,c=0,然后计算即可a+b+c;先解出2x+1=3的值,然后代入可得出k.解答:解:∵方程ax2+3x2b﹣1+cy=2是关于x的一元一次方程,∴a=0,2b﹣1=1,c=0,解得:a=0,b=1,c=0,故可得a+b+c=1;方程2x+1=﹣3的解为:x=﹣2,代入可得:=0,解得:k=﹣2.故答案为:1、﹣2.点评:此题考查了同解方程的知识,关键是掌握使方程左右两边相等的未知数的值是该方程的解,难度一般.19.若3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解,则(a﹣b+c)2009=﹣1.考点:同解方程.专题:计算题;整体思想.分析:答题时首先解出一元一次方程的解,把一元一次方程的解代入另一个方程中,求得a﹣b+c的值.解答:解:∵3x﹣4=﹣1与ax﹣b+1=﹣c有相同的解,∴x=1也是ax﹣b+1=﹣c的解,∴a﹣b+c=﹣1,∴(a﹣b+c)2009=﹣1.点评:本题主要考查解一元一次方程,利用整体法求值是解答本题的关键.20.若以为未知数的方程3x=5x﹣8和有相同的解,则a=.考点:同解方程.专题:计算题.分析:解方程3x=5x﹣8就可以求出方程的解,这个解也是方程的解,根据方程的解的定义,把这个解代入就可以求出a的值.解答:解:首先解方程3x=5x﹣8得:x=4;把x=4代入方程,得到2+4a=a﹣5;解得:a=﹣.点评:本题的关键是正确解一元一次方程以及同解方程的意义.理解方程的解的定义,就是能够使方程左右两边相等的未知数的值.21.已知方程2x﹣3=+x的解满足|x|﹣1=0,则m﹣6或﹣12.考点:同解方程.分析:通过解绝对值方程可以求得x=±1.然后把x的值分别代入方程2x﹣3=+x来求m的值.解答:解:由|x|﹣1=0,得x=±1..当x=1时,由,得,解得m=﹣6;当x=﹣1时,由,得,解得m=﹣12.综上可知,m=﹣6或﹣12.故答案是:﹣6或﹣12.点评:本题考查了同解方程的定义.如果第一个方程的解都是第二个方程的解,并且第二个方程的解也都是第一个方程的解,那么这两个方程叫做同解方程.22.关于x的方程3x=9与x+4=k的解相同,则代数式1﹣2|k|的值为﹣13.考点:同解方程.专题:计算题.分析:根据3x=9与x+4=k的解相同可得出k的值,代入即可得出答案.解答:解:3x=9,解得:x=3,将x=3代入x+4=k可得:3+4=k,k=7,∴1﹣2|k|=﹣13.故填:﹣13.点评:本题考查同解方程的定义,难度不大,理解同解的概念是关键.23.关于x的方程3mx+7=0和2 x+3n=0是同解方程,那么(mn)2=.考点:同解方程;代数式求值.分析:分别解出两个方程的解,使这两个解相等,即可得出mn的值,从而可得出答案.解答:解:由3mx+7=0与2x+3n=0是关于x的同解方程,可知m≠0,n≠0解得∴,.故填:2.点评:本题考查了同解方程的知识,属于比较简单的题目,注意掌握解答此类题目的方法.24.已知:一元一次方程2x﹣2=3的解是方程的解,则m=.考点:同解方程.分析:先求出方程2x﹣2=3的解,然后把x的值代入方程,求解m的值.解答:解:解方程2x﹣2=3得:x=,把x=,代入方程,得,m+=4,解得:m=.故答案为:.点评:本题考查了同解方程,解决本题的关键是能够求解关于x的方程,要正确理解方程解的含义.三.解答题(共6小题)25.已知:关于x的方程4x﹣k=2与3(2+x)=2k的解相同,求k的值及相同的解.考点:同解方程.专题:计算题.分析:由已知关于x的方程4x﹣k=2与3(2+x)=2k的解相同,所以得关于x、k的方程组,解方程组即可.解答:解:已知:关于x的方程4x﹣k=2与3(2+x)=2k的解相同,∴,解得,,所以k的值为6,相同的解为2.点评:此题考查的知识点是同解方程,本题解决的关键是能够求解关于x的方程,根据同解的定义建立方程组.26.已知关于x的方程2x+1=a和2x+2=0的解相同,求的值.考点:同解方程.专题:计算题.分析:先求出方程2x+2=0的解,代入方程2x+1=a求出a的值,代入代数式即可得出答案.解答:解:2x+2=0,解得:x=﹣1,将x=﹣1代入2x+1=a,得a=﹣1,则=1﹣1=0.点评:本题考查了同解方程的知识,关键是理解方程解得含义,另外在代入计算时要细心,不要出错.27.若关于x的方程2x﹣3=1和=k﹣3x有相同的解,求k的值.考点:同解方程.分析:求出方程2x﹣3=1中x的值,再把k当作已知条件求出方程=k﹣3x中x的值,再根据两方程有相同的解列出关于k的方程,求出k的值即可.解答:解:解方程2x﹣3=1得,x=2,解方程=k﹣3x得,x=k,∵两方成有相同的解,∴k=2,解得k=.点评:本题考查的是同解方程,熟知如果两个方程的解相同,那么这两个方程叫做同解方程是解答此题的关键.28.如果方程的解与方程4y﹣(3m+1)=6y+2m﹣1的解相同,求式子的值.考点:同解方程.分析:求出方程的解y=10,代入第二个方程求出m=﹣4,代入求出即可.解答:解:,2(y﹣4)﹣48=﹣3(y+2),2y﹣8﹣48=﹣3y﹣6,5y=50,y=10,即方程4y﹣(3m+1)=6y+2m﹣1的解也是y=10,代入得:40﹣(3m+1)=60+2m﹣1,m=﹣4,所以=4﹣=.点评:本题考查了一元一次方程的解,解一元一次方程,求出代数式的值的应用,关键是求出y、m的值.29.方程4+2(x﹣1)=0的解与关于x的方程的解相同,求k的值.考点:同解方程.专题:方程思想.分析:先求方程4+2(x﹣1)=0的解,再代入,求得k的值.解答:解:解方程4+2(x﹣1)=0,得x=﹣1,把x=﹣1代入,得﹣3k﹣2=﹣2,解得k=﹣.点评:此题主要考查了一元一次方程解的定义.解答此题的关键是熟知方程组有公共解的含义,考查了学生对题意的理解能力.30.当k为何值时,方程与方程有相同的解?考点:同解方程.分析:先解第二个方程,得x的值,因为这个解也是第一个方程的解,根据方程的解的定义,把x代入第一个方程中求出k的值.解答:解:解方程,得x=1,把x=1代入方程,得4﹣,解得k=﹣13,∴当k=﹣13时,方程与方程有相同的解.点评:此题考查同解方程,关键是正确解方程的解的定义,就是能够使方程左右两边相等的未知数的值.。
