立体几何定理总结_百度文库.

合集下载

立体几何相关定理汇总

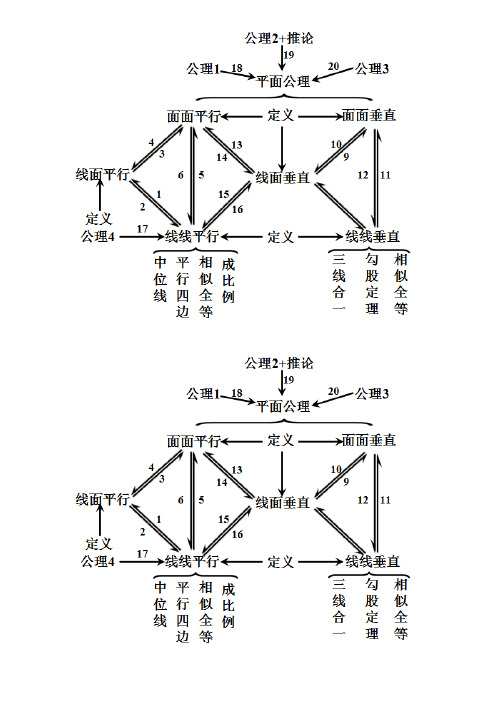
（16）
文字说明图像描述符号说明如果两条平行直线中的一条与平面垂直，则另一条也和平面垂直
（17）
如果两条直线都和第三条直线平行，则这两条直线平行
l // m m l
l // m l n m // n
A AB B
（14）
如果两个平面平行，则垂直于一个平面的直线垂直于另一个平面
m l
lm
（11）
文字说明图像描述符号说明如果两个平面内都垂直于交线的两条直线垂直，则两个平面垂直
（12）
如果两个平面垂直，则两个平面内都垂直于交线的两条直线垂直
（4）
如果两个平面平行，则一个平面内的任意直线都与另一个平面平行
（5）
如果一个平面内两条相交直线和另一个平面内两条相交直线都平行，那么这两个平面平行
符号说明
Hale Waihona Puke l m l // l // m
（6）
l l // m m
（15）
如果两条直线同垂直于一个平面，那么这两条直线平行
n l ,l n m , m n lm
n l m l ,l n m , m n
l // l
立体几何定理汇总
（1）
文字说明图像描述符号说明
（2）
（3）
（4）
（5）
（6）
文字说明图像描述符号说明
（7）
（8）
（9）

立体几何常考定理的总结(八大定理)

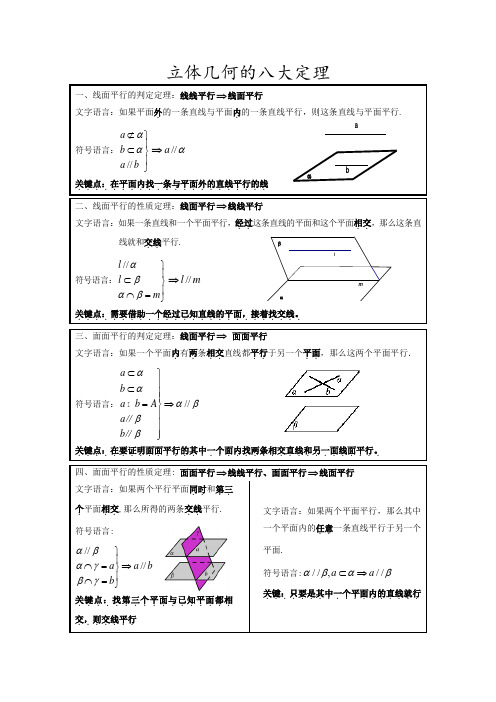
lmβααba立体几何的八大定理一、线面平行的判定定理：线线平行⇒线面平行文字语言：如果平面外．的一条直线与平面内．的一条直线平行，则这条直线与平面平行. 符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点：在平面内找一条与平面外的直线平行的线．．．．．．．．．．．．．．．．．．．．．．二、线面平行的性质定理：线面平行⇒线线平行文字语言：如果一条直线和一个平面平行，经过．．这条直线的平面和这个平面相交．．，那么这条直线就和交线．．平行. 符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点：需要借助一个经过已知直线的平面，接着找交线。

．．．．．．．．．．．．．．．．．．．．．．．．．．三、面面平行的判定定理：线面平行⇒ 面面平行文字语言：如果一个平面内．有两．条相交．．直线都平行．．于另一个平面．．，那么这两个平面平行．符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点：在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行文字语言：如果两个平行平面同时．．和第三．．个．平面相交．．,那么所得的两条交线．．平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点：找第三个平面与已知平面都相．．．．．．．．．．．．．．．．．交，则交线平行．．．．．．．文字语言：如果两个平面平行，那么其中一个平面内的任意．．一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键：只要是其中一个平面内的直线就行．．．．．．．．．．．．．．．．．．nmAαaBA l βαaβα五、线面垂直的判定定理：线线垂直⇒线面垂直文字语言：如果一条直线和一个平面内．的两．条相交．．直线垂直．．，那么这条直线垂直于这个平面. 符号语言：,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点：在平面内找两条相交直线与所要证的直线垂直．．．．．．．．．．．．．．．．．．．．．．．．六、线面垂直的性质定理：线面垂直⇒线线垂直文字语言：若一条直线垂直于一个平面，则这条直线垂直平面内的任意．．一条直线. 符号语言：l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点：往往线面垂直中的线线垂直需要用这个定理推出．．．．．．．．．．．．．．．．．．．．．．．．．七、平面与平面垂直的判定定理：线面垂直⇒面面垂直文字语言：如果一个平面经过．．另一个平面的一条垂线，则这两个平面互相垂直. （如果一条直线垂直于一个平面，并且有另一个平面经过这条直线，那么这两个平面垂直）符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点：．．．．在需要证明的两个平面中找线面垂直．．．．．．．．．．．．．．．．八、平面与平面垂直的性质定理：面面垂直⇒线面垂直文字语言：如果两个平面互相垂直，那么在一个平面内垂直．．于它们的交线．．的直线垂直于另一个平面.符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点：先找交线，再在其中一个面内找与交线垂直的线。

高中立体几何八大定理

lmβααba线面位置关系的八大定理一、直线与平面平行的判定定理：文字语言：如果平面外的一条直线与平面内的一条直线平行，则这条直线与平面平行图形语言：符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α 作用：线线平行⇒线面平行二、直线与平面平行的性质定理：文字语言：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行。

图形语言：符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用：线面平行⇒线线平行三、平面与平面平行的判定定理文字语言：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．图形语言：符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 作用：线线平行⇒ 面面平行四、平面与平面平行的性质定理:文字语言：如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行nmAαaαbaBA l βαaβα五、直线与平面垂直的判定定理：文字语言：如果一条直线和一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面图形语言：符号语言： ,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭作用：线线垂直⇒线面垂直六、直线与平面垂直的性质定理：文字语言：若两条直线垂直于同一个平面，则这两条直线平行图形语言：符号语言：//a a b b αα⊥⎫⇒⎬⊥⎭作用：线面垂直⇒线线平行七、平面与平面垂直的判定定理：文字语言：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。

图形语言：符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭注：线面垂直⇒面面垂直八、平面与平面垂直的性质定理：文字语言：如果两个平面互相垂直，那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言：符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用：面面垂直⇒线面垂直Welcome !!! 欢迎您的下载，资料仅供参考！。

立体几何公理定理总结

立体几何公理定理总结
一．公理
公理1：如果一条直线上两点在一个平面内，那么这条直线在此平面内.
公理2：过不在一条直线上的三点，有且只有一个平面.
公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.
公理4：平行于同一条直线的两条直线平行.
二．空间位置关系
面面平行：
判定：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行．
性质：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．
四．垂直
线线垂直：
平面上的判定如果直线与平面垂直，则该直线与平面内任意
一条直线垂直．
线面垂直：
定义：如果一条直线垂直于一个平面内的任意一条直线，那பைடு நூலகம்就说这条直线和这个平面垂直.
判定：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直.
性质：垂直于同一个平面的两条直线平行．
面面垂直：
定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．
判定：一个平面经过另一个平面的一条垂线，则这两个平面垂直．
性质：两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面．
线线位置关系：平行、相交、异面．定理：空间中如果两个角的两边分别对应
平行，那么这两个角相等或互补. 线面位置关系：线在平面内、线与平面相
交、线与平面平行．面面位置关系：平行、相交．
三．平行
线面平行：
判定：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．
性质：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行．

立体几何所有的定理大总结绝对全

（二）异面直线所成角1.定义：不一样在任何一个平面内的两条直线或既不平行也不订交的两条直线叫异面直线。

2.画法：借助协助平面。

1.定义：关于异面直线 a 和 b，在空间任取一点 P，过 P 分别作 a 和 b 的平行线a1和b1，我们把 a1和b1所成的锐角或许叫做异面直线 a 和 b 所成的角。

2.范围： (0 °， 90°】( ★空间两条直线所成角范围：【0°， 90°】 )（三）线面角1. 定义：当直线 l 与平面α订交且不垂直时，叫做直线 l 与平面α斜交，直线 l 叫做平面α的斜线。

设直线 l 与平面α斜交与点 M，过 l 上随意点 A，做平面α的垂线，垂足为O，把点 O叫做点 A 在平面α上的射影，直线 OM叫做直线 l 在平面α上的射影。

1.定义：把直线 l 与其在平面α上的射影所成的锐角叫做直线 l 和平面α所成的角。

2.范围【 0°， 90°】（★斜线与平面所成角范围：【0°， 90°】）（三）二面角1.定义：（1）半平面：平面内的一条直线把这个平面分红两个部分，此中每一个部分叫做半平面。

（3）二面角的棱：这一条直线叫做二面角的棱。

（4）二面角的面：这两个半平面叫做二面角的面。

（5）二面角的平面角：以二面角的棱上随意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。

（6）直二面角：平面角是直角的二面角叫做直二面角。

1.定义：从一条直线出发的两个半平面所构成的图形叫做二面角。

2. 表示：以下列图，可记作 α-AB- β或 P-AB-Q3. 范围为【 0°， 180°】（五）六种距离1. 点到点的距离：两点之间的线段 PQ 的长。

2. 点到线的距离：过 P 点作 PPl ，交 l 于 P ，线段 PP 的长。

1 1 13. 点到面的距离：过 P 点作 PP 1，交于 P 1 ，线段 PP 1 的长。

(完整版)高中立体几何八大定理

线面位置关系的八大定理一、直线与平面平行的判定定理：文字语言：如果平面外的一条直线与平面内的一条直线平行，则这条直线与平面平行a 图形语言：符号语言：a ⊄α⎫⎪b ⊂α⎬⇒a //αa //b ⎪⎭αb作用：线线平行⇒线面平行二、直线与平面平行的性质定理：文字语言：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行。

图形语言：β⎫⎪符号语言：l ⊂β⎬⇒l //mα⋂β=m ⎪⎭作用：线面平行⇒线线平行三、平面与平面平行的判定定理l //αl m α文字语言：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．图形语言：符号语言：a ⊂αb ⊂αa I b =a ∥βb ∥β⎫⎪⎪⎪A ⎬⇒α//β⎪⎪⎪⎭作用：线线平行⇒面面平行四、平面与平面平行的性质定理:文字语言：如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行图形语言:α//β⎫⎪符号语言:α⋂γ=a ⎬⇒a //bβ⋂γ=b ⎪⎭作用:面面平行⇒线线平行五、直线与平面垂直的判定定理：文字语言：如果一条直线和一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面图形语言：符号语言：aa ma nam n Am,n作用：线线垂直线面垂直六、直线与平面垂直的性质定理：文字语言：若两条直线垂直于同一个平面，则这两条直线平行图形语言：符号语言：Amnabaa//bb作用：线面垂直线线平行七、平面与平面垂直的判定定理：文字语言：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。

图形语言：a符号表示：aa注：线面垂直面面垂直八、平面与平面垂直的性质定理：文字语言：如果两个平面互相垂直，那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言：I l符号语言：ABABAB l作用：面面垂直线面垂直Al B。

立体几何中的所有结论

第九章：直线、平面、简单几何体小结一、重要的概念和定理 1.公理和推论公理1.如果一条直线上的两个点在一个平面内，那么这条直线上的所有点都在这个平面内。

作用：判断直线在平面内的依据。

公理2.如果两个平面有一个公共点，那么它们还有其它公共点，且这些公共点的集合是通过该公共点的一条直线。

作用：判断两个平面相交和共线的依据。

公理3.经过不在同一直线上的三个点，有且只有一个平面。

推论1.经过一条直线和这条直线外一点，有且作用：确定平面的依据。

只有一个平面。

推论2.经过两条相交直线，有且只有一个平面。

推论3.经过两条平行直线，有且只有一个平面。

公理4.同平行于一条直线的两条直线互相平行。

作用：判断平行的依据。

2.概念⑴直线与直线 ①异面直线：不在任何一个平面内的两条直线叫做异面直线。

②异面直线所成角：如果a 、b 是异面直线，经过空间任意一点0作a '∥a ，b '∥b ，那么把a '和b '所成的锐角（或直角）叫做异面直线a 和b 所成的角。

如果两条异面直线所成的角是直角，就称这两条异面直线互相垂直。

显然若设异面直线所成角为α，则0<α≤2π。

③异面直线间的距离：和异面直线都垂直相交的直线叫做两条异面直线的公垂线。

两条异面直线的公垂线在这两条异面直线间的线段的长度，叫做两条异面直线的距离。

⑵直线和平面①直线和平面平行：如果一条直线和一个平面没有公共点，那么就说这条直线和这个平面平行。

②直线和平面垂直：如果一条直线和一个平面内的任何一条直线都垂直，那么就说这条直线和这个平面垂直，这条直线叫做平面的垂线，平面叫做直线的垂面。

③射影：自一点P 向平面α引垂线，垂足P ' 叫做点P 在平面α内的正射影（简称射影）。

如果图形F 上的所有点在一平面内射影构成图形F '，则F '叫做图形F 在这个平面内的射影。

过斜线上斜足以外的一点向平面引垂线，过垂足和斜足的直线叫做斜线在这个平面上的射影。

(完整版)高中立体几何八大定理

线面地址关系的八大定理一、直线与平面平行的判判定理：文字语言：若是平面外的一条直线与平面内的一条直线平行，那么这条直线与平面平行a图形语言：符号语言：a bb a //a // b作用：线线平行线面平行二、直线与平面平行的性质定理：文字语言：若是一条直线和一个平面平行，经过这条直线的平面和这个平面订交，那么这条直线就和交线平行。

图形语言：l //l符号语言： l l // mm m作用：线面平行线线平行三、平面与平面平行的判判定理文字语言：若是一个平面内有两条订交直线都平行于另一个平面，那么这两个平面平行．图形语言：符号语言：aba Ib A//a∥b∥作用：线线平行面面平行四、平面与平面平行的性质定理:文字语言：若是两个平行平面同时和第三个平面订交, 那么所得的两条交线平行图形语言 ://符号语言 :a a // bb作用 :面面平行线线平行五、直线与平面垂直的判判定理：文字语言：若是一条直线和一个平面内的两条订交直线垂直，那么这条直线垂直于这个平面图形语言：符号语言：aa ma na m n Am, nAn m作用：线线垂直线面垂直六、直线与平面垂直的性质定理：文字语言：假设两条直线垂直于同一个平面，那么这两条直线平行图形语言：符号语言：aa //b b ab作用：线面垂直线线平行七、平面与平面垂直的判判定理：文字语言：若是一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

图形语言：a a符号表示：a注：线面垂直面面垂直八、平面与平面垂直的性质定理：文字语言：若是两个平面互相垂直，那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言：I l符号语言：ABABAB l Al B作用：面面垂直线面垂直。

立体几何公理定理总结

性质：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行．
面面平行：
判定：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行．
性质：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．
四．垂直
线线垂直：
平面上的判定如果直线与平面垂直，则该直线与平面内任意
判定：一个平面经过另一个平面的一条垂线，则这两个平面垂直．
性质：两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面．
立体几何公理定理ห้องสมุดไป่ตู้结
一．公理
公理1：如果一条直线上两点在一个平面内，那么这条直线在此平面内.
公理2：过不在一条直线上的三点，有且只有一个平面.
公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.
公理4：平行于同一条直线的两条直线平行.
二．空间位置关系
线线位置关系：平行、相交、异面．定理：空间中如果两个角的两边分别对应
平行，那么这两个角相等或互补. 线面位置关系：线在平面内、线与平面相
交、线与平面平行．面面位置关系：平行、相交．
三．平行
线面平行：
判定：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．
一条直线垂直．
线面垂直：
定义：如果一条直线垂直于一个平面内的任意一条直线，那么就说这条直线和这个平面垂直.
判定：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直.
性质：垂直于同一个平面的两条直线平行．
面面垂直：
定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．

立体几何定理总结

(1)平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行。

(2)一个平面内两条相交直线与另一个平面平行，则这两个平面平行。

(3)一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。

(4)一个平面过另一个平面的垂线，则这两个平面垂直。

(5)一条直线和一个平面平行，则过这条直线的任一平
面与此平面的交线与该直线平行。

(6)如果两个平行平面同时与第三个平面相交，那么它
们的交线平行。

(7)垂直于同一个平面的两条直线平行。

(8)两个平面垂直，则一个平面内垂直于交线的直线与
另一个平面垂直。

(9)两个平面平行，一个平面内的任意一条直线与另一
平面平行。

(10)一条直线与一个平面垂直，则这条直线垂直于这
个平面内的任意一条直线。

(11)如果一个平面内的两条相交直线与另一个平面
内的两条相交直线分别平行，则两平面平行。

(12)如果两条平行直线中的一条垂直于一个平面，那
么另一条也垂直于这个平面。

(13)垂直于同一条直线的两个平面平行。

(14)如果一条直线垂直于两平行平面中的一个，那么
此直线也垂直于另一个。

数学立体几何八大定理

数学立体几何八大定理
1. 柿子定理：一个作为平面多边形底面的凸多面体的侧面积等
于这个凸多面体表面积的一半加上这个多面体面数目乘以它的底面积。

2. 欧拉定理：一个简单凸多面体的面数、顶点数和边数满足公式：面
数+顶点数=边数+2。

3. 狄利克雷定理：如果一个立体角的每个边界面都可以划分成互不相
交有限个平凡的平面角，则这个立体角为平凡的。

一个立体角被称为
平凡的，当且仅当它可以被划分成三角形。

4. 菲赫斯定理：一个多面体的每条棱所在的平面相交于一点（称为多
面体的菲赫斯点）。

5. 球冠切割定理：一个球的表面可以被三个平面分割成球冠。

6. 萨公定理：任何一个超过120度的立体角可以被切割成平凡的立体角。

7. 凸多面体的交角定理：凸多面体中任意两个面交角的余角的总和等
于360度。

8. 柯西・切比雪夫定理：如果两个凸多面体的交集不为空，则它们的
交界面至少有一点。