串、数组和广义表结构特点和储存方法
数据结构各章概要

数据结构各章概要数据结构是计算机科学中非常重要的一个学科,其主要研究各种数据的组织方式和操作方法。
善于运用合适的数据结构可以提高算法的效率,并优化程序的性能。
本文将对数据结构的各个章节进行概要介绍,帮助读者了解不同章节的主要内容和应用。
第一章:引论在引论章节,我们将引入数据结构的基本概念和术语,例如什么是数据、数据项、数据对象等等。
同时,还将介绍数据结构的分类和基本操作,如搜索、遍历、插入、删除和排序。
这些基础知识是后续章节的基础。
第二章:线性表线性表是数据结构中最简单、最基本的一种结构。
其特点是数据元素之间的前驱和后继关系非常明确。
线性表可以用数组和链表两种方式实现。
在本章节中,我们将分别介绍顺序表和链表的实现原理、插入、删除、合并以及应用场景。
第三章:栈和队列栈和队列是两种特殊的线性表结构,它们对数据的访问具有限制性。
栈具有“先进后出”的特点,而队列则具有“先进先出”的特点。
在本章节中,我们将介绍栈和队列的实现方式以及常见的应用场景,如递归、表达式求值、广度优先搜索等。
第四章:串串是由零个或多个字符组成的有限序列,其长度可以为零。
在本章节中,我们将介绍串的定义和操作,包括字符串的模式匹配、模式识别和编辑操作。
串的相关算法在文本处理、计算机网络等领域具有广泛的应用。
第五章:数组和广义表数组是一种在内存中以连续方式存储的数据结构,它具有高效的随机访问特性。
广义表是线性表的一种扩展,可以包含表结构、原子结构以及其他广义表。
本章节将介绍数组和广义表的定义、操作和应用。
第六章:树树是一种非线性的数据结构,具有分层次、递归和层次遍历等特点。
在本章节中,我们将介绍树的基本概念、二叉树、树的遍历算法、平衡树以及树的应用,如编译器中的语法树、文件系统的目录结构等。
第七章:图图是一种复杂的非线性数据结构,由顶点集合和边集合组成。
在本章节中,我们将介绍图的各种表示方式,图的遍历算法、最短路径算法以及常用的图算法,如最小生成树算法和拓扑排序。
四种基本的存储结构

四种基本的存储结构在计算机科学中,有四种基本的存储结构,分别是:顺序存储结构、链式存储结构、索引存储结构和散列存储结构。
这四种存储结构在不同场景下都有各自的优势和适用性。
1. 顺序存储结构(Sequential Storage Structure)顺序存储结构是将数据元素按照其逻辑顺序依次存放在一块连续的存储空间中。
这种结构依赖于元素本身的物理顺序,使得数据的访问和处理更为高效。
数组就是一种典型的顺序存储结构,可以通过下标进行随机访问。
优点:存取速度快,适用于静态数据。
缺点:插入和删除操作需要移动大量元素,不适用于频繁的插入和删除操作。
2. 链式存储结构(Linked Storage Structure)链式存储结构是通过指针将数据元素连接起来,每个元素都包含一个指向下一个元素的指针。
这种结构可以在任意位置插入和删除元素,不需要移动其他元素。
链表就是一种典型的链式存储结构。
优点:插入和删除操作高效,适用于动态数据。
缺点:访问一些特定元素需要遍历整个链表,存储和访问效率相对较低。
3. 索引存储结构(Indexed Storage Structure)索引存储结构通过建立索引表来提供对数据元素的快速访问。
索引表包含了数据元素的关键字和对应的物理地址,用户可以通过关键字直接访问到相应的数据元素。
常见的索引存储结构包括有序索引、散列索引等。
优点:访问速度快,适用于查找频繁的场景。
缺点:需要额外的存储空间来维护索引表,使得存储空间开销增加。
4. 散列存储结构(Hash Storage Structure)散列存储结构通过哈希函数将关键字映射到存储位置,可以快速定位到数据元素。
散列表是在实际应用中广泛使用的散列存储结构。
优点:快速查找,存取速度均匀稳定。
缺点:对存储空间的利用率较低,冲突处理可能会引起性能问题。
以上四种基本的存储结构都有各自的优缺点,在不同的应用场景下可以选择适合的存储结构来优化数据的存储和访问效率。
第四章数组、矩阵、广义表

数组、矩阵、广义表数组的概念和逻辑结构模糊定义:它就是数据类型相同的元素按一定顺序排列的集合,可以看作是广义表的推广数组具有的三个特征:1.数据元素类型必须一致2.数组在内存中占用一段连续的存储空间,数组元素的逻辑顺序和物理顺序一致3.数组中的元素本身可以是具有某种结构的数据,如整型,字符型,自定义结构体类型多维数组可以被看做是一维数组,n维数组(n>=2)可以看做是一维数组,它的每个数组元素都是一个n-1维的数组二维数组中每一个数组元素最多可以有两个直接前驱和两个直接后继(边界元素除外)——>在n维数组中,每个数组元素最多可以有n个直接前驱和n个直接后继,所以多维数组是一种非线性结构清晰定义:数组是一个具有固定格式和数量的数据有序集,每个数据元素由唯一的数组下标标识,因此,在数组上不适合做插入、删除数据元素的操作数组中两个主要操作:取值操作:给定数组下标,读取其对应的数据元素;赋值操作:给定数组下标,存储或修改与其对应的数据元素;数组的基本操作(书上P75面)数组的物理结构(是数组在计算机中的存储表示):实质是讨论数组在内存中的映像。
通常,数组在内存中被映像为向量,即用向量作为数组的一种存储结构。
因为内存的地址空间是一维的,用一维的连续存储空间存放多维数组,就必须通过某种次序将数组中的元素排成一个线性序列,然后将这个线性序列顺序存放在计算机中。
当数组的行列固定后,通过一个映像函数,则可根据数组元素下表得到它的存储地址:1.对于一维数组按下标顺序分配地址即可ai=a0+(n-1)d2.对于二维数组分配地址时,需要把它的元素映像存储在一维存储器中,如(BASIC,Pascal,C等)采用以行为主(先行后列)的方式顺序存放,即一行分配结束之后,再分配下一行,物理地址:aij=a00+(i*n+j)d3.“以行为主序”的分配规律:最右边的下标先从小到大变化,循环一遍后,右边第二个下标再变,……,按照此规律从右往左,最后变化的是数组元素最左边的下标特殊矩阵需要原因:二维数组很适合来表示矩阵结构,可是某些特殊矩阵中含有许多重复或无效的数据,如三角矩阵,对称矩阵,对角矩阵,稀疏矩阵。
数据结构第五章 数组与广义表

压缩存储方法:只需要存储下三角 (含对角线)上的元素。可节省一 半空间。
可以使用一维数组Sa[n(n+1)/2]作为n阶对称矩阵A的存 储结构,且约定以行序为主序存储各个元素,则在Sa[k]和矩
阵元素aij之间存在一一对应关系: (下标变换公式)
i(i+1)/2 + j 当i≥j k = j(j+1)/2 + i 当i<j
q = cpot[col];
T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i; T.data[q].e = M.data[p].e; ++cpot[col]; }
分析算法FastTransposeSMatrix的时间 复杂度:
for (col=1; col<=M.nu; ++col) … … for (t=1; t<=M.tu; ++t) … … for (col=2; col<=M.nu; ++col) … … for (p=1; p<=M.tu; ++p) … …
//对当前行中每一个非零元
处
brow=M.data[p].j;
理
if (brow < N.nu ) t = N.rpos[brow+1];
M
else { t = N.tu+1 }
的
for (q=N.rpos[brow]; q< t; ++q) { ccol = N.data[q].j; // 乘积元素在Q中列号
一、三元组顺序表
对于稀疏矩阵,非零元可以用三元组表示, 整个稀疏矩阵可以表示为所有非零元的三元组所 构成的线性表。例如:
数组广义表

数组广义表数组广义表是一种数据结构,用于表示多层次的数据组织关系。
它可以看作是一种多叉树的扩展形式,其中每个节点可以有任意多个子节点。
数组广义表在计算机科学中具有重要的应用价值,特别是在数据库管理和树结构算法中。
一、数组广义表的定义和特点数组广义表由若干个元素组成,每个元素可以是一个原子元素,也可以是一个数组广义表。
这种嵌套的结构使得数组广义表可以表示复杂的数据关系。
数组广义表通过使用方括号和逗号来表示各个元素之间的层次关系。
例如,[1, [2,3], 4]表示一个包含三个元素的数组广义表,其中第一个元素是1,第二个元素是一个包含两个元素的数组广义表,其第一个元素是2,第二个元素是3,第三个元素是4。
数组广义表具有以下特点:1. 多层次结构:数组广义表可以表示多个层次的数据组织关系,使得数据的嵌套和层次化处理成为可能。
2. 可变长度:数组广义表的每个节点可以包含任意多个子节点,使得数据的组织形式更加灵活。
3. 多用途性:数组广义表既可以表示简单的数据结构,也可以表示复杂的数据关系,适用于各种不同的应用场景。
二、数组广义表的应用1. 数据库管理:数组广义表可以用于表示和管理数据库中的复杂数据结构,如树形结构、图形结构等。
通过使用数组广义表,可以方便地对数据库中的数据进行增、删、改、查等操作。
2. 树结构算法:数组广义表可以作为树结构的一种扩展形式,用于表示和处理树形数据结构。
通过使用数组广义表,可以简化树结构的操作和管理,提高算法的效率。
3. 文件系统:数组广义表可以用于表示和管理文件系统中的目录结构。
通过使用数组广义表,可以方便地对文件和目录进行组织和管理,实现快速的文件查找和访问。
4. 网络路由:数组广义表可以用于表示和管理网络中的路由表。
通过使用数组广义表,可以方便地对网络路由进行组织和管理,实现高效的数据传输和路由选择。
5. 图形图像处理:数组广义表可以用于表示和处理图形图像中的复杂结构,如图形对象、图像分割等。
数据结构 5数组和广义表A
1 Status Locate(Array A,va_list ap,int &off) 2{ 3 //若ap指示的各下标值合法,则求出该元素在A中,相对地
址off
4 off=0; 5 for(i=0;i<A.dim;++i) 6 { 7 ind=va_arg(ap,int); 8 if(ind<0||ind>A.bounds[i]) return OVERFLOW; 9 off+=A.constants[i] *ind; 10 } 11 return OK; 12 }
行数 总列数,即 第2维长度 元素个数
ij
补充:计算二维数组元素地址的通式
设一般的二维数组是A[c1..d1, c2..d2],这里c1,c2不一定是0。
单个元素 长度
二维数组列优先存储的通式为: LOC(aij)=LOC(ac1,c2)+[(j-c2)*(d1-c1+1)+i-c1)]*L
6
例1〖软考题〗:一个二维数组A[1..6, 0..7],每个数组元素
16
5.4
1、定义:
广义表的定义
广义表是线性表的推广,也称为列表(lists) 记为: LS = ( a1 , a2 , ……, an ) 广义表名 表头(Head) 表尾 (Tail) n是表长
在广义表中约定:
① 第一个元素是表头,而其余元素组成的表称为表尾; ② 用小写字母表示原子类型,用大写字母表示列表。
13
1 Status Value(Array A,ElemType &e,…){ 2 //A是n维数组,e为元素变量,随后是n个下标值,若各下
标不超界,则e赋值为所指定的A的元素值,即将指定元素值 读到e变量中。
串的知识点总结

串的知识点总结1. 串的基本概念串是由零个或多个字符组成的有限序列,通常用来表示文本数据。
在编程语言中,串通常被定义为一个字符数组或字符串变量。
例如,在C语言中,字符串通常被定义为char类型的数组,而在Java语言中,字符串则是一个类对象。
2. 串的存储结构串的存储结构有两种常见形式:一是定长顺序存储结构,二是链式存储结构。
定长顺序存储结构是将串的字符按照顺序存储在一块连续的存储空间中,这种方式可以通过下标来访问任意位置的字符,但是需要预先分配足够的存储空间。
链式存储结构则是使用链表来存储串的字符,这种方式可以动态分配内存空间,但是访问任意位置的字符需要从链表头开始遍历,效率较低。
3. 串的基本操作串的基本操作包括串的创建、复制、连接、比较、插入和删除等。
创建串是指将一组字符转换成串的操作;复制是指将一个串的内容复制到另一个串中;连接是指将两个串连接在一起形成一个新的串;比较是指比较两个串的大小关系;插入是指在一个串中的指定位置插入一个子串;删除是指删除一个串中的指定子串。
这些操作都是串的基本操作,它们在实际应用中有着重要的作用。
4. 串的模式匹配串的模式匹配是指在一个主串中查找与给定模式串相匹配的子串的过程。
常见的模式匹配算法有暴力匹配算法、KMP算法和Boyer-Moore算法等。
暴力匹配算法是最简单的模式匹配算法,它的时间复杂度为O(m*n),其中m为主串长度,n为模式串长度;KMP算法是一种高效的模式匹配算法,它的时间复杂度为O(m+n),其中m为主串长度,n为模式串长度;Boyer-Moore算法是一种更加高效的模式匹配算法,它的时间复杂度为O(m*n),其中m为主串长度,n为模式串长度。
5. 串的应用串在计算机科学中有着广泛的应用,它在各种应用中都有着重要的作用。
例如,在文本编辑器中,串被用来表示文本文件的内容;在数据库系统中,串被用来表示数据的各种属性;在网络通信中,串被用来表示网页的URL地址等。
《数据结构》课程标准

《数据结构》课程标准学时:72学时(其中:讲课学时:36 上机学时:36 )先修课程:高等数学、C语言程序设计后续课程:软件开发相关的应用性课程(Android应用开发、软件工程等)适用专业:软件技术、移动应用开发、软件与信息服务等开课部门:信息工程与大数据学院一、课程的性质《数据结构》是面向软件技术相关专业的一门专业基础课,课程要求:熟练掌握线性表、栈和队的存储结构及基本操作,并能在相应的应用中正确地选用,培养学生用链式结构编写程序的能力;了解串和广义表的定义和存储结构;掌握数组的存储结构,熟悉稀疏矩阵的两种压缩存储方法的特点及适用范围;了解树的存储结构及特点,掌握二叉树和图的存储结构及其相应算法,培养学生用非线性结构解决实际问题的能力;掌握各种查找、排序方法,培养学生灵活应用已有排序方法的能力,开拓思路编写新的排序算法。
二、课程设计理念数据结构是计算机存储、组织数据的方式。
数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
精心选择的数据结构可以带来更高的运行或存储效率,数据结构往往同高兴的检索算法和索引技术有关。
1、课程地位理念在许多类型的程序设计中,数据结构的选择是一个基本的设计考虑因素。
许多大型的构造经验表明,系统实现的困难程度和系统构造的质量都严重的依赖于是否选择了最优的数据结构。
许多时候,确定了数据结构后,算法就容易得到了。
有些时候事情也会反过来,我们根据特定算法来选择数据结构与之适应。
不论哪种情况,选择合适的数据结构都是非常重要的。
选择了数据结构,算法随之确定,是数据而不是算法是系统构造的关键因素。
2、课程学情理念本课程开设在嵌入式系统工程专科第一学期,学生在学习本课程前已具备计算机基础、C语言基础等知识,本课程力图让学生学会在C语言环境下,运用面向对象的思想编写规范的代码,实现经典的数据结构和算法。
熟悉常用的数据结构和算法,使学生初步具备一个优秀的软件开发人员所应有的基本能力。
《数据结构与算法》第五章-数组和广义表学习指导材料

《数据结构与算法》第五章数组和广义表本章介绍的数组与广义表可视为线性表的推广,其特点是数据元素仍然是一个表。
本章讨论多维数组的逻辑结构和存储结构、特殊矩阵、矩阵的压缩存储、广义表的逻辑结构和存储结构等。
5.1 多维数组5.1.1 数组的逻辑结构数组是我们很熟悉的一种数据结构,它可以看作线性表的推广。
数组作为一种数据结构其特点是结构中的元素本身可以是具有某种结构的数据,但属于同一数据类型,比如:一维数组可以看作一个线性表,二维数组可以看作“数据元素是一维数组”的一维数组,三维数组可以看作“数据元素是二维数组”的一维数组,依此类推。
图5.1是一个m行n列的二维数组。
5.1.2 数组的内存映象现在来讨论数组在计算机中的存储表示。
通常,数组在内存被映象为向量,即用向量作为数组的一种存储结构,这是因为内存的地址空间是一维的,数组的行列固定后,通过一个映象函数,则可根据数组元素的下标得到它的存储地址。
对于一维数组按下标顺序分配即可。
对多维数组分配时,要把它的元素映象存储在一维存储器中,一般有两种存储方式:一是以行为主序(或先行后列)的顺序存放,如BASIC、PASCAL、COBOL、C等程序设计语言中用的是以行为主的顺序分配,即一行分配完了接着分配下一行。
另一种是以列为主序(先列后行)的顺序存放,如FORTRAN语言中,用的是以列为主序的分配顺序,即一列一列地分配。
以行为主序的分配规律是:最右边的下标先变化,即最右下标从小到大,循环一遍后,右边第二个下标再变,…,从右向左,最后是左下标。
以列为主序分配的规律恰好相反:最左边的下标先变化,即最左下标从小到大,循环一遍后,左边第二个下标再变,…,从左向右,最后是右下标。
例如一个2×3二维数组,逻辑结构可以用图5.2表示。
以行为主序的内存映象如图5.3(a)所示。
分配顺序为:a11 ,a12 ,a13 ,a21 ,a22,a23 ; 以列为主序的分配顺序为:a11 ,a21 ,a12 ,a22,a13 ,a23 ; 它的内存映象如图5.3(b)所示。
串的两种基本存储方式

串的两种基本存储方式
串是由字符组成的有序序列。
在计算机中,串的存储方式可以分为两种基本形式:数组形式和链表形式。
1. 数组形式:基于数组的存储方式是最常见和简单的方式。
在数组中,每个字符占据一个存储位置,通过数组的下标来访问每个字符。
例如,字符串 "Hello" 可以用一个字符数组 [H, e, l, l, o] 来表示。
优点是随机访问速度快,可以通过索引快速访问任意位置的字符;缺点是插入和删除字符时需要移动数组的元素,效率较低。
2. 链表形式:基于链表的存储方式是通过节点之间的指针来链接字符。
每个字符都被封装在一个节点中,节点之间通过指针进行连接。
例如,字符串 "Hello" 可以用以下节点形成的链表来表示:H -> e -> l -> l -> o。
优点是插入和删除字符时只需要修改指针,效率较高;缺点是访问字符时需要遍历链表,访问速度较慢。
需要根据具体的需求和场景来选择适合的存储方式,数组形式适合对字符串的随机访问较多的场景,而链表形式适合对字符串的插入和删除操作较多的场景。
串的顺序存储结构

串的顺序存储结构串是由零个或多个字符组成的有限序列,是一种特殊的线性表。
在计算机中,字符串的存储可以使用顺序存储结构来实现。
顺序存储结构是将数据元素存放在一块连续的存储空间中,通过元素在内存中的物理地址来表示元素之间的关系。
对于串的顺序存储结构来说,就是将串中的字符按照顺序存放在一块连续的存储空间中。
在串的顺序存储结构中,通常使用一个字符数组来存储串的字符,同时需要记录串的长度。
数组中的每个元素都对应着串中的一个字符,通过下标可以直接访问和操作对应的字符。
由于顺序存储结构中的元素是连续存储的,所以可以实现快速的查找和修改操作。
在实际应用中,串的顺序存储结构常用于处理字符串的操作。
例如,在字符串匹配算法中,需要对两个字符串进行比较,通过顺序存储结构可以方便地获取和比较字符,从而判断两个字符串是否相等或者是否包含某个子串。
在字符串的操作中,还可以使用顺序存储结构来实现插入、删除和替换等操作。
通过将插入或删除的字符后面的字符依次向后或向前移动,可以实现字符串的动态修改。
顺序存储结构对于串的访问操作也是十分方便的。
通过下标可以直接访问和操作对应的字符,可以快速地获取字符串中的某个字符,也可以通过循环遍历整个串来进行特定操作,如统计字符出现的次数、查找子串的位置等。
但是,顺序存储结构也存在一些限制和问题。
首先,由于顺序存储结构需要预先分配一定大小的存储空间,所以对于长度不确定的串来说,需要事先估计好串的最大长度,以避免空间浪费或者内存溢出的问题。
由于顺序存储结构中的元素是连续存储的,所以在插入和删除操作时,需要移动大量的元素,时间复杂度较高。
这就导致了在实际应用中,对于频繁进行插入和删除操作的串来说,顺序存储结构并不适合。
顺序存储结构也无法灵活地改变串的长度。
当需要插入或删除大量字符时,可能需要重新分配更大或更小的存储空间,并将原有的字符复制到新的存储空间中。
串的顺序存储结构是一种常见的字符串存储方式,适用于对字符串进行查找、修改和访问等操作。
数据结构数组与广义表知识点总结

数据结构数组与广义表知识点总结数组是一种线性数据结构,可以存储多个相同类型的元素。
它的特点是元素的大小固定,并且在内存中是连续存储的。
数组的访问方式是通过下标来访问,下标从0开始。
数组可以在编程中应用于各种情况,比如存储一组数字、一组字符串等。
广义表是一种扩展的线性数据结构,可以存储不同类型的元素。
它由元素和表构成,其中表可以是空表、原子或子表。
广义表可以递归定义,即子表可以包含更多的子表。
广义表的访问方式是通过递归来访问,可以对表的元素进行遍历和操作。
在数据结构中,数组和广义表都有自己的特点和用途,下面对它们的知识点进行总结:1.数组的特点及应用:-数组是一种线性数据结构,可以存储多个相同类型的元素。
-数组的内存分配是连续的,可以通过下标来访问元素。
-数组的大小固定,一旦定义后不能改变。
-数组的访问速度快,可以通过下标直接访问元素。
-数组适合用于存储一组相同类型的数据,比如一组数字、一组字符串等。
-数组的应用场景包括但不限于:排序算法、查找算法、图像处理、矩阵运算等。
2.数组的操作和常用算法:-初始化:可以直接赋值或使用循环初始化数组。
-访问元素:通过下标访问元素,下标从0开始。
-修改元素:直接通过下标修改元素的值。
-插入元素:需要移动插入位置之后的元素。
-删除元素:需要移动删除位置之后的元素。
-查找元素:可以使用线性查找或二分查找等算法。
-排序算法:比如冒泡排序、选择排序、插入排序等。
-数组还有一些常用的属性和方法,比如长度、最大值、最小值等。
3.广义表的特点及应用:-广义表是一种扩展的线性数据结构,可以存储不同类型的元素。
-广义表由元素和表构成,表可以是空表、原子或子表。
-广义表可以递归定义,即子表可以包含更多的子表。
-广义表的访问方式是通过递归遍历和操作。
-广义表适合存储一组不同类型的数据,比如存储学生信息、函数调用栈等。
-广义表的应用场景包括但不限于:函数式编程、树的表示、图的表示等。
数据结构课件总结

1. 掌握栈和队列这两种抽象数据类型的特点,并能相应的 应用问题中正确选用它们。
2. 熟练掌握栈类型的两种实现方法,即两种存储结构表示时 的基本操作实现算法,特别应注意栈满和栈空的条件以及 它们的描述方法。
3. 熟练掌握循环队列和链队列的基本操作实现算法,特别注 意队满和队空的描述方法。
4. 理解递归算法执行过程中栈的状态变化过程。
第四章 数组和广义表的学习要点:
1. 了解数组的两种存储表示方法,并掌握数组在以行为主的存 储结构中的地址计算方法。
2. 掌握对特殊矩阵进行压缩存储时的下标变换公式。 3. 了解稀疏矩阵的压缩存储方法的特点,领会以三元组表示稀
疏矩阵时进行矩阵运算采用的处理方法。 4. 掌握广义表的结构特点及其存储表示方法,可将一个非空广
3. 理解教科书中讨论的各种图的算法。
第八章 查找表的学习要点:
1. 熟练掌握顺序表和有序表的查找方法,理解分块查找的方法 和索引存储结构。
2. 熟练掌握二叉排序树的构造和查找方法。 3. 理解在二叉排序树上删除结点的过程。 3. 掌握二叉平衡树的维护平衡方法。 4. 掌握B-树的概念,理解建树、查找和删除结点的过程。 5. 掌握B+树和键树的概念及其特点,以及在其上查找关键字的
义表分解为表头和表尾两部分。
第五章 串的学习要点:
1. 熟悉串的七种基本操作的定义,并能利用这些基本 操作来实现串的其它各种操作。
2. 熟练掌握在串的定长顺序存储结构上实现串的各种 操作的方法。
3. 了解串操作的应用方法和特点。
第六章 树的学习要点:
1. 熟练掌握树、二叉树中的基本概念和性质。 2. 遍历二叉树是二叉树各种操作的基础。不仅要熟练掌握各
数据结构(C语言)第五章

假设以一维数组sa[0..n(n+1)/2-1]作为n阶对称矩阵A的
存储结构,则sa[k]和矩阵元aij之间存在着一一对应的关系。
0
1
2
3
4
5
6
7
8
……
n(n+1)/2-1
sa a00 a10 a11 a20 a21 a22 a30 a31 a32
an-1n-1
27
若i≥j,则aij在下三角形中。aij之前的i行(从第0 行到第i-1行)共有1+2+…+i=i*(i+1)/2个元素,在第i行 上,aij之前恰有j个元素(即ai0,ai1,…,ai,j-1 ),因此aij之 前共有k个元素:
=2000+(3*4+2)*4 =2056
21
例2:二维数组A中,每个元素的长度为3个字节,行下标i 从0到7,列下标j从0到9,从首地址SA开始存放在存储 器内,该数组按列存放时,元素A[4][7]的起始地址 为 。
A. SA+141 C. SA+222 B. SA+180 D. SA+225
解:LOC(a47)=LOC(a00)+(j *m+ i)*L = SA+(7*8+4)*3
以行序为主序(行优先顺序) 以列序为主序(列优先顺序)
13
一、以行序为主序:
1.存放规则 行优先顺序也称为低下标优先或右边下标优先于左 边下标。具体实现时,按行号从小到大的顺序,先将第 一行中元素全部存放好,再存放第二行元素,第三行元 素,依次类推……
BASIC语言、PASCAL语言、C/C++语言都是按行优先
第5章 数据结构 多维数组和广义表

按列优先存储的寻址方法与此类似。
数据结构(C版)
广义线性表——多维数组
数组的存储结构与寻址——多维数组
n(n>2)维 数组一般也采用 按行优先和按列 优先两种存储方 法。请自行推导 任一元素存储地 址的计算方法。 Loc(aijk ) = Loc(a000) +( i×m2×m3 + j×m3 + k )×c
如何压缩存储?
只存储上三角(或下三角)部分的元素。
数据结构(C版)
a00 a10 a 20 a30
a01 a11 a21 a31
a02 a12 a22 a32
a03 a13 a23 a33
上 三 角 矩 阵
a00 a01 a02 a10 a11 a12 a a a 20 21 22
(a) 三对角矩阵
按行 存储
元素aij在一维数组中的序号 =2 + 3(i-1)+( j-i + 1)+1 =2i+ j+1 ∵一维数组下标从0开始 ∴元素aij在一维数组中的下标 =2i+ j (b) 寻址的计算方法
0
1
2
3
4
5
6
7
8
9 10
11 12
a00 a01 a10 a11 a12 a21 a22 a23 a32 a33 a34 a43 a44
数组——线性表的推广
a11 a21 … am1 a12 a22 … am2 … … … … a1n a2n … amn
A=(A1,A2,……,An)
其中: Ai=(a1i,a2i,……,ami) (1≤i≤n)
A=
二维数组是数据元素为线性表的线性表。
数据结构数组和广义表

数据结构05数组与广义表数组与广义表可以看做是线性表地扩展,即数组与广义表地数据元素本身也是一种数据结构。
5.1 数组地基本概念5.2 数组地存储结构5.3 矩阵地压缩存储5.4 广义表地基本概念数组是由相同类型地一组数据元素组成地一个有限序列。
其数据元素通常也称为数组元素。
数组地每个数据元素都有一个序号,称为下标。
可以通过数组下标访问数据元素。
数据元素受n(n≥1)个线性关系地约束,每个数据元素在n个线性关系地序号 i1,i2,…,in称为该数据元素地下标,并称该数组为n维数组。
如下图是一个m行,n列地二维数组A矩阵任何一个元素都有两个下标,一个为行号,另一个为列号。
如aij表示第i行j列地数据元素。
数组也是一种线性数据结构,它可以看成是线性表地一种扩充。
一维数组可以看作是一个线性表,二维数组可以看作数据元素是一维数组(或线性表)地线性表,其一行或一列就是一个一维数组地数据元素。
如上例地二维数组既可表示成一个行向量地线性表: A1=(a11,a12,···,a1n)A2=(a21,a22, ···,a2n)A=(A1,A2, ···,Am) ············Am=(am1,am2, ···,amn)也可表示成一个列向量地线性表:B1=(a11,a21,···,am1)B2=(a12,a22, ···,am2)A=(B1,B2, ···,Bm) ············Bn=(a1n,a2n, ···,amn)数组地每个数据元素都与一组唯一地下标值对应。
数据结构知识点归纳

一、数据结构的章节结构及重点构成数据结构学科的章节划分基本上为:概论,线性表,栈和队列,串,多维数组和广义表,树和二叉树,图,查找,内排,外排,文件,动态存储分配。
对于绝大多数的学校而言,“外排,文件,动态存储分配”三章基本上是不考的,在大多数高校的计算机本科教学过程中,这三章也是基本上不作讲授的。
数据结构的章节比重大致为:1.概论:概念,时间复杂度。
2.线性表:基础章节,必考内容之一。
概念,算法设计题。
3.栈和队列:基本概念。
4.串:基本概念。
5.多维数组及广义表: 基本概念。
6.树和二叉树:重点难点章节,各校必考章节。
概念,问答,算法设计题。
7.图:重点难点章节,各校必考章节。
概念,问答,算法设计题。
8.查找:重点难点章节,概念,问答。
9.排序:重点难点章节,问答各种排序算法的排序过程二、各章节的主要内容:第一章概述主要内容:本章主要起到总领作用,为读者进行数据结构的学习进行了一些先期铺垫。
大家主要注意以下几点: (1)数据结构的基本概念。
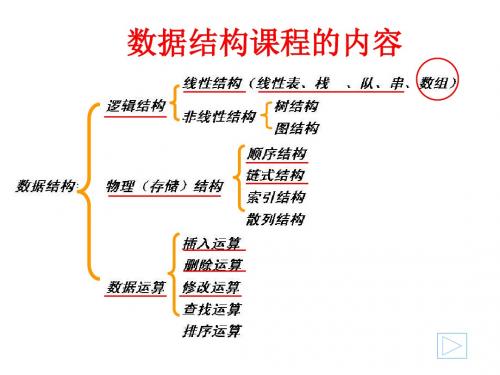
(数据;数据元素;数据项;数据结构;数据的逻辑结构:线性和非线性,具体分为集合、线性结构、树形结构和图状结构;数据的存储结构:顺序存储和链式存储;运算)(2)算法的度量:时间效率和空间效率,分别用时间复杂度和空间复杂度度量,掌握时间复杂度的度量方法量方法。
(大O表示法)参考题目:填空题:1、数据结构是相互之间存在一种或多种特定关系的数据元素的集合,它包括三方面的内容,分别是数据的逻辑结构、()和()。
2、数据结构按逻辑结构可分为两大类,它们分别是()和()3. 数据的物理结构主要包括()和()两种情况。
4.线性表,栈,队列和二叉树四种数据结构中()是非线性结构,()是线性结构。
5、线性结构中元素之间存在()关系,树形结构中元素之间存在()关系,图形结构中元素之间存在()关系。
6、程序段的时间复杂度是_______。
for(i=1;i<=n;i++){ k++;for(j=1;j<=n;j++)x=x+k;}7.下列算法的时间复杂度是_____。
北京师范大学数据结构教学资料 第4章——数组、串与广义表

精选ppt
25
设矩阵 A 中有 s 个非零元素。令 e = s/(m*n), 称 e 为矩阵的稀疏因子。
有人认为 e≤0.05 时称之为稀疏矩阵。 在存储稀疏矩阵时,为节省存储空间,应只
存储非零元素。但由于非零元素的分布一般 没有规律,故在存储非零元素时,必须记下 它所在的行和列的位置 ( i, j )。 每一个三元组 (i, j, aij) 唯一确定了矩阵A的一 个非零元素。因此,稀疏矩阵可由表示非零 元的一系列三元组及其行列数唯一确定。
精选ppt
26
稀疏矩阵的定义
const int drows = 6, dcols = 7, dterms = 9;
template<class E>
struct Triple {
//三元组
int row, col;
//非零元素行号/列号
E value;
//非零元素的值
void operator = (Triple<E>& R) //赋值
a1 1
a2 1 an1 1
a1 2
a2 2 an1 2
aaan12n1nn111
下 三 角 矩 阵
01 2 3 4 5 6 7 8
n(n+1)/2-1
B a00 a10 a11 a20 a21 a22 a30 a31 a32 …… an-1n-1
若 i j, 数组元素A[i][j]在数组B中的存放位置 为 1 + 2 + + i + j = (i + 1)* i / 2 + j
前i行(0~i-1)元素总数 第i行第j个元素前元素个数
精选ppt
18
数据结构讲义第5章-数组和广义表

5.4 广义表
5)若广义表不空,则可分成表头和表尾,反之,一对表头和表尾 可唯一确定广义表 对非空广义表:称第一个元素为L的表头,其余元素组成的表称 为LS的表尾; B = (a,(b,c,d)) 表头:a 表尾 ((b,c,d)) 即 HEAD(B)=a, C = (e) D = (A,B,C,f ) 表头:e 表尾 ( ) TAIL(B)=((b,c,d)),
5.4 广义表
4)下面是一些广义表的例子; A = ( ) 空表,表长为0; B = (a,(b,c,d)) B的表长为2,两个元素分别为 a 和子表(b,c,d); C = (e) C中只有一个元素e,表长为1; D = (A,B,C,f ) D 的表长为4,它的前三个元素 A B C 广义表, 4 A,B,C , 第四个是单元素; E=( a ,E ) 递归表.
以二维数组为例:二维数组中的每个元素都受两个线性关 系的约束即行关系和列关系,在每个关系中,每个元素aij 都有且仅有一个直接前趋,都有且仅有一个直接后继. 在行关系中 aij直接前趋是 aij直接后继是 在列关系中 aij直接前趋是 aij直接后继是
a00 a01 a10 a11
a0 n-1 a1 n-1
a11 a21 ┇ a12 a22 ┇ ai2 ┇ … amj … amn … aij … ain … … a1j a2j … … a1n a2n β1 β2 ┇ βi ┇ βm
数组结构的特点

数组结构的特点
数组结构是一种常见的数据结构,其特点包括以下几个方面: 1. 存储连续性:数组在内存中是一段连续的存储空间,元素之间的地址是相邻的,这种特性使数组的存储和访问效率非常高。
2. 随机访问性:由于元素在数组中的位置是固定的,因此可以通过下标直接访问数组中的任意元素,这种随机访问性是数组结构的一个重要特点。
3. 固定长度:数组的长度是固定的,一旦创建了一个数组,它的长度就不能再改变。
如果需要存储更多的元素,就必须重新创建一个更大的数组,并将原来的元素复制到新的数组中。
4. 同种数据类型:数组中的元素必须是同种数据类型,这是因为数组的内存空间是连续的,不同类型的数据占用的字节数可能不同,会导致地址计算错误。
5. 内存空间的浪费:由于数组的长度是固定的,因此可能会出现内存空间浪费的情况。
如果数组的长度过大,而实际存储的元素很少,就会浪费大量的内存空间。
综上所述,数组结构具有存储连续性、随机访问性、固定长度、同种数据类型和内存空间浪费等特点。
在实际应用中,我们需要根据具体的需求来选择不同的数据结构,以达到最优的效果。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构
s'a1a2an'
串名
串值
串长
n
空串
n=0
4.1.1 串的基本概念
a=‘BEI’, b=‘JING’ c=‘BEIJING’ d=‘BEI JING’
a和b是c和d的子串 a在c和d中的位置是1。 b在c中的位置是4,在d中的位置为5。 ‘ ’是空格串Φ
基本操作:
⑴ StrLength (s):求串s的长度。
⑵ StrAssign (s1, s2):赋值,将s2的值赋值给串s1。
⑶ StrConcat (s1, s2, s):连接,将串s2放在串s1的后面连接 成一个新串s。
⑷ SubStr (s, i, len):求子串,返回从串s的第i个字符开始取 长为 len 的子串。
串、数组和广义表结构特 点和储存方法
教学目标
数据结构
了解串的存储方法,理解串的两种模式匹配算法,重点掌 握BF算法。
明确数组和广义表这两种数据结构的特点,掌握数组地址 计算方法,了解几种特殊矩阵的压缩存储方法。
掌握广义表的定义、性质及其GetHead和GetTail的操作 。
数据结构
第一节
串
补充:C语言中常用的串运算
调用标准库函数 #include<string.h>
串比较,strcmp(char s1,char s2) 串复制,strcpy(char to,char from) 串连接,strcat(char to,char from) 求串长,strlen(char s) ……
数据结构
4.1.1 串的基本概念
数据结构
子串 主串 字符位置 子串位置 串相等 空格串
4.1.2 串的抽象数据类型
数据结构
ADT String{
数据对象:D = { ai|ai∈CharacterSet, i=1,2,…,n, n ≥0 }
数据关系:R = {<ai-1, ai>| ai-1, ai∈D, i=2,3,…,n }
按这种串的表示方法实现的串的运算时,其基本操作为 “字符序 列的复制”。
定长顺序存储结构定义为:
#define MAX_STRLEN 256 typedef struct
{ char str[MAX_STRLEN] ; int length;
} StringType ;
4.1.4 串的存储结构
T[0] = MAXSTRLEN; uncut = FALSE; } else { // s1截断(仅取S1)
T[1..MAXSTRLEN] = S1[1..MAXSTRLEN];
T[0] = MAXSTRLEN
uncut = FALSE;
T[1..S1[0]] = S1[1..S1[0]]; T[S1[0]+1..S1[0]+S2[0]] = S2[1..S2[0]];
T[0] = S1[0]+S2[0]; uncut = TRUE; } else if (S1[0] <MAXSTRLEN) { // s2截断,s1未截断
T[1..S1[0]] = S1[1..S1[0]]; T[S1[0]+1..MAXSTRLEN] = S2[1..MAXSTRLEN-S1[0]];
数据结构
如何表示串的长度?
方案1:用一个变量来表示串的实际长度。 方案2:在串尾存储一个不会在串中出现的特殊字符 作为串的终结符,表示串的结尾。 方案3:用数组的0号单元存放串的长度,从1号单 元开始存放串值。
0 1 2 3 4 5 6 …77…………M…ax-M1ax-1
a9 ab bc cd de ef gf \g0空 闲空 闲9
4.1.2 串的抽象数据类型
数据结构
⑸ StrCmp (s1, s2):串比较,若s1=s2,返回0;若s1<s2, 返 回-1;若s1>s2, 返回1。
⑹ StrIndex (s, t):定,则返回0。
⑺ StrInsert (s, i, t):插入,将串t插入到串s中的第i个位置。
⑻ StrDelete (s, i, len):删除,在串s中删除从第i个字符开始 的连续len个字符。
⑼ StrRep (s, t, r):替换,在串s中用串r替换所有与串t相等 的子串。
}ADT String
4.1.2 串的抽象数据类型
数据结构
求子串操作SubStr(s, i, len)示例
i = 3, len = 3
块链存储方式:是一种链式存储结构表示。
4.1.4 串的存储结构
数据结构
串的定长顺序存储表示
这种存储结构又称为串的顺序存储结构。是用一组连续的存储单元来 存放串中的字符序列。所谓定长顺序存储结构,是直接使用定长的字 符数组来定义,数组的上界预先确定。
特点:
串的实际长度可在这个予定义长度的范围内随意设定,超过予定义 长度的串值则被舍去,称之为“截断” 。
4.1.4 串的存储结构
数据结构
串的联接算法中需分三种情况处理:
Status Concat(SString S1, SString S2, SString &T) { // 用T返回由S1和S2联接而成的新串。若未截断, 则返回TRUE,否则FALSE。 if (S1[0]+S2[0] <= MAXSTRLEN) {// 未截断
4.1.4 串的存储结构
数据结构
串是一种特殊的线性表,其存储表示和线性表类似,但又 不完全相同。串的存储方式取决于将要对串所进行的操作 。串在计算机中有3种表示方式:
定长顺序存储表示:将串定义成字符数组,利用串名可 以直接访问串值。用这种表示方式,串的存储空间在编 译时确定,其大小不能改变。
堆分配存储方式:仍然用一组地址连续的存储单元来依 次存储串中的字符序列,但串的存储空间是在程序运行 时根据串的实际长度动态分配的。
abcdefge
i = 7, len = 4
abcdefge
空串
cde
ge
4.1.3 串与线性表的比较
数据结构
逻辑结构 串的逻辑结构和线性表极为相似,区别仅在于串的数据对 象约束为字符集。
基本操作
在线性表的基本操作中,大多以“单个元素”作为操作 对象;
在串的基本操作中,通常以“串的整体”作为操作对象 。
