电压电流有效值,平均值的计算
单相、三相整流的输入电流、平均电流、电流有效值、峰值电流与输出电流的关系
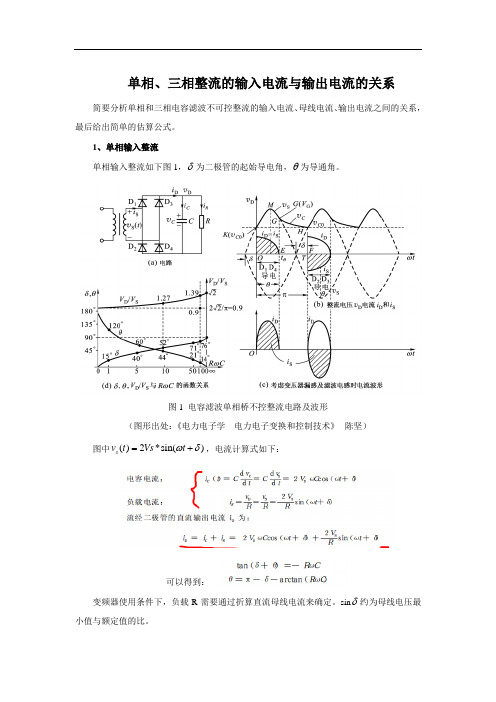
单相、三相整流的输入电流与输出电流的关系简要分析单相和三相电容滤波不可控整流的输入电流、母线电流、输出电流之间的关系,最后给出简单的估算公式。
1、单相输入整流单相输入整流如下图1,δ为二极管的起始导电角,θ为导通角。
图1 电容滤波单相桥不控整流电路及波形(图形出处:《电力电子学---电力电子变换和控制技术》--陈坚)图中()2*sin()s v t Vs t ωδ=+,电流计算式如下:可以得到:变频器使用条件下,负载R 需要通过折算直流母线电流来确定。
sin δ约为母线电压最小值与额定值的比。
起始导电角、导通角、负载、电容间的关系如下表:sin()in t ωδ+。
(1)单相输入电流有效值忽略效率,假设输入功率等于输出功率,则Pin=Pout 。
Pin=Uin*Iin ,(电流电压均为有效值)。
*Uo*Io ,(Uo 为输出的线电压,Io 为输出电流)。
可得到*Io ,即单相输入的变频器,倍。
考虑功率因数时,Iin= *Io/cos γ。
(2)单相母线电流平均值in ,根据母线提供的功率等于输出功率,则**in d o o I I =,(S2变频器,Uin 为220V ,Uo 为220V ),2d o I I =,( 1.22d o I I =) 单个二极管承受的电流平均值为母线电流平均值的一半。
(3)单相输入电流峰值输入电流类似与正弦波,只是导通角度减小,但周期和输入电压一致。
将输入电流的方向电流变为正后即为母线电流,所以输入电流峰值即为母线电流峰值。
输入电流峰值与负载和滤波电容有关,它们决定了导通角θ。
当负载在有感性负载如电机或直流电抗器的情况下,输入电流的波形类似于正弦半波。
函数y=Asin(wt),通过积分计算可得到正弦半波的最大值与平均值的关系为2AV Ay π=,2AV MAX y y π=单相整流的输出电流周期为π,最大导通角为π,当导通角为θ时,2*AV MAXy y θππ=输出功率逆推得到母线电流平均值与波形计算值相等,d AV I y =,则输入电流最大值:()*in MAX o I I ππθ=考虑功率因数,则()**4cos o in MAX I I ππθλ=,(()*1.92*cos o in MAX I I πθλ=)根据经验,输入电流峰值为输出电流有效值的4-6倍左右,当有直流电抗器时,导通角度会增加,峰值会稍微降低。
电压有效值计算

电压有效值计算
电压有效值是指一段时间内电压平方的平均值再开根号,也称为方均根值(RMS值)。
在交流电路中,电压是周期性变化的,因此不能简单地使用最大值或平均值来描述电压大小。
电压有效值是描述电压大小的常用方法,它表示为:
Vrms = sqrt(1/T ∫(0->T) V^2(t) dt)
其中,Vrms表示电压有效值,V(t)表示在时间t上的电压值,T 表示电压周期,dt表示时间微元。
计算电压有效值的方法:
1. 将电压波形平方
2. 对平方后的波形进行时间平均
3. 对时间平均后的波形开根号
例如,对于一段时间内的正弦电压,其有效值可以通过以下公式计算:
Vrms = Vm/√2
其中,Vm为该正弦波形的最大峰值,√2是正弦波形的有效值与峰值的比例。
对于复杂的波形,可以采用数值计算或采样方法来计算其有效值。
交流电压的有效值平均值瞬时值最大值

交流电压的有效值、平均值和瞬时值引言交流电是我们日常生活中常见的一种电力形式,它具有周期性变化的特点。
在分析交流电时,我们常常关注其有效值、平均值和瞬时值。
本文将对这三个概念进行详细解释,并探讨它们之间的关系。
交流电的特点交流电是指电流和电压随时间变化而周期性地改变方向和大小的电信号。
在交流电中,电流和电压都是随时间而变化的,且其波形通常呈正弦曲线。
有效值(RMS)有效值又称为均方根(Root Mean Square,简称RMS),是衡量交流电大小的一个重要参数。
它表示一个周期内正弦波振幅平方的平均数,并且与相同大小的直流电产生相同效果。
对于一个正弦波来说,其有效值等于其峰-峰值(peak-to-peak value)除以2倍根号2。
峰-峰值即为波形从最低点到最高点所经历的全部变化。
例如,一个正弦波的峰-峰值为10伏特,则其有效值为10 / (2 * √2) ≈ 3.54伏特。
有效值在电力系统中有着重要的应用,例如计算功率、电流负载等。
平均值平均值是指一个周期内交流电信号的平均数。
对于正弦波来说,其平均值为0,因为正弦波在一个周期内上升和下降的部分面积相等。
然而,在实际应用中,我们通常关注交流电信号的绝对值平均数。
这个平均数可以通过将正弦波进行整个周期的积分,并除以一个周期的长度来计算得到。
对于一个正弦波来说,其绝对值平均数等于其有效值乘以根号2 / π。
即:绝对值平均数 = 有效值* √2 / π。
例如,一个正弦波的有效值为3伏特,则其绝对值平均数为3 * √2 / π ≈1.35伏特。
瞬时值瞬时值是指交流电信号在某一时刻的具体数值。
由于交流电信号是随时间变化的,所以瞬时值可以看作是时间的函数。
对于正弦波来说,瞬时值可以表示为:V(t) = Vm * sin(ωt + φ)其中,V(t)表示瞬时值,Vm表示峰值,ω表示角频率,t表示时间,φ表示相位差。
三者之间的关系在一个周期内,交流电信号的瞬时值是不断变化的,而有效值和平均值则是对这些瞬时值进行综合考虑得到的。
交流电有效值计算公式

交流电有效值计算公式交流电是指电流和电压在大小和方向上都随时间变化的电信号。
在实际应用中,我们常常需要计算交流电的有效值,以便更好地了解电信号的特性。
交流电的有效值是指与该交流电对应的同样功率的直流电所产生的电压或电流的大小。
有效值可以反映交流电信号的平均功率。
计算交流电有效值的公式如下:有效值 = 平方根(周期内各时刻电压或电流的平方和的平均值)在实际计算中,我们通常使用下列公式来计算交流电的有效值:有效值 = 平方根(1/周期* ∫(0到周期) 电压或电流的平方 dt)其中,周期是指一个完整的波形所经历的时间,通常以秒为单位。
电压或电流的平方和的平均值可以通过对一个周期内的电压或电流进行平方和的累加,再除以周期来得到。
积分符号∫表示对时间的积分。
通过这个公式,我们可以方便地计算交流电的有效值。
下面我们通过一个例子来说明如何应用这个公式进行计算。
假设我们有一个正弦波形的交流电,频率为50Hz,峰值电压为220V。
我们希望计算这个交流电的有效值。
我们需要确定一个周期内的时间范围。
由于频率为50Hz,一个周期的时间为1/50秒,即0.02秒。
接下来,我们可以将这个周期内的电压波形表示为一个函数,例如:V(t) = 220*sin(2π*50t)其中,V(t)表示时刻t的电压值。
我们可以通过对V(t)进行平方,再对整个周期进行积分来计算电压的平方和的平均值。
然后,我们将上述公式代入计算,得到有效值的计算公式为:有效值 = 平方根(1/0.02 * ∫(0到0.02) (220*sin(2π*50t))^2 dt)接下来,我们可以进行具体的计算。
通过对上述积分进行计算,我们可以得到电压的平方和的平均值。
然后,将平方和的平均值除以周期,再开平方根,即可得到交流电的有效值。
通过这个计算过程,我们可以得到这个正弦波形交流电的有效值。
总结起来,交流电的有效值计算公式是通过对一个周期内的电压或电流进行平方和的积分,再除以周期,再开平方根来得到的。
电流平均值和有效值计算公式

电流平均值和有效值计算公式
电流平均值和有效值是电流的基本参数,也是电路设计和计算中常用的参数。
电流平均值是指一段时间内电流大小的平均值,通常用于直流电路分析;有效值是指交流电流大小的平均值,通常用于交流电路分析。
下面是电流平均值和有效值的计算公式:
1. 直流电流平均值的计算公式:
I平均 = (I1 + I2 + … + In) / n
其中,I1、I2、…、In为电流的各个采样值,n为采样值的个数。
2. 交流电流有效值的计算公式:
Irms = √[(I1 + I2 + … + In) / n]
其中,I1、I2、…、In为电流的各个采样值,n为采样值的个数。
根据以上公式,可以计算出电流的平均值和有效值,从而为电路设计和计算提供基础数据。
需要注意的是,在实际应用中,电流的波形和频率也会对平均值和有效值的计算产生影响,因此需要对具体情况进行分析和计算。
- 1 -。
电压电流有效值平均值的计算

电压电流有效值平均值的计算
电压的有效值计算公式为:Vrms=Vpeak/√2,其中Vpeak为电压的峰值;电压的平均值计算公式为:Vaverage=
(V1+V2+V3+...+Vn)/n,其中V1~Vn为电压的采样值,n为采样数量。
这两个公式在电路分析和计算中非常常用,电压的平均值表示电压信号的平均水平,而电压的有效值则表示电压信号的等效振幅,二者的计算可以帮助我们更好地理解和分析电路的运作状态,从而进行合适的调整和优化。
同时,我们也可以通过这些公式计算出能够稳定供电的电压范围,并制定相应的安全措施。
交流电有效值的计算

交流电有效值的计算交流电有效值的计算是指通过测量或计算得出交流电信号在一定时间内的平均能量大小。
在交流电中,电流和电压都是随时间变化的,因此不能直接使用最大值或峰值来表示电流或电压的大小。
有效值的概念旨在提供一个与直流电相同功率的参考值。
要计算交流电的有效值,可以使用以下三种方法:平均值法、功率法和积分法。
1. 平均值法:交流电的有效值可通过将电流或电压的平方信号取平均并开方来计算。
假设电流的波形为I(t),则交流电的有效值表示为Irms,可用以下公式计算:Irms = √(1/T ∫[0 to T] I(t)²dt)其中,T表示一个完整的周期。
例如,如果电流的波形是正弦波,那么该方法可以简化为使用最大峰值电流的70.71%:Irms = Imax/√22.功率法:根据交流电功率的定义,可以使用功率计来测量电流和电压之间的功率输出。
根据功率的平方等于电流和电压乘积的平均值,可以将交流电的有效值表示为:Irms = √(Pavg/Vrms)其中,Pavg表示平均功率输出,Vrms表示电压的有效值。
这种方法适用于通过功率计间接测量交流电的有效值。
3.积分法:通过将电流或电压信号与一个参考信号进行积分,并将结果除以积分时间来计算有效值。
该方法需要使用一些数学和信号处理技术,通常在数字信号处理领域使用。
这些方法可以适用于各种交流电信号的有效值计算。
但需要注意的是,对于非线性或非周期性的波形,这些方法可能不适用。
在这种情况下,可以借助计算机和数值计算技术进行数值模拟和数据处理。
除了计算交流电的有效值,也可以使用示波器等检测设备来显示电流和电压的波形,并通过与标准波形进行比较来估计有效值。
交流电有效值计算在电力系统分析、电路设计和实际应用中具有重要意义。
它能够描述交流电信号的实际能量,为电力传输、电能计量和电气设备的设计和使用提供准确的参考值。
有效值计算也是交流电工程中一项基本的测量和分析技术。
电流有效值的计算公式

电流有效值的计算公式
1什么是电流有效值
电流有效值,也叫直流有效值,是指单位时间内,电流一种周期一次变化曲线的绝对值的期望称之为电流有效值。
也就是说,一个完全扭曲的交流电流的有效值等于该曲线的实际平均值。
另外,一个电流的有效值可以表达实际发生的功率。
2计算电流有效值的公式
电流有效值计算的公式如下:I_eff=√(I_max²+I_min²)/2其中,I_eff代表电流的有效值,I_max代表电流曲线的最大值,I_min 代表曲线的最小值。
3为什么需要计算电流有效值
正是由于电流有效值可以反映电流实际发生的功率,所以通常情况下我们都会计算曲线的电流有效值来获取真正可用的功率,从而将这些功率用在日常生活中。
例如,由电流曲线形象地表示家用电力,用电流有效值可以准确地表示可使用的功率。
4电流有效值的应用
电流有效值主要用于电力系统,可以用来计算家用电力的可使用功率以及功率最大化等;并且可用于故障测试或维护,例如集中控制系统,生产流程控制中对部分设备功耗计量等。
当然,电流有效值也
可以应用于电子设备中,例如电磁兼容、电磁辐射等,以更好的表示电源的有效功率。
电压有效值 方均值 平均值

电压有效值方均值平均值
在我们生活中,我们经常接触到电器和电子设备。
电器和电子设备的使用离不开电压,而电压的有效值、方均值、平均值也是我们需要了解的常见概念。
一、电压有效值
电压的有效值是指交流电压在一个完整周期内的平方均值的平方根,通常用符号Vm表示。
有效值是指交流电的能量含量。
在交流电的正、负半周中,电压值的大小是不同的,因此需经过计算才能得到电压的有效值。
通常,标准的交流电压是以其有效值来表示的,例如220V的交流电表示其电压的有效值是220V。
二、电压方均值
电压的方均值是指交流电压在一定时间范围内每个瞬时值的平方值的平均值,通常用符号Vrms表示。
方均值是交流电的一个参数,用来描述电压的大小。
交流电的周期恒定不变,因此可以用积分的方式计算出每个瞬时点的电压平方,然后再将它们平均,得到电压的方均值。
三、电压平均值
电压的平均值是指交流电压在一个完整周期内各瞬时值的平均数,通常用符号Vavg表示。
电压的平均值可以是正数、负数或零。
交流电的正半周和负半周都有正、负值的部分,因此,当求得的电压平均值为零时,称为电压平衡。
总之,电压的有效值、方均值和平均值是我们需要了解的重要参数。
在实际使用中,根据需要选择不同的电压参数,以达到更好的电器电子设备的使用效果。
交流电平均值、最大值、有效值的详细区别

交流电平均值、瞬时值、最大值、有效值林永德在交流电教学中,历届学生对交流电的瞬时值、最大值、有效值、平均值的理解容易出错,有的乱用方式,有的忽视条件,如果在教学中注意以下两个方面,可以有效地防止学生所出的错误。
1.以交流发电模式为主体,揭示概念的实值。
① 发电模式:N 匝线圈,其面积为S ,总电阻为r ,在一匀强磁场中(磁感应强度为B ),绕垂直于B 的轴,以角速度ω匀速转动;即构成交流电源;交流电源通过滑环和电刷引到外电路,即构成交流全电路。
② 概念的理解:A 、最大值,当线圈平面与磁场平行时,出现最大值。
最大电动势Em=NB ωS 最大电流Im=rR Em +,R 两端的最大电压Um=I m ·R 。
B 、瞬时值:交流全路中,其电动势、电流、电压、均随时间发生周期性变化,如从中性面开始计时,其瞬时值分别为:e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值:对于正弦(或余弦)交流电,有效值=2最大值。
即 E=2EmI=2ImU=2UmD 、 平均值: 对于某一段时间或某一过程,其平均感应电动势: I tN E 平均电流→∆∆•=φ=U r R E 平均电压→+=I R • 2、学生容易出现的错误:(1)有效值的理解:有效值=2最大值,学生容易把条件“正弦或余弦”交流电忽视,对于非正弦或余弦交流电,学生很难建立起电流热效应方程,以求解有效值。
如:求以下交流电的有效值。
学生容易出现以下几种答案: a : U=25, b : U=23c: U=28正确的解法: 建立电流热效应方程: 2.01.031.05222⨯=⨯+⨯RU R R 即: U=17 (V )(2)平均值的理解:如:交流发电模式中,从中性面开始,转过060,求此过程的平均电动势。
学生容易出现以下错误,把平均电动势理解为电动势的平均值,即E =S NB Em e e ω43260sin 02021=+=+ 正确的解法: E =N πωωπφ2326160cos 0S NB BS BS N t =•-=∆∆ (3)求解功率或电热用交流电源给外电路供电,在求解功率或电热问题的时候,学生很容易把平均值与有效值混淆。
三相电压有效值平均值

三相电压有效值平均值
摘要:
1.三相电压的基本概念
2.三相电压的有效值定义
3.三相电压有效值平均值的计算方法
4.我国常用的三相电压等级及应用场景
5.三相电压在工业生产和生活中的重要性
正文:
三相电压,是指电力系统中三个相位之间的电压。
在电力系统中,电压是一个非常重要的参数,它直接影响到电力设备的运行和电力系统的稳定性。
因此,对于三相电压的计算和分析尤为重要。
首先,我们需要了解什么是三相电压的有效值。
有效值,又称均方根值,是指一个交流信号的平方值的平均值的平方根。
对于正弦波,其有效值等于其峰值的0.707 倍。
对于三相电压,其有效值定义为三个相位电压的平方值的平均值的平方根。
那么,如何计算三相电压的有效值平均值呢?其计算公式为:U_rms = (Ua^2 + Ub^2 + Uc^2) / 3,其中,Ua、Ub、Uc 分别为三相电压的峰值。
在我国,常用的三相电压等级有220V、380V、6kV、10kV 等。
其中,220V 和380V 主要用于居民用电和低压工业用电;6kV 和10kV 主要用于中压工业用电。
这些电压等级在工业生产和生活中都扮演着重要的角色。
例如,在工业生产中,三相电压被广泛应用于各类电动机、变压器等电力
设备。
通过调整三相电压的大小和相位,可以实现电动机的正反转和调速等功能。
在生活中,我们常用的家用电器,如空调、洗衣机、电饭煲等,也都是使用三相电压进行工作的。
总的来说,三相电压在工业生产和生活中的应用非常广泛,它直接影响到电力设备的运行和电力系统的稳定性。
电压电流有效值_平均值的计算
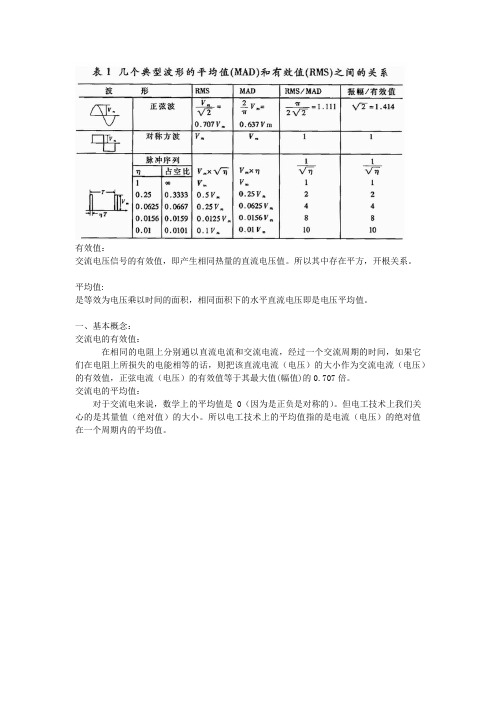
有效值:
交流电压信号的有效值,即产生相同热量的直流电压值。
所以其中存在平方,开根关系。
平均值:
是等效为电压乘以时间的面积,相同面积下的水平直流电压即是电压平均值。
一、基本概念:
交流电的有效值:
在相同的电阻上分别通以直流电流和交流电流,经过一个交流周期的时间,如果它们在电阻上所损失的电能相等的话,则把该直流电流(电压)的大小作为交流电流(电压)的有效值,正弦电流(电压)的有效值等于其最大值(幅值)的0.707倍。
交流电的平均值:
对于交流电来说,数学上的平均值是0(因为是正负是对称的)。
但电工技术上我们关心的是其量值(绝对值)的大小。
所以电工技术上的平均值指的是电流(电压)的绝对值
在一个周期内的平均值。
电流(或电压)的平均值与有效值

谈电流(或电压)的平均值与有效值测量同一个物体的长度,用米尺测量和用市尺测量的出得数椐不一样,其原因就是米尺与市尺的量制(即单位长度)不同所造成的。
为此人们找出它们之间的转换关系,使得米尺与市尺都可用于测量长度。
同样在电路中测量电流(或电压)的大小时,也有二种制式,即电流(或电压)的平均值与电流(或电压)的有效值。
何谓电流(或电压)的平均值?其定义为:在某一时间段内,用等长间隔时间连续采集电流(或电压)值并将其累加,其累加值除以采集次数,其商即为该电流(或电压)的平均值。
它适用于直流电的计量,无论是恒定的或是脉动的直流电都可用它计量电流(或电压)的大小。
但是平均值却不适用于交流电,其原因就是;我们常用的交流电,其波形为正弦波,即其电流(或电压)是按固定周期变化,而且其值在正负半波的变化是大小相等方向相反,故其平均值=0。
但是交流电同直流电一样,是可以做功的:可以使灯泡发光,可以使电机转动,而且作功可大可小,那么用什么来计量交流电的大小呢?这就引来“有效值”的概念。
对同一个负载,在相同的时间内,用一恒定直流电作功与用一交流电作功相等时,我们用这直流电的电流(或电压)值代表这交流电的电流(或电压)的值,此值即为交流电的有效值。
交流电的有效值是如何求得的,请见如下推导:据有效值定义可列: RU 2·π=R U m 2·x ⎰20sin πdx = R U m 22故得交流电的有效值: U =2m U 即:交流电的有效值 = 其峰值除以2。
交流电通过整流方式可将交流电转变为脉动的直流电,那么该直流电与转变它的交流电有什么关系呢?下面分几种情况来分析:一、单相半波整流电路Bπ2π一、交流半波整流 电压平均值推导公式交流半波电压波形图π2πu uω tω tU = 1Um sinωt dωt= (-cosωt)1Um=12Π2Uo2Π2ΠΠ0ΠΠUo=2平2= 0.45 UoU = 1Um sin ωt dωt= (1-cos2ωt) d(2ωt)2Um =8Π28Π2ΠΠUm 22ΠUmΠ222开放得:U = 0.5Um =0.71Uo 二、交流半波整流 电压有效值推导公式有有Um : 交流电的峰值Uo : 交流电的有效值U : 直流电的有效值U : 直流电的平均值平有=4单相半波整流:平均值U = 0.45 U 0有效值•U = 0.71 U 0 (U 0为交流电的有效值)二、单相全波整流电路Bπ2π一、交流全波整流 电压平均值推导公式交流全波电压波形图π2πuuω tω tU = 1Um sinωt dωt= (-cosωt)1Um=1Π2UoΠΠΠ0ΠΠUo=2平2= 0.9 UoU = 1Um sin ωt dωt= (1-cos2ωt) d(2ωt)2Um =4Π24ΠΠΠ= 0.5 Um = Uo22ΠUmΠ222开放得:U = 0.71Um =Uo 二、交流全波整流 电压有效值推导公式有有Um : 交流电的峰值Uo : 交流电的有效值U : 直流电的有效值U : 直流电的平均值平有22单相全波整流:平均值U = 0.9 U 0 有效值•U = U 0 (U 0为交流电的有效值)三、三相半波整流电路与三相全波整流综上推导汇总如下:1、 单相交流电: 平均值U = 0 有效值U 0 =21 U m (U m 为交流电的峰值电压)2、单相半波整流:平均值U = 0.45 U 0 有效值•U = 0.71 U 0 (U 0为交流电的有效值)3、单相全波整流:平均值U= 0.9 U0有效值•U= U(U为交流电的有效值)4、三相半波整流:平均值U= 1.17 U0有效值•U=1.19 U(U为相电压的有效值)5、三相全波整流:平均值U= 2.34 U0有效值•U= 1.68U(U为相电压的有效值)6、三相全波整流的平均值与三相半波整流的平均值之比= 27、三相全波整流的有效值与三相半波整流的有效值之比= 2。
交流电的有效值和平均值定义及其计算

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间内,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期内的平均值为零,而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值.也等于交流电在正半个周期内的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。
峰值有效值平均值之间的计算公式

峰值有效值平均值之间的计算公式在我们的物理世界中,峰值、有效值和平均值这三个概念就像是三位性格各异的小伙伴,它们各自有着独特的特点,同时又相互关联。
要搞清楚它们之间的关系,那咱们就得先从它们的定义入手。
峰值,顾名思义,就是在一个周期内信号的最大值。
比如说,咱们想象一下荡秋千。
当你荡到最高的那个点时,那就是秋千运动的峰值。
有效值呢,它可有点特别。
如果一个交流电流和一个直流电流分别通过相同的电阻,在相同的时间内产生相同的热量,那么这个直流电流的值就被称为交流电流的有效值。
平均值就更好理解啦,就是在一个周期内,对信号进行算术平均得到的值。
那它们之间的计算公式是怎样的呢?咱们先来说说正弦交流电的情况。
对于正弦交流电,峰值等于有效值乘以根号 2 。
这就好比是一个神秘的魔法公式,把峰值和有效值紧紧地联系在了一起。
记得有一次,我在给学生们讲解这个知识点的时候,有个学生就特别迷糊,怎么都理解不了。
我就给他举了个例子,假设我们有一个正弦交流电压,它的峰值是 10 伏特。
那么根据公式,它的有效值就是 10 除以根号 2 ,约等于 7.07 伏特。
为了让学生们更直观地感受,我还专门用示波器给他们展示了不同的电压波形。
当看到示波器上那跳动的线条,同学们的眼睛都瞪得大大的,充满了好奇和探索的欲望。
再来说说平均值的计算。
对于正弦交流电,它的平均值是峰值的0.637 倍。
在实际的电路中,这三个值都有着非常重要的应用。
比如说,我们在选择电器元件的时候,就要考虑到电压和电流的峰值,以确保元件不会被损坏。
而在计算功率的时候,通常用到的就是有效值。
总之,峰值、有效值和平均值这三个小伙伴,虽然有时候会让我们感到有点头疼,但只要我们掌握了它们之间的计算公式和相互关系,就能在物理的世界里游刃有余啦。
不管是在复杂的电路中,还是在日常生活中的各种电现象里,理解和运用好这三个值,都能帮助我们更好地理解和解决问题。
所以,小伙伴们,加油吧,让我们一起在物理的海洋中畅游,探索更多的奥秘!。
正弦电压和电流的有效值、平均值、瞬时值及峰值
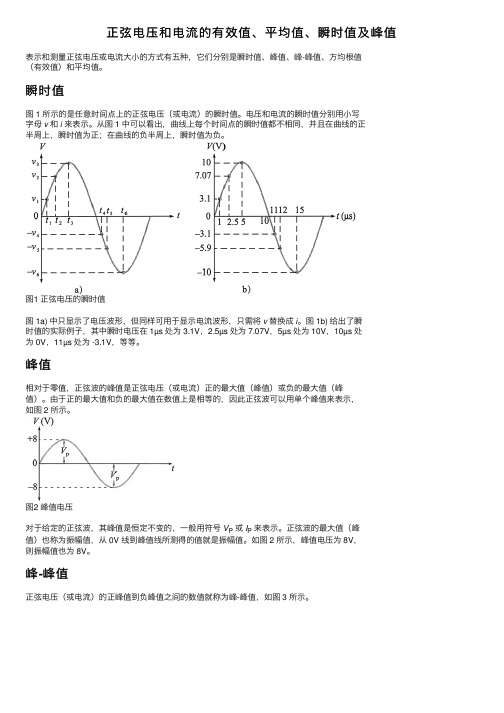
正弦电压和电流的有效值、平均值、瞬时值及峰值表⽰和测量正弦电压或电流⼤⼩的⽅式有五种,它们分别是瞬时值、峰值、峰-峰值、⽅均根值(有效值)和平均值。
瞬时值图 1 所⽰的是任意时间点上的正弦电压(或电流)的瞬时值。
电压和电流的瞬时值分别⽤⼩写字母v和i来表⽰。
从图 1 中可以看出,曲线上每个时间点的瞬时值都不相同,并且在曲线的正半周上,瞬时值为正;在曲线的负半周上,瞬时值为负。
图1 正弦电压的瞬时值图 1a) 中只显⽰了电压波形,但同样可⽤于显⽰电流波形,只需将v 替换成i。
图 1b) 给出了瞬时值的实际例⼦,其中瞬时电压在 1µs 处为 3.1V,2.5µs 处为 7.07V,5µs 处为 10V,10µs 处为 0V,11µs 处为 -3.1V,等等。
峰值相对于零值,正弦波的峰值是正弦电压(或电流)正的最⼤值(峰值)或负的最⼤值(峰值)。
由于正的最⼤值和负的最⼤值在数值上是相等的,因此正弦波可以⽤单个峰值来表⽰,如图 2 所⽰。
图2 峰值电压对于给定的正弦波,其峰值是恒定不变的,⼀般⽤符号V P或I P来表⽰。
正弦波的最⼤值(峰值)也称为振幅值,从 0V 线到峰值线所测得的值就是振幅值。
如图 2 所⽰,峰值电压为 8V,则振幅值也为 8V。
峰-峰值正弦电压(或电流)的正峰值到负峰值之间的数值就称为峰-峰值,如图 3 所⽰。
图3 峰-峰值电压峰-峰值通常是峰值的两倍,⽤公式表⽰为:⽅均根值(有效值)⽅均根(RMS)值也称为有效值,其中 RMS 是英语⽅均根⾸字母的缩写。
⼤多数交流电压表显⽰的都是电压的有效值,例如,墙壁插座引出的 120V 电压就是有效电压值。
电压的有效值是正弦电压热效应的度量值。
如图 4a) 所⽰,当把电阻器连接到交流(正弦波形)电压源上时,电阻器会以热量的形式消耗⼀部分能量。
如图 4b) 所⽰,将同样的电阻器连接到直流电压源上,调整交流电压源的电压值,可使连接在交流电压源上的电阻器产⽣和连接在直流电压源上的电阻器相等的热量。
交流电有效值计算方法

交流电有效值计算方法交流电一般可以表示为一个周期性变化的正弦函数,即I(t) = I_m * sin(ωt+θ)其中,I(t)表示交流电流随时间变化的函数,I_m表示电流的峰值,ω表示角频率,t表示时间,θ表示相位。
有效值的计算方法有两种:平方平均法和积分法。
一、平方平均法:平方平均法是最常用的计算方法,它的基本思想是对交流电流或电压进行平方运算,并求取其平均值的平方根。
1.对交流电流或电压进行平方运算:I^2(t) = I_m^2 * sin^2(ωt+θ)或U^2(t) = U_m^2 * sin^2(ωt+θ)2.求取平均值并开根号:I_rms = sqrt(1/T * ∫[0, T] (I^2(t)) dt)或U_rms = sqrt(1/T * ∫[0, T] (U^2(t)) dt)其中,T是一个周期的时间长度。
二、积分法:积分法是直接对交流电流或电压进行积分运算,并求取积分结果与周期长度的比值的平方根。
1.对交流电流或电压进行积分运算:∫[0, T] (I(t)) dt或∫[0, T] (U(t)) dt2.求取积分结果与周期长度的比值的平方根:I_rms = sqrt(1/T * (∫[0, T] (I(t)) dt)^2)或U_rms = sqrt(1/T * (∫[0, T] (U(t)) dt)^2)其中,T是一个周期的时间长度。
无论是平方平均法还是积分法,求取有效值的步骤是类似的,只是具体的计算过程有所差别。
需要注意的是,对于其他波形,如方波、三角波等,求取有效值的方法可能会稍有不同,但基本思想是一致的。
在实际应用中,计算交流电有效值非常重要,因为有效值是描述交流电大小的一个重要指标,也是进行电路设计、电能计量和电能消耗分析等的基础。
总结起来,交流电有效值的计算方法可以通过平方平均法或积分法来实现,根据具体情况选择合适的方法进行计算。
电流(或电压)的平均值与有效值

用心专注,负责专业!谈电流(或电压)的平均值与有效值测量同一个物体的长度,用米尺测量和用市尺测量的出得数椐不一样,其原因就是米尺与市尺的量制(即单位长度)不同所造成的。
为此人们找出它们之间的转换关系,使得米尺与市尺都可用于测量长度。
同样在电路中测量电流(或电压)的大小时,也有二种制式,即电流(或电压)的平均值与电流(或电压)的有效值。
何谓电流(或电压)的平均值?其定义为:在某一时间段内,用等长间隔时间连续采集电流(或电压)值并将其累加,其累加值除以采集次数,其商即为该电流(或电压)的平均值。
它适用于直流电的计量,无论是恒定的或是脉动的直流电都可用它计量电流(或电压)的大小。
但是平均值却不适用于交流电,其原因就是;我们常用的交流电,其波形为正弦波,即其电流(或电压)是按固定周期变化,而且其值在正负半波的变化是大小相等方向相反,故其平均值=0。
但是交流电同直流电一样,是可以做功的:可以使灯泡发光,可以使电机转动,而且作功可大可小,那么用什么来计量交流电的大小呢?这就引来“有效值”的概念。
对同一个负载,在相同的时间内,用一恒定直流电作功与用一交流电作功相等时,我们用这直流电的电流(或电压)值代表这交流电的电流(或电压)的值,此值即为交流电的有效值。
交流电的有效值是如何求得的,请见如下推导:据有效值定义可列: RU 2·π=R U m 2·x 20sin πdx =R U m22 故得交流电的有效值: U =2m U 即:交流电的有效值 = 其峰值除以2。
交流电通过整流方式可将交流电转变为脉动的直流电,那么该直流电与转变它的交流电有什么关系呢?下面分几种情况来分析:一、单相半波整流电路用心专注,负责专业!Bπ2π一、交流半波整流 电压平均值推导公式交流半波电压波形图π2πu uω tω tU = 1Um sinωt dωt= (-cosωt)1Um=12Π2Uo2Π2ΠΠ0ΠΠUo=2平2= 0.45 UoU = 1Um sin ωt dωt= (1-cos2ωt) d(2ωt)2Um =8Π28Π2ΠΠUm 22ΠUmΠ222开放得:U = 0.5Um =0.71Uo 二、交流半波整流 电压有效值推导公式有有Um : 交流电的峰值Uo : 交流电的有效值U : 直流电的有效值U : 直流电的平均值平有=4单相半波整流:平均值U = 0.45 U 0有效值•U = 0.71 U 0 (U 0为交流电的有效值)二、单相全波整流电路Bπ2π一、交流全波整流 电压平均值推导公式交流全波电压波形图π2πuuω tω tU = 1Um sinωt dωt= (-cosωt)1Um=1Π2UoΠΠΠ0ΠΠUo=2平2= 0.9 UoU = 1Um sin ωt dωt= (1-cos2ωt) d(2ωt)2Um =4Π24ΠΠΠ= 0.5 Um = Uo22ΠUmΠ222开放得:U = 0.71Um =Uo 二、交流全波整流 电压有效值推导公式有有Um : 交流电的峰值Uo : 交流电的有效值U : 直流电的有效值U : 直流电的平均值平有22单相全波整流:平均值U = 0.9 U 0 有效值•U = U 0 (U 0为交流电的有效值)三、三相半波整流电路与三相全波整流用心专注,负责专业!用心专注,负责专业!用心专注,负责专业!用心专注,负责专业!综上推导汇总如下:1、单相交流电:平均值U= 0 有效值U0 =21Um(Um为交流电的峰值电压)2、单相半波整流:平均值U= 0.45 U0有效值•U= 0.71 U(U为交流电的有效值)3、单相全波整流:平均值U= 0.9 U0有效值•U= U(U为交流电的有效值)4、三相半波整流:平均值U= 1.17 U0有效值•U=1.19 U(U为相电压的有效值)5、三相全波整流:平均值U= 2.34 U0有效值•U= 1.68U(U为相电压的有效值)6、三相全波整流的平均值与三相半波整流的平均值之比= 27、三相全波整流的有效值与三相半波整流的有效值之比= 2。
