材料科学基础第一章 作业
材料科学基础习题库第一章-晶体结构

(一).填空题1.同非金属相比,金属的主要特性是__________2.晶体与非晶体的最根本区别是__________3.金属晶体中常见的点缺陷是__________ ,最主要的面缺陷是__________ 。
4.位错密度是指__________ ,其数学表达式为__________ 。
5.表示晶体中原子排列形式的空间格子叫做__________ ,而晶胞是指__________ 。
6.在常见金属晶格中,原子排列最密的晶向,体心立方晶格是__________ ,而面心立方晶格是__________ 。
7.晶体在不同晶向上的性能是__________,这就是单晶体的__________现象。
一般结构用金属为__________ 晶体,在各个方向上性能__________ ,这就是实际金属的__________现象。
8.实际金属存在有__________ 、__________ 和__________ 三种缺陷。
位错是__________ 缺陷。
实际晶体的强度比理想晶体的强度__________ 得多。
9.常温下使用的金属材料以__________ 晶粒为好。
而高温下使用的金属材料在一定范围内以__________ 晶粒为好。
‘10.金属常见的晶格类型是__________、__________ 、__________ 。
11.在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为__________ ,OC晶向指数为__________ ,OD晶向指数为__________ 。
12.铜是__________ 结构的金属,它的最密排面是__________ ,若铜的晶格常数a=0.36nm,那么最密排面上原子间距为__________ 。
13 α-Fe、γ-Fe、Al、Cu、Ni、Pb、Cr、V、Mg、Zn中属于体心立方晶格的有__________ ,属于面心立方晶格的有__________ ,属于密排六方晶格的有__________ 。
(完整版)材料科学基础第1-2章作业及解答彭

第一章作业——材料结构的基本知识1、简述一次键与二次键的差异及各键的特点。
2、简述三大类材料中的结合键类型及性能(物性、力性)特点。
3、为什么金属材料的密度比陶瓷材料及高分子材料密度高?4、用金属键的特征解释金属材料的性能-----①良好的导电;②良好的导热性;③正的电阻温度系数;④不透明性及具有金属光泽;⑤良好的塑性⑥金属之间的溶解性(固溶能力)。
5、简述晶体与非晶体的主要区别。
6、简述原子结构、原子结合键、原子的排列方式及显微组织对材料性能的影响。
第一章作业解答1、述一次键与二次键的差异及各键的特点。
解答:(1)一次键结合力较强,包括金属键、离子键、共价键;二次键结合力较弱,包括范德华键和氢键。
一次键主要依靠外壳层电子转移或共享以形成稳定的电子壳层;二次键是借原子之间的偶极吸引力结合而成。
(2)金属键电子共有化,没有方向性和饱和性;离子键没有方向性,但要满足正负电荷平衡要求;共价键有明显的方向性和饱和性;范德华键没有方向性、饱和性;氢键(X-H…Y)有饱和性、方向性。
2、简述三大类材料中的结合键类型及性能(物性、力性)特点。
解答:(1)三大类材料主要指金属材料、陶瓷材料和高分子材料。
(2)金属材料中的结合键主要是金属键,其次是共价键、离子键,使金属材料具有较高的熔点、密度,良好的导电、导热性能及较高的弹性模量、强度和塑性。
陶瓷材料中的结合键主要是离子键和共价键,使其熔点高、密度低,具有良好的绝缘性能和绝热性能,高的弹性模量和强度,但塑性差,脆性大。
高分子材料中分子链内部虽为共价键结合,但分子链之间为二次键结合,使其具有较低的熔点、密度,良好的绝缘性能、绝热性能及较低的弹性模量、强度和塑性。
3、为什么金属材料的密度比陶瓷材料及高分子材料密度高?金属材料的密度较高是因为①金属元素具有较高的相对原子质量,②金属材料主要以金属键结合,金属键没有方向性和饱和性,使金属原子总是趋于密集排列,达到密堆结构。
材料科学基础-作业参考答案与解析
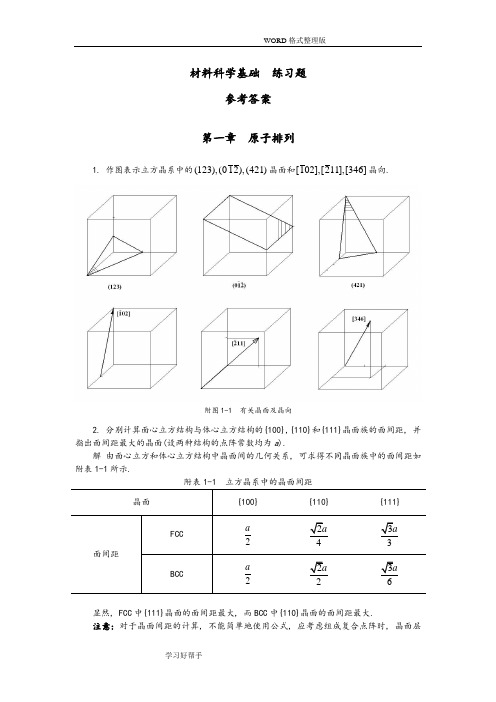
材料科学基础练习题参考答案第一章原子排列1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向.附图1-1 有关晶面及晶向2. 分别计算面心立方结构与体心立方结构的{100},{110}和{111}晶面族的面间距, 并指出面间距最大的晶面(设两种结构的点阵常数均为a).解由面心立方和体心立方结构中晶面间的几何关系, 可求得不同晶面族中的面间距如附表1-1所示.附表1-1 立方晶系中的晶面间距晶面{100} {110} {111}面间距FCC2a24a33aBCC2a22a36a显然, FCC中{111}晶面的面间距最大, 而BCC中{110}晶面的面间距最大.注意:对于晶面间距的计算, 不能简单地使用公式, 应考虑组成复合点阵时, 晶面层数会增加.3. 分别计算fcc和bcc中的{100},{110}和{111}晶面族的原子面密度和<100>,<110>和<111>晶向族的原子线密度, 并指出两种结构的差别. (设两种结构的点阵常数均为a) 解原子的面密度是指单位晶面内的原子数; 原子的线密度是指晶面上单位长度所包含的原子数. 据此可求得原子的面密度和线密度如附表1-2所示.附表1-2 立方晶系中原子的面密度和线密度晶面/晶向{100} {110} {111} <100> <110> <111>面/线密度BCC21a22a233a1a22a233aFCC22a22a2433a1a2a33a可见, 在BCC中, 原子密度最大的晶面为{110}, 原子密度最大的晶向为<111>; 在FCC 中, 原子密度最大的晶面为{111}, 原子密度最大的晶向为<110>.4. 在(0110)晶面上绘出[2113]晶向.解详见附图1-2.附图1-2 六方晶系中的晶向5. 在一个简单立方二维晶体中, 画出一个正刃型位错和一个负刃型位错. 试求:(1) 用柏氏回路求出正、负刃型位错的柏氏矢量.(2) 若将正、负刃型位错反向时, 说明其柏氏矢量是否也随之反向.(3) 具体写出该柏氏矢量的方向和大小.(4) 求出此两位错的柏氏矢量和.解正负刃型位错示意图见附图1-3(a)和附图1-4(a).(1) 正负刃型位错的柏氏矢量见附图1-3(b)和附图1-4(b).(2) 显然, 若正、负刃型位错线反向, 则其柏氏矢量也随之反向.(3) 假设二维平面位于YOZ坐标面, 水平方向为Y轴, 则图示正、负刃型位错方向分别为[010]和[010], 大小均为一个原子间距(即点阵常数a).(4) 上述两位错的柏氏矢量大小相等, 方向相反, 故其矢量和等于0.6. 设图1-72所示立方晶体的滑移面ABCD平行于晶体的上下底面, 该滑移面上有一正方形位错环. 如果位错环的各段分别与滑移面各边平行, 其柏氏矢量b // AB, 试解答:(1) 有人认为“此位错环运动离开晶体后, 滑移面上产生的滑移台阶应为4个b”, 这种说法是否正确? 为什么?(2) 指出位错环上各段位错线的类型, 并画出位错移出晶体后, 晶体的外形、滑移方向和滑移量. (设位错环线的方向为顺时针方向)图1-72 滑移面上的正方形位错环 附图1-5 位错环移出晶体引起的滑移解 (1) 这种看法不正确. 在位错环运动移出晶体后, 滑移面上下两部分晶体相对移动的距离是由其柏氏矢量决定的. 位错环的柏氏矢量为b , 故其相对滑移了一个b 的距离.(2) A ′B ′为右螺型位错, C ′D ′为左螺型位错, B ′C ′为正刃型位错, D ′A ′为负刃型位错. 位错运动移出晶体后滑移方向及滑移量见附图1-5.7. 设面心立方晶体中的(111)晶面为滑移面, 位错滑移后的滑移矢量为[110]2a .(1) 在晶胞中画出此柏氏矢量b 的方向并计算出其大小.(2) 在晶胞中画出引起该滑移的刃型位错和螺型位错的位错线方向, 并写出此二位错线的晶向指数.解 (1) 柏氏矢量等于滑移矢量, 因此柏氏矢量的方向为[110], 大小为2/2a .(2) 刃型位错与柏氏矢量垂直, 螺型位错与柏氏矢量平行, 晶向指数分别为[112]和[110], 详见附图1-6.附图1-6 位错线与其柏氏矢量、滑移矢量8. 若面心立方晶体中有[101]2a b =的单位位错及[121]6a b =的不全位错, 此二位错相遇后产生位错反应.(1) 此反应能否进行? 为什么?(2) 写出合成位错的柏氏矢量, 并说明合成位错的性质.解 (1) 能够进行.因为既满足几何条件:[111]3a b b ==∑∑后前,又满足能量条件: . 22222133b a b a =>=∑∑后前. (2) [111]3a b =合, 该位错为弗兰克不全位错. 9. 已知柏氏矢量的大小为b = 0.25nm, 如果对称倾侧晶界的取向差θ = 1° 和10°, 求晶界上位错之间的距离. 从计算结果可得到什么结论?解 根据bD θ≈, 得到θ = 1°,10° 时, D ≈14.3nm, 1.43nm. 由此可知, θ = 10°时位错之间仅隔5~6个原子间距, 位错密度太大, 表明位错模型已经不适用了.第二章 固体中的相结构1. 已知Cd, In, Sn, Sb 等元素在Ag 中的固熔度极限(摩尔分数)分别为0.435, 0.210, 0.130, 0.078; 它们的原子直径分别为0.3042 nm, 0.314 nm, 0.316 nm, 0.3228 nm; Ag 的原子直径为0.2883 nm. 试分析其固熔度极限差异的原因, 并计算它们在固熔度极限时的电子浓度.答: 在原子尺寸因素相近的情况下, 熔质元素在一价贵金属中的固熔度(摩尔分数)受原子价因素的影响较大, 即电子浓度e /a 是决定固熔度(摩尔分数)的一个重要因素, 而且电子浓度存在一个极限值(约为1.4). 电子浓度可用公式A B B B (1)c Z x Z x =-+计算. 式中, Z A , Z B 分别为A, B 组元的价电子数; x B 为B 组元的摩尔分数. 因此, 随着熔质元素价电子数的增加, 极限固熔度会越来越小.Cd, In, Sn, Sb 等元素与Ag 的原子直径相差不超过15%(最小的Cd 为5.5%, 最大的Sb 为11.96%), 满足尺寸相近原则, 这些元素的原子价分别为2, 3, 4, 5价, Ag 为1价, 据此推断它们的固熔度极限越来越小, 实际情况正好反映了这一规律; 根据上面的公式可以计算出它们在固熔度(摩尔分数)极限时的电子浓度分别为1.435, 1.420, 1.390, 1.312.2. 碳可以熔入铁中而形成间隙固熔体, 试分析是α-Fe 还是γ-Fe 能熔入较多的碳. 答: α-Fe 为体心立方结构, 致密度为0.68; γ-Fe 为面心立方结构, 致密度为0.74. 显然, α-Fe 中的间隙总体积高于γ-Fe, 但由于α-Fe 的间隙数量多, 单个间隙半径却较小, 熔入碳原子将会产生较大的畸变, 因此, 碳在γ-Fe 中的固熔度较α-Fe 的大.3. 为什么只有置换固熔体的两个组元之间才能无限互熔, 而间隙固熔体则不能?答: 这是因为形成固熔体时, 熔质原子的熔入会使熔剂结构产生点阵畸变, 从而使体系能量升高. 熔质原子与熔剂原子尺寸相差越大, 点阵畸变的程度也越大, 则畸变能越高, 结构的稳定性越低, 熔解度越小. 一般来说, 间隙固熔体中熔质原子引起的点阵畸变较大,故不能无限互熔, 只能有限熔解.第三章 凝固1. 分析纯金属生长形态与温度梯度的关系.答: 纯金属生长形态是指晶体宏观长大时固-液界面的形貌. 界面形貌取决于界面前沿液相中的温度梯度.(1) 平面状长大: 当液相具有正温度梯度时, 晶体以平直界面方式推移长大. 此时, 界面上任何偶然的、小的凸起深入液相时, 都会使其过冷度减小, 长大速率降低或停止长大, 而被周围部分赶上, 因而能保持平直界面的推移. 长大过程中晶体沿平行温度梯度的方向生长, 或沿散热的反方向生长, 而其它方向的生长则受到限制.(2) 树枝状长大: 当液相具有负温度梯度时, 晶体将以树枝状方式生长. 此时, 界面上偶然的凸起深入液相时, 由于过冷度的增大, 长大速率越来越大; 而它本身生长时又要释放结晶潜热, 不利于近旁的晶体生长, 只能在较远处形成另一凸起. 这就形成了枝晶的一次轴, 在一次轴成长变粗的同时, 由于释放潜热使晶枝侧旁液体中也呈现负温度梯度, 于是在一次轴上又会长出小枝来, 称为二次轴, 在二次轴上又长出三次轴……由此而形成树枝状骨架, 故称为树枝晶(简称枝晶).2. 简述纯金属晶体长大机制及其与固-液界面微观结构的关系.答: 晶体长大机制是指晶体微观长大方式, 即液相原子添加到固相的方式, 它与固-液界面的微观结构有关.(1) 垂直长大方式: 具有粗糙界面的物质, 因界面上约有50% 的原子位置空着, 这些空位都可以接受原子, 故液相原子可以进入空位, 与晶体连接, 界面沿其法线方向垂直推移, 呈连续式长大.(2) 横向(台阶)长大方式: 包括二维晶核台阶长大机制和晶体缺陷台阶长大机制, 具有光滑界面的晶体长大往往采取该方式. 二维晶核模式, 认为其生长主要是利用系统的能量起伏, 使液相原子在界面上通过均匀形核形成一个原子厚度的二维薄层状稳定的原子集团, 然后依靠其周围台阶填充原子, 使二维晶核横向长大, 在该层填满后, 则在新的界面上形成新的二维晶核, 继续填满, 如此反复进行.晶体缺陷方式, 认为晶体生长是利用晶体缺陷存在的永不消失的台阶(如螺型位错的台阶或挛晶的沟槽)长大的.第四章 相图1. 在Al-Mg 合金中, x Mg 为0.15, 计算该合金中镁的w Mg 为多少.解 设Al 的相对原子量为M Al , 镁的相对原子量为M Mg , 按1mol Al-Mg 合金计算, 则镁的质量分数可表示为Mg MgMg Al Al Mg Mg 100%x M w x M x M =⨯+.将x Mg = 0.15, x Al = 0.85, M Mg = 24, M Al = 27代入上式中, 得到w Mg = 13.56%.2. 根据图4-117所示二元共晶相图, 试完成:(1) 分析合金I, II的结晶过程, 并画出冷却曲线.(2) 说明室温下合金I, II的相和组织是什么, 并计算出相和组织组成物的相对量.(3) 如果希望得到共晶组织加上相对量为5%的β初的合金, 求该合金的成分.图4-117 二元共晶相图附图4-1 合金I的冷却曲线附图4-2 合金II的冷却曲线解 (1) 合金I的冷却曲线参见附图4-1, 其结晶过程如下:1以上, 合金处于液相;1~2时, 发生匀晶转变L→α, 即从液相L中析出固熔体α, L和α的成分沿液相线和固相线变化, 达到2时, 凝固过程结束;2时, 为α相;2~3时, 发生脱熔转变, α→βII.合金II的冷却曲线参见附图4-2, 其结晶过程如下:1以上, 处于均匀液相;1~2时, 进行匀晶转变L →β;2时, 两相平衡共存, 0.50.9L β;2~2′ 时, 剩余液相发生共晶转变0.50.20.9L βα+;2~3时, 发生脱熔转变α→βII .(2) 室温下, 合金I 的相组成物为α + β, 组织组成物为α + βII .相组成物相对量计算如下:αβ0.900.20100%82%0.900.050.200.05100%18%0.900.05w w -=⨯=--=⨯=- 组织组成物的相对量与相的一致.室温下, 合金II 的相组成物为α + β, 组织组成物为β初 + (α+β).相组成物相对量计算如下:αβ0.900.80100%12%0.900.050.800.05100%88%0.900.05w w -=⨯=--=⨯=- 组织组成物相对量计算如下:β(α+β)0.800.50100%75%0.900.500.900.80100%25%0.900.50w w -=⨯=--=⨯=-初 (3) 设合金的成分为w B = x , 由题意知该合金为过共晶成分, 于是有β0.50100%5%0.900.50x w -=⨯=-初 所以, x = 0.52, 即该合金的成分为w B = 0.52.3. 计算w C 为0.04的铁碳合金按亚稳态冷却到室温后组织中的珠光体、二次渗碳体和莱氏体的相对量, 并计算组成物珠光体中渗碳体和铁素体及莱氏体中二次渗碳体、共晶渗碳体与共析渗碳体的相对量.解 根据Fe-Fe 3C 相图, w C = 4%的铁碳合金为亚共晶铸铁, 室温下平衡组织为 P + Fe 3C II + L d ′, 其中P 和Fe 3C II 系由初生奥氏体转变而来, 莱氏体则由共晶成分的液相转变而成, 因此莱氏体可由杠杆定律直接计算, 而珠光体和二次渗碳体则可通过两次使用杠杆定律间接计算出来.L d ′ 相对量: d L 4 2.11100%86.3%4.3 2.11w '-=⨯=-. Fe 3C II 相对量: 3II Fe C 4.34 2.110.77100% 3.1%4.3 2.11 6.690.77w --=⨯⨯=--.P 相对量: P 4.34 6.69 2.11100%10.6%4.3 2.11 6.690.77w --=⨯⨯=--. 珠光体中渗碳体和铁素体的相对量的计算则以共析成分点作为支点, 以w C = 0.001%和w C = 6.69%为端点使用杠杆定律计算并与上面计算得到的珠光体相对量级联得到.P 中F 相对量: F P 6.690.77100%9.38%6.690.001w w -=⨯⨯=-. P 中Fe 3C 相对量: 3Fe C 10.6%9.38% 1.22%w =-=.至于莱氏体中共晶渗碳体、二次渗碳体及共析渗碳体的相对量的计算, 也需采取杠杆定律的级联方式, 但必须注意一点, 共晶渗碳体在共晶转变线处计算, 而二次渗碳体及共析渗碳体则在共析转变线处计算.L d ′ 中共晶渗碳体相对量: d Cm L 4.3 2.11100%41.27%6.69 2.11w w '-=⨯⨯=-共晶L d ′ 中二次渗碳体相对量: d Cm L 6.69 4.3 2.110.77100%10.2%6.69 2.11 6.690.77w w '--=⨯⨯⨯=--II L d ′ 中共析渗碳体相对量:d Cm L 6.69 4.3 6.69 2.110.770.0218100% 3.9%6.69 2.11 6.690.77 6.690.0218w w '---=⨯⨯⨯⨯=---共析 4. 根据下列数据绘制Au-V 二元相图. 已知金和钒的熔点分别为1064℃和1920℃. 金与钒可形成中间相β(AuV 3); 钒在金中的固熔体为α, 其室温下的熔解度为w V = 0.19; 金在钒中的固熔体为γ, 其室温下的熔解度为w Au = 0.25. 合金系中有两个包晶转变, 即1400V V V 1522V V V (1) β(0.4)L(0.25)α(0.27)(2) γ(0.52)L(0.345)β(0.45)w w w w w w =+===+==℃℃解 根据已知数据绘制的Au-V 二元相图参见附图4-3.附图4-3 Au-V 二元相图第五章 材料中的扩散1. 设有一条直径为3cm 的厚壁管道, 被厚度为0.001cm 的铁膜隔开, 通过输入氮气以保持在膜片一边氮气浓度为1000 mol/m 3; 膜片另一边氮气浓度为100 mol/m 3. 若氮在铁中700℃时的扩散系数为4×10-7 cm 2 /s, 试计算通过铁膜片的氮原子总数.解 设铁膜片左右两边的氮气浓度分别为c 1, c 2, 则铁膜片处浓度梯度为7421510010009.010 mol /m 110c c c c x x x --∂∆-≈===-⨯∂∆∆⨯ 根据扩散第一定律计算出氮气扩散通量为 722732410(10)(9.010) 3.610 mol/(m s)c J D x---∂=-=-⨯⨯⨯-⨯=⨯∂ 于是, 单位时间通过铁膜片的氮气量为 3-22-63.610(310) 2.5410 mol/s 4J A π-=⨯⨯⨯⨯=⨯最终得到单位时间通过铁膜片的氮原子总数为-62318-1A () 2.5410 6.02102 3.0610 s N J A N =⨯=⨯⨯⨯⨯=⨯第六章 塑性变形1. 铜单晶体拉伸时, 若力轴为 [001] 方向, 临界分切应力为0.64 MPa, 问需要多大的拉伸应力才能使晶体开始塑性变形?解 铜为面心立方金属, 其滑移系为 {111}<110>, 4个 {111} 面构成一个八面体, 详见教材P219中的图6-12.当拉力轴为 [001] 方向时, 所有滑移面与力轴间的夹角相同, 且每个滑移面上的三个滑移方向中有两个与力轴的夹角相同, 另一个为硬取向(λ = 90°). 于是, 取滑移系(111)[101]进行计算.222222222222k s cos 3001111cos 2001(1)01cos cos 60.646 1.57 MPa.m mϕλϕλτσ==++⨯++==++⨯-++=====即至少需要1.57 MPa 的拉伸应力才能使晶体产生塑性变形.2. 什么是滑移、滑移线、滑移带和滑移系? 作图表示α-Fe, Al, Mg 中的最重要滑移系. 那种晶体的塑性最好, 为什么?答: 滑移是晶体在切应力作用下一部分相对于另一部分沿一定的晶面和晶向所作的平行移动; 晶体的滑移是不均匀的, 滑移部分与未滑移部分晶体结构相同. 滑移后在晶体表面留下台阶, 这就是滑移线的本质. 相互平行的一系列滑移线构成所谓滑移带. 晶体发生滑移时, 某一滑移面及其上的一个滑移方向就构成了一个滑移系.附图6-1 三种晶体点阵的主要滑移系α-Fe具有体心立方结构, 主要滑移系可表示为 {110}<111>, 共有6×2 = 12个; Al 具有面心立方结构, 其滑移系可表示为 {111}<110>, 共有4×3 = 12个; Mg具有密排六方结构, 主要滑移系可表示为{0001}1120<>, 共有1×3 = 3个. 晶体的塑性与其滑移系的数量有直接关系, 滑移系越多, 塑性越好; 滑移系数量相同时, 又受滑移方向影响, 滑移方向多者塑性较好, 因此, 对于α-Fe, Al, Mg三种金属, Al的塑性最好, Mg的最差, α-Fe 居中. 三种典型结构晶体的重要滑移系如附图6-1所示.3. 什么是临界分切应力? 影响临界分切应力的主要因素是什么? 单晶体的屈服强度与外力轴方向有关吗? 为什么?答:滑移系开动所需的作用于滑移面上、沿滑移方向的最小分切应力称为临界分切应力.临界分切应力τk的大小主要取决于金属的本性, 与外力无关. 当条件一定时, 各种晶体的临界分切应力各有其定值. 但它是一个组织敏感参数, 金属的纯度、变形速度和温度、金属的加工和热处理状态都对它有很大影响.如前所述, 在一定条件下, 单晶体的临界分切应力保持为定值, 则根据分切应力与外加轴向应力的关系: σs= τk/ m, m为取向因子, 反映了外力轴与滑移系之间的位向关系, 因此, 单晶体的屈服强度与外力轴方向关系密切. m越大, 则屈服强度越小, 越有利于滑移.4. 孪生与滑移主要异同点是什么? 为什么在一般条件下进行塑性变形时锌中容易出现挛晶, 而纯铁中容易出现滑移带?答: 孪生与滑移的异同点如附表6-1所示.附表6-1 晶体滑移与孪生的比较锌为密排六方结构金属, 主要滑移系仅3个, 因此塑性较差, 滑移困难, 往往发生孪生变形, 容易出现挛晶; 纯铁为体心立方结构金属, 滑移系较多, 共有48个, 其中主要滑移系有12个, 因此塑性较好, 往往发生滑移变形, 容易出现滑移带.第七章 回复与再结晶1. 已知锌单晶体的回复激活能为8.37×104J/mol, 将冷变形的锌单晶体在-50 ℃进行回复处理, 如去除加工硬化效应的25% 需要17 d, 问若在5 min 内达到同样效果, 需将温度提高多少摄氏度?解 根据回复动力学, 采用两个不同温度将同一冷变形金属的加工硬化效应回复到同样程度, 回复时间、温度满足下述关系:122111exp t Q t R T T ⎛⎫⎛⎫=-- ⎪ ⎪ ⎪⎝⎭⎝⎭整理后得到221111ln T t R T Q t =+.将41211223 K,/5/(172460),8.3710 J/mol, 8.314 J/(mol K)4896T t t Q R ==⨯⨯==⨯=⋅代入上式得到2274.7 K T =.因此, 需将温度提高21274.722351.7 T T T ∆=-=-=℃.2. 纯铝在553 ℃ 和627 ℃ 等温退火至完成再结晶分别需要40 h 和1 h, 试求此材料的再结晶激活能.解 再结晶速率v 再与温度T 的关系符合阿累尼乌斯(Arrhenius)公式, 即exp()Q v A RT=-再 其中, Q 为再结晶激活能, R 为气体常数.如果在两个不同温度T 1, T 2进行等温退火, 欲产生同样程度的再结晶所需时间分别为t 1, t 2, 则122112122111exp[()]ln(/)t Q t R T T RTT t t Q T T =--⇒=-依题意, 有T 1 = 553 + 273 = 826 K, T 2 = 627 + 273 = 900 K, t 1 = 40 h, t 2 = 1 h, 则58.314826900ln(40/1)3.0810J/mol 900826Q ⨯⨯⨯=⨯-3. 说明金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别.答: 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别详见附表7-1.附表7-1 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能第八章固态相变。
材料科学基础课后作业及答案(分章节)

材料科学基础课后作业及答案(分章节)第一章8.计算下列晶体的离于键与共价键的相对比例(1)NaF (2)CaO (3)ZnS 解:1、查表得:XNa=,XF= 根据鲍林公式可得NaF中离子键比例为:[1?e共价键比例为:%=% 2、同理,CaO中离子键比例为:[1?e共价键比例为:%=% 12?(?)412?(?)4]?100%?% ]?100%? % 23、ZnS中离子键比例为:ZnS 中离子键含量?[1?e?1/4(?)]?100%?% 共价键比例为:%=% 10说明结构转变的热力学条件与动力学条件的意义.说明稳态结构与亚稳态结构之间的关系。
答:结构转变的热力学条件决定转变是否可行,是结构转变的推动力,是转变的必要条件;动力学条件决定转变速度的大小,反映转变过程中阻力的大小。
稳态结构与亚稳态结构之间的关系:两种状态都是物质存在的状态,材料得到的结构是稳态或亚稳态,取决于转交过程的推动力和阻力(即热力学条件和动力学条件),阻力小时得到稳态结构,阻力很大时则得到亚稳态结构。
稳态结构能量最低,热力学上最稳定,亚稳态结构能量高,热力学上不稳定,但向稳定结构转变速度慢,能保持相对稳定甚至长期存在。
但在一定条件下,亚稳态结构向稳态结构转变。
第二章1.回答下列问题:(1)在立方晶系的晶胞内画出具有下列密勒指数的晶面和晶向:(001)与[210],(111)与[112],(110)与[111],(132)与[123],(322)与[236](2)在立方晶系的一个晶胞中画出晶面族各包括多少晶面?写出它们的密勒指数。
[1101]4.写出六方晶系的{1012}晶面族中所有晶面的密勒指数,在六方晶胞中画出[1120]、晶向和(1012)晶面,并确定(1012)晶面与六方晶胞交线的晶向指数。
5.根据刚性球模型回答下列问题:(1)以点阵常数为单位,计算体心立方、面心立方和密排六方晶体中的原子半径及四面体和八面体的间隙半径。
材料科学基础习题与答案

第一章 原子排列与晶体结构1. fcc 结构的密排方向是 ,密排面是 ,密排面的堆垛顺序是 ,致密度为 ,配位数是 ,晶胞中原子数为 ,把原子视为刚性球时,原子的半径r 与点阵常数a 的关系是 ;bcc 结构的密排方向是 ,密排面是 ,致密度为 ,配位数是 ,晶胞中原子数为 ,原子的半径r 与点阵常数a 的关系是 ;hcp 结构的密排方向是 ,密排面是 ,密排面的堆垛顺序是 ,致密度为 ,配位数是 ,晶胞中原子数为 ,原子的半径r 与点阵常数a 的关系是 。
2. Al 的点阵常数为0.4049nm ,其结构原子体积是 ,每个晶胞中八面体间隙数为 ,四面体间隙数为 。
3. 纯铁冷却时在912ε 发生同素异晶转变是从 结构转变为 结构,配位数 ,致密度降低 ,晶体体积 ,原子半径发生 。
4. 在面心立方晶胞中画出)(211晶面和]211[晶向,指出﹤110﹥中位于(111)平面上的方向。
在hcp 晶胞的(0001)面上标出)(0121晶面和]0121[晶向。
5. 求]111[和]120[两晶向所决定的晶面。
6 在铅的(100)平面上,1mm 2有多少原子?已知铅为fcc 面心立方结构,其原子半径R=0.175×10-6mm 。
第二章 合金相结构一、 填空1) 随着溶质浓度的增大,单相固溶体合金的强度 ,塑性 ,导电性 ,形成间隙固溶体时,固溶体的点阵常数 。
2) 影响置换固溶体溶解度大小的主要因素是(1) ;(2) ;(3) ;(4) 和环境因素。
3) 置换式固溶体的不均匀性主要表现为 和 。
4) 按照溶质原子进入溶剂点阵的位置区分,固溶体可分为 和 。
5) 无序固溶体转变为有序固溶体时,合金性能变化的一般规律是强度和硬度 ,塑性 ,导电性 。
6)间隙固溶体是 ,间隙化合物是 。
二、 问答1、 分析氢,氮,碳,硼在α-Fe 和γ-Fe 中形成固溶体的类型,进入点阵中的位置和固溶度大小。
已知元素的原子半径如下:氢:0.046nm ,氮:0.071nm ,碳:0.077nm ,硼:0.091nm ,α-Fe :0.124nm ,γ-Fe :0.126nm 。
[2017年整理]《材料科学基础》作业题
![[2017年整理]《材料科学基础》作业题](https://img.taocdn.com/s3/m/61e23e93ed3a87c24028915f804d2b160a4e8657.png)
第一章 原子结构与键合1、说明量子力学中有关原子结构的玻尔模型和几率波模型。
2、给出下列离子的电子组态:Fe 2+, Fe 3+, Cu +, Ba 2+, Br -, S 2-。
3、对于K +—Cl -离子对,吸引能E A 和排斥能E R 分别表示为:计算平衡距离r 0和结合能E 0。
(提示:净能对原子间距r 的微分为0时,r= r 0。
r 的单位为nm ) 4、净能有时可表示为其中,r 为离子间距,C ,D 和r 为常数。
试推出结合能E 0对于平衡距离r 0的表达式。
5、计算下列化合物中,离子键的百分含量:TiO ,ZnTe ,CsCl ,InSb ,MgCl 。
6、下列物质含有何种键:黄铜(brass )、橡胶(rubber )、金刚石(diamond )、SiO 2、单晶Si 、NaCl 。
7、 HF (hydrogen fluoride )的分子量小于 HCl (hydrogen chloride ),为什么HF 具有比HCl 更高的沸点。
8、画出下列物质单体单元的结构图:(1)聚乙烯(polyethylene PV );(2)聚四氟乙烯(polytetrafluorethylene PTFE );(3)聚苯乙烯(polystyrene PS );(4)聚甲基丙烯酸甲酯 [俗]有机玻璃(polymethyl methacrylate PMMA )。
9、(1)计算聚乙烯结构单元的分子量;(2)聚乙烯的数均分子重量为1,000,000 g/mol ,计算其数均聚合度。
10、两种聚四氟乙烯样品的密度及其晶化率如下:i) 2.144 g/cm 3, 51.3%; ii) 2.215 g/cm 3, 74.2%.计算晶态聚四氟乙烯和非晶态聚四氟乙烯的密度。
简述高分子链结构的形态特征以及与性能的定性关系。
r E A 436.1-=961086.5r E R -⨯=)exp(ρr D r C E N -+-=第二章 固体结构1、锆(Zr ,Zirconium )具有HCP 结构,密度为6.51 g/cm 3,(a )计算晶胞体积;(b )如果c /a 为1.593,计算c 和a 。
材料科学基础第一章习题答案

材料科学基础第一章习题答案1. (P80 3-3) Calculate the atomic radius in cm for the following:(a) BCC metal with a 0=0.3294nm and one atom per lattice point; and(b) FCC metal with a 0=4.0862Å and one atom per lattice point.Solution:(a) In BCC structures, atoms touch along the body diagonal, which is 3a 0 in length. There are two atomic radii from the center atom and one atomic radius from each of the corner atoms on the body diagonal,so 340ra =430a r ==0.14263nm=1.4263810-⨯cm (b) In FCC structures, atoms touch along the face diagonal of the cube, which is02a in length. There are four atomic radii along this length —two radii from the face-centered atom and one radius from each corner, so240r a =, 420a r ==1.44447 Å=1.44447810-⨯cm2.(P80 3-4) determine the crystal structure for the following:(a) a metal with a0=4.9489Å, r=1.75Å, and one atom per lattice point; and (b) a metal with a0=0.42906nm, r=0.1858nm, and one atom per lattice point.Solution:We know the relationships between atomic radii and lattice parameters are 430a r =in BCC and 420a r =in FCC. (a) 420a r ==⨯=49489.42 1.75 so its crystal structure is FCC;(b) 430a r ==44296.03⨯=0.186nm so its crystal structure is BCC.3. (P80 3-5) the density of potassium, which has the BCC structure and oneatom per lattice point, is 0.855g/cm 3.the atomic weight of potassium is 39.09g/mol. Calculate(a) the lattice parameter; and(b) the atomic radius of potassium.Solution(a) For a BCC unit cell, there are twoatoms in per unit cell,atomic mass is 39.09g/mol,density ρ=0.855g/cm 3Avogadro ’s number N A =6.022310⨯atoms/mol())'()()(/snumber Avogadro cell unit of volume mass atomic cell atoms of numbers =ρ0.855g/cm 3=)/()1002.6()/(09.392233mol atoms a mol g atoms ⨯⨯⨯ So a=3231002.6855.009.392⨯⨯⨯=0.53cm710-⨯=5.3Å(b)then r=a 43=0.229710-⨯cm=2.29Å4. (P81 3-20) determine the indices forthe directions in the cubic unit cell shown in Figure 3-32.The procedure for finding the Miller indices for directions is as follows:ing a right-handed coordinatesystem, determine the coordinates of two points, which lie on the direction.2.Subtract the coordinates of the “tail”point from the coordinates of the “head”point to obtain the number oflattice parameters traveled in the direction of each axis of the coordinate system.3.Clear fractions and/or reduce the results obtained from the subtraction to lowest integers.4.Enclose the number in square brackets[ ]. If a negative sign is produced, represent the negative sign with a bar over the number.SolutionDirection A1.Two points are 0,0,1 and 1,0,02.0,0,1-1,0,0=-1,0,13.no fraction to clear or integers to reduce4.[]011Direction B 1.Two points are 1,0,1 and 21,1,0 2.1,0,1-21,1,0=21,-1,1 3.2(21,-1,1)=1,-2,24.[]221Direction C 1.Two points are 1,0,0 and 0,43,1 2.1,0,0-0,43,1=1, -43,-1 3.4(1, -43,-1)=4, -3, -4 4.[]434Direction D 1.Two points are 0,1,21 and 1,0,0 2.0,1,21 -1,0,0=-1,1, 21 3.2(-1,1, 21)=-2,2,1 4.[]2125.(P82 3-22) Determine the indices for the planes in the cubic unit cell shown in Figure 3-34.The procedure for finding the Miller indices for planes is as follows:1. Identify the points at which the plane intercepts the x, y, and z coordinates in terms of the number of lattice parameters. If the plane passes throughthe origin, the origin of the coordinate system must be moved!2. Take reciprocals of these intercepts.3. Clear fractions but not reduce to lowest integers.4. Enclose the resulting numbers in parentheses (). Again, negative numbers should be written with a bar over the number.SolutionPlane A 1. x=-1, y=21, z=43 2. 341,21,11==-=z y x3. Clear fractions: -3, 6, 44. (643)Plane B 1. x=1, y=-43, z=∞ 2. 01,341,11=-==z y x3. Clear fractions: 3, -4, 04. ()043Plane C 1. x=2, y=23, z=1 2. 11,321,211===z y x3. Clear fractions: 3, 4, 64. (346)6.(P82 3-23) Sketch the following planes and directions within a cubic unit cell:(a) [101] (b) [010] (c) [122] (d)[301] (e) [201] (f) [213](g) (011) (h) (102) (i) (002) (j) (130) (k) (212) (l) (321)7. Calculate the angle between [100] and [111] in Al.Solution: The crystal structure of Al is Fcc. We can calculate the angle between [100] and [111] as31111001101011''''''cos 222222222222=+++++⨯+⨯+⨯=+++++++=w v u w v u ww vv uu θ73.54=θ8. Use a calculation to verify that theatomic packing factor for the FCC structure is 0.74.Solution:In an FCC, there are four lattice points per cell: if there is one atom per lattice point, there are also four atoms per cell. Thevolume of one atom is 4πr 3/3 and thevolume of the unit cell is a 3:Packing factor = 4×4πr 3/3 a 3Since for FCC unit cell, a=4r/2, packingfactor =o.749. 写出溶解在γ-Fe 中碳原子所处的位置,若此类位置全部被碳原子占据,那么试问在这种情况下,γ-Fe 能溶解多少重量百分数的碳?而实际上在γ-Fe 中最大溶解度是多少?两者在数值上有差异的原因是什么?解答:γ-Fe 是fcc ,八面体间隙尺寸大,故C 的存在位置为八面体间隙。
《材料科学基础》作业-答案全

绪论一、填空题1、材料科学主要研究的核心问题是结构和性能的关系。
材料的结构是理解和控制性能的中心环节,结构的最微细水平是原子结构,第二个水平是原子排列方式,第三个水平是显微组织。
2. 根据材料的性能特点和用途,材料分为结构材料和功能材料两大类。
根据原子之间的键合特点,材料分为金属、陶瓷、高分子和复合材料四大类。
第一章材料的原子结构一、填空题1. 金属材料中原子结合以金属键为主,陶瓷材料(无机非金属材料)以共价键和离子键结合键为主,聚合物材料以共价键和氢键以及范德华键为主。
第二章材料的结构一、填空题1、晶体是基元(原子团)以周期性重复方式在三维空间作有规则的排列的固体。
2、晶体与非晶体的最根本区别是晶体原子排布长程有序,而非晶体是长程无序短程有序。
3、晶胞是晶体结构中的最小单位。
4、根据晶体的对称性,晶系有三大晶族,七大晶系,十四种布拉菲Bravais点阵,三十二种点群,230种空间群。
5、金属常见的晶格类型有体心立方、面心立方、密排六方。
6、fcc晶体的最密排方向为<110>,最密排面为{111},最密排面的堆垛顺序为ABCABCABCABC……。
7、fcc晶体的致密度为0.74,配位数为12,原子在(111)面上的原子配位数为6。
8、bcc晶体的最密排方向为<111>,最密排面为{110},致密度为0.68,配位数为8。
9、晶体的宏观对称要素有对称点、对称轴、对称面。
10、CsCl型结构属于简单立方格子,NaCl型结构属于面心立方格子,CaF2型结构属于面心立方格子。
11、MgO晶体具有NaCl型结构,其对称型是3 L44L36L29PC,晶族是高级晶族,晶系是立方晶系,晶体的键型是离子键。
12、硅酸盐晶体结构中的基本结构单元是硅氧四面体[SiO4]。
?13、几种硅酸盐晶体的络阴离子分别为[Si2O7]6-、[Si2O6]4-、[Si4O10]4-、[AlSi3O8]1-,它们的晶体结构类型分别为组群状,链状,层状,和架状。
完整版材料科学基础习题库第一章 晶体结构

(一).填空题1.同非金属相比,金属的主要特性是___________2.晶体与非晶体的最根本区别是____________3.金属晶体中常见的点缺陷是___________ ,最主要的面缺陷是__________ 。
4.位错密度是指___________ ,其数学表达式为 __________ 。
5.表示晶体中原子排列形式的空间格子叫做__________________ ,而晶胞是指6.在常见金属晶格中,原子排列最密的晶向,体心立方晶格是____________ ,而面心立方晶格是__________ 。
7.晶体在不同晶向上的性能是___________ ,这就是单晶体的__________ 现象。
一般结构用金属为___________ 晶体,在各个方向上性能 ____________ ,这就是实际金属的___________ 现象。
8.实际金属存在有__________ 、__________ 和__________ 三种缺陷。
位错是___________ 缺陷。
实际晶体的强度比理想晶体的强度___________ 得多。
9.常温下使用的金属材料以__________ 晶粒为好。
而高温下使用的金属材料在一定范围内以___________ 晶粒为好。
‘10.金属常见的晶格类型是_________ 、____________ 、__________ 。
11.在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C(1,1,1/2),D(1/2 ,1,1/2),那么AB晶向指数为________ ,0(晶向指数为_________ , 0E晶向指数为___________ 。
1 2.铜是__________ 结构的金属,它的最密排面是 __________ 若铜的晶格常数a=0.36nm,那么最密排面上原子间距为 ___________ 。
13 a -Fe、丫-Fe、Al、Cu、Ni、Pb Cr、V、Mg Zn中属于体心立方晶格的有 ,属于面心立方晶格的有 _________________________ ,属于密排六方晶格的有3 14. ________________________________________________________ 已知Cu 的原子直径为0. 256nm那么铜的晶格常数为_______________________ 。
(完整版)材料科学基础习题及答案

第一章材料的结构一、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离子键、金属键、组元、合金、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第二相强化.二、填空题1、材料的键合方式有四类,分别是(),( ),(),().2、金属原子的特点是最外层电子数(),且与原子核引力(),因此这些电子极容易脱离原子核的束缚而变成( )。
3、我们把原子在物质内部呈( )排列的固体物质称为晶体,晶体物质具有以下三个特点,分别是(),( ),( ).4、三种常见的金属晶格分别为(),( )和().5、体心立方晶格中,晶胞原子数为( ),原子半径与晶格常数的关系为( ),配位数是(),致密度是( ),密排晶向为(),密排晶面为( ),晶胞中八面体间隙个数为(),四面体间隙个数为( ),具有体心立方晶格的常见金属有()。
6、面心立方晶格中,晶胞原子数为( ),原子半径与晶格常数的关系为(),配位数是( ),致密度是(),密排晶向为( ),密排晶面为(),晶胞中八面体间隙个数为( ),四面体间隙个数为(),具有面心立方晶格的常见金属有()。
7、密排六方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为( ),密排晶面为(),具有密排六方晶格的常见金属有( )。
8、合金的相结构分为两大类,分别是()和( )。
9、固溶体按照溶质原子在晶格中所占的位置分为()和(),按照固溶度分为()和(),按照溶质原子与溶剂原子相对分布分为()和()。
10、影响固溶体结构形式和溶解度的因素主要有()、()、()、()。
11、金属化合物(中间相)分为以下四类,分别是( ),( ),( ),( )。
12、金属化合物(中间相)的性能特点是:熔点()、硬度( )、脆性(),因此在合金中不作为()相,而是少量存在起到第二相()作用。
13、CuZn、Cu5Zn8、Cu3Sn的电子浓度分别为(),( ),( ).14、如果用M表示金属,用X表示非金属,间隙相的分子式可以写成如下四种形式,分别是( ),(),( ),( ).15、Fe3C的铁、碳原子比为(),碳的重量百分数为(),它是( )的主要强化相。
《材料科学基础》作业1

Ch1 习题及思考题1.名词解释晶体液晶非晶体长程有序短程有序等同点空间点阵结构基元晶体结构晶体点阵空间格子布拉菲点阵单胞(晶胞) 点阵常数晶系2.体心单斜和底心正方是否皆为新点阵?3.绘图说明面心正方点阵可表示为体心正方点阵。
4.试证明金刚石晶体不是布拉菲点阵,而是复式面心立方点阵。
金刚石晶体属于立方晶系,其中碳原子坐标是(000)、(0 1/2 1/2)、(1/2 1/2 0)、(1/20 1/2)、(1/4 1/4 1/4)、(3/4 1/4 3/4)、(1/4 3/4 3/4)、(3/4 3/4 1/4)。
5.求金刚石结构中通过(0,0,0)和(3/4,3/4,1/4)两碳原子的晶向,及与该晶向垂直的晶面。
6.画出立方晶系中所有的{110}和{111}。
7.写出立方晶系中属于{123}晶面族的所有晶面和属于〈110〉晶向族的所有晶向。
8.画出立方晶系中具有下列密勒指数的晶面和晶向:(130)、(211)、(131)、(112)、(321)晶面和[210]、[111]、[321]、[121]晶向。
9.试在完整的六方晶系的晶胞中画出(1012)晶面和[1120]、[1101],并列出{1012}晶面族中所有晶面的密勒指数。
10.点阵平面(110)、(311)和(132)是否属于同一晶带?如果是的话,试指出其晶带轴,另外再指出属于该晶带的任一其它点阵平面;如果不是的话,为什么?11.求(121)和(100)决定的晶带轴与(001)和(111)所决定的晶带轴所构成的晶面的晶面指数。
12.计算立方晶系[321]与[120]夹角,(111)与(111)之间的夹角。
13.写出镍晶体中面间距为0.1246nm的晶面族指数。
镍的点阵常数为0.3524nm。
14. 1)计算fcc结构的(111)面的面间距(用点阵常数表示);2)欲确定一成分为18%Cr,18%Ni的不锈钢晶体在室温下的可能结构是fcc还是bcc,由X射线测得此晶体的(111)面间距为0.21nm,已知bcc铁的a=0.286nm,fcc铁的a=0.363nm,试问此晶体属何种结构?Ch2.1-2 习题及思考题1.分别说明什么是过渡族金属、镧系金属和锕系金属?2.什么是一次键、二次键?它们分别包括哪些键?3.什么是离子键、共价键和金属键?它们有何特性,并给予解释。
材料科学基础 张晓燕1-5章作业及题解.

第一章 作业题解1. 原子中一个电子的空间位置和能量可用哪四个量子数来决定?2. 在多电子的原子中,核外电子的排布应遵循哪些个原则?3. 在元素周期表中,同一周期或同一主族元素原子结构有什么共同特点?从左到右或从上到下元素结构有什么区别?性质如何递变?解、同一周期元素具有相同原子核外电子层数,但从左到右,核电荷依次增多,原子半径逐渐减小,电离能增加,失去电子的能力降低,得到电子能力增加,金属性减弱,非金属性增强,同一主族元素最外层电子数相同,但从上→下,电子层数最多,原子半径增大,电离能降低,失去电子能力增加,得到电子能力降低,金属性增加,非金属性降低。
4. 铬的原子序数为24,共有四种同位数:4.31%的Cr 原子含有26个中子,83.76%含有28个中子,9.55%含有29个中子,且2.38%含有30个中子。
试求铬的原子量。
解、=Ar 0.0431X (24+26)+0.8376X (24+28)+0.0955X (24+29)+0.0238X(24+30)=52.0575. 原子间的结合键共有几种?各自特点如何? 解、6. 按分子材料受热的表现分类可分为热塑性和热固性两大类,试从高分子链结构角度加以解释之。
解、热塑性;具有线性和枝化高分子链结构,加热后变软,可反复加工再成形;热固性;具有体型(立体网状)高分子链结构,不溶于任何溶剂,也不能熔融,一旦定型后不能再改变形状,无法再生。
第二章 作业题解1、归纳总结三种典型的晶体结构的晶体学特征。
解、2、试证明理想密排六方结构的轴比c/a=1.633。
解、见图所示,等边三角形的高 a h ⋅=43 氢键;分子间作用力,氢桥,具有饱和性结合键化学键;主价键 物理键;次价键,也称范德华健 金属键;电子共有化,无饱和性,无方向性。
离子键;以离子而不是以原子为结合单元,无饱和性,无方向性。
共价键;共用电子对,有饱和性方向性。
hd2c343222222a c h c d +=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛= 理想密排六方晶体结构中a d = 故633.138==a c 3、Ni 的晶体结构为面心立方结构,其原子半径为r=0.1243nm ,试求Ni 的晶格常数和密度。
材料科学基础经典习题及答案

第一章 材料科学根底1.作图表示立方晶体的()()()421,210,123晶面及[][][]346,112,021晶向。
2.在六方晶体中,绘出以下常见晶向[][][][][]0121,0211,0110,0112,0001等。
3.写出立方晶体中晶面族{100},{110},{111},{112}等所包括的等价晶面。
4.镁的原子堆积密度和所有hcp 金属一样,为。
试求镁单位晶胞的体积。
Mg 的密度3Mg/m 74.1=m g ρ,相对原子质量为,原子半径。
5.当CN=6时+Na 离子半径为,试问:1) 当CN=4时,其半径为多少?2) 当CN=8时,其半径为多少?6. 试问:在铜〔〕的<100>方向及铁(bcc,a=0.286nm)的<100>方向,原子的线密度为多少?7.镍为面心立方构造,其原子半径为nm 1246.0=Ni r 。
试确定在镍的〔100〕,〔110〕及〔111〕平面上12mm 中各有多少个原子。
8. 石英()2SiO 的密度为3Mg/m 。
试问: 1) 13m 中有多少个硅原子〔与氧原子〕?2) 当硅与氧的半径分别为与时,其堆积密度为多少〔假设原子是球形的〕?9.在800℃时1010个原子中有一个原子具有足够能量可在固体内移动,而在900℃时910个原子中那么只有一个原子,试求其激活能〔J/原子〕。
10.假设将一块铁加热至850℃,然后快速冷却到20℃。
试计算处理前后空位数应增加多少倍〔设铁中形成一摩尔空位所需要的能量为104600J 〕。
11.设图1-18所示的立方晶体的滑移面ABCD 平行于晶体的上、下底面。
假设该滑移面上有一正方形位错环,如果位错环的各段分别与滑移面各边平行,其柏氏矢量b ∥AB 。
1) 有人认为“此位错环运动移出晶体后,滑移面上产生的滑移台阶应为4个b ,试问这种看法是否正确?为什么?2)指出位错环上各段位错线的类型,并画出位错运动出晶体后,滑移方向及滑移量。
材料科学基础经典习题及答案

第一章材料科学基础1.作图表示立方晶体的晶面及晶向。
2.在六方晶体中,绘出以下常见晶向等。
3.写出立方晶体中晶面族{100},{110},{111},{112}等所包括的等价晶面。
4.镁的原子堆积密度和所有hcp金属一样,为。
试求镁单位晶胞的体积。
已知Mg的密度,相对原子质量为,原子半径r=。
5.当CN=6时离子半径为,试问:1) 当CN=4时,其半径为多少?2) 当CN=8时,其半径为多少?6. 试问:在铜(fcc,a=)的<100>方向及铁(bcc,a=的<100>方向,原子的线密度为多少?7.镍为面心立方结构,其原子半径为。
试确定在镍的(100),(110)及(111)平面上1中各有多少个原子。
8. 石英的密度为。
试问:1) 1中有多少个硅原子(与氧原子)?2) 当硅与氧的半径分别为与时,其堆积密度为多少(假设原子是球形的)?9.在800℃时个原子中有一个原子具有足够能量可在固体内移动,而在900℃时个原子中则只有一个原子,试求其激活能(J/原子)。
10.若将一块铁加热至850℃,然后快速冷却到20℃。
试计算处理前后空位数应增加多少倍(设铁中形成一摩尔空位所需要的能量为104600J)。
11.设图1-18所示的立方晶体的滑移面ABCD平行于晶体的上、下底面。
若该滑移面上有一正方形位错环,如果位错环的各段分别与滑移面各边平行,其柏氏矢量b∥AB。
1) 有人认为“此位错环运动移出晶体后,滑移面上产生的滑移台阶应为4个b,试问这种看法是否正确?为什么?2)指出位错环上各段位错线的类型,并画出位错运动出晶体后,滑移方向及滑移量。
12.设图1-19所示立方晶体中的滑移面ABCD平行于晶体的上、下底面。
晶体中有一条位错线段在滑移面上并平行AB,段与滑移面垂直。
位错的柏氏矢量b与平行而与垂直。
试问:1) 欲使段位错在ABCD 滑移面上运动而不动,应对晶体施加怎样的应力?2) 在上述应力作用下位错线如何运动?晶体外形如何变化?13.设面心立方晶体中的为滑移面,位错滑移后的滑移矢量为。
材料科学基础第一章全部作业

材料科学基础第⼀章全部作业(⼀)1 谈谈你对材料学科及材料四要素之间的关系的认识2 ⾦属键与其它结合键有何不同,如何解释⾦属的某些特性?3 说明空间点阵、晶体结构、晶胞三者之间的关系。
4 晶向指数和晶⾯指数的标定有何不同?其中有何须注意的问题?5 画出三种典型晶胞结构⽰意图,其表⽰符号、原⼦数、配位数、致密度各是什么?6 画出⽴⽅晶系中(011),(312),[211],[211],[101],(101)7, 画出六⽅晶系中(1120),(0110),(1012),(110),(1012)8. 原⼦间的结合键共有⼏种?各⾃特点如何?9.在⽴⽅系中绘出{110}、{111}晶⾯族所包括的晶⾯,及(112)和(120)晶⾯。
标出具有下列密勒指数的晶⾯和晶向:a)⽴⽅晶系(421),()123,(130),[211],[311];10.在⽴⽅系中绘出{110}、{111}晶⾯族所包括的晶⾯,及(112)和(120)晶⾯。
11.计算⾯⼼⽴⽅结构(111)、(110)与(100)⾯的⾯密度和⾯间距。
12. 标出具有下列密勒指数的晶⾯和晶向:a)⽴⽅晶系(421),()123,(130),[211],[311];b)六⽅晶系()2111, ()1101,()3212,[2111],1213。
13 在体⼼⽴⽅晶系中画出{111}晶⾯族的所有晶⾯。
14 画出<110>晶向族所有晶向15.写出密排六⽅晶格中的[0001],(0001),()1120,()1100,()121016. 在⼀个简单⽴⽅晶胞内画出⼀个(110)晶⾯和⼀个[112]晶向。
17. 标出具有下列密勒指数的晶⾯和晶向:⽴⽅晶系(421),()123,(130),[211],[311];18.计算晶格常数为a 的体⼼⽴⽅结构晶体中⼋⾯体间隙的⼤⼩。
19.画出⾯⼼⽴⽅晶体中(111)⾯上的[112]晶向。
20.已知某⼀⾯⼼⽴⽅晶体的晶格常数为a ,请画出其晶胞模型并分别计算该晶体的致密度、{111}晶⾯的⾯密度以及{110}晶⾯的⾯间距。
《材料科学基础》作业
出位错分解的反应式。
5.在外力作用下,fcc结构的晶体在(11 )晶面上沿[ 10]方向滑移,试回答下列问题:
若晶体的滑移是由单位位错的运动引起的,写出该单位位错的柏氏矢量。
若此单位位错是纯刃型位错,写出位错线方向及在外力作用下滑移运动的方向。
1.画图并计算fcc和bcc结构晶体的八面体间隙半径大小。
2.画图并说明hcp结构不是一种空间点阵的原因,并计算 ≌1.633。
3.作图表示( 11)、(11 )、(112)晶面及[11 ]、[112]晶向。
4.求bcc结构(111)、(100)及(110)晶面的面间距大小,并指出面间距最大的晶面。
图中标出,并说明原因。图a)图b)
2.画图说明在fcc结构晶体的( 11)晶面上,可以运动的单位位错的柏氏矢量有哪些?
它们相应能在哪些晶面上运动?
3.在面心立方结构的晶体中,沿[ 01]晶向上有一单位位错与沿[12 ]晶向的一个肖克莱
部分位错反应合成一个弗兰克部分位错:
(1)求合成后的弗兰克部分位错的柏氏矢量。
5.在体心立方结构晶体内的(011)晶面上有一个b1= [1 1]刃型位错,在(01 )晶
面上有一个b2= [111]刃型位错,它们分别沿所在晶面进行滑移,当彼此相遇时,
能否发生位错反应?
第一章纯金属的晶ห้องสมุดไป่ตู้结构单元练习题
一.判断是非题,对的在括号中划“∨”,错的划“×”:
1.布拉非点阵与晶体结构是同一概念,因此不管离子晶体,分子晶体,还是原子晶体,
向和晶面。
5.在六方晶系中,画图表示(11 0)、( 010)晶面及[11 3]晶向。并用三坐标系写
(完整版)材料科学基础习题库第一章-晶体结构

(一).填空题1.同非金属相比,金属的主要特性是__________2.晶体与非晶体的最根本区别是__________3.金属晶体中常见的点缺陷是__________ ,最主要的面缺陷是__________ 。
4.位错密度是指__________ ,其数学表达式为__________ 。
5.表示晶体中原子排列形式的空间格子叫做__________ ,而晶胞是指__________ 。
6.在常见金属晶格中,原子排列最密的晶向,体心立方晶格是__________ ,而面心立方晶格是__________ 。
7.晶体在不同晶向上的性能是__________,这就是单晶体的__________现象。
一般结构用金属为__________ 晶体,在各个方向上性能__________ ,这就是实际金属的__________现象。
8.实际金属存在有__________ 、__________ 和__________ 三种缺陷。
位错是__________ 缺陷。
实际晶体的强度比理想晶体的强度__________ 得多。
9.常温下使用的金属材料以__________ 晶粒为好。
而高温下使用的金属材料在一定范围内以__________ 晶粒为好。
‘10.金属常见的晶格类型是__________、__________ 、__________ 。
11.在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为__________ ,OC晶向指数为__________ ,OD晶向指数为__________ 。
12.铜是__________ 结构的金属,它的最密排面是__________ ,若铜的晶格常数a=0.36nm,那么最密排面上原子间距为__________ 。
13 α-Fe、γ-Fe、Al、Cu、Ni、Pb、Cr、V、Mg、Zn中属于体心立方晶格的有__________ ,属于面心立方晶格的有__________ ,属于密排六方晶格的有__________ 。
材料科学基础习题库第一章-晶体结构

(一).填空题1.同非金属相比,金属的主要特性是__________2.晶体与非晶体的最根本区别是__________3.金属晶体中常见的点缺陷是__________ ,最主要的面缺陷是__________ 。
4.位错密度是指__________ ,其数学表达式为__________ 。
5.表示晶体中原子排列形式的空间格子叫做__________ ,而晶胞是指__________ 。
6.在常见金属晶格中,原子排列最密的晶向,体心立方晶格是__________ ,而面心立方晶格是__________ 。
7.晶体在不同晶向上的性能是__________,这就是单晶体的__________现象。
一般结构用金属为__________ 晶体,在各个方向上性能__________ ,这就是实际金属的__________现象。
8.实际金属存在有__________ 、__________ 和__________ 三种缺陷。
位错是__________ 缺陷。
实际晶体的强度比理想晶体的强度__________ 得多。
9.常温下使用的金属材料以__________ 晶粒为好。
而高温下使用的金属材料在一定范围内以__________ 晶粒为好。
‘10.金属常见的晶格类型是__________、__________ 、__________ 。
11.在立方晶格中,各点坐标为:A (1,0,1),B (0,1,1),C (1,1,1/2),D(1/2,1,1/2),那么AB晶向指数为__________ ,OC晶向指数为__________ ,OD晶向指数为__________ 。
12.铜是__________ 结构的金属,它的最密排面是__________ ,若铜的晶格常数a=0.36nm,那么最密排面上原子间距为__________ 。
13 α-Fe、γ-Fe、Al、Cu、Ni、Pb、Cr、V、Mg、Zn中属于体心立方晶格的有__________ ,属于面心立方晶格的有__________ ,属于密排六方晶格的有__________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 a 3 d (111) a 2 2 2 2 6 1 1 1
所以,体心立方晶体中考虑附加面因素,(110)面的面间距为最大。
4) 立方晶系的各{111}晶面构成一个八面体,试作图画 出该八面体,并注出这些具体晶面的指数。
<111>晶向族包括: [111]、[11 1]、[1 11]、 [ 111]、[1 1 1]、[ 111]
2) 画出立方晶系中下列密勒指数的晶面 (321) 和晶向 [1 3] 1
ቤተ መጻሕፍቲ ባይዱ
3) 体心立方结构的晶格常数为a,试求出 (100)、(110)、(111)晶面的面间距,并 指出面间距最大的面。
答: 在体心立方晶格中,当h+k+l=奇数时,有附加面:
1 a a d (100 ) 2 12 0 0 2 d (110 ) 2 a 2 2 2 1 1 0 a
[ 111 ]、[1 1 1 ]
1) 何谓晶面、晶向,它们的表示方法如何? 立方晶格的晶面指数如何确定?
答:晶面(crystal plane):晶体结构一系列原子所构成的平面。 晶向(crystal directions):通过晶体中任意两个原子中心连成直线来表示 晶体结构的空间的各个方向。 晶向和晶面一般用晶向指数(indices of directions)和晶面指数(indices of crystal- plane)来表示,国际上用Miller指数(Miller indices )来统一标定。如晶向指数用[u v w]来表示,晶面指数记为( h k l )。 确定立方晶系(cubic crystal systems) 晶面指数(hkl)的步骤如下: 1、设坐标:原点设在待求晶面以外。 2、求截距:求晶面在三个轴上的截距。 3、取倒数 4、化整数:h、k、l 5、加括号:(hkl),如果所求晶面在晶轴上截距为负数则在指数上加一负号。
第二章 作业题
1)何谓晶面、晶向,它们的表示方法如何?立 方晶格的晶面指数如何确定?
2)画出立方晶系中下列密勒指数的晶面 (321) 和晶向 [1 3] 。 1 3) 体心立方结构的晶格常数为a,试求出 (100)、(110)、(111)晶面的面间距,并 指出面间距最大的面。 4) 立方晶系的各{111}晶面构成一个八面体,试 作图画出该八面体,并注出这些具体晶面的指 数。
