裸导线膨胀系数和弹性系数计算
热膨胀系数

热膨胀量=温度差X热胀系数X长度=5.802X长度(mm)长度单位: m参考资料:GB/T20801.2-2006 表B.1(东北大学,辽宁沈阳 110006)2.2 材料的其它性能①机械强度如上所述,系统的器壁必须承受得住大气的压力。
因此它必须满足最低机械强度和刚度的要求,应考虑相应尺寸的结构所能承受的总压力(当然,容器结构形状也有较大的影响。
例如,圆柱形和球面形结构的强度就大于平面形结构的强度)。
②热学性能许多真空系统要承受温度的变化,如加热和冷却或二者兼备。
因而必须对所用材料的热学性能十分熟悉。
不仅要考虑到熔点,还要考虑到强度随温度的变化。
例如,铜的机械性能远在低于熔点温度之前就开始下降,因而不宜用铜制做真空容器的承压器壁。
另外,真空系统的材料除了受到温度缓慢变化的影响外,还会受到温度突变的影响。
因此,还要考虑材料的抗热冲击的特性。
③电磁性能许多真空系统中的部件必须具备能完成某项功能或工序所要求的电性能,同时这些性能又不能与真空系统的要求相矛盾。
例如,元件在真空室中工作,是靠辐射放热冷却的,因此元件的工作温度将会很高,使得元件的电性能可能受到影响,因此在选材及结构设计上要考虑工作部件的耐高温及冷却问题。
在许多真空系统中,往往要应用带电粒子束。
但这些带电粒子束往往容易受到某些不必要磁场的干扰。
因此在有电子束或离子束的系统中,必须认真考虑系统材料的磁性能,在某些情况下,即使很小的磁场也可能造成很严重的问题。
因此必须考虑用非磁性材料。
④其它性能光学性能(例观察窗)、硬度、抗腐蚀性、热导率和热膨胀等性能也常常起着十分重要的作用。
2.3 真空材料的选材原则2.3.1 对真空容器壳体及内部零件材料的要求①有足够的机械强度和刚度来保证壳体的承压能力。
②气密性好。
要保持一个完好的真空环境,器壁材料不应存在多孔结构、裂纹或形成渗漏的其它缺陷。
有较低的渗透速率和出气速率。
③在工作温度和烘烤温度下的饱和蒸气压要足够低(对超高真空系统来说尤其重要)。
什么是线膨胀系数

什么是线膨胀系数一般指由于外界温度、压力(主要指温度)变化时,物体的线性尺寸随温度、压力(主要指温度)的变化率。
如铁温度每升高1度,长或宽或高尺寸增加12X10^-6,即增加0.0012%。
对应地还有体膨胀系数,即物体的体积随温度的变化率。
对于各向同性的物体,线膨胀系数较小时,体膨胀系数是线膨胀系数的3倍略多一点。
金属材料线膨胀系数的测量线膨胀系数在数值上等于当温度升高1℃时固体材料单位长度的伸长量。
对于不同的物质,线膨胀系数不同。
一般来说,塑料的线膨胀系数较大,金属的次之,熔凝石英的较小。
常见几种材料的线膨胀系数的数量级物质在一定的温度和压力下具有一定的体积。
温度变化时,物质的体积亦相应地变化。
物质的体积随温度升高而增大的现象称为热膨胀。
物质的热膨胀是由于构成物质的原子间的平均距离随温度升高而增大造成的。
物质的热膨胀性质与物质的结构、键型、键力、比热容、熔点等密切相关。
因此,不同的物质或者组成相同结构不同的物质,具有不同的热膨胀性质,常用体积膨胀系数这一物理量来表征物质的不同热膨胀性质。
固体材料在一维方向上的热膨胀伸长称为线膨胀,用线膨胀系数来描述不同物质的线膨胀特性。
物体的热膨胀性质反映了材料本身的属性,测量材料的线膨胀系数,不仅对新材料的研制具有重要意义,而且也是选用材料的重要指标之一。
在工程结构设计(如桥梁、铁路轨道、电缆工程等)、机械和仪表的制造、材料的加工和焊接等过程中都必须考虑材料的热膨胀特性。
材料的热膨胀特性也有许多有利方面的应用,如液体温度计、喷墨打印机等等。
在测量材料线膨胀系数的常用方法中,关键是测量材料受热膨胀后的微小长度伸长量。
这一微小长度变化量用一般的长度测量仪器很难测准,一般需要采用放大测量方法、借助测微装置或仪器来测量,如光杠杆光学放大法、千分尺螺旋放大法、光学干涉法等。
本实验采用非电量电测法通过霍尔位移传感器测量微小的长度变化。
【预习提示】1.什么是线膨胀系数?测量线膨胀系数需要测量哪些相关物理量?2.霍尔位移传感器的基本工作原理是什么?3.什么是定标?4.怎样设计测量数据记录表?【实验目的】1.掌握测量线膨胀系数的基本原理。
(新)架空输电线路设计-孟遂民版--答案

第二章 4.求[例2-2]中沈阳地区50年一遇的30m 高度的最大设计风速是多少? 【解】(1)计算样本中的48个年最大风速的均值ν和标准差S 分别为:)/(9375.184890911s m v n n i i ===∑=ν)/(3402.41483525.885)(1112s m v v n S n i i=-=--=∑= (2)进行重现期的概率计算,由于风速个数48=n ,查表2-7并进行线性插值,得到修正系数C 1、C 2为:15714.1)4548(455015185.116066.115185.11=-⨯--+=C54764.0)4548(455054630.054853.054630.02=-⨯--+=C分布的尺度参数a 和位置参数b 为:1)/(26661.03402.415714.11-===s m S C a )/(8834.1626661.054764.09375.182s m a C v b =-=-=重现期R=50年20m 高度的年最大风速为:)/(519.31)15050ln(ln 2661.018834.16)1ln(ln 150s m R R a b v =⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--= (3)进行高度换算,B 类地区,故0.1,16.0==βz ,则067025.1)2030(0.1)(16.0=⨯==z h h 仪设计βα所以,30m 设计高度处50年重现期的年最大风速为:)/(632.33519.31067025.15050s m v v m =⨯==α第三章 6.试计算LGJ-150/35钢芯铝绞线的弹性系数、温度线膨胀系数和计算拉断力,并与查表值进行比较(以相对误差表示)。
【解】:查附录A 得35/150-LGJ(根数30/7)可知:铝部截面积226.147mm A a =, 直径mm d a 5.2=;钢部截面积236.34mm A s =,直径mm d s5.2=;计算截面积262.181mm A =,导线外径25.17mm d =, 计算拉断力[]N T j 65020=。
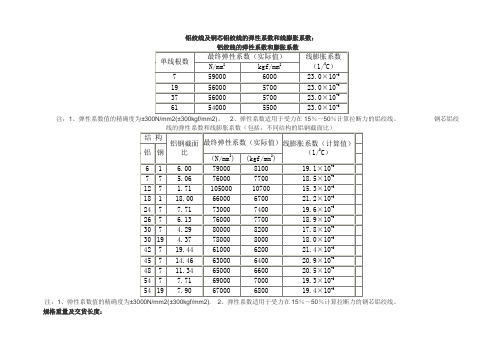
铝绞线及钢芯铝绞线的弹性系数和线膨胀系数
34.36
181.62
17.50
0.1962
65020
676.2
2000
185/10
18/3.60
1/3.60
183.22
10.18
193.40
18.00
0.1572
40880
584.0
2000
185/25
24/3.15
7/2.10
187.04
24.25
211.29
18.90
0.1542
204.14
11.34
215.48
19.00
0.1411
45140
650.7
2000
210/25
24/3.33
7/2.22
209.02
27.10
236.12
19.98
0.1380
65990
789.1
2000
210/35
26/3.22
7/2.50
211.73
34.36
246.09
20.38
0.1363
54
19
7.90
67000
6800
19.4×10-6
注:1、弹性系数值的精确度为±3000N/mm2(±300kgf/mm2).2、弹性系数适用于受力在15%~50%计算拉断力的钢芯铝绞线。
规格重量及交货长度:
LJ型铝绞线
标称截面
(mm2)
结构根数/直径
(mm)
计算截面
(mm2)
外径(mm)
直流电阻不大于
1
6.00
79000
8100
19.1×10-6
7
架空线常用计算公式和应用举例

架空线常⽤计算公式和应⽤举例架空线常⽤计算公式和应⽤举例前⾔在基层电⼒部门从事输电线路专业⼯作的技术⼈员,需要掌握导线的基本的计算⽅法。
这些⽅法可以从教材或⼿册中找到。
但是,教材⼀般从原理开始叙述,⽤于实际计算的公式夹在⼤量的⽂字和推导公式中,⼿册的计算实例较少,给应⽤带来⼀些不便。
本书根据个⼈在实际⼯作中的经验,摘取了⼀些常⽤公式,并主要应⽤Excel⼯作表编制了⼀些例⼦,以供相关⼈员参考。
本书的基本内容主要取材于参考⽂献,部分取材于⽹络。
所⽤参考⽂献如下:1. GB50545 -2010《110~750kV架空输电线路设计规程》。
2. GB50061-97 《66kV及以下架空电⼒线路设计规范》。
3. DL/T5220-2005 《10kV及以下架空配电线路设计技术规程》。
4. 邵天晓著,架空送电线路的电线⼒学计算,中国电⼒出版社,2003。
5.刘增良、杨泽江主编,输配电线路设计, 中国⽔利⽔电出版社,2004。
6.李瑞祥编,⾼压输电线路设计基础,⽔利电⼒出版社,1994。
7.电机⼯程⼿册编辑委员会,电机⼯程⼿册,机械⼯业出版社,1982。
8.张殿⽣主编,电⼒⼯程⾼压送电线路设计⼿册,中国电⼒出版社,2003。
9.浙西电⼒技⼯学校主编,输电线路设计基础,⽔利电⼒出版社,1988。
10.建筑电⽓设计⼿册编写组,建筑电⽓设计⼿册,中国建筑⼯业出版社,1998。
11.许建安主编,35-110kV输电线路设计,中国⽔利⽔电出版社,2003。
由于个⼈⽔平所限,书中难免出现错误,请识者不吝指正。
四川安岳供电公司李荣久2015-9-16⽬录第⼀章电⼒线路的导线和设计⽓象条件第⼀节导线和地线的型式和截⾯的选择⼀、导线型式⼆、导线截⾯选择及校验的⽅法三、地线的选择第⼆节架空电⼒线路的设计⽓象条件⼀、设计⽓象条件的选⽤⼆、⽓象条件的换算第⼆章导线(地线)张⼒(应⼒)弧垂计算第⼀节导线和地线的机械物理特性及单位荷载⼀、导线的机械物理特性⼆、导线的单位荷载第⼆节导线的最⼤使⽤张⼒和平均运⾏张⼒⼀、导线的最⼤使⽤张⼒⼆、导线的平均运⾏张⼒第三节导线张⼒弧垂的精确计算⼀、导线的悬链线解析⽅程式⼆、导线的张⼒、弧垂及线长三、导线的允许档距和允许⾼差四、导线悬挂点等⾼时的张⼒弧垂计算五、架空线的等效张⼒(平均张⼒)第四节导线张⼒弧垂的近似计算⼀、导线的抛物线解析⽅程式⼆、导线的张⼒、弧垂及线长第五节⽔平档距和垂直档距⼀、⽔平档距和⽔平荷载⼆、垂直档距和垂直荷载第六节导线的状态⽅程式⼀、孤⽴档的状态⽅程式⼆、连续档的状态⽅程式和代表档距第七节临界档距⼀、⽤斜抛物线状态⽅程式求临界档⼆、⽤临界档距判别控制条件所控制的档距范围第⼋节导线张⼒弧垂计算步骤第九节导线应⼒弧垂分析⼀、导线和地线的破坏应⼒及⽐载⼆、导线的悬链线公式三、导线应⼒弧垂的近似计算四、⽔平档距和垂直档距五、导线的斜抛物线状态⽅程式六、临界档距第三章特殊情况导线张⼒弧垂的计算第⼀节档距中有⼀个集中荷载时导线张⼒弧垂的计算⼀、档距中有⼀个集中荷载的弧垂和张⼒⼆、导线强度及对地或交叉跨越物距离的校验第⼆节孤⽴档导线的计算⼀、耐张绝缘⼦串的单位荷载⼆、孤⽴档导线的张⼒和弧垂三、孤⽴档的临界档距第三节导线紧线时的过牵引计算⼀、紧线施⼯⽅法及过牵引长度⼆、过牵引引起的伸长和变形三、不考虑耐张绝缘⼦串的导线过牵引计算四、孤⽴档考虑耐张绝缘⼦串的导线过牵引计算第四节连续倾斜档的安装计算⼀、连续倾斜档导线安装时的受⼒分析⼆、连续倾斜档观测弧垂的确定三、悬垂线夹安装位置的调整四、地线的安装第五节耐张绝缘⼦串倒挂的校验第六节悬垂线夹悬垂⾓的计算第四章导线和地线的防振计算第⼀节防振锤和阻尼线⼀、防振锤的安装⼆、阻尼线的安装第⼆节分裂导线的防振第五章架空线的不平衡张⼒计算第⼀节刚性杆塔固定横担线路不平衡张⼒的计算⼀、线路产⽣不平衡张⼒时的⼏种关系⼆、不均匀覆冰或不同时脱冰时的不平衡张⼒求解⽅法三、断线张⼒求解⽅法四、导线从悬垂线夹松落时的不平衡张⼒第⼆节固定横担线路考虑杆塔挠度时不平衡张⼒的计算⼀、线路产⽣不平衡张⼒时的⼏种关系⼆、不均匀覆冰或不同时脱冰时考虑杆塔挠度的不平衡张⼒求解⽅法三、考虑杆塔挠度时的断线张⼒求解⽅法第三节转动型横担线路断线张⼒的计算⼀、断线张⼒的求解⽅程⼆、断线张⼒的计算机试凑求解⽅法第四节相分裂导线不平衡张⼒的计算⼀、计算分裂导线的不平衡张⼒的公式⼆、计算公式中⼏个参数的取值及计算三、不平衡张⼒的求解⽅法四、⽤Excel⼯作表进⾏计算的⽅法第五节地线⽀持⼒的计算⼀、电杆的刚度和刚度系数⼆、电杆的挠度三、地线⽀持⼒的计算四、地线⽀持⼒的计算机试凑求解⽅法第六章架空线弧垂观测计算第⼀节弧垂观测概述⼀、观测档的选择⼆、导线初伸长的处理三、弧垂的观测⽅法四、弧垂的调整及检查五、观测弧垂时应该注意的问题第⼆节均布荷载下的弧垂的观测参数计算⼀、⽤悬链线法求弧垂观测参数⼆、弧垂观测⾓的近似计算公式三、⽤异长法和等长法观测弧垂时a、b及弧垂f的关系第三节观测档内联有耐张绝缘⼦串时弧垂的观测参数计算⼀、观测档弧垂的计算公式⼆、⽤等长法和异长法观测弧垂三、⽤⾓度法观测弧垂架空线常⽤计算公式和应⽤举例安岳供电公司李荣久第⼀章电⼒线路的导线和设计⽓象条件第⼀节导线和地线的型式和截⾯的选择⼀、导线型式常⽤导线的型号和名称如表1-1-1。
材料线膨胀系数

材料线膨胀系数材料线膨胀系数是指材料在温度变化时,单位温度变化下长度的增加量与原长度的比值。
在工程实践中,了解材料的线膨胀系数对于设计和制造具有温度变化环境的设备和结构至关重要。
本文将介绍材料线膨胀系数的概念、计算方法以及实际应用。
一、概念。
材料线膨胀系数是描述材料在温度变化时长度变化的物理量。
通常用α表示,单位为1/℃。
材料线膨胀系数的大小与材料的种类、结构和温度有关。
一般来说,固体材料的线膨胀系数在常温下是一个固定值,但随着温度的升高,线膨胀系数也会随之增大。
二、计算方法。
材料线膨胀系数的计算方法可以通过实验测定得到,也可以通过理论计算进行估算。
实验测定的方法是将材料样品置于恒定温度下,测量其长度随温度变化的变化量,然后根据公式α=(ΔL/L0) / ΔT计算得到。
其中,α为线膨胀系数,ΔL为长度变化量,L0为原长度,ΔT为温度变化量。
理论计算方法则需要考虑材料的晶格结构、原子间作用力等因素,通过热力学和固体物理学的理论模型进行计算。
三、实际应用。
材料线膨胀系数在工程实践中有着广泛的应用。
例如,在建筑工程中,由于温度变化会导致建筑材料的线膨胀,因此在设计建筑结构时需要考虑材料的线膨胀系数,以避免由于温度变化而引起的结构变形和损坏。
在机械制造领域,由于温度变化会引起零件的尺寸变化,因此需要在设计和加工过程中考虑材料的线膨胀系数,以保证零件在不同温度下的尺寸精度。
此外,在航空航天、汽车制造、电子设备等领域,对材料线膨胀系数的要求也非常严格,因为温度变化可能会对设备的性能和稳定性产生重要影响。
综上所述,材料线膨胀系数是描述材料在温度变化时长度变化的重要物理量,对于工程设计和制造具有重要意义。
通过了解材料的线膨胀系数,可以更好地应对温度变化对设备和结构的影响,保证其性能和稳定性。
因此,对于工程师和设计人员来说,掌握材料线膨胀系数的基本概念和计算方法是非常重要的。
线膨胀系数3.3 -回复

线膨胀系数3.3 -回复线膨胀系数是材料在温度改变下线性膨胀或收缩的程度的指标。
它是一个表示材料热膨胀性质的物理常数,用于计算在温度变化下材料尺寸的变化。
线膨胀系数为3.3的材料在温度改变时会有比较显著的尺寸变化。
本文将逐步解析线膨胀系数3.3的几个关键问题,包括线膨胀系数的定义、计算方法、影响因素以及示例应用。
一、线膨胀系数的定义线膨胀系数是指材料在单位温度变化下长度或体积的相对变化比例。
它通常用α表示,单位为1/。
线膨胀系数可用公式表示如下:γ= ΔL / (L * ΔT)其中,γ为线膨胀系数,ΔL为温度变化下的长度变化,L为初始长度,ΔT 为温度变化。
二、线膨胀系数的计算方法对于线膨胀系数为3.3的材料,可以通过实验测量或从相关文献中获取。
实验测量通常采用热膨胀仪等设备,在不同温度下测量材料的长度变化。
计算线膨胀系数的方法已在上述定义中给出。
三、影响线膨胀系数的因素线膨胀系数受到多个因素的影响,包括材料的晶格结构、化学成分、温度变化范围等。
晶格结构的不同会导致材料在不同方向上的膨胀系数不同。
化学成分的改变也会影响材料的热膨胀性质。
此外,温度变化范围对材料的膨胀系数也有一定影响,通常情况下,在较广的温度范围内,材料的线膨胀系数是变化的。
四、示例应用线膨胀系数是材料工程和结构设计中的一个重要参数,广泛应用于各个领域。
以线膨胀系数为3.3的材料为例,它的尺寸变化在温度改变时较为显著。
在建筑中,对于长跨度的梁、桥等结构,考虑到温度变化引起的尺寸变化,需要合理选择材料和结构设计,以满足安全要求。
在航空航天领域,线膨胀系数是设计和制造高温部件时必须考虑的因素,如发动机涡轮叶片的设计和材料选择。
此外,线膨胀系数还可以应用于材料研究和加工过程中对材料的性能和稳定性进行评估。
综上所述,线膨胀系数是一个重要的材料性质指标,对于理解材料在温度变化下的尺寸变化、工程设计和材料选择具有重要意义。
线膨胀系数为3.3的材料在温度改变时尺寸变化较大,因此需要在应用中充分考虑其影响,以确保材料及结构的稳定性和可靠性。
管材的线膨胀及伸缩量的计算

第一节 管材的线膨胀及伸缩量的计算一、热膨胀量的计算管道安装完毕投入运行时,常因管内介质的温度与安装时环境温度的差异而产生伸缩。
另外,由于管道本身工作温度的高低,也会引起管道的伸缩。
实验证明,温度变化而引起管道长度成比例的变化。
管道温度升高,由于膨胀,长度增加;温度下降,则由于收缩,长度缩短。
温度变化1度相应的长度成比例变化量称为管材的线膨胀系数。
不同材质的材料线膨胀系数也不同。
碳素钢的线膨胀系数为12×10—6/℃,而硬质聚氯乙烯管的线膨胀系数为80X10—6/℃,约为碳素钢的七倍。
管材受热后的线膨胀量,按下式进行计算:()L t t L 21-=∆α式中△L ——管道热膨胀伸长量(m);α——管材的线膨胀系数(1/K)或(1/℃); t 2——管道运行时的介质温度(℃);t l ——管道安装时的温度(℃),安装在地下室或室内时取t 1=—5℃;当室外架空敷设时,t 1应取冬季采暖室外计算温度;L ——计算管段的长度(m)。
不同材质管材的。
值见表2—1。
表2—1不同材质管材的线膨胀系数在管道工程中,碳素钢管应用最广,其伸长量的计算公式为()L t t L 2161012-⨯=∆-式中12×10—6——常用钢管的线膨胀系数(1/)。
根据式(2—2)制成管道的热伸长量△L 表(见表2—2),由表中可直接查出不同温度下相应管长的热伸长量。
例有一段室内热水采暖碳素钢管道,管长70m ,输送热水温度为95℃,试计算此段管道的热伸长量。
解根据钢管的热膨胀伸长量计算式(2—2)△L=12×10—6(t 1—t 2)L=12×10—6(95+5)×70=0.084m由已知管长及送水温度,直接查表2—2,也可得管道的热伸长量△L 。
如果管道中通过介质的温度低于环境温度,则计算出来的是缩短量。
二、热应力计算如果管道两端不固定,允许它自由伸缩,则热伸缩量对管予的强度没有什么影响。
28.架空导线的机械物理特性、应力及安全系数有关计算

架空导线的机械物理特性、应力及安全系数有关计算架空导线的机械物理特性,与线路设计密切相关的主要是弹性系数、线性温度膨胀系数、抗拉强度极限(瞬时破坏应力)以及抗弯强度。
由于钢芯铝绞线是常用的架空线,其结构也比较复杂,故作重点介绍,其它类型架空线的机械物理特性可类似研究得到。
一、钢芯铝绞线的综合弹性系数钢芯铝绞线的弹性系数E,指的是在弹性限度内,导线受拉时,其应力与应变的比例系数。
计算方法如下:二、钢芯铝绞线的线性温度膨胀系数钢芯铝绞线的线性温度膨胀系数,指的是温度升高1℃时其单位长度的伸长量。
计算方法如下:三、钢芯铝绞线的瞬时破坏应力架空线在均匀增大的拉力作用下,缓慢伸长至拉断,此时的拉力称为拉断力。
对于钢芯铝绞线来说,拉断力由钢部和铝部共同承受,为二者的综合拉断力。
影响综合拉断力的因素主要有:(1)铝和钢的机械性能不同,铝的延伸率远低于钢的延伸率。
当铝部被拉断时,钢部的强度还未得到充分发挥,通常认为此时钢线的变形量为1%左右。
(2)绞合后单线与整体绞合线轴线间存在扭绞角,综合拉断力是各单线拉断力在轴线方向的分力构成。
(3)各层单线之间的应力分布不均匀。
(4)相邻两层单线间存在正应力和摩擦力。
抗拉强度(瞬时破坏应力)是指导线的计算拉断力与导线的计算截面积的比值。
对导线做拉伸试验,将测得的瞬时破坏拉断力除以导线的截面积,就得到瞬时破坏应力,即四、架空线的许用应力架空线的许用应力是指架空线弧垂最低点所允许使用的最大应力,工程中称之为最大使用应力,计算公式如下:五、架空线的安全系数影响安全系数的因素很多,如悬挂点的应力大于弧垂最低点的应力,补偿初伸长需增大应力,振动时产生附加应力而且断股后架空线强度降低,因腐蚀、挤压损伤造成强度降低以及设计、施工中的误差等等。
各因素对架空线许用应力的影响程度示于下表。
最小安全系数值公式:k=(1+k1+k2+k3+k6+k7)/(1-k4-k5)由上表可以看出,即使不考虑悬挂点附加弯曲应力和振动时的附加动应力的影响,最小安全系数也要求达到1.86。
管材的线膨胀及伸缩量的计算

第一节管材的线膨胀及伸缩量的计算一、热膨胀量的计算管道安装完毕投入运行时,常因管内介质的温度与安装时环境温度的差异而产生伸缩。
另外,由于管道本身工作温度的高低,也会引起管道的伸缩。
实验证明,温度变化而引起管道长度成比例的变化。
管道温度升高,由于膨胀,长度增加;温度下降,则由于收缩,长度缩短。
温度变化1度相应的长度成比例变化量称为管材的线膨胀系数。
不同材质的材料线膨胀系数也不同。
碳素钢的线膨胀系数为12×10—6/℃,而硬质聚氯乙烯管的线膨胀系数为80X10—6/℃,约为碳素钢的七倍。
管材受热后的线膨胀量,按下式进行计算:式中△L——管道热膨胀伸长量(m);?——管材的线膨胀系数(1/K)或(1/℃);t2——管道运行时的介质温度(℃);t l——管道安装时的温度(℃),安装在地下室或室内时取t1=—5℃;当室外架空敷设时,t1应取冬季采暖室外计算温度;L——计算管段的长度(m)。
不同材质管材的。
值见表2—1。
表2—1不同材质管材的线膨胀系数在管道工程中,碳素钢管应用最广,其伸长量的计算公式为式中12×10—6——常用钢管的线膨胀系数(1/)。
根据式(2—2)制成管道的热伸长量△L表(见表2—2),由表中可直接查出不同温度下相应管长的热伸长量。
例有一段室内热水采暖碳素钢管道,管长70m,输送热水温度为95℃,试计算此段管道的热伸长量。
解根据钢管的热膨胀伸长量计算式(2—2)△L=12×10—6(t1—t2)L=12×10—6(95+5)×70=0.084m由已知管长及送水温度,直接查表2—2,也可得管道的热伸长量△L。
如果管道中通过介质的温度低于环境温度,则计算出来的是缩短量。
表2—2水和蒸汽管道的热伸长量△L表(m)如果管道两端不固定,允许它自由伸缩,则热伸缩量对管予的强度没有什么影响。
若在管子的两端加以限制,阻止管子伸缩,这时在管道内部将产生很大的热应力,热应力的计算式为式中σ——管材受热时所产生的热应力(MN/m2);E——管材的弹性模量(MN/m2),碳素钢的弹性模量 E=20.104×104MN /m2;ε——管段的相对变形量,ε=△L/L为管段的热膨胀量(m);L为在室温下安装的管段原长度(m)。
管材的线膨胀及伸缩量的计算

第一节 管材的线膨胀及伸缩量的计算一、热膨胀量的计算管道安装完毕投入运行时,常因管内介质的温度与安装时环境温度的差异而产生伸缩。
另外,由于管道本身工作温度的高低,也会引起管道的伸缩。
实验证明,温度变化而引起管道长度成比例的变化。
管道温度升高,由于膨胀,长度增加;温度下降,则由于收缩,长度缩短。
温度变化1度相应的长度成比例变化量称为管材的线膨胀系数。
不同材质的材料线膨胀系数也不同。
碳素钢的线膨胀系数为12×10—6/℃,而硬质聚氯乙烯管的线膨胀系数为80X10-6/℃,约为碳素钢的七倍。
管材受热后的线膨胀量,按下式进行计算:()L t t L 21-=∆α式中△L ——管道热膨胀伸长量(m );α——管材的线膨胀系数(1/K )或(1/℃); t 2——管道运行时的介质温度(℃); t l -—管道安装时的温度(℃),安装在地下室或室内时取t 1=—5℃;当室外架空敷设时,t 1应取冬季采暖室外计算温度;L —-计算管段的长度(m )。
不同材质管材的.值见表2-1。
表2—1不同材质管材的线膨胀系数在管道工程中,碳素钢管应用最广,其伸长量的计算公式为()L t t L 2161012-⨯=∆-式中12×10—6——常用钢管的线膨胀系数(1/)。
根据式(2—2)制成管道的热伸长量△L 表(见表2—2),由表中可直接查出不同温度下相应管长的热伸长量.例有一段室内热水采暖碳素钢管道,管长70m ,输送热水温度为95℃,试计算此段管道的热伸长量。
解根据钢管的热膨胀伸长量计算式(2-2)△L=12×10—6(t 1—t 2)L=12×10—6(95+5)×70=0.084m由已知管长及送水温度,直接查表2—2,也可得管道的热伸长量△L 。
如果管道中通过介质的温度低于环境温度,则计算出来的是缩短量.二、热应力计算如果管道两端不固定,允许它自由伸缩,则热伸缩量对管予的强度没有什么影响。
02 m,求金属的线膨胀系数。

02 m,求金属的线膨胀系数。
02M 金属的线膨胀系数
简介
金属的线膨胀系数是描述金属材料随温度变化时线性尺寸变化的一个物理量。
知道金属材料的线膨胀系数有助于在工程设计和热力学计算中预测和控制金属材料的尺寸变化。
定义
线膨胀系数是指单位温度变化时,单位长度的金属材料在长度方向上的尺寸变化量。
通常用符号α表示,单位是1/℃。
计算方法
通常计算金属的线膨胀系数有两种常用方法:
1. 直线膨胀系数法:通过测量金属材料在不同温度下的尺寸变化,然后使用线性回归方法计算出线膨胀系数。
α = (L2 - L1) / (L1 * (T2 - T1))
其中,α为线膨胀系数,L1和L2为金属材料在温度T1和T2下的长度,T1和T2为温度。
2. 热膨胀系数法:通过已知金属材料的热膨胀系数和初始长度来计算线膨胀系数。
α = β * ΔT
其中,α为线膨胀系数,β为热膨胀系数,ΔT为温度变化量。
应用
金属材料的线膨胀系数在工程设计和热力学计算中有着广泛的应用。
以下是一些应用场景:
- 构建桥梁和建筑物时,需要考虑材料的线膨胀系数以预测材料的尺寸变化,避免因温度变化引起的结构变形。
- 制造长管道时,需要考虑管道材料的线膨胀系数,以避免因温度变化引起的管道伸缩问题。
- 在热力学计算中,需要考虑材料的线膨胀系数,以准确计算热传导、热膨胀和热变形等热力学过程。
结论
金属材料的线膨胀系数是描述金属材料随温度变化时尺寸变化的重要物理量。
通过测量或计算金属材料的线膨胀系数,可以在工程设计和热力学计算中预测和控制金属材料的尺寸变化,避免由温度变化引起的问题。
02 m,求金属的线膨胀系数。

02 m,求金属的线膨胀系数。
02 m,求金属的线膨胀系数引言线膨胀是指物质在温度改变下长度或体积的变化。
对于金属材料来说,线膨胀系数是一个重要的物理性质,它描述了金属材料在温度变化下单位长度的变化量。
了解金属的线膨胀系数有助于我们在设计和制造中合理选择材料,避免因温度变化导致的问题。
本文将介绍金属线膨胀系数的计算方法和几种常见金属的线膨胀系数。
计算方法金属的线膨胀系数可以通过实验测量或理论计算获得。
实验测量是通过在不同温度下测量金属样品的长度变化,并根据实验数据计算膨胀系数。
理论计算可以使用线膨胀系数的经验公式或基于晶格结构的理论模型。
经验公式常见的经验公式用于计算金属的线膨胀系数包括线性膨胀系数和体积膨胀系数。
线性膨胀系数描述了长度的变化,而体积膨胀系数描述了体积的变化。
线性膨胀系数的计算公式为:α = (L₂ - L₁) / (L₁ * ΔT)其中,α为线膨胀系数,L₂为温度为T₂时的长度,L₁为温度为T₁时的长度,ΔT为温度变化量。
体积膨胀系数的计算公式为:β = (V₂ - V₁) / (V₁ * ΔT)其中,β为体膨胀系数,V₂为温度为T₂时的体积,V₁为温度为T₁时的体积,ΔT为温度变化量。
理论模型除了经验公式,金属的线膨胀系数可以通过基于晶格结构的理论模型进行计算。
这些模型基于金属晶格的几何和力学性质,可用于计算不同温度下的线膨胀系数。
常见金属的线膨胀系数金属的线膨胀系数因金属种类而异。
下面是一些常见金属的线膨胀系数的示例:1. 铝(Aluminum):线膨胀系数为2.4×10^-5 /℃。
2. 铜(Copper):线膨胀系数为1.7×10^-5 /℃。
3. 铁(Iron):线膨胀系数为1.2×10^-5 /℃。
4. 钢(Steel):线膨胀系数为1.2×10^-5 /℃。
这只是一些常见金属的线膨胀系数的示例,实际上每种金属都有不同的线膨胀系数,并且可能随温度的变化而变化。
2195线膨胀系数 -回复

2195线膨胀系数-回复什么是2195线膨胀系数?为何它如此重要?2195线膨胀系数是指金属材料在特定温度下的线膨胀率。
线膨胀系数用于描述材料随着温度的变化所引起的尺寸变化。
这个系数是一个物理常数,表示材料在温度变化时单位长度的线性变化率。
线膨胀系数对于工程和科学领域非常重要。
首先,了解材料的线膨胀特性可以帮助工程师预测和解决由温度变化引起的尺寸变化问题。
例如,在建筑工程中,建筑物的材料会因为季节性的温度变化而发生膨胀和收缩。
如果不考虑线膨胀系数,建筑物可能会出现裂缝、变形或其他结构问题。
因此,使用2195线膨胀系数可以帮助工程师选择适当的材料,并在设计和施工过程中做出合理的调整。
其次,线膨胀系数在热学和材料科学的研究中也起着重要的作用。
通过研究不同材料的线膨胀系数,科学家可以深入了解材料的热传导和热膨胀机制。
这项研究对于开发新型材料、改善热传导性能以及设计高温设备等方面具有重要意义。
了解2195线膨胀系数的计算方法也非常重要。
线膨胀系数通常用ΔL 表示,表示在温度变化ΔT下,单位长度的线性变化。
ΔL的计算公式如下:ΔL = α×L ×ΔT其中,α表示线膨胀系数,L表示初始长度,ΔT表示温度变化。
通过计算ΔL,可以得到材料在温度变化下的尺寸变化。
在实际应用中,每种材料都有不同的线膨胀系数。
例如,铝的线膨胀系数为23 ×10-6-1,而钢的线膨胀系数为13 ×10-6-1。
这意味着,在相同的温度变化下,铝材料的尺寸变化将更大。
因此,在工程设计中,通过选择具有适当线膨胀系数的材料,可以更好地应对温度变化。
此外,值得注意的是,线膨胀系数还可能随温度的变化而变化。
这是因为不同材料在不同温度下的结构和性质会发生变化。
因此,在进行线膨胀系数计算时,需要考虑这种温度依赖性,并使用相应的数据和公式。
综上所述,2195线膨胀系数是描述金属材料在温度变化下尺寸变化的一个重要参数。
平均线胀系数

平均线胀系数
(最新版)
目录
1.介绍平均线胀系数
2.解释线胀系数的计算方法
3.探讨线胀系数的应用
4.说明线胀系数的重要性
正文
一、介绍平均线胀系数
平均线胀系数(Average Line Expansion Coefficient)是一种描述材料在温度变化时,其长度变化情况的物理量。
它是衡量材料在温度变化过程中,单位长度的变化量与原始长度之比,通常用百分比表示。
平均线胀系数可以用来评估材料的热膨胀性能,对于工程应用和科学研究具有重要的意义。
二、解释线胀系数的计算方法
线胀系数的计算公式为:
α = ΔL / L0 * 100%
其中,α表示线胀系数,ΔL 表示材料长度的变化量,L0 表示原始长度。
三、探讨线胀系数的应用
1.在金属材料中的应用:线胀系数是金属材料在高温环境下重要的性能指标。
对于金属材料,在其使用过程中,往往需要承受高温环境,因此,了解材料的线胀系数对于设计和生产具有重要意义。
2.在陶瓷材料中的应用:陶瓷材料在高温环境下的线胀系数对于材料
的稳定性和可靠性至关重要。
陶瓷材料的线胀系数越小,其抗热震性能越强,使用寿命越长。
3.在聚合物材料中的应用:聚合物材料在生产和加工过程中,往往需要考虑其线胀系数。
因为聚合物材料的线胀系数会影响材料的尺寸稳定性和使用寿命。
四、说明线胀系数的重要性
平均线胀系数是衡量材料在温度变化时长度变化的物理量,对于材料的设计、生产和使用具有重要意义。
了解材料的线胀系数可以帮助工程师更好地评估材料的性能,为工程应用提供依据。
架空绝缘配电线路设计技术规程(导线部分)

架空绝缘配电线路设计技术规程(导线部分)1架空绝缘配电线路所采用的导线应符合GB12527、GB14049的规定。
供计算用的导线性能参数见附录B附录B导线的性能参数Bl铝线的性能参数见表Bl。
2)弹性系数适用于导线受力在15%~50%导线计算拉断力时。
B2铝合金线的性能参数见表B2。
注:1)铝合金线根据其所含合金成分不同而最终弹性系数有差别,故可在此范围内选择。
3)弹性系数适用于导线受力在15%~50%导线计算拉断力时。
B3铜线的性能参数见表B3。
注:1)弹性系数值的精确度为±3000N∕mm2;4)弹性系数适用于导线受力在15%~50%导线计算拉断力时。
2绝缘导线及悬挂绝缘导线的钢绞线的设计安全系数均不应小于33绝缘导线截面的确定应符合下列要求。
3.1应结合地区配电网发展规划选定导线截面,无配电网规划城镇地区的绝缘导线设计最小截面见表1。
表1无配电网规划城镇地区绝缘导线设计最小截面mm23.2采用允许电压降校验时:a)中压绝缘配电线路,自供电的变电所二次侧出口至线路末端变压器或末端受电变电所一次侧入口的允许电压降为供电变电所二次侧额定电压(6、IOkV)的5%;b)低压绝缘配电线路,自配电变压器二次侧出口至线路末端(不包括接户线)的允许电压降为额定低压配电电压(220、380V)的4%。
4校验导线的载流量时,PE、PVC绝缘的导线的允许温度采用+70°C,XLPE绝缘的导线的允许温度采用+90°CO绝缘导线载流量的参考数据见附录C5三相四线制低压绝缘配电线路的最小零线截面见表2。
单相制的零线截面,应与相线截面相同。
26悬挂绝缘线的钢绞线的自重荷载应包括绝缘线、钢绞线、绝缘支架质量及200kg施工荷重。
钢绞线的最小截面不应小于50mm2o7绝缘导线的连接,应符合下列要求。
7.1不同金属、不同规格、不同绞向的导线及无承力线的集束线严禁在档距内连接。
7.2在一个档距内,每根导线不应超过一个承力接头。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
架空导线线膨胀系数计算
线膨胀系数概括铝线膨胀系数0.000023/℃钢芯膨胀系数0.0000115/℃铝计算截面积300.09mm2
钢计算截面积38.9mm2
铝线弹性系数6700kg/mm2
需要更改钢芯弹性系数20500kg/mm2
计算结果等价线膨胀系数 1.97342E-05
/℃架空导线弹性系数计算
(精确度±3000N/mm2)弹性系数概括铝计算截面积
300.09mm2钢计算截面积
38.9mm2铝线弹性系数
6800kgf/mm2钢芯弹性系数
20700kgf/mm2等价弹性系数8395.061801kgf/mm2
线膨胀系数N/mm 2kgf/mm 2(1/0C)759000600023.0×10-61956000570023.0×10-63756000570023.0×10-66154000550023.0×10-6
铝绞线的弹性系数和膨胀系数
最终弹性系数(实单线根数
线膨胀系数概括
铝23*10-6/℃
钢11.5*10-6/℃
镀锌殷钢 3.0*10-6/℃
铝包殷钢 3.7*10-6/℃导线名称
铝合金23.0*10-6/℃铝绞线
碳纤维 1.6*10-6/℃铝合金绞线
铝包钢13*10-6/℃铝合金芯铝绞线
铜17*10-6/℃钢芯铝绞线
铝基陶瓷纤维6.3*10-6/℃钢绞线
弹性系数概括
铝6800kgf/mm2
钢20700kgf/mm2
镀锌殷钢16500kgf/mm2
铝包殷钢15500kgf/mm2
铝合金6300kgf/mm2。
