人工智能天气决策树源代码

合集下载

天气决策树ID3

一、上机目的及内容1.上机内根据下列给定的14个样本数据,运用ID3算法构造一个是否适宜打网球的天气决策树。

2.上机目的（1）学习用Information Gain构造决策树的方法；（2）在给定的例子上，构造出正确的决策树；（3）理解并掌握构造决策树的技术要点。

二、实验原理及基本技术路线图（方框原理图或程序流程图）1、决策树通过把实例从根节点排列到某个叶子节点来分类实例，叶子节点即为实例所属的分类。

树上的每一个节点说明了对实例的某个属性的测试，并且该节点的每一个后继分支对应于该属性的一个可能值。

构造好的决策树的关键在于如何选择好的逻辑判断或属性。

对于同样一组例子，可以有很多决策树能符合这组例子。

人们研究出，一般情况下或具有较大概率地说，树越小则树的预测能力越强。

要构造尽可能小的决策树，关键在于选择恰当的逻辑判断或属性。

由于构造最小的树是NP-难问题，因此只能采取用启发式策略选择好的逻辑判断或属性。

用信息增益度量期望熵最低，来选择分类属性。

公式为算法：创建树的Root 结点如果Examples 都为正，那么返回label=+中的单结点Root 如果Examples 都为反，那么返回lable=-单结点树Root如果Attributes 为空，那么返回单节点树Root ，lable=Examples 中最普遍的目标属性值否则开始∑∑=∈⨯-=-=ci ii v A Values v v p p S Entropy S Entropy SS S Entropy A S Gain 12)(log )()()(),(A<-Attributes中分类能力最好的属性Root的决策属性<-A对于每个可能值在Root下加一个新的分支对应测试A=vi令Example-vi为Examples中满足A属性值为vi的子集如果Examples-vi为空在这个新分支下加一个叶子结点，节点的lable=Examples中最普遍的目标属性值否则在这个新分支下加一个子树ID3(example-vi,target-attribute,attributes-|A|)结束返回 Root算法实现:天气数据存放在data.txt 中；第一行为样本数量14和每个样本中属性的数量4；第二行为每个属性取值的数量；后面n行皆为例子；节点数据结构struct DTNode{int name; //用 1,2,3,4表示选择的属性，0表示不用分类，即叶节点int data[D_MAX+1]; //表示此节点包含的数据,data[i]=1,表示包含二维数组data[][]中的第i条数据int leaf; //leaf=1 正例叶节点；leaf=2 反例叶节点；leaf=0不是节点 int c; //c=1 正类；c=0 反类DTNode *child[P+1]; //按属性值的个数建立子树};定义函数void Read_data() //从数据文件data.txt中读入训练数据DT_pointer Create_DT(DT_pointer Tree,int name,int value) //创建决策树int chose(int *da) //选择分类属性float Gain(int *da,int p) //计算以p属性分类的期望熵float Entropy(int *da) //计算数据的熵int test_leaf(int *da) //测试节点属性void Out_DT(DT_pointer Tree) //用线性表形式输出建立的决策树int Class(int *da) //对输入的测试样本分类全局变量FILE *fp;int p_num; //属性的数量int pi[P_MAX+1]; //每个属性有几种取值int d_num; //数据的数量int data[P_MAX+1][D_MAX+1];//存储训练数据三、所用仪器、材料（设备名称、型号、规格等或使用软件）1台PC及VISUAL C++6.0软件四、实验方法、步骤（或：程序代码或操作过程）#include "stdio.h"#include "math.h"int trnum;struct tr{int key,childs,father,kind;int child[4];}tree[100];int n=14,c[100][5],keykind[10][2],keykind_num;int p,q;int captionnum=4;float mc;int outtree[5];int caption[10]={3,3,2,2};char caption_name[5][10]={"天况","温度","湿度","风况","分类"};char key_name[5][3][10]={{"晴","多云","雨"},{"热","中","冷"},{"大","正常"},{"无","有"},{"-","+"}};void initdata()//初始化数据c[0][0]=1: 表示第一个实例的天况为晴{c[0][0]=1;c[0][1]=1;c[0][2]=1;c[0][3]=1;c[0][4]=1;c[1][0]=1;c[1][1]=1;c[1][2]=1;c[1][3]=2;c[1][4]=1;c[2][0]=2;c[2][1]=1;c[2][2]=1;c[2][3]=1;c[2][4]=2;c[3][0]=3;c[3][1]=2;c[3][2]=1;c[3][3]=1;c[3][4]=2;c[4][0]=3;c[4][1]=3;c[4][2]=2;c[4][3]=1;c[4][4]=2;c[5][0]=3;c[5][1]=3;c[5][2]=2;c[5][3]=2;c[5][4]=1;c[6][0]=2;c[6][1]=3;c[6][2]=2;c[6][3]=2;c[6][4]=2;c[7][0]=1;c[7][1]=2;c[7][2]=1;c[7][3]=1;c[7][4]=1;c[8][0]=1;c[8][1]=3;c[8][2]=2;c[8][3]=1;c[8][4]=2;c[9][0]=3;c[9][1]=2;c[9][2]=2;c[9][3]=1;c[9][4]=2;c[10][0]=1;c[10][1]=2;c[10][2]=2;c[10][3]=2;c[10][4]=2;c[11][0]=2;c[11][1]=2;c[11][2]=1;c[11][3]=2;c[11][4]=2;c[12][0]=2;c[12][1]=1;c[12][2]=2;c[12][3]=1;c[12][4]=2;c[13][0]=3;c[13][1]=2;c[13][2]=1;c[13][3]=2;c[13][4]=1;tree[0].father=-1;}void calculate_pq()//计算在当前条件限制下，p=正例多少个，q=反例多少个，{int u,k,i;p=0;q=0;for (i=0;i<n;i++){u=1;for (k=1;k<=keykind_num;k++)if (c[i][keykind[k][0]]!=keykind[k][1]){u=0;break;}if (u)if (c[i][4]==1) q++;else p++;}}void calculate_keykind(int x)//找出从当前节点出发，所有父节点的属性{int i;i=x;keykind_num=0;while (tree[i].father>=0){keykind_num++;keykind[keykind_num][0]=tree[tree[i].father].key;keykind[keykind_num][1]=tree[i].kind;i=tree[i].father;}}float calculate_mc(float x,float y)//计算相对于当前正例和反例的熵{if (x==0||y==0) return 0;return -(x/(x+y))*(log(x/(x+y))/log(2))-(y/(x+y))*(log(y/(x+y))/log(2));}float calculate_gain(int x,int num,float mc1)//计算以属性x对当前节点进行决策的gain值{float bc=0;int i;keykind[keykind_num][0]=x;for (i=0;i<caption[x];i++)//计算B(C,属性X){keykind[keykind_num][1]=i+1;calculate_pq();bc=bc+((p+q)/(num+0.0))*calculate_mc(p,q);}return mc1-bc;}int findkey(int x)//找出当前点x的决策属性{int not_use[10],i;calculate_keykind(x);//找出X节点及其父节点的所有决策calculate_pq();//计算正反实例的个数if (p==0||q==0) return -1;mc=calculate_mc(p,q);//计算正反实例的熵int num=p+q,nowkey=-2;float max=-1,ans;for (i=0;i<=captionnum;i++) not_use[i]=1;for (i=1;i<=keykind_num;i++) not_use[keykind[i][0]]=0;keykind_num++;for (i=0;i<captionnum;i++)//枚举法一次讨论每个可用属性对X节点进行决策的gain值，取gain 值最大的属性为决策属性if (not_use[i]){ans=calculate_gain(i,num,mc);if (ans>max){max=ans;nowkey=i;}}return nowkey;}void output_con(int x)//输出满足X节点以及其所有父节点的决策的实例集合{calculate_keykind(x);int u,k,i;p=0;q=0;for (i=0;i<n;i++){u=1;for (k=1;k<=keykind_num;k++)if (c[i][keykind[k][0]]!=keykind[k][1]){u=0;break;}if (u){for (k=0;k<captionnum;k++)printf("%s,",key_name[k][c[i][k]-1]);printf("%s\n",key_name[k][c[i][k]-1]);}}}void output(int x,int deep)//输出X节点的实例，如果X不是叶子节点，则递归，一直找到叶节点才输出满足相应决策的实例集合{outtree[deep]=x;if (tree[x].childs>=0){for (int i=0;i<=tree[x].childs;i++)output(tree[x].child[i],deep+1);}else{printf("\n");for (int j=0;j<=deep-1;j++){printf("%s(%s)-->",caption_name[tree[outtree[j]].key],key_name[tree[outtree[j]].key][tree[outtree[j+1]].ki nd-1]);}printf("\n");output_con(outtree[deep]);}}void main(){int i;initdata();trnum=0;int open=0;while (open<=trnum)//open用来一次访问决策树的每个节点//每次访问一个节点，就对其进行决策，如果决策成功，则将新的点加入到决策树中，直至不能再扩展{tree[open].key=findkey(open);//寻找决策属性tree[open].childs=-1;if (tree[open].key>=0){for (i=0;i<caption[tree[open].key];i++)//决策成功，向决策树加入新的节点{trnum++;tree[trnum].kind=i+1;tree[open].childs++;tree[open].child[tree[open].childs]=trnum;tree[trnum].father=open;}}open++;}output(0,0);}五、实验过程原始记录( 测试数据、图表、计算等)六、实验结果、分析和结论（误差分析与数据处理、成果总结等。

决策树算法python代码

决策树算法python代码决策树是一种常见的机器学习算法，它可以用来做分类和回归问题。

决策树算法可以帮助我们从一组数据中找出有用的信息，并且可以把这些信息用来做出决策。

一般来说，决策树算法的基本思想是：从一组数据中提取最重要的特征，并根据这些特征来做出决策。

这些特征可以是数值型的，也可以是类别型的，也可以是组合型的。

下面我们来看一下决策树算法的python代码：## 一、导入库首先，我们需要导入相关的库，比如`numpy`，`pandas`，`sklearn`等。

```pythonimport numpy as npimport pandas as pdfrom sklearn.tree import DecisionTreeClassifier```## 二、准备数据然后，我们需要准备用于训练决策树的数据。

我们可以使用`pandas`库读取数据，并将其转换为`numpy`数组。

```python# 读取数据data = pd.read_csv('data.csv')# 将数据转换为numpy数组X = data.iloc[:,:-1].valuesy = data.iloc[:,-1].values```## 三、构建决策树接下来，我们就可以构建决策树了。

我们可以使用`sklearn`库中的`DecisionTreeClassifier`类来构建决策树。

```python# 创建决策树clf = DecisionTreeClassifier()# 训练决策树clf.fit(X,y)```## 四、预测结果最后，我们可以使用训练好的决策树来做预测。

```python# 预测结果y_pred = clf.predict(X)```## 五、评估模型最后，我们还可以使用`sklearn`库中的`accuracy_score`函数来评估模型的准确率。

```python# 评估模型from sklearn.metrics import accuracy_scoreprint(accuracy_score(y, y_pred))```以上就是决策树算法的python代码。

id3决策树算法python程序

id3决策树算法python程序关于ID3决策树算法的Python程序。

第一步：了解ID3决策树算法ID3决策树算法是一种常用的机器学习算法，用于解决分类问题。

它基于信息论的概念，通过选择最佳的特征来构建决策树模型。

ID3算法的核心是计算信息增益，即通过选择最能区分不同类别的特征来构建决策树。

第二步：导入需要的Python库和数据集在编写ID3决策树算法的Python程序之前，我们需要导入一些必要的Python库和准备好相关的数据集。

在本例中，我们将使用pandas库来处理数据集，并使用sklearn库的train_test_split函数来将数据集拆分为训练集和测试集。

pythonimport pandas as pdfrom sklearn.model_selection import train_test_split# 读取数据集data = pd.read_csv('dataset.csv')# 将数据集拆分为特征和标签X = data.drop('Class', axis=1)y = data['Class']# 将数据集拆分为训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) 第三步：实现ID3决策树算法的Python函数在此步骤中，我们将编写一个名为ID3DecisionTree的Python函数来实现ID3决策树算法。

该函数将递归地构建决策树，直到满足停止条件。

在每个递归步骤中，它将计算信息增益，并选择最佳特征作为当前节点的分裂依据。

pythonfrom math import log2from collections import Counterclass ID3DecisionTree:def __init__(self):self.tree = {}def calc_entropy(self, labels):label_counts = Counter(labels)entropy = 0for count in label_counts.values():p = count / len(labels)entropy -= p * log2(p)return entropydef calc_info_gain(self, data, labels, feature):feature_values = data[feature].unique()feature_entropy = 0for value in feature_values:subset_labels = labels[data[feature] == value]feature_entropy += len(subset_labels) / len(labels) * self.calc_entropy(subset_labels)return self.calc_entropy(labels) - feature_entropydef choose_best_feature(self, data, labels):best_info_gain = 0best_feature = Nonefor feature in data.columns:info_gain = self.calc_info_gain(data, labels, feature)if info_gain > best_info_gain:best_info_gain = info_gainbest_feature = featurereturn best_featuredef build_tree(self, data, labels):if len(set(labels)) == 1:return labels[0]elif len(data.columns) == 0:return Counter(labels).most_common(1)[0][0] else:best_feature = self.choose_best_feature(data, labels)sub_data = {}for value in data[best_feature].unique():subset = data[data[best_feature] == value].drop(best_feature, axis=1)sub_labels = labels[data[best_feature] == value]sub_data[value] = (subset, sub_labels)tree = {best_feature: {}}for value, (subset, sub_labels) in sub_data.items():tree[best_feature][value] = self.build_tree(subset, sub_labels)return treedef fit(self, data, labels):self.tree = self.build_tree(data, labels)def predict(self, data):predictions = []for _, row in data.iterrows():node = self.treewhile isinstance(node, dict):feature = list(node.keys())[0]value = row[feature]node = node[feature][value]predictions.append(node)return predictions第四步：使用ID3决策树模型进行训练和预测最后一步是使用我们实现的ID3DecisionTree类进行训练和预测。

人工智能c语言源代码

人工智能c语言源代码人工智能是一个广泛的领域，涉及多种算法和技术。

在C语言中，可以实现一些基本的人工智能功能。

下面是一个简单的示例，展示了如何使用C语言编写一个简单的决策树算法：c.#include <stdio.h>。

// 定义决策树节点结构。

typedef struct DecisionTreeNode {。

char question;struct DecisionTreeNode yesNode;struct DecisionTreeNode noNode;} DecisionTreeNode;// 创建决策树节点。

DecisionTreeNode createNode(char question) {。

DecisionTreeNode node = (DecisionTreeNode)malloc(sizeof(DecisionTreeNode));node->question = question;node->yesNode = NULL;node->noNode = NULL;return node;}。

// 决策树算法。

void decisionTree() {。

DecisionTreeNode root = createNode("Is it a mammal?");root->yesNode = createNode("Does it have fur?");root->yesNode->yesNode = createNode("It's amammal!");root->yesNode->noNode = createNode("It's not a mammal!");root->noNode = createNode("Does it have feathers?");root->noNode->yesNode = createNode("It's a bird!");root->noNode->noNode = createNode("It's not abird!");printf("%s\n", root->question);char answer;scanf(" %c", &answer);DecisionTreeNode currentNode = root;while (currentNode != NULL) {。

人工智能决策树例题经典案例

人工智能决策树例题经典案例一、经典案例：天气预测决策树在天气预测中有广泛应用，下面是一个关于是否适宜进行户外运动的示例：1. 数据收集：- 温度：高（>30℃）/中（20℃-30℃）/低（<20℃）- 降水：是/否- 风力：高/中/低- 天气状况：晴朗/多云/阴天/雨/暴雨- 应该户外运动：是/否2. 构建决策树：- 根据温度将数据分为三个分支：高温、中温、低温- 在每个分支中，继续根据降水、风力和天气状况进行划分，最终得到是否适宜户外运动的决策3. 决策树示例：温度/ / \高温中温低温/ | | \ |降水无降水风力适宜/ \ | | / \是否高中低| |不适宜适宜- 如果温度是高温且有降水，则不适宜户外运动- 如果温度是高温且无降水，则根据风力判断，如果风力是高，则不适宜户外运动，如果风力是中或低，则适宜户外运动 - 如果温度是中温，则不论降水和风力如何，都适宜户外运动- 如果温度是低温，则需要考虑风力，如果风力是高，则适宜户外运动，如果风力是中或低，则不适宜户外运动4. 参考内容：决策树的构建和应用：决策树通过对输入特征进行划分，构建了一棵树形结构，用于解决分类或回归问题。

构建决策树主要包括数据预处理、特征选择、划分策略和停止条件等步骤。

特征选择可以使用信息增益、基尼指数等算法，划分策略可以使用二叉划分或多叉划分，停止条件可以是叶子节点纯度达到一定阈值或达到预定的树深度。

决策树的应用包括数据分类、特征选择和预测等任务。

天气预测案例中的决策树：将天气预测问题转化为分类问题，通过构建决策树，可以得到识别是否适宜户外运动的规则。

决策树的决策路径可以用流程图或树状图表示，帮助理解和解释决策过程。

决策树的节点表示特征值，分支表示判断条件，叶子节点表示分类结果。

决策树的生成算法可以基于启发式规则或数学模型，如ID3、C4.5、CART等。

决策树的优缺点：决策树具有可解释性强、易于理解和实现、能处理非线性关系等优点。

机器学习-ID3决策树算法（附matlaboctave代码）

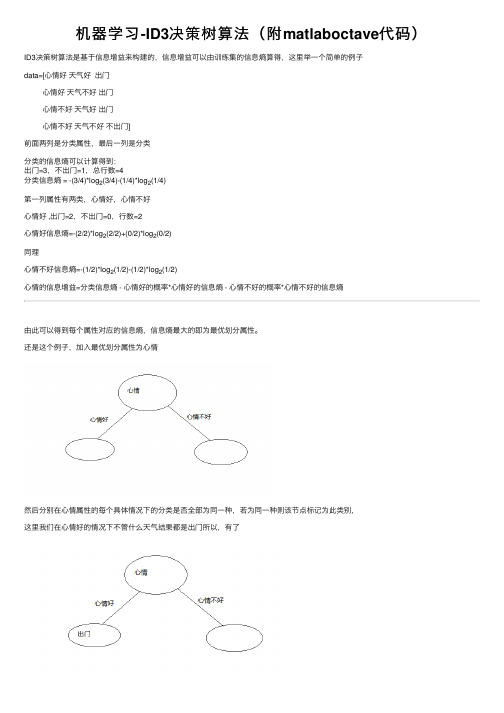
机器学习-ID3决策树算法（附matlaboctave代码）ID3决策树算法是基于信息增益来构建的，信息增益可以由训练集的信息熵算得，这⾥举⼀个简单的例⼦data=[⼼情好天⽓好出门⼼情好天⽓不好出门⼼情不好天⽓好出门⼼情不好天⽓不好不出门]前⾯两列是分类属性，最后⼀列是分类分类的信息熵可以计算得到：出门=3，不出门=1，总⾏数=4分类信息熵 = -(3/4)*log2(3/4)-(1/4)*log2(1/4)第⼀列属性有两类，⼼情好，⼼情不好⼼情好 ,出门=2，不出门=0，⾏数=2⼼情好信息熵=-(2/2)*log2(2/2)+(0/2)*log2(0/2)同理⼼情不好信息熵=-(1/2)*log2(1/2)-(1/2)*log2(1/2)⼼情的信息增益=分类信息熵 - ⼼情好的概率*⼼情好的信息熵 - ⼼情不好的概率*⼼情不好的信息熵由此可以得到每个属性对应的信息熵，信息熵最⼤的即为最优划分属性。

还是这个例⼦，加⼊最优划分属性为⼼情然后分别在⼼情属性的每个具体情况下的分类是否全部为同⼀种，若为同⼀种则该节点标记为此类别，这⾥我们在⼼情好的情况下不管什么天⽓结果都是出门所以，有了⼼情不好的情况下有不同的分类结果，继续计算在⼼情不好的情况下，其它属性的信息增益，把信息增益最⼤的属性作为这个分⽀节点，这个我们只有天⽓这个属性，那么这个节点就是天⽓了，天⽓属性有两种情况，如下图在⼼情不好并且天⽓好的情况下，若分类全为同⼀种，则改节点标记为此类别有训练集可以，⼼情不好并且天⽓好为出门，⼼情不好并且天⽓不好为不出门，结果⼊下图对于分⽀节点下的属性很有可能没有数据，⽐如，我们假设训练集变成data=[⼼情好晴天出门⼼情好阴天出门⼼情好⾬天出门⼼情好雾天出门⼼情不好晴天出门⼼情不好⾬天不出门⼼情不好阴天不出门]如下图：在⼼情不好的情况下，天⽓中并没有雾天，我们如何判断雾天到底是否出门呢？我们可以采⽤该样本最多的分类作为该分类，这⾥天⽓不好的情况下，我们出门=1，不出门=2，那么这⾥将不出门，作为雾天的分类结果在此我们所有属性都划分了，结束递归，我们得到了⼀颗⾮常简单的决策树。

机器学习经典算法详解及Python实现–决策树(Decision Tree) _ 数盟

人工智能
作者:Adan
℃
0评论
（一）认识决策树
1，决策树分类原理
决策树是通过一系列规则对数据进行分类的过程。它提供一种在什么条件下会得到什么值的类似规则的方法。决策树分为分类树和回归树两种，分类树对离散变量做决策树，回归树对连续变量做决策树。近来的调查表明决策树也是最经常使用的数据挖掘算法，它的概念非常简单。决策树算法之所以如此流行，一个很重要的原因就是使用者基本上不用了解机器学习算法，也不用深究它是如何工作的。直观看上去，决策树分类器就像判断模块和终止块组成的流程图，终止块表示分类结果（也就是树的叶子）。判断模块表示对一个特征取值的判断（该特征有几个值，判断模块就有几个分支）。如果不考虑效率等，那么样本所有特征的判断级联起来终会将某一个样本分到一个类终止块上。实际上，样本所有特征中有一些特征在分类时起到决定性作用，决策树的构造过程就是找到这些具有决定性作用的特征，根据其决定性程度来构造一个倒立的树–决定性作用最大的那个特征作为根节点，然后递归找到各分支下子数据集中次大的决定性特征，直至子数据集中所有数据都属于同一类。所以，构造决策树的过程本质上就是根据数据特征将数据集分类的递归过程，我们需要解决的第一个问题就是，当前数据集上哪个特征在划分数据分类时起决定性作用。为了找到决定性的特征、划分出最好的结果，我们必须评估数据集中蕴含的每个特征，寻找分类数据集的最好特征。完成评估之后，原始数据集就被划分为几个数据子集。这些数据子集会分布在第一个决策点的所有分支上。如果某个分支下的数据属于同一类型，则则该分支处理完成，称为一个叶子节点，即确定了分类。如果数据子集内的数据不属于同一类型，则需要重复划分数据子集的过程。如何划分数据子集的算法和划分原始数据集的方法相同，直到所有具有相同类型的数据均在一个数据子集内（叶子节点）。如下图就是一个决策树实例（目标是两类–见或者不见，每个样本有年龄、长相、收入、是否公务员四个特征）：

matlab决策树代码例子

matlab决策树代码例子当涉及到决策树的代码示例时，MATLAB提供了一个强大的工具箱，称为Statistics and Machine Learning Toolbox。

下面是一个使用MATLAB的决策树分类器的简单代码示例：matlab.% 导入数据。

load fisheriris.X = meas;Y = species;% 创建决策树模型。

tree = fitctree(X, Y);% 可视化决策树。

view(tree, 'Mode', 'Graph');% 预测新样本。

newX = [5 3.5 1.4 0.2; 6 3 4.5 1.5];predictedY = predict(tree, newX);disp(predictedY);这个示例中，我们首先导入了经典的鸢尾花数据集（fisheriris），其中包含了鸢尾花的测量数据（花萼长度、花萼宽度、花瓣长度和花瓣宽度）以及对应的鸢尾花种类。

然后，我们使用`fitctree`函数创建了一个决策树分类器模型，其中`X`是输入特征矩阵，`Y`是对应的目标变量。

接下来，我们使用`view`函数可视化生成的决策树模型，可以以图形方式展示决策树的结构。

最后，我们使用新的样本数据`newX`来预测其所属的鸢尾花种类，并使用`predict`函数进行预测。

这只是一个简单的决策树代码示例，你可以根据自己的需求进行更复杂的决策树模型构建和预测。

MATLAB的决策树工具箱提供了更多的选项和功能，例如控制树的最大深度、最小叶节点数等参数，以及交叉验证和剪枝等技术来优化模型。

决策树算法代码

决策树算法代码
简单来说，决策树算法是一种基于特征的方法，能够从训练数据中按照某种规则构建出决策树，用于预测未知数据。

它是非参数研究算法，不需要设定任何参数，只需要使用训练数据和特征，就可以构建出一个决策树。

决策树算法的基本思想是将数据集分解为更小的子集，每个子集都可以用一个决策来表示。

决策树算法通过不断地将数据集分解，最终形成一个“决策树”，用于预测未知数据。

决策树算法的基本步骤如下：
1. 从训练集中选择一个最优特征；
2. 根据最优特征的不同值，将训练集分成多个子集；
3. 对每一个子集，如果子集中的所有实例属于同一类，则该子集为“叶子结点”；否则，选择一个新的最优特征，重复1-2步；
4. 重复1-3步，直到所有子集都属于同一类，形成一棵决策树；
5. 利用决策树预测未知数据。

决策树算法具有许多优点，如容易理解、可视化和实现简单等。

决策树算法也有一些缺点，如容易过拟合、对异常数据敏感等。

总之，决策树算法是一种非常有用的机器研究算法，它可以用来解决分类和回归问题，它的优点和缺点都要注意，在使用时要谨慎，以达到最佳的效果。

实验二.天气决策树 PPT

Biblioteka 输入数据生成的决策树
算法
• 选择一个属性，把数据分割为K份。 • 选择的准则：Information Gain
Ga(iSn,A)Entr(oS)py vValu(eA)s SSv Entr(oSvp)y
c
Entr(oS)py pilo2gpi i1
原始数据的熵
• 本题中物体集C有十四个例子，9个正例，5 个反例。于是：
048bits大家应该也有点累了稍作休息大家有疑问的可以询问和交流生成的决策树继续划分晴的分支?gainc晴温度m天况为晴b天况为晴温度0571?gainc晴湿度m天况为晴b天况为晴湿度0971?gainc晴风况m天况为晴b天况为晴风况0420继续划分多云的分支?全部为正例无须划分
实验二.天气决策树
继续划分“多云 ”的分支
• 全部为正例，无须划分。
继续划分“雨 ”的分支
• Gain(C雨, “温度”) ＝ M(天况为雨)－B(天况为雨，“温度”) ＝０.０２０
• Gain(C雨, “湿度”) ＝ M(天况为雨)－B(天况为雨，“湿度”) ＝０.０２０
• Gain(C雨, “风况”) ＝ M(天况为雨)－B(天况为雨，"风况") ＝０.９７１
– “多云”的分支，含4个正例0个反例： M(天况为多云)＝0
– “雨”的分支，含３个正例２个反例： M(天况为雨)＝－3/5 * log2 (3/5)－2/5 * log2 (2/5) ＝ 0. 971 bits
• 则以“天况”作划分后，对应决策树的信息量为：
B(C，“天况”)＝5/14 * 0. 971 ＋4/14 * 0 ＋5/14 * 0. 971 ＝0. 694 bits
M(C)＝－9/14 * log2 (9/14) －5/14 * log2 (5/14)

机器学习决策树ID3算法的源代码

机器学习决策树ID3算法的源代码决策树算法（ID3）是一种机器学习算法，利用决策树的方式来学习和预测数据。

它是一种递归算法，可以根据现有的数据对分类功能进行估计。

ID3算法一般包括以下几个步骤：1、首先从所有的可能的特征中选择一个最好的分类特征，这个特征会从样本中提取出最有区分度的分类特征；2、接着把训练数据集按照这个特征的取值，划分成若干个小数据集；3、然后，从小数据集中，继续选择一个具有最大信息增益的特征作为子节点分裂依据；4、将节点分裂后，立即分类节点，叶子节点的样本类型应经过多数投票法，确定这个节点所属的分类；5、再把上述过程应用到每一个子节点上，一直迭代直到每一个节点只包含单一类别的样本；6、最后，根据决策树规则，得到一个分类模型，用于预测新的样本属于哪一类；下面是实现ID3算法的源代码：# -*- coding: utf-8 -*-import pandas as pdimport numpy as npfrom math import log2"""计算基尼不纯度parameters:dfData - 训练数据class_col - 分类的列returns:giniIndex - 基尼不纯度"""def giniIndex(dfData, class_col):giniIndex = 1class_count = dfData[class_col].value_counts( #计算每个类别出现的次数sum_count = dfData.shape[0] #数据的总条数for k in class_count:giniIndex -= (k / sum_count)**2 #基尼不纯度公式return giniIndex"""计算信息增益parameters:。

人工智能天气决策树源代码

昆明理工大学信息工程与自动化学院学生实验报告（ 2011 — 2012 学年第 1 学期）课程名称：人工智能开课实验室：信自楼计算机机房444 2011 年12月 16 日专业班级0 学号200 姓名成绩实验名称天气决策树指导教师教师评语该同学是否了解实验原理： A.了解□ B.基本了解□ C.不了解□该同学的实验能力： A.强□ B.中等□ C.差□该同学的实验是否达到要求： A.达到□ B.基本达到□ C.未达到□实验报告是否规范： A.规范□ B.基本规范□ C.不规范□实验过程是否详细记录： A.详细□ B.一般□ C.没有□教师签名：2011 年12 月日一、上机目的及内容1.上机内容根据下列给定的14个数据,运用Information Gain构造一个天气决策树。

例子编号属性分类天况温度湿度风况1 晴热大无N2 晴热大有N3 多云热大无P4 雨中大无P5 雨冷正常无P6 雨冷正常有N7 多云冷正常有P8 晴中大无N9 晴冷正常无P10 雨中正常无P11 晴中正常有P12 多云中大有P13 多云热正常无P14 雨中大有N2.上机目的（1）学习用Information Gain构造决策树的方法；（2）在给定的例子上，构造出正确的决策树；（3）理解并掌握构造决策树的技术要点。

二、实验原理及基本技术路线图（方框原理图或程序流程图）（1）设计并实现程序，构造出正确的决策树；（2）对所设计的算法采用大O符号进行时间复杂性和空间复杂性分析；主函数流程图：Attributevalue.cpp流程图Basefun流程图：Datapiont.cpp流程图：Dataset主要流程图：三、所用仪器、材料（设备名称、型号、规格等或使用软件）1台PC及VISUAL C++6.0软件四、实验方法、步骤（或：程序代码或操作过程）工程源代码：Main.cpp:#include <fstream>#include <iostream>#include <list>#include <sstream>#include <string>#include <vector>#include "AttributeValue.h"#include "DataPoint.h"#include "DataSet.h"DataPoint processLine(std::string const& sLine){std::istringstream isLine(sLine, std::istringstream::in);std::vector<AttributeValue> attributes;// TODO: need to handle beginning and ending empty spaces.while( isLine.good() ){std::string rawfield;isLine >> rawfield;attributes.push_back( AttributeValue( rawfield ) );}AttributeValue v = attributes.back();attributes.pop_back();bool type = v.GetType();return DataPoint(attributes, type);}void main(){std::ifstream ifs("in.txt", std::ifstream::in);DataSet initDataset;while( ifs.good() ){// TODO: need to handle empty lines.std::string sLine;std::getline(ifs, sLine);initDataset.addDataPoint( processLine(sLine) );}std::list<DataSet> processQ;std::vector<DataSet> finishedDataSet;processQ.push_back(initDataset);while ( processQ.size() > 0 ){std::vector<DataSet> splittedDataSets;DataSet dataset = processQ.front();dataset.splitDataSet(splittedDataSets);processQ.pop_front();for (int i=0; i<splittedDataSets.size(); ++i){float prob = splittedDataSets[i].getPositiveProb();if (prob == 0.0 || prob == 1.0){finishedDataSet.push_back(splittedDataSets[i]);}else{processQ.push_back(splittedDataSets[i]);}}}std::cout << "The dicision tree is:" << std::endl;for (int i = 0; i < finishedDataSet.size(); ++i){finishedDataSet[i].display();}}Attributevalue.cpp：#include "AttributeValue.h"#include "base.h"AttributeValue::AttributeValue(std::string const& instring): m_value(instring){}bool AttributeValue::GetType(){if (m_value == "P"){return true;}else if (m_value == "N"){return false;}else{throw DataErrException();}}Basefun.cpp:#include <math.h>float log2 (float x){return 1.0 / log10(2) * log10(x);}float calEntropy(float prob){float sum=0;if (prob == 0 || prob == 1){return 0;}sum -= prob * log2(prob);sum -= (1 - prob) * log2 ( 1 - prob );return sum;}Datapiont.cpp:#include <iostream>#include "DataPoint.h"DataPoint::DataPoint(std::vector<AttributeValue> const& attributes, bool type) : m_type(type){for (int i=0; i<attributes.size(); ++i){m_attributes.push_back( attributes[i] );}}void DataPoint::display(){for (int i=0; i<m_attributes.size(); ++i){std::cout << "\t" << m_attributes[i].getValue();}if (true == m_type){std::cout << "\tP";}else{std::cout << "\tN";}std::cout << std::endl;}Dataset.cpp:#include <iostream>#include <map>#include "base.h"#include "DataSet.h"void SplitAttributeValue::display(){std::cout << "\tSplit attribute ID(" << m_attributeIndex << ")\t";std::cout << "Split attribute value(" << m_v.getValue() << ")" << std::endl; }void DataSet::addDataPoint(DataPoint const& datapoint){m_data.push_back(datapoint);}float DataSet::getPositiveProb(){float nPositive = 0;for(int i=0; i<m_data.size(); ++i){if ( m_data[i].isPositive() ){nPositive++;}}return nPositive / m_data.size();}struct Stat{int nPos;int nNeg;int id;};void DataSet::splitDataSet(std::vector<DataSet>& splittedSets){// find all available splitting attributesint nAttributes = m_data[0].getNAttributes();int i, j;std::vector<bool> splittingAttributeBV;splittingAttributeBV.resize(nAttributes);for (i=0; i<nAttributes; ++i){splittingAttributeBV[i] = true;}for (i=0; i<m_splitAttributes.size(); ++i){splittingAttributeBV[ m_splitAttributes[i].getAttributeIndex() ] = false;}std::vector<int> splittingAttributeIds;for (i=0; i<nAttributes; ++i){if (true == splittingAttributeBV[i]){splittingAttributeIds.push_back(i);}}typedef std::map<AttributeValue, Stat, AttributeValueCmp> AttributeValueStat;typedef std::map<AttributeValue, Stat, AttributeValueCmp>::iterator AttributeValueStat_iterator;typedef std::map<AttributeValue, Stat, AttributeValueCmp>::const_iterator AttributeValueStat_const_iterator;// go through data once, and collect needed statistics to calculate entropystd::vector< AttributeValueStat > splittingStats;splittingStats.resize( splittingAttributeIds.size() );for (i=0; i<m_data.size(); ++i){for (j=0; j<splittingAttributeIds.size(); ++j){AttributeValue const& v = m_data[i].getAttribute(splittingAttributeIds[j]);AttributeValueStat_iterator it = splittingStats[j].find(v);if ( splittingStats[j].end() == it ){Stat stat;if ( m_data[i].isPositive() ){stat.nPos = 1;stat.nNeg = 0;stat.id = 0;}else{stat.nPos = 0;stat.nNeg = 1;stat.id = 0;}splittingStats[j].insert(std::pair<AttributeValue, Stat>(v, stat));}else{if ( m_data[i].isPositive() ){it->second.nPos++;}else{it->second.nNeg++;}}}}// display collected statisticsfor (j=0; j<splittingAttributeIds.size(); ++j){std::cout << "Attribute(" << splittingAttributeIds[j] << "):" << std::endl;std::cout << "\tValue \t nPos \t nNeg" << std::endl;for (AttributeValueStat_const_iterator it = splittingStats[j].begin();it != splittingStats[j].end(); ++it)std::cout << "\t" << it->first.getValue() << " \t " << it->second.nPos << " \t " << it->second.nNeg << std::endl;}}// find splitting attributefloat minEntropy = 0.0;int splitAttributeId = -1;for (j=0; j<splittingStats.size(); ++j){int n = m_data.size();float entropy = 0.0;for (AttributeValueStat_iterator it = splittingStats[j].begin();it != splittingStats[j].end(); ++it){int nSamples = it->second.nPos + it->second.nNeg;float p = it->second.nPos;p /= nSamples;entropy += calEntropy(p) * nSamples / n;}if (entropy < minEntropy || -1 == splitAttributeId){minEntropy = entropy;splitAttributeId = j;}}std::cout << "Split at attribute(" << splittingAttributeIds[splitAttributeId] << ")" << std::endl << std::endl;// splitint attrId = splittingAttributeIds[splitAttributeId];AttributeValueStat const& attVStat = splittingStats[splitAttributeId];splittedSets.clear();int k = 0;for (AttributeValueStat_iterator it = splittingStats[splitAttributeId].begin();it != splittingStats[splitAttributeId].end(); ++it){it->second.id = k++;}splittedSets.resize( k);for (i=0; i<k; ++i){for (j=0; j<m_splitAttributes.size(); ++j)splittedSets[i].m_splitAttributes.push_back( m_splitAttributes[j] );}}for (AttributeValueStat_iterator itt = splittingStats[splitAttributeId].begin();itt != splittingStats[splitAttributeId].end(); ++itt) {splittedSets[itt->second.id].m_splitAttributes.push_back(SplitAttributeValue(itt ->first, attrId));}for (i=0; i<m_data.size(); ++i){AttributeValue const& v = m_data[i].getAttribute(attrId);AttributeValueStat_const_iterator it = attVStat.find(v);if ( attVStat.end() != it ){splittedSets[it->second.id].addDataPoint(m_data[i]);}else{throw DataErrException();}}}void DataSet::display(){int i;std::cout << "Dataset(" << this << ")" << std::endl;for (i=0; i<m_splitAttributes.size(); ++i){m_splitAttributes[i].display();}std::cout << "Data:" << std::endl;for (i=0; i<m_data.size(); ++i){m_data[i].display();}std::cout << std::endl;}五、实验过程原始记录( 测试数据、图表、计算等)六、实验结果、分析和结论（误差分析与数据处理、成果总结等。

机器学习之决策树一-ID3原理与代码实现

机器学习之决策树⼀-ID3原理与代码实现决策树之系列⼀ID3原理与代码实现本⽂系作者原创，转载请注明出处:应⽤实例：你是否玩过⼆⼗个问题的游戏，游戏的规则很简单：参与游戏的⼀⽅在脑海⾥想某个事物，其他参与者向他提问题，只允许提20个问题，问题的答案也只能⽤对或错回答。

问问题的⼈通过推断分解，逐步缩⼩待猜测事物的范围。

决策树的⼯作原理与20个问题类似，⽤户输⼈⼀系列数据，然后给出游戏的答案。

如下表假如我告诉你，我有⼀个海洋⽣物，它不浮出⽔⾯可以⽣存，并且没有脚蹼，你来判断⼀下是否属于鱼类？通过决策树，你就可以快速给出答案不是鱼类。

决策树的⽬的就是在⼀⼤堆⽆序的数据特征中找出有序的规则，并建⽴决策树（模型）。

决策树⽐较⽂绉绉的介绍决策树学习是⼀种逼近离散值⽬标函数的⽅法。

通过将⼀组数据中学习的函数表⽰为决策树，从⽽将⼤量数据有⽬的的分类，从⽽找到潜在有价值的信息。

决策树分类通常分为两步---⽣成树和剪枝；树的⽣成 --- ⾃上⽽下的递归分治法；剪枝 --- 剪去那些可能增⼤错误预测率的分枝。

决策树的⽅法起源于概念学习系统CLS（Concept Learning System）, 然后发展最具有代表性的ID3（以信息熵作为⽬标评价函数）算法，最后⼜演化为C4.5, C5.0,CART可以处理连续属性。

这篇⽂章主要介绍ID3算法原理与代码实现（属于分类算法）分类与回归的区别回归问题和分类问题的本质⼀样，都是针对⼀个输⼊做出⼀个输出预测，其区别在于输出变量的类型。

分类问题是指，给定⼀个新的模式，根据训练集推断它所对应的类别（如：+1，-1），是⼀种定性输出，也叫离散变量预测；回归问题是指，给定⼀个新的模式，根据训练集推断它所对应的输出值（实数）是多少，是⼀种定量输出，也叫连续变量预测。

举个例⼦：预测明天的⽓温是多少度，这是⼀个回归任务；预测明天是阴、晴还是⾬，就是⼀个分类任务。

分类模型可将回归模型的输出离散化，回归模型也可将分类模型的输出连续化。

决策树算法编程

决策树算法编程决策树算法是一种常用的机器学习算法，它通过构建一棵树来解决分类和回归问题。

决策树算法具有易于理解、可解释性强的特点，因此在实际应用中被广泛使用。

本文将介绍决策树算法的基本原理，并以编程的方式实现一个简单的决策树模型。

一、决策树算法的原理决策树算法的基本思想是通过对数据集进行递归划分，构建一棵树来表示数据的分类或回归关系。

决策树的每个内部节点表示一个属性，每个叶节点表示一个类别或一个回归值。

决策树的构建过程可以分为三个步骤：特征选择、划分准则和停止条件。

特征选择是指从当前节点的属性集合中选择一个最优的属性作为划分属性。

常用的特征选择准则有信息增益、信息增益比、基尼系数等。

信息增益是指在划分属性前后，数据集的信息熵的差值。

信息增益比是信息增益除以划分属性的固有信息。

基尼系数是指数据集中一个随机选中的样本被错误分类的概率。

划分准则是指根据特征选择得到的划分属性将数据集划分成若干个子集。

划分准则的选择与特征选择密切相关，常用的划分准则有ID3、C4.5、CART等。

ID3算法使用信息增益作为划分准则，C4.5算法使用信息增益比作为划分准则，CART算法使用基尼系数作为划分准则。

停止条件是指决策树的构建过程何时停止。

常用的停止条件有：节点中的样本个数小于某个阈值、节点中的样本属于同一类别、节点中的样本属性值相同等。

二、决策树算法的编程实现下面以Python编程语言为例，介绍决策树算法的编程实现。

首先，我们需要定义一个节点类，用来表示决策树的节点。

```pythonclass Node:def __init__(self, attr=None, value=None, label=None, children=None):self.attr = attr # 节点划分属性self.value = value # 节点划分属性的取值bel = label # 叶节点的类别或回归值self.children = children # 子节点```然后，我们可以定义一个决策树类，用来表示整棵决策树。

决策树分类算法及python代码实现案例

决策树分类算法及python代码实现案例决策树分类算法1、概述决策树（decision tree）——是⼀种被⼴泛使⽤的分类算法。

相⽐贝叶斯算法，决策树的优势在于构造过程不需要任何领域知识或参数设置在实际应⽤中，对于探测式的知识发现，决策树更加适⽤。

2、算法思想通俗来说，决策树分类的思想类似于找对象。

现想象⼀个⼥孩的母亲要给这个⼥孩介绍男朋友，于是有了下⾯的对话：⼥⼉：多⼤年纪了？母亲：26。

⼥⼉：长的帅不帅？母亲：挺帅的。

⼥⼉：收⼊⾼不？母亲：不算很⾼，中等情况。

⼥⼉：是公务员不？母亲：是，在税务局上班呢。

⼥⼉：那好，我去见见。

这个⼥孩的决策过程就是典型的分类树决策。

实质：通过年龄、长相、收⼊和是否公务员对将男⼈分为两个类别：见和不见假设这个⼥孩对男⼈的要求是：30岁以下、长相中等以上并且是⾼收⼊者或中等以上收⼊的公务员，那么这个可以⽤下图表⽰⼥孩的决策逻辑上图完整表达了这个⼥孩决定是否见⼀个约会对象的策略，其中：◊绿⾊节点表⽰判断条件◊橙⾊节点表⽰决策结果◊箭头表⽰在⼀个判断条件在不同情况下的决策路径图中红⾊箭头表⽰了上⾯例⼦中⼥孩的决策过程。

这幅图基本可以算是⼀颗决策树，说它“基本可以算”是因为图中的判定条件没有量化，如收⼊⾼中低等等，还不能算是严格意义上的决策树，如果将所有条件量化，则就变成真正的决策树了。

决策树分类算法的关键就是根据“先验数据”构造⼀棵最佳的决策树，⽤以预测未知数据的类别决策树：是⼀个树结构（可以是⼆叉树或⾮⼆叉树）。

其每个⾮叶节点表⽰⼀个特征属性上的测试，每个分⽀代表这个特征属性在某个值域上的输出，⽽每个叶节点存放⼀个类别。

使⽤决策树进⾏决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分⽀，直到到达叶⼦节点，将叶⼦节点存放的类别作为决策结果。

3、决策树构造假如有以下判断苹果好坏的数据样本：样本红⼤好苹果0 1 1 11 1 0 12 0 1 03 0 0 0样本中有2个属性，A0表⽰是否红苹果。

python实现ID3决策树算法

python实现ID3决策树算法决策树之ID3算法及其Python实现，具体内容如下主要内容决策树背景知识决策树⼀般构建过程ID3算法分裂属性的选择ID3算法流程及其优缺点分析ID3算法Python代码实现1. 决策树背景知识决策树是数据挖掘中最重要且最常⽤的⽅法之⼀，主要应⽤于数据挖掘中的分类和预测。

决策树是知识的⼀种呈现⽅式，决策树中从顶点到每个结点的路径都是⼀条分类规则。

决策树算法最先基于信息论发展起来，经过⼏⼗年发展，⽬前常⽤的算法有：ID3、C4.5、CART算法等。

2. 决策树⼀般构建过程构建决策树是⼀个⾃顶向下的过程。

树的⽣长过程是⼀个不断把数据进⾏切分细分的过程，每⼀次切分都会产⽣⼀个数据⼦集对应的节点。

从包含所有数据的根节点开始，根据选取分裂属性的属性值把训练集划分成不同的数据⼦集，⽣成由每个训练数据⼦集对应新的⾮叶⼦节点。

对⽣成的⾮叶⼦节点再重复以上过程，直到满⾜特定的终⽌条件，停⽌对数据⼦集划分，⽣成数据⼦集对应的叶⼦节点，即所需类别。

测试集在决策树构建完成后检验其性能。

如果性能不达标，我们需要对决策树算法进⾏改善，直到达到预期的性能指标。

注：分裂属性的选取是决策树⽣产过程中的关键，它决定了⽣成的决策树的性能、结构。

分裂属性选择的评判标准是决策树算法之间的根本区别。

3. ID3算法分裂属性的选择——信息增益属性的选择是决策树算法中的核⼼。

是对决策树的结构、性能起到决定性的作⽤。

ID3算法基于信息增益的分裂属性选择。

基于信息增益的属性选择是指以信息熵的下降速度作为选择属性的⽅法。

它以的信息论为基础，选择具有最⾼信息增益的属性作为当前节点的分裂属性。

选择该属性作为分裂属性后，使得分裂后的样本的信息量最⼤，不确定性最⼩，即熵最⼩。

信息增益的定义为变化前后熵的差值，⽽熵的定义为信息的期望值，因此在了解熵和信息增益之前，我们需要了解信息的定义。

信息：分类标签xi 在样本集 S 中出现的频率记为 p(xi)，则 xi 的信息定义为：−log2p(xi) 。

id3决策树算法代码

id3决策树算法代码ID3决策树算法是一种常用的机器学习算法，它可以根据给定的训练数据集构建决策树模型，用于分类和预测任务。

下面我们将详细介绍ID3决策树算法的实现过程。

决策树是一种树结构模型，它由节点和有向边组成。

在决策树中，每个内部节点表示一个特征或属性，每条边表示一个特征取值，叶节点表示一个类别。

决策树的构建过程是一个递归的过程，通过选择最优的特征来划分数据集，使得每个子节点上的样本尽可能属于同一类别。

在ID3算法中，选择最优的特征是通过计算信息增益来实现的。

信息增益表示在特征F的条件下，样本集D的不确定性减少的程度。

具体计算公式如下：信息增益(Gain) = Entropy(D) - ∑(|Dv|/|D|) * Entropy(Dv)其中，Entropy(D)表示样本集D的信息熵，Entropy(Dv)表示在特征F的取值为v时，样本集Dv的信息熵，|Dv|表示样本集Dv的样本个数，|D|表示样本集D的样本个数。

信息熵表示样本集的不确定性，熵越大表示样本集的不确定性越高。

ID3算法的实现步骤如下：1. 若样本集D中的所有样本属于同一类别C，则将该节点标记为C，并返回。

2. 若特征集A为空集，或者样本集D中的所有样本在特征集A上取值相同，则将该节点标记为D中样本数最多的类别，并返回。

3. 计算特征集A中每个特征的信息增益，选择信息增益最大的特征F。

4. 将节点标记为特征F，并根据特征F的取值将样本集D划分为多个子集Dv。

5. 对于每个子集Dv，递归调用ID3算法，构建子节点。

6. 返回决策树模型。

ID3算法的实现过程比较简单，但也存在一些问题。

首先，ID3算法倾向于选择具有较多取值的特征，导致决策树过于复杂。

其次，ID3算法不能处理连续型特征，需要将其离散化。

此外，ID3算法容易产生过拟合问题，可以通过剪枝来解决。

为了避免决策树过于复杂，可以使用剪枝技术对决策树进行优化。

剪枝分为预剪枝和后剪枝两种方式。

决策树算法（1）含java源代码

决策树算法（1）含java源代码信息熵：变量的不确定性越⼤，熵越⼤。

熵可⽤下⾯的公式描述：-（p1*logp1+p2*logp2+...+pn*logpn)pi表⽰事件i发⽣的概率ID3：GAIN(A)=INFO(D)-INFO_A(D)节点A的信息增益为不加节点A时的信息量INFO(D)-加上A后的信息量INFO_A(D)算法步骤：1、树以代表训练样本的某个结点开始2、如果样本都在同⼀类，则将该节点设置为叶⼦，并使⽤该类标号3、否则，算法使⽤熵度量每个样本的分类结点，选择可以获得最⼤信息的节点4、所有的属性都是分类的，连续值必须离散化停⽌条件：该节点上所有的样本都属于⼀个类没有剩余的属性没有属性时，⽐如已经分到第三个属性，但是没有第四个属性，这时将样本分到最多的那类C4.5与ID3区别在于属性度量⽅式的不同优点：直观、便于理解、⼩规模数据有效缺点：处理连续变量不好类别较多时，错误增加⽐较快可规模性⼀般package dTree;import java.util.ArrayList;import java.util.HashMap;import java.util.Iterator;import java.util.List;import java.util.Map;import java.util.Set;public class dataClass {public static void main(String[] args) {double [][]exerciseData = {{1,1,0,0},{1,3,1,1},{3,2,1,1},{2,2,1,1},{3,2,1,1},{2,3,0,1},{2,1,0,0},{3,2,0,1},{2,1,0,1},{1,1,1,0}};//每⼀列表⽰⼀个属性值，最后⼀列表⽰决策层int[] index = gainResult(exerciseData);//输出的结果表⽰按照决策树规则所对应的属性参考顺序for(int i = 0;i<index.length;i++){System.out.print(" "+(index[i]+1));}}private static int[] gainResult(double[][] exerciseData) {int dataQuantity = exerciseData.length;int attributeQuantity = exerciseData[0].length-1;int []attribute = new int[attributeQuantity];int []newAttribute = new int [attributeQuantity];double [][]newExerciseData = exerciseData ;double [][]maxgainIndexData = new double[dataQuantity][attributeQuantity];for(int i = 0;i<attributeQuantity;i++){attribute[i] = MaxgainIndex(newExerciseData);for(int j = 0;j<maxgainIndexData.length;j++){maxgainIndexData[j][i] = newExerciseData[j][attribute[i]];}newExerciseData = NewData(newExerciseData,attribute[i]);}boolean flag =true;for(int i = 0;i<maxgainIndexData[0].length;i++){//寻找第i列所对应的exerciseDatafor(int k = 0;k<exerciseData[0].length-1;k++){flag = true;for(int j = 0;j<exerciseData.length;j++){if(maxgainIndexData[j][i]!=exerciseData[j][k]){flag = false;break;}}if(flag==true){newAttribute[i] = k;}}}return newAttribute;}//矩阵转置private static double[][] Transpose(double[][] exerciseData){int rows = exerciseData.length;int columns = exerciseData[0].length;double [][]newData = new double [columns][rows];for(int i = 0;i<columns;i++){for(int j= 0;j<rows;j++){newData[i][j] = exerciseData[j][i];}}return newData;}private static double[][] NewData(double[][] exerciseData,int maxIndex) {//删除exerciseData中maxindex列的数据，产⽣新数据double [][]newExerciseData = new double[exerciseData.length][];for(int i = 0;i<exerciseData.length;i++){newExerciseData[i] = new double[exerciseData[i].length-1];for(int j = 0;j<newExerciseData[i].length;j++){if(j>=maxIndex){newExerciseData[i][j] = exerciseData[i][j+1];}else{newExerciseData[i][j] = exerciseData[i][j];}}}return newExerciseData;}private static int MaxgainIndex(double[][] exerciseData) {//获取exerciseData最⼤增益率所对应的⼀列double []gainRatio = gainAll(exerciseData);double maxGain = gainRatio[0];//最⼤增益率int maxIndex = 0;//最⼤增益率所对应的索引值for(int i=1;i<gainRatio.length-1;i++){if(maxGain<gainRatio[i]){maxGain = gainRatio[i];maxIndex = i;}}return maxIndex;}public static double[] gainAll(double [][]Data){//得到Data中每⼀列的增益值int col = Data.length;//数据个数int vol = Data[0].length;//属性个数double [][]count = new double[vol][];double []info = new double[vol];double Lcount[][] = new double[vol][];//第i个属性的第j个分类的⽐率double Mcount[][] = new double[vol][];List <List<Map1>>listM = new ArrayList<List<Map1>>();List <List<Map1>>listM2 = new ArrayList<List<Map1>>();double []gain;//矩阵的属性统计for (int i = 0;i<vol;i++){//属性i的不重复的分类集（mapList加⼊了属性i以及对应的决策层的值）List<Map> mapList = new ArrayList<Map>();for(int j = 0;j<col;j++){Map y = new HashMap();y.put(Data[j][i],Data[j][vol-1]);if(!mapList.contains(y)){mapList.add(y);}}//属性i全部分类集（重复，listM2加⼊了i值以及决策层的值）List<Map> AllmapList = new ArrayList<Map>();for(int j = 0;j<col;j++){Map y = new HashMap();y.put(Data[j][i],Data[j][vol-1]);AllmapList.add(y);}count[i] = new double[mapList.size()];double sum = 0;double num = 0;List<Map1>LM = new ArrayList<Map1>();for(int j=0;j<mapList.size();j++){Iterator it =((Map)(mapList.get(j))).keySet().iterator(); num = (Double) it.next();for(int k = 0;k<AllmapList.size();k++){if(mapList.get(j).equals(AllmapList.get(k))){count[i][j] = count[i][j]+1;}}Map1 p = new Map1();p.setKey(count[i][j]);p.setValue(num);LM.add(p);}listM2.add(LM);}for( int k = 0;k<vol;k++){List <Double>list = new ArrayList<Double>();for(int i = 0;i<col;i++){if(!list.contains(Data[i][k])){list.add(Data[i][k]);}}Lcount[k] = new double[list.size()];Mcount[k] = new double[list.size()];for(int j = 0;j<col;j++){int index = list.indexOf(Data[j][k]);Lcount[k][index] = Lcount[k][index]+1;Mcount[k][index] = Mcount[k][index]+1;}double LastSum = 0;for(int i = 0;i<Lcount[k].length;i++){LastSum = LastSum+Lcount[k][i];}for(int j = 0;j<Lcount[k].length;j++){Lcount[k][j] = Lcount[k][j]/LastSum;}List<Map1> LM = new ArrayList<Map1>();for(int i = 0;i<Lcount[k].length;i++){Map1 p = new Map1();p.setKey(Mcount[k][i]);p.setValue(list.get(i));LM.add(p);}listM.add(LM);}gain = new double[listM2.size()];for(int i = 0; i<listM2.size()-1;i++){List listi = new ArrayList();listi = listM.get(i);double sum = 0;for(int j=0;j<listi.size();j++){Map1 p = (Map1) listi.get(j);double key = p.getKey();double value = p.getValue();for(int k = 0;k<listM2.get(i).size();k++){Map1 p1 = (Map1) listM2.get(i).get(k);if(p1.value==value){sum = sum+xlog2(p1.key/p.key);}//System.out.println(sum);}gain[i]+=sum*Lcount[i][j];sum = 0;}}for(int i = 0;i<Lcount[Lcount.length-1].length;i++){gain[listM2.size()-1] += -xlog2(Lcount[Lcount.length-1][i]); }for(int j = 0;j<gain.length-1;j++){gain[j] = gain[gain.length-1]+gain[j];}double[]Scount = new double [Lcount.length-1];for(int j= 0;j<Lcount.length-1;j++){double sum = 0;for(int k = 0;k<Lcount[j].length;k++){sum += xlog2(Lcount[j][k]);}Scount[j] = -sum;}for(int j= 0;j<Scount.length;j++){gain[j] = gain[j]/Scount[j];}return gain;}public static boolean contain(Map mapList,double key,double value){ if(value==Double.parseDouble(mapList.get(key).toString())){return true;}else{return false;}}public static double xlog2(double x){return x*(Math.log(x)/Math.log((double)2));}}。