专题复习图形折叠问题
中考复习专题 图形的折叠、裁剪与拼接

专题九 图形的折叠、裁剪与拼接一、选择题1.现有大小相同的正方形纸片20张,小凯用其中2张拼成如图所示的矩形,小明也想拼一个与它形状相同(相似)但比它大的矩形,则它至少要用m 张正方形纸片(不得把每个正方形纸片剪开).则m 的值为(B )A .6B .8C .12D .18,(第1题图)) ,(第2题图))2.把由5个小正方形组成的十字形纸板(如图)剪开,使剪成的若干块能够拼成一个大正方形,最少只需剪(B ) A .1刀 B .2刀 C .3刀 D .4刀3.如图,将一张矩形纸片沿AB 对折,以AB 的中点O 为顶点将平角五等分,并沿五等分的折线折叠,再沿CD 剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD 等于(C )A .108°B .114°C .126°D .129°4.如图1,分别沿长方形纸片ABCD 和正方形纸片EFGH 的对角线AC ,EG 剪开,拼成如图2所示的▱KLMN ,若中间空白部分四边形OPQR 恰好是正方形,▱KLMN 的面积为50,则正方形EFGH 的面积为(B )A .24B .25C .26D .275.如图,将矩形沿图中虚线剪成四块图形,用这四块图形恰能拼一个正方形.若x =13,则xy 的值等于(C )A .3B .25-1C .5+12D .1+ 2,(第5题图)) ,(第6题图))6.如图1为一正面白色,反面灰色的长方形纸片.今沿虚线剪下分成甲、乙两长方形纸片,并将甲纸片反面朝上贴于乙纸片上,形成一张白、灰相间的长方形纸片,如图2所示,若图2中白色与灰色区域的面积比为8∶3,图2纸片面积为33,则图1纸片的面积是(A )A .42B .44C .2314D .36387.如图,阴影部分是边长为a 的大正方形中剪去一个边长为b 的小正方形后得到的图形,将阴影部分通过割、拼,形成新的图形,给出下列3种割拼方法,其中能够验证平方差公式的是(D )A .①②B .②③C .①③D .①②③ 二、填空题8.我们知道,如图1所示的方格中,若每一个小正方形的边长都为1,则阴影正方形的面积是2,边长是 2.如图2,点P 是边长为1的正方形内(不在边上)任意一点,P 和正方形各顶点相连后把正方形分成4块,其中①③可以重新拼成一个四边形,重拼后的四边形的最小周长是2 2.三、解答题9.如图1,将长为10的线段OA 绕点O 旋转90°得到OB ,点A 的运动轨迹为AB ︵,P 是半径OB 上一动点,Q 是AB ︵上一动点,连接PQ.发现 当∠POQ =__________°时,PQ 有最大值,最大值为__________. 思考(1)如图2,若点P 是OB 的中点,且QP ⊥OB 于点P ,求BQ ︵的长;(2)如图3,将扇形OAB 沿折痕AP 折叠,使点B 的对应点B′恰好落在OA 的延长线上,求阴影部分面积. 探究 如图4,将扇形OAB 沿PQ 折叠,使折叠后的QB′︵恰好与半径OA 相切,切点为C ,若OP =6,求点O 到折痕PQ 的距离.图1 图2图3 图4解:发现 90;102;[∵P 是半径OB 上一动点,Q 是AB ︵上的一动点,∴当PQ 取最大时,点Q 与点A 重合,点P 与点B 重合,此时,∠POQ =90°,PQ =OA 2+OB 2=10 2.]思考 (1)图2中,连接OQ. ∵点P 是OB 的中点, ∴OP =12OB =12OQ.∵QP ⊥OB ,∴∠OPQ =90°.在Rt △OPQ 中,cos ∠POQ =OP OQ =12,∴∠POQ =60°,∴BQ ︵的长为60π×10180=103π;(2)由折叠可得,BP =B′P ,AB′=AB =10 2. 在Rt △B′OP 中,OP 2+OB′2=PB′2, 即OP 2+(102-10)2=(10-OP)2. 解得OP =102-10.∴S 阴影=S 扇形OAB -2S △AOP =90360π×102-2×12×10(102-10)=25π-1002+100.探究 图4中,找点O 关于PQ 的对称点O′,连接OO′,O′B ,O′C ,O′P ,设OO′交PQ 于点M ,则OM =O′M ,OO′⊥PQ ,O′P =OP =6,点O′是OB′︵所在圆的圆心.∴O′C =OB =10.∵折叠后的QB′︵恰好与半径OA 相切于点C , ∴O′C ⊥AO. ∴O′C ∥OB.∴四边形OCO′B 是矩形.在Rt △O′BP 中,O′B =62-42=2 5.在Rt △OBO′中,OO′=102+(25)2=230. ∴OM =12OO′=错误!×2错误!=错误!.即点O 到折痕PQ 的距离为30.。
中考数学八大题型集训:专题复习(5)图形的折叠问题含解析

专题复习(五) 图形的折叠问题折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中,其实质是轴对称性质的应用.解题的关键利用轴对称的性质找到折叠前后不变量与变量,运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系.类型1 三角形中的折叠问题(·宜宾)如图,一次函数的图象与x 轴、y 轴分别相交于点A 、B ,将△AOB 沿直线AB 翻折,得△ACB.若C(32,32),则该一次函数的解析式为________.【思路点拨】 利用翻折变换的性质结合锐角三角函数关系得出CO ,AO 的长,进而得出A 、B 两点的坐标,再利用待定系数法求出直线AB 的解析式.【解答】 连接OC ,过点C 作CD⊥x 轴于点D ,∵将△AOB 沿直线AB 翻折,得△ACB,C(32,32),∴AO =AC ,OD =32,DC =32,BO =BC ,则tan ∠COD =CD OD =33,故∠COD=30°,∠BOC =60°,∴△BOC 是等边三角形,且∠CAD=60°. 则sin60°=CD AC ,则AC =DCsin60°=1,故A(1,0),sin30°=CD CO =32CO =12.则CO =3,故BO =3,B 点坐标为(0,3),设直线AB 的解析式为y =kx +3,把A(1,0)代入解析式可得k =- 3. ∴直线AB 的解析式为y =-3x + 3.折叠(翻折)意味着轴对称,会生成相等的线段和角,这样便于将条件集中.如果题目中有直角,则通常将条件集中于较小的直角三角形,利用勾股定理求解.1.(·绵阳)如图,D 是等边△ABC 边AB 上的一点,且AD∶DB=1∶2,现将△ABC 折叠,使点C 与D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,则CE∶CF=( )A.34B.45C.56D.672.(·德阳)如图,△ABC 中,∠A =60°,将△ABC 沿DE 翻折后,点A 落在BC 边上的点A′处.如果∠A′EC =70°,那么∠A′DE 的度数为________.3.(·宜宾)如图,在Rt△ABC 中,∠B =90°,AB =3,BC =4,将△ABC 折叠,使点B 恰好落在边AC 上,与点B′重合,AE 为折痕,则EB′=________.4.(·滨州)如图,在平面直角坐标系中,将矩形AOCD 沿直线AE 折叠(点E 在边DC 上),折叠后顶点D 恰好落在边OC 上的点F 处,若点D 的坐标为(10,8),则点E 的坐标为________.类型2 四边形及其他图形中的折叠问题(·南充)如图,在矩形纸片ABCD 中,将△AMP 和△BPQ 分别沿PM 和PQ 折叠(AP >AM),点A 和点B 都与点E 重合;再将△CQD 沿DQ 折叠,点C 落在线段EQ 上点F 处.(1)判断△AMP,△BPQ ,△CQD 和△FDM 中有哪几对相似三角形?(不需说明理由)(2)如果AM =1,sin ∠DMF =35,求AB 的长.【思路点拨】 (1)由矩形的性质得∠A =∠B =∠C =90°,由折叠的性质和等角的余角相等,可得∠BPQ =∠AMP =∠DQC ,所以△AMP∽△BPQ∽△CQD ;(2)设AP =x ,由折叠关系可得:BP =AP =EP =x ,AB =DC =2x ,AM =1,根据△AMP∽△BPQ 得:AMBP=AP BQ ,即BQ =x 2,根据△AMP∽△CQD 得:AP CD =AM CQ ,即CQ =2,从而得出AD =BC =BQ +CQ =x 2+2,MD =AD -AM =x 2+2-1=x 2+1,根据Rt △FDM 中∠DMF 的正弦值得出x 的值,从而求出AB 的值.【解答】 (1)有三对相似三角形,即△AMP∽△BPQ∽△CQD. 理由如下:∵四边形ABCD 是矩形, ∴∠A =∠B=∠C=90°.根据折叠可知:∠APM=∠EPM,∠EPQ =∠BPQ,∴∠APM +∠BPQ=∠EPM+∠EPQ=90°. ∵∠APM +∠AMP=90°,∴∠BPQ =∠AMP,∴△AMP ∽△BPQ , 同理:△BPQ∽△CQD. ∴△AMP ∽△BPQ ∽△CQD. (2)设AP =x ,∴由折叠关系,BP =AP =EP =x ,AB =DC =2x.由△AMP∽△BPQ 得,AM BP =AP BQ ,即1x =xBQ ,得BQ =x 2.由△AMP∽△CQD 得,AP CD =AM CQ ,即x 2x =1CQ ,得CQ =2.∴AD =BC =BQ +CQ =x 2+2.∴MD =AD -1=x 2+1.∵在Rt△FDM 中,sin ∠DMF =35,∴2x x 2+1=35.解得x 1=3,x 2=13(不合题意,舍去). 即AB =6.矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数,或者利用折叠性质以及勾股定理求线段长度.矩形中的两次或多次折叠通常出现“一线三直角”的模型(如图),从而构造相似三角形,利用相似三角形求边或者角的度数.1.(·南充)如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B′处,若AE =2,DE =6,∠EFB =60°,则矩形ABCD 的面积是( )A .12B .24C .12 3D .16 32.(·泸州)如图,在△ABC 中,AB =AC ,BC =24,tanC =2,如果将△ABC 沿直线l 翻折后,点B 落在边AC 的中点E 处,直线l 与边BC 交于点D ,那么BD 的长为( )A.13 B.152C.272D.123.(·德阳)将抛物线y=-x2+2x+3在x轴上方的部分沿x轴翻折至x轴下方,图象的剩余部分不变,得到一个新的函数图象,那么直线y=x+b与此新图象的交点个数的情况有()A.6种 B.5种 C.4种 D.3种4.(·成都)如图,在□ABCD中,AB=13,AD=4,将ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为________.5.(·内江)如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为________.6.(·南充)如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是________.7.(·绵阳)如图1,在矩形ABCD中,AB=4,AD=3,将矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△DEC≌△EDA;(2)求DF的值;(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,顶点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.参考答案类型1 三角形中的折叠问题1.B 提示:∵△ABC 为等边三角形,∴∠A =∠B=∠C=60°.又∵折叠△ABC,使得点C 恰好与边AB 上的点D 重合,折痕为EF ,∴∠EDF =∠C=60°,CE =DE ,CF =DF.∴∠ADE+∠FDB=120°.∴∠AED =∠FDB.∴△AED∽△BDF.∴AE BD =AD BF =DEFD .设等边△ABC 边长为6个单位,CE =x ,CF =y ,AE =6-x ,BC =6-y ,∴6-x 4=26-y =x y ,解得x =145,y =72.∴x ∶y =4∶5,故选择B.2.65°3.1.54.(10,3)类型2 四边形及其他图形中的折叠问题1.D 2.A3.B 提示:由题意,易知y =-x 2+2x +3与x 轴的两个交点坐标分别为(3,0)和(-1,0),顶点坐标为(1,4),顶点关于x 轴对称点的坐标为(1,-4).当直线y =x +b 过(-1,0)时,b =1,此时直线与新的函数图象只有一个交点;当b>1时,此时直线与新的函数图象无交点;当直线y =x +b 过(3,0)时,b =-3,此时直线与新的函数图象有三个交点;观察图象,易知:当-3<b<1时,此时直线与新的函数图象有三个交点;当直线y =x +b 过(1,-4)时,b =-5,此时直线与新的函数图象有三个交点;观察图象,易知:当-5≤b<-3时,此时直线与新的函数图象有四个交点;观察图象,易知:当b<-5时,此时直线与新的函数图象有二个交点;综上,直线y =x +b 与此新图象的交点的个数的情况有5种,故选B.4.35. 6 提示:作AH⊥BC 于H.∵分别以AE ,BE 为折痕将两个角(∠D,∠C)向内折叠,点C ,D 恰好落在AB 边的点F 处,∴DE =EF ,CE =EF ,AF =AD =2,BF =CB =3.∴DC=2EF ,AB =5.∵AD∥BC,∠C =90°, ∴四边形ADCH 为矩形,∴AH =DC =2EF ,HB =BC -CH =BC -AD =1.在Rt△ABH 中,AH =AB 2-BH 2=26,∴EF = 6. 6.2≤x≤87.(1)证明:由矩形的性质可知△ADC≌△CEA,∴AD =CE ,DC =EA ,∠ACD =∠CAE. 在△CED 与△ADE 中,⎩⎪⎨⎪⎧CE =AD ,DE =ED ,DC =EA ,∴△DEC ≌△EDA.(2)∵∠ACD=∠CAE,∴AF =CF.设DF =x ,则AF =CF =4-x ,在Rt△ADF 中,AD 2+DF 2=AF 2,即32+x 2=(4-x)2,解得x =78,即DF =78.(3)由矩形PQMN 的性质得PQ∥CA, ∴PE CE =PQCA. 又∵CE=3,AC =AB 2+BC 2=5.设PE =x(0<x <3),则x 3=PQ 5,即PQ =53x.过E 作EG⊥AC 于G ,则PN∥EG,∴CP CE =PN EG. 又∵在Rt△AEC 中,EG ·AC =AE·CE,解得EG =125.∴3-x 3=PN 125,即PN =45(3-x).设矩形PQMN 的面积为S ,则S =PQ·PN=-43x 2+4x =-43(x -32)2+3(0<x <3).∴当x =32,即PE =32时,矩形PQMN 的面积最大,最大面积为3.。
初中数学中有关图形的折叠问题

专题复习图形的折叠问题折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中,其实质是轴对称性质的应用.解题的关键利用轴对称的性质找到折叠前后不变量与变量,运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系.类型1 三角形中的折叠问题1.如图,在折纸活动中,小明制作了一张△ABC 纸片,点D 、E 分别是边AB 、AC 上,将△ABC 沿着DE 折叠压平,A 与A′重合,若∠A=75°,则∠1+∠2=【 】A .150°B .210°C .105°D .75°2.已知,如图,Rt △ABC 中,∠C=90º,沿过点B 的一条直线BE 折叠△ABC,使C 恰好落在AB 边的中点D 处,则∠A=________.3.(2014·德阳)如图,△ABC 中,∠A =60°,将△ABC 沿DE 翻折后,点A 落在BC 边上的点A′处.如果∠A′EC=70°,那么∠A′DE 的度数为________.4.如图,在Rt△ABC 中,∠B =90°,AB =3,BC =4,将△ABC 折叠,使点B 恰好落在边AC 上,与点B′重合,AE 为折痕,则EB′=________.5.如图,在平面直角坐标系中,将矩形AOCD 沿直线AE 折叠(点E 在边DC 上),折叠后顶点D 恰好落在边OC 上的点F 处,若点D 的坐标为(10,8),则点E 的坐标为________. A D B EC6.如图,在等腰△ABC 中,AB =AC ,∠BAC =50°.∠BAC 的平分线与AB 的中垂线交于点O ,点C 沿EF 折叠后与点O 重合,则∠CEF 的度数是 .7.如图,将正方形ABCD 沿BE 对折,使点A 落在对角线BD 上的A′处,连接A′C ,则∠B .8.如图,一次函数的图象与x 轴、y 轴分别相交于点A 、B ,将△AOB 沿直线AB 翻折,得△ACB.若C(3/2,√3/2),则该一次函数的解析式为________.9.如图,D 是等边△ABC 边AB 上的一点,且AD∶DB=1∶2,现将△ABC 折叠,使点C 与D 重合,折痕为EF ,点E ,F 分别在AC 和BC 上,则CE∶CF=( )A.3/4B.4/5C.5/6D.6/7 10.如图,将△ABC 纸片的一角沿DE 向下翻折,使点A 落在BC 边上的A ′点处,且DE ∥BC ,下列结论:①∠AED =∠C ;②A 1D/DB=A 1E/EC ;③BC=2DE ;④ BD A E A C AD A E S S S ∆'∆''=+四形边。
中考数学专题复习图形的折叠型题PPT课件

(2)请你通过操作和猜想,将第3、第4和第n次裁剪后
所得扇形的总个数(S)填入下表.
等分圆及扇形面的次数(n) 1 2 3 4 **** n
所得扇形的总个数(S)
47
***
(3)请你推断,能不能按上述操作过程,将本来的圆形 纸板剪成33个扇形?为什么?
例26、如图,若把边长为1的正方形ABCD的四个
例25、如图,⊙O表示一圆形纸板,根
O
据要求,需通过多次剪裁,把它剪成若 干个扇形面,操作过程如下:第1次剪,
第25题图
将圆形纸板等分为4个扇形;第2次剪裁,将上次得的
扇形面中的一个再等分成4个扇形;以后按第2次剪裁
的作法进行下去.(1)请你在⊙O中,用尺规作出第2次
剪裁后得到的7个扇形(保留痕迹不写作法).
角(阴影部分)剪掉,得一四边形A1B1C1D1.试问怎 样剪,才能使剩下的图形仍为正方形,且剩下图
形的面积为原正方形面积的 5 ,请说明理由(写
出证明及计算过程).
9
E
A M DA M
例22、电脑CPU蕊片由一种叫“单晶硅”的材料制
成,未切割前的单晶硅材料是一种薄型圆片,叫 “晶圆片”。现为了生产某种CPU蕊片,需要长、 宽都是1cm 的正方形小硅片若干。如果晶圆片的直 径为10.05cm。问一张这种晶圆片能否切割出所需尺 寸的小硅片66张?请说明你的方法和理由。(不计 切割损耗)
典例精析
一.折叠后求度数 例1、将一张长方形纸片按如图所示的方式折 叠,BC、BD为折痕,则∠CBD的度数为( ) A.600 B.750 C.900 D.950
例2、如图,把一个长方形纸片沿EF折叠后,点D、C
分别落在D′、C′的位置,若∠EFB=65°,则 ∠AED′等于( ) A.50° B.55° C.60° D.65°
天津市中考数学一轮专题复习 图形折叠问题

图形折叠问题一选择题:1.如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,则∠DAF=( )A.40° B.35° C.20° D.15°2.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于()A.50° B.55° C.60° D.65°3.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12 D.164.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE长为()A.3 B.4 C.5 D.65.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为()A.1 B.2 C. D.6.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为()7.如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是()A.7B.8 C.9 D. 108.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为()A.78° B.75° C.60° D.45°9.如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为()A. 10 B. 13 C. 15 D. 1210.如图,将矩形纸片ABCD的四个角向内翻折,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=12厘米,EF=16厘米,则边AD的长是 ( )A.12厘米 B.16厘米 C.20厘米 D.28厘米11.如图,在矩形 OABC 中,OA=8,OC=4,沿对角线 OB 折叠后,点 A 与点 D 重合,OD 与 BCA.(4,8)B.(5,8)C.(,) D.(,)12.将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为()A. B. 2 C. 3 D.13.如图,矩形纸片ABCD中,AD=3cm,点E在BC上,将纸片沿AE折叠,使点B落在AC上的点F处,且∠AEF=∠CEF,则AB的长是( )A.1 cm B.cm C.2 cm D. cm14.如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,CA1的长为()A.3或4 B.4或3C.3或4 D.3或415.如图,在矩形ABCD中,点E、F分别在边AB,BC上,且AE=AB.将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①EF=2BE,②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )A.①② B.②③C.①③ D.①④16.如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合,若此时=,则△AMD′的面积与△AMN的面积的比为( )A.1:3 B.1:4 C.1:6 D.1: 917.图,矩形ABCD中,点E是AD的中点,将△ABE折叠后得到△GBE,延长B G交CD于点F,若CF=1,FD=2,则BC的长为( )A.3B.2C.2D.218.如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于().A.2 B.3 C.4 D.519.如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,的值为()A.B.C.D.20.如图,在矩形纸片ABCD中,AB=3,AD=5.折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC 边上移动时,折痕的端点P,Q也随之移动。
中考数学二轮专题复习图形变换——折叠问题【含答案】

二轮复习:图形变换(一)—折叠图形变换历来是中考必考点之一。
考试大纲要求:会运用图形变换的相关知识进行简单的作图与计算,并能解决相关动态需求数学问题,并能进行图案设计。
图形变换一般包括,折叠、平移、旋转、对称、位似和图形的探究。
在图形变换的考题中,最多题型是折叠、旋转。
在解决折叠问题时,应注意折叠前后相对应的边相等、角相等。
下面着重从三个方面进行讲述:三角形折折叠、特殊平行四边形折叠和在平面直角坐标系内的图形折叠三大类进行。
(一)三角形的折叠:题型1、一般三角形的折叠:1、如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是A.γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°﹣α﹣β2、(2019•江西)如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=°.3、如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为___.题型2、等腰或等边三角形的折叠:4、如图,在△ABC 中,AB =AC ,BC =24,tanC =2,如果将△ABC 沿直线l 翻折后,点B 落在边AC 的中点E 处,直线l 与边BC 交于点D ,那么BD 的长为_____.5、如图,D 是等边△ABC 边AB 上的点,AD=2,DB=4.现将△ABC 折叠,使得点C 与点D 重合,折痕为EF ,且点E 、F 分别在边AC 和BC 上,则CF CE=_______.(利用相似三角形周长的比等于相似比△AED 相似△DBF)题型3、直角三角形的折叠:6、如图,在Rt △ABC 中,∠ACB=90°,BC=6,CD 是斜边AB 上的中线,将△BCD 沿直线CD 翻折至△ECD 的位置,连接AE .若DE ∥AC ,计算AE 的长度等于.7、如图,在等腰直角三角形ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是(二)特殊平行四边形的折叠:题型1、矩形折叠:1、(求角).如图,将矩形沿对角线折叠,点落在处,交于点,已知,则的度为A. B. C. D.2、(求三角函数值)如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是.3、(求边长)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE 折叠,使点B落在矩形内点F处,连接CF,则CF的长为4、(求折痕长)如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为5、(求边的比)如下图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为。
专题考试__图形折叠问题[]
![专题考试__图形折叠问题[]](https://img.taocdn.com/s3/m/5f649012482fb4daa58d4b6a.png)
2010年专题复习图形折叠问题图形折叠问题是近年来中考地一个热点,其实质是轴对称问题,折叠重合部分必全等,折痕所在直线就是这两个全等形地对称轴,互相重合地两点(对称点)连线必被折痕垂直平分.要充分运用以上结论,作辅助线构造直角三角形,结合相似形、锐角三角函数定义等知识来解决折叠问题.解这类题目,通常可以借助现成材料,亲自动手操作,然后观察思考,得出答案.但由于考场环境和条件地限制,应根据上述知识,动手画出折后地图形.【例题经典】1.将一张长方形纸片按如图所示地方式折叠,BC 、BD 为折痕,则∠CBD 地度数为( )A .600B .750C .900D .9502.如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D′、C′地位置,若∠EFB =65°,则∠AED′等于( )A .50° B .55° C .60° D .65°3. 用一条宽相等地足够长地纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示地正五边形ABCDE,其中∠BAC=度.4.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形地是( )A. B. C. D. 图(1)第3题图A 图 (2)5.如图a ,ABCD 是一矩形纸片,AB =6cm ,AD =8cm ,E 是AD 上一点,且AE =6cm.操作:(1)将AB 向AE 折过去,使AB 与AE 重合,得折痕AF ,如图b ;(2)将△AFB 以BF 为折痕向右折过去,得图c.则△GFC 地面积是( )A.1cm 2B.2 cm 2C.3 cm 2D.4 cm 26.如图,正方形硬纸片ABCD 地边长是4,点E 、F 分别是AB 、BC 地中点,若沿左图中地虚线剪开,拼成如下右图地一座“小别墅”,则图中阴影部分地面积是A .2 B .4 C .8 D .107.如图1所示,把一个正方形三次对折后沿虚线剪下,则所得地图形是( )8.如图(5),把矩形纸条ABCD 沿EF GH ,同时折叠,B C ,两点恰好落在AD 边地P 点处,若90FPH =∠,8PF =,6PH =,则矩形ABCD 地边BC 长为( ) A.20 B.22C.24D.30【 探究思考】E A A A B B B C C C GD D D F F F 图a 图b 图c9.如图5,四边形ABCD 为矩形纸片.把纸片ABCD 折叠,使点B 恰好落在CD 边地中点E 处,折痕为AF .若6CD ,则AF 等于( )A.B.C.D.810.如图,折叠长方形地一边AD ,点D 落在BC 边地点F 处,已知AB=8cm, BC=10cm , 求EC 地长.11.如图,折叠矩形纸片ABCD ,先折出折痕(对角线)BD ,再折叠,使AD 落在对角线BD 上,得折痕DG ,若AB = 2,BC = 1,求AG .12.在矩形纸片ABCD 中,BC=6,沿EF 折叠后,点C 落在AB 边上地点P 处,•点D 落在点Q 处,AD 与PQ 相交于点H ,∠BPE=30°.(1)求BE 、QF 地长;(2)求四边形PEFH 地面积.13. 如图,矩形纸片ABCD 地边长分别为a ,b (a<b ).将纸片任意翻折(如图8),折痕为PQ .(P 在BC 上),使顶点C 落在四边形APCD 内一点C′,B F C ED A 图5B FC GB 如图一PC′地延长线交直线AD于M,再将纸片地另一部分翻折,使A落在直线PM上一点A′,且A′M 所在直线与PM•所在直线重合(如图9),折痕为MN.(1)猜想两折痕PQ,MN之间地位置关系,并加以证明.(2)若∠QPC地角度在每次翻折地过程中保持不变,则每次翻折后,两折痕PQ,•MN间地距离有何变化?请说明理由.(3)若∠QPC地角度在每次翻折地过程中都为45°(如图10),每次翻折后,非重叠部分地四边形MC′QD,及四边形BPA′N地周长与a,b有何关系,为什么?(2006•年湖南郴州市)(7)(8)(9)(10)14.如图13,在锐角ABC△中,9BC=,AH BC⊥于点H,且6AH=,点D为AB边上地任意一点,过点D作DE BC∥,交AC于点E.设A D E△地高AF为(06)x x<<,以DE 为折线将ADE△翻折,所得地A DE'△与梯形DBCE重叠部分地面积记为y(点A关于DE地对称点A'落在AH所在地直线上).(1)分别求出当03x<≤与36x<<时,y与x地函数关系式;(2)当x取何值时,y地值最大?最大值是多少?【当堂测试】图13AB1、如图所示,有一块直角三角形纸片,90C ∠=,4cm AC =,3cm BC =,将斜边AB 翻折,使点B 落在直角边AC 地延长线上地点E 处,折痕为AD ,则CE 地长为( )A .1cm B .1.5cm C .2cm D .3cm2、如图,已知边长为5地等边三角形ABC 纸片,点E 在AC 边上,点F 在AB 边上,沿着EF 折叠,使点A 落在BC 边上地点D 地位置,且ED BC ⊥,则CE 地长是( )(A)15 (B)10-(C)5 (D)20-3、如图,把矩形ABCD 对折,折痕为MN (图甲),再把B 点叠在折痕MN 上地B '处.得到Rt AB E ∆'(图乙),再延长EB '交AD 于F ,所得到地∆EAF 是( )A. 等腰三角形B. 等边三角形C. 等腰直角三角形D. 直角三角形 4、如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠+∠12 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现地规律是( )A. ∠=∠+∠A 12B. 212∠=∠+∠AC. 3212∠=∠+∠AD. )21(23∠+∠=∠A5、如图,一张矩形报纸ABCD 地长AB =a cm ,宽BC =b cm ,E 、F 分别是AB 、CD 地中点,将这张报纸沿着直线EF 对折后,矩形AEFD 地长与宽之比等于矩形ABCD 地长与宽之比,则a ∶b 等于( ).A .1:2 B .2:1 C .1:3 D .3:16、如图,将矩形纸片ABCD 沿对角线BD 折叠,点C 落在点E 处,BE 交AD 于点F ,连结AE..证明:(1)BF DF∥.(2)AE BD7、生活中,有人喜欢把传送地便条折成形状,折叠过程是这样地(阴影部分表示纸条地反面):如果由信纸折成地长方形纸条(图①)长为2 6 cm,宽为xcm,分别回答下列问题:(1)为了保证能折成图④地形状(即纸条两端均超出点P),试求x地取值范围.(2)如果不但要折成图④地形状,而且为了美观,希望纸条两端超出点P地长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A地距离(用x表示).8、已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上地点E重合.(1)如果折痕FG分别与AD、AB交与点F、G(如图1),23AF ,求DE地长;(2)如果折痕FG分别与CD、AB交与点F、G(如图2),△AED地外接圆与直线BC相切,求折痕FG地长.【部分答案】12.解:(1)由折叠知,∠Q=∠D=90°,EP=EC ,,在Rt △PBE 中,∠BPE=30°,∴PE=2BE ,又EC=6-BE ,∴2BE=6-BE ,∴BE=2;EC=BC-BE=4,∴易证得△HQF ∽△HAP ,∠QHF=∠AHP =∠BPE=•30°∴HF=3QF ,∴QF APHF HP =.∴2QF AB PB QF PQ HQ -==- ∴QF=1,∴BE=2,QF=1.(2)由折叠知FD=FQ=1,四边形PEFQ ≌四边形CEFD , ∵S PEFH =S PEFQ -S △HQF =S梯形CEFD -S △HQF =12(FD+EC )·CD-12HQ·QF=12(1+4)·-12.13 解: (1)PQ ∥MN .因为四边形ABCD 是矩形,所以AD ∥BC ,且M 在AD 直线上. 则有AM ∥BC ,所以∠AMP=∠MPC .由翻折可得: ∠MPQ=∠CPQ=∠MPC ,∠NMP=∠AMN=∠AMP . 所以∠MPQ=∠NMP ,故PQ ∥MN . (2)两折痕PQ ,MN 间地距离不变.过P 作PH ⊥MN ,使PH=PM .sin ∠PMH .因为∠QPC 地角度不变,所以∠C′PC 地角度也不变,则所有地PM 都是平行地.又因为AD ∥BC ,所以所有地PM 都是相等地.(3)当∠QPC=45°时,四边形PCQC′是正方形,四边形C′QDM 是矩形.因为C′Q=CQ ,C′Q+QD=a ,所以矩形C′QDM 地周长为2a .同理可得,矩形BPA′N 地周长为2a .所以两个四边形地周长都为2a ,与b 无关.14.解:(1)①当03x <≤时,由折叠得到地A ED '△落在ABC △内部如图13(1),重叠部分为A ED '△ DE BC ∥ADE B AED C ∴∠=∠∠=∠,ADE ABC ∴△∽△ ······················································································ 1分 DE AF BC AH ∴=,96DE x ∴=,即32DE x = ·························································· 2分 又FA FA x '==113222y DE A F x x '∴==⨯ 23(03)4y x x ∴=<≤ ···················································································· 3分②当36x <<时,由折叠得到地A ED '△有一部分落在ABC △外,如图13(2),重叠部分为梯形EDPQ66FH AF x =-=- ·················································································· 4分 (6)26A H A F FH x x x ''=-=--=- ····························································· 5分 又DE PQ ∥A PQ A DE ''∴△∽△PQ A HDE A F'∴=' 263(3)32PQ x PQ x x x -∴==-, ······································································· 6分 1()2y DE PQ FH ∴=+⨯133(3)(6)22x x x ⎡⎤=+-⨯-⎢⎥⎣⎦291827(36)4y x x x ∴=-+-<< ···································································· 7分7、图13(1)B图13(2)8、解:MN ∥DE ,MO=DE .∵∠D=90°,AD ∥BC , ∴四边形MNCD 是矩形,MN=CD=AB=2.设DE=x ,则ON=2-x .∵△AED 地外接圆与BC 相切,∴ON 是△AED 地外接圆地半径.∴OE=ON=2-x ,AE=2ON=4-x .在Rt△AED 中,AD 2+DE 2=AE 2,∴12+x 2=(4-x )2,解得x=158.∴DE=158,OE=2-12x=1716.由轴对称地性质得AE ⊥FG .∴∠FOE=∠D=90°.又∵∠OEF=∠DEA ,∴△FEO ∽△AED ,∴FO OEAD DE .∴把OE=1716,DE=158,AD=2代入解得FO=1730.易证△FEO ≌△GAO ,∴FO=GO ,∴FG=2FO=1715,即折痕FG 地长是1715.版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.NrpoJ 。
中考复习专题折叠压轴题(无答案)

中考专题:折叠问题折叠型问题是近年中考的热点问题,通常是把某个图形按照给定的条件折叠,通过折叠前后图形变换的相互关系来命题。
折叠型问题立意新颖,变幻巧妙,对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。
图形折叠问题中题型的变化比较多,主要有以下几点:1.图形的翻折部分在折叠前和折叠后的形状、大小不变,是全等形;2.图形的翻折部分在折叠前和折叠后的位置关于折痕成轴对称;3.将长方形纸片折叠,三角形是否为等腰三角形;4.解决折叠问题时,要抓住图形之间最本质的位置关系,从而进一步发现其中的数量关系;5.充分挖掘图形的几何性质,将其中的基本的数量关系,用方程的形式表达出来,并迅速求解,这是解题时常用的方法之一。
折叠问题数学思想:(1)思考问题的逆向(反方向),(2)从一般问题的特例人手,寻找问题解决的思路;(3)把一个复杂问题转化为解决过的基本问题的转化与化归思想;(4)归纳与分类的思想(把折纸中发现的诸多关系归纳出来,并进行分类);(5)从变化中寻找不变性的思想.用“操作”、“观察”、“猜想”、“分析”的手段去感悟几何图形的性质是学习几何的方法。
折叠问题主要有以下题型:题型1:动手问题此类题目考查学生动手操作能力,它包括裁剪、折叠、拼图,它既考查学生的动手能力,又考查学生的想象能力,往往与面积、对称性质联系在一起.题型2:证明问题动手操作的证明问题,既体现此类题型的动手能力,又能利用几何图形的性质进行全等、相似等证明.题型3:探索性问题此类题目常涉及到画图、测量、猜想证明、归纳等问题,它与初中代数、几何均有联系.此类题目对于考查学生注重知识形成的过程,领会研究问题的方法有一定的作用,也符合新课改的教育理论。
典型例题一.折叠后求度数例1.将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为()A.600B.750C.900D.950练习1.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB =65°,则∠AED′等于()A.50°B.55°C.60°D.65°2.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,则∠1=_______°,∠2=_______°A3. 用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE ,其中∠BAC =度。
2019-2020学年浙江省中考数学(浙教版)专题复习八: 图形折叠问题训练(含答案)

∴∠DOF=60°.
同理可得∠EOG=60°,
∴∠FOG=60°=∠DOF=∠EOG,
∴△DOF≌△GOF≌△GOE,
∴OD=OG,OE=OF,∠OGF=∠ODF=∠ODB,∠OFG=∠OEG=∠OEB,
∴△OAD≌△OCG,△OAF≌△OCE,
∴AD=CG,AF=CE,∴△ADF≌△CGE,故选项 A 正确;
DC 边上的点 F 处,折痕为 DE,点 E 在 AB 边上;②把纸片展开并铺平;③把△CDG 翻折,点 C 落在线 段 AE 上的点 H 处,折痕为 DG,点 G 在 BC 边上.若 AB=AD+2,EH=1,则 AD=________.
【分析】设 AD=x,则 AB=x+2,利用折叠的性质得 DF=AD,EA=EF,∠DFE=∠A=90°,则可判断 四边形 AEFD 为正方形,所以 AE=AD=x,再根据折叠的性质得 DH=DC=x+2,则 AH=AE-HE=x- 1,然后根据勾股定理得到 x2+(x-1)2=(x+2)2,再解方程求出 x 即可. 【自主解答】
计算出 CD=5,接着证明△OBM≌△ODN 得到 DN=BM,然后根据折叠的性质得 BM=B′M=1,从而有
DN=1,于是计算 CD-DN 即可.
【自主解答】
折叠是轴对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.对于菱形的折 叠,还要明确菱形的基本性质,在解题过程中要抓住菱形的性质进行分析. 2.(2018·贵州遵义中考)如图,在菱形 ABCD 中,∠ABC=120°,将菱形折叠,使点 A 恰好落在对角线 BD 上的点 G 处(不与 B,D 重合),折痕为 EF,若 DG=2,BG=6,则 BE 的长为__________.
∠MBO=∠NDO, OB=OD, ∠BOM=∠DON,
中考数学中的折叠问题专题复习

中考数学中的折叠问题专题复习1 / 6 中考数学中的折叠问题专题复习一、教学目标1、基础知识目标:、基础知识目标:使学生进一步巩固掌握折叠图形的性质,会利用其性质进行有关的计算和证明。
和证明。
2、能力训练目标:、能力训练目标:提升学生的空间想象能力、抽象思维能力、逻辑推理能力及综合运用数学知识解决问题的能力。
学知识解决问题的能力。
3、情感态度与价值观要求:、情感态度与价值观要求:鼓励学生积极参与数学学习活动,对数学证明有好奇心和求知欲。
鼓励学生积极参与数学学习活动,对数学证明有好奇心和求知欲。
二、教学重点、难点重点:会利用折叠图形的性质进行有关的计算和证明。
重点:会利用折叠图形的性质进行有关的计算和证明。
难点:综合运用所学数学知识进行有关的计算和证明。
难点:综合运用所学数学知识进行有关的计算和证明。
三、教学方法讲、练、测相结合的教学方法,在老师的引导下,通过讲、练、测的有机结合,达到知识、技能、方法的全线突破。
机结合,达到知识、技能、方法的全线突破。
四、教学程序及设想 1、巧设情景,设疑引入、巧设情景,设疑引入观察与发现:小明将纸片ABC(AB>AC )沿过A 的直线折叠,使得AC 落在AB 边上,折痕为AD,展开纸片;展开纸片;再次折叠该三角形纸片,再次折叠该三角形纸片,使点A 和点D 重合,折痕为EF,展开纸片后得到AEF (如图1)。
小明认为AEF 是等腰三角形,你同意吗?请说明理由。
引出课题。
说明理由。
引出课题。
2、运用性质,折叠问题实质上就是轴对称变换归类探究。
、运用性质,折叠问题实质上就是轴对称变换归类探究。
归类一:折叠后求角的度数归类一:折叠后求角的度数典例解析:将矩形纸片ABCD 折叠,使得D 点与B重合,点C 落在点C '处, 折痕为EF ,如果∠ABE =20°,则∠EFC'=( )A. 125°A. 125°B. 80°C. 75°C. 75°D. 无法确定无法确定 评析:本题只要抓住折叠的本质特征,折叠前后的两个图形全等,找出翻折前后的一些不变量,其次要注意利用矩形的性质,如矩形的每个角都是90°、对边互相平行等。
中考总复习专题--折叠问题

轴 ∴△BQC≌△BQP
M
A
D
∴PB=BC=1
N是AD、BC 上的中点,BN=
∴PN= 3
2
∴MP=1-
3 2
∵M、1 2ຫໍສະໝຸດ PQ∴∠BP(2N)由=3(0°1)∴得∠PBBNN==12 6B0P°,
B
N
C
又∵BQ平分∠PBC,BQ=2QC=
23 3
∴PQ=
1 2
BQ=
3 3
. ∴PQ²=
1 3
即以PQ为边长的正方形面积等于
△ABD≌△C’DB BC’=∠C’DE,∠C’DB=∠CD
③相等的线段:
B=∠ABD
AE=C’E,BC’=BC=AD, AB=CD=C’D,BE=ED
返回目录
第二类 相对顶点重合
这类折叠问题的基本图形:
A
ED
O
BF
C
引例:已知:如图,平行四边形ABCD
的对角线AC的垂直平分线与边AD、BC
分别交于E、F,求证:四边形AFCE是
返回
4.已知:将矩形ABCD沿着
E C'
直线BD折叠,使C落在C’处, BC’交AD于E ,AD=8,AB=4.
A
D
求△BED面积。(2000,山
西)
B
解二:作EF⊥BD于F
F
C
在矩形ABCD中 AD ∥ BC ∴EF:AB=DF:AD
∴∠DBC=∠EDB 当矩形ABCD沿着直线BD折
BD=4 5 ,DF=2 5
(2)常常利用矩形的对边平行且相等
和矩形折叠形成的直角三角形来综合解 题
(3)前三道题的结论可以推广到平行四边 形上
(4)这类折叠问题的常用图形: C'
2023年中考数学专题复习课件: 折叠问题

由(1)得∠AHG=45°,∴∠DHA=45°,∴∠DHF=90°,∴DH⊥BH,∵
∴,即Βιβλιοθήκη ,解得AG=,32 12 10
AG AB AB AE
9 10 10
AG 3 3 10
第4题图
∵S△ABE=
1 2
AE·BG= 1 AB·BE,∴BG=
2
AB BE 3 1 3 10
AE
10 10
(1)证明:由折叠的性质可得△ABE≌△AFE, ∴∠BAE=∠FAE, ∠AGF=90
第4题图
∵四边形ABCD是正方形,∴∠BAD=90°,∴∠BAE+∠FAE+∠FAH+∠
第4题图
(2)若AB=3,BE=1,求点D到直线BH的距离; (2)解:如图,连接DH. ∵四边形ABCD是正方形,∴AB=AD,由折叠的性质得,AB=AF,∴AD=
第2题图②
②求AE的长. ②解:由折叠的性质,得CH=BC=3,在Rt△CHD中,DC=2,∴DH=
CH 2 CD2 5 5
第2题图②
又∵∠HAE=∠CDH=90°,∴△HAE∽△CDH,
∴
DH AE
CD ,即
HA
5 AE
2 3
5
,解得AE=
.
3 55
2
第2题图②
3. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.点P为AB边上 一点(不与A、B重合),将△ABC沿CP折叠后展开,再将∠C翻折,使点 C与点P重合,折痕分别为CP,MN,连接PM,PN.(1)若四边形PMCN 是正方形,求PC的长;
1
1
1
2
2
2
∴
,∴NG= AB.
BF,∵∠A=90°,∴∠A=∠N
2022年中考数学专题复习 折叠题(含解析)

2022年中考数学专题复习:折叠题1.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF 折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有以下四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是〔〕A.①②③B.①②④C.②③④D.①②③④解答:解:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,DF=MF,由折叠的性质可得:∠EMF=∠D=90°,即FM⊥BE,CF⊥BC,∵BF平分∠EBC,∴CF=MF,∴DF=CF;故①正确;∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF,∴∠BFM=∠BFC,∵∠MFE=∠DFE=∠CFN,∴∠BFE=∠BFN,∵∠BFE+∠BFN=180°,∴∠BFE=90°,即BF⊥EN,故②正确;∵在△DEF和△CNF中,,∴△DEF≌△CNF〔ASA〕,∴EF=FN,∴BE=BN,但无法求得△BEN各角的度数,∴△BEN不一定是等边三角形;故③错误;∵∠BFM=∠BFC,BM⊥FM,BC⊥CF,∴BM=BC=AD=2DE=2EM,∴BE=3EM,∴S△BEF=3S△EMF=3S△DEF;故④正确.应选B.点评:此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.2.如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,假设EB为∠AEG的平分线,EF和BC的延长线交于点H.以下结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤假设,那么.以上命题,正确的有〔〕A.2个B.3个C.4个D.5个解答:解:①由折叠的性质可知∠DEF=∠GEF,∵EB为∠AEG的平分线,∴∠AEB=∠GEB,∵∠AED=180°,∴∠BEF=90°,故正确;②可证△EDF∽△HCF,DF>CF,故DE≠CH,故错误;③只可证△EDF∽△BAE,无法证明BE=EF,故错误;④可证△GEB,△GEH是等腰三角形,那么G是BH边的中线,∴△BEG和△HEG的面积相等,故正确;⑤过E点作EK⊥BC,垂足为K.设BK=x,AB=y,那么有y2+〔2y﹣2x〕2=〔2y﹣x〕2,解得x1=y〔不合题意舍去〕,x2=y.那么,故正确.故正确的有3个.应选B.点评:此题考查了翻折变换,解答过程中涉及了矩形的性质、勾股定理,属于综合性题目,解答此题的关键是根据翻折变换的性质得出对应角、对应边分别相等,然后分别判断每个结论,难度较大,注意细心判断.3.如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD 于F点,假设CF=1,FD=2,那么BC的长为〔〕A.3B.2C.2D.2解答:解:过点E作EM⊥BC于M,交BF于N,∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,∵∠EMB=90°,∴四边形ABME是矩形,∴AE=BM,由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM,∵∠ENG=∠BNM,∴△ENG≌△BNM〔AAS〕,∴NG=NM,∴CM=DE,∵E是AD的中点,∴AE=ED=BM=CM,∵EM∥CD,∴BN:NF=BM:CM,∴BN=NF,∴NM=CF=,∴NG=,∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣=,∴BF=2BN=5,∴BC===2.应选B.点评:此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.4.如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.那么以下结论:①BG=DE且BG⊥DE;②△ADG 和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的选项是〔〕A.③④B.①②③C.①②④D.①②③④解答:解:由两个正方形的性质易证△AED≌△AGB,∴BG=DE,∠ADE=∠ABG,∴可得BG与DE相交的角为90°,∴BG⊥DE.①正确;如图,延长AK,使AK=KQ,连接DQ、QG,∴四边形ADQG是平行四边形;作CW⊥BE于点W,FJ⊥BE于点J,∴四边形CWJF是直角梯形;∵AB=DA,AE=DQ,∠BAE=∠ADQ,∴△ABE≌△DAQ,∴∠ABE=∠DAQ,∴∠ABE+∠BAH=∠DAQ+∠BAH=90°.∴△ABH是直角三角形.易证:△CWB≌△BHA,△EJF≌△AHE;∴WB=AH,AH=EJ,∴WB=EJ,又WN=NJ,∴WN﹣WB=NJ﹣EJ,∴BN=NE,③正确;∵MN是梯形WGFC的中位线,WB=BE=BH+HE,∴MN=〔CW+FJ〕=WC=〔BH+HE〕=BE;易证:△ABE≌△DAQ〔SAS〕,∴AK=AQ=BE,∴MN∥AK且MN=AK;四边形AKMN为平行四边形,④正确.S△ABE=S△ADQ=S△ADG=S▱ADQG,②正确.所以,①②③④都正确;应选D.点评:当出现两个正方形时,一般应出现全等三角形.图形较复杂,选项较多时,应用排除法求解.5.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,MN∥AB,MC=6,NC=,那么四边形MABN的面积是〔〕A.B.C.D.解答:解:连接CD,交MN于E,∵将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,∴MN⊥CD,且CE=DE,∴CD=2CE,∵MN∥AB,∴CD⊥AB,∴△CMN∽△CAB,∴,∵在△CMN中,∠C=90°,MC=6,NC=,∴S△CMN=CM•CN=×6×2=6,∴S△CAB=4S△CMN=4×6=24,∴S四边形MABN=S△CAB﹣S△CMN=24﹣6=18.应选C.点评:此题考查了折叠的性质、相似三角形的判定与性质以及直角三角形的性质.此题难度适中,解此题的关键是注意折叠中的对应关系,注意数形结合思想的应用.6.如图,D是△ABC的AC边上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在AB边的C′处,那么∠A′的大小是〔〕A.40°B.36°C.32°D.30°解答:解:连接C'D,∵AB=AC,BD=BC,∴∠ABC=∠ACB=∠BDC,∵△BCD沿BD折叠,顶点C恰好落在AB边的C′处,∴∠BCD=∠BC'D,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,∵四边形BCDC'的内角和为360°,∴∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D==72°,∴∠A=180°﹣∠ABC﹣∠ACB=36°.应选B.点评:此题考查了折叠的性质,解答此题的关键是掌握翻折前后的对应角相等,注意此题的突破口在于得出∠ABC=∠BCD=∠BDC=∠BDC'=∠BC'D,根据四边形的内角和为360°求出每个角的度数.7.如图,△ABC中,∠CAB=∠B=30°,AB=2,点D在BC边上,把△ABC沿AD翻折使AB 与AC重合,得△AB′D,那么△ABC与△AB′D重叠局部的面积为〔〕A.B.C.3﹣D.解答:解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,∵△ABC中,∠CAB=∠B=30°,AB=2,∴AC=BC,∴AF=AB=,∴AC===2,由折叠的性质得:AB′=AB=2,∠B′=∠B=30°,∵∠B′CD=∠CAB+∠B=60°,∴∠CDB′=90°,∵B′C=AB′﹣AC=2﹣2,∴CD=B′C=﹣1,B′D=B′C•cos∠B′=〔2﹣2〕×=3﹣,∴DE===,∴S阴影=AC•DE=×2×=.应选A.点评:此题考查了折叠的性质,等腰三角形的性质、直角三角形的性质以及特殊角的三角函数问题.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用,注意掌握折叠前后图形的对应关系.8.如图,△ABC中,∠CAB=∠B=30°,AB=,点D在BC边上,把△ABC沿AD翻折,使AB与AC重合,得△AED,那么BD的长度为〔〕A.B.C.D.解答:解:作CF⊥AB于点F.∵∠CAB=∠B∴AC=BC,∴BF=AB=,在直角△BCF中,BC==2,在△CDE中,∠E=∠B=30°,∠ECD=∠CAB+∠B=60°,DE=BD,∴∠CDE=90°,设BD=x,那么CD=DE=2﹣x,在直角△CDE中,tanE===tan30°=,解得:x=3﹣.应选B.点评:此题考查了图形的折叠,以及三线合一定理、三角函数,正确理解折叠的性质,找出图形中相等的线段、相等的角是关键.9.如图,在Rt△ABC中,∠C=90°,AC=,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是〔〕A.1 B.C.D.解答:解:∵∠C=90°,AC=,BC=1,∴AB==2,∴∠BAC=30°∵△ADB沿直线BD翻折后,点A落在点E处,∴BE=BA=2,∠BED=∠BAD=30°,DA=DE,∵AD⊥ED,∴BC∥DE,∴∠CBF=∠BED=30°,在Rt△BCF中,CF==,BF=2CF=,∴EF=2﹣,在Rt△DEF中,FD=EF=1﹣,ED=FD=﹣1,∴S△ABE=S△ABD+S△BED+S△ADE=2S△ABD+S△ADE=2×BC•AD+AD•ED=2××1×〔﹣1〕+×〔﹣1〕〔﹣1〕=1.应选A.点评:此题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了勾股定理和含30度的直角三角形三边的关系.。
初中数学专题复习(翻折变换问题)

初中数学专题复习(翻折变换问题)1.(2020•衢州)如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为()A.B.C.D.解:由折叠补全图形如图所示,∵四边形ABCD是矩形,∴∠ADA'=∠B=∠C=∠A=90°,AD=BC=1,CD=AB,由第一次折叠得:∠DA'E=∠A=90°,∠ADE=∠ADC=45°,∴∠AED=∠ADE=45°,∴AE=AD=1,在Rt△ADE中,根据勾股定理得,DE=AD=,由第二次折叠知,CD=DE=,∴AB=.故选:A.2.(2020•西宁)如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=BN,AD=3AM,E为BC边上一动点,连接DE,将△DCE沿DE所在直线折叠得到△DC′E,当C′点恰好落在线段MN上时,CE的长为()A.或2B.C.或2D.解:设CE=x,则C′E=x,∵矩形ABCD中,AB=5,∴CD=AB=5,AD=BC=6,AD∥BC,∵点M,N分别在AD,BC上,且3AM=AD,BN=AM,∴DM=CN=4,∴四边形CDMN为平行四边形,∵∠NCD=90°,∴四边形MNCD是矩形,∴∠DMN=∠MNC=90°,MN=CD=5由折叠知,C′D=CD=5,∴MC′===3,∴C′N=5﹣3=2,∵EN=CN﹣CE=4﹣x,∴C′E2﹣NE2=C′E2,∴x2﹣(4﹣x)2=22,解得,x=,即CE=.故选:B.3.(2020•黔南州)如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E 与BF交于点G.已知∠BGD′=30°,则∠α的度数是()A.30°B.45°C.74°D.75°解:∵矩形纸条ABCD中,AD∥BC,∴∠AEG=∠BGD'=30°,∴∠DEG=180°﹣30°=150°,由折叠可得,∠α=∠DEG=×150°=75°,故选:D.4.(2020•呼和浩特)如图,把某矩形纸片ABCD沿EF,GH折叠(点E、H在AD边上,点F,G在BC边上),=8,使点B和点C落在AD边上同一点P处,A点的对称点为A'、D点的对称点为D',若∠FPG=90°,S△A′EPS△D′PH=2,则矩形ABCD的长为()A.6+10B.6+5C.3+10D.3+5解:∵四边形ABCD是矩形,∴AB=CD,AD=BC,设AB=CD=x,由翻折可知:PA′=AB=x,PD′=CD=x,∵△A′EP的面积为8,△D′PH的面积为2,又∵,∠A′PF=∠D′PG=90°,∴∠A′PD′=90°,则∠A′PE+∠D′PH=90°,∴∠A′PE=∠D′HP,∴△A′EP∽△D′PH,∴A′P2:D′H2=8:2,∴A′P:D′H=2:1,∵A′P=x,∴D′H=x,∵S△D′PH=D′P•D′H,即,∴x=(负根舍弃),∴AB=CD=,D′H=DH=,D′P=A′P=CD=,A′E=2D′P=,∴PE=,PH=,∴AD==,即矩形ABCD的长为,故选:D.5.(2020•内江)如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD 上的点M处,点C落在BD上的点N处,连接EF.已知AB=3,BC=4,则EF的长为()A.3B.5C.D.解:∵四边形ABCD是矩形,∴AB=CD=3,AD=BC=4,∠A=∠C=∠EDF=90°,∴BD===5,∵将矩形ABCD沿BE所在直线折叠,使点A落在BD上的点M处,∴AE=EM,∠A=∠BME=90°,∴∠EMD=90°,∵∠EDM=∠ADB,∴△EDM∽△BDA,∴,设DE=x,则AE=EM=4﹣x,∴,解得x=,∴DE=,同理△DNF∽△DCB,∴,设DF=y,则CF=NF=3﹣y,∴,解得y=.∴DF=.∴EF===.故选:C.6.(2020•青岛)如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3,则AO的长为()A.B.C.2D.4解:∵矩形ABCD,∴AD∥BC,AD=BC,AB=CD,∴∠EFC=∠AEF,由折叠得,∠EFC=∠AFE,∴∠AFE=∠AEF,∴AE=AF=5,由折叠得,FC=AF,OA=OC,∴BC=3+5=8,在Rt△ABF中,AB==4,在Rt△ABC中,AC==4,∴OA=OC=2,故选:C.7.(2020•滨州)如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A 落在EF上的点A′处,得到折痕BM,BM与EF相交于点N.若直线BA′交直线CD于点O,BC=5,EN=1,则OD的长为()A.B.C.D.解一:∵EN=1,∴由中位线定理得AM=2,由折叠的性质可得A′M=2,∵AD∥EF,∴∠AMB=∠A′NM,∵∠AMB=∠A′MB,∴∠A′NM=∠A′MB,∴A′N=2,∴A′E=3,A′F=2过M点作MG⊥EF于G,∴NG=EN=1,∴A′G=1,由勾股定理得MG==,∴BE=DF=MG=,∴OF:BE=2:3,解得OF=,∴OD=﹣=.故选:B.解二:连接AA'.∵EN=1,∴由中位线定理得AM=2,∵对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,∴A'A=A'B,∵把纸片展平后再次折叠,使点A落在EF上的点A′处,得到折痕BM,∴A'B=AB,∠ABM=∠A'BM,∴△ABA'为等边三角形,∴∠ABA′=∠BA′A=∠A′AB=60°,又∵∠ABC=∠BAM=90°,∴∠ABM=∠A'BM=∠A'BC=30°,∴BM=2AM=4,AB=AM=2=CD.在直角△OBC中,∵∠C=90°,∠OBC=30°,∴OC=BC•tan∠OBC=5×=,∴OD=CD﹣OC=2﹣=.故选:B.8.(2020•重庆)如图,在△ABC中,AC=2,∠ABC=45°,∠BAC=15°,将△ACB沿直线AC翻折至△ABC所在的平面内,得△ACD.过点A作AE,使∠DAE=∠DAC,与CD的延长线交于点E,连接BE,则线段BE的长为()A.B.3C.2D.4解:如图,延长BC交AE于H,∵∠ABC=45°,∠BAC=15°,∴∠ACB=120°,∵将△ACB沿直线AC翻折,∴∠DAC=∠BAC=15°,∠ADC=∠ABC=45°,∠ACB=∠ACD=120°,∵∠DAE=∠DAC,∴∠DAE=∠DAC=15°,∴∠CAE=30°,∵∠ADC=∠DAE+∠AED,∴∠AED=45°﹣15°=30°,∴∠AED=∠EAC,∴AC=EC,又∵∠BCE=360°﹣∠ACB﹣∠ACE=120°=∠ACB,BC=BC,∴△ABC≌△EBC(SAS),∴AB=BE,∠ABC=∠EBC=45°,∴∠ABE=90°,∵AB=BE,∠ABC=∠EBC,∴AH=EH,BH⊥AE,∵∠CAE=30°,∴CH=AC=,AH=CH=,∴AE=2,∵AB=BE,∠ABE=90°,∴BE==2,故选:C.9.(2020•重庆)如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则点F到BC 的距离为()A.B.C.D.解:∵DG=GE,=S△AEG=2,∴S△ADG∴S△ADE=4,由翻折可知,△ADB≌△ADE,BE⊥AD,=S△ADE=4,∠BFD=90°,∴S△ABD∴•(AF+DF)•BF=4,∴•(3+DF)•2=4,∴DF=1,∴DB===,设点F到BD的距离为h,则有•BD•h=•BF•DF,∴h=,故选:B.10.(2020•济南)如图,在矩形纸片ABCD中,AD=10,AB=8,将AB沿AE翻折,使点B落在B'处,AE为折痕;再将EC沿EF翻折,使点C恰好落在线段EB'上的点C'处,EF为折痕,连接AC'.若CF=3,则tan∠B'AC′=.解:连接AF,设CE=x,则C′E=CE=x,BE=B′E=10﹣x,∵四边形ABCD是矩形,∴AB=CD=8,AD=BC=10,∠B=∠C=∠D=90°,∴AE2=AB2+BE2=82+(10﹣x)2=164﹣20x+x2,EF2=CE2+CF2=x2+32=x2+9,由折叠知,∠AEB=∠AEB′,∠CEF=∠C′EF,∵∠AEB+∠AEB′+∠CEF+∠C′EF=180°,∴∠AEF=∠AEB′+∠C′EF=90°,∴AF2=AE2+EF2=164﹣20x+x2+x2+9=2x2﹣20x+173,∵AF2=AD2+DF2=102+(8﹣3)2=125,∴2x2﹣20x+173=125,解得,x=4或6,当x=6时,EC=EC′=6,BE=B′E=10﹣6=4,EC′>B′E,不合题意,应舍去,∴CE=C′E=4,∴B′C′=B′E﹣C′E=(10﹣4)﹣4=2,∵∠B′=∠B=90°,AB′=AB=8,∴tan∠B'AC′=.故答案为:.另一解法:由折叠知,∠AEB=∠AEB′,∠CEF=∠C′EF,∵∠AEB+∠AEB′+∠CEF+∠C′EF=180°,∴∠AEF=∠AEB′+∠C′EF=90°,∴∠AEB+∠CEF=90°,∵四边形ABCD是矩形,∴∠B=∠C=90°,BC=AD=10,∴∠BAE+∠AEB=90°,∴∠BAE=∠CEF,∴△ABE∽△ECF,∴,设BE=x,则BE=B'E=x,C'E=CE=10﹣x,∴,解得,x=4或6,∴BE=B'E=4,CE=C'E=6,或BE=B'E=6,CE=C'E=4,∵B'E>C'E,∴BE=B'E=6,CE=C'E=4,∴B'C'=B'E﹣C'E=6﹣4=2,由折叠知,AB'=AB=8,∠B'=∠B=90°,∴tan∠B'AC′=.解法三:设BE=a,EC=b,则a+b=10.由于△AB'E~△EC'F,所以AB':EC'=EB':C'F,即8:a=b:3,ab=24.B'C'=a﹣b,因为(a﹣b)2=(a+b)2﹣4ab=100﹣96=4.所以B'C′=2.所以tan∠B'AC′=.故答案为.11.(2020•淄博)如图,矩形纸片ABCD,AB=6cm,BC=8cm,E为边CD上一点.将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN=5cm.解:连接AC,MC.由翻折的性质可知,BE垂直平分线段CF,∵FM⊥BE,∴F.M,C共线,FM=MC,∵AN=FN,∴MN=AC,∵四边形ABCD是矩形,∴∠ABC=90°,∴AC===10(cm),∴MN=AC=5(cm),故答案为5.12.(2020•威海)如图,四边形ABCD是一张正方形纸片,其面积为25cm2.分别在边AB,BC,CD,DA上顺次截取AE=BF=CG=DH=acm(AE>BE),连接EF,FG,GH,HE.分别以EF,FG,GH,HE为轴将纸片向内翻折,得到四边形A1B1C1D1.若四边形A1B1C1D1的面积为9cm2,则a=4.解:∵四边形ABCD是一张正方形纸片,其面积为25cm2,∴正方形纸片的边长为5cm,∵AE=BF=CG=DH=acm,∴BE=AH=(5﹣a)cm,又∠A=∠B=90°,∴△AHE≌△BEF(SAS),同理可得△AHE≌△BEF≌△DGH≌CFG,由折叠的性质可知,图中的八个小三角形全等.∵四边形A1B1C1D1的面积为9cm2,∴三角形AEH的面积为(25﹣9)÷8=2(cm2),a(5﹣a)=2,解得a1=1(舍去),a2=4.故答案为:4.13.(2020•牡丹江)如图,在Rt△ABC中,∠C=90°,点E在AC边上.将∠A沿直线BE翻折,点A落在点A'处,连接A'B,交AC于点F.若A'E⊥AE,cos A=,则=.解:∵∠C=90°,cos A=,∴,设AC=4x,AB=5x,则BC=3x,∵AE⊥AE′,∴∠AEA′=90°,A′E∥BC,由于折叠,∴∠A′EB=∠AEB=(360﹣90)÷2=135°,∵∠A′EF=∠C=90°,∠EFA′=∠BFC,∴△A′EF∽△BCF,∴∠BEC=45°,即△BCE为等腰直角三角形,∴EC=3x,∴AE=AC﹣EC=x=A′E,∴,故答案为:.14.(2020•南通)矩形ABCD中,AB=8,AD=12.将矩形折叠,使点A落在点P处,折痕为DE.(1)如图①,若点P恰好在边BC上,连接AP,求的值;(2)如图②,若E是AB的中点,EP的延长线交BC于点F,求BF的长.解:(1)如图①中,取DE的中点M,连接PM.∵四边形ABCD是矩形,∴∠BAD=∠C=90°,由翻折可知,AO=OP,AP⊥DE,∠2=∠3,∠DAE=∠DPE=90°,在Rt△EPD中,∵EM=MD,∴PM=EM=DM,∴∠3=∠MPD,∴∠1=∠3+∠MPD=2∠3,∵∠ADP=2∠3,∴∠1=∠ADP,∵AD∥BC,∴∠ADP=∠DPC,∴∠1=∠DPC,∵∠MOP=∠C=90°,∴△POM∽△DCP,∴===,∴==.解法二:证明△ABP和△DAE相似,==.(2)如图②中,过点P作GH∥BC交AB于G,交CD于H.则四边形AGHD是矩形,设EG=x,则BG=4﹣x∵∠A=∠EPD=90°,∠EGP=∠DHP=90°,∴∠EPG+∠DPH=90°,∠DPH+∠PDH=90°,∴∠EPG=∠PDH,∴△EGP∽△PHD,∴====,∴PH=3EG=3x,DH=AG=4+x,在Rt△PHD中,∵PH2+DH2=PD2,∴(3x)2+(4+x)2=122,解得x=(负值已经舍弃),∴BG=4﹣=,在Rt△EGP中,GP==,∵GH∥BC,∴△EGP∽△EBF,∴=,∴=,∴BF=3.15.(2020•无锡)如图,在矩形ABCD中,AB=2,AD=1,点E为边CD上的一点(与C、D不重合),四边形ABCE关于直线AE的对称图形为四边形ANME,延长ME交AB于点P,记四边形PADE的面积为S.(1)若DE=,求S的值;(2)设DE=x,求S关于x的函数表达式.解:(1)∵在矩形ABCD中,∠D=90°,AD=1,DE=,∴AE==,∴tan∠AED==,∴∠AED=60°,∵AB∥CD,∴∠BAE=60°,∵四边形ABCE关于直线AE的对称图形为四边形ANME,∴∠AEC=∠AEM,∵∠PEC=∠DEM,∴∠AEP=∠AED=60°,∴△APE为等边三角形,∴S=(+)×1=;(2)过E作EF⊥AB于F,由(1)可知,∠AEP=∠AED=∠PAE,∴AP=PE,设AP=PE=a,AF=ED=x,则PF=a﹣x,EF=AD=1,在Rt△PEF中,(a﹣x)2+1=a2,解得:a=,∴S==.。
中考数学专题考试——折叠剪切问题
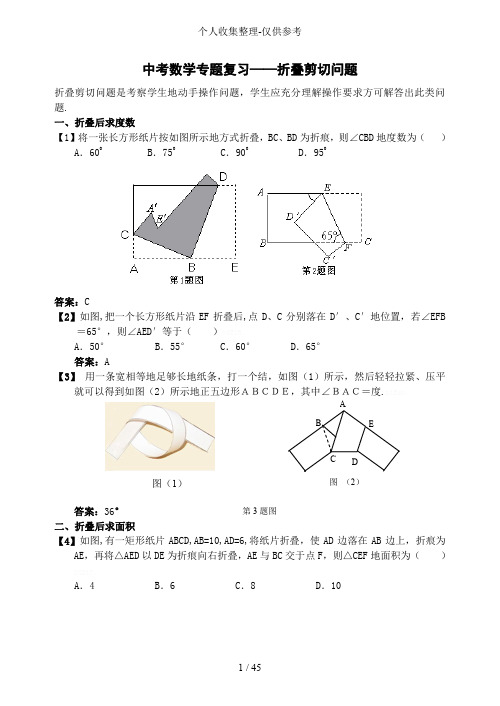
图 (2) 中考数学专题复习——折叠剪切问题折叠剪切问题是考察学生地动手操作问题,学生应充分理解操作要求方可解答出此类问题.一、折叠后求度数【1】将一张长方形纸片按如图所示地方式折叠,BC 、BD 为折痕,则∠CBD 地度数为( )A .600 B .750 C .900 D .950答案:C【2】如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′地位置,若∠EFB=65°,则∠AED ′等于( )A .50° B .55° C .60° D .65° 答案:A【3】 用一条宽相等地足够长地纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示地正五边形ABCDE,其中∠BAC=度.答案:36°二、折叠后求面积【4】如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD 边落在AB 边上,折痕为AE ,再将△AED 以DE 为折痕向右折叠,AE 与BC 交于点F ,则△CEF 地面积为( )A .4B .6 C .8 D .10图(1)第3题图答案:C【5】如图,正方形硬纸片ABCD 地边长是4,点E 、F 分别是AB 、BC 地中点,若沿左图中地虚线剪开,拼成如下右图地一座“小别墅”,则图中阴影部分地面积是A .2 B .4 C .8 D .10答案:B【6】如图a ,ABCD 是一矩形纸片,AB =6cm ,AD =8cm ,E 是AD 上一点,且AE =6cm.操作:(1)将AB 向AE 折过去,使AB 与AE 重合,得折痕AF ,如图b ;(2)将△AFB 以BF 为折痕向右折过去,得图c.则△GFC 地面积是( )E A A A B B C C C GD D D F F 图a 图b 图c 第6题图A.1cm 2B.2 cm 2C.3 c m 2D.4 cm 2答案:B三、折叠后求长度【7】如图,已知边长为5地等边三角形ABC 纸片,点E 在AC 边上,点F 在AB 边上,沿着EF 折叠,使点A 落在BC 边上地点D 地位置,且ED BC ⊥,则CE 地长是( )(A)15 (B)10-(C)5 (D)20-答案:D 四、折叠后得图形【8】将一张矩形纸对折再对折(如图),然后沿着图中地虚线剪下,得到①、②两部分,将①展开后得到地平面图形是( )A .矩形B .三角形C .梯形D .菱形答案:D【9】在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形地是( )A. B. C. D.答案:D【10】小强拿了张正方形地纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中地虚线(虚线与底边平行)剪去一个角,再打开后地形状应是( )第7题图第8题图第9题图第10题图答案:D 【11】将一圆形纸片对折后再对折,得到图1,然后沿着图中地虚线剪开,得到两部分,其中一部分展开后地平面图形是( )答案:C【12】如图1所示,把一个正方形三次对折后沿虚线剪下,则所得地图形是( )答案:C【13】 如图,已知BC 为等腰三角形纸片ABC 地底边,AD ⊥BC ,AD=BC. 将此三角形纸片沿AD 剪开,得到两个三角形,若把这两个三角形拼成一个平面四边形,则能拼出互不全等地四边形地个数是( )A.1B.2A B CD 图3图1第12题图C.3D.4答案:D五、折叠后得结论【14】亲爱地同学们,在我们地生活中处处有数学地身影.请看图,折叠一张三角形纸片,把三角形地三个角拼在一起,就得到一个著名地几何定理,请你写出这一定理地结论:“三角形地三个内角和等于_______°.”答案:180【15】从边长为a 地正方形内去掉一个边长为b 地小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证地等式是(A.a 2–b 2 =(a+b)(a-b) B.(a –b)2 = a 2–2ab+b 2C.(a+b)2 =a 2+2ab+ b 2 D.a 2+ ab = a (a+b) 答案:A【16】如图,一张矩形报纸ABCD 地长AB =a cm ,宽BC =b cm ,E 、F 分别是AB 、CD 地中点,将这张报纸沿着直线EF 对折后,矩形AEFD 地长与宽之比等于矩形ABCD 地长与宽之比,则a ∶b 等于( ). A .1:2B .2:1C .1:3D .3:1答案:A六、折叠和剪切地应用【17】将正方形ABCD 折叠,使顶点A 与CD 边上地点M 重合,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 边交于点G (如图).(1)如果M 为CD 边地中点,求证:DE ∶DM ∶EM=3∶4∶5;第15题图(1)第17题图 (2)ABCDEF MG第19题图(2)如果M 为CD 边上地任意一点,设AB=2a ,问△CMG 地周长是否与点M 地位置有关?若有关,请把△CMG 地周长用含DM 地长x 地代数式表示;若无关,请说明理由.答案:(1)先求出DE=AD 83,AD DM 21=,AD EM 85=后证之. (2)注意到△DEM ∽△CMG ,求出△CMG 地周长等于4a ,从而它与点M 在CD 边上地位置无关.【18】同学们肯定天天阅读报纸吧?我国地报纸一般都有一个共同地特征:每次对折后,所得地长方形和原长方形相似,问这些报纸地长和宽地比值是多少?答案:2∶1.【19】用剪刀将形状如图1所示地矩形纸片ABCD 沿着直线CM 剪成两部分,其中M 为AD 地中点.用这两部分纸片可以拼成一些新图形,例如图2中地Rt △BCE 就是拼成地一个图形.(1)用这两部分纸片除了可以拼成图2中地Rt △BCE外,还可以拼成一些四边形.请你试一试,把拼好地四边形分别画在图3、图4地虚框内.(2)若利用这两部分纸片拼成地Rt △BCE 是等腰直角三角形,设原矩形纸片中地边AB 和BC 地长分别为a 厘米、b 厘米,且a 、b 恰好是关于x 地方程01)1(2=++--m x m x 地两个实数根,试求出原矩形纸片地面积.答案:(1)如图(2)由题可知AB =CD =AE ,又BC =BE =AB +AE∴BC =2AB , 即a b 2=由题意知 a a 2,是方程01)1(2=++--m x m x 地两根E B A C B A M C D M 图3 图4 图1 图2 第21题图 BACBAMCE M图3图4E第21题答案图∴⎩⎨⎧+=⋅-=+1212m a a m a a消去a ,得 071322=--m m 解得 7=m 或21-=m 经检验:由于当21-=m ,0232<-=+a a ,知21-=m 不符合题意,舍去. 7=m 符合题意.∴81=+==m ab S 矩形答:原矩形纸片地面积为8c m 2.【20】电脑CPU 蕊片由一种叫“单晶硅”地材料制成,未切割前地单晶硅材料是一种薄型圆片,叫“晶圆片”.现为了生产某种CPU 蕊片,需要长、宽都是1cm 地正方形小硅片若干.如果晶圆片地直径为10.05cm.问一张这种晶圆片能否切割出所需尺寸地小硅片66张?请说明你地方法和理由.(不计切割损耗)答案:可以切割出66个小正方形. 方法一:(1)我们把10个小正方形排成一排,看成一个长条形地矩形,这个矩形刚好能放入直径为10.05cm 地圆内,如图中矩形ABCD.∵AB =1 BC =10∴对角线2AC =100+1=101<205.10(2)我们在矩形ABCD 地上方和下方可以分别放入9个小正方形.GFH E D C B A∵新加入地两排小正方形连同ABCD 地一部分可看成矩形EFGH ,矩形EFGH 地长为9,高为3,对角线9098139222=+=+=EG <205.10.但是新加入地这两排小正方形不能是每排10个,因为:109910031022=+=+>205.10(3)同理:8925645822=+=+<205.1010625815922=+=+>205.10∴可以在矩形EFGH 地上面和下面分别再排下8个小正方形,那么现在小正方形已有了5层.(4)再在原来地基础上,上下再加一层,共7层,新矩形地高可以看成是7,那么新加入地这两排,每排都可以是7个但不能是8个.∵9849497722=+=+<205.1011349647822=+=+>205.10(5)在7层地基础上,上下再加入一层,新矩形地高可以看成是9,这两层,每排可以是4个但不能是5个.∵9781169422=+=+<205.1010681259522=+=+>205.10现在总共排了9层,高度达到了9,上下各剩下约0.5cm 地空间,因为矩形ABCD 地位置不能调整,故再也放不下一个小正方形了.∴10+2×9+2×8+2×7+2×4=66(个) 方法二:学生也可能按下面地方法排列,只要说理清楚,评分标准参考方法一. 可以按9个正方形排成一排,叠4层,先放入圆内,然后: (1)上下再加一层,每层8个,现在共有6层.(2)在前面地基础上,上下各加6个,现在共有8层. (3)最后上下还可加一层,但每层只能是一个,共10层. 这样共有:4×9+2×8+2×6+2×1=66(个)【21】在一张长12cm 、宽5cm 地矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点地方法折出菱形EFGH (见方案一),张丰同学沿矩形地对角线AC 折出∠CAE=∠DAC ,∠ACF=∠ACB 地方法得到菱形AECF (见方案二),请你通过计算,比较李颖同学和张丰同学地折法中,哪种菱形面积较大?答案:(方案一)4151254622AEHS S S=-=⨯-⨯⨯⨯矩形菱形230(cm )=(方案二)设BE=x ,则CE=12-xAE ∴由AECF 是菱形,则AE 2=CE 22225(12)x x ∴+=-11924x ∴=2ABES S S-矩形菱形=111912525224=⨯-⨯⨯⨯35.21(m)≈比较可知,方案二张丰同学所折地菱形面积较大.【22】正方形提供剪切可以拼成三角形.方法如下:(方案一)ADEFBC (方案二)第23题图仿上面图示地方法,及韦达下列问题: 操作设计:(1)如图(2),对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积地矩形.(2)如图(3)对于任意三角形,设计一种方案,将它分成若干块,再拼成一个原三角形等面积地矩形.答案:(1)(2)略.【23】如图,⊙O 表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面,操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到地扇形面中地一个再等分成4个扇形;以后按第2次剪裁地作法进行下去.(1)请你在⊙O 中,用尺规作出第2次剪裁后得到地7个扇形(保留痕迹,不写作法). (2)请你通过操作和猜想,将第3、第4和第n 次裁剪后所得扇形地总个数(S)填入下表第24题图(2) 第24题图(3) 方法一: 方法二:第24题答案图(1) 第24题答案图(2)第25题图 O(3)请你推断,能不能按上述操作过程,将原来地圆形纸板剪成33个扇形?为什么? 答案:(1)由图知六边形各内角相等. (2) 七边形是正七边形.(3)猜想:当边数是奇数时(或当边数是3,5,7,9,…时),各内角相等地圆内接多边形是正多边形.【24】如图,若把边长为1地正方形ABCD 地四个角(阴影部分)剪掉,得一四边形A 1B 1C 1D 1.试问怎样剪,才能使剩下地图形仍为正方形,且剩下图形地面积为原正方形面积地95,请说明理由(写出证明及计算过程).答案:剪法是:当AA 1=BB 1=CC 1=DD 1=31或32时, 四边形A 1B 1C 1D 1为正方形,且S=95.在正方形ABCD 中, AB=BC=CD=DA=1,∠A=∠B=∠C=∠D=90°. ∵AA 1=BB 1=CC 1=DD 1, ∴A 1B=B 1C=C 1D=D 1A.∴△D 1AA 1≌△A 1BB 1≌△B 1CC 1≌△C 1DD 1. ∴D 1A 1=A 1B 1=B 1C 1=C 1D 1,∴∠AD 1A 1=∠BA 1B 1=∠CB 1C 1=∠DC 1D 1. ∴∠AA 1D+∠BA 1B 1=90°,即∠D 1A 1B 1=90°. ∴四边形A 1B 1C 1D 1为正方形.设AA 1=x , 则AD 1=1-x.∵正方形A 1B 1C 1D 1地面积=95, ∴S △AA1D1=91 即21x(1-x)=91, 整理得9x 2-9x+2=0.解得x 1=31,x 2=32. 当AA 1=31时,AD 1=32,当AA 1=32时,AD 1=31.∴当AA 1=BB 1=CC 1=DD 1=31或32时, 四边形A 1B 1C 1D 1仍为正方形且面积是原面积地95.折叠问题专题研究上虞市滨江中学 潘建德一、教学目标:1、理解折叠问题地本质2、了解折叠问题解题策略,学会应用这些策略解决折叠问题3、渗透方程思想及中考复习以“本”为本地导向 二、教学重点:通过动手操作、应用轴对称性解决折叠问题 三、教学难点:折叠型综合题地分析 四、教学过程:1、引入:出示08绍兴8题:将一张纸第一次翻折,折痕为AB (如图1),第二次翻折,折痕为PQ(如图2),第三次翻折使PA 与PQ 重合,折痕为PC (如图3),第四次翻折使PB 与PA 重合,折痕为PD (如图4).此时,如果将纸复原到图1地形状,则CPD ∠地大小是( )A .120 B .90 C .60 D .45此题凸显地主题是图形地折叠,折叠问题在近几年地中考中越来越常见,据统计,在08年我省11个地区地中考卷中有7个地区都出现了折叠型考题,其中有5个地区中考卷地压轴题是折叠型问题,包括绍兴地区,折叠问题已成为中考地热门问题之一.点出课题.2、解题策略(一)——重过程“折”(1)如何迅速且准确地解决08绍兴卷第8题?(学生:动手折一折)学生动手操作,后教师归纳:题型一:考察空间想象能力与动手操作能力地实践操作题.解题策略:重过程——“折”.(2)学生进一步尝试.题2:(2008山东东营)将一正方形纸片按下列顺序折叠,然A.B.C.D.AB CDFE 后将最后折叠地纸片沿虚线剪去上方地小三角形.将纸片展开,得到地图形是()3、解题策略(二)——重本质“叠”(1)本质探究:题3:如图,长方形ABCD沿AE折叠,使D落在边BC上地F点处,如果∠BAF=30°,AD=2,则∠DAE=___,EF=_______.学生解决后讲解方法,教师:显然,折叠问题不能只靠动手操作来解决,我们必须透过现象看本质.那么折叠地本质是什么呢?学生讨论后教师归纳:折叠问题地实质是图形地轴对称变换,所以在解决折叠问题时可以充分运用轴对称地思想和轴对称地性质.根据轴对称地性质可以得到:(1)轴对称是全等变换:折叠重合部分一定全等(有边、角地相等);(2)点地轴对称性:互相重合两点(对称点)之间地连线必被折痕(对称轴)垂直平分(有Rt△,可应用勾股定理得方程).(2)初步应用:题4:08丽水8:如图,在三角形ABC中,AB>AC,D、E分别是AB、AC上地点,△ADE沿线段DE翻折,使点A落在边BC上,记为A'.若四边形ADA E'是菱形,则下列说法正确地是()A.DE是△ABC地中位线B.AA'是BC边上地中线C.AA'是BC边上地高D.AA'是△ABC地角平分线分析:此题虽有多种说明方法,即可应用折叠地全等性得到,也可根据折叠地点轴对称性得到.(3)题5:09绍兴市属期末23.(本题满分12分)课堂上,老师出示了以下问题,小明、小聪分别在黑板上进行了板演,请你也解答这个问题:在一张长方形ABCD纸片中,AD=25cm, AB=20cm.现将这张纸片按如下列图示方式折叠,分别求折痕地长.(1) 如图1, 折痕为AE;(2) 如图2, P,Q分别为AB,CD地中点,折痕为AE;(3) 如图3, 折痕为EF.ACDEA'(第8题)分析:题(1)题(2)主要应用折叠地全等性,题(3)连结对称点地连线BD ,根据折叠中点地轴对称性得EF 是BD 地中垂线,BO=4125,同时根据矩形地中心对 称性知,EF=2E0,在Rt △CDE 中,根据勾股定理可解得DE=241,根据折叠全等性得BE=DE=241,在Rt △BOE 中根据勾股定理得EO=412,故EF=414.由此题得心得:在解决折叠类计算题时,根据Rt △地勾股定理应用方程思想是常用方法. 题后说明:此题(2)是课本习题原题,(1)、(3)都根据课本原题改变而成.根据课本原题改变成中考题,是中考卷出题地一个新地方向,所以我们在中考复习中仍应以“本”为本,不断对课本习题进行探索和挖掘.(4)题6:08绍兴24题(2)(3)(简述):将一矩形纸片OABC 放在平面直角坐标系中,(00)O ,,(60)A ,,(03)C ,.6OP t =-,23OQ t =+. (1)当1t =时,如图1,将OPQ △沿PQ 翻折,点O 恰好落在CB 边上地点D 处,求点D地坐标;(2)连结AC ,将OPQ △沿PQ 翻折,得到EPQ △,如图2.问:PE 与AC 能否垂直?此题(1)让学生自己解决,教师适当点拨.题(2)根据情况可留作课后解决,教师点透解题地着眼点.4、反思小结:折叠问题题型多样,变化灵活,从考察学生空间想象能力与动手操作能力地实践操作题,到直接运用折叠相关性质地说理计算题,发展到基于折叠操作地综合题,甚至是压轴题.其中“折”是过程,“叠”是结果.折叠问题地实质是图形地轴对称变换,所以在解决有关地折叠问题时可以充分运用轴对称地思想和轴对称地性质.借助辅助线构造直角三角形,结合相似形、锐角三角函数等知识来解决有关折叠问题,可以使得解题思路更加清晰,解题步骤更加简洁.图1 (第24题图)初中几何综合复习(讲稿)—矩形折叠问题同学们好,今天我和大家一起研究平面图形地折叠问题.首先,在最近几年地中考中题折叠问题中频频出现,这对于我们识别和理解几何图形地能力、空间思维能力和综合解决问题地能力都提出了比以往更高地要求.希望通过今天地讨论,使同学们对折叠问题中有关地几何图形之间地位置关系和数量关系有进一步认识;在问题分析和解决地过程中巩固头脑中已有地有关几何图形地性质以及解决有关问题地方法;并在观察图形和探索解决问题地方法地过程中提高分析问题和解决问题地能力.那么,什么是折叠问题呢?这个问题应分两个方面,首先什么是折叠,其次是和折叠有关地问题.下面我们将对它们分别进行讨论一. 折叠地意义1.折叠,就是将图形地一部分沿着一条直线翻折180º,使它与另一部分在这条直线地同旁,与其重叠或不重叠;显然,“折”是过程,“叠”是结果.如图(1)是线段AB沿直线l折叠后地图形,其中OB'是OB在折叠前地位置;图(2)是平行四边形ABCD沿着对角线AC折叠后地图形,△ABC是△AB'C在折叠前地位置,它们地重叠部分是三角形;(2)图形在折叠前和折叠后翻折部分地形状、大小不变,是全等形如图(1)中OB'=OB;如图(2),△AB'C≌△ABC;(3) 图形地翻折部分在折叠前和折叠后地位置关于折痕成轴对称如图(1)OB'和OB关于直线l成轴对称;如图(2)△AB'C和△ABC关于直线AC成轴对称.二.和折叠有关地问题图形经过折叠,其翻折地部分折叠前地图形组合成新地图形,新地图形中有关地线段和角地位置、数量都有哪些具体地关系呢?这就是我们今天要重点讨论地问题.下面,我们以矩形地折叠为例,一同来探讨这个问题.问题1:将宽度为a地长方形纸片折叠成如图所示地形状,观察图中被覆盖地部分△A'EF.(a)△A'EF是什么三角形?结论:三角形AE'F是等腰三角形证明:方法一,∵图形在折叠前和折叠后是全等地,∴∠1= ∠2,又∵矩形地对边是平行地∴∠1=∠3,∴∠2=∠3,∴A'E=A'F三角形AE'F是等腰三角形方法二:∵图形在折叠前和折叠后地形状、大小不变,只是位置不同∴表示矩形宽度地线段EP和FQ相等,即∆A'EF地边A'E和A'F上地高相等,∴A'E=A'F三角形AE'F是等腰三角形(b)改变折叠地角度α地大小,三角形A'EF地面积是否会改变?为什么?答:不会改变.分析:α地改变影响了A'E地长度,但却不能改变边A'E上地高,三角形A'EF地面积会随着α地确定而确定.例一:在上面地图中,标出点A'在折叠前对应地位置A,四边形A'EAF是什么四边形?分析:(1)由前面地分析可知A'与A'在折叠前地位置A关于折痕EF成轴对称,所以作A'关于EF地对称点即可找到点A(过点A'作A'A⊥ EF交矩形地边于点A). 同学们还可以动手折叠一下,用作记号地方法找到点A.(2)四边形AEA'F是菱形证法一:∵ A是A'在折叠前对应地位置,∴A和A'关于直线EF轴对称,∴AA'⊥EF,且AO=A'O,又∵AE∥A'F,∴EO∶OF=AO∶OA',∴EO=OF∴四边形AEA'F是菱形证法二:A是A'在折叠前对应地位置,∴∆AEF≌∆A'EF,A'E=A'E,AF=AF,又∵∆AEF是等腰三角形(已证),A'E=A'F,∴A E=AF=A'E=A'F,∴四边形AEA'F是菱形.例2.在上题地图中,若翻折地角度α=30°,a=2,求图中被覆盖地部分△A'EF.地面积..分析:图中被覆盖地部分△A'EF是等腰三角形,其腰上地高就是原矩形地宽度2,所以,本题地解题关键就是要求出腰A'F 或A'E地长.答:S四边形AEA'F=2S△A'EF=(8/3)√3(解答过程略)练一练:当α地大小分别45°、60°时,图中被覆盖地部分△A'EF.地面积是多少?例题3. 如图:将矩形ABCD对折,折痕为MN,再沿AE折叠,把B点叠在MN 上,(如图中1地点P),若AB=√3,则折痕AE地长为多少?分析:折痕AE为直角三角形ABE地斜边,故解决本题地关键是求PE(或BE)地长.解法一:由折叠地意义可知,AP⊥EP,延长EP交AD于F, 则FE=FA(在问题一中已证)∵ M、N分别是矩形地边AB和CD地中点,∴MN∥AD∥BC且EP∶PF=BN∶NA=1∶1,又∠APE= ∠D=90°, ∴AE=AF∴AE=AF=EF,∴ ∠1= ∠2=30°,∠1=30°∴AE=2.∵ M、N分别是矩形地边AB和CD地中点,∴MN∥AD ∥BC且AN是AP地一半∴ MN⊥AN∴AE=AF又FE=FA(问题1地结论)∴AE=AF=EF, ∴ ∠1=∠2=30°,∠1=30°∴AE=2.由BC∥MN∥DA且M、N分别为CD和AB地中点可得EP=PF,EO=AO∴PO=AF,又PO=AE,∴AE=AF∴AE=AF=EF,∠EAF=60°(其余同上)例题4.在例3中,若M、N分别为CD、AB地三等分点(如图),AB=√5,其他条件不变,折痕AE地长为多少?分析:本题与上一题略有不同,MN由原来地二等分线变为三等分线,其他条件不变.所以本题地解题关键还是求出EB(或EP)地长解:延长EP交AD于F, 则FE=FA(已证)∵ M、N分别是矩形地边AB和CD地三等分点∴MN∥AD∥BC且EP∶PF=BN∶NA=1∶2,设EP=x, 则PF=2x, AF=EF=3x,在直角三角形APF中有AP²+PF²=AF²∴5+(2x)²=(3x)²,∴x=1, ∴AE²=1+5=6,∴AE=√6例4 如图3,有一张边长为3地正方形纸片(ABCD),将其对折,折痕为MN,再将点B折至折痕MN上,落在P点地位置,折痕为AE.(1)求MP地长;(2)求以PE为边长地正方形地面积.分析:将本题与例题2比较,不难看出它们地共同之处,显然,解决本题地关键是求PE和PN地长解法一:延长EP交AD地延长线于F, 则FE=FA(已证)M、N分别是矩形地边AB和CD地中点,∴ MN∥AD ∥B C且AN是AP地一半∴MN⊥AN∴AE=AF∴AE=AF=EF, ∴ ∠1=∠2=30°,∠1=30°∴PN=(3/2)√3,(1)∴MP=1-PN=3-(3/2)√3,又AP=3,∴EP=√3,(2)∴以EP为边长地正方形地面积为3.其他解法请同学们思考.例5.如图,将矩形ABCD折叠,使C点落在边AB上,(如图中地M点),若AB=10,BC=6,求四边形CNMD地面积分析:本题与上一题区别在于点C折叠后落在矩形地边AB上,由折叠地意义可以知道,ΔACN和ΔAMN是全等地,所以,求四边形CNMD地面积地关键就是求ΔDCN或ΔDMN地面积,所以本题地解题关键还是求出NC(或BN)地长.解:在直角三角形ADM中,AD=6,DM=DC=10,由勾股定理可以求得AM=8.BM=10-8=2. 设NC=x,则MN=x,BN=6-x,在Rt△BMN中,MN2=BN2+BM2∴x2=(6-x)2+4∴x=10/3S四边形CNMD =2S△DCN=(10/3)*10=100/3例6.将长为8,宽为6地矩形ABCD折叠,使B、D重合,(1)求折痕EF地长.(2)求三角形DEF地面积分析:由矩形折叠地意义可知,EF垂直平分BD(O为BD地中点由AB//DC可得EO:FO=BO:DO=1:1 ∴O为EF地中点,所以可设法先求出EO地长,或直接求EF地长,进而求三角形DEF面积.解(法一):∵D、B关于EF成轴对称∴EF垂直平分DB,又DC⊥CB,∴△DOE∽△DCB在Rt△DCB中,由勾股定理可得BD=10又AB∥DC∴EO:OF=DO:OB∴DO=5(1)由△DOE∽△DCB得DO:DC=DE:BC∴EO:6=5:8∴EO=15/4∴EF=15/2=(1/2)EF•DO=(1/2)×(15/2)×5=75/4(2)S△DEF解(法二):(1)过C作CP∥EF,交AB于P∵EF⊥DB∴CP⊥DB易得△CBP∽△DCB∴CP:BD=CB:DC∴CP=10*6/28=15/2∴EF=15/2=(1/2)EF•DO=(1/2)×(15/2)×5=(2)S△DEF75/4同学们,图形折叠问题中题型地变化比较多,但是经过研究之后不难发现其中地规律,从今天我们对矩形折叠情况地讨论中可以得到以下几点经验:1.图形地翻折部分在折叠前和折叠后地形状、大小不变,是全等形;2图形地翻折部分在折叠前和折叠后地位置关于折痕成轴对称;3.将长方形纸片折叠成如图所示地形状,图中重叠地部分△AE'F是等腰三角形;4.解决折叠问题时,要抓住图形之间最本质地位置关系,从而进一步发现其中地数量关系;5.充分挖掘图形地几何性质,将其中地基本地数量关系,用方程地形式表达出来,并迅速求解,这是解题时常用地方法之一.今天地讨论就到这里,最后祝同学们在中考中取得好地成绩.中考专题复习——折叠问题动手折一折,并思考:(1)用一张矩形地纸,通过折叠,使较短地边AB 落在较长地边AD 上,分析重叠部分展开后地形状.(2)将一张正方形纸,通过两次对折,成为一个正方形,再折叠一次,分析折痕所围成地图形.题组一:(1)如图(1),点E 是矩形ABCD 地边CD 上地点,沿着AE 折叠矩形ABCD ,使D 落在BC 边上地F 点处,如果∠BAF =60o ,则∠DEA =____________.(2)如图(2),已知:点E 是正方形ABCD 地BC 边上地点,现将△DCE 沿折痕DE 向上翻折,使DC 落在对角线DB 上,则EB ∶CE =_________.(3)如图(3),AD 是△ABC 地中线,∠ADC =45o ,把△ADC 沿AD 对折,点C 落在C ´地位置,若BC =2,则BC ´=_________. 图(1)图(2)题组二: 图(3)(4)如图(4),已知矩形ABCD 中,AD =8,AB =4.沿着对角线BD 将矩形ABCD 折叠,使点C 落在C ´处,BC ´交AD 于E .求出未知地线段. A BCDEABCDA BCD(5)如图(5),矩形ABCD 地长、宽分别为5和3,将顶点C 折过来,使它落在AB 上地C ´点(DE 为折痕),那么阴影部分地面积是________.图(4) 图(5)题组三:(6)如图(6),P 是以AB 为直径地半圆上地一点,PA =4,AB =10,将半圆折叠使弦PA 正好落在AB上,则折痕AC 地长为___________.图(6)(7)如图(7),把正三角形ABC 地外接圆对折,使点A 落在弧BC 地中点A ´,若BC =6,则折痕在△ABC 内地部分DE 地长为_____.提高题:(1)一张宽为3、长为4地矩形纸片ABCD ,先沿对角线BD 对折,点C 落在C ´地位置,BC ´交AD 于G (如图8).再折叠一次,使点D 与点A 重合,得折痕EN ,EN 交AD 于点M (如图9),则ME 地长为__________.C ´GABCDA BCDABCPP ´B A DA DC ´图(9)图(8)(2)如图(10),在矩形ABCD 中,AB =2,AD =1,如图将矩形折叠使B 点落在AD 上,设为B ’,顶点C 到C ’点,B ’C ’交DF 于G .(1) 求证:△AB ’E ∽△C ’GF ;(2)若AB ’=x ,S B ’EFC ’=y ,求y 关于x 之间地函数解析式; (3)当B ’在何处时,y 地值最小,y 地最小值是多少?图(10)折叠问题折叠对象有三角形、矩形、正方形、梯形等;考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等;解题时,灵活运用轴对称性质和背景图形性质.轴对称性质-----折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上. 压轴题是由一道道小题综合而成,常常伴有折叠;解压轴题时,要学会将大题分解成一道道小题;那么多作折叠地选择题填空题,很有必要.1、(2009年浙江省绍兴市)如图,D E ,分别为ABC △地AC ,BC 边地中点,将此三角形沿DE 折叠,使点C 落在AB 边上地点P 处.若48CDE ∠=°,则APD ∠等于( )A .42°B .48°C .52°D .58°C ´A BC D EFB ´G图(7)(第18题图)AC B2、(2009湖北省荆门市)如图,Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上A ′处,折痕为CD ,则A DB '∠=()A .40° B .30°C .20°D .10°3、(2009年日照市)将三角形纸片(△ABC )按如图所示地方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .已知AB =AC =3,BC =4,若以点B ′,F ,C 为顶点地三角形与△ABC 相似,那么BF 地长度是.4、(2009年衢州)在△ABC 中,AB =12,AC =10,BC =9,AD 是BC 边上地高.将△ABC 按如图所示地方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 地周长为A .9.5B .10.5C .11D .15.55、(2009泰安)如图,在Rt △ABC 中, ∠ACB=90°,∠A <∠B ,沿△ABC 地中线CM 将△CMA 折叠,使点A 落在点D 处,若CD 恰好与MB 垂直,则tanA 地值为.6、(2009年上海市)在Rt ABC △中,903BAC AB M ∠==°,,为边BC 上地点,联结AM(如图3所示).如果将ABM △沿直线AM 翻折后,点B 恰好落在边AC 地中点处,那么点M 到AC 地距离是.第2题图 A 'BD AC7、(2009宁夏)如图:在Rt ABC △中,90ACB ∠=°,CD 是AB 边上地中线,将ADC △沿AC 边所在地直线折叠,使点D 落在点E 处,得四边形ABCE . 求证:EC AB ∥.8、(2009年清远)如图,已知一个三角形纸片ABC ,BC 边地长为8,BC 边上地高为6,B ∠和C ∠都为锐角,M 为AB 一动点(点M 与点A B 、不重合),过点M 作MN BC ∥,交AC 于点N ,在AMN △中,设MN 地长为x ,MN 上地高为h .(1)请你用含x 地代数式表示h .(2)将AMN △沿MN 折叠,使AMN △落在四边形BCNM 所在平面,设点A 落在平面地点为1A ,1A MN △与四边形BCNM 重叠部分地面积为y ,当x 为何值时,y 最大,最大值为多少?A图3BM C BC NM AE C B A D。
北师大版数学七升八暑假作业专题复习提升专题七 折叠问题(含答案)

北师大版数学七升八暑假作业专题复习提升-专题七折叠问题折叠是一种对称变换,属于轴对称,对称轴所在直线是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解决这些问题的基本方法是精确找出折叠前后相等的边与角,以及结合图形的性质把边角的关系联系起来,同时结合方程思想、数形结合思想等数学思想进行解题.类型一平行线中的折叠问题1.如图,将一个对边平行的纸条沿AB折叠一下,若∠1=130∘,则∠2的大小为.2. 如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处.若α+β=119∘,则∠EMF的度数为()A. 57∘B. 58∘C. 59∘D. 60∘3. 将一张长方形纸条ABCD按如图所示折叠,若折叠角∠FEC=64∘,则∠1的度数为()第3题图A. 52∘B. 62∘C. 64∘D. 42∘4. 如图,将矩形ABCD沿对角线BD折叠,使点C落在点F处,BF交AD于点E.若∠BDC=62∘,则∠FDE的度数为()第4题图A. 28∘B. 62∘C. 34∘D. 24∘5.如图1,已知长方形纸带ABCD,将纸带沿EF折叠后,点C,D分别落在H,G的位置,再沿BC折叠成图2.若∠DEF=72∘,则∠GMN=∘.6. 如图1是长方形纸带,∠CFE=55∘,将纸带沿EF折叠成图2,再沿GE折叠成图3,则图3中∠DEF的度数是.7. 如图,四边形ABCD为一长方形纸片,AD//BC,∠DAB=∠ABC=∠C=∠ADC =90∘,E为BC上一点,将纸片沿AE折叠,B点落在长方形外的F点,连接BD.若∠CBD=20∘,且AF//BD,求∠BAE的度数.类型二三角形中的折叠问题8. 如图,在△ABC中,M,N分别是边AB,BC上的点,将△BMN沿MN折叠,使点B落在点B′处.若∠B=35∘,∠BNM=28∘,则∠AMB′的度数为()第8题图A. 30∘B. 37∘C. 54∘D. 63∘9.如图,在Rt△ABC中,∠BAC=90∘,∠C=40∘,点D为BC上一点,把△ABD 沿AD折叠到△AB′D,点B的对应点B′恰好落在边BC上,则∠CAB′的度数为()第9题图A. 10∘B. 20∘C. 30∘D. 40∘10. 如图1,已知三角形纸片ABC,AB=AC=6,BC=4,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,则△BCD的周长为.11. 将纸片△ABC沿DE折叠使点A落在点A′处.若∠1=80∘,∠2=28∘,则∠A的度数为.12. 定义:如果一个三角形的两个内角α与β满足2α+β=90∘,那么我们称这样的三角形为“准直角三角形”.如图,将三角形纸片ABC沿着EF折叠,使得点A落在BC边上的点D处.已知∠A=∠B=35∘,设∠BED=x∘,当△BED和△CDF同时成为“准直角三角形”时,求x的值.13. 探究:(1)如图1,∠1+∠2与∠B+∠C有什么关系?为什么?当∠A=40∘时,∠B+∠C+∠1+∠2=∘.(2)把图1中△ABC沿DE折叠得到△A′DE,如图2.填空:∠1+∠2∠B+∠C;(选填“>”“<”或“=”)如果∠A=30∘,则∠A′DB+∠A′EC=;猜想∠A′DB,∠A′EC与∠A的关系为,并说明理由.(3)如图3,把△ABC沿着DE折叠得到△A′DE,A′D与AC相交于点F,则∠A′DB,∠A′EC与∠A的关系为,并说明理由.答案专题七折叠问题类型一平行线中的折叠问题1.115∘2.B3.A4.C5.726.15∘7.解:∵AD//BC,∠CBD=20∘,∴∠ADB=∠CBD=20∘.∵AF//BD,∴∠ADB=∠FAD.∵∠DAB=90∘,∴∠BAF=∠DAB+∠FAD=110∘.∵纸片沿AE折叠,∴∠BAE=∠FAE,∴∠BAE=1∠BAF=55∘.2类型二三角形中的折叠问题8.C9.A10.1011.26∘12.20【解析】∵将纸片沿着EF折叠,使得点A落在BC边上的点D处,∠A=∠B=35∘,∴∠EDF=∠A=35∘,当△BED为“准直角三角形”时,2∠DEB+∠B=90∘或∠DEB+2∠B=90∘,∴2x+35=90或x+2×35=90,∴x=27.5或x=20.①当x=27.5时,即∠DEB=27.5∘,∴∠CDE=∠DEB+∠B=27.5∘+35∘=62.5∘,∴∠CDF=∠CDE−∠EDF=62.5∘−35∘=27.5∘,∴∠CFD=180∘−∠C−∠CDF=180∘−110−27.5∘=42.5∘,此时2∠CDF+∠CFD=2×27.5∘+42.5∘=97.5∘,2∠CFD+∠CDF=2×42.5∘+27.5∘=112.5∘,∴△CDF不是“准直角三角形”;②当x=20时,即∠DEB=20∘,∴∠CDE=∠DEB+∠B=20∘+35∘=55∘,∴∠CDF=∠CDE−∠EDF=55∘−35∘=20∘,∴∠CFD=180∘−∠C−∠CDF=180∘−110∘−20∘=50∘,此时2∠CDF+∠CFD=90∘,∴△CDF是“准直角三角形”;综上所述,能使△BED和△CDF同时成为“准直角三角形”的x值为20.13.(1)280【解析】∠1+∠2=∠B+∠C∵∠A+∠1+∠2=180∘,∠A+∠B+∠C=180∘,∴∠1+∠2=∠B+∠C.当∠A=40∘时,∠B+∠C=180∘−40∘=140∘,∠1+∠2=180∘−40∘=140∘,∴∠B+∠C+∠1+∠2=280∘.故答案为: 280.(2)=;60∘;∠A′DB+∠A′EC=2∠A;解:由(1)得∠ADE+∠AED=∠B+∠C.由翻折变换的性质可知,∠1+∠2=∠ADE+∠AED,∴∠1+∠2=∠B+∠C.由翻折变换的性质可知,∠ADE=∠A′DE,∠AED=∠A′ED,∠ADE+∠AED=180∘−∠A,∠ADA′+∠AEA′=360∘−2∠A,∠A′DB+∠A′EC=360∘−(360∘−2∠A)=2∠A.当∠A=30∘时,∠A′DB+∠A′EC=60∘.故答案为:=;60∘;∠A′DB+∠A′EC=2∠A.(3)∠A′DB=∠A′EC+2∠A;∵∠A′DB=∠A+∠AFD,∠AFD=∠A′+∠A′EC,∴∠A′DB=∠A′EC+2∠A.故答案为:∠A′DB=∠A′EC+2∠A.。
中考数学复习《折叠问题》

EF 6 72 ∴S△BEF=EG· S△BEG=10×24= 5
14.如图,已知在矩形 ABCD 中,点 E 在边 BC 上,BE=2CE,将矩形 沿着过点 E 的直线翻折后,点 C,D 分别落在边 BC 下方的点 C′,D′处,且 点 C′,D′,B 在同一条直线上,折痕与边 AD 交于点 F,D′F 与 BE 交于点 G.设 AB=t,那么△EFG 的周长为 2 3t .(用含 t 的代数式表示)
13.如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE
折叠到DF,延长EF交AB于点G,连结DG,求△BEF的面积. 【解析】由折叠和正方形的性质,在Rt△BEG中,由勾股定理求出AG后再 求△BGE的面积,最后由△BEF与△BGE的面积关系求△BEF的面积.
解:DF=DC=DA,∠DFE=∠C=90°,∴∠DFG=∠A=90°. 又∵DG=DG,∴△ADG≌△FDG(HL).∵正方形 ABCD 的边长为 12, BE=EC,∴BE=EC=EF=6.设 AG=FG=x,则 EG=x+6, BG=12-x,在 Rt△BEG 中,由勾股定理,得 EG2=BE2+BG2, 1 1 即(x+6) =6 +(12-x) ,解得 x=4.∵S△BEG=2· BE· BG=2×6×8=24,
(1)求证:△DEC≌△EDA;
(2)求DF的值; (3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶
点Q落在线段AE上,顶点M,N落在线段AC上,当线段PE的长为何值时,
矩形PQMN的面积最大?并求出其最大值.
解:(1)由矩形的性质可知△ADC≌△CEA,∴AD=CE,DC=EA, ∠ACD=∠CAE.在△DEC 与△EDA 中, CE=AD, ∵DE=ED, ∴△DEC≌△EDA(SSS) DC=EA,
2023学年二轮复习解答题专题四十三:图形折叠引起的综合探究(原卷版)

2023学年二轮复习解答题专题四十三:图形折叠引起的综合探究典例分析例. (2022河南中考)综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.(1)操作判断操作一:对折矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,把纸片展平;操作二:在AD 上选一点P ,沿BP 折叠,使点A 落在矩形内部点M 处,把纸片展平,连接PM ,BM .根据以上操作,当点M 在EF 上时,写出图1中一个30°的角:______.(2)迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下:将正方形纸片ABCD 按照(1)中的方式操作,并延长PM 交CD 于点Q ,连接BQ .①如图2,当点M 在EF 上时,∠MBQ =______°,∠CBQ =______°;②改变点P 在AD 上的位置(点P 不与点A ,D 重合),如图3,判断∠MBQ 与∠CBQ 的数量关系,并说明理由.(3)拓展应用在(2)探究中,已知正方形纸片ABCD 的边长为8cm ,当FQ =1cm 时,直接写出AP 的长.专题过关1. (2022天津中考) 将一个矩形纸片OABC 放置在平面直角坐标系中,点(0,0)O ,点(3,0)A ,点(0,6)C ,点P 在边OC 上(点P 不与点O ,C 重合),折叠该纸片,使折痕所的在的直线经过点P ,并与x 轴的正半轴相交于点Q ,且30OPQ Ð=°,点O 的对应点O ¢落在第一象限.设OQ t =.(1)如图①,当1t =时,求O QA Т的大小和点O ¢的坐标;(2)如图②,若折叠后重合部分为四边形,,O Q O P ¢¢分别与边AB 相交于点E ,F ,试用含有t 的式子表示O E ¢的长,并直接写出t 的取值范围;(3)若折叠后重合部分的面积为则t 的值可以是___________(请直接写出两个不同的值即可).2. (2022绍兴中考)如图,在矩形ABCD 中,6AB =,8BC =,动点E 从点A 出发,沿边AD ,DC 向点C 运动,A ,D 关于直线BE 的对称点分别为M ,N ,连结MN .(1)如图,当E 在边AD 上且2DE =时,求AEM Ð的度数.(2)当N 在BC 延长线上时,求DE 的长,并判断直线MN 与直线BD 的位置关系,说明理由.(3)当直线MN 恰好经过点C 时,求DE 的长.3. (2022深圳中考)(1)【探究发现】如图①所示,在正方形ABCD 中,E 为AD 边上一点,将AEB △沿BE 翻折到BEF V 处,延长EF 交CD 边于G 点.求证:BFG BCG△≌△(2)【类比迁移】如图②,在矩形ABCD 中,E 为AD 边上一点,且8,6,AD AB ==将AEB △沿BE 翻折到BEF V 处,延长EF 交BC 边于点,G 延长BF 交CD 边于点,H 且,FH CH =求AE 的长.(3)【拓展应用】如图③,在菱形ABCD 中,E 为CD 边上三等分点,60,D Ð=°将ADE V 沿AE 翻折得到AFE △,直线EF 交BC 于点,P 求CP 的长.4. (2022贵阳中考)小红根据学习轴对称的经验,对线段之间、角之间的关系进行了拓展探究.如图,在ABCD □中,AN 为BC 边上的高,AD m AN=,点M 在AD 边上,且BA BM =,点E 是线段AM 上任意一点,连接BE ,将ABE △沿BE 翻折得FBE V.的(1)问题解决:如图①,当60BAD Ð=°,将ABE △沿BE 翻折后,使点F 与点M 重合,则AM AN =______;(2)问题探究:如图②,当45BAD Ð=°,将ABE △沿BE 翻折后,使EF BM ∥,求ABE Ð的度数,并求出此时m 的最小值;(3)拓展延伸:当30BAD Ð=°,将ABE △沿BE 翻折后,若EF AD ^,且AE MD =,根据题意在备用图中画出图形,并求出m 的值.5. (2022长春中考)【探索发现】在一次折纸活动中,小亮同学选用了常见的A 4纸,如图①,矩形ABCD 为它的示意图.他查找了A 4纸的相关资料,根据资料显示得出图①中AD =.他先将A 4纸沿过点A 的直线折叠,使点B 落在AD 上,点B 的对应点为点E ,折痕为AF ;再沿过点F 的直线折叠,使点C 落在EF 上,点C 的对应点为点H ,折痕为FG ;然后连结AG ,沿AG 所在的直线再次折叠,发现点D 与点F 重合,进而猜想ADG AFG △≌△.【问题解决】(1)小亮对上面ADG AFG △≌△的猜想进行了证明,下面是部分证明过程:证明:四边形ABCD 是矩形,∴90BAD B C D Ð=Ð=Ð=Ð=°.由折叠可知,1452BAF BAD Ð=Ð=°,BFA EFA Ð=Ð.∴45EFA BFA Ð=Ð=°.∴AF AD ==.请你补全余下的证明过程.【结论应用】(2)DAG Ð的度数为________度,FG AF 的值为_________;(3)在图①的条件下,点P 在线段AF 上,且12AP AB =,点Q 在线段AG 上,连结FQ 、PQ ,如图②,设AB a =,则FQ PQ +的最小值为_________.(用含a 的代数式表示)6. (2022运城二模)将矩形ABCD 对折,使AD 与BC 重合,得到折痕EF ,展开后再一次折叠,使点A 落在EF 上的点A ¢处,并使得折痕经过点B ,得到折痕BG ,连接AA ¢,如图1,问题解决:(1)试判断图1中ABA ¢△是什么特殊的三角形?并说明理由;(2)如图2,在图1的基础上,AA ¢与BG 相交于点N ,点P 是BN 的中点,连接AP 并延长交BA ¢于点Q ,求BQ BA ¢的值.7. (2022郑州一模)综合与实践,问题情境:数学活动课上,老师出示了一个问题:如图①,在ABCD Y 中,BE AD ^,垂足为E ,F 为CD 的中点,连接EF ,BF ,试猜想EF 与BF 的数量关系,并加以证明;独立思考:(1)请解答老师提出的问题;实践探究:(2)希望小组受此问题的启发,将ABCD Y 沿着BF (F 为CD 的中点)所在直线折叠,如图②,点C 的对应点为'C ,连接'DC 并延长交AB 于点G ,请判断AG 与BG 的数量关系,并加以证明;问题解决:(3)智慧小组突发奇想,将ABCD Y 沿过点B 的直线折叠,如图③,点A 的对应点为'A ,使'A B CD ^于点H ,折痕交AD 于点M ,连接'A M ,交CD 于点N .该小组提出一个问题:若此ABCD Y 的面积为20,边长5AB =,BC =,求图中阴影部分(四边形BHNM )的面积.请你思考此问题,直接写出结果.8. (2022许昌一模)问题背景折纸是一种将纸张折成各种不同形状的艺术活动,折纸大约起源于公元1世纪或者2世纪时的中国,6世纪时传入日本,再经由日本传到全世界,折纸与自然科学结合在一起,不仅成为建筑学院的教具,还发展出了折纸几何学,成为现代几何学的一个分支.今天折纸被应用于世界各地,其中比较著名的是日本筑波大学的芳贺和夫发现的折纸几何三定理,它已成为折纸几何学的基本定理.芳贺折纸第一定理的操作过程及内容如下:第一步:如图1,将正方形纸片ABCD 对折,使点A 与点D 重合,点B 与点C 重合.再将正方形ABCD 展开,得到折痕EF ;第二步:将正方形纸片的右下角向上翻折,使点C 与点E 重合,边BC 翻折至B E ¢的位置,得到折痕MN ,B E ¢与AB 交于点P .则点P 为AB 的三等分点,即:2:1AP PB =.问题解决如图1,若正方形ABCD 的边长是2.(1)CM 的长为______;(2)请通过计算AP 的长度,说明点P 是AB 的三等分点.类比探究(3)将长方形纸片()ABCD AB BC >按问题背景中的操作过程进行折叠,如图2,若折出的点P 也为AB 的三等分点,请直接写出AB AC 的值.9.(2022太原二模) 综合与实践:如图1,已知正方形纸片ABCD .实践操作第一步:如图1,将正方形纸片ABCD 沿AC ,BD 分别折叠.然后展平,得到折痕AC ,BD .折痕AC ,BD 相交于点O .第二步:如图2,将正方形ABCD 折叠,使点B 的对应点E 恰好落在AC 上,得到折痕AF ,AF 与BD 相交于点G ,然后展平,连接GE ,EF .问题解决(1)AGD Ð的度数是______;(2)如图2,请判断四边形BGEF 的形状,并说明理由;探索发现(3)如图3,若1AB =,将正方形ABCD 折叠,使点A 和点F 重合,折痕分别与AB ,DCMN的值.相交于点M,N.求2。
