中考数学轨迹问题精选
中考的数学轨迹问题集锦
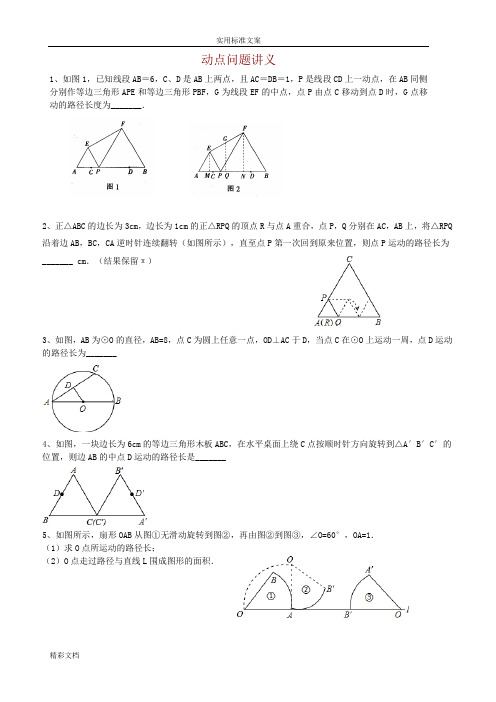
动点问题讲义1、如图1,已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_______.2、正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ 沿着边AB,BC,CA逆时针连续翻转(如图所示),直至点P第一次回到原来位置,则点P运动的路径长为_______ cm.(结果保留π)3、如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为_______4、如图,一块边长为6cm的等边三角形木板ABC,在水平桌面上绕C点按顺时针方向旋转到△A′B′C′的位置,则边AB的中点D运动的路径长是_______5、如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.(1)求O点所运动的路径长;(2)O点走过路径与直线L围成图形的面积.6、如图,OA ⊥OB ,垂足为O ,P 、Q 分别是射线OA 、OB 上两个动点,点C 是线段PQ 的中点,且PQ=4.则动点C 运动形成的路径长是______7、如图,半径为2cm ,圆心角为90°的扇形OAB 的弧AB 上有一运动的点P .从点P 向半径OA 引垂线PH 交OA 于点H .设△OPH 的内心为I ,当点P 在弧AB 上从点A 运动到点B 时,内心I 所经过的路径长为______ .8.如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止.连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG .(1)设AE =x 时,△EGF 的面积为y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (2)P是MG 的中点,请直接写出点P 运动路线的长.9、某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.问题思考:如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.问题拓展:(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.10、如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t ≥0).(1)直接用含t的代数式分别表示:QB=____ ,PD=____(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.11、在直角坐标系中,O是坐标原点,点A坐标为(0,-1),点C是x轴上一个动点。
中考数学轨迹问题集锦

合用标准文案动点问题讲义1、如图 1,已知线段AB = 6, C、 D 是 AB 上两点,且AC = DB = 1, P 是线段 CD 上一动点,在AB 同侧分别作等边三角形APE 和等边三角形PBF, G 为线段 EF 的中点,点P 由点 C 搬动到点D 时, G 点搬动的路径长度为_______.2 、正△ABC 的边长为3cm ,边长为1cm 的正△RPQ 的极点 R 与点 A 重合,点 P, Q 分别在 AC ,AB 上,将△RPQ 沿着边 AB ,BC,CA 逆时针连续翻转(以下列图),直至点P 第一次回到原来地址,则点P 运动的路径长为_______ cm.(结果保留π)3 、如图, AB 为⊙ O 的直径, AB=8 ,点 C 为圆上任意一点,OD ⊥ AC 于 D ,当点 C 在⊙ O 上运动一周,点 D 运动的路径长为 _______4 、如图,一块边长为6cm 的等边三角形木板ABC ,在水平桌面上绕 C 点按顺时针方向旋转到△ A ′B′C′的位置,则边AB 的中点 D 运动的路径长是_______5 、以下列图,扇形OAB 从图①无滑动旋转到图②,再由图②到图③,∠O=60 °,OA=1 .(1 )求 O 点所运动的路径长;(2 )O 点走过路径与直线 L 围成图形的面积.6 、如图, OA ⊥OB ,垂足为O , P、 Q 分别是射线OA 、 OB 上两个动点,点 C 是线段 PQ 的中点,且PQ=4 .则动点 C 运动形成的路径长是______7 、如图,半径为2cm ,圆心角为90 °的扇形 OAB 的弧 AB 上有一运动的点P.从点 P 向半径 OA 引垂线PH 交 OA 于点 H .设△OPH 的内心为I,当点 P 在弧 AB 上从点 A 运动到点 B 时,内心 I 所经过的路径长为______ .8 .如图,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点 B 停止.连接 EM 并延长交射线 CD 于点 F,过 M 作 EF 的垂线交射线BC 于点 G,连接 EG、 FG.( 1 )设AE=x时,△EGF的面积为y,求y关于x的函数关系式,并写出自变量x 的取值范围;( 2 )P是MG的中点,请直接写出点P 运动路线的长.FFAMA MD DEEP PBB C GC G9 、某数学兴趣小组对线段上的动点问题进行研究,已知AB=8 .问题思虑:如图 1,点 P 为线段 AB 上的一个动点,分别以AP 、BP 为边在同侧作正方形APDC 、 BPEF.(1)当点 P 运动时,这两个正方形的面积之和是定值吗?若是,央求出;若不是,央求出这两个正方形面积之和的最小值.(2)分别连接 AD 、 DF、 AF ,AF 交 DP 于点 K,当点 P 运动时,在△ APK 、△ADK 、△DFK 中,可否存在两个面积向来相等的三角形?请说明原由.问题拓展:(3 )如图 2,以 AB 为边作正方形ABCD ,动点 P、 Q 在正方形ABCD 的边上运动,且PQ=8 .若点 P 从点 A 出发,沿 A → B→ C→D 的线路,向点 D 运动,求点 P 从 A 到 D 的运动过程中, PQ 的中点 O 所经过的路径的长.(4)如图 3,在“问题思虑”中,若点M 、 N 是线段 AB 上的两点,且 AM=BN=1 ,点 G、H 分别是边CD 、EF 的中点,请直接写出点P 从 M 到 N 的运动过程中, GH 的中点 O 所经过的路径的长及OM+OB的最小值.10 、如图 1 ,在 Rt △ABC 中,∠C=90 °,AC=6 , BC=8 ,动点 P 从点 A 开始沿边AC 向点 C 以 1 个单位长度的速度运动,动点 Q 从点 C 开始沿边CB 向点 B 以每秒 2个单位长度的速度运动,过点P作PD∥BC,交AB 于点 D,连接 PQ 分别从点 A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为 t 秒( t ≥0).(1 )直接用含 t 的代数式分别表示: QB=____ ,PD=____(2 )可否存在 t 的值,使四边形 PDBQ 为菱形?若存在,求出 t 的值;若不存在,说明原由.并研究如何改变 Q 的速度(匀速运动),使四边形PDBQ 在某一时辰为菱形,求点Q 的速度;( 3 )如图 2 ,在整个运动过程中,求出线段PQ 中点 M 所经过的路径长.11 、在直角坐标系中,O 是坐标原点,点 A 坐标为( 0 , -1 ),点 C 是 x 轴上一个动点。
中考数学轨迹问题集锦

【中考数学综合7】1、如图1,已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_______.2、正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA逆时针连续翻转(如图所示),直至点P第一次回到原来位置,则点P运动的路径长为_______ cm.(结果保留π)3、如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为_______4、如图,一块边长为6cm的等边三角形木板ABC,在水平桌面上绕C点按顺时针方向旋转到△A′B′C′的位置,则边AB的中点D运动的路径长是_______5、如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.(1)求O点所运动的路径长;(2)O点走过路径与直线L围成图形的面积.6、如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是______7、如图,半径为2cm ,圆心角为90°的扇形OAB 的弧AB 上有一运动的点P .从点P 向半径OA 引垂线PH 交OA 于点H .设△OPH 的内心为I ,当点P 在弧AB 上从点A 运动到点B 时,内心I 所经过的路径长为______ .8.如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止.连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG .(1)设AE =x 时,△EGF 的面积为y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)P 是MG 的中点,请直接写出点P 运动路线的长.F D A M P E F D A M P E9、某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.问题思考:如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.问题拓展:(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.10、如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB 于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).(1)直接用含t的代数式分别表示:QB=____ ,PD=____(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.11、在直角坐标系中,O是坐标原点,点A坐标为(0,-1),点C是x轴上一个动点。
初中中考数学轨迹问题集锦.doc

动点问题讲义1 、如图 1 ,已知线段AB = 6 , C、 D 是 AB 上两点,且AC = DB = 1 , P 是线段 CD 上一动点,在AB 同侧分别作等边三角形APE 和等边三角形PBF, G 为线段 EF 的中点,点P 由点 C 移动到点 D 时, G 点移动的路径长度为_______.2 、正△ABC 的边长为3cm ,边长为1cm 的正△RPQ 的顶点 R 与点 A 重合,点 P, Q 分别在 AC ,AB 上,将△RPQ 沿着边 AB ,BC,CA 逆时针连续翻转(如图所示),直至点P 第一次回到原来位置,则点P 运动的路径长为_______ cm.(结果保留π)3 、如图, AB 为⊙ O 的直径, AB=8 ,点 C 为圆上任意一点,OD ⊥ AC 于 D ,当点 C 在⊙ O 上运动一周,点D 运动的路径长为 _______4 、如图,一块边长为6cm 的等边三角形木板ABC ,在水平桌面上绕 C 点按顺时针方向旋转到△ A ′B′C′的位置,则边AB 的中点 D 运动的路径长是_______5 、如图所示,扇形OAB 从图①无滑动旋转到图②,再由图②到图③,∠O=60 °,OA=1 .(1 )求 O 点所运动的路径长;(2 )O 点走过路径与直线 L 围成图形的面积.6 、如图, OA ⊥OB ,垂足为O , P、 Q 分别是射线OA 、 OB 上两个动点,点 C 是线段 PQ 的中点,且PQ=4 .则动点 C 运动形成的路径长是______7 、如图,半径为2cm ,圆心角为90 °的扇形 OAB 的弧 AB 上有一运动的点P.从点 P 向半径 OA 引垂线PH 交 OA 于点 H .设△OPH 的内心为I,当点 P 在弧 AB 上从点 A 运动到点 B 时,内心 I 所经过的路径长为______ .8 .如图,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点 B 停止.连接EM 并延长交射线CD于点,过M作EF的垂线交射线BC于点G,连结、.F EG FG( 1 )设AE=x时,△EGF的面积为y ,求 y 关于 x 的函数关系式,并写出自变量x 的取值范围;( 2 )P是MG的中点,请直接写出点P 运动路线的长.FFAM DA M DEEP PB C GB C G9 、某数学兴趣小组对线段上的动点问题进行探究,已知AB=8 .问题思考:如图 1,点 P 为线段 AB 上的一个动点,分别以AP 、BP 为边在同侧作正方形APDC 、 BPEF.(1)当点 P 运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.(2)分别连接 AD 、 DF、 AF ,AF 交 DP 于点 K,当点 P 运动时,在△ APK 、△ADK 、△DFK 中,是否存在两个面积始终相等的三角形?请说明理由.问题拓展:(3 )如图 2,以 AB 为边作正方形ABCD ,动点 P、 Q 在正方形ABCD 的边上运动,且PQ=8 .若点 P 从点A 出发,沿 A → B→ C→D 的线路,向点 D 运动,求点 P 从 A 到 D 的运动过程中, PQ 的中点 O 所经过的路径的长.(4)如图 3,在“问题思考”中,若点M 、 N 是线段 AB 上的两点,且 AM=BN=1 ,点 G、H 分别是边CD 、EF 的中点,请直接写出点P 从 M 到 N 的运动过程中, GH 的中点 O 所经过的路径的长及OM+OB的最小值.10 、如图 1 ,在 Rt △ABC 中,∠C=90 °,AC=6 , BC=8 ,动点 P 从点 A 开始沿边AC 向点 C 以 1 个单位长度的速度运动,动点 Q 从点 C 开始沿边CB 向点 B 以每秒 2个单位长度的速度运动,过点P作PD∥BC,交AB 于点 D,连接 PQ 分别从点 A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为 t 秒( t ≥0).(1 )直接用含 t 的代数式分别表示: QB=____ ,PD=____(2 )是否存在 t 的值,使四边形 PDBQ 为菱形?若存在,求出 t 的值;若不存在,说明理由.并探究如何改变 Q 的速度(匀速运动),使四边形PDBQ 在某一时刻为菱形,求点Q 的速度;( 3 )如图 2 ,在整个运动过程中,求出线段PQ 中点 M 所经过的路径长.11 、在直角坐标系中,O 是坐标原点,点 A 坐标为( 0 , -1 ),点 C 是 x 轴上一个动点。
中考数学压轴题轨迹问题

与路径有关的问题姓名1.如图,已知点A是第一象限内横坐标为2的一个定点,⊥x轴于点M,交直线﹣x于点N.若点P是线段上的一个动点,∠30°,⊥,则点P在线段上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径是.2.如图,E,F是正方形的边上两个动点,满足.连接交于点G,连接交于点H.若正方形的边长为2,则线段长度的最小值是.3.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A,B两点,与y 轴交于C,D两点,点E为⊙G上一动点,CF AE⊥于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为()A.32πB.33π C.34πD.36πyxGFOEDCBA5.如图,正方形的边长是2,M 是的中点,点E 从点A 出发,沿运动到点B 停止.连接并延长交射线于点F ,过M 作的垂线交射线于点G ,连结、.(1)设=x 时,△的面积为y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)P 是的中点,请直接写出点P 运动路线的长.6x上,=4,=2.点P 从点O A 匀速运动,当点P到达点A 时停止运动,设点P 运动的时间是t 秒.将线段的中点绕点P 按顺时针方向旋转90°得点D ,点D 随点P 的运动而运动,连接、.(1)请用含t 的代数式表示出点D 的坐标; (2)求t 为何值时,△的面积最大,最大为多少?(3)在点P 从O 向A 运动的过程中,△能否成为直角三角形?若能,求t 的值;若不能,请说明理由; (4)请直接写出随着点P 的运动,点D 运动路线的长.7.如图,直角坐标系中,已知点A(2,4),B(5,0),动点P从B点出发沿向终点O运动,动点Q从A点出发沿向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了x秒.(1)Q点的坐标为( , )(用含x的代数式表示);(2)当x为何值时,△是一个以为腰的等腰三角形?(3)记的中点为G.请你直接写出点G随点P,Q运动所经过的路线的长度.G G9.如图1,已知正方形的边长为2,顶点A、C分别在x、y轴的正半轴上,M是的中点.P(0,m)是线段上一个动点(点C除外),直线交的延长线于点D.(1)求点D的坐标(用含m的代数式表示);(2)当△是等腰三角形时,求m的值;(3)设过点P、M、B的抛物线与x轴的正半轴交于点E,过点O作直线图1图2备用图1备用图2的垂线,垂足为H (如图2).当点P 从原点O 向点C 运动时,点H 也随之运动.请直接写出点H 所经过的路径长(不写解答过程).10、问题探究:(1)请在图①的正方形内,画出使∠90°的一个点,并说明理由.(2)请在图②的正方形内(含边),画出使∠60°的所有的点P,并说明理由.问题解决:(3)如图③,现在一块矩形钢板,4,3.工人师傅想用它裁出两块全等的、面积最大的△和△′D钢板,且∠∠'60度.请你在图③中画出符合要求的点和,并求出△的面积(结果保留根号).。
中考数学轨迹问题集锦77659
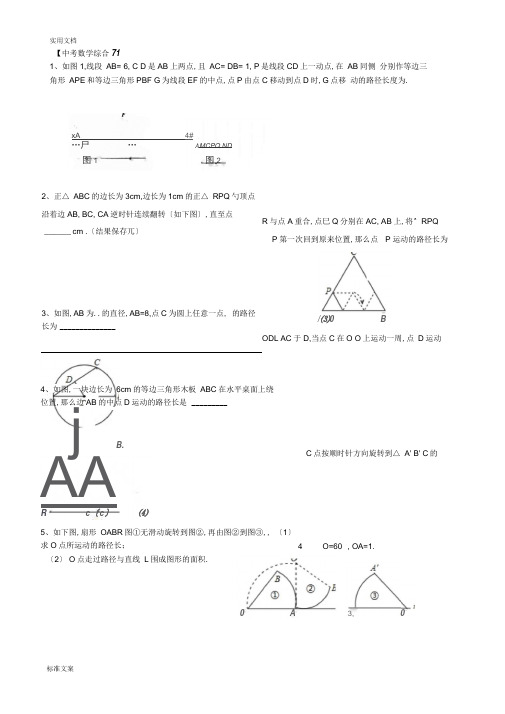
实用文档【中考数学综合711、如图1,线段AB= 6, C D是AB上两点,且AC= DB= 1, P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为.xA 4#…尸…A MCPQ ND图1 图22、正△ ABC的边长为3cm,边长为1cm的正△ RPQ勺顶点沿着边AB, BC, CA逆时针连续翻转〔如下图〕,直至点______ cm .〔结果保存兀〕3、如图,AB为..的直径,AB=8,点C为圆上任意一点, 的路径长为______________ R与点A重合,点巳Q分别在AC, AB上,将^ RPQ P第一次回到原来位置,那么点P运动的路径长为/⑶0 BODL AC于D,当点C在O O上运动一周,点D运动4、如图,一块边长为6cm的等边三角形木板ABC在水平桌面上绕位置,那么边AB的中点D运动的路径长是_________j B.AAR c〔c〕⑷5、如下图,扇形OABR图①无滑动旋转到图②,再由图②到图③,, 〔1〕求O点所运动的路径长;C点按顺时针方向旋转到△ A' B' C的4 O=60° , OA=1.〔2〕 O点走过路径与直线L围成图形的面积.标准文案0 A3, 0点C 运动形成的路径长是 90°的扇形OABW 弧AB 上有一运动的点 P.从点P 向半径OA 弓|垂线PH 交 当点P 在弧AB 上从点A 运动到点B 时,内心I 所经过的路径长为8.如图,正方形 ABCD 勺边长是2, M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止.连接EM 并延长交射线 CDT 点F,过M 作EF 的垂线交射线 BC 于点G 连结EG FG(1)设AE= x 时,△ EGF 勺面积为V ,求y 关于x 的函数关系式,并写出自变量 x 的取值范围;(2) P 是MG 勺中点,请直接写出点 P 运动路线的长.6、如图, O4 OB,垂足为O, P 、Q 分别是射线OA OB 上两个动点,点 C 是线段PQ 的中点,且PQ=4那么动B7、如图,半径为2cm,圆心角为OA 于点H.设△ OPH 的内心为I ,9、某数学兴趣小组对线段上的动点问题进行探究, AB=8.问题思考:如图1,点P为线段AB上的一个动点,分别以AR BP为边在同侧作正方形APDC BPEF(1)当点P运动时,这两个正方形的面积之和是定值吗?假设是,请求出;假设不是,请求出这两个正方形面积之和的最小值.(2)分别连接AR DF、AF, AF交DP于点K,当点P运动时,在^ APK △ ADK 4DFK中,是否存在两个面积始终相等的三角形?请说明理由.问题拓展:(3)如图2,以AB为边作正方形ABCD动点P、Q在正方形ABCD勺边上运动,且PQ=8假设点P从点A出发, 沿A- B-O D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.(4)如图3,在“问题思考〞中,假设点M N是线段AB上的两点,且AM=BN=1点G H分别是边CD EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+O的最小值.Si肆图310、如图1,在Rt^ABC中,/ 0=90° , AC=6 BC=8动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD// BC交AB于点D,连接PQ分别从点A C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t >0).(1)直接用含t的代数式分别表示:QB=,PD=(2)是否存在t的值,使四边形PDBQ^菱形?假设存在,求出t的值;假设不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQB某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.11、在直角坐标系中, O是坐标原点,点A坐标为(0, -1 ),点C是x轴上一个动点.(1)如图1, 4AO*口△BCD^B是等边三角形,当点C在x轴上运动时,请探究点D的运动轨迹;(2)如图2, 4ABO和^ACD^B是等腰直角三角形,当点C在x轴上运动时,请探究点D的运动轨迹;(3)如图3,四边形OABE^正方形,请你画出正方形BCDF( BCDF根据逆时针顺序),并探究当点C 上运动时,点D的运动轨迹.12、如图,在直角坐标系中, A点坐标为(0, 6), B点坐标为(8, 0),点P沿射线BO以每秒2个单位的速度匀速运动,同时点Q从A到O以每秒1个单位的速度匀速运动,当点Q运动到点O时两点同时停止运动.(1)设P点运动时间为t秒,M为PQ的中点,请用t表示出M点的坐标为(2)设^ BPM勺面积为S,当t为何值时,S有最大值,最大值为多少?(3)请画出M点的运动路径,并说明理由;(4)假设以A为圆心,AQ为半径画圆,t为何值时.A与点M的运动路径只有一个交点?13、如图,抛物线y=ax2+bx+3过点A (1, 0), B (3, 0),与y轴相交于点C. (1)求抛物线的解析式;(2)假设点E为抛物线对称轴上的一点,请探索抛物线上是否存在点F,使以A, B, E, F为顶点的四边形为平行四边形?假设存在,请求出所有点F的坐标;假设不存在,请说明理由;J | ,(3)假设点P为线段OC上的动点,连接BP,过点C作CN垂直于直线BP,i : 1垂足为N,当点P从点O运动到点C时,求点N运动路径的长.14、如图,在直角坐标系中,点 A 的坐标是〔0.3〕,点C 是x 轴上的一个动点,点 C 在x 轴上移动时,始终 保持△ AC 幅等边三角形.当点 C 移动到点O 时,得到等边三角形 AOB 〔此时点P 与点B 重合〕.〔1〕点C 在移动的过程中,当等边三角形 ACP 的顶点P 在第三象限时〔如图〕,求证:△ AOC2△ ABFP 由此 你发现什么结论?〔2〕求点C 在x 轴上移动时,点 P 所在函数图象的解析式.15、如图,边长为4的等边三角形 AOB 勺顶点O 在坐标原点,点 A 在x 轴正半轴上,点 B 在第一象限.一动 点P 沿x 轴以每秒1个单位长的速度向点 A 匀速运动,当点 P 到达点A 时停止运动,设点 P 运动的时间是t 秒.将线段BP 的中点绕点P 按顺时针方向旋转 60.得点C,点C 随点P 的运动而运动,连接 CP CA 过点 P 作PDL O 时点D.,用含t 的代数式表示〕;〔2〕求点C 的坐标〔用含t 的代数式表示〕; 在点P 从O 向A 运动的过程中,△ PCAf 归否成为直角三角形?求 t 的值.假设不能,说理由; 填空:在点 P 从O 向A 运动的过程中,点 C 运动路线的长为 —. 16、等边三角形 ABC 勺边长为6,在AG BC 边上各取一点 E, F,连结AF, BE 相交于点P. (1)假设AE=CF ①求证:AF =BE 并求/ APB 勺度数.②假设AE=2,试求AP ,AF 的值.(1)(3)(4) 填空:PD 的长为(2)假设AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.s F C17、如图,E, F是正方形ABCM边AD上两个动点,满足AE=DF连接CF交BD于点G,连接BE交AG于点H.假设正方形的边长为2,那么线段DH长度的最小值是 .20、在平面直角坐标系中, O为原点,点A (- 2, 0),点B (0, 2),点E,点F分别为OA OB的中点.假设正方形OED嗓点O顺时针旋转,得正方形OE D' F',记旋转角为a .F(I)如图①,当“二90°时,求AE' , BF'的长;(II)如图②,当a =135°时,求证AE'=BF',且AE',BF';(出)假设直线AE'与直线BF'相交于点P,求点P的纵坐标的最大值(直接写出结果即可)18、如图,矩形ABCD的边AB=3cn^ AD=4^ 点E从点A出发,沿射线AD移动,以CE为直径作.O,点F为.O与射线BD的公共点,连接EF、CF,过点E作EG!EF, EG与..相交于点G,连接CG(1) 试说明四边形EFC比矩形;(2) 当.O与射线BD相切时,点E停止移动.在点E移动的过程中,①矩形EFCG勺面积是否存在最大值或最小值?假设存在,求出这个最大值或最小值;假设不存在,说明理由;②求点G移动路线的长.19 .如图,在平面直角坐标系中,矩形OABC勺两边OA OC分别在x轴、y轴的正半轴上,O44,OG= 2 .点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90.得点D,点D随点P的运动而运动,连接DR DA 标准文案实用文档(1)请用含t的代数式表示出点D的坐标;(2)求t为何值时,△ DPA勺面积最大,最大为多少?(3)在点P从O向A运动的过程中,△ DP厢归否成为直角三角形?假设能,求t的值;假设不能,请说明理由;(4)请直接写出随着点P的运动,点D运动路线的长20 .如图,直角坐标系中,点A (2, 4) , B (5, 0),动点P从B点出发沿BO向终点O运动, 动点Q从A点出发沿AB向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了x秒.(1) Q点的坐标为( ) (用含x的代数式表示);(2)当x为何值时,△ APQ是一个以AP为腰的等腰三角形?(3)记PQ的中点为G请你直接写出点G随点P, Q运动所经过的路线的长度.21、问题探究:(1)请在图①的正方形ABCXJ,画出使/ APB=90的一个点,并说明理由.(2)请在图②的正方形ABCXJ (含边),画出使/ APB=60°的所有的点P,并说明理由.问题解决:(3)如图③,现在一块矩形钢板ABCD AB=4, BC=3工人师傅想用它裁出两块全等的、面积最大的4APB和^CP D钢板,且/ APB=Z CP'D=60度.请你在图③中画出符合要求的点和, 并求出△ APB 22.:矩形纸片2BCD中,2B=26厘米,BC=18.5厘米,点E在2D上,且2E=6厘米,点P是2B 边上一动点.按如下操作:的面积(结果保存根号)步骤一,折叠纸片,使点P与点E重合,展开纸片得折痕MN〔如了1所示〕;步骤二,过点P作PT± AB,交MN^在的直线于点Q,连接QE 〔手图9所示〕〔1〕无论点P在AB边上任何位置,都有PQ QE 〔填“>〞、"="、“<〞号〕;〔2〕如图3所示,将纸片ABCD^在直角坐标系中,按上述步骤一、二进行操作:①当点P在A点时,P3与MN交于点55, Q点的坐标是〔 , 〕;②当PA=6厘米日PT与MN^于点r2, Q点的坐标是〔 , 〕;③当PA=d2厘米时,在图3中画出MN PT 〔不要求写画法〕,并求出MN与PT的交点Q的坐标;〔3〕点P在运动过程,PT与MN^成一系列着交点Q, Q, Q,…观察、猜测:众的的交点形成的图象是什么并直接写出该图象的函数表达式.C图1 图2 图3。
中考数学轨迹问题集锦

【中考数学综合7】1、如图1,已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_______.2、正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA逆时针连续翻转(如图所示),直至点P第一次回到原来位置,则点P运动的路径长为_______ cm.(结果保留π)3、如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D 运动的路径长为_______4、如图,一块边长为6cm的等边三角形木板ABC,在水平桌面上绕C点按顺时针方向旋转到△A′B′C′的位置,则边AB的中点D运动的路径长是_______5、如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.(1)求O点所运动的路径长;(2)O点走过路径与直线L围成图形的面积.6、如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是______7、如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为______ .8.如图,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点B停止.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG、FG.(1)设AE=x时,△EGF的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;(2)P是MG的中点,请直接写出点P运动路线的长.FDA MPGEFDA MPGE9、某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.问题思考:如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.(1)当点P运动时,这两个正方形的面积之和是定值吗若是,请求出;若不是,请求出这两个正方形面积之和的最小值.(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形请说明理由.问题拓展:(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A 出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.10、如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒(t≥0).(1)直接用含t的代数式分别表示:QB=____ ,PD=____(2)是否存在t的值,使四边形PDBQ为菱形若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.11、在直角坐标系中,O是坐标原点,点A坐标为(0,-1),点C是x轴上一个动点。
中考数学轨迹问题集锦

【中考数学综合7】1、如图1,已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_______.2、正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ 沿着边AB,BC,CA逆时针连续翻转(如图所示),直至点P第一次回到原来位置,则点P运动的路径长为_______ cm.(结果保留π)3、如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为_______4、如图,一块边长为6cm的等边三角形木板ABC,在水平桌面上绕C点按顺时针方向旋转到△A′B′C′的位置,则边AB的中点D运动的路径长是_______5、如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.(1)求O点所运动的路径长;(2)O点走过路径与直线L围成图形的面积.6、如图,OA ⊥OB ,垂足为O ,P 、Q 分别是射线OA 、OB 上两个动点,点C 是线段PQ 的中点,且PQ=4.则动点C 运动形成的路径长是______7、如图,半径为2cm ,圆心角为90°的扇形OAB 的弧AB 上有一运动的点P .从点P 向半径OA 引垂线PH 交OA 于点H .设△OPH 的内心为I ,当点P 在弧AB 上从点A 运动到点B 时,内心I 所经过的路径长为______ .8.如图,正方形ABCD 的边长是2,M 是AD 的中点,点E 从点A 出发,沿AB 运动到点B 停止.连接EM 并延长交射线CD 于点F ,过M 作EF 的垂线交射线BC 于点G ,连结EG 、FG .(1)设AE =x 时,△EGF 的面积为y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (2)P 是MG 的中点,请直接写出点P 运动路线的长.9、某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.问题思考:如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.问题拓展:(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.10、如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t ≥0).(1)直接用含t的代数式分别表示:QB=____ ,PD=____(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.11、在直角坐标系中,O是坐标原点,点A坐标为(0,-1),点C是x轴上一个动点。
中考数学轨迹问题集锦

中考数学轨迹问题集锦(总13页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--【中考数学综合7】1、如图1,已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_______.2、正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA逆时针连续翻转(如图所示),直至点P第一次回到原来位置,则点P运动的路径长为_______ cm.(结果保留π)3、如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为_______4、如图,一块边长为6cm的等边三角形木板ABC,在水平桌面上绕C点按顺时针方向旋转到△A′B′C′的位置,则边AB的中点D运动的路径长是_______5、如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.(1)求O点所运动的路径长;(2)O点走过路径与直线L围成图形的面积.6、如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是______7、如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P.从点P向半径OA 引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I 所经过的路径长为______ .8.如图,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点B停止.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG、FG.(1)设AE=x时,△EGF的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;(2)P是MG的中点,请直接写出点P运动路线的长.FDCABMPGEFDCABMPGE9、某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.问题思考:如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.问题拓展:(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.10、如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).(1)直接用含t的代数式分别表示:QB=____ ,PD=____(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.11、在直角坐标系中,O是坐标原点,点A坐标为(0,-1),点C是x轴上一个动点。
初中中考常考轨迹问题整理
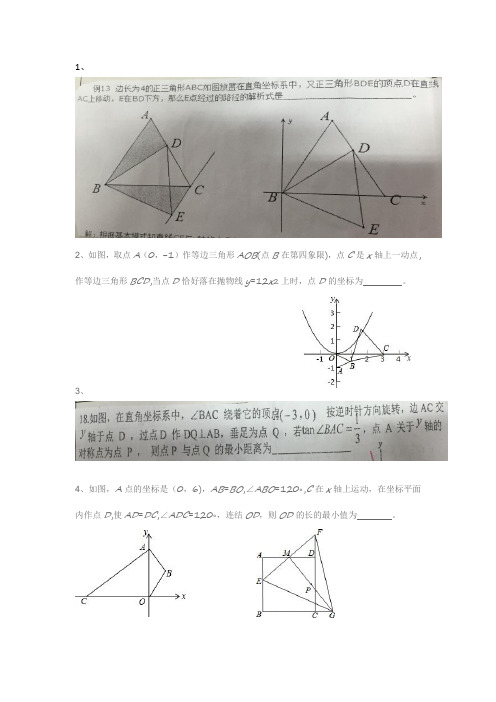
1、
2、如图,取点A(0,−1)作等边三角形AOB(点B在第四象限),点C是x轴上一动点,作等边三角形BCD,当点D恰好落在抛物线y=12x2上时,点D的坐标为。
3、
4、如图,A点的坐标是(0,6),AB=BO,∠ABO=120∘,C在x轴上运动,在坐标平面内作点D,使AD=DC,∠ADC=120∘,连结OD,则OD的长的最小值为。
5、如图,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点B停止,连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连接EG、FG.
(1)设AE=x时,△EGF的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(2)P是MG的中点,请直接写出点P的运动路线的长。
6、如图①,已知∠MON=Rt∠,点A,P分别是射线OM,ON上两定点,且OA=2,OP=6,动点B从点O向点P运动,以AB为斜边向右侧作等腰直角△ABC,设线段OB的长x,点C到射线ON的距离为y.
(1)若OB=2,直接写出点C到射线ON的距离;
(2)求y关于x的函数表达式,并在图②中画出函数图象;
(3)当动点B从点O运动到点P,求点C运动经过的路径长。
中考数学轨迹问题集锦77659
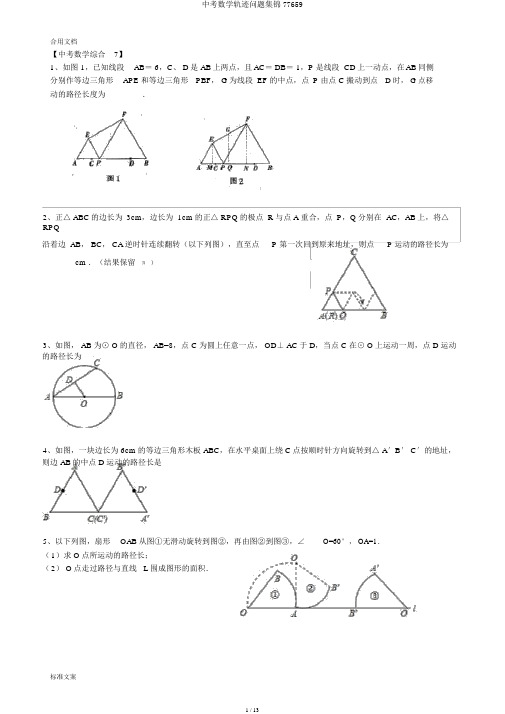
【中考数学综合7】1、如图 1,已知线段AB= 6,C、 D是 AB上两点,且 AC= DB= 1,P 是线段 CD上一动点,在AB同侧分别作等边三角形APE 和等边三角形PBF, G为线段 EF 的中点,点P 由点 C 搬动到点 D 时, G点移动的路径长度为_______.2、正△ ABC的边长为3cm,边长为 1cm 的正△ RPQ的极点 R与点 A 重合,点 P,Q分别在 AC,AB上,将△RPQ沿着边 AB, BC, CA逆时针连续翻转(以下列图),直至点P 第一次回到原来地址,则点P 运动的路径长为_______ cm .(结果保留π )3、如图, AB 为⊙ O的直径, AB=8,点 C 为圆上任意一点, OD⊥ AC于 D,当点 C 在⊙ O上运动一周,点 D 运动的路径长为 _______4、如图,一块边长为 6cm 的等边三角形木板 ABC,在水平桌面上绕 C点按顺时针方向旋转到△ A′B′ C′的地址,则边 AB的中点 D 运动的路径长是 _______5、以下列图,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°, OA=1.(1)求 O点所运动的路径长;(2) O点走过路径与直线 L 围成图形的面积.6、如图, OA⊥ OB,垂足为 O, P、 Q分别是射线 OA、 OB上两个动点,点 C 是线段 PQ的中点,且 PQ=4.则动点 C 运动形成的路径长是 ______7、如图,半径为 2cm,圆心角为 90°的扇形 OAB的弧 AB上有一运动的点 P.从点 P 向半径 OA引垂线 PH交OA于点H.设△ OPH的内心为 I ,当点 P 在弧 AB上从点 A 运动到点 B 时,内心 I 所经过的路径长为 ______ .8.如图,正方形ABCD的边长是2,M是 AD的中点,点E从点 A 出发,沿 AB运动到点 B停止.连接EM并延长交射线CD于点 F,过 M 作(1)设AE=x时,△EGF的面积为(2)P是MG的中点,请直接写出点EF的垂线交射线BC于点G,连接EG、FG.y,求 y 关于 x 的函数关系式,并写出自变量P运动路线的长.Fx的取值范围;FA M DA M DEE PPB C GB C G9、某数学兴趣小组对线段上的动点问题进行研究,已知AB=8.问题思虑:如图 1,点 P 为线段 AB上的一个动点,分别以AP、 BP为边在同侧作正方形APDC、 BPEF.(1)当点 P 运动时,这两个正方形的面积之和是定值吗?若是,央求出;若不是,央求出这两个正方形面积之和的最小值.(2)分别连接 AD、DF、 AF, AF交 DP于点 K,当点 P 运动时,在△ APK、△ ADK、△ DFK中,可否存在两个面积向来相等的三角形?请说明原由.问题拓展:(3)如图 2,以 AB 为边作正方形 ABCD,动点 P、Q在正方形 ABCD的边上运动,且 PQ=8.若点 P 从点 A 出发,沿 A→ B→ C→ D的线路,向点 D运动,求点 P 从 A 到 D 的运动过程中, PQ的中点 O所经过的路径的长.(4)如图 3,在“问题思虑”中,若点 M、 N 是线段 AB上的两点,且 AM=BN=1,点 G、 H分别是边 CD、 EF 的中点,请直接写出点 P 从 M到 N 的运动过程中, GH的中点 O所经过的路径的长及 OM+OB的最小值.10、如图 1,在 Rt △ ABC中,∠ C=90°, AC=6, BC=8,动点 P从点 A 开始沿边 AC向点 C以 1个单位长度的速度运动,动点Q从点 C开始沿边CB向点 B 以每秒 2个单位长度的速度运动,过点P 作 PD∥ BC,交 AB于点 D,连接 PQ分别从点A、 C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒( t≥ 0).(1)直接用含 t 的代数式分别表示: QB=____ ,PD=____(2)可否存在 t 的值,使四边形 PDBQ为菱形?若存在,求出 t 的值;若不存在,说明原由.并研究如何改变 Q的速度(匀速运动),使四边形PDBQ在某一时辰为菱形,求点Q的速度;( 3)如图 2,在整个运动过程中,求出线段PQ中点 M所经过的路径长.11、在直角坐标系中,O是坐标原点,点 A 坐标为( 0, -1 ),点 C 是 x 轴上一个动点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运动轨迹
1、如图1,已知线段AB=6,C、D是AB上两点,且AC=DB=1,P是线段CD上一动点,在AB同侧分别作等边三角
形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为_______.
2、正△ABC的边长为3cm,边长为1cm的正△RPQ的顶点R与点A重合,点P,Q分
别在AC,AB上,将△RPQ沿着边AB,BC,CA逆时针连续翻转(如图所示),直至点P
第一次回到原来位置,则点P运动的路径长为_______ cm.(结果保留π)
3、如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,
当点C在⊙O上运动一周,点D运动的路径长为_______
4、如图,一块边长为6cm的等边三角形木板ABC,在水平桌面上绕C点按顺
时针方向旋转到△A′B′C′的位置,则边AB的中点D运动的路径长是_______
5、如图所示,扇形OAB从图①无滑动旋转到图②,再由图②到图③,∠O=60°,OA=1.
(1)求O点所运动的路径长;(2)O点走过路径与直线L围成图形的面积.
6、如图,OA⊥OB,垂足为O,P、Q分别是射线OA、OB上两个动点,点C是线段PQ的中点,且PQ=4.则动点C运动形成的路径长是______
7、如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为______ .
8、某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C →D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
9、如图,抛物线y=ax2+bx+3过点A(1,0),B(3,0),与y轴相交于点C.
(1)求抛物线的解析式;
(2)若点E为抛物线对称轴上的一点,请探索抛物线上是否存在点F,使以A,B,E,F为顶点的四边形为平行四边形?若存在,请求出所有点F的坐标;若不存在,请说明理由;
(3)若点P为线段OC上的动点,连接BP,过点C作CN垂直于直线BP,垂足为N,当点P从点O运动到点C时,求点N运动路径的长.
10、等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.
的值.
(1)若AE=CF.①求证:AF=BE,并求∠APB的度数.②若AE=2,试求AP AF
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
11、如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作⊙O,点F为⊙O与射线BD 的公共点,连接EF、CF,过点E作EG⊥EF,EG与⊙O相交于点G,连接CG.
(1)试说明四边形EFCG是矩形;
(2)当⊙O与射线BD相切时,点E停止移动.在点E移动的过程中,
①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.。
