中考基础训练每天一练(3)
2025年中考数学总复习前17题基础训练 (6)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
11. (2023·东营)分解因式:3ma2-6mab+3mb2=
3m(a-b)2 .
解析:3ma2-6mab+3mb2=3m(a2-2ab+b2)=3m(a-b)2.
12. (2023·天津)不透明的袋子中装有10个球,其中有7个绿球、3个红
交于点C.∴ CD=CE.易得当涂色部分周长取得最小值时,AC+CD=
AC+CE=AE.在扇形AOB中,∠AOB=60°,OD平分∠AOB,
∴ ∠AOD=∠BOD=30°.由轴对称的性质,得∠BOE=∠BOD=30°,
OE=OD.∴ ∠AOE=90°.∴ △AOE是等腰直角三角形.∵ OA=1,∴
×
8. (2023·眉山)若关于x的不等式组ቊ
的整数解仅有4
5 − 2 < 4 + 1
个,则m的取值范围是( A )
A. -5≤m<-4
B. -5<m≤-4
C. -4≤m<-3
D. -4<m≤-3
解析:∵ 不等式组有解,∴ 解不等式组,得m+3<x<3.由题意,得-
2≤m+3<-1,解得-5≤m<-4.
AE= .∵ 的长=
= ,∴ 涂色部分周长的最小值为 + .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
10. (2023·达州)如图,抛物线y=ax2+bx+c(a,b,c为常数)关于
2021年中考数学复习专题之三角形03-【三角形的面积】基础训练

2021中考数学复习专题之三角形03【三角形的面积】基础训练一.选择题1.△ABC中,BC=10,AC﹣AB=4.过C作∠BAC的角平分线的垂线,垂足为D,连结BD,CD,则S的最大值为()△BDCA.10B.15C.12D.142.如图,在四边形ABCD中,对角线AC,BD交于点O,∠CBD=90°,BC=4,OB=OD=3,AC=10,则四边形ABCD的面积为()A.48B.36C.24D.123.在平面直角坐标系中,由点A(a,3),B(a+4,3),C(b,﹣3)组成的△ABC的面积是()A.6B.12C.24D.不确定4.如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为()A.6B.7C.8D.95.如图,在△ABC中,AG=BG,BD=DE=EC,CF=4AF,若四边形DEFG的面积为14,则△ABC的面积为()A.24B.28C.35D.306.如图,点P在直线m上移动,A,B是直线n上的两个定点,且直线m∥n.对于下列各值:①点P到直线n的距离;②△PAB的周长:③△PAB的面积:④∠APB的大小.其中不会随点p 的移动而变化的是()A.①②B.①③C.②④D.③④7.如图,△ABC中,AD是BC上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是20,则△ABE的面积是()A .10B .6C .5D .48.活动课上,小华将两张直角三角形纸片如图放置,已知AC =8,O 是AC 的中点,△ABO 与△CDO 的面积之比为4:3,则两纸片重叠部分即△OBC 的面积为( )A .4B .6C .2D .29.如图,已知△ABC 中,CN =3BN ,AM =CM ,AN 交BM 于O .若S △ABC =40,则下列正确的是( )①S △ABO =2;②BO :MO =2:3;③AO :NO =4;④S △AMO =12:⑤S △CMO =13.A .①②④B .②③④C .②③④⑤D .①②③④10.已知点A (1,2a +1),B (﹣a ,a ﹣3),若线段AB ∥x 轴,则三角形AOB 的面积为( ) A .21B .28C .14D .10.5二.填空题11.如图,点E 、F 都在线段AB 上,分别过点A 、B 作AB 的垂线AD 、BC ,连接DE 、DF 、CE 、CF ,DF 交CE 于点G ,已知AD =BE =7.5,AE =BF =CB =2.5.如果△DEG 的面积为S 1,△CFG 的面积为S 2,则S 1﹣S 2= .12.如图,在△ABC 中,∠BAC =90°,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法中正确的序号是 .①△ABE 的面积等于△BCE 的面积;②∠AFG =∠AGF ;③∠FAG =2∠ACF ;④BH =CH .13.如图,△ABC 中,D 是AB 的中点,且AE :CE =3:1,S △CEP =1,则S △BPC = .14.如图,已知△ABC 中,∠BAC =120°,点D 在边BC 上,且AD =4.BD :CD =3:2.当△ABD 面积最大时,AB 的长为 .15.如图,AD 是△ABC 的中线,G 是AD 上的一点,且AG =2GD ,连结BG ,若S △ABC =12,则S △ABG 为 .三.解答题16.在平面直角坐标系中,已知点A,B,C的坐标分别为A(﹣1,0),B(3,﹣2),C(a,b),且+|a+2b﹣7|=0.(1)求点C的坐标;(2)画出△ABC并求△ABC的面积;(3)若BC与x轴交点为点M,求点M坐标.17.如图,长方形ABCD中,AB=10cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x为何值时,△APE的面积等于32cm2?(提醒:同学们,要分类讨论哦!)18.如图,在△ABC中,AD是BC边上的中线,AE是BC边上的高线,已知AE=4,△ABD的面积是6,求BC的长.19.在平面直角坐标系中,已知以A(﹣1,0)或以B(3,0)为直角顶点的直角三角形ABC的面积为6,求顶点C的坐标.20.已知A(0,2),B(4,0),C(6,6)(1)在图中的直角坐标系中画出△ABC;(2)求△ABC的面积.参考答案一.选择题1.解:如图:延长AB ,CD 交点于E ,∵AD 平分∠BAC ,∴∠CAD =∠EAD ,∵CD ⊥AD ,∴∠ADC =∠ADE =90°,在△ADE 和△ADC 中,,∴△ADE ≌△ADC (ASA ),∴AC =AE ,DE =CD ;∵AC ﹣AB =4,∴AE ﹣AB =4,即BE =4;∵DE =DC ,∴S △BDC =S △BEC ,∴当BE ⊥BC 时,S △BDC 面积最大,即S △BDC 最大面积=××10×4=10.故选:A .2.解:在Rt△OBC中,由勾股定理,得CO===5.∵AC=10,∴AO=5,∴OA=OC,∵OB=OD=3,∴四边形ABCD是平行四边形.四边形ABCD的面积为BC•BD=4×(3+3)=24,故选:C.3.解:∵点A(a,3),B(a+4,3),∴AB=4,∵C(b,﹣3),∴点C在直线y=﹣3上,∵AB :y =3与直线y =﹣3平行,且平行线间的距离为6, ∴S =×4×6=12,故选:B .4.解:连接OC ,OB ,OA ,OD ,∵E 、F 、G 、H 依次是各边中点,∴△AOE 和△BOE 等底等高,所以S △OAE =S △OBE , 同理可证,S △OBF =S △OCF ,S △ODG =S △OCG ,S △ODH =S △OAH , ∴S 四边形AEOH +S 四边形CGOF =S 四边形DHOG +S 四边形BFOE , ∵S 四边形AEOH =6,S 四边形BFOE =7,S 四边形CGOF =8, ∴6+8=7+S 四边形DHOG ,解得S 四边形DHOG =7.故选:B .5.解:连接EG ,CG ,∵BD =DE =EC ,∴BD =BC ,∵AG =BG =AB ,∴S △BDG =S △BCG =S △ABC =S △ABC ,同理S △ECF =S △ABC =S △ABC ,S △AFG =×S △ABC =S △ABC ,∴S 四边形DEFG =S △ABC ﹣S BDG ﹣S △CEF ﹣S △AGF =S △ABC =14,∴S △ABC =30.故选:D .6.解:①∵直线m ∥n ,∴点P 到直线n 的距离不变;②∵PA 、PB 的长度随点P 的移动而变化,∴△PAB 的周长会随点P 的移动而变化;③∵点P 到直线n 的距离不变,AB 的大小,∴△PAB 的面积不变;④直线m 、n 之间的距离不随点P 的移动而变化,∠APB 的大小随点P 的移动而变化; 故不会随点p 的移动而变化的是①③,故选:B .7.解:∵AD 是BC 上的中线,∴S △ABD =S △ACD =S △ABC ,∵BE 是△ABD 中AD 边上的中线,∴S △ABE =S △BED =S △ABD ,∴S △ABE =S △ABC ,∵△ABC 的面积是20,∴S △ABE ==5. 故选:C .8.解:∵点O 是直角△ABC 斜边AC 的中点,∴S △ABO =S △CBO ,OB =OA =OC ,∵△ABO 与△CDO 的面积之比为4:3,∴△CBO 与△CDO 的面积之比为4:3,∴OB :OD =4:3,设OB =4x ,则OD =3x ,∴OA =OC =4x ,∵AC =8,∴4x +4x =8,解得x =1,在Rt △ODC 中,OD =3,OC =4,∴CD ==,∴S △ODC =×3×=,而△CBO 与△CDO 的面积之比为4:3,∴S △OBC =×=2.故选:D .9.解:过M 点作MD ∥BC ,交AN 于点N ,连接OC ,则△DOM ∽△NOB ,∴DM :BN =DO :ON =MO :BO ,∵AM =CM ,∴DM 为△ANC 的中位线,∴AD =DN ,BC =2DM ,∵CN =3BN ,∴DM :BN =3:2,BN :BC =1:4,∴DO :ON =MO :BO =3:2,∴BO :MO =2:3,故②正确;AO :NO =4:1,故③正确;AO :AN =4:5,OM :BM =3:5,∵S △ABC =40,AM =CM ,BN :BC =1:4,∴S △ABN =10,S △ABM =20,∵S △ABO :S △ABN =AO :AN =4:5,S △AMO :S △ABM =MO :BM =3:5,∴S △ABO =8,故①错误;S △AMO =12,故④正确;∵AM =CM ,∴S △CMO =S △AMO =12,故⑤错误.故选:B .10.解:∵AB ∥x 轴,∴2a +1=a ﹣3.解得a =﹣4.∴A (1,﹣7),B (4,﹣7).∴AB =3.∴△AOB 的面积为:×3×7=10.5,故选:D .二.填空题11.解:∵AD =BE =7.5,AE =BF =CB =2.5.∴AF =BE ,∴AD =AF =7.5,在△ADE 和△BEC 中,,∴△ADE ≌△BEC (SAS ),∴S △DAE =S △CBE ,∵S 1=S △DAF ﹣S △DAE ﹣S △EFG ,S 2=S △CBE ﹣S △EFG ﹣S △CBF ,∴S 1﹣S 2=S △DAE +S △CBF =+=.故答案为.12.解:∵BE是中线,∴AE=CE,∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;∵CF是角平分线,∴∠ACF=∠BCF,∵AD为高,∴∠ADC=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,∴∠ABC=∠CAD,∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,∴∠AFG=∠AGF,故②正确;∵AD为高,∴∠ADB=90°,∵∠BAC=90°,∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,∴∠ACB=∠BAD,∵CF是∠ACB的平分线,∴∠ACB=2∠ACF,∴∠BAD=2∠ACF,即∠FAG =2∠ACF ,故③正确;根据已知条件不能推出∠HBC =∠HCB ,即不能推出BH =CH ,故④错误;故答案为:①②③.13.解:连接PA ,∵D 是AB 的中点,∴S △ADC =S △BCD ,S △PAD =S △PBD ,∴S △BPC =S △APC ,∵AE :CE =3:1,S △CEP =1,∴S △AEP =3S △CEP =3,∴S △APC =4,∴S △BPC =4,故答案为4.14.解:作DE ⊥AB 于E ,∴S △ABD =AB •DE ,∵DE ⊥AB ,∴DE ≤AD .当DA ⊥AB 时,DE 与DA 重合,此时,DE 取得最大值4,△ABD 面积最大,作CF ⊥AB ,交BA 的延长线于F ,∴DE ∥CF ,∴△BDE ∽△BCF , ∴=,即=, ∴=,∴CF =,∵∠BAC =120°,∴∠CAF =60°,∴∠ACF =30°∴AF =tan30°•CF =×=,∵AD ∥CF , ∴==,∴AB =. 故答案为.15.解:∵AD 是△ABC 的中线,S △ABC =12,∴S △ABD =S △ABC =×12=6,∵AG =2GD ,∴S △ABG =S △ABD =×6=4,故答案为:4.三.解答题16.解:(1)∵+|a +2b ﹣7|=0, ∴, 解得:,∴C (1,3);(2)如图,△ABC 为所作,如图,分别过点B ,点C 作x 轴的平行线BF ,DE ,过点A ,点B 作y 轴的平行线DF ,EB , ∴S △ABC =S 四边形DFBE ﹣S △ADC ﹣S △BCE ﹣S △ABF ,=4×5﹣﹣﹣,=8;(3)设点M 的坐标为(m ,0),∵S△ABC =S△AMC+S△ABM,S△ABC=8,∴,∴AM=,∴m﹣(﹣1)=,∴m=,∴M(,0).17.解:①如图1,当P在AB上时,∵△APE的面积等于32,∴×2x•8=32,解得:x=4;②当P在BC上时,∵△APE的面积等于32,∴S 矩形ABCD ﹣S △CPE ﹣S △ADE ﹣S △ABP =32,∴10×8﹣(10+8﹣2x )×5﹣×8×5﹣×10×(2x ﹣10)=32, 解得:x =6.6;③当P 在CE 上时,∴(10+8+5﹣2x )×8=32,解得:x =7.5<(10+8+5),x =7.5时2x =15,P 在BC 边,∴舍去;答:4或6.6.18.解:∵AD 为△ABC 的中线,∴S △ABC =2S △ABD =2×6=12, ∴×AE •BC =12,即4•BC =12,∴BC =6.19.解:设C 点的纵坐标为t ,∵A (﹣1,0),B (3,0),∴AB =4,∵S=×4×|t|=6,解得|t|=3,△ABC∴点C的坐标为(﹣1,3)或(3,3)或(﹣1,﹣3)或(3,﹣3).20.解:(1)在平面直角坐标系中画出△ABC如图所示:(2)△ABC的面积=6×6﹣×4×2﹣﹣=36﹣4﹣6﹣12=14.21 / 21。
中考填空 计算题专题基础训练(附录答案)

中考填空 计算题专题基础训练填空题专题训练(一)声学1、在中考考场里,开考前监考老师正在强调考试要求.(1)监考老师的声音是由声带的 产生的,是通过 传播传入考生耳中的,考生能分辨出两位老师的声音是因为他们发出声音的 不同.(2)考试期间,考点周边禁止鸣笛、禁止附近工地开工,这种措施属于在 处减弱噪声.(二)光学2、如图1所示,要反射光线水平射出,镜子应顺时针转动 o 或逆时针转动 o .3、小蔡在一家商场通过光亮的瓷砖地面看到了挂在天花板上的吊灯.他看到的其实是吊灯的________(选填“虚”、“实”)像.如果吊灯到地面的距离为6m ,则像到地面的距离为________m .小蔡发现通过地毯就看不到吊灯的像,这是因为光照射到地毯时发生了________(选填“镜面”、“漫”)反射.4、如图2所示,在“研究凸透镜成像规律”的实验中,若在透镜右侧的光屏上(光屏未画出)得到清晰放大的实像,则蜡烛可能置于透镜左侧a 、b、c 、三点中的 点处, 就是利用此成像特点制成的.5、在如图3所示实验中,凸透镜焦距为10cm .把蜡烛和透镜放在图中位置时,移动光屏,能在光屏上成一个清晰的 、 实像.利用该成像原理可以制成 (选填“放大镜”、“投影仪”、“照相机”).为了得到更大的清晰像,应将蜡烛向凸透镜靠近,同时应将光屏向 的方向移动(选填“远离透镜”、“靠近透镜”).6、人眼的晶状体相当于一个凸透镜,视网膜相当于光屏.当物体在很远的地方时,物体成像在视网膜上.当物体靠近人眼时,若晶状体的焦距不变,则它的像将会落在视网膜_______(选填“前”、“后”)而导致看不清物体,但实际上,人眼在由远到近观察物体时,晶状体的焦距会___________(选填“变大”、“不变”、“变小”),所以人还能清晰地观察到物体. 300 图1图3图2图4 图5(三)热学7、我国北方地区冬季贮菜时,人们常在地窖里放几桶水,这是利用水的 (填物态变化名称) 热,以防止地窖里的菜被冻坏;暑季在空调房间里,人们也常会放盆水,这是利用水的 (填物态变化名称)来提高房间里的空气湿度. 8、物理课上老师进行了下列的实验:(1)向一个透明塑料袋中吹气,塑料袋鼓起.将袋挤瘪,排出袋中空气后把袋口扎紧,放入80℃以上的热水中,发现塑料袋仅鼓起一点点,将袋取出,在透明塑料袋中滴入几滴酒精,排出袋中空气后把袋口扎紧,再放入80℃以上的热水中,发现塑料袋明显鼓起(如图4所示);从热水中拿出鼓起的塑料袋,放入冷水中,发现塑料袋又变瘪了.以上过程是因为酒精发生了 和 两种物态变化.(酒精的沸点:78℃) (2)将装有固态碘的试管浸入热水中(如图5所示),试管中出现紫色的烟雾,这是碘的 现象.(碘的熔点:114℃)9、小蔡把柚子皮放到冰箱的保鲜层,把猪肉放到冰冻层.过一段时间,打开冰箱会闻到柚皮的香味,香味的存在说明了_______________________________________________________________________;看到柚子皮又干又瘪,说明柚子皮在这段时间内发生的物态变化是______________;冰冻的猪肉上面有一层白霜,这是冰冻层中的水蒸气___________而成的. 10、如图6所示,烧杯内装有2kg 的某种液体:(1)酒精燃烧时放出的热量是通过_____________________(选填“做功”、“热传递”)的方式传递给该液体的,该液体________________(选填“已经”、“还未”)沸腾.(2)酒精的热值为3×107J/kg ,完全燃烧0.1kg 的酒精,共放出 J 的热量.如果酒精放出的热量有14%被液体吸收,液体的温度升高了50℃(液体还未沸腾),则该液体的比热容为 J/(kg·℃).(四)电学11、如图7甲所示电路中,电流表A 1、A 2的指针位置如图7乙所示,则电流表A 1示数为________A ,电流表A 2示数为________A .图6图712、如图8甲所示电路中,开关S 闭合后,两电压表指针偏转位置均如图8乙所示,则电阻R 1两端的电压为_______V ,电阻R 2两端的电压为_______V .13、已知电阻R 1=20Ω,R 2=30Ω,求:(1)将它们串联后接在12V 的电源上,通过R 1的电流为 _____A ,通过R 1、R 2的电流之比I 1:I 2=_____,R 1、R 2两端的电压之比U 1:U 2=_______ .(2)将它们并联后接在12V的电源上,通过R 1的电流为____A ,通过R 2的电流为____A ,电路的总电阻为________Ω,通过R 1、R 2的电流之比I 1:I 2=______,R 1、R 2两端的电压之比U 1:U 2=_____.14、如图9所示,滑片P 左移时,电流表A 示数 ,电压表V 1示数 ,电压表V 2示数.(选填“增大”、“不变”、“减小”)15、如图10所示,滑片P 右移时,电流表A 1示数 ,电流表A 2示数 ,电压表V 1示数 ,电压表V 2示数 .(选填“增大”、“不变”、“减小”)16、某家用电能表表盘上标有“3000revs/(kW·h)”的字样,将某用电器单独接在该电能表上工作20min ,电能表表盘转动了330转.该用电器在上述时间内消耗的电能为__________kW·h ,它的电功率为__________W ,正常工作电流为_______A .17、如图11所示为某玩具汽车的控制电路,小蔡对其进行测量和研究发现:电动机线圈电阻为1Ω,保护电阻R 为4Ω,闭合开关S ,两电压表示数分别为6V 和2V ,则电路电流为_______A ,电动机两端的电压为_______V ,电动机功率为_________W ,电动机工作1s 产生的热量为_______J .8图1518、如图12所示的三幅图中,A 图是研究____________________________的实验,B 图是研究______________________________的实验,C 图是研究____________________________的实验.19、(1)对着话筒(图13甲)唱歌时,声音使膜片及与之相连的线圈在磁场中____________,使线圈中产生随声音变化的____________;此过程中____________能转化为____________能.(2)录音机录音时,变化的电流通过录音磁头(图13乙),录音磁头产生变化的____________,使磁带上带有磁性材料的小颗粒被____________,记录下声音所携带的信息.20、电磁波中真空中的传播速度为____________m/s ,甲电磁波(频率为106.1MHz)、乙电磁波(频率为1098kHz),_____电磁波的波长较长.(五)力学21、体积为100cm 3的冰全部熔化成水后,水的体积为__________cm 3,质量为_________ g .(ρ冰=0.9g/cm 3) 22、为测定某轿车在平直路面上行驶的速度,小蔡同学利用数码相机拍摄了一张在同一张底片上多次曝光的照片,如图14所示.已知拍摄时间间隔设定为1s ,轿车车身长为3.6m . (1)轿车在AC 段做______运动,这段时间内的速度大小为______m/s .(2)轿车在CF 段做______运动, CD 、DF 两段相比较,汽车通过_______段的平均速度大,此段的平均速度等于_____m/s .图11图13甲乙图12图17图1623、如图15所示,(1)物体P 的质量为1.5kg ,则水平桌面对物体P 的支持力为____N .(2)水平拉力F 为5N 时,物体P 未被拉动,此时物体P 受到的摩擦力为____N . (3)水平拉力F 为10N 时,物体P 匀速直线运动,此时物体P 受到的摩擦力为____N . (4)水平拉力F 为15N 时,物体P 加速直线运动,此时物体P 受到的摩擦力为____N .24、图16所示为列车上出售食品的手推车,当前轮遇到障碍物时,售货员向下按扶把,若把手推车视为杠杆,这时杠杆的支点为_________(选填“前轮”、“后轮”);当后轮遇到障碍物时,售货员向上抬扶把,这时杠杆的支点为___________(选填“前轮”、“后轮”);此时手推车可视为_________(选填“省力”、“费力”)杠杆.25、如图17所示,物体A 在水平拉力F 的作用下匀速向右滑动,弹簧测力计的示数为10N ,不计滑轮重量及轮、绳摩擦,则水平拉力F 为 N ,物体A 与水平地面间的摩擦力f 的大小为 N . 26、(1)坦克利用 的方式来 (选填“增大”、“减小”)对地面的压强.一重量为4×105N 的坦克,履带着地总面积为5m 2,该坦克对地面的压强为 Pa .(2)潜水员潜入水中越深,所受水的压强就__________,水对潜水员的压力就___________,所以潜水员潜入水中的深度有一定的限度.当一个潜水员身穿潜水服下潜到水下20m 深处,该处水产生的压强为_____________Pa ,此压强对潜水服上面积为0.02m 2的视窗玻璃的压力为_________N .(3)氢气球升到高空会破裂是因为球内压强________(选填“大于”、“等于”、“小于”)球外压强,破裂的原因是_____________(选填“胀破”、“压破”).27、把重量为4.5N 、密度为0.9×103kg/m 3的木块投入煤油中,则木块静止时处于_____(选填“漂浮”、“悬浮”、“沉没”)状态,所受的浮力为________N ,若将木块投入硫酸中,则木块静止时处于_____(选填“漂浮”、“悬浮”、“沉没”)状态,所受的浮力为________N .(ρ煤油=0.8×103kg/m 3、ρ硫酸=1.8×103kg/m 3)28、小蔡利用如图18所示的滑轮组以150N 的拉力将一个重量为270N 的重物提升了1m ,用时10s .此过程中绳子自由端移动的距离为_____m ;有用功为_______J ;总功为__________J ;机械效率为 ,拉力做功的功率为______W .29、如图19所示,小蔡同学在1min 内引体向上15次,若小蔡同学体重为600N ,每次身体上升高度为50cm ,则小蔡同学完成一次引体向上所做的功为 J ;这1min 内,小蔡同学做功的功率为 W . 30、如图20所示,小球从光滑轨道上的E 点滚落下来,在圆形轨道上运动了一周,最后经过H 点被抛出去,则小球动能最大的位置为 点,重力势能最大的位置为 点,G 点位置的机械能 (选填“大于”、“等于”、“小于”)H 点位置的机械能.计算题专题训练(一)电学1、如图1所示的电路中,电源电压为9V ,标有“6 V 6 W”字样的灯泡正常发光,求电阻的阻值. 解:指定灯泡为用电器1,电阻为用电器2,两用电器 联.2、如图2所示的电路中,电阻R 1=20Ω.当开关S 接位置1时,电流表示数I=0.6A ;当开关S 接位置2时,电流表示数I /=0.2A .求: (1)电源电压.(2)开关S 接位置2时,电阻R 2的电功率. 解:图1图23、如图3所示为某品牌家用电饭锅的工作原理图,已知R2=44Ω;单独闭合开关S1时,电饭锅处于保温状态,保温功率P1=100W.求:(1)R1的阻值.(2)同时闭合开关S1、S2,电饭锅工作1min消耗的电能.解:4、图4甲为通过灯泡的电流随其两端电压变化的图像,将此灯泡接入图4乙所示电路中,闭合开关S后,灯泡实际功率为1 W;再闭合开关S1后,电流表示数变化了0.1 A,求:(1)定值电阻的阻值.(2)电路的总功率.解:指定泡灯为用电器1,电阻为用电器2.图3(二)力学5、小蔡在滑冰场上10s内滑行了80m,他和冰刀的总质量为60kg,已知每把冰刀与冰面的接触面积为10cm2.求:(1)小蔡和冰刀的总重量.(2)小蔡滑行的平均速度.(3)小蔡单脚滑行时对冰面的压强.解:6、小蔡同学在“测定滑轮组机械效率”的实验中,用如图5所示的装置匀速吊起钩码,并记录了如下实验数据.求该滑轮组的机械效率.图5图77、如图6所示,把一个长a=30cm 、宽b=20cm 、高c=100cm 的长方体物体竖立在水平地面上,已知该物体密度ρ=2g/cm 3.(1)求该物体对地面的压强.(2)若某工人利用高h=1m ,长s=2m 的斜面以平行于斜面的大小为800N 的拉力F 把物体匀速拉上斜面,求拉力做的功W 总及工人做功的机械效率η. 解:8、如图7所示为北京残奥会开幕式最后一棒火炬手侯斌靠自己双手的力量攀爬到火炬台底部并最终点燃圣火的照片.已知侯斌和轮椅总质量为80kg ,攀爬高度为40m ,历时约3min20s . (1)不计机械装置的额外功,求侯斌的平均功率.(2)小蔡同学看到火炬手攀爬很费劲,想到物理课上学过利用滑轮组可以省力,小蔡同学如果站在地面上,用如图8所示的哪组滑轮组拉起火炬手侯斌最合适?如果该滑轮组的机械效率为80%,求小蔡同学的拉力. 解:A B C D图8图6图9(三)热学9、如图9所示,一太阳能热水器内装有质量m=200kg ,温度t 0=20℃的水,在阳光照射一段时间后,水温升高到t=70℃.求: (1)水吸收的太阳能.(2)要得到同等的热量,要完全燃烧多少kg 的干木柴.(q 干木柴=1.2×107J/kg) 解:10、如图10所示,某型号汽车在一段平直的公路上匀速行驶s=5.6km ,所受阻力f=3×103N ,消耗燃油v=1.5×10-3m 3(假设燃油完全燃烧).若燃油密度ρ=0.8×103kg/m 3,热值q=4×107J/kg .求: (1)汽车牵引力所做的功W .(2)汽车的热机效率.{热机效率η=WQ (W 为热机在某段时间内对外所做的功,Q 为热机在这段时间内所消耗的燃油完全燃烧产生的热量.)} 解:图10填空 计算题专题训练参考答案填空题专题训练1、(1)振动 空气 音色 (2)声源2、75 153、虚 6 漫4、b 投影仪(幻灯机)5、倒立 缩小 照相机 远离透镜6、后 变小7、凝固 放 汽化(蒸发)8、(1)汽化(沸腾) 液化 (2)升华 9、一切物质的分子都在不停地做无规则运动 汽化(蒸发) 凝华 10、(1)热传递 已经 (2)3×106 4.2×103 11、0.5 1.5 12、4.8 1.213、(1)0.24 1:1 2:3 (2) 0.6 0.4 12 3:2 1:1 14、增大 增大 减小15、减小 减小 不变 不变 16、0.11 330 1.5 17、0.5 4 2 0.2518、电流磁效应 通电导体在磁场中受力 电磁感应现象 19、(1)振动 电流 机械 电(2)磁场 磁化 20、3×108 乙 21、90 90 22、(1)匀速 9 (2) 减速 CD 6.323、(1)15 (2)5 (3)10 (4)10 24、后轮 前轮 省力 25、20 10 26、(1)增大受力面积 减小 8×104 (2)越大 越大 2×105 4×103 (3)大于 胀破 27、沉没 4 漂浮 4.5 28、3 270 450 60% 45 29、300 75 30、F E 等于计算题专题训练1、解:指定灯泡为用电器1,电阻为用电器2,两用电器串联.I 1=P 1U 1=6W 6V=1A I 1=I 2=I=1AU 2=U-U 1=9V -6V=3VR 2=U 2I 2=3V 1A=3Ω 2、解:(1) U=IR 1=0.6A×20Ω=12V(2) 开关S 接位置2时,两电阻串联.I 1=I 2=I /=0.2AU 1=I 1R 1=0.2A×20Ω=4VU 2=U-U 1=12V -4V=8VP 2=U 2 I 2=8V×0.2A=1.6W3、解:(1) R 1=U 2P =(220V)2100W=484Ω(2) P 2=U 2R 2=(220V)244Ω=1100W P=P 1+P 2=100W+1100W=1200WW=Pt=1200W×60s=7.2×104J4、解:指定灯泡为用电器1,电阻为用电器2,两开关均闭合时,两用电器并联.(1) 由图甲可知,U 1=2V 时,I 1=0.5A .P 1=U 1I 1=2V×0.5A=1WU=U 1=U 2=2VR 2=U 2I 2=2V 0.1A=20Ω (2) I=I 1+I 2=0.5A+0.1A=0.6AP=UI=2V×0.6A=1.2W5、解:(1) G=mg=60kg×10N/kg=600N(2) v=s t =80m 10s=8m/s (3) 小蔡滑行时对冰面的压力等于小蔡和冰刀的总重量.p=F S =G S =600N 1×10-3m 2=6×105Pa 6、解:W 有用=G 1h=4N×0.1m=0.4JW 总=Fs=1.6N×0.3m=0.48Jη=W 有用W 总=0.4J 0.48J=83.3% 7、解:(1) V=abc=0.3m×0.2m×1m=0.06m 3G=mg=ρVg=2×103kg/m 3×0.06m 3×10N/kg=1.2×103N物体竖立在水平地面上时,地面受到的压力等于物体的重量.S=ab=0.3m×0.2m=0.06m 2p=F S =G S =1.2×103N 0.06m 2=2×104Pa (2) W 有用=Gh=1.2×103N×1m=1.2×103JW =Fs=800N×2m=1.6×103Jη=W 有用W 总=1.2×103J 1.6×103J =75% 8、解:(1) W 有用=Gh=mgh=80kg×10N/kg×40m=3.2×104JP=W 有用t =3.2×104J 200s=160W (2) 使用D 滑轮组时拉力向下且更省力(有效绳子段数n=4).W 总=W 有用η=3.2×104J 0.8=4×104J F=W 总s =W 总nh =4×104J 4×40m=250N 9、解:(1) Q 吸=cm(t-t 0)=4.2×103J/(kg·℃)×200kg×(70℃-20℃)=4.2×107J(2) Q 放=Q 吸=4.2×107J m=Q 放q =4.2×107J 1.2×107J/kg =3.5kg 10、解:(1) 汽车匀速运动 F=f=3×103NW=Fs=3×103N×5.6×103m=1.68×107J(2) Q=mq=ρVq=0.8×103kg/m 3×1.5×10-3m 3×4×107J/kg=4.8×107Jη=W Q =1.68×107J 4.8×107J=35%。
2022年中考数学人教版基础训练:全等三角形

2022年中考数学人教版基础训练:全等三角形一、选择题(本大题共10道小题)1. AD是△ABC的角平分线,自D点向AB、AC两边作垂线,垂足为E、F,那么下列结论中错误的是( )A.DE = DFB. AE = AFC.BD = CDD. ∠ADE =∠ADF2. 两个三角形有两个角对应相等,正确说法是()A.两个三角形全等B.两个三角形一定不全等C.如果还有一角相等,两三角形就全等D.如果一对等角的角平分线相等,两三角形全等3. 在下列结论中, 正确的是( )A.全等三角形的高相等B.顶角相等的两个等腰三角形全等C. 一角对应相等的两个直角三角形全等D.一边对应相等的两个等边三角形全等4. 如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )A.∠B=∠EB.∠BAD=∠EACC.∠BAC=∠EADD.BC=ED5. 如图,在△ABC中,AB=AC,AD⊥BC于点D,下列结论不正确的是( )A.∠B=∠C B.BD=CDC.AB=2BD D.AD平分∠BAC6. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A.∠A与∠D互为余角 B.∠A=∠2 C.△ABC≌△CED D.∠1=∠27. 如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=()A.40° B.50° C.60° D.75°8. 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( ).A.PD=PE B.OD=OE C.∠DPO=∠EPO D.PD=OD9. 平面上有△ACD与△BCE,其中AD与BE相交于P点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为()A.110°B.125°C.130°D.155°10. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是()A.15 B.30 C.45 D.60二、填空题11. 杜师傅在做完门框后,为防止门框变形常常需钉两根斜拉的木条,这样做的数学原理是12. 如图,在图中的两个三角形是全等三角形,其中A和D、B和E是对应点.(1)用符号“≌“表示这两个三角形全等(要求对应顶点写在对应位置上);(2)写出图中相等的线段和相等的角;(3)写出图中互相平行的线段,并说明理由.13. 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=______14. 如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“______”.15.如图,△ABC是三边均不等的三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画个.16. 如图所示,∠AOB=60°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DCO=________.17. 如图,已知△ABC(AC>AB),DE=BC,以D,E为顶点作三角形,使所作的三角形与△ABC全等,则这样的三角形最多可以作出________个.AA BB的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳), 18. 把两根钢条','如图,若测得AB=5厘米,则槽宽为厘米.三、解答题19. 如图,已知AB DC AC DB==,.求证:12∠=∠.20. 已知,在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠E=∠C.21. 如图,木工师傅常用角尺来作任意一个角的平分线,请你设计一个方案,只用角尺来作∠AOB的平分线,并说明理由.22. 已知:如图所示,BF与CE相交于点D,BD=CD,BF⊥AC于点F,CE⊥AB于点E,求证:点D 在∠BAC的平分线上.23.如图,两根旗杆AC、BD间相距12m,某人从A点沿AB走向B,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1/m s,求这个人运动了多长时间?24. 在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC 的平分线交BC于点G,连接FG.(1)求∠DFG的度数;(2)设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.25.如图①,点A,E,F,C在一条直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.(1)若BD与EF交于点G,试证明BD平分EF;(2)若将△DEC沿AC方向移动到图②的位置,其余条件不变,上述结论是否仍然成立?请说明理由.26. 在△ABC中,,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE;(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系?请写出这个等量关系,并加以证明.。
2023年中考物理基础训练——电功率的计算

2023年中考物理基础训练——电功率的计算一、计算题1.(1)1度电可以供20W 的灯泡工作多长时间?(2)一台电视机10h 耗电1度,这台电视机的功率是多少?2.如图所示,电源电压恒定,电阻R 的阻值为30Ω。
闭合开关后,通过R 的电流为0.1A ,通过灯L 的电流为0.2A 。
求:(1)R 两端的电压;(2)灯泡L 的实际功率。
3.用额定功率为250W 的电加热器将质量为300g 的水由18℃加热至38℃用了2min ,电加热器正常工作。
()()34210J /kg c =⨯⋅水.℃求: (1)水吸收的热量。
(2)电加热器的效率。
4.如图所示为某款电热水龙头电路图,a 、b 、c 、d 为四个固定触点,绕O 点转动的扇形金属触片P 可同时接触两个触点。
触片P 置于不同位置时,有冷水、温水和热水三种状态,正常工作时出温水的电功率为1100W ,出热水的电功率为2200W 。
(1)求出温水时电路中的电流;(2)求出热水时2分钟内消耗的电能;(3)若水龙头只能出冷水和温水,电路可能存在的故障。
(写出一条即可)5.如图甲所示的电路中,R 0为定值电阻,R 1为滑动变阻器(其最大阻值为40Ω).闭合开关S 后,当滑动变阻器的滑片P 从a 端移至b 端的过程中,R 1消耗的电功率随R 1电阻变化关系如图乙所示,根据图像信息.求:(1)电路中最小电流;(2)电源电压;(3)R0消耗的最大电功率.6.如图所示电路中,小灯泡L上标有“3V 0.9W”字样,R1和R2均为定值电阻,其中R1=15Ω。
闭合开关S1,开关S2接a,小灯泡L正常发光;开关S2接b,小灯泡L的电功率只有正常发光时的14,忽略温度变化对小灯泡电阻的影响。
求:(1)电源电压U;(2)定值电阻R2的阻值;7.如图所示,电源电压恒为12V,小灯泡上标有“6V 3.6W”字样且灯丝电阻保持不变,当只闭合开关S、S1时,小灯泡正常发光;当所有开关都闭合,且滑动变阻器的滑片滑到最右端时,电流表A的示数是1.8A。
苏科版2019-2020九年级数学第一学期期中综合复习基础训练3(附答案)

苏科版2019-2020九年级数学第一学期期中综合复习基础训练3(附答案)1.下列说法:①如果a 2>b 2,那么a>b ;4;③过一点有且只有一条直线与已知直线平行;④关于x 的方程2210mx x ++=没有实数根,那么m 的取值范围是m>1且m≠0;正确的有( )A .0个B .1个C .2个D .3个2.如图,如果从半径为9cm 的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径为( )A .6cmB .3cmC .5cm D .3cm 3.如图,AB 是O 的直径,120BOD =∠,点C 为BD 的中点,AC 交OD 于点E ,1DE =,则AE 的长为( )A B C .D .4.若关于x 的一元二次方程mx 2﹣2x +1=0有两个实数根,则实数m 的取值范围是( )A .m ≤1B .m ≤﹣1C .m ≤1且m ≠0D .m ≥1且m ≠0 5.下列说法正确的是( )A .一个游戏中奖的概率是1100,则做100次这样的游戏一定会中奖 B .为了了解全国中学生的心理健康状况,应采用普查的方式C .一组数据0,1,2,1,1的众数和中位数都是1D .若甲组数据的方差为2s 甲,乙组数据的方差为2s 乙,则乙组数据比甲组数据稳定6.某型号的手机连续两次降阶,每台手机售价由原来的1185元降到580元,设平均每次降价的百分率为,则列出方程正确的是( )A .580(1+x)2=1185B .1185(1-x)2=580C.580(1-x)2=1185 D.1185(1+x)2=5807.如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为()A B.2 C.D.(1+8.一组数据2,3,5,4,5的众数是()A.2 B.3 C.4 D.59.如图,已知⊙O的半径为5,点A到圆心O的距离为3,则过点A的所有弦中,最短弦的长为( )A.4 B.6 C.8 D.1010.通过测试从9位书法兴趣小组的同学中,择优挑选5位去参加中学生书法表演,若测试结果每位同学的成绩各不相同.则被选中同学的成绩,肯定不少于这9位同学测试成绩统计量中的()A.平均数B.众数C.中位数D.方差11.在如图所示的电路图中,在开关全部断开的情况下,闭合其中任意一个开关,灯泡发亮的概率是______.12.如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为O.以点C为圆心,BC为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是_____.13.一组数据2,4,5,,1的平均数为,那么这组数据的方差是___.14.关于x 的方程x 2+2(m ﹣1)x ﹣4m =0的两个实数根分别是x 1,x 2,且x 1﹣x 2=2,则m 的值是_____.15.已知圆锥的母线长为5cm ,侧面积为15π2cm ,则这个圆锥的底面圆半径为_____cm.16.已知a ,b 是方程x 2+2017x +2=0的两个根,则(2+2019a +a 2)(2+2019b +b 2)的值为______.17.如图,四边形ABCD 为⊙O 的内接四边形,点E 在DA 的延长线上,已知∠BCD=110°,则∠BAE =_______°.18.已知O 的半径为4cm ,点P 在直线l 上,且点P 到圆心O 的距离为4cm ,则直线l 与O ______.19.如图,△ABC 中,AB =8,BC =10,AC =7,∠ABC 和∠ACB 的平分线交于点 I ,IE ⊥BC 于E ,则 BE 的长为________.20.一元二次方程290x x +=的解是______.21.如图,已知Rt △ABC 中,∠ACB=90°,以AC 为直径的圆O 交斜边AB 于D .过D 作DE ⊥AC 于E ,将△ADE 沿直线AB 翻折得到△ADF .(1)求证:DF 是⊙O 的切线;(2)若⊙O 的半径为10,sin ∠FAD=35,延长FD 交BC 于G ,求BG 的长.22.已知:关于x 的方程()222120x m x m -+++=. ()1若方程总有两个实数根,求m 的取值范围;()2在(1)的条件下,若两实数根1x 、2x 满足1212x x x x +=,求m 的值.23.每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x≤85,B.85≤x≤90,C.90≤x≤95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:90,80,90,86,99,96,96,100,89,82八年级10名学生的竞赛成绩在C组中的数据是:94,90,94根据以上信息,解答下列问题:(1)直接写出上述图表中a,b,c的值;(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);(3)该校七、八年级共730人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≧90)的学生人数是多少?24.已知ABC,()1用无刻度的直尺和圆规作ABD,使A D B A C B.∠∠=且ABD的面积为ABC 面积的一半,只需要画出一个ABD即可(作图不必写作法,但要保留作图痕迹) ()2在ABC中,若ACB45∠=,AB4=,则ABC面积的最大值是______25.足球训练场上,教练在球门前画了一个圆圈进行无人防守的射门训练.如图,甲、乙两名运动员分别在C,D两处,他们争论不休,都说自己所在的位置对球门AB的张角大,如果你是教练,请评一评他们两个人谁的位置对球门AB的张角大?为什么?26.如图①,四边形ABCD 与四边形CEFG 都是矩形,点E ,G 分别在边CD ,CB 上,点F 在AC 上,AB =3,BC =4(1)求AF BG的值; (2)把矩形CEFG 绕点C 顺时针旋转到图②的位置,P 为AF ,BG 的交点,连接CP (Ⅰ)求AF BG 的值; (Ⅱ)判断CP 与AF 的位置关系,并说明理由.27.解下列方程(1)x 2+12x +27=0(2)3x 2-2=5x28.如图1,四边形ADBC 内接于O ,AB 为O 的直径,对角线AB 、CD 相交于点E .图1 图2图3(1)求证:90BCD ABD ∠+∠=︒;(2)如图2,点G 在AC 的延长线上,连接BG ,交O 于点Q ,CA CB =,ABD ABG ∠=∠,作GH CD ⊥,交DC 的延长线于点H ,求证:GQ = (3)如图3,在(2)的条件下,过点B 作//BF AD ,交CD 于点F ,3GH CH =,若CF =O 的半径.参考答案1.A【解析】【分析】①当a是负数且绝对值大于b(正数)时,不成立;②4,再求其算术平方根即可;③当点在直线上时,没有与已知直线平等的直线;④根据一元二次方程根的判别式进行判断.【详解】①当a=-5时,b=2时,a2>b2,a<b,故①错误;=4,故其算术平方根为2,故②错误;③当点在直线上时,没有与已知直线平行的直线,正确说法是:过直线外一点有且只有一条直线与已知直线平行,故③错误;④关于x的方程mx2+2x+1=0没有实数根,那么m的取值范围是m>1,故此选项错误.所以正确的有0个.故选:A.【点睛】考查了算术平方根的定义、一元二次方程根的判别式等知识,正确把握相关性质是解题关键.2.A【解析】【分析】设圆锥的底面圆半径为r,先利用圆的周长公式计算出剩下的扇形的弧长,然后把它作为圆锥的底面圆的周长进行计算即可.【详解】设圆锥的底面圆半径为r,∵半径为9cm的圆形纸片剪去一个圆周的扇形,∴剩下的扇形的弧长=×2π×9=12π,∴2πr=12π,∴r=6.【点睛】本题考查了圆锥的有关计算:圆锥的侧面展开图为扇形,圆锥的底面圆的周长等于扇形的弧长.也考查了圆的周长公式.3.A【解析】【分析】连接OC ,证明OD ⊥AC 即可解决问题.【详解】解:连接OC ,∵弧CD=弧BC ,∴60DOC BOC ∠=∠=︒,60AOD ∠=︒,∴AOD DOC ∠=∠,∴弧AD=弧CD ,∴OD AC ⊥,90AEO ∠=︒,设AO r =,则1OE r =-,∵·cos60OE AO =︒, ∴112r r -=,2r =,∴AE =故选:A.【点睛】本题考查圆周角定理,垂径定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.4.C【解析】利用一元二次方程的定义和判别式的意义得到m≠0且△=(﹣2)2﹣4m≥0,然后求出两不等式的公共部分即可.【详解】根据题意得m≠0且△=(﹣2)2﹣4m≥0,解得m≤1且m≠0.故选:C.【点睛】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.5.C【解析】【分析】根据调查方式,可判断A,根据概率的意义一,可判断B根据中位数、众数,可判断c,根据方差的性质,可判断D.【详解】A、一个游戏中奖的概率是1100,做100次这样的游戏有可能中奖,而不是一定中奖,故A错误;B、为了了解全国中学生的心理健康状况,应采用抽查方式,故B错误;C、一组数据0,1,2,1,1的众数和中位数都是1,故C正确;D. 若甲组数据的方差为2s甲,乙组数据的方差为2s乙,无法比较甲乙两组的方差,故无法确定那组数据更加稳定,故D错误.故选:C.【点睛】本题考查了概率、抽样调查及普查、中位数及众数、方差等,熟练的掌握各知识点的概念及计算方法是关键.6.B【解析】根据降价后的价格=原价(1-降低的百分率),本题可先用x表示第一次降价后商品的售价,再根据题意表示第二次降价后的售价,即可列出方程.【详解】设平均每次降价的百分率为x,由题意得出方程为:1185(1−x)2=580.故选:B.【点睛】本题考查的是由实际问题列出一元二次方程,正确列出方程是解题的关键.7.C【解析】【分析】过O作OC⊥AB,交圆O于点D,连接OA,由垂径定理得到C为AB的中点,再由折叠得到CD=OC,求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,即可确定出AB的长.【详解】过O作OC⊥AB,交圆O于点D,连接OA,由折叠得到CD=OC=12OD=1cm,在Rt△AOC中,根据勾股定理得:AC2+OC2=OA2,即AC2+1=4,解得:,则.故选C.【点睛】此题考查了垂径定理,勾股定理,以及翻折的性质,熟练掌握垂径定理是解本题的关键.8.D【解析】【分析】根据众数的定义:一组数据中出现次数最多的数据即可得出答案.【详解】解:这组数据中出现次数最多的数据为:5.故众数为5,故选:D.【点睛】本题考查了众数的知识,属于基础题,解答本题的关键是熟练掌握一组数据中出现次数最多的数据叫做众数.9.C【解析】【分析】最短弦是过A点垂直于OA的弦.根据垂径定理和勾股定理求解.【详解】由垂径定理得,该弦应该是以OA为中垂线的弦BC.连接OB.已知OB=5,OA=3,由勾股定理得AB=4.所以弦BC=8.故选C.【点睛】此题主要考查了学生对垂径定理及勾股定理的理解运用.10.C【解析】【分析】由于从9个人中挑选5位,则应根据中位数的意义进行解答.【详解】∵从9位书法兴趣小组的同学中,择优挑选5位去参加中学生书法表演,∴则被选中同学的成绩,肯定不少于这9位同学测试成绩统计量中的中位数,故选C .【点睛】本题考查了统计的相关知识,涉及了平均数、中位数、众数、方差等,要结合具体的问题对统计量进行合理的选择和恰当的运用.11.13【解析】【分析】根据概率公式知,共有3个开关,只闭一个开关时,只有闭合S 3时才发光,所以小灯泡发光的概率等于1.3【详解】根据题意,三个开关,只有闭合3S 小灯泡才发光,所以小灯泡发光的概率等于13. 故答案为:13【点睛】考查概率的计算,明确概率的意义是解题的关键,概率等于所求情况数与总情况数的比.12.53π﹣ 【解析】【分析】如图,图中S 阴影=S 扇形BCE ﹣S 扇形BOD ﹣S △OCE .根据已知条件易求得OB =OC =OD =2,BC=CE =4.∠ECB=60°,∠OEC=30°,所以由扇形面积公式、三角形面积公式进行解答即可 【详解】解:如图,连接CE .∵AC ⊥BC ,AC =BC =4,以BC 为直径作半圆,圆心为点O ;以点C 为圆心,BC 为半径作弧AB ,∴∠ACB =90°,OB =OC =OD =2,BC =CE =4.又∵OE ∥AC ,∴∠ACB =∠COE =90°.∴在直角△OEC 中,OC =2,CE =4,∴∠CEO =30°,∠ECB =60°,OE =∴S 阴影=S 扇形BCE ﹣S 扇形BOD ﹣S △OCE =2604360 π ﹣14 π×22﹣12×2×=53π﹣,故答案为:53π﹣【点睛】此题考查扇形面积的计算,掌握运算法则是解题关键13.2【解析】【分析】根据平均数的计算方法求得a 的值,再利用方差公式计算这组数据的方差即可.【详解】∵数据2,4,5,a ,1的平均数为a , ∴(2 +4+5+a+1)=a ,∴a=3,∴s 2=[(2-3)2+(4-3)2+(5-3)2+(3-3)2+(1-3)2]=2.故答案为:2.【点睛】本题考查了平均数及方差的计算公式,熟知平均数及方差的计算公式是解决问题的关键. 14.m =0或m =﹣2.【解析】【分析】由韦达定理得出x 1+x 2=﹣2(m ﹣1),x 1x 2=﹣4m ,结合x 1﹣x 2=2知122x m x m =-+⎧⎨=-⎩,代入x 1x 2=﹣4m 可得关于m 的方程,解之可得答案.【详解】解:∵关于x 的方程x 2+2(m ﹣1)x ﹣4m =0的两个实数根分别是x 1,x 2,∴x 1+x 2=﹣2(m ﹣1),x 1x 2=﹣4m ,又∵x 1﹣x 2=2,∴1212222x x m x x +=-+⎧⎨-=⎩, 解得:122x m x m =-+⎧⎨=-⎩, 代入x 1x 2=﹣4m 得﹣m (﹣m+2)=﹣4m ,解得:m =0或m =﹣2,故答案为:m =0或m =﹣2.【点睛】本题主要考查一元二次方程根与系数的关系,根据韦达定理及x 1﹣x 2=2得出关于m 的方程是解题的关键.15.3【解析】【分析】根据圆锥的侧面积和圆锥的母线长求得圆锥的弧长,利用圆锥的侧面展开扇形的弧长等于圆锥的底面周长求得圆锥的底面半径即可.【详解】∵圆锥的母线长是5cm ,侧面积是15πcm2,∴圆锥的侧面展开扇形的弧长为:215=65ππ⨯, ∵锥的侧面展开扇形的弧长等于圆锥的底面周长,∴r=62ππ=3cm , 故答案为:3.【点睛】本题考查了圆锥的计算,解题的关键是正确地进行圆锥与扇形的转化.16.8.【解析】【分析】根据已知条件得到2+2017a+a2=0,2+2017b+b2=0,ab=2,代入代数式即可得到结论.【详解】∵a,b是方程x2+2017x+2=0的两个根,∴2+2017a+a2=0,2+2017b+b2=0,ab=2,∴(2+2019a+a2)(2+2019b+b2)=(2+2017a+2a+a2)(2+2017b+2b+b2)=4ab=8,故答案为:8.【点睛】本题考查了一元二次方程根与系数的关系,熟练掌握根与系数的关系是解题的关键.17.110【解析】【分析】根据圆内接四边形的任意一个外角等于它的内对角解答.【详解】∵四边形ABCD是⊙O的内接四边形,∴∠BAE=∠BCD=110°,故答案为:110.【点睛】本题考查了圆内接四边形的性质,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键.18.相交或相切【解析】【分析】根据直线与圆的位置关系即可得出结论.【详解】解:∵点P在直线l上,且点P到圆心O的距离为4cm,等于直径,∴点P在⊙O上∴直线l与⊙O相交或相切故答案为:相交或相切【点睛】本题考查直线与圆的位置关系,解题的关键是熟知直线与圆的三种位置关系.19.【解析】【分析】如图作△ABC 的内切圆,切点分别为 E ,F ,G ,根据切线长定理即可解决问题;【详解】解:如图作△ABC 的内切圆,切点分别为 E ,F ,G ,∵BE =BF ,AF =AG ,CE =CG ,∴BE ==, 故答案为. 【点睛】本题考查角平分线的性质,三角形的内切圆,切线长定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.20.0x =或9x =-【解析】【分析】因式分解法求解可得.【详解】解:()90x x +=,0x ∴=或90x +=,解得:0x =或9x =-,故答案为:0x =或9x =-.【点睛】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.21.(1)见解析(2)15 4【解析】【分析】(1)由△ADE沿直线AB翻折得到△ADF,得到∠DAE=∠DAF,∠AED=∠F=90°,由于OA=OD,于是得到∠DAE=∠ODA,根据平行线的判定定理得到OD∥AF,根据平行线的性质得到OD⊥DF,于是得到结论;(2)连接DC,由于AC是O的直径,即CD⊥AB;又FD与BC均是O的切线且相交于点G由切线长定理可得:GD=GC,于是得到∠GDC=∠GCD,由于GD是Rt△BDC斜边上的中线,即GD=12BC,由于△ADE沿直线AB翻折得到△ADF,得到sin∠DAE=sin∠DAF=35,解直角三角形得到sin∠DAC=DCAC=10DC=35,得DC=6,由勾股定理得AD=8;根据三角形相似即可得到结论.【详解】(1)证明:∵△ADE沿直线AB翻折得到△ADF,∴∠DAE=∠DAF,∠AED=∠F=90°,又∵OA=OD,∴∠DAE=∠ODA,∴∠DAF=∠ODA,∴OD∥AF,∴∠ODF+∠F=180°,∴∠ODF=90°,∴OD⊥DF,∴DF是O的切线;(2)连接DC,∵AC是圆O的直径,∴∠ADC=90°,即CD⊥AB;又∵FD与BC均是圆O的切线且相交于点G,由切线长定理可得:GD=GC,∴∠GDC=∠GCD,又∵Rt△BDC中,∠GCD+∠B=90°,∠GDC+∠GDB=90°,∴∠B=∠GDB,∴GD=GB,∴GD是Rt△BDC斜边上的中线,即GD=12 BC,∵△ADE沿直线AB翻折得到△ADF,∴∠DAE=∠DAF,∴sin∠DAE=sin∠DAF=35,又∵圆O的半径为5,∴AC=10,Rt△DAC中,∠ADC=90°,∴sin∠DAC=DCAC=DC10=35,得DC=6,由勾股定理得AD=8;在Rt △ADC 与Rt △ACB 中,∠ADC=∠ACB=90°,∠DAC=∠BAC ,∴Rt △ADC ∽Rt △ACB , ∴CD AD BC AC =,即6810BC =,解得BC=152; ∴GB=GD=12BC=154. 【点睛】本题考查的知识点是切线的判定, 翻折变换(折叠问题), 相似三角形的判定与性质,解题的关键是熟练的掌握切线的判定, 翻折变换(折叠问题), 相似三角形的判定与性质. 22.(1)12m >;(2)2m =. 【解析】【分析】 ()1由0>得840m ->,解之可得;()2由()1221x x m +=+,2122x x m =+,结合1212x x x x +=得()2212m m +=+,解之可得m 的值,依据()1中的结果取舍即可得.【详解】解:()()()221[21]412m m =-+-⨯⨯+ 2248448m m m =++--840m =->,12m ∴>; ()()12221x x m +=+,2122x x m =+,∴由1212x x x x +=得()2212m m +=+,解得:10m =,22m =, 12m >, 2m ∴=.【点睛】本题主要考查根的判别式、根与系数的关系,关键是掌握1x ,2x 是方程20x px q ++=的两根时,12x x p +=-,12x x q =.23.(1)a=40,b=94,c=99;(2)八年级,见解析;(3)参加此次竞赛活动成绩优秀的人数是468人.【解析】【分析】(1)根据中位数和众数的定义即可得到结论;(2)根据八年级的中位数和众数均高于七年级于是得到八年级学生掌握防溺水安全知识较好;(3)利用样本估计总体思想求解可得.【详解】解:(1)3120%10%1004010a ⎛⎫=---⨯= ⎪⎝⎭, ∵八年级10名学生的竟赛成绩的中位数是第5和第6个数据的平方数,∴ 9494942b +== ∵在七年级10名学生的竟赛成绩中99出现的次数最多,∴c=99;(2)八年级学生掌握防溺水安全知识较好,理由:虽然七、八年级的平均分均为92分,但八年级的中位数和众数均高于七年级.(3)参加此次竞赛活动成绩优秀(x≥90)的学生人数=720×1320=468人, 答:参加此次竞赛活动成绩优秀(x≥90)的学生人数是468人.【点睛】本题考查读扇形统计图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问24.(1)详见解析;(2)4+【解析】【分析】(1)先作出ABC 的外接圆,再作AB 边上的高,继而作出此高的中垂线,与外接圆的交点即为所求;(2)作以AB 为弦且AB 所对圆心角为90°的O ,则垂直于弦AB 的直径与优弧的交点即为使三角形面积最大的点C ,根据作图得出AB 边上的高可得答案.【详解】∠即为所求.解:()1如图1所示,ABD()2如图2所示,作以AB为弦,且AB所对圆心角为90的O,C点轨迹为圆上不与AB重合的任一点,∴当C在位置上时,高最长,故面积最大,=,AB4AP BP OP2∴===,则OC OA==∴=+PC2ABC ∴的面积为(11AB PC 42422⋅⋅=⨯⨯+=+故答案为:4+.【点睛】 本题主要考查作图复杂作图,解题的关键判断出点C 是以AB 为弦的圆上、圆的确定及线段的中垂线的尺规作图等知识点.25.一样大,理由见解析.【解析】【分析】根据圆周角定理,即可确定两角的大小.【详解】解:甲、乙两个人所在的位置对球门AB 的张角一样大.根据圆周角定理的推论可得∠ADB=∠ACB.【点睛】本题的解答关键是对圆周角定理的灵活运用.圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半;即同弦或等弦所对的圆周角相等.26.(1)54AF BG =;(2)(Ⅰ)54AF BG =;(Ⅱ)CP ⊥AF ,理由:见解析. 【解析】【分析】(1)根据矩形的性质得到∠B =90°,根据勾股定理得到AC =5,根据相似三角形的性质即可得到结论;(2)(Ⅰ)连接CF ,根据旋转的性质得到∠BCG =∠ACF ,根据相似三角形的判定和性质定理得到结论;(Ⅱ)根据相似三角形的性质得到∠BGC =∠AFC ,推出点C ,F ,G ,P 四点共圆,根据圆周角定理得到∠CPF =∠CGF =90°,于是得到结论.【详解】(1)∵四边形ABCD 是矩形,∴∠B =90°,∵AB =3,BC =4,∴AC=5,∴54 ACBC=,∵四边形CEFG是矩形,∴∠FGC=90°,∴GF∥AB,∴△CGF∽△CBA,∴54 CF CACG CB==,∵FG∥AB,∴54 AF CFBG CG==;(2)(Ⅰ)连接CF,∵把矩形CEFG绕点C顺时针旋转到图②的位置,∴∠BCG=∠ACF,∵54 AC CFBC CG==,∴△BCG∽△ACF,∴54 AF ACBG BC==;(Ⅱ)CP⊥AF,理由:∵△BCG∽△ACF,∴∠BGC=∠AFC,∴点C,F,G,P四点共圆,∴∠CPF=∠CGF=90°,∴CP⊥AF.【点睛】本题考查了相似三角形的判定和性质,矩形的性质,平行线分线段成比例定理,旋转的性质,熟练掌握相似三角形的判定定理是解题的关键.27.(1)x 1=-3,x 2=-9;(2)x 1=2,x 2=-13. 【解析】【分析】 (1)直接把等号左边进行因式分解,然后可得x+3=0,x+9=0,再解即可;(2)先整理成一般形式,然后用公式法解答即可.【详解】(1)(x+3)(x+9)=0,x+3=0,x+9=0,解得:x 1=-3,x 2=-9;(2) 3x 2-2=5x整理为:3x 2-5x-2=0,这里,a=3,b=-5,c=-2,b 2-4ac=(-5)2-4×3×(-2)=49>0,∴ ∴x 1=2,x 2=13-.【点睛】本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程.28.(1)证明见解析;(2)证明见解析;(3).【解析】【分析】(1)根据圆周角定理即可证明;(2)作AM AD ⊥交DC 延长线于点M ,连接MG ,AQ ,证明AMG QAG ∆≅∆,得到45GMH AMD ∠=∠=︒,易求得GQ =;(3)延长MG 交DB 于N ,延长BF 交6030m n =⎧⎨=-⎩于W ,则四边形AMND 是正方形,求出13EF ED =,设EF x =,则3ED x =,列式求出EF ,易得AB ,问题得解. 【详解】解:(1)证明:AB Q 是直径90BCD ABD ∴∠+∠=︒BCD DAB ∠=∠90DAB DBA ∴∠+∠=︒(2)证明:作AM AD ⊥交DC 延长线于点M ,连接MG ,AQ,AB Q 是直径,90AQB ∴∠=︒,90ACB ∠=︒ABD ABG ∠=∠AQ AD ∴=CA CB =45CBA CAB ∴∠=∠=︒45ADM ∴∠=︒AM AD ∴=AM AQ ∴=BAD BAQ ∠=∠,45BAQ QAG ∠+∠=︒45BAD GAM ∴∠+∠=︒GAQ GAM ∴∠=∠AMG QAG ∴∆≅∆90AMG ∴∠=︒45GMH AMD ∴∠=∠=︒MG ∴=GQ ∴=(3)延长MG 交DB 于N ,∴四边形AMND 是正方形延长BF 交6030m n =⎧⎨=-⎩于W //BW MN BWG MGA ∴∠=∠BWG BGW ∴∠=∠BG BW ∴=MG BD BW +=WF MG ∴=FC MC ∴=BAD BCD HGC ∠=∠=∠,3HG CH =1tan 3BAD ∴∠=13BD BF AD AD ∴== 13EF ED ∴= 设EF x =,则3ED x =222EC CM DE =+222((3)x x ∴+=+x ∴=DF =4BD =,12AD =AB ∴=r =【点睛】本题是圆和四边形的综合问题,考查了圆周角定理、三角形全等的判定和性质以及三角函数等知识点,涉及知识点较多,图形较为复杂,能够作出辅助线是解题关键.。
中考语文基础训练试卷答案

一、选择题1. 下列词语中字形、字音、字义完全正确的一项是()A. 谦虚(qiān xū)妩媚(wǔ mèi)精神抖擞(jīng shén dǒu sǒu)B. 沉着(chén zhù)端庄(duān zhuāng)息息相关(xī xī xiāng guān)C. 狂妄(kuáng wàng)纤细(xiān xì)风驰电掣(fēng chí diàn chè)D. 神秘(shén mì)娇艳(jiāo yàn)蹦蹦跳跳(bèng bèng tiào tiào)答案:D2. 下列句子中,加点词解释错误的一项是()A. 他神情恍惚,好像刚从梦中醒来。
(恍:模糊不清)B. 这本书的内容十分丰富,引人入胜。
(入胜:吸引人)C. 她那双明亮的眼睛里闪烁着智慧的光芒。
(闪烁:闪耀)D. 春天的阳光温暖而明媚,万物复苏。
(明媚:鲜明可爱)答案:A3. 下列词语中,加点字音、字形、字义都正确的一项是()A. 沉思(chén)深思熟虑(shēn)沉着冷静(zhù)B. 恍惚(huǎng)恍若隔世(wǎng)恍然大悟(huǎng)C. 精湛(zhàn)精益求精(jīng)精疲力尽(jīng)D. 狂妄(kuáng)狂风暴雨(kuáng)狂热(kuáng)答案:B二、填空题4. 下列词语中,加点字音、字形、字义都正确的一项是()A. 沉思(chén)深思熟虑(shēn)沉着冷静(zhù)B. 恍惚(huǎng)恍若隔世(wǎng)恍然大悟(huǎng)C. 精湛(zhàn)精益求精(jīng)精疲力尽(jīng)D. 狂妄(kuáng)狂风暴雨(kuáng)狂热(kuáng)答案:C5. 下列句子中,加点词语解释错误的一项是()A. 他神情恍惚,好像刚从梦中醒来。
【每日一练】经典高考数学基础训练(3)(含参考答案)

【每日一练】经典高考数学基础训练(3)(含参考答案)一、选择题:1.设集合{ EMBED Equation.DSMT4 |{2,1,0,1,2},{|12},()S T x R x S T =--=∈+≤= S 则CA .B .C .D .2.已知向量,若与共线,则等于A .B .C .D .43.函数在=1处的导数等于A .2B .3C .4D .54.设:,:关于的方程有实数根,则是的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.已知函数的最小正周期为,则该函数的图象A .关于点对称B .关于直线对称C .关于点对称D .关于直线对称6.一个四边形的四个内角成等差数列,最小角为,则最大角为A .B .C .D .7.函数的零点所在的区间是A .B .C .D .8.函数的值域是A .B .C .D .9.如果我们定义一种运算: 已知函数,那么函数的大致图象是10.4只笔与5本书的价格之和小于22元,而6只笔与3本书的价格之和大于24元,则2只笔与3本书的价格比较( )A .2只笔贵B .3本书贵C .二者相同D .无法确定二、填空题:11.函数的单调减区间是;12.定义在R上的奇函数f(x)满足,若则________;13.知抛物线和双曲线都经过点,它们在轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是.14.设是等比数列的前项和,对于等比数列,有真命题若成等差数列,则成等差数列。
请将命题补充完整,使它也是真命题,命题若成等差数列,则成等差数列(只要一个符合要求的答案即可) 三、解答题已知数列是等差数列,且,是数列的前项和.() 求数列的通项公式及前项和;() 若数列满足,且是数列的前项和,求与.答案一、选择题1.B2.A3.C4.A5.B 6。
A 7.B 8.D 9.B 10.A10.设每支笔x元,每本书y元,有二、填空题:11.(-1,1)12. -1 13.14.案不唯一三、解答题:解:()设数列的公差为,由题意可知:,解得:…………………………3分∴……………………………………5分…………………………………………7分() ………………………………9分……12分。
九年级数学中考复习第一轮复习基础训练三角函数(一)三角函数与解直角三角形 课时作业同步练习含答案解析

微专题8 三角函数(一)三角函数与解直角三角形考点1锐角三角函数的定义1.如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,则 sin A 等于( ) A.35 B.45 C.34 D.432.如图,边长为1的小正方形网格中, ⊙O 的圆心在格点上,cos ∠AED = .3.如图,在△ABC 中,CA=CB =4, cos C =14,则sinB 的值为 . 考点2 特殊角的三角函数值4.(1) sin 30°= ; cos 60°= ;tan 45"= ;(2)3sin 60"—2cos 30°—tan 60°= .5.在△ABC 中,∠A ,∠B 为锐角,若|sinA 一22|+(32-cosB )2=0,则∠C = 度. 考点3 解直角三角形及其实际应用6.如图,在△ABC 中,∠B =30°,AC=2,cosC =35.则AB 边的长为 .7.如图,某地修建高速公路,要从B 地向C 地修一座隧道(B,C 在同一水平面上),为了测量B ,C 两地之间的距离,某工程队员乘坐热气球从C 地出发垂直上升100m 到达A 处,在A 处观察B 地的俯角为30°,则B,C 两地间的距离为 m .8.如图,一艘船由A 港沿北偏东65°方向航行302km 至B 港,然后再沿北偏西40°方向航行至C 港,C 港在A 港北偏东20°方向,则A,C 两港之间的距离为 km.DOB AECAC ABCB第1题图第2题图第3题图30°30°B CC A CAB AB 第6题图 第7题图 第8题图9.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD.10.某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1.(1)求新坡面的坡角α的度数;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由. :C BC微专题8 三角函数(一)三角函数与解直角三角形考点精练精练1锐角三角函数的定义1.如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,则 sin A 等于( A ) A.35 B.45 C.34 D.432.如图,边长为1的小正方形网格中, ⊙O 的圆心在格点上,cos ∠AED =255. 3.如图,在△ABC 中,CA=CB =4, cos C =14,则sinB 的值为104.精练2 特殊角的三角函数值4.(1) sin 30°=12; cos 60°=12;tan 45"= 1 ;(2)3sin 60"—2cos 30°—tan 60°= 32 .5.在△ABC 中,∠A ,∠B 为锐角,若|sinA 一22|+(32-cosB )2=0,则∠C =105度. 精练3 解直角三角形及其实际应用6.如图,在△ABC 中,∠B =30°,AC=2,cosC =35.则AB 边的长为165.DOB AECAC ABCB第1题图第2题图第3题图30°30°BC CACABAB第6题图第7题图第8题图7.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程队员乘坐热气球从C地出发垂直上升100m到达A处,在A处观察B地的俯角为30°,则B,C两地间的距离为.8.如图,一艘船由A港沿北偏东65°方向航行至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为(30+km.9.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD.解:设AD=x米,则BDx米.CD=AD=xx-x=100.解得:x=50.答:山高为(50)米.10.某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1.(1)求新坡面的坡角α的度数;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由. 解:(1)30°:(2)过点C作CD⊥AB于点D.则BD=CD=6.AD∴AB=AD-BD一6<8∴文化培PM不需要拆除.C B。
上海市2020年中考物理一模复习知识手册与必刷题 压强(基础练习题)(原卷版)

专题6.2 压强 02 基础训练题一、填空题1.在物理学中把_______作用在物体表面上的力叫压力,它是物体间由于挤压发生______而产生的。
2.如图1所示,放在水平面上的物体受到的重力为G ,在等大的力F 的作用下,则物体对支撑面的压力大于物体重力的是图_______,小于物体重力的是图 ,与物体重力无关的是图_______,与力F 无关的是图________。
(已知F<G )3.如图2所示,物体G A=10牛,G B=20牛,A 对B 的压力是______牛,B 对地面的压力是______牛,用力的图示法表示地面所受的压力。
4.如图3所示,物体G A=6牛,物体对斜面的压力为4牛,用力的图示法作出物体对斜面的压力。
5.如图4(a )所示,重力为5牛的柱形容器内盛有10牛顿的水,则容器对地面的压力______牛。
如图4(b )所示,重力为5牛的杯形容器内盛有10牛顿的水,则容器对地面的压力为_______牛。
6.压力作用的效果不仅跟__________的大小有关系,还跟__________的大小有关系。
物理上用________表示压力作用的效果。
物体_________上受到的压力叫做压强,国际单位制中,压强的单位是“牛/米2”,读作 __________,它的专门名称叫_________。
7.2帕=________牛/米2,表示的物理意义是:______________________________。
一张报纸平放在水平桌图3图2(1)(2)图1(4)F 图4(b)图4(a )面上,对水平桌面的压强约________帕。
我们所用的九年级第一学期物理教科书共有70页纸,当它平放在水平桌面上时,对水平桌面的压强约为_______帕,若书本的长和宽为0.2米和0.3米,则书本对水平桌面压力约为______牛。
8.由压强的计算公式P=__________可知:当压力F 不变时,增大受力面积S ,则压强P 会_______;减小S 时,压强P 会__________。
升初三准备的练习题

升初三准备的练习题练习题一:语文1. 下面句子中的“所”字,在以下各句中的意义分别为:(5分)a. 看到老师进来,所坐的同学立刻站起来。
b. 在操场上跑步锻炼是我们每天早晨所做的事情。
c. 这个问题所涉及的范围非常广。
d. 我们所读的这篇文章写的是一个真实的故事。
e. 她的中国话所掌握的不错。
2. 根据阅读理解回答问题:“发热真材料”是一款教育玩具,它可以帮助孩子学习不同的科学原理。
玩具包括一个烧杯、一根温度计和一些可能的材料。
当把材料装进烧杯中、点燃并测量温度时,孩子可以观察和记录实验的结果。
下列哪个原理与“发热真材料”最相关?(5分)练习题二:数学1. 用余角的概念,计算下列各问题:a. 45°的余角是多少?b. 140°的余角是多少?c. 315°的余角是多少?(5分)2. 有两块积木,一块有 6 个阶梯,另一块有 8 个阶梯。
Tom 想用它们组成一个长方形。
那么这个长方形面积的最小值是多少呢?(10分)练习题三:英语阅读下面的短文, 根据短文内容完成后面的题目。
I like Sunday because I can play and have fun. In the morning, I always get up early and have breakfast with my family. Then we go to the park together. I play on the swings and slides. My dad always pushes me very high on the swing. It's so much fun! Sometimes I bring my kite to the park. I can fly it with my dad's help. We have a picnic in the park too. We bring sandwiches, fruits and juice. I love eating under the big tree.1. Why does the author like Sunday? (5分)2. What does the family do in the morning? (5分)3. What does the author do in the park? (5分)4. What does the author do with his dad? (5分)5. What do they bring for the picnic? (5分)练习题四:物理1. 示波器上显示的周期数是10个,振动频率是20Hz,求振动周期T和角频率ω。
人教版九年级数学中考基础训练每天一练15)

基础训练(15)时间:(10分钟)姓名________一、填空题(本大题共10小题,每小题2分,共20分.) 1.如果a 与2-互为相反数,那么a = .2.龙滩电站第一期工程年发电量为157亿千瓦时,用科学记数法表示,157亿千瓦时= 千瓦时. 3.如图1,直线AB ,CD 被EF 所截,且AB ∥CD , 如果∠1=135°,那么∠2= .4.分解因式:22242x xy y -+= .5.函数2y x =-的自变量x 的取值范围是 .6.化简:23-= .7.若两圆的半径分别为5cm 和3cm ,圆心距为1cm ,则这两个圆的位置关系是 .8.如图2,BD 是⊙O 的直径,∠A = 30°,则∠CBD = .9.已知梯形的两底边长分别为6和8,一腰长为7,则另一腰长a 的取值范围是 . 10.填在下面三个田字格内的数有相同的规律,根据此规律,C = .二、选择题(本大题共8小题,每小题3分,共24分;在每小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得零分) 11. 下列运算正确的是( )A. 236a a a =gB. 842a a a ÷= C.3362a a a +=D . 236()a a =12.为了了解本校初三年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并将其绘制成如图3所示的频数分布直方图.那么仰卧起坐次数在25~30次的频率是( )A. 0.4 B. 0.3 C. 0.2 D. 0.1CBA 55675320531图2O CDBA21FDCE B A 图1图313.若不等式组的解集在数轴上表示如图4,则这个不等式组是( )A.21x x >⎧⎨-⎩≤ B.21x x <⎧⎨>-⎩ C.21x x <⎧⎨-⎩≥ D.21x x <⎧⎨-⎩≤14.如果反比例函数ky x=的图象经过点(34)--,,那么该函数的图象位于( ) A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限15. 顺次连结菱形的各边中点所得到的四边形是 ( )A . 平行四边形B . 菱形C . 矩形16. 已知等腰三角形的两条边长分别为2和5A . 9 B . 12 C . 9或17. 已知二次函数2y ax bx c =++的图象如图A .00b c >>, B .00b c ><,C .00b c <>, D .00b c <<,18. 如图6,在矩形ABCD 中,AB =3,AD =4上,PE ⊥AC 于E ,PF ⊥BD 于F ,则PE+PF A.75 B.125 C.135 D.145图4。
中考化学复习基础训练卷——化学方程式
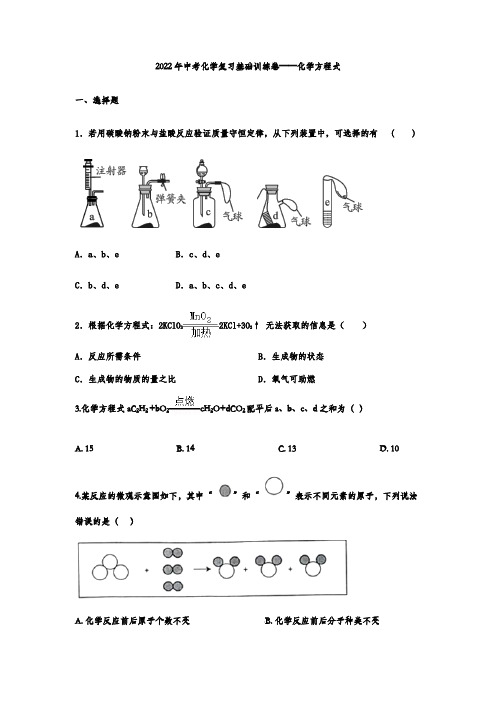
2022年中考化学复习基础训练卷——化学方程式一、选择题1.若用碳酸钠粉末与盐酸反应验证质量守恒定律,从下列装置中,可选择的有( )A.a、b、e B.c、d、eC.b、d、e D.a、b、c、d、e2.根据化学方程式:2KClO32KCl+3O2↑无法获取的信息是()A.反应所需条件B.生成物的状态C.生成物的物质的量之比D.氧气可助燃3.化学方程式aC2H2 +bO2cH2O+dCO2配平后a、b、c、d之和为()A. 15B. 14C. 13D. 104.某反应的微观示意图如下,其中“”和“”表示不同元素的原子,下列说法错误的是()A. 化学反应前后原子个数不变B. 化学反应前后分子种类不变C. 化学反应前后元素种类不变D. 化学反应前后质子总数不变5.洁厕灵、84消毒液是两种常见的清洁、消毒用品,混合使用时会发生如图反应:下列说法正确的是()A.该反应是分解反应B.有毒气体是Cl2C.反应前后元素化合价不变D.84消毒液、洁厕灵能混合使用6.实验中有些变化虽然是“<”或“>”的,但仍然符合质量守恒定律,其中不符合的是()A.铜丝的质量为m g,在火焰上灼烧后的质量为n g,则m<nB.木炭的质量为m g,在火焰上灼烧后所有灰烬的质量为n g,则m>nC.浓盐酸的质量为m g,敞口放置于空气中一段时间后质量为n g,则m>nD.氢氧化钠溶液的质量为m g,敞口放置于空气中一段时间后质量为n g,则m<n7.下列化学方程式中符合题意且书写正确的是()A.军事上利用镁作燃烧弹: Mg+O2MgO2B.生活中利用氢气作燃料: H2+O2H2OC.古代利用湿铁炼铜法制铜:Fe+CuSO4═Cu↓+FeSO4D.工业上用石灰石制生石灰:CaCO3CO2↑+CaO8.在“新型状冠病毒”的疫情防控过程中,场室常用“84消毒液”进行消毒。
但如果将洁厕灵和“84消毒液”同时使用,则会产生一种有毒的气体,发生该反应的化学方程式是:2HCl+NaClO=X+NaCl+H O,则X的化学式为2A.ClO B.Cl2C.O2D.CO9.高纯度的单晶硅是制作电子集成电路的基础材料。
2022年中考化学复习基础训练卷——身边的化学物质

2022年中考化学复习基础训练卷——身边的化学物质一、选择题1.下列关于氧气性质的描述,正确的是A.氧气的密度比空气略大B.氧气极易溶于水C.氧气可以燃烧D.氧气能与所有的物质发生化学反应2.两支试管中各注入5ml滴有石蕊试液的蒸馏水,通入CO2气体,然后将一只试管加热,另一支试管中撒入少量活性炭,其颜色变化分别为:①红—紫—无;②紫—红—紫;③紫—红—无;④无—红—无,其中正确的是A.①②B.②④C.②③D.①③3.下列关于CO2 实验室制法的说法中,不正确的是()A.制CO2的药品B.发生装置C.收集装置D.验满4.电解水实验如图,下列说法正确的是A.试管1中得到的气体为O2B.产生氢气与氧气的质量比为2:1C.可用带火星的木条检验生成的氢气D.该实验可说明水由氢元素和氧元素组成5.水是生命之源。
成市生活用水经自来水厂净化处理的过程如下图。
下列说法错误的是()A.通过反应沉淀池、过滤池除去水中不溶性杂质B.吸附池内常用活性炭吸附色素和异味C.自来水厂投入明矾进行消毒D.硬度较高的自来水,用户可用煮沸的方法来降低其硬度6.实验室用双氧水制氧气和大理石与盐酸反应制二氧化碳相比较,正确的是A.反应都需要催化剂B.反应基本类型都是分解反应C.所用药品的状态相同D.收集的方法不相同7.比较、推理是化学学习常用的方法。
以下是根据一些实验事实推理出的影响化学反应的序号实验事实影响化学反应的因素A 铁丝在空气中很难燃烧,而在氧气中能剧烈燃烧反应物浓度B 碳在常温下不与氧气发生反应,而在点燃时能与氧气反应反应温度C 双氧水在常温下缓慢分解,而在加入二氧化锰后迅速分解有、无催化剂D 铜片在空气中很难燃烧,铜粉在空气中较易燃烧反应物的种类8.小强同学在用氯酸钾制取氧气时,误把高锰酸钾当作二氧化锰加入了。
下列对该实验的分析错误的是() A. 生成氧气的速度加快了 B. 产生的氧气质量增加了C. 反应中高锰酸钾起催化作用D. 反应过程中,试管中的固体种类最多5种,最少3种9.下图装置中哪些可以控制反应的发生和停止()A.①③B.②③C.①④D.②④10.通常条件下水的沸点是100℃。
中考语文专题复习基础训练及答案

中考语文专题复习基础训练及答案一、选择题1. 下面哪个成语使用不当?A. 垂涎三尺B. 目不转睛C. 无济于事D. 人模狗样答案:D2. “功夫不负有心人”中的“功夫”是指什么?A. 功夫片B. 武术表演C. 努力研究的过程D. 身体素质训练答案:C3. 下列哪种标点符号用法不正确?A. 这个问题,不用考虑了。
B. 老师说:“你们好!”C. 看到了么?我的裙子……D. 他叹了口气,深深地吸了口烟。
答案:C4. 下列《西游记》中的人物,属于仙界的是:A. 孙悟空B. 白骨精C. 玉皇大帝D. 黑熊精答案:C5. “什么是快乐?”这个问题的提出者是:A. 李白B. 杜甫C. 白居易D. 王之涣答案:B二、填空题1. “沉舟侧畔千帆过,病树前头万木春。
”出自唐代诗人()的《题李凝幽居》。
答案:刘禹锡2. “云想衣裳花想容,春风拂槛露华浓。
”这是唐代()的诗句。
答案:李清照3. “大江东去,浪淘尽,千古风流人物。
”是()的诗句。
答案:苏轼4. “黄河远上白云间,一片孤城万仞山。
”是明代()的诗句。
答案:杨慎5. “问君能有几多愁?恰似一江春水向东流。
”是元代()的诗句。
答案:白朴三、简答题1. 理解古诗《静夜思》中的“床前明月光”?答案:床前的明月光是来自窗子的,因为窗子外头没有遮拦物,即没有阻挡物。
所以暗示的意思就是将自己渴望达到的目标比喻为明月。
2. 解释诗句“人生若只如初见”中的“初见”?答案:初见是指第一次见到的时候,这里比喻一件事情第一次发生时的新鲜感和美好感受。
3. 赏析文言文《论语》中的“温故而知新,可以为师矣。
”答案:孔子在这里表达出研究的方法,先回忆旧知识,再研究新知识,才能掌握更多的知识,从而为人们能够成为优秀的老师提供了一个有效的方法。
4. 解释成语“百年树人”的意思?答案:百年树人是一个比喻,意思是培养人才需要长期的投资和努力。
因为培养人才不是一朝一夕的事情,需要长期耕耘和培养,才能最终得到优秀人才的收获。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础训练(3)时间:(30分钟)姓名______
一.仔细选一选(本题有10个小题。
每小题4分。
共40分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的宇母填在答题卷中相应的格子内.注意可以用多种不同的方法来选取正确答案.
1.下列运算的结果中,是正数的是 ( )
(A)(-2007)-1 (B)(-1)2007 (C)(-1)×(-2007) (D)(-2007)÷2007
2.点P在第二象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )
(A)(-4,3) (B)(-3,-4) (C)(-3,4) (D)(3,-4)
3.如图1,用放大镜将图形放大,应该属于( )
(A)相似变换 (B)平移变换 (C)对称变换 (D)旋转变换
(1) (2) (3)
4.有一组数据如下:3,6,5,2,3,4,3,6.那么,这组数据的中位数是( ) (A)3或4 (B)4 (C)3 (D)3.5
5.因式分解(x-1)2-9的结果是( )
(A)(x+8)(x+1) (B)(x+2)(x-4) (C)(x-2)(x+4) (D)(x-10)(x+8) 6.如图2,正三角形ABC内接于圆0,动点P在圆周的劣弧AB上,且不与A,B重合,则∠BPC等于( )
(A)30o (B)60o (C)90o (D)45o
7.如图3,在高楼前D点测得楼顶的仰角为30o,向高楼前进60米到C点,又测得仰角为45o,则该高楼的高度大约为( ).
(A)82米 (B)163米 (C)52米 (D)30米
8.如果函数y=ax+b(a<0,b<O)和y=kx(k>0)的图象交于点P,那么点P应该位于( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
9.右图背景中的点均为大小相同的小正方形的顶点,
其中画有两个四边形,下列叙述中正确的是( )
(A)这两个四边形面积和周长都不相同
(B)这两个四边形面积和周长都相同
(C)这两个四边形有相同的面积,但I的周长大于Ⅱ的周长
(D)这两个四边形有相同的面积,但I的周长小于Ⅱ的周长
10.将三粒均匀的分别标有1,2,3,4,5,6的正六面体骰子同时掷出,出现的数字分别为a,b,c,则a,b,c正好是直角三角形三边长的概率是( )
(A)
1
216
(B)
1
72
(C)
1
36
(D)
1
12
二、认真填一填(本题有6个小题,每小题5分,共30分)
要注意认真看清题目的条件和要填写的内容。
尽量完整地填写答案.
11.两圆的半径分别为3和5,当这两圆相交
时,圆心距d的取值范围是.
12.抽取某校学生一个容量为150的样本,测
得学生身高后,得到身高频数分布直方图
如右,已知该校有学生1500人,则可以估
计出该校身高位于160cm至165cm之间的
学生大约有人.
13.一个等腰三角形的一个外角等于110o,则这个三角形的三个角应该为.14.抛物线y=2(x-2)2-6的顶点为C,已知y=-kx+3的图象经过点C,则这个一次函数图象与两坐标轴所围成的三角形面积为.
15.三个同学对问题“若方程组111
222
a x
b y c
a x
b y c
+=
⎧
⎨
+=
⎩
的解是
3
4
x
y
=
⎧
⎨
=
⎩
,求方程组
111
222
325
325
a x
b y c
a x
b y c
+=
⎧
⎨
+=
⎩
的解.”提出各自的想法.甲说:“这个题目好象条件不够,
不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”.参考他们的讨论,你认为这个题目的解应该是.
16.如图,P1是一块半径为1的半圆形纸板,在P1的左下端剪去一个半径为
1
2
的半圆后得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形P3,P4,…,P n,…,记纸板P n的面积为S n,试计算求出S2= ;
S3= ;并猜测得到S n-S n-1= (n≥2)。
