材料力学题目及答案
材料力学拉伸与扭转题目答案

75
2
3
1
A
B
C
P
40
80
80
变形相容条件 变形后三根杆与梁 仍绞接在一起。 变形几何方程
2 l2 l1 l3
2
3
1
A
B
C
l1
P
l2
l3
40
80
80
75
2 l2 l1 l3
补充方程
2 N 2 l2 N1l1 N3l3 EA EA EA
静力平衡方程
N1 N2 N3 P 0 2N2 4N3 P 0
2
3
1
A
B
C
P
40
80
80
N1
N2
N3
P
75
3、阶梯形圆杆AE段为空心,外径 D =140mm,内径 d=100mm。BC段为实心,直径 d=100mm。外力偶矩 mA=18KN.m,mB=32KN.m,mC=14KN.m。已知许用切应力 []=80MPa 。试校核轴的强度。
mA
D
d
A
E
mB mC
二、计算题
1:悬臂吊车如图所示。G=20KN,许用应力 []=120MPa,弹性模量E=200GPa。AB杆为圆钢。试设计 AB杆的直径并计算其伸长量l
A
C
300
3m
D B
2m
G
1、解:计算AB杆的轴力
A
mc 0
3N AB sin300 5G 0
C
300
D
NAB=66.7KN (1) 设计AB杆的直径
d
C B
mAB =18KN.m ,mBD =14KN.m
BC
M nBC Wn
材料力学习题01拉压剪切

拉伸与压缩一、 选择题 (如果题目有5个备选答案选出其中2—5个正确答案,有4个备选答案选出其中一个正确答案。
)1.若两等直杆的横截面面积为A ,长度为l ,两端所受轴向拉力均相同,但材料不同,那么下列结论正确的是( )。
A .两者轴力相同应力相同B .两者应变和仲长量不同C .两者变形相同D .两者强度相同E .两者刚度不同2.一圆截面直杆,两端承受拉力作用,若将其直径增大一倍,其它条件不变,则( )。
A .其轴力不变B .其应力将是原来的1/4C .其强度将是原来的4倍D .其伸长量将是原来的1/4E .其抗拉强度将是原来的4倍3.设ε和1ε分别表示拉压杆的轴向线应变和横向线应变,μ为材料的泊松比,则下列结论正确的是( )。
A .εεμ1=B .εεμ1-=C .εεμ1= D .εεμ1-= E .常数时,=≤μσσ p 4.钢材经过冷作硬化处理后,其性能的变化是( )。
A .比例极限提高 B .屈服极限提高C .弹性模量降低D .延伸率提高E .塑性变形能力降低5.低碳钢的拉伸σ-ε曲线如图1-19所示若加载至强化阶段的C 点,然后卸载,则应力回到零值的路径是( )。
A .曲线cbaoB .曲线cbf (bf ∥oa )C .直线ce (ce ∥oa )D .直线cd (cd ∥o σ轴)6.低碳钢的拉伸σ-ε曲线如图l —19,若加载至强化阶段的C 点时,试件的弹性应变 和塑性应变分别是( )。
A .弹性应变是ofB .弹性应变是oeC .弹性应变是edD .塑性应变是ofE .塑性应变是oe7.图l-2l 表示四种材料的应力—应变曲线,则: (1)弹性模量最大的材料是( );(2)强度最高的材料是( ); (3)塑性性能最好的材料是( )。
8.等截面直杆承受拉力,若选用三种不同的截面形状:圆形、正方形、空心圆,比较材料用量,则( )。
A .正方形截面最省料B .圆形截面最省料C .空心圆截面最省料D .三者用料相同9.若直杆在两外力作用下发生轴向拉伸(压缩)变形,则此两外力应满足的条件是 A .等值 B .反向 C .同向D .作用线与杆轴线重合E .作用线与轴线垂直 10.轴向受拉杆的变形特征是( )。
材料力学试题及答案期末

材料力学试题及答案期末期末考试是学生们在学期结束时面临的一项重要考核。
在材料力学这门课程中,试题的设计和答案的准确性对于学生的学习成绩至关重要。
本文将为大家提供一套材料力学试题,并给出详细的答案解析。
试题一:弹性模量的计算1. 弹簧的伸长量随外力的大小而变化,如果给定外力-伸长量的关系图,如下图所示,试求该材料的弹性模量。
(图略)解答:根据胡克定律,应力与应变之间的关系为:σ = Eε其中,σ为应力,E为弹性模量,ε为应变。
弹性模量E的计算公式为:E = σ/ε根据图中的数据,我们可以求得外力-伸长量的关系为:外力(F):10 N,20 N,30 N伸长量(ΔL):0.5 mm,1 mm,1.5 mm根据胡克定律以及弹性模量的计算公式,我们可以得到如下关系式:E = σ/ε = F/A / ΔL/L其中,A为横截面积,L为原长。
假设A与L的值为常数,则可以推导得到:E = F/ΔL * L/A根据给定的数据代入公式计算,可以得到:当F = 10 N 时,E = 10 N / 0.5 mm * L/A = 20 / mm * L/A当F = 20 N 时,E = 20 N / 1 mm * L/A = 20 / mm * L/A当F = 30 N 时,E = 30 N / 1.5 mm * L/A = 20 / mm * L/A由此可见,无论外力的大小,材料的弹性模量均为20 / mm * L/A。
试题二:杨氏模量的测定2. 某学生通过实验测得一块金属试样在受力时的应变与应力之间的关系如下图所示。
试求该金属试样的杨氏模量。
(图略)解答:根据实验数据绘制的应力-应变曲线,可以看出,在线段OA区域内,应力与应变呈线性关系。
通过直线OA的斜率可以求得该材料的杨氏模量。
根据图中的数据,我们可以计算出斜率为:斜率K = Δσ/Δε = (350 MPa - 250 MPa) / (0.0025 - 0.0020) = 400 MPa / 0.0005 = 8 * 10^5 Pa根据公式,杨氏模量E等于斜率K乘以应变ε,即:E = K * ε根据给定的数据代入公式计算,可以得到:E = 8 * 10^5 Pa * 0.0025 = 2 * 10^3 Pa所以该金属试样的杨氏模量为2 * 10^3 Pa。
考研材料力学考试题及答案

考研材料力学考试题及答案# 考研材料力学考试题及答案## 一、选择题1. 材料力学中,下列哪一项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案: D2. 在单向拉伸试验中,材料的屈服强度是指:A. 材料开始发生永久变形的应力B. 材料发生断裂的应力C. 材料发生弹性变形的应力D. 材料发生塑性变形的应力答案: A## 二、简答题1. 简述材料力学中弹性模量和剪切模量的定义及其物理意义。
答案:弹性模量(E)是指材料在单向拉伸或压缩时,应力与应变的比值。
它反映了材料抵抗变形的能力,数值越大,材料的刚度越大。
剪切模量(G)是材料在剪切状态下,剪切应力与剪切应变的比值,它描述了材料抵抗剪切变形的能力。
2. 描述材料的疲劳破坏现象及其影响因素。
答案:疲劳破坏是指材料在反复加载和卸载过程中,即使应力水平低于材料的屈服强度,也可能发生断裂的现象。
影响疲劳破坏的因素包括应力幅度、循环次数、加载频率、材料的微观结构和环境因素等。
## 三、计算题1. 某材料的弹性模量E=200 GPa,泊松比ν=0.3。
当该材料的一端受到100 MPa的拉伸应力时,求另一端的正应变。
答案:根据胡克定律,正应变ε可以由以下公式计算:\[\epsilon = \frac{\sigma}{E}\]其中,σ为应力,E为弹性模量。
代入数值得到:\[\epsilon = \frac{100 \times 10^6 \text{ Pa}}{200 \times10^9 \text{ Pa}} = 5 \times 10^{-4}\]2. 一个直径为d的圆杆,受到轴向拉伸力P,若材料的许用应力为σ,求该圆杆的许用长度L。
答案:圆杆的许用长度L可以通过以下公式计算:\[L = \frac{P}{\sigma \cdot \frac{\pi d^2}{4}}\]其中,P为轴向拉伸力,σ为许用应力,d为圆杆直径。
## 四、论述题1. 论述材料力学在工程结构设计中的应用及其重要性。
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
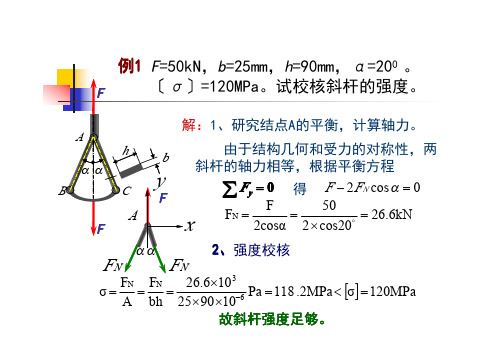
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
第五版材料力学答案

第五版材料力学答案1. 什么是材料的弹性模量?材料的弹性模量是描述材料在受力作用下的变形能力的物理量,它是应力和应变之间的比值。
弹性模量越大,材料的刚度越大,变形能力越小;弹性模量越小,材料的刚度越小,变形能力越大。
常见的弹性模量有弹性模量、剪切模量和体积模量等。
2. 什么是材料的屈服强度?材料的屈服强度是指材料在受到外力作用下开始发生塑性变形的应力值。
超过屈服强度后,材料将发生不可逆的塑性变形。
屈服强度是材料的重要力学性能参数,对于材料的强度和使用性能有重要影响。
3. 什么是材料的断裂韧性?材料的断裂韧性是描述材料在受到外力作用下抵抗断裂的能力。
断裂韧性越大,材料在受到外力作用下越不容易发生断裂。
断裂韧性是衡量材料抗断裂能力的重要指标,对于材料的使用安全性具有重要意义。
4. 什么是材料的疲劳强度?材料的疲劳强度是指材料在交变应力作用下能够承受的最大应力值。
材料在长期交变应力作用下容易发生疲劳破坏,疲劳强度是描述材料抗疲劳破坏能力的重要参数,对于材料的使用寿命具有重要影响。
5. 什么是材料的弹性极限?材料的弹性极限是指材料在受到外力作用下发生弹性变形的极限应力值。
超过弹性极限后,材料将发生塑性变形。
弹性极限是描述材料在受力作用下的弹性变形能力的重要参数,对于材料的设计和使用具有重要意义。
6. 什么是材料的刚度?材料的刚度是描述材料在受力作用下的变形能力的物理量,它是应力和应变之间的比值。
刚度越大,材料在受力作用下的变形能力越小;刚度越小,材料在受力作用下的变形能力越大。
刚度是描述材料力学性能的重要参数,对于材料的设计和使用具有重要影响。
7. 什么是材料的蠕变强度?材料的蠕变强度是指材料在高温和持续应力作用下发生蠕变变形的能力。
蠕变强度是描述材料在高温条件下的稳定性能的重要参数,对于材料在高温环境下的使用具有重要影响。
总结,材料力学是工程学、材料学和力学的交叉学科,对于材料的性能分析和设计具有重要意义。
材料力学本科

材料力学作业一一、填空题1、轴向拉伸的等直杆,杆内的任一点处最大剪应力的方向与轴线成( )。
2、受轴向拉伸的等直杆,在变形后其体积将( )。
3、低碳钢经过冷做硬化处理后,它的( )极限得到了明显的提高。
4、工程上通常把延伸率δ>( )的材料成为塑性材料。
5、一空心圆截面直杆,其内、外径之比为0.8,两端承受力力作用,如将内外径增加一倍,则其抗拉刚度将是原来的( )倍。
二、选择题1、理论力学中的“力和力偶可传性原理”在下面成立的是( ) A 在材料力学中仍然处处适用 B 在材料力学中根本不能适用C 在材料力学中研究变形式可以适用D 在材料力学研究平衡问题时可以适用 2、 下列结论中正确的是( ) A 外力指的是作用与物体外部的力 B 自重是外力C 支座约束反力不属于外力D 惯性力不属于外力3、下列结论中正确的是( )A 影响材料强度的是正应力和切应力的大小。
B 影响材料强度的是内力的大小。
C 同一截面上的正应力必是均匀分布的。
D 同一截面上的剪应力必定是均匀分布的。
4、下列结论中正确的是( )A 一个质点的位移可以分为线位移和角位移B 一个质点可以有线位移,但没有角位移。
C 一根线或一个面元素可以有角位移但没线位移D 一根线或一个面元素可以有线位移但没角位移5、设低碳钢拉伸试件工作段的初始横截面面积为0A ,试件被拉断后端口的最小横截面面积为1A ,试件断裂后所能承受的最大荷载为b P 。
则下列结论正确是( )A 材料的强度极限1/b b P A σ=B 材料的强度极限0/b b P A σ=C 试件应力达到强度极限的瞬时,试件横截面面积为0APD 试件开始断裂时,试件承受的荷载是b参考答案一、填空题1、45度2、增大3、比例4、5%5、4二、选择题1、D2、B3、A4、B5、B材料力学作业二一、是非判断题1、圆杆受扭时,杆内各点处于纯剪切状态。
()2、圆杆扭转变形实质上是剪切变形。
()3、非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
材料力学试的题目及答案

一、判断题(正确打“√”,错误打“X ”,本题满分为10分) 1、拉杆伸长后,横向会缩短,这是因为杆有横向应力的存在。
( )2、圆截面杆件受扭时,横截面上的最大切应力发生在横截面离圆心最远处。
( )3、两梁的跨度、承受载荷及支承相同,但材料和横截面面积不同,因而两梁的剪力图和弯矩图不一定相同。
( )4、交变应力是指构件内的应力,它随时间作周期性变化,而作用在构件上的载荷可能是动载荷,也可能是静载荷。
( )5、弹性体的应变能与加载次序无关,只与载荷的最终值有关。
( )6、单元体上最大切应力作用面上必无正应力。
( )7、平行移轴公式表示图形对任意两个相互平行轴的惯性矩和惯性积之间的关系。
( ) 8、动载荷作用下,构件内的动应力与材料的弹性模量有关。
( )9、构件由突加载荷所引起的应力,是由相应的静载荷所引起应力的两倍。
( ) 10、包围一个点一定有一个单元体,该单元体各个面上只有正应力而无切应力。
( ) 二、选择题(每个2分,本题满分16分)1.应用拉压正应力公式A FN =σ的条件是( )。
A 、应力小于比例极限;B 、外力的合力沿杆轴线;C 、应力小于弹性极限;D 、应力小于屈服极限。
2.梁拟用图示两种方式搁置,则两种情况下的最大弯曲正应力之比 )(m ax )(m ax b a σσ 为( )。
A 、1/4; B 、1/16; C 、1/64; D、16。
3、关于弹性体受力后某一方向的应力与应变关系有如下论述:正确的是 。
A 、有应力一定有应变,有应变不一定有应力; B 、有应力不一定有应变,有应变不一定有应力; C 、有应力不一定有应变,有应变一定有应力; D 、有应力一定有应变,有应变一定有应力。
4、火车运动时,其轮轴横截面边缘上危险点的应力有四种说法,正确的是 。
A :脉动循环应力: B :非对称的循环应力; C :不变的弯曲应力;D :对称循环应力h4h(a) h4h(b)5、如图所示的铸铁制悬臂梁受集中力F 作用,其合理的截面形状应为图( )6、对钢制圆轴作扭转校核时,发现强度和刚度均比规定的要求低了20%,若安全因数不变,改用屈服极限提高了30%的钢材,则圆轴的( ) A 、 强度、刚度均足够;B 、强度不够,刚度足够; C 、强度足够,刚度不够;D 、强度、刚度均不够。
材料力学复习

1. 两圆杆的尺寸、受力及支撑情况均相同,但其一为钢,另一为铝,若G[钢]=3G[铝],则两轴的最大剪应力之比τmax [钢]: τmax [铝]= 1:1 ,φ[钢]: φ[铝]= 1:3 。
2. 受外力而发生变形的构件,在外力消除后能够恢复的变形称为 弹性变形 ,而不能恢复的变形则称为 塑性变形 。
3. 在材料力学中,对可变形固体采用 连续性 、 均匀性 、 各向同性 三个基本假设。
4. 静定结构的支反力可通过___静力平衡方程___方程求得,超静定结构的支反力要通过____静力平衡方程和变形协调方程____方程求得。
5. 某段梁在均布荷载作用下M 图和Fs 图如图,则梁上的分布荷载集度为 2 kN/m 。
第5题图 第6题图6. 图示梁用积分法求变形时的边界条件为 W A =0, θA =0, W B =0 光滑连续条件为 W C+=W C 。
7.材料力学强度方面的三类问题是校核强度,设计截面,确定荷载。
8.外径为D 、内外径之比为α的圆环形截面的扭转截面系数()16143απ-=D W p 。
9. 在材料力学中,对可变形固体采用 连续性 、 均匀性 、 各向同性 三个基本假设。
10.使用强度理论对脆性材料进行强度计算时,对以 拉 应力为主的应力状态宜采用第一强度理论;对以 压 应力为主的应力状态宜采用第二强度理论。
11. 阶梯形轴的尺寸及受力如图所示,其AB 段的最大剪应力τmax1与BC 段的最大剪应力τmax2之比ττmax max 12=____3/8___。
图5 图7 12.纯剪切状态属于 双 (单、双、三)向应力状态。
13. 铸铁梁受载荷如图所示,截面为T 字型。
(a )、(b)两种方式,哪种放置更合理 b 。
14.对于超静定结构,当未知力个数多于平衡方程个数时,需补充 变形协调 条件,来求解问题。
15.用积分法求图示梁的挠度时,确定积分常数的条件是右左=B B C A A ωωωθω000===。
材料力学试卷(手动组卷)

材料力学试卷(手动组卷)题目部分,(卷面共有53题,314.0分,各大题标有题量和总分)一、选择题(24小题,共72.0分)(3分)[1]下列结论中哪些是正确的?(1)荷载的量纲可以是[力],[力] [长度],[力][长度]-1,[力][长度]-2或[力][长度]-3.(2)内力的量纲可以是[力]或[力][长度].(3)应力的量纲只能是[力]/[长度]2.A、(1),(2)B、(2),(3).C、(1),(3).D、全对.(3分)[2]若采用O xyz坐标系,并使x轴与杆轴重合.则下列结论中哪些是正确的?(1)杆件横截面上一点处,总应力P可分解为正应力和剪应力,它们之间存在下列关系:(2)杆件横截面上一点处,剪应力可分解为方向的分量和z方向的分量,且。
(3)设横截面面积为A,则该截面上的轴力,剪力.(3分)[5]铸铁试件扭转破坏的破坏面为_______。
A、沿横截面Ⅰ-Ⅰ剪断B、沿螺旋面Ⅱ(与试件轴线夹角)拉断C、沿螺旋面Ⅲ(与试件轴线夹角)拉断D、沿横截面Ⅰ-Ⅰ拉断(3分)[6]根据均匀性假设,可认为构件的_____在各点处相同。
A、应力B、应变C、材料的弹性常数D、位移(3分)[7]钢制实心轴和铝制空心圆轴(内外径之比α=d/D=0.6)的长度及横截面积均相等,钢的许可切应力[τ1]=80MPa,铝的许可切应力[τ2]=50MPa。
仅从强度条件考虑,能承受较大扭矩的是_______。
A、铝制空心轴B、钢制实心轴C、承载能力相同D、无法判断(3分)[8]对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是_____。
A、②③对B、①③对C、①②对D、全对(3分)[9]在图示四个轴力中,_____________。
A、为正,为负;B、为正,为负;C、和为正,为负;D、为正,为负。
考研材料力学试题及答案

考研材料力学试题及答案一、选择题(每题2分,共10分)1. 在拉伸试验中,材料的弹性模量E可以通过应力-应变曲线中的哪一点来确定?A. 弹性极限B. 屈服点C. 断裂点D. 比例极限答案:D2. 根据材料力学的理论,下列哪一项不是材料的力学性能?A. 硬度B. 韧性C. 密度D. 弹性答案:C3. 在剪切应力作用下,材料的剪切模量G可以通过以下哪个公式计算?A. G = τ/γB. G = σ/εC. G = τ/εD. G = σ/γ答案:A4. 材料在受力后,其内部各点处的应力状态可以用哪种理论来描述?A. 拉梅理论B. 圣维南理论C. 莫尔圆理论D. 虎克定律答案:C5. 对于理想塑性材料,当其达到屈服点后,以下哪种说法是正确的?A. 应力不再增加,但应变继续增加B. 应力和应变都会继续增加C. 应力会突然下降,但应变继续增加D. 应力和应变都会突然下降答案:A二、简答题(每题5分,共20分)1. 简述材料力学中的弹性变形和塑性变形的区别。
答:弹性变形是指材料在受到外力作用后,材料内部的分子或原子结构发生可逆的变化,当外力去除后,材料能恢复到原来的形状和尺寸。
塑性变形则是指材料在受到外力作用后,材料内部的分子或原子结构发生不可逆的变化,即使外力去除,材料也不能恢复到原来的形状和尺寸。
2. 什么是应力集中?它对材料的强度有何影响?答:应力集中是指在材料的某些局部区域,由于几何形状、载荷方式或材料不均匀性等原因,应力值显著高于周围区域的现象。
应力集中会导致材料在这些高应力区域更容易发生断裂,从而降低材料的整体强度。
3. 何为材料的屈服强度?它在工程应用中有何意义?答:屈服强度是指材料在受到外力作用后,从弹性变形过渡到塑性变形的临界应力值。
在工程应用中,屈服强度是设计和选材的重要参数,它直接关系到结构的安全性能和承载能力。
4. 描述一下泊松比的概念及其在实际应用中的作用。
答:泊松比是材料在受到拉伸或压缩力时,横向应变与纵向应变的比值。
材料力学考试试题及答案

材料力学考试试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性能?A. 弹性B. 塑性C. 韧性D. 硬度2. 材料在拉伸过程中,若应力超过屈服点后继续增加,材料将进入:A. 弹性阶段B. 塑性阶段C. 断裂阶段D. 疲劳阶段3. 材料的弹性模量E表示的是:A. 材料的硬度B. 材料的韧性C. 材料的弹性程度D. 材料的屈服强度4. 根据材料力学理论,下列哪一项不是材料的疲劳破坏特点?A. 疲劳破坏是局部的B. 疲劳破坏是突然的C. 疲劳破坏是可预测的D. 疲劳破坏是累积的5. 在材料力学中,下列哪一项不是材料的失效模式?A. 屈服B. 断裂C. 腐蚀D. 疲劳6. 材料的屈服强度和抗拉强度之间的关系是:A. 屈服强度总是大于抗拉强度B. 屈服强度总是小于抗拉强度C. 屈服强度等于抗拉强度D. 两者之间没有固定关系7. 材料的疲劳寿命与下列哪一项无关?A. 应力水平B. 材料的微观结构C. 环境温度D. 材料的密度8. 材料的冲击韧性通常用下列哪一项来表示?A. 抗拉强度B. 屈服强度C. 硬度D. 冲击吸收能量9. 材料的疲劳寿命与加载频率的关系是:A. 正相关B. 负相关C. 无关D. 先正相关后负相关10. 在材料力学中,下列哪一项不是材料的应力-应变曲线的特点?A. 弹性阶段B. 屈服阶段C. 塑性阶段D. 线性阶段二、简答题(每题10分,共20分)1. 请简述材料的弹性模量和屈服强度的区别和联系。
2. 材料的疲劳破坏与静载下的破坏有何不同?三、计算题(每题15分,共30分)1. 已知一材料的弹性模量E=200 GPa,泊松比ν=0.3。
若材料受到拉伸力F=10 kN,试计算材料的应变ε和应力σ。
2. 某材料的疲劳寿命S-N曲线已知,当应力水平为σ=200 MPa时,疲劳寿命N=1000次。
若应力水平降低到150 MPa,根据Basis Goodman关系,计算新的疲劳寿命。
材料力学1 (答案)

材料力学请在以下五组题目中任选一组作答,满分100分。
第一组:计算题(每小题25分,共100分)1. 梁的受力情况如下图,材料的a。
若截面为圆柱形,试设计此圆截面直径。
10kNq/m2. 求图示单元体的:(1)图示斜截面上的应力;(2)主方向和主应力,画出主单元体;(3)主切应力作用平面的位置及该平面上的正应力,并画出该单元体。
60x解:(1)、斜截面上的正应力和切应力:MPa MPa o 95.34,5.6403030=-=--τσ(2)、主方向及主应力:最大主应力在第一象限中,对应的角度为0067.70=α,则主应力为:MPa MPa 0.71),(0.12131-==σσ(3)、主切应力作用面的法线方向:0/20/167.115,67.25==αα 主切应力为:/2/104.96ααττ-=-=MPa此两截面上的正应力为:)(0.25/2/1MPa ==αασσ,主单元体如图3-2所示。
x图3-10.MPa0.25图3-23. 图中所示传动轴的转速n=400rpm,主动轮2输入功率P2=60kW,从动轮1,3,4和5的输出功率分别为P1=18kW,P3=12kW,P4=22kW,P5=8kW。
试绘制该轴的扭矩图。
4. 用积分法求图所示梁的挠曲线方程和转角方程,并求最大挠度和转角。
各梁EI均为常数。
第二组:计算题(每小题25分,共100分)1. 简支梁受力如图所示。
采用普通热轧工字型钢,且已知= 160MPa。
试确定工字型钢型号,并按最大切应力准则对梁的强度作全面校核。
(已知选工字钢No.32a:W = 692.2 cm3,Iz = 11075.5 cm4)解:1.FRA = FRB= 180kN(↑)kN·mkN·mkNm3由题设条件知:W = 692.2 cm2,Iz = 11075.5 cm4cmE截面:MPaMPa2. A+、B-截面:MPaMPa3.C-、D+截面:MPaMPa∴选No.32a工字钢安全。
材料力学作业及答案

【A】
【B】
【C】
【D】 解:正确答案为【D】; 【A】 分离体上不能带有支座,因为支座处的支反力要影响分离体的平衡(如下图所示),
因此必须将支座去除,用相应的支反力取而代之; 【B】 用截面法计算轴力时,不要在集中力作用点上取截面,因为此处的受力比较复杂,
为了保险起见,建议大家用 的公式来计算线应变。从这个公式可以看出,当材料相同的时, E
线应变的变化规律与正应力的变化规律相同,正应力发生变化的截面上,线应变也将发生变化。
三、图示立柱由横截面面积分别为 A 和 2A 的 AB 和 BC 段组成,已知材料的容重为 ,弹性模量为 E,则
解:正确答案为【A】。 [B]问题出在分子上的 3,在用胡克定律计算变形时分子上要用轴力,而不能用杆件上作用的外力。 [C]这是一个常见的错误,很多同学会仿照对变形进行分段累加的算法来计算线应变,要注意变形有累 加意义,即一段杆件的总的变形量等于每个分段变形量的代数和;但是线应变指的是在一个很小的范围 内杆件的变形程度,可以简单地将线应变理解成是属于某个截面的。当一段杆件受力均匀时,这段杆件 各个横截面上的线应变都是相等的,你可以笼统地说这段杆件的线应变是多少,但是当两段杆件的轴力 不同时,只能说两段杆件的线应变个各是多少,而不能把两段杆件的线应变加起来。不要说是两段杆件 的线应变,即便是把两个截面不同的线应变加起来都没有任何力学意义。就像汽车在公路上行驶,在第 一段上是一个速度,在第二段上是另一个速度,显然把这两个速度加起来是没有什么意义的。 [D]当两段杆件的变形程度不同时,不能像本选项那样将两段杆件连在一起,一次性计算线应变,必须 是各算各的。
在材料力学中采用“突变”的形式来处理。在这种处理方式下,这个截面上的轴力 是不确定的,在材料力学中绘制出来的集中力作用截面附近的轴力图,如下图所示, 此时只需要求出集中力作用截面左右两条线代表的轴力值即可,因此,应该在集中 力作用截面的左右两侧取计算截面。,而不要把计算截面取在集中力的作用截面上。
材料力学习题()

7、在所有相互平行的坐标轴中,对(形心轴)的惯性矩为最小。
8、在平行移轴公式 中,z轴和z1轴互相平行,则z轴通过(形心轴)
9.在弯曲正应力公式 中,y表示欲求应力点到(中性轴)的距离。
10.两梁的几何尺寸和材料相同,由正应力强度条件可得B的承载能力是A的( 5 )倍。
(a) (b)
(a)
(b)
(d)
11.不列剪力方程和弯矩方程,画出图示各梁的剪力图和弯矩图,并求出FS,max和Mmax。
(a) (b) (c)
(a)(b)(c)解:
弯曲应力
一、选择题(如果题目有5个备选答案,选出2~5个正确答案,有4个备选答案选出一个正确答案。)
1.等强度梁的截面尺寸( C )
A、与载荷和许用应力均无关
(1)试确定AB段的直径d1和BC段的直径d2。
(2)若AB和BC两段选用同一直径,试确定直径d。
(3)主动轮和从动轮应如何安排才比较合理?
统一直径取
4. 阶梯轴AB如图所示,AC段直径d1=40mm,CB段直径d2=70mm,外力偶矩MB=1500N·m,MA=600N·m,MC=900N·m,G=80GPa,[τ]=60MPa,[φ/]=2(º)/m。试校核该轴的强度和刚度。
3.实心圆轴横截面上(半径)处剪应力最大,中心处剪应力(为零)。
4.外径为D,内径为d= 0.5D的空心圆轴,两端受扭转外力偶矩m作用时,轴内最大剪应力为 。若轴的外径不变,内径改为 ,则轴内的最大剪应力变为(0.6 )。
5.扭转应力公式 适用(实心圆)或(空心圆)截面直杆。
6.材料相同的两根圆轴,一根为实心轴,直径为 ;另一根为空心轴,内径 ,外径为 , 。若两轴横截面上的扭矩T和最大剪应 均相同,则两轴的横截面积之比 ()。
材料力学考研真题答案

材料力学考研真题答案一、选择题1. 材料力学中,描述材料弹性特性的物理量是( A )。
A. 杨氏模量B. 泊松比C. 剪切模量D. 屈服强度2. 在材料力学中,当材料受到拉伸时,其内部的应力与应变之间的关系是( B )。
A. 线性关系B. 非线性关系C. 没有关系D. 反比关系二、简答题1. 请简述材料的弹性模量和剪切模量的区别。
弹性模量是指材料在单轴拉伸或压缩时,应力与应变的比值,它反映了材料抵抗形变的能力。
剪切模量则是指材料在剪切状态下,剪切应力与剪切应变的比值,它反映了材料抵抗剪切形变的能力。
两者都是描述材料刚度的物理量,但应用的力学状态不同。
2. 解释什么是材料的屈服现象,并说明其在工程应用中的重要性。
屈服现象是指材料在受到一定的应力后,即使应力不再增加,材料也会发生明显的塑性变形。
屈服点是材料从弹性阶段过渡到塑性阶段的临界点。
在工程应用中,了解材料的屈服点对于设计结构的安全性和可靠性至关重要,可以避免结构在实际使用中发生不可逆的变形或破坏。
三、计算题1. 某材料的杨氏模量为200 GPa,泊松比为0.3。
若该材料的一根杆件受到100 MPa的拉伸应力,请计算其纵向应变。
根据胡克定律,\( \varepsilon = \frac{\sigma}{E} \),其中\( \varepsilon \) 为应变,\( \sigma \) 为应力,\( E \) 为杨氏模量。
代入数据得:\( \varepsilon = \frac{100 \times 10^6 \text{Pa}}{200\times 10^9 \text{Pa}} = 5 \times 10^{-4} \)。
2. 一根直径为20 mm的圆杆,在受到轴向拉伸力作用下,其横截面面积减小了1%。
如果材料的屈服强度为300 MPa,计算该圆杆是否处于屈服状态。
首先计算圆杆的横截面面积变化量:\( A_0 = \frac{\pi}{4}\times (20 \times 10^{-3})^2 \),\( A = A_0 \times (1 - 0.01) \)。
材料力学的试题及答案

材料力学的试题及答案一、选择题(每题2分,共20分)1. 材料力学研究的对象是什么?A. 材料的化学性质B. 材料的力学性质C. 材料的热学性质D. 材料的电学性质2. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 韧性C. 硬度D. 塑性3. 材料力学中,应力的定义是什么?A. 力与面积的比值B. 力与体积的比值C. 力与长度的比值D. 面积与力的比值4. 材料力学中,下列哪一项不是材料的基本变形形式?A. 拉伸B. 压缩C. 扭转D. 膨胀5. 材料力学中,弹性模量表示什么?A. 材料的硬度B. 材料的韧性C. 材料的弹性D. 材料的塑性二、简答题(每题10分,共30分)6. 简述材料力学中材料的三种基本力学性质。
7. 解释材料力学中的应力-应变曲线,并说明其各阶段的意义。
8. 什么是材料的屈服强度,它在工程设计中的重要性是什么?三、计算题(每题25分,共50分)9. 一根直径为20mm,长度为200mm的圆杆,在两端受到100kN的拉伸力。
如果材料的弹性模量为200GPa,求圆杆的伸长量。
10. 一个直径为50mm,长为100mm的空心圆筒,内径为40mm,受到一个扭矩为500N·m。
如果材料的剪切模量为80GPa,求圆筒的最大剪切应力。
答案一、选择题1. B. 材料的力学性质2. C. 硬度3. A. 力与面积的比值4. D. 膨胀5. C. 材料的弹性二、简答题6. 材料力学中材料的三种基本力学性质包括弹性、塑性和韧性。
弹性是指材料在受到外力作用后能恢复原状的能力;塑性是指材料在达到一定应力后,即使撤去外力也不会完全恢复原状的性质;韧性是指材料在断裂前能吸收和分散能量的能力。
7. 应力-应变曲线是描述材料在受力过程中应力与应变之间关系的曲线。
它通常包括弹性阶段、屈服阶段、强化阶段和颈缩阶段。
弹性阶段表示材料在受力后能够完全恢复原状;屈服阶段是材料开始产生永久变形的点;强化阶段是材料在屈服后继续承受更大的应力而不断裂;颈缩阶段是材料接近断裂前发生的局部变细现象。
材料力学题目

材料力学题目第一章单向静拉伸力学性能1、金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。
合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小,但是不改变金属原子的本性和晶格类型。
组织虽然改变了,原子的本性和晶格类型未发生改变,故弹性模量对组织不敏感。
1、决定金属屈服强度的因素有哪些?【P12】答:内在因素:金属本性及晶格类型、晶粒大小和亚结构、溶质元素、第二相。
外在因素:温度、应变速率和应力状态。
2、试述韧性断裂与脆性断裂的区别。
为什么脆性断裂最危险?【P21】答:韧性断裂是金属材料断裂前产生明显的宏观塑性变形的断裂,这种断裂有一个缓慢的撕裂过程,在裂纹扩展过程中不断地消耗能量;而脆性断裂是突然发生的断裂,断裂前基本上不发生塑性变形,没有明显征兆,因而危害性很大。
3、剪切断裂与解理断裂都是穿晶断裂,为什么断裂性质完全不同?【P23】答:剪切断裂是在切应力作用下沿滑移面分离而造成的滑移面分离,一般是韧性断裂,而解理断裂是在正应力作用以极快的速率沿一定晶体学平面产生的穿晶断裂,解理断裂通常是脆性断裂。
4、何谓拉伸断口三要素?影响宏观拉伸断口性态的因素有哪些?答:宏观断口呈杯锥形,由纤维区、放射区和剪切唇三个区域组成,即所谓的断口特征三要素。
上述断口三区域的形态、大小和相对位置,因试样形状、尺寸和金属材料的性能以及试验温度、加载速率和受力状态不同而变化。
第二章金属在其他静载荷下的力学性能说明下列力学性能指标的意义(1)σbc——材料的抗压强度(2)σbb——材料的抗弯强度(3)τs——材料的扭转屈服点(4)τb——材料的抗扭强度(5)σbn——材料的抗拉强度(6)NSR——材料的缺口敏感度(7)HBW——压头为硬质合金球的材料的布氏硬度(8)HRA——材料的洛氏硬度(9)HRB——材料的洛氏硬度(10)HRC——材料的洛氏硬度(11)HV——材料的维氏硬度缺口试样拉伸时的应力分布有何特点?在弹性状态下的应力分布:薄板:在缺口根部处于单向拉应力状态,在板中心部位处于两向拉伸平面应力状态。
材料力学考试常见大题目
0.4m
3
m3
φ13 = φ12 + φ23 = 1.85×10−3 − 9.75×10−3 = −7.9 ×10−3 rad
x
155
跟踪训练
6.发电量为15000KW的水轮机主轴如图,轴是空心
的,外径D = 550mm,d = 300mm,转速n = 250r / min。
材料的许用应力[τ ] = 50MPa.试校核该轴的强度。
F
N1 ≤ [σ ]A1
查表得斜杆AC的面积为A1=2×4.8cm2
F
≤
1 2
[σ
]A1
=
1 × 120 × 106 × 2 × 4.8 × 10−4 2
= 57.6 × 103 N = 57.6kN
N1
N2 α
3、根据水平杆的强度,求许可载荷
查表得水平杆AB的面积为A2=2×12.74cm2
N2 ≤ [σ ]A2
力为[τ ]= 60M Pa ,许用挤压应力为[σbs]= 100M Pa, 试校核键的强度。
解:1.键的受力分析如图
m
h
2
∑d
Mo = 0
FS ⋅ − m = 0 2
剪力FS = 57KN
挤压m力Fbs
F{
FS
=
}
F F
=
57KN
h
o
L
b d
2.切应力和挤压应力的强度校核
AS = bL
Abs = Lh 2
试确定轴的直径;并求齿轮3对齿轮1的扭转角。
3
1
2
解:1.计算外力偶矩
m1
m1
=
9549
p1 n
=
9549× 0.756 183.5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学题目及答案Revised on November 25, 2020习题3-1图(a)习题3-2图(a)习题3-3图 习题3-4图 第3章 弹性杆件横截面上的正应力分析3-1 桁架结构受力如图示,其上所有杆的横截面均为20mm ×50mm 的矩形。
试求杆CE 和杆DE 横截面上的正应力。
解:图(a )中,54cos =θ (1)截面法受力图(a )0=∑D M ,03)515(4=⨯+-⨯CE F (2) F CE = 15 kN0=∑x F ,40cos =θDE F (3) (1)代入(3),得F DE = 50 kN∴ 1505.002.010153=⨯⨯==A F CE CE σMPa 50==AFDE DE σMPa3-2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷,其集度p = 10kN/m ,在自由端D 处作用有集中呼F P = 20 kN 。
已知杆的横截面面积A = ×10-4m 2,l = 4m 。
试求:1.A 、B 、E 截面上的正应力;2.杆内横截面上的最大正应力,并指明其作用位置。
解:由已知,用截面法求得 F N A = 40 kN F N B = 20 kN F N E = 30 kN(1)200100.2104043N =⨯⨯==-A F A A σMPa 100N ==A FB B σMPa150N ==AFE E σMPa(2)200max ==A σσMPa (A 截面)3-3 图示铜芯与铝壳组成的复合材料杆,轴向拉伸载荷F P 通过两端的刚性板加在杆上。
试: 1.写出杆横截面上的正应力与F P 、d 、D 、E c 、E a 的关系式;2.若已知d = 25mm ,D = 60mm ;铜和铝的单性模量分别为E c = 105GPa 和E a = 70GPa ,F P = 171 kN 。
试求铜芯与铝壳横截面上的正应力。
解:1.变形谐调:a a Na c c Nc A E F A E F = (1)P Na Nc F F F =+(2)∴ ⎪⎪⎪⎩⎪⎪⎪⎨⎧-+==-⋅+⋅=+==4)(π4π)(4π4π22a 2c P a a Na a 22a 2c P a a c c P c c Nc cd D E d E F E A F d D E d E F E A E A E F E A F c σσ2. 5.83)025.006.0(π1070025.0π10105101711010542292939c =-⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯=σMPa6.55105705.83c a c a =⨯==E E σσMPa 3-4 图示由铝板钢板组成的复合材料柱,纵向截荷F P 通过刚性平板沿着柱的中心线施加在其上。
试:1.导出复合材料柱横截面上正应力与F P 、b 0、b 1、h 和E a 、E s 之间的关系式;2.已知F P = 385kN ;E a = 70GPa ,E s = 200GPa ;b 0 = 30mm ,b 1 = 20mm ,h = 50mm 。
求铝板与钢板横截面上的最大正应力。
解:变形谐调:aa Na s s Ns A E F A E F = (1)习题3-5图 习题3-6图习题3-7图习题3-8图 (a)P Na Ns F F F =+ (2)1. a1s 0Ps 1a 0s P s s Ns s 22hE b hE b F E h b E h b E F E A F +=⋅+=-=σ 2. 175107005.002.021020005.003.01038502009939s -=⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯-=σMPa (压)25.6120070175175s a a -=-=-=E E σMPa (压) 3-5 从圆木中锯成的矩形截面梁,受力及尺寸如图所示。
试求下列两种情形下h 与b 的比值:1.横截面上的最大正应力尽可能小; 2.曲率半径尽可能大。
解:1.)(66222b d b M bh M W M zz z z -===σ ∴2=bh(正应力尽可能小) 2.zz z EI M =ρ10d d =h I z ,得2243d h = ∴ 3=bh(曲率半径尽可能大)3-6 梁的截面形状为正方形去掉上、下角,如图所示。
梁在两端力偶M z 作用下发生弯曲。
设正方形截面时,梁内最大正应力为0σ;去掉上、下角后,最大正应力变为0max σσk =,试求:1.k 值与h 值之间的关系;2.max σ为尽可能小的h 值,以及这种情形下的k 值。
解:3400h I zh =,3300h W z = )34()34(3)34(3023002300230max h h h h h h h h h h h h k -=-=-==σσ (1)0)338(0=-h h h ,h = 0(舍去),098h h =代入(1):9492.0)812(64381)384()98(1)9834()98(200203=-⨯⨯=-=⨯-=h h h h k3-7 工字形截面钢梁,已知梁横截面上只承受M z = 20 kN ·m 一个内力分量,I z = ×106mm 4,其他尺寸如图所示。
试求横截面中性轴以上部分分布力系沿x 方向的合力。
解:⎰⎰⎰-+-==21 2N d d d A z z A z z A x x A y I MA y I M A F σ 143101433-=⨯-=kN即上半部分布力系合力大小为143 kN (压力),作用位置离中心轴y = 70mm 处,即位于腹板与翼缘交界处。
3-8 图示矩形截面(b ·h )直梁,在弯矩M z 作用的Oxy 平面内发生平面弯曲,且不超出弹性范围,假定在梁的纵截面上有y 方向正应力y σ存在,且沿梁长均匀分布。
试: 1.导出)(y y y σσ=的表达式; 2.证明:max max 4x y hσρσ-≈,ρ为中性面的曲率半径。
解:1.先求)(y y σ表达式:⎰⎰--=⋅⋅+⋅⋅⋅⋅=∑yh x y y y y F 2220d 12sin2cos d 1θσϕϕρσθθ习题3-9图习题3-10图 (a) h t即 0d 2sin 22sin22=-+⎰-y y I M yh z z y y θθρσ,(y I M z z x -=σ)即 0)4(212sin 22sin 222=-⋅-h y I M z z y y θθρσ∴ )4(222y h I M z y z y --=ρσ(a )2.由(a )式,令0d d =yy σ,得y = 0,则max 2max ,44248x z z y z z y z y z y hW M h h I M h I M h σρρρρσ-≈⋅-=⋅-=-= (b )3-9 图示钢管和铝管牢固地粘成复合材料管,在两端力偶M z 作用下发生平面弯曲,试: 1.导出管横截面上正应力与M z 、D 1、D 2、D 3和钢的E s 、铝的E a 之间的关系式;2.已知D 1 = 20mm ,D 2 = 36mm ,D 3 = 44mm ;M z = 800N ·m ;E s = 210GPa ,E a = 70GPa 。
求钢管和铝和铝管横截面上的最大正应力max σ。
解:静力平衡: z M M M =+s a (1)变形谐调:s a ρρ=得ss sa a a I E M I E M =(2) 64)(π4243a D D I -=,64)(π4142s D D I -=(3) 由(2)s ss a a a M I E IE M =(4)代入(1),得 z M M I E I E =+s ss aa )1( aa s s s s s I E I E M I E M z+=(5) ∴ z M I E I E I E M aa s s aa a +=(6)1. )]()([ π644243a 4142s s a a s s s s s s D D E D D E yM E y I E I E M E y I M z z -+--=+-=-=σ,(2221D y D ≤≤) )]()([ π644243a 4142s a a a s s a a a a D D E D D E yM E y I E I E M E y I M z z -+--=+-=-=σ,(2232D y D ≤≤) 2. 13310)]3644(70)2036(210[π1018800210641244443maxs =⨯-⨯+-⨯⨯⨯⨯⨯=--σMPa 1.5410)]3644(70)2036(210[π102280070641244443max a =⨯-⨯+-⨯⨯⨯⨯⨯=--σMPa3-10 由塑料制成的直梁,在横截面上只有M z 作用,如图所示。
已知塑料受拉和受压时的弹性模量分别为E t 和E c ,且已知E c = 2E t ;M z = 600N ·m 。
试求: 1.梁内最大拉、压正应力; 2.中性轴的位置。
解:根据平面假设,应变沿截面高度作直线变化 ∵ E c = 2E t ,εσE =∴ σ沿截面高度直线的斜率不同 ∴中性轴不过截面形心。
1.确定中性轴位置。
设拉压区高度分别为h t 、h c由0=∑x F ,得:02121t max t c max c =⋅⋅+⋅⋅-b h b h σσ即 ccc t max t max c h h h h h -==σσ (1)习题3-11图 习题3-12图 又∵tc max t max c max t t max c c max t max c 22h hE E ===εεεεσσ (2)由(1)、(2),得cc t c c c 22h h h h h h h h -==- 即 2c 2c 2)(h h h =- ⎪⎭⎪⎬⎫=-=∴=-=∴mm 6.58)22(mm 4.41)12(t c h h h h (中性轴的位置)2.⎰⎰⎰⎰⎰⎰⋅+=+=+=ctctctd 2d d d d d c t t t c c t t c t A A A A A A z A E y A yE A yE A yE A y A y M εεεεσσ其中)246(3323233c 3t c t -=⨯+=+bh bh bh I I ∴ )2(1c t t I I E M z +=ρ∴ c ct c c t t c c cmax c 222h I I M h I I M E E h E zz +=+==ρσ69.810)246(310050104.4160021233=⨯-⨯⨯⨯⨯=--MPa (压)∴ 15.6)246(1031005010100)22(60021233t c t t tmax t =-⨯⨯⨯⨯-⨯=+==--h I I M h E z ρσMPa (拉) 3-11 试求图a 、b 中所示的二杆横截面上最大正应力的比值。
