《几何画板》课件制作——圆锥曲线的形成和画法
圆锥曲线PPT优秀课件

y 2 x2 2 1( a b 0 ) , 2 a b
解析: (2)∵椭圆焦点在 y 轴上,故设椭圆的标准方程为
由椭圆的定义知,
3 5 3 5 3 1 2a ( )2 ( 2)2 ( )2 ( 2)2 10 10 2 10 , 2 2 2 2 2 2
A1
.F . . O M . F
2
0
A2
x
F1
其中 a2 b2 c2 , a 0, b c 0 , F0 , F1 , F2 是对应的焦点。 B1 (1)若三角形 F0 F1 F2 是边长为 1 的等边三角形,求“果圆”的方程;
b (2)若 A1 A B1 B ,求 的取值范围; a
焦点分别为 F1 , F2 ,点 P 在双曲线的右支上,且
| PF1 | 4 | PF2 | ,则此双曲线的离心率 e 的最大值为
8 解一:由定义知 | PF1 | | PF2 | 2a ,又已知 | PF1 | 4 | PF2 | ,解得 PF1 a , 3 2 PF2 a , 在 PF1F2 中 , 由 余 弦 定 理 , 得 3
1 1 1 1 a 2 16 将 2 和 2 看着整体,解得 , a b 1 1 b2 9
2 a y 2 x2 16 ∴ 2 即双曲线的标准方程为 1 。 16 9 b 9
点评:本题只要解得 a 2 , b 2 即可得到双曲线的方程,没有 必要求出 a , b 的值;在求解的过程中也可以用换元思想, 可能会看的更清楚。
x2 y2 1 有共同渐近线, (4) 与双曲线 9 16
且过点 (3,2 3) 。
利用几何画板辅助圆锥曲线曲线的统一定义

利用“几何画板”辅助圆锥曲线曲线的统一定义炎陵一中范林华圆锥曲线曲线的定义统一为:平面内与一个定点的距离和一条定直线的距离之比等于常数e的点的轨迹,当0<e<1时,它是椭圆;当e=1时,它是抛物线;当e>1时,它是双曲线。
利用几何画板这一动态几何工具辅助教学,能更好地揭示圆锥曲线的规律,利于学生的认识和掌握。
下面介绍该课件的制作方法和步骤:一、确定对称轴、焦点、准线。
1.1 打开《几何画板》,新建文件;1.2 画一条水平直线x;1.3 作出直线x对象上的点K、F(焦点);1.4 过K作直线x的垂线l(准线)。
二、设置离心率。
2.1 画一条线段AB;2.2 作出线段AB对象上的点E;2.3 通过度量、计算,求得线段AE与EB的比(离心率);2.4 将比值标签改为e。
三、设置作轨迹所需的动态半径。
3.1 过任一点D作出两条相交直线m、n;3.2 以D为圆心,AE为半径画圆交直线m于M;3.3 以D为圆心,EB为半径画圆交直线n于N;作直线MN;3.4 作直线m上一点G,过G作MN的平行线交n于H;3.5 作出线段DG、DH。
四、作出轨迹。
4.1 以F为圆心,线段DG为半径画圆;4.2 以K为圆心,线段DH为半径画圆交直线x于P、Q两点,分别过P、Q 作x的垂线p 、q;4.3 改变E的位置或改变F的位置使圆F与直线p、q都相交,交点分别为P1、P2、P3、P4;4.4 选取P1(或P2、P3、P4)、点G、直线m,构造轨迹,即可作出所需轨迹。
4.5 添加操作按钮、隐藏不必显示的对象。
(若轨迹失真,可增加图象的采样数量)。
几何画板制作 圆锥曲线的画法
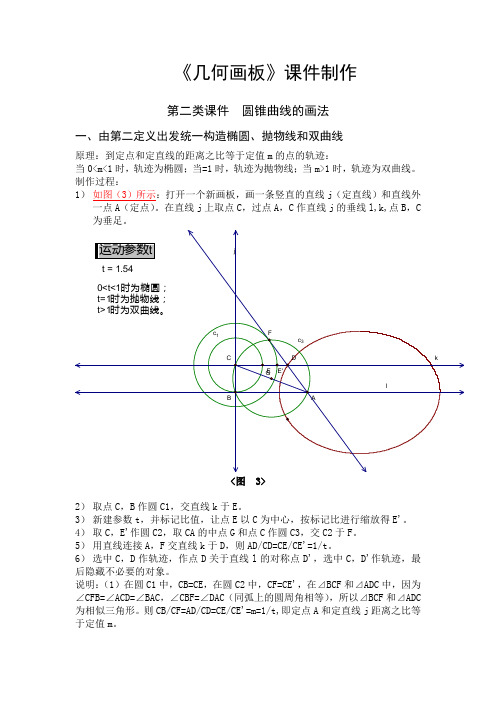
《几何画板》课件制作第二类课件圆锥曲线的画法一、由第二定义出发统一构造椭圆、抛物线和双曲线原理:到定点和定直线的距离之比等于定值m的点的轨迹:当0<m<1时,轨迹为椭圆;当=1时,轨迹为抛物线;当m>1时,轨迹为双曲线。
制作过程:1)如图(3)所示:打开一个新画板,画一条竖直的直线j(定直线)和直线外一点A(定点)。
在直线j上取点C,过点A,C作直线j的垂线l,k,点B,C 为垂足。
<图 3>2)取点C,B作圆C1,交直线k于E。
3)新建参数t,并标记比值,让点E以C为中心,按标记比进行缩放得E'。
4)取C,E'作圆C2,取CA的中点G和点C作圆C3,交C2于F。
5)用直线连接A,F交直线k于D,则AD/CD=CE/CE'=1/t。
6)选中C,D作轨迹,作点D关于直线l的对称点D',选中C,D'作轨迹,最后隐藏不必要的对象。
说明:(1)在圆C1中,CB=CE,在圆C2中,CF=CE',在⊿BCF和⊿ADC中,因为∠CFB=∠ACD=∠BAC,∠CBF=∠DAC(同弧上的圆周角相等),所以⊿BCF和⊿ADC 为相似三角形。
则CB/CF=AD/CD=CE/CE'=m=1/t,即定点A和定直线j距离之比等于定值m。
(2)单击"运动参数t"按钮,比值m 随之改变,这时可以动态地看到,当m 小于1的值逐渐变为1时,轨迹由椭圆变成抛物线;当m 大于1时,轨迹变成双曲线。
二、由第一定义出发,构造椭圆和双曲线及抛物线原理:椭圆(双曲线)——到定点的距离和定直线的距离之和(差)等于定值的点的轨迹;抛物线——到定点的距离和定直线的距离相等的点的轨迹。
制作过程:1.椭圆(或双曲线)的制作:<图 4> <图 5>()()1211221121,2()()x F x F F M F M MN N F M F N MN A B AB F F A F B 作出平面直角坐标系,在轴上任取两点作圆标记圆心的点记为,另一点隐藏。
几何画板制作 圆锥曲线的画法

《几何画板》课件制作第二类课件圆锥曲线的画法一、由第二定义出发统一构造椭圆、抛物线和双曲线原理:到定点和定直线的距离之比等于定值m的点的轨迹:当0<m<1时,轨迹为椭圆;当=1时,轨迹为抛物线;当m>1时,轨迹为双曲线。
制作过程:1)如图(3)所示:打开一个新画板,画一条竖直的直线j(定直线)和直线外一点A(定点)。
在直线j上取点C,过点A,C作直线j的垂线l,k,点B,C 为垂足。
<图 3>2)取点C,B作圆C1,交直线k于E。
3)新建参数t,并标记比值,让点E以C为中心,按标记比进行缩放得E'。
4)取C,E'作圆C2,取CA的中点G和点C作圆C3,交C2于F。
5)用直线连接A,F交直线k于D,则AD/CD=CE/CE'=1/t。
6)选中C,D作轨迹,作点D关于直线l的对称点D',选中C,D'作轨迹,最后隐藏不必要的对象。
说明:(1)在圆C1中,CB=CE,在圆C2中,CF=CE',在⊿BCF和⊿ADC中,因为∠CFB=∠ACD=∠BAC,∠CBF=∠DAC(同弧上的圆周角相等),所以⊿BCF和⊿ADC 为相似三角形。
则CB/CF=AD/CD=CE/CE'=m=1/t,即定点A和定直线j距离之比等于定值m。
(2)单击"运动参数t"按钮,比值m 随之改变,这时可以动态地看到,当m 小于1的值逐渐变为1时,轨迹由椭圆变成抛物线;当m 大于1时,轨迹变成双曲线。
二、由第一定义出发,构造椭圆和双曲线及抛物线原理:椭圆(双曲线)——到定点的距离和定直线的距离之和(差)等于定值的点的轨迹;抛物线——到定点的距离和定直线的距离相等的点的轨迹。
制作过程:1.椭圆(或双曲线)的制作:<图 4> <图 5>()()1211221121,2()()x F x F F M F M MN N F M F N MN A B AB F F A F B 作出平面直角坐标系,在轴上任取两点作圆标记圆心的点记为,另一点隐藏。
3D课件分享——圆锥曲线的形成

3D课件分享——圆锥曲线的形成
写在前面:
本文动态课件下载方式:
(长按屏幕,直接复制粗体字在后台回复)
后台回复:圆锥曲线
圆锥曲线的形成
主要内容:
1、主要从3D模型以及2D平面给大家动态展示高中圆锥曲线的形成。
2、动态课件的打开方式以及使用方式。
多图预警!第一part
首先给大家介绍各个滑条的作用,
第一、改变平面的旋转角度
第二、改变圆锥的形态
接着给大家看个总汇,
各个曲线如何形成。
下面逐个介绍:
在β=30°,b=4.1的时候,只改变平面旋转角度,
一、椭圆
先来个椭圆的形成的动态图
静态图——俯视图
二、抛物线
静态图
三、双曲线
静态图
下面再来个平面内的圆锥曲线形成
一、椭圆第一定义
二、抛物线定义
第二part课件打开方式以及使用方式
课件打开分成两种模式:
一、用geogebra软件打开(需要安装geogebra软件)
二、用IE浏览器或者是谷歌浏览器打开(无需安装软件;适用于无网络情况)
使用方式:
直接用IE浏览器打开“HTML”格式的文档,拖动滑条即可。
几何画板下的圆锥曲线的三合一的作图讲解

2008-2-2几何画板构造圆锥曲线2008-10-01 15:43分类:默认分类字号:大中小{Copyright by LhfcwsCopied from Helped by PestJust for fun.}可以说算是拓展的新定义。
如直接用所给的按钮画圆锥曲线,难以对其有较深的理解,因此尝试自己通过定义构造。
原始定义(必须了解):1、椭圆:平面内与两个定点(焦点)的距离之和等于常数的点的轨迹2、双曲线:平面内与两个定点(焦点)的距离之差绝对值等于常数的点的轨迹3、抛物线:平面内与一定点(焦点)和一定直线(准线)的距离相等的点的轨迹1、椭圆的画法。
根据定义,我们需要确定的两个点O1,O2以及一个动点P。
O1P+O2P=k(k为常数)。
如上图,作一个圆O1,取圆内一定点O2,取圆上一动点M。
连结O1M,O2M。
作O2M中垂线L,交O1M于点P。
追踪交点P。
当M在圆上移动一周时,点P运动轨迹为一个椭圆。
直线L刚好与椭圆相切。
证明:其实很简单。
作圆的目的就是为了能够找到一个定值k,而此时,k=r。
连结O2P,根据中垂线定理,O2P=MP,又因为O1P+MP=r,所以O1P+O2P=r=k回到了椭圆定义上去了。
2、双曲线和椭圆一样。
根据定义,我们需要确定的两个点O1,O2以及一个动点P。
O1P-O2P=k(k为常数)。
如上图,作一个圆O1,取圆外一定点O2,取圆上一动点M。
连结O1M,O2M。
作O2M中垂线L,交O1M于点P。
追踪交点P。
当M在圆上移动一周时,点P运动轨迹为双曲线。
直线L刚好与曲线相切。
证明:其实也很简单。
根据中垂线定理,O2P=MP,MP=O1P+r。
所以O2P=O1P+r,即O2P-O1P=r=k。
回到双曲线定义,证毕。
可以看到,画双曲线和画椭圆基本上差不多,原理几乎一样。
3、抛物线由于定义中,没有定值,只有等量关系,因此我们很难用到圆,但是中垂线仍是可以运用的,其等量关系可以通过中垂线实现。
运用几何画板动态构造圆锥曲线的方法

运用几何画板动态构造圆锥曲线的方法贵州省平塘民族中学刘光宜(558300)摘要本文根据圆锥曲线的第一定义、第二定义以及标准方程,运用尺规作图原理结合几何画板动态生成轨迹的功能,详尽而系统地阐述圆锥曲线的画法和构造。
每一类画法及构造的步骤,极富操作性和实践性。
直接运用于教学,能够达到激活数学课堂,启迪学生思维,拓展学生数学视野,提升数学教学效率的目的。
关键词圆锥曲线尺规作图原理几何画板动态生成轨迹一、根据圆锥曲线的第一定义构造圆锥曲线(一)椭圆1、椭圆第一定义一般地,平面内到两个定点F1、F2的距离之和等于常数2a(2a>︱F1F2︱)的点M的轨迹叫做椭圆。
其中,定点F1、F2叫做椭圆的焦点,两定点F1、F2间的距离︱F1F2︱叫做椭圆的焦距,常数2a叫做椭圆的长轴的长。
特别地,当2a=︱F1F2︱时,点M的轨迹是线段F1F2;当2a<︱F1F2︱时,点M的轨迹不存在。
2、画法步骤(1)按住shift 键,在画图区上部画一条直线l(隐藏控制点)。
再在直线l上构造线段AB,度量线段AB的长度并改为用2a表示。
(2)在线段AB上取一点C,并构造线段AC 和线段BC。
(3)按住shift键在画图区中部画一条线段F 1F2,隐藏线段,保留端点,然后度量两端点的距离︱F1F2︱,并调整大小使之小于2a。
(4)以F1为圆心,线段AC为半径画圆,以F2为圆心,线段BC为半径画圆。
构造两圆的交点M和M',并设置成“追踪交点”。
(5)构造线段MF1、MF2并度量长度,然后计算MF1+MF2。
(6)设置点C双向在线段AB上滑动,并编辑生成操作按钮“动画生成轨迹”。
或用选择工具拖动点C 在线段AB上滑动生成椭圆(如图1-1)。
(7)用选择工具拖动点B或点A调整线段AB与F1F2的大小关系:当2a=︱F1F2︱时,动点M与两个定点F1、F2共线,其轨迹是线段F1F2;当2a<︱F1F2︱时,动点M消失,表示其轨迹不存在。
几何画板下的圆锥曲线的三合一的作图概要

2008-2-2几何画板构造圆锥曲线2008-10-01 15:43分类:默认分类字号:大中小{Copyright by LhfcwsCopied from Helped by PestJust for fun.}可以说算是拓展的新定义。
如直接用所给的按钮画圆锥曲线,难以对其有较深的理解,因此尝试自己通过定义构造。
原始定义(必须了解):1、椭圆:平面内与两个定点(焦点)的距离之和等于常数的点的轨迹2、双曲线:平面内与两个定点(焦点)的距离之差绝对值等于常数的点的轨迹3、抛物线:平面内与一定点(焦点)和一定直线(准线)的距离相等的点的轨迹1、椭圆的画法。
根据定义,我们需要确定的两个点O1,O2以及一个动点P。
O1P+O2P=k(k为常数)。
如上图,作一个圆O1,取圆内一定点O2,取圆上一动点M。
连结O1M,O2M。
作O2M中垂线L,交O1M于点P。
追踪交点P。
当M在圆上移动一周时,点P运动轨迹为一个椭圆。
直线L刚好与椭圆相切。
证明:其实很简单。
作圆的目的就是为了能够找到一个定值k,而此时,k=r。
连结O2P,根据中垂线定理,O2P=MP,又因为O1P+MP=r,所以O1P+O2P=r=k回到了椭圆定义上去了。
2、双曲线和椭圆一样。
根据定义,我们需要确定的两个点O1,O2以及一个动点P。
O1P-O2P=k(k为常数)。
如上图,作一个圆O1,取圆外一定点O2,取圆上一动点M。
连结O1M,O2M。
作O2M中垂线L,交O1M于点P。
追踪交点P。
当M在圆上移动一周时,点P运动轨迹为双曲线。
直线L刚好与曲线相切。
证明:其实也很简单。
根据中垂线定理,O2P=MP,MP=O1P+r。
所以O2P=O1P+r,即O2P-O1P=r=k。
回到双曲线定义,证毕。
可以看到,画双曲线和画椭圆基本上差不多,原理几乎一样。
3、抛物线由于定义中,没有定值,只有等量关系,因此我们很难用到圆,但是中垂线仍是可以运用的,其等量关系可以通过中垂线实现。
如何用几何画板统一作出圆锥曲线

如何用几何画板统一作出圆锥曲线包汉忠(贵州都匀三中)我们见到的关于圆锥曲线的课件,通常都是作椭圆、双曲线、抛物线中单纯的一个曲线,没有使用一个课件同时展示三种圆锥曲线的。
那么用一个课件是否能同时展示这三种圆锥曲线呢?经过对几种常用的课件制作软件工具的试验与比较,借助于几何画板,笔者完成了一个制作统一圆锥曲线的几何画板课件。
以下谈一下这个课件的设计目的、思想与方法。
这个课件的制作目的很简单,就是想让学生直观地观察椭圆、双曲线、抛物线这三种圆锥曲线的变化规律,以及它们之间的离心率变化引起的图象变化。
这个课件的理论基础是圆锥曲线的第二定义(即统一定义):一个动点到一个定点的距离与这个动点到一条定直线的距离的比值等于定值(即常数),我们知道,这个常数就是离心率e,并且,当01ee>时,<<时,这个动点的轨迹就是椭圆;当1这个动点的轨迹就是双曲线;当1e=时,这个动点的轨迹就是抛物线。
那么,如何在作图过程中确定这个常数e ,如何才能使两条线段的比值等于事先想要的或者预先设定的离心率呢?这个问题成为了这个课件的制作的关键。
其实要得到两条线段的比值等于事先想要的或者预先设定的离心率e 并不难,因为这可以从初中数学中的相似三角形中得到。
如右图所示,若//BC DE ,则可以得到AB AD BC DE =,因此,可以把AB BC作离心率e 的参考值,在作图的过程中可使BC AB ⊥,这会使作图变得更方便。
由此,可以得到确定e 的方法。
制作的步骤如下:①作两互相垂直的直线m 、l ,设定点F 在直线l 上,定直线为m ,②在定直线m 上取一定点B 和一个可调动点A ,过点B 作l 的平行线BC ,在BC 上取一点C,过A、C作直线AC,则三角形ABC为直角三角形,此时,把BC固定,通过调节AB的长度,则可调节AB的取值BC作为离心率e的标准值范围,用ABBC③在m上又取一动点D,过动点D作DE m⊥,交直线AC 于E,此时,用AD作为动点P到定点F的距离,用DE作为到定直线m的距离,则离心率AD AB===定值eDE BC④以点F为圆心,AD为半径,作圆F交过点E作m的平行线于点P此时通过调节AD与DE的长度关系,追踪点P的轨迹,即可得到圆锥曲线的图形。
圆锥曲线定义(适合公开课) PPT

第三章Biblioteka 2019/09/301 圆锥曲线 前世今生
•圆锥面
•定义
两直线相交,其中一条直线
以另外一条直线为旋转轴进
行旋转所形成的曲面,称为
圆锥面。
也可以理解为两个全等的圆 锥顶点重合,高线重合,相 对放置时,两个侧面所形成 的的整体。
母线和圆锥的夹角为半顶角α。
•圆锥曲线
平面截圆锥面所得到的曲线,叫做圆锥曲线。 根据平面与圆锥轴线所成的角θ不同,所截圆锥曲线也不同。
•圆
•椭圆
大家应该也有点累了,稍作休息
大家有疑问的,可以询问和交流
•抛物线
•双曲线
2 圆锥曲线 平面定义
•圆锥曲线
•圆
平面内,到一个定点的距离为定长的点构成的集
合.
椭圆 平面内,到两个定点的距离之和为定长(大于两 定点之间的距离)的点构成的集合.
抛物线 平面内,到一个定点的距离与到一条定直线(不 过定点)的距离相等的点构成的集合.
双曲线 平面内,到两个定点的距离之差为定长(小于两 定点之间的距离)的点构成的集合.
•椭圆
•抛物线
•双曲线
3 圆锥曲线 光学性质
•椭圆
一个焦点处出发的 光,经反射后汇聚 到另一个焦点。
•抛物线
焦点处出发的光, 经反射后变成平 行光。
•双曲线
一个焦点处出发的光, 经反射后看上去就好像 是从另一个焦点处出发 的光。
其实,这哪里是什么悲伤的双曲线? •悲伤的双曲线 渐近线,越走越近,又给了彼此空间!
词、曲、唱:王渊超 如果我是双曲线,恩~你就是那渐近线 如果我是反比例函数,你就是那坐标轴 虽然我们有缘,能够生在同一个平面 然而我们又无缘,恩~慢慢长路无交点 为何看不见,等式成立要条件 难到正如书上说的,无限接近不能达到 如果我是双曲线,恩~你就是那渐近线
用几何画板做圆锥曲线

用几何画板做圆锥曲线圆锥曲线曲线的定义统一为:平面内与一个定点的距离和一条定直线的距离之比等于常数e的点的轨迹,当0<e<1时,它是椭圆;当e=1时,它是抛物线;当e>1时,它是双曲线。
利用几何画板这一动态几何工具辅助教学,能更好地揭示圆锥曲线的规律,利于学生的认识和掌握。
下面介绍该课件的制作方法和步骤:一、确定对称轴、焦点、准线。
1.1 打开《几何画板》,新建文件;1.2 画一条水平直线x;1.3 作出直线x对象上的点K、F(焦点);1.4 过K作直线x的垂线l(准线)。
二、设置离心率。
2.1 画一条线段AB;2.2 作出线段AB对象上的点E;2.3 通过度量、计算,求得线段AE与EB的比(离心率);2.4 将比值标签改为e。
三、设置作轨迹所需的动态半径。
3.1 过任一点D作出两条相交直线m、n;3.2 以D为圆心,AE为半径画圆交直线m于M;3.3 以D为圆心,EB为半径画圆交直线n于N;作直线MN;3.4 作直线m上一点G,过G作MN的平行线交n于H;3.5 作出线段DG、DH。
作者:Fanlinhua 第 1 页共 2 页四、作出轨迹。
4.1 以F为圆心,线段DG为半径画圆;4.2 以K为圆心,线段DH为半径画圆交直线x于P、Q两点,分别过P、Q作x的垂线p 、q;4.3 改变E的位置或改变F的位置使圆F与直线p、q都相交,交点分别为P1、P2、P3、P4;4.4 选取P1(或P2、P3、P4)、点G、直线m,构造轨迹,即可作出所需轨迹。
4.5 添加操作按钮、隐藏不必显示的对象。
(若轨迹失真,可增加图象的采样数量)。
圆锥曲线PPT课件

2021/3/7
CHENLI
26
(1)若设动点M到F1,F2的距离之和为2a,则 当0<F1F2<2a时,动点M的轨迹是椭圆;当 F1F2=2a>0时,动点M的轨迹是线段F1F2; 当0<2a<F1F2时,动点M的轨迹不存在.
(2)椭圆的定义可以表述为PF1+PF2= 2a(0<F1F2<2a),它是点P在椭圆上的充要条 件.
2021/3/7
CHENLI
19
抛物线的定义
根据抛物线的定义判断动点轨迹是否为抛物 线,关键看两点:
(1)定点是否在定直线l上; (2)到定Байду номын сангаас的距离和到定直线的距离是否相等 .
2021/3/7
CHENLI
20
例3 若动圆与定圆(x-2)2+y2=1外切,又 与直线x+1=0相切,则动圆圆心的轨迹是 ________.
2021/3/7
CHENLI
16
例2 (本题满分14分)曲线上的点到两个定点 F1(-5,0),F2(5,0)的距离之差的绝对值分别 等于(1)6,(2)10,(3)12.若满足条件的曲线 存在,则是什么样的曲线;若不存在,请说 明理由.
【思路点拨】 本题中已知条件与两定点距 离差的绝对值有关,因此可结合双曲线定义 求解.
2021/3/7
CHENLI
14
自我挑战1 平面内有定点A、B及动点P,命 题甲:|PA|+|PB|是定值,命题乙:点P的轨 迹是以A、B为焦点的椭圆,那么甲是乙的 ________条件.
解析:由椭圆定义知,甲 乙且乙⇒甲.
答案:必要不充分
2021/3/7
CHENLI
15
双曲线的定义
运用几何画板绘制圆锥曲线的十种方法

运用几何画板绘制圆锥曲线的十种方法几何画板是一种非常好用的工具,可以完成许多复杂的几何图形绘制任务。
几何画板中最常用的图形之一就是圆锥曲线,它的形状像一个山的状况,是很多几何形状中最有趣的一种。
本文介绍了如何使用几何画板绘制圆锥曲线的十种方法。
第一种方法:使用半圆锥曲线半圆锥曲线是一种特殊的圆锥曲线,它只有一个顶点。
要使用几何画板绘制半圆锥曲线,首先需要确定它的顶点和两个曲线的大小,然后就可以开始绘图了。
要绘制半圆锥曲线,需要用几何画板的“圆锥曲线”工具,来连接左右两边的端点,并填充它们。
第二种方法:使用等腰三角形等腰三角形是一种特殊的圆锥曲线,有三个顶点,其形状很像一个等腰三角形。
要绘制等腰三角形,首先需要确定三个顶点,然后使用几何画板的“圆锥曲线”工具,将它们连接起来,并填充它们。
第三种方法:使用平行四边形对于平行四边形,需要确定它的四个顶点,然后使用几何画板的“圆锥曲线”工具,将它们连接起来,并填充它们。
第四种方法:使用椭圆形椭圆形也可以用来绘制圆锥曲线,需要确定它的四个顶点,然后使用几何画板的“圆锥曲线”工具,将它们连接起来,并填充它们。
第五种方法:使用五边形五边形也可以作为圆锥曲线的基础,需要确定它的五个顶点,然后使用几何画板的“圆锥曲线”工具,将它们连接起来,并填充它们。
第六种方法:使用六边形六边形也可以作为圆锥曲线的基础,需要确定它的六个顶点,然后使用几何画板的“圆锥曲线”工具,将它们连接起来,并填充它们。
第七种方法:使用七边形七边形也可以作为圆锥曲线的基础,需要确定它的七个顶点,然后使用几何画板的“圆锥曲线”工具,将它们连接起来,并填充它们。
第八种方法:使用多边形如果要绘制多边形圆锥曲线,需要确定它的多个顶点,然后使用几何画板的“圆锥曲线”工具,将它们连接起来,并填充它们。
第九种方法:使用多段弧形如果要绘制多段弧形的圆锥曲线,需要确定它的多个顶点,然后使用几何画板的“圆锥曲线”工具,将其中的多段弧形连接起来,并填充它们。
圆锥曲线形成与画法

雙曲線畫法-焦點法
2. 以F1為圓心,任意大於線段AB之長為半徑(R)畫弧, 再以F2為圓心,(R-AB)之長為半徑畫弧,而與前 弧相交得C、D兩點。
資料來源:華興書局
雙曲線畫法-焦點法
3. 以相同的方法再求諸多點,用曲線板連接即得。
資料來源:華興書局
雙曲線畫法-等軸法
已知雙曲線之兩漸近線OA、OB及雙曲線上一點P,求 作雙曲線
外擺線: 一滾圓在另一圓外側滾動,滾圓上一點所經過的
軌跡。Leabharlann 擺線 內擺線: 一滾圓在另一圓內側滾動,滾圓上一點所經過的
軌跡。
漸開線
將一繩繞在圓形上,當一端放鬆轉開時,此端點 所形成的軌跡稱為漸開線,如下圖所示,常用於 齒輪輪齒之曲線繪製,為一種平面曲線。
4. 以相同方法,求得諸多點,,以曲線板連接即得。
資料來源:華興書局
拋物線畫法-包絡線法
已知X軸與Y軸,求作拋物線。 1. 在X軸及Y軸上作相同之等分與編號(X軸編號由
左向右,Y軸由上往下)。
資料來源:華興書局
拋物線畫法-包絡線法
2. 以相同號碼點連接。 3. 用曲線板畫曲線與各線段相切即得拋物線。
資料來源:華興書局
雙曲線畫法-等軸法
1. 過P點畫FG線平行OA線,畫DE線平行OB線。 2. 由O點畫數條傾斜線(於此設畫三條)與DE線相交得
1、2、3各點,與FG線相交得1' 、2' 、3'各點。
雙曲線畫法-等軸法
3. 由1、2、3各點畫與OA線之平行線,1' 、2' 、3' 各點畫與OB線之平行線。對應數字平行線之相交 點,即為雙曲線上之點。 (如點3之平利線與點3'之平行線相交於點3'' )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《几何画板》课件制作——圆锥曲线的形成和画法作者:马现岭摘要《几何画板》是一个适用于几何(平面几何,解析几何,射影几何,立体几何)、部分物理、天文教学的专业学科优秀平台软件,它能辅助教师在教学中使用现代化教育技术并进行教学试验,也可以帮助学生在实际操作中把握学科的在实质,培养其观察能力,问题解决能力,并发展思维能力。
它代表了当代专业工具平台类教学软件的发展方向。
在对《几何画板》进行系统的学习之后,我利用有关知识制作了两大类综合的数学课件。
主要包括:用动态效果展示圆锥曲线及截面的形成和圆锥曲线的画法。
这两类课件在教学上都有很重要的应用。
最新的《普通中学数学课程标准》中强调“教师应向学生展示平面截圆锥得到的椭圆的过程,使学生加深对圆锥曲线的理解,有条件的学校应充分发挥现代教育技术的作用,利用计算机演示平面截圆锥所得的圆锥曲线。
”这表明圆锥曲线的教学在以往的教学过程中存在着很大的困难,由于以往教育技术的落后,无法生动直观的进行讲解。
现在有了这个课件,我们就能达到既生动又直观的教学效果。
第二类利用《几何画板》实现了轨迹、函数图像的变换以及图像变换的动态演示,并由此法制作了几个有关函数图像变换的课件。
第二类课件系统介绍了圆锥曲线的画法,为在教学中提高学生学习兴趣,开展对圆锥曲线的研究,提供了良好的方法和方便的途径。
全文由三部分组成:第一部分:《几何画板》课件制作的选题原则。
第二部分:详细介绍了我所选择制作的数学课件及其制作过程。
第三部分:学习及应用《几何画板》的体会。
关键词:几何画板、标记向量、椭圆、圆锥曲线、圆锥截面、轨迹。
AbstractThe Geometer' s Sketchpad is an excellent platform for teaching of geometry (plane geometry, analytic geometry, projection geometry and solid geometry). It also applies to teaching of partial physics and astronomy. This platform not only can help teachers use the modern education technology in the course of teaching, but also can help students grasp the inwardness of science, and cultivate their ability of observation, solving question, and progressing their ideation. It represents the developing direction of the educative tool software.After I learn the Geometer’s Sketchpad, I have made kinds of comprehensive mathematics course wares, mainly including: Demonstrate the development of cone curve. These kinds of course wares have very important application on teaching. In "The newest ordinary middle school mathematics course standard ", it is emphasized that " teacher should demonstrate to student the plane section ellipse that cone gets, make student deepen the understanding for cone curve, under certain condition schools should play the role of modern educational technology fully, using computer to demonstration incoming of cone curve from cone by the plane. It shows that the teaching of cone curve has great difficulty in former teaching course, just because that educating technology fall behind before, and it can not be active and visual to explain. Now, here are these course wares, we can reach active and visual teaching effect. The second kind of side spread out problem is concerned with in former lesson, but the method to produce is fussy. The biggest advantage of my lesson lies in the method that I have used a unification to carry out, so that the time to produce is shortened greatly, and has reached very good demonstration effect.The paper text is composed of three parts:In the first part: I write some fundamental about what kinds of problem we can make the coursewares in the Geometer’s Sketchpad.In the second part: The mathematics coursewares and its produce course that I select to make are introduced in detail.In the last part: I relate the experience study by using the Geometer’s Sketchpad.Keywords:The Geometer’s Sketchpad、mark vector、ellipse、cone curve、cone section、trace.引言The Geometer’s Sketchpad 是美国优秀的教育软件。
由美国Nicholas Jackiw 和Scott Steketee程序实现,Steven Rasmussen领导的Key Curriculum出版。
它的中文名是《几何画板─21世纪的动态几何》,以下简称《几何画板》。
它小巧玲珑,操作简单,是数学学习的有力助手。
它可以说是我们的数学实验室,因为它能够有效地使数形结合,使我们在数学学习中既理解了数学结论,又得到了数学经验。
众所周知数学是训练逻辑思维的,尤其几何。
通过教师的辅导,我们在自己的记忆中形成—套逻辑思维体系。
那么怎样才能使我们更好地理解几何知识、掌握逻辑思维方法呢?一个方法是多看、多想,增加我们的学习经验,另一个方法就是寻找良好的辅助工具,帮助我们在动态的几何之中,去观察,探索。
《几何画板》就是一个适用于几何(平面几何,解析几何,射影几何,立体几何)、部分物理、天文教学的专业学科优秀平台软件,它能辅助教师在教学中使用现代化教育技术并进行教学试验,也可以帮助学生在实际操作中把握学科的在实质,培养其观察能力,问题解决能力,并发展思维能力。
它代表了当代专业工具平台类教学软件的发展方向。
在对《几何画板》进行系统的学习之后,我利用有关知识制作了两大类综合的数学课件,主要包括:用动态效果展示圆锥曲线的形成和圆锥曲线的画法。
这两类课件在教学上都有很重要的应用。
这里我所选择的《几何画板》版本为4.04版,目前最高的版本为5.0英文版,此外还有3.03版、4.03版和4.06版.下面我就课件的选题、制作及使用《几何画板》的感受几方面来展开我的论文。
第一部分几何画板的选题原则在数学教学过程中,不论是代数教学还是几何教学,遇到的最大困难就是:教师在教学过程重使用常规工具(如黑板,粉笔,圆规和直尺等)作图或是演示都有一定的局限性,而且无法达到动态地、任意地展示的目的,更多的时候无法揭示事物变化过程中的规律。
《几何画板─21世纪的动态几何》。
顾名思义,《几何画板》就是一个可以很好的解决以上难题的辅助教学工具。
《几何画板》在中学数学教学中有很多应用,不论在代数教学还是在几何教学中都显示出它的超凡魅力。
例如,在代数学教学中,它对函数、极限、复数和不等式等的教学起到了很大的作用。
在几何学教学中,平面、立体和解析几何更让《几何画板》大显身手。
当然,并不是所有教学都要利用《几何画板》来完成,也并不是所有教学容都适合利用《几何画板》达到最好的效果,这就要遵循《几何画板》的选题原则:第一:《几何画板》可以动态地演示图形的变化过程。
例如:下面要展示的圆锥曲线和函数图象的变换的课件都体现了动态的特点;第二:《几何画板》可以有效地使数形结合。
例如:大量极值问题都可以通过《几何画板》来动态模拟。
第三:《几何画板》可以精确画出函数图形并表现其全部情况。
例如:函数教学量的绘图工作可以轻而易举地通过《几何画板》来完成。
而且对于一类函数,《几何画板》可以通过改变系数及参数而达到表现其全部情况的目的。
例如:三角函数中正弦函数y=A sin(ωx+φ)+d 的图像可以通过调整A,ω,φ,d的值得到不同的精确图像。
第四:《几何画板》最重要的是可以很好的表现图形的任意性。
例如:在让学生掌握三角形重心,心,外心等概念时,在以往的教学过程中只能在黑板上画出几个三角形作代表,不能很好地说明三角形的任意性,而利用《几何画板》就可以任意拖动三角形的顶点以达到任意三角形的目的。
总之,在所做课件中我们能够充分体现出《几何画板》的以上优势,并能够恰当的应用到教学实践中,为教学服务。
