初二数学几何练习题

合集下载

初二数学几何图形练习题

初二数学几何图形练习题1. 设△ABC 为等腰直角三角形，其中∠BAC = 90°，∠ABC =∠ACB。

已知 AB = 5cm。

(a) 求 BC 的长度。

(b) 求△ABC 的面积。

2. 在△ABC 中，AD 是边 BC 的中线，且 AB = 3cm，BC = 4cm。

连接 BD，BD 的延长线交 AC 于 E 点。

(a) 求 BD 和 DE 的长度。

(b) 求△ADE 的面积。

3. 在△ABC 中，D、E 两点分别在边 AB、AC 上。

若DE ║ BC，则证明：AD/BD + AE/CE = 1。

4. 已知△ABC 中，∠BAC = 40°，∠ABC = 70°，点 D 在边 BC 上，且满足 BD = AC。

(a) 求∠BDC 的度数。

(b) 求∠ADB 的度数。

5. 在△ABC 中，D、F 分别是边 AB、AC 上的两个点，连接 BF、CD。

已知 AF = 6cm，BF = 4cm，CF = 3cm，FD = 1.5cm。

(a) 求△BFD 的面积。

(b) 求△ABC 的面积。

6. △ABC 的三个内角分别为 60°、75°、45°。

(a) 将△ABC 分别绕着顶点 A，边 BC，边 AC 旋转 90°，分别得到△A'B'C'、△AB'C'、△A'BC。

求△A'B'C'、△AB'C'、△A'BC 的内角。

(b) 证明△A'B'C' 是等腰三角形。

7. 在平面直角坐标系中，点 A(3, 4)、B(-1, -2)、C(-2, 6) 是顶点坐标。

连接 AB、AC，垂直平分 AC 的线段交 AB 的延长线于点 D。

求点 D 的坐标。

8. 已知△ABC 中，点 D、E 分别是边 AB、BC 上的两个点，且 DE ║ AC。

初二数学几何题50道,要带答案带过程

初二数学几何题50道,要带答案带过程选择题：1. 若两角互为补角，则它们的差是（）。

A.0°B.45°C.60°D.90°2. 在图中，如点S、T分别在边AB的延长线上，且∠ASP=60°，∠BAT=20°，则∠AST为（）。

A.40°B.50°C.80°D.110°3. 已知正方形ABCD的边长为5cm，点E、F分别在边AD、AB上，且AE=BF，则三角形CEF的面积为（）。

A.(5/8) cm²B.(9/8) cm²C.(13/8) cm²D.(15/8) cm²4. 如果一个圆心角的度数为30°，则它所对的弧度数是（）。

A.π/6B.π/3C.π/4D.π/2填空题：1.如图，已知BC平分∠ABD，设∠BAC=a°，∠BCA=b°，则∠CBD=\_\_\_\_°。

2.如图，点A、B、C在同一条直线上，则对于ΔABC来说，以下说法正确的是：①AB＝AC；②\angleBAC是钝角；③\angleABC＋\angleACB ＝180^\circ，所以\angleABC＝\_\_\_\_°，\angleACB＝\_\_\_\_°。

3. 已知直角三角形ABC，其中\angleC=90°，BC＝3，AC＝4，则AB=\_\_\_\_。

4.如图，长方形ABCD中，点E、F分别为BC、CD上的点，若∠BAE=∠EFD，AB=10cm，则DF=\_\_\_\_cm。

解答题：1.如图，在\triangleABC中，垂足分别为D、E、F。

若AC＝6，BD＝8，DE＝5，EF＝9，则BC＝（）。

2.如图，已知\angleBAC=60°，AD平分\angleBAC，且BD=AD，点E为AD的延长线上的点，且\angleBEC=140°，则\angleACD=\_\_\_\_\_\_°。

初二数学几何难题训练题及答案

初二数学几何难题训练题及答案1.已知⊙O的直径AB=10cm，点C、D、E、F分别在弧AB 上，若AC=3cm，BE=2cm，CF=4cm，求DE+FA的长度。

解：∠ABC=90°，∠AOC=180°，所以∠AFC=90°。

同理，∠ADE=90°。

又因为△ABC与△AED相似，所以$\frac{DE}{AC}=\frac{AB}{BC} \RightarrowDE=\frac{AB\times AC}{BC}$同理，因为△ABE与△AFC相似，所以$\frac{FA}{BE}=\frac{AB}{BC} \RightarrowFA=\frac{AB\times BE}{BC}$代入已知数据得到$DE=\frac{10\times 3}{7},FA=\frac{10\times 2}{7}$ 所以 DE+FA=4cm。

答案：4cm。

2.在△ABC中，D、E分别在AB、AC上，DE//BC，已知AB=6cm，AC=9cm，BD:DA=1:2，CE:EA=2:3，求BC的长。

解：因为DE//BC，所以$\frac{BD}{DA}=\frac{CE}{EA}=\frac{DB+BC}{DA+AC}$ 代入已知数据得到$\frac{1}{2}=\frac{2P+BC}{3P+9} \RightarrowBC=\frac{9}{2}$所以BC的长为4.5cm。

答案：4.5cm。

3.在四棱锥ABCD-P中，AB=BC=CD=l，PA=2l，PB=3l，PC=4l，且四棱锥的底面ABCD是个正方形，求四棱锥的体积V。

解：设△PAB与底面平行，交底面为E，△PAD与底面平行，交底面为F。

则有$PE=2l,PF=3l$由于ABCD是个正方形，所以$AE=BF=CF=DF=l$又因为連接PC与數直BD平行，所以$\frac{BD}{PC}=\frac{AE}{AF}$带入已知数据得到$\frac{BD}{4l}=\frac{l}{PF} \RightarrowBD=\frac{l^2}{PF}\times 4l=\frac{16l^3}{9}$所以四棱锥的高为$h=\sqrt{(PA-BD/3)^2-PF^2}=\sqrt{(2l-\frac{16l^3}{3\times 9l^2})^2-9l^2}=(8\sqrt{3}-9)l$ 最后利用公式$V=\frac{1}{3}S\times h$求出四棱锥的体积V，其中S为底面积，S=AB×BC=l²。

初二数学几何角度练习题

初二数学几何角度练习题1. 已知一直角三角形的一个锐角的度数是30°，求另外两个角的度数。

解答：由直角三角形的性质可知，三角形的三个角度之和为180°。

其中一个角是90°，另一个角度为30°，设第三个角度为x°，则有 90°+ 30° + x° = 180°。

解方程可得 x° = 180° - 90° - 30°，即 x° = 60°。

所以，另外两个角的度数分别为30°和60°。

2. 两条直线相交，交点角度为65°，求与其中一条直线垂直的直线与另一条直线成的角度。

解答：根据直线相交的性质，交点的角度为其对应角的互补角。

即，与其中一条直线垂直的直线与另一条直线成的角度为 90° - 65° = 25°。

3. 在菱形中，已知一个锐角的度数是40°，求其他三个角的度数。

解答：由菱形的性质可知，每个角的度数相等。

设每个角的度数为x°，则有 40° + x° + x° + x° = 360°。

解方程可得 x° = (360° - 40°) / 4，即x° = 80°。

所以，其他三个角的度数分别为80°、80°和80°。

4. 两条平行线之间的夹角是120°，与其中一条平行线垂直的直线与另一条平行线成的角度是多少？解答：根据平行线性质可知，同位角的度数相等。

即，与其中一条平行线垂直的直线与另一条平行线成的角度也是120°。

5. 在正方形中，一个内角的度数是60°，求其他三个角的度数。

解答：由正方形的性质可知，每个内角的度数都是90°。

初二数学几何试题及答案

初二数学几何试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项不是三角形的内角和？A. 180°B. 360°C. 540°D. 720°2. 如果一个三角形的两条边长分别为3和4，第三边的长度可能为：A. 1B. 5C. 7D. 93. 一个圆的半径为5厘米，那么它的周长是：A. 10π cmB. 20π cmC. 30π cmD. 40π cm4. 一个正方形的对角线长度为10厘米，那么它的边长是：A. 5 cmB. 7.07 cmC. 10 cmD. 14.14 cm5. 一个长方形的长和宽分别是8厘米和6厘米，那么它的面积是：A. 48 cm²B. 36 cm²C. 24 cm²D. 12 cm²二、填空题（每题2分，共10分）6. 一个等腰三角形的底角是45°，那么它的顶角是________度。

7. 如果一个正多边形的每个内角都是120°，那么它是________边形。

8. 一个圆的直径是14厘米，那么它的半径是________厘米。

9. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的斜边长是________厘米。

10. 如果一个平行四边形的对角线互相平分，那么它是一个________。

三、计算题（每题10分，共20分）11. 一个正六边形的边长为2厘米，求它的周长和面积。

12. 已知一个圆的半径为7厘米，求它的面积和周长。

四、解答题（每题15分，共30分）13. 在一个等边三角形ABC中，点D是边AB上的一点，且AD=2，BD=1。

求∠ADC的度数。

14. 一个圆的半径为10厘米，圆心到一个点P的距离为8厘米，求点P到圆上任意一点的距离的最大值和最小值。

答案：一、选择题1. B2. B3. B4. B5. A二、填空题6. 907. 68. 79. 510. 矩形三、计算题11. 周长：2×6=12厘米；面积：(3√3)×2²=12√3平方厘米。

几何题目初二数学3篇

几何题目初二数学题目1：求扇形的面积扇形是一个常见的几何图形，它由一个圆心和两条半径组成，圆心角的度数决定了扇形的大小。

我们可以通过以下公式来求解一个扇形的面积：S = (θ / 360) × πr^2其中，θ代表圆心角的度数，r代表扇形的半径，π是一个常数，约等于3.14。

举个例子，如果一个扇形的半径为5cm，圆心角的度数为60°，那么它的面积应该为：S = (60 / 360) × 3.14 × 5^2 ≈ 13.09(cm^2)注意：在使用这个公式时，需要将度数换算成弧度，即用角度×π/180来计算角度的弧度值。

例如60°的弧度值应该是60×π/180=π/3。

题目2：求直角三角形的斜边长度直角三角形是一个有一条直角边的三角形，我们可以利用勾股定理来求解它的斜边长度。

勾股定理指出：在一个直角三角形中，直角边的两个平方和等于斜边的平方，即a^2+b^2=c^2。

（其中a和b分别为直角边，c为斜边）例如，如果一个直角三角形的直角边长度分别为3cm和4cm，那么它的斜边长度应该为：c = √(3^2 + 4^2) ≈ 5(cm)注意：在使用勾股定理时，必须要保证直角边的长度已知，且只能求解斜边长度，不能求解其他两个角或两个边的长度。

题目3：求圆柱的表面积和体积圆柱是一个由一个圆形底面和一个长方形侧面组成的几何体，我们可以通过以下公式来求解一个圆柱的表面积和体积：表面积S = 2πr^2 + 2πrh体积V = πr^2h其中，r代表圆柱的半径，h代表圆柱的高，π是一个常数，约等于3.14。

举个例子，如果一个圆柱的半径为3cm，高为5cm，那么它的表面积应该为：S = 2π×3^2 + 2π×3×5 ≈ 113.1(cm^2)它的体积应该为：V = π×3^2×5 ≈ 141.3(cm^3)注意：在使用这些公式时，需要将所有的长度单位统一转换成同一单位，例如上述例子中，半径和高都是用厘米表示，因此得到的表面积和体积单位也是厘米的平方和立方。

初二上数学几何题10题

初二上数学几何题10题
以下是10道适合初二学生练习的几何题目：
已知等腰三角形的两边长分别为5和2，求该三角形的周长。

在平行四边形ABCD中，若∠A = 60°，AB = 5cm，BC = 8cm，求平行四边形ABCD的面积。

在△ABC中，若∠A = ∠B = ∠C，则△ABC是什么三角形？请说明理由。

在△ABC中，若∠A = 30°，∠B = 60°，AB = 4cm，求BC的长。

在矩形ABCD中，若AB = 6cm，BC = 8cm，E是AD的中点，求CE的长。

在菱形ABCD中，若∠A = 60°，AB = 4cm，求菱形ABCD的面积。

在△ABC中，若∠A = 90°，AB = AC，D为BC的中点，E、F分别为AB、AC上的点，且DE⊥DF，求∠EDF的度数。

已知圆O的半径为5cm，A、B是圆O上的两点，且∠AOB = 60°，求弦AB的长。

在梯形ABCD中，AD∥BC，AB = CD，若∠B = 60°，AD = 2cm，BC = 6cm，求梯形ABCD的面积。

已知一个直角三角形的两条直角边分别为3cm和4cm，求该直角三角形的外接圆的半径。

这些题目涵盖了初二数学几何的多个方面，包括等腰三角形、平行四边形、菱形、矩形、圆等基本图形的性质和计算。

通过练习这些题目，学生可以加深对几何知识的理解和应用，提高解题能力。

希望这些题目对初二学生的数学学习有所帮助！。

五四制初二下册数学几何练习题

五四制初二下册数学几何练习题第一题：求下列各组数的最小公倍数和最大公约数。

1) 12，202) 18，27，363) 25，40，504) 8，14，20解答：1) 12和20的最小公倍数为60，最大公约数为4。

2) 18，27，36的最小公倍数为108，最大公约数为9。

3) 25，40，50的最小公倍数为200，最大公约数为5。

4) 8，14，20的最小公倍数为280，最大公约数为2。

第二题：计算下列各组数的平均值。

1) 12，18，24，302) 6，10，14，18，223) 15，20，25，30，35，40解答：1) 12，18，24，30的平均值为21。

2) 6，10，14，18，22的平均值为14。

3) 15，20，25，30，35，40的平均值为27.5。

第三题：已知两个角的度数互为补角，其中一个角的度数为70度，请计算另一个角的度数。

解答：根据补角的定义，两个角的度数之和为90度。

设另一个角的度数为x度，则有70 + x = 90。

解方程可得x = 20。

所以另一个角的度数为20度。

第四题：已知一条直线上的两个点A(-2, 3)和B(4, -1)，求AB的长度和斜率。

解答：AB的长度可以通过计算两点之间的距离得到。

设AB的长度为L，利用两点间距离公式可得L = √((4 - (-2))^2 + (-1 - 3)^2)= √(6^2 + (-4)^2)= √(36 + 16)= √52= 2√13斜率可以通过计算直线AB的斜率得到。

设AB的斜率为k，利用斜率公式可得k = (y2 - y1) / (x2 - x1)= (-1 - 3) / (4 - (-2))= (-4) / (4 + 2)= -4 / 6= -2 / 3所以AB的长度为2√13，斜率为-2/3。

第五题：已知△ABC，AB = 6cm，BC = 8cm，AC = 10cm。

判断△ABC的类型，并说明理由。

解答：根据三角形边长的关系，AB + BC > AC，AB + AC > BC，BC + AC > AB。

初二数学几何难题练习题含答案

初二数学几何难题练习题含答案1. 题目：已知直角三角形ABC中，AB = 6cm，BC = 8cm。

求AC 的长度。

解析：根据直角三角形的勾股定理，可得AC^2 = AB^2 + BC^2。

代入数值计算可得AC = √(6^2 + 8^2) = √(36 + 64) = √100 = 10cm。

答案：AC的长度为10cm。

2. 题目：四边形ABCD是一个矩形，AB = 5cm，BC = 8cm。

如果∠CBD = 90°，求AD的长度。

解析：由于ABCD是一个矩形，所以AD = BC = 8cm。

答案：AD的长度为8cm。

3. 题目：在平面直角坐标系中，点A(3, 4)和点B(7, 2)分别为直角三角形ABC的两个顶点，求直角三角形ABC的斜边长。

解析：利用两点间距离公式，设A(x1, y1)和B(x2, y2)，则AB的长度为√[(x2 - x1)^2 + (y2 - y1)^2]。

代入数值计算可得AB = √[(7 - 3)^2 + (2 - 4)^2] = √[16 + 4] = √20 ≈ 4.47。

答案：直角三角形ABC的斜边长约为4.47。

4. 题目：已知平行四边形ABCD的边长分别为AB = 6cm，BC =8cm。

如果∠BCD = 120°，求对角线AC的长度。

解析：根据平行四边形的性质，对角线互相平分。

因此，对角线AC的长度等于边长DC的长度。

由已知信息可得DC = BC = 8cm。

答案：对角线AC的长度为8cm。

5. 题目：已知等腰梯形ABCD，AB || CD，AB = 6cm，CD = 10cm，AD = 5cm。

求BD的长度。

解析：由等腰梯形的性质可知，AB和CD的中点M处于同一条水平线上。

连接AM和CM，得到直角三角形AMC。

利用勾股定理可得AC的长度为√[(AD + CD)^2 - (2AB)^2] = √[(5 + 10)^2 - (2 * 6)^2] = √225 - 144 = √81 = 9。

初二数学几何试题及答案

初二数学几何试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是直角三角形的判定条件？A. 两角之和为90°B. 两边之和大于第三边C. 斜边的平方等于两直角边的平方和D. 任意两边之和大于第三边2. 一个圆的半径是5厘米，那么它的直径是：A. 10厘米B. 15厘米C. 20厘米D. 25厘米3. 如果一个三角形的三个内角分别为40°、60°和80°，那么这个三角形是：A. 直角三角形B. 钝角三角形C. 锐角三角形D. 不能确定4. 一个矩形的长是10厘米，宽是6厘米，那么它的面积是：A. 60平方厘米B. 100平方厘米C. 120平方厘米D. 150平方厘米5. 一个等腰三角形的底边长为8厘米，腰长为5厘米，那么它的高是：A. 3厘米B. 4厘米C. 6厘米D. 8厘米6. 一个正方形的对角线长度为10厘米，那么它的边长是：A. 5厘米B. 7.07厘米C. 8厘米D. 10厘米7. 一个梯形的上底是4厘米，下底是8厘米，高是6厘米，那么它的面积是：A. 12平方厘米B. 24平方厘米C. 30平方厘米D. 40平方厘米8. 一个平行四边形的对角线互相垂直，那么这个平行四边形是：A. 矩形B. 菱形C. 正方形D. 梯形9. 一个正五边形的内角和是：A. 540°B. 720°C. 900°D. 1080°10. 一个圆的周长是62.8厘米，那么它的半径是：A. 10厘米B. 11厘米C. 12厘米D. 13厘米二、填空题（每题4分，共20分）1. 如果一个三角形的两个内角分别为30°和60°，那么第三个内角是______°。

2. 一个圆的周长是31.4厘米，那么它的直径是______厘米。

3. 一个直角三角形的两条直角边长分别为3厘米和4厘米，那么它的斜边长是______厘米。

初二比较难的数学练习题

初二比较难的数学练习题在初二的数学学习中，遇到一些难题是很常见的。

这些题目需要我们掌握一定的数学知识和解题技巧才能顺利解答。

下面，我将为大家列举一些初二比较难的数学练习题。

一、立体几何题1. 某矩形纸片的长是宽的四倍，将该矩形剪成两个正方形，剪下的两个正方形面积之和是矩形面积的81%，求矩形的长和宽分别是多少？2. 下面的解析几何图形中，点A、B、C、D、E、F六点不在同一平面中，求ADE面与BCF面的夹角。

3. 设一条直线通过坐标轴上的点A(a, 0)和B(0, b)，且直线与y轴交于点C(0, c)，若三点A、B、C共线，求a、b、c之间的关系。

二、初中代数题4. 已知方程组：2x + 3y = 114x + ky = 15求k的值，使得方程组有唯一解。

5. 某数学题库有机试题100道，其中单选题每个题目的正确答案有4个选项，多选题每个题目的正确答案有5个选项，则这100道题中的选择题正确答案选项总数为多少？三、数列题6. 在等差数列{an}中，已知a1 = 3，a2 = 7，a4 = 17，则an的通项公式是什么？7. 若等比数列{bn}满足b1 = 2，b2 = 6，b4 = 90，则bn的通项公式是什么？四、概率题8. 一件商品的质量服从正态分布，已知其平均值为μ，标准差为σ。

若70%的商品质量在80kg到100kg之间，求μ和σ的值。

9. 一枚正六面体骰子有6个面，分别刻有1、2、3、4、5、6这6个数字。

现随机扔一枚骰子，连续扔5次，且每次都得到数字4的概率是多少？五、面积和体积题10. 在长方体中，一条对角线为18，长和宽的比为3:2，求长方体的体积和表面积。

以上是初二比较难的数学练习题，希望通过解题过程，能帮助大家加深对数学知识的理解和运用。

在解答这些题目时，我们要掌握相应的数学概念，并善于运用所学的数学方法和技巧进行推导和计算。

祝愿大家在数学学习中取得优异的成绩！。

初二上册数学几何试题(附答案)

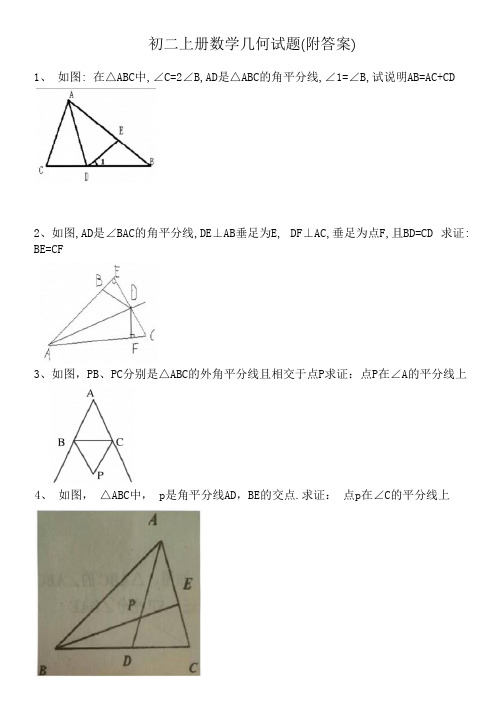
初二上册数学几何试题(附答案)1、如图: 在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E, DF⊥AC,垂足为点F,且BD=CD 求证: BE=CF3、如图，PB、PC分别是△ABC的外角平分线且相交于点P求证：点P在∠A的平分线上4、如图，△ABC中， p是角平分线AD，BE的交点.求证：点p在∠C的平分线上5、下列说法中，错误的是( )A. 三角形任意两个角的平分线的交点在三角形的内部B. 三角形两个角的平分线的交点到三边的距离相等C. 三角形两个角的平分线的交点在第三个角的平分线上D. 三角形任意两个角的平分线的交点到三个顶点的距离相等6、如图在三角形ABC 中BM=MC∠ABM=∠ACM 求证 AM平分∠BAC7、如图, AP、CP分别是△ABC外角∠MAC与∠NCA的平分线, 它们相交于点P, PD⊥BM 于点D, PF⊥BN于点F. 求证: BP为∠MBN的平分线。

8、如图,在∠AOB的两边OA, OB上分别取 OM=ON, OD=OE, DN 和EM 相交于点C. 求证: 点C在∠AOB的平分线上.9、如图, ∠B=∠C=90° , M是BC的中点, DM平分∠ADC.(1)若连接AM，则AM是否平分∠BAD?请你证明你的结论；(2)线段 DM与AM有怎样的位置关系?请说明理由.参考答案：1、因为∠1=∠B所以∠DEA=2∠B=∠C因为 AD是△ABC的角平分线所以∠CAD=∠EAD 因为 AD=AD所以△ADC 全等于△ADE 所以 AC=AE CD=DE 因为∠1=∠B 所以△EDB 为等腰三角形所以 EB=DE 因为 AB=AE+EB AC=AE CD=DE EB=DE所以 AB=AC+CD2、因为 ad是∠bac的角平分线, ,DE⊥AB, DF⊥AC, 所以DE=DF三角形DEB和三角形DFC均为直角三角形,又因为 BD=CD 所以BE=CF3、作PF⊥AD, PH⊥BC, PG⊥AE∵PB 平分∠DBC, PC平分∠ECB, PF⊥AD, PH⊥BC, PG⊥AE∴PF=PH，PG=PH(角平分线上的点到这个角的两边的距离相等)∴PF=PG∵PF⊥AD, PG⊥AE, PF=PG∴PA平分∠BAC(在一个角的内部，且到角的两边距离相等的点，在这个角的平分线上)4、作PG⊥BC,PH⊥AC,PQ⊥AB,垂足分别为G、H、Q,AD为∠A的平分线,PH=PQ;BE为∠B 的平分线, PQ=PG;所以PG=PH,又CP为RT△CGP和RT△CEP的公共斜边,所以△CGP≌△CHP,所以∠GCP=∠ECP,CP为∠的平分线，P点在∠C的平分线上5、 A6、∵BM=MC, ∴∠MBC=∠MCB, ∵∠ABM=∠ACM, ∴∠ABM+∠MBC=∠ACM+∠MCB, 即∠ABC=∠ACB,∴AB=AC, 在△AMB与△AMC中, AB=AC, ∠ABM=∠ACM, MB=MC, ∴△AMB≌△AMC(SAS),∴ ∠MAB=∠MAC, 即AM平分∠BAC。

2024年数学八年级上册几何基础练习题(含答案)

2024年数学八年级上册几何基础练习题（含答案）试题部分一、选择题1. 在一个等腰三角形中，如果底边长为10cm，腰长为13cm，那么这个三角形的周长是多少？A. 26cmB. 36cmC. 46cmD. 56cm2. 一个直角三角形的两个锐角分别是30度和60度，如果斜边长为20cm，那么直角边长是多少？A. 10cmB. 10√3 cmC. 20cmD. 20√3 cm3. 一个圆的半径为5cm，那么它的直径是多少？A. 2.5cmB. 5cmC. 10cmD. 20cm4. 一个正方形的对角线长为10cm，那么它的边长是多少？B. 10cmC. 10√2 cmD. 20cm5. 一个等边三角形的边长为6cm，那么它的高是多少？A. 3cmB. 3√3 cmC. 6cmD. 6√3 cm6. 一个长方形的长是宽的两倍，如果长方形的周长是30cm，那么长和宽分别是多少？A. 长为15cm，宽为7.5cmB. 长为10cm，宽为5cmC. 长为20cm，宽为10cmD. 长为12cm，宽为6cm7. 一个圆的周长是31.4cm，那么它的半径是多少？A. 5cmB. 10cmC. 15cmD. 20cm8. 一个正方形的面积是36cm²，那么它的边长是多少？A. 6cmB. 9cmC. 12cm9. 一个等腰三角形的底边长为8cm，腰长为10cm，那么这个三角形的周长是多少？A. 16cmB. 20cmC. 24cmD. 28cm10. 一个直角三角形的两个锐角分别是45度和45度，如果斜边长为10cm，那么直角边长是多少？A. 5cmB. 5√2 cmC. 10cmD. 10√2 cm二、判断题1. 一个圆的半径是直径的一半。

（）2. 一个等腰三角形的底边和腰的长度相等。

（）3. 一个直角三角形的两个锐角之和是90度。

（）4. 一个正方形的对角线长等于边长的两倍。

（）5. 一个等边三角形的高等于边长的根号3倍。