UMAT以及depvar整理
最新黄永刚单晶塑性有限元umat子程序

SUBROUTINE UMAT(stress,statev,ddsdde,sse,spd,scd,1 rpl, ddsddt, drplde, drpldt,2 stran,dstran,time,dtime,temp,dtemp,predef,dpred,cmname,3 ndi,nshr,ntens,nstatv,props,nprops,coords,drot,pnewdt,4 celent,dfgrd0,dfgrd1,noel,npt,layer,kspt,kstep,kinc)c WRITE (6,*) 'c NOTE: MODIFICATIONS TO *UMAT FOR ABAQUS VERSION 5.3 (14 APR '94)cc (1) The list of variables above defining the *UMAT subroutine,c and the first (standard) block of variables dimensioned below,c have variable names added compared to earlier ABAQUS versions.cc (2) The statement: include 'aba_param.inc' must be added as below.cc (3) As of version 5.3, ABAQUS files use double precision only.c The file aba_param.inc has a line "implicit real*8" and, sincec it is included in the main subroutine, it will define the variablesc there as double precision. But other subroutines still need thec definition "implicit real*8" since there may be variables that arec not passed to them through the list or common block.cc (4) This is current as of version 5.6 of ABAQUS.cc (5) Note added by J. W. Kysar (4 November 1997). This UMAT has beenc modified to keep track of the cumulative shear strain in eachc individual slip system. This information is needed to correct anc error in the implementation of the Bassani and Wu hardening law.c Any line of code which has been added or modified is precededc immediately by a line beginning CFIXA and succeeded by a linec beginning CFIXB. Any comment line added or modified will beginc with CFIX.cc The hardening law by Bassani and Wu was implemented incorrectly.c This law is a function of both hyperbolic secant squared and hyperbolicc tangent. However, the arguments of sech and tanh are related to the *total* c slip on individual slip systems. Formerly, the UMAT implemented thisc hardening law by using the *current* slip on each slip system. Thereinc lay the problem. The UMAT did not restrict the current slip to be ac positive value. So when a slip with a negative sign was encountered, the c term containing tanh led to a negative hardening rate (since tanh is anc odd function).c The UMAT has been fixed by adding state variables to keep track of thec *total* slip on each slip system by integrating up the absolute valuec of slip rates for each individual slip system. These "solution dependent c variables" are available for postprocessing. The only required changec in the input file is that the DEPVAR command must be changed.cC----- Use single precision on Cray byC (1) deleting the statement "IMPLICIT*8 (A-H,O-Z)";C (2) changing "REAL*8 FUNCTION" to "FUNCTION";C (3) changing double precision functions DSIGN to SIGN.CC----- Subroutines:CC ROTATION -- forming rotation matrix, i.e. the directionC cosines of cubic crystal [100], [010] and [001]C directions in global system at the initialC stateCC SLIPSYS -- calculating number of slip systems, unitC vectors in slip directions and unit normals toC slip planes in a cubic crystal at the initialC stateCC GSLPINIT -- calculating initial value of current strengthsC at initial stateCC STRAINRATE -- based on current values of resolved shearC stresses and current strength, calculatingC shear strain-rates in slip systemsCC LATENTHARDEN -- forming self- and latent-hardening matrixCC ITERATION -- generating arrays for the Newton-RhapsonC iterationCC LUDCMP -- LU decompositionCC LUBKSB -- linear equation solver based on LUC decomposition method (must call LUDCMP first)C----- Function subprogram:C F -- shear strain-rates in slip systemsC----- Variables:CC STRESS -- stresses (INPUT & OUTPUT)C Cauchy stresses for finite deformationC STATEV -- solution dependent state variables (INPUT & OUTPUT) C DDSDDE -- Jacobian matrix (OUTPUT)C----- Variables passed in for information:CC STRAN -- strainsC logarithmic strain for finite deformationC (actually, integral of the symmetric part of velocity C gradient with respect to time)C DSTRAN -- increments of strainsC CMNAME -- name given in the *MATERIAL optionC NDI -- number of direct stress componentsC NSHR -- number of engineering shear stress componentsC NTENS -- NDI+NSHRC NSTATV -- number of solution dependent state variables (asC defined in the *DEPVAR option)C PROPS -- material constants entered in the *USER MATERIALC optionC NPROPS -- number of material constantsCC----- This subroutine provides the plastic constitutive relation of C single crystals for finite element code ABAQUS. The plastic slip C of single crystal obeys the Schmid law. The program gives the C choice of small deformation theory and theory of finite rotation C and finite strain.C The strain increment is composed of elastic part and plastic C part. The elastic strain increment corresponds to latticeC stretching, the plastic part is the sum over all slip systems of C plastic slip. The shear strain increment for each slip system is C assumed a function of the ratio of corresponding resolved shear C stress over current strength, and of the time step. The resolved C shear stress is the double product of stress tensor with the slip C deformation tensor (Schmid factor), and the increment of current C strength is related to shear strain increments over all slipC systems through self- and latent-hardening functions.C----- The implicit integration method proposed by Peirce, Shih and C Needleman (1984) is used here. The subroutine provides an option C of iteration to solve stresses and solution dependent stateC variables within each increment.C----- The present program is for a single CUBIC crystal. However, C this code can be generalized for other crystals (e.g. HCP,C Tetragonal, Orthotropic, etc.). Only subroutines ROTATION and C SLIPSYS need to be modified to include the effect of crystalC aspect ratio.CC----- Important notice:CC (1) The number of state variables NSTATV must be larger than (or CFIX equal to) TEN (10) times the total number of slip systems in C all sets, NSLPTL, plus FIVE (5)CFIX NSTATV >= 10 * NSLPTL + 5C Denote s as a slip direction and m as normal to a slip plane.C Here (s,-m), (-s,m) and (-s,-m) are NOT consideredC independent of (s,m). The number of slip systems in each set C could be either 6, 12, 24 or 48 for a cubic crystal, e.g. 12 C for {110}<111>.CC Users who need more parameters to characterize theC constitutive law of single crystal, e.g. the frameworkC proposed by Zarka, should make NSTATV larger than (or equal C to) the number of those parameters NPARMT plus nine timesC the total number of slip systems, NSLPTL, plus fiveCFIX NSTATV >= NPARMT + 10 * NSLPTL + 5CC (2) The tangent stiffness matrix in general is not symmetric if C latent hardening is considered. Users must declare "UNSYMM"C in the input file, at the *USER MATERIAL card.CPARAMETER (ND=150)C----- The parameter ND determines the dimensions of the arrays inC this subroutine. The current choice 150 is a upper bound for a C cubic crystal with up to three sets of slip systems activated.C Users may reduce the parameter ND to any number as long as larger C than or equal to the total number of slip systems in all sets.C For example, if {110}<111> is the only set of slip systemC potentially activated, ND could be taken as twelve (12).cinclude 'aba_param.inc'cCHARACTER*8 CMNAMEEXTERNAL Fdimension stress(ntens),statev(nstatv),1 ddsdde(ntens,ntens),ddsddt(ntens),drplde(ntens),2 stran(ntens),dstran(ntens),time(2),predef(1),dpred(1),3 props(nprops),coords(3),drot(3,3),dfgrd0(3,3),dfgrd1(3,3)DIMENSION ISPDIR(3), ISPNOR(3), NSLIP(3),2 SLPDIR(3,ND), SLPNOR(3,ND), SLPDEF(6,ND),3 SLPSPN(3,ND), DSPDIR(3,ND), DSPNOR(3,ND),4 DLOCAL(6,6), D(6,6), ROTD(6,6), ROTATE(3,3),5 FSLIP(ND), DFDXSP(ND), DDEMSD(6,ND),6 H(ND,ND), DDGDDE(ND,6),7 DSTRES(6), DELATS(6), DSPIN(3), DVGRAD(3,3),8 DGAMMA(ND), DTAUSP(ND), DGSLIP(ND),9 WORKST(ND,ND), INDX(ND), TERM(3,3), TRM0(3,3), ITRM(3)DIMENSION FSLIP1(ND), STRES1(6), GAMMA1(ND), TAUSP1(ND),2 GSLP1(ND), SPNOR1(3,ND), SPDIR1(3,ND), DDSDE1(6,6),3 DSOLD(6), DGAMOD(ND), DTAUOD(ND), DGSPOD(ND),4 DSPNRO(3,ND), DSPDRO(3,ND),5 DHDGDG(ND,ND)C----- NSLIP -- number of slip systems in each setC----- SLPDIR -- slip directions (unit vectors in the initial state) C----- SLPNOR -- normals to slip planes (unit normals in the initial C state)C----- SLPDEF -- slip deformation tensors (Schmid factors)C SLPDEF(1,i) -- SLPDIR(1,i)*SLPNOR(1,i)C SLPDEF(2,i) -- SLPDIR(2,i)*SLPNOR(2,i)C SLPDEF(3,i) -- SLPDIR(3,i)*SLPNOR(3,i)C SLPDEF(4,i) -- SLPDIR(1,i)*SLPNOR(2,i)+C SLPDIR(2,i)*SLPNOR(1,i)C SLPDEF(5,i) -- SLPDIR(1,i)*SLPNOR(3,i)+C SLPDIR(3,i)*SLPNOR(1,i)C SLPDEF(6,i) -- SLPDIR(2,i)*SLPNOR(3,i)+C SLPDIR(3,i)*SLPNOR(2,i)C where index i corresponds to the ith slip systemC----- SLPSPN -- slip spin tensors (only needed for finite rotation) C SLPSPN(1,i) -- [SLPDIR(1,i)*SLPNOR(2,i)-C SLPDIR(2,i)*SLPNOR(1,i)]/2C SLPSPN(2,i) -- [SLPDIR(3,i)*SLPNOR(1,i)-C SLPDIR(1,i)*SLPNOR(3,i)]/2C SLPSPN(3,i) -- [SLPDIR(2,i)*SLPNOR(3,i)-C SLPDIR(3,i)*SLPNOR(2,i)]/2C where index i corresponds to the ith slip systemC----- DSPDIR -- increments of slip directionsC----- DSPNOR -- increments of normals to slip planesCC----- DLOCAL -- elastic matrix in local cubic crystal systemC----- D -- elastic matrix in global systemC----- ROTD -- rotation matrix transforming DLOCAL to DCC----- ROTATE -- rotation matrix, direction cosines of [100], [010] C and [001] of cubic crystal in global systemCC----- FSLIP -- shear strain-rates in slip systemsC----- DFDXSP -- derivatives of FSLIP w.r.t x=TAUSLP/GSLIP, whereC TAUSLP is the resolved shear stress and GSLIP is the C current strengthCC----- DDEMSD -- double dot product of the elastic moduli tensor with C the slip deformation tensor plus, only for finiteC rotation, the dot product of slip spin tensor with C the stressCC----- H -- self- and latent-hardening matrixC H(i,i) -- self hardening modulus of the ith slipC system (no sum over i)C H(i,j) -- latent hardening molulus of the ith slip C system due to a slip in the jth slip system C (i not equal j)CC----- DDGDDE -- derivatice of the shear strain increments in slipC systems w.r.t. the increment of strainsCC----- DSTRES -- Jaumann increments of stresses, i.e. corotationalC stress-increments formed on axes spinning with the C materialC----- DELATS -- strain-increments associated with lattice stretching C DELATS(1) - DELATS(3) -- normal strain incrementsC DELATS(4) - DELATS(6) -- engineering shear strainC incrementsC----- DSPIN -- spin-increments associated with the material element C DSPIN(1) -- component 12 of the spin tensorC DSPIN(2) -- component 31 of the spin tensorC DSPIN(3) -- component 23 of the spin tensorCC----- DVGRAD -- increments of deformation gradient in the currentC state, i.e. velocity gradient times the increment of C timeCC----- DGAMMA -- increment of shear strains in slip systemsC----- DTAUSP -- increment of resolved shear stresses in slip systems C----- DGSLIP -- increment of current strengths in slip systemsCCC----- Arrays for iteration:CC FSLIP1, STRES1, GAMMA1, TAUSP1, GSLP1 , SPNOR1, SPDIR1,C DDSDE1, DSOLD , DGAMOD, DTAUOD, DGSPOD, DSPNRO, DSPDRO,C DHDGDGCCC----- Solution dependent state variable STATEV:C Denote the number of total slip systems by NSLPTL, whichC will be calculated in this code.CC Array STATEV:C 1 - NSLPTL : current strength in slip systemsC NSLPTL+1 - 2*NSLPTL : shear strain in slip systemsC 2*NSLPTL+1 - 3*NSLPTL : resolved shear stress in slip systems CC 3*NSLPTL+1 - 6*NSLPTL : current components of normals to slip C slip planesC 6*NSLPTL+1 - 9*NSLPTL : current components of slip directions CCFIX 9*NSLPTL+1 - 10*NSLPTL : total cumulative shear strain on each CFIX slip system (sum of the absolute CFIX values of shear strains in each slip CFIX system individually)CFIXCFIX 10*NSLPTL+1 : total cumulative shear strain on all C slip systems (sum of the absoluteC values of shear strains in all slipC systems)CCFIX 10*NSLPTL+2 - NSTATV-4 : additional parameters users may need C to characterize the constitutive law C of a single crystal (if there areC any).CC NSTATV-3 : number of slip systems in the 1st set C NSTATV-2 : number of slip systems in the 2nd set C NSTATV-1 : number of slip systems in the 3rd set C NSTATV : total number of slip systems in all C setsCCC----- Material constants PROPS:CC PROPS(1) - PROPS(21) -- elastic constants for a general elastic C anisotropic materialCC isotropic : PROPS(i)=0 for i>2C PROPS(1) -- Young's modulusC PROPS(2) -- Poisson's ratioCC cubic : PROPS(i)=0 for i>3C PROPS(1) -- c11C PROPS(2) -- c12C PROPS(3) -- c44CC orthotropic : PORPS(i)=0 for i>9C PROPS(1) - PROPS(9) are D1111, D1122, D2222, C D1133, D2233, D3333, D1212, D1313, D2323, C respectively, which has the same definition C as ABAQUS for orthotropic materialsC (see *ELASTIC card)CC anisotropic : PROPS(1) - PROPS(21) are D1111, D1122,C D2222, D1133, D2233, D3333, D1112, D2212, C D3312, D1212, D1113, D2213, D3313, D1213, C D1313, D1123, D2223, D3323, D1223, D1323, C D2323, respectively, which has the sameC definition as ABAQUS for anisotropicC materials (see *ELASTIC card)CCC PROPS(25) - PROPS(56) -- parameters characterizing all slipC systems to be activated in a cubicC crystalCC PROPS(25) -- number of sets of slip systems (maximum 3),C e.g. (110)[1-11] and (101)[11-1] are in the C same set of slip systems, (110)[1-11] andC (121)[1-11] belong to different sets of slip C systemsC (It must be a real number, e.g. 3., not 3 !) CC PROPS(33) - PROPS(35) -- normal to a typical slip plane in C the first set of slip systems, C e.g. (1 1 0)C (They must be real numbers, e.g.C 1. 1. 0., not 1 1 0 !)C PROPS(36) - PROPS(38) -- a typical slip direction in the C first set of slip systems, e.g.C [1 1 1]C (They must be real numbers, e.g.C 1. 1. 1., not 1 1 1 !)CC PROPS(41) - PROPS(43) -- normal to a typical slip plane in C the second set of slip systemsC (real numbers)C PROPS(44) - PROPS(46) -- a typical slip direction in the C second set of slip systemsC (real numbers)CC PROPS(49) - PROPS(51) -- normal to a typical slip plane in C the third set of slip systemsC (real numbers)C PROPS(52) - PROPS(54) -- a typical slip direction in the C third set of slip systemsC (real numbers)CCC PROPS(57) - PROPS(72) -- parameters characterizing the initial C orientation of a single crystal inC global systemC The directions in global system and directions in local C cubic crystal system of two nonparallel vectors are needed C to determine the crystal orientation.CC PROPS(57) - PROPS(59) -- [p1 p2 p3], direction of first C vector in local cubic crystalC system, e.g. [1 1 0]C (They must be real numbers, e.g.C 1. 1. 0., not 1 1 0 !)C PROPS(60) - PROPS(62) -- [P1 P2 P3], direction of first C vector in global system, e.g.C [2. 1. 0.]C (It does not have to be a unit C vector)CC PROPS(65) - PROPS(67) -- direction of second vector inC local cubic crystal system (real C numbers)C PROPS(68) - PROPS(70) -- direction of second vector inC global systemCCC PROPS(73) - PROPS(96) -- parameters characterizing the visco-C plastic constitutive law (shearC strain-rate vs. resolved shearC stress), e.g. a power-law relationCC PROPS(73) - PROPS(80) -- parameters for the first set of C slip systemsC PROPS(81) - PROPS(88) -- parameters for the second set of C slip systemsC PROPS(89) - PROPS(96) -- parameters for the third set of C slip systemsCCC PROPS(97) - PROPS(144)-- parameters characterizing the self-C and latent-hardening laws of slipC systemsCC PROPS(97) - PROPS(104)-- self-hardening parameters for the C first set of slip systemsC PROPS(105)- PROPS(112)-- latent-hardening parameters for C the first set of slip systems and C interaction with other sets of C slip systemsCC PROPS(113)- PROPS(120)-- self-hardening parameters for the C second set of slip systemsC PROPS(121)- PROPS(128)-- latent-hardening parameters for C the second set of slip systems C and interaction with other sets C of slip systemsCC PROPS(129)- PROPS(136)-- self-hardening parameters for the C third set of slip systemsC PROPS(137)- PROPS(144)-- latent-hardening parameters for C the third set of slip systems and C interaction with other sets ofC slip systemsCCC PROPS(145)- PROPS(152)-- parameters characterizing forward time C integration scheme and finiteC deformationCC PROPS(145) -- parameter theta controlling the implicitC integration, which is between 0 and 1C 0. : explicit integrationC 0.5 : recommended valueC 1. : fully implicit integrationCC PROPS(146) -- parameter NLGEOM controlling whether theC effect of finite rotation and finite strain C of crystal is considered,C 0. : small deformation theoryC otherwise : theory of finite rotation and C finite strainCCC PROPS(153)- PROPS(160)-- parameters characterizing iteration C methodCC PROPS(153) -- parameter ITRATN controlling whether theC iteration method is used,C 0. : no iterationC otherwise : iterationCC PROPS(154) -- maximum number of iteration ITRMAXCC PROPS(155) -- absolute error of shear strains in slipC systems GAMERRCC----- Elastic matrix in local cubic crystal system: DLOCALDO J=1,6DO I=1,6DLOCAL(I,J)=0.END DOEND DOCHECK=0.DO J=10,21CHECK=CHECK+ABS(PROPS(J))END DOIF (CHECK.EQ.0.) THENDO J=4,9CHECK=CHECK+ABS(PROPS(J))END DOIF (CHECK.EQ.0.) THENIF (PROPS(3).EQ.0.) THENC----- Isotropic materialGSHEAR=PROPS(1)/2./(1.+PROPS(2))E11=2.*GSHEAR*(1.-PROPS(2))/(1.-2.*PROPS(2)) E12=2.*GSHEAR*PROPS(2)/(1.-2.*PROPS(2))DO J=1,3DLOCAL(J,J)=E11DO I=1,3IF (I.NE.J) DLOCAL(I,J)=E12END DODLOCAL(J+3,J+3)=GSHEAREND DOELSEC----- Cubic materialDO J=1,3DLOCAL(J,J)=PROPS(1)DO I=1,3IF (I.NE.J) DLOCAL(I,J)=PROPS(2)END DODLOCAL(J+3,J+3)=PROPS(3)END DOEND IFELSEC----- Orthotropic metarialDLOCAL(1,1)=PROPS(1)DLOCAL(1,2)=PROPS(2)DLOCAL(2,1)=PROPS(2)DLOCAL(2,2)=PROPS(3)DLOCAL(1,3)=PROPS(4)DLOCAL(3,1)=PROPS(4)DLOCAL(2,3)=PROPS(5)DLOCAL(3,2)=PROPS(5)DLOCAL(3,3)=PROPS(6)DLOCAL(4,4)=PROPS(7)DLOCAL(5,5)=PROPS(8)DLOCAL(6,6)=PROPS(9)END IFELSEC----- General anisotropic materialID=0DO J=1,6DO I=1,JID=ID+1DLOCAL(I,J)=PROPS(ID)DLOCAL(J,I)=DLOCAL(I,J)END DOEND DOEND IFC----- Rotation matrix: ROTATE, i.e. direction cosines of [100], [010] C and [001] of a cubic crystal in global systemCCALL ROTATION (PROPS(57), ROTATE)C----- Rotation matrix: ROTD to transform local elastic matrix DLOCAL C to global elastic matrix DCDO J=1,3J1=1+J/3J2=2+J/2DO I=1,3I1=1+I/3I2=2+I/2ROTD(I,J)=ROTATE(I,J)**2ROTD(I,J+3)=2.*ROTATE(I,J1)*ROTATE(I,J2)ROTD(I+3,J)=ROTATE(I1,J)*ROTATE(I2,J)ROTD(I+3,J+3)=ROTATE(I1,J1)*ROTATE(I2,J2)+2 ROTATE(I1,J2)*ROTATE(I2,J1)END DOEND DOC----- Elastic matrix in global system: DC {D} = {ROTD} * {DLOCAL} * {ROTD}transposeCDO J=1,6DO I=1,6D(I,J)=0.END DOEND DODO J=1,6DO I=1,JDO K=1,6DO L=1,6D(I,J)=D(I,J)+DLOCAL(K,L)*ROTD(I,K)*ROTD(J,L) END DOEND DOD(J,I)=D(I,J)END DOEND DOC----- Total number of sets of slip systems: NSETNSET=NINT(PROPS(25))IF (NSET.LT.1) THENWRITE (6,*) '***ERROR - zero sets of slip systems'STOPELSE IF (NSET.GT.3) THENWRITE (6,*)2 '***ERROR - more than three sets of slip systems'STOPEND IFC----- Implicit integration parameter: THETATHETA=PROPS(145)C----- Finite deformation ?C----- NLGEOM = 0, small deformation theoryC otherwise, theory of finite rotation and finite strain, Users C must declare "NLGEOM" in the input file, at the *STEP cardCIF (PROPS(146).EQ.0.) THENNLGEOM=0ELSENLGEOM=1END IFC----- Iteration?C----- ITRATN = 0, no iterationC otherwise, iteration (solving increments of stresses andC solution dependent state variables)CIF (PROPS(153).EQ.0.) THENITRATN=0ELSEITRATN=1END IFITRMAX=NINT(PROPS(154))GAMERR=PROPS(155)NITRTN=-1DO I=1,NTENSDSOLD(I)=0.END DODO J=1,NDDGAMOD(J)=0.DTAUOD(J)=0.DGSPOD(J)=0.DO I=1,3DSPNRO(I,J)=0.DSPDRO(I,J)=0.END DOEND DOC----- Increment of spin associated with the material element: DSPIN C (only needed for finite rotation)CIF (NLGEOM.NE.0) THENDO J=1,3DO I=1,3TERM(I,J)=DROT(J,I)TRM0(I,J)=DROT(J,I)END DOTERM(J,J)=TERM(J,J)+1.D0TRM0(J,J)=TRM0(J,J)-1.D0END DOCALL LUDCMP (TERM, 3, 3, ITRM, DDCMP)DO J=1,3CALL LUBKSB (TERM, 3, 3, ITRM, TRM0(1,J))END DODSPIN(1)=TRM0(2,1)-TRM0(1,2)DSPIN(2)=TRM0(1,3)-TRM0(3,1)DSPIN(3)=TRM0(3,2)-TRM0(2,3)END IFC----- Increment of dilatational strain: DEVDEV=0.D0DO I=1,NDIDEV=DEV+DSTRAN(I)END DOC----- Iteration starts (only when iteration method is used)1000 CONTINUEC----- Parameter NITRTN: number of iterationsC NITRTN = 0 --- no-iteration solutionCNITRTN=NITRTN+1C----- Check whether the current stress state is the initial stateIF (STATEV(1).EQ.0.) THENC----- Initial stateCC----- Generating the following parameters and variables at initialC state:C Total number of slip systems in all the sets NSLPTLC Number of slip systems in each set NSLIPC Unit vectors in initial slip directions SLPDIRC Unit normals to initial slip planes SLPNORCNSLPTL=0DO I=1,NSETISPNOR(1)=NINT(PROPS(25+8*I))ISPNOR(2)=NINT(PROPS(26+8*I))ISPNOR(3)=NINT(PROPS(27+8*I))ISPDIR(1)=NINT(PROPS(28+8*I))ISPDIR(2)=NINT(PROPS(29+8*I))ISPDIR(3)=NINT(PROPS(30+8*I))CALL SLIPSYS (ISPDIR, ISPNOR, NSLIP(I), SLPDIR(1,NSLPTL+1), 2 SLPNOR(1,NSLPTL+1), ROTATE)NSLPTL=NSLPTL+NSLIP(I)END DOIF (ND.LT.NSLPTL) THENWRITE (6,*)2 '***ERROR - parameter ND chosen by the present user is less than3 the total number of slip systems NSLPTL'STOPEND IFC----- Slip deformation tensor: SLPDEF (Schmid factors)DO J=1,NSLPTLSLPDEF(1,J)=SLPDIR(1,J)*SLPNOR(1,J)SLPDEF(2,J)=SLPDIR(2,J)*SLPNOR(2,J)SLPDEF(3,J)=SLPDIR(3,J)*SLPNOR(3,J)SLPDEF(4,J)=SLPDIR(1,J)*SLPNOR(2,J)+SLPDIR(2,J)*SLPNOR(1,J) SLPDEF(5,J)=SLPDIR(1,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(1,J) SLPDEF(6,J)=SLPDIR(2,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(2,J) END DOC----- Initial value of state variables: unit normal to a slip plane C and unit vector in a slip directionCSTATEV(NSTATV)=FLOAT(NSLPTL)DO I=1,NSETSTATEV(NSTATV-4+I)=FLOAT(NSLIP(I))END DOIDNOR=3*NSLPTLIDDIR=6*NSLPTLDO J=1,NSLPTLDO I=1,3IDNOR=IDNOR+1STATEV(IDNOR)=SLPNOR(I,J)IDDIR=IDDIR+1STATEV(IDDIR)=SLPDIR(I,J)END DOEND DOC----- Initial value of the current strength for all slip systemsCCALL GSLPINIT (STATEV(1), NSLIP, NSLPTL, NSET, PROPS(97))C----- Initial value of shear strain in slip systemsCFIX-- Initial value of cumulative shear strain in each slip systemsDO I=1,NSLPTLSTATEV(NSLPTL+I)=0.CFIXASTATEV(9*NSLPTL+I)=0.CFIXBEND DOCFIXASTATEV(10*NSLPTL+1)=0.CFIXBC----- Initial value of the resolved shear stress in slip systemsDO I=1,NSLPTLTERM1=0.DO J=1,NTENSIF (J.LE.NDI) THENTERM1=TERM1+SLPDEF(J,I)*STRESS(J)ELSETERM1=TERM1+SLPDEF(J-NDI+3,I)*STRESS(J)END IFEND DOSTATEV(2*NSLPTL+I)=TERM1END DOELSEC----- Current stress stateCC----- Copying from the array of state variables STATVE the following C parameters and variables at current stress state:C Total number of slip systems in all the sets NSLPTLC Number of slip systems in each set NSLIPC Current slip directions SLPDIRC Normals to current slip planes SLPNORCNSLPTL=NINT(STATEV(NSTATV))DO I=1,NSETNSLIP(I)=NINT(STATEV(NSTATV-4+I))END DOIDNOR=3*NSLPTLIDDIR=6*NSLPTLDO J=1,NSLPTLDO I=1,3IDNOR=IDNOR+1SLPNOR(I,J)=STATEV(IDNOR)IDDIR=IDDIR+1SLPDIR(I,J)=STATEV(IDDIR)END DOEND DOC----- Slip deformation tensor: SLPDEF (Schmid factors)DO J=1,NSLPTLSLPDEF(1,J)=SLPDIR(1,J)*SLPNOR(1,J)SLPDEF(2,J)=SLPDIR(2,J)*SLPNOR(2,J)SLPDEF(3,J)=SLPDIR(3,J)*SLPNOR(3,J)SLPDEF(4,J)=SLPDIR(1,J)*SLPNOR(2,J)+SLPDIR(2,J)*SLPNOR(1,J) SLPDEF(5,J)=SLPDIR(1,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(1,J) SLPDEF(6,J)=SLPDIR(2,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(2,J) END DOEND IFC----- Slip spin tensor: SLPSPN (only needed for finite rotation)IF (NLGEOM.NE.0) THENDO J=1,NSLPTLSLPSPN(1,J)=0.5*(SLPDIR(1,J)*SLPNOR(2,J)-2 SLPDIR(2,J)*SLPNOR(1,J))SLPSPN(2,J)=0.5*(SLPDIR(3,J)*SLPNOR(1,J)-2 SLPDIR(1,J)*SLPNOR(3,J))SLPSPN(3,J)=0.5*(SLPDIR(2,J)*SLPNOR(3,J)-2 SLPDIR(3,J)*SLPNOR(2,J))END DOEND IFC----- Double dot product of elastic moduli tensor with the slipC deformation tensor (Schmid factors) plus, only for finiteC rotation, the dot product of slip spin tensor with the stress: C DDEMSDCDO J=1,NSLPTLDO I=1,6DDEMSD(I,J)=0.DO K=1,6DDEMSD(I,J)=DDEMSD(I,J)+D(K,I)*SLPDEF(K,J)END DOEND DOEND DOIF (NLGEOM.NE.0) THENDO J=1,NSLPTLDDEMSD(4,J)=DDEMSD(4,J)-SLPSPN(1,J)*STRESS(1)DDEMSD(5,J)=DDEMSD(5,J)+SLPSPN(2,J)*STRESS(1)IF (NDI.GT.1) THENDDEMSD(4,J)=DDEMSD(4,J)+SLPSPN(1,J)*STRESS(2)DDEMSD(6,J)=DDEMSD(6,J)-SLPSPN(3,J)*STRESS(2)END IFIF (NDI.GT.2) THENDDEMSD(5,J)=DDEMSD(5,J)-SLPSPN(2,J)*STRESS(3)DDEMSD(6,J)=DDEMSD(6,J)+SLPSPN(3,J)*STRESS(3)END IFIF (NSHR.GE.1) THENDDEMSD(1,J)=DDEMSD(1,J)+SLPSPN(1,J)*STRESS(NDI+1)DDEMSD(2,J)=DDEMSD(2,J)-SLPSPN(1,J)*STRESS(NDI+1)DDEMSD(5,J)=DDEMSD(5,J)-SLPSPN(3,J)*STRESS(NDI+1)DDEMSD(6,J)=DDEMSD(6,J)+SLPSPN(2,J)*STRESS(NDI+1)END IFIF (NSHR.GE.2) THENDDEMSD(1,J)=DDEMSD(1,J)-SLPSPN(2,J)*STRESS(NDI+2)DDEMSD(3,J)=DDEMSD(3,J)+SLPSPN(2,J)*STRESS(NDI+2)DDEMSD(4,J)=DDEMSD(4,J)+SLPSPN(3,J)*STRESS(NDI+2)DDEMSD(6,J)=DDEMSD(6,J)-SLPSPN(1,J)*STRESS(NDI+2)END IFIF (NSHR.EQ.3) THENDDEMSD(2,J)=DDEMSD(2,J)+SLPSPN(3,J)*STRESS(NDI+3)DDEMSD(3,J)=DDEMSD(3,J)-SLPSPN(3,J)*STRESS(NDI+3)DDEMSD(4,J)=DDEMSD(4,J)-SLPSPN(2,J)*STRESS(NDI+3)DDEMSD(5,J)=DDEMSD(5,J)+SLPSPN(1,J)*STRESS(NDI+3)END IFEND DOEND IFC----- Shear strain-rate in a slip system at the start of increment: C FSLIP, and its derivative: DFDXSPCID=1DO I=1,NSETIF (I.GT.1) ID=ID+NSLIP(I-1)CALL STRAINRATE (STATEV(NSLPTL+ID), STATEV(2*NSLPTL+ID),2 STATEV(ID), NSLIP(I), FSLIP(ID), DFDXSP(ID),3 PROPS(65+8*I))END DOC----- Self- and latent-hardening laws。
UMAT全过程技术篇

UMAT全过程-"技术篇"[写在前面:这篇文章是UMAT全过程-感想篇的姊妹篇,答应要给大家写的一篇帖子,同时也是为了记录自己的学习过程,与大家分享!首先指出,俺的"技术篇"--是加了引号的,因为确实称不上有多么大的技术含量,还望大家莫笑偶!只不过一是跟那个感想篇形成一个对照,同时主要内容为自己编子程序过程中涉及的技术边边上的小问题的一些解决方法,供仿友们参考!偶不是谦虚,也不是一个低调的人,大家谢谢和支持的话,我先行谢过啦!更希望大家能提出质疑或者别的更好的办法,大家相互交流,共同进步!]----------------------------------------------------------------------------*转*入*正*题*第一部分:相关知识[特别声明,这部分来自于华中科技大学杨曼娟同学的硕士学位论文,在此对作者表示感谢!--大家可以去知网下载]----------------------------------------------------------------------------1.ABAQUS中材料非线性问题的处理ABAQUS中材料非线性问题用Newton-Raphson法来求解。
首先将载荷分为若干个微小增量,结构受到一个微小增量△P。
ABAQUS用与初始结构位移相对应的初始刚度矩阵K0和荷载增量△P计算出结构的在这一步增量后的位移修正Ca、修正后的位移值Ua和相应的新的刚度矩阵Ka。
ABAQUS用新的刚度矩阵计算结构的内力Ia,荷载P和Ia的差值为迭代的残余力Ra,即Ra=P-Ia。
如果Ra在模型内的每个自由度上的值都为零,如图2-2中的a点,则结构处于平衡状态。
但在非线性问题中,通常Ra是不可能为零,ABAQUS为此设置了一个残余力容差。
如果Ra小于这个数字,ABAQUS就认为结构的内外力是平衡的。
一般这个缺省值取为平均内力的0.5%(如图2-2)。
ABAQUS-UMAT-自学知识整理贴

各个楼层及内容索引2-------------------------------------什么是UMAT3-------------------------------------UMAT功能简介4-------------------------------------UMAT开始的变量声明5-------------------------------------UMAT中各个变量的详细解释6-------------------------------------关于沙漏和横向剪切刚度7-------------------------------------UMAT流程和参数表格实例展示8-------------------------------------FORTRAN语言中的接口程序Interface 9-------------------------------------关于UMAT是否可以用Fortran90编写的问题10-17--------------------------------Fortran77的一些有用的知识简介20-25\30-32-----------------------弹塑性力学相关知识简介34-37--------------------------------用户材料子程序实例JOhn-cook模型压缩包下载38-------------------------------------JOhn-cook模型本构简介图40-------------------------------------用户材料子程序实例JOhn-cook模型完整程序+david详细注解[欢迎大家来看看,并提供意见,完全是自己的diy的,不保证完全正确,希望共同探讨,以便更正,带"?"部分,还望各位大师\同仁指教]什么是UMAT程序,真正的定义材料的力学行为即属性,是用户自己编译的FORTRAN 程序来实现的!UMAT通过与ABAQUS主求解程序的接口实现与ABAQUS的数据交流UMAT功能简介[-摘自庄茁老师的书]UMAT子程序具有强大的功能,使用UMAT子程序:(1)可以定义材料的本构关系,使用ABAQUS材料库中没有包含的材料进行计算,扩充程序功能。
UMAT以及depvar整理

UMAT以及depvar整理UMAT以及depvar整理by warmwormdk最近一直在论坛查资料,对自己感兴趣的一些问题专门进行了整理,希望对大家有所帮助,也希望能获得小小的奖励啊,哈哈1UMAT的状态变量问题Q:用DEPVAR定义的状态变量个数假设为10个。
是不是说一个积分点的状态变量是10个,单元的积分点是4的话,那么单元的状态变量就是40个。
也就是自己要存储单元变量的话,就得按40个状态变量来。
是不是呢?A:有人说跟我说,DEPVAR定义的状态变量个数指每个积分点的状态变量个数。
abaqus 会自动为每个单元的每个积分点开辟这样大小的状态变量数组,abaqus调用umat时能够自动根据单元好和积分点向umat提供状态变量,在此基础上umat修改状态变量。
2umat里的STATEV变量怎么输出到odb文件中Q:比如我想知道statev(10)的odb文件,怎么输出?又怎么打开.statev(10)是我自己定义的damage变量,请各位赐教A在element关键词中添加SDV,就像下面这样。
*Element Output,directions=YESALPHA,LE,PE,PEEQ,PEMAG,PS,S,STH,SE,SF,VE,VEEQ,VS,SDV3Q statev(?)请问这个状态变量()内的数字代表什么含义?对应的变量是不是固定的?各自对应着哪些变量?A:括号中的数代表这个变量矩阵的维数,这个值等于depvar的值。
4umat中DEPVAR有几种定义方式?Q;UMAT中状态变量的定义方式,一般有两种形式,一是在inp文件中采用*initial conditions定义,二是特殊情况下可以采用SDVINI来定义;目前的疑问是,是否还有其他定义状态变量的方式?请专家针对上传的附件给于指点多谢!附件中的例子来自ABAQUS HELP中的例子!请问例子中INP文件中是如何定义状态变量的THANKS A:初值可以采用SDVINI来定义程序运行中用以下代码更新DO310K1=1,NTENSSTATEV(K1)=EELAS(K1)STATEV(K1+NTENS)=EPLAS(K1)310CONTINUESTATEV(1+2*NTENS)=EQPLASCRETURNEND5umat子程序定义问题?Q:在umat中定义的参数在材料中需不需再定义了?比如我umat 中已经给了密度了。
用户子程序UMAT设置

ABAQUS用户子程序UMAT的设置在property模块进行。
Creat material→General→User Material,输入Mechanical Constants,即为子程序中需要输入的参数,如下图所示。
Creat material→General→Depvar,在这里面设置状态变量的个数,与子程序中变量STATEV(NSTATEV)有关,如下图所示。
而用户子程序的格式可以通过搜索ABAQUS Documentation,在该文档中可以找到子程序UMAT的书写方法以及相关变量的含义。
SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,1 RPL,DDSDDT,DRPLDE,DRPLDT,2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)CINCLUDE 'ABA_PARAM.INC'CCHARACTER*80 CMNAMEDIMENSION STRESS(NTENS),STATEV(NSTATV),1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),4 JSTEP(4)user coding to define DDSDDE, STRESS, STATEV, SSE, SPD, SCDand, if necessary, RPL, DDSDDT, DRPLDE, DRPLDT, PNEWDTRETURNEND必须在子程序UMAT中提供材料本构的雅可比(Jacobian)矩阵(即变量DDSDDE),即应力增量对应变增量的变化率。
UMAT全过程技术篇

UMAT全过程-"技术篇"[写在前面:这篇文章是UMAT全过程-感想篇的姊妹篇,答应要给大家写的一篇帖子,同时也是为了记录自己的学习过程,与大家分享!首先指出,俺的"技术篇"--是加了引号的,因为确实称不上有多么大的技术含量,还望大家莫笑偶!只不过一是跟那个感想篇形成一个对照,同时主要内容为自己编子程序过程中涉及的技术边边上的小问题的一些解决方法,供仿友们参考!偶不是谦虚,也不是一个低调的人,大家谢谢和支持的话,我先行谢过啦!更希望大家能提出质疑或者别的更好的办法,大家相互交流,共同进步!]----------------------------------------------------------------------------*转*入*正*题*第一部分:相关知识[特别声明,这部分来自于华中科技大学杨曼娟同学的硕士学位论文,在此对作者表示感谢!--大家可以去知网下载]----------------------------------------------------------------------------1.ABAQUS中材料非线性问题的处理ABAQUS中材料非线性问题用Newton-Raphson法来求解。
首先将载荷分为若干个微小增量,结构受到一个微小增量△P。
ABAQUS用与初始结构位移相对应的初始刚度矩阵K0和荷载增量△P计算出结构的在这一步增量后的位移修正Ca、修正后的位移值Ua和相应的新的刚度矩阵Ka。
ABAQUS用新的刚度矩阵计算结构的内力Ia,荷载P和Ia的差值为迭代的残余力Ra,即Ra=P-Ia。
如果Ra在模型内的每个自由度上的值都为零,如图2-2中的a点,则结构处于平衡状态。
但在非线性问题中,通常Ra是不可能为零,ABAQUS为此设置了一个残余力容差。
如果Ra小于这个数字,ABAQUS就认为结构的内外力是平衡的。
一般这个缺省值取为平均内力的0.5%(如图2-2)。
一起学习UMAT 的一些公式注释

一起学习UMAT的一些公式注释ZHANG chunyuherrliubs comments in formulas知识积累和储备在进行ABAQUS子程序UMAT的编写前,要弄清楚:ABAQUS调用UMAT子程序流程;要建立的材料模型的本构关系和屈服准则等;UMAT子程序中相关参数、以及矩阵的表达。
主要求解过程:每一个增量步开始,ABAQUS主程序在单元积分点上调用UMAT 子程序,并转入应变增量、时间步长及荷载增量,同时也传入当前已知的状态的应力、应变及其他求解过程相关的变量;UMAT子程序根据本构方程求解应力增量及其他相关的变量,提供Jacobian矩阵给ABAQUS主程序以形成整体刚度矩阵;主程序结合当前荷载增量求解位移增量,继而进行平衡校核;如果不满足指定的误差,ABAQUS将进行迭代直到收敛,然后进行下一增量步的求解。
弹性力学相关知识(基本)仿真论坛(/forum.php ... &highlight=UMAT)ABAQUS二次开发版块这个人帖子结合例子,列出了弹性力学的基本公式。
UMAT变量含义UMAT中可以得到的量增量步开始时刻的,应力(Stress),应变(Strain), 状态变量(Solution-dependent state variables (SDVs))增量步开始时刻的,应变增量(Strain increment),转角增量(Rotation increment),变形梯度(Deformation gradient)时间总值及增量(Total and incremental values of time),温度(Temperature),用户定义场变量材料常数,材料点的位置,特征单元长度当前分析步,增量步必须定义的变量应力,状态变量,材料Jacobian矩阵(本构关系)可以定义的变量应变能,塑性耗能,蠕变耗能新建议的时间增量变量分类UMAT中可以直接调用(Call ……)的子程序或子函数SINV(STRESS,SINV1,SINV2,NDI,NSHR)——用于计算应力不变量。
清华大学bbs的abaqus精华

清华大学bbs的abaqus精华大家看看吧: air1大侠,本人给你作广告,为何不可?: 请问:弹塑性矩阵【D]与ddsdde有何联系,: 你用过板壳单元吗?stress=D*stran?d(stress)=ddsdde*d(stran)--那应该就是一样的,因为全量理论,Sij=DijklEkl(满足张量求和约定)即Stress=D*Strain;而在增量理论中,△S=D*△E(在有限变形中,△其实应该为应力的客观率)--似乎不对吧大变形下此D非彼D你看过黄克智的固体本构关系这本书么如果你从全量理论和增量理论的角度上讲那似乎第一个Digkl就不对你有第一个式子么如果有,求导不久完了?: 那应该就是一样的,因为全量理论,: Sij=DijklEkl(满足张量求和约定): 即Stress=D*Strain;: 而在增量理论中,: △S=D*△E(在有限变形中,△其实应该为应力的客观率)是啊,大变形下的[D]与普通意义下的[D]在构型上是不一样的,毕竟[D]大是变形历史的函数,而[D]小则不是,我推导一种新的本构关系,△Sij=Dijkl△Ekl (其中△为Jaumann率)假设材料一开始就屈服(即屈服面为0)想用壳单元,: 似乎不对吧: 大变形下此D非彼D: 你看过黄克智的固体本构关系这本书么: 如果你从全量理论和增量理论的角度上讲: 那似乎第一个Digkl就不对: 你有第一个式子么: 如果有,求导不久完了?: 是啊,大变形下的[D]与普通意义下的[D]在构型上是不一样的,: 毕竟[D]大是变形历史的函数,而[D]小则不是,: 我推导一种新的本构关系,: △Sij=Dijkl△Ekl (其中△为Jaumann率): 假设材料一开始就屈服(即屈服面为0): 想用壳单元,唉,别提了,问题就出在,在abaqus中,明明写着可以考虑剪切效应,可我打印出剪切力个数是,nshr=1,即只有S12,那我的S13,S23就不知怎么计算,(DDSDDE(5,5)无法计算,因为ntens=3,最多只能计算DDSDDE(3,3))你编umat编进去不久行了他让用NDI,NSHR,NTENS表示变量,你就用这些表示变量这样他就可以任意的计算了呀,而不在意实际计算的变量数: 唉,别提了,问题就出在,在abaqus中,明明写着可以考虑剪切效应,: 可我打印出剪切力个数是,nshr=1,即只有S12,: 那我的S13,S23就不知怎么计算,: (DDSDDE(5,5)无法计算,因为ntens=3,最多只能计算DDSDDE(3,3)) 因为我的UMAT从abaqus传来的变量(当我选用壳单元时)ntens=3, ndi=2,nshr=1,这样的话,STRESS为3个,STRESS(3),不可能计算STRESS(4),STRESS(5),同理,STRAIN,DDSDDE也存在同样的情况在中厚度板壳元中(MINDLIN)中,DDSDDE为5×5你的FOR文件收到,可惜研究的对象相差太大,看不懂!不过你在文件中定义的变量有的根本就没有用到,还有有的地方似乎是毫无用处的代码,比如:SMISES一段我觉得你不应该太急,第一步应该保证代码的正确性。
ABAQUS-UMAT-自学知识整理贴

各个楼层及内容索引2-------------------------------------什么是UMAT3-------------------------------------UMAT功能简介4-------------------------------------UMAT开始的变量声明5-------------------------------------UMAT中各个变量的详细解释6-------------------------------------关于沙漏和横向剪切刚度7-------------------------------------UMAT流程和参数表格实例展示8-------------------------------------FORTRAN语言中的接口程序Interface 9-------------------------------------关于UMAT是否可以用Fortran90编写的问题10-17--------------------------------Fortran77的一些有用的知识简介20-25\30-32-----------------------弹塑性力学相关知识简介34-37--------------------------------用户材料子程序实例JOhn-cook模型压缩包下载38-------------------------------------JOhn-cook模型本构简介图40-------------------------------------用户材料子程序实例JOhn-cook模型完整程序+david详细注解[欢迎大家来看看,并提供意见,完全是自己的diy的,不保证完全正确,希望共同探讨,以便更正,带"?"部分,还望各位大师\同仁指教]什么是UMAT程序,真正的定义材料的力学行为即属性,是用户自己编译的FORTRAN 程序来实现的!UMAT通过与ABAQUS主求解程序的接口实现与ABAQUS的数据交流UMAT功能简介[-摘自庄茁老师的书]UMAT子程序具有强大的功能,使用UMAT子程序:(1)可以定义材料的本构关系,使用ABAQUS材料库中没有包含的材料进行计算,扩充程序功能。
子程序(UMAT)基本操作过程1
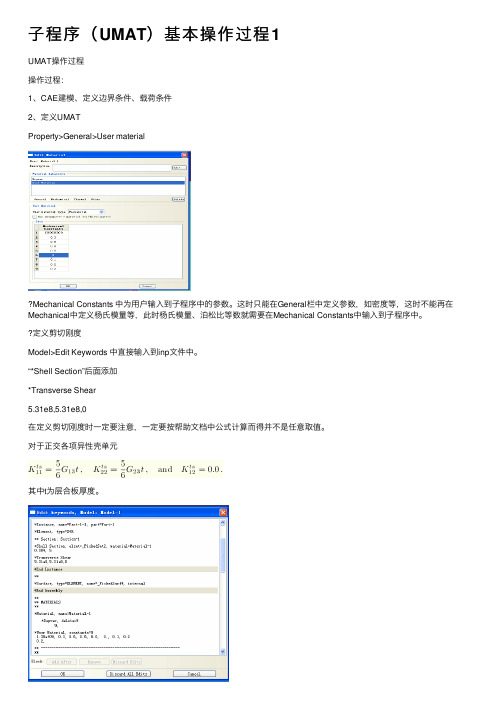
⼦程序(UMAT)基本操作过程1UMAT操作过程操作过程:1、CAE建模、定义边界条件、载荷条件2、定义UMATProperty>General>User materialMechanical Constants 中为⽤户输⼊到⼦程序中的参数。
这时只能在General栏中定义参数,如密度等,这时不能再在Mechanical中定义杨⽒模量等,此时杨⽒模量、泊松⽐等数就需要在Mechanical Constants中输⼊到⼦程序中。
定义剪切刚度Model>Edit Keywords 中直接输⼊到inp⽂件中。
“*Shell Section”后⾯添加*Transverse Shear5.31e8,5.31e8,0在定义剪切刚度时⼀定要注意,⼀定要按帮助⽂档中公式计算⽽得并不是任意取值。
对于正交各项异性壳单元其中t为层合板厚度。
Depvar 中的数字与Mechanical Constants栏中定义的参数数量相等。
3编辑.for后缀的⼦程序3.1 推导出本构关系建⽴刚度矩阵时最好是直接指定刚度阵的每⼀项的⽅法得到刚度阵。
3.2更新应⼒下⾯是各项同性弹性本构关系(刚度阵)及应⼒更新。
DO K1=1,NTENSDO K2=1,NTENSDDSDDE(K1,K2)=ZEROEND DOEND DODO K1=1,NDIDO K2=1,NDIDDSDDE(K2,K1)=EBULK3END DOEND DODO K1=1,NDIDO K2=1,NDIDDSDDE(K1,K1)=EG2END DOEND DODO K1=NDI+1,NTENSDDSDDE(K1,K1)=EG3END DODO K1=1,NTENSDO K2=1,NTENSSTRESS(K1)=STRESS(K1)+DDSDDE(K1,K2)*DSTRAN(K2)END DOEND DO注意:UMAT⼦程序中并不是⼀定要写成增量形式,建⽴Jacobian矩阵,只要能做到更新应⼒即可,写成全量形式也可以。
ABAQUS-二次开发资料-UMAT

各个楼层及内容索引2-------------------------------------什么是UMAT3-------------------------------------UMAT功能简介4-------------------------------------UMAT开始的变量声明5-------------------------------------UMAT中各个变量的详细解释6-------------------------------------关于沙漏和横向剪切刚度7-------------------------------------UMAT流程和参数表格实例展示8-------------------------------------FORTRAN语言中的接口程序Interface9-------------------------------------关于UMAT是否可以用Fortran90编写的问题10-17--------------------------------Fortran77的一些有用的知识简介20-25\30-32-----------------------弹塑性力学相关知识简介34-37--------------------------------用户材料子程序实例JOhn-cook模型压缩包下载38-------------------------------------JOhn-cook模型本构简介图40-------------------------------------用户材料子程序实例JOhn-cook模型完整程序+david详细注解[欢迎大家来看看,并提供意见,完全是自己的diy的,不保证完全正确,希望共同探讨,以便更正,带"?"部分,还望各位大师\同仁指教]1 什么是UMAT???1.1 UMAT功能简介!!
3.前推后拉及Lie导数
Lie导数
后拉和前推的概念为定义张量的时间导数提供了数学上的一致性 -Lie导数。如框5.17,Kirchhoff应力的Lie导数是其应力的后拉的时 间导数的前推。
D D Lv τ * ( * τ) F (F1 τ) Dt Dt
Lagrangian矢量dX和Eulerian矢量dx定义的二阶张量
可以由后拉和前推运算给出E-L张量之间映射的统一描述。 例如,L矢量dX由F前推到当前构形给出E矢量dx
dx F dX * dX
Eulerian-Lagrangian 前推运算
1 E矢量dx由 F 后拉到参考构形给出L矢量dX
Jaumann率 发生有限剪切时 慎用Jaumann率
Green-Naghdi率
2.几种客观率的关系
如何得到正确的结果? 切线模量之间的关系
次弹性本构关系共同应用的形式为
σ J CsJ : D
σ T CsT : D
σ G CsG : D
对于各向同性材料Jaumann率的切线模量为
退化
Ω σ σ ΩT σG σ
=W 简化
Assume
W σ σ WT σJ σ
2.几种客观率的关系
总结一: Comparison of different objective stress rate
Truesdell •Difficult to implement •Not used in commercial software •Kinematically consistent with the rate of Cauchy stress •Must accurately determine the rotation tensor R •Relatively easy to implement •Produces symmetric tangent moduli
ABAQUS用户材料子程序UMAT介绍

(一)UMAT简介
用户可以定义包括:边界条件、荷载条件、 接触条件、材料特性以及利用用户子程序 和其它应用软件进行数值交换等等。这些 用户子程序接口使得用户解决一些问题时 有很大的灵活性,同时大大的扩充了 ABAQUS 的功能。
(一)UMAT简介
通过用户材料子程序(User-defined Material Mechanical Behavior,简称UMAT) 接口,用户可定义任何补充的材料模型, 不但任意数量的材料常数都可以作为资料 被读取,而且ABAQUS 对于任何数量的与 解相关的状态变量在每一材料计数点都提 供了存储功能,以便在这些子程序中应用。
(四)子程序的调用
将这两个文件拷贝到分析目录D:>Temp下,将 子程序的后缀改为.for,然后在D:\Temp下面 用运行 在command中: abaqus job=your job name user=your umat
在cae中调用子程序可以采用以下方法:打开 job下面的edit菜单,点general,点击user subroutine后面的select,即可选择你所需要的 用户子程序。
PROPS(NPROPS)材料常数矩阵,矩阵中 元素的数值对应于关键字“*USER MATERIAL”下面的数据行。 SSE , SPD , SCD分别定义每一增量步 的弹性应变能,塑性耗散和蠕变耗散。 它们对计算结果没有影响,仅仅作为能 量输出。
(三)编程思路
其他变量: STRAN ( NTENS ) :应变矩阵; DSTRAN ( NTENS ) :应变增量矩阵; DTIME :增量步的时间增量; NDI :直接应力分量的个数; NSHR :剪切应力分量的个数; NTENS :总应力分量的个数, NTENS = NDI + NSHR 。
黄永刚单晶塑性有限元umat子程序

SUBROUTINE UMAT(stress,statev,ddsdde,sse,spd,scd,1 rpl, ddsddt, drplde, drpldt,2 stran,dstran,time,dtime,temp,dtemp,predef,dpred,cmname,3 ndi,nshr,ntens,nstatv,props,nprops,coords,drot,pnewdt,4 celent,dfgrd0,dfgrd1,noel,npt,layer,kspt,kstep,kinc)c WRITE (6,*) 'c NOTE: MODIFICATIONS TO *UMAT FOR ABAQUS VERSION 5.3 (14 APR '94) cc (1) The list of variables above defining the *UMAT subroutine,c and the first (standard) block of variables dimensioned below,c have variable names added compared to earlier ABAQUS versions.cc (2) The statement: include 'aba_param.inc' must be added as below.cc (3) As of version 5.3, ABAQUS files use double precision only.c The file aba_param.inc has a line "implicit real*8" and, sincec it is included in the main subroutine, it will define the variablesc there as double precision. But other subroutines still need thec definition "implicit real*8" since there may be variables that arec not passed to them through the list or common block.cc (4) This is current as of version 5.6 of ABAQUS.cc (5) Note added by J. W. Kysar (4 November 1997). This UMAT has beenc modified to keep track of the cumulative shear strain in eachc individual slip system. This information is needed to correct anc error in the implementation of the Bassani and Wu hardening law.c Any line of code which has been added or modified is precededc immediately by a line beginning CFIXA and succeeded by a linec beginning CFIXB. Any comment line added or modified will beginc with CFIX.cc The hardening law by Bassani and Wu was implemented incorrectly.c This law is a function of both hyperbolic secant squared and hyperbolicc tangent. However, the arguments of sech and tanh are related to the *total*c slip on individual slip systems. Formerly, the UMAT implemented thisc hardening law by using the *current* slip on each slip system. Thereinc lay the problem. The UMAT did not restrict the current slip to be ac positive value. So when a slip with a negative sign was encountered, thec term containing tanh led to a negative hardening rate (since tanh is anc odd function).c The UMA T has been fixed by adding state variables to keep track of thec *total* slip on each slip system by integrating up the absolute valuec of slip rates for each individual slip system. These "solution dependentc variables" are available for postprocessing. The only required changec in the input file is that the DEPV AR command must be changed.cC----- Use single precision on Cray byC (1) deleting the statement "IMPLICIT*8 (A-H,O-Z)";C (2) changing "REAL*8 FUNCTION" to "FUNCTION";C (3) changing double precision functions DSIGN to SIGN.CC----- Subroutines:CC ROTATION -- forming rotation matrix, i.e. the directionC cosines of cubic crystal [100], [010] and [001]C directions in global system at the initialC stateCC SLIPSYS -- calculating number of slip systems, unitC vectors in slip directions and unit normals toC slip planes in a cubic crystal at the initialC stateCC GSLPINIT -- calculating initial value of current strengthsC at initial stateCC STRAINRA TE -- based on current values of resolved shearC stresses and current strength, calculatingC shear strain-rates in slip systemsCC LATENTHARDEN -- forming self- and latent-hardening matrixCC ITERATION -- generating arrays for the Newton-RhapsonC iterationCC LUDCMP -- LU decompositionCC LUBKSB -- linear equation solver based on LUC decomposition method (must call LUDCMP first) C----- Function subprogram:C F -- shear strain-rates in slip systemsC----- Variables:CC STRESS -- stresses (INPUT & OUTPUT)C Cauchy stresses for finite deformationC STATEV -- solution dependent state variables (INPUT & OUTPUT) C DDSDDE -- Jacobian matrix (OUTPUT)C----- Variables passed in for information:CC STRAN -- strainsC logarithmic strain for finite deformationC (actually, integral of the symmetric part of velocityC gradient with respect to time)C DSTRAN -- increments of strainsC CMNAME -- name given in the *MATERIAL optionC NDI -- number of direct stress componentsC NSHR -- number of engineering shear stress componentsC NTENS -- NDI+NSHRC NSTATV -- number of solution dependent state variables (asC defined in the *DEPVAR option)C PROPS -- material constants entered in the *USER MA TERIAL C optionC NPROPS -- number of material constantsCC----- This subroutine provides the plastic constitutive relation ofC single crystals for finite element code ABAQUS. The plastic slipC of single crystal obeys the Schmid law. The program gives theC choice of small deformation theory and theory of finite rotationC and finite strain.C The strain increment is composed of elastic part and plasticC part. The elastic strain increment corresponds to latticeC stretching, the plastic part is the sum over all slip systems ofC plastic slip. The shear strain increment for each slip system isC assumed a function of the ratio of corresponding resolved shearC stress over current strength, and of the time step. The resolvedC shear stress is the double product of stress tensor with the slipC deformation tensor (Schmid factor), and the increment of currentC strength is related to shear strain increments over all slipC systems through self- and latent-hardening functions.C----- The implicit integration method proposed by Peirce, Shih andC Needleman (1984) is used here. The subroutine provides an option C of iteration to solve stresses and solution dependent stateC variables within each increment.C----- The present program is for a single CUBIC crystal. However,C this code can be generalized for other crystals (e.g. HCP,C Tetragonal, Orthotropic, etc.). Only subroutines ROTATION andC SLIPSYS need to be modified to include the effect of crystalC aspect ratio.CC----- Important notice:CC (1) The number of state variables NSTATV must be larger than (or CFIX equal to) TEN (10) times the total number of slip systems inC all sets, NSLPTL, plus FIVE (5)CFIX NSTATV >= 10 * NSLPTL + 5C Denote s as a slip direction and m as normal to a slip plane.C Here (s,-m), (-s,m) and (-s,-m) are NOT consideredC independent of (s,m). The number of slip systems in each setC could be either 6, 12, 24 or 48 for a cubic crystal, e.g. 12C for {110}<111>.CC Users who need more parameters to characterize theC constitutive law of single crystal, e.g. the frameworkC proposed by Zarka, should make NSTATV larger than (or equal C to) the number of those parameters NPARMT plus nine timesC the total number of slip systems, NSLPTL, plus fiveCFIX NSTATV >= NPARMT + 10 * NSLPTL + 5CC (2) The tangent stiffness matrix in general is not symmetric ifC latent hardening is considered. Users must declare "UNSYMM"C in the input file, at the *USER MATERIAL card.CPARAMETER (ND=150)C----- The parameter ND determines the dimensions of the arrays inC this subroutine. The current choice 150 is a upper bound for aC cubic crystal with up to three sets of slip systems activated.C Users may reduce the parameter ND to any number as long as larger C than or equal to the total number of slip systems in all sets.C For example, if {110}<111> is the only set of slip systemC potentially activated, ND could be taken as twelve (12).cinclude 'aba_param.inc'cCHARACTER*8 CMNAMEEXTERNAL Fdimension stress(ntens),statev(nstatv),1 ddsdde(ntens,ntens),ddsddt(ntens),drplde(ntens),2 stran(ntens),dstran(ntens),time(2),predef(1),dpred(1),3 props(nprops),coords(3),drot(3,3),dfgrd0(3,3),dfgrd1(3,3)DIMENSION ISPDIR(3), ISPNOR(3), NSLIP(3),2 SLPDIR(3,ND), SLPNOR(3,ND), SLPDEF(6,ND),3 SLPSPN(3,ND), DSPDIR(3,ND), DSPNOR(3,ND),4 DLOCAL(6,6), D(6,6), ROTD(6,6), ROTATE(3,3),5 FSLIP(ND), DFDXSP(ND), DDEMSD(6,ND),6 H(ND,ND), DDGDDE(ND,6),7 DSTRES(6), DELATS(6), DSPIN(3), DVGRAD(3,3),8 DGAMMA(ND), DTAUSP(ND), DGSLIP(ND),9 WORKST(ND,ND), INDX(ND), TERM(3,3), TRM0(3,3), ITRM(3)DIMENSION FSLIP1(ND), STRES1(6), GAMMA1(ND), TAUSP1(ND),2 GSLP1(ND), SPNOR1(3,ND), SPDIR1(3,ND), DDSDE1(6,6),3 DSOLD(6), DGAMOD(ND), DTAUOD(ND), DGSPOD(ND),4 DSPNRO(3,ND), DSPDRO(3,ND),5 DHDGDG(ND,ND)C----- NSLIP -- number of slip systems in each setC----- SLPDIR -- slip directions (unit vectors in the initial state)C----- SLPNOR -- normals to slip planes (unit normals in the initialC state)C----- SLPDEF -- slip deformation tensors (Schmid factors)C SLPDEF(1,i) -- SLPDIR(1,i)*SLPNOR(1,i)C SLPDEF(2,i) -- SLPDIR(2,i)*SLPNOR(2,i)C SLPDEF(3,i) -- SLPDIR(3,i)*SLPNOR(3,i)C SLPDEF(4,i) -- SLPDIR(1,i)*SLPNOR(2,i)+C SLPDIR(2,i)*SLPNOR(1,i)C SLPDEF(5,i) -- SLPDIR(1,i)*SLPNOR(3,i)+C SLPDIR(3,i)*SLPNOR(1,i)C SLPDEF(6,i) -- SLPDIR(2,i)*SLPNOR(3,i)+C SLPDIR(3,i)*SLPNOR(2,i)C where index i corresponds to the ith slip systemC----- SLPSPN -- slip spin tensors (only needed for finite rotation)C SLPSPN(1,i) -- [SLPDIR(1,i)*SLPNOR(2,i)-C SLPDIR(2,i)*SLPNOR(1,i)]/2C SLPSPN(2,i) -- [SLPDIR(3,i)*SLPNOR(1,i)-C SLPDIR(1,i)*SLPNOR(3,i)]/2C SLPSPN(3,i) -- [SLPDIR(2,i)*SLPNOR(3,i)-C SLPDIR(3,i)*SLPNOR(2,i)]/2C where index i corresponds to the ith slip systemC----- DSPDIR -- increments of slip directionsC----- DSPNOR -- increments of normals to slip planesCC----- DLOCAL -- elastic matrix in local cubic crystal systemC----- D -- elastic matrix in global systemC----- ROTD -- rotation matrix transforming DLOCAL to DCC----- ROTATE -- rotation matrix, direction cosines of [100], [010]C and [001] of cubic crystal in global systemCC----- FSLIP -- shear strain-rates in slip systemsC----- DFDXSP -- derivatives of FSLIP w.r.t x=TAUSLP/GSLIP, whereC TAUSLP is the resolved shear stress and GSLIP is the C current strengthCC----- DDEMSD -- double dot product of the elastic moduli tensor withC the slip deformation tensor plus, only for finiteC rotation, the dot product of slip spin tensor withC the stressCC----- H -- self- and latent-hardening matrixC H(i,i) -- self hardening modulus of the ith slipC system (no sum over i)C H(i,j) -- latent hardening molulus of the ith slipC system due to a slip in the jth slip system C (i not equal j)CC----- DDGDDE -- derivatice of the shear strain increments in slipC systems w.r.t. the increment of strainsCC----- DSTRES -- Jaumann increments of stresses, i.e. corotationalC stress-increments formed on axes spinning with theC materialC----- DELATS -- strain-increments associated with lattice stretchingC DELATS(1) - DELATS(3) -- normal strain increments C DELATS(4) - DELATS(6) -- engineering shear strain C incrementsC----- DSPIN -- spin-increments associated with the material elementC DSPIN(1) -- component 12 of the spin tensorC DSPIN(2) -- component 31 of the spin tensorC DSPIN(3) -- component 23 of the spin tensorCC----- DVGRAD -- increments of deformation gradient in the currentC state, i.e. velocity gradient times the increment ofC timeCC----- DGAMMA -- increment of shear strains in slip systemsC----- DTAUSP -- increment of resolved shear stresses in slip systemsC----- DGSLIP -- increment of current strengths in slip systemsCCC----- Arrays for iteration:CC FSLIP1, STRES1, GAMMA1, TAUSP1, GSLP1 , SPNOR1, SPDIR1,C DDSDE1, DSOLD , DGAMOD, DTAUOD, DGSPOD, DSPNRO, DSPDRO, C DHDGDGCCC----- Solution dependent state variable STATEV:C Denote the number of total slip systems by NSLPTL, whichC will be calculated in this code.CC Array STATEV:C 1 - NSLPTL : current strength in slip systemsC NSLPTL+1 - 2*NSLPTL : shear strain in slip systemsC 2*NSLPTL+1 - 3*NSLPTL : resolved shear stress in slip systemsCC 3*NSLPTL+1 - 6*NSLPTL : current components of normals to slipC slip planesC 6*NSLPTL+1 - 9*NSLPTL : current components of slip directionsCCFIX 9*NSLPTL+1 - 10*NSLPTL : total cumulative shear strain on eachCFIX slip system (sum of the absoluteCFIX values of shear strains in each slipCFIX system individually)CFIXCFIX 10*NSLPTL+1 : total cumulative shear strain on allC slip systems (sum of the absoluteC values of shear strains in all slipC systems)CCFIX 10*NSLPTL+2 - NSTA TV-4 : additional parameters users may needC to characterize the constitutive lawC of a single crystal (if there areC any).CC NSTATV-3 : number of slip systems in the 1st setC NSTATV-2 : number of slip systems in the 2nd setC NSTATV-1 : number of slip systems in the 3rd setC NSTATV : total number of slip systems in allC setsCCC----- Material constants PROPS:CC PROPS(1) - PROPS(21) -- elastic constants for a general elasticC anisotropic materialCC isotropic : PROPS(i)=0 for i>2C PROPS(1) -- Young's modulusC PROPS(2) -- Poisson's ratioCC cubic : PROPS(i)=0 for i>3C PROPS(1) -- c11C PROPS(2) -- c12C PROPS(3) -- c44CC orthotropic : PORPS(i)=0 for i>9C PROPS(1) - PROPS(9) are D1111, D1122, D2222, C D1133, D2233, D3333, D1212, D1313, D2323,C respectively, which has the same definitionC as ABAQUS for orthotropic materialsC (see *ELASTIC card)CC anisotropic : PROPS(1) - PROPS(21) are D1111, D1122,C D2222, D1133, D2233, D3333, D1112, D2212,C D3312, D1212, D1113, D2213, D3313, D1213,C D1313, D1123, D2223, D3323, D1223, D1323,C D2323, respectively, which has the sameC definition as ABAQUS for anisotropicC materials (see *ELASTIC card)CCC PROPS(25) - PROPS(56) -- parameters characterizing all slipC systems to be activated in a cubicC crystalCC PROPS(25) -- number of sets of slip systems (maximum 3),C e.g. (110)[1-11] and (101)[11-1] are in theC same set of slip systems, (110)[1-11] andC (121)[1-11] belong to different sets of slipC systemsC (It must be a real number, e.g. 3., not 3 !)CC PROPS(33) - PROPS(35) -- normal to a typical slip plane inC the first set of slip systems,C e.g. (1 1 0)C (They must be real numbers, e.g.C 1. 1. 0., not 1 1 0 !)C PROPS(36) - PROPS(38) -- a typical slip direction in theC first set of slip systems, e.g.C [1 1 1]C (They must be real numbers, e.g.C 1. 1. 1., not 1 1 1 !)CC PROPS(41) - PROPS(43) -- normal to a typical slip plane inC the second set of slip systemsC (real numbers)C PROPS(44) - PROPS(46) -- a typical slip direction in theC second set of slip systemsC (real numbers)CC PROPS(49) - PROPS(51) -- normal to a typical slip plane inC the third set of slip systemsC (real numbers)C PROPS(52) - PROPS(54) -- a typical slip direction in theC third set of slip systemsC (real numbers)CCC PROPS(57) - PROPS(72) -- parameters characterizing the initialC orientation of a single crystal inC global systemC The directions in global system and directions in localC cubic crystal system of two nonparallel vectors are neededC to determine the crystal orientation.CC PROPS(57) - PROPS(59) -- [p1 p2 p3], direction of firstC vector in local cubic crystalC system, e.g. [1 1 0]C (They must be real numbers, e.g.C 1. 1. 0., not 1 1 0 !)C PROPS(60) - PROPS(62) -- [P1 P2 P3], direction of firstC vector in global system, e.g.C [2. 1. 0.]C (It does not have to be a unitC vector)CC PROPS(65) - PROPS(67) -- direction of second vector inC local cubic crystal system (real C numbers)C PROPS(68) - PROPS(70) -- direction of second vector inC global systemCCC PROPS(73) - PROPS(96) -- parameters characterizing the visco-C plastic constitutive law (shearC strain-rate vs. resolved shearC stress), e.g. a power-law relationCC PROPS(73) - PROPS(80) -- parameters for the first set ofC slip systemsC PROPS(81) - PROPS(88) -- parameters for the second set of C slip systemsC PROPS(89) - PROPS(96) -- parameters for the third set ofC slip systemsCCC PROPS(97) - PROPS(144)-- parameters characterizing the self-C and latent-hardening laws of slipC systemsCC PROPS(97) - PROPS(104)-- self-hardening parameters for the C first set of slip systemsC PROPS(105)- PROPS(112)-- latent-hardening parameters for C the first set of slip systems and C interaction with other sets ofC slip systemsCC PROPS(113)- PROPS(120)-- self-hardening parameters for the C second set of slip systemsC PROPS(121)- PROPS(128)-- latent-hardening parameters for C the second set of slip systems C and interaction with other sets C of slip systemsCC PROPS(129)- PROPS(136)-- self-hardening parameters for the C third set of slip systemsC PROPS(137)- PROPS(144)-- latent-hardening parameters for C the third set of slip systems and C interaction with other sets ofC slip systemsCCC PROPS(145)- PROPS(152)-- parameters characterizing forward time C integration scheme and finiteC deformationCC PROPS(145) -- parameter theta controlling the implicitC integration, which is between 0 and 1C 0. : explicit integrationC 0.5 : recommended valueC 1. : fully implicit integrationCC PROPS(146) -- parameter NLGEOM controlling whether the C effect of finite rotation and finite strainC of crystal is considered,C 0. : small deformation theoryC otherwise : theory of finite rotation andC finite strainCCC PROPS(153)- PROPS(160)-- parameters characterizing iterationC methodCC PROPS(153) -- parameter ITRATN controlling whether theC iteration method is used,C 0. : no iterationC otherwise : iterationCC PROPS(154) -- maximum number of iteration ITRMAXCC PROPS(155) -- absolute error of shear strains in slipC systems GAMERRCC----- Elastic matrix in local cubic crystal system: DLOCALDO J=1,6DO I=1,6DLOCAL(I,J)=0.END DOEND DOCHECK=0.DO J=10,21CHECK=CHECK+ABS(PROPS(J))END DOIF (CHECK.EQ.0.) THENDO J=4,9CHECK=CHECK+ABS(PROPS(J))END DOIF (CHECK.EQ.0.) THENIF (PROPS(3).EQ.0.) THENC----- Isotropic materialGSHEAR=PROPS(1)/2./(1.+PROPS(2))E11=2.*GSHEAR*(1.-PROPS(2))/(1.-2.*PROPS(2))E12=2.*GSHEAR*PROPS(2)/(1.-2.*PROPS(2))DO J=1,3DLOCAL(J,J)=E11DO I=1,3IF (I.NE.J) DLOCAL(I,J)=E12END DODLOCAL(J+3,J+3)=GSHEAREND DOELSEC----- Cubic materialDO J=1,3DLOCAL(J,J)=PROPS(1)DO I=1,3IF (I.NE.J) DLOCAL(I,J)=PROPS(2)END DODLOCAL(J+3,J+3)=PROPS(3)END DOEND IFELSEC----- Orthotropic metarialDLOCAL(1,1)=PROPS(1)DLOCAL(1,2)=PROPS(2)DLOCAL(2,1)=PROPS(2)DLOCAL(2,2)=PROPS(3)DLOCAL(1,3)=PROPS(4)DLOCAL(3,1)=PROPS(4)DLOCAL(2,3)=PROPS(5)DLOCAL(3,2)=PROPS(5)DLOCAL(3,3)=PROPS(6)DLOCAL(4,4)=PROPS(7)DLOCAL(5,5)=PROPS(8)DLOCAL(6,6)=PROPS(9)END IFELSEC----- General anisotropic materialID=0DO J=1,6DO I=1,JID=ID+1DLOCAL(I,J)=PROPS(ID)DLOCAL(J,I)=DLOCAL(I,J)END DOEND DOEND IFC----- Rotation matrix: ROTA TE, i.e. direction cosines of [100], [010]C and [001] of a cubic crystal in global systemCCALL ROTATION (PROPS(57), ROTA TE)C----- Rotation matrix: ROTD to transform local elastic matrix DLOCAL C to global elastic matrix DCDO J=1,3J1=1+J/3J2=2+J/2DO I=1,3I1=1+I/3I2=2+I/2ROTD(I,J)=ROTATE(I,J)**2ROTD(I,J+3)=2.*ROTATE(I,J1)*ROTA TE(I,J2)ROTD(I+3,J)=ROTA TE(I1,J)*ROTATE(I2,J)ROTD(I+3,J+3)=ROTA TE(I1,J1)*ROTA TE(I2,J2)+2 ROTA TE(I1,J2)*ROTA TE(I2,J1)END DOEND DOC----- Elastic matrix in global system: DC {D} = {ROTD} * {DLOCAL} * {ROTD}transposeCDO J=1,6DO I=1,6D(I,J)=0.END DOEND DODO J=1,6DO I=1,JDO K=1,6DO L=1,6D(I,J)=D(I,J)+DLOCAL(K,L)*ROTD(I,K)*ROTD(J,L) END DOEND DOD(J,I)=D(I,J)END DOEND DOC----- Total number of sets of slip systems: NSETNSET=NINT(PROPS(25))IF (NSET.LT.1) THENWRITE (6,*) '***ERROR - zero sets of slip systems'STOPELSE IF (NSET.GT.3) THENWRITE (6,*)2 '***ERROR - more than three sets of slip systems'STOPEND IFC----- Implicit integration parameter: THETATHETA=PROPS(145)C----- Finite deformation ?C----- NLGEOM = 0, small deformation theoryC otherwise, theory of finite rotation and finite strain, Users C must declare "NLGEOM" in the input file, at the *STEP card CIF (PROPS(146).EQ.0.) THENNLGEOM=0ELSENLGEOM=1END IFC----- Iteration?C----- ITRATN = 0, no iterationC otherwise, iteration (solving increments of stresses andC solution dependent state variables)CIF (PROPS(153).EQ.0.) THENITRATN=0ELSEITRATN=1END IFITRMAX=NINT(PROPS(154))GAMERR=PROPS(155)NITRTN=-1DO I=1,NTENSDSOLD(I)=0.END DODO J=1,NDDGAMOD(J)=0.DTAUOD(J)=0.DGSPOD(J)=0.DO I=1,3DSPNRO(I,J)=0.DSPDRO(I,J)=0.END DOEND DOC----- Increment of spin associated with the material element: DSPIN C (only needed for finite rotation)CIF (NLGEOM.NE.0) THENDO J=1,3DO I=1,3TERM(I,J)=DROT(J,I)TRM0(I,J)=DROT(J,I)END DOTERM(J,J)=TERM(J,J)+1.D0TRM0(J,J)=TRM0(J,J)-1.D0END DOCALL LUDCMP (TERM, 3, 3, ITRM, DDCMP)DO J=1,3CALL LUBKSB (TERM, 3, 3, ITRM, TRM0(1,J)) END DODSPIN(1)=TRM0(2,1)-TRM0(1,2)DSPIN(2)=TRM0(1,3)-TRM0(3,1)DSPIN(3)=TRM0(3,2)-TRM0(2,3)END IFC----- Increment of dilatational strain: DEVDEV=0.D0DO I=1,NDIDEV=DEV+DSTRAN(I)END DOC----- Iteration starts (only when iteration method is used)1000 CONTINUEC----- Parameter NITRTN: number of iterationsC NITRTN = 0 --- no-iteration solutionCNITRTN=NITRTN+1C----- Check whether the current stress state is the initial stateIF (STATEV(1).EQ.0.) THENC----- Initial stateCC----- Generating the following parameters and variables at initialC state:C Total number of slip systems in all the sets NSLPTLC Number of slip systems in each set NSLIPC Unit vectors in initial slip directions SLPDIRC Unit normals to initial slip planes SLPNORCNSLPTL=0DO I=1,NSETISPNOR(1)=NINT(PROPS(25+8*I))ISPNOR(2)=NINT(PROPS(26+8*I))ISPNOR(3)=NINT(PROPS(27+8*I))ISPDIR(1)=NINT(PROPS(28+8*I))ISPDIR(2)=NINT(PROPS(29+8*I))ISPDIR(3)=NINT(PROPS(30+8*I))CALL SLIPSYS (ISPDIR, ISPNOR, NSLIP(I), SLPDIR(1,NSLPTL+1),2 SLPNOR(1,NSLPTL+1), ROTATE)NSLPTL=NSLPTL+NSLIP(I)END DOIF (ND.LT.NSLPTL) THENWRITE (6,*)2 '***ERROR - parameter ND chosen by the present user is less than3 the total number of slip systems NSLPTL'STOPEND IFC----- Slip deformation tensor: SLPDEF (Schmid factors)DO J=1,NSLPTLSLPDEF(1,J)=SLPDIR(1,J)*SLPNOR(1,J)SLPDEF(2,J)=SLPDIR(2,J)*SLPNOR(2,J)SLPDEF(3,J)=SLPDIR(3,J)*SLPNOR(3,J)SLPDEF(4,J)=SLPDIR(1,J)*SLPNOR(2,J)+SLPDIR(2,J)*SLPNOR(1,J)SLPDEF(5,J)=SLPDIR(1,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(1,J)SLPDEF(6,J)=SLPDIR(2,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(2,J) END DOC----- Initial value of state variables: unit normal to a slip planeC and unit vector in a slip directionCSTATEV(NSTATV)=FLOAT(NSLPTL)DO I=1,NSETSTA TEV(NSTA TV-4+I)=FLOAT(NSLIP(I))END DOIDNOR=3*NSLPTLIDDIR=6*NSLPTLDO J=1,NSLPTLDO I=1,3IDNOR=IDNOR+1STA TEV(IDNOR)=SLPNOR(I,J)IDDIR=IDDIR+1STA TEV(IDDIR)=SLPDIR(I,J)END DOEND DOC----- Initial value of the current strength for all slip systemsCCALL GSLPINIT (STATEV(1), NSLIP, NSLPTL, NSET, PROPS(97))C----- Initial value of shear strain in slip systemsCFIX-- Initial value of cumulative shear strain in each slip systemsDO I=1,NSLPTLSTA TEV(NSLPTL+I)=0.CFIXASTA TEV(9*NSLPTL+I)=0.CFIXBEND DOCFIXASTATEV(10*NSLPTL+1)=0.CFIXBC----- Initial value of the resolved shear stress in slip systemsDO I=1,NSLPTLTERM1=0.DO J=1,NTENSIF (J.LE.NDI) THENTERM1=TERM1+SLPDEF(J,I)*STRESS(J)ELSETERM1=TERM1+SLPDEF(J-NDI+3,I)*STRESS(J) END IFEND DOSTA TEV(2*NSLPTL+I)=TERM1END DOELSEC----- Current stress stateCC----- Copying from the array of state variables STA TVE the following C parameters and variables at current stress state:C Total number of slip systems in all the sets NSLPTLC Number of slip systems in each set NSLIPC Current slip directions SLPDIRC Normals to current slip planes SLPNORCNSLPTL=NINT(STA TEV(NSTATV))DO I=1,NSETNSLIP(I)=NINT(STATEV(NSTATV-4+I))END DOIDNOR=3*NSLPTLIDDIR=6*NSLPTLDO J=1,NSLPTLDO I=1,3IDNOR=IDNOR+1SLPNOR(I,J)=STATEV(IDNOR)IDDIR=IDDIR+1SLPDIR(I,J)=STA TEV(IDDIR)END DOEND DOC----- Slip deformation tensor: SLPDEF (Schmid factors)DO J=1,NSLPTLSLPDEF(1,J)=SLPDIR(1,J)*SLPNOR(1,J)SLPDEF(2,J)=SLPDIR(2,J)*SLPNOR(2,J)SLPDEF(3,J)=SLPDIR(3,J)*SLPNOR(3,J)SLPDEF(4,J)=SLPDIR(1,J)*SLPNOR(2,J)+SLPDIR(2,J)*SLPNOR(1,J)SLPDEF(5,J)=SLPDIR(1,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(1,J)SLPDEF(6,J)=SLPDIR(2,J)*SLPNOR(3,J)+SLPDIR(3,J)*SLPNOR(2,J) END DOEND IFC----- Slip spin tensor: SLPSPN (only needed for finite rotation)IF (NLGEOM.NE.0) THENDO J=1,NSLPTLSLPSPN(1,J)=0.5*(SLPDIR(1,J)*SLPNOR(2,J)-2 SLPDIR(2,J)*SLPNOR(1,J))SLPSPN(2,J)=0.5*(SLPDIR(3,J)*SLPNOR(1,J)-2 SLPDIR(1,J)*SLPNOR(3,J))SLPSPN(3,J)=0.5*(SLPDIR(2,J)*SLPNOR(3,J)-2 SLPDIR(3,J)*SLPNOR(2,J))END DOEND IFC----- Double dot product of elastic moduli tensor with the slipC deformation tensor (Schmid factors) plus, only for finiteC rotation, the dot product of slip spin tensor with the stress:C DDEMSDCDO J=1,NSLPTLDO I=1,6DDEMSD(I,J)=0.DO K=1,6DDEMSD(I,J)=DDEMSD(I,J)+D(K,I)*SLPDEF(K,J)END DOEND DOEND DOIF (NLGEOM.NE.0) THENDO J=1,NSLPTLDDEMSD(4,J)=DDEMSD(4,J)-SLPSPN(1,J)*STRESS(1)DDEMSD(5,J)=DDEMSD(5,J)+SLPSPN(2,J)*STRESS(1)IF (NDI.GT.1) THENDDEMSD(4,J)=DDEMSD(4,J)+SLPSPN(1,J)*STRESS(2)DDEMSD(6,J)=DDEMSD(6,J)-SLPSPN(3,J)*STRESS(2)END IFIF (NDI.GT.2) THENDDEMSD(5,J)=DDEMSD(5,J)-SLPSPN(2,J)*STRESS(3)DDEMSD(6,J)=DDEMSD(6,J)+SLPSPN(3,J)*STRESS(3)END IFIF (NSHR.GE.1) THENDDEMSD(1,J)=DDEMSD(1,J)+SLPSPN(1,J)*STRESS(NDI+1)DDEMSD(2,J)=DDEMSD(2,J)-SLPSPN(1,J)*STRESS(NDI+1)DDEMSD(5,J)=DDEMSD(5,J)-SLPSPN(3,J)*STRESS(NDI+1)DDEMSD(6,J)=DDEMSD(6,J)+SLPSPN(2,J)*STRESS(NDI+1) END IFIF (NSHR.GE.2) THENDDEMSD(1,J)=DDEMSD(1,J)-SLPSPN(2,J)*STRESS(NDI+2)DDEMSD(3,J)=DDEMSD(3,J)+SLPSPN(2,J)*STRESS(NDI+2)DDEMSD(4,J)=DDEMSD(4,J)+SLPSPN(3,J)*STRESS(NDI+2)DDEMSD(6,J)=DDEMSD(6,J)-SLPSPN(1,J)*STRESS(NDI+2) END IFIF (NSHR.EQ.3) THENDDEMSD(2,J)=DDEMSD(2,J)+SLPSPN(3,J)*STRESS(NDI+3)DDEMSD(3,J)=DDEMSD(3,J)-SLPSPN(3,J)*STRESS(NDI+3)DDEMSD(4,J)=DDEMSD(4,J)-SLPSPN(2,J)*STRESS(NDI+3)DDEMSD(5,J)=DDEMSD(5,J)+SLPSPN(1,J)*STRESS(NDI+3) END IFEND DOEND IFC----- Shear strain-rate in a slip system at the start of increment:C FSLIP, and its derivative: DFDXSPCID=1DO I=1,NSETIF (I.GT.1) ID=ID+NSLIP(I-1)CALL STRAINRATE (STATEV(NSLPTL+ID), STATEV(2*NSLPTL+ID),2 STA TEV(ID), NSLIP(I), FSLIP(ID), DFDXSP(ID),3 PROPS(65+8*I))END DOC----- Self- and latent-hardening laws。
Abaqus材料属性定义部分翻译《User-definedmechanicalmateri

淤Abaqus材料属性定义部分翻译« User-defined mechanical materiUser-defined mechanical material behavior 翻译产品Abaqus /Standard Abaqus/Explicit Abaqus /CAE 参考“UMAT ,Abaqus User Subroutines Reference Manual 的部分“VUMAT ,Abaqus User Subroutines Reference Manual 的部分*USER MATERIAL * DEPVAR“指定解决方案的参考状态变虽,“节“为用户材料定义常虽”,节概述在ABAQUS^用户自定义材料力学行为:通过一个接口,任何力学本构模型可以添加到库中;要求一个本构模型是在用户子程序UMA械VUMA冲编程;和需要相当大的努力和专业知识:这种方法的特点是非常通用和有效的,但这并不是一个较常规的用法。
应力分H和应变增H接口子程序一直采用柯西应力组件实现。
土壤问题的“应力”应理解为有效应力。
应变增虽是位移增虽梯度对称部分定义在用户子程序UMAT的应力和应变分虽的方向取决于局部方向(a Orientations, ” Section ).。
在用户子程序VUMATff有的应变值是中间增虽配置计算得到。
所有的张虽坐标与材料点旋转定义。
为了说明应力在这方面的定义,参照杆,如图,通过拉伸和旋转,从原来的位置AB,到其新的位置AB'。
这种变形可以两个阶段获得;第一,拉伸杆件,如图,然后运用刚体转动,如图。
Figure - 1 Stretched and rotated bar.Figure - 2 Stretching of bar. Figure - 3 Rigidbody rotation of bar.杆件的应力在拉伸后达到,这个应力并没有改变刚体转动。
坐标系的旋转是于刚体旋转在自转坐标系统导致的。
UMAT子程序详解

写UMAT或VUMAT概览目的书写UMAT或VUMAT所需要采取

第六讲写UMAT或VUMAT概览目的书写UMAT或VUMAT所需要采取的步骤UMAT接口例子VUMAT接口例子概览ABAQUS / Standard和ABAQUS /显有接口,使用户执行本构方程。
-在ABAQUS /标准用户定义的材料通过用户子程序UMAT模型实施。
-在ABAQUS /明确的用户定义的材料通过用户子程序VUMAT模型实施。
当在ABAQUS素材库中没有任何一种已经存在的材料,能够准确反映当前用来建模所用材料的特性时,就需要使用UMAT和VUMAT进行建模。
这些接口能够确定各种复杂本构关系的材料模型。
用户定义的材料模型可用于任何ABAQUS结构元素类型。
多用户材料可通过一个单一的UMAT或VUMAT或一起使用。
在这个讲座,在UMAT或VUMAT中的材料模型的实施将会被讨论并举例说明目的为了模拟实验结果而进行地高级的本构模行测试往往需要复杂的有限元模型。
-先进的结构element-复杂加载条件-热负荷-接触和摩擦条件-静态和动态分析如果本构模型模拟不稳定性和具有本地化现象的材料,特别的分析问题就会产生。
-准静态分析需要特别的解决方案。
-鲁棒元素配方应当提供。
-显式动态的解决方案以及强大矢量联系算法需要改进。
此外,强大的功能要求随时的可视化结果。
(就是可以动态的可视化结果)-轮廓和路径图的状态变量。
-函数地块。
-列表的结果。
材料模型的开发者应当只关注的材料模型的发展,而不是有限元软件的开发和维持。
-发展和材料没关系的建模方法-新系统的移植问题-用户开发的代码长期的计划维持书写UMAT或VUMAT所需要采取的步骤需要采取的步骤书面UMAT或VUMAT:这就需要定义一个适当的本构方程,如下:-明确定义应力(柯西应力大变形应用)-定义的应力变化率(仅在corotational框架)此外,它很可能需要:-时间,温度,或外地变量这些所依赖东西的定义-内部状态变量的定义,显式的或者用带有偏微分的函数。
复合材料渐进失效UMAT程序中公式详细解释(精品)

《UMAT 子程序详解》各页公式详解********************************************************************************* P2:STATEV 状态变量矩阵STATEV(5:10) TEMPORARY ARRAYS TO SA VE DOLD_STRESS********************************************************************************* P2:更新初始状态的应变分量On entry to the UMAT subroutine, an estimate of the current total strains for the current iteration is determined:11n n n εεε++=+∆参考文献:Knight, Norman F. User-Defined Material Model for Progressive Failure Analysis . National Aeronautics and Space Administration, Langley Research Center, 2006.*********************************************************************************P3:计算刚度阵[C] The glass/epoxy layer shows transverse isotropy. Therefore, the modulus stiffness values:21123221221112233222212122322231221121323441255126623(1)(1);; ; ()();;;;;E E C C C C a a E E C C C a aC G C G C G ννννννννν--===++======其中,2122123122123122a νννννν=---注:此处材料为transverse isotropic ,如为其他材料,此处则需要修改。
【免费下载】黄永刚单晶塑性有限元umat子程序

C
shear strain-rates in slip systems
SUBROUTINE UMAT(stress,statev,ddsdde,sse,spd,scd, 1 rpl, ddsddt, drplde, drpldt, 2 stran,dstran,time,dtime,temp,dtemp,predef,dpred,cmname, 3 ndi,nshr,ntens,nstatv,props,nprops,coords,drot,pnewdt, 4 celent,dfgrd0,dfgrd1,noel,npt,layer,kspt,kstep,kinc)
c The UMAT has been fixed by adding state variables to keep track of the c *total* slip on each slip system by integrating up the absolute value
c of slip rates for each individual slip system. These "solution dependent
c WRITE (6,*) ' c NOTE: MODIFICATIONS TO *UMAT FOR ABAQUS VERSION 5.3 (14 APR '94) c c (1) The list of variables above defining the *UMAT subroutine, c and the first (standard) block of variables dimensioned below, c have variable names added compared to earlier ABAQUS versions. c c (2) The statement: include 'aba_param.inc' must be added as below. c c (3) As of version 5.3, ABAQUS files use double precision only. c The file aba_param.inc has a line "implicit real*8" and, since c it is included in the main subroutine, it will define the variables c there as double precision. But other subroutines still need the c definition "implicit real*8" since there may be variables that are c not passed to them through the list or common block. c c (4) This is current as of version 5.6 of ABAQUS. c c (5) Note added by J. W. Kysar (4 November 1997). This UMAT has been c modified to keep track of the cumulative shear strain in each c individual slip system. This information is needed to correct an c error in the implementation of the Bassani and Wu hardening law. c Any line of code which has been added or modified is preceded c immediately by a line beginning CFIXA and succeeded by a line c beginning CFIXB. Any comment line added or modified will begin c with CFIX. c c The hardening law by Bassani and Wu was implemented incorrectly. c This law is a function of both hyperbolic secant squared and hyperbolic c tangent. However, the arguments of sech and tanh are related to the *total* c slip on individual slip systems. Formerly, the UMAT implemented this c hardening law by using the *current* slip on each slip system. Therein c lay the problem. The UMAT did not restrict the current slip to be a c positive value. So when a slip with a negative sign was encountered, the c term containing tanh led to a negative hardening rate (since tanh is an c odd function).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最近一直在论坛查资料,对自己兴趣的一些问题专门进行了整理,希望对大家有所帮助,也希望能获得小小的奖励啊,哈哈
1 UMAT的状态变量问题
Q:用DEPVAR定义的状态变量个数假设为10个。是不是说一个积分点的状态变量是10个,单元的积分点是4的话,那么单元的状态变量就是40个。也就是自己要存储单元变量的话,就得按40个状态变量来。是不是呢?
A:
那是有可能的,因为所有在umat中出现的问题,本身的原因就是inp文件,变量数组设置的不够也可能是原因,这个我也遇到过,其实之所以error code 5出错,就是inp文件中材料参数设置的不合理造成的。
A:
肯定是UMAT中发生了一些比如说divide by zero的illegal operation. 这种情况是code abort.
5 调试过程中,可以增加write语句帮助检查错误。write(6,*) 表示将输出信息保存到dat文件。
1 在调用UMAT之前,ABAQUS传递给UMAT本次增量开始时的应力sigma(0),总应变E,应变增
量delta(E)。
状态变量保存:弹性应变,塑性应变,等效塑性应变。
Q:
最近在用umat编写abaqus的材料模型,其中碰到一些问题,总是无法通过编译,自己总结了一下,特向高手们请教……
1、应变梯度dfgrd在变量声明中以及存在,那么在编程中是否可以用应变梯度dfgrd以及dfgrd0和dfgrd1来代替strain来进行本构模型的表示?具体用法是什么?
2、ddsdde也就是雅克比矩阵可以用梯度增量来代替应变增量dstran吗?
帮助里面看了,还是不明白。*HOURGLASS STIFFNESS 来定义 nondefault hourglass stiffness 时,下面的参数怎么取呢,帮助里面说不输入或者输入0,会采用默认的值,但是我试了发现不行啊,还是出错
出错信息如下:
***ERROR: ABAQUS CALCULATES ZERO HOURGLASS STIFFNESS FOR ELEMENT 1. USE
*HOURGLASS STIFFNESS OR CHANGE ELEMENT TYPE. 不知道怎么修改,请各位大佬赐教啊。
不知道有没有在umat中用过减缩积分单元,能否共享一下材料定义这部分是怎么做的,谢谢!
A:
不管有没有人回,我还是把自己的试验结果写出来,和大家一起讨论下。
_说明,在UMAT中,不能像不采用子程序那样来控制沙漏问题, 个人认为,可能还是帮助里面说的那样,必须用*HOURGLASS STIFFNESS 来控制
我用了
*HOURGLASS STIFFNESS
10,0,0
计算没有出错,可以完成。但是10,0,0这数据是我瞎写的,没有什么根据,所以也不知道结果会相差多大。
A:有人说跟我说,DEPVAR定义的状态变量个数指每个积分点的状态变量个数。abaqus会自动为每个单元的每个积分点开辟这样大小的状态变量数组,abaqus调用umat时能够自动根据单元好和积分点向umat提供状态变量,在此基础上umat修改状态变量。
2 umat里的STATEV变量怎么输出到odb文件中
等物理量可以参与ddsdde更新,但是计算时还是 dstress=ddsdde*dstrain这个dstrain是abaqus主程序根据收敛性自定义的,用户不能改变.同时,经过以前我计算验证,调用F计算应变,与主程序计算的应变,是相等的
以上是我结合自己UMAT对F的使用一点看法,欢迎指正
A:实际上dfgrd是用于层合板的,而对于超弹性材料主要是使用dfgrd0和dfgrd1,而这两个光看名字就可以猜到一个是增量前,一个是增量后,而且后者只有在出现几何非线性时才有意义,但是这只是定性的解释,可以在document里面找到。
aborted with system error "拒绝访问。error code 5)
为什么log文件显示错误,而Job Moniter却没有提示?
另外我在UMAT中加入了一句输出,我可以发现总是第一个单元可以成功调用UMAT,此后就出问题了??
希望高手能解决,若需要的话,我可以上传UMAT和INPUT文件
当然最好的方法就是在两者之间选择平衡了。
其实您还可以在进行umat计算时,用debug检查一下每个变量的输出,或者使用write(*,*)命令在for文件中,来监控整个程序。
A:
问题已解决,主要是INP文件的问题。。。。。!!!所以inp文件也会引起error code 5
我这里主要是由于depvar的值设置的有些问题。。。。。
有没有一个更为详细的解释呢?让我们可以放心大胆的使用这个东东
而且我没有找到过用dfgrd的增量作为ddsdde的自变量的umat,不知道能不能用
8 请教,umat中如何使用缩减积分单元(已解决,与大家分享)
Q: 查了一些资料,说要定义×HOURGLASS STIFFNESS: ~- ^, Z+ t- w$ p/ J9 `4 h& v8 a
A:
f当时我以为是硬件或者软件本身的毛病。
我从装过系统,abaqus,fortran。visual studio。结果是一样的。
最后我开始在子程序本身寻找问题。我发现我在用umat中如果使用mewton迭代进行一个数值的求解,当循环次数设置过高的话就会出现这一问题(我当时让他循环1000次)。但是如果循环次数较小又满足不了要求。所以面对这一问题时就只好牺牲精度,换取计算继续下去。
3、状态变量statev个数有没有限制?其作用是不是对当前计算步的结果进行保存,以便下一个计算步使用?那么其他变量如stress以及strain和它的区别是什么?
4、fortran中的计算有什么限制,例如式子的长度,变量的个数什么的?
A:在此过程中本人积累了一点经验,仅供大家参考。
1 首先要明确已知的量:stress,strain以及可以据此求得的volumetric strain。在 编写umat的时候,stress,strain 就直接可以当成当前步的应力和应变。这一点非常重要。个人觉得。
A:
error code 5一般不是内部的bug 主要是参数设置的不合理或子程序的问题
A:
做了很长时间后我发现, 无论是多么奇怪的错误, 99.999%是自已在什么地方没有做对,而不是硬件软件的问题
A:
有时候是两个物体的网格划分的比例相差很大造成的!
7
Q:比如我想知道statev(10)的odb文件,怎么输出?又怎么打开.
statev(10)是我自己定义的damage变量,
请各位赐教
A 在element关键词中添加SDV,就像下面这样。
*Element Output, directions=YES
ALPHA, LE, PE, PEEQ, PEMAG, PS, S, STH,SE, SF, VE, VEEQ, VS, SDV
我试了用*SECTION CONTROL,NAME=***,HOURGLASS=ENHANCED结果还是出现错误:
***ERROR: ABAQUS CALCULATES ZERO HOURGLASS STIFFNESS FOR ELEMENT 1. USE *HOURGLASS STIFFNESS OR CHANGE ELEMENT TYPE.
3. 有没有限制不知道, 但要用到多少个你要在INP文件里面设置的, 估计楼主用到的数量绝对达不到上限
4. fortran的计算有它自已的语法和格式, 其中的限制什么的太多不能详诉, 变量的个数是没有限制的.
A: 大变形问题,在UMAT中可以使用DFGRD,从而导出速度梯度L 等等参与材料本构的计算.
A:
初值可以采用SDVINI来定义
程序运行中用以下代码更新
DO 310 K1=1,NTENS
STATEV(K1)=EELAS(K1)
STATEV(K1+NTENS)=EPLAS(K1)
310 CONTINUE
STATEV(1+2*NTENS)=EQPLAS
C
RETURN
6 怪异的ABAQUS错误
Q: 做UMAT的时候,总是在第一个单元所有积分点调用完UMAT后,ABAUQS显示RUNNING,但实际上没有运行,查看Log文件,显示下面的错误:
ABAQUS Error: The executable C:\ABAQUS\6.5-1\exec\standard.exe,
×Depvar
5,
{这一行是写在input文件中的
A: density在哪个地方定义并不重要, 重要的是你在什么地方要用到, 如果你在UMAT中定义了, 但是你想加重力荷载怎么办呢, 所以要看需要定义
depvar是让ABAQUS主程序知道要分配多少内存给每个积分点来存储状态变量, 以实现增量步之间的数据传递, 比如自编的弹塑性模型中的塑性应变, 必须从一个增量步传到下一个, 以实现累加.
3
Q statev(?)请问这个状态变量()内的数字代表什么含义?对应的变量是不是固定的?各自对应着哪些变量?
A:括号中的数代表这个变量矩阵的维数,这个值等于depvar的值。
4 umat中DEPVAR有几种定义方式?
Q;UMAT中状态变量的定义方式,一般有两种形式,一是在inp文件中采用*initial conditions定义,二是特殊情况下可以采用SDVINI来定义; 目前的疑问是,是否还有其他定义状态变量的方式? 请专家针对上传的附件给于指点 多谢! 附件中的例子来自ABAQUS HELP中的例子! 请问例子中INP文件中是如何定义状态变量的 THANKS
