七年级数学不等式应用题专项练习
初一不等式试题及答案

初一不等式试题及答案1. 若不等式 \(2x - 5 < 3\),求 \(x\) 的取值范围。
答案:首先将不等式 \(2x - 5 < 3\) 进行移项,得到 \(2x < 8\)。
然后将两边同时除以2,得到 \(x < 4\)。
因此,\(x\) 的取值范围是\(x < 4\)。
2. 已知 \(a > 0\),\(b < 0\),判断不等式 \(a - b > 0\) 是否成立。
答案:由于 \(a > 0\) 且 \(b < 0\),即 \(a\) 是正数,\(b\) 是负数。
根据不等式的性质,正数减去负数结果为正数,所以 \(a - b > 0\) 成立。
3. 解不等式组:\[\begin{cases}x + 2 > 0 \\3x - 4 \leq 5\end{cases}\]答案:首先解第一个不等式 \(x + 2 > 0\),得到 \(x > -2\)。
接着解第二个不等式 \(3x - 4 \leq 5\),得到 \(x \leq 3\)。
因此,不等式组的解集为 \(-2 < x \leq 3\)。
4. 若不等式 \(3x - 7 > 0\),求 \(x\) 的最小整数值。
答案:首先解不等式 \(3x - 7 > 0\),得到 \(3x > 7\)。
然后将两边同时除以3,得到 \(x > \frac{7}{3}\)。
因为 \(x\) 必须是整数,所以 \(x\) 的最小整数值是 3。
5. 已知不等式 \(5x - 2 \geq 8\),求 \(x\) 的取值范围。
答案:将不等式 \(5x - 2 \geq 8\) 进行移项,得到 \(5x \geq10\)。
然后将两边同时除以5,得到 \(x \geq 2\)。
因此,\(x\) 的取值范围是 \(x \geq 2\)。
6. 判断不等式 \(-3x + 4 > 0\) 是否有解。
七年级下册解不等式习题(总3页)

七年级下册解不等式习题(总3页)1. 解不等式x-5\geqslant7。
解:将不等式变形得x\geqslant12。
2. 解不等式3x+2<11。
解:将不等式变形得3x<9,再除以3 得x<3。
3. 解不等式-2x+3>1-x。
解:将不等式变形得-2x+x>1-3,即-x>-2。
两边同乘以-1 得x<2。
4. 解不等式4x+5\leqslant3x+10。
解:将不等式变形得x\leqslant5。
5. 解不等式2x+3>5x-2。
解:将不等式变形得-3x>-5,两边同除以-3 得x<\frac{5}{3}。
6. 解不等式0.5x+1\leqslant0.7x-2。
解:将不等式变形得-0.2x\leqslant-3,两边同除以-0.2 得x\geqslant15。
7. 解不等式-3(x+1)>6。
解:将不等式变形得-3x-3>6,再将式子两边都加上3 得-3x>9,最后两边都除以-3 得x<-3。
8. 解不等式1+(x+2)\geqslant2(x-1)。
解:将不等式变形得1+x+2\geqslant2x-2,即-x\geqslant-5,两边同时乘以-1 得x\leqslant5。
9. 解不等式\frac{5x+1}{3}\leqslant\frac{4x-3}{2}。
解:将不等式变形得10(5x+1)\leqslant12(4x-3),即50x+10\leqslant48x-36,再将式子两边都减去48x+36 得2x\leqslant-46,最后两边都除以2 得x\leqslant-23。
10. 解不等式\frac{3x-5}{2}\geqslant\frac{2x+1}{3}。
解:将不等式变形得9(3x-5)\geqslant4(2x+1),即27x-45\geqslant8x+4,再将式子两边都减去8x+45 得19x\geqslant-41,最后两边都除以19 得x\geqslant-\frac{41}{19}。
最新人教版七年级数学下册第九章 :不等式组应用题专项训练

一、选填题1、雯雯同学到文具店买中性笔和笔记本,中性笔每支0.8元,笔记本每本1.2元,雯雯带了10元钱,则可供她选择的购买方案数为(两种文具都买,且余下的钱少于0.8元)()A. 6B. 7C. 8D. 92、雯雯去文具店买文具,练习本每个卖2元,水性笔每支卖3元,两种文具至少各买1个,买文具的总钱数不能超过15元,则不同的购买方案的个数为()A. 11B. 12C. 13D. 143、某商品的售价是150元,商家售出一件这种商品可获利润是进价的10%~20%,则进价的范围是()(精确到1元).4、甲、乙两队进行篮球对抗赛,规定每队胜一场得3分,平一场得1分,负一场得0分.一共进行了10场比赛,甲队保持不败,且得分不低于24分,则甲队至少胜了()场.二、解答题5、把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?6、把一些糖果分给小朋友,如果分给每个小朋友4颗糖,那么剩下28颗糖;如果分给每个小朋友5颗糖,那么最后一位小朋友分得的糖果不到4颗,但至少1颗.至少有多少个小朋友?7、商场销售甲、乙两种商品,它们的进价和售价如下表:(1)若该商场购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?(2)该商场为使销售甲、乙两种商品共100件的总利润(利润=售价−进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.8、某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.(1)A、B两种商品的单价分别是多少元?(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且商店购买A、B两处商品的总费用不超过296元,那么该商店有哪几种购买方案?9、某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元. (1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?(2)如果购买乙种奖品的数量不超过甲种奖品数量的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案?10、某省计划对A,B两类学校的校舍进行改造,根据预算,改造一所A类学校和三所B类学校的校舍共需资金480万元;改造三所A 类学校和一所B类学校的校舍共需资金400万元.(1)改造一所A类学校的校舍和一所B类学校的校舍所需资金分别是多少万元?(2)该省计划共改造8所A,B两类学校的校舍.改造资金由国家财政和地方财政共同承担,若国家财政投入的资金不超过770万元,地方财政投入的奖金不少于210万元,其中地方财政投入到A,B两类学校的改造资金分别为每所20万元和30万元.请你通过计算说明有几种改造方案?11、江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?12、“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书贵440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).(1)求每本文学名著和动漫书各多少元;(2)若学校要求采购动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请写出所有符合条件的购书方案.13、现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.(1)求A,B两种商品每件各是多少元?(2)如果雯雯准备购买A,B两种商品共10件,总费用不超过350元,且不低于300元,问有几种购买方案?哪种方案费用最低?14、雯雯的妈妈开了一家糕点店,现有10.2千克面粉和10.2千克鸡蛋,计划加工普通糕点和精制糕点两种产品共50盒.已知加工一盒普通糕点需0.3千克面粉和0.1千克鸡蛋,加工一盒精制糕点需0.1千克面粉和0.3千克鸡蛋.(1)有哪几种不同的加工方案?(2)若销售一盒普通糕点和一盒精制糕点的利润分别为3元和4元,则按哪种方案加工,雯雯的妈妈可获得的利润最大?最大利润是多少?15、在某河流污水网管改造建设中,需要确保在汛期来临前将建设过程中产生的渣土清运完毕,每天至少需要清运渣土12720 m3.施工方准备每天租用大、小两种运输车共80辆,已知每辆大车每天运送渣土200 m3,每辆小车每天运送渣土120 m3,大、小车每天每辆租车费用分别为1200元、900元,且要求每天租车的总费用不超过85300元.(1)施工方共有多少种租车方案?(2)哪种租车方案费用最低,最低费用是多少?16、公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B 型公交车1辆,共需350万元.(1)求购买A型和B型公交车每辆各需多少万元?(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路上的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?17、某中学开学初到商场购买A,B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元.(1)求购买一个A种品牌、一个B种品牌的足球各需要多少元?(2)为了进一步丰富同学们的体育活动,学校决定再次购进A,B两种品牌的足球共50个,正好赶上商场对商品价格进行调整,A种品牌的足球售价比第一次购买时提高4元,B种品牌的足球按第一次购买时售价的九折出售,如果学校要求此次购买A,B两种品牌的足球的总费用不超过第一次花费的70%,且这次购买的B种品牌的足球不少于23个,则这次学校有哪几种购买方案?(3)请你求出学校在第二次购买活动中最多需要多少资金.18、求分式不等式5x+12x−3<0的解集.一、选填题1、B2、D3、125元~136元4、7二、解答题5、这些书有26本,共有6人.6、至少有30个小朋友.7、(1)甲40件,乙60件;(2)该商场有三种进货方案:方案一:购进甲种商品14件,购进乙种商品86件;方案二:购进甲种商品15件,购进乙种商品85件;方案三:购进甲种商品16件,购进乙种商品84件.8、(1)A商品的单价是16元,B商品的单价是4元;(2)该商店有两种购买方案:方案一:购买12件A商品,购买20件B商品;方案二:购买13件A商品,购买22件B商品.9、(1)甲奖品5件、乙奖品15件;(2)有两种不同的购买方案:方案一:购买甲种奖品7件,乙种奖品13件;方案二:购买甲种奖品8件,乙种奖品12件.10、(1)改造一所A类校舍需90万元,改造一所B类校舍需130万元;(2)有三种不同的改造方案:方案一:改造1所A类学校,7所B类学校;方案二:改造2所A类学校,6所B类学校;方案三:改造3所A类学校,5所B类学校;11、(1)每台大型收割机每小时收割小麦0.5公顷,每台小型收割机每小时收割小麦0.3公顷;(2)有三种方案:方案一:5台大小型收割机,5台小型收割机;方案二:6台大小型收割机,4台小型收割机;方案三:7台大小型收割机,3台小型收割机.12、(1)每本文学名著40元,每本动漫书18元;(2)该学校有三种进货方案:方案一:采购文学名著26本,采购动漫书46本;方案二:采购文学名著27本,采购动漫书47本;方案三:采购文学名著28本,采购动漫书48本.13、(1)A,B两种商品每件各20元、50元;(2)有两种购买方案:方案一:购买A种商品5件,B种商品5件;方案二:购买A种商品6件,B种商品4件.方案二费用最低.14、(1)有三种不同的加工方案:方案一:加工普通糕点24盒,精制糕点26盒;方案二:加工普通糕点25盒,精制糕点25盒;方案三:加工普通糕点26盒,精制糕点24盒.(2)方案一的利润最大,最大利润为176元.15、(1)施工方共有6种租车方案:方案一:大车39辆,小车41辆;方案二:大车40辆,小车40辆;方案三:大车41辆,小车39辆;方案四:大车42辆,小车38辆;方案五:大车43辆,小车37辆;方案六:大车44辆,小车36辆;(2)方案一的费用最低,最低费用为83700元.16、(1)购买A型和B型公交车每辆各需100万元、150万元;(2)该公司有3种购车方案:方案一:购买A型公交车6辆,B型公交车7辆;方案二:购买A型公交车7辆,B型公交车3辆;方案三:购买A型公交车8辆,B型公交车2辆.方案三总费用最少,最少总费用为1100万元.17、(1)A种品牌的足球单价为50元,B种品牌的足球单价为80元.(2)学校有3种购买方案:方案一:购买A种品牌的足球25个,购买B种品牌的足球25个;方案二:购买A种品牌的足球26个,购买B种品牌的足球24个;方案三:购买A种品牌的足球27个,购买B种品牌的足球23个. (3)学校在第二次购买活动中最多需要3150元.18、分式不等式5x+12x−3<0的解集为−15<x<32.。
人教版七年级下册数学不等式与不等式组应用题训练(word,含答案)

人教版七年级下册数学不等式与不等式组应用题训练1.列方程组或不等式解决问题:2022年北京冬奥会、冬残奥会已圆满结束,活泼敦厚的“冰墩墩”,喜庆祥和的“雪容融”引起广大民众的喜爱.王老师想要购买两种吉祥物作为本次冬奥会的纪念品,已知购买2件“冰墩墩”和1件“雪容融”共需150元,购买3件“冰墩墩”和2件“雪容融”共需245元.(1)求“冰墩墩”和“雪容融”的单价;(2)学校现需一次性购买上述型号的“冰墩墩”和“雪容融”纪念品共100个,要求购买的总费用不超过5000元,则最多可以购买多少个“冰墩墩”?2.为支援上海抗击新冠肺炎,甲地捐赠多批救援物资并联系了一家快递公司进行运送.快递公司准备安排A、B两种车型把这批物资从甲地快速送到上海.其中,从甲地到上海,A型货车1辆、B型货车1辆,一共需补贴油费1000元;A型货车10辆、B 型货车6辆,一共需补贴油费8400元.(1)从甲地到上海,A、B两种型号的货车,每辆车需补贴的油费分别是多少元?(2)如果需派出20辆车,并且预算油费补贴不超过9600元,那么该快递公司至多能派出几辆A型货车?3.开学前夕,某书店计划购进A、B两种笔记本共350 本.已知A种笔记本的进价为12 元/本,B种笔记本的进价为15 元/本,共计4800 元.(1)请问购进了A种笔记本多少本?(2)在销售过程中,A、B两种笔记本的标价分别为20元/本、25元/本.受疫情影响,两种笔记本按标价各卖出m本以后,该店进行促销活动,剩余的A种笔记本按标价的七折全部售出,剩余的B种笔记本按成本价清货,若两种笔记本的总利润不少于2348元,请求出m的最小值.4.抗击新型冠状肺炎疫情期间,84消毒液和酒精都是重要的防护物资.某药房根据实际需要采购了一批84消毒液和酒精,共花费11000元,84消毒液和酒精的进价和售价如下:(1)该药房销售完这批84消毒液和酒精后共获利5400元,则84消毒液和酒精各销售了多少瓶?(2)随着疫情的发展,结合药房实际,该药房打算用不超过6600元钱再次采购84消毒液和酒精共300瓶,已知84消毒液和酒精价格不变,则第二批最多采购84消毒液多少瓶?5.小玉计划购买A、B两种饮料,若购买8瓶A种饮料和5瓶B种饮料需用220元;若购买4瓶A种饮料和6瓶B种饮料需用152元.(1)求每瓶A种饮料和B种饮料各多少元;(2)小玉决定购买A种饮料和B种饮料共15瓶,总费用不超过260元,那么最多可以购买多少瓶A种饮料?6.小明家新买了一套住房,打算装修一下,春节前住进去.现有甲、乙两家装修公司可供选择,这两家装修公司提供的信息如下表所示:若设需要x天装修完毕,请解答下列问题:(1)请分别用含x的代数式,写出甲、乙两家公司的装修总费用;(2)当装修天数为多少时,两家公司的装修总费用一样多?(3)根据装修天数x讨论选择哪家装修公司更合算(提示:结合(2)中的结论进行分类解决问题).7.每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.(1)求甲、乙两种型号设备的价格;(2)公司决定购买甲、乙两种型号的设备共10台,且该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司甲种型号的设备至多购买几台?8.为庆祝“元旦”,光明学校统一组织合唱比赛,七、八年级共92人(其中七年级的人数多于八年级的人数,且七年级的人数不足90人)准备统一购买服装参加比赛.如表是某服装厂给出服装的价格表:(1)如果两个年级分别单独购买服装一共应付5000元,求七、八年级各有多少学生参加合唱比赛;(2)如果七年级参加合唱比赛的学生中,有10名同学抽调去参加绘画比赛,不能参加合唱比赛,请你为两个年级设计一种最省钱的购买服装方案.9.某电器超市销售每台进价分别为140元、100元的A、B两种型号的电风扇,如表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)(1)求A、B两种型号的电风扇的销售单价.(2)若超市准备用不多于6500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过2850元的目标?若能,请给出相应的采购方案:若不能,请说明理由.10.某商店欲购进A、B两种商品,若购进A种商品5件和B种商品4件需300元;购进A种商品6件和B种商品8件需440元.(1)A、B两种商品每件的进价分别为多少元?(2)若该商店A种商品每件的售价为48元,B种商品每件的售价为31元,该商店准备购进A、B两种商品共50件,且这两种商品全部售出后总获利不低于344元,则至少购进多少件A种商品?11.学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买A、B两种道具.已知购买1件A道具比购买1件B道具多10元,购买2件A道具和3件B道具共需要45元.(1)购买一件A道具和一件B道具各需要多少元?(2)根据班级情况,需要这两种道具共60件,且购买两种道具的总费用不超过620元.求道具A最多购买多少件?12.对于企业来说:科学技术永远是第一生产力,在长沙市里程最长、站点最多的地铁6号线建设过程中,某知名运输集团承包了地铁6号线多标段的土方运输任务,该集团为了出色完成承接任务,拟派出该集团自主研发的A、B两种新型运输车运输土方.已知4辆A型运输车与3辆B型运输车一次共运输土方64吨,2辆A型运输车与4辆B型运输车一次共运输土方52吨.(1)请问一辆A型运输车和一辆B型运输车一次各运输土方多少吨?(2)该运输集团决定派出A、B两种型号新型运输车共18辆参与运输土方,若每次运输土方总量不小于169吨,且B型运输车至少派出4辆,则有哪几种派车方案?13.某商店欲购进A、B两种商品,若购进A种商品5件和B种商品4件需300元;若购进A种商品6件和B种商品8件需440元.(1)求A、B两种商品每件的进价分别为多少元?(2)商店准备用不超过1615元购进50件这两种商品,求购进A种商品最多是多少件?14.某超市共用24000元同时购进甲、乙两种型号书包各200个,购进甲型号书包40个比购进乙型书包30个少用100元.(1)求甲、乙两种型号书包的进价各为多少元?(2)若超市把甲、乙两种型号书包均按每个90元定价进行零售,同时为扩大销售,拿出一部分书包按零售价的8折进行优惠销售.商场在这批背包全部售完后,若总获利不低于10200元,则超市用于优惠销售的书包数量最多为多少个?15.某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.(1)求A,B两种工艺品的单价;(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?16.每年的4月22日是世界地球日.某校为响应“携手为保护地球投资”的号召计划购入,A B两种规格的分类垃圾桶,用于垃圾分类.若购买A种垃圾桶30个和B种垃圾桶20个共需1020元;若购买A种垃圾桶50个和B种垃圾桶40个共需1860元.(1),A B两种垃圾桶的单价分别是多少元?(2)若该校最多有4360元用于购买这两种规格的垃圾桶共200个,则B种垃圾桶最多可以买________个.17.某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B 商品共用了880元.(1)A,B两种商品的单价分别是多少元?(2)已知该商店购买A,B两种商品共30件,要求购买B商品的数量不高于A商品数量的2倍,且该商店购买的A,B两种商品的总费用不超过276元,那么该商店有几种购买方案?18.每年一度的中考牵动着数万家长的心,为了给考生一个良好的环境,某市教委规定每个考场安排考生数是固定的人数,该市A 区的9000 名考生安排的考场数比B 区3000人安排的考场数多200个.(1)求每个考场安排固定考生的人数;(2)该市C区共有可作为考场的大小教室共300 间,由于今年疫情影响,该市教委要求大教室按原固定人数的80%安排考生,小教室按原固定人数的50%安排考生,若该市C 区共有考生6300 人,则至少需要有多少间大教室.19.2022年北京冬奥会吉祥物冰墩墩和雪容融在一开售时,就深受大家的喜欢.某供应商今年2月购进一批冰墩墩和雪容融,已知一个冰墩墩的进价比一个雪容融的进价多40元,并且购买20个冰墩墩和30个雪容融的价格相同.(1)问每个冰墩墩和雪容融的进价分别是多少元?(2)根据市场实际,供应商计划用20000元购进这两种吉祥物200个,则他本次采购时最多可以购进多少个冰墩墩?20.某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.已知工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?参考答案:1.(1)“冰墩墩”和“雪容融”的单价分别为55元,40元(2)最多可以购买66个“冰墩墩”2.(1)每辆A型货车补贴油费600元,每辆B型货车补贴油费400元.(2)该快递公司至多能派出8辆A型货车.3.(1)购进了A种笔记本150本;(2)m的最小值128.4.(1)84消毒液销售了200瓶,酒精销售了300瓶;(2)120瓶5.(1)每瓶A种饮料20元,每瓶B种饮料12元(2)10瓶6.(1)甲公司的总费用为(900x+2700)元,乙公司的总费用为(960x+1500)元;(2)当装修天数为20天时,两家公司的装修总费用一样多;(3)当x<20时,乙装修公司更合算;当x=20时,两家装修公司一样;当x>20时,甲装修公司更合算.7.(1)甲、乙两种型号设备每台的价格分别为12万元和10万元(2)至多购买5台8.(1)七年级52人,八年级40人;(2)两个年级一起买91套时最省钱;9.(1)A、B两种型号的电风扇的销售单价分别为200元和150元(2)A种型号的电风扇最多能采购37台(3)能实现利润超过2850元的目标,相应方案有两种:方案一:购买A种型号的电风扇36台,购买B种型号的电风扇14台;方案二:购买A种型号的电风扇37台,购买B种型号的电风扇13台10.(1)A种商品每件的进价为40元,B种商品每件的进价为25元(2)至少购进22件A种商品11.(1)购买1件A道具需要15元,1件B道具需要5元(2)道具A最多购买32件12.(1)一辆A型运输车一次运土10吨,一辆B型运输车一次运土8吨(2)有两种派送方案,方案一:派出A型号的新型运输车13辆,B型号的新型运输车5辆;方案二:派出A型号的新型运输车14辆,B型号的新型运输车4辆.13.(1)A种商品每件进价40元,B种商品每件进价25元(2)24件14.(1)A、B两种型号书包的进货单价各为50元、70元;(2)商场用于优惠销售的书包数量为100个.15.(1)A种工艺品的单价为80元,B种工艺品的单价为120元(2)共有3种进货方案16.(1)A种垃圾桶的单价熟练掌握18元,B种垃圾桶的单价是24元.(2)12617.(1)A种商品的单价为16元、B种商品的单价为4元(2)有四种方案,方案一:购买A商品的件数为10件,购买B商品的件数为20件;方案二:购买A商品的件数为11件,购买B商品的件数为19件;方案三:购买A商品的件数为12件,购买B商品的件数为18件;方案四:购买A商品的件数为13件,购买B商品的件数为17件.18.(1)每个考场安排固定考生的人数为30人;(2)至少需要有200间大教室.19.(1)今年2月第一周每个冰墩墩的进价为120元,每个雪容融的进价为80元(2)最多可以购进100个冰墩墩20.共有如下四种方案:A种21件,B种39件;A种20件,B种40件;A种19件,B种41件;A种18件,B种42件。
七年级数学不等式应用题专项练习(含答案解析)

七年级数学不等式应用题专项练习(含答案解析)1. 两名教师带学生去旅游,联系了两家标价相同的旅游公司。
甲公司优惠条件是1名教师全额收费,其余7.5折收费;乙公司的优惠条件是全部师生8折收费。
问当学生人数超过多少人时,甲旅游公司比乙旅游公司更优惠?2. 一位老师所教班级的学生人数,一半学数学,四分之一学音乐,七分之一学外语,还剩不足6位学生在玩足球。
求这个班有多少位学生?3. 某工程队要招聘甲、乙两种工人150人,甲、乙两种工种的月工资分别为600元和1000元。
现要求乙种工种的人数不少于甲种工种人数的2倍。
问甲、乙两种工种各招聘多少人时,可使得每月所付工资最少?4. 某商店以每辆300元的进价购入200辆自行车,并以每辆400元的价格销售。
两个月后自行车的销售款已超过这批自行车的进货款。
问这时至少已售出多少辆自行车?5. 某校为奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们。
如果每人送3本,则还余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本。
设该校买了m本课外读物,有x名学生获奖。
请解答下列问题:(1)用含x的代数式表示m;(2)求出该校的获奖人数及所买课外读物的本数。
6. 某果品公司要请汽车运输公司或火车货运站将60t水果从A地运到B地。
已知汽车和火车从A地到B地的运输路程都是Skm,两家运输单位除都要收取运输途中每吨每小时5元的冷藏费用外,其他收取的费用和有关运输资料由表列出。
问:(1)分别写出这两家运输单位运送这批水果所要收取的总费用y1元和y2元(用含S的式子表示);(2)为减少费用,当s=100km时,你认为果品公司应该选择哪一家运输单位更为合算?7. 用甲、乙两种原料配制成某种果汁,已知这两种原料的维生素C的含量及购买这两种原料的价格如表。
现制作这种果汁200kg,要求至少含有52,000单位的维生素C。
试写出所需甲种原料的质量x(kg)应满足的不等式。
(2)在方案一中果农应付运输费:5*2000+5*1300=元,在方案二中果农应付运输费:6*2000+4*1300=元。
解不等式例题50道

解不等式例题50道一、一元一次不等式1. 解不等式:2x + 5>9- 解析:- 首先对不等式进行移项,将常数项移到右边,得到2x>9 - 5。
- 计算右边式子得2x>4。
- 两边同时除以2,解得x > 2。
2. 解不等式:3x-1<8- 解析:- 移项可得3x<8 + 1。
- 即3x<9。
- 两边同时除以3,解得x<3。
3. 解不等式:5x+3≤slant2x + 9- 解析:- 移项,把含x的项移到左边,常数项移到右边,得到5x-2x≤slant9 - 3。
- 计算得3x≤slant6。
- 两边同时除以3,解得x≤slant2。
4. 解不等式:4x-7≥slant3x+1- 解析:- 移项得4x - 3x≥slant1+7。
- 即x≥slant8。
5. 解不等式:(1)/(2)x+3>x - 1- 解析:- 移项可得(1)/(2)x-x>-1 - 3。
- 通分计算,((1)/(2)-(2)/(2))x>-4,即-(1)/(2)x>-4。
- 两边同时乘以 - 2,不等号变向,解得x < 8。
6. 解不等式:(2)/(3)x-1≤slant(1)/(3)x+2- 解析:- 移项得(2)/(3)x-(1)/(3)x≤slant2 + 1。
- 计算得(1)/(3)x≤slant3。
- 两边同时乘以3,解得x≤slant9。
7. 解不等式:2(x + 3)>3(x - 1)- 解析:- 先展开括号,得到2x+6>3x - 3。
- 移项得2x-3x>-3 - 6。
- 计算得-x>-9。
- 两边同时乘以 - 1,不等号变向,解得x < 9。
8. 解不等式:3(x - 2)≤slant2(x+1)- 解析:- 展开括号得3x-6≤slant2x + 2。
- 移项得3x-2x≤slant2+6。
- 计算得x≤slant8。
人教版七年级下册数学不等式与不等式组应用题训练

人教版七年级下册数学不等式与不等式组应用题训练1.随着夏季的到来,某床上用品店准备新进A,B两种不同型号的凉席.在进货时,发现购进10件A种凉席和15件B种凉席的费用是4250元;购进22件A种凉席和30件B种凉席的费用是8900元.(1)求A,B两种凉席每件进价是多少元?(2)已知A种凉席每件的售价是300元,B种凉席每件的售价是220元,现在准备购进A种和B种凉席共60件,若使全部售完后获取的利润不低于5000元,则最少需要购进A种凉席多少件,并说明理由.2.立体书兼具了传统书的内容和形式,也拥有玩具的趣味和功能.某工厂生产了一款立体书,按标价销售此立体书,每本可获利30元;若按标价的八折销售6本此立体书与将标价降低10元销售3本此立体书获得的利润相同.(1)该工厂生产的这款立体书的标价与成本分别为多少元?(2)该工厂原计划按标价销售这款立体书共600本,销售一部分后发现生意火爆,于是将每本立体书提价10元,很快全部销售完,最后发现总利润不低于22000元,求提价前最多销售多少本此款立体书?3.某汽车租赁公司要购买轿车和面包车共10辆,已知轿车每辆7万元,面包车每辆4万元,其中轿车至少要购买3辆,且公司可投入的购车款不超过55万元.(1)符合公司要求的购买方案有哪几种?(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金不低于1500元,那么该租赁公司应选择以上哪种购买方案?4.莆田市校园阅读研究中心开展“教师共读”活动:计划购买甲乙两种书籍共100套,其中甲种书籍每套售价120元,乙种书籍每套售价80元.(1)如果购买甲乙两种书籍一共花费了9600元,求购买甲乙两种书籍各多少套?(2)设购买甲种书籍m套,如果购买乙种书籍的套数不超过甲种书籍的2倍,并且总费用不超过9440元,问购买甲乙两种书籍共有几种方案?哪种方案所需总费用最少?最少总费用是多少?5.某零食店销售牛轧糖、雪花酥2种糖果,如果用800元可购买5千克牛轧糖和4千克雪花酥,用760元可购买7千克牛轧糖和2千克雪花酥.(1)求牛轧糖、雪花酥每千克的价格分别为多少元?(2)已知该零食店在12月共售出牛轧糖50千克、雪花酥30千克.春节将近,1月份超市将牛轧糖每千克的售价提升43m元,雪花酥的价格不变,结果与12月相比,牛轧糖只销售了45千克,雪花酥销量上升1m5千克,销售总额超过了12月份销售总额;求m的取值范围.6.某地面对形势异常严峻的新冠疫情,遵从党和国家部署,最大程度保障人民群众的健康,将所在区域划分为封控区、管控区和防范区. 现要将一批蔬菜运往封控区,已知用3辆A型车和1辆B型车装满蔬菜一次可运26吨;用1辆A型车和2辆B型车装满蔬菜一次可运22吨.(1)求一辆A型车和一辆B型车装满蔬菜分别可运多少吨?(2)若一辆A型车的租金是180元,一辆B型车的租金是220元,该地计划租用A型车和B型车共7辆,且租金不超过1400元,问最多可租用几辆B型车?7.为了减少疫情带来的损失,某市决定加快复工复产.该市一企业需要运输一批物小货车一次可运输650箱物资.(1)1辆大货车与1辆小货车一次分别可运输多少箱物资?(2)该企业计划用这两种货车共12辆一次性运输这批物资,每辆大货车运输一次需5000元运费,每辆小货车运输一次需3000元运费.若运输物资不少于1500箱,且总费用小于53000元.请你列出所有运输方案,并指出哪种方案所需要费用最少,最少费用是多少元?8.用甲、乙两种原料配制成某种饮料,已知两种原料的维生素C 的含量以及购买这两种原料的价格如下表所示:现配制这种饮料10kg ,所需乙种原料的质量为()kg 0x x ≠.(1)当配制成的饮料,维生素C 的含量不少于4200单位,求配制这种饮料需乙种原料的质量范围;(2)在(1)的条件下,为了称量方便,所需甲、乙两种原料的质量均为整数,请你判断配制这种饮料共有几种方案,并计算哪种方案所需费用较少.9.国内某航空公司为提高经济效益,准备一次性购买国内A 品牌飞机和国际B 品牌飞机若干架.若购买2架国内A 品牌飞机和3架国际B 品牌飞机共需36亿元;购买4架国内A 品牌飞机和1架国际B 品牌飞机共需32亿元.(1)求购买一架国内A 品牌飞机与一架国际B 品牌飞机各需多少亿元;(2)根据该航空公司的实际情况,需一次性购买国内A 品牌飞机和国际B 品牌飞机共10架(两种品牌飞机均需购买),要求购买国内A 品牌飞机和国际B 品牌飞机的总费用不超过64亿元,共有哪几种购买方案?10.某水果店主计划采购A、B两种水果100kg进行销售,其中A水果的进货量(取整数)不小于28kg,下表为这两种水果的进货价、销售价及损耗率:经预算,该店主准备采购的总资金不高于950元.(1)请你为店主设计有几种采购方案,请写出具体方案;(2)设采购A水果akg,请用含有a字母的代数式(化简后)表示采购A、B两种水果销售后所获取的利润;在(1)方案中,最多获取利润是多少元?11.“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,并写出各种方案.12.张家口市某校为了普及推广冰雪活动进校园,准备购进速滑冰鞋和花滑冰鞋用于开展冰雪运动,若购进30双速滑冰鞋和20双花滑冰鞋共需8500元;若购进40双速滑冰鞋和10双花滑冰鞋共需8000元.(1)求速滑冰鞋和花滑冰鞋每双购进价格分别为多少元?(2)若该校购进两种冰鞋共50双,其中花滑冰鞋的数量不少于速滑冰鞋的数量,且用于购置两种冰鞋的总经费不超过8900元,则该校本次购买两种冰鞋共有哪几种方案?13.历经7年艰辛努力,北京冬奥会、冬残奥会胜利举办,激发了亿万人民的体育热情,推动了我国体育业发展.某校为了普及推广冰雪活动进校园,准备购买滑雪镜和滑雪手套用于开展冰雪运动,已知购买20副滑雪镜和60副滑雪手套共需7800元,购买40副滑雪镜和50副滑雪手套共需10000元.(1)求滑雪镜和滑雪手套每副购买的价格分别为多少元?(2)学校准备购买滑雪镜和滑雪手套共100副,购买的总费用不能超过12000元,则该校最多购买滑雪镜多少副?14.2022年冬奥会吉祥物“冰墩墩”与冬残奥会吉祥物“雪容融”深受人们的喜爱.某玩具店预购进这两款吉祥物玩具100个进行销售.若购进20个“冰墩墩”和10个“雪容融”共需1000元;若购进10个“冰墩墩”和20个“雪容融”共需950元.(1)求“冰墩墩”和“雪容融”单价;(2)若购买“冰墩墩”不少于60个,所需费用总额不超过3310元,请你求出满足要求的所有进货方案,并直接写出最省钱的进货方案.15.某商场在“双11”前准备从供货商家处新选购一批商品,已知按进价购进1件甲种商品和2件乙种商品共需320元,购进3件甲种商品和2件乙种商品共需520元.(1)求甲、乙两种商品每件的进价分别是多少元?(2)若甲种商品的售价为每件120元,乙种商品的售价为每件140元,该商场准备购进甲、乙两种商品共50件,且这两种商品全部售出后总利润不少于1350元,不高于1375元.若购进甲种商品m件,请问该商场共有哪几种进货方案?(3)根据往年销售情况,商场计划在“双11”当天将现有的甲、乙两种商品共46件按(2)中的售价全部售完.但因受拉尼娜现象形成的冷空气持续影响,当天出现的雨雪天气使得46件商品没有全部售完,两种商品的实际销售利润总和为1220元.那么,“双11”当天商场至少卖出乙种商品多少件?16.篮球赛单循环赛一般按积分确定名次.胜一场得2分,负一场得1分.如果积分相同,再比较相互间胜负记录.某次篮球联赛中,太阳队与蓝天队要争夺一个出线权,太阳队目前的战绩是12胜8负(与蓝天队无比赛),后面还要比赛5场(其中与蓝天队有一场比赛);蓝天队目前的战绩是10胜10负,后面还要比赛5场.探究以下问题:(1)为确保出线,太阳队在后面的比赛中至少要胜多少场?(2)如果太阳队在后面的比赛中3胜2负,未能出线,那么蓝天队后续战果如何?17.河南某校为做好新型冠状病毒感染的预防工作,计划为教职工购买一批洗手液(每人1瓶).学校派王老师去商场购买,他在商场了解到,某个牌子的洗手液,售价为每瓶14元,有两种优惠活动:活动一:一律打9折;活动二:当购买量不超过50瓶时,按原价销售;当购买量超过50瓶时,超过的部分打8折.如果该校共有m名教职工,请你帮王老师设计最省钱的购买方案.18.炎炎夏日,雪糕成为降暑解渴的必需品,小王通过市场调查,准备购进甲乙两种口味的雪糕进行销售.已知购进30支甲种口味雪糕和25支乙种口味雪糕共需215元;购进40支甲种口味雪糕和50支乙种口味雪糕共需370元.(1)求两种雪糕的进价分别为每支多少元?(2)甲种口味雪糕售价为每支4.5元,乙种口味雪糕售价为每支7元,在销售过程中,小王发现甲种口味的雪糕更受人们喜爱,所以打算再次购进两种雪糕共800支,并且乙种口味雪糕的数量不多于甲种口味雪糕数量13,则乙种口味雪糕最多购进多少支?此时的利润是多少元?19.疫情期间为了满足口罩需求,某药店计划购买同一品牌的甲型口罩和乙型口罩.已知购买1个甲型口罩和2个乙型口罩需花费8元,购买2个甲型口罩和3个乙型口罩需花费13元.(1)求购买该品牌一个甲型口罩、一个乙型口罩各需花费多少元?(2)如果药店需要甲型口罩的个数是乙型口罩个数的2倍还多8个,且该药店购买甲型口罩和乙型口罩的总费用不超过5000元,那么该药店最多可购买多少个该品牌乙型口罩?20.随着“一带一路”的进一步推进,我国瓷器更是“一带一路”沿线人民所推崇的,某商户看准这一商机,准备经销瓷器茶具,计划购进青瓷茶具和白瓷茶具共80套.已知青瓷茶具每套280元,白瓷茶具每套250元,设购进x套青瓷茶具,购进青瓷茶具和白瓷茶具的总费用为y.(1)求出y与x之间的函数关系式;(2)该商户想要用不多于20900元的钱购进这两种茶具,且购买白瓷茶具的数量不超过青瓷茶具的两倍,请问有哪几种购进方案.。
初中不等式经典例题

初中不等式经典例题一、例题11. 若不等式3x - a ≤ 0的正整数解是1、2、3,求a的取值范围。
这题啊,可有点小绕呢。
首先我们来解这个不等式3x - a ≤ 0,把它变形一下就得到x ≤ a/3。
正整数解是1、2、3,那就是说3肯定是满足这个不等式的,所以3 ≤ a/3,这就得出a ≥ 9。
但是呢,4就不满足这个不等式了,要是4满足的话正整数解就不止1、2、3了,所以4 > a/3,也就是a < 12。
所以啊,a的取值范围就是9 ≤ a < 12。
2. 已知关于x的不等式组{x - a > 0,1 - x > 0}的整数解共有3个,求a的取值范围。
先看这个不等式组,x - a > 0,那就是x > a;1 - x > 0,变形一下就是x < 1。
这个不等式组的解集就是a < x < 1。
它的整数解共有3个,那这三个整数解肯定是 - 2, - 1,0啊。
所以 - 3 ≤ a < - 2。
为什么呢?要是a < - 3的话,整数解就不止3个了,要是a ≥ - 2的话,整数解就没3个了,是不是很有趣呢?二、例题21. 解不等式2(x - 1) + 5 < 3x。
这题看着简单,可也有不少同学会犯错哦。
我们先把括号展开,2x - 2 + 5 < 3x,然后把含有x的项移到一边,常数项移到另一边,就得到2x - 3x < 2 - 5,也就是 - x < - 3。
两边同时除以 - 1,注意哦,除以一个负数的时候,不等式要变号,所以x > 3。
2. 若不等式组{x + 8 < 4x - 1,x > m}的解集是x > 3,求m 的取值范围。
先解x + 8 < 4x - 1,移项得到x - 4x < - 1 - 8, - 3x < - 9,x > 3。
这个不等式组的解集是x > 3,还有个x > m,那m肯定是小于等于3的。
七年级数学不等式(组)应用题——分配问题

不等式(组)应用题——分配问题
1、某校安排寄宿生住宿舍,如果每间住7人,那么有一间不空也不满;如果每间宿舍住4人,那么有100个人住不下。
问该校寄宿生几人?宿舍有几间?
2、若干苹果分给几只猴子,若每只猴子分3个,则余8个;每只猴分5个,则最后一只猴分得的数不足5个,问共有多少只猴子?多少个苹果?
3、我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房。
如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?
4、学校将若干间宿舍分配给七年级一班的女生住宿,已知该班女生少于35人,若每个房间住5人,则剩下5人没处可住;若每个房间住8人,则空出一间房,并且还有一间房也不满。
有多少间宿舍,多少名女生?
5、现有住宿生若干人,分住若干间宿舍,若每间住4人,则还有19人无宿舍住;若每间住6人,则有一间宿舍不空也不满,求住宿生人数和宿舍间数。
6、课外阅读课上,老师将43本书分给各小组,每组8本,还有剩余;每组9本却又不够。
问有几个小组?
7、有学生若干人,住若干间宿舍,若每间住4人,则有20人无法安排住宿;若每间住8人,则有一间宿舍不满也不空,问宿舍间数是多少?
1。
不等式解决问题练习题

不等式解决问题练习题一、一元一次不等式1. 解不等式:3x 5 > 22. 解不等式:4 2x ≤ 13. 解不等式:5x + 8 > 34. 解不等式:7 3x < 45. 解不等式:2x 6 ≥ 4二、一元一次不等式组1. 解不等式组:\[\begin{cases}x 2 > 0 \\3x + 1 < 4\end{cases}\]2. 解不等式组:\[\begin{cases}2x 3 < 5 \\4x + 7 > 11\end{cases}\]3. 解不等式组:\[\begin{cases}5x + 4 > 2x 1 \\3x 2 ≤ 8\end{cases}\]三、一元二次不等式1. 解不等式:x^2 5x + 6 > 02. 解不等式:2x^2 4x 6 < 03. 解不等式:x^2 + 3x 4 ≥ 04. 解不等式:x^2 + 2x + 3 ≤ 05. 解不等式:4x^2 12x + 9 > 0四、分式不等式1. 解不等式:\(\frac{1}{x2} > 0\)2. 解不等式:\(\frac{2}{x+3} < 1\)3. 解不等式:\(\frac{3}{x1} + \frac{1}{x+2} ≥ 0\)4. 解不等式:\(\frac{4}{x+1} \frac{2}{x3} ≤ 2\)5. 解不等式:\(\frac{5}{x^2 4x + 3} > 0\)五、绝对值不等式1. 解不等式:|x 4| < 32. 解不等式:|2x + 1| ≥ 53. 解不等式:|3x 7| > 24. 解不等式:|4 x| ≤ 65. 解不等式:|5x + 3| < 8六、综合应用题1. 某企业生产一种产品,每件产品的成本为50元,售价为80元。
若该企业每月固定开支为2000元,要使企业不亏损,每月至少需要销售多少件产品?2. 一辆汽车以60km/h的速度行驶,行驶过程中,速度每增加10km/h,油耗增加1L/100km。
七下数学不等式应用题

七下数学不等式应用题
1、一只纸箱质量为1 kg,放入一些苹果(每个苹果质量为0.25 kg)后,纸箱和苹果的总质量不超过10 kg,这只纸箱最多只能装多少个苹果?
2、某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案.方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠.已知小敏5月1日前不是该商店的会员.
(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?
(2)请帮小敏算一算,所购买商品的价格在什么范围内时,采用方案一更合算?
3、为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1 220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
4、某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案:方案一,用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二,若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠,已知小敏5月1日前不是该商店的会员.
(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?
(2)请帮小敏算一算,所购买商品的价格在什么范围内时,采用方案一更合算?。
初一数学不等式与不等式组30道典型题(含答案和解析及相关考点)

初一数学不等式与不等式组30道典型题(含答案和解析)1、在式子 -3<0,x ≥2,x=a,x 2-2x,x ≠3,x+1>y 中,是不等式的有( ).A. 2个B. 3个C. 4个D. 5个 答案:C.解析:式子 -3<0,x ≥2,x ≠3,x+1>y 这四个是不等式.考点:方程与不等式——不等式与不等式组——不等式的基础——不等式的定义.2、下列结论正确的有 (填序号).①如果a >b,c <d,那么a-c >b-d. ②如果a >b,那么ab >1.③如果a >b,那么1a <1b.④如果a c2<bc2,那么a <b.答案:①④.解析:①∵c <d,∴-c >-d,∵a >b,∴a-c >b-d, 故①正确.②当b <0时,ab <1, 故②错.③若a=2,b= -1,满足a >b,但1a >1b , 故③错. ④∵ac2<bc 2,∴c 2>0,∴a <b.考点:方程与不等式——不等式与不等式组——不等式的基础——不等式的性质.3、若0<m <1,m ,m 2,1m的大小关系是( ).A. m <m 2<1m B. m 2<m <1m C. 1m <m <m 2D. 1m <m 2<m答案:B.解析:可用特殊值.考点:方程与不等式——不等式与不等式组——不等式的基础——不等式的性质.4、若a <b,则下列各式中一定成立的是( ).A.a-1<b-1B. a 3>b3 C.-a <-b D.ac <bc 答案:A.解析:根据不等式的性质可得:不等式两边加(或减)同一个数(或式子),不等号的方不变.A. a-1<b-1,故A 选项是正确的.B.a >b,不成立,故B 选项是错误的.C. a >-b,不一定成立,故 选项是错误的.D. C 的值不确定,故D 选项是错误的.考点:方程与不等式——不等式与不等式组——不等式的基础——不等式的性质.5、下列式子中,是一元一次不等式的有( ).①x 2+x <1 ②1x +2>0 ③x-3>y+4 ④2x+3<8 A.1个 B.2个 C.3个 D.4个 答案:A.解析:①不是,因为它的未知数的最高次数是2.②不是,因为不等式的左边是1x +2,它不是整式.③不是,因为不等式中含有两个未知数.④是,因为它符合一元一次不等式定义中的三个条件. 故答案为A.考点:方程与不等式——不等式与不等式组——一元一次不等式的定义.6、如果(m+1)x >2是一元一次不等式,则m = . 答案:1. 解析:∵(m+1)x∣m ∣>2是一元一次不等式.∴m+1≠0.︱m ︱=1,解得:m=1.考点:数——有理数——绝对值——方程与不等式——不等式与不等式组——一元一次不等式的定义.7、解不等式3-4(2x-3)≥3(3-2x),并把它的解集在数轴上表示出来.答案:原不等式的解集为x≤3.画图见解析.解析:去括号,得3-8x+12≥9-6x.移项,得-8x+6x≥9-3-12.合并同类项,得-2x≥-6.系数化1 ,得x≤3.把它的解集在数轴上表示为:考点:方程与不等式——不等式与不等式组——在数轴上表示不等式的解集——解一元一次不等式.8、当a<3时,不等式ax≥3x+7的解集是..答案:x≤7a−3解析:ax≥3x+7.ax-3x≥7.(a-3)x≥7.∵a<3.∴a-3<0..∴x≤7a−3考点:方程与不等式-不等式与不等式组-含参不等式(组)-解含参不等式.(x-5)-1>x+m的解集为x<2,则m的值为.9、已知不等式12答案:-4.5.解析:1(x-5)-1>x+m.212x-52-1-x >m.-12x >m+72. x <-2m-7. ∵解集为x <2. 则-2m-7=2. m=-4.5.考点:方程与不等式——不等式与不等式组——含参不等式(组)——已知解集反求参数.10、若不等式4x-a <0只有三个正整数解,则 的取值范围 . 答案:12<a ≤16.解析::将4x-a <0变形为x <a4.不等式只有三个正整数解.即x 的正整数解为1,2,3,所以3<a4≤4,解得a 的取值范围为12<a ≤16.考点:方程与不等式——不等式与不等式组——一元一次不等式的整数解.11、若关于x 的不等式mx-n >0的解集是x <15,则关于x 的不等式(m+n )x >n-m 的解集是( ).A. x <-23B. x >-23C. x <23D. x >23答案:A.解析:∵不等式mx-n >0的解集是x <15.∴m <0且n m= 15.∴m=5n,n <0.∴不等式(m+n )x >n-m 可整理为6nx >-4n 的解集是x <-23.考点:方程与不等式——不等式与不等式组——解一元一次不等式.12、若方程3(x+1)-m = 3m-5x 的解是负数,则 的取值范围是( ).A. m <34 B. m >34 C. m <−34 D. m >−34答案:A.解析:3(x+1)-m = 3m-5x.3x+5x = 3m+m-3. 8x = 4m-3. ∵解是负数. ∴8x <0. ∴4m-3<0. m <34.考点:方程与不等式—一元一次方程—含字母参数的一元一次方程—含参一元一次方程.不等式与不等式组—一元一次不等式的应用.13、若关于x ,y 的二元一次方程组 {3x +y =1+ax +3y =3的解满足x+y <2,则a 的取值范围是 . 答案:a <4.解析:将二元一次方程组两个等式相加,得4x+4y=a+4,即x+y=a+44.∵x+y <2. ∴a+44<2.∴a <4.考点:方程与不等式——二元一次方程组——含字母参数的二元一次方程组.14、关于x,y 的二元一次方程组{3x −y =ax −3y =5−4a的解满足x <y,则a 的取值范围是( ).A. a >35B. a <13C. a <53D. a >53答案:D. 解析:解法一:解不等式组得{x =7a−58y =13a−158.∵x <y.∴7a−58<13a−158.解得a >53. 解法二:两式相加得4(x-y )=5-3a. ∵x <y. ∴x-y <0. ∴5-3a <0. ∴a >53.考点:方程与不等式——不等式与不等式组——解一元一次不等式组.15、解不等式2x−13-5x+12≥1,并把它的解集在数轴上表示出来.答案:不等式的解集为x ≤-1,在数轴上表示如图所示:解析:去分母,得2(2x-1)-3(5x+1)≥6.去括号,得4x-2-15-3≥6. 移项合并同类项,得-11x ≥11. 系数化为1,得x ≤-1.∴此不等式的解集为x ≤-1,在数轴上表示如图所示:考点:方程与不等式——不等式与不等式组——在数轴上表示不等式的解集——解一元一次不等式.16、解不等式12(x+1)≤23x-1,并把它的解集表示在数轴上,再写出它的最小整数解. 答案:最小整数解为x=9. 解析:12(x+1)≤23x-1.3(x+1)≤4x-6.3x+3≤4x-6.3x-4x≤-6-3.-x≤-9.x≥9.将它的解集表示在数轴上:∴它的最小整数解为x=9.考点:方程与不等式——不等式与不等式组——解一元一次不等式.17、若m>6,则(6-m)x<m-6的解集为.答案:x>-1.解析:∵m>6.∴(6-m)x<m-6.∴x>-1.考点:方程与不等式——不等式与不等式组——含参不等式(组)——解含参不等式. 18、关于x的不等式2x-a≤-1的解集如图所示,则a的值是( ).A.4B.3C.2D.1答案:B.解析:解不等式2x-a≤-1得,x≤a−1,根据数轴可知x≤1.2=1,即a=3.∴a−12考点:方程与不等式——不等式与不等式组——在数轴上表示不等式的解集——解一元一次不等式.19、已知a、b为常数,若ax+b>0的解集是x<1,则bx-a<0的解集是( ).4A.x >-4B.x <-4C.x >4D.x <4 答案:B.解析:∵ax+b >0的解集x <14.∴x <-ba . 则-ba = 14. ∴a <0. 又∵a=-4b. ∴b >0. ∴bx-a <0. ∴bx+4b <0. ∴x+4<0. ∴x <-4.考点:方程与不等式——不等式与不等式组——含参不等式(组)——解含参不等式.20、已知方程组{2x +3y =3m +72x +y =4m +1的解满足x+y >0,求m 的取值范围.答案:m >-87.解析:{2x +3y =3m +7①2x +y =4m +1 ②.解:①+②得. 4x+4y=7m+8. 4(x+y)=7m+8. x+y=7m+84.∵x+y >0. ∴7m+84>0.∴7m+8>0. ∴7m >-8. ∴m >-87.考点:方程与不等式——二元一次方程组——含字母参数的二元一次方程组.不等式与不等式组——一元一次不等式的应用.21、解不等式组{2(x +8)≤10−4(x −3)x+12−4x+16<1,并写出该不等式组的整数解. 答案:-4<x ≤1,整数解有-3,-2,-1,0,1. 解析:{2(x +8)≤10−4(x −3)①x+12−4x+16<1 ②. 由①得:x ≤1. 由②得:x >-4. ∴-4<x ≤1.整数解有-3,-2,-1,0,1.考点:方程与不等式——不等式与不等式组——解一元一次不等式组.22、解不等式组:{7(x −5)+2(x +1)>−152x+13−3x−12<0答案:x >2.解析:{7(x −5)+2(x +1)>−15①2x+13−3x−12<0②. 解①得:x >2. 解②得:x >1. ∴x >2.考点:方程与不等式——不等式与不等式组——解一元一次不等式组.23、解不等式组:{2(x +1)>5x −7x+103>2x 答案:x <2.解析:解不等式2(x+1)>5x-7得.2x+2>5x-7. 3x <9.x <3. 解不等式x+103>2x 得.x+10>6x. 5x <10. x <2.∴原不等式的解集为x <2.考点:方程与不等式——不等式与不等式组——解一元一次不等式组.24、不等式组{x +9<5x +1x >m +1的解集是x >2,则m 的取值范围是 .答案:m ≤1.解析:由不等式组可得{x >2x >m +1,其解集为x >2,则m+1≤2,m ≤1.考点:方程与不等式——不等式与不等式组——解一元一次不等式组.25、若关于x 的不等式组{x −2<5x −a >0无解,则 的取值范围是 .答案:a ≥7.解析:解不等式组得{x <7x >a,由不等式组无解可知a ≥7.考点:方程与不等式——不等式与不等式组——解一元一次不等式组.26、已知关于x 的不等式组{x −a ≥b 2x −a <2b +1的解集为3≤x <5,则ba 的值为 .答案:-2.解析::由x-a ≥b 得x ≥a+b.由2x-a <2b+1得x <a+2b+12.∵解集为3≤x <5. ∴{a +b =3a+2b+12=5.解b=6,a=-3.∴ba = 6−3= -2.考点:方程与不等式——不等式与不等式组——解一元一次不等式组.27、已知方程组{x+y=m+3x−y=3m−1的解是一对正数,试化简∣2m+1∣+∣2-m∣.答案:化简得:m+3.解析:{x+y=m+3①x−y=3m−1②.①+②:2x=4m+2.x=2m+1.①-②:2y=-2m+4.y=-m+2.∵方程组的解是一对正数.∴{x>0 y>0.∴{2m+1>0−m+1>0.解得:-12<m<2.∴∣2m+1∣+∣2-m∣.=2m+1+2-m.=m+3.考点:数——有理数——绝对值化简——已知范围化简绝对值.方程与不等式——二元一次方程组——含字母参数的二元一次方程组——含参方程组解的分类讨论.不等式与不等式组——含参不等式(组)——方程根的取值范围.28、若关于x的不等式组{x−m<07−2x≤1的整数解有且只有4个,则m的取值范围是( ).A.6<m <7B.6≤m <7C.6≤m ≤7D.6<m ≤7 答案:D解析:{x −m <07−2x ≤1.由x-m <0得:x <m . 有7-2x ≤1得:x ≥3. ∴不等式的解集为:3≤x <m .∴不等式的整数解为:3 、4 、5 、6 . ∴m 的取值范围是6<m ≤7.考点:方程与不等式——不等式与不等式组——解一元一次不等式组——一元一次不等式组的整数解.29、对x,y 定义一种新运算T,规定:T(x,y )= ax+by2x+y (其中a 、b 均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= a×0+b×12×0+1 = b .(1) 已知T(1,-1)= -2,T(4,2)= 1.① 求 a,b 的值.② 若关于m 的不等式组{T(2m,5−4m )≤4T(m,3−2m )>p恰好有3个整数解,求实数p 的取值范围.(2) 若T(x,y )=T(y,x )对任意实数x,y 都成立(这里T(x,y )和T(y,x )均有意义),则a,b 应满足怎样的关系式?答案: (1) ① a=1,b=3 .② -2≤p <−13 . (2) a=2b .解析: (1)① 根据题意得:T(1,-1)=a−b 2−1=-2,即a-b=-2.T(4,2)=4a+2b 8+2=1,即2a+b=5.解得: a=1,b=3.② 根据题意得:{2m+(5−4m )4m+(5−4m )≤4 ①m+3(3−2m )2m+3−2m>p ②.由①得:m ≥−12. 由②得:m <−9−3p 5.∴不等式组的解集为−12≤m <−9−3p 5.∵不等式组恰好有3个整数解,即m=0,1,2. ∴2<9−3p 5≤3.解得: -2≤p <-13.(2) 由T(x,y )=T(y,x ),得到ax+by 2x+y = ay+bx2y+x .整理得:(x 2-y 2)(2b-a )=0.∵T(x,y )=T(y,x )对任意实数x,y 都成立. ∴2b-a=0,即 a=2b.考点:式——探究规律——定义新运算.方程与不等式——不等式与不等式组——解一元一次不等式组.30、如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.(1) 在方程① 3x-1=0,② 23x+1=0,③ x-(3x+1)=-5中,不等式组{−x +2>x −53x −1>−x +2的关联方程是 .(填序号) (2)若不等式组{x −12<11+x >−3x +2的一个关联方程的根是整数,则这个关联方程可以是 (写出一个即可).(3)若方程3-x=2x,3+x=2(x+12)都是关于x 的不等式组{x <2x −m x −2≤m的关联方程,直接写出m 的取值范围.答案: (1) ③.(2)2x-1=1.(3)m 的取值范围为0≤m <1 .解析: (1)解不等式组{−x +2>x −53x −1>−x +2.解−x +2>x −5得x <312. 解3x −1>−x +2得x >34. ∴不等式的解为34<x <312.解方程① 3x-1=0得x=13,② 23x+1=0得x=-32 ,③ x-(3x+1)=-5得x=2. 根据一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程. ∴关联方程为③. (2) 解不等式{x −12<11+x >−3x +2.解x −12<1,得x <112. 解1+x >−3x +2,得x >14. ∴不等式得解集为14<x <112.∵关联方程的根是整数,∴方程的根为1. ∵2x-1=1的方程的解为1. ∴2x-1=1满足.答案不唯一,只要解为1一元一次方程即可. (3) 解方程3-x=2x,得x=1.解方程3+x=2(x+12),得x=2.∵方程3-x=2x,3+x=2(x+12),都是关于x 的不等式组{x <2x −m x −2≤m的关联方程.∴满足{1<2×1−m 1−2≤m ,即-1<m <1.且{2<2×2−m 2−2≤m ,即0≤m <2.∴m 的取值范围为0≤m <2.考点:方程与不等式——一元一次方程——一元一次方程的解.不等式与不等式组——解一元一次不等式组.。
初一不等式试题及答案

初一不等式试题及答案一、选择题1. 如果a > b,且c < 0,那么下列不等式中正确的是:A. ac > bcB. ac < bcC. a + c > b + cD. a - c < b - c答案:A2. 对于任意实数x,下列不等式一定成立的是:A. x + 1 > xB. x - 1 < xC. x × 1 = xD. x ÷ 1 = x答案:C二、填空题1. 如果x > 5,那么-3x _______ -15。
答案:<2. 已知2x - 3 < 7,解得x _______ 5。
答案:<三、解答题1. 已知不等式3x + 5 > 14,求x的取值范围。
解:首先将不等式两边同时减去5,得到3x > 9。
然后将不等式两边同时除以3,得到x > 3。
所以x的取值范围是x > 3。
2. 如果一个数的一半加上3等于这个数减去4,求这个数。
解:设这个数为x,根据题意可得:\( \frac{x}{2} + 3 = x - 4 \)将等式两边同时乘以2,得到:\( x + 6 = 2x - 8 \)将等式两边同时减去x,得到:\( 6 = x - 8 \)将等式两边同时加上8,得到:\( x = 14 \)所以这个数是14。
四、应用题1. 某工厂计划在一个月内生产至少100件产品,已知每天可以生产10件产品,问至少需要多少天完成生产计划?解:设需要x天完成生产计划。
根据题意,每天生产10件产品,至少需要生产100件产品,可以得到不等式:\( 10x \geq 100 \)将不等式两边同时除以10,得到:\( x \geq 10 \)所以至少需要10天完成生产计划。
结束语:通过本试题的练习,同学们应该对不等式的概念、性质以及解法有了更深入的理解。
希望同学们能够通过不断的练习,提高解决实际问题的能力。
不等式应用题(带答案)

不等式应用题(带答案)不等式应用题1. 某商场正在举行打折活动,标有原价为x元的商品打7折出售,小明买了一个售价为y元的商品打了折后用了z元购买,设不等式x>y>z,请计算头一个不等式。
解: 原价为x元的商品打7折后的价格为0.7x元,由题意可知小明买的商品在打折后售价为0.7x元,且小明用z元购买了该商品。
根据不等式的性质,可得到如下关系式:0.7x > z即,x > z/0.7所以,头一个不等式为x > z/0.7。
2. 一辆汽车每小时以v公里的速度行驶,已知行驶t小时后行驶了s 公里,求不等式v < s/t。
解: 汽车行驶t小时后行驶的路程为vt公里,已知行驶了s公里,则可得到如下关系式:vt > s即,v > s/t所以,不等式为v > s/t。
3. 小明参加了一场马拉松比赛,他总共用时t小时,已知他的平均速度为v千米每小时,求不等式t > d/v,其中d为比赛的总路程。
解: 小明参加马拉松比赛用时t小时,根据速度的定义可知,平均速度v等于总路程d除以用时t,即:v = d/t由于不等式是要求t > d/v,将v的表达式代入可得:t > d/(d/t)化简后得到:t > t,该不等式恒成立。
所以,不等式为t > d/v。
4. 一个三角形的两边长分别为a和b,夹角为θ (0° < θ < 180°),求不等式a + b > 2absin(θ)。
解: 根据三角形的余弦定理可得 a² = b² + c² - 2bc cos(θ),将此式代入不等式中可得:a +b > 2ab sin(θ) + 2bc cos(θ)又因为sin(θ) ≤ 1,所以2ab sin(θ) ≤ 2ab,化简后得到:a +b > 2bc cos(θ)由于夹角θ位于 (0°, 180°) 之间,所以cos(θ) > 0,即2bc cos(θ) > 0。
七年级数学不等式解应用题练习
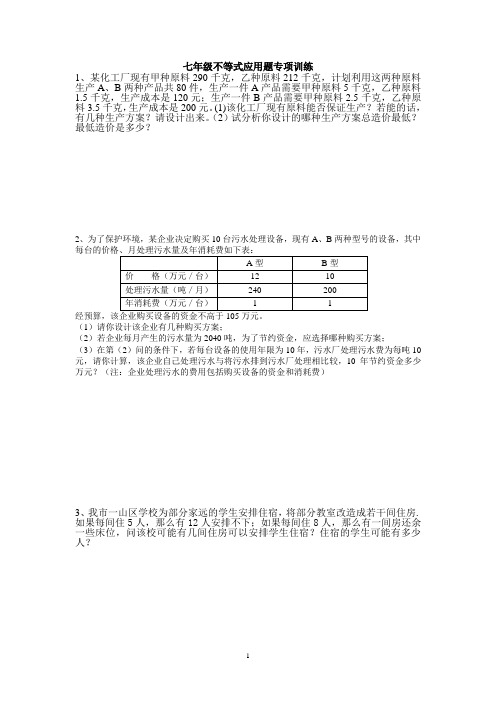
七年级不等式应用题专项训练1、某化工厂现有甲种原料290千克,乙种原料212千克,计划利用这两种原料生产A、B两种产品共80件,生产一件A产品需要甲种原料5千克,乙种原料1.5千克,生产成本是120元;生产一件B产品需要甲种原料2.5千克,乙种原料3.5千克,生产成本是200元。
(1)该化工厂现有原料能否保证生产?若能的话,有几种生产方案?请设计出来。
(2)试分析你设计的哪种生产方案总造价最低?最低造价是多少?2、为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,其中(1)请你设计该企业有几种购买方案;(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案;(3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)3、我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?4、某园林的门票每张10,一次使用。
考虑到人们的不同需求,也为了吸收更多的少游客,该园林除保留原有的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购买日起,可供持票者使用一年)。
年票分A、B、C三类:A类年票每张120元,持票者是入该园林时,无需再购买门票;B类门票每张60元,持票者进入该园林时,需再购买门票,每次2元;C类门票每张40元,持票者进入该园林时,需再购买门票,每次3元。
(1)如果您只选择一种购买门票的方式,并且您计划在一年中花80元在该园林的门票上,试通过计算,找出可使进入该园林的次数最多的购票方式。
(2)求一年中进入该园林至少超过多少次时,购买A类年票比较合算。
7年级不等式解应用题(含答案)

七年级不等式应用题专项训练1、某化工厂现有甲种原料290千克,乙种原料212千克,计划利用这两种原料生产A、B两种产品共80件,生产一件A产品需要甲种原料5千克,乙种原料1.5千克,生产成本是120元;生产一件B产品需要甲种原料2.5千克,乙种原料3.5千克,生产成本是200元。
(1)该化工厂现有原料能否保证生产?若能的话,有几种生产方案?请设计出来。
(2)试分析你设计的哪种生产方案总造价最低?最低造价是多少?(1)设生产A产品m件,生产B产品n件.5m+2.5n<=2901.5m+3.5n<=212m+n=80m=34,35,36n=46,45,44共3种(2)其中一种的件数为x,另一种的件数为(80-x)若A的件数为x,则y=16000-80x若B的件数为x,则y=9600+80x因为y=16000-80x是减函数,所以x越大,值越小.所以x=36时,有最小值此时y=13120y=9600+80x是增函数,所以x越小,值越小,所以x=44时值最小,此时y=13120所以这时都是A是36件,B是44件,此时最少为131202、为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的(1)请你设计该企业有几种购买方案;(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案;(3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)解:(1)设购买污水处理设备A型x台,则B型(10-x)台。
由题意知,12x+10(10-x)≤105,x≥2.5∵x取非负整数,∴x可取0,1,2.∴有三种购买方案:购A型0台,B型10台;购A型1台;B型9,购A型2台,B型8台。
(2)由题意得240x+200(10-x)≥2040,x≥1,∴x为1或2当x=1时,购买资金为12×1+10×9=102(万元)当x=2时,购买资金为12×2+10×8=104(万元)∴为了节约资金,应选购A型1台,B型9台3、我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?解:设有x间住房,有y名学生住宿,则有y=5x+12,根据题意得:8x-(5x+12)>0 8x-(5x+12)<8 解得4<x<6 2/ 3 .因为x为整数,所以x可取5,6,把x的值代入y=5x+12得:y的值为37,42.答:该校可能有5间或6间住房,当有5间住房时,住宿学生有37人;当有6间住房时,住宿学生有42人.4、某园林的门票每张10,一次使用。
不等式应用题专项练习

应用题专题训练(关于不等式方案应用)1、兴发服装店老板用4500元购进一批某款T 恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T 恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.(1)第一批该款式T 恤衫每件进价是多少元?(2)老板以每件120元的价格销售该款式T 恤衫,当第二批T 恤衫售出 54时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T 恤衫每件售价至少要多少元?(利润=售价﹣进价)2、(2013•六盘水)为了抓住2013年凉都消夏文化节的商机,某商场决定购进甲,乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.(1)购进甲、乙两种纪念品每件各需要多少元?(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6000元,同时又不能超过6430元,则该商场共有几种进货方案?(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?3、(2013•益阳)“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.4、(2003•苏州)我国东南沿海某地的风力资源丰富,一年内日平均风速不小于3m/s的时间共约160天,其中日平均风速不小于6m/s的时间约占60天,为了充分利用“风能”这种“绿色资源”,该地拟建一个小型风力发电厂,决定选用A、B两种型号的风力发电机.根据产品说明,这两种风力发电机在各种风速下的日发电量(即一天的发电量)如下表:日平均风速v(m/s)v<3 3≤v<6 v≥6A 型0 ≥36 ≥150日发电量/kw.hB型0 ≥24 ≥90根据上面的数据回答:(1)若这个发电厂购买x台A型风力发电机,则预计这些A型风力发电机一年的发电总量至少为千瓦•时;(2)已知A型风力发电机每台0.3万元,B型风力发电机每台0.2万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9. 为了抓住世博会商机,某商店决定购进 A,B 两种世博会纪念品,若购进 A 种纪念品 10 件, B 种纪念品 5 件,需要
1000 元;若购进 A 种纪念品 4 件, B 种纪念品 3 件,需要 550 元,
( 1)求购进 A, B 两种纪念品每件需多少元
( 2)若该商店决定拿出 1 万元全部用来购进这两种纪念品,考虑到市场需求,要求购进
根据题意得:敲击 2 次后铁钉进入木块的长度是 2+1=3cm,
而此时还要敲击 1 次故长度要大于 3cm,
第三次敲击进去最大长度是前一次的二分之一,也就是第二次的一半
所以 a 的最大长度为 2+1+=3.5cm,
3 次后全部进入木块(木块足够厚) ,且第 =0.5cm
故 a 的取值范围是: 3<a≤.
26 本.
6.
解:( 1) y 1=(2×60)s+5×× 60+3000=126s+3000;
y2=(× 60)s+5×× 60+4620=+4620;
(2)当 s=100km 时, y1=3000+126×100=15600(元) ,y 2=×100+4620=15195(元) . 故为减少费用,果品公司应选择火车货运站运送这批水果更为合算.
又∵ 0≤x≤50,∴当 x=50 时,∴y 最小 =﹣400×50+150000=130000(元)
∴150﹣ x=150﹣ 50=100(人)
答:甲、乙两种工种分别招聘 50, 100 人时,可使得每月所付的工资最少为 130000 元.
4.
解:设已售出 x 辆自行车,两个月后自行车的销售款已超过这批自行车的进货款,
(3)结合( 2)知:要使新工人的数量多于熟练工,则
n=8,a=1;或 n=6, a=2;或 n=4, a=3.
根据题意,得
W=2000a+1200n=2000a+1200( 10﹣ 2a)=12000 ﹣400a.
要使工厂每月支出的工资总额 W(元)尽可能地少,则 a 应最大.
显然当 n=4, a=3 时,工厂每月支出的工资总额 W(元)尽可能地少.
一个不等式.
8.如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当未进入木块的钉
子长度足够时,每次钉入木块的钉子长度是前一次.已知这个铁钉被敲击
3 次后全部进入木块(木块足够厚)
次敲击后铁钉进入木块的长度是 2cm,若铁钉总长度为 acm,求 a 的取值范围.
,且第一
(3)解法一:方案 1 利润为: 226×20+29×30=5390(元) ; 方案 2 利润为: 220×20+30×30=5300(元) ; 方案 3 利润为: 214×20+30×31=5210(元) ; 方案 4 利润为: 208×20+30×32=5120(元) ; 方案 5 利润为: 202×20+30×33=5030(元) ; 故 A 种纪念品 226 件, B 种纪念品 29 件利润较大为 5390 元.
/ 个) (单位:万元
/ 个)
A 15
18
2
B 20
30
已知可供建造沼气池的占地面积不超过
3 365m2,该村农户共有 492 户.
( 1)满足条件的方案共有几种写出解答过程;
( 2)通过计算判断,哪种建造方案最省钱
A、B 两种型号的沼气池共
20 个,
参考答案
1.
解:设学生人数为 x 人,每人旅游价格为 a 元,
汽车
50
2
3000
火车
80
4620
( 1)分别写出这两家运输单位运送这批水果所要收取的总费用
y 1 元和 y 2 元(用含 S 的式子表示) ;
( 2)为减少费用,当 s=100km 时,你认为果品公司应该选择哪一家运输单位更为合算
7.用甲、乙两种原料配制成某种果汁,已知这两种原料的维生素
C 的含量及购买这两种原料的价格如表:
甲种原料 维生素 C 含量(单位 / 千克) 800
乙种原料 200
原料价格(元 /kg )
18
14
( 1)现制作这种果汁 200kg,要求至少含有 52 000 单位的维生素 C,试写出所需甲种原料的质量 x( kg)应满足的不
等式;
( 2)如果还要求购买甲、乙两种原料的费用不超过
1 800 元,那么请你写出所需甲种原料的质量 x( kg)应满足的另
一元一次不等式应用题专项练习
1.某校两名教师带若干名学生去旅游,联系了两家标价相同的旅游公司,经洽谈后,甲公司优惠条件是
1 名教师全额
收费,其余折收费;乙公司的优惠条件是全部师生
8 折收费.试问:当学生人数超过多少人时,甲旅游公司比乙旅游
公司更优惠
2.有人问一位老师:“您所教的班级有多少名学生”老师说一半学生在学数学,四分之一的学生在学音乐,七分之一 的学生在学外语,还剩不足 6 位学生在玩足球.”求这个班有多少位学生
( 2)如果工厂招聘 n( 0< n< 10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工
厂有哪几种新工人的招聘方案
( 3)在( 2)的条件下,工厂给安装电动汽车的每名熟练工每月发
2000 元的工资,给每名新工人每月发 1200 元的工
资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额
10.
解:( 1)设每名熟练工和新工人每月分别可以安装
x、 y 辆电动汽车.
根据题意,得,
解得.
答:每名熟练工和新工人每月分别可以安装
4、 2 辆电动汽车.
(2)设工厂有 a 名熟练工. 根据题意,得 12( 4a+2n) =240, 2a+n=10, n=10﹣ 2a, 又 a, n 都是正整数, 0< n<10, 所以 n=8,6, 4, 2. 即工厂有 4 种新工人的招聘方案. ①n=8, a=1,即新工人 8 人,熟练工 1 人; ②n=6, a=2,即新工人 6 人,熟练工 2 人; ③n=4, a=3,即新工人 4 人,熟练工 3 人; ④n=2, a=4,即新工人 2 人,熟练工 4 人.
3.某工程队要招聘甲、乙两种工人 150 人,甲、乙两种工种的月工资分别为 600 元和 1000 元,现要求乙种工种的人 数不少于甲种工种人数的 2 倍,问甲、乙两种工种各招聘多少人时,可使得每月所付工资最少
4.某商店以每辆 300 元的进价购入 200 辆自行车,并以每辆 400 元的价格销售.两个月后自行车的销售款已超过这批 自行车的进货款,问这时至少已售出多少辆自行车
5.某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们,如果每人送 前面每人送 5 本,则最后一人得到的课外读物不足 3 本,设该校买了 m本课外读物,有 题:( 1)用含 x 的代数式表示 m;
( 2)求出该校的获奖人数及所买课外读物的本数.
3 本,则还余 8 本;如果 x 名学生获奖,请解答下列问
9.
解:( 1)设 A, B 两种纪念品每件需 x 元, y 元. , 解得:. 答: A, B 两种纪念品每件需 25 元, 150 元;
(2)设购买 A 种纪念品 a 件, B 种纪念品 b 件. , 解得≤ b≤. 则 b=29; 30; 31; 32; 33; 则 a 对应为 226 , 220; 214; 208, 202. 答:商店共有 5 种进货方案:进 A 种纪念品 226 件, B 种纪念品 29 件;或 A 种纪念品 220 件, B 种纪念品 30 件;或 A 种纪念品 214 件, B 种纪念品 31 件;或 A 种纪念品 208 件, B 种纪念品 32 件;或 A 种纪念品 202 件, B 种纪念品 33 件;
7.
解:( 1)若所需甲种原料的质量为 xkg ,则需乙种原料( 200﹣ x) kg.
根据题意,得 800x+200( 200﹣ x)≥ 52000;
(2)由题意得, 18x+14( 200﹣ x)≤ 1800.
8.
解:∵每次钉入木块的钉子长度是前一次的.已知这个铁钉被敲击
一次敲击后铁钉进入木块的长度是 2cm,
运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案请你一一写出.
13. 为执行中央“节能减排, 美化环境, 建设美丽新农村”的国策, 我市某村计划建造
以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
型号 占 地面积
使用农户数
造价
2
(单位: m/ 个
) (单位:户
A 种纪念品的数量不少于 B 种
纪念品数量的 6 倍,且不超过 B 种纪念品数量的 8 倍,那么该商店共有几种进货方案
( 3)若销售每件 A 种纪念品可获利润 20 元,每件 B 种纪念品可获利润 30 元,在第( 2)问的各种进货方案中,哪一
种方案获利最大最大利润是多少元
10. 某汽车制造厂开发了一款新式电动汽车,计划一年生产安装
W(元)尽可能地少
11. 某地区果农收获草莓 30 吨,枇杷 13 吨,现计划租用甲、乙两种货车共 10 辆将这批水果全部运往省城,已知甲种 货车可装草莓 4 吨和枇杷 1 吨,乙种货车可装草莓、枇杷各 2 吨. ( 1)该果农安排甲、乙两种货车时有几种方案请您帮助设计出来; ( 2)若甲种货车每辆要付运输费 2 000 元,乙种货车每辆要付运输费 1 300 元,则该果农应选择哪种运输方案才能使 运费最少,最少运费是多少元
240 辆.由于抽调不出足够的熟练工来完成新式电动汽
车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门
