整式的加减重难点和易错点
中考数学知识辅导:整式的加减

中考数学知识辅导:整式的加减
2019中考数学知识辅导:整式的加减
中考复习最忌心浮气躁,急于求成。
指导复习的教师,应给学生一种乐观、镇定、自信的精神面貌。
要扎扎实实地复习,一步一步地前进,下文为大家准备了2019中考数学知识辅导的内容。
一、重点
单项式及其相关的概念;
多项式及其相关的概念;
去括号法则,准确应用法则将整式化简。
二、难点
区别单项式的系数和次数;
区别多项式的次数和单项式的次数;
括号前面是-号去括号时,括号内各项变号容易产生错误。
三、知识点、概念总结
1.单项式:在代数式中,若只含有乘法(包括乘方)运算。
或虽含有除法运算,但除式中不含字母的一类代数式叫单项式;数字或字母的乘积叫单项式(单独的一个数字或字母也是单项式)。
2.系数:单项式中的数字因数叫做这个单项式的系数。
所有字母的指数之和叫做这个单项式的次数。
任何一个非零数的零次方等于1.
3.多项式:几个单项式的和叫多项式。
的项叫做同类项。
10.合并同类项:多项式中的同类项可以合并,叫做合并同类项,合并同类项的法则是:同类项的系数相加,所得的结果作为系数,字母与字母的指数不变。
这篇2019中考数学知识辅导的内容,希望会对各位同学带来很大的帮助。
整式的加减重点、难点、例题解析

整式的加减重点、难点、例题解析重点、难点例题解析】例1指出下列各式哪些是单项式?哪些是多项式?并指出单项式的系数、次数,多项式是几次几项式.分析:判断一个代数式是单项式还是多项式,要根据它们的定义来判定.要注意区别单项式的次数与多项式的次数概念的不同之处.单项式的次数是单项式中所有字母指数的和,而多项式的次数是多项式里次数最高项的次数.解:(1)5x2y是单项式,系数是5,次数是3(3)-2x2+3x+1是多项式,是二次三项式(5)a是单项式,系数是1,次数是1例2排列下列多项式:(1)9x-7x2+3 按x的升幂排列(3)y4-1+x4+3x2y+3xy2分别按x降幂排列和y的升幂排列分析:排列可以方便计算,但只能“按某一字母”排列,在排列中利用加法交换律交换多项式各项的次序,一定要注意每一项与它的前边符号一起移动.解:(1)3+9x-7x2(2)-3a2+5a+6(3)x4+3x2y+3xy2+y4-1,-1+x4+3x2y+3xy2+y4例3选择题:(1)[a-(b-c)]-[(a-b)-c]应等于[ ]A.2b B.2c C.-2b D.-2c(2)下列说法正确的是[ ]D.am2与bm2是同类项(3)三角形的第一条边是a+b,第二条边比第一条边大a+5,第三条边等于2b,那么这个三角形的周长是[ ]A.3a+3b+5 B.2a+4b+5(4)使(Ax2-2xy+y2)-(-x2+Bxy+2y2)=5x2-10xy+Cy2成立的A、B、C依次为[ ]A.4,-8,-1 B.-4,-8,-1C.4,8,-1 D.4,8,1分析:(1)根据去括号法则去掉括号后再合并:[a-(b-c)]-[(a-b)-c]=[a-b+c]-[a-b-c]=a-b+c-a+b+c=2c∴答案选B.∴答案是C.(3)求三角形的周长,实际上是求多项式与多项式的和,第二边比第一边大a+5,则第二边长为(a +b)+(a+5)=2a+b+5,那么三角形的周长是(a+b)+(2a+b+5)+2b=3a+4b+5 ∴答案是C.(4)题,把等式左边化简:Ax2-2xy+y2+x2-Bxy-2y2=(A+1)x2+(-2-B)xy-y2又∵(Ax2-2xy+y2)-(-x2+Bxy+2y2)=5x2-10xy+Cy2∴(A+1)x2+(-2-B)xy-y2=5x2-10xy+Cy2根据多项式恒等的意义,它们的同次项系数对应相等∴A+1=5,-2-B=-10,-1=C即A=4,B=8,C=-1.∴答案选C.例4 计算:(1)-[-(-2a2)-3b2]-[+(-b)2](2)3(x-y)4-{(x-y)4-[2(x-y)4-5(x-y)4]}分析:(1)去括号的关键是看括号前边是“+”号还是“-”号来决定括号内的各项是否变号.(2)要把(x-y)看作一个整体,合并以(x-y)为整体的同类项.解:(1)-[-(-2a2)-3b2]-[+(-b)2]=-[2a2-3b2]-(-b)2=-2a2+3b2-b2=-2a2+2b2(2)3(x-y)4-{(x-y)4-[2(x-y)4-5(x-y)4]}=3(x-y)4-{(x-y)4-2(x-y)4+5(x-y)4}=3(x-y)4-(x-y)4+2(x-y)4-5(x-y)4=(3-1+2-5)(x-y)4=-(x-y)4例5 合并下列各题的同类项:(1)7x-4x2-1-9x+5x2(2)a3-3a2b+5ab2-1+a2b-2ab2-4-a3分析:合并时要不重不漏,合并后一般按字母降幂排列.解:(1)7x-4x2-1-9x+5x2=(-4x2+5x2)+(7x-9x)-1=x2-2x-1(2)a3-3a2b+5ab2-1+a2b-2ab2-4-a3=(a3-a3)+(-3a2b+a2b)+(5ab2-2ab2)+(-1-4)=-2a2b+3ab2-5求5a2-3b2-(a2-b2)-(3a2+4b2)的值.分析:要先合并同类项再代入数值计算,代入的数值是分数或负数时要加括号.解:5a2-3b2-(a2-b2)-(3a2+4b2)=5a2-3b2-a2+b2-3a2-4b2=a2-6b2求A-(B+C).分析:由于A、B、C都是代数式,只要把已知代入即可,代入时要正确使用括号,运算时注意去括号法则.解:A-(B+C)=(3x3-2x2-5x-7)-例8 已知(2a-3)2+|2a+4b+1|=0求3(4a+5b-b2)-2(5a-3b+b2)的值.分析:此题要用到()2≥0,||≥0等知识,欲求代数式的值,必须先求出a、b的值由(2a -3)2+|2a+4b+1|=0和(2a-3)2≥0,|2a+4b+1|≥0可以得出2a-3=0,即解:∵(2a-3)2≥0 |2a+4b+1|≥0(2a-3)2+|2a+4b+1|=0∴2a-3=0,2a+4b+1=0得b=-13(4a+5b-b2)-2(5a-3b+b2)=12a+15b-3b2-10a+6b-2b2=2a+21b-5b2=3-21-5=-23例9已知:m(m+n)=-5,n(m+n)=-1求2(2m2-n2)-3(m2-mn-n2)-mn的值.分析:此题要用到乘法分配律和它的逆向应用,合并同类项,拆项、整体代入等知识.先把要求的多项式化简,得到m2+n2+2mn,如何把m2+n2+2mn通过折项化为含有m(m+n)和n(m+n)形式是关键,那么由2mn=mn+mn,得m2+n2+2mn=m2+mn+n2+mn然后根据乘法分配律的逆向应用得m(m +n)+n(m+n)最后把已知条件整体代入求解.解:2(2m2-n2)-3(m2-mn-n2)-mn=4m2-2n2-3m2+3mn+3n2-mn=m2+n2+2mn=m2+n2+mn+mn=(m2+mn)+(n2+mn)=m(m+n)+n(m+n)当m(m+n)=-5,n(m+n)=-1时原式=-5-1=-6其中a>0,b<0解:∵a>0,b<0。
《整式的加减》易错点剖析

例 7 写 出三个 多项式 , 各满足下列 三类
8 +…依次下 去 , 你发现 了什么规律? 请根据 情况 中 的一种 :① 用任 意数代 替字母 时 , 只 你发现 的规律写出第 n 项.
得正值 ; ②用任意数代替字母时, 只得负值 ;
解析 : 此题 的规 律特点 如下 : ① 的各 项 ③用任意数代换字母时, 能得正值 , 也能得负 指数从 1 开始 往后为连续整数 ;②后 一项系 值. 数依次为前 一项 系数 的一2 ; 倍 ③奇次项 的符 号为正 , 偶次项 的符号为负.
的次数. 正解 : 的系数是 , 次数是 2 ;
一
剖 析 : 1 错 误 的原 因是 违 背 了合并 同 () 类 项 的法则 , 合并 同类项 时 , 是字 母 以及 应
字母 的指数不变 , 只是 系数相加 ;2 误认 为 () 3 和 是 同类项 .
正解 :1 3 2 ; ( ) a=5
整 式 的加减 实质 上是 去括 号和 合并 同
类项 , 是做好 整式 的加 减 的关 键 , 中去 也 其
二三× _
)
的系数是一 0次数是 2 4, .
括号是至关重要的一环. 去括号法则是: 括号
前是“ ” , + 号 把括 号 和 它前 面 的 “ ” 去 + 号 掉, 括号 里各项 都不 变符 号 ; 号前 是 “ 括 一” 号, 把括 号和 它前 面的 “ 号 去掉 , 一” 括号 里
系数是 3 ,次 数是 4 ;二
是一 , 次数是 4 .
合并 同类项时, 系数相加是关键 , 及其指 字母
数都不变.
例 4 合并下列各式的 同类项 : f )a 22 ( )x 2 32 a; 2 3+ x. 1 + 误解 :1 3222 a; 2 3 +x=5 ( )a+a=5 4 ( )x 2 x.
专题1 整式的加减(8个常考点+9种重难点题型+4个易错)七年级数学上学期期中考点(沪教版2024)

考点六: 去括号
【例6】下列变形中,正确的是( D )
A.a+b+c-d=a+(b+c+d)
B.a-(b-c+d)=a-b+c+d
C.a-b-c-d=a-b-(c-d)
D.a+b-(-c-d)=a+b+c+d
【解析】解:A.a+b+c-d=a+(b+c-d),故本选项错误;
=2×3+21=6+21=27;
(2)∵a+2b=6,
-3a+2(a+2b)-6b-3=2(a+2b)-3(a+2b)-3
=2×6-3×6-3=12-18-3=-6-3=-9;
2
2
2
2
(3)∵a +2ab=20,b +2ab=8,∴a +2b +6ab
2
2
=a +2ab+2b +4ab
2
2
=a +2ab+2(b +2ab)
当 =
= -
=-2.
− ,
2
= 时,原式=(- ) + ×(- )×3
− )2
+ | +
1
|
2
=0
【变式8-1】先化简,再求值:2mn-[3mn -2(mn +mn)]+mn ,其中m=-3, =
2
2
2
2
整式加减的常见错误及避免方法教案

整式加减的常见错误及避免方法教案。
一、常见错误1.没有化简式子在学习整式加减的过程中,很多时候都需要先将式子化简一下,然后再进行加减操作。
但是很多学生经常会忘记这个步骤,导致最后的答案错误。
例如:2x+3y+4x-5y=3x-2y如果不进行化简,直接进行加减操作,那么就会得到错误的答案。
2.不注意正负号在整式加减中,很多学生都容易犯的一个错误就是不注意正负号。
这个错误很容易发生,有时候只是因为粗心大意,有时候是因为基础不扎实。
例如:3x-4xy-2x-5xy=?如果不注意正负号,很容易出现错误。
3.没有将同类项合并在进行整式加减的过程中,很多时候需要将同类项合并,然后再进行加减操作。
但是有些学生经常会忘记这个步骤,导致最后的答案错误。
例如:3x+5y-2x+4y=?如果不合并同类项直接进行加减操作,就会出现错误。
二、避免方法1.认真阅读题目在进行整式加减的时候,首先需要认真阅读题目,弄清楚需要进行何种运算以及需要注意哪些细节问题。
只有认真阅读题目,才能够避免犯一些低级错误。
2.多思考多练习整式加减是需要思考的,如果想要避免犯错误,那么就需要多思考多练习。
多做一些有思考性的题目,多总结自己的思考方法和错误点,有助于提高整式加减的水平。
3.化简式子、合并同类项、注意正负号在进行整式加减的时候,一定要记得先化简式子、合并同类项,然后再进行加减操作,最后注意正负号。
只有按照这样的基本方法进行整式加减,才能够避免犯低级错误。
4.扎实基础知识整式加减是代数知识的一部分,如果想要做好整式加减,就必须要扎实代数基础知识。
只有掌握了代数的基础知识,才能够更好地理解和运用整式加减。
如果基础不扎实,那么即使掌握了整式加减的方法,也很容易出现错误。
学好整式加减需要认真对待每个细节问题,遇到错误要时刻反思,掌握正确的避免方法。
只有这样,才能够在整式加减这个知识点上取得好的成绩。
整式的加减重难点和易错点

整式的加减重难点和易错点一、选择题1、整式-(a-(b-c))去括号为()A。
-a-b+cB。
-a+b-cC。
-a+b+cD。
-a-b-c2、在(a-b+c)(a+b-c)=[a+(b-c)][a-(b-c)]的括号内填入的代数式分别()A。
c-b,c-bB。
b+c,b+cC。
b+c,b-cD。
c-b,c+b3、当k取1/3时,多项式x^2-3kxy-3y^2+xy-8中不含xy 项。
A。
0B。
1C。
1/9D。
-1/34、如果多项式(a+1)x^4-bx-3x-5是关于x的四次三项式,则ab的值是()A、4B、-4C、5D、-55、若|a|=2,|b|=3,且a>b,则|a-b|的值是()A、-5或-1B、1或-1C、5或3D、5或16、若|m|=3,|n|=7.且m-n>0,则m+n的值()A、10B、4C、-10或-4D、4或-47、若M=3x^2-5x-2,N=3x^2-4x-2,则M,N的大小关系()A、M>NB、M=NC、M<ND、以上都有可能8、设a是最小的自然数,b是最大的负整数,c,d分别是单项式-xy^2的系数和次数,则a,b,c,d四个数的和是()A、-1B、0C、1D、39、若多项式y^2+(m-3)xy+2x|m|是三次三项式,则m的值为()A、-3B、3C、3或-3D、210、如果a是最小的正整数,b是绝对值最小的数,c与a^2互为相反数,那么(a+b)^2009-c^2009=11、当a<3时,|a-3|+a=12、有理数a,b满足a|b|,则代数式|a+b|+|2a-b|化简后结果为___________13、去括号a-b)-(-c-d)a-b)+(c-d)________________14、化简(x+2)-(x-3x)4x-(-6x)+(-9x)=15、化简3-5x-4(x-x+3x)/22=16、当a^2+b^2=1时,(a+b)^2的最小值为__________17、计算m+n-(m-n)的结果为2n。
整式的加减重难点题型

整式的加减-重难点题型【题型1 整式的加减(比较大小)】【例1】(2020秋•铜官区期末)设M=x2+3x+7,N=﹣x2+3x﹣4,那么M与N的大小关系是()A.M<N B.M=N C.M>N D.无法确定【变式1-1】(2020秋•澄海区期末)若A=2x2﹣x+1,B=x2﹣x﹣m2,则A,B的大小关系是()A.A<B B.A=BC.A>B D.与x的值有关【变式1-2】(2020秋•南京期末)若M=3x2+5x+2,N=4x2+5x+3,则M与N的大小关系是()A.M<N B.M>N C.M≤N D.不能确定【变式1-3】(2020秋•广信区期中)设A=x2﹣4x﹣3,B=2x2﹣4x﹣1,若x取任意有理数.则A与B的大小关系为()A.A<B B.A=B C.A>B D.无法比较【题型2 整式的加减(项与系数)】【例2】(2021春•萧山区月考)若P和Q都是关于x的五次多项式,则P+Q是()A.关于x的五次多项式B.关于x的十次多项式C.关于x的四次多项式D.关于x的不超过五次的多项式或单项式【变式2-1】(2020秋•射洪市期末)两个三次多项式相加,和的次数是()A.三B.六C.大于或等于三D.小于或等于三【变式2-2】(2020秋•凤凰县期末)若A与B都是二次多项式,则关于A﹣B的结论,下列选项中正确的有()A.一定是二次式B.可能是四次式C.可能是一次式D.不可能是零【变式2-3】(2020秋•铜官区期末)若A是五次多项式,B是三次多项式,则A﹣B一定是次式.【题型3 整式的加减(错看问题)】【例3】(2020秋•来宾期末)小文在做多项式减法运算时,将减去2a2+3a﹣5误认为是加上2a2+3a﹣5,求得的答案是a2+a﹣4(其他运算无误),那么正确的结果是()A.﹣a2﹣2a+1B.﹣3a2+a﹣4C.a2+a﹣4D.﹣3a2﹣5a+6【变式3-1】(2020秋•罗庄区期末)有一道题目是一个多项式减去x2+14x﹣6,小强误当成了加法计算,结果得到2x2﹣x+3,则原来的多项式是.【变式3-2】(2020秋•伊通县期末)某同学做一道数学题,“已知两个多项式A、B,B=2x2+3x﹣4,试求A﹣2B”.这位同学把“A﹣2B”误看成“A+2B”,结果求出的答案为5x2+8x﹣10.请你替这位同学求出“A﹣2B”的正确答案.【变式3-3】(2020秋•新邵县期末)一位同学做一道题:已知两个多项式A、B,计算A﹣3B他误将“A﹣3B”看成“3A﹣B”,求得的结果为x2﹣14xy﹣4y2,其中B=2x2+2xy+y2,(1)请你计算出多项式A.(2)若x=﹣3,y=2,计算A﹣3B的正确结果.【题型4 整式的加减(遮挡问题)】【例4】(2020秋•海淀区校级期末)下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面.(﹣x2+3xy−12y2)﹣(−12x2+4xy−32y2)=−12x2+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是()A.﹣7xy B.+7xy C.﹣xy D.+xy【变式4-1】(2020秋•卫辉市期末)下面是小明做的一道多项式的加减运算题,但他不小心把一滴墨水滴在了上面.(﹣x2+3xy−12y2)﹣(−12x2+4xy−12y2)=−12x2●,黑点处即为被墨迹弄污的部分,那么被墨汁遮住的一项应是()A.﹣xy B.+xy C.﹣7xy D.+7xy【变式4-2】(2020秋•喀喇沁旗期末)某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:(2a2+3ab﹣b2)﹣(﹣3a2+ab+5b2)=5a2﹣6b2,空格的地方被墨水弄脏了,请问空格中的一项是()A.+2ab B.+3ab C.+4ab D.﹣ab【变式4-3】(2020秋•射洪市期末)印卷时,工人不小心把一道化简题前面一个数字遮住了,结果变成:■x2y−[5xy2−2(−23xy+32x2y)−43xy]+5xy2.(1)某同学辨认后把“■”猜成10,请你帮他算算化简后该式是多少;(2)老师说:“你猜错了,我看到该题目遮挡部分是单项式−4m2n3的系数和次数之积.”遮挡部分是多少?(3)若化简结果是一个常数,请算算遮挡部分又该是多少?【题型5 整式的加减(不含某项)】【例5】(2020秋•鹿邑县期末)若多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3的差不含二次项,则m 等于()A.2B.﹣2C.4D.﹣4【变式5-1】已知多项式4x2﹣2kxy﹣3(x2﹣5xy+x)不含xy项,则k的值为.【变式5-2】(2020秋•九龙坡区校级期末)已知关于x,y的多项式x2+mx﹣2y+n与nx2﹣3x+4y﹣7的差的值与字母x的取值无关,则n﹣m=.【变式5-3】(2020秋•清涧县期末)已知代数式A=a4﹣3a2b2﹣ab3+5,B=2b4﹣2a2b2+ab3,C=a4﹣5a2b2+2b4﹣2.小丽说:“代数式A+B﹣C的值与a,b的值无关.”她说得对吗?说说你的理由.【题型6 整式的加减的应用】【例6】(2020秋•南充期末)计算:(1)3(a+b)﹣(3a﹣2b);(2)xy2﹣[x+12(6y+2xy2)﹣3x].【变式6-1】(2020秋•陇县期末)化简:(1)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b);(2)﹣2(mn﹣3m2)﹣[m2﹣5(mn﹣m2)+2mn].【变式6-2】(2020秋•渝中区期末)已知A=m2﹣3mn+n2,B=﹣2m2+8mn﹣3n2.计算:(1)B+2A;(2)4A﹣3B.【变式6-3】(2021秋•织金县期末)已知:A=x2﹣2xy+y2,B=x2+2xy+y2.(1)求﹣A+B;(2)如果2A﹣3B+C=0,那么C的表达式是什么。
整式的加减知识点总结和重难点精析

七年级数学整式的加减知识点总结
1、整式:单项式和多项式统称整式。
2、单项式:数与字母的积叫做单项式;单独的一个数或一个字母也叫单项式;单项式中的数字因数叫做这个单项式的系数,所有字母指数和叫做这个单项式的次数。
3、多项式:几个单项式的和叫做多项式;多项式中的每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数。
4、整式的加减法:根据去括号、合并同类项化简整式。
重难点精析
1、重点
(1)掌握单项式、多项式的概念,熟练地进行单项式、多项式的读写。
(2)掌握单项式系数、次数的概念,熟练判断一个代数式是否是单项式以及确定单项式的系数和次数。
(3)掌握多项式项、次数的概念,熟练判断一个和式是否是多项式以及确定多项式的项和次数。
(4)掌握合并同类项的概念,熟练地进行合并同类项。
(5)掌握去括号法则,熟练地进行去括号。
2、难点
(1)合并同类项时,把各项系数相加减而字母和字母的指数不变,特别是含有未知数的系数相加减时,指数的处理容易出错。
(2)去括号时,括号前是“+”号,如果括号前是代数式,往往看不出是加法还是减法,容易出错。
特别是当括号很长时,更容易出错。
(3)往往容易忽视系数为0的情况。
整式的加减知识点归纳

整式的加减知识点归纳关于整式的加减练习题很多同学都觉得做起来有一定的难度,主要在于变号、移项等问题。
整式的加减练习题做起来觉得难,是因为对于知识点掌握的不够好,所以想要做好有关于整式的加减练习题,首先还是要从知识点开始。
下面是小编为大家整理的关于整式的加减知识点归纳,希望对您有所帮助。
欢迎大家阅读参考学习!整式的加减知识点归纳1.单项式:在代数式中,若只含有乘法(包括乘方)运算。
或虽含有除法运算,但除式中不含字母的一类代数式叫单项式;数字或字母的乘积叫单项式(单独的一个数字或字母也是单项式)。
2.系数:单项式中的数字因数叫做这个单项式的系数。
所有字母的指数之和叫做这个单项式的次数。
任何一个非零数的零次方等于1.3.多项式:几个单项式的和叫多项式。
4.多项式的项数与次数:多项式中所含单项式的个数就是多项式的项数,每个单项式叫多项式的项;多项式里,次数最高项的次数叫多项式的次数。
5.常数项:不含字母的项叫做常数项。
6.多项式的排列(1)把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列。
(2)把一个多项式按某一个字母的指数从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列。
7.多项式的排列时注意:(1)由于单项式的项,包括它前面的性质符号,因此在排列时,仍需把每一项的性质符号看作是这一项的一部分,一起移动。
(2)有两个或两个以上字母的多项式,排列时,要注意:a.先确认按照哪个字母的指数来排列。
b.确定按这个字母向里排列,还是向外排列。
(3)整式:单项式和多项式统称为整式。
8. 多项式的加法:多项式的加法,是指多项式的同类项的系数相加(即合并同类项)。
9.同类项:所含字母相同,并且相同字母的次数也分别相同的项叫做同类项。
10.合并同类项:多项式中的同类项可以合并,叫做合并同类项,合并同类项的法则是:同类项的系数相加,所得的结果作为系数,字母与字母的指数不变。
11.掌握同类项的概念时注意:(1)判断几个单项式或项,是否是同类项,就要掌握两个条件:①所含字母相同。
整式的加减全章知识点总结

整式的加减全章知识点总结一、整式的基本概念整式是代数式的一部分,为有理式的一部分,在有理式中可以包含加、减、乘、除、乘方五种运算,但在整式中除数不能含有字母。
1、单项式由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式。
单项式中的数字因数叫做这个单项式的系数,一个单项式中,所有字母的指数的和叫做这个单项式的次数。
例如,单项式 5x 的系数是 5,次数是 1;单项式-3xy²的系数是-3,次数是 3。
2、多项式几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。
多项式中次数最高的项的次数,叫做这个多项式的次数。
例如,多项式 2x²+ 3x 1 有三项,分别是 2x²、3x 和-1,其中-1 是常数项,该多项式的次数是 2。
3、整式单项式和多项式统称为整式。
二、整式的加减运算整式的加减实质上就是合并同类项。
1、同类项所含字母相同,并且相同字母的指数也相同的项叫做同类项。
几个常数项也是同类项。
例如,2x²y 和-5x²y 是同类项;3 和-7 是同类项。
2、合并同类项把多项式中的同类项合并成一项,叫做合并同类项。
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
例如,计算 3x²+ 2x²=(3 + 2)x²= 5x²。
三、整式加减的步骤1、去括号如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
例如,a +(b c) = a + b c;a (b c) = a b +c 。
2、合并同类项将同类项的系数相加,字母和字母的指数不变,得到最简结果。
四、整式加减的应用整式的加减在解决实际问题中有着广泛的应用。
例如,在行程问题中,如果已知速度和时间,可以用整式表示路程,然后通过整式的加减来计算不同情况下的路程和。
整式的加减专题知识点 常考(典型)题型 重难点题型(含详细答案)

整式的加减专题知识点常考(典型)题型重难点题型(含详细答案)一、目录二、知识点1.整式的加减定义2.整式的加减原则3.整式的加减步骤三、常考题型1.基础练题2.提高练题四、重难点题型1.含有分式的整式加减2.含有根式的整式加减3.含有绝对值的整式加减五、详细答案二、知识点1.整式的加减定义整式加减是指将同类项合并,最终得到一个简化的整式的过程。
整式是由各种数的积和和式构成,包括常数项、一次项、二次项等。
2.整式的加减原则在整式加减中,只有同类项才能相加减。
同类项是指变量的指数相同的项,例如2x^2和5x^2就是同类项,但2x^2和5x^3不是同类项。
3.整式的加减步骤整式加减的步骤如下:1.将同类项放在一起。
2.对同类项的系数进行加减运算。
3.将结果合并,得到简化后的整式。
三、常考题型1.基础练题例题:将3x^2+5x-2和2x^2-3x+1相加。
解题思路:将同类项放在一起,得到5x^2+2x-1,即为答案。
答案:5x^2+2x-12.提高练题例题:将4x^2+3x-1和2x^2-5x+3相减。
解题思路:将同类项放在一起,得到2x^2+8x-4,即为答案。
答案:2x^2+8x-4四、重难点题型1.含有分式的整式加减例题:将(2x^2+3)/(x+1)和(3x-1)/(x+1)相加。
解题思路:先将分式化简为同分母,得到(2x^2+3+3x-1)/(x+1),化简后得到(2x^2+3x+2)/(x+1),即为答案。
答案:(2x^2+3x+2)/(x+1)2.含有根式的整式加减例题:将3√2x+5和5√2x-2相减。
解题思路:将同类项放在一起,得到(3-5)√2x+7,化简后得到-2√2x+7,即为答案。
答案:-2√2x+73.含有绝对值的整式加减例题:将|2x+1|+|3x-2|和|4x-3|相减。
解题思路:考虑绝对值的取值范围,将式子拆分为两部分,得到(2x+1+3x-2)-(4x-3)和(4x-3)-(2x+1+3x-2),化简后得到5x-1和-x,即为答案。
专题整式的加减(2个常考点 9种重难点题型 8个易错 点)七年级数学上学期期中考点(人教版2024)

C. 3,4
D. 8,4
C
【变式1-3】【易错题】若多项式3 x| m|+( m +2) x -7是关于 x 的
二次三项式,则 m 的值是(
A )
A. 2
B. -2
C. 2或-2
D. 以上均不对
)
【变式1-4】 [2024西安高新一中期末]记多项式2 m3-7-3 mn 的次数为
a ,二次项系数为 b ,常数项为 c ,则 a + b + c = -7
2 − − − =(2-2 b ) x2+(3+ a ) x +6+ b .
因为当 x 取任意值, A -2 B 的值是一个定值,
所以2-2 b =0,3+ a =0,
所以 b =1, a =-3.所以 A -2 B =7.
+
-
+
= a -2 b +
-(- a )= b - a - c + a + a = a + b - c .
(3)若| c -5|+( a +1)2=0,且 BC =2 AB ,求点 B 表示
的数.
解: (3)由题意得 c -5=0, a +1=0,所以 c =5, a =-1.
又因为 A , B , C 对应的数分别是 a , b , c ,且 a < b < c ,
(2) (3
x2
y -2
xy2)-2(
2
xy -
x2 y ),其中 x , y 满足( x -1)2
+| y +2|=0.
解: 原式=2 x 2 y -3 xy 2 .
因为( x -1) 2 +| y +2|=0,所以 x -1=0, y +2=0.
第08讲整式的加减(3大考点)(原卷版)

第08讲整式的加减(3大考点)考点考向一、去(添)括号法则括号前是“+”,去括号后,括号内的符号不变括号前是“”,去括号后,括号内的符号全部要变号。
括号前有系数的,去括号后,括号内所有因素都要乘此系数。
解题技巧:去多重括号,可以先去大括号,在去中括号,后去小括号;也可以先从最内层开始,先去小括号,在去中括号,最后去大括号。
可依据简易程度,选择合适顺序。
二、整式的加减(合并同类项)整式的加减运算实际就是合并同类项的过程,具体步骤为:①将同类项找出,并置与一起;②合并同类项。
解题技巧:(1)当括号前面有数字因数时,应先利用乘法分配律计算,然后再去括号,注意不要漏乘括号内的任一项。
(2)合并同类项时,只能把同类项合并,不是同类项的不能合并,合并同类项实际上就是有理数的加减运算。
合并同类项要完全、彻底,不能漏项考点精讲一.去括号与添括号(共5小题)1.(2022春•宁波期末)下列添括号正确的是()A.﹣b﹣c=﹣(b﹣c)B.﹣2x+6y=﹣2(x﹣6y)C.a﹣b=+(a﹣b)D.x﹣y﹣1=x﹣(y﹣1)2.(2021秋•嘉兴期末)代数式x﹣2(y﹣1)去括号正确的是()A.x﹣2y﹣1B.x﹣2y+1C.x﹣2y﹣2D.x﹣2y+23.(2021秋•江干区校级期中)化简:(1);(2)3x2﹣3x3﹣5x﹣4+2x+x2.4.(2021秋•青田县期末)去括号等于()A.B.C.D.5.(2020秋•西湖区校级期中)已知:代数式A=2x2﹣2x﹣1,代数式B=﹣x2+xy+1,代数式M=4A﹣(3A ﹣2B)(1)当(x+1)2+|y﹣2|=0时,求代数式M的值;(2)若代数式M的值与x的取值无关,求y的值;(3)当代数式M的值等于5时,求整数x、y的值.二.整式的加减(共11小题)6.(2022春•萧山区期中)若x+y=8,y+z=6,x2﹣z2=20,则x+y+z的值为()A.10B.12C.14D.207.(2021秋•上虞区期末)代数式a﹣b,b+c,﹣(a+c)的和是.8.(2021秋•宁波期末)已知x=﹣5﹣y,xy=2,计算3x+3y﹣4xy的值为.9.(2021秋•金东区校级期中)化简:3ab﹣(2ab﹣1)=.10.(2021秋•泗阳县期末)A、B、C、D四个车站的位置如图所示,求:(1)A、D两站的距离;(2)A、C两站的距离.11.(2022春•丽水期末)如图,以a,b为边长的矩形面积为S1,以c为边长的正方形面积为S2,已知S1+4S2=32.(1)当a=b=2c时,则c的值是;(2)若c为整数,2a﹣b+4=0,则矩形和正方形的周长之和的值是.12.(2021秋•瓯海区月考)在边长为8cm的正方形ABCD底座中,放置两张大小相同的正方形纸板,边EF 在AB上,点K,I分别在BC,CD上,若区域Ⅰ的周长比区域Ⅱ与区域Ⅲ的周长之和还大4cm,则正方形纸板的边长为cm.13.(2022春•新昌县期末)已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形,小明把这2个小长方形按如图所示放置在大长方形中,小明经过推理得知,要求出图中阴影部分的周长之和,只需知道a、b、m、n中的一个量即可,则要知道的那个量是()A.a B.b C.m D.n14.(2021秋•西湖区期末)已知A=a2﹣2ab+b2,B=a2+2ab+b2.(1)求A+B;(2)求(A﹣B);(3)若2A﹣2B+9C=0,当a,b互为倒数时,求C的值.15.(2017秋•天门期末)一般情况下不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;(3)若(m,n)是“相伴数对”,求代数式m﹣﹣[4m﹣2(3n﹣1)]的值.16.(2017秋•义乌市月考)已知A﹣2B=7a2﹣7ab,且B=﹣4a2+6ab+7(1)求A等于多少?(2)若|a+1|+(b﹣2)2=0,求A的值.三.整式的加减—化简求值(共9小题)17.(2021秋•龙泉市期末)先化简,再求值:2(a2﹣2a)﹣(2a2﹣3a)+1,其中a=﹣3.18.(2021秋•新昌县期末)化简求值:(3a2﹣ab)+(3ab﹣b)﹣(3a2﹣b),其中a=3,b=﹣5.19.(2021秋•上虞区期末)对于任意实数a和b,如果满足+=+那么我们称这一对数a,b 为“友好数对”,记为(a,b).若(x,y)是“友好数对”,则2x﹣3[6x+(3y﹣4)]=()A.﹣4B.﹣3C.﹣2D.﹣120.(2021秋•温州期末)先化简再求值:2(a2﹣ab)﹣3(a2﹣ab),其中a=2,b=﹣5.21.(2021秋•椒江区期末)先化简,再求值:2(x﹣2y2)﹣(x﹣y2),其中x=﹣1,y=2.22.(2021秋•临海市期末)先化简,再求值:2(x2﹣2x+1)﹣(2﹣4x),其中x=3.23.(2021秋•金华期末)已知x,y满足(x﹣2)2+|y+1|=0.(1)求x,y的值.(2)先化简,再求值:2(x2﹣xy)﹣3(x2﹣2xy).24.(2021秋•定海区期末)先化简,再求值:﹣(a2+6ab+9)+2(a2+4ab﹣4.5),其中a=﹣2,b=6.25.(2021秋•普陀区期末)求值:(1)已知5x﹣2y=3,求15x﹣6y﹣8的值.(2)已知a﹣b=5,﹣ab=3,求的值.一、单选题1.(2021·浙江七年级期末)若M 和N 都是3次多项式,则M N +为( )A .3次多项式B .6次多项式C .次数不超过3的整式D .次数不低于3的整式 2.(2021·浙江)若四个有理数a b c d ,,,满足:11112017201820192020a b c d ===-+-+,则a b c d ,,,的大小关系是( )A .a c b d >>>B .b d a c >>>C .d b a c >>>D .c a b d >>>3.(2021·浙江)大于10小于100的整数,当数字交换位置后(即个位数字变为十位数字,而十数位学变为个位数字),新数比原数大9,这样的数共有( )个A .10B .9C .8D .74.(2021·浙江七年级期末)把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为n ,宽为m )的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是( )A .4nB .4mC .22n m +D .24n m +5.(2021·浙江七年级期末)如图,长为y ,宽为x 的大长方形被分割为5小块,除D 、E 外,其余3块都是正方形,若阴影E 的周长为8,下列说法中正确的是( )①x 的值为4;②若阴影D 的周长为6,则正方形A 的面积为1;③若大长方形的面积为24,则三个正方形周长的和为24.巩固提升A .①②③B .①②C .①③D .②③6.(2021·浙江)把四张大小相同的长方形卡片(如图①按图②、图③两种放在一个底面为长方形(长比宽多6cm )的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长2C ,图③中阴影部分的周长为3C ,则( )A .23C C =B .2C 比3C 大12cm C .2C 比3C 小6cmD .2C 比3C 大3cm二、填空题 7.(2020·浙江七年级月考)某同学做一道题,已知两个多项式AB 、,求2A B -的值.他误将2A B -看成2A B -,经过正确计算求得结果为2335x x -+,已知21B x x =--,则正确答案是__________.8.(2020·浙江杭州·)已知7,22x y a b -=-=,则(32)2(3)b y a x ---=________.9.(2020·浙江)某同学把6(4)a -错抄成了64a -,抄错后的答案为y ,正确答案为x ,则x y -的值为________.10.(2020·浙江七年级期末)关于x 的多项式222514x mx nx x x -++--+,它的值与x 的取值无关,则m n +=________.11.(2021·浙江七年级期末)如图是一个书报柜截面的示意图,每一个转角都是直角.数据如图所示.则该图形的周长为_______,面积为_______.用含,,m n b 的代数式表示)12.(2021·浙江七年级期中)若实数x ,y ,z 满足132345x y z --+==,则代数式3x y z --=_______. 13.(2021·浙江)如图,在长方形内有三块面积分别是13,35,49的图形.则阴影部分的面积为______.三、解答题14.(2020·浙江七年级期末)先化简,后求值:()22214342233x xy y y xy ⎛⎫--++-- ⎪⎝⎭,其中12x =,1y =-.15.(2021·浙江七年级期末)(1)已知2223,1A x x B x x =-=-+,求当1x =-时代数式3A B -的值.(2)已知,a b 为常数,且三个单项式234,,3b xy axy xy -相加得到的和仍然是单项式.那么a b +的值可能是多少?请你说明理由.16.(2021·浙江)一位同学做一道题:“已知两个多项式,A B ,计算2A B +”.他误将“2A B +”看成:“2A B +”,求得的结果为2927x x +-.已知232B x x =-+(1)求多项式A 是多少?(2)若x 的平方等于4,求原题正确的结果是多少?17.(2021·浙江)化简求值:(5x 2y +5xy ﹣7x )﹣12(4x 2y +10xy ﹣14x ),其中x ,y 满足(x ﹣1)2+|y +2|=0.18.(2021·诸暨市开放双语实验学校七年级期中)先化简再求值. ()232623x x x x ⎡⎤----⎣⎦,其中x 是最大的负整数.19.(2020·浙江七年级期中)已知 A −B =7a 2−7ab +1,且B =−4a 2+6ab +5,(1)求A ;(2)若2|1|(2)0a b ++-=,求A B +的值.20.(2020·浙江七年级期末)我国是世界上淡水资源匮乏的国家之一,为节约用水,不少城市作出了用水规定,某城市规定:每一个用水大户,月用水量不超过规定标准a 吨时,按每吨1.6元的价格收费;如果超过了标准,超标部分每吨加收0.4元的附加费用.(1)某户在3月份用水()x x a >吨,则该户应交水费多少元?(2)若规定标准用水量为100吨,某用户在4月份用水150吨,则该用户应交水费多少元?21.(2020·浙江七年级期末)小方家住房户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区域铺设地砖.(1)a 的值为_______.(2)铺设地面需要木地板和地砖各多少平方米(用含x 的代数式表示)?(3)已知卧室2的面积为21平方米,按市场价格,木地板单价为400元/平方米,地砖单价为10元/平方米,求铺设地面总费用.22.(2021·浙江七年级期中)定义;任意两个数a 、b ,按规则c a b ab =+-扩充得到一个新数c ,称所得的新数c 为“如意数”.(1)若2,3a b ==-,直接写出a 、b 的“如意数”c =_______;(2)若22,1a b x ==+,求a 、b 的“如意数”c ,并比较b 与c 的大小;(3)已知2a =,且a 、b 的“如意数”3231c x x =+-,则b =_______(用含x 的式子表示).23.(2021·浙江)阅读材料:我们知道,4x ﹣2x +x =(4﹣2+1)x =3x ,类似地,我们把(a +b )看成一个整体,则4(a +b )﹣2(a +b )+(a +b )=(4﹣2+1)(a +b )=3(a +b ).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用整体思想解决下列问题:(1)把(a ﹣b )2看成一个整体,合并2(a ﹣b )2﹣6(a ﹣b )2+3(a ﹣b )2;(2)已知x 2﹣2y =4,求6x 2﹣12y ﹣27的值;(3)已知a ﹣2b =3,2b ﹣c =﹣5,c ﹣d =10,求(a ﹣c )+(2b ﹣d )﹣(2b ﹣c )的值.。
整式的加减知识要点归纳

整式的加减知识要点归纳一、根底知识:知识点一:用字母表示数用字母表示数就是用字母或含字母的式子表示数和数量关系,它是从算术到代数的重要转变。
而用字母表示数之后,有些数量之间的关系用含有字母的式子表示,看上去更加简明,更具有普遍意义了.举例:如果用a 、b 表示任意两个有理数,那么加法交换律可以用字母表示为:a +b =b +a .乘法交换律可以用字母表示为:ab =ba要点诠释:〔1〕当数字与字母相乘时,乘号通常省略不写或简写为“·〞,且数字在前,字母在后,假设数字是带分数,要化为假分数,如112 ×a 写成32 ·a 或32 a ;〔2〕字母与字母相乘时,乘号通常省略不写或简写为“·〞,如a ×b 写成a ·b 或ba ;〔3〕除法运算写成分数形式,如1÷a 通常写作1a (a ≠0) 知识点二:单项式 由数与字母的积组成的式子叫做单项式,例如, 13 r 2h 、、abc 、-m 都是单项式.其中,单项式中的数字因数叫做这个单项式的系数,所有字母的指数的和叫做这个单项式的次数。
例如,13 r 2h 的系数是13 ,次数是3;的系数是,次数是1;abc 的系数是1,次数是3;-m 的系数是-1,次数是1.要点诠释:1、特别地,单独一个数或一个字母也是单项式.2、单项式的系数包括它前面的符号。
3、单项式的系数是1或-1时,通常1省略不写,如-k ,pq 2等,单项式的系数是带分数时,通常化成假分数。
如写成4、单项式的次数仅仅与字母有关,是单项式中所有字母的指数的和。
特别地,单项式b 的次数是1,常数-5的次数是0,而9×103a 2b 3c 的次数是6,与103无关。
5、要正确区分单项式的次数与单项式中字母的次数,如6p 2q 的次数是3,其中字母p 的次数是2。
6、圆周率π是常数。
知识点三:多项式几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项.其中,不含字母的项,叫做常数项.例如,多项式有三项,它们是,-2x,5.其中5是常数项.多项式的项数与次数:一个多项式含有几项,就叫几项式.多项式里,次数最高项的次数,就是这个多项式的次数.例如,多项式是一个二次三项式.要点诠释:1、多项式的每一项都包括它前面的符号。
整式的加减》单元重难点知识树
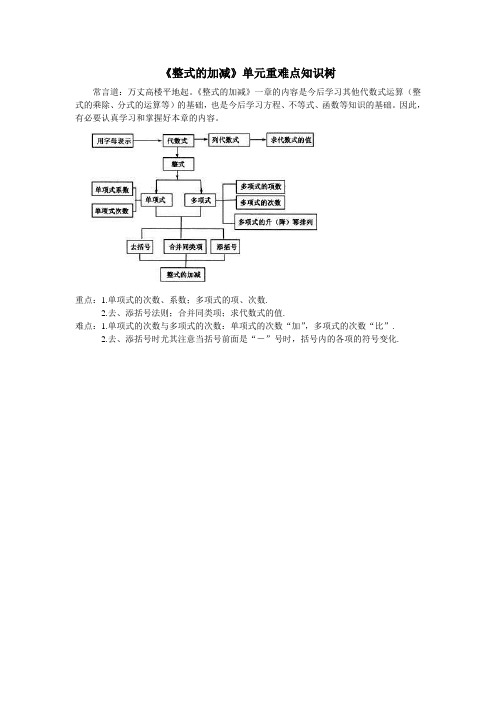
《整式的加减》单元重难点知识树
常言道:万丈高楼平地起。
《整式的加减》一章的内容是今后学习其他代数式运算(整式的乘除、分式的运算等)的基础,也是今后学习方程、不等式、函数等知识的基础。
因此,有必要认真学习和掌握好本章的内容。
重点:1.单项式的次数、系数;多项式的项、次数.
2.去、添括号法则;合并同类项;求代数式的值.
难点:1.单项式的次数与多项式的次数:单项式的次数“加”,多项式的次数“比”.
2.去、添括号时尤其注意当括号前面是“-”号时,括号内的各项的符号变化.。
整式的加减知识点归纳

整式的加减知识点归纳一、整式的基本概念1、单项式由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式。
例如,3x,-5,a 等都是单项式。
单项式中的数字因数叫做这个单项式的系数,所有字母指数的和叫做这个单项式的次数。
比如,单项式 3x 的系数是 3,次数是 1;单项式-5 的系数是-5,次数是 0。
2、多项式几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。
多项式中次数最高的项的次数,叫做这个多项式的次数。
例如,多项式 2x²+ 3x 1 中,有三项,分别是 2x²、3x、-1,其中-1 是常数项,次数最高的项是 2x²,次数为 2,所以这个多项式的次数是 2。
3、整式单项式和多项式统称为整式。
二、同类项1、定义所含字母相同,并且相同字母的指数也相同的项叫做同类项。
几个常数项也是同类项。
例如,2x²y 和5x²y 是同类项,3 和-7 是同类项。
2、合并同类项把多项式中的同类项合并成一项,叫做合并同类项。
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
例如,计算 3x²+ 2x²,因为 3x²和 2x²是同类项,所以可以合并为(3 + 2)x²= 5x²。
三、去括号法则1、括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变。
例如,a +(b c) = a + b c2、括号前是“”号,把括号和它前面的“”号去掉后,原括号里各项的符号都要改变。
例如,a (b c) = a b + c四、整式的加减运算整式的加减的实质就是合并同类项。
一般步骤是:1、如果有括号,先去括号。
2、然后找出同类项,将同类项合并。
例如,计算(2x² 3x + 1) (3x²+ 5x 2)先去括号:2x² 3x + 1 3x² 5x + 2然后合并同类项:(2x² 3x²) +(-3x 5x) +(1 + 2)= x² 8x + 3再比如,计算 3a²b + 2ab² 5a²b ab²合并同类项:(3a²b 5a²b) +(2ab² ab²)=-2a²b + ab²五、整式加减的应用整式的加减在解决实际问题中有着广泛的应用。
中考数学知识点归纳:整式的加减

中考数学知识点归纳:整式的加减
2019中考数学知识点归纳:整式的加减
2019中考复习最忌心浮气躁,急于求成。
指导复习的教师,应给学生一种乐观、镇定、自信的精神面貌。
要扎扎实实地复习,一步一步地前进,下文为大家准备了2019中考数学知识点归纳:整式的加减。
一、重点
单项式及其相关的概念;
多项式及其相关的概念;
去括号法则,准确应用法则将整式化简。
二、难点
区别单项式的系数和次数;
区别多项式的次数和单项式的次数;
括号前面是“-”号去括号时,括号内各项变号容易产生错误。
三、知识点、概念总结
1.单项式:在代数式中,若只含有乘法(包括乘方)运算。
或虽含有除法运算,但除式中不含字母的一类代数式叫单项式;数字或字母的乘积叫单项式(单独的一个数字或字母也是单项式)。
2.系数:单项式中的数字因数叫做这个单项式的系数。
所有字母的指数之和叫做这个单项式的次数。
任何一个非零数的零次方等于1.
9.同类项:所含字母相同,并且相同字母的次数也分别相同的项叫做同类项。
10.合并同类项:多项式中的同类项可以合并,叫做合并同类项,合并同类项的法则是:同类项的系数相加,所得的结果作为系数,字母与字母的指数不变。
以上就是查字典数学网为大家整理的2019中考数学知识点归纳:整式的加减,怎么样,大家还满意吗?希望对大家有所帮助,同时也祝大家学习进步,考试顺利!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1、整式---[()]a b c 去括号为( )
A. --+a b c
B. -+-a b c
C. -++a b c
D. ---a b c
2、在()()[(
)][()]a b c a b c a a -++-=+-的括号内填入的代数式分别( ) A. c b c b --,
B. b c b c ++,
C. b c b c +-,
D. c b c b -+,
3、当k 取 ( )时,多项式8313322-+
--xy y kxy x 中不含xy 项。
A. 0 B. 13 C. 19 D. -19
4、如果多项式(a+1)x 4- x b -3x-5是关于x 的四次三项式,则ab 的值是( )
A 、4
B 、-4
C 、5
D 、-5
已知a+b=-c ,则代数式(a+b )(b+c )(c+a )+abc 的值为( )
A 、-1
B 、1
C 、0
D 、2
5、若|a|=2,|b|=3,且a >b ,则|a-b|的值是( )
A 、-5或-1
B 、1或-1
C 、5或3
D 、5或1
6、若|m|=3,|n|=7。
且m-n >0,则m+n 的值( )
A 、10
B 、4
C 、-10或-4
D 、4或-4
7、若M=3x 2-5x-2,N=3x 2-4x-2,则M ,N 的大小关系( )
A 、M >N
B 、M=N
C 、M <N
D 、以上都有可能
8、设a 是最小的自然数,b 是最大的负整数,c ,d 分别是单项式-x y 2的系数和次数,则a ,b ,c ,d 四个数的和是( )
A 、-1
B 、0
C 、1
D 、3
9、若多项式y 2+(m-3)xy+2x ∣m∣是三次三项式,则m 的值为( )
A 、-3
B 、3
C 、3或-3
D 、2
10、如果a 是最小的正整数,b 是绝对值最小的数,c 与a 2互为相反数,那么(a +b)2009-c 2009=________________
11、当a <3时,|a-3|+a=_______________
12、有理数a ,b 满足a <0<b ,且|a|>|b|,则代数式|a+b|+|2a-b|化简后结果为___________-
13、去括号)()(d c b a ----=__________ )()(d c b a -+--=________________
14、化简 )3()2(232x x x --+=__________
)9()6(4333x x x -+--=______ 15、化简 =+---)3(4532
2x x x x ________________ 16、当的值为+时,-ab ab ab b a 87631,9-==_____________
17、计算m+n-(m-n )的结果为_________________________
18、有一道题目是一个多项式减去x 2+14x-6,小强误当成了加法计算,结果得到2x 2-x+3,则原来的多项式是________________________________ .
19、某校为适应电化教学的需要新建阶梯教室,教室的第一排有a 个座位,后面每一排都比前一排多一个座位,若第n 排有m 个座位,则a 、n 和m 之间的关系为m=________________
20、若a <0,则|1-a|+|2a-1|+|a-3|=______________________
21、化简(2m 2+2m-1)-(5-m 2+2m )=________________________
22、若(a+2)2+|b+1|=0,则5a b 2-{2a 2b-[3a b 2-(4a b 2-2a 2b )]}=____________________
23、化简
x x x x x 2)4
365()213222++---+
( )34(5)132(322x x x x ---+-
24、化简并求值 2.0,2),32(2)(432222==-+-++b a b ab a b a ab 其中
(
五、简答题
11、求的差减去-354.61422-+++-x x x x
12、有一个三位数,百、十、个位上的数字恰好是顺次连续的奇数,且个位上的数字最大,设十位上的数字为52-n ,求这个三位数。
(用n 的代数式表示)
13、一根铁丝长2a 米,第一次用去它的一半少2米,第二次用去剩下的一半多3米,结果还剩下多少米呢?
二、1.若a 为有理数,当a=( )时,多项式
不含项。
A 、0 B 、 C 、 D 、2
a x ax x x ++++2232312x 2-31-
2.当时,代数式=18,这时:( )
A 、20
B 、22
C 、26
D 、36
3.有理数a ,b 。
满足:,且,代数式:化简结果( )
A 、
B 、
C 、
D 、
4.代数式:的系数是
5.如果代数式2235y y ++=8,则代数式的2463y y +-值________.
6.若两个单项式:与是同类项,则:=
7.计算:=
8.化简
① ②
9.化简并求值:①,其中
②已知,求代数式.的值。
(3)若()0232=++-y x ,求代数式2222224])32(2[3xy y x y x xy xy y x ++---的值
10.某一种商品若按标价的八折出售商品,可获利20%,若按标价出售,则可获利( )
1-=x 8323+-bx ax =+-246a b b o a <<b a >a b b a -++a 2-b 2a 2b 2-m y x 22331
y x n -n m 2012
20112332⎪⎭⎫
⎝⎛-⋅⎪⎭⎫
⎝⎛)2(3)32(2y x y x x +--+⎥⎦⎤
⎢⎣⎡++--2222)34
(34ab b a ab ab b a [])3(348222m m m m +-+23
-=m 021
)2(2=++-y x []12)12(35222+----xy x x xy 5 2 2 y
x -
A . 25%
B . 40%
C . 50%
D . 66.7%
11.主城某楼盘11月份的房价为元/m 2,预计12月份房价为8000元/m 2
,比11月份减少了,则11月份的房价为( )元/m 2
A 、
B 、
C 、
D 、
12.某地居民生活用电基本价格为0.5元/度, 规定每月基本用电量为a 度,超出部分电量的每度电价比基本用电量
的每度电价高20%. 某用户在6月份用电100度,共缴电费58元,则基本用电量a 是 度.
13.如图,将一张长为1、宽为a 的长方形纸片()折一下,剪下一个边长等于宽度a 的正方形(称为第一次操作);再将剩下的长方形如图折一下,再次剪下一个边长等于该长方形宽度的正方形(称为第二次操作)……如此反复操作下去,直到第n 次操作后,剩下的小长方形为正方形时停止操作.当3=n 时,a 的值为________.
a
14.在“十、一”黄金周期间,小刚拿着妈妈给的800元钱到运动商城购买运动服和运动鞋,他来到了自己最喜欢的“某品牌”专柜前看到该品牌打出的优惠条件:(1)标价200以内(含200元)不打折;标价200元以上的按如下方式打折:(1)200~500元(含500元)的部分打9折;(2)500~800元(含800元)的部分打8折;(3)800元以上的部分打7折(商品金额可累计),他又看到运动服标价a 元/件(),运动鞋标价b 元/双();
(1)计算他单独购买一件运动服需多少钱(用含a 的代数式表示);
(2)计算他一次性购买一件运动服和一双运动鞋共需多少钱(用a 、b 的代数式表示)
(3)小刚准备留20元钱打车回家,请问他能一次性购买一件运动服和一双运动鞋吗? a %x ()%18000x +%18000x +%)1(8000x -%18000x -12
1<<a 500400≤≤a 400300≤≤b 第一次操作 第二次操作。
