人教版七年级数学上册期未复习(二)整式的加减
新人教版七年级数学上册第2章整式的加减复习教材全解(重难点、例题解析)
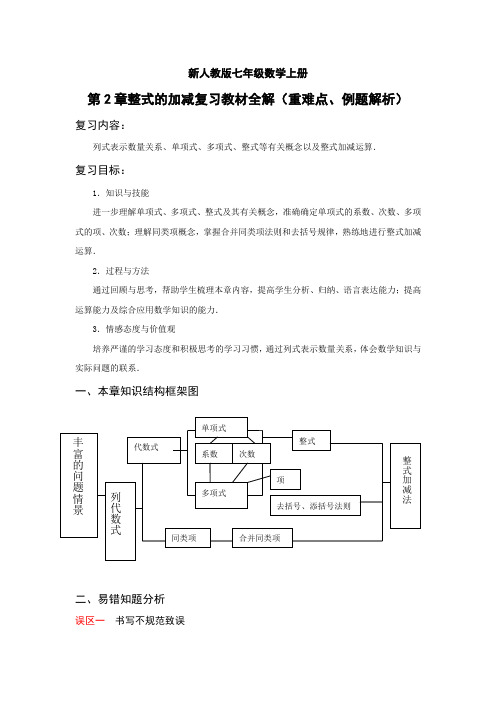
新人教版七年级数学上册第2章整式的加减复习教材全解(重难点、例题解析)复习内容:列式表示数量关系、单项式、多项式、整式等有关概念以及整式加减运算.复习目标:1.知识与技能进一步理解单项式、多项式、整式及其有关概念,准确确定单项式的系数、次数、多项式的项、次数;理解同类项概念,掌握合并同类项法则和去括号规律,熟练地进行整式加减运算.2.过程与方法通过回顾与思考,帮助学生梳理本章内容,提高学生分析、归纳、语言表达能力;提高运算能力及综合应用数学知识的能力.3.情感态度与价值观培养严谨的学习态度和积极思考的学习习惯,通过列式表示数量关系,体会数学知识与实际问题的联系.一、本章知识结构框架图二、易错知题分析误区一书写不规范致误例1 用代数式表示下列语句:(1)比x 与y 的和的平方小x 与y 的和的数 (2)a 的2倍与b 的31的差除以a 与b 的差的立方。
错解(1)(22y x +)-(x+y ) (2)(2a-1/3b )÷(x+y)剖析:(1)要表示的是“比x 与y 的和的平方小x 与y 的和的数”,应该先求和再求平方即应该是)()(2y x y x +-+,而不应该是(22y x +)-(x+y )。
(2)是书写不规范,除号要用分数线代替,即应该写成3)(312b a ba --。
正解:(1))()(2y x y x +-+ (2)3)(312b a ba -- 误区二 概念不清致误例2、判断下列各组是否是同类项:(1)0.2x 2y 与0.2xy 2 (2)4abc 与4ac (3)-130与15 (4)-532m n 与423n m(5)-++()()a b a b 332与 (6)7311pq p q n n n n ++与错解:(1)(3)(4)(6)是同类项,(2)(5)不是同类项。
剖析:(1)0.2x 2y 与0.2xy 2因为字母x 的指数不同,字母y 的指数也不同,所以不是同类项。
人教版初一上册数学第二章整式的加减总结(共66张PPT)

合并同类项概念: _把__多__项_式__中__的__同__类_项__合__并__成__一_项_.
合并同类项法则: 1.__系_数___相加减;
2._字__母__和__字_母__的__指__数___不变。
掌握同类项的概念时注意:
1.判断几个单项式或项,是否是同类项,就 要掌握两个条件: ①所含字母相同。 ②相同字母的次数也相同.
=(3x2 3x2 2x2 ) 2x 3
=4x 2 2 x 3
注意:有多重括号的,一般先去小括号,再去中括号, 最后再去大括号;
求多项式3(x2 4x 1) 1 (3x3 4x2 6)的值,其中x 2; 3
(先去括号) (降幂排列)
(合并同类项,化简完成) 当x=-2时(代入)
是单项式。 • 4,0也是数字,也属于单项式。 • 5,有分数也属于单项式。
• 单项式的次数是指单项式中所有字母因数的指数和
•
这个名词是清代数学家李善兰译书时根据原词概念汉
化的。
•
单项式是字母与数的乘积。
•
单项式的次数:一个单项式中,所有字母的指数的和
叫做这个单项式的次数。
•
单项式的系数:单项式中的数字因数。如:2xy的系
3、 –xmy与45ynx3是同类项,则 m=__3_____. n=__1____
1.填空,并解释其中依据:
(1) 79t 21t (79 21)t 100t
(2) 3ab2 4ab2 ( 3 4)ab2 ab2
(3) 1.618 x 0.118 x 0.5x ( 1.618 0.118 0.5 )x x
呀!!
1、找出同类项
用不同的线标记出各组同类项,注意每一项的符号。
人教版七年级数学上册 第二章 整式的加减 2.2 整式的加减 考点与题型归纳 讲义

人教版七年级数学上册考点与题型归纳第二章:整式的加减2.2 整式的加减一:考点归纳考点一:同类项所含字母相同,并且相同字母的指数也相同的项。
与字母前面的系数(≠0)无关。
2、同类项必须同时满足两个条件:(1)所含字母相同;(2)相同字母的次数相同,二者缺一不可.同类项与系数大小、字母的排列顺序无关考点二:合并同类项把多项式中的同类项合并成一项。
可以运用交换律,结合律和分配律。
合并同类项法则:合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变;考点三:去括号法则去括号,看符号:是正号,不变号;是负号,全变号。
考点四:整式加减的一般步骤:一去、二找、三合(1)如果遇到括号按去括号法则先去括号. (2)结合同类项. (3)合并同类项二:【题型归纳】题型一:去括号法则1.计算:(1)()()2824-+---(2)()()2224133⎡⎤-+---⨯⎣⎦ (3)21(32)xy xy +-+(4)()()223222a ab a ab ---+ 2.去括号,合并同类项(1)(5)3(23)x y x y -+-- (2)2()2()a a b a b ++-+(3)1(3)2(23)xy x x yz ⎡⎤--+-+⎣⎦题型二:整式加减的一般步骤3.先化简,再求值.(1)225[3(23)4]a a a a ---+,其中1a =-;(2)22225(3)4(3)a b ab ab a b ---+,其中1a =-,2b =-.4.如图所示,化简|a ﹣c|+|a ﹣b|+|c|三:基础巩固和培优一、单选题1.下列去括号正确的是( )A .223()333x x y z x x y z --+=-++B .[]35(21)3521x x x x x x ---=--+C .(321)321a x y a x y +-+-=-+-D .(2)(21)221x y x y --+-=--+-2.一个长方形的周长为6a ,一边长为2a b -,则另一边长为( )A .5a b +B .42a b +C .+a bD .2+a b 3.一多项式与2237a a 的和为249a a ,则这个多项式为( ) A .22a a --+ B .2716a a C .216a a D .232a a4.去括号后等于a-b+c 的是() A .()a b c -+B .()a b c --C .()a c b --D .()a b c ++5.下列运算正确的是( )A .326=B .880a a --=C .2416-=-D .523xy xy -+=-6.已知1312a x y -与43b xy +的和是单项式,那么a 、b 的值分别是( ) A .21a b =⎧⎨=⎩ B .21a b =⎧⎨=-⎩ C .21a b =-⎧⎨=-⎩ D .21a b =-⎧⎨=⎩7.下列各组中的两项,属于同类项的是( )A .a 2与aB .﹣3ab 与2abC .a 2b 与ab 2D .a 与b8.化简22(2x +3x-2)-(-x +2)正确的是( )A .2-x +3xB .2-x +3x-4C .23x +3x-4D .2-3x 3x +9.下列说法正确的个数有( )①﹣0.5x2y3与5y2x3是同类项 ②单项式2323x y π-的次数是5次,系数是23- ③倒数等于它本身的数有1,相反数是本身的数是0④2223a b a -+是四次三项式A .1个B .2个C .3个D .4个10.数轴上A 、B 、C 三点表示的数分别是a 、b 、c ,若|a -c |-|a -b |=|c -b |.则下列选项中,表示A 、B 、C 三点在数轴上的位置关系正确的是( )A .B .C .D .二、填空题11.已知223m mn ,24mn n ,则222m n -的值为______.12.已知当2x =时,代数式32ax bx ++的值为7,则当2x =-时,代数式32ax bx ++的值为______.13.单项式523n x y +-与21716m x y -是同类项,则m-n=__________14.已知有理数a 、b 在数轴上的位置如图所示:化简||||()||++--+a b a b ab 结果是______________ .15.定义a b c d 为二阶行列式,规定它的运算法则为abc d =ad -bc .那么二阶行列式2322x yy x---=______________________.三、解答题16.已知2 231A x xy y =++-,2B x xy =-, 若(x +2)2+|y -3|=0,求2A B -的值.17.先化简,再求值:2211(23)4()22x x x x -+--+,其中x=-218.计算(1)15(8)(11)12---+--;(2)71133663145⎛⎫⨯-⨯÷ ⎪⎝⎭;(3)222(2)4(3)(4)(2)-+⨯---÷-;(4)3222[(4)(13)3]-+---⨯;(5)221112()3233ab a a ab --+--; (6)22314[(3)3]22x x x x ---+. 19.先化简,再求值:()331131122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭,其中1,2x y =-=-. ()2已知关于xy 的多项式22262351xax y bx x y +-+-+--的值与字母x 的取值无关,求32323243a b a b --+的值. 20.对于有理数a ,b ,定义一种新运算“★”,规定a ★b a b ab =++﹣.(1)计算:3★()5-的值;(2)当a ,b 在数轴上的位置如图所示时,化简:a ★b .7参考答案题型归纳1.(1)14;(2)18;(3)1xy --;(4)277a ab -2.(1)118x y -+;(2)a b -;(3)1336xy x yz ---3.(1)23a a --;1-;(2)223a b ab -;2-.4.b-2c三:基础巩固和培优1.C2.C3.B4.B5.C6.B7.B8.C9.A10.B11.5- 12.3- 13.8- 14.﹣ab 15.-x-4y .16.2A B -的值为10-17.2562x x --;1232. 18.(1)-30;(2)-572(3)48;(4)32;(5)13ab-16a 2;(6)x 2-x-3. 19.(1)33x y -+,5-;(2)28.20.(1)10;(2)2b -。
人教版七年级数学上册第二章整式的加减复习小结课件

xy2 4;
a 2 1 b; 2
1a;
1 1 xy; 3
e f ; 5
3 b2
(9)下列各式中哪些是单项式(系数、次数), 哪些是多项式(项、次数)?
(1) 3abc 2
(2) x 2 y 3
(3) 4 R3
3
(4)0
(5)3x2y - 3xy 2 y3 - x3
5 (6)
x2 y
z3
4
(4)单项式的系数是带分数时,还常写成假分
数,如1 1 x2 y写成 5 x2 y 。
4
4
(5)单独的数字不含字母,所以它的次数是零次.
(1)列式表示:p的3倍的
1 4
是
.
(2) 0.4 xy 3的次数是
.
2b 1 ab2 5ab 1
(3) 多项式 4
的次数为
,项为 ,
第三项的系数是 ,三次项是
(7) 25 x2 y2
(8) q (9) x 1
p
பைடு நூலகம்
a
回顾:
1、同类项
(1) 所含字母相同; (2)相同字母的指数也分别相同;
(满足这样条件)的项,叫同类项; (3)所有的常数项也是同类项。
2、合并同类项法则:
系数相加,字母和字母的指数不变。
3、去括号法则:
➢括号前面带“+”的括号,去括号时括号内的各 项都不变符号。
(1) a-b与b-a (3) –(a-b)与b-a
(2) -a-b与-(b-a) (4) –(a-b)与b-a
2.
若3x 2 2 x 3的值是 9, 则9 x 2 6 x 7的值是
本章知识结构图:
用字母表示数
列式表示 数量关系
七年级数学上册2整式的加减复习课课件新版新人教版

多项式的次数:_多__项__式_中__次__数__最__高_的__项__的__次_项式的项时,要连同它前面的符号.
2.一个多项式的次数最高项的次数是几,就说这个
多项式是几次多项式.
3.在多项式中,每个单项式都是这个多项式的项,
每一项都有系数,但对整个多项式来说,没有系
(2) - 102与22
(3)2x 2 y3与3 y2 x 3
(4)2x 2 y与 - 3 yx2
点拨: 对于(1)(3),考查的是同类项的定义,所含 字母相同 , 相同字母 的指数也相同 的称为同类项 ;所以(1)(3)不是同类项; 对于(2),虽然好像它们的次数不一样,但其实它们都是 常数 项,所以,它们都 是同类项 ;对于(4),虽然它们的 系数不同 ,
第二章 整式的加减 复习课
1.引导学生梳理整式的相关概念,通过让学生回顾单项式、 多 项式、整式及有关的概念,归纳概念之间的区别与联系.
2.在正确合并同类项、准确运用去括号时的符号变化规律的基础 上,使学生达到可以熟练地进行整式的加减运算的目的.
3.通过分析实际问题中的数量关系,让学生进一步体会用字母表 示数的意义,通过对数与式运算的分析,体会“数式通性”, 体会蕴含在具体问题中的数学思想和规律,以及数学知识之间
“具体”与“抽象”的内在联系和数学的内在统一性.
减加的式整
知识结构:
整式的概念
整式的计算
单项式 多项式
系数
次数 项,项数,常数项, 最高次项 次数
同类项与合并同类项 去括号 化简求值
用字母来表示生活中的量
单项式:
定义:由__数__字__或__字__母__的_乘__积__ 组成的式子 . 单独的一__个__数__ 或一__个__字__母__ 也是单项式 .
人教版七年级上册2整式的加减复习课件

=18xy-6x+3
=(18y-6)x+3.
因为 3A+6B 的值与 x 无关,所以 18y-6=0,解得 y=13
(2).若x2+ax-2y+7-(bx2-2x+9y-1)的值与x无关,求-a-b的值. 解: x2+ax-2y+7-(bx2-2x+9y-1)
=x2+ax-2y+7-bx2+2x-9y+1 =(1-b)x2+(a+2)x-11y+8. 因为该整式的值与x无关,所以1-b=0,a+2=0,得b=1,a=-2. 所以-a-b=-(-2)-1=1
练习:去掉下列各式中的括号: (1) (x+y)-z=_____x_+__y_-__z____; (2) x-(y+z)=___x_-__y_-__z_____; (3) -1-2(x-y)=__-__1_-__2_x+__2_y____; (4) 2(a-b)-3(x+y)=2_a_-__2_b_-__3_x_-__3.y
同类型题:《新课程》45页 能力提升 第九题
C
(解题技能:将x代入具体数值,例:x=0)
(3)黑板上有一道题,是一个多项式减去3x2-5x+1,某同学由于大意,将 减号抄成了加号,得出的结果是5x2+3x-7,求出这道题的正确结果.
分析: 原题: - (2-5x+1)=
大意抄错: +(3x2-5x+1)= 5x2+3x-7
解:该多项式为(5x2+3x-7)-(3x2-5x+1)=2x2+8x-8.所以正确的结 果为(2x2+8x-8)-(3x2-5x+1)=-x2+13x-9
3.求相反数
-x+y-z的相反数是( B )
A.-x-y+z
B.x-y+z
C.x+y-z
D.x+y+z
解题关键:求某个数的相反数,在整体前添上负号,然后去括号化简 -x+y-z的相反数是- ( - x+y-z)= x-y+z
人教版 七年级数学上册 第二章 整式的加减 知识点+易错题

七年级数学上册期末复习整式的加减知识点+易错题整式的加减知识点整式知识点1.单项式:在代数式中,若只含有乘法(包括乘方)运算。
或虽含有除法运算,但除式中不含字母的一类代数式叫单项式.2.单项式的系数与次数:单项式中不为零的数字因数,叫单项式的数字系数,简称单项式的系数;系数不为零时,单项式中所有字母指数的和,叫单项式的次数.3.多项式:几个单项式的和叫多项式.4.多项式的项数与次数:多项式中所含单项式的个数就是多项式的项数,每个单项式叫多项式的项;多项式里,次数最高项的次数叫多项式的次数;注意:(若a、b、c、p、q是常数)ax2+bx+c和x2+px+q是常见的两个二次三项式.5.整式:凡不含有除法运算,或虽含有除法运算但除式中不含字母的代数式叫整式.整式分类为:错误!未找到引用源。
.6.同类项:所含字母相同,并且相同字母的指数也相同的单项式是同类项.7.合并同类项法则:系数相加,字母与字母的指数不变.8.去(添)括号法则:去(添)括号时,若括号前边是“+”号,括号里的各项都不变号;若括号前边是“-”号,括号里的各项都要变号.9.整式的加减:整式的加减,实际上是在去括号的基础上,把多项式的同类项合并.10.多项式的升幂和降幂排列:把一个多项式的各项按某个字母的指数从小到大(或从大到小)排列起来,叫做按这个字母的升幂排列(或降幂排列).注意:多项式计算的最后结果一般应该进行升幂(或降幂)排列.11. 列代数式列代数式首先要确定数量与数量的运算关系,其次应抓住题中的一些关键词语,如和、差、积、商、平方、倒数以及几分之几、几成、倍等等.抓住这些关键词语,反复咀嚼,认真推敲,列好一般的代数式就不太难了.12.代数式的值根据问题的需要,用具体数值代替代数式中的字母,按照代数式中的运算关系计算,所得的结果是代数式的值.13. 列代数式要注意①数字与字母、字母与字母相乘,要把乘号省略;②数字与字母、字母与字母相除,要把它写成分数的形式;③如果字母前面的数字是带分数,要把它写成假分数。
【优选整合】人教版数学七年级上册第2章整式的加减小结与复习教案.doc

第2章整式的加减小结与复习教案教学目标1•使学生对本章内容的认识更全面、更系统化.2.进一步加深学生对本章基础知识的理解以及基本技能(主要是计算)的掌握. 教学重点和难点重点:本章基础知识的归纳、总结;基础知识的运用;整式的加减运算.难点:本章基础知识的归纳、总结;基础知识的运用.一、复习1.怎样进行整式的加减?整式的加减实际上就是去括号、合并同类项这两个知识的综合.2.整式的加减的一般步骤:(1)如果有括号,那么先去括号.(2)如果有同类项,那么先合并同类项.3.求多项式的值,一般先将多项式化简,再代入求值,这样可使计算简便.二、新课lo知识框图,整体把握2、释疑解惑,加深理解1.学习单项式应注意的问题:(1)单项式的系数包括它前面的符号;(2)单项式的系数是1或一1时,通常1省略不写,如一k, pq2等,单项式的系数是带分数时,通常写成假分数;(3)单项式的次数仅仅与字母有关,是单项式中所有字母指数的和,特别地,单个字母的次数是1.常数的次数是0.而7X 102ab2c的次数是4,与IO?无关;(4)要正确区分单项式的次数与单项式中字母的次数,如6p2q的次数是3,其中字母p的次数是2. 例1丄ab (填“是”或“不是”)单项式,一空(填“是”或“不是”)单项式.3【分析】本题出现了两个极易被混淆的单项式,兀只是一个数的代号,易被误认为是一个字母,而分母中是非零数时,因为乘除的运算是统一的,实际表示的是乘法运算,这与单项式定义并不冲突.【答案】是是例2单项式一4. 3X10;i ab2c是次单项式.【分析】单项式的次数只与字母因数有关,1(/是数字因数的一部分,指数3不能参与指数和的计算.【答案】四2.学习多项式应注意儿个问题:(1)多项式中,每个单项式叫做多项式的项,项包括它前面的符号;(2)多项式的次数不是所有项的次数Z和,而是次数最高项的次数;(3)多项式没有系数概念,但对多项式中的每一项来说都有系数.例3判断下列多项式是几次几项式.(1)—3x+5y —7;(2)a3b — a2b2c+abc — 5c2+7.【分析】判断一个多项式是儿次儿项式时,首先要看哪一项的次数最高,则这一项的次数就是多项式的次数;再确定这个多项式所含不为同类项的项的个数,则就是儿项式.【答案】(1)一次三项式(2)五次五项式3.整式的加减运算是重点,准确求得结果先得把握两个前提:(1)认准同类项,从“相同字母”和“同一字母次数相同”两方面考察;(2)谨慎处理去括号时符号的变与不变.3、典例精析,复习新知例1找出下列代数式中的单项式、多项式和整式.—Z -- , TH、— 2. ()1 X 105:x2-2x解:羊项式冇4忙岂一2. 01 x 1()';多项式冇二4上;2整式右 4.小罟,(),/, - 2. 01 x 1()5,X + V +Z丿3 •此题由学生口答,并说明理由.通过此题,进一步加深学生对于单项式、多项式、整式的定义的理解.例2指出下列单项式的系数、次数:解:M:系数足1,次数是2;—/:系数是—1,次数是2;3 5討■系数是斗,次数是6 ;二^:系数是—次数是9.此题在学生回答过程中,及时强调“系数”及“次数”定义屮应注意的问题:系数应包括前面的“+” 号或“一”号,次数是“指数之和” •例3指出多项式a3-a2b-abW-l是几次几项式,最高次项、常数项各是什么?解:是三次五项式,最高次项有:a\ — a2b—ab\ b3,常数项是一1.例4化简:例4化简:(1)(1/— 5.r2— 4x + I )—(3.v3— 5/ — 3-r);〔2) —[―(―(w— 1);2_ 2xy + , | 十 *( 2,_ X)—2/).解:(1)原式 ~ 2r4—— A 4-1 ;〔2)原式=—2x+-y;(3)原或=—4" + ¥巧一4込通过此题强调:(1)去括号(包括去多重括号)的问题;(2)数字与多项式相乘时分配律的使用问题.1 1 9例 5 化简、求值:5ab —2 E3ab — (4ab 2+ — ab ) ] — 5ab\ 其中 a 二一,b=——. 2 2 32解:化简的结果是:3ab 2,求值的结果是土. 3例6 —个多项式加上—2x 3+4x 2y+5y 3后,M x 3—x 2y+3y 3,求这个多项式,并求当x 二一丄,y 二丄时,这2 2 个多项式的值.解:此多项式为3x 3—5x"y —2y 3;值为一一.4例7己知当x = l 时,代数式ax°+bx'+cx —8 = 6,求当x = —1时,ax s +bx 3+cx —8的值.【分析】观察ax 5+bx 3+cx 中x 的指数均为奇数,当x = l, x = —1时,它的值正好互为相反数,以整体 代入的方法可达到求值的目的.解:•・•当 x=l 时,代数式 ax 5+bx 3+cx-8=6,a+b+c —8=6,即 a+b+c =14.当x= —1时,代数式的值为a (-1) 5+b (-1) '+c (-1) -8=—a —b —c —8 = — (a+b+c ) —8②把①代入②得原式=_ 14 _ 8 = _ 22,即当 x= — 1 时,ax 3+bx 3+cx —8=—22.三、练习 1. 下列各式中是多项式的是(B)A1_ _ ab A. ---- B. x 4* y C ・— 2 32. 下列说法中正确的是(C)B. 丄是单项式 y C ・丄是单项式 D. -5口的系数是5 23. 如图1,为做一个试管架,在dem 长的木条上钻了 4个圆孔,每个孔直径2cm,则兀等于(D )D. -a 2b 2A.兀的次数是04. d — (b + c — d) — (d — c) + (A6. 化间 2a — [3b — 5a — (2a — 7/?)J 的结果是(D)C. (1 + 25%)(1-70%加元D. (l + 25% + 70%)d 元 8. 下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面. (,o 1 J ( 1 2 彳-x" +3xv ——-——x +4xy- I 2,丿 I 2 部分•那么被墨汁遮住的一项应是(C )A. - IxyB. +7xyC. - xyD. +xy9. 把(X -3)2-2(X -3)-5(X -3)2+(X -3)中的(兀一3)看成一个因式合并同类项,结果应(D )A. 一4(无一3尸+(兀一3)B. 4(兀一3产一x (兀一3)C. 4(X -3)2-(X -3) D . -4(X -3)2-(X -3)四、 小结通过本节课的复习,你还有哪些困惑和疑问?说说看.五、 作业a + 8 A. ------- 5cm c a —16 小 a-4 B. -------- cmC. -------- cm 5 cm A. d-b B> — b — d C. b — dD. b + d 5.只含有九”z 的三次多项式中,不可能含有的项是(D) A. 2x 3B. 5xyzC. -7/D. -x 2yz 4 A. - 7a + 10b B. 5a + 4b C. - a-4b D. 9a-10b 7. 一•台电视机成本价为a 元,销售价比成本价增加了 25%, 因库存积压,所以就按销售价的70%出售, 那么每台实际售价为(B)A. (1 + 25%)(1 + 70%)Q 元B. 70%(l + 25%)a 元 扑*+几阴影部分即为被墨迹弄污的教科书76页10、11题。
期末复习——整式的加减人教版七年级数学上册PPT精品课件

考点6.整式的加减在实际问题中的应用
12. 已知小明的年龄是m岁,小红的年龄比小明的年龄 的2倍少4岁,小华的年龄比小红的年龄的 还多 1岁,求这三名同学的年龄的和.
核心考题
13. 甲乙两人岁数的年龄和等于甲乙两人年龄差的3倍,
甲x岁,乙y岁(x>y),则他们的年龄和如何用年
龄差表示( C )
A. (x+y)
(2)-3(2x2-xy)+4(x2+xy-6). (2)解:原式=-6x2+3xy+4x2+4xy-24=-2x2+7xy-24.
20. 先化简,再求值: 2(3x2-2x)-(-4x+5),其中x=-1.
解:原式=6x2-4x+4x-5=6x2-5. 当x=-1时,原式=6×(-1)2-5=1.
(2)-2(2mn2-mn)-(-3mn2+2mn). (2)解:原式=-4mn2+2mn+3mn2-2mn=-mn2.
考点5.求代数式的值 11. 先化简,再求值: 3(2x2-5x)-2(-3x-2+3x2),其中x=-3.
解:原式=6x2-15x+6x+4-6x2=-9x+4. 当x=-3时,原式=27+4=31.
•
6.石壕吏和老妇人是诗中的主要人物 ,要立 于善于 运用想 像来刻 画他们 各自的 动作、 语言和 神态; 还要补 充一些 事实上 已经发 生却被 诗人隐 去的故 事情节 。
•
7.文学本身就是将自己生命的感动凝 固成文 字,去 唤醒那 沉睡的 情感, 饥渴的 灵魂, 也许已 是跨越 千年, 但那人 间的真 情却亘 古不变 ,故事 仿佛就 在昨日 一般亲 切,光 芒没有 丝毫的 暗淡减 损。
人教版数学七年级上册第二章整式的加减复习课件

(3)、7x 3x 4 =4x 求多项式2x2-5x+x2+4x-3x2-2的值,其中x=2
2
2
2
☺
(4)、9a2b9b2 a0✓ ☺
例:化简
1 .4 (x 3 y 9 y 3 ) 3 ( x 2 y 2 8 y 3 )
2 . 1 3 ( 1 4 a 3 ) ( 1 a 2 a 2 ) ( 1 a a 2 a 3 ) 2.题,很多同学在化简为 : 14 33a3 1 a 2a2 1- a a2 - a3, 由于项比较多, 合并的时候存在漏项和 符号错误, 那么我们怎么处理呢?
同类项:所含字母相同,且相同字母的指数也相同的项
(1)、2x3x 5x =5x2 ☺ 2 2 把同类项的系数相加,所得的结果作为系数,
雄鹰必须比鸟飞得高,因为它的猎物就是鸟。
4
这个式子从和式的角度理解,可以避免我们符号错误,读作:“17,-3a3,+2a2,+a2,-a3的和,即把式子前面的符号理解为性质符号,
=-3-a43a-3a+33合a2并+1,7+2a2+a2合并,17不能合并写在后边,最后用“+”连接 不注是意, :保几持个不常变数,项放也后是面同!类项
无这钱个之 式人子脚从杆和硬式,的有角钱度之理人解骨,头可酥以。避免我们符号错误,读作:“17,-3a3,+2a2,+a2,-a3的和,即把式子前面的符号理解为性质符号, 2不(y作+1运)-算5(符1-0号. 无 2(y钱+1之)-人5(脚1-0杆. 硬,有钱之人骨头酥。 —这(个式)子(从负和括式号的)角。度理解,可以避免我们符号错误,读作:“17,-3a3,+2a2,+a2,-a3的和,即把式子前面的符号理解为性质符号, 这不个作式 运子算从符和号式的角度理解,可以避免我们符号错误,读作:“17,-3a3,+2a2,+a2,-a3的和,即把式子前面的符号理解为性质符号, 不如作果运 括算号符前号有系数,则先用乘法分配律运算后进行转化。
人教版七年级数学上册第二章《整式的加减》复习课课件

知识框架
用字母表示数 整 整 单项式:系数、次数
式 式 多项式: 项、次数、常数项 同类项: 定义、“两相同、两无关”
方法技能:
在求多项式的值时,一般情况是先化简,然后再 把字母的值代入化简后的式子中求值,化简的过 程就是整式运算的过程.
针对训练
5.化简后再求值:5x2-2y-8(x2-2y)+3(2x2-3y),其中 |x+12|+(y-13)2=0. 分析:原式去括号合并得到最简结果,利用非负 数的性质求出x与y的值,代入计算即可求出值. 解:原式=5x2-2y-8x2+16y+6x2-9y=3x2-5y. 因为|x+2|+(y-3)2=0,所以x+2=0,y-3=0, 即x=-2,y=3,则原式=12-15= -3.
s=1002×(1002+1)=1005006.
即2+4+6+8+……+2004=1005006.
考点讲授
小结:视察是解题的前提条件,当已知数据有很多组 时,需要仔细视察,反复比较,才能发现其中的规律.
针对训练
6. 视察下列图形:它们是按一定规律排列的,依照 此规律,第202X个图形中共有__6_0_5_2___个五角星.
易错警示:
单项式的次数和系数、多项式的次数和项是 容易混淆的概念,须辨别清楚.
考点2 同类项
考点讲授
例2 若3xm+5y2与x3yn的和是单项式,求mn的值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
期未复习(二)整式的加减01知识结构图02重难点突破重难点1 整式的相关概念【例1】(通辽中考)下列说法中,正确的是( ) A.43x -的系数是43 B.332a π的系数是32C.23ab 的系数是3aD.225xy 的系数是25方法指导确定单项式的系数与次数时,要紧扣概念进行判断,同时要注意“π”是一个数,而不是表示任意数的字母.变式训练1.多项式2253a a -+是_________次__________项式.重难点2 同类项【例2】(雅安中考)如果单项式212a x y -与313b x y 是同类项,那么a ,b 的值分别为( )A. 2,2B. 3,2C. 2,3D. 3,2-方法指导本题考查同类项的知识,注意掌握同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同.变式训练2.若关于x ,y 的单项式1232b a mxy x y +--与的和为0,则()m a b -=____________. 重难点3 整式的运算【例3】(淮安中考)计算:3(2)a a b --=____________.方法指导整式的加减的实质是先去括号,再合并同类项.变式训练3.一个整式减去22a b -等于22a b +,则这个整式为( )2222A. 2 B. 2 C. 2 D. 2b a b a --重难点4 化简求值【例4】化简求值:22113122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭,其中22,3x y =-=. 【解答】方法指导本题考查了整式的化简.整式的加减运算实质是去括号、合并同类项,这是各地中考的常考点.变式训练4.先化简,再求值:(222532()5)a ab a ab a ab b ++--+-,其中a ,b 满足21|1|02a b ⎛⎫++-= ⎪⎝⎭. 重难点5 整式加减的应用【例5】某单位准备组织部分员工到某地旅游,现在联系了甲、乙两家旅行社,两家旅行社报价均为2000元/人,两家旅行社同时都对10人以上的团体推出了优惠措施:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队员工的费用,其余员工八折优惠.(1)若设参加旅游的员工共有()10m m >人,则甲旅行社的费用为________元,乙旅行社的费用为_________元;(用含m 的式子表示并化简)(2)假如这个单位组织包括带队员工在内的共20名员工到某地旅游,该单位选择哪一家旅行社比较优惠?说明理由.【解答】方法指导解答整式运算的应用题的关键是通过建立整式运算模型,把实际问题转化为整式加减运算问题来解决.变式训练5.(遵义中考)如图,从边长为1a +()cm 的正方形纸片中剪去一个边长为1a -()cm 的正方形(1a >),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则长方形的长为( )(). 2cm . 2cmC. 4 cmD. 22 cma a a A B -03思想方法突破 【例6】如图,由若干根火柴棒摆成正方形,第1个图用了4根火柴棒,第2个图用了7根火柴棒,第3个图用了10根火柴棒,依次类推,第10个图要用了_________根火柴棒,摆第n 个图时,要用__________根火柴棒.【思路点拨】第1个图可拆为即1+3=4(根),第2个图可拆为即1+3×2=7(根);第3个图可拆为即1+3×3=10(根),由此可知图形中所用火柴棒的根数与n 之间的关系,列式计算即可得出答案.方法指导本题采用拆图法,探索发现有关图形所具有的规律性或不变性的问题,它往往给出一组变化了的图形或条件,通过拆图,观察、分析、猜想出图形的相同点或不同点,找出图形之间的变化规律.【例7】(日照中考)已知26m m -=,则2122m m -+=__________.【思路点拨】观察题中的两个式子2m m -和2122m m -+,可以发现,()22222m m m m -+=-,因此将2m m -的值整体代入即可求出结果.方法指导式子中的字母表示的数没有明确告知,而是隐含在已知条件中,可从已知条件中将式子进行变形,利用“整体代入法”求式子的值.04复习自测一、选择题(每小题4分,共32分)1.下列式子符合书写要求的是( )2A. B. 121C. 4 D. 33xy a b xy ab --÷⨯ 2.多项式2112x x ---的各项分别是( ) 222211A.,,1 B.,,12211C.,,1 D. ,,122x x x x x x x x ------ 3.若23232m x y x y -与是同类项,则m 等于( )A. 1B. 2C. 3D. 44.(泸州中考)计算223a a -的结果是( )222A. 4 B. 3C. 2 D. 3a a a5.[()]a b c ---去括号正确的是( )A. B. C. D. a b ca b c a b c a b c--+-+-----++ 6.数x ,y 在数轴上对应点的位置如图所示,则化简||||x y y x +--的结果是( )A. 0B. 2C. 2D. 22x y x y- 7.如果关于x 的式子22421x x ax x a +-++与的和没有2x 项,那么这个和为( )A. 35B. 33C. 44D. 33x x x x -+-- 8.已知整式61x -的值是22y ,的值是4,则()()22557457x y xy x x y xy x +--+-=( )11. B. 22111C. D. 2222A ---或或 二、填空题(每小题4分,共24分)9.(桂林中考)单项式327a b 的次数是__________. 10.254143a b ab --+是_____次______项式,其中常数项是______,最高次项是_______,二次项系数是_______.11.一家体育器材商店将某种品牌的篮球按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出.已知每个篮球的成本价为a 元,则该商店卖出个一篮球可获利润_______元.12.当3x =时,()()2221x x x x --++的值等于_________.13.若24513m n a b a b +--与的和仍是一个单项式,则m n +=________.14.(滨州中考)观察下列各式的计算过程:550110025⨯=⨯⨯+,151********⨯=⨯⨯+,25252310025⨯=⨯⨯+,35353410025⨯=⨯⨯+,⋅⋅⋅请猜测,第n 个算式(n 为正整数)应表示为_____________.三、解答题(共44分)15.(20分)化简:(1)()()227357x x x x ----;(2)()()222422ab b a ab b --+-;(3)[2()]x y x x y ----;(4)3()2()5()4(3)()x y x y x y x y x y --+--+++-.16.(6分)化简求值:22113122223a a b a b ⎛⎫----- ⎪⎝⎭⎛⎫ ⎪⎝⎭,其中32,2a b =-=. 17.(8分)已知2222335, x 32y 4 A x y xy B x y =+-=-+,当11x y =-=,时,计算23A B -的值.18.(10分)某超市在春节期间对顾客实行优惠,规定如下:(1)王老师十次性购物600元,他实际付款________元;(2)若顾客在该超市一次性购物x 元,当x 小于500但不小于200时,他实际付款__________元,当x 大手或等于500时,他实际付款______元(用含x 的式子表示);(3)如果王老师两次购物货款合计820元,第一次购物的货款为a 元(200300<<),用含a的式子表示:两次购物王老师实际付款多少元?a参考答案【例1】D【例2】D【例3】a b +【例4】原式=23x y -+.当2x =-,23y =时,原式=469. 【例5】(1)1500 16001m m -()(2)选择甲旅行社比较优惠.理由如下:当20m =时,甲旅行社的费用为1500×20=30000(元);乙旅行社的费用为1600×19=30400(元),因为30000<30400,所以该单位选择甲旅行社比较优惠.【例6】31 31n +()【例7】11-变式训练1.二 三2.13.B4.解:原式=22a b +.因为21|1|02a b ++-=(),所以11002a b +=-=,,即1a =-,12b =.所以原式=2117212244⨯-+=-+=-()() 5.B 复习自测1.A2.B3.C4.C5.B6.C7.A 8C 9.5 10.254 1 43a b --三三 11.0.12a 12.8- 13.8 14.[10(1)5][10(1)5]100(1)25n n n n -+⨯-+=-+15.解:(1)原式=225x -+.(2)原式=222b a -.(3)原式=42x y -.(4)原式3x y =+.16.解:原式=2443a b -+.当32,2a b =-=时,原式=11. 17.解:因为2222335,432A x y xy B x y xy =+-=-+,所以222222236610129661516A B x y xy x y xy x y xy -=+--+-=-+-.当1,1x y =-=时,原式=6151625-++=.18.解:(1)530(2)0.9 0.850x x +()(3)0.90.8(820)500.96560.850(0.1706)a a a a a +-+=+-+=+元.。
