Lingo_简单教程
lingo基础教程

LINGO 使用指南LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口: 外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO 中求解如下的LP 问题:0,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码: min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如下表。
使用LINGO软件,编制程序如下:model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
lingo入门教程(共55张)

3 3
A2
8 67
A3 4
7
B2
8 9
5 C2 6
T
第18页,共55页。
分析
(fēnxī)
6 A1 5 6
B1 6 C1
S
3 3
A2
8 67
A3 4
7
B2
8 9
5 C2 6
T
假设从S到T的最优行驶路线 P 经过城市C1, 则P中从S到C1的子路也一定 是从S到C1的最优行驶路线; 假设 P 经过城市C2, 则P中从S到C2的子路也一定是从S到C2的最优行驶路线. 因此, 为得到从S到T的最优行驶路线, 只需要先求出从S到Ck(k=1,2)的最 优行驶路线, 就可以方便地得到从S到T的最优行驶路线.
第19页,共55页。
分析
(fēnxī)
6 A1 5 6
B1 6 C1
S
3 3
A2
8 67
A3 4
7
B2
8 9
5 C2 6
T
此例中可把从S到T的行驶过程分成4个阶段,即 S→Ai (i=1,2 或3), Ai → Bj(j=1或2), Bj → Ck(k=1或2), Ck → T. 记d(Y,X)为城 市Y与城市X之间的直接距离(若这两个城市之间没有道路直 接相连,则可以认为直接距离为∞),用L(X)表示城市S到城市
L B2 minL A1 5, L A2 6, L A3 4 7 L A3 4; L C1 minL B1 6, L B2 8 15 L B2 8;
略2去),最小运量136.2275(吨公里)。
1
3
5
0
0
1
2
3
4
5
6
LINGO快速入门

概率函数
• 7.@phg(pop,g,n,x) • 超几何(Hypergeometric)分布的累积分布函数。pop表示产品总数,g是正
品数。从所有产品中任意取出n(n≤pop)件。pop,g,n和x都可以是非整数, 这时采用线性插值进行计算。
变量界定函数
• 变量界定函数实现对变量取值范围的附加限制,共4种: • @bin(x) 限制x为0或1 • @bnd(L,x,U) 限制L≤x≤U • @free(x) 取消对变量x的默认下界为0的限制,即x可
以取任意实数 • @gin(x) 限制x为整数 • 在默认情况下,LINGO规定变量是非负的,也就是说下界
• @smax(x1,x2,...,xn)返回 x1 , x2 , … , xn 中的 最大值
• @smin(x1,x2,...,xn)返回 x1 , x2 , … , xn 中的最 小值
例 给定一个直角三角形,求包含该三角形的最小正方形。
解:如图所示。ABCDDAEabx
求最小的正方形就相当于求如下的最优化问题:
• data:
• sex,age = 1 16
•
0 14
•
0 17
•
0 13;
• friend = 0.3 0.5 0.6;
• enddata
基本运算符
• ^ 乘方 •﹡ 乘 •/ 除 •﹢ 加 •﹣ 减
: LINGO具有9种逻辑运算符
• #not# 否定该操作数的逻辑值,# not #是一个一元运算符 • #eq# 若两个运算数相等,则为 true ;否则为 flase • #ne# 若两个运算符不相等,则为 true ;否则为 flase • #gt# 若左边的运算符严格大于右边的运算符,则为 true ;否则
LINGO教程(PDF)
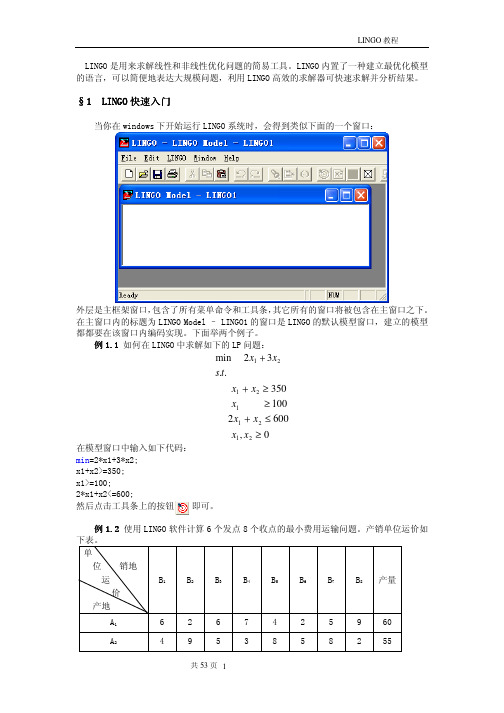
例 2.3
sets: product/A B/; machine/M N/; week/1..2/; allowed(product,machine,week):x; endsets
LINGO 生成了三个父集的所有组合共八组作为 allowed 集的成员。列表如下: 编号 成员 1 (A,M,1)
共 53 页 4
注意:用“[]”表示该部分内容可选。下同,不再赘述。
Setname 是你选择的来标记集的名字,最好具有较强的可读性。集名字必须严格符合标 准命名规则:以拉丁字母或下划线(_)为首字符,其后由拉丁字母(A—Z) 、下划线、阿拉 伯数字(0,1,…,9)组成的总长度不超过 32 个字符的字符串,且不区分大小写。
LINGO 教程
LINGO 是用来求解线性和非线性优化问题的简易工具。LINGO 内置了一种建立最优化模型 的语言,可以简便地表达大规模问题,利用 LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门
当你在 windows 下开始运行 LINGO 系统时,会得到类似下面的一个窗口:
共 53 页 3
LINGO 教程
MonthM..MonthN MonthYearM..MonthYearN
Oct..Jan Oct2001..Jan2002
Oct,Nov,Dec,Jan Oct2001,Nov2001,Dec2001,Jan2002
③ 集成员不放在集定义中,而在随后的数据部分 数据部分来定义。 数据部分 例 2.2
共 53 页 1
LINGO 教程
A3 A4 A5 A6 销量
5 7 2 5 35
2 6 3 5 37
1 7 9 2 22
9 3 5 2 32
lingo教程

使用LINGO软件,编制程序如下:
model:
!6发点8收点运输问题;
sets:
warehouses/wh1..wh6/: capacity;
vendors/v1..v8/: demand;
links(warehouses,vendors): cost, volume;
endsets !目标函数;
Mon..Fri
Mon,Tue,Wed,Thu,Fri
MonthM..MonthN
Oct..Jan
Oct,Nov,Dec,Jan
MonthYearM..MonthYearN Oct2001..Jan2002 Oct2001,Nov2001,Dec2001,Jan2002
③ 集成员不放在集定义中,而在随后的数据部分来定义。
23
(A,N,1)
34
(A,N,2)
45
(B,M,1)
56
(B,M,2)
67
(B,N,1)
78
(B,N,2)
成员列表被忽略时,派生集成员由父集成员所有的组合构成,这样
的派生集成为稠密集。如果限制派生集的成员,使它成为父集成员所有
组合构成的集合的一个子集,这样的派生集成为稀疏集。同原始集一
样,派生集成员的声明也可以放在数据部分。一个派生集的成员列表有
许多稀疏集的成员都满足一些条件以和非成员相区分。我们可以把这些
逻辑条件看作过滤器,在LINGO生成派生集的成员时把使逻辑条件为假
的成员从稠密集中过滤掉。
例2.4
sets:
!学生集:性别属性sex,1表示男性,0表示女性;年龄属性age. ;
students/John,Jill,Rose,Mike/:sex,age;
LINGO使用教程
LINGO 使用教程LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例 如何在LINGO 中求解如下的LP 问题: ⎪⎪⎩⎪⎪⎨⎧≥≤+≥≥++0,6002100350..32min212112121x x x x x x x t s x x 在模型窗口中输入如下代码:min =2*x1+3*x2; x1+x2>=350; x1>=100; 2*x1+x2<=600;然后点击工具条上的按钮即可。
例使用LINGO软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如下表。
使用LINGO软件,编制程序如下:model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
lingo基本用法(精华版)20分钟学会

lingo基本⽤法(精华版)20分钟学会Lingo基本⽤法总结(除集函数部分)LINGO是⽤来求解线性和⾮线性优化问题的简易⼯具。
Lingo免费版可以⽀持30个未知数,lingo破解版可以⽀持⼏万个未知数、⼏万个约束条件。
当你在windows下开始运⾏LINGO系统时,会得到类似下⾯的⼀个窗⼝:外层是主框架窗⼝,包含了所有菜单命令和⼯具条,其它所有的窗⼝将被包含在主窗⼝之下。
在主窗⼝内的标题为LINGO Model – LINGO1的窗⼝是LINGO的默认模型窗⼝,建⽴的模型都都要在该窗⼝内编码实现。
下⾯举两个例⼦。
例1.1 如何在LINGO中求解如下的LP问题:在模型窗⼝中输⼊如下代码:min=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后点击⼯具条上的按钮即可。
得到如下结果:所以当x1为250,x2为100时⽬标函数得到最⼤值。
算术运算符Lingo 中变量不区分⼤⼩写,以字母开头不超过32个字符算术运算符是针对数值进⾏操作的。
LINGO 提供了5种⼆元运算符:^乘⽅﹡乘/除﹢加﹣减LINGO 唯⼀的⼀元算术运算符是取反函数“﹣”。
这些运算符的优先级由⾼到底为:⾼﹣(取反)^﹡/低﹢﹣运算符的运算次序为从左到右按优先级⾼低来执⾏。
运算的次序可以⽤圆括号“()”来改变。
例:在x1+x2>=350,x1>=100,2*x1+x2<=600的条件下求2*x1+3*x2的最⼩值在代码窗⼝中编写min=2*x1+3*x2;x1+x2>=350;x1>=100;2*x1+x2<=600;然后单击上⾯菜单lingo菜单下solve键即可。
数学函数标准数学函数:@abs(x) 返回x的绝对值@sin(x) 返回x的正弦值,x采⽤弧度制@cos(x) 返回x的余弦值@tan(x) 返回x的正切值@exp(x) 返回常数e的x次⽅@log(x) 返回x的⾃然对数@lgm(x) 返回x的gamma函数的⾃然对数@sign(x) 如果x<0返回-1;否则,返回1@floor(x) 返回x的整数部分。
lingo基础教程

LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO 中求解如下的LP 问题:在模型窗口中输入如下代码: min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x xmodel:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
Lingo教程

LINGO教程LINGO是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
§1 LINGO快速入门●安装:实验室的所有电脑都已经事先安装好了Lingo 8(或者9, 10, 11)。
如果要在自己的电脑上安装这个软件,建议从网上下载一个破解版的,按照提示一步一步地安装完毕。
●简单例子:当你在windows系统下开始运行LINGO时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口,建立的模型都要在该窗口内编码实现。
下面举两个例子。
例 1 某工厂在计划期内要安排生产I、II两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表所示。
产品I 产品II设备 1 2 8台时原材料A 4 0 16kg原材料B 0 4 12kg该工厂每生产一件产品I可获利2元,每生产一件产品II可获利3元,问应该如何安排生产计划使该厂获利最多?我们用下面的数学模型来描述这个问题。
设x_1、x_2分别表示在计划期内产品I、II的产量。
因为设备的有效台时是8,这是一个限制产量的条件,所以在确定产品I、II的产量时,要考虑不超过设备的有效台时数,即可用不等式表示为x_1 + 2x_2 <=8同理,因原材料A、B的限量,可以得到以下不等式4x_1 <=164x_2 <=12该工厂的目标是在不超过所有资源限量的条件下,如何确定产量x_1、x_2以得到最大的利润。
若用z表示利润,这时z=2x_1+3x_2.综合上述,该计划问题可用数学模型表示为:目标函数 max z=2x_1+3x_2约束条件 x_1 + 2x_2 <=84x_1 <=164x_2 <=12x_1、x_2 >=0一个优化模型一般有三部分组成:1.目标函数(Objective Function):要达到的目标。
LINGO教程(图文版)

LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门1.1 应用实例当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO 中求解如下的LP 问题:0,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码:min =2*x1+3*x2; x1+x2>=350; x1>=100; 2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2使用LINGO软件计算6个发点8个收点的最小费用运输问题。
产销单位使用LINGO软件,编制程序如下:model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;v endors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I, J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I, J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost= 6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
LINGO教程(基本语法)

H
3
LINGO软件的安装
安装过程: 与LINDO for Windows类似.
安装文件20M多一点,需要接受安装协议、选择安装目录(缺省C:\LINGO9)。
安装完成前,在出现的对话框(如图)中选择缺省的建模(即编程)语言,系统推荐的 是采用LINGO。安装后可通过“LINGO|Options|File Format”命令修改缺省的建模 (即编程)语言。
H
7
在LINGO中使用LINDO模型
LINGO的界面
• LINGO软件的主窗口(用 户界面),所有其他窗口 都在这个窗口之内。
• 状态行(最左边显 示“Ready”,表示 “准备就绪”)
• 当前光标 的位置
• 模型窗口(Model Window),用于输入 LINGO优化模型(即 LINHGO程序)。
H
18
一个简单的LINGO程序
例 直接用LINGO来解如下二次规划问题:
Max98x127x72x120.3x1x22x22 1
s.t. x1x2100
2
x12x2
3
x1,x2 0 为整数
4
输入窗口如下:
H
19
程序语句输入的备注:
•LINGO总是根据“MAX=”或“MIN=”寻找目标函数,而除注释语句和TITLE语句外的其 他语句都是约束条件,因此语句的顺序并不重要 。
目前为止的 迭代次数
当前约束不满足的总量(不是不 满足的约束的个数):实数(即使 该值=0,当前解也可能不可行, 因为这个量中没有考虑用上下界 命令形式给出的约束)
H
14
• 运行状态窗口
扩展 的求 解器 (求解 程序) 状态 框
使用的特殊求解程序 : B-and-B (分枝定界算法) Global (全局最优求解程序) Multistart(用多个初始点求解的程序)
lingo入门

lingo入门lingo入门教程之一--- 初识lingoingo对于一些线性或者非线性的规划,优化问题非常有效首先介绍一下,在lingo中运行程序时出现的页面(在工具栏点击类似靶子一样的图标便可运行)Solver status:求解器(求解程序)状态框Model Class:当前模型的类型:LP,QP,ILP,IQP,PILP,PIQP,NLP,INLP,PINLP(以I开头表示IP,以PI 开头表示PIP)State:当前解的状态:"Global Optimum", "LocalOptimum", "Feasible", "Infeasible“(不可行), "Unbounded “(无界), "Interrupted“(中断), "Undetermined“(未确定)Object:解的目标函数值Infeasibility:当前约束不满足的总量(不是不满足的约束的个数):实数(即使该值=0,当前解也可能不可行,因为这个量中没有考虑用上下界命令形式给出的约束)Iteration:目前为止的迭代次数Extend solverstatus:扩展的求解器(求解程序)状态框Solver type:使用的特殊求解程序:Bestobj :目前为止找到的可行解的最佳目标函数值Objbound:目标函数值的界Steps:特殊求解程序当前运行步数:Active:有效步数Variables(变量数量):变量总数(T otal)、非线性变量数(Nonlinear)、整数变量数(Integer)。
Constraints(约束数量):约束总数(T otal)、非线性约束个数(Nonlinear)。
Nonzeros(非零系数数量):总数(Total)、非线性项系数个数(Nonlinear)。
GeneratorMemory Used (K) (内存使用量)ElapsedRuntime (hh:mm:ss)(求解花费的时间)运行之后页面介绍(这里的运行界面并不是与上面的运行过程中出现界面一致,即并非来自于同一个程序运行出现)第一行表示在经过457次迭代后得到局部最优解第二行给出该局部最优解的具体值下面给出取局部最优值时,x1 x2的具体取值这里求解的是局部最优解,如果想求出全局最优解,可以进行页面设置:lingo --> option --> global solver --> 勾选use globalsolver对于运行结果也可以另存为,格式一般为ldt,因为有时候对于求解一个问题,或许需要运行很久才可以得出结果,所以没必要每次为了看结果都运行,而是运行成功一次后便把结果保存下来注意事项LINGO总是根据“MAX=”或“MIN=”寻找目标函数;程序语句的顺序一般不重要,既可以随意调换;程序运用函数时都是以@开头;程序中的变量默认为非负数,想要改变变量类型必须有相应函数调整程序中变量不区分大小写;语句必须以分号结尾;注释以!开始,且注释语句后面必须也有分号,注释默认注释到第一个分号处,意思是分号前面会全部被注释掉。
lingo软件简单教程

下料方案
下料根数 方案 ⅠⅡⅢⅣⅤⅥ
料长
2.9 2.1 1.5 合计 料头
1
2
0
1
0
1
0
0
2
2
1
1
3
1
2
0
3
1
7.4 7.3 7.2 7.1 6.6 6.5
0 0.1 0.2 0.3 0.8 0.9
哇!这样分析就好建 立数学模型了!
设 xi 为选用方案i 下料的原材料根数,
其中i Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ.
运行状态窗口
求解 器(求 解程 序)状 态框
当前模型的类型 :LP,QP,ILP,IQP,PILP, PIQP,NLP,INLP,PINLP (以I开头表示 IP,以PI开头表示PIP)
解的目标函数值
当前解的状态 : "Global
Optimum", "Local Optimum", "Feasible", "Infeasible“(不可 行), "Unbounded“(无界), "Interrupted“(中断), "Undetermined“(未确定)
运 行该程序 后,立 即可以 得到最优 解为
x (0, 40, 30, 20, 0, 0) , 最 优 值 为
z 16 。即按方案 B 下料 40 根,方案 C 下料
目前为止的 迭代次数
当前约束不满足的总量(不是不 满足的约束的个数):实数(即使 该值=0,当前解也可能不可行, 因为这个量中没有考虑用上下界 命令形式给出的约束)
运行状态窗口
使用的特殊求解程序 : B-and-B (分枝定界算法) Global (全局最优求解程序) Multistart(用多个初始点求解的程序)
Lingo教程(一)
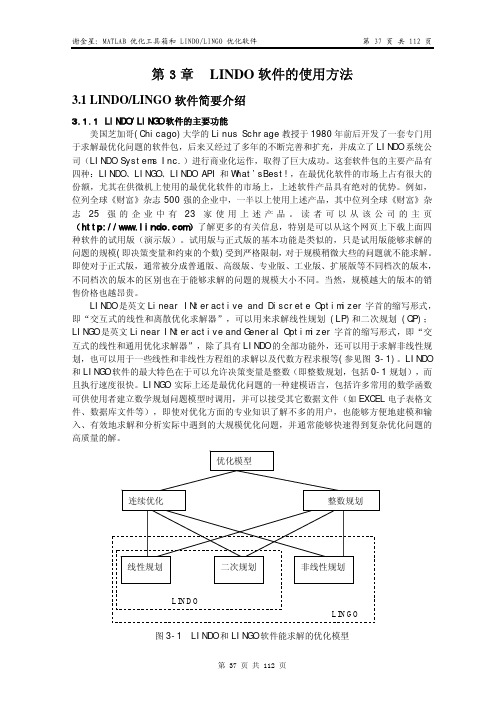
NLP
IP
分枝定界管理程序
ILPBiblioteka INLPIQP线性优化求解程序
非线性优化求解程序
图 3-2 LINDO/LINGO 软件的求解过程
第 38 页 共 112 页
谢金星:MATLAB 优化工具箱和 LINDO/LINGO 优化软件
第 39 页 共 112 页
2、识别优化模型的类型:对等式约束的预处理完成后,预处理程序能自动识别优化模型 的类型,从而决定下一步采用什么求解程序。如果模型是连续线性规划,下一步直接调用线 性优化求解程序;如果模型是连续非线性规划,下一步直接调用非线性优化求解程序;如果 模型是整数规划,则下一步直接调用分枝定界管理程序。
优化模型
连续优化
整数规划
线性规划
二次规划
非线性规划
LINDO
LINGO
图 3-1 LINDO 和 LINGO 软件能求解的优化模型
第 37 页 共 112 页
谢金星:MATLAB 优化工具箱和 LINDO/LINGO 优化软件
第 38 页 共 112 页
此外,LINDO 系统公司还提供了 LINDO/LINGO 软件与其它开发工具(如 C++和 Java 等语言)的接口软件 LINDO API(Application Program Interface),因此使 LINDO 和 LINGO 软件还能方便地融入到用户应用软件的开发中去。
线性优化求解程序通常使用单纯形算法,对高级版本的 LINDO/LINGO 软件,为了能解 大规模问题,也可以使用内点算法。非线性优化求解程序采用的是顺序线性规划法(Sequential Linear Programming, 简称 SLP),即通过迭代求解一系列线性规划来达到求解非线性规划的 目的。非线性优化求解程序也可以使用其他算法,如广义既约梯度法(Generalized Reduced Gradient, 简称 GRG),并可以自动选用多个初始点开始进行迭代,以便增加找到全局最优解 的可能性。分枝定界管理程序用于管理整数规划问题的分枝定界算法,在运行中还要不断调 用线性优化求解程序和非线性优化求解程序进行定界处理。
Lingo教程

L i n g o教程-CAL-FENGHAI.-(YICAI)-Company One1LINGO教程LINGO是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
?§1 LINGO快速入门安装:实验室的所有电脑都已经事先安装好了Lingo 8(或者9, 10,11)。
如果要在自己的电脑上安装这个软件,建议从网上下载一个破解版的,按照提示一步一步地安装完毕。
简单例子:当你在windows系统下开始运行LINGO时,会得到类似于下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口,建立的模型都要在该窗口内编码实现。
下面举两个例子。
例 1某工厂在计划期内要安排生产I、II两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表所示。
产品I产品II设备 1 28台时原材料A 4 016kg原材料B 0 412kg该工厂每生产一件产品I可获利2元,每生产一件产品II可获利3元,问应该如何安排生产计划使该厂获利最多我们用下面的数学模型来描述这个问题。
设x_1、x_2分别表示在计划期内产品I、II的产量。
因为设备的有效台时是8,这是一个限制产量的条件,所以在确定产品I、II的产量时,要考虑不超过设备的有效台时数,即可用不等式表示为x_1 + 2x_2 <=8同理,因原材料A、B的限量,可以得到以下不等式4x_1 <=164x_2 <=12该工厂的目标是在不超过所有资源限量的条件下,如何确定产量x_1、x_2以得到最大的利润。
若用z表示利润,这时z=2x_1+3x_2.综合上述,该计划问题可用数学模型表示为:目标函数 max z=2x_1+3x_2约束条件 x_1 + 2x_2 <=84x_1 <=164x_2 <=12x_1、x_2 >=0一般来说,一个优化模型将由以下三部分组成:1.目标函数(Objective Function):要达到的目标。
LINGO教程数据输入输出

10
Lingo程序exam0402.LG4 :
MODEL: SETS: MYSET / @FILE(myfile.ldt) / : @FILE(myfile.ldt); ENDSETS MIN = @SUM( MYSET( I):
• LINGO系统与EXCEL文件传递数据旳函数旳一般使用方法是
经过@OLE函数。 • 调用格式:
电子表格文件名
数据旳单元 范围
@OLE(spreadsheet_file [, range_name_list]) • 输入数据 :“属性(或变量)=@OLE(...)” • 输出数据 :“@OLE(...)=属性(或变量)”
LLIINNGGOO 教 程
LINGO软件与外部文件旳接口
1
LLIINNGGOO 教 程
经过文件输入输出数据
• 经过文件输入输出数据能够将LINGO程序和程 序处理旳数据分离开来。
• “程序和数据旳分离”是构造化程序设计、面 对对象编程旳基本要求。
• 实际问题一般需要处理大规模旳实际数据,而 这些数据一般都是在其他应用系统中生成旳, 或者已经存储在其他应用系统中旳某个文件或 数据库中。
LLIINNGGOO 教 程
LINGO与数据库互换数据
• 不同旳数据库有不同旳数据库管理系统(DBMS: DataBase Management System)
• WINDOWS环境下能够用ODBC(Open DataBase Connectivity)进行连接
• LINGO中能够使用函数@ODBC,格式为 :
数据单元定义措施:选择EXCEL旳菜单命令“插入|名称|定义” ,才谈出对话框中输入单元名称
lingo教程
LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO 中求解如下的LP 问题:0,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码: min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。
产销model :!6发点8收点运输问题; sets :warehouses/wh1..wh6/: capacity; vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume; endsets !目标函数;min =@sum (links: cost*volume); !需求约束;@for (vendors(J):@sum (warehouses(I): volume(I,J))=demand(J)); !产量约束;@for (warehouses(I):@sum (vendors(J): volume(I,J))<=capacity(I));!这里是数据; data :capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38; cost=6 2 6 7 4 2 9 5 4 9 5 3 8 5 8 2 5 2 1 9 7 4 3 3 7 6 7 3 9 2 7 1 2 3 9 5 7 2 6 5 5 5 2 2 8 1 4 3; enddata end然后点击工具条上的按钮 即可。
lingo入门教程

lingo入门教程Lingo是一种广泛应用于计算机编程和计算机科学领域的编程语言。
它是用于Adobe Director(一种多媒体应用程序)中的脚本语言,用于控制多媒体元素和动画。
Lingo的语法比较简单易懂,有助于创建交互式和多媒体项目。
下面是一些Lingo的基本概念和用法。
1. 变量(Variables): 在Lingo中,变量用于存储数据值。
变量可以是数字、文本或其他数据类型。
要创建变量,可以使用关键字`global`或`local`,后跟变量名和初始值(可选)。
例如:```global myVariable = 10local myText = "Hello World"```2. 条件语句(Conditional statements): 条件语句用于根据条件执行特定的代码块。
常用的条件语句有`if-then`和`if-then-else`。
例如:```if myVariable > 5 thenalert "Value is greater than 5"elsealert "Value is less than or equal to 5"end if```3. 循环(Loops): 循环用于重复执行一段代码块,直到满足指定条件为止。
Lingo提供了`repeat`和`repeat while`循环语句。
例如:```repeat with i = 1 to 5put iend repeat```4. 函数(Functions): 函数是一组预定义的代码,用于执行特定的任务。
Lingo提供了许多内置函数,如`alert`、`put`等。
您还可以创建自己的函数。
例如:```on multiplyNumbers(a, b)return a * bend multiplyNumbersput multiplyNumbers(2, 4) -- 输出8```这些只是Lingo的一些基本概念和用法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通过“LINGO | Generate | Display Model
(Ctrl +G)”命令可以看到完整的模型以及每行语 句对应的行号了。
可使用“ LINGO |
Picture ”命令检查模型中 的简单错误,该命令将 目标函数和约束表达式 中的非零系数通过列表 (或图形)显示出来。
用“LINGO | Solve
LINDO格式的模型文 件
· 后缀“ldt”表示LINGO数据 文件; · 后缀“ltf”表示LINGO命令 脚本文件; · 后缀“lgr”表示LINGO报告 文件; · 后缀“mps”表示MPS(数 学规划系统)格式的模型文 件; ·“*.*”表示所有文件。
2 用Lingo求解 二次规划( QP)模型
(4)初始段(INIT)——赋初值 (5)计算段(CALC)——预处理
例4.2 建筑工地的位置(用平面坐标a,b表示,距离单位:
km)及水泥日用量d(单位:t)由下表给出。目前有两 个临时料场位于P(5,1),Q(2,7),日储量各有 20t,求从A,B两料场分别向各工地运送多少吨水泥,使 总的吨公里数最小。两个新的料场应建在何处,节省的 吨公里数有多大?
优化模型
决策变量:
设每天用x1桶牛奶生产A1,用x2桶牛奶生产A2
目标函数:
设每天获利为z(元),x1桶牛奶生产3x1(kg)A1,获利 24×3x1,x2桶牛奶生产4x2(kg) A2,获利16×4x1,故 z=72x1+64x2.
约束条件:
原料供应:生产A1,A2的原料(牛奶)总量不得超过每 天的供应,即x1+x2≤50(桶); 劳动时间:生产A1,A2的总加工时间不得超过每天正式 工人总的劳动时间,即 12x1+8x2≤480(h); 设备能力:A1的产量不得超过甲车间设备每天的加工 能力,即3x1≤100; 非负约束:x1,x2均不能为负值。
Max
z 72 x1 64 x 2
l5
Z=0
x1 D Z=2400
z=c (常数) ~等值线
在B(20,30)点得到最优解 最优解一定在凸多边 形的某个顶点取得。
目标函数和约束条件是线性函数 可行域为直线段围成的凸多边形 目标函数的等值线为直线
Lingo优化模型
这是一个(连 续)线性规划(LP)问题
献给忠诚愿为数学付出的人
Come onபைடு நூலகம்!
Lingo 入门
广西大学数学与信息科学学院 韦琳娜 j_wln@
1 在Lingo中使用Lindo模型
Lindo与Lingo都是LINDO系统公司开发的专门用
于求解最优化问题的软件包。与Lindo相比, Lingo软件主要具有两大优点: (1)除具有LINDO的全部功能外,还可用于求解 非线性规划问题,包括非线性整数规划问题。 (2)LINGO包含了内置的建模语言,允许以简 练、直观的方式描述较大规模的优化问题,模型 中所需的数据可以以一定格式保存在独立的文件 中。
DEM——需求量,RP——正常生产的产量,OP——加班 生产的产量,INV——库存量 目标函数:
约束条件: 能力限制 RP(I)≤40,I=1,2,3,4 产品数量的平衡方程 INV(I)=INV(I-1)+RP(I)+OP(I)- DEM(I) I=1,2,3,4 INV(0)=10; 变量的非负约束
修改运行时的 内存限制
激活敏感 性分析
例3.1 一奶制品加工厂用牛奶生产A1,A2两种奶制品, 1桶牛奶可以在甲车间用12h加工成3kgA1,或者在乙车 间用8h加工成4kg A2。根据市场需求,生产出的A1,A2 全部能售出,且每千克A1获利24元,每千克A2获利16 元。现在加工厂每天能得到50桶牛奶的供应,每天正式 工人总的劳动时间为480h,并且甲车间的设备每天至多 能加工100kg A1,乙车间的设备的加工能力可以认为没 有上限限制(即加工能力足够大)。试为该厂制定一个 生产计划,使每天获利最大,并进一步讨论以下3个附 加问题: (1)若用35元可以买到1桶牛奶,是否作这项投资?若 投资,每天最多购买多少桶牛奶? (2)若可以聘用临时工人以增加劳动时间,付给临时 工人的工资最多是每小时几元? (3)由于市场需求变化,每千克A1的获利增加到30元, 是否应该改变生产计划?
1 在Lingo中使用Lindo模型
Lingo 9.0完全支持Lindo模型程序的书写格式。
在Lingo 9.0模型窗口中选择菜单命令 “File|Open (F3)” 注意 在Lingo 9.0以前的版本中(如Lingo 8.0), “File|Import LINDO File (F12)”命 令可以将Lindo模型文件转化成Lingo模型。 这个菜单命令的意思是“导入Lindo文件” (在LINGO 9.0中已无必要,所以该命令已 经被取消了)。
Lingo优化模型
集合
属性
集合的属性相当于以集合的元素为下标的数组
Lingo模型的基本要素
(1)集合段(SETS) (2)目标与约束段 (3)数据段(DATA):作用在于对集合的属性(数
组)输入必要的常数数据。格式为: attribute(属性)=value _list(常数列表); 常数列表(value _list)中数据之间可以用逗号“,” 分 开,也可以用空格分开(回车的作用也等价于一个 空 格) “变量名=?;” ——运行时赋值
工地的位置(a,b)及水泥日用量d
1
2 8.75 0.75 5
3 0.5 4.75 4
4 5.75 5 7
5 3 6.5 6
6 7.25 7.75 11
a b d
1.25 1.25 3
优化模型
记工地的位置为(ai,bi),水泥日用量为di, i=1,2,…,6;料场位置为(xj,yj),日储量为ej, j=1,2;从料场j向工地i的运送量为cij。 决策变量: 在问题(1)中,决策变量就是料场j向工地i的 运送量cij,该问题是个LP问题;在问题(2)中, 决策变量除了料场j向工地i的运送量cij,新建料场 位置(xj,yj)也是决策变量,该问题是个NLP问 题。 目标函数: f是总吨公里数(运量乘以运输距离)
结 论
应该批准用35元买1桶牛奶的投资,但每天
最多购买10桶牛奶。
可以用低于2元/h的工资聘用临时工人以增
加劳动时间,但最多增加53.3333h。
若每千克A1的获利增加到30元,则x1系数
变为30×3=90,在允许的范围内,所以不 应改变生产计划,但最优值变为 90×20+64×30=3720。
线性规划模型
A1,A2每公斤的获利是与各 自产量无关的常数 每桶牛奶加工出A1,A2的数量 和时间是与各自产量无关的常 数 A1,A2每公斤的获利是与相 互产量无关的常数 每桶牛奶加工出A1,A2的数量和 时间是与相互产量无关的常数 加工A1,A2的牛奶桶数是实数
模型求解
约 束 12 x 1 8 x 2 条 3 x 1 100 件
综上所述
max z=98 x1+277 x2-x12-0.3 x1 x2-2x22 (1.1) s.t. x1+x2≤100 x1≤2x2 x1,x2≥0 (1.2) (1.3) (1.4)
LINGO中的变量名
由字母和数字组成, 但必须以字母开头, 长度不能超过32个 字符(只能是英文字 符,不能含有中文字 符) 行号、“TITLE”语 句和注释语句是 LINGO中唯一可以 使用汉字字符的地方 行号必须以字母或下 划线开头; LINGO中不区分大 小写字母 LINGO中已假定所 有变量非负
(1)若用35元可以买到1桶牛奶,是否作这项投资?若投资,每天最多购买多 少桶牛奶? (2)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时 几元? (3)由于市场需求变化,每千克A1的获利增加到30元,是否应该改变生产计 划?
“LINGO| Solve”求解结果报告
“LINGO| Range”敏感性分析
例2.1 某厂生产的一种产品有甲、乙两个牌号,讨论在产
销平衡的情况下如何确定各自的产量,使总的利润最大。 所谓产销平衡指工厂的产量等于市场上的销量,没有卖不 出去的产品的情况。显然,销售总利润既取决于两种牌号 产品的销量和(单件)价格,也依赖于产量和(单件)成 本,按照市场经济规律,甲的价格p1固然会随其销量x1的 增长而降低,同时乙的销量x2的增长也会使甲的价格有稍 微的下降,可以简单地假设价格与销量成线性关系,即 p1=b1-a11x1-a12x2,b1,a11,a12>0,a11>a12;类似地,乙 的价格p2遵循同样的规律,即有p2=b2-a21x1-a22x2, b2,a21,a22>0,a22>a21.例如,假定实际中b1=100,a11=1, a12=0.1,b2=280;a21=0.2,a22=2。此外,假设工厂的生 产能力有限,两种牌号产品的产量之和不可能超过100件, 且甲的产量不可能超过乙的产量的两倍,甲乙的单件生产 成本分别是q1=2和q2=3(假定为常数)。求甲、乙两个牌号 的产量 x1,x2使总利润最大。
x1 , x 2 0 x 1 x 2 50
480
图解法
l1 : x1 x 2 50
l 2 : 12 x1 8 x 2 480
x2 A
l1 B l4 c l2 C Z=3600 l3
l 3 : 3 x1 100
l 4 : x1 0 , l 5 : x 2 0
0
目标 函数
(Ctrl +S)”命令来运 行这个程序。 (如果想要了解运行状 态窗口中各项的含义, 可先点击工具栏上的图 标 ,再点击运行状态 窗口,屏幕上自动弹出 运行状态窗口的帮助信 息。)
求解结果报告窗口
