重复测量的数据方差分析
心理学统计第五部分重复测量方差分析

心理学统计第五部分重复测量方差分析在心理学研究中,有时候研究者需要评估一个或多个因素对参与者的多个测量结果的影响。
这种情况下,重复测量方差分析(Repeated Measures Analysis of Variance,简称为RM ANOVA)是一种常用的统计方法。
重复测量方差分析是一种比较多个组内变量平均数差异的方法,它比较了每个组内变量的差异以及每个组间变量的差异。
与传统的方差分析不同,重复测量方差分析考虑了相同参与者在不同条件下的多次测量结果,因此能够更准确地评估因素对测量结果的影响。
首先,我们需要明确的是,在重复测量方差分析中,我们的因变量是一个连续的测量结果,而自变量是一个或多个处理条件。
例如,我们可能想要评估一个新药物是否对人们的注意力产生影响,我们可以将注意力测量结果作为因变量,而药物与安慰剂作为自变量。
重复测量方差分析有三个基本的假设。
首先,我们假设不同处理条件下的测量结果的总平均数相等,即每组的平均值相等。
其次,我们假设各个处理条件下的测量结果有一定的方差。
最后,我们假设不同处理条件下的测量结果相互独立。
重复测量方差分析有一些优点和注意事项。
首先,这种方法可以减少误差变异,因为我们可以通过比较同一参与者在不同条件下的测量结果来消除参与者间的差异。
其次,重复测量方差分析可以提高统计功效,以便检测到小的差异。
然而,我们需要注意确保多次测量结果之间的独立性,以及在数据分析中正确处理可能的违反方差齐性和正态分布的情况。
总结起来,重复测量方差分析是一种常用的心理学统计方法,用于评估一个或多个因素对参与者的多个测量结果的影响。
它是一种有效的方法,可以提供关于不同处理条件之间差异的信息。
在分析数据时,我们需要检查数据的正态性和方差齐性,并使用适当的修正方法来应对违反这些假设的情况。
重复测量方差分析为心理学研究提供了一个强有力的统计工具,使得研究者能够更好地理解和解释影响行为和心理过程的因素。
方差分析(重复测量)

诱导
患者
方法
序号
T0
t3
A
1
120
A
2
118
A
3
119
A
4
121
A
5
127
B
6
121
B
7
122
B
8
128
B
9
117
B
10
118
C
11
131
C
12
129
C
13
123
C
14
123
C
15
125
麻醉诱导时相
t1 t2 t4
108
112
120
117
109
115
H uy nh-F eldt
2336.453
Low er-bound
2336.453
B * G RO U PS phericity A ssum ed 837.627
G reenhouse-G eisser 837.627
H uy nh-F eldt
837.627
Low er-bound
837.627
T es ts of Within-Sub je cts Effe cts
M easure: M E A S U RE _1
S ource
Ty pe III Sum of S quares
B
S phericity A ssum ed 2336.453
G reenhouse-G eisser 2336.453
Within SubjectsMEfafuecthly 's WC hi-Square
重复测量方差分析

重复测量方差分析1. 引言重复测量方差分析(Repeated Measures Analysis of Variance, RM-ANOVA)是一种统计方法,用于分析在不同时间点或不同处理条件下对同一组个体或样本进行多次测量的数据。
通过比较不同时间点或处理条件下的测量结果,我们可以确定是否存在显著的差异,并了解时间或处理对测量结果的潜在影响。
本文档将介绍重复测量方差分析的基本原理、假设条件、计算方法和结果解读,并提供使用Markdown格式编写重复测量方差分析报告的示例。
2. 基本原理重复测量方差分析的基本原理是基于方差分析(ANOVA)方法,但相对于普通的单因素方差分析,重复测量方差分析考虑了测量数据间的相关性。
在重复测量设计中,同一个个体或样本在不同时间点或处理条件下进行多次测量,因此测量数据之间存在一定的相关性。
为了解决相关性的问题,重复测量方差分析使用了独特的矩阵分解方法,将总体方差分解为组内方差和组间方差。
通过计算组间方差与组内方差的比值,可以判断不同时间点或处理条件下的测量结果是否存在显著差异。
3. 假设条件在进行重复测量方差分析之前,需要满足以下假设条件:•正态性假设:每个时间点或处理条件下的测量结果应当服从正态分布。
•同方差性假设:每个时间点或处理条件下的测量结果应具有相同的方差。
•相关性假设:各个时间点或处理条件下的测量结果之间应具有一定的相关性。
如果数据不满足正态性、同方差性或相关性假设,需要采取适当的数据转换、方差齐性检验或相关性分析等方法进行处理。
4. 计算方法重复测量方差分析的计算方法可以通过计算F统计量来进行。
具体步骤如下:步骤1:计算总体方差首先计算总体方差SSTotal,即测量数据的总体波动情况。
步骤2:计算组间方差然后计算组间方差SSBetween,即不同时间点或处理条件下的测量结果之间的差异。
步骤3:计算组内方差接下来计算组内方差SSWithin,即测量数据在同一个时间点或处理条件下的波动情况。
重复测量资料的方差分析

ˆ ˆ ˆ2 2k 式中中的 s 是协方差矩阵中的第 k 行第 l 列元素, s = ( = (∑ s ) / a 是主对角线元素的平均值, s = (∑ s ) / a 是第 k 行的平均值。
ε ˆ 的取值在 1.0 与 1/(a -1)之间。
ε =ˆˆ ˆ分子自由度ν 1 =ν 1 ⨯ε 分母自由度ν 2 =ν 2 ⨯ε 。
具体计算时可用或ε 代替。
用 调整所得的ν 1 及ν 2 的 F 值查临界值表,得 F α (ν ' ,ν ' ) 。
由于ε≤ 1.0,所以调整后的重复测量资料方差分析重复测量(repeated measure )是指对同一观察对象的同一观察指标在不同时间 点上进行的多次测量,用于分析该观察指标在不同时间上的变化特点。
这类测量 资料在临床和流行病学研究中比较常见,例如,为研究某种药物对高血压病人的 治疗效果,需要定时多次测量受试者的血压,以分析其血压的变动情况。
1、 重复测量资料方差分析中自由度调整方法1.调整系数 ε 的计算有两个调整系数,第一个是 Greenhouse-Geisser 调整系数 ε (G - G ε ) ,计算 公式为ε =a 2(s kl - s 2) 2(a -1)[∑ ∑ (s kl ) 2 - (2a )(∑ (s 2 ) 2 ) + a 2 (s 2 ) 2 ]k l kkl 2 2 ∑∑ s k l 2 kl ) / a 2 是所有元素的总平均值, s 2 kk l2 2 ll2 2 kkll 第 2 个系数是 Huynh-Feldt 调整系数 ε (H - F ε ) 。
研究表明,当 ε 真值在 0.7 以上时,用 ε 进行自由度调整后的统计学结论偏于保守,故 Huynh 和 Feldt 提 出用平均调整值 ε 值进行调整。
ε 值的计算公式为ng (a - 1)ε - 2 (a - 1)[(n - 1)g - (a - 1)ε ]式中中的 g 是对受试对象的某种特征(如年龄或性别)进行分组的组数,n 是每组的观察例数。
重复测量设计的方差分析

u 随机区组设计 ●处理因素在区组内随机分配; 每个区组内实验单位彼此独立。
第二节
重复测量数据 的两因素两水平分析
高血压患者治疗前后的舒张压(mmHg)
处理组 a1
对照组(安慰剂组)a2
顺序号 治疗前 治疗后 合计(Mj) 顺序号 治疗前 治疗后 合计(Mj)
●处理因素在区组内随b机1分配; b2
118
124
-6
132
122
10
134
132
2
114
96
18
118
124
-6
128
118
10
118
116
2
132
122
10
120
124
-4
134
128
6
1248
1206
42
124.8
120.6
4.2
7.90
9.75
8.02
三、重复测同相量一关受的设试。计者的(单血样因重素复测)量的结果是高度
受试者血糖浓度(mmol/L)
214
17
118
明“服8药”有效; 138
122
260
18
132
重复测量设计与随机区组设计区别
降压药9物与安慰剂间疗12效6差别无统计学1意08义;
234
19
120
注若意球事 对1项称0 1性、质单不因能素满实足1验2,重4则复方测差量分数析据的1分F0析值6是偏大的,2增3大0了犯第一类错2误0 的概率。 134
重复测量设计的方差分析
讲课内容
第一节 重复测量资料的数据特征 第二节 重复测量数据的两因素两水平分析
方差分析三重复测量资料的方差分析

缺点
实验成本高
需要进行多次测量,增加了实验成本和时间。
数据处理复杂
三重复测量资料的方差分析需要处理大量的数据,并且需要进行复 杂的统计分析,对数据分析的要求较高。
样本量要求高
为了获得更可靠的结果,需要较大的样本量,增加了实验难度。
06
三重复测量资料的方差分析的未来 发展
研究方向
1 2
拓展应用领域
通过比较组间方差和组内 方差的差异,判断各组之
间的差异是否显著。
01
02
03
04
05
1. 建立假设
确定要检验的原假设(H0) 和备择假设(H1)。
3. 计算方差
根据数据计算组间方差和 组内方差。
5. 解读结果
根据统计结果解释实验结 果,确定处理因素对实验 结果的影响是否显著。
03
三重复测量资料的方差分析
感谢您的观看
THANKS
5. 结果解释
根据模型的拟合结果, 解释三重复测量资料 的变化情况,并给出 相应的结论和建议。
04
三重复测量资料的方差分析实例
实例一:药物效果研究
总结词
药物效果研究是三重复测量资料方差分析的重要应用领域之一,主要用于评估药物治疗前后的效果差 异。
详细描述
在药物效果研究中,通常会对同一组受试者在药物治疗前、治疗中、以及治疗后的不同时间点进行测 量,以评估药物对受试者的影响。通过三重复测量资料的方差分析,可以比较不同时间点上受试者的 生理指标、症状改善程度等方面的差异,从而为药物的疗效提供科学依据。
02
方差分析概述
方差分析的定义
方差分析(ANOVA)是一种统计方 法,用于比较两个或多个组之间的平 均值差异是否显著。
重复测量数据方差分析

74.4
77.0
75.2 77.4
82.6
80.4
81.2 79.6
68.6
65.0
63.2 63.4
79.0
77.0
73.8 72.5
69.4
66.8
64.4 60.8
72.6
71.0
68.2 70.2
72.4
72.6
72.8 72.6
75.6
73.4
73.4 72.2
80.0
78.0
76.4 74.8
7.90
9.75 8.02
经检验处理组与对照组的差值 d 方差不齐(F S12 / S22 6.58 , P 0.01),不符合两均数比较 t 检验的前提条件。
设置对照旳前后测量设计
前后测量数据间存在明显差别时,并不能阐明这种差 别是由前后测量之间施加旳处理所产生,还是因为存 在于前后两次测量之间旳时间效应所致。
比较
表9-2 两种措施对乳酸饮料中脂肪含量旳测定成果(%)
编号
1 2 3 4 5 6 7 8 9 10
哥特里-罗紫法
0.840 0.591 0.674 0.632 0.687 0.978 0.750 0.730 1.200 0.870
脂肪酸水解法
0.580 0.509 0.500 0.316 0.337 0.517 0.454 0.512 0.997 0.506
受试 对象j
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
剂型 k
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
服药后测定时间i(周)
重复测量方差分析

重复测量方差分析1.理论重复测量:指对同一批研究对象先后施加不同的实验(或在不同的场合)进行测量。
重复测量方差分析:研究在不同的实验或(不同场合)之间是否有差异,或条件和处理间交互项是否有差异。
变量应满足:因变量为连续型随机变量,因素为分类变量。
正态性:不同条件下的个体取自相互独立的随机样本,其总体需满足近似正态分布。
方差齐性:不同条件下的总体方差相等。
满足球形假设:因变量的方差-协方差矩阵满足球形交互项项两两比较结果需要借助语法。
图1交互项两两比较语法2.重复测量方差分析操作步骤操作步骤第一步:首先将数据导入spss中并进行赋值,后点击分析、一般线性模型、重复测量。
图2重复测量方差分析操作步骤第一步操作步骤第二步:进入图中对话框后首先定义主体因子名及实验次数点击添加,后添加测量名称(先在测量名称框中输入名称、后点击添加)点击定义。
图3定义因子操作步骤第三步:定义完成后进入图中对话框后、先将对应的变量放入对应的变量框中,点击事后比较将因子框内的因子放入事后比较框中,勾选假定等方差(LSD)、不假定等方差(塔姆黑尼),点击继续。
图4事后比较勾选操作步骤第四步:点击选项将因子框中的因子放入平均值框中,勾选描述统计、齐性检验,点击继续、确定。
图5选项勾选然后重复测量方差分析的主体间因子、描述统计、等同性检验、主体内效应检验、主体因子事后比较结果就出来了。
图6描述统计结果图7主体内效应操作步骤第一步:点击分析、一般线性模型、重复测量。
图8操作步骤第一步第二步:点击定义。
图9点击定义第三步:进入图中对话框后,点击粘贴。
图10点击粘贴第四步:进入语法编辑窗:在红色框内放入对应的语法(可参考图中语法进行编辑),后选中语法点击红色框内的绿色箭头。
图11语法编写5.交互项结果然后重复测量方差分析的主体因子和因子交互项的主体内因子、主体间因子、描述统计、博克斯等同性酱油结果就出来了。
图12描述统计主体内效应检验、主体内对比检验、误差方差的莱文等同性检验。
第十四章 重复测量的资料方差分析

编号
治疗前
治疗后
差值
1
130
114
16
2
124
110
14
3
136
126
10
4
128
116
12
5
122
102
20
6
118
100
18
7
116
98
18
8
138
122
16
9
126
108
18
10
124
106
18
X
126.2
110.2
16.0
S
7.08
9.31
3.13
比较
表3-3 两种方法对乳酸饮料中脂肪含量的测定结果(%)
SS
MS
F
P
总变异
14 0.5328
处理间
2 0.2280 0.1140 11.88 <0.01
区组间
4 0.2284 0.0571 5.95 <0.05
误差
8 0.0764 0.0096
2.重复测量设计区组内即同一受试者 的重复测量数据是高度相关的。例如,计 算表 12-3 中各时间点数据间的相关系数 结果见表 12-6。
表12-4 表 12-3数据的方差分析表
变异来源 自由度 SS MS F
P
总变异
31 5.751
区组(受试者)
7
2.828 0.361 27.77 <0.01
放置时间
3
2.959 0.986 75.85 <0.01
误差
21 0.264 0.013
表12-7 表12-3数据“球对称”检验结果
单因素重复测量方差分析

单因素重复测量方差分析单因素重复测量方差分析是统计学中常用的一种方法,用于比较在同一组个体上进行多次测量所得到的数据之间的差异。
本文将从介绍单因素重复测量方差分析的基本概念、假设条件、计算方法和结果解读等方面进行详细阐述。
一、基本概念单因素重复测量方差分析是通过比较同一组个体在不同时间点或条件下的多次测量结果,判断这些测量结果是否存在显著差异。
在进行单因素重复测量方差分析时,通常需要有一个待测因素(也称为处理因素),以及一个或多个水平(也称为处理水平)。
二、假设条件在进行单因素重复测量方差分析时,需要满足以下假设条件:1. 观测值之间相互独立;2. 测量误差服从正态分布;3. 同方差性:不同处理水平下的观测值方差应相等。
三、计算方法进行单因素重复测量方差分析时,需要先计算各个处理水平下的观测值的均值和总平均值,并构建方差分析表。
方差分析表包含总平方和、处理平方和、误差平方和、总均方、处理均方、误差均方和F值等信息。
通过比较F值与临界值(一般为0.05),来判断各处理水平之间是否存在显著差异。
四、结果解读在进行单因素重复测量方差分析后,如F值小于临界值,则说明各处理水平之间没有显著差异,即处理因素对测量结果没有影响;反之,如F值大于临界值,则可以认为各处理水平之间存在显著差异,即处理因素对测量结果有影响。
需要注意的是,在进行单因素重复测量方差分析时,存在一种可能的误解,即称F值大于临界值就代表存在显著差异。
事实上,F值较大仅表明处理因素对测量结果有影响,而具体哪些处理水平之间存在显著差异,还需要进行进一步的事后多重比较。
五、应用案例为了更好地理解单因素重复测量方差分析的应用,下面举一个简单的应用案例来说明。
假设我们要比较三种不同肥料对植物生长的影响,我们在相同的土壤条件下,随机选取了10个种子进行种植,并分别施加三种不同的肥料。
每天测量植物的生长量,连续记录了10天。
现在我们想知道这三种肥料对植物生长是否有影响。
第三讲重复测量资料的方差分析
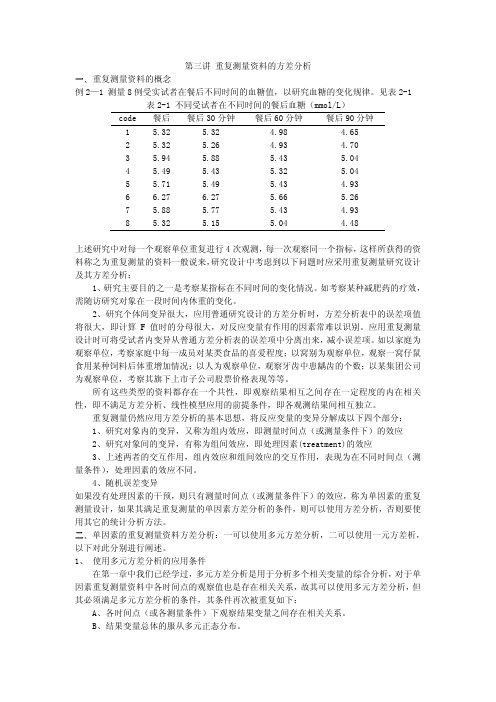
第三讲 重复测量资料的方差分析一、重复测量资料的概念例2—1 测量8例受实试者在餐后不同时间的血糖值,以研究血糖的变化规律。
见表2-1 表2-1 不同受试者在不同时间的餐后血糖(mmol/L)code 餐后 餐后30分钟 餐后60分钟 餐后90分钟1 5.32 5.32 4.98 4.652 5.32 5.26 4.93 4.703 5.94 5.88 5.43 5.044 5.49 5.43 5.32 5.045 5.71 5.49 5.43 4.936 6.27 6.27 5.66 5.267 5.88 5.77 5.43 4.938 5.32 5.15 5.04 4.48上述研究中对每一个观察单位重复进行4次观测,每一次观察同一个指标,这样所获得的资料称之为重复测量的资料一般说来,研究设计中考虑到以下问题时应采用重复测量研究设计及其方差分析:1、研究主要目的之一是考察某指标在不同时间的变化情况。
如考察某种减肥药的疗效,需随访研究对象在一段时间内休重的变化。
2、研究个体间变异很大,应用普通研究设计的方差分析时,方差分析表中的误差项值将很大,即计算F值时的分母很大,对反应变量有作用的因素常难以识别。
应用重复测量设计时可将受试者内变异从普通方差分析表的误差项中分离出来,减小误差项。
如以家庭为观察单位,考察家庭中每一成员对某类食品的喜爱程度;以窝别为观察单位,观察一窝仔鼠食用某种饲料后体重增加情况;以人为观察单位,观察牙齿中患龋齿的个数;以某集团公司为观察单位,考察其旗下上市子公司股票价格表现等等。
所有这些类型的资料都存在一个共性,即观察结果相互之间存在一定程度的内在相关性,即不满足方差分析、线性模型应用的前提条件,即各观测结果间相互独立。
重复测量仍然应用方差分析的基本思想,将反应变量的变异分解成以下四个部分:1、研究对象内的变异,又称为组内效应,即测量时间点(或测量条件下)的效应2、研究对象间的变异,有称为组间效应,即处理因素(treatment)的效应3、上述两者的交互作用,组内效应和组间效应的交互作用,表现为在不同时间点(测量条件),处理因素的效应不同。
定量数据重复测量的方差分析

定量数据重复测量的方差分析引言。
在科学研究中,我们经常需要对同一组对象进行多次测量,以便得到更加准确和可靠的数据。
在这种情况下,我们需要进行方差分析来确定测量结果的差异是否显著。
本文将介绍定量数据重复测量的方差分析方法及其应用。
一、方差分析的基本原理。
方差分析是一种用于比较两个或多个组之间差异的统计方法。
在定量数据重复测量的情况下,我们通常使用重复测量方差分析(Repeated Measures ANOVA)来分析数据。
重复测量方差分析可以用于比较同一组对象在不同时间点或不同条件下的测量结果之间的差异。
重复测量方差分析的基本原理是利用组内变异和组间变异之间的比较来判断测量结果的差异是否显著。
组内变异是指同一组对象在不同时间点或不同条件下的测量结果之间的差异,而组间变异是指不同组对象之间的测量结果之间的差异。
通过比较组内变异和组间变异的大小,我们可以判断测量结果的差异是否由于不同时间点或不同条件引起。
二、重复测量方差分析的假设。
在进行重复测量方差分析时,我们需要满足以下几个假设:1. 同质性方差假设,不同组对象在不同时间点或不同条件下的测量结果的方差相等;2. 正态分布假设,测量结果符合正态分布;3. 独立性假设,不同组对象在不同时间点或不同条件下的测量结果相互独立。
如果以上假设不成立,我们需要采取相应的方法来处理数据,例如进行变换或者使用非参数方法进行分析。
三、重复测量方差分析的步骤。
进行重复测量方差分析的步骤如下:1. 确定研究设计,确定需要比较的组别以及重复测量的时间点或条件;2. 收集数据,收集不同组对象在不同时间点或不同条件下的测量结果;3. 检验假设,对数据进行正态性检验和同质性方差检验,如果假设不成立,则需要进行相应的数据处理;4. 进行方差分析,利用统计软件进行重复测量方差分析,得出组间变异和组内变异的比较结果;5. 进行事后检验,如果方差分析结果显著,我们需要进行事后检验来确定具体哪些组别或时间点之间存在显著差异;6. 结果解释,根据方差分析和事后检验的结果,对测量结果的差异进行解释和讨论。
重复测量资料的方差分析

重复测量资料的方差分析什么是重复测量资料?重复测量资料是指在同一物件上,经过多次测量所得的一组数据。
它可以用于评估测量装置或人员的准确度和可靠性,或对同一样品在不同时间或不同实验条件下的实验测量结果进行比较。
方差分析方差分析是一种分析比较不同组别之间差异的统计方法,它可以判断一个因素对实验结果的影响是否显著。
在重复测量资料的分析中,方差分析可以用于确定是否存在个体之间的显著差异。
重复测量资料的方差分析方法在重复测量资料的方差分析中,采用的是双因素重复测量资料的方差分析方法。
这种方法包括两个因素:测量因素和重复因素。
测量因素是要分析的因素,重复因素是指对同一物件进行多次测量,每次测量之间都存在一定程度的差异,重复因素会产生误差。
以下是双因素重复测量资料的方差分析步骤:步骤一:确定方差来源方差来源包括测量因素、重复因素以及随机误差。
其中测量因素和重复因素可以用于计算方差,而随机误差则不能。
步骤二:计算平方和平方和是指每个因素所产生的方差之和。
计算平方和的公式如下:•总平方和(TSS):TSS=SSA+SSB+SSAB+SSE•因素A的平方和(SSA):SSA=n∑(yij-y··)2/a-1•因素B的平方和(SSB):SSB=n∑(yij-y··)2/b-1•因素AB的平方和(SSAB):SSAB=n∑(yij-yi·-y·j+y··)2/(a-1)(b-1)•误差平方和(SSE):SSE=TSS-SSA-SSB-SSAB其中,n是每组数据的测量次数,a和b是因素A和因素B的水平数,yij是第i个个体在第j次测量中的数据,yi·是第i个个体在所有测量中的均值,y·j是所有个体在第j次测量中的均值,y··是所有测量数据的均值。
步骤三:计算自由度自由度是指某一因素或误差中可变的部分,计算自由度的公式如下:•总自由度(DFS):dfs=nab-1•因素A的自由度(DFA):DFA=a-1•因素B的自由度(DFB):DFB=b-1•因素AB的自由度(DFAB):DFAB=(a-1)(b-1)•误差自由度(DFE):DFE=dfs-DFA-DFB-DFAB步骤四:计算均方值均方值是平方和与自由度的比值,计算均方值的公式如下:•因素A的均方值(MSA):MSA=SSA/DFA•因素B的均方值(MSB):MSB=SSB/DFB•因素AB的均方值(MSAB):MSAB=SSAB/DFAB•误差的均方值(MSE):MSE=SSE/DFE步骤五:计算F值F值是均方值之比,计算F值的公式如下:•因素A的F值(FA):FA=MSA/MSE•因素B的F值(FB):FB=MSB/MSE•因素AB的F值(FAB):FAB=MSAB/MSE步骤六:计算P值P值是指一个F分布的概率值,计算P值需要使用F分布表。
重复测量方差分析

SPSS学习笔记之——重复测量的多因素方差分析1、概述重复测量数据的方差分析是对同一因变量进行重复测量的一种试验设计技术。
在给予一种或多种处理后,分别在不同的时间点上通过重复测量同一个受试对象获得的指标的观察值,或者是通过重复测量同一个个体的不同部位(或组织)获得的指标的观察值。
重复测量数据在科学研究中十分常见。
分析前要对重复测量数据之间是否存在相关性进行球形检验。
如果该检验结果为P﹥0.05,则说明重复测量数据之间不存在相关性,测量数据符合Huynh-Feldt条件,可以用单因素方差分析的方法来处理;如果检验结果P﹤0.05,则说明重复测量数据之间是存在相关性的,所以不能用单因素方差分析的方法处理数据。
在科研实际中的重复测量设计资料后者较多,应该使用重复测量设计的方差分析模型。
球形条件不满足时常有两种方法可供选择:(1)采用MANOVA(多变量方差分析方法);(2)对重复测量ANOVA检验结果中与时间有关的F值的自由度进行调整。
2、问题新生儿胎粪吸入综合征(MAS)是由于胎儿在子宫内或着生产时吸入了混有胎粪的羊水,从而导致呼吸道和肺泡发生机械性阻塞,并伴有肺泡表面活性物质失活,而且肺组织也会发生化学性炎症,胎儿出生后出现的以呼吸窘迫为主,同时伴有其他脏器受损现象的一组综合征[11]。
血管内皮生长因子(vascular endothelial growth factor,VEGF)是一种有丝分裂原,它特异作用于血管内皮细胞时,能够调节血管内皮细胞的增殖和迁移,从而使血管通透性增加。
而本实验旨在通过观察分析给予外源性肺表面活性物质治疗前后胎粪吸入综合征患儿血清中VEGF的含量变化,评价药物治疗的效果。
将收治的诊断胎粪吸入综合症的新生儿共42名。
将患儿随机分为肺表面活性物质治疗组(PS组)和常规治疗组(对照组),每组各21例。
PS组和对照组两组所有患儿均给予除用药外的其他相应的对症治疗。
PS组患儿给予牛肺表面活性剂PS70mg/kg治疗。
重复测量设计资料的方差分析SPSS操作

8.000 104.703 19.101
2.000 418.813 19.101
48
5.482
32. 577
8.077
48. 000
5.482
12. 000
21. 927
不同诱导时相之间收缩
Sig. .0ቤተ መጻሕፍቲ ባይዱ0
压存在差别,
.000
.000 F=106.558,P<0.01;
.000
.000
.000 诱导时相与诱导方法之
Corre cted
t ests
are
b.
满足了协方差矩阵
Design: Inte rcept+GROUP Within Subjects Design: FACTOR1
球对称的条件,不 需对结果进行校正;
Te sts of Within-Subje cts Effect s
Measure: MEASURE_1
患者序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
T 0
T 1
麻醉诱导时相
T 2 T 3
120
108
112
120
118
109
115
126
119
112
119
124
121
112
119
126
127
121
127
133
121
120
118
131
122
121
119
129
128
129
126
Lower-bound
263. 120
df Mean Square F
重复测量资料的方差分析

浙江大学医学院流行病与卫生统计学教研室 沈毅
协方差阵的球形性质是指该矩阵主对角线元素(方差)
相等、非主对角线元素(协方差)为零。用Mauchly氏法
检验协方差阵的球形性质。Mauchly氏检验的 P值若大于
研究者所选择的显著性水准α时,说明协方差阵的球形性
质得到满足。否则,必须对与时间有关的F统计量的分子、
(1)Greenhouse-Geisser调整系数
(G
G
)
为:
a2 (sk2k s2 )2
(a
1)
k
l
(sk2l )2 (2a)(
k
(sk2
)2
)
a
2
(
s
2
)2
(10 2)
式(10-2)中的 sk2l 是矩阵(10-1)中第k行第l列元素,
浙江大学医学院流行病与卫生统计学教研室 沈毅
SAS程序给出本例的协方差阵Mauchly球形性检验的结果为P
=0.1628,故不必进行自由度的调整。查F界值表得:F0.01(3,24) =3.01,F0.01(3,24)=4.72。本例处理因素的F值为8.22,大于 F0.01(3,24),故拒绝无效假设,说明处理因素间的差别具有统计 学意义。
当 1.0时,取=1.0。
浙江大学医学院流行病与卫生统计学教研室 沈毅
2.调整规则 只对具有重复测定性质的时间效应的
F值的自由度,和处理时间交互作用的F值的自由度进行
调整。由于F值有两个自由度v1和v2,调整的分子自由
度
v1' v1× ,
,分母自由度 v2'
重复测量方差分析报告

前后测量设计和配对设计的区别
配对设计可随机分配同一对子的试验单位,同 期观察试验结果,而前后测量设计则不能同期 观察试验结果;
配对设计比较两种处理的差别,前后测量设计 比较某种处理前后的差别;
前后测量设计在推断处理是否有效时需假定 测量时间对观察结果没有影响.
前后测量设计和配对设计的区别
配对设计要求每组观察结果和差值相互独立, 且差值服从正态分布,前后测量设计差值通常 与前一次观察存在相关关系;
重复测量设计
当前后测量设计的重复测量次数≥3时,则所得 观察结果称为重复测量数据.
表12-5 20例患者手术前后症状评分
处理 分组
A A …… B B
手术 前
0.60 1.42 …… 2.71 1.80
10天 0.67 3.40 …… 2.04 1.40
手术后 2月 4月 6月 2.84 2.10 2.00 4.10 2.92 2.65 …… …… …… 2.61 2.17 2.15 1.00 1.30 2.40
18 128.633
Sig. .000
.226
处理<A>的检验结果,F=1.574,P=0.226 组间误差项
表12-10 重复测量设计两因素两水平的方差分析表
变异来源 组间(对象)
干预(A) 组间误差 组内(重复) 时间(B) AB交互作用 组内误差
自由度 19 1 18 20 1 1 18
SS MS 2517.9 202.5 202.5 2314.5 128.6 1702.0 1020.1 1020.1 348.1 348.1 333.8 18.54
5
4 0
45
90
135
放置时间(分钟)
重复测量方差分析

课件
53
表9-13
课件
54
可以看出重复测量资料中同一受试对象 (看成区组)的数据高度相关
无论哪位受试对象服用曲明片剂或是胶囊,其服药后8 周、16周和24周的体重均和前面时间点(含服药前 的0周)的体重相关。不同时点数据其相关性较强。
课件
55
重复测量资料方差分析的基本步骤 分为三步:
课件
56
⑵计算检验统计量:使用统计软件进行计算结果如下 :
1 50.10 58.20 64.50 2 47.80 48.50 62.40 3 53.10 53.80 58.60 4 63.50 64.20 72.50 5 71.20 68.40 79.30 6 41.40 45.70 38.40 7 61.90 53.00 51.20 课8件 42.20 39.80 46.2015
常用的调整方法
课件
30
4. 计算F值
时间点间 误差
课件
31
球对称性通常采用 Mauchly’s test检验来判断
其结果按α=0.1水准检验,不满足球对称性, 对系数ε进行校正,其结果如下:
结果显示:治疗前与治疗后不课同件 时间转氨酶平均水平不同。32
5.单组重复测量方 差分析数据结构
6.基本程序格式
run; 提示:显示不同水平比较时的结构
课件
48
显示不同水平比较时的结构
课件
49
当兴趣在于1个水平与以后的所有水平 的比较时,可选helmert
………….; repeated time helmert /printm summary ; ………….;
课件
50
小结: 两两比较参数选择
Printe 产生Mauchly’s 的χ2值和P值 Printm 产生不同水平比较结构阵
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 完全随机设计资料的方差分析 二、 随机区组设计资料的方差分析 三、 析因设计资料的方差分析 四、重复测量资料的方差分析 五、 多个样本均数的两两比较 六、方差分析前提条件和数据转换
• 学习要求:
1.掌握方差分析的基本思想; 2.掌握单因素、双因素方差分析的应用条件、
意义及计 算方法; 3.熟悉多个均数间两两比较的意义及方法; 4.了解方差齐性检验和t’检验的意义及方法; 5.熟悉变量变换的意义和方法。
两实验单位
可随机分配
N
观测时间
同期
两时间点
试验数据与差值关系 独立
N
分析指标
平均差值 平均差值、相关回归
推断
组间差别
前后差别
二、设立对照的前后测量设计
表 9-1 中高血压患者治疗后的舒张压平均下 降 了 16 mmHg , 虽 然 经 配 对 t 检 验 : t 16.18, P 0.01 ,也未必能说明治疗有效,因为 住院休息、环境和情绪的改变同样可以使血压恢 复平稳。因此,确定疗效的前后测量设计必须增 加平行对照,如将 20 位轻度高血压患者随机分 配到处理组和对照组,试验结果见表 9-3。
2. 配对 t 检验要求同一对子的两个实验 单位的观察结果分别与差值相互独立,差值服 从正态分布。
前后测量设计前后两次观察结果通常与 差值不独立,大多数情况第一次观察结果与差 值存在负相关的关系,如表9-1中,治疗前舒 张压与差值的相关系数为-0.602。
3. 配对设计用平均差值推论处理的作用,而 前后测量设计除了分析平均差值外,还可进行相 关回归分析。
表9-3 高血压患者治疗前后的舒张压(mmHg)
顺序号
处理组
顺序号
对照组
治疗前 治疗后 差值 (d )
治疗前 治疗后 差值 (d )
1 130
114
2 124
110
3 136
126
4 128
116
5 122
102
6 118
100
7 116
98
8 138
122
9 126
108
10 124
106
11
118
124
12
132
122
13
134
132
14
114
96
15
118
124
16
128
118
17
118
116
18
132
122
19
120
124
20
134
128
合 计 1262
1102
合 计 1248
1206
均 数 126.2
110.2 16.0 均 数 124.8
120.6 4.2
重复测量设计的优缺点
• 优点:
每一个体作为自 身的对照,克服了个 体间的变异。分析时 可更好地集中于处理 效应.
因重复测量设计 的每一个体作为自身 的对照,所以研究所 需的个体相对较少, 因此更加经济。
• 缺点:
滞留效应(Carry-over effect)
前面的处理效应有可能 滞留到下一次的处理.
潜隐效应(Latent effect)
前面的处理效应有可能 激活原本以前不活跃的效 应.
学习效应(Learning effect)
由于逐步熟悉实验,研 究对象的反应能力有可能 逐步得到了提高。
一、重复测量资料的数据特征
目的:推断处理、时间、处理×时间作用于试 验对象的试验指标的作用。
资料特征:
处理因素 g (≥1 )个水平,每个水平有n个
试验对象,共计 gn个试验对象。
时间因素 同一试验对象在m(≥2 )个时
点获得m个测量值,共计gnm个测量值。 方法:方差分析
前后测量设计
前后测量设计资料是重复测量资料中最为常见 的资料类型,即g=1, m=2, 如表9-1。
和配对设计的数据形式相同,但两者属于完全 不同的实验设计类型。区别如下: 1. 是否随机分配处理(分组); 2. 差值的独立性问题; 3. 数据处理方式的差异。
比较
表9-2 两种方法对乳酸饮料中脂肪含量的测定结果(%)
编号
1 2 3 4 5 6 7 8 9 10
哥特里-罗紫法
0.840 0.591 0.674 0.632 0.687 0.978 0.750 0.730 1.200 0.870
脂肪酸水解法
0.580 0.509 0.500 0.316 0.337 0.517 0.454 0.512 0.997 0.506
差值 d 0.260 0.082 0.174 0.316 0.350 0.461 0.296 0.218 0.203 0.364
与配对设计设计的区别
1.配对设计中同一对子的两个实验单位可 以随机分配处理,两个实验单位同期观察试验 结果,可以比较处理组间差别。
前后测量设计不能同期观察试验结果,虽 然可以在前后测量之间安排处理,但本质上比 较的是前后差别,推论处理是否有效是有条件 的,即假定测量时间对观察结果没有影响。
• 连续型的重复测量资料较为常见,可以采用方差分
析方法进行处理,离散型重复测量资料比较少见, 分析方法更为复杂。此处我们主要讨论连续型重复 测量资料的统计学处理问题。
每一根线代表1位病人
实例举例
血药浓度(μ mol/L)
180 150 120
90 60 30
0
旧剂型 新剂型
4பைடு நூலகம்
8
12
时间(小时)
图10.附2 某药新旧剂型血药浓度随时间的变化
第四节 重复测量资料的方差分析
重复测量资料:
• 重复测量资料是同一受试对象的同一个观察指标在
不同时间点上进行多次测量所得的资料,常用来分 析该观察指标在不同时间点上的变化特点。这类资 料在临床试验和流行病学研究中较常见。
• 重复测量资料的反应变量(即被重复测量的观察指
标)可以为连续型(定量指标)或离散型(定性或 分类指标)。
表9-1 高血压患者治疗前后的舒张压(mmHg)
编号
治疗前
治疗后
差值
1
130
114
16
2
124
110
14
3
136
126
10
4
128
116
12
5
122
102
20
6
118
100
18
7
116
98
18
8
138
122
16
9
126
108
18
10
124
106
18
X
126.2
110.2
16.0
S
7.08
9.31
3.13
如由表 12-1 计算,治疗前后舒张压的相关系 数为 0.963,P<0.01,用治疗前舒张压(X ) 推论治疗 后舒张压(Y ) 的回归方程为:Yˆ 49.534 1.266X , 截距检验 P=0.014,回归系数检验 P 0.01。
单组前后测量设计与配对设计的区别区别
区别点
配对设计 单组前后测量设计
