《工程力学(静力学与材料力学)》第6章静力学专题

合集下载

《静力学专题》课件

02 静力学分析方法
力的平衡分析
力的平衡分析
通过分析物体所受的力，确定物体在静止或匀速直线运动状态下的受力情况。
力的平衡分析步骤
确定研究对象、分析受力情况、建立平衡方程、求解未知量。
力的平衡分析的应用
解决各种工程实际问题，如桥梁、建筑、机械等领域的结构稳定性问题。
力矩平衡分析
力矩平衡分析
01
通过分析物体所受到的力矩，确定物体在旋转或角速度运动状
态下的受力情况。
力矩平衡分析步骤
02
确定研究对象、分析受力情况、建立力矩平衡方程、求解未知
量。
力矩平衡分析的应用
03
解决各种工程实际问题，如旋转机械、航空航天、车辆等领域
的设计和稳定性问题。
力的分布分析
力的分布分析
通过分析物体上力的分布情况，了解物体在不同位置的受力情况。
学提供了更深入的理解和更广泛的应用。
静力学与流体力学
要点一
总结词
静力学与流体力学在研究流体平衡和稳定性方面有共同之处，两者在理论和方法上相互借鉴。
要点二
详细描述
流体力学主要关注流体（液体和气体）的运动状态和受力情况，而静力学则关注物体在静止或平衡状态下所受的力。在研究流体平衡和稳定性方面，静力学中的一些基本原理，如力的平衡和力矩平衡，可以应用于流体的平衡和稳定性分析。此外，流体力学中的一些概念，如流体压力、流速和流量等，也为静力学提供了更深入的理解和更广泛的应用。
《静力学专题》ppt课件
目录
Contents
• 静力学基础 • 静力学分析方法 • 静力学应用 • 静力学与其他学科的交叉
01 静力学基础
静力学的基本概念

工程力学(静力学与材料力学)第四版习题答案

静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P Nθ==+=∑故： 161.2R F N==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有故：3R F KN== 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ）由平衡方程有：0.577AB F W=（拉力）1.155AC F W=（压力）（b ）由平衡方程有：1.064AB F W=（拉力）0.364AC F W=（压力）（c ）由平衡方程有：0.5AB F W= (拉力)0.866AC F W=（压力）（d ）由平衡方程有：0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ cos 450RA F P -=由Y =∑ sin 450RA RB F F P +-=(b)解：受力分析如图所示：由联立上二式，得：2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=由0Y =∑sin 0AC N F F W α+-=2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：取E 为研究对象：由0Y =∑cos 0NH CEF F α'-=CECE F F '= 故有：2-11解：取A 点平衡：联立后可得：2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：由对称性及ADAD F F '=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡联立上二式得：1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡联立方程后解得： RD F = （2）取ABCE 部分，对C 点列平衡且RE REF F '=联立上面各式得： RA F = （3）取BCE 部分。

单辉祖工力-6静力学专题1

yC
yili li
yi li l
xC
zili li
zi li l
z
C Pi
P
zi
zC
O
yi
xi
xC y
x
yC
2. 确定重心的常用方法
• 当物体具有对称轴、对称面或对称中心时，它的重心一定在对称轴、对称面或对称中心上。
• 对于几何形状较复杂的均质物体，往往采用分割法和负面积法
S 3 = 9. 81kN
YA +S2 ·sin 60°－P1 = 0 S 2 = 1. 15kN
● 零力杆的判断零力杆：杆件内力为零的杆件
节点只连接两根不共线的杆件
0 0
节点无外力则此两根杆为零力杆
节点只连接两根不共线的杆件
0
外力作用线沿某一根杆
则另一根杆为零力杆
节点连接三根杆件
0
若其中两根共线且节点无外力
称重法
• 然后将其一端支承于 A 点，另一端放在磅称 B上，测得两点的水平距离 l 及 B 处的约束反力 FB , 假定为 G , 由
∑MA( F ) = 0 ， P xC － FB l = 0
xc
FBl P
G P
l
O x
zi
yi yC
P
zC
xi
xC y
为了求坐标 zC，将物体连同直角坐标系 Oxyz 一起绕 x 轴逆时针旋转90°
重力的方向并无改变对 x 轴取矩，有
P zC = (P1z1 + P2z2 + …+ Pnzn) = ∑Pi zi
重心的坐标公式
z
y
Mi
△Vi Mi
PCi P

06静力学专题——桁架、摩擦、重心(阅读版)

China University of Mining & Technology
§6-2 摩擦
摩擦滚动摩擦静滚动摩擦动滚动摩擦
滑动摩擦静滑动摩擦动滑动摩擦摩擦
湿摩擦
干摩擦
《摩擦学》
一、滑动摩擦
Fx 0 FT Fs 0
F s FT
静滑动摩擦力的特点 1 方向：沿接触处的公切线，与相对滑动趋势反向； 2 大小：0 F s Fmax 3 Fmax f s FN（库仑摩擦定律）
取节点Ｅ
Fiy 0 FEG Fix 0 FEF

例6-4 已知：P1,P2,P3, 尺寸如图。求：１，２，３杆所受力。解：求支座约束力
M 0 F 0
A
iy
F Ay
FBy
从1，2，3杆处截取左边部分
F F
iy
0
0
F2 F1 F3
动滑动摩擦的特点 1 方向：沿接触处的公切线，与相对滑动趋势反向； 2 大小：F d f d F N
f d f s （对多数材料，通常情况下）
二、摩擦角和自锁现象
1 摩擦角
F RA
全约束力
物体处于临界平衡状态时，全约束力和法线间的夹角。摩擦角
tan f
Fmax f s FN fs FN FN
FA max f sA FNA FB max f sA FNB
(3) (4) (5) (6) (7)
FBmax smax P

解上述5个方程，得
f sA (tan f sB ) smax l 1 f sA f sB 所求 s 值为 f (tan f sB ) 0 s sA l 1 f sA f sB

工程力学终于知识点

三、扭转轴的内力扭矩 ——T 扭矩的正负规定：
按右手螺旋法则，扭矩矢量沿截面外法线方
向为正；反之为负。
3、扭矩图
扭矩图——表示扭矩沿杆件轴线变化规律的图线。
要求：
①扭矩图和受力图对齐； ②扭矩图上标明扭矩的大小、正负和单位。
快速作扭矩图
上上下下
四、薄壁圆筒的扭转
r0/d≥10 时，称为薄壁圆筒。
作用于杆上的合外力的作用线与杆的轴线重合。
2、变形特点
杆件产生轴向的伸长或缩短。
二、内力·截面法·轴力和轴力图 1、内力
指截面上分布内力系的合力。
2、截面法
截面法四部曲 —截开 —取出 —代替 —平衡
3、轴力FN
沿杆轴线方向作用的内力，称为轴力。
轴力正负规定：
以使脱离体受拉为正，使脱离体受压为负。
F N3
一定为零力杆。
F N2
3
3、两杆相结，不共线，且节点处的载荷沿其中某一杆件，则另一杆为零力杆。
2 A 1 FN1 F N2
2
F A 1 F N1
三、重心坐标的一般公式
xc
Pi xi P
yc
Pi yi P
zc
Pi zi P
四、组合形体的重心
1、分割法
如果一个物体由几个简单形状的物体组合而成，而
此法适合于求桁架部分杆件的内力。
注:
（1）所有杆件均假设受拉。（2）每次对象只能列出三个方程。（3）合理确定坐标方位、矩心位置及方程次序。
两种方法并不相互独立，可配合使用。
二、桁架零力杆的判断方法
F N2
1、两杆相结，不共线，且节点
2
处没载荷，则此两杆均为零力杆。

工程力学(静力学与材料力学)-1-静力学基础

力偶及其性质
力偶－最简单、最基本的力系
工程中的
力偶实例
F1
F2
1. 力偶的定义
两个力大小相等、方向相反、作用线互相平行、
但不在同一直线上，这两个力组成的力系称为力
偶(couple)。
（F,F）
力偶臂
dF F
力偶的作用面
平面力偶及其性质
m
B
F
o
dA
F’
力偶没有合力，不能用一个力来代替，也不能用一个力与之平
力偶及其性质
力偶及其性质
力偶－最简单、最基本的力系力偶的性质力偶系及其合成
力偶及其性质
力偶－最简单、最基本的力系
力偶及其性质
力偶－最简单、最基本的力系
工程中的力偶实例
钳工用绞杠丝锥攻螺纹时，两手施于绞杆上的力和，如果大小相等、方向相反，且作用线互相平行而不重合时，便组成一力偶。
O
d1
d d2
F1
力和力矩
合力之矩定理
FR
n
mOFR＝mOFi
i1
F2
例1 已知：如图 F、R、r, a , 求：MA(F)
解：应用合力矩定理
R Fy
F
r
a
a
Fx
M A ( F ) M A ( F x ) M A ( F y )
A
a a
M A ( F ) F x ( R r c) o F y r s sin
解 : 可以直接应用力矩公式计算力F 对O点之矩。但是，在本例的情形下，不易计算矩心O到力F作用线的垂直距离h。
如果将力F分解为互相垂直的
两个分力Fl和F2，二者的数值分别
为
F1＝Fcos45

工程力学第6章弹性静力学基本概念

第6章　弹性静力学的基本概念　刚体静力学研究力系的等效、简化与力系的平衡，并且应用这些基本概念和理论，分析、确定物体的受力。

刚体静力学的模型是质点和质点系以及刚体和刚体系。

弹性静力学则主要研究变形体受力后发生的变形，以及由于变形而产生的附加内力。

分析方法上，弹性静力学与理论力学刚体静力学也不完全相同。

建立在实验基础上的假定、简化计算，是弹性静力学分析方法的主要特点。

本章介绍弹性静力学的基本概念、研究方法以及弹性静力学对于工程设计的重要意义。

　§6-1　弹性静力学概述　§6-2　弹性体及其理想化　６－２－１　各向同性与各向异性弹性体　６－２－２　各向同性弹性体的均匀连续性　§6-3　弹性体受力与变形特征　§6-4　应力及其与内力分量之间的关系　６－４－１　分布内力集度－应力　６－４－２　应力与内力分量之间的关系　§6-5　正应变与切应变　§6-6　线弹性材料的物性关系　§6-7工程结构与构件　§6-8　杆件变形的基本形式　§6-9　结论与讨论　６－９－１关于刚体静力学模型与弹性静力学模型　６－９－２关于弹性体受力与变形特点　６－９－３关于刚体静力学概念与原理在弹性静力学中的　可用性与限制性　习题　本章正文返回总目录第6章　弹性静力学的基本概念　§６—１　弹性静力学概述　弹性静力学(elastic statics)又称材料力学(strength of materials)，其研究内容分属于两个学科。

第一个学科是固体力学(solid mechanics)，即研究物体在外力作用下的应力、变形和能量，统称为应力分析(stress analysis)。

但是，弹性静力学所研究的仅限于杆、轴、梁等物体，其几何特征是纵向尺寸远大于横向尺寸，这类物体统称为杆或杆件（bars或rods）。

大多数工程结构的构件或机器的零部件都可以简化为杆件。

工程力学课件第6章(静力学专题)

空间问题的平衡方程
03
根据平衡条件，可以建立空间问题的平衡方程，通过求解平衡
方程可以得到物体的平衡位置。
静力学的进一步研究
静力学的应用领域
静力学在工程领域中有着广泛的应用，如建筑、机械、航空航天等。
静力学的理论体系
静力学作为力学的一个分支，有着完整的理论体系，包括基本概念、原理、定理和公式等。
析力的作用效果等。
运动状态的分析
利用平衡方程可以分析物体的运动状态，如确定物体的位移、速度和加速度等。
实际问题的应用
平衡方程在实际问题中有着广泛的应用，如工程设计、机械制造、航空航天等领域都需要用到平衡方程来解决实际问题。
03
力矩与力矩平衡
力矩的概念
力矩
力对物体产生转动作用的物理量，用M表示，单位是牛顿·米（N·m）。
几何方程
描述了物体在受力后产生的应变与位移的关系。
本构方程
描述了物体内部的应力与应变之间的关系，涉及到材料的弹性模量等物理性质。
06
静力学专题研究
平面问题的平衡
1 2
平面问题概述
平面问题是指物体在平面内的受力情况，其平衡是指物体在平面内受到的合力为零。
平面问题的平衡条件
平面问题的平衡条件是所有外力的矢量和为零，即∑FX=0和∑FY=0。
受力分析的步骤
受力分析的步骤包括标出主动力、分析约束反力、画受力图等。主动力是使物体运动的力，约束反力是约束物体运动的力，画受力图是将物体受到的力在图上表示出来。
平衡方程的建立
平衡方程的定义
平衡方程的应用
平衡方程是描述物体在力作用下处于平衡状态的方程，其形式为∑F=0和 ∑M=0。∑F=0表示合力为零，∑M=0 表示合力矩为零。

《工程力学》(静力学部分)

力系的分类：
平面力系：力的作用线均在同一个平面内

汇交力系：力的作用线汇交于一点；平行力系：力的作用线相互平行；一般力系：力的作用线既不完全汇交，又不完全平行；汇交力系平行力系一般力系

空间力系

平衡

定义：
物体相对于惯性参考系处于静止或匀速直线运动状态。建立在地球上，并相对于地球不动的参考系称为惯性参考系。

力的三要素：

三力平衡条件
静力学公理四、五

公理四：作用于反作用公理
任何两个物体相互的作用力和反作用力总是大小相等，方向相反，沿着同一条直线，分别作用在这两个物体上。作用力和反作用力的作用对象

公理五：刚化原理
若变形体在某一力系作用下平衡，则可将此受力的变形体视为刚体，其平衡状态仍保持不变。
《工程力学》
（静力学部分）
云南交通职业技术学院李昆华副教授
总第一讲
教学要求： 1、熟悉工程力学的研究对象、内容，
2、掌握刚体、平衡、力的概念
3、掌握五个公理
第一章静力学基础绪论 §1-1 刚体和力的概念 §1-2 静力学公理
刚体和力的概念

刚体

在力的作用下，其物体内部任意两点之间的距离始终保持不变刚体是静力学中对物体进行分析所简化的力学模型
3. 正负规定： 4. 投影和分力关系
合力投影定理

合力在某一轴的投影，等于各分力在同一轴上投影的代数和。
F Rx F1 x F 2 x ... F nx F F1 y F 2 y ... F ny Ry

《工程力学》(静力学)教学大纲

《工程力学》〔静力学〕教学大纲适用专业：工程监理专业参考学时：30学时一、教学内容：第一章绪论<2学时>本章主要介绍理论力学〔静力学〕的研究对象,研究任务和研究方法,并指出工程监理专业学生学习理论力学〔静力学〕的目的及其重要性.静力学研究物体机械运动的特殊情况,即物体的平衡问题.研究物体的平衡就是研究物体在外力作用下平衡应满足的条件,以及如何应用这些条件解决工程实际问题.所以,静力学主要解决以下两个基本问题：〔1〕力系的简化；〔2〕力系的平衡条件及其应用.静力学的理论和方法,特别是对物体进行受力分析和画受力图的方法是学习后续许多课程的基础,在工程技术中也有广泛的应用. 第二章静力学基本概念和静力学公理〔4学时〕一、基本要求1、掌握静力学基本概念,力的概念、刚体的概念、平衡的概念.2、理解并掌握静力学公理的内容.3、掌握约束和约束反力的概念.4、熟练掌握受力分析和画受力分析图的方法.二、重点、难点1、力、刚体、平衡、约束的概念.2、理解五个公理两个推论.3、对研究对象进行受力分析并画出受力图.第三章平面力系〔14学时〕一、基本要求1、掌握平面汇交力系的几何法和解析法合成的方法.2、掌握平面汇交力系平衡的几何条件,应用力系的力多边形封闭和静力平衡方程解平面汇交力系的平衡问题.3、掌握力矩的概念,合力矩定理,掌握力偶和力偶矩的概念和性质.掌握平面力偶系的合成方法和平衡条件,应用平衡方程解决平面力偶系的平衡问题.4、熟悉力的平移定理及适用X围.5、掌握平面任意力系向作用面内任一点简化的方法,分析简化结果.6、掌握固定端约束的特性和约束反力的表示方法.7、掌握平面任意力系的平衡条件；掌握应用平衡条件解平面任意力系的平衡问题；熟悉平衡方程的三种形式.8、掌握静定的物体系统平衡问题的分析方法.9、熟悉平面平衡力系的平衡问题.二、重点、难点1、掌握力的分解与力的投影.2、掌握平面汇交力系的合成.3、掌握平面汇交力系的平衡.4、熟练掌握用解析法求解平面汇交力系的平衡问题.5、掌握力矩和力偶矩的概念.6、力矩的计算.7、力偶的性质.8、平面力偶系平衡方程的应用.9、主矢和主矩概念的理解.10、主矢、主矩以及力系合成的最后结果计算.11、熟练掌握三种形式的平衡方程求解单个物体的平衡问题.12、熟练掌握求解物体系统的平衡问题.第四章空间力系〔4学时〕一、基本要求1、掌握力在空间直角坐标轴上投影的计算方法.2、了解在空间力系中,力对点之矩的矢量表示,力对点之矩与力对轴之矩的关系.3、掌握力对轴之矩的计算及符号表示.4、了解空间汇交力系的解析法合成、平衡条件,用平衡方程解空间汇交力系的平衡问题.5、了解空间一般力系平衡的解析条件,了解用平衡方程求解空间一般力系的平衡问题.二、重点、难点1、空间力在坐标轴上的投影计算.2、空间力对轴之矩的计算及符号表示.二、参考学时分配表：三、能力及技能培养内容：注：习题练习是培养学生实际能力和技能培养的重要内容,习题要切合实际,力求简单.学生的平时作业成绩占总成绩的20%.《工程力学》〔材料力学〕教学大纲适用专业：工程监理专业参考学时：35学时一、教学内容第一章绪论一、基本要求1、明确材料力学的任务和研究对象.2、初步了解构件的强度、刚度和稳定性等基本概念.3、了解变形固体及其基本假设.4、初步了解杆件的基本变形形式.二、重点、难点1、材料力学的任务2、变形固体及其基本假设3、杆件变形的基本形式第二章轴向拉伸和压缩一、基本要求1、建立内力的概念,能熟练地运用截面法求轴力,并画出轴力图.2、建立应力的概念,能灵活地运用强度条件解决强度计算的三类问题.3、建立变形和位移的概念,明确虎克定律的物理含义及其适用X围；并能正确计算拉压杆的变形和位移.4、低碳钢的应力应变曲线,明确塑性材料和脆性材料的力学性能及其差别.5、了解超静定问题的基本概念,会分析超静定次数.二、重点、难点1、拉压杆的概念2、内力和应力的概念3、拉压杆的内力和应力4、材料的力学性质5、许用应力和强度计算6、拉压杆的变形计算7、超静定问题第三章剪切与扭转一、基本要求1、明确剪切和挤压的概念,能正确地确定剪切面积和挤压面积,掌握简单的连接件的强度计算.2、熟练地确定外力偶矩、扭矩和扭矩图.3、牢固地掌握实心和空心圆轴横截面上剪应力的分布规律和计算公式,并准确地计算最大剪应力.4、运用扭转角计算公式计算圆轴的相对扭转角.5、运用圆轴的强度条件,对圆轴进行强度计算.6、正确理解剪应力互等定理和剪切虎克定律的含义.二、重点、难点1、剪切的概念2、铆接件的破坏形式及相应的强度计算3、剪应力互等定理4、剪切虎克定律5、扭转变形及内力图6、圆轴扭转时的剪应力计算7、圆轴扭转时的相对扭转角的计算第四章梁的内力一、基本要求1、准确地计算梁的支座反力,并会校核.2、熟练地计算梁上任意指定截面的内力〔剪力和弯矩〕.会确定弯矩为极值的截面位置并计算弯矩极值.3、正确地列出剪力方程和弯矩方程,了解根据内力方程画内力图的方法.4、掌握M、Q与q之间的微分关系,并理解其几何意义.5、牢固地掌握荷载与剪力图、弯矩图之间应服从的规律；并熟练地运用这些规律画Q图、M图和校核Q图、M图.二、重点、难点1、平面弯曲的概念2、梁及其反力计算3、平面弯曲梁的内力4、内力方程和内力图5、弯矩M、剪力Q与荷载集度q之间的微分关系及其应用第五章截面的几何性质一、基本要求1、掌握静矩、惯性矩、极惯性矩、惯性积、主轴和形心主轴的定义及特征2、会确定截面的形心位置,尤其能熟练地确定具有对称轴的截面的形心位置3、牢记矩形截面、圆形截面的极惯性矩计算公式.二、重点、难点1、静矩、形心及其关系2、惯性矩、惯性积、极惯性矩3、惯性矩的平行移轴公式4、形心主轴和形心主惯性矩第六章梁的应力及强度计算一、基本要求1、掌握有关梁弯曲的基本概念2、正确理解和掌握梁弯曲时的正应力计算公式；了解公式的推导过程；明确公式的适用X围和正应力沿截面高度的分布规律；能熟练地运用该公式计算梁任一横截面上任意点处的正应力以及最大正应力.3、掌握梁弯曲时的剪应力计算公式；明确剪应力沿截面高度的分布规律；能熟练地计算矩形截面梁和工字型、T型截面梁腹板上任一点处的剪应力以及最大剪应力.4、灵活运用梁的正应力强度条件,解决三类强度计算问题：强度校核、截面设计、确定许用荷载.5、掌握梁的剪应力强度条件,并会进行剪应力强度校核.二、重点、难点1、有关梁弯曲的基本概念2、纯弯曲梁横截面上的正应力计算公式3、梁弯曲时的剪应力计算公式4、梁的强度计算5、弯曲中心的概念第七章弯曲变形一、基本要求1、掌握挠曲线、挠度、转角的概念及挠度、转角间的关系.2、熟练应用积分法、叠加法计算梁的位移,会对梁进行刚度校核.3、了解超静定梁的概念.二、重点、难点1、挠曲线概念2、平面弯曲时梁横截面的位移3、挠曲线近似微分方程4、积分法求位移5、叠加法求位移6、刚度校核7、求解简单超静定梁第八章应力状态和强度理论一、基本要求1、建立应力状态概念及其研究方法.2、掌握平面应力状态下,斜截面上的应力计算法；熟练掌握主应力和最大剪应力的计算.3、明确空间应力状态下三个应力的排法,正确理解、应用广义虎克定律.4、了解强度理论的概念以及金属材料破坏的主要形式；理解四个强度理论的基本观点、强度条件；掌握用强度理论对杆件进行强度校核.二、重点、难点1、基本概念2、平面应力状态的分析3、空间应力状态下任一点的主应力和最大剪应力4、广义虎克定律5、强度理论第九章压杆稳定一、基本要求1、掌握压杆稳定、失稳现象、临界力、临界应力、长度系数、柔度、稳定安全系数和折减系数的概念.2、掌握细长压杆临界力的计算公式.3、掌握欧拉公式的适用X围及临界应力的公式,熟练地计算细长压杆的临界应力和临界力.4、掌握压杆的稳定条件.会运用安全系数法和折减系数法对压杆进行稳定性计算.二、重点、难点1、压杆稳定性的概念.2、细长压杆的临界力公式〔欧拉公式〕.3、临界应力、柔度、欧拉公式的适用X围.4、经验公式、临界应力总图.5、压杆稳定的实用计算.6提高压杆稳定性的措施.二、参考学时分配表：三、能力及技能培养内容：注：习题练习是培养学生实际能力和技能培养的重要内容,习题要切合实际,力求简单.学生的平时作业成绩占总成绩的20%.实训课为加深学生对基本理论的理解,增强感性认识,在授课中间穿插一些实验.《建筑力学》〔结构力学部分〕教学大纲适用专业：工程监理专业参考学时：40学时一、课程内容第一章绪论§1-1 杆件结构力学的研究对象和任务.内容：结构的概念,结构的分类,杆件结构力学的对象和任务.§1-2 杆件结构的计算简图.内容：计算简图,杆件结构的简化要点包括杆件的简化,支座的简化和分类及结点的简化.§1-3 平面杆件结构的分类.内容：梁、刚架、桁架、拱、组合结构.§1-4 荷载的分类.内容：分布荷载和集中荷载,恒载和活载、静力荷载和动力荷载. 第二章平面体系的几何组成§2-1 几何组成分析的目的.内容：几何组成分析的目的,几何可变体系和几何不变体系.§2-2 平面体系自由度的概念.内容：刚片、自由度、约束的概念.§2-3 平面几何不变体系的简单组成规律.内容：两刚片的组成规那么,三刚片的组成规那么,二元体规那么,瞬变体系的概念.§2-4 几何组成分析举例.§2-5 静定结构和超静定结构.第三章静定结构的内力分析§3-1 静定梁.内容：单跨静定梁,斜梁,多跨静定梁.§3-2 静定平面刚架.内容：静定平面刚架的类型,静定平面刚架的内力计算.§3-3 三铰拱.内容：概述,三绞拱的内力计算,拱的合理线概念.§3-4 静定平面桁架、组合结构内力计算方法.内容：桁架的有关概念,用结点法和截面法解算桁架结构内力.组合结构的概念和内力计算.§3-5 静定结构的内力分析和受力特点.内容：静定结构的基本特征,静定结构的受力分析,常用静定结构的受力特点.第四章静定结构的位移计算§4-1 计算结构位移的目的.内容：位移的概念,计算位移的目的,位移计算的假定.§4-2 功广义力和广义位移.内容：功、实功和虚功、广义力和广义位移的概念.§4-3 计算结构位移得一般公式.内容：外力虚功和虚应变能,虚功原理,利用虚功原理计算结构的位移.§4-4 静定结构由于荷载引起的位移.内容：荷载作用下的位移计算公式,不同类型的结构位移计算公式,位移计算举例.§4-5 图乘法.内容：图乘法适用条件及图乘公式,图乘计算中的几个问题.§4-6 静定结构由于支座移动和温度变化下的位移计算.§4-7 线形变形体系的几个互等定理.内容：功的互等定理,位移互等定理,反力互等定理.第五章力法§5-1 超静定结构的概念和超静定次数的确定.§5-2 力法的基本概念.内容：基本结构和基本体系的概念.§5-3 超静定次数的确定.内容：超静定次数的概念.§5-4 力法的典型方程.内容：主系数、副系数、自由项的概念,力法的典型方程.§5-5 用力法计算超静定刚架.§5-6 对称性的利用.内容：结构的正对称和反对称,荷载的正对称和反对称.§5-7 用力法计算绞接排架§5-8 等截面单跨超静定梁的杆端内力.内容：固端弯矩和剪力、线抗弯刚度〔线刚度〕的概念,转角位移方程和旋转角的概念.第六章位移法§6-1 位移法的基本概念.§6-2 位移法基本未知量数目的确定.内容：位移法计算的基本未知量,位移法基本结构.§6-3 用位移法计算刚架的步骤和示例.内容：直接利用平衡条件建立位移法方程.§6-4 位移法的典型方程.内容：附加刚臂和附加链杆的概念,位移法的典型方程.§6-5 用剪力分配法计算等高饺结排架.内容：柱顶作用水平集中力时的单阶柱绞接排架,一般荷载作用时的单阶柱绞接排架.第七章渐近法与近似法§7-1 概述§7-2 力矩分配法的基本概念.内容：力矩分配法的解题思路,转动刚度、分配系数、传递系数的概念.§7-3 用力矩分配法计算连续梁及无结点线位移的刚架.§7-4 无剪力分配法.内容：无剪力分配法的应用条件,固端弯矩,转动刚度和传递系数.无剪力分配法的解题方法.§7-5 用近似法计算多跨多层刚架.内容：竖向荷载作用下的近似计算—分层法,水平荷载作用下的近似计算法—反弯点法.§7-6 超静定结构的受力分析和变形特点.第八章影响线和内力包络图§8-1 影响线的概念.§8-2 用静力法作简支梁的影响线.内容：支座反力影响线、弯距影响线、剪力影响线.§8-3 利用影响线求量值.§8-4 最不利荷载位置.§8-5 简支梁的内力包络图. 内容：包络图的概念,弯距包络图和剪力包络图.§8-6 连续梁的内力包络图.二、能力及技能培养的内容1、习题及习题课注：习题是学生能力及技能培养的重要内容,习题课中讲解例题要力求简单、切合实际,要分析学生作业中碰到的难点问题和容易出错的内容,并可在课堂上布置一部分习题让学生当堂完成.对于指定完成的习题,学生必须按时独立完成,对学生要求做到计算方法正确,字、图整洁规整,结果无误,平时作业成绩占总成绩的20%〔优：20~18,良：17~16,中：15~14,及格：13~12〕,平时成绩不及格者不得参加期末考试.习题讨论课形式可以采用教师讲授和集体讨论的形式进行教学,教师要列出讨论课的提纲,并且课后应对讨论课的内容进行总结.2、实训课为加深学生对基本理论的理解,增加感性认识,可以用现有的计算机软件如结构力学求解器、建筑科学研究院PKPM系列软件来校核手算结果,做到手算和机算相结合,调动学生的学习兴趣,增强学生的动手能力.可根据学生完成的质量评定成绩,计入平时成绩.三、学时分配表。

【工程力学课后习题及答案全解】第6章弹性静力学的基本概念习题解

— 31
—
习题6-1图习题6-3图习题6-4图习题6-2图工程力学（1）习题全解
第6章弹性静力学的基本概念
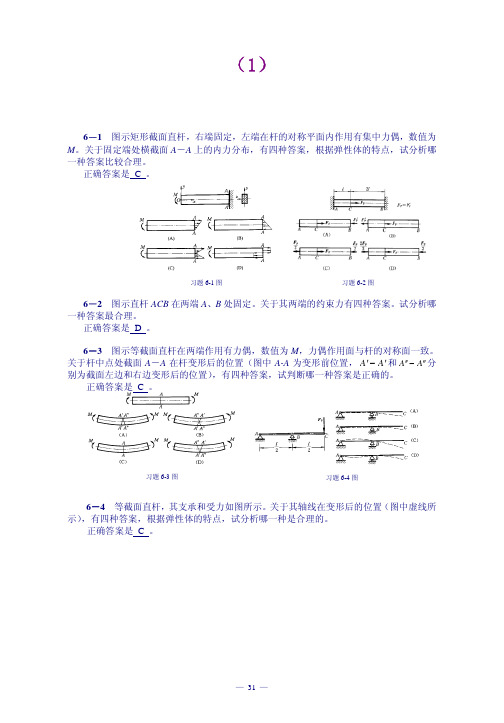
6－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

6－2 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

6－3 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（图中A-A 为变形前位置，A A ′−′和A A ′′−′′分别为截面左边和右边变形后的位置），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

6－4 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

《工程力学》课件第6章截面图形的几何性质

Ip
r2dA A
D 2
r2
2
rdr
D4
0
32
Ip Iy Iz
Iy
பைடு நூலகம்
Iz
Ip 2
D4
64
四、组合截面的惯性矩与惯性积
z
I
例如工字型截面 A AI AII AIII
II
y
III
Iy
z 2 dA
A
z2dA z2dA z2dA
AI
AII
AIII
m
I yI I yII I yIII I yi
包括：形心、静矩、极惯性矩、惯性矩、惯性半径、惯性积、主轴和形心主轴、主矩和形心主矩等
6.1 静矩和形心
一、静矩
截面对z轴的静矩
z
Sz
ydA
A
截面对y轴的静矩
y
dA
A
z
Sy
zdA
A
o
单位： m3
y
静矩的数值可大于零、等于零或小于零。
二、形心
如图所示均质薄板，重心与形心C重合，
由静力学可知形心坐标在yoz：
何关系， y R sin , dy R cosd ,
dA 2R cosdy 2R2 cos2 d
Sz
A
（2）形心
ydA yC
2 0
Sz A
R sin 2R2 cos2 d
2 R3 3
4R
1 R2 3
zC
2 3
0
R3
2
三、组合截面的静矩和形心 z
D d
y
整个图形对某一轴的静矩等于各个分图形对同一轴的静矩之和。
z1
y1 z

工程力学课后习题答案（静力学和材料力学）

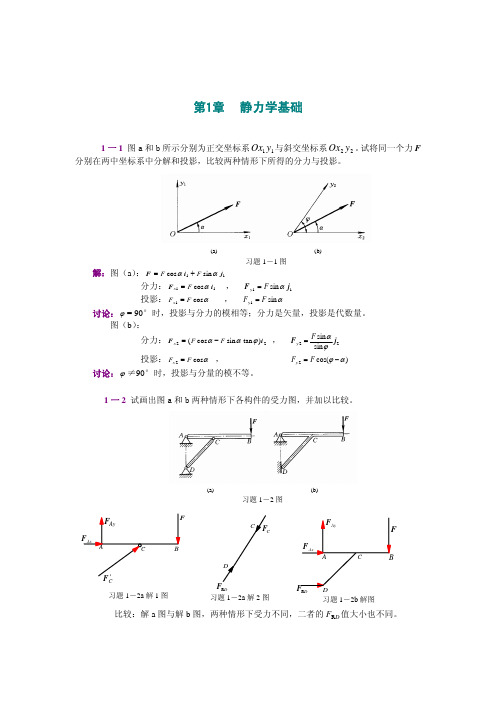
1 一 3 试画出图示各构件的受力图。
F
D
习题 1－3 图
C
F
D
C
A
B
FA
FB
习题 1－3a 解 1 图
F Ax
A
B
FAy
FB
习题 1－3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1－3b 解 2 图
W
FAx
FAy
习题 1－3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1－3d 解 2 图
FB2 x
B
FDy
C FB2 y
F Dx D
W
习题 1－4b 解 2 图
F'B1
B
F'B2x
F'B2 y F1
A B
F'B2x
习题 1－4c 解 1 图
F1 F'B2 y
FDx D FDy
F'B2x B
C
F'B2 y
W
F'B2 B
习题 1－4c 解 2 图
习题 1－4b 解 3 图
FA
A
B
F B1
习题 1－4d 解 1 图
可推出图（b）中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1－12 解 1 图
F AB 习题 1－12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点，滚子搁置在倾斜的光滑刚性平面上，如

工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第6章_圆轴扭转

该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6－5 图
解：1． τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2． M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3． τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
16 M x
3 π d1
=
16 M x
3 π D2 (1 − α 4 )
即
d1 = (1 − α 4 ) 3 D2
1
（a）
二者重量之比
W1 A1 d2 = = 2 1 2 W2 A2 D2 (1 − α )
（b）
式（a）代入式（b），得
W1 (1 − α 4 ) = W2 1−α2
2 3
所以，正确答案是
16 M x 3 16 × 10.53 × 10 6 = = 96.3 π [τ ] π × 60
（3）按刚度条件求轴的直径
θ=
Mx ≤ [θ ] GI P
[θ ] = 1D / 2m =
π
180 × 2 × 10 3
rad/mm
6
D≥4
32M x 32 × 10.53 × 10 6 =4 = 110.6mm Gπ [θ ] 82 × 10 3 π [θ ]

工程力学静力学与材料力学

工程力学静力学与材料力学工程力学是研究物体在外力作用下的平衡、运动和变形规律的一门学科，它是工程学的基础和核心课程之一。

而工程力学又分为静力学和动力学两个部分，其中静力学是研究物体在静止状态下受力和力的平衡条件的学科，而材料力学则是研究材料的性质、行为和应用的学科。

本文将重点介绍工程力学静力学与材料力学的相关内容。

首先，我们来谈谈静力学。

静力学是研究物体在静止状态下受力和力的平衡条件的学科。

在工程实践中，静力学的理论常常被用于分析和计算各种结构的受力情况，比如建筑物、桥梁、机械设备等。

静力学的基本原理包括力的平衡条件、力的合成与分解、力的作用点、力的性质等。

在学习静力学的过程中，我们需要掌握平衡条件的原理，了解各种受力情况下物体的平衡条件，并能够运用相关理论进行实际问题的分析和计算。

其次，我们来看看材料力学。

材料力学是研究材料的性质、行为和应用的学科。

材料力学的内容非常广泛，包括材料的力学性能、材料的应力应变关系、材料的疲劳与断裂、材料的塑性变形等。

在工程实践中，材料力学的理论常常被用于材料的选用、结构的设计和材料的加工等方面。

学习材料力学需要掌握材料的基本力学性能，了解材料的应力应变关系，并能够运用相关理论进行材料的性能分析和计算。

工程力学静力学与材料力学是工程学的基础课程，它们为我们理解和掌握工程实践中的力学问题提供了重要的理论基础。

通过学习工程力学静力学与材料力学，我们能够更好地理解和应用力学原理，为工程实践提供科学的理论支持。

同时，工程力学静力学与材料力学的学习也是提高我们工程素质和解决工程实际问题能力的重要途径。

总之，工程力学静力学与材料力学是工程学习的重要基础课程，它们的学习对我们掌握工程学科知识、提高工程素质和解决工程实际问题能力具有重要意义。

希望大家能够认真学习，掌握其中的基本原理和方法，为将来的工程实践打下坚实的理论基础。

工程力学静力学与材料力学

铸铁二向断裂试验
第10页/共49页
例2-1 铸铁构件危险点处受力如图, 试校核强度，[s]=30 MPa
宜用第一强度理论考虑强度问题
例题
解：
第11页/共49页
§3 关于屈服的强度理论
最大切应力理论畸变能理论试验验证
第12页/共49页
最大切应力理论（第三强度理论）
பைடு நூலகம்
第24页/共49页
弯扭组合强度计算
弯扭组合
危险截面: 截面A
危险点: a 与 b
应力状态－单向＋纯剪切
强度条件（塑性材料, 圆截面）
第25页/共49页
弯拉(压)扭组合强度计算
弯拉扭组合
危险截面－截面A
危险点－ a
应力状态－单向＋纯剪切
强度条件（塑性材料）
第26页/共49页
例5-1 图示钢质传动轴，Fy = 3.64 kN, Fz= 10 kN, F’z =1.82 kN, F’y = 5 kN, D1 = 0.2 m, D2 = 0.4 m, [s] = 100 MPa, 轴径 d=52 mm, 试按第四强度理论校核轴的强度
平面应变断裂韧度
当板厚大于某一数值 bmin 后，Kc 趋于某一稳定值，称为平面应变断裂韧度，对于Ⅰ型裂纹，并用 KIc 表示。
Kc与板厚 b 有关。
几种材料的KIc 与 bmin
断裂韧度代表含裂纹材料抵抗断裂失效的能力。
第46页/共49页
断裂判据概念
断裂判据 Ⅰ型裂纹开始扩展的条件为
经研究，由于冶炼、加工与使用等原因，构件中往往存在裂纹甚至宏观裂纹，而低应力脆断，就是在一定应力条件下发生迅速扩展所致。这种情况在高强度材料中尤为突出。
断裂力学是固体力学的一个新分支，主要研究含裂纹材料与结构的宏观裂纹扩展规律。

第六章静力学专题-桁架、摩擦、中心

桁架上每个节点的平衡。
2、截面法：应用平面任意力系的平衡条件，研究桁架由截面切出的部分的平衡。
§6-1 桁架
一、节点法：
例题已知P=10kN，试求各杆内力。
解：1) 研究整体，求支座约束力：
FAy
FBy
Fx 0 : FBx 0
FBx
MA(F) 0:
4FBy 2P 0
M B (F ) 0 : 2P 4FAy 0
第六章静力学专题
• §1 桁架 • §2 摩擦 • §3 重心
§6-1 桁架
建筑
通讯
桥梁
输电
§6-1 桁架
桁架:
由一些细长直杆按适当方式分别在两端连接而成的几何形状不变的结构。
§6-1 桁架桁架是工程中常见的一种结构。
桁架的优点：结构“轻”；能充分发挥材料的力学性能。
§6-1 桁架
Q F1' F1 F4 10kN （受压）
F’1
F4
F’3
注意：节点法的理论基础是平面汇交力系的平衡理论。在应用节点法时,所选取节点的未知量一般不应超过两个。
§6-1 桁架
二、截面法：
例题已知h，a，P。求：4，5，6杆内力。
解：首先求支座约束力： FAy
I
Fx 0 : FAx 0
二力杆
A
FA
A
FC
C
B
FB
B
轴向力
FB
B
§6-1 桁架平面简单静定桁架模型：基本三角形
总杆数：3 节点数：3
总杆数：5 节点数：4
总杆数：7 节点数：5
若设总杆件数目为m ，而对应的总节点数目为n，则有：m-3 = 2(n – 3 )，即m=2n-3 。因此有下面的结论：

《工程力学》课程专升本考试大纲(供参考)

《工程力学》课程专升本考试大纲2012年版本第一部分课程性质与目标一、课程性质与特点《工程力学》课程是土木建筑及工程管理类专业的一门重要技术基础课。

通过本课程的学习，使学生掌握构件的受力分析和平衡规律，对构件的强度、刚度和稳定性问题有明确的概念，具有一定的分析和计算能力，能解决简单的建筑工程中的力学问题，为学习后继课程打下必要的理论基础。

二、课程目标与基本要求本课程的设置目标是使学生通过学习，掌握静力学和材料力学两部分内容的基本概念、基本定律和原理及具备一定的分析、计算能力。

课程的基本要求如下：1、熟悉静力学的基本概念、公理、推论和定理。

2、掌握各种约束及约束反力的性质和特点，会画单个构件及物体系统的受力图。

3、掌握各种力系的简化和平衡问题的计算，着重解决物体的平衡问题。

4、理解材料力学的基本概念和有关的定律和定理。

掌握轴向拉压、剪切、扭转和弯曲的四种基本变形的强度和刚度计算，着重解决强度计算。

5、了解点的应力状态的概念和内容，理解强度理论的知识，能初步解决组合变形的强度计算。

6、掌握压杆稳定问题的基本概念和计算。

三、与本专业其它课程的关系本课程要求考生具有一定的数学和物理基础，并有较强的分析和计算能力。

先修课程为：《高等数学》、《大学物理》第二部分考核内容与考核目标第一篇静力学第一章静力学基本概念与物体的受力分析一、学习目的与要求了解工程力学的研究对象、内容及研究方法，掌握静力学的基本概念和理论，了解各类型约束的特点，能正确地对单个物体和物体系统进行受力分析，并画出其受力图。

二、考核知识点和考核目标1、画单个构件或整体的受力图第二章汇交力系一、学习目的与要求理解力的可传性原理以及在直角坐标轴上的投影方法,掌握求汇交力系合成与平衡的几何法和解析法。

二、考核知识点与考核目标1、计算平面汇交力系的平衡问题第三章力偶系一、学习目的与要求理解力矩的概念和计算，理解力偶的性质和特点，能求解力偶系的合成与平衡问题。

《工程力学(静力学与材料力学)》第6章 静力学专题

《静力学专题》课件

工程力学(静力学与材料力学)第四版习题答案

单辉祖工力-6静力学专题1

06静力学专题——桁架、摩擦、重心(阅读版)

工程力学终于知识点

工程力学(静力学与材料力学)-1-静力学基础

工程力学 第6章 弹性静力学基本概念

工程力学课件第6章(静力学专题)

《工程力学》(静力学部分)

《工程力学》(静力学)教学大纲

【工程力学 课后习题及答案全解】第6章弹性静力学的基本概念习题解

《工程力学》课件第6章 截面图形的几何性质

工程力学课后习题答案（静力学和材料力学）

工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第6章_圆轴扭转

工程力学静力学与材料力学

工程力学静力学与材料力学

第六章 静力学专题-桁架、摩擦、中心

《工程力学》课程专升本考试大纲(供参考)

《工程力学(静力学与材料力学)》第6章静力学专题

工程力学第6章弹性静力学基本概念

【工程力学课后习题及答案全解】第6章弹性静力学的基本概念习题解

《工程力学》课件第6章截面图形的几何性质

第六章静力学专题-桁架、摩擦、中心