高考数学(解三角形)第一轮复习
高考数学第一轮章节复习课件 第三章 三角函数 解三角形

【注意】 若角α的终边落在某条直线上,一般要分类讨论.
已知角α的终边在直线3x+4y=0上,求sinα, cosα,tanα的值.
.
解析:tan= 答案:
5.某时钟的秒针端点A到中心点O的距离为5 cm,秒针均匀 地绕点O旋转,当时间t=0时,点A与钟面上标12的点B
重
合.将A、B两点间的距离d(cm)表示成t(s)的函数,则d
=
,其中t∈[0,60].
解析:∵经过t(s)秒针转了 弧度
d
5. t
, d
t
10 sin
.
2 60
)内的单调性.
知识点
考纲下载
考情上线
函数y= Asin(ωx +φ)的图 象
1.考查图象的变换和 1.了解函数y=Asin(ωx+φ)
解析式的确定,以 的
及通过图象描绘, 物理意义;能画出y=
观察讨论有关性质. Asin(ωx+φ)的图象,了解
2.以三角函数为载体, 参数A、ω、φ对函数图象
考查数形结合的思想. 变化的影响.
当且仅当α= ,即α=2时取等号, 此时 故当半径r=1 cm,圆心角为2弧度时,扇形面积最大, 其最大值为1 cm2.
法二:设扇形的圆心角为α(0<α<2π),半径为r,面积为S,
则扇形的弧长为rα,由题意有:2r+rα=4⇒α=
×r2=2r-r2=-(r-1)2+1,
∴当r=1(cm)时,S有最大值1(cm2),
为余弦线
有向线段 AT 为正切线
数学一轮复习第4章三角函数解三角形第1讲三角函数的基本概念同角三角函数的基本关系与诱导公式试题1理

第四章三角函数、解三角形第一讲三角函数的基本概念、同角三角函数的基本关系与诱导公式练好题·考点自测1.已知下列命题:①第二象限角大于第一象限角;②不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关;③若sin α=sin β,则α与β的终边相同;④若cos θ<0,则θ是第二或第三象限的角.其中正确的个数是()A.1B.2 C。
3 D。
42。
sin 2·cos 3·tan 4的值()A。
小于0 B。
大于0C。
等于0 D.不存在3.已知点P(cos 300°,sin 300°)是角α终边上一点,则sin α—cos α= ()A.√32+12B。
-√32+12C。
√32−12D。
-√32−124.[2019全国卷Ⅰ,7,5分]tan 255°= ()A.-2—√3B。
—2+√3C。
2—√3 D.2+√35.[2020全国卷Ⅱ,2,5分][理]若α为第四象限角,则 ( ) A 。
cos 2α>0 B 。
cos 2α〈0 C 。
sin 2α>0 D.sin 2α<06。
已知sin α+cos α=12,α∈(0,π),则1-tanα1+tanα= ( )A.—√7B.√7C.√3 D 。
-√3图4-1—17。
[2019北京,8,5分]如图4—1-1,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,∠APB 是锐角,大小为β.图中阴影区域的面积的最大值为 ( ) A 。
4β+4cos β B.4β+4sin β C.2β+2cos β D.2β+2sin β8.[2018全国卷Ⅰ,11,5分]已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A (1,a ),B (2,b ),且cos 2α=23,则|a -b |=( )A.15B .√55C 。
2√55D.1拓展变式1.在一块顶角为120°、腰长为2的等腰三角形厚钢板废料OAB 中用电焊切割成扇形,现有如图4-1—3所示两种方案,既要充分利用废料,又要切割时间更短,则方案更优.2.(1)[2021洛阳市联考]已知角α的顶点为坐标原点,始边与x轴非负半轴重合,终边与直线y=3x重合,且sin α<0,P(m,n)是角α终边上一点,且|OP|=√10(O为坐标原点),则m-n 等于()A.2B.-2C.4 D。
数学一轮复习第四章三角函数解三角形4.2同角三角函数的基本关系及诱导公式学案理

4。
2同角三角函数的基本关系及诱导公式必备知识预案自诊知识梳理1。
同角三角函数的基本关系(1)平方关系:sin2α+cos2α=。
(2)商数关系:sinαcosα=(α≠π2+kπ,k∈Z)。
2.三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)π+α-απ-απ2-απ2+α正弦sin α余弦cos α正切tan α续表公式一二三四五六口诀函数名不变,符号看象限函数名改变,符号看象限1。
特殊角的三角函数值2.同角三角函数基本关系式的常用变形(1)(sin α±cos α)2=1±2sin αcos α;(2)sin α=tan αcos αα≠π2+kπ,k∈Z;(3)sin2α=sin2αsin2α+cos2α=tan2αtan2α+1;(4)cos 2α=cos 2αsin 2α+cos 2α=1tan 2α+1。
考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”。
(1)对任意的角α,β有sin 2α+cos 2β=1。
( ) (2)若α∈R ,则tan α=sinαcosα恒成立.( )(3)sin (π+α)=-sin α成立的条件是α为锐角。
( )(4)若cos(n π—θ)=13(n ∈Z ),则cos θ=13.( )2。
(2020河北衡水中学模拟一,理3)已知cos α-π2=-2√55,α∈π,3π2,则tan α=( )A 。
2B 。
32C.1D.123。
(2020河北唐山模拟,理4)已知角α的顶点在原点,始边与x 轴的正半轴重合,终边上一点A (2sin α,3)(sin α≠0),则cos α=( )A.12B 。
-12C 。
√32D.-√324。
函数f (x )=15sin x+π3+cos x —π6的最大值为( ) A.65B.1C.35D.15关键能力学案突破考点同角三角函数基本关系式的应用【例1】(1)若tan(α-π)=12,则sin 2α+1cos 2α-sin 2α=( )A。
2024年高考数学一轮复习课件(新高考版) 第4章 必刷大题9 解三角形

(2)若c=6,△ABC的面积S=6bsin B,求S.
123456
由 S=6bsin B,根据面积公式得 6bsin B=12acsin B=3asin B, 所以a=2b. 由余弦定理得 cos C=a2+2ba2b-c2=12, 整理得a2+b2-ab=36,即3b2=36, 所以 b=2 3,a=4 3. 所以△ABC 的面积 S=12absin C=12×4 3×2 3sin π3=6 3.
123456
(2)若△ABC是锐角三角形,且AB=4 km,求养殖区△ABC面积(单位: km2)的取值范围.
123456
因为AB=4,∠BAC=60°, 所以△ABC 的面积 S=12AB·ACsin∠BAC= 3AC. 在△ABC 中,由正弦定理可得sin∠ABACB=sin∠ACABC, 则 AC=ABsisni∠n∠ACABBC=4sin1si2n0∠°-AC∠BACB=tan∠ 2 A3CB+2. 因为△ABC 是锐角三角形,所以00°°<<∠ 12A0°C-B<∠9A0°C,B<90°,
1-2
5
52=
55,
sin∠ADC=sin∠ACB-4π
= 22(sin∠ACB-cos∠ACB)= 22×255- 55= 1100,
在△ACD 中,由正弦定理得sin∠CDDAC=sinπ-A∠D ACB=sin∠ACADC,
123456
即CD2 = A1C0=2105=5 5,解得 CD=5 210,AC=522, 2 10 5
123456
2.(2023·唐山模拟)如图,在锐角△ABC中,内角A,B,C所对的边分别为 a,b,c,4 5 a=bsin 2C+2c(sin A-sin Bcos C).
高三数学第一轮复习 解三角形教案

高三数学第一轮复习解三角形教案三角形是几何学中研究的一个重要的图形,它拥有许多特征和性质,因此在数学中被广泛地研究和应用。
在高三数学第一轮复习中,对于三角形的解题方法和相关知识的掌握是非常重要的。
本文将为大家介绍三角形的基本概念、常用定理和解题技巧。
一、三角形的基本概念1. 三角形的定义:三角形是由三条线段组成的图形,其中任意两条线段的长度之和大于第三条线段的长度。
2. 三角形的分类:(1) 根据边长分类:等边三角形、等腰三角形、一般三角形。
(2) 根据角度分类:锐角三角形、直角三角形、钝角三角形。
(3) 根据边角关系分类:外角、内角、对角、邻角等。
3. 三角形的元素:三角形的边、角和顶点。
二、三角形的常用定理1. 三角形内角和定理:一个三角形的三个内角的和为180°。
2. 直角三角形的性质:(1) 斜边平方等于两直角边平方和的定理(勾股定理)。
(2) 直角三角形内角的关系:直角对顶角为90°,直角三角形的其它两个内角为锐角。
三、三角形的解题技巧1. 判断三角形的类型:(1) 根据边长关系判断三角形的类型:边长相等的三角形为等边三角形,两边相等的三角形为等腰三角形,其余为一般三角形。
(2) 根据角度关系判断三角形的类型:有一个角大于90°的三角形为钝角三角形,有一个角等于90°的三角形为直角三角形,其余为锐角三角形。
2. 运用三角形的性质和定理解题:(1) 利用三角形内角和定理解决求角度的问题。
(2) 运用勾股定理解决用已知信息求三角形边长的问题。
(3) 利用等腰三角形的性质解决求角度或边长的问题。
四、三角形解题的思路1. 首先,根据问题中给出的已知条件判断三角形的类型,并利用已知信息列写方程。
2. 其次,根据三角形的性质和定理对三角形进行推导和运算,求解未知量。
3. 最后,验证解答的合理性,并作出结论。
通过掌握三角形的基本概念、常用定理和解题技巧,我们不仅可以更好地理解三角形的属性和性质,还能够灵活运用这些知识解决实际问题。
高考数学一轮复习 第四章 三角函数与解三角形 4
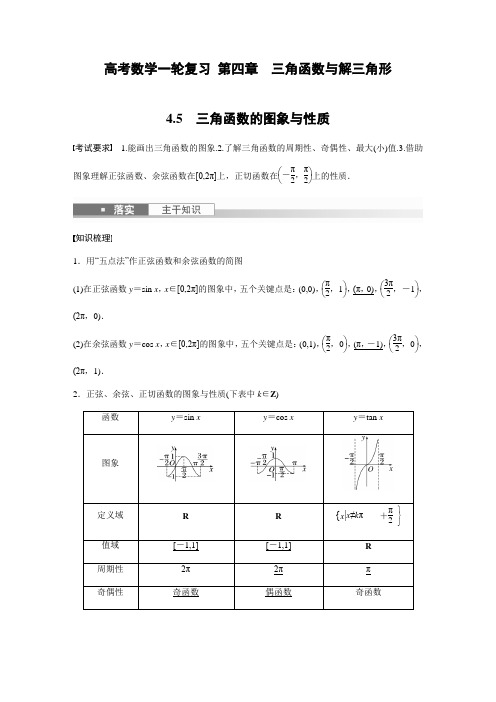
高考数学一轮复习 第四章 三角函数与解三角形4.5 三角函数的图象与性质考试要求 1.能画出三角函数的图象.2.了解三角函数的周期性、奇偶性、最大(小)值.3.借助图象理解正弦函数、余弦函数在[0,2π]上,正切函数在⎝⎛⎭⎫-π2,π2上的性质.知识梳理1.用“五点法”作正弦函数和余弦函数的简图(1)在正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0).(2)在余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )函数y =sin xy =cos xy =tan x图象定义域 R R {x | x ≠k π ⎭⎬⎫+π2 值域 [-1,1] [-1,1] R 周期性 2π 2π π 奇偶性奇函数偶函数奇函数递增区间⎣⎡ 2k π-π2,⎦⎤2k π+π2[2k π-π,2k π]⎝⎛ k π-π2,⎭⎫k π+π2递减区间⎣⎡ 2k π+π2,⎦⎤2k π+3π2[2k π,2k π+π]对称中心 (k π,0) ⎝⎛⎭⎫k π+π2,0⎝⎛⎭⎫k π2,0对称轴方程 x =k π+π2x =k π常用结论1.对称性与周期性(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是12个周期,相邻的对称中心与对称轴之间的距离是14个周期.(2)正切曲线相邻两对称中心之间的距离是半个周期. 2.奇偶性若f (x )=A sin(ωx +φ)(A ,ω≠0),则(1)f (x )为偶函数的充要条件是φ=π2+k π(k ∈Z ).(2)f (x )为奇函数的充要条件是φ=k π(k ∈Z ). 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)正切函数y =tan x 在定义域内是增函数.( × ) (2)已知y =k sin x +1,x ∈R ,则y 的最大值为k +1.( × ) (3)y =sin|x |是偶函数.( √ )(4)若非零实数T 是函数f (x )的周期,则kT (k 是非零整数)也是函数f (x )的周期.( √ ) 教材改编题1.若函数y =2sin 2x -1的最小正周期为T ,最大值为A ,则( )A .T =π,A =1B .T =2π,A =1C .T =π,A =2D .T =2π,A =2 答案 A2.函数f (x )=-2tan ⎝⎛⎭⎫2x +π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪x ≠π6B.⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪x ≠-π12 C.⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪x ≠k π+π6k ∈Z D.⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪x ≠k π2+π6k ∈Z答案 D解析 由2x +π6≠k π+π2,k ∈Z ,得x ≠k π2+π6,k ∈Z .3.函数y =3cos ⎝⎛⎭⎫2x -π3的单调递减区间是________. 答案 ⎣⎡⎦⎤k π+π6,k π+2π3,k ∈Z 解析 因为y =3cos ⎝⎛⎭⎫2x -π3, 令2k π≤2x -π3≤2k π+π,k ∈Z ,求得k π+π6≤x ≤k π+2π3,k ∈Z ,可得函数的单调递减区间为⎣⎡⎦⎤k π+π6,k π+2π3,k ∈Z .题型一 三角函数的定义域和值域例1 (1)函数y =1tan x -1的定义域为________.答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠π4+k π,且x ≠π2+k π,k ∈Z 解析 要使函数有意义, 则⎩⎪⎨⎪⎧tan x -1≠0,x ≠π2+k π,k ∈Z ,即⎩⎨⎧x ≠π4+k π,k ∈Z ,x ≠π2+k π,k ∈Z .故函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠π4+k π,且x ≠π2+k π,k ∈Z .(2)函数y =sin x -cos x +sin x cos x 的值域为________.答案 ⎣⎢⎡⎦⎥⎤-1+222,1解析 设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x ·cos x ,sin x cos x =1-t 22, 且-2≤t ≤ 2.∴y =-t 22+t +12=-12(t -1)2+1,t ∈[-2,2]. 当t =1时,y max =1; 当t =-2时,y min =-1+222. ∴函数的值域为⎣⎢⎡⎦⎥⎤-1+222,1.教师备选1.函数y =sin x -cos x 的定义域为________.答案 ⎣⎡⎦⎤2k π+π4,2k π+5π4(k ∈Z ) 解析 要使函数有意义,必须使sin x -cos x ≥0.利用图象,在同一坐标系中画出[0,2π]上y =sin x 和y =cos x 的图象, 如图所示.在[0,2π]内,满足sin x =cos x 的x 为π4,5π4,再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π+π4≤x ≤2k π+5π4,k ∈Z . 2.函数f (x )=sin 2x +3cos x -34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0,π2的最大值是________. 答案 1解析 由题意可得 f (x )=-cos 2x +3cos x +14=-⎝⎛⎭⎫cos x -322+1. ∵x ∈⎣⎡⎦⎤0,π2, ∴cos x ∈[0,1]. ∴当cos x =32,即x =π6时,f (x )取最大值为1. 思维升华 (1)三角函数定义域的求法求三角函数的定义域实际上是构造简单的三角不等式(组),常借助三角函数的图象来求解. (2)三角函数值域的不同求法①把所给的三角函数式变换成y =A sin(ωx +φ)的形式求值域. ②把sin x 或cos x 看作一个整体,转换成二次函数求值域. ③利用sin x ±cos x 和sin x cos x 的关系转换成二次函数求值域.跟踪训练1 (1)(2021·北京)函数f (x )=cos x -cos 2x ,试判断函数的奇偶性及最大值( ) A .奇函数,最大值为2 B .偶函数,最大值为2 C .奇函数,最大值为98D .偶函数,最大值为98答案 D 解析 由题意,f (-x )=cos (-x )-cos (-2x ) =cos x -cos 2x =f (x ), 所以该函数为偶函数,又f (x )=cos x -cos 2x =-2cos 2x +cos x +1=-2⎝⎛⎭⎫cos x -142+98, 所以当cos x =14时,f (x )取最大值98.(2)函数y =lg(sin 2x )+9-x 2的定义域为________. 答案 ⎣⎡⎭⎫-3,-π2∪⎝⎛⎭⎫0,π2 解析 ∵函数y =lg(sin 2x )+9-x 2,∴应满足⎩⎪⎨⎪⎧sin 2x >0,9-x 2≥0, 解得⎩⎪⎨⎪⎧k π<x <π2+k π,-3≤x ≤3,其中k ∈Z ,∴-3≤x <-π2或0<x <π2,∴函数的定义域为⎣⎡⎭⎫-3,-π2∪⎝⎛⎭⎫0,π2.题型二 三角函数的周期性、奇偶性、对称性例2 (1)(2019·全国Ⅱ)下列函数中,以π2为周期且在区间⎝⎛⎭⎫π4,π2上单调递增的是( ) A .f (x )=|cos 2x | B .f (x )=|sin 2x |答案 A解析 A 中,函数f (x )=|cos 2x |的周期为π2,当x ∈⎝⎛⎭⎫π4,π2时,2x ∈⎝⎛⎭⎫π2,π,函数f (x )单调递增,故A 正确;B 中,函数f (x )=|sin 2x |的周期为π2,当x ∈⎝⎛⎭⎫π4,π2时,2x ∈⎝⎛⎭⎫π2,π,函数f (x )单调递减,故B 不正确;C 中,函数f (x )=cos|x |=cos x 的周期为2π,故C 不正确;D 中,f (x )=sin|x |=⎩⎪⎨⎪⎧sin x ,x ≥0,-sin x ,x <0,由正弦函数图象知,在x ≥0和x <0时,f (x )均以2π为周期,但在整个定义域上f (x )不是周期函数,故D 不正确.(2)函数f (x )=3sin ⎝⎛⎭⎫2x -π3+φ+1,φ∈(0,π),且f (x )为偶函数,则φ=________,f (x )图象的对称中心为________. 答案5π6 ⎝⎛⎭⎫π4+k π2,1,k ∈Z 解析 若f (x )=3sin ⎝⎛⎭⎫2x -π3+φ+1为偶函数,则-π3+φ=k π+π2,k ∈Z , 即φ=5π6+k π,k ∈Z ,又∵φ∈(0,π), ∴φ=5π6.∴f (x )=3sin ⎝⎛⎭⎫2x +π2+1=3cos 2x +1, 由2x =π2+k π,k ∈Z 得x =π4+k π2,k ∈Z ,∴f (x )图象的对称中心为⎝⎛⎭⎫π4+k π2,1,k ∈Z . 教师备选1.下列函数中,是周期函数的为( ) A .y =sin|x |B .y =cos|x |答案 B解析 ∵cos|x |=cos x ,∴y =cos|x |是周期函数.其余函数均不是周期函数. 2.函数f (x )=3sin ⎝⎛⎭⎫2x -π3+φ,φ∈(0,π),若f (x )为奇函数,则φ=________. 答案 π3解析 若f (x )=3sin ⎝⎛⎭⎫2x -π3+φ为奇函数, 则-π3+φ=k π,k ∈Z ,即φ=π3+k π,k ∈Z ,又∵φ∈(0,π), ∴φ=π3.思维升华 (1)奇偶性的判断方法:三角函数中奇函数一般可化为y =A sin ωx 或y =A tan ωx 的形式,而偶函数一般可化为y =A cos ωx 的形式.(2)周期的计算方法:利用函数y =A sin(ωx +φ),y =A cos(ωx +φ)(ω>0)的周期为2πω,函数y =A tan(ωx +φ)(ω>0)的周期为πω求解.跟踪训练2 (1)(2021·全国乙卷)函数f (x )=sin x 3+cos x3最小正周期和最大值分别是( )A .3π和 2B .3π和2C .6π和 2D .6π和2答案 C解析 因为函数f (x )=sin x 3+cos x3=2⎝⎛⎭⎫22sin x 3+22cos x 3=2⎝⎛⎭⎫sin x 3cos π4+cos x 3sin π4 =2sin ⎝⎛⎭⎫x 3+π4,所以函数f (x )的最小正周期T =2π13=6π,最大值为 2.(2)已知f (x )=A cos(ωx +φ)(A >0,ω>0,0<φ<π)是定义域为R 的奇函数,且当x =3时,f (x )取得最小值-3,当ω取得最小正数时,f (1)+f (2)+f (3)+…+f (2 022)的值为( ) A.32 B .-6-3 3 C .1 D .-1答案 B解析 ∵f (x )=A cos(ωx +φ)(A >0,ω>0,0<φ<π)是定义域为R 的奇函数, ∴φ=π2+k π,k ∈Z ,则φ=π2,则f (x )=-A sin ωx .当x =3时,f (x )取得最小值-3, 故A =3,sin 3ω=1, ∴3ω=π2+2k π,k ∈Z .∴ω的最小正数为π6,∴f (x )=-3sin π6x ,∴f (x )的周期为12,∴f (1)+f (2)+f (3)+…+f (12)=0, ∴f (1)+f (2)+f (3)+…+f (2 022) =168×0+f (1)+f (2)+…+f (6) =-6-3 3.(3)(2022·郑州模拟)设函数f (x )=2sin ⎝⎛⎭⎫2x -π3+34,则下列叙述正确的是( ) A .f (x )的最小正周期为2π B .f (x )的图象关于直线x =π12对称 C .f (x )在⎣⎡⎦⎤π2,π上的最小值为-54 D .f (x )的图象关于点⎝⎛⎭⎫2π3,0对称 答案 C解析 对于A ,f (x )的最小正周期为2π2=π,故A 错误;对于B ,∵sin ⎝⎛⎭⎫2×π12-π3=-12≠±1, 故B 错误;对于C ,当x ∈⎣⎡⎦⎤π2,π时,2x -π3∈⎣⎡⎦⎤2π3,5π3, ∴sin ⎝⎛⎭⎫2x -π3∈⎣⎡⎦⎤-1,32, ∴2sin ⎝⎛⎭⎫2x -π3+34∈⎣⎡⎦⎤-54,3+34, ∴f (x )在⎣⎡⎦⎤π2,π上的最小值为-54,故C 正确; 对于D ,∵f ⎝⎛⎭⎫2π3=2sin ⎝⎛⎭⎫2×2π3-π3+34=34, ∴f (x )的图象关于点⎝⎛⎭⎫2π3,34对称,故D 错误. 题型三 三角函数的单调性 命题点1 求三角函数的单调区间例3 函数f (x )=sin ⎝⎛⎭⎫-2x +π3的单调递减区间为________.答案 ⎣⎡⎦⎤k π-π12,k π+5π12(k ∈Z ) 解析 f (x )=sin ⎝⎛⎭⎫-2x +π3 =sin ⎣⎡⎦⎤-⎝⎛⎭⎫2x -π3 =-sin ⎝⎛⎭⎫2x -π3, 由2k π-π2≤2x -π3≤2k π+π2,k ∈Z , 得k π-π12≤x ≤k π+5π12,k ∈Z . 故所求函数的单调递减区间为⎣⎡⎦⎤k π-π12,k π+5π12(k ∈Z ). 延伸探究 f (x )=sin ⎝⎛⎭⎫-2x +π3在[0,π]上的单调递减区间为________. 答案 ⎣⎡⎦⎤0,5π12和⎣⎡⎦⎤11π12,π 解析 令A =⎣⎡⎦⎤k π-π12,k π+5π12,k ∈Z , B =[0,π],∴A ∩B =⎣⎡⎦⎤0,5π12∪⎣⎡⎦⎤11π12,π, ∴f (x )在[0,π]上的单调递减区间为⎣⎡⎦⎤0,5π12和⎣⎡⎦⎤11π12,π. 命题点2 根据单调性求参数例4 (1)若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω=________.答案 32解析 ∵f (x )=sin ωx (ω>0)过原点,∴当0≤ωx ≤π2, 即0≤x ≤π2ω时,y =sin ωx 单调递增; 当π2≤ωx ≤3π2, 即π2ω≤x ≤3π2ω时,y =sin ωx 单调递减. 由f (x )=sin ωx (ω>0)在⎣⎡⎦⎤0,π3上单调递增, 在⎣⎡⎦⎤π3,π2上单调递减,知π2ω=π3, ∴ω=32. (2)已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是________. 答案 ⎣⎡⎦⎤12,54解析 由π2<x <π,ω>0, 得ωπ2+π4<ωx +π4<ωπ+π4, 因为y =sin x 的单调递减区间为⎣⎡⎦⎤2k π+π2,2k π+3π2,k ∈Z , 所以⎩⎨⎧ ωπ2+π4≥π2+2k π,ωπ+π4≤3π2+2k π,k ∈Z ,解得4k +12≤ω≤2k +54,k ∈Z . 又由4k +12-⎝⎛⎭⎫2k +54≤0,k ∈Z , 且2k +54>0,k ∈Z , 解得k =0,所以ω∈⎣⎡⎦⎤12,54.教师备选(2022·定远县育才学校月考)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|≤π2,x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在⎝⎛⎭⎫π18,5π36上单调,则ω的最大值为( ) A .11 B .9 C .7 D .1答案 B解析 因为x =-π4为f (x )的零点, x =π4为y =f (x )图象的对称轴, 所以2n +14·T =π2(n ∈N ), 即2n +14·2πω=π2(n ∈N ), 所以ω=2n +1(n ∈N ),即ω为正奇数.因为f (x )在⎝⎛⎭⎫π18,5π36上单调,则5π36-π18=π12≤T 2, 即T =2πω≥π6, 解得ω≤12.当ω=11时,-11π4+φ=k π,k ∈Z , 因为|φ|≤π2, 所以φ=-π4,此时f (x )=sin ⎝⎛⎭⎫11x -π4. 当x ∈⎝⎛⎭⎫π18,5π36时,11x -π4∈⎝⎛⎭⎫13π36,46π36, 所以f (x )在⎝⎛⎭⎫π18,5π36上不单调,不满足题意;当ω=9时,-9π4+φ=k π,k ∈Z , 因为|φ|≤π2, 所以φ=π4, 此时f (x )=sin ⎝⎛⎭⎫9x +π4. 当x ∈⎝⎛⎭⎫π18,5π36时,9x +π4∈⎝⎛⎭⎫3π4,3π2, 此时f (x )在⎝⎛⎭⎫π18,5π36上单调递减,符合题意.故ω的最大值为9.思维升华 (1)已知三角函数解析式求单调区间求形如y =A sin(ωx +φ)或y =A cos(ωx +φ)(其中ω>0)的单调区间时,要视“ωx +φ”为一个整体,通过解不等式求解.但如果ω<0,可借助诱导公式将ω化为正数,防止把单调性弄错.(2)已知三角函数的单调区间求参数.先求出函数的单调区间,然后利用集合间的关系求解.跟踪训练3 (1)(2021·新高考全国Ⅰ)下列区间中,函数f (x )=7sin ⎝⎛⎭⎫x -π6的单调递增区间是( )A.⎝⎛⎭⎫0,π2 B.⎝⎛⎭⎫π2,π C.⎝⎛⎭⎫π,3π2 D.⎝⎛⎭⎫3π2,2π答案 A解析 令-π2+2k π≤x -π6≤π2+2k π,k ∈Z ,得-π3+2k π≤x ≤2π3+2k π,k ∈Z .取k =0,则-π3≤x ≤2π3.因为⎝⎛⎭⎫0,π2⎣⎡⎦⎤-π3,2π3,所以区间⎝⎛⎭⎫0,π2是函数f (x )的单调递增区间. (2)(2022·开封模拟)已知函数y =sin ⎝⎛⎭⎫ωx +π3 (ω>0)在区间⎝⎛⎭⎫-π6,π3上单调递增,则ω的取值范围是( ) A.⎝⎛⎦⎤0,12 B.⎣⎡⎦⎤12,1 C.⎝⎛⎦⎤13,23D.⎣⎡⎦⎤23,2答案 A解析 当-π6<x <π3时, -πω6+π3<ωx +π3<πω3+π3, 当x =0时,ωx +π3=π3. 因为函数y =sin ⎝⎛⎭⎫ωx +π3(ω>0)在区间⎝⎛⎭⎫-π6,π3上单调递增, 所以⎩⎨⎧ -πω6+π3≥-π2,πω3+π3≤π2,解得ω≤12, 因为ω>0,所以ω的取值范围是⎝⎛⎦⎤0,12. 课时精练1.y =|cos x |的一个单调递增区间是( )A.⎣⎡⎦⎤-π2,π2 B .[0,π]C.⎣⎡⎦⎤π,3π2 D.⎣⎡⎦⎤3π2,2π 答案 D 解析 将y =cos x 的图象位于x 轴下方的部分关于x 轴对称向上翻折,x 轴上方(或x 轴上)的图象不变,即得y =|cos x |的图象(如图).故选D.2.函数f (x )=2sin π2x -1的定义域为( ) A.⎣⎡⎦⎤π3+4k π,5π3+4k π(k ∈Z ) B.⎣⎡⎦⎤13+4k ,53+4k (k ∈Z ) C.⎣⎡⎦⎤π6+4k π,5π6+4k π(k ∈Z ) D.⎣⎡⎦⎤16+4k ,56+4k (k ∈Z ) 答案 B解析 由题意,得2sin π2x -1≥0, π2x ∈⎣⎡⎦⎤π6+2k π,5π6+2k π(k ∈Z ), 则x ∈⎣⎡⎦⎤13+4k ,53+4k (k ∈Z ). 3.函数f (x )=sin ⎝⎛⎭⎫x +5π12cos ⎝⎛⎭⎫x -π12是( ) A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为2π的非奇非偶函数D .最小正周期为π的非奇非偶函数答案 D解析 由题意可得f (x )=sin ⎝⎛⎭⎫x +5π12cos ⎝⎛⎭⎫x -π12 =sin ⎝⎛⎭⎫x +5π12cos ⎝⎛⎭⎫x +5π12-π2 =sin 2⎝⎛⎭⎫x +5π12, ∴f (x )=12-12cos ⎝⎛⎭⎫2x +5π6, 故f (x )的最小正周期T =2π2=π,由函数奇偶性的定义易知,f (x )为非奇非偶函数. 4.函数f (x )=sin x +x cos x +x 2在[-π,π]的图象大致为( )答案 D解析 由f (-x )=sin -x +-x cos -x +-x2 =-sin x -x cos x +x 2=-f (x ),得f (x )是奇函数,其图象关于原点对称,排除A ; 又f ⎝⎛⎭⎫π2=1+π2⎝⎛⎭⎫π22=4+2ππ2>1, f (π)=π-1+π2>0,排除B ,C. 5.关于函数f (x )=sin 2x -cos 2x ,下列命题中为假命题的是( )A .函数y =f (x )的周期为πB .直线x =π4是y =f (x )图象的一条对称轴 C .点⎝⎛⎭⎫π8,0是y =f (x )图象的一个对称中心D .y =f (x )的最大值为 2答案 B解析 因为f (x )=sin 2x -cos 2x =2sin ⎝⎛⎭⎫2x -π4, 所以f (x )的最大值为2,故D 为真命题;因为ω=2,故T =2π2=π,故A 为真命题; 当x =π4时,2x -π4=π4,终边不在y 轴上,故直线x =π4不是y =f (x )图象的一条对称轴, 故B 为假命题;当x =π8时,2x -π4=0,终边落在x 轴上, 故点⎝⎛⎭⎫π8,0是y =f (x )图象的一个对称中心,故C 为真命题.6.(2022·广州市培正中学月考)关于函数f (x )=sin|x |+|sin x |,下列叙述正确的是( )A .f (x )是奇函数B .f (x )在区间⎝⎛⎭⎫π2,π上单调递增C .f (x )的最大值为2D .f (x )在[-π,π]上有4个零点答案 C解析 f (-x )=sin|-x |+|sin(-x )|=sin|x |+|sin x |=f (x ),f (x )是偶函数,A 错误;当x ∈⎝⎛⎭⎫π2,π时,f (x )=sin x +sin x =2sin x ,单调递减,B 错误;f (x )=sin|x |+|sin x |≤1+1=2,且f ⎝⎛⎭⎫π2=2,C 正确;在[-π,π]上,当-π<x <0时,f (x )=sin(-x )+(-sin x )=-2sin x >0,当0<x <π时,f (x )=sin x +sin x =2sin x >0,f (x )的零点只有π,0,-π共三个,D 错误.7.写出一个周期为π的偶函数f (x )=________.(答案不唯一) 答案 cos 2x8.(2022·上外浦东附中检测)若在⎣⎡⎦⎤0,π2内有两个不同的实数值满足等式cos 2x +3sin 2x =k +1,则实数k 的取值范围是________.答案 0≤k <1解析 函数f (x )=cos 2x +3sin 2x=2sin ⎝⎛⎭⎫2x +π6, 当x ∈⎣⎡⎦⎤0,π6时, f (x )=2sin ⎝⎛⎭⎫2x +π6单调递增; 当x ∈⎣⎡⎦⎤π6,π2时,f (x )=2sin ⎝⎛⎭⎫2x +π6单调递减, f (0)=2sin π6=1, f ⎝⎛⎭⎫π6=2sin π2=2, f ⎝⎛⎭⎫π2=2sin 7π6=-1,所以在⎣⎡⎦⎤0,π2内有两个不同的实数值满足等式cos 2x +3sin 2x =k +1, 则1≤k +1<2,所以0≤k <1.9.已知函数f (x )=4sin ωx sin ⎝⎛⎭⎫ωx +π3-1(ω>0)的最小正周期为π. (1)求ω及f (x )的单调递增区间;(2)求f (x )图象的对称中心.解 (1)f (x )=4sin ωx ⎝⎛⎭⎫12sin ωx +32cos ωx -1 =2sin 2ωx +23sin ωx cos ωx -1 =1-cos 2ωx +3sin 2ωx -1 =3sin 2ωx -cos 2ωx=2sin ⎝⎛⎭⎫2ωx -π6. ∵最小正周期为π,∴2π2ω=π, ∴ω=1,∴f (x )=2sin ⎝⎛⎭⎫2x -π6, 令-π2+2k π≤2x -π6≤π2+2k π,k ∈Z , 解得-π6+k π≤x ≤π3+k π,k ∈Z , ∴f (x )的单调递增区间为⎣⎡⎦⎤-π6+k π,π3+k π (k ∈Z ).(2)令2x -π6=k π,k ∈Z , 解得x =π12+k π2,k ∈Z ,∴f (x )图象的对称中心为⎝⎛⎭⎫π12+k π2,0,k ∈Z .10.(2021·浙江)设函数f (x )=sin x +cos x (x ∈R ).(1)求函数y =⎣⎡⎦⎤f ⎝⎛⎭⎫x +π22的最小正周期; (2)求函数y =f (x )f ⎝⎛⎭⎫x -π4在⎣⎡⎦⎤0,π2上的最大值. 解 (1)因为f (x )=sin x +cos x ,所以f ⎝⎛⎭⎫x +π2=sin ⎝⎛⎭⎫x +π2+cos ⎝⎛⎭⎫x +π2 =cos x -sin x ,所以y =⎣⎡⎦⎤f ⎝⎛⎭⎫x +π22=(cos x -sin x )2 =1-sin 2x .所以函数y =⎣⎡⎦⎤f ⎝⎛⎭⎫x +π22的最小正周期T =2π2=π. (2)f ⎝⎛⎭⎫x -π4=sin ⎝⎛⎭⎫x -π4+cos ⎝⎛⎭⎫x -π4 =2sin x ,所以y =f (x )f ⎝⎛⎭⎫x -π4 =2sin x (sin x +cos x ) =2(sin x cos x +sin 2x ) =2⎝⎛⎭⎫12sin 2x -12cos 2x +12 =sin ⎝⎛⎭⎫2x -π4+22. 当x ∈⎣⎡⎦⎤0,π2时,2x -π4∈⎣⎡⎦⎤-π4,3π4, 所以当2x -π4=π2,即x =3π8时, 函数y =f (x )f ⎝⎛⎭⎫x -π4在⎣⎡⎦⎤0,π2上取得最大值,且y max =1+22.11.(2022·苏州模拟)已知函数f (x )=sin ⎝⎛⎭⎫2x +π3,则下列结论不正确的是( ) A .x =-π6是函数f (x )的一个零点 B .函数f (x )在区间⎣⎡⎦⎤-5π12,π12上单调递增 C .函数f (x )的图象关于直线x =π12对称 D .函数f ⎝⎛⎭⎫x -π3是偶函数 答案 D解析 对于A 选项,因为f ⎝⎛⎭⎫-π6=sin 0=0, 故x =-π6是函数f (x )的一个零点,A 对; 对于B 选项,当-5π12≤x ≤π12时, -π2≤2x +π3≤π2, 所以函数f (x )在区间⎣⎡⎦⎤-5π12,π12上单调递增,B 对; 对于C 选项,因为对称轴满足2x +π3=π2+k π,k ∈Z , 解得x =π12+k π2,k ∈Z ,当k =0时,x =π12,C 对; 对于D 选项,令g (x )=f ⎝⎛⎭⎫x -π3=sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π3+π3 =sin ⎝⎛⎭⎫2x -π3, 则g ⎝⎛⎭⎫π6=0,g ⎝⎛⎭⎫-π6=sin ⎝⎛⎭⎫-2π3≠0, 故函数f ⎝⎛⎭⎫x -π3不是偶函数,D 错. 12.(2022·厦门模拟)已知函数f (x )=cos 2⎝⎛⎭⎫x -π6-cos 2x ,则下列结论正确的是( ) A .f (x )的最大值为3-12B .f (x )的图象关于点⎝⎛⎭⎫7π6,0对称C .f (x )的图象的对称轴方程为x =5π12+k π2(k ∈Z ) D .f (x )在[0,2π]上有2个零点答案 C解析 f (x )=1+cos ⎝⎛⎭⎫2x -π32-cos 2x =12+12⎝⎛⎭⎫12cos 2x +32sin 2x -cos 2x =34sin 2x -34cos 2x +12=32sin ⎝⎛⎭⎫2x -π3+12, 则f (x )的最大值为1+32,A 错误; 易知f (x )图象的对称中心的纵坐标为12, B 错误;令2x -π3=π2+k π(k ∈Z ), 得x =5π12+k π2(k ∈Z ), 此即f (x )图象的对称轴方程,C 正确;由f (x )=32sin ⎝⎛⎭⎫2x -π3+12=0, 得sin ⎝⎛⎭⎫2x -π3=-33, 当x ∈[0,2π]时,2x -π3∈⎣⎡⎦⎤-π3,11π3, 作出函数y =sin x ⎝⎛⎭⎫x ∈⎣⎡⎦⎤-π3,11π3的图象,如图所示.所以方程sin ⎝⎛⎭⎫2x -π3=-33在[0,2π]上有4个不同的实根, 即f (x )在[0,2π]上有4个零点,D 错误.13.(2022·绵阳中学实验学校模拟)已知sin x +cos y =14,则sin x -sin 2y 的最大值为______. 答案 916解析 ∵sin x +cos y =14,sin x ∈[-1,1], ∴sin x =14-cos y ∈[-1,1], ∴cos y ∈⎣⎡⎦⎤-34,54, 即cos y ∈⎣⎡⎦⎤-34,1, ∵sin x -sin 2y =14-cos y -(1-cos 2y ) =cos 2y -cos y -34=⎝⎛⎭⎫cos y -122-1, 又cos y ∈⎣⎡⎦⎤-34,1,利用二次函数的性质知,当cos y =-34时, (sin x -sin 2y )max =⎝⎛⎭⎫-34-122-1=916. 14.(2022·苏州八校联盟检测)已知f (x )=sin x +cos x ,若y =f (x +θ)是偶函数,则cos θ=________.答案 ±22解析 因为f (x )=2sin ⎝⎛⎭⎫x +π4, 所以f (x +θ)=2sin ⎝⎛⎭⎫x +θ+π4, 又因为y =f (x +θ)是偶函数,所以θ+π4=π2+k π,k ∈Z , 即θ=π4+k π,k ∈Z , 所以cos θ=cos ⎝⎛⎭⎫π4+k π=±22.15.(2022·江西九江一中模拟)已知函数f (x )=sin ⎝⎛⎭⎫ωx +π3(ω>0),若方程f (x )=0在[0,2π]上有且仅有6个根,则实数ω的值可能为( )A .2B .3C .4D .5答案 B解析 令f (x )=sin ⎝⎛⎭⎫ωx +π3=0, 则ωx +π3=k π,k ∈Z , 所以x =-π3ω+k πω,k ∈Z , 所以当x ≥0时,函数f (x )的第一个零点为x 1=-π3ω+πω=2π3ω,第六个零点为x 6=-π3ω+6πω=17π3ω,第七个零点为x 7=-π3ω+7πω=20π3ω, 因为方程f (x )=0在[0,2π]上有且仅有6个根等价于函数y =f (x )在[0,2π]上有且仅有6个零点,所以17π3ω≤2π<20π3ω, 所以176≤ω<103. 16.已知f (x )=sin 2⎝⎛⎭⎫x +π8+2sin ⎝⎛⎭⎫x +π4·cos ⎝⎛⎭⎫x +π4-12. (1)求f (x )的单调递增区间;(2)若函数y =|f (x )|-m 在区间⎣⎡⎦⎤-5π24,3π8上恰有两个零点x 1,x 2. ①求m 的取值范围;②求sin(x 1+x 2)的值.解 (1)f (x )=sin 2⎝⎛⎭⎫x +π8+2sin ⎝⎛⎭⎫x +π4·cos ⎝⎛⎭⎫x +π4-12=1-cos ⎝⎛⎭⎫2x +π42+22sin ⎝⎛⎭⎫2x +π2-12 =12-24cos 2x +24sin 2x +22cos 2x -12=24sin 2x +24cos 2x =12sin ⎝⎛⎭⎫2x +π4, 结合正弦函数的图象与性质, 可得当-π2+2k π≤2x +π4≤π2+2k π(k ∈Z ), 即-3π8+k π≤x ≤π8+k π(k ∈Z )时,函数单调递增, ∴函数y =f (x )的单调递增区间为⎣⎡⎦⎤-3π8+k π,π8+k π(k ∈Z ). (2)①令t =2x +π4,当x ∈⎣⎡⎦⎤-5π24,3π8时,t ∈⎣⎡⎦⎤-π6,π,12sin t ∈⎣⎡⎦⎤-14,12, ∴y =⎪⎪⎪⎪12sin t ∈⎣⎡⎦⎤0,12(如图).∴要使y =|f (x )|-m 在区间⎣⎡⎦⎤-5π24,3π8上恰有两个零点,m 的取值范围为14<m <12或m =0. ②设t 1,t 2是函数y =⎪⎪⎪⎪12sin t -m 的两个零点⎝⎛⎭⎫即t 1=2x 1+π4,t 2=2x 2+π4, 由正弦函数图象性质可知t 1+t 2=π,即2x 1+π4+2x 2+π4=π. ∴x 1+x 2=π4,∴sin(x 1+x 2)=22.。
2022版高考数学一轮复习第3章三角函数解三角形36正弦定理和余

2022版高考数学一轮复习第3章三角函数解三角形36正弦定理和余3.6正弦定理和余弦定理[知识梳理]1.正弦定理、余弦定理在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则2.在△ABC中,已知a,b和A时,三角形解的情况3.三角形中常用的面积公式1(1)S=ah(h表示边a上的高).2111(2)S=bcinA=acinB=abinC.222(3)S=r(a+b+c)(r为三角形的内切圆半径).24.在△ABC中,常有的结论(1)∠A+∠B+∠C=π.(2)在三角形中大边对大角,大角对大边.(3)任意两边之和大于第三边,任意两边之差小于第三边.[诊断自测]1.概念思辨(1)在三角形中,已知两角和一边或已知两边和一角都能解三角形.()aa+b-c(2)在△ABC中,=.()inAinA+inB-inC(3)若a,b,c是△ABC的三边,当b+c-a>0时,△ABC为锐角三角形;当b+c-22222a2=0时,△ABC为直角三角形;当b2+c2-a2<0时,△ABC为钝角三角形.()(4)在△ABC中,若inAinBin2A(1)(必修A5P10A组T4)在△ABC中,a=4,b=5,c=6,则=________.inC答案1解析由正弦定理得inA∶inB∶inC=a∶b∶c=4∶5∶6,又由余弦定理知coA=b2+c2-a225+36-163in2A2inAcoA43==,所以==2某某=1.2bc2某5某64inCinC64(2)(必修A5P20A组T11)若锐角△ABC的面积为103,且AB=5,AC=8,则BC等于________.答案711解析因为△ABC的面积S△ABC=AB·ACinA,所以103=某5某8inA,解得inA=223122222,因为角A为锐角,所以coA=.根据余弦定理,得BC=5+8-2某5某8coA=5+8221-2某5某8某=49,所以BC=7.23.小题热身(1)(2022·天津高考)在△ABC中,若AB=13,BC=3,∠C=120°,则AC=()A.1B.2C.3D.4答案A解析在△ABC中,设A,B,C所对的边分别为a,b,c,则由c=a+b-2abcoC,222122得13=9+b-2某3b某-,即b+3b-4=0,解得b=1(负值舍去),即AC=1.故选A.24(2)(2022·全国卷Ⅲ)△ABC的内角A,B,C的对边分别为a,b,c,若coA=,coC55=,a=1,则b=________.13答案21133123541263inAinB3135题型1利用正、余弦定理解三角形b(2022·郑州预测)在△ABC中,角A,B,C所对的边分别为a,b,c,若典例13coB=,则coB=()inA1133A.-B.C.-D.2222a边角互化法.答案B解析由正弦定理知inBinAπ==1,即tanB=3,由B∈(0,π),所以B=,33coBinAπ1所以coB=co=.故选B.32典例2(2022·重庆期末)在△ABC中,已知AB=43,AC=4,∠B=30°,则△ABC的面积是()A.43B.83C.43或83D.3注意本题的多解性.答案C解析在△ABC中,由余弦定理可得AC=4=(43)+BC-2某43BCco30°,解得BC=4或BC=8.当BC=4时,AC=BC,∠B=∠A=30°,△ABC为等腰三角形,∠C=120°,111△ABC的面积为AB·BCinB=某43某4某=43.222111当BC=8时,△ABC的面积为AB·BCinB=某43某8某=83.故选C.222方法技巧正、余弦定理在解三角形中的应用技巧1.已知两边和一边的对角或已知两角和一边都能用正弦定理解三角形,正弦定理的形式多样,其中a=2RinA,b=2RinB,c=2RinC能够实现边角互化.见典例1.2.已知两边和它们的夹角、已知两边和一边的对角或已知三边都能直接运用余弦定理解三角形.见典例2.3.已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.见典例2.冲关针对训练1.(2022·河西五市联考)在△ABC中,角A,B,C的对边分别为a,b,c,且满足(b-a)inA=(b-c)·(inB+inC),则角C等于() A.πππ2πB.C.D.36432222答案Aa2+b2-c21解析由题意,得(b-a)a=(b-c)(b+c),∴ab=a+b-c,∴coC==,2ab2222π∴C=.故选A.32.(2022·山东师大附中模拟)在△ABC中,角A,B,C的对边分别是a,b,c,已知1co2A=-,c=3,inA=6inC.3(1)求a的值;(2)若角A为锐角,求b的值及△ABC的面积.解(1)在△ABC中,c=3,inA=6inC,由正弦定理=,得a=6c=6inAinC某3=32.12π622(2)由co2A=1-2inA=-得,inA=,由03323则coA=1-inA=2222ac3.3由余弦定理a=b+c-2bccoA,化简,得b-2b-15=0,解得b=5(b=-3舍去).11652所以S△ABC=bcinA=某5某3某=.22322题型2利用正、余弦定理判断三角形的形状典例(2022·陕西模拟)设△ABC的内角A,B,C所对的边分别为a,b,c,若bcoC+ccoB=ainA,则△ABC的形状为()A.锐角三角形C.钝角三角形B.直角三角形D.不确定用边角互化法.答案B解析∵bcoC+ccoB=ainA,由正弦定理得inBcoC+inCcoB=inA,∴in(Bπ22+C)=inA,即inA=inA.又inA>0,∴inA=1,∴A=,故△ABC为直角三角形.故2选B.[条件探究1]将本典例条件变为“若2inAcoB=inC”,那么△ABC一定是()A.直角三角形C.等腰直角三角形B.等腰三角形D.等边三角形2答案B解析解法一:由已知得2inAcoB=inC=in(A+B)=inAcoB+coAinB,即in(A-B)=0,因为-πa2+c2-b222由余弦定理得2a·=ca=ba=b.故选B.2ac[条件探究2]将本典例条件变为“若△ABC的三个内角满足inA∶inB∶inC=5∶11∶13”,则△ABC()A.一定是锐角三角形B.一定是直角三角形C.一定是钝角三角形D.可能是锐角三角形,也可能是钝角三角形答案C解析在△ABC中,inA∶inB∶inC=5∶11∶13,∴a∶b∶c=5∶11∶13,故设a=5k,b=11k,c=13k(k>0),由余弦定理可得a2+b2-c225k2+121k2-169k223coC===-<0,22ab2某5某11k110π又∵C∈(0,π),∴C∈,π,2∴△ABC为钝角三角形.故选C.[条件探究3]将本典例条件变为“若bcoB+ccoC=acoA”,试判断三角形的形状.解由已知得a2+c2-b2a2+b2-c2b2+c2-a2b·+c·=a·,2ac2ab2bc∴b(a+c-b)+c(a+b-c)=a(b+c-a).∴(a+c-b)(b +a-c)=0.ππ222222∴a+c=b或b+a=c,即B=或C=.22∴△ABC为直角三角形.方法技巧判定三角形形状的两种常用途径222222222222222222提醒:“角化边”后要注意用因式分解、配方等方法得出边的相应关系;“边化角”后答案B解析解法一:由已知得2inAcoB=inC=in(A+B)=inAcoB+coAinB,即in(A-B)=0,因为-πa2+c2-b222由余弦定理得2a·=ca=ba=b.故选B.2ac[条件探究2]将本典例条件变为“若△ABC的三个内角满足inA∶inB∶inC=5∶11∶13”,则△ABC()A.一定是锐角三角形B.一定是直角三角形C.一定是钝角三角形D.可能是锐角三角形,也可能是钝角三角形答案C解析在△ABC中,inA∶inB∶inC=5∶11∶13,∴a∶b∶c=5∶11∶13,故设a=5k,b=11k,c=13k(k>0),由余弦定理可得a2+b2-c225k2+121k2-169k223coC===-<0,22ab2某5某11k110π又∵C∈(0,π),∴C∈,π,2∴△ABC为钝角三角形.故选C.[条件探究3]将本典例条件变为“若bcoB+ccoC=acoA”,试判断三角形的形状.解由已知得a2+c2-b2a2+b2-c2b2+c2-a2b·+c·=a·,2ac2ab2bc∴b(a+c-b)+c(a+b-c)=a(b+c-a).∴(a+c-b)(b +a-c)=0.ππ222222∴a+c=b或b+a=c,即B=或C=.22∴△ABC为直角三角形.方法技巧判定三角形形状的两种常用途径222222222222222222提醒:“角化边”后要注意用因式分解、配方等方法得出边的相应关系;“边化角”后。
高考数学一轮总复习教学课件第四章 三角函数、解三角形第二课时 解三角形的综合问题

个角的三角函数,利用函数思想求解,此时要特别注意题目隐含条件
的应用,如锐角三角形、钝角三角形、三角形内角和为π等.
[针对训练] (2024·山东青岛模拟)记△ABC的内角A,B,C的对边
分别为a,b,c,已知acos B+b·cos A=2ccos C.
-
-
=
=
=
+
+ ( -) +- - +
=
2
=4cos B+ -5≥2
=
·
-5
的最小值.
解:(2)由(1)得 cos(A+B)=sin B,
所以 sin[ -(A+B)]=sin B,
且 0<A+B<,
所以 0<B<,0<-(A+B)<,
所以-(A+B)=B,解得 A=-2B,
由正弦定理得
+
=
+
( -)+
提升·关键能力
类分考点,落实四翼
考点一
以多个三角形为载体的解三角形问题
[例1] (2024·江苏南通质量监测)在△ABC中,点D在边BC上,AB=3,
AC=2.
(1)若AD是∠BAC的平分线,求BD∶DC;
解:(1)法一 因为点D在边BC上,AB=3,AC=2,
所以在△ABD和△ACD中,由正弦定理,得
高考一轮复习第3章三角函数解三角形第1讲任意角和蝗制及任意角的三角函

第一讲 任意角和弧度制及任意角的三角函数
知识梳理·双基自测
知识点一 角的有关概念
(1)从运动的角度看,角可分为正角、负角和零角.
(2)从终边位置来看,角可分为象限角与轴线角.
(3)若β与α是终边相同的角,则β用α表示为β=2kπ+α,k∈Z.
知识点二 弧度制及弧长、扇形面积公式
知识点三 任意角的三角函数
(1)定义:设α是一个任意角,它的终边与单位圆交于点P(x,y),那么sin α=y,cos α=x,tan α= (x≠0).
(2)几何表示:三角函数线可以看作是三角函数的几何表示.正弦线的起点都在x轴上,余弦线的起点都是原点,正切线的起点都是点(1,0).如图中有向线段MP,OM,AT分别叫做角α的正弦线,余弦线和正切线.
[解析]由角α的终边过点P 得sin α=- ,所以sin(α+π)=-sin α= .
考点突破·互动探究
考点一 角的基本概念——自主练透
例1 (1)若角θ的终边与 角的终边相同,则在区间[0,2π)内终边与 角的终边相同的角为 , , .
(2)若角α的顶点为坐标原点,始边在x轴的非负半轴上,终边在直线y=- x上,则角α的取值集合是( D )
考点三 三角函数的定义——多维探究
角度1 定义的直接应用
例3 (1)(2020·北京海淀期中)在平面直角坐标系xOy中,点A的纵坐标为2,点C在x轴的正半轴上.在△AOC中,若cos∠AOC=- ,则点A的横坐标为( A )
A.- B.
C.-3D.3
(2)若角θ的终边经过点P(- ,m)(m≠0)且sin θ= m,则cos θ的值为- .
所以 终边在第三象限,综上, 的终边在第一或三象限.故选A、C.
(浙江专版)高考数学一轮复习 第3章 三角函数、解三角形 第2节 同角三角函数的基本关系与诱导公式教

第二节 同角三角函数的基本关系与诱导公式1.同角三角函数的基本关系式 (1)平方关系:sin 2α+cos 2α=1; (2)商数关系:tan α=sin αcos α.2.诱导公式组序一 二三四五六 角 2k π+α(k ∈Z )π+α -απ-απ2-απ2+α 正弦 sin α-sinα-sinαsin α cosαcos_α余弦 cos α-cosαcos α -cos_α sinα -sin α正切 tan αtan α-tanα-tan_α口诀 函数名不变,符号看象限 函数名改变符号看象限记忆规律奇变偶不变,符号看象限1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.( ) (2)若α∈R ,则tan α=sin αcos α恒成立.( )(3)sin(π+α)=-sin α成立的条件是α为锐角.( )(4)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指π2的奇数倍、偶数倍,变与不变指函数名称是否变化.( )[答案] (1)× (2)× (3)× (4)√2.(教材改编)已知α是第二象限角,sin α=513,则cos α等于( )A .-513B .-1213C.513D.1213B [∵sin α=513,α是第二象限角,∴cos α=-1-sin 2α=-1213.]3.(2017·某某质检(二))若tan α=12,则sin 4α-cos 4α的值为( )A .-15B .-35C.15D.35B [sin 4α-cos 4α=(sin 2α-cos 2α)(sin 2α+cos 2α)=sin 2α-cos 2αsin 2α+cos 2α=tan 2α-1tan 2α+1=-35,故选B.]4.sin 750°=________.12 [sin 750°=sin(750°-360°×2)=sin 30°=12.] 5.已知sin ⎝ ⎛⎭⎪⎫π2+α=35,α∈⎝⎛⎭⎪⎫0,π2,则sin(π+α)=________.【导学号:51062098】-45 [因为sin ⎝ ⎛⎭⎪⎫π2+α=cos α=35,α∈⎝ ⎛⎭⎪⎫0,π2,所以sin α=1-cos 2α=45,所以sin(π+α)=-sin α=-45.]同角三角函数基本关系式的应用(1)已知sin αcos α=18,且5π4<α<3π2,则cos α-sin α的值为( )A .-32B.32C .-34D.34(2)若tan α=34,则cos 2α+2sin 2α=( )A.6425B.4825 C .1D.1625(1)B (2)A [(1)∵5π4<α<3π2,∴cos α<0,sin α<0且cos α>sin α, ∴cos α-sin α>0.又(cos α-sin α)2=1-2sin αcos α=1-2×18=34,∴cos α-sin α=32. (2)∵tan α=34,则cos 2α+2sin 2α=cos 2α+4sin αcos αsin 2α+cos 2α=1+4tan αtan 2α+1=1+4×34⎝ ⎛⎭⎪⎫342+1=6425,故选A.] [规律方法] 1.利用sin 2α+cos 2α=1可以实现角α的正弦、余弦的互化,利用sin αcos α=tan α可以实现角α的弦切互化.2.应用公式时要注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.3.注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α.[变式训练1] 设θ为第二象限角,若tan ⎝ ⎛⎭⎪⎫θ+π4=12,则sin θ+cos θ=________. -105 [∵tan ⎝⎛⎭⎪⎫θ+π4=12,∴1+tan θ1-tan θ=12,解得tan θ=-13.∴(sin θ+cos θ)2=sin 2θ+cos 2θ+2sin θ·cos θsin 2θ+cos 2θ =tan 2θ+2tan θ+1tan 2θ+1=19-23+119+1=25. ∵θ为第二象限角,tan θ=-13,∴2k π+3π4<θ<2k π+π,∴sin θ+cos θ<0,∴sin θ+cos θ=-105.]诱导公式的应用(1)已知A =sin k π+αsin α+cos k π+αcos α(k ∈Z ),则A 的值构成的集合是( )A .{1,-1,2,-2}B .{-1,1}C .{2,-2}D .{1,-1,0,2,-2}(2)已知tan ⎝ ⎛⎭⎪⎫π6-α=33,则tan ⎝ ⎛⎭⎪⎫5π6+α=________.(1)C (2)-33 [(1)当k 为偶数时,A =sin αsin α+cos αcos α=2; k 为奇数时,A =-sin αsin α-cos αcos α=-2.(2)tan ⎝⎛⎭⎪⎫5π6+α=tan ⎝ ⎛⎭⎪⎫π-π6+α =tan ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6-α=-tan ⎝ ⎛⎭⎪⎫π6-α=-33.][规律方法] 1.利用诱导公式应注意已知角或函数名称与所求角或函数名称之间存在的关系,尤其是角之间的互余、互补关系,选择恰当的公式,向所求角和三角函数进行化归.2.诱导公式的应用原则:负化正、大化小、小化锐、锐求值.[变式训练2] 已知cos ⎝ ⎛⎭⎪⎫π6-α=33,则cos ⎝ ⎛⎭⎪⎫5π6+α-sin 2⎝ ⎛⎭⎪⎫α-π6的值为________. 【导学号:51062099】-2+33 [∵cos ⎝ ⎛⎭⎪⎫5π6+α=cos ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6-α=-cos ⎝ ⎛⎭⎪⎫π6-α=-33,sin 2⎝ ⎛⎭⎪⎫α-π6=sin 2⎣⎢⎡⎦⎥⎤-⎝ ⎛⎭⎪⎫π6-α=sin 2⎝ ⎛⎭⎪⎫π6-α=1-cos 2⎝ ⎛⎭⎪⎫π6-α=1-⎝ ⎛⎭⎪⎫332=23,∴cos ⎝⎛⎭⎪⎫5π6+α-sin 2⎝ ⎛⎭⎪⎫α-π6=-33-23=-2+33.]同角关系式与诱导公式的综合应用(1)已知θ是第四象限角,且sin ⎝ ⎛⎭⎪⎫θ+π4=35,则tan ⎝ ⎛⎭⎪⎫θ-π4=________. (2)(2017·某某质检)已知cos ⎝ ⎛⎭⎪⎫π2+α=2sin ⎝⎛⎭⎪⎫α-π2,则sin3π-α+cos α+π5cos ⎝ ⎛⎭⎪⎫5π2-α+3sin ⎝ ⎛⎭⎪⎫7π2-α的值为________.(1)-43 (2)335 [(1)由题意知sin ⎝ ⎛⎭⎪⎫θ+π4=35,θ是第四象限角,所以cos ⎝⎛⎭⎪⎫θ+π4>0,所以cos ⎝ ⎛⎭⎪⎫θ+π4=1-sin 2⎝⎛⎭⎪⎫θ+π4=45.tan ⎝ ⎛⎭⎪⎫θ-π4=tan ⎝ ⎛⎭⎪⎫θ+π4-π2=-1tan ⎝⎛⎭⎪⎫θ+π4=-cos ⎝⎛⎭⎪⎫θ+π4sin ⎝⎛⎭⎪⎫θ+π4=-4535=-43.(2)∵cos ⎝ ⎛⎭⎪⎫π2+α=2sin ⎝⎛⎭⎪⎫α-π2,∴-sin α=-2cos α,则sin α=2cos α, 代入sin 2α+cos 2α=1,得cos 2α=15.sin3π-α+cos α+π5cos ⎝ ⎛⎭⎪⎫52π-α+3sin ⎝ ⎛⎭⎪⎫72π-α=sin 3α-cos α5sin α-3cos α=8cos 3α-cos α7cos α=87cos 2α-17=335.][规律方法] 利用同角三角函数基本关系式和诱导公式化简三角函数的基本思路和化简要求:(1)基本思路:①分析结构特点,选择恰当公式;②利用公式化成单角三角函数;③整理得最简形式.(2)化简要求:①化简过程是恒等变形;②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值.[变式训练3] (2016·某某模拟训练卷(三))已知cos ⎝ ⎛⎭⎪⎫π2+α=23,则sin α=________,sin ⎝ ⎛⎭⎪⎫π2+2α=________.-2319 [由cos ⎝ ⎛⎭⎪⎫π2+α=23,得sin α=-23;sin ⎝ ⎛⎭⎪⎫π2+2α=cos 2α=1-2sin 2α=19.][思想与方法]三角函数求值与化简的常用方法(1)弦切互化法:主要利用公式tan α=sin αcos α进行弦、切互化.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化. (3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=tan π4等.(4)利用相关角的互补、互余等特殊关系可简化解题步骤. [易错与防X]1.利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐.应特别注意函数名称和符号的确定.2.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.课时分层训练(十六)同角三角函数的基本关系与诱导公式A 组 基础达标 (建议用时:30分钟)一、选择题1.若cos α=13,α∈⎝ ⎛⎭⎪⎫-π2,0,则tan α等于( )A .-24B.24C .-22D .2 2C [∵α∈⎝ ⎛⎭⎪⎫-π2,0,∴sin α=-1-cos 2α=-1-⎝ ⎛⎭⎪⎫132=-232,∴tan α=sin αcos α=-2 2.]2.已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于( )A .-π6B .-π3C.π6D.π3D [∵sin(π+θ)=-3cos(2π-θ),∴-sin θ=-3cos θ,∴tan θ= 3.∵|θ|<π2,∴θ=π3.]3.cos 350°-2sin 160°sin -190°=( )A .- 3B .-32C.32D. 3D [原式=cos360°-10°-2sin 180°-20°-sin 180°+10°=cos 10°-2sin 30°-10°--sin 10°=cos 10°-2⎝ ⎛⎭⎪⎫12cos 10°-32sin 10°sin 10°= 3.]4.(2017·某某镇海中学二诊)已知sin θ+cos θ=43⎝ ⎛⎭⎪⎫0<θ<π4,则sin θ-cos θ的值为( )A.23B .-23C.13 D .-13B [∵sin θ+cos θ=43,∴1+2sin θcos θ=169,∴2sin θcos θ=79.又0<θ<π4,故sin θ-cos θ=-sin θ-cos θ2=-1-2sin θcos θ=-23,故选B.] 5.(2017·某某某某五校联盟高三一诊)已知倾斜角为θ的直线与直线x -3y +1=0垂直,则23sin 2θ-cos 2θ=( ) A.103 B .-103C.1013D .-1013C [直线x -3y +1=0的斜率为13,因此与此直线垂直的直线的斜率k =-3,∴tan θ=-3,∴23sin 2θ-cos 2θ=2sin 2θ+cos 2θ3sin 2θ-cos 2θ=2tan 2θ+13tan 2θ-1,把tan θ=-3代入得,原式=2×[-32+1]3×-32-1=1013.故选C.]二、填空题6.若sin ⎝ ⎛⎭⎪⎫π6-α=13,则cos ⎝ ⎛⎭⎪⎫π3+α=________. 【导学号:51062100】 13 [cos ⎝ ⎛⎭⎪⎫π3+α=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π6-α=sin ⎝ ⎛⎭⎪⎫π6-α=13.]7.已知α是三角形的内角,且sin α+cos α=15,则tan α=________.-43[由⎩⎪⎨⎪⎧sin α+cos α=15,sin 2α+cos 2α=1,消去cos α整理,得 25sin 2α-5sin α-12=0,解得sin α=45或sin α=-35.因为α是三角形的内角, 所以sin α=45.又由sin α+cos α=15,得cos α=-35,所以tan α=-43.]8.已知α为第二象限角,则cos α1+tan 2α+sin α·1+1tan 2α=________. 【导学号:51062101】0 [原式=cos α1+sin 2αcos 2α+sin α1+cos 2αsin 2α=cos α1cos 2α+sin α1sin 2α=cos α⎝ ⎛⎭⎪⎫1-cos α+sin α1sin α=0.] 三、解答题9.求值:sin(-1 200°)·cos 1 290°+cos(-1 020°)·sin(-1 050°)+tan 945°. [解] 原式=-sin 1 200°·cos 1 290°+cos 1 020°·(-sin 1 050°)+tan 945°4分=-sin 120°·cos 210°+cos 300°·(-sin 330°)+tan 225°8分 =(-sin 60°)·(-cos 30°)+cos 60°·sin 30°+tan 45°12分 =⎝ ⎛⎭⎪⎫-32×⎝ ⎛⎭⎪⎫-32+12×12+1=2.14分 10.已知sin(3π+α)=2sin ⎝ ⎛⎭⎪⎫3π2+α,求下列各式的值:(1)sin α-4cos α5sin α+2cos α; (2)sin 2α+sin 2α.[解] 由已知得sin α=2cos α.2分 (1)原式=2cos α-4cos α5×2cos α+2cos α=-16.7分(2)原式=sin 2α+2sin αcos αsin 2α+cos 2α=sin 2α+sin 2αsin 2α+14sin 2α=85.14分B 组 能力提升 (建议用时:15分钟)1.设函数f (x )(x ∈R )满足f (x +π)=f (x )+sin x ,当0≤x <π时,f (x )=0,则f ⎝ ⎛⎭⎪⎫23π6=( )A.12B.32C .0D .-12A [由f (x +π)=f (x )+sin x ,得f (x +2π)=f (x +π)+sin(x +π)=f (x )+sin x -sin x =f (x ), 所以f ⎝⎛⎭⎪⎫236π=f ⎝ ⎛⎭⎪⎫116π+2π=f ⎝ ⎛⎭⎪⎫116π=f ⎝ ⎛⎭⎪⎫π+56π=f ⎝ ⎛⎭⎪⎫56π+sin 56π. 因为当0≤x <π时,f (x )=0, 所以f ⎝⎛⎭⎪⎫236π=0+12=12.] 2.(2016·某某高考冲刺卷(二))若θ∈⎝ ⎛⎭⎪⎫π2,π,且sin 2θ=sin ⎝ ⎛⎭⎪⎫θ+π4,则sin 2θ=________,tan θ=________.-12 -2+3 [由sin 2θ=sin ⎝ ⎛⎭⎪⎫θ+π4,得sin 2θ=22(sin θ+cos θ),两边平方得sin 22θ=12(1+sin 2θ),解得sin 2θ=-12或sin 2θ=1.又θ∈⎝ ⎛⎭⎪⎫π2,π,∴2θ∈(π,2π),则sin 2θ<0,故sin 2θ=-12,则有sin ⎝⎛⎭⎪⎫θ+π4=sin 2θ=-12.显然3π4<θ+π4<5π4,∴cos ⎝ ⎛⎭⎪⎫θ+π4=-32,∴tan ⎝⎛⎭⎪⎫θ+π4=33.word 11 / 11 ∴tan θ=tan ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫θ+π4-π4=33-11+33=-2+ 3.]3.已知f (α)=sin π-αcos 2π-αtan ⎝ ⎛⎭⎪⎫-α+3π2tan ⎝ ⎛⎭⎪⎫π2+α·sin -π-α. (1)化简 f (α);(2)若α是第三象限角,且cos ⎝ ⎛⎭⎪⎫α-3π2=15,求f (α)的值.【导学号:51062102】 [解] (1)f (α)=sin α·cos α·ta n ⎝ ⎛⎭⎪⎫-α+3π2-2πtan ⎝ ⎛⎭⎪⎫π2+α·si n α=sin α·cos α·⎣⎢⎡⎦⎥⎤-tan ⎝ ⎛⎭⎪⎫π2+αtan ⎝ ⎛⎭⎪⎫π2+α·sin α=-cos α.7分(2)∵cos ⎝ ⎛⎭⎪⎫α-3π2=-sin α=15,∴sin α=-15,10分又α是第三象限角,∴cos α=-1-sin 2α=-265,故f (α)=265.14分。
高考数学一轮总复习第3章三角函数解三角形3.5两角和与差的正弦余弦和正切公式课件文

例 1 (1)[2017·衡水中学二调]cos130°-sin1170°=(
)
A.4
B.2
C.-2
D.-4
[解析]
3- 1 =
3- 1 =
cos10° sin170° cos10° sin10°
3ssiinn1100°°c-osc1o0s°10°=2sin110°-30°=-12sin20°=-4.
3 2
,1,f(x)∈0,1+
23.
故
f(x)的值域为0,1+
23.
核心规律 重视三角函数的“三变”:“三变”是指“变角、变名、变式”; 变角:对角的拆分要尽可能化成同名、同角、特殊角;变名: 尽可能减少函数名称;变式:对式子变形一般要尽可能有理 化、整式化、降低次数等.在解决求值、化简、证明问题时, 一般是观察角度、函数名、所求(或所证明)问题的整体形式 中的差异,再选择适当的三角公式恒等变形.
2sin20°
2sin20°
(2)4cos50°-tan40°=(
)
A. 2
B.
2+ 2
3
C. 3 [解析]
D.2 2-1
4cos50°-
tan40°=
4sin40°cos40°-sin40°= cos40°
2sin80°-sin40°
=
cos40°
2sin100°-sin40°
=
cos40°
2sin60°+ cos4400°°-sin40°=2×
23cos10°+12sin10° cos20°
考向 三角函数的条件求值
命题角度 1 给值求值问题
例 2 [2016·全国卷Ⅱ]若 cosπ4-α=35,则 sin2α=(
高考数学一轮复习 解三角形(1)导学案 文

高考数学一轮复习解三角形(1)导学案文文知识梳理:1、直角三角形各元素之间的关系:如图1,在RtABC中,C= ,BC=a,AC=b,Ab=c。
(1)、三边之间的关系:(2)、锐角之间的关系:(3)、边角之间的关系:(锐角三角函数的定义):sinA=cosB= sinB=cosA= ,tanA2、斜三角形各元素之间的关系:如图2,ABC中,A、B、C为其内角,a、b、c分别表示A、B、C的对边。
(1)、三角形内角之间的关系:A+B+C= ;sin(A+B)=sinC, cos(A+B)=-cosC;tan(A+B)=-tanC sin; cos;(2)、三边之间的关系:两边之和大于第三边,两边之差小于第三边;(3)、正弦定理:正弦定理变形:a=2R ;;;;; a:b:c= (4)、余弦定理:余弦定理变形:cosA= ; cosB=; cosC=3、三角形的面积公式:(1)、=a=b=c(,,分别表示a,b,c三边上的高)(2)、=absinC=bcsinA=casinB(3)、=2= (4)、= ;(5)、=rs(r为内切圆半径,)4、解三角形:由三角形的六个元素(即三个内角和三条边)中的三个元素(其中至少有一个是边)求其它未知元素的问题叫做解三角形,这里所说的元素还可以包括三角形的高、中线、角平分线、内切圆半径、外接圆半径、面积等等,解三角形问题一般可以分为下面两个情形:若给出是直角三角形,则称为解直角三角形;若给出的三角形为斜三角形,则称为解斜三角形。
5、实际问题中的应用。
(1)、仰角和俯角:与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标线在水平线上方的角叫做仰角,目标线在水平线下方的角叫俯角。
(2)、方位角:指从正北方向顺时针转到目标方向线的角。
(3)、坡度角:坡面与水平面所成的二面角的度数。
(4)、距离、角度的测量测量距离问题;测量高度问题;测量角度问题。
二、题型探究探究一:利用正余弦定理解三角形例1:在中,已知a= ,c=+ ,B= ,求b及A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学(解三角形)第一轮复习资料1、正弦定理:在C ∆AB 中,a 、b 、c 分别为角A 、B 、C 的对边,R 为C ∆AB 的外接圆的半径,则有2sin sin sin a b cR C===A B . 2、正弦定理的变形公式:①2sin a R =A ,2sin b R =B ,2sin c R C =;②sin 2a R A =,sin 2b R B =,sin 2cC R=;③::sin :sin :sin a b c C =A B ;④sin sin sin sin sin sin a b c a b cC C++===A +B +A B .3、三角形面积公式:111sin sin sin 222C S bc ab C ac ∆AB =A ==B .4、余弦定理:在C ∆AB 中,有2222cos a b c bc =+-A ,2222cos b a c ac =+-B ,2222cos c a b ab C =+-.5、余弦定理的推论:222cos 2b c a bc +-A =,222cos 2a c b ac+-B =,222cos 2a b c C ab +-=.6、设a 、b 、c 是C ∆AB 的角A 、B 、C 的对边,则:①若222a b c +=,则90C =; ②若222a b c +>,则90C <;③若222a b c +<,则90C >.第一节 正弦定理与余弦定理1.(2008·陕西理,3)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若c =2,b =6,B =120°,则 a 等于 ( ) A.6 B.2 C.3 D.2答案 D2.(2008·福建理,10)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则角B 的值为( ) A.6πB.3π C.6π或65π D.3π或32π答案 D3.下列判断中正确的是 ( )A .△ABC 中,a =7,b =14,A =30°,有两解B .△ABC 中,a =30,b =25,A =150°,有一解C .△ABC 中,a =6,b =9,A =45°,有两解D .△ABC 中,b =9,c =10,B =60°,无解 答案 B4. 在△ABC 中,若2cos B sin A =sin C ,则△ABC 一定是( )A.等腰直角三角形B.等腰三角形C.直角三角形D.等边三角形 答案 B5. 在△ABC 中,A =120°,AB =5,BC =7,则CBsin sin 的值为( )A.58 B.85C.35D.53答案 D6.△ABC 中,若a 4+b 4+c 4=2c 2(a 2+b 2),则∠C 的度数是 ( ) A.60° B.45°或135° C.120°D.30°答案 B7.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =1,b =7,c =3,则B = . 答案65π 8. 在△ABC 中,A =60°,AB =5,BC =7,则△ABC 的面积为 . 答案 3109. (2008·浙江理,13)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c .若(3b -c )cos A =a cos C ,则cos A = . 答案33 10. 在△ABC 中,已知a =3,b =2,B =45°,求A 、C 和c . 解 ∵B =45°<90°且a sin B <b <a ,∴△ABC 有两解. 由正弦定理得sin A =b B a sin =245sin 3︒=23, 则A 为60°或120°.①当A =60°时,C =180°-(A +B )=75°, c =B C b sin sin =︒︒45sin 75sin 2=︒︒+︒45sin )3045sin(2=226+.②当A =120°时,C =180°-(A +B )=15°, c =B C b sin sin =︒︒45sin 15sin 2=︒︒-︒45sin )3045sin(2=226-.故在△ABC 中,A =60°,C =75°,c =226+或A =120°,C =15°,c =226-.11. 在△ABC 中,a 、b 、c 分别是角A ,B ,C 的对边,且C B cos cos =-ca b+2.(1)求角B 的大小;(2)若b =13,a +c =4,求△ABC 的面积.解 (1)由余弦定理知:cos B =ac b c a 2222-+,cos C =ab c b a 2222-+.将上式代入C Bcos cos =-c a b +2得:ac b c a 2222-+·2222c b a ab -+=-ca b +2整理得:a 2+c 2-b 2=-ac ∴cos B =acb c a 2222-+=ac ac 2- =-21∵B 为三角形的内角,∴B =32π. (2)将b =13,a +c =4,B =32π代入b 2=a 2+c 2-2ac cos B ,得b 2=(a +c )2-2ac -2ac cos B ∴b 2=16-2ac ⎪⎭⎫⎝⎛-211,∴ac =3.∴S △ABC =21ac sin B =433. 12. 在△ABC 中,a 、b 、c 分别表示三个内角A 、B 、C 的对边,如果(a 2+b 2)sin (A -B )=(a 2-b 2)sin (A +B ),判断三角形的形状.解 方法一 已知等式可化为a 2[sin (A -B )-sin (A +B )]=b 2[-sin (A +B )-sin(A -B )]∴2a 2cos A sin B =2b 2cos B sin A由正弦定理可知上式可化为:sin 2A cos A sin B =sin 2B cos B sin A∴sin A sin B (sin A cos A -sin B cos B )=0∴sin2A =sin2B ,由0<2A ,2B <2π 得2A =2B 或2A =π-2B ,即A =B 或A =2π-B ,∴△ABC 为等腰或直角三角形. 方法二 同方法一可得2a 2cos A sin B =2b 2sin A cos B由正、余弦定理,可得a 2b bc a c b 2222-+= b 2a acb c a 2222-+ ∴a 2(b 2+c 2-a 2)=b 2(a 2+c 2-b 2)即(a 2-b 2)(a 2+b 2-c 2)=0∴a =b 或a 2+b 2=c 2∴△ABC 为等腰或直角三角形.13. 已知△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,若△ABC 的面积为S ,且2S =(a +b )2-c 2,求tan C 的值.解 依题意得ab sin C =a 2+b 2-c 2+2ab ,由余弦定理知,a 2+b 2-c 2=2ab cos C . 所以,ab sin C =2ab (1+cos C ),即sin C =2+2cos C ,所以2sin2C cos 2C =4cos 22C 化简得:tan 2C =2.从而tan C =2tan 12tan22C C-=-34. 14. 已知△ABC 的三个内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c 成等差数列,且2cos2B -8cos B +5=0,求角B 的大小并判断△ABC 的形状.解 方法一 ∵2cos2B -8cos B +5=0,∴2(2cos 2B -1)-8cos B +5=0.∴4cos 2B -8cos B +3=0, 即(2cos B -1)(2cos B -3)=0. 解得cos B =21或cos B =23(舍去).∴cos B =21.∵0<B <π,∴B =3π. ∵a ,b ,c 成等差数列,∴a +c =2b .∴cos B =acbc a 2222-+=acc a c a 2)2(222+-+=21,化简得a 2+c 2-2ac =0,解得a =c .又∵B =3π,∴△ABC 是等边三角形. 方法二 ∵2cos2B -8cos B +5=0,∴2(2cos 2B -1)-8cos B +5=0.∴4cos 2B -8cos B +3=0,即(2cos B -1)(2cos B -3)=0.解得cos B =21或cos B =23(舍去).∴cos B =21,∵0<B <π,∴B =3π, ∵a ,b ,c 成等差数列,∴a +c =2b .由正弦定理得sin A +sin C =2sin B =2sin 3π=3. ∴sin A +sin ⎪⎭⎫⎝⎛-A 32π=3,∴sin A +sin A cos 32π-cos A sin 32π=3. 化简得23sin A +23cos A =3,∴sin ⎪⎭⎫⎝⎛+6πA =1. ∴A +6π=2π,∴A =3π,∴C =3π,∴△ABC 为等边三角形. 15. (2008·广东五校联考)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知a +b =5,c =7,且4sin22B A +-cos2C =27. (1)求角C 的大小;(2)求△ABC 的面积. 解 (1)∵A +B +C =180°,由4sin 22B A +-cos2C =27,得4cos 22C-cos2C =27,∴4·2cos 1C +-(2cos 2C -1)=27,整理,得4cos 2C -4cos C +1=0,解得cos C =21, ∵0°<C <180°,∴C =60°.(2)由余弦定理得c 2=a 2+b 2-2ab cos C ,即7=a 2+b 2-ab ,∴7=(a +b )2-3ab , 由条件a +b =5,得7=25-3ab ,ab =6,∴S △ABC =21ab sin C =21×6×23=233. 第二节 正弦定理、余弦定理的应用1.从A 处望B 处的仰角为α,从B 处望A 处的俯角为β,则βα、的关系为( ) A.α>βB.α=βC.α+β=90°D.α+β=180°答案 B2.已知A 、B 两地的距离为10 km,B 、C 两地的距离为20 km,现测得∠ABC =120°,则A 、C 两地的距离为 ( ) A.10 km B.3 km C.510 km D.107 km答案 D3. 为测量某塔AB 的高度,在一幢与塔AB 相距20 m 的楼顶处测得塔顶A 的仰角为30°,测得塔基B 的俯角为45°,那么塔AB 的高度是 ( )A.)331(20+m B.)231(20+ m C.)31(20+ m D.30 m答案 A4.如图,位于港口O 正东20海里B 处的渔船回港时出现故障.位于港口南偏西30°,距港口10海里C 处的拖轮接到海事部门营救信息后以30海里/小时的速度沿直线CB 去营救渔船,则拖轮到达B 处需要________小时.解析:由余弦定理得BC =202+102-2×10×20cos120°=107,从而需73小时到达B 处.答案:735.(2010年南京市高中联考)如图,海岸线上有相距5海里的两座灯塔A ,B ,灯塔B 位于灯塔A 的正南方向.海上停泊着两艘轮船,甲船位于灯塔A 的北偏西75°,与A 相距32海里的D 处;乙船位于灯塔B 的北偏西60°方向,与B 相距5海里的C 处.则两艘轮船之间的距离为________海里.解析:连结AC .则AC =5,在△ACD 中,AD =32,AC =5,∠DAC =45°,由余弦定理得CD =13.答案:136.(2010年宁波十校联考)一船向正北方向匀速行驶,看见正西方向两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西60°方向上,另一灯塔在南偏西75°方向上,则该船的速度是________海里/小时.解析:假设该船从A 处航行到了D 处,两座灯塔分别在B 、C 位置,如图,设AD 长为x ,则AB =x tan60°,AC =x tan75°,所以BC =x tan75°-x tan60°=10,解得x =5,所以该船的速度v =50.5=10(海里/小时).答案:107.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB ,C 是该小区的一个出入口,且小区里有一条平行于AO 的小路CD .已知某人从O 沿OD 走到D 用了2分钟,从D 沿着DC 走到C 用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为________米.解析:连结OC ,在三角形OCD 中,OD =100,CD =150,∠CDO =60°,由余弦定理可得OC 2=1002+1502-2×100×150×12=17500,∴OC =507.答案:5078.(原创题)在Rt △ABC 中,斜边AB =2,内切圆的半径为r ,则r 的最大值为________.解析:∵r =a +b -c 2=a +b 2-1,∵4=a 2+b 2≥(a +b )22,∴(a +b )2≤8,∴a +b ≤22,∴r ≤2-1.答案:2-19.(2009年高考辽宁卷)如图,A 、B 、C 、D 都在同一个与水平面垂直的平面内,B 、D 为两岛上的两座灯塔的塔顶,测量船于水面A 处测得B 点和D 点的仰角分别为75°、30°,于水面C 处测得B 点和D 点的仰角均为60°,AC =0.1 km.试探究图中B 、D 间距离与另外哪两点间距离相等,然后求B 、D 的距离(计算结果精确到0.01 km ,2≈1.414,6≈2.449).解:在△ACD 中,∠DAC =30°, ∠ADC =60°-∠DAC =30°,所以CD =AC =0.1.又∠BCD =180°-60°-60°=60°, 故CB 是△CAD 底边AD 的中垂线,所以BD =BA .在△ABC 中,AB sin ∠BCA =AC sin ∠ABC,所以AB =AC sin60°sin15°=32+620. 同理,BD =32+620≈0.33(km),故B 、D 的距离约为0.33 km.。
