理论力学扭转例题
(仅供参考)第3章扭转作业参考解答
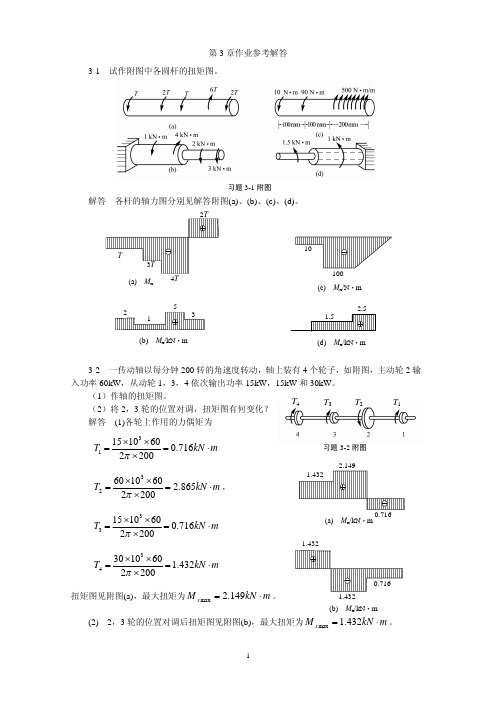
第3章作业参考解答3-1 试作附图中各圆杆的扭矩图。
习题3-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
3-2 一传动轴以每分钟200转的角速度转动,轴上装有4个轮子,如附图,主动轮2输入功率60kW ,从动轮1,3,4依次输出功率15kW ,15kW 和30kW 。
(1)作轴的扭矩图。
(2)将2,3轮的位置对调,扭矩图有何变化? 解答 (1)各轮上作用的力偶矩为m kN T ×=´´´=716.0200260101531pm kN T ×=´´´=865.2200260106032p ,m kN T ×=´´´=716.0200260101533pm kN T ×=´´´=432.1200260103034p扭矩图见附图(a),最大扭矩为m kN M x ×=149.2max 。
(2) 2,3轮的位置对调后扭矩图见附图(b),最大扭矩为m kN M x ×=432.1max 。
(a) M x(c) M x /N ·m(b)M x /kN ·m(d) M x /kN ·m习题3-2附图T 1T 2 T 3 T 4 (a)M x /kN ·m1.432(b) M x /kN ·m3-3 一直径d =60mm 的圆杆,其两端受T =2kN·m 的外力偶矩作用而发生扭转,如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
解答 1,2,3点处的切应力分别为MPaMPa W T p 4.313/22.4716/06.014.320000.031332===´===t t t t 切应力方向见附图(1)。
扭转典型习题解析

扭转典型习题解析1 一内径d =100mm 的空心圆轴如图示,已知圆轴受扭矩m kN 5⋅=T ,许用切应力][τ=80MPa ,试确定空心圆轴的壁厚。
解题分析:因为不知道壁厚,所以不能确定是不是薄壁圆管。
分别按薄壁圆管和空心圆轴设计。
解: 1、按薄壁圆管设计薄壁圆管扭转时,假设切应力沿壁厚均匀分布,设壁厚为δ,平均半径为2/0)(δ+=d R ,则扭转切应力为 δτ20π2R T=强度条件为][ττ≤,于是得][π22τδδTd =+)( ][π22223τδδδTd d =++ ()Pa1080πm N 1052m 10100m 1010026323233××⋅××=×+××+−−δδδ解得 mm 70.3m 1070.33=×=−δ 2、按空心圆轴设计强度条件为 ][pmax ττ≤=W T将δ216π44p +=−=d D d D DW );(代入得][π16][π][π164444=−−≤−τττd TD D d D DT,)(0Pa)108(m 1.0πm N 10516Pa 1080π64346=××−×⋅××−×××)(D D解得mm 107.7m 10107.73=×=−Dmm 85.32mm100mm 7.1072=−=−=d D δ 比较可知,两种设计的结果非常接近。
讨论: 当10/0R ≤δ时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD 截取下半部分为研究对象,如图b 所示。
试问截面ABCD 上的切向内力所形成的力偶矩将由哪个力偶矩来平衡?解题分析:由切应力互等定理可知截面ABCD 上的切向内力分布及其大小。
该截面上切向内力形成一个垂直向上的力偶矩。
在图b 中,左右两个横截面上的水平切向内力分量形成垂直于截面ABCD 的竖直向下的力偶矩,正好与截面ABCD 上切向内力的合力偶矩平衡。
材料力学扭转详细讲解和题目非常好

材料力学 扭转扭转的概念扭转是杆件变形的一种基本形式。
在工程实际中以扭转为主要变形的杆件也是比较多的,例如图6-1所示汽车方向盘的操纵杆,两端分别受到驾驶员作用于方向盘上的外力偶和转向器的反力偶的作用;图6-2所示为水轮机与发电机的连接主轴,两端分别受到由水作用于叶片的主动力偶和发电机的反力偶的作用;图6-3所示为机器中的传动轴,它也同样受主动力偶和反力偶的作用,使轴发生扭转变形。
图6—1 图6—2 图6—3这些实例的共同特点是:在杆件的两端作用两个大小相等、方向相反、且作用平面与杆件轴线垂直的力偶,使杆件的任意两个截面都发生绕杆件轴线的相对转动。
这种形式的变形称为扭转变形(见图6-4)。
以扭转变形为主的直杆件称为轴。
若杆件的截面为圆形的轴称为圆轴。
图6—4扭矩和扭矩图6.2.1 外力偶矩作用在轴上的外力偶矩,可以通过将外力向轴线简化得到,但是,在多数情况下,则是通过轴所传递的功率和轴的转速求得。
它们的关系式为 nP M 9550= (6-1) 其中:M ——外力偶矩(N ·m );P ——轴所传递的功率(KW );n ——轴的转速(r /min )。
外力偶的方向可根据下列原则确定:输入的力偶矩若为主动力矩则与轴的转动方向相同;输入的力偶矩若为被动力矩则与轴的转动方向相反。
6.2.2 扭矩圆轴在外力偶的作用下,其横截面上将产生连续分布内力。
根据截面法,这一分布内力应组成一作用在横截面内的合力偶,从而与作用在垂直于轴线平面内的外力偶相平衡。
由分布内力组成的合力偶的力偶矩,称为扭矩,用n M 表示。
扭矩的量纲和外力偶矩的量纲相同,均为N·m 或kN·m。
当作用在轴上的外力偶矩确定之后,应用截面法可以很方便地求得轴上的各横截面内的扭矩。
如图6-5(a )所示的杆,在其两端有一对大小相等、转向相反,其矩为M 的外力偶作用。
为求杆任一截面m-m 的扭矩,可假想地将杆沿截面m-m 切开分成两段,考察其中任一部分的平衡,例如图6-5(b )中所示的左端。
理论力学 第三章扭转07.8.28

侧边平行。
τ max
=T Wt
=
T β b3
=
3×103 0.346× 0.063
= 40.14×106 Pa =
40.14MPa
2.横截面短边中点处的切应力:τ =ντ max = 0.858× 40.14 = 34.44MPa
3.的单位长度扭转角:
-4-
第三章
扭转习题答案
ϕ′ = T = T =
解:1.扭矩图
2.切应力强度条件
AB段:
τ AE
=
TAE Wp
=
π
16 ×18000 × 0.143(1− (100 /140)4 )
= 45.2MPa < [τ ]
T图 (kN.m)
14 ⊕
CB段:τ CB
= TCB Wp
= 16×14000 π × 0.13
= 71.3MPa < [τ ]
18
3.刚度条件
/ m) ×1800
/π
= 0.460 / m < [ϕ′] ,所以轴的强度和刚度安全
3-20 一端固定的圆截面杆AB,承受集度为m的均布外力偶作 用,如图所示。试求杆内积蓄的应变能。已知材料的切变 模量为G。 解:杆内积蓄的应变能
∫ Vε =
l (mx)2 dx = m2l3 = 16m2l3 0 2GI p 6GI p 3Gπ d 4
( 3 16T )2
πd2
=
d2
=
π[τ ]
= (1− 0.84 )2/3 = 1.95
π D2 (1− 0.82 )
D2 (1− 0.82 )
(3
π
16T (1− 0.84 )[τ
)2 (1− ]
材料力学-扭转-计算公式及例题

求 AB段Mn(1-1剖面)
K N·m 4.50 背向剖切面为正
求 BC段Mn(2-2剖
面) K N·m
-4.50
求 CD段Mn(3-3剖面)
K N·m -1.50
D>=103mm
已知 CD段Mn(3-3剖面)
K N·m -1.5
求
IP m4 1.19E-05
求 φB-A
° 0.216
求 ΦC-B
K N·m
K N·m
K N·m
K N·m
数值
0.62
2.05
1.43
0.62
横截面上的力偶矩的方向,为外力偶矩(如T1,T2,T3)指向剖切面为负,背向剖切面为正
校核AC段 的强度(实
数据状态
代号
单位
数值 校核DB段 的强度(实
数据状态
代号
单位
已知 d1 mm 40
已知 d2 mm
已知 Mn(AC) K N·m 0.62
°/m
m4
1.05E+01 5.00E-01 1.50E-08
,试设 计截面的内
求 D0 mm 63.38
求 d mm 60.44
求 A1/A2
mm 0.51
d2=70mm。 。材料的许用切应 轴的强度和刚度。
。材料的许用切应 轴的强度和刚度。
求 CD段Mn(2-2剖面)
K N·m 0.62 背向剖切面为正
° -0.270
求 φD-C
° -0.108
强度计算 序号
名称
代号
单位
max
M n max Wp
[ ]
1
横截面上的最大扭 矩
Mn max
扭转习题

第三章 扭转习题一、单项选择题1、横截面都为圆的两个杆,直径分别为d 和D ,并且d=。
两杆横截面上扭矩相等两杆横截面上的最大切应力之比maxDmaxdττ为A 、2倍,B 、4倍,C 、8倍,D 、16倍。
二、1、扭转变形时,公式pTlGI τ=中的 表示单位长度的扭转角,公式中的T 表示横截面上的 ;G 表示杆材料的 弹性模量;I P 表示杆横截面对形心的 ;GI P 表示杆的抗扭 。
2、截面为圆的杆扭转变形时,所受外力偶的作用面与杆的轴线 .3、实心圆轴扭转时,横截面上的切应力分布是否均匀,横截面上离圆心愈远的点处切应力 ,圆心处的切应力为 ,圆周上切应力4、两根实心圆轴的直径d 和长度L 都相同,而材料不同,在相同扭矩作用下,它们横截面上的最大切应力是否相同 ,单位长度的扭转角是否相同 。
5、剪切虎克定律的表达式 G τγ=,式中的G 表示材料的 模量,式中的γ称为 。
6、根据切应力互等定理,单元体两互相垂直截面上在其相交处的切应力成对存在, 且 相等,而 现反。
三、 1、如图所示圆轴,一端固定。
圆轴横截面的直径D=100mm ,所受的外力偶矩M 1=6kN•m,M 2=4kN•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:圆轴横截面上的最大扭矩为 kN•m;圆轴横截面上的最大切应力为 Mpa 。
2、如图所示阶梯形圆轴,一端固定。
圆轴横截面的直径分别为外力偶矩M C =1200 N•m,M B =1800 N•m。
试求BC 段横截面上的扭矩和该阶梯轴的最 大切应力。
答:BC 段横截面上的扭矩为 N•m;该阶梯轴的最大切应力为 Mpa 。
3、如图所示圆轴,一端固定。
圆轴横截面的直径d=100mm ,所受的外力偶矩M 1=7000 N•mM 2=5000 N•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:最大扭矩为 N •m 。
最大切应力为 Mpa 。
4、某传动轴为实心圆轴,轴内的最大扭矩=1.5kN m T g,许用切应力[]=50MPa τ,试确定该轴的横截面直径。
第三章扭转(习题解答)

3-1ab 作图求各杆的扭矩图 解:(1)轴的扭矩图分成二段,整个轴上无均布荷载扭矩图为间断水平线。
左段:m kN ⋅=6左T (背正)右段: m kN ⋅-=-=4106右T (指负背正),或m kN ⋅-=4右T (指负) (2)画扭矩图如图题3-1(a)所示。
从左至右,扭矩图的突变与外力偶矩转向一至,突变之值为外力偶的大小(从前往后看)m10kN 4kN mT (b )(a 题3-1(a )(b)T 图(kN m )4+题3-1(b )2m2m解:(1)轴的扭矩图分成二段,轴上的右段有均布荷载,该段扭矩图向下倾斜线段。
左段无均布荷载,扭矩图为水平线段。
左段:m kN ⋅=⨯=422AB T 右段: 0422=⋅=⨯=C B T T mkN(2)画扭矩图如图题3-1(b)所示。
扭矩图集中力偶处发生突变,而有均布力偶段扭矩图呈线性。
显而易见,A 端有大小为m kN ⋅4,力偶矩矢向左的外力偶。
3-2图示钢质圆轴,m kN m m l mm D ⋅===15,2.1,100。
试求:(1)n-n 截面上A 、B 、C 三点的剪应力数值及其方向(保留n-n 截面左段);(2)最大剪应力m ax τ;(3)两端截面的相对扭转角。
解:(1)圆轴受力偶作用面与轴线垂直的一对外力偶作用,发生扭转变形。
由于扭矩在整个轴内无变化,可不画扭矩图。
(2)扭转圆轴上各点的剪应力应在各自的横截面内,垂直于所在的“半径”,与扭矩的转向一致,如图3-2(c)所示。
由求扭转剪应力的公式知:MPa Pa D D T I T P B A 43.7621.0321.014.31015232434=⨯⨯⨯=⋅=⋅==πρττ MPa Pa D D T I T P C 21.3841.0321.014.31014432434=⨯⨯⨯=⋅=⋅=πρτ(2)最大剪应力m ax τ,圆轴发生扭转时,边缘各点的剪应力最大。
MPa B A 43.76max ===τττ(3)由公式求两端截面的相对扭转角。
材料力学作业参考题解扭转

17.76MPa [ ]
(3)如图取坐标系,有:
T (x) m0 x
AB
l T (x) dx
m0
0 GI p
GI p
l
xdx
m0l 2
M 0l
0
2GI p 2GI p
32 389.9 40
0.064 [1
(5 /
6)4 ]
0.148弧度
8.48
3-16 如图所示,将空心圆杆(管)A套在实心圆杆B旳一端。两杆在同一横截面处有一直径 相同旳贯穿孔,但两孔旳中心线构成一β角,目前杆B上施加扭力偶使之扭转,将杆A和B旳 两孔对齐,装上销钉后卸去所施加旳扭力偶。试问两杆横截面上旳扭矩为多大?已知两杆旳 极惯性矩分别为 IpA和 IpB,且材料相同,切变模量为G。
620.7 16
0.043
49.4MPa [ ]
max 2
TDB W pDB
1432.4 16
0.073
21.3MPa [ ]
max
TAC GI pAC
180
80
32 620.7
109
180
0.044
1.77 / m [ ]
该轴满足强度与刚度要求
3-13 已知钻探机钻杆旳外径D=60mm,内径d=50mm,功率P=7.35kW,转速n=180r/min,钻 杆入土深度l=40m,材料旳G=80GPa,[ τ ]=40MPa。假设土壤对钻杆旳阻力沿长度均匀分布, 试求:(1)单位长度上土壤对钻杆旳阻力矩;(2)作钻杆旳扭矩图,并进行强度校核; (3)A、B两截面旳相对扭转角。
d 4
d 8
32 100 103
8 0.13
127MPa
LC-CHAPTER03-扭转-课堂例题

N Me 9549 (牛顿米) n
例2
试分析图示轴的扭矩 (m-轴单位长度内的扭力偶矩)
dx
复习:角应变
复习:角应变
ty
tz
tx
• 扭转的实例和工程运用
• 外力偶矩、扭矩和扭矩图 • 纯剪切、切应力互等定理、 剪切胡克定律 • 圆轴扭转时的应力和强度条件
• 圆轴扭转时的变形和刚度条件 • 其他扭转
“压缩为负”
3、内力图(扭矩图)表示构件各横截面扭矩沿轴线变化的图形。 扭矩图作法:同轴力图: 例 1 一传动轴如图,转速n = 300r/min; 主动轮输入的功 率P1= 500kW,三个从动轮输出的功率分别为: N2= 150kW, N3= 150kW, N4= 200kW。试作轴的扭矩图。
• 圆柱形密圈螺旋弹簧的应力和变形 • 非圆截面杆扭转的概念 • 薄壁杆件的自由扭转
扭转超静定问题
例: T , G, A, l 均相同的两根轴,分别为圆截面和正方形截面。 试求:两者的最大扭转切应力与扭转变形,并进行比较。
d
a a
例 比较闭口与开口薄壁圆管的抗扭性能, 设 R0=20d
二、截面法
圆轴受扭时其横截面上的内力偶矩称为扭矩,用符号T 表示。 扭矩大小可利用截面法来确定。源自Me A1 1 1
Me B
Me
T
1 1
A
x
T Me
Me B
T
1
二、扭转杆件的内力——扭矩及扭矩图
1、扭转杆件的内力(截面法)
取左段为研究对象:
Me
Me
m
x
0, T M e 0
Me T
60 (秒) 电机做功 W = N × t W N (千瓦) N (1000牛顿米) 60 (秒)
扭转的强度计算—例题分析

扭转的强度条件—例题分析例题1-1 一电机传动钢轴,直径d = 40mm ,轴传递的功率30kW ,转速n = 1400r/min 。
轴的许用切应力[]τ= 40MPa ,试校核此轴的强度。
解:(1)计算扭力偶矩和扭矩。
扭力偶距为x m = 9550n P = 9550140030⨯= 204×103 (N ·mm ) 由截面法求得轴横截面上的扭矩为:320410(N mm)x T m ==⨯⋅(2) 强度校核。
轴的抗扭截面系数为 334320 1.25510(mm )22R W ρππ⨯===⨯3maxmax 42041016.3(MPa)1.25510T W ρτ⨯==⨯ 因为 max []40(MPa)ττ<=轴满足扭转强度条件。
例题1-2 如图所示为汽车传动轴简图,轴选用无缝钢管,其外半径45mm R =,内半径42.5mm r =。
许用剪应力[]τ=60MPa ,根据强度条件,求轴能承受的最大扭矩。
例题1-2图解:按强度条件确定最大扭矩。
42.50.94445r R α=== 3344345(1)(10.944)29400(mm )22R W ρππα⨯=-=-=由强度条件得3max []6029400176410(N mm)1764(N m)T W ρτ≤=⨯=⨯⋅=⋅轴能承受的最大扭矩为1764N m ⋅。
例题1-3 某传动轴,轴内的最大扭矩max 1.5kN m T =⋅,若许用切应力[]τ=50MPa ,试按下列两种方案确定轴的横截面尺寸,并比较其重量。
①实心圆截面轴;②空心圆截面轴,其内、外半径的比值9.022=R r 。
解:(1)确定实心圆轴的半径。
根据强度条公式可得 max T W ρτ≥ 将实心圆轴的抗扭截面系数32R W ρπ=代入上式得126.73(mm)R ≥= 取 )(271mm R =(2)确定空心圆轴的内、外半径。
将空心圆轴的抗扭截面系数()3412R W ρπα=-代入强度条件式可得238.15(mm)R = 其内半径相应为220.90.938.1534.34(mm)r R ==⨯=取 239(mm)R = 234(mm)r =(3)重量比较。
圆轴的扭转习题+答案

13、一空心圆轴在产生扭转变形时,其危险截面外缘处具有全轴的最大剪应力,而危险截面内缘处的剪应力为零。 ( )
14、粗细和长短相同的二圆轴,一为钢轴,另一为铝轴,当受到相同的外力偶作用产生弹性扭转变形时,其横截面上最大剪应力是相同的。 ( )
5、圆轴扭转时,横截面上任意点的剪应变与该点到圆心的距离成___________。
6、试观察圆轴的扭转变形,位于同一截面上不同点的变形大小与到圆轴轴线的距离有关,显然截面边缘上各点的变形为最_______,而圆心的变形为__________。
7、圆轴扭转时,在横截面上距圆心等距离的各点其剪应变必然_________。
13、横截面面积相等的实心轴和空心轴相比,虽材料相同,但_________轴的抗扭承载能力要强些。
16、直径和长度均相等的两根轴,其横截面扭矩也相等,而材料不同,因此它们的最大剪应力是________同的,扭转角是_______同的。
17、产生扭转变形的实心圆轴,若使直径增大一倍,而其他条件不改变,则扭转角将变为原来的_________。
17、内外径比值d/D=的空心圆轴受扭转,若将内外径都减小到原尺寸的一半,同时将轴的长度增加一倍,则圆轴的抗扭刚度会变成原来的( )。
A、1/2 B、1/4 C、1/8 D、1/16
18、等截面圆轴扭转时的单位长度扭转角为θ,若圆轴的直径增大一倍,则单位长度扭转角将变为( )。
A、θ/16 B、θ/8 C、θ/4 D、θ/2
5、扭矩就是受扭杆件某一横截面在、右两部分在该横截面上相互作用的分布内力系合力偶矩。 ( )
7、扭矩的正负号可按如下方法来规定:运用右手螺旋法则,四指表示扭矩的转向,当拇指指向与截面外法线方向相同时规定扭矩为正;反之,规定扭矩为负。 ( )
6第六章 圆轴的扭转习题+答案

一、填空题1、圆轴扭转时的受力特点是:一对外力偶的作用面均_______于轴的轴线,其转向______。
2、圆轴扭转变形的特点是:轴的横截面积绕其轴线发生________。
3、在受扭转圆轴的横截面上,其扭矩的大小等于该截面一侧(左侧或右侧)轴段上所有外力偶矩的_______。
4、在扭转杆上作用集中外力偶的地方,所对应的扭矩图要发生________,_________值的大小和杆件上集中外力偶之矩相同。
5、圆轴扭转时,横截面上任意点的剪应变与该点到圆心的距离成___________。
6、试观察圆轴的扭转变形,位于同一截面上不同点的变形大小与到圆轴轴线的距离有关,显然截面边缘上各点的变形为最_______,而圆心的变形为__________。
7、圆轴扭转时,在横截面上距圆心等距离的各点其剪应变必然_________。
8、从观察受扭转圆轴横截面的大小、形状及相互之间的轴向间距不改变这一现象,可以看出轴的横截面上无____________力。
9、圆轴扭转时,横截面上剪应力的大小沿半径呈______规律分布。
11、受扭圆轴横截面内同一圆周上各点的剪应力大小是_______的。
12、产生扭转变形的一实心轴和空心轴的材料相同,当二者的扭转强度一样时,它们的_________截面系数应相等。
13、横截面面积相等的实心轴和空心轴相比,虽材料相同,但_________轴的抗扭承载能力要强些。
16、直径和长度均相等的两根轴,其横截面扭矩也相等,而材料不同,因此它们的最大剪应力是________同的,扭转角是_______同的。
17、产生扭转变形的实心圆轴,若使直径增大一倍,而其他条件不改变,则扭转角将变为原来的_________。
18、两材料、重量及长度均相同的实心轴和空心轴,从利于提高抗扭刚度的角度考虑,以采用_________轴更为合理些。
二、判断题1、只要在杆件的两端作用两个大小相等、方向相反的外力偶,杆件就会发生扭转变形。
测试题-扭转-答案
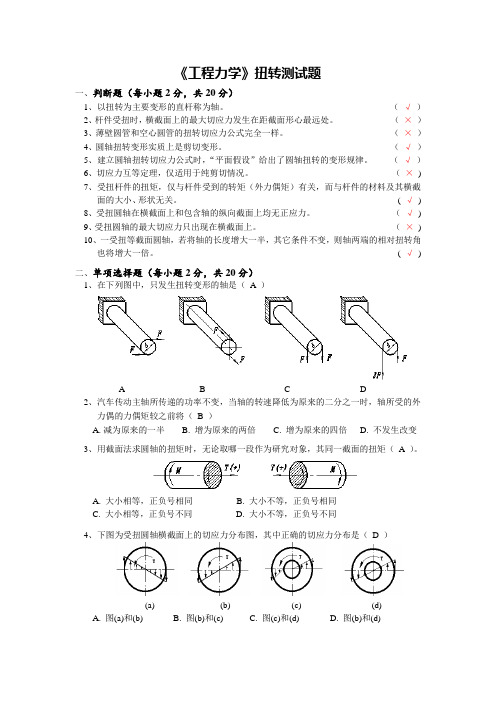
《工程力学》扭转测试题一、判断题(每小题2分,共20分)1、以扭转为主要变形的直杆称为轴。
(√)2、杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
(×)3、薄壁圆管和空心圆管的扭转切应力公式完全一样。
(×)4、圆轴扭转变形实质上是剪切变形。
(√)5、建立圆轴扭转切应力公式时,“平面假设”给出了圆轴扭转的变形规律。
(√)6、切应力互等定理,仅适用于纯剪切情况。
(×)7、受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √)8、受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
(√)9、受扭圆轴的最大切应力只出现在横截面上。
(×)10、一受扭等截面圆轴,若将轴的长度增大一半,其它条件不变,则轴两端的相对扭转角也将增大一倍。
( √)二、单项选择题(每小题2分,共20分)1、在下列图中,只发生扭转变形的轴是(A )A B C D2、汽车传动主轴所传递的功率不变,当轴的转速降低为原来的二分之一时,轴所受的外力偶的力偶矩较之前将(B )A.减为原来的一半B. 增为原来的两倍C. 增为原来的四倍D. 不发生改变3、用截面法求圆轴的扭矩时,无论取哪一段作为研究对象,其同一截面的扭矩(A )。
A. 大小相等,正负号相同B. 大小不等,正负号相同C. 大小相等,正负号不同D. 大小不等,正负号不同4、下图为受扭圆轴横截面上的切应力分布图,其中正确的切应力分布是(D )(a) (b) (c) (d)A. 图(a)和(b)B. 图(b)和(c)C. 图(c)和(d)D. 图(b)和(d)5、一内径为d ,外径为D 的空心圆轴,其扭转截面系数为( C )A. 16π16π33p d D W −=B. 32π32π33p d D W −= C. Dd D W 16)(π44p −= D. 32π32π44p d D W −=6、建立圆轴的扭转切应力公式p I T ρτρ=时,以下哪个关系式没有用到?( C ) A. 变形的几何协调关系 B. 剪切胡克定律C. 切应力互等定理D. 切应力ρτ与扭矩的关系A T A d ρτρ⎰=7、图示等截面圆轴上装有四个皮带轮,如何合理安排?( B ) A. 将轮B 与轮D 对调 B. 将轮C 与轮D 对调 C. 将轮B 与轮C 对调D. 将轮B 与轮D 对调,然后再将轮B 与轮C 对调8、一圆轴用碳钢制作,校核其扭转角时,发现单位长度扭转角超过了许用值。
材料力学专项习题练习扭转

扭 转1. 一直径为1D 的实心轴,另一内径为d , 外径为D , 内外径之比为22d D α=的空心轴,若两轴横截面上的扭矩和最大切应力均分别相等,则两轴的横截面面积之比12/A A 有四种答案:(A) 21α-; (B)(C); (D)。
2. 圆轴扭转时满足平衡条件,但切应力超过比例极限,有下述四种结论: (A) (B) (C) (D) 切应力互等定理: 成立 不成立 不成立 成立 剪切胡克定律: 成立 不成立 成立 不成立3. 一内外径之比为/d D α=的空心圆轴,当两端承受扭转力偶时,若横截面上的最大切应力为τ,则内圆周处的切应力有四种答案:(A) τ ; (B) ατ; (C) 3(1)ατ-; (D) 4(1)ατ-。
4. 长为l 、半径为r 、扭转刚度为p GI 的实心圆轴如图所示。
扭转时,表面的纵向线倾斜了γ角,在小变形情况下,此轴横截面上的扭矩T 及两端截面的相对扭转角ϕ有四种答案:料的切变模量(A) 43π128d G a ϕ(C) 43π32d G a ϕ8. 一直径为D 重量比21W W 9. 10. 矩形截面杆扭转变形的主要特征是 。
1-10题答案:1. D 2. D 3. B 4. C 5. B 6. C 7. B 8. 0.479. 横截面上的切应力都达到屈服极限时圆轴所能承担的扭矩;4/3 10. 横截面翘曲11. 已知一理想弹塑性材料的圆轴半径为R ,扭转加载到整个截面全部屈服,将扭矩卸掉所产生的残余应力如图所示,试证明图示残余应力所构成的扭矩为零。
证:截面切应力 4103s R R ρρττρ⎛⎫=-≤≤ ⎪⎝⎭截面扭矩 04d 12πd 03Rs s A T A R ρρτρτρρ⎛⎫==-⋅= ⎪⎝⎭⎰⎰ 证毕。
12. 图示直径为d 的实心圆轴,两端受扭转力偶e M 用1/m C τγ=表示,式中C ,m 式为:证:几何方面 d d xρϕγρ=物理方面 1/1/d d mmC C x ρϕτγρ⎛⎫== ⎪⎝⎭静力方面 1//21/e 0d d 2πd d md mAM T A C x ρϕρτρρρρ⎛⎫==⋅⋅=⋅⋅ ⎪⎝⎭⎰⎰所以 1/e (31)/2π()23m 1mm mM m d ρρτ+=+ 证毕。
机械扭转例题

②计算并校核剪应力强度
τ max
③此轴满足强度要求。
T 1.55 ×103 = = = 23MPa ≤ [τ ] 3 Wt π ⋅ 0.07 16
1
[例2]已知: d1=100 mm,d2=60 mm, τ 已知: mm,d mm,
G = 80 GPa ,试校核强度、刚度. ,试校核强度、刚度.
7kN·m 3kN·m
32T ×180 4 32×7024×180 1 d1 ≥ 4 = = 84.6 m m 2 9 2 Gπ [θ ] 80×10 ×π ×1
取 d1= 84.6 mm BC段: 同理,由强度条件, d2≥67 mm BC段 同理,由强度条件, 由刚度条件, 由刚度条件,d2≥74.5 mm 取 d2=74.5 mm.
l1m mC = l1 + l2
l2m mB = l1 + l2
9
非圆截面杆的扭转
一、非圆截面杆扭转变形特点
截面翘曲
warping!
10
二、自由扭转和约束扭转
1. 自由扭转 free torsion 当杆件两端各有一个扭转力偶, 当杆件两端各有一个扭转力偶,且端面可 翘曲时,相邻两截面翘曲程度相同, 自由 翘曲时,相邻两截面翘曲程度相同,这种 情况下横截面上只有剪应力而无正应力。 情况下横截面上只有剪应力而无正应力。称这种 扭转为自由扭转。 扭转为自由扭转。
结论:第一段满足强度和刚度要求,第二 结论:第一段满足强度和刚度要求, 段则都不满足。 段则都不满足。
3
[例3]
mA
1
mB
2
B
mC
C
A
400
200
(N·m)
T
已知: 已知: mA = 7024 N·m mB = 2809.6 N·m mC = 4214.4 N·m G = 80 GPa, [τ] = 70 MPa, [θ ] = 1 º/m 求:AB 和 BC 段直径 解:1. 内力分析 T1 =-mA =- 7024 N·m T2 =-mC =- 4214.4 N·m 作扭矩图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
题解:
由于B端固定,φB¹ 则有: =0
B
T1 a GI P T2 (a b) GI P TB (a b c) GI P
2
0
T1 2
式中设TB与T1同向,代入 T 其中: a c 得 T 5T1 B
8
4
b
2
(与假设方向相反)
画出图如图所示。
12tl
2
题13:图示一实心钢轴插入一铜管中,设彼此之间无摩 擦力,A端用一销钉连接,此时B端轴与管的销钉相差φ 角,施加外力偶使轴与管相对转动,插入另一销钉,已 知:轴长为l,实心钢轴的抗扭刚度为GIp,铜管的抗扭刚 度为轴的2倍,求移去外力偶后轴与管的内力。
题解:
设轴和管的扭矩分别为T1 和T2
39、题解:
M x 0
有
T 0
Dt
D 2
2T
D t
2
'
由剪应力互等定律,纵截面上的 纵向截面上的总剪力
'
,
Q l t l t
n Q A 2T
由铆钉的剪切强度条件,有
D A
2
一、剪应力流的方向与扭矩的方向一致。
x
4
1 32T l 1 1 d d d d 3 d 3 0 GI x 3G b p a a b Tdx
题7:若圆截面轴AB,其左端固定,承受 均布力矩 t 作用,试导出该轴B端的扭转 角。 题解:
二、开口薄壁截面杆在自由扭转时的剪应力分布如图(a),厚 度中点处,应力为零。
当h/b>10时,截面为狭长矩形: =1/3
max
T
hb
T
2
T 1 3 h
2
h
G hb
3
T GI
n
G
T 1 3 h
3
三、闭口薄壁截面杆在自由扭转时的剪应力分布如图(b),同
一厚度处,应力均匀分布。
题解:
题5:若将实心圆轴的直径增加一倍, 则其强度增加 倍,刚度增加 倍。
• 题解: 8 、 16
题6:实心圆截面锥形杆,受T 作用而扭转,求杆的 扭转角φ。
题解:
Mt T
dx单元的扭转角
d Tdx GI p x
I p x
da 32
l
db d a L
M t x t l x
d t l x dx GI p
d
l
t l x dx GI p
t l
2
0
2GI p
题8:两段同直径的圆轴用凸缘和8个同直 径的螺栓连接,轴的[τ]=70MPa,螺栓的 [τ]=60MPa ,求许用扭矩[T]的值。
题10:已知[τ]=60MPa ,求图 示轴的外力偶矩[T]。
题解:T
B
A
TB T 1
TB 1.5 GI P1 TB 1 GI P2
12
A
B
T 1.5 GI P1
I P2
0 2
式中:
50
32
4
10
I P1
70
32
4
轴的[τ]=70MPa, 螺栓的[τ]=60MPa , 求 [T]
题解:
按轴的强度计算:T WP 轴 13.7kN m 按螺栓的强度计算: 设每一螺栓受力 Q,按剪切强度Байду номын сангаас件 Q A栓 栓 则:
T 8Q
应取:
D 2
8 A栓 栓
10
12
联解(1)(2)式,得 AC段: max BC段:
max
TA 0.719T
,T
TB 0.281T
0.719T WP1
[ ]
5.62 KN m
0.281T WP2
[ ]
,
T 5.24 KN m
T 5.24 KN m
题11:图示圆截面轴,设已 知截面B的转角为φ,材料 的剪切弹性模量G,轴直径 为d,计算所加力矩T 的值。
题解:
即: TA a
GI P
TA TC T (1)
变形协调条件:
AB CB
TC 2a GI P
TA 2TC (2)
联解(1)、(2)式得:
TA
2T 3
TC
3GI P 2a
T 3
3d G
4
2aT 3GI P
T
64a
题12:图示圆轴,在AB段受 均布转矩t 的作用,材料的弹 性模量G,试作轴的扭矩图, 并计算横截面A的扭转角φA。
题解:
T l 2 GI P txdx 2 GI P
l
16
tl
l
16t
l
2
A
0
2 2 4 4 4 Gd Gd Gd
题1:设一钢杆扭转900角时,其最大 剪应力仍小于许用剪应力, [τ]=90MPa, G=80GPa。求该杆长 度与直径d 的比值关系是多少? 题解:
T l GI P T d max 2I P
解得:
l 0.5Gd
l
d
G
2
698
题2:为截面上的扭矩,空心圆轴截面上剪 应力分布应是图 。
• 题解:(C)
题3:内外径分别为d和D的一空心圆 轴,其抗扭截面模量。( )
题4:指出矩形截 面杆扭转时,横截 面上哪些点的τ=0。
题解:截面的角点处和形心处,剪应力均为零。
题5:一根铸铁圆轴,在扭矩T 作用下发生 扭转破坏。断口如图所示。试按右手螺旋 法则,用矢量表示扭矩T。
D 2
15.1kN m
T 13.7kN m
题9:图示薄板卷成筒后,用一排铆钉固定, 设此时无初应力。若铆钉的[τ]和横截面积A均 已知。当薄圆筒受扭矩T作用时,导出计算铆 钉个数n的公式。
题39:设此时无初应力。若铆 钉的[τ]和横截面积A均已知。当 薄圆筒受扭矩T作用时,导出计 算铆钉个数n的公式。
则: T1 = T2
变形条件: 1 2
T1l GI P T2 l 2GI P
180
(设的单位为度)
解得
T1 T2
GI P
270l
外管与内轴承受的扭矩相等,设为T
m
m l G I p内
T l G I p内
T l G I p外
14:图示圆轴两端固 1 1 T 定, 1 2T2 , a c , b 4 2 作轴的扭矩图。
