立体几何常考定理总结
高中立体几何八大定理

a mnA m ,n
作用:线线垂直 线面垂直
那么这条直线垂直于这个平面
a
A n
m
六、直线与平面垂直的性质定理:
文字语言:若两条直线垂直于同一个平面,则这两条直线平行
图形语言: 符号语言:
a a // b
b
a b
作用:线面垂直 线线平行 七、平面与平面垂直的判定定理: 文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。 图形语言:
线就和交线平行。 图形语言:
l // 符号语言: l
l // m m
l m
作用:线面平行 线线平行 三、平面与平面平行的判定定理 文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言:
a
b
abA
//
a∥
b∥
作用:线线平行
面面平行
四、平面与平面平行的性质定理 : 文字语言:如果两个平行平面同时和第三个平面相交 图形语言 :
//
符号语言 :
a a // b
b
作用 : 面面平行 线线平行
, 那么所得的两条交线平行
1
更多资料请加三好网小好师弟微信:sanhao1001
更多资料请加三好网小好师弟微信:sanhao1001
五、直线与平面垂直的判定定理: 文字语言: 如果一条直线和一个平面内的两条相交直线垂直, 图形语言: 符号语言:
a
符号表示:
a
a
注:线面垂直 面面垂直 八、 平面与平面垂直的性质定理: 文字语言: 如果两个平面互相垂直, 那么在一个平面内垂直与它们的交线的直线垂直于另一
个平面 图形语言:
A
常考定理总结(八大定理)

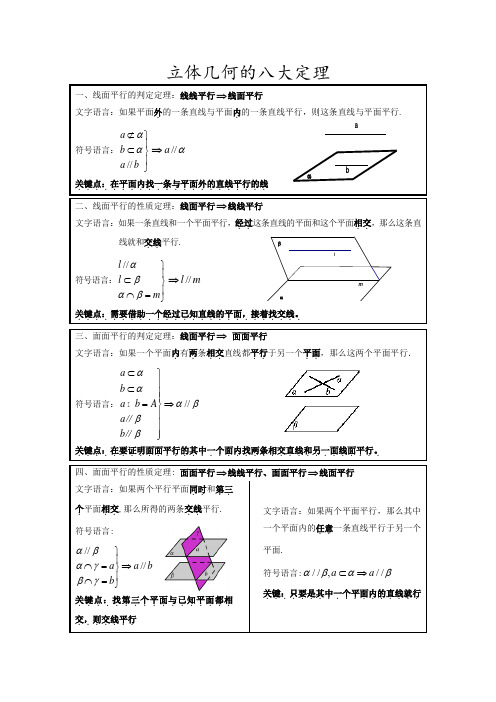
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键..点:在需要证明的两个平面中找线面垂直..................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
立体几何常考定理的总结(八大定理)
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点:....在需要证明的两个平面中找线面垂直................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
高中立体几何八大定理

线面位置关系的八大定理之南宫帮珍创作一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行 图形语言: 符号语言:作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m 作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言:作用:线线平行⇒ 面面平行 四、平面与平面平行的性质定理: 文字语言:如果两个平行平面同时和第三个平αbalmβα面相交,那么所得的两条交线平行图形语言:符号语言:////a a bbαβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面图形语言:符号语言:作用:线线垂直⇒线面垂直六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行图形语言:符号语言:作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号暗示:aaααββ⊥⎫⇒⊥⎬⊂⎭aβααbanmAαa注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:lAB ABAB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直BAlβα。
立体几何的八个判定定理

立体几何的八个判定定理立体几何的八个判定定理是指由英国数学家约翰·威尔逊(John Wallis)在17th century所提出的一套定理。
其中包括:(1)贝瑟尔定理:任意一个平面三角形的内角之和等于180度。
(2)杨氏定理:任意一个对角相交的多边形,其内部角之和等于其外部角之和。
(3)特斯克定理:在同样边上的三个面有关的角相加等于180度。
(4)柯尔定理:在同样边上的四个面有关的角相加等于360度。
(5)高斯定理:任意一个多面体的角之和等于360度乘以面的数量。
(6)伯尔定理:任意一个多边形的角之和大于360度。
(7)双旋定理:任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。
(8)欧几里得定理:任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。
贝瑟尔定理是最重要的立体几何判定定理,表明任意一个平面三角形的三个内角之和都等于180度。
这个定理是用来表示平面三角形的构成的,而这个定理也被用来表示一个多边形的构成。
杨氏定理是贝瑟尔定理的推广,即任意一个对角相交的多边形,其内部角之和等于其外部角之和。
特斯克定理是杨氏定理的一个特殊情况,表示在同样边上的三个面有关的角相加等于180度。
柯尔定理也是杨氏定理的一个特殊情况,表示在同样边上的四个面有关的角相加等于360度。
高斯定理是一个重要的立体几何判定定理,即任意一个多面体的角之和等于360度乘以面的数量。
这个定理与贝瑟尔定理的相似之处在于,它们都可以用来表明多面体的构成,它们都表示了一个多面体的性质。
伯尔定理是高斯定理的一个推广,表明任意一个多边形的角之和大于360度。
双旋定理是一个重要的立体几何判定定理,表明任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。
欧几里得定理也是一个重要的立体几何判定定理,表明任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。
总的来说,立体几何的八个判定定理是一个重要的数学工具,它们不仅可以帮助人们更好地理解多面体和多边形的构造,还可以帮助人们解决一些复杂的问题,比如求解三角形的面积,求解多面体的体积等等。
高中立体几何八大定理

lmβααba线面位置关系的八大定理一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行图形语言: 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α 作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 作用:线线平行⇒ 面面平行四、平面与平面平行的性质定理:文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行nmAαaαbaBA l βαaβα五、直线与平面垂直的判定定理: 文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言: 符号语言: ,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭作用:线线垂直⇒线面垂直六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行 图形语言: 符号语言://a a b b αα⊥⎫⇒⎬⊥⎭作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理: 文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直Welcome !!! 欢迎您的下载,资料仅供参考!。
高中立体几何八大定理
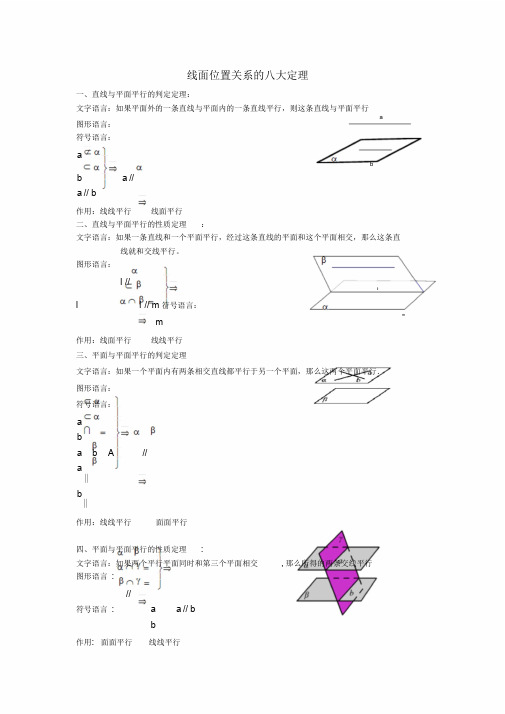
线面位置关系的八大定理一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行a图形语言:符号语言:abb a //a // b作用:线线平行线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:l //ll l // m 符号语言:m m作用:线面平行线线平行三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.图形语言:符号语言:aba b A //a∥b∥作用:线线平行面面平行四、平面与平面平行的性质定理:文字语言:如果两个平行平面同时和第三个平面相交, 那么所得的两条交线平行图形语言://符号语言: a a // bb作用: 面面平行线线平行1五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面图形语言:符号语言:aa ma nm n A m ,n amAn作用:线线垂直线面垂直六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行图形语言:符号语言:ab aba// b作用:线面垂直线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号表示:aaa注:线面垂直面面垂直八、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:All符号语言:ABABBAB l作用:面面垂直线面垂直2。
立体几何所有的定理大总结绝对全

(二)异面直线所成角1.定义:不一样在任何一个平面内的两条直线或既不平行也不订交的两条直线叫异面直线。
2.画法:借助协助平面。
1.定义:关于异面直线 a 和 b,在空间任取一点 P,过 P 分别作 a 和 b 的平行线a1和b1,我们把 a1和b1所成的锐角或许叫做异面直线 a 和 b 所成的角。
2.范围: (0 °, 90°】( ★空间两条直线所成角范围:【0°, 90°】 )(三)线面角1. 定义:当直线 l 与平面α订交且不垂直时,叫做直线 l 与平面α斜交,直线 l 叫做平面α的斜线。
设直线 l 与平面α斜交与点 M,过 l 上随意点 A,做平面α的垂线,垂足为O,把点 O叫做点 A 在平面α上的射影,直线 OM叫做直线 l 在平面α上的射影。
1.定义:把直线 l 与其在平面α上的射影所成的锐角叫做直线 l 和平面α所成的角。
2.范围【 0°, 90°】(★斜线与平面所成角范围:【0°, 90°】)(三)二面角1.定义:(1)半平面:平面内的一条直线把这个平面分红两个部分,此中每一个部分叫做半平面。
(3)二面角的棱:这一条直线叫做二面角的棱。
(4)二面角的面:这两个半平面叫做二面角的面。
(5)二面角的平面角:以二面角的棱上随意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
(6)直二面角:平面角是直角的二面角叫做直二面角。
1.定义:从一条直线出发的两个半平面所构成的图形叫做二面角。
2. 表示:以下列图,可记作 α-AB- β或 P-AB-Q3. 范围为【 0°, 180°】(五)六种距离1. 点到点的距离:两点之间的线段 PQ 的长。
2. 点到线的距离:过 P 点作 PPl ,交 l 于 P ,线段 PP 的长。
1 1 13. 点到面的距离:过 P 点作 PP 1,交 于 P 1 ,线段 PP 1 的长。
立体几何经典定理概述(八大定理)

立体几何经典定理概述(八大定理)立体几何经典定理概述(八大定理)本文将概述立体几何中的八大经典定理。
立体几何是研究三维空间中的图形和形体的数学学科,定理是在研究过程中得出的具有重要意义的数学命题。
1. 欧拉定理欧拉定理是立体几何中最著名的定理之一。
它规定了三维物体的面、顶点和边的关系。
具体来说,如果一个多面体满足面+顶点-边=2的关系,那么它就是一个封闭的多面体。
欧拉定理形象地描述了三维世界中多面体的特性。
2. 柯西定理柯西定理是关于立体几何中平行四边形的定理。
它指出,对于一个平行四边形,其对角线互相平分彼此。
这个定理在解决平行四边形的性质和关系时非常有用,能够帮助我们更好地理解平面几何的性质。
3. 形心定理形心定理是关于多边形形心的定理。
形心是多边形中所有顶点的连线的交点,该定理指出,任意多边形的形心一定在多边形的重心和质心连线的上面。
形心定理可以帮助我们确定多边形的形心位置,从而研究多边形的性质和变形。
4. 二等分线定理二等分线定理是关于立体几何中等分线的定理。
它规定了等分线在多面体中的特性,即等分线和相应的两个面以及它们的交点构成的平面垂直。
这个定理在解决多面体的等分线问题时非常有用,能够帮助我们进一步理解多面体的性质。
5. 范恩艾克线定理范恩艾克线定理是关于球面上切线和交角的定理。
它指出,在球面上,任意切线与相应交角的正弦值等于球心到交点的距离和切线长的比值。
这个定理在解决球面上的切线和交角问题时非常有用,能够帮助我们研究球面的性质和切线关系。
6. 斯坦纳定理斯坦纳定理是关于三维空间中图的生成树的定理。
生成树是一个无圈连通图的子图,其中包含了所有顶点并且边的数量最少。
斯坦纳定理指出,在三维空间中的图中,生成树的条数等于顶点数减去连通分量的数量。
这个定理在解决三维空间图的生成树问题时非常有用。
7. 勾股定理勾股定理是立体几何中最基础的定理之一。
它规定了直角三角形边长之间的关系,即直角三角形的两个直角边的平方和等于斜边的平方。
高中立体几何八大定理

1/2lmβααbanmA αa线面位置关系的八大定理(一)一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行图形语言: 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α 作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 作用:线线平行⇒ 面面平行四、平面与平面平行的性质定理:文字语言:如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言:2/2αbaBA l βαaβα符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭作用:线线垂直⇒线面垂直 六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行 图形语言: 符号语言://a a b b αα⊥⎫⇒⎬⊥⎭作用:线面垂直⇒线线平行七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理: 文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直。
立体几何定理大全

立体几何公式大全基本观点公义 1:假如一条直线上的两点在一个平面内,那么这条直线上的全部的点都在这个平面内。
公义 2:假如两个平面有一个公共点,那么它们有且只有一条经过这个点的公共直线。
公义 3:过不在同一条直线上的三个点,有且只有一个平面。
推论 1:经过一条直线和这条直线外一点,有且只有一个平面。
推论 2:经过两条订交直线,有且只有一个平面。
推论 3:经过两条平行直线,有且只有一个平面。
公义 4 :平行于同一条直线的两条直线相互平行。
等角定理:假如一个角的两边和另一个角的两边分别平行而且方向同样,那么这两个角相等。
空间两直线的地点关系:空间两条直线只有三种地点关系:平行、订交、异面1、按能否共面可分为两类:(1)共面:平行、订交(2)异面:异面直线的定义:不一样在任何一个平面内的两条直线或既不平行也不订交。
异面直线判断定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线所成的角:范围为 ( 0 °, 90° ) esp. 空间向量法两异面直线间距离 : 公垂线段 ( 有且只有一条 ) esp. 空间向量法2、若从有无公共点的角度看可分为两类:(1)有且仅有一个公共点——订交直线;(2)没有公共点——平行或异面直线和平面的地点关系:直线和平面只有三种地点关系:在平面内、与平面订交、与平面平行①直线在平面内——有无数个公共点②直线和平面订交——有且只有一个公共点直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp. 空间向量法 ( 找平面的法向量 )规定: a、直线与平面垂直时,所成的角为直角, b、直线与平面平行或在平面内,所成的角为 0°角由此得直线和平面所成角的取值范围为[0 °, 90° ]最小角定理 :斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理:假如平面内的一条直线, 与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直esp. 直线和平面垂直直线和平面垂直的定义:假如一条直线 a 和一个平面内的随意一条直线都垂直,我们就说直线 a 和平面相互垂直 . 直线 a 叫做平面的垂线,平面叫做直线 a 的垂面。
高中立体几何八大定理

lmβααba线面位置关系的八大定理之欧侯瑞魂创作一、直线与平面平行的判定定理:文字语言:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行 图形语言: 符号语言:作用:线线平行⇒线面平行二、直线与平面平行的性质定理:文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
图形语言:符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m作用:线面平行⇒线线平行 三、平面与平面平行的判定定理文字语言:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行. 图形语言: 符号语言:作用:线线平行⇒ 面面平行 四、平面与平面平行的性质定理: 文字语言:如果两个平行平面同时和第三个平nmAαaαbaaβα面相交,那么所得的两条交线平行 图形语言:符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭作用: 面面平行⇒线线平行五、直线与平面垂直的判定定理:文字语言:如果一条直线和一个平面内的两条相交直线垂直,那么这条直线垂直于这个平面 图形语言:符号语言:作用:线线垂直⇒线面垂直六、直线与平面垂直的性质定理:文字语言:若两条直线垂直于同一个平面,则这两条直线平行图形语言: 符号语言:作用:线面垂直⇒线线平行 七、平面与平面垂直的判定定理:文字语言:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直。
图形语言:符号暗示:a a ααββ⊥⎫⇒⊥⎬⊂⎭B A lβα注:线面垂直⇒面面垂直八、平面与平面垂直的性质定理:文字语言:如果两个平面互相垂直,那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言:符号语言:l AB AB AB l αβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭作用:面面垂直⇒线面垂直。
立体几何所有的定理大总结(绝对全)

(二)异面直线所成角1.定义:不同在任何一个平面内的两条直线或既不平行也不相交的两条直线叫异面直线。
2.画法:借助辅助平面。
1.定义:对于异面直线a 和b ,在空间任取一点P ,过P 分别作a 和b 的平行线1a 和1b ,我们把1a 和1b 所成的锐角或者叫做异面直线a 和b 所成的角。
2.范围:(0°,90°】(★空间两条直线所成角范围:【0°,90°】)(三)线面角1.定义:当直线l 与平面α相交且不垂直时,叫做直线l 与平面α斜交,直线l 叫做平面α的斜线。
设直线l 与平面α斜交与点M ,过l 上任意点A ,做平面α的垂线,垂足为O ,把点O 叫做点A 在平面α上的射影,直线OM 叫做直线l 在平面α上的射影。
1.定义:把直线l 与其在平面α上的射影所成的锐角叫做直线l 和平面α所成的角。
2.范围【0°,90°】(★斜线与平面所成角范围:【0°,90°】)(三)二面角1.定义:(1) 半平面:平面内的一条直线把这个平面分成两个部分,其中每一个部分叫做半平面。
(3) 二面角的棱:这一条直线叫做二面角的棱。
(4) 二面角的面:这两个半平面叫做二面角的面。
(5) 二面角的平面角:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
(6) 直二面角:平面角是直角的二面角叫做直二面角。
1.定义:从一条直线出发的两个半平面所组成的图形叫做二面角。
2.表示:如下图,可记作α-AB-β或P-AB-Q3.范围为【0°,180°】(五)六种距离1.点到点的距离:两点之间的线段PQ 的长。
2.点到线的距离:过P 点作1PP ⊥l ,交l 于1P ,线段1PP 的长。
3.点到面的距离:过P 点作1PP ⊥α,交α于1P ,线段1PP 的长。
两条平行线的距离4.线到线的距离:异面直线的距离:公垂线段PQ ⊥1l , PQ ⊥2l ,则 线段PQ 的长。
立体几何定理总结
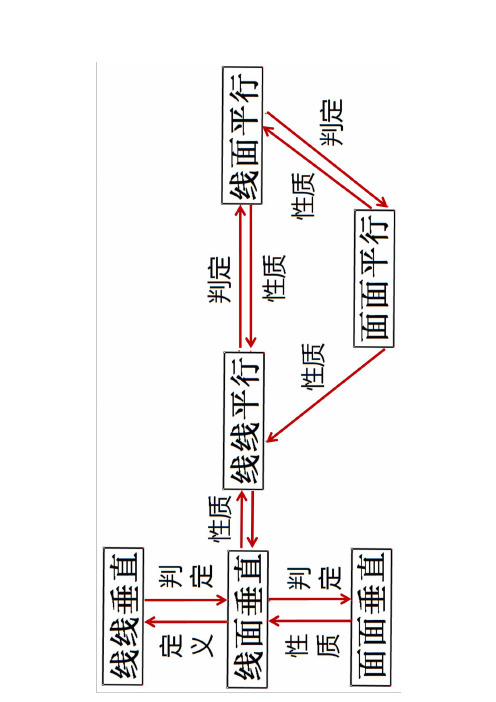
文字语言:如果一条直线和一个平面平行,经.过.这条直线的平面和这个平面相.交.,
那么这条直线就和交.线.平行.
l //
符号语言:l
l
//
m
m
关.键.点.:.必.须.产.生.交.线.才.能.判.定.线.线.平.行.
三、面面平行的判定定理:线面平行 面面平行
文字语言:如果一个平面.内.有两.条相.交.直线都平.行.于另一个平.面.,那么这两个平
关.键.:.只.要.是.其.中.一.个.平.面.内.的.直.线.就.行.
五、线面垂直的判定定理:线线垂直 线面垂直
文字语言:如果一条直线和一个平面内.的两.条相.交.直线垂.直.,那么这条直线垂直
于这个平面.
am
an 符号语言:
mn A
a
m , n
关.键.点.:.在.平.面.内.找.两.条.相.交.直.线.与.所.要.证.的.直.线.垂.直.
立体几何定理总结
一、线面平行的判定定理:线线平行 线面平行
文字语言:如果平面.外.的一条直线与平面.内.的一条直线平行,则这条直线与平面
平.行..
a
符号b
关.键.点.:.在.平.面.内.找.一.条.与.平.面.外.的.直.线.平.行.的.线.
二、线面平行的性质定理:线面平行 线线平行
面平行.
a
符号语言:
b a
b
A
//
a∥
b∥
关.键.点.:.在.要.证.明.面.面.平.行.的.其.中.一.个.面.内.找.两.条.相.交.直.线.和.另.一.面.线.面.平.行.。.
四、面面平行的性质定理(2 个):
面面平行 线线平行 文字语言:如果两个平行平面同.时.和第.三.个.平面相.交.,那么所得的两条交.线.平行.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l
m
β
α
α
b
a
立体几何的八大定理
一、线面平行的判定定理:线线平行⇒线面平行
文字语言:如果平面外.的一条直线与平面内.
的一条直线平行,则这条直线与平面平行、 符号语言://a b a b αα⊄⎫
⎪
⊂⎬⎪⎭
⇒//a α
关键点...:.在.平面内...找一条与....平面外...的.直线平行的线...... 二、线面平行的性质定理:线面平行⇒线线平行
文字语言:如果一条直线与一个平面平行,经过..这条直线的平面与这个平面相交..
,那么这条直线就与交线..
平行、 符号语言://l l m α
βαβ⎫
⎪
⊂⎬⎪⋂=⎭
⇒//l m
关键点...:.需要..借助一个....经过已知直线......的.平面..,.接着找交线。
...... 三、面面平行的判定定理:线面平行⇒ 面面平行
文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..
,那么这两个平面平行. 符号语言://a b a b A a b αα
αβββ
⊂⎫⎪⊂⎪⎪
=
⇒⎬⎪⎪⎪⎭
I ∥∥ 关键..点.:.在要证明面面平行的其中一个面内找两条相交直线与另一面线面平行。
...............................
四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行文字语言:如果两个平行平面同时..与第三..个.平面相交..,那么所得的两条交线..平行、 符号语言:
////a a b b αβαγβγ⎫
⎪
⋂=⇒⎬⎪⋂=⎭
关键点...:.找.第三个平面.....与已知平面都相交........,.则交线平行.....
文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面、
符号语言://,//a a αβαβ⊂⇒ 关键..:.只要就是其中一个平面内的直线就...............行.
n
m
A
α
a
五、线面垂直的判定定理:线线垂直⇒线面垂直
文字语言:如果一条直线与一个平面内.的两.条相交..直线垂直..
,那么这条直线垂直于这个平面、 符号语言:,a m a n a m n A m n ααα⊥⎫
⎪⊥⎪
⇒⊥⎬⋂=⎪⎪⊂⊂⎭
关键点...:.在平面内找两条相交直线与所要证的直线垂直.................... 六、线面垂直的性质定理:线面垂直⇒线线垂直
文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..
一条直线、 符号语言:l l a a αα⊥⎫
⇒⊥⎬⊂⎭
关键点...:.往往线面垂直中的线线垂直需要用这个定理推出.....................
两直线位置关系
a b
a b
a b
⎧⎧
⎨
⎪
⎨⎩
⎪
⎩
I=A
共面
//
异面-----与异面
线面位置关系
//
l
l A
l l
l
α
α
αα
α
⊂
⎧
⎪
⎧⎧
⎪
=
⎪
⎨⎨
⊄⊥
⎨⎩
⎪
⎪
⎪
⎩
⎩
I
斜交
垂直:
面面的位置关系
a
αβ
αβ
αβ
⎧
⎪
⎧
⎨
⎨
⎪⊥
⎩
⎩
I
平行://
斜交:=
相交
垂直:
二、有关平行的证明
线
∥
线
⑴
//
//
//
a
c
a
c
b
b⎫
⇒
⎬
⎭
线∥线⇒线
∥线
(都就是直
线)
⑵
//
//
a
a a b
b
α
β
αβ
⎫
⎪
⎬
⎪
⎭
⊂⇒
=
I
线∥面⇒线∥线
(相交平面)
⑶
//
//
a a b
b
αβ
αγ
βγ
=⇒
=
⎫
⎪
⎬
⎪
⎭
I
I
面∥面⇒线∥线
(平行平面)
⑷
//
a
a b
b
α
α
⎫
⎬⇒
⎭
⊥
⊥
同垂直于一个
平面
⇒线∥线
(线面垂直)
线
∥
面
⑴
//
//
a
b a
a b
α
αα
⎫
⎪
⎭
⇒
⎪
⎬
⊄
⊂
线∥线⇒线
∥面
⑵
//
//
a
a
αβ
β
α
⎫
⇒
⎬
⎭
⊂
面∥面⇒线∥面
面∥面
,
//
//,//
a b
a b O
a b
αα
αβ
ββ
⎫
⎪
⎬
⎪
⎭
⊂⊂
=⇒
I
线∥面⇒面∥
面
线
⊥
线
//
a c
b c
a b
⊥⎫
⇒⊥
⎬
⎭
线⊥线⇒线⊥线
a
a b
b
α
α
⊥⎫
⇒⊥
⎬
⊂⎭
线⊥面⇒线⊥线
线
⊥
面
,
,
l a l b
a b P l
a b
α
αα
⊥⊥⎫
⎪
=⇒⊥
⎬
⎪
⊂⊂⎭
I
线⊥线⇒线⊥面
l
a
a
a l
αβ
αβ
β
α
⊥⎫
⎪
=⎪
⇒⊥
⎬
⊂⎪
⎪
⊥⎭
I
面⊥面⇒线⊥面
面
⊥
面
a
a
β
αβ
α
⊥⎫
⇒⊥
⎬
⊂⎭
线⊥面⇒面⊥面
四、三种角的范围
异面直线所成角
(]
0,90
θ∈︒︒
直线与平
面所成角
[0,90]
PAO
∠∈︒︒
二面角
[0,180]
AOB
∠∈︒︒
五、三角形的四心六、平面几何中结论
外心:中垂线的交点
外接圆的圆心
中位线定理——中位线平行且等于底边的一半
内心:角平分线的交点
内切圆的圆心
线段对应成比例⇔线线平行重心:中线的交点
(2比1)
两组对边平行或一组对边平行且相等的四边形为平行四
边形
垂心:高的交点一组对边平行且不相等的四边形为梯形。
