【精选】八年级数学三角形解答题易错题(Word版 含答案)
八年级上册数学 全等三角形易错题(Word版 含答案)

八年级上册数学全等三角形易错题(Word版含答案)一、八年级数学轴对称三角形填空题(难)∥,1.如图所示,ABC为等边三角形,P是ABC内任一点,PD AB,PE BC++=____cm.∥,若ABC的周长为12cm,则PD PE PFPF AC【答案】4【解析】【分析】先说明四边形HBDP是平行四边形,△AHE和△AHE是等边三角形,然后得到一系列长度相等的线段,最后求替换求和即可.【详解】∥解:∵PD AB,PE BC∴四边形HBDP是平行四边形∴PD=HB∵ABC为等边三角形,周长为12cm∴∠B=∠A=60°,AB=4∥∵PE BC∴∠AHE=∠B=60°∴∠AHE=∠A=60°∴△AHE是等边三角形∴HE=AH∵∠HFP=∠A=60°∴∠HFP=∠AHE=60°∴△AHE是等边三角形,∴FP=PH∴PD+PE+PF=BH+(HP+PE)=BH+HE=BH+AH=AB=4cm故答案为4cm.【点睛】本题考查了平行四边形的判定和性质以及等边三角形的性质,掌握等边三角形的性质是解答本题的关键.2.如图,在锐角△ABC中,AB=5,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.【答案】5【解析】【分析】作BH ⊥AC ,垂足为H ,交AD 于M 点,过M 点作MN ⊥AB ,垂足为N ,则BM+MN 为所求的最小值,再根据AD 是∠BAC 的平分线可知MH=MN ,再由等腰直角三角形的性质即可得出结论.【详解】如图,作BH ⊥AC ,垂足为H ,交AD 于M 点,过M 点作MN ⊥AB ,垂足为N ,则BM+MN 为所求的最小值.∵AD 是∠BAC 的平分线,∴MH=MN ,∴BH 是点B 到直线AC 的最短距离(垂线段最短). ∵AB=5,∠BAC=45°,∴BH== 5.∵BM+MN 的最小值是BM+MN=BM+MH=BH=5.故答案为5.【点睛】本题考查了轴对称﹣最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.3.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D 在第二象限,且ABD 与ABC 全等,点D 的坐标是______.【答案】(-4,2)或(-4,3)【解析】【分析】【详解】把点C 向下平移1个单位得到点D (4,2),这时△ABD 与△ABC 全等,分别作点C ,D 关于y 轴的对称点(-4,3)和(-4,2),所得到的△ABD 与△ABC 全等.故答案为(-4,2)或(-4,3).4.如图,线段AB ,DE 的垂直平分线交于点C ,且72ABC EDC ∠=∠=︒,92AEB ∠=︒,则EBD ∠的度数为 ________ .【答案】128︒【解析】【分析】连接CE ,由线段AB ,DE 的垂直平分线交于点C ,得CA=CB ,CE=CD ,ACB=∠ECD=36°,进而得∠ACE=∠BCD ,易证∆ACE ≅∆BCD ,设∠AEC=∠BDC=x ,得则∠BDE=72°-x ,∠CEB=92°-x ,BDE 中,∠EBD=128°,根据三角形内角和定理,即可得到答案.【详解】连接CE ,∵线段AB ,DE 的垂直平分线交于点C ,∴CA=CB ,CE=CD ,∵72ABC EDC ∠=∠=︒=∠DEC ,∴∠ACB=∠ECD=36°,∴∠ACE=∠BCD ,在∆ACE与∆BCD中,∵CA CBACE BCDCE CD=⎧⎪∠=∠⎨⎪=⎩,∴∆ACE≅∆BCD(SAS),∴∠AEC=∠BDC,设∠AEC=∠BDC=x,则∠BDE=72°-x,∠CEB=92°-x,∴∠BED=∠DEC-∠CEB=72°-(92°-x)=x-20°,∴在∆BDE中,∠EBD=180°-(72°-x)-(x-20°)=128°.故答案是:128︒.【点睛】本题主要考查中垂线的性质,三角形全等的判定和性质定理以及三角形内角和定理,添加辅助线,构造全等三角形,是解题的关键.5.如图,己知30MON∠=︒,点1A,2A,3A,…在射线ON上,点1B,2B,3B,…在射线OM上,112A B A∆,223A B A∆,334A B A∆,…均为等边三角形,若12OA=,则556A B A∆的边长为________.【答案】32【解析】【分析】根据底边三角形的性质求出130∠=︒以及平行线的性质得出112233////A B A B A B ,以及22122A B B A =,得出332212244A B A B B A ===,441288A B B A ==,551216A B B A =⋯进而得出答案.【详解】解:△112A B A 是等边三角形,1121A B A B ∴=,341260∠=∠=∠=︒,2120∴∠=︒,30MON ∠=︒,11801203030∴∠=︒-︒-︒=︒,又360∠=︒,5180603090∴∠=︒-︒-︒=︒,130MON ∠=∠=︒,1112OA A B ∴==,212A B ∴=,△223A B A 、△334A B A 是等边三角形,111060∴∠=∠=︒,1360∠=︒,41260∠=∠=︒,112233////A B A B A B ∴,1223//B A B A ,16730∴∠=∠=∠=︒,5890∠=∠=︒,22122242A B B A =∴==,33232B A B A =,33312428A B B A ∴===,同理可得:444128216A B B A ===,⋯∴△1n n n A B A +的边长为2n ,∴△556A B A 的边长为5232=.故答案为:32.【点睛】本题考查了等边三角形的性质以及30°直角三角形的性质,根据已知得出33124A B B A =,44128A B B A =,551216A B B A =进而发现规律是解题关键.6.如图,点A,B,C 在同一直线上,△ABD 和△BCE 都是等边三角形,AE,CD 分别与BD,BE 交于点F,G ,连接FG ,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG ;④AD ⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)【答案】①②③⑤【解析】【分析】易证△ABE ≌△DBC ,则有∠BAE =∠BDC ,AE =CD ,从而可证到△ABF ≌△DBG ,则有AF =DG ,BF =BG ,由∠FBG =60°可得△BFG 是等边三角形,证得∠BFG =∠DBA =60°,则有FG ∥AC ,由∠CDB ≠30°,可判断AD 与CD 的位置关系.【详解】∵△ABD 和△BCE 都是等边三角形,∴BD =BA =AD ,BE =BC =EC ,∠ABD =∠CBE =60°. ∵点A 、B 、C 在同一直线上,∴∠DBE =180°﹣60°﹣60°=60°,∴∠ABE =∠DBC =120°. 在△ABE 和△DBC 中,∵BD BAABE DBCBE BC∠∠=⎧⎪=⎨⎪=⎩,∴△ABE≌△DBC,∴∠BAE=∠BDC,∴AE=CD,∴①正确;在△ABF和△DBG中,60BAF BDGAB DBABF DBG∠∠∠∠=⎧⎪=⎨⎪==︒⎩,∴△ABF≌△DBG,∴AF=DG,BF=BG.∵∠FBG=180°﹣60°﹣60°=60°,∴△BFG是等边三角形,∴∠BFG=60°,∴②正确;∵AE=CD,AF=DG,∴EF=CG;∴③正确;∵∠ADB=60°,而∠CDB=∠EAB≠30°,∴AD与CD不一定垂直,∴④错误.∵△BFG是等边三角形,∴∠BFG=60°,∴∠GFB=∠DBA=60°,∴FG∥AB,∴⑤正确.故答案为①②③⑤.【点睛】本题考查了等边三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质、平行线的判定和性质,证得△ABE≌△DBC是解题的关键.7.如图,在△ABC中,P,Q分别是BC,AC上的点,PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ PQ=,PR PS=,那么下面四个结论:①AS AR=;②QP//AR;③△BRP≌△QSP;④BR QS,其中一定正确的是(填写编号)_____________.【答案】①,②【解析】【分析】连接AP,根据角平分线性质即可推出①,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP∥AB即可;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断△BRP≌△QSP也无法证明BR QS.【详解】解:连接AP①∵PR⊥AB,PS⊥AC,PR=PS,∴点P在∠BAC的平分线上,∠ARP=∠ASP=90°,∴∠SAP=∠RAP,在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2-PR2,AS2=AP2-PS2,∵AP=AP,PR=PS,∴AR=AS,∴①正确;②∵AQ=QP,∴∠QAP=∠QPA,∵∠QAP=∠BAP,∴∠QPA=∠BAP,∴QP∥AR,∴②正确;③在Rt△BRP和Rt△QSP中,只有PR=PS,不满足三角形全等的条件,故③④错误;故答案为:①②.【点睛】本题主要考查了角平分线的性质与勾股定理的应用,熟练掌握根据垂直与相等得出点在角平分线上是解题的关键.8.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 ______cm.【答案】8.【解析】【分析】作出辅助线后根据等边三角形的判定得出△BDM为等边三角形,△EFD为等边三角形,从而得出BN的长,进而求出答案.【详解】解:延长DE交BC于M,延长AE交BC于N,作EF∥BC于F,∵AB=AC,AE平分∠BAC,∴AN⊥BC,BN=CN,∵∠DBC=∠D=60°,∴△BDM为等边三角形,∴△EFD为等边三角形,∵BD=5,DE=3,∴EM=2,∵△BDM为等边三角形,∴∠DMB=60°,∵AN⊥BC,∴∠ENM=90°,∴∠NEM=30°,∴NM=1,∴BN=4,∴BC=2BN=8(cm),故答案为8.【点睛】本题考查等边三角形的判定与性质;等腰三角形的性质.9.如图,在Rt△ABC中,∠C=30°,将△ABC绕点B旋转α(0<α<60°)到△A′BC′,边AC 和边A′C′相交于点P,边AC和边BC′相交于Q.当△BPQ为等腰三角形时,则α=__________.【答案】20°或40°【解析】【分析】过B作BD⊥AC于D,过B作BE⊥A'C'于E,根据旋转可得△ABC≌△A'BC',则BD=BE,进而得到BP平分∠A'PC,再根据∠C=∠C'=30°,∠BQC=∠PQC',可得∠CBQ=∠C'PQ=θ,即可得出∠BPQ=12(180°-∠C'PQ)=90°-12θ,分三种情况讨论,利用三角形内角和等于180°,即可得到关于θ的方程,进而得到结果.【详解】如图,过B作BD⊥AC于D,过B作BE⊥A'C'于E,由旋转可得,△ABC≌△A'BC',则BD=BE,∴BP平分∠A'PC,又∵∠C=∠C'=30°,∠BQC=∠PQC',∴∠CBQ=∠C'PQ=θ,∴∠BPQ=12(180°-∠C'PQ)=90°-12θ,分三种情况:①如图所示,当PB=PQ时,∠PBQ=∠PQB=∠C+∠QBC=30°+θ,∵∠BPQ+∠PBQ+∠PQB=180°,∴90°-12θ+2×(30°+θ)=180°,解得θ=20°;②如图所示,当BP=BQ时,∠BPQ=∠BQP,即90°-12θ=30°+θ,解得θ=40°;③当QP=QB时,∠QPB=∠QBP=90°-12θ,又∵∠BQP=30°+θ,∴∠BPQ+∠PBQ+∠BQP=2(90°-12θ)+30°+θ=210°>180°(不合题意),故答案为:20°或40°.【点睛】本题主要考查了等腰三角形的性质以及旋转的性质的运用,解决问题的关键是利用全等三角形对应边上高相等,得出BP平分∠A'PC,解题时注意分类思想的运用.10.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为_________【答案】8 5【解析】【分析】首先根据折叠可得CD=AC=6,B′C=BC=8,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,然后求得△ECF是等腰直角三角形,进而求得∠B′FD=90°,CE=EF=4.8,由勾股定理求出AE,得出BF 的长,即B′F的长.【详解】解:根据折叠的性质可知:DE=AE,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,B′F=BF,∴B′D=8-6=2,∠DCE+∠B′CF=∠ACE+∠BCF,∵∠ACB=90°,∴∠ECF=45°,∴△ECF是等腰直角三角形,∴EF=CE,∠EFC=45°,∴∠BFC=∠B′FC=135°,∴∠B′FE=90°,∵S△ABC=12AC•BC=12AB•CE,∴AC•BC=AB•CE , ∵根据勾股定理得:22226810AB AC BC ∴ 4.8AC BC CE AB⋅== ∴EF=4.8,22 3.6AE AC EC =-=∴B′F=BF=AB -AE-EF=10-3.6-4.8=1.6=85,故答案是:85.【点睛】此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理等知识;熟练掌握翻折变换的性质,由直角三角形的性质和勾股定理求出CE 、AE 是解决问题的关键.二、八年级数学轴对称三角形选择题(难)11.边长为a 的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )A .511a 32⨯() B .511a 23⨯() C .611a 32⨯() D .611a 23⨯() 【答案】A【解析】 连接AD 、DB 、DF ,求出∠AFD=∠ABD=90°,根据HL 证两三角形全等得出∠FAD=60°,求出AD ∥EF ∥GI ,过F 作FZ ⊥GI ,过E 作EN ⊥GI 于N ,得出平行四边形FZNE 得出EF=ZN=13a ,求出GI 的长,求出第一个正六边形的边长是13a ,是等边三角形QKM 的边长的13;同理第二个正六边形的边长是等边三角形GHI 的边长的13;求出第五个等边三角形的边长,乘以13即可得出第六个正六边形的边长. 连接AD 、DF 、DB .∵六边形ABCDEF是正六边形,∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,∴∠EFD=∠EDF=∠CBD=∠BDC=30°,∵∠AFE=∠ABC=120°,∴∠AFD=∠ABD=90°,在Rt△ABD和RtAFD中AF=AB{AD=AD∴Rt△ABD≌Rt△AFD(HL),∴∠BAD=∠FAD=12×120°=60°,∴∠FAD+∠AFE=60°+120°=180°,∴AD∥EF,∵G、I分别为AF、DE中点,∴GI∥EF∥AD,∴∠FGI=∠FAD=60°,∵六边形ABCDEF是正六边形,△QKM是等边三角形,∴∠EDM=60°=∠M,∴ED=EM,同理AF=QF,即AF=QF=EF=EM,∵等边三角形QKM的边长是a,∴第一个正六边形ABCDEF的边长是13a,即等边三角形QKM的边长的13,过F作FZ⊥GI于Z,过E作EN⊥GI于N,则FZ∥EN,∵EF∥GI,∴四边形FZNE是平行四边形,∴EF=ZN=13a,∵GF=12AF=12×13a=16a,∠FGI=60°(已证),∴∠GFZ=30°,∴GZ=12GF=112a,同理IN=112a,∴GI=112a+13a+112a=12a,即第二个等边三角形的边长是12a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是13×12a;同理第第三个等边三角形的边长是12×12a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是13×12×12a;同理第四个等边三角形的边长是12×12×12a,第四个正六边形的边长是13×12×12×12a;第五个等边三角形的边长是12×12×12×12a,第五个正六边形的边长是1 3×12×12×12×12a;第六个等边三角形的边长是12×12×12×12×12a,第六个正六边形的边长是1 3×12×12×12×12×12a,即第六个正六边形的边长是13×512()a,故选A.12.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )A.32B.332C.32D.不能确定【答案】B【解析】已知,如图,P为等边三角形内任意一点,PD、PE、PF分别是点P到边AB、BC、AC的距离,连接AP、BP、CP,过点A作AH⊥BC于点H,已知等边三角形的边长为3,可求得高线AH=332,因S△ABC=12BC•AH=12AB•PD+12BC•PE+12AC•PF,所以1 2×3×AH=12×3×PD+12×3×PE+12×3×PF,即可得PD+PE+PF=AH=332,即点P到三角形三边距离之和为332.故选B.点睛:本题考查了等边三角形的性质,根据三角形的面积求点P到三边的距离之和等于等边三角形的高是解题的关键,作出图形更形象直观.13.在一个33的正方形网格中,A,B是如图所示的两个格点,如果C也是格点,且ABC是等腰三角形,则符合条件的C点的个数是()A.6B.7C.8D.9【答案】C【解析】【分析】根据题意、结合图形,画出图形即可确定答案.【详解】解:根据题意,画出图形如图:共8个.故答案为C.【点睛】本题主要考查了等腰三角形的判定,根据题意、画出符合实际条件的图形是解答本题的关键.14.在平面直角坐标系中,等腰△ABC 的顶点A 、B 的坐标分别为(1,0)、(2,3),若顶点C 落在坐标轴上,则符合条件的点C 有( )个.A .9B .7C .8D .6【答案】C【解析】【分析】要使△ABC 是等腰三角形,可分三种情况(①若CA =CB ,②若BC =BA ,③若AC =AB )讨论,通过画图就可解决问题.【详解】①若CA =CB ,则点C 在AB 的垂直平分线上.∵A (1,0),B (2,3),∴AB 的垂直平分线与坐标轴有2个交点C 1,C 2.②若BC =BA ,则以点B 为圆心,BA 为半径画圆,与坐标轴有3个交点(A 点除外)C 3,C 4,C 5;③若AC =AB ,则以点A 为圆心,AB 为半径画圆,与坐标轴有4个交点C 6,C 7,C 8,C 9.而C 8(0,-3)与A 、B 在同一直线上,不能构成三角形,故此时满足条件的点有3个.综上所述:符合条件的点C 的个数有8个.故选C .【点睛】本题考查了等腰三角形的判定、垂直平分线的性质的逆定理等知识,还考查了动手操作的能力,运用分类讨论的思想是解答本题的关键.15.已知:如图,ABC ∆、CDE ∆都是等腰三角形,且CA CB =,CD CE =,ACB DCE α∠=∠=,AD 、BE 相交于点O ,点M 、N 分别是线段AD 、BE 的中点.以下4个结论:①AD BE =;②180DOB α∠=-;③CMN ∆是等边三角形;④连OC ,则OC 平分AOE ∠.正确的是( )A .①②③B .①②④C .①③④D .①②③④【答案】B【解析】【分析】 ①根据∠ACB=∠DCE 求出∠ACD=∠BCE,证出ACD BCE ≅△△即可得出结论,故可判断; ②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB ,故可判断;③根据已知条件可求出AM=BN,根据SAS 可求出CAM CBN ≅,推出CM=CN ,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断CMN ∆的形状;④在AD 上取一点P 使得DP=EO,连接CP ,根据ACD BCE ≅△△,可求出∠CEO=∠CDP ,根据SAS 可求出 CEO CDP ≅,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE ,故可判断.【详解】①正确,理由如下:∵ACB DCE α∠=∠=,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,又∵CA=CB,CD=CE,∴ACD BCE ≅△△(SAS),∴AD=BE,故①正确;②正确,理由如下:由①知,ACD BCE ≅△△,∴∠CAD=∠CBE,∵∠DOB 为ABO 的外角,∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC, ∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,∴∠CBA+∠BAC=180°-α,即∠DOB=180°-α,故②正确;③错误,理由如下:∵点M 、N 分别是线段AD 、BE 的中点,∴AM=12AD,BN= 12BE, 又∵由①知,AD=BE,∴AM=BN,又∵∠CAD=∠CBE,CA=CB,∴CAM CBN ≅(SAS), ∴CM=CN ,∠ACM=∠BCN,∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,∴MCN △为等腰三角形且∠MCN=α,∴MCN △不是等边三角形,故③错误;④正确,理由如下:如图所示,在AD 上取一点P 使得DP=EO,连接CP ,由①知,ACD BCE ≅△△,∴∠CEO=∠CDP ,又∵CE=CD,EO=DP ,∴CEO CDP ≅(SAS),∴∠COE=∠CPD,CP=CO,∴∠CPO=∠COP ,∴∠COP=∠COE,即OC 平分∠AOE,故④正确;故答案为:B.【点睛】本题考查了三角形全等的判定和性质,三角形内角和定理和外角定理,等边三角形的判定,根据已知条件作出正确的辅助线,找出全等三角形是解题的关键.16.如图, 在△DAE 中, ∠DAE =40°, B 、C 两点在直线DE 上,且∠BAE =∠BEA ,∠CAD =∠CDA ,则∠BAC 的大小是( )A.100°B.90°C.80°D.120°【答案】A【解析】【分析】由已知条件,利用了中垂线的性质得到线段相等及角相等,再结合三角形内角和定理求解.【详解】解:如图,∵BG是AE的中垂线,CF是AD的中垂线,∴AB=BE,ACECD∴∠AED=∠BAE=∠BAD+∠DAE,∠CDA=∠CAD=∠DAE+∠CAE,∵∠DAE+∠ADE+∠AED=180°∴∠BAD+∠DAE+∠DAE+∠CAE+∠DAE=3∠DAE+∠BAD+∠EAC=120°+∠BAD+∠EAC=180°∴∠BAD+∠EAC=60°∴.∠BAC=∠BAD+∠EAC+∠DAE=60°+40°=100°;故选:A【点睛】本题考查了中垂线的性质、三角形内角和定理及等腰三角形的判定与性质;找着各角的关系利用内角和列式求解是正确解答本题的关键.17.如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠MPN=110°,则∠AOB=()A.35°B.40°C.45°D.50°【答案】A【解析】【分析】作P 关于OA ,OB 的对称点P 1,P 2.连接OP 1,OP 2.则当M ,N 是P 1P 2与OA ,OB 的交点时,△PMN 的周长最短,根据对称的性质可以证得:∠OP 1M=∠OPM=50°,OP 1=OP 2=OP ,根据等腰三角形的性质求解.【详解】作P 关于OA ,OB 的对称点P 1,P 2.连接OP 1,OP 2.则当M ,N 是P 1P 2与OA ,OB 的交点时,△PMN 的周长最短,连接P 1O 、P 2O ,∵PP 1关于OA 对称,∠MPN=110°∴∠P 1OP=2∠MOP ,OP 1=OP ,P 1M=PM ,∠OP 1M=∠OPM ,同理可得:∠P 2OP=2∠NOP ,OP=OP 2,∴∠P 1OP 2=∠P 1OP+∠P 2OP=2(∠MOP+∠NOP )=2∠AOB ,OP 1=OP 2=OP ,∴△P 1OP 2是等腰三角形.∴∠OP 2N=∠OP 1M ,∴∠P 1OP 2=180°-110°=70°,∴∠AOB=35°,故选A .【点睛】考查了对称的性质,解题关键是正确作出图形和证明△P 1OP 2是等腰三角形是.18.如图,ABC △是等边三角形,ABD △是等腰直角三角形,∠BAD =90°,AE ⊥BD 于点E .连CD 分别交AE ,AB 于点F ,G ,过点A 做AH ⊥CD 交BD 于点H ,则下列结论:①∠ADC =15°;②AF =AG ;③AH =DF ;④△ADF ≌△BAH ;⑤DF =2EH .其中正确结论的个数为( )A .5B .4C .3D .2【答案】B【解析】【分析】①根据△ABC 为等边三角形,△ABD 为等腰直角三角形,可以得出各角的度数以及DA=AC ,即可作出判断;②分别求出∠AFG 和∠AGD 的度数,即可作出判断;④根据三角形内角和定理求出∠HAB 的度数,求证EHG DFA ∠=∠,利用AAS 即可证出两个三角形全等;③根据④证出的全等即可作出判断;⑤证明∠EAH=30°,即可得到AH=2EH ,又由③可知AH DF =,即可作出判断.【详解】①正确:∵ABC △是等边三角形,∴60BAC ︒∠=,∴CA AB =.∵ABD △是等腰直角三角形,∴DA AB =.又∵90BAD ︒∠=,∴150CAD BAD BAC ︒∠=∠+∠=,∴DA CA =,∴()1180150152ADC ACD ︒︒︒∠=∠=-=; ②错误:∵∠EDF=∠ADB-∠ADC=30°∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG∵∠AGD=90°-∠ADG=90°-15°=75°∠AFG≠∠AGD∴AF≠AG③,④正确,由题意可得45DAF ABH ︒∠=∠=,DA AB =,∵AE BD ⊥,AH CD ⊥.∴180EHG EFG ︒∠+∠=.又∵180?DFA EFG ∠+∠=,∴EHG DFA ∠=∠,在DAF △和ABH 中 ()AFD BHA DAF ABHAAS DA AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴DAF △≌ABH .∴DF AH =.⑤正确:∵150CAD ︒∠=,AH CD ⊥,∴75DAH ︒∠=,又∵45DAF ︒∠=,∴754530EAH ︒︒︒∠=-=又∵AE DB ⊥,∴2AH EH =,又∵=AH DF ,∴2DF EH =【点睛】本题考查了等边三角形的性质,等腰三角形的性质,三角形的内角和定理,三角形外角的性质,全等三角形的判定与性质,综合性较强,属于较难题目.19.如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x 轴上取点C ,使△ABC 为等腰三角形,则满足条件的点C 的个数是( )A.1 B.2 C.3 D.4【答案】D【解析】【分析】由点A、B的坐标可得到AB=22,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.【详解】∵点A、B的坐标分别为(2,2)、B(4,0).∴AB=22,如图,①若AC=AB,以A为圆心,AB为半径画弧与x轴有2个交点(含B点),即(0,0)、(4,0),∴满足△ABC是等腰三角形的C点有1个;②若BC=AB,以B为圆心,BA为半径画弧与x轴有2个交点,即满足△ABC是等腰三角形的C点有2个;③若CA=CB,作AB的垂直平分线与x轴有1个交点,即满足△ABC是等腰三角形的C点有1个;综上所述:点C在x轴上,△ABC是等腰三角形,符合条件的点C共有4个.故选D.【点睛】本题主考查了等腰三角形的判定以及分类讨论思想的运用,分三种情况分别讨论,注意等腰三角形顶角的顶点在底边的垂直平分线上.20.如图,在△ABC中,AB=AC=8,BC=5,AB的垂直平分线交AC于D,则△BCD的周长为()A.13B.15C.18D.21【答案】A【解析】根据线段垂直平分线的性质,可由AB=AC=8,BC=5,AB的垂直平分线交AC于D,得到AD=BD,进而得出△BCD的周长为:CD+BD+BC=AC+BC=8+5=13.故选A.点睛:此题主要考查了线段垂直平分线的性质,关键是掌握垂直平分线上任意一点,到线段两端点的距离相等.。
八年级上册数学 全册全套试卷易错题(Word版 含答案)

八年级上册数学全册全套试卷易错题(Word版含答案)一、八年级数学全等三角形解答题压轴题(难)1.(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=12∠BAD,上述结论是否仍然成立,并说明理由;(3)结论应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O 之间夹角∠EOF=70°,试求此时两舰艇之间的距离.(4)能力提高:如图4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,试求出MN的长.【答案】(1)EF=BE+FD;(2)EF=BE+FD仍然成立;(3)210;(4)MN10.【解析】试题分析:(1)由△AEF≌△AGF,得EF=GF,又由BE=DG,得EF=GF=DF+DG=DF+BE;(2)延长FD到点G,使DG=BE,连接AG,证明△ABE≌△ADG,再证△AEF≌△AGF,得EF=FG,即可得到答案;(3)连接EF,延长AE,BF相交于点C,根据探索延伸可得EF=AE+FB,即可计算出EF的长度;(4)在△ABC外侧作∠CAD=∠BAM,截取AD=A M,连接CD,DN,证明△ACD≌△ABM,得到CD=BM,再证MN=ND,则求出ND的长度,即可得到答案.解:(1)由△AEF≌△AGF,得EF=GF,又由BE=DG,得EF=GF=DF+DG=DF+BE;(2)EF=BE+FD仍然成立.证明:如答图1,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,∴∠B=∠ADG,在△ABE与△ADG中,AB=AD,∠B=∠ADG,BE=DG,∴△ABE≌△ADG.∴AE=AG,∠BAE=∠DAG.又∵∠EAF=12∠BAD,∴∠F AG=∠F AD+∠DAG=∠F AD+∠BAE=∠BAD-∠EAF=∠BAD-12∠BAD=12∠BAD,∴∠EAF=∠GAF.在△AEF与△AGF中,AE=AG,∠EAF=∠GAF,AF=AF,∴△AEF≌△AGF.∴EF=FG.又∵FG=DG+DF=BE+DF.∴EF=BE+FD.(3)如答图2,连接EF,延长AE,BF相交于点C,在四边形AOBC中,∵∠AOB=30°+90°+20°=140°,∠FOE=70°=12∠AOB,又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,∴结论EF=AE+FB成立.∴EF=AE+FB=1.5×(60+80)=210(海里).答:此时两舰艇之间的距离为210海里;(4)如答图3,在△ABC外侧作∠CAD=∠BAM,截取AD=AM,连接CD,DN,在△ACD与△ABM中,AC=AB,∠CAD=∠BAM,AD=AM,则△ACD≌△ABM,∴CD=BM=1,∠ACD=∠ABM=45°,∵∠NAD=∠NAC+∠CAD=∠NAC+∠BAM=∠BAC-∠MAN=45°,∴∠MAD=∠MAN+∠NAD=90°=2∠NAD,又∵AM=AD,∠NCD+∠MAD=(∠ACD+∠ACB)+90°=180°,∴对于四边形AMCD符合探索延伸,则ND=MN ,∵∠NCD=90°,CD=1,CN=3,∴MN=ND=10.2.在ABC ∆中,90,BAC AB AC ∠=︒=,点D 为直线BC 上一动点(点D 不与点,B C 重合),以AD 为腰作等腰直角DAF ∆,使90DAF ∠=︒,连接CF .(1)观察猜想如图1,当点D 在线段BC 上时, ①BC 与CF 的位置关系为__________;②CF DC BC 、、之间的数量关系为___________(提示:可证DAB FAC ∆≅∆)(2)数学思考如图2,当点D 在线段CB 的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;(3)拓展延伸如图3,当点D 在线段BC 的延长线时,将DAF ∆沿线段DF 翻折,使点A 与点E 重合,连接CE CF 、,若4,22CD BC AC ==CE 的长.(提示:做AH BC ⊥于H ,做EM BD ⊥于M )【答案】(1)①BC ⊥CF ;②BC =CF +DC ;(2)C ⊥CF 成立;BC =CF +DC 不成立,正确结论:DC =CF +BC ,证明详见解析;(3)32【解析】【分析】(1)①根据正方形的性质得,∠BAC =∠DAF =90°,推出△DAB ≌△FAC (SAS );②由正方形ADEF 的性质可推出△DAB ≌△FAC ,根据全等三角形的性质可得到=CF BD ,ACF ABD ∠=∠ ,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC =∠DAF =90°,推出△DAB ≌△FAC ,根据全等三角形的性质以及等腰三角形的角的性质可得到结论;(3)过A 作AH BC ⊥ 于H ,过E 作EM BD ⊥ 于M ,证明ADH DEM △≌△ ,推出3EM DH == ,2DM AH == ,推出3CM EM == ,即可解决问题.【详解】(1)①正方形ADEF 中,AD AF =∵90BAC DAF ==︒∠∠∴BAD CAF ∠=∠在△DAB 与△FAC 中AD AF BAD CAF AB AC =⎧⎪∠=∠⎨⎪=⎩∴()DAB FAC SAS △≌△∴B ACF ∠=∠∴90ACB ACF +=︒∠∠ ,即BC CF ⊥ ;②∵DAB FAC △≌△∴=CF BD∵BC BD CD =+∴BC CF CD =+(2)BC ⊥CF 成立;BC =CF +DC 不成立,正确结论:DC =CF +BC证明:∵△ABC 和△ADF 都是等腰直角三角形∴AB =AC ,AD =AF ,∠BAC =∠DAF =90°,∴∠BAD =∠CAF在△DAB 和△FAC 中AD AF BAD CAF AB AC =⎧⎪∠=∠⎨⎪=⎩∴△DAB ≌△FAC (SAS )∴∠ABD =∠ACF ,DB =CF∵∠BAC =90°,AB =AC ,∴∠ACB =∠ABC =45°∴∠ABD =180°-45°=135°∴∠ACF =∠ABD =135°∴∠BCF =∠ACF -∠ACB =135°-45°=90°,∴CF ⊥BC∵CD =DB +BC ,DB =CF∴DC =CF +BC(3)过A 作AH BC ⊥ 于H ,过E 作EM BD ⊥ 于M ,∵90BAC ∠=︒ ,22AB AV ==∴12422BC AB AH BH CH BC ======, ∴114CD BC == ∴3DH CH CD =+=∵四边形ADEF 是正方形∴90AD DE ADE ==︒,∠∵BC CF EM BD EN CF ⊥⊥⊥,,∴四边形CMEN 是矩形∴NE CM EM CN ==,∵90AHD ADC EMD ===︒∠∠∠∴90ADH EDM EDM DEM +=+=︒∠∠∠∠∴ADH DEM =∠∠在△ADH 和△DEM 中ADH DEM AHD DME AD DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ADH DEM △≌△∴32EM DH DM AH ====,∴3CM EM ==∴2232CE EM CM =-=【点睛】本题考查了三角形的综合问题,掌握正方形的性质、全等三角形的性质以及判定、余角的性质、等腰三角形的角的性质是解题的关键.3.如图,∠BAD=∠CAE=90°,AB=AD ,AE=AC ,AF ⊥CB ,垂足为F .(1)求证:△ABC ≌△ADE ;(2)求∠FAE 的度数;(3)求证:CD=2BF+DE .【答案】(1)证明见解析;(2)∠FAE=135°;(3)证明见解析.【解析】【分析】(1)根据已知条件易证∠BAC=∠DAE ,再由AB=AD ,AE=AC ,根据SAS 即可证得△ABC ≌△ADE ;(2)已知∠CAE=90°,AC=AE ,根据等腰三角形的性质及三角形的内角和定理可得∠E=45°,由(1)知△BAC ≌△DAE ,根据全等三角形的性质可得∠BCA=∠E=45°,再求得∠CAF=45°,由∠FAE=∠FAC+∠CAE 即可得∠FAE 的度数;(3)延长BF 到G ,使得FG=FB ,易证△AFB ≌△AFG ,根据全等三角形的性质可得AB=AG ,∠ABF=∠G ,再由△BAC ≌△DAE ,可得AB=AD ,∠CBA=∠EDA ,CB=ED ,所以AG=AD ,∠ABF=∠CDA ,即可得∠G=∠CDA ,利用AAS 证得△CGA ≌△CDA ,由全等三角形的性质可得CG=CD ,所以CG=CB+BF+FG=CB+2BF=DE+2BF .【详解】(1)∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE ,在△BAC 和△DAE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩, ∴△BAC ≌△DAE (SAS );(2)∵∠CAE=90°,AC=AE ,∴∠E=45°,由(1)知△BAC ≌△DAE ,∴∠BCA=∠E=45°,∵AF ⊥BC ,∴∠CFA=90°,∴∠CAF=45°,∴∠FAE=∠FAC+∠CAE=45°+90°=135°;(3)延长BF 到G ,使得FG=FB ,∵AF ⊥BG ,∴∠AFG=∠AFB=90°,在△AFB和△AFG中,BF FAFB AFGAF AFG=⎧⎪∠=∠⎨⎪=⎩,∴△AFB≌△AFG(SAS),∴AB=AG,∠ABF=∠G,∵△BAC≌△DAE,∴AB=AD,∠CBA=∠EDA,CB=ED,∴AG=AD,∠ABF=∠CDA,∴∠G=∠CDA,在△CGA和△CDA中,GCA DCACGA CDAAG AD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CGA≌△CDA,∴CG=CD,∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE.【点睛】本题考查全等三角形的判定与性质,解决第3问需作辅助线,延长BF到G,使得FG=FB,证得△CGA≌△CDA是解题的关键.4.如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD 的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.探究:当∠ACB多少度时,CE⊥BC?请说明理由.【答案】(1)①垂直,相等.②都成立,理由见解析;(2)45°,理由见解析【解析】【分析】(1)①根据∠BAD=∠CAE ,BA=CA ,AD=AE ,运用“SAS ”证明△ABD ≌△ACE ,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE 、BD 之间的关系;②先根据“SAS ”证明△ABD ≌△ACE ,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;(2)先过点A 作AG ⊥AC 交BC 于点G ,画出符合要求的图形,再结合图形判定△GAD ≌△CAE ,得出对应角相等,即可得出结论.【详解】(1):(1)CE 与BD 位置关系是CE ⊥BD ,数量关系是CE=BD .理由:如图1,∵∠BAD=90°-∠DAC ,∠CAE=90°-∠DAC ,∴∠BAD=∠CAE .又 BA=CA ,AD=AE ,∴△ABD ≌△ACE (SAS )∴∠ACE=∠B=45°且 CE=BD .∵∠ACB=∠B=45°,∴∠ECB=45°+45°=90°,即 CE ⊥BD .故答案为垂直,相等;②都成立,理由如下:∵∠BAC =∠DAE =90°,∴∠BAC +∠DAC =∠DAE +∠DAC ,∴∠BAD =∠CAE ,在△DAB 与△EAC 中,AD AE BAD CAE AB AC ⎧⎪∠∠⎨⎪⎩=== ∴△DAB ≌△EAC ,∴CE =BD ,∠B =∠ACE ,∴∠ACB +∠ACE =90°,即CE ⊥BD ;(2)当∠ACB=45°时,CE⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,在△GAD与△CAE中,AC AGDAG EACAD AE⎧⎪∠∠⎨⎪⎩===∴△GAD≌△CAE,∴∠ACE=∠AGC=45°,∠BCE=∠ACB+∠ACE=45°+45°=90°,即CE⊥B C.5.在等边ABC中,点D是边BC上一点.作射线AD,点B关于射线AD的对称点为点E.连接CE并延长,交射线AD于点F.(1)如图,连接AE,①AE与AC的数量关系是__________;②设BAFα∠=,用α表示BCF∠的大小;(2)如图,用等式表示线段AF,CF,EF之间的数量关系,并证明.【答案】(1)①AB=AE;②∠BCF=α;(2) AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案;②由轴对称性,得:AE=AB,∠BAF=∠EAF=α,由ABC是等边三角形,得AB=AC,∠BAC=∠ACB=60°,再根据等腰三角形的性质和三角形内角和等于180°,即可求解;(2)作∠FCG=60°交AD于点G,连接BF,易证∆FCG是等边三角形,得GF=FC,再证∆ACG≅∆BCF(SAS),从而得AG=BF,进而可得到结论.【详解】(1)①∵点B关于射线AD的对称点为点E,∴AB和AE关于射线AD的对称,∴AB=AE.故答案是:AB=AE;②∵点B关于射线AD的对称点为点E,∴AE=AB,∠BAF=∠EAF=α,∵ABC是等边三角形,∴AB=AC,∠BAC=∠ACB=60°,∴∠EAC=60°-2α,AE=AC,∴∠ACE=1180(602)602αα⎡⎤--=+⎣⎦,∴∠BCF=∠ACE-∠ACB=60α+-60°=α.(2)AF-EF=CF,理由如下:作∠FCG=60°交AD于点G,连接BF,∵∠BAF=∠BCF=α,∠ADB=∠CDF,∴∠ABC=∠AFC=60°,∴∆FCG是等边三角形,∴GF=FC,∵ABC是等边三角形,∴BC=AC,∠ACB=60°,∴∠ACG=∠BCF=α.在∆ACG和∆BCF中,∵CA CBACG BCFCG CF=⎧⎪∠=∠⎨⎪=⎩,∴∆ACG≅∆BCF(SAS),∴AG=BF,∵点B关于射线AD的对称点为点E,∴AG=BF=EF,∵AF-AG=GF,∴AF-EF=CF.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.二、八年级数学轴对称解答题压轴题(难)6.已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求ABFACFSS的值.【答案】(1)①见解析;②见解析;(2)2【解析】【分析】(1)①只要证明∠2+∠BAF=∠1+∠BAF=60°即可解决问题;②只要证明△BFC≌△ADB,即可推出∠BFC=∠ADB=90°;(2)在BF上截取BK=AF,连接AK.只要证明△ABK≌CAF,可得S△ABK=S△AFC,再证明AF=FK=BK,可得S△ABK=S△AFK,即可解决问题;【详解】(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴ABFAFCS2S∆∆=.【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识,解题的关键是能够正确添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.7.问题探究:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.(1)证明:AD=BE;(2)求∠AEB的度数.问题变式:(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.【答案】(1)见详解;(2)60°;(3)(Ⅰ)90°;(Ⅱ)AE=BE+2CM,理由见详解.【解析】【分析】(1)由条件△ACB和△DCE均为等边三角形,易证△ACD≌△BCE,从而得到对应边相等,即AD=BE;(2)根据△ACD≌△BCE,可得∠ADC=∠BEC,由点A,D,E在同一直线上,可求出∠ADC=120°,从而可以求出∠AEB的度数;(3)(Ⅰ)首先根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°;(Ⅱ)根据DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM.【详解】解:(1)如图1,∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE.在△ACD和△BCE中,AC BCACD BCE CD CE=⎧⎪∠=∠⎨⎪=⎩∴△ACD≌△BCE(SAS),∴AD=BE;(2)如图1,∵△ACD≌△BCE,∴∠ADC=∠BEC,∵△DCE为等边三角形,∴∠CDE=∠CED=60°,∵点A,D,E在同一直线上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB=∠BEC-∠CED=60°;(3)(Ⅰ)如图2,∵△ACB和△DCE均为等腰直角三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE,在△ACD和△BCE中,AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△BCE(SAS),∴BE=AD,∠BEC=∠ADC,∵点A,D,E在同一直线上,∴∠ADC=180-45=135°,∴∠BEC=135°,∴∠AEB=∠BEC-∠CED=135°-45°=90°,故答案为:90°;(Ⅱ)如图2,∵∠DCE=90°,CD=CE,CM⊥DE,∴CM=DM=EM,∴DE=DM+EM=2CM,∵△ACD≌△BCE(已证),∴BE=AD,∴AE=AD+DE=BE+2CM,故答案为:AE=BE+2CM.【点睛】本题属于三角形综合题,主要考查了全等三角形的判定方法和性质,等边三角形的性质以及等腰直角三角形的性质的综合应用.在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.8.八年级的小明同学通到这样一道数学题目:△ABC为边长为4的等边三角形,E是边AB 边上任意一动点,点D在CB的延长线上,且满足AE=BD.(1)如图①,当点E 为AB 的中点时,DE = ;(2)如图②,点E 在运动过程中,DE 与EC 满足什么数量关系?请说明理由;(3)如图③,F 是AC 的中点,连接EF .在AB 边上是否存在点E ,使得DE +EF 值最小?若存在,求出这个最小值;若不存在,请说明理由.(直角三角形中,30°所对的边是斜边的一半)【答案】(1)23;(2)DE =CE ,理由见解析;(3)这个最小值为27;【解析】【分析】(1)如图①,过点E 作EH ⊥BC 于H ,由等边三角形的性质可得BE =DB =AE =2,由直角三角形的性质可求BH =1,EH 3=,由勾股定理可求解;(2)如图②,过E 作EF ∥BC 交AC 于F ,可证△AEF 是等边三角形,AE =EF =AF =BD ,由“SAS ”可证△DBE ≌△EFC ,可得DE =CE ;(3)如图③,将△ABC 沿AB 翻折得到△ABC ',连接C 'F 交AB 于点E ',连接CE ',DE ',过点F 作FH ⊥AC '于点H ,由“SAS ”可证△ACE '≌△AC 'E ',可得C 'E '=CE ',可得当点C ',点E ',点F 三点共线时,DE +EF 的值最小,由勾股定理可求最小值.【详解】(1)如图①,过点E 作EH ⊥BC 于H ,∵△ABC 为边长为4的等边三角形,点E 是AB 的中点,∴AE =BE =2=DB ,∠ABC =60°,且EH ⊥BC ,∴∠BEH =30°,∴BH =1,EH 3=3=∴DH =DB +BH =2+1=3,∴DE 2293DH EH =+=+=23故答案为:3(2)DE =CE.理由如下:如图②,过E 作EF ∥BC 交AC 于F .∵△ABC 是等边三角形,∴∠ABC =∠ACB =∠A =60°,AB =AC =BC.∵EF ∥BC ,∴∠AEF =∠ABC =60°,∠AFE =∠ACB =60°,∴∠AEF =∠AFE =∠A =60°,∴△AEF 是等边三角形,∴AE =EF =AF ,∴AB ﹣AE =AC ﹣AF ,∴BE =CF.∵∠ABC =∠ACB =∠AFE =60°,∴∠DBE =∠EFC =120°,且AE =EF =DB ,BE =CF ,∴△DBE ≌△EFC (SAS),∴DE =CE ,(3)如图③,将△ABC 沿AB 翻折得到△ABC ',连接C 'F 交AB 于点E ',连接CE ',DE ',过点F 作FH ⊥AC '于点H.∵将△ABC 沿AB 翻折得到△ABC ',∴AC =AC '=BC =BC '=4,∠BAC =∠BAC '=60°,且AE '=AE ',∴△ACE '≌△AC 'E '(SAS),∴C 'E '=CE ',由(2)可知:DE '=CE ',∴C 'E '=CE '=DE '.∵DE +EF =C 'E +EF =C 'E '+EF ,∴当点C ',点E ',点F 三点共线时,DE +EF 的值最小.∵F 是AC 的中点,∴AF =CF =2,且HF ⊥AC ',∠FAH =180°﹣∠CAB ﹣∠C 'AB =60°,∴AH =1,HF 3=3=∴C 'H =4+1=5,∴C'F22'253C H HF=+=+=27,∴DE+EF的最小值为27.【点睛】本题是三角形综合题,考查了等边三角形的判定和性质,直角三角形的性质,全等三角形的判定和性质,折叠的性质,添加恰当辅助线是解答本题的关键.9.已知等边△ABC的边长为4cm,点P,Q分别是直线AB,BC上的动点.(1)如图1,当点P从顶点A沿AB向B点运动,点Q同时从顶点B沿BC向C点运动,它们的速度都为lcm/s,到达终点时停止运动.设它们的运动时间为t秒,连接AQ,PQ.①当t=2时,求∠AQP的度数.②当t为何值时△PBQ是直角三角形?(2)如图2,当点P在BA的延长线上,Q在BC上,若PQ=PC,请判断AP,CQ和AC之间的数量关系,并说明理由.【答案】(1)①∠AQP=30°;②当t=43秒或t=83秒时,△PBQ为直角三角形;(2)AC=AP+CQ,理由见解析.【解析】【分析】(1)①由△ABC是等边三角形知AQ⊥BC,∠B=60°,从而得∠AQB=90°,△BPQ是等边三角形,据此知∠BQP=60°,继而得出答案;②由题意知AP=BQ=t,PB=4﹣t,再分∠PQB=90°和∠BPQ=90°两种情况分别求解可得.(2)过点Q作QF∥AC,交AB于F,知△BQF是等边三角形,证∠QFP=∠PAC=120°、∠BPQ=∠ACP,从而利用AAS可证△PQF≌△CPA,得AP=QF,据此知AP=BQ,根据BQ+CQ=BC=AC可得答案.【详解】解:(1)①根据题意得AP=PB=BQ=CQ=2,∵△ABC是等边三角形,∴AQ⊥BC,∠B=60°,∴∠AQB=90°,△BPQ是等边三角形,∴∠BQP=60°,∴∠AQP=∠AQB﹣∠BQP=90°﹣60°=30°;②由题意知AP=BQ=t,PB=4﹣t,当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得:4﹣t=2t,解得t=43;当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2(4﹣t),解得t=83;∴当t=43秒或t=83秒时,△PBQ为直角三角形;(2)AC=AP+CQ,理由如下:如图所示,过点Q作QF∥AC,交AB于F,则△BQF是等边三角形,∴BQ=QF,∠BQF=∠BFQ=60°,∵△ABC为等边三角形,∴BC=AC,∠BAC=∠BFQ=60°,∴∠QFP=∠PAC=120°,∵PQ=PC,∴∠QCP=∠PQC,∵∠QCP=∠B+∠BPQ,∠PQC=∠ACB+∠ACP,∠B=∠ACB,∴∠BPQ=∠ACP,在△PQF和△CPA中,∵BPQ ACPQFP PAC PQ PC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△PQF≌△CPA(AAS),∴AP=QF,∴AP=BQ,∴BQ+CQ=BC=AC,∴AP+CQ=AC.【点睛】考核知识点:等边三角形的判定和性质.利用全等三角形判定和性质分析问题是关键.10.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A.点B同时出发,沿三角形的边运动,已知点M的速度为2cm/s,点N的速度为3cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动秒后,△AMN是等边三角形?(2)点M、N在BC边上运动时,运动秒后得到以MN为底边的等腰三角形△AMN?(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.【答案】(1)125;(2)485;(3)点M、N运动3秒或127秒或10秒或9秒后,△AMN为直角三角形.【解析】【分析】(1)当AM=AN时,△MNA是等边三角形.设运动时间为t秒,构建方程即可解决问题;(2)点M、N在BC边上运动时,满足CM=BN时,可以得到以MN为底边的等腰三角形△AMN.构建方程即可解决问题;(3)据题意设点M、N运动t秒后,可得到直角三角形△AMN,分四种情况讨论即可.【详解】(1)当AM=AN时,△MNA是等边三角形,设运动时间为t秒则有:2t=12﹣3t解得t=12 5故点M、N运动125秒后,△AMN是等边三角形;(2)点M、N在BC边上运动时,满足CM=BN时,可以得到以MN为底边的等腰三角形△AMN则有:2t﹣12=36﹣3t解得t=48 5故运动485秒后得到以MN为底边的等腰三角形△AMN;(3)设点M、N运动t秒后,可得到直角三角形△AMN ①当M在AC上,N在AB上,∠ANM=90°时,如图∵∠A=60°∴∠AMN=30°∴AM=2AN则有2t=2(12﹣3t)∴t=3;②当M在AC上,N在AB上,∠AMN=90°时,如图∵∠A=60°∴∠ANM=30°∴2AM=AN∴4t=12﹣3t∴t=127;③当M、N都在BC上,∠ANM=90°时,如图CN=3t﹣24=6解得t=10;④当M、N都在BC上,∠AMN=90°时,则N与B重合,M正好处于BC的中点,如图此时2t =12+6解得t =9;综上所述,点M 、N 运动3秒或127秒或10秒或9秒后,△AMN 为直角三角形. 【点睛】本题主要考查了等边三角形的性质、等腰三角形的判定、全等三角形的判定与性质,熟练掌握相关知识点是解决本题的关键.三、八年级数学整式的乘法与因式分解解答题压轴题(难)11.阅读下列材料:利用完全平方公式,可以将多项式2(0)ax bx c a ++≠变形为2()a x m n ++的形式,我们把这种变形方法,叫做配方法.运用配方法及平方差公式能对一些多项式进行因式分解.例如:22222111111251151151124112422242222x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++=++-+=+-=+++- ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭根据以上材料,解答下列问题:(1)用配方法将281x x +-化成2()x m n ++的形式,则281=x x +- ________;(2)用配方法和平方差公式把多项式228x x --进行因式分解;(3)对于任意实数x ,y ,多项式222416x y x y +--+的值总为______(填序号).①正数②非负数 ③ 0【答案】(1)2(4)17x +-;(2)(2)(4)x x +-;(3)①【解析】【分析】(1)根据材料所给方法解答即可;(2)材料所给方法进行解答即可;(3)局部进行因式分解,最后写成非负数的积的形式即可完成解答.【详解】解:(1)281x x +-=2816116x x ++--2(4)17x +-.(2)原式=22118x x -+--=2(1)9x --=(13)(13)x x -+--=(2)(4)x x +-.(3)222416x y x y +--+=()()22214411x x y y -++-++=()()221211x y -+-+>11故答案为①.【点睛】本题考查了配方法,根据材料学会配方法并灵活运用配方法解题是解答本题的关键.12.(阅读材料)因式分解:()()221x y x y ++++.解:将“x y +”看成整体,令x y A +=,则原式()22211A A A =++=+.再将“A ”还原,原式()21x y =++.上述解题用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法.(问题解决)(1)因式分解:()()2154x y x y +-+-;(2)因式分解:()()44a b a b ++-+;(3)证明:若n 为正整数,则代数式()()()21231n n n n ++++的值一定是某个整数的平方.【答案】(1)()()144x y x y +-+-1.(2)()22a b +-;(3)见解析. 【解析】【分析】(1)把(x-y )看作一个整体,直接利用十字相乘法因式分解即可;(2)把a+b 看作一个整体,去括号后利用完全平方公式即可将原式因式分解;(3)将原式转化为()()223231n n n n ++++,进一步整理为(n 2+3n+1)2,根据n 为正整数得到n 2+3n+1也为正整数,从而说明原式是整数的平方.【详解】(1)()()[][]21541()14()(1)(144)x y x y x y x y x y x y +-+-=+-+-=+-+-; (2)()()2244()4()4(2)a b a b a b a b a b ++-+=+-++=+-; (3)原式()()223231n n n n =++++()()2223231n n n n =++++ ()2231n n =++. ∵n 为正整数,∴231n n ++为正整数.∴代数()()()21231n n n n ++++的值一定是某个整数的平方.【点睛】本题考查因式分解的应用,解题的关键是仔细读题,理解题意,掌握整体思想解决问题的方法.13.阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.根据你的观察,探究下面的问题:(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC 的最大边c的值;(3)已知a﹣b=8,ab+c2﹣16c+80=0,求a+b+c的值.【答案】(1)9;(2)△ABC的最大边c的值可能是6、7、8、9、10;(3)8.【解析】试题分析:(1)直接利用配方法得出关于x,y的值即可求出答案;(2)直接利用配方法得出关于a,b的值即可求出答案;(3)利用已知将原式变形,进而配方得出答案.试题解析:(1)∵x2﹣2xy+2y2+6y+9=0,∴(x2﹣2xy+y2)+(y2+6y+9)=0,∴(x﹣y)2+(y+3)2=0,∴x﹣y=0,y+3=0,∴x=﹣3,y=﹣3,∴xy=(﹣3)×(﹣3)=9,即xy的值是9.(2)∵a2+b2﹣10a﹣12b+61=0,∴(a2﹣10a+25)+(b2﹣12b+36)=0,∴(a﹣5)2+(b﹣6)2=0,∴a﹣5=0,b﹣6=0,∴a=5,b=6,∵6﹣5<c<6+5,c≥6,∴6≤c<11,∴△ABC的最大边c的值可能是6、7、8、9、10.(3)∵a﹣b=8,ab+c2﹣16c+80=0,∴a(a﹣8)+16+(c﹣8)2=0,∴(a﹣4)2+(c﹣8)2=0,∴a﹣4=0,c﹣8=0,∴a=4,c=8,b=a﹣8=4﹣8=﹣4,∴a+b+c=4﹣4+8=8,即a+b+c的值是8.14.材料阅读:若一个整数能表示成a 2+b 2(a 、b 是正整数)的形式,则称这个数为“完美数”.例如:因为13=32+22,所以13是“完美数”;再如:因为a 2+2ab +2b 2=(a +b)2+b 2(a 、b 是正整数),所以a 2+2ab +2b 2也是“完美数”.(1)请你写出一个大于20小于30的“完美数”,并判断53是否为“完美数”;(2)试判断(x 2+9y 2)·(4y 2+x 2)(x 、y 是正整数)是否为“完美数”,并说明理由.【答案】(1)25,53是完美数; (2)是,理由见解析.【解析】【分析】(1)根据“完美数”的定义判断即可;(2)根据多项式的乘法法则计算出结果后,根据“完美数”的定义判断即可.【详解】(1)25=4²+3²,∵53=49+4=7²+2²,∴53是“完美数”;(2)(x²+9y²)⋅(4y²+x²)是“完美数”,(x²+9y²)⋅(4y²+x²)=4x 2y²+364y +4x +9x²y²=13x²y²+364y +4x =(6y²+x²) ²+x²y²,∴(x²+9y²)⋅(4y²+x²)是“完美数”.【点睛】本题考查了因式分解的应用,正确的理解新概念“完美数”是解题的关键.15.观察:22213-=;2222432110-+-=;22222265432121-+-+-=. 探究:(1)2222222287654321-+-+-+-= .(直接写出答案)(2)222222(2)(21)(22)(23)21n n n n --+---+-= .(直接写出答案)应用:(3)如图,20个圆由小到大套在一起,从外向里相间画阴影,最外面一层画阴影,最外面的圆的半径为20cm ,向里依次为19cm 、18cm 、……1cm ,那么在这个图形中,所有阴影部分的面积和是多少?(结果保留π)【答案】(1)36;(2)83n -;(3)210π【解析】【分析】(1)根据已知条件,直接结算可得;(2)根据观察可得规律:结果就是底数和;其实是运用平方差公式得到;(3)根据题意列出式子,()()()()()22222222222019181716154321ππππππππππ-+-+-++-+-,再根据上面规律简便运算.【详解】(1)2222222287654321-+-+-+-=15+21=36;(2)222222(2)(21)(22)(23)21n n n n --+---+-=[][][][]()()2(21)2(21)(22)(23)(22)(23)2121n n n n n n n n +-•--+-+-•---++•-2(21)(22)(23)21n n n n =+-+-+-++=83n -;(3)由题意可得阴影面积是:()()()()()22222222222019181716154321ππππππππππ-+-+-++-+- =2019181716154321ππππππππππ++++++++++ =()1202012π⨯⨯+ =210π【点睛】 考核知识点:因式分解在运算中的应用.观察并找出规律,利用平方差公式分析问题是关键.四、八年级数学分式解答题压轴题(难)16.按要求完成下列题目.()1求:()11111223341n n +++⋯+⨯⨯⨯+的值. 对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成()11n n +的形式,而()11111n n n n =-++,这样就把()11n n +一项(分)裂成了两项. 试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出111112233420162017+++⋯+⨯⨯⨯⨯的值. ()2若()()()()()112112A B n n n n n n n =++++++①求:A 、B 的值:②求:()()11112323412n n n ++⋯+⨯⨯⨯⨯++的值. 【答案】()()()3412n n n n +++【解析】【分析】(1)根据题目的叙述的方法即可求解;(2)①把等号右边的式子通分相加,然后根据对应项的系数相等即可求解; ②根据()()()()()11111..1221212n n n n n n n =-+++++把所求的每个分式化成两个分式的差的形式,然后求解.【详解】解:(1)112⨯+123⨯+134⨯+…+120161017⨯ =1-12+12-13+13-14+…+12016-12017 =1-12017=20162017; (2)①∵()1A n n ++()()12B n n ++=()()()2n 12A B n A n n ++++ =()()1n 12n n ++, ∴120A B B ⎧=⎪⎨⎪+=⎩, 解得1212A B ⎧=⎪⎪⎨⎪=-⎪⎩. ∴A 和B 的值分别是12和-12; ②∵()()1n 12n n ++=12•()11n n +-12•()()1n 12n n ++ =12•(1n -1n 1+)-12(11n +-12n +)∴原式=12•112⨯-12•123⨯+12•123⨯-12•134⨯+…+12•()11n n +-12•()()112n n ++ =12•112⨯-12•()()112n n ++ =14-()()1212n n ++ =()()()3412n n n n +++.【点睛】本题考查了分式的化简求值,正确理解()()1n 12n n ++=12•()1n 1n +-12•()()112n n ++是关键.17.阅读后解决问题:在“15.3分式方程”一课的学习中,老师提出这样的一个问题:如果关于x 的分式方程3111a x x+=--的解为正数,那么a 的取值范围是什么? 经过交流后,形成下面两种不同的答案:小明说:解这个关于x 的分式方程,得到方程的解为x=a ﹣2.因为解是正数,可得a ﹣2>0,所以a >2.小强说:本题还要必须a≠3,所以a 取值范围是a >2且a≠3.(1)小明与小强谁说的对,为什么?(2)关于x 的方程11222mx x x-+=--有整数解,求整数m 的值. 【答案】(1)小强的说法对,理由见解析;(2)m=3,4,0.【解析】【分析】 (1)先根据解分式方程的步骤和解法解分式方程可得x =a ﹣2,根据分式方程有解和解是正数可得:x >0且x ≠1, 即a ﹣2>0, a ﹣2≠1,即可求解,(2) 先根据解分式方程的步骤和解法解分式方程可得(m ﹣2)x =﹣2, 当m ≠2时,解得:x =﹣22m -,根据分式方程有整数解可得: m ﹣2=±1,m ﹣2=±2,继而求m 的值. 【详解】解:(1)小强的说法对,理由如下:解这个关于x 的分式方程,得到方程的解为x =a ﹣2,因为解是正数,可得a ﹣2>0,即a >2,同时a ﹣2≠1,即a ≠3,则a 的范围是a >2且a≠3,(2)去分母得:mx ﹣1﹣1=2x ﹣4,整理得:(m ﹣2)x =﹣2,当m ≠2时,解得: x =﹣22m -,由方程有整数解,得到m ﹣2=±1,m ﹣2=±2,解得:m =3,4,0.【点睛】本题主要考查分式方程解是正数和解是整数问题,解决本题的关键是要熟练掌握解分式方程的解法.18.甲、乙两商场自行定价销售某一商品.(1)甲商场将该商品提价25%后的售价为1.25元,则该商品在甲商场的原价为 元;(2)乙商场定价有两种方案:方案①将该商品提价20%;方案②将该商品提价1元。
八年级数学全册全套试卷易错题(Word版 含答案)

八年级数学全册全套试卷易错题(Word版含答案)一、八年级数学全等三角形解答题压轴题(难)1.在平面直角坐标系中,直线AB分别交x轴,y轴于A(a,0),B(0,b),且满足a2+b2+4a﹣8b+20=0.(1)求a,b的值;(2)点P在直线AB的右侧;且∠APB=45°,①若点P在x轴上(图1),则点P的坐标为;②若△ABP为直角三角形,求P点的坐标.【答案】(1)a=﹣2,b=4;(2)①(4,0);②P点坐标为(4,2),(2,﹣2).【解析】【分析】(1)利用非负数的性质解决问题即可.(2)①根据等腰直角三角形的性质即可解决问题.②分两种情形:如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.分别利用全等三角形的性质解决问题即可.【详解】(1)∵a2+4a+4+b2﹣8b+16=0∴(a+2)2+(b﹣4)2=0∴a=﹣2,b=4.(2)①如图1中,∵∠APB=45°,∠POB=90°,∴OP=OB=4,∴P(4,0).故答案为(4,0).②∵a=﹣2,b=4∴OA=2OB=4又∵△ABP为直角三角形,∠APB=45°∴只有两种情况,∠ABP=90°或∠BAP=90°①如图2中,若∠ABP=90°,过点P作PC⊥OB,垂足为C.∴∠PCB=∠BOA=90°,又∵∠APB=45°,∴∠BAP=∠APB=45°,∴BA=BP,又∵∠ABO+∠OBP=∠OBP+∠BPC=90°,∴∠ABO=∠BPC,∴△ABO≌△BPC(AAS),∴PC=OB=4,BC=OA=2,∴OC=OB﹣BC=4﹣2=2,∴P(4,2).②如图3中,若∠BAP=90°,过点P作PD⊥OA,垂足为D.∴∠PDA=∠AOB=90°,又∵∠APB=45°,∴∠ABP=∠APB=45°,∴AP=AB,又∵∠BAD+∠DAP=90°,∠DPA+∠DAP=90°,∴∠BAD=∠DPA,∴△BAO≌△APP(AAS),∴PD=OA=2,AD=OB=4,∴OD=AD﹣0A=4﹣2=2,∴P(2,﹣2).综上述,P点坐标为(4,2),(2,﹣2).【点睛】本题属于三角形综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题.2.如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD 的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.探究:当∠ACB多少度时,CE⊥BC?请说明理由.【答案】(1)①垂直,相等.②都成立,理由见解析;(2)45°,理由见解析【解析】【分析】(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.【详解】(1):(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,∴∠BAD=∠CAE.又 BA=CA,AD=AE,∴△ABD≌△ACE (SAS)∴∠ACE=∠B=45°且 CE=BD.∵∠ACB=∠B=45°,∴∠ECB=45°+45°=90°,即 CE⊥BD.故答案为垂直,相等;②都成立,理由如下:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC,∴∠BAD=∠CAE,在△DAB与△EAC中,AD AEBAD CAEAB AC⎧⎪∠∠⎨⎪⎩===∴△DAB≌△EAC,∴CE=BD,∠B=∠ACE,∴∠ACB+∠ACE=90°,即CE⊥BD;(2)当∠ACB=45°时,CE⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,在△GAD与△CAE中,AC AGDAG EACAD AE⎧⎪∠∠⎨⎪⎩===∴△GAD≌△CAE,∴∠ACE=∠AGC=45°,∠BCE=∠ACB+∠ACE=45°+45°=90°,即CE⊥B C.3.已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.(1)如图1,求证:OA是第一象限的角平分线;(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作A E⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.【答案】(1)证明见解析(2)答案见解析(3)8【解析】【分析】(1)过点A分别作x轴,y轴的垂线,垂足分别为M、N,则AN=AM,根据非负数的性质求出a、b的值即可得结论;(2)如图2,过A作AH平分∠OAB,交BM于点H,则△AOE≌△BAH,可得AH=OE,由已知条件可知ON=AM,∠MOE=∠MAH,可得△ONE≌△AMH,∠ABH=∠OAE,设BM 与NE交于K,则∠MKN=180°﹣2∠ONE=90°﹣∠NEA,即2∠ONE﹣∠NEA=90°;(3)如图3,过H作HM⊥OF,HN⊥EF于M、N,可证△FMH≌△FNH,则FM=FN,同理:NE=EK,先得出OE+OF﹣EF=2HK,再由△APF≌△AQE得PF=EQ,即可得OE+OF=2OP=8,等量代换即可得2HK+EF的值.【详解】解:(1)∵|a﹣b|+b2﹣8b+16=0∴|a﹣b|+(b﹣4)2=0∵|a﹣b|≥0,(b﹣4)2≥0∴|a﹣b|=0,(b﹣4)2=0∴a=b=4过点A分别作x轴,y轴的垂线,垂足分别为M、N,则AN=AM∴OA平分∠MON即OA是第一象限的角平分线(2)过A作AH平分∠OAB,交BM于点H∴∠OAH=∠HAB=45°∵BM⊥AE∴∠ABH=∠OAE在△AOE 与△BAH 中OAE ABH OA ABAOE BAH ==∠∠⎧⎪=⎨⎪∠∠⎩, ∴△AOE ≌△BAH (ASA )∴AH =OE在△ONE 和△AMH 中OE AH NOE MAH ON AM =⎧⎪∠∠⎨⎪=⎩=, ∴△ONE ≌△AMH (SAS )∴∠AMH =∠ONE设BM 与NE 交于K∴∠MKN =180°﹣2∠ONE =90°﹣∠NEA∴2∠ONE ﹣∠NEA =90°(3)过H 作HM ⊥OF ,HN ⊥EF 于M 、N可证:△FMH ≌△FNH (SAS )∴FM =FN同理:NE =EK∴OE+OF ﹣EF =2HK过A 作AP ⊥y 轴于P ,AQ ⊥x 轴于Q可证:△APF ≌△AQE (SAS )∴PF =EQ∴OE+OF =2OP =8∴2HK+EF =OE+OF =8【点睛】本题考查非负数的性质,平面直角坐标系中点的坐标,等腰直角三角形,全等三角形的判定和性质.4.如图,在ABC ∆中,903, 7C AC BC ∠=︒==,,点D 是BC 边上的动点,连接AD ,以AD 为斜边在AD 的下方作等腰直角三角形ADE .(1)填空:ABC ∆的面积等于 ;(2)连接CE ,求证:CE 是ACB ∠的平分线;(3)点O 在BC 边上,且1CO =, 当D 从点O 出发运动至点B 停止时,求点E 相应的运动路程.【答案】(1)212;(2)证明见解析;(3)32【解析】【分析】 (1)根据直角三角形的面积计算公式直接计算可得;(2)如图所示作出辅助线,证明△AEM ≌△DEN (AAS ),得到ME=NE ,即可利用角平分线的判定证明;(3)由(2)可知点E 在∠ACB 的平分线上,当点D 向点B 运动时,点E 的路径为一条直线,再根据全等三角形的性质得出CN=1()2AC CD +,根据CD 的长度计算出CE 的长度即可.【详解】解:(1)903, 7C AC BC ∠=︒==, ∴112137222ABC S AC BC =⨯=⨯⨯=, 故答案为:212 (2)连接CE ,过点E 作EM ⊥AC 于点M ,作EN ⊥BC 于点N ,∴∠EMA=∠END=90°,又∵∠ACB=90°,∴∠MEN=90°,∴∠MED+∠DEN=90°,∵△ADE 是等腰直角三角形∴∠AED=90°,AE=DE∴∠AEM+∠MED=90°,∴∠AEM=∠DEN∴在△AEM 与△DEN 中,∠EMA=∠END=90°,∠AEM=∠DEN ,AE=DE∴△AEM≌△DEN(AAS)∴ME=NE∴点E在∠ACB的平分线上,即CE是ACB∠的平分线(3)由(2)可知,点E在∠ACB的平分线上,∴当点D向点B运动时,点E的路径为一条直线,∵△AEM≌△DEN∴AM=DN,即AC-CM=CN-CD在Rt△CME与Rt△CNE中,CE=CE,ME=NE,∴Rt△CME≌Rt△CNE(HL)∴CM=CN∴CN=1() 2AC CD+,又∵∠MCE=∠NCE=45°,∠CME=90°,∴CE=22()2CN AC CD=+,当AC=3,CD=CO=1时,CE=2(31)22+=当AC=3,CD=CB=7时,CE=2(37)52+=∴点E的运动路程为:522232-=,【点睛】本题考查了全等三角形的综合证明题,涉及角平分线的判定,几何中动点问题,全等三角形的性质与判定,解题的关键是综合运用上述知识点.5.操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;(2)在(1)的条件下,求∠BEC的度数;拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.【答案】(1)见解析;(2)70°;(3)2【解析】【分析】(1)根据SAS证明△BAD≌△CAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证△BAD≌△CAE,推出EC=BD=4,由∠BEC=∠BAC=120°,推出∠FCE=30°即可解决问题.【详解】(1)证明:如图1中,∵∠ABC=∠ACB=∠ADE=∠AED,∴∠EAD=∠CAB,∴∠EAC=∠DAB,∵AE=AD,AC=AB,∴△BAD≌△CAE(SAS).(2)解:如图1中,设AC交BE于O.∵∠ABC=∠ACB=55°,∴∠BAC=180°﹣110°=70°,∵△BAD≌△CAE,∴∠ABO=∠ECO,∵∠EOC=∠AOB,∴∠CEO=∠BAO=70°,即∠BEC=70°.(3)解:如图2中,∵∠CAB=∠EAD=120°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴∠BAD=∠ACE,BD=EC=4,同理可证∠BEC=∠BAC=120°,∴∠FEC=60°,∵CF⊥EF,∴∠F=90°,∴∠FCE=30°,∴EF=12EC=2.【点睛】本题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.二、八年级数学轴对称解答题压轴题(难)6.如图,在平面直角坐标系中,已知点A(2,3),点B(﹣2,1).(1)请运用所学数学知识构造图形求出AB的长;(2)若Rt△ABC中,点C在坐标轴上,请在备用图1中画出图形,找出所有的点C后不用计算写出你能写出的点C的坐标;(3)在x轴上是否存在点P,使PA=PB且PA+PB最小?若存在,就求出点P的坐标;若不存在,请简要说明理由(在备用图2中画出示意图).【答案】(1)AB=52)C2(0,7),C4(0,-4),C5(-1,0)、C6(1,0);(3)不存在这样的点P.【解析】【分析】(1)如图,连结AB,作B关于y轴的对称点D,利用勾股定理即可得出AB;(2)分别以A,B,C为直角顶点作图,然后直接得出符合条件的点的坐标即可;(3)作AB的垂直平分线l3,则l3上的点满足PA=PB,作B关于x轴的对称点B′,连结AB′,即x轴上使得PA+PB最小的点,观察作图即可得出答案.【详解】解:(1)如图,连结AB,作B关于y轴的对称点D,由已知可得,BD=4,AD=2.∴在Rt△ABD中,AB=5(2)如图,①以A为直角顶点,过A作l1⊥AB交x轴于C1,交y轴于C2.②以B为直角顶点,过B作l2⊥AB交x轴于C3,交y轴于C4.③以C为直角顶点,以AB为直径作圆交坐标轴于C5、C6、C7.(用三角板画找出也可)由图可知,C2(0,7),C4(0,-4),C5(-1,0)、C6(1,0).(3)不存在这样的点P.作AB的垂直平分线l3,则l3上的点满足PA=PB,作B关于x轴的对称点B′,连结AB′,由图可以看出两线交于第一象限.∴不存在这样的点P.【点睛】本题考查了勾股定理,构造直角三角形,中垂线和轴对称--路径最短问题的综合作图分析,解题的关键是学会分类讨论,学会画好图形解决问题.7.如图,在ABC △中,已知AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于点F ,求证:AF EF =.【答案】证明见解析【解析】【分析】延长AD 到点G ,使得AD DG =,连接BG ,结合D 是BC 的中点,易证△ADC 和△GDB 全等,利用全等三角形性质以及等量代换,得到△AEF 中的两个角相等,再根据等角对等边证得AE=EF.【详解】如图,延长AD 到点G ,延长AD 到点G ,使得AD DG =,连接BG .∵AD 是BC 边上的中线,∴DC DB =. 在ADC 和GDB △中,AD DG ADC GDB DC DB =⎧⎪∠=∠⎨⎪=⎩(对顶角相等), ∴ADC ≌GDB △(SAS ).∴CAD G ∠=∠,BG AC =.又BE AC =,∴BE BG =.∴BED G ∠=∠.∵BED AEF ∠=∠∴AEF CAD ∠=∠,即AEF FAE ∠=∠∴AF EF =.【点睛】本题考查的是全等三角形的判定与性质,根据题意构造全等三角形是解答本题的关键.8.已知等边△ABC 的边长为4cm ,点P ,Q 分别是直线AB ,BC 上的动点.(1)如图1,当点P 从顶点A 沿AB 向B 点运动,点Q 同时从顶点B 沿BC 向C 点运动,它们的速度都为lcm /s ,到达终点时停止运动.设它们的运动时间为t 秒,连接AQ ,PQ . ①当t =2时,求∠AQP 的度数.②当t 为何值时△PBQ 是直角三角形?(2)如图2,当点P在BA的延长线上,Q在BC上,若PQ=PC,请判断AP,CQ和AC之间的数量关系,并说明理由.【答案】(1)①∠AQP=30°;②当t=43秒或t=83秒时,△PBQ为直角三角形;(2)AC=AP+CQ,理由见解析.【解析】【分析】(1)①由△ABC是等边三角形知AQ⊥BC,∠B=60°,从而得∠AQB=90°,△BPQ是等边三角形,据此知∠BQP=60°,继而得出答案;②由题意知AP=BQ=t,PB=4﹣t,再分∠PQB=90°和∠BPQ=90°两种情况分别求解可得.(2)过点Q作QF∥AC,交AB于F,知△BQF是等边三角形,证∠QFP=∠PAC=120°、∠BPQ=∠ACP,从而利用AAS可证△PQF≌△CPA,得AP=QF,据此知AP=BQ,根据BQ+CQ=BC=AC可得答案.【详解】解:(1)①根据题意得AP=PB=BQ=CQ=2,∵△ABC是等边三角形,∴AQ⊥BC,∠B=60°,∴∠AQB=90°,△BPQ是等边三角形,∴∠BQP=60°,∴∠AQP=∠AQB﹣∠BQP=90°﹣60°=30°;②由题意知AP=BQ=t,PB=4﹣t,当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得:4﹣t=2t,解得t=43;当∠BPQ=90°时,∵∠B=60°,∴BQ=2BP,得t=2(4﹣t),解得t=83;∴当t=43秒或t=83秒时,△PBQ为直角三角形;(2)AC=AP+CQ,理由如下:如图所示,过点Q作QF∥AC,交AB于F,则△BQF是等边三角形,∴BQ=QF,∠BQF=∠BFQ=60°,∵△ABC为等边三角形,∴BC=AC,∠BAC=∠BFQ=60°,∴∠QFP=∠PAC=120°,∵PQ=PC,∴∠QCP=∠PQC,∵∠QCP=∠B+∠BPQ,∠PQC=∠ACB+∠ACP,∠B=∠ACB,∴∠BPQ=∠ACP,在△PQF和△CPA中,∵BPQ ACPQFP PAC PQ PC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△PQF≌△CPA(AAS),∴AP=QF,∴AP=BQ,∴BQ+CQ=BC=AC,∴AP+CQ=AC.【点睛】考核知识点:等边三角形的判定和性质.利用全等三角形判定和性质分析问题是关键.9.如图,在等边三角形ABC右侧作射线CP,∠ACP=α(0°<α<60°),点A关于射线CP 的对称点为点D,BD交CP于点E,连接AD,AE.(1)求∠DBC的大小(用含α的代数式表示);(2)在α(0°<α<60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;(3)用等式表示线段AE,BD,CE之间的数量关系,并证明.【答案】(1)∠DBC60α=︒-;(2)∠AEB的大小不会发生变化,且∠AEB=60°;(3)BD=2AE+CE,证明见解析.【解析】【分析】(1)如图1,连接CD,由轴对称的性质可得AC=DC,∠DCP=∠ACP=α,由△ABC是等边三角形可得AC=BC,∠ACB=60°,进一步即得∠BCD=602α︒+,BC=DC,然后利用三角形的内角和定理即可求出结果;(2)设AC、BD相交于点H,如图2,由轴对称的性质可证明△ACE≌△DCE,可得∠CAE=∠CDE,进而得∠DBC=∠CAE,然后根据三角形的内角和可得∠AEB=∠BCA,即可作出判断;(3)如图3,在BD上取一点M,使得CM=CE,先利用三角形的外角性质得出∠BEC60=︒,进而得△CME是等边三角形,可得∠MCE=60°,ME=CE,然后利用角的和差关系可得∠BCM=∠DCE,再根据SAS证明△BCM≌△DCE,于是BM=DE,进一步即可得出线段AE,BD,CE之间的数量关系.【详解】解:(1)如图1,连接CD,∵点A关于射线CP的对称点为点D,∴AC=DC,∠DCP=∠ACP=α,∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,∴∠BCD=602α︒+,BC=DC,∴∠DBC=∠BDC()1806021806022BCDαα︒-︒+︒-∠===︒-;(2)∠AEB的大小不会发生变化,且∠AEB=60°.理由:设AC、BD相交于点H,如图2,∵点A关于射线CP的对称点为点D,∴AC=DC,AE=DE,又∵CE=CE,∴△ACE≌△DCE(SSS),∴∠CAE=∠CDE,∵∠DBC=∠BDC,∴∠DBC=∠CAE,又∵∠BHC=∠AHE,∴∠AEB=∠BCA=60°,即∠AEB的大小不会发生变化,且∠AEB=60°;(3)AE ,BD ,CE 之间的数量关系是:BD =2AE +CE .证明:如图3,在BD 上取一点M ,使得CM=CE ,∵∠BEC =∠BDC +∠DCE =6060αα︒-+=︒,∴△CME 是等边三角形,∴∠MCE =60°,ME=CE ,∴60260BCM BCD MCE DCE ααα∠=∠-∠-∠=︒+-︒-=,∴∠BCM =∠DCE ,又∵BC=DC ,CM=CE ,∴△BCM ≌△DCE (SAS ),∴BM=DE ,∵AE=DE ,∴BD=BM+ME+DE =2DE+ME =2AE+CE .【点睛】本题考查了等边三角形的判定和性质、全等三角形的判定和性质、三角形的内角和定理和轴对称的性质等知识,熟练掌握并运用上述知识解题的关键.10.(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.【答案】(1)见解析;(2)见解析;(3)∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【解析】【分析】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,根据垂直平分线的性质及外角的性质求出各角度数即可;(2)分别作AB、BC的垂直平分线,交于点O,连接OA、OB、OC可得三角形OAB、OAC、OBC为等腰三角形,根据等腰三角形的性质及外角性质求出各角度数即可;(3)分PB=PA、AB=AP、BA=BP时,PB=PQ、BP=BQ、QB=QP,PQ=QC、PC=QC、PQ=PC等10种情况,根据等腰三角形的性质分别求出∠C的度数即可.【详解】(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,如图1,∵∠ABC=23°,∠BAC=90°,∴∠C=90°-23°=67°,∵MN垂直平分AB,∴BD=AD,∴△ABD是等腰三角形,∴∠BAD=∠ABC=23°,∴∠ADC=2∠ABC=46°,∵∠BAC=90°,∴∠DAC=∠BAC-∠BAD=67°,∴∠DAC=∠C,∴△DAC是等腰三角形,同理:图2中,∠ADC=46°,∠DAC=88°,∠C=46°,△ABD和△ACD是等腰三角形,图3中,∠BCD=23°,∠ADC=46°,∠ACD=46°,△BCD和△ACD是等腰三角形.(2)作AB、BC的垂直平分线,交于点O,连接OA、OB、OC,∵点O是三角形垂直平分线的交点,∴OA=OB=OC,∴△OAB、△OAC、△OBC是等腰三角形,∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB=67.5°,∴AD是BC的垂直平分线,∴∠BAD=∠CAD=22.5°,∴∠OBA=∠OAB=22.5°,∠OCA=∠OAC=22.5°,∴∠OBC=∠OCB=45°.(3)①如图,当PB=PA,PB=PQ,PQ=CQ时,∵∠A=30°,PB=PQ,∴∠ABP=∠A=30°,∴∠APB=120°,∵PB=PQ,PQ=CQ,∴∠PQB=∠PBQ,∠C=∠CPQ,∴∠PBQ=2∠C,∴∠APB=∠PBQ+∠C=3∠C=120°,解得:∠C=40°.②如图,当PB=PA,PB=BQ,PQ=CQ时,∴∠PQB=2∠C,∠PQB=∠BPQ,∴∠PBQ=180°-2∠PQB=180°-4∠C,∴180°-4∠C+∠C=120°,解得:∠C=20°,③如图,当PA=PB,BQ=PQ,CQ=CP时,∵∠PQC=2∠PBQ,∠PQC=12(180°-∠C),∴∠PBQ=14(180°-∠C),∴14(180°-∠C)+∠C=120°,解得:∠C=100°.④如图,当PA=PB,BQ=PQ,PQ=CP时,∵∠PQC=∠C=2∠PBQ,又∵∠C+∠PBQ=120°,∴∠C=80°;⑤如图,当AB=AP,BP=BQ,PQ=QC时,∵∠A=30°,∴∠APB=12(180°-30°)=75°,∵BP=BQ,PQ=CQ,∴∠BPQ=∠BQP,∠QPC=∠QCP,∴∠BQP=2∠C,∴∠PBQ=180°-4∠C,∴∠C+180°-4∠C=75°,解得:∠C=35°.⑥如图,当AB=AP,BQ=PQ,PC=QC时,∴∠PQC=2∠PBC,∠PQC=12(180°-∠C),∴∠PBC=14(180°-∠C),∴14(180°-∠C)+∠C=75°,解得:∠C=40°.⑦如图,当AB=AP,BQ=PQ,PC=QP时,∵∠C=∠PQC=2∠PBC,∠C+∠PQC=75°,∴∠C=50°;⑧当AB=AP,BP=PQ,PQ=CQ时,∵AB=BP,∠A=30°,∴∠ABP=∠APB=75°,又∵∠PBQ=∠PQB=2∠C,且有∠PBQ+∠C=180°-30°-75°=75°,∴3∠C=75°,∴∠C=25°;⑨当AB=BP,BP=PQ,PQ=CQ时,∵AB=BP,∴∠BPA=∠A=30°,∵∠PBQ=∠PQB=2∠C,∴2∠C+∠C=30°,解得:∠C=10°.⑩当AB=BP,BQ=PQ,PQ=CQ时,∴∠PQC=∠C=2∠PBQ,∴12∠C+∠C=30°,解得:∠C=20°.综上所述:∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.【点睛】本题考查复杂作图及等腰三角形的性质,熟练掌握等腰三角形的性质是解题关键.三、八年级数学整式的乘法与因式分解解答题压轴题(难)11.先阅读下列材料,然后解后面的问题.材料:一个三位自然数abc(百位数字为a,十位数字为b,个位数字为c),若满足a+c=b,则称这个三位数为“欢喜数”,并规定F(abc)=ac.如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F(374)=3×4=12.(1)对于“欢喜数abc”,若满足b能被9整除,求证:“欢喜数abc”能被99整除;(2)已知有两个十位数字相同的“欢喜数”m ,n (m >n ),若F (m )﹣F (n )=3,求m ﹣n 的值.【答案】(1)详见解析;(2)99或297.【解析】【分析】(1)首先由题意可得a +c =b ,将欢喜数展开,因为要证明“欢喜数abc ”能被99整除,所以将展开式中100a 拆成99a +a ,这样展开式中出现了a +c ,将a +c 用b 替代,整理出最终结果即可;(2)首先设出两个欢喜数m 、n ,表示出F (m )、F (n )代入F (m )﹣F (n )=3中,将式子变形分析得出最终结果即可.【详解】(1)证明:∵abc 为欢喜数,∴a +c =b . ∵abc =100a +10b +c =99a +10b +a +c =99a +11b ,b 能被9整除,∴11b 能被99整除,99a 能被99整除,∴“欢喜数abc ”能被99整除;(2)设m =11a bc ,n =22a bc (且a 1>a 2),∵F (m )﹣F (n )=a 1•c 1﹣a 2•c 2=a 1•(b ﹣a 1)﹣a 2(b ﹣a 2)=(a 1﹣a 2)(b ﹣a 1﹣a 2)=3,a 1、a 2、b 均为整数,∴a 1﹣a 2=1或a 1﹣a 2=3.∵m ﹣n =100(a 1﹣a 2)﹣(a 1﹣a 2)=99(a 1﹣a 2),∴m ﹣n =99或m ﹣n =297.∴若F (m )﹣F (n )=3,则m ﹣n 的值为99或297.【点睛】做此类阅读理解类题目首先要充分理解题目,会运用因式分解将式子变形.12.(1)填空:()()a b a b -+= ;22()()a b a ab b -++= ;3223()()a b a a b ab b -+++= .(2)猜想:1221()(...)n n n n a b a a b ab b -----++++= (其中n 为正整数,且2n ≥).(3)利用(2)猜想的结论计算:98732222...222-+-+-+.【答案】(1)22a b -,33a b -,44a b -;(2)n n a b -;(3)342.【解析】试题分析:(1)根据平方差公式与多项式乘以多项式的运算法则运算即可;(2)根据(1)的规律可得结果;(3)原式变形后,利用(2)得出的规律计算即可得到结果.试题解析:(1)()()a b a b -+=22a b -;3223()()a b a a b ab b -+++=33a b -;3223()()a b a a b ab b -+++=44a b -;故答案为22a b -,33a b -,44a b -;(2)由(1)的规律可得:原式=n n a b -,故答案为n n a b -;(3)令98732222...222S =-+-+-+,∴987321222...2221S -=-+-+-+-=98732[2(1)](222...2221)3---+-+-+-÷=10(21)3(10241)3341-÷=-÷=,∴S=342.考点:1.平方差公式;2.规律型.13.阅读下列因式分解的过程,解答下列问题:1+x +x (x +1)+x (x +1)2=(1+x )[1+x +x (x +1)]=(1+x )2(1+x )=(1+x )3.(1)上述分解因式的方法是____________,共应用了________次;(2)若分解因式1+x +x (x +1)+x (x +1)2+…+x (x +1)2019,则需要应用上述方法________次,结果是________;(3)分解因式:1+x +x (x +1)+x (x +1)2+…+x (x +1)n (n 为正整数).【答案】(1)提取公因式法,2;(2)2019,(1+x)2020;(3) (1+x)n +1.【解析】【分析】(1)根据已知计算过程直接得出因式分解的方法即可;(2)根据已知分解因式的方法可以得出答案;(3)由(1)中计算发现规律进而得出答案.【详解】(1)提取公因式法,2(因式分解的方法是提公因式法,共应用了2次)(2)2019,(1+x)2020(分解因式1+x+x(x+1)+x(x+1)2+…+x(x+1)2019,则需应用上述方法2019次,结果是(1+x)2020)(3)原式=(1+x)[1+x +x(x +1)+x(x +1)2+…+x(x +1)n -1]=(1+x)2[1+x +x(x +1)+x(x +1)2+…+x(x +1)n -2]=(1+x)3[1+x +x(x +1)+x(x +1)2+…+x(x +1)n -3]=(1+x)n (1+x)=(1+x)n +1.【点睛】本题考查的知识点是因式分解-提公因式法,解题的关键是熟练的掌握因式分解-提公因式法.14.(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式:.(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2=.(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=.(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:.【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)30;(3)9;(4)x3﹣x=(x+1)(x﹣1)x【解析】【分析】(1)依据正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,可得等式;(2)依据a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,进行计算即可;(3)依据所拼图形的面积为:xa2+yb2+zab,而(2a+b)(a+2b)=2a2+4ab+ab+2b2=2a2+5b2+2ab,即可得到x,y,z的值.(4)根据原几何体的体积=新几何体的体积,列式可得结论.【详解】(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,∵a+b+c=10,ab+ac+bc=35,∴102=a2+b2+c2+2×35,∴a2+b2+c2=100﹣70=30,故答案为:30;(3)由题意得:(2a+b)(a+2b)=xa2+yb2+zab,∴2a2+5ab+2b2=xa2+yb2+zab,∴225xyz=⎧⎪=⎨⎪=⎩,∴x+y+z=9,故答案为:9;(4)∵原几何体的体积=x3﹣1×1•x=x3﹣x,新几何体的体积=(x+1)(x﹣1)x,∴x3﹣x=(x+1)(x﹣1)x.故答案为:x3﹣x=(x+1)(x﹣1)x.【点睛】本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的体积或面积,然后根据它们的体积或面积相等列出等式是解题的关键.15.阅读材料:小明发现一些含根号的式子可以写成另一个式子的平方,如=()2,善于思考的小明进行了以下探索:设=()2(其中a、b、m、n均为正整数)则有:=m2+2n2,所以a=m2+2n2,b=2mn.这样小明就找到了一种把的式子化为平方式的方法.请仿照小明的方法探索并解决下列问题:(1)当a、b、m、n均为正整数时,若()2,用含m、n的式子分别表示a、b,得a=,b=(2)若(2(其中a、b、m、n均为正整数),求a的值.【答案】(1)m2+3n2,2mn;(2)13.【解析】试题分析:(1)根据完全平方公式运算法则,即可得出a、b的表达式;(2)根据题意,4=2mn,首先确定m、n的值,通过分析m=2,n=1或者m=1,n=2,然后即可确定好a的值.试题解析:(1)∵)2,∴2+3n2∴a=m2+3n2,b=2mn.故a=m2+3n2,b=2mn;(2)由题意,得223 {42a m nmn=+=∵4=2mn,且m、n为正整数,∴m=2,n=1或m=1,n=2,∴a=22+3×12=7或a=12+3×22=13四、八年级数学分式解答题压轴题(难)16.小明和小强两名运动爱好者周末相约到滨江大道进行跑步锻炼.(1)周六早上6点,小明和小强同时从家出发,分别骑自行车和步行到离家距离分别为4500米和1200米的滨江大道入口汇合,结果同时到达.若小明每分钟比小强多行220米,求小明和小强的速度分别是多少米/分?(2)两人到达滨江大道后约定先跑1000米再休息.小强的跑步速度是小明跑步速度的m 倍,两人在同起点,同时出发,结果小强先到目的地n 分钟.①当3m =,6n =时,求小强跑了多少分钟?②小明的跑步速度为_______米/分(直接用含m n ,的式子表示).【答案】(1)小强的速度为80米/分,小明的速度为300米/分;(2)①小强跑的时间为3分;②1000(1)m mn-. 【解析】【分析】 (1)设小强的速度为x 米/分,则小明的速度为(x+220)米/分,根据路程除以速度等于时间得到方程,解方程即可得到答案;(2)①设小明的速度为y 米/分,由m =3,n =6,根据小明的时间-小强的时间=6列方程解答;②根据路程一定,时间与速度成反比,可求小强的时间进而求出小明的时间,再根据速度=路程除以时间得到答案.【详解】(1)设小强的速度为x 米/分,则小明的速度为(x+220)米/分, 根据题意得:1200x =4500220x +. 解得:x =80.经检验,x =80是原方程的根,且符合题意.∴x+220=300.答:小强的速度为80米/分,小明的速度为300米/分.(2)①设小明的速度为y 米/分,∵m =3,n =6, ∴1000100063y y -=,解之得10009y =. 经检验,10009y =是原方程的解,且符合题意,∴小强跑的时间为:10001000(3)39÷⨯=(分) ②小强跑的时间:1n m -分钟,小明跑的时间:11n mn n m m +=--分钟, 小明的跑步速度为: 1000(1)10001mn m m mn -÷=-分. 故答案为:1000(1)m mn-. 【点睛】 此题考查分式方程的应用,正确理解题意根据路程、时间、速度三者的关系列方程解答是解题的关键.17.(1)请你写出五个正的真分数,____,____,____,____,____,给每个分数的分子和分母加上同一个正数得到五个新分数:____,____,____,_____,____.(2)比较原来每个分数与对应新分数的大小,可以得出下面的结论:一个真分数是a b (a 、b 均为正数),给其分子分母同加一个正数m ,得a m b m++,则两个分数的大小关系是a mb m ++_____a b . (3)请你用文字叙述(2)中结论的含义:(4)你能用图形的面积说明这个结论吗?(5)解决问题:如图1,有一个长宽不等的长方形绿地,现给绿地四周铺一条宽相等的路,问原来的长方形与现在铺过小路后的长方形是否相似?为什么?(6)这个结论可以解释生活中的许多现象,解决许多生活与数学中的问题.请你再提出一个类似的数学问题,或举出一个生活中与此结论相关例子.【答案】(1) 12;14;16;18;19;23;25;27;29;15;(2)>;(3)给一个正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数;(4)答案见解析;(5)不相似,理由见解析;(6)答案见解析.【解析】【分析】(1)小于1的数叫做真分数;(2)根据实例易得规律;(3)抓住新分数大于原分数即可;(4)根据图形进行分析解答;(5)利用相关规律解决问题即可;(6)结合生活中的现象进行解答. 【详解】 解:(1)12、14、16、18、19,23、25、27、29、15;(2)a m a b m b+>+; (3)给一个正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数; (4)思路1:如图2所示,由a b <,得12s s s s +>+,即ab bm ab am +>+,()().a b m b a m +=+,可推出a m a b m b+>+; 思路2:构造两个面积为1的长方形(如图3),将它们分成两部分,比较右侧的两个长方形面积可以发现:1a b a b b --=,1a m b a b m b m+--=++,因为a 、b 、0m >,且a b <,故1a b - 1a m b m +>-+,即a m a b m b+>+ (5)不相似.因为两个长方形长与宽的比值不相等;(6)数学问题举例:①若a b是假分数,会有怎样的结论? ②a 、b 不是正数,或不全是正数,情况如何?【点睛】本题实际考查了分式的基本性质,熟练掌握分式的基本性质是解题的关键.18.某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.(1)求每件甲种、乙种玩具的进价分别是多少元?(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?【答案】(1)甲,乙两种玩具分别是15元/件,25元/件;(2)共有四种方案.【解析】【分析】(1)设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解.(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,根据甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,可列出不等式组求解.【详解】解:设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,x=15,经检验x=15是原方程的解.∴40﹣x=25.甲,乙两种玩具分别是15元/件,25元/件;(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,,解得20≤y<24.因为y是整数,甲种玩具的件数少于乙种玩具的件数,∴y取20,21,22,23,共有4种方案.考点:分式方程的应用;一元一次不等式组的应用.19.杨梅是漳州的特色时令水果.杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价每件比第一批多了5元.(1)第一批杨梅每件进价多少元?(2)老板以每件150元的价格销售第二批杨梅,售出80%后,为了尽快售完,决定打折促销.要使得第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折(利润-售价-进价)?【答案】(1)120元(2)至少打7折.【解析】【分析】(1)设第一批杨梅每件进价是x元,则第二批每件进价是(x+5)元,再根据等量关系:。
八年级数学三角形填空选择易错题(Word版 含答案)

八年级数学三角形填空选择易错题(Word版含答案)一、八年级数学三角形填空题(难)1.若△ABC三条边长为a,b,c,化简:|a-b-c|-|a+c-b|=__________.【答案】2b-2a【解析】【分析】【详解】根据三角形的三边关系得:a﹣b﹣c<0,c+a﹣b>0,∴原式=﹣(a﹣b﹣c)﹣(a+c﹣b)=﹣a+b+c﹣a﹣c+b=2b﹣2a.故答案为2b﹣2a【点睛】本题考查了绝对值得化简和三角形三条边的关系:三角形任意两边之和大于第三边,任意两边之差小于第三边;一个正数的绝对值等于它的本身,零的绝对值还是零,一个负数的绝对值等于它的相反数,据此解答即可.2.某多边形内角和与外角和共1080°,则这个多边形的边数是__________.【答案】6【解析】∵多边形内角和与外角和共1080°,∴多边形内角和=1080°−360°=720°,设多边形的边数是n,∴(n−2)×180°=720°,解得n=6.故答案为6.点睛:先根据多边形的外角和为360°求出其内角和,再根据多边形内角和定理即可求出多边形的边数.3.直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_______.【答案】30°【解析】【分析】设较小的锐角是x,然后根据直角三角形两锐角互余列出方程求解即可.【详解】设较小的锐角是x,则另一个锐角是2x,由题意得,x+2x=90°,解得x=30°,即此三角形中最小的角是30°.故答案为:30°.【点睛】本题考查了直角三角形的性质,熟练掌握该知识点是本题解题的关键.4.一个多边形的内角和与外角和的差是180°,则这个多边形的边数为_____.【答案】5【解析】【分析】根据多边形的内角和公式(n﹣2)•180°与外角和定理列式求解即可【详解】解:设这个多边形的边数是n,则(n﹣2)•180°﹣360°=180°,解得n=5.故答案为5.【点睛】本题考查了多边形的内角和与外角和定理,任意多边形的外角和都是360°,与边数无关.5.等腰三角形一边长是10cm,一边长是6cm,则它的周长是_____cm或_____cm.【答案】22cm,26cm【解析】【分析】题目给出等腰三角形有两条边长为10cm和6cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【详解】(1)当腰是6cm时,周长=6+6+10=22cm;(2)当腰长为10cm时,周长=10+10+6=26cm,所以其周长是22cm或26cm.故答案为:22,26.【点睛】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.6.如图,李明从A点出发沿直线前进5米到达B点后向左旋转的角度为α,再沿直线前进5米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了45米,则每次旋转的角度α为_____.【答案】40︒.【解析】【分析】根据共走了45米,每次前进5米且左转的角度相同,则可计算出该正多边形的边数,再根据外角和计算左转的角度.【详解】连续左转后形成的正多边形边数为:4559÷=,则左转的角度是360940︒÷=︒.故答案是:40︒.【点睛】本题考查了多边形的外角计算,正确理解多边形的外角和是360°是关键.7.如果一个n 边形的内角和是1440°,那么n=__.【答案】10【解析】∵n 边形的内角和是1440°,∴(n−2)×180°=1440°,解得:n=10.故答案为:10.8.如图,在ABC ∆中,AD 是BC 边上的高,AE 平分BAC ∠,若130∠=,220∠=,则B ∠=__________.【答案】50°【解析】【分析】由角平分线的定义和已知可求出∠BAC ,由AD 是BC 边上的高和已知条件可以求出∠C,然后运用三角形内角和定理,即可完成解答.【详解】解:∵AE 平分BAC ∠,若130∠=∴BAC ∠=2160∠=;又∵AD 是BC 边上的高,220∠=∴C ∠=90°-270∠= 又∵BAC ∠+∠B+∠C=180°∴∠B=180°-60°-70°=50°故答案为50°.【点睛】本题考查了角平分线、高的定义以及三角形内角和的知识,考查知识点较多,灵活运用所学知识是解答本题的关键.9.如图,小亮从A 点出发前进5m ,向右转15°,再前进5m ,又向右转15°…,这样一直走下去,他第一次回到出发点A 时,一共走了______m .【答案】120.【解析】【分析】由题意可知小亮所走的路线为正多边形,根据多边形的外角和定理即可求出答案.【详解】解:∵小亮从A 点出发最后回到出发点A 时正好走了一个正多边形,∴该正多边形的边数为n=360°÷15°=24,则一共走了24×5=120米,故答案为:120.【点睛】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°,用外角和求正多边形的边数可直接用360°除以一个外角度数.10.如图,BP 是△ABC 中∠ABC 的平分线,CP 是∠ACB 的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=______°.【答案】30【解析】【分析】根据角平分线的定义可得∠PBC=20°,∠PCM=50°,根据三角形外角性质即可求出∠P 的度【详解】∵BP是∠ABC的平分线,CP是∠ACM的平分线,∠ABP=20°,∠ACP=50°,∴∠PBC=20°,∠PCM=50°,∵∠PBC+∠P=∠PCM,∴∠P=∠PCM-∠PBC=50°-20°=30°,故答案为:30【点睛】本题考查及角平分线的定义及三角形外角性质,三角形的外角等于和它不相邻的两个内角的和,熟练掌握三角形外角性质是解题关键.二、八年级数学三角形选择题(难)11.若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()A.n·180°B.(n+2)·180°C.(2n-1)·180°D.(2n+1)·180°【答案】D【解析】【分析】当△ABC内的点的个数是1时,三角形内互不重叠的小三角形的个数是3;当△ABC内的点的个数是2时,三角形内互不重叠的小三角形的个数是5;依此类推得到当△ABC内的点的个数是3时,三角形内互不重叠的小三角形的个数是7;当△ABC内的点的个数是n 时,三角形内互不重叠的小三角形的个数2n+1,所以这些小三角形的内角和为(2n+1)·180°【详解】】解:图1中,当△ABC内只有1个点时,可分割成3个互不重叠的小三角形;图2中,当△ABC内只有2个点时,可分割成5个互不重叠的小三角形;图3中,当△ABC内只有3个点时,可分割成7个互不重叠的小三角形;根据以上规律,当△ABC内有n个点(P1,P2,…,P n)时,可以把△ABC分割成S=2n+1个互不重叠的三角形,所以这些小三角形的内角和为(2n+1)·180°.【点睛】此题考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳并发现其中的规律,并应用规律解决问题是解题的关键.12.如图,CD 是ABC 的一条中线,E 为BC 边上一点且2,BE CE AE CD 、相交于,F 四边形BDFE 的面积为6,则ABC 的面积是( )A .14B .14.4C .13.6D .13.2【答案】B【解析】【分析】 连结BF ,设S △BDF =x ,则S △BEF =6-x ,由CD 是中线可以得到S △ADF =S △BDF ,S △BDC =S △ADC ,由BE =2CE 可以得到S △CEF =12S △BEF ,S △ABE =23S △ABC ,进而可用两种方法表示△ABC 的面积,由此可得方程,进而得解.【详解】解:如图,连接BF ,设S △BDF =x ,则S △BEF =6-x ,∵CD 是中线,∴S △ADF =S △BDF =x ,S △BDC = S △ADC =12△ABC , ∵BE =2CE ,∴S △CEF =12S △BEF =12(6-x),S △ABE =23S △ABC , ∵S △BDC = S △ADC =12△ABC ,∴S△ABC=2S△BDC=2[x+32(6-x)]=18-x,∵S△ABE=23S△ABC,∴S△ABC=32S△ABE=32[2x+ (6-x)]=1.5x+9,∴18-x =1.5x+9,解得:x=3.6,∴S△ABC=18-x,=18-3.6=14.4,故选:B.【点睛】本题考查了三角形的中线能把三角形的面积平分,等高三角形的面积比等于底的比,熟练掌握这个结论记以及方程思想是解题的关键.13.如图,小明从A点出发,沿直线前进10米后向左转10°再沿直线前进10米后向左转20°再沿直线前进10米后向左转30°……照这样下去,他第一次回到出发地A点时,一共走了()A.80米B.160米C.300米D.640米【答案】A【解析】【分析】利用多边形的外角和得出小明回到出发地A点时左转的次数,即可求出多边形的边数,即可解决问题.【详解】解:由题意可知,小明第一次回到出发地A点时,他一共转了360 ,由题意得10°+20°+30°+40°+50°+60°+70°+80°=360°,所以共转了8次,每次沿直线前进10米,所以一共走了80米.故选:A.【点睛】本题考查根据多边形的外角和解决实际问题,注意多边形的外角和是360 ,要注意第一次转了10°,第二次转了20°,第三次转了30°……,利用好规律解题.14.能够铺满地面的正多边形组合是()A.正三角形和正五边形B.正方形和正六边形C.正方形和正五边形D.正五边形和正十边形【答案】D【解析】【分析】正多边形的组合能否铺满地面,关键是要看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.【详解】解:A、正五边形和正三边形内角分别为108°、60°,由于60m+108n=360,得m=6-95 n,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;B、正方形、正六边形内角分别为90°、120°,不能构成360°的周角,故不能铺满,故此选项错误;C、正方形、正五边形内角分别为90°、108°,当90n+108m=360,显然n取任何正整数时,m不能得正整数,故不能铺满,故此选项错误;D、正五边形和正十边形内角分别为108、144,两个正五边形与一个正十边形能铺满地面,故此选项正确.故选:D.【点睛】此题主要考查了平面镶嵌,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°-360°÷边数.15.如图,在△ABC中,点D、E分别是边AC,AB的中点,BD,CE相交于点O,连接O在AO上取一点F,使得OF=12AF若S△ABC =12,则四边形OCDF的面积为()A .2B .83C .3D .103【答案】B【解析】【分析】 重心定理:三角形的三条边的中线交于一点,该点叫做三角形的重心.重心和三角形任意两个顶点组成的3个三角形面积相等.【详解】解:∵点D 、E 分别是边AC,AB 的中点,∴O 为△ABC 的重心,∴13AOC S=ABC S =4, ∴12DOC DOA S S ==AOC S =2,∵OF=12AF , ∴13DOF S =AOD S =23, ∴S 阴=DOC S +DOF S =83.故选:B.【点睛】本题考查了重心及重心定理,熟练掌握相关定理是解题关键.16.如图所示,小华从A 点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A 点时,一共走的路程是( )A .140米B .150米C .160米D .240米【答案】B【解析】【分析】 由题意可知小华走出了一个正多边形,根据正多边形的外角和公式可求解.【详解】已知多边形的外角和为360°,而每一个外角为24°,可得多边形的边数为360°÷24°=15,所以小明一共走了:15×10=150米.故答案选B .【点睛】本题考查多边形内角与外角,熟记公式是关键.17.已知正多边形的一个外角等于40,那么这个正多边形的边数为()A.6 B.7 C.8 D.9【答案】D【解析】【分析】根据正多边形的外角和以及一个外角的度数,即可求得边数.【详解】正多边形的一个外角等于40,且外角和为360,÷=,则这个正多边形的边数是:360409故选D.【点睛】本题主要考查了多边形的外角和定理,熟练掌握多边形的外角和等于360度是解题的关键.18.如果一个多边形的内角和是1800°,这个多边形是()A.八边形B.十四边形C.十边形D.十二边形【答案】D【解析】【分析】n边形的内角和可以表示成(n﹣2)•180°,设这个正多边形的边数是n,就得到方程,从而求出边数.【详解】这个正多边形的边数是n,根据题意得:(n﹣2)•180°=1800°解得:n=12.故选D.【点睛】本题考查了多边形的内角和定理.注意多边形的内角和为:(n﹣2)×180°.19.已知三角形的两边长分别为4和9,则下列数据中能作为第三边长的是( )A.13 B.6 C.5 D.4【答案】B【解析】【分析】首先根据三角形的三边关系定理,求得第三边的取值范围,再进一步找到符合条件的数值.【详解】解:设这个三角形的第三边为x.根据三角形的三边关系定理“两边之和大于第三边,两边之差小于第三边”,得:-<<+,94x94解得5x13<<.故选:B.【点睛】本题考查了三角形的三边关系定理.一定要注意构成三角形的条件:两边之和>第三边,两边之差<第三边.20.如图,ABC△是一块直角三角板,90,30C A∠=︒∠=︒,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D,E,AB与直尺的两边分别交于点F,G,若∠1=40°,则∠2的度数为()A.40º B.50º C.60º D.70º【答案】D【解析】【分析】依据平行线的性质,即可得到∠1=∠DFG=40°,再根据三角形外角性质,即可得到∠2的度数.【详解】∵DF∥EG,∴∠1=∠DFG=40°,又∵∠A=30°,∴∠2=∠A+∠DFG=30°+40°=70°,故选D.【点睛】本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,内错角相等.。
全等三角形易错题(Word版 含答案)

一、八年级数学全等三角形解答题压轴题(难)1.如图,已知△ABC中,AB=AC=20cm,BC=16cm,点D为AB的中点.(1)如果点P在线段BC上以6cm/s的速度由B点向C点运动,同时点Q在线段CA上由C向A点运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?【答案】(1)①△BPD≌△CQP,理由见解析;②V7.5Q(厘米/秒);(2)点P、Q在AB边上相遇,即经过了803秒,点P与点Q第一次在AB边上相遇.【解析】【分析】(1)①先求出t=1时BP=BQ=6,再求出PC=10=BD,再根据∠B=∠C证得△BPD≌△CQP;②根据V P≠V Q,使△BPD与△CQP全等,所以CQ=BD=10,再利用点P的时间即可得到点Q的运动速度;(2)根据V Q>V P,只能是点Q追上点P,即点Q比点P多走AB+AC的路程,设运动x秒,即可列出方程1562202x x,解方程即可得到结果.【详解】(1)①因为t=1(秒),所以BP=CQ=6(厘米)∵AB=20,D为AB中点,∴BD=10(厘米)又∵PC=BC﹣BP=16﹣6=10(厘米)∴PC=BD∵AB=AC,∴∠B=∠C,在△BPD与△CQP中,BP CQ B C PC BD =⎧⎪∠=∠⎨⎪=⎩, ∴△BPD ≌△CQP (SAS ),②因为V P ≠V Q ,所以BP ≠CQ ,又因为∠B =∠C ,要使△BPD 与△CQP 全等,只能BP =CP =8,即△BPD ≌△CPQ ,故CQ =BD =10.所以点P 、Q 的运动时间84663BPt (秒), 此时107.543Q CQ V t (厘米/秒).(2)因为V Q >V P ,只能是点Q 追上点P ,即点Q 比点P 多走AB +AC 的路程设经过x 秒后P 与Q 第一次相遇,依题意得1562202x x , 解得x=803(秒) 此时P 运动了8061603(厘米) 又因为△ABC 的周长为56厘米,160=56×2+48, 所以点P 、Q 在AB 边上相遇,即经过了803秒,点P 与点Q 第一次在AB 边上相遇. 【点睛】此题考查三角形全等的证明,三角形与动点相结合的解题方法,再证明三角形全等时注意顶点的对应关系是证明的关键.2.(1)如图1,在Rt △ABC 中,AB AC =,D 、E 是斜边BC 上两动点,且∠DAE=45°,将△ABE 绕点A 逆时针旋转90后,得到△AFC ,连接DF .(1)试说明:△AED ≌△AFD ;(2)当BE=3,CE=9时,求∠BCF 的度数和DE 的长;(3)如图2,△ABC 和△ADE 都是等腰直角三角形,∠BAC=∠DAE=90°,D 是斜边BC 所在直线上一点,BD=3,BC=8,求DE 2的长.【答案】(1)略(2)∠BCF=90° DE=5 (3)34或130【解析】试题分析:()1由ABE AFC ≌, 得到AE AF =,BAE CAF ∠=∠,45,EAD ∠=45,BAE CAD ∴∠+∠=45,CAF CAD ∴∠+∠=即45.DAF ∠=EAD DAF ∠=∠,从而得到.AED AFD ≌ ()2 由△AED AFD ≌得到ED FD =,再证明90DCF ∠=︒,利用勾股定理即可得出结论. ()3过点A 作AH BC ⊥于H ,根据等腰三角形三线合一得,1 4.2AH BH BC === 1DH BH BD =-=或7,DH BH BD =+=求出AD 的长,即可求得2DE .试题解析:()1ABE AFC ≌,AE AF =,BAE CAF ∠=∠,45,EAD ∠=90,BAC ∠=45,BAE CAD ∴∠+∠=45,CAF CAD ∴∠+∠=即45.DAF ∠=在AED 和AFD 中,{AF AEEAF DAE AD AD ,=∠=∠=.AED AFD ∴≌()2AED AFD ≌,ED FD ∴=,,90.AB AC BAC =∠=︒45B ACB ∴∠=∠=︒,45ACF ,∠=︒ 90.BCF ∴∠=︒设.DE x =,9.DF DE x CD x ===- 3.FC BE ==222,FC DC DF +=()22239.x x ∴+-=解得: 5.x =故 5.DE = ()3过点A 作AH BC ⊥于H ,根据等腰三角形三线合一得,1 4.2AH BH BC === 1DH BH BD =-=或7,DH BH BD =+= 22217AD AH DH =+=或65.22234DE AD ==或130.点睛:D 是斜边BC 所在直线上一点,注意分类讨论.3.如图,∠BAD=∠CAE=90°,AB=AD ,AE=AC ,AF ⊥CB ,垂足为F .(1)求证:△ABC ≌△ADE ;(2)求∠FAE 的度数;(3)求证:CD=2BF+DE .【答案】(1)证明见解析;(2)∠FAE=135°;(3)证明见解析.【解析】【分析】(1)根据已知条件易证∠BAC=∠DAE ,再由AB=AD ,AE=AC ,根据SAS 即可证得△ABC ≌△ADE ;(2)已知∠CAE=90°,AC=AE ,根据等腰三角形的性质及三角形的内角和定理可得∠E=45°,由(1)知△BAC ≌△DAE ,根据全等三角形的性质可得∠BCA=∠E=45°,再求得∠CAF=45°,由∠FAE=∠FAC+∠CAE 即可得∠FAE 的度数;(3)延长BF 到G ,使得FG=FB ,易证△AFB ≌△AFG ,根据全等三角形的性质可得AB=AG ,∠ABF=∠G ,再由△BAC ≌△DAE ,可得AB=AD ,∠CBA=∠EDA ,CB=ED ,所以AG=AD ,∠ABF=∠CDA ,即可得∠G=∠CDA ,利用AAS 证得△CGA ≌△CDA ,由全等三角形的性质可得CG=CD ,所以CG=CB+BF+FG=CB+2BF=DE+2BF .【详解】(1)∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE ,在△BAC 和△DAE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩, ∴△BAC ≌△DAE (SAS );(2)∵∠CAE=90°,AC=AE ,∴∠E=45°,由(1)知△BAC ≌△DAE ,∴∠BCA=∠E=45°,∵AF ⊥BC ,∴∠CFA=90°,∴∠CAF=45°,∴∠FAE=∠FAC+∠CAE=45°+90°=135°;(3)延长BF 到G ,使得FG=FB ,∵AF ⊥BG ,∴∠AFG=∠AFB=90°,在△AFB 和△AFG 中,BF F AFB AFG AF AF G =⎧⎪∠=∠⎨⎪=⎩, ∴△AFB ≌△AFG (SAS ),∴AB=AG ,∠ABF=∠G ,∵△BAC ≌△DAE ,∴AB=AD ,∠CBA=∠EDA ,CB=ED ,∴AG=AD ,∠ABF=∠CDA ,∴∠G=∠CDA ,在△CGA 和△CDA 中,GCA DCA CGA CDA AG AD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△CGA ≌△CDA ,∴CG=CD ,∵CG=CB+BF+FG=CB+2BF=DE+2BF ,∴CD=2BF+DE .【点睛】本题考查全等三角形的判定与性质,解决第3问需作辅助线,延长BF到G,使得FG=FB,证得△CGA≌△CDA是解题的关键.4.如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD 的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.探究:当∠ACB多少度时,CE⊥BC?请说明理由.【答案】(1)①垂直,相等.②都成立,理由见解析;(2)45°,理由见解析【解析】【分析】(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.【详解】(1):(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,∴∠BAD=∠CAE.又 BA=CA,AD=AE,∴△ABD≌△ACE (SAS)∴∠ACE=∠B=45°且 CE=BD.∵∠ACB=∠B=45°,∴∠ECB=45°+45°=90°,即 CE⊥BD.故答案为垂直,相等;②都成立,理由如下:∵∠BAC=∠DAE=90°,∴∠BAC+∠DAC=∠DAE+∠DAC,∴∠BAD=∠CAE,在△DAB与△EAC中,AD AEBAD CAEAB AC⎧⎪∠∠⎨⎪⎩===∴△DAB≌△EAC,∴CE=BD,∠B=∠ACE,∴∠ACB+∠ACE=90°,即CE⊥BD;(2)当∠ACB=45°时,CE⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,在△GAD与△CAE中,AC AGDAG EACAD AE⎧⎪∠∠⎨⎪⎩===∴△GAD≌△CAE,∴∠ACE=∠AGC=45°,∠BCE=∠ACB+∠ACE=45°+45°=90°,即CE⊥B C.5.如图1,在ABC ∆中,ACB ∠是直角,60B ∠=︒,AD 、CE 分别是BAC ∠、BCA ∠的平分线,AD 、CE 相交于点F .(1)求出AFC ∠的度数;(2)判断FE 与FD 之间的数量关系并说明理由.(提示:在AC 上截取CG CD =,连接FG .)(3)如图2,在△ABC ∆中,如果ACB ∠不是直角,而(1)中的其它条件不变,试判断线段AE 、CD 与AC 之间的数量关系并说明理由.【答案】(1)∠AFC =120°;(2)FE 与FD 之间的数量关系为:DF =EF .理由见解析;(3)AC =AE+CD .理由见解析.【解析】【分析】(1)根据三角形的内角和性质只要求出∠FAC ,∠ACF 即可解决问题;(2)根据在图2的 AC 上截取CG=CD ,证得△CFG ≌△CFD (SAS),得出DF= GF ;再根据ASA 证明△AFG ≌△AFE ,得EF=FG ,故得出EF=FD ;(3)根据(2) 的证明方法,在图3的AC 上截取AG=AE ,证得△EAF ≌△GAF (SAS)得出∠EFA=∠GFA ;再根据ASA 证明△FDC ≌△FGC ,得CD=CG 即可解决问题.【详解】(1)解:∵∠ACB =90°,∠B =60°,∴∠BAC =90°﹣60°=30°,∵AD 、CE 分别是∠BAC 、∠BCA 的平分线,∴∠FAC =15°,∠FCA =45°,∴∠AFC =180°﹣(∠FAC+∠ACF )=120°(2)解:FE 与FD 之间的数量关系为:DF =EF .理由:如图2,在AC 上截取CG =CD ,∵CE 是∠BCA 的平分线,∴∠DCF =∠GCF ,在△CFG和△CFD中,CG CDDCF GCFCF CF=⎧⎪∠=∠⎨⎪=⎩,∴△CFG≌△CFD(SAS),∴DF=GF.∠CFD=∠CFG由(1)∠AFC=120°得,∴∠CFD=∠CFG=∠AFE=60°,∴∠AFG=60°,又∵∠AFE=∠CFD=60°,∴∠AFE=∠AFG,在△AFG和△AFE中,AFE AFGAF AFEAF GAF∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AFG≌△AFE(ASA),∴EF=GF,∴DF=EF;(3)结论:AC=AE+CD.理由:如图3,在AC上截取AG=AE,同(2)可得,△EAF≌△GAF(SAS),∴∠EFA=∠GFA,AG=AE∵∠BAC+∠BCA=180°-∠B=180°-60°=120°∴∠AFC=180°﹣(∠FAC+∠FCA)=180°-12(∠BAC+∠BCA)=180°-12×120°=120°,∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,∴∠CFG=∠CFD=60°,同(2)可得,△FDC≌△FGC(ASA),∴CD=CG,∴AC=AG+CG=AE+CD.【点睛】本题考查了全等三角形的判定和性质的运用,全等三角形的判定和性质是证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.6.综合实践如图①,90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥,垂足分别为点D E 、,2.5, 1.7AD cm DE cm ==.(1)求BE 的长;(2)将CE 所在直线旋转到ABC ∆的外部,如图②,猜想AD DE BE 、、之间的数量关系,直接写出结论,不需证明;(3)如图③,将图①中的条件改为:在ABC ∆中,,AC BC D C E =、、三点在同一直线上,并且BEC ADC BCA α∠=∠=∠=,其中α为任意钝角.猜想AD DE BE 、、之间的数量关系,并证明你的结论.【答案】(1)0.8cm;(2)DE=AD+BE;(3)DE=AD+BE ,证明见解析.【解析】【分析】(1)本小题只要先证明ACD CBE ≅,得到AD CE =,CD BE =,再根据2.5, 1.7AD cm DE cm ==,CD CE DE =-,易求出BE 的值;(2)先证明ACD CBE ≅,得到AD CE =,CD BE =,由图②ED=EC+CD ,等量代换易得到AD DE BE 、、之间的关系;(3)本题先证明EBC DCA ∠=∠,然后运用“AAS”定理判定BEC CDA ≅,从而得到,BE CD EC AD ==,再结合图③中线段ED 的特点易找到AD DE BE 、、之间的数量关系.【详解】解:(1)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∵90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中,90ADC E ACD BCEAC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ 2.5, 1.7AD cm DE cm ==, 2.5 1.70.8()CD CE DE AD DE cm =-=-=-= ∴0.8BE cm =(2)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∴90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中,90ADC E ACD BCE AC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ED EC CD =+∴ED AD BE =+(3)∵BEC ADC BCA α∠=∠=∠=∴180BCE ACD a ︒∠+∠=-180BCE BCE a ︒∠+∠=-∴ACD BCE ∠=∠在ACD 与CBE △中, ADC E a ACD BCE AC BC ∠=∠=⎧⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ED EC CD =+∴ED AD BE =+【点睛】本题考查的知识点是全等三角形的判定,确定一种判定定理,根据已知条件找到判定全等所需要的边相等或角相等的条件是解决这类题的关键.7.(1)问题发现:如图(1),已知:在三角形ABC ∆中,90BAC ︒∠=,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点,D E ,试写出线段,BD DE 和CE 之间的数量关系为_________________.(2)思考探究:如图(2),将图(1)中的条件改为:在ABC ∆中, ,,,AB AC D A E =三点都在直线l 上,并且BDA AEC BAC α∠=∠=∠=,其中α为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.(3)拓展应用:如图(3),,D E 是,,D A E 三点所在直线m 上的两动点,(,,D A E 三点互不重合),点F 为BAC ∠平分线上的一点,且ABF ∆与ACF ∆均为等边三角形,连接,BD CE ,若BDA AEC BAC ∠=∠=∠,试判断DEF ∆的形状并说明理由.【答案】(1)DE=CE+BD ;(2)成立,理由见解析;(3)△DEF 为等边三角形,理由见解析.【解析】【分析】(1)利用已知得出∠CAE=∠ABD ,进而根据AAS 证明△ABD 与△CAE 全等,然后进一步求解即可;(2)根据BDA AEC BAC α∠=∠=∠=,得出∠CAE=∠ABD ,在△ADB 与△CEA 中,根据AAS 证明二者全等从而得出AE=BD ,AD=CE ,然后进一步证明即可;(3)结合之前的结论可得△ADB 与△CEA 全等,从而得出BD=AE ,∠DBA=∠CAE ,再根据等边三角形性质得出∠ABF=∠CAF=60°,然后进一步证明△DBF 与△EAF 全等,在此基础上进一步证明求解即可.【详解】(1)∵BD ⊥直线l ,CE ⊥直线l ,∴∠BDA=∠AEC=90°,∴∠BAD+∠ABD=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∴∠CAE=∠ABD ,在△ABD 与△CAE 中,∵∠ABD=∠CAE ,∠BDA=∠AEC ,AB=AC ,∴△ABD ≌△CAE(AAS),∴BD=AE ,AD=CE ,∵DE=AD+AE ,∴DE=CE+BD ,故答案为:DE=CE+BD ;(2)(1)中结论还仍然成立,理由如下:∵BDA AEC BAC α∠=∠=∠=,∴∠DBA+∠BAD=∠BAD+∠CAE=180°−α,∴∠CAE=∠ABD ,在△ADB 与△CEA 中,∵∠ABD=∠CAE ,∠ADB=∠CEA ,AB=AC ,∴△ADB ≌△CEA(AAS),∴AE=BD ,AD=CE ,∴BD+CE=AE+AD=DE ,即:DE=CE+BD ,(3)DEF ∆为等边三角形,理由如下:由(2)可知:△ADB ≌△CEA ,∴BD=EA ,∠DBA=∠CAE ,∵△ABF 与△ACF 均为等边三角形,∴∠ABF=∠CAF=60°,BF=AF ,∴∠DBA+∠ABF=∠CAE+CAF ,∴∠DBF=∠FAE ,在△DBF 与△EAF 中,∵FB=FA ,∠FDB=∠FAE ,BD=AE ,∴△DBF ≌△EAF(SAS),∴DF=EF ,∠BFD=∠AFE ,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF 为等边三角形.【点睛】本题主要考查了全等三角形性质与判定的综合运用,熟练掌握相关概念是解题关键.8.如图,在ABC ∆中,5BC = ,高AD 、BE 相交于点O , 23BD CD =,且AE BE = . (1)求线段 AO 的长;(2)动点 P 从点 O 出发,沿线段 OA 以每秒 1 个单位长度的速度向终点 A 运动,动点 Q 从 点 B 出发沿射线BC 以每秒 4 个单位长度的速度运动,,P Q 两点同时出发,当点 P 到达 A 点时,,P Q 两点同时停止运动.设点 P 的运动时间为 t 秒,POQ ∆的面积为 S ,请用含t 的式子表示 S ,并直接写出相应的 t 的取值范围;(3)在(2)的条件下,点 F 是直线AC 上的一点且 CF BO =.是否存在t 值,使以点 ,,B O P 为顶 点的三角形与以点 ,,F C Q 为顶点的三角形全等?若存在,请直接写出符合条件的 t 值; 若不存在,请说明理由.【答案】(1)5;(2)①当点Q 在线段BD 上时,24QD t =-,t 的取值范围是102t <<;②当点Q 在射线DC 上时,42QD t =-,,t 的取值范围是152t <≤;(3)存在,1t =或53. 【解析】【分析】(1)只要证明△AOE ≌△BCE 即可解决问题;(2)分两种情形讨论求解即可①当点Q 在线段BD 上时,QD=2-4t ,②当点Q 在射线DC 上时,DQ=4t-2时;(3)分两种情形求解即可①如图2中,当OP=CQ 时,BOP ≌△FCQ .②如图3中,当OP=CQ 时,△BOP ≌△FCQ ;【详解】解:(1)∵AD 是高,∴90ADC ∠=∵BE 是高,∴90AEB BEC ∠=∠=∴90EAO ACD ∠+∠=,90EBC ECB ∠+∠=,∴EAO EBC ∠=∠在AOE ∆和BCE ∆中,EAO EBC AE BEAEO BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴AOE ∆≌BCE ∆∴5AO BC ==;(2)∵23BD CD =,=5BC ∴=2BD ,=3CD ,根据题意,OP t =,4BQ t =,①当点Q 在线段BD 上时,24QD t =-,∴21(24)22S t t t t =-=-+,t 的取值范围是102t <<. ②当点Q 在射线DC 上时,42QD t =-,∴21(42)22S t t t t =-=-,t 的取值范围是152t <≤ (3)存在. ①如图2中,当OP=CQ 时,∵OB=CF ,∠POB=∠FCQ ,∴△BOP ≌△FCQ .∴CQ=OP ,∴5-4t ═t ,解得t=1,②如图3中,当OP=CQ 时,∵OB=CF ,∠POB=∠FCQ ,∴△BOP ≌△FCQ .∴CQ=OP ,∴4t-5=t ,解得t=53. 综上所述,t=1或53s 时,△BOP 与△FCQ 全等. 【点睛】 本题考查三角形综合题、全等三角形的判定和性质、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.9.如图,ABC ∆是等腰直角三角形,090BAC ∠=,点D 是直线BC 上的一个动点(点D 与点B C 、不重合),以AD 为腰作等腰直角ADE ∆,连接CE .(1)如图①,当点D 在线段BC 上时,直接写出,BC CE 的位置关系,线段,BC CD ,CE 之间的数量关系;(2)如图②,当点D 在线段BC 的延长线上时,试判断线段BC ,CE 的位置关系,线段,,BC CD CE 之间的数量关系,并说明理由;(3)如图③,当点D 在线段CB 的延长线上时,试判断线段,BC CE 的位置关系,线段,,BC CD CE 之间的数量关系,并说明理由.【答案】(1)见解析;(2)BC CE ⊥,CE BC CD =+,理由见解析;(3),BC CE CD BC CE ⊥=+,理由见解析【解析】【分析】(1)根据条件AB=AC ,∠BAC=90°,AD=AE ,∠DAE=90°,判定△ABD ≌△ACE (SAS ),利用两角的和即可得出BC CE ⊥;利用线段的和差即可得出BC CE CD =+;(2)同(1)的方法根据SAS 证明△ABD ≌△ACE ,得出BD=CE ,∠ACE=∠ABD ,从而得出结论;(3)先根据SAS 证明△ABD ≌△ACE ,得出ADB AEC ∠=∠,BD CE =,从而得出结论.【详解】(1)∵△ABC 、△ADE 是等腰直角三角形,∴AB=AC ,AE =AD ,在△△ABD 和△ACE 中90AB AC BAC DAE AD AE ⎧⎪∠∠=︒⎨⎪⎩=== , ∴△ABD ≌△ACE (SAS ),∴∠B =∠ACE ,BD=CE,又∵△ABC 是等腰直角三角形,∴∠B+∠ACB=90︒,∴∠ACE +∠ACB=90︒,即BC CE ⊥,∵BC=BD+CD, BD=CE ,∴BC CE CD =+;(2)BC CE ⊥,CE BC CD =+,理由如下:∵ABC ∆、ADE ∆是等腰直角三角形,∴0,,90AB AC AD AE BAC DAE ==∠=∠=,∴BAC DAC DAE DAC ∠+∠=∠+∠即BAD CAE ∠=∠,在ABD ∆和ACE ∆中AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪⎩== ∴()ABD ACE SAS ∆≅∆∴BD CE =∵BD BC CD =+∴CE BC CD =+,∴ABD ACE ∠=∠,∵090ABD ACE ∠+∠=∴090ACE ACB ∠+∠=∴BC CE ⊥.(3),BC CE CD BC CE ⊥=+,理由如下:∵ABC ADE ∆∆、是等腰直角三角形,∴0,,90AB AC AD AE BAC DAE ==∠=∠=,∴BAC BAE DAE BAE ∠-∠=∠-∠,即BAD CAE ∠=∠,在ABD ∆和ACE ∆中 AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪⎩== ∴()ABD ACE SAS ∆≅∆,∴ADB AEC ∠=∠,BD CE =,∵CD BD BC =+,∴CD CE BC =+,∵090ADE AED ∠+∠=,即090ADB CDE AED ∠+∠+∠=∴090AEC CDE AED ∠+∠+∠=,∴090DCE ∠=,即BC CE ⊥.【点睛】考查了全等三角形的判定与性质以及等腰直角三角形的性质的运用,解题关键是根据利用两边及其夹角分别对应相等的两个三角形全等判定三角形全等.10.综合与实践:我们知道“两边及其中一边的对角分别对应相等的两个三角形不一定全等”.但是,乐乐发现:当这两个三角形都是锐角三角形时,它们会全等.(1)请你用所学知识判断乐乐说法的正确性.如图,已知ABC ∆、111A B C ∆均为锐角三角形,且11AB A B =,11BC B C =,1C C ∠=∠. 求证:111ABC A B C ∆∆≌.(2)除乐乐的发现之外,当这两个三角形都是______时,它们也会全等.【答案】(1)见解析;(2)钝角三角形或直角三角形.【解析】【分析】(1)过B 作BD ⊥AC 于D ,过B 1作B 1D 1⊥B 1C 1于D 1,得出∠BDA=∠B 1D 1A 1=∠BDC=∠B 1D 1C 1=90°,根据SAS 证△BDC ≌△B 1D 1C 1,推出BD=B 1D 1,根据HL 证Rt △BDA ≌Rt △B 1D 1A 1,推出∠A=∠A 1,根据AAS 推出△ABC ≌△A 1B 1C 1即可.(2)当这两个三角形都是直角三角形时,直接利用HL 即可证明;当这两个三角形都是钝角三角形时,与(1)同理可证.【详解】(1)证明:过点B 作BD AC ⊥于D ,过1B 作1111B D A C ⊥于1D ,则11111190BDA B D A BDC B D C ∠=∠=∠=∠=︒.在BDC ∆和111B D C ∆中,1C C ∠=∠,111BDC B D C ∠=∠,11BC B C =,∴111BDC B D C ∆∆≌,∴11BD B D =.在Rt BDA ∆和111Rt B D A ∆中,11AB A B =,11BD B D =,∴111Rt Rt (HL)BDA B D A ∆∆≌,∴1A A ∠=∠.在ABC ∆和111A B C ∆中,1C C ∠=∠,1A A ∠=∠,11AB A B =,∴111(AAS)ABC A B C ∆∆≌.(2)如图,当这两个三角形都是直角三角形时,∵11AB A B =,11BC B C =,190C C ∠==∠︒.∴Rt ABC ∆≌111Rt A B C ∆(HL );∴当这两个三角形都是直角三角形时,它们也会全等;如图,当这两个三角形都是钝角三角形时,作BD ⊥AC ,1111B D A C ⊥,与(1)同理,利用AAS 先证明111BDC B D C ∆∆≌,得到11BD B D =,再利用HL 证明111Rt Rt BDA B D A ∆∆≌,得到1A A ∠=∠,再利用AAS 证明111ABC A B C ∆∆≌;∴当这两个三角形都是钝角三角形时,它们也会全等;故答案为:钝角三角形或直角三角形.【点睛】本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力.解题的关键是熟练掌握证明三角形全等的方法.。
【精选】八年级数学上册三角形解答题易错题(Word版 含答案)

【精选】八年级数学上册三角形解答题易错题(Word 版 含答案)一、八年级数学三角形解答题压轴题(难)1.如图①所示,在三角形纸片ABC 中,70C ∠=︒,65B ∠=︒,将纸片的一角折叠,使点A 落在ABC 内的点A '处.(1)若140∠=︒,2∠=________.(2)如图①,若各个角度不确定,试猜想1∠,2∠,A ∠之间的数量关系,直接写出结论.②当点A 落在四边形BCDE 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,A ∠,1∠,2∠之间又存在什么关系?请说明.(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的123456∠+∠+∠+∠+∠+∠和是________.【答案】(1)50°;(2)①见解析;②见解析;(3)360°.【解析】【分析】(1)根据题意,已知70C ∠=︒,65B ∠=︒,可结合三角形内角和定理和折叠变换的性质求解;(2)①先根据折叠得:∠ADE=∠A ′DE ,∠AED=∠A ′ED ,由两个平角∠AEB 和∠ADC 得:∠1+∠2等于360°与四个折叠角的差,化简得结果;②利用两次外角定理得出结论;(3)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去(∠B'GF+∠B'FG)以及(∠C'DE+∠C'ED)和(∠A'HL+∠A'LH),再利用三角形的内角和定理即可求解.【详解】解:(1)∵70C ∠=︒,65B ∠=︒,∴∠A ′=∠A=180°-(65°+70°)=45°,∴∠A ′ED+∠A ′DE =180°-∠A ′=135°,∴∠2=360°-(∠C+∠B+∠1+∠A ′ED+∠A ′DE )=360°-310°=50°;(2)①122A ∠+∠=∠,理由如下由折叠得:∠ADE=∠A ′DE ,∠AED=∠A ′ED ,∵∠AEB+∠ADC=360°,∴∠1+∠2=360°-∠ADE-∠A ′DE-∠AED-∠A ′ED=360°-2∠ADE-2∠AED ,∴∠1+∠2=2(180°-∠ADE-∠AED )=2∠A ;②221A ∠=∠+∠,理由如下:∵2∠是ADF 的一个外角∴2A AFD ∠=∠+∠.∵AFD ∠是A EF '△的一个外角∴1AFD A '∠=∠+∠又∵A A '∠=∠∴221A ∠=∠+∠(3)如图由题意知,∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠B'GF+∠B'FG)-(∠C'DE+∠C'ED)-(∠A'HL+∠A'LH)=720°-(180°-∠B')-(180°-C')-(180°-A')=180°+(∠B'+∠C'+∠A')又∵∠B=∠B',∠C=∠C',∠A=∠A',∠A+∠B+∠C=180°,∴∠1+∠2+∠3+∠4+∠5+∠6=360°.【点睛】题主要考查了折叠变换、三角形、四边形内角和定理.注意折叠前后图形全等;三角形内角和为180°;四边形内角和等于360度.2.如图,△ABC 的三条角平分线相交于点I ,过点I 作DI ⊥IC ,交AC 于点D .(1)如图①,求证:∠AIB =∠ADI ;(2)如图②,延长BI ,交外角∠ACE 的平分线于点F.①判断DI 与CF 的位置关系,并说明理由;②若∠BAC =70°,求∠F 的度数.【答案】(1)证明见解析;(2)解:①结论:DI ∥CF ,②35°.【解析】分析:(1)只要证明∠AIB=90°+12∠ACB ,∠ADI=90°+12∠ACB 即可; (2)①只要证明∠IDC=∠DCF 即可; ②首先求出∠ACE-∠ABC=∠BAC=70°,再证明∠F=12∠ACE-12∠ABC=12(∠ACE-∠ABC )即可解决问题;详解:(1)证明:∵AI ,BI 分别平分∠BAC ,∠ABC ,∴∠BAI =12∠BAC ,∠ABI =12∠ABC , ∴∠BAI +∠ABI =12 (∠BAC +∠ABC)=12 (180°-∠ACB)=90°-12∠ACB. 在△ABI 中,∠AIB =180°-(∠BAI +∠ABI)=180°-(90°-12∠ACB)=90°+12∠ACB. ∵CI 平分∠ACB ,∴∠DCI =12∠ACB.∵DI ⊥IC , ∴∠DIC =90°,∴∠ADI =∠DIC +∠DCI =90°+12∠ACB. ∴∠AIB =∠ADI.(2)解:①结论:DI ∥CF.理由:∵∠IDC =90°-∠DCI =90°-12∠ACB ,CF 平分∠ACE , ∴∠ACF=12∠ACE =12 (180°-∠ACB)=90°-12∠ACB ,∴∠IDC =∠ACF ,∴DI ∥CF. ②∵∠ACE =∠ABC +∠BAC ,∴∠ACE -∠ABC =∠BAC =70°.∵∠FCE =∠FBC +∠F ,∴∠F =∠FCE -∠FBC.∵∠FCE =12∠ACE ,∠FBC =12∠ABC , ∴∠F =12∠ACE -12∠ABC =12(∠ACE -∠ABC)=35°. 点睛:本题考查了三角形的外角性质:三角形的一个外角等于另外两个内角之和,三角形内角和定理:三角形的内角和为180°,难度适中,此类题型的关键在于结合题目条件与三角形的外角性质,三角形内角和定理.3.(1)在ABC ∆中,AD BC ⊥,BE AC ⊥,CF AB ⊥,16BC =,3AD =,4BE =,6CF =,则ABC ∆的周长为______.(2)如图①,在ABC ∆中,已知点D ,E ,F 分别为边BC ,BD ,CD 的中点,且4ABC S ∆=2cm ,则AEF S ∆等于______2cm .① ②(3)如②图,三角形ABC 的面积为1,点E 是AC 的中点,点O 是BE 的中点,连接AO 并延长交BC 于点D ,连接CO 并延长交AB 于点F ,则四边形BDOF 的面积为______.【答案】(1)36(2)2(3)16 【解析】【分析】(1)利用三角形面积公式,求出AB 、AC 的长,再计算三角形的周长即可;(2)设ABC ∆在BC 边上的高为h ,则12ABC S BC h ∆=⋅,根据线段中点的定义以及线段的和差得出12EF BC =,继而再根据三角形面积公式进行求解即可; (3)设BOF S x ∆=,BOD S y ∆=,根据三角形中线将三角形分成两个面积相等的三角形可得14AOE COE AOB COB S S S S ∆∆∆∆====,从而得14AOF S x ∆=-,34ACF S x ∆=-,14BCF S x ∆=+,14COD S y ∆=-,34ACD S y ∆=-,14ABD S y ∆=+,利用等高的两三角形面积之比等于底边之比分别列出关于x 、y 的方程,求出x 、y 的值即可求得答案.【详解】 (1)111222ABC S BC AD AC BE AB CF ∆=⋅=⋅=⋅, ∴BC AD AC BE AB CF ⋅=⋅=⋅,即16346AC AB ⨯=⋅=⋅,∴12AC =,8AB =,∴△ABC 的周长=AB+BC+AC=36;(2)设ABC ∆在BC 边上的高为h ,则12ABC S BC h ∆=⋅, ∵E 为BD 中点,∴12ED BD =, ∵F 为DC 中点,∴12DF DC =, ∴111222EF BD DC BC =+=,∴211112cm 2222AEF ABC S EF h BC h S ∆∆=⋅=⋅⋅==; (3)设BOF S x ∆=,BOD S y ∆=,∵点E ,O 分别是AC ,BE 的中点,1ABC S ∆=,∴14AOE COE AOB COB S S S S ∆∆∆∆====, ∴14AOF S x ∆=-,34ACF S x ∆=-,14BCF S x ∆=+, ∴134414x x x x --=+,即2213164x x x -=-, 解得112x =, 又14COD S y ∆=-,34ACD S y ∆=-,14ABD S y ∆=+, ∴141344y y y y +=--,得112y =, 故11112126BDOF S x y =+=+=四边形. 【点睛】本题考查了三角形面积的应用,三角形的周长,解题关键在于找出等高的两三角形面积与底边的对应关系.4.Rt △ABC 中,∠C=90°,点D 、E 分别是△ABC 边AC 、BC 上的点,点P 是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P 在线段AB 上,如图(1)所示,且∠α=50°,则∠1+∠2= °;(2)若点P 在边AB 上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;(3)若点P 运动到边AB 的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:.【答案】(1)140°;(2)∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α.【解析】试题分析:(1)根据四边形内角和定理以及邻补角的定义,得出∠1+∠2=∠C+∠α,进而得出即可;(2)利用(1)中所求的结论得出∠α、∠1、∠2之间的关系即可;(3)利用三角外角的性质,得出∠1=∠C+∠2+α=90°+∠2+α;(4)利用三角形内角和定理以及邻补角的性质可得出∠α、∠1、∠2之间的关系.试题分析:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,∴∠1+∠2=140°,故答案为140;(2)由(1)得∠α+∠C=∠1+∠2,∴∠1+∠2=90°+∠α.故答案为∠1+∠2=90°+∠α.(3)∠1=90°+∠2+∠α.理由如下:如图③,设DP与BE的交点为M,∵∠2+∠α=∠DME,∠DME+∠C=∠1,∴∠1=∠C+∠2+∠α=90°+∠2+∠α.(4)如图④,设PE与AC的交点为F,∵∠PFD=∠EFC,∴180°-∠PFD=180°-∠EFC,∴∠α+180°-∠1=∠C+180°-∠2,∴∠2=90°+∠1-∠α.故答案为∠2=90°+∠1-∠α点睛:本题考查了三角形内角和定理和外角的性质、对顶角相等的性质,熟练掌握三角形外角的性质是解决问题的关键.5.数学活动课上,老师提出了一个问题:我们知道,三角形的一个外角等于和它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系?(1)独立思考,请你完成老师提出的问题:如图所示,已知∠DBC和∠BCE分别为△ABC的两个外角,试探究∠A和∠DBC,∠BCE之间的数量关系.解:⑵合作交流,“创新小组”受此问题的启发:分别作外角∠CBD和∠BCE的平分线BF和CF,交于点F(如图所示),那么∠A与∠F之间有何数量关系?请写出解答过程.【答案】(1)∠DBC+∠BCE-∠A=180º(2)12∠A+∠F=90º【解析】【分析】(1)根据三角形的一个外角等于和它不相邻的两个内角的和,三角形内角和定理计算即可.(2)根据角平分线可知∠FBC+∠FCB=12(∠DBC+∠BCE,)再根据三角形内角和定理,结合(1)即可解答.【详解】⑴∠DBC+∠BCE-∠A=180º.∠DBC+∠BCE=∠ABC+∠A+∠ACB+∠A=180°+∠A即∠DBC+∠BCE-∠A=180º.(2)12∠A+∠F=90°∵BF和CF分别平分∠CBD和∠BCE,∴∠CBF=12∠CBD,∠BCF=12∠BCE.∴∠CBF+∠BCF=12(∠CBD+∠BCE).∵∠CBF+∠BCF=180º-∠F,∠DBC+∠BCE=180º+∠A.∴180º-∠F =12(∠CBD+∠BCE)=12(180º+∠A)∴12∠A+∠F=90º.【点睛】本题考查了三角形外角性质及三角形内角和定理,熟练掌握三角形外角性质是解题的关键.6.如图①,在△ABC中,AE平分∠BAC,∠C>∠B,F是AE上一点,且FD⊥BC于D点.(1)试猜想∠EFD,∠B,∠C的关系,并说明理由;(2)如图②,当点F在AE的延长线上时,其余条件不变,(1)中的结论还成立吗?说明理由.①②【答案】(1)∠EFD=12∠C-12∠B.()成立,理由见解析.【解析】【分析】先根据AE平分∠BAC推出∠BAE=12∠BAC=12[180°-(∠B+∠C)],再根据外角的定义求出∠FED=∠B+∠BAE,然后利用直角三角形的性质求出∠EFD=90°-∠FED.【详解】解:(1)∠EFD=12∠C-12∠B.理由如下:由AE是∠BAC的平分线知∠BAE=12∠BAC.由三角形外角的性质知∠FED=∠B+12∠BAC,故∠B+12∠BAC+∠EFD=90°①.在△ABC中,由三角形内角和定理得∠B+∠BAC+∠C=180°,即12∠C+12∠B+12∠BAC=90°②.②-①,得∠EFD=12∠C-12∠B.(2)成立.理由如下:由对顶角相等和三角形的外角性质知:∠FED=∠AEC=∠B+12∠BAC,故∠B+12∠BAC+∠EFD=90°①.在△ABC中,由三角形内角和定理得:∠B+∠BAC+∠C=180°,即12∠B+12∠BAC+12∠C=90°②.②-①,得∠EFD=12∠C-12∠B.【点睛】此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质,命题时经常将多个知识点联系在一起进行考查,这样更能训练学生的解题能力.7.如图1,在△ABC中,∠B=90°,分别作其内角∠ACB与外角∠DAC的平分线,且两条角平分线所在的直线交于点E.(1)∠E= °;(2)分别作∠EAB与∠ECB的平分线,且两条角平分线交于点F.①依题意在图1中补全图形;②求∠AFC的度数;(3)在(2)的条件下,射线FM在∠AFC的内部且∠AFM=∠AFC,设EC与AB的交点为H,射线HN在∠AHC的内部且∠AHN=∠AHC,射线HN与FM交于点P,若∠FAH,∠FPH和∠FCH满足的数量关系为∠FCH=m∠FAH+n∠FPH,请直接写出m,n的值.【答案】(1)45;(2)67.5°;(3)m=2,n=﹣3.【解析】【分析】(1)根据角平分线的定义可得∠CAF=12∠DAC,∠ACE=12∠ACB,设∠CAF=x,∠ACE=y,根据已知可推导得出x﹣y=45,再根据三角形外角的性质即可求得答案;(2)①根据角平分线的尺规作图的方法作出图形即可;②如图2,由CF平分∠ECB可得∠ECF=12y,再根据∠E+∠EAF=∠F+∠ECF以及∠E+∠EAB=∠B+∠ECB,可推导得出45°+452y+=∠F+12y,由此即可求得答案;(3)如图3,设∠FAH=α,根据AF平分∠EAB可得∠FAH=∠EAF=α,根据已知可推导得出∠FCH=α﹣22.5①,α+22.5=30+23∠FCH+∠FPH②,由此可得∠FPH=22.53α+,再根据∠FCH=m∠FAH+n∠FPH,即可求得答案.【详解】(1)如图1,∵EA平分∠DAC,EC平分∠ACB,∴∠CAF=12∠DAC,∠ACE=12∠ACB,设∠CAF=x,∠ACE=y,∵∠B=90°,∴∠ACB+∠BAC=90°,∴2y+180﹣2x=90,x﹣y=45,∵∠CAF=∠E+∠ACE,∴∠E=∠CAF﹣∠ACE=x﹣y=45°,故答案为:45;(2)①如图2所示,②如图2,∵CF平分∠ECB,∴∠ECF=12 y,∵∠E+∠EAF=∠F+∠ECF,∴45°+∠EAF=∠F+12y ①,同理可得:∠E+∠EAB=∠B+∠ECB,∴45°+2∠EAF=90°+y,∴∠EAF=452y+②,把②代入①得:45°+452y+=∠F+12y,∴∠F=67.5°,即∠AFC=67.5°;(3)如图3,设∠FAH=α,∵AF平分∠EAB,∴∠FAH=∠EAF=α,∵∠AFM=13∠AFC=13×67.5°=22.5°, ∵∠E+∠EAF=∠AFC+∠FCH ,∴45+α=67.5+∠FCH ,∴∠FCH=α﹣22.5①, ∵∠AHN=13∠AHC=13(∠B+∠BCH )=13(90+2∠FCH )=30+23∠FCH , ∵∠FAH+∠AFM=∠AHN+∠FPH , ∴α+22.5=30+23∠FCH+∠FPH ,② 把①代入②得:∠FPH=22.53α+, ∵∠FCH=m ∠FAH+n ∠FPH ,α﹣22.5=mα+n 22.5·3α+,解得:m=2,n=﹣3.【点睛】本题考查了三角形内角和定理、三角形外角的性质、基本作图——角平分线等,熟练掌握三角形内角和定理以及三角形外角的性质、结合图形进行求解是关键.8.如图 (1)所示,AB ,CD 是两条线段,M 是AB 的中点,连接AD ,MD ,BC ,BD , MC ,AC ,S △DMC ,S △DAC 和S △DBC 分别表示△DMC ,△DAC ,△DBC 的面积,当AB ∥CD 时,有S △DMC =2DAC DBC S S+.(1)如图 (2)所示,当图6-9(1)中AB 与CD 不平行时,S △DMC =2DBC DAC S S +是否仍然成立?请说明理由; (2)如图 (3)所示,当图6-9(1)中AB 与CD 相交于点O 时,S △DMC 与S △DAC ,S △DBC 有什么样的数量关系?试说明你的结论.【答案】(1) S △DMC =2DAC DBC S S +仍成立,理由见解析; (2)S △DMC =2DBC DAC S S -,理由见解析.【解析】【分析】(1)先看题中给出的条件为何成立,由于三角形ADC ,DMC ,DBC 都是同底,而由于AB ∥DC ,因此高相等,就能得出题中给出的结论,那么本题也要用高来求解,过A ,M ,B 分别作BC 的垂线AE ,MN ,BF ,AE ∥MN ∥BF ,由于M 是AB 中点,因此MN 是梯形AEFB 的中位线,因此MN=12(AE+BF ),三个三角形同底因此结论①是成立的. (2)本题可以利用AM=MB ,让这两条边作底边来求解,三角形ADB 中,小三角形的AB 边上的高都相等,那么三角形ADM 和DBM 的面积就相等(等底同高),因此三角形OAD ,OMD 的和就等于三角形BMD 的面积,同理三角形AOC 和OMC 的面积和等于三角形CMB 的面积.根据这些等量关系即可得出题中三个三角形的面积关系.【详解】(1)当AB 与CD 不平行时,S △DMC =2DAC DBC S S+仍成立.分别过点A ,M ,B 作CD 的垂线AE ,MN ,BF ,垂足分别为E ,N ,F.∵M 为AB 的中点,∴MN =12(AE+BF),∴S △DAC +S △DBC =12DC·AE+12DC·BF =12DC·(AE+BF)= 12DC·2MN=DC·MN=2S △DMC .∴S △DMC =2DAC DBC S S +; (2)S △DMC =2DBC DAC S S-.理由:∵M 是AB 的中点,∴S △ADM =S △BDM ,S △ACM =S △BCM ,而S △DBC =S △BDM +S △BCM +S △DMC ,① S △DAC =S △ADM +S △ACM -S △DMC ,②∴①-②得S △DBC -S △DAC =2S △DMC ,故S △DMC =2DBC DAC S S-.【点睛】本题考查了三角形中位线和梯形,解题的关键是掌握三角形中位线定理和梯形的概念.9.如图①.ABC 中,AB AC =,P 为底边BC 上一点,PE AB ⊥,PF AC ⊥,CH AB ⊥,垂足分别为E 、F 、H .易证PE PF CH +=.证明过程如下:如图①,连接AP .∵PE AB ⊥,PF AC ⊥,CH AB ⊥,∴12ABP S AB PE =⋅,12ACP S AC PF =⋅,12ABC S AB CH =⋅ 又∵ABP ACP ABC S S S +=,∴AB PE AC PF AB CH ⋅+⋅=⋅∵AB AC =,∴PE PF CH +=.如图②,P 为BC 延长线上的点时,其它条件不变,PE 、PF 、CH 又有怎样的数量关系?请写出你的猜想,并加以证明.【答案】PE PF CH -=【解析】【分析】参考题设的证明过程,主要思路就是等面积法:ABP ACP ABC SS S +=,同样,P 为BC 延长线上的点时,也可以用类似的等面积法:ABP ACP ABC SS S =-,即可得出结论. 【详解】∵PE AB ⊥,PF AC ⊥,CH AB ⊥,∴12ABP S AB PE =⋅,12ACP S AC PF =⋅,12ABC S AB CH =⋅ 又∵ABP ACP ABC S S S =-,∴AB PE AC PF AB CH ⋅-⋅=⋅∵AB AC =,∴PE PF CH -=.故答案为:PE PF CH -=.【点睛】本题考查几何图形中等面积法的应用,读懂题目,灵活运用题设条件是解题的关键.10.图1,线段AB 、CD 相交于点O ,连接AD 、CB ,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ,并且与CD 、AB 分别相交于M 、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D 之间的数量关系: ;(2)图2中,当∠D=50度,∠B=40度时,求∠P 的度数.(3)图2中∠D 和∠B 为任意角时,其他条件不变,试问∠P 与∠D、∠B 之间存在着怎样的数量关系.【答案】(1)∠A+∠D=∠C+∠B;(2)∠P=45°;(3)2∠P=∠D+∠B.【解析】【分析】(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;(2)由(1)得,∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义可得∠DAP=∠PAB,∠DCP=∠PCB,将①+②整理可得2∠P=∠D+∠B,进而求得∠P的度数;(3)同(2)根据“8字形”中的角的规律和角平分线的定义,即可得出2∠P=∠D+∠B.【详解】解(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,∴∠A+∠D=∠C+∠B;(2)由(1)得,∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠PAB+∠P,②∵∠DAB和∠BCD的平分线AP和CP相交于点P,∴∠DAP=∠PAB,∠DCP=∠PCB,①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,即2∠P=∠D+∠B=50°+40°,∴∠P=45°;(3)关系:2∠P=∠D+∠B;证明过程同(2).。
八年级数学上册三角形解答题易错题(Word版 含答案)

八年级数学上册三角形解答题易错题(Word版含答案)一、八年级数学三角形解答题压轴题(难)1.探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX等于多少度;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.【答案】(1)详见解析;(2)①50°;②85°;③63°.【解析】【分析】(1)连接AD并延长至点F,根据外角的性质即可得到∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,即可得出∠BDC=∠A+∠B+∠C;(2)①根据(1)得出∠ABX+∠ACX+∠A=∠BXC,再根据∠A=40°,∠BXC=90°,即可求出∠ABX+∠ACX的度数;②先根据(1)得出∠ADB+∠AEB=90°,再利用DC平分∠ADB,EC平分∠AEB,即可求出∠DCE的度数;③由②得∠BG1C=110(∠ABD+∠ACD)+∠A,设∠A为x°,即可列得110(133-x)+x=70,求出x的值即可.【详解】(1)如图(1),连接AD并延长至点F,根据外角的性质,可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,∴∠BDC=∠A+∠B+∠C;(2)①由(1),可得∠ABX+∠ACX+∠A=∠BXC,∵∠A=40°,∠BXC=90°,∴∠ABX+∠ACX=90°-40°=50°;②由(1),可得∠DBE=∠DAE+∠ADB+∠AEB,∴∠ADB+∠AEB=∠DBE-∠DAE=130°-40°=90°,∴12(∠ADB+∠AEB)=90°÷2=45°,∵DC平分∠ADB,EC平分∠AEB,∴12ADC ADB∠=∠,12AEC AEB∠=∠,∴∠DCE=∠ADC+∠AEC+∠DAE,=12(∠ADB+∠AEB)+∠DAE,=45°+40°, =85°;③由②得∠BG1C=110(∠ABD+∠ACD)+∠A,∵∠BG1C=70°,∴设∠A为x°,∵∠ABD+∠ACD=133°-x°∴110(133-x)+x=70,∴13.3-110x+x=70,解得x=63,即∠A的度数为63°.【点睛】此题考查三角形外角的性质定理,三角形的外角等于与它不相邻的内角的和,,根据此定理得到角度的规律,由此解决问题,此题中得到平分角的变化规律是解题的难点.2.如图,在△ABC 中,记∠A=x 度,回答下列问题:(1)图中共有三角形个.(2)若 BD,CE 为△ABC 的角平分线,则∠BHC= 度(结果用含 x 的代数式表示),并证明你的结论.(3)若 BD,CE 为△ABC 的高线,则∠BHC= 度(结果用含 x 的代数式表示),并证明你的结论.【答案】(1)图中共有三角形 8 个;(2)(90+12x ) ;(3)(180-x).【解析】【分析】本题考查的是三角形内角和定理,分析题意观察图形,根据三角形内角和为180°可知∠ABC=180-2x,根据角平分线的性质可以求出∠BHC,根据高线的性质可知∠CDB=∠BEC=90º,再次利用三角形内角和定理可以求答案【详解】解:(1)图中共有三角形 8 个;(2)∠BHC=(90+ 12x )度.∵BD,CE 分别是∠ABC,∠ACB 的平分线,∴∠BHC=180º-∠HBC-∠HCB=180º-12(∠ABC+∠ACB)= (90+12x )度.(3)∠BHC=(180-x)度,∵BD,CE 为△ABC 的高线,∴BD⊥AC,CE⊥AB,∴∠CDB=∠BEC=90º,∵∠BEC+∠ABC+∠BCH=180°∠CDB+∠ACB+∠CBH=180°∴∠BEC+∠ABC+∠BCH+∠CDB+∠ACB+∠CBH=360°∠ABC+∠BCH+∠ACB+∠CBH=180°∵∠ABC+∠ACB=180°-∠A∠BCH+∠CBH=180°-∠BHC∴180°-∠A+180°-∠BHC=180°∴∠BHC=(180-x)度【点睛】本题的关键是掌握三角形内角和定理3.如图, A为x轴负半轴上一点, B为x轴正半轴上一点, C(0,-2),D(-3,-2).(1)求△BCD的面积;(2)若AC⊥BC,作∠CBA的平分线交CO于P,交CA于Q,判断∠CPQ与∠CQP的大小关系, 并证明你的结论.【答案】(1)3;(2)∠CPQ=∠CQP,理由见解析;【解析】【分析】(1)求出CD的长度,再根据三角形的面积公式列式计算即可得解;(2)根据角平分线的定义可得∠ABQ=∠CBQ,然后根据等角的余角相等解答;【详解】解:(1)∵点C(0,-2),D(-3,-2),∴CD=3,且CD//x轴∴△BCD面积=12×3×2=3;(2)∠CPQ=∠CQP,∵AC⊥BC,∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°∴∠OAC=∠BCO,又BQ平分∠CBA,∴∠ABQ=∠CBQ,∵∠CQP=∠OAC+∠ABQ∠CPQ=∠CBQ+∠BCO,∴∠CQP=∠CPQ(2)∠CPQ=∠CQP,∵AC⊥BC,∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°∴∠OAC=∠BCO,又BQ平分∠CBA,∴∠ABQ=∠CBQ,∵∠CQP=∠OAC+∠ABQ∠CPQ=∠CBQ+∠BCO,∴∠CQP=∠CPQ【点睛】本题考查了坐标与图形性质,三角形的角平分线,三角形的面积,三角形的内角和定理,三角形的外角性质,综合题,熟记性质并准确识图是解题的关键.4.如图①,在平面直角坐标系中,点A 的坐标为()0,4,4OC OB =.① ②(1)若ABC ∆的面积为20,求点B ,C 的坐标.(2)如图①,向x 轴正方向移动点B ,使90ABC ACB ∠-∠=︒,作BAC ∠的平分线AD 交x 轴于点D ,求ADO ∠的度数.(3)如图②,在(2)的条件下,线段AD 上有一动点Q ,作AQM DQP ∠=∠,它们的边分别交x 轴、y 轴于点M ,P ,作FMG DMQ ∠=∠,试判断FM 与PQ 的位置关系,并说明理由.【答案】(1)10,03B ⎛⎫⎪⎝⎭,40,03C ⎛⎫ ⎪⎝⎭;(2)45°;(3)FM PQ ⊥ 【解析】【分析】(1)设OB=a ,根据三角形的面积公式列式求出a ,即可得到点B 、C 的坐标;(2)设ACB α∠=,根据题意得到∠ABC=90°+α,根据三角形内角和定理得到∠BAC=90°-2α,再根据角平分线的定义、三角形外角的性质即可得到答案;(3)延长FM 交QP 于H ,设∠DQP=∠AQM=α,∠FMG=∠DMQ=β,根据三角形外角的性质、三角形内角和定理求出∠2+∠DMH=90°即可得到答案.【详解】(1)设OB=a ,则OC=4a ,∴BC=3a ,由题意得,134202a ⨯⨯=, 解得:a=103, ∴OB=103,OC=403,∴10,03B ⎛⎫ ⎪⎝⎭,40,03C ⎛⎫ ⎪⎝⎭; (2)设ACB α∠=,∵90ABC ACB ∠-∠=︒,∴90ABC α∠=︒+,∴180BAC ABC ACB ∠=︒-∠-∠()18090αα=︒-︒+-902α=︒-,∵AD 平分BAC ∠,∴1452DAC BAC α∠=∠=︒-, ∴4545ADO DAC ACB αα∠=∠+∠=︒-+=︒;(3)FM ⊥PQ ,理由如下:延长FM 交PQ 于点H ,.设∠DQP=∠AQM=α,∠FMG=∠DMQ=β,则∠DMH=∠FMG=β,∠AQM=∠QMD+∠QDM ,即α=β+45°,∴∠1=180°-∠DQP-∠ADO=90°-β,∴∠2=∠1=90°-β,∴∠2+∠DMH=β+90°-β=90°,∴∠MHQ=90°,即FM ⊥PQ.【点睛】本题考查了角平分线的定义,三角形外角的性质,三角形内角和定理,熟练掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.5.已知:点D 是△ABC 所在平面内一点,连接AD 、CD .(1)如图1,若∠A =28°,∠B =72°,∠C =11°,求∠ADC ;(2)如图2,若存在一点P ,使得PB 平分∠ABC ,同时PD 平分∠ADC ,探究∠A ,∠P ,∠C 的关系并证明;(3)如图3,在 (2)的条件下,将点D 移至∠ABC 的外部,其它条件不变,探究∠A ,∠P ,∠C 的关系并证明.【答案】(1) 111º ;(2) ∠A-∠C=2∠P,理由见解析;(3) ∠A+∠C=2∠P,理由见解析.【解析】【分析】(1)延长AD交BC于E,利用三角形外角的性质即可求解;(2)∠A-∠C=2∠P,由三角形外角等于不相邻的两个内角的和以及(1)结论即可求解;(3)∠A+∠C=2∠P,由(2)结论以及角平分线的性质即可得到.【详解】(1)如图1,延长AD交BC于E,在△ABE中,∠AEC=∠A+∠B=28º+72º=100º,在△DEC中,∠ADC=∠AEC+∠C=100º+11º=111º ;(2)∠A-∠C=2∠P,理由如下:如图2,∠5=∠A+∠1,∠5=∠P+∠3∴∠A+∠1=∠P+∠3∵PB平分∠ABC,PD平分∠ADC∴∠1=∠2,∠3=∠4∴∠A+∠2=∠P+∠4由(1)知∠4=∠2+∠P+∠C∴∠A+∠2=∠P+∠2+∠P+∠C∴∠A-∠C=2∠P(3)∠A+∠C=2∠P,理由如下:如图3,同(2)理知∠A+∠1=∠P+∠3,∠C+∠4=∠P+∠2∴∠A+∠C+∠1+∠4=2∠P+∠2+∠3∵PB平分∠ABC,PD平分∠ADC∴∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3∴∠A+∠C=2∠P【点睛】本题考查了三角形外角的性质,角平分线的定义,整体思想的利用是解题的关键.6.(1)如图1,有一块直角三角板XYZ(其中∠X=90°)放置在△ABC上,恰好三角板XYZ 的两条直角边XY,XZ分别经过B,C两点,且直角顶点X在△ABC内部.①若∠A=40°,∠ABC+∠ACB= °;∠XBC+∠XCB= °;②试判断∠A与∠XBA+∠XCA之间存在怎样数量关系?并写出证明过程.(2)如图2,如果直角顶点X在△ABC外部,试判断∠A、∠XBA、∠XCA之间又存在怎样的数量关系?(只写出答案,无需证明).【答案】(1)①140,90;②∠A+∠XBA+∠XCA=90°,证明见解析;(2)∠A+(∠XBA-∠XCA)=90°【解析】试题分析:(1)①根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=140°,∠XBC+∠XCB=180°﹣∠XBC=90°,进而可求出∠ABX+∠ACX 的度数;②根据三角形内角和定义有90°+(∠ABX+∠ACX)+∠A=180°,则可得出结论.(2)由②的解题思路可得:∠A+(∠XBA-∠XCA)=90°.(1)①若∠A=40°,∠ABC+∠ACB= 140 °;∠XBC+∠XCB= 90 °;②∠A+∠XBA+∠XCA=90°(或等式的变形也可以)证明:∵∠X=90°∴∠XBC+∠XCB=180°-∠X=90°∵∠A+∠ABC+∠ACB=180°,∴∠A+(∠XBA+∠XCA)+(∠XBC+∠XCB)=180°,∴∠A+(∠XBA+∠XCA)=180°-90°=90°,∴∠A=90°-(∠XBA+∠XCA)(2)∠A+(∠XBA-∠XCA) =90°.点睛:本题考查三角形外角的性质及三角形的内角和定理,解答的关键是熟练掌握三角形的内角和为180°以及沟通外角和内角的关系.7.(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.x=____________°;x=____________°;x=____________°;(3)如图③,一个六角星,其中∠BOD=70°,则∠A+∠B+∠C+∠D+∠E+∠F=________°.【答案】(1)证明见解析. (2)180;180;180;(3)140【解析】【分析】(1)首先延长BO交AC于点D,可得BOC=∠BDC+∠C,然后根据∠BDC=∠A+∠B,判断出∠BOC=∠B+∠C+∠A即可.(2)a、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.b、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.c、首先延长EA交CD于点F,EA和BC交于点G,然后根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B,再根据∠GFC+∠FGC+∠C=180°,可得x=∠A+∠B+∠C+∠D+∠E=180°,据此解答即可.(3)根据∠BOD=70°,可得∠A+∠C+∠E=70°,∠B+∠D+∠F=70°,据此求出∠A+∠B+∠C+∠D+∠E+∠F的度数是多少即可.【详解】(1)证明:如图,延长BO交AC于点D,则∠BOC=∠BDC+∠C,又∵∠BDC=∠A+∠B,∴∠BOC=∠B+∠C+∠A.(2)180;180;180(3)140【点睛】(1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.(2)此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.8.如图,将一块三角板ABC的直角顶点C放在直尺的一边PQ上,直尺的另一边MN与三角板的两边AC、BC分别交于两点E、D,且AD为∠BAC的平分线,∠B=300,∠ADE=150.(1)求∠BDN的度数;(2)求证:CD=CE.【答案】(1)∠BDN=∠CDE=450(2)CD=CE【解析】试题分析:(1)根据直角三角形的性质,求出∠BAC=60°,然后根据角平分线的性质求出∠CAD=30°,进而根据三角形的内角和求出∠CDA=60°,最后根据角的和差求解即可;(2)结合(1)的关系,由“等角对等边”得出结论.试题解析:(1)在直角三角形ABC中,∠ACB=900,∠B=300,∴∠BAC=600,又AD平分∠BAC,∴∠CAD=300,又∠ACD=900,∴∠CDA=600又∠ADE=150,∴∠CDE=∠CDA-∠ADE=600-150=450∴∠BDN=∠CDE=450(2)在△CED中,∠ECD=900,∠CDE=450∴∠CED=450∴ CD=CE点睛:此题主要考查了直角三角形、角平分线的性质,三角形的内角和定理,解题关键是利用三角形的外角和内角求解角之间的和差关系即可.9.根据题意解答:(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.(2)阅读下面的内容,并解决后面的问题:如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.解:∵AP、CP分别平分∠BAD、∠BCD∴∠1=∠2,∠3=∠4由(1)的结论得:∠P+∠3=∠1+∠B①,∠P+∠2=∠4+∠D②,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D∴∠P= 12(∠B+∠D)=26°.①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.【答案】(1)证明见解析;(2)①∠P=26゜;②∠P=180°﹣12(∠B+∠D);③∠P=90°+ 12(∠B+∠D).【解析】试题分析:(1)根据三角形的内角和等于180°列式整理即可得证;(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;①表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;②根据四边形的内角和等于360°,可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解;③根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.试题解析:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜,∴∠A+∠B+∠AOB=∠C+∠D+∠COD.∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D.(2)①∠P=26゜.∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4.由(1)的结论得:∠PAD+∠P=∠PCD+∠D①,∠PAB+∠P=∠PCB+∠B②,∵∠PAB=∠1,∠1=∠2,∴∠PAB=∠2,∴∠2+∠P=∠3+∠B③,①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,∴∠P=12(∠B+∠D)=26°.②如图4,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,∴2∠P+∠B+∠D=360°,∴∠P=180°﹣12(∠B+∠D);③如图5,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∵(∠1+∠2)+∠B=(180°﹣2∠3)+∠D,∠2+∠P=(180°﹣∠3)+∠D,∴2∠P=180°+∠D+∠B,∴∠P=90°+ 12(∠B+∠D).点睛:本题考查了三角形的内角和定理,角平分线的定义,准确识图并运用好“8字形”的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.10.等边△ABC边长为6,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转。
八年级数学三角形解答题易错题(Word版 含答案)

八年级数学三角形解答题易错题(Word 版 含答案)一、八年级数学三角形解答题压轴题(难)1.直线MN 与直线PQ 垂直相交于O ,点A 在直线PQ 上运动,点B 在直线MN 上运动. (1)如图1,已知AE 、BE 分别是∠BAO 和∠ABO 角的平分线,点A 、B 在运动的过程中,∠AEB 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB 的大小.(2)如图2,已知AB 不平行CD ,AD 、BC 分别是∠BAP 和∠ABM 的角平分线,又DE 、CE 分别是∠ADC 和∠BCD 的角平分线,点A 、B 在运动的过程中,∠CED 的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.(3)如图3,延长BA 至G ,已知∠BAO 、∠OAG 的角平分线与∠BOQ 的角平分线及延长线相交于E 、F ,在△AEF 中,如果有一个角是另一个角的3倍,试求∠ABO 的度数.【答案】(1)135°;(2)67.5°;(3)60°, 45°【解析】【分析】(1)根据直线MN 与直线PQ 垂直相交于O 可知∠AOB=90°,再由AE 、BE 分别是∠BAO 和∠ABO 的角平分线得出1BAE OAB 2∠=∠,1ABE ABO 2∠=∠,由三角形内角和定理即可得出结论;(2)延长AD 、BC 交于点F ,根据直线MN 与直线PQ 垂直相交于O 可得出∠AOB=90°,进而得出OAB OBA 90∠+∠=︒ ,故PAB MBA 270∠+∠=︒,再由AD 、BC 分别是∠BAP 和∠ABM 的角平分线,可知1BAD BAP 2∠=∠,1ABC ABM 2∠=∠,由三角形内角和定理可知∠F=45°,再根据DE 、CE 分别是∠ADC 和∠BCD 的角平分线可知CDE DCE 112.5∠+∠=︒,进而得出结论;(3))由∠BAO 与∠BOQ 的角平分线相交于E 可知1EAO BAO 2∠=∠,1EOQ BOQ 2∠=∠ ,进而得出∠E 的度数,由AE 、AF 分别是∠BAO 和∠OAG 的角平分线可知∠EAF=90°,在△AEF 中,由一个角是另一个角的3倍分四种情况进行分类讨论.【详解】(1)∠AEB 的大小不变,∵直线MN 与直线PQ 垂直相交于O ,∴∠AOB=90°, ∴OAB OBA 90∠+∠=︒,∵AE 、BE 分别是∠BAO 和∠ABO 角的平分线,∴1BAE OAB 2∠=∠,1ABE ABO 2∠=∠, ∴()1BAE ABE OAB ABO 452∠+∠=∠+∠=°, ∴∠AEB=135°;(2)∠CED 的大小不变.如图2,延长AD 、BC 交于点F .∵直线MN 与直线PQ 垂直相交于O ,∴90∠=AOB °,∴OAB OBA 90∠+∠=°,∴PAB MBA 270∠+∠=°,∵AD 、BC 分别是∠BAP 和∠ABM 的角平分线,∴1BAD BAP 2∠=∠,1ABC ABM 2∠=∠, ∴()1BAD ABC PAB ABM 1352∠+∠=∠+∠=°,F 45∠=°, ∴FDC FCD 135∠+∠=°,∴CDA DCB 225∠+∠=°,∵DE 、CE 分别是∠ADC 和∠BCD 的角平分线,∴CDE DCB 112.5∠+∠=°,∴E 67.5∠=°;(3)∵∠BAO 与∠BOQ 的角平分线相交于E ,∴1EAO BAO 2∠=∠,1EOQ BOQ 2∠=∠ , ∴()11E EOQ EAO BOQ BAQ ABO 22∠=∠-∠=∠-∠=∠, ∵AE 、AF 分别是∠BAO 和∠OAG 的角平分线,∴EAF 90∠=°.在△AEF 中,∵有一个角是另一个角的3倍,故有:①EAF 3E ∠=∠,E 30∠=°,ABO 60∠=°;②EAF 3F ∠=∠,E 60∠=°,ABO 120∠=°;③EAF 3E ∠=∠,E 22.5∠=°,ABO 45∠=°;④EAF 3F ∠=∠,E 67.5∠=°,ABO 135∠=°.∴∠ABO 为60°或45°.【点睛】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.2.已知在四边形ABCD 中,∠A =∠C =90°.(1)∠ABC +∠ADC = °;(2)如图①,若DE 平分∠ADC ,BF 平分∠ABC 的外角,请写出DE 与BF 的位置关系,并证明;(3)如图②,若BE ,DE 分别四等分∠ABC 、∠ADC 的外角(即∠CDE =14∠CDN ,∠CBE =14∠CBM ),试求∠E 的度数.【答案】(1)180°;(2)DE ⊥BF ;(3)450【解析】【分析】(1)根据四边形内角和等于360°列式计算即可得解;(2)延长DE 交BF 于G ,根据角平分线的定义可得∠CDE=12∠ADC ,∠CBF=12∠CBM ,然后求出∠CDE=∠CBF ,再利用三角形的内角和定理求出∠BGE=∠C=90°,最后根据垂直的定义证明即可;(3)先求出∠CDE+∠CBE ,然后延长DC 交BE 于H ,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可.【详解】(1)解:∵∠A=∠C=90°,∴∠ABC+∠ADC=360°-90°×2=180°;故答案为180°;(2)解:延长DE 交BF 于G ,∵DE 平分∠ADC ,BF 平分∠CBM ,∴∠CDE=12∠ADC ,∠CBF=12∠CBM , 又∵∠CBM=180°-∠ABC=180°-(180°-∠ADC )=∠ADC ,∴∠CDE=∠CBF ,又∵∠BED=∠CDE+∠C=∠CBF+∠BGE ,∴∠BGE=∠C=90°,∴DG ⊥BF ,即DE ⊥BF ;(3)解:由(1)得:∠CDN+∠CBM=180°,∵BE 、DE 分别四等分∠ABC 、∠ADC 的外角,∴∠CDE+∠CBE=14×180°=45°, 延长DC 交BE 于H , 由三角形的外角性质得,∠BHD=∠CDE+∠E ,∠BCD=∠BHD+∠CBE ,∴∠BCD=∠CBE+∠CDE+∠E ,∴∠E=90°-45°=45°【点睛】本题考查了三角形的内角和定理,四边形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键,要注意整体思想的利用.3.已知:线段AB ,以AB 为公共边,在AB 两侧分别作ABC ∆和ABD ∆,并使C D ∠=∠.点E 在射线CA 上.(1)如图l ,若ACBD ,求证:AD BC ∥; (2)如图2,若BD BC ⊥,请探究DAE ∠与C ∠的数量关系,写出你的探究结论,并加以证明; (3)如图3,在(2)的条件下,若BAC BAD ∠=∠,过点D 作DF BC ∥交射线于点F ,当8DFE DAE ∠=∠时,求BAD ∠的度数.【答案】(1)见详解;(2)DAE ∠+2C ∠=90°,理由见详解;(3)99°.【解析】【分析】(1)根据平行线的性质和判定定理,即可得到结论;(2)设CE 与BD 交点为G ,由三角形外角的性质得∠CGB=∠D+∠DAE ,由BD BC ⊥,得∠CGB+∠C=90°,结合C D ∠=∠,即可得到结论;(3)设∠DAE=x ,则∠DFE=8x ,由DF BC ∥,DAE ∠+2C ∠=90°,得关于x 的方程,求出x 的值,进而求出∠C ,∠ADB 的度数,结合∠BAD=∠BAC ,即可求解.【详解】(1)∵AC BD ,∴∠C+∠CBD=180°,∵C D ∠=∠,∴∠D+∠CBD=180°,∴AD BC ∥;(2)DAE ∠+2C ∠=90°,理由如下:设CE 与BD 交点为G ,∵∠CGB 是∆ADG 的外角,∴∠CGB=∠D+∠DAE ,∵BD BC ⊥,∴∠CBD=90°,∴在∆BCG 中,∠CGB+∠C=90°,∴∠D+∠DAE+∠C=90°,又∵C D ∠=∠,∴DAE ∠+2C ∠=90°;(3)设∠DAE=x ,则∠DFE=8x ,∴∠AFD=180°-8x ,∵DF BC ∥,∴∠C=∠AFD=180°-8x ,又∵DAE ∠+2C ∠=90°,∴x+2(180°-8x)=90°,解得:x=18°,∴∠C=180°-8x=36°=∠ADB ,又∵∠BAD=∠BAC ,∴∠ABC=∠ABD=12∠CBD=45°, ∴∠BAD=180°-45°-36°=99°.【点睛】本题主要考查平行线的性质和判定定理,三角形的内角和定理与外角的性质,掌握平行线的性质和三角形外角的性质,是解题的关键.4.探究:(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB.求证:∠P=90°+12∠A.(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE.猜想∠P和∠A有何数量关系,并证明你的结论.(3)如图3,BP平分∠CBF,CP平分∠BCE.猜想∠P和∠A有何数量关系,请直接写出结论.【答案】(1)见解析;(2)12∠A=∠P,理由见解析;(3)∠P=90°﹣12∠A,理由见解析【解析】【分析】(1)根据三角形内角和定理以及角平分线的性质进行解答即可:(2)根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果,(3)根据三角形的外角性质、内角和定理、角平分线的定义探求并证明.【详解】证明:(1)∵△ABC中,∠ABC+∠ACB=180°﹣∠A.又∵BP平分∠ABC,CP平分∠ACB,∴∠PBC=12∠ABC,∠PCB=12∠ACB,∴∠PBC+∠PCB=12(180°﹣∠A),根据三角形内角和定理可知∠BPC=180°﹣12(180°﹣∠A)=90°+12∠A;(2)12∠A=∠P,理由如下:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠PBC=12∠ABC,∠PCE=12∠ACE.∵∠ACE是△ABC的外角,∠PCE是△BPC的外角,∴∠ACE=∠ABC+∠A,∠PCE=∠PBC+∠P,∴12∠ACP=12∠ABC+12∠A,∴12∠ABC+12∠A=∠PBC+∠P,∴12∠A=∠P.(3)∠P=90°﹣12∠A,理由如下:∵P点是外角∠CBF和∠BCE的平分线的交点,∠P+∠PBC+∠PCB=180°∴∠P=180°﹣(∠PBC+∠PCB)=180°﹣12(∠FBC+∠ECB)=180°﹣12(∠A+∠ACB+∠A+∠ABC)=180°﹣12(∠A+180°)=90°﹣12∠A.【点睛】本题考查了角平分线的定义,一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为180°,此类题解题的关键是找出角平分线平分的两个角的和的度数,从而利用三角形内角和定理求解.5.已知:点D是△ABC所在平面内一点,连接AD、CD.(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;(3)如图3,在(2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.【答案】(1) 111º ;(2) ∠A-∠C=2∠P,理由见解析;(3) ∠A+∠C=2∠P,理由见解析.【解析】【分析】(1)延长AD交BC于E,利用三角形外角的性质即可求解;(2)∠A-∠C=2∠P,由三角形外角等于不相邻的两个内角的和以及(1)结论即可求解;(3)∠A+∠C=2∠P,由(2)结论以及角平分线的性质即可得到.【详解】(1)如图1,延长AD交BC于E,在△ABE中,∠AEC=∠A+∠B=28º+72º=100º,在△DEC中,∠ADC=∠AEC+∠C=100º+11º=111º ;(2)∠A-∠C=2∠P,理由如下:如图2,∠5=∠A+∠1,∠5=∠P+∠3∴∠A+∠1=∠P+∠3∵PB平分∠ABC,PD平分∠ADC∴∠1=∠2,∠3=∠4∴∠A+∠2=∠P+∠4由(1)知∠4=∠2+∠P+∠C∴∠A+∠2=∠P+∠2+∠P+∠C∴∠A-∠C=2∠P(3)∠A+∠C=2∠P,理由如下:如图3,同(2)理知∠A+∠1=∠P+∠3,∠C+∠4=∠P+∠2∴∠A+∠C+∠1+∠4=2∠P+∠2+∠3∵PB平分∠ABC,PD平分∠ADC∴∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3∴∠A+∠C=2∠P【点睛】本题考查了三角形外角的性质,角平分线的定义,整体思想的利用是解题的关键.6.如图①,在△ABC中,AE平分∠BAC,∠C>∠B,F是AE上一点,且FD⊥BC于D点.(1)试猜想∠EFD,∠B,∠C的关系,并说明理由;(2)如图②,当点F在AE的延长线上时,其余条件不变,(1)中的结论还成立吗?说明理由.①②【答案】(1)∠EFD=12∠C-12∠B.()成立,理由见解析.【解析】【分析】先根据AE 平分∠BAC 推出∠BAE=12∠BAC=12[180°-(∠B+∠C )],再根据外角的定义求出∠FED=∠B+∠BAE ,然后利用直角三角形的性质求出∠EFD=90°-∠FED . 【详解】 解:(1)∠EFD =12∠C -12∠B . 理由如下:由AE 是∠BAC 的平分线知∠BAE =12∠BAC . 由三角形外角的性质知∠FED =∠B +12∠BAC , 故∠B +12∠BAC +∠EFD =90°①. 在△ABC 中,由三角形内角和定理得∠B +∠BAC +∠C =180°, 即12∠C +12∠B +12∠BAC =90°②. ②-①,得∠EFD =12∠C -12∠B . (2)成立.理由如下:由对顶角相等和三角形的外角性质知:∠FED =∠AEC =∠B +12∠BAC , 故∠B +12∠BAC +∠EFD =90°①. 在△ABC 中,由三角形内角和定理得: ∠B +∠BAC +∠C =180°,即12∠B +12∠BAC +12∠C =90°②.②-①,得∠EFD =12∠C -12∠B . 【点睛】 此题主要考查了角平分线的性质、三角形内角和定理和直角三角形的性质,命题时经常将多个知识点联系在一起进行考查,这样更能训练学生的解题能力.7.如图 (1)所示,AB ,CD 是两条线段,M 是AB 的中点,连接AD ,MD ,BC ,BD , MC ,AC ,S △DMC ,S △DAC 和S △DBC 分别表示△DMC ,△DAC ,△DBC 的面积,当AB ∥CD 时,有S △DMC =2DAC DBC S S.(1)如图 (2)所示,当图6-9(1)中AB 与CD 不平行时,S △DMC =2DBC DAC S S +是否仍然成立?请说明理由; (2)如图 (3)所示,当图6-9(1)中AB 与CD 相交于点O 时,S △DMC 与S △DAC ,S △DBC 有什么样的数量关系?试说明你的结论.【答案】(1) S △DMC =2DAC DBC S S +仍成立,理由见解析; (2)S △DMC =2DBC DAC S S -,理由见解析.【解析】【分析】(1)先看题中给出的条件为何成立,由于三角形ADC ,DMC ,DBC 都是同底,而由于AB ∥DC ,因此高相等,就能得出题中给出的结论,那么本题也要用高来求解,过A ,M ,B 分别作BC 的垂线AE ,MN ,BF ,AE ∥MN ∥BF ,由于M 是AB 中点,因此MN 是梯形AEFB 的中位线,因此MN=12(AE+BF ),三个三角形同底因此结论①是成立的. (2)本题可以利用AM=MB ,让这两条边作底边来求解,三角形ADB 中,小三角形的AB 边上的高都相等,那么三角形ADM 和DBM 的面积就相等(等底同高),因此三角形OAD ,OMD 的和就等于三角形BMD 的面积,同理三角形AOC 和OMC 的面积和等于三角形CMB 的面积.根据这些等量关系即可得出题中三个三角形的面积关系.【详解】(1)当AB 与CD 不平行时,S △DMC =2DAC DBC S S+仍成立.分别过点A ,M ,B 作CD 的垂线AE ,MN ,BF ,垂足分别为E ,N ,F.∵M 为AB 的中点,∴MN =12(AE+BF),∴S △DAC +S △DBC =12DC·AE+12DC·BF =12DC·(AE+BF)= 12DC·2MN=DC·MN=2S △DMC .∴S △DMC =2DAC DBC S S +; (2)S △DMC =2DBC DAC S S-.理由:∵M 是AB 的中点,∴S △ADM =S △BDM ,S △ACM =S △BCM ,而S △DBC =S △BDM +S △BCM +S △DMC ,① S △DAC =S △ADM +S △ACM -S △DMC ,②∴①-②得S △DBC -S △DAC =2S △DMC ,故S △DMC =2DBC DAC S S-.【点睛】本题考查了三角形中位线和梯形,解题的关键是掌握三角形中位线定理和梯形的概念.8.学习几何的一个重要方法就是要学会抓住基本图形,让我们来做一次研究性学习.(1)如图①所示的图形,像我们常见的学习用品一圆规,我们常把这样的图形叫做“规形图”.请你观察“规形图”,试探究∠BOC与∠A、∠B、∠C之间的关系,并说明理由:(2)如图②,若△ABC中,BO平分∠ABC,CO平分∠ACB,且它们相交于点O,试探究∠BOC与∠A的关系;(3)如图③,若△ABC中,∠ABO=13∠ABC,∠ACO=13∠ACB,且BO、CO相交于点O,请直接写出∠BOC与∠A的关系式为_.【答案】(1)∠BOC=∠BAC+∠B+∠C.理由见解析;(2)∠BOC=90°+12∠A.理由见解析;(3)∠BOC=60°+23∠A.理由见解析.【解析】【分析】(1)如图1,连接AO,延长AO到H.由三角形的外角的性质证明即可得到结论:∠BOC=∠BAC+∠B+∠C;(2)利用角平分线的定义,三角形的内角和定理证明可得到结论:∠BOC=90°+12∠A;(3)类似(2)可证明结论:∠BOC=60°+23∠A.【详解】解:(1)∠BOC=∠BAC+∠B+∠C.理由:如图1,连接AO,延长AO到H.∵∠BOH=∠B+∠BAH,∠CAH=∠C+∠CAH,∴∠BOC=∠B+∠BAH+∠CAH+∠C=∠BAC+∠B+∠C,∴∠BOC=∠BAC+∠B+∠C;(2)∠BOC=90°+12∠A.理由:如图2,∵OB,OC是△ABC的角平分线,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∴∠BOC=180°-12(∠ABC+∠ACB)=180°-(180°-∠A)=90°+12∠A,∴∠BOC=90°+12∠A;(3)∠BOC=60°+23∠A.理由:∵∠ABO=13∠ABC,∠ACO=13∠ACB,∴∠BOC=180°-23(∠ABC+∠ACB)=180°-23(180°-∠A)=60°+23∠A.故答案为:∠BOC=60°+23∠A.【点睛】本题考查三角形的内角和定理,三角形的外角的性质等知识,解题的关键是熟练掌握三角形的角的基本知识.9.动手操作,探究:探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系.已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.并说明理由.探究二:若将△ADC改为任意四边形ABCD呢?已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,请你利用上述结论探究∠P与∠A+∠B的数量关系,并说明理由.探究三:若将上题中的四边形ABCD改为六边形ABCDEF如图(3)所示,请你直接写出∠P 与∠A+∠B+∠E+∠F的数量关系.【答案】探究一: 90°+12∠A;探究二:12(∠A+∠B);探究三:∠P=12(∠A+∠B+∠E+∠F)﹣180°.【解析】试题分析:探究一:根据角平分线的定义可得∠PDC=12∠ADC,∠PCD=12∠ACD,然后根据三角形内角和定理列式整理即可得解.探究二:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究一解答即可.探究三:根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理探究一解答即可.试题解析:探究一:∵DP、CP分别平分∠AD C和∠ACD,∴∠PDC=12∠ADC,∠PCD=12∠ACD,∴∠DPC=180°-∠PDC-∠PCD,=180°-12∠ADC-12∠ACD,= 180°-12(∠ADC+∠ACD),=180°-12(180°-∠A),=90°+12∠A;探究二:∵DP、CP分别平分∠ADC和∠BCD,∴∠PDC=12∠ADC,∠PCD=12∠BCD,∴∠DPC=180°-∠PDC-∠PCD,=180°-12∠ADC-12∠BCD,=180°-12(∠ADC+∠BCD),=180°-12(360°-∠A-∠B),=12(∠A+∠B);探究三:六边形ABCDEF的内角和为:(6-2)×180°=720°,∵DP、CP分别平分∠EDC和∠BCD,∴∠PDC=12∠EDC,∠PCD=12∠BCD,∴∠P=180°-∠PDC-∠PCD,=180°-12∠EDC-12∠BCD,=180°-12(∠EDC+∠BCD),=180°-12(720°-∠A-∠B-∠E-∠F),=12(∠A+∠B+∠E+∠F)-180°,即∠P=12(∠A+∠B+∠E+∠F)-180°.点睛:本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,在此类题目中根据同一个解答思路求解是解题的关键.10.已知:如图,等边三角形ABD与等边三角形ACE具有公共顶点A,连接CD,BE,交于点P.(1)观察度量,BPC的度数为____.(直接写出结果)(2)若绕点A 将△ACE 旋转,使得180BAC ∠=︒,请你画出变化后的图形.(示意图)(3)在(2)的条件下,求出BPC ∠的度数.【答案】(1)120°;(2)作图见解析;(3)∠BPC =120°.【解析】分析:(1)∠BPC 的度数为120°,理由为:由△ABD 与△ACE 都是等边三角形,利用等边三角形的性质得到∠DAB=∠ABD=∠CAE=60°,AD=AB ,AC=AE ,利用等式的性质得到夹角相等,利用SAS 得出三角形DAC 与三角形BAE 全等,由全等三角形的对应角相等得到∠ADC=∠ABE ,利用外角性质,等量代换即可得到所求;(2)作出相应的图形,如图所示;(3)解法同(1),求出∠BPC 的度数即可.本题解析:(1)∠BPC 的度数为120°,理由为:证明:∵△ABD 与△ACE 都是等边三角形,∴∠DAB=∠ABD=∠CAE=60°,AD=AB ,AC=AE ,∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,在△DAC 与△BAE 中,{AD ABDAC BAE AC AE=∠=∠=,∴△DAC≌△BAE(SAS ),∴∠ADC=∠ABE,∵∠ADC+∠CDB=60°,∴∠ABE+∠CDB=60°,∴∠BPC=∠DBP+∠PDB=∠ABE+∠CDB+∠ABC=120°;(2)作出相应的图形,如图所示;(3)∵△ABD 与△ACE 都是等边三角形,∴∠ADB=∠BAD=∠ABD=∠CAE=60°,AD=AB ,AC=AE ,∴∠DAB+∠DAE=∠CAE+∠DAE,即∠DAC=∠BAE,在△DAC 与△BAE 中,{AD ABDAC BAC AC AE=∠=∠=,∴△DAC≌△BAE(SAS ),∴∠ADC=∠ABE,∵∠ABE+∠DBP=60°, ∴∠ADC+∠DBP=60°,∴∠BPC=∠BDP+∠PBD=∠ADC+∠DBP+∠ADB=120°.点睛:本题考查了等边三角形的性质,外角性质,以及全等三角形的判定与性质,熟练掌握等边三角形的性质是解本题的关键.。
八年级上册数学 全等三角形易错题(Word版 含答案)

八年级上册数学全等三角形易错题(Word版含答案)一、八年级数学轴对称三角形填空题(难)1.在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=12BC,则△ABC的顶角的度数为_____.【答案】30°或150°或90°【解析】试题分析:分两种情况;①BC为腰,②BC为底,根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°,然后分AD在△ABC内部和外部两种情况求解即可.解:①BC为腰,∵AD⊥BC于点D,AD=12 BC,∴∠ACD=30°,如图1,AD在△ABC内部时,顶角∠C=30°,如图2,AD在△ABC外部时,顶角∠ACB=180°﹣30°=150°,②BC为底,如图3,∵AD⊥BC于点D,AD=12 BC,∴AD=BD=CD,∴∠B=∠BAD,∠C=∠CAD,∴∠BAD+∠CAD=12×180°=90°,∴顶角∠BAC=90°,综上所述,等腰三角形ABC的顶角度数为30°或150°或90°.故答案为30°或150°或90°.点睛:本题考查了含30°交点直角三角形的性质,等腰三角形的性质,分类讨论是解题的关键.2.△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=6.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF 运动过程中,若△AEM能构成等腰三角形,则BE的长为______.【答案】363【解析】【分析】分若AE=AM 则∠AME=∠AEM=45°;若AE=EM;若MA=ME 则∠MAE=∠AEM=45°三种情况讨论解答即可;【详解】解:①若AE=AM 则∠AME=∠AEM=45°∵∠C=45°∴∠AME=∠C又∵∠AME>∠C∴这种情况不成立;②若AE=EM∵∠B=∠AEM=45°∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°∴∠BAE=∠MEC在△ABE和△ECM中,B BAE CEN AE EIIC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABE ≌△ECM (AAS ),∴CE =AB =6,∵AC =BC =2AB =23,∴BE =23﹣6;③若MA =ME 则∠MAE =∠AEM =45°∵∠BAC =90°,∴∠BAE =45° ∴AE 平分∠BAC∵AB =AC ,∴BE =12BC =3. 故答案为23﹣6或3.【点睛】本题考查了等腰三角形的判定,掌握分类讨论的数学思想是解答本题的关键.3.已知A 、B 两点的坐标分别为 (0,3),(2,0),以线段AB 为直角边,在第一象限内作等腰直角三角形ABC ,使∠BAC =90°,如果在第二象限内有一点P (a ,12),且△ABP 和△ABC 的面积相等,则a =_____.【答案】-83. 【解析】【分析】先根据AB 两点的坐标求出OA 、OB 的值,再由勾股定理求出AB 的长度,根据三角形的面积公式即可得出△ABC 的面积;连接OP ,过点P 作PE ⊥x 轴,由△ABP 的面积与△ABC 的面积相等,可知S △ABP =S △POA +S △AOB ﹣S △BOP =132,故可得出a 的值.∵A 、B 两点的坐标分别为 (0,3),(2,0),∴OA =3,OB =2,∴223+213AB ==,∵△ABC 是等腰直角三角形,∠BAC =90°,∴1113•1313222ABC S AB AC ⨯⨯===, 作PE ⊥x 轴于E ,连接OP ,此时BE =2﹣a ,∵△ABP 的面积与△ABC 的面积相等,∴111•••222ABP POA AOB BOP S S S S OA OE OB OA OB PE ++=﹣=﹣, 111113332222222a ⨯⨯+⨯⨯⨯⨯=(﹣)﹣=,解得a =﹣83.故答案为﹣83.【点睛】本题考查等腰直角三角形的性质,坐标与图象性质,三角形的面积公式,解题的关键是根据S △ABP =S △POA +S △AOB -S △BOP 列出关于a 的方程.4.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D 在第二象限,且ABD 与ABC 全等,点D 的坐标是______.【答案】(-4,2)或(-4,3)【分析】【详解】把点C 向下平移1个单位得到点D (4,2),这时△ABD 与△ABC 全等,分别作点C ,D 关于y 轴的对称点(-4,3)和(-4,2),所得到的△ABD 与△ABC 全等.故答案为(-4,2)或(-4,3).5.在平面直角坐标系xOy 中,已知点A (2,3),在x 轴上找一点P ,使得△AOP 是等腰三角形,则这样的点P 共有_____个.【答案】4【解析】【分析】以O 为圆心,OA 为半径画弧交x 轴于点P 1、P 3,以A 为圆心,AO 为半径画弧交x 轴于点P 4,作OA 的垂直平分线交x 轴于P 2.【详解】解:如图,使△AOP 是等腰三角形的点P 有4个.故答案为4.【点睛】本题考查了在平面直角坐标系中寻找等腰三角形,掌握两圆一线找等腰三角形是解题的关键.6.如图,在ABC ∆和DBC ∆中,40A ∠=,2AB AC ==,140BDC ∠=,BD CD =,以点D 为顶点作70MDN ∠=,两边分别交,AB AC 于点,M N ,连接的周长为_______.MN,则AMN【答案】4【解析】【分析】延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△CDN,及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.【详解】延长AB至F,使BF=CN,连接DF.∵BD=CD,且∠BDC=140°,∴∠BCD=∠DBC=20°.∵∠A=40°,AB=AC=2,∴∠ABC=∠ACB=70°,∴∠DBA=∠DCA=90°.在Rt△BDF和Rt△CND中,∵BF=CN,∠DBA=∠DCA,DB=DC,∴△BDF≌△CDN,∴∠BDF=∠CDN,DF=DN.∵∠MDN=70°,∴∠BDM+∠CDN=70°,∴∠BDM+∠BDF=70°,∴∠FDM=70°=∠MDN.∵DF=DN,∠FDM=∠MDN,DM=DM,∴△DMN≌△DMF,∴MN=MF,∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=4.故答案为:4.【点睛】本题主要利用等腰三角形的性质来证明三角形全等,构造全等三角形是解答本题的关键.7.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△A n B n A n+1的边长为_____.【答案】2n.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2…进而得出答案.【详解】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∵∠MON=30°,∵OA2=4,∴OA1=A1B1=2,∴A2B1=2,∵△A2B2A3、△A3B3A4是等边三角形,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴A 2B 2=2B 1A 2,B 3A 3=2B 2A 3,∴A 3B 3=4B 1A 2=8,A 4B 4=8B 1A 2=16,A 5B 5=16B 1A 2=32,以此类推△A n B n A n +1的边长为 2n .故答案为:2n .【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA 5=2OA 4=4OA 3=8OA 2=16OA 1是解题的关键.8.如图,已知AB AC =,AD 平分BAC ∠,60DEB EBC ∠=∠=︒,若3BE =,3DE =,则BC =____________.【答案】33+【解析】【分析】延长ED 交BC 于点M ,延长AD 交BC 于点N ,作DF ∥BC 于点F.由已知条件推出△BEM 是等边三角形,△FDE 是等边三角形,在△DNM 中求出NM 的长度,即可求出BC 的长度.【详解】如图,延长ED 交BC 于点M ,延长AD 交BC 于点N ,作DF ∥BC 于点F ,∵AB AC =,AD 平分BAC ∠,∴AN ⊥BC ,BN=CN ,∵60DEB EBC ∠=∠=︒,∴△BEM 是等边三角形,∴△FDE 是等边三角形,∵3BE =,3DE =,∴33DM =-,∵△BEM 是等边三角形,∴∠EMB=60°,∵AN ⊥BC ,∴∠DNM=90°,∴∠NDM=30°,∴13322NM DM -==, ∴3333322BN BM NM -+=-=-=, ∴233BC BN ==+.【点睛】本题考查了等边三角形的性质,解题的关键是作出辅助线构造等边三角形.9.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC 为格点三角形,在图中最多能画出_____个格点三角形与△ABC 成轴对称.【答案】6【解析】【分析】根据网格结构分别确定出不同的对称轴,然后作出轴对称三角形即可得解.【详解】如图,最多能画出6个格点三角形与△ABC 成轴对称.故答案为:6. 【点睛】本题考查了利用轴对称变换作图,熟练掌握网格结构并准确找出对应点的位置是解题的关键,本题难点在于确定出不同的对称轴.10.如图,在边长为6的菱形ABCD 中,∠DAB=60°,E 是AB 的中点,F 是AC 上一个动点,则EF+BF 的最小值是________ .【答案】33【解析】试题解析:∵在菱形ABCD 中,AC 与BD 互相垂直平分,∴点B 、D 关于AC 对称,连接ED ,则ED 就是所求的EF+BF 的最小值的线段,∵E 为AB 的中点,∠DAB=60°,∴DE ⊥AB ,∴ED=22AD AE -=2263-=33,∴EF+BF 的最小值为33.二、八年级数学轴对称三角形选择题(难)11.如图,ABC ∆中,3AC DC ==,BD 垂直BAC ∠的角平分线于D ,E 为AC 的中点,则图中两个阴影部分面积之差的最大值为( )A .1.5B .3C .4.5D .9【答案】C【解析】【分析】首先证明两个阴影部分面积之差=S△ADC,然后由DC⊥AC时,△ACD的面积最大求出结论即可.【详解】延长BD交AC于点H.设AD交BE于点O.∵AD⊥BH,∴∠ADB=∠ADH=90°,∴∠ABD+∠BAD=90°,∠H+∠HAD=90°.∵∠BAD=∠HAD,∴∠ABD=∠H,∴AB=AH.∵AD⊥BH,∴BD=DH.∵DC=CA,∴∠CDA=∠CAD.∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,∴∠CDH=∠H,∴CD=CH=AC.∵BD=DH,AC=CH,∴S△CDH=12S△ADH14=S△ABH.∵AE=EC,∴S△ABE14=S△ABH,∴S△CDH=S△ABE.∵S△OBD﹣S△AOE=S△ADB﹣S△ABE=S△ADH﹣S△CDH=S△ACD.∵AC=CD=3,∴当DC⊥AC时,△ACD的面积最大,最大面积为12⨯3×392=.故选C.【点睛】本题考查了等腰三角形的判定和性质,三角形中线的性质等知识,解题的关键是学会用转化的思想思考问题,属于中考选择题中的压轴题.12.等边△ABC,在平面内找一点P,使△PBC、△PAB、△PAC均为等腰三角形,具备这样条件的P点有多少个?()A.1个B.4个C.7个D.10个【答案】D【解析】试题分析:根据点P在等边△ABC内,而且△PBC、△PAB、△PAC均为等腰三角形,可知P点为等边△ABC的垂心;由此可得分别以三角形各顶点为圆心,边长为半径,交垂直平分线的交点就是满足要求的.解:由点P在等边△ABC内,而且△PBC、△PAB、△PAC均为等腰三角形,可知P点为等边△ABC的垂心;因为△ABC是等边三角形,所以分别以三角形各顶点为圆心,边长为半径画弧,交垂直平分线的交点就是满足要求的,每条垂直平分线上得3个交点,再加三角形的垂心,一共10个.故选D.点评:此题主要考查等腰三角形的性质和等边三角形的性质,有一定的拔高难度,属于中档题.13.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.随x,m,n的值而定【答案】C【解析】【分析】将△ABM绕点B顺时针旋转60°得到△CBH.连接HN.想办法证明∠HCN=120°HN=MN=x即可解决问题.【详解】将△ABM绕点B顺时针旋转60°得到△CBH.连接HN.∵△ABC是等边三角形,∴∠ABC=∠ACB=∠A=60°.∵∠MON=30°,∴∠CBH+∠CBN=∠ABM+∠CBN=30°,∴∠NBM=∠NBH.∵BM=BH,BN=BN,∴△NBM≌△NBH,∴MN=NH=x.∵∠BCH=∠A=60°,CH=AM=n,∴∠NCH=120°,∴x,m,n为边长的三角形△NCH是钝角三角形.故选C.【点睛】本题考查了等边三角形的性质、全等三角形的判定和性质、旋转的性质等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考常考题型.14.如图,∠AOB=60°,点P是∠AOB内的定点且OP=3,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是()A 36B33C.6 D.3【答案】D【解析】分析:作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,利用轴对称的性质得MP=MC,NP=ND,3∠BOP=∠BOD,∠AOP=∠AOC,所以∠COD=2∠AOB=120°,利用两点之间线段最短判断此时△PMN周长最小,作OH⊥CD于H,则CH=DH,然后利用含30度的直角三角形三边的关系计算出CD即可.详解:作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,则MP=MC,NP=ND,3∠BOP=∠BOD,∠AOP=∠AOC,∴PN+PM+MN=ND+MN+MC=DC,∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°,∴此时△PMN周长最小,作OH⊥CD于H,则CH=DH,∵∠OCH=30°,∴OH=1233OH=3 2 ,∴CD=2CH=3.故选D.点睛:本题考查了轴对称﹣最短路线问题:熟练掌握轴对称的性质,会利用两点之间线段最短解决路径最短问题.15.如图,Rt ACB ∆中,90ACB ∠=︒,ABC ∠的平分线BE 和BAC ∠的外角平分线AD 相交于点P ,分别交AC 和BC 的延长线于E ,D .过P 作PF AD ⊥交AC 的延长线于点H ,交BC 的延长线于点F ,连接AF 交DH 于点G .下列结论:①45APB ∠=︒;②PB 垂直平分AF ;③BD AH AB -=;④2DG PA GH =+;其中正确的结论有( )A .4个B .3个C .2个D .1个【答案】A【解析】【分析】 ①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP ,再根据角平分线的定义∠ABP =12∠ABC ,然后利用三角形的内角和定理整理即可得解;②先求出∠APB =∠FPB ,再利用“角边角”证明△ABP 和△FBP 全等,根据全等三角形对应边相等得到AB =BF ,AP =PF ;③根据直角的关系求出∠AHP =∠FDP ,然后利用“角角边”证明△AHP 与△FDP 全等,根据全等三角形对应边相等可得DF =AH ;④求出∠ADG =∠DAG =45°,再根据等角对等边可得DG =AG ,再根据等腰直角三角形两腰相等可得GH =GF ,然后根据即可得到DG GH =+. 【详解】解:①∵∠ABC 的角平分线BE 和∠BAC 的外角平分线,∴∠ABP =12∠ABC , ∠CAP =12(90°+∠ABC )=45°+12∠ABC , 在△ABP 中,∠APB =180°−∠BAP−∠ABP ,=180°−(45°+12∠ABC +90°−∠ABC )−12∠ABC , =180°−45°−12∠ABC−90°+∠ABC−12∠ABC , =45°,故本小题正确;②∵PF ⊥AD ,∠APB =45°(已证),∴∠APB =∠FPB =45°,∵∵PB 为∠ABC 的角平分线,∴∠ABP =∠FBP ,在△ABP 和△FBP 中,APB FPB PB PBABP FBP ∠∠⎧⎪⎨⎪∠∠⎩===, ∴△ABP ≌△FBP (ASA ),∴AB =BF ,AP =PF ;∴PB 垂直平分AF ,故②正确;③∵∠ACB =90°,PF ⊥AD ,∴∠FDP +∠HAP =90°,∠AHP +∠HAP =90°,∴∠AHP =∠FDP ,∵PF ⊥AD ,∴∠APH =∠FPD =90°,在△AHP 与△FDP 中,90AHP FDP APH FPD AP PF ∠∠⎧⎪∠∠︒⎨⎪⎩====,∴△AHP ≌△FDP (AAS ),∴DF =AH ,∵BD =DF +BF ,∴BD=AH+AB,∴BD−AH=AB,故③小题正确;④∵AP=PF,PF⊥AD,∴∠PAF=45°,∴∠ADG=∠DAG=45°,∴DG=AG,∵∠PAF=45°,AG⊥DH,∴△ADG与△FGH都是等腰直角三角形,∴DG=AG,GH=GF,∴DG=GH+AF,∴FG=GH,AF=2PA故2=+.DG PA GH综上所述①②③④正确.故选:A.【点睛】本题考查了直角三角形的性质,全等三角形的判定,以及等腰直角三角形的判定与性质,等角对等边,等边对等角的性质,综合性较强,难度较大,做题时要分清角的关系与边的关系.16.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①AP⊥BC;②AS=AR;③QP∥AR;④△BRP≌△QSP.正确的有( )A.1个B.2个C.3个D.4个【答案】D【解析】【分析】根据到角的两边的距离相等的点在角的平分线上可得AP平分∠BAC,根据等腰三角形“三线合一”的性质判断出①正确;根据HL证明Rt△APR≌Rt△APS,即可判断②正确;根据等边对等角的性质可得∠APQ=∠PAQ,根据三角形外角的性质得到然后得到∠PQC=2∠PAC=60°=∠BAC,然后根据同位角相等两直线平行可得QP∥AB,从而判断出③正确,④由③易证△QPC是等边三角形,得到PQ=PC,等量代换得到BP=PQ,用HL证明Rt△BRP≌Rt△QSP,即可得到④正确.【详解】∵△ABC是等边三角形,PR⊥AB,PS⊥AC,且PR=PS,∴P在∠A的平分线上.∵AB=AC,∴AP⊥BC,故①正确;∵PA =PA ,PR =PS ,∴Rt △APR ≌Rt △APS ,∴AS =AR ,故②正确;∵AQ =PQ ,∴∠APQ =∠PAQ ,∴∠PQC =2∠PAC =60°=∠BAC ,∴PQ ∥AR ,故③正确; 由③得:△PQC 是等边三角形,∴△PQS ≌△PCS ,∴PQ =PC .又∵AB =AC ,AP ⊥BC ,∴BP =PC ,∴BP =PQ .∵PR =PS ,∴Rt △BRP ≌Rt △QSP ,故④也正确.∵①②③④都正确.故选D .【点睛】本题考查了等腰三角形的性质、全等三角形的判定与性质以及等边三角形的判定与性质,准确识图并熟练掌握全等三角形的判定方法与性质是解题的关键.17.如图,Rt ABC ∆中,90ACB ∠=,3AC =,4BC =,5AB =,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B ′处,两条折痕与斜边AB 分别交于点E 、F ,则线段EF 的长为( )A .52B .125C .4D .53【答案】B【解析】【分析】先利用折叠的性质证明出△ECF 是一个等腰直角三角形,因此EF=CE ,然后再根据文中条件综合得出S △ABC =12AC∙BC=12AB∙CE ,求出CE 进而得出答案即可. 【详解】根据折叠性质可知:CD=AC=3,BC=B C '=4,∠ACE=∠DCE ,∠BCF=∠B 'CF ,CE ⊥AB , ∴∠DCE+∠B 'CF=∠ACE+∠BCF ,∵∠ACB=90°,∴∠ECF=45°,又∵CE ⊥AB ,∴△ECF 是等腰直角三角形,∴EF=CE ,又∵S △ABC =12AC∙BC=12AB∙CE , ∴AC∙BC=AB∙CE ,∵3AC =,4BC =,5AB =,∴125 CE=,∴EF12 5 =.所以答案为B选项.【点睛】本题主要考查了直角三角形与等腰三角形性质的综合运用,熟练掌握相关概念是解题关键.18.如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为()A.(-2012,2)B.(-2012,-2)C.(-2013,-2)D.(-2013,2)【答案】A【解析】试题分析:首先由正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),继而求得把正方形ABCD连续经过2014次这样的变换得到正方形ABCD的对角线交点M的坐标.试题解析:∵正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).∴对角线交点M的坐标为(2,2),根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),∴连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(-2012,2).故选A.考点:1.翻折变换(折叠问题);2.正方形的性质;3.坐标与图形变化-平移.19.如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠MPN=110°,则∠AOB=()A.35°B.40°C.45°D.50°【答案】A【解析】【分析】作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA,OB的交点时,△PMN的周长最短,根据对称的性质可以证得:∠OP1M=∠OPM=50°,OP1=OP2=OP,根据等腰三角形的性质求解.【详解】作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA,OB的交点时,△PMN的周长最短,连接P1O、P2O,∵PP1关于OA对称,∠MPN=110°∴∠P1OP=2∠MOP,OP1=OP,P1M=PM,∠OP1M=∠OPM,同理可得:∠P2OP=2∠NOP,OP=OP2,∴∠P1OP2=∠P1OP+∠P2OP=2(∠MOP+∠NOP)=2∠AOB,OP1=OP2=OP,∴△P1OP2是等腰三角形.∴∠OP2N=∠OP1M,∴∠P1OP2=180°-110°=70°,∴∠AOB=35°,故选A.【点睛】考查了对称的性质,解题关键是正确作出图形和证明△P1OP2是等腰三角形是.20.已知等边△ABC中,在射线BA上有一点D,连接CD,并以CD为边向上作等边△CDE,连接BE和AE,试判断下列结论:①AE=BD;②AE与AB所夹锐夹角为60°;③当D在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2,正确的序号有()A.①②B.①②③C.①②④D.①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°,∠ACE=∠ACD+60°可得∠BCD=∠ACE,利用SAS可证明△BCD≌△ACE,可得AE=BD,①正确;∠CBD=∠CAE=60°,进而可得∠EAD=60°,②正确,当∠BCD=90°时,可得∠ACD=∠ADC=30°,可得AD=AC,即可得CE2+AD2=AC2+DE2,④正确;当D点在BA延长线上时,∠BDE-∠BDC=60°,根据△BCD≌△ACE可得∠AEC=∠BDC,进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,即可证明∠BDE-∠BDC=∠BDC+∠AED,即∠BDE-∠AED=2∠BDC,当点D在AB上时可证明∠BDE-∠AED=120°,③错误,综上即可得答案.【详解】∵∠BCA=∠DCE=60°,∴∠BCA+∠ACD=∠DCE+∠ACD,∴∠BCD=∠ACE,又∵AC=BC,CE=CD,∴△BCD≌△ACE,∴AE=BD,∠CBA=∠CAE=60°,∠AEC=∠BDC,①正确,∴∠BAE=120°,∴∠EAD=60°,②正确,∵∠BCD=90°,∠BCA=60°,∴∠ACD=∠ADC=30°,∴AC=AD,∵CE=DE,∴CE2+AD2=AC2+DE2,④正确,当D点在BA延长线上时,∠BDE-∠BDC=60°,∵∠AEC=∠BDC,∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°,∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC,如图,当点D在AB上时,∵△BCD≌△∠ACE,∴∠CAE=∠CBD=60°,∴∠DAE=∠BAC+∠CAE=120°,,③错误∴∠BDE-∠AED=∠DAE=120°故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握。
八年级全等三角形易错题(Word版 含答案)
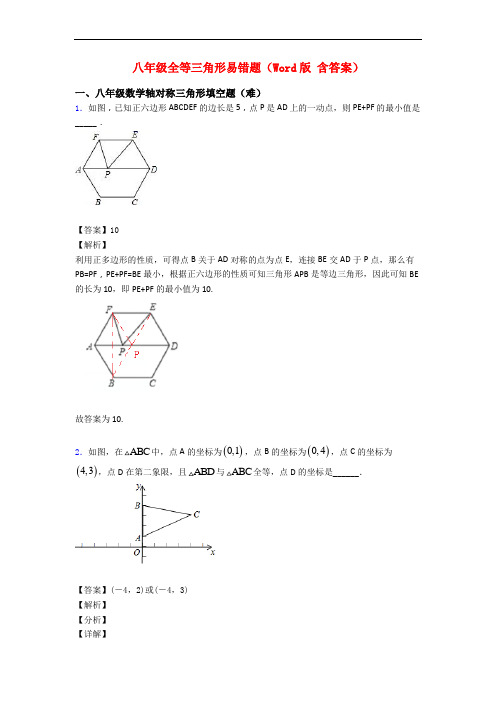
八年级全等三角形易错题(Word 版 含答案)一、八年级数学轴对称三角形填空题(难)1.如图,已知正六边形 ABCDEF 的边长是 5,点 P 是 AD 上的一动点,则 PE+PF 的最小值是_____.【答案】10【解析】利用正多边形的性质,可得点B 关于AD 对称的点为点E ,连接BE 交AD 于P 点,那么有PB=PF ,PE+PF=BE 最小,根据正六边形的性质可知三角形APB 是等边三角形,因此可知BE 的长为10,即PE+PF 的最小值为10.故答案为10.2.如图,在ABC 中,点A 的坐标为()0,1,点B 的坐标为()0,4,点C 的坐标为()4,3,点D 在第二象限,且ABD 与ABC 全等,点D 的坐标是______.【答案】(-4,2)或(-4,3)【解析】【分析】【详解】把点C 向下平移1个单位得到点D (4,2),这时△ABD 与△ABC 全等,分别作点C ,D 关于y 轴的对称点(-4,3)和(-4,2),所得到的△ABD 与△ABC 全等.故答案为(-4,2)或(-4,3).3.如图,△ABC 是等边三角形,高AD 、BE 相交于点H ,BC=43,在BE 上截取BG=2,以GE 为边作等边三角形GEF ,则△ABH 与△GEF 重叠(阴影)部分的面积为_____.【答案】53 【解析】试题分析:如图所示,由△ABC 是等边三角形,BC=43,得到AD=BE=3BC=6,∠ABG=∠HBD=30°,由直角三角的性质,得∠BHD=90°﹣∠HBD=60°,由对顶角相等,得∠MHE=∠BHD=60°,由BG=2,得EG=BE ﹣BG=6﹣2=4.由GE 为边作等边三角形GEF ,得FG=EG=4,∠EGF=∠GEF=60°,△MHE 是等边三角形;S △ABC =12AC•BE=12AC×EH×3EH=13BE=13×6=2.由三角形外角的性质,得∠BIF=∠FGE ﹣∠IBG=60°﹣30°=30°,由∠IBG=∠BIG=30°,得IG=BG=2,由线段的和差,得IF=FG ﹣IG=4﹣2=2,由对顶角相等,得∠FIN=∠BIG=30°,由∠FIN+∠F=90°,得∠FNI=90°,由锐角三角函数,得FN=1,IN=3.S 五边形NIGHM =S △EFG ﹣S △EMH ﹣S △FIN =2233142312⨯-⨯-⨯⨯=53,故答案为53.考点:1.等边三角形的判定与性质;2.三角形的重心;3.三角形中位线定理;4.综合题;5.压轴题.4.如图,在ABC 中,AB AC >,按以下步骤作图:分别以点B 和点C 为圆心,大于BC 一半长为半径作画弧,两弧相交于点M 和点N ,过点M N 、作直线交AB 于点D ,连接CD ,若10AB =,6AC =,则ADC 的周长为_____________________.【答案】16【解析】【分析】利用基本作图可以判定MN 垂直平分BC ,则DC=DB ,然后利用等线段代换得到ACD ∆的周长=AB+AC ,再把10AB =,6AC =代入计算即可.【详解】解:由作法得MN 垂直平分BC ,则DC=DB ,10616ACD C CD AC AD DB AD AC AB AC ∆=++=++=+=+=故答案为:16.【点睛】本题考查了基本作图和线段垂直平分线的性质,熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线)是本题的关键.5.如图,1AB A B =,1112A B A A =,2223A B A A =,3334A B A A =,…,当2n ≥,70A ∠=︒时,11n n n A A B --∠=__________.【答案】1702n -︒ 【解析】【分析】先根据三角形外角的性质及等腰三角形的性质分别求出121B A A ∠,232B A A ∠及343B A A ∠的度数,再找出规律即可得出11n n n A A B --∠的度数.【详解】解:∵在1ABA ∆中,70A ∠=︒,1AB A B =∴170BA A A ∠==︒∠∵1112A A A B =,1BA A ∠是121A A B ∆的外角∴12111211703522B A A A B A BA A ︒∠=∠===︒∠ 同理可得,2321217017.542B A A BA A ︒∠===︒∠,343131708.7582B A A BA A ︒∠===︒∠ ∴111702n n n n A A B ---︒∠=. 故答案为:1702n -︒ 【点睛】本题考查的是等腰三角形的性质及三角形外角的性质,根据特殊情况找出规律是解题关键.6.如图,在Rt △ABC 中,∠ACB =90°,AB 的垂直平分线DE 交BC 的延长线于F ,若∠F =30°,DE =1,则EF 的长是_____.【答案】2【解析】【分析】连接BE ,根据垂直平分线的性质、直角三角形的性质,说明∠CBE =∠F ,进一步说明BE =EF ,,然后再根据直角三角形中,30°所对的直角边等于斜边的一半即可.【详解】解:如图:连接BE∵AB的垂直平分线DE交BC的延长线于F,∴AE=BE,∠A+∠AED=90°,∵在Rt△ABC中,∠ACB=90°,∴∠F+∠CEF=90°,∵∠AED=∠FEC,∴∠A=∠F=30°,∴∠ABE=∠A=30°,∠ABC=90°﹣∠A=60°,∴∠CBE=∠ABC﹣∠ABE=30°,∴∠CBE=∠F,∴BE=EF,在Rt△BED中,BE=2DE=2×1=2,∴EF=2.故答案为:2.【点睛】本题考查了垂直平分线的性质、直角三角形的性质,其中灵活利用垂直平分线的性质和直角三角形30°角所对的边等于斜边的一半是解答本题的关键.7.如图,在△ABC中,AB=AC,点D、E在BC的延长线上,G是AC上一点,且CG=CD,F是GD上一点,且DF=DE.若∠A=100°,则∠E的大小为_____度.【答案】10【解析】【分析】由DF=DE,CG=CD可得∠E=∠DFE,∠CDG=∠CGD,再由三角形的外角的意义可得∠GDC=∠E+∠DFE=2∠E,∠ACB=∠CDG+∠CGD=2∠CD G,进而可得∠ACB=4∠E,最后代入数据即可解答.【详解】解:∵DF=DE,CG=CD,∴∠E=∠DFE,∠CDG=∠CGD,∵GDC=∠E+∠DFE,∠ACB=∠CDG+∠CGD,∴GDC=2∠E,∠ACB=2∠CDG,∴∠ACB=4∠E,∵△ABC中,AB=AC,∠A=100°,∴∠ACB=40°,∴∠E=40°÷4=10°.故答案为10.【点睛】本题考查等腰三角形的性质以及三角形外角的定义,解题的关键是灵活运用等腰三角形的性质和三角形的外角的定义确定各角之间的关系.8.如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 CD 相交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F ,则 BE 的长为_____.【答案】3【解析】【分析】连接CD,BD,由∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,根据角平分线的性质与线段垂直平分线的性质,易得CD=BD,DF=DE,继而可得AF=AE,易证得Rt△CDF≌Rt△BDE,则可得BE=CF,继而求得答案.【详解】如图,连接CD,BD,∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,∴AE=AF,∵DG是BC的垂直平分线,∴CD=BD,在Rt △CDF 和Rt △BDE 中,CD BD DF DE ⎧⎨⎩==,∴Rt △CDF ≌Rt △BDE (HL ),∴BE=CF ,∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE ,∵AB=11,AC=5,∴BE=12(11-5)=3. 故答案为:3.【点睛】 此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.9.如图,在边长为6的菱形ABCD 中,∠DAB=60°,E 是AB 的中点,F 是AC 上一个动点,则EF+BF 的最小值是________ .【答案】33【解析】试题解析:∵在菱形ABCD 中,AC 与BD 互相垂直平分,∴点B 、D 关于AC 对称,连接ED ,则ED 就是所求的EF+BF 的最小值的线段,∵E 为AB 的中点,∠DAB=60°,∴DE ⊥AB ,∴22AD AE -2263-3∴EF+BF 的最小值为3.10.如图, 在Rt △ABC 中,∠ACB =90°,AC =6,BC =8,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B′处,两条折痕与斜边AB 分别交于点E 、F ,则线段B′F 的长为_________【答案】85【解析】【分析】 首先根据折叠可得CD=AC=6,B′C=BC=8,∠ACE=∠DCE ,∠BCF=∠B′CF ,CE ⊥AB ,然后求得△ECF 是等腰直角三角形,进而求得∠B′FD=90°,CE=EF=4.8,由勾股定理求出AE ,得出BF 的长,即 B′F 的长.【详解】 解:根据折叠的性质可知:DE=AE ,∠ACE=∠DCE ,∠BCF=∠B′CF ,CE ⊥AB ,B′F=BF ,∴B′D=8-6=2,∠DCE+∠B′CF=∠ACE+∠BCF ,∵∠ACB=90°,∴∠ECF=45°,∴△ECF 是等腰直角三角形, ∴EF=CE ,∠EFC=45°,∴∠BFC=∠B′FC=135°,∴∠B′FE=90°,∵S △ABC =12AC•BC=12AB•CE , ∴AC•BC=AB•CE , ∵根据勾股定理得:22226810ABAC BC ∴ 4.8AC BC CE AB⋅== ∴EF=4.8,22 3.6AE AC EC -=∴B′F=BF=AB -AE-EF=10-3.6-4.8=1.6=85,故答案是:8 5 .【点睛】此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理等知识;熟练掌握翻折变换的性质,由直角三角形的性质和勾股定理求出CE、AE是解决问题的关键.二、八年级数学轴对称三角形选择题(难)11.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )A.3B.33C.32D.不能确定【答案】B【解析】已知,如图,P为等边三角形内任意一点,PD、PE、PF分别是点P到边AB、BC、AC的距离,连接AP、BP、CP,过点A作AH⊥BC于点H,已知等边三角形的边长为3,可求得高线AH=332,因S△ABC=12BC•AH=12AB•PD+12BC•PE+12AC•PF,所以1 2×3×AH=12×3×PD+12×3×PE+12×3×PF,即可得PD+PE+PF=AH=332,即点P到三角形三边距离之和为332.故选B.点睛:本题考查了等边三角形的性质,根据三角形的面积求点P到三边的距离之和等于等边三角形的高是解题的关键,作出图形更形象直观.12.如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有()个A.1 B.2 C.3 D.4【答案】C【解析】【分析】由已知条件可知∠ABC+∠ACB=90°,又因为CD、BE分别是△ABC的角平分线,所以得到∠FBC+∠FCB=45°,所以求出∠CFB=135°;有平行线的性质可得到:∠ABG=∠ACB,∠BAG=2∠ABF.所以可知选项①③④正确.【详解】∵AB⊥AC.∴∠BAC=90°,∵∠BAC+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=90°∵CD、BE分别是△ABC的角平分线,∴2∠FBC+2∠FCB=90°∴∠FBC+∠FCB=45°∴∠BFC=135°故④正确.∵AG∥BC,∴∠BAG=∠ABC∵∠ABC=2∠ABF∴∠BAG=2∠ABF 故①正确.∵AB⊥AC,∴∠ABC+∠ACB=90°,∵AG⊥BG,∴∠ABG+∠GAB=90°∵∠BAG=∠ABC,∴∠ABG=∠ACB 故③正确.故选C.【点睛】本题考查了等腰三角形的判定与性质,平行线的性质.掌握相关的判定定理和性质定理是解题的关键.的正方形网格中,A,B是如图所示的两个格点,如果C也是格点,且13.在一个33ABC是等腰三角形,则符合条件的C点的个数是()A.6B.7C.8D.9【答案】C【解析】【分析】根据题意、结合图形,画出图形即可确定答案.【详解】解:根据题意,画出图形如图:共8个.故答案为C.【点睛】本题主要考查了等腰三角形的判定,根据题意、画出符合实际条件的图形是解答本题的关键.14.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC 于F,AD交CE于G.则下列结论中错误的是( )A.AD=BE B.BE⊥ACC.△CFG为等边三角形D.FG∥BC【答案】B【解析】试题解析:A.ABC和CDE△均为等边三角形,60AC BC EC DC ACB ECD∴==∠=∠=︒,,,在ACD与BCE 中,{AC BCACD BCECD CF=∠=∠=,ACD BCE∴≌,AD BE∴=,正确.B.据已知不能推出F是AC中点,即AC和BF不垂直,所以AC BE⊥错误,故本选项符合题意.C.CFG是等边三角形,理由如下:180606060ACG BCA∠=︒-︒-︒=︒=∠,ACD BCE≌,CBE CAD∴∠=∠,在ACG和BCF中,{CAG CBFAC BCBCF ACG∠=∠=∠=∠,ACG BCF∴≌,CG CH∴=,又∵∠ACG=60°CFG∴是等边三角形,正确.D.CFG是等边三角形,60CFG ACB∴∠︒=∠﹦,.FG BC∴正确.故选B.15.如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①AP⊥BC;②AS=AR;③QP∥AR;④△BRP≌△QSP.正确的有( )A.1个B.2个C.3个D.4个【答案】D【解析】【分析】根据到角的两边的距离相等的点在角的平分线上可得AP平分∠BAC,根据等腰三角形“三线合一”的性质判断出①正确;根据HL证明Rt△APR≌Rt△APS,即可判断②正确;根据等边对等角的性质可得∠APQ=∠PAQ,根据三角形外角的性质得到然后得到∠PQC=2∠PAC=60°=∠BAC,然后根据同位角相等两直线平行可得QP∥AB,从而判断出③正确,④由③易证△QPC是等边三角形,得到PQ=PC,等量代换得到BP=PQ,用HL证明Rt△BRP≌Rt△QSP,即可得到④正确.【详解】∵△ABC是等边三角形,PR⊥AB,PS⊥AC,且PR=PS,∴P在∠A的平分线上.∵AB=AC,∴AP⊥BC,故①正确;∵PA=PA,PR=PS,∴Rt△APR≌Rt△APS,∴AS=AR,故②正确;∵AQ=PQ,∴∠APQ=∠PAQ,∴∠PQC=2∠PAC=60°=∠BAC,∴PQ∥AR,故③正确;由③得:△PQC是等边三角形,∴△PQS≌△PCS,∴PQ=PC.又∵AB=AC,AP⊥BC,∴BP=PC,∴BP=PQ.∵PR=PS,∴Rt△BRP≌Rt△QSP,故④也正确.∵①②③④都正确.故选D.【点睛】本题考查了等腰三角形的性质、全等三角形的判定与性质以及等边三角形的判定与性质,准确识图并熟练掌握全等三角形的判定方法与性质是解题的关键.16.如果一个三角形能被一条线段分割成两个等腰三角形,那么称这个三角形为特异三角形.若△ABC是特异三角形,∠A=30°,∠B为钝角,则符合条件的∠B有()个.A.1 B.2 C.3 D.4【答案】B【解析】【分析】【详解】如下图,当30°角为等腰三角形的底角时有两种情况:∠B=135°或90°,当30°角为等腰三角形的顶角时有一种情况:∠B=112.5°,所以符合条件的∠B有三个.又因为∠B为钝角,则符合答案的有两个,故本题应选B.点睛:因为不确定这个等腰三角形的底边,所以应当以点A为一个确定点进行分类讨论:①当以B为顶点时,即以B为圆心,AB长为半径画弧交AC于点D,构成等腰△BAD;②当以点A为顶点时,即以点A为圆心,AB长为半径画弧,交AC于点D,构成等腰△ABD;或作线段AB的垂直平分线交AC于点D构成等腰△DAB.17.如图,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为( )A.1 B.2 C.3 D.4【答案】D【解析】【分析】根据题意,结合图形,对选项一一求证,即可得出正确选项.【详解】(1)△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,∴AC=BC,EC=DC,∠ACB=∠DCE=60°,∴∠ACE=∠BCD=120°.在△BCD和△ACE中,∵AC BCBCD ACECD CE=⎧⎪∠=∠⎨⎪=⎩,∴△BCD≌△ACE,∴AE=BD,故结论①正确;(2)∵△BCD≌△ECA,∴∠GAC=∠FBC.又∵∠ACG=∠BCF=60°,AC=BC,∴△ACG≌△BCF,∴AG=BF,故结论②正确;(3)∵△ACG≌△BCF,∴CG=CF.∵∠ACB=∠DCE=60°,∴∠ACD=60°,∴△FCG为等边三角形,∴∠FGC=60°,∴∠FGC=∠DCE,∴FG∥BE,故结论③正确;(4)过C作CN⊥AE于N,CZ⊥BD于Z,则∠CNE=∠CZD=90°.∵△ACE≌△BCD,∴∠CDZ=∠CEN.在△CDZ和△CEN中,CZD CNECDZ CENCD CE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CDZ≌△CEN,∴CZ=CN.∵CN⊥AE,CZ⊥BD,∴∠BOC=∠EOC,故结论④正确.综上所述:四个结论均正确.故选D.【点睛】本题综合考查了等边三角形的判定与性质,全等三角形的判定与性质,角平分线的判定定理等重要几何知识点,有一定难度,需要学生将相关知识点融会贯通,综合运用.18.如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )A.1 B.2 C.3 D.4【答案】D【解析】【分析】由点A、B的坐标可得到AB=22,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.【详解】∵点A、B的坐标分别为(2,2)、B(4,0).∴AB=22,如图,①若AC=AB,以A为圆心,AB为半径画弧与x轴有2个交点(含B点),即(0,0)、(4,0),∴满足△ABC是等腰三角形的C点有1个;②若BC=AB,以B为圆心,BA为半径画弧与x轴有2个交点,即满足△ABC是等腰三角形的C点有2个;③若CA=CB,作AB的垂直平分线与x轴有1个交点,即满足△ABC是等腰三角形的C点有1个;综上所述:点C在x轴上,△ABC是等腰三角形,符合条件的点C共有4个.故选D.【点睛】本题主考查了等腰三角形的判定以及分类讨论思想的运用,分三种情况分别讨论,注意等腰三角形顶角的顶点在底边的垂直平分线上.19.如图,已知长方形ABCD,AB=1,BC=2,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为( )A.1 B.1+3C.2+3D.3【答案】B【解析】【分析】将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,推出AM=MM’可得MA+MD+ME=D’M+MM’+ME,共线时最短;由于点E 也为动点,可得当D’E⊥BC时最短,此时易求得D’E=DG+GE的值.【详解】将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,∴AM=MM’,∴MA+MD+ME=D’M+MM’+ME,∴D′M、MM′、ME共线时最短,由于点E也为动点,∴当D’E⊥BC时最短,此时易求得D’E=DG+GE=4+33,∴MA+MD+ME的最小值为4+33.故选B.【点睛】本题考查轴对称、旋转变换、矩形的性质等知识,解题的关键是学会添加常用辅助线,构造等边三角形解决问题,学会用转化的思想思考问题.20.如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有()A.①③B.①②④C.①②③④D.①③④【答案】C【解析】【分析】①易证∠CBE=∠DAE,即可求证:△ADE≌△BCE;②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;③证明△AEF≌△BED即可;④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.【详解】①∵AD为△ABC的高线,∴∠CBE+∠ABE+∠BAD=90°.∵Rt△ABE是等腰直角三角形,∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,∴∠CBE+∠BAD=45°,∴∠DAE=∠CBE.在△DAE和△CBE中,∵AE BEDAE CBEAD BC=⎧⎪∠=∠⎨⎪=⎩,∴△ADE≌△BCE(SAS);故①正确;②∵△ADE≌△BCE,∴∠EDA=∠ECB.∵∠ADE+∠EDC=90°,∴∠EDC+∠ECB=90°,∴∠DEC=90°,∴CE⊥DE;故②正确;③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,∴∠BDE=∠AFE.∵∠BED+∠BEF=∠AEF+∠BEF=90°,∴∠BED=∠AEF.在△AEF和△BED中,∵BDE AFEBED AEFAE BE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEF≌△BED(AAS),∴BD=AF;故③正确;④∵AD=BC,BD=AF,∴CD=DF.∵AD⊥BC,∴△FDC是等腰直角三角形.∵DE⊥CE,∴EF=CE,∴S△AEF=S△ACE.∵△AEF≌△BED,∴S△AEF=S△BED,∴S△BDE=S△ACE.故④正确.故选C.【点睛】本题考查了全等三角形的判定与性质,本题中求证△BFE≌△CDE是解题的关键.。
初中数学八年级数学《全等三角形》易错题精选附答案
全等三角形易错题精选,附答案第1节 全等三角形1.易错点:对应边不确定,需要分类讨论1、已知△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1,若这两个三角形全等,则x 为( ) A .37B .4C .3D .3或37参考答案 1、C2.易错点:忽略隐藏的8字形(一)1、如图,△ABC△△AEF ,AB=AE ,△B=△E ,则下列结论:△AC=AF ;△△FAC=△EAB ;△EF=BC ;△△EAB=△EFB ,其中正确的是_________.2、【变式1】如图,△ABC△△AEF ,AB=AE ,△B=△E ,则下列结论中不一定成立的是( )A .AC=AFB .△EAB=△EFBC .△FAB=△EABD .△EAB=△FAC3、【变式2】如图,在△ABC 与△AEF 中,AB=AE ,BC=EF ,△B=△E ,AB 交EF 于D .给出下列结论:△△AFC=△C ;△DE=CF ;△△EAD=△BFD ;△△BFD=△CAF .其中正确的结论是( ) A .△△ B .△△ C .△△ D .△△△4、【变式3】如图,△ABC△△ADE ,△DAC=60°,△BAE=100°,BC 、DE 相交于点F ,则△DFB 的度数是_______.参考答案1、△△△△2、B3、D4、20°3.易错点:忽略隐藏的8字形(二)1、如图,△ABC△△ADE ,BC 的延长线交DA 于F ,交DE 于G ,△ACB=△AED=105°,△CAD=10°,△B=△D=25°,求△DFB 、△DGB 的度数.2、【变式1】如图所示,△ABC△△ADE ,延长BC 分别交AD ,DE 于F ,G ,△CAD=10°,△B=△D=25°,△EAB=120°.求△DFB 和△DGB 的度数.3、【变式2】如图,△ABC△△ADE ,BC 的延长线过点E ,△ACB=△AED=105°,△CAD=10°,△B=50°,则△DEF 的度数为________.参考答案1、△DFB=85°;△DGB=60°.2、△DFB=90°;△DGB=65°3、35°第2节 全等三角形的判定一、用SSS 边边边判定三角形全等二、用SAS 边角边判定三角形全等 4.易错点:误用SSA 判定三角形全等 1、如图,AB=AC ,AE=AD ,要使△ACD△△ABE ,需要补充的一个条件是( )A .△B=△CB .△D=△EC .△BAC=△EAD D .△B=△E参考答案 1、C5.易错点:乱用中点的各种结论1、如图所示,AB=AC,D,E分别是AB,AC的中点.求证:△ABE△△ACD.证明:∵D、E分别是AB、AC的中点∴AD=BD,AE=CE∵AB=AC∴AE=AD在△ABE和△ACD中AE=AD△A=△AAB=AC∴△ABE△△ACD以上证明过程是否有误?若有,请将错误的地方改正.参考答案1、有错,AD=BD,AE=CE应改为AD=1/2AB,AE=1/2AC6.易错点:对应边的关系不确定1、如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=________时,△ABC和△PQA全等.2、【变式1】如图(1),AB=5cm,AC⊥AB,BD⊥AB,AC=BD=4cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B 向点D运动.它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1,△ACP与△BPQ是否全等,请说明理由,并推导出此时线段PC和线段PQ的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=a°”,其他条件不变.设点Q 的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.参考答案1、5或10.2、提示:(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.解:(1)(1)当t=1时,AP=BQ=1,BD=AC=4,∵AB=5,∴BP=5-1=4=AC,又∵AC⊥AB,BD⊥AB,∴∠A=∠B=90°,在△ACP和△BPQ中,AP=BQ,∠A=∠B,AC=BP,∴△ACP≌△BPQ(SAS),∴∠ACP=∠BPQ,∴∠APC+∠BPQ=∠APC+∠ACP=90°,∴∠CPQ=90°,即线段PC与线段PQ垂直;(2)△若△ACP△△BPQ,则AC=BP,AP=BQ,△4=5-t,t=xt,解得t=1,x=1,△存在x=1,t=1,使得△ACP与△BPQ全等;△若△ACP△△BQP,则AC=BQ,AP=BP,△t=5-t,4=xt,解得t=2.5,x=1.6,△存在t=2.5,x=1.6,使得△ACP与△BPQ全等;综上所述,存在x=1,t=1或t=2.5,x=1.6,使得△ACP 与△BPQ全等.三、用ASA角边角或AAS角角边判定三角形全等7.易错点:误以为AAS就是两个角和一条边相等1、下列说法正确的是()A.有三个角对应相等的两个三角形全等B.有两边对和其中一边的对角对应相等的两个三角形全等C.有两个角和其中一个角的对边对应相等的两个三角形全等D.有两个角对应相等,还有一条边也相等的两个三角形全等2、【变式1】下列条件不能判断两个直角三角形全等的是()A.有两条直角边对应相等B.有两个锐角对应相等C.斜边和一条直角边对应相等D.斜边和一个锐角对应相等参考答案1、C2、B四、用HL斜边直角边判定三角形全等8.易错点:判定直角三角形全等时将HL与SSA混淆1、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:△BDF≌△ADC.证明:∵AD⊥BC∴∠BDF=∠ADC=90°在Rt△BDF和Rt△ADC中BF=AC,FD=CD,∠BDF=∠ADC,∴Rt△BDF≌Rt△ADC以上证明是否有错?如果有错,请将错误改正.2、【变式1】如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,则∠ABC=_____.3、【变式2】如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE ⊥AC.参考答案1、有错,证明三角形全等应该用HL,不是SSA需要把∠BDF=∠ADC删掉.2、45°3、证明:△AD△BC,△△BDF=△ADC=90°在Rt△BDF和Rt△ADC中,BF=AC,FD=CD,△Rt△BDF△Rt△ADC(HL),△△C=△BFD,△△DBF+△BFD=90°,,△△C+△DBF=90°,△△C+△DBF+△BEC=180°,△△BEC=90°,△BE△AC.9.易错点:全等三角形的判定定理混淆1、如图,在正方形网格中,△ABC的三个顶点及点D、E、F、G、H都在格点上,现以D、E、F、G、H中的三点为顶点画三角形,则下列与△ABC面积相等但不全等的三角形是()A.△EHD B.△EGF C.△EFH D.△HDF 参考答案1、D第3节角平分线的性质10.易错点:不理解点到直线的距离1、如图,PD△AB,PE△AC,垂足分别为D、E,且PA 平分△BAC,则△APD与△APE全等的理由是()A.SAS B.AAS C.SSS D.ASA2、如图,在△AOB和△COD中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD交于点M,连接OM.下列结论:①∠AMB=36°;②AC=BD;③OM平分∠AOD;④MO平分∠AMD.其中正确的有______________.参考答案1、B2、①②④。
八年级上册数学 全册全套试卷易错题(Word版 含答案)

八年级上册数学全册全套试卷易错题(Word版含答案)一、八年级数学全等三角形解答题压轴题(难)1.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m 上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.【答案】(1)见解析(2)成立(3)△DEF为等边三角形【解析】解:(1)证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=900.∵∠BAC=900,∴∠BAD+∠CAE=900.∵∠BAD+∠ABD=900,∴∠CAE=∠ABD.又AB="AC" ,∴△ADB≌△CEA(AAS).∴AE=BD,AD=CE.∴DE="AE+AD=" BD+CE.(2)成立.证明如下:∵∠BDA =∠BAC=α,∴∠DBA+∠BAD=∠BAD +∠CAE=1800—α.∴∠DBA=∠CAE.∵∠BDA=∠AEC=α,AB=AC,∴△ADB≌△CEA(AAS).∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.(3)△DEF为等边三角形.理由如下:由(2)知,△ADB≌△CEA,BD=AE,∠DBA =∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=600.∴∠DBA+∠ABF=∠CAE+∠CAF.∴∠DBF=∠FAE.∵BF=AF,∴△DBF≌△EAF(AAS).∴DF=EF,∠BFD=∠AFE.∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600.∴△DEF为等边三角形.(1)因为DE=DA+AE,故由AAS证△ADB≌△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证明△ADB≌△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD.(3)由△ADB≌△CEA得BD=AE,∠DBA =∠CAE,由△ABF和△ACF均等边三角形,得∠ABF=∠CAF=600,FB=FA ,所以∠DBA+∠ABF=∠CAE+∠CAF ,即∠DBF=∠FAE ,所以△DBF ≌△EAF ,所以FD=FE ,∠BFD=∠AFE ,再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF 是等边三角形.2.(1)如图(a )所示点D 是等边ABC 边BA 上一动点(点D 与点B 不重合),连接DC ,以DC 为边在BC 上方作等边DCF ,连接AF .你能发现线段AF 与BD 之间的数量关系吗?并证明.(2)如图(b )所示当动点D 运动至等边ABC 边BA 的延长线上时,其他作法与(1)相同,猜想AF 与BD 在(1)中的结论是否仍然成立?(直接写出结论)(3)①如图(c )所示,当动点D 在等边ABC 边BA 上运动时(点D 与点B 不重合),连接DC ,以DC 为边在BC 上方、下方分别作等边DCF 和等边DCF ',连接AF 、BF ',探究AF 、BF '与AB 有何数量关系?并证明.②如图(d )所示,当动点D 在等边ABC 边BA 的延长线上运动时,其他作法与(3)①相同,①中的结论是否成立?若不成立,是否有新的结论?并证明.【答案】(1)AF=BD ,理由见解析;(2)AF=BD ,成立;(3)①AF BF AB '+=,证明见解析;②①中的结论不成立新的结论是AF AB BF '=+,理由见解析【解析】【分析】(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS 可证得BCD ACF △≌△,然后由全等三角形的对应边相等知AF BD = .(2)通过证明BCD ACF △≌△,即可证明AF BD =.(3)①'AF BF AB += ,利用全等三角形BCD ACF △≌△的对应边BD AF = ,同理'BCF ACD △≌△ ,则'BF AD = ,所以'AF BF AB +=;②①中的结论不成立,新的结论是'AF AB BF =+ ,通过证明BCF ACD △≌△,则'BF AD =(全等三角形的对应边相等),再结合(2)中的结论即可证得'AF AB BF =+ .【详解】(1)AF BD =证明如下:ABC 是等边三角形,BC AC ∴=,60BCA ︒∠=.同理可得:DC CF =,60DCF ︒∠=.BCA DCA DCF DCA ∴∠-∠=∠-∠.即BCD ACF ∠=∠.BCD ACF ∴△≌△.AF BD ∴=.(2)证明过程同(1),证得BCD ACF △≌△,则AF BD =(全等三角形的对应边相等),所以当动点D 运动至等边△ABC 边BA 的延长线上时,其他作法与(1)相同,AF BD =依然成立.(3)①AF BF AB '+=证明:由(1)知,BCD ACF △≌△.BD AF ∴=.同理BCF ACD '△≌△.BF AD '∴=.AF BF BD AD AB '∴+=+=.②①中的结论不成立新的结论是AF AB BF '=+;BC AC =,BCF ACD '∠=∠,F C DC '=,BCF ACD '∴△≌△.BF AD '∴=.又由(2)知,AF BD =.AF BD AB AD AB BF '∴==+=+.即AF AB BF '=+.【点睛】本题考查了三角形的综合问题,掌握等边三角形的三条边、三个内角都相等的性质、全等三角形的判定定理、全等三角形的对应边相等是解题的关键.3.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图(1)观察“规形图(1)”,试探究∠BDC 与∠A 、∠B 、∠C 之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下问题:①如图(2),把一块三角尺XYZ 放置在△ABC 上使三角尺的两条直角边XY 、XZ 恰好经过点B 、C ,若∠A =40°,则∠ABX+∠ACX = °.②如图(3),DC 平分∠ADB ,EC 平分∠AEB ,若∠DAE =40°,∠DBE =130°,求∠DCE 的度数.【答案】(1)∠BDC=∠BAC+∠B+∠C,理由见解析;(2)①50;②∠DCE=85°.【解析】【分析】(1)首先连接AD并延长至点F,然后根据外角的性质,即可判断出∠BDC=∠BAC+∠B+∠C;(2)①由(1)可得∠A+∠ABX+∠ACX=∠X,然后根据∠A=40°,∠X=90°,即可求解;(3)②由∠A=40°,∠DBE=130°,求出∠ADE+∠AEB的值,然后根据∠DCE=∠A+∠ADC+∠AEC,求出∠DCE的度数即可.【详解】(1)如图,∠BDC=∠BAC+∠B+∠C,理由是:过点A、D作射线AF,∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,即∠BDC=∠BAC+∠B+∠C;(2)①如图(2),∵∠X=90°,由(1)知:∠A+∠ABX+∠ACX=∠X=90°,∵∠A=40°,∴∠ABX+∠ACX=50°,故答案为:50;②如图(3),∵∠A=40°,∠DBE=130°,∴∠ADE+∠AEB=130°﹣40°=90°,∵DC平分∠ADB,EC平分∠AEB,∴∠ADC=12∠ADB,∠AEC=12∠AEB,∴∠ADC+∠AEC=1(ADB AEB)2∠+∠=45°,∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.【点睛】本题主要考查了三角形外角性质以及角平分线的定义的运用,熟知三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.4.操作发现:如图,已知△ABC和△ADE均为等腰三角形,AB=AC,AD=AE,将这两个三角形放置在一起,使点B,D,E在同一直线上,连接CE.(1)如图1,若∠ABC=∠ACB=∠ADE=∠AED=55°,求证:△BAD≌△CAE;(2)在(1)的条件下,求∠BEC的度数;拓广探索:(3)如图2,若∠CAB=∠EAD=120°,BD=4,CF为△BCE中BE边上的高,请直接写出EF的长度.【答案】(1)见解析;(2)70°;(3)2【解析】【分析】(1)根据SAS证明△BAD≌△CAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证△BAD≌△CAE,推出EC=BD=4,由∠BEC=∠BAC=120°,推出∠FCE=30°即可解决问题.【详解】(1)证明:如图1中,∵∠ABC=∠ACB=∠ADE=∠AED,∴∠EAD=∠CAB,∴∠EAC=∠DAB,∵AE=AD,AC=AB,∴△BAD≌△CAE(SAS).(2)解:如图1中,设AC交BE于O.∵∠ABC=∠ACB=55°,∴∠BAC=180°﹣110°=70°,∵△BAD≌△CAE,∴∠ABO=∠ECO,∵∠EOC=∠AOB,∴∠CEO=∠BAO=70°,即∠BEC=70°.(3)解:如图2中,∵∠CAB=∠EAD=120°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴∠BAD=∠ACE,BD=EC=4,同理可证∠BEC=∠BAC=120°,∴∠FEC=60°,∵CF⊥EF,∴∠F=90°,∴∠FCE=30°,∴EF=12EC=2.【点睛】本题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.5.如图,ABC∆是等边三角形,点D在边AC上(“点D不与,A C重合),点E是射线BC上的一个动点(点E不与点,B C重合),连接DE,以DE为边作作等边三角形DEF∆,连接CF.(1)如图1,当DE 的延长线与AB 的延长线相交,且,C F 在直线DE 的同侧时,过点D 作//DG AB ,DG 交BC 于点G ,求证:CF EG =;(2)如图2,当DE 反向延长线与AB 的反向延长线相交,且,C F 在直线DE 的同侧时,求证:CD CE CF =+;(3)如图3, 当DE 反向延长线与线段AB 相交,且,C F 在直线DE 的异侧时,猜想CD 、CE 、CF 之间的等量关系,并说明理由.【答案】(1)证明见详解;(2)证明见详解;(3)CF =CD +CE ,理由见详解.【解析】【分析】(1)由ABC ∆是等边三角形,//DG AB ,得∠CDG=∠A=60°,∠ACB=60°,CDG ∆是等边三角形,易证∆ GDE ≅ ∆ CDF(SAS),即可得到结论;(2)过点D 作DG ∥AB 交BC 于点G ,易证∆ GDE ≅ ∆ CDF(SAS),即可得到结论;(3)过点D 作DG ∥AB 交BC 于点G ,易证∆ GDE ≅ ∆ CDF(SAS),即可得到结论.【详解】(1)∵ABC ∆是等边三角形,//DG AB ,∴∠CDG=∠A=60°,∠ACB=60°,∴CDG ∆是等边三角形,∴DG=DC.∵DEF ∆是等边三角形,∴DE=DF ,∠EDF=60°,∴∠CDG-∠GDF=∠EDF-∠GDF ,即:∠GDE=∠CDF ,在∆ GDE 和∆ CDF 中,∵DE DF GDE CDF DG DC =⎧⎪∠=∠⎨⎪=⎩,∴∆ GDE ≅ ∆ CDF(SAS),∴CF EG =;(2)过点D 作DG ∥AB 交BC 于点G ,如图2,∵ABC ∆是等边三角形,//DG AB ,∴∠CDG=∠A=60°,∠ACB=60°,∴CDG ∆是等边三角形,∴DG=DC.∵DEF∆是等边三角形,∴DE=DF,∠EDF=60°,∴∠CDG-∠CDE=∠EDF-∠CDE,即:∠GDE=∠CDF,在∆ GDE和∆ CDF中,∵DE DFGDE CDFDG DC=⎧⎪∠=∠⎨⎪=⎩,∴∆ GDE≅∆ CDF(SAS),∴CF GE=,∴CD CG CE GE CE CF==+=+(3)CF=CD+CE,理由如下:过点D作DG∥AB交BC于点G,如图3,∵ABC∆是等边三角形,//DG AB,∴∠CDG=∠A=60°,∠ACB=60°,∴CDG∆是等边三角形,∴DG=DC=GC.∵DEF∆是等边三角形,∴DE=DF,∠EDF=60°,∴∠CDG+∠CDE=∠EDF+∠CDE,即:∠GDE=∠CDF,在∆ GDE和∆ CDF中,∵DE DFGDE CDFDG DC=⎧⎪∠=∠⎨⎪=⎩,∴∆ GDE≅∆ CDF(SAS),∴CF GE==GC+CE=CD+CE.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.二、八年级数学轴对称解答题压轴题(难)6.如图,在ABC△中,已知AD是BC边上的中线,E是AD上一点,且BE AC=,延长BE交AC于点F,求证:AF EF=.【答案】证明见解析【解析】【分析】延长AD到点G,使得AD DG=,连接BG,结合D是BC的中点,易证△ADC和△GDB全等,利用全等三角形性质以及等量代换,得到△AEF中的两个角相等,再根据等角对等边证得AE=EF.【详解】如图,延长AD到点G,延长AD到点G,使得AD DG=,连接BG.∵AD是BC边上的中线,∴DC DB=.在ADC和GDB△中,AD DGADC GDBDC DB=⎧⎪∠=∠⎨⎪=⎩(对顶角相等),∴ADC≌GDB△(SAS).∴CAD G∠=∠,BG AC=.又BE AC=,∴BE BG=.∴BED G∠=∠.∵BED AEF∠=∠∴AEF CAD ∠=∠,即AEF FAE ∠=∠∴AF EF =.【点睛】本题考查的是全等三角形的判定与性质,根据题意构造全等三角形是解答本题的关键.7.(1)如图①,D 是等边△ABC 的边BA 上一动点(点D 与点B 不重合),连接DC ,以DC 为边,在BC 上方作等边△DCF ,连接AF ,你能发现AF 与BD 之间的数量关系吗?并证明你发现的结论;(2)如图②,当动点D 运动至等边△ABC 边BA 的延长线时,其他作法与(1)相同,猜想AF 与BD 在(1)中的结论是否仍然成立?若成立,请证明;(3)Ⅰ.如图③,当动点D 在等边△ABC 边BA 上运动时(点D 与B 不重合),连接DC ,以DC 为边在BC 上方和下方分别作等边△DCF 和等边△DCF ′,连接AF ,BF ′,探究AF ,BF ′与AB 有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D 在等边△ABC 的边BA 的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.【答案】(1)AF =BD ,理由见解析;(2)AF 与BD 在(1)中的结论成立,理由见解析;(3)Ⅰ. AF +BF ′=AB ,理由见解析,Ⅱ.Ⅰ中的结论不成立,新的结论是AF =AB +BF ′,理由见解析.【解析】【分析】(1)由等边三角形的性质得BC =AC ,∠BCA =60°,DC =CF ,∠DCF =60°,从而得∠BCD =∠ACF ,根据SAS 证明△BCD ≌△ACF ,进而即可得到结论;(2)根据SAS 证明△BCD ≌△ACF ,进而即可得到结论;(3)Ⅰ.易证△BCD ≌△ACF (SAS ),△BCF ′≌△ACD (SAS ),进而即可得到结论;Ⅱ.证明△BCF ′≌△ACD ,结合AF =BD ,即可得到结论.【详解】(1)结论:AF =BD ,理由如下:如图1中,∵△ABC 是等边三角形,∴BC =AC ,∠BCA =60°,同理知,DC =CF ,∠DCF =60°,∴∠BCA -∠DCA =∠DCF -∠DCA ,即:∠BCD =∠ACF ,在△BCD 和△ACF 中,∵BC AC BCD ACF DC FC =∠=∠=⎧⎪⎨⎪⎩,∴△BCD ≌△ACF (SAS ),∴BD =AF ;(2)AF 与BD 在(1)中的结论成立,理由如下:如图2中,∵△ABC 是等边三角形,∴BC =AC ,∠BCA =60°,同理知,DC =CF ,∠DCF =60°,∴∠BCA +∠DCA =∠DCF +∠DCA ,即∠BCD =∠ACF ,在△BCD 和△ACF 中,∵BC AC BCD ACF DC FC =∠=∠=⎧⎪⎨⎪⎩,∴△BCD ≌△ACF (SAS ),∴BD =AF ;(3)Ⅰ.AF +BF ′=AB ,理由如下:由(1)知,△BCD ≌△ACF (SAS ),则BD =AF ;同理:△BCF ′≌△ACD (SAS ),则BF ′=AD ,∴AF +BF ′=BD +AD =AB ;Ⅱ.Ⅰ中的结论不成立,新的结论是AF =AB +BF ′,理由如下:同理可得:BCF ACD ∠=∠′,F C DC =′,在△BCF ′和△ACD 中,BC AC BCF ACD F C DC =∠⎧⎪=∠=⎪⎨⎩′′, ∴△BCF ′≌△ACD (SAS ),∴BF ′=AD ,又由(2)知,AF =BD ,∴AF =BD =AB +AD =AB +BF ′,即AF =AB +BF ′.【点睛】本题主要考查等边三角形的性质定理,三角形全等的判定和性质定理,熟练掌握三角形全等的判定和性质定理,是解题的关键.8.已知:三角形ABC 中,∠A=90°,AB=AC,D 为BC 的中点.(1)如图,E 、F 分别是AB 、AC 上的点,且BE=AF,求证:△DEF 为等腰直角三角形.(2)若E 、F 分别为AB,CA 延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF 是否仍为等腰直角三角形?画出图形,写出结论不证明.【答案】(1)见解析;(2)见解析【解析】【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.【详解】解:(1)连结AD ,∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD⊥BC ,BD=AD ,∴∠B=∠BAD=∠DAC=45°,又∵BE=AF ,∴△BDE≌△ADF(SAS),∴ED=FD ,∠BDE=∠ADF,∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,∴△DEF为等腰直角三角形.(2)连结AD∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD=BD ,AD⊥BC ,∴∠DAC=∠ABD=45° ,∴∠DAF=∠DBE=135°,又∵AF=BE ,∴△DAF ≌△DBE (SAS ),∴FD=ED ,∠FDA=∠EDB,∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.∴△DEF 为等腰直角三角形.【点睛】本题利用了等腰直角三角形底边上的中线平分顶角,并且等于底边的一半,还利用了全等三角形的判定和性质,及等腰直角三角形的判定.9.如图,在等边ABC ∆中,点D ,E 分别是AC ,AB 上的动点,且AE CD =,BD 交CE 于点P .(1)如图1,求证120BPC ︒∠=;(2)点M 是边BC 的中点,连接PA ,PM .①如图2,若点A ,P ,M 三点共线,则AP 与PM 的数量关系是 ; ②若点A ,P ,M 三点不共线,如图3,问①中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.【答案】(1)证明过程见详解;(2)①2AP PM =;②结论成立,证明见详解【解析】【分析】(1)先证明()AEC CDB SAS ≌,得出对应角相等,然后利用四边形的内角和和对顶角相等即可得出结论;(2)①2AP PM =;由等边三角形的性质和已知条件得出AM ⊥BC ,∠CAP =30°,可得PB =PC ,由∠BPC =120°和等腰三角形的性质可得∠PCB =30°,进而可得AP =PC ,由30°角的直角三角形的性质可得PC =2PM ,于是可得结论;②延长BP 至D ,使PD =PC ,连接AD 、CD ,根据SAS 可证△ACD ≌△BCP ,得出AD =BP ,∠ADC =∠BPC =120°,然后延长PM 至N ,使MN =MP ,连接CN ,易证△CMN ≌△BMP (SAS ),可得CN =BP =AD ,∠NCM =∠PBM ,最后再根据SAS 证明△ADP ≌△NCP ,即可证得结论.【详解】(1)证明:因为△ABC为等边三角形,所以60A ACB∠=∠=︒∵AC BCA ACBAE CD=⎧⎪∠=∠⎨⎪=⎩,∴()AEC CDB SAS≌,∴AEC CDB∠=∠,在四边形AEPD中,∵360AEC EPD PDA A∠+∠+∠+∠=︒,∴18060360AEC EPD CDB∠+∠+︒-∠+︒=︒,∴120EPD∠=︒,∴120BPC∠=︒;(2)①如图2,∵△ABC是等边三角形,点M是边BC的中点,∴∠BAC=∠ABC=∠ACB=60°,AM⊥BC,∠CAP=12∠BAC=30°,∴PB=PC,∵∠BPC=120°,∴∠PBC=∠PCB=30°,∴PC=2PM,∠ACP=60°﹣30°=30°=∠CAP,∴AP=PC,∴AP=2PM;故答案为:2AP PM=;②AP=2PM成立,理由如下:延长BP至D,使PD=PC,连接AD、CD,如图4所示:则∠CPD=180°﹣∠BPC=60°,∴△PCD是等边三角形,∴CD=PD=PC,∠PDC=∠PCD=60°,∵△ABC是等边三角形,∴BC=AC,∠ACB=60°=∠PCD,∴∠BCP=∠ACD,∴△ACD≌△BCP(SAS),∴AD=BP,∠ADC=∠BPC=120°,∴∠ADP=120°﹣60°=60°,延长PM至N,使MN=MP,连接CN,∵点M是边BC的中点,∴CM=BM,∴△CMN≌△BMP(SAS),∴CN=BP=AD,∠NCM=∠PBM,∴CN∥BP,∴∠NCP+∠BPC=180°,∴∠NCP=60°=∠ADP,在△ADP和△NCP中,∵AD=NC,∠ADP=∠NCP,PD=PC,∴△ADP ≌△NCP (SAS ),∴AP =PN =2CM ;【点睛】本题是三角形的综合题,主要考查了等边三角形的判定与性质、全等三角形的判定与性质、含30°角的直角三角形的性质等知识;熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.10.如果一个三角形能被一条线段割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.(1)如图1,ABC ∆是等腰锐角三角形,()AB AC AB BC =>,若ABC ∠的角平分线BD 交AC 于点D ,且BD 是ABC ∆的一条特异线,则BDC ∠= 度.(2)如图2,ABC ∆中,2B C ∠=∠,线段AC 的垂直平分线交AC 于点D ,交BC 于点E ,求证:AE 是ABC ∆的一条特异线;(3)如图3,若ABC ∆是特异三角形,30A ∠=,B 为钝角,不写过程,直接写出所有可能的B 的度数.【答案】(1)72;(2)证明见解析;(3)∠B 度数为:135°、112.5°或140°.【解析】【分析】(1)根据等腰三角形性质得出∠C=∠ABC=∠BDC=2∠A ,据此进一步利用三角形内角和定理列出方程求解即可;(2)通过证明△ABE 与△AEC 为等腰三角形求解即可;(3)根据题意分当BD 为特异线、AD 为特异线以及CD 为特异线三种情况分类讨论即可.【详解】(1)∵AB=AC,∴∠ABC=∠C,∵BD平分∠ABC,∴∠ABD=∠CBD=12∠ABC,∵BD是△ABC的一条特异线,∴△ABD与△BCD为等腰三角形,∴AD=BD=BC,∴∠A=∠ABD,∠C=∠BDC,∴∠ABC=∠C=∠BDC,∵∠BDC=∠A+∠ABD=2∠A,设∠A=x,则∠C=∠ABC=∠BDC=2x,在△ABC中,∠A+∠ABC+∠C=180°,即:x+2x+2x=180°,∴x=36°,∴∠BDC=72°,故答案为:72;(2)∵DE是线段AC的垂直平分线,∴EA=EC,∴△EAC为等腰三角形,∴∠EAC=∠C,∴∠AEB=∠EAC+∠C=2∠C,∵∠B=2∠C,∴∠AEB=∠B,∴△EAB为等腰三角形,∴AE是△ABC的一条特异线;(3)如图3,当BD 是特异线时,如果AB=BD=DC ,则∠ABC=∠ABD+∠DBC=120°+15°=135°;如果AD=AC ,DB=DC ,则∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°;如果AD=DB ,DC=DB ,则∠ABC=∠ABD+∠DBC=30°+60°=90°,不符合题意,舍去;如图4,当AD 是特异线时,AB=BD ,AD=DC ,则:∠ABC=180°−20°−20°=140°;当CD 为特异线时,不符合题意;综上所述,∠B 度数为:135°、112.5°或140°.【点睛】本题主要考查了等腰三角形性质的综合运用,熟练掌握相关概念是解题关键.三、八年级数学整式的乘法与因式分解解答题压轴题(难)11.阅读下列材料,然后解答问题:问题:分解因式:3245x x +-.解答:把1x =带入多项式3245x x +-,发现此多项式的值为0,由此确定多项式3245x x +-中有因式()1x -,于是可设()()322451x x x x mx n +-=-++,分别求出m ,n 的值.再代入()()322451x x x x mx n +-=-++,就容易分解多项式3245x x +-,这种分解因式的方法叫做“试根法”.(1)求上述式子中m ,n 的值;(2)请你用“试根法”分解因式:3299x x x +--.【答案】(1)5m =,5n =;(2)()()()133x x x ++-【解析】【分析】(1)先找出一个x 的值,进而找出一个因式,再将多项式设成分解因式的形式,即可得出结论;(2)先找出x=-1时,得出多项式的值,进而找出一个因式,再将多项式设成分解因式的形式,即可得出结论.【详解】解:(1)把1x =带入多项式3245x x +-,发现此多项式的值为0,∴多项式3245x x +-中有因式()1x -,于是可设322451xx x x mx n , 得出:3232451x x x m x n m x n ,∴14m ,0n m,∴5m =,5n =, (2)把1x =-代入3299x x x +--,多项式的值为0,∴多项式3299x x x +--中有因式()1x +,于是可设322329911x x x x x mx n x m x n m x n ,∴11m +=,9n m,9n =- ∴0m =,9n =-,∴3229133991x x x x x x x x【点睛】此题是分解因式,主要考查了试根法分解因式的理解和掌握,解本题的关键是理解试根法分解因式.12.观察下列各式:()()2111,x x x -+=-()()23 111,x x x x -++=-()()324 111,x x x x x -+++=-()()4325 1 11,x x x x x x -++++=-······()1根据规律()()122 1 ...1n n x x x x x ---+++++=(其中n 为正整数) ;()()3029282(51)5555251-+++++()3计算:201920182017321(2)(2)(2)(2)(2)(2)1-+-+-++-+--++ 【答案】(1)1n x -;(2)311-5;(3)2020213-- 【解析】【分析】(1)归纳总结得到一般性规律,即可得到结果;(2)根据一般性结果,将n=31,x=5代入(1)中即可;(3)将代数式适当变形为(1)的形式,根据前面总结的规律即可计算出结果.【详解】(1)根据上述规律可得()()122 1 ...1n n x x x x x ---+++++=1n x -,故填:1n x -;(2)由(1)可知()3029282(51)555551-+++++=311-5()3 201920182017321(2)(2)(2)(2)(2)(2)1-+-+-+⋅+-+-+-+ =201920182011732[(2)1](2)(2)(2)(2)(2)(2)13⎡⎤---+-+-+⋯+-+--+⎣⎦-+ =2020(2)13--- =2020213-- 【点睛】本题考查整式的乘法,能根据题例归纳总结出一般性规律是解题关键,(3)中能对整式适当变形是解题关键,但需注意变形时要为等量变形.13.先阅读下列材料,然后解后面的问题. 材料:一个三位自然数abc (百位数字为a ,十位数字为b ,个位数字为c ),若满足a+c=b ,则称这个三位数为“欢喜数”,并规定F (abc )=ac .如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F (374)=3×4=12. (1)对于“欢喜数abc ”,若满足b 能被9整除,求证:“欢喜数abc ”能被99整除; (2)已知有两个十位数字相同的“欢喜数”m ,n (m >n ),若F (m )﹣F (n )=3,求m ﹣n 的值.【答案】(1)详见解析;(2)99或297.【解析】【分析】(1)首先由题意可得a +c =b ,将欢喜数展开,因为要证明“欢喜数abc ”能被99整除,所以将展开式中100a 拆成99a +a ,这样展开式中出现了a +c ,将a +c 用b 替代,整理出最终结果即可;(2)首先设出两个欢喜数m 、n ,表示出F (m )、F (n )代入F (m )﹣F (n )=3中,将式子变形分析得出最终结果即可.【详解】(1)证明:∵abc 为欢喜数,∴a +c =b . ∵abc =100a +10b +c =99a +10b +a +c =99a +11b ,b 能被9整除,∴11b 能被99整除,99a 能被99整除,∴“欢喜数abc ”能被99整除;(2)设m =11a bc ,n =22a bc (且a 1>a 2),∵F (m )﹣F (n )=a 1•c 1﹣a 2•c 2=a 1•(b ﹣a 1)﹣a 2(b ﹣a 2)=(a 1﹣a 2)(b ﹣a 1﹣a 2)=3,a 1、a 2、b 均为整数,∴a 1﹣a 2=1或a 1﹣a 2=3.∵m ﹣n =100(a 1﹣a 2)﹣(a 1﹣a 2)=99(a 1﹣a 2),∴m ﹣n =99或m ﹣n =297.∴若F (m )﹣F (n )=3,则m ﹣n 的值为99或297.【点睛】做此类阅读理解类题目首先要充分理解题目,会运用因式分解将式子变形.14.阅读以下文字并解决问题:对于形如222x ax a ++这样的二次三项式,我们可以直接用公式法把它分解成()2x a +的形式,但对于二次三项式2627x x +-,就不能直接用公式法分解了。
人教版八年级上册数学 三角形解答题易错题(Word版 含答案)

人教版八年级上册数学 三角形解答题易错题(Word 版 含答案)一、八年级数学三角形解答题压轴题(难)1.如图1,直线MN 与直线AB 、CD 分别交于点E 、F ,1∠与2∠互补.(1)试判断直线AB 与直线CD 的位置关系,并说明理由.(2)如图2,BEF ∠与EFD ∠的角平分线交于点P ,EP 与CD 交于点G ,点H 是MN 上一点,且GH EG ⊥,求证://PF GH .(3)如图3,在(2)的条件下,连接PH ,K 是GH 上一点使PHK HPK ∠=∠,作PQ 平分EPK ∠,求HPQ ∠的度数.【答案】(1)AB//CD ,理由见解析;(2)证明见解析;(3)45HPQ ∠=.【解析】【分析】(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF 、∠CFE 互补,即可证明; (2)利用(1)中平行线的性质、角平分线的性质、三角形内角和定理可得∠EPF=90°,即EG ⊥PF ,再结合GH ⊥EG ,即可证明;(3)利用三角形外角定理、三角形内角和定理求得∠A=90°-∠3=90°-2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK=-12∠EPK=45°+∠2,最后根据角与角间的和差关系即可求解.【详解】(1)//AB CD ,理由如下:如图1, 图1∵1∠与2∠互补,∴12180∠+∠=︒,又∵1AEF ∠=∠,2CFE ∠=∠,∴180AEF CFE ∠+∠=︒,∴//AB CD ;(2)如图2,由(1)知,//AB CD ,图2∴180BEF EFD ∠+∠=︒.又∵BEF ∠与EFD ∠的角平分线交于点P ,∴1(2)90FEP EFP BEF EFD ∠+∠=∠+∠=︒, ∴90EPF ∠=︒,即EG PF ⊥.∵GH EG ⊥,∴//PF GH ;(3)如图3,∵PHK HPK ∠=∠,2PKG HPK ∴∠=∠.又∵GH EG ⊥,∴90902KPG PKG HPK ∠=-∠=-∠.∴180902EPK KPG HPK ∠=-∠=+∠.∵PQ 平分EPK ∠,∴1452QPK EPK HPK ∠=∠=+∠. ∴45HPQ QPK HPK ∠=∠-∠=.【点睛】本题主要考查了平行线的判定与性质、角平分线的性质、三角形内角和定理等知识.解题过程关注中“数形结合”思想是解答本题的关键.2.如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+D;(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.①以线段AC为边的“8字型”有个,以点O为交点的“8字型”有个;②若∠B=100°,∠C=120°,求∠P的度数;③若角平分线中角的关系改为“∠CAP=13∠CAB,∠CDP=13∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.【答案】(1)证明见解析;(2)①3, 4;②∠P=110°;③3∠P=∠B+2∠C,理由见解析.【解析】【分析】(1)由三角形内角和得到∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,由对顶角相等,得到∠AOC=∠BOD,因而∠A+∠C=∠B+∠D;(2)①以线段AC为边的“8字形”有3个,以O为交点的“8字形”有4个;②根据(1)的结论,以M为交点“8字型”中,∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,∠P+∠BAP=∠B+∠BDP,两等式相加得到2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,由AP和DP是角平分线,得到∠BAP=∠CAP,∠CDP=∠BDP,从而∠P=12(∠B+∠C),然后将∠B=100º,∠C=120º代入计算即可;③与②的证明方法一样得到3∠P=∠B+2∠C.【详解】解:(1)在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,∵∠AOC=∠BOD,∴∠A+∠C=∠B+∠D;(2)解:①以线段AC为边的“8字型”有3个:以点O为交点的“8字型”有4个:②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,∵AP、DP分别平分∠CAB和∠BDC,∴∠BAP=∠CAP,∠CDP=∠BDP,∴2∠P=∠B+∠C,∵∠B=100°,∠C=120°,∴∠P=12(∠B+∠C)=12(100°+120°)=110°;③3∠P=∠B+2∠C,其理由是:∵∠CAP=13∠CAB,∠CDP=13∠CDB,∴∠BAP=23∠CAB,∠BDP=23∠CDB,以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP∴∠C﹣∠P=∠CDP﹣∠CAP=13(∠CDB﹣∠CAB),∠P﹣∠B=∠BDP﹣∠BAP=23(∠CDB﹣∠CAB).∴2(∠C﹣∠P)=∠P﹣∠B,∴3∠P=∠B+2∠C.故答案为:(1)证明见解析;(2)①3, 4;②∠P=110°;③3∠P=∠B+2∠C,理由见解析.【点睛】本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线的定义.3.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).(1)∠ABO的度数为°,△AOB(填“是”或“不是”灵动三角形);(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;(3)当△ABC为“灵动三角形”时,求∠OAC的度数.【答案】(1)30°;(2)详见解析;(3)∠OAC=80°或52.5°或30°.【解析】【分析】(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“智慧三角形”的概念判断;(2)根据“智慧三角形”的概念证明即可;(3)分点C在线段OB和线段OB的延长线上两种情况,根据“智慧三角形”的定义计算.【详解】(1)答案为:30°;是;(2)∵AB⊥OM∴∠B AO=90°∵∠BAC=60°∴∠OAC=∠B AO-∠BAC=30°∵∠MON=60°∴∠ACO=180°-∠OAC-∠MON=90°∴∠ACO=3∠OAC,∴△AOC为“灵动三角形”;(3)设∠OAC= x°则∠BAC=90-x, ∠ACB=60+x ,∠ABC=30°∵△ABC为“智慧三角形”,Ⅰ、当∠ABC=3∠BAC时,°,∴30=3(90-x),∴x=80Ⅱ、当∠ABC=3∠ACB时,∴30=3(60+x)∴x= -50 (舍去)∴此种情况不存在,Ⅲ、当∠BCA=3∠BAC时,∴60+x=3(90-x),∴x=52.5°,Ⅳ、当∠BCA=3∠ABC时,∴60+x=90°,∴x=30°,Ⅴ、当∠BAC=3∠ABC时,∴90-x=90°,∴x=0°(舍去)Ⅵ、当∠BAC =3∠ACB 时,∴90-x =3(60+x ),∴x= -22.5(舍去),∴此种情况不存在,∴综上所述:∠OAC=80°或52.5°或30°。
八年级上册期中精选试卷易错题(Word版 含答案)

八年级上册期中精选试卷易错题(Word版含答案)一、八年级数学全等三角形解答题压轴题(难)1.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F(1)证明:PC=PE;(2)求∠CPE的度数;(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.【答案】(1)证明见解析(2)90°(3)AP=CE【解析】【分析】(1)、根据正方形得出AB=BC,∠ABP=∠CBP=45°,结合PB=PB得出△ABP ≌△CBP,从而得出结论;(2)、根据全等得出∠BAP=∠BCP,∠DAP=∠DCP,根据PA=PE得出∠DAP=∠E,即∠DCP=∠E,易得答案;(3)、首先证明△ABP和△CBP全等,然后得出PA=PC,∠BAP=∠BCP,然后得出∠DCP=∠E,从而得出∠CPF=∠EDF=60°,然后得出△EPC是等边三角形,从而得出AP=CE.【详解】(1)、在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,在△ABP和△CBP中,又∵ PB=PB ∴△ABP ≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE;(2)、由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPF=∠EDF=90°;(3)、AP=CE理由是:在菱形ABCD中,AB=BC,∠ABP=∠CBP,在△ABP和△CBP中,又∵ PB=PB ∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠DCP,∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,∵PA=PC ∴∠DAP=∠E,∴∠DCP=∠E∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,∴△EPC是等边三角形,∴PC=CE,∴AP=CE考点:三角形全等的证明2.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,他们的运动时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由(2)判断此时线段PC和线段PQ的关系,并说明理由。
八年级上册三角形解答题易错题(Word版 含答案)

八年级上册三角形解答题易错题(Word版含答案)一、八年级数学三角形解答题压轴题(难)1.(1)如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,①写出图中一对全等的三角形,并写出它们的所有对应角;②设AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.(2)如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.【答案】(1)①△EAD≌△EA′D,其中∠EAD=∠EA′D,∠AED=∠A′ED,∠ADE=∠A′DE;②∠1=180°−2x,∠2=180°−2y;③∠A=12(∠1+∠2);(2)变化,∠A=12(∠2-∠1),见详解【解析】【分析】(1)①根据翻折方法可得△ADE≌△A′DE;②根据翻折方法可得∠AEA′=2x,∠ADA′=2y,再根据平角定义可得∠1=180°-2x,∠2=180°-2y;③首先由∠1=180°-2x,2=180°-2y,可得x=90-12∠1,y=90-12∠2,再根据三角形内角和定理可得∠A=180°-x-y,再利用等量代换可得∠A=12(∠1+∠2);(2)根据折叠的性质和三角形内角和定理解答即可.【详解】(1)①根据翻折的性质知△EAD≌△EA′D,其中∠EAD=∠EA′D,∠AED=∠A′ED,∠ADE=∠A′DE;②)∵∠AED=x,∠ADE=y,∴∠AEA′=2x,∠ADA′=2y,∴∠1=180°-2x,∠2=180°-2y;③∠A=12(∠1+∠2);∵∠1=180°-2x ,∠2=180°-2y ,∴x=90-12∠1,y=90-12∠2, ∴∠A=180°-x-y=190-(90-12∠1)-(90-12∠2)=12(∠1+∠2). (2))∵△A′DE 是△ADE 沿DE 折叠得到,∴∠A′=∠A,又∵∠AEA′=180°-∠2,∠3=∠A′+∠1,∴∠A+∠AEA′+∠3=180°,即∠A+180°-∠2+∠A′+∠1=180°,整理得,2∠A=∠2-∠1. ∴∠A=12(∠2-∠1). 【点睛】 此题主要考查了翻折变换,关键是掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.2.如图①,在△ABC 中,CD 、CE 分别是△ABC 的高和角平分线,∠BAC =α,∠B =β(α>β).(1)若α=70°,β=40°,求∠DCE 的度数; (2)试用α、β的代数式表示∠DCE 的度数(直接写出结果);(3)如图②,若CE 是△ABC 外角∠ACF 的平分线,交BA 延长线于点E ,且α﹣β=30°,求∠DCE 的度数.【答案】(1)15°;(2)DCE 2αβ-∠=;(3)75°. 【解析】【分析】(1)三角形的内角和是180°,已知∠BAC 与∠ABC 的度数,则可求出∠BAC 的度数,然后根据角平分线的性质求出∠BCE ,再利用三角形的一个外角等于和它不相邻的两个内角的和求出∠DEC 的度数,进而求出∠DCE 的度数;(2)∠DCE =2αβ- .(3)作∠ACB 的内角平分线CE′,根据角平分线的性质求出∠ECE′=∠ACE+∠ACE′=12∠ACB+12∠ACF=90°,进而求出∠DCE 的度数.【详解】 解:(1)因为∠ACB =180°﹣(∠BAC+∠B )=180°﹣(70°+40°)=70°,又因为CE 是∠ACB 的平分线,所以1352ACE ACB ∠=∠=︒. 因为CD 是高线,所以∠ADC =90°,所以∠ACD =90°﹣∠BAC =20°, 所以∠DCE =∠ACE ﹣∠ACD =35°﹣20°=15°.(2)DCE 2αβ-∠=.(3)如图,作∠ACB 的内角平分线CE′,则152DCE αβ-'==︒∠.因为CE 是∠ACB 的外角平分线,所以∠ECE′=∠ACE+∠ACE′=11+22ACB ACF ∠∠=1(+)2ACB ACF ∠∠=90°, 所以∠DCE =90°﹣∠DCE′=90°﹣15°=75°.即∠DCE 的度数为75°.【点睛】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.解决(3),作辅助线是关键.3.如图, A 为x 轴负半轴上一点, B 为x 轴正半轴上一点, C(0,-2),D(-3,-2).(1)求△BCD 的面积;(2)若AC ⊥BC,作∠CBA 的平分线交CO 于P ,交CA 于Q,判断∠CPQ 与∠CQP 的大小关系, 并证明你的结论.【答案】(1)3;(2)∠CPQ=∠CQP,理由见解析;【解析】【分析】(1)求出CD的长度,再根据三角形的面积公式列式计算即可得解;(2)根据角平分线的定义可得∠ABQ=∠CBQ,然后根据等角的余角相等解答;【详解】解:(1)∵点C(0,-2),D(-3,-2),∴CD=3,且CD//x轴∴△BCD面积=12×3×2=3;(2)∠CPQ=∠CQP,∵AC⊥BC,∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°∴∠OAC=∠BCO,又BQ平分∠CBA,∴∠ABQ=∠CBQ,∵∠CQP=∠OAC+∠ABQ∠CPQ=∠CBQ+∠BCO,∴∠CQP=∠CPQ(2)∠CPQ=∠CQP,∵AC⊥BC,∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°∴∠OAC=∠BCO,又BQ平分∠CBA,∴∠ABQ=∠CBQ,∵∠CQP=∠OAC+∠ABQ∠CPQ=∠CBQ+∠BCO,∴∠CQP=∠CPQ【点睛】本题考查了坐标与图形性质,三角形的角平分线,三角形的面积,三角形的内角和定理,三角形的外角性质,综合题,熟记性质并准确识图是解题的关键.4.如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β(1)如图,若α+β=120°,求∠MBC+∠NDC的度数;(2)如图,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;(3)如图,若α=β,判断BE、DF的位置关系,并说明理由.【答案】(1)120°;(2)β﹣α=60° 理由见解析;(3)平行,理由见解析.【解析】【分析】(1)利用四边形的内角和求出∠ABC与∠ADC的和,利用角平分线的定义以及α+β=120°推导即可;(2)由(1)得,∠MBC+∠NDC=α+β,利用角平分线的定义得∠CBG+∠CDG=12(α+β),在△BCD中利用三角形的内角和定理得∠BDC+∠CDB =180°﹣β,在△BDG中利用三角形的内角和定理得出关于α、β的等式整理即可得出结论;(3)延长BC交DF于H,由(1)得∠MBC+∠NDC=α+β,利用角平分线的定义得∠CBE+∠CDH=12(α+β),利用三角形的外角的性质得∠CDH=β﹣∠DHB,然后代入∠CBE+∠CDH=12(α+β)计算即可得出一组内错角相等.【详解】(1)解:(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,∴∠ABC+∠ADC=360°-(α+β),∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,∵α+β=120°,∴∠MBC+∠NDC=120°;(2)β﹣α=60°理由:如图1,连接BD,由(1)得,∠MBC+∠NDC=α+β,∵BE、DF分别平分四边形的外角∠MBC和∠NDC,∴∠CBG=12∠MBC,∠CDG=12∠NDC,∴∠CBG+∠CDG=12∠MBC+12∠NDC=12(∠MBC+∠NDC)=12(α+β),在△BCD中,∠BDC+∠CDB=180°﹣∠BCD=180°﹣β,在△BDG中,∠GBD+∠GDB+∠BGD=180°,∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,∴12(α+β)+180°﹣β+30°=180°,∴β﹣α=60°,(3)平行,理由:如图2,延长BC交DF于H,由(1)有,∠MBC+∠NDC=α+β,∵BE、DF分别平分四边形的外角∠MBC和∠NDC,∴∠CBE=12∠MBC,∠CDH=12∠NDC,∴∠CBE+∠CDH=12∠MBC+12∠NDC=12(∠MBC+∠NDC)=12(α+β),∵∠BCD=∠CDH+∠DHB,∴∠CDH=∠BCD﹣∠DHB=β﹣∠DHB,∴∠CBE+β﹣∠DHB=12(α+β),∵α=β,∴∠CBE+β﹣∠DHB=12(β+β)=β,∴∠CBE=∠DHB,∴BE∥DF.【点睛】此题是三角形综合题,主要考查了平角的意义,四边形的内角和,三角形内角和,三角形的外角的性质,角平分线的意义,用整体代换的思想是解本题的关键,整体思想是初中阶段的一种重要思想,要多加强训练.5.(1)在ABC ∆中,AD BC ⊥,BE AC ⊥,CF AB ⊥,16BC =,3AD =,4BE =,6CF =,则ABC ∆的周长为______.(2)如图①,在ABC ∆中,已知点D ,E ,F 分别为边BC ,BD ,CD 的中点,且4ABC S ∆=2cm ,则AEF S ∆等于______2cm .① ②(3)如②图,三角形ABC 的面积为1,点E 是AC 的中点,点O 是BE 的中点,连接AO 并延长交BC 于点D ,连接CO 并延长交AB 于点F ,则四边形BDOF 的面积为______.【答案】(1)36(2)2(3)16【解析】【分析】(1)利用三角形面积公式,求出AB 、AC 的长,再计算三角形的周长即可; (2)设ABC ∆在BC 边上的高为h ,则12ABC S BC h ∆=⋅,根据线段中点的定义以及线段的和差得出12EF BC =,继而再根据三角形面积公式进行求解即可; (3)设BOF S x ∆=,BOD S y ∆=,根据三角形中线将三角形分成两个面积相等的三角形可得14AOE COE AOB COB S S S S ∆∆∆∆====,从而得14AOF S x ∆=-,34ACF S x ∆=-,14BCF S x ∆=+,14COD S y ∆=-,34ACD S y ∆=-,14ABD S y ∆=+,利用等高的两三角形面积之比等于底边之比分别列出关于x 、y 的方程,求出x 、y 的值即可求得答案.【详解】(1)111222ABC S BC AD AC BE AB CF ∆=⋅=⋅=⋅, ∴BC AD AC BE AB CF ⋅=⋅=⋅,即16346AC AB ⨯=⋅=⋅,∴12AC =,8AB =,∴△ABC 的周长=AB+BC+AC=36;(2)设ABC ∆在BC 边上的高为h ,则12ABC S BC h ∆=⋅, ∵E 为BD 中点,∴12ED BD =, ∵F 为DC 中点,∴12DF DC =, ∴111222EF BD DC BC =+=, ∴211112cm 2222AEF ABC S EF h BC h S ∆∆=⋅=⋅⋅==; (3)设BOF S x ∆=,BOD S y ∆=,∵点E ,O 分别是AC ,BE 的中点,1ABC S ∆=, ∴14AOE COE AOB COB S S S S ∆∆∆∆====, ∴14AOF S x ∆=-,34ACF S x ∆=-,14BCF S x ∆=+, ∴134414x x x x --=+,即2213164x x x -=-, 解得112x =, 又14COD S y ∆=-,34ACD S y ∆=-,14ABD S y ∆=+, ∴141344y y y y +=--,得112y =, 故11112126BDOF S x y =+=+=四边形. 【点睛】本题考查了三角形面积的应用,三角形的周长,解题关键在于找出等高的两三角形面积与底边的对应关系.6.如图1:ABC 中,AD 是高,AE 是BAC ∠的平分线,=40=70ABC ACB ,∠︒∠︒.(1)求EAD ∠的度数(2)当==ABC ACB αβ∠∠,,请用αβ,表示EAD ∠,并写出推导过程(3)当AE 是BAC ∠的外角FAC ∠的平分线,如图2则此时EAD ∠的度数是多少,用,αβ表示,直接写出结果.【答案】(1)15o ;(2) -2EAD βα∠=;(3) 902EAD αβ-∠=︒+【解析】【分析】(1)先根据三角形的内角和定理求得∠BAC=180°-∠B-∠C=70°,利用角平分线的定义得∠EAC=12∠BAC=35°,而∠DAC=90°-∠C=20°,通过∠EAD=∠EAC-∠DAC 即可得到结果. (2)猜想∠DAE=12(β-α),重复(1)的过程找出∠BAD 和∠BAE 的度数,二者做差即可得出结论; (3)作∠BAC 的内角平分线AE ′,根据角平分线的性质求出∠EAE′=∠CAE+∠CAE′=12∠CAB+12∠CAF=90°,进而求出∠DAE 的度数. 【详解】解:(1)40,70,ABC ACB ∠=︒∠=︒180704070BAC ∴∠=︒-︒-︒=︒, AE 是BAC ∠的平分线,1=352BAE CAE BAC ∴∠=∠=∠︒, 在ACD Rt 中,9020CAD C ∠=︒-∠=︒,15EAD EAC CAD ∴∠=∠-∠=︒.(2),,ABC ACB αβ∠=∠=180BAC αβ∴∠=︒--, AE 是BAC ∠的平分线,1111=180--=90--2222BAE CAE BAC αβαβ∴∠=∠=∠︒︒(), 在Rt △ACD 中,90CAD β∠=︒-,-=2EAD CAE CAD βα∴∠=∠-∠. (3)902EAD αβ-∠=︒+.如图,作∠CAB 的内角平分线AE′,则∠DAE′=-2βα.因为AE 是∠ACB 的外角平分线,所以∠EAE′=∠CAE+∠CAE′=12∠CAB+12∠CAF=12(∠CAB+∠CAF )=90°, 所以∠DAE=90°-∠DAE′=90°--2βα=902αβ-︒+. 即∠DAE 的度数为902αβ-︒+. 【点睛】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.解决(3)作辅助线是关键.7.操作示例:如图1,在△ABC 中,AD 为BC 边上的中线,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1=S 2.解决问题:在图2中,点D 、E 分别是边AB 、BC 的中点,若△BDE 的面积为2,则四边形ADEC 的面积为 .拓展延伸:(1)如图3,在△ABC 中,点D 在边BC 上,且BD =2CD ,△ABD 的面积记为S 1,△ADC 的面积记为S 2.则S 1与S 2之间的数量关系为 .(2)如图4,在△ABC 中,点D 、E 分别在边AB 、AC 上,连接BE 、CD 交于点O ,且BO =2EO ,CO =DO ,若△BOC 的面积为3,则四边形ADOE 的面积为 .【答案】解决问题:6; 拓展延伸:(1)S 1=2S 2 (2)10.5【解析】试题分析:解决问题:连接AE ,根据操作示例得到S △ADE =S △BDE ,S △ABE =S △AEC ,从而得到结论;拓展延伸:(1)作△ABD 的中线AE ,则有BE =ED =DC ,从而得到△ABE 的面积=△AED 的面积=△ADC 的面积,由此即可得到结论;(2)连接AO.则可得到△BOD的面积=△BOC的面积,△AOC的面积=△AOD的面积,△EOC的面积=△BOC的面积的一半,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,求出a、b的值,即可得到结论.试题解析:解:解决问题连接AE.∵点D、E分别是边AB、BC的中点,∴S△ADE=S△BDE,S△ABE=S△AEC.∵S△BDE=2,∴S△ADE =2,∴S△ABE=S△AEC=4,∴四边形ADEC的面积=2+4=6.拓展延伸:解:(1)作△ABD的中线AE,则有BE=ED=DC,∴△ABE的面积=△AED的面积=△ADC的面积= S2,∴S1=2S2.(2)连接AO.∵CO=DO,∴△BOD的面积=△BOC的面积=3,△AOC的面积=△AOD的面积.∵BO=2EO,∴△EOC的面积=△BOC的面积的一半=1.5,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,解得:a=6,b=4.5,∴四边形ADOE的面积为=a+b=6+4.5=10.5.8.等边△ABC边长为6,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转。
全等三角形易错题(Word版 含答案)

全等三角形易错题(Word版含答案)一、八年级数学轴对称三角形填空题(难)1.在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=12BC,则△ABC的顶角的度数为_____.【答案】30°或150°或90°【解析】试题分析:分两种情况;①BC为腰,②BC为底,根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°,然后分AD在△ABC内部和外部两种情况求解即可.解:①BC为腰,∵AD⊥BC于点D,AD=12 BC,∴∠ACD=30°,如图1,AD在△ABC内部时,顶角∠C=30°,如图2,AD在△ABC外部时,顶角∠ACB=180°﹣30°=150°,②BC为底,如图3,∵AD⊥BC于点D,AD=12 BC,∴AD=BD=CD,∴∠B=∠BAD,∠C=∠CAD,∴∠BAD+∠CAD=12×180°=90°,∴顶角∠BAC=90°,综上所述,等腰三角形ABC的顶角度数为30°或150°或90°.故答案为30°或150°或90°.点睛:本题考查了含30°交点直角三角形的性质,等腰三角形的性质,分类讨论是解题的关键.2.在直角坐标系中,O 为坐标原点,已知点 A(1,2),点 P 是 y 轴正半轴上的一点,且△AOP 为等腰三角形,则点P 的坐标为_____________.【答案】5 4),0,4⎛⎫⎪⎝⎭【解析】【分析】有三种情况:①以O为圆心,以OA为半径画弧交y轴于D,求出OA即可;②以A为圆心,以OA为半径画弧交y轴于P,求出OP即可;③作OA的垂直平分线交y轴于C,则AC=OC,根据勾股定理求出OC即可.【详解】有三种情况:①以O为圆心,以OA为半径画弧交y轴于D,则OA=OD==∴D(0);②以A为圆心,以OA为半径画弧交y轴于P,OP=2×y A=4,∴P(0,4);③作OA的垂直平分线交y轴于C,则AC=OC,由勾股定理得:OC=AC,∴OC=54,∴C(0,54);故答案为:5 4),0,4⎛⎫⎪⎝⎭.【点睛】本题主要考查对线段的垂直平分线,等腰三角形的性质和判定,勾股定理,坐标与图形性质等知识点的理解和掌握,能求出符合条件的所有情况是解此题的关键.3.△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=6.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF 运动过程中,若△AEM能构成等腰三角形,则BE的长为______.【答案】363【解析】【分析】分若AE=AM 则∠AME=∠AEM=45°;若AE=EM;若MA=ME 则∠MAE=∠AEM=45°三种情况讨论解答即可;【详解】解:①若AE=AM 则∠AME=∠AEM=45°∵∠C=45°∴∠AME=∠C又∵∠AME>∠C∴这种情况不成立;②若AE=EM∵∠B=∠AEM=45°∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°∴∠BAE=∠MEC在△ABE和△ECM中,BBAE CENAE EIIC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE≌△ECM(AAS),∴CE=AB=6,∵AC=BC=2AB=23,∴BE=23﹣6;③若MA=ME 则∠MAE=∠AEM=45°∵∠BAC=90°,∴∠BAE=45°∴AE平分∠BAC∵AB=AC,∴BE=12BC=3.故答案为23﹣6或3.【点睛】本题考查了等腰三角形的判定,掌握分类讨论的数学思想是解答本题的关键.4.如图,在ABC∆中,点D是BC的中点,点E是AD上一点,BE AC=.若70C∠=︒,50DAC∠=︒则EBD∠的度数为______.【答案】10︒【解析】【分析】延长AD 到F 使DF AD =,连接BF ,通过ACD FDB ≅,根据全等三角形的性质得到CAD BFD ∠=∠,AC BF =, 等量代换得BF BE =,由等腰三角形的性质得到F BEF ∠=∠,即可得到BEF CAD ∠=∠,进而利用三角形的内角和解答即可得.【详解】如图,延长AD 到F ,使DF AD =,连接BF :∵D 是BC 的中点∴BD CD =又∵ADC FDB ∠=∠,AD DF =∴ACD FDB ≅∴AC BF =, CAD F ∠=∠,C DBF ∠=∠∵AC BE =, 70C ︒∠=, 50CAD ︒∠=∴BE BF =, 70DBF ︒∠=∴50BEF F ︒∠=∠=∴180180505080EBF F BEF ︒︒︒︒︒∠=-∠-∠=--=∴807010EBD EBF DBF ︒︒︒∠=∠-∠=-=故答案为:10︒【点睛】本题主要考查的知识点有全等三角形的判定及性质、等腰三角形的性质及三角形的内角和定理,解题的关键在于通过倍长中线法构造全等三角形.5.如图,已知△ABC 中,AB=AC ,∠BAC=90°,直角∠EPF 的顶点P 是BC 中点,两边PE 、PF 分别交AB 、AC 于点E 、F ,给出下列四个结论:①AE=CF ;②△EPF 是等腰直角三角形;③EF=AB;④12ABCAEPFS S∆=四边形,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).【答案】①②④【解析】试题分析:∵∠APE、∠CPF都是∠APF的余角,∴∠APE=∠CPF,∵AB=AC,∠BAC=90°,P是BC中点,∴AP=CP,∴∠PAE=∠PCF,在△APE与△CPF中,{?PAE PCFAP CPEPA FPC∠=∠=∠=∠,∴△APE≌△CPF(ASA),同理可证△APF≌△BPE,∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF=12S△ABC,①②④正确;而AP=12BC,当EF不是△ABC的中位线时,则EF不等于BC的一半,EF=AP,∴故③不成立.故始终正确的是①②④.故选D.考点:1.全等三角形的判定与性质;2.等腰直角三角形.6.如图,在ABC∆中,AB AC=,点D和点A在直线BC的同侧,,82,38BD BC BAC DBC=∠=︒∠=︒,连接,AD CD,则ADB∠的度数为__________.【答案】30°【解析】【分析】先根据等腰三角形的性质和三角形的内角和定理以及角的和差求出ABD ∠的度数,然后作点D 关于直线AB 的对称点E ,连接BE 、CE 、AE ,如图,则BE=BD ,∠EBA=∠DB ,∠BEA =∠BDA ,进而可得∠EBC=60°,由于BD=BC ,从而可证△EBC 是等边三角形,可得∠BEC =60°,EB=EC ,进一步即可根据SSS 证明△AEB ≌△AEC ,可得∠BEA 的度数,问题即得解决.【详解】解:∵AB AC =,82BAC ∠=︒,∴180492BAC ABC ︒-∠∠==︒, ∵38DBC ∠=︒,∴493811ABD ∠=︒-︒=︒,作点D 关于直线AB 的对称点E ,连接BE 、CE 、AE ,如图,则BE=BD ,∠EBA=∠DBA =11°,∠BEA =∠BDA ,∴∠EBC=11°+11°+38°=60°,∵BD=BC ,∴BE=BC ,∴△EBC 是等边三角形,∴∠BEC =60°,EB=EC ,又∵AB=AC ,EA=EA ,∴△AEB ≌△AEC (SSS ),∴∠BEA =∠CEA =1302BEC ∠=︒, ∴∠ADB =30°.【点睛】本题考查了等腰三角形的性质、三角形的内角和定理、等边三角形的判定和性质、全等三角形的判定和性质以及轴对称的性质等知识,涉及的知识点多、综合性强,难度较大,作点D 关于直线AB 的对称点E ,构造等边三角形和全等三角形的模型是解题的关键.7.如图,BD 是ABC 的角平分线,AE BD ⊥,垂足为F ,且交线段BC 于点E ,连结DE ,若50C ∠=︒,设 ABC x CDE y ∠=︒∠=︒,,则y 关于x 的函数表达式为_____________.【答案】80y x =-【解析】【分析】 根据题意,由等腰三角形的性质可得BD 是AE 的垂直平分线,进而得到AD =ED ,求出BED ∠的度数即可得到y 关于x 的函数表达式.【详解】∵BD 是ABC ∆的角平分线,AE BD ⊥∴1122ABD EBD ABC x ∠=∠=∠=︒,90AFB EFB ∠=∠=︒ ∴1902BAF BEF x ∠=∠=︒-︒ ∴AB BE =∴AF EF =∴AD ED =∴DAF DEF ∠=∠∵180BAC ABC C ∠=︒-∠-∠,50C ∠=︒∴130BAC x ∠=︒-︒∴130BED BAD x ∠=∠=︒-︒∵CDE BED C ∠=∠-∠∴1305080y x x ︒=-︒-︒=︒-︒∴80y x =-,故答案为:80y x =-.【点睛】本题主要考查了等腰三角形的性质及判定,三角形的内角和定理,三角形外角定理,角的和差倍分等相关知识,熟练运用角的计算是解决本题的关键.8.如图,已知∠MON =30°,点A 1,A 2,A 3,…在射线ON 上,点B 1,B 2,B 3,…在射线OM 上,△A 1B 1A 2,△A 2B 2A 3,△A 3B 3A 4,…均为等边三角形,若OA 2=4,则△A n B n A n +1的边长为_____.【答案】2n.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2…进而得出答案.【详解】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∵∠MON=30°,∵OA2=4,∴OA1=A1B1=2,∴A2B1=2,∵△A2B2A3、△A3B3A4是等边三角形,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2=32,以此类推△A n B n A n+1的边长为 2n.故答案为:2n.【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键.9.已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30 ,CF=43,则DH=______.【答案】23【解析】连接AF.∵△ABC是等边三角形,∴AB=BC,∠ABC=∠ACB=∠BAC=60°.∵DE=DC,∠EDC=30°,∴∠DEC=∠DCE=75°,∴∠ACF=75°-60°=15°.∵BF平分∠ABC,∴∠ABF=∠CBF.在△ABF和△CBF中,AB BCABF CBFBF BF⎧⎪∠∠⎨⎪⎩===,∴△ABF≌△CBF,∴AF=CF,∴∠FAC=∠ACF=15°,∴∠AFH=15°+15°=30°.∵AH⊥CD,∴AH=12AF=12CF=23.∵∠DEC=∠ABC+∠BDE,∴∠BDE=75°-60°=15°,∴∠ADH=15°+30°=45°,∴∠DAH=∠ADH=45°,∴DH=AH=23.故答案为23.点睛:本题考查了全等三角形的判定与性质;证明三角形全等是解决问题的关键,注意辅助线的作法.10.如图:在ABC ∆中,D ,E 为边AB 上的两个点,且BD BC =,AE AC =,若108ACB ∠=︒,则DCE ∠的大小为______.【答案】036【解析】【分析】根据三角形内角和求出∠A+∠B,再根据AC=AE,BC=BD ,用∠A 表示∠AEC,用∠B 表示∠BDC,然后根据内角和求出∠DCE 的度数.【详解】∵∠ACB=1080,∴∠A+∠B=1800-1080=720,∵AC=AE,BC=BD,∴∠ACE=∠AEC,∠BCD=∠BDC,∴01(180)2AEC A ∠=-∠01902A =-∠ 01(180)2BDCB ∠=-∠ =01902B -∠ ∵∠DCE+∠CDE+∠DEC=1800,∴0180DCE CDE CED ∠=-∠-∠= 00011180(90)(90)22A B --∠--∠ =1122A B ∠+∠ =1()2A B ∠+∠ =360【点睛】此题考察等腰三角形的性质,注意两条等边所在三角形,依此判断对应的两个底角相等.二、八年级数学轴对称三角形选择题(难)11.如图,平面直角坐标系中存在点A (3,2),点B (1,0),以线段AB 为边作等腰三角形ABP ,使得点P 在坐标轴上.则这样的P 点有( )A .4个B .5个C .6个D .7个【答案】D【解析】【分析】 本题是开放性试题,由题意知A 、B 是定点,P 是动点,所以要分情况讨论:以AP 、AB 为腰、以AP 、BP 为腰或以BP 、AB 为腰.则满足条件的点P 可求.【详解】由题意可知:以AP 、AB 为腰的三角形有3个;以AP 、BP 为腰的三角形有2个;以BP 、AB 为腰的三角形有2个.所以,这样的点P 共有7个.故选D .【点睛】本题考查了等腰三角形的判定及坐标与图形的性质;分类别寻找是正确解答本题的关键.12.已知40MON ∠=︒,P 为MON ∠内一定点,OM 上有一点A ,ON 上有一点B ,当PAB ∆的周长取最小值时,APB ∠的度数是( )A .40︒B .50︒C .100︒D .140︒【答案】C【解析】【分析】 设点P 关于OM 、ON 对称点分别为P '、P '',当点A 、B 在P P '''上时,PAB ∆周长为PA AB BP P P ++=''',此时周长最小.根据轴对称的性质,可求出APB ∠的度数.【详解】分别作点P 关于OM 、ON 的对称点P '、P '',连接OP '、OP ''、P P ''',P P '''交OM 、ON 于点A 、B ,连接PA 、PB ,此时PAB ∆周长的最小值等于P P '''.由轴对称性质可得,OP OP OP '=''=,P OA POA ∠'=∠,P OB POB ∠''=∠,224080P OP MON ∴∠'''=∠=⨯︒=︒,(18080)250OP P OP P ∴∠'''=∠'''=︒-︒÷=︒,又50BPO OP B ∠=∠''=︒,50APO AP O ∠=∠'=︒,100APB APO BPO ∴∠=∠+∠=︒.故选:C .【点睛】此题考查轴对称作图,最短路径问题,将三角形周长最小转化为最短路径问题,根据轴对称作图是解题的关键.13.如图,坐标平面内一点A(2,-1),O 为原点,P 是x 轴上的一个动点,如果以点P 、O 、A 为顶点的三角形是等腰三角形,那么符合条件的动点P 的个数为( )A .2B .3C .4D .5【答案】C【解析】 以O 点为圆心,OA 为半径作圆与x 轴有两交点,这两点显然符合题意.以A 点为圆心,OA 为半径作圆与x 轴交与两点(O 点除外).以OA 中点为圆心OA 长一半为半径作圆与x 轴有一交点.共4个点符合,14.如图,AB ⊥AC ,CD 、BE 分别是△ABC 的角平分线,AG ∥BC ,AG ⊥BG ,下列结论:①∠BAG =2∠ABF ;②BA 平分∠CBG ;③∠ABG =∠ACB ;④∠CFB =135°,其中正确的结论有( )个A .1B .2C .3D .4【解析】【分析】由已知条件可知∠ABC+∠ACB=90°,又因为CD 、BE 分别是△ABC 的角平分线,所以得到∠FBC+∠FCB=45°,所以求出∠CFB=135°;有平行线的性质可得到:∠ABG=∠ACB ,∠BAG=2∠ABF .所以可知选项①③④正确.【详解】∵AB ⊥AC .∴∠BAC =90°,∵∠BAC+∠ABC+∠ACB =180°,∴∠ABC+∠ACB =90°∵CD 、BE 分别是△ABC 的角平分线,∴2∠FBC+2∠FCB =90°∴∠FBC+∠FCB =45°∴∠BFC =135°故④正确.∵AG ∥BC ,∴∠BAG =∠ABC∵∠ABC =2∠ABF∴∠BAG =2∠ABF 故①正确.∵AB ⊥AC ,∴∠ABC+∠ACB =90°,∵AG ⊥BG ,∴∠ABG+∠GAB =90°∵∠BAG =∠ABC ,∴∠ABG =∠ACB 故③正确.故选C .【点睛】本题考查了等腰三角形的判定与性质,平行线的性质.掌握相关的判定定理和性质定理是解题的关键.15.在Rt ABC ∆中,90ACB ∠=︒,点D E 、是AB 边上两点,且CE 垂直平分,AD CD 平分,6BCE AC cm ∠=,则BD 的长为( )A .6cmB .7cmC .8cmD .9cm【答案】A【分析】根据CE 垂直平分AD ,得AC=CD ,再根据等腰在三角形的三线合一,得ACE ECD ∠=∠,结合角平分线定义和90ACB ︒∠=,得30ACE ECD DCB ︒∠=∠=∠=,则BD CD AC ==.【详解】∵CE 垂直平分AD∴AC=CD =6cm ,ACE ECD ∠=∠∵CD 平分BCE ∠∴BCD ECD ∠=∠∴30ACE ECD DCB ︒∠=∠=∠=∴60A ︒∠=∴30B BCD ︒∠==∠∴6CD BD AC cm ===故选:A【点睛】本题考查的知识点主要是等腰三角形的性质的“三线合一”性质定理及判定“等角对等边”,熟记并能熟练运用这些定理是解题的关键.16.在Rt ABC ∆中,90ACB ∠=︒,以ABC ∆的一边为边画等腰三角形,使得它的第三个顶点在ABC ∆的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个?( )A .9个B .7个C .6个D .5个【答案】B【解析】【分析】先以Rt ABC ∆三个顶点分别为圆心,再以每个顶点所在的较短边为半径画弧,即可确定等腰三角形的第三个顶点;也可以作三边的垂直平分线确定等腰三角形的第三个顶点即得.【详解】解:①如图1,以B为圆心,BC长为半径画弧,交AB于点D,则∆BCD就是等腰三角形;②如图2,以A为圆心,AC长为半径画弧,交AB于点E,则∆ACE就是等腰三角形;③如图3,以C为圆心,BC长为半径画弧,交AB于M,交AC于点F,则∆BCM、∆BCF是等腰三角形;④如图4,作AC的垂直平分线交AB于点H,则∆ACH就是等腰三角形;⑤如图5,作AB的垂直平分线交AC于点G,则∆AGB就是等腰三角形;⑥如图6,作BC的垂直平分线交AB于I,则∆BCI就是等腰三角形.故选:B.【点睛】本题考查等腰三角形的判定的应用,通过作垂直平分线或者画弧的方法确定相等的边是解题关键.17.如图,△ABC、△CDE都是等腰三角形,且CA=CB, CD=CE,∠ACB=∠DCE=α,AD,BE相交于点O,点M,N分别是线段AD,BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC,则OC平分∠AOE.正确的是()A.①②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】①根据全等三角形的判定定理得到△ACD≌△BCE(SAS),由全等三角形的性质得到AD=BE;故①正确;②设CD与BE交于F,根据全等三角形的性质得到∠ADC=∠BEC,得到∠DOE=∠DCE=α,根据平角的定义得到∠BOD=180°-∠DOE=180°-α,故②正确; ③根据全等三角形的性质得到∠CAD=∠CBE ,AD=BE ,AC=BC 根据线段的中点的定义得到AM=BN ,根据全等三角形的性质得到CM=CN ,∠ACM=∠BCN ,得到∠MCN=α,推出△MNC 不一定是等边三角形,故③不符合题意;④过C 作CG ⊥BE 于G ,CH ⊥AD 于H ,根据全等三角形的性质得到CH=CG ,根据角平分线的判定定理即可得到OC 平分∠AOE ,故④正确.【详解】解:①∵CA=CB ,CD=CE ,∠ACB=∠DCE=α,∴∠ACB+∠BCD=∠DCE+∠BCD ,∴∠ACD=∠BCE ,在△ACD 和△BCE 中AC BC ACD BCE CD CE ⎪∠⎪⎩∠⎧⎨=== ∴△ACD ≌△BCE (SAS ),∴AD=BE ;故①正确;②设CD 与BE 交于F ,∵△ACD ≌△BCE ,∴∠ADC=∠BEC ,∵∠CFE=∠DFO ,∴∠DOE=∠DCE=α,∴∠BOD=180°-∠DOE=180°-α,故②正确;③∵△ACD ≌△BCE ,∴∠CAD=∠CBE ,AD=BE ,AC=BC又∵点M 、N 分别是线段AD 、BE 的中点,∴AM=12AD ,BN=12BE , ∴AM=BN ,在△ACM 和△BCN 中 AC BC CAM CBN AM BN ⎪∠⎪⎩∠⎧⎨=== ∴△ACM ≌△BCN (SAS ),∴CM=CN ,∠ACM=∠BCN ,又∠ACB=α,∴∠ACM+∠MCB=α,∴∠BCN+∠MCB=α,∴∠MCN=α,∴△MNC 不一定是等边三角形,故③不符合题意;④过C 作CG ⊥BE 于G ,CH ⊥AD 于H ,∴∠CHD=∠ECG=90°,∵∠CEG=∠CDH ,CE=CD ,∴△CGE ≌△CHD (AAS ),∴CH=CG ,∴OC 平分∠AOE ,故④正确,故选:B .【点睛】本题综合考查了全等三角形的性质和判定,三角形的内角和定理,等边三角形的性质和判定等知识点的应用,解此题的关键是根据性质进行推理,此题综合性比较强,有一定的代表性.18.如图,等腰ABC ∆中,AB AC =,120BAC ∠=,AD BC ⊥于点D ,点P 是BA 延长线上一点,点O 是线段AD 上一点,OP OC =.下列结论:①30APO DCO ∠+∠=;②APO DCO ∠=∠;③OPC ∆是等边三角形;④AB AO AP =+.其中正确结论的个数是( )A .1B .2C .3D .4【答案】D【解析】【分析】 ①②连接OB ,根据垂直平分线性质即可求得OB=OC=OP ,即可解题;③根据周角等于360°和三角形内角和为180°即可求得∠POC=2∠ABD=60°,即可解题;④AB 上找到Q 点使得AQ=OA ,易证△BQO≌△PAO,可得PA=BQ ,即可解题.【详解】连接OB ,∵AB AC =,AD ⊥BC ,∴AD 是BC 垂直平分线,∴OB OC OP ==,∴APO ABO ∠=∠,DBO DCO ∠=∠,∵AB=AC ,∠BAC =120∘∴30ABC ACB ∠=∠=︒∴30ABO DBO ∠+∠=︒,∴30APO DCO ∠+∠=.故①②正确;∵OBP ∆中,180BOP OPB OBP ∠=︒-∠-∠,BOC ∆中,180BOC OBC OCB ∠=︒-∠-∠,∴360POC BOP BOC OPB OBP OBC OCB ∠=︒-∠-∠=∠+∠+∠+∠,∵OPB OBP ∠=∠,OBC OCB ∠=∠,∴260POC ABD ∠=∠=︒,∵PO OC ,∴OPC ∆是等边三角形,故③正确;在AB 上找到Q 点使得AQ=OA ,则AOQ ∆为等边三角形,则120BQO PAO ∠=∠=︒,在BQO ∆和PAO ∆中,BQO PAO QBO APO OB OP ∠∠⎧⎪∠∠⎨⎪⎩===∴BQO PAO AAS ∆∆≌(),∴PA BQ =,∵AB BQ AQ =+,∴AB AO AP =+,故④正确.故选:D.【点睛】本题主要考查全等三角形的判定与性质、线段垂直平分线的性质,本题中求证BQO PAO ∆∆≌是解题的关键.19.如图,在Rt △ABC 中,AC =BC ,∠ACB =90°,D 为AB 的中点,E 为线段AD 上一点,过E 点的线段FG 交CD 的延长线于G 点,交AC 于F 点,且EG =AE ,分别延长CE ,BG 交于点H ,若EH 平分∠AEG ,HD 平分∠CHG 则下列说法:①∠GDH =45°;②GD =ED ;③EF =2DM ;④CG =2DE +AE ,正确的是( )A .①②③B .①②④C .②③④D .①②③④【答案】B【解析】【分析】 首先证明△AEC ≌△GEC (SAS ),推出CA =CG ,∠A =∠CGE =45°,推出DE =DG ,故②正确;再证明△EDC ≌△GDB ,推出∠CED =∠BGD ,ED =GD ,由三角形外角的性质得出∠HDG =∠HDE ,进而得出∠GDH =∠EDH =45°,即可判断①正确;通过证明△EDC 和△EMD 是等腰直角三角形,得到ED 2MD ,再通过证明△EFC ≌△EDC ,得到EF =ED ,从而可判断③错误;由CG =CD +DG ,CD =AD ,ED =GD ,变形即可判断④正确.【详解】∵AC =BC ,∠ACB =90°,AD =DB ,∴CD ⊥AB ,CD =AD =DB ,∠A =∠CBD =45°.∵EH 平分∠AEG ,∴∠AEH =∠GEH .∵∠AEH +∠AEC =180°,∠GEH +∠CEG =180°,∴∠AEC =∠CEG .∵AE=GE,EC=EC,∴△AEC≌△GEC(SAS),∴CA=CG,∠A=∠CGE=45°.∵∠EDG=90°,∴∠DEG=∠DGE=45°,∴DE=DG,∠AEF=∠DEG=∠A=45°,故②正确;∵DE=DG,∠CDE=∠BDG=90°,DC=DB,∴△EDC≌△GDB(SAS),∴∠CED=∠BGD,ED=GD.∵HD平分∠CHG,∴∠GHD=∠EHD.∵∠CED=∠EHD+∠HDE,∠BGD=∠GHD+∠HDG,∴∠HDG=∠HDE.∵∠EDG=∠ADC=90°,∴∠GDH=∠EDH=45°,故①正确;∵∠EDC=90°,ED=GD,∴△EDC是等腰直角三角形,∴∠DEG=45°.∵∠GDH=45°,∴∠EDH=45°,∴△EMD是等腰直角三角形,∴ED MD.∵∠AEF=∠DEG=∠A=45°,∴∠AFE=∠CFG=90°.∵∠EDC=90°,∴∠EFC=∠EDC=90°.∵EH平分∠AEG,∴∠AEH=∠GEH.∵∠FEC=∠GEH,∠DEC=∠AEH,∴∠FEC=∠DEC.∵EC=EC,∴△EFC≌△EDC,∴EF=ED,∴EF MD.故③错误;∵CG=CD+DG=AD+ED=AE+ED+ED,∴CG=2DE+AE,故④正确.故选B.【点睛】本题考查了等腰直角三角形的性质和判定,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考选择题中的压轴题.20.如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为()A.(-2012,2)B.(-2012,-2)C.(-2013,-2)D.(-2013,2)【答案】A【解析】试题分析:首先由正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),继而求得把正方形ABCD连续经过2014次这样的变换得到正方形ABCD的对角线交点M的坐标.试题解析:∵正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).∴对角线交点M的坐标为(2,2),根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),∴连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为(-2012,2).故选A.考点:1.翻折变换(折叠问题);2.正方形的性质;3.坐标与图形变化-平移.。
八年级数学三角形填空选择易错题(Word版 含答案)

八年级数学三角形填空选择易错题(Word 版 含答案)一、八年级数学三角形填空题(难)1.如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限,且MA 平分∠BAO ,做射线MB ,若∠1=∠2,则∠M 的度数是_______。
【答案】45︒【解析】【分析】根据三角形内角与外角的关系可得2M MAB ∠∠∠=+由角平分线的性质可得MAB MAO ∠∠=根据三角形内角和定理可得OBA OAB BOA 180∠∠∠++=︒易得∠M 的度数。
【详解】在ABM 中,2∠是ABM 的外角∴2M MAB ∠∠∠=+由三角形内角和定理可得OBA OAB BOA 180∠∠∠++=︒∵BOA 90∠=︒∴OBA OAB 90∠∠+=︒∵MA 平分BAO ∠∴BAO 2MAB ∠∠=由三角形内角与外角的关系可得12BAO BOA 90BAO ∠∠∠∠∠+=+=︒+ ∵12∠∠=∴2290BAO ∠∠=︒+又∵2M MAB ∠∠∠=+∴222M 2MAB 2M BAO ∠∠∠∠∠=+=+∴90BAO 2M BAO ∠∠∠︒+=+2M 90∠=︒M 45∠=︒【点睛】本题考查三角形外角的性质,即三角形的外角等于与之不相邻的两个内角的和。
2.如图,将一副直角三角板,按如图所示叠放在一起,则图中∠COB =____.【答案】105°.【解析】【分析】先根据直角三角形的特殊角可知:∠ECD=45°,∠BDC=60°,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】如图,∠ECD=45°,∠BDC=60°,∴∠COB=∠ECD+∠BDC=45°+60°=105°.故答案为:105°.【点睛】此题考查三角形外角的性质,掌握三角形的一个外角等于与它不相邻的两个内角的和的性质是解题的关键.3.如图,在△ABC中,∠B和∠C的平分线交于点O,若∠A=50°,则∠BOC=_____.【答案】115°.【解析】【分析】根据三角形的内角和定理得出∠ABC+∠ACB=130°,然后根据角平分线的概念得出∠OBC+∠OCB,再根据三角形的内角和定理即可得出∠BOC的度数.【详解】解;∵∠A=50°,∴∠ABC+∠ACB=180°﹣50°=130°,∵∠B和∠C的平分线交于点O,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∴∠OBC+∠OCB=12×(∠ABC+∠ACB)=12×130°=65°,∴∠BOC=180°﹣(∠OBC+∠OCB)=115°,故答案为:115°.【点睛】本题考查了三角形的内角和定理和三角形的角平分线的概念,关键是求出∠OBC+∠OCB 的度数.4.如图所示,∠1+∠2+∠3+∠4+∠5+∠6=__________度.【答案】360 °【解析】如图所示,根据三角形外角的性质可得,∠1+∠5=∠8,∠4+∠6=∠7,根据四边形的内角和为360°,可得∠2+∠3+∠7+∠8=360°,即可得∠1+∠2+∠3+∠4+∠5+∠6=360°.点睛:本题考查的知识点:(1)三角形的内角和外角之间的关系:三角形的外角等于与它不相邻的两个内角和;(2)四边形内角和定理:四边形内角和为360°.5.如果一个n边形的内角和是1440°,那么n=__.【答案】10【解析】∵n边形的内角和是1440°,∴(n−2)×180°=1440°,解得:n=10.故答案为:10.6.如图,A、B、C三点在同一条直线上,∠A=50°,BD垂直平分AE,垂足为D,则∠EBC 的度数为_____.【答案】100°【解析】【分析】根据线段垂直平分线的性质,得BE BA =,根据等腰三角形的性质,得50E A ∠=∠=︒,再根据三角形外角的性质即可求解.【详解】∵BD 垂直平分AE ,∴BE BA =,∴50E A ∠=∠=︒,∴100EBC E A ∠=∠+∠=︒,故答案为100°.【点睛】考查线段垂直平分线的性质以及三角形外角的性质,掌握线段垂直平分线的性质是解题的关键.7.如图,在△ABC 中,∠ABC 、∠ACB 的平分线BE 、CD 相交于点F ,∠A=60°,则∠BFC=______.【答案】120【解析】【分析】根据角平分线的定义可得出∠CBF =12∠ABC 、∠BCF =12∠ACB ,再根据内角和定理结合∠A =60°即可求出∠BFC 的度数.【详解】∵∠ABC 、∠ACB 的平分线BE 、CD 相交于点F ,∴∠CBF =12∠ABC ,∠BCF =12∠ACB .∵∠A =60°,∴∠ABC +∠ACB =180°﹣∠A =120°,∴∠BFC =180°﹣(∠CBF +BCF )=180°﹣12(∠ABC +∠ACB )=120°. 故答案为120°.【点睛】 本题考查了三角形内角和定理,根据角平分线的定义结合三角形内角和定理求出角的度数是解题的关键.8.如图,在△ABC 中,∠A =60°,若剪去∠A 得到四边形BCDE ,则∠1+∠2=______.【答案】240.【解析】【详解】试题分析:∠1+∠2=180°+60°=240°.考点:1.三角形的外角性质;2.三角形内角和定理.9.如图所示,请将12A ∠∠∠、、用“>”排列__________________.【答案】21A ∠∠∠>>【解析】【分析】根据三角形的外角的性质判断即可.【详解】解:根据三角形的外角的性质得,∠2>∠1,∠1>∠A∴∠2>∠1>∠A ,故答案为:∠2>∠1>∠A .【点睛】本题考查了三角形的外角的性质,掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键.10.如图,BP 是△ABC 中∠ABC 的平分线,CP 是∠ACB 的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=______°.【答案】30【解析】【分析】根据角平分线的定义可得∠PBC=20°,∠PCM=50°,根据三角形外角性质即可求出∠P的度数.【详解】∵BP是∠ABC的平分线,CP是∠ACM的平分线,∠ABP=20°,∠ACP=50°,∴∠PBC=20°,∠PCM=50°,∵∠PBC+∠P=∠PCM,∴∠P=∠PCM-∠PBC=50°-20°=30°,故答案为:30【点睛】本题考查及角平分线的定义及三角形外角性质,三角形的外角等于和它不相邻的两个内角的和,熟练掌握三角形外角性质是解题关键.二、八年级数学三角形选择题(难)11.一个多边形除了一个内角外,其余各内角的和为2100°则这个多边形的对角线共有()A.104条B.90条C.77条D.65条【答案】C【解析】【分析】n边形的内角和是(2)180n-︒,即内角和一定是180度的整数倍,即可求解,据此可以求出多边形的边数,在根据多边形的对角线总条数公式()32n n-计算即可.【详解】解:22100180113÷=,则正多边形的边数是11+2+1=14.∴这个多边形的对角线共有()()314143==7722n n--条.故选:C.【点睛】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理;要注意每一个内角都应当大于0︒而小于180度.同时要牢记多边形对角线总条数公式()32n n-.12.在多边形内角和公式的探究过程中,主要运用的数学思想是()A.化归思想B.分类讨论C.方程思想D.数形结合思想【答案】A【解析】【分析】根据多边形内角和定理:(n-2)·180(n≥3)且n为整数)的推导过程即可解答.【详解】解:多边形内角和定理:(n-2)·180(n≥3)且n为整数),该公式推导的基本方法是从n 边形的一个顶点出发引出(n-3)条对角线,将n边形分割为(n-2)个三角形,这(n-2)个三角形的所有内角之和正好是n边形的内角和,体现了化归思想.故答案为A.【点睛】本题主要考查了在数学的学习过程应用的数学思想,弄清推导过程是解答此题的关键.13.马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830,则该多边形的边数是( )A.7B.8C.7或8D.无法确定【答案】C【解析】【分析】n边形的内角和是(n-2)•180°,即为180°的(n-2)倍,多边形的内角一定大于0度,小于180度,因而多边形中,除去2个内角外,其余内角和与180度的商加上2,以后所得的数值,比这个数值大1或2的整数就是多边形的边数.【详解】设少加的2个内角和为x度,边数为n.则(n-2)×180=830+x,即(n-2)×180=4×180+110+x,因此x=70,n=7或x=250,n=8.故该多边形的边数是7或8.故选C.【点睛】本题考查了多边形的内角和定理,正确理解多边形内角的大小的特点,以及多边形的内角和定理是解决本题的关键.14.如图,△ABC 中,E 是 AC 的中点,延长BC 至D,使BC :CD=3:2,以CE,CD 为邻边做▱CDFE,连接 AF,BE,BF,若△ABC 的面积为 9,则阴影部分面积是()A .6B .4C .3D .2【答案】A【解析】【分析】根据三角形中位线性质结合三角形面积去解答.【详解】 解:在ABC 中,E 是 AC 的中点,S ABC 9=, BC :CD =3:2▱CDFE 中,CD=EF 1S BCE 4.52S ABC ∴== 设BCE 的高为1h , ABC 的高为2.h11S BCE 4.52BC h ∴=⨯⨯= 13h =12:1:2h h =26h ∴=S AEF S EFB s ∴=+阴()2111122EF h h EF h =⨯⨯-+⨯⨯ 212EF h =⨯⨯ 1262=⨯⨯ 6.=【点睛】此题重点考察学生对三角形中位线和面积的理解,熟练掌握三角形面积计算方法是解题的关键.15.已知△ABC 的两条高分别为4和12,第三条高也为整数,则第三条高所有可能值为( )A .3和4B .1和2C .2和3D .4和5 【答案】D【解析】【分析】先设长度为4、12的高分别是a 、b 边上的,边c 上的高为h ,△ABC 的面积是S ,根据三角形面积公式,可求a=24S ;b=212S ;c=2S h,结合三角形三边的不等关系,可得关于h 的不等式,解不等式即可.【详解】 设长度为4、12的高分别是a ,b 边上的,边c 上的高为h ,△ABC 的面积是S ,那么a=24S ;b=212S ;c=2S h∵a-b <c <a+b , ∴24S -212S <c <24S +212S , 即 3S <2S h <23S , 解得3<h <6,∴h=4或h=5,故选D.【点睛】主要考查三角形三边关系;利用三角形面积的表示方法得到相关等式是解决本题的关键.16.适合下列条件的△ABC 中, 直角三角形的个数为 ①111345a b c ,,;===②6a =,∠A =45°;③∠A =32°, ∠B =58°; ④72425a b c ===,,;⑤22 4.a b c ===,,⑥::3:4:5a b c =⑦::12:13:15A B C ∠∠∠=⑹5a b c === A .2个B .3个C .4个D .5个【答案】C【解析】 根据勾股定理的逆定理,可分别求出各边的平方,然后计算判断:222111+345≠()()(),故①不能构成直角三角形;当a=6,∠A=45°时,②不足以判定该三角形是直角三角形;根据直角三角形的两锐角互余,可由∠A+∠B=90°,可知③是直角三角形;根据72=49,242=576,252=625,可知72+242=252,故④能够成直角三角形;由三角形的三边关系,2+2=4可知⑤不能构成三角形;令a=3x ,b=4x ,c=5x ,可知a 2+b 2=c 2,故⑥能够成直角三角形;根据三角形的内角和可知⑦不等构成直角三角形;由a 2=5,b 2=20,c 2=25,可知a 2+b 2=c 2,故⑧能够成直角三角形.故选:C.点睛:此题主要考查了直角三角形的判定,解题关键是根据角的关系,两锐角互余,和边的关系,即勾股定理的逆定理,可直接求解判断即可,比较简单.17.如图P 为ABC ∆内一点,070,BAC ∠=0120,BPC ∠=BD 是ABP ∠的平分线,CE 是ACP ∠的平分线,BD 与CE 交于F ,则BFC ∠=( )A .085B .090C .095D .0100【答案】C【解析】 ∵070,BAC ∠= 0120,BPC ∠=∴∠ABC+∠ACB=110°,∠PBC+∠PCB=60°,∴∠ABP+∠ACP=(∠ABC+∠ACB)-(∠PBC+∠PCB)=110°-60°=50°,∵BD 是ABP ∠的平分线,CE 是ACP ∠的平分线,∴∠FBP+∠FCP=12 (∠ABP+∠ACP)=00150252⨯=; ∴∠FBC+∠FCB=∠FBP+∠FCP+∠PBC+∠PCB=25°+60°=85°,∴BFC ∠=180°-(∠FBC+∠FCB )=180°-85°=95°.故选C.点睛:本题主要考查了三角形的内角和定理和角平分线的定义,根据图形正确找出角与角之间的数量关系是解题的关键.18.已知△ABC 的两条高的长分别为5和20,若第三条高的长也是整数,则第三条高的长的最大值为( )A .5B .6C .7D .8【答案】B【解析】设△ABC 的面积为S ,所求的第三条高线的长为h ,则三边长分别为,,,根据三角形的三边关系为 ,解得 ,所以h 的最大整数值为6,即第三条高线的长的最大值为6.故选B .点睛:本题主要考查了三角形的面积公式,三角形三边关系定理及不等式组的解法,有一定难度.利用三角形的面积公式,表示出△ABC 三边的长度,从而运用三角形三边关系定理,列出不等式组是解题的关键,难点是解不等式组.19.有下列说法:①有一个角为60°的等腰三角形是等边三角形;②三边长为、、3的三角形为直角三角形;③等腰三角形的两边长为3、4,则等腰三角形的周长为10;④一边上的中线等于这边长的一半的三角形是等腰直角三角形.其中正确的个数是()A.4个 B.3个 C.2个 D.1个【答案】C【解析】试题分析:根据等边三角形的性质可知,有一个角为60°的等腰三角形是等边三角形,故①正确;根据三边可知:,,3²=9,因此可知:,由勾股定理的逆定理可知其是直角三角形,故②正确;由等腰三角形的三边可知其边长为:3,3,4或3,4,4,则周长为10或11,故③不正确;由一边上的中线等于这边长的一半的直角三角形是等腰直角三角形,故④不正确.故选:C20.若一个凸多边形的内角和为720°,则这个多边形的边数为()A.4 B.5 C.6 D.7【答案】C【解析】【分析】设这个多边形的边数为n,根据多边形的内角和定理得到(n﹣2)×180°=720°,然后解方程即可.【详解】设这个多边形的边数为n,由多边形的内角和是720°,根据多边形的内角和定理得(n-2)180°=720°.解得n=6.故选C.【点睛】本题主要考查多边形的内角和定理,熟练掌握多边形的内角和定理是解答本题的关键.。
八年级全等三角形易错题(Word版 含答案)

一、八年级数学全等三角形解答题压轴题(难)1.如图,在ABC 中,45ABC ∠=,AD ,BE 分别为BC ,AC 边上的高,连接DE ,过点D 作DF DE ⊥与点F ,G 为BE 中点,连接AF ,DG .(1)如图1,若点F 与点G 重合,求证:AF DF ⊥;(2)如图2,请写出AF 与DG 之间的关系并证明.【答案】(1)详见解析;(2)AF=2DG,且AF ⊥DG,证明详见解析.【解析】【分析】(1) 利用条件先△DAE ≌△DBF,从而得出△FDE 是等腰直角三角形,再证明△AEF 是等腰直角三角形,即可.(2) 延长DG 至点M,使GM=DG,交AF 于点H,连接BM, 先证明△BGM ≌△EGD,再证明△BDM ≌△DAF 即可推出.【详解】解:(1)证明:设BE 与AD 交于点H..如图,∵AD,BE 分别为BC,AC 边上的高,∴∠BEA=∠ADB=90°.∵∠ABC=45°,∴△ABD 是等腰直角三角形.∴AD=BD.∵∠AHE=∠BHD,∴∠DAC=∠DBH.∵∠ADB=∠FDE=90°,∴∠ADE=∠BDF.∴△DAE ≌△DBF.∴BF=AE,DF=DE.∴△FDE是等腰直角三角形.∴∠DFE=45°.∵G为BE中点,∴BF=EF.∴AE=EF.∴△AEF是等腰直角三角形.∴∠AFE=45°.∴∠AFD=90°,即AF⊥DF.(2)AF=2DG,且AF⊥DG.理由:延长DG至点M,使GM=DG,交AF于点H,连接BM,∵点G为BE的中点,BG=GE.∵∠BGM∠EGD,∴△BGM≌△EGD.∴∠MBE=∠FED=45°,BM=DE.∴∠MBE=∠EFD,BM=DF.∵∠DAC=∠DBE,∴∠MBD=∠MBE+∠DBE=45°+∠DBE.∵∠EFD=45°=∠DBE+∠BDF,∴∠BDF=45°-∠DBE.∵∠ADE=∠BDF,∴∠ADF=90°-∠BDF=45°+∠DBE=∠MBD.∵BD=AD,∴△BDM≌△DAF.∴DM=AF=2DG,∠FAD=∠BDM.∵∠BDM+∠MDA=90°,∴∠MDA+∠FAD=90°.∴∠AHD=90°.∴AF⊥DG.∴AF=2DG,且AF⊥DG【点睛】本题考查三角形全等的判定和性质,关键在于灵活运用性质.2.在四边形ABCD 中,E 为BC 边中点.(Ⅰ)已知:如图,若AE 平分∠BAD,∠AED=90°,点F 为AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD(Ⅱ)已知:如图,若AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点F,G 均为AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+12BC+CD.【答案】(Ⅰ)(1)证明见解析;(2)证明见解析;(Ⅱ)(1)证明见解析;(2)证明见解析.【解析】【分析】(Ⅰ)(1)运用SAS证明△ABE≌AFE即可;(2)由(1)得出∠AEB=∠AEF,BE=EF,再证明△DEF≌△DEC(SAS),得出DF=DC,即可得出结论;(Ⅱ)(1)同(Ⅰ)(1)得△ABE≌△AFE(SAS),△DGE≌△DCE(SAS),由全等三角形的性质得出BE=FE,∠AEB=∠AEF,CE=GE,∠CED=∠GED,进而证明△EFG是等边三角形;(2)由△EFG是等边三角形得出GF=EE=BE=12BC,即可得出结论.【详解】(Ⅰ)(1)∵AE平分∠BAD,∴∠BAE=∠FAE,在△ABE 和△AFE 中,AB AF BAE FAE AE AE ⎪∠⎪⎩∠⎧⎨===,∴△ABE ≌△AFE (SAS ),(2)∵△ABE ≌△AFE ,∴∠AEB=∠AEF ,BE=EF ,∵E 为BC 的中点,∴BE=CE ,∴FE=CE ,∵∠AED=∠AEF+∠DEF=90°,∴∠AEB+∠DEC=90°,∴∠DEF=∠DEC ,在△DEF 和△DEC 中,FE CE DEF DEC DE DE ⎪∠⎪⎩∠⎧⎨===,∴△DEF ≌△DEC (SAS ),∴DF=DC ,∵AD=AF+DF ,∴AD=AB+CD ;(Ⅱ)(1)∵E 为BC 的中点,∴BE=CE=12BC , 同(Ⅰ)(1)得:△ABE ≌△AFE (SAS ),△DEG ≌△DEC (SAS ),∴BE=FE ,∠AEB=∠AEF ,CE=GE ,∠CED=∠GED ,∵BE=CE ,∴FE=GE ,∵∠AED=120°,∠AEB+∠CED=180°-120°=60°,∴∠AEF+∠GED=60°,∴∠GEF=60°,∴△EFG 是等边三角形,(2)∵△EFG 是等边三角形,∴GF=EF=BE=12BC , ∵AD=AF+FG+GD ,∴AD=AB+CD+12BC . 【点睛】 本题考查了全等三角形的判定与性质、等边三角形的判定与性质等知识;熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.3.如图1,在等边△ABC 中,E 、D 两点分别在边AB 、BC 上,BE =CD ,AD 、CE 相交于点F .(1)求∠AFE 的度数;(2)过点A 作AH ⊥CE 于H ,求证:2FH +FD =CE ;(3)如图2,延长CE 至点P ,连接BP ,∠BPC =30°,且CF =29CP ,求PF AF的值. (提示:可以过点A 作∠KAF =60°,AK 交PC 于点K ,连接KB ) 【答案】(1)∠AFE =60°;(2)见解析;(3)75【解析】【分析】(1)通过证明 BCE CAD ≌ 得到对应角相等,等量代换推导出60AFE ∠=︒;(2)由(1)得到60AFE ∠=︒,CE AD = 则在Rt AHF △ 中利用30°所对的直角边等于斜边的一半,等量代换可得;(3)通过在PF 上取一点K 使得KF =AF ,作辅助线证明ABK 和ACF 全等,利用对应边相等,等量代换得到比值.(通过将ACF 顺时针旋转60°也是一种思路.)【详解】(1)解:如图1中.∵ABC 为等边三角形,∴AC=BC,∠BAC=∠ABC=∠ACB=60°,在BCE和CAD中,60BE CDCBE ACDBC CA=⎧⎪∠=∠=︒⎨⎪=⎩,∴BCE CAD≌(SAS),∴∠BCE=∠DAC,∵∠BCE+∠ACE=60°,∴∠DAC+∠ACE=60°,∴∠AFE=60°.(2)证明:如图1中,∵AH⊥EC,∴∠AHF=90°,在Rt△AFH中,∵∠AFH=60°,∴∠FAH=30°,∴AF=2FH,∵EBC DCA≌,∴EC=AD,∵AD=AF+DF=2FH+DF,∴2FH+DF=EC.(3)解:在PF上取一点K使得KF=AF,连接AK、BK,∵∠AFK=60°,AF=KF,∴△AFK为等边三角形,∴∠KAF=60°,∴∠KAB=∠FAC,在ABK和ACF中,AB ACKAB ACFAK AF=⎧⎪∠=∠⎨⎪=⎩,∴ABK ACF≌(SAS),BK CF=∴∠AKB=∠AFC=120°,∴∠BKE=120°﹣60°=60°,∵∠BPC=30°,∴∠PBK=30°,∴29BK CF PK CP===,∴79PF CP CF CP=-=,∵45()99AF KF CP CF PK CP CP CP==-+=-=∴779559CPPFAF CP== .【点睛】掌握等边三角形、直角三角形的性质,及三角形全等的判定通过一定等量代换为本题的关键.4.如图(1),在ABC中,90A∠=︒,AB AC=,点D是斜边BC的中点,点E,F分别在线段AB,AC上,且90EDF∠=︒.(1)求证:DEF为等腰直角三角形;(2)若ABC的面积为7,求四边形AEDF的面积;(3)如图(2),如果点E运动到AB的延长线上时,点F在射线CA上且保持90EDF∠=︒,DEF还是等腰直角三角形吗.请说明理由.【答案】(1)证明见解析;(2)3.5;(3)是,理由见解析.【解析】【分析】(1)由题意连接AD,并利用全等三角形的判定判定△BDE≌△ADF(ASA),进而分析证得DEF为等腰直角三角形;(2)由题意分析可得S四边形AEDF=S∆ADF+S∆ADE=S∆BDE+S∆CDF,以此进行分析计算求出四边形AEDF的面积即可;(3)根据题意连接AD,运用全等三角形的判定判定△BDE≌△ADF(ASA),进而分析证得DEF为等腰直角三角形.【详解】解:(1)证明:如图①,连接AD.∵∠BAC=90˚,AB=AC,点D是斜边BC的中点,∴AD⊥BC,AD=BD,∴∠1=∠B=45°,∵∠EDF=90°,∠2+∠3=90°,又∵∠3+∠4=90°,∴∠2=∠4,在△BDE 和△ADF中,∠1=∠B,AD=BD,∠2=∠4,∴△BDE≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°,∴ΔDEF为等腰直角三角形.(2)由(1)可知DE=DF,∠C=∠6=45°,又∵∠2+∠3=90°,∠2+∠5=90°,∴∠3=∠5,∴△ADE≌△CDF,∴S四边形AEDF=S∆ADF+S∆ADE=S∆BDE+S∆CDF,∴ S∆ABC=2 S四边形AEDF,∴S四边形AEDF=3.5 .(3)是.如图②,连接AD.∵∠BAC=90°,AB=AC,D是斜边BC的中点,∴AD⊥BC,AD=BD ,∴∠1=45°,∵∠DAF=180°-∠1=180°—45°=135°,∠DBE=180°-∠ABC=180°-45°=135°,∴∠DAF=∠DBE,∵∠EDF=90°,∴∠3+∠4=90°,又∵∠2+∠3=90°,∴∠2=∠4,在△BDE和△ADF中,∠DAF=∠DBE,AD=BD,∠2=∠4,∴△BDE ≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°,∴△DEF 为等腰直角三角形.【点睛】本题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图1,在长方形ABCD 中,AB=CD=5 cm , BC=12 cm ,点P 从点B 出发,以2cm/s 的速度沿BC 向点C 运动,设点P 的运动时间为ts .(1)PC=___cm ;(用含t 的式子表示)(2)当t 为何值时,△ABP ≌△DCP ?.(3)如图2,当点P 从点B 开始运动,此时点Q 从点C 出发,以vcm/s 的速度沿CD 向点D 运动,是否存在这样的v 值,使得某时刻△ABP 与以P ,Q ,C 为顶点的直角三角形全等?若存在,请求出v 的值;若不存在,请说明理由.【答案】(1)()122t -;(2)3t =;(3)存在,2v =或53v =【解析】【分析】(1)根据P 点的运动速度可得BP 的长,再利用BC 的长减去BP 的长即可得到PC 的长; (2)先根据三角形全等的条件得出当BP=CP ,列方程求解即得;(3)先分两种情况:当BP=CQ ,AB=PC 时,△ABP ≌△PCQ ;或当BA=CQ ,PB=PC 时,△ABP ≌△QCP ,然后分别列方程计算出t 的值,进而计算出v 的值.【详解】解:(1)当点P 以2cm/s 的速度沿BC 向点C 运动时间为ts 时2BP tcm =∵12BC cm =∴()122PC BC BP t cm =-=-故答案为:()122t -(2)∵ABP DCP ∆≅∆∴BP CP =∴2122t t =-解得3t =.(3)存在,理由如下:①当BP=CQ ,AB=PC 时,△ABP ≌△PCQ ,∴PC=AB=5∴BP=BC-PC=12-5=7∵2BP tcm =∴2t=7解得t=3.5∴CQ=BP=7,则3.5v=7解得2v =.②当BA CQ =,PB PC =时,ABP QCP ∆≅∆∵12BC cm =∴162BP CP BC cm === ∵2BP tcm =∴26t = 解得3t =∴3CQ vcm =∵5AB CQ cm ==∴35v =解得53v =. 综上所述,当2v =或53v =时,ABP ∆与以P ,Q ,C 为顶点的直角三角形全等. 【点睛】本题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.6.如图1,在ABC ∆中,90ACB ∠=,AC BC =,直线MN 经过点C ,且AD MN ⊥于点D ,BE MN ⊥于点E .易得DE AD BE =+(不需要证明).(1)当直线MN 绕点C 旋转到图2的位置时,其余条件不变,你认为上述结论是否成立?若成立,写出证明过程;若不成立,请写出此时DE AD BE 、、之间的数量关系,并说明理由;(2)当直线MN 绕点C 旋转到图3的位置时,其余条件不变,请直接写出此时DE AD BE 、、之间的数量关系(不需要证明).【答案】(1) 不成立,DE=AD-BE,理由见解析;(2) DE=BE-AD【解析】【分析】(1)DE、AD、BE之间的数量关系是DE=AD-BE.由垂直的性质可得到∠CAD=∠BCE,证得△ACD≌△CBE,得到AD=CE,CD=BE,即有DE=AD-BE;(2)DE、AD、BE之间的关系是DE=BE-AD.证明的方法与(1)一样.【详解】(1)不成立.DE、AD、BE之间的数量关系是DE=AD-BE,理由如下:如图,∵∠ACB=90°,BE⊥CE,AD⊥CE,AC CB=,∴∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ACD和△CBE中,90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ACD≌△CBE(AAS),∴AD=CE,CD=BE,∴DE=CE-CD=AD-BE;(2)结论:DE=BE-AD.∵∠ACB=90°,BE⊥CE,AD⊥CE,AC CB=,∴∠ACD+∠CAD=90°,又∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ACD和△CBE中,90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△ADC≌△CEB(AAS),∴AD=CE,DC=BE,∴DE=CD-CE=BE-AD.【点睛】本题考查了旋转的性质、直角三角形全等的判定与性质,旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.7.在等边ABC中,点D是边BC上一点.作射线AD,点B关于射线AD的对称点为点E.连接CE并延长,交射线AD于点F.(1)如图,连接AE,①AE与AC的数量关系是__________;②设BAFα∠=,用α表示BCF∠的大小;(2)如图,用等式表示线段AF,CF,EF之间的数量关系,并证明.【答案】(1)①AB=AE;②∠BCF=α;(2) AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案;②由轴对称性,得:AE=AB,∠BAF=∠EAF=α,由ABC是等边三角形,得AB=AC,∠BAC=∠ACB=60°,再根据等腰三角形的性质和三角形内角和等于180°,即可求解;(2)作∠FCG=60°交AD于点G,连接BF,易证∆FCG是等边三角形,得GF=FC,再证∆ACG≅∆BCF(SAS),从而得AG=BF,进而可得到结论.【详解】(1)①∵点B关于射线AD的对称点为点E,∴AB和AE关于射线AD的对称,∴AB=AE.故答案是:AB=AE;②∵点B关于射线AD的对称点为点E,∴AE=AB,∠BAF=∠EAF=α,∵ABC是等边三角形,∴AB=AC,∠BAC=∠ACB=60°,∴∠EAC=60°-2α,AE=AC,∴∠ACE=1180(602)602αα⎡⎤--=+⎣⎦,∴∠BCF=∠ACE-∠ACB=60α+-60°=α.(2)AF-EF=CF,理由如下:作∠FCG=60°交AD于点G,连接BF,∵∠BAF=∠BCF=α,∠ADB=∠CDF,∴∠ABC=∠AFC=60°,∴∆FCG是等边三角形,∴GF=FC,∵ABC是等边三角形,∴BC=AC,∠ACB=60°,∴∠ACG=∠BCF=α.在∆ACG和∆BCF中,∵CA CBACG BCF CG CF=⎧⎪∠=∠⎨⎪=⎩,∴∆ACG≅∆BCF(SAS),∴AG=BF,∵点B关于射线AD的对称点为点E,∴AG=BF=EF,∵AF-AG=GF,∴AF-EF=CF.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.8.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m 上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:△DEF是等边三角形.【答案】(1)见解析;(2)成立,理由见解析;(3)见解析【解析】【分析】(1)因为DE=DA+AE ,故通过证BDA AEC ≅△△,得出DA=EC ,AE=BD ,从而证得DE=BD+CE.(2)成立,仍然通过证明BDA AEC ≅△△,得出BD=AE ,AD=CE ,所以DE=DA+AE=EC+BD.(3)由BDA AEC ≅△△得BD=AE ,=BDA AEC ∠∠,ABF 与ACF 均等边三角形,得==60BA AC ︒∠F ∠F ,FB=FA ,所以=BA BA AC AC ∠F +∠D ∠F +∠E ,即FBD FAB ≅∠∠,所以BDF AEF ≅△△,所以FD=FE ,BFD AFE ≅∠∠,再根据=60BFD FA BFA =︒∠+∠D ∠,得=60AF FA =︒∠E +∠D ,即=60FE =︒∠D ,故DFE △是等边三角形.【详解】证明:(1)∵BD ⊥直线m ,CE ⊥直线m∴∠BDA =∠CEA=90°,∵∠BAC =90°∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°∴∠CAE=∠ABD ,又AB=AC ,∴△ADB ≌△CEA∴AE=BD ,AD=CE ,∴DE=AE+AD= BD+CE(2)∵∠BDA =∠BAC=α,∴∠DBA+∠BAD=∠BAD +∠CAE=180°—α∴∠DBA=∠CAE ,∵∠BDA=∠AEC=α,AB=AC∴△ADB ≌△CEA ,∴AE=BD ,AD=CE∴DE=AE+AD=BD+CE(3)由(2)知,△ADB≌△CEA, BD=AE,∠DBA =∠CAE∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE∵BF=AF,∴△DBF≌△EAF∴DF=EF,∠BFD=∠AFE∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°∴△DEF为等边三角形.【点睛】利用全等三角形的性质证线段相等是证两条线段相等的重要方法.9.如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE⊥AC,连结DF 交射线 AC 于点 G(1)当 DF⊥AB 时,求 t 的值;(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
八年级全等三角形易错题(Word版 含答案)

八年级全等三角形易错题(Word 版 含答案)一、八年级数学轴对称三角形填空题(难)1.在ABC ∆中,边AB 、AC 的垂直平分线分别交边BC 于点D 、点E ,20DAE ∠=︒,则BAC ∠=______°.【答案】80或100【解析】【分析】根据题意,点D 和点E 的位置不确定,需分析谁靠近B 点,则有如下图(图见解析)两种情况:(1)图1中,点E 距离点B 近,根据垂直平分线性质可知,,BD AD AE CE ==,从而有1,2B DAE C DAE ∠=∠+∠∠=∠+∠,再根据三角形的内角和定理可得180B C BAC ∠+∠+∠=︒,联立即可求得;(2)图2中,点D 距离点B 近,根据垂直平分线性质可知,,BD AD AE CE ==,从而有3,4B C ∠=∠∠=∠,由三角形的内角和定理得180B C BAC ∠+∠+∠=︒,联立即可求得.【详解】由题意可分如下两种情况:(1)图1中,根据垂直平分线性质可知,,BD AD AE CE ==,1,2B DAE C DAE ∴∠=∠+∠∠=∠+∠(等边对等角),两式相加得12B C DAE DAE ∠+∠=∠+∠+∠+∠,又12DAE BAC ∠+∠+∠=∠20B C BAC DAE BAC ∴∠+∠=∠+∠=∠+︒,由三角形内角和定理得180B C BAC ∠+∠+∠=︒,20180BAC BAC ∴∠+︒+∠=︒,80BAC ∴∠=︒;(2)图2中,根据垂直平分线性质可知,,BD AD AE CE ==,3,4B C ∴∠=∠∠=∠(等边对等角),两式相加得34B C ∠+∠=∠+∠,又34DAE BAC ∠+∠+∠=∠,3420BAC DAE BAC ∴∠+∠=∠-∠=∠-︒,20B C BAC ∴∠+∠=∠-︒由三角形内角和定理得180B C BAC ∠+∠+∠=︒,20180BAC BAC ∴∠-︒+∠=︒,100BAC ∴∠=︒.故答案为80或100.【点睛】本题考查了垂直平分线的性质(垂直平分线上的点到线段两端点的距离相等)、等腰三角形的定义和性质(等边对等角)、以及三角形内角和定理,本题的难点在于容易漏掉第二种情况,出现漏解.2.如图,在01A BA △中,20B ∠=︒,01A B A B =,在1A B 上取点C ,延长01A A 到2A ,使得121A A AC =;在2A C 上取一点D ,延长12A A 到3A ,使得232A A A D =;…,按此做法进行下去,第n 个等腰三角形的底角n A ∠的度数为__________.【答案】11()802n -︒⋅.【解析】 【分析】 先根据等腰三角形的性质求出∠BA 1 A 0的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1,∠DA 3A 2及∠EA 4A 3的度数,找出规律即可得出第n 个等腰三角形的底角∠A n 的度数.【详解】解:∵在△A 0BA 1中,∠B=20°,A 0B=A 1B ,∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°, ∵A 1A 2=A 1C ,∠BA 1 A 0是△A 1A 2C 的外角,∴∠CA 2A 1= 108022BA A ︒∠= =40°; 同理可得,∠DA 3A 2=20°,∠EA 4A 3=10°,∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠CA 2A 1,∠DA 3A 2及∠EA 4A 3的度数,找出规律是解答此题的关键.3.在锐角三角形ABC 中.BC=32,∠ABC=45°,BD 平分∠ABC .若M ,N 分别是边BD ,BC 上的动点,则CM +MN 的最小值是____.【答案】4【解析】【分析】过点C 作CE ⊥AB 于点E ,交BD 于点M′,过点M′作M′N′⊥BC 于N′,则CE 即为CM+MN 的最小值,再根据32ABC=45°,BD 平分∠ABC 可知△BCE 是等腰直角三角形,由锐角三角函数的定义即可求出CE 的长.【详解】解:过点C 作CE ⊥AB 于点E ,交BD 于点M′,过点M′作M′N′⊥BC 于N′,则CE 即为CM+MN 的最小值,∵32ABC=45°,BD 平分∠ABC ,∴△BCE 是等腰直角三角形,∴CE=BC•cos45°=32×22=4. ∴CM+MN 的最小值为4.【点睛】本题考查了轴对称最短路线问题,难度较大,根据题意作出辅助线,构造出等腰直角三角形,利用锐角三角函数的定义求解是解答此题的关键.4.如图,已知△ABC 中,AB=AC ,∠BAC=90°,直角∠EPF 的顶点P 是BC 中点,两边PE 、PF 分别交AB 、AC 于点E 、F ,给出下列四个结论:①AE=CF ;②△EPF 是等腰直角三角形;③EF=AB ;④12ABC AEPF S S ∆=四边形,当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A 、B 重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).【答案】①②④【解析】试题分析:∵∠APE 、∠CPF 都是∠APF 的余角,∴∠APE=∠CPF ,∵AB=AC ,∠BAC=90°,P 是BC 中点,∴AP=CP ,∴∠PAE=∠PCF ,在△APE 与△CPF 中,{?PAE PCFAP CPEPA FPC ∠=∠=∠=∠,∴△APE ≌△CPF (ASA ),同理可证△APF ≌△BPE ,∴AE=CF ,△EPF 是等腰直角三角形,S 四边形AEPF =12S △ABC ,①②④正确; 而AP=12BC ,当EF 不是△ABC 的中位线时,则EF 不等于BC 的一半,EF=AP , ∴故③不成立.故始终正确的是①②④.故选D .考点:1.全等三角形的判定与性质;2.等腰直角三角形.5.如图,点A,B,C 在同一直线上,△ABD 和△BCE 都是等边三角形,AE,CD 分别与BD,BE 交于点F,G ,连接FG ,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG ;④AD ⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)【答案】①②③⑤【解析】【分析】易证△ABE ≌△DBC ,则有∠BAE =∠BDC ,AE =CD ,从而可证到△ABF ≌△DBG ,则有AF =DG ,BF =BG ,由∠FBG =60°可得△BFG 是等边三角形,证得∠BFG =∠DBA =60°,则有FG ∥AC ,由∠CDB ≠30°,可判断AD 与CD 的位置关系.【详解】∵△ABD 和△BCE 都是等边三角形,∴BD =BA =AD ,BE =BC =EC ,∠ABD =∠CBE =60°. ∵点A 、B 、C 在同一直线上,∴∠DBE =180°﹣60°﹣60°=60°,∴∠ABE =∠DBC =120°. 在△ABE 和△DBC 中,∵BD BA ABE DBC BE BC ∠∠=⎧⎪=⎨⎪=⎩,∴△ABE ≌△DBC ,∴∠BAE =∠BDC ,∴AE =CD ,∴①正确; 在△ABF 和△DBG中,60BAF BDG AB DBABF DBG ∠∠∠∠=⎧⎪=⎨⎪==︒⎩,∴△ABF ≌△DBG ,∴AF =DG ,BF =BG . ∵∠FBG =180°﹣60°﹣60°=60°,∴△BFG 是等边三角形,∴∠BFG =60°,∴②正确; ∵AE =CD ,AF =DG ,∴EF =CG ;∴③正确;∵∠ADB =60°,而∠CDB =∠EAB ≠30°,∴AD 与CD 不一定垂直,∴④错误.∵△BFG 是等边三角形,∴∠BFG =60°,∴∠GFB =∠DBA =60°,∴FG ∥AB ,∴⑤正确.故答案为①②③⑤.【点睛】本题考查了等边三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质、平行线的判定和性质,证得△ABE ≌△DBC 是解题的关键.6.如图,在ABC ∆中,ABC ∠和ACB ∠的平分线相交于点O ,过点O 作//EF BC 交AB 于E ,交AC 于F ,过点O 作OD AC ⊥于D 下列结论:①EF BE CF =+;②点O 到ABC ∆各边的距离相等;③1902BOC A ∠=+∠;④设OD m =,AE AF n +=,则AEF S mn ∆=;⑤1()2AD AB AC BC =+-.其中正确的结论是.__________.【答案】①②③⑤【解析】【分析】由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC =90°+12∠A 正确;由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF =BE +CF 故①正确;由角平分线的性质得出点O 到△ABC 各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD =m ,AE +AF =n ,则S △AEF =12mn ,故④错误,根据HL 证明△AMO ≌△ADO 得到AM =AD ,同理可证BM =BN ,CD =CN ,变形即可得到⑤正确.【详解】 ∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =12∠ABC ,∠OCB =12∠ACB ,∠A +∠ABC +∠ACB =180°,∴∠OBC +∠OCB =90°﹣12∠A ,∴∠BOC =180°﹣(∠OBC +∠OCB )=90°+12∠A ;故③正确; ∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =∠OBE ,∠OCB =∠OCF . ∵EF ∥BC ,∴∠OBC =∠EOB ,∠OCB =∠FOC ,∴∠EOB =∠OBE ,∠FOC =∠OCF ,∴BE =OE ,CF =OF ,∴EF =OE +OF =BE +CF ,故①正确;过点O 作OM ⊥AB 于M ,作ON ⊥BC 于N ,连接OA .∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴ON =OD =OM =m ,∴S △AEF =S △AOE +S △AOF =12AE •OM +12AF •OD =12OD •(AE +AF )=12mn ;故④错误; ∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴点O 到△ABC 各边的距离相等,故②正确;∵AO =AO ,MO =DO ,∴△AMO ≌△ADO (HL ),∴AM =AD ;同理可证:BM =BN ,CD =CN .∵AM +BM =AB ,AD +CD =AC ,BN +CN =BC ,∴AD =12(AB +AC ﹣BC )故⑤正确. 故答案为:①②③⑤.【点睛】本题考查了角平分线的定义与性质,等腰三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用.7.如图,在直角坐标系中,点()8,8B -,点()2,0C -,若动点P 从坐标原点出发,沿y 轴正方向匀速运动,运动速度为1/cm s ,设点P 运动时间为t 秒,当BCP ∆是以BC 为腰的等腰三角形时,直接写出t 的所有值__________________.【答案】2秒或6秒或14秒【解析】【分析】分两种情况:PC 为腰或BP 为腰.分别作出符合条件的图形,计算出OP 的长度,即可求出t 的值.【详解】解:如图所示,过点B 作BD ⊥x 轴于点D ,作BE ⊥y 轴于点E ,分别以点B 和点C 为圆心,以BC长为半径画弧交y轴正半轴于点F,点H和点G∵点B(-8,8),点C(-2,0),∴DC=6cm,BD=8cm,由勾股定理得:BC=10cm∴在直角三角形COG中,OC=2cm,CG=BC=10cm,∴OP=OG= 22-=,10246(cm)当点P运动到点F或点H时,BE=8cm,BH=BF=10cm,∴EF=EH=6cm∴OP=OF=8-6=2(cm)或OP=OH=8+6=14(cm),故答案为:2秒,46秒或14秒.【点睛】本题综合考查了勾股定理和等腰三角形在平面直角坐标系中的应用,通过作图找出要求的点的位置,利用勾股定理来求解是本题的关键.8.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交BC的延长线于F,若∠F =30°,DE=1,则EF的长是_____.【答案】2【解析】【分析】连接BE,根据垂直平分线的性质、直角三角形的性质,说明∠CBE=∠F,进一步说明BE =EF,,然后再根据直角三角形中,30°所对的直角边等于斜边的一半即可.【详解】解:如图:连接BE∵AB的垂直平分线DE交BC的延长线于F,∴AE=BE,∠A+∠AED=90°,∵在Rt△ABC中,∠ACB=90°,∴∠F+∠CEF=90°,∵∠AED=∠FEC,∴∠A=∠F=30°,∴∠ABE=∠A=30°,∠ABC=90°﹣∠A=60°,∴∠CBE=∠ABC﹣∠ABE=30°,∴∠CBE=∠F,∴BE=EF,在Rt△BED中,BE=2DE=2×1=2,∴EF=2.故答案为:2.【点睛】本题考查了垂直平分线的性质、直角三角形的性质,其中灵活利用垂直平分线的性质和直角三角形30°角所对的边等于斜边的一半是解答本题的关键.9.如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,按此做法继续下去,第2019个等腰三角形的底角度数是______________.【答案】20181802⎛⎫⨯ ⎪⎝⎭【解析】【分析】 根据等腰三角形的性质求出∠BA 1C 的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA 2A 1,∠EA 3A 2及∠FA 4A 3的度数,找出规律即可得出第2019个三角形中以A 2019为顶点的内角度数.【详解】解:∵在△CBA 1中,∠B=20°,A 1B=CB ,∴∠BA 1C=°180-2B ∠=80°, ∵A 1A 2=A 1D ,∠BA 1C 是△A 1A 2D 的外角,∴∠DA 2A 1=12∠BA 1C=12×80°; 同理可得∠EA 3A 2=(12)2×80°,∠FA 4A 3=(12)3×80°, ∴第n 个三角形中以A n 为顶点的底角度数是(12) n-1×80°. ∴第2017个三角形中以A 2019为顶点的底角度数是(12)2018×80°, 故答案为:(12) 2018×80°. 【点睛】 本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠DA 2A 1,∠EA 3A 2及∠FA 4A 3的度数,找出规律是解答此题的关键.10.如图:在ABC ∆中,D ,E 为边AB 上的两个点,且BD BC =,AE AC =,若108ACB ∠=︒,则DCE ∠的大小为______.【答案】036【解析】【分析】根据三角形内角和求出∠A+∠B,再根据AC=AE,BC=BD ,用∠A 表示∠AEC,用∠B 表示∠BDC,然后根据内角和求出∠DCE 的度数.【详解】∵∠ACB=1080,∴∠A+∠B=1800-1080=720,∵AC=AE,BC=BD,∴∠ACE=∠AEC,∠BCD=∠BDC, ∴01(180)2AEC A ∠=-∠01902A =-∠ 01(180)2BDCB ∠=-∠ =01902B -∠ ∵∠DCE+∠CDE+∠DEC=1800,∴0180DCE CDE CED ∠=-∠-∠ = 00011180(90)(90)22A B --∠--∠ =1122A B ∠+∠ =1()2A B ∠+∠ =360【点睛】此题考察等腰三角形的性质,注意两条等边所在三角形,依此判断对应的两个底角相等.二、八年级数学轴对称三角形选择题(难)11.在Rt ABC ∆中,90ACB ∠=︒,以ABC ∆的一边为边画等腰三角形,使得它的第三个顶点在ABC ∆的其他边上,则可以画出的不同的等腰三角形的个数最多可画几个?( )A .9个B .7个C .6个D .5个【答案】B【解析】【分析】先以Rt ABC ∆三个顶点分别为圆心,再以每个顶点所在的较短边为半径画弧,即可确定等腰三角形的第三个顶点;也可以作三边的垂直平分线确定等腰三角形的第三个顶点即得.【详解】解:①如图1,以B 为圆心,BC 长为半径画弧,交AB 于点D ,则∆BCD 就是等腰三角形;②如图2,以A 为圆心,AC 长为半径画弧,交AB 于点E ,则∆ACE 就是等腰三角形; ③如图3,以C 为圆心,BC 长为半径画弧,交AB 于M ,交AC 于点F ,则∆BCM 、∆BCF 是等腰三角形;④如图4,作AC 的垂直平分线交AB 于点H ,则∆ACH 就是等腰三角形;⑤如图5,作AB 的垂直平分线交AC 于点G ,则∆AGB 就是等腰三角形;⑥如图6,作BC 的垂直平分线交AB 于I ,则∆BCI 就是等腰三角形.故选:B .【点睛】本题考查等腰三角形的判定的应用,通过作垂直平分线或者画弧的方法确定相等的边是解题关键.12.如图所示,等边三角形的边长依次为2,4,6,8,……,其中1(0,1)A ,()21,13A --,()31,13A -,4(0,2)A ,()52,223A --,……,按此规律排下去,则2019A 的坐标为( )A .(673,6736733-B .(673,6736733--C .(0,1009)D .(674,6746743- 【答案】A【解析】【分析】根据等边三角形的边长依次为2,4,6,8,……,及点的坐标特征,每三个点一个循环,2019÷3=673,A2019的坐标在第四象限即可得到结论.【详解】∵2019÷3=673,∴顶点A2019是第673个等边三角形的第三个顶点,且在第四象限.第673个等边三角形边长为2×673=1346,∴点A2019的横坐标为12⨯1346=673.点A2019的纵坐标为673-134632⨯=673﹣6733.故点A2019的坐标为:()673,6736733-.故选:A.【点睛】本题考查了点的坐标、等边三角形的性质,是点的变化规律,主要利用了等边三角形的性质,确定出点A2019所在三角形是解答本题的关键.13.如图,在平面直角坐标系中,A(a,0),B(0,a),等腰直角三角形ODC的斜边经过点B,OE⊥AC,交AC于E,若OE=2,则△BOD与△AOE的面积之差为()A.2 B.3 C.4 D.5【答案】A【解析】【分析】首先证明△DOB≌△COA(SAS),推出S△DOB﹣S△AOE=S△EOC,再证明△OEC是等腰直角三角形即可解决问题.【详解】∵A(a,0),B(0,a),∴OA=OB.∵△ODC是等腰直角三角形,∴OD=OC,∠D=∠DCO=45°.∵∠DOC=∠BOA=90°,∴∠DOB=∠COA.在△DOB和△COA中,∵OD=OC,∠DOB=∠COA,OB=OA,∴△DOB≌△COA(SAS),∴∠D=∠OCA=45°,S△DOB﹣S△AOE=S△EOC.∵OE⊥AC,∴∠OEC=90°,∴△CEO是等腰直角三角形,∴OE=EC=2,∴S△DOB﹣S△AOE=S△EOC12=⨯2×2=2.故选A.【点睛】本题考查了等腰直角三角形的性质和判定,全等三角形的判定和性质等知识,解题的关键是证明△OEC是等腰直角三角形.14.如图,C 是线段 AB 上一点,且△ACD 和△BCE 都是等边三角形,连接 AE、BD 相交于点O,AE、BD 分别交 CD、CE 于 M、N,连接 MN、OC,则下列所给的结论中:①AE=BD;②CM=CN;③MN∥AB;④∠AOB=120º;⑤OC 平分∠AOB.其中结论正确的个数是()A.2 B.3 C.4 D.5【答案】D【解析】【分析】由题意易证:△ACE≅△DCB,进而可得AE=BD;由△ACE≅△DCB,可得∠CAE=∠CDB,从而△ACM ≅△DCN,可得:CM=CN;易证△MCN是等边三角形,可得∠MNC=∠BCE,即MN∥AB;由∠CAE=∠CDB,∠AMC=∠DMO,得∠ACM=∠DOM=60°,即∠AOB=120º;作CG⊥AE,CH⊥BD,易证CG=CH,即:OC 平分∠AOB.【详解】∵△ACD 和△BCE 都是等边三角形,∴AC=DC,CE=CB,∠ACE=∠DCB=120°,∴△ACE≅△DCB(SAS)∴AE=BD,∴①正确;∵△ACE≅△DCB,∴∠CAE=∠CDB,∵△ACD 和△BCE 都是等边三角形,∴∠ACD=∠BCE=∠DCE=60°,AC=DC,在△ACM 和△DCN中,∵60CAE CDB AC DCACD DCE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴△ACM ≅△DCN (ASA ),∴CM =CN ,∴②正确;∵CM =CN ,∠DCE=60°,∴△MCN 是等边三角形,∴∠MNC=60°,∴∠MNC=∠BCE ,∴MN ∥AB ,∴③正确;∵△ACE ≅△DCB ,∴∠CAE=∠CDB ,∵∠AMC=∠DMO ,∴180°-∠CAE-∠AMC=180°-∠CDB-∠DMO ,即:∠ACM=∠DOM=60°,∴∠AOB =120º,∴④正确;作CG ⊥AE ,CH ⊥BD ,垂足分别为点G ,点H ,如图,在△ACG 和△DCH 中,∵90?AMC DHC CAE CDB AC DC ∠=∠=⎧⎪∠=∠⎨⎪=⎩∴△ACG ≅△DCH (AAS ),∴CG =CH ,∴OC 平分∠AOB ,∴⑤正确.故选D.【点睛】本题主要考查全等三角形的判定定理和性质定理,等边三角形的性质定理以及角平分线性质定理的逆定理,添加合适的辅助线,是解题的关键.15.如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是()A.4 B.245C.5 D.6【答案】C【解析】试题解析:如图,∵AD是∠BAC的平分线,∴点B关于AD的对称点B′在AC上,过点B′作B′N⊥AB于N交AD于M,由轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,过点B作BE⊥AC于E,∵AC=10,S△ABC=25,∴12×10•BE=25,解得BE=5,∵AD是∠BAC的平分线,B′与B关于AD对称,∴AB=AB′,∴△ABB′是等腰三角形,∴B′N=BE=5,即BM+MN的最小值是5.故选C.16.如图,等腰三角形ABC的底边BC长为4,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,若△CDM周长的最小值为8,则△ABC的面积为()A.12 B.16 C.24 D.32【答案】A【解析】【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,再根据三角形的周长求出AD的长,由此即可得出结论.【详解】连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴AD的长为CM+MD的最小值,∵△CDM周长的最小值为8,∴AD=8-12BC=8-2=6∴S△ABC=12BC•AD=12×4×6=12,故选A.【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.17.如图,已知等边△ABC的面积为43, P、Q、R分别为边AB、BC、AC上的动点,则PR+QR的最小值是()A.3B.3C15D.4【答案】B【解析】如图,作△ABC关于AC对称的△ACD,点E与点Q关于AC对称,连接ER,则QR=ER,当点E,R,P在同一直线上,且PE⊥AB时,PE的长就是PR+QR的最小值,设等边△ABC的边长为x,则高为32x,∵等边△ABC的面积为43,∴12x×3x=43,解得x=4,∴等边△ABC的高为32x=23,即PE=23,所以PR+QR的最小值是23,故选B.【点睛】本题考查了轴对称的性质,最短路径问题等,解题的关键是正确添加辅助线构造出最短路径.18.如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.有下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD.其中正确的选项是()A.①③B.②③C.①②③D.①②【答案】D【解析】①、∵∠A=36°,AB=AC,∴∠C=∠ABC=72°,∴∠C=2∠A,正确;②、∵DO是AB垂直平分线,∴AD=BD.∴∠A=∠ABD=36°.∴∠DBC=72°﹣36°=36°=∠ABD.∴BD是∠ABC的角平分线,正确;③,根据已知不能推出△BCD的面积和△BOD面积相等,错误;故选:D.19.如图,已知,点A(0,0)、B(43,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于()A.3B.3C.2017327D.3【答案】A【解析】【分析】【详解】根据锐角三函数的性质,由OB=43,OC=1,可得∠OCB=90°,然后根据等边三角形的性质,可知∠A1AB=60°,进而可得∠CAA1=30°,∠CA1O=90°,因此可推导出∠A2A1B=30°,同理得到∠CA2B1=∠CA3B2=∠CA4B3=90°,∠A2A1B=∠A3A2B2=∠A4A3B3=30°,故可得后一个等边三角形的边长等于前一个等边三角形的边长的一半,即OA1=OCcos∠CAA1=23,B1A2=1232⨯,以此类推,可知第2017个等边三角形的边长为:201713()432⨯=.故选A.【点睛】此题主要考查了等边三角形的性质,属于规律型题目,解题关键是仔细审图,得出:后一个等边三角形的边长等于前一个等边三角形的边长的一半.20.等腰三角形中有一个角是40°,则另外两个角的度数是()A.70°,70°B.40°,100°C.70°,40°D.70°,70°或40°,100°【答案】D【解析】分析:由等腰三角形的一个角是40度,可以分为若40°的角是顶角与若40°的角是底角去分析求解,小心别漏解.详解:若40°的角是顶角,则底角为:(180°﹣40°)=70°,∴此时另外两个角的度数是70°,70°;若40°的角是底角,则另一底角为40°,∴顶角为:180°﹣40°﹣40°=100°,∴此时另外两个角的度数是100°,40°.∴另外两个角的度数是:70°、70°或40°、100°.故选:D.点睛:此题考查了等腰三角形的性质.解题的关键是注意分类讨论思想的应用,注意别漏解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【精选】八年级数学三角形解答题易错题(Word 版 含答案)一、八年级数学三角形解答题压轴题(难)1.直线MN 与直线PQ 垂直相交于O ,点A 在直线PQ 上运动,点B 在直线MN 上运动. (1)如图1,已知AE 、BE 分别是∠BAO 和∠ABO 角的平分线,点A 、B 在运动的过程中,∠AEB 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB 的大小.(2)如图2,已知AB 不平行CD ,AD 、BC 分别是∠BAP 和∠ABM 的角平分线,又DE 、CE 分别是∠ADC 和∠BCD 的角平分线,点A 、B 在运动的过程中,∠CED 的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.(3)如图3,延长BA 至G ,已知∠BAO 、∠OAG 的角平分线与∠BOQ 的角平分线及延长线相交于E 、F ,在△AEF 中,如果有一个角是另一个角的3倍,试求∠ABO 的度数.【答案】(1)135°;(2)67.5°;(3)60°, 45°【解析】【分析】(1)根据直线MN 与直线PQ 垂直相交于O 可知∠AOB=90°,再由AE 、BE 分别是∠BAO 和∠ABO 的角平分线得出1BAE OAB 2∠=∠,1ABE ABO 2∠=∠,由三角形内角和定理即可得出结论;(2)延长AD 、BC 交于点F ,根据直线MN 与直线PQ 垂直相交于O 可得出∠AOB=90°,进而得出OAB OBA 90∠+∠=︒ ,故PAB MBA 270∠+∠=︒,再由AD 、BC 分别是∠BAP 和∠ABM 的角平分线,可知1BAD BAP 2∠=∠,1ABC ABM 2∠=∠,由三角形内角和定理可知∠F=45°,再根据DE 、CE 分别是∠ADC 和∠BCD 的角平分线可知CDE DCE 112.5∠+∠=︒,进而得出结论;(3))由∠BAO 与∠BOQ 的角平分线相交于E 可知1EAO BAO 2∠=∠,1EOQ BOQ 2∠=∠ ,进而得出∠E 的度数,由AE 、AF 分别是∠BAO 和∠OAG 的角平分线可知∠EAF=90°,在△AEF 中,由一个角是另一个角的3倍分四种情况进行分类讨论.【详解】(1)∠AEB 的大小不变,∵直线MN 与直线PQ 垂直相交于O ,∴∠AOB=90°, ∴OAB OBA 90∠+∠=︒,∵AE 、BE 分别是∠BAO 和∠ABO 角的平分线,∴1BAE OAB 2∠=∠,1ABE ABO 2∠=∠, ∴()1BAE ABE OAB ABO 452∠+∠=∠+∠=°, ∴∠AEB=135°;(2)∠CED 的大小不变.如图2,延长AD 、BC 交于点F .∵直线MN 与直线PQ 垂直相交于O ,∴90∠=AOB °,∴OAB OBA 90∠+∠=°,∴PAB MBA 270∠+∠=°,∵AD 、BC 分别是∠BAP 和∠ABM 的角平分线,∴1BAD BAP 2∠=∠,1ABC ABM 2∠=∠, ∴()1BAD ABC PAB ABM 1352∠+∠=∠+∠=°,F 45∠=°, ∴FDC FCD 135∠+∠=°,∴CDA DCB 225∠+∠=°,∵DE 、CE 分别是∠ADC 和∠BCD 的角平分线,∴CDE DCB 112.5∠+∠=°,∴E 67.5∠=°;(3)∵∠BAO 与∠BOQ 的角平分线相交于E ,∴1EAO BAO 2∠=∠,1EOQ BOQ 2∠=∠ , ∴()11E EOQ EAO BOQ BAQ ABO 22∠=∠-∠=∠-∠=∠, ∵AE 、AF 分别是∠BAO 和∠OAG 的角平分线,∴EAF 90∠=°.在△AEF 中,∵有一个角是另一个角的3倍,故有:①EAF 3E ∠=∠,E 30∠=°,ABO 60∠=°;②EAF 3F ∠=∠,E 60∠=°,ABO 120∠=°;③EAF 3E ∠=∠,E 22.5∠=°,ABO 45∠=°;④EAF 3F ∠=∠,E 67.5∠=°,ABO 135∠=°.∴∠ABO 为60°或45°.【点睛】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.2.(问题探究)将三角形ABC 纸片沿DE 折叠,使点A 落在点A '处.(1)如图,当点A 落在四边形BCDE 的边CD 上时,直接写出A ∠与1∠之间的数量关系;(2)如图,当点A 落在四边形BCDE 的内部时,求证:122A ∠+∠=∠;(3)如图,当点A 落在四边形BCDE 的外部时,探索1∠,2∠,A ∠之间的数量关系,并加以证明;(拓展延伸)(4)如图,若把四边形ABCD 纸片沿EF 折叠,使点A 、D 落在四边形BCFE 的内部点A '、D 的位置,请你探索此时1∠,2∠,A ∠,D ∠之间的数量关系,写出你发现的结论,并说明理由.【答案】【问题探究】(1)∠1=2∠A ;(2)证明见详解;(3)∠1=2∠A+∠2;【拓展延伸】(4)()212360A D ∠+∠=∠+∠+︒.【解析】【分析】(1)运用折叠原理及三角形的外角性质即可解决问题,(2)运用折叠原理及四边形的内角和定理即可解决问题,(3)运用三角形的外角性质即可解决问题,(4)先根据翻折的性质求出∠AEF、∠EFD,再根据四边形的内角和定理列式整理即可得解.【详解】解:(1)如图,∠1=2∠A .理由如下:由折叠知识可得:∠EA′D=∠A ;∵∠1=∠A+∠EA′D ,∴∠1=2∠A .(2)∵∠1+∠A′EA+∠2+∠A′DA=360°,由四边形的内角和定理可知:∠A+∠A′+∠A′EA+∠A′DA=360°,∴∠A′+∠A=∠1+∠2,由折叠知识可得∠A=∠A′,∴2∠A=∠1+∠2.(3)如图,∠1=2∠A+∠2理由如下:∵∠1=∠EFA+∠A ,∠EFA=∠A′+∠2,∴∠1=∠A+∠A′+∠2=2∠A+∠2,(4)如图,根据翻折的性质,()3181201∠=-∠,()4181202∠=-∠, ∵34360A D ∠+∠+∠+∠=︒, ∴()()180118023601122A D ∠+∠+-∠+-∠=︒, 整理得,()212360A D ∠+∠=∠+∠+︒.【点睛】本题考查了折叠的性质,三角形外角性质,三角形内角和定理及四边形内角和的应用,主要考查学生运用定理进行推理和计算的能力.3.探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,(1)观察“规形图”,试探究∠BDC 与∠A 、∠B 、∠C 之间的关系,并说明理由; (2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ 放置在△ABC 上,使三角尺的两条直角边XY 、XZ 恰好经过点B 、C ,∠A=40°,则∠ABX+∠ACX 等于多少度;②如图3,DC 平分∠ADB ,EC 平分∠AEB ,若∠DAE=40°,∠DBE=130°,求∠DCE 的度数; ③如图4,∠ABD ,∠ACD 的10等分线相交于点G 1、G 2…、G 9,若∠BDC=133°,∠BG 1C=70°,求∠A 的度数.【答案】(1)详见解析;(2)①50°;②85°;③63°.【解析】【分析】(1)连接AD 并延长至点F ,根据外角的性质即可得到∠BDF=∠BAD+∠B ,∠CDF=∠C+∠CAD ,即可得出∠BDC=∠A+∠B+∠C ;(2)①根据(1)得出∠ABX+∠ACX+∠A=∠BXC ,再根据∠A=40°,∠BXC=90°,即可求出∠ABX+∠ACX 的度数;②先根据(1)得出∠ADB+∠AEB=90°,再利用DC 平分∠ADB ,EC 平分∠AEB ,即可求出∠DCE 的度数;③由②得∠BG 1C=110(∠ABD+∠ACD )+∠A ,设∠A 为x°,即可列得110(133-x )+x=70,求出x 的值即可.【详解】(1)如图(1),连接AD 并延长至点F ,根据外角的性质,可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,∴∠BDC=∠A+∠B+∠C;(2)①由(1),可得∠ABX+∠ACX+∠A=∠BXC,∵∠A=40°,∠BXC=90°,∴∠ABX+∠ACX=90°-40°=50°;②由(1),可得∠DBE=∠DAE+∠ADB+∠AEB,∴∠ADB+∠AEB=∠DBE-∠DAE=130°-40°=90°,∴12(∠ADB+∠AEB)=90°÷2=45°,∵DC平分∠ADB,EC平分∠AEB,∴12ADC ADB∠=∠,12AEC AEB∠=∠,∴∠DCE=∠ADC+∠AEC+∠DAE,=12(∠ADB+∠AEB)+∠DAE,=45°+40°, =85°;③由②得∠BG1C=110(∠ABD+∠ACD)+∠A,∵∠BG1C=70°,∴设∠A为x°,∵∠ABD+∠ACD=133°-x°∴110(133-x)+x=70,∴13.3-110x+x=70,解得x=63,即∠A的度数为63°.【点睛】此题考查三角形外角的性质定理,三角形的外角等于与它不相邻的内角的和,,根据此定理得到角度的规律,由此解决问题,此题中得到平分角的变化规律是解题的难点.4.如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.(1)求证:∠BAG=∠BGA;(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.①若点E在线段AD上,求∠AFC的度数;②若点E在DA的延长线上,直接写出∠AFC的度数;(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.【答案】(1)证明见解析;(2)①20°;②160°;(3)13或73【解析】【分析】(1)根据AD//BC可知∠GAD=∠BGA,由AG平分∠BAD可知∠BAG=∠GAD,即可得答案.(2)①根据CF平分∠BCD,∠BCD=90°,可求出∠GCF的度数,由AD//BC可求出∠AEF 和∠DAB的度数,根据三角形外角的性质求出∠AFC的度数即可;②根据三角形外角性质求出即可;(3)根据M点在BP的上面和下面两种情况讨论,分别求出∠PBM和∠ABM 的值即可.【详解】(1)∵AD∥BC,∴∠GAD=∠BGA,∵AG平分∠BAD,∴∠BAG=∠GAD,∴∠BAG=∠BGA;(2)①∵CF平分∠BCD,∠BCD=90°,∴∠GCF=45°,∵AD∥BC,∠ABC=50°,∴∠AEF=∠GCF=45°;∠DAB=180°﹣50°=130°,∵AG平分∠BAD,∴∠BAG=∠GAD=65°,∴∠AFC=65°﹣45°=20°;②如图:∵∠AGB=65°,∠BCF=45°,∴∠AFC=∠CGF+∠BCF=115°+45°=160°;(3)有两种情况:①当M在BC的下方时,如图:∵∠ABC=50°,∠ABP=2∠PBG,∴∠ABP=(1003)°,∠PBG=(503)°,∵AG∥CH,∴∠BCH=∠AGB=65°,∵∠BCD=90°,∴∠DCH=∠PBM=90°﹣65°=25°,∴∠ABM=∠ABP+∠PBM=(1003+25)°=(1753)°,∴∠ABM:∠PBM=(1753)°:25°=73;②当M在BC的上方时,如图:同理得:∠ABM=∠ABP﹣∠PBM=(1003﹣25)°=(253)°,∴∠ABM:∠PBM=(253)°:25°=13;综上,∠ABM:∠PBM的值是13或73.【点睛】本题考查平行线的性质和三角形外角性质,熟练掌握平行线性质是解题关键.5.已知:点D是△ABC所在平面内一点,连接AD、CD.(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;(3)如图3,在(2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.【答案】(1) 111º ;(2) ∠A-∠C=2∠P,理由见解析;(3) ∠A+∠C=2∠P,理由见解析.【解析】【分析】(1)延长AD交BC于E,利用三角形外角的性质即可求解;(2)∠A-∠C=2∠P,由三角形外角等于不相邻的两个内角的和以及(1)结论即可求解;(3)∠A+∠C=2∠P,由(2)结论以及角平分线的性质即可得到.【详解】(1)如图1,延长AD交BC于E,在△ABE中,∠AEC=∠A+∠B=28º+72º=100º,在△DEC中,∠ADC=∠AEC+∠C=100º+11º=111º ;(2)∠A-∠C=2∠P,理由如下:如图2,∠5=∠A+∠1,∠5=∠P+∠3∴∠A+∠1=∠P+∠3∵PB平分∠ABC,PD平分∠ADC∴∠1=∠2,∠3=∠4∴∠A+∠2=∠P+∠4由(1)知∠4=∠2+∠P+∠C∴∠A+∠2=∠P+∠2+∠P+∠C∴∠A-∠C=2∠P(3)∠A+∠C=2∠P,理由如下:如图3,同(2)理知∠A+∠1=∠P+∠3,∠C+∠4=∠P+∠2∴∠A+∠C+∠1+∠4=2∠P+∠2+∠3∵PB平分∠ABC,PD平分∠ADC∴∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3∴∠A+∠C=2∠P【点睛】本题考查了三角形外角的性质,角平分线的定义,整体思想的利用是解题的关键.6.(1)如图1,有一块直角三角板XYZ(其中∠X=90°)放置在△ABC上,恰好三角板XYZ 的两条直角边XY,XZ分别经过B,C两点,且直角顶点X在△ABC内部.①若∠A=40°,∠ABC+∠ACB= °;∠XBC+∠XCB= °;②试判断∠A与∠XBA+∠XCA之间存在怎样数量关系?并写出证明过程.(2)如图2,如果直角顶点X在△ABC外部,试判断∠A、∠XBA、∠XCA之间又存在怎样的数量关系?(只写出答案,无需证明).【答案】(1)①140,90;②∠A+∠XBA+∠XCA=90°,证明见解析;(2)∠A+(∠XBA-∠XCA)=90°【解析】试题分析:(1)①根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=140°,∠XBC+∠XCB=180°﹣∠XBC=90°,进而可求出∠ABX+∠ACX 的度数;②根据三角形内角和定义有90°+(∠ABX+∠ACX)+∠A=180°,则可得出结论.(2)由②的解题思路可得:∠A+(∠XBA-∠XCA)=90°.(1)①若∠A=40°,∠ABC+∠ACB= 140 °;∠XBC+∠XCB= 90 °;②∠A+∠XBA+∠XCA=90°(或等式的变形也可以)证明:∵∠X=90°∴∠XBC+∠XCB=180°-∠X=90°∵∠A+∠ABC+∠ACB=180°,∴∠A+(∠XBA+∠XCA)+(∠XBC+∠XCB)=180°,∴∠A+(∠XBA+∠XCA)=180°-90°=90°,∴∠A=90°-(∠XBA+∠XCA)(2)∠A+(∠XBA-∠XCA) =90°.点睛:本题考查三角形外角的性质及三角形的内角和定理,解答的关键是熟练掌握三角形的内角和为180°以及沟通外角和内角的关系.7.根据题意解答:(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.(2)阅读下面的内容,并解决后面的问题:如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.解:∵AP、CP分别平分∠BAD、∠BCD∴∠1=∠2,∠3=∠4由(1)的结论得:∠P+∠3=∠1+∠B①,∠P+∠2=∠4+∠D②,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D∴∠P= 12(∠B+∠D)=26°.①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.【答案】(1)证明见解析;(2)①∠P=26゜;②∠P=180°﹣12(∠B+∠D);③∠P=90°+ 12(∠B+∠D).【解析】试题分析:(1)根据三角形的内角和等于180°列式整理即可得证;(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;①表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;②根据四边形的内角和等于360°,可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解;③根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.试题解析:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜,∴∠A+∠B+∠AOB=∠C+∠D+∠COD.∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D.(2)①∠P=26゜.∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4.由(1)的结论得:∠PAD+∠P=∠PCD+∠D①,∠PAB+∠P=∠PCB+∠B②,∵∠PAB=∠1,∠1=∠2,∴∠PAB=∠2,∴∠2+∠P=∠3+∠B③,①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,∴∠P=12(∠B+∠D)=26°.②如图4,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,∴2∠P+∠B+∠D=360°,∴∠P=180°﹣12(∠B+∠D);③如图5,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∵(∠1+∠2)+∠B=(180°﹣2∠3)+∠D,∠2+∠P=(180°﹣∠3)+∠D,∴2∠P=180°+∠D+∠B,∴∠P=90°+ 12(∠B+∠D).点睛:本题考查了三角形的内角和定理,角平分线的定义,准确识图并运用好“8字形”的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.8.等边△ABC边长为6,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转。
