MATLAB程序运行结果
matlab实验报告总结精选

matlab实验报告总结电气工程学院自动化102班 2012年12月21日实验一 MATLAB环境的熟悉与基本运算一、实验目的1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令变量与运算符变量命名规则如下:变量名可以由英语字母、数字和下划线组成变量名应以英文字母开头长度不大于31个区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式的基本运算表7 两种运算指令形式和实质内涵的异同表的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、新建一个文件夹2、启动,将该文件夹添加到MATLAB路径管理器中。
3、保存,关闭对话框4、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye5、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
6、初步程序的编写练习,新建M-file,保存,学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
注意:每一次M-file的修改后,都要存盘。
练习A:help rand,然后随机生成一个2×6的数组,观察command window、command history和workspace等窗口的变化结果。
学习使用clc、clear,了解其功能和作用。
答:clc是清除命令窗体内容 clear是清除工作区间输入C=1:2:20,则C表示什么?其中i=1,2,3,?,10。
matlab实验报告

2015秋2013级《MATLAB程序设计》实验报告实验一班级:软件131姓名:陈万全学号:132852一、实验目的1、了解MATLAB程序设计的开发环境,熟悉命令窗口、工作区窗口、历史命令等窗口的使用。
2、掌握MATLAB常用命令的使用。
3、掌握MATLAB帮助系统的使用。
4、熟悉利用MATLAB进行简单数学计算以及绘图的操作方法。
二、实验内容1、启动MATLAB软件,熟悉MATLAB的基本工作桌面,了解各个窗口的功能与使用。
图1 MATLAB工作桌面2、MATLAB的常用命令与系统帮助:(1)系统帮助help:用来查询已知命令的用法。
例如已知inv是用来计算逆矩阵,键入help inv即可得知有关inv命令的用法。
lookfor:用来寻找未知的命令。
例如要寻找计算反矩阵的命令,可键入lookfor inverse,MATLAB即会列出所有和关键字inverse相关的指令。
找到所需的命令後,即可用help进一步找出其用法。
(2)数据显示格式:常用命令:说明format short 显示小数点后4位(缺省值)format long 显示15位format bank 显示小数点后2位format + 显示+,-,0format short e 5位科学记数法format long e 15位科学记数法format rat 最接近的有理数显示(3)命令行编辑:键盘上的各种箭头和控制键提供了命令的重调、编辑功能。
具体用法如下:↑----重调前一行(可重复使用调用更早的)↓----重调后一行→----前移一字符←----后移一字符home----前移到行首end----移动到行末esc----清除一行del----清除当前字符backspace----清除前一字符(4)MATLAB工作区常用命令:who--------显示当前工作区中所有用户变量名whos--------显示当前工作区中所有用户变量名及大小、字节数和类型disp(x) -----显示变量X的内容clear -----清除工作区中用户定义的所有变量save文件名-----保存工作区中用户定义的所有变量到指定文件中load文件名-----载入指定文件中的数据三、源程序和实验结果1、在命令窗口执行命令完成以下运算,观察workspace 的变化,记录运算结果。
程序设计实验报告(matlab)

程序设计实验报告(matlab)实验一: 程序设计基础实验目的:初步掌握机器人编程语言Matlab。
实验内容:运用Matlab进行简单的程序设计。
实验方法:基于Matlab环境下的简单程序设计。
实验结果:成功掌握简单的程序设计和Matlab基本编程语法。
实验二:多项式拟合与插值实验目的:学习多项式拟合和插值的方法,并能进行相关计算。
实验内容:在Matlab环境下进行多项式拟合和插值的计算。
实验方法:结合Matlab的插值工具箱,进行相关的计算。
实验结果:深入理解多项式拟合和插值的实现原理,成功掌握Matlab的插值工具箱。
实验三:最小二乘法实验目的:了解最小二乘法的基本原理和算法,并能够通过Matlab进行计算。
实验内容:利用Matlab进行最小二乘法计算。
实验方法:基于Matlab的线性代数计算库,进行最小二乘法的计算。
实验结果:成功掌握最小二乘法的计算方法,并了解其在实际应用中的作用。
实验六:常微分方程实验目的:了解ODE的基本概念和解法,并通过Matlab进行计算。
实验内容:利用Matlab求解ODE的一阶微分方程组、变系数ODE、高阶ODE等问题。
实验方法:基于Matlab的ODE工具箱,进行ODE求解。
实验结果:深入理解ODE的基本概念和解法,掌握多种ODE求解方法,熟练掌握Matlab的ODE求解工具箱的使用方法。
总结在Matlab环境下进行程序设计实验,使我对Matlab有了更深刻的认识和了解,也使我对计算机科学在实践中的应用有了更加深入的了解。
通过这些实验的学习,我能够灵活应用Matlab进行各种计算和数值分析,同时也能够深入理解相关的数学原理和算法。
这些知识和技能对我未来的学习和工作都将有着重要的帮助。
MATlab 仿真部分习题答案
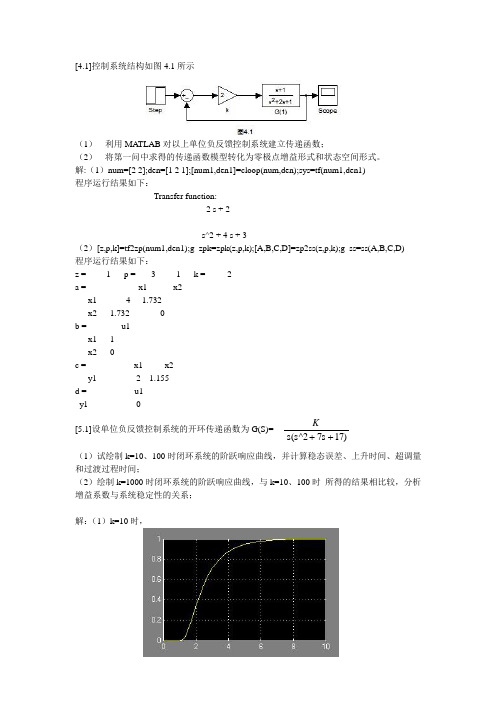
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
MATLAB程序运行结果
closeall %关闭打开了的所有图形窗口clc %清屏命令clear%清除工作空间中所有变量%定义时间范围t=[0:pi/10:8*pi];y=sin(t);plot(t,y,'b:square')closeallclcclear%定义时间范围t=[0:pi/20:9*pi];grid onhold on %允许在同一坐标系下绘制不同的图形plot(t,sin(t),'r:*')plot(t,cos(t))plot(t,-cos(t),'k')%grid on %在所画出的图形坐标中添加栅格,注意用在pl ot之后4-1:closeallclcclear%定义时间范围t=[0:pi/20:9*pi];hold on %允许在同一坐标系下绘制不同的图形plot(t,sin(t),'r:*')plot(t,cos(t))plot(t,-cos(t),'k')grid on %在所画出的图形坐标中添加栅格,注意用在pl ot之后hold off %覆盖旧图,自动把栅格去掉,且若要在加入栅格就%必须把gri d on加在pl ot后面plot(t,-sin(t))grid on%主程序exp2_10.mglobal a %声明变量a为全局变量x=1:100;a=3;c=prods(x) %调用子程序p rods.m%子程序pro d s.m% functi on result=prods(x)% global a% result=a*sum(x);%声明了与主程序一样的全局变量a,以便在子程序中可以%使用主程序中定义的变量答案:15150exmdl2_1.mclearcloseallclct=[0:pi/20:5*pi];figure(1)plot(t,out)grid onxlabel('time')ylabel('magnit ude')exp2_1.mclc %清屏clear%从内存中清除变量和函数more onecho on%求矩阵与矩阵的乘积,矩阵与向量的乘积A=[5 6 7;9 4 6;4 3 6]B=[3 4 5;5 7 9;7 3 1]C=A*BY=A*Xmore offecho off答案:%求矩阵与矩阵的乘积,矩阵与向量的乘积A=[5 6 7;9 4 6;4 3 6]A =5 6 79 4 64 3 6B=[3 4 5;5 7 9;7 3 1]B =3 4 55 7 97 3 1X=[5 ;7;8]X =578C=A*BC =94 83 8689 82 8769 55 53Y=A*XY =12189more offecho offexp2_2.mclcclearmore onecho on%为便于理解,在程序等执行过程中显示程序的表达式a=16;b=12;c=3;d=4;e=a+b-c*df=e/2k=e\2h=c^3g=e+f+ ...2+1-9aa=sin(g)abs(aa)bb=2+3jcc=conj(bb)rbb=real(bb) log(rbb) sqrt(rbb) exp(rbb) echo off more offa=16;b=12;c=3;d=4;e=a+b-c*de =16f=e/2f =8k=e\2k =0.1250h=c^3h =27g=e+f+ ...2+1-9g =18aa=sin(g)aa =-0.7510abs(aa)ans =0.7510bb=2+3jbb =2.0000 +3.0000icc=conj(bb)cc =2.0000 -3.0000irbb=real(bb)rbb =2log(rbb)ans =0.6931sqrt(rbb)ans =1.4142exp(rbb)ans =7.3891echo offans =7.3891exp2_5.m%绘制单位圆clearcloseallclc%定义时间范围t=[0:0.01:2*pi];x=sin(t);y=cos(t);plot(x,y)axis([-1.5 1.5 -1.5 1.5])%限定x轴和y轴的显示范围grid onaxis('equal')%axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围:答案:exp2_5_.mclearcloseallclct=[0:pi/20:5*pi];plot(t,sin(t),'r:*')axis([0 5*pi -1.5 1.5 ])%给x轴和y轴命名xlabel('t(deg)')ylabel('magnit ude')%给图形加标题title('sine wave from zero to 5\pi')%在指定位置创建说明性文字text(pi/2,sin(pi/2),'\bullet\leftar row The sin(t) at t=2')%图形文字标示命令的使用clearcloseallclct=[0:pi/20:5*pi];plot(t,sin(t),'r:*')axis([0 5*pi -1.5 1.5 ])%给x轴和y轴命名xlabel('t(deg)')ylabel('magnit ude')%给图形加标题title('sine wave from zero to 5\pi')%在指定位置创建说明性文字text(pi/2,sin(pi/2),'\bullet\leftar row The sin(t) at t=2') %输入特定的字符%\pi%\alpha%\leftar row%\righta rrow%\bullet(点号)hold onplot(t,cos(t))%区分图形上不同的曲线legend('sin(t)','cos(t)')%用鼠标在特定位置输入文字gtext('文字标示命令举例') hold offexp2_6.m%图形分割命令的使用clearcloseallclct=[0:pi/20:5*pi];subplo t(321)plot(t,sin(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnit ude') grid ontitle('sin(t)')subplo t(322)plot(t,-sin(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnit ude') grid ontitle('-sin(t)') subplo t(323)plot(t,cos(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnit ude') grid ontitle('cos(t)')subplo t(324)plot(t,-cos(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnit ude') grid ontitle('-cos(t)') subplo t(325) subplo t(326)exp2_7.mclcclear%绘制对应于每个输入x的输出y的高度条形图subplo t(221)x=[1 2 3 4 5 6 7 8 9 10];y=[5 6 3 4 8 1 10 3 5 6];bar(x,y)%绘制x1在以y1为中心的区间中分布的个数条形图subplo t(222)x1=randn(1,1000);%生成1000个各随机数y1=-3:0.1:3;hist(x1,y1)%绘制y2对应于x2的梯形图subplo t(223)x2=0:0.1:10;y2=1./(x2.^3-2.*x2+4);stairs(x2,y2)%绘制y3对应于x3的散点图subplo t(224)x3=0:0.1:10;y3=1./(x2.^3-2.*x2+4);stem(x3,y3)exp2_8.mecho off % 不显示程序内容%clearallclearclca=4;b=6disp('暂停,请按任意键继续') % disp指令可以用来显示字符pause% 暂停,直到用户按任意键echo on% 显示程序内容,注意matl ab默认是不显示c=a+b% 暂时把控制权交给键盘(在命令窗口中出现k提示符), % 输入retu rn,回车后退出,继续执行下面的语句。
多元线性回归及显著性检验Matlab程序

多元线性回归及显著性检验Matlab程序(完美版)一、说明:1、本程序是研究生教材《数理统计》(杨虎、刘琼、钟波编著)例(P133)的Matlab编程解答程序。
教材上的例题只做了回归方程显著性分析和一次回归系数显著性分析(剔除x1后没有再检验x2和x3)。
2、本程序在以上的基础之上,还分别检验了x2和x3,并且计算精度更高。
3、本程序可根据用户的需要,在输入不同的显著性水平α之下得到相应的解答。
4、本程序移植性强,对于其他数据,只需要改变excel中的数据即可。
5、本程序输出的可读性强,整洁美观。
二、数据入下(将数据存入excel表格,文件名为。
注意数据是按x1,x2,…,xk,y这样来列来存储。
若不是3个变量,则相应增减数据列就行。
):三、完整程序如下:%----------------------------by ggihhimm----------------------------%《数理统计》杨虎、刘琼、钟波编著例多元线性回归及显著性检验完整解答% 输入需要的显著水平α(默认α=),计算出不同结果(见运行结果)% 该程序也适合其他维数的数据分析(只需改变excel表格中的数据即可)%----------------------------by ggihhimm----------------------------clear;clc;data=xlsread('','sheet1');xi=data(:,1:end-1);[n,k]=size(data);k=k-1;index_of_xi_array=ones(1,k);X=[ones(n,1) xi];Y=data(:,end);fprintf('第1次计算结果:\r')beta_mao=((X'*X)\X'*Y)';fmt_str0='';for i0=1:k+1fmt_str0=[fmt_str0 'β' num2str(i0-1) ' = %\r'];endfprintf(fmt_str0,beta_mao)fprintf('\r')%%检验回归方程的显著性x_ba=mean(xi);y_ba=mean(Y);St_square=sum(Y.^2)-n*y_ba^2;lxy=sum((xi-ones(n,1)*x_ba).*((Y-y_ba)*ones(1,k)));Sr_square=sum(beta_mao(2:end).*lxy);Se_square=St_square-Sr_square;c_flag=Sr_square/Se_square;F_alpha=input('>>>>>>请输入您要求的显著性水平(0<α<1)α= ');while ~(isscalar(F_alpha) && F_alpha<1 && F_alpha>0)F_alpha=input('您的输入有误,请重新输入一个大于0,小于1的数,α= ');endF_fenweidian=finv(1-F_alpha,k,n-k-1);c=k/(n-k-1)*F_fenweidian;if c_flag>cfprintf(['\r--------------------回归方程显著性检验(H0:β1=β2=...=βk=0)' ...'--------------------\r经过计算:拒绝H0,原假设不成立。
牛顿插值法matlab程序例题

牛顿插值法是一种常用的数值分析方法,用于构造一个多项式函数,以便在给定的数据点上进行插值。
这个主题在数学和工程领域中有着广泛的应用,特别是在数据拟合和函数逼近方面。
牛顿插值法的核心思想是通过不断地添加新的数据点来构造一个多项式,并利用已知数据点来确定多项式的系数,从而实现对未知数据点的插值预测。
在Matlab中,实现牛顿插值法并不困难,我们可以利用已有的函数和工具来简化计算过程。
下面,我们将通过一个具体的例题来讲解如何使用Matlab编写牛顿插值法的程序,并分析其结果。
我们需要明确牛顿插值法的数学原理。
给定n个互不相同的节点\(x_0, x_1, ... , x_n\),以及在这些节点上的函数值\(f(x_0), f(x_1), ... , f(x_n)\),我们希望构造一个n次插值多项式p(x),满足p(x_i) = f(x_i),i=0,1,...,n。
牛顿插值多项式的一般形式为:\[p(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)(x - x_1) + ... + a_n(x -x_0)(x - x_1)...(x - x_{n-1})\]其中,\[a_i\]表示插值多项式的系数。
通过牛顿插值法的迭代过程,可以逐步求解出这些系数,进而得到插值多项式的表达式。
接下来,我们将以一个具体的例题来演示如何在Matlab中实现牛顿插值法。
假设我们有如下的数据点和函数值:\(x = [1, 2, 3, 4]\)\(f(x) = [1, 4, 9, 16]\)我们希望利用这些数据点来构造一个插值多项式,并在给定的区间上进行插值计算。
在Matlab中,可以通过interp1函数来进行插值计算,该函数支持多种插值方法,包括牛顿插值法。
下面是一个简单的Matlab程序示例:```matlabx = [1, 2, 3, 4];y = [1, 4, 9, 16];xi = 2.5;yi = interp1(x, y, xi, 'spline');disp(['在x=',num2str(xi),'处的插值结果为:',num2str(yi)]);```在这段代码中,我们首先定义了给定的数据点x和对应的函数值y,然后利用interp1函数对x=2.5处的插值结果进行计算。
自动控制原理MATLAB分析与设计-仿真实验报告

兰州理工大学《自动控制原理》MATLAB分析与设计仿真实验报告院系:电气工程与信息工程学院班级:电气工程及其自动化四班姓名:学号:时间:年月日电气工程与信息工程学院《自动控制原理》MATLAB 分析与设计仿真实验任务书(2014) 一、仿真实验内容及要求 1.MATLAB 软件要求学生通过课余时间自学掌握MATLAB 软件的基本数值运算、基本符号运算、基本程序设计方法及常用的图形命令操作;熟悉MATLAB 仿真集成环境Simulink 的使用。
2.各章节实验内容及要求1)第三章 线性系统的时域分析法∙ 对教材第三章习题3-5系统进行动态性能仿真,并与忽略闭环零点的系统动态性能进行比较,分析仿真结果;∙ 对教材第三章习题3-9系统的动态性能及稳态性能通过仿真进行分析,说明不同控制器的作用;∙ 在MATLAB 环境下选择完成教材第三章习题3-30,并对结果进行分析; ∙ 在MATLAB 环境下完成英文讲义P153.E3.3;∙ 对英文讲义中的循序渐进实例“Disk Drive Read System”,在100=a K 时,试采用微分反馈控制方法,并通过控制器参数的优化,使系统性能满足%5%,σ<3250,510s ss t ms d -≤<⨯等指标。
2)第四章 线性系统的根轨迹法∙ 在MATLAB 环境下完成英文讲义P157.E4.5; ∙ 利用MATLAB 绘制教材第四章习题4-5;∙ 在MATLAB 环境下选择完成教材第四章习题4-10及4-17,并对结果进行分析;∙ 在MATLAB 环境下选择完成教材第四章习题4-23,并对结果进行分析。
3)第五章 线性系统的频域分析法∙ 利用MATLAB 绘制本章作业中任意2个习题的频域特性曲线;4)第六章 线性系统的校正∙ 利用MATLAB 选择设计本章作业中至少2个习题的控制器,并利用系统的单位阶跃响应说明所设计控制器的功能;∙ 利用MATLAB 完成教材第六章习题6-22控制器的设计及验证;∙ 对英文讲义中的循序渐进实例“Disk Drive Read System”,试采用PD控制并优化控制器参数,使系统性能满足给定的设计指标ms t s 150%,5%<<σ。
matlab打印函数

matlab打印函数MATLAB印函数是MATLAB中一种重要的工具,它是用于将 MATLAB 序运行后产生的结果输出到屏幕或文件中的函数。
用户可以根据自己的要求,组合一系列 MATLAB置的打印函数,实现用户自定义的输出格式。
本文将介绍 MATLAB 中的常用的打印函数,并举例说明如何正确使用它们,最终使得 MATLAB序的输出更加清晰,便于用户阅读。
MATLAB 为用户提供了一些特定用途的打印函数,例如 disp()、fprintf()、printf()、sprintf()、fscanf() scanf()。
这些函数有其各自独特的用法,下面将介绍它们的用法和功能:disp()数:主要用于输出字符串或变量值,例如 disp(Hello World!,它将在命令窗口中输出‘Hello World!’。
printf()数:用于输出变量值或格式化字符串,它可以实现在命令行窗口中按照特定的格式输出变量或字符串,例如 printf(%fx),可以指定输出 x值,且保留小数点后 6 位。
fprintf()数:类似于 printf()数,它可以实现在指定文件中按照特定格式输出变量或字符串,例如 fprintf(%dx) x值以 10制的格式输出至指定文件中。
sprintf()数:实现将变量按照特定格式放入一个字符串中,例如,sprintf(x值是 %dx) x值以 10制的格式放入字符串中。
fscanf()数:用于从指定文件中读取变量的值,例如,fscanf(fileID, %f 3)从文件中读取 3 个浮点数,并将它们以实数形式存放在变量中。
scanf()数:类似于 fscanf()数,只不过读取的内容从标准输入(stdin)而非文件中读取,例如,scanf(%f 3)从标准输入设备中读取 3 个浮点数,并将它们存放在变量中。
以上就是 MATLAB 中常用的打印函数,供用户根据实际需求选择使用。
当然,要正确使用这些函数,用户需要熟悉它们的参数说明,以及掌握正确的输出格式,这样才能将程序运行的结果输出得更加清晰易读,以满足自己的需求。
bpsk调制的matlab程序

题目:BPSK调制的MATLAB程序一、BPSK调制技术介绍BPSK(Binary Phase Shift Keying)调制是一种数字调制技术,它使用两个不同的相位来表示数字比特0和1。
在BPSK调制中,0和1分别映射到正弦波的两种相位,通常为0°和180°。
二、MATLAB程序编写流程在MATLAB中实现BPSK调制的程序主要包括以下几个步骤:1. 生成要调制的数字比特序列2. 将数字比特序列转化为相应的正弦波信号3. 添加高斯白噪声4. 绘制调制后的信号波形图三、MATLAB程序实现下面是一个简单的MATLAB程序,实现了BPSK调制的过程:```matlab生成随机的数字比特序列bitStream = randi([0,1],1,1000);将数字比特序列映射为正弦波信号t = 0:0.01:length(bitStream)-1;t = t/100;carrier = sin(2*pi*t);BPSK调制bpskSignal = (1-2*bitStream).*carrier;添加高斯白噪声noise = 0.1*randn(1,length(bpskSignal)); noisyBpskSignal = bpskSignal + noise;绘制调制后的信号波形图subplot(2,1,1);plot(t,carrier);title('Carrier Signal');xlabel('Time');ylabel('Amplitude');grid on;subplot(2,1,2);plot(t,noisyBpskSignal);title('Noisy BPSK Signal');xlabel('Time');ylabel('Amplitude');grid on;```四、MATLAB程序运行结果分析通过上述程序,我们可以得到BPSK调制后的信号波形图。
MATLAB实训报告

一、实训目的1. 熟悉MATLAB语言的使用2. 了解MATLAB在电子信息课程中的应用3. 掌握MATLAB矩阵输入、运算以及MATLAB数值的运算功能4.掌握各种数据的创建、访问、扩建及缩减5.了解利用MATLAB计算系统响应的方法;验证信号与系统的基本概念、基本理论,掌握信号与系统的分析方法。
二、实训任务和要求1、熟练利用MATLAB语言编程对系统S平面分析2、掌握利用MATLAB分析系统时域的方法,熟悉系统的零输入响应,零状态响应及冲击响应的步骤。
3、MATLAB是目前国际上最流行,应用最广泛的科学与工程计算软件,它由MATLAB语言,MATLAB工作环境,MATLAB图像处理系统,MATLAB数据函数库,MATLAB应用程序接口五大部分组成的集数值计算,图形处理,程序开发为一体的功能强大的系统.它应用于自动控制,数学计算,信号分析,计算机技术,图像信号处理,财务分析,航天工业,汽车工业,生物医学工程,语音处理和雷达工程等各行业,也是国高校和研究部门进行许多科学研究的重要工具。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学,工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完相同的事情简捷得多。
MATLAB是“矩阵实验室”(MATrix LABoratoy)的缩写,它是以矩阵运算为基础的交互式程序语言,能够满足科学、工程计算和绘图的需求。
与其它计算机语言相比,其特点是简洁和智能化,适应科技专业人员的思维方式和书写习惯,使得编程和调试效率大大提高。
它用解释方式工作,键入持续后立即得出结果,人机交互性能好,易于调试并被科技人员所乐于接受。
特别是它可适应多种平台,并且随着计算机硬软件的更新及时升级,因此MATLAB语言在国外的大学工学院中,特别是频繁进行数值计算的电子信息类学科中,已经成为每个学生都掌握的工具了。
它大大提高了课程教学、解题作业、分析研究的效率。
matlab disp的用法

matlab disp的用法MatlabDisp函数是Matlab中语句输出的有效工具。
在Matlab编程中,disp函数用于显示字符串、向量或矩阵,这样可以清晰地显示程序运行的结果。
本文将主要讨论Matlab disp函数的使用方法,以及用于调试程序的技巧。
1、Matlab disp函数基本用法在Matlab中,disp函数的基本用法是打印字符串或显示变量的值,如下所示:a = 10;disp(a);上述代码将输出字符串中的“10”,这表明变量“a”的值为10。
此外,我们也可以使用disp函数显示向量或矩阵,如下所示:b = [1 2 3; 4 5 6];disp(b);上述代码将打印一个2 x 3的矩阵,即1 2 34 5 6此外,在disp函数的调用中,我们可以使用任意数量的参数,以用于分隔字符串或矩阵中的元素,如下所示:c = [1 2 3 4 5 6];disp(c, -);上述代码将输出1-2-3-4-5-6。
2、使用Matlab disp函数进行调试Matlab disp函数不仅可用于显示字符串或矩阵,它还可以用于检查变量的值以及程序的执行过程。
例如,我们可以在程序运行的不同阶段调用disp函数,显示相应的值,这样可以更清楚地了解每一阶段程序正在做什么。
例如,下面的示例代码计算了一个值的平方和立方:a = 10;b = a * a;disp(b);c = a * b;disp(c);上述代码将输出“100”和“1000”,其中“100”是a的平方,“1000”是a的立方。
另一个使用disp函数进行调试的例子是,可以通过将disp函数放在循环中来确定循环体内变量的值是否正确:for i=1:5a(i) = i * 10;disp(a(i));end上述代码将输出以下内容:1020304050从输出的结果可以看出,变量a的值是按预期增长的。
3、总结本文介绍了如何使用Matlab disp函数,以及如何将其用于调试程序。
matlab显示程序进度

关于matlab中的waitbar(用于显示程序运行的进度)应用1:h = waitbar(x,'message'); %其中x必须为0到1之间的数,message为显示的信息,其实这个x大于1也可以啊,但是进度条总在满的状态,x是多少就对应进度条显示的比例是多少举例: hwait=waitbar(0,'请等待>>>>>>>>'); %这个0显示的是进度条的位置,因为是0,就在起始位置,还有就是这个hwait就是这个waitbar函数的句柄得到:应用2:waitbar(x,h,'updated message'); % x为显示的进度,必须在0到1之间;h为所建立的waitbar的句柄,updated message为实时显示的信息,此语句经常地用于for循环中举例:steps=100;hwait=waitbar(0,'请等待>>>>>>>>');for k=1:stepsif steps-k<=5waitbar(k/steps,hwait,'即将完成'); %因为k/steps在逐步增大,所有进度条在往右走,另外,如果这个hwait不加上的话,会显示n多个进度条窗口,让你关闭不过来啊,加上之后就只显示一个了pause(0.05); %延时一下啊否则太快看不出来变化,一般有个0.01就能看出变化,但还是比较快的elsestr=['正在运行中',num2str(k),'%']; %用于显示如下图中“正在运行中46%”等比例数据waitbar(k/steps,hwait,str);pause(0.05); %pause(n)函数是程序停止n秒后继续,n可以使分数或小数。
函数的分辨率根据平台而定,大多数平台都能满足0.01秒的精度。
机械优化可靠性设计第三次作业

1.用进退法确定f(x)=x 2-7x+10的初始搜索区间.设x 0=0,h 0=1. 解:()()000()10,()0+1(1)40f x f f x h f f ==+===,因为000f x f x h >+()(),搜索成功,步长加倍;计算0000023 031 32f x h h f x h f f ++=+=+⨯==-()()()(), 因为00003f x h f x h +>+()(),搜索成功,步长加倍; 计算00000347 071 710f x h h f x h f f ++=+=+⨯==()()()(), 因为00003 7f x h f x h +<+()(),搜索失败,停止迭代;得到初始搜索区间为[]][0000, 71[,7]a b x h x h =++=,。
function [a, b]=jtf(varargin) if numel(varargin)<1 h0=input(' h0= ' ); x0=input(' x0= ' ); fx=@(x)x^2-7*x+10; elseinput_num= cell2mat (varargin(1, 1:2)); h0=input_num(1) ; x0=input_num(2) ; fx=varargin{3}; endh=h0;x1=x0;f1=fx(x1);x2=x1+h;f2=fx(x2); if f2>f1h=-h;x3=x1;f3=f1;x1=x2;f1=f2;x2=x3;f2=f3; endh=2*h;x3=x2+h;f3=fx(x3); while f2>=f3x1=x2;f1=f2;x2=x3;f2=f3; h=2*h;x3=x2+h;f3=fx(x3); end if h<0a=x3;b=x1; elsea=x1;b=x3; endresult=[a,b]MATLAB 程序运行结果: h0= 1 x0= 0 result =1 72.用0.618法求函数f(x)=x 2-7x+10的最优解.已知初始搜索区间为[2,8],精度为0.4。
MATLAB程序设计与应用(第二版)课后实验答案

Matlab课后实验题答案实验一 MATLAB运算基础1. 先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。
(1)0 122sin851ze =+(2)21ln(2z x=,其中2120.455ix+⎡⎤=⎢⎥-⎣⎦(3)0.30.330.3sin(0.3)ln, 3.0, 2.9,,2.9,3.0 22a ae e az a a--+=++=--(4)2242011122123t tz t tt t t⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t=0:0.5:2.52. 已知:1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1) A+6*B 和A —B+I(其中I 为单位矩阵) (2) A*B 和A.*B (3) A^3和A.^3 (4) A/B 及B\A(5) [A,B ]和[A ([1,3],:);B^2] 解:3. 设有矩阵A 和B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D 。
(3) 查看MATLAB 工作空间的使用情况。
4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2).建立一个字符串向量 例如: ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1。
设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
实验一MATLAB基础资料

if (sum>1000)
break;
end
end
45
2)编写函数文件:分别用for和while循环结构编写程序,求2的0到n次幂的和。
m=0:n;
(m<=n)
3、矩阵的基本操作
(1)设有矩阵A和B
016
2345
69
78910
0234
12131415
、向量乘法
2 3 ; 4 5 6 ; 7 8 9]
2 2 ; 2 2 2 ; 2 2 2]
运行结果为:
2 4 6 D= 2 4 6
%指定2号为活动区
subplot(2,1,1);
01234567-1-0.500.51sin(x)01234567-1-0.500.51cos (x)
123456-1-0.500.51
1234567-1-0.500.51
、多项式运算
数 功 能 函 数 功 能
多项式求根 conv
多项式乘法(卷积) 多项式除法(解卷)
由根式求多项式 residue 分式多项式的部分分式展开(留数)
多项式求值 polyder 多项式求导数
1:求多项式 P (x)=x4+2x3+3x2+4x+5 的根。
21 22 23 24 25
3 0 16
17 -6 9
0 23 -4
9 7 0
4 13 11
93 150 77
258 335 237
…', 'eqn', 'var1', '…', 'varn'):计算方程组,eq1,…eqn为输入的方程组;var1,…varn用来指
Matlab实验报告13

301,302,303,304,305,306,307,308,309];
(3)
仿照问题
1
中方法找出数组
A
4 3
2 1
0 1
2 3
4
5
中所有绝对值大于
3
的元素。
(4)在命令窗口执行下面指令,体味二维数组的子数组寻访和赋值
A=zeros(2,4)
% 创建(2*4)的全零数组
二行是“ has multiple rows. ”。
6 .利用串操作函数 char、str2mat、strvcat 分别写出使以下这段文字成为字符串的程序,
注意保持这段文字的格式。
在英式用法中,引号通常是单引号,如‘Fire!’。
In GB usage quotation marks are usually single: ’Fire!’ .
whos
% 观察变量 a,b 在内存中所占字节
2 .已知串数组 a=”This is an example.”, 试将其到序输出。
3 .接上题,试执行 ascii_a=double(a),观察其 ASCII 码,并将 ASCII 码变回字符串。
4 .设 A=”这是一个算例”,重复上面的 2-3。
5 .尝试用直接输入法在命令窗口创建字符串 s ,第一行时“ This string array ” , 第
全赋为 1
(5) 运行指令
rand(‘state ’,11),A=rand(3,10000);B=(A>0.5);C=2*B-1;
首先预测( C*C’)/100 的运行结果,然后再在机器上验证。(本方法提供了产
生通信等仿真中常需若干独立的双随机码的方法原型。)
多普勒走动matlab程序

多普勒走动matlab程序1.引言1.1 概述本文将介绍多普勒走动的Matlab程序设计和实现。
首先,我们需要了解多普勒效应的原理和应用。
多普勒效应是流体中物体运动引起的频率变化现象,广泛应用于医学、气象、交通等领域。
在医学方面,多普勒效应常被用于心血管疾病的诊断和治疗。
通过使用超声波检测心脏或血管中血液的流动情况,可以获取血液速度和流量信息,从而帮助医生判断病情和制定治疗方案。
在气象领域,多普勒雷达常被用于探测和跟踪风暴的运动。
通过测量风暴中雨滴、冰粒等物质的运动速度,可以分析出风暴的强度、大小和移动方向,为气象预测和防灾减灾提供重要信息。
在交通领域,多普勒效应被广泛应用于雷达测速仪。
当汽车驶向或远离雷达测速仪时,其速度会引起雷达所接收到的回波频率的变化。
通过测量这一频率变化,可以准确计算出汽车的速度,以实现道路交通的管理和监控。
本文将重点介绍如何使用Matlab编写多普勒走动的程序,并实现对多普勒效应的模拟和分析。
我们将详细讲解程序设计的步骤和关键技术,以及如何利用Matlab的强大功能进行数据处理和可视化展示。
总结而言,本文旨在帮助读者理解多普勒效应的原理和应用,并通过Matlab程序设计和实现,实现对多普勒走动的模拟和分析。
希望读者通过本文的学习,能够深入掌握多普勒走动的特点和优势,并对未来多普勒走动的发展有所展望。
文章结构部分的内容可以编写为:1.2 文章结构文章将分为三个主要部分:引言、正文和结论。
在引言部分,我们将概述本文的主题——多普勒走动,并介绍本文的结构和目的。
首先,我们将提供对多普勒效应原理和应用的概述,以帮助读者了解多普勒走动的背景和原理。
其次,我们将介绍本文的重点——Matlab程序设计与实现,包括算法和相关的编程技巧。
在正文部分,我们将详细讨论多普勒效应的原理和应用。
首先,我们将简要介绍多普勒效应的基本原理和公式。
然后,我们将探讨多普勒走动在不同领域的应用,如气象雷达、医学诊断和无线通信等。
香农熵的matlab程序

香农熵的Matlab程序1. 引言香农熵(Shannon Entropy)是信息论中一个重要的概念,用于衡量一个随机变量的不确定性或者信息量。
在信息论和通信领域,香农熵被广泛应用于数据压缩、信号处理、密码学等方面。
本文将介绍如何使用Matlab编写程序来计算香农熵。
2. 算法原理香农熵的计算公式如下:其中,H表示香农熵,p(x)表示随机变量X取某个值x的概率。
根据该公式,我们需要计算每个可能取值的概率,并将其代入公式中求和,即可得到香农熵的值。
3. Matlab程序实现下面是一个简单的Matlab程序,用于计算给定随机变量的香农熵:function entropy = shannon_entropy(probabilities)entropy = 0;for i = 1:length(probabilities)if probabilities(i) ~= 0entropy = entropy - probabilities(i) * log2(probabilities(i));endendend以上程序定义了一个名为shannon_entropy的函数,该函数接受一个概率向量作为输入参数,并返回计算得到的香农熵。
程序的实现思路是遍历概率向量中的每个元素,如果该元素不为0,则将其代入香农熵的计算公式中进行计算,并累加到最终的结果中。
4. 使用示例为了演示程序的使用,我们将计算一个简单的示例。
假设有一个随机变量X,其可能取值为[1, 2, 3],对应的概率分别为[0.3, 0.5, 0.2]。
我们可以使用上述程序来计算该随机变量的香农熵。
probabilities = [0.3, 0.5, 0.2];entropy = shannon_entropy(probabilities);disp(['Entropy: ', num2str(entropy)]);运行上述代码,程序将输出以下结果:Entropy: 1.4854753这表明给定的随机变量X的香农熵为1.4854753。
matlab中,计算,记录,程序运行,起始,结束时间,间隔matlab中tic,toc函数的用法

matlab中,计算,记录,程序运⾏,起始,结束时间,间隔matlab
中tic,toc函数的⽤法
Tic和toc函数可以计算运⾏⼀段时间的代码。
例如:
clc
tic
d=zeros(1,10000);
for i=1:10000
d(i)=i;
end
toc
tic
c=1;
for i=1:10000
c=[c:i];
end
toc
运⾏结果如下:
Elapsed time is 0.000158 seconds.
Elapsed time is 0.152307 seconds.
只要⽤tic和toc函数,不需要⾃⼰计算前后时间的差,tic函数会记录起始时刻,toc函数会⾃动计算时间差。
通过这个程序,可以发现,先把矩阵的⼤⼩确定再给矩阵的赋值的⽅法⽐边赋值边改变矩阵维数的⽅法更节省时间。
%本程序⽤来⽐较两种计算恰定⽅程的时间和精确度
%第⼀种使⽤矩阵求逆的⽅法
%第⼆种使⽤矩阵的除法
clc;
a=rand(100)+1.e10;
x=ones(100,1);
b=a*x;
tic
y=inv(a)*b;
toc
err=norm(y-x) %结果与精确解的范2误差
res=norm(a*y-b) %⽅程的范2误差
tic
y=a\b;
toc
err=norm(y-x) res=norm(a*y-b) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
close all %关闭打开了的所有图形窗口clc %清屏命令clear %清除工作空间中所有变量%定义时间范围t=[0:pi/10:8*pi];y=sin(t);plot(t,y,'b:square')close allclcclear%定义时间范围t=[0:pi/20:9*pi];grid onhold on %允许在同一坐标系下绘制不同的图形plot(t,sin(t),'r:*')plot(t,cos(t))plot(t,-cos(t),'k')%grid on %在所画出的图形坐标中添加栅格,注意用在plot之后4-1:close allclcclear%定义时间范围t=[0:pi/20:9*pi];hold on %允许在同一坐标系下绘制不同的图形plot(t,sin(t),'r:*')plot(t,cos(t))plot(t,-cos(t),'k')grid on %在所画出的图形坐标中添加栅格,注意用在plot之后hold off %覆盖旧图,自动把栅格去掉,且若要在加入栅格就%必须把grid on加在plot后面plot(t,-sin(t))grid on%主程序exp2_10.mglobal a %声明变量a为全局变量x=1:100;a=3;c=prods(x) %调用子程序prods.m%子程序prods.m% function result=prods(x)% global a% result=a*sum(x);%声明了与主程序一样的全局变量a,以便在子程序中可以%使用主程序中定义的变量答案:15150exmdl2_1.mclearclose allclct=[0:pi/20:5*pi];figure(1)plot(t,out)grid onxlabel('time')ylabel('magnitude')exp2_1.mclc %清屏clear %从内存中清除变量和函数more onecho on%求矩阵与矩阵的乘积,矩阵与向量的乘积A=[5 6 7;9 4 6;4 3 6]B=[3 4 5;5 7 9;7 3 1]C=A*BY=A*Xmore offecho off答案:%求矩阵与矩阵的乘积,矩阵与向量的乘积A=[5 6 7;9 4 6;4 3 6]A =5 6 79 4 64 3 6B=[3 4 5;5 7 9;7 3 1]B =3 4 55 7 97 3 1X=[5 ;7;8]X =578C=A*BC =94 83 8689 82 8769 55 53Y=A*XY =12189more offecho offexp2_2.mclcclearmore onecho on%为便于理解,在程序等执行过程中显示程序的表达式a=16;b=12;c=3;d=4;e=a+b-c*df=e/2k=e\2h=c^3g=e+f+ ...2+1-9aa=sin(g)abs(aa)bb=2+3jcc=conj(bb)rbb=real(bb) log(rbb) sqrt(rbb) exp(rbb) echo off more offa=16;b=12;c=3;d=4;e=a+b-c*de =16f=e/2f =8k=e\2k =0.1250h=c^3h =27g=e+f+ ...2+1-9g =18aa=sin(g)aa =-0.7510abs(aa)ans =0.7510bb=2+3jbb =2.0000 +3.0000i cc=conj(bb)cc =2.0000 -3.0000i rbb=real(bb)rbb =2log(rbb)ans =0.6931sqrt(rbb)ans =1.4142exp(rbb)ans =7.3891echo offans =7.3891exp2_5.m%绘制单位圆clearclose allclc%定义时间范围t=[0:0.01:2*pi];x=sin(t);y=cos(t);plot(x,y)axis([-1.5 1.5 -1.5 1.5])%限定x轴和y轴的显示范围grid onaxis('equal')%axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围:答案:exp2_5_.mclearclose allclct=[0:pi/20:5*pi];plot(t,sin(t),'r:*')axis([0 5*pi -1.5 1.5 ])%给x轴和y轴命名xlabel('t(deg)')ylabel('magnitude')%给图形加标题title('sine wave from zero to 5\pi')%在指定位置创建说明性文字text(pi/2,sin(pi/2),'\bullet\leftarrow The sin(t) at t=2')%图形文字标示命令的使用clearclose allclct=[0:pi/20:5*pi];plot(t,sin(t),'r:*')axis([0 5*pi -1.5 1.5 ])%给x轴和y轴命名xlabel('t(deg)')ylabel('magnitude')%给图形加标题title('sine wave from zero to 5\pi')%在指定位置创建说明性文字text(pi/2,sin(pi/2),'\bullet\leftarrow The sin(t) at t=2') %输入特定的字符%\pi%\alpha%\leftarrow%\rightarrow%\bullet(点号)hold onplot(t,cos(t))%区分图形上不同的曲线legend('sin(t)','cos(t)')%用鼠标在特定位置输入文字gtext('文字标示命令举例') hold offexp2_6.m%图形分割命令的使用clearclose allclct=[0:pi/20:5*pi];subplot(321)plot(t,sin(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnitude') grid ontitle('sin(t)') subplot(322)plot(t,-sin(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnitude') grid ontitle('-sin(t)') subplot(323)plot(t,cos(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnitude') grid ontitle('cos(t)') subplot(324)plot(t,-cos(t))axis([0 16 -1.5 1.5]) xlabel('t(deg)') ylabel('magnitude') grid ontitle('-cos(t)') subplot(325) subplot(326)exp2_7.mclcclear%绘制对应于每个输入x的输出y的高度条形图subplot(221)x=[1 2 3 4 5 6 7 8 9 10];y=[5 6 3 4 8 1 10 3 5 6];bar(x,y)%绘制x1在以y1为中心的区间中分布的个数条形图subplot(222)x1=randn(1,1000);%生成1000个各随机数y1=-3:0.1:3;hist(x1,y1)%绘制y2对应于x2的梯形图subplot(223)x2=0:0.1:10;y2=1./(x2.^3-2.*x2+4);stairs(x2,y2)%绘制y3对应于x3的散点图subplot(224)x3=0:0.1:10;y3=1./(x2.^3-2.*x2+4);stem(x3,y3)exp2_8.mecho off % 不显示程序内容%clear allclearclca=4;b=6disp('暂停,请按任意键继续') % disp指令可以用来显示字符pause % 暂停,直到用户按任意键echo on% 显示程序内容,注意matlab默认是不显示c=a+b% 暂时把控制权交给键盘(在命令窗口中出现k提示符), % 输入return,回车后退出,继续执行下面的语句。
keyboardd=input('Enter the value of d=');%提示用户输入d的值e=a*24+b*8+d*6-cf=e/ddisp('work pause 30 second') % disp指令可以用来显示字符pause(10) %暂停10秒disp(f) % 显示指定变量的结果,而不显示变量名称echo off答案:b =6暂停,请按任意键继续% 显示程序内容,注意matlab默认是不显示c=a+bc =10% 暂时把控制权交给键盘(在命令窗口中出现k提示符), % 输入return,回车后退出,继续执行下面的语句。
keyboardK>> returnd=input('Enter the value of d=');%提示用户输入d的值Enter the value of d=10e=a*24+b*8+d*6-ce =194f=e/df =19.4000disp('work pause 30 second') % disp指令可以用来显示字符work pause 30 secondpause(10) %暂停10秒disp(f) % 显示指定变量的结果,而不显示变量名称19.4000echo offexp2_9.msumhe.m函数% sumhe.mfunction result=sumhe(a,b)% sumhe(a,b) sum the serial of numbers from a tobresult=sum(a:b);主程序exp2_9.ma=input('please input value of a=');b=input('please input value of b=');c=sumhe(a,b)% 在此例中,主程序exp2_9.m设定了两个参数a和b来调用% 子程序sumhe.m(为一个函数文件),% 所以执行主程序时,子程序就会调用主程序传递过来的% a和b值进行计算,再将结果返回主程序。
